面积问题(中考数学压轴)

合集下载

中考数学压轴题(重叠面积问题)

(1）求∠OＡB得度数,并求当点Ａ′在线段AB上时,S关于t得函数关系式;
(２)当纸片重叠部分得图形就就是四边形时,求t得取值范围;
（3)Ｓ存在最大值吗?若存在,求出这个最大值,并求此时ｔ得值;若不存在,请说明理由。
解:(1）∵A,B两点得坐标分别就就是Ａ(１0，０）与Ｂ(8，),
∴,
∴
当点A´在线段AB上时,∵,ＴＡ＝TＡ´,
(4)在(３)得条件下，抛物线与正方形一起平移，同时停止,求抛物线上两点间得抛物线弧所扫过得面积、
（14分)(1）；…………………………………………………2分
(2)设抛物线为,抛物线过,
解得…………………………………………………２分
∴、……………………………………………………………１分
（３)①当点A运动到点Ｆ时,
例1: 在梯形ABCD中,AＤ∥ＢC，AB=AＤ＝ＤC=２cm,BＣ=4ｃm,在等腰△PQR中,∠QPR=1２0°,底边QR＝６cm,点B、Ｃ、Q、Ｒ在同一直线l上,且C、Q两点重合,如果等腰△ＰQR以1cm/秒得速度沿直线l箭头所示方向匀速运动，t秒时梯形AＢCＤ与等腰△PQR重合部分得面积记为S平方厘米
∴S=(CE+ＯF)·EＦ
=(t－4+ｔ)×(8－t)
=－+4t－８ﻩﻩﻩﻩ………………9分
②当０<ｔ≤4时,S=，t=4时,S最大=2
当4<ｔ＜8时,S=-+４ｔ-8＝－(t－)+
ｔ＝时,S最大=
∵>2，∴当t=时,S最大＝ﻩ………………１２分
例４: 已知直角梯形纸片OABＣ在平面直角坐标系中得位置如图所示，四个顶点得坐标分别为Ｏ(0，0），A(10,0),B(8,),C(0,),点T在线段OA上(不与线段端点重合）,将纸片折叠，使点A落在射线AB上(记为点A′),折痕经过点Ｔ,折痕ＴＰ与射线AB交于点P,设点T得横坐标为ｔ,折叠后纸片重叠部分(图中得阴影部分）得面积为S;

中考数学总复习《二次函数压轴题(面积问题)》专题训练-附含答案

中考数学总复习《二次函数压轴题（面积问题）》专题训练-附含答案学校：___________班级：___________姓名：___________考号：___________1．如图，在平面直角坐标系中，抛物线2y ax x c =-+与y 轴交于点()0,4A -，与x 轴交于点()4,0B ，连接AB .(1)求抛物线的解析式．(2)P 是AB 下方抛物线上的一动点，过点P 作x 轴的平行线交AB 于点C ，过点P 作PD x ⊥轴于点D ．①求PC PD +的最大值．①连接PA ，PB ，是否存在点P ，使得线段PC 把PAB 的面积分成3:5两部分？若存在，请直接写出点P 的坐标；若不存在，请说明理由．2．综合与探究如图1，抛物线212y x bx c =-++经过点(4,0)B 和(0,2)C ，与x 轴的另一个交点为A ，连接AC ，BC ．(1)求该抛物线的解析式及点A 的坐标；(2)如图1，点D 是线段AC 的中点，连接BD ．点E 是抛物线上一点，若ABE BCD S S =△△，设点E 的横坐标为x ，请求出x 的值；(3)试探究在抛物线上是否存在一点P ，使得45PBO OBC ∠+∠=︒？若存在，请直接写出点P 的坐标；若不存在，请说明理由．3．如图抛物线2y ax bx c =++经过点()1,0A -，点()0,3C ，且OB OC =．(1)求抛物线的解析式及其对称轴；(2)点D 、E 是直线1x =上的两个动点，且1DE =，点D 在点E 的上方，求四边形ACDE 的周长的最小值．(3)点P 为抛物线上一点，连接CP ，直线CP 把四边形CBPA 的面积分为3:5两部分，求点P 的坐标．4．已知二次函数23y ax bx a =+-经过点()1,0A -和()0,3C ，与x 轴交于另一点B ，抛物线的顶点为D ．(1)求此二次函数解析式；(2)连接DC 、BC 和DB ，判断BCD △的形状并说明理由；(3)在对称轴右侧抛物线上找一点P ，使得P 、D 、C 构成以PC 为底边的等腰三角形，求出点P 的坐标及此时四边形PBCD 的面积．5．如图，抛物线214y x bx c =-++与x 轴交于点,A B 两点（点A 在点B 的右侧），点()()8,02,0A B -、，与y 轴交于点C ．(1)求抛物线的解析式； (2)点D 为抛物线的顶点，过点D 作DE AC ∥交抛物线于点E ，点P 为抛物线上点,D E 之间的一动点，连接,,,,AC AE AP CE CP ，线段,AP CE 交于点G ，记CPG △的面积为1,S AEG △的面积为2S ，且12S S S =-，求S 的最大值及此时点P 的坐标；(3)在（2）的条件下，将拋物线沿射线AC 方向平移5个单位长度后得到新抛物线，点Q 是新拋物线对称轴上一动点，在平面内确定一点R ，使得以点P Q B R 、、、为顶点的四边形是矩形．直接写出所有符合条件的点R 的坐标．6．如图，有一个长为30米的篱笆，一面利用墙（墙的最大可用长度18a =米）围成的中间隔有一道篱笆的长方形花圃设花圃的宽AB 为x 米，面积为y 平方米．(1)求y 与x 的函数关系式，并直接写出自变量x 的取值范围；(2)如何设计才能使长方形花圃面积最大；并求其最大面积．7．如图，过原点的抛物线212y x bx c =-++与x 轴的另一个交点为A ，且抛物线的对称轴为直线2x =，点B 为顶点(1)求抛物线的解析式(2)如图（1），点C 为直线OB 上方抛物线上一动点，连接AB，BC 和AC ，线段AC 交直线OB 于点E ，若CBE △的面积为1S ，ABE 的面积为2S ，求12S S 的最大值 (3)如图（2），设直线()20y kx k k =-≠与抛物线交于D ，F 两点，点D 关于直线2x =的对称点为D ，直线D F '与直线2x =交于点P ，求证：BP 的长是定值．8．抛物线2y x bx c =-++经过点A ，B ，C ，已知()1,0A -和()0,3C ．(1)求抛物线的解析式及顶点E 的坐标；(2)点D 在BC 上方的抛物线上．①如图1，若CAB ABD ∠=∠，求点D 的坐标；①如图2，直线BD 交y 轴于点N ，过点B 作AD 的平行线交y 轴于点M ，当点D 运动时，求CBD AMNS S △△的最大值及此时点D 的坐标． 9．在平面直角坐标系中，O 为坐标原点，抛物线244y ax ax =-+交x 轴于点A 、B （A 左B右），交y 轴于点C ，直线123y x =-+，经过B 点，交y 轴于点D ．(1)如图1，求a 的值；(2)如图2，点P 在第一象限内的抛物线上，过点A 、B 作x 轴的垂线，分别交直线PD 于点E 和F ，若PF DE =，求点P 的坐标；(3)如图3，在（2）的条件下，点Q 在第一象限内的抛物线上，过点Q 作QH DP ⊥于点H ，交直线BD 于点R ，连接EQ 和ER ，当QE ER =时，求ERQ △的面积．10．已知抛物线213222y x x =-++与x 轴交于B 、C 两点（点B 在点C 的左侧），与y 轴交于点A ．(1)判断ABC 的形状，并说明理由．(2)设点(,)P m n 是抛物线在第一象限部分上的点，过点P 作PH x ⊥轴于H ，交AC 于点Q ，设四边形OAPC 的面积为S ，求S 关于m 的函数关系式，并求使S 最大时点P 的坐标和QHC △的面积；(3)在（2）的条件下，点N 是坐标平面内一点，抛物线的对称轴上是否存在点M ，使得以P 、C 和M 、N 为顶点的四边形是菱形，若存在，写出点M 的坐标，并选择一个点写出过程，若不存在，请说明理由．11．已知，如图，在平面直角坐标系中，点O 为坐标原点，直线6y x =+与x 轴相交于点B ，与y 轴交于点C ，点A 是x 轴正半轴上一点，且满足2tan 3ACO ∠=．(1)若抛物线2y ax bx c =++经过A 、B 和C 三点，求抛物线的解析式；(2)若点M 是第二象限内抛物线上的一个动点，过点M 作MP y ∥轴，交BC 于点P ，连接OP ，在第一象限内找一点Q ，过点Q 作⊥OQ OP 且OQ OP =，连接PQ ，MQ ，设MPQ 的面积为S ，点P 的横坐标为t ，求S 与t 的函数关系式，并直接写出自变量的取值范围；(3)在（2）的条件下，设PQ 与y 轴相交于点R ，若53=PR PC 时，求点P 的坐标． 12．已知抛物线22y ax ax c =-+过点()10A -，和()03C ，，与x 轴交于另一点B ．(1)求抛物线的解析式；(2)若抛物线的顶点为D ，在直线BC 上方抛物线上有一点P （与D 不重合），BCP 面积与BCD △面积相等，求点P 的坐标；(3)若点E 为抛物线对称轴上一点，在平面内是否存在点F ，使得以E 、F 和B 、C 为顶点的四边形是菱形，若存在，请直接写出F 点的坐标；若不存在，请说明理由．13．如图，抛物线过点()08D ，，与x 轴交于()20A -，，()40B ，两点．(1)求抛物线的解析式；(2)若点C 为二次函数的顶点，求BCD S △．14．如图，O 为平面直角坐标系坐标原点，抛物线22y ax ax c =-+经过点()6,0B ，点()0,6C 与x 轴交于另一点A ．(1)求抛物线的解析式；(2)D 点为第一象限抛物线上一点，连接AD 和BD ，设点D 的横坐标为t ，ABD △的面积为S ，求S 关于t 的函数解析式（不要求写出自变量t 的取值范围）；(3)在（2）的条件下，P 为第四象限抛物线上一点，连接PA 交y 轴于点E ，点F 在线段BC 上，点G 在直线AD 上，若1tan 2DAO ∠=，四边形BEFG 为菱形，求点P 的坐标． 15．已知抛物线2()20y ax x c a =++≠与x 轴交于点(1,0)A -和点B ，与直线3y x =-+交于点B 和点C ，M 为抛物线的顶点，直线ME 是抛物线的对称轴．(1)求抛物线的解析式及点M 的坐标；(2)点P 为直线BC 上方抛物线上一点，连接PB ，PC ，当PBC 的面积取最大值时，求点P 的坐标．参考答案：1．(1)2142y x x =-- (2)① PC PD +取得最大值254 ① 53,2⎛⎫- ⎪⎝⎭或 316,2⎛⎫+- ⎪⎝⎭2．(1)213222y x x =-++ (1,0)-； (2)3172+或3172-或3332+或3332- (3)存在，517(,)39--或113(,)39-3．(1)故抛物线的表达式为：223y x x =-++，函数的对称轴为：1x =；(2)10113++(3)()4,5-或()8,45-4．(1)223y x x =-++(2)BCD △为直角三角形(3)点P 的坐标为()2,3，四边形PBCD 的面积为45．(1)213442y x x =-++ (2)S 的最大值为1，()4,6P(3)()7,3或()5,3-6．(1)2330S x x =-+ 410x ≤＜；(2)当宽AB 为5米，长15BC =米时，长方形花圃的最大面积为75平方米.7．(1)2122y x x =-+ (2)188．(1)()1,4(2)①()2,3D ；①CBD AMN S S △△的最大值为916，此时315,24D ⎛⎫ ⎪⎝⎭9．(1)13a =- (2)()4,4P(3)1010．(1)直角三角形(2)244S m m =-++ (2,3)P 1QHC S =(3)存在，点M 坐标为3651(,)22+或3651(,)22-或333(,)22或333(,)22-或31(,)22，理由见解析11．(1)211642=--+y x x (2)()2396042S t t t =---<< (3)()()124,2,2,4P P --12．(1)223y x x =-++(2)()23P ，(3)存在，点F 的坐标为()417，或()417-，或()2314-+，或()2314--，13．(1)228y x x =-++(2)614．(1)211642y x x =-++ (2)2553042S t t =-++ (3)()8,6P -15．(1)抛物线的解析式为223y x x =-++，点M 的坐标为(1,4)(2)315,24P ⎛⎫ ⎪⎝⎭。

中考数学压轴题---增长率(面积问题)例题讲解

中考数学压轴题---增长率（面积问题）例题讲解例1、（2022•无锡）某农场计划建造一个矩形养殖场，为充分利用现有资源，该矩形养殖场一面靠墙（墙的长度为10m），另外三面用栅栏围成，中间再用栅栏把它分成两个面积为1：2的矩形，已知栅栏的总长度为24m，设较小矩形的宽为xm（如图）．（1）若矩形养殖场的总面积为36m2，求此时x的值；（2）当x为多少时，矩形养殖场的总面积最大？最大值为多少？【解答】解：（1）根据题意知：较大矩形的宽为2xm，长为＝（8﹣x）m，∴（x+2x）×（8﹣x）＝36，解得x＝2或x＝6，经检验，x＝6时，3x＝18＞10不符合题意，舍去，∴x＝2，答：此时x的值为2；（2）设矩形养殖场的总面积是ym2，∵墙的长度为10m，根据题意得：y＝（x+2x）×（8﹣x）＝﹣3x2+24x＝﹣3（x﹣4）2+48，∵﹣3＜0，∴当x＝时，y取最大值，最大值为﹣3×（﹣4）2+48＝（m2），答：当x＝时，矩形养殖场的总面积最大，最大值为m2．【变式1-1】（2022•湘潭）为落实国家《关于全面加强新时代大中小学劳动教育的意见》，某校准备在校园里利用围墙（墙长12m）和21m长的篱笆墙，围成Ⅰ、Ⅱ两块矩形劳动实践基地．某数学兴趣小组设计了两种方案（除围墙外，实线部分为篱笆墙，且不浪费篱笆墙），请根据设计方案回答下列问题：（1）方案一：如图①，全部利用围墙的长度，但要在Ⅰ区中留一个宽度AE＝1m 的水池，且需保证总种植面积为32m2，试分别确定CG、DG的长；（2）方案二：如图②，使围成的两块矩形总种植面积最大，请问BC应设计为多长？此时最大面积为多少？【解答】解：（1）∵（21﹣12）÷3＝3（m），∴Ⅰ、Ⅱ两块矩形的面积为12×3＝36（m2），设水池的长为am，则水池的面积为a×1＝a（m2），解得a＝4，∴DG＝4m，∴CG＝CD﹣DG＝12﹣4＝8（m），即CG的长为8m、DG的长为4m；（2）设BC长为xm，则CD长度为21﹣3x，∴总种植面积为（21﹣3x）•x＝﹣3（x2﹣7x）＝﹣3（x﹣）2+，∵﹣3＜0，∴当x＝时，总种植面积有最大值为m2，即BC应设计为m总种植面积最大，此时最大面积为m2．【变式1-2】（2021•重庆）重庆小面是重庆美食的名片之一，深受外地游客和本地民众欢迎．某面馆向食客推出经典特色重庆小面，顾客可到店食用（简称“堂食”小面），也可购买搭配佐料的袋装生面（简称“生食”小面）．已知3份“堂食”小面和2份“生食”小面的总售价为31元，4份“堂食”小面和1份“生食”小面的总售价为33元．（1）求每份“堂食”小面和“生食”小面的价格分别是多少元？（2）该面馆在4月共卖出“堂食”小面4500份，“生食”小面2500份．为回馈广大食客，该面馆从5月1日起每份“堂食”小面的价格保持不变，每份“生食”小面的价格降低a%．统计5月的销量和销售额发现：“堂食”小面的销量与4月相同，“生食”小面的销量在4月的基础上增加a%，这两种小面的总销售额在4月的基础上增加a%．求a的值．【解答】解：（1）设每份“堂食”小面的价格为x元，每份“生食”小面的价格为y元，根据题意得：，解得：，答：每份“堂食”小面的价格为7元，每份“生食”小面的价格为5元；（2）由题意得：4500×7+2500（1+a%）×5（1﹣a%）＝（4500×7+2500×5）（1+a%），设a%＝m，则方程可化为：9×7+25（1+m）（1﹣m）＝（9×7+25）（1+ m），375m2﹣30m＝0，m（25m﹣2）＝0，解得：m1＝0（舍），m2＝，∴a＝8．【变式1-3】（2022•大渡口区校级模拟）草莓是大家非常喜欢的水果，3月份是草莓上市的旺季．某水果超市销售草莓，第一周每千克草莓的销售单价比第二周销售单价高10元，该水果超市这两周共销售草莓180千克，且第一周草莓的销量与第二周的销量之比为4：5，该水果超市这两周草莓销售总额为11600元．（1）第二周草莓销售单价是每千克多少元？（2）随着草莓的大量上市，3月份第三周，草莓定价与第二周保持一致，且该水果超市推出会员优惠活动，所有的会员均可享受每千克直降a元的优惠，而非会员需要按照原价购买，第三周草莓的销量比第二周增加了20%，其中通过会员优惠活动购买的销量占第三周草莓总销量的，而第三周草莓的销售总额为（6200+100a）元，求a的值．【解答】解：（1）设第一周草莓销售单价是每千克x元，第二周草莓销售单价是每千克y元，依题意得：，解得：，答：第二周草莓销售单价是每千克60元．（2）依题意可知，3月份第三周草莓的销售单价为60元/千克，第三周草莓的销售量为：180×（1+20%）＝120（千克），其中会员购买的销量为：120×＝20a（千克），非会员购买的销量为：（120﹣20a）千克，由题意得：20a（60﹣a）+（120﹣20a）×60＝6200+100a，整理得：a2+5a﹣50＝0，解得：a1＝5，a2＝﹣10（不符合题意，舍去）．答：a的值为5．【变式1-4】（2021•湖州）今年以来，我市接待的游客人数逐月增加，据统计，游玩某景区的游客人数三月份为4万人，五月份为5.76万人．（1）求四月和五月这两个月中该景区游客人数平均每月增长百分之几；（2）若该景区仅有A，B两个景点，售票处出示的三种购票方式如下表所示：并且当甲、乙两种门票价格不变时，丙种门票价格每下降1元，将有600人原计划购买甲种门票的游客和400人原计划购买乙种门票的游客改为购买丙种门票．①若丙种门票价格下降10元，求景区六月份的门票总收入；②问：将丙种门票价格下降多少元时，景区六月份的门票总收入有最大值？最大值是多少万元？【解答】解：（1）设四月和五月这两个月中该景区游客人数平均每月增长率为x，由题意，得4（1+x）2＝5.76，解这个方程，得x1＝0.2，x2＝﹣2.2（舍去），答：四月和五月这两个月中该景区游客人数平均每月增长率为20%；（2）①由题意，得100×（2﹣10×0.06）+80×（3﹣10×0.04）+（160﹣10）×（2+10×0.06+10×0.04）＝798（万元）．答：景区六月份的门票总收入为798万元．②设丙种门票价格降低m元，景区六月份的门票总收入为W万元，由题意，得W＝100（2﹣0.06m）+80（3﹣0.04m）+（160﹣m）（2+0.06m+0.04m），化简，得W＝﹣0.1（m﹣24）2+817.6，∵﹣0.1＜0，∴当m＝24时，W取最大值，为817.6万元．答：当丙种门票价格下降24元时，景区六月份的门票总收入有最大值，最大值是817.6万元．。

【中考压轴题专项练习】最新中考数学压轴大题冲刺专项训练：《面积的最值问题》含答案与解析

中考数学压轴大题冲刺专项训练面积的最值问题1．如图三角形ABC，BC＝12，AD是BC边上的高AD＝10．P，N分别是AB，AC边上的点，Q，M是BC 上的点，连接PQ，MN，PN交AD于E．求（1）若四边形PQMN是矩形，且PQ：PN＝1：2．求PQ、PN的长；（2）若四边形PQMN是矩形，求当矩形PQMN面积最大时，求最大面积和PQ、PN的长．2．如图，四边形ABCD的两条对角线AC、BD互相垂直，10AC BD，当AC、BD的长是多少时，四边形ABCD的面积最大？3．已知，如图，矩形ABCD中，AD＝6，DC＝7，菱形EFGH的三个顶点E，G，H分别在矩形ABCD的边AB，CD，AD上，AH＝2，连接CF．（1）当四边形EFGH为正方形时，求DG的长；（2）当DG ＝6时，求△FCG 的面积；（3）求△FCG 的面积的最小值．4．如图，已知点P 是∠AOB 内一点，过点P 的直线MN 分别交射线OA ，OB 于点M ，N ，将直线MN 绕点P 旋转，△MON 的形状与面积都随之变化．（1）请在图1中用尺规作出△MON ，使得△MON 是以OM 为斜边的直角三角形；（2）如图2，在OP 的延长线上截取PC ＝OP ，过点C 作CM ∥OB 交射线OA 于点M ，连接MP 并延长交OB 于点N ．求证：OP 平分△MON 的面积；（3）小亮发现：在直线MN 旋转过程中，（2）中所作的△MON 的面积最小．请利用图2帮助小亮说明理由．5．如图，现有一张矩形纸片ABCD ，2AB =，6BC =，点M ，N 分别在矩形的边AD ，BC 上，将矩形纸片沿直线MN 折叠，使点C 落在矩形的边AD 上，记为点P ，点D 落在G 处，连接PC ，交MN 于点Q ，连接CM ．（1）求证：PM PN =；（2）当P ，A 重合时，求MN 的值；（3）若PQM ∆的面积为S ，求S 的取值范围．6．某公司对办公大楼一块墙面进行如图所示的图案设计．这个图案由四个全等的直角三角形和一个小正方形拼接而成的大正方形，设小正方形的边长m ，直角三角形较短边长n ，且n ＝2m ﹣4，大正方形的面积为S ．（1）求S 关于m 的函数关系式．（2）若小正方形边长不大于3，当大正方形面积最大时，求m 的值．7．如图：已知矩形ABCD 中，AB =3cm ，BC =3cm ，点O 在边AD 上，且AO =1cm.将矩形ABCD 绕点O 逆时针旋转α角(0180α<<)，得到矩形A ′B ′C ′D ′(1)求证：AC ⊥OB ；(2)如图1, 当B ′落在AC 上时，求AA ′；(3)如图2，求旋转过程中△CC ′D ′的面积的最大值.8．[问题提出]（1）如图①，在ABC 中，6,BC D =为BC 上一点，4,AD =则ABC 面积的最大值是（2）如图②，已知矩形ABCD 的周长为12，求矩形ABCD 面积的最大值[实际应用]（3）如图③，现有一块四边形的木板余料ABCD ，经测量60.80,70,AB cm BC cm CD cm ===且60,B C ∠=∠=︒木匠师傅从这块余料中裁出了顶点,M N 在边BC 上且面积最大的矩形,PQMN 求该矩形的面积9．如图，已知A ，B 是线段MN 上的两点，4MN =，1MA =，1MB >，以A 为中心顺时针旋转点M ，以B 为中心逆时针旋转点N ，使M ，N 两点重合成一点C ，构成ABC ，设AB x =．（1）求x的取值范围；（2）求ABC面积的最大值．10．如图，已知AB为半圆O的直径，P为半圆上的一个动点（不含端点），以OP、OB为一组邻边作▱POBQ，连接OQ、AP，设OQ、AP的中点分别为M、N，连接PM、ON．（1）试判断四边形OMPN的形状，并说明理由．（2）若点P从点B出发，以每秒15°的速度，绕点O在半圆上逆时针方向运动，设运动时间为ts．①试求：当t为何值时，四边形OMPN的面积取得最大值？并判断此时直线PQ与半圆O的位置关系（需说明理由）；②是否存在这样的t，使得点Q落在半圆O内？若存在，请直接写出t的取值范围；若不存在，请说明理由．11．如图①，在△ABC中，∠C＝90°，AB＝10，BC＝8．点D，E分别是边AC，BC上的动点，连接DE．设CD＝x（x＞0），BE＝y，y与x之间的函数关系如图②所示．（1）求出图②中线段PQ所在直线的函数表达式；（2）将△DCE沿DE翻折，得△DME．①点M是否可以落在△ABC的某条角平分线上？如果可以，求出相应x的值；如果不可以，说明理由；②直接写出△DME与△ABC重叠部分面积的最大值及相应x的值．12．问题提出（1）如图①，已知线段AB，请以AB为斜边，在图中画出一个直角三角形；（2）如图②，已知点A是直线l外一点，点B、C均在直线l上，AD⊥l且AD=3，∠BAC=60°，求△ABC 面积的最小值；问题解决（3）如图③，某园林单位要设计把四边形花园划分为几个区域种植不同花草，在四边形ABCD中，∠A=45°，∠B=∠D=90°，CB=CD=6m，点E、F分别为AB、AD上的点，若保持CE⊥CF，那么四边形AECF的面积是否存在最大值?若存在，请求出面积的最大值；若不存在，请说明理由．参考答案与试题解析1．如图三角形ABC，BC＝12，AD是BC边上的高AD＝10．P，N分别是AB，AC边上的点，Q，M是BC 上的点，连接PQ，MN，PN交AD于E．求（1）若四边形PQMN是矩形，且PQ：PN＝1：2．求PQ、PN的长；（2）若四边形PQMN是矩形，求当矩形PQMN面积最大时，求最大面积和PQ、PN的长．【解析】解：（1）设PQ＝y，则PN＝2y，∵四边形PQMN是矩形，∴PN∥BC，∴△APN∽△ABC，∵AD⊥BC，∴AD⊥PN，∴PNBC＝AEAD，即212y＝1010y，解得y＝154，∴PQ＝154，PN＝152．（2）设AE＝x．∵四边形PQMN是矩形，∴PN∥BC，∴△APN∽△ABC，∵AD⊥BC，∴AD⊥PN，∴PN BC ＝AE AD， ∴PN ＝65x ，PQ ＝DE ＝10﹣x ， ∴S 矩形PQMN ＝65x （10﹣x ）＝﹣65（x ﹣5）2+30， ∴当x ＝5时，S 的最大值为30，∴当AE ＝5时，矩形PQMN 的面积最大，最大面积是30，此时PQ ＝5，PN ＝6．2．如图，四边形ABCD 的两条对角线AC 、BD 互相垂直，10ACBD ，当AC 、BD 的长是多少时，四边形ABCD 的面积最大？【解析】解：设AC=x ，四边形ABCD 面积为S ，则BD=10-x ，则：211125(10)(5)2222S AC BD x x x =⋅=-=--+， ∴当x=5时，S 最大=252，所以当AC=BD=5时，四边形ABCD 的面积最大．3．已知，如图，矩形ABCD 中，AD ＝6，DC ＝7，菱形EFGH 的三个顶点E ，G ，H 分别在矩形ABCD 的边AB，CD，AD上，AH＝2，连接CF．（1）当四边形EFGH为正方形时，求DG的长；（2）当DG＝6时，求△FCG的面积；（3）求△FCG的面积的最小值．【解析】解：（1）∵四边形EFGH为正方形，∴HG=HE，∠EAH=∠D=90°，∵∠DHG+∠AHE=90°，∠DHG+∠DGH=90°，∴∠DGH=∠AHE，∴△AHE≌△DGH（AAS），∴DG=AH=2；（2）过F作FM⊥DC，交DC延长线于M，连接GE，∵AB∥CD，∴∠AEG=∠MGE，∵HE∥GF，∴∠HEG=∠FGE，∴∠AEH=∠MGF，在△AHE和△MFG中，∠A=∠M=90°，HE=FG，∴△AHE≌△MFG（AAS），∴FM=HA=2，即无论菱形EFGH如何变化，点F到直线CD的距离始终为定值2，因此S△FCG=12×FM×GC=12×2×（7-6）=1；（3）设DG=x，则由（2）得，S△FCG=7-x，在△AHE中，AE≤AB=7，∴HE2≤53，∴x2+16≤53，∴x≤37，∴S△FCG的最小值为7-37，此时DG=37，∴当DG=37时，△FCG的面积最小为（7-37）．4．如图，已知点P是∠AOB内一点，过点P的直线MN分别交射线OA，OB于点M，N，将直线MN绕点P旋转，△MON的形状与面积都随之变化．（1）请在图1中用尺规作出△MON，使得△MON是以OM为斜边的直角三角形；（2）如图2，在OP的延长线上截取PC＝OP，过点C作CM∥OB交射线OA于点M，连接MP并延长交OB于点N．求证：OP平分△MON的面积；（3）小亮发现：在直线MN旋转过程中，（2）中所作的△MON的面积最小．请利用图2帮助小亮说明理由．【解析】（1）①在OB下方取一点K，②以P为圆心，PK长为半径画弧，与OB交于C、D两点，③分别以C 、D为圆心，大于12CD 长为半径画弧，两弧交于E 点， ④作直线PE ，分别与OA 、OB 交于点M 、N ，故△OMN 就是所求作的三角形；（2）∵CM ∥OB ，∴∠C ＝∠PON ，在△PCM 和△PON 中，C PON PC POCPH OPN ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△PCM ≌△PON （ASA ），∴PM ＝PN ，∴OP 平分△MON 的面积；（3）过点P 作另一条直线EF 交OA 、OB 于点E 、F ，设PF ＜PE ，与MC 交于于G ，∵CM ∥OB ，∴∠GMP ＝∠FNP ，在△PGM 和△PFM 中，PMG PNF PM PNMPG NPF ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△PGM ≌△PFN （ASA ），∴S △PGM ＝S △PFN∴S 四边形MOFG ＝S △MON ．∵S 四边形MOFG ＜S △EOF ，∴S △MON ＜S △EOF ，∴当点P 是MN 的中点时S △MON 最小．5．如图，现有一张矩形纸片ABCD ，2AB =，6BC =，点M ，N 分别在矩形的边AD ，BC 上，将矩形纸片沿直线MN 折叠，使点C 落在矩形的边AD 上，记为点P ，点D 落在G 处，连接PC ，交MN 于点Q ，连接CM ．=；（1）求证：PM PN（2）当P，A重合时，求MN的值；∆的面积为S，求S的取值范围．（3）若PQM【解析】（1）证明：如图1中，∵四边形ABCD是矩形，∴PM∥CN，∴∠PMN=∠MNC，∵∠MNC=∠PNM，∴∠PMN=∠PNM，∴PM=PN．（2）解：点P与点A重合时，如图2中，设BN=x ，则AN=NC=6-x ，在Rt △ABN 中，AB 2+BN 2=AN 2，即22+x 2=（6-x ）2，解得x=83， ∴CN=6-83=103，222226210AC AB BC =+=+=， ∴1102CQ AC ==， ∴222210()(10)310QN CN CQ =-=-=， ∴10223MN QN ==．（3）解：当MN 过点D 时，如图3所示，此时，CN 最短，四边形CMPN 的面积最小，则S 最小为14S S =菱形CMPN =12214⨯⨯=，当P点与A点重合时，CN最长，四边形CMPN的面积最大，则S最大为11210152102223S=⨯⨯⨯⨯=，∴513S≤≤．6．某公司对办公大楼一块墙面进行如图所示的图案设计．这个图案由四个全等的直角三角形和一个小正方形拼接而成的大正方形，设小正方形的边长m，直角三角形较短边长n，且n＝2m﹣4，大正方形的面积为S．（1）求S关于m的函数关系式．（2）若小正方形边长不大于3，当大正方形面积最大时，求m的值．【解析】解：（1）∵小正方形的边长m，直角三角形较短边长n，∴直角三角形较长边长为m+n，∴由勾股定理得：S＝（m+n）2+n2，∵n＝2m﹣4，∴S＝（m+2m﹣4）2+（2m﹣4）2，＝13m2﹣40m+32，∵n＝2m﹣4＞0，∴m＞2，∴S关于m的函数关系式为S＝13m2﹣40m+32（m＞2）；（2）∵S＝13m2﹣40m+32（2＜m≤3），∴S ＝13(m-2013)2+1613∵m≥2013时，S 随x 的增大而增大， ∴m ＝3时，S 取最大．∴m ＝3．7．如图：已知矩形ABCD 中，AB =3cm ，BC =3cm ，点O 在边AD 上，且AO =1cm.将矩形ABCD 绕点O 逆时针旋转α角(0180α<<)，得到矩形A ′B ′C ′D ′(1)求证：AC ⊥OB ；(2)如图1, 当B ′落在AC 上时，求AA ′；(3)如图2，求旋转过程中△CC ′D ′的面积的最大值.【解析】解：(1)Rt △OAB 中，tan 3AB AOB OA∠== ∴∠AOB ＝60° R t △ACD 中，3tan CD CAD AD ∠== ∴∠CAD ＝30°∴∠OMA ＝180°－60°－30°＝90°即AC ⊥OB(2)Rt △OAM 中，1•sin 1sin 302OM OA CAD =∠=⨯︒= Rt △OAB 中，OB ′＝OB ＝60OA COS ︒＝2， Rt △O B ′M 中，B ′M ＝2215OB OM -='， BM ＝OB －OM ＝32， Rt △B B ′M 中，2222153()()622BB B M BM =++''== ,,OA OB AOB A OB AOA BOB OA OB'''=∠=∴∆'∆''∽ ∴1,26AA OA BB OB ==''， ∴62AA '=(3)如图，过C 点作CH ⊥于C ′D ′点H ，连结OC ，则CH ≤OC ＋OD ′只有当D ′在CO 的延长线上时，CH 才最大.又C ′D ′长一定，故此时△CC ′D ′的面积的最大.而2222OC CD OD =+=∴△CC ′D ′的最大面积为1(222)3632+⨯=+ 8．[问题提出]（1）如图①，在ABC 中，6,BC D =为BC 上一点，4,AD =则ABC 面积的最大值是（2）如图②，已知矩形ABCD 的周长为12，求矩形ABCD 面积的最大值[实际应用]（3）如图③，现有一块四边形的木板余料ABCD ，经测量60.80,70,AB cm BC cm CD cm ===且60,B C ∠=∠=︒木匠师傅从这块余料中裁出了顶点,M N 在边BC 上且面积最大的矩形,PQMN 求该矩形的面积【解析】解：（1）过点A 作AE ⊥BC ，如图所示：∴12ABCS BC AE=⋅，∵D为BC上一点，∴AD AE≥，∴要使△ABC的面积最大，则需满足AD=AE，∵BC=6，AD=4，∴△ABC的面积最大为：16412 2⨯⨯=；故答案为12；（2）∵四边形ABCD是矩形，∴AB=DC，AD=BC，∵矩形ABCD的周长是12，∴设AB=x，则有AD=6-x，矩形ABCD的面积为S，则有：()()226639S x x x x x=-=-+=--+，此函数为二次函数，由10a=-<，二次函数的开口向下，∴当x=3时，矩形ABCD的面积有最大值为：S9=；（3）如图所示：∵四边形PQMN 是矩形，∴QM=PN ，PQ=MN ，∠QMN=∠PNM=90°，∵∠B=∠C=60°，∠QMB=∠PNC=90°，∴△BMQ ≌△CNP ，∴BM=NC ，设BM=NC=x ，则有MN=PQ=80-2x ， ∴603QM BM tan x =⋅︒=，∴()()2380223208003PQMN S PQ QM x x x =⋅=⋅-=--+矩形，此函数关系为二次函数，由230a =-<可得开口向下， ∴当x=20时，矩形PQMN 的面积有最大，即8003PQMN S =矩形． 9．如图，已知A ，B 是线段MN 上的两点，4MN =，1MA =，1MB >，以A 为中心顺时针旋转点M ，以B 为中心逆时针旋转点N ，使M ，N 两点重合成一点C ，构成ABC ，设AB x =．（1）求x 的取值范围；（2）求ABC 面积的最大值．【解析】解：（1）∵4MN =，1MA =，AB x =，∴413BN x x =--=-．由旋转的性质，得1MA AC ==，3BN BC x ==-，由三角形的三边关系，得31,31,x x x x --<⎧⎨-+>⎩①② 解不等式①得1x >，解不等式②得2x <，∴x 的取值范围是12x <<．（2）如图，过点C 作CD AB ⊥于点D ，设CD h =，由勾股定理，得2221AD AC CD h -=-=2222(3)BD BC CD x h =-=--∵BD AB AD =-， 222(3)1x h x h --=-2134-=-h x ，两边平方整理，得()222832=x x h x -+-．∵ABC 的面积为1122AB CD xh ⋅=， ∴()2222113183222422S xh x x x ⎛⎫⎛⎫==-⨯-+=--+ ⎪ ⎪⎝⎭⎝⎭，∴当32x 时，ABC面积最大值的平方为12，∴ABC面积的最大值为22．10．如图，已知AB为半圆O的直径，P为半圆上的一个动点（不含端点），以OP、OB为一组邻边作▱POBQ，连接OQ、AP，设OQ、AP的中点分别为M、N，连接PM、ON．（1）试判断四边形OMPN的形状，并说明理由．（2）若点P从点B出发，以每秒15°的速度，绕点O在半圆上逆时针方向运动，设运动时间为ts．①试求：当t为何值时，四边形OMPN的面积取得最大值？并判断此时直线PQ与半圆O的位置关系（需说明理由）；②是否存在这样的t，使得点Q落在半圆O内？若存在，请直接写出t的取值范围；若不存在，请说明理由．【解析】（1）四边形OMPN为矩形，理由如下：∵四边形POBQ为平行四边形，∴PQ∥OB，PQ=OB．又∵OB=OA，∴PQ=AO．又∵PQ∥OA，∴四边形PQOA为平行四边形，∴P A∥QO，P A=QO．又∵M、N分别为OQ、AP的中点，∴OM=12OQ，PN=12AP，∴OM=PN，∴四边形OMPN为平行四边形．∵OP=OA，N是AP的中点，∴ON⊥AP，即∠ONP=90°，∴四边形OMPN为矩形；（2）①∵四边形OMPN为矩形，∴S矩形OMPN =ON·NP=ON·12AP，即S矩形OMPN=S△AOP．∵△AOP的底AO为定值，∴当P旋转运动90°（运动至最高点）时，△AOP的AO边上的高取得最大值，此时△AOP的面积取得最大值，∴t=90÷15=6秒，∴当t=6秒时，四边形OMPN面积最大．此时，PQ与半圆O相切．理由如下：∵此时∠POB=90°，PQ//OB，∴∠OPQ=90°，∴PQ与半圆O相切；②当点Q在半圆O上时，∵四边形POBQ为平行四边形，且OB=OP，∴四边形POBQ为菱形，∴OB=BQ=OQ=OP=PQ，∴∠POQ=∠BOQ=60°，即：∠BOP=120°，∴此时，t=120°÷15°=8秒，当点P与点A重合时，t=180°÷15°=12秒，综上所述：当8＜t＜12时，点Q在半圆O内．11．如图①，在△ABC中，∠C＝90°，AB＝10，BC＝8．点D，E分别是边AC，BC上的动点，连接DE．设CD＝x（x＞0），BE＝y，y与x之间的函数关系如图②所示．（1）求出图②中线段PQ所在直线的函数表达式；（2）将△DCE沿DE翻折，得△DME．①点M是否可以落在△ABC的某条角平分线上？如果可以，求出相应x的值；如果不可以，说明理由；②直接写出△DME与△ABC重叠部分面积的最大值及相应x的值．【解析】解：（1）设线段PQ 所在直线的函数表达式为y ＝kx +b ，将P （3，4）和Q （6，0）代入得，0306k b k b =+⎧⎨=+⎩，解得438k b ⎧=-⎪⎨⎪=⎩， ∴线段PQ 所在直线的函数表达式为483y x =-+；（2）①如图1，连接CM 并延长CM 交AB 于点F ，∵∠C ＝90°，AB ＝10，BC ＝8，∴AC 22AB BC -＝6，由（1）得BE ＝()2221624248DEKP S x x x =-+-=--+四边形，∴CE ＝43x ，∴34DC AC CE BC ==， ∵∠DCE ＝∠ACB ，∴△DCE ∽△ACB ，∴∠DEC ＝∠ABC ，∴DE//AB，∵点C和点M关于直线DE对称，∴CM⊥DE，∴CF⊥AB，∵1122ABCS AC BC AB CF==△，∴6×8＝10×CF，∴CF＝24 5,∵∠C＝90°，CD＝x，CE＝43x，∴DE53x =，∴CM＝85x，MF＝24855x-，过点M作MG⊥AC于点M，过点M作MH⊥BC于点H，则四边形GCHM为矩形，∵∠GCM+∠BCF＝∠BCF+∠ABC＝90°，∴∠GCM＝∠ABC，∵∠MGC＝∠ACB＝90°，∴△CGM∽△BCA，∴MG CG CM AC BC AB==，即85 6810x MG CG==，∴MG ＝2425x ，CG ＝3225x ， ∴MH ＝3225x ，（Ⅰ）若点M 落在∠ACB 的平分线上，则有MG ＝MH ，即24322525x x =，解得x ＝0（不合题意舍去），（Ⅱ）若点M 落在∠BAC 的平分线上，则有MG ＝MF ，即242482555x x =-，解得x ＝158，（Ⅲ）若点M 落在∠ABC 的平分线上，则有MH ＝MF ，即322482555x x =-，解得x ＝53．综合以上可得，当x ＝158或x ＝53时，点M 落在△ABC 的某条角平分线上． ②当0＜x ≤3时，点M 不在三角形外，△DME 与△ABC 重叠部分面积为△DME 的面积，∴2142233S x x x ==，当x ＝3时，S 的最大值为22363⨯=．当3＜x ≤6时，点M 在三角形外，如图2，由①知CM ＝2CQ ＝85x ， ∴MT ＝CM ﹣CF ＝82455x -， ∵PK//DE ，∴△MPK ∽△MDE ，∴()2222824265545MPKMDE x x S MF S MQ x x ⎛⎫- ⎪-⎛⎫=== ⎪ ⎪⎝⎭ ⎪⎝⎭△△ ， ∴()2226MPK MDE x S S x -=△△，∵DEKP MDE MPK S S S =-△△四边形，∴()()2222226262113DEKP MDE x x S S x x x ⎡⎤⎡⎤--=-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦△四边形，即：()2221624248DEKP S x x x =-+-=--+四边形，∴当x ＝4时，△DME 与△ABC 重叠部分面积的最大值为8．综合可得，当x ＝4时，△DME 与△ABC 重叠部分面积的最大值为8．13．问题提出（1）如图①，已知线段AB ，请以AB 为斜边，在图中画出一个直角三角形；（2）如图②，已知点A 是直线l 外一点，点B 、C 均在直线l 上，AD ⊥l 且AD=3，∠BAC=60°，求△ABC 面积的最小值；问题解决（3）如图③，某园林单位要设计把四边形花园划分为几个区域种植不同花草，在四边形ABCD 中，∠A=45°，∠B=∠D=90°，CB=CD=6m ，点E 、F 分别为AB 、AD 上的点，若保持CE ⊥CF ，那么四边形AECF 的面积是否存在最大值?若存在，请求出面积的最大值；若不存在，请说明理由．【解析】解：（1）如图，Rt△ACB即为所求．（2）如图，作△ABC的外接圆⊙O，连接OA，OB，OC，过点O作OE⊥BC于点E，则∠BOC=2∠BAC，OA=OB=OC，BE=CE=12 BC，∵∠BAC=60°，∴∠BOC=120°，∠OBC=∠OCB=30°，设OA=OB=OC=r，则OE=12r，3，∵AO+OE≥A D，AD=3，∴r+12r≥3，解得r≥2，∴323∴S△ABC=12BC·AD≥12×33=33∴△ABC 面积的最小值为33．（3）存在；如图，分别延长AB 、DC 交于点M ，则△ADM 、△CBM 均为等腰直角三角形， ∵CB=CD=6m ，∴BM=6m ，CM=62，AD=DM=（6+2m ， ∴S 四边形ABCD=S △ADM -S △CBM=12DM 2-12BC 2 =12×（6+622-12×62 =（36+362）m 2．将△CBE 绕点C 顺时针旋转135°得到△CDE′，则A 、D 、E′三点共线．∴S 四边形AECF =S 四边形ABCD –（S △CBE +S △CDF ）=S 四边形ABCD –S △CE ′F ∵S 四边形ABCD 为定值，∴当S △CE ′F 取得最小值时，S 四边形AECF 取得最大值．∵∠E′CF=135°-90°=45°，∴以E′F为斜边作等腰Rt△OE′F，则△CE′F的外接圆是以点O为圆心，OF长为半径的圆，设△CE′F的外接圆半径为rm，∴E′F=2rm，又∵OC+OD≥CD，∴22r+r≥6，∴r≥12-62，当点O在CD上时，E′F最短，此时E′F=2r=（122-12）m，∴S△CE′F最小=12×（122-12）×6=（362-36）m2，∴S四边形AECF最大=S四边形ABCD-S△CE’F最小=36+362-（362-36）=72m2．。

中考数学压轴题：二次函数中的面积问题(含答案)

学生/课程年级日期学科时段课型数学授课教师核心内容二次函数中求面积最值，图形平移或折叠面积问题1.会利用函数的图象性质来研究几何图形的面积最值问题；教学目标重、难点2.掌握几种求图形面积的常见解题方法与技巧，如：割补法、平行等积变换法等。

3.掌握图形平移或折叠变换过程中找等量关系列函数解析式求图形面积问题的一般方法．割补法求三角形面积，动态问题一般解题思路。

了解学生的学习情况S△ = a h或S△ = a d (d表示已知点到直线的距离)以动点作垂直(平行)x轴的直线，即铅垂高，再分别过点A,C作PF的高，即和为水平宽。

S△ = ×水平宽×铅垂高如下图：①等底等高的两个三角形面积相等．②底在同一条直线上并且相等，该底所对角的顶点是同一个点或在与底平行的直线上，这两个三角形面积相等．如图，AD∥BC中，AC与BD交点O，则S△ABC = S△DBC，S△AOB = S△COD2如图，在平面直角坐标系中，抛物线y＝mx －8mx＋4m＋2（m＞0）与y轴的交点为A，与x轴的交点分别为B（x ，10），C（x ，0），且x －x ＝4，直线AD∥x轴，在x轴上有一动点E（t，0）过点E作平行于y轴的直线l与抛物线，直线AD2 2 1的交点分别为P，Q．（1）求抛物线的解析式；（2）当0＜t≤8时，求△APC面积的最大值．图形面积的求法常见有三种，分别是：(1)_______________________________(2)_______________________________(3)_______________________________[学有所获答案] (1)直接公式求法割补法平行线等积变换法(2)(3) 2 如图，已知抛物线y ＝x ＋bx ＋c 与轴交于A ，B 两点（点A 在点B 的左侧）与轴交于点C （0，－3），对称轴是直线x＝1，直线BC 与抛物线的对称轴交于点D ，点E 为y 轴上一动点，CE 的垂直平分线交抛物线于P ，Q 两点（点P 在第三象限）（1）求抛物线的函数表达式和直线BC 的函数表达式；（2）当△CDE 是直角三角形，且∠CDE ＝90°时，求出点P 的坐标；（3）当△PBC 的面积为时，求点E 的坐标．2 如图，已知抛物线y ＝ x ＋ax ＋4a 与x 轴交于点A ，B ，与y 轴负半轴交于点C 且OB ＝OC ，点P 为抛物线上的一个动点，且点P 位于x 轴下方，点P 与点C 不重合．（1）求该抛物线的解析式；（2）若△PAC 的面积为，求点P 的坐标；（3）若以A ，B ，C ，P 为顶点的四边形面积记作S ，则S 取何值时，对应的点P 有且只有2个?将（）的图像如何平移到的图像。

2023年中考数学高频压轴题突破——二次函数与面积问题

2023年中考数学高频压轴题突破——二次函数与面积问题一、单选题1．如图，已知AB=8，点P是线段AB上的动点，以AP为边作正方形APCD，以PB 为底作等腰△PBE，连接CE，则△PCE的面积的最大值是（）A．B．4C．4.2D．2．下列函数关系中，是二次函数的为（）A．在弹性限度内，弹簧的长度y与所挂物体的质量x之间的关系.B．距离一定时，火车行驶的时间t与速度v之间的关系C．等边三角形的周长C与边长a之间的关系D．圆的面积S与半径之间的关系3．用48米木料制作成一个如图所示的“目”形长方形大窗框（横档EF，GH也用木料）．其中AB∥EF∥GH∥CD，要使窗框ABCD的面积最大，则AB的长为（）A．6米B．8米C．12米D．4．将抛物线y＝x2﹣4x+1向左平移至顶点落在y轴上，如图所示，则两条抛物线直线y＝﹣3和x轴围成的图形的面积S（图中阴影部分）是（）A．5B．6C．7D．85．如图，抛物线与x轴交于点A，B，与y轴交于点G，正方形CDEF的边CD在x轴上，E，F在抛物线上，连结GA ，GB ，ABG 是正三角形，2AB =，则阴影部分的面积为（）A．12 B．3 C．22- D．2-6．如图，点A （1，16），B （2，12），C （3，8），D （4，4）均在函数l 图象上，P 为该函数在第一象限内图象上一点，PE ⊥x 轴于点E ，当△OEP 的面积取最大值时，OE 的长为（）A ．1.5B ．2.5C ．3.5D ．4.5二、填空题7．如图，2=23y x x --与x 轴交于A ，B 两点（在左边）与y 轴交于C 点，P 是线段AC 上的一点，连结BP 交轴于点Q ，连结OP ，当OAP 和PQC 的面积之和与OBQ 的面积相等时，点的坐标为 .A y P8．用长12m 的铝合金条制成矩形窗框（如图所示），那么这个窗户的最大透光面积是（中间横框所占的面积忽略不计）9．如图所示，用一段长30m 的木栏围成一个一边靠墙的矩形菜园，墙长14m ，这个矩形菜园的面积最大为 2m ．10．如图，正方形的边长为4，以正方形中心为原点建立平面直角坐标系，作出函数213y x =与213y x =-的图象，则阴影部分的面积是．11．如图，菱形ABCD 的两条对角线AC 和BD 满足AC+BD ＝16，则这个菱形的面积最大值是．12．如图，在Rt △ABC 中，∠BAC =90°，AB =AC =16cm ，AD 为BC 边上的高，动点P 从点A 出发，沿A →D 方向以 cm /s 的速度向点D 运动，过P 点作PE ∥BC 交AC 于点E ，过E 点作EF ⊥BC 于点F ，设△ABP 的面积为S 1，四边形PDFE 的面积为S 2，则点P 在运动过程中，S 1+S 2的最大值为．三、解答题13．如图，用一段30米长的篱笆围出一个一边靠墙的矩形菜园，墙长为18米.求当平行于墙的边长为多少米时，围成的矩形面积最大，并求出面积的最大值.14．如图，矩形绿地的长、宽各增加 m x ，写出扩充后的绿地的面积y 与x 的关系式．15．如图，二次函数 223y x x =-++ 的图象与x 轴交于A 、B 两点，与y 轴交于点C ，顶点为D ，求 BCD 的面积．16．如图，四边形 ABCD 的两条对角线 AC 、 BD 互相垂直， 10AC BD += ，当、的长是多少时，四边形的面积最大？17．在平面直角坐标系中，若抛物线 22y x = 与直线 1y x =+ 交于点 (,)A a b 和点 (,)B c d ，其中 a c > ，点 O 为原点，求 ABO ∆ 的面积.18．如图所示的正方形区域ABCD 是某公园健身广场示意图，公园管理处想在其四个角的三角形区域内种植草皮加以绿化（阴影部分），剩余部分安装健身器材作为市民健身活动场所（四边形EFGH ）其中AB=100米，且AE=AH=CF=CG ．则当AE 的长度为多少时，市民健身活动场所的面积达到最大？AC BDABCD19．如图，已知二次函数y=﹣ 12x 2+bx ﹣6的图象与x 轴交于一点A （2，0），与y 轴交于点B ，对称轴与x 轴交于点C ，连接BA ，BC ，求△ABC 的面积．20．为了“创建文明城市，建设美丽家园”，我市某社区将辖区内的一块面积为1000m 2的空地进行绿化，一部分种草，剩余部分栽花，设种草部分的面积为x （m 2），种草所需费用y 1（元）与x （m 2）的函数关系式为 ()()11206006001000k x x y k x b x ≤<⎧⎪=⎨+≤≤⎪⎩ ，其图象如图所示：栽花所需费用y 2（元）与x （m 2）的函数关系式为y 2=﹣0.01x 2﹣20x+30000（0≤x≤1000）．（1）请直接写出k 1、k 2和b 的值；（2）设这块1000m 2空地的绿化总费用为W （元），请利用W 与x 的函数关系式，求出绿化总费用W 的最大值；（3）若种草部分的面积不少于700m 2，栽花部分的面积不少于100m 2，请求出绿化总费用W 的最小值．21．已知二次函数y ＝x 2+bx+c.(Ⅰ)若二次函数的图象经过(3，﹣2)，且对称轴为x＝1，求二次函数的解析式；(Ⅱ)如图，在(Ⅰ)的条件下，过定点的直线y＝﹣kx+k﹣4(k≤0)与(1)中的抛物线交于点M，N，且抛物线的顶点为P，若△PMN的面积等于3，求k的值；(Ⅲ)当c＝b2时，若在自变量x的值满足b≤x≤b+3的情况下，与其对应的函数值y的最小值为21，求此时二次函数的解析式.。

2023年九年级数学中考专题：二次函数综合压轴题(面积问题)(含简单答案)

2023年九年级数学中考专题：二次函数综合压轴题（面积问题）1．如图，二次函数25y ax bx =++的图象经过点(1,8)，且与x 轴交于A 、B 两点，与y 轴交于点C ，其中点(1,0)A -，M 为抛物线的顶点．(1)求二次函数的解析式； (2)求MCB △的面积；(3)在坐标轴上是否存在点N ，使得BCN △为直角三角形？若存在，求出点N 的坐标；若不存在，请说明理由．2．如图，抛物线212y x bx c =-++（b 、c 为常数）经过()4,0A 和()0,4B 两点，其顶点为C ．(1)求该抛物线的表达式及其顶点坐标；(2)若点M 是拋物线上第一象限的一个动点．设ABM 的面积为S ，试求S 的最大值； (3)若抛物线222y mx mx m =-++与线段AB 有两个交点，直接写出m 的取值范围． 3．如图，抛物线22(0)y ax ax c a =-+>与y 轴交于点C ，与x 轴交于A ，B 两点，点A 在点B 左侧．点A 的坐标为(1,0),3OC OA -=．(1)求抛物线的解析式；(2)在直线BC 下方的抛物线上是否存在一点P ，使得PBC 的面积等于ABC 面积的三分之二？若存在，求出此时OP 的长；若不存在，请说明理由．(3)将直线AC 绕着点C 旋转45︒得到直线l ，直线l 与抛物线的交点为M （异于点C ），求M 点坐标．4．如图1，抛物线24y ax bx a =+-经过()10A -，，()04C ，两点，与x 轴交于另一点B ．(1)求抛物线和直线BC 的解析式；(2)如图2，点P 为第一象限抛物线上一点，是否存在使四边形PBOC 面积最大的点P ？若存在，求出点P 的坐标；若不存在，请说明理由；(3)如图3，若抛物线的对称轴EF （E 为抛物线顶点）与直线BC 相交于点F ，M 为直线BC 上的任意一点，过点M 作MN EF ∥交抛物线于点N ，以E ，F ，M ，N 为顶点的四边形能否为平行四边形？若能，请求出点N 的坐标；若不能，请说明理由． 5．如图，抛物线24y ax bx =+-与x 轴交于点()2,0A -，()4,0B ，与y 轴交于点C ，顶点为D ．(1)求抛物线的解析式和顶点D 的坐标；(2)动点P ，Q 以相同的速度从点O 同时出发，分别在线段,OB OC 上向点B ，C 方向运动，过点P 作x 轴的垂线，交抛物线于点E ． ①当四边形OQEP 为矩形时，求点E 的坐标；①过点E 作EM BC ⊥于点M ，连接,PM QM ，设BPM △的面积为1S ，CQM 的面积为2S ，当PE 将BCE 的面积分成1:3两部分时，请直接写出12S S 的值． 6．如图，抛物线2(0)y ax bx c a =++≠与x 轴相交于A ，B 两点，抛物线的对称轴为直线=1x -，其中点A 的坐标为(3,0)-．(1)求点B 的坐标；(2)已知1a =，C 为抛物线与y 轴的交点，求抛物线的解析式； (3)若点P 在抛物线上，且4POCBOCSS=，求点P 的坐标；(4)设点Q 是线段AC 上的动点，过点Q 作QD y 轴交抛物线于点D ，求线段QD 长度的最大值．7．如图，在平面直角坐标系中，二次函数22y ax bx =++的图象与x 轴交于()30A -,，()10B ,两点，与y 轴交于点C ．(1)求二次函数的解析式；(2)点P 是直线AC 上方的抛物线上一动点，当ACP △的面积最大时，求点P 的坐标；(3)Q 是x 轴上一动点，M 是第二象限内抛物线上一点，若以A ，C ，M ，Q 为顶点的四边形是平行四边形，直接写出点Q 的坐标．8．如图，直线132y x =-+交y 轴于点A ，交x 轴于点C ，抛物线214y x bx c =-++经过点A ，点C ，且交x 轴于另一点B ．(1)直接写出点A ，点B ，点C 的坐标及抛物线的解析式；(2)在直线AC 上方的抛物线上有一点M ，求四边形ABCM 面积的最大值及此时点M 的坐标；(3)将线段OA 绕x 轴上的动点(),0P m 顺时针旋转90°得到线段O A ''，若线段O A ''与抛物线只有一个公共点，请结合函数图象，求m 的取值范围．9．如图，已知抛物线与x 轴交于()1,0A - 、()4,0B 两点，与y 轴交于点()0,3C ．(1)求抛物线的解析式； (2)求直线BC 的函数解析式；(3)在抛物线上，是否存在一点P ，使PAB 的面积等于ABC 的面积？若存在，求出点P 的坐标；若不存在，请说明理由．10．如图，抛物线26y ax bx =++与x 轴交于点()6,0B ，()2,0C -，与y 轴交于点A ，点P 是线段AB 上方抛物线上的一个动点．(1)求抛物线的解析式；(2)当点P 运动到什么位置时，PAB 的面积最大？(3)过点P 作x 轴的垂线，交线段AB 于点D ，再过点P 作PE x ∥轴交抛物线于点E ，连接DE ．是否存在点P ，使PDE △为等腰直角三角形？若存在，求点P 的坐标；若不存在，请说明理由．11．如图，直线l ：112y x =-+与x 轴，y 轴分别交于点B ，C ，经过B ，C 两点的抛物线2y x bx c =++与x 轴的另一个交点为A ．(1)求该抛物线的解析式；(2)若点P 在直线l 下方的抛物线上，过点P 作PD ①x 轴交l 于点D ，PE ①y 轴交l 于点E ，求PD PE +的最大值；(3)若点P 在直线l 下方的抛物线上，F 为直线l 上的点，以A ，B ，P ，F 为顶点的四边形能否构成平行四边形？若能，直接写出点F 的坐标；若不能，请说明理由． 12．已知顶点为()1,5A 的抛物线2y ax bx c =++经过点()5,1B ，(1)求抛物线的解析式；(2)设C ，D 分别是x 轴、y 轴上的两个动点．①当四边形ABCD 的周长最小时，在图1中作直线CD ，保留作图痕迹并直接写出直线CD 的解析式；①点()(),>0P m n m 是直线y x =上的一个动点，Q 是OP 的中点，以PQ 为斜边按图2所示构造等腰Rt PQR △．在①的条件下，记PQR 与COD △的公共部分的面积为S ，求S 关于m 的函数关系式，并求S 的最大值．13．抛物线24y x x =-与直线y x =交于原点O 和点B ，与x 轴交于另一点A ，顶点为D ．(1)填空：点B 的坐标为___________，点D 的坐标为___________．(2)如图1 ，连结OD P ，为x 轴上的动点，当以O D P ，，为顶点的三角形是等腰三角形时，请直接写出点P 的坐标；(3)如图2， M 是点B 关于拋物线对称轴的对称点， Q 是拋物线上的动点，它的横坐标为 (05)m m <<，连结MQ BQ MQ ，，与直线OB 交于点E ．设BEQ 和BEM △的面积分别为1S 和2S ，设12S t s =，试求t 关于m 的函数解析式并求出t 的最值． 14．如图，二次函数的图象经过点()10A -，，()30B ，，()03C -，，直线22y x =-与x 轴、y 轴交于点D ，E ．(1)求该二次函数的解析式(2)点M 为该二次函数图象上一动点．①若点M 在图象上的B ，C 两点之间，求DME 的面积的最大值． ①若MED EDB ∠∠=，求点M 的坐标．15．如图，在平面直角坐标系中，抛物线24y ax bx =+-与x 轴交于()2,0A -，B 两点，其对称轴直线2x =与x 轴交于点D ．(1)求该抛物线的函数表达式为______；(2)如图1，点P 为抛物线上第四象限内的一动点，连接CD ，PB ，PC ，求四边形BDCP 面积最大值和点P 此时的坐标；(3)如图2，将该抛物线向左平移得到抛物线y '，当抛物线y '经过原点时，与原抛物线的对称轴相交于点E ，点F 为抛物线y '对称轴上的一点，点M 是平面内一点，若以点A ，E ，F ，M 为顶点的四边形是以AE 为边的菱形，请直接写出满足条件的点M 的坐标______．16．如图，已知抛物线2y x bx c =++与x 轴交于点()21,0A m -和点()2,0B m +，与y 轴交于点C ，对称轴轴为直线=1x -．(1)求抛物线的解析式；(2)点P 是直线AC 上一动点，过点P 作PQ y ∥轴，交抛物线于点Q ，以P 为圆心，PQ 为半径作P ，当P 与坐标轴相切时，求P 的半径；(3)直线()340y kx k k =++≠与抛物线交于M ，N 两点，求AMN 面积的最小值．17．如图，在平面直角坐标系中，抛物线23y ax bx =+-与x 轴交于两点()1,0A -和()3,0B ，与y 轴交于点C ，抛物线上有一动点P ，抛物线的对称轴交x 轴于点E ，连接EC ，作直线BC ．(1)求抛物线的解析式；(2)若点P 为直线BC 上方抛物线上一动点时，连接,PB PC ，当23EBC PBC S S =△△时，求点P 坐标；(3)如果抛物线的对称轴上有一动点Q ，x 轴上有一动点N ，是否存在四边形PQCN 是矩形？若存在，在横线上直接写出点N 的坐标，若不存在，请说明理由． 18．如图，直线122y x =-+交y 轴于点A ，交x 轴于点C ，抛物线214y x bx c=-++经过点A ，点C ，且交x 轴于另一点B ．(1)直接写出点A ，点B ，点C 的坐标及抛物线的解析式；(2)在直线AC 上方的抛物线上有一点M ，求三角形ACM 面积的最大值及此时点M 的坐标；(3)将线段OA 绕x 轴上的动点(),0P m 顺时针旋转90︒得到线段O A ''，若线段O A ''与抛物线只有一个公共点，请结合函数图象，求m 的取值范围（直接写出结果即可）．参考答案：1．(1)245y x x =-++； (2)15(3)存在，点N 的坐标为(5,0)-或(0,5)-或(0,0)．2．(1)2142y x x =-++，91,2⎛⎫⎪⎝⎭(2)S 的最大值为4 (3)2m ≥或1249m -<≤-3．(1)抛物线的解析式为2=23y x x -- (2)不存在这样的点P ， (3)M 点坐标是(45)，或315()24-，4．(1)抛物线的解析式：234y x x =-++；直线BC 的解析式为4y x =-+；(2)当()26P ，时，四边形PBOC 面积最大； (3)能，点N 的坐标为52124⎛⎫ ⎪⎝⎭，或724⎛- ⎝或724⎛- ⎝．5．(1)2142y x x =--，91,2D ⎛⎫- ⎪⎝⎭．(2)①(-；①1215S S =或1279S S =6．(1)(1,0) (2)223y x x =+- (3)(4,21)或()4,5- (4)947．(1)224233y x x =--+(2)3(2P -，5)2(3)(5,0)-或(1,0)-8．(1)03A （，），20B -（，），60C （，），抛物线解析式为：2134y x x =-++； (2)3a =时，四边形ABCM 面积最大，其最大值为754，此时M 的坐标为153,4⎛⎫⎪⎝⎭；(3)当3m -≤≤-33m ≤≤时，线段O A ''与抛物线只有一个公共点．9．(1)239344y x x =-++(2)334y x =-+(3)存在，点P 的坐标为：()13,3P ，23P ⎫-⎪⎪⎝⎭，33P ⎫-⎪⎪⎝⎭10．(1)21262y x x =-++(2)153,2P ⎛⎫ ⎪⎝⎭(3)点P 坐标为()46，或()55．11．(1)2512y x x =-+ (2)3(3)13,2⎛⎫- ⎪⎝⎭或1(1,)212．(1)21119424y x x =-++(2)①4y x =-+；①当02m <≤时，218PQRSm =；当823m <≤时，27448S m m =-+-；当843m ≤≤时，21244S m m =-+；S 的最大值为：47答案第3页，共3页 13．(1)()5,5；()2,4-；(2)点P的坐标为()或()-或()4,0或()5,0； (3)()2150566t m m m =-+<<，当52m =时，t 的最大值为2524．14．(1)该二次函数的解析式是()()21323y x x x x =+-=--；(2)①DME 的面积的最大值为52；①点M的坐标为⎝⎭或()12--．15．(1)214433y x x =-- (2)PBDC S 四边形的最大值为17，此时点P 的坐标为()3,5-(3)⎛ ⎝⎭或⎛ ⎝⎭或⎛- ⎝⎭或8,⎛- ⎝⎭16．(1)223y x x =+-(2)2或4(3)817．(1)2=23y x x --(2)⎝⎭或⎝⎭ (3)存在，⎫⎪⎪⎝⎭或⎫⎪⎪⎝⎭18．(1)()0,2A ，()2,0B -，()4,0C ，211242y x x =-++ (2)2，()2,2(3)34m -≤≤-或32m -+≤。

初三数学压轴题及答案

⼀、图形运动产⽣的⾯积问题知识点睛研究_基本_图形分析运动状态：①由起点、终点确定t的范围；②对t分段，根据运动趋势画图，找边与定点，通常是状态转折点相交时的特殊位置．分段画图，选择适当⽅法表达⾯积．⼆、精讲精练已知，等边三⾓形ABC的边长为4厘⽶，长为1厘⽶的线段MN在△ABC的边AB上，沿AB⽅向以1厘⽶/秒的速度向B点运动（运动开始时，点与点重合，点N到达点时运动终⽌），过点M、N分别作边的垂线，与△ABC的其他边交于P、Q两点，线段MN 运动的时间为秒．（1）线段MN在运动的过程中，为何值时，四边形MNQP恰为矩形？并求出该矩形的⾯积．（2）线段MN在运动的过程中，四边形MNQP的⾯积为S，运动的时间为t．求四边形MNQP的⾯积S随运动时间变化的函数关系式，并写出⾃变量t的取值范围．1题图 2题图如图，等腰梯形ABCD中，AB∥CD，AB＝， CD＝，⾼CE＝，对⾓线AC、BD交于点H．平⾏于线段BD的两条直线MN、RQ 同时从点A出发，沿AC⽅向向点C匀速平移，分别交等腰梯形ABCD的边于M、N和R、Q，分别交对⾓线AC于F、G，当直线RQ到达点C时，两直线同时停⽌移动．记等腰梯形ABCD被直线MN扫过的⾯积为，被直线RQ扫过的⾯积为，若直线MN平移的速度为1单位/秒，直线RQ平移的速度为2单位/秒，设两直线移动的时间为x秒．（1）填空：∠AHB＝____________；AC＝_____________；（2）若，求x．如图，△ABC中，∠C＝90°，AC=8cm，BC=6cm，点P、Q同时从点C出发，以1cm/s的速度分别沿CA、CB匀速运动，当点Q到达点B时，点P、Q同时停⽌运动．过点P作AC的垂线l交AB于点R，连接PQ、RQ，并作△PQR关于直线l对称的图形，得到△PQ'R．设点Q的运动时间为t（s），△PQ'R与△PAR重叠部分的⾯积为S（cm2）．（1）t为何值时，点Q' 恰好落在AB上？（2）求S与t的函数关系式，并写出t的取值范围．（3）S能否为？若能，求出此时t的值；若不能，请说明理由．如图，在△ABC中，∠A=90°，AB=2cm，AC=4cm，动点P从点A出发，沿AB⽅向以1cm/s的速度向点B运动，动点Q从点B同时出发，沿BA⽅向以1cm/s的速度向点A运动．当点P到达点B时，P，Q两点同时停⽌运动．以AP为边向上作正⽅形APDE，过点Q作QF∥BC，交AC于点F．设点P的运动时间为ts，正⽅形APDE和梯形BCFQ重叠部分的⾯积为Scm2．（1）当t=_____s时，点P与点Q重合；（2）当t=_____s时，点D在QF上；（3）当点P在Q，B两点之间（不包括Q，B两点）时，求S与t之间的函数关系式．如图，在平⾯直⾓坐标系中，已知点A（0，1）、D（-2，0），作直线AD并以线段AD为⼀边向上作正⽅形ABCD．（1）填空：点B的坐标为________，点C的坐标为_________．（2）若正⽅形以每秒个单位长度的速度沿射线DA向上平移，直⾄正⽅形的顶点C落在y轴上时停⽌运动．在运动过程中，设正⽅形落在y轴右侧部分的⾯积为S，求S关于平移时间t（秒）的函数关系式，并写出相应的⾃变量t的取值范围．如图，在平⾯直⾓坐标系xOy中，已知直线l1：y=x与直线l2：y=-x+6相交于点M，直线l2与x轴相交于点N．　（1）求M，N的坐标．（2）已知矩形ABCD中，AB=1，BC=2，边AB在x轴上，矩形ABCD沿x轴⾃左向右以每秒1个单位长度的速度移动．设矩形ABCD与△OMN重叠部分的⾯积为S，移动的时间为t（从点B与点O重合时开始计时，到点A与点N重合时计时结束）．求S与⾃变量t之间的函数关系式，并写出相应的⾃变量t的取值范围．⼆、⼆次函数中的存在性问题⼀、知识点睛解决“⼆次函数中存在性问题”的基本步骤：①画图分析．研究确定图形，先画图解决其中⼀种情形．②分类讨论.先验证①的结果是否合理，再找其他分类，类⽐第⼀种情形求解．③验证取舍.结合点的运动范围，画图或推理，对结果取舍．⼆、精讲精练如图，已知点P是⼆次函数y=-x2+3x图象在y轴右侧部分上的⼀个动点，将直线y=-2x沿y轴向上平移，分别交x轴、y轴于A、B 两点. 若以AB为直⾓边的△PAB与△OAB相似，请求出所有符合条件的点P的坐标．抛物线与y轴交于点A，顶点为B，对称轴BC与x轴交于点C．点P在抛物线上，直线PQ//BC交x轴于点Q，连接BQ．（1）若含45°⾓的直⾓三⾓板如图所⽰放置，其中⼀个顶点与点C重合，直⾓顶点D在BQ上，另⼀个顶点E在PQ上，求直线BQ的函数解析式；（2）若含30°⾓的直⾓三⾓板的⼀个顶点与点C重合，直⾓顶点D在直线BQ上（点D不与点Q重合），另⼀个顶点E在PQ上，求点P的坐标．如图，矩形OBCD的边OD、OB分别在x轴正半轴和y轴负半轴上，且OD＝10，OB＝8．将矩形的边BC绕点B逆时针旋转，使点C恰好与x轴上的点A重合．（1）若抛物线经过A、B两点，求该抛物线的解析式：______________；（2）若点M是直线AB上⽅抛物线上的⼀个动点，作MN⊥x轴于点N．是否存在点M，使△AMN与△ACD相似？若存在，求出点M的坐标；若不存在，说明理由．已知抛物线经过A、B、C三点，点P（1，k）在直线BC：y=x3上，若点M在x轴上，点N在抛物线上，是否存在以A、M、N、P为顶点的四边形为平⾏四边形？若存在，请求出点M的坐标；若不存在，请说明理由．抛物线与y轴交于点C，与直线y=x交于A(-2，-2)、B(2，2)两点．如图，线段MN在直线AB上移动，且，若点M的横坐标为m，过点M作x轴的垂线与x轴交于点P，过点N作x轴的垂线与抛物线交于点Q．以P、M、Q、N为顶点的四边形否为平⾏四边形？若能，请求出m的值；若不能，请说明理由．三、⼆次函数与⼏何综合⼀、知识点睛 “⼆次函数与⼏何综合”思考流程：整合信息时，下⾯两点可为我们提供便利：①研究函数表达式．⼆次函数关注四点⼀线，⼀次函数关注k、b； ②)关键点坐标转线段长．找特殊图形、特殊位置关系，寻求边和⾓度信息．⼆、精讲精练如图，抛物线y=ax2-5ax+4（a＜0）经过△ABC的三个顶点，已知BC∥x轴，点A在x轴上，点C在y轴上，且AC=BC．（1）求抛物线的解析式．（2）在抛物线的对称轴上是否存在点M，使|MA-MB|？若存在，求出点M的坐标；若不存在，请说明理由．如图，已知抛物线y=ax2-2ax-b（a>0）与x轴交于A、B两点，点A在点B的右侧，且点B的坐标为(-1，0)，与y轴的负半轴交于点C，顶点为D．连接AC、CD，∠ACD=90°．　（1）求抛物线的解析式；（2）点E在抛物线的对称轴上，点F在抛物线上，且以B、A、F、E四点为顶点的四边形为平⾏四边形，求点的坐标．如图，在平⾯直⾓坐标系中，直线与抛物线交于A、B两点，点A在x轴上，点B的横坐标为-8．（1）求该抛物线的解析式；（2）点P是直线AB上⽅的抛物线上⼀动点（不与点A、B重合），过点P作x轴的垂线，垂⾜为C，交直线AB于点D，作PE⊥AB于点E．设△PDE的周长为l，点P的横坐标为x，求l关于x的函数关系式，并求出l的值．已知，抛物线经过A(-1，0)，C(2，)两点，与x轴交于另⼀点B．（1）求此抛物线的解析式；（2）若抛物线的顶点为M，点P为线段OB上⼀动点（不与点B重合），点Q在线段MB上移动，且∠MPQ=45°，设线段OP=x，MQ=，求y2与x的函数关系式，并直接写出⾃变量x的取值范围．已知抛物线的对称轴为直线，且与x轴交于A、B两点，与y轴交于点C，其中A(1，0)，C(0，-3). （1）求抛物线的解析式；（2）若点P在抛物线上运动（点P异于点A），①如图1，当△PBC的⾯积与△ABC的⾯积相等时，求点P的坐标； ②如图2，当∠PCB =∠BCA时，求直线CP的解析式．四、中考数学压轴题专项训练1.如图，在直⾓梯形OABC中，AB∥OC，BC⊥x轴于点C，A(1，1)，B(3，1)．动点P从点O出发，沿x轴正⽅向以每秒1个单位长度的速度移动．过点P作PQ⊥OA，垂⾜为Q．设点P移动的时间为t秒（0△OPQ与直⾓梯形OABC重叠部分的⾯积为S．（1）求经过O，A，B三点的抛物线解析式．（2）求S与t的函数关系式．（3）将△OPQ绕着点P顺时针旋转90°，是否存在t，使得△OPQ的顶点O或Q在抛物线上？若存在，直接写出t的值；若不存在，请说明理由．2.如图，抛物线与x轴交于A(-1，0)，B(4，0)两点，与y轴交于点C，与过点C且平⾏于x轴的直线交于另⼀点D，点P是抛物线上⼀动点．（1）求抛物线的解析式及点D的坐标．（2）点E在x轴上，若以A，E，D，P为顶点的四边形是平⾏四边形，求此时点P的坐标．（3）过点P作直线CD的垂线，垂⾜为Q．若将△CPQ沿CP翻折，点Q的对应点为Q′，是否存在点P，使点Q′恰好在x轴上？若存在，求出此时点P的坐标；若不存在，请说明理由． 3.（11分）如图，已知直线与坐标轴交于A，B两点，以线段AB为边向上作正⽅形ABCD，过点A，D，C的抛物线与直线的另⼀个交点为E．（1）请直接写出C，D两点的坐标，并求出抛物线的解析式；（2）若正⽅形以每秒个单位长度的速度沿射线AB下滑，直⾄顶点D落在x轴上时停⽌，设正⽅形落在x轴下⽅部分的⾯积为S，求S关于滑⾏时间t的函数关系式，并写出相应⾃变量t的取值范围；（3）在（2）的条件下，抛物线与正⽅形⼀起平移，同时停⽌，求抛物线上C，E两点间的抛物线弧所扫过的⾯积．4.（11分）如图，抛物线y=ax2+bx+c交x轴于点A(-3，0)，点B(1，0)，交y轴于点E(0，-3)．点C是点A关于点B的对称点，点F 是线段BC的中点，直线l过点F且与y轴平⾏．直线y=-x+m过点C，交y轴于点D．（1）求抛物线的解析式；（2）点K为线段AB上⼀动点，过点K作x轴的垂线，交直线CD于点H，交抛物线于点G，求线段HG长度的值；（3）在直线l上取点M，在抛物线上取点N，使以A，C，M，N为顶点的四边形是平⾏四边形，求点N的坐标．5.（11分）如图，在平⾯直⾓坐标系中，直线与抛物线交于A，B两点，点A在x轴上，点B的横坐标为-8．（1）求抛物线的解析式．（2）点P是直线AB上⽅的抛物线上⼀动点（不与点A，B重合），过点P作x轴的垂线，垂⾜为C，交直线AB于点D，作PE⊥AB于点E．①设△PDE的周长为l，点P的横坐标为x，求l关于x的函数关系式，并求出l的值．②连接PA，以PA为边作图⽰⼀侧的正⽅形APFG．随着点P的运动，正⽅形的⼤⼩、位置也随之改变．当顶点F或G恰好落在y轴上时，直接写出对应的点P的坐标．6.（11分）如图1，点A为抛物线C1：的顶点，点B的坐标为　(1，0)，直线AB交抛物线C1于另⼀点C．（1）求点C的坐标；（2）如图1，平⾏于y轴的直线x=3交直线AB于点D，交抛物线C1于点E，平⾏于y轴的直线x=a交直线AB于点F，交抛物线C1于点G，若FG:DE=4:3，求a的值；（3）如图2，将抛物线C1向下平移m（m>0）个单位得到抛物线C2，且抛物线C2的顶点为P，交x轴负半轴于点M，交射线AB于点N，NQ⊥x轴于点Q，当NP平分∠MNQ时，求m的值．附：参考答案⼀、图形运动产⽣的⾯积问题1. （1）当t=时，四边形MNQP恰为矩形．此时，该矩形的⾯积为平⽅厘⽶．（2）当0＜t≤1时，；当1＜t≤2时，；当2＜t＜3时，2．（1）90°；4 （2）x=2.3．（1）当t=时，点Q' 恰好落在AB上. （2）当0＜t≤时，；当＜t≤6时，（3）由（2）问可得，当0＜t≤时，；当＜t≤6时，；解得，或，此时.4．（1）1 （2）（3）当1＜t≤时，；当＜t＜2时，.5．（1）（﹣1，3），（﹣3，2）（2）当0＜t≤时，；当＜t≤1时，；当1＜t≤时，.6．（1）M（4，2） N（6，0）（2）当0≤t≤1时，；当1＜t≤4时，；当4＜t≤5时，；当5＜t≤6时，；当6＜t≤7时，⼆、⼆次函数中的存在性问题1.解：由题意，设OA=m，则OB=2m；当∠BAP=90°时，△BAP∽△AOB或△BAP∽△BOA；若△BAP∽△AOB，如图1，可知△PMA∽△AOB，相似⽐为2：1；则P1（5m，2m），代⼊，可知，若△BAP∽△BOA，如图2，可知△PMA∽△AOB，相似⽐为1：2；则P2（2m，），代⼊，可知，当∠ABP=90°时，△ABP∽△AOB或△ABP∽△BOA；若△ABP∽△AOB，如图3，可知△PMB∽△BOA，相似⽐为2：1；则P3（4m，4m），代⼊，可知，若△ABP∽△BOA，如图4，可知△PMB∽△BOA，相似⽐为1：2；则P4（m，），代⼊，可知，2.解：（1）由抛物线解析式可得B点坐标（1，3）.要求直线BQ的函数解析式，只需求得点Q坐标即可，即求CQ长度.过点D作DG⊥x轴于点G，过点D作DF⊥QP于点F.则可证△DCG≌△DEF.则DG=DF，∴矩形DGQF为正⽅形.则∠DQG=45°，则△BCQ为等腰直⾓三⾓形.∴CQ=BC=3，此时，Q点坐标为（4，0）可得BQ解析式为y=－x+4.（2）要求P点坐标，只需求得点Q坐标，然后根据横坐标相同来求点P坐标即可.⽽题⽬当中没有说明∠DCE=30°还是∠DCE=60°，所以分两种情况来讨论.当∠DCE=30°时，a）过点D作DH⊥x轴于点H，过点D作DK⊥QP于点K.则可证△DCH∽△DEK.则，在矩形DHQK中，DK=HQ，则.在Rt△DHQ中，∠DQC=60°.则在Rt△BCQ中，∴CQ=，此时，Q点坐标为（1+,0）则P点横坐标为1+.代⼊可得纵坐标.∴P（1+,）.b）⼜P、Q为动点，∴可能PQ在对称轴左侧，与上⼀种情形关于对称轴对称.由对称性可得此时点P坐标为（1－,）当∠DCE=60°时，过点D作DM⊥x轴于点M，过点D作DN⊥QP于点N.则可证△DCM∽△DEN.则，在矩形DMQN中，DN=MQ，则.在Rt△DMQ中，∠DQM=30°.则在Rt△BCQ中，∴CQ=BC=，此时，Q点坐标为（1+，0）则P点横坐标为1+.代⼊可得纵坐标.∴P（1+,）.b）⼜P、Q为动点，∴可能PQ在对称轴左侧，与上⼀种情形关于对称轴对称.由对称性可得此时点P坐标为（1－,）综上所述，P点坐标为（1+,），（1－,），（1+,）或（1－,）.3．解：（1）∵AB=BC=10，OB=8 ∴在Rt△OAB中，OA=6 ∴ A（6，0）将A（6，0），B（0，-8）代⼊抛物线表达式，得，（2）存在：如果△AMN与△ACD相似，则或设M（0假设点M在x轴下⽅的抛物线上，如图1所⽰：当时，，即∴∴如图2验证⼀下当时，，即∴（舍）2）如果点M在x轴上⽅的抛物线上：当时，，即∴∴M此时, ∴∴△AMN∽△ACD ∴M满⾜要求当时，，即∴m=10（舍）综上M1,M24.解：满⾜条件坐标为：思路分析：A、M、N、P四点中点A、点P为顶点，则AP可为平⾏四边形边、对⾓线；(1)如图，当AP为平⾏四边形边时，平移AP；∵点A、P纵坐标差为2 ∴点M、N纵坐标差为2；∵点M的纵坐标为0 ∴点N的纵坐标为2或-2①当点N的纵坐标为2时解：得⼜∵点A、P横坐标差为2 ∴点M的坐标为：、　②当点N的纵坐标为-2时　解：得⼜∵点A、P横坐标差为2 ∴点M的坐标为：、(2)当AP为平⾏四边形边对⾓线时；设M5（m,0）MN⼀定过AP的中点（0，-1）则N5（-m，-2），N5在抛物线上∴（负值不符合题意，舍去）∴∴综上所述:符合条件点P的坐标为：5．解：分析题意，可得：MP∥NQ，若以P、M、N、Q为顶点的四边形为平⾏四边形，只需MP=NQ即可。

最新九年级数学中考复习：二次函数综合压轴题题(面积问题)含答案

(1)求抛物线的表达式；
(2)点是线段上的动点（除、外），过点作轴的垂线交抛物线于点．
①当点的横坐标为2时，求四边形的面积；
②如图2，直线，分别与抛物线对称轴交于、两点．试问，是否为定值？如果是，请求出这个定值；如果不是，请说明理由．
20．如图，在平面直角坐标系中，直线AB交x轴于点A（﹣4，0），交y轴于点B，抛物线经过A，B两点，其对称轴交x轴于点M．P是线段AM上的一动点，过点P作PC⊥x轴交直线AB于点C，交抛物线于点D．
(2)如图，点在轴的负半轴上，且，连接，并延长交抛物线于点，点为直线上方抛物线上一动点，连接，，当的面积最大时，请求出的最大值及点的坐标；
(3)如图，将抛物线沿射线方向平移个单位到新抛物线，此时新抛物线顶点记为，为新抛物线上一点，若是以为直角边的直角三角形，请直接写出满足条件的点的横坐标．
(3)平行于DE的一条动直线l与直线BC相交于点P，与抛物线相交于点Q，若以D、E、P、Q为顶点的四边形是平行四边形，求P点的坐标．
(4)探究对称轴上是否存在一点P，使得以点P，C，A为顶点的三角形是等腰三角形？若存在，请求出所有符合条件的P点的坐标，若不存在，请说明理由．
18．已知抛物线与轴交于点和点，直线交轴于点和轴于点．
①连接，当的面积最大时，求此时点F的坐标；
②探究是否存在点D使得为直角三角形？若存在，求出点F的坐标；若不存在，说明理由．
8．如图，抛物线：与轴交于，两点，且顶点为，直线经过，两点．
(1)求直线的表达式与抛物线的表达式；
(2)如图，将抛物线沿射线方向平移一定距离后，得到抛物线为，其顶点为，抛物线与直线的另一交点为，与轴交于，两点点在点右边，若，求点的坐标；

专题03 二次函数中面积问题压轴真题训练(解析版)-挑战2023年中考数学选择、填空压轴真题汇编

挑战2023年中考数学解答题压轴真题汇编专题03二次函数中面积问题压轴真题训练1．（2022•连云港）已知二次函数y＝x2+（m﹣2）x+m﹣4，其中m＞2．（1）当该函数的图象经过原点O（0，0），求此时函数图象的顶点A的坐标；（2）求证：二次函数y＝x2+（m﹣2）x+m﹣4的顶点在第三象限；（3）如图，在（1）的条件下，若平移该二次函数的图象，使其顶点在直线y ＝﹣x﹣2上运动，平移后所得函数的图象与y轴的负半轴的交点为B，求△AOB面积的最大值．【解答】（1）解：把O（0，0）代入y＝x2+（m﹣2）x+m﹣4得：m﹣4＝0，解得m＝4，∴y＝x2+2x＝（x+1）2﹣1，∴函数图像的顶点A的坐标为（﹣1，﹣1）；（2）证明：由抛物线顶点坐标公式得y＝x2+（m﹣2）x+m﹣4的顶点为（，），∵m＞2，∴2﹣m＜0，∴＜0，∵＝﹣（m﹣4）2﹣1≤﹣1＜0，∴二次函数y＝x2+（m﹣2）x+m﹣4的顶点在第三象限；（3）解：设平移后图像对应的二次函数表达式为y＝x2+bx+c，其顶点为（﹣，），当x＝0时，B（0，c），将（﹣，）代入y＝﹣x﹣2得：＝﹣2，∴c＝，∵B（0，c）在y轴的负半轴，∴c＜0，∴OB＝﹣c＝﹣，过点A作AH⊥OB于H，如图：∵A（﹣1，﹣1），∴AH＝1，在△AOB中，S△AOB＝OB•AH＝×（﹣）×1＝﹣b2﹣b+1＝﹣（b+1）2+，∵﹣＜0，取最大值，最大值为，∴当b＝﹣1时，此时c＜0，S△AOB答：△AOB面积的最大值是．2．（2022•成都）如图，在平面直角坐标系xOy中，直线y＝kx﹣3（k≠0）与抛物线y＝﹣x2相交于A，B两点（点A在点B的左侧），点B关于y轴的对称点为B'．（1）当k＝2时，求A，B两点的坐标；（2）连接OA，OB，AB'，BB'，若△B'AB的面积与△OAB的面积相等，求k 的值；（3）试探究直线AB'是否经过某一定点．若是，请求出该定点的坐标；若不是，请说明理由．【解答】解：（1）当k＝2时，直线为y＝2x﹣3，由得：或，∴A（﹣3，﹣9），B（1，﹣1）；（2）当k＞0时，如图：∵△B'AB的面积与△OAB的面积相等，∴OB'∥AB，∴∠OB'B＝∠B'BC，∵B、B'关于y轴对称，∴OB＝OB'，∠ODB＝∠ODB'＝90°，∴∠OB'B＝∠OBB'，∴∠OBB'＝∠B'BC，∵∠ODB＝90°＝∠CDB，BD＝BD，∴△BOD≌△BCD（ASA），∴OD＝CD，在y＝kx﹣3中，令x＝0得y＝﹣3，∴C（0，﹣3），OC＝3，∴OD＝OC＝，D（0，﹣），在y＝﹣x2中，令y＝﹣得﹣＝﹣x2，解得x＝或x＝﹣，∴B（，﹣），把B（，﹣）代入y＝kx﹣3得：﹣＝k﹣3，解得k＝；当k＜0时，过B'作B'F∥AB交y轴于F，如图：在y＝kx﹣3中，令x＝0得y＝﹣3，∴E（0，﹣3），OE＝3，∵△B'AB的面积与△OAB的面积相等，∴OE＝EF＝3，∵B、B'关于y轴对称，∴FB＝FB'，∠FGB＝∠FGB'＝90°，∴∠FB'B＝∠FBB'，∵B'F∥AB，∴∠EBB'＝∠FB'B，∴∠EBB'＝∠FBB'，∵∠BGE＝90°＝∠BGF，BG＝BG，∴△BGF≌△BGE（ASA），∴GE＝GF＝EF＝，∴OG＝OE+GE＝，G（0，﹣），在y＝﹣x2中，令y＝﹣得﹣＝﹣x2，解得x＝或x＝﹣，∴B（，﹣），把B（，﹣）代入y＝kx﹣3得：﹣＝k﹣3，解得k＝﹣，综上所述，k的值为或﹣；（3）直线AB'经过定点（0，3），理由如下：由得：x2+kx﹣3＝0，设x2+kx﹣3＝0二根为a，b，∴a+b＝﹣k，ab＝﹣3，A（a，﹣a2），B（b，﹣b2），∵B、B'关于y轴对称，∴B'（﹣b，﹣b2），设直线AB'解析式为y＝mx+n，将A（a，﹣a2），B'（﹣b，﹣b2）代入得：，解得：，∵a+b＝﹣k，ab＝﹣3，∴m＝﹣（a﹣b）＝b﹣a＝＝，n＝﹣ab＝﹣（﹣3）＝3，∴直线AB'解析式为y＝•x+3，令x＝0得y＝3，∴直线AB'经过定点（0，3）．3．（2022•巴中）如图1，抛物线y＝ax2+2x+c，交x轴于A、B两点，交y轴于点C，F为抛物线顶点，直线EF垂直于x轴于点E，当y≥0时，﹣1≤x≤3．（1）求抛物线的表达式；（2）点P是线段BE上的动点（除B、E外），过点P作x轴的垂线交抛物线于点D．①当点P的横坐标为2时，求四边形ACFD的面积；②如图2，直线AD，BD分别与抛物线对称轴交于M、N两点．试问，EM+EN是否为定值？如果是，请求出这个定值；如果不是，请说明理由．【解答】解：（1）∵当y≥0时，﹣1≤x≤3，∴x1＝﹣1，x2＝3是ax2+2x+c＝0的两根，A（﹣1，0），B（3，0），∴，解得：，∴抛物线的表达式为：y＝﹣x2+2x+3；（2）①把x＝2代入y＝﹣x2+2x+3得：y＝3，∴D（2，3）．又当x＝0，y＝3，∴C（0，3），∴线段CD∥x轴．∵y＝﹣x2+2x+3＝﹣（x﹣1）2+4，∴F（1，4），；②设D（m，﹣m2+2m+3）（1＜m＜3），直线AD：y＝k1x+b1，BD：y＝k2x+b2，因此可得：或，解得：或，∴直线AD：y＝（3﹣m）x+（3﹣m），BD：y＝﹣（m+1）x+3（m+1）．令x＝1得y M＝6﹣2m，y N＝2m+2，∴ME＝6﹣2m，NE＝2m+2，∴NE+ME＝8．4．（2022•阜新）如图，已知二次函数y＝﹣x2+bx+c的图象交x轴于点A（﹣1，0），B（5，0），交y轴于点C．（1）求这个二次函数的表达式；（2）如图1，点M从点B出发，以每秒个单位长度的速度沿线段BC向点C运动，点N从点O出发，以每秒1个单位长度的速度沿线段OB向点B运动，点M，N同时出发．设运动时间为t秒（0＜t＜5）．当t为何值时，△BMN 的面积最大？最大面积是多少？（3）已知P是抛物线上一点，在直线BC上是否存在点Q，使以A，C，P，Q为顶点的四边形是平行四边形？若存在，直接写出点Q坐标；若不存在，请说明理由．【解答】解：（1）将点A（﹣1，0），B（5，0）代入y＝﹣x2+bx+c中，得，解这个方程组得，∴二次函数的表达式为y＝﹣x2+4x+5；（2）过点M作ME⊥x轴于点E，如图：设△BMN面积为S，根据题意得：ON＝t，BM＝．∵B（5，0），∴BN＝5﹣t，在y＝﹣x2+4x+5中，令x＝0得y＝5，∴C（0，5），∴OC＝OB＝5，∴∠OBC＝45°．∴ME＝BM sin45°＝，∴S＝BN•ME＝（5﹣t）•t＝﹣t2+t＝﹣（t﹣）2+，∵0＜t＜5，∴当时，△BMN的面积最大，最大面积是；（3）存在点Q，使以A，C，P，Q为顶点的四边形是平行四边形，理由如下：由B（5，0），C（0，5）得直线BC解析式为y＝﹣x+5，设Q（m，﹣m+5），P（n，﹣n2+4n+5），又A（﹣1，0），C（0，5），①当PQ，AC是对角线，则PQ，AC的中点重合，∴，解得m＝0（与C重合，舍去）或m＝﹣7，∴Q（﹣7，12）；②当QA，PC为对角线，则QA，PC的中点重合，∴，解得m＝0（舍去）或m＝7，∴Q（7，﹣2）；③当QC，PA为对角线，则QC，PA的中点重合，∴，解得m＝1或m＝2，∴Q（1，4）或（2，3），综上所述，Q的坐标为（﹣7，12）或（7，﹣2）或（1，4）或（2，3）．5．（2022•鞍山）如图，抛物线y＝﹣x2+bx+c与x轴交于A（﹣1，0），B两点，与y轴交于点C（0，2），连接BC．（1）求抛物线的解析式．（2）点P是第三象限抛物线上一点，直线PB与y轴交于点D，△BCD的面积为12，求点P的坐标．（3）在（2）的条件下，若点E是线段BC上点，连接OE，将△OEB沿直线OE翻折得到△OEB'，当直线EB'与直线BP相交所成锐角为45°，时，求点B'的坐标．【解答】解：（1）将A（﹣1，0），C（0，2）代入y＝﹣x2+bx+c，∴，解得，∴y＝﹣x2+x+2；（2）令y＝0，则﹣x2+x+2＝0，解得x＝﹣1或x＝4，∴B（4，0），∴OB＝4，＝×4×（2+OD）＝12，∴S△BCD∴OD＝4，∴D（0，﹣4），设直线BD的解析式为y＝kx+b，∴，解得，∴y＝x﹣4，联立方程组，解得或，∴P（﹣3，﹣7）；（3）如图1，当B'在第一象限时，设直线BC的解析式为y＝k'x+b'，∴，解得，∴y＝﹣x+2，设E（t，﹣t+2），∴OH＝t，EH＝﹣t+2，∵D（0，﹣4），B（4，0），∴OB＝OD，∴∠ODB＝45°，∵直线EB'与直线BP相交所成锐角为45°，∴EB'∥CD，由折叠可知，OB'＝BO＝4，BE＝B'E，在Rt△OHB'中，B'H＝，∴B'E＝﹣（﹣t+2）＝+t﹣2，∴BE＝+t﹣2，在Rt△BHE中，（+t﹣2）2＝（4﹣t）2+（﹣t+2）2，解得t＝，∵0≤t≤4，∴t＝，∴B'（，）；如图2，当B'在第二象限，∠BGB'＝45°时，∵∠ABP＝45°，∴B'G∥x轴，∵将△OEB沿直线OE翻折得到△OEB'，∴BE＝B'E，OB＝OB'，∠BOE＝∠B'OE，∴∠BOE＝∠B'EO，∴B'E∥B'O，∵B'E＝BO，∴四边形B'OBE是平行四边形，∴B'E＝4，∴B'（t﹣4，﹣t+2），由折叠可知OB＝OB'＝4，∴平行四边形OBEB'是菱形，∴BE＝OB，∴＝4，解得t＝4+或t＝4﹣，∵0≤t≤4，∴t＝4﹣，∴B'（﹣，）；综上所述：B'的坐标为（，）或（﹣，）．方法2：在Rt△BCO中，BC＝2，CO：OB：BC＝1：2：，∵BP与x轴和y轴的夹角都是45°，BP与B'E的夹角为45°，∴B'E∥x轴或B'E∥y轴，当B'E∥y轴时，延长B'E交x轴于F，∴B'F⊥OB，∵∠CBA＝∠OB'E，∴△OB'F∽△CBO，∴OF：FB'：B'O＝1：2：，∵OB＝OB'＝4，∴FO＝，B'F＝，∴B'（，）；当B'E∥x轴时，过B'作B'F⊥x中交于F，∴B'F⊥OF，B'E∥OB，∵B'E和BE关于OE对称，OB和OB'关于OE对称，∴BE∥OB'，∵∠FOB'＝∠OBC，∴△OB'F∽△BCO，∴B'F：FO：OB'＝1：2：，∵OB＝OB'＝4，∴B'F＝，OF＝，∴B'（﹣，）；综上所述：B'坐标为（，）或（﹣，）．6．（2022•菏泽）如图，抛物线y＝ax2+bx+c（a≠0）与x轴交于A（﹣2，0）、B（8，0）两点，与y轴交于点C（0，4），连接AC、BC．（1）求抛物线的表达式；（2）将△ABC沿AC所在直线折叠，得到△ADC，点B的对应点为D，直接写出点D的坐标，并求出四边形OADC的面积；（3）点P是抛物线上的一动点，当∠PCB＝∠ABC时，求点P的坐标．【解答】解：（1）∵抛物线y＝ax2+bx+c（a≠0）与x轴交于A（﹣2，0）、B（8，0）两点，与y轴交于点C（0，4），∴，解得：．∴抛物线的表达式为y＝﹣+x+4；（2）点D的坐标为（﹣8，8），理由：将△ABC沿AC所在直线折叠，得到△ADC，点B的对应点为D，如图，过点D作DE⊥x轴于点E，∵A（﹣2，0）、B（8，0），C（0，4），∴OA＝2，OB＝8，OC＝4．∵，，∴．∵∠AOC＝∠COB＝90°，∴△AOC∽△COB，∴∠ACO＝∠CBO．∵∠CBO+∠OCB＝90°，∴∠ACO+∠OCB＝90°，∴∠ACB＝90°，∵将△ABC沿AC所在直线折叠，得到△ADC，点B的对应点为D，∴点D，C，B三点在一条直线上．由轴对称的性质得：BC＝CD，AB＝AD．∵OC⊥AB，DE⊥AB，∴DE∥OC，∴OC为△BDE的中位线，∴OE＝OB＝8，DE＝2OC＝8，∴D（﹣8，8）；＝S△ABC，由题意得：S△ACD+S△ADC ∴四边形OADC的面积＝S△OAC+S△ABC＝S△OAC＝OC•OA+AB•OC＝4×2+10×4＝4+20＝24；（3）①当点P在BC上方时，如图，∵∠PCB＝∠ABC，∴PC∥AB，∴点C，P的纵坐标相等，∴点P的纵坐标为4，令y＝4，则﹣+x+4＝4，解得：x＝0或x＝6，∴P（6，4）；②当点P在BC下方时，如图，设PC交x轴于点H，∵∠PCB＝∠ABC，∴HC＝HB．设HB＝HC＝m，∴OH＝OB﹣HB＝8﹣m，在Rt△COH中，∵OC2+OH2＝CH2，∴42+（8﹣m）2＝m2，解得：m＝5，∴OH＝3，∴H（3，0）．设直线PC的解析式为y＝kx+n，∴，解得：．∴y＝﹣x+4．∴，解得：，．∴P（，﹣）．综上，点P的坐标为（6，4）或（，﹣）．7．（2022•沈阳）如图，在平面直角坐标系中，抛物线y＝ax2+bx﹣3经过点B （6，0）和点D（4，﹣3），与x轴的另一个交点为A，与y轴交于点C，作直线AD．（1）①求抛物线的函数表达式；②直接写出直线AD的函数表达式；（2）点E是直线AD下方的抛物线上一点，连接BE交AD于点F，连接BD，DE，△BDF的面积记为S1，△DEF的面积记为S2，当S1＝2S2时，求点E的坐标；（3）点G为抛物线的顶点，将抛物线图象中x轴下方的部分沿x轴向上翻折，与抛物线剩下的部分组成新的曲线记为C1，点C的对应点为C′，点G的对应点为G′，将曲线C1沿y轴向下平移n个单位长度（0＜n＜6）．曲线C1与直线BC的公共点中，选两个公共点记作点P和点Q，若四边形C′G′QP 是平行四边形，直接写出点P的坐标．【解答】解：（1）①∵抛物线y＝ax2+bx﹣3经过点B（6，0）和点D（4，﹣3），∴，解得：，∴抛物线的函数表达式为y＝x2﹣x﹣3；②由①得y＝x2﹣x﹣3，当y＝0时，x2﹣x﹣3＝0，解得：x1＝6，x2＝﹣2，∴A（﹣2，0），设直线AD的函数表达式为y＝kx+d，则，解得：，∴直线AD的函数表达式为y＝x﹣1；（2）如图1，过点B作BG∥y轴交直线AD于G，过点E作EH∥y轴交直线AD于H，∵S1＝2S2，即＝2，∴＝2，∵BG∥y轴，EH∥y轴，∴BG∥EH，∴△BFG∽△EFH，∴＝＝2，即BG＝2EH，∵点G在直线y＝x﹣1上，BG∥y轴，∴G（6，﹣4），∴BG＝4，∴EH＝2，设E（x，x2﹣x﹣3），则H（x，x﹣1），∴EH＝x﹣1﹣（x2﹣x﹣3）＝﹣x2+x+2，∴﹣x2+x+2＝2，解得：x1＝0，x2＝2，∴E（0，﹣3）或（2，﹣4）；（3）∵y＝x2﹣x﹣3＝（x﹣2）2﹣4，∴顶点坐标为G（2，﹣4），当x＝0时，y＝3，即点C（0，﹣3），∴点C′（0，3），G′（2，4），∴向上翻折部分的图象解析式为y＝﹣（x﹣2）2+4，∴向上翻折部分平移后的函数解析式为y＝﹣（x﹣2）2+4﹣n，平移后抛物线剩下部分的解析式为y＝（x﹣2）2﹣4﹣n，设直线BC的解析式为y＝k′x+d′（k′≠0），把点B（6，0），C（0，﹣3）代入得：，解得：，∴直线BC的解析式为y＝x﹣3，同理直线C′G′的解析式为y＝x+3，∴BC∥C′G′，设点P的坐标为（s，s﹣3），∵点C′（0，3），G′（2，4），∴点C′向右平移2个单位，再向上平移1个单位得到点G′，∵四边形C′G′QP是平行四边形，∴点Q（s+2，s﹣2），当点P，Q均在向上翻折部分平移后的图象上时，则，解得：，∵0＜n＜6，∴s＝0，n＝6不符合题意，舍去；当点P在向上翻折部分平移后的图象上，点Q在平移后抛物线剩下部分的图象上时，则，解得：或（不合题意，舍去），当点P在平移后抛物线剩下部分的图象上，点Q在向上翻折部分平移后的图象上时，则，解得：或（不合题意，舍去），综上所述，点P的坐标为（1+，）或（1﹣，）．8．（2022•西藏）在平面直角坐标系中，抛物线y＝﹣x2+（m﹣1）x+2m与x 轴交于A，B（4，0）两点，与y轴交于点C，点P是抛物线在第一象限内的一个动点．（1）求抛物线的解析式，并直接写出点A，C的坐标；（2）如图甲，点M是直线BC上的一个动点，连接AM，OM，是否存在点M 使AM+OM最小，若存在，请求出点M的坐标，若不存在，请说明理由；（3）如图乙，过点P作PF⊥BC，垂足为F，过点C作CD⊥BC，交x轴于点D，连接DP交BC于点E，连接CP．设△PEF的面积为S1，△PEC的面积为S2，是否存在点P，使得最大，若存在，请求出点P的坐标，若不存在，请说明理由．【解答】解：（1）将B（4，0）代入y＝﹣x2+（m﹣1）x+2m，∴﹣8+4（m﹣1）+2m＝0，解得m＝2，∴y＝﹣x2+x+4，令x＝0，则y＝4，∴C（0，4），令y＝0，则﹣x2+x+4＝0，解得x＝4或x＝﹣2，∴A（﹣2，0）；（2）存在点M使AM+OM最小，理由如下：作O点关于BC的对称点O'，连接AO'交BC于点M，连接BO'，由对称性可知，OM＝O'M，∴AM+OM＝AM+O'M≥AO'，当A、M、O'三点共线时，AM+OM有最小值，∵B（4，0），C（0，4），∴OB＝OC，∴∠CBO＝45°，由对称性可知∠O'BM＝45°，∴BO'⊥BO，∴O'（4，4），设直线AO'的解析式为y＝kx+b，∴，解得，∴y＝x+，设直线BC的解析式为y＝k'x+4，∴4k'+4＝0，∴k'＝﹣1，∴y＝﹣x+4，联立方程组，解得，∴M（，）；（3）存在点P，使得最大，理由如下：连接PB，过P点作PG∥y轴交CB于点G，设P（t，﹣t2+t+4），则G（t，﹣t+4），∴PG＝﹣t2+2t，∵OB＝OC＝4，∴BC＝4，＝×4×（﹣t2+2t）＝﹣t2+4t＝×4×PF，∴S△BCP∴PF＝﹣t2+t，∵CD⊥BC，PF⊥BC，∴PF∥CD，∴＝，∵＝，∴＝，∵B、D两点关于y轴对称，∴CD＝4，∴＝﹣（t2﹣4t）＝﹣（t﹣2）2+，∵P点在第一象限内，∴0＜t＜4，∴当t＝2时，有最大值，此时P（2，4）．9．（2022•青海）如图1，抛物线y＝x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C．（1）求该抛物线的解析式；（2）若点E是抛物线的对称轴与直线BC的交点，点F是抛物线的顶点，求EF的长；＝6的点P？（3）设点P是（1）中抛物线上的一个动点，是否存在满足S△P AB 如果存在，请求出点P的坐标；若不存在，请说明理由．（请在图2中探讨）【解答】解：（1）将A（﹣1，0），B（3，0）代入y＝x2+bx+c，得：，解得：，∴该抛物线的解析式为y＝x2﹣2x﹣3．（2）∵抛物线的解析式为y＝x2﹣2x﹣3，∴抛物线的顶点F的坐标为（1，﹣4），抛物线的对称轴为直线x＝1．当x＝0时，y＝02﹣2×0﹣3＝﹣3，∴点C的坐标为（0，﹣3）．设直线BC的解析式为y＝mx+n（m≠0），将B（3，0），C（0，﹣3）代入y＝mx+n，得：，解得：，∴直线BC的解析式为y＝x﹣3．当x＝1时，y＝1﹣3＝﹣2，∴点E的坐标为（1，﹣2），∴EF＝|﹣2﹣（﹣4）|＝2．（3）∵点A的坐标为（﹣1，0），点B的坐标为（3，0），∴AB＝|3﹣（﹣1）|＝4．设点P的坐标为（t，t2﹣2t﹣3）．＝6，∵S△P AB∴×4×|t2﹣2t﹣3|＝6，即t2﹣2t﹣3＝3或t2﹣2t﹣3＝﹣3，解得：t1＝1﹣，t2＝1+，t3＝0，t4＝2，＝6的点P，点P的坐标为（1﹣，3）或（1+，3）或∴存在满足S△P AB（0，﹣3）或（2，﹣3）．10．（2022•上海）在平面直角坐标系xOy中，抛物线y＝x2+bx+c过点A（﹣2，﹣1），B（0，﹣3）．（1）求抛物线的解析式；（2）平移抛物线，平移后的顶点为P（m，n）（m＞0）．＝3，设直线x＝k，在这条直线的右侧原抛物线和新抛物线均ⅰ．如果S△OBP呈上升趋势，求k的取值范围；ⅱ．点P在原抛物线上，新抛物线交y轴于点Q，且∠BPQ＝120°，求点P 的坐标．【解答】解：（1）将A（﹣2，﹣1），B（0，﹣3）代入y＝x2+bx+c，得：，解得：，∴抛物线的解析式为y＝x2﹣3．（2）i．∵y＝x2﹣3，∴抛物线的顶点坐标为（0，﹣3），即点B是原抛物线的顶点，∵平移后的抛物线顶点为P（m，n），∴抛物线平移了|m|个单位，＝×3|m|＝3，∴S△OPB∵m＞0，∴m＝2，即平移后的抛物线的对称轴为直线x＝2，∵在x＝k的右侧，两抛物线都上升，原抛物线的对称轴为y轴，开口向上，∴k≥2；ii．把P（m，n）代入y＝x2﹣3，∴n＝﹣3，∴P（m，﹣3），由题意得，新抛物线的解析式为y＝+n＝﹣3，∴Q（0，m2﹣3），∵B（0，﹣3），∴BQ＝m2，+，PQ2＝，∴BP＝PQ，如图，过点P作PC⊥y轴于C，则PC＝|m|，∵PB＝PQ，PC⊥BQ，∴BC＝BQ＝m2，∠BPC＝∠BPQ＝×120°＝60°，∴tan∠BPC＝tan60°＝＝，∴m＝2或m＝﹣2（舍），∴n＝﹣3＝3，∴P点的坐标为（2，3）．轴交于A，B两点，A（1，0），AB＝4，点P为线段AB上的动点，过P作PQ∥BC交AC于点Q．（1）求该抛物线的解析式；（2）求△CPQ面积的最大值，并求此时P点坐标．【解答】（1）∵抛物线y＝x2+bx+c（b，c是常数）的顶点为C，与x轴交于A，B两点，A（1，0），AB＝4，∴B（﹣3，0），∴，解得，∴抛物线的解析式为y＝x2+2x﹣3；（2）过Q作QE⊥x轴于E，过C作CF⊥x轴于F，设P（m，0），则P A＝1﹣m，∵y＝x2+2x﹣3＝（x+1）2﹣4，∴C（﹣1，﹣4），∴CF＝4，∵PQ∥BC，∴△PQA∽△BCA，∴，即，∴QE＝1﹣m，＝S△PCA﹣S△PQA∴S△CPQ＝PA•CF﹣PA•QE＝（1﹣m）×4﹣（1﹣m）（1﹣m）＝﹣（m+1）2+2，∵﹣3≤m≤1，有最大值2，∴当m＝﹣1时S△CPQ∴△CPQ面积的最大值为2，此时P点坐标为（﹣1，0）．11．（2022•福建）在平面直角坐标系xOy中，已知抛物线y＝ax2+bx经过A（4，0），B（1，4）两点．P是抛物线上一点，且在直线AB的上方．（1）求抛物线的解析式；（2）若△OAB面积是△PAB面积的2倍，求点P的坐标；（3）如图，OP交AB于点C，PD∥BO交AB于点D．记△CDP，△CPB，△CBO的面积分别为S1，S2，S3．判断+是否存在最大值．若存在，求出最大值；若不存在，请说明理由．【解答】解：（1）将A（4，0），B（1，4）代入y＝ax2+bx，∴，解得．∴抛物线的解析式为：y＝﹣x2+x．（2）设直线AB的解析式为：y＝kx+t，将A（4，0），B（1，4）代入y＝kx+t，∴，解得．∵A（4，0），B（1，4），＝×4×4＝8，∴S△OAB＝2S△P AB＝8，即S△P AB＝4，∴S△OAB过点P作PM⊥x轴于点M，PM与AB交于点N，过点B作BE⊥PM于点E，如图，＝S△PNB+S△PNA＝PN×BE+PN×AM＝PN＝4，∴S△P AB∴PN＝．设点P的横坐标为m，∴P（m，﹣m2+m）（1＜m＜4），N（m，﹣m+），∴PN＝﹣m2+m﹣（﹣m+）＝．解得m＝2或m＝3；∴P（2，）或（3，4）．（3）∵PD∥OB，∴∠DPC＝∠BOC，∠PDC＝∠OBC，∴△DPC∽△BOC，∴CP：CO＝CD：CB＝PD：OB，∵＝＝，＝＝，∴+＝．设直线AB交y轴于点F．则F（0，），过点P作PH⊥x轴，垂足为H，PH交AB于点G，如图，∵∠PDC＝∠OBC，∴∠PDG＝∠OBF，∵PG∥OF，∴∠PGD＝∠OFB，∴△PDG∽△OBF，∴PD：OB＝PG：OF，设P（n，﹣n2+n）（1＜n＜4），由（2）可知，PG＝﹣n2+n﹣，∴+＝＝＝PG＝﹣（n﹣）2+．∵1＜n＜4，∴当n＝时，+的最大值为．12．（2022•岳阳）如图1，在平面直角坐标系xOy中，抛物线F1：y＝x2+bx+c 经过点A（﹣3，0）和点B（1，0）．（1）求抛物线F1的解析式；（2）如图2，作抛物线F2，使它与抛物线F1关于原点O成中心对称，请直接写出抛物线F2的解析式；（3）如图3，将（2）中抛物线F2向上平移2个单位，得到抛物线F3，抛物线F1与抛物线F3相交于C，D两点（点C在点D的左侧）．①求点C和点D的坐标；②若点M，N分别为抛物线F1和抛物线F3上C，D之间的动点（点M，N与点C，D不重合），试求四边形CMDN面积的最大值．【解答】解：（1）将点A（﹣3，0）和点B（1，0）代入y＝x2+bx+c，∴，解得，∴y＝x2+2x﹣3；（2）∵y＝x2+2x﹣3＝（x+1）2﹣4，∴抛物线的顶点（﹣1，﹣4），∵顶点（﹣1，﹣4）关于原点的对称点为（1，4），∴抛物线F2的解析式为y＝﹣（x﹣1）2+4，∴y＝﹣x2+2x+3；（3）由题意可得，抛物线F3的解析式为y＝﹣（x﹣1）2+6＝﹣x2+2x+5，①联立方程组，解得x＝2或x＝﹣2，∴C（﹣2，﹣3）或D（2，5）；②设直线CD的解析式为y＝kx+b，∴，解得，∴y＝2x+1，过点M作MF∥y轴交CD于点F，过点N作NE∥y轴交CD于点E，设M（m，m2+2m﹣3），N（n，﹣n2+2n+5），则F（m，2m+1），E（n，2n+1），∴MF＝2m+1﹣（m2+2m﹣3）＝﹣m2+4，NE＝﹣n2+2n+5﹣2n﹣1＝﹣n2+4，∵﹣2＜m＜2，﹣2＜n＜2，∴当m＝0时，MF有最大值4，当n＝0时，NE有最大值4，＝S△CDN+S△CDM＝×4×（MF+NE）＝2（MF+NE），∵S四边形CMDN∴当MF+NE最大时，四边形CMDN面积的最大值为16．13．（2023•沛县模拟）如图，已知抛物线y＝﹣x2+ax经过点A（4，0）和B（1，m）点，其对称轴交x轴于点H，点C是抛物线在直线AB上方的一个动点（不含A，B两点）．（1）求a、m的值．（2）连接AB、OB，若△AOB的面积是△ABC的面积的2倍，求点C的坐标．（3）若直线AC、OC分别交该抛物线的对称轴于点E、F，试问EH+FH是否为定值，若是，请求出该定值；若不是，请说明理由．【解答】解：（1）将点A的坐标代入抛物线表达式得：0＝﹣16+4a，解得：a＝4，即抛物线的表达式为：y＝﹣x2+4x，当x＝1时，y＝﹣x2+4x＝3，即点B（1，3），即m＝3，故a＝4，m＝3；（2）延长AB交y轴于点N，过点C作CM∥AB交y轴于点M，设直线AB的表达式为：y＝kx+b，则，解得：，即点N（0，4），即ON＝4，∵△AOB的面积是△ABC的面积的2倍，∴MN＝ON＝2，即点M（0，6），∵CM∥AB，故直线CM的表达式为：y＝﹣x+6，联立上式和抛物线的表达式得：﹣x2+4x＝﹣x+6，解得：x＝2或3，即点C（2，4）或（3，3）；（3）是定值，理由：设点C（t，﹣t2+4t），由点A、C的坐标得：直线AC的表达式为：y＝﹣t（x﹣4），当x＝2时，y＝2t，即点E（2，2t），则EH＝2t，由点C的坐标得，直线CO的表达式为：y＝（﹣t+4）x，当x＝2时，y＝（﹣t+4）x＝﹣2t+8，即点F（2，﹣2t+8），则FH＝﹣2t+8，则EH+FH＝2t﹣2t+8＝8，为定值．14．（2023•柳南区一模）如图，已知抛物线的图象经过点C（0，3），与x轴交于A，B两点，顶点坐标D（1，4），连接BC交对称轴于点E．（1）求抛物线的解析式；（2）若点P是抛物线上的一个动点，位于直线BC的上方（点P与B，C不重合），过P作y轴的平行线交BC于F点；①设点P的横坐标为m，当四边形DEFP是平行四边形时，求m的值；②在①的条件下，抛物线上是否存在点Q，使得△QBC的面积与△PBC的面积相等，若存在，请求出点Q坐标；若不存在，请说明理由．【解答】解：（1）∵顶点坐标D（1，4），∴设二次函数解析式y＝a（x﹣1）2+4，把C（3，0）代入y＝a（x﹣1）2+4，解得a＝﹣1，∴抛物线解析式为y＝﹣x2+2x+3；（2）①当y＝0时，则﹣x2+2x+3＝0，∴x1＝1，x2＝3，∴点B（3，0），∵点C（0，3），设直线BC的解析式为y＝kx+b（k≠0），把B（3，0），C（0，3）代入直线y＝kx+b（k≠0）得，解得，∴BC解析式为y＝﹣x+3，∵点D（1，4），∴点E（1，2），∴DE＝2，设点P（m，﹣m2+2m+3），则点F（m，﹣m+3），∴PF＝（﹣m2+2m+3）﹣（m+3）＝﹣m2+3m，∵四边形DEFP是平行四边形，∴PF＝DE，∴﹣2+4＝﹣m2+3m，解得m1＝1（不合题意舍去），m2＝2，∴m＝2；②当点Q、点P在直线BC的同侧时，如图所示：∵四边形DEFP是平行四边形，∴PD∥BC，＝S△DBC，∴S△BPC＝S△QBC，∴当点Q与点D重合时，S△BPC∴点Q（1，4）；当点P与点Q在直线BC的异侧时，延长PD交y轴于H，在OC上截取CN ＝CH＝2，则N（0，1），过点N作BC的平行线交抛物线于点Q，如图所示：∵DP∥BC，∴设直线DP的解析式为y＝﹣x+d，将D（1，4）代入y＝﹣x+d得到4＝﹣1+d，解得d＝5，∴直线DP的解析式为y＝﹣x+5，∴点H（0，5），∵C（0，3），∴CH＝2，∵BC∥QN，NC＝CH，∴QN与BC的距离与DP与BC的距离相等，＝S△BCP，∴S△BCQ∵QN∥BC，点N（0，1），∴直线QN的解析式为y＝﹣x+1，联立方程组得，解得或，综上所述，满足题意的点，点，点Q3（1，4）．15．（2022•淄博）如图，抛物线y＝﹣x2+bx+c与x轴相交于A，B两点（点A 在点B的左侧），顶点D（1，4）在直线l：y＝x+t上，动点P（m，n）在x轴上方的抛物线上．（1）求这条抛物线对应的函数表达式；（2）过点P作PM⊥x轴于点M，PN⊥l于点N，当1＜m＜3时，求PM+PN 的最大值；（3）设直线AP，BP与抛物线的对称轴分别相交于点E，F，请探索以A，F，B，G（G是点E关于x轴的对称点）为顶点的四边形面积是否随着P点的运动而发生变化，若不变，求出这个四边形的面积；若变化，说明理由．【解答】解：（1）∵抛物线的顶点D（1，4），∴可以假设抛物线的解析式为y＝﹣（x﹣1）2+4＝﹣x2+2x+3；（2）如图，设直线l交x轴于点T，连接PT，BD，BD交PM于点J．设P （m，﹣m2+2m+3）．点D（1，4）在直线l：y＝x+t上，∴4＝+t，∴t＝，∴直线DT的解析式为y＝x+，令y＝0，得到x＝﹣2，∴T（﹣2，0），∴OT＝2，∵B（3，0），∴OB＝3，∴BT＝5，∵DT＝＝5，∴TD＝TB，∵PM⊥BT，PN⊥DT，∴四边形DTBP的面积＝△PDT的面积+△PBT的面积＝×DT×PN+×TB×PM＝（PM+PN），∴四边形DTBP的面积最大时，PM+PN的值最大，∵D（1，4），B（3，0），∴直线BD的解析式为y＝﹣2x+6，∴J（m，﹣2m+6），∴PJ＝﹣m2+4m﹣3，∵四边形DTBP的面积＝△DTB的面积+△BDP的面积＝×5×4+×（﹣m2+4m﹣3）×2＝﹣m2+4m+7＝﹣（m﹣2）2+11∵﹣1＜0，∴m＝2时，四边形DTBP的面积最大，最大值为11，∴PM+PN的最大值＝×11＝；解法二：延长MP交直线l与点H，易得直线l：y＝x+，∴H（m，m+）设直线l交x轴于点C，交y轴于点L，∴C（﹣2，0），L（0，），∴CL＝，∴sin∠CLO＝，由LO∥HM，∴∠NHM＝∠CLO，∴sin∠NHM＝，∴PH＝m++m2﹣2m﹣3＝m2﹣m﹣，∴PN＝PH，∴PM+PN＝﹣m2+2m+3+（m2﹣m﹣）＝﹣（m﹣2）2+，∵﹣＜0，∴m＝2时，PM+PN的值最小，最小值为；（3）四边形AFBG的面积不变．理由：如图，设P（m，﹣m2+2m+3），∵A（﹣1，0），B（3，0），∴直线AP的解析式为y＝﹣（m﹣3）x﹣m+3，∴E（1，﹣2m+6），∵E，G关于x轴对称，∴G（1，2m﹣6），∴直线PB的解析式y＝﹣（m+1）x+3（m+1），∴F（1，2m+2），∴GF＝2m+2﹣（2m﹣6）＝8，∴四边形AFBG的面积＝×AB×FG＝×4×8＝16．∴四边形AFBG的面积是定值．16．（2022•烟台）如图，已知直线y＝x+4与x轴交于点A，与y轴交于点C，抛物线y＝ax2+bx+c经过A，C两点，且与x轴的另一个交点为B，对称轴为直线x＝﹣1．（1）求抛物线的表达式；（2）D是第二象限内抛物线上的动点，设点D的横坐标为m，求四边形ABCD 面积S的最大值及此时D点的坐标；（3）若点P在抛物线对称轴上，是否存在点P，Q，使以点A，C，P，Q为顶点的四边形是以AC为对角线的菱形？若存在，请求出P，Q两点的坐标；若不存在，请说明理由．【解答】解：（1）当x＝0时，y＝4，∴C（0，4），当y＝0时，x+4＝0，∴x＝﹣3，∴A（﹣3，0），∵对称轴为直线x＝﹣1，∴B（1，0），∴设抛物线的表达式：y＝a（x﹣1）•（x+3），∴4＝﹣3a，∴a＝﹣，∴抛物线的表达式为：y＝﹣（x﹣1）•（x+3）＝﹣x2﹣x+4；（2）如图1，作DF⊥AB于F，交AC于E，∴D（m，﹣﹣m+4），E（m，m+4），∴DE＝﹣﹣m+4﹣（m+4）＝﹣m2﹣4m，＝OA＝•（﹣m2﹣4m）＝﹣2m2﹣6m，∴S△ADC＝＝＝8，∵S△ABC∴S＝﹣2m2﹣6m+8＝﹣2（m+）2+，∴当m＝﹣时，S＝，最大当m＝﹣时，y＝﹣＝5，∴D（﹣，5）；（3）存在点P和点Q，使以点A，C，P，Q为顶点的四边形是以AC为对角线的菱形，理由如下：设P（﹣1，n），∵以A，C，P，Q为顶点的四边形是以AC为对角线的菱形，∴P A＝PC，即：P A2＝PC2，∴（﹣1+3）2+n2＝1+（n﹣4）2，∴n＝，∴P（﹣1，），∵x P+x Q＝x A+x C，y P+y Q＝y A+y C∴x Q＝﹣3﹣（﹣1）＝﹣2，y Q＝4﹣＝，∴Q（﹣2，）．17．（2022•内江）如图，抛物线y＝ax2+bx+c与x轴交于A（﹣4，0），B（2，0），与y轴交于点C（0，2）．（1）求这条抛物线所对应的函数的表达式；（2）若点D为该抛物线上的一个动点，且在直线AC上方，求点D到直线AC的距离的最大值及此时点D的坐标；（3）点P为抛物线上一点，连接CP，直线CP把四边形CBP A的面积分为1：5两部分，求点P的坐标．【解答】解：（1）∵抛物线y＝ax2+bx+c与x轴交于A（﹣4，0），B（2，0），与y轴交于点C（0，2）．∴，解得：，∴抛物线的解析式为y＝﹣x2﹣x+2；（2）过点D作DH⊥AB于H，交直线AC于点G，过点D作DE⊥AC于E，如图．设直线AC的解析式为y＝kx+t，则，解得：，∴直线AC的解析式为y＝x+2．设点D的横坐标为m，则点G的横坐标也为m，∴DH＝﹣m2﹣m+2，GH＝m+2∴DG＝﹣m2﹣m+2﹣m﹣2＝﹣m2﹣m，∵DE⊥AC，DH⊥AB，∴∠EDG+∠DGE＝∠AGH+∠CAO＝90°，∵∠DGE＝∠AGH，∴∠EDG＝∠CAO，∴cos∠EDG＝cos∠CAO＝＝，∴，∴DE＝DG＝（﹣m2﹣m）＝﹣（m2+4m）＝﹣（m+2）2+，∴当m＝﹣2时，点D到直线AC的距离取得最大值．此时y D＝﹣×（﹣2）2﹣×（﹣2）+2＝2，即点D的坐标为（﹣2，2）；（3）如图，设直线CP交x轴于点E，直线CP把四边形CBP A的面积分为1：5两部分，：S△PCA＝EB×（y C﹣y P）：AE×（y C﹣y P）＝BE：AE，又∵S△PCB则BE：AE＝1：5或5：1则AE＝5或1，即点E的坐标为（1，0）或（﹣3，0），将点E的坐标代入直线CP的表达式：y＝nx+2，解得：n＝﹣2或，故直线CP的表达式为：y＝﹣2x+2或y＝x+2，联立方程组或，解得：x＝6或﹣，故点P的坐标为（6，﹣10）或（﹣，﹣）．18．（2021•西宁）如图，在平面直角坐标系xOy中，一次函数y＝﹣x+3的图象与x轴交于点A，与y轴交于点B，点C的坐标为（﹣2，0），抛物线经过A，B，C三点．（1）求抛物线的解析式；（2）直线AD与y轴负半轴交于点D，且∠BAO＝∠DAO，求证：OB＝OD；（3）在（2）的条件下，若直线AD与抛物线的对称轴l交于点E，连接BE，在第一象限内的抛物线上是否存在一点P，使四边形BEAP的面积最大？若存在，请求出点P的坐标及四边形BEAP面积的最大值；若不存在，请说明理由．【解答】解：（1）令y＝0，则﹣x+3＝0，解得x＝6，令x＝0，则y＝3，∴A（6，0），B（0，3），设抛物线的解析式为y＝ax2+bx+c，把A，B，C三点坐标代入解析式，得：，解得：，∴抛物线的解析式为y＝x2+x+3；（2）证明：∵在平面直角坐标系xOy中，∴∠BOA＝∠DOA＝90°，在△BOA和△DOA中，。

最新九年级中考数学专题：二次函数综合压轴题(面积问题)附答案

2023年九年级中考数学专题：二次函数综合压轴题（面积问题）1．已知抛物线27 32y ax x=++的对称轴是直线3x=，与x轴相交于A，B两点（点B在点A右侧），与y轴交于点C．(1)求抛物线的解析式和A，B两点的坐标；(2)如图1，若点P是抛物线上B、C两点之间的一个动点（不与B、C重合），是否存在点P，使四边形PBOC的面积最大？若存在，求点P的坐标及四边形PBOC面积的最大值；若不存在，请说明理由；(3)如图2，若点M是抛物线上任意一点；过点M作y轴的平行线，交直线BC于点N，当3MN=时，求点M的坐标．2．如图，在平面直角坐标系中，抛物线y=ax2+4x+c（a≠0）与x轴交于点A、B，与y 轴交于点C，连接BC，OA=1，对称轴为x=2，点D为抛物线的顶点．(1)求抛物线的解析式；(2)抛物线上C，D两点之间的距离是__________；(3)点E是第一象限内抛物线上的动点，连接BE和CE．求△BCE面积的最大值；(4)平面内存在点Q，使以点B、C、D、Q为顶点的四边形为平行四边形，请直接写出点Q的坐标．3．综合与探究：如图，抛物线y＝ax²＋bx＋3与x轴交于A，B（3，0）两点（点A在点B的左侧），与y轴交于点C，且OA＝13OB，点D是抛物线上一动点，设点D的横坐标为m（0<m<3）．连接AC，BC，BD，CD．(1)求抛物线的函数表达式；(2)当△ BCD 的面积等于△AOC的面积时，求m的值；(3)当m＝2时，若点P是x轴上一动点，点Q是抛物线上一动点．试判断是否存在这样的点P，使得以点B，D，P，Q为顶点的四边形是平行四边形．若存在，请直接写出点P的坐标，若不存在，请说明理由．4．如图，抛物线223y x x=-++与x轴交于点A、B（点A在点B左侧），与y轴交于点C，连接BC．(1)求线段BC的长；(2)过点A作AE//BC，与y轴交于点D，与抛物线第四象限的图象交于点E，P为抛物线上位于第一象限的点，连接PE交BC于点H，连接DH，求四边形PCDH面积的最大值及此时点P的坐标；(3)将原抛物线沿射线BC y'，y'与原抛物线交于点M，点N在直线BC上，且位于y轴右侧，在平面直角坐标系中是否存在点Q，使以点A、M、N、Q为顶点的四边形为菱形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．5．如图，抛物线2(0)y ax bx c a=++≠交坐标轴于A、B、C三点，1,4,90OA OB ACB==∠=︒，点D是直线BC下方抛物线上一点，设点D的横坐标为t，DE BC ⊥交直线BC 于点E ．(1)求抛物线的函数关系式；(2)求当t 为何值时，线段DE 的长度最大？最大长度是多少？(3)是否存在点D 的位置，使CDE 与AOC 相似？若存在，请求出相应点D 的坐标，若不存在，请说明理由．6．如图，平面直角坐标系xOy 中，抛物线y ＝12-x 2+bx +c 与x 轴交于点A （﹣1，0），B （4，0），与y 轴交于点C ．(1)b ＝______；c ＝_______；(2)若直线l 经过点C ，点A 关于直线l 的对称点A ′恰好在线段BC 上，直线AA ′与抛物线交于另一点E ．△求点E 的坐标；△点P （x 0，y 0）是直线BE 上一点，若对于在第一象限内的抛物线y ＝12-x 2+bx +c 上的动点Q ，始终有S △QCA ′≤S △PCA ′，直接写出x 0的取值范围．7．在平面直角坐标系中，直线2y x =+与x 轴交于点A ，与y 轴交于点B ，抛物线2y ax bx c =++（a ，b ，c 为常数，0a <）经过点A 、B ．(1)c ＝；a 、b 之间的关系式为：；(2)当0x <时，若2y ax bx c =++（0a <）的函数值随x 的增大而增大，求a 的取值范围；(3)如图，当1a =-时，在抛物线上是否存在点P ，使△P AB 的面积为1？若存在，请求出符合条件的所有点P 的坐标；若不存在，请说明理由．8．如图，已知抛物线2y x bx c =-++与一直线相交于1,0A ，()2,3C -两点，与y 轴交于点N ．(1)求抛物线的函数关系式；(2)求直线AC 的函数关系式；(3)若P 是抛物线上位于直线AC 上方的一个动点．求APC △面积的最大值． 9．已知抛物线2y ax bx =+（a ，b 为常数，且0a ≠）的对称轴为1x =，且过点(1，12)．点P 是抛物线上的一个动点，点P 的横坐标为t ，直线AB ：4y x =-+与x 轴相交于点A ，与y 轴相交于点B ．(1)求抛物线的解析式；(2)若点P 在第一象限内或x 轴上，连接PA ，PB ，当PAB ∆面积最小时，求此时点P 的坐标；(3)对于函数2y ax bx =+，当1t x t ≤≤+时，此函数的最大值为m ，最小值为n ，是否存在t 的值使23m n -=．若存在，请直接写出t 的值；若不存在，请说明理由． 10．如图，开口向上的抛物线与x 轴交于()1,0A x ，()2,0B x 两点，与y 轴交于点C ，且AC BC ⊥，其中1x ，2x 是方程2340x x +-=的两个根．(1)求点C 的坐标，并求出抛物线的表达式；(2)垂直于线段BC 的直线l 交x 轴于点D ，交线段BC 于点E ，连接CD ，求CDE 的面积的最大值及此时点D 的坐标．11．如图抛物线y ＝ax 2+bx +6的开口向下与x 轴交于点A （﹣6，0）和点B （2，0），与y 轴交于点C ，点P 是抛物线上一个动点（不与点C 重合）(1)求抛物线的解析式；(2)当点P 是抛物线上一个动点，若△PCA 的面积为12，求点P 的坐标；(3)如图2，抛物线的顶点为D ，在抛物线上是否存在点E ，使得△EAB ＝2△DAC ，若存在请直接写出点E 的坐标；若不存在请说明理由．12．如图1，抛物线214y x bx c =-++经过点A (4，3)，对称轴是直线x =2，顶点为B ．抛物线与y 轴交于点C ，连接AC ，过点A 作AD △x 轴于点D ，点E 是线段AC 上的动点(点E 不与A 、C 两点重合)．(1)求抛物线的函数解析式和顶点B 的坐标；(2)若直线BE 将四边形ACOD 分成面积比为1:3的两个四边形，求点E 的坐标；(3)如图2，连接DE ，作矩形DEFG ，在点E 的运动过程中，是否存在点G 落在y 轴上的同时点F 也恰好落在抛物线上?若存在，求出此时AE 的长；若不存在，请说明理由．13．如图，在平面直角坐标系中，抛物线y ＝x 2+bx +c 与直线AB 交于A ，B 两点，其中A （0，1），B （4，﹣1）．(1)求该抛物线的函数表达式；(2)点P ，Q 为直线AB 下方抛物线上任意两点，且满足点P 的横坐标为m ，点Q 的横坐标为m +1，过点P 和点Q 分别作y 轴的平行线交直线AB 于C 点和D 点，连接PQ ，求四边形PQDC 面积的最大值；(3)在（2）的条件下，将抛物线y ＝x 2+bx +c 沿射线AB 平移线y 1，点E 为点P 的对应点，点F 为y 1的对称轴上任意一点，点G 为平面直角坐标系内一点，当点B ，E ，F ，G 构成以EF 为边的菱形时，直接写出所有符合条件的点G 的坐标，并任选其中一个点的坐标，写出求解过程．14．已知抛物线234y x bx c =-++与x 轴交于A 、B 两点，与y 轴交于C 点，且点A 的坐标为(1,0)-、点C 的坐标为(0,3)；(1)求该抛物线的函数表达式及顶点坐标；(2)如图1，有两动点D 、E 在COB △的边上运动，速度均为每秒1个单位长度，它们分别从点C 和点B 同时出发，点D 沿折线COB 按C O B →→方向向终点B 运动，点E 沿线段BC 按B C →方向向终点C 运动，当其中一个点到达终点时，另一个点也随之停止运动．设运动时间为t 秒，请解答下列问题：△当t= 时，BDE △的面积等于3310； △在点D 、E 运动过程中，该抛物线上存在点F ，使得依次连接AD 、DF 、FE 、EA 得到的四边形ADFE是平行四边形，请直接写出所有符合条件的点F的坐标．15．如图，在平面直角坐标系中，抛物线y=2x bx c-++与x轴交于A（-1，0），B（4，0）两点，与y轴交于点C，点P为直线BC上方抛物线上一动点．(1)求抛物线的解析式；(2)过点A作AD//BC交抛物线于点D，点Q为直线AD上一动点，连接CP，CQ，BP，BQ，求四边形BPCQ面积的最大值及此时点P的坐标；(3)将抛物线沿射线CB个单位，M为平移后的抛物线的对称轴上一动点，在平面直角坐标系中是否存在点N，使以点B，C，M，N为顶点的四边形为菱形？若存在，请直接写出所有符合条件的点N的坐标，若不存在，请说明理由．16．如图，对称轴为x=﹣1的抛物线y=ax2+bx+c（a≠0）与x轴相交于A，B两点，其中点A的坐标为（﹣3，0）．(1)求点B的坐标．(2)已知a=1，C为抛物线与y轴的交点．△求抛物线的解析式．△若点P在抛物线上，且S△POC=4S△BOC，求点P的坐标．△设点Q是线段AC上的动点，作QD△x轴交抛物线于点D，请直接写出线段QD长度的最大值和对应的点Q的坐标．17．如图，把两个全等的Rt△AOB和Rt△COD分别置于平面直角坐标系中，使直角边OB ，OD 在x 轴上，已知点A （2，4），过点A 、C 两点的直线分别交x 轴、y 轴于点E 、F ，抛物线2y ax bx c =++经过O ，A ，C 三点．(1)求该抛物线的函数解析式；(2)点G 为抛物线上位于线段OC 所在直线上方部分的一动点，求点G 到直线OC 的最大距离和此时点G 的坐标；(3)点P 为线段OC 上一个动点，过点P 作y 轴的平行线交抛物线于点M ，交x 轴于点N ，问是否存在这样的点P ，使得四边形ABPM 是等腰梯形？若存在，求出此时点P 的坐标；若不存在，请说明理由．18．如图，抛物线y ＝34x 2+bx +c 交x 轴于A ，B 两点，交轴于点C ，点A ，B 的坐标分别为（-1，0），（4，0）．(1)求抛物线的解析式；(2)点P 是直线BC 下方的抛物线上一动点，求△CPB 的面积最大时点P 的坐标；(3)若M 是抛物线上一点，且△MCB ＝△ABC ，请直接写出点M 的坐标．19．已知抛物线214y x bx c =-++与直线AC 相交于A 、C 两点，且()2,0A -、()4,3C ．(1)填空：b=______，c=______；(2)DE在线段AC上移动，点G与点F在上述抛物线上，且线段DG 与EF始终平行于y轴．△连接FG，求四边形DEFG的面积的最大值，并求出对应点D的坐标；△CH AB⊥，垂足为点H，线段DE在移动的过程中，是否存在点D，使△DEG与△ACH 相似？若存在，请求出此时点D的坐标；若不存在，试说明理由．20．综合与探究：如图，抛物线y1＝ax2﹣6ax+c（a≠0）与x轴交于点A，B（点A在点B的右侧），与y轴交于点C，顶点为N，直线y212=-x﹣1与x轴交于点B，与抛物线交于点D，连接BC，DN，sin△OCB=．(1)求抛物线的解析式；(2)△点D的坐标为______，DN＝______；△当y1＜y2时，自变量x的取值范围是______；(3)若点P在直线AC上，且S△ABP：S△BCP＝1：3，求ABAP的值；(4)在第四象限内存在点E，使△ACE与△ABC相似，且AC为△ACE的直角边，请直接写出点E的坐标．参考答案：1．(1)217322y x x =-++；A （-1，0），B （7，0） (2)763(,)28P ，四边形PBOC 的面积最大为53916(3)点M 或M 或M （1，6）或M （6，72） 2．(1)245y x x =-++(2)(3)1258(4)()()()1237,4,3,4,3,14Q Q Q --3．(1)223y x x =-++(2)1m =2m =(3))1P ，()250P ，，()310P ，，()4P4．(1)线段BC 的长为(2)四边形PCDH 面积的最大值为8，及此时点P 的坐标为（2，3）；(3)存在，Q （1，﹣4）或Q （﹣2，3）．5．(1)213222y x x =--(2)2t =时，DE 最大，此时DE (3)存在，(3,2)D -或325,28D ⎛⎫- ⎪⎝⎭6．(1)32，2 (2)△E （103，139）；△x 0≤145或x 0≥2657．(1)2，21b a =+ (2)102a -≤< (3)存在，P （﹣1，2）或（1-1-，）8．(1)y ＝−x 2−2x ＋3(2)y ＝−x ＋1 (3)2789．(1)212y x x =-+ (2)P (2，0) (3)16-或7610．(1)()0,2C -，213222y x x =+-； (2)CDE S △最大为54，3,02D ⎛⎫- ⎪⎝⎭11．(1)21262y x x =--+；(2)P 的坐标为（﹣2，8）或（﹣4，6）或（﹣31）或（﹣31）(3)E （12，398）或（72，578）12．(1)2134y x x =-++；()2,4 (2)835⎛⎫ ⎪⎝⎭，或1235⎛⎫ ⎪⎝⎭， (3)存在，4313．(1)y ＝x 2﹣92x +1(2)最大值为154(3)G 坐标为（194194）或（134，﹣154），求解过程见解析14．(1)239344y x x =-++，375,216⎛⎫ ⎪⎝⎭△1013,36⎛⎫ ⎪⎝⎭或(3,3) 15．(1)234y x x =-++(2)当m ＝2时，四边形BPCQ 的面积最大为18，此时P （2，6）．(3)(2,42,4-+---16．(1)点B 的坐标为(1,0)(2)△223y x x =+-；△(4,21)或()4,5-；△QD 有最大值94，点Q 的坐标为3(2-，9)2-．17．(1)23742y x x =-+；(2)G 点到直线OC G (2，4)； (3)存在，P 点的坐标为4233⎛⎫ ⎪⎝⎭，．18．(1)239344y x x =-- (2)92,2P ⎛⎫- ⎪⎝⎭ (3)M 的坐标为()3,3-或531125,749⎛⎫ ⎪⎝⎭19．(1)1，3；(2)△4；D (0，1)；△存在这样的D 使△DEG 与△ACH 相似，坐标为1⎛ ⎝⎭20．(1)y 114=x 232-x ﹣4 (2)△（6，﹣4），154；△﹣2＜x ＜6(3)AB AP的值为(4)点E 的坐标为（2，﹣8）或（8，﹣20）或（10，﹣4）或（16，﹣16）。

最新九年级中考数学复习：几何探究压轴题(面积问题)

14．（1）如图1，在等腰直角三角形ABC中，∠C＝90°，点O为AB的中点，点M为AC上一点，将射线OM绕点O顺时针旋转90°交BC于点N，则OM与ON的数量关系为；
（2）如图2，在等腰三角形ABC中，∠C＝120°，点O为AB的中点，点M为AC上一点，将射线OM绕点O顺时针旋转60°交BC于点N，则OM与ON的数量关系是否改变，请说明理由；
9．在△ABC中，CA＝CB，∠ACB＝a，将△CAD绕点C按逆时针方向旋转角a得到△CBE，点A，D的对应点分别为点B，E．
(1)如图1，若A，D，E三点在同一直线上，则∠CDE=（用含a的代数式表示）；
(2)如图2，若A，D，E三点在同一直线上，a=60°，过点C作CF⊥AE于点F，然后探究线段CF，AE，BE之间的数量关系，并证明你的结论；
(3)拓展延伸：把△ADE绕点A在平面内自由旋转，若AD=3，AB=7，请直接写出△PMN面积的最大值．
18．如图1，在等腰三角形ABC中，∠A＝120°，AB＝AC，点D、E分别在边AB、AC上，AD＝AE，连接BE，点M、N、P分别为DE、BE、BC的中点．
(1)观察猜想：图1中，线段NM、NP的数量关系是，∠MNP的大小为；
(2)在三角板旋转的过程中，边与AB所在直线交于点D，过点D作DE∥ 交边于点E，连接BE．
①当时，设AD= ，BE= ，求与之间的函数解析式及自变量的取值范围；
②当时，求AD的长．
13．在中中．，，点E在射线CB上运动．连接AE，将线段AE绕点E顺时针旋转90°得到EF，连接CF．
②如图3，连接AF，若AC＝3，CD＝1，求S△ADF的取值范围．
2．如图，矩形中，为等边三角形．点E，F分别为边上的动点，且，P为上一动点，连接，将线段绕点B顺时针旋转至，连接．

2020年中考数学压轴题：图形面积计算

2020年中考数学压轴题：图形面积计算【例1】（2019·南阳模拟）如图，在扇形AOB中，∠AOB＝90°，半径OA＝6，将扇形AOB沿过点B 的直线折叠，点O恰好落在弧AB上点D处，折痕交OA于点C，则整个阴影部分的面积为（）A．9π﹣9 B．9π﹣63C．9π﹣18 D．9π﹣123【答案】D.【解析】解：连接OD，由折叠的性质知：CD＝CO，BD＝BO，∠DBC＝∠OBC，∴OB＝OD＝BD，即△OBD是等边三角形，∴∠DBO＝60°，∴∠CBO＝30°，∴OC＝33OB＝23，∴S阴影=S扇形AOB﹣S△BDC﹣S△OBCS△BDC＝S△OBC＝12×OB×OC＝12×6×23＝63，S扇形AOB＝9π，∴S阴影=S扇形AOB﹣S△BDC﹣S△OBC=9π﹣63﹣63＝9π﹣123．所以答案为：D．【变式1-1】（2019·开封模拟）如图，把半径为2的⊙O沿弦AB，AC折叠，使弧AB和弧BC都经过圆心O，则阴影部分的面积为（）A．3B．3C．23D．43【答案】C．【解析】解：过O作OD⊥AC于D，连接AO、BO、CO，∴OD＝12AO＝1，AD＝12AC3∴∠OAD＝30°，∴∠AOC＝2∠AOD＝120°，同理∠AOB＝120°，∠BOC＝120°，∴S阴＝2S△AOC＝2×34×22＝23，所以答案为：C ．【变式1-2】如图，半径为1的半圆形纸片，按如图方式折叠，使对折后半圆弧的中点M 与圆心O 重合，则图中阴影部分的面积是．【答案】326π-．【解析】解：设折痕为AB ，连接OM 交AB 于点C ，连接OA 、OB ，由题意知，OM ⊥AB ，且OC =MC =12，在RT △AOC 中，OA =1，OC =12，∴∠AOC =60°，AC =3，AB =2AC =3， ∴∠AOB =2∠AOC =120°， S 阴影=S 半圆﹣2S 弓形ABM=12π×12﹣2（2120111336022π⨯-⨯⨯）=36π-．故答案为：36π-．【例2】（2019·郑州外外国语测试）如图所示，在Rt △ABC 中，∠ACB =90°，AC =BC ，将Rt △ABC 绕点A 逆时针旋转30°后得到Rt △ADE ，若图中阴影部分面积为3π，则AB =【答案】2.【解析】S 阴影=S △ADE +S 扇形BAD －S △ABC ∵S △ADE = S △ABC ∴S 阴影= S 扇形BAD =3π，∴230360AB π⨯=3π,解得：AB =2，故答案为：2.【变式2-1】（2019·河南南阳一模）如图，在正方形ABCD 中，AB =3，点M 在CD 边上，且DM =1，△AEM 与△ADM 关于AM 所在直线对称，将△ADM 按顺时针方向绕点A 旋转90°得到△ABF ，连接EF ，则线段EF 的长为（）D MA . 3B .C .D . 【分析】求线段的长度，常用方法是将所求线段放在直角三角形中借助勾股定理求解，如图作出辅助线，通过分析可知，△ADM ≌△ABF ≌△AEM ，可得DM =EM =1，AE =AD =AB =3，进而利用△AEK ∽△EMH ，求得EH ，MH 的长，再计算出EG ，FG 的长，在Rt △EFG 中，利用勾股定理求EF 的长度即可.【解析】过点E 作EG ⊥BC 于G ，作EH ⊥CD 于H ，延长HE 交AB 于K ，如图所示，D FMH由题意知，△ADM ≌△ABF ≌△AEM ，∴DM =EM =1，AE =AD =AB =3，由△AEK ∽△EMH ，得：AE AK EKEM EH MH===3，∴设EH=x，则AK=3x，即DH=3x，MH=3x－1，在Rt△EMH中，由勾股定理得：()22311x x-+=，解得：x=0（舍）或x=35，∴MH=45，AK=DH=95，CH=3－DH=65，KE=BG=3MH=125，∴FG=BF+BG=175，EG=CH=65，在Rt△EFG中，由勾股定理得：EF=22221761355FG EG⎛⎫⎛⎫+=+=⎪ ⎪⎝⎭⎝⎭,故答案为：C.【变式2-2】（2019·洛阳二模）如图，矩形ABCD中，AB=2，BC=1，将矩形ABCD绕点A旋转得到矩形AB′C′D′，点C的运动路径为弧CC′，当点B′落在CD上时，则图中阴影部分的面积为．【答案】532 12π+-.【解析】解：连接AC’，AC，过点B’作B’E⊥AB于E，如图图所示，由旋转性质，得：AC=AC’，AB’=AB=2，∠CAB=∠C’AB’，∵BC=B’E=1，∴∠B’AB=30°，∴∠C’AC=30°，∴AE=3，B’C=2－3，在Rt△ABC中，由勾股定理得：AC=5, ∴S阴影=S扇形C’AC－S△AB’C’－S△B’CA=()()23051121231 36022π⨯-⨯⨯-⨯-⨯=532 122π+-.故答案为：532 12π+-.【例3】（2019·河南南阳一模）如图，在△ABC中，AB=BC，∠ABC=90°，CA=4，D为AC的中点，以D为圆心，以DB的长为半径作圆心角为90°的扇形EDF，则图中阴影部分的面积为.【分析】设DE与BC交于M，DF与AB交于N，S阴影=S扇形EDF－S四边形DMBN，根据△DBM≌△DAN，得S四边形DMBN=S△BDA，再利用扇形面积公式及三角形面积公式求解即可.【解析】解：设DE与BC交于M，DF与AB交于N，∵AB=BC，∠ABC=90°，D是AC中点，∴∠A=∠C=∠CBD=∠DBA=45°，AD=BD=2，∠BDA=90°，∵∠EDF=90°，∴∠BDM=∠ADF，∴△DBM≌△DAN，即S△DBM=S△DAN，∴S四边形DMBN=S△BDA，S阴影=S扇形EDF－S四边形DMBN=213602n rAD BD π-⋅⋅=2902122 3602π⨯-⨯⨯=π－2，故答案为：π－2.【变式3-1】（2018·洛阳三模）如图，在扇形OAB中，C是OA的中点，CD⊥OA，CD与弧AB交于点D，以O为圆心，OC的长为半径作弧CE交OB于点E，若OA=6，∠AOB=120°，则图中阴影部分的面积为.【答案】93 32π+.【解析】解：连接OD，交弧CE于F，连接AD，∵OC=AC=3，CD⊥OA，∴CD是线段OA的垂直平分线，∴OD=AD，∵OD=OA，∴△OAD是等边三角形，∵∠AOB=120°，∴∠DOA=∠BOD=60°，∴CD33∴S阴影=S扇形BOD－S扇形EOF+S△COD－S扇形COF=222 6066031603333 3603602360πππ⨯⨯⨯-+⨯⨯=3π93.即答案为：3π93.【变式3-2】（2018·河南第一次大联考）如图，O是边长为a的正方形ABCD的中心，将一块半径足够长、圆心为直角的扇形纸板的圆心放在O点处，并将纸板的圆心绕O旋转，则正方形ABCD被纸板覆盖部分的面积为（）A ．13a 2 B ．14a 2 C ．12a 2 D ．14a 【答案】B .【解析】解：如图，过O 作OE ⊥AD 于E ，OF ⊥CD 于F ，∴OE =OF ，∠EOF =90°，∴四边形OEDF 是正方形，OF =12a ，∵扇形的圆心角为直角， ∴△OME ≌△ONF ， ∴S 阴影=S 正方形OEDF =214a ，故答案为：B ．1.（2018·河南师大附中模拟）如图，菱形ABCD 和菱形ECGF 的边长分别为2和3，∠A =120°，则图中阴影部分（△BDF ）的面积等于.3【解析】解：由题意得：S △BDF =S 菱形ABCD +S 菱形ECGF －S △BGF －S △EDF －S △ABD 菱形ECGF 边CG 边上的高为：GF ·sin 60°33，菱形ECGF 边CE 边上的高为：EF ·sin 60°=332， ∴S △BDF =222331331333235122222224⨯+⨯-⨯⨯-⨯⨯-⨯ =3，故答案为：3.2.（2019·济源一模）汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝，如图所示的弦图中，中间的小正方形 ABCD 的边长为 1，分别以A ，C 为圆心，1为半径作圆弧，则图中阴影部分的面积为【答案】12π-.【解析】解：连接BD ， S 阴影=2（S 扇形BAD －S △ABD ）=2（29011113602π⨯-⨯⨯）=12π-，故答案为：12π-.3.（2019·偃师一模）如图，正方形ABCD 中，AB =1，将线段 CD 绕点 C 顺时针旋转 90°得到线段CE ，线段 BD 绕点 B 顺时针旋转 90°得到线段 BF ，连接 EF ，则图中阴影部分的面积是【答案】32－4π.【解析】解：过F作FM⊥BE于M，则∠FME=∠FMB=90°，∵四边形ABCD是正方形，AB=1，∴∠DCB=90°，DC=BC=AB=1，∠DCB=45°，由勾股定理得：BD=2，由旋转性质得：∠DCE=90°，BF=BD=2，∠FBE=90°－45°=45°，∴BM=FM=1，即C点与M点重合，ME=1，∴阴影部分的面积：S=S△BCD+S△BFE+S扇形DCE－S扇形DBF=12+1+2901360π⨯－()2902360π⨯=32－4π，故答案为：32－4π．4.（2019·洛阳三模）如图，已知矩形ABCD的两条边AB=1，AD=3，以B为旋转中心，将对角线BD顺时针旋转60°得到线段BE，再以C为圆心将线段CD顺时针旋转90°得到线段CF，连接EF，则图中阴影部分面积为．15 3212π-.【解析】解：连接CE，由CD=AB=1，AD3BD=2，∴∠DBC =30°，由旋转知∠DBE =60°，BE =BD =2， ∴∠DBC =∠EBC =30°，此时D 、C 、E 共线，∴S 阴影=S 扇形DCF +S △BCD +S △BEF －S 扇形DBE=()22901160113131236022360ππ⨯+⨯⨯+⨯+⨯-⨯ =153212π+-.故答案为：153212π+-.5.（2019·周口二模）如图，△AOB 中，∠AOB =90°，AO =3，BO =6，△AOB 绕点O 逆时针旋转到△A ′OB ′处，此时线段A ′B ′与BO 的交点E 为BO 的中点，则线段B ′E 的长度为（）A ．35B ．95C ．65D ．35A′B′OB AE【答案】B .【解析】解：过O 作OF ⊥A ’B ’于F ，由旋转性质得：OA =OA ’=3，OB =OB ’=6， ∴F 为A ’E 的中点， ∵E 为OB 中点，在Rt△A’OB’中，由勾股定理得：A’B’=35，∴OF=6535=，在Rt△A’OF中，由勾股定理得：A’F=35，∴A’E=65∴B’E=A’B’－A’E=95，故答案为：B.6.（2019·周口二模）如图，等腰直角三角形ABC，绕点C顺时针旋转得到△A′B′C，AB′所在的直线经过A′C的中点时，若AB=2，则阴影部分的面积为_________．A′B′A【答案】4313π--.【解析】解：延长AB’交A’C于E，由题意知E为A’C的中点，∵A’B’=B’C=AB=BC=2，∴B’E⊥A’C，在Rt△ABC中，由勾股定理得：AC2，∴CE=A’E2，∴∠CAE=30°，∠ACE=60°，∴S阴影=S扇形ACA’－S△ACE－S△A’B’E=()26022112622 36022π⨯-⨯⨯-⨯⨯=431 3π--.故答案为：431 3π--.7.如图，在扇形OAB中，∠O=60°，OA=43，四边形OECF是扇形OAB中最大的菱形，其中点E，C，F分别在OA，弧AB，OB上，则图中阴影部分的面积为．【答案】8π﹣83.【解析】解：连接EF、OC交于点H，则OH=12OC3FOH=∠AOC=30°，在Rt△FOH中，FH=OH×tan30°=2，∴菱形FOEC的面积=12×33扇形OAB的面积=(26043360π⨯=8π，则阴影部分的面积为8π﹣3故答案为：8π﹣38.（2019·开封二模）如图，在圆心角为120°的扇形OAB中，半径OA＝2，C为弧AB的中点，D为OA 上任意一点（不与点O、A重合），则图中阴影部分的面积为．【答案】23π．【解析】解：连接OC，BC，由题意知∠BOC＝∠AOC＝60°，∵OB＝OC，∴△BOC为等边三角形，∴∠OCB＝∠COA＝60°，∴BC∥OA，∴S△BOC=S△BCD，∴S阴影＝S弓形BC+S△BCD＝S弓形BC+S△BOC＝S扇形BOC＝23π，故答案为：23π.9.（2019·安阳一模）如图，在正方形ABCD中，AD=3，将线段AB绕点B逆时针旋转90°得到线段BE，将线段AC绕点C逆时针旋转90°得到线段CF，连接EF，则图中阴影部分的面积是___________．AB CF【答案】27924π-.【解析】解：由图知：S阴影=S扇形ABE+S△BEF－S弓形AFS弓形AF=S扇形ACF－S△ACF由题意知，AD=3，AC=CF=32，AB=BC=BF=BE=3，∠EBA=∠ACF=90°，∴S弓形AF=S扇形ACF－S△ACF=()29032360π⨯－132322⨯⨯=92π－9，S阴影=S扇形ABE+S△BEF－S弓形AF=2903360π⨯+1332⨯⨯－（92π－9）=279 24π-.10.（2019·省实验一模）如图，将半径为1的半圆O，绕着其直径的一端点A顺时针旋转30°，直径的另一端点B的对应点为B'，O的对应点为O'，则图中阴影部分的面积是．【答案】3 2π-.【解析】解：连接O′D、B′D，∵∠B′AB＝30°，∴∠AO′D＝120°，∵AB′是直径，∴∠ADB′＝90°，由∠B ′AB ＝30°，得B ′D ＝12AB ′＝1，在Rt △ADB ’中，由勾股定理得，AD ＝3，∴S 阴影＝S 扇形BAB ’－S △AO ’D －S 扇形DO ’B ’+S 扇形AO ’D －S △AO ’D=222223023601120131136043603604πππ⨯⨯⨯-⨯-+-⨯ =322π- 故答案为：322π-．11.（2019·叶县一模）如图，在平行四边形ABCD 中，以点A 为圆心，AB 的长为半径的圆恰好与CD 相切于点C ，交AD 于点E ，延长BA 与⊙A 相交于点F ．若弧EF 的长为2π，则图中阴影部分的面积为．【答案】22π-.【解析】解：连接AC ，∵DC 是⊙A 的切线， ∴AC ⊥CD ， ∵AB ＝AC ＝CD ，∴△ACD 是等腰直角三角形， ∴∠CAD ＝45°，∵四边形ABCD 是平行四边形， ∴AD ∥BC ，∴∠CAD ＝∠ACB ＝45°，∴∠ACB ＝∠B ＝45°， ∴∠F AD ＝∠B ＝45°， ∵弧EF 的长为2π，∴45=2180rππ，解得：r ＝2，∴S 阴影＝S △ACD ﹣S 扇形ACE＝21452222360π⨯⨯⨯- =22π-．故答案为：22π-．12.（2019·濮阳二模）如图，在Rt △ABC 中，∠ACB ＝90°，AC ＝BC ＝2，以点A 为圆心，AC 的长为半径作弧CE 交AB 于点E ，以点B 为圆心，BC 的长为半径作弧CD 交AB 于点D ，则阴影部分的面积为．【答案】π﹣2．【解析】解：S 阴影＝S △ABC ﹣S 空白， ∵∠ACB ＝90°，AC ＝BC ＝2，∴S △ABC ＝12×2×2＝2，S 扇形BCD ＝2452360π⨯＝12π，S 空白＝2×（2﹣12π）＝4﹣π，S 阴影＝S △ABC ﹣S 空白＝2﹣4+π ＝π﹣2，故答案为：π﹣2．13.（2019·南阳模拟）如图，在△ABC 中，BC ＝4，以点A 为圆心，2为半径的⊙A 与BC 相切于点D ，交AB 于点E ，交AC 于点F ，点P 是⊙A 上的一点，且∠EPF ＝45°，则图中阴影部分的面积为．【答案】4﹣π．【解析】解：连接AD∵⊙A与BC相切于点D，∴AD⊥BC，∵∠EPF＝45°，∴∠BAC＝2∠EPF＝90°．∴S阴影＝S△ABC﹣S扇形AEF＝12×4×2﹣2902360π⨯＝4﹣π．故答案是：4﹣π．14.（2019·商丘二模）如图，在扇形OAB中，∠AOB＝90°，点C为OB的中点，CD⊥OB交弧AB于点D．若OA＝2，则阴影部分的面积为．【答案】23 3π【解析】解：连接DO，则OD＝OA＝OB＝2，∵CD∥OA，∠AOB＝90°，∴∠OCD＝90°，∵C为OB的中点，∴CO＝12OB＝12DO，∴∠CDO=30°，∠COD＝60°，则CD＝3，∴S阴影＝S扇形BOD－S△OCD=2602113 3602π⨯-⨯⨯=233π-，故答案为：23 32π-．15.（2019·开封二模）如图，在▱ABCD中，以点A为圆心，AB的长为半径的圆恰好与CD相切于点C，交AD于点E，延长BA与⊙O相交于点F．若弧EF的长为π，则图中阴影部分的面积为．【答案】8﹣2π．【解析】解：连结AC，∵CD是圆A的切线，∴AC⊥CD，即∠ACD＝90°，∵四边形ABCD为平行四边形，∴AB∥CD，AD∥BC，∴∠CAF＝90°，∠F AE＝∠B，∠EAC＝∠ACB，∵AB＝AC，∴∠B＝∠ACB，∴∠F AE＝∠EAC＝45°，∵弧EF的长为π，设圆A的半径为r，∴45180rππ⨯=，得：r＝4，∴S阴影＝S△ACD﹣S扇形CAE=12×4×4﹣2454360π⨯＝8﹣2π．故答案为：8﹣2π．16.（2019·安阳二模）如图，点C为弧AB的三等分点（弧BC<弧AC），∠AOB＝90°，OA＝3，CD⊥OB，则图中阴影部分的面积为．【答案】393 28π-．【解析】解：连接OC，AC，由题意知：∠COD＝30°，∠AOC＝60°，∵CD⊥OB，∴S△OCD＝S△ACD，∵∠CDO＝90°，OC＝OA＝3，∠COD＝30°，∴CD＝32，OD＝332，S阴影＝S△ACD+S弓形AC ＝S△OCD+S弓形AC＝12×332×32+2603360π⨯－34×32=393 28π-.故答案为：393 28π-．17.（2019·平顶山三模）如图，长方形纸片ABCD的长AB＝3，宽BC＝2，以点A为圆心，以AB的长为半径作弧；以点C为圆心，以BC的长为半径作弧．则图中阴影部分的面积是．【答案】134π－6．【解析】解：由图可知：S阴影=2903360π⨯+2902360π⨯－S矩形ABCD= 94π+π－6=134π－6，故答案为：134π－6．18.（2019·名校模考）如图，在△ABC中，∠ABC＝45°，∠ACB＝30°，AB＝2，将△ABC绕点C顺时针旋转60°得△CDE，则图中线段AB扫过的阴影部分的面积为．【答案】233π．【解析】解：过A作AF⊥BC于F，∵∠ABC＝45°，∴AF＝BF＝22AB＝2，在Rt△AFC中，∠ACB＝30°，AC＝2AF＝22，FC＝6，由旋转的性质可知，S△ABC＝S△EDC，S阴影＝S扇形DCB+S△EDC﹣S△ABC﹣S扇形ACE＝S扇形DCB﹣S扇形ACE＝()()22 60266022360360ππ⨯+⨯-=233π,故答案为：233π．19.（2019·枫杨外国语三模）如图，在矩形ABCD中，AB＝3，AD＝4，将矩形ABCD绕点D顺时针旋转90°得到矩形A′B′C′D，连接A′B，则图中阴影部分的面积为.【答案】25144π-．【解析】解：连接BD，B’D，由题意知：∠BDB’=90°，A’C=A’D－CD=1，由勾股定理得：BD=B’D=5，∴S阴影=S扇形DBB’－S△BCD－S△A’B’D－S△A’BC=2905111343414 360222π⨯-⨯⨯-⨯⨯-⨯⨯=2514 4π-.故答案为：2514 4π-.20.（2019·中原名校大联考）如图，在菱形ABCD中，AB＝2，∠BAC＝30°，将菱形ABCD绕点A逆时针旋转120°，点B的对应点为点B′，点C的对应点为点C′，点D的对应点为点D′，则图中阴影部分的面积为．【答案】83π．【解析】解：连接BD，与AC相交于点O，则BD＝2BO＝2，AC3AD＝3S扇形＝S扇形CAC′+S△ABC+S△AC′D′﹣S菱形ABCD﹣S扇形DAD′＝S扇形CAC′﹣S扇形DAD′＝(22 120231202360360ππ⨯⨯-=83π．故答案为：83π．21.（2019·三门峡一模）如图，在平行四边形ABCD中，AD=2，AB=4，∠A=30°，以点A为圆心，AD 的长为半径画弧交AB于点E，连接CE，则阴影部分的面积是__________．ACE30°【答案】33－3π．【解析】解：∵∠A=30°，AD=2，∴平行四边形AB边上的高为：AD·sin30°=3，∵AB=4，∴BE=2，S阴影=S平行四边形ABCD－S扇形AED－S△BEC=43－2302360π⨯－1232⨯⨯=33－3π故答案为：33－3π.22.（2019·周口二模）如图，P A、PB是半径为1的⊙O的两条切线，点A、B分别为切点，∠APB＝60°，OP与弦AB交于点C，与⊙O交于点D．阴影部分的面积是（结果保留π）．【答案】6π.【解析】解：∵P A、PB是⊙O的切线，∴OA⊥P A，OB⊥PB，OP平分∠APB，∵∠APB＝60°，∴∠APO＝30°，∠POA＝60°，由AP=BP，OA=OB得：OP垂直平分AB，∴AC=BC，∴S△AOC＝S△BOC，∴S阴影部分＝S扇形OAD＝26013606ππ⨯=．故答案为：．6。

2023年中考数学高频压轴题突破——二次函数与面积问题

2023年中考数学高频压轴题突破——二次函数与面积问题1．如图，抛物线y＝ax2+bx+c经过点A（﹣2，0），B（4，0），与y轴正半轴交于点C，且OC＝2OA，抛物线的顶点为D，对称轴交x轴于点E，直线y＝mx+n经过B，C两点．（1）求抛物线的解析式；（2）点F是第一象限内抛物线上一点，当△BCF面积最大时，求此时点F点到直线BC 的距离；（3）连接AC，若点P是抛物线上对称轴右侧一点，点Q是直线BC上一点，试探究是否存在以点E为直角顶点的Rt△PEQ，且满足tan∠EQP＝tan∠OCA．若存在，求出点P 的坐标；若不存在，请说明理由．2．如图，抛物线交x轴于A、B两点（点A在点B的左边），交y轴于点C，直线y＝﹣x+3经过点C与x轴交于点D，抛物线的顶点坐标为（2，4）．（1）求CD的长及抛物线的函数关系式；（2）若点P是抛物线位于第一象限部分上的一个动点，则当点P运动至何处时，△PCD 的面积最大？（3）若点P是抛物线位于第一象限部分上的一个动点，则当点P运动至何处时，恰好使∠PDC＝45°？请你求出此时的P点坐标．3．如图1，在平面直角坐标系中，抛物线y＝ax2+bx+c（a≠0）与直线交于x轴上的点B，y轴上的点C，且其对称轴为直线．该抛物线与x轴的另一交点为点A，顶点为M．（1）求抛物线的解析式及顶点M的坐标；（2）如图2，长度为的线段DF在线段BC上滑动（点D在点F的左侧），过D，F 分别作y轴的平行线，交抛物线于E，P两点，连接PE．求四边形PFDE面积的最大值及此时点P坐标；（3）在（2）问条件下，当四边形PFDE面积有最大值时，记四边形PFDE为四边形P1F1D1E1．将四边形P1F1D1E1沿直线BC平移，点P1，E1关于直线BC的对称点分别是点P2，E2．在平移过程中，当点P2，E2中有一点落到抛物线上时，请直接写出点P2，E2的坐标．4．在平面直角坐标系中，点O为坐标原点，抛物线y＝ax2+bx+3交x轴负半轴于点A，交x轴正半轴于点B，交y轴于点C，且OA＝OC＝3OB．（1）求这个抛物线的解析式；（2）如图1，点P为第三象限抛物线上的点，设点P的横坐标为t，△P AC面积为S，求S与t的函数解析式（直接写出自变量t的取值范围）；（3）如图2，在（2）的条件下，Q为CA延长线上的一点，若P到x轴的距离为d，△PQB的面积为2d，且∠P AQ＝∠AQB，求点P的坐标．5．如图，在平面直角坐标系中，直线y＝2x+4与x轴，y轴分别交于A，B两点，抛物线y ＝ax2+x+c（a≠0）经过A，B两点与x轴相交于点C．（1）求抛物线的解析式；（2）若点M为直线BC上方抛物线上任意一点，当△MBC面积最大时，求出点M的坐标；（3）若点P在抛物线上，连接PB，当∠PBC+∠OBA＝45°时，请直接写出点P的坐标．6．如图，已知抛物线y＝ax2+c过点（﹣2，2），（4，5），过定点F（0，2）的直线l：y ＝kx+2与抛物线交于A、B两点，点B在点A的右侧，过点B作x轴的垂线，垂足为C．（1）求抛物线的解析式；（2）当点B在抛物线上运动时，判断线段BF与BC的数量关系（＞、＜、＝），并证明你的判断；（3）若k＝1，在直线l下方的抛物线上是否存在点Q，使得△QBF的面积最大？若存在，求出点Q的坐标及△QBF的最大面积；若不存在，请说明理由．7．如图，对称轴为直线x＝﹣1的抛物线y＝a（x﹣h）2+k（a≠0）图象与x轴交于点A、B （点A在点B的左侧），与y轴交于点C，其中点B的坐标为（2，0），点C的坐标为（0，4）．（1）求该抛物线的解析式；（2）如图1，若点P为抛物线上第二象限内的一个动点，点M为线段CO上一动点，当△APC的面积最大时，求△APM周长的最小值；（3）如图2，将原抛物线绕点A旋转180°，得新抛物线y'，在新抛物线y'的对称轴上是否存在点Q使得△ACQ为等腰三角形？若存在，请直接写出点Q的坐标；若不存在，说明理由．8．已知抛物线与x轴交于A，B两点，且经过点C（0，﹣2），顶点坐标为（，）．（1）求抛物线的解析式；（2）如图1，点D为第四象限抛物线上一点，连接AD，BC交于点E，连接BD，记△BDE的面积为S1，△ABE的面积为S2，当最大时，求D点坐标；（3）如图2，连接AC，BC，过点O作直线l∥BC，点P，Q分别为直线l和抛物线上的点．试探究：在y轴右侧是否存在这样的点P，Q，使以点A，B，P，Q为顶点的四边形为平行四边形？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由．9．如图，定义：直线l：y＝mx+n（m＜0，n＞0）与x轴、y轴分别相交于A，B两点，将△AOB绕着点O逆时针旋转90°得到△COD，过点A，B，D的抛物线叫做直线l的“纠缠抛物线”，反之，直线叫做抛物线的“纠缠直线”，两线“互为纠缠线”．（1）若l：y＝﹣2x+2，则求它的纠缠抛物线的函数解析式；（2）判断并说明y＝﹣2x+2k与y＝﹣x2﹣x+2k是否“互为纠缠线”；（3）在（1）中，P是l的纠缠抛物线在第二象限上的一个动点，求△PCD的最大面积．10．如图，已知抛物线y＝x2+bx+c经过点A（﹣3，0）和点C（0，﹣3）．解答下列问题．（1）求抛物线的解析式；（2）抛物线的顶点为D，对称轴与x轴的交点为E，求线段BD的长；（3）点F在抛物线上运动，是否存在点F使△F AB的面积等于6？如果存在，求出点F 的坐标；如果不存在，说明理由．11．如图①，在平面直角坐标系中，抛物线y＝ax2+bx+c与x轴交于A（﹣1，0）、B（4，0）两点，与y轴交于点C（0，﹣2），点P在直线BC下方的抛物线上，过点P作PD ⊥x轴于点D，交直线BC于点E，并连接AC、CP．（1）求抛物线的解析式；（2）连接BP，设四边形ABPC的面积为S，当S最大时，求点P的坐标及最大值；（3）如图②，过点P作PF⊥BC于点F，当以C、P、F为顶点的三角形与△AOC相似时，求点P的坐标．12．如图，直线y＝﹣x+3与x轴交于点C，与y轴交于点B，抛物线y＝ax2+x+c经过B、C两点，且与x轴的另一个交点为A．（1）求抛物线的解析式；（2）如图，点E是直线BC上方抛物线上的一动点，当△BEC面积最大时，请求出点E 的坐标和△BEC面积的最大值？（3）在（2）的结论下，过点E作y轴的平行线交直线BC于点M，连接AM，点Q是抛物线对称轴上的动点，在抛物线上是否存在点P，使得以P、Q、A、M为顶点的四边形是平行四边形？如果存在，请求出点P的坐标；如果不存在，请说明理由．13．如图，在平面直角坐标系xOy中，抛物线y＝x2+x﹣2与x轴交于A、B两点（点A 在点B的左侧），与y轴交于点C．（1）求点A的坐标；（2）如图1，连接AC，点D为线段AC下方抛物线上一动点，过点D作DE∥y轴交线段AC于E点，连接EO，记△ADC的面积为S1，△AEO的面积为S2，求S1﹣S2的最大值及此时点D的坐标；（3）如图2，将抛物线沿射线CB方向平移个单位长度得到新抛物线，动点N在原抛物线的对称轴上，点M为新抛物线与y轴的交点，当△AMN为以AM为腰的等腰三角形时，请直接写出点N的坐标．14．如图，在平面直角坐标系中，抛物线y＝ax2+bx﹣4与x轴交于点A（﹣2，0），B（4，0），与y轴交于点C，点D为BC的中点．（1）求该抛物线的函数表达式；（2）若点P是第四象限内该抛物线上一动点，求△BDP面积的最大值；（3）M是抛物线的对称轴上一点，N是抛物线上一点，直接写出所有使得以点A，D，M，N为顶点的四边形是平行四边形的点N的坐标，并把求其中一个点N的坐标的过程写出来．15．如图，在平面直角坐标系中，抛物线y＝﹣x2+2x与x轴正半轴交于点A，点B在抛物线的对称轴上，点D在抛物线上，且在对称轴右侧，点C是平面内一点，四边形OBCD 是平行四边形．（1）求点A的坐标及抛物线的对称轴；（2）若点B的纵坐标是﹣3，点D的横坐标是，则S▱OBCD＝；（3）若点C在抛物线上，且▱OBCD的面积是12，请直接写出点C的坐标．16．已知直线y＝﹣x+3与x轴相交于点A，与y轴相交于点B．经过A，B两点的抛物线y ＝ax2+bx+c的对称轴为直线x＝1，与x轴的另一个交点为D（D在A的左侧），点P为y轴右侧抛物线上的一动点．（1）求抛物线的解析式；（2）若Q为OA的中点，当PQ∥y轴时，求点P的坐标；（3）当点P位于直线AB上方的抛物线上时，求四边形P ADB面积的最大值．17．如图，已知抛物线y＝ax2+bx﹣4与x轴交于A，B两点，与y轴交于点C，且点A的坐标为（﹣2，0），直线BC的解析式为y＝x﹣4．（1）求抛物线的解析式．（2）如图1，过点A作AD∥BC交抛物线于点D（异于点A），P是直线BC下方抛物线上一点，过点P作PQ∥y轴，交AD于点Q，过点Q作QR⊥BC于点R，连接PR．求△PQR面积的最大值及此时点P的坐标．（3）如图2，点C关于x轴的对称点为点C′，将抛物线沿射线C′A的方向平移2个单位长度得到新的抛物线y′，新抛物线y′与原抛物线交于点M，原抛物线的对称轴上有一动点N，平面直角坐标系内是否存在一点K，使得以D，M，N，K为顶点的四边形是矩形？若存在，请直接写出点K的坐标；若不存在，请说明理由．18．若直线y＝﹣2x+4与y轴交于点A，与x轴交于点B，二次函数y＝ax2+3x+c的图象经过点A，交x轴于C、D两点，且抛物线的对称轴为直线x＝．（1）求二次函数的解析式；（2）过点C作直线CE∥AB交y轴于点E，点P是直线CE上一动点，点Q是第一象限抛物线上一动点，求四边形APBQ面积的最大值与此时点Q的坐标；（3）在（2）的结论下，点E是抛物线的顶点，对称轴与x轴交于点G，直线EQ交x 轴于点F，在抛物线的对称轴上是否存在一点M，使得∠MFQ+∠CAO＝45°，求点M 的坐标．19．如图，抛物线y＝﹣x2+bx+c经过A（4，0），C（﹣1，0）两点，与y轴交于点B，P 为第一象限抛物线上的动点，连接AB，BC，P A，PC，PC与AB相交于点Q．（1）求抛物线的解析式；（2）设△APQ的面积为S1，△BCQ的面积为S2，当S1﹣S2＝5时，求点P的坐标；（3）是否存在点P，使△P AQ为直角三角形，若存在，直接写出点P的坐标；若不存在，说明理由．20．如图，边长为8的正方形OABC的两边在坐标轴上，以点C为顶点的抛物线经过点A，点P是抛物线上点A，C间的一个动点（含端点），过点P作PF⊥BC于点F，点D、E 的坐标分别为（0，6），（4，0），连接PD、PE、DE．（1）求出抛物线的解析式；（2）小明探究点P的位置发现：当点P与点A或点C重合时，PD与PF的差为定值，进而猜想：对于任意一点P，PD与PF的差为定值，请你判断该猜想是否正确，请说明理由；（3）小明进一步探究得出结论：若将“使△PDE的面积为整数”的点P记作“好点”，则存在多个“好点”，且使△PDE的周长最小的点P也是一个“好点”．请直接写出所有“好点”的个数．并求出△PDE周长最小时“好点”的坐标．参考答案与试题解析1．【解答】解：（1）∵A（﹣2，0），∴OA＝2，∵OC＝2OA，∴CO＝4，∴C（0，4），将点A（﹣2，0），B（4，0），C（0，4）代入y＝ax2+bx+c，得，∴，∴y＝﹣x2+x+4；（2）设直线BC的解析式为y＝kx+b，∴，∴，∴y＝﹣x+4，过点F作FH⊥x轴交BC于点G，F点到直线BC的距离为h，设F（t，﹣t2+t+4），则G（t，﹣t+4），∴FG＝﹣t2+t+4+t﹣4＝﹣t2+2t，∴S△BCF＝×4×（﹣t2+2t）＝﹣t2+4t＝﹣（t﹣2）2+4，∴当t＝2时，△BCF的面积有最大值4，∵B（4，0），C（0，4），∴BC＝4，∴4＝×BC×h，∴h＝，∴点F点到直线BC的距离为；（3）存在以点E为直角顶点的Rt△PEQ，且满足tan∠EQP＝tan∠OCA，理由如下：∵A（﹣2，0），C（0，4），∴OA＝2，OC＝4，∴tan∠OCA＝，∵tan∠EQP＝tan∠OCA，∴tan∠EQP＝，∵y＝﹣x2+x+4＝﹣（x﹣1）2+5，∴D（1，5），E（1，0），当P点在Q点左侧时，如图2，过点P作PM⊥DE交于M，过点Q作QN⊥DE交于N，∵∠PEQ＝90°，∴∠MEP+∠NEQ＝90°，∵∠MEP+∠MPE＝90°，∴∠NEQ＝∠MPE，∴△MEP∽△NQE，∴＝＝，∵＝，∴＝＝，设P（m，﹣m2+m+4），∴PM＝m﹣1，EM＝﹣m2+m+4，∴EN＝2m﹣2，NQ＝﹣m2+2m+8，∴Q（﹣m2+2m+9，2﹣2m），∴2﹣2m＝﹣（﹣m2+2m+9）+4，解得m＝，∵点P是抛物线上对称轴右侧，∴m＝，∴P（，+）；当点P在点Q的右侧时，同理可得P（，﹣）；综上所述：P点坐标为（，+）或（，﹣）．2．【解答】解：（1）∵直线y＝﹣x+3经过点C与x轴交于点D，∴C（0，3），D（4，0），∴CD＝，∵抛物线的顶点坐标为（2，4），∴设抛物线的解析式为y＝a（x﹣2）2+4，将C（0，3）代入，得3＝a（0﹣2）2+4，得a＝﹣，∴抛物线的解析式为y＝﹣（x﹣2）2+4＝﹣x2+x+3，（2）过点P作一条关于CD的平行线，当该直线与抛物线只有一个交点时，该交点即为P，此时△PCD的面积最大，∵直线CD的解析式为y＝﹣x+3，∴设过P点且与直线CD平行的直线解析式为y＝，∵直线y＝与抛物线y＝﹣x2+x+3，有且只有一个交点，∴当﹣x+b＝﹣x2+x+3时，△＝0，解得b＝，∴该直线的解析式为y＝﹣x+，∴﹣x+＝﹣+x+3，解得x＝，∴﹣×+＝，∴P（，）时，有△PCD的面积最大值，（3）如图，以CD为底，向上作等腰直角三角形CDE，则ED与抛物线的交点即为点P，过点E作EM⊥y轴于点M，过点D作DN⊥ME的延长线于N，∵△ECD为等腰直角三角形，∴EC＝ED，∠CED＝90°，∴∠MEC+∠DEN＝180°﹣90°＝90°，∵△EMC中，∠EMC＝90°，∴∠MEC+∠MCE＝90°，∴∠MCE＝∠NED，在△MCE和△NED中，，∴△MCE≌△NED（AAS），∴MC＝EN，ME＝ND，设MC＝EN＝x，ME＝ND＝y，则x+y表示D点和C点横坐标的差的绝对值，y﹣x表示D点和C点纵坐标的差的绝对值，∴x+y＝4，y﹣x＝3解得x＝，y＝，∴E点是由C向上平移个单位长度，再向右平移个单位长度得到，∴E（，），∴设DE解析式为y＝mx+n，得，解得，∴DE的解析式为y＝﹣7x+28，∴﹣7x+28＝﹣x2+x+3，解得x＝16±2，此时取x＝16﹣2，∴﹣7x+28＝14﹣84，∴当∠PDC＝45°时，P点的坐标为（16﹣2.14﹣84）．3．【解答】解：（1）对，当x＝0时，y＝2，当y＝0时，x＝4，∴点B（4，0），点C（0，2），将点B和点C的坐标代入y＝ax2+bx+c，得，化简得：，∵对称轴为直线x＝，∴﹣＝，即有b＝﹣3a，∴﹣4a﹣＝﹣3a，∴a＝﹣，b＝，∴抛物线的解析式为y＝﹣x2+x+2＝﹣（x﹣）2+，∴顶点M的坐标（，）．（2）如图2，过点F作FQ⊥PF于点Q，过点P作PN⊥DE于点N，∵PF⊥x轴，ED⊥x轴，∴∠DQF＝∠BOC＝90°，∠QDF＝∠OBC，DQ＝PN，∴△DQF∽△BOC，∵B（4，0），C（0，2），∴OB＝4，OC＝2，∴BC＝2，∵DF＝，∴，即，∴DQ＝PN＝2，FQ＝1，设点D的坐标为（x，﹣x+2），则点E（x，﹣x2+x+2），F（x+2，﹣x+1），P （x+2，﹣x2﹣x+3），∴ED＝﹣x2+2x，PF＝﹣x2+2，∴S四边形PFDE＝S△DPF+S△PDE＝＝PF+ED＝﹣x2+2﹣x2+2x＝﹣x2+2x+2＝﹣（x﹣1）2+3，∴当x＝1时，四边形PFDE面积的最大值为3，此时，点E的坐标为（1，3），点P坐标为（3，2）．（3）由（2）得到点P1（3，2），E1（1，3），D1（1，），F1（3，），∴E1D1＝，P1F1＝，∴E1D1＝P1F1，∵E1D1∥P1F1，∴四边形E1D1F1P1是平行四边形，∴直线P1E1与直线BC平行，∴直线P2E2与直线BC平行，如图3，记直线P1E1和直线P2E2与y轴的交点分别为G、H，则CG＝CH，设直线P1E1的解析式为y＝﹣x+m，则﹣×1+m＝3，解得：m＝，∴直线P1E1的解析式为y＝﹣x+，∴点G（0，），∴CG＝CH＝，∴点H（0，），∴直线P2E2的解析式为y＝﹣x+，由，解得：或，当点P2落在抛物线上时，点P2（2﹣，﹣），E2（﹣，+）或点P2（2+，﹣﹣），E2（，﹣+）；当点E2落在抛物线上时，点E2（2﹣，﹣），P2（4﹣，﹣）或点E2（2+，﹣﹣），P2（4+，﹣﹣）；综上所述：点P2（2﹣，﹣），E2（﹣，+）或点P2（2+，﹣﹣），E2（，﹣+）或P2（4﹣，﹣），点E2（2﹣，﹣）或P2（4+，﹣﹣），点E2（2+，﹣﹣）．4．【解答】解：（1）对y＝ax2+bx+3，当x＝0时，y＝3，∴点C（0，3），∴OA＝OC＝3，∴A（﹣3，0），OB＝1，∴B（1，0），设抛物线的解析式为y＝a（x+3）（x﹣1），代入点C（0，3）得，﹣3a＝3，∴a＝﹣1，∴抛物线的解析式为y＝﹣（x+3）（x﹣1）＝﹣x2﹣2x+3；（2）如图1，过P作PM⊥x轴交直线AC于点M，设直线CA的解析式为y＝kx+b，则，解得：，∴直线AC的解析式为y＝x+3，设点P的坐标为（t，﹣t2﹣2t+3），则M的坐标为（t，3+t），∴PM＝t+3﹣（﹣t2﹣2t+3）＝t2+3t，∴S△P AC＝S△PMC﹣S△PMA＝PM•（x C﹣x P）﹣PM•（x A﹣x P）＝PM•（x C﹣x A）＝PM，∴S＝（t2+3t）＝t2+t（t＜﹣3）．（3）如图2，过A作AE⊥PB于点E，过Q作QF⊥PB于点F，则QF∥AE，∵AB＝4，点P到x轴的距离为d，∴S△APB＝AB•d＝2d，∴S△P AB＝S△PBQ，又∵S△P AB＝PB•AE，S△PBQ＝PB•QF，∴AE＝QF，∵AE∥QF，∴四边形AEFQ为平行四边形，∴AQ∥PB，设直线PB的解析式为y＝x+b，则1+b＝0，∴b＝﹣1，∴直线PB的解析式为y＝x﹣1，∵点P在抛物线y＝﹣x2﹣2x+3上，∴x﹣1＝﹣x2﹣2x+3，解得：x＝﹣4或x＝1（舍去），∴P的坐标为（﹣4，﹣5）．5．【解答】解：（1）直线y＝2x+4，当x＝0时，y＝4；当y＝0时，则2x+4＝0，解得x＝﹣2，∴A（﹣2，0），B（0，4），∵抛物线y＝ax2+x+c点B（0，4），∴c＝4，把A（﹣2，0）代入y＝ax2+x+4，得4a﹣2+4＝0，解得a＝﹣，∴抛物线的解析式的解析式为y＝﹣x2+x+4．（2）如图1，作MG⊥x轴于点G，交BC于点F，抛物线y＝﹣x2+x+4，当y＝0时，则﹣x2+x+4＝0，解得x1＝﹣2，x2＝4，∴C（4，0），OC＝4，设直线BC的解析式为y＝kx+4，把C（4，0）代入y＝kx+4，得4k+4＝0，解得k＝﹣1，∴y＝﹣x+4，设M（m，﹣m2+m+4），则F（m，﹣m+4），∴MF＝（﹣m2+m+4）﹣（﹣m+4）＝﹣m2+2m，∵S△MBC＝OG•MF+CG•MF＝OC•MF，∴S△MBC＝×4（﹣m2+2m）＝﹣m2+4m＝﹣（m﹣2）2+4，∴当m＝2时，S△MBC最大＝4，∴点M标为（2，4）．（3）如图2，在x轴上取点D（2，0），作射线BD交抛物线于另一点P，∵OB＝OC＝4，∠BOC＝90°，∴∠OBC＝∠OCB＝45°，∵OB⊥AD，OA＝OD＝2，∴AB＝DB，CD＝OC﹣OD＝4﹣2＝2，∴∠OBA＝∠OBP，∴∠PBC+∠OBA＝∠PBC+∠OBP＝∠OBC＝45°，设直线BP的解析式为y＝nx+4，则2n+4＝0，解得n＝﹣2，∴y＝﹣2x+4，由得，，∴P（6，﹣8）；如图2，作CE⊥x轴，使CE＝CD＝2，连接BE交抛物线于另一点P′，则E（4，2），∵∠OCE＝90°，∠OCB＝45°，∴∠BCE＝∠BCD＝45°，∵BC＝BC，∴△BCE≌△BCD（SAS），∴∠P′BC＝∠PBC，∴∠P′BC+∠OAB＝∠PBC+∠OBA＝45°，设直线BP′的解析式为y＝rx+4，则4r+4＝2，解得r＝﹣，∴y＝﹣x+4，由得，，∴P′（3，），综上所述，点P的坐标为（6，﹣8）或（3，）．6．【解答】解：（1）把点（﹣2，2），（4，5）代入y＝ax2+c得，解得，所以抛物线解析式为y＝x2+1；（2）BF＝BC．理由如下：设B（x，x2+1），而F（0，2），∴BF2＝x2+（x2+1﹣2）2＝x2+（x2﹣1）2＝（x2+1）2，∴BF＝x2+1，∵BC⊥x轴，∴BC＝x2+1，∴BF＝BC；（3）作QE∥y轴交AB于E，如图，当k＝1时，一次函数解析式为y＝x+2，解方程组得或，∴B（2+2，4+2），设Q（t，t2+1），则E（t，t+2），∴EQ＝t+2﹣（t2+1）＝﹣t2+t+1，∴S△QBF＝S△EQF+S△EQB＝•（2+2）•EQ＝（+1）（﹣t2+t+1）＝﹣（t ﹣2）2+2+2，当t＝2时，S△QBF的最大值为2+2，此时Q点坐标为（2，2）．7．【解答】解：（1）∵抛物线y＝a（x﹣h）2+k（a≠0）的对称轴为直线x＝﹣1，∴x＝h＝﹣1，∵抛物线过点B（2，0），点C（0，4），∴，解得，∴抛物线的解析式为：y＝﹣（x+1）2+．（2）由（1）知函数解析式为：y＝﹣（x+1）2+．∴A（﹣4，0），∴直线AC：y＝x+4，过点P作PN∥AC，设直线PN的解析式为：y＝x+m，当△APC的面积最大时，直线PN与抛物线有且仅有一个交点，令x+m＝﹣（x+1）2+，整理得x2+4x+2m﹣8＝0，∴Δ＝42﹣4（2m﹣8）＝0，解得m＝6，∴x2+4x+4＝0，∴x＝﹣2，即P（﹣2，4）；作点A关于y轴的对称点A′，连接A′P交y轴于点M，如图1，此时△APM的周长最小，∵A（﹣4，0），∴A′（4，0），∴A′P＝＝2，AP＝＝2，∴△APM周长的最小值为：2+2．（3）由（1）知原抛物线的顶点坐标D（﹣1，），绕点A旋转后的顶点D′（﹣7，﹣），∴y′的对称轴为直线x＝﹣7；设点Q的坐标为（﹣7，t），若△ACQ是等腰三角形，则需要分类讨论：①当AC＝AQ时，如图2；∴（﹣4﹣0）2+（0﹣4）2＝（﹣4+7）2+（0﹣t）2，解得t＝±；∴Q（﹣7，）或（﹣7，﹣）；②当CA＝CQ时；∴（﹣4﹣0）2+（0﹣4）2＝（0+7）2+（4﹣t）2，无解；③当QA＝QC时，如图3，∴（﹣4+7）2+（0﹣t）2＝（0+7）2+（4﹣t）2，解得t＝7，∴Q（﹣7，7）．综上可知，存在，点Q的坐标为（﹣7，）或（﹣7，﹣）或（﹣7，7）．8．【解答】解：（1）设抛物线的解析式为y＝a（x﹣）2﹣，∵将C（0，﹣2）代入得：4a＝2，解得a＝，∴抛物线的解析式为y＝（x﹣）2﹣，即y＝x2﹣x﹣2；（2）过点D作DG⊥x轴于点G，交BC于点F，过点A作AK⊥x轴交BC的延长线于点K，∴AK∥DG，∴△AKE∽△DFE，∴，∴＝＝＝，设直线BC的解析式为y＝kx+b，∴，解得，∴直线BC的解析式为y＝x﹣2，∵A（﹣1，0），∴y＝﹣﹣2＝﹣，∴AK＝，设D（m，m2﹣m﹣2），则F（m，m﹣2），∴DF＝m﹣2﹣（m2﹣m﹣2）＝﹣m2+2m．∴＝＝＝．∴当m＝2时，有最大值，最大值是，此时D（2，﹣3）；（3）存在．理由如下：∵l∥BC，∴直线l的解析式为y＝x，设P（n，n），∵P，Q在y轴右侧，∴n＞0①当AB为边时，则PQ∥AB，PQ＝AB＝5，若点Q在点P左侧时，∴点Q（n﹣5，n），∴n＝（n﹣5）2﹣（n﹣5）﹣2，∴n＝+7或﹣+7，∴点P（+7，）或（﹣+7，）若点Q在点P右侧时，∴点Q（n+5，n），∴n＝（n+5）2﹣（5+n）﹣2，∴n＝﹣﹣3（舍去）或﹣+3∴点P（﹣+3，），②当AB为对角线时，∵AB与PQ互相平分，∴点Q（3﹣n，﹣n）∴﹣n＝（3﹣n）2﹣（3﹣n）﹣2，∴n＝+1或﹣+1（舍去），∴点P（+1，），此时点P的坐标为（+1，）或（﹣1，）综上所述，点P的坐标为（+1，）或（﹣+3，）或（+7，）或（﹣+7，）9．【解答】解：（1）在y＝﹣2x+2中，令y＝0得x＝2，令x＝0得y＝2，∴A（1，0），B（0，2），∵将△AOB绕着点O逆时针旋转90°得到△COD，∴OD＝OB，∴D（﹣2，0），∵直线y＝﹣2x+2的纠缠抛物线过A（1，0），D（﹣2，0），设纠缠抛物线函数解析式为y＝a（x+2）（x﹣1），把B（0，2）代入得：2＝﹣2a，∴a＝﹣1，∴纠缠抛物线函数解析式为y＝﹣（x+2）（x﹣1）＝﹣x2﹣x+2，答：直线y＝﹣2x+2的纠缠抛物线的函数解析式是y＝﹣x2﹣x+2；（2）y＝﹣2x+2k与y＝﹣x2﹣x+2k是“互为纠缠线”，理由如下：在y＝﹣2x+2k中，令x＝0得y＝2k，令y＝0得x＝k，∴A（k，0），B（0，2k），∵将△AOB绕着点O逆时针旋转90°得到△COD，∴D（﹣2k，0），∵直线y＝﹣2x+2k的纠缠抛物线过A（k，0），D（﹣2k，0），设纠缠抛物线函数解析式为y＝a（x﹣k）（x+2k），将B（0，2k）代入得：2k＝﹣2k2a，解得a＝﹣，∴纠缠抛物线函数解析式为y＝﹣（x﹣k）（x+2k）＝﹣x2﹣x+2k，∴y＝﹣2x+2k与y＝﹣x2﹣x+2k是“互为纠缠线”；（3）过点P作y轴的平行线交DC于E，如图：由（1）知A（1，0），B（0，2），D（﹣2，0），∵将△AOB绕着点O逆时针旋转90°得到△COD，∴OC＝OA＝1，∴C（0，1），设直线CD为y＝tx+1，将D（﹣2，0）代入得：0＝﹣2t+1，解得t＝，∴直线CD为y＝x+1，设P（x，﹣x2﹣x+2），则E（x，x+1），∴PE＝﹣x2﹣x+2﹣（x+1）＝﹣x2﹣x+1，∴△PCD的面积＝PE•|x C﹣x D|＝×（﹣x2﹣x+1）×2＝﹣x2﹣x+1＝﹣（x+）2+，∵﹣1＜0，∴x＝﹣时，△PCD的面积最大为，答：△PCD的最大面积是．10．【解答】解：（1）∵抛物线y＝x2+bx+c经过点A（﹣3，0），C（0，﹣3），∴9﹣3b+c＝0，0+0+c＝﹣3，即得b＝2，c＝﹣3，∴抛物线的表达式为：y＝x2+2x﹣3；（2）∵y＝x2+2x﹣3＝（x+1）2﹣4；∴函数的对称轴为直线x＝﹣1，顶点D（﹣1，﹣4），∵A（﹣3，0），∴B（1，0），∴BD＝＝2；（3）存在，理由：△BF A的面积＝×BA×|y F|＝2|y F|＝6，解得：y F＝±3，故：x2+2x﹣3＝±3，解得：x＝0或﹣2或﹣1±，故点F的坐标为：（0，﹣3）或（2，﹣3）或（﹣1﹣，3）或（﹣1+，3）．11．【解答】解：（1）设抛物线的解析式为y＝a（x+1）（x﹣4）．∵将C（0，﹣2）代入得：﹣4a＝﹣2，解得a＝，∴抛物线的解析式为y＝（x+1）（x﹣4），即y＝x2﹣x﹣2；（2）设P（m，m2﹣m﹣2），∵A（﹣1，0）、B（4，0），C（0，﹣2），点P在直线BC下方的抛物线上，∴S四边形ABPC＝S△OAC+S△OPB+S△OPC＝×2×1+×4（﹣m2+m+2）+×2m＝﹣m2+4m+5＝﹣（m﹣2）2+9，∴当m＝2时，S最大是9，∴点P的坐标为（2，﹣3）；（3）设P（x，x2﹣x﹣2），∵A（﹣1，0）、B（4，0），C（0，﹣2），∴BC＝＝2，PC＝，AC＝，∵S△PCB＝S四边形ABPC﹣S△ABC＝﹣x2+4x+5﹣×5×2＝﹣x2+4x＝BC•PF＝PF，∴PF＝，∵PF⊥BC于点F，∴∠PFC＝∠AOC＝90°，①△PCF∽△CAO时，∴，∴，解得：x1＝0（与点C重合，舍去），x2＝，∴点P的坐标为（，﹣）；②△PCF∽△ACO时，∴，∴，解得：x1＝（不合题意，舍去），x2＝3，∴点P的坐标为（3，﹣2）；综上，点P的坐标为（，﹣）或（3，﹣2）．12．【解答】解：（1）令y＝0，则x＝4，∴C（4，0），令x＝0，则y＝3，∴B（0，3），将点B、点C代入y＝ax2+x+c，∴，∴，∴y＝﹣x2+x+3；（2）令x＝0，则y＝3，∴B（0，3），令y＝0，则x＝4，∴C（4，0），令y＝0，则﹣x2+x+3＝0，∴x＝4或x＝﹣2，∴A（﹣2，0），如图：过点E作EF⊥x轴交BC于点F，设E（t，﹣t2+t+3），则F（t，﹣t+3），∴EF＝﹣t2+t，∴S△BCE＝×4×（﹣t2+t）＝﹣（t﹣2）2+3，∴当t＝2时，△BCE面积的最大值为3，此时E（2，3）；（3）存在点P，使得以P、Q、A、M为顶点的四边形是平行四边形，理由如下：∵E（2，3），∴M（2，），设Q（1，n），P（m，﹣m2+m+3），①当AM为平行四边形的对角线时，1+m＝0，∴m＝﹣1，∴P（﹣1，）；②当AQ为平行四边形的对角线时，2+m＝﹣1，∴m＝﹣3，∴P（﹣3，﹣）；③当AP为平行四边形的对角线时，1+2＝﹣2+m，∴m＝5，∴P（5，﹣）；综上所述：P点坐标为（﹣1，）或（﹣3，﹣）或（5，﹣）．13．【解答】解：（1）∵抛物线，与x轴交于A、B两点，令y＝0，得，解得x1＝﹣3，x2＝1，∵点A在点B的左侧，∴点A的坐标为（﹣3，0）；（2）如图1，延长DE交x轴于点K，∵抛物线与y轴交于点C，∴C（0，﹣2），设直线AC的函数表达式为y＝kx+n（k≠0），∵A（﹣3，0），C（0，﹣2），∴，解得，∴直线AC的函数表达式为，设，其中﹣3＜t＜0，∴，K（t，0），∴DE＝﹣t2﹣2t，∵＝（﹣t2﹣2t）＝﹣t2﹣3t，＝（t+2）＝t+3，∴S1﹣S2＝﹣t2﹣3t﹣t﹣3＝﹣t2﹣4t﹣3＝﹣（t+2）2+1，∴当t＝﹣2时，S1﹣S2取得最大值，最大值为1，此时点D的坐标为（﹣2，﹣2）；（3）∵C（0，﹣2），B（1，0），∴＝，∵抛物线沿射线CB方向平移个单位长度，∴抛物线向右平移个单位长度，向上平移3个单位长度，∴平移后的抛物线解析式为y＝（x+1﹣）2﹣+3＝（x﹣）2+，当x＝0时，y＝，∴M（0，），∵原抛物线的对称轴为直线x＝﹣1，设N（﹣1，n），①当AM＝AN时，9+＝4+n2，∴n＝±，∴N（﹣1，）或N（﹣1，﹣）；②当AM＝MN时，9+＝1+（﹣n）2，∴n＝或n＝，∴N（﹣1，）或N（﹣1，）；综上所述：N点坐标为（﹣1，）或（﹣1，﹣）或（﹣1，）或（﹣1，）．14．【解答】解：（1）将A（﹣2，0），B（4，0）代入y＝ax2+bx﹣4得：∴，解得，∴抛物线的函数表达式为y＝x2﹣x﹣4；（2）在y＝x2﹣x﹣4中，当x＝0时，y＝﹣4，∴C（0，﹣4），设直线BC为y＝kx﹣4，将B（4，0）代入得：0＝4k﹣4，解得k＝1，∴直线BC为y＝x﹣4，∵B（4，0），C（0，﹣4），D是BC中点，∴D（2，﹣2），过点P作PQ⊥x轴交BC于点Q，如图：设P（t，t2﹣t﹣4），（0＜t＜4），则Q（t，t﹣4），∴PQ＝t2﹣t﹣4﹣（t﹣4）＝﹣t2+2t，∴S△BDP＝PQ•|x B﹣x D|＝×（﹣t2+2t）×（4﹣2）＝﹣t2+2t＝﹣（t﹣2）2+2，∵﹣＜0，0＜t＜4，∴t＝2时，S△PBD有最大值为2；答：△BDP面积的最大值是2；（3）由y＝x2﹣x﹣4得抛物线对称轴是直线x＝1，设M（1，m），N（n，n2﹣n﹣4），而A（﹣2，0），D（2，﹣2），①当MN、AD为对角线时，MN的中点即是AD中点，∴，解得n＝﹣1，∴N（﹣1，﹣），②当MA、ND为对角线时，MA的中点即是ND中点，∴，解得n＝﹣3，∴N（﹣3，），③当MD、AN为对角线时，MD的中点即是AN中点，∴，解得n＝5，∴N（5，），综上所述，N的坐标为（﹣1，﹣）或（﹣3，）或（5，）．15．【解答】解：（1）在y＝﹣x2+2x中，令y＝0，得：﹣x2+2x＝0，解得：x1＝0，x2＝2，∴A（2，0）；∵x＝﹣＝1，抛物线的对称轴为直线x＝1；（2）如图1，连接BD，∵点B在抛物线的对称轴上，且点B的纵坐标是﹣3，∴B（1，﹣3），∵点D在抛物线上，且点D的横坐标是，∴D（，），设直线OD的解析式为y＝kx，则：＝k，解得：k＝﹣，∴直线OD的解析式为y＝x，设抛物线的对称轴交OD于点H，∴H（1，），∴BH＝﹣﹣（﹣3）＝，∴S▱OBCD＝2S△OBD＝2××BH×|x D﹣x O|＝2×××＝，故答案为：；（3）如图2，设B（1，b），C（c，﹣c2+2c），设抛物线的对称轴交x轴于点G，交OD于点H，过点D作DK∥x轴，过点C作CK∥y 轴，连接BD，则∠CKD＝∠BGO＝90°，∵四边形OBCD是平行四边形，∴OB∥CD，OB＝CD，∵BG∥CK，且∠OBG与∠DCK均为锐角，∴∠OBG＝∠DCK，∴△BOG≌△CDK（AAS），∴DK＝OG＝1，CK＝BG＝﹣b，∴D（c﹣1，﹣c2+4c﹣3），设直线OD的解析式为y＝ax，则：﹣c2+4c﹣3＝a（c﹣1），∴a＝3﹣c，∴直线OD的解析式为y＝（3﹣c）x，∴H（1，3﹣c），∴BH＝3﹣c﹣b，∵▱OBCD的面积是12，∴S△OBD＝6，∴×（3﹣c﹣b）×（c﹣1）＝6，即（3﹣c﹣b）（c﹣1）＝12①，∵CK＝BG＝﹣b，∴﹣c2+4c﹣3﹣（﹣c2+2c）＝﹣b，即b+2c﹣3＝0②，由①②组成方程组，解得：（舍去），，∴点C的坐标为C（4，﹣8）．16．【解答】解：（1）对于y＝﹣x+3，令y＝0，即0＝﹣x+3，解得x＝3；令x＝0，得y ＝3；∴A（3，0），B（0，3），∵抛物线y＝ax²+bx+c经过A（3，0），B（0，3）两点，且对称轴为直线x＝1，∴，解得，∴抛物线的解析式为：y＝﹣x²+2x+3；（2）∵A（3，0），∴OA＝3，∵Q为OA的中点，∴OQ＝OA＝×3＝，∴Q（，0），∵PQ∥y轴，∴点P的横坐标为，当x＝时，y＝﹣x²+2x+3＝﹣+2×+3＝，∴点P的坐标为（，）；（3）过点P作PN∥y轴交直线AB于N，如图：对于y＝﹣x²+2x+3，令y＝0，即0＝﹣x²+2x+3，解得x1＝3，x2＝﹣1，∴A（3，0），D（﹣1，0），∴AD＝3﹣（﹣1）＝4，∵B（0，3），∴OB＝3，∴S△ADB＝AD•OB＝×4×3＝6，设P（m，﹣m²+2m+3），则N（m，﹣m+3），∴PN＝﹣m²+2m+3﹣（﹣m+3）＝﹣m²+3m，∴S△P AB＝S△PNB+S△PNA＝PN•m+PN•（3﹣m）＝PN＝（﹣m²+3m），∴S四边形P ADB＝S△P AB+S△ABD＝（﹣m²+3m）+6＝﹣+，∵﹣＜0，∴当m＝时，S四边形P ADB有最大值，最大值为，∴四边形P ADB面积的最大值为．17．【解答】解：（1）∵B点在x轴上，且B点在y＝x﹣4上，∴B（8，0），∵A（﹣2，0），B（8，0），都在抛物线y＝ax2+bx﹣4上，∴x＝﹣2，x＝8是方程ax2+bx﹣4＝0的两个根，∴﹣16＝﹣，＝6，∴a＝，b＝﹣，∴y＝x2﹣x﹣4；（2）∵AD∥BC，直线BC的解析式为y＝x﹣4，∴直线AD的解析式为y＝x+1，过点B作BG⊥AD交点G，∵QR⊥BC，∴QR＝BG，在Rt△ABG中，AB＝10，tan∠BAG＝，∴BG＝2，设P（m，m2﹣m﹣4），R（n，n﹣4），则Q（m，m+1），∵QR＝2，∴20＝（m﹣n）2+，∴n﹣m＝2，∴R（m+2，m﹣3），S△PQR＝×（m+1﹣m2+m+4）×2＝﹣m2+2m+5＝﹣（m﹣4）2+9，∴当m＝4时，S△PQR有最大值9，∴P（4，﹣6）；（3）∵点C关于x轴的对称点为点C′，∴C'（0，﹣4），∴直线AC的解析式为y＝2x+4，∵抛物线沿射线C′A的方向平移2个单位长度，∴抛物线沿着x轴负方向平移2个单位长度，沿着y轴负方向平移4个单位长度，∵y＝x2﹣x﹣4＝（x﹣3）2﹣，∴y'＝（x﹣1）2﹣，联立（x﹣3）2﹣＝（x﹣1）2﹣，解得x＝6，∴M（6，﹣4），联立x+1＝x2﹣x﹣4，解得x＝10或x＝﹣2，∵D异于点A，∴D（10，6），∵y＝x2﹣x﹣4的对称轴为直线x＝3，设N（3，t），K（x，y），①当DM与KN为矩形对角线时，DM的中点与KN的中点重合，∴8＝，1＝，∴x＝13，t＝2﹣y，∵DM＝KN，∴16+100＝（3﹣x）2+（t﹣y）2，∴y＝﹣1或y＝3，∴K（13，﹣1）或K（13，3）；②当DN与MK为矩形对角线时，DN的中点与MK的中点重合，∴＝，＝，∴x＝7，t＝y﹣10，∵DN＝MK，∴49+（6﹣t）2＝（6﹣x）2+（y+4）2，∴y＝，∴K（7，）；③当KD与MN为矩形对角线时，KD的中点与MN的中点重合∴＝，＝，∴x＝﹣1，t＝10+y，∵KD＝MN，∴（x﹣10）2+（6﹣y）2＝9+（t+4）2，∴y＝﹣，∴K（﹣1，﹣）；综上所述：以D，M，N，K为顶点的四边形是矩形时，K点坐标为（﹣1，﹣）或（7，）或（13，﹣1）或（13，3）．18．【解答】解：（1）由直线y＝﹣2x+4与y轴交于点A，得A（0，4），又抛物线经过点A且对称轴为直线x＝，则c＝4，由﹣＝，得a＝﹣1，∴二次函数的解析式为y＝﹣x2+3x+4．（2）如图1，作QH⊥AB于点H，QN∥y轴交直线AB于点N．设点Q（x，﹣x2+3x+4），则F（x，﹣2x+4）；当y＝0时，由﹣x2+3x+4＝0得，x1＝﹣1，x2＝4，∴C（﹣1，0），D（4，0）；由﹣2x+4＝0，得x＝2，∴B（2，0），∴AB＝．∵∠HNQ＝∠OAB，∴，∴HQ＝QN＝（﹣x2+3x+4+2x﹣4）＝（﹣x2+5x），由CE∥AB，可得，∴S四边形APBQ＝S△ABQ+S△ABP＝（﹣x2+5x）+6＝﹣x2+5x+6＝﹣（x﹣）2+，∴当x＝时，四边形APBQ的面积最大，四边形APBQ的最大面积为，此时Q（，）．（3）存在．如图2，由y＝﹣x2+3x+4＝﹣（x﹣）2+，得E（，），又Q（，），设直线EF的解析式为y＝kx+b，则，解得，∴F（，0），GF＝＝＝GE，∴△EGF是等腰直角三角形．若点M在直线EF下方，当时，则∠GFM＝∠CAO，∴∠MFQ+∠CAO＝45°，此时MG＝×＝，∴M（，）．若点M在直线EF上方，作点M关于直线EF的对称点J，连接EJ，则△MEJ是等腰直角三角形，∴EJ∥x轴．∵EJ＝EM＝，∴J（，）．设直线FJ的解析式为y＝mx+n，则，解得，∴y＝﹣4x+31，当x＝时，y＝﹣4×+31＝25，此时，M（，25）．综上所述，点M的坐标为（，）或（，25）19．【解答】解：（1）∵抛物线y＝﹣x2+bx+c经过A（4，0），C（﹣1，0）两点，∴．解得．∴抛物线的解析式是y＝﹣x2+3x+4；（2）设P（x，y），对于抛物线y＝﹣x2+3x+4．令x＝0，则y＝4，∴B（0，4）．∵S1﹣S2＝5，∴S1＝S2+5．∴S1+S△AQC＝S2+S△AQC+5，即S△APC＝S△ABC+5．∴＝+5．∴y＝6．∴﹣x2+3x+4＝6．解得x1＝1，x2＝2．∴点P的坐标是（1，6）或（2，6）．（3）存在，点P的坐标是（3，4）或（，1）．理由：若∠AQP＝90°时，即AB⊥CP．由A（4，0），B（0，4）知，OA＝OB，∴∠OAB＝∠OBA＝45°．∴∠PCA＝45°．∴设直线PC解析式为：y＝x+t．把C（﹣1，0）代入，得﹣1+t＝0．解得t＝1．故直线PC的解析式为y＝x+1．联立，解得（舍去）或．∴P（3，4）；若∠APQ＝90°时，△APC是直角三角形，设P（m，n），则n＝﹣m2+3m+4．则由AP2+CP2＝AC2，即（m+1）2+n2+（m﹣4）2+n2＝（4+1）2．整理，得m2﹣3m﹣4+n2＝0．∴﹣n+n2＝0．解得n1＝0，n2＝1．当n＝0时，﹣m2+3m+4＝0，即（m﹣4）（m+1）＝0．解得m1＝﹣1，m2＝4．当n＝1时，﹣m2+3m+4＝1，即m2﹣3m﹣3＝0，解得m1＝，m2＝（舍去）．此时点P的坐标分别是（﹣1，0）（舍去），（4，0）（舍去），（，1）．若∠QAP＝90°时，该种情况不存在．综上所述，符合条件的点P的坐标是（3，4）或（，1）．20．【解答】解：（1）∵边长为8的正方形OABC的两边在坐标轴上，以点C为顶点的抛物线经过点A，∴C（0，8），A（8，0），设抛物线解析式为：y＝ax2+c，则，解得：．故抛物线的解析式为：y＝﹣x2+8；（2）正确，理由如下：设P（a，﹣a2+8），则F（a，8），∵D（0，6），∴PD＝＝＝a2+2，PF＝8﹣（a2+8）＝a2，∴PD﹣PF＝2；（3）在点P运动时，DE大小不变，则PE与PD的和最小时，△PDE的周长最小，∵PD﹣PF＝2，∴PD＝PF+2，∴PE+PD＝PE+PF+2，∴当P、E、F三点共线时，PE+PF最小，此时点P，E的横坐标都为4，将x＝4代入y＝﹣x2+8，得y＝6，∴P（4，6），此时△PDE的周长最小，且△PDE的面积为12，点P恰为“好点，∴△PDE的周长最小时”好点“的坐标为：（4，6），由（2）得：P（a，﹣a2+8），∵点D、E的坐标分别为（0，6），（4，0），①当0≤a≤4时，S△PDE＝×（a+4）×（﹣a2+8）﹣×4×6﹣a（﹣a2+8﹣6）＝﹣a2+3a+4；∴4＜S△PDE≤12，②当4＜a≤8时，S△PDE＝a（﹣a2+8﹣6）﹣×（a﹣4）×（﹣a2+8）﹣×4×6+＝﹣a2+3a+4；∴4＜S△PDE≤12，∴12≤S△PDE≤13，∴△PDE的面积可以等于4到13所有整数，在面积为12时，a的值有两个，所以面积为整数时好点有11个，经过验证周长最小的好点包含这11个之内，所以好点共11个，综上所述：11个好点，P（4，6）．。

中考数学压轴题---因动点产生的面积问题[含答案]

因动点产生的面积问题例1（ 2011年南通市中考第28题）如图1，直线l 经过点A (1，0)，且与双曲线m y x=(x ＞0)交于点B (2，1)．过点(,1)P p p -(p ＞1)作x轴的平行线分别交曲线m y x=(x ＞0)和m y x=-(x ＜0)于M 、N 两点．（1）求m 的值及直线l 的解析式；（2）若点P 在直线y ＝2上，求证：△PMB ∽△PNA ；（3）是否存在实数p ，使得S △AMN ＝4S △AMP ？若存在，请求出所有满足条件的p 的值；若不存在，请说明理由．图1满分解答（1）因为点B (2，1)在双曲线m y x=上，所以m ＝2．设直线l 的解析式为y kx b =+，代入点A (1，0)和点B (2，1)，得0,2 1.k b k b +=⎧⎨+=⎩ 解得1,1.k b =⎧⎨=-⎩ 所以直线l 的解析式为1y x =-．（2）由点(,1)P p p -(p ＞1)的坐标可知，点P 在直线1y x =-上x 轴的上方．如图2，当y ＝2时，点P 的坐标为(3，（2）．此时点M 的坐标为(1，2)，点N 的坐标为(－1，2)．由P (3，2)、M (1，2)、B (2，1)三点的位置关系，可知△PMB 为等腰直角三角形．由P (3，2)、N (－1，2)、A (1，0)三点的位置关系，可知△PNA 为等腰直角三角形．所以△PMB ∽△PNA ．图2 图3 图4（3）△AMN 和△AMP 是两个同高的三角形，底边MN 和MP 在同一条直线上．当S △AMN ＝4S △AMP 时，MN ＝4MP ．①如图3，当M 在NP 上时，x M －x N ＝4(x P －x M )．因此222()4(1)x x x x ⎛⎫⎛⎫--=-- ⎪ ⎪⎝⎭⎝⎭．解得1132x +=或1132x -=（此时点P 在x 轴下方，舍去）．此时1132p +=．②如图4，当M 在NP 的延长线上时，x M －x N ＝4(x M －x P )．因此222()4(1)x xx x⎛⎫⎛⎫--=-- ⎪ ⎪⎝⎭⎝⎭．解得152x +=或152x -=（此时点P 在x 轴下方，舍去）．此时152p +=．考点伸展在本题情景下，△AMN 能否成为直角三角形？情形一，如图5，∠AMN ＝90°，此时点M 的坐标为（1，2），点P 的坐标为（3，2）．情形二，如图6，∠MAN ＝90°，此时斜边MN 上的中线等于斜边的一半．不存在∠ANM ＝90°的情况．图5 图6例2（2011年上海市松江区中考模拟第24题）如图1，在平面直角坐标系xOy 中，直角梯形OABC 的顶点O 为坐标原点，顶点A 、C 分别在x 轴、y 轴的正半轴上，CB ∥OA ，OC ＝4，BC ＝3，OA ＝5，点D 在边OC 上，CD ＝3，过点D 作DB 的垂线DE ，交x 轴于点E ．（1）求点E 的坐标；（2）二次函数y ＝－x 2＋bx ＋c 的图像经过点B 和点E ． ①求二次函数的解析式和它的对称轴；②如果点M 在它的对称轴上且位于x 轴上方，满足S △CEM ＝2S △ABM ，求点M 的坐标．图1满分解答（1）因为BC ∥OA ，所以BC ⊥CD ．因为CD ＝CB ＝3，所以△BCD 是等腰直角三角形．因此∠BCD ＝45°．又因为BC ⊥CD ，所以∠ODE ＝45°．所以△ODE 是等腰直角三角形，OE ＝OD ＝1．所以点E 的坐标是（1，0）．（2）①因为抛物线y ＝－x 2＋bx ＋c 经过点B （3，4）和点E （1，0），所以934,10.b c b c -++=⎧⎨-++=⎩ 解得6,5.b c =⎧⎨=-⎩所以二次函数的解析式为y ＝－x 2＋6x －5，抛物线的对称轴为直线x ＝3．②如图2，如图3，设抛物线的对称轴与x 轴交于点F ，点M 的坐标为（3，t ）．C EM M EF C O E O FM C S S S S ∆∆∆=--梯形111(4)321442222t t t =+⨯-⨯⨯-⨯⨯=+．（ⅰ）如图2，当点M 位于线段BF 上时，t t S ABM -=⨯-=∆42)4(21．解方程)4(242t t -=+，得58=t ．此时点M 的坐标为（3，58）．（ⅱ）如图3，当点M 位于线段FB 延长线上时，42)4(21-=⨯-=∆t t S ABM ．解方程)4(242-=+t t ，得8=t ．此时点M 的坐标为（3，8）．图2 图3考点伸展对于图2，还有几个典型结论：此时，C 、M 、A 三点在同一条直线上；△CEM 的周长最小．可以求得直线AC 的解析式为445y x =-+，当x ＝3时，85y =．因此点M （3，58）在直线AC 上．因为点A 、E 关于抛物线的对称轴对称，所以ME ＋MC ＝MA ＋MC ．当A 、M 、C 三点共线时，ME ＋MC 最小，△CEM 的周长最小．例3（2010年广州市中考第25题）如图1，四边形OABC 是矩形，点A 、C 的坐标分别为(3,0)，(0,1)．点D 是线段BC 上的动点（与端点B 、C 不重合），过点D 作直线12y x b =-+交折线OAB 于点E ．（1）记△ODE 的面积为S ，求S 与b 的函数关系式；（2）当点E 在线段OA 上时，若矩形OABC 关于直线DE 的对称图形为四边形O 1A 1B 1C 1，试探究四边形O 1A 1B 1C 1与矩形OABC 的重叠部分的面积是否发生变化？若不变，求出重叠部分的面积；若改变，请说明理由．图1满分解答(1)①如图2，当E 在OA 上时，由12y x b =-+可知，点E 的坐标为(2b ,0)，OE ＝2b ．此时S ＝S △ODE ＝112122O E O C b b ⋅=⨯⨯=．②如图3，当E 在AB 上时，把y ＝1代入12y x b =-+可知，点D 的坐标为(2b －2,1)，CD ＝2b －2，BD ＝5－2b ．把x ＝3代入12y x b =-+可知，点E 的坐标为3(3,)2b -，AE ＝32b -，BE ＝52b -．此时S ＝S 矩形OABC －S △OAE － S △BDE －S △OCD ＝1315133()()(52)1(22)22222b b b b -⨯-----⨯⨯- 252b b =-+．(2)如图4，因为四边形O 1A 1B 1C 1与矩形OABC 关于直线DE 对称，因此DM ＝DN ，那么重叠部分是邻边相等的平行四边形，即四边形DMEN 是菱形．作DH ⊥OA ，垂足为H ．由于CD ＝2b －2，OE ＝2b ，所以EH ＝2．设菱形DMEN 的边长为m ．在Rt △DEH 中，DH ＝1，NH ＝2－m ，DN ＝m ，所以12＋(2－m )2＝m 2．解得54m =．所以重叠部分菱形DMEN 的面积为54．图2 图3 图4考点伸展把本题中的矩形OABC 绕着它的对称中心旋转，如果重叠部分的形状是菱形（如图5），那么这个菱形的最小面积为1，如图6所示；最大面积为53，如图7所示．图5 图6 图7例4（ 2010年扬州市中考第28题）如图1，在△ABC 中，∠C ＝90°，A C ＝3，BC ＝4，CD 是斜边AB 上的高，点E 在斜边AB 上，过点E 作直线与△ABC 的直角边相交于点F ，设AE ＝x ，△AEF 的面积为y ．（1）求线段AD 的长；（2）若EF ⊥AB ，当点E 在斜边AB 上移动时，①求y 与x 的函数关系式（写出自变量x 的取值范围）； ②当x 取何值时，y 有最大值？并求出最大值．（3）若点F 在直角边AC 上（点F 与A 、C 不重合），点E 在斜边AB 上移动，试问，是否存在直线EF 将△ABC 的周长和面积同时平分？若存在直线EF ，求出x 的值；若不存在直线EF ，请说明理由．图1 备用图满分解答(1) 在Rt △ABC 中， AC ＝3，BC ＝4，所以AB ＝5．在Rt △ACD 中，39cos 355AD AC A ==⨯=．(2) ①如图2，当F 在AC 上时，905x <<．在Rt △AEF 中，4tan 3EF AE A x ==．所以21223y AE EF x =⋅=．如图3，当F 在BC 上时，955x <≤．在Rt △BEF 中，3tan (5)4E F B E B x ==-．所以21315288y A E E F x x =⋅=-+．②当905x <<时，223y x =的最大值为5425；当955x <≤时，231588y x x =-+23575)8232x =--+(的最大值为7532．因此，当52x =时，y 的最大值为7532．图2 图3 图4(3)△ABC 的周长等于12，面积等于6．先假设EF 平分△ABC 的周长，那么AE ＝x ，AF ＝6－x ，x 的变化范围为3＜x ≤5．因此1142s i n (6)(6)2255AEF S AE AF A xx x x ∆=⋅⋅=-⨯=--．解方程2(6)35x x --=，得1362x =±．因为1362x =+在3≤x ≤5范围内（如图4），因此存在直线EF 将△ABC 的周长和面积同时平分．考点伸展如果把第（3）题的条件“点F 在直角边AC 上”改为“点F 在直角边BC 上”，那么就不存在直线EF 将△ABC 的周长和面积同时平分．先假设EF 平分△ABC 的周长，那么AE ＝x ，BE ＝5－x ，BF ＝x ＋1．因此21133sin (5)(1)(45)22510BEF S BE BF B x x x x ∆=⋅⋅=-+⨯=---．解方程23(45)310x x ---=．整理，得2450x x -+=．此方程无实数根．例5（2009年兰州市中考第29题）如图1，正方形 ABCD 中，点A 、B 的坐标分别为（0，10），（8，4），点C 在第一象限．动点P 在正方形ABCD 的边上，从点A 出发沿A →B →C →D 匀速运动，同时动点Q 以相同速度在x 轴上运动，当P 点到D 点时，两点同时停止运动，设运动的时间为t 秒．（1）当P 点在边AB 上运动时，点Q 的横坐标x （长度单位）关于运动时间t （秒）的函数图象如图2所示，请写出点Q 开始运动时的坐标及点P 运动速度；（2）求正方形边长及顶点C 的坐标；（3）在（1）中当t 为何值时，△OPQ 的面积最大，并求此时P 点的坐标．（4）如果点P 、Q 保持原速度速度不变，当点P 沿A →B →C →D 匀速运动时，OP 与PQ 能否相等，若能，写出所有符合条件的t 的值；若不能，请说明理由．图1 图2满分解答（1）Q (1,0)，点P 每秒钟运动1个单位长度．（2）过点B 作BE ⊥y 轴于点E ，过点C 作x 轴的垂线交直线BE 于F ，交x 轴于H ．在Rt △ABE 中，BE ＝8，AE ＝10－4＝6，所以AB ＝10．由△ABE ≌△BCF ，知BF ＝AE ＝4，CF ＝BE ＝6．所以EF ＝8＋6＝14，CH ＝8＋4＝12．因此点C 的坐标为（14，12）．（3）过点P 作PM ⊥y 轴于M ，PN ⊥x 轴于N ．因为PM //BE ，所以AP AM M P ABAFBF==，即1068t A M M P ==．因此34,55A M t P M t==．于是3410,55P NO M t O N P M t==-==．设△OPQ 的面积为S (平方单位)，那么2113347(1)(10)52251010S O Q PN t t t t =⋅⋅=+-=-++，定义域为0≤t ≤10．因为抛物线开口向下，对称轴为直线476t =，所以当476t=时，△OPQ 的面积最大．此时P 的坐标为(9415，5310)．（4）当53t =或29513t=时, OP 与PQ 相等．图3 图4附加题的一般思路是：点Q的横坐标是点P的横坐标的2倍．先求直线AB、BC、CD的解析式，根据直线的解析式设点P的坐标，再根据两点间的距离公式列方程PO＝PQ．附加题也可以这样解：①如图4，在Rt△AMP中，设AM＝3m，MP＝4 m，AP＝5m，那么OQ＝8m．根据AP、OQ的长列方程组5, 81,m tm t=⎧⎨=+⎩解得53t=．②如图5，在Rt△GMP中，设GM＝3m，MP＝4 m，GP＝5m，那么OQ＝8m．在Rt△GAD中，GD＝7.5．根据GP、OQ的长列方程组537.5,81,m tm t=-⎧⎨=+⎩解得29513t=．③如图6，设MP＝4m，那么OQ＝8m．根据BP、OQ的长列方程组51010,81,m tm t-=-⎧⎨=+⎩解得53t=，但这时点P不在BC上．图5 图6例6（2008年长春市中考第25题）在直角坐标系中，抛物线cbxxy++=2经过点（0，10）和点（4，2）．（1）求这条抛物线的解析式.（2）如图1，在边长一定的矩形ABCD中，CD＝1，点C在y轴右侧沿抛物线cbxxy++=2滑动，在滑动过程中CD∥x轴，AB在CD的下方.当点D在y轴上时，AB落在x轴上.①求边BC的长.②当矩形ABCD在滑动过程中被x轴分成两部分的面积比为1:4时，求点C的坐标.图1（1）因为抛物线cbxxy++=2经过点（0，10）和点（4，2），所以10,164 2.cb c=⎧⎨++=⎩解得6b=-，10c=．因此抛物线的解析式为y＝x2－6x＋10．（2）①因为CD＝1，点D在y轴上，所以点C的横坐标为1．在y＝x2－6x＋10中，当x＝1时，y＝5．所以边BC 的长为5．②因为矩形边长一定，所以BC＝5．如图2，当矩形ABCD在x轴上方部分的面积与这个矩形面积的比为1:5时，点C的纵坐标为1．解方程x2－6x＋10＝1，得123x x==．此时点C的坐标为(3，1)．如图3，当矩形ABCD在x轴上方部分的面积与这个矩形面积的比为5:1时，点C的纵坐标为4．解方程x2－6x＋10＝4，得133x=+，233x=-．此时点C的坐标为(3＋3，4)或(3－3，4)．图2 图3考点伸展在本题情景下，以CD为半径的⊙C如果与坐标轴相切，那么符合条件的点C有哪些？解：由于CD＝1，抛物线的顶点为（3，1），因此与坐标轴相切的⊙C有三个，点C的坐标分别为（1，5），（－1，17），（3，1）．在本题情景下，以CB为半径的⊙C如果与坐标轴相切，那么符合条件的点C有哪些？解：由于点（5，5）恰好在抛物线上，因此与坐标轴相切的⊙C有两个，点C的坐标分别为（5，5），（－5，65）．。

中考数学压轴题提升训练：图形面积计算

精品基础教育教学资料，仅供参考，需要可下载使用！中考数学压轴题提升训练：图形面积计算【例1】如图，在扇形AOB 中，∠AOB ＝90°，半径OA ＝6，将扇形AOB 沿过点B 的直线折叠，点O 恰好落在弧AB 上点D 处，折痕交OA 于点C ，则整个阴影部分的面积为（）A ．9π﹣9B ．9π﹣C ．9π﹣18D ．9π﹣【答案】D .【解析】解：连接OD ，由折叠的性质知：CD ＝CO ，BD ＝BO ，∠DBC ＝∠OBC ， ∠OB ＝OD ＝BD ，即∠OBD 是等边三角形， ∠∠DBO ＝60°， ∠∠CBO ＝30°，∠OC OB ＝， ∠S 阴影=S 扇形AOB ﹣S ∠BDC ﹣S ∠OBCS ∠BDC ＝S ∠OBC ＝12×OB ×OC ＝12S 扇形AOB ＝9π，∠S 阴影=S 扇形AOB ﹣S ∠BDC ﹣S ∠OBC=9π﹣﹣＝9π﹣．所以答案为：D ．【变式1-1】如图，把半径为2的∠O 沿弦AB ，AC 折叠，使弧AB 和弧BC 都经过圆心O ，则阴影部分的面积为（）ABC ．D ．【答案】C ．【解析】解：过O 作OD ∠AC 于D ，连接AO 、BO 、CO ，∠OD ＝12AO ＝1，AD ＝12AC ， ∠∠OAD ＝30°，∠∠AOC ＝2∠AOD ＝120°，同理∠AOB ＝120°，∠BOC ＝120°， ∠S 阴＝2S ∠AOC＝×22＝，所以答案为：C ．【变式1-2】如图，半径为1的半圆形纸片，按如图方式折叠，使对折后半圆弧的中点M 与圆心O 重合，则图中阴影部分的面积是．【答案】26π-．【解析】解：设折痕为AB ，连接OM 交AB 于点C ，连接OA 、OB ，由题意知，OM ⊥AB ，且OC =MC =12，在RT △AOC 中，OA =1，OC =12，∴∠AOC =60°，AC =2，AB =2AC ∴∠AOB =2∠AOC =120°， S 阴影=S 半圆﹣2S 弓形ABM=12π×12﹣2（212011136022π⨯-⨯6π-．6π-．【例2】如图所示，在Rt △ABC 中，∠ACB =90°，AC =BC ，将Rt △ABC 绕点A 逆时针旋转30°后得到Rt △ADE ，若图中阴影部分面积为3π，则AB =【答案】2.【解析】S 阴影=S ∠ADE +S 扇形BAD －S ∠ABC∠S ∠ADE = S ∠ABC ∠S 阴影= S 扇形BAD =3π，∠230360AB π⨯=3π,解得：AB =2，故答案为：2.【变式2-1】如图，在正方形ABCD 中，AB =3，点M 在CD 边上，且DM =1，∠AEM 与∠ADM 关于AM 所在直线对称，将∠ADM 按顺时针方向绕点A 旋转90°得到∠ABF ，连接EF ，则线段EF 的长为（）A . 3B.C.D.【分析】求线段的长度，常用方法是将所求线段放在直角三角形中借助勾股定理求解，如图作出辅助线，通过分析可知，∠ADM ∠∠ABF ∠∠AEM ，可得DM =EM =1，AE =AD =AB =3，进而利用∠AEK ∠∠EMH ，求得EH ，MH 的长，再计算出EG ，FG 的长，在Rt ∠EFG 中，利用勾股定理求EF 的长度即可.【解析】过点E 作EG ∠BC 于G ，作EH ∠CD 于H ，延长HE 交AB 于K ，如图所示，由题意知，∠ADM ∠∠ABF ∠∠AEM ，∠DM =EM =1，AE =AD =AB =3，由∠AEK ∠∠EMH ，得：AE AK EKEM EH MH===3， ∠设EH =x ，则AK =3x ，即DH =3x ，MH =3x －1，在Rt ∠EMH 中，由勾股定理得：()22311x x -+=，D FMD MH解得：x =0（舍）或x =35， ∠MH =45，AK =DH =95，CH =3－DH =65， KE =BG =3MH =125，∠FG =BF +BG =175，EG =CH =65，在Rt ∠EFG 中，由勾股定理得：EF ==,故答案为：C .【变式2-2】.如图，矩形 ABCD 中，AB =2，BC =1，将矩形 ABCD 绕点 A 旋转得到矩形AB ′C ′D ′，点 C 的运动路径为弧 CC ′，当点 B ′落在 CD 上时，则图中阴影部分的面积为．【答案】5212π. 【解析】解：连接AC ’，AC ，过点B ’作B ’E ∠AB 于E ，如图图所示，由旋转性质，得：AC =AC ’， AB ’=AB =2，∠CAB =∠C ’AB ’， ∠BC =B ’E =1， ∠∠B ’AB =30°， ∠∠C ’AC =30°，∠AE ，B ’C =2，在Rt ∠ABC 中，由勾股定理得：AC∠S 阴影=S 扇形C ’AC －S ∠AB ’C ’－S ∠B ’CA=(23011212136022π⨯-⨯⨯-⨯⨯=52122π+-.故答案为：5212π+. 【例3】.如图，在∠ABC 中，AB =BC ，∠ABC =90°，CA =4，D 为AC 的中点，以D 为圆心，以DB 的长为半径作圆心角为90°的扇形EDF ，则图中阴影部分的面积为.【分析】设DE 与BC 交于M ，DF 与AB 交于N ，S 阴影=S 扇形EDF －S 四边形DMBN ，根据∠DBM ∠∠DAN ，得S 四边形DMBN =S ∠BDA ，再利用扇形面积公式及三角形面积公式求解即可.【解析】解：设DE 与BC 交于M ，DF 与AB 交于N ， ∠AB =BC ，∠ABC =90°，D 是AC 中点，∠∠A =∠C =∠CBD =∠DBA =45°，AD =BD =2，∠BDA =90°， ∠∠EDF =90°， ∠∠BDM =∠ADF ， ∠∠DBM ∠∠DAN ，即S ∠DBM =S ∠DAN ， ∠S 四边形DMBN =S ∠BDA ， S 阴影=S 扇形EDF －S 四边形DMBN=213602n r AD BD π-⋅⋅=29021223602π⨯-⨯⨯=π－2，故答案为：π－2.【变式3-1】.如图，在扇形OAB 中，C 是OA 的中点，CD ∠OA ，CD 与弧AB 交于点D ，以O 为圆心，OC 的长为半径作弧CE 交OB 于点E ，若OA =6，∠AOB =120°，则图中阴影部分的面积为.【答案】3π 【解析】解：连接OD ，交弧CE 于F ，连接AD ，∠OC =AC =3，CD ∠OA ， ∠CD 是线段OA 的垂直平分线， ∠OD =AD ， ∠OD =OA ，∠∠OAD 是等边三角形， ∠∠AOB =120°， ∠∠DOA =∠BOD =60°，∠CD∠S 阴影=S 扇形BOD －S 扇形EOF +S ∠COD －S 扇形COF=222606603160333603602360πππ⨯⨯⨯-+⨯⨯=3π.即答案为：3π. 【变式3-2】.如图，O 是边长为a 的正方形ABCD 的中心，将一块半径足够长、圆心为直角的扇形纸板的圆心放在O 点处，并将纸板的圆心绕O 旋转，则正方形ABCD 被纸板覆盖部分的面积为（）A ．13a 2 B ．14a 2 C ．12a 2 D ．14a 【答案】B .【解析】解：如图，过O 作OE ∠AD 于E ，OF ∠CD 于F ，∠OE =OF ，∠EOF =90°，∠四边形OEDF 是正方形，OF =12a ，∠扇形的圆心角为直角， ∠∠OME ∠∠ONF ， ∠S 阴影=S 正方形OEDF =214a ，故答案为：B ．1..如图，菱形ABCD 和菱形ECGF 的边长分别为2和3，∠A =120°，则图中阴影部分（∠BDF ）的面积等于.【解析】解：由题意得：S ∠BDF =S 菱形ABCD +S 菱形ECGF －S ∠BGF －S ∠EDF －S ∠ABD菱形ECGF 边CG 边上的高为：GF ·sin ，菱形ECGF 边CE 边上的高为：EF ·sin ，∠S ∠BDF 222112351222+-⨯⨯2..汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝，如图所示的弦图中，中间的小正方形 ABCD 的边长为 1，分别以A ，C 为圆心，1为半径作圆弧，则图中阴影部分的面积为【答案】12π-.【解析】解：连接BD ， S 阴影=2（S 扇形BAD －S ∠ABD ）=2（29011113602π⨯-⨯⨯）=12π-，故答案为：12π-.3..如图，正方形ABCD 中，AB =1，将线段 CD 绕点 C 顺时针旋转 90°得到线段CE ，线段 BD 绕点 B 顺时针旋转 90°得到线段 BF ，连接 EF ，则图中阴影部分的面积是【答案】32－4π. 【解析】解：过F 作FM ∠BE 于M ，则∠FME =∠FMB =90°， ∠四边形ABCD 是正方形，AB =1，∠∠DCB =90°，DC =BC =AB =1，∠DCB =45°，由勾股定理得：BD 由旋转性质得：∠DCE =90°，BF =BD ，∠FBE =90°－45°=45°， ∠BM =FM =1，即C 点与M 点重合，ME =1， ∠阴影部分的面积：S =S ∠BCD +S ∠BFE +S 扇形DCE －S 扇形DBF=12+1+2901360π⨯－290360π⨯=32－4π，故答案为：32－4π．4..如图，已知矩形 ABCD 的两条边 AB =1，AD B 为旋转中心，将对角线BD 顺时针旋转60°得到线段BE ，再以C 为圆心将线段CD 顺时针旋转90°得到线段CF ，连接EF ，则图中阴影部分面积为．15212π-. 【解析】解：连接CE ，由CD =AB =1，AD ，得：BD =2，∠∠DBC =30°，由旋转知∠DBE =60°，BE =BD =2，∠∠DBC =∠EBC =30°，此时D 、C 、E 共线，∠S 阴影=S 扇形DCF +S ∠BCD +S ∠BEF －S 扇形DBE=(229011601111236022360ππ⨯+⨯⨯⨯-⨯15212π-.15212π-. 5..如图，∠AOB 中，∠AOB =90°，AO =3，BO =6，∠AOB 绕点O 逆时针旋转到∠A ′OB ′处，此时线段A ′B ′与BO 的交点E 为BO 的中点，则线段B ′E 的长度为（）A． B．5 C．5 D．5【答案】B . 【解析】解：过O 作OF ∠A ’B ’于F ，由旋转性质得：OA =OA ’=3，OB =OB ’=6，∠F 为A ’E 的中点，∠E 为OB 中点，A′B′OB AE在Rt ∠A ’OB ’中，由勾股定理得：A ’B’=∠OF= 在Rt ∠A ’OF 中，由勾股定理得：A ’F， ∠A ’E∠B ’E =A ’B ’－A ’E，故答案为：B .6..如图，等腰直角三角形ABC ，绕点C 顺时针旋转得到∠A ′B ′C ，AB ′所在的直线经过A ′C 的中点时，若AB =2，则阴影部分的面积为_________．【答案】413π. 【解析】解：延长AB ’交A ’C 于E ，由题意知E 为A ’C 的中点，∠A ’B ’=B ’C =AB =BC =2，∠B ’E ∠A ’C ，在Rt ∠ABC 中，由勾股定理得：AC，A′∠CE =A ’E ，∠∠CAE =30°，∠ACE =60°，∠S 阴影=S 扇形ACA ’－S ∠ACE －S ∠A ’B ’E=(2601136022π⨯-=413π.故答案为：413π.7.如图，在扇形OAB 中，∠O =60°，OA 四边形OECF 是扇形OAB 中最大的菱形，其中点E ，C ，F 分别在OA ，弧AB ，OB 上，则图中阴影部分的面积为．【答案】8π﹣【解析】解：连接EF 、OC 交于点H ，则OH =12OC ，∠FOH =∠AOC =30°，在Rt ∠FOH 中，FH =OH ×tan 30°=2，∠菱形FOEC 的面积=12扇形OAB 的面积=(260360π⨯=8π，则阴影部分的面积为8π﹣，故答案为：8π﹣8..如图，在圆心角为120°的扇形OAB 中，半径OA ＝2，C 为弧AB 的中点，D 为OA 上任意一点（不与点O 、A 重合），则图中阴影部分的面积为．【答案】23π．【解析】解：连接OC ，BC ，由题意知∠BOC ＝∠AOC ＝60°，∠OB ＝OC ，∠∠BOC 为等边三角形，∠∠OCB ＝∠COA ＝60°，∠BC ∠OA ，∠S ∠BOC =S ∠BCD ，∠S 阴影＝S 弓形BC +S ∠BCD＝S 弓形BC +S ∠BOC＝S 扇形BOC ＝23π，故答案为：23π. 9..如图，在正方形ABCD 中，AD =3，将线段AB 绕点B 逆时针旋转90°得到线段BE ，将线段AC 绕点C 逆时针旋转90°得到线段CF ，连接EF ，则图中阴影部分的面积是___________．E【答案】27924π-. 【解析】解：由图知：S 阴影=S 扇形ABE +S ∠BEF －S 弓形AFS 弓形AF =S 扇形ACF －S ∠ACF由题意知，AD =3，AC =CF AB =BC =BF =BE =3，∠EBA =∠ACF =90°，∠S 弓形AF =S 扇形ACF －S ∠ACF=(290360π⨯－12⨯92π－9， S 阴影=S 扇形ABE +S ∠BEF －S 弓形AF=2903360π⨯+1332⨯⨯－（92π－9） =27924π-. 10..如图，将半径为1的半圆O ，绕着其直径的一端点A 顺时针旋转30°，直径的另一端点B 的对应点为B '，O 的对应点为O '，则图中阴影部分的面积是．【答案】2π【解析】解：连接O ′D 、B ′D ，∠∠B ′AB ＝30°，∠∠AO ′D ＝120°，∠AB ′是直径，∠∠ADB ′＝90°，由∠B ′AB ＝30°，得B ′D ＝12AB ′＝1，在Rt ∠ADB ’中，由勾股定理得，AD ，∠S 阴影＝S 扇形BAB ’－S ∠AO ’D －S 扇形DO ’B ’+S 扇形AO ’D －S ∠AO ’D=22222302601120111360360360πππ⨯⨯⨯-+=22π-故答案为：2π-． 11..如图，在平行四边形ABCD 中，以点A 为圆心，AB 的长为半径的圆恰好与CD 相切于点C ，交AD 于点E ，延长BA 与∠A 相交于点F ．若弧EF 的长为2π，则图中阴影部分的面积为．【答案】22π-.【解析】解：连接AC ，∠DC 是∠A 的切线，∠AC ∠CD ，∠AB ＝AC ＝CD ，∠∠ACD 是等腰直角三角形，∠∠CAD ＝45°，∠四边形ABCD 是平行四边形，∠AD ∠BC ，∠∠CAD ＝∠ACB ＝45°，∠∠ACB ＝∠B ＝45°，∠∠F AD ＝∠B ＝45°，∠弧EF 的长为2π， ∠45=2180r ππ，解得：r ＝2，∠S 阴影＝S ∠ACD ﹣S 扇形ACE ＝21452222360π⨯⨯⨯- =22π-．故答案为：22π-．12..如图，在Rt ∠ABC 中，∠ACB ＝90°，AC ＝BC ＝2，以点A 为圆心，AC 的长为半径作弧CE 交AB 于点E ，以点B 为圆心，BC 的长为半径作弧CD 交AB 于点D ，则阴影部分的面积为．【答案】π﹣2．【解析】解：S 阴影＝S ∠ABC ﹣S 空白，∠∠ACB ＝90°，AC ＝BC ＝2，∠S ∠ABC ＝12×2×2＝2， S 扇形BCD ＝2452360π⨯＝12π， S 空白＝2×（2﹣12π）＝4﹣π， S 阴影＝S ∠ABC ﹣S 空白＝2﹣4+π＝π﹣2，故答案为：π﹣2．13..如图，在∠ABC 中，BC ＝4，以点A 为圆心，2为半径的∠A 与BC 相切于点D ，交AB 于点E ，交AC 于点F ，点P 是∠A 上的一点，且∠EPF ＝45°，则图中阴影部分的面积为．【答案】4﹣π．【解析】解：连接AD∠∠A 与BC 相切于点D ，∠AD ∠BC ，∠∠EPF ＝45°，∠∠BAC ＝2∠EPF ＝90°．∠S 阴影＝S ∠ABC ﹣S 扇形AEF ＝12×4×2﹣2902360π⨯ ＝4﹣π．故答案是：4﹣π．14..如图，在扇形OAB 中，∠AOB ＝90°，点C 为OB 的中点，CD ∠OB 交弧AB 于点D ．若OA ＝2，则阴影部分的面积为．【答案】23π【解析】解：连接DO ，则OD ＝OA ＝OB ＝2，∠CD ∠OA ，∠AOB ＝90°，∠∠OCD ＝90°，∠C 为OB 的中点，∠CO ＝12OB ＝12DO ， ∠∠CDO =30°，∠COD ＝60°，则CD ，∠S 阴影＝S 扇形BOD －S ∠OCD=2602113602π⨯-⨯=23π-故答案为：23π- 15..如图，在∠ABCD 中，以点A 为圆心，AB 的长为半径的圆恰好与CD 相切于点C ，交AD 于点E ，延长BA 与∠O 相交于点F ．若弧EF 的长为π，则图中阴影部分的面积为．【答案】8﹣2π．【解析】解：连结AC ，∠CD 是圆A 的切线，∠AC ∠CD ，即∠ACD ＝90°，∠四边形ABCD 为平行四边形，∠AB ∠CD ，AD ∠BC ，∠∠CAF ＝90°，∠F AE ＝∠B ，∠EAC ＝∠ACB ，∠AB ＝AC ，∠∠B ＝∠ACB ，∠∠F AE ＝∠EAC ＝45°，∠弧EF 的长为π，设圆A 的半径为r ， ∠45180r ππ⨯=，得： r ＝4， ∠S 阴影＝S ∠ACD ﹣S 扇形CAE =12×4×4﹣2454360π⨯ ＝8﹣2π．故答案为：8﹣2π．16..如图，点C 为弧AB 的三等分点（弧BC <弧AC ），∠AOB ＝90°，OA ＝3，CD ∠OB ，则图中阴影部分的面积为．【答案】328π-．【解析】解：连接OC ，AC ，由题意知：∠COD ＝30°，∠AOC ＝60°，∠CD ∠OB ，∠S ∠OCD ＝S ∠ACD ，∠∠CDO ＝90°， OC ＝OA ＝3，∠COD ＝30°，∠CD ＝32，OD ， S 阴影＝S ∠ACD +S 弓形AC＝S ∠OCD +S 弓形AC＝12×2×32+2603360π⨯－4×32=32π.故答案为：328π-． 17..如图，长方形纸片ABCD 的长AB ＝3，宽BC ＝2，以点A 为圆心，以AB 的长为半径作弧；以点C 为圆心，以BC 的长为半径作弧．则图中阴影部分的面积是．【答案】134π－6．【解析】解：由图可知：S 阴影=2903360π⨯+2902360π⨯－S 矩形ABCD = 94π+π－6=134π－6，故答案为：134π－6． 18..如图，在∠ABC 中，∠ABC ＝45°，∠ACB ＝30°，AB ＝2，将∠ABC 绕点C 顺时针旋转60°得∠CDE ，则图中线段AB 扫过的阴影部分的面积为．．【解析】解：过A 作AF ∠BC 于F ，∠∠ABC ＝45°，∠AF ＝BF AB ，在Rt ∠AFC 中，∠ACB ＝30°，AC ＝2AF ＝FC由旋转的性质可知，S ∠ABC ＝S ∠EDC ，S 阴影＝S 扇形DCB +S ∠EDC ﹣S ∠ABC ﹣S 扇形ACE＝S 扇形DCB ﹣S 扇形ACE＝(226060360360ππ⨯⨯-=3,．19..如图，在矩形ABCD中，AB＝3，AD＝4，将矩形ABCD绕点D顺时针旋转90°得到矩形A′B′C′D，连接A′B，则图中阴影部分的面积为.【答案】25144π-．【解析】解：连接BD，B’D，由题意知：∠BDB’=90°，A’C=A’D－CD=1，由勾股定理得：BD=B’D=5，∠S阴影=S扇形DBB’－S∠BCD－S∠A’B’D－S∠A’BC=2905111343414 360222π⨯-⨯⨯-⨯⨯-⨯⨯=2514 4π-.故答案为：2514 4π-.20..如图，在菱形ABCD中，AB＝2，∠BAC＝30°，将菱形ABCD绕点A逆时针旋转120°，点B的对应点为点B′，点C的对应点为点C′，点D的对应点为点D′，则图中阴影部分的面积为．【答案】83π．【解析】解：连接BD，与AC相交于点O，则BD ＝2BO ＝2，AC＝，S 扇形＝S 扇形CAC ′+S ∠ABC +S ∠AC ′D ′﹣S 菱形ABCD ﹣S 扇形DAD ′＝S 扇形CAC ′﹣S 扇形DAD ′＝(221201202360360ππ⨯⨯- =83π．故答案为：83π． 21..如图，在平行四边形ABCD 中，AD =2，AB =4，∠A =30°，以点A 为圆心，AD 的长为半径画弧交AB 于点E ，连接CE ，则阴影部分的面积是__________．【答案】3π．【解析】解：∵∠A =30°，AD =2，∴平行四边形AB 边上的高为：AD ·sin 30°∵AB =4，∴BE =2，S 阴影=S 平行四边形ABCD －S 扇形AED －S △BEC－2302360π⨯－122⨯－3π故答案为：3π.22..如图，P A 、PB 是半径为1的⊙O 的两条切线，点A 、B 分别为切点，∠APB ＝60°，OP 与弦AB 交于点C ，与⊙O 交于点D ．阴影部分的面积是（结果保留π）．A E【答案】6π.【解析】解：∵P A 、PB 是⊙O 的切线， ∴OA ⊥P A ，OB ⊥PB ，OP 平分∠APB ， ∵∠APB ＝60°，∴∠APO ＝30°，∠POA ＝60°，由AP =BP ，OA =OB 得：OP 垂直平分AB ， ∴AC =BC ，∴S △AOC ＝S △BOC ，∴S 阴影部分＝S 扇形OAD ＝26013606ππ⨯=．故答案为：6π．。

2023年九年级数学中考复习：旋转(面积问题)综合压轴题(Word版,含答案)

2023年九年级数学中考复习：旋转（面积问题）综合压轴题1．一节数学课上，老师提出一个这样的问题：如图，点P是正方形ABCD内一点，P A=1，PB=2，PC=3，你能求出∠APB的度数吗？小明通过观察、分析、思考，形成了如下思路：思路一：将∠PBC绕点B逆时针旋转90°，得到∠P'BA，连接P P'，求出∠APB的度数．思路二：将∠APB绕点B顺时针旋转90°，得到∠C P'B，连接P P'，求出∠APB的度数．请参考小明的思路，任选一种写出完整的解答过程．2．如图，已知在∠ABC中，AB＝AC，D、E是BC边上的点，将∠ABD绕点A旋转，得到∠AC D，连接D E．(1)当∠BAC＝120°，∠DAE＝60°时，求证：DE＝D E；(2)当DE＝D E时，∠DAE与∠BAC有怎样的数量关系？请写出，并说明理由．(3)在（2）的结论下，当∠BAC＝90°，BD与DE满足怎样的数量关系时，∠D EC是等腰直角三角形？（直接写出结论，不必证明）AC BD相交于点O，3．如图，平行四边形ABCD中，,1,5AB AC AB BC⊥==,BC AD于点E，F．将直线AC绕点O顺时针旋转，分别交,(1)证明：当旋转角为90°时，四边形ABEF 是平行四边形；(2)证明：在旋转过程中，线段AF 与EC 总保持相等；(3)在旋转过程中，当AC 绕点O 顺时针旋转多少度时，四边形BEDF 是菱形，请给出证明．4．如图1所示，将一个边长为2的正方形ABCD 和一个长为2、宽为1的长方形CEFD 拼在一起，构成一个大的长方形ABEF ．现将小长方形CEFD 绕点C 顺时针旋转至''CE FD ，旋转角为α．(1)当点D 恰好落在边EF 上时，点D 到边DC 的距离为____________，旋转角α=____________︒；(2)如图2，G 为BC 的中点，且090α︒<<︒，求证：GD E D ''=；(3)小长方形CEFD 绕点C 顺时针旋转一周的过程中，DCD '与CBD '△能否全等？若能，直接写出旋转角α的值；若不能，说明理由．5．将两块完全相同的且含60°角的直角三角板ABC 和AFE 按如图1所示位置放置，现将Rt AEF 绕A 点按逆时针方向旋转()090αα︒<<︒．如图2，AE 与BC 交于点M ，AC 与EF 交于点N ，BC 与EF 交于点P ．(1)若AMC 是等腰三角形，则旋转角α的度数为______．(2)在旋转过程中，连接AP ，CE ，求证：AP 所在的直线是线段CE 的垂直平分线．(3)在旋转过程中，CPN是否能成为直角三角形？若能，直接写出旋转角α的度数；若不能，说明理由．6．旋转是一种重要的图形变换，当图形中有一组邻边相等时，往往可以通过旋转解决问题．如图∠，在四边形ABCD中，AD CDADC∠=︒，2∠=︒，60=，120ABCAB=，1BC=．【问题提出】(1)如图∠，在图∠的基础上连接BD，由于AD CD=，所以可将DCB绕点D顺时针方向旋转60°，得到DAB'，则BDB'的形状是_______；【尝试解决】(2)在（1）的条件下，求四边形ABCD的面积；【类比应用】(3)如图∠，等边ABC的边长为2，BDC是顶角120∠=︒的等腰三角形，以D为顶BDC点作一个60°的角，角的两边分别交AB于点M，交AC于点N，连接MN，求AMN的周长．7．如图1，在等腰三角形ABC中，∠A＝120°，AB＝AC，点D、E分别在边AB、AC上，AD＝AE，连接BE，点M、N、P分别为DE、BE、BC的中点．。

中考数学分面积类压轴题集锦

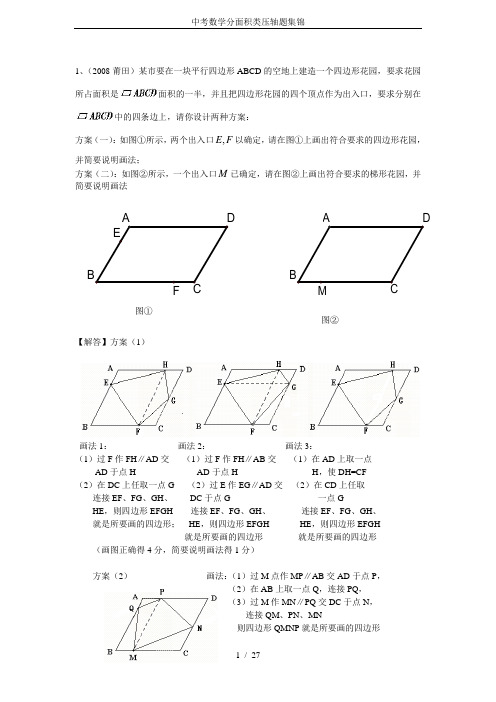
1、（2008莆田）某市要在一块平行四边形ABCD 的空地上建造一个四边形花园，要求花园所占面积是面积的一半，并且把四边形花园的四个顶点作为出入口，要求分别在中的四条边上，请你设计两种方案：方案（一）：如图①所示，两个出入口F E ,以确定，请在图①上画出符合要求的四边形花园，并简要说明画法；方案（二）：如图②所示，一个出入口M 已确定，请在图②上画出符合要求的梯形花园，并简要说明画法【解答】方案（1）画法1：画法2：画法3：（1）过F 作FH ∥AD 交（1）过F 作FH ∥AB 交（1）在AD 上取一点AD 于点H AD 于点H H ，使DH=CF （2）在DC 上任取一点G （2）过E 作EG ∥AD 交（2）在CD 上任取连接EF 、FG 、GH 、 DC 于点G 一点GHE ，则四边形EFGH 连接EF 、FG 、GH 、连接EF 、FG 、GH 、就是所要画的四边形； HE ，则四边形EFGH HE ，则四边形EFGH 就是所要画的四边形就是所要画的四边形（画图正确得4分，简要说明画法得1分）方案（2）画法：（1）过M 点作MP ∥AB 交AD 于点P ，（2）在AB 上取一点Q ，连接PQ ，（3）过M 作MN ∥PQ 交DC 于点N ，连接QM 、PN 、MN则四边形QMNP 就是所要画的四边形（画图正确的2分，简要说明画法得1分）（本题答案不唯一，符合要求即可）2、问题发现：（1）在我们学习过的几何图形里，有很多图形的面积和周长能同时被某条直线平分，如图1，⊙O 的周长和面积能被过圆心的任意一条直线同时平分.请你在图2和图3中分别做两条．．不同的直线将矩形ABCD 和等腰梯形ABCD 的周长和面积同时平分，并简要说明作法.问题解决如图4，在等腰梯形ABCD 中，AB=DC=5，AD=4，BC=10. 点E ．在下底边．．．．BC ．．上，点．．．F ．在腰．．AB ．．上．. （2）是否存在线段EF 将等腰梯形ABCD 的周长和面积同时平分？若存在，求出此时BE 的长；若不存在，请说明理由；（3）是否存在线段EF 将等腰梯形ABCD 的周长和面积同时分成1∶2的两部分？若存在，求出此时BE 的长；若不存在，请说明理由.【解答】（1）如图（图2）（图3）（图4）(语言描述略)（2）存在.设BE=x, 由已知条件得：梯形周长为24，高4，面积为28。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

面积问题（中考数学压轴）
一、解答题(共1道，每道100分)
1.如图，在锐角三角形ABC中，BC=12，△ABC的面积为48，D，E分别是边AB，AC上的两个动点（D不与A，B重合），且保持DE∥BC，以DE为边，在点A的异侧作正方形DEFG．（1）当正方形DEFG的边GF在BC上时，求正方形DEFG的边长；（2）设DE=x，△ABC与正方形DEFG重叠部分的面积为y，试求y关于x的函数关系式，写出x的取值范围，并求出y的最大值．
答案：（1）当正方形DEFG的边GF在BC上时，如图（1），
过点A作BC边上的高AM，交DE于N，垂足为M．
∵S△ABC=48，BC=12，
∴AM=8，
∵DE∥BC，△ADE∽△ABC，
∴，
而AN=AM－MN=AM－DE，
∴，解之得DE=4.8．
∴当正方形DEFG的边GF在BC上时，正方形DEFG的边长为4.8，
（2）分两种情况：
①当正方形DEFG在△ABC的内部时，如图（2），
△ABC与正方形DEFG重叠部分的面积为正方形DEFG的面积，
∵DE=x，
∴y=x2，
此时x的范围是0＜x≤4.8，
②当正方形DEFG的一部分在△ABC的外部时，
如图（2），设DG与BC交于点Q，EF与BC交于点P，△ABC的高AM交DE于N，
∵DE=x，DE∥BC，
∴△ADE∽△ABC，
即，
而AN=AM－MN=AM－EP，
∴，
解得．
所以，即，
由题意，x＞4.8，且x＜12，所以4.8＜x＜12；
因此△ABC与正方形DEFG重叠部分的面积需分两种情况讨论，
当0＜x≤4.8时，△ABC与正方形DEFG重叠部分的面积的最大值为4.82=23.04，
当4.8＜x＜12时，因为，
所以当时，△ABC与正方形DEFG重叠部分的面积的最大值为二次函数的
最大值：；因为24＞23.04，所以△ABC与正方形DEFG重叠部分
的面积的最大值为24．
解题思路：（1）根据题意，作出图示；分析可得：AM=8，且△ADE∽△ABC，进而可得
，解可得答案．（2）分两种情况：①当正方形DEFG在△ABC的内部时，②
当正方形DEFG的一部分在△ABC的外部时，依据平行线以及正方形的性质，可得二次函数，再根据二次函数的性质，解可得重合部分的面积，比较可得面积的最大值．
试题难度：三颗星知识点：中考压轴之面积问题。

面积问题(中考数学压轴)

中考数学压轴题(重叠面积问题)

中考数学总复习《二次函数压轴题(面积问题)》专题训练-附含答案

中考数学压轴题---增长率(面积问题)例题讲解

【中考压轴题专项练习】最新中考数学压轴大题冲刺专项训练：《 面积的最值问题 》含答案与解析

中考数学压轴题：二次函数中的面积问题(含答案)

2023年中考数学高频压轴题突破——二次函数与面积问题

2023年九年级数学中考专题：二次函数综合压轴题(面积问题)(含简单答案)

初三数学压轴题及答案

最新九年级数学中考复习：二次函数综合压轴题题(面积问题)含答案

专题03 二次函数中面积问题压轴真题训练(解析版)-挑战2023年中考数学选择、填空压轴真题汇编

最新九年级中考数学专题：二次函数综合压轴题(面积问题)附答案

最新九年级中考数学复习：几何探究压轴题(面积问题)

2020年中考数学压轴题： 图形面积计算

2023年中考数学高频压轴题突破——二次函数与面积问题

中考数学压轴题---因动点产生的面积问题[含答案]

中考数学压轴题提升训练：图形面积计算

2023年九年级数学中考复习：旋转(面积问题)综合压轴题(Word版,含答案)

中考数学分面积类压轴题集锦

【中考压轴题专项练习】最新中考数学压轴大题冲刺专项训练：《面积的最值问题》含答案与解析

2020年中考数学压轴题：图形面积计算