第3章 5 裁剪算法
梁友栋裁剪算法

梁友栋裁剪算法
梁友栋裁剪算法是一种常用的计算机图形学算法,用于将线段或多边形裁剪成可见部分。
该算法由梁钰栋和友松教授于1978年提出,因此得名为梁友栋裁剪算法。
在计算机图形学中,裁剪是指将一个图形对象的一部分或全部从视图中删除,以便在屏幕上显示。
裁剪算法是计算机图形学中的一个重要问题,因为它可以提高图形渲染的效率和质量。
梁友栋裁剪算法的基本思想是将线段或多边形与裁剪窗口进行比较,确定它们的可见部分。
裁剪窗口是一个矩形,表示屏幕上显示的区域。
如果线段或多边形完全在裁剪窗口内部,则它们是可见的,否则需要进行裁剪。
梁友栋裁剪算法的具体步骤如下:
1. 将线段或多边形的两个端点坐标表示为(x1,y1)和(x2,y2)。
2. 计算线段或多边形与裁剪窗口的交点,得到交点坐标(x,y)。
3. 判断交点是否在裁剪窗口内部,如果是,则将交点加入可见部分的点集合中。
4. 重复步骤2和3,直到所有交点都被处理完毕。
5. 根据可见部分的点集合,绘制线段或多边形的可见部分。
梁友栋裁剪算法的优点是简单易懂,计算量小,适用于各种类型的线段和多边形。
它可以用于计算机图形学中的各种应用,如计算机辅助设计、计算机游戏、虚拟现实等。
梁友栋裁剪算法是计算机图形学中的一种重要算法,它可以提高图形渲染的效率和质量,是计算机图形学领域不可或缺的一部分。
简单多边形裁剪算法

摘 要 :为 了尽量 降低任意 多边形裁剪复杂度,提 出了一种基 于多边形顶点遍历 的简单 多边形裁 剪算 法。该 算法将 多边形
交 点插 入 到裁 剪 多边 形 和 被 裁 减 多边 形 顶 点 矢 量数 组 中 ,通 过 记 录 交 点及 其 前 驱 、 后 继 信 息 ,可 快 速 生 成 结 果 多边 形 。其
2 .C h i n a C e n t r e f o r R e s o u r c e s S a t e l l i t e Da t a a n d Ap p l i c a t i o n , B e i j i n g 1 0 0 0 9 4 , C h i n a ;3 .C h i n a C o a l Te c h n o l o g i e s G r o u p or C p o r a t i o n ,B e i j i n g 1 0 0 0 1 3 , C h i n a ; 4 .B e i j i n g I n s t i t u t e o f A p p l i e d Me t e o r o l o g y , B e i j i n g 1 0 0 0 2 9 , C h i n a )
中,时间复杂度 为 ( ) ( ( m+k ) ×k ) ,m 是两 多边形 中顶点数较 大者 ,k是 两 多边形的 交点数 。该算 法简化 了交点的数据 结 构 ,节省 了存储 空间,降低 了算法的时间复杂度 ,具有 简单 、易于编程 实现 、运行效 率高的特点 。
关 键 词 : 多边 形 裁 剪 ; 交点 ;前 驱 ;后 继 ;矢 量数 组 中图 法 分 类 号 :TP 3 9 1 文 献 标 识 号 :A 文章 编 号 :1 0 0 0 — 7 0 2 4( 2 0 1 4 )0 1 - 0 1 9 2 - 0 6
裁剪算法——cohen-sutherland算法

裁剪算法——cohen-sutherland算法实验环境:VC6.0算法思想: 延长窗⼝的边,将⼆维平⾯分成9个区域,每个区域赋予4位编码C t C b C r C l,裁剪⼀条线段P1P2时,先求出所在的区号code1,code2。
若code1=0,且code2=0,则线段P1P2在窗⼝内,应取之。
若按位与运算code1&code2,则说明两个端点同时在窗⼝的上⽅、下⽅、左⽅或右⽅,则可判断线段完全在窗⼝外,可弃之;否则,按第三种情况处理,求出线段与窗⼝某边的交点,在交点处把线段⼀分为⼆,其中必有⼀段在窗⼝外,可弃之,再对另⼀段重复上述处理。
100110001010000100000010010********* 多边形裁剪编码程序实现:#include "stdafx.h"#include<stdio.h>#include<conio.h>#include<graphics.h>#define LEFT 1#define RIGHT 2#define BOTTOM 4#define TOP 8void midpointLine(int x0,int y0,int x1,int y1,int color)//中点画线算法{int a,b,d1,d2,d,x,y;a=y0-y1;b=x1-x0;d=2*a+b;d1=2*a;d2=2*(a+b);x=x0;y=y0;putpixel(x,y,color);while(x<x1){if(d<0){x++;y++;d+=d2;}else{x++;d+=d1;}putpixel(x,y,color);}}int encode(int x,int y,int XL,int XR,int YB,int YT)//编码{int c=0;if(x<XL) c|=LEFT;if(x>XR) c|=RIGHT;if(y<YB) c|=BOTTOM;if(y>YT) c|=TOP;return c;}void C_SLineClip(int x1,int y1,int x2,int y2,int XL,int XR,int YB,int YT){int code1,code2,code,x,y;code1=encode(x1,y1,XL,XR,YB,YT);code2=encode(x2,y2,XL,XR,YB,YT);while((code1 != 0) || (code2 != 0)){if((code1 & code2) != 0){midpointLine(x1,y1,x2,y2,RGB(0, 255, 0));//如果直线在裁剪窗⼝外就⽤绿⾊画出printf("线段在窗⼝外!");return;}if(code1 != 0) code=code1;else code=code2;if((LEFT & code) != 0){x=XL;y=y1+(y2-y1)*(XL-x1)/(x2-x1);}else if((RIGHT & code) != 0){x=XR;y=y1+(y2-y1)*(XR-x1)/(x2-x1);}else if((BOTTOM & code) != 0){y=YB;x=x1+(x2-x1)*(YB-y1)/(y2-y1);}else if((TOP & code) != 0){y=YT;x=x1+(x2-x1)*(YT-y1)/(y2-y1);}if(code == code1){x1=x; y1=y; code1=encode(x,y,XL,XR,YB,YT);}else{x2=x; y2=y; code2=encode(x,y,XL,XR,YB,YT);}}midpointLine(x1,y1,x2,y2,RGB(255,0,0));//将裁减的直线⽤红⾊标注return;}int main(int argc, char* argv[]){int gdriver=DETECT,gmode;int x1=20,y1=30,x2=250,y2=300,XL=10,XR=200,YT=400,YB=30;initgraph(&gdriver,&gmode,"c:\\tc");//setbkcolor(WHITE);cleardevice();midpointLine(x1,y1,x2,y2,RGB(0,255,0));//将被裁剪直线⽤绿⾊画出rectangle(10,400,200,30);//rectangle(int left,int top,int right,int bottom);//裁剪窗⼝ C_SLineClip(x1,y1,x2,y2,XL,XR,YB,YT);// cohen sutherland算法getch();closegraph();return0;}显⽰效果:将在窗⼝内的线段设为红⾊,窗⼝外的线段设为绿⾊。
计算机图形学基础实验指导书

计算机图形学基础实验指导书目录实验一直线的生成 ............................................................... -..2.-实验二圆弧及椭圆弧的生成........................................................ -..3 -实验三多边形的区域填充 ......................................................... - (4)-实验四二维几何变换 ............................................................. -..5.-实验五裁剪算法 ................................................................. -..6.-实验六三维图形变换 ............................................................. -..7.-实验七BEZIER 曲线生成......................................................... -..8.-实验八交互式绘图技术实现........................................................ -..10-实验一直线的生成一、实验目的掌握几种直线生成算法的比较,特别是Bresenham 直线生成算法二、实验环境实验设备:计算机实验使用的语言: C 或Visual C++ 、OpenGL三、实验内容用不同的生成算法在屏幕上绘制出直线的图形,对不同的算法可设置不同的线形或颜色表示区别。
四、实验步骤直线Bresenham 生成算法思想如下1)画点(x i, y i), dx=x2-x i, dy=y2-y i,计算误差初值P i=2dy-dx , i=1;2)求直线下一点位置x i+i=x i+i 如果P i>0,贝U y i+i=y i+i,否则y i+i=y i;3)画点(x i+i ,y i+i );4)求下一个误差P i+i 点,如果P i>0,贝U P i+i=P i+2dy-2dx,否则P i+i=P i+2dy;i=i+i ,如果i<dx+i 则转步骤2,否则结束操作。
自学裁剪100例公式

自学裁剪100例公式自学裁剪公式是学习裁剪技术的基础,掌握了这些公式,可以帮助我们更好地理解裁剪的原理和技巧,提升我们的裁剪技能。
本文将介绍100个常用的自学裁剪公式,通过逐步思考和举例说明,帮助你掌握这些公式。
一、裁剪公式的基础知识在开始介绍具体的裁剪公式之前,我们先来了解一些基础知识。
裁剪公式是通过数学计算来确定裁剪点和线段的位置,以实现准确、精细的裁剪效果。
了解以下几个概念对于理解后续的裁剪公式非常重要:1. 坐标系:裁剪过程中需要使用坐标系来确定点的位置。
常用的坐标系有笛卡尔坐标系和极坐标系。
在笛卡尔坐标系中,x轴和y轴垂直,以原点为基准,用(x, y)表示点的位置;在极坐标系中,以原点为基准,用(r, θ)表示点的位置,其中r表示点到原点的距离,θ表示点与正方向x轴的夹角。
2. 裁剪窗口:裁剪窗口是一个定义了裁剪区域的矩形。
在裁剪时,只有位于裁剪窗口内的图形部分会被显示,位于裁剪窗口外的部分会被裁剪掉。
通常,裁剪窗口的左下角坐标为(w_min_x, w_min_y),右上角坐标为(w_max_x, w_max_y)。
3. 裁剪对象:裁剪对象是指需要进行裁剪操作的图形。
常见的裁剪对象包括线段、多边形、圆等。
二、裁剪公式的具体应用下面我们将具体介绍100个常用的自学裁剪公式,并结合示例进行说明。
这些公式涵盖了不同类型的裁剪对象,帮助你了解裁剪技术的全貌。
1. 线段裁剪公式:- Cohen-Sutherland裁剪算法- Liang-Barsky裁剪算法2. 多边形裁剪公式:- Sutherland-Hodgman裁剪算法- Weiler-Atherton裁剪算法3. 圆裁剪公式:- 椭圆裁剪算法4. 曲线裁剪公式:- Bezier曲线裁剪算法5. 文本裁剪公式:- 文本溢出裁剪算法以线段裁剪公式为例,我们来演示Cohen-Sutherland裁剪算法的应用。
这个算法将线段裁剪为窗口内的可见部分。
哈工大chapter 05裁剪、反走样

Pm B P1
中点分割裁剪算法
中点分割裁剪算法
ϒ 对分辩率为2N次。 ϒ 主要过程只用到加法和除法运算,适合硬件 实现,它可以用左右移位来代替乘除法,这 样就大大加快了速度。
梁友栋-Barsky算法
设要裁剪的线段是P0P1。 P0P1和 窗口边界交于A,B,C,D四点,见图。 算法的基本思想是从A,B和P0三点中 找出最靠近的P1点,图中要找的点 是P0。从C,D和P1中找出最靠近P0的 点。图中要找的点是C点。那么P0C 就是P0P1线段上的可见部分。
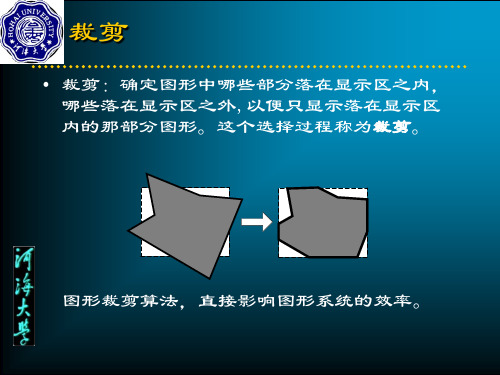
哪些落在显示区之外,以便只显示落在显示区 内的那部分图形。这个选择过程称为裁剪。
图形裁剪算法,直接影响图形系统的效率。
点的裁剪
ϒ 图形裁剪中最基本的问题。
为(xL,yB),右上角坐标 为(xR,yT),对于给定点 P(x,y),则P点在窗口内的条 件是要满足下列不等式: xL <= x <= xR (xL,yB ϒ 并且yB <= y <= yT ) 否则,P点就在窗口外。 ϒ 问题:对于任何多边形窗口, 如何判别?
第五章 裁剪、反走样 方法
反走样方法 裁剪算法
反走样
ϒ 用离散量表示连续量引起的失真现象称之为走样
(aliasing) 。 光栅图形的走样现象
阶梯状边界; 图形细节失真; 狭小图形遗失:动画序列中时隐时现,产生闪烁。
时间上的混淆现象
轮子的转速是:1r/s(1HZ)
每0.75s采一次样(1/0.75HZ)
1
P0P1至少部分可见的充分条件是 max(0, t 0) ≤ min(1, t1 ) 且可见部分的参数区间为[max(0, t 0 ),min(1, t1)]。
t0 Q0 0 P0 t1 Q1 1 P1
计算机图形学 第三章 二维图形的裁剪概述

3.2.3 梁友栋-Barsky裁剪算法
式中,Δx=x2-x1,Δy=y2-y1,参数u在0~1 之间取值,P(x,y)代表了该线段上的一个 点,其值由参数u确定,由公式可知,当u=0 时,该点为P1(x1,y1),当u=1时,该点 为P2(x2,y2)。如果点P(x,y)位于由 坐标(xwmin,ywmin)和(xwmax,ywmax)所 确定的窗口内,那么下式成立: xwmin≤x1+ u· Δx≤xwmax ywmin≤y1+ u· Δy≤ywmax(3-10)
3.2.1 Cohen-Sutherland算法
► Code(int ►{
x,int y,int *c)
*c=0; if(y>ymax) /*(xmin,ymin)和(xmax,ymax) 为窗口左下角、右上角坐标。*/ *c=*c|0x08; else if(y<ymin) *c=*c|0x04; if(x>xmax) *c=*c|0x02; else if(x<xmin) *c=*c|0x01; }
► 根据直线两点式方程:
►
2)
(3-
3.2 线段的裁剪
► 整理后得通用交点公式: ►
(3-3)
► ►
1、与上边界的求交公式: (3-4)
3.2 线段的裁剪
► ►
2、与下边界的求交公式:
(3-5)
►
► ►
3、与右边界的求交公式:
(3-6) 4、与左边界的求交公式:
►
(3-7)
3.2.1 Cohen-Sutherla2、判别 根据C1和C2的具体值,可以有三种情况: (1)C1=C2=0,表明两端点全在窗口内,因而 整个线段也在窗内,应予保留。 (2)C1&C2≠0(两端点代码按位作逻辑乘不为 0),即C1和C2至少有某一位同时为1,表明两端点 必定处于某一边界的同一外侧,因而整个线段全在 窗外,应予舍弃。 (3)不属于上面两种情况,均需要求交点。
多边形裁剪算法
则tu即为三者中离p0最近的 0
点的参数
– 若tu > tl,则可见线段区间 [tl , tu]
1
t3
梁友栋-Barsky算法
始边和终边的确定及交点计算:
令 QL= - △x
DL= x0-xLQR= △xDR= 来自R-x0QB= - △y
DB= y0-yB
QT= △y
DT= yT-y0
交点为
ti= Di / Qi
可弃之。然后对另一段重复上述处理。
1001
1000
1010
0001
0000
0010
0101
0100
0110
–
编码
P1 P3 P4
P2
线段裁剪
Cohen-Sutherland裁剪
如何判定应该与窗口的哪条边求交呢? 编码中对应位为1的边。
• 计算线段P1(x1,y1)P2(x2,y2)与窗口边界的交点 if(LEFT&code !=0) { x=XL; y=y1+(y2-y1)*(XL-x1)/(x2-x1);} else if(RIGHT&code !=0) { x=XR; y=y1+(y2-y1)*(XR-x1)/(x2-x1);} else if(BOTTOM&code !=0) { y=YB; x=x1+(x2-x1)*(YB-y1)/(y2-y1);} else if(TOP & code !=0) { y=YT; x=x1+(x2-x1)*(YT-y1)/(y2-y1);}
直接求交算法
直线与窗口边都 写成参数形式, 求参数值。
Cohen-Sutherland裁剪
• 基本思想:
第3章 5 裁剪算法

80年代初提出了著名的Liang-Barsky裁剪算法,通过 线段的参数化表示,实现快速裁剪,至今仍是计算机 图形学中最经典的算法之一; 80年代末到90年代,梁友栋先生致力于几何连续性的 研究,提出了一系列几何连续性方面的理论和方法,成 为国际上几何连续性研究的重要力量; 1991年梁友栋先生为首完成的成果“计算机图形生 成与几何造型研究”获国家自然科学三等奖;
1
2 3 4
Sutherlan-Cohen算法 中点分割算法
梁友栋-Barsky算法 Sutherlan-Hodgman逐边裁剪算法
裁剪的意义 为了描述图形对象,我们必须存储它的全部信息,但有时 为了达到分区描述或重点描述某一部分的目的,往往将 要描述的部分置于一个窗口内,而将窗口外的部分“剪 掉”,这个处理过程叫做裁剪,裁剪在计算机图形处理中 具有十分重要的意义。 裁剪就是将指定窗口作为图形边界,将窗口内的图形保 留,而窗口外的图形则被舍弃。 裁剪处理过程 1、图元在窗口内外的判别; 2、图形元素与窗口的求交。
直线裁剪方法
◦ Cohen-Sutherland裁剪算法
◦ 中点分割算法 ◦ 梁友栋-barskey算法
多边形裁剪方法
◦ Sutherland-Hodgman逐次多边形裁剪算法 ◦ Weiler-Atherton多边形裁剪算法
对于线段的裁剪基本思想是:
线段是否全不在窗口里,若是,转5 ② 线段是否全在窗口,若是,转4 ③ 计算该线段与窗口边界的交点,以此将线段分为两部分, 丢弃不可见的部分,剩余线段转2 ④ 保留并显示该线段 ⑤ 算法结束 可以看到算法的核心有两个:
区域编码
◦ 由窗口四条边所在直线把二维平面分成9个区域,每个区域 赋予一个四位编码,CtCbCrCl,上下右左
梁友栋裁剪算法

梁友栋裁剪算法梁友栋裁剪算法是计算机图形学中的一种裁剪算法,主要用于将一个多边形或直线段与一个矩形框进行裁剪。
该算法由梁友栋提出,因此得名。
该算法的基本思想是:将线段或多边形的端点表示为参数方程式,并通过求解参数方程式与裁剪边界的交点来确定裁剪后的线段或多边形。
具体来说,对于一条线段(或多边形的一条边),假设其起点为P1(x1,y1),终点为P2(x2,y2),则可以将其表示为以下参数方程式:x = x1 + t * (x2 - x1)y = y1 + t * (y2 - y1)其中t取值范围为[0,1]。
这个参数方程式描述了从P1到P2之间所有可能的点。
现在需要判断这条线段是否与矩形框相交,如果相交,则需要找到相交部分并输出。
对于矩形框上下左右四条边,可以分别用以下参数方程式表示:左:x = xmin右:x = xmax上:y = ymax下:y = ymin接下来需要求解线段和每条矩形边界的交点。
以左侧矩形边界为例,将其参数方程式代入线段参数方程式中,得到以下两个方程:x1 + t * (x2 - x1) = xminy1 + t * (y2 - y1) = y解这个方程组可以得到t的值,进而可以求出相交点的坐标。
对于其他边界也是类似的求解过程。
求解出所有相交点后,需要判断哪些部分需要被保留。
对于线段而言,如果起点和终点都在矩形框内,则整条线段需要被保留;如果起点和终点都在矩形框外,则整条线段需要被裁剪掉;如果只有一端在矩形框内,则需要根据相交点位置判断哪一部分需要被保留。
对于多边形而言,可以将每条边看作一个线段,然后分别进行裁剪操作。
裁剪后的所有线段再组合成新的多边形。
梁友栋裁剪算法的优势在于其简单易懂、高效快速、适用范围广泛。
它不仅可以用于二维图形的裁剪,还可以扩展到三维图形中去。
此外,在实际应用中,该算法还常常和其他算法结合使用,如多边形填充算法、图像变换算法等。
总之,梁友栋裁剪算法是计算机图形学中一种重要的裁剪算法,具有广泛的应用前景和研究价值。
裁剪算法设计实验报告(3篇)

第1篇一、实验目的本次实验旨在深入理解并掌握裁剪算法的基本原理,通过编程实现Cohen-Sutherland算法和Liang-Barsky算法,对图形进行窗口裁剪,从而提高图形处理效率,优化显示效果。
二、实验环境1. 开发环境:Visual Studio 20192. 编程语言:C++3. 图形库:OpenGL三、实验内容1. 理解裁剪算法的基本原理;2. 实现Cohen-Sutherland算法;3. 实现Liang-Barsky算法;4. 对图形进行窗口裁剪,并展示裁剪效果。
四、实验过程1. 理解裁剪算法的基本原理裁剪算法是计算机图形学中的一个重要技术,用于将一个图形或图像中不需要的部分去除,只保留需要的部分。
常见的裁剪算法有Cohen-Sutherland算法、Liang-Barsky算法等。
Cohen-Sutherland算法是一种编码线段裁剪算法,通过将线段端点相对于窗口的位置进行编码,判断线段是否与窗口相交,从而实现裁剪。
Liang-Barsky算法是一种参数化线段裁剪算法,通过计算线段参数,判断线段是否与窗口相交,从而实现裁剪。
2. 实现Cohen-Sutherland算法(1)定义窗口边界首先,定义窗口边界,包括左边界、右边界、上边界和下边界。
(2)编码线段端点将线段端点相对于窗口的位置进行编码,编码规则如下:- 如果端点在窗口内,则编码为0;- 如果端点在窗口左侧,则编码为1;- 如果端点在窗口右侧,则编码为2;- 如果端点在窗口上方,则编码为4;- 如果端点在窗口下方,则编码为8。
(3)判断线段是否与窗口相交将线段两端点的编码进行异或运算,如果结果为0,则线段与窗口相交;否则,线段与窗口不相交。
(4)裁剪线段如果线段与窗口相交,则根据端点编码,将线段分为两部分,分别进行裁剪。
3. 实现Liang-Barsky算法(1)定义窗口边界首先,定义窗口边界,包括左边界、右边界、上边界和下边界。
计算机图形学-第三章-变换及裁剪

(x,y)点对应的齐次坐标为三维空间的一条 直线
xh hx
yh
hy
zh h
7
齐次坐标的作用
1. 将各种变换用阶数统一的矩阵来表示。提供了用矩阵 运算把二维、三维甚至高维空间上的一个点从一个坐 标系变换到另一坐标系的有效方法。
2. 便于表示无穷远点。
例如:(x h, y h, h),令h等于0
25
3 规格化设备坐标系 用于用户的图形是定义在用户坐标系里,
而图形的输出定义在设备坐标系里,它依赖于 基体的图形设备。由于不同的图形设备有不同 的设备坐标系,且不同设备间坐标范围也不尽 相同, 例如:分辨率为1024*768的显示器其屏幕坐标的 范围:x方向为0~1023,y方向为0~767,分辨 率为640*480的显示器,其屏幕坐标范围为:x 方向0~639,y方向0~479
y 1),则
1 0 0
P'x' y' 1 x y 1 0 1 0 x
Tx1
Ty1
1
y 1Tt1
经第二次平移变换后的坐标为P*(x* y* 1)
P * x *
y * 1 x'
y'
1
1 0
0 0 1 0
Tx
2
Ty 2
1
1 0 0 1 0 0
x y 1 0 1 0 0 1 0 x y 1 Tt1Tt2
44
关于透视投影
一点透视投影
两点透视投影
三点透视投影
45
内容
二维变换 三维变换 裁剪
二维线裁剪 二维多边形裁剪 文本裁剪 三维裁剪 关于三维变换与裁剪
46
三维变换流程图
计算机图形学--第五讲 裁剪的基本概念与直线裁剪

12直线生成算法圆与椭圆的绘制算法5图元的概念436区域填充算法裁剪反走样技术4.5 裁剪—4.5 裁剪—4.5 裁剪—4.5 裁剪—4.5 裁剪—4.5 裁剪—算法实现◆第一步◆第二步4.5 裁剪—编码实现(第一步)九个区域,每一个区域采用四位编码对于任一端点左),赋予一个◆左:若◆右:若◆下:若◆上:若4.5 裁剪—编码实现(第一步)对要被裁剪的线段的两个端点,如果其所在的区域的编码均是如果两个编码的见的,可简弃之;如果两个编码的少一个端点非在交点处把线段一分为二,其中必有一段完全在窗口外,可弃之。
再对另一段重复进行上述处理,直到该线段完全被舍弃或找到位于窗口内的一段线段为止。
4.5 裁剪—析出点。
求出其交点见的,因而只要对上述处理步骤。
y=裁剪结束。
算法步骤界坐标:code2(0100)之,转则交换段与窗口边界的交点除p算法的编码实现到另一端点间的线段重复上述过程直到接受或拒绝;计算线段if(LEFT&codeelse if(RIGHT&codeelse if(BOTTOM&code {y=YB;else if(TOP & code !=0) {y=YT;Cohen-SutherlandNicholl et al. An efficient new algorithm for 2-D line clipping: its4.5 裁剪—4.5 裁剪—4.5 裁剪—(((4.5 裁剪—)界L上;要条件A和该处内法向量P(t)4.5 裁剪—)。
4.5 裁剪—)终点组:N i ⋅(P 2-P 1)<0 起点组:N i ⋅(P 2-P 1)>0 特殊情况:N i ⋅(P 2-P 1)=0这时,,P 1P 2与对应边平行, 这时有两种情况:线段在区域外侧或内侧:前一种情况对应于N i ⋅(P 2-P 1)<0,可直接判断线段在多边形之外前一种情况对应于N i ⋅(P 2-P 1)>0,则不于考虑,继续处理其他边。
三维裁剪算法

三维裁剪算法三维裁剪算法是计算机图形学中的一种重要算法,它可以用来对三维模型进行裁剪,从而实现对三维模型的显示和处理。
在计算机图形学中,三维裁剪算法是非常重要的,因为它可以帮助我们实现对三维模型的精确处理和显示,从而提高计算机图形学的应用效果和实用性。
三维裁剪算法的基本原理是将三维模型分割成多个小块,然后对每个小块进行裁剪,最后将所有小块合并起来,得到完整的三维模型。
这个过程需要使用到一些数学知识和计算机图形学的基本算法,比如平面方程、向量运算、矩阵变换等等。
三维裁剪算法的实现过程可以分为以下几个步骤:1. 将三维模型分割成多个小块。
这个过程需要根据三维模型的形状和大小来确定分割的方式和数量。
一般来说,可以将三维模型分割成多个立方体或长方体,然后对每个小块进行裁剪。
2. 对每个小块进行裁剪。
这个过程需要使用到平面方程和向量运算等数学知识。
首先,需要确定裁剪面的位置和方向,然后将裁剪面转换成平面方程的形式。
接着,需要将小块中的每个顶点和面都进行裁剪,得到裁剪后的顶点和面。
这个过程需要使用到向量运算和矩阵变换等计算机图形学的基本算法。
3. 将所有小块合并起来,得到完整的三维模型。
这个过程需要将每个小块的裁剪结果进行合并,得到完整的三维模型。
这个过程需要使用到三维模型的拼接和合并算法,以及一些计算机图形学的基本算法。
三维裁剪算法的应用非常广泛,可以用来实现对三维模型的显示和处理。
比如,在计算机游戏中,三维裁剪算法可以用来实现对游戏场景的裁剪,从而提高游戏的运行效率和流畅度。
在工业设计和建筑设计中,三维裁剪算法可以用来实现对产品和建筑模型的裁剪,从而提高设计的精度和效率。
在医学图像处理中,三维裁剪算法可以用来实现对医学图像的裁剪和分割,从而提高医学诊断的准确性和效率。
三维裁剪算法是计算机图形学中非常重要的一种算法,它可以帮助我们实现对三维模型的精确处理和显示,从而提高计算机图形学的应用效果和实用性。
在未来的发展中,三维裁剪算法将会得到更广泛的应用和发展,成为计算机图形学领域中的重要技术和工具。
计算机图形学第3章

第3章 基本图形生成算法
3.1 生成直线的常用算法
均假定所画直线的斜率k∈[0,1]。
3.1.1 DDA画线算法
DDA(Digital Differential Analyzer)画线 算法也称数值微分法,是一种增量算法。它的算 法实质是用数值方法解微分方程,通过同时对x和 y各增加一个小增量,计算下一步的x、y值。
边界表示的四连通区域种子填充算法 内点表示的四连通区域种子填充算法 边界表示的八连通区域种子填充算法 内点表示的八连通区域种子填充算法
第3章 基本图形生成算法
1.边界表示的四连通区域种子填充算法
基本思想:从多边形内部任一点(像素)出发,依“左 上右下”顺序判断相邻像素,若其不是边界像素且没有被填 充过,对其填充,并重复上述过程,直到所有像素填充完毕。 可以使用栈结构来实现该算法,算法的执行步骤如下: 种子像素入栈,当栈非空时,重复执行如下三步操作: (1)栈顶像素出栈; (2)将出栈像素置成多边形填充的颜色; (3)按左、上、右、下的顺序检查与出栈像素相邻的 四个像素,若其中某个像素不在边界上且未置成多边形色, 则把该像素入栈。
过各行各列像素中心构造一组虚拟网格线,按直 线从起点到终点的顺序计算直线与各垂直网格线的交 点,然后确定该列像素中与此交点最近的像素。 由图3-5不难看出:若s<t, 则Si比较靠近理想直线,应 选Si;若s≥t,则Ti比较靠近 理想直线,应选Ti。
第3章 基本图形生成算法
令dx=x2-x1,dy=y2-y1 递推公式 :di 1 di 2dy 2dx( yi yi 1 ) di的初值: d1 2dy dx 当di≥0时,选Ti,
第3章 基本图形生成算法
圆形窗口裁剪算法_计算机图形学实用教程(第3版)_[共2页]
![圆形窗口裁剪算法_计算机图形学实用教程(第3版)_[共2页]](https://img.taocdn.com/s3/m/02a0c5d7a6c30c2258019e96.png)
对于直线和圆不相交和相切两种情况,由于直线在圆内不可能有可见线段,因此,这两种情
况可以不考虑,只考虑直线与圆相交的情况即可。
设线段的方程为
直线的方程为
x y
= =
x1 y1
+ +
( (
x2 y2
− −
x1 )t y1 )t
0≤t ≤1
(5-52)
圆的方程为
x y
= =
x1 y1
+ +
( x2 ( y2
max(x1, x2 ) < xcw − R min(x1, x2 ) > xcw + R max( y1, y2 ) < ycw − R min( y1, y2 ) > ycw + R 步骤 2:计算参数 t 以及判别式 WD。
为计算直线与圆形窗口的交,将式(5-52)代入式(5-54)得
[(x2 − x1)2 + ( y2 − y1)2 ]t 2 + 2[(x1 − xcw ) ⋅ (x2 − x1) + ( y1 − ycw ) ⋅ ( y2 − y1)]t
第 5 章 图形变换与裁剪
5.5.2 圆形窗口裁剪算法
在实际应用中,如工程制图,经常会用到局部放大圆形窗口内图形的问题,因此,本节介绍
圆形窗口的裁剪方法。
将被裁剪的线段的方程代入圆的方程中,可得如下形式的方程。
at2 + bt + c = 0
< 0 ∆ = b2 − 4ac = 0
> 0
直线与圆不相交 直线与圆相切 直线与圆相交
− −
x1 )t y1 )t
−∞≤ t ≤∞
(5-53)
sutherland-hodgman裁剪算法

Sutherland-Hodgman裁剪算法是一种用于裁剪凸多边形的算法。
该算法的基本思想是在多边形的每一条边上进行裁剪,逐步得到裁剪后的多边形。
以下是详细的Sutherland-Hodgman裁剪算法的步骤:
步骤:
1.确定裁剪窗口:定义一个裁剪窗口(clipping window),它是一个矩形,
用来指定裁剪区域。
2.初始化:对于输入多边形的每一条边,按顺序执行以下步骤:
–记录当前边的起点和终点。
–将裁剪窗口的一个边作为“裁剪边”。
–初始化一个空的输出多边形。
3.迭代裁剪:遍历每一条输入多边形的边,依次进行以下操作:
–对于当前边,判断其与裁剪边的相对位置关系(在窗口内、窗口外或跨越窗口边界)。
–根据相对位置关系,更新输出多边形:
•如果边完全在窗口内,则将边的终点添加到输出多边形中。
•如果边跨越窗口边界,则计算边与裁剪边的交点,并将交点添
加到输出多边形中。
•如果边完全在窗口外,则不添加任何点。
4.更新裁剪边:对于每一轮迭代,更新裁剪边为下一条窗口的边。
依次遍历
裁剪窗口的四个边。
5.重复直到完成:重复步骤3和步骤4,直到遍历完所有输入多边形的边。
6.输出结果:输出多边形即为裁剪后的结果。
示例代码:
以下是一个简单的示例代码,用C语言实现Sutherland-Hodgman裁剪算法:
请注意,这只是一个简单的示例,实际应用中可能需要更多的边界条件和错误处理。
计算机图形学裁剪算法详解

计算机图形学裁剪算法详解裁剪算法详解在使⽤计算机处理图形信息时,计算机内部存储的图形往往⽐较⼤,⽽屏幕显⽰的只是图的⼀部分。
因此需要确定图形中哪些部分落在显⽰区之内,哪些落在显⽰区之外,以便只显⽰落在显⽰区内的那部分图形。
这个选择过程称为裁剪。
最简单的裁剪⽅法是把各种图形扫描转换为点之后,再判断各点是否在窗内。
但那样太费时,⼀般不可取。
这是因为有些图形组成部分全部在窗⼝外,可以完全排除,不必进⾏扫描转换。
所以⼀般采⽤先裁剪再扫描转换的⽅法。
(a)裁剪前 (b) 裁剪后图1.1 多边形裁剪1直线段裁剪直线段裁剪算法⽐较简单,但⾮常重要,是复杂图元裁剪的基础。
因为复杂的曲线可以通过折线段来近似,从⽽裁剪问题也可以化为直线段的裁剪问题。
常⽤的线段裁剪⽅法有三种:Cohen-Sutherland,中点分割算法和梁友栋-barskey 算法。
1.1 Cohen-Sutherland裁剪该算法的思想是:对于每条线段P1P2分为三种情况处理。
(1)若P1P2完全在窗⼝内,则显⽰该线段P1P2简称“取”之。
(2)若P1P2明显在窗⼝外,则丢弃该线段,简称“弃”之。
(3)若线段既不满⾜“取”的条件,也不满⾜“弃”的条件,则在交点处把线段分为两段。
其中⼀段完全在窗⼝外,可弃之。
然后对另⼀段重复上述处理。
为使计算机能够快速判断⼀条直线段与窗⼝属何种关系,采⽤如下编码⽅法。
延长窗⼝的边,将⼆维平⾯分成九个区域。
每个区域赋予4位编码CtCbCrCl.其中各位编码的定义如下:图1.2 多边形裁剪区域编码图5.3线段裁剪裁剪⼀条线段时,先求出P1P2所在的区号code1,code2。
若code1=0,且code2=0,则线段P1P2在窗⼝内,应取之。
若按位与运算code1&code2≠0,则说明两个端点同在窗⼝的上⽅、下⽅、左⽅或右⽅。
可判断线段完全在窗⼝外,可弃之。
否则,按第三种情况处理。
求出线段与窗⼝某边的交点,在交点处把线段⼀分为⼆,其中必有⼀段在窗⼝外,可弃之。
裁剪算法——中点分割算法Liang-Barsky算法

裁剪算法——中点分割算法Liang-Barsky算法三、中点分割法⾸先对直线段的端点进⾏编码。
【核⼼思想:通过⼆分逼近来确定直线段与窗⼝的交点。
】具体⽅法:1、若中点不在窗⼝内,则把【中点】和离窗⼝边界【最远点】构成的线段丢掉,以线段上的另⼀点和该中点再构成线段求其中点。
2、如果中点在窗⼝内,则⼜以中点和最远点构成线段,并求其中点,直到中点与窗⼝边界的坐标值在规定的误差范围内想等。
【问题】中点分割算法会不会⽆限循环⼆分下去?由于屏幕像素是有限的⽽且会规定误差范围,⼀般计算次数不会太多。
四、Liang-Barsky裁剪算法——>【基本出发点:直线的参数⽅程】Liang-Barsky算法是写进国内外主流《计算机图形学》教科书⾥唯⼀⼀个亿中国⼈命名的算法。
【主要思想】(1)⽤参数⽅程表⽰⼀条直线;(2)把被裁剪的红⾊直线段看成是⼀条【有⽅向】的【线段】,把窗⼝的四条边分成两类:⼊边和出边;裁剪线段的起点是直线和两条⼊边的交点以及始端点三个点⾥最前⾯的⼀个点,即参数u【最⼤】的那个点;裁剪线段的终点是直线和两条出边的交点以及端点最后⾯的⼀个点,即参数u【最⼩】的那个点;【梁先⽣的重⼤发现】如果⽤u1,u2分别表⽰线段(u1<=u2)可见部分的开始和结束——>由直线的参数⽅程可知:线段和窗⼝边界⼀共有四个交点,根据Pk的符号,可以知道那两个是⼊交点,那两个是出交点。
:【Liang-Barsky裁剪算法步骤】(1)输⼊直线段的两端点坐标(x1,y1)、(x2,y2),以及窗⼝的四条边界坐标:wxl,wxr,wyb,wyt;(2)若Δx=0,则p1=p2=0,此时进⼀步判断是否满⾜q1<0或q2<0,若满⾜,则直线段不在窗⼝内,算法转(7)结束,否则,进⼀步计算Umax=max(0,Uk|pk<0)和Umin=min(Uk|pk>0,1),其中,Uk=qk/pk;(pk≠0,k=3,4)算法转(5);(3)若Δy=0,则p3=p4=0,此时进⼀步判断是否满⾜q3<0或q4<0,若满⾜,则直线段不在窗⼝内,算法转(7),否则,进⼀步计算Umax=max(0,Uk|pk<0)和Umin=min(Uk|pk>0,1),其中,Uk=qk/pk;(pk≠0,k=3,4)算法转(5);(4)若上述两个条件均不满⾜,则有pk≠0(k=1,2,3,4),此时计算Umax=max(0,Uk|pk<0,Uk|pk<0)和Umin=min(Uk|pk>0,Uk|pk>0,1)其中,Uk=qk/pk;(pk≠0,k=1,2,3,4);(5)求得Umax和Umin后,进⾏判断:若Umax>Umin,则直线段在窗⼝外,算法转(7)若Umax≤Umin,带⼊直线段参数⽅程;(6)利⽤直线的扫描转换算法绘制在窗⼝内的直线段;(7)算法结束。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
xmin≤x0+ t· Δx≤xmax
ymin≤y0+ t· Δy≤ymax
t· Dk ≤Mk , k=1,2,3,4 其中: ① D1=-Δx, M1=x0-xmin ② D2= Δx, M2=xmax-x0 ③ D3=-Δy, M3=y0-ymin ④ D4= Δy, M4=ymax-y0 进行公式验证:
第一,当code1&code2≠0,能判断出直 线段显然在窗口之外. 然而这个条件
并没有包含所有的在窗口之外的直线段,比如: code1=0001,code2=0100,如图 中直线段P3P4,此时,
如何改进? code1&code2=0,但直线段也是完全在窗口之外.这就意
味着这类型的直线必须计算与窗口的边线求交,其实是 一种无意义操作;
Cohen-Sutherland算法的实现
算法优点: 1) 简单将不需剪裁的直线舍弃。法则是:若是
一条直线的两头在同一地区,则该直线不需裁剪, 不然,该直线为也许剪裁直线。
算法的缺点? 2) 对也许剪裁的直线缩小了与之求交的边框范
畴。法则是:若是直线的一个端点在上(下、左、 右)域,则此直线与上边框求交,然后移除上边框 以上的局部。该法则对直线的另一端点也实用。这 样,一条直线至多只需与两条边框求交。
第三章
裁剪是抽取数据的一部分,或者识别一个指定区域 内部或外部的画面或图片的成分的过程。
按照被裁剪的图形可以分为:二维裁剪算法和三维 裁剪算法
按照裁剪区域的形状可以分为:规则区域和不规则 区域
本章二维裁剪算法只考虑举行和多边形,裁剪的对 象只考虑点、线段、多边形、字符等。
三维裁剪算法只考虑正方体和平截头正四棱锥两种 裁剪盒,裁剪对象只考虑线段。
裁剪就是将指定窗口作为图形边界,将窗口内的图形保 留,而窗口外的图形则被舍弃。
裁剪处理过程
1、图元在窗口内外的判别;
2、图形元素与窗口的求交。
直线裁剪方法
◦ Cohen-Sutherland裁剪算法 ◦ 中点分割算法 ◦ 梁友栋-barskey算法
多边形裁剪方法
◦ Sutherland-Hodgman逐次多边形裁剪算法 ◦ Weiler-Atherton多边形裁剪算法
对于线段的裁剪基本思想是:
① 线段是否全不在窗口里,若是,转5 ② 线段是否全在窗口,若是,转4
③ 计算该线段与窗口边界的交点,以此将线段分为两部分, 丢弃不可见的部分,剩余线段转2
④ 保留并显示该线段 ⑤ 算法结束 可以看到算法的核心有两个:
① 判断线段与窗口的关系。 ② 获取线段与窗口的交点。
Dk =0
任何平行于窗口某边界的直线,其Dk=0,k值对应于相应 的边界(k=1,2,3,4对应于左、右、下、上边界)。如 果还满足Mk<0,则线段完全在边界外,应舍弃该线段。如 果Dk=0并且Mk≥0,则线段平行于窗口某边界并在窗口内, 见图中所示。
公式还告诉我们:
1、当Dk<0时,线段从裁剪边界延长线的外部延伸到内部; 2、当Dk>0时,线段从裁剪边界延长线的内部延伸到外部;
区域编码
◦ 由窗口四条边所在直线把二维平面分成9个区域,每个区域
赋予一个四位编码,CtCbCrCl,上下右左
例端如点Ct : 编1给码0 出。当el直yse线y mAaxB的
A
问端AB::题点C10b2的00:10区01给10 域定当码e一lyse,条该y线m如in段何
B
判断属于1 哪当一x 种 x情ma况x ?
算法的思想:
① 对线段p1p2进行编码,如果p1p2可以直接保留或者舍弃, 算法结束,否则进入步骤2.
② 从p1出发寻找离p1最远的可见点B; ③ 从p2出发寻找离p2最远的可见点A; ④ AB之间的线段就是可见的线段。
1. 输入线段端点P1,P2 对于端点P0:
① P2是否可见,若可见,则它为离P1最远的可见点,算法 结束
最后汇聚成一点。计算该点的编码。对 p2进行同样处理。
梁友栋-Barsky算法(Liang-Barsky算法) 写入图形学教科书的唯一中国人的算 法 梁有栋教授的贡献
Liang-Barsky算法 几何连续理论 从几何学与纤维缠绕理论到基因工程
梁友栋先生出生于1935年7月,福建福州人. 19561960年于复旦大学作为研究生,师从苏步青先生学 习几何理论,1960年研究生毕业后任教于浙江大学 数学系,1984-1990年任数学系主任.
问题1:用什么方法解决该问题?
区域编码
◦ 由窗口四条边所在直线把二维平面分成9个区域,每个区域
赋予一个四位编码,CtCbCrCl,上下右左
1
Ct
0
1 Cb 0
当y y max else 当y y min else
1 当x x max
Cr
0
else
1 当x x min Cl 0 else
1 Sutherlan-Cohen算法 2 中点分割算法
3 梁友栋-Barsky算法 4 Sutherlan-Hodgman逐边裁剪算法
裁剪的意义
为了描述图形对象,我们必须存储它的全部信息,但有时 为了达到分区描述或重点描述某一部分的目的,往往将 要描述的部分置于一个窗口内,而将窗口外的部分“剪 掉”,这个处理过程叫做裁剪,裁剪在计算机图形处理中 具有十分重要的意义。
右: x=XR
下:y=YB
y=k(XR-x1)+y1
x=x1+(1/k)(YB-y1)
◦ 对于那些非完全可见、又非显然不可见的线段, 需要求交(如,线段CD) 求交前先测试与窗口哪条边所在直线有交?
规则:判断端点编码中各位的值CtCbCrCl
分别对应:上、下、右和左边 端点码位值等于1时,说明线段与对应窗口边
1991年梁友栋先生为首完成的成果“计算机图形生 成与几何造型研究”获国家自然科学三等奖;
九十年代后期,六十多岁的他积极开展纤维缠绕几何 设计的研究,为我国几何设计与计算机图形学的研究 做出了杰出贡献.
鉴于梁友栋先生的杰出贡献和成就,中国工业与应用 数学学会几何设计与计算专委会授予梁友栋先生第 二届“中国几何设计与计算贡献奖”。
之。然后对另一段重复上述处理。
问题3:如何求交点?
问题4:如何才能使 算法效率高?
求交点:
① 已知线段的两个端点(x1,y1),(x2,y2),直线的方程 为y=k(x-x1)+y1,其中k=(y2-y1)/(x2-x1)
② 交点为: 左: x=XL
y=k(XL-x1)+y1
上:y=YT x=x1+(1/k)(YT-y1)
第二,对于p1p2,当code 码中同时有两位不等于0 时,求 交运算的次数多达四次. 如图2中直线P1P2 与窗口的四 条边的交点分别为A、B、C、D。而实际上,直线只与窗 口的两条边相交,另外两个交点发生在边的延长线上。
编码裁剪算法需要求线段与边界的交点
如果使用将线段一分为二,那么求交点的过程可以 用二分法逐渐逼近来得到
② Pa=p1,pb=p2,得papb的中点pm,若pm可见,pm代替p1, 否则pm代替p2.
③ 如果papb的长度小于系统设定的一个很小的数,该点即 为找到的点.
④ 算法必须对P2做相同的处理,找到点A。 ⑤ 计算AB的可见性,决定是否显示AB线段.
示例:
对于A线段, P1(0000).p2(0000),显示出来
p2
b
p1
p1
c
对于线段B P1(1000),p2(1000),非零,丢弃 对于线段C
p1
p2
p1
d a p2
P1(1000),p2(0010),“与”为零,不可判断,对P1
开始,pa=p1,pb=p2,求得pm1(1000),pb与pm1
p2
“与”为零,不可判断, pa=pm1,求得pm2(0010),Pb与pm2
“与”非零,丢弃,pb变为pm2。直到线段长度小于一个给定的值,计算该 点的 编码。对于p2做同样处理,最后得出线段C不可见。
对于选段D: P1(0001),p2(0100), “与”为零,不可判断。
从p1开始, pa=p1,pb=p2,pm1(0100),pbpm1丢弃,pm1代替pb,求 得pm2(0000),pm2与pb“与”,为零 ,pa=pm2,计算pm3(0000),
线段p1(x1,y1)p2(x2,y2)的参数方程可以表示为:
x=x1+t△x y=y1+t△y 其中,△x=x2-x1, △y=y2-y1,0<=t<=1
P(x,y)代表了该线段上的一个点,其值由参数t确定。 由公式可知,当t=0时,该点为P1(x1,y1),当t=1时,该
点为P2(x2,y2)。 如果点P(x,y)位于由坐标(xmin,ymin)和(xmax,ymax)
相交 次序:上、下、右和左边 以交点为界,丢弃外侧线段,
以交点为新端点判断另一线段, 重复上述过程
如:CD C:0000 D:1000 Dt位等于1,与上边相交
9
8
10
AB:与窗口左边相交,求交点H, AH和BH显然不可见
1
2 0
5
4
6
EF:与窗口上边交点I,弃EI
与窗口下边交点K,弃KF
与窗口右边交点J,弃KJ
CrLeabharlann 0else1 当x x min Cl 0 else
若P1P2完全在窗口内, code1=0,且code2=0,则“取”; 若P1P2明显在窗口外code1&code2≠0,则“弃” ; 若P1P2明显在窗口外code1&code2=0,则不确定 ; 在交点处把线段分为两段。其中一段完全在窗口外,可弃
