2020年中考数学题型专练一 动点问题的函数图像(含答案)
2020年浙江省中考数学题型专练一 动点问题的函数图像含答案
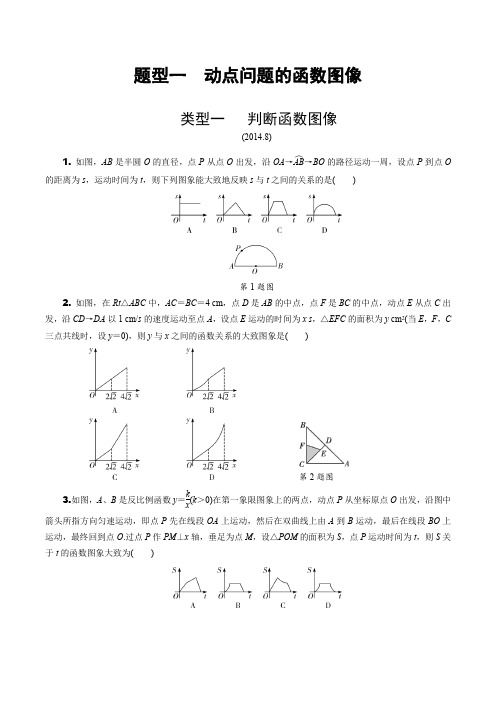
题型一 动点问题的函数图像类型一 判断函数图像(2014.8)1. 如图，AB 是半圆O 的直径，点P 从点O 出发，沿OA →AB ︵→BO 的路径运动一周，设点P 到点O的距离为s ，运动时间为t ，则下列图象能大致地反映s 与t 之间的关系的是( )第1题图2. 如图，在Rt △ABC 中，AC ＝BC ＝4 cm ，点D 是AB 的中点，点F 是BC 的中点，动点E 从点C 出发，沿CD →DA 以1 cm/s 的速度运动至点A ，设点E 运动的时间为x s ，△EFC 的面积为y cm 2(当E ，F ，C 三点共线时，设y ＝0)，则y 与x 之间的函数关系的大致图象是( )第2题图3.如图，A 、B 是反比例函数y ＝k x(k ＞0)在第一象限图象上的两点，动点P 从坐标原点O 出发，沿图中 箭头所指方向匀速运动，即点P 先在线段OA 上运动，然后在双曲线上由A 到B 运动，最后在线段BO 上运动，最终回到点O .过点P 作PM ⊥x 轴，垂足为点M ，设△POM 的面积为S ，点P 运动时间为t ，则S 关于t 的函数图象大致为( )第3题图4.如图，在菱形ABCD中，∠B＝60°，AB＝2，动点P从点B出发，以每秒1个单位长度的速度沿折线BA→AC运动到点C，同时动点Q从点A出发，以相同速度沿折线AC→CD运动到点D，当一个点停止运动时，另一个点也随之停止.设△APQ的面积为y，运动时间为x秒，则下列图象能大致反映y与x之间函数关系的是()第4题图5.如图，在矩形ABCD中，对角线AC与BD交于点O，点M为线段AC上一个动点，过点M作EF∥BD 交AD(或DC)于点E，交AB(或BC)于点F，已知AC＝5，设AM＝x，EF＝y，则y关于x的函数图象大致为()第5题图6. (2019衢州)如图，正方形ABCD的边长为4，点E是AB的中点，点P从点E出发，沿E→A→D→C 移动至终点C，设点P经过的路径长为x，△CPE的面积为y，则下列图象能大致反映y与x函数关系的是()第6题图类型二分析函数图像1.如图①，点P从矩形ABCD的顶点B出发，沿射线BC的方向以每秒1个单位长度的速度运动，过点P作PG⊥AP交射线DC于点G.如图②是点P运动时CG的长度y随时间t变化的图象，其中点Q是第一段曲线(抛物线的一部分)的最高点，则AB的长度是()第1题图A. 2B. 3C. 4D. 232.(2019郑州模拟)如图①，四边形ABCD中，AB∥CD，∠B＝90°，AC＝A D.动点P从点B出发，沿折线B－A－D－C方向以 1 cm/s的速度匀速运动，在整个运动过程中，△BCP的面积S(cm2)与运动时间t(s)的函数图象如图②所示，则AD等于()第2题图A. 5 cmB. 34 cmC. 8 cmD. 2 3 cm3.如图①，菱形ABCD中，∠B＝60°，动点P以每秒1个单位的速度自点A出发沿线段AB运动到点B，同时动点Q以每秒2个单位的速度自点B出发沿折线B－C－D运动到点D.图②是点P、Q运动时，△BPQ的面积S随时间t变化关系图象，则a的值是()第3题图A. 2B. 2.5C. 3D. 234.如图①，在正方形ABCD中，动点E从点A出发，沿A－B－C运动，当点E到达点C时停止运动，过点E作EF⊥AE，交CD于点F，设点E运动的路程为x，FC＝y(当点A，E重合时，点D，F重合；当点C，E重合时，不妨设y＝0)，y与x的函数关系的大致图象如图②，当点E在BC上运动时，FC的最大长度是1，则正方形ABCD的面积是()第4题图A. 8B. 12C. 16D. 4.85.如图①，在矩形ABCD中，动点P从点A出发，沿A→B→C运动，设P A＝x，点D到直线P A的距离为y，且y关于x的函数图象如图②所示，则当△PCD和△P AB的面积相等时，y的值为.第5题图6.如图①，已知点E，F，G，H是矩形ABCD各边的中点，动点M从点E出发，沿E→F→G匀速运动，设点M运动的路程为x，点M到矩形顶点B的距离为y，如果表示y关于x函数关系的图象如图②所示，那么四边形EFGH的面积是.第6题图参考答案类型一 判断函数图象1. C 【解析】点P 在OA 上从点O 向点A 运动的过程中，s 随着t 的增大而增大，点P 在AB ︵上运动时，s ＝OP ＝12AB (定值)，点P 在OB 上从点B 向点O 运动的过程中，s 随着t 的增大而减小． 2. A 【解析】∵在Rt △ABC 中，AC ＝BC ＝4，∴AB ＝42，AD ＝CD ＝22，CF ＝2，当点E 在CD 上时，CE ＝x ，点E 到BC 的距离h 1＝22x ，∴y ＝12×2×22x ＝22x (0≤x ≤22)；当点E 在AD 上时，BE ＝BD ＋DE ＝CD ＋DE ＝x ，∴点E 到FC 的距离h 2＝22BE ＝22x ，∴y ＝12×2×22x ＝22x (22≤x ≤42)． 3. D 【解析】设∠AOM ＝α，点P 运动的速度为a ，当点P 从点O 运动到点A 的过程中，S ＝12OM ·PM ＝12at ·cos α·at ·sin α＝12a 2·cos α·sin α·t 2，由于α及a 均为常量，从而可知图象本段应为抛物线，且S 随着t 的增大而增大；当点P 从A 运动到B 时，由反比例函数性质可知△OPM 的面积为12k ，保持不变，本段图象应为与x 轴平行的线段；同理可得，当点P 从B 运动到O 过程中，S 也是t 的二次函数，且S 随着t 的增大而减小．4. B 【解析】∵四边形ABCD 为菱形，且∠B ＝60°，AB ＝2，∴当0＜t ＜2时，△APQ 的面积y ＝12t ·(2－t )·sin60°＝－34t 2＋32t ，函数图象为开口向下的一段抛物线，且当t ＝1时，y 最大值为34；当2＜t ＜4时，△APQ 的面积y ＝12(t －2)·(t －2)·sin60°＝34(t －2)2，函数图象为开口向上的一段抛物线，且当t ＝4时，y 最大值为3，故选B .5. B 【解析】当0≤x ≤2.5时，如解图①，∵四边形ABCD 是矩形，∴OA ＝OB ＝OC ＝OD ，∴∠OAD ＝∠ODA ，∵EF ∥BD ，∴∠ODA ＝∠MEA ，∴∠OAD ＝∠MEA ，∴ME ＝MA ，同理可得AM ＝MF ，∴EM ＝AM ＝MF ，∴EF ＝2AM ，即y ＝2x ；当2.5<x ≤5时，如解图②，由题意知CM ＝AC －AM ＝5－x ，∵ME＝MC ＝MF ，∴EF ＝2MC ，即y ＝2(5－x )＝10－2x .综上所述，y ＝⎩⎪⎨⎪⎧2x （0≤x ≤2.5）10－2x （2.5<x ≤5）.图① 图②第5题解图6. C 【解析】∵AB ＝4，点E 是AB 的中点，∴AE ＝BE ＝2，当0≤x ≤2时，如解图①，y ＝S △CPE ＝12PE·BC＝2x，∴此段函数图象是正比例函数的一部分；当2<x≤6时，如解图②，y＝S△CPE＝S正方形ABCD－S△BCE －S△APE－S△PCD＝42－12×4×2－12×2×(x－2)－12×4×[4－(x－2)]＝x＋2，∴此段函数图象是一次函数的一部分；当6<x≤10时，如解图③，y＝S△CPE＝12PC·BC＝12(10－x)×4＝－2x＋20，∴此段函数图象是一次函数的一部分，综上所述，根据各段图象及x的取值范围，可得函数图象如选项C所示．图①图②图③第6题解图类型二 分析函数图象1. B 【解析】结合图形分析函数图象可得：当点P 运动到点C 的位置时，CG ＝0，∴BC ＝4.当点P运动到线段BC 的中点时，CG ＝43.∵∠B ＝90°，∴∠BAP ＋∠APB ＝90°，∵PG ⊥AP ，∴∠APG ＝90°，∴∠APB ＋∠CPG ＝90°，∴∠BAP ＝∠CPG ，又∵∠ABP ＝∠PCG ＝90°，∴△ABP ∽△PCG ，∴AB PC ＝BP CG，当点P 为BC 的中点时，BP ＝PC ＝2，∴AB 2＝243，解得AB ＝3. 2. B 【解析】结合图形分析函数图象可得，当t ＝3时，点P 到达A 处，即AB ＝3；如解图，过点A作AE ⊥CD 于点E ，则四边形ABCE 为矩形，∵AC ＝AD ，∴DE ＝CE ＝12CD .当S ＝15时，点P 到达点D 处，则S ＝12CD ·BC ＝12·2AB ·BC ＝3×BC ＝15，则BC ＝5，在Rt △ABC 中，由勾股定理得，AD ＝AC ＝AB 2＋BC 2＝34.第2题解图3. D 【解析】由题图②得，t ＝4时两点停止运动，∴点P 以每秒1个单位的速度从点A 运动到点B 用了4秒，∴AB ＝4，∵点Q 运动到点C 之前和之后，△BPQ 面积算法不同，即t ＝2时，S 的解析式发生变化，∴题图②中点M 对应的横坐标为2，此时P 为AB 中点，点C 与点Q 重合，如解图，连接AC ，∵菱形ABCD 中，AB ＝BC ＝4，∠B ＝60°，∴△ABC 是等边三角形，∴CP ⊥AB ，BP ＝12AB ＝2，∴CP ＝BC 2－BP 2＝42－22＝23，∴a ＝12BP ·CP ＝12×2×23＝2 3.第3题解图4. C 【解析】如解图，设AB ＝a ，当点E 在BC 上运动时(不与点B 、C 重合)，∵AE ⊥EF ，∴△EFC∽△AEB ，∴EC AB ＝FC EB ，即2a －x a ＝y x －a ，∴y ＝－1a x 2＋3x －2a ，－1a <0，当x ＝－32×（－1a ）＝32a 时，y 取得最大值，此时点E 为BC 的中点，y ＝1，把(32a ，1)代入y ＝－1ax 2＋3x －2a ，解得a ＝4，即AB ＝4，故正方形ABCD 的面积为4×4＝16.第4题解图5. 121313【解析】当P 点在AB 上运动时，D 点到AP 的距离不变，始终是AD 长，从图象可以看出AD ＝4，当P 点到达B 点时，从图象看出x ＝3，即AB ＝3.当△PCD 和△P AB 的面积相等时，P 点在BC 中点处，此时△ADP 面积为12×4×3＝6，在Rt △ABP 中，AP ＝AB 2＋BP 2＝13，则12AP ·y ＝6，解得y ＝121313. 6. 24 【解析】如解图，连接BD ，EG ，FH ，∵点E ，F ，G ，H 是矩形ABCD 各边的中点，∴EF ∥BD ∥GH ，EF ＝GH ＝12BD ，∴四边形EFGH 是平行四边形，又∵EF ＝EH ，∴平行四边形EFGH 是菱形，由题图②得BE ＝3，点M 运动到点G 时，运动路程为10，又∵EF ＝FG ，则可知菱形的边长为5，即EF ＝FG ＝GH ＝HE ＝5，∴AF ＝4，AD ＝8，∴S 菱形EFGH ＝12EG ·FH ＝24.第6题解图。
2020年浙江省中考数学题型专练一 动点问题的函数图像含答案
题型一 动点问题的函数图像类型一 判断函数图像(2014.8)1. 如图，AB 是半圆O 的直径，点P 从点O 出发，沿OA →AB ︵→BO 的路径运动一周，设点P 到点O的距离为s ，运动时间为t ，则下列图象能大致地反映s 与t 之间的关系的是( )第1题图2. 如图，在Rt △ABC 中，AC ＝BC ＝4 cm ，点D 是AB 的中点，点F 是BC 的中点，动点E 从点C 出发，沿CD →DA 以1 cm/s 的速度运动至点A ，设点E 运动的时间为x s ，△EFC 的面积为y cm 2(当E ，F ，C 三点共线时，设y ＝0)，则y 与x 之间的函数关系的大致图象是( )第2题图3.如图，A 、B 是反比例函数y ＝k x(k ＞0)在第一象限图象上的两点，动点P 从坐标原点O 出发，沿图中 箭头所指方向匀速运动，即点P 先在线段OA 上运动，然后在双曲线上由A 到B 运动，最后在线段BO 上运动，最终回到点O .过点P 作PM ⊥x 轴，垂足为点M ，设△POM 的面积为S ，点P 运动时间为t ，则S 关于t 的函数图象大致为( )第3题图4.如图，在菱形ABCD中，∠B＝60°，AB＝2，动点P从点B出发，以每秒1个单位长度的速度沿折线BA→AC运动到点C，同时动点Q从点A出发，以相同速度沿折线AC→CD运动到点D，当一个点停止运动时，另一个点也随之停止.设△APQ的面积为y，运动时间为x秒，则下列图象能大致反映y与x之间函数关系的是()第4题图5.如图，在矩形ABCD中，对角线AC与BD交于点O，点M为线段AC上一个动点，过点M作EF∥BD 交AD(或DC)于点E，交AB(或BC)于点F，已知AC＝5，设AM＝x，EF＝y，则y关于x的函数图象大致为()第5题图6. (2019衢州)如图，正方形ABCD的边长为4，点E是AB的中点，点P从点E出发，沿E→A→D→C 移动至终点C，设点P经过的路径长为x，△CPE的面积为y，则下列图象能大致反映y与x函数关系的是()第6题图类型二分析函数图像1.如图①，点P从矩形ABCD的顶点B出发，沿射线BC的方向以每秒1个单位长度的速度运动，过点P作PG⊥AP交射线DC于点G.如图②是点P运动时CG的长度y随时间t变化的图象，其中点Q是第一段曲线(抛物线的一部分)的最高点，则AB的长度是()第1题图A. 2B. 3C. 4D. 232.(2019郑州模拟)如图①，四边形ABCD中，AB∥CD，∠B＝90°，AC＝A D.动点P从点B出发，沿折线B－A－D－C方向以 1 cm/s的速度匀速运动，在整个运动过程中，△BCP的面积S(cm2)与运动时间t(s)的函数图象如图②所示，则AD等于()第2题图A. 5 cmB. 34 cmC. 8 cmD. 2 3 cm3.如图①，菱形ABCD中，∠B＝60°，动点P以每秒1个单位的速度自点A出发沿线段AB运动到点B，同时动点Q以每秒2个单位的速度自点B出发沿折线B－C－D运动到点D.图②是点P、Q运动时，△BPQ的面积S随时间t变化关系图象，则a的值是()第3题图A. 2B. 2.5C. 3D. 234.如图①，在正方形ABCD中，动点E从点A出发，沿A－B－C运动，当点E到达点C时停止运动，过点E作EF⊥AE，交CD于点F，设点E运动的路程为x，FC＝y(当点A，E重合时，点D，F重合；当点C，E重合时，不妨设y＝0)，y与x的函数关系的大致图象如图②，当点E在BC上运动时，FC的最大长度是1，则正方形ABCD的面积是()第4题图A. 8B. 12C. 16D. 4.85.如图①，在矩形ABCD中，动点P从点A出发，沿A→B→C运动，设P A＝x，点D到直线P A的距离为y，且y关于x的函数图象如图②所示，则当△PCD和△P AB的面积相等时，y的值为.第5题图6.如图①，已知点E，F，G，H是矩形ABCD各边的中点，动点M从点E出发，沿E→F→G匀速运动，设点M运动的路程为x，点M到矩形顶点B的距离为y，如果表示y关于x函数关系的图象如图②所示，那么四边形EFGH的面积是.第6题图参考答案类型一 判断函数图象1. C 【解析】点P 在OA 上从点O 向点A 运动的过程中，s 随着t 的增大而增大，点P 在AB ︵上运动时，s ＝OP ＝12AB (定值)，点P 在OB 上从点B 向点O 运动的过程中，s 随着t 的增大而减小． 2. A 【解析】∵在Rt △ABC 中，AC ＝BC ＝4，∴AB ＝42，AD ＝CD ＝22，CF ＝2，当点E 在CD 上时，CE ＝x ，点E 到BC 的距离h 1＝22x ，∴y ＝12×2×22x ＝22x (0≤x ≤22)；当点E 在AD 上时，BE ＝BD ＋DE ＝CD ＋DE ＝x ，∴点E 到FC 的距离h 2＝22BE ＝22x ，∴y ＝12×2×22x ＝22x (22≤x ≤42)． 3. D 【解析】设∠AOM ＝α，点P 运动的速度为a ，当点P 从点O 运动到点A 的过程中，S ＝12OM ·PM ＝12at ·cos α·at ·sin α＝12a 2·cos α·sin α·t 2，由于α及a 均为常量，从而可知图象本段应为抛物线，且S 随着t 的增大而增大；当点P 从A 运动到B 时，由反比例函数性质可知△OPM 的面积为12k ，保持不变，本段图象应为与x 轴平行的线段；同理可得，当点P 从B 运动到O 过程中，S 也是t 的二次函数，且S 随着t 的增大而减小．4. B 【解析】∵四边形ABCD 为菱形，且∠B ＝60°，AB ＝2，∴当0＜t ＜2时，△APQ 的面积y ＝12t ·(2－t )·sin60°＝－34t 2＋32t ，函数图象为开口向下的一段抛物线，且当t ＝1时，y 最大值为34；当2＜t ＜4时，△APQ 的面积y ＝12(t －2)·(t －2)·sin60°＝34(t －2)2，函数图象为开口向上的一段抛物线，且当t ＝4时，y 最大值为3，故选B .5. B 【解析】当0≤x ≤2.5时，如解图①，∵四边形ABCD 是矩形，∴OA ＝OB ＝OC ＝OD ，∴∠OAD ＝∠ODA ，∵EF ∥BD ，∴∠ODA ＝∠MEA ，∴∠OAD ＝∠MEA ，∴ME ＝MA ，同理可得AM ＝MF ，∴EM ＝AM ＝MF ，∴EF ＝2AM ，即y ＝2x ；当2.5<x ≤5时，如解图②，由题意知CM ＝AC －AM ＝5－x ，∵ME＝MC ＝MF ，∴EF ＝2MC ，即y ＝2(5－x )＝10－2x .综上所述，y ＝⎩⎪⎨⎪⎧2x （0≤x ≤2.5）10－2x （2.5<x ≤5）.图① 图②第5题解图6. C 【解析】∵AB ＝4，点E 是AB 的中点，∴AE ＝BE ＝2，当0≤x ≤2时，如解图①，y ＝S △CPE ＝12PE·BC＝2x，∴此段函数图象是正比例函数的一部分；当2<x≤6时，如解图②，y＝S△CPE＝S正方形ABCD－S△BCE －S△APE－S△PCD＝42－12×4×2－12×2×(x－2)－12×4×[4－(x－2)]＝x＋2，∴此段函数图象是一次函数的一部分；当6<x≤10时，如解图③，y＝S△CPE＝12PC·BC＝12(10－x)×4＝－2x＋20，∴此段函数图象是一次函数的一部分，综上所述，根据各段图象及x的取值范围，可得函数图象如选项C所示．图①图②图③第6题解图类型二 分析函数图象1. B 【解析】结合图形分析函数图象可得：当点P 运动到点C 的位置时，CG ＝0，∴BC ＝4.当点P运动到线段BC 的中点时，CG ＝43.∵∠B ＝90°，∴∠BAP ＋∠APB ＝90°，∵PG ⊥AP ，∴∠APG ＝90°，∴∠APB ＋∠CPG ＝90°，∴∠BAP ＝∠CPG ，又∵∠ABP ＝∠PCG ＝90°，∴△ABP ∽△PCG ，∴AB PC ＝BP CG，当点P 为BC 的中点时，BP ＝PC ＝2，∴AB 2＝243，解得AB ＝3. 2. B 【解析】结合图形分析函数图象可得，当t ＝3时，点P 到达A 处，即AB ＝3；如解图，过点A作AE ⊥CD 于点E ，则四边形ABCE 为矩形，∵AC ＝AD ，∴DE ＝CE ＝12CD .当S ＝15时，点P 到达点D 处，则S ＝12CD ·BC ＝12·2AB ·BC ＝3×BC ＝15，则BC ＝5，在Rt △ABC 中，由勾股定理得，AD ＝AC ＝AB 2＋BC 2＝34.第2题解图3. D 【解析】由题图②得，t ＝4时两点停止运动，∴点P 以每秒1个单位的速度从点A 运动到点B 用了4秒，∴AB ＝4，∵点Q 运动到点C 之前和之后，△BPQ 面积算法不同，即t ＝2时，S 的解析式发生变化，∴题图②中点M 对应的横坐标为2，此时P 为AB 中点，点C 与点Q 重合，如解图，连接AC ，∵菱形ABCD 中，AB ＝BC ＝4，∠B ＝60°，∴△ABC 是等边三角形，∴CP ⊥AB ，BP ＝12AB ＝2，∴CP ＝BC 2－BP 2＝42－22＝23，∴a ＝12BP ·CP ＝12×2×23＝2 3.第3题解图4. C 【解析】如解图，设AB ＝a ，当点E 在BC 上运动时(不与点B 、C 重合)，∵AE ⊥EF ，∴△EFC∽△AEB ，∴EC AB ＝FC EB ，即2a －x a ＝y x －a ，∴y ＝－1a x 2＋3x －2a ，－1a <0，当x ＝－32×（－1a ）＝32a 时，y 取得最大值，此时点E 为BC 的中点，y ＝1，把(32a ，1)代入y ＝－1ax 2＋3x －2a ，解得a ＝4，即AB ＝4，故正方形ABCD 的面积为4×4＝16.第4题解图5. 121313【解析】当P 点在AB 上运动时，D 点到AP 的距离不变，始终是AD 长，从图象可以看出AD ＝4，当P 点到达B 点时，从图象看出x ＝3，即AB ＝3.当△PCD 和△P AB 的面积相等时，P 点在BC 中点处，此时△ADP 面积为12×4×3＝6，在Rt △ABP 中，AP ＝AB 2＋BP 2＝13，则12AP ·y ＝6，解得y ＝121313. 6. 24 【解析】如解图，连接BD ，EG ，FH ，∵点E ，F ，G ，H 是矩形ABCD 各边的中点，∴EF ∥BD ∥GH ，EF ＝GH ＝12BD ，∴四边形EFGH 是平行四边形，又∵EF ＝EH ，∴平行四边形EFGH 是菱形，由题图②得BE ＝3，点M 运动到点G 时，运动路程为10，又∵EF ＝FG ，则可知菱形的边长为5，即EF ＝FG ＝GH ＝HE ＝5，∴AF ＝4，AD ＝8，∴S 菱形EFGH ＝12EG ·FH ＝24.第6题解图。
2020中考数学 函数及其图象综合训练(含答案)
2020中考数学函数及其图象综合训练（含答案）一、选择题（本大题共6道小题）1. 已知A，B两地相距3千米，小黄从A地到B地，平均速度为4千米/时，若用x表示行走的时间(小时)，y表示余下的路程(千米)，则y关于x的函数解析式是()A.y=4x(x≥0)B.y=4x-3x≥34C.y=3-4x(x≥0)D.y=3-4x0≤x≤342. 二次函数y=x2-ax+b的图象如图所示，对称轴为直线x=2，下列结论不正确的是()A.a=4B.当b=-4时，顶点的坐标为(2，-8)C.当x=-1时，b>-5D.当x>3时，y随x的增大而增大3. 正比例函数y=kx(k≠0)的函数值y随着x的增大而减小，则一次函数y=x+k的图象大致是()4. 在平面直角坐标系中，点P(-3，m2+1)关于原点的对称点在()A.第一象限B.第二象限C.第三象限D.第四象限5. 已知二次函数y=(x-a-1)(x-a+1)-3a+7(其中x是自变量)的图象与x轴没有公共点，且当x<-1时，y随x的增大而减小，则实数a的取值范围是()A.a<2B.a>-1C.-1<a≤2D.-1≤a<26. 已知m>0，关于x的一元二次方程(x+1)(x-2)-m=0的解为x1，x2(x1<x2)，则下列结论正确的是()A.x1<-1<2<x2B.-1<x1<2<x2C.-1<x1<x2<2D.x1<-1<x2<2二、填空题（本大题共6道小题）7. 若二次函数y=ax2+bx的图象开口向下，则a0(填“=”或“>”或“<”).8. 如图所示，一次函数y=ax+b的图象与x轴相交于点(2，0)，与y轴相交于点(0，4)，结合图象可知，关于x的方程ax+b=0的解是x=.x x时，x的取值范围9. 如图，直线y=kx+b(k<0)经过点A(3，1)，当kx+b<13为.10. 已知抛物线y=ax2+4ax+4a+1(a≠0)过点A(m，3)，B(n，3)两点，若线段AB的长不大于4，则代数式a2+a+1的最小值是.的图象的交11. 如图，点A，C分别是正比例函数y=x的图象与反比例函数y=4x点，过A点作AD⊥x轴于点D，过C点作CB⊥x轴于点B，则四边形ABCD的。
(中考数学)动点问题专题训练(含答案)
中考专题训练 动点问题例1. 如图， 在ABC ∆中，AB AC =，AD BC ⊥于点D ，10BC cm =，8AD cm =． 点P 从点B 出发， 在线段BC 上以每秒3cm 的速度向点C 匀速运动， 与此同时， 垂直于AD 的直线m 从底边BC 出发， 以每秒2cm 的速度沿DA 方向匀速平移， 分别交AB 、AC 、AD 于E 、F 、H ，当点P 到达点C 时， 点P 与直线m 同时停止运动， 设运动时间为t 秒(0)t >．（1） 当2t =时， 连接DE 、DF ，求证： 四边形AEDF 为菱形；（2） 在整个运动过程中， 所形成的PEF ∆的面积存在最大值， 当PEF ∆的面积最大时， 求线段BP 的长；（3） 是否存在某一时刻t ，使PEF ∆为直角三角形？若存在， 请求出此时刻t 的值；若不存在， 请说明理由 ．【解答】（1） 证明： 当2t =时，4DH AH ==，则H 为AD 的中点， 如答图 1 所示 ． 又EF AD ⊥ ，EF ∴为AD 的垂直平分线，AE DE ∴=，AF DF =．AB AC = ，AD BC ⊥于点D ，AD BC ∴⊥，B C ∠=∠．//EF BC ∴，AEF B ∴∠=∠，AFE C ∠=∠，AEF AFE ∴∠=∠，AE AF ∴=，AE AF DE DF ∴===，即四边形AEDF 为菱形 ．（2） 解： 如答图 2 所示， 由 （1） 知//EF BC ，AEF ABC ∴∆∆∽， ∴EF AH BC AD =，即82108EF t -=，解得：5102EF t =-． 221155510(10)210(2)10(0)222223PEF S EF DH t t t t t t ∆==-=-+=--+<< ， ∴当2t =秒时，PEF S ∆存在最大值， 最大值为210cm ，此时36BP t cm ==．（3） 解： 存在 ． 理由如下：①若点E 为直角顶点， 如答图 3①所示，此时//PE AD ，2PE DH t ==，3BP t =．//PE AD ，∴PE BP AD BD =，即2385t t =，此比例式不成立， 故此种情形不存在； ②若点F 为直角顶点如答图 3②所示，此时//PF AD ，2PF DH t ==，3BP t =，103CP t =-．//PF AD ，∴PF CP AD CD =，即210385t t -=，解得4017t =；③若点P 为直角顶点，如答图③所示 ．过点E 作EM BC ⊥于点M ，过点F 作FN BC ⊥于点N ，则2EM FN DH t ===，////EM FN AD ．//EM AD ，∴EM BM AD BD =，即285t BM =，解得54BM t =， 57344PM BP BM t t t ∴=-=-=． 在Rt EMP ∆中， 由勾股定理得：2222227113(2)()416PE EM PM t t t =+=+=． //FN AD ，∴FN CN AD CD =，即285t CN =，解得54CN t =， 5171031044PN BC BP CN t t t ∴=--=--=-． 在Rt FNP ∆中， 由勾股定理得：22222217353(2)(10)85100416PF FN PN t t t t =+=+-=-+． 在Rt PEF ∆中， 由勾股定理得：222EF PE PF =+， 即：2225113353(10)()(85100)21616t t t t -=+-+ 化简得：21833508t t -=， 解得：280183t =或0t =（舍 去） 280183t ∴=． 综上所述， 当4017t =秒或280183t =秒时，PEF ∆为直角三角形 ．例2. 如图， 在同一平面上， 两块斜边相等的直角三角板Rt ABC ∆和Rt ADC ∆拼在一起，使斜边AC 完全重合， 且顶点B ，D 分别在AC 的两旁，90ABC ADC ∠=∠=︒，30CAD ∠=︒，4AB BC cm ==（1） 填空：AD = )cm ，DC = ()cm（2） 点M ，N 分别从A 点，C 点同时以每秒1cm 的速度等速出发， 且分别在AD ，CB 上沿A D →，C B →方向运动， 当N 点运动到B 点时，M 、N 两点同时停止运动， 连接MN ，求当M 、N 点运动了x 秒时， 点N 到AD 的距离 （用 含x 的式子表示）（3） 在 （2） 的条件下， 取DC 中点P ，连接MP ，NP ，设PMN ∆的面积为2()y cm ，在整个运动过程中，PMN ∆的面积y 存在最大值， 请求出y 的最大值 ．（参考数据sin 75︒=sin15︒=【解答】解： （1）90ABC ∠=︒ ，4AB BC cm ==，AC ∴===，90ADC ∠=︒ ，30CAD ∠=︒，12DC AC ∴==，AD ∴==；故答案为：，；（2） 过点N 作NE AD ⊥于E ，作NF DC ⊥，交DC 的延长线于F ，如图所示：则NE DF =，90ABC ADC ∠=∠=︒ ，AB BC =，30CAD ∠=︒，45ACB ∴∠=︒，60ACD ∠=︒，180456075NCF ∴∠=︒-︒-︒=︒，15FNC ∠=︒，sinFC FNCNC ∠=，NC x=，FC x∴=，NE DF x∴==+，∴点N到ADx+；（3）sinFN NCFNC ∠=，FN x∴=，P为DC的中点，PD CP∴==PF x∴=PMN∴∆的面积y=梯形MDFN的面积PMD-∆的面积PNF-∆的面积111)) 222x x x x=+-+--+2x x=+，即y是x的二次函数，0<，y∴有最大值，当x==时，y=．例3. 如图，BD 是正方形ABCD 的对角线，2BC =，边BC 在其所在的直线上平移， 将通过平移得到的线段记为PQ ，连接PA 、QD ，并过点Q 作QO BD ⊥，垂足为O ，连接OA 、OP ．（1） 请直接写出线段BC 在平移过程中， 四边形APQD 是什么四边形？（2） 请判断OA 、OP 之间的数量关系和位置关系， 并加以证明；（3） 在平移变换过程中， 设OPB y S ∆=，(02)BP x x =……，求y 与x 之间的函数关系式，并求出y 的最大值 ．【解答】（1） 四边形APQD 为平行四边形；（2）OA OP =，OA OP ⊥，理由如下：四边形ABCD 是正方形，AB BC PQ ∴==，45ABO OBQ ∠=∠=︒，OQ BD ⊥ ，45PQO ∴∠=︒，45ABO OBQ PQO ∴∠=∠=∠=︒，OB OQ ∴=，在AOB ∆和OPQ ∆中，AB PQABO PQO BO QO=⎧⎪∠=∠⎨⎪=⎩()AOB POQ SAS ∴∆≅∆，OA OP ∴=，AOB POQ ∠=∠，90AOP BOQ ∴∠=∠=︒，OA OP ∴⊥；（3） 如图， 过O 作OE BC ⊥于E ．①如图 1 ，当P 点在B 点右侧时，则2BQ x =+，22x OE +=， 1222x y x +∴=⨯，即211(1)44y x =+-， 又02x ……，∴当2x =时，y 有最大值为 2 ；②如图 2 ，当P 点在B 点左侧时，则2BQ x =-，22x OE -=， 1222x y x -∴=⨯ ，即211(1)44y x =--+， 又02x ……，∴当1x =时，y 有最大值为14； 综上所述，∴当2x =时，y 有最大值为 2 ．例4. 如图， 在平面直角坐标系中，O 为原点， 四边形ABCO 是矩形， 点A ，C 的坐标分别是(0,2)A 和C ，0)，点D 是对角线AC 上一动点 （不 与A ，C 重合） ，连结BD ，作DE DB ⊥，交x 轴于点E ，以线段DE ，DB 为邻边作矩形BDEF ．（1） 填空： 点B 的坐标为 ；（2） 是否存在这样的点D ，使得DEC ∆是等腰三角形？若存在， 请求出AD 的长度；若不存在， 请说明理由；（3）①求证：DE DB =； ②设AD x =，矩形BDEF 的面积为y ，求y 关于x 的函数关系式 （可 利用①的结论） ，并求出y 的最小值 ．【解答】解： （1） 四边形AOCB 是矩形，2BC OA ∴==，OC AB ==90BCO BAO ∠=∠=︒，B ∴2)．故答案为2)．（2） 存在 ． 理由如下：2OA = ，OC =，tan AO ACO OC ∠== ， 30ACO ∴∠=︒，60ACB ∠=︒①如图 1 中， 当E 在线段CO 上时，DEC ∆是等腰三角形， 观察图象可知， 只有ED EC =，30DCE EDC ∴∠=∠=︒，60DBC BCD ∴∠=∠=︒，DBC ∴∆是等边三角形，2DC BC ∴==，在Rt AOC ∆中，30ACO ∠=︒ ，2OA =，24AC AO ∴==，422AD AC CD ∴=-=-=．∴当2AD =时，DEC ∆是等腰三角形 ．②如图 2 中， 当E 在OC 的延长线上时，DCE ∆是等腰三角形， 只有CD CE =，15DBC DEC CDE ∠=∠=∠=︒，75ABD ADB ∴∠=∠=︒，AB AD ∴==，综上所述， 满足条件的AD 的值为 2 或（3）①如图 1 ，过点D 作MN AB ⊥交AB 于M ，交OC 于N ，(0,2)A 和C ，0)，∴直线AC 的解析式为2y x =+，设(,2)D a +，2DN ∴=+，BM a =90BDE ∠=︒ ，90BDM NDE ∴∠+∠=︒，90BDM DBM ∠+∠=︒，DBM EDN ∴∠=∠，90BMD DNE ∠=∠=︒ ，BMD DNE ∴∆∆∽，∴DE DN BD BM ===②如图 2 中， 作DH AB ⊥于H ．在Rt ADH ∆中，AD x = ，30DAH ACO ∠=∠=︒，1122DH AD x ∴==，AH x ==，BH x ∴=， 在Rt BDH ∆中，BD ==，DE ∴==， ∴矩形BDEF的面积为22612)y x x ==-+，即2y x =-+，23)y x ∴=-+，0>，3x ∴=时，y ．例5. 已知Rt OAB ∆，90OAB ∠=︒，30ABO ∠=︒，斜边4OB =，将Rt OAB ∆绕点O 顺时针旋转60︒，如图 1 ，连接BC ．（1） 填空：OBC ∠= 60 ︒；（2） 如图 1 ，连接AC ，作OP AC ⊥，垂足为P ，求OP 的长度；（3） 如图 2 ，点M ，N 同时从点O 出发， 在OCB ∆边上运动，M 沿O C B →→路径匀速运动，N 沿O B C →→路径匀速运动， 当两点相遇时运动停止， 已知点M 的运动速度为 1.5 单位/秒， 点N 的运动速度为 1 单位/秒， 设运动时间为x 秒，OMN ∆的面积为y ，求当x 为何值时y 取得最大值？最大值为多少？【解答】解： （1） 由旋转性质可知：OB OC =，60BOC ∠=︒，OBC ∴∆是等边三角形，60OBC ∴∠=︒．故答案为 60 ．（2） 如图 1 中，4OB = ，30ABO ∠=︒，122OA OB ∴==，AB ==11222AOC S OA AB ∆∴==⨯⨯=BOC ∆ 是等边三角形，60OBC ∴∠=︒，90ABC ABO OBC ∠=∠+∠=︒，AC ∴==2AOC S OP AC ∆∴===．（3）①当803x <…时，M 在OC 上运动，N 在OB 上运动，此时过点N 作NE OC ⊥且交OC 于点E ．则sin 60NE ON x =︒= ，11 1.522OMN S OM NE x x ∆∴==⨯ ，2y x ∴=．83x ∴=时，y 有最大值， 最大值=． ②当843x <…时，M 在BC 上运动，N 在OB 上运动 ．作MH OB ⊥于H ． 则8 1.5BM x =-，sin 60 1.5)MH BM x =︒=- ，212y ON MH x ∴=⨯⨯=+．当83x =时，y 取最大值，y < ③当4 4.8x <…时，M 、N 都在BC 上运动， 作OG BC ⊥于G ．12 2.5MN x =-，OG AB ==，12y MN OG ∴== ，当4x =时，y 有最大值， 最大值=，综上所述，y 有最大值， ．。
2020中考数学 函数图象的性质(包含答案)
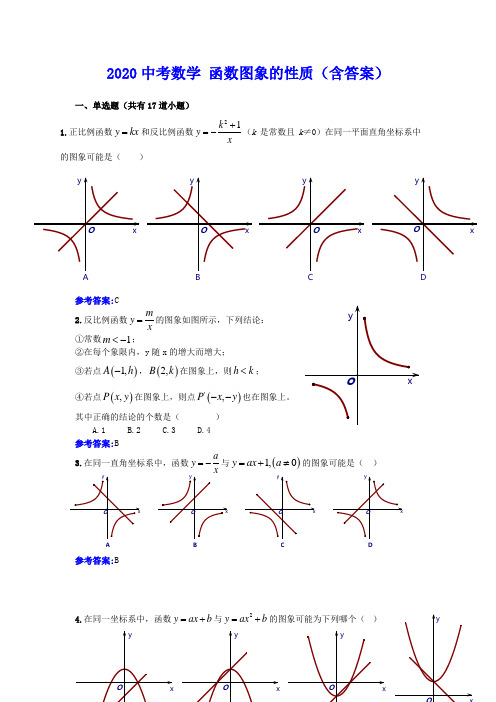
2020中考数学 函数图象的性质（含答案）一、单选题（共有17道小题）1.正比例函数y kx =和反比例函数21y k x=-+（k 是常数且k ≠0）在同一平面直角坐标系中的图象可能是（ ）参考答案:C2.反比例函数my x=的图象如图所示，下列结论： ①常数1m <-；②在每个象限内，y 随x 的增大而增大； ③若点()1,A h -，()2,B k 在图象上，则h k <； ④若点(),P x y 在图象上，则点()',P x y --也在图象上。
其中正确的结论的个数是（ ）A.1B.2C.3D.4参考答案:B3.在同一直角坐标系中，函数ay=-与()1,0y ax a =+≠的图象可能是（ ）参考答案:B4.在同一坐标系中，函数y ax b=+与2y ax b =+的图象可能为下列哪个（ ）yxDOy xC Oy x A O y xB O参考答案:C5.如果函数()0,2≠-=k kx y 的图象不经过第一象限，那么函数xky=的图象一定在（ ） A.第一、二象限 B.第三、四象限 C.第一、三象限 D.第二、四象限 参考答案:D6.在同一直角坐标系中，反比例函数()0ky k x=≠和正比例函数()0y kx k =≠的图象可能是（）A. B. C. D. 参考答案:C7.在同一坐标系中，函数xky =和2+=kx y 的图象大致可能是（ ）x yO xyO xyOxyOC. D.参考答案:A8.在同一平面直角坐标系内，一次函数b ax y +=与二次函数b x ax y ++=82的图象可能是( )参考答案:C9.若0ab <，则正比例函数y ax =和反比例函数y bx=在同一坐标系中的大致图象可能是（ ）参考答案:B10.若正比例函数()0y mx m =≠，y 随x 的增大而减小，则它和二次函数2y mx m =+的图象大致可能是（ ）y x A O yxBOyxDOyxCOyxDO yx COyxB OB参考答案:B12.如图，在同一直角坐标系中，一次函数y ax c =-和二次函数2y ax c =-+的图象大致可能为( )参考答案:D13.在同一平面直角坐标系中，一次函数b ax y +=和二次函数c bx ax y ++=2的图象可能为（ ）参考答案:A14.二次函数bx ax y +=2的图象如图所示，那么一次函数y ）参考答案:C15.已知0b <，二次函数22y ax bx a =++-A A BCDyxDOyxCOyxBOy xAOC D试根据图象分析，a 的值应等于（ ）A ．－2B ．－1C ．1D ．2参考答案:C16.二次函数2y ax bx c =++的图象如图所示，反比例函数by x=与一次函数y cx a =+在同一平面直角坐标系中的大致图象是（ ）参考答案:B17.在同一平面直角坐标系中，函数y mxm =+,和函数222,)0y mx x m m =-++≠（是常数,且的图象可能是( )参考答案:D。
中考数学复习----《动点问题的函数图像》压轴真题练习(含答案解析)
中考数学复习----《动点问题的函数图像》压轴真题练习（含答案解析）1．（2021•益阳）如图，已知▱ABCD的面积为4，点P在AB边上从左向右运动（不含端点），设△APD的面积为x，△BPC的面积为y，则y关于x的函数图象大致是（）A．B．C．D．【答案】B【解答】解：∵▱ABCD的面积为4，x+y是平行四边形面积的一半，∴x+y＝2，∴y＝2﹣x，∴y是x的一次函数，且当x＝0时，y＝2；x＝2时，y＝0；故只有选项B符合题意．2．（2021•河南）如图1，矩形ABCD中，点E为BC的中点，点P沿BC从点B运动到点C，设B，P两点间的距离为x，PA﹣PE＝y，图2是点P运动时y随x变化的关系图象，则BC的长为（）A．4B．5C．6D．7【答案】C【解答】解：由函数图象知：当x＝0，即P在B点时，BA﹣BE＝1．利用三角形两边之差小于第三边，得到PA﹣PE≤AE．∴y的最大值为AE，∴AE＝5．在Rt△ABE中，由勾股定理得：BA2+BE2＝AE2＝25，设BE的长度为t，则BA＝t+1，∴（t+1）2+t2＝25，即：t2+t﹣12＝0，∴（t+4）（t﹣3）＝0，由于t＞0，∴t+4＞0，∴t﹣3＝0，∴BC＝2BE＝2t＝2×3＝6．故选：C．3．（2022•鞍山）如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，AB＝4cm，CD⊥AB，垂足为点D，动点M从点A出发沿AB方向以cm/s的速度匀速运动到点B，同时动点N从点C出发沿射线DC方向以1cm/s的速度匀速运动．当点M停止运动时，点N也随之停止，连接MN．设运动时间为ts，△MND的面积为Scm2，则下列图象能大致反映S与t之间函数关系的是（）A．B．C．D．【答案】B【解答】解：∵∠ACB＝90°，∠A＝30°，AB＝4，∴∠B＝60°，BC＝AB＝2，AC＝BC＝6，∵CD⊥AB，∴CD＝AC＝3，AD＝CD＝3，BD＝BC＝，∴当M在AD上时，0≤t≤3，MD＝AD﹣AM＝3﹣t，DN＝DC+CN＝3+t，∴S＝MD•DN＝（3﹣t）（3+t）＝﹣t2+，当M在BD上时，3＜t≤4，MD＝AM﹣AD＝t﹣3，∴S＝MD•DN＝（t﹣3）（3+t）＝t2﹣，故选：B．4．（2022•菏泽）如图，等腰Rt△ABC与矩形DEFG在同一水平线上，AB＝DE ＝2，DG＝3，现将等腰Rt△ABC沿箭头所指方向水平平移，平移距离x是自点C到达DE之时开始计算，至AB离开GF为止．等腰Rt△ABC与矩形DEFG的重合部分面积记为y，则能大致反映y与x的函数关系的图象为（）A．B．C．D．【答案】B【解答】解：如图，作CH⊥AB于点H，∵AB＝2，△ABC是等腰直角三角形，∴CH＝1，当0≤x≤1时，y＝×2x•x＝x2，当1＜x≤3时，y＝＝1，当3＜x≤4时，y＝1﹣＝﹣（x﹣3）2+1，故选：B．5．（2022•鄂尔多斯）如图①，在正方形ABCD中，点M是AB的中点，点N 是对角线BD上一动点，设DN＝x，AN+MN＝y，已知y与x之间的函数图象如图②所示，点E（a，2）是图象的最低点，那么a的值为（）A．B．2C．D．【答案】 A【解答】解：如图，连接AC交BD于点O，连接NC，连接MC交BD于点N′．∵四边形ABCD是正方形，∴O是BD的中点，∵点M是AB的中点，∴N′是△ABC的重心，∴N′O＝BO，∴N′D＝BD，∵A、C关于BD对称，∴NA＝NC，∴AN+MN＝NC+MN，∵当M、N、C共线时，y的值最小，∴y的值最小就是MC的长，∴MC＝2，设正方形的边长为m，则BM＝m，在Rt△BCM中，由勾股定理得：MC2＝BC2+MB2，∴20＝m2+（m）2，∴m＝4，∴BD＝4，∴a＝N′D＝BD＝×4＝，故选：A．6．（2021•鞍山）如图，△ABC是等边三角形，AB＝6cm，点M从点C出发沿CB方向以1cm/s的速度匀速运动到点B，同时点N从点C出发沿射线CA 方向以2cm/s的速度匀速运动，当点M停止运动时，点N也随之停止．过点M作MP∥CA交AB于点P，连接MN，NP，作△MNP关于直线MP对称的△MN′P，设运动时间为ts，△MN′P与△BMP重叠部分的面积为Scm2，则能表示S与t之间函数关系的大致图象为（）A．B．C．D．【答案】A【解答】解：如图1中，当点N′落在AB上时，取CN的中点T，连接MT．∵CM＝t（cm），CN＝2t（cm），CT＝TN，∴CT＝TN＝t（cm），∵△ABC是等边三角形，∴∠C＝∠A＝60°，∴△MCT是等边三角形，∴TM＝TC＝TN，∴∠CMN＝90°，∵MP∥AC，∴∠BPM＝∠A＝∠MPN＝60°，∠BMP＝∠C＝60°，∠C+∠CMP＝180°，∴∠CMP＝120°，△BMP是等边三角形，∴BM＝MP，∵∠CMP+∠MPN＝180°，∴CM∥PN，∵MP∥CN，∴四边形CMPN是平行四边形，∴PM＝CN＝BM＝2t，∴3t＝6，∴t＝2，如图2中，当0＜t≤2时，过点M作MK⊥AC于K，则MK＝CM•sin60°＝t，∴S＝•（6﹣t）•t＝﹣t2+t．如图3中，当2＜t≤6时，S＝•MQ•PQ＝×（6﹣t）×（6﹣t）＝×（6﹣t）2，观察图象可知，选项A符合题意，故选：A．7．（2021•威海）如图，在菱形ABCD中，AB＝2cm，∠D＝60°，点P，Q同时从点A出发，点P以1cm/s的速度沿A﹣C﹣D的方向运动，点Q以2cm/s 的速度沿A﹣B﹣C﹣D的方向运动，当其中一点到达D点时，两点停止运动．设运动时间为x（s），△APQ的面积为y（cm2），则下列图象中能大致反映y与x之间函数关系的是（）A．B．C．D．【答案】A【解答】解：∵四边形ABCD为菱形，∴AB＝BC＝CD＝DA＝2cm，∠B＝∠D＝60°．∴△ABC、△ACD都是等边三角形，∴∠CAB＝∠ACB＝∠ACD＝60°．如图1所示，当0≤x≤1时，AQ＝2xcm，AP＝xcm，作PE⊥AB于E，∴PE＝sin∠PAE×AP＝（cm），∴y＝AQ•PE＝×2x×＝，故D选项不正确；如图2，当1＜x≤2时，AP＝xcm，CQ＝（4﹣2x）cm，作QF⊥AC于点F，∴QF＝sin∠ACB•CQ＝（cm），∴y＝＝＝，故B选项不正确；如图3，当2＜x≤3时，CQ＝（2x﹣4）cm，CP＝（x﹣2）cm，∴PQ＝CQ﹣CP＝2x﹣4﹣x+2＝（x﹣2）cm，作AG⊥DC于点G，∴AG＝sin∠ACD•AC＝×2＝（cm），∴y＝＝＝．故C选项不正确，故选：A．8．（2021•日照）如图，平面图形ABD由直角边长为1的等腰直角△AOD和扇形BOD组成，点P在线段AB上，PQ⊥AB，且PQ交AD或交于点Q．设AP＝x（0＜x＜2），图中阴影部分表示的平面图形APQ（或APQD）的面积为y，则函数y关于x的大致图象是（）A．B．C．D．【答案】D【解答】解：当Q在AD上时，即点P在AO上时，有0＜x≤1，此时阴影部分为等腰直角三角形，∴y＝，该函数是二次函数，且开口向上，排除B，C选项；当点Q在弧BD上时，补全图形如图所示，阴影部分的面积等于等腰直角△AOD的面积加上扇形BOD的面积，再减去平面图形PBQ的面积即减去弓形QBF的面积，设∠QOB＝θ，则∠QOF＝2θ，∴，S弓形QBF＝﹣S△QOF，当θ＝45°时，AP＝x＝1+≈1.7，S弓形QBF＝﹣＝﹣，y＝+﹣（﹣）＝≈1.14，当θ＝30°时，AP＝x≈1.87，S弓形QBF＝﹣＝﹣，y＝+﹣（﹣）＝≈1.24，当θ＝60°时，AP＝x≈1.5，y≈0.98，在A，D选项中分别找到这两个特殊值，对比发现，选项D符合题意．故选：D．法二、当1＜x＜2时，即P在OB之间时，设∠QOD＝θ，则θ∈（0，），则PQ＝cosθ，OP＝sinθ，则弧QD的长为θπ，此时S阴影＝+θπ+sinθcosθ＝+θ+sin2θ，∴y随x的增大而增大，而且增加的速度越来越慢，分析四个选项中的图象，只有选项D符合．故选：D．9．（2021•辽宁）如图，在矩形ABCD中，AB＝6，AD＝4，E是CD的中点，射线AE与BC的延长线相交于点F，点M从A出发，沿A→B→F的路线匀速运动到点F停止．过点M作MN⊥AF于点N．设AN的长为x，△AMN 的面积为S，则能大致反映S与x之间函数关系的图象是（）A．B．C．D．【答案】B【解答】解：如图，∵E是CD的中点，∴CE＝DE，∵四边形ABCD是矩形，∴∠D＝∠DCF＝90°，AD＝BC＝4，在△ADE与△FCE中，，∴△ADE≌△FCE（SAS），∴CF＝AD＝4，∴BF＝CF+BC＝8，∴AF＝，当点M在AB上时，在Rt△AMN和Rt△AFB中，tan∠NAM＝，∴NM＝x＝x，∴△AMN的面积S＝×x×x＝x2，∴当点M在AB上时，函数图象是开口向上、经过原点的抛物线的一部分；当点M在BF上时，如图，AN＝x，NF＝10﹣x，在Rt△FMN和Rt△FBA中，tan∠F＝，∴＝﹣，∴△AMN的面积S＝＝﹣，∴当点M在BF上时，函数图象是开口向下的抛物线的一部分；故选：B．10．（2021•苏州）如图，线段AB＝10，点C、D在AB上，AC＝BD＝1．已知点P从点C出发，以每秒1个单位长度的速度沿着AB向点D移动，到达点D后停止移动．在点P移动过程中作如下操作：先以点P为圆心，PA、PB的长为半径分别作两个圆心角均为60°的扇形，再将两个扇形分别围成两个圆锥的侧面，设点P的移动时间为t（秒），两个圆锥的底面面积之和为S，则S关于t的函数图象大致是（）A．B．C．D．【答案】D【解答】解：∵AB＝10，AC＝BD＝1，∴CD＝10﹣1﹣1＝8，∵PC＝t，∴AP＝t+1，PB＝8﹣t+1＝9﹣t，设围成的两个圆锥底面圆半径分别为r和R则：2πr＝；．解得：r＝，R＝，∴两个圆锥的底面面积之和为S＝＝＝，根据函数关系式可以发现该函数图象是一个开口向上的二次函数．故选：D．11．（2021•甘肃）如图1，在△ABC中，AB＝BC，BD⊥AC于点D（AD＞BD）．动点M从A点出发，沿折线AB→BC方向运动，运动到点C停止．设点M的运动路程为x，△AMD的面积为y，y与x的函数图象如图2，则AC的长为（）A．3B．6C．8D．9【答案】B【解答】解：由图2知，AB+BC＝2，∵AB＝BC，∴AB＝，∵AB＝BC，BD⊥AC，∴AC＝2AD，∠ADB＝90°，在Rt△ABD中，AD²+BD²＝AB²＝13①，设点M到AC的距离为h，∴S△ADM＝AD•h，∵动点M从A点出发，沿折线AB→BC方向运动，∴当点M运动到点B时，△ADM的面积最大，即h＝BD，由图2知，△ADM的面积最大为3，∴AD•BD＝3，∴AD•BD＝6②，①+2×②得，AD²+BD²+2AD•BD＝13+2×6＝25，∴（AD+BD）²＝25，∴AD+BD＝5（负值舍去），∴BD＝5﹣AD③，将③代入②得，AD（5﹣AD）＝6，∴AD＝3或AD＝2，∵AD＞BD，∴AD＝3，∴AC＝2AD＝6，故选：B．12．（2021•百色）如图，矩形ABCD各边中点分别是E、F、G、H，AB＝2，BC＝2，M为AB上一动点，过点M作直线l⊥AB，若点M从点A开始沿着AB方向移动到点B即停（直线l随点M移动），直线l扫过矩形内部和四边形EFGH外部的面积之和记为S．设AM＝x，则S关于x的函数图象大致是（）A．B．C．D．【答案】D【解答】解：①当M点运动在AE段，此时S＝S△HAE+S△GHD﹣S△EOM﹣S△GPS，∵四边形ABCD是矩形，直线l⊥AB，H、E、F、G为AD、AB、BC、CD的中点，∴AH＝AD＝＝1，AE＝AB＝，S△HAE＝S△GHD，S△EOM＝S△GPS，∴S＝2S△HAE﹣2S△EOM，∴S△HAE＝AE•AH＝；∵直线l⊥AB，∴∠OME＝∠A＝90°，∠HEA＝∠OEM，∴△HAE∽△OME，∴，∴OM＝，又∵ME＝AE﹣AM＝﹣x，∴OM＝ME＝，∴S△EOM＝，∴S＝2S△HAE﹣2S△EOM＝，此时，对应抛物线开口向下；②当M点运动到在BE段，此时，S＝S△HAE+S△GHD+S△EO1M1+S△GP1S1，即S＝2S△HAE+2S△EO1M1，与①同理，O1M1＝，又∵M1E＝AM1﹣AE＝x﹣，∴O1M1＝M1E＝，∴S△EO1M1＝，∴S＝2S△HAE+2S△EO1M1＝，此时，对应抛物线开口向上，故选：D．13．（2021•鄂尔多斯）如图①，在矩形ABCD中，H为CD边上的一点，点M 从点A出发沿折线AH﹣HC﹣CB运动到点B停止，点N从点A出发沿AB 运动到点B停止，它们的运动速度都是1cm/s，若点M、N同时开始运动，设运动时间为t（s），△AMN的面积为S（cm2），已知S与t之间函数图象如图②所示，则下列结论正确的是（）①当0＜t≤6时，△AMN是等边三角形．②在运动过程中，使得△ADM为等腰三角形的点M一共有3个．③当0＜t≤6时，S＝．④当t＝9+时，△ADH∽△ABM．⑤当9＜t＜9+3时，S＝﹣3t+9+3．A．①③④B．①③⑤C．①②④D．③④⑤【答案】A【解答】解：由图②可知：点M、N两点经过6秒时，S最大，此时点M在点H处，点N在点B处并停止不动，如图，①∵点M、N两点的运动速度为1cm/s，∴AH＝AB＝6cm，∵四边形ABCD是矩形，∴CD＝AB＝6 cm．∵当t＝6s时，S＝9cm2，∴×AB×BC＝9．∴BC＝3cm．∵当6≤t≤9时，S＝且保持不变，∴点N在B处不动，点M在线段HC上运动，运动时间为（9﹣6）秒，∴HC＝3 cm，即点H为CD的中点．∴BH＝cm．∴AB＝AH＝BH＝6cm，∴△ABM为等边三角形．∴∠HAB＝60°．∵点M、N同时开始运动，速度均为1cm/s，∴AM＝AN，∴当0＜t≤6时，△AMN为等边三角形．故①正确；②如图，当点M在AD的垂直平分线上时，△ADM为等腰三角形：此时有两个符合条件的点；当AD＝AM时，△ADM为等腰三角形，如图：当DA＝DM时，△ADM为等腰三角形，如图：综上所述，在运动过程中，使得△ADM为等腰三角形的点M一共有4个．∴②不正确；③过点M作ME⊥AB于点E，如图，由题意：AM＝AN＝t，由①知：∠HAB＝60°．在Rt△AME中，∵sin∠MAE＝，∴ME＝AM•sin60°＝tcm，∴S＝AN×ME＝cm2．∴③正确；④当t＝9+时，CM＝cm，如图，由①知：BC＝3cm，∴MB＝BC﹣CM＝2cm．∵AB＝6cm，∴tan∠MAB＝，∴∠MAB＝30°．∵∠HAB＝60°，∴∠DAH＝90°﹣60°＝30°．∴∠DAH＝∠BAM．∵∠D＝∠B＝90°，∴△ADH∽△ABM．∴④正确；⑤当9＜t＜9+3时，此时点M在边BC上，如图，此时MB＝9+3﹣t，∴S＝×AB×MB＝×6×（9+3﹣t）＝27+9﹣3t．∴⑤不正确；综上，结论正确的有：①③④．故选：A．14．（2021•通辽）如图，在矩形ABCD中，AB＝4，BC＝3，动点P，Q同时从点A出发，点P沿A→B→C的路径运动，点Q沿A→D→C的路径运动，点P，Q的运动速度相同，当点P到达点C时，点Q也随之停止运动，连接PQ．设点P的运动路程为x，PQ2为y，则y关于x的函数图象大致是（）A．B．C．D．【答案】C【解答】解：当0≤x≤3时，在Rt△APQ中，∠QAP＝90°，AP＝AQ＝x，∴PQ2＝2x2．∴y＝PQ2＝2x2；当3≤x≤4时，DQ＝x﹣3，AP＝x，∴y＝PQ2＝32+32＝18；当4≤x≤7时，CP＝7﹣x，CQ＝7﹣x，∴y＝PQ2＝CP2+CQ2＝2x2﹣28x+98．故选：C．15．（2021•湖北）如图，AC为矩形ABCD的对角线，已知AD＝3，CD＝4，点P沿折线C﹣A﹣D以每秒1个单位长度的速度运动（运动到D点停止），过点P作PE⊥BC于点E，则△CPE的面积y与点P运动的路程x间的函数图象大致是（）A．B．C．D．【答案】D【解答】解：∵BC∥AD，∴∠ACB＝∠DAC，∵∠PEC＝∠D＝90°，∴△PCE∽△CAD，∴＝＝，∵AD＝3，CD＝4，∴AC＝＝5，∴当P在CA上时，即当0＜x≤5时，PE＝＝x，CE＝＝x，∴y＝PE•CE＝＝x2，当P在AD上运动时，即当5＜x≤8时，PE＝CD＝4，CE＝8﹣x，∴y＝PE•CE＝×4×（8﹣x）＝16﹣2x，综上，当0＜x≤5时，函数图象为二次函数图象，且y随x增大而增大，当5＜x≤8时，函数图象为一次函数图象，且y随x增大而减小，故选：D．16．（2021•衡阳）如图1，菱形ABCD的对角线AC与BD相交于点O，P、Q 两点同时从O点出发，以1厘米/秒的速度在菱形的对角线及边上运动．点P 的运动路线为O﹣A﹣D﹣O，点Q的运动路线为O﹣C﹣B﹣O．设运动的时间为x秒，P、Q间的距离为y厘米，y与x的函数关系的图象大致如图2所示，当点P在A﹣D段上运动且P、Q两点间的距离最短时，P、Q两点的运动路程之和为厘米．【答案】（2+3）【解答】解：由图分析易知：当点P从O→A运动时，点Q从O→C运动时，y不断增大，当点P运动到A点，点Q运动到C点时，由图象知此时y＝PQ＝2cm，∴AC＝2cm，∵四边形ABCD为菱形，∴AC⊥BD，OA＝OC＝＝cm，当点P运动到D点，Q运动到B点，结合图象，易知此时，y＝BD＝2cm，∴OD＝OB＝BD＝1cm，在Rt△ADO中，AD＝＝＝2（cm），∴AD＝AB＝BC＝DC＝2cm，如图，当点P在A﹣D段上运动，点P运动到点E处，点Q在C﹣B段上运动，点Q运动到点F处时，P、Q两点的距离最短，此时，OE＝OF＝＝，AE＝CF＝＝＝，∴当点P在A﹣D段上运动且P、Q两点间的距离最短时，P、Q两点的运动路程之和为：（cm），故答案为：（2+3）．17．（2021•武汉）如图（1），在△ABC中，AB＝AC，∠BAC＝90°，边AB上的点D从顶点A出发，向顶点B运动，同时，边BC上的点E从顶点B出发，向顶点C运动，D，E两点运动速度的大小相等，设x＝AD，y＝AE+CD，y 关于x的函数图象如图（2），图象过点（0，2），则图象最低点的横坐标是．【答案】﹣1【解答】解：∵图象过点（0，2），即当x＝AD＝BE＝0时，点D与A重合，点E与B重合，此时y＝AE+CD＝AB+AC＝2，∵△ABC为等腰直角三角形，∴AB＝AC＝1，过点A作AF⊥BC于点F，过点B作NB⊥BC，并使得BN＝AC，如图所示：∵AD＝BE，∠NBE＝∠CAD，∴△NBE≌△CAD（SAS），∴NE＝CD，又∵y＝AE+CD，∴y＝AE+CD＝AE+NE，当A、E、N三点共线时，y取得最小值，如图所示，此时：AD＝BE＝x，AC＝BN＝1，∴AF＝AC•sin45°＝，\又∵∠BEN＝∠FEA，∠＝∠AFE∴△NBE∽△AFE∴，即，解得：x＝，∴图象最低点的横坐标为：﹣1．故答案为：．18．（2022•营口）如图1，在四边形ABCD中，BC∥AD，∠D＝90°，∠A＝45°，动点P，Q同时从点A出发，点P以cm/s的速度沿AB向点B运动（运动到B点即停止），点Q以2cm/s的速度沿折线AD→DC向终点C运动，设点Q的运动时间为x（s），△APQ的面积为y（cm2），若y与x之间的函数关系的图象如图2所示，当x＝（s）时，则y＝cm2．【答案】【解答】解：过点D作DE⊥AB，垂足为E，在Rt△ADE中，∵∠AED＝90°，∠EAD＝45°，∴，∵点P的速度为cm/s，点Q的速度为2cm/s，∴AP＝x，AQ＝2x，∴，在△APQ和△AED中，＝，∠A＝45°，∴△AED∽△APQ，∴点Q在AD上运动时，△APQ为等腰直角三角形，∴AP＝PQ＝x，∴当点Q在AD上运动时，y＝AP•AQ＝×x×x＝x2，由图像可知，当y＝9此时面积最大，x＝3或﹣3（负值舍去），∴AD＝2x＝6cm，当3＜x≤4时，过点P作PF⊥AD于点F，如图：此时S△APQ＝S△APF+S四边形PQDF﹣S△ADQ，在Rt△APF中，AP＝x，∠PAF＝45°，∴AF＝PF＝x，FD＝6﹣x，QD＝2x﹣6，∴S△APQ＝x2+（x+2x﹣6）•（6﹣x）﹣×6×（2x﹣6），即y＝﹣x2+6x，当x＝时，y＝﹣（）2+6×＝，故答案为：．。
2020中考数学-动点问题专题训练(含答案)
中考专题训练 动点问题例1. 如图， 在ABC ∆中，AB AC =，AD BC ⊥于点D ，10BC cm =，8AD cm =． 点P 从点B 出发， 在线段BC 上以每秒3cm 的速度向点C 匀速运动， 与此同时， 垂直于AD 的直线m 从底边BC 出发， 以每秒2cm 的速度沿DA 方向匀速平移， 分别交AB 、AC 、AD 于E 、F 、H ，当点P 到达点C 时， 点P 与直线m 同时停止运动， 设运动时间为t 秒(0)t >．（1） 当2t =时， 连接DE 、DF ，求证： 四边形AEDF 为菱形；（2） 在整个运动过程中， 所形成的PEF ∆的面积存在最大值， 当PEF ∆的面积最大时， 求线段BP 的长；（3） 是否存在某一时刻t ，使PEF ∆为直角三角形？若存在， 请求出此时刻t 的值；若不存在， 请说明理由 ．【解答】（1） 证明： 当2t =时，4DH AH ==，则H 为AD 的中点， 如答图 1 所示 ． 又EF AD ⊥Q ，EF ∴为AD 的垂直平分线，AE DE ∴=，AF DF =．AB AC =Q ，AD BC ⊥于点D ，AD BC ∴⊥，B C ∠=∠．//EF BC ∴，AEF B ∴∠=∠，AFE C ∠=∠，AEF AFE ∴∠=∠，AE AF ∴=，AE AF DE DF ∴===，即四边形AEDF 为菱形 ．（2） 解： 如答图 2 所示， 由 （1） 知//EF BC ，AEF ABC ∴∆∆∽， ∴EF AH BC AD =，即82108EF t -=，解得：5102EF t =-． 221155510(10)210(2)10(0)222223PEF S EF DH t t t t t t ∆==-=-+=--+<<g g ， ∴当2t =秒时，PEF S ∆存在最大值， 最大值为210cm ，此时36BP t cm ==．（3） 解： 存在 ． 理由如下：①若点E 为直角顶点， 如答图 3①所示，此时//PE AD ，2PE DH t ==，3BP t =．//PE AD Q ，∴PE BP AD BD =，即2385t t =，此比例式不成立， 故此种情形不存在； ②若点F 为直角顶点如答图 3②所示，此时//PF AD ，2PF DH t ==，3BP t =，103CP t =-．//PF AD Q ，∴PF CP AD CD =，即210385t t -=，解得4017t =；③若点P 为直角顶点，如答图③所示 ．过点E 作EM BC ⊥于点M ，过点F 作FN BC ⊥于点N ，则2EM FN DH t ===，////EM FN AD ．//EM AD Q ，∴EM BM AD BD=，即285t BM =，解得54BM t =， 57344PM BP BM t t t ∴=-=-=． 在Rt EMP ∆中， 由勾股定理得：2222227113(2)()416PE EM PM t t t =+=+=． //FN AD Q ，∴FN CN AD CD=，即285t CN =，解得54CN t =， 5171031044PN BC BP CN t t t ∴=--=--=-． 在Rt FNP ∆中， 由勾股定理得：22222217353(2)(10)85100416PF FN PN t t t t =+=+-=-+． 在Rt PEF ∆中， 由勾股定理得：222EF PE PF =+， 即：2225113353(10)()(85100)21616t t t t -=+-+ 化简得：21833508t t -=， 解得：280183t =或0t =（舍 去） 280183t ∴=． 综上所述， 当4017t =秒或280183t =秒时，PEF ∆为直角三角形 ．例2. 如图， 在同一平面上， 两块斜边相等的直角三角板Rt ABC ∆和Rt ADC ∆拼在一起，使斜边AC 完全重合， 且顶点B ，D 分别在AC 的两旁，90ABC ADC ∠=∠=︒，30CAD ∠=︒，4AB BC cm ==（1） 填空：AD = )cm ，DC = ()cm（2） 点M ，N 分别从A 点，C 点同时以每秒1cm 的速度等速出发， 且分别在AD ，CB 上沿A D →，CB →方向运动，当N 点运动到B 点时，M 、N 两点同时停止运动， 连接MN ，求当M 、N 点运动了x 秒时， 点N 到AD 的距离 （用 含x 的式子表示）（3） 在 （2） 的条件下， 取DC 中点P ，连接MP ，NP ，设PMN ∆的面积为2()y cm ，在整个运动过程中，PMN ∆的面积y 存在最大值， 请求出y 的最大值 ．（参考数据sin 75︒=sin15︒=【解答】解： （1）90ABC ∠=︒Q ，4AB BC cm ==，AC ∴== 90ADC ∠=︒Q ，30CAD ∠=︒，12DC AC ∴==AD ∴==故答案为：，（2） 过点N 作NE AD ⊥于E ，作NF DC ⊥，交DC 的延长线于F ，如图所示：则NE DF =，90ABC ADC ∠=∠=︒Q ，AB BC =，30CAD ∠=︒，45ACB ∴∠=︒，60ACD ∠=︒，180456075NCF ∴∠=︒-︒-︒=︒，15FNC ∠=︒，sin FC FNC NC∠=Q ，NC x =，4FC x ∴=，4NE DF x ∴==+ ∴点N 到ADx +； （3）sin FN NCF NC∠=Q ，FN x ∴=， P Q 为DC 的中点，PD CP ∴==4PF x ∴=+ PMN ∴∆的面积y =梯形MDFN 的面积PMD -∆的面积PNF -∆的面积111))222x x x =++-2784x x =++ 即y 是x 的二次函数，Q 08<， y ∴有最大值，当7x ==时，y=例3. 如图，BD 是正方形ABCD 的对角线，2BC =，边BC 在其所在的直线上平移， 将通过平移得到的线段记为PQ ，连接PA 、QD ，并过点Q 作QO BD ⊥，垂足为O ，连接OA 、OP ．（1） 请直接写出线段BC 在平移过程中， 四边形APQD 是什么四边形？（2） 请判断OA 、OP 之间的数量关系和位置关系， 并加以证明；（3） 在平移变换过程中， 设OPB y S ∆=，(02)BP x x =剟，求y 与x 之间的函数关系式，并求出y 的最大值 ．【解答】（1） 四边形APQD 为平行四边形；（2）OA OP =，OA OP ⊥，理由如下：Q 四边形ABCD 是正方形，AB BC PQ ∴==，45ABO OBQ ∠=∠=︒，OQ BD ⊥Q ，45PQO ∴∠=︒，45ABO OBQ PQO ∴∠=∠=∠=︒，OB OQ ∴=，在AOB ∆和OPQ ∆中，AB PQABO PQO BO QO=⎧⎪∠=∠⎨⎪=⎩()AOB POQ SAS ∴∆≅∆，OA OP ∴=，AOB POQ ∠=∠，90AOP BOQ ∴∠=∠=︒，OA OP ∴⊥；（3） 如图， 过O 作OE BC ⊥于E ．①如图 1 ，当P 点在B 点右侧时，则2BQ x =+，22x OE +=， 1222x y x +∴=⨯g ，即211(1)44y x =+-， 又02x Q 剟， ∴当2x =时，y 有最大值为 2 ；②如图 2 ，当P 点在B 点左侧时，则2BQ x =-，22x OE -=， 1222x y x -∴=⨯g ，即211(1)44y x =--+， 又02x Q 剟， ∴当1x =时，y 有最大值为14； 综上所述，∴当2x =时，y 有最大值为 2 ．例4. 如图， 在平面直角坐标系中，O 为原点， 四边形ABCO 是矩形， 点A ，C 的坐标分别是(0,2)A 和C 0)，点D 是对角线AC 上一动点 （不 与A ，C 重合） ，连结BD ，作DE DB ⊥，交x 轴于点E ，以线段DE ，DB 为邻边作矩形BDEF ．（1） 填空： 点B 的坐标为 ；（2） 是否存在这样的点D ，使得DEC ∆是等腰三角形？若存在， 请求出AD 的长度；若不存在， 请说明理由；（3）①求证：DE DB = ②设AD x =，矩形BDEF 的面积为y ，求y 关于x 的函数关系式 （可 利用①的结论） ，并求出y 的最小值 ．【解答】解： （1）Q 四边形AOCB 是矩形，2BC OA ∴==，OC AB ==90BCO BAO ∠=∠=︒，B ∴2)．故答案为2)．（2） 存在 ． 理由如下：2OA =Q ，OC =tan AO ACO OC ∠==Q 30ACO ∴∠=︒，60ACB ∠=︒①如图 1 中， 当E 在线段CO 上时，DEC ∆是等腰三角形， 观察图象可知， 只有ED EC =， 30DCE EDC ∴∠=∠=︒，60DBC BCD ∴∠=∠=︒，DBC ∴∆是等边三角形，2DC BC ∴==，在Rt AOC ∆中，30ACO ∠=︒Q ，2OA =，24AC AO ∴==，422AD AC CD ∴=-=-=．∴当2AD =时，DEC ∆是等腰三角形 ．②如图 2 中， 当E 在OC 的延长线上时，DCE ∆是等腰三角形， 只有CD CE =，15DBC DEC CDE ∠=∠=∠=︒，75ABD ADB ∴∠=∠=︒，AB AD ∴==综上所述， 满足条件的AD 的值为 2 或（3）①如图 1 ，过点D 作MN AB ⊥交AB 于M ，交OC 于N ，(0,2)A Q 和C 0)，∴直线AC 的解析式为23y x =-+，设(,2)3D a a -+，2DN ∴=+，BM a =90BDE ∠=︒Q ，90BDM NDE∴∠+∠=︒，90BDM DBM∠+∠=︒，DBM EDN∴∠=∠，90BMD DNE∠=∠=︒Q，BMD DNE∴∆∆∽，∴23DE DNBD BM+===．②如图 2 中，作DH AB⊥于H．在Rt ADH∆中，AD x=Q，30DAH ACO∠=∠=︒，1122DH AD x∴==，AH x==，2BH x∴=，在Rt BDH∆中，BD==，DE∴==∴矩形BDEF的面积为22612)y x x==-+，即2y=-+23)3y x∴=-+Q03>，3x ∴=时，y ．例5. 已知Rt OAB ∆，90OAB ∠=︒，30ABO ∠=︒，斜边4OB =，将Rt OAB ∆绕点O 顺时针旋转60︒，如图 1 ，连接BC ．（1） 填空：OBC ∠= 60 ︒；（2） 如图 1 ，连接AC ，作OP AC ⊥，垂足为P ，求OP 的长度；（3） 如图 2 ，点M ，N 同时从点O 出发， 在OCB ∆边上运动，M 沿O C B →→路径匀速运动，N 沿O B C →→路径匀速运动， 当两点相遇时运动停止， 已知点M 的运动速度为1.5 单位/秒， 点N 的运动速度为 1 单位/秒， 设运动时间为x 秒，OMN ∆的面积为y ，求当x 为何值时y 取得最大值？最大值为多少？【解答】解： （1） 由旋转性质可知：OB OC =，60BOC ∠=︒，OBC ∴∆是等边三角形，60OBC ∴∠=︒．故答案为 60 ．（2） 如图 1 中，4OB =Q ，30ABO ∠=︒，122OA OB ∴==，AB ==11222AOC S OA AB ∆∴==⨯⨯=g gBOC ∆Q 是等边三角形，60OBC ∴∠=︒，90ABC ABO OBC ∠=∠+∠=︒，AC ∴==27AOC S OP AC ∆∴===．（3）①当803x <…时，M 在OC 上运动，N 在OB 上运动，此时过点N 作NE OC ⊥且交OC 于点E ．则sin 60NE ON x =︒=g ，11 1.522OMN S OM NE x x ∆∴==⨯g g ，28y x ∴=．83x ∴=时，y 有最大值， 最大值=． ②当843x <„时，M 在BC 上运动，N 在OB 上运动 ．作MH OB ⊥于H ． 则8 1.5BM x =-，sin 60(8 1.5)2MH BM x =︒=-g，212y ON MH x ∴=⨯⨯=+．当83x =时，y 取最大值，y < ③当4 4.8x <„时，M 、N 都在BC 上运动， 作OG BC ⊥于G ．12 2.5MN x =-，OG AB ==，122y MN OG x ∴==g g ，当4x =时，y 有最大值， 最大值=，综上所述，y 有最大值， ．。
中考数学专题复习《动点问题的函数图象》测试卷-附带答案
中考数学专题复习《动点问题的函数图象》测试卷-附带答案学校:___________班级:___________姓名:___________考号:___________1．用一个乒乓球垂直向上抛出则下列描述乒乓球的运动速度v与运动时间t关系的函数图像中正确的是（）A．B．C．D．2．一辆小车从甲地匀速行驶到乙地到达乙地后按原来的速度返回若x表示行驶的时间y表示小车与甲地的距离．则下列图象能反映y与x的函数关系的是（）A．B．C．D．3．吴老师家公园学校依次在同一条直线上家到公园公园到学校的距离分别为400m 600m．他从家出发匀速步行8min到公园后停留4min 然后匀速步行6min到学校设吴老师离公园的距离为y（单位：m）所用时间为x（单位：min）则下列表示y与x之间函数关系的图象中正确的是（）A．B．C．D．4．如图正方形ABCD的边长为2cm 动点P从点A出发在正方形的边上沿A→B→C的方向运动到点C停止．设点P的运动路程为x(cm) 在下列图象中能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是（）A．B．C．D．5．如图1 Rt△ABC中点P从点C出发匀速沿CB−BA向点A运动连接AP设点P 的运动距离为x AP的长为y y关于x的函数图象如图2所示则当点P为BC中点时AP 的长为（）A．5B．8C．5√2D．2√136．如图1 在△ABC中CA=CB直线l经过点A且垂直于AB．现将直线l以1cm/s的速度向右匀速平移直至到达点B时停止运动直线l与边AB交于点M与边AC（或CB）交于点N．设直线l移动的时间是x(s)△AMN的面积为．y(cm²)，若y关于x的函数图象如图2所示则△ABC的周长为（）A．16cm B．17cm C．18cm D．20cm7．如图1 四边形ABCD中AD∥BC直线l⊥AB当直线l沿射线BC的方向从点B开始向右平移时直线l与四边形ABCD的边分别相交于点E,F．设直线l向右平移的距离为x线段EF的长为y且y与x的函数关系如图2．则下列结论：①BC的长为5 ②AB的长为3√2③当4≤x≤5时△BEF的面积不变其中正确的个数为（）A．0B．1C．2D．38．如图1 正方形ABCD中点E在边BC上连接AE动点P从A点出发沿A→D→C 的路径以1cm/s的速度匀速运动到C点在此过程中△APE的面积y(cm2)随运动时间x(s)变化的函数关系图象如图2所示则当x=5时y的值为（）A．2.5B．3C．3.2D．3.59．“龟兔赛跑”讲述了这样的故事：领先的兔子看着缓慢爬行的乌龟骄傲起来睡了一觉．当它醒来时发现乌龟快到终点了于是急忙追赶但为时已晩乌龟还是先到达了终点．下图中与故事情节相吻合的是（）A．B．C．D．10．如图1 点P从△ABC的顶点B出发沿B→C→A匀速运动到点A图2是点P运动时线段BP的长度y随时间x变化的关系图象其中曲线部分为轴对称图形M为最低点则△ABC的面积是（）A．6B．9C．12D．1511．如图正方形ABCD的边长为2cm动点P Q同时从点A出发在正方形的边上分别按A→D→C A→B→C的方向都以1cm/s的速度运动到达点C运动终止连接PQ 设运动时间为xs△APQ的面积为ycm2则下列图象中能大致表示y与x的函数关系的是（）A．B．C．D．12．如图：菱形ABCD的对角线AC上有一动点P BP的长y关于点P运动的路程x的函数图像如图则该菱形的面积为（）A．12B．24C．48D．9613．如图在四边形ABDC中CD∥AB,DB⊥AB矩形EFGH的边EH与AB同在直线l上且点A,E重合已知EH=4,AB=13,CD=4,EF=BD=6．将矩形EFGH沿直线l向右平移当点E,B重合时停止．设点E平移的距离为x矩形EFGH与四边形ABDC重合部分的面积为y 则y关于x的函数图象大致为()A．B．C．D．14．如图在矩形ABCD中对角线AC=4,AC的垂直平分线EH交CD于点E交AC于点H．设AB=x,CE=y则y关于x的函数图像大致为（）A．B．C．D．15．如图1 在△ABC中点D是边AB的中点动点E从点A出发沿A→C→B运动设点E运动的路程为x△BED的面积为y y与x之间的函数图象如图2所示．有下列结论：①AC=2②△ABC的面积为1 ③当x=3时y=1．其中正确的有（）2A．①②B．①③C．②③D．①②③16．如图点A的坐标为（01）点B是x轴正半轴上的一动点把线段AB以A为旋转中心逆时针方向旋转90°得到线段AC设点B的横坐标为x点C的纵坐标为y能表示y与x的函数关系的图象大致是（）A．B．C．D．17．如图（a）A B是△O上两定点∠AOB=90°圆上一动点P从点B出发沿逆时针方向匀速运动到点A运动时间是x(s)线段AP的长度是y(cm)．图（b）是y随x变化的关系图象其中图象与x轴交点的横坐标记为m则m的值是（）A．8B．6C．4√2D．14318．已知动点P以2cm s⁄的速度沿图①所示的边框从B→C→D→E→F→A的路径运动记三角形ABP的面积为S S（cm2）与运动时间t（s）的关系如图②所示．若AB=6cm根据图中提供的信息给出下列结论：①m=24②n=17③S的最大值为42 ④当S= 30时t=7．其中结论正确的有（）A．4个B．3个C．2个D．1个19．如图AC，BD是△O直径且AC⊥BD动点P从圆心O出发沿O→C→D→O路线作匀速运动设运动时间为t（秒）∠APB=y（度）则下列图象中表示y与t之间的函数关系最恰当的是（）A．B．C．D．．动点P沿路径20．如图在四边形ABCD中AD//BC∠D=90°,AB=BC=5,tanA=43A→B→C→D从点A出发以每秒1个单位长度的速度向点D运动．过点P作PH⊥AD 垂足为H．设点P运动的时间为x（单位：s）△APH的面积为y则y关于x的函数图象大致是（）A．B．C．D．参考答案1．解：根据分析知运动速度v先减小后增大．故选：C．2．解：从甲地匀速行驶到乙地y随x的增大而增大到达乙地后按原来的速度返回y 随x的增大而减小．故选：A．3．解：吴老师家出发匀速步行8min到公园表示从(0 400)运动到(8 0)在公园停留4min 然后匀速步行6min到学校表示从(12 0)运动到(18 600)故选：C．×2x=x4．解：当P点由A运动到B点时即0≤x≤2时y=12×2×2=2当P点由B运动到C点时即2＜x＜4时y=12符合题意的函数关系的图象是A故选：A．5．解：因为P点是从C点出发的C为初始点观察图象x=0时y=6则AC=6P从C向B移动的过程中AP是不断增加的而P从B向A移动的过程中AP是不断减少的因此转折点为B点P运动到B点时即x=a时BC=PC=a此时y=a+2即AP=AB=a+2AC=6,BC=a,AB=a+2△∠C=90°由勾股定理得：(a+2)2=62+a2解得：a=8△AB=10,BC=8当点P为BC中点时CP=4△AP=√AC2+CP2=√62+42=2√13故选：D．6．解：过C作CD⊥AB于D如图由函数图像知当直线l与CD重合时y的值最大为6AD⋅CD=6此时AM=AD=412△CD=3△AC=BC CD⊥AB△AB=2AD=8由勾股定理得：AC=√AD2+CD2=5△△ABC的周长为AC+BC+AB=2AC+AB=18(cm)故选：C．7．解：从图2知：△当4≤x≤5时y的值不变△相应的对应图1是：直线EF从过点A开始到经过C点结束EF的值不变即当BE=4FE经过点A当BE=5时EF经过点C△BC=5△①正确从图1知BE1=4，E1F1=2，∠BF1E1=90°△AB=√42−22=2√3△②不正确如图2当4≤x≤5时S△BEF=12BE⋅FH△FH不变BE变化△△BEF的面积变化△③不正确△正确的有1个故选：B8．解：①当点P在点D时设正方形的边长为a(a>0)y=12AB·AD=12a2=4.5a2=9a=3②当点P在点C时y=12EP·AB=12×3EP=3,解得EP=2即EC=2,BE=1③当x=5时如图所示则PD=5−3=2PC=3−PD=3−2=1即y=S正方形ABCD −(S△ABE+S△ECP+S)△APD=3×3−12×(3×1+2×1+3×2)=9−12×11=3.5故选：D．9．解：由图可知：乌龟的路程一直匀速增加兔子的路程变化有三个阶段 1 匀速增加 2 睡了一觉不变 3 当它醒来时发现乌龟快到终点了于是急忙追赶加速增加但没超过乌龟即在乌龟下方△符合题意的图象是C故选C．10．解：由图得当点P运动到点C和店A处时BP长都是5 即BC=BA=5当BP最短时即BP垂直AC时长为4如图在Rt△BCP中∵BC=5BP=4∴PC=√BC2−BP2=3∵BC=BA BP⊥AC∴CP=AP=3∴AC=6∴S△ABC=12AC⋅BP=12×6×4=12．故选：C．11．解：①当0≤x≤2时∵正方形的边长为2cm∴y=S△APQ=12AQ•AP=12x2②当2<x≤4时y=S△APQ=S正方形ABCD−S△CP′Q′−S△ABQ′−S△AP′D=2×2−12(4−x)2−12×2×(x−2)−12×2×(x−2) =−12x2+2x所以y与x之间的函数关系可以用两段二次函数图象表示纵观各选项只有A选项图象符合．故选：A．12．解：连接BD交BD于点O由函数图象知当BP⊥AC时BP最短此时BP=6即BO=6AO=8∴BD=12,AC=16∴该菱形的面积为：12AC⋅BD=96故选：D．13．解：过点C作CM⊥AB于点M．当0≤x<4时如图1,AE=x即∵PECM=AEAM∴PE6=x9PE=23x∴y=12x⋅23x=13x2当4≤x<9时如图2 AH=x−4∵AHAM=HQCM∴x−49=HQ6HQ=23(x−4)∴x9=PE6∵AEAM =PECM,即PE=23x∴y=12[23(x−4)+23x]×4=83x−163当9≤x≤13时如图3∵AHAM=HQCM∴x−49=HQ6即HQ=23(x−4)∴GQ=6−23(x−4)=−23(x−13)CG=4−(x−9)=−x+13∴y=4×6−1 2(−x+13)⋅[−23(x−13)]=−13(x−13)2+24．综上所述D项正确．故选：D．14．解：△四边形ABCD是矩形∴DC∥AB,∠B=90°∴∠ECH=∠CAB．∵AC的垂直平分线EH交CD于点E交AC于点H∴∠EHC=90°CH=12AC=2△△ECH∽△CAB△EC CA =CHAB即y4=2x∴y=8x(0<x<4)．△对应函数图像为A选项．故选：A．15．解：△在△ABC中点D是边AB的中点△当点E在AC上时S△ADE=S△BDE过点E作EH⊥BA于H则EH=AE⋅sinA=x⋅sinA△y=12x⋅sinA⋅AD△此过程中y随着x的增大而增大由图2可知当x=2时y在0≤x≤2有最大值1 即此时点E运动到了点C即AC=2故①正确△S△ACD=1△S△ABC=2S△ACD=2故②错误同理可知当x=4时点E运动到了点B△BC=4−AC=2当x=3时此时点E为BC的中点△S△BAE=12S△ABC=1又△点D是边AB的中点△S△BDE=12S△ABE=12故③正确故选：B．16．解：过点C作CD⊥y轴于点D∵∠AOB=90°∴∠CDA=∠AOB∠OBA+∠OAB=90°∵∠CAB=90°∴∠CAD+∠OAB=90°∴∠CAD=∠OBA又∵AB=AC∴ΔAOB≌ΔCDA(AAS)∴DA=OB=x∴y=OD=DA+OA=x+1又∵点B是x轴正半轴上的一动点∴x＞0故选：A.17．解：如图当点P运动到PA过圆心O即PA为直径时AP最长由图（b）得AP最长时为6 此时x=2∵∠AOB=90°∴∠POB=90°∴此时点P路程为90度的弧∵点P从点B运动到点A的弧度为270度∴运动时间为2×3=6故选：B．18．解：由图2可知从B→C运动时间为4s△BC=2×4=8cm同理：CD=2×(6−4)=4cm DE=2×(9−6)=6cm△EF=AB−CD=6−4=2cm AF=BC+DE=8+6=14cm×AB×BC=24cm2△m=S△ABC=12n=(BC+CD+DE+EF+AF)÷2=17s×AB×AF=42cm2当P运动到点E时S最大且为12△S 的最大值为42 m =24△当S =30时 t 的值有两个故①②③正确 ④错误故选：B ．19．解：△AC ⊥BD△∠AOB =90°根据题意 分3个阶段P 在线段OC 上时 ∠APB 逐渐减小 到C 点时 ∠APB =45° 所以图像是下降的线段 ②P 在弧CD 之间 ∠APB 保持45° 大小不变 所以图像是水平的线段③P 在DO 之间 ∠APB 逐渐增大 到O 点时 ∠APB =90° 所以图像是上升的线段 分析可得：C 符合3个阶段的描述故选C ．20．解：①当点P 在AB 上运动时△AB =BC =5 tanA =43△AP ：PH ：AH =5：4：3△AP =x△PH =45x AH =35xy =12AH ⋅PH =12⋅35x ⋅45x =625x 2 图象为二次函数且当x =5时 y =6 故B C D 不正确 则A 正确②当点P 在BC 上运动时 如下图 过点B 作BE △AD 于点E△tanA=43 AB =5△BE =4 AE =3△AB +BP =x△BP =EH =x -5△AH =2+x -5=x -2△y=12AH⋅PH=12⋅(x−2)⋅4=2x−4为一次函数且当x=10时y=16③当点P在CD上运动时此时AD=AH=3+5=8△AB+BC+CP=x△PH=AB+BC+CD-x=14-x△y=12AH⋅PH=12×8⋅(14−x)=−4x+56故选：A．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
题型一 动点问题的函数图像类型一 判断函数图像(2014.8)1. 如图，AB 是半圆O 的直径，点P 从点O 出发，沿OA →AB ︵→BO 的路径运动一周，设点P 到点O的距离为s ，运动时间为t ，则下列图象能大致地反映s 与t 之间的关系的是( )第1题图2. 如图，在Rt △ABC 中，AC ＝BC ＝4 cm ，点D 是AB 的中点，点F 是BC 的中点，动点E 从点C 出发，沿CD →DA 以1 cm/s 的速度运动至点A ，设点E 运动的时间为x s ，△EFC 的面积为y cm 2(当E ，F ，C 三点共线时，设y ＝0)，则y 与x 之间的函数关系的大致图象是( )第2题图3.如图，A 、B 是反比例函数y ＝k x(k ＞0)在第一象限图象上的两点，动点P 从坐标原点O 出发，沿图中 箭头所指方向匀速运动，即点P 先在线段OA 上运动，然后在双曲线上由A 到B 运动，最后在线段BO 上运动，最终回到点O .过点P 作PM ⊥x 轴，垂足为点M ，设△POM 的面积为S ，点P 运动时间为t ，则S 关于t 的函数图象大致为( )第3题图4.如图，在菱形ABCD中，∠B＝60°，AB＝2，动点P从点B出发，以每秒1个单位长度的速度沿折线BA→AC运动到点C，同时动点Q从点A出发，以相同速度沿折线AC→CD运动到点D，当一个点停止运动时，另一个点也随之停止.设△APQ的面积为y，运动时间为x秒，则下列图象能大致反映y与x之间函数关系的是()第4题图5.如图，在矩形ABCD中，对角线AC与BD交于点O，点M为线段AC上一个动点，过点M作EF∥BD 交AD(或DC)于点E，交AB(或BC)于点F，已知AC＝5，设AM＝x，EF＝y，则y关于x的函数图象大致为()第5题图6. (2019衢州)如图，正方形ABCD的边长为4，点E是AB的中点，点P从点E出发，沿E→A→D→C 移动至终点C，设点P经过的路径长为x，△CPE的面积为y，则下列图象能大致反映y与x函数关系的是()第6题图类型二分析函数图像1.如图①，点P从矩形ABCD的顶点B出发，沿射线BC的方向以每秒1个单位长度的速度运动，过点P作PG⊥AP交射线DC于点G.如图②是点P运动时CG的长度y随时间t变化的图象，其中点Q是第一段曲线(抛物线的一部分)的最高点，则AB的长度是()第1题图A. 2B. 3C. 4D. 2 32.(2019郑州模拟)如图①，四边形ABCD中，AB∥CD，∠B＝90°，AC＝A D.动点P从点B出发，沿折线B－A－D－C方向以 1 cm/s的速度匀速运动，在整个运动过程中，△BCP的面积S(cm2)与运动时间t(s)的函数图象如图②所示，则AD等于()第2题图A. 5 cmB. 34 cmC. 8 cmD. 2 3 cm3.如图①，菱形ABCD中，∠B＝60°，动点P以每秒1个单位的速度自点A出发沿线段AB运动到点B，同时动点Q以每秒2个单位的速度自点B出发沿折线B－C－D运动到点D.图②是点P、Q运动时，△BPQ的面积S随时间t变化关系图象，则a的值是()第3题图A. 2B. 2.5C. 3D. 2 34.如图①，在正方形ABCD中，动点E从点A出发，沿A－B－C运动，当点E到达点C时停止运动，过点E作EF⊥AE，交CD于点F，设点E运动的路程为x，FC＝y(当点A，E重合时，点D，F重合；当点C，E重合时，不妨设y＝0)，y与x的函数关系的大致图象如图②，当点E在BC上运动时，FC的最大长度是1，则正方形ABCD的面积是()第4题图A. 8B. 12C. 16D. 4.85.如图①，在矩形ABCD中，动点P从点A出发，沿A→B→C运动，设P A＝x，点D到直线P A的距离为y，且y关于x的函数图象如图②所示，则当△PCD和△P AB的面积相等时，y的值为.第5题图6.如图①，已知点E，F，G，H是矩形ABCD各边的中点，动点M从点E出发，沿E→F→G匀速运动，设点M运动的路程为x，点M到矩形顶点B的距离为y，如果表示y关于x函数关系的图象如图②所示，那么四边形EFGH的面积是.第6题图参考答案类型一 判断函数图象1. C 【解析】点P 在OA 上从点O 向点A 运动的过程中，s 随着t 的增大而增大，点P 在AB ︵上运动时，s ＝OP ＝12AB (定值)，点P 在OB 上从点B 向点O 运动的过程中，s 随着t 的增大而减小． 2. A 【解析】∵在Rt △ABC 中，AC ＝BC ＝4，∴AB ＝42，AD ＝CD ＝22，CF ＝2，当点E 在CD 上时，CE ＝x ，点E 到BC 的距离h 1＝22x ，∴y ＝12×2×22x ＝22x (0≤x ≤22)；当点E 在AD 上时，BE ＝BD ＋DE ＝CD ＋DE ＝x ，∴点E 到FC 的距离h 2＝22BE ＝22x ，∴y ＝12×2×22x ＝22x (22≤x ≤42)． 3. D 【解析】设∠AOM ＝α，点P 运动的速度为a ，当点P 从点O 运动到点A 的过程中，S ＝12OM ·PM ＝12at ·cos α·at ·sin α＝12a 2·cos α·sin α·t 2，由于α及a 均为常量，从而可知图象本段应为抛物线，且S 随着t 的增大而增大；当点P 从A 运动到B 时，由反比例函数性质可知△OPM 的面积为12k ，保持不变，本段图象应为与x 轴平行的线段；同理可得，当点P 从B 运动到O 过程中，S 也是t 的二次函数，且S 随着t 的增大而减小．4. B 【解析】∵四边形ABCD 为菱形，且∠B ＝60°，AB ＝2，∴当0＜t ＜2时，△APQ 的面积y ＝12t ·(2－t )·sin60°＝－34t 2＋32t ，函数图象为开口向下的一段抛物线，且当t ＝1时，y 最大值为34；当2＜t ＜4时，△APQ 的面积y ＝12(t －2)·(t －2)·sin60°＝34(t －2)2，函数图象为开口向上的一段抛物线，且当t ＝4时，y 最大值为3，故选B .5. B 【解析】当0≤x ≤2.5时，如解图①，∵四边形ABCD 是矩形，∴OA ＝OB ＝OC ＝OD ，∴∠OAD ＝∠ODA ，∵EF ∥BD ，∴∠ODA ＝∠MEA ，∴∠OAD ＝∠MEA ，∴ME ＝MA ，同理可得AM ＝MF ，∴EM ＝AM ＝MF ，∴EF ＝2AM ，即y ＝2x ；当2.5<x ≤5时，如解图②，由题意知CM ＝AC －AM ＝5－x ，∵ME＝MC ＝MF ，∴EF ＝2MC ，即y ＝2(5－x )＝10－2x .综上所述，y ＝⎩⎪⎨⎪⎧2x （0≤x ≤2.5）10－2x （2.5<x ≤5）.图① 图②第5题解图6. C【解析】∵AB＝4，点E是AB的中点，∴AE＝BE＝2，当0≤x≤2时，如解图①，y＝S△CPE＝1 2PE·BC＝2x，∴此段函数图象是正比例函数的一部分；当2<x≤6时，如解图②，y＝S△CPE＝S正方形ABCD－S△BCE －S△APE－S△PCD＝42－12×4×2－12×2×(x－2)－12×4×[4－(x－2)]＝x＋2，∴此段函数图象是一次函数的一部分；当6<x≤10时，如解图③，y＝S△CPE＝12PC·BC＝12(10－x)×4＝－2x＋20，∴此段函数图象是一次函数的一部分，综上所述，根据各段图象及x的取值范围，可得函数图象如选项C所示．图①图②图③第6题解图类型二 分析函数图象1. B 【解析】结合图形分析函数图象可得：当点P 运动到点C 的位置时，CG ＝0，∴BC ＝4.当点P运动到线段BC 的中点时，CG ＝43.∵∠B ＝90°，∴∠BAP ＋∠APB ＝90°，∵PG ⊥AP ，∴∠APG ＝90°，∴∠APB ＋∠CPG ＝90°，∴∠BAP ＝∠CPG ，又∵∠ABP ＝∠PCG ＝90°，∴△ABP ∽△PCG ，∴AB PC ＝BP CG，当点P 为BC 的中点时，BP ＝PC ＝2，∴AB 2＝243，解得AB ＝3. 2. B 【解析】结合图形分析函数图象可得，当t ＝3时，点P 到达A 处，即AB ＝3；如解图，过点A作AE ⊥CD 于点E ，则四边形ABCE 为矩形，∵AC ＝AD ，∴DE ＝CE ＝12CD .当S ＝15时，点P 到达点D 处，则S ＝12CD ·BC ＝12·2AB ·BC ＝3×BC ＝15，则BC ＝5，在Rt △ABC 中，由勾股定理得，AD ＝AC ＝AB 2＋BC 2＝34.第2题解图3. D 【解析】由题图②得，t ＝4时两点停止运动，∴点P 以每秒1个单位的速度从点A 运动到点B 用了4秒，∴AB ＝4，∵点Q 运动到点C 之前和之后，△BPQ 面积算法不同，即t ＝2时，S 的解析式发生变化，∴题图②中点M 对应的横坐标为2，此时P 为AB 中点，点C 与点Q 重合，如解图，连接AC ，∵菱形ABCD 中，AB ＝BC ＝4，∠B ＝60°，∴△ABC 是等边三角形，∴CP ⊥AB ，BP ＝12AB ＝2，∴CP ＝BC 2－BP 2＝42－22＝23，∴a ＝12BP ·CP ＝12×2×23＝2 3.第3题解图4. C 【解析】如解图，设AB ＝a ，当点E 在BC 上运动时(不与点B 、C 重合)，∵AE ⊥EF ，∴△EFC∽△AEB ，∴EC AB ＝FC EB ，即2a －x a ＝y x －a ，∴y ＝－1a x 2＋3x －2a ，－1a <0，当x ＝－32×（－1a ）＝32a 时，y 取得最大值，此时点E 为BC 的中点，y ＝1，把(32a ，1)代入y ＝－1ax 2＋3x －2a ，解得a ＝4，即AB ＝4，故正方形ABCD 的面积为4×4＝16.第4题解图5. 121313【解析】当P 点在AB 上运动时，D 点到AP 的距离不变，始终是AD 长，从图象可以看出AD ＝4，当P 点到达B 点时，从图象看出x ＝3，即AB ＝3.当△PCD 和△P AB 的面积相等时，P 点在BC 中点处，此时△ADP 面积为12×4×3＝6，在Rt △ABP 中，AP ＝AB 2＋BP 2＝13，则12AP ·y ＝6，解得y ＝121313. 6. 24 【解析】如解图，连接BD ，EG ，FH ，∵点E ，F ，G ，H 是矩形ABCD 各边的中点，∴EF ∥BD ∥GH ，EF ＝GH ＝12BD ，∴四边形EFGH 是平行四边形，又∵EF ＝EH ，∴平行四边形EFGH 是菱形，由题图②得BE ＝3，点M 运动到点G 时，运动路程为10，又∵EF ＝FG ，则可知菱形的边长为5，即EF ＝FG ＝GH ＝HE ＝5，∴AF ＝4，AD ＝8，∴S 菱形EFGH ＝12EG ·FH ＝24.第6题解图。