场地设计标高的确定
场地设计标高确定方法

场地设计标高确定方法一、收集基础资料1. 地形地貌:了解项目所在地的地形特征,如山地、丘陵、平原等,为后续标高设计提供依据。
2. 水文地质:收集项目周边的水文地质资料,包括地下水位、地表水系、土壤类型等。
3. 气象资料:了解项目所在地的气候特点,如年降水量、蒸发量、气温等。
4. 邻近设施:调查周边建筑物、道路、管网等设施的标高情况,以便于场地标高与周边设施的衔接。
二、确定设计原则1. 安全性:确保场地设计标高能够满足防洪、排涝、防塌陷等安全要求。
2. 经济性:在满足使用功能的前提下,尽量降低土石方工程量,减少投资。
3. 合理性:充分考虑地形地貌、水文地质等因素,使场地标高与周边环境相协调。
4. 可实施性:确保场地标高设计在施工过程中具有可行性,便于施工操作。
三、计算场地设计标高1. 初步确定场地设计标高范围:根据地形地貌、水文地质等基础资料,初步确定场地设计标高的上限和下限。
2. 确定设计标高计算方法:根据项目特点,选择合适的设计标高计算方法,如平均高程法、最小二乘法、加权平均法等。
3. 计算场地设计标高:运用所选计算方法,结合地形地貌、水文地质等因素,计算出场地设计标高。
四、场地设计标高调整与优化1. 分析计算结果:对比初步确定的场地设计标高范围,分析计算结果的合理性。
2. 考虑影响因素:结合地形地貌、水文地质、邻近设施等因素,对场地设计标高进行调整。
3. 优化设计:在确保安全、经济、合理的前提下,对场地设计标高进行优化,使其更加符合项目需求。
场地设计标高确定方法五、实地踏勘与验证1. 实地考察:设计团队需亲自前往现场,对地形地貌、水文地质等情况进行实地考察,验证前期收集资料的准确性。
2. 采样分析:对土壤、水体等进行采样分析,以获取更详细的地质信息,为标高设计提供科学依据。
3. 评估风险:根据实地考察结果,评估可能存在的风险,如地质灾害、环境污染等,并在标高设计中予以考虑。
六、多方沟通与协调1. 与政府部门沟通:了解当地规划、水利、环保等政策要求,确保场地设计标高符合法律法规。
浅析工业建设场地设计标高的确定

4 根 据 厂 外 现 有 或 规 划 的排 水 接 口标
高 来 确 定
确 定场 地设 计 标 高 的首 要 条件是 满 足场 地排 水 要 求 , 区应该 有 安 全 、 靠 的排 水 方 向 , 厂 可 以保 证 厂
区在遇 暴雨 时不 出现 大 面积 积 水 , 免 厂 外 雨 水 倒 避 灌, 而影 响正 常 的生 产 或造 成财 产损 失 。
社 。9 8 19 .
t e S h e d rn w e e ain s f ha d r u o t n h c n i e e g n r t o r wa e a t ma i o t o p afr — Un t a d d d c td e eo lto m — iy n a e ia e d v lpme t o l n t o UAG. T p p r e p ans t e c nsiu in, ln he a e x l i h o tt to ie
划 。这种 方 法适合 于 场地 一 面或 多面 I 的情 况 。 临路
的措 施 , 只需 使堤 顶 标 高 至少 高 出汇 水 区域 内设 计
内涝水位 05m, . 这时场地雨水 、 污水必须依靠排水
泵站 才 能排 出厂 外 。这 种 情 况 下 , 地 设计 标 高 不 场 受 内涝水 位 的影 响 , 根据 原 始 地 形 按 照 土方 量 平 可 衡原 则 确定场 地设 计 标 高 , 必 须 保 证 不 淹 没有 重 但
山区地段时, 为了保证企业 的安全 , 保证厂区不被洪
水、 潮水 或 内涝水 淹没 , 计 中必 须 采 取 有效 、 设 可靠
的防洪 设施 。
一
般情 况 下 , 与企业 规 模 相 对应 的 防洪设 计 以
场地标高选择计算

场地标高选择计算场地标高选择是一个重要的工程设计问题,涉及到土方工程、场地排水、建造成本等多个方面。
在选择场地标高时,需要综合考虑以上因素,以得出最优的标高方案。
以下是一些计算方法,可供参考。
1.考虑土方工程量在选择场地标高时,一个重要的因素是土方工程量。
土方工程量可以根据场地的高程和设计标高计算得出,计算公式如下:Q = [(h1-h2)×Axbyc] - (A1x1b1y1c1) - (A2x2b2y2c2)其中:Q为土方工程量,单位为立方米;h1为场地最低点的高程,单位为米;h2为场地最高点的高程,单位为米;Axbyc为场地的面积,其中A为长度,B为宽度,C为平均填挖深度,单位为平方米;(Ax1by1c1)为挖方区域的面积及平均填挖深度,单位为平方米;(A2x2by2c2)为填方区域的面积及平均填挖深度,单位为平方米;x1、y1为挖方区域的长度和宽度,单位为米;x2、y2为填方区域的长度和宽度,单位为米。
在计算土方工程量时,需要以图纸为基础,综合考虑各因素对标高的影响。
在确定最优标高时,应当尽可能使土方工程量最小化。
2.考虑场地排水标高的选择也直接影响到场地的排水情况。
为了保证场地排水顺畅,应尽量选择较高的标高,以减少场地内部的汇水面积。
但是,如果标高过高,可能会导致雨水无法顺利排出,从而影响场地的使用效果。
因此,在选择标高时,需要充分考虑场地的地形、气候等条件,以得出最优方案。
3.考虑建造成本除了土方工程量和场地排水之外,建造成本也是选择场地标高时需要考虑的因素之一。
较高的标高意味着需要更多的土方工程量,进而增加建设成本。
因此,在选择标高时,需要综合考虑土方工程量、场地排水和建造成本三个因素,以得出最优方案。
在实际操作中,可以采用一些软件工具来进行计算。
例如,AutoCAD软件可以根据设计图纸进行精确计算,可以大大提高计算效率和准确性。
同时,一些专门针对场地设计计算的软件也可以提供更为全面和准确的服务。
确定竖向场地设计标高考虑五大因素

确定竖向场地设计标高考虑五大因素发帖人: my198442 点击率: 972在竖向布置中,合理确定场地标高和建筑物、构筑物、铁路、道路的标高,是一项重要任务。
而在确定设计标高时,必须综合考虑以下主要因素:(一)方便生产上的联系生产上的联系要求,保证车间之间有良好的运输装卸条件。
对于生产上有密切联系的车间、仓库、堆场,其设计标高要与相互之间所采用的运输方式相适应,使进入车间的铁路、道路具有合适的标高和坡度。
对于管线较多的工厂,还要考虑地下管道的埋没深度对竖向标高的要求。
在坡地,联系密切的建筑物宜组合布置在同一台阶上。
为了保证生产使用要求,生产车间的地面,一般不宜设台阶或斜坡。
但当场地地形复杂,进入车间的运输线路标高不能与车间地面标高相同时,若生产上的联系许可,车间的地面方可采用台阶。
(二)与交通运输及排水设施相协调符合厂内、外铁路、道路、排水设施等对连接点的竖向标高要求,并使厂内外运输线路具有合理的横、纵断面。
在改、扩建工厂中,还须考虑新旧厂区的衔接问题。
(三)满足排水和防洪要求场地应该考虑排水系统对设计标高的要求。
一般平整场地的表面,均应具有不小于3‰的坡度,以保证排除雨水。
在确定道路标高时,应使雨水从车间、仓库、堆场排向路面或道路两侧的明构。
室内外地坪的高差,应保证雨水不倒灌到建筑物内,并考虑生产联系和运输装卸的方便。
一般建筑物的室内地坪标高,应高出建筑物室外散水坡脚标高15厘米以上。
露天堆场等的地面标高应高出周围场地,并没有≥5‰的排水坡度。
有贵重设备、材料或受水淹后对生产损失很大的车间、仓库地坪标高,宜略高于一般车间、仓库。
对于全厂起控制作用的主要生产车间或重型厂房,在考虑车间设计标高时,应注意地基下沉,以免造成今后室内地坪低于室外地坪的不合理现象。
引入建筑物的铁路轨顶标高,应根据生产和铁路运输装卸要求而定。
一般情况下,轨顶标高宜与建筑物地坪标高相同。
(四)土石方工程量较小尽量使全厂土石方平衡和工程量较小。
场地设计标高H的确定

•同济大学版《土木工程施工》给出了用最小二 施 乘法原理求最佳设计平面的方法。
•并不是总会将挖填平衡作为目标或主要约束条 工件
7
2019/11/21
土木与建筑学院
第一章 土方工程 第二节 土方量计算
2、场地设计标高H0的调整
土
上述公式所计算的设计标高H0系一理论值,实际上
第一章 土方工程 第二节 土方量计算
场地平整: 土 通过挖填后,将自然地面 改造成 要求的场
地
木
工 • 场地平整土方量的计算思路: 先确定一个场地设计标高,以此标高为基准
程 分别计算标高以下的填方量和标高以上的挖方 量。
施
工
3
2019/11/21
土木与建筑学院
第一章 土方工程 第二节 土方量计算
•确定方法和步骤:
土 l、初步确定场地设计标高H0 (1)在具有等高线的地形图上将
木
施工区域划分方格(边长
工 a=10m~50m);
(2)确定各小方格的角点高程。 程 A.插值法:根据地形图相邻两
等高线的高程求得。
施
B.测量法:无地形图时,在 工 现场地面用木桩或钢钎打好方
格网,用仪器测出角点标高。 场地设计标高计算
则属于两个方格公共的角点标
工
高,H22则属于四个方格公共
的角点标高,它们分别在上式
中要加一次、二次、四次。
场地设计标高计算
5
2019/11/21
土木与建筑学院
第一章 土方工程 第二节 土方量计算
土 因此,上式可改写成下列 形式:
木
H
土木施工工程学场地设计标高计算的一般方法
1.2 场地设计标高的确定
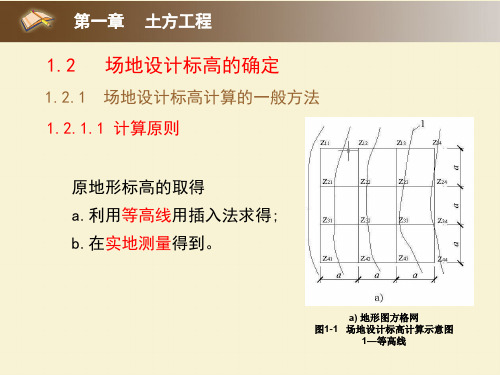
1.2.1 场地设计标高计算的一般方法 1.2.1.1 计算原则
原地形标高的取得 a.利用等高线用插入法求得; b.在实地测量得到。
a) 地形图方格网 图1-1 场地设计标高计算示意图
1—等高线
第一章 土方工程
1.2.1.1 计算原则
按照挖填土方量相等的 原则(图1-1b),场地设计 标高可按下式计算:
泄水坡度。
zo
1 4n
(
z1 2
z2 3
z3 4
z4 )
因此,应根据泄水要求计算出实际施工时所采用的设计标高。
第一章 土方工程
1.2.1.2 计算步骤
设计标高调整 以 zo 作为场地中心的
标高(图1-2),则场地任 意点的设计 标高为:
z'i zo lxix lyiy
Hi 为负值,则该点为挖方。
(1-3)
第一章 土方工程
1.2.1.1 计算原则
zo
1 4n
n i 1
( zi1
zi 2
zi3
zi4 )
(1-3)
角点的标高在计算过程中被应用的次数( Pi ) 反映 了各角点标高对计算结果的影响程度,测量上的术语 称为“权”。
考虑各角点标高的“权”,式(1-3)可改写成更 便于计算的形式:
1
zo 4n ( z1 2 z2 3 z3 4 z4 )
式中
z1 — 一个方格独有的角点标高; z2、z3、z4 — 分别为二、三、四个方格
所共有的角点标高。
(1-4)
第一章 土方工程
1.2.1.2 计算步骤
场地平整设计标高的确定

场地设计标高的调整与施工高度的确定
计算步骤:
1. 划分场地方格网;
2. 计算或实测各角点的原地形标高; 3. 按上式计算场地设计标高; 4. 设计标高调整; 5. 施工高度计算。
下面分别讨论:
设计标高调整与施工高度计算问题
场地设计标高H0的调整 按上述公式所计算的设计标高H0系一理论值,实际上还需要考虑以
方就近取于场外而引起挖、填土方量的变化后,需增减设计标高。 上述四方面因素对H0的影响同时出现的机会较小,可根据现场情
况适当考虑。
考虑泄水坡度对设计标高的调整
实际场地都有一定的泄水坡度。应考虑泄水坡度对设计标高的 影响,最后确定场地各方格角点的设计标高。
以计算出的设计标高H0作为场地中心点的标高,场地内任意一个 角点的设计标高为:
H’i=H0±lx ix±ly iy H’i——场地内任意一个角点的设计标高(m)
±——该点比H0高则取“+”,反之取“-” 离(m) 于2‰) lx 、 ly——该点于 x——x 、 y——y 方向距场地中心点的距
ix 、 iy——场地在 x——x 、 y——y 方向的泄水坡度(不小
例如 H42=H0-1.5a ix-0.5a iy
场地设计标高的确定,一般有两种方法: 1.一般方法:如场地比较平缓,对场地设计标高无特殊要 求,可按照“挖填土方量相等”的原则确定场地设计标高; 2.用最小二乘法原理求最佳设计平面: 不仅可满足土方挖填平衡、还可做到土方的总工程量最小。
l. 初步确定场地设计标高H0
(1)在具有等高线的地形图上将施工区域划分 为边长a=10m~40m的若干方格如图所示; (2)确定各小方格的角点高程。可根据地形图 上相邻两等高线的高程,用插值法求得。在无地形 图的情况下,也可以在地面用木桩或钢钎打好方格 网,然后用仪器直接测出方格角点标高。 计算场地设计标高的原则:
场地、建(构)筑物、道路和排水沟标高的确定

场地、建(构)筑物、道路和排水沟标高的确定场地、建(构)筑物、道路和排水沟标高的确定注意:在同一张图中应采用同一高程系统。
4.1.1场地标高1.当场地临水时,场地标高的最低点应高出河流常年洪水位标高0.5m,对于湖泊和海洋尚应增加波浪侵袭和壅水高度。
否则应采取工程措施,如砌筑防洪堤、防浪堤等。
其中河流常年洪水位标高系根据防洪标准确定。
2.当场地与城市道路有一段距离时,场地标高与已有城市道路标高应衔接,该段道路的坡度应控制在 0.3%~8%之间。
3.当场地紧挨城市道路时,场地红线处的标高应高出城市道路中心线标高 200~400mm。
4.场地的地面坡度、道路坡度、场地的地面形式;5.地形坡度比较大的地方,先要进行场地平整,在平整时应当注意地下水的深度和土方量的平衡。
必要时用方格网或断面图来计算土方量。
4.1.2建筑物室内±0.00标高建筑物室内±0.00 标高,应根据该建筑物所处的场地整平最高点标高确定,而该建筑物散水的标高一般宜高出该点200mm 左右,散水的标高可以随室外场地坡度的变化而变化。
但散水标高不应高于室内陆坪的防潮层,也不能使建筑物的基础埋深小于当地的冰冻线深度。
散水标高加上室内外高差就是室内±0.00 标高。
室内外高差可以根据该建筑物是否通行车辆决定,需要通行车辆的,室内外高差宜为 150m;不需要通行车辆的,可为 300~900mm;有半地下室或有特殊要求的例外。
4.1.3道路标高确定场地设计标高和建筑物±0.00 标高后,进而确定道路标高。
因为建筑物占地面积大,标高定得是否合理,不但涉及土方量的大小,对环境、美观也会有所影响,而道路标高的影响则较小。
确定道路标高时,应使道路有合理的横、纵断面,但更重要的是,应使建筑物周围的雨水及场地的雨水,能够顺畅便捷地排向路面或道路两侧的明沟。
这就要求建筑物的室外地坪至路边应有0.5%~2%的坡度,以及场地有大于0.3%的坡度坡向道路或路边沟。
土方工程场地设计标高的确定

土方工程场地设计标高的确定场地设计标高是进行场地平整和土方量计算的依据,也是总施工图规划和土方竖向设计的依据。
合理确定场地的设计标高,对减少土方量、节约土方运输费用、加快施工进度等都有重要的意义。
选择设计标高时应满足生产工艺和运输的要求;尽量利用地形,使场内挖填平衡,以减少土方运输费用;要有一定的泄水坡度(≥2‰),满足排水要求;考虑最高洪水位的影响。
场地设计标高一般应在设计文件上规定,若设计文件没有规定,可按下述步骤和方法确定。
一、划分土方计算方格网划分方格网的基本步骤:①在一定比例尺的地形图上,根据平整场地的范围划分方格网;②根据地形变化程度及要求的计算精度,确定方格网的边长,一般取10~40m,地形复杂取小值,地形平坦取大值,一般取边长为20m;③在各方格的左上方逐一标出其角点的编号,以便进行计算。
二、计算各角点的实际标高各角点的实际标高也称为角点的自然地面标高,可根据地形图上相邻两等高线的高程,用“数解法”或“图解法”求得各角点的标高。
三、计算场地的设计标高按照场地内挖填方平衡的原则,用下式计算场地平整的设计标高。
——一个方格独有的角点标高;式中H1H——两个方格共有的角点标高;2——三个方格共有的角点标高;H3——四个方格共有的角点标高;H4N——方格数;∑——表示代数和。
四、场地设计标高的调整是一理论值,实际上还需要考虑以下因素进行调按上式计算的设计标高H整。
1.土的可松性影响由于土具有可松性,按理论计算出的H进行施工,填土会有剩余,需相应地提高设计标高,如图1.1所示。
若Δh 为土的可松性引起设计标高的增加值,则设计标高调整后的总挖方体积V′W为总填方体积为而所以移项整理得当VW =Vt时,上式化为故考虑土的可松性后,场地设计标高应调整为图1.1 设计标高调整计算(a)理论设计标高;(b)调整设计标高2.借土或弃土的影响由于场地内大型基坑挖出的土方、修筑路堤填高的土方,以及从经济角度比较,将部分挖方就近弃于场外(简称弃土)或将部分填方就近取土于场外(简称借土)等,均会引起挖填土方量的变化。
运动场竖向标高设计的确定方法及步骤

运动场竖向标高设计的确定方法及步骤1).根据场地竖向标高设计确定基准点的图纸设计标高值。
2).定义基准点实物的标高设计值。
3).确定实物参照点与排水井的高差,以及实物参照点与内环排水沟最低点的高差。
4).确保实物参照点与排水井的高差大于实物参照点与内环排水沟最低点的高差。
5).同时保证运动场与实际地形结合最不利位置的条件,即保证运动场地形比结合部(比如结合部道路)地形要高。
实际操作中可以找出结合部最高点,确保运动场在此位置处标高高于结合部最高点。
竖向标高上限的确定
1).确定接合部道路最高点与实物基准点之间的高差。
2).根据场地结合部区域(比如铺砖区)的坡度值确定道路最高点与相应塑胶区域边缘的高差。
3).确定运动场塑胶区域边缘与实物处设计高差。
4).确保实物处运动场标高值与道路最高点处运动场标高值的差值(计算出)小于实物参考点与道路最高点的高程差(测量出)。
5).可以根据实际需要调整铺砖区的坡度。
场地设计标高的确定

[Ph]
第一章
土方工程
应用上述准则方程时,若已知 c 或 ix ,或 iy 时,只要把这些已知值作为常数代入,即可求 得该条件下的最佳设计平面。
23
第一章
土方工程
1.2.2.3 设计标高的调整
实际工程中,对计算所得的设计标高,还应考虑下述 因素进行调整,这工作在完成土方量计算后进行。 (1) 考虑土的最终可松性,需相应提高设计标高,以达到 土方量的实际平衡。
11
第一章
土方工程
1.2.2 最佳设计平面
最佳设计平面即设计标高满足规划、 生产工艺及运输、排水及最高洪水位等要 求,并做到场地内土方挖填平衡,且挖填 的总土方工程量最小。
12
第一章
土方工程
1.2.2.1 最佳设计平面设计原理
任何一个平面在直角坐标体系中都可以用三
个参数 c、i 、
x
iy
来确定(图1-3)。
21
1 2 3 点 x y 号
4
z
5
p
6
pz
7
py
8
pz
9
pxx
10
pxy
11
pyy
12
pxz
13
pyz
1 4
15
H pH
0 …… … … … … … 1 2 3
…
…
…
…
… … …
……… … … … … … …
…
…
…
… … …
22
[p] [ pz ] [py ] [pz ] [ pxx ] [ pxy ] [ pyy ] [ pxz ] [pyz ]
c — 原点标高; c i x tan , a x 方向的坡度; c i y tan , b y 的方向坡度
场地平整设计标高的确定

土方平衡因素
土方量计算
土方平衡是确定设计标高的重要考虑因素,需要精确计算土方量,以实现填挖 平衡,降低工程成本。
土方调配
土方调配也是确定设计标高的关键因素,需要考虑土方的来源和去向,合理调 配土方,以降低运输成本和避免二次搬运。
场地规划因素
规划功能需求
场地规划的功能需求会影响设计标高的确定,例如停车场需要较低的设计标高以 便于车辆进出。
地面坡度
地面坡度的大小也会影响设计标 高的确定,坡度较大的地方需要 适当提高设计标高,以保证场地 的平整。
排水因素
排水方向
排水方向是确定设计标高的重要因素 ,应确保场地平整后的标高与排水方 向相符合,避免出现积水问题。
排水坡度
排水坡度的大小会影响场地平整的设 计标高,需要根据排水要求合理设置 坡度,以保证排水顺畅。
案例三:某公共设施场地平整设计标高确定
• 总结词:注重功能性与景观效果 • 详细描述:在某公共设施场地平整设计中,设计标高的确定需注重功能
性和景观效果。根据公共设施的功能需求和使用特点,合理确定不同功 能分区的场地标高,以满足使用安全、交通组织及景观效果的需求。同 时,应考虑排水设计的要求,确保场地排水顺畅,防止积水对公共设施 的正常使用造成影响。此外,应结合景观设计的需求,使场地标高与周 边环境相协调,提升公共设施的整体环境品质和形象。在满足功能性的 前提下,注重景观效果的营造,为公众提供一个舒适、美观的公共空间。
考虑景观需求
根据景观设计要求,调整 设计标高,使场地与周围 环境相协调。
计算土方量
计算填挖量
根据场地现状标高和初步 确定的设计标高,计算填 土或挖土的工程量。
考虑土方调配
根据施工条件和土方来源, 合理调配土方,降低施工 成本。
场地设计中,如何确定室内±0.000标高

关于室外地面标高的确定应考虑的因素及室内±0.000标高确定(一)对外与交通、市政设施相协调,对内方便生产、使用上的联系。
与周边道路交通相接轨,坡度合理,保持交通顺畅,遇到交通问题能及时分流。
(二)满足排水和防洪要求 1).防洪排涝:应保证场地设计地面的标高高出设计频率洪水位o.5m以上,一般城市防洪规划中有明确的最低场地标高和室内±0.000标高。
当场地与城市道路相临时,用地红线处的标高应高于城市道路中心线标高0.20~0.40m。
各设计标高之间的协调:一般的应使道路设计标高低于建筑物室外地坪标高,满足场地不积水的要求即可。
2)市政下水管道接入点标高:地面及地下管道排水坡度满足排水规范要求。
地下管道起点还应满足最低覆土深度要求。
(三)考虑地下水位高低、土方量及基础埋置深度及建筑物沉降的影响。
地下水较高的地段不宜挖方,减少处理地下水位造成的防水施工费用;地下水较低的地段,可考虑适当挖方,以获得较高地耐力,减少基础埋深。
最好使建筑基础、设备基础、管沟在地下水位0.5米以上。
减少土石填、挖方量和基础工程量。
(四)、环境景观要求,室内外地坪设计标高确定,应有一个与相邻建筑物谐和又考虑城市发展变化的前瞻性,营造美丽景观。
(五)、室内±0.000标高确定建筑物室内外地坪高差:一般应根据各种建筑物的使用性质、出人口要求、场地地形和地质条件等因素确定,其室内外最小高差满足相关规范要求。
含有地下室的建筑物,其室内地坪标高一般应比室外地坪高o.5m,以免雨水倒灌。
建筑物室内外地坪的设计标高确定设计地面的标高是指场地经过平整后形成的设计地面的控制性高程。
1)对于较为平坦不进行平整的场地,建筑物的室内地坪标高取建筑物室外场地设计标高(散水坡脚标高)的最大值加上室内外地坪的最小高差,建筑物室外散水坡脚标高可根据地形读取。
2)对于建筑群两端的地形标高落差较大、未加平整的场地,建筑物的室内地坪标高取建筑物室外场地设计标高的平均值加上室内外地坪的最小高差3)对于经过平整的场地,建筑物的室外地坪标高等于设计地面标高,建筑物室内地坪标高的确定可根据最高点、平均值或最低处标高加上室内外地坪的最小高差来确定。
场地设计标高H0的确定

土木与建筑学院
第二节 土方量计算
•一般方法的求解步骤:
1)初步确定场地设计标高H0 (1)在具有等高线的地形图上将 施工区域划分方格(边长 a=10m~50m); (2)确定各小方格的角点高程。 A.插值法:根据地形图相邻两 等高线的高程求得。 B.测量法:无地形图时,在 现场地面用木桩或钢钎打好方 格网,用仪器测出角点标高。
由图 可看出,H11只属于一 个方格的角点标高,H12和H21 则属于两个方格公共的角点标 高,H22则属于四个方格公共 的角点标高,它们分别在上式 中要加一次、二次、四次。
土木与建筑学院
场地设计标高计算
第二节 土方量计算
因此,上式可改写成下列 形式:
土 木
H 1 2 H 2 3 H 3 4 H 4 H0 4N
土木与建筑学院
土 木
工
程 施 工
场地设计标高计算
第二节 土方量计算
(3)按填挖方平衡原则确定设 计标高H0;
土 木
工
程 施 工
H 11 H 12 H 21 H 22 H 0 Na ( a ) 4 ( H 11 H 12 H 21 H 22 ) H0 4N
2 2
土 木
c.满足排水(泄水坡度)及最高洪水位要求; d.力求使场地内土方挖填平衡,且土方量最小。
工
程 施 工
•场地设计标高确定方法:
a.一般方法:如场地比较平整,对场地设计标高无特殊要 求,可按照“土方挖填平衡”的原满足土方挖填平衡,还可以做到土方的总工程量最小。
第二节 土方量计算
场地设计标高H0的确定
土 木
工
程 施 工
•确定场地设计标高的目的: 场地平整和土方量计算依据; 总图规划和竖向设计的依据; 根据场地设计标高与原地形标高确定土方填 挖量; 找到最佳设计平面,利于减少挖填工作量。
场地平整设计标高的确定

Y 2
z0
ix 1 z 42 lx iy
a a
X 1
iy
a 2
a
aY
a
a
a
iy
z 42 2-2
a ix
a
z 42
1-1
H′i=H0±lx ix±ly iy
z0
施工高度计算 求得 H'i 后,即可按下式计算各角点的施工高度 hi 。 施工高度的含义是该角点的设计标高与原地形标高的差 值:
hi= H'i -Hi
下因素进行调整:
(1)由于土的可松性,会使填土有剩余—— H0 (2)考虑场地泄水坡度对角点设计标高的影响;
(3)设计标高以上的各种填方工程(如场区上填筑路堤)——
ห้องสมุดไป่ตู้
H0 ;或者由于设计标高以下的各种挖方工程(如挖河道、水池、基坑
等) —— H0
(4)根据经济比较的结果,将部分挖方就近弃于场外,或部分填
场地平整的概念
场地平整——就是将自然地面改造成人们所要求的平面, 达到设计标高,并满足泻水坡度的要求。
在场地平整中,需要确定场地的设计标高。
场地设计标高的确定 场地设计标高的确定,应考虑以下因素: (1)满足生产工艺和运输的要求; (2)尽量利用地形,减少挖填方数量;
(3)场地内挖填方平衡,土方运费最少;
场地设计标高的调整与施工高度的确定
计算步骤:
1. 划分场地方格网;
2. 计算或实测各角点的原地形标高; 3. 按上式计算场地设计标高; 4. 设计标高调整; 5. 施工高度计算。
下面分别讨论:
设计标高调整与施工高度计算问题
场地设计标高H0的调整 按上述公式所计算的设计标高H0系一理论值,实际上还需要考虑以
场地设计中,如何确定室内±0.000标高

场地设计中,如何确定室内±0.000标高(总1页) -CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除关于室外地面标高的确定应考虑的因素及室内±0.000标高确定(一)对外与交通、市政设施相协调,对内方便生产、使用上的联系。
与周边道路交通相接轨,坡度合理,保持交通顺畅,遇到交通问题能及时分流。
(二)满足排水和防洪要求1).防洪排涝:应保证场地设计地面的标高高出设计频率洪水位o.5m以上,一般城市防洪规划中有明确的最低场地标高和室内±0.000标高。
当场地与城市道路相临时,用地红线处的标高应高于城市道路中心线标高0.20~0.40m。
各设计标高之间的协调:一般的应使道路设计标高低于建筑物室外地坪标高,满足场地不积水的要求即可。
2)市政下水管道接入点标高:地面及地下管道排水坡度满足排水规范要求。
地下管道起点还应满足最低覆土深度要求。
(三)考虑地下水位高低、土方量及基础埋置深度及建筑物沉降的影响。
地下水较高的地段不宜挖方,减少处理地下水位造成的防水施工费用;地下水较低的地段,可考虑适当挖方,以获得较高地耐力,减少基础埋深。
最好使建筑基础、设备基础、管沟在地下水位0.5米以上。
减少土石填、挖方量和基础工程量。
(四)、环境景观要求,室内外地坪设计标高确定,应有一个与相邻建筑物谐和又考虑城市发展变化的前瞻性,营造美丽景观。
(五)、室内±0.000标高确定建筑物室内外地坪高差:一般应根据各种建筑物的使用性质、出人口要求、场地地形和地质条件等因素确定,其室内外最小高差满足相关规范要求。
含有地下室的建筑物,其室内地坪标高一般应比室外地坪高o.5m,以免雨水倒灌。
建筑物室内外地坪的设计标高确定设计地面的标高是指场地经过平整后形成的设计地面的控制性高程。
1)对于较为平坦不进行平整的场地,建筑物的室内地坪标高取建筑物室外场地设计标高(散水坡脚标高)的最大值加上室内外地坪的最小高差,建筑物室外散水坡脚标高可根据地形读取。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 土方工程
场地设计标高的两种方法:
1.一般方法:如场地比较平缓,对场地设计 标高无特殊要求,可按照“挖填土方量相等”的原则 确定场地设计标高;
2.用最小二乘法原理求最佳设计平面:应用 最小二乘 法的原理,不仅可满足土方挖填平衡、还 可做到土方的总工程量最小。
3
第一章 土方工程
1.2.1 场地设计标高计算的一般方法
考虑各角点标高的“权”,式(1-3)可改写 成更便于计算的形式:
z o 4 1 n z 1 2z 2 3z 3 4z 4 (1-4)
式中
z1 —— 一个方格独有的角点标高; z2、z3、z4 —— 分别为二、三、四个方格
所共有的角点标高。
7
第一章 土方工程
1.2.1.2 计算步骤
1. 划分场地方格网; 2. 计算或实测各角点的原地形标高; 3. 按式(1-4)计算场地设计标高; 4. 设计标高调整; 5. 施工高度计算。
1.2.1.1 计算原则 将场地划分成边长
为a 的若干方格,并将方 格网点的原地形标高标在 图上(图1-1a)。原地形 高可利用等高线用插入法 求得或在实地测量得到。
a) 地形图方格网 图1-1 场地设计标高计算示意图
1—等高线
4
第一章 土方工程
1.2.1 场地设计标高 计算的一般方法
1.2.1.1 计算原则
以Zo 作为场地中心的标高(图1-2),则场地任 意点的设计标高为:
z'izolxixlyiy
(1-5)
图1-2 场地泄水坡度
10
z i
第一章 土方工程
施工高度计算
求得
z
' i
后,即可按下式计算各角点的施工高度
Hi,施工高度的含义是该角点的设计标高与原地形
标高的差值:
Hi zi' zi
(1-6)
式中 z i —— 角点的原地形标高。
按照挖填土方量相等的
z12
z11
z z 21
22
2
3
z0
a a a
原则(图1-1b),场地设计 标高可按下式计算:
aa a b)
b)设计标高示意图 图1-1 场地设计标高计算示意图
2—自然地面;3—设计平面
na2zoi n1 a2zi1zi2 4zi3zi4 (1-2)
5
第一章 土方工程
由式1-2可得到:
i y
n i 1
pi yi (c xiix
第一章 土方工程
第一章 土方工程
1.2 场地设计标高的确 定
1
第一章 土方工程
1.2 场地设计标高的确定
大型工程项目通常都要确定场地设计平面, 进行场地平整。场地平整就是将自然地面改造 成人们所要求的平面。
场地设计标高应满足规划、生产工艺及运 输、排水及最高洪水位等要求,并力求使场地 内土方挖填平衡且土方量最小。
(1-8)
式中
H
—方格网各角点的施工高度;
i
z
' i
—方格网各角点的设计平面标高;
z i —方格网各角点的原地形标高;
n —方格角点总数。
15
第一章 土方工程
土方工程量与施工高度之和成正比。 施工高度之和为零时,则表明该场地土方 的填挖平衡, 但由于施工高度有正有负,当但它不能反 映出填方和挖方的绝对值之和为多少。
18
第一章 土方工程
1.2.2.2 最佳设计平面的计算方法
为了求得σ最小时的设计平面参数c、i x 、i y 可以
对式1-9的ci、x
i
、
y
分别求偏导数,并令其为0,于是
得:
n
c
pi (c xiix yii y zi ) 0
i 1
n
ix i1 pi xi (c xi ix yi i y zi ) 0
i 1
17
第一章 土方工程
将公式(1-8)代入上式,得:
p1(c x1ix y1iy z1)2
p2(c x2ix y2iy z2)2
2
L pn c xnix yniy zn
当σ的值最小时,该设计平面既能使土方工程
量最小,又能保证填挖方量相等(填挖方不平衡时, 上式所得数值不可能最小)。这就是用最小二乘法 求最佳设计平面的方法。
16
第一章 土方工程
为了不使施工高度正负相互抵消,若把施工 高度平方之后再相加,则其总和能反映土方工程 填挖方绝对值之和的大小。
但要注意,在计算施工高度总和时,应考虑 方格网各点施工高度在计算土方量时被应用的次
数Pi,令σ为土方施工高度之平方和,则:
n
p iH i2p 1 H 1 2p 2 H 2 2 L p n H n 2 (1-9)
个参数 c、i x 、i y 来确定(图1-3)。
c — 原点标高;
ix
tan
c, a
x 方向的坡度;
iy
tan
c, b
y 的方向坡度
13
第一章 土方工程 1.2.2.1 最佳设计平面设计原理
在(图1-3)所示的这个平面上任何一
点
i
的标高
z
' i
,可以根据下式求出:
zicxiixyiiy (1-7)
若Hi为正值,则该点为填方,Hi为负值则为
挖方。
11
第一章 土方工程
1.2.2 最佳设计平面
最佳设计平面即设计标高满足规划、 生产工艺及运输、排水及最高洪水位等要 求,并做到场地内土方挖填平衡,且挖填 的总土方工程量最小。
12
第一章 土方工程
1.2.2.1 最佳设计平面设计原理
任何一个平面在直角坐标体系中都可以用三
其中
yi
x i — i 点在 x 方向的坐标;
— i 点在 y 方向的坐标。
式(1-7)为最佳设计平面的方程形式。
14
第一章 土方工程
与前述方法类似,将场地划分成方格网,并
将 点的原施地工形高标度高为z :i' 标于图上,则该场地方格网角
H i z i z i c x i i x y i i y z i ( i 1 , L , n )
6. 下面分别讨论: 7. 设计标高调整与施工高度计算问题
8.
8
第一章 土方工程
设计标高调整
设计标高的调整主要是泄水坡度的调整, 由于按式(1-4)得到的设计平面为一水平的 挖填方相等的场地,实际场地均应有一定的泄 水坡度。因此,应根据泄水要求计算出实际施 工时所采用的设计标高。
9
第一章 土方工程
zo41ni n1 zi1zi2zi3zi4
(1-3)
式中
zo——所计算场地的设计标高(m); n ——方格数; zi1、zi2、zi3、zi4——第i个方格四个角点的原地形
标高(m)。
6
第一章 土方工程
点的标高在计算过程中被应用的次数( Pi ) 反映 了各角点标高对计算结果的影响程度,测量上的 术语称为“权”。
