新人教版八年级数学竞赛试题
八年级(上)数学竞赛试题及答案(新人教版)
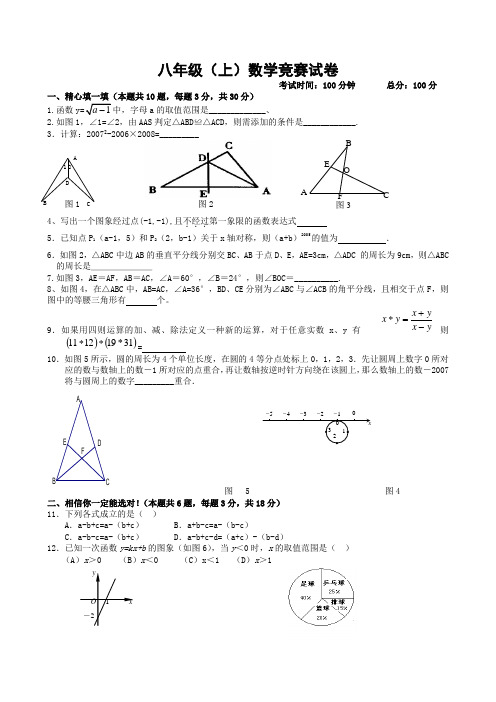
八年级(上)数学竞赛试卷考试时间:100分钟 总分:100分一、精心填一填(本题共10题,每题3分,共30分)1.函数a 的取值范围是_____________、2.如图1,∠1=∠2,由AAS 判定△ABD ≌△ACD ,则需添加的条件是____________. 3.计算:20072-2006×2008=_________图1 图24、写出一个图象经过点(-1,-1),且不经过...第一象限的函数表达式 5.已知点P 1(a-1,5)和P 2(2,b-1)关于x 轴对称,则(a+b )2005的值为 .6.如图2,△ABC 中边AB 的垂直平分线分别交BC 、AB于点D 、E ,AE=3cm ,△ADC•的周长为9cm ,则△ABC 的周长是_______7.如图3,AE =AF ,AB =AC ,∠A =60°,∠B =24°,则∠BOC =__________.8、如图4,在△ABC 中,AB=AC ,∠A=36°,BD 、CE 分别为∠ABC 与∠ACB 的角平分线,且相交于点F ,则图中的等腰三角形有 个。
9.如果用四则运算的加、减、除法定义一种新的运算,对于任意实数x 、y 有y x y x y x -+=* 则()()31*191211**=10.如图5所示,圆的周长为4个单位长度,在圆的4等分点处标上0,1,2,3.先让圆周上数字0所对应的数与数轴上的数-1所对应的点重合,再让数轴按逆时针方向绕在该圆上,那么数轴上的数-2007将与圆周上的数字_________重合.FEDACB图 5图4 二、相信你一定能选对!(本题共6题,每题3分,共18分) 11.下列各式成立的是( )A .a-b+c=a-(b+c )B .a+b-c=a-(b-c )C .a-b-c=a-(b+c )D .a-b+c-d=(a+c )-(b-d ) 12.已知一次函数y=kx+b 的图象(如图6),当y <0时,x 的取值范围是( )(A )x >0 (B )x <0 (C )x <1 (D )x >1A B C D12 AEBO F C图3图6 图713.在△ABC 中,∠B =∠C ,与△ABC 全等的三角形有一个角是100°,那么在△ABC 中与这100°角对应相等的角是 ( )A.∠AB.∠BC.∠CD.∠B 或∠C 14.某校八(2)班的全体同学喜欢的球类运动用图7所示的扇形统计图来表示,下面说法正确的是( ) A 、从图中可以直接看出喜欢各种球类的具体人数; B 、从图中可以直接看出全班的总人数;C 、从图中可以直接看出全班同学初中三年来喜欢各种球类的变化情况;D 、从图中可以直接看出全班同学现在喜欢各种球类的人数的大小关系 15.已知一次函数y=mx+│m+1│的图像与y 轴交于点(0,3),且y 随x 的增大而减小,则m 的值为( ). A .2 B .-4 C .-2或-4 D .2或-416.设y=ax 15+bx 13+cx 11-5(a 、b 、c 为常数),已知当x=7时,y=7,则x= -7时,y 的值等于( )A 、-7B 、-17C 、17D 、不确定 三、认真解答,一定要细心哟!(各6分,共18分) 17. 先化简再求值:[]y y x y x y x 4)4()2)(2(2÷+--+,其中x =5,y=2。
八年级数学竞赛试题及参考答案

八年级数学竞赛试题及参考答案八年级数学竞赛试题(一)一、选择题(每小题5分,共30分) 1.已知2220082008,2ca b a b c k k +=-==++=,且那么的值为( ). A .4 B .14 C .-4 D .14- 2.若方程组312433x y k x y k x y x y +=+⎧<<-⎨+=⎩的解为,,且,则的取值范围是( ). A .102x y <-<B .01x y <-<C .31x y -<-<-D .11x y -<-< 3.计算:2399100155555++++++=( ).A .10151- B .10051- C .101514- D .100514-4.如图,已知四边形ABCD 的四边都相等,等边△AEF 的顶点E 、F 分别在BC 、CD 上,且AE=AB ,则∠C=( ). A .100° B .105° C .110° D .120°5.已知5544332222335566a b c d a b c d ====,,,,则、、、的大小关系是( ). A .a b c d >>> B .a b d c >>> C .b a c d >>> D .a d b c >>> 6.如果把分数97的分子、分母分别加上正整数913a b 、,结果等于,那么a b +的最小 值是( ).A .26B .28C .30D .32 二、填空题:(每小题5分,共30分)(第4题图)DCB(第15题图)EDCBA7.方程组200820092007200720062008x y x y -=⎧⎨-=⎩的解是 .8.如图,已知AB 、CD 、EF 相交于点O ,EF ⊥AB ,OG 为∠COF 的平分线,OH 为∠DOG 的平分线,若∠AOC :∠COG=4:7,则∠GOH= .9.小张和小李分别从A 、B 两地同时出发,相向而行,第一次在距A 地5千米处相遇,继续往前走到各地(B 、A )后又立即返回,第二次在距B 地4千米处两人再次相遇,则A 、B 两地的距离是 千米.10.在△ABC 中,∠A 是最小角,∠B 是最大角,且2∠B=5∠A ,若∠B 的最大值为m °,最小值为n °,则m °+n °= .11.已知21()()()04b c b c a b c a a a+-=--≠=,且,则 . 12.设p q ,均为正整数,且7111015p q <<,当q 最小时,pq 的值为 . 以下三、四、五题要求写出解题过程. 三、(本题满分20分)13.在一次抗击雪灾而募捐的演出中,晨光中学有A 、B 、C 、D 四个班的同学参加演出,已知A 、B 两个班共16名演员,B 、C 两个班共20名演员,C 、D 两个班共34名演员,且各班演员的人数正好按A 、B 、C 、D 次序从小到大排列,求各班演员的人数. 四、(本题满分20分)14.已知2211x x y y x y =+=+≠,,且. ⑴ 求证:1x y +=. ⑵ 求55x y +的值.五、(本题满分20分)15.如图,在△ABC 中AC >BC ,E 、D 分别是AC 、BC 上的点,且∠BAD=∠ABE ,AE=BD .求证:∠BAD=12∠C .G(第8题图)HOFED CBA参考答案一、选择题1.A 2.B 3.C 4.A 5.A 6.B 二、填空题: 7、21x y =⎧⎨=⎩ 8、72.5° 9、11 10、175° 11、2 12、68213、解:依题意得:A+B=16,B+C=20,C+D=34∵A <B <C <D ,∴A <8,B >8,B <10,C >10,C <17,D >17 由8<B <10且B 只能取整数得,B=9 ∴C=11,D=23,A=7答:A 、B 、C 、D 各班演员人数分别是7人、9人、11人、23人。
初中数学竞赛试卷人教版

一、选择题(每题3分,共30分)1. 下列各数中,正数是()A. -1/2B. -√2C. √2D. 02. 下列各数中,绝对值最小的是()A. -1/2B. -√2C. √2D. 03. 若a=3,b=-3,则a-b的值为()A. 0B. 6C. -6D. -94. 已知等差数列{an}的前三项分别为1,4,7,则第10项an的值为()A. 19B. 23C. 27D. 315. 在直角坐标系中,点A(2,3),点B(-1,-4),则线段AB的中点坐标是()A. (1,-1)B. (3,2)C. (1,2)D. (2,3)6. 若x^2+4x+4=0,则x的值为()A. -2B. 2C. -4D. 47. 在△ABC中,∠A=30°,∠B=45°,则∠C的度数是()A. 105°B. 120°C. 135°D. 150°8. 若a+b=5,ab=4,则a^2+b^2的值为()A. 21B. 25C. 29D. 339. 已知一元二次方程x^2-3x+2=0的两个根为x1,x2,则x1+x2的值为()A. 1B. 2C. 3D. 410. 在等腰三角形ABC中,AB=AC,∠B=50°,则∠A的度数是()A. 40°B. 50°C. 60°D. 70°二、填空题(每题5分,共25分)11. 若a=√2,b=√3,则a^2+b^2的值为______。
12. 已知等差数列{an}的前三项分别为2,5,8,则第10项an的值为______。
13. 在直角坐标系中,点P(3,4),点Q(-2,-1),则线段PQ的长度为______。
14. 若x^2-6x+9=0,则x的值为______。
15. 在△ABC中,∠A=40°,∠B=60°,则∠C的度数是______。
三、解答题(每题10分,共20分)16. (10分)已知等差数列{an}的前三项分别为1,4,7,求该数列的通项公式。
新人教版八年级数学竞赛试题

永川中学片区初2019级桂山杯数学竞赛试题(总分:100分时间:100分钟)考号:班级:姓名:一、选择题(共10小题,每小题4分)1.下列计算中,正确的是()A .B .C .D .2.已知一次函数()22m-1-+=mxy,函数y随着x的增大而减小,且其图象不经过第一象限,则m的取值范围是()A.21>m B.2≤m C.221<<m D.221≤<m3.如图,△ABC中,AD是∠BAC内的一条射线,BE⊥AD,且△CHM可由△BEM旋转而得,延长CH交AD于F,则下列结论错误的是()A.BM=CMB.FM=21EH C.CF⊥AD D. FM⊥BC4.如图所示,两个边长都为2的正方形ABCD和OPQR,如果O点正好是正方形ABCD的中心,而正方形OPQR可以绕O点旋转,那么它们重叠部分的面积为()A.4B.2C.1D.215.若关于x的方程22x cx c+=+的解是1x c=,22xc=,则关于x的方程2211x ax a+=+--的解是()A.a,2cB.1a-,21a-C.a,21a-D. a,11aa+-6.△ABC的三边为a、b、c,且满足cbacba5.1225.3222+⨯=++,则△ABC是 ( )A.直角三角形B.等腰三角形C.等边三角形D.以上答案都不对7.如图大正方形中有2个小正方形,如果它们的面积分别是 S1、 S2,那么 S1、 S2的大小关系是()A.S1>S2 B.S1= S2 C. S1< S2D. S1、 S2的大小关系不确定8.如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以OA1对角线为边作正方形OA1A2B1,再以正方形的对角线OA2作正方形OA1A2B1,…,依此规律,则点A8的坐标是()A.(﹣8,0) B.(0,8) C.(0,8) D.(0,16)9.已知三角形的边长为n,n+1,m(其中m2=2n+1),则此三角形()A.一定是等边三角形B.一定是等腰三角形C.一定是直角三角形D.无法确定10.在某火车站托运物品时,不超过3kg的物品需付1.5元,以后每增加1kg(不足1kg按1kg计)需增加托运费0.5元,则下列图象能表示出托运费y与物品重量x之间的函数关系式的是().A B C D二.填空题(共10小题,每小题4分)11.如图,直线1l:1y x=+与直线2l:y mx n=+相交于点P(a,2),则关于x的不等式1x+≥mx n+的解集为.12.在平面直角坐标系xOy中,点A的坐标为(3,2),若将线段OA绕点O顺时针旋转90°得到线段AO',则点A'的坐标是.13.如图是重叠的两个直角三角形,将其中一个直角三角形沿BC方向平移BE距离就得到此图,已知AB=8cm,BE=4cm,DH=3cm,则图中阴影部分的面积是_____14.如果关于x的不等式3x-m≤0只有三个正整数解,则m的取值范围为_________.15.已知:如图, ABCD中,E,F两点在对角线BD上,BE=DF.当四边形AECF为矩形时,直接写出BD ACBE-= .第3题4题7题8题16.如图,在平面直角坐标系xOy 中,直线与x 轴交于点A ,与y 轴交于点B ,将△AOB沿过点A 的直线折叠,使点B 落在x 轴负半轴上,记作点C ,折痕与y 轴交点交于点D ,则点D 的坐标为_________ .17.在一次越野赛跑中,当小明跑了1600m 时,小刚跑了1450m ,此后两人分别调整速度,并以各自新的速度匀速跑,又过100s 时小刚追上小明,200s 时小刚到达终点,300s 时小明到达终点.他们赛跑使用时间t (s )及所跑距离如图s (m ),这次越野赛的赛跑全程为 m ? 18.如果两个数x 和y 满足385x y x y ++=---,则x+y 的最小值是________, 最大值是19.如图,正方形ABCD 的边长为a ,E 是AB 的中点,CF 平分∠DCE ,交AD 于F ,则AF 的长为 .20.已知非负实数a 、b 、c 满足条件:3a +2b +c=4, 2a +b +3c=5, 设S =5a +4b +7c 的最大值为m ,最小值为n ,则n -m 等于 。
人教版初二数学竞赛试卷

一、选择题(每题5分,共25分)1. 下列各数中,不是有理数的是()A. -2.5B. 3/4C. √16D. √22. 下列各式中,正确的是()A. a + b = b + aB. a - b = b - aC. a × b = b × aD. a ÷ b = b ÷ a3. 若x² - 3x + 2 = 0,则x的值为()A. 1B. 2C. 1或2D. 1和34. 已知等腰三角形底边长为6,腰长为8,则该三角形的面积为()A. 24B. 32C. 36D. 405. 若a、b、c、d为等差数列,且a + b + c + d = 24,则d的值为()A. 6C. 8D. 9二、填空题(每题5分,共25分)6. 已知一元二次方程x² - 5x + 6 = 0,则其因式分解为______。
7. 若等边三角形的一边长为a,则其面积为______。
8. 若x + 1/x = 5,则x² + 1的值为______。
9. 若等差数列的第一项为a₁,公差为d,则第n项为______。
10. 若a、b、c、d为等比数列,且a + b + c + d = 16,则d的值为______。
三、解答题(每题15分,共45分)11. (10分)已知一元二次方程x² - 4x + 3 = 0,求:(1)方程的解;(2)方程的判别式。
12. (15分)已知等腰三角形底边长为8,腰长为10,求:(1)该三角形的周长;(2)该三角形的面积。
13. (15分)已知等差数列的第一项为3,公差为2,求:(1)该数列的前10项和;(2)该数列的第n项。
答案:一、选择题1. D2. A4. B5. D二、填空题6. (x - 3)(x - 1)7. (√3/4)a²8. 269. a₁ + (n - 1)d10. 2三、解答题11. (1)x₁ = 1,x₂ = 3;(2)判别式为Δ = 16 - 4×3×1 = 4。
人教版初二数学竞赛试题及答案

八 年 级 数 学 竞 赛 试 题一、精心选一选,相信你选得准!(每小题5分,共30分)1.三角形的三边长分别为6,1-3a ,10,则a 的取值范围是( )A .-6<a <-3B .5<a <1C .-5<a <-1D .a >-1或a <-52.使分式xx y z x 5201020092010201020092008--+有意义的x 的取值范围是( )A .x ≠0B .x ≠0且x ≠±402C .x ≠0且x ≠402D .x ≠0且x ≠-402 3.如图,将纸片△ABC 沿着DE 折叠压平,且∠1+∠2=72°,则∠A =( )A .72°B .24°C .36°D .18° 4.已知一个梯形的四条边长分别为2、3、4、5,则此梯形的面积为( )A .5B .8C .3310 D .3514 5.如图,E 、F 分别是矩形ABCD 的边AB 、BC 的中点,连CE 、AF ,设CE 、AF相交于G ,则S BEGF 四边形∶S ABCD 四边形等于( )A .41B .92C .61 D .1036.已知x 为实数,且13-x +14-x +15-x +…+117-x 的值是一个确定的常数,则这个常数是( ) A .5 B .10 C .15 D .75二、细心填一填,相信你填得对!(每小题5分,共30分)7.已知实数x 、y 满足x 2—3x +4y =7,则3x +4y 的最大值为__________. 8.如果a 、b 是整数,且x 2+x —1是a x 3+b x +1的因式,则b 的值为__________. 9.如图,E 、F 分别是矩形ABCD 的BC 边和CD 边上的点,且S △ABE =3,S △ECF =8,S △ADF =5,则矩形ABCD 的面积为__________. 10.如图△ABC 中,AD 平分∠BAC ,且AB +BD =AC ,若∠B =62°,则∠C =__________. 11.已知k =acb a bc b a c c b a ++-=+-=-+,且n 2+16+ BDECA 12(第3题图) C(第9题图) (第10题图)ABCDC FB(第5题图)6 m =8n ,则关于x 的一次函数y =-kx +n -m 的图象一定经过第__________象限.12.若a +x 2=2008,b +x 2=2009,c +x 2=2010,且abc =24,则bc a +ac b +abc -a1-b1-c1的值为__________.三、用心做一做,试试你能行!(共40分) 13.(8分)蕲春红人电器行“家电下乡”指定型号的冰箱彩电的进价和售价如右表所示: ⑴按国家政策,农民购买“家电下乡”产品可享受售价13%的政府补贴;农民蕲大伯到该电器行购买了冰箱一台,彩电两台,可以享受多少元的政府补贴?(2分)⑵为满足农民需求,红人电器行决定用不超过85000元采购冰箱和彩电共40台,且冰箱的数量不少于彩电数量的65.①请你帮助该电器行设计相应的进货方案;(3分)②哪种进货方案电器行获得的利润最大?(利润=售价-进价)最大利润是多少?(3分)14.(8分)如图,已知 :正△OAB 的面积为34,双曲线y =xk经过点B ,点P (m ,n )(m >0)在双曲线y =xk 上,PC ⊥x 轴于点C ,PD ⊥y 轴于点D ,设矩形OCPD 与正△OAB 不重叠部分的面积为S . ⑴求点B 的坐标及k 的值; ⑵求m =1和m =3时,S 的值.15.(8分)已知a 、b 、c 均为正数,且满足如下两个条件:⎪⎩⎪⎨⎧=-++-++-+=++4132ab c b a ac b a c bca cbc b a证明:以a 、b 、c 为三边长可构成一个直角三角形.16.(加油啊!加油!加油!!)(8分)2010年4月14日青海省玉树发生了7.1级大地震,驻军某部(位于距玉树县城结古镇91公里处的上拉秀镇)接到上级命令,须火速前往结古镇救援.已知该部有120名官兵,且步行的速度为每小时10公里,现仅有一辆时速为80公里的卡车,可乘坐40人,请你设计一个乘车兼步行方案,使该部120人能在最短时间内赶往重灾区结古镇救x援.其中中途换车(上、下车)的时间均忽略不计,最快多少时间可以赶到?(可用分数表示)17.(6分)计算:2sin 45°+sin 2α+cos 2α+330cos 2360tan ︒-︒18.(8分)如图,△ABC 的边AB =3,AC =2,Ⅰ、Ⅱ、Ⅲ 分别表示以AB 、AC 、BC 为边的正方形,求图中三个阴影部分的面积之和的最大值是多少?H(第18题图)。
八年级(上)数学竞赛试题及答案(新人教版)

一、精心填一填(本题共 10题,每题3分,共30分) 1. 函数y= JT 万中,字母a 的取值范围是 ______________ 2. 如图1, 3. 计算:4、写出一个图象经过点(-1,-1),且不经过第一象限的函数表达式5. 已知点P 1 (a-1 , 5)和P 2 (2, b-1 )关于x 轴对称,则(a+b ) 2005的值为6. 如图2,A ABC 中边AB 的垂直平分线分别交 BC AB 于点D 、E , AE=3cm △ ADC?勺周长为9cm 则厶ABC 的周长是 ________________7. 如图 3, AE = AF , AB = AC, / A = 60°,/ B = 24°,则/ BOC= ___________ . 8.如图4,在厶ABC 中,AB=AC / A=36°, BD CE 分别为/ ABC 与/ ACB 的角平分线,且相交于点 F ,贝U 图中的等腰三角形有 个。
9 •如果用四则运算的加、减、除法定义一种新的运算,对于任意实数11 12 19*31 =10•如图5所示,圆的周长为 4个单位长度,在圆的4等分点处标上0, 1, 2, 应的数与数轴上的数一1所对应的点重合, 将与圆周上的数字 __________ 重合./戴尊7 *J)八年级(上)数学竞赛试卷考试时间:100分钟总分:100分/仁/ 2,由AAS 判定△ ABD^A ACD 则需添加的条件 20072-2006 X 2008=3 •先让圆周上数字0所对 那么数轴上的数一2007 再让数轴按逆时针方向绕在该圆上, 、相信你一定能选对! 下列各式成立的是( a-b+c=a- a-b-c=a- 已知一次函数 (A ) x > 0 11.A C 12. (b+c ) (b+c ) (本题共 ) B 6题,每题 图 53分,共18分).a+b-c=a- (b-c ) .a-b+c-d= (a+c ) - (b-d ) y=kx+b 的图象(如图6),当y v 0时,x 的取值范围是()(B ) x v 0(C ) x v 1( D ) x > 1图3图6图713.在厶ABC 中,/ B =Z 。
人教版八年级数学上册(三角形、全等三角形、轴对称、整式的乘法)竞赛培优题(含答案)

人教版八年级数学上册(三角形、全等三角形、轴对称、整式的乘法)竞赛培优题分数:100 考试时间:80分钟一、选择题(10×3=30分)1. 下列运算正确的是 ( )A 、x 2 + x 3 = x 5B 、-2x ·x 2 =-2x 3C 、x 6÷x 2 = x 3D 、(- x 2 )3 = x 62. (−2)m +2⋅(−2)m−1的值是( )A 、0B 、-2C 、2D 、(−2)m+1 3. 下列各组图形中,是全等形的是( )A.两个含60°角的直角三角形B.腰对应相等的两个等腰直角三角形C.边长为3和4的两个等腰三角形D.一个钝角相等的两个等腰三角形 4. 若二次三项式26x ax +-可分解成(x −2)(x +b),则a ,b 的值分别为( ) A . 1,3 B . 1-,3 C . 1,3- D . 1-,3-5.要使二次三项式25x x p -+在整数范围内能进行因式分解,那么整数p 的取值可以有( ) A . 2个 B . 4个 C . 6个 D .无数个6.如图,△ABC 中,∠C=90°,AC=3,∠B=30°,点P 是BC 边上的动点,则AP 的长不可能是( ) A 、3.5 B 、4.2 C 、5.8 D 、77.如图,把矩形纸片ABCD 纸沿对角线折叠,设重叠部分为△EBD ,对于下列结论,其中说法错误的是( )A.△EBD 是等腰三角形,EB =ED ;B .折叠后∠ABE 和∠CBD 一定相等;C .折叠后得到的图形是轴对称图形 ; D.△EBA 和△EDC 一定是全等三角形。
8.如图,等边三角形△ABC 的边长是6,面积是9√3,AD 是BC 边上的高, 点E 是AB 的中点,在AD 上求一点P ,则P B +PE 的和的最小值为( )A 、3B 、6C 、3√3D 、6√39. 如图,AD 是△ABC 的角平分线,DE ⊥AB 于E ,已知△ABC 的 面积为28.AC =6,DE =4,则AB 的长为( ) A .6 B .8 C .4 D .1010. 如图,四边形ABCD 中,AB =AD ,点B 关于AC 的对 称点B ′恰好落在CD 上,若∠BAD =100°,则∠ACB 的 度数为( )A .40°B .45° C .60° D .80° 二、填空题(5×3=15分)11. a 4b −6a 3b +9a 2b 分解因式得正确结果为 . 12. 满足(n −1)n+2=1的整数n 的值是 .13. 如图:在△FHI 中,HF +FG=GI ,HG ⊥FI ,∠F=058,则∠FHI= 度。
新人教版八年级下数学竞赛试题

八年级数学竞赛试题 (时间:60分 满分:120分) 一、 填空题(每空3分,共36分) 1、 分式392--x x 当x _________时分式的值为零,当x ________时,分式x x 2121-+有意义 2、 =-0)5( . =-23 . =-1a (a ≠0) 3、利用分式的基本性质填空:(1)())0(,10 53≠=a axy xy a (2)() 1422=-+a a 4、写一个反比例函数,使得它所在的象限内函数值y 随着自变量x 的增加而增加,这个函数解析式可以为 .(只写一个即可) 5、计算:=+-+3932a a a __________ 6、反比例函数6y x =-图象上一个点的坐标是 7、斜边长为17cm ,一条直角边长为15cm 的直角三角形的面积为_________8、若正方形的面积为16cm 2,则正方形对角线长为__________cm二、选择题(每小题3分,共24分)9、在代数式23451,,,,23xb x x y x y a π+-+-中,分式有( )A 、 2个B 、3个C 、4 个D 、5个 班别姓名10、对于反比例函数2y x=,下列说法不正确...的是( ) A .点(21)--,在它的图象上 B .它的图象在第一、三象限C .当0x >时,y 随x 的增大而增大D 当0x <时,y 随x 的增大而减小11、若把分式xyy x 2+中的x 和y 都扩大3倍,那么分式的值( ) A .扩大3倍 B .不变 C .缩小3倍 D .缩小6倍12、 三角形的三边长分别为6,8,10,它的斜边上的高为 ( )A. 6B. 4.8C. 2.4D. 813、 若函数12k y x -=是反比例函数,则k 为( )A 、1B 、0C 、2D 、-214、解分式方程4223=-+-xx x 时,去分母后得( ). A. )2(43-=-x x B. )2(43-=+x xC. 4)2()2(3=-+-x x xD. 43=-x15、化简2293m m m --的结果是( ) A.3+m m B.3+-m m C.3-m m D.mm -3 16、如图中字母A 所代表的正方形的面积为 ( )A 、4B 、8C 、16D 、64 三、解答题(共60分) 17、计算(每小题10分,共20分)(1) 11124x x x ++A 2892253 (16题图)(2)2224369 a aa a a--÷+++18、(12分)解方程1052 2112xx x+=--19、(14分)某工人原计划在规定时间内恰好加工1500个零件,改进了工具和操作方法后,工作效率提高为原来的2倍,因此加工1500个零件时,比原计划提前了5小时,问原计划每小时加工多少个零件?20、(14分)如图所示,在平面直角坐标系中,第一象限的角平分线OM 与反比例函数的图象相交于点M,已知OM的长是22.(1)求点M的坐标;(2)求此反比例函数的关系式.。
初二数学竞赛试题及答案

初二数学竞赛试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是无理数?A. 4B. 2/3C. √2D. 0.5答案:C2. 如果一个三角形的两边长分别为3和4,且第三边长为整数,那么第三边长可能是:A. 1B. 2C. 5D. 7答案:C3. 计算下列表达式的值:(3x - 2) / (x + 1),当x = 2时,结果为:A. 1/3B. 1C. 4D. 5答案:C4. 一个数的平方是其本身的数有:A. 0和1B. 0和-1C. 1和-1D. 0和2答案:A5. 一个圆的直径是10厘米,那么它的半径是:A. 5厘米B. 10厘米C. 15厘米D. 20厘米答案:A6. 一个数的立方是-8,这个数是:A. 2B. -2C. 3D. -3答案:B7. 一个数的绝对值是其本身,这个数可能是:A. 正数B. 负数C. 0D. 正数或08. 计算下列表达式的值:(2x + 3) / (x - 1),当x = 2时,结果为:A. 5B. 7C. 9D. 11答案:B9. 一个等腰三角形的两边长分别为5和8,那么其周长可能是:A. 18B. 21C. 26D. 30答案:C10. 一个数的相反数是-3,这个数是:A. 3B. -3C. 0D. 6答案:A二、填空题(每题4分,共20分)11. 一个数的平方根是4,那么这个数是______。
12. 一个数的立方根是2,那么这个数是______。
答案:813. 如果一个角的补角是120°,那么这个角的度数是______。
答案:60°14. 一个数的倒数是1/2,那么这个数是______。
答案:215. 一个数的绝对值是5,那么这个数可能是______或______。
答案:5或-5三、解答题(每题10分,共50分)16. 已知一个直角三角形的两个直角边长分别为6和8,求斜边的长度。
答案:根据勾股定理,斜边的长度为√(6² + 8²) = √(36 + 64) = √100 = 10。
人教八年级数学竞赛试题

人教八年级数学竞赛试题一、选择题(每题5分,共40分)1. 下列哪个数是无理数?A. 3.14159B. πC. 0.33333...(无限循环)D. √22. 如果一个三角形的三边长分别为a、b、c,且满足a^2 + b^2 = c^2,那么这个三角形是什么类型的三角形?A. 等边三角形B. 等腰三角形C. 直角三角形D. 钝角三角形3. 已知一个数列的前三项为1, 2, 3,从第四项开始,每一项都是前三项的和。
这个数列的第10项是多少?A. 144B. 145C. 146D. 1474. 一个圆的半径为r,那么它的面积是多少?A. πrB. πr^2C. 2πrD. 4πr^25. 一个长方体的长、宽、高分别为a、b、c,它的体积是多少?A. abcB. a + b + cC. 2(ab + bc + ac)D. 3(a + b + c)6. 一个函数f(x) = 3x^2 - 2x + 1,当x = 2时,f(x)的值是多少?A. 7B. 8C. 9D. 107. 一个正整数n,如果它能够被2整除,但不能被3整除,那么n的最小值是多少?A. 2B. 4C. 6D. 88. 一个数的平方根是它本身,这个数是什么?A. 0B. 1C. -1D. 2二、填空题(每题5分,共30分)9. 如果一个数的立方根等于它本身,那么这个数可以是_________。
10. 一个数的绝对值是它本身,这个数可以是正数或_________。
11. 如果一个分数的分子和分母都乘以同一个数,那么这个分数的值_________。
12. 已知一个数列的前三项为2, 3, 5,从第四项开始,每一项都是前两项的平均值。
这个数列的第5项是_________。
13. 一个直角三角形的两条直角边分别为3和4,那么它的斜边长是_________。
14. 如果一个数的相反数是-5,那么这个数是_________。
三、解答题(每题15分,共30分)15. 已知一个二次方程x^2 - 5x + 6 = 0,求它的根。
人教版初二数学竞赛试题

第一学期八年级数学竞赛练习题一、选择题:1.下列四个式子中与(a-3)a-31相等的是( ) A.a -3 B.-a -3 C.-3-a D.3-a2.若a+b=4,a 3+b 3=28,则a 2+b 2的值是( )A.14B.12C.10D.83.在⊿ABC 中,∠C=900,∠A=150,AB=12,则⊿ABC 的面积是( )A.18B.12C.10D.84.已知方程x =ax+1有一个负根,且没有正根,则a 的取值范围是( )A.a >-1B.a=1C.a ≥1D.a >15.⊿ABC 的周长是24,M 是AB 的中点,MC=MA=5,则⊿ABC 的面积是( )A.30B.24C.16D.126.如果一条直线l 经过不同的三点A(a,b),B(b,a),C(a-b,b-a),那么直线l 经过第( )象限.A.二、四B.一、三C.二、三、四D.一、三、四二、填空题:7.已知8=a ,70=b ,则6.5=______________.8.已知x=1-3,则x 5-2x 4-2x 3+x 2-2x+1的值是______________.9. 某人将一本书的页码按1,2,3,…的顺序相加,其中有一个页码被多加了一次,结果得到一个错误的总和2005,则被多加的页码是 。
10. 如图,点C 在线段AB 上,DA ⊥AB ,EB ⊥AB ,FC ⊥AB ,且DA=BC ,EB=AC ,FC=AB ,∠AFB=51°,则∠DFE= .11.一个六边形六个内角都是1200,连续四边的长依次是1、3、3、2,则该六边形的周长是___________.12.已知⊿ABC 的三边长分别为AB=13,BC=5,CA=12,CT 是∠ACB 的内角平分线, ⊿ABC 关于直线CT 的对称图形是⊿A 1B 1C 1,⊿ABC 和⊿A 1B 1C 1,的公共面积是nm ,m,n 是互质的正整数,则m+n=__________.三、解答题:13.已知方程组27234ax y x y -=-⎧⎨+=⎩中的系数a 是不等式组513(1)131722a a a a ->+⎧⎪⎨-<-⎪⎩的整数解,求代数式(x-y)(x 2-xy+y 2)的值.14.如图,已知∠ACB=900,AD 平分∠CAB,BC= 4,CD=23,求AC 的长。
湖北省武汉市八年级数学竞赛试题 新人教版

八年级数学竞赛试题一、选择题(每小题4分,共40分)1、计算)21(22x x x -÷-的结果是( )A x B x 1- C x x 2-- D x1 2、下列命题正确的是( ) A 若a >0,则aa 1> B 若a>a 2,则a>1 C 若0a 2 D 若a a =,则0>a 3、已知,81002022=+-+-x x x 则3x 的最大整数值是( )A 0B 1C 2D 34、已知a-b=1,则a 2-b 2-2b 的值是( ) A 0 B 1 C 2 D 45、在平面直角坐标系内,A 、B 、C 三点的坐标分别是(0,0),(4,0),(3,2),以 A 、B 、C 三点为顶点画平行四边形,则第四个顶点不可能在( )A 第一象限B 第二象限C 第三象限D 第四象限6、已知三角形三边长分别是2、3、4,三边上的高分别是h a , h b , h c则 )111()cb ac b a h h h h h h ++⋅++(的值是( ) A 641 B 538 C 738 D 439 7、 If 0<m <1,then m mut be maer than itA. Ober B invere vaue(英汉词典:invere 倒数;aboute 绝对)8、若,k cb a b ac a c b =+=+=+则直线=-必经过( ) A 第一、二象限 B 第二、三象限 C 第三、四象限 D 第一、四象限9、四个人的年龄分别为a,b,c,d,任取三个人的平均年龄加上余下一人的年龄分别是w,,,,则zy x w d c b a ++++++的值是( ) A 1 B 2 C 21 D 32 10、如图,将△ABC 沿DE 折叠,使点A 与边BC 的中点F 重合,有下面四个结论:①EF ∥AB,且EF=21AB ②AF 平分∠DFE ③S 四边形ADFE =21AF ·DE ④∠BDF ∠FEC=2∠BAC 其中正确的是( )A ①②③B ②③④C ③④D ①②③④二、A 组填空题(每小题4分,共40分)11、若1<x <2022,则2)2014(1-+-x x = 12、若4292=8800,=-100,则2-3=13、若(-4)(n=2-m24,则mn=14、已知一次函数=m-3-2的图象不经过第二象限,一次函数=m-43的图象不 经过第三象限,化简:m m m m 6916822-+-+-=15、关于的分式方程234222+=-+-x x mx x 会产生增根,则m = 16、如果要(-2232=15,则(2-3的值是 。
新初二数学竞赛试题及答案

新初二数学竞赛试题及答案一、选择题(每题3分,共30分)1. 下列哪个数是最小的正整数?A. 0B. 1C. -1D. 2答案:B2. 如果一个数的平方等于其本身,这个数可能是:A. 0B. 1C. -1D. 2答案:B3. 一个三角形的三个内角之和是多少度?A. 180度B. 360度C. 90度D. 120度答案:A4. 以下哪个是二次方程的解法?A. 直接开平方法B. 配方法C. 因式分解法D. 所有以上答案:D5. 一个数的绝对值是其本身,这个数是:A. 正数B. 零C. 负数D. 正数或零答案:D6. 以下哪个是不等式的解集?A. 所有实数B. 所有正数C. 所有负数D. 所有非零数答案:A7. 一个圆的周长是其直径的多少倍?A. π倍B. 2倍C. 3倍D. 4倍答案:A8. 以下哪个是整式除法的运算法则?A. 同底数幂相除B. 幂的乘方C. 积的乘方D. 所有以上答案:D9. 以下哪个是几何级数的通项公式?A. \( a_n = a_1 \times r^{(n-1)} \)B. \( a_n = a_1 \times n \)C. \( a_n = a_1 \times (n-1) \)D. \( a_n = a_1 \times r \)答案:A10. 以下哪个是勾股定理的表述?A. 直角三角形的斜边平方等于两直角边平方和B. 直角三角形的两直角边平方和等于斜边平方C. 直角三角形的斜边等于两直角边之和D. 直角三角形的两直角边等于斜边的平方根答案:A二、填空题(每题4分,共20分)11. 如果 \( a \) 和 \( b \) 是两个连续的整数,且 \( a > b \),那么 \( a \) 的值是 \( b \) 加上 ______ 。
答案:112. 一个数的平方根是 \( \sqrt{a} \),那么这个数是 \( \sqrt{a} \) 的 ______ 。
答案:平方13. 如果一个三角形的三边长分别为 \( a \),\( b \) 和 \( c \),且满足 \( a^2 + b^2 = c^2 \),那么这个三角形是 ______ 三角形。
人教版初二数学竞赛练习题

八年级数学竞赛练习题一、选择题1. 当 x 为任意实数时,下列分式一定有意义的是-----------()1111( A ) x22 ; ( B ) x 21 ;(C )| x |; (D )x 2.2. 商品的原售价为 m 元,若按该价的 8 折出售,仍获利 n%,则该商品的进价为( )元.(A)0.8 m ×n% (B)0.8m (1+n%)(C)0.8m (D)0.8m1 n%n%x 8 )3. 如果不等式无解 , 那么 m 的取值范围是 (xmA .m>8B .m ≥8C .m<8D . m ≤ 84. 已知点 P 1(a-1 ,5)和 P 2( 2,b-1 )关于 x 轴对称,则( a+b )2005 的值为( ).A .0B .-1C . 1D .(-3 ) 20055. △ABC 为等腰直角三角形,∠ C=90°, D 为 BC 上一点,且 AD=2CD ,则∠ DAB=( ). A .30° B .45° C .60° D .15°6. 若 m >-1 ,则多项式 m 3 m 2 m 1 的值为( )(A) 正数 (B) 负数 (C) 非负数 (D) 非正数7. 如果 x 1 1 x, 3x 2 3x 2, 那么 x 的取值范围是 ( )A. 1 x2 B. x1 C.x2 D. 2 133x0 ,则分式1138. 若 xyx y( )yxA 、1B、 yxC、1D、- 1xy二、填空题1. 分解因式 :x ( a-b ) 2n +y (b-a )2n+1=_______________________.2. 若1x 3,则x 2 1__________。
xx 4x 23. 如图,Rt △ ABC 中, ACB 90°,直线 EF ∥ BD ,交 AB 于点 E ,交 AC 于点 G ,交AD于点若1 S 四边形,则CF.EBCGF , S △ AEG3AD4.一次函数 y kx 6的图象经过第三象限,且它与两条坐标轴构成的直角三角形面积等于 9 ,则 k。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
永川中学片区初2019级桂山杯数学竞赛试题(总分:100分时间:100分钟)考号:班级:姓名:一、选择题(共10小题,每小题4分)1.下列计算中,正确的是()A .B .C .D .2.已知一次函数()22m-1-+=mxy,函数y随着x的增大而减小,且其图象不经过第一象限,则m的取值范围是()A.21>m B.2≤m C.221<<m D.221≤<m3.如图,△ABC中,AD是∠BAC内的一条射线,BE⊥AD,且△CHM可由△BEM旋转而得,延长CH交AD于F,则下列结论错误的是()A.BM=CMB.FM=21EH C.CF⊥AD D. FM⊥BC4.如图所示,两个边长都为2的正方形ABCD和OPQR,如果O点正好是正方形ABCD的中心,而正方形OPQR可以绕O点旋转,那么它们重叠部分的面积为()A.4B.2C.1D.215.若关于x的方程22x cx c+=+的解是1x c=,22xc=,则关于x的方程2211x ax a+=+--的解是()A.a,2cB.1a-,21a-C.a,21a-D. a,11aa+-6.△ABC的三边为a、b、c,且满足cbacba5.1225.3222+⨯=++,则△ABC是 ( )A.直角三角形B.等腰三角形C.等边三角形D.以上答案都不对7.如图大正方形中有2个小正方形,如果它们的面积分别是 S1、 S2,那么 S1、 S2的大小关系是()A.S1>S2 B.S1= S2 C. S1< S2D. S1、 S2的大小关系不确定8.如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以OA1对角线为边作正方形OA1A2B1,再以正方形的对角线OA2作正方形OA1A2B1,…,依此规律,则点A8的坐标是()A.(﹣8,0) B.(0,8) C.(0,8) D.(0,16)9.已知三角形的边长为n,n+1,m(其中m2=2n+1),则此三角形()A.一定是等边三角形B.一定是等腰三角形C.一定是直角三角形D.无法确定10.在某火车站托运物品时,不超过3kg的物品需付1.5元,以后每增加1kg(不足1kg按1kg计)需增加托运费0.5元,则下列图象能表示出托运费y与物品重量x之间的函数关系式的是().A B C D二.填空题(共10小题,每小题4分)11.如图,直线1l:1y x=+与直线2l:y mx n=+相交于点P(a,2),则关于x的不等式1x+≥mx n+的解集为.12.在平面直角坐标系xOy中,点A的坐标为(3,2),若将线段OA绕点O顺时针旋转90°得到线段AO',则点A'的坐标是.13.如图是重叠的两个直角三角形,将其中一个直角三角形沿BC方向平移BE距离就得到此图,已知AB=8cm,BE=4cm,DH=3cm,则图中阴影部分的面积是_____14.如果关于x的不等式3x-m≤0只有三个正整数解,则m的取值范围为_________.15.已知:如图, ABCD中,E,F两点在对角线BD上,BE=DF.当四边形AECF为矩形时,直接写出BD ACBE-= .第3题4题7题8题16.如图,在平面直角坐标系xOy 中,直线与x 轴交于点A ,与y 轴交于点B ,将△AOB沿过点A 的直线折叠,使点B 落在x 轴负半轴上,记作点C ,折痕与y 轴交点交于点D ,则点D 的坐标为_________ .17.在一次越野赛跑中,当小明跑了1600m 时,小刚跑了1450m ,此后两人分别调整速度,并以各自新的速度匀速跑,又过100s 时小刚追上小明,200s 时小刚到达终点,300s 时小明到达终点.他们赛跑使用时间t (s )及所跑距离如图s (m ),这次越野赛的赛跑全程为 m ? 18.如果两个数x 和y 满足385x y x y ++=---,则x+y 的最小值是________, 最大值是19.如图,正方形ABCD 的边长为a ,E 是AB 的中点,CF 平分∠DCE ,交AD 于F ,则AF 的长为 .20.已知非负实数a 、b 、c 满足条件:3a +2b +c=4, 2a +b +3c=5, 设S =5a +4b +7c 的最大值为m ,最小值为n ,则n -m 等于 。
三.解答题(共2小题,每题10分)21、图1为学校运动会终点计时台侧面示意图,已知:AB=1米,DE=5米,BC ⊥DC ,∠ADC=30°,∠BEC=60°(1)求AD 的长度.(2)如图2,为了避免计时台AB 和AD 的位置受到与水平面成45°角的光线照射,计时台上方应放直径是多少米的遮阳伞(即求DG 长度)?22.为了保护环境,某企业决定购买10台污水处理设备,现有A、B 两种型号的设备,其中每台的价格,月处理污水量及年消耗费用如下表:经预算,该企业购买设备的资金不高于105万元。
(1)求购买设备的资金y 万元与购买A 型x 台的函数关系,并设计该企业有哪几种购买方案? (2)若企业每月产生的污水量为2040吨,为了节约购买资金,利用函数知识说明应选择哪种购买方案?(3)在第(2)问的条件下,若每台设备的使用年限为10年,污水厂处理污水费为每吨10元,请你计算,该企业自己处理污水与排到污水厂处理相比较,10年共节约资金多少万元?(注:企业处理污水的费用包括购买设备的资金和消耗费)AB CDEF16题 17题 19题一、选择题(40用2B 铅笔将题号右侧正确答案所对应的方框涂黑)二、填空题(40 请用0.5毫米黑色签字笔书写)11.___________ 12.___________ 13.___________ 14.___________ 15.___________ 16.___________ 17.___________ 18.___________ 19.___________20.___________21.(10分)1 [A] [B] [C] [D] 5 [A] [B] [C] [D] 9 [A] [B] [C] [D]2 [A] [B] [C] [D] 6 [A] [B] [C] [D] 10 [A] [B] [C] [D]3 [A] [B] [C] [D] 7 [A] [B] [C] [D]4 [A] [B] [C] [D] 8 [A] [B] [C] [D] 缺考标记,考生禁填!由监考老师填涂。
重庆市红炉初级中学校初2017级期末质量模拟检测数学试题 答题卡请 在 各 题 目 的 答 题 区 域 内 作 答, 超 出 黑 色 矩 形 边 框 限 定 区 域 的 答 案 无 效!22.(10分)参考答案: 一.选择题 1.D2.D(∵y 随着x 的增大而减小∴1-2m<0, ∵图象不经过第一象限 ∴m -2≤0,∴221≤<m ) 3、D 4、D(旋转至OP 、OR 过点A 、B)5、D(∵x -1+2x-1 =a -1+2a-1 ∴x -1=a -1或x -1=2a-1 ∴x=a 或x=2a-1 +1=a+1a-1)6、B(a 2+b 2+134 c 2=2ac+3bc ∴(a 2-2ac+c 2)+(b 2-3bc+94 c 2)=0,即(a -c )2+(b - 32c)2=0)7.A 8.D 9.C 10.D 二.填空题11. x ≥1 12.(2,-3) 13.26 14.9≤m <12 15.216. (0,34) 17.205018.∵│x+y+3│+│5-x -y │=8,而(x+y+3)+(5-x -y )=8,∴x+y+3≥0 且5-x -y ≥0 ∴-3≤x+y ≤5,∴最小值为-3,最大值为5。
19.延长CE 交DA 的延长线于点G ,过F 作FH ⊥CG 于H ,易求得 AG=CB=a ,CG= 5 a,∵CH=CD=a,∴HG=( 5 -1)a,设AF=x,则FH=DF=a -x,FG=a+x,由勾股定理得(a+x )2-(a -x)2=[ 5 -1)a]2,∴4ax=(6-2 5 )a 2,∴AF=x=3-52 a.20.∵3a +2b +c=4, 2a +b +3c=5,∴a=6-5c,b=7c -7,∴S =5a +4b +7c=10c+2, ∵非负实数a 、b 、c ∴a=6-5c ≥0,b=7c -7≥0,∴1≤c ≤65 ,∵S=10c+2,∴当c =65时,S 最大=14,当c =1时,S 最小=12,即m=14,n=12,∴n -m=-2 三.解答题21.解:(1)如图,过点B 作BF ∥AD ,交DC 于点F , 直角梯形ABCD 中,AB ∥DF , ∴四边形ABFD 为平行四边形. ∴∠BFE=∠D=30°,AB=DF=1米, ∴EF=DE-DF=4米,在Rt △BCF 中,设BC=x 米,则BF=2x ,CF=,在Rt △BCE 中,∠BEC=60°,CE=,∴EF=CF-CE=,解得:,∴AD=BF=2x=米.(2)由题意知,∠BGE=45°, 在Rt △BCG 中,BC=CG=米,∴GE=GC-EC=()米,DG=DE-GE=()米,即应放直径是()米的遮阳伞.22.解:(1)∵购买污水处理设备A 型x 台,则购买B 型(10-x )台。
由题意知: 1002)10(1012+=-+=x x x y ∵1051002≤+x ∴解得,∵x 取非负整数,∴x=0,1,2。
即有三种购买方案:(2)由题意得,解得,∵∴5.21≤≤x 且x 为整数, ∴x=1或2, 当x=1时,购买资金:y=2×1+100=102(万元), 当x=2时,购买资金:y=2×2+100=104(万元), ∴为了节约资金,应选购A 型1台,B 型9台; (3)10年企业自己处理污水的总资金为: 102+1×10×10=202(万元),若将污水排到污水厂处理,10年所需费用为:2040×12×10×10=2448000(元)=244.8(万元) 244.8-202=42.8(万元), ∴能节约资金42.8万元。
A B C D E F G H。
