一阶纯滞后系统的不完全微分PID控制
不完全微分PID算法

设数字微分调节器的输入 为单位阶跃序列 ek 1 普通的数字调节器的微分作用
普通的数字调节器
LOGO
只在第一个采样周期里起作用 不能按照偏差变换的趋势在整个调节 过程中起作用。 微分作用在第一个采样周期时作用很 强,容易溢出。
LOGO
不完全微分PID算法
不完全数字PID 能抑制高频干扰 数字控制器输出的微分作 用能在各个采样周期按照误 差变化的趋势均匀地输出 改善了系统的系能。
《计算机控制技术》讨论课
不完全微分PID算法
1 PID控制器的结构简单,参数易 于通过编制计算机语言实现调整, 在长期应用中已积累了丰富的经验。
2 执行机构都存在一个线性工作区 。在此线性区内,它可以线性地跟踪 控制信号,而当控制信号过大,超过 这个线性区,就进入饱和区或截止区 ,其特性将变成非线性特性。从而使 系统出现过大的超调和持续振荡,动 态品质变坏。
输出控制曲线
图一 :不完全微分PID算法输出控制曲线
图二:普通PID算法输出控制曲线
计算得:
在第一个采样周期里 不完全微分数字控制器 的
输出比 完全微分数字控制器 的输出幅度小得 多,而且控制器的输出十分近似于理想的微分控
制器。
10
比较输出控制曲线
能够抑制控制系 统的高频干扰,有 效地改善干扰对系 统的影响。
不完全微分 PID算法复杂
UPDATES
改善系统的动 态性能,提高了系 统的控制精度。
11
谢谢观赏
计算机控制技术
3 微分控制器根据偏差变化的 趋向进行控制,它能够预测偏差, 产生超前的校正作用,有助于减小 超调,克服振荡,使系统趋于稳定。
5 串接一个低通滤波器(一阶 惯性环节)来抑制高频影响,形。 成不完全微分PID控制算法
一阶惯性加纯滞后过程的分数阶PID的脆弱性剖析

一阶惯性加纯滞后过程的分数阶PID的脆弱性摘要本文对在一阶惯性加纯滞后模型采用的分数阶PID控制器进行了分析。
尤其是对控制器参数对已获得控制系统的鲁棒性和性能的影响的研究。
结果表明,这种控制器跟标准PID控制器比起来更加脆弱,因此用户在整定的时候需要格外的慎重。
关键词:分数阶控制器,PID控制,整定,脆弱性1 引言众所周知,一个合理的控制系统必须同时兼顾性能和鲁棒性。
然而,也应该认识到另外很重要的一点那就是控制器参数变化对脆弱性的影响,也就是说,控制器参数改变会影响控制系统的鲁棒性和性能的敏感程度。
这个问题已经在其他文章中提及(见,例,[1]),尤其在[2]强调基于的最小化设计技术,和规范服从于高阶的健壮性(yield to high-order robust),最优的但极其脆弱的控制器,换言之,控制器系数非常小的变化会导致不稳定的系统。
然而,在[3,4]中指出,这个问题可以通过采用合适的控制器参数来解决。
就如在工业界使用最广的整数阶PID,这类控制器的脆弱性已经被解决。
其中,为了是控制器参数向量在给定的范围内的稳定域最大化,作者建议调整整数阶PID控制器的参数。
然而典型的工业性能的测量(关系到对设定值的跟踪和对负载干扰的抑制任务)并不考虑。
并且,在图[7]中显示,这种办法已经被应用到一阶惯性加纯滞后模型,产生了与采用Ziegler-Nichols阶跃响应方法相似的调谐,从各方面看都是有改善的。
因此,在文献中已被公认,研究整数阶PID的一个主要原因就是让使用者明白怎样调整好控制器[10,11,12]。
换句话说,整数阶PID的参数有明确的物理含义,操作者可以通过修改它们来改变控制系统的性能。
在文中,当参数微调对评估鲁棒性和性能的敏感性很有用。
为此,引入了一个叫做脆弱性环的图形化工具,它可以对评估控制器的鲁棒性/脆弱性提供了一种可视化帮助。
近年来,一些学术和工业界团体对分数阶PID控制器很感兴趣,因为他们在控制系统设计中能够更灵活(仅有5个参数需要整定)(见,例[14]-[17])。
纯滞后系统PID-模糊控制

4 1
纯滞后系统 P I D 一 模糊控制
PI D— — f u z z y Co n t r o l S y s t e m wi t h P u r e L a g
尹 超 李 茂 军 张 静 ( 长沙理工大学电气与信息工程学院, 湖南 长沙 4 1 0 0 7 6 )
I n o r de r t o e ns u r e t he qu al i t y o f u r b an wa t er s u ppl y, t h e wa t er s uppl y wi t h f r e qu e n cy c on v er s i on an d co n s t an t pr e s s ur e i s o f t en u se d.A PI D-f u z z y c on t r o l s t r a t eg y wi t h Smi t h p r e di c t or i s pr op os e d f or t h e co n s t a n t p r e s s ur e wa t e r s u ppl y s y s t em . wh i c h ha s t he c ha r a c t e r s of n on l i n e ar i t y, r a ndo mi ci t y, l ar g e i n er t i a a n d bi g del ay T hi s co n t r ol s t r a t eg y co m bi ne s t h e a d va n — r a ges of go od d yn a mi c r e s po n se o f f u z z y c on t r o l , h i gh r eg ul at i o n ac cu r ac y o f PI D co n t r ol an d pu r e l ag c o mp en s a t i on o f Smi l h pr edi c t or On t h e ba s i s of r e t a i n i n g t h e s y s t em S s t at i o n ar i t y, d yn a mi c p r o c es s an d s t ea dy s t at e pe r f o r man c e, t hi s c o n — t r o l s t r a t e gy c an e v i de n t l y i mp r o v e t h e s pe ed abi l i t y of d yn ami c pr oc e s s, h a s go od r o bu s t n e s s a nd ha s wel l a da pt ab i l i t y t o
一阶惯性加纯滞后过程的分数阶PID的脆弱性剖析

一阶惯性加纯滞后过程的分数阶PID的脆弱性摘要本文对在一阶惯性加纯滞后模型采用的分数阶PID控制器进行了分析。
尤其是对控制器参数对已获得控制系统的鲁棒性和性能的影响的研究。
结果表明,这种控制器跟标准PID控制器比起来更加脆弱,因此用户在整定的时候需要格外的慎重。
关键词:分数阶控制器,PID控制,整定,脆弱性1 引言众所周知,一个合理的控制系统必须同时兼顾性能和鲁棒性。
然而,也应该认识到另外很重要的一点那就是控制器参数变化对脆弱性的影响,也就是说,控制器参数改变会影响控制系统的鲁棒性和性能的敏感程度。
这个问题已经在其他文章中提及(见,例,[1]),尤其在[2]强调基于的最小化设计技术,和规范服从于高阶的健壮性(yield to high-order robust),最优的但极其脆弱的控制器,换言之,控制器系数非常小的变化会导致不稳定的系统。
然而,在[3,4]中指出,这个问题可以通过采用合适的控制器参数来解决。
就如在工业界使用最广的整数阶PID,这类控制器的脆弱性已经被解决。
其中,为了是控制器参数向量在给定的范围内的稳定域最大化,作者建议调整整数阶PID控制器的参数。
然而典型的工业性能的测量(关系到对设定值的跟踪和对负载干扰的抑制任务)并不考虑。
并且,在图[7]中显示,这种办法已经被应用到一阶惯性加纯滞后模型,产生了与采用Ziegler-Nichols阶跃响应方法相似的调谐,从各方面看都是有改善的。
因此,在文献中已被公认,研究整数阶PID的一个主要原因就是让使用者明白怎样调整好控制器[10,11,12]。
换句话说,整数阶PID的参数有明确的物理含义,操作者可以通过修改它们来改变控制系统的性能。
在文中,当参数微调对评估鲁棒性和性能的敏感性很有用。
为此,引入了一个叫做脆弱性环的图形化工具,它可以对评估控制器的鲁棒性/脆弱性提供了一种可视化帮助。
近年来,一些学术和工业界团体对分数阶PID控制器很感兴趣,因为他们在控制系统设计中能够更灵活(仅有5个参数需要整定)(见,例[14]-[17])。
PID控制算法详细讲解

PID控制算法详细讲解5.1 PID控制原理与程序流程5.1.1过程控制的基本概念过程控制一一对生产过程的某一或某些物理参数进行的自动控制。
一、模拟控制系统图5-1-1基本模拟反馈控制回路被控量的值由传感器或变送器来检测,这个值与给定值进行比较,得到偏差,模拟调节器依一定控制规律使操作变量变化,以使偏差趋近于零,其输出通过执行器作用于过程。
控制规律用对应的模拟硬件来实现,控制规律的修改需要更换模拟硬件。
二、微机过程控制系统微型计算机图5-1-2微机过程控制系统基本框图以微型计算机作为控制器。
控制规律的实现,是通过软件来完成的。
改变控制规律,只要改变相应的程序即可。
三、数字控制系统DDC图5-1-3 DDC系统构成框图DDC(Direct Digital Congtrol)系统是计算机用于过程控制的最典型的一种系统。
微型计算机通过过程输入通道对一个或多个物理量进行检测,并根据确定的控制规律(算法)进行计算,通过输出通道直接去控制执行机构,使各被控量达到预定的要求。
由于计算机的决策直接作用于过程,故称为直接数字控制。
DDC系统也是计算机在工业应用中最普遍的一种形式。
5.1.2模拟PID 调节器 一、模拟PID 控制系统组成二、模拟PID 调节器是一种线性调节器,它将给定值r(t)与实际输出值c(t)的偏差的比例(P)、积分(I)、微分(D)通过线性组合构成控制量,对控制对象进行控制。
、PID 调节器的微分方程u(t)二 K p e(t) T .0e (t)dt T D 售)式中 e(t)二 r(t) 一c(t)2 、PID 调节器的传输函数 三、PID 调节器各校正环节的作用1、 比例环节:即时成比例地反应控制系统的偏差信号e(t),偏差一旦产生,调节器 立即产生控制作用以减小偏差。
2、 积分环节:主要用于消除静差,提高系统的无差度。
积分作用的强弱取决于积分 时间常数TI ,TI越大,积分作用越弱,反之则越强。
不完全微分PID算法与标准PID算法的比较与分析
· 43 ·不完全微分PID 算法与标准PID 算法的比较与分析王 斌 李 伟 刘世军新疆电力科学研究院(乌鲁木齐 830011)摘要:在PID 算法的微分环节中加入一阶惯性环节,通过不完全微分PID 来改善干扰对系统的影响,改善系统的动态特性。
关键词:不完全微分,PID,matlab,锅炉主控 0 前言在PID 控制中,微分作用的引入可以改善系统的动态特性,加快系统的动作速度,减少调节时间。
但是目前新疆火电厂的自动控制系统中很少应用到微分作用,其主要原因是(1)微分作用容易引入高频干扰,当系统出现高频扰动时会破坏系统的稳定性。
(2)当被控参数以阶跃函数改变时,微分项仅在第一个采样周期起作用,对于惯性较大的系统其调节作用很小,不能达到超前调节的目的。
1 不完全微分PID 优点分析标准PID 算法的微分项为()D D U s T s =, 微分项对阶跃输入的响应为脉冲函数,但应用到工业生产的计算机控制系统中时,输出是一个有限的量,即()[()(1)]/D D U k T e k e k T =−−Δ,这一输出只在第一个采样周期内有效,而且作用很强。
在一个采样周期后微分输出将回到零。
执行机构实际是不可能这么快速地动作的,因此这时的微分作用形同虚设。
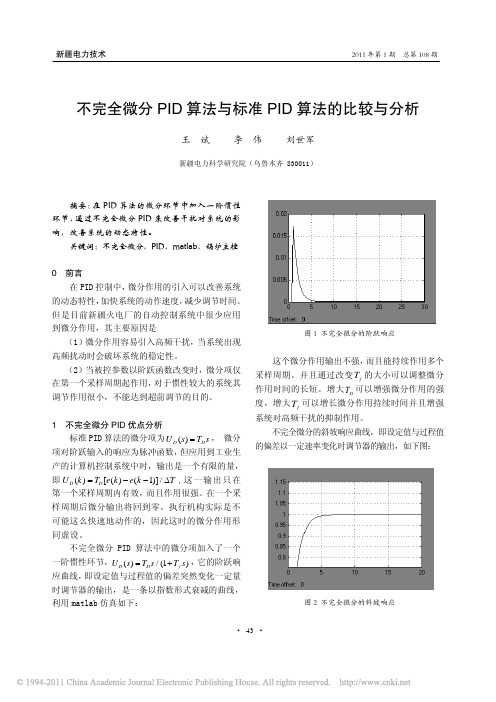
不完全微分PID 算法中的微分项加入了一个一阶惯性环节,()/(1)D D f U s T s T s =+,它的阶跃响应曲线,即设定值与过程值的偏差突然变化一定量时调节器的输出,是一条以指数形式衰减的曲线,利用matlab 仿真如下:图1 不完全微分的阶跃响应这个微分作用输出不强,而且能持续作用多个采样周期。
并且通过改变f T 的大小可以调整微分作用时间的长短。
增大D T 可以增强微分作用的强度,增大f T 可以增长微分作用持续时间并且增强系统对高频干扰的抑制作用。
不完全微分的斜坡响应曲线,即设定值与过程值的偏差以一定速率变化时调节器的输出,如下图:图2不完全微分的斜坡响应· 44 ·由上图可见,不完全微分能够实现标准PID 算法中微分环节的功能,并且响应曲线比前述微分项平滑。
一阶加纯滞后对象的PID控制器参数整定方法的比较研究

一阶加纯滞后对象的PID控制器参数整定方法的比较研究【摘要】在工业控制领域,以一阶加纯滞后控制过程为研究对象,分别采用Z-N法、粒子群、模糊控制对PID控制器的参数进行整定,并且从稳定性、跟踪性、以及抗干扰性等方面通过MATLAB仿真,分析比较各自的优缺点。
研究结果表明粒子群算法以及模糊控制法对于PID参数的整定在综合性能方面有一定的优势,并对现代工业控制的PID整定设计方面有一定实用价值。
【关键词】参数整定;Z-N;粒子群算法;模糊PID;MATLAB仿真Abstract:In the field of industrial control,to a first order plus dead time control process for the study,were used Z-N method,PSO,fuzzy control parameters were tuning PID controllers,and from stability,tracking,as well as other aspects of immunity by MATLAB simulation,analysis and comparison of their advantages and disadvantages.The results show that particle swarm optimization and fuzzy PID control method for the whole parameter set in terms of overall performance has certain advantages and tuning PID control of modern industrial design has some practical value.Keywords:Parameter tuning;Z-N;Particle Swarm Optimization;Fuzzy PID control;MATLAB simulation引言PID控制器是目前在工业控制中应用最广泛的控制策略之一[1]。
不完全微分pid的微分表达形式

不完全微分PID的微分表达形式在探讨不完全微分PID的微分表达形式之前,我们需要先了解什么是不完全微分以及PID控制器的基本概念。
不完全微分是指在多元函数微分中,只有部分变量被微分,而其他变量被视为常数。
PID控制器是一种常见的控制系统,由比例(proportional)、积分(integral)和微分(derivative)三部分组成,用于调节系统的输出,以使其达到所需的状态。
不完全微分PID的微分表达形式即是对PID控制器中微分部分的具体表达方式。
我们来看一个简单的不完全微分的例子:假设有一个二元函数f(x,y),其中y是x的函数,即y=y(x)。
那么f(x,y)对x的不完全微分即为∂f/∂x,在此过程中,y被视为常数。
同理,对y的不完全微分为∂f/∂y,其中x被视为常数。
接下来,我们来探讨不完全微分PID的微分表达形式。
在PID控制器中,微分项通常表示系统的瞬时状态变化率。
对于不完全微分PID,我们需要将微分表达形式分别应用到各个部分,以得到整体的微分表达。
1. 对于比例项(P部分):P部分的微分表达形式可以直接写为Proportional * ∂e/∂t,其中e表示误差项。
这里的∂e/∂t即表示对误差随时间的变化率进行微分。
比例项的微分表达形式简单直观,反映了误差的瞬时变化对输出的影响。
2. 对于积分项(I部分):I部分的微分表达形式需要考虑积分运算对误差的积累效果。
一般来说,积分项的微分表达形式为Integral * e。
这里的e表示误差项,而Integral则反映了误差随时间的积累效果。
在不完全微分的情况下,积分项的微分表达形式需要特别注意误差对时间的影响,以避免积分效果的不完全微分。
3. 对于微分项(D部分):D部分的微分表达形式通常为Derivative * ∂e/∂t,其中e也表示误差项。
微分项的微分表达形式主要反映了误差的瞬时变化率对输出的影响,与比例项类似。
然而,需要特别注意的是,由于微分本身就是一种关于时间变化率的操作,因此微分项的微分表达形式在不完全微分中更加注重误差随时间的瞬时变化。
不完全微分pid1

1 引言智能车系统是一个时变且非线性的系统,采用传统PID算法的单一的反馈控制会使系统存在不同程度的超调和振荡现象,无法得到理想的控制效果。
本文将前馈控制引入到了智能车系统的控制中,有效地改善了系统的实时性,提高了系统的反应速度[1];并且根据智能车系统的特点,对数字PID算法进行了改进,引入了微分先行和不完全微分环节,改善了系统的动态特性;同时,利用模糊控制具有对参数变化不敏感和鲁棒性强的特点[2],本文将模糊算法与PID算法相结合,有效地提高了智能车的适应性和鲁棒性,改善了系统的控制性能。
2 改进PID算法智能车的控制是由飞思卡尔公司的S12芯片完成,所以对智能车的控制要采用计算机控制方法。
本文针对智能车控制的特殊性,对传统数字PID算法做了一些改进,这样可以更好地满足智能车控制的需要。
2.1不完全微分PID将微分环节引入智能车的方向和速度控制,明显地改善了系统的动态性能,但对于误差干扰突变也特别敏感,对系统的稳定性有一定的不良影响。
为了克服上述缺点,本文在PID算法中加入了一阶惯性环节[3] ,不完全微分PID算法结构如图1所示。
图1 不完全微分PID算法机构图将一阶惯性环节直接加到微分环节上,可得到系统的传递函数为:(1)将(1)式的微分项推导并整理,得到方程如下:(2)式中,,由系统的时间常数和一阶惯性环节时间常数决定的一个常数。
为了编程方便,可以将2-2式写成如下形式:(3)式中,。
分析式(3)可知,引入不完全微分以后,微分输出在第一个采样周期内被减少了,此后又按照一定比例衰减[3][4]。
实验表明,不完全微分有效克服了智能车的偏差干扰给速度控制带来的不良影响,具有较好的控制效果。
图2为不完全微分PID算法的程序流程图。
2.2 微分先行PID由于智能车在跑道上行驶时,经常会遇到转弯的情况,所以智能车的速度设定值和方向设定值都会发生频繁的变化,从而造成系统的振荡。
为了解决设定值的频繁变化给系统带来的不良影响,本文在智能车的速度和方向控制上引入了微分先行PID算法,其特点是只对输出量进行微分,即只对速度测量值和舵机偏转量进行微分,而不对速度和方向的设定值进行微分。
不完全微分PID算法

不完全微分PID算法不完全微分PID算法是一种改进的PID控制算法,它比传统的PID控制算法有更好的稳定性和鲁棒性。
不完全微分PID算法是在控制系统中引入微分操作的一个改进,通过将差分器的输出与积分因子相乘,得到一个不完全微分PID控制器,从而使系统响应速度更快、误差更小。
PID控制器是由比例项、积分项和微分项组成的。
比例项用来调整控制器的输出与误差之间的线性关系,积分项用来修正系统的稳态误差,微分项用来提高系统的稳定性和响应速度。
然而,传统的PID控制器在实际应用中存在一些不足之处。
比如,微分项通常会引入控制器的噪声放大因子,导致控制器的输出过于敏感,容易产生震荡。
此外,传统的PID控制器在存在大量干扰或参数变化的情况下,容易产生较大的误差。
不完全微分PID算法通过引入微分操作的改进,可以有效地解决传统PID控制器的不足之处。
不完全微分PID算法的核心思想是将差分器的输出与积分因子相乘,得到一个不完全微分PID控制器。
通过不完全微分操作,可以有效地抑制控制器的输出过于敏感,减小系统的震荡。
具体地说,不完全微分PID算法可以通过以下几个步骤来实现:1.根据控制对象的特性和性能指标,确定合适的比例增益、积分增益和微分增益。
2.在传统PID算法的基础上,将微分器的输出与积分因子相乘,得到一个不完全微分项。
3.将不完全微分项与比例项、积分项相加,得到一个新的控制器输出。
4.根据实际系统的反馈信号和期望输出信号,计算系统的误差。
5.根据误差和控制器增益,计算控制器的输出。
通过以上步骤,不完全微分PID算法就可以实现对系统的精确控制。
不完全微分PID算法在很多实际应用中取得了较好的效果,具有较好的稳定性和鲁棒性。
需要注意的是,不完全微分PID算法的实现需要根据具体的系统特性和性能指标进行调整和优化。
此外,不完全微分PID算法也需要根据实际应用的需求进行参数调整,以获得最佳的控制效果。
一阶加纯滞后对象的PID控制器参数整定方法的比较研究

一阶加纯滞后对象的PID控制器参数整定方法的比较研究【摘要】在工业控制领域,以一阶加纯滞后控制过程为研究对象,分别采用Z-N法、粒子群、模糊控制对PID控制器的参数进行整定,并且从稳定性、跟踪性、以及抗干扰性等方面通过MATLAB仿真,分析比较各自的优缺点。
研究结果表明粒子群算法以及模糊控制法对于PID参数的整定在综合性能方面有一定的优势,并对现代工业控制的PID整定设计方面有一定实用价值。
【关键词】参数整定;Z-N;粒子群算法;模糊PID;MATLAB仿真Abstract:In the field of industrial control,to a first order plus dead time control process for the study,were used Z-N method,PSO,fuzzy control parameters were tuning PID controllers,and from stability,tracking,as well as other aspects of immunity by MATLAB simulation,analysis and comparison of their advantages and disadvantages.The results show that particle swarm optimization and fuzzy PID control method for the whole parameter set in terms of overall performance has certain advantages and tuning PID control of modern industrial design has some practical value.Keywords:Parameter tuning;Z-N;Particle Swarm Optimization;Fuzzy PID control;MATLAB simulation引言PID控制器是目前在工业控制中应用最广泛的控制策略之一[1]。
一阶纯滞后系统的不完全微分PID控制

目录0.前言 (1)1. 不完全微分PID算法设计 (2)2.算法仿真研究 (3)3.一阶纯滞后系统的不完全微分PID控制程序 (4)4.实验结果 (7)5.结论及总结 (8)参考文献 (8)课设体会 (10)$一阶纯滞后系统的不完全微分PID控制沈阳航空航天大学北方科技学院摘要:提出在PID算法中加入一阶惯性环节,通过不完全微分PID算法来改善干扰对系统的影响,用MATLAB仿真分析说明该算法在改善过程的动态性能方面具有良好的控制精度。
在现代工业生产中,自动控制技术的使用越来越多,而随着工业和控制技术的发展,自动控制理论也在发展和完善,出现了多种控制方法如最基础的PID控制以及微分先行控制、中间微分控制、史密斯补偿控制、模糊控制、神经网络控制等。
自动控制技术的发展在工业生产中遇到了一系列的问题:如在本文中所研究的一阶纯滞后系统的控制就是控制理论中一个较为重要的问题。
由控制理论可知,无滞后控制系统(简单点说就是没有延迟)比有滞后系统更加稳定,更加容易控制。
因此如何解决生产中滞后的问题在当前工业大生产中尤其重要。
论文在常规PID控制也就是比例-积分-微分控制的基础上提出了三种控制方法即:微分先行控制、中间微分反馈控制、史密斯补偿控制。
并对这三种方案进行Simulink 仿真,检测其抗干扰性能。
为便于分析,论文将所得仿真结果以图形的方式给予显示出来,形象生动便于理解。
关键词:一阶纯滞后 ;不完全微分;仿真;PID…0.前言在多数工业过程当中,控制对象普遍存在着纯时间滞后现象,如化工,热工过程等.这种滞后时间的存在,会使系统产生明显的超调量和较长的调节时间,滞后严重时甚至会破坏系统的稳定性,在工业生产上产生事故.因此长期以来,纯滞后系统就一直是工业过程中的难控制对象,人们也对它进行了大量的研究.在现代工业生产和理论研究中出现了多种控制方法,如PID控制、PID改进控制、Smith 预估算法控制以及模糊控制、神经网络控制等.而对于最基础的一阶纯滞后系统常用的控制方法主要是PID 控制、不完全微分PID 控制.1. 不完全微分PID 算法设计为了克服上述缺点, 在PID 算法中加一个一阶惯性环节(低通滤波器)G f (S )=1/[1+T f (S )],将低通滤波器直接加在微分环节上,构成如图1的不完全微分PID 控制:式中,T 为采样时间,T f 为滤波器系数,T 1和T D 分别为积分时间常数和微分时间常数,令 ɑ=T f /(T f +T),则T/(T+T f )=1-ɑ;显然有1<α,1−α<1成立,不完全微分项为:若e(k)为单位阶跃(即e(k)=1,k=0,1,2,∧)由此得出不完全微分项为:(可见,引入不完全微分后,微分输出按ɑk U D(0)的规律)(ɑ(1)逐渐衰减,所以不完全微分能有效地克服前述微分项的不足。
不完全微分PID 算法在纯滞后系统中的应用

不完全微分PID 算法在纯滞后系统中的应用朱仲邃嘉应学院 物理系,广东 梅州 514015摘要:提出在PID 算法中加入一阶惯性环节,通过不完全微分PID 算法来改善干扰对系统的影响,用MATLAB 仿真分析说明该算法在改善过程的动态性能方面具有良好的控制精度。
关键词:纯滞后,不完全微分,PID 算法中图分类号:TP273 文献标识码:AApplication of PID Algorithm with Incomplete Derivationin Time-delay SystemZHU ZhongsuiDepartment of Physics ,Jiaying University ,Meizhou 514015,ChinaAbstract : A digital PID control algorithm with incomplete derivation is presented. MATLAB simulations show this algorithm has good dynamic performance such as control accuracy.Key Word : Time-delay ,Incomplete derivation , PID algorithm1.引言在PID 控制中,微分信号的引入可改善系统的动态特性,加快系统的动作速度,减少调节时间,但也易引入高频干扰,在误差扰动突变时尤其显出微分项的不足。
微分输出项为:[])1()()(−−=k e k e TT K k U D P D 当)(k e 为阶跃函数时,)(k U D 输出的特点: (1)微分项的输出仅在第一个周期起激励作用,对于时间常数较大的系统,其调节作用很小,不能达到超前控制误差的目的。
(2)D U 的幅值T T K D P /一般比较大,容易造成计算机中数据溢出;此外,D U 过大、过快的变化,对执行机构也会造成不利的影响(通常D T T <<)。
一阶纯滞后系统控制

The control method research of the first-order delay system Abstract
The automatic control technology use more and more in modern industrial production, and as the industrial and control technology development, the automatic control theory are developed and perfected, a lot of controlled methods appear such as PID control which is the most basic control and differential first control, intermediate differential control, Smith compensation control, fuzzy control, nerve network control. Automatic control technology had experienced a series of questions in industrial production: as the first-order delay system control in this article which is a more important issue in the control theory. Known by the control theory,a no lag control system (simple say is no delay) is more stable and more easily controlled than a delay system . So it is particularly important of how to solve the lagging problem in the current industrial production . The articles propose three control methods such as differential first control 、 the middle of differential feedback control 、 smith compensation control base the conventional PID control in the other word is proportional - integral - derivative controller .And simulate this three programs by the simulink, testing its interference fearure. For convenient analyze the simulation result , the paper of the study derive from the simulation results by the graphical ,which we can easy understand and clear know the mean in the article. Key Words:automatic control; simulation; PID; complicated control
一阶惯性环节的模糊PID自整定控制算法的设计

= K P e ( k ) + K i ∑ e ( j ) + K d [ e ( k ) − e ( k − 1)]
j =0
k
比例环节作用在于加快系统的响应速度 节精度 越高 Kp 越大 系统的响应速度越快 也就是对误差的分辨率越高
提高系统调 甚
K
P
为比例系数
Ki = K P
T Ti
为积分系数
系统的调节精度
万方数据
第 15 卷第 2 期 的控制规则表如表 2 所示 表2
Ki E NB NM NS O PS PM PB NB NB NB NM NM O O NB NB NM NM NS O O NM NM NS NS O PS PS NM NS NS O PS PS PM NS NS O PS PS PM PM E NB NM
常将积分环节分离出来 调 KI 取零值
率 在 0 值附近的函数形状取得更陡一些 形式如图 2 所 示 各变量的模糊量分别为 E 46 EC Kp KI KD 其模糊集合的论域为[-6 -5 -4 -3 -2 -1 0 1 2 3
入积分环节 因此 当偏差|e|大或较大时 为避免系统超 当|e|较小时 积分环节有效 随|e|的减 KI 小而增大 以消除系统的稳态误差 提高控制精度
控制效果 数 中
PID 调节器便可实现作用
大多数工业过程都不同程度地存在非线性
性和模型不确定性 因而一般的 PID 控制无法实现对这样 过程的精确控制 型 由于模糊控制不需要建立过程的精确模 针对 PID 控制和模糊
所以得到了越来越广泛的应用
控制的各自特点
国内外学者分别采用不同的方法将模糊 研究出了多种模糊 PID 控制
但容易产生超调
力控的策略控制器PID算法介绍及应用

力控的策略控制器PID算法介绍及应用力控的策略控制器可以方便地实施多种控制算法,在这里我们以PID为例介绍如何在力控中组建一个PID 控制系统。
多年以来,在过程控制中,按偏差的比例(P)、积分(I)和微分(D)进行控制的PID控制器(亦称PID调节器)是应用最为广泛的一种自动控制器。
它具有原理简单,易于实现,适用面广,控制参数相互独立,参数的选定比较简单等优点;而且在理论上可以证明,对于过程控制的典型对象──“一阶滞后+纯滞后”与“二阶滞后+纯滞后”的控制对象,PID控制器是一种最优控制。
PID调节规律是连续系统动态品质校正的一种有效方法,它的参数整定方式简便,结构改变灵活(PI、PD、…)。
长期以来被广大科学技术人员及现场操作人员所采用,并积累了大量的经验。
连续系统PID调节器为对误差的比例、积分和微分控制,即或式中:Ti、Td分别为积分和微分时间常数;Kp、Ki、Kd分别为比例系数、积分系数、微分系数。
在计算机控制系统中使用的是PID数字调节器,就是对式(1)离散化,令式中,T是采样周期。
由式(1)与式(3)可得式(4)称为位置式PID控制算法。
由于位置式算法输出在计算过程中容易产生积分饱和作用,导致控制器的响应速度变慢,而且由于积分的累积作用,在手动和自动切换时,很难做到无扰动切换。
因此,人们又提出一种新的控制算法,PID增量式控制算法:在力控的策略控制器中采用的是增量式算法,但是输出采用位置式输出。
即把上次输出加上本次计算的增量输出即得到本次的位置式输出。
PID控制回路有三种方式,手动,自动和串级,在手动状态下,PID控制回路相当于手动调节器。
在自动状态下,PID控制回路完成PID算法,设定值由操作站给定,在串级状态,设定值由主回路的输出给定。
当回路处于手动状态下时,设定值具有自动跟踪测量值功能,以便从手动切换到自动状态时,切换时是无扰动的;当回路处自动状态时,主回路的输出自动跟踪副回路的设定,以便当下一级控制回路从自动切换到串级时,切换时是无扰动的。
微分先行PID和不完全微分

5.2.1 微分项的改进
1.不完全微分型PID控制算法: 不完全微分就是用实际PD环节来代替理想PD环节,
使微分作用对于偏差的变化不会有太大的反应. 同时减小理想微分带来的系统剧烈动作. 在比例积分作用的基础上串接一个
令微分部分的传递函数为:
则:
u (s) T s 1
D
D
y(s) TDs 1
1
TD
duD dt
uD
TD
dy dt
y
差分得: duD uD(k) u 1)
dt
T
T uD(k) uD(k 1) u (k) T y(k) y(k 1) y(k)
P
不稳定。
5.1.6 积分调节器
积分作用是指调节器的输出与输入偏差的积分成 比例的作用,其作用是消除静差。
积分方程为:
1
y(t) TI e(t)d (t)
e(t)
积分作用的响应特
0
t
性曲线如右图:
y
0
t
由图中曲线看出积分作用的特点:
只要偏差不为零就会产生对应的控制量并依此影 响被控量。
TD S 1 (TD / KD )S 1
环节。
传递函数框图如下:
图5-2-1 传递函数框图
完全和不完全微分的作用
微分先行PID控制算法及仿真
基本思想:微分先行PID控制的结构如下图所示,其特点是只对输 出量 y(t) 进行微分,而对给定值 r(t)不作微分。这样,在改变给定 值时,输出不会改变,而被控量的变化通常总是比较缓和的。这 种输出量先行微分控制适用于给定值 r(t) 频繁升降的场合,可以 避免给定值升降时所引起的系统振荡,明显地改善了系统的动态 特性。
PID调节比例积分微分作用的特点和规律总结

PID调节比例积分微分作用的特点和规律总结一在自动控制系统中,P、I、D调节是比例调节,积分调节和微分调节作用。
调节控制质量的好坏取决于控制规律的合理选取和参数的整定。
在控制系统中总是希望被控参数稳定在工艺要求的范围内。
但在实际中被控参数总是与设定值有一定的差别。
调节规律的选取原则为:调节规律有效,能迅速克服干扰。
比例、积分、微分之间的联系与相匹配使用效果比例调节简单,控制及时,参数整定方便,控制结果有余差。
因此,比例控制规律适应于对象容量大负荷变化不大纯滞后小,允许有余差存在的系统,一般可用于液位、次要压力的控制。
比例积分控制作用为比例及时加上积分可以消除偏差。
积分会使控制速度变慢,系统稳定性变差。
比例积分适应于对象滞后大,负荷变化较大,但变化速度缓慢并要求控制结果没有余差。
广泛使用于流量,压力,液位和那些没有大的时间滞后的具体对象。
比例微分控制作用:响应快、偏差小,能增加系统稳定性,有超前控制作用,可以克服对象的惯性,控制结果有余差。
适应于对象滞后大,负荷变化不大,被控对象变化不频繁,结果允许有余差的系统。
在自动调节系统中,E=SP-PV。
其中,E为偏差,SP为给定值,PV为测量值。
当SP大于PV时为正偏差,反之为负偏差。
比例调节作用的动作与偏差的大小成正比;当比例度为100时,比例作用的输出与偏差按各自量程范围的1:1动作。
当比例度为10时,按lO:l动作。
即比例度越小。
比例作用越强。
比例作用太强会引起振荡。
太弱会造成比例欠调,造成系统收敛过程的波动周期太多,衰减比太小。
其作用是稳定被调参数。
积分调节作用的动作与偏差对时间的积分成正比。
即偏差存在积分作用就会有输出。
它起着消除余差的作用。
积分作用太强也会引起振荡,太弱会使系统存在余差。
微分调节作用的动作与偏差的变化速度成正比。
其效果是阻止被调参数的一切变化,有超前调节的作用。
对滞后大的对象有很好的效果。
但不能克服纯滞后。
适用于温度调节。
使用微分调节可使系统收敛周期的时间缩短。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目录
0.前言 (1)
1. 不完全微分PID算法设计 (2)
2.算法仿真研究 (3)
3.一阶纯滞后系统的不完全微分PID控制程序 (4)
4.实验结果 (7)
5.结论及总结 (8)
参考文献 (8)
课设体会 (10)
一阶纯滞后系统的不完全微分PID控制
沈阳航空航天大学北方科技学院
摘要:提出在PID算法中加入一阶惯性环节,通过不完全微分PID算法来改善干扰对系统的影响,用MATLAB仿真分析说明该算法在改善过程的动态性能方面具有良好的控制精度。
在现代工业生产中,自动控制技术的使用越来越多,而随着工业和控制技术的发展,自动控制理论也在发展和完善,出现了多种控制方法如最基础的PID控制以及微分先行控制、中间微分控制、史密斯补偿控制、模糊控制、神经网络控制等。
自动控制技术的发展在工业生产中遇到了一系列的问题:如在本文中所研究的一阶纯滞后系统的控制就是控制理论中一个较为重要的问题。
由控制理论可知,无滞后控制系统(简单点说就是没有延迟)比有滞后系统更加稳定,更加容易控制。
因此如何解决生产中滞后的问题在当前工业大生产中尤其重要。
论文在常规PID控制也就是比例-积分-微分控制的基础上提出了三种控制方法即:微分先行控制、中间微分反馈控制、史密斯补偿控制。
并对这三种方案进行Simulink 仿真,检测其抗干扰性能。
为便于分析,论文将所得仿真结果以图形的方式给予显示出来,形象生动便于理解。
关键词:一阶纯滞后 ;不完全微分;仿真;PID
0.前言
在多数工业过程当中,控制对象普遍存在着纯时间滞后现象,如化工,热工过程等.
这种滞后时间的存在,会使系统产生明显的超调量和较长的调节时间,滞后严重时甚至会破坏系统的稳定性,在工业生产上产生事故.因此长期以来,纯滞后系统就一直是工业过程中的难控制对象,人们也对它进行了大量的研究.在现代工业生产和理论研究中出现了多种控制方法,如PID控制、PID改进控制、Smith 预估算法控制以及模糊
控制、神经网络控制等.而对于最基础的一阶纯滞后系统常用的控制方法主要是PID 控制、不完全微分PID 控制.
1. 不完全微分PID 算法设计
为了克服上述缺点, 在PID 算法中加一个一阶惯性环节(低通滤波器)G f (S )=1/[1+T f (S )],将低通滤波器直接加在微分环节上,构成如图1的不完全微分PID 控制:
式中,T 为采样时间,T f 为滤波器系数,T 1和T D 分别为积分时间常数和微分时间常数,令 ɑ=T f /(T f +T),则T/(T+T f )=1-ɑ;显然有1<α,1−α<1成立,不完全微分项为:
若e(k)为单位阶跃(即e(k)=1,k=0,1,2,∧)由此得出不完全微分项为:
可见,引入不完全微分后,微分输出按ɑk U D(0)的规律)(ɑ(1)逐渐衰减,所以不完全微分能有效地克服前述微分项的不足。
2.算法仿真研究
设被控对象为含纯滞后的一阶惯性环节,其传递函数为: G(S)=e-80S/50S+1
在对象的输出端加幅值为0.01的随机干扰信号,
采样时间为20s 低通滤波器为G f(S)=1/(180S+1)
控制器取K P=0.30,T1=55,T D=140
控制算法程序框图如图2;
图2 控制算法程序框图
3.一阶纯滞后系统的不完全微分PID控制程序PID的MATLAB仿真程序:
%PID Controler 不完全微分
clear all;
close all;
ts=20;
sys=tf([1],[60,1],'inputdelay',80);
dsys=c2d(sys,ts,'zoh');
[num,den]=tfdata(dsys,'v');
u_1=0;u_2=0;u_3=0;u_4=0;u_5=0;
ud_1=0;
y_1=0;y_2=0;y_3=0;
error_1=0;
ei=0;
for k=1:1:100
time(k)=k*ts;
rin(k)=1.0;
%Linear model
yout(k)=-den(2)*y_1+num(2)*u_5;
D(k)=0.01*rands(1);
yout(k)=yout(k)+D(k);
error(k)=rin(k)-yout(k);
%PID Controller with partly differential
ei=ei+error(k)*ts;
kc=0.30;
ki=0.0055;
TD=140;
kd=kc*TD/ts;
Tf=180;
Q=tf([1],[Tf,1]); %Low Freq Signal Filter
M=2; %M=1不完全微分,
%M=2普通Pid控制!!
if M==1
%Using PID with Partial differential
alfa=Tf/(ts+Tf);
ud(k)=kd*(1-alfa)*(error(k)-error_1)+alfa*ud_1;
u(k)=kc*error(k)+ud(k)+ki*ei;
ud_1=ud(k);
elseif M==2 %Using Simple PID
u(k)=kc*error(k)+kd*(error(k)-error_1)+ki*ei; end
%Restricting the output of controller
if u(k)>=10
u(k)=10;
end
if u(k)<=-10
u(k)=-10;
end
u_5=u_4;u_4=u_3;u_3=u_2;u_2=u_1;u_1=u(k);
y_3=y_2;y_2=y_1;y_1=yout(k);
error_1=error(k);
end
figure(1);
plot(time,rin,'b',time,yout,'r');
xlabel('time(s)');ylabel('rin,yout');
4.实验结果
系统的设定输入值r(K)取单位阶跃函数,跟踪输出控制曲线如图3,比较采用普通PID算法的输出控制曲线图4。
可以看出,尽管不完全微分PID算法要复杂一些,但能有效地改善干扰对系统的影响,改善系统的动态特性,提高了系统的控制精度。
图3 普通PID算法输出控制曲线
图4 不完全微分PID算法输出控制曲线
5.结论及总结
由仿真结果可以看出,采用不完全微分型PID算法,引入不完全微分后能有效克服普通PID的不足,尽管不完全微分算法比普通PID控制算法要复杂的多,但由于其良好的控制特性,近年来越来越广泛的应用。
研究本课题的课题背景和课题综述即课题在工业生产中的应用有一个初步的了解,以及自动控制的背景知识,为后面纯滞后问题的提出和研究做好铺垫。
参考文献
[1] 《MATLAB仿真技术与应用》作者:张德丰杨文茵出版社:清华大学出版社出版年份:2012 年
[2] 《微型计算机控制技术》第二版作者:于海生丁军航潘松峰吴贺荣出版社:清华大学出版社出版年份:1999年
[3]金以慧. 过程控制[M].清华大学出版社,1993年:196-202
[4]潘新民,王燕芳.微型计算机控制技术[M].电子工业出版社,2002年:281-282
沈阳航空航天大学北方科技学院课程设计论文
课设体会
通过本次课设,我学会了matlab软件的运用,对直线插补与逐点比较法平有了一个深刻的认识,遇到问题是,在解决问题的过程中使我对知识有了更深刻的认识,不再像知识把书本上的习题学来考试。
课程设计诚然是一门专业课,给我很多专业知识以及专业技能上的提升,同时又是一门讲道课,一门辩思课,给了我许多道,给了我很多思,给了我莫大的空间。
同时,设计让我感触很深。
使我对抽象的理论有了具体的认识。
通过这次课程设计,我掌握了的识别和测试;熟悉了;了解了方法;以及如何提高的性能等等,掌握了的方法和技术,通过查询资料,也了解了原理。
我认为,在这学期的实验中,不仅培养了独立思考、动手操作的能力,在各种其它能力上也都有了提高。
更重要的是,在实验课上,我们学会了很多学习的方法。
而这是日后最实用的,真的是受益匪浅。
要面对社会的挑战,只有不断的学习、实践,再学习、再实践。
这对于我们的将来也有很大的帮助。
以后,不管有多苦,我想我们都能变苦为乐,找寻有趣的事情,发现其中珍贵的事情。
就像中国提倡的艰苦奋斗一样,我们都可以在实验结束之后变的更加成熟,会面对需要面对的事情。
回顾起此课程设计,至今我仍感慨颇多,从理论到实践,在这段日子里,可以说得是苦多于甜,但是可以学到很多很多的东西,同时不仅可以巩固了以前所学过的知识,而且学到了很多在书本上所没有学到过的知识。
通过这次课程设计使我懂得了理论与实际相结合是很重要的,只有理论知识是远远不够的,只有把所学的理论知识与实践相结合起来,从理论中得出结论,才能真正为社会服务,从而提高自己的实际动手能力和独立思考的能力。
在设计的过程中遇到问题,可以说得是困难重重,但可喜的是最终都得到了解决。
[2014年7月11日完成]
第10 页。
