曲面建模讲解与实例
CAD软件中的曲面建模技巧与实例解析

CAD软件中的曲面建模技巧与实例解析曲面建模是CAD软件中一个重要的技术,应用广泛,可以用来设计复杂的表面形状和曲线。
在本文中,我将分享一些曲面建模的技巧和实例,帮助读者更好地使用CAD软件。
1. 使用面实体建模面实体是曲面建模的基础,是由一系列边和顶点组成的。
在CAD 软件中,我们可以通过绘制直线、圆弧等基本形状,然后通过面命令将其组合成面实体。
这样可以快速创建出复杂的曲面形状。
2. 使用曲线命令曲线命令是曲面建模中一个非常重要的工具,可以用来绘制多种不同类型的曲线。
例如,我们可以使用样条曲线、贝塞尔曲线等来描述复杂的曲线形状。
在CAD软件中,我们可以通过指定曲线的控制点或参数方程的形式来创建曲线。
3. 使用曲面命令曲面命令是创建曲面实体的主要工具。
在CAD软件中,我们可以通过指定曲线边界或曲线路径来创建曲面。
同时,我们还可以使用曲面修剪、曲面布尔运算等命令来对曲面进行进一步的编辑和修饰。
4. 使用曲面编辑工具CAD软件中还提供了一些强大的曲面编辑工具,可以帮助我们对曲面实体进行精确调整和修改。
例如,我们可以使用曲面拉伸、曲面扫掠等命令来改变曲面的形状和方向。
同时,我们还可以使用曲面偏置、曲面平滑等命令来实现曲面的精确调整。
下面通过一个实例来具体说明曲面建模的应用。
实例:设计一款汽车车身假设我们要设计一款新型的汽车车身,其中包含复杂的曲面形状和曲线。
我们可以通过CAD软件中的曲面建模技巧来实现这一目标。
首先,我们可以使用面命令将车身分为多个面实体,例如车门、车顶、车窗等。
然后,我们可以使用曲线命令来绘制车身的曲线边界,例如车顶弧线、车窗边界等。
接下来,通过曲面命令将曲线边界转化为曲面实体,例如将车顶弧线转化为车顶的曲面。
在创建曲面实体时,我们可以根据需要调整曲面的曲度和光滑度。
最后,使用曲面编辑工具来精确调整和修改曲面实体,确保车身的曲线和曲面符合设计要求。
通过这个实例,我们可以看到曲面建模技巧在设计汽车车身中的重要性。
曲面建模经典案例

曲面建模是三维建模中非常重要的一种技术,可以用于创建曲面形状,如汽车、飞机、船舶、家具等。
以下是一些曲面建模的经典案例:
1. 法拉利F430
法拉利F430是一款流线型跑车,由曲面造型的流线型外观著称。
通过曲面建模技术,设计师们可以创建如此复杂的曲线和曲面形状。
2. 波音787飞机
波音787飞机是一款高科技、高性能的现代化飞机,曲面建模技术被广泛应用于其设计和制造过程中。
通过曲面建模技术,设计师们可以创建飞机机身的复杂曲线和曲面形状。
3. 雀巢咖啡机
雀巢咖啡机是一款现代化的家用电器,其具有精致的曲面设计,尤其是圆弧形的壳体和曲面按钮。
通过曲面建模技术,设计师们可以创建精细的产品外观和曲面形状。
4. 华盛顿巴伦山庄
华盛顿巴伦山庄是美国华盛顿特区的一座历史建筑,建筑外
观拥有大量的曲线、曲面和褶皱。
曲面建模技术可以帮助设计师们精确地重建其复杂的外观和曲面形状。
5. Zaha Hadid设计的建筑
Zaha Hadid是著名的建筑师和设计师,她通过曲面建模技术,在多个项目中展现出其标志性的曲线和曲面造型。
比如著名的Guangzhou Opera House、Heydar Aliyev Cultural Center 等,都是曲面建模技术的经典案例。
曲面建模技术在许多领域都得到了广泛应用,比如汽车工业、航天工业、室内设计、建筑设计等。
通过曲面建模技术,人们可以创造出更加复杂、更加先进的产品和建筑。
ug-曲面建模实例教程-茶壶建模步骤
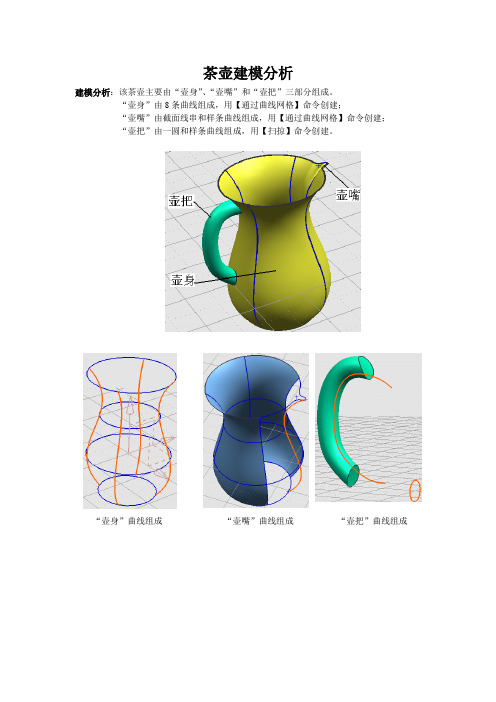
茶壶建模分析建模分析:该茶壶主要由“壶身”、“壶嘴”和“壶把”三部分组成。
“壶身”由8条曲线组成,用【通过曲线网格】命令创建;“壶嘴”由截面线串和样条曲线组成,用【通过曲线网格】命令创建;“壶把”由一圆和样条曲线组成,用【扫掠】命令创建。
“壶身”曲线组成“壶嘴”曲线组成“壶把”曲线组成壶身曲线的构建1、选择【俯视图】,并在【艺术曲线】工具栏中选择【直线和圆弧工具条】,在工具条中选择按钮,绘制半径为70的圆。
2、将图形转换到【正二侧视图】,选择【编辑】-【变换】-【平移】-【增量】命令,分别将该圆向上平移2个圆,下平移1个圆,距离均为100mm。
3、用功能修改第1、3圆的半径至100mm。
4、选择命令,将以上四个圆弧分割成四段。
5、选择命令,创建如下四条艺术样条。
6、用命令创建XZ平面与最上端圆弧的交点。
壶嘴曲线的构建7、分别用等工具按照下列步骤绘制图形。
要点:在【直线】绘制过程中注意“终点选项”中矢量的选择;在圆弧R5的绘制过程中,“起点和终点”的选择中分别选择“点”。
将如下三个图素隐藏后绘制半径为15的切弧。
将如下两条直线隐藏后,绘制两圆弧之间的连接直线。
8、选择【编辑】-【变换】-【用直线做镜像】命令镜像如下曲线。
9、选择命令,修剪掉中间多余的曲线。
要点:在【设置】-“输入曲线”中选择“隐藏”方式。
10、用命令创建如下曲面,并用相同方法创建另外2个曲面。
11、用命令绘制如下样条曲线。
12、用命令创建如下曲面。
(如上端圆弧不能选择,可将以前的圆弧隐藏后,重新绘制一半径为100mm的圆,并将其分割成2段后再修剪;或者在选择器中将激活。
)13、用命令将上下两平面封闭,并用命令将所有曲面进行缝合,最后用命令将曲面向内抽1mm的厚度。
壶把曲线的构建14、在XZ平面上,用命令创建如下样条曲线。
15、在YZ平面上,创建直径为30 mm的圆。
16、用命令创建茶壶的手柄17、用命令修茶壶手柄多余的部分。
注意【类选择器】应选择【单个面】18、选择【编辑】-【对象显示】功能,将茶壶设置成需要的颜色。
ug-曲面建模实例教程-茶壶建模步骤

茶壶建模分析建模分析:该茶壶主要由“壶身”、“壶嘴"和“壶把"三部分组成。
“壶身”由8条曲线组成,用【通过曲线网格】命令创建;“壶嘴"由截面线串和样条曲线组成,用【通过曲线网格】命令创建;“壶把”由一圆和样条曲线组成,用【扫掠】命令创建.“壶身”曲线组成“壶嘴”曲线组成“壶把”曲线组成壶身曲线的构建1、选择【俯视图】,并在【艺术曲线】工具栏中选择【直线和圆弧工具条】,在工具条中选择按钮,绘制半径为70的圆。
2、将图形转换到【正二侧视图】,选择【编辑】—【变换】-【平移】—【增量】命令,分别将该圆向上平移2个圆,下平移1个圆,距离均为100mm。
3、用功能修改第1、3圆的半径至100mm.4、选择命令,将以上四个圆弧分割成四段。
5、选择命令,创建如下四条艺术样条.6、用命令创建XZ平面与最上端圆弧的交点。
壶嘴曲线的构建7、分别用等工具按照下列步骤绘制图形。
要点:在【直线】绘制过程中注意“终点选项”中矢量的选择;在圆弧R5的绘制过程中,“起点和终点”的选择中分别选择“点”.将如下三个图素隐藏后绘制半径为15的切弧.将如下两条直线隐藏后,绘制两圆弧之间的连接直线。
8、选择【编辑】-【变换】-【用直线做镜像】命令镜像如下曲线。
9、选择命令,修剪掉中间多余的曲线。
要点:在【设置】-“输入曲线"中选择“隐藏”方式。
10、用命令创建如下曲面,并用相同方法创建另外2个曲面。
11、用命令绘制如下样条曲线.12、用命令创建如下曲面。
(如上端圆弧不能选择,可将以前的圆弧隐藏后,重新绘制一半径为100mm的圆,并将其分割成2段后再修剪;或者在选择器中将激活。
)13、用命令将上下两平面封闭,并用命令将所有曲面进行缝合,最后用命令将曲面向内抽1mm的厚度。
壶把曲线的构建14、在XZ平面上,用命令创建如下样条曲线.15、在YZ平面上,创建直径为30 mm的圆。
16、用命令创建茶壶的手柄17、用命令修茶壶手柄多余的部分。
第8章 曲面建模

8.3.8 偏置曲面
偏置曲面用于创建原有曲面的偏置平面,即沿指定平面的法向偏置点来生成用户所需 的曲面。其主要用于从一个或多个已有的面生成曲面,已有面称之为基面,指定的距 离称为偏置距离。 创建偏置曲面,执行“插入”|“偏置\缩放”|“偏置曲面”命令(或者单击“曲面” 工具栏中的“偏置平面”按钮),打开“偏置平面”对话框,如图8-57所示。 偏置曲面操作比较简单,选取基面后,设置偏置距离,单击“确定”按钮便完成偏置 曲面操作。 举例介绍用“偏置曲面”创建曲面的操作步骤如下。
8.3.4 扫掠
扫掠是使用轮廓曲线沿空间路径扫掠而成,其中扫掠路径称为引导线(最 多3根),轮廓线称为截面线。引导线和截面线均可以由多段曲线组成, 但引导线必须一阶导数连续。 该方法是所有曲面建模中最复杂、最强大的一种,在工业设计设计中使用 广泛。 创建扫掠曲面,执行“插入”|“扫掠”|“扫掠”命令(或者单击“曲面” 工具栏中的“扫掠”按钮),打开“扫掠”对话框,如图8-19所示。
“从极点创建曲面”使用方法与“通过点构造曲面”命令相同, 但这个命令可以通过极点更好的控制曲面的外形。在逆向工程中, 由测量仪扫描获得的成行排列的点,经过数据交换输入到NX中, 然后利用“从极点”操作创建曲面。 单击“曲面”工具栏中的“从极点”按钮 ,系统弹出“从极点” 对话框,如图8-8所示。
8.3.3 通过曲线网格
该方法是指用主曲线和交叉曲线创建曲面的一种方法。其中主曲线是一组同方向的截 面线串,而交叉曲线是另一组大致垂直于主曲线的截面线。通常把第一组曲线线串称 为主曲线,把第二组曲线线串称为交叉曲线。由于没有对齐选项,在生成曲面,主曲 线上的尖角不会生成锐边。“通过曲线网格”曲面建模有以下几个特点。 生成曲面或体与主曲线和交叉曲线相关联。 生成曲面为双多次三项式,即曲面在行与列两个方向均为3次。 主曲线环状封闭,可重复选择第一条交叉线作为最后一条交叉线,可形成封闭实体。 选择主曲线时,点可以作为第一条截面线和最后一条截面线的可选对象。
solidworks叶子形状曲面建模_概述说明

solidworks叶子形状曲面建模概述说明1. 引言1.1 概述在工程设计和制造领域,使用CAD软件进行建模是一项常见且必要的工作。
SolidWorks作为一种流行的三维建模软件,提供了许多功能强大而灵活的工具,在各个行业中都得到了广泛应用。
本文将重点介绍SolidWorks中叶子形状曲面建模的方法和技巧。
1.2 文章结构本文按照以下结构进行组织:引言、solidworks叶子形状曲面建模、示例应用、结论和致谢。
在solidworks叶子形状曲面建模部分,我们将详细介绍该建模过程的简介、步骤以及常用工具和技巧。
示例应用部分将展示几个实际案例以帮助读者更好地理解如何应用所学内容。
1.3 目的通过撰写本文,旨在向读者提供有关SolidWorks叶子形状曲面建模的详细概述。
我们将介绍这种特殊类型的曲面建模方法,并解释其在实际应用中的重要性和优势。
此外,我们还将分享一些常用于叶子形状曲面建模的工具和技巧,希望能够帮助读者提升他们的建模技能并掌握这一特定领域的技术。
请注意,以上内容为普通文本格式。
2. solidworks叶子形状曲面建模:2.1 叶子形状曲面建模简介:SolidWorks是一款功能强大的三维建模软件,它可以用于创建复杂的曲面模型。
在本节中,我们将重点介绍如何使用SolidWorks进行叶子形状的曲面建模。
叶子是自然界中常见的物体之一,其形状变化多样,这对于设计师来说可能是一个挑战。
但通过SolidWorks提供的工具和技巧,我们可以轻松地创建出各种形状丰富的叶子模型。
2.2 建模过程步骤:在进行叶子形状曲面建模之前,需要先准备好计划和参考图。
下面是一般的建模过程步骤:第一步:导入或绘制基础草图:根据参考图纸或者实际测量数据,在SolidWorks 中创建基础草图。
可以使用线、圆、弧等基本几何元素进行绘制。
第二步:使用草图工具构建表面曲线:利用Spline、Bezier Curve、Boundary Surface等工具,在基础草图上绘制并调整出符合要求的平滑曲线。
ug曲面建模实例教程

ug曲面建模实例教程UG(Unigraphics)是由美国UGS公司开发的一种三维计算机辅助设计(CAD)软件,是当前工程设计中常用的软件之一。
曲面建模是UG软件中的一个重要功能,在工程设计中有广泛的应用。
本教程将向您介绍UG软件中曲面建模的基本概念和操作步骤,帮助您快速上手。
首先,需要明确曲面建模的概念。
曲面建模是指通过控制点和曲线来创建复杂的三维曲面。
UG软件提供了多种曲面建模工具和功能,使得用户可以灵活地创建不同形状和复杂度的曲面。
在UG软件中,曲面建模的基本步骤如下:1.创建曲线:在曲面建模中,曲线是最基本的构建单元。
通过选择线段工具或曲线工具来创建基础曲线。
用户可以选择直线、圆弧、样条曲线等不同类型的曲线进行建模。
2.曲面边界:使用曲线工具创建曲面的边界。
根据具体要求,可以使用一条或多条曲线构建曲面的边界。
3.创建曲面:通过选择曲面工具,根据边界曲线和辅助曲线创建具体的曲面。
UG软件提供了多种曲面创建工具,如旋转曲面、扫描曲面、放样曲面等,可以根据具体需要选择合适的工具进行操作。
4.编辑曲面:在创建曲面之后,可以使用编辑工具对曲面进行调整和修改。
UG软件提供了丰富的编辑工具,如移动、拉伸、旋转等,可以通过简单的操作来实现对曲面的编辑。
5.曲面修复:在曲面建模过程中,可能会出现曲面断裂或不完整的情况。
UG软件提供了曲面修复工具,可以自动检测和修复曲面的问题。
6.曲面分割:在建模过程中,需要将曲面分割成多个部分来进一步进行操作。
UG软件提供了曲面分割工具,可以根据用户指定的分割曲线将曲面分割成不同的部分。
7.曲面求交和连接:在建模过程中,可能需要对多个曲面进行求交和连接。
UG软件提供了曲面求交和连接的工具,可以实现曲面的精确求交和连接。
除了上述基本步骤,UG软件还提供了很多高级功能和工具,如曲面平滑、曲面展开、曲面偏差分析等,可以根据具体需求进行使用。
总结一下,UG曲面建模是一种功能强大且灵活的工程设计方法,通过控制点和曲线可以创建各种形状和复杂度的曲面。
综合实例曲面建模技巧

4 使用Loft 指令以模型中的三条曲线新建放样曲面。
Loft 指令会记忆上次使用的设置,所以必需确定放 样型式是设置为标准,并选择不要简化。
5 我们将新建通过这三条曲线的曲面,而中间那条 曲线是曲面的渐消边缘。使用中间的曲线将曲面分 割成两半。
17 使用FilletEdge 指令(实体:边缘圆角> 边缘圆 角),将目前的半径设为15,选取四个垂直的边缘。
将目前的半径设为10,选取四个上方的边缘,按 Enter,新建圆角。
新建的曲面结构非常简洁,而且没有锐边。
渐消面通常是指两个曲面相接边缘的一端为锐边,
往另一端渐变为相切或更平滑的造型,稍后的练习 将举出两种可能的情况。
与自动修剪,设置曲面的U 与V 方 向跨距数为10,硬度为2。
当要填补的缺口超过四个边缘时必需使用Patch 指令, NetworkSrf 指令只能填补四个边缘的缺口。
新建一个类似立方体但有弧度的曲面(一)
可以使用许多方法新建像下图一样上方有弧度的 曲面,通常新建这样的曲面会以圆弧曲线做为参 考线。
7 隐藏下方的曲面,并关闭Curve 图层。
新建替代曲面 我们会将上方的曲面与新新建的替代曲面衔接。 这个替代曲面是由一条或以上的不同角度的直线线
段沿着上方曲面的下方边缘新建的。要新建一条与 相切方向差距某个角度的直线线段最简单的方法是 使用变动工具放置相切直线线段,再旋转某个角度。
1 设置Dummy Curve图层为目前的图层。 2 在Top 工作视窗新建一条长度为20 单位的直线。 3 执行OrientCrvToEdge 指令(变动:定位> 曲线至边缘)。 4 选取刚才新建的直线为要定位的曲线。 5 选取曲面的下方边缘为目标曲面边缘。 6 锁定边缘的一个端点,放置第一条直线。 7 锁定边缘的另一个端点,放置第二条直线。 8 按Enter 结束指令。 定位后的两条直线应该与图一样。
ProE高级曲面建模实例

ProE⾼级曲⾯建模实例⼀、前⾔因本⼈⽔平有限,理论上没有什么⼤的建树,现就⼀些实际的曲⾯构建题⽬写出我⾃⼰的解法,与⼤家⼀起探讨,希望对⼤家有所帮助,共同进步!⼆、知识准备1. 主要涉及模块:Style(ISDX模块)、⾼级曲⾯设计模块主要涉及概念:活动平⾯、曲⾯相切(G1连续)、曲⾯曲率连续(G2连续)、Style中的⾃由曲线/平⾯曲线/cos曲线、⾃由曲线端点状态(相切、法向、曲率连续等)2. 主要涉及命令:⾼级曲⾯命令(边界曲⾯)、曲线命令及Style中的操作命令三、实例操作下⾯我们结合实际题⽬来讲述。
1. 1. 题⽬⼀:带翅膀的飞梭,完成效果见图1:图1 飞梭最终效果图原始架构线如图2所⽰:图2 飞梭原始架构线图⾸先我们门分析⼀下,先看效果图应该是⼀个关于通过其中⼼三个基准⾯的对称图形,那么从原始架构线出发,我们只要做出⼋分之⼀就可以了。
很容易想到应该在中⼼添加于原有曲线垂直⾯上边界曲线,根据实际情况,我先进⼊Style中做辅助线,如图3所⽰:图3 Style辅助线操作图图3中标⽰1处选择绘制曲线为平⾯曲线(此时绘制的曲线在活动平⾯上,活动平⾯为图中⽹格状显⽰平⾯),标⽰2设置曲线端点处垂直于平⾯,标⽰3处设置曲线端点曲率连续。
设置⽅法为,左键点击要设置的端点,出现黄⾊操纵杆,⿏标放于黄⾊操纵杆上,按住右键1秒钟以上便会出现菜单,如图4左图所⽰。
图4 绘制曲线操作图设置时先选设置属性(相切、曲率连续等),再选相关联的曲⾯或平⾯(含基准平⾯),黄⾊操纵杆长短可调整,同时可打开曲率图适时注意曲率变化,如图4右图所⽰。
有了图4辅助线后就可以做⾯了,此处我⽤⾼级曲⾯命令(boundaries),注意线的选取顺序,第⼀⽅向选取曲线1,2,第⼆⽅向选曲线3(如不能直接利⽤曲线选项选取,可⽤链选项,另⼀个选项也可⾃⼰尝试⼀下),见图5。
图5 构⾯时线的选取顺序图如选择完边界直接完成,则⽣成的曲⾯并不满⾜要求,因此我们必须定义边界条件,如图6左图所⽰。
PROE经典曲面实例(共60张PPT)

PNT0
直线,距 离为1
画直线
首先创建辅助基准点:依次选取 / 【曲线】/【长度比例】选项,用 【查询选取】选取图中的曲线段,输 入比例值为“0”,完成的基准点 PNT0如图所示
步骤2:创建汤匙轮廓线的主视图
画样条曲线
生成 的曲 线
然后创建轮廓曲线:以临时基准 面(FRONT基准面偏距25)为草 绘平面,绘制图线
上偏距40)为曲面延伸的终止面
步骤4:对扫描曲面和延伸 的曲面作镜像
步骤5:将3个曲面合并:注意选择曲面 的保留部分,合并结果如图所示
12-3
倒圆角
剖截面
步骤6:创建薄板实体特征:依次选 取【创建】/【实体】/【加材料】/ 【使用面组】/【薄板】选项,选曲面
任意处,薄壳厚度为1.5
步骤7:创建圆角特征:在凹槽 顶部的4条边倒圆角,半径为1。
步骤5:创建汤匙的骨架曲线(续):创建第3条曲线(续)
12-34
曲线2
首先创建辅助基准面:过 PNT0点且平行RIGHT基准面, 生成基准平面DTM4
曲线1
创建辅助基准点:以【曲线×曲面】方 式,选取图中的曲线1和DTM4创建点 PNT7;选取曲线2和DTM4创建点PNT8
第4条曲线
创建基准曲线:以【经过点】方式,依 次选取PNT7、PNT0与PNT8三个点,生 成第4条曲线
/ 【曲线】/【长度比例】选项,用【查询选取】
步步骤骤选54::取创创建建图汤汤中匙匙的的的骨轮架 廓曲曲线线线(段续,):输创入建第比5条例曲线值(为续)“0.5”,生成基准点PNT9
步骤4:创建汤匙的轮廓线(续)
步骤9:创建笔筒外围四周所有面的拔模面:用【中平面】拔模,利用【环曲面】选取笔筒四周曲面,TOP基准面为中平面,拔模角度为“-4”
CATIA曲面建模教程

CATIA曲面建模教程CATIA(计算机辅助三维交互应用)是一种广泛使用的计算机辅助设计(CAD)软件,被广泛应用于工程设计、汽车设计、航空航天等领域。
曲面建模是CATIA的重要功能之一,通过曲面建模,可以创建复杂的三维曲面模型。
本教程将带您逐步学习如何在CATIA中进行曲面建模。
1. 准备工作在开始之前,您需要确保已经安装并正确运行了CATIA软件。
如果您还没有安装CATIA,您可以从官方网站下载并按照指引进行安装。
2. 创建曲面在CATIA中,可以使用多种命令和工具来创建曲面。
最常用的是通过绘制曲线和曲面来建模。
2.1 创建曲线曲线是曲面建模的基础。
在CATIA中,有多种绘制曲线的方法,例如使用点绘制、直线绘制、圆弧绘制等。
您可以根据具体的设计需求选择适合的方法。
2.2 创建曲面一旦绘制完成曲线,就可以使用曲面命令将这些曲线转换为曲面。
在CATIA中,有多种曲面命令可供选择,例如拉伸、旋转、变形等。
根据需要选择合适的命令进行曲面建模。
3. 曲面编辑在创建曲面之后,您可能需要对曲面进行进一步编辑和修改。
CATIA提供了一系列的编辑工具,帮助您对曲面进行平移、旋转、缩放等操作。
您可以根据具体的设计需求使用这些工具进行曲面编辑。
4. 曲面分析在进行曲面建模时,有时需要对曲面进行分析和评估。
CATIA提供了一些曲面分析工具,帮助您评估曲面的质量和几何特征。
例如,您可以使用曲面诊断工具来检查曲面的连续性和光滑度。
5. 曲面修复在进行曲面建模时,有时会出现曲面中的错误或缺陷。
CATIA提供了一些曲面修复工具,帮助您修复曲面中的问题。
例如,您可以使用曲面修复工具来填充曲面中的孔洞或修复曲面的边缘。
6. 曲面导入和导出CATIA支持多种文件格式的导入和导出,使您可以与其他CAD软件进行兼容。
您可以将CATIA中创建的曲面导出为常见的文件格式,例如STEP、IGES等。
同样,您也可以从其他CAD软件中导入曲面到CATIA进行编辑和建模。
CAD曲面建模技巧及实例展示

CAD曲面建模技巧及实例展示CAD(计算机辅助设计)是现代设计师们常用的工具之一,它能够帮助设计师们快速、精确地完成各种设计任务。
而曲面建模则是CAD 设计中非常重要的一部分,它能够帮助我们创建出流线型、有机形状的物体,例如汽车外壳、家电产品等。
在CAD软件中,曲面建模可以通过多种方式实现,下面我将为大家介绍几种常见的曲面建模技巧,并通过实例展示其应用。
1. 曲面拉伸技巧曲面拉伸是一种常用的建模技巧,它能够帮助我们创建出复杂的曲面物体。
在CAD软件中,我们可以选取一个曲面或曲线作为路径,然后根据设计需求,在该路径上拉伸出所需的物体形状。
例如,我们要设计一个扁平的弧形玻璃顶盖。
首先,我们可以在CAD软件中绘制一个弧线,然后使用曲面拉伸工具,以该弧线作为路径,拉伸出我们需要的弧形玻璃顶盖。
通过调整拉伸的参数,我们可以得到不同曲率的顶盖形状。
2. 曲面平移技巧曲面平移是另一种常用的建模技巧,它可以帮助我们在曲面上创建出新的物体。
在CAD软件中,我们可以选取一个曲面作为基准面,然后在该曲面上绘制一个曲线,接着使用曲面平移工具,以该曲线作为路径,在基准面上平移出新的物体形状。
例如,我们要设计一个流线型的汽车车身。
首先,我们可以在CAD软件中绘制出汽车的侧视图,并将其转换为曲面。
接着,我们在该曲面上绘制出一条曲线,以该曲线为路径,使用曲面平移工具,平移出整个汽车车身的截面。
通过不断平移多个截面,并进行调整,最终可以得到一个流线型完整的汽车车身。
3. 曲面修剪技巧曲面修剪是一种常用的曲面建模技巧,它可以帮助我们在复杂的曲面中去除不需要的部分。
在CAD软件中,我们可以绘制一个封闭的曲线作为修剪边界,然后使用曲面修剪工具,将曲面中与修剪边界相交的部分去除。
例如,我们要设计一个双曲面形状的家具面板。
首先,我们可以在CAD软件中绘制出两个封闭的曲线,分别作为家具面板的上下边界。
接着,我们使用曲面工具,将两个封闭曲线连接起来,形成一个双曲面。
ug曲面建模实例教程茶壶建模步骤

茶壶建模分析建模分析:该茶壶主要由“壶身”、“壶嘴”和“壶把”三部分组成。
“壶身”由8条曲线组成,用【通过曲线网格】命令创建;“壶嘴”由截面线串和样条曲线组成,用【通过曲线网格】命令创建;“壶把”由一圆和样条曲线组成,用【扫掠】命令创建。
“壶身”曲线组成“壶嘴”曲线组成“壶把”曲线组成壶身曲线的构建1、选择【俯视图】,并在【艺术曲线】工具栏中选择【直线和圆弧工具条】,在工具条中选择按钮,绘制半径为70的圆。
2、将图形转换到【正二侧视图】,选择【编辑】-【变换】-【平移】-【增量】命令,分别将该圆向上平移2个圆,下平移1个圆,距离均为100mm。
3、用功能修改第1、3圆的半径至100mm。
4、选择命令,将以上四个圆弧分割成四段。
5、选择命令,创建如下四条艺术样条。
6、用命令创建XZ平面与最上端圆弧的交点。
壶嘴曲线的构建7、分别用等工具按照下列步骤绘制图形。
要点:在【直线】绘制过程中注意“终点选项”中矢量的选择;在圆弧R5的绘制过程中,“起点和终点”的选择中分别选择“点”。
将如下三个图素隐藏后绘制半径为15的切弧。
将如下两条直线隐藏后,绘制两圆弧之间的连接直线。
8、选择【编辑】-【变换】-【用直线做镜像】命令镜像如下曲线。
9、选择命令,修剪掉中间多余的曲线。
要点:在【设置】-“输入曲线”中选择“隐藏”方式。
10、用命令创建如下曲面,并用相同方法创建另外2个曲面。
11、用命令绘制如下样条曲线。
12、用命令创建如下曲面。
(如上端圆弧不能选择,可将以前的圆弧隐藏后,重新绘制一半径为100mm的圆,并将其分割成2段后再修剪;或者在选择器中将激活。
)13、用命令将上下两平面封闭,并用命令将所有曲面进行缝合,最后用命令将曲面向内抽1mm的厚度。
壶把曲线的构建14、在XZ平面上,用命令创建如下样条曲线。
15、在YZ平面上,创建直径为30 mm的圆。
16、用命令创建茶壶的手柄17、用命令修茶壶手柄多余的部分。
注意【类选择器】应选择【单个面】18、选择【编辑】-【对象显示】功能,将茶壶设置成需要的颜色。
SolidWorks曲面实例操作|案例讲解

SolidWorks曲⾯实例操作|案例讲解在利⽤SOLIDWORKS绘制您的产品模型时,初期您的产品由产品设计师进⾏初步概念设计,经由简单的⼿绘图绘制出⼀个外观雏型图。
接下来您可由不同的基准⾯将这些图⽚来输⼊到SOLIDWORKS内(图1),输⼊后您可以发现SOLIDWORKS中将出现⼀个⽐例尺线段,您可以拖曳该线段⾄您所需绘制的图⽚前后端,可直接输⼊尺⼨来定义该图⽚的实际⼤⼩,以便您后续绘制相同尺⼨模型(图2)。
以下我们使⽤SOLIDWORKS曲⾯功能来完成⼀个砂铸开瓶器的建置。
图1图2输⼊完所需的图⽚后,您可利⽤草图⼯具在不同视⾓基准⾯依实际图⽚的外观轮廓线段来描绘出所需的草图线段(图3),完成这些前置作业后可开始进⼊实体建模阶段。
图3⾸先我们可参考Top Layout草图来绘制⼀个头部实体模型(图4),接着我们可利⽤曲⾯中”删除⾯”的功能(图5),模型将由⼀个实体转为曲⾯本体,保留我们后续所需之曲⾯后,可再利⽤Right Layout草图绘制把柄的草图,伸长曲⾯完成⼀曲⾯外型(图6),并利⽤Top Flat Layout草图,修剪该曲⾯完成柄⾝造型(图7)。
图4图5图6图7接下来我们将使⽤不同绘制⽅式与技巧来完成把柄柄⾝的外部⾯,使⽤”边界曲⾯”功能时,我们需要完成曲⾯的边缘界线,这些边界线可为既有的曲⾯边线或是⾃⾏绘制的草图线段,⼀样使⽤Top Layout草图参考出侧⾯轮廓线并伸长曲⾯(图8),我们可定义⼀新的基准⾯来绘制⼀弧形草图,并使⽤边界曲⾯功能将草图与不同曲⾯边缘之线段直接⽣柄⾝侧⾯曲⾯(图9)。
图8图9另外我们在尾端也绘制⼀草图并伸长曲⾯(图10),以备稍后的⾯的填补。
使⽤”曲⾯填补”时,选择的边线需要是实际存在的曲⾯边线⽽⽆法使⽤草图线段,接着我们可先缝织曲⾯(图11)来简化需填补的曲⾯边界以利后续填补曲⾯,在填补曲⾯时,您可选择所需填补的边界线段,不同线段可给定接触、相切、曲率等不同的边线设定,设定好后选择确定完成曲⾯的填补(图12)。
CAD中的曲面建模技巧与应用示例

CAD中的曲面建模技巧与应用示例CAD(计算机辅助设计)软件在现代工程和设计领域中扮演着重要的角色。
曲面建模是CAD软件中一个重要的技术,它广泛应用于汽车设计、航空航天、产品设计等领域。
本篇文章将介绍CAD中的曲面建模技巧,并提供一些应用示例。
首先,我们来了解几个曲面建模中常用的工具和操作。
在CAD软件中,创建曲面通常有两种方法:点云建模和造型建模。
点云建模是通过一系列散点来构建曲面,在处理复杂的有机形状时很有用。
而造型建模则是通过创建基础几何体并进行变形、截取等操作来生成曲面。
在进行曲面建模时,掌握一些常用的工具和技巧是非常重要的。
例如,在CAD软件中,可以使用插值函数来创建曲线和曲面。
插值函数可以根据已知的控制点和插值方法来生成平滑的曲线和曲面。
此外,还可以使用曲线修剪、领域变形和扩展等操作来调整曲面的形状。
下面我们将通过一些应用示例来展示这些曲面建模技巧和工具的实际应用。
示例一:汽车外壳设计在汽车设计中,曲面建模被广泛应用于外壳的设计和造型。
通过CAD软件中的曲面建模技巧,设计师可以根据汽车品牌和用户需求来创建独特的外观,如流线型车身和曲线美感。
同时,通过利用曲面修剪等操作,设计师可以对外壳进行细微的调整和优化,以实现更佳的空气动力学性能和美观度。
示例二:航空航天设计在航空航天领域,曲面建模技巧的应用更加复杂和关键。
例如,在飞机机翼的设计中,曲面建模可以帮助工程师创建流线型的空气动力学理想形状,以减少阻力和提高飞行性能。
通过插值函数和曲线修剪等操作,工程师可以实现机翼的复杂曲面设计,并满足性能和安全要求。
示例三:产品设计除了汽车和航空航天领域,曲面建模技巧在产品设计中也得到广泛应用。
例如,在电子产品的外观设计中,曲面建模可以帮助设计师实现流线型外壳和舒适的握持感。
通过CAD软件中的曲面建模工具,设计师可以调整产品的曲面斜度、曲率和转角等参数,以实现更好的人机工程学和视觉效果。
综上所述,曲面建模技巧在CAD软件中的应用非常广泛,并在各种设计领域中发挥重要作用。
proe曲面建模实例

proe曲面建模实例
以下是一个Proe曲面建模的实例:
1. 创建一个新的Proe文档,并设置工作单位和精度。
2. 在Proe中创建一个新的曲面,可以通过使用“填充曲面”命令来完成。
选择两个或多个边界曲线,并设置曲面的属性,例如厚度和拔模角度。
3. 使用“偏移曲面”命令来创建另一个曲面,该曲面与原始曲面平行。
输入偏移距离,并设置其他属性,例如拔模角度和偏移方向。
4. 使用“倒圆角”命令来对两个曲面之间的边界进行圆角处理。
输入圆角半径,并选择要倒角的边线。
5. 创建一个新的拉伸曲面,选择一个草绘作为基础,然后进行拉伸操作。
输入拉伸长度和方向,并设置其他属性,例如拔模角度和拉伸方向。
6. 使用“拉伸切除曲面”命令来创建一个切除曲面。
选择一个基础草绘,然后进行拉伸操作。
输入切除长度和方向,并设置其他属性,例如拔模角度和切除方向。
7. 对曲面进行圆角处理,可以选择多个边线进行圆角处理。
输入圆角半径,并选择要倒角的边线。
8. 使用“加厚”命令来对曲面进行加厚操作。
输入厚度值,并选择要加厚的曲面。
可以选择不同的方向和偏移距离进行加厚操作。
9. 最后,使用“渲染”命令来对模型进行渲染,以查看最终效果。
以上是一个简单的Proe曲面建模实例,您可以根据需要进行修改和调整。
请注意,在使用Proe进行建模时,需要具备一定的几何知识和空间想象力。
CATIA曲面设计实例

CATIA曲面设计实例CATIA(Computer-Aided Three-Dimensional Interactive Application)是一款功能强大的三维建模软件,广泛应用于航空航天、汽车、工业设计等领域。
本文将介绍一些CATIA曲面设计的实例,帮助读者更好地理解和应用CATIA软件。
一、简介CATIA曲面设计是基于NURBS曲面理论,通过控制曲线和面的形状进行曲面建模。
NURBS曲线是一种数学公式,具有灵活性和精确性,非常适合用于创建复杂的曲面。
二、实例1:汽车车身设计在汽车设计领域,曲面设计是至关重要的环节。
CATIA可以帮助设计师通过曲面构建模块来创建车身曲面。
首先,设计师可以使用曲线工具创建车身的主要曲线轮廓,如车顶线和车身侧面线。
然后,通过曲面工具将这些曲线连接起来,形成完整的车身曲面。
设计师可以根据需要调整曲面的形状和光滑度,以满足美学和工程要求。
三、实例2:飞机机身设计在航空航天领域,CATIA的曲面设计功能也发挥着重要作用。
例如在飞机机身设计中,设计师可以利用CATIA的曲面工具创建机身曲面,并特别关注飞机的气动外形和结构强度。
设计师可以通过控制曲面的形状和光滑度来优化机身外形,以减少阻力和提高飞行性能。
此外,CATIA还可以帮助设计师进行机身的结构分析和飞行模拟,以确保飞机的安全和性能。
四、实例3:产品外观设计CATIA还广泛应用于产品外观设计领域。
无论是汽车、手机还是家电产品,外观设计是吸引消费者的重要因素。
通过CATIA的曲面设计工具,设计师可以快速创建产品的流线型曲面,并进行实时渲染和观察。
设计师可以根据市场需求和用户偏好,灵活调整产品的曲面形状和色彩,实现最佳的外观效果。
五、总结CATIA曲面设计是一项重要的工程技术,广泛应用于各个行业。
在汽车、航空航天和产品设计领域,CATIA的曲面设计工具为设计师提供了强大的功能和灵活性,帮助他们创造出优秀的产品和解决方案。
综合实例曲面建模技巧

新建一个类似立方体但有弧度的曲面(二)
1 将02 Separate Curves 图层设为目前的图层,并关闭其它图层。 2 隐藏白色与绿色的圆弧曲线。 3 锁定红色曲线。 4 使用Extend 指令(曲线:延伸曲线>延伸曲线),输入10 设置延伸长度。
延伸两条青色圆弧曲线的四个端点及四条黑色圆弧曲线的上方端点。每一条 圆弧曲线都以原来的半径延伸。
当要填补的缺口超过四个边缘时必需使用Patch 指令, NetworkSrf 指令只能填补四个边缘的缺口。
新建一个类似立方体但有弧度的曲面(一)
可以使用许多方法新建像下图一样上方有弧度的 曲面,通常新建这样的曲面会以圆弧曲线做为参 考线。
这个练习里,将使用两种方法以同样的参考曲 新建这个曲面。
1创建文件Soft Corners.3dm,建立如图曲线 2 使用Join 指令(编辑:组合) 组合圆滑立方体底
面边缘的所有圆弧曲线。
3 将03 Sweeps 图层设为目前的图层。 4 使用Sweep1 指令(曲面:单轨扫掠)新建第一
个曲面。
5 在单轨扫掠选项对话框勾选封闭扫掠,按确定。
9 在Perspective 工作视窗,从工作视窗菜单选择 设置工作平面> 与曲线垂直,选取曲面下方边缘,
设置工作平面与曲面下方边缘垂直。锁定前方直线 的上方端点,放置工作平面原点。
10 执行Rotate 指令,以自定义工作平面原点为旋 转中心点,将靠近工作平面原点的直线线段旋转10 度(依据实际情况不同,可能需要将直线线段旋转10度)。
2 选取上方曲面的下方边缘。
3 选取替代曲面的上方边缘。
4 在衔接曲面对话框,选取相切,并勾选以最接近 点衔接边缘。使衔接时曲面变形程度降到最小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
多边形建模现在被越来越多的人喜爱并使用。
了解这些特性并在建模当中巧妙的使用能起到很好的效果,本教程详细的讲解曲面建模。
作者:asdf
在火星人上看到了很多人在讨论软件中的曲面建模方法,这其中包括NURBS、PATCH、SURFACE,和SUB DIVETION(细分)先介绍几个连续性的概念,需小小的高数基础,但为了让我们更好地理解曲线建模,不要畏惧它!LET’S BEGIN 某节点两端曲线在该点重合,则该点具有C0、G0级连续;该点两端曲线重合,切矢量方向相同,大小不等,称为G1级连续,该点两端曲线重合,切矢量方向相同,大小相等,称为C1级连续,如果两端曲线重合,切矢量导数方向相同,大小不等称为G2级连续,如果两端曲线重合,切矢量导数方向相同,大小相等称为C2级连续,至二阶三阶有C2、G2、C3、G3等连续方式。
一般默认的NURBS(MAX中MAYA中)连续,是C23级别,控制点(CV、EP)的权重反映了切线的大小数值,而在高精度的工业设计中可应用于更高的连续级别。
而把这些概念应用于BRZEIL上,我们可以看到,MAX中的BREZIL曲线可以较为自由地改变其节点连续性,将之转化成CORNER形或是BREZIL CORNER,就是C0G0级别,将之转成BEZIL 形就是两端曲线切线柄方向一致就是G1形,转成SMOOTH,因切线柄两端方向一致大小一致因此是C1形,因为都属于有理化样条曲线,所以BREZEIL和NURBS之间是可以转换的,也就是说PATCH和NURBS曲面是可以转换的,所以正像我前面说了,MAYA中NURBS面片建模的原理其实和PATCH原理极其相似,不过一般要满足四边面的拓朴关系,而PATCH也是一样的,如果出现三角面,曲面的光滑度很难控制,像是A:M和MAX中的基于样条曲建模手段,在MAX叫做SURFACE,其实也就连续性。
细分是从多边形和NURBS中演生出的一种建模手段,在MAX中叫做NURMS,可以用少量的点、线、面是PATCH的快速方法,类似的方法其实用NURBS也可以实现,比如说在RHINOS中可织成曲线网,然后用三边线成面或四边线成面并要注意其子物体控制曲面的形态,并可以调整其子物体上的权重(WEIGHT)。
因为是个人分析,可能有错误,希望高手斧正!
点击放大
接下来是实例,我觉得初学者要掌握曲面建模技术,,最主要的是要理解连续性的问题,也就是在转折处有转折,在平滑处有光滑,怎样做到呢?一般较为复杂的曲面最好不要由单独一块面片(NURBS或PATCH)生成,而要由分片来实现,,网上很多人头和汽车建模的例子说明了这一点。
不过在这里我们不讨论那么复杂的过程,,我们来尝试做一个鼠标,是我正在用的鼠标,,XMAN牌鼠标,(XMAN是我另一个网名)来吧,初学者也很快入门的.
1.绘出底线轮廓和几条关键曲线,注意拐角方式。
织网,在关键的转折处可调整BREZIL杆来改变曲率大小。
