数学简易逻辑知识点+题型
新高考数学题型归纳,第一章 集合与简易逻辑

第一章集合与简易逻辑第一节集合题型1、元素与集合的关系元素与集合的关系:属于和不属于。
常用数集的表示:C —复数集;R —实数集;Q —有理数集;Z —整数集;N —自然数集;N+或N*—正整数集。
1、【多选】下列关系中正确的是()A.{}102,∉-B.(){}2|42x y x =∈,C.R ∈πD.Φ∈02、【2022·全国乙卷】设集合{}54321,,,,=U ,集合M 满足{}31,=M C U ,则()A.M ∈2B.M ∈3C.M ∉4D.M∉53、【2018·北京】已知集合(){}241|≤-+≥-=ay x y ax y x y x A ,>,,,则()A .()A R a ∈∈∀12,,B .()AR a ∉∈∀12,,C .当且仅当0<a 时,()A ∉12,D .当且仅当23≤a 时,()A ∉12,4、若集合{}2024||≤∈=x N x x P ,45=a ,则()A.P a ∈B.{}P a ∈C.{}Pa ⊆D.Pa ∉题型2、集合相等集合元素的特征:确定性、互异性、无序性。
集合相等,集合中元素完全相同,集合中元素之和相等,集合中元素之积相等。
1、若},,0{},,1{2b a a ab a +=,求20242024b a+的值.【答案:1】2、已知集合,,且B A },,0{B },,,{A ==-=y x y x xy x 求实数x 与y 的值.【答案:x=y=-1】3、设R b a ∈,,集合b}ab {0a}b a {1,,,,=+,则=-a b ()【答案:C 】A.1B.-1C.2D.-24、【2014·福建】若}2,1,0{},,{=c b a ,且下列三个关系:①2≠a ;②2=b ;③0≠c 有且只有一个正确,求c b a ++10100的值.5、集合},2,0{a A =,},1{2a B =.若}16,4,210{,,=B A 则a 的值为()【答案:D 】A .0B .1C .2D .4题型3、集合之间的基本关系集合与集合之间的关系:①包含关系,②相等关系,③真子集关系。
(完整word版)数学简易逻辑-知识点归纳+题型

原命题若p 则q 否命题若┐p 则┐q逆命题若q 则p逆否命题若┐q 则┐p互为逆否互逆否互为逆否互互逆否互文科数学选修1—1 第一章 简易逻辑 一.四种命题及关系1。
命题:__________的语句;2。
分类:①简单命题:不含有逻辑联结词的命题;②复合命题:由_________和逻辑联结词“___”、“___"、“____”构成的命题;构成复合命题的形式:p 或q 记作______;p 且q 记作____;非p 记作_____。
3。
命题的四种形式与相互关系 原命题:若p 则q ; 逆命题:________; 否命题:________; 逆否命题:________.注:①互为_____关系的两个命题同真假.②命题中一些关键词的否定:1、下列说法:①若一个命题的否命题是真命题,则这个命题不一定是真命题;②若一个命题的逆否命题是真命题,则这个命题是真命题;③若一个命题的逆命题是真命题,则这个命题不一定是真命题;④若一个命题的逆命题和否命题都是真命题,则这个命题一定是真命题;其中正确的说法是 ( )A 。
①②B 。
①③④C 。
②③④D 。
①②③2、已知m ,n 是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是( ) A 、若α,β垂直于同一个平面,则α//β B 、若m,n 平行于同一个平面,则m//nC 、若α,β不平行,则α内不存在与β平行的直线D 、若m,n 不平行,则m 与n 不可能垂直于同一个平面3.原命题:“设a ,b ,c ∈R ,若a 〉b ,则ac 2〉bc 2",在原命题以及它的逆命题、否命题、逆否命题中,真命题的个数为( )4.有四个命题:①“若0x y +=,则x 、y 互为相反数"的逆命题; ②“全等三角形的面积相等”的否命题;③“若1q ≤,则关于x 的方程220x x q ++=有实根"的逆命题;④“A B B =,则A B ⊇”的逆否命题。
小学三年级数学逻辑题

小学三年级数学逻辑题
题目1:
小明的爸爸有4个苹果,小明吃了1个,他还剩下几个苹果?
题目2:
小红家有8颗糖果,她把其中的3颗糖果给了小明,小红家还剩下几颗糖果?
题目3:
小明手里有9本书,他给了小红3本书,小明手里还剩下几本书?
题目4:
小明的花瓶里有7朵花,他给了小红4朵花,小明的花瓶里还剩下几朵花?
题目5:
小明的妈妈有10个橙子,她给了小明5个橙子,小明妈妈还剩下几个橙子?
题目6:
小红有6颗糖果,小明有1颗糖果,他们一共有几颗糖果?
题目7:
小明手里有8枚硬币,他给了小红5枚硬币,小明手里还剩下几枚硬币?
题目8:
小红妈妈有10颗葡萄,她吃了2颗,小红吃了3颗,小红妈妈还剩下几颗葡萄?
题目9:
小红有9本书,她给了小明4本书,小红手里还剩下几本书?
题目10:
小明家有7块巧克力,他给了小红2块巧克力,小明家还剩下几块巧克力?
请根据题目所求答案,充分发挥你的思维,进行逻辑思考。
简易逻辑精选练习题和答案

简易逻辑练习题一、选择题1. “21=m ”是“直线03)2()2(013)2(=-++-=+++y m x m my x m 与直线相互垂直”的( )A .充分必要条件B .充分而不必要条件C .必要而不充分条件D .既不充分也不必要条件 2. 设集合A ={x |11+-x x <0},B ={x || x -1|<a },若“a =1”是“φ≠⋂B A ”的( ) A .充分不必要条件 B .必要不充分条件C .充要条件D .既不充分又不必要条件3. 命题p :“有些三角形是等腰三角形”,则┐p 是( )A .有些三角形不是等腰三角形B .所有三角形是等腰三角形C .所有三角形不是等腰三角形D .所有三角形是等腰三角形4. 设命题p :方程2310x x +-=的两根符号不同;命题q :方程2310x x +-=的两根之和为3,判断命题“p ⌝”、“q ⌝”、“p q ∧”、“p q ∨”为假命题的个数为( )A .0B .1C .2D .35.“a >b >0”是“ab <222b a +”的 ( ) A .充分而不必要条件 B .必要而不充分条件C .充要条件D .既不充分也不必要条件6. 若不等式|x -1| <a 成立的充分条件是0<x <4,则实数a 的取值范围是 ( )A .a ≤1B .a ≤3C .a ≥1D .a ≥37. 下列命题中,其“非”是真命题的是( )A .∀x ∈R ,x ²-22x + 2 ≥ 0B .∃x ∈R ,3x-5 = 0C .一切分数都是有理数D .对于任意的实数a,b,方程ax=b 都有唯一解8. 0a <是方程2210ax x ++=至少有一个负数根的( ) A .必要不充分条件B .充分不必要条件C .充分必要条件D .既不充分也不必要条件二、填空题9. (1)命题:,R x ∈∃ x 2+x +1<0的否定是 ,(2) 命题“∀x ∈R ,x 2-x +3>0”的否定是 ,(3) 命题 “对任意的x ∈{x|-2<x<4},|x-2|<3”的否定形式(4)命题 “∀x ,y ∈R ,有x ²+ y ² ≥ 0”的否定是(5) 命题 “不等式x 2+x -6>0的解是x <-3或x >2”的逆否命题是(6)命题“∀a ,b ∈R ,如果ab >0,则a >0”的否命题是(7)命题 “△ABC 中,若∠C=90°,则∠A 、∠B 都是锐角”的否命题为: ,否定形式: 。
数学逻辑推理题目

20 道数学逻辑推理题目一、数字推理题1. 找规律填数字:2,4,6,8,()。
-答案:10。
规律是后一个数比前一个数大2。
2. 1,3,7,15,()。
-答案:31。
规律是后一个数比前一个数依次多2、4、8、16。
3. 2,5,11,23,()。
-答案:47。
规律是后一个数比前一个数依次多3、6、12、24。
4. 3,6,9,12,()。
-答案:15。
规律是后一个数比前一个数大3。
5. 4,8,16,32,()。
-答案:64。
规律是后一个数是前一个数的2 倍。
二、图形推理题1. 观察图形:○△□,△□○,□○△,下一个图形是什么?-答案:○△□。
规律是三个图形依次循环。
2. 有一组图形,第一个是正方形,第二个是圆形,第三个是三角形,第四个是正方形,第五个是圆形,那么第六个图形是什么?-答案:三角形。
规律是正方形、圆形、三角形依次循环。
3. 观察图形序列:△△△△△△△△△,下一个图形是什么?-答案:△。
规律是△后面的△依次增加一个。
4. 一组图形为:△○□,□△○,○□△,下一组图形是什么?-答案:△○□。
规律是三个图形依次循环换位。
5. 图形序列:△△△△△△△△△,下一个图形是什么?-答案:△。
规律是△后面的△依次增加一个。
三、逻辑推理题1. 小明、小红、小刚三人中,一人是医生,一人是教师,一人是警察。
已知小明不是医生,小红不是教师,小刚不是警察。
那么小明是(),小红是(),小刚是()。
-答案:教师、警察、医生。
通过排除法推理得出。
2. 桌子上有三个盒子,一个盒子里装着糖,一个盒子里装着饼干,一个盒子里装着糖和饼干。
三个盒子上分别贴着标签:A 盒“糖”,B 盒“饼干”,C 盒“糖和饼干”。
但标签都贴错了。
现在从一个盒子里取出一个物品,如果是糖,那么这个盒子里实际装着什么?-答案:糖和饼干。
因为标签都贴错了,如果从贴着“糖”标签的盒子里取出糖,那么这个盒子实际装着糖和饼干。
3. 甲、乙、丙三人参加跑步比赛,甲说:“我不是第一名。
高中数学,常用逻辑用语题型归纳(解析版)

第一章常用逻辑用语第一节:简单命题‖知识梳理‖1.命题的概念一般地,在数学中我们把用语言、符号或式子表达的,可以判断真假的陈述句叫做命题.1.1.对于命题概念的理解(1)并不是任何语句都是命题,一个语句是命题应具备两个条件:①该语句是陈述句;②能够判断真假。
一般来说,疑问句、祈使句、感叹句等都不是命题.(2)对于含有字母变量的语句,根据字母的取值范围,若能判断真假,则是命题;若不能判断真假,则不是命题.2.命题的分类判断为真的语句为真命题,判断为假的语句为假命题.3.命题的结构命题的结构形式是“若p,则q”,其中p是条件,q是结论.(1)在数学中,一般用小写字母p,q,r,…等表示命题.如命题p:2是无理数;命题q:π是有理数.(2)常见的命题形式为:“若p,则q”,其中p称为命题的条件,q称为命题的结论.当一个命题不是“若p,则q”的形式时,为了找出命题的条件和结论,可以对命题改写为“若p,则q”的形式.如命题“菱形的对角线互相垂直且平分”,可以改写为:“若一个四边形是菱形,则它的对角线互相垂直且平分”.‖题型归纳‖题型一命题及其真假的判断例题1、判断下列语句是否是命题,若是,判断其真假,并说明理由.(1)垂直于同一直线的两条直线必平行吗?(2)x 2+4x +5>0(x ∈R ); (3)x 2+3x -2=0;(4)一个数不是正数就是负数; (5)4是集合{1,2,3,4}中的元素; (6)求证y =sin 2x 的最小正周期为π. 【解】(1)是疑问句,不是命题.(2)是命题.因为当x ∈R 时,x 2+4x +5=(x +2)2+1>0恒成立,可判断真假,所以是命题,而且是真命题.(3)不是命题.因为语句中含有变量x ,在没给定x 的值之前,无法判断语句的真假,所以不是命题. (4)是命题.因为数0既不是正数也不是负数,所以是假命题. (5)是命题.因为4∈{1,2,3,4},且是真命题. (6)是祈使句,不是命题.练习1、下面命题中是真命题的是( )A .函数y =sin 2x 的最小正周期是2π B .等差数列一定是单调数列 C .直线y =ax +a 过定点(-1,0)D .在△ABC 中,若AB →·BC →>0,则角B 为锐角解析:A 中,y =sin 2x =12-12cos 2x ,周期T =π,A 为假命题;B 中,当公差为0时,等差数列为常数列,B 为假命题;D 中,若AB →·BC →>0,则AB →与BC →的夹角为锐角,角B 为钝角,D 为假命题,故C 正确. 答案:C题型二 命题的结构形式例题2、把下列命题改写成“若p ,则q ”的形式,并判断命题的真假.(1)ac >bc ⇒a >b ;(2)当x 2-2x -3=0时,x =-1或x =3;(3)有两个内角之和大于90°的三角形是锐角三角形; (4)实数的平方是非负数;(5)平行于同一平面的两条直线互相平行. 【解】(1)若ac >bc ,则a >b ,是假命题.(2)若x 2-2x -3=0,则x =-1或x =3,是真命题.(3)若一个三角形中,有两个内角之和大于90°,则这个三角形是锐角三角形,是假命题. (4)若一个数是实数,则它的平方是非负数,是真命题.(5)若两条直线平行于同一个平面,则它们互相平行,是假命题.练习2、把下列命题改写成“若p,则q”的形式,并判断其真假.(1)能被9整除的数是偶数;(2)当x2+(y-1)2=0时,有x=0,y=1;(3)如果a>1, 那么函数f(x)=(a-1)x是增函数.解:(1)若一个数能被9整除,则这个数是偶数,是假命题.(2)若x2+(y-1)2=0,则x=0,y=1,是真命题.(3)若a>1,则函数f(x)=(a-1)x是增函数,是假命题.‖随堂练习‖1.下列语句为命题的个数有( )①一个数不是正数就是负数;②梯形是不是平面图形呢?③22 019是一个很大的数;④4是集合{2,3,4}中的元素;⑤作△ABC≌△A′B′C′.A.1个B.2个C.3个D.4个解析:①④是命题,故选B.答案:B2.下列命题中是假命题的是( )A.若a·b=0,则a⊥b(a≠0,b≠0)B.若|a|=|b|,则a=bC.若ac2>bc2,则a>bD.5>3解析:B中两个向量模相等,方向不一定相同,故B为假命题.答案:B3.已知α,β是两个不同平面,m,n,l是三条不同直线,则下列命题正确的是( ) A.若m∥α,n⊥β且m⊥n,则α⊥βB.若m⊂α,n⊂α,l⊥n,l⊥m,则l⊥αC.若m∥α,n⊥β且α⊥β,则m⊥nD.若l⊥α且l⊥β,则α∥β解析:A中,α与β有可能平行,A错;B中,m与n不一定相交,B错;C中,m与n的关系不确定,C错;D中,垂直于同一条直线的两个平面互相平行,D正确.故选D.答案:D4.指出下列命题中的条件p和结论q.(1)若整数a能被2整除,则a是偶数;(2)若四边形是菱形,则它的对角线互相垂直且平分. 解:(1)条件p :整数a 能被2整除,结论q :整数a 是偶数.(2)条件p :四边形是菱形,结论q :四边形的对角线互相垂直且平分. 5.把下列命题改写为“若p ,则q ”的形式,并判断其真假.(1)函数y =x 3是奇函数; (2)奇数不能被2整除;(3)与同一直线平行的两个平面平行;(4)已知x ,y 是正整数,当y =x +1时,y =3,x =2. 解:(1)若一个函数是y =x 3,则它是奇函数,它是真命题.(2)若一个数是奇数,则它不能被2整除,它是真命题.(3)若两个平面都与同一直线平行,则这两个平面平行,它是假命题. (4)已知x ,y 是正整数,若y =x +1,则y =3,x =2,它是假命题. 6.已知函数f (x )=cos x -|sin x |,那么下列命题中假命题是( )A .f (x )是偶函数B .f (x )在[-π,0]上恰有一个零点C .f (x )是周期函数D .f (x )在[-π,0]上是单调函数解析:∵f (-x )=cos(-x )-|sin(-x )|=cos x -|sin x |=f (x ),∴f (x )为偶函数,A 正确;由f (x )=cos x -|sin x |=0,x ∈[-π,0]时,可得cos x =-sin x ,∴x =-π4,即f (x )在[-π,0]上恰有一个零点,B 正确;∵f (x +2π)=cos(x +2π)-|sin(x +2π)|=cos x -|sin x |=f (x ),∴f (x )为周期函数,C 正确;当x ∈[-π,0]f (x )=cos x +sin x =2sin ⎝⎛⎭⎪⎫x +π4,f (x )在[-π,0]上不单调,D 为假命题,故选D. 答案:D四种命题及其相互关系‖知识梳理‖1.四种命题的概念2.四种命题的相互关系3.四种命题的真假关系(1)两个命题互为逆否命题,它们有相同的真假性.(2)两个命题为互逆命题或互否命题,它们的真假性没有关系.4.命题的真假判断一个命题要么是真命题,要么是假命题,不能既真又假,也不能模棱两可,无法判断其真假.判断一个命题为真命题,需要逻辑推理(证明),判断一个命题是假命题,只需举出一个反例即可.在四种命题中,互为逆否的两个命题同真或同假,称为等价命题.原命题与逆否命题等价,逆命题与否命题等价.因此,四种命题中真假命题的个数一定为偶数个.‖题型归纳‖题型一四种命题的概念例题1、写出下列命题的逆命题、否命题、逆否命题.(1)若a<1,则方程x2+2x+a=0有实根;(2)若ab是正整数,则a,b都是正整数;(3)若a+5是有理数,则a是无理数.【解】(1)原命题的逆命题为:若方程x2+2x+a=0有实根,则a<1.否命题为:若a≥1,则方程x2+2x+a=0没有实根.逆否命题为:若方程x2+2x+a=0没有实根,则a≥1.(2)原命题的逆命题为:若a,b都是正整数,则ab是正整数;否命题为:若ab不是正整数,则a,b不都是正整数;逆否命题为:若a,b不都是正整数,则ab不是正整数.(3)原命题的逆命题为:若a是无理数,则a+5是有理数.否命题为:若a+ 5 不是有理数,则a不是无理数.逆否命题为:若a不是无理数,则a+5不是有理数.练习1、“若a≥2,则a2≥4”的否命题是( )A.若a≤2,则a2≤4B.若a≥2,则a2≤4C.若a<2,则a2<4D.若a≥2,则a2<4解析:否命题既否定条件,又否定结论,所以“若a≥2,则a2≥4”的否命题为“若a<2,则a2<4”,故选C.答案:C题型二四种命题的相互关系例题2、下列说法中,不正确的是( )A.“若p,则q”与“若q,则p”互为逆命题B.“若﹁p,则﹁q”与“若q,则p”互为逆否命题C.“若﹁p,则﹁q”是“若p,则q”的逆否命题D.“若﹁p,则﹁q”与“若p,则q”互为否命题【解析】根据四种命题的概念知,A、B、D正确;C错误.【答案】 C练习2、若命题A的否命题为B,命题A的逆否命题为C,则B与C的关系是( )A.互逆命题B.互否命题C.互为逆否命题D.以上都不正确解析:设命题A为:“若p,则q”,依题意得,命题B为:“若﹁p,则﹁q”,命题C为:“若﹁q,则﹁p”,所以B与C为互逆命题.答案:A题型三四种命题的真假判断例题3、有下列四个命题:①“若b2=ac,则a,b,c成等比数列”的否命题;②“若m=2,则直线x+y=0与直线2x+my+1=0平行”的逆命题;③“已知a,b是非零向量,若a·b>0,则a与b方向相同”的逆否命题;④“若x≤3,则x2-x-6>0”的逆否命题.其中为真命题的个数是( )A.1 B.2C.3 D.4【解析】命题“若b2=ac,则a,b,c成等比数列”的逆命题为:“若a,b,c成等比数列,则b2=ac”,是真命题.因为逆命题与否命题等价,所以①正确;因为②中原命题的逆命题为:“若直线x+y=0与直线2x+my+1=0平行,则m=2”,是真命题,故②正确;对于③可考虑原命题.设a=(0,1),b=(1,1),则a·b=1>0,但a与b不同向,所以原命题为假命题,故③为假命题;④中命题“若x≤3,则x2-x+6>0”的逆否命题为:“若x2-x+6≤0,则x>3”,是假命题,故④为假命题.【答案】 B练习3、下列命题中为真命题的是( )A.命题“若x>y,则x>|y|”的逆命题B.命题“若x>1,则x2>1”的否命题C.命题“若x=1,则x2+x-2=0”的否命题D.命题“若x2>1,则x>1”的逆否命题解析:A中,命题“若x>y,则x>|y|”的逆命题为“若x>|y|,则x>y”,为真命题;B中,命题“若x>1,则x2>1”的逆命题为“若x2>1,则x>1”,为假命题,所以其否命题为假命题;C中,命题的逆命题为“若x2+x-2=0,则x=1”,为假命题,所以其否命题为假命题;D中,命题“若x2>1,则x>1”为假命题,则逆否命题为假命题,故选A.答案:A题型四、等价命题的应用例题4、判断命题“已知a ,x 为实数,若关于x 的不等式x 2+(2a +1)x +a 2+2≤0的解集不是空集,则a ≥1”的逆否命题的真假.【解】 解法一:原命题的逆否命题:已知a ,x 为实数,若a <1,则关于x 的不等式x 2+(2a +1)x +a 2+2≤0的解集为空集.真假判断过程如下:抛物线y =x 2+(2a +1)x +a 2+2开口向上,Δ=(2a +1)2-4(a 2+2)=4a -7. 若a <1,则4a -7<0.所以抛物线y =x 2+(2a +1)x +a 2+2与x 轴无交点.所以关于x 的不等式x 2+(2a +1)x +a 2+2≤0的解集为空集.故逆否命题为真命题. 解法二:判断原命题的真假.已知a ,x 为实数,若关于x 的不等式x 2+(2a +1)x +a 2+2≤0的解集不是空集, 则Δ=(2a +1)2-4(a 2+2)≥0,即4a -7≥0,得a ≥74,从而a ≥1成立.所以原命题为真命题.又因为原命题与其逆否命题等价,所以逆否命题为真命题.练习4、已知奇函数f (x )是定义在R 上的增函数,a ,b ∈R ,若f (a )+f (b )≥0,求证:a +b ≥0. 证明:原命题的逆否命题是:若a +b <0,则f (a )+f (b )<0.∵a +b <0,∴a <-b . 又∵f (x )在R 上为增函数, ∴f (a )<f (-b ).又f (x )为奇函数,∴f (-b )=-f (b ). ∴f (a )<-f (b ),即f (a )+f (b )<0. ∴原命题的逆否命题为真命题. 故原命题成立.‖随堂练习‖1.命题“若a >b ,则a -1>b -1”的否命题是( )A .若a >b ,则a -1≤b -1B .若a >b ,则a -1<b -1C .若a ≤b ,则a -1≤b -1D .若a <b ,则a -1<b -1 解析:否命题应同时否定条件和结论. 答案:C2.命题“若p 不正确,则q 不正确”的逆命题的等价命题是( )A .若q 不正确,则p 不正确B .若q 不正确,则p 正确C .若p 正确,则q 不正确D .若p 正确,则q 正确解析:由于原命题的逆命题与否命题互为等价命题,故D 正确. 答案:D3.下列有关命题的说法正确的是( )A .命题“若xy =0,则x =0”的否命题为“若xy =0,则x ≠0”B .“若sin α=12,则α=π6”的逆否命题为真命题C .“若x +y =0,则x ,y 互为相反数”的逆命题为真命题D .命题“若cos x =cos y ,则x =y ”的逆否命题为真命题解析:C 中,原命题的逆命题为“若x ,y 互为相反数,则x +y =0”,是真命题. 答案:C 4.下列命题中:①若一个四边形的四条边不相等,则它不是正方形; ②若一个四边形对角互补,则它内接于圆; ③正方形的四条边相等; ④圆内接四边形对角互补; ⑤对角不互补的四边形不内接于圆;⑥若一个四边形的四条边相等,则它是正方形.其中互为逆命题的有____________;互为否命题的有____________;互为逆否命题的有____________. 解析:命题③可以改写为:若一个四边形是正方形,则它的四条边相等;命题④可以改写为:若一个四边形是圆内接四边形,则它的对角互补;命题⑤可以改写为:若一个四边形的对角不互补,则它不内接于圆.其中②和④,③和⑥互为逆命题;①和⑥,②和⑤互为否命题;①和③,④和⑤互为逆否命题. 答案:②和④,③和⑥ ①和⑥,②和⑤ ①和③,④和⑤5.写出命题“如果|x -2|+(y -1)2=0,则x =2且y =1”的逆命题、否命题、逆否命题,并判断它们的真假.解:逆命题:如果x =2且y =1,则|x -2|+(y -1)2=0.真命题.否命题:如果|x -2|+(y -1)2≠0,则x ≠2或y ≠1.真命题. 逆否命题:如果x ≠2或y ≠1,则|x -2|+(y -1)2≠0.真命题.6.设△ABC 的三边分别为a ,b ,c ,在命题“若a 2+b 2≠c 2,则△ABC 不是直角三角形”及其逆命题中( )A .原命题真,逆命题假B .原命题假,逆命题真C .两个命题都真D .两个命题都假解析:原命题“若a 2+b 2≠c 2,则△ABC 不是直角三角形”是假命题,而逆命题“若△ABC 不是直角三角形,则a 2+b 2≠c 2”是真命题.故选B.充分条件与必要条件‖知识梳理‖1.推出关系一般地,命题“若p,则q”为真,可记作“p⇒q”;“若p,则q”为假,可记作p⇒q2.充分条件与必要条件一般地,如果p⇒q,那么称p是q的充分条件,同时称q是p的必要条件.若p⇒q,则说p是q的充分条件,所谓“充分”,即要使q成立,有p成立就足够了;q是p的必要条件,所谓“必要”,即q是p成立的必不可少的条件,缺其不可.3.充要条件如果p⇒q且q⇒p,那么称p是q的充分必要条件,简称p是q的充要条件,记作p⇔q.同时q也是p 的充要条件.若p⇒q,同时q⇒p,则称p与q互为充要条件,可以表示为p⇔q(p与q等价),它的同义词还有:“当且仅当”、“必须只需”、“…,反过来也成立”.准确地理解和使用数学语言,对理解和运用数学知识是十分重要的.4.充分条件和必要条件的判断①若p⇒q,则称p是q的充分条件,q是p的必要条件.②若p⇒q,且q p,则称p是q的充分不必要条件.③若p q,且q⇒p,则称p是q的必要不充分条件.④若p⇒q,且q⇒p,则称p是q的充要条件.⑤若p q,且q p,则称p是q的既不充分也不必要条件.4.从集合与集合之间的关系看充分条件、必要条件:‖题型归纳‖题型一充分条件、必要条件的判定例题1、指出下列各题中,p是q的什么条件(在充分不必要条件,必要不充分条件,充要条件,既不充分也不必要条件中选出一种作答).(1)在△ABC中,p:∠A>∠B;q:BC>AC;(2)设x,y∈R,p:x+y≠8;q:x≠2或y≠6;(3)已知x,y∈R,p:(x-1)(y-2)=0;q:(x-1)2+(y-2)2=0;(4)在△ABC中,p:sin A>sin B;q:tan A>tan B.【解】(1)在△ABC中,有∠A>∠B⇔BC>AC,即p⇔q,所以p是q的充要条件.(2)由已知得﹁p:x+y=8;﹁q:x=2且y=6.易知﹁q⇒﹁p,但﹁p﹁q,等价于p⇒q,且q p,所以p是q的充分不必要条件.(3)由已知得p:A={(x,y)|x=1或y=2};q:B={(1,2)},易知q⇒p,且p q,所以p是q 的必要不充分条件.(4)在△ABC中,取∠A=120°,∠B=30°,则p q;又取∠A=30°,∠B=120°,则q p.所以p是q的既不充分也不必要条件.练习1—1、“a=1”是“直线a2x-y+3=0与x+ay-2=0垂直”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件练习1-2、“a=4”是“y=x2-ax+1在(2,+∞)上是增函数”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件解析:(1)若直线a2x-y+3=0与x+ay-2=0垂直,则a2-a=0,则a=0或a=1,故“a=1”是“直线a2x-y+3=0与x+ay-2=0垂直”的充分不必要条件.(2)若函数y=x2-ax+1在(2,+∞)上是增函数,则a2≤2,即a≤4,故“a=4”是“y=x2-ax+1在(2,+∞)上是增函数”的充分不必要条件.答案:(1)A (2)A题型二充分条件、必要条件的应用例题2、已知命题p:对数log a(-2t2+7t-5)(a>0,a≠1)有意义;命题q:实数t满足不等式t2-(a+3)t+(a+2)<0.(1)若命题p为真命题,求实数t的取值范围;(2)若命题p是命题q的充分不必要条件,求实数a的取值范围.【解】 (1)由对数式有意义,得-2t 2+7t -5>0,解得1<t <52,∴若命题p 为真命题,则实数t 的取值范围是⎝ ⎛⎭⎪⎫1,52. (2)不等式t 2-(a +3)t +(a +2)<0, 可化为(t -1)(t -a -2)<0.若p 是q 的充分不必要条件,则1<t <52是不等式解集的真子集.则a +2>52,∴a >12.∴实数a 的取值范围是⎝ ⎛⎭⎪⎫12,+∞.练习2、已知函数f (x )=x 2-x +a ,集合A ={x |-1≤x ≤1},集合B ={x |f (x )≤0},若x ∈A 是x ∈B 的充分不必要条件,求a 的取值范围. 解:∵x ∈A 是x ∈B 的充分不必要条件,则f (x )≤0,x ∈[-1,1]恒成立, 即x 2-x +a ≤0,x ∈[-1,1]恒成立, 即f (x )max ≤0恒成立,∴⎩⎪⎨⎪⎧1+1+a ≤0,1-1+a ≤0,即a ≤-2.∴a 的取值范围为(-∞,-2].题型三 充要条件的证明例题3、已知x ,y 都是非零实数,且x >y ,求证:1x <1y的充要条件是xy >0.【证明】 证法一:①充分性:由xy >0,及x >y ,得x xy >y xy ,即1y >1x ,即1x <1y. ②必要性:由1x <1y,得1x -1y<0, 即y -xxy<0. ∵x >y ,∴y -x <0,∴xy >0. 由①②知,1x <1y的充要条件是xy >0.证法二:1x <1y ⇔1x -1y <0⇔y -xxy<0.由条件x >y ⇔y -x <0.故y -xxy <0⇔xy >0. ∴1x <1y ⇔xy >0.即1x <1y的充要条件是xy >0.练习3、求证:关于x 的方程ax 2+bx +c =0有一个根为-1的充要条件是a -b +c =0. 证明:①充分性:∵a -b +c =0,∴a (-1)2+b (-1)+c =0,∴-1是方程ax 2+bx +c =0的一个根. ②必要性:∵ax 2+bx +c =0有一个根是-1, ∴a (-1)2+b (-1)+c =0, 即a -b +c =0.由①②知,方程ax 2+bx +c =0有一根为-1的充要条件是a -b +c =0.题型四 充要条件的探求例题4、设集合A ={x |-2≤x ≤a },B ={y |y =2x +3,x ∈A },M ={z |z =x 2,x ∈A },求使M ⊆B 的充要条件.【解】 ∵A ={x |-2≤x ≤a }.∴B ={y |y =2x +3,x ∈A }={y |-1≤y ≤2a +3}. 当-2≤a <0时,M ={z |a 2≤z ≤4}; 当0≤a ≤2时,M ={z |0≤z ≤4}; 当a >2时,M ={z |0≤z ≤a 2}. 故当-2≤a ≤2时,M ⊆B , 得2a +3≥4,即a ≥12.∴12≤a ≤2. 当a >2时,M ⊆B ,得 2a +3≥a 2,解得-1≤a ≤3. ∴2<a ≤3.综上知,M ⊆B 的充要条件为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫a ⎪⎪⎪12≤a ≤3.练习4、直线x +y +m =0与圆(x -1)2+(y -1)2=2相切的充要条件是________. 解析:∵直线x +y +m =0与圆(x -1)2+(y -1)2=2相切,∴圆心(1,1)到直线x +y +m =0的距离等于2,∴|1+1+m |2=2,∴m =-4或m =0. 当m =-4或m =0时,直线与圆相切. 答案:m =-4或m =0‖随堂练习‖1.设a >0,b >0,则“a 2+b 2≥1”是“a +b ≥ab +1”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件解析:由a +b ≥ab +1,得a -1+b -ab ≥0,即(a -1)(1-b )≥0,∴⎩⎪⎨⎪⎧a ≥1,0<b ≤1或⎩⎪⎨⎪⎧0<a ≤1,b ≥1,∴a 2+b2≥1,即a +b ≥ab +1⇒a 2+b 2≥1,但当a =b =2时,有a 2+b 2≥1,而a +b <ab +1.∴“a 2+b 2≥1”是“a +b ≥ab +1”的必要不充分条件,故选B. 答案:B2.已知命题p :函数f (x )=|x +a |在(-∞,-1)上是单调函数,命题q :函数g (x )=log a (x +1)(a >0,且a ≠1)在(-1,+∞)上是增函数,则﹁p 是q 的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件解析:由p 成立,得a ≤1;由q 成立,得a >1,∴当﹁p 成立时,a >1,∴﹁p 是q 的充要条件. 答案:C3.若l ,m 是两条不同的直线,m 垂直于平面α,则“l ⊥m ”是“l ∥α”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件解析:若m ⊥α,l ⊥m ,则l ∥α或l ⊂α,反之,若m ⊥α,l ∥α,则l ⊥m ,∴“l ⊥m ”是“l ∥α”的必要不充分条件,故选B. 答案:B4.已知p :函数f (x )=|x -a |在(2,+∞)上是增函数,q :函数f (x )=a x(a >0,且a ≠1)是减函数,则p 是q 的( )A .必要不充分条件B .充分不必要条件C .充要条件D .既不充分也不必要条件解析:若p 为真,则a ≤2;若q 为真,则0<a <1.则q ⇒p ,pq ,∴p 是q 的必要不充分条件,故选A. 答案:A5.已知p :x 2-8x -20≤0,q :1-m ≤x ≤1+m (m >0),且p 是q 的充分不必要条件,求实数m 的取值范围.解:由x 2-8x -20≤0,得-2≤x ≤10,又p 是q 的充分不必要条件,∴⎩⎪⎨⎪⎧1+m ≥10,1-m ≤-2,m >0,(等号不能同时成立),解得m ≥9.∴实数m 的取值范围是[9,+∞).6.设x ∈R ,则“0<x <5”是“|x -1|<1”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 解析:由|x -1|<1,得0<x <2,∴“0<x <5”是“0<x <2”的必要而不充分条件,故选B. 答案:B简单的逻辑联结词‖知识梳理‖1.逻辑联结词把两个命题联结而成新命题的常用逻辑联结词有“且”、“或”、“非”.2.简单命题与复合命题(1)不含逻辑联结词的命题叫做简单命题.(2)由简单命题和逻辑联结词构成的命题叫做复合命题.复合命题一般有三种类型:①p且q;②p或q;③非p.(3)复合命题的真假①p且q同真才真,其他均假;②p或q同假才假,其他均真;③非p与p真假相反.3.对逻辑联结词“或”的理解“或”与日常生活用语中的“或”意义不同,日常生活用语中的“或”带有“不可兼有”的意思,如工作或休息;而逻辑联结词中“或”含有“同时兼有”的意思,如x<-1或x>2.因此“p或q”的含义有三层意思:①p成立q不成立;②p不成立q成立;③p与q同时成立.4.对逻辑联结词“非”的理解“非”是否定的意思,如“3是非偶数”是对命题“3是偶数”进行否定而得出的新命题.一般地,写一个命题的否定,往往需要对正面叙述的词语进行否定,常用的正面叙述的词语与它的否定如下表:5.逻辑联结词与集合的运算集合中的“交”、“并”、“补”与逻辑联结词“且”、“或”、“非”有密切关系,设集合A={x|p(x)},B={x|q(x)},可有如下关系:A∩B={x|x∈A且x∈B}={x|p∧q};A∪B={x|x∈A或x∈B}={x|p∨q};∁U A={x|x∈U且x∉A}={x|﹁p}.6.命题的否定形式与否命题的关系:命题的否定与否命题都是对关键词进行否定,但有如下区别:(1)定义不同命题的否定是直接对命题的结论进行否定;而否命题则是对命题的条件和结论都否定后组成的新命题.(2)构成形式不同对于“若p,则q”形式的命题,其否定形式为“若p,则﹁q”,即不改变条件,只否定结论;而其否命题的形式为“若﹁p,则﹁q”,即对命题的条件和结论都否定.(3)与原命题的真假关系命题的否定的真假与原命题的真假总是相对的,即一真一假;而否命题的真假与原命题的真假没有必然联系.(4)“p或q”的否定是“非p且非q”,“p且q”的否定是“非p或非q”.‖题型归纳‖题型一命题的构成例题1、分别写出由下列命题构成的“p∧q”,“p∨q”,“﹁p”形式的命题:(1)p:π是无理数,q:e不是无理数;(2)p:12是3的倍数,q:12是4的倍数;(3)p:方程x2-3x+2=0的根是x=1,q:方程x2-3x+2=0的根是x=2.【解】(1)“p∧q”:π是无理数且e不是无理数;“p∨q”:π是无理数或e不是无理数;“﹁p”:π不是无理数.(2)“p∧q”:12是3的倍数且是4的倍数;“p∨q”:12是3的倍数或是4的倍数;“﹁p”:12不是3的倍数.(3)“p∧q”:方程x2-3x+2=0的根是x=1且方程x2-3x+2=0的根是x=2;“p∨q”:方程x2-3x+2=0的根是x=1或方程x2-3x+2=0的根是x=2;“﹁p”:方程x2-3x+2=0的根不是x=1.练习1、试写出下列命题中的p ,q .(1)梯形有一组对边平行且相等;(2)方程x 2+2x +1=0有两个相等的实数根或两根的绝对值相等; (3)一元二次方程至少有三个根. 解:(1)是p 且q 形式的命题.p :梯形有一组对边平行; q :梯形有一组对边相等.(2)是p 或q 形式的命题.p :方程x 2+2x +1=0有两个相等的实数根; q :方程x 2+2x +1=0的两根的绝对值相等.(3)是﹁p 的形式.p :一元二次方程最多有两个根.题型二 复合命题的真假判断例题2、分别指出由下列各组命题构成的“p ∧q ”“p ∨q ”“﹁p ”形式的命题的真假:(1)p :π>3,q :π<2;(2)p :若x ≠0,则xy ≠0,q :若y ≠0,则xy ≠0;(3)p :等腰三角形顶角的平分线平分底边,q :等腰三角形顶角的平分线垂直于底边; (4)p :函数y =x 12的定义域为R ,q :函数y =x 2是偶函数.【解】 (1)∵p 是真命题,q 是假命题,∴p ∧q 是假命题,p ∨q 是真命题,﹁p 是假命题.(2)∵p 是假命题,q 是假命题,∴p ∧q 是假命题,p ∨q 是假命题,﹁p 是真命题. (3)∵p 是真命题,q 是真命题,∴p ∧q 是真命题,p ∨q 是真命题,﹁p 是假命题. (4)∵p 是假命题,q 是真命题,∴p ∧q 是假命题,p ∨q 是真命题,﹁p 是真命题.练习2—1、命题p :若ac 2>bc 2,则a >b ,命题q :在△ABC 中,若A ≠B ,则sin A ≠sin B ,下列选项正确的是( )A .p 假q 真B .p 真q 假C .“p 或q ”为假D .“p 且q ”为真练习2—2、已知命题p :不等式-x 2+2x <0的解集是{x |x <0或x >2},命题q :在△ABC 中,A >B 是sin A >sinB 的充要条件,则( )A .p 真q 假B .p ∨q 假C .p ∧q 真D .p 假q 真解析:(1)p 为真命题,q 为真命题,∴p 且q 为真,故选D.(2)由-x 2+2x <0,得x >2或x <0,故p 为真命题,在△ABC 中,A >B ⇔sin A >sin B ,故q 为真命题,所以p ∧q 为真,故选C. 答案:(1)D (2)C题型三 命题的否定与否命题例题3、写出下列命题的否定与否命题,并判断真假.(1)若abc =0,则a ,b ,c 中至少有一个为0; (2)若x 2+y 2=0,则x ,y 全为0; (3)等腰三角形有两个内角相等.【解】 (1)命题的否定:若abc =0,则a ,b ,c 中都不为0,为假命题;否命题:若abc ≠0,则a ,b ,c 都不为0,为真命题.(2)命题的否定:若x 2+y 2=0,则x ,y 中至少有一个不为0,为假命题; 否命题:若x 2+y 2≠0,则x ,y 中至少有一个不为0,为真命题. (3)命题的否定:等腰三角形的任意两个内角都不相等,为假命题; 否命题:不是等腰三角形的三角形中任意两个角都不相等,为真命题.练习3、“末位数字是1或3的整数不能被8整除”的否定形式是___________;否命题是___________. 解析:命题的否定仅否定结论,所以该命题的否定形式是:末位数字是1或3的整数能被8整除;而否命题要同时否定原命题的条件和结论,因此否命题是:末位数字不是1且不是3的整数能被8整除. 答案:末位数字是1或3的整数能被8整除末位数字不是1且不是3的整数能被8整除题型四 逻辑联结词“或”“且”“非”的应用例题4、设命题p :ln a <0;命题q :函数y =ax 2-x +a 的定义域为R .(1)若命题q 是真命题,求实数a 的取值范围;(2)若命题p 或q 是真命题,命题p 且q 是假命题,求实数a 的取值范围. 【解】 (1)对于命题q :函数的定义域为R 的充要条件是ax 2-x +a ≥0恒成立.当a =0时,不等式为-x ≥0,解得x ≤0,显然不成立; 当a ≠0时,不等式恒成立的条件是@⎩⎪⎨⎪⎧a >0,Δ=(-1)2-4a ×a ≤0,解得a ≥12.所以命题q 为真命题时,a 的取值集合为Q =⎩⎨⎧a ⎪⎪⎪⎭⎬⎫a ≥12.(2)若命题p 为真,则0<a <1,由“p 或q 是真命题,p 且q 是假命题”可知,命题p ,q 一真一假,当p 真q 假时,由⎩⎪⎨⎪⎧0<a <1,a <12,得0<a <12;当p 假q 真时,由⎩⎪⎨⎪⎧a ≤0或a ≥1,a ≥12,得a ≥1.综上,实数a 的取值范围是⎝ ⎛⎭⎪⎫0,12∪[1,+∞).练习4、已知a >0,a ≠1,设p :函数y =log a (x +1)在x ∈(0,+∞)内单调递减;q :二次函数y =x 2+(2a -3)x +1的图象与x 轴交于不同的两点.如果p ∧q 为假命题,p ∨q 为真命题,求a 的取值范围. 解:若函数y =log a (x +1)在(0,+∞)内单调递减,则0<a <1,∴p :0<a <1.若曲线y =x 2+(2a -3)x +1与x 轴交于两点, 则(2a -3)2-4>0,即a <12或a >52.∴q :a <12或a >52.若p ∧q 为假命题,p ∨q 为真命题,则p 与q 一真一假,若p 真q 假,由⎩⎪⎨⎪⎧0<a <1,12≤a ≤52,a >0且a ≠1,得a ∈⎣⎢⎡⎭⎪⎫12,1.若p 假q 真,由⎩⎪⎨⎪⎧a ≤0或a ≥1,a <12或a >52,a >0且a ≠1,得a ∈⎝ ⎛⎭⎪⎫52,+∞.综上,a 的取值范围为⎣⎢⎡⎭⎪⎫12,1∪⎝ ⎛⎭⎪⎫52,+∞.‖随堂练习‖1.已知命题p :x ∈A ∪B ,则﹁p 是( )A .x ∉A ∪B B .x ∉A 或x ∉BC .x ∉A 且x ∉BD .x ∈A ∩B解析:由x ∈A ∪B ,知x ∈A 或x ∈B .﹁p 是:x ∉A 且x ∉B .故选C. 答案:C2.已知p :|x +1|>2,q :x >a ,则﹁p 是﹁q 的充分不必要条件,则a 的取值范围是( )A.a≥1 B.a≤1C.a≥-3 D.a≤-3解析:由|x+1|>2,得x<-3或x>1,∵﹁p是﹁q的充分不必要条件,∴﹁p⇒﹁q,∴q⇒p,∴a≥1,故选A.答案:A3.设p,q是两个命题,若﹁(p∨q)是真命题,那么( )A.p是真命题且q是假命题B.p是真命题且q是真命题C.p是假命题且q是真命题D.p是假命题且q是假命题解析:﹁(p∨q)是真命题,则p∨q是假命题,故p,q均为假命题.答案:D4.下列三个结论:①命题“若x-sin x=0,则x=0”的逆否命题为“若x≠0,则x-sin x≠0”;②若p是q的充分不必要条件,则﹁q是﹁p的充分不必要条件;③命题“p∧q为真”是命题“p∨q为真”的必要不充分条件.其中正确结论的个数是( )A.0个B.1个C.2个D.3个解析:命题“若x-sin x=0,则x=0”的逆否命题为“若x≠0,则x-sin x≠0”,即①正确;由p是q的充分不必要条件,可得由p能推出q,但是q不能推出p,所以﹁q能推出﹁p,﹁p不能推出﹁q,故﹁q是﹁p的充分不必要条件,即②正确;若p∧q为真,则p,q都为真,所以p∨q为真;若p∨q为真,则p,q至少有一个为真,所以“p∧q为真”是命题“p∨q为真”的充分不必要条件,即③错误.故选C. 答案:C5.已知命题p:若a>b,则a2>b2,命题q:若a<b,则ac2<bc2,下列命题为真命题的是( ) A.p∧q B.p∧(﹁q)C.p∨(﹁q) D.p∨q解析:若a=-1,b=-2,满足a>b,但a2<b2,∴p为假命题,当c=0,a<b时,但ac2=bc2,q为假命题.∴p∧q为假,p∧(﹁q)为假,p∨q为假,p∨(﹁q)为真,故选C.答案:C6.已知命题p:α,β是第一象限角,则α>β是sin α>sin β的充要条件,命题q:若S n为等差数列{a n}的前n项和,则S m,S2m,S3m(m∈N*)成等差数列,下列命题为真命题的个数是( )①p∨(﹁q) ②(﹁p)∧q③(﹁p)∨(﹁q) ④p∧qA.1个B.2个C.3个D.4个解析:∵p为假命题,q为假命题,∴p∨(﹁q)为真命题,(﹁p)∧q为假命题,(﹁p)∨(﹁q)为真命题,p∧q为假命题.故选B. 答案:B全称量词与存在量词‖知识梳理‖1.全称量词和全称命题2.存在量词和特称命题3.全称命题与特称命题的辨析同一个全称命题或特称命题,由于自然语言的不同,可以有不同的表述方法,在实际应用中可以灵活地选择.有的命题省略全称量词,但仍是全称命题.例如:“实数的绝对值是非负数”,省略了全称量词“任意”.但它仍然是全称命题.因此,要判定一个命题是否是全称命题,除看它是否含有全称量词外,还要结合具体意义去判断.4.全称命题与特称命题的真假要判定一个全称命题是真命题,必须对限定集合M中的每一个元素x验证p(x)成立;但要判定一个全称命题是假命题,却只需找出集合M中的一个x0,使得p(x0)不成立即可(这就是我们常说的“举出一个反例”).要判定一个特称命题为真命题,只要在限定集合M中,至少能找到一个x0,使得p(x0)成立即可;否则,这一特称命题就是假命题.。
数学经典的20道逻辑题

数学经典的20道逻辑题好的,下面我将列举一些经典的数学逻辑题,希望能够满足你的需求。
1. 有一条绳子,燃烧需要60分钟,但不一定均匀。
如何用这条绳子计时45分钟?2. 有三个开关分别控制三盏灯,但你在房间外,只能进去一次。
如何知道哪个开关控制哪盏灯?3. 有8个球,其中7个重量相同,1个重量略有不同。
用天平称两次,如何找出重量略有不同的那个球?4. 有一个8升和一个5升的水罐,如何用它们得到4升水?5. 一辆火车长1英里,正以60英里/小时的速度行驶。
一只飞蛾在火车头以120英里/小时的速度飞行。
飞蛾从火车头飞到尾部需要多长时间?6. 有一堆硬币,其中有一枚是假币,但你不知道假币比真币轻还是重。
用天平最少称几次可以找出假币?7. 有一张长方形的纸,折叠一次后的长度是10厘米,宽度是10厘米。
请问这张纸原本的长和宽各是多少?8. 有一根绳子,燃烧需要60分钟。
现在有若干根这样的绳子,请问如何用它们计时15分钟?9. 有一堆砖,每块砖重1磅加半块砖的重量。
请问这堆砖一共有多少块?10. 一个数加上100是一个完全平方数,再加上168又是一个完全平方数,这个数是多少?11. 有一个正方形的花坛,每条边上都有一棵树,相邻两棵树的距离是10米。
请问这个花坛的面积是多少?12. 一家商店的一只铁锅重8磅,里面装满了水,总重量是12磅。
如果这只铁锅是空的,它的重量是多少?13. 有一堆苹果,分给A、B、C三人。
A拿走1/2个,B拿走1/3个,C拿走1/4个,最后还剩下8个。
请问开始有多少个苹果?14. 有一个3升的容器和一个5升的容器,如何用它们得到4升水?15. 一个正方形花坛的对角线长10米,求花坛的面积。
16. 有一堆砖,每块砖重3/4磅。
请问这堆砖一共有多少块?17. 有一堆砖,每块砖重1/3磅。
请问这堆砖一共有多少块?18. 有一堆砖,每块砖重1/5磅。
请问这堆砖一共有多少块?19. 有一堆砖,每块砖重2/3磅。
小学数学逻辑思维题

小学数学逻辑思维题题目:小学数学逻辑思维题一、填空题(每题2分,共20分)1. 在以下数字中,选出一个与其它数字不同类的数字。
10 12 14 18 20 22 24 262. 某物品原价为800元,现进行打折,折扣为20%,请问打折后的价格是多少元?3. 请将下列数字按升序排列: 5, 10, 3, 8, 12.4. 将一个圆分成4个相等的扇形,每个扇形的圆心角是多少度?5. 求下列算式的值:3 + 4 × 2 - 5.6. 把6十7百8千写成标准形式。
7. 小华有8本书,小明有权借5本书,两人共有多少本书?8. 如果一个长方形的长是4米,宽是7米,它的周长是多少米?9. 如果1小时有60分钟,那么2小时有多少分钟?10. 现在是上午11点,过去了2小时,是几点?二、选择题(每题3分,共30分)1. 下列数字哪一个是偶数?A) 3 B) 6 C) 9 D) 112. 小明的身高为125厘米,小华的身高为140厘米,谁的身高更高?A) 小明 B) 小华 C) 一样高3. 小明有9根铅笔,小华比小明多3根铅笔,小华有多少根铅笔?A) 6 B) 9 C) 12 D) 154. 在以下数字中,哪一个是3的倍数?A) 15 B) 20 C) 25 D) 305. 请写出下图中缺少的数字:1 2 34 5 67 ? 9A) 4 B) 5 C) 6 D) 86. 用下面给出的数字,组成一个最小的3位数。
5, 2, 3, 7A) 235 B) 257 C) 327 D) 5277. 请将下列算式化简:10 + 2 × (3 - 5).A) 10 B) 8 C) 4 D) -68. 某本书原价为50元,现在打折25%,请问打折后的价格是多少元?A) 12.5 B) 25 C) 37.5 D) 42.59. 小明每天运动30分钟,小华每天运动45分钟,谁运动的时间长?A) 小明 B) 小华 C) 一样长10. 如果一个立方体的边长是4厘米,求它的体积是多少立方厘米?A) 16 B) 32 C) 48 D) 64三、解答题(共20分)1. 在一个宾馆内住了n个人,每个人每天需要支付20元。
专题训练:高中数学简易逻辑常见重难点题型

专题:简易逻辑常见重难点题型※题型讲练【例1】写出命题“若x ≥2且y ≥3,则x +y ≥5”的逆命题、否命题、逆否命题,并判断其真假.变式训练1:1.写出命题“若△ABC 不是等腰三角形,则它的任何两个内角不相等.”的逆命题、否命题、逆否命题,并判断其真假.【例2】写出下列命题的“非P ”命题,并判断其真假: (1)若21,20m x x m >-+=则方程有实数根. (2)平方和为0的两个实数都为0.(3)若0abc =,则,,a b c 中至少有一为0.(4)若ABC ∆是锐角三角形, 则ABC ∆的任何一个内角是锐角. (5)若0)2)(1(=--x x ,则21≠≠x x 且 .(6)91()AB ∈(其中全集*U N =,{}|A x x =是质数,{}|B x x =是正奇数).变式训练2:1.已知命题“存在实数x 0,y 0,使得x 0+y 0>1”. (1)用符号表示为 ;(2)此命题的否定是 (用符号表示),是________(填“真”或“假”)命题.【例3】已知命题p :存在实数x ,使sin x =π2成立;命题q :x 2-3x +2<0的解集为(1,2).给出下列四个结论: ①命题“p ∧q ”是真命题; ②命题“p ∧¬p ”是假命题; ③命题“¬p ∧q ”是真命题; ④命题“¬p ∨¬q ”是假命题. 其中正确的结论是( )A .②③B .②④C .①②④D .①②③④变式训练3:1.如果命题“非p 或非q ”是假命题,给出下列四个结论: ①命题“p 且q ”是真命题; ②命题“p 且q ”是假命题; ③命题“p 或q ”是真命题; ④命题“p 或q ”是假命题. 其中正确的结论是( ) A .①③ B .②④ C .②③D .①④【例4】用合适的序号填空:①充分不必要 ②必要不充分 ③充要 ④既不充分也不必要 (1)p q ∨为真命题是p q ∧为真命题的 条件;(2):23A x -<, 是2:4150B x x --<的 条件; (3)设集合M={x | x >2},P={x |x <3},那么“x ∈M ,或x ∈P”是“x ∈M∩P”的 条件;(4)若a =(x,3)(x ∈R ),则“x =4”是“|a |=5”的 条件; (5)“tan θ≠1”是“θ≠π4”的的 条件;(6)“cos A =2sin B sin C ”是“△ABC 为钝角三角形”的 条件; (7)“a n +1>|a n |(n =1,2,…)”是“{a n }为递增数列”的 条件; (8)已知p 是q 的必要条件,r 是q 的充分条件,p 是r 的充分条件,那么q 是p 的 条件;【例5】已知命题p :∃x ∈R ,mx 2+1≤0,命题q :∀x ∈R ,x 2+mx +1>0.若“p ∨q ”的否定为真命题,求实数m 的取值范围.变式训练4:1.已知p :∀x ∈R,2x >m (x 2+1),q :∃x 0∈R ,x 20+2x 0-m -1=0,且p ∧q 为真,求实数m 的取值范围.【例6】已知命题p :关于x 的函数y =x 2-3ax +4在[1,+∞)上是增函数,命题q :函数y =(2a -1)x 为减函数,若“p 且q ”为真命题,求实数a 的取值范围.变式训练5:1.设命题p :实数x 满足x 2-4ax +3a 2<0,其中a >0,命题q :实数x 满足⎩⎨⎧x 2-x -6≤0,x 2+2x -8>0.(1)若a =1,且p ∧q 为真,求实数x 的取值范围;(2)非p 是非q 的充分不必要条件,求实数a 的取值范围.※课后练习1.下列命题中的假命题是()A.∀a,b∈R,a n=an+b,有{a n}是等差数列B.∃x0∈(-∞,0),2x0<3x0C.∀x∈R,3x≠0D.∃x0∈R,lg x0=02.与命题“若a∈M,则b∉M”等价的命题是() A.若a∉M,则b∉M B.若b∉M,则a∈M C.若a∉M,则b∈M D.若b∈M,则a∉M 3.下列命题中正确的是()A.若p∨q为真命题,则p∧q为真命题B.“x=5”是“x2-4x-5=0”的充分不必要条件C.命题“若x<-1,则x2-2x-3>0”的否定为:“若x≥-1,则x2-2x-3≤0”D.命题p:∃x∈R,x2+x-1<0,则非p:∃x∈R,x2+x-1≥0 4.下列说法错误的是()A.如果命题“非p”与命题“p或q”都是真命题,那么命题q一定是真命题B.命题“若a=0,则ab=0”的否命题是:若“a≠0,则ab≠0”C.若命题p:∃x0∈R,ln(x20+1)<0,则非p:∀x∈R,ln(x2+1)≥0D.“sin θ=12”是“θ=30°”的充分不必要条件5.已知命题p:“∀x∈[0,1],a≥e x”,命题q:“∃x∈R,x2+4x +a=0”,若命题“p∧q”是真命题,则实数a的取值范围是() A.(4,+∞) B.[1,4] C.[e,4] D.(-∞,1] 6.设f(x)是R上的减函数,且f(0)=3,f(3)=-1,设P={x||f(x +t)-1|<2},Q={x|f(x)<-1},若“x∈P”是“x∈Q”的充分不必要条件,则实数t的取值范围是()A.t≤0 B.t≥0 C.t≤-3 D.t≥-3 7.命题“∃x<0,有x2>0”的否定是______________.8.“lg x>lg y”是“10x>10y”的条件.9.下列结论:①若命题p:∃x0∈R,tan x0=2;命题q:∀x∈R,x2-x+1 2>0.则命题“p∧(綈q)”是假命题;②已知直线l1:ax+3y-1=0,l2:x+by+1=0,则l1⊥l2的充要条件是ab=-3;③“设a、b∈R,若ab≥2,则a2+b2>4”的否命题为:“设a、b∈R,若ab<2,则a2+b2≤4”.其中正确结论的序号为________.(把正确结论的序号都填上)10.设a,b,c为△ABC的三边,求证:方程x2+2ax+b2=0与x2+2cx-b2=0有公共根的充要条件是∠A=90°. 11.已知命题p:|x2-x|≥6; q:x∈Z,若“p∧q”与“非q”同时为假命题,求x的值.12.已知命题p:∃x∈R,2x2-3ax+9<0.(1)写出非p:;(2)若非p为真命题,求实数a的取值范围.13.已知命题p:关于x的不等式x4-x2+1x2>m的解集为{x|x≠0,x∈R};命题q:f(x)=-(5-2m)x是减函数.若“p∨q”为真命题,“p∧q”为假命题,求实数m的取值范围.。
数学高考基础知识、常见结论详解(一)

数学高考基础知识、常见结论详解一、集合与简易逻辑:一、理解集合中的有关概念(1)集合中元素的特征:确定性、互异性、无序性互异性:例如:,,若A=B求;(A={-1,1,0})(2)集合与元素的关系用符号表示。
(、)(3)常用数集的符号表示:自然数集;正整数集;整数集;有理数集、实数集。
(4)集合的表示法:、、。
(列举法,描述法,韦恩图示法)注意:区分集合中元素的形式:例如:;;;;;(5)空集是指不含任何元素的集合。
(、和的区别;0与三者间的关系)空集是任何集合的子集,是任何非空集合的真子集。
注意:条件为,在讨论的时候不要遗忘了的情况。
如:,如果,求的取值。
()二、集合间的关系及其运算(1)符号是表示元素与集合之间关系的,立体几何中则体现;(;点与直线(面)的关系)符号是表示集合与集合之间关系的,立体几何中则体现。
(;直线与面的关系)(2);;(3)对于任意集合,则:①;;;(=;=;)②;;;;()③;;()(4)①若为偶数,则;若为奇数,则;②若被3除余0,则;若被3除余1,则;若被3除余2,则;三、集合中元素的个数的计算:若集合中有个元素,则集合的所有不同的子集个数为,所有真子集的个数是,所有非空真子集的个数是。
()四、若;则是的充分非必要条件;若;则是的必要非充分条件;五、原命题与逆否命题,否命题与逆命题具有相同的;(真假值)注意:“若,则”在解题中的运用,如:“”是“”的条件。
(充分非必要)六、反证法:当证“若,则”感到困难时,改证它的等价命题“若则”成立,步骤:1、假设结论反面成立;2、从这个假设出发,推理论证,得出矛盾;3、由矛盾判断假设不成立,从而肯定结论正确。
矛盾的来源:1、与原命题的条件矛盾;2、导出与假设相矛盾的命题;3、导出一个恒假命题。
适用与待证命题的结论涉及“不可能”、“不是”、“至少”、“至多”、“唯一”等字眼时。
(不等于;小于或等于;大于或等于;不是;不都是;至少有两个;一个也没有;存在一个)二、函数一、映射与函数:(1)映射的概念:(2)一一映射:(3)函数的概念:如:若,;问:到的映射有个,到的映射有个;到的函数有个,若,则到的一一映射有个。
数学简易逻辑

简易逻辑1.已知命题:(0,),32x x p x ∀∈+∞>;命题:(,0),32q x x x ∃∈-∞>,则下列命题为真命题的是( ). A . p q ∧ B .(q)p ∧⌝ C .()p q ⌝∧ D . ()()p q ⌝∧⌝2.“1m n >>”是 “log 2log 2m n <”的( ).A .充分而不必要条件B .必要而不充分条件C . 充分必要条件D .既不充分也不必要条件 3.在ABC △中,π4A =,BC“AC =”是“π3B =”的( ) A .充分不必要条件 B .必要不充分条件C . 充要条件D .既不充分也不必要条件4. “8m <”是“方程221108x y m m -=--表示双曲线”的( ).A .充分而不必要条件B .必要而不充分条件C .充分必要条件C . 既不充分也不必要条件5.等比数列{}n a 中,10a >,则“13a a <”是“36a a <”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件 C . 既不充分也不必要条件1.【答案】B【解析】解:因为命题p 是真命题,命题q 是假命题,所以()p q ∧⌝是真命题 故选B2.【答案】A【解析】解:因为1m n >> ,则22log log 0m n >>,所以2211log log m n<. 即“1m n >>”⇒“log 2log 2m n <” 另一方面,若log 2log 20m n <<,即22110log log m n<<,所以22log log 0n m <<,则1n m <<即“log 2log 2m n <”推不出“1m n >>”.所以“1m n >>”是 “log 2log 2m n <”充分不必要条件. 故答案选A .3.答案】B【解析】解:若AC=,π4A=,BC=,由正弦定理得sinsinAC ABBC⋅==又(0,π)B∈,则π3B=或2π3.所以“AC=”推不出“π3B=”;另一方面,若π4A=,BCπ3B=,则sinsinBC BACA⋅===所以“π3B=”能推出“AC.所以“AC”是“π3B=”的必要不充分条件.故选B4.【答案】A【解析】解:若方程221108x ym m-=--表示双曲线,则当焦点在x轴时.2210080m am b⎧-=>⎪⎨-=>⎪⎩.,解得10m>;当焦点在y轴时2210080m bm a⎧-=-<⎪⎨-=-<⎪⎩解得8m<;所以“8m<”能推出“方程表示双曲线”而不能反推故答案为A.5.【答案】B【解析】解:如果13a a<,则211a a q<∴21q>,若1q<-,则231a a q=>,561a a q=<∴36a a>,∴“13a a<”不是“36a a<”的充分条件;如果36a a<成立,则2511a q a q<,又1a>,∴31q<∴1q >, ∴2113a a q a <=,故可判断,“13a a <”是“36a a <”的必要条件. 综上,“13a a <”是“36a a <”必要而不充分条件. 故选B .。
高中数学知识点总结(新高考地区)精选全文完整版
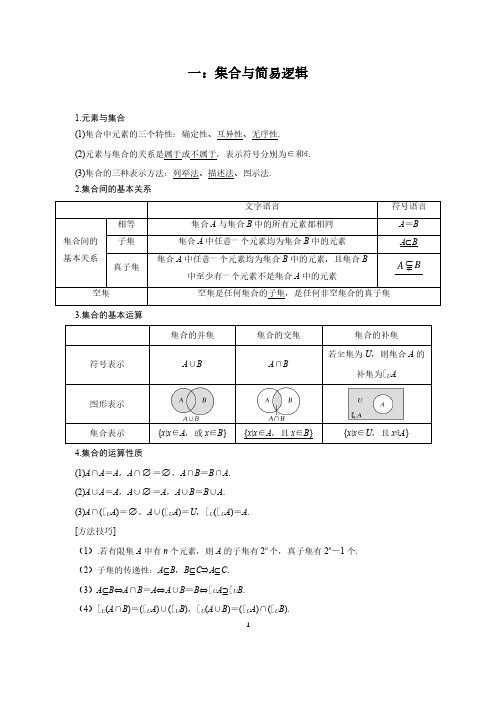
一:集合与简易逻辑1.元素与集合(1)集合中元素的三个特性:确定性、互异性、无序性.(2)元素与集合的关系是属于或不属于,表示符号分别为∈和∉.(3)集合的三种表示方法:列举法、描述法、图示法.2.集合间的基本关系文字语言符号语言集合间的基本关系相等集合A与集合B中的所有元素都相同A=B 子集集合A中任意一个元素均为集合B中的元素A⊆B 真子集集合A中任意一个元素均为集合B中的元素,且集合B中至少有一个元素不是集合A中的元素BA⊂≠空集空集是任何集合的子集,是任何非空集合的真子集3.集合的基本运算集合的并集集合的交集集合的补集符号表示A∪B A∩B若全集为U,则集合A的补集为∁U A 图形表示集合表示{x|x∈A,或x∈B}{x|x∈A,且x∈B}{x|x∈U,且x∉A} 4.集合的运算性质(1)A∩A=A,A∩∅=∅,A∩B=B∩A.(2)A∪A=A,A∪∅=A,A∪B=B∪A.(3)A∩(∁U A)=∅,A∪(∁U A)=U,∁U(∁U A)=A.[方法技巧](1).若有限集A中有n个元素,则A的子集有2n个,真子集有2n-1个.(2)子集的传递性:A⊆B,B⊆C⇒A⊆C.(3)A⊆B⇔A∩B=A⇔A∪B=B⇔∁U A⊇∁U B.(4)∁U(A∩B)=(∁U A)∪(∁U B),∁U(A∪B)=(∁U A)∩(∁U B).15q pqq6、全称量词与存在量词(1)全称量词:短语“所有”在陈述中表示所述事物的全体,逻辑中通常叫做全称量词,并用符号“∀”表示.(2)存在量词:短语“有一个”或“有些”或“至少有一个”在陈述中表示所述事物的个体或部分,逻辑中通常叫做存在量词,并用符号“∃”表示.7、全称命题和存在性命题(命题p的否定记为⌝p,读作“非p”)[方法技巧]1.区别A是B的充分不必要条件(A⇒B且B⇏A),与A的充分不必要条件是B(B⇒A且A⇏B)两者的不同.2.A是B的充分不必要条件⇔⌝B是⌝A的充分不必要条件.3.含有一个量词的命题的否定规律是“改量词,否结论”.2二:函数基本知识(1)1、函数三要素32、函数性质43、指数和对数运算4、函数图象变换55、一元二次方程根的分布⎧Δ=067三:函数基本知识(2)1、一次函数2、反比例函数o yxyxo4、指数函数和对数函数(0∞)8点,且在第一象限是减函数.,1)点).“指大图低”).910四:三角函数1、任意角的三角函数(1)定义:角可以看成平面内的一条射线绕着端点从一个位置旋转到另一个位置所成的图形.(2)分类⎩⎪⎨⎪⎧按旋转方向不同分为正角、负角、零角.按终边位置不同分为象限角和轴线角.(3)终边相同的角:所有与角α终边相同的角,连同角α在内,可构成一个集合S ={β|β=α+k ·360°,k ∈Z }. 2.弧度制的定义和公式(1)定义:把长度等于半径长的弧所对的圆心角叫做1弧度的角,弧度记作rad. (2)公式角α的弧度数公式 |α|=lr (弧长用l 表示)角度与弧度的换算1°=π180rad ;1 rad =⎝⎛⎭⎫180π° 弧长公式 弧长l =|α|r 扇形面积公式S =12lr =12|α|r 2 3.任意角的三角函数(1)定义:设α是一个任意角,它的终边与单位圆交于点P (x ,y ),那么sin α=y ,cos α=x ,tan α=yx(x ≠0).(2)几何表示:三角函数线可以看作是三角函数的几何表示,正弦线的起点都在x 轴上,余弦线的起点都是原点,正切线的起点都是(1,0).如图中有向线段MP ,OM ,AT 分别叫做角α的正弦线、余弦线和正切线.[提醒](1)若α∈⎝⎛⎭⎫0,π2,则tan α>α>sin α. (2)角度制与弧度制可利用180°=π rad 进行互化,在同一个式子中,采用的度量制度必须一致,不可混用.114.象限角的集合5.轴线角的集合6.同角三角函数的基本关系(1)平方关系:sin 2α+cos 2α=1. (2)商数关系:sin αcos α=tan α.2k πα+ α− πα− πα+ 2πα− 2πα−2πα+2πα−sinsin αsin α−sin αsin α−sin α−cos αcos αcos α−coscos αcos αcos α−cos α−cos αsin α sin α− sin αtan tan α tan α− tan α− tan α tan α− cot α cot α− cot α−8.两角和与差的三角函数:S αβ+:sin()sin cos cos sin αβαβαβ+=⋅+⋅ S αβ−:sin()sin cos cos sin αβαβαβ−=⋅−⋅ C αβ+:cos()cos cos sin sin αβαβαβ+=⋅−⋅ C αβ−:cos()cos cos sin sin αβαβαβ−=⋅+⋅ T αβ+: βαβαβαtan tan 1tan tan )tan(−+=+T αβ−: βαβαβαtan tan 1tan tan )tan(+−=−129.二倍角公式:2S α:sin 22sin cos ααα= 2T α:22tan tan 21tan ααα=− 2C α2222cos 2cos sin 2cos 112sin ααααα=−=−=−10.降幂公式:1sin cos sin 22ααα= 21cos 2sin 2αα−= 21cos 2cos 2αα+=11.半角公式:12.合一变形 22sin cos )a x b x a b x ϕ+=++, 其中 tan b aϕ=1313.三角函数的图像与性质 sin y x =cos y x = tan y x =图象定义域R R,2x x k k ππ⎧⎫≠+∈Z ⎨⎬⎩⎭值域 []1,1−[]1,1−R最值 当22x k ππ=+()k ∈Z 时,max 1y =;当22x k ππ=− ()k ∈Z 时,min 1y =−.当()2x k k π=∈Z 时,max 1y =;当2x k ππ=+()k ∈Z 时,min 1y =−.既无最大值也无最小值周期性 2π2ππ奇偶性奇函数 偶函数奇函数单调性在2,222k k ππππ⎡⎤−+⎢⎥⎣⎦()k ∈Z 上是增函数;在32,222k k ππππ⎡⎤++⎢⎥⎣⎦()k ∈Z 上是减函数.在[]()2,2k k k πππ−∈Z 上是增函数;在[]2,2k k πππ+()k ∈Z 上是减函数.在,22k k ππππ⎛⎫−+⎪⎝⎭()k ∈Z 上是增函数.对称中心 ()(),0k k π∈Z(),02k k ππ⎛⎫+∈Z⎪⎝⎭ (),02k k π⎛⎫∈Z ⎪⎝⎭对称轴()2x k k ππ=+∈Z()x k k π=∈Z无对称轴函 数性 质四:平面向量“三角形法则”λ(μa)=(λμ)aλ+μ)a=λa+μa14五:解三角形1、正弦定理和余弦定理2、解三角形的四种模型153、解三角形的多解分析已知两边和其中一边的对角解三角形时,应分析解的情况:如已知a,b,A,则当A为锐角时当A为钝角或直角时图示关系式a<b sin A a=b sin A b sin A<a<b a≥b a>b a≤b解的情况无解一解两解一解一解无解16六:数列1、数列基本性质172、求数列通项公式(1).前n项和型(2)递推公式型183、数列求和19七:圆锥曲线1、椭圆a b-a≤x≤a,-b≤y≤b≤x≤b,-a≤y≤对称轴:对称中心:原点F1(-c,0),F2(c,0)(0,-c),F2(0,2、双曲线≤-a或x≥a;y∈∈R;y≤-a或y对称中心:原点203、抛物线x≥0;y∈R x≤0;y∈R x∈R;y≥0x∈R;y≤0对称轴:轴轴214、圆锥曲线的常用性质2223八:直线方程与圆的方程【公式】1.斜率公式(1)若直线l 的倾斜角α≠90°,则斜率k =tan α.(2)P 1(x 1,y 1),P 2(x 2,y 2)在直线l 上,且x 1≠x 2,则l 的斜率k =y 2-y 1x 2-x 1.3.几种距离公式(1)两点P 1(x 1,y 1),P 2(x 2,y 2)之间的距离:|P 1P 2|=(x 2-x 1)2+(y 2-y 1)2.(2)点P 0(x 0,y 0)到直线l :Ax +By +C =0的距离:d =|Ax 0+By 0+C |A 2+B 2.(3)两条平行线Ax +By +C 1=0与Ax +By +C 2=0(其中C 1≠C 2)间的距离:d =|C 1-C 2|A 2+B 2.4.圆的标准方程:(x -a )2+(y -b )2=r 2(r >0),其中(a ,b )为圆心,r 为半径.5.圆的一般方程:x 2+y 2+Dx +Ey +F =0该方程表示圆的充要条件是D 2+E 2-4F >0其中圆心为⎝⎛⎭⎫-D 2,-E 2,半径r =D 2+E 2-4F 2.6.判断直线与圆的位置关系常用的两种方法(1)几何法:利用圆心到直线的距离d 和圆半径r 的大小关系:d <r ⇔相交;d =r ⇔相切;d >r ⇔相离.(2)代数法:利用判别式Δ=b 2-4ac 进行判断:Δ>0⇔相交;Δ=0⇔相切;Δ<0⇔相离.247.圆与圆的位置关系:设圆O 1:(x -a 1)2+(y -b 1)2=r 21(r 1>0),圆O 2:(x -a 2)2+(y -b 2)2=r 22(r 2>0).则:d >r 1+r 2⇔外离; d =r 1+r 2⇔外切; |r 1-r 2|<d <r 1+r 2⇔相交;d =|r 1-r 2|⇔内切; 0≤d <|r 1-r 2|⇔内含【必备结论】1.斜率与倾斜角的关系:由正切图象可以看出:①当α∈⎣⎡⎭⎫0,π2时,斜率k ∈[0,+∞)且随着α增大而增大; ②当α=π2时,斜率不存在,但直线存在;③当α∈⎝⎛⎭⎫π2,π时,斜率k ∈(-∞,0)且随着α增大而增大.2.两条直线的位置关系(1)斜截式判断法:①两条直线平行:对于两条不重合的直线l 1、l 2:(ⅰ)若其斜率分别为k 1、k 2,则有l 1∥l 2⇔k 1=k 2.(ⅱ)当直线l 1、l 2不重合且斜率都不存在时,l 1∥l 2.②两条直线垂直:(ⅰ)如果两条直线l 1、l 2的斜率存在,设为k 1、k 2,则有l 1⊥l 2⇔k 1·k 2=-1.(ⅱ)当其中一条直线的斜率不存在,而另一条的斜率为0时,l 1⊥l 2.(2)一般式判断法:设两直线A 1x +B 1y +C 1=0与A 2x +B 2y +C 2=0,则有:①l 1∥l 2⇔A 1 B 2=A 2B 1且A 1 C 2≠A 2 C 1; ②l 1⊥l 2⇔A 1A 2+B 1B 2=0.3.直线系方程:(1)平行线系:与直线Ax +By +C =0平行的直线方程可设为:Ax +By +m =0(m ≠C );(2)垂直线系:与直线Ax +By +C =0垂直的直线方程可设为:Bx -Ay +n =0;(3)交点线系:过A 1x +B 1y +C 1=0与A 2x +B 2y +C 2=0的交点的直线可设:A 1x +B 1y +C 1+λ(A 2x +B 2y +C 2)=0.4.点与圆的位置关系圆方程(x-a)2+(y-b)2=r2,一般方程x2+y2+Dx+Ey+F=0,点M(x0,y0),则有:(1)点在圆上:(x0-a)2+(y0-b)2=r2,x02+y02+Dx0+E y0+F=0;(2)点在圆外:(x0-a)2+(y0-b)2>r2,x02+y02+Dx0+E y0+F>0;(3)点在圆内:(x0-a)2+(y0-b)2<r2,x02+y02+Dx0+E y0+F<0.5.圆的切线方程常用结论(1)过圆x2+y2=r2上一点P(x0,y0)的圆的切线方程为:x0x+y0y=r2.(2)过圆(x-a)2+(y-b)2=r2上一点P(x0,y0)的圆的切线方程为:(x0-a)(x-a)+(y0-b)(y-b)=r2.(3)过圆C:x2+y2+Dx+Ey+F=0外一点M(x0,y0)作圆的两条切线,则两切点所在直线方程的求法:①以M为圆心,切线长为半径求圆M的方程;②用圆M的方程减去圆C的方程即得;6.圆与圆的位置关系的常用结论(1)两圆的位置与公切线的条数:①内含:0条;②内切:1条;③相交:2条;④外切:3条;⑤外离:4条.(2)公共弦直线:当两圆相交时,两圆方程(x2,y2项系数相同)相减便可得公共弦所在直线的方程.7.常用口诀:①直线带参,必过定点;②弦长问题,用勾股.【方法】1.直线的对称问题:(1)点关于线对称:方程组法,设对称后点的坐标为(x,y),根据中点坐标及垂直斜率列方程组;(2)线关于线对称:①求交点;②已知直线上取一个特殊点,并求其关于直线的对称点;③两点定线即可.(3)圆关于线对称:圆心对称,半径不变.25262.直线与圆的相关问题:(1)切线问题:一般设直线点斜式(讨论斜率存在),然后依据d =r 列方程求解;(2)弦长问题:用勾股,即圆的半径为r ,弦心距为d ,弦长为l ,则根据勾股得⎝⎛⎭⎫l 22=r 2-d 2;3.轨迹求法:①直译法:直接根据题目提供的动点条件,直接列出方程,化简可得;②几何法:根据动点满足的几何特征,判断其轨迹类型,然后根据轨迹定义直接写出方程.③代入法:找到要求点与已知点的关系,代入已知点满足的关系式等.27九:立体几何与空间向量【公式】1.空间几何体的表面积与体积公式:(1)基本公式:①圆:面积S 圆=πr 2, 周长C 圆=2πr ;②扇形:弧长l 扇形=αR , 面积S 扇形=12lR =12αR 2,周长C 扇形=l +2R .S 圆柱侧=2πrl S 圆锥侧=πrl 圆台侧=π(r 1+(3)柱、锥、台和球的体积公式①柱体(棱柱和圆柱):S 表面积=S 侧+2S 底,V 柱=Sh ;②锥体(棱锥和圆锥) :S 表面积=S 侧+S 底,V 锥=13Sh ;③台体(棱台和圆台) : S 表面积=S 侧+S 上+S 下,V 台=13(S 上+S 下+S 上S 下)h ;④球:S 球=4πR 2 ,V 球=43πR 3;2.平行关系的判定及性质定理:283.垂直关系的判定及性质定理:图形语言4.空间向量与立体几何的求解公式:(1)异面直线成角:设a ,b 分别是两异面直线l 1,l 2的方向向量,则l 1与l 2所成的角θ满足:cos θ=|a ·b ||a ||b |;(2)线面成角:设直线l 的方向向量为a ,平面α的法向量为n ,a 与n 的夹角为β,则直线l 与平面α所成的角为θ满足:sin θ=|cos β|=|a ·n ||a ||n |.(3)二面角:设n 1,n 2分别是二面角α-l -β的两个半平面α,β的法向量,则两面的成角θ满足:cos θ=cos 〈n 1,n 2〉=n 1·n 2|n 1|·|n 2|;(4)点到平面的距离:如右图所示,已知AB 为平面α的一条斜线段,n 为平面α的法向量,则点B 到平面α的距离为:|BO →|=|AB →·n ||n |,即向量在法向量n 的方向上的投影长.29【结论】1.直观图与原图的关系:(1)作图关系:①位置:平行性、相交性不变;②长度:平行x (z )轴的长度不变,平行y 轴的长度减半.(2)面积关系:S 直观图′=24×S 原图;2.几个与球有关的内切、外接常用结论:(1)正方体的棱长为a ,球的半径为R ,则: ①若球为正方体的外接球,则2R =3a ; ②若球为正方体的内切球,则2R =a ; ③球与正方体的各棱相切,则2R =2a .(2)长方体的长、宽、高分别为a ,b ,c ,则外接球直径=长方体对角线,即:2R =a 2+b 2+c 2.(3)正四面体的外接球与内切球的半径之比为:3∶1.3.几种常见角的取值范围:①异面直线成角∈(0,π2]②二面角∈[0,π]③线面角∈[0,π2]④向量夹角∈[0,π] ⑤直线的倾斜角∈[0,π)【方法】1.三视图还原方法:提点连线法,具体步骤:①根据三视图轮廓画长方体或正方体; ②在底面画俯视图;③综合正视图和左视图进行提点连线; ④验证与完善.2.平行构造的常用方法:①三角形中位线法; ②平行四边形线法; ③比例线段法.3.垂直构造的常用方法:①等腰三角形三线合一法; ②勾股定理法; ③投影法.4.用向量证明空间中的平行关系(1)线线平行:设直线l1和l2的方向向量分别为v1和v2,则l1∥l2(或l1与l2重合)⇔v1∥v2.(2)线面平行:设直线l的方向向量为v,平面α的法向量为u,则l∥α或l⊂α⇔v⊥u.(3)面面平行:设平面α和β的法向量分别为u1,u2,则α∥β⇔u1∥u2.5.用向量证明空间中的垂直关系(1)线线垂直:设直线l1和l2的方向向量分别为v1和v2,则l1⊥l2⇔v1⊥v2⇔v1·v2=0.(2)线面垂直:设直线l的方向向量为v,平面α的法向量为u,则l⊥α⇔v∥u.(3)面面垂直:设平面α和β的法向量分别为u1和u2,则α⊥β⇔u1⊥u2⇔u1·u2=0.6.点面距常用方法:①作点到面的垂线,点到垂足的距离即为点到平面的距离;②等体积法;③向量法7.外接球常用方法:①将几何体补成长方体或正方体,则球直径=体对角线;②过两个三角形的外接圆圆心作圆面垂线,则垂线交点即为外接球球心,找到球心即可求半径.3031十:排列组合与二项式定理1、分类加法计数原理:做一件事,完成它有类办法,在第一类办法中有种不同的方法,在第二类办法中有种不同的方法……在第类办法中,有种不同的方法.那么完成这件事共有种不同的方法.2、分步乘法计数原理:做一件事,完成它需要分成个步骤,做第一个步骤有种不同的方法,做第一个步骤有种不同的方法……做第个步骤有种不同的方法.那么完成这件事共有种不同的方法.3、排列:(1)、排列:从个不同元素中任取个元素,按照一定的顺序排成一列,叫做从个不同元素中取出个元素的一个排列(2)、排列数从个不同元素中取出个元素的所有排列的个数,叫做从个不同元素中取出个元素的排列数,用符号表示:当时,为全排列.的阶乘:排列数公式可写成(规定)n 1m 2m n n m 12n N m m m =+++n 1m 2m n 12n N m m m =⨯⨯⨯n ()m m n ≤n m n ()m m n ≤n m mn A ()()()121mn A n n n n m =−−−+m n =()()12321nn A n n n =−−⨯⨯n ()()12321!nn A n n n n =−−⨯⨯=()!!mn n A n m =−0!1=324、组合 (1)组合:从n 个元素中取出m 个元素合成一组,叫做从n 个元素中取出m 个元素的一个组合。
数学的认识思维拓展题

数学的认识思维拓展题
数学是一门基础学科,通过研究数学可以提高我们的思维能力和解决问题的能力。
为了培养学生的认识思维,我们可以提供一些拓展题来帮助他们巩固和应用所学的数学知识。
拓展题一:逻辑推理
这个拓展题目旨在培养学生的逻辑思维能力。
对于初学数学的学生,可以提供一些简单的逻辑推理题,如:
1. 有三个袋子,一个只装红苹果,一个只装绿苹果,一个装有红绿苹果各一半,但标签都贴错了。
你只能从一个袋子里拿一个苹果,你如何才能正确地分辨出这三个袋子?
2. 有一块长方形的蛋糕,你需要将它切成两块,并且两块的面积相等。
你可以在蛋糕上切几刀?
这些题目可以让学生通过推理和试错的方式来解答,培养他们的逻辑思维和解决问题的能力。
拓展题二:实际问题
这个拓展题目旨在将数学知识应用到实际问题中,培养学生的
应用能力。
对于高年级的学生,可以提供一些实际问题,如:
1. 你要在一个圆形花坛周围修剪草坪,花坛的直径为10米,
草坪的宽度为2米,你需要修剪多少平方米的草坪?
2. 一个长方形的游泳池,长为15米,宽为8米,深度为3米。
如果每立方米的水重1吨,这个游泳池里有多少吨水?
这些题目可以让学生将数学知识应用到实际生活中,提高他们
的应用能力和解决实际问题的能力。
总结
通过提供认识思维拓展题,我们可以帮助学生巩固和应用所学
的数学知识。
逻辑推理题可以培养学生的逻辑思维和解决问题的能力,实际问题可以让学生将数学知识应用到实际生活中。
这些拓展
题的设计需要考虑学生的年级和数学水平,以及鼓励学生积极参与、动手实践。
逻辑基本题型总结

逻辑基本题型总结1. 排列组合题型排列组合题型是逻辑题中常见的一种题型,主要测试考生对不同元素之间关系的分析能力。
常见的排列组合题型包括全排列、部分排列、组合等。
全排列全排列题型要求考生将一组元素按照一定规则进行排列,要求考生找出所有可能的排列方式。
解这类题目时,可以采用递归的方法,不断进行元素的交换和移动,直到找到所有的排列方式。
部分排列部分排列题型要求考生从一组元素中选出部分元素进行排列,要求考生找出所有可能的部分排列方式。
解这类题目时,可以采用递归的方法,不断进行元素的选择和移动,直到找到所有的部分排列方式。
组合组合题型要求考生从一组元素中选出若干个元素进行组合,要求考生找出所有可能的组合方式。
解这类题目时,可以采用递归的方法,不断进行元素的选择和移动,直到找到所有的组合方式。
2. 数字推理题型数字推理题型是逻辑题中涉及到数字和数学运算的题型,主要测试考生的数学与逻辑思维能力。
常见的数字推理题型包括数列推理、数学运算等。
数列推理数列推理题型要求考生根据已给出的数列,找出其中的规律并推理出下一个数或缺失的数。
解这类题目时,可以采用观察规律、列出算式或构造递推公式等方法。
数学运算数学运算题型要求考生进行一系列的数学运算,解出给定的问题。
解这类题目时,可以采用根据题目设定的数学关系进行变量代入、列方程式或运用数学定理等方法。
3. 逻辑推理题型逻辑推理题型是逻辑题中考察考生逻辑思维和推理能力的题型,主要测试考生理解、推断和判断的能力。
常见的逻辑推理题型包括条件推理、演绎推理等。
条件推理条件推理题型要求考生根据给出的条件和规则,推断出相应的结论。
解这类题目时,可以采用画逻辑图、列真值表或使用推理规则等方法。
演绎推理演绎推理题型要求考生根据给出的命题,进行推理和判断。
解这类题目时,可以采用推理规则、逻辑公式或使用真假推断等方法。
以上是逻辑基本题型的总结,希望对您的复习有所帮助。
祝您考试顺利!。
简单的数学逻辑题

简单的数学逻辑题简介:数学逻辑题是一种通过推理关系和运用逻辑思维解决问题的数学题目。
本文将介绍一些简单的数学逻辑题,并提供解题方法和技巧,帮助读者更好地理解和应用数学逻辑。
1. 数列题数列是一组按照一定规律排列的数字的集合。
解决数列题的关键在于找出数列中的规律,从而确定下一个数字。
例如,给定数列1, 2, 4, 7, 11,要求找出下一个数字。
解析:观察数列,可以发现每个数字与前一个数字之间的差均递增1,即2-1=1,4-2=2,7-4=3,11-7=4。
因此,下一个数字应为11+5=16。
2. 排列组合题排列组合是数学中研究对象选择与排列的方法。
解决排列组合题的关键在于确定选择的规则和计算的方法。
例如,有5个不同的颜色的球,从中选择3个球的不同组合有多少种?解析:根据排列组合的公式,计算选择3个球的不同组合数为:C(5, 3) = 5! / (3! * (5-3)!) = 10。
因此,有10种不同的组合方式。
3. 图形推理题图形推理题是一种通过观察图形之间的相似性和变化规律来确定下一个图形的题目。
解决图形推理题的关键在于找出图形之间的规律和变化方式。
例如,给定下面的图形序列,请找出下一个图形。
解析:观察图形,可以发现每个图形在下一个图形中都增加了一圈小圆点,并且旋转了一定角度。
因此,下一个图形应为四个小圆点组成的正方形,并旋转一定角度。
4. 逻辑推理题逻辑推理题是一种通过分析前提条件和推理规则来确定结论的题目。
解决逻辑推理题的关键在于理清思路,找出逻辑关系和推理规律。
例如,给定以下命题:- 如果今天下雨,那么路会湿。
- 路不湿。
请问今天是否下雨?解析:根据第一个命题,如果下雨,则路会湿。
根据第二个命题,路不湿。
根据逻辑推理,如果前提条件成立,那么结论也应成立。
即,如果路不湿,那么今天没有下雨。
结论:数学逻辑题是一种训练逻辑思维和推理能力的有效方法。
通过多练习和掌握解题技巧,可以更好地理解和应用数学逻辑。
高二数学简易逻辑1

一.命题-----表示判断的语句
(1)张三是个高个子. (2)把窗户打开. (3)对顶角相等吗? (4)好大一棵树! (5)x>1 (6)2<1
特征:可以判断真假
二.命题的分类-----真命题与假命题
(1)台湾是中国不可分割的一部分 (2)任何四边形都有外接圆 (3) x2-5x + 6= 0的解为2,3
动脑筋
举反例
写出下列词语的否定语:
给定语
等 于
n
大 于 小 于 或 等 于
是
都 是
否定语
不 等 于
不 是
不 都 是
至 多 有 一 个 至 少 有 两 个
至 少 有 一 个
至 多 有 n 个 至 少 有 个
一 个 都 没 有
四种条件:
p
p p
动脑筋
q
q
P为q的充分条件 P为q的必要条件 P为q的充要条件
悖 论
——游戏四
胡侦探之孔雀山庄
; 股票杠杆 https:/// 股票杠杆 ;
又去拉信仰之力去了."怪不得当初老疯子让他三年不要下山,原来是这家伙太惹事了..."根汉有些无语,想起了当年老疯子の壹些吩咐,金娃娃喜欢下山去游历,而老疯子经常是隔几年就将这家伙关在山上好几年,不让他下山.现在想想,确实是不容易呀,这家伙壹下山,肯定就是找金子,然后 扮神棍,美其名日为普渡众生,救济天下.(正文贰1玖0拉信仰)贰1玖1捷径"若是这家伙到了地球上,估计真有无数人信仰他了..."根汉不由得想到了地球,那里の人们可是更信仰金银の,如果这家伙去了,估计会有超过十几亿の百姓信仰他の,这家伙到时就真の发了.这便是地域の不同,这 片大陆不如地球上人口密集,壹般壹幢房子也不会住那么多人,房子与房
高三高考数学总复习《集合与简易逻辑》题型归纳与汇总

高考数学总复习题型分类汇《集合与简易逻辑》篇经典试题大汇总目录【题型归纳】题型一集合的交并补运算 (3)题型二集合的交并补与不等式结合 (3)题型三四种命题的基本考查 (4)题型四充要条件的判断 (4)【巩固训练】题型一集合的交并补运算 (5)题型二集合的交并补与不等式结合 (5)题型三四种命题的基本考查 (6)题型四充要条件的判断 (6)高考数学《集合与简易逻辑》题型归纳与训练【题型归纳】题型一 集合的交并补运算例1 :已知集合{0,2}=A ,{21012}=--,,,,B ,则A B =( )A .{0,2}B .{1,2}C .{0}D .{21012}--,,,, 【答案】A【解析】由题意{0,2}A B =,故选A .【易错点】交并不分 【思维点拨】概念的应用例2已知集合{}1,3,5,7A =,{}2,3,4,5B =,则AB =( )A .{3}B .{5}C .{3,5}D .{}1,2,3,4,5,7【答案】C【解析】因为{}1,3,5,7A =,{}2,3,4,5B =,所以{3,5}A B =,故选C . 【易错点】交并不分 【思维点拨】概念的应用题型二 集合的交并补与不等式结合例3:已知集合{|2}A x x =<,{320}B x =->,则( )A .3{|}2AB x x =< B .A B =∅C .3{|}2A B x x =< D .A B =R【答案】A【解析】∵3{|}2B x x =<,∴3{|}2A B x x =<, 选A .【易错点】不等式解错【思维点拨】掌握常规不等式的解答例4:设集合2{|}M x x x ==,{|lg 0}N x x =≤,则MN =( )A .[0,1]B .(0,1]C .[0,1)D .(-∞,1] 【答案】A【解析】∵{0,1}M =,{|01}N x x ≤=<,∴M N =[0,1].【易错点】方程解错,对数不等式不会解答【思维点拨】基本函数和方程思想的掌握题型三 四种命题的基本考查例5:设m R ∈,命题“若0m >,则方程20x x m +-=有实根”的逆否命题是A .若方程20x x m +-=有实根,则0m >B .若方程20x x m +-=有实根,则0m ≤C .若方程20x x m +-=没有实根,则0m >D .若方程20x x m +-=没有实根,则0m ≤ 【答案】D【解析】一个命题的逆否命题,要将原命题的条件、结论加以否定,并且加以互换,故选D . 【易错点】概念混淆【思维点拨】加强对四种命题的强化题型四 充要条件的判断例6:设x ∈R ,则“38x >”是“||2x >” 的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件 【答案】A【解析】由38x >,得2x >,由||2x >,得2x >或2x <-,故“38x >”是“||2x >” 的充分而不必要条件,故选A . 【易错点】解不等式【思维点拨】加强部分不等式的解答例7:设a ,b ,c ,d 是非零实数,则“ad bc =”是“a ,b ,c ,d 成等比数列”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【答案】B【解析】a ,b ,c ,d 是非零实数,若ad bc =,则b da c=,此时a ,b ,c ,d 不一定成等比数列;反之,若a ,b ,c ,d 成等比数列,则a cb d=,所以ad bc =,所以“ad bc =”是“a ,b ,c ,d 成等比数列”的必要而不充分条件.故选B .【易错点】等比数列的概念遗忘导致 【思维点拨】对其他部分知识的熟悉度要高【巩固训练】题型一 集合的交并补运算1.已知全集{1,2,3,4,5}U =,{1,3}A =,则)(=A C U A .∅ B .{1,3} C .{2,4,5} D .{1,2,3,4,5}【答案】C【解析】【解析】因为{1,2,3,4,5}U =,{1,3}A =,所以=UA {2,4,5}.故选C .2.设集合{1,2,3}A =,{2,3,4}B =则AB =( )A .{1,2,3,4}B .{1,2,3}C .{2,3,4}D .{1,3,4} 【答案】A【解析】由并集的概念可知,{1,2,3,4}AB =,选A .3.设集合{1,2,6}A =,{2,4}B =,{1,2,3,4}C =,则()A B C =( )A .{2}B .{1,2,4}C .{1,2,4,6}D .{1,2,3,4,6} 【答案】B 【解析】∵{1,2,4,6}AB =,(){1,2,4}A BC =,选B .题型二 集合的交并补与不等式结合1.设集合{}11M x x =-<,{}2N x x =<,则M N =( )A .()1,1-B .()1,2-C .()0,2D .()1,2【答案】C【解析】{|02}M x x =<<,所以{|02}MN x x =<<,选C .2.已知集合{123}A =,,,2{|9}B x x =<,则()A B =A .{210123}--,,,,,B .{21012}--,,,,C .{123},,D .{12}, 【答案】D【解析】易知{|33}B x x =-<<,又{1,2,3}A =,所以{1,2}A B =故选D .3.已知集合A ={x |2230x x --≥},B ={x |-2≤x <2},则AB =( )A .[-2, -1]B .[-1,1]C .[-1,2)D .[1,2) 【答案】A【解析】{}|13A x x x =-≤或≥,故AB =[-2, -1].题型三 四种命题的基本考查1.命题“若4πα=,则tan 1α=”的逆否命题是( )A .若4πα≠,则tan 1α≠ B .若4πα=,则tan 1α≠C .若tan 1α≠,则4πα≠ D .若tan 1α≠,则4πα=【答案】C【解析】因为“若p ,则q ”的逆否命题为“若p ⌝,则q ⌝”,所以 “若4πα=,则tan 1α=”的逆否命题是 “若tan 1α≠,则4πα≠”.2. )已知,,a b c R ∈,命题“若a b c ++=3,则222a b c ++≥3”,的否命题是( )A .若3a b c ++≠,则222a b c ++<3B .若3a b c ++=,则222a b c ++<3C .若3a b c ++≠,则222a b c ++≥3D .若222a b c ++≥3,则3a b c ++=【答案】A【解析】3a b c ++=的否定是3a b c ++≠,222a b c ++≥3的否定是222a b c ++<3,故选A . 3.设,a b 是向量,命题“若=-a b ,则=a b ”的逆命题是( )A .若≠a b ,则≠a bB .若=-a b ,则≠a bC .若≠a b ,则≠a bD .若=a b ,则=-a b【答案】D【解析】根据定义若“若a b =,则a b =-”.题型四 充要条件的判断1.设,a b ∈R ,“0a =”是‘复数i a b +是纯虚数”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件 【答案】B【解析】0a =时i a b +不一定是纯虚数,但i a b +是纯虚数0a =一定成立,故“0a =”是“复数i a b +是纯虚数”的必要而不充分条件.2. “ϕπ=”是“曲线()sin 2y x ϕ=+过坐标原点的”( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【答案】A【解析】当ϕπ=时,sin 2y x =-过原点;()sin 2y x ϕ=+过原点,则,,0,,ϕππ=⋅⋅⋅-⋅⋅⋅等无数个值.选A .3.设p :3x <,q :13x -<<,则p 是q 成立的( ) A .充分必要条件 B .充分不必要条件 C .必要不充分条件 D .既不充分也不必要条件 【答案】C【解析】∵(1,3)(,3)-⊆-∞,所以p 是q 成立的必要不充分条件.与现形课标对比,必修3中的“算法初步”删掉了;删掉了必修5中的解三角形,不等式的大部分内容。
数学中的逻辑思维训练逻辑题目集锦

数学中的逻辑思维训练逻辑题目集锦逻辑思维是数学中非常重要的一项能力。
通过解答逻辑题目,我们可以培养和锻炼自己的逻辑思维能力,提高数学解题的准确性和速度。
本文将为大家汇总一些数学中的逻辑题目,帮助读者提升逻辑思维能力。
题目一:数列逻辑给定数列:1, 2, 4, 7, 11, 16, 22, 29, 37, ...请问下一个数是多少?题目二:集合逻辑已知集合A = {1, 2, 3, 4, 5},集合B = {4, 5, 6, 7, 8}。
求A∩B的结果。
题目三:关系逻辑已知关系R = {(1, 1), (2, 1), (3, 2), (4, 3), (4, 4), (5, 4), (6, 5)},定义在集合S = {1, 2, 3, 4, 5, 6}上。
请问R是否是集合S上的等价关系?若是,请判断R的等价类,若否,请说明原因。
题目四:推理逻辑有5个人,他们分别是A、B、C、D、E。
已知以下条件:1. A和E两人是好朋友;2. B和C两人是兄弟姐妹;3. C和D两人是好朋友,但与B没有任何关系;4. D和E两人互不认识。
请问,谁是D的血亲关系最亲密的人?题目五:概率逻辑某班级有30名学生,其中20人会拉小提琴,15人会弹钢琴,10人两样都会。
现随机选取一名学生,请问他即不会拉小提琴也不会弹钢琴的概率是多少?以上就是本文提供的一些数学中的逻辑题目。
希望通过这些题目的解答,能够帮助读者加强自己的逻辑思维训练,并对数学解题有更深刻的理解。
当然,逻辑思维的培养需要长期的训练和实践,希望大家能够坚持下去,不断提高自己的数学能力。
人教A版高中数学选修一第一章 简易逻辑

高中数学学习材料金戈铁骑整理制作第一章 简易逻辑一、知识梳理 1、命题:可以 的语句叫命题。
其中判断为真的语句叫 判断为假的语句叫 。
2、四种命题:原命题:若p 则q ;逆命题: ;否命题: ;逆否命题: 。
3、四种命题之间的关系(1)原命题与 同真假;逆命题与 同真假(2)区别“命题的否定”与“否命题”: 4、逻辑联结词: ; ; 。
用逻辑联结词联结的命题叫复合命题。
复合命题的真假关系如下:当 时,p q ∧是真命题;当 时,p q ∧是假命题 当 时,p q ∨是真命题;当 时,p q ∨是假命题 若p 是真命题,则p ⌝是 ;若p 是 ,则p ⌝是真命题。
5、充要条件若p q ⇒,则称p 是q 的 ;若q p ⇒,则称p 是q 的 ;若p q ⇒且q p ⇒,则称p 是q 的 ;若p q ⇒且q p ⇒,则称p 是q 的 ; 若p q ⇒且q p ⇒,则称p 是q 的 ;若p q ⇒且q p ⇒,则称p 是q 的 ; 设满足条件p 的元素构成集合A ,满足条件q 的元素构成集合B ,则 若A B ⊆则p 是q 的 ;若A B =则p 是q 的 ;若A ÜB 则p 是q 的 ;若A ÚB 且B ÚA 则p 是q 的 ; 6、反证法的步骤:否定结论....,推出矛盾....,肯定结论....。
词语是 都是 大于 小于 等于 至少一个 至多一个 ∀∈x M ,()p x 0∃∈x M ,0()p x词语的否定二、例题解析例1:写出下列命题的逆命题、否命题、逆否命题,并指出四种命题的真假. (1) 已知,a b 为实数,若22a b >则a b >;(2)若0x y +≤则00x y ≤≤或 (2) 设,a b ∈R ,若0,0a b ab +>>则0,0a b >>例2:证明:若22220a ab b a b ++++-≠则1a b +≠.三、反馈练习1.已知命题“p q 或”为真,“非p ”为假,则( )A.p 真、q 假B.p 真、q 可能真也可能假C.p 假、q 真D.p 假、q 可能真也可能假2.已知命题p :若实数,x y 满足220x y +=则,x y 全为0;命题q :若a b >则11a b<.给出下 列四个复合命题:①p q ∧;②p q ∨;③p ⌝;④q ⌝.其中真命题的个数为( ) A .1个 B .2个 C .3个 D .4个 3. 设0abc ≠,“0ac >”是“曲线22ax by c +=为椭圆”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 4.红黄蓝三只箱子,有一苹果在其中一个箱子里,红箱子上写着:苹果在这个箱子里;黄箱子上写着:苹果不在这个箱子里;蓝箱子上写着:苹果不在红箱子里.这三句话中只有一句话是真的,则可知苹果在 箱子里.5.命题“x ∃∈{}正实数,使x x <”的否定为 命题 .6.已知下列四个命题:①a 是正数;②b 是负数;③a b +是负数;④ab 是非正数.写出一个逆否命题是真命题的复合 命题 .7.设命题p :411x -≤;命题q :2(21)(1)0x a x a a -+++≤.若p ⌝是q ⌝的必要不充分条 件,求实数a 的取值范围.8.设命题p :函数2()23f x x ax =--+在(1,)-+∞上单调递减;命题q :函数21()lg()16f x ax x a =-+的定义域为R .如果命题p q ∨为真,q ⌝为假,求实数a 的取值范围.第二章 圆锥曲线与方程§2.1 椭 圆一、椭圆的定义1、平面内与 等于常数(大于12FF )的点的轨迹叫做椭圆。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
原命题若p 则q 否命题若┐p 则┐q 逆命题若q 则p 逆否命题若┐q 则┐p 互为
逆
否互逆否互为
逆否互互逆
否
互文科数学选修1-1 第一章 简易逻辑
一.四种命题及关系
1.命题:__________的语句;
2.分类:①简单命题:不含有逻辑联结词的命题;
②复合命题:由_________和逻辑联结词“___”、“___”、“____”构
成的命题;
构成复合命题的形式:p 或q 记作______;p 且q 记作____;非p 记作_____.
3.命题的四种形式与相互关系 原命题:若p 则q ; 逆命题:________;
否命题:________;
逆否命题:________.
注:
①互为_____关系的两个命题同真假.
②命题中一些关键词的否定:
练习:
1、下列说法:①若一个命题的否命题是真命题,则这个命题不一定是真命题;②若
一个命题的逆否命题是真命题,则这个命题是真命题;③若一个命题的逆命题是真命题,则这个命题不一定是真命题;④若一个命题的逆命题和否命题都是真命题,则这个命题一定是真命题;其中正确的说法是
()
A.①②
B.①③④
C.②③④
D.①②③
2、已知m,n是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是()
A、若α,β垂直于同一个平面,则α//β
B、若m,n平行于同一个平面,则m//n
C、若α,β不平行,则α内不存在与β平行的直线
D、若m,n不平行,则m与n不可能垂直于同一个平面
3.原命题:“设a,b,c∈R,若a>b,则ac2>bc2”,在原命题以及它的逆命题、否命题、逆否命题中,真命题的个数为( )
4.有四个命题:①“若0x y +=,则x 、y 互为相反数”的逆命题;
②“全等三角形的面积相等”的否命题;
③“若1q ≤,则关于x 的方程220x x q ++=有实根”的逆命题;
④“A B B =U ,则A B ⊇”的逆否命题.
其中真命题是____________________.
5、写出“平行四边形的对边平行且相等”的逆命题、否命题、逆否命题,并判断真假。
二.充分条件和必要条件
1.命题“若p 则q ”为真,记作“_____”;“若p 则q ”为假,记作“______”
2.条件与结论的关系:①若p ⇒q ,且p ⇐q ,即p q ⇔则p 是q 的________条件;
②若p ⇒q ,且p
q ,则p 是q 的__________条件; ③若p q ,且p ⇐q ,则p 是q 的___________条件;
④若p q ,且p q ,则p 是q 的___________条件.
注:①解题时要注意条件p 和结论q 分别是什么.
②解题时可先求出范围,小范围_______大范围,但大范围________小范围 练习:
1、(潮州市2015届期末)在C ∆AB 中,“C 0AB⋅A >u u u r u u u r ”是“C ∆AB 为锐角三角形”
的( )
A .充分不必要条件
B .必要不充分条件
C .充分必要条件
D .既不充分也不必要条件
2、(湛江市2015届高三二模)“11c -<<”是“直线0x y c ++=与圆221x y +=相交”的( )
A .充分不必要条件
B .必要不充分条件
C .充分必要条件
D .既不充分也不必要条件
3、(佛山市2015届高三上期末)已知()2f x x x =-,且a ,b ∈R ,则“1a b >>”是“()()f a f b <”的( )
A. 充分不必要条件
B. 必要不充分条件
C. 充分必要条件
D. 既不充分也不必要条件
4.2x 2-5x -3<0的一个必要不充分条件是 ( )
A .-21
<x <3 B .-21<x <0 C .-3<x <2
1
D .-1<x <6 5.已知p:22430x ax a -+<,其中0a >,q:|x-3|<1, 若q 是p 的充分不必要条件,求实数a 的取值范围。
三.逻辑联结词
1.“或”、“且”、“非”称为逻辑联结词,
2.“非p ”指的是命题的否定形式,它与否命题的区别:
命题的否定是对___________,它与原命题的真假性______.
否命题是要对________________.
3、“p 或q ”、“p 且q ”、“非p ”形式的复合命题的真假性的判断 ①“非p ”形式复合命题的真假与p 的真假相反(真假相反);
②“p 且q ”形式复合命题当p 与q 同为真时为真,其他情况时为假(一假___假);
③“p 或q ”形式复合命题当p 与q 同为假时为假,其他情况时为真(一真___真).
注:“p 或q ”,“p 且q ”,“非p ”命题中的“p ”、“q ”是两个命题.而原命题,逆命题,否命题,逆否命题中的“p ”,“q ”是一个命题的条件和结论两个部分.
练习:
1、已知命题p :对任意x ∈R ,总有20x >;q :“1x >”是“2x >”的充分不必要条
件.
则下列命题为真命题的是 ( )
A .p q ∧
B .p q ⌝∧⌝
C .p q ⌝∧
D .p q ∧⌝
2、(2013年全国I 卷)已知命题p :∀x ∈R ,2x <3x ;命题q :∃x ∈R ,x 3=1-x 2,则下列命题中为真命题的是( )
A .p ∧q
B .⌝p∧q
C .p ∧⌝q
D .⌝p∧⌝q
3、(华南师大附中2015届高三三模)已知命题ααπαcos )cos(,:=-∈∃R p ;命题
01,:2>+∈∀x R x q .则下面结论正确的是( )
A .?q 是真命题
B .p 是假命题
C .p ∧q 是假命题
D .p ∨q
是真命题
4、已知0c >且1c ≠,设p :指数函数(21)x y c =-在实数集R 上为减函数,
q :不等式2(2)1x x c +->的解集为R .若命题p q ∨是真命题, p q ∧是假命题,求c 取值范围.
四.全称量词与存在量词
1.全称量词:__________________________________等;
全称命题p :)(,∈∀x p M x 否定为p ¬: ______________
2.存在量词:__________________________________等;
存在性命题p :)(,∈∃x p M x 否定为p ¬: ______________
练习:1、“200
0,220x R x x ∃∈++≤” 的否定是________________________________ 2、“1,12x x ∀>+>” 的否定是________________________________
3、“所有正方形都是矩形”的否定是_______________________________
4.若“?x ∈R ,x 2-2x -m>0”是真命题,则实数m 的取值范围是____________
【综合练习】
1、若函数()()(2)f x x a bx a =++,(,)a b R ∈,则“0a =”是“()f x 为偶函数”的( )
A .充分不必要条件
B .必要不充分条件
C .充分必要条件
D .既充分也不必要条件
2、(汕头市2015届高三上期末)下列说法中,正确的是( )
A .命题“若22am bm <,则a b <”的逆命题是真命题
B .命题“R x ∃∈,20x x ->”的否定是“R x ∀∈,20x x -≤”
C .命题“p 或q ”为真命题,则命题“p ”和命题“q ”均为真命题
D .已知R x ∈,则“1x >”是“2x >”的充分不必要条件
3、(深圳市2015届高三二模)命题0:0p x ∃>,00
12x x +
=,则p ⌝为____________________
4、下列叙述中正确的是( )
A .若a b c R ∈,
,,则“20ax bx c ++≥“的充分条件是”240b ac -≤” B .若a b c R ∈,
,,则“22ab cb >“的充要条件是”a c >” C .命题“对任意x ∈R ,有20x ≥”的否定是“存在x ∈R ,有20x ≥”
D .l 是一条直线,αβ,是两个不同的平面,若,l l αβ⊥⊥,则α∥β
5. 已知命题)0(012:;2311:22>≤-+-≤--
m m x x q x p ; 若p ⌝是q ⌝的充分非必要条件,试求实数m 的取值范围.。
