CT实验平行束投影与反投影重建报告
CT实验

前 射 准 线 直 源 器
后 探 准 测 直 器 器
计 算 机
机械扫描运动系统
控制系统
图像 拷贝
显示
图 58-8
CT 实验系统组成方框
【实验内容】
注意事项】
• • • • • • 资格(具有上岗证的专人操作) 。 个人防护须知:更衣、换鞋、手套、眼镜。 保护实验环境 。 使用防护板 ;专用用具。 废弃物处理原则:尽量少、统一废弃。 使用检测器 。
CT实验
重庆大学物理实验中心
【实验背景】
Tomography),分为 医学CT(MCT)和工业CT(ICT),它是与一般辐射成像完全不 同的成像方法。一般辐射成像是将三维物体投影到二维平 面成像,各层面影像重叠,造成相互干扰,不仅图像模糊, 且损失了深度信息,不能满足分析评价要求。CT是把被测 体所检测断层孤立出来成像,避免了其余部分的干扰和影 响,图像质量高,能清晰、准确地展示所测部位内部的结 构关系、物质组成及缺陷状况,检测效果是其它传统的无 损检测方法所不及的。
3 图像重建
断层图像重建过程是以扫描检测所得的衰减系数线积分
数据集为基础,经必要的数据校正,按一定的图像重建算法,通 过计算机运算,得到衰减系数具体的二维分布,再将其以灰度形 式显示,从而生成断层图像。 (1)重建的初步概念 (2)反投影法 (3)卷积反投影法
【实验仪器】
教学ICT实验机
数据 采集 系统
CT即计算机断层成像技术(Computed
【实验目的】
理解ICT的基本原理;
掌握ICT的使用方法; 能够应用ICT实验装置进行工件 扫描和图像处理。
【实验原理】
1.CT的基本原理
μ (x,y) I0 L 图 58-1 射线穿过衰减系数为μ (x,y)的物质面 I
实验二CT重建实验报告

实验二CT重建实验报告一、实验目的1.了解CT重建的基本原理;2.熟悉医学图像处理软件ImageJ的使用方法;3.掌握CT重建算法的实现过程;4.验证重建算法的正确性。
二、实验原理实验中使用的CT重建算法有多种,本实验选择了最基本的滤波反投影算法。
该算法首先对投影数据进行滤波处理,然后通过逆Radon变换得到重建图像。
三、实验步骤1.准备工作a.从CT设备上获取一系列X射线投影图像;b.使用软件ImageJ导入投影数据;c.调整图像的对比度和亮度,尽可能提高图像质量。
2.投影数据的滤波a.选择合适的滤波函数,如Ram-Lak函数或Shepp-Logan函数等;b.对每一条投影数据进行滤波处理,得到滤波后的投影数据。
3.逆Radon变换a.根据滤波后的投影数据,使用逆Radon变换算法得到重建图像;b.重复上述步骤,得到所有投影的重建图像;c.将所有重建图像叠加起来,得到最终的重建图像。
4.结果分析a.使用ImageJ软件查看重建图像,观察图像的清晰度和准确性;b.与原始图像进行对比,验证重建算法的正确性。
四、实验结果经过上述步骤,得到了一幅重建图像。
通过ImageJ软件的查看,发现重建图像清晰度较高,能够明显显示出被检对象的内部结构。
与原始图像进行对比,可以发现重建图像与原始图像基本吻合,验证了重建算法的正确性。
五、实验总结本实验通过实际操作CT重建的流程,深入理解了CT重建的基本原理和算法。
通过使用ImageJ软件进行图像处理,掌握了图像的调整和分析方法。
通过与原始图像进行对比,验证了重建算法的正确性。
在实验过程中,需要注意调整图像的对比度和亮度,以提高图像质量。
此外,选择合适的滤波函数也是重建的关键步骤,不同的滤波函数对图像质量有很大影响,需要根据具体情况进行选择。
本实验在CT重建实验中使用了最基本的滤波反投影算法,实际应用中还有更复杂的算法和技术。
进一步深入研究和了解这些算法和技术,将有助于提高CT重建的准确性和图像质量。
医学成像原理实验报告
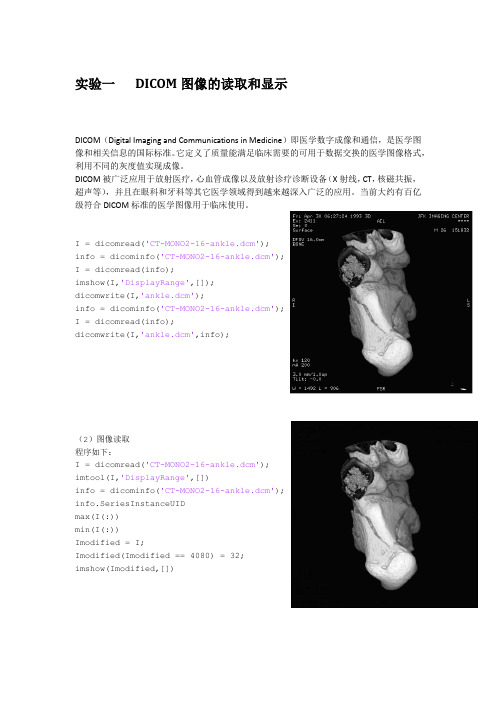
实验一DICOM图像的读取和显示DICOM(Digital Imaging and Communications in Medicine)即医学数字成像和通信,是医学图像和相关信息的国际标准。
它定义了质量能满足临床需要的可用于数据交换的医学图像格式,利用不同的灰度值实现成像。
DICOM被广泛应用于放射医疗,心血管成像以及放射诊疗诊断设备(X射线,CT,核磁共振,超声等),并且在眼科和牙科等其它医学领域得到越来越深入广泛的应用。
当前大约有百亿级符合DICOM标准的医学图像用于临床使用。
I = dicomread('CT-MONO2-16-ankle.dcm');info = dicominfo('CT-MONO2-16-ankle.dcm');I = dicomread(info);imshow(I,'DisplayRange',[]);dicomwrite(I,'ankle.dcm');info = dicominfo('CT-MONO2-16-ankle.dcm');I = dicomread(info);dicomwrite(I,'ankle.dcm',info);(2)图像读取程序如下:I = dicomread('CT-MONO2-16-ankle.dcm');imtool(I,'DisplayRange',[])info = dicominfo('CT-MONO2-16-ankle.dcm');info.SeriesInstanceUIDmax(I(:))min(I(:))Imodified = I;Imodified(Imodified == 4080) = 32;imshow(Imodified,[])2040608010012020406080100120204060801001202040608010012020406080100120204060801001202040608010012020406080100120实验二 MRI 图像显示和读取MRI 可获得人体横面、冠状面、矢状面及任何方向断面的图像,实现三维定位图像。
CT反投影滤波重建算法设计

地理与生物信息学院2012 / 2013 学年第二学期实验报告课程名称:医学图像处理和成像技术实验名称:CT反投影滤波重建算法设计班级学号: B10090405学生姓名: 陈洁指导教师: 戴修斌日期:2013 年 5 月一、实验题目:CT反投影滤波重建算法设计二、实验内容:1.显示图像;2.获得仿真投影数据;3.基于获得的仿真投影数据重建图像。
三、实验要求:1.Shepp-Logan头模型:画出Shepp-Logan头模型,简称S-L模型,头模型尺寸设定为128×128;2.仿真投影数据的获得:从头模型中获得投影数据,投影数据格式为180×185,即[0,179°]范围内角度每隔1°取样,每个角度下有185个探测器;3.卷积反投影重建算法的实现:基于获得的仿真投影数据重建图像,使用R-L卷积函数,重建尺寸为128×128。
四、实验过程:实验1. Shepp-Logan头模型①算法实现流程:I. S-L头模型由10个位置、大小、方向、密度各异的椭圆组成,象征一个脑断层图像。
Shepp-Logan头模型中的椭圆参数:II. 使用循环语句给像素赋值:for i=1:10for x….for y…..判断点(x, y)是否在第i个椭圆内;如是,则将第i个椭圆折射指数赋给点(x, y);endendendIII. 显示仿真头模型:使用imshow(f,[])函数显示出图像。
②实验代码:clear all;p=[0 0 0.92 0.69 pi/2 10 -0.0184 0.874 0.6624 pi/2 20.22 0 0.31 0.11 72/180*pi 0-0.22 0 0.41 0.16 108/180*pi 40 0.35 0.25 0.21 pi/2 50 0.1 0.046 0.046 0 60 -0.1 0.046 0.046 0 7-0.08 -0.605 0.046 0.023 0 80 -0.605 0.023 0.023 0 80.06 -0.605 0.046 0.023 pi/2 8];N=256;x=linspace(-1,1,N);y=linspace(-1,1,N);f=zeros(N,N);for i=1:Nfor j=1:Nfor k=1:10A=p(k,3);B=p(k,4);x0=p(k,1);y0=p(k,2);x1=(x(i)-x0)*cos(p(k,5))+(y(j)-y0)*sin(p(k,5));y1=-(x(i)-x0)*sin(p(k,5))+(y(j)-y0)*cos(p(k,5));if((x1*x1)/(A*A)+(y1*y1)/(B*B)<=1) %判断条件f(i,j)=p(k,6);endendendendf=rot90(f);imshow(f,[])③运行结果:实验2. 获得仿真投影数据:①算法实现流程:I. θ∈ [00, 10, ..., 1790], s ∈[-92, -91, ..., 91,92];II. 对于第i 个椭圆求出对应θ和s 的仿真投影数据:其中,(x 0, y 0)为中心坐标,A 为长轴,B 为短轴,a 为旋转角度,ρ为折射指数。
CT实验报告

计算机断层扫描成像摘要:利用已经掌握的γ射线衰减原理以及γ射线测厚仪原理,了解计算机断层成像的基本原理,并通过本实验能够对铜块进行测量;同时了解工业CT 机的基本结构以及组成部分。
关键字:CT γ射线 计算机断层成像 图像重建引言自七十年代初第一台电子计算机断层扫描装置面世以来,成像技术发展异常迅速,设备不断。
以医学成像为例,以实现了三大飞跃,即脏器清晰图像的获得,把生化病理研究推向分子结构的水平和直接提供有关成像组织的化学成分的信息,步入了断层显像的新时代。
计算机断层扫描的分布情况显示出来的一种实验方法,都是利用计算机图像重建的方法来得到物体内部信息。
人们对射线成像的最早认识是从X 光机开始的。
医用X 光机成像技术的发展和应用已有近百年的历史,它是利用X 射线的物理性能和物理效应,来对人体器官组织进行检查。
由于普通X 光机只能把人体内部形态投影在二维平面上,因此会引起成像器官和骨骼的前后重叠,造成影像模糊。
为了克服这一缺点,英国ENI 公司的工程师好恩斯非得(G..N.Hounsfield )运用了美国物理学家马克(Cormack )于1963年发表图像重建数学建模,推出了第一台X 射线计算机断层图像重建技术(X-CT )装置,并1977年9月在英国Ackinson Morleg 医院投入运用。
1979年该技术的发明者为此获得了诺贝尔医学奖。
X-CT 的出现时X 射线成像技术的一个重大的突破。
经过多代的发展,CT 已经获得广泛的应用。
除了在医学上。
在线实时无损检测工业CT 的中也有广泛的应用。
[1]1 CT 的成像原理1.1 概述窄束γ射线在穿过物质时,由于光电效应、康普顿效应、电子对效应这三种效应,其强度就会减弱,这种现象称为γ射线的吸收。
γ射线强度随物质厚度的衰减服从指数规律,即x Nx e I e I I r μσ--==00其中,I 0、I 分别是穿过物质前、后的γ射线强度,x 是γ射线穿过的物质的厚度(单位cm ),σr 是光电、康普顿、电子对三种效应截面之和,N 是吸收物质单位体积中的原子数,μ是物质的线性吸收系数(μ=σr N ,单位为cm )。
CT图像重建技术

CT图像重建技术CT图像重建技术000计算机层析成像(Computed Tomography,CT)是通过对物体进行不同角度的射线投影测量而获取物体横截面信息的成像技术,涉及到放射物理学、数学、计算机学、图形图像学和机械学等多个学科领域。
CT技术不但给诊断医学带来革命性的影响.还成功地应用于无损检测、产品反求和材料组织分析等工业领域。
CT技术的核心是由投影重建图像的理论,其实质是由扫描所得到的投影数据反求出成像平面上每个点的衰减系数值。
图像重建的算法有很多,本文根据CT扫描机的发展对不同时期CT所采用重建算法分别进行介绍。
第一代和第二代CT机获取一个单独投影的采样数据是从一组平行射线获取的,这种采样类型叫平行投影。
平行投影重建算法一般分为直接法与间接法两大类。
直接法是直接计算线性方程系数的方法,如矩阵法、迭代法等。
间接法是先计算投影的傅立叶变换,再导出吸收系数的方法,如反投影法、二维傅立叶重建法和滤波反投影法等[1]。
2.1 直接法2.1.1 矩阵法设一个物体的内部吸收系数矩阵为:(1)为了求得该矩阵中的元素值,我们可以先计算该矩阵在T个角度下的T组投影值 ,如设水平方向时 ,则:(2)同样其它角度下也有类似方程,把所有方程联立得到求解,即可求得所有u值。
通常情况下,由于联立方程组的数目往往不同于未知数个数,且可能有不少重复的方程,这样形成的不是方阵,所以一般不满秩,此时需要利用广义逆矩阵法进行求解。
2.1.2 迭代法实际应用中,由于图像尺寸较大,联立的方程个数较多,采用直接采用解析法难度较大,因此提出了迭代重建方法。
迭代法的主要思想是:从一个假设的初始图像出发,采用迭代的方法,将根据人为设定并经理论计算得到的投影值同实验测得的投影值比较,不断进行逼近,按照某种最优化准则寻找最优解[2]。
通常有两种迭代公式,一种是加法迭代公式[2]:(3)另一种是乘法迭代公式[2]:(4)两式中是相邻两次迭代的结果;是某一角度的实测投影值,是计算过程的计算投影值, 是投影的某一射线穿过点的点数,即计算投影值的射线所经过的像素的数目,是松弛因子。
CT平行投影的快速重建算法研究与实现

MA e x n,JANG a, Ch n.i I HH YAN n Bi
(n tueo nomain E gn eig,Ifr t nEn iern iest,Z e gh u4 0 0 Is tt fIfr t n ie r i o n nomai gn eigUnv ri o y h n zo 5 0 2,C ia hn ) Absr c : n o d rt p e p CT r c n tu t n o t a t I r e o s e d u e o sr ci n PC, a e n t e n lss o h o v n in l o b s d o h a ay i f te c n e to a
b c p oe t n ag r h a k rjci loi m,ti p p rp o oe n i rv d ag r h n p lr codn t , rsns o t hs a e rp s sa mpo e loi m i oa o r iae pee t t
关 键 词 :T; 行 束 ; C 平 重建 算 法 ; 速 加 中 图 分 类 号 :P 9 . 1 R 4 T 3 14 ; 4 5 文 献 标 识 码 : 文 章 编 号 :6 1 0 7 ( 0 0 0 0 0 0 A 1 7 — 6 3 2 1 ) 2— 2 6— 4
R e e r h a e lz to f Fa tPa al lBe m e o s r c i n Al o ih n CT s a c nd R a ia i n o s r le - a R c n t u to g rt m i
函数 ,) 0 射线 A Y ,是 B的法 线与 轴 的夹 角 , 则射线 方程 :
P=X O O+y i0 CS sn () 1
CT断层图像重建算法研究.

CT断层图像重建算法研究专业:通信工程姓名:刘明帅指导教师:骆岩红摘要CT技术是一种融合了射线光电子学、信息学、微电子学等学科的新兴技术,因为其先进的无损检测技术,所以被广泛地应用于医学、航天、生物等多个领域。
随着科技的进步,图像重建技术开始应用于X射线中,这是数字图像处理的一个重大进步。
如何能重建出高质量的图像,取决于所采用的重建算法。
从图像重建的角度来看,主要分为解析法与迭代法。
解析法是利用解析、变换重建公式来构建重建图像。
它具有容易实现,速度较快,且能重建出高质量的图像的特点,但是对投影数据完备性要求高。
迭代法是利用求解线性方程组来重建图像,它能够在投影数据信噪较低条件下,获得高质量图像。
本文将从原理、应用、与优缺点的角度来分析两种算法,重点对解析法中的滤波反投影算法从平行束与扇束投影方式进行研究,最后通过Visual C++与MATLAB软件相结合的方式对图像重建,并分析各参数对重建图像的影响。
关键字:CT技术图像重建算法滤波反投影算法AbstractCT technology is a emerging technology that blend of the Ray optoelectronics, microelectronics and informatics subject. Because of its advanced nondestructive testing technology, it is widely used in medical, aerospace, biological and otherfields. With the progress of science and technology, Image reconstruction technology is applied to the X ray, This is a major progress of digital image processing. How to rebuild the high quality images, depends on the reconstruction algorithm you adopt. From the perspective of image reconstruction, it mainly divided into the analytical method and iteration method.Analytical method use the analysis and transform formula to build image reconstruction.It has the characteristics of implementating easily and fast,and reconstructing out high quality images,but the demand of the projection data is high. Iterative method is used to solve the linear system of equations to reconstruction image, the projection data under the condition of low signal-to-noise, it can get high quality image.This article we will be from the point of view of the principle ,application,and the advantages and disadvantages to analysis the two kinds of algorithms, focusing on studying the analytical method of filter back projection algorithm from the parallel beam and fan beam projection methods , finally, combining the software of Visual c + + with MATLAB software to image reconstruction, and analyzes the influence of various parameters on the reconstruction imageKey words: CT technology image reconstruction algorithmFiltered Backprojection Algorithm目录第一章绪论........................................................................................ - 6 -1.1 CT技术与图像重建概述 ...................................................... - 6 -1.2 CT和重建技术的发展及研究现状 ...................................... - 6 -1.3 研究的目的与意义 ............................................................... - 8 - 第二章 CT成像原理和图像重建算法 ................................................ - 9 -2.1 CT成像原理与系统组成 ........................................................ - 9 -2.2 CT成像系统扫描方式的发展 .............................................. - 10 -2.3 CT断层图像原理 .................................................................. - 11 -2.4图像重建算法概述 ................................................................ - 13 -2.4.1解析类方法 .................................................................. - 13 -2.4.2传统迭代类方法 .......................................................... - 13 - 第三章 CT图像重建算法实现原理的研究 ................................ - 14 -3.1图像重建系统中的数学概念及变换 .................................... - 14 -3.1.1 投影与反投影 ............................................................. - 14 -3.1.2 Radon变换及其反变换 .............................................. - 15 -3.1.3傅里叶变换 .................................................................. - 16 -3.1.4中心切片定理 .............................................................. - 16 -3.2解析类重建算法 .................................................................... - 17 -3.2.1直接傅里叶变换算法 .................................................. - 17 -3.2.2反投影重建算法 .......................................................... - 18 -3.3 迭代类重建算法 ................................................................... - 20 -3.3.1 代数迭代重建算法 ..................................................... - 21 -(1) ART算法 ...................................................................... - 21 -(2)同时代数重建算法 ....................................................... - 22 -3.3.2 影响代数迭代重建算法的因素 ................................. - 22 -3.3.3 ART重建算法与SART ................................................. - 25 -3.3.4 统计迭代重建算法 ..................................................... - 27 -(1)最小二乘图像重建算法 ............... 错误!未定义书签。
医学成像系统实验-X-CT图像重建

医学成像系统实验:X-CT图像重建实验目的:Sheep-Logan模型是由10个位置、大小、方向、密度各异的椭圆组成,用来模拟一个脑断层的图像。
通过该模型,可以获得各个投影方向上数据的解析表达式。
利用matlab产生Sheep-Logan模型的仿真投影数据,重建X-CT图像,从而理解图像重建算法。
实验内容:基本要求部分1.利用Sheep-Logan头部模型生成平行束投影。
本部分要求:写出平行束投影表达式,根据Sheep-Logan模型自行编程生成各个方向上投影离散数据,与matlab函数所生成的数据加以比较,充分理解X-CT 投影数据获得的过程。
2.根据平行束投影数据重建图像。
本部分要求:自行编写利用滤波反投影法、R-L函数卷积反投影法、S-L函数重建图像的程序,比较重建的效果,并与matlab提供的函数相比较,充分的理解平行束投影重建算法。
3.在重建过程中,引入噪声、检测器损坏、旋转中心偏移等问题,对重建的结果加以比较和探讨。
可获得免试资格的选做部分(仍选其一即可获得免试资格,根据完成的水平给与相当于期末考试的分数,多选多得分)1.扇形束重建:利用Sheep-Logan模型,根据扇形束投影的原理自行编程生成投影数据,与matlab函数比较;利用数据重排方法和直接加权反投影方法重建图像,比较效果;在重建过程中,同样引入一些误差来源加以分析;理解共轭采样对,分析重建所需的最小数据集。
2.三维螺旋X-CT仿真:自行生成一组重叠或者相套的椭球模型作为体数据,设计一组螺旋X-CT的参数(多排/单排、p=d/W),根据投影原理,生成一套投影数据,利用360°差值和180°差值重建若干个断面的图像,与仿真数据比较,分析重建效果;改变一些配置的参数,比较重建效果。
3.迭代重建算法:自行查阅文献,理解迭代中间算法的基本原理,根据投影数据实现迭代重建算法,与各类反投影算法加以比较,分析优、缺点。
CT重建实验报告

平行光照射的CT重建艾文书220171807一、实验目的认识并熟悉CT重建的原理和成像基础。
通过编写CT图像重建程序,进一步了解CT重建过程,同时加强图像处理程序的编程训练。
二、实验软件:MATLAB三、实验要求1.递交整个过程的源程序。
比较原图和旋转360次(一度一次)2.采用频率滤波反投影和时域卷积反投影得到重建结果。
四、算法原理及结果1.CT重建原理在CT成像中,物体对X线吸收起主要作用,在一个均匀的物体中,X线的衰减服从指数规律。
在X线穿透人体器官或组织时,由于人体器官或组织是由多种物质成分和不同的密度构成的,所以各点对X线的吸收系数是不同的。
将沿着X线束通过的物体分割成许多小单元体(体素),令每个体素的厚度相等(l)。
设足够小,使得每个体素均匀,每个体素的吸收系数为常值,如果X线的入射强度I0、透射强度I和物体体素的厚度l均为已知,沿着X线通过路径上的吸收系数之和μ1+μ2+……+μn就可计算出来。
吸收系数是一个物理量,它是CT影像中每个像素所对应的物质对X线线性平均衰减量大小的表示。
再将图像面上各像素的CT值转换为灰度,就得到了图像面上的灰度分布,就是CT影像。
CT重建过程可以采用直接反投影和卷积反投影来实现。
卷积反投影重建图像时,先把由检测器上获得的原始数据与一个滤波函数进行了卷积运算,得到各方向卷积的投影函数;然后再把它们从各方向进行反投影,即按其原路径平均分配到每一个矩阵元上,进行叠加后得到每一矩阵元的CT值;再经过适当处理后就可以得到被扫描物体的断层图像,卷积反投影可消除单纯的反投影产生的边缘失锐效应,补偿投影中的高频成分和降低投影中心密度,并保证重建图像边缘清晰和内部分布均匀。
2.图示CT重建原理(重要步骤部分原理)五、MATLAB程序算法及结果六、结果评估本次实验,总体上实现了老师的要求,但是由于程序简单,对实现的效果并不是特别明显,在图形重建方面知识还是有待于加强与提高。
医学影像系统实验PART II部分报告 U201012579 生医1002班刘志

医学影像系统实验PART II部分报告专业:生物医学工程*名:**学号:U*********班级:1002班邮箱:****************指导老师:张日欣(老师)完成时间:2013年6月23号实验一CT投影数据采集、反投影重建实验一、实验目的:1. 用Matlab实现模拟CT投影数据采集、反投影重建;2. 掌握反投影重建的方法步骤;3. 掌握Matlab进行模拟CT图像重建方法。
二、实验器材与设备:计算机或图形工作站、Matlab 6.5软件。
三、实验方法与步骤:(1)Matlab的Image processing工具箱中有radon、iradon和fanbeam、ifanbeam两组函数,可以分别进行对图像和体模的投影数据采集和反投影重建。
•其中radon、iradon是对对象进行平行直线束投影重建。
•Fanbeam、ifanbeam是进行扇型束投影重建,函数提供多种参数选择,如:图像和体模的灰阶,投影角度间隔,重建图像的矩阵等。
(2)本实验采用matlab 7.0版进行实验操作,选取shepp-logan图像,进行两种投影实验,获得投影数据图像和重建图像。
函数的具体功能可参看相关M文件。
四、实验要求:1.注释实验中各步骤命令。
2.记录获得的各步影像,分析函数所用的重建方法。
3.观察投影数据和重建图线,比较重建效果和伪影对图像的影响。
4.在实验各步骤中尝试选用其他参数,比较实验结果(如何提高投影和重建图像的精度)。
5.选用shepp_logan体模或自己采集一幅CT图像,进行实验。
五、实验结果显示及其分析:在m文件中输入如下程序代码:(对对象进行平行直线束投影重建)clear %清楚工作空间的所有原有变量P=phantom('Modified Shepp-Logan',256);%使用函数得到修改后的体模图像imshow(P);%显示体模图像title('Shepp-Logan体模图像');%对图像进行主题标明imwrite(P,'C:\MATLAB7\work\shepp-logan.png');%将体模图像写入到自定义的路径文件夹里进行保存%对对象进行平行直线束投影重建%CT=imread('shepp-logan.png');%读入一个图像扩展名为shepp-logan.png的图像,并将其图像矩阵赋给变量CTfigure;imshow(CT);%显示该CT图像title('CT-Shepp-Logan体模图像');%对图像进行主题标明thetal1=0:10:170;%定义一个thetal角度变量,其范围为0-170度,步长为10度thetal2=0:5:170;%定义一个theta2角度变量,其范围为0-170度,步长为5度[R1,Xp1]=radon(CT,thetal1);%对该CT图像进行rason变换,得到投影数据1[R2,Xp2]=radon(CT,thetal2);%对该CT图像进行rason变换,得到投影数据2Num_angles_R1=size(R1,2);%取矩阵R1的列数Num_angles_R2=size(R2,2);%取矩阵R2的列数N_R1=size(R1,1);%取矩阵R1的行数N_R2=size(R2,1);%取矩阵R2的行数Output_size=max(size(CT));%取CT图像矩阵中行数与列数两者的最大值figure;imagesc(thetal1,Xp1,R1);%显示该投影数据图像1title('用平行直线束投影所得到的投影数据图像1(thetal1=0:10:170)');%对图像进行主题标明figure;imagesc(thetal2,Xp2,R2);%显示该投影数据图像2title('用平行直线束投影所得到的投影数据图像2(thetal2=0:5:170)');%对图像进行主题标明Dthetal1=thetal1(2)-thetal1(1);%定义反变换1的步长Dthetal2=thetal2(2)-thetal2(1);%定义反变换2的步长I1=iradon(R1,Dthetal1,Output_size);%对图像数据1进行radon反变换I2=iradon(R2,Dthetal2,Output_size);%对图像数据2进行radon反变换figure;imshow(uint8(I1));%显示重建后的图像1title('用平行直线束投影所重建的图像1(thetal1=0:10:170)');%对图像进行主题标明figure;imshow(uint8(I2));%显示重建后的图像2title('用平行直线束投影所重建的图像2(thetal1=0:5:170)');%对图像进行主题标明%对对象进行扇型束投影重建%D=285;%将D赋值为285,表示从扇束顶点到旋转中心的像素dsensor1=0.5;%正实数指定扇束传感器的间距为0.5dsensor2=1;%正实数指定扇束传感器的间距为1dsensor3=2;%正实数指定扇束传感器的间距为2F1=fanbeam(CT,D,'FanSensorSpacing',dsensor1);%对CT图像进行fanbeam变换,得到投影数据1F2=fanbeam(CT,D,'FanSensorSpacing',dsensor2);%对CT图像进行fanbeam变换,得到投影数据2F3=fanbeam(CT,D,'FanSensorSpacing',dsensor3);%对CT图像进行fanbeam变换,得到投影数据3[F1,sensor_pos1,fan_rot_angles1]=fanbeam(CT,D,'FanSensorSpacing',dsensor1);%对CT图像进行fanbeam变换,并得到扇束传感器的位置sensor_pos1和旋转角度fan_rot_angles1[F2,sensor_pos2,fan_rot_angles2]=fanbeam(CT,D,'FanSensorSpacing',dsensor2);%对CT图像进行fanbeam变换,并得到扇束传感器的位置sensor_pos2和旋转角度fan_rot_angles2[F3,sensor_pos3,fan_rot_angles3]=fanbeam(CT,D,'FanSensorSpacing',dsensor3);%对CT图像进行fanbeam变换,并得到扇束传感器的位置sensor_pos3和旋转角度fan_rot_angles3 figure;imagesc(fan_rot_angles1,sensor_pos1,F1);%根据计算出的位置和角度展示F1的图像colormap(hot);%设置色图为hotcolorbar;%显示色栏xlabel('Fan Rotation angle(degress)');%标注x轴ylabel('Fan Sensor Position(deress)');%标注y轴title('用扇型束投影所得到的投影数据图像1(dsensor1=0.5)');%对图像进行主题标明figure;imagesc(fan_rot_angles2,sensor_pos2,F2);%根据计算出的位置和角度展示F2的图像colormap(hot);%设置色图为hotcolorbar;%显示色栏xlabel('Fan Rotation angle(degress)');%标注x轴ylabel('Fan Sensor Position(deress)');%标注y轴title('用扇型束投影所得到的投影数据图像2(dsensor1=1)');%对图像进行主题标明figure;imagesc(fan_rot_angles3,sensor_pos3,F3);%根据计算出的位置和角度展示F3的图像colormap(hot);%设置色图为hotcolorbar;%显示色栏xlabel('Fan Rotation angle(degress)');%标注x轴ylabel('Fan Sensor Position(deress)');%标注xy轴title('用扇型束投影所得到的投影数据图像3(dsensor1=2)');%对图像进行主题标明output_size=max(size(CT));%得到图像CT维数的最大值,并赋值给变量output_size Ifan1=ifanbeam(F1,D,'FanSensorSpacing',dsensor1,'Outputsize',output_size);%根据扇束投影数据F1及D,desensor1重建图像1Ifan2=ifanbeam(F2,D,'FanSensorSpacing',dsensor2,'Outputsize',output_size);%根据扇束投影数据F2及D,desensor2重建图像2Ifan3=ifanbeam(F3,D,'FanSensorSpacing',dsensor3,'Outputsize',output_size);%根据扇束投影数据F3及D,desensor3重建图像3figure;imshow(uint8(Ifan1));%显示重建图像1title('用扇型束投影所重建的图像1(dsensor1=0.5)');%对图像进行主题标明figure;imshow(uint8(Ifan2));%显示重建图像2title('用扇型束投影所重建的图像2(dsensor1=1)');%对图像进行主题标明figure;imshow(uint8(Ifan3));%显示重建图像3title('用扇型束投影所重建的图像3(dsensor1=2)');%对图像进行主题标明(1)见上述代码,均已做了注释。
CT实验一

实验课程:现代医学影像设备生物医学工程学院实验技术管理中心1.运行matlab程序,在命令窗口输入以下exit moxing 输入以下代码:I=phantom(512); //生成shepp-logan体模H=imrotate(I,270); //figure,imshow(I);figure,imshow(H);显示图像如下:图1 shepp-ladon体模512X512图2体模旋转180度矩阵512X5122、X线以与Y轴平行的方向进行投影,根据傅立叶切片定理知道θ=180度,1)获取在θ=180度角度下的体模的投影数据projection=sum(H,1);figure,plot(1:512,projection);图如下:2)再把此角度下的投影数据进行傅立叶变换,图如下f=fft(projection); %进行傅立叶变换fab=f.*conj(f); %由于变换是复数,取模f3=fftshift(fab); %对所得的傅立叶变换进行频谱转移figure,plot(1:512,f3); %显示图像图33)直接把原旋转180角度下的体模进行一维傅立叶变换,图如下:f4=fft2(H); %直接对原图傅立叶变换fab1=f4.*conj(f4); %取模f5=fftshift(fab1);figure,plot(f5);图4行BP实验内容:1.实验步骤1)通过 help radon 和 help iradon 了解radon与iradon函数的用法;然后编写生成图像的m文件;程序:P = phantom(256);C = radon(P,0:179);I = iradon(C, 0:179);imshow(C,[]);figure,imshow(I,[]);得出结果如图2-1所示。
图2-1 a 弦图 b iradon重建图像2)首先,我们分别对前面所创建的shepp-logan进行平行束反投影重建以及滤波反投影重建。
CT系统标定参数与图像重建的探究

CT系统标定参数与图像重建的探究摘要:CT(计算机层析成像)是通过对物体进行多角度的射线投影测量,从而获得物体横断面信息的成像技术。
为将此技术在多个领域进行推广,本文简述了对CT系统的标定参数和图像重建展开研究,关键词:射线光学;图像重建模型;像素矩阵;平行束投影引言自20世纪70年代初第一台CT扫描系统问世以来,其结构和扫描方式不断革新,且性能逐渐强大,至今已发展到第五代电子束CT机。
本文所研究的对象为第一代CT机。
第一代CT机采用平行光束[2]的扫描的方式,按照旋转-平移的方法工作,属于头颅专用机,且工作周期较长,得到的图像较为粗糙。
此外,在CT系统的安装过程中,往往存在误差,其影响图像质量,需引入已知模板来确定CT系统的标定参数,并根据此在图像重建的过程中,对重建后的图像进行修正。
1 模型建立1.1 问题一根据标定模板的几何信息以及其接收数据信息,利用统计学和几何学原理,逐步确定探测器单元之间的距离、CT系统旋转中心在正方形托盘中的位置和CT系统所使用的X射线的180个方向。
1.1.1 探测器单元间距的确定根据统计学知识,对附件2中的数据进行分析,发现规律:标定模板中的小圆在多个方向上的投影中,其所对应的探测器数目恒为29个(极少数数目为28个的情况忽略不计),即其宽度始终不变。
结合题干中提供的标定模板的几何信息,取模板中小圆的直径为8mm。
又因为探测器单元等距排列,从而可在忽略探测器长度的情况下,确定探测器单元的间距。
1.1.2 CT系统旋转中心位置的确定CT系统的旋转中心是必需的标定参数,其在图像重建中起着至关重要的作用,若不对该参数进行精准确定,所得到的重建图像将存在伪影,易造成测量人员判断错误。
由于本文所研究的第一代CT机与第二代在原理上无本质的区别,遂结合标定模板的几何信息以及原始投影数据,借鉴了李堡磊和孟凡勇等人的方法,基于原始平行束投影数据的旋转中心确定法。
1.1.3 系统中X射线的180个方向的确定为简化计算的步骤,利用几何学的原理,以标定模型中的椭圆中点为原点再次建立平面直角坐标系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.3反投影的计算机实现:
for(x=0;x<256;x++)
for(y=0;y<256;y++)
{
sum1=0;
for(i=0;i<180;i++)
{
intn;
floatm;
m=128*(1-cos(pi*i/180)-sin(pi*i/180))+(x-1)*cos(pi*i/180)+(y-1)*sin(pi*i/180);
二、设备及原理
1)已有的数字图像平台
2)二维平行束计算机层析成像原理
3)二维扇束计算机层析成像原理
三、内容与步骤
1.学习二维平行束计算机层析成像原理(2周)
2.编制二维平行束投影,滤波与重建程序(2周)
3.将二维平行束CT程序融于数字图像平台软件(1周)
4.学习二维扇束计算机层析成像原理(2周)
5.编制二维扇束投影,滤波与重建程序(1周)
先讨椭圆中心在坐标原点,长轴与y轴重叠时,穿过椭圆的某一射线投影 的求法。
1.2 投影的计算机算法实现:
for(i=0;i<180;i++)//角度,从0到180
{
for(d=-128, j=0;d<128;j++,d++)//距离,从-128到128
{
r=p.a*p.a*cos(pi*i/180-pi*p.angle/180)*cos(pi*i/180-pi*p.angle/180)
else
pa[i*256+j] = 0;
}
}
1.3得到的投影效果图:
以长轴100,短轴50,中心坐标(0,0),偏转角45度为例:
二、滤波投影
2.1滤波的原理及滤波函数的选取:
2.2滤波投影的计算机实现:
for(i=0;i<180;i++)//补全投影数据
{
for(j=0;j<256;j++)
q[j]=(pa[i*256]+pa[i*256+1])/2;//前255个点取投影0和1的平均值
m=m+1;
if(m<0||m>255)continue;
else
{
n=floor(m);
m=m-n;
sum1+=((1-m)*pa[i*256+n]+m*pa[i*256+n+1]);
}
}
a[x*256+y]=sum1 *pi/180;
}
3.4反投影效果图:
四、对本课程的感想
CT的投影与重建是在完成数字图像处理平台后进行的,在经过了对位图的理解和对MFC编程的纠结之后,这个上手还比较容易,其难点在于对公式的理解。
专业课程实验报告
------“CT成像及原理”
******
******
学 号:********
院 系:机械工程及自动化
2012年11月15日
专业课程实验任务书
CT成像原理及算法
一、教学目标
结合计算机层析成像原理(CT)与数字图像软件平台,让学生在层析成像理论和软件调试等方面得到综合训练,提高学生对所学知识的综合应用能力,为毕业设计及今后从事相关工作培养分析和解决工程实际问题的能力。
6.将二维扇束CT程序融于数字图像平台软件。(1周)
7.写出课程设计报告(1周)
四、参考书目:
1.《CT原理与算法》庄天戈编著上海交通大学出版社
2.《由投影重建图像》赫尔曼编著科学出版社
3.《计算机断层成像技术》Jiang Hsieh编著科学出版社
4.《C语言程序设计》谭浩强编著清华大学出版社
一、真实投影数据的模拟
for(j=256;j<511;j++)
q[j]=pa[i*256+j-256];//中间255个点不变
for(j=511;j<766;j++)
q[j]=(pa[i*256+254]+pa[i*256+255])/2;//后255个点取投影254和255的平均值
for(int l=0;l<256;l++)//用S-L滤波函数滤波
比如说如何求得投影数据?这是通过不同距离d和角度α的一系列平行束照到椭圆上,再求得直线与椭圆交线的长度,用长度乘以密度就可以得到投影。而求直线与椭圆的交线则要经过一系列的数学运算。如何把数学运算转化为计算机语言,这就是我们要做的内容。
然后比较难的就是滤波的实现以及滤波函数的选择。这里我选择的是S-L滤波函数。通过将卷积转化为累加求和,然后方便计算机语言的编写。
+p.b*p.b*sin(pi*i/180-pi*p.angle/180)*sin(pi*i/180-pi*p.angle/180);
d1=d-p.x*cos(pi*i/180)-p.y*sin(pi*i/180);
if((r-d1*d1)> 0)
pa[i*256+j]=2*p.a*p.b*sqrt(r-d1*d1)/r;//代入公式求出投影数据
最后就是反投影了。他是基于中心切片定理而来的。中心切片定理告诉我们:一个物体的一个角度上的投影的一维傅立叶变换是他二维傅立叶变换在这个方向上的一个切片。根据这个定理,我们可以对投影进行重建,从而得到原图像。在实验过程中是通过内插的方法实现的。
总体来说在这个上面花的时间比在图像处理上少,因为做图像处理时什么都不懂,做这个的时候有了图像处理的经验和方法,做起来就得心应手了。所以说我们应该认真地学好每一门课,在以后的学习过程中遇到了,就会少花很多时间。
{
sum=0;
for(int k=0;k<511;k++)
sum+=q[k+l]*(-2)/(pi*pi*(4*(k-255)*(k-255)-1));
pa[i*256+l]=sum;
}
}
2.3滤波投影效果图:
以长轴100,短轴50,中心坐标(0,0),偏转角45度为例:
三、反投影重建
3.1反投影重建基础——中心切片定理:
1.1投影的原理:
实际的投影数据及真实的投影数据是由检测器得到的,在计算机模拟时,则取自仿真模型。仿真模型常由一系列大小不同、位置各异,具有给定密度的椭圆组成,以模拟脑部不同的组织(图A.1)。
每一椭圆的位置,用其中心坐标(G、H),长轴与y轴的交角α来表示(图A.3)。其大小自然由长轴2a与短轴2b确定。
