一阶逻辑基本概念
一阶逻辑基本概念

问:(司能否将Q)符号化为
Vx(M(x) AF(x)) ?
常项或变项之间数量关系的词。称表示个体常项或变项之间数量关系的词为 量词。量词可分两种:
(1)全称*i司 日常生活和数学中所用的〃一切的〃,〃所有的〃,〃每一个〃,"任意 的",〃凡〃,〃都〃等词可统称为全称量词,将它们符号化为7'。并用 Vx , Vy等表示个体域里斤有个依,而用VxF(x) , VyG(y)等分别表示个体 域里所有 个体都有性质F和都有性质G。
S P
H
用d
KI
3 、 茹
7 a1 3回 A国 m今
Tt
R鄂
由例4.2可知,命题(1) , (2)在不同的个体域D]和D2中符号化的形式不
I 一样。主要区别在于,在使用个体域D2时,要将人与其他事物区分开来。
\ 为此引进了谓词M(x),像这样的谓词称为特性谓词。在命题符号化时一定 荽
正确使用特性谓词。
域可以是有穷集合,例如,{:1,2,3}, {a , b , c , d}, {a , b , c,…,x , y ,
z};也可以是无穷集合,例如,自然数 集合N={0,1,2 ,…},实数集合R={x|x是实数}。有一个特殊的个体域, 它是由宇宙间一切事物组成的,称它为全总个
体域。本书在论述或推理中如没有指明 所采用的个体域,都是使用全总个体域。
( ()
赣 炀
m
s e
S 般
m 畏、、
、 ^ 任、
w 1Mx
m §、
、、 q
葛屈 倒蟹
c
I H 腐、
5 -孵I
C @暇 l
妇犯色 6
屈 型 、 挝 |
挝 , € 眠
离散数学第二章一阶逻辑知识点总结

离散数学第二章一阶逻辑知识点总结数理逻辑部分第2章一阶逻辑2.1 一阶逻辑基本概念个体词(个体): 所研究对象中能够独立存在的具体或抽象的客体个体常项:具体的事物,用a, b, c表示个体变项:抽象的事物,用x, y, z表示个体域: 个体变项的取值范围有限个体域,如{a, b, c}, {1, 2}无限个体域,如N, Z, R, …全总个体域: 宇宙间一切事物组成谓词: 表示个体词性质或相互之间关系的词谓词常项:F(a):a是人谓词变项:F(x):x具有性质F一元谓词: 表示事物的性质多元谓词(n元谓词, n2): 表示事物之间的关系如L(x,y):x与y有关系L,L(x,y):x y,…0元谓词: 别含个体变项的谓词, 即命题常项或命题变项量词: 表示数量的词全称量词: 表示任意的, 所有的, 一切的等如x 表示对个体域中所有的x存在量词: 表示存在, 有的, 至少有一具等如x表示在个体域中存在x一阶逻辑中命题符号化例1 用0元谓词将命题符号化要求:先将它们在命题逻辑中符号化,再在一阶逻辑中符号化(1) 墨西哥位于南美洲在命题逻辑中, 设p:墨西哥位于南美洲符号化为p, 这是真命题在一阶逻辑中, 设a:墨西哥,F(x):x位于南美洲符号化为F(a)例2 在一阶逻辑中将下面命题符号化(1) 人都爱美; (2) 有人用左手写字分不取(a) D为人类集合, (b) D为全总个体域.解:(a) (1) 设G(x):x爱美, 符号化为x G(x)(2) 设G(x):x用左手写字, 符号化为x G(x)(b) 设F(x):x为人,G(x):同(a)中(1) x (F(x)G(x))(2) x (F(x)G(x))这是两个基本公式, 注意这两个基本公式的使用.例3 在一阶逻辑中将下面命题符号化(1) 正数都大于负数(2) 有的无理数大于有的有理数解注意: 题目中没给个体域, 一律用全总个体域(1) 令F(x): x为正数, G(y): y为负数, L(x,y): x>y x(F(x)y(G(y)L(x,y))) 或x y(F(x)G(y)L(x,y)) 两者等值(2) 令F(x): x是无理数, G(y): y是有理数,L(x,y):x>yx(F(x)y(G(y)L(x,y)))或x y(F(x)G(y)L(x,y)) 两者等值几点注意:1元谓词与多元谓词的区分无特殊要求,用全总个体域量词顺序普通别能随便颠倒否定式的使用考虑:①没有别呼吸的人②别是所有的人都喜爱吃糖③别是所有的火车都比所有的汽车快以上命题应怎么符号化?2.2 一阶逻辑合式公式及解释字母表定义字母表包含下述符号:(1) 个体常项:a, b, c, …, a i, b i, c i, …, i1(2) 个体变项:x, y, z, …, x i, y i, z i, …, i 1(3) 函数符号:f, g, h, …, f i, g i, h i, …, i1(4) 谓词符号:F, G, H, …, F i, G i, H i, …, i1(5) 量词符号:,(6) 联结词符号:, , , ,(7) 括号与逗号:(, ), ,定义项的定义如下:(1) 个体常项和个体变项是项.(2) 若(x1, x2, …, x n)是任意的n元函数,t1,t2,…,t n是任意的n个项,则(t1, t2, …, t n) 是项.(3) 所有的项基本上有限次使用(1), (2) 得到的.个体常项、变项是项,由它们构成的n元函数和复合函数依然项定义设R(x1, x2, …, x n)是任意的n元谓词,t1,t2,…, t n 是任意的n个项,则称R(t1, t2, …, t n)是原子公式.原子公式是由项组成的n元谓词.例如,F(x,y), F(f(x1,x2),g(x3,x4))等均为原子公式定义合式公式(简称公式)定义如下:(1) 原子公式是合式公式.(2) 若A是合式公式,则(A)也是合式公式(3) 若A, B是合式公式,则(A B), (A B), (A B),(A B)也是合式公式(4) 若A是合式公式,则xA, xA也是合式公式(5) 惟独有限次地应用(1)~(4)形成的符号串是合式公式.请举出几个合式公式的例子.定义在公式xA和xA中,称x为指导变元,A为相应量词的辖域. 在x和x的辖域中,x的所有浮现都称为约束浮现,A中别是约束浮现的其他变项均称为是自由浮现的.例如, 在公式x(F(x,y)G(x,z)) 中,A=(F(x,y)G(x,z))为x的辖域,x为指导变元, A中x的两次浮现均为约束浮现,y与z均为自由浮现.闭式: 别含自由浮现的个体变项的公式.给定公式A=x(F(x)G(x))成真解释: 个体域N, F(x): x>2, G(x): x>1代入得A=x(x>2x>1) 真命题成假解释: 个体域N, F(x): x>1, G(x): x>2 代入得A=x(x>1x>2) 假命题咨询: xF(x)x F(x) 有成真解释吗?xF(x)x F(x) 有成假解释吗?被解释的公式别一定全部包含解释中的4部分.闭式在任何解释下基本上命题,注意别是闭式的公式在某些解释下也也许是命题.永真式(逻辑有效式):无成假赋值矛盾式(永假式):无成真赋值可满脚式:至少有一具成真赋值几点讲明:永真式为可满脚式,但反之别真谓词公式的可满脚性(永真性,永假性)是别可判定的利用代换实例可判某些公式的类型定义设A0是含命题变项p1, p2, …,p n的命题公式,A1,A2,…,A n是n个谓词公式,用A i处处代替A0中的p i (1i n),所得公式A称为A0的代换实例.例如:F(x)G(x), xF(x)yG(y) 等基本上p q的换实例,x(F(x)G(x)) 等别是p q 的代换实例.定理重言式的代换实例基本上永真式,矛盾式的代换实例基本上矛盾式.2.3 一阶逻辑等值式等值式定义若A B为逻辑有效式,则称A与B是等值的,记作A B,并称A B 为等值式.基本等值式:命题逻辑中16组基本等值式的代换实例如,xF(x)yG(y) xF(x)yG(y)(xF(x)yG(y)) xF(x)yG(y) 等消去量词等值式设D={a1,a2,…,a n} xA(x)A(a1)A(a2)…A(a n)xA(x)A(a1)A(a2)…A(a n)量词否定等值式设A(x)是含x自由浮现的公式xA(x)x A(x)xA(x)x A(x)量词分配等值式x(A(x)B(x))xA(x)xB(x)x(A(x)B(x))xA(x)xB(x)注意:对无分配律,对无分配律例将下面命题用两种形式符号化(1) 没有别犯错误的人(2) 别是所有的人都爱看电影解(1) 令F(x):x是人,G(x):x犯错误.x(F(x)G(x))x(F(x)G(x))请给出演算过程,并讲明理由.(2) 令F(x):x是人,G(x):爱看电影.x(F(x)G(x))x(F(x)G(x))给出演算过程,并讲明理由.前束范式定义设A为一具一阶逻辑公式, 若A具有如下形式Q1x1Q2x2…Q k x k B, 则称A为前束范式, 其中Q i(1i k)为或,B为别含量词的公式.例如,x y(F(x)(G(y)H(x,y)))x(F(x)G(x))是前束范式, 而x(F(x)y(G(y)H(x,y)))x(F(x)G(x))别是前束范式.定理(前束范式存在定理)一阶逻辑中的任何公式都存在与之等值的前束范式注意:公式的前束范式别惟一求公式的前束范式的办法: 利用重要等值式、置换规则、换名规则、代替规则举行等值演算.换名规则: 将量词辖域中浮现的某个约束浮现的个体变项及对应的指导变项,改成其他辖域中未曾浮现过的个体变项符号,公式中其余部分别变,则所得公式与原来的公式等值.代替规则: 对某自由浮现的个体变项用与原公式中所有个体变项符号别同的符号去代替,则所得公式与原来的公式等值.例求下列公式的前束范式(1) x(M(x)F(x))解x(M(x)F(x))x(M(x)F(x)) (量词否定等值式)x(M(x)F(x))两步结果基本上前束范式,讲明前束范式别惟一.(2) xF(x)xG(x)解xF(x)xG(x)xF(x)x G(x) (量词否定等值式)x(F(x)G(x)) (量词分配等值式)另有一种形式xF(x)xG(x)xF(x)x G(x)xF(x)y G(y) ( 换名规则) x y(F(x)G(y)) ( 量词辖域扩张) 两种形式是等值的(3) xF(x)xG(x)解xF(x)xG(x)xF(x)x G(x)x(F(x)G(x)) (为啥?)或x y(F(x)G(y)) (为啥?)(4) xF(x)y(G(x,y)H(y))解xF(x)y(G(x,y)H(y))zF(z)y(G(x,y)H(y)) (换名规则)z y(F(z)(G(x,y)H(y))) (为啥?)或xF(x)y(G(z,y)H(y)) (代替规则)x y(F(x)(G(z,y)H(y)))(5) x(F(x,y)y(G(x,y)H(x,z)))解用换名规则, 也可用代替规则, 这个地方用代替规则 x(F(x,y)y(G(x,y)H(x,z)))x(F(x,u)y(G(x,y)H(x,z)))x y(F(x,u)G(x,y)H(x,z)))注意:x与y别能颠倒。
第二章一阶逻辑

练习2 在一阶逻辑中将下列命题符号化。 ⑴ 兔子比乌龟跑得快。 ⑵ 每个人都有自己喜欢的职业。 ⑶ 不存在同样高的两个人。 ⑷ 存在最小的自然数。 解 ⑴兔子比乌龟跑得快。 令F(x):x是兔子, G(x):x是乌龟, H(x,y):x比y跑得快。 本命题符号化为 x(F(x)→ y(G(y)→H(x,y))), 或 x y(F(x)∧G(y)→H(x,y))。
⑷ 存在着偶素数。
⑸ 在北京工作的人未必都是北京人。
解 ⑴有的有理数是整数。
令Q(x):x是有理数。 P(x):x是整数。 本命题符号化为 x (Q(x)∧P(x))。
⑵每个计算机系的学生都学离散数学。
令P(x):x是计算机系的学生。
R(x):x学离散数学。
本命题符号化为x (P(x)→R(x))。
⑶ 每个人都会犯错误。
令 R(x):x是人。 P(x):x会犯错误。 本命题符号化为 x (R(x)→P(x))。
⑷ 存在着偶素数。
令E(x):x是偶数。
P(x):x是素数。
本命题符号化为 x(E(x)∧P(x))。
⑸在北京工作的人未必都是北京人。
令W(x):x在北京工作。
B(x):x是北京人。
母a, b, c, d 等表示常元。
个体变项(也称个体变元,简称变元):泛指
个体域中个体的符号。一般用小写英文字母x, y,
z 等表示变元。
例
2是有理数。 这是一个简单命题。 “2”是个体词 “…是有理数”是谓词,它表示个体的性 质。 个体词:是表示个体的符号。 谓词:用来刻画个体的性质或个体之间的关 系。一般用大写英文字母表示谓词。 例 张三比李四高。 有两个个体词:张三,李四 “…比…高”是谓词,表示两个体之间的关 系。
4一阶逻辑公式及解释

4一阶逻辑公式及解释一阶逻辑(First-Order Logic, FOL)是数理逻辑中的一个重要分支,它被广泛应用于数学、计算机科学和人工智能等领域。
在一阶逻辑中,逻辑公式是推理的基础,能够对命题进行符号化的描述和推理。
本文将介绍一阶逻辑的基本概念和常见的一阶逻辑公式,并对其进行解释。
一、一阶逻辑基本概念1. 常量:在一阶逻辑中,常量是指代具体对象的符号,如a、b、c 等。
常量一般用小写字母表示。
2. 变量:变量是用来占位的符号,可以代表任意对象。
在一阶逻辑中,变量一般用大写字母表示,如X、Y、Z等。
3. 函数:函数是一种从一个或多个参数到一个值的映射关系。
在一阶逻辑中,常用的函数包括算术函数、关系函数等。
函数一般用小写字母或希腊字母表示,如f(x)、g(x)等。
4. 谓词:谓词是描述对象性质的符号,可以表示真假的陈述。
在一阶逻辑中,常用的谓词包括等于、大于、小于等。
谓词一般用小写字母或希腊字母表示,如P(x)、Q(x)等。
二、一阶逻辑公式在一阶逻辑中,公式是用符号表示的逻辑陈述,包括原子公式和复合公式两类。
1. 原子公式原子公式是一阶逻辑中最基本的公式,它不再含有其他公式作为子公式。
原子公式由一个谓词和一个或多个常量、变量组成,形式为P(t1,t2,...,tn),其中P为谓词,t1,t2,...,tn为常量、变量。
举例:P(a,b)表示P是一个二元谓词,a和b是其两个参数。
2. 复合公式复合公式由一个或多个公式通过逻辑连接词(如否定、合取、析取、蕴含等)组合而成。
- 否定(¬):如果φ是一个一阶逻辑公式,则¬φ也是一个一阶逻辑公式。
- 合取(∧):如果φ和ψ是两个一阶逻辑公式,则(φ∧ψ)也是一个一阶逻辑公式。
- 析取(∨):如果φ和ψ是两个一阶逻辑公式,则(φ∨ψ)也是一个一阶逻辑公式。
- 蕴含(→):如果φ和ψ是两个一阶逻辑公式,则(φ→ψ)也是一个一阶逻辑公式。
举例:如果P(x)表示“x是人”,Q(x)表示“x是聪明的”,那么复合公式可以表示为:(P(x)∧Q(x)),表示“x是人且x是聪明的”。
《离散数学》-一阶逻辑-基本概念

《离散数学》-⼀阶逻辑-基本概念⼀阶逻辑这个⼀块属于离散数学的内容,它的功能就是将⾃然事物给符号化以为体系的确⽴奠定语⾔基础。
回想⽆论学汉语还是英语的语法,我们都是从句⼦的主⼲学起,那么数学作为⼀门语⾔,它的句⼦当然也有所谓的主⼲。
个体词:个体次是所研究对象可以独⽴存在的具体的或者抽象的客体。
具体⽽特定的客体个体成为个体常项,⼀般⽤⼩写字母a、b、c表⽰。
⽽将抽象或泛指的个体词成为个体变项,⼀般⽤英⽂字母x、y、z表⽰,并称个体变项的取值范围为个体域。
举例说明:(1)“5是素数”,5、素数都是个体词语,5是个体常项⽽素数是个体变项.(2)“x>y”,x、y都是个体变项.谓词:这⾥似乎类似于⾃然语⾔中谓语动词,往往是形容“⼀个动作”,但是在这⾥,谓词是形容“⼀种关系”,当然和个体词类似,根据这种描绘个体之间的关系的确定与否(具体或者抽象泛指),我们也可以把谓词分为常项和变项。
举例说明:(1) X是有理数。
“是有理数”是常项谓词。
(2) X与y有具体关系L。
这⾥及其迷惑⼈的是语句“有具体关系L”,但是本质上关系L还是抽象的不确定的,因此这⾥“有具体关系L”是变项谓词。
下⾯要做的就是将这种描述关系的语句进⾏符号化,这⾥其实有点类似于函数的概念,因为谓词描述的是个体之间的关系,因此它必须依赖于个体。
我们⽤F、G、H来进⾏符号化的表⽰。
F(a)、F(x)分别表⽰个体常项a、个体变项x满⾜的性质F(a)和F(x).更⼀般的情况,P(x1,x2,x3…xn)表⽰个体x1,x2,…xn具有关系P。
对于不含个体变项的谓词,我们成为0元谓词。
Ex1:将下列命题在⼀阶逻辑中⽤0元谓词符号化,并讨论他们的真值(1) 只有2是素数,4才是素数。
G(2)表⽰2是素数,G(4)表⽰4是素数,则我们将这个命题符号化的结果: G(2) —> G(4),由于命题的条件为假,因此该命题为真。
(2) 如果5⼤于4,则4⼤于6G(5,4)表⽰“5⼤于4”,命题符号化之后的结果: G(5,4) —> G(4,6),条件为真结论为假,因此命题为假。
《离散数学》第二章 一阶逻辑 讲稿分析

2.1 一阶逻辑基本概念一、本节主要内容基本概念——个体词、谓词、量词命题符号化二、教学内容个体词(个体): 所研究对象中可以独立存在的具体或抽象的客体,它可以是一个具体的事物,也可以是一个抽象的概念. 表示主语的词(名词或代词):苏格拉底,2,黑板,自然数,思想,定理.个体常项:具体的或特定的个体词,用a, b, c表示个体变项:抽象的或泛指的个体词,用x, y, z表示个体域: 个体变项的取值范围有限个体域,如{a, b, c}, {1, 2}无限个体域,如N, Z, R, …全总个体域: 宇宙间一切事物组成基本概念谓词: 表示个体词的性质或相互之间关系的词谓词常项:表示具体性质或关系的谓词F: …是人,F(a):a是人G:…是自然数,F(2):2是自然数谓词变项:表示抽象的或泛指的谓词F: …具有性质F,F(x):x具有性质F元数:谓词中所包含的个体词数一元谓词: 表示事物的性质多元谓词(n元谓词, n 2): 表示个体词之间的关系如L(x,y):x与y有关系L,L(x,y):x比y高2厘米注意:多元谓词中,个体变项的顺序不能随意改动个体变项和谓词的联合体,F(x),L(x,y),也称为谓词n元谓词L(x1, x2,…, xn)可看作一个函数,定义域为个体变项的个体域,值域为{0,1}n元谓词L(x1, x2,…, xn)的真值不确定,不是命题, 如:L(x,y)如果L(x,y)表示“x小于y”,谓词部分已经是常项,但还不是命题.考虑L(2,3)和L(3,2)L(x1, x2,…, xn)是命题:只有当L是常项,x1, x2,…, xn是个体常项0元谓词: 不含个体变项的谓词, 如L(a, b)如L的意义明确,则0元谓词都是命题一阶逻辑中命题符号化例1 用0元谓词将命题符号化要求:先将它们在命题逻辑中符号化,再在一阶逻辑中符号化(1) 墨西哥位于南美洲在命题逻辑中, 设p: 墨西哥位于南美洲符号化为p, 这是真命题在一阶逻辑中, 设a:墨西哥,F(x):x位于南美洲符号化为F(a)例1(续)(2) 是无理数仅当是有理数在命题逻辑中, 设p:是无理数,q:是有理数.符号化为p → q, 这是假命题在一阶逻辑中, 设F(x): x是无理数, G(x): x是有理数符号化为(3) 如果2>3,则3<4在命题逻辑中, 设p:2>3,q:3<4.符号化为p→q, 这是真命题在一阶逻辑中, 设F(x,y):x>y,G(x,y):x<y,符号化为F(2,3)→G(3,4)(4)如果张明比李民高,李民比赵亮高,则张明比赵亮高.在命题逻辑中, 设p:张明比李民高,q:李民比赵亮高, r:张明比赵亮高.符号化为:p ∧ q → r在一阶逻辑中, 设F(x,y):x比y高a:张明,b:李民,c:赵亮符号化为:F(a, b) ∧ F(b, c) → F(a, c)基本概念(续)量词: 表示数量的词例如(1)所有的人都要死的;(2)有的人活一百岁以上;全称量词∀: 表示任意的, 所有的, 一切的等∀x 表示对个体域中所有的个体,∀x F(x)表示个体域中所有的个体都有性质F.∀x F(x),其中F(x):x是要死的,个体域为人类集合存在量词∃: 表示存在着, 有的, 有一个,至少有一个等∃x 表示存在个体域中的个体,∃x F(x)表示存在着个体域中的个体具有有性质F ∃x G(x),其中G (x):x活一百岁以上,个体域为人类集合如果个体域D为全总个体域,则∀x F(x),其中F(x):x是要死的,表示宇宙间的一切事物都要死的.∃x G(x),其中G (x):x活一百岁以上,表示宇宙间的一切事物中存在活一百岁以上的. 特性谓词:M(x): x是人符号化为:(1)∀x (M(x) → F(x))(2)∃x (M(x) ∧ G(x))考虑:(1)∀x (M(x) ∧ F(x))(2)∃x (M(x) → G(x))一阶逻辑中命题符号化(续)例2 在一阶逻辑中将下面命题符号化(1) 人都爱美; (2) 有人用左手写字分别取(a) D为人类集合, (b) D为全总个体域.解:(a) (1) 设G(x):x爱美, 符号化为∀x G(x)(2) 设G(x):x用左手写字, 符号化为∃x G(x)(b) 设F(x):x为人,G(x):同(a)中(1) ∀x (F(x)→G(x))(2) ∃ x (F(x)∧G(x))这是两个基本公式, 注意这两个基本公式的使用.一阶逻辑中命题符号化(续)例3 在一阶逻辑中将下面命题符号化(1) 正数都大于负数(2) 有的无理数大于有的有理数解注意: 题目中没给个体域, 一律用全总个体域(1) 令F(x): x为正数, G(y): y为负数, L(x,y): x>y∀x(F(x)→∀y(G(y)→L(x,y))) 或∀x∀y(F(x)∧G(y)→L(x,y)) 两者等值(2) 令F(x): x是无理数, G(y): y是有理数,L(x,y):x>y∃x(F(x)∧∃y(G(y)∧L(x,y)))或∃x∃y(F(x)∧G(y)∧L(x,y)) 两者等值一阶逻辑中命题符号化(续)几点注意:1元谓词与多元谓词的区分无特别要求,用全总个体域量词顺序一般不要随便颠倒例:对任意x,存在着y,使得x+y=5. 个体域为实数集.符号化为:∀x ∃y H(x,y), 其中H(x,y):x+y=5考虑∃y ∀x H(x,y) 否定式的使用例:在一界逻辑中命题符号化①没有不呼吸的人②不是所有的人都喜欢吃糖③不是所有的火车都比所有的汽车快①⌝∃x( F(x)∧⌝G(x))其中F(x):x是人,G(x):x呼吸或者:∀x( F(x) →G(x))②⌝∀x( F(x) →G(x))其中F(x):x是人,G(x):x喜欢吃糖或者:∃x( F(x)∧⌝G(x))③⌝∀x( F(x) →∀y (G(y) →H(x,y)) )或者:∃x( F(x)∧∃y (G(y) ∧⌝ H(x,y)) )例:在一界逻辑中命题符号化①一切人都不一样高②每个自然数都有后继数③有的自然数无先驱数①∀x ∀y( F(x) ∧F(y) ∧ G(x,y) →⌝H(x,y))其中F(x):x是人,G(x,y) :x和y不是同一个人,H(x,y):x和y一样高或者:⌝∃x ∃y( F(x) ∧F(y) ∧ G(x,y) ∧H(x,y))②∀x( F(x) →∃y(G(y) ∧ H(x,y))其中F(x):x是自然数,H(x,y) :y是x的后继数或者:∀x( F(x) →L(x)) ,L(x) :x有后继数③∃x( F(x) ∧∀y(G(y) →⌝ H(x,y))或者:∃x( F(x)∧⌝L(x) ) ,L(x) :x有先驱数2.2 一阶逻辑公式及解释一、本节主要内容字母表合式公式(简称公式)个体变项的自由出现和约束出现解释永真式(逻辑有效式)矛盾式(永假式)可满足式二、教学内容字母表定义字母表包含下述符号:(1) 个体常项:a, b, c, …, ai, bi, ci, …, i ≥1(2) 个体变项:x, y, z, …, xi, yi, zi, …, i ≥1(3) 函数符号:f, g, h, …, fi, gi, hi, …, i ≥1(4) 谓词符号:F, G, H, …, Fi, Gi, Hi, …, i ≥1(5) 量词符号:∀, ∃(6) 联结词符号:⌝, ∧, ∨, →, ↔(7) 括号与逗号:( , ), ,项定义项的定义如下:(1) 个体常项和个体变项是项.(2) 若ϕ(x1, x2, …, xn)是任意的n元函数,t1,t2,…,tn是任意的n个项,则ϕ(t1, t2, …, tn) 是项.(3) 所有的项都是有限次使用(1), (2) 得到的.例:a,b,x,y,f(x,y)=x+y,g(x,y)=x-y都是项f(a, g(x,y))=a+ (x-y)是项其实, 个体常项、变项是项,由它们构成的n元函数和复合函数还是项原子公式定义设R(x1, x2, …, xn)是任意的n元谓词,t1,t2,…, tn是任意的n个项,则称R(t1, t2, …, tn)是原子公式.其实,原子公式是由项组成的n元谓词.例如,F(x,y), F(f(x1,x2),g(x3,x4))等均为原子公式合式公式定义合式公式(简称公式)定义如下:(1) 原子公式是合式公式.(2) 若A是合式公式,则(⌝A)也是合式公式(3) 若A, B是合式公式,则(A∧B), (A∨B), (A→B),(A↔B)也是合式公式(4) 若A是合式公式,则∀xA, ∃xA也是合式公式(5) 只有有限次地应用(1)~(4)形成的符号串才是合式公式(谓词公式).个体变项的自由出现与约束出现定义在公式∀xA和∃xA中,称x为指导变元,A为相应量词的辖域. 在∀x和∃x的辖域中,x的所有出现都称为约束出现,A中不是约束出现的其他变项均称为是自由出现的.例如, 在公式∀x(F(x,y)→G(x,z)) 中,A=(F(x,y)→G(x,z))为∀x的辖域,x为指导变项, A中x的两次出现均为约束出现,y与z均为自由出现.闭式: 不含自由出现的个体变项的公式.例1:∀x(F(x)→∃y H(x,y) )∃y H(x,y)中,y为指导变项,∃的辖域为H(x,y),其中y为约束出现的,x为自由出现的. 在整个合式公式中,x为指导变项,∀的辖域为(F(x)→∃y H(x,y) ),其中x与y都是约束出现的,x约束出现2次,y约束出现1次.例2:∀x ∀y(R(x,y) ∨L(y,z) ) ∧∃x H(x,y)∀x ∀y(R(x,y) ∨L(y,z) )中,x,y都是指导变项,辖域为(R(x,y) ∨L(y,z) ),x与y都是约束出现的,z为自由出现的.∃x H(x,y)中,x为指导变项,∃的辖域为H(x,y),其中x为约束出现的,y为自由出现的在此公式中,x为约束出现的,y为约束出现的,又为自由出现的. z为自由出现的.换名规则将量词辖域中出现的某个约束出现的个体变项及对应的指导变项,改成另一个辖域中未出现过的个体变项符号,公式中的其余部分不变。
F4一阶逻辑基本概念

第四章一阶逻辑基本概念
§4.1 一阶逻辑命题的符号化 §4.2 一阶逻辑公式及解释
091离散数学(60). W&M. §4.2 一阶逻辑公式及解释
命题逻辑形式系统 I = A, E, AX, R, 其中A, E是语言系统. 谓词逻辑形式系统的语言 , 它便于翻译自然语言. (下一章
Dx2Dx1A(x1, x2, …, xn) 可记为 A2(x3, x4, …, xn), …… ,
Dxn…Dx1A(x1, x2, …, xn) 中没有自由出现的个体变项, 可z) = x(F(x, y) G(x, z)) B(z) = yA(y, z) = yx(F(x, y) G(x, z)) C =zyA(y, z) = zyx(F(x, y) G(x, z))
(3) H(a, b), 其中 H: “…与…同岁”, a: 小王, b: 小 李.
(4) L(x, y), 其中L: “…与…具有关系L”.
091离散数学(60). W&M. §4.1 一阶逻辑命题的符号化
一元谓词 F(x) 表示 x 具有性质 F.
二元谓词 F(x, y) 表示个体变项 x, y 具有关系 F.
xy(x + y = 0) 与 yx(x + y = 0) 含义不同. ‡†句子的符号化形式不止一种. 设 H(x): x 是人, P(x): x 是完美的, 则 “人无完人”可 符号化为
第四章一阶逻辑的基本概念
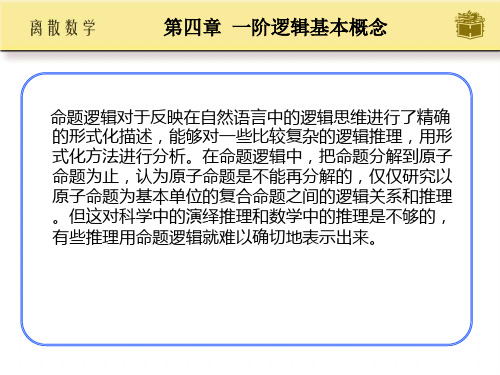
(2) 令F(x):x是无理数,G(y):y是有理数,L(x,y):x>y x(F(x)y(G(y)L(x,y) ) )
或者 xy(F(x)G(y)L(x,y))
14
实例4
例4 在一阶逻辑中将下面命题符号化 (1) 没有不呼吸的人 (2) 不是所有的人都喜欢吃糖 解 (1) M(x): x是人, G(x): x呼吸
合式公式 (4) 若A是合式公式,则xA, xA也是合式公式 (5) 只有有限次地应用(1)—(4)形成的符号串才是合式公式. 合式公式简称公式
如, F(x), F(x)G(x,y), x(F(x)G(x)) xy(F(x)G(y)L(x,y))等都是合式公式
19
量词的辖域
定义4.5 在公式 xA 和 xA 中,称x为指导变元,A为相应 量词的辖域. 在x和 x的辖域中,x的所有出现都称为约束 出现,A中不是约束出现的其他变项均称为是自由出现的.
9
(3)存在唯一量词!,用来表达“恰有一个”、“存在唯一”等词语。
“(!x)R(x)”表示命题:“在个体域中恰好有一个个体使谓词R(x)为
真”。(了解)
全称量词、存在量词统称量词。量词是由逻辑学家Fray引入的,有了量 词之后,用逻辑符号表示命题的能力大大增强。
实例1
例1 用0元谓词将命题符号化 (1) 墨西哥位于南美洲
(2) 2 是无理数仅当 3 是有理数
(3) 如果2>3,则3<4
解:在命题逻辑中: (1) p, p为墨西哥位于南美洲(真命题)
(2) p→q, 其中, p:2 是无理数, q: 3 是有理数. 是假命题
(3) pq, 其中, p:2>3, q:3<4. 是真命题
离散数学 第二章:一阶逻辑

(2) xF(x) G(x, y);
(3) xyR(x, y) L(y, z) xH(x, y).
2.闭式
定义6. 设A为任一公式,若A中无自由出现的个体变项,则称A是 封闭的合式公式,简记闭式.
例: xF(x) G(x),xyF(x) G(x, y) 闭式, 但 xF(x) G(x, y),zyL(x, y, z) 不是闭式.
(1)所有的人都要死的. (2)有的人活百岁以上.
全称量词:一切,所有,任意. 用 表示.
1.量词
x:表示对个体域中的所有个
xF(x)体:表. 示个体域中的所有个体都具有性质F.
存在量词:存在着,有一个,至少有一个. 用 表示.
x:表示存在个体域里的个体.
xF ( x):表示存在着个体域中的个体具有性质F.
(2)xR(x) G(x), 其中 G(x): x是整数.
3) 同2).
例3. 将下面命题符号化. (1)对所有的x ,均有 x2-1=(x+1)(x-1). (2)存在x,使得 x+5=2.
要求: 1)个体域为自然数集合. 2)个体域为实数集合.
解:1) 不用引入特性谓词.
(1)xF(x), 其中 F(x): x2-1=(x+1)(x-1). 真命题
(3) xF(x) yF(y) L(x, y),
其中 F(x): x是自然数, L(x,y): y是 x的先驱数.
§2.2 一阶逻辑合式公式及解释
一、合式公式
1.字母表 定义1.字母表如下: (1)个体常项: a,b,c,… (2)个体变项: x,y,z,… (3)函数符号: f,g,h,… (4)谓词符号: F,G,H,…
第二章 一阶逻辑

或 xy F ( x) G( y) H ( x, y)
例4、在一阶逻辑中将下列命题符号化。
(6) 每列火车都比某些汽车快。
某些汽车比所有的火车慢。
G ( y ) :y 是汽车, x 是火车, 解: F ( x) :
H ( x, y) : x 比 y 快,
第二句为:y G( y) x F ( x) H ( x, y) 或 yx G( y) F ( x) H ( x, y)
x Q( x) Z ( x)
注:若本题指定的个体域为有理数集,
则(1),(2)分别符号化为xF ( x)
和 xZ ( x) 。
例4、在一阶逻辑中将下列命题符号化。
(1) 凡偶数均能被2整除。
x 是偶数,G ( x) : x 能被2整除, 解:F ( x) :
x F ( x) G( x)
均以全总个体域为个体域,
2、量词——表示数量的词。 量词 全称量词 存在量词
使用量词时,应注意以下6点:
(3) 在引入特性谓词后,使用全称量词用“ ”, 使用存在量词用“ ”, (4) n 元谓词化为命题至少需要 n 个量词,
2、量词——表示数量的词。 量词 全称量词 存在量词
( A B),( A B) 也是合式公式;
3、原子公式。
设 R( x1 , x2 , xn )是任意 n 元谓词,
t1 , t2 ,, tn 是项,则称 R(t1 , t2 ,, tn ) 为原子公式。
4、合式公式的递归定义。
(4) 若 A 是合式公式,则xA, xA 也是合式公式;
(2) 存在着偶素数。
x 是偶数,H ( x ) : x 是素数, 解:F ( x) :
一阶逻辑基本概念知识点总结

一阶逻辑基本概念知识点总结一阶逻辑是一种形式化的逻辑系统,也称为一阶谓词演算。
它由一组基本的概念组成,包括:1. 项(Term):一阶逻辑中的项是指个体或对象,可以是常量、变量或函数应用。
常量是指已知的个体,变量是指代未知个体,函数应用是将一个函数应用于一组参数得到的结果。
2. 公式(Formula):一阶逻辑中的公式是用来描述真假性的陈述。
公式可以是原子公式或复合公式。
原子公式是一个谓词应用,谓词是一个描述性的关系符号,用来描述个体之间的关系。
复合公式是由逻辑连接词(如否定、合取、析取、蕴含等)连接的一个或多个公式。
3. 量词(Quantifier):一阶逻辑中的量词用来描述一个谓词在某个个体集合上的性质。
常见的量词包括全称量词(∀,表示对所有个体都成立)和存在量词(∃,表示存在至少一个个体成立)。
4. 推理规则(Inference Rule):一阶逻辑中的推理规则用来进行逻辑推理,在给定一组前提条件的情况下,得出结论的过程。
常用的推理规则包括引入规则(例如全称引入和存在引入)、消去规则(例如全称消去和存在消去)、逆反法和假设法等。
5. 自由变量和限定变量:一阶逻辑中的变量可以分为自由变量和限定变量。
自由变量是没有被量词约束的变量,限定变量是被量词约束的变量。
6. 全称有效性和存在有效性:一阶逻辑中的一个论断是全称有效的,如果它在所有模型中都为真;一个论断是存在有效的,如果它在某个模型中为真。
这些是一阶逻辑的基本概念,它们提供了一种描述和推理关于个体和关系之间的真假性的形式化方法。
一阶逻辑在数学、人工智能、计算机科学等领域有广泛的应用。
离散数学第二章一阶逻辑

(2) ∀x∀y(x+0=y →y+0=x) 真命题 (3) ∀x∀y∃z(x+y=z) 真命题 (4) ∀x∀y(x+y=x*y) 假命题 (5)x+y=y+z,它的真值不确定,因而不是命题. 注)非闭式,在有的解释中不是命题.
定义:设A为一公式(谓词公式),如果A在任何解释下都是 真的,则称A为逻辑有效式(永真式);如果A在任何解释下 都是假的,则称A是矛盾式(永假式);若至少存在一个解 释使A为真,则称A是可满足式. 2.代换实例 设A0是含命题变项p1,p2,…,pn的命题公式,A1,A2,…,An 是n个谓词公式,用Ai(1≤i≤n)处处代换pi,所得公式A 称为A0的代换实例. 例如:F(x)→G(x),∀xF(x)→∃xG(x)等都是p→q的代换实例; 命题公式中的重言式的代换实例在谓词公式中可仍称为重言式 ,这样的重言式都是逻辑有效式. 命题公式中的矛盾式的代换实例仍为矛盾式.
例2.7 给定解释I如下: 1)DI={2,3} 2)DI中特定元素a=2 3)函数f(x)为f(2)=3,f(3)=2 4)谓词F(x)为F(2)=0,F(3)=1 G(x,y)为G(i,j)=1,i,j=2,3 L(x,y)为L(2,2)=L(3,3)=1,L(2,3)=L(3,2)=0 在解释I下,求下列各式的真值 (1) ∀ ∀x(F(x)∧G(x,a)) (2)∃x(F(f(x))∧G(x,f(x))) ∃ (3)∀x∃yL(x,y) ∀ ∃
例2.2 在一阶逻辑中将下面命题符号化 (1)凡有理数均可表成分数; (2)有的有理数是整数; 要求:1)个体域为有理数集合, 2)个体域为实数集合, 3)个体域为全总个体域. 解: 1)个体域为有理数集合(不用引入特性谓词): (1) 设 F(x):x可表成分数; 则命题符号化为∀xF(x). ∀ (2) 设 G(x):x是整数;则命题符号化为∃xG(x). 2)个体域为实数集合(引入特性谓词):令 R(x):x是有理数; (1) 设F(x):x可表成分数;则命题符号化为∀x(R(x)→F(x)) (2) 设G(x):x是整数;则命题符号化为∃x(R(x)∧G(x))。
一阶逻辑基本概念

将下列命题符号化,并讨论真值。 例4.4 将下列命题符号化,并讨论真值。 (1)所有的人都长着黑头发 )所有的人都长着黑头发. (2)有的人登上过月球 )有的人登上过月球. (3)没有人登上过木星 )没有人登上过木星. (4)在美国留学的学生未必都是亚洲人 )在美国留学的学生未必都是亚洲人. 解:由于本题没提出个体域,因而应采用全 由于本题没提出个体域, 总个体域,并令 为人。 总个体域,并令M(x): x为人。 为人
∀x ∀y (F(x) ∧ G(y) →H(x,y)) ∃x (F(x) ∧ ∀y( G(y) →H(x,y) ) ) ¬∀x ∀y( F(x) ∧ G(y) →H(x,y) ) ¬ ∃x ∃y( F(x) ∧ G(y) ∧ L(x,y) )
补充) 例(补充 在一阶逻辑中将下面命题符号化 补充 (1) 正数都大于负数 (2) 有的无理数大于有的有理数
下面讨论n(n≥2)元谓词的符号化 问题
将下列命题符号化: 例4.5 将下列命题符号化: (1)兔子比乌龟跑的快 ) 2) (2)有的兔子比所有的乌龟跑的快 (3)并不是所有的兔子都比乌龟跑的快 ) (4)不存在跑得同样快的两只兔子 )
解:因为本题没有指明个体域,因而采用全总个体 因为本题没有指明个体域, 因为本例中出现二元谓词, 域,因为本例中出现二元谓词,因而引入两个个 体变项x与y。 体变项 与 。 是兔子, 令F(x):x是兔子,G(y):y是乌龟 : 是兔子 : 是乌龟 H(x,y):x比y跑的快, L(x,y):x与y跑得同样快 : 比 跑的快 跑的快, : 与 跑得同样快 这四个命题分别符号化为: 这四个命题分别符号化为:
例4.1 将下列命题在一阶逻辑中用0元谓词符 号化,并讨论它们的真值: (1)如果2是素数,4才是素数。 解:设一元谓词F(x):x是素数。 a:2 b:4 则(1)中命题符号化为0元谓词的蕴涵 式: F(a) → F(b)。 由于此蕴涵式前件为假,所以命题为真.
离散数学(一阶逻辑的基本概念)

多个量词的使用
xyG(x,y):对于每一个x,都存在一个y, 真命题 x与y能配成一对。
yxG(x,y):存在一个y,对于每一个x,x 假命题 与y能配成一对。
28
小结
一元谓词用以描述某一个个体的某种特性, 而n元谓词则用以描述n个个体之间的关系; 如有多个量词,则读的顺序按从左到右的顺 序;另外,量词对变元的约束,往往与量词 的次序有关,不同的量词次序,可以产生不 同的真值,此时对多个量词同时出现时,不 能随意颠倒它们的顺序,颠倒后会改变原有 的含义。
20
实例
例 2 在一阶逻辑中将下面命题符号化 (1) 人都爱美 (2) 有人用左手写字 个体域分别为 (a) D为人类集合 (b) D为全总个体域 解:(a) D为人类集合 (1) xG(x), G(x):x爱美 (2) xG(x), G(x):x用左手写字
21
ቤተ መጻሕፍቲ ባይዱ 实例
(b) D为全总个体域 F(x):x为人,G(x):x爱美 (1) x(F(x)G(x)) (2) x(F(x)G(x)) 1. 引入特性谓词F(x) 2. (1),(2)是一阶逻辑中两个“基本”公式
29
小结
根据命题的实际意义,选用全称量词或存在 量词。全称量词加入时,其刻划个体域的特 性谓词将以蕴涵的前件加入,存在量词加入 时,其刻划个体域的特性谓词将以合取项加 入; 有些命题在进行符号化时,由于语言叙述不 同,可能翻译不同,但它们表示的意思是相 同的,即句子符号化形式可不止一种。
30
22
实例
例3 在一阶逻辑中将下面命题符号化 (1) 正数都大于负数 (2) 有的无理数大于有的有理数 解: 注意:题目中没给个体域,一律用全总个体域 (1) 令F(x):x为正数,G(y):y为负数, L(x,y):x>y x(F(x)y(G(y)L(x,y))) 或者 xy(F(x)G(y)L(x,y))
一阶逻辑基本概念讲解

一阶逻辑在处理多主体系统时可能存在挑战,需要借助其他逻辑系 统如交互逻辑或认知逻辑等来扩展其表达能力。
一阶逻辑的未来发展方向与趋势
扩展表达能力
为了克服一阶逻辑的局限性,未来的研究可以探索扩展其表达能力和推理规则,例如通过引入新的量词或扩展模态、 时态等逻辑系统。
融合其他逻辑系统
为了更好地处理复杂问题,未来的研究可以探索一阶逻辑与其他逻辑系统的融合,例如将一阶逻辑与模态、时态、认 知等逻辑系统相结合。
02
CATALOGUE
一阶逻辑的基本概念
命题与量词
命题
表示一个陈述句,具有真假性,是逻 辑推理的基本单位。
量词
表示数量的符号,如“所有”、“存 在”等,用于限定命题的范围。
逻辑联结词
逻辑联结词
表示命题之间关系的符号,如“并且”、“或者”、“如果...那么...”等。
否定词
表示否定关系的符号,用于改变命题的真假性。
推理过程
通过否定某个命题,根据逻辑规则或推理规则,推导出结论。
归结推理
归结推理
将复杂命题逐步简化为简单命题,然后 通过简单命题的推理得出结论的推理方
法。
结论
根据前提条件推导出的结果或结论。
前提条件
已知的前提或命题。
推理过程
将复杂命题逐步简化为简单命题,然 后通过简单命题的直接推理或间接推 理,得出结论。
一阶逻辑的重要性
逻辑基础
一阶逻辑是形式化逻辑的基础, 为数学、计算机科学和哲学等领 域提供了逻辑推理的框架。
精确表达
一阶逻辑能够精确地表达命题之 间的逻辑关系,有助于避免歧义 和误解。
推理工具
一阶逻辑是进行逻辑推理和数学 证明的重要工具,有助于发现和 证明新的数学定理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单又常见的推理
1 一阶逻辑命题符号化
• 一阶逻辑
– 对命题做进一步分解 – 揭示命题的内部结构以及命题间的内在联系
• 命题分解
– 个体词(名词、代词) – 谓词 – 量词
– 不带个体变项的谓词为0元谓词,当为谓词常项时,即命题
1 一阶逻辑命题符号化
• 例:将下列命题用0元谓词符号化
– 2既是素数又是偶数
• F(x):x是素数 • G(x):x是偶数 • a:2 • F(a) G(a)
• 例:将下列命题用0元谓词符号化
– 如果3>5,则2>3
• F(x,y):x>y • a:3, b:5, c:2 • F(a,b) F(c,a)
– 有的人用左手写字(个体域为全总个体域) • G(x): x用左手写字, M(x): x是人 • x(M(x) G(x))
1 一阶逻辑命题符号化
• 例:将下列命题符号化并判断真假值
– 所有有理数都是整数 (个体域为有理数集合)
• F(x): x是整数 • xF(x)
– 所有有理数都是整数 (个体域为实数集合)
• 全称量化中,特性谓词常作为蕴涵式的前件 • x(M(x) F(x)) • 存在量化中,特性谓词常作为合取项之一 • x (M(x) G(x))
1 一阶逻辑命题符号化
• 例:将下列命题符号化并判断真假值
– 凡是学生都需要学习和考试 – 在北京工作的人未必是北京人 – 没有人登上过木星
1 一阶逻辑命题符号化
1 一阶逻辑命题符号化
• 量词:表示个体常项或变项之间数量关系的词
• 全称量词 : x表示个体域里的所有个体x
– 对应日常语言中的“一切的”、“所有的”等
– 一元谓词F(x)个体域为D, xF(x)真值
• xF(x)为真:F(a)为真,对所有a D • xF(x)为假:F(a)为假,对某个a D
– x yG(x,y):个体域里所有个体x,y有关系G
– x yG(x,y):个体域里存在个体x,y有关系G
• 全称量词与存在量词联合
– x yG(x,y): 个体域里任意x,存在个体y, x, y有关系G
– x yG(x,y): 个体域里存在x和所有个体y都有关系G
1 一阶逻辑命题符号化
• 讨论: xF(x), xF(x), F(x)的联系、区别
– F(x)是不能确定真值的谓词 – xF(x), xF(x)都是命题 – x称为约束变元
• x yG(x,y)为真:G(a,b)为真,对所有a,b D • x yG(x,y)为假:G(a,b)为假,对某对a,b D
1 一阶逻辑命题符号化
• 存在量词 : x表示个体域里有一个个体x
– 对应日常语言中的“存在”、“有一个”等
– 一元谓词F(x)个体域为D, xF(x)真值
• xF(x)为真:F(a)为真,存在某个a D • xF(x)为假:F(a)为假,对任意a D
1 一阶逻辑命题符号化
• 谓词:刻画个体词性质及个体词之间的关系的词
– 谓词常项:具体性质或关系的谓词
• F(a,b):小王和小李是同学 • G(x):x是有理数
– 谓词变项:抽象或泛指的性质或关系的谓词
• L(x,y):x,y具有关系L
• n元谓词P(x1,…,xn)
– P(x1,…,xn): Dn {F,T},D为个体域
• M(x): x是人; H(x):x登上过木星
•
x(M(x) H(x))
1 一阶逻辑命题符号化
• 例:将下列命题符号化
– 不存在跑得同样快的两只兔子 – 有的兔子比所有的乌龟跑得快 – 尽管有些人聪明,未必所有人都聪明
1 一阶逻辑命题符号化
• 例:将下列命题符号化
– 不存在跑得同样快的两只兔子
一阶逻辑基本概念
• 本章的主要内容 一阶逻辑命题符号化 一阶逻辑公式、解释及分类 • 本章与其他章的联系 克服命题逻辑的局限性 是第五章的先行准备
第一节:一阶逻辑命题符号化
1 一阶逻辑命题符号化
• 例子
凡是人都要死 p q 苏格拉底是人 r
推出:苏格拉底要死?
• 命题逻辑命的题表示之能间力的缺联陷系无法刻画
• F(x): x是整数, Q(x): x是有理数 • x(Q(x) F(x))
1 一阶逻辑命题符号化
• 例:将下列命题符号化并判断真假值
– 任意x,x2-3x+2=(x-1)(x-2) (个体域为自然数集合)
• F(x): x2-3x+2=(x-1)(x-2) • xF(x)
– 存在x, x+5=3 (个体域为自然数集合)
• G(x): x+5=3
• xG(x) – 任意x,x2-3x+2=(x-1)(x-2) (个体域为实数集合) – 存在x, x+5=3 (个体域为实数集合)
1 一阶逻辑命题符号化
• 谓式可能不一样,命题真值也可能不 同
– 一般默认是全总个体域,即包含一切个体 – 特性谓词:描述个体变元取值范围的谓词
1 一阶逻辑命题符号化
• 例:将下列命题符号化
– 凡是人都呼吸 (个体域为人类集合) • F(x): x呼吸 • xF(x)
– 有的人用左手写字(个体域为人类集合) • G(x): x用左手写字 • xG(x)
– 凡是人都呼吸(个体域为全总个体域) • F(x): x呼吸, M(x): x是人 • x(M(x) F(x))
• 例:
– 南京是城市 – 个体词:南京 – 谓词:是城市
1 一阶逻辑命题符号化
• 个体词:研究对象中独立存在的具体或抽象的个体
– 个体常项:具体或特定的个体词
• 南京,东南大学,1,2
– 个体变项:抽象或泛指的个体词
• x,y,z • 取值范围称为个体域或论域
– 空集不能作为论域
– 全总个体域:宇宙间一切事物
• 例:将下列命题符号化并判断真假值
– 凡是学生都需要学习和考试
• F(x): x是学生;G(x):x学习;H(x):x考试
• x(F(x) G(x) H(x))
– 在北京工作的人未必是北京人
• F(x): x在北京工作;G(x):x是北京人
•
x(F(x) G(x))
• x(F(x)
G(x))
– 没有人登上过木星
