常用统计量分布表
统计量及其分布

样本均值的抽样分布 (例题分析)
【例】设一个总体含有4 个个体,分别为X1=1、X2=2、 X3=3 、X4=4 。总体的均值、方差及分布如下。
总体均值和方差
总体的频数分布
X
i 1
N
i
N
N
2.5
2
2 ( X ) i i 1
0.02 0 2 1 0.1
21 Φ0.2
0.8414
(4) 样本 k 阶(原点)矩
1 n k Ak X i , k 1, 2, ; n i 1
1 n k 其观察值 k x i , k 1, 2, . n i 1
n n 1 2 1 2 2 E( S ) E X i nX (Xi X ) E n 1 i 1 n 1 i 1
2
1 n 2 2 E ( X i ) nE ( X ) n 1 i 1 2 1 n 2 2 2 ( ) n 2 n 1 i 1 n
n
k 1
n
2
2
n
,
定理 设总体X的期望E(X) = ,方差D(X) = 2,X1, X2,…,Xn为总体X的样本, X,S2分别为样本均值 和样本方差,则
E( X ) E( X )
D( X ) 2 D( X ) n n
E( S 2 ) D( X ) 2
思考:在分组样本场合,样本均值如何计算? 二者结果相同吗?
x1 f1 x n f n 其中 x n
常用统计量与计算方法

代入公式(3—5)得:
Md
L
i
n
15 68
( c) 57 ( 16) 70.5
(天)
f2
20 2
即间隔时间的中位数为70.5天。
L — 频数最多所在组的下限
i — 组距 (即全距/组数)
f — 频数最多所在组的频数
n — 总频数(即总次数)
c — 小于频数最多所在组的累加频数
19
(三)众数 (mode) M0 (书 P17)
26
为 了 准 确 地 表示样本内各个观测值的变异 程度 ,人们 首 先会考虑到以平均数为标准,求 出各个观测值与平均数的离差,(x x) ,称为 离均差。
虽然离均差能表示一个观测值偏离平均数的 性质和程度,但因为离均差有正、有负 ,离均 差之和 为零,即Σx( x ) = 0 ,因 而 不 能 用离均差之和Σ(x x )来 表 示 资料中所有观 测值的总偏离程度。
注: 小样本的自由度为n-1
x x 2
n 1
n 30
35
标准差的计算方法
上述计算方法需先求出平均数(一般为约数),容易 引起计算误差,因此采用原始数据进行计算 (书P20)
大样本: S x 2 x 2 / n
n
小样本: S x 2 x 2 / n
n -1
为简化计算过程,若试验观测数值较大(小)时,可将各观测值
乙组的变异明显低于甲组, R 不能反映 组内其它数据的 变异度 25
二、变异数
缺点
c. 样本较大时, 抽到较大值与较小值的可能性也较大, 因而样本极差也较大,故样本含量相差较大时,不宜用 极差来比较分布的离散度。
当资料很多,而又要迅速对资料的变异程度作出判断 用途 时,有时可先利用极差判断。
第五章-正态分布、常用统计分布和极限定理

的面积, 然后根据1 0.125 0.875查附表4, 对应
Z 1.15,那么录取分数线
x X Z X 74 1.1511 86.65(分)
表5-2
例11:
0Z 图5-11
(1)求Z 1分数以上的概率是多少 ?
解:Z 1时, (Z) 0.34134, Z以上的概率为
(Z) Z
1
t2
e 2 dt
2
(Z 2 ) 图5-8 Z 2
(Z2 Z1)
图5-9Z1 Z 2
例4:已知服从标准正态分布 N(0,1), 求P( 1.3) ? 解:因为() 1,() P( 1.3) P( 1.3) 所以( 1.3) 1 P( 1.3) 1 (1.3) 1 - 0.9032 0.0968
2
如果把u 0, 1代入(x)
1
e
(
xu)2
2 2
2
(x)
1
x2
e2
2
标准正态分布其实是一般正态分布的一个特 例,记作N(0,1),一般正态分布记作N(μ,σ2)。
一般正态分布之所以能变成唯一的标准正态 分布,就是把原来坐标中的零点沿着X轴迁到μ点, 并且以σ为单位记分。
σ=1
0
图5-5
13.6%
13.6%
2.16% 0.11%
3 2 1 图05-6 1
2.16% 0.11%
23
三、标准分的实际意义
例1:甲、乙、丙3个同学《社会统计学》分数 都是80分,甲同学所在班平均成绩μ甲=80分, μ 乙=75分, μ丙=70分,标准差都是10,比较甲、乙、 丙3个同学在班上的成绩。
SPSS统计分析汇总一览表
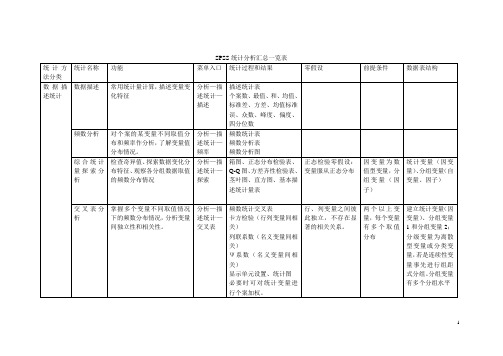
频数统计表
频数分析表
频数分析图
综合统计量探索分析
检查奇异值、探索数据变化分布特征、观察各分组数据取值的频数分布情况
分析—描述统计—探索
箱图、正态分布检验表、Q-Q图、方差齐性检验表、茎叶图、直方图、基本描述统计量表
正态检验零假设:变量服从正态分布
因变量为数值型变量,分组变量(因子)
连续型数值变量作因变量
单样本T检验
检验某个变量的总体均值与某指定值之间是否存在显著差异
分析—比较均值—单样本T检验
单样本统计表
单样本检验表
总体均值的指点定检验值之间不存在显著差异。
样本总体服从正态分布
建立考察指标变量和分组变量
两独立样本T检验
了解两个样本之间是否有显著差异
分析—比较均值—独立样本T检验
两个以上变量,每个变量有多个取值分布
建立统计变量(因变量)、分组变量1和分组变量2;分级变量为离散型变量或分类变量,若是连续性变量事先进行组距式分组。分组变量有多个分组水平
均值比较及参数检验
均值比较过程
按用户指定条件对样本进行分组计算均值和标准差。也可进行方差分析
分析—比较均值—均值
统计量报告表
方差分析表
分析—比较均值—配对样本T检验
分析变量的简单描述统计表
分析变量的相关系数表
两配对样本检验表
两个样本在某变量上不存在显著的线性相关。
两个总体均值间不存在显著差异。
两个样本观察数目相同且观察值顺序不能随意改变;样本来自的两个总体服从正态分布。
按不同总体(组别)建立两个变量,将观察量数据按其顺序对应放在相应的变量名下。
单因素方差分析
用于测试某一个控制变量的不同水平是否给指标变量造成了显著差异和变动。即检验不同水平下各总体均值是否有显著差异(考察不同水平的K个总体是否具有相同的正态分布)。用于两个以上样本均值的差别检测。
spss教程-常用的数据描述统计:频数分布表等--统计学

第二节常用的数据描述统计本节拟讲述如何通过SPSS菜单或命令获得常用的统计量、频数分布表等。
1.数据这部分所用数据为第一章例1中学生成绩的数据,这里我们加入描述学生性别的变量“sex”和班级的变量“class”,前几个数据显示如下(图2-2),将数据保存到名为“2—6—1.sav”的文件中。
图2-2:数据输入格式示例1.Frequencies语句(1)操作打开数据文件“2—6—1。
sav",单击主菜单Analyze /Descriptive Statistics / F requencies…,出现频数分布表对话框如图2-3所示。
图2-3:Frequencies定义窗口把score变量从左边变量表列中选到右边,并请注意选中下方的Display frequency table复选框(要求显示频数分布表)。
如果您只要求得到一个频数分布表,那么就可以点OK按钮了。
如果您想同时获得一些统计量,及统计图表,还需要进一步设置。
①Statistics选项单击Statistics按钮,打开对话框,请按图2—4自行设置。
有关说明如下:(ⅰ)在定义百分位值(percentile value)的矩形框中,选择想要输出的各种分位数,SPSS提供的选项有:●Quartiles四分位数,即显示25%、50%、75%的百分位数。
●Cut points equal 把数据平均分为几份。
如本例中要求平均分为3份.●Percentile显示用户指定的百分位数,可重复多次操作。
本例中要求15%、50%、85%的百分位数。
(ⅱ)在定义输出集中趋势(Central Tendency)的矩形框中,选择想要输出的集中统计量,常用的选项有: ●Mean 算术平均数●Median 中数●Mode 众数●Sum 算术和(ⅲ)在定义输出离散统计量(Dispersion)的矩形框中,选择想要输出的离散统计量,常用的选项有:●Std。
Deviation 标准差●Variance 方差●Range 全距●Minimum 最小值●Maximum 最大值●S。
顺序统计量

−1 ! − !
−1
1−
−
()
证明: 对任意的实数 x ,考虑次序统计量 x(k) 取值
落在小区间 (x , x + x ] 内这一事件,它等价于
“样本容量为 n 的样本中有 1 个观测值落在区间
(x , x + x ] 之间,而有 k-1 个观测值小于等于 x ,
100
•T1 X i 是不合格品率p的充分统计量
i 1
1 n
( X i )2
•来自正态总体的样本,若总体期望已知,
n i 1
1 n
是总体方差的充分统计量,若总体方差已知,n X i
i 1
•是总体期望的充分统计量。
3、分位数
设(1) ≤ (1) ≤ ⋯ ≤ () 为取自总体 X 的
次序统计量,称 Mp为p分位数。
+1 ,
= ൞1
+
2
若不是整数
+1
,
若是整数
4、四分位数:
① 排序后处于25%和75%位置上的值
25%
25%
QL
25%
QM
② 不受极端值的影响
③ 计算公式
布,
X
0
1
2
设总体 X 的分布如下:
p
1/3 1/3 1/3
现抽取容量为 3 的样本, 共有 27 种可能取值, 列表如下
x1
x2 x3 x(1) x(2) x(3) x1 x2 x3 x(1) x(2) x(3) x1 x2 x3 x(1) x(2) x(3)
0
0
0
0
0
0
1
1
0
统计学中常见分布的应用

1引言
在数理统计中,常见的分布包括指数分布,普哇松分布,正态分布, 分布, 分布, 分布.这些常见分布的参数的区间估计和假设检验问题是在日常生产生活中我们常用到的问题,在大部分的文献资料中对正态分布的这一问题讨论较多,本文将就其它五个常见分布的参数的区间估计和假设检验问题进行详细的介绍.其中包括这五种分布的密度函数、性质及其在数理统计中的应用.
那么
~ ,
所以假设拒绝域:对于给定的 和 ,由
,
是自由度为 的 分布之 水平双侧分位数,假设 之 水平的拒绝域是
,
接受域是
.
例某种中药饮片中成分 的含量规定为 ,现在抽验了该药物一批成品中的五个片剂,测得其中成分 的含量分别为: 假设该药物中成分 的含量 服从正态分布,问在 的显著性水平下,抽验结果是否与片剂中成分 的含量为 要求相符?
其中 为常数,这种分布叫作指数分布.显然,我们有
指数分布含有一个参数 ,通常把这分种分布记作 .如果随机变量 服从指数分布 ,则记为 ~ ,因为
(连续随机变量的分布函数 等于概率密度 在区间 上的反常积分)由此可得指数分布 的分布函数为
=
2.5 普哇松分布
定义5[3](P64)称随机变量 服从普哇松分布,如果
2五中常见分布的定义及其相关性质
2.1 分布
定义1[1](P225)称随机变量 服从 分布,自由度为 ,如果它有密度函数
性质假设 独立同标准正态分布,则随机变量
服从 分布,自由度等于 .
2.2 分布
定义2[1](P228)称随机变量 服从 分布,自由度为 ,如果它有密度函数
.
性质假设 服从标准正态分布, 服从 分布,自由度为 ,而且 和 相互独立,那么随机变量 ,服从 分布,自由度为 .
第3节 常用统计分布(三个常用分布)

例2
设X
~
N
(
,
2
),
Y
2
~
2 (n),且X ,Y相互独立,
试求 T X 的概率分布.
Yn
解 因为X ~ N(, 2),所以 X ~ N(0,1)
又Y
2
~
2 (n),且X ,Y独立,则
X
与Y
2
独立,
由定理得
T (X ) / X ~ t(n) (Y / 2) / n Y n
n
事实上,它们受到一个条件的约束:
Xi nX
i 1
n
i 1
Xi
X
1
n
(
i 1
Xi
nX )
1
0
0.
例1
设X1 ,
X 2 ,
,
X
为
6
来
自
正
态
总
体N
(0,1)的
一
组
样
本,
求C1
,
C
使
2
得
Y C1( X1 X 2 )2 C2( X 3 X4 X5 X6 )2
服 从 2分 布.
解
X1
2
4
则C1 1 2 ,C2 1 4 .
3. t 分布 定义 设 X ~ N (0, 1), Y ~ 2 (n), 且 X , Y
独立,则称随机变量 T X 服从自由度为 n Y /n
的 t 分布, 记为T ~ t(n).
t 分布又称学生氏(Student)分布. t(n) 分布的概率密度函数为
2. 2分布(卡方分布)
定义、设 X1, X 2 ,L , X n 相互独立,同服从 N (0, 1)
频数分布表及图形描述

生成交叉频数分布表
列联表的描述性分析
(例题分析—SPSS)
饮 料 类 型* 顾 客 性 别Crosstabulation
列 联 表 的 统 计 描 述
顾 客 性 别 男 饮 料 类 型 果 汁 Count % withi n 饮 料 类 型 % withi n 顾 客 性 别 % of Total Count % withi n 饮 料 类 型 % withi n 顾 客 性 别 % of Total Count % withi n 饮 料 类 型 % withi n 顾 客 性 别 % of Total Count % withi n 饮 料 类 型 % withi n 顾 客 性 别 % of Total Count % withi n 饮 料 类 型 % withi n 顾 客 性 别 % of Total Count % withi n 饮 料 类 型 % withi n 顾 客 性 别 % of Total 1 16.7% 4.5% 2.0% 6 60.0% 27.3% 12.0% 7 63.6% 31.8% 14.0% 2 25.0% 9.1% 4.0% 6 40.0% 27.3% 12.0% 22 44.0% 100.0% 44.0% 女 5 83.3% 17.9% 10.0% 4 40.0% 14.3% 8.0% 4 36.4% 14.3% 8.0% 6 75.0% 21.4% 12.0% 9 60.0% 32.1% 18.0% 28 56.0% 100.0% 56.0% Total 6 100.0% 12.0% 12.0% 10 100.0% 20.0% 20.0% 11 100.0% 22.0% 22.0% 8 100.0% 16.0% 16.0% 15 100.0% 30.0% 30.0% 50 100.0% 100.0% 100.0%
f分布表计算

标题:F分布表计算方法及应用在统计学中,F分布是一种常用的统计分布,用于衡量两组观测数据之间的关联程度。
F分布表是进行统计推断和数据分析的重要工具。
本文将介绍F分布表的计算方法,并应用于实际案例。
一、F分布表的基本概念F分布是一种连续概率分布,其概率质量函数具有两个自由度。
在统计学中,F统计量是一种常用的统计量,用于衡量两组观测数据之间的关联程度。
F分布表则提供了F统计量的概率质量函数。
二、F分布表计算方法1. 查找F分布表:根据所研究的自由度组合,在F分布表中查找对应的概率值。
2. 计算F统计量:根据样本数据,计算两组观测数据的F统计量。
3. 确定概率质量函数:根据所查找的F分布表中的概率值,确定F统计量的概率质量函数。
三、实际案例应用假设我们有一组样本数据,其中包含两组观测数据x和y,我们想知道这两组数据之间是否存在显著关联。
为此,我们可以使用F分布表进行统计分析。
步骤1:收集样本数据x和y,计算它们的平均值和标准差。
步骤2:根据样本数据,计算F统计量F=(x-μ1)/σ1,(y-μ2)/σ2,其中μ1和μ2分别为两组数据的均值,σ1和σ2分别为两组数据的标准差。
步骤3:查找F分布表,查找自由度为(n1-1, n2-1)对应的概率值p。
其中n1和n2分别为样本x和样本y的个数。
步骤4:根据概率值p,判断两组数据之间是否存在显著关联。
如果p小于显著性水平(如0.05),则认为两组数据之间存在显著关联;否则,认为两组数据之间不存在显著关联。
四、总结通过以上介绍,我们可以了解到F分布表计算方法及其在统计学中的应用。
在实际案例中,我们可以通过收集样本数据、计算F统计量、查找F分布表和判断显著性水平等方法,对两组观测数据进行统计分析,从而得出有意义的结论。
F分布表是进行统计学研究的重要工具之一,掌握其计算方法和应用技巧对于提高统计学研究的质量具有重要意义。
χ2分布查表举例

χ2分布查表举例χ2分布是概率统计学中常用的一种分布,它是根据正态分布的平方和而得到的。
在实际应用中,我们经常需要查找χ2分布表来计算一些与χ2分布相关的概率或统计量。
本文将以一个具体的例子来详细介绍如何使用χ2分布表进行查表。
1. 问题描述假设有一批产品,我们想要检验其质量是否符合标准。
我们从这批产品中随机抽取了100个样本,并对每个样本进行了质量检测。
现在我们想要判断这批产品的整体质量是否符合标准,即判断总体质量是否服从某个特定的分布。
2. 假设检验为了判断总体质量是否符合某个特定的分布,我们需要进行假设检验。
假设我们已经知道总体质量服从一个特定的理论分布(比如正态分布),那么我们可以通过观察样本数据来判断这个假设是否成立。
3. 计算χ2统计量在进行假设检验时,我们需要计算一个统计量来衡量观察值与理论值之间的差异程度。
对于χ2检验而言,该统计量就是χ2统计量。
4. 计算自由度在计算χ2统计量之前,我们需要先确定自由度。
自由度是指可以独立取值的变量的个数。
对于χ2检验而言,自由度的计算方法是样本个数减去1。
5. 查找临界值根据假设检验的要求,我们需要设定一个显著性水平(一般为0.05),来判断观察值与理论值之间的差异是否显著。
为了确定是否拒绝原假设,我们需要查找χ2分布表来找到与给定显著性水平相对应的临界值。
6. 比较统计量与临界值将计算得到的χ2统计量与查找得到的临界值进行比较。
如果统计量大于临界值,则拒绝原假设;如果统计量小于等于临界值,则接受原假设。
7. 例子假设我们观察到样本数据中有60个产品符合标准,40个产品不符合标准。
我们想要判断这批产品整体质量是否符合标准。
根据样本数据,我们可以计算出χ2统计量。
根据公式:χ2 = Σ((O-E)^2 / E)其中,O表示观察到的频数,E表示期望的频数。
假设这批产品整体质量符合标准,那么我们可以根据标准来计算期望频数。
假设有100个样本,60%符合标准,40%不符合标准。
excel 2017 基本统计量

一、引言Excel是微软公司推出的一套电子表格软件,被广泛应用于数据分析、数据可视化、数据处理等领域。
在数据分析中,基本统计量是对数据进行描述和分析的重要手段,可以帮助人们了解数据的分布、集中趋势和离散程度。
本文将介绍如何使用Excel 2017进行基本统计量的计算,并以具体的例子进行说明。
二、平均数1. 平均数是一组数据的算术平均值,可以用来表示数据的集中趋势。
2. 在Excel 2017中,可以使用AVERAGE函数来计算一组数据的平均数。
若要计算A1到A10的平均数,在一个空白单元格中输入“=AVERAGE(A1:A10)”并按下回车即可得到结果。
三、中位数1. 中位数是一组数据按大小排序后的中间数值,可以用来表示数据的位置关系。
2. 在Excel 2017中,可以使用MEDIAN函数来计算一组数据的中位数。
若要计算A1到A10的中位数,在一个空白单元格中输入“=MEDIAN(A1:A10)”并按下回车即可得到结果。
四、众数1. 众数是一组数据中出现次数最多的数值,可以用来表示数据的集中趋势。
2. 在Excel 2017中,可以使用MODE函数来计算一组数据的众数。
若要计算A1到A10的众数,在一个空白单元格中输入“=MODE(A1:A10)”并按下回车即可得到结果。
五、标准差和方差1. 标准差和方差是用来表示数据的离散程度的统计量,可以用来衡量数据的波动情况。
2. 在Excel 2017中,可以使用STDEV.S函数和VAR.S函数来计算一组数据的标准差和方差。
若要计算A1到A10的标准差和方差,在一个空白单元格中分别输入“=STDEV.S(A1:A10)”和“=VAR.S(A1:A10)”并按下回车即可得到结果。
六、相关系数1. 相关系数是用来衡量两组数据之间线性关系强弱的统计量,可以用来表示数据之间的关联程度。
2. 在Excel 2017中,可以使用CORREL函数来计算两组数据的相关系数。
统计量及其分布ppt课件

图5.1.1 SONY彩电彩色浓度分布图q
表5.1.1 各等级彩电的比例(%)
等级
I
|X-m|<5/3
II
III
5/3<|X-m|<10/3 10/3 <|X-m|<5
IV
|X-m|>5
美产 33.3 33.3 33.3
0
日产 68.3 27.1 4.3
0.3
抽样 :
5.1.2 样本
要了解总体的分布规律,在统计分析工作中,往往 是从总体中抽取一部分个体进行观测,这个过程称为抽 样。样本
x 344 344 x 347 347 x 351 351 x 355
x 355
由伯努里大数定律:
第25页
两点分布,只要 n 相当大,Fn(x)依概率收敛于F(x) 。
更深刻的结论:格里纹科定理
定理5.2.1 设 x1,x2,L,xn 是取自总体分布函数为F(x) 的样本F,n ( x ) 为其经验分布函数,当n 时,有
若以 p 表示这堆数中1的比例(不合格品率), 则该总体可由一个二点分布表示:
X01 P 1p p
比如:两个生产同类产品的工厂的产品 的总体分布:
例5.1.2 在二十世纪七十年代后期,美国消费者购买
日产SONY彩电的热情高于购买美产 SONY彩电,原因何在?
原因在于总体的差异上!
➢ 1979年4月17日日本《朝日新闻》刊登调查报 告指出N(m, (5/3)2),日产SONY彩电的彩色浓 度服从正态分布,而美产SONY彩电的彩色浓 度服从(m5 , m+5)上的均匀分布。
元件数 4 8 6 5 3 4 5 4
寿命范围 (192 216] (216 240] (240 264] (264 288] (288 312] (312 336] (336 360] (360 184]
方差和标准差,频数分布表

方差和标准差1一、自学指导:看书P 140-P145 回答下列问题:1、一组数据中_____________________的差,叫做这组数据的极差,极差是表示两组数据变化范围的大小,极差大的变化范围______,极差小的变化范围______2、n x x x x ...,,,321为一组数据x 为它们的平均数,方差的基本公式2S =_______________,方差描述了一组数据__________的大小,方差的值越小,数据的波动越小,越________,越__________3、标准差就是____________的算术平方根,公式为σ=___________,它能更精确的描述了一组数据波动的大小4、表示一组数据波动大小的量有____________________二、自学书P143例1、P144例2并完成书后练习三、自学反馈:1.已知某样本的方差是4,则这个样本的标准差是_____.2.已知一个样本1,3,2,x ,5,其平均数是3,则这个样本的标准差是_____.极差是______3.甲、乙两名战士在射击训练中,打靶的次数相同,且打中环数的平均数 乙甲x x =如果甲的射击成绩比较稳定,那么方差的大小关系是S 甲2___S 乙2。
4.已知一个样本的方差的平均数是S 2=51[(X 1-4)2+(x 2-4)2+…+(x 5-4)2],这个样本的平均数是____,样本的容量是_____② 请根据这两名射击手的成绩在图中画出折线图(说明极差的概念)③你认为挑选哪一位比较适宜?为什么?6八年级(5)班要从黎明的张军两位获选人中选出一人去参加学科竞赛,他们在平时的5次测试中成绩如下(单位:分)黎明:652 652 654 652 654张军:667 662 653 640 643如果你是班主任,在收集了上述数据或,你将利用哪些统计的知识来决定这一个名额?四、拓展提高:1、已知一组5个数据的和为100,平方和为2010,求方差和标准差2、若1,2,3,x 的平均数为3,又4,5,x ,y 的平均数为5,则样本0,1,2,3,4,x ,y 的方差是_________五、检测:求 -4,-3, 0, 4 , 3的极差,方差,标准差和平均数方差和标准差2 射击次序2543211、甲、乙两人在相同条件下各射10(1)请填写下表:(2)请你就下列四个不同的角度对这次测试结果进行分析:从平均数和方差相结合看,谁的成绩好?从平均数和命中9环以上的次数相结合看,谁的成绩较好?从折线图上两人射击命中环数的走势看,谁更有潜力?2、探究:1、分别求下列各组数据的平均数、方差、标准差:①已知两组数据1,2,3,4,5,和101,102,103,104,105.②已知两组数据为1,2,3,4,5和3,6,9,12,15.通过以上两题的计算,你发现的结论是________________________③用你发现的结论来解决以下的问题: 十九八七六五四三二一987654321已知数据x 1,x 2,x 3………,x n 的平局数为a ,方差为b ,标准差为c 则 数据x 1+3,x 2+3,x 3+3,……,x n +3的平均数为_______,方差为_______,标准差为___________.(2)x 1-3,x 2-3,x 3-3,,……,x n -3的平均数为________,方差为________,标准差为__________.(3)数据4x 1,4x 2,4x 3,…,4x n 的平均数为_________, 方差为_________, 标准差为__________(4)数据2x 1-3,2x 2-3,2x 3-3,…,2x n -3的平均数为_________, 方差为________, 标准差为__________。
常用统计量数

第三十九页,课件共有81页
累积百分数
100.00 99.32 97.89 85.21 91.53 86.37 79.32 72.42 65.84 58.00 50.84 43.79 37.16 29.89 22.58 14.84 6.89 1.74 0.37
P90=73.52
X=82, PR=96.28
(3) 由于i=10.2不是整数, 向上取整,所以第85百分位数对应的是第 11项,其值为2630。
同理,计算第50百分位(中位数)。i=(50/100) ×12=6,是整数,第50 第三十五页,课件共有81页
百分位分数的计算
1. 组下限:
2. 组上限:
第三十六页,课件共有81页
二、百分等级分数
方差与标准差事最经常用于描述次数分布 离散程度的差异量数。 (一)总体方差与总体标准差 (二)样本方差与样本标准差 (三)标准差的合成 (四)方差与标准差的意义
第二十页,课件共有81页
方差与标准差的定义
方差:每个数据与该组数据平均数之差乘方 后的均值,即离均差平方和的平均数。 标准差:方差的算术平方根,表示一列数据 的平均差距。
限制,就只有(n-k)个自由度了 。计算样本方差时, n个变量值本 身有n个自由度。但受到样本均 数的限制,任何一个“离均差” 均可以用另外的(n-1)个“离均 差”表示,所以只有(n-1)个独 立的“离均差”,因此只有(n
-1)个自由度。
第二十三页,课件共有81页
(三)标准差的合成
方差具有可加性。在已知几个组方差或标准差的情况下,
Mo=3Mdn-2M
第十五页,课件共有81页
众数
Mode,Mo
众数:一组数据中出现次数最多的数
第一节基本统计分析一`频数分布表

以下,我们介绍的主要是SPSS。
SPSS(PASW)基础
软件名称
Statistical Package for Social Science (1975-2000年) Statistical Product and Service Solutions(2000年-2009年4月) Predictive Analytics Software(2009年4月起)
Cumulativ e P erc en t 27.8 44.7 69.5 83.8 92.2 95.8 97.3 98.9 100.0
Statistics:
Dispersion(离差栏):
Std.Deviation 标准差
Variance
方差
Range
全距
Minimum
最小值
Maximum
最大值
Valid Percent 27.8 16.9 24.9 14.2 8.4 3.6 1.6 1.5 1.1 100.0
Cumulative Percent 27.8 44.7 69.5 83.8 92.2 95.8 97.3 98.9 100.0
还可直接作出图形(Charts): Bar charts:条形图 Pie Charts:圆图、饼图 Histograms:直方图,只适用于连续的
4、关于相关系数统计意义的检验:由于抽样误差的存在。 检验的零假设——总体中两个变量间的关系为0。
SPSS只给出给假设成立的概率P值。
(1)Analyze ——Correlations—— Bivariate
计算指定的两个变量之间的相关系数,可选择 Pearson相关、Spearman和
正态分布分位数表

正态分布分位数表正态分布分位数表是统计学中一种重要的分位数表,用于计算随机变量的分位值,根据随机变量的概率密度函数得到。
正态分布分位数表的缩写形式常用于统计分析,是计算抽样统计量的非常重要的工具。
正态分布分位数表是由正态分布函数(即钟形曲线)和对应的分位值所组成。
正态分布函数是一个具有很强特征的双峰函数,最大值出现在中间,两边是渐缓收敛由最大值向两边减小。
正态分布分位数表可以用来表示正态分布函数的概率密度函数,用于描述一组随机变量的分布。
正态分布分位数表的使用在统计学中属于一种应用的技术,主要是为了计算一组随机变量的分位值,而不管这一组随机变量是否符合正态分布,其概率值可以从正态分布分位数表得出。
例如,根据正态分布分位数表,如果检测结果的观测值低于第25%分位数,说明这个观测值处于分布的低限,也就是说,这个观测值有着更低几率出现在这个组中。
同样,如果检测结果的观测值高于第75%分位数,说明这个观测值处于分布的高限,也就是说,这个观测值有着更高几率出现在这个组中。
正态分布分位数表是一种应用技术,其中以概率密度函数来表示正态分布函数,可以计算随机变量的分位值,而这些分位值可以用于统计学中的抽样统计分析,从而更好地评估和比较数据分布,推断更多不同组数据之间的差异。
正态分布分位数表广泛应用于各种数据分析,在实验中,可以用它来检验样本是否满足正态分布假定,检验分组的数据分布情况,以及对样本的偏斜进行检验等。
此外,它还可以用于数据预测,计算样本的测试统计量等。
总而言之,正态分布分位数表对于统计数据的分析和预测至关重要。
正态分布分位数表的使用有其显著的优点,首先,它可以实现对一组随机变量的定量分析,例如可以检验数据的分布情况;其次,它可以用于检验一组样本数据满足正态分布假定,以及检验数据的预测能力等;最后,它可以提供对随机变量分位值的定量预测,从而更加有效地评估不同组数据之间的差异。
正态分布分位数表在实际应用中具有重要意义,它可以为统计学究提供重要的参考,帮助我们更好地理解一组样本的分布情况,支持数据分析的结论,提高计量统计学的可信度,从而使得更有效、更准确地把握统计数据的变化趋势,辅助决策分析。
