2017重庆中考数学17题一次函数行程问题
一次函数行程问题及答案详解
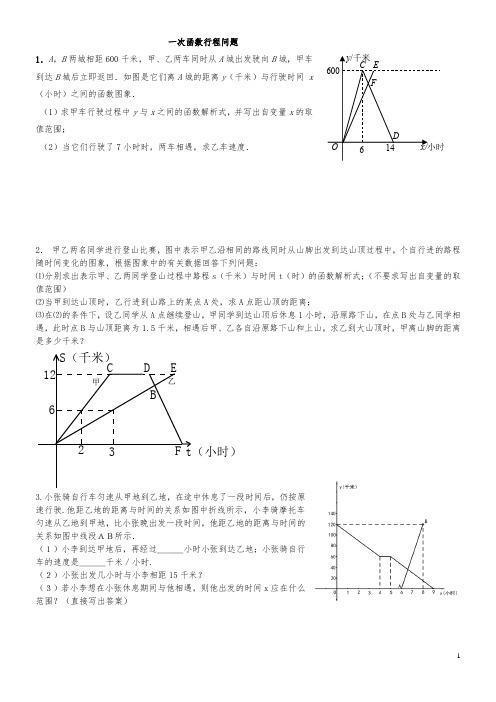
一次函数行程问题1.A ,B 两城相距600千米,甲、乙两车同时从A 城出发驶向B 城,甲车到达B 城后立即返回.如图是它们离A 城的距离y (千米)与行驶时间 x (小时)之间的函数图象.(1)求甲车行驶过程中y 与x 之间的函数解析式,并写出自变量x 的取值范围;(2)当它们行驶了7小时时,两车相遇,求乙车速度.2. 甲乙两名同学进行登山比赛,图中表示甲乙沿相同的路线同时从山脚出发到达山顶过程中,个自行进的路程随时间变化的图象,根据图象中的有关数据回答下列问题:⑴分别求出表示甲、乙两同学登山过程中路程s (千米)与时间t (时)的函数解析式;(不要求写出自变量的取值范围)⑵当甲到达山顶时,乙行进到山路上的某点A 处,求A 点距山顶的距离;⑶在⑵的条件下,设乙同学从A 点继续登山,甲同学到达山顶后休息1小时,沿原路下山,在点B 处与乙同学相遇,此时点B 与山顶距离为1.5千米,相遇后甲、乙各自沿原路下山和上山,求乙到大山顶时,甲离山脚的距离是多少千米?12623S(千米)t(小时)CD EF B甲乙3.小张骑自行车匀速从甲地到乙地,在途中休息了一段时间后,仍按原速行驶.他距乙地的距离与时间的关系如图中折线所示,小李骑摩托车匀速从乙地到甲地,比小张晚出发一段时间,他距乙地的距离与时间的关系如图中线段AB所示.(1)小李到达甲地后,再经过___小时小张到达乙地;小张骑自行车的速度是___千米/小时.(2)小张出发几小时与小李相距15千米?(3)若小李想在小张休息期间与他相遇,则他出发的时间x 应在什么范围?(直接写出答案)4.周六上午8:00小明从家出发,乘车1小时到郊外某基地参加社会实践活动,在基地活动2.2小时后,因家里有急事,他立即按原路以4千米/时的平均速度步行返回.同时爸爸开车从家出发沿同一路线接他,在离家28千米处与小明相遇。
接到小明后保持车速不变,立即按原路返回.设小明离开家的时间为x 小时,小名离家的路程y (干米) 与x (小时)之间的函致图象如图所示,(1)小明去基地乘车的平均速度是________千米/小时,爸爸开车的平均速度应是________千米/小时; (2)求线段CD 所表示的函敛关系式;(3)问小明能否在12:0 0前回到家?若能,请说明理由:若不能,请算出12:00时他离家的路程,5.一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(时),两车之间的距离为y (千米),图中的折线表示从两车出发至快车到达乙地过程中y 与x 之间的函数关系. (1)根据图中信息,求线段AB 所在直线的函数解析式和甲乙两地之间的距离;(2)已知两车相遇时快车比慢车多行驶40千米,若快车从甲地到达乙地所需时间为t 时,求t 的值;(3)若快车到达乙地后立刻返回甲地,慢车到达甲地后停止行驶,请你在图中画出快车从乙地返回到甲地过程中y 关于x 的函数的大致图像. (温馨提示:请画在答题卷相对应的图上)6. 在一条直线上依次有A 、B 、C 三个港口,甲、乙两船同时分别从A 、B 港口出发,沿直线匀速驶向C 港,最终达到C 港.设甲、乙两船行驶x (h )后,与.B .港的距离....分别为1y 、2y (km ),1y 、2y 与x 的函数关系如图所示. (1)填空:A 、C 两港口间的距离为 km , a ; (2)求图中点P 的坐标,并解释该点坐标所表示的实际意义;(3)若两船的距离不超过10 km 时能够相互望见,求甲、乙两船可以相互望见时x 的取值范围.(第23题图)x (小时)7.某物流公司的甲、乙两辆货车分别从A 、B 两地同时相向而行,并以各自的速度匀速行驶,途径配货站C ,甲车先到达C 地,并在C 地用1小时配货,然后按原速度开往B 地,乙车从B 地直达A 地,图16是甲、乙两车间的距离(千米)与乙车出发(时)的函数的部分图像(1)A 、B 两地的距离是 千米,甲车出发 小时到达C 地; (2)求乙车出发2小时后直至到达A 地的过程中,与的函数关系式及的取值范围,并在图16中补全函数图像;(3)乙车出发多长时间,两车相距150千米8.小聪和小明沿同一条路同时从学校出发到宁波天一阁查阅资料,学校与天一阁的路程是4千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达天一阁,图中折线O -A -B -C 和线段OD 分别表示两人离学校的路程s (千米)与所经过的时间t (分钟)之间的函数关系,请根据图象回答下列问题:(1)小聪在天一阁查阅资料的时间为________分钟,小聪返回学校的速度为_______千米/分钟。
2017年重庆市中考《2.1一次方程组及其应用》课件+真题演练中考数学考点试卷分类汇编_OK

一 料共100瓶
列方程为① x y 100
A饮料每瓶需加该 x瓶A种饮料需加该添加剂
二
添加剂2克,B饮料 ② 2x
克;
每瓶需加该添加剂3 y瓶B种饮料需加该添加剂
克
③ 3y
克
需加入同种添加剂
三
270克
列方程为④ 2x 3y 270
15
解:设饮料加工厂生产了A 种饮料 x 瓶,生产了B 种饮料y 瓶.
根据题意得:2x + 3100- x 270,
解得:x = 30则,
100- x = 70.
答:饮料加工厂生产了A种饮料30瓶,生产了B种饮
料70瓶.
17
一 次 方
定义:方程组有⑧ 两个未知数,含有每个 未知数的项的次数都是1,并且一共有两个 方程,一般形式:
a1 x b1 y 0 ①
a2 x b2 y 0 ②( ,x 为y未知数)
解二元一次方程组的基本思想:消元思想,即
二元一次方程组 消元一元一次方程
转化
两种基本解法
6
法两 种 基
1.代入消元法:步骤:(1)变形:将方程①变形为含 x y 的代数式表示 y的x方程③ (2)代入:将方程③代入方程②,得关于 x的y一元
3.列:根据等量关系,列方程(组);
步 4.解:解方程(组);
骤 5.验:检验所解答案是否正确,是否符合题意;
6.答:规范作答,注意单位名称.
9
售价=标价×折扣,销售额=售价×销量
系 常 利润问题 利润=售价-进价,利润率=利润进价×100% 式见
类 工程问题:工作量=工作效率×⑨工作时间
型
路程=速度×时间
(4)代回:求解另一未知数的值
2017年全国中考数学真题《函数与一次函数》分类汇编解析

2017年全国中考数学真题《函数与一次函数》分类汇编解析函数与一次函数考点一、平面直角坐标系 (3分) 1、平面直角坐标系在平面内画两条互相垂直且有公共原点的数轴,就组成了平面直角坐标系。
其中,水平的数轴叫做x 轴或横轴,取向右为正方向;铅直的数轴叫做y 轴或纵轴,取向上为正方向;两轴的交点O (即公共的原点)叫做直角坐标系的原点;建立了直角坐标系的平面,叫做坐标平面。
为了便于描述坐标平面内点的位置,把坐标平面被x 轴和y 轴分割而成的四个部分,分别叫做第一象限、第二象限、第三象限、第四象限。
注意:x 轴和y 轴上的点,不属于任何象限。
2、点的坐标的概念点的坐标用(a ,b )表示,其顺序是横坐标在前,纵坐标在后,中间有“,”分开,横、纵坐标的位置不能颠倒。
平面内点的坐标是有序实数对,当b a ≠时,(a ,b )和(b ,a )是两个不同点的坐标。
考点二、不同位置的点的坐标的特征 (3分) 1、各象限内点的坐标的特征 点P(x ,y )在第一象限0,0>>⇔y x点P(x ,y )在第二象限0,0><⇔y x 点P(x ,y )在第三象限0,0<<⇔y x 点P(x ,y )在第四象限0,0<>⇔y x 2、坐标轴上的点的特征点P(x ,y )在x 轴上0=⇔y ,x 为任意实数 点P(x ,y )在y 轴上0=⇔x ,y 为任意实数点P(x ,y )既在x 轴上,又在y 轴上⇔x ,y 同时为零,即点P 坐标为(0,0) 3、两条坐标轴夹角平分线上点的坐标的特征点P(x ,y )在第一、三象限夹角平分线上⇔x 与y 相等 点P(x ,y )在第二、四象限夹角平分线上⇔x 与y 互为相反数 4、和坐标轴平行的直线上点的坐标的特征 位于平行于x 轴的直线上的各点的纵坐标相同。
位于平行于y 轴的直线上的各点的横坐标相同。
5、关于x 轴、y 轴或远点对称的点的坐标的特征点P 与点p’关于x 轴对称⇔横坐标相等,纵坐标互为相反数 点P 与点p’关于y 轴对称⇔纵坐标相等,横坐标互为相反数 点P 与点p’关于原点对称⇔横、纵坐标均互为相反数 6、点到坐标轴及原点的距离点P(x ,y )到坐标轴及原点的距离: (1)点P(x ,y )到x 轴的距离等于y(2)点P(x ,y )到y 轴的距离等于x(3)点P(x ,y )到原点的距离等于22y x +考点三、函数及其相关概念 (3~8分) 1、变量与常量在某一变化过程中,可以取不同数值的量叫做变量,数值保持不变的量叫做常量。
2017中考数学真题汇编一次函数

( 5) y=x ﹣1.2.若函数 y=(k+1)x+k ﹣1 是正比例函数,则 k 的值为( 2017 中考数学真题汇编 ----一次函数一.选择题1.下列函数中,是一次函数的有()( 1) y=πx ( 2) y=2x ﹣ 1(3)y=(4)y=2﹣3x2A .4 个B .3 个C .2 个D .1 个2)A .0B .1C .± 1D .﹣ 13.下列关系中的两个量成正比例的是()A .从甲地到乙地,所用的时间和速度B .正方形的面积与边长C .买同样的作业本所要的钱数和作业本的数量D .人的体重与身高4.已知函数 y=(1﹣3m )x 是正比例函数,且 y 随 x 的增大而增大,那么 m 的取值范围是()A .m >B .m <C .m >1D .m < 15.若 2y+1 与 x ﹣ 5 成正比例,则(A .y 是 x 的一次函数B .y 与 x 没有函数关系C .y 是 x 的函数,但不是一次函数D .y 是 x 的正比例函数)6.已知函数 y=( m+1)的值是()是正比例函数,且图象在第二、四象限内,则mA .2B .﹣ 2C .± 2D .7.一次函数 y=kx+3 的自变量取值增加 2,函数值就相应减少 2,则 k 的值为()A .2B .﹣ 2C .﹣ 1D .48.y=(m ﹣1)x| m | +3m 表示一次函数,则 m 等于()A .1B .﹣ 1C .0 或﹣ 1D .1 或﹣ 19.下列问题中,是正比例函数的是()y=f ( x ),若已知 f (3x ) =3x +b ,且 f ( 1) =0,则C .f (x ) =3x ﹣ 311.已知 y=(k ﹣1)x+k ﹣1 是正比例函数,则 k=+4x ﹣5(x ≠0)是一次函数. 时,函数y=(m+3) x 15.如果对于一切实数 x ,有 f ( x )=x ﹣2x+5,则 f (x ﹣1)的解析式是 18.当 m ,n 为何值时, y=( 5m ﹣ 3)x 19.已知 y=(k ﹣1)x ﹣k 是一次函数. A .矩形面积固定,长和宽的关系B .正方形面积和边长之间的关系C .三角形的面积一定,底边和底边上的高之间的关系D .匀速运动中,速度固定时,路程和时间的关系10.我们可以把一个函数记作2()A .B .2D .二.填空题 2.12.若函数 y=( m+1)x | m |是正比例函数,则该函数的图象经过第象限. 13.当 m=2m +114.下列函数关系式:① y=2x ﹣ 1;②函数的有(填序号);③;④ s=20t .其中表示一次2.16.某商人购货,进价已按原价a 扣去 25%,他希望对货物订一新价格,以便按 新价让利 20%销售后仍可获得 25%的利润,则此商人经营这种货物的件数x 与按新价让利总额 y 之间的函数关系式为 17.潍坊市出租车计价方式如下:行驶距离在.2.5km 以内(含 2.5km )付起步价6 元,超过 2.5km 后,每多行驶 1km 加收 1.4 元,试写出乘车费用 y (元)与乘车距离 x (km )(x >2.5)之间的函数关系为 三.解答题.2﹣nn 为何值时, y 是关于 x 的正比例函数?| k |( 1)求 k 的值;+( m+n )是关于 x 的一次函数?当 m ,( 2)若点( 2, a )在这个一次函数的图象上,求a 的值.______________________________________________________________________________________________________________义,我们来证明函数 f (x )=x +1 是偶函数. 20.已知,若函数 y=(m ﹣1)+3 是关于 x 的一次函数( 1)求 m 的值,并写出解析式.( 2)判断点( 1,2)是否在此函数图象上,说明理由.21.已知一次函数y=(2m+4)x+(3﹣n )( 1)求 m , n 为何值时,函数是正比例函数?( 2)求 m , n 是什么数时, y 随 x 的增大而减小?( 3)若图象经过第一,二,三象限,求m ,n 的取值范围.22.阅读下列材料:现给如下定义:以 x 为自变量的函数用 y=f ( x )表示,对于自变量 x 取值范围内的一切值,总有 f (﹣ x )=f (x )成立,则称函数y=f (x )为偶函数.用上述定2证明:∵ f (﹣ x )=(﹣ x ) 2+1=x 2+1=f ( x )∴ f (x )是偶函数.根据以上材料,解答下面的问题:已知函数①若 f (x )是偶函数,且,求 f (﹣ 1);②若 a=1,求证: f (x )是偶函数.是2.若函数 y=(k+1)x+k ﹣1 是正比例函数,则 k的值为( 参考答案与解析一.选择题1.下列函数中,是一次函数的有()( 1) y=πx ( 2) y=2x ﹣ 1(3)y=(4)y=2﹣3x( 5) y=x 2﹣1.A .4 个B .3 个C .2 个D .1 个【分析】 根据一次函数的定义对各选项进行逐一分析即可.【解答】 解:(1)y=πx 一次函数;( 2) y=2x ﹣ 1 是一次函数;( 3) y= 是反比例函数,不是一次函数; ( 4) y=2﹣ 3x 是一次函数;( 5) y=x 2﹣ 1 是二次函数,不是一次函数. 是一次函数的有 3 个.故选: B .【点评】 本题考查的是一次函数的定义,即一般地,形如是常数)的函数,叫做一次函数.2y=kx+b ( k ≠0, k 、b)A .0B .1C .± 1D .﹣ 1【分析】 先根据正比例函数的定义列出关于k 的方程组,求出 k 的值即可. 【解答】 解:∵函数 y=(k+1)x+k 2﹣ 1 是正比例函数, ∴ 解得 k=1.故选 B .,【点评】 本题考查的是正比例函数的定义,即形如 函数.y=kx ( k ≠ 0)的函数叫正比例 3.下列关系中的两个量成正比例的是(A .从甲地到乙地,所用的时间和速度)B 、根据面积 =边长 ,不是正比例函数,故本选项错误; B .正方形的面积与边长C .买同样的作业本所要的钱数和作业本的数量D .人的体重与身高【分析】 根据正比例函数的定义计算.【解答】 解: A 、从甲地到乙地,所用的时间和速度,用关系式表达为 是正比例函数,故本选项错误;2s=vt ,不C 、买同样的作业本所要的钱数和作业本的数量,是正比例函数, 故本选项正确;D 、人的体重与身高不成正比例关系,故本选项错误.故选 C .【点评】 本题主要考查正比例函数的定义:一般地,两个变量x ,y 之间的关系式可以表示成形如 y=kx ( k 为常数,且 k ≠0)的函数,那么 y 就叫做 x 的正比例 函数.4.已知函数 y=(1﹣3m )x 是正比例函数,且 y 随 x 的增大而增大,那么 m 的取值范围是()A .m >B .m <C .m >1D .m <1【分析】 先根据正比例函数的性质列出关于m 的不等式,求出 m 的取值范围即 可.【解答】 解:∵正比例函数 y=(1﹣3m )x 中, y 随 x 的增大而增大, ∴ 1﹣ 3m > 0,解得 m < . 故选: B .【点评】 本题考查的是正比例函数的性质,即正比例函数> 0 时, y 随 x 的增大而增大.y=kx (k ≠0)中,当 k5.若 2y+1 与 x ﹣ 5 成正比例,则(A .y 是 x 的一次函数B .y 与 x 没有函数关系C .y 是 x 的函数,但不是一次函数)D.y 是x 的正比例函数【分析】根据2y+1 与x﹣ 5 成正比例可得出2y+1=k(x﹣5)k≠0),据此可得出结论.【解答】解:∵2y+1 与x﹣ 5 成正比例,∴2y+1=k(x﹣5)(k≠0),∴y= x﹣,∴y 是x 的一次函数.故选A.【点评】本题考查的是正比例函数的定义,熟知一般地,形如y=kx(k 是常数,k≠0)的函数叫做正比例函数,其中k 叫做比例系数是解答此题的关键.6.已知函数y=(m+1)的值是()A.2B.﹣ 2 C.±2 D.是正比例函数,且图象在第二、四象限内,则m【分析】根据正比例函数的定义得出【解答】解:∵函数y=(m+1)∴m2﹣3=1,m+1<0,解得:m=±2,则m 的值是﹣2.故选:B.2是正比例函数,且图象在第二、四象限内,【点评】此题主要考查了正比例函数的定义以及其性质,得出题关键.m+1 的符号是解7.一次函数y=kx+3 的自变量取值增加2,函数值就相应减少2,则k 的值为()A.2 B.﹣ 2 C.﹣ 1 D.4【分析】先根据自变量取值增加2,函数值就相应减少2,得到ka+3﹣[ k(a+2)+3] =2,据此求得k 的值.______________________________________________________________________________________________________________【解答】解:当x=a 时,y=ka+3,(m﹣3=1,m+1<0,进而得出即可.B 、∵ S=a ,∴正方形面积和边长是二次函数,故本选项错误; 当 x=a+2 时, y=k (a+2)+3,∵ ka+3﹣[ k (a+2)+3] =2,∴ ka+3﹣[ ka+2k+3] =2,∴﹣ 2k=2,∴ k=﹣1, 故选: C .【点评】本题考查了一次函数的定义以及待定系数法的运用,上的点满足函数解析式.注意理解函数解析8.y=(m ﹣1)x| m |+3m 表示一次函数,则 m 等于()A .1B .﹣ 1C .0 或﹣ 1D .1 或﹣ 1【分析】 根据一次函数的定义,自变量x 的次数为 1,一次项系数不等于 0 列式解答即可.【解答】 解:由题意得, | m| =1 且 m ﹣ 1≠ 0,解得 m=±1 且 m ≠1,所以, m=﹣1.故选 B .【点评】 本题主要考查了一次函数的定义,一次函数 b 为常数, k ≠0,自变量次数为 1.y=kx+b 的定义条件是: k 、9.下列问题中,是正比例函数的是()A .矩形面积固定,长和宽的关系B .正方形面积和边长之间的关系C .三角形的面积一定,底边和底边上的高之间的关系D .匀速运动中,速度固定时,路程和时间的关系【分析】 根据正比例函数的定义对各选项进行逐一分析即可.【解答】 解: A 、∵ S=ab ,∴矩形的长和宽成反比例,故本选项错误;2C 、∵ S= ah ,∴三角形的面积一定,底边和底边上的高是反比例关系,故本选y=f ( x ),若已知 f (3x )=3x +b ,且f ( 1) =0,则C .f (x ) =3x ﹣ 3【分析】 将 x=1 代入 f (3x )=3x +b 可以求得 b=﹣ 3,然后将 3x代入四个答案验 11.已知 y=(k ﹣1)x+k ﹣1 是正比例函数,则 k= ﹣ 1【解答】 解:∵ y=(k ﹣1)x+k ﹣1 是正比例函数,项错误;D 、∵ S=vt ,∴速度固定时,路程和时间是正比例关系,故本选项正确.故选 D .【点评】 本题考查的是正比例函数的定义,即一般地,形如≠ 0)的函数叫做正比例函数.y=kx ( k 是常数, k10.我们可以把一个函数记作2()A .B . 2D . 2证即可得到答案.【解答】 解:∵ f (3x ) =3x 2+b= (3x ) 2+b ∴ f (x )= x 2+b , ∵ f (1)=0, ∴ ×12+b=0, 解得 b=﹣ , ∴ f (x )= x 2﹣ . 故选 A .【点评】本题考查了函数的关系式, 解题的关键是对函数关系式进行正确的变形.二.填空题 2【分析】 让 x 的系数不为 0,常数项为 0 列式求值即可.2∴ k ﹣ 1≠0,k 2﹣ 1=0,解得 k ≠1,k=± 1,∴ k=﹣1,.+4x ﹣5( x ≠0)是一次函时,函数y=(m+3)x 【解答】 解:①由 y=( m+3)x 时, y=(m ﹣3)x 2m 1+4x ﹣5 是一次函数.故答案为﹣ 1.【点评】 考查正比例函数的定义:一次项系数不为0,常数项等于 0.| m |12.若函数 y=(m+1) x是正比例函数,则该函数的图象经过第一、三象限.【分析】 根据一次函数定义可得: | m| =1,且 m+1≠0,计算出 m 的值,再根据一次函数的性质进而可得答案.【解答】 解:由题意得: | m| =1,且 m+1≠0,解得: m=1,则 m+1=2>0,则该函数的图象经过第一、三象限,故答案为:一、三.【点评】此题主要考查了正比例函数定义和性质,关键是掌握正比例函数是一次 函数,因此自变量的指数为1.13.当 m=﹣3,0,﹣2m +1数.【分析】 根据二次项的系数为零,可得一次函数.m+3=0. 解得 m=﹣3;2m +1+4x ﹣5(x ≠0)是一次函数,得②,解得 m=0;③ 2m+1=0,解得: m=﹣ ; 综上所述,当 m=﹣3,0,﹣ 故答案为:﹣ 3,0,﹣ .+【点评】 本题考查了一次函数的定义,一次函数常数, k ≠0,自变量次数为 1.y=kx+b 的定义条件是: k 、b 为______________________________________________________________________________________________________________x ,有f (x )=x ﹣2x+5,则f ( x ﹣ 1)的解析式是﹣ 1) =x ﹣ 4x+8【解答】 解:∵ f (x )=x ﹣2x+5,∴ f (x ﹣1)=(x ﹣1) ﹣ 2( x ﹣ 1) +5=x ﹣4x+8.14.下列函数关系式:① y=2x ﹣ 1;②;③;④ s=20t .其中表示一次函数的有①②④(填序号)【分析】 根据一次函数和反比例函数的定义可找出: 函数有③.此题得解.一次函数有①②④; 反比例 【解答】 解:一次函数有:① y=2x ﹣1、②、④ s=20t 是一次函数;反比例函数有:③ 故答案为:①②④.【点评】本题考查了一次函数的定义以及反比例函数的定理,函数的定义是解题的关键.牢记一次(反比例)15.如果对于一切实数2.2f (x【分析】 将( x ﹣1)当作自变量代入 f (x )的函数解析式即可得出答案. 2 2 2故答案为: f ( x ﹣1)=x 2﹣4x+8.【点评】 此题考查了函数关系式的知识, 解答本题关键是理解自变量的含义, ( x ﹣1)当作自变量代入.将 16.某商人购货,进价已按原价a 扣去 25%,他希望对货物订一新价格,以便按 新价让利 20%销售后仍可获得 25%的利润,则此商人经营这种货物的件数x 与按 新价让利总额 y 之间的函数关系式为y= x.【分析】 根据题意得出:新价让利总额=新价× 20%×售出件数,进而得出等量关系.【解答】 解:设新价为 b 元,则销售价为:(1﹣20%)b ,进价为 a ( 1﹣ 25%),则( 1﹣20%)b ﹣( 1﹣ 25%)a 是每件的纯利,∴ b ( 1﹣ 20%)﹣ a (1﹣25%)=b ( 1﹣ 20%)× 25%,化简得: b= a ,______________________________________________________________________________________________________________18.当 m ,n 为何值时, y=( 5m ﹣ 3)x【解答】 解:若 y=(5m ﹣3)x 2 n +(m+n )是关于 x 的一次函数, 所以当 m ≠ 且 n=1 时, y=(5m ﹣3)x 2 n +(m+n )是关于 x 的一次函数. 若 y=(5m ﹣ 3) x 2 n +( m+n )是关于 x 的正比例函数,所以当 m=﹣ 1 且 n=1 时, y=( 5m ﹣ 3) x 2 n +(m+n )是关于 x 的正比例函数.∴ y=b?20%?x= a?20%?x , 即 y= x .故答案为: y= x .【点评】此题主要考查了函数关系式的应用, 得出进件与利润之间的关系是解题 关键.17.潍坊市出租车计价方式如下:行驶距离在2.5km 以内(含 2.5km )付起步价6 元,超过 2.5km 后,每多行驶 1km 加收 1.4 元,试写出乘车费用 y (元)与乘车距离 x (km )(x >2.5)之间的函数关系为1.4x+2.5.【分析】 根据乘车费用 =起步价 +超过 2.5km 的付费得出.【解答】 解:依题意有: y=6+1.4(x ﹣ 2.5)=6+1.4x ﹣ 1.4× 2.5=1.4x+2.5,故答案为: 1.4x+2.5.【点评】此题考查的知识点是函数关系式, 找到所求量的等量关系是解决问题的关键.本题乘车费用 =起步价 +超过 3 千米的付费.三.解答题 2﹣n+( m+n )是关于 x 的一次函数?当 m ,n 为何值时, y 是关于 x 的正比例函数?【分析】 根据一次函数的定义,正比例函数的定义求解即可.﹣则有解得﹣﹣则有解得 ﹣【点评】 本题考查了正比例函数, 利用一次函数的定义、 正比例函数的定义求解是解题关键.______________________________________________________________________________________________________________19.已知y=(k﹣1)x﹣k是一次函数.| k|(1)求k 的值;(2)若点(2,a)在这个一次函数的图象上,求a 的值.【分析】(1)由一次函数的定义可知:k﹣1≠0 且| k| =1,从而可求得k 的值;a 的值.(2)将点的坐标代入函数的解析式,从而可求得【解答】解:(1)∵y 是一次函数,∴| k| =1,解得k=±1.又∵k﹣1≠0,∴k≠1.∴k=﹣1.y=﹣2x+1.(2)将k=﹣ 1 代入得一次函数的解析式为∵(2,a)在y=﹣2x+1 图象上,∴a=﹣4+1=﹣3.依据一次函数的定义求得k 的值是【点评】本题主要考查的是一次函数的定义,解题的关键.20.已知,若函数y=(m﹣1)+3 是关于x 的一次函数(1)求m 的值,并写出解析式.(2)判断点(1,2)是否在此函数图象上,说明理由.【分析】(1)根据一次函数的定义,可得答案;(2)根据点的坐标满足函数解析式,点在函数图象上,可得答案.+3 是关于x 的一次函数,得【解答】解:(1)由y=(m﹣1),解得m=﹣1,函数解析式为y=﹣2x+3(2)将x=1 代入解析式得y=1≠2,故不在函数图象上.y=kx+b 的定义条件是:k、【点评】本题主要考查了一次函数的定义,一次函数b 为常数,k≠0,自变量次数为1.______________________________________________________________________________________________________________证明:∵ f (﹣ x )=(﹣ x ) +1=x +1=f ( x ) 21.已知一次函数y=(2m+4)x+(3﹣n )( 1)求 m , n 为何值时,函数是正比例函数?( 2)求 m , n 是什么数时, y 随 x 的增大而减小?( 3)若图象经过第一,二,三象限,求m ,n 的取值范围.【分析】(1)根据正比例函数的定义来求出 ( 2)根据一次函数的性质即可得出结论;m ,n 的值即可; ( 3)根据一次函数所经过的象限判定m , n 的取值范围.【解答】 解:(1)依题意得: 2m+4≠ 0,且 3﹣n=0,解得 m ≠﹣ 2,且 n=3;( 2)依题意得: 2m+4<0,且 3﹣n 是任意实数.解得 m <﹣ 2,n 是任意实数;( 3)∵一次函数y=(2m+4) x+(3﹣n )的图象经过第一,二,三象限,∴ 2m+4>0 且 3﹣n > 0,解得 m >﹣ 2,n <3.【点评】本题考查的是一次函数的定义和正比例函数的性质,解题的关键是熟悉函数图象与系数的关系.22.阅读下列材料:现给如下定义:以 x 为自变量的函数用 y=f ( x )表示,对于自变量 x 取值范围内的一切值,总有f (﹣ x )=f (x )成立,则称函数y=f (x )为偶函数.用上述定 义,我们来证明函数 f (x )=x 2+1 是偶函数.2 2∴ f (x )是偶函数.根据以上材料,解答下面的问题:已知函数①若 f (x )是偶函数,且,求 f (﹣ 1);②若 a=1,求证: f (x )是偶函数.【分析】 ①根据偶函数定义, f (﹣ 1)=f ( 1),进行求解即可;②把 a=1 代入,求出 f (﹣ x )的表达式,整理后再与 f (x )进行比较即可进行判______________________________________________________________________________________________________________断.【解答】解:①∵f(x)是偶函数,f(1)= ,∴f(﹣1)=f(1)= ;②证明:a=1 时,f(﹣x)=﹣x(+ ),=﹣x(+ ),=x(=x(=f(x),﹣+ ),),即对于自变量x 取值范围内的一切值,总有∴f(x)是偶函数.f(﹣x)=f(x)成立,【点评】本题考查了偶函数的概念,读懂题目信息,整理出解题的关键.f(﹣x)的表达式是______________________________________________________________________________________________________________Welcome To Download !!!欢迎您的下载,资料仅供参考!。
重庆中考数学17题----行程问题

重庆中考17题----行程问题1.甲、乙两车分别从A,B两地同时相向匀速行驶.当乙车到达A地后,继续保持原速向远离B的方向行驶,而甲车到达B地后立即掉头,并保持原速与乙车同向行驶,经过一段时间后两车同时到达C地.设两车行驶的时间为x(小时),两车之间的距离为y(千米),y与x之间的函数关系如图所示,则B,C两地相距千米.2.甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:①A,B两城相距300千米;②乙车比甲车晚出发1小时,却早到1小时;③乙车出发后2小时追上甲车;④当甲、乙两车相距50千米时,t=或.其中正确的结论有.3.甲乙两地相距50千米.星期天上午8:00小聪同学在父亲陪同下骑山地车从甲地前往乙地.2小时后,小明的父亲骑摩托车沿同一路线也从甲地前往乙地,他们行驶的路程y(千米)与小聪行驶的时间x(小时)之间的函数关系如图所示,小明父亲出发小时时,行进中的两车相距8千米.4.点A、B、C表示同一笔直公路上的三个不同的车站,甲,乙两人分别从A、B车站同时出发,匀速直线运动到C站,到达C站就停下来.甲、乙两人与B站的距离y(千米)与时间(小时)之间的函数关系如图所示,则当甲出发小时时,甲乙两人距离为5千米.5.A、B两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入(城区与入口的距离忽略不计),并始终在高速公路上正常行驶.甲车驶往B城,乙车驶往A城,已知甲车以90千米/时的速度匀速行驶.两车之间的距离s(千米)与行驶时间x(小时)之间的关系如图.给出下列结论:①A、B两城相距300千米②乙车与甲车相遇之前速度为60千米/时③C点的横坐标为④两车相遇时距离A城180千米⑤乙车与甲车相遇后,速度改为90千米/时以上结论中正确的是(填序号)6.某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后缷完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下4个结论:①快递车从甲地到乙地的速度为100千米/时;②甲、乙两地之间的距离为120千米;③图中点B的坐标为(3,75);④快递车从乙地返回时的速度为90千米/时,以上4个结论正确的是.7.在同一条直线上依次有A、B、C三地,甲、乙二人同时分别从A、B两地同向去C地,若甲、乙二人x小时候与B地的距离分别为y1千米、y2千米,且其图象如图所示,则甲、乙相遇时,甲走了千米.8.一名考生步行前往考场,10分钟走了总路程的,估计步行不能准时到达,于是他改乘出租车赶往考场,他的行程与时间关系如图所示(假定总路程为1),则他到达考场所花的时间比一直步行提前了分钟.9.李明骑自行车去上学途中,经过先上坡后下坡的一条路段,在这段路上所走的路程s(米)与时间t(分钟)之间的函数关系如图所示,若李明放学后按原路返回,且往返过程中,上坡的速度相同,下坡的速度也相同,问李明返回时走这段路所用的时间为分钟.10.学生甲、乙两人跑步的路程s与所用时间t的函数关系图象表示如图(甲为实线,乙为虚线).根据图象判断:如果两人进行一百米赛跑,当甲跑到终点时,乙落后甲米.11.“国际龙舟节”在岳阳汩罗江举行.某龙舟队在1000米比赛项目中,路程y(米)与时间x(分钟)之间的函数图象如图所示.根据图中提供的信息,该龙舟队的比赛成绩是分钟.12.某人从甲地出发,骑摩托车去乙地,途中因车出现故障而停车修理,到达乙埋正好用了2小时,已知摩托车行驶的路程S(千米)与行驶的时间t(小时)之间的函数关系由如图的图象ABCD给出,若这辆摩托车平均每行驶100千米的耗油量为2升,根据图中给出的信息,从甲地到乙地,这辆摩托车共耗油量升.13.甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则下列结论:(1)a=40,m=1;(2)乙的速度是80km/h;(3)甲比乙迟h到达B地;(4)乙车行驶小时或小时,两车恰好相距50km.正确的个数是()A.1B.2C.3D.414.甲、乙两人从科技馆出发,沿相同的路线分别以不同的速度匀速跑向极地馆,甲先跑一段路程后,乙开始出发,当乙超出甲150米时,乙停在此地等候甲,两人相遇后乙又继续以原来的速度跑向极地馆.如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)的函数图象.则下列四种说法:①甲的速度为1.5米/秒;②a=750;③乙在途中等候甲100秒;④乙出发后第一次与甲相遇时乙跑了375米.其中正确的个数是()A.1个B.2个C.3个D.4个15.小明家、公交车站、学校在一条笔直的公路旁(小明家、学校到这条公路的距离忽略不计),一天,小明从家出发去上学,沿这条公路步行到公交车站恰好乘上一辆公交车,公交车沿这条公路匀速行驶,小明下车时发现还有4分钟上课,于是他沿这条公路跑步赶到学校(上、下车时间忽略不计),小明与家的距离s(单位:米)与他所用时间t(单位:分钟)之间的函数关系如图所示,已知小明从家出发7分钟时与家的距离为1200米,从上公交车到他到达学校共用10分钟,下列说法:①小明从家出发5分钟时乘上公交车②公交车的速度为400米/分钟③小明下公交车后跑向学校的速度为100米/分钟④小明上课没有迟到其中正确的个数是()A.1个B.2个C.3个D.4个16.一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后分别按原速同时驶往甲地,两车之间的距离S(km)与慢车行驶时间t(h)之间的函数图象如图所示,下列说法:①甲、乙两地之间的距离为560km;②快车速度是慢车速度的1.5倍;③快车到达甲地时,慢车距离甲地60km;④相遇时,快车距甲地320km其中正确的个数是()A.1个B.2个C.3个D.4个17.一辆货车从A地开往B地,一辆小汽车从B地开往A地.同时出发,都匀速行驶,各自到达终点后停止.设货车、小汽车之间的距离为s(千米),货车行驶的时间为t(小时),S与t之间的函数关系如图所示.下列说法中正确的有()①A、B两地相距60千米:②出发1小时,货车与小汽车相遇;③出发1.5小时,小汽车比货车多行驶了60千米;④小汽车的速度是货车速度的2倍.A.1个B.2个C.3个D.4个18.为增强学生体质,某中学在体育课中加强了学生的长跑训练.在一次女子800米耐力测试中,小静和小茜在校园内200米的环形跑道上同时起跑,同时到达终点;所跑的路程S(米)与所用的时间t(秒)之间的函数图象如图所示,则她们第一次相遇的时间是起跑后的第秒.19.在一条笔直的公路上有A,B,C三地,C地位于A,B两地之间,甲,乙两车分别从A,B两地出发,沿这条公路匀速行驶至C地停止.从甲车出发至甲车到达C地的过程,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图表示,当甲车出发h时,两车相距350km.20.一辆汽车由A地开往B地,它距离B地的路程s(km)与行驶时间t(h)的关系如图所示,如果汽车一直快速行驶,那么可以提前小时到达B地.21.甲、乙两人在直线道路上同起点、同终点、同方向,分别以不同的速度匀速跑步1500米,先到终点的人原地休息,已知甲先出发30秒后,乙才出发,在跑步的整个过程中,甲、乙两人的距离y(米)与甲出发的时间x(秒)之间的关系如图所示,则乙到终点时,甲距终点的距离是米.22.如图,在一次自行车越野赛中,甲、乙两名选手所走的路程y(千米)随时间x(分钟)变化的图象(全程)分别用实线(O→A→B→C)与虚线(OD)表示,那么,在本次比赛过程中,乙领先甲时的x的取值范围是.23.设甲、乙两车在同一直线公路上相向匀速行驶,相遇后两车停下来,把乙车的货物卸到甲车用了100秒,然后两车分别按原路原速返回.设x秒后两车之间的距离为y米,y关于x的函数关系如图所示,则a=米.24.小丽的家和学校在一条笔直的马路旁,某天小丽沿着这条马路上学,先从家步行到公交站台甲,再乘车到公交站如乙下车,最后步行到学校(在整个过程中小丽步行的速度不变).图中折线ABCDE表示小丽和学校之间的距离y(米)与她离家时间x(分钟)之间的函数关系.(1)小丽步行的速度为;(2)写出y与x之间的函数关系式:.25.某校八年级的学生到距学校6千米的郊外旅游,一部分学生步行,另一部分学生骑自行车沿相同线路前往,如图,l1、l2分别表示步行和骑车的学生前往目的地所走的路程y(千米)与所用的时间x(分钟)之间的函数图象,给出下列判断:①骑车的学学比步行的学生晚出发30分钟;②步行的速度是每小时6千米;③骑车的学生从出发到追上步行的学生用了20分钟;④骑车的学生和步行的学生同时到达目的地.则正确的判断有个.26.一辆快车从甲地开往乙地,一辆慢车从乙地开往甲地,两车同时出发,分别以各自的速度在甲乙两地间匀速行驶,行驶1小时后,快车司机发现有重要文件遗忘在出发地,便立即返回出发地,拿上文件后(取文件时间不计)立即再从甲地开往乙地,结果快车先到达乙地,慢车继续行驶到甲地.设慢车行驶时间x(h),两车之间的距离为y(km),y与x的函数图象如图所示,则a=.27.甲、乙两车都从同一地点沿同一路线驶向同一目的地,甲车先行,一段时间后,乙车开始行驶,甲车到达目的地后,乙车走完了全程的,下图反应的是从甲车开始行驶到乙车到达目的地整个过程中两车之间的距离与时间的函数关系图象,则a=.28.甲、乙两车同时从A地出发,以各自的速度匀速向B地行驶.甲车先到达B地后,立即按原路以相同速度匀速返回(停留时间不作考虑),直到两车相遇.若甲、乙两车之间的距离y(千米)与两车行驶的时间x(小时)之间的函数图象如图所示,则A、B两地之间的距离为千米.29.甲、乙两车从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,则当乙车到达B城时,甲车离B城的距离为km.30.小明骑自行车从家出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96米/分钟的速度从邮局沿一条道路步行回家,小明在邮局停留2分钟后沿原理以原速返回,设他们出发后经过t分钟时,小明与家之间的距离为S1米,小明爸爸与家之间的距离为S2米,图中折线OABD、线段EF分别是表示S1、S2与t之间函数关系的图象,则小明从家出发,追上爸爸所用的时间是分钟.31.甲、乙两名自行车爱好者准备在一段长为3400m的笔直公路上进行比赛,比赛开始时乙在起点,甲在乙的前面,他们同时出发,匀速前进,已知甲的速度为15m/s,设甲、乙两人之间的距离为y(米),比赛时间为x(秒),图中的折线表示从两人出发至乙先到达终点的过程中y (米)与x(秒)的函数关系,根据图中信息,乙到终点时,甲离终点还有米.32.一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象.当快车到达甲地时,慢车离甲地的距离为千米.33.甲、乙两人同时从A地出发到B地去,已知甲骑自行车,乙步行,甲到达B地后用半小时办完事后按原速返回.甲、乙两人之间的距离y(单位:千米)与行驶时间t(单位:时)之间的函数关系如图所示,则图中a的值是.34.某天,为按计划准点到达指定海域,某巡逻艇凌晨1:00出发,匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达.如图是该艇行驶的路程y(海里)与所用时间t(小时)的函数图象,则该巡逻艇原计划准点到达的时刻是.35.在一平直公路上依次有A、C、B三地,客车、货车分别从A、B两地同时出发,匀速相向行驶.货车2小时可到达途中C站,14小时到达A地,客车需6小时到达C站.已知客车、货车到C站的距离与它们行驶时间x(小时)之间的函数关系如图所示,客车的速度比货车的速度快千米/小时.36.甲乙两人在一笔直的公路上,沿同一方向骑自行车同时出发前往A地,到A地后停止,他们距A地的路程ykm 与甲行驶的时间x小时之间的关系如图所示,则出发小时甲乙二人相距5km.37.已知A、B、C是同一条笔直公路上的三个不同的车站,甲、乙两人分别从A、B车站同时出发,匀速直线运动到C站,到达C站就停下来,甲、乙两人与B站的距离y(千米)与时间x(小时)之间的函数关系的图象如图,当甲出发小时,甲、乙两人相距5千米.38.一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,两车的距离y(千米)与慢车行驶的时间为x(小时)之间的函数关系如图所示,则快车到达乙地时慢车离乙地距离为.39.从甲地到乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即原路返回甲地,途中休息了一段时间,假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比在平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km.设小明出发x h后,到达离甲地y km的地方,图中的折线OABCDE表示y与x之间的函数关系.如果小明两次经过途中某一地点的时间间隔为0.12h,那么该地点离甲地km.40.甲地宏达物流公司的快递车和货车同时从甲地出发,以各自的速度沿快速通道向乙地匀速行驶,快递车到达乙地后,卸完物资并另装货物共用了45分钟,然后按原路以另一速度返回,直至与货车相遇,已知货车行驶速度为60km/h,两车间的距离y(km)与货车行驶时间x(h)之间的函数图象如图所示给出以下四个结论:①快递车从甲地到乙地的速度是100km/h②甲、乙两地之间的距离是80km③图中点B的坐标为(2,35)④快递车从乙地返回时的速度为90km/h其中正确的是(填序号)41.小华和爷爷在一环形跑道上匀速跑步,两人在同一起点顺时针出发,两人离起点较近的环形距离y与时间t之间关系如图所示,出发后小华第一次与爷爷相遇的时间为分.42.某天,小明来到体育馆看球赛,进场时,发现门票还在家里,此时离比赛开始还有25分钟,于是立即步行回家取票.同时,他父亲从家里出发骑自行车以他3倍的速度给他送票,两人在途中相遇,相遇后小明立即坐父亲的自行车赶回体育馆.下图中线段AB、OB分别表示父、子俩送票、取票过程中,离体育馆的路程S(米)与所用时间t(分钟)之间的函数关系,骑自行车和步行的速度始终保持不变,则小明在比赛开始前分钟到达体育馆.43.甲、乙两车从A地出发以各自的速度匀速开往450km外的B地,甲车先行0.5h后乙车出发,乙车到达B地后原地休息.甲、乙两车的距离s与乙车行驶的时间t之间的函数关系如图,则此次行程中,甲、乙两车两次相遇的时间间隔为h.44.如图,已知A地在B地正南方3千米处,甲乙两人同时分别从A、B两地向正北方向匀速直行,他们的距离s (千米)与所用的时间t(小时)之间的函数关系分别如图中的射线OC和ED,当他们行走4小时后,他们之间的距离为千米.45.学校组织学生外出踏青,学生队伍从学校先步行出发,一段时间后王老师从学校骑车追赶学生,追上学生时接到电话要求王老师返回,因此王老师又立即按原速返回,当王老师回到学校时,学生还在继续前行,直到目的地.设王老师和学生队伍间的距离为y米,从王老师出发开始计时,设时间为x分钟,图中折线表示y与x的函数关系,则王老师的速度是米/分.46.在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终到达C港,设甲乙两船行驶的时间为x(h),与B港的距离为y(km),它们间的函数关系如图所示,若两船的距离不超过10km时能够相互望见,则甲乙两船可以互相望见的时间共有小时.47.一次越野跑中,当小明跑了1000米时,小刚跑了800米,小明、小刚在此后所跑的路程y(米)与时间t(秒)之间的函数关系如图所示,则这次越野跑的全程为米.48.如图,小明从A地出发向B地行走,同时小亮从B地出发向A地行走,线段l1,l2分别表示小明、小亮离B 地的距离与已用时间之间的关系,当x=h时,小明与小亮相距7.7km.49.周末,小华骑自行车从家里出发到植物园游玩,从家出发0.5小时后,因自行车损坏修理了一段时间后,按原速前往植物园,小华离家1小时20分钟后,爸爸开车沿相同路线前往植物园,如图是他们离家的路程y(km)与小华离家时间x(h)的函数图象.已知爸爸开车的速度是小华骑车速度的3倍,若爸爸比小华早10分钟到达植物园,则从小华家到植物园的路程是km.50.沿河岸有A,B,C三个港口,甲、乙两船同时分别从A,B港口出发,匀速驶向C港,最终到达C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.考察下列结论:①甲船的速度是25km/h;②从A港到C港全程为120km;③甲船比乙船早1.5小时到达终点;④图中P点为两者相遇的交点,P点的坐标为();⑤如果两船相距小于10km能够相互望见,那么,甲、乙两船可以相互望见时,x的取值范围是<x<2.其中正确的结论有.51.甲乙两地相距50千米,星期天上午8:00小明同学骑山地自行车从甲地前往乙地.2小时后,小明的父亲骑摩托车沿同一路线也从甲地前往乙地,他们行驶的路程y(千米)与小明行驶的时间x(小时)之间的函数关系如图所示,则小明父亲出发小时后,行进中的两车相距24千米.52.某渔船计划从码头出发到指定海域捕鱼,匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该渔船加快速度仍匀速前进,结果恰好准点到达,如图是该渔船行驶的路程y(海里)与所用时间t(小时)的函数图象,则该渔船从码头到捕鱼海域的路程是海里.53.早晨,小刚沿着通往学校唯一的一条路(直路)上学,途中发现忘带饭盒,停下往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即赶往学校,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达学校,小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的函数关系如图,下列四种说法:①打电话时,小刚和妈妈的距离为1250米;②打完电话后,经过23分钟小刚到达学校;③小刚和妈妈相遇后,妈妈回家的速度为150米/分;④小刚家与学校的距离为2550米.其中正确的结论是.54.甲、乙两人都从光明学校出发,去距离光明学校1500m远的篮球馆打球,他们沿同一条道路匀速行走,乙比甲晚出发4min.设甲行走的时间为t(单位:min),甲、乙两人相距y(单位:m),表示y与t的函数关系的图象如图所示,根据图中提供的信息,下列说法:①甲行走的速度为30m/min②乙在距光明学校500m处追上了甲③甲、乙两人的最远距离是480m④甲从光明学校到篮球馆走了30min正确的是(填写正确结论的序号).55.一辆货车从甲地匀速驶往乙地用了2.7小时,到达后用了0.5小时卸货,随即匀速返回,已知货车返回的速度是它从甲地驶往乙地的速度的1.5倍,货车离甲地的距离y(千米)关于时间x(小时)的函数图象如图所示,则a=(小时).56.甲、乙二人从学校出发去科技馆,甲步行一段时间后,乙骑自行车沿相同路线行进,两人均匀速前行,他们的路程差s(米)与甲出发时间t(分)之间的函数关系如图所示.下列说法:①乙先到达青少年宫;②乙的速度是甲速度的2.5倍;③b=480;④a=24.其中正确的是(填序号).57、甲、乙两人骑自行车匀速同向行驶,乙在甲前面100米处,同时出发去距离甲1300米的目的地,其中甲的速度比乙的速度快.设甲、乙之间的距离为米,乙行驶的时间为秒,与之间的关系如图所示.若丙也从甲出发的地方沿相同的方向骑自行车行驶,且与甲的速度相同,当甲追上乙后45秒时,丙也追上乙,则丙比甲晚出发_____▲_____秒.58、如图:小明和小亮同时从学校放学,两人以各自速度匀速步行回家,小明的家在学校的正西方向,小亮的家在学校的正东方向,小明准备一回家就开始做作业,打开书包时发现错拿了小亮的练习册,于是立即跑步去追小亮,终于在途中追上了小亮并交还了练习册,然后再以先前的速度步行回家,(小明在家中耽搁和交还作业的时间忽略不计)结果小明比小亮晚回到家中。
题目一次函数行程问题图象

1. 已知:甲、乙两车分别从相距300千米的A B ,两地同时出发相向而行,甲到B 地后立即返回,下图是它们离各自出发地的距离y (千米)与行驶时间x (小时)之间的函数图象. (1)请直接写出甲、乙两车离各自出发地的距离y (千米)与行驶时间x (小时)之间的函数关系式,并标明自变量x 的取值范围;(2)它们在行驶的过程中有几次相遇?并求出每次相遇的时间.2. 周华早起锻炼,往返于家与体育场之间,离家的距离y (米)与时间x (分)的关系如图所示.回答下列问题:(1)填空:周华从体育场返回的行走速度是 米/分;(2)刘明与周华同时出发,按相同的路线前往体育场,刘明离周华家的距离y (米)与时间x (分)的关系式为400y kx =+.当周华回到家时,刘明刚好到达体育场.①直接在图中画出刘明离周华家的距离y (米)与时间x (分)的函数图象;②填空:周华与刘明在途中共相遇 次;③求周华出发后经过多少分钟与刘明最后一次相遇.3. 2007年4月18日,我国铁路第六次大提速,在甲、乙两城市之间开通了动车组高速列车.已知每隔1h 有一列速度相同的动车组列车从甲城开往乙城.如图所示,OA 是第一列动车组列车离开甲城的路程s (单位:km )与运行时间t (单位:h )的函数图象,BC 是一列从乙城开往甲城的普通快车距甲城的路程s (单位:km )与运行时间t (单位:h )的函数图象.请根据图中信息,解答下列问题:(1)点B 的横坐标0.5的意义是普通快车发车时间比第一列动车组列车发车时间 h ,点B 的纵坐标300的意义是 . (2)请你在原图中直接画出第二列动车组列车离开甲城的路程s (单位:km )与时间t (单位:h )的函数图象.(3)若普通快车的速度为100km/h ,①求BC 的解析式,并写出自变量t 的取值范围. ②求第二列...动车组列车出发后多长时间与普通快车相遇.③直接..写出这列普通快车在行驶途中与迎面而来的相邻两列动车组列车相遇的间隔时间.)x /分y /米 s4. 小明早晨从家里出发匀速步行去上学,小明的妈妈在小明出发后10分钟,发现小明的数学课本没带,于是她带上课本立即匀速骑车按小明上学的路线追赶小明,结果与小明同时到达学校.已知小明在整个上学途中,他出发后t 分钟时,他所在的位置与家的距离为s 千米,且s 与t 之间的函数关系的图像如图中的折线段OA AB -所示.(1)试求折线段OA AB -所对应的函数关系式;(2)请解释图中线段AB 的实际意义; (3)请在所给的图中画出小明的妈妈在追赶小明的过程中,她所在位置与家的距离s (千米)与小明出发后的时间t (分钟)之间函数关系的图像.(友情提醒:请对画出的图像用数据作适当的标注)5. 星期天,小强骑自行车到郊外与同学一起游玩.从家出发2小时到达目的地,游玩3小时后按原路以原速返回,小强离家4小时40分钟后,妈妈驾车沿相同路线迎接小强,如图是他们离家的路程y (千米)与时间x (时)的函数图象.已知小强骑车的速度为15千米/时,妈妈驾车的速度为60千米/时.(1)小强家与游玩地的距离是多少? (2)妈妈出发多长时间与小强相遇?6. 甲、乙二人骑自行车同时从张庄出发,沿同一路线去李庄.甲行驶20分钟因事耽误一会儿,事后继续按原速行驶.下图表示甲、乙二人骑自行车行驶的路程y (千米)随时间x (分)变化的图像(全程),根据图像回答下列问题: (1)乙比甲晚多长时间到达李庄? (2)甲因事耽误了多长时间?(3)x 为何值时,乙行驶的路程比甲行驶的路程多1千米?(分钟))y 甲 乙7. 小王骑车往返于甲、乙两地,距甲地的路程y (千米)与时间x (小时)的函数图象如图所示.(1) 小王在路上停留了______小时,他从乙地返回时骑车的速度为_______千米/时; (2) 小李与小王同时从甲地出发,按相同路线匀速前往乙地,到乙地停止,途中小李与小王共相遇3次,请在图中画出小李距甲地的路程y (千米)与时间x (小时)的函数的大致图象;(3) 小刘与小王同时出发,按相同的路线匀速前往乙地, 距甲地的路程y (千米)与时间x (小时)的函数关系为y =12x +10,小刘与小王在途中共相遇几次?请你计算第一次相遇的时间.(千米)(小时)y 543216050403020108. 2007年5月,第五届中国宜昌长江三峡国际龙舟拉力赛在黄陵庙揭开比赛帷幕.20日上午9时,参赛龙舟从黄陵庙同时出发.其中甲、乙两队在比赛时,路程y (千米)与时间x (小时)的函数关系如图所示.甲队在上午11时30分到达终点黄柏河港.(1)哪个队先到达终点?乙队何时追上甲队? (2)在比赛过程中,甲、乙两队何时相距最远?路程/千米C B A ED40 35 20 16 00.5 1 1.5 2 2.5。
2017重庆中考数学第17题专题复习

2017重庆中考数学第17题专题复习1.(2016贵州黔南)XXX购买一种笔记本,其付款金额y(元)与购买量x(本)之间的函数图象由线段OB和射线BE组成。
求一次购买8个笔记本比分8次购买每次购买1个可节省多少钱。
2.(2016辽宁沈阳)在一条直线上有A、B、C三地,C 地位于A、B两地之间。
甲、乙两车分别从A、B地出发沿直线匀速行至C地停止。
从出发至甲车到达C地过程,甲、乙两车各自与C的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示。
当甲车出发多少小时时,两车相距350km。
3.(2016贵州遵义)如图,四边形ABCD,AB∥CD,∠ADC=90°,P从A出发,以每秒1个位长的速度,按A→B→C→D的顺序在上匀速运动。
设P点的运动时为t秒,△PAD的面积为S,S关于t的函数图象如图所示。
当P运动到C时,△PAD的面积为多少。
4.(2017级南开入学)甲、乙两车分别从A、B两地同时相向匀速行驶。
当乙车到达A地后,继续保持原速原方向向远离B的方向行驶,而甲车到达B地后立即掉头,并保持原速与乙车同向行驶。
经过一段时间后两车同进到达C地。
设两车行驶的时间为x(小时),两车之间的距离为y(千米),y与x之间的函数关系如图所示。
求B、C两地相距多少千米。
5.(2017级南开第一次)今年夏天,重庆各区持续高温日数达到历史之最。
受持续高温和连日无雨的影响,重庆某水库的蓄水量随时间的增加而减少。
已知原有蓄水量y(万m3)与干旱持续时间x(天)的关系如图中线段l1所示。
针对这种干旱情况,从第20天开始向水库注水,注水量y2(万m3)与时间x(天)的关系如图中线段l2所示(不考虑其他因素)。
若总蓄水量不多于900万m3为严重干旱,则该水库发生严重干旱时的天数为多少天。
6.(2016年XXX三模)甲、乙两车分别从A、B两地同时出发,相向而行。
甲车从A地行驶到B地后,立即按原速度返回A地。
乙车从B地行驶到A地,两车到达A地均停止运动。
(完整word版)重庆中考专题训练第17题(行程问题)
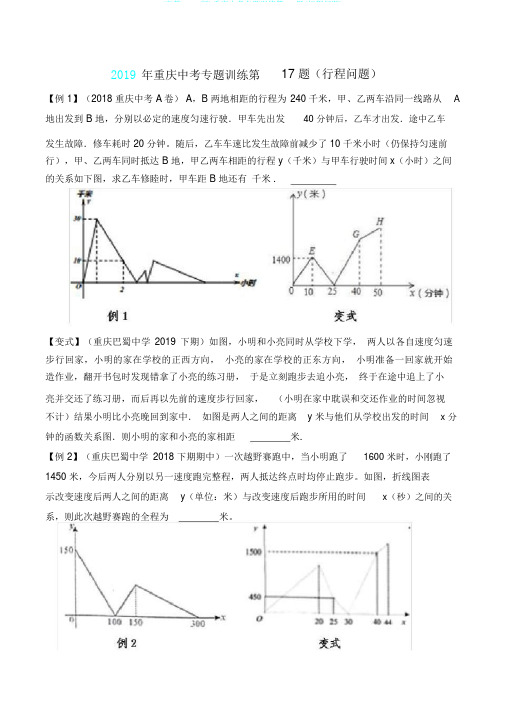
2019年重庆中考专题训练第17 题(行程问题)【例 1】(2018 重庆中考 A卷) A,B 两地相距的行程为 240 千米,甲、乙两车沿同一线路从 A 地出发到 B 地,分别以必定的速度匀速行驶.甲车先出发40 分钟后,乙车才出发.途中乙车发生故障.修车耗时 20 分钟。
随后,乙车车速比发生故障前减少了 10 千米小时(仍保持匀速前行),甲、乙两车同时抵达 B 地,甲乙两车相距的行程 y(千米)与甲车行驶时间 x(小时)之间的关系如下图,求乙车修睦时,甲车距 B 地还有千米 .【变式】(重庆巴蜀中学2019 下期)如图,小明和小亮同时从学校下学,两人以各自速度匀速步行回家,小明的家在学校的正西方向,小亮的家在学校的正东方向,小明准备一回家就开始造作业,翻开书包时发现错拿了小亮的练习册,于是立刻跑步去追小亮,终于在途中追上了小亮并交还了练习册,而后再以先前的速度步行回家,(小明在家中耽误和交还作业的时间忽视不计)结果小明比小亮晚回到家中.如图是两人之间的距离y 米与他们从学校出发的时间x 分钟的函数关系图.则小明的家和小亮的家相距米.【例 2】(重庆巴蜀中学2018 下期期中)一次越野赛跑中,当小明跑了1600 米时,小刚跑了1450 米,今后两人分别以另一速度跑完整程,两人抵达终点时均停止跑步。
如图,折线图表示改变速度后两人之间的距离y(单位:米)与改变速度后跑步所用的时间x(秒)之间的关系,则此次越野赛跑的全程为米。
【变式】(2017 重庆八中 4 月一模)小兵清晨从家匀速步行去学校,走到途中发现数学书忘在家里了,随即打电话给爸爸,爸爸立刻送书去,小兵掉头以原速往回走,几分钟后,经过一家信店,此时还未碰到爸爸,小兵便在书店精选了几支笔,刚付完款,爸爸正好赶到,将书交给了小兵。
而后,小兵以原速持续上学,爸爸也以原速返回家,爸爸到家后,过一会小兵才抵达学校。
两人之间的距离 y(米)与小兵从家出发的时间 x(分钟)的函数关系如下图,则家与学校相距米。
一次函数行程问题

三、跟踪训练
四、课堂总结:
横、纵坐标的意 过
程
速度是关键
注 意
过程
转化线段图
事 项
计算要细心
五、课后巩固
y(米)
A 2500
0 10
D
B 45 C
a x(分钟)
五、课后巩固
《一次函数行程问题》专题复习
初二中 饶建明
一、基础知识
速度、时间、路程之间的关系: 速度×时间=路程
追及问题时间关系:
速度差×时间=路程
相遇问题时间关系:
速度和×时间=路程
二、直击中考
☞题型1“行程问题单线型” 例题:已知A、B两地相距810千米,甲车从A地匀速前往B地,到达B 地后停止.甲车出发1小时后,乙车从B地沿同一公路匀速前往A地,到 达A地后停止.设甲乙两车之间的距离为y(千米),甲车出发的时间为x (小时),y与x的关系如图所示,对于以下说法:①乙车的速度为90 千米/时;②点F的坐标为(9,540);③图中a的值是13.5;④当甲乙两 车相遇时,两车相遇地距A地的距离为360千米.其中正确的结论是 () A.①②③ B. ①②④ C. ②③④ D. ①③④
一次函数行程问题(附答案详细讲解)
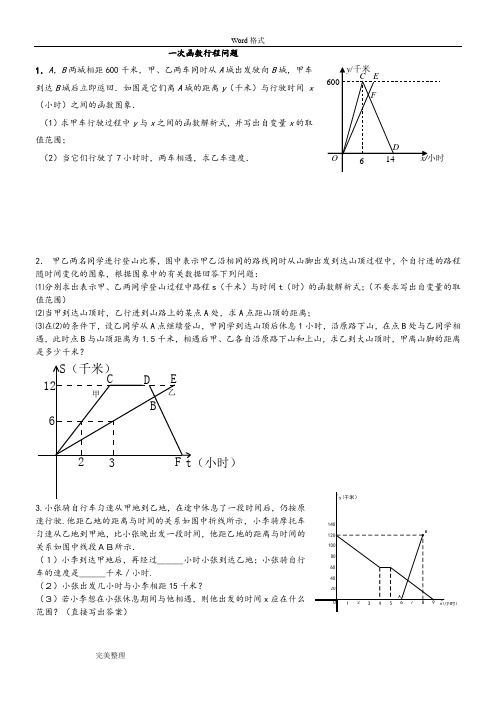
BA O80140120x(小时)1006040y(千米)20987654321一次函数行程问题1.A ,B 两城相距600千米,甲、乙两车同时从A 城出发驶向B 城,甲车到达B 城后立即返回.如图是它们离A 城的距离y (千米)与行驶时间 x (小时)之间的函数图象.(1)求甲车行驶过程中y 与x 之间的函数解析式,并写出自变量x 的取值范围;(2)当它们行驶了7小时时,两车相遇,求乙车速度.2. 甲乙两名同学进行登山比赛,图中表示甲乙沿相同的路线同时从山脚出发到达山顶过程中,个自行进的路程随时间变化的图象,根据图象中的有关数据回答下列问题:⑴分别求出表示甲、乙两同学登山过程中路程s (千米)与时间t (时)的函数解析式;(不要求写出自变量的取值范围)⑵当甲到达山顶时,乙行进到山路上的某点A 处,求A 点距山顶的距离;⑶在⑵的条件下,设乙同学从A 点继续登山,甲同学到达山顶后休息1小时,沿原路下山,在点B 处与乙同学相遇,此时点B 与山顶距离为1.5千米,相遇后甲、乙各自沿原路下山和上山,求乙到大山顶时,甲离山脚的距离是多少千米?12623S(千米)t(小时)CD EF B甲乙3.小张骑自行车匀速从甲地到乙地,在途中休息了一段时间后,仍按原速行驶.他距乙地的距离与时间的关系如图中折线所示,小李骑摩托车匀速从乙地到甲地,比小张晚出发一段时间,他距乙地的距离与时间的关系如图中线段AB所示.(1)小李到达甲地后,再经过___小时小张到达乙地;小张骑自行车的速度是___千米/小时.(2)小张出发几小时与小李相距15千米?(3)若小李想在小张休息期间与他相遇,则他出发的时间x 应在什么范围?(直接写出答案)4.周六上午8:00小明从家出发,乘车1小时到郊外某基地参加社会实践活动,在基地活动2.2小时后,因家里有急事,他立即按原路以4千米/时的平均速度步行返回.同时爸爸开车从家出发沿同一路线接他,在离家28千米处与小明相遇。
2017年重庆市中考数学试卷(b卷)(含答案解析版)

7.( 4 分)若分式 有意义,则 x 的取值范围是(
)
A.x>3 B.x<3C. x≠ 3D.x=3
8.( 4 分)已知△ ABC∽△ DEF,且相似比为 1:2,则△ ABC与△ DEF的面积比
为( )
A.1:4 B.4:1 C.1:2 D.2:1
9.( 4 分)如图,在矩形 ABCD中, AB=4,AD=2,分别以 A、C 为圆心, AD、
第 6 页(共 36 页)
( 1)求直线 AE 的解析式; ( 2)点 P 为直线 CE下方抛物线上的一点,连接 PC,PE.当△ PCE的面积最大 时,连接 CD, CB,点 K 是线段 CB的中点,点 M 是 CP上的一点,点 N 是 CD上 的一点,求 KM+MN+NK 的最小值; ( 3)点 G 是线段 CE的中点,将抛物线 y= x2﹣ x﹣ 沿 x 轴正方向平移得 到新抛物线 y′,y′经过点 D, y′的顶点为点 F.在新抛物线 y′的对称轴上,是否存 在一点 Q,使得△ FGQ为等腰三角形?若存在,直接写出点 Q 的坐标;若不存 在,请说明理由.
第 5 页(共 36 页)
但销售均价比去年减少了 m%,该果农今年运往市场销售的这部分樱桃和枇杷 的销售总金额与他去年樱桃和枇杷的市场销售总金额相同,求 m 的值. 24.( 10 分)如图,△ ABC中,∠ ACB=90°,AC=BC,点 E 是 AC上一点,连接 BE. ( 1)如图 1,若 AB=4 ,BE=5,求 AE 的长; ( 2)如图 2,点 D 是线段 BE延长线上一点,过点 A 作 AF⊥BD于点 F,连接 CD、 CF,当 AF=DF时,求证: DC=BC.
2017 年重庆市中考数学试卷( B 卷)
一、选择题(每小题 4 分,共 48 分)
2017中考数学真题汇编一次函数

( 5) y=x ﹣1.2.若函数 y=(k+1)x+k ﹣1 是正比例函数,则 k 的值为( 2017 中考数学真题汇编 ----一次函数一.选择题1.下列函数中,是一次函数的有()( 1) y=πx ( 2) y=2x ﹣ 1(3)y=(4)y=2﹣3x 2A .4 个B .3 个C .2 个D .1 个2)A .0B .1C .± 1D .﹣ 13.下列关系中的两个量成正比例的是()A .从甲地到乙地,所用的时间和速度B .正方形的面积与边长C .买同样的作业本所要的钱数和作业本的数量D .人的体重与身高4.已知函数 y=(1﹣3m )x 是正比例函数,且 y 随 x 的增大而增大,那么 m 的取值范围是( )A .m >B .m <C .m >1D .m < 15.若 2y+1 与 x ﹣5 成正比例,则(A .y 是 x 的一次函数B .y 与 x 没有函数关系C .y 是 x 的函数,但不是一次函数D .y 是 x 的正比例函数)6.已知函数 y=( m+1)的值是()是正比例函数,且图象在第二、四象限内,则mA .2B .﹣ 2C .± 2D .7.一次函数 y=kx+3 的自变量取值增加 2,函数值就相应减少 2,则 k 的值为()A .2B .﹣ 2C .﹣ 1D .48.y=(m ﹣1)x| m | +3m 表示一次函数,则 m 等于()A .1B .﹣ 1C .0 或﹣ 1D .1 或﹣ 19.下列问题中,是正比例函数的是()y=f ( x ),若已知 f (3x ) =3x +b ,且 f ( 1) =0,则 C .f (x ) =3x ﹣ 3 11.已知 y=(k ﹣1)x+k ﹣1 是正比例函数,则 k= +4x ﹣5(x ≠0)是一次函数.时,函数 y=(m+3) x 15.如果对于一切实数 x ,有 f ( x )=x ﹣2x+5,则 f (x ﹣1)的解析式是18.当 m ,n 为何值时, y=( 5m ﹣ 3)x 19.已知 y=(k ﹣1)x ﹣k 是一次函数.A .矩形面积固定,长和宽的关系B .正方形面积和边长之间的关系C .三角形的面积一定,底边和底边上的高之间的关系D .匀速运动中,速度固定时,路程和时间的关系10.我们可以把一个函数记作 2()A .B .2D .二.填空题2.12.若函数 y=( m+1)x| m | 是正比例函数,则该函数的图象经过第象限.13.当 m=2m +114.下列函数关系式:① y=2x ﹣ 1;②函数的有(填序号);③;④ s=20t .其中表示一次2.16.某商人购货,进价已按原价a 扣去 25%,他希望对货物订一新价格,以便按 新价让利 20%销售后仍可获得 25%的利润,则此商人经营这种货物的件数x 与按 新价让利总额 y 之间的函数关系式为 17.潍坊市出租车计价方式如下:行驶距离在.2.5km 以内(含 2.5km )付起步价6 元,超过 2.5km 后,每多行驶 1km 加收 1.4 元,试写出乘车费用 y (元)与乘车距离 x (km )(x >2.5)之间的函数关系为 三.解答题.2﹣nn 为何值时, y 是关于 x 的正比例函数? | k |( 1)求 k 的值;+( m+n )是关于 x 的一次函数?当 m ,( 2)若点( 2, a )在这个一次函数的图象上,求a 的值.义,我们来证明函数 f (x )=x +1 是偶函数. 20.已知,若函数 y=(m ﹣1)+3 是关于 x 的一次函数( 1)求 m 的值,并写出解析式.( 2)判断点( 1,2)是否在此函数图象上,说明理由.21.已知一次函数y=(2m+4)x+(3﹣n ) ( 1)求 m , n 为何值时,函数是正比例函数? ( 2)求 m , n 是什么数时, y 随 x 的增大而减小? ( 3)若图象经过第一,二,三象限,求m ,n 的取值范围.22.阅读下列材料:现给如下定义:以 x 为自变量的函数用 y=f ( x )表示,对于自变量 x 取值范围内 的一切值,总有f (﹣ x )=f (x )成立,则称函数y=f (x )为偶函数.用上述定 2证明:∵ f (﹣ x )=(﹣ x ) 2+1=x 2+1=f ( x ) ∴ f (x )是偶函数.根据以上材料,解答下面的问题: 已知函数①若 f (x )是偶函数,且,求 f (﹣ 1);②若 a=1,求证: f (x )是偶函数.是 2.若函数 y=(k+1)x+k ﹣1 是正比例函数,则 k 的值为(参考答案与解析一.选择题1.下列函数中,是一次函数的有()( 1) y=πx ( 2) y=2x ﹣ 1(3)y=(4)y=2﹣3x( 5) y=x 2﹣1.A .4 个B .3 个C .2 个D .1 个【分析】 根据一次函数的定义对各选项进行逐一分析即可. 【解答】 解:(1)y=πx 一次函数; ( 2) y=2x ﹣1 是一次函数;( 3) y= 是反比例函数,不是一次函数; ( 4) y=2﹣ 3x 是一次函数;( 5) y=x 2﹣1 是二次函数,不是一次函数. 是一次函数的有 3 个. 故选: B .【点评】 本题考查的是一次函数的定义,即一般地,形如 是常数)的函数,叫做一次函数.2y=kx+b ( k ≠0, k 、b)A .0B .1C .± 1D .﹣ 1【分析】 先根据正比例函数的定义列出关于k 的方程组,求出 k 的值即可. 【解答】 解:∵函数 y=(k+1)x+k 2﹣ 1 是正比例函数, ∴ 解得 k=1. 故选 B .,【点评】 本题考查的是正比例函数的定义,即形如 函数.y=kx ( k ≠ 0)的函数叫正比例 3.下列关系中的两个量成正比例的是(A .从甲地到乙地,所用的时间和速度)B 、根据面积 =边长 ,不是正比例函数,故本选项错误; B .正方形的面积与边长C .买同样的作业本所要的钱数和作业本的数量D .人的体重与身高【分析】 根据正比例函数的定义计算.【解答】 解: A 、从甲地到乙地,所用的时间和速度,用关系式表达为 是正比例函数,故本选项错误;2s=vt ,不C 、买同样的作业本所要的钱数和作业本的数量,是正比例函数, 故本选项正确;D 、人的体重与身高不成正比例关系,故本选项错误.故选 C .【点评】 本题主要考查正比例函数的定义:一般地,两个变量x ,y 之间的关系式可以表示成形如 y=kx ( k 为常数,且 k ≠0)的函数,那么 y 就叫做 x 的正比例 函数.4.已知函数 y=(1﹣3m )x 是正比例函数,且 y 随 x 的增大而增大,那么 m 的 取值范围是()A .m >B .m <C .m >1D .m <1【分析】 先根据正比例函数的性质列出关于m 的不等式,求出 m 的取值范围即 可.【解答】 解:∵正比例函数 y=(1﹣3m )x 中, y 随 x 的增大而增大, ∴ 1﹣ 3m > 0,解得 m < . 故选: B .【点评】 本题考查的是正比例函数的性质,即正比例函数 > 0 时, y 随 x 的增大而增大.y=kx (k ≠0)中,当 k5.若 2y+1 与 x ﹣5 成正比例,则(A .y 是 x 的一次函数B .y 与 x 没有函数关系C .y 是 x 的函数,但不是一次函数)( m ﹣3=1, m+1<0,进而得出即可.D .y 是 x 的正比例函数【分析】 根据 2y+1 与 x ﹣5 成正比例可得出 2y+1=k (x ﹣5) k ≠ 0),据此可得出 结论.【解答】 解:∵ 2y+1 与 x ﹣5 成正比例, ∴ 2y+1=k ( x ﹣ 5)(k ≠0), ∴ y= x ﹣,∴ y 是 x 的一次函数. 故选 A .【点评】 本题考查的是正比例函数的定义,熟知一般地,形如y=kx ( k 是常数,k ≠0)的函数叫做正比例函数,其中k 叫做比例系数是解答此题的关键.6.已知函数 y=( m+1)的值是()A .2B .﹣ 2C .± 2D .是正比例函数,且图象在第二、四象限内,则m【分析】 根据正比例函数的定义得出 【解答】 解:∵函数 y=( m+1) ∴ m 2﹣3=1, m+1<0, 解得: m=±2, 则 m 的值是﹣ 2. 故选: B .2是正比例函数,且图象在第二、四象限内,【点评】 此题主要考查了正比例函数的定义以及其性质,得出 题关键.m+1 的符号是解7.一次函数 y=kx+3 的自变量取值增加 2,函数值就相应减少 2,则 k 的值为()A .2B .﹣ 2C .﹣ 1D .4【分析】 先根据自变量取值增加 2,函数值就相应减少 2,得到 ka+3﹣ [ k (a+2) +3] =2,据此求得 k 的值.【解答】 解:当 x=a 时, y=ka+3,B 、∵ S=a ,∴正方形面积和边长是二次函数,故本选项错误;当 x=a+2 时, y=k (a+2)+3, ∵ ka+3﹣[ k (a+2)+3] =2, ∴ ka+3﹣[ ka+2k+3] =2, ∴﹣ 2k=2, ∴ k=﹣1, 故选: C .【点评】本题考查了一次函数的定义以及待定系数法的运用, 上的点满足函数解析式.注意理解函数解析8.y=(m ﹣1)x| m |+3m 表示一次函数,则 m 等于()A .1B .﹣ 1C .0 或﹣ 1D .1 或﹣ 1【分析】 根据一次函数的定义,自变量x 的次数为 1,一次项系数不等于 0 列式 解答即可.【解答】 解:由题意得, | m| =1 且 m ﹣ 1≠ 0, 解得 m=±1 且 m ≠1, 所以, m=﹣1. 故选 B .【点评】 本题主要考查了一次函数的定义,一次函数 b 为常数, k ≠0,自变量次数为 1.y=kx+b 的定义条件是: k 、9.下列问题中,是正比例函数的是()A .矩形面积固定,长和宽的关系B .正方形面积和边长之间的关系C .三角形的面积一定,底边和底边上的高之间的关系D .匀速运动中,速度固定时,路程和时间的关系【分析】 根据正比例函数的定义对各选项进行逐一分析即可.【解答】 解: A 、∵ S=ab ,∴矩形的长和宽成反比例,故本选项错误; 2C 、∵ S= ah ,∴三角形的面积一定,底边和底边上的高是反比例关系,故本选y=f ( x ),若已知 f (3x ) =3x +b ,且 f ( 1) =0,则 C .f (x ) =3x ﹣ 3 【分析】 将 x=1 代入 f (3x )=3x +b 可以求得 b=﹣ 3,然后将 3x 代入四个答案验 11.已知 y=(k ﹣1)x+k ﹣1 是正比例函数,则 k= ﹣ 1 【解答】 解:∵ y=(k ﹣1)x+k ﹣1 是正比例函数, 项错误;D 、∵ S=vt ,∴速度固定时,路程和时间是正比例关系,故本选项正确.故选 D .【点评】 本题考查的是正比例函数的定义,即一般地,形如 ≠ 0)的函数叫做正比例函数.y=kx ( k 是常数, k10.我们可以把一个函数记作 2()A .B .2D .2证即可得到答案.【解答】 解:∵ f (3x ) =3x 2+b= (3x ) 2+b ∴ f (x )= x 2+b , ∵ f (1)=0, ∴ ×12+b=0, 解得 b=﹣ , ∴ f (x )= x 2﹣ . 故选 A .【点评】本题考查了函数的关系式, 解题的关键是对函数关系式进行正确的变形.二.填空题2【分析】 让 x 的系数不为 0,常数项为 0 列式求值即可. 2∴ k ﹣ 1≠0,k 2﹣ 1=0, 解得 k ≠1,k=± 1,∴ k=﹣1,.+4x ﹣ 5( x ≠0)是一次函时,函数 y=(m+3)x 【解答】 解:①由 y=( m+3)x 时, y=(m ﹣3)x 2m 1+4x ﹣5 是一次函数.故答案为﹣ 1.【点评】 考查正比例函数的定义:一次项系数不为0,常数项等于 0.| m |12.若函数 y=(m+1) x是正比例函数,则该函数的图象经过第一、三象限.【分析】 根据一次函数定义可得: | m| =1,且 m+1≠0,计算出 m 的值,再根据 一次函数的性质进而可得答案.【解答】 解:由题意得: | m| =1,且 m+1≠0, 解得: m=1, 则 m+1=2>0,则该函数的图象经过第一、三象限, 故答案为:一、三.【点评】此题主要考查了正比例函数定义和性质,关键是掌握正比例函数是一次 函数,因此自变量的指数为1.13.当 m=﹣3,0,﹣2m +1 数.【分析】 根据二次项的系数为零,可得一次函数.m+3=0. 解得 m=﹣3;2m +1+4x ﹣5(x ≠0)是一次函数,得 ②,解得 m=0;③ 2m+1=0,解得: m=﹣ ; 综上所述,当 m=﹣3,0,﹣ 故答案为:﹣ 3,0,﹣ .+【点评】 本题考查了一次函数的定义,一次函数常数, k ≠0,自变量次数为 1.y=kx+b 的定义条件是: k 、b 为x ,有 f (x )=x ﹣2x+5,则 f ( x ﹣ 1)的解析式是 ﹣ 1) =x ﹣ 4x+8 【解答】 解:∵ f (x )=x ﹣2x+5,∴ f (x ﹣1)=(x ﹣1) ﹣ 2( x ﹣ 1) +5=x ﹣4x+8. 14.下列函数关系式:① y=2x ﹣ 1;②;③;④ s=20t .其中表示一次函数的有①②④(填序号)【分析】 根据一次函数和反比例函数的定义可找出: 函数有③.此题得解.一次函数有①②④; 反比例 【解答】 解:一次函数有:① y=2x ﹣1、②、④ s=20t 是一次函数;反比例函数有:③ 故答案为:①②④.【点评】本题考查了一次函数的定义以及反比例函数的定理, 函数的定义是解题的关键.牢记一次(反比例)15.如果对于一切实数 2.2f (x 【分析】 将( x ﹣1)当作自变量代入 f (x )的函数解析式即可得出答案. 22 2故答案为: f ( x ﹣1)=x 2﹣4x+8.【点评】 此题考查了函数关系式的知识, 解答本题关键是理解自变量的含义, ( x ﹣1)当作自变量代入.将 16.某商人购货,进价已按原价a 扣去 25%,他希望对货物订一新价格,以便按 新价让利 20%销售后仍可获得 25%的利润,则此商人经营这种货物的件数x 与按 新价让利总额 y 之间的函数关系式为y= x.【分析】 根据题意得出:新价让利总额=新价× 20%×售出件数,进而得出等量 关系.【解答】 解:设新价为 b 元,则销售价为:(1﹣20%)b ,进价为 a ( 1﹣ 25%), 则( 1﹣20%)b ﹣( 1﹣ 25%)a 是每件的纯利,∴ b ( 1﹣ 20%)﹣ a (1﹣25%)=b ( 1﹣ 20%)× 25%,化简得: b= a ,18.当 m ,n 为何值时, y=( 5m ﹣ 3)x 【解答】 解:若 y=(5m ﹣3)x 2 n +(m+n )是关于 x 的一次函数, 所以当 m ≠ 且 n=1 时, y=(5m ﹣3)x 2 n +(m+n )是关于 x 的一次函数.若 y=(5m ﹣ 3) x 2 n+( m+n )是关于 x 的正比例函数, 所以当 m=﹣ 1 且 n=1 时, y=( 5m ﹣ 3) x 2 n +(m+n )是关于 x 的正比例函数. ∴ y=b?20%?x= a?20%?x , 即 y= x .故答案为: y= x .【点评】此题主要考查了函数关系式的应用, 得出进件与利润之间的关系是解题 关键.17.潍坊市出租车计价方式如下:行驶距离在2.5km 以内(含 2.5km )付起步价6 元,超过 2.5km 后,每多行驶 1km 加收 1.4 元,试写出乘车费用 y (元)与乘 车距离 x (km )(x >2.5)之间的函数关系为1.4x+2.5.【分析】 根据乘车费用 =起步价 +超过 2.5km 的付费得出.【解答】 解:依题意有: y=6+1.4(x ﹣2.5)=6+1.4x ﹣ 1.4× 2.5=1.4x+2.5, 故答案为: 1.4x+2.5.【点评】此题考查的知识点是函数关系式, 找到所求量的等量关系是解决问题的 关键.本题乘车费用 =起步价 +超过 3 千米的付费.三.解答题2﹣n+( m+n )是关于 x 的一次函数?当 m , n 为何值时, y 是关于 x 的正比例函数?【分析】 根据一次函数的定义,正比例函数的定义求解即可.﹣则有解得﹣﹣则有解得﹣【点评】 本题考查了正比例函数, 利用一次函数的定义、 正比例函数的定义求解是解题关键.| k|19.已知y=(k﹣1)x﹣k是一次函数.(1)求k的值;(2)若点(2,a)在这个一次函数的图象上,求a的值.【分析】(1)由一次函数的定义可知:k﹣1≠0且| k| =1,从而可求得k的值;(2)将点的坐标代入函数的解析式,从而可求得a的值.【解答】解:(1)∵y是一次函数,∴| k| =1,解得k=±1.又∵k﹣1≠0,∴k≠1.∴k=﹣1.(2)将k=﹣1代入得一次函数的解析式为y=﹣2x+1.∵(2,a)在y=﹣2x+1图象上,∴a=﹣4+1=﹣3.依据一次函数的定义求得k的值是【点评】本题主要考查的是一次函数的定义,解题的关键.20.已知,若函数y=(m﹣1)+3是关于x的一次函数(1)求m的值,并写出解析式.(2)判断点(1,2)是否在此函数图象上,说明理由.【分析】(1)根据一次函数的定义,可得答案;(2)根据点的坐标满足函数解析式,点在函数图象上,可得答案.【解答】解:(1)由y=(m﹣1)+3是关于x的一次函数,得,解得m=﹣1,函数解析式为y=﹣2x+3(2)将x=1代入解析式得y=1≠2,故不在函数图象上.【点评】本题主要考查了一次函数的定义,一次函数y=kx+b的定义条件是:k、b为常数,k≠0,自变量次数为1.证明:∵ f (﹣ x )=(﹣ x ) +1=x +1=f ( x ) 21.已知一次函数y=(2m+4)x+(3﹣n ) ( 1)求 m , n 为何值时,函数是正比例函数? ( 2)求 m , n 是什么数时, y 随 x 的增大而减小? ( 3)若图象经过第一,二,三象限,求m ,n 的取值范围. 【分析】(1)根据正比例函数的定义来求出 ( 2)根据一次函数的性质即可得出结论;m ,n 的值即可; ( 3)根据一次函数所经过的象限判定m , n 的取值范围. 【解答】 解:(1)依题意得: 2m+4≠ 0,且 3﹣n=0, 解得 m ≠﹣ 2,且 n=3;( 2)依题意得: 2m+4<0,且 3﹣n 是任意实数. 解得 m <﹣ 2,n 是任意实数;( 3)∵一次函数y=(2m+4) x+(3﹣n )的图象经过第一,二,三象限, ∴ 2m+4>0 且 3﹣n > 0, 解得 m >﹣ 2,n <3.【点评】本题考查的是一次函数的定义和正比例函数的性质,解题的关键是熟悉函数图象与系数的关系.22.阅读下列材料:现给如下定义:以 x 为自变量的函数用 y=f ( x )表示,对于自变量 x 取值范围内 的一切值,总有f (﹣ x )=f (x )成立,则称函数y=f (x )为偶函数.用上述定义,我们来证明函数 f (x )=x 2+1 是偶函数.2 2∴ f (x )是偶函数.根据以上材料,解答下面的问题: 已知函数①若 f (x )是偶函数,且,求 f (﹣ 1);②若 a=1,求证: f (x )是偶函数.【分析】 ①根据偶函数定义, f (﹣ 1)=f ( 1),进行求解即可;②把 a=1 代入,求出 f (﹣ x )的表达式,整理后再与 f (x )进行比较即可进行判断.【解答】解:①∵f(x)是偶函数,f(1)=,∴f(﹣1)=f(1)=;②证明:a=1时,f(﹣x)=﹣x(+),=﹣x(+),=x(=x(=f(x),﹣+),),即对于自变量x取值范围内的一切值,总有∴f(x)是偶函数.f(﹣x)=f(x)成立,【点评】本题考查了偶函数的概念,读懂题目信息,整理出解题的关键.f(﹣x)的表达式是。
2017重庆中考数学第17题专题复习

2017重庆中考数学第17题专题复习1、(2016贵州黔南)如图,小明购买一种笔记本所付款金额y(元)与购买量x(本)之间的函数图象由线段OB和射线BE组成,则一次购买8个笔记本比分8次购买每次购买1个可节省_______。
2、(2016辽宁沈阳)在一条直公上有A,B,C三地,C地位于A、B两地之间,甲、乙两车分别从A,B地出发沿条匀速行至C地停止.从出发至甲车到达C地过程,甲、乙两车各自C 的距离y(km)与甲车行驶时间t(h)之间的函数关系如图,当甲车出发_____h时,两车相距350km。
2、(2016贵州遵义)如图①,四边形ABCD,AB∥CD,∠ADC=90°,P从A出发,以每秒1个位长的速,按A→B→C→D的顺序在上匀速运动,设P点的运动时为t秒,△PAD的面积为S,S关于t的函数图象如图②所示,当P运动到C时,△PAD的面积为_________.4、(2017级南开入学)甲、乙两车分别从A ,B 两地同时相向匀速行驶,当乙车到达A 地后,继续保持原速原方向向远离B 的方向行驶,而甲车到达B 地后立即掉头,并保持原速与乙车同向行驶,经过一段时间后两车同进到达C 地。
设两车行驶的时间为x (小时),两车之间的距离为y (千米),y 与x 之间的函数关系如图所示,则B 、C 两地相距________千米。
5、(2017级南开第一次)今年夏天,重庆各区持续高温日数达到历史之最,受持续高温和连日无雨的影响,重庆某水库的蓄水量随时间的增加而减少,已知原有蓄水量y 1(万m 3)与干旱持续时间x (天)的关系如图中线段l 1所示,针对这种干旱情况,从第20天开始向水库注水,注水量y 2(万m 3)与时间x (天)的关系如图中线段l 2所示(不考虑其他因素)。
若总蓄水量不多于900m 3万为严重干旱,则该水库发生严重干旱时的天数为_________天6、(2016年重庆一中三模)甲、乙两车分别从A 、B 两地同时出发,相向而行,甲车从A 地行驶到B 地后,立即按原速度返回A 地,乙车从B 地行驶到A 地,两车到达A 地均停止运动。
重庆中考17题----行程问题

重庆中考17题----行程问题1.甲、乙两车分别从A,B两地同时相向匀速行驶.当乙车到达A地后,继续保持原速向远离B的方向行驶,而甲车到达B地后立即掉头,并保持原速与乙车同向行驶,经过一段时间后两车同时到达C地.设两车行驶的时间为x(小时),两车之间的距离为y(千米),y与x之间的函数关系如图所示,则B,C两地相距千米.2.甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:①A,B两城相距300千米;②乙车比甲车晚出发1小时,却早到1小时;③乙车出发后2小时追上甲车;④当甲、乙两车相距50千米时,t=或.其中正确的结论有.3.甲乙两地相距50千米.星期天上午8:00小聪同学在父亲陪同下骑山地车从甲地前往乙地.2小时后,小明的父亲骑摩托车沿同一路线也从甲地前往乙地,他们行驶的路程y(千米)与小聪行驶的时间x(小时)之间的函数关系如图所示,小明父亲出发小时时,行进中的两车相距8千米.4.点A、B、C表示同一笔直公路上的三个不同的车站,甲,乙两人分别从A、B车站同时出发,匀速直线运动到C站,到达C站就停下来.甲、乙两人与B站的距离y(千米)与时间(小时)之间的函数关系如图所示,则当甲出发小时时,甲乙两人距离为5千米.5.A、B两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入(城区与入口的距离忽略不计),并始终在高速公路上正常行驶.甲车驶往B城,乙车驶往A城,已知甲车以90千米/时的速度匀速行驶.两车之间的距离s(千米)与行驶时间x(小时)之间的关系如图.给出下列结论:①A、B两城相距300千米②乙车与甲车相遇之前速度为60千米/时③C点的横坐标为④两车相遇时距离A城180千米⑤乙车与甲车相遇后,速度改为90千米/时以上结论中正确的是(填序号)6.某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后缷完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下4个结论:①快递车从甲地到乙地的速度为100千米/时;②甲、乙两地之间的距离为120千米;③图中点B的坐标为(3,75);④快递车从乙地返回时的速度为90千米/时,以上4个结论正确的是.7.在同一条直线上依次有A、B、C三地,甲、乙二人同时分别从A、B两地同向去C地,若甲、乙二人x小时候与B地的距离分别为y1千米、y2千米,且其图象如图所示,则甲、乙相遇时,甲走了千米.8.一名考生步行前往考场,10分钟走了总路程的,估计步行不能准时到达,于是他改乘出租车赶往考场,他的行程与时间关系如图所示(假定总路程为1),则他到达考场所花的时间比一直步行提前了分钟.9.李明骑自行车去上学途中,经过先上坡后下坡的一条路段,在这段路上所走的路程s(米)与时间t(分钟)之间的函数关系如图所示,若李明放学后按原路返回,且往返过程中,上坡的速度相同,下坡的速度也相同,问李明返回时走这段路所用的时间为分钟.10.学生甲、乙两人跑步的路程s与所用时间t的函数关系图象表示如图(甲为实线,乙为虚线).根据图象判断:如果两人进行一百米赛跑,当甲跑到终点时,乙落后甲米.11.2006年5月29日﹣6月1日,“国际龙舟节”在岳阳汩罗江举行.某龙舟队在1000米比赛项目中,路程y(米)与时间x(分钟)之间的函数图象如图所示.根据图中提供的信息,该龙舟队的比赛成绩是分钟.12.某人从甲地出发,骑摩托车去乙地,途中因车出现故障而停车修理,到达乙埋正好用了2小时,已知摩托车行驶的路程S(千米)与行驶的时间t(小时)之间的函数关系由如图的图象ABCD给出,若这辆摩托车平均每行驶100千米的耗油量为2升,根据图中给出的信息,从甲地到乙地,这辆摩托车共耗油量升.13.甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则下列结论:(1)a=40,m=1;(2)乙的速度是80km/h;(3)甲比乙迟h到达B地;(4)乙车行驶小时或小时,两车恰好相距50km.正确的个数是()A.1 B.2 C.3 D.414.甲、乙两人从科技馆出发,沿相同的路线分别以不同的速度匀速跑向极地馆,甲先跑一段路程后,乙开始出发,当乙超出甲150米时,乙停在此地等候甲,两人相遇后乙又继续以原来的速度跑向极地馆.如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)的函数图象.则下列四种说法:①甲的速度为1.5米/秒;②a=750;③乙在途中等候甲100秒;④乙出发后第一次与甲相遇时乙跑了375米.其中正确的个数是()A.1个B.2个C.3个D.4个15.小明家、公交车站、学校在一条笔直的公路旁(小明家、学校到这条公路的距离忽略不计),一天,小明从家出发去上学,沿这条公路步行到公交车站恰好乘上一辆公交车,公交车沿这条公路匀速行驶,小明下车时发现还有4分钟上课,于是他沿这条公路跑步赶到学校(上、下车时间忽略不计),小明与家的距离s(单位:米)与他所用时间t(单位:分钟)之间的函数关系如图所示,已知小明从家出发7分钟时与家的距离为1200米,从上公交车到他到达学校共用10分钟,下列说法:①小明从家出发5分钟时乘上公交车②公交车的速度为400米/分钟③小明下公交车后跑向学校的速度为100米/分钟④小明上课没有迟到其中正确的个数是()A.1个B.2个C.3个D.4个16.一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后分别按原速同时驶往甲地,两车之间的距离S(km)与慢车行驶时间t(h)之间的函数图象如图所示,下列说法:①甲、乙两地之间的距离为560km;②快车速度是慢车速度的1.5倍;③快车到达甲地时,慢车距离甲地60km;④相遇时,快车距甲地320km其中正确的个数是()A.1个B.2个C.3个D.4个17.一辆货车从A地开往B地,一辆小汽车从B地开往A地.同时出发,都匀速行驶,各自到达终点后停止.设货车、小汽车之间的距离为s(千米),货车行驶的时间为t(小时),S与t之间的函数关系如图所示.下列说法中正确的有()①A、B两地相距60千米:②出发1小时,货车与小汽车相遇;③出发1.5小时,小汽车比货车多行驶了60千米;④小汽车的速度是货车速度的2倍.A.1个B.2个C.3个D.4个18.为增强学生体质,某中学在体育课中加强了学生的长跑训练.在一次女子800米耐力测试中,小静和小茜在校园内200米的环形跑道上同时起跑,同时到达终点;所跑的路程S(米)与所用的时间t(秒)之间的函数图象如图所示,则她们第一次相遇的时间是起跑后的第秒.19.在一条笔直的公路上有A,B,C三地,C地位于A,B两地之间,甲,乙两车分别从A,B两地出发,沿这条公路匀速行驶至C地停止.从甲车出发至甲车到达C地的过程,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图表示,当甲车出发h时,两车相距350km.20.一辆汽车由A地开往B地,它距离B地的路程s(km)与行驶时间t(h)的关系如图所示,如果汽车一直快速行驶,那么可以提前小时到达B地.21.甲、乙两人在直线道路上同起点、同终点、同方向,分别以不同的速度匀速跑步1500米,先到终点的人原地休息,已知甲先出发30秒后,乙才出发,在跑步的整个过程中,甲、乙两人的距离y(米)与甲出发的时间x(秒)之间的关系如图所示,则乙到终点时,甲距终点的距离是米.22.如图,在一次自行车越野赛中,甲、乙两名选手所走的路程y(千米)随时间x(分钟)变化的图象(全程)分别用实线(O→A→B→C)与虚线(OD)表示,那么,在本次比赛过程中,乙领先甲时的x的取值范围是.23.设甲、乙两车在同一直线公路上相向匀速行驶,相遇后两车停下来,把乙车的货物卸到甲车用了100秒,然后两车分别按原路原速返回.设x秒后两车之间的距离为y米,y关于x的函数关系如图所示,则a=米.24.小丽的家和学校在一条笔直的马路旁,某天小丽沿着这条马路上学,先从家步行到公交站台甲,再乘车到公交站如乙下车,最后步行到学校(在整个过程中小丽步行的速度不变).图中折线ABCDE表示小丽和学校之间的距离y(米)与她离家时间x(分钟)之间的函数关系.(1)小丽步行的速度为;(2)写出y与x之间的函数关系式:.25.某校八年级的学生到距学校6千米的郊外旅游,一部分学生步行,另一部分学生骑自行车沿相同线路前往,如图,l1、l2分别表示步行和骑车的学生前往目的地所走的路程y(千米)与所用的时间x(分钟)之间的函数图象,给出下列判断:①骑车的学学比步行的学生晚出发30分钟;②步行的速度是每小时6千米;③骑车的学生从出发到追上步行的学生用了20分钟;④骑车的学生和步行的学生同时到达目的地.则正确的判断有个.26.一辆快车从甲地开往乙地,一辆慢车从乙地开往甲地,两车同时出发,分别以各自的速度在甲乙两地间匀速行驶,行驶1小时后,快车司机发现有重要文件遗忘在出发地,便立即返回出发地,拿上文件后(取文件时间不计)立即再从甲地开往乙地,结果快车先到达乙地,慢车继续行驶到甲地.设慢车行驶时间x(h),两车之间的距离为y(km),y与x的函数图象如图所示,则a=.27.甲、乙两车都从同一地点沿同一路线驶向同一目的地,甲车先行,一段时间后,乙车开始行驶,甲车到达目的地后,乙车走完了全程的,下图反应的是从甲车开始行驶到乙车到达目的地整个过程中两车之间的距离与时间的函数关系图象,则a=.28.甲、乙两车同时从A地出发,以各自的速度匀速向B地行驶.甲车先到达B地后,立即按原路以相同速度匀速返回(停留时间不作考虑),直到两车相遇.若甲、乙两车之间的距离y(千米)与两车行驶的时间x(小时)之间的函数图象如图所示,则A、B两地之间的距离为千米.29.甲、乙两车从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,则当乙车到达B城时,甲车离B城的距离为km.30.小明骑自行车从家出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96米/分钟的速度从邮局沿一条道路步行回家,小明在邮局停留2分钟后沿原理以原速返回,设他们出发后经过t分钟时,小明与家之间的距离为S1米,小明爸爸与家之间的距离为S2米,图中折线OABD、线段EF分别是表示S1、S2与t之间函数关系的图象,则小明从家出发,追上爸爸所用的时间是分钟.31.甲、乙两名自行车爱好者准备在一段长为3400m的笔直公路上进行比赛,比赛开始时乙在起点,甲在乙的前面,他们同时出发,匀速前进,已知甲的速度为15m/s,设甲、乙两人之间的距离为y(米),比赛时间为x(秒),图中的折线表示从两人出发至乙先到达终点的过程中y (米)与x(秒)的函数关系,根据图中信息,乙到终点时,甲离终点还有米.32.一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象.当快车到达甲地时,慢车离甲地的距离为千米.33.甲、乙两人同时从A地出发到B地去,已知甲骑自行车,乙步行,甲到达B地后用半小时办完事后按原速返回.甲、乙两人之间的距离y(单位:千米)与行驶时间t(单位:时)之间的函数关系如图所示,则图中a的值是.34.某天,为按计划准点到达指定海域,某巡逻艇凌晨1:00出发,匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达.如图是该艇行驶的路程y(海里)与所用时间t(小时)的函数图象,则该巡逻艇原计划准点到达的时刻是.35.在一平直公路上依次有A、C、B三地,客车、货车分别从A、B两地同时出发,匀速相向行驶.货车2小时可到达途中C站,14小时到达A地,客车需6小时到达C站.已知客车、货车到C站的距离与它们行驶时间x(小时)之间的函数关系如图所示,客车的速度比货车的速度快千米/小时.36.甲乙两人在一笔直的公路上,沿同一方向骑自行车同时出发前往A地,到A地后停止,他们距A地的路程ykm 与甲行驶的时间x小时之间的关系如图所示,则出发小时甲乙二人相距5km.37.已知A、B、C是同一条笔直公路上的三个不同的车站,甲、乙两人分别从A、B车站同时出发,匀速直线运动到C站,到达C站就停下来,甲、乙两人与B站的距离y(千米)与时间x(小时)之间的函数关系的图象如图,当甲出发小时,甲、乙两人相距5千米.38.一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,两车的距离y(千米)与慢车行驶的时间为x(小时)之间的函数关系如图所示,则快车到达乙地时慢车离乙地距离为.39.从甲地到乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即原路返回甲地,途中休息了一段时间,假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比在平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km.设小明出发x h后,到达离甲地y km的地方,图中的折线OABCDE表示y与x之间的函数关系.如果小明两次经过途中某一地点的时间间隔为0.12h,那么该地点离甲地km.40.甲地宏达物流公司的快递车和货车同时从甲地出发,以各自的速度沿快速通道向乙地匀速行驶,快递车到达乙地后,卸完物资并另装货物共用了45分钟,然后按原路以另一速度返回,直至与货车相遇,已知货车行驶速度为60km/h,两车间的距离y(km)与货车行驶时间x(h)之间的函数图象如图所示给出以下四个结论:①快递车从甲地到乙地的速度是100km/h②甲、乙两地之间的距离是80km③图中点B的坐标为(2,35)④快递车从乙地返回时的速度为90km/h其中正确的是(填序号)41.小华和爷爷在一环形跑道上匀速跑步,两人在同一起点顺时针出发,两人离起点较近的环形距离y与时间t之间关系如图所示,出发后小华第一次与爷爷相遇的时间为分.42.某天,小明来到体育馆看球赛,进场时,发现门票还在家里,此时离比赛开始还有25分钟,于是立即步行回家取票.同时,他父亲从家里出发骑自行车以他3倍的速度给他送票,两人在途中相遇,相遇后小明立即坐父亲的自行车赶回体育馆.下图中线段AB、OB分别表示父、子俩送票、取票过程中,离体育馆的路程S(米)与所用时间t(分钟)之间的函数关系,骑自行车和步行的速度始终保持不变,则小明在比赛开始前分钟到达体育馆.43.甲、乙两车从A地出发以各自的速度匀速开往450km外的B地,甲车先行0.5h后乙车出发,乙车到达B地后原地休息.甲、乙两车的距离s与乙车行驶的时间t之间的函数关系如图,则此次行程中,甲、乙两车两次相遇的时间间隔为h.44.如图,已知A地在B地正南方3千米处,甲乙两人同时分别从A、B两地向正北方向匀速直行,他们的距离s (千米)与所用的时间t(小时)之间的函数关系分别如图中的射线OC和ED,当他们行走4小时后,他们之间的距离为千米.45.学校组织学生外出踏青,学生队伍从学校先步行出发,一段时间后王老师从学校骑车追赶学生,追上学生时接到电话要求王老师返回,因此王老师又立即按原速返回,当王老师回到学校时,学生还在继续前行,直到目的地.设王老师和学生队伍间的距离为y米,从王老师出发开始计时,设时间为x分钟,图中折线表示y与x的函数关系,则王老师的速度是米/分.46.在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终到达C港,设甲乙两船行驶的时间为x(h),与B港的距离为y(km),它们间的函数关系如图所示,若两船的距离不超过10km时能够相互望见,则甲乙两船可以互相望见的时间共有小时.47.一次越野跑中,当小明跑了1000米时,小刚跑了800米,小明、小刚在此后所跑的路程y(米)与时间t(秒)之间的函数关系如图所示,则这次越野跑的全程为米.48.如图,小明从A地出发向B地行走,同时小亮从B地出发向A地行走,线段l1,l2分别表示小明、小亮离B 地的距离与已用时间之间的关系,当x=h时,小明与小亮相距7.7km.49.周末,小华骑自行车从家里出发到植物园游玩,从家出发0.5小时后,因自行车损坏修理了一段时间后,按原速前往植物园,小华离家1小时20分钟后,爸爸开车沿相同路线前往植物园,如图是他们离家的路程y(km)与小华离家时间x(h)的函数图象.已知爸爸开车的速度是小华骑车速度的3倍,若爸爸比小华早10分钟到达植物园,则从小华家到植物园的路程是km.50.沿河岸有A,B,C三个港口,甲、乙两船同时分别从A,B港口出发,匀速驶向C港,最终到达C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.考察下列结论:①甲船的速度是25km/h;②从A港到C港全程为120km;③甲船比乙船早1.5小时到达终点;④图中P点为两者相遇的交点,P点的坐标为();⑤如果两船相距小于10km能够相互望见,那么,甲、乙两船可以相互望见时,x的取值范围是<x<2.其中正确的结论有.51.甲乙两地相距50千米,星期天上午8:00小明同学骑山地自行车从甲地前往乙地.2小时后,小明的父亲骑摩托车沿同一路线也从甲地前往乙地,他们行驶的路程y(千米)与小明行驶的时间x(小时)之间的函数关系如图所示,则小明父亲出发小时后,行进中的两车相距24千米.52.某渔船计划从码头出发到指定海域捕鱼,匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该渔船加快速度仍匀速前进,结果恰好准点到达,如图是该渔船行驶的路程y(海里)与所用时间t(小时)的函数图象,则该渔船从码头到捕鱼海域的路程是海里.53.早晨,小刚沿着通往学校唯一的一条路(直路)上学,途中发现忘带饭盒,停下往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即赶往学校,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达学校,小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的函数关系如图,下列四种说法:①打电话时,小刚和妈妈的距离为1250米;②打完电话后,经过23分钟小刚到达学校;③小刚和妈妈相遇后,妈妈回家的速度为150米/分;④小刚家与学校的距离为2550米.其中正确的结论是.54.甲、乙两人都从光明学校出发,去距离光明学校1500m远的篮球馆打球,他们沿同一条道路匀速行走,乙比甲晚出发4min.设甲行走的时间为t(单位:min),甲、乙两人相距y(单位:m),表示y与t的函数关系的图象如图所示,根据图中提供的信息,下列说法:①甲行走的速度为30m/min②乙在距光明学校500m 处追上了甲③甲、乙两人的最远距离是480m④甲从光明学校到篮球馆走了30min正确的是 (填写正确结论的序号).55.一辆货车从甲地匀速驶往乙地用了2.7小时,到达后用了0.5小时卸货,随即匀速返回,已知货车返回的速度是它从甲地驶往乙地的速度的1.5倍,货车离甲地的距离y (千米)关于时间x (小时)的函数图象如图所示,则a= (小时).56.甲、乙二人从学校出发去科技馆,甲步行一段时间后,乙骑自行车沿相同路线行进,两人均匀速前行,他们的路程差s (米)与甲出发时间t (分)之间的函数关系如图所示.下列说法:①乙先到达青少年宫;②乙的速度是甲速度的2.5倍;③b=480;④a=24.其中正确的是 (填序号).57、甲、乙两人骑自行车匀速同向行驶,乙在甲前面100米处,同时出发去距离甲1300米的目的地,其中甲的速度比乙的速度快.设甲、乙之间的距离为米,乙行驶的时间为秒,与之间的关系如图所示.若丙也从甲出发的地方沿相同的方向骑自行车行驶,且与甲的速度相同,当甲追上乙后45秒时,丙也追上乙,则丙比甲晚出发_____▲_____秒.58、如图:小明和小亮同时从学校放学,两人以各自速度匀速步行回家,小明的家在学校的正西方向,小亮的家在学校的正东方向,小明准备一回家就开始做作业,打开书包时发现错拿了小亮的练习册,于是立即跑步去追小亮,终于在途中追上了小亮并交还了练习册,然后再以先前的速度步行回家,(小明在家中耽搁和交还作业的y x yx时间忽略不计)结果小明比小亮晚回到家中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一次函数行程问题
1、在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时x(h)之间的函数图象,若两人之间保持的距离不超过3km时,能够用无线对讲机保持联系,甲、乙两人能够用无线对讲机保持联系时x围__________
2、甲、乙两车分别从A,B两地同时出发相向而行.并以各自的速度匀速行驶,甲车途经C地时休息一小时,然后按原速度继续前进到达B地;乙车从B地直接到达A地,如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.当两车相距120千米时,乙车行驶了__________小时。
3、甲、乙两名大学生去距学校36千米的某乡镇进行社会调查.他们从学校出发,骑电动车行驶20分钟时发现忘带相机,甲下车前往,乙骑电动车按原路返回.乙取相机后(在学校取相机所用时间忽略不计),骑电动车追甲.在距乡镇13.5千米处追上甲后同车前往乡镇.乙电动车的速度始终不变.设甲与学校相距y甲(千米),乙与学校相离y乙(千米),甲离开学校的时间为x(分钟).y甲、y乙与x之间的函数图象如图所示,结合图象解答下列问题:求乙返回到学校时,甲与学校相距__________km
4、甲、乙两地之间有一条笔直的公路L,小明从甲地出发沿公路L步行前往乙地,同时小亮从乙地出发沿公路L 骑自行车前往甲地,小亮到达甲地停留一段时间,原路原速返回,追上小明后两人一起步行到乙地.设小明与甲地的距离为y1米,小亮与甲地的距离为y2米,小明与小亮之间的距离为s米,小明行走的时间为x分钟.y1、y2与x 之间的函数图象如图1,s与x之间的函数图象(部分)如图2.a=______。
5、2016年秋季,某省部分地区遭受严重的雨雪自然灾害,兴化农场34800亩的农作物面临着收割困难的局面.兴华农场积极想办法,决定采取机械收割和人工收割两种方式同时进行抢收,工作了4天,由于雨雪过大,机械收割
被迫停止,此时,人工收割的工作效率也减少到原来的,第8天时,雨雪停止附近的胜利农场前来支援,合作6
天,完成了兴化农场所有的收割任务.图1是机械收割的亩数y1(亩)和人工收割的亩数y2(亩)与时间x(天)之间的函数图象.图2是剩余的农作物的亩数w(亩)与时间x天之间的函数图象,x=_______时,机械收割的总量是人工收割总量的10倍?
6、甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y (千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.轿车到达乙地后,马上沿原路以CD段速度返回,货车从甲地出发后__ ___小时再与轿车相遇。
7、甲、乙两车从A地将一批物品匀速运往B地,甲出发0.5h后乙开始出发,结果比甲早1h到达B地.如图,线段OP、MN分别表示甲、乙两车离A地的距离S(km)与时间t(h)的关系,乙车到达B地后以原速立即返回,甲车到达B地后以__________km\h速度立即匀速返回,才能与乙车同时回到A地?
8、甲、乙两人从少年宫出发,沿相同的路线分别以不同的速度匀速跑向体育馆,甲先跑一段路程后,乙开始出发,当乙超出甲150米时,乙停在此地等候甲,两人相遇后乙又继续以原来的速度跑向体育馆.如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)的函数图象.甲出发_______秒第一次与乙相遇?此时乙跑了多少米?
9、甲、乙两车在连通A、B、C三地的公路上行驶,甲车从A地出发匀速向C地行驶,同时乙车从C地出发匀速向b 地行驶,到达B地并在B地停留1小时后,按原路原速返回到C地.在两车行驶的过程中,甲、乙两车距B地的路程y(千米)与行驶时间x(小时)之间的函数图象如图所示,请结合图象回答下列问题:
当甲、乙两车行驶到距B地的路程相等时,甲、乙两车距B地__________km
10、邮递员小王从县城出发,骑自行车到A村投递,途中遇到县城中学的学生明从A村步行返校.小王在A村完成投递工作后,返回县城途中又遇到明,便用自行车载上明,一起到城,结果小王比预计时间晚到1分钟.二人与县城间的距离s(千米)和小王从县城出发后所用的时间t(分)之间的函数关系如图,假设二人之间交流的时间忽略不计.明从A村到县城共用分
因长期干旱,甲水库蓄水量降到了正常水位的最低值.为灌溉需要,由乙水库向甲水库匀速供水,20h后,甲水库打开一个排灌闸为农田匀速灌溉,又经过20h,甲水库打开另一个排灌闸同时灌溉,再经过40h,乙水库停止供水.甲水库每个排泄闸的灌溉速度相同,图中的折线表示甲水库蓄水量Q(万m3)与时间t(h)之间的函数关系.乙水库停止供水后,__________h甲水库蓄水量又降到了正常水位的最低值
11、汶川灾后重建工作受到全社会的广泛关注,全国各省对口支援省受灾市县.我省援建剑阁县,建筑物资先用火车源源不断的运往距离剑阁县180千米的市火车站,再由汽车运往剑阁县.甲车在驶往剑阁县的途中突发故障,司机马上通报剑阁县总部并立即检查和维修.剑阁县总部在接到通知后第12分钟时,立即派出乙车前往接应.经过抢修,甲车在乙车出发第8分钟时修复并继续按原速行驶,两车在途中相遇.为了确保物资能准时运到,随行人员将物资全部转移到乙车上,乙车按原速原路返回,并按预计时间准时到达剑阁县.下图是甲、乙两车离剑阁县的距离y(千米)与时间x(小时)之间的函数图象.乙车的行驶速度________km/h
12小骑自行车匀速从甲地到乙地,在途中休息了一段时间后,仍按原速行驶.他距乙地的距离与时间的关系如图中折线所示,小骑摩托车匀速从乙地到甲地,比小晚出发一段时间,他距乙地的距离与时间的关系如图中线段AB所示.小想在小休息期间与他相遇,则他出发的时间x取值围__________。
13、快车甲和慢车乙分别从A、B两站同时出发,相向而行.快车到达B站后,停留1小时,然后原路原速返回A 站,慢车到达A站即停运休息.下图表示的是两车之问的距离y(千米)与行驶时间x(小时)的函数图象.请结合图象信息.出发__________小时,两车相距200千米
14、甲乙两名同学进行登山比赛,图中表示甲乙沿相同的路线同时从山脚出发到达山顶过程中,个自行进的路程随时间变化的图象,当甲到达山顶时,乙行进到山路上的某点A处,乙同学从A点继续登山,甲同学到达山顶后休息1小时,沿原路下山,在点B处与乙同学相遇,此时点B与山顶距离为1.5千米,相遇后甲、乙各自沿原路下山和上山,当乙到大山顶时,甲离山脚的距离是__________千米
12
6
23
S(千米)
t(小时)
C D E
F
B
甲乙
15、小聪和小明沿同一条路同时从学校出发到天一阁查阅资料,学校与天一阁的路程是4千米,小聪骑自行车,小
明步行,当小聪从原路回到学校时,小明刚好到达天一阁,图中折线O-A-B-C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系,请根据图象回答下列问题:当小聪与小明迎面相遇时,他们离学校的路程是______千米?
16、周末,小明骑自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.妈妈比小明早10分钟到达乙地家到乙地______km.
17、黄岩岛是我国南沙群岛的一个小岛,渔产丰富.一天某渔船离开港口前往该海域捕鱼.捕捞一段时间后,发现一外国舰艇进入我国水域向黄岩岛驶来,渔船向渔政部门报告,并立即返航,渔政船接到报告后,立即从该港口出发赶往黄岩岛.下图是渔政船及渔船与港口的距离s和渔船离开港口的时间t之间的函数图象.(假设渔船与渔政船沿同一航线航行)在渔政船驶往黄岩岛的过程中,渔船从港口出发 h与渔政船相距30海里?。
