第三章 语法分析(5). pda
pda编译原理

pda编译原理
2. 语法分析:语法分析是将词法单元序列转化为语法结构的过程。在PDA编译原理中, 可以使用上下文无关文法(Context-Free Grammar)和PDA来实现语法分析器,将词法单 元序列转化为语法树或语法分析树。
3. 语义分析:语义分析是对语法结构进行语义检查和语义动作的过程。在PDA编译原理 中,可以使用符号表(Symbol Table)和PDA来实现语义分析器,对语法结构进行类型检查 、计算表达式的值等语义操作。
a编译原理
4. 中间代码生成:中间代码生成是将语法树或语法分析树转化为中间代码的过程。在 PDA编译原理中,可以使用PDA和转换规则来实现中间代码生成器,将语法结构转化为中间 代码表示形式,如三地址码、四元式等。
5. 代码优化:代码优化是对中间代码进行优化的过程,以提高程序的性能和效率。在 PDA编译原理中,可以使用PDA和优化规则来实现代码优化器,对中间代码进行常量折叠、 循环优化、公共子表达式提取等优化操作。
pda编译原理
PDA(Pushdown Automaton)是一种计算模型,它是有限状态自动机(Finite State Automaton)的扩展,具有一个栈(stack)作为额外的存储器。PDA编译原理是指将编译 原理的概念和技术应用于PDA的设计和实现。
PDA编译原理主要涉及以下几个方面:
1. 词法分析:词法分析是将输入的字符序列划分为词法单元(tokens)的过程。在PDA 编译原理中,可以使用正则表达式或有限状态自动机来实现词法分析器,将输入的字符序列 转化为词法单元序列。
pda编译原理
6. 目标代码生成:目标代码生成是将中间代码转化为目标机器代码的过程。在PDA编译 原理中,可以使用PDA和目标机器的指令集来实现目标代码生成器,将中间代码转化为目标 机器代码。
在线分析设备PDA的使用方法1

在线分析设备PDA的使用方法1在线分析设备PDA的使用方法1在线分析设备PDA(Personal Digital Assistant)是一种便携式的电子设备,具有数据收集、处理和传输等功能。
它可以帮助用户更高效地进行数据采集和分析,并提供实时的数据反馈和分析结果。
以下是使用PDA的详细方法:1.掌握PDA的基本功能2.收集和导入数据3.数据处理和分析一旦数据导入到PDA中,可以进行数据处理和分析。
PDA通常提供了多种数据处理和分析方法,如统计分析、图表分析、模型建立等。
用户可以根据分析目的选择适合的方法,并设置相关参数。
在进行数据处理前,建议先备份数据,以防止误操作导致数据丢失。
4.实时监控和反馈在线分析设备PDA具有实时监控功能,可以随时监测数据的变化情况,并提供实时的反馈和预警信息。
用户可以设置监控参数和界限值,一旦数据超过设定的阈值,PDA将通过声音、震动等方式向用户发出警报,以便用户及时采取相应的措施。
5.数据传输和共享PDA可以通过无线网络、蓝牙等方式将数据传输到远程设备或电脑上。
用户可以选择合适的传输方式,并设置传输参数。
在数据传输过程中,保证网络和设备的稳定性,并注意数据的安全性和隐私保护。
此外,PDA还可以支持数据共享和协作,用户可以将数据分享给其他用户进行协同分析。
6.数据存储和管理7.设备维护和更新为了保证PDA的正常运行和性能,需要定期对设备进行维护和更新。
例如,清理设备内存、升级系统软件、检查传感器和电池状态等。
同时,需要定期更新分析算法和相关软件,以获得更准确和高效的分析结果。
8.遵守安全和法律规定在使用在线分析设备PDA时,需要遵守相关的安全和法律规定。
例如,在采集和处理数据时,应确保数据的合法性和隐私保护。
在数据传输过程中,需要采用安全的传输协议和加密技术,以防止数据泄露和篡改。
总之,使用在线分析设备PDA需要熟悉设备的基本功能,掌握数据采集、处理和传输等方法。
在使用过程中,需要注意数据的安全性和隐私保护,并定期进行设备维护和更新。
sdd编译原理

sdd编译原理
SDD(Simple Directive Diagram)是一种用于描述编译器和解释器等计算机程序中语法分析器和语法分析过程的图形化表示方法。
SDD 是一种基于文法的描述方法,通过SDD可以方便地描述出语言的语法结构,从而方便进行语法分析。
SDD的编译原理主要包括以下几个步骤:
1.词法分析:将输入的源代码转换为一个个的单词或符号,称为
“令牌”(token),并将令牌序列存储在内存中。
2.语法分析:使用SDD描述的语法规则,对词法分析得到的令牌
序列进行解析,生成语法树或句法树(parse tree)。
3.语义分析:对生成的语法树或句法树进行语义分析,检查语法
的正确性,并进行类型检查、符号表管理等操作。
4.中间代码生成:将语法树或句法树转换为中间代码
(intermediate code),以便后续的代码生成和优化。
5.代码生成:将中间代码转换为目标机器的机器码(object
code),以便执行。
6.优化:对生成的代码进行优化,以使得程序的执行效率更高。
以上是SDD编译原理的主要步骤,其中SDD主要用于语法分析阶段,通过SDD描述语法规则,生成语法树或句法树,为后续的编译过程提供基础。
大学英语三级语法详解

英语语法:被动语态的“一般”和“特殊”在被动句中,主语是动作的承受者,它主要用于强调动作的承受者或因为动作的执行者难以说出或不必说出时。
我们在学习运用它时,应注意以下两个方面:一、掌握被动语态的一般结构被动语态基本形式为:助动词be +过去分词。
助动词be有时态、人称和数的变化,我们可以通过be的不同变化形式推出各种时态的被动语态形式。
如:The film is being shown now.电影正在放映。
(现在进行时的被动语态)Dr. Smith had been mentally disturbed by his long years alone in prison.多年孤独的监狱生活使史密斯医生的精神受到了刺激。
(过去完成时的被动语态)二、掌握几种特殊的被动语态结构1. 带情态动词的被动结构。
其形式为:情态动词+be +过去分词。
The baby should be taken good care of by the baby-sitter.婴儿应该由临时保姆好好照看。
2. 当使役动词have, make, get以及感官动词see, watch, notice, hear, feel, observe等后面的不定式作宾语补足语时,在主动结构中不定式to要省略,但变为被动结构时,要加to。
Someone saw a stranger walk into the building.有人看见一个陌生人走进了大楼。
变为被动句为:A stranger was seen to walk into the building.3. 非谓语动词的被动语态。
动词-ing形式及不定式to do 也有被动语态。
I don’t like being laughed at in the public.我不喜欢当众被人嘲笑。
What is to be done next?下一步要做什么?4. 短语动词的被动语态。
有些相当于及物动词的动词词组,如“动词+介词”、“动词+副词”等,也可以用于被动结构,但要把它们看作一个整体,不能分开,其中的介词或副词也不能省略。
语法知识在阅读理解中的应用与分析总结

语法知识在阅读理解中的应用与分析总结无题语法知识在阅读理解中的应用与分析总结语法是语言的基础,它规范了词语的搭配和句子的结构,为我们准确地传达思想提供了保障。
在阅读理解中,语法知识的应用和分析起着至关重要的作用。
本文将从句子结构、词性、语序和语态等方面讨论语法知识在阅读理解中的应用,并总结有效的分析方法。
一、句子结构的应用句子是表达完整意思的最基本单位,其结构的准确理解对于阅读理解至关重要。
句子的基本结构包括主语、谓语和宾语。
通过分析句子结构,我们可以理解句子中各个成分之间的关系,从而准确地理解句子的意思。
例如,在阅读中遇到复杂的长句时,我们可以通过找出主语和谓语,确定句子的核心内容,并进一步分析其他成分的修饰关系,帮助我们更好地理解句子的意思。
此外,掌握句子结构可以帮助我们发现并理解悬垂修饰、省略等现象,从而避免误解句子的真实含义。
二、词性的分析词性是词语的基本属性,对于理解句子各个成分在句子中的作用非常重要。
通过分析词性,我们可以确定句子中各个词语的词义和语法功能,从而准确地理解句子的含义。
比如,在阅读中遇到生词时,通过分析其词性,我们可以推测出其基本含义和在句子中的作用,从而帮助我们理解整个句子的意思。
此外,掌握词性还可以帮助我们区分词义相近的词语,避免混淆和误解。
三、语序和语态的运用句子的语序和语态对于句子的意思和表达方式起着至关重要的作用。
通过分析句子的语序和语态,我们可以准确地理解句子的句意,帮助我们更好地理解文章的主旨和作者的观点。
在阅读理解中,我们可以根据句子的语序推测出重要信息的排列顺序,以及从句和主句的关系。
同时,了解常见的语态变化规律,将有助于我们快速理解句子中的被动语态,进一步理解句子的意思。
四、有效的分析方法总结在应用语法知识分析阅读理解时,我们可以采用以下有效的分析方法:1. 逐句分析:对于长句子或复杂句子,逐句分析可以帮助我们理清各个句子之间的逻辑关系和修饰关系。
2. 上下文推测:通过仔细阅读上下文,推测词语的含义和句子的意思,从而帮助我们理解句子中的难点。
编译原理语法分析(1)

例如, 考虑句子 i+i*i 按文法G[E]的推导 最左推导: EE+Ei+Ei+E*E i+i*E i+i*i 最右推导: EE+EE+E*EE+E*i E+i*ii+i*i 注意: 推导过程不唯一, 通常只考虑最左 推导或最右推导。 最右推导又称为规范推导。 规范推导的逆过程称为规范归约。
+ 。 * 意味着或 = , 或 即1 n 1 n 1 n
例如,考虑算术表达式文法G[E]: E→E+E∣E*E∣(E)│i 非终结符E代表一类算术表达式, 从E出发可进行一系列推导, 表达式 i+i*i 的推导如下: E E+E E+E*E E+E*i E+i*i i+i*I 注意: 在每一步推 导中,只能对其中一个 非终结符用其对应的产生式右部的 一个候选式来替换。
文法可表示为 VN为非空非终结符集,且VT∩VN=Φ; (3) S为文法开始符, S∈VN; (4)ξ是产生式的非空有限集, 其中每个 产生式(规则)记作 → 或 ::= 左部∈(VT∪VN)+至少含一非终结符, 右部∈(VT∪VN)*。
B
3.1.3 正规式与上下文无关文法 1. 正规式到上下文无关文法的转换 由正规式构造CFG的一种方法: (1)构造正规式的NFA; (2)若0为初始状态, 则A0为开始符; (3)若存在映射关系f(i,a)=j, 则定义产生式Ai →aAj; (4)若存在映射关系f(i,ε)=j, 则定义产生式Ai →Aj; (5) 若i为终态, 则定义产生式Ai →ε。
产生式 (也称产生式规则或规则) 是 定义语法实体的一种书写规则。一个语 法实体的相关规则可能不止一个, 如: P→1, P→2 , P→n 相同左部的产生式可合并为一个: P→ 1| 2|„| n 其中, i(i=1,2,„,n)称为P的候选式。
第三章 语法分析3精品PPT课件

②归约-归约冲突
–存在两个可选的句柄可对栈顶符号进行归约。 例如上述第12)步,可以用T→F进行归约,又可 以按T→T*F进行归约。
各种分析方法中处理冲突的技术不同!
3.5 LR分析法
• 本节重点:
为了识别非终结符A,就要识别符号 串aBc。为此,构造一个DFA如图3-27所 示。
栈 输入 #S #
【例】文法G[S]: SaAcBe 待分析的句子为:abbcde
分析栈 # #a #ab #aA
输入串 abbcde#
bbcde# bcde# bcde#
A bAb B d
动作 移进 移进 归约 A b 移进
分析栈 #aAb #aA #aAc #aAcd #aAcB #aAcBe #S
关键:如何识别可归约的符号串? 通过不同的自下而上的分析算法来解释,不同 的算法对可归约串的定义是不同的,但分析过 程都有一个共同的特点:边移进边归约。
规范归约:使用句柄来定义可归约串
算符优先:使用最左素短语来定义可归约串
自下而上语法分析主要有以下三种方法 ①简单优先分析法(规范归约)——文法按 一定原则规定文法符号的优先关系。 ②算符优先分析法(非规范归约)——规定 算符之间的优先关系。 ③ LR分析法(规范归约)—— LR(0)、 LR(1)、SLR(1)和LALR(1)。
• 句型→ 短语→ 直接短语 →句柄
注: 采用规范归约的算法,每次归约的部分就是分析为句柄 的字符串。 因此,在规范归约中,关键问题就转化为如何识别句柄?
练习பைடு நூலகம்
有文法如下: (1)E→E+T|T (2)T→T*F|F (3)F→(E)|id
PDA具体介绍内容相当全面

GZHU
1999年7月,由于与管理层意见不合,杰夫•霍金 1999年 由于与管理层意见不合,杰夫• Hawkins)和唐娜•杜宾斯基( 斯(Jeff Hawkins)和唐娜•杜宾斯基(Donna Dubinsky)离开原来公司, Dubinsky)离开原来公司,并成立了一家新的企 Handspring(有人直接翻译为:掌上春天), 业 Handspring(有人直接翻译为:掌上春天), 继续生产Palm OS,但比Palm便宜的PDA 1999年 Palm便宜的PDA。 继续生产Palm OS,但比Palm便宜的PDA。1999年9 月,发布了第一款产品--Visor Delux,5种颜 发布了第一款产品--Visor Delux, -- 色炫丽的外型,搭配略为透明的外壳, 色炫丽的外型,搭配略为透明的外壳,如同苹果 电脑那般,深受年轻时尚人群喜爱。 电脑那般,深受年轻时尚人群喜爱。
GZHU
1997年2月,Palm OS 2.0发布。与1.0相比,主要 1997年 2.0发布。 1.0相比, 发布 相比 改进在增加了TCP/IP支持,能使Palm Pilot在 TCP/IP支持 改进在增加了TCP/IP支持,能使Palm Pilot在 TCP/IP网络上通信 网络上通信。 TCP/IP网络上通信。 1998年 3.0随着工业史上的又一个 1998年4月,Palm OS 3.0随着工业史上的又一个 里程碑式的产品――Palm III一起发布 一起发布。 里程碑式的产品――Palm III一起发布。
GZHU
1999年年初,palm最经典的产品 Palm V发布。出 1999年年初,palm最经典的产品 V发布。 年年初 发布 色的外型设计,颇具质感的铝合金外壳, 色的外型设计,颇具质感的铝合金外壳,内置可 方便充电的锂电池,超轻超薄的机身, 方便充电的锂电池,超轻超薄的机身,都让每一 个看到的人爱不释手。 个看到的人爱不释手。当年获得工业设计大奖的 外形在今天看来依然是一代典范, 外形在今天看来依然是一代典范,所以后来的 M500系列也沿用其外形设计。 M500系列也沿用其外形设计。 系列也沿用其外形设计
编译原理第三版 第五章 自下而上语法分析

a
b a
A a
b A A a a
c A a
d c A a
e B B c c A A a a
S
(2) 分析树: 用树表示“移进 - 归约 ”过程
A A B S
b
A
b
b
d
a
A
直接短语
T i F
句柄
T
T * F F ( E ) i
E + T T F
规范归约
设α是文法G的一个句子, 若序列αn, αn-1, …, α0,满足: (1)αn = α; (2) α0 = S; (3)对任 意i , 0< i ≤n , αi-1 是从αi 将句柄替换成 相应产生左部符号而得到的;则称该序列是一个 规范归约。
1、归约与分析树
(1)移进-归约法: 使用符号栈, 把输入符号逐一移 进栈, 栈顶出现某个产生式右部时归约为左部。
例 :给定文法 G: (1) S→aAcBe (2) A→b (3) A→Ab (4) B→d 输入串 abbcde是否为句子? 归约过程如下: 步骤: 1. 2. 进 进 动作: a b
例:文法G: G[E]: E→E+E|E*E |(E) |i (1) E→E+T│T (2) T→T*F│F (3) F→P↑F│P (4) P→(E)│i 算符优先关系为: 由(4): P→(E) ∴( =) 由(1) (2): E→E+T, T => T*F ∴+<* 由(2) (3): T→T*F, F => P↑F ∴ *<↑ 由(1): E→E+T, E => E+T ∴ +>+ 由(3): F→P↑F, F=> P↑F ∴ ↑ <↑ 由(4): P→(E), E => E+T ∴ ( < +, +>) ... ∴ G为算符优先文法(优先关系表如表5.1所示,P90) #看作终结符号
自下而上语法分析

自下而上语法分析1、规约:自下而上的语法分析过程:分为简单优先分析法,算符优先分析法,LR分析法。
2、自下而上的语法分析过程思想:自下而上的语法分析过程是一个最左规约的过程,从输入串开始,朝着文法的开始符号进行规约,直到文法的开始符号为止的过程。
输入串在这里是指词法分析器送来的单词符号组成的二元式的有限序列。
3、自下而上的PDA(下推自动机)工作方式:“移近-规约”方式注:初态时栈内仅有栈顶符“#”,读头指在最左边的单词符号上。
语法分析程序执行的动作:◆移进:读入一个单词并压入栈内,读头后移◆规约:检查栈顶若干符号能否进行规约,若能,就以产生式左部代替该符号串,同时输出产生式编号。
◆识别成功:移近-规约的结局是栈内只剩下栈底符号和文法的开始符号,读头也指向语句的结束符。
◆识别失败。
4、判读一语句是否是该文法的合法语句(可以用语法树)5、优先分析器:简单优先分析法(理论简单,实际比较麻烦)算符优先分析法6、LR分析器7、相邻文法符号之间的优先关系◆在句型中,句柄内各相邻符号之间具有相同的优先级。
◆由于句柄要先规约,所以规定句柄两端符号的优先级要比位于句柄之外的相邻符号的优先级高。
(#的优先级是最低的。
)9、简单优先文法:定义:一个文法G,如果它不含ε的产生式,也不含任何右部相同的不同产生式,并且它的任何符号(X,Y)-X,Y是非终结符或终结符—或者没有关系,或者存在优先级相同或低于、高于等关系之一,则这是一个简单优先文法。
10、简短优先分析的思想1)简单优先矩阵:根据优先关系的定义:将简单优先文法中各文法符号之间的这种关系用一个矩阵表示,称作简单优先矩阵。
2)PDA读入一个单词后,比较栈顶符号和该单词的优先级,若栈顶符号优先级低于该单词,继续读入;若栈顶符号优先级高于或者等于读入符号,则找句柄进行规约,找不到句柄继续读入11、简单优先法的优缺点:1、优点:算法比较好理解。
2、缺点:适用范围小,分析表尺寸太大。
阅读理解题中的语法分析技巧课件

阅读理解题中的语法分析技巧课件在我们学习语文或者英语等语言类学科时,阅读理解题是经常会遇到的题型。
而要准确理解和回答这些题目,掌握语法分析技巧是非常重要的。
接下来,就让我们一起深入探讨一下阅读理解题中的语法分析技巧。
一、句子成分分析句子成分包括主语、谓语、宾语、定语、状语和补语。
理解这些成分对于我们理解句子的意思至关重要。
主语通常是句子中表示动作的执行者或者被描述的对象。
比如,“小明在公园里玩耍”,“小明”就是主语。
谓语则是表示主语的动作或状态。
在上面的例子中,“玩耍”就是谓语。
宾语是动作的承受者。
例如,“我吃苹果”,“苹果”就是宾语。
定语用于修饰主语或宾语,一般由形容词、名词等充当。
像“漂亮的花朵”,“漂亮的”就是定语。
状语用来修饰谓语,表明动作发生的时间、地点、方式等。
比如“他快速地跑”,“快速地”就是状语。
补语则是对谓语进行补充说明。
例如“他跑得很快”,“很快”就是补语。
在阅读理解中,通过分析句子成分,我们能够更清晰地理解句子的结构和含义。
二、词性的判断词性包括名词、动词、形容词、副词、介词、连词等。
名词表示人、事物、地点或抽象概念。
比如“学校”“友谊”等。
动词表示动作或状态的词,如“跑”“思考”。
形容词用于描述或修饰名词,“美丽的风景”中的“美丽的”。
副词用于修饰动词、形容词或其他副词,“非常好”中的“非常”。
介词用于表示名词、代词等与句中其他词的关系,“在桌子上”的“在”。
连词用于连接单词、短语或句子,“因为……所以……”“虽然……但是……”。
正确判断词性有助于我们理解词语在句子中的作用和含义。
三、句式结构常见的句式结构有简单句、复合句和复杂句。
简单句只有一个主谓结构,“他笑了”就是一个简单句。
复合句由两个或多个简单句通过连词连接而成,比如“我喜欢读书,而且我每天都会读一些”。
复杂句则包含一个主句和一个或多个从句,“当我回到家时,妈妈正在做饭”,“当我回到家时”就是一个从句。
了解不同的句式结构,能够帮助我们更好地把握句子之间的逻辑关系和语义。
大学英语三级语法知识总结汇总(可编辑修改word版)

大学英语三级语法知识总结汇总(可编辑修改word版)三级语法考点归纳一.虚拟语气1.if 句中虚拟形式if 引导的非真实条件句(纯粹假设或发生的可能性不大):条件从句主句与现在相反did (be were) would/ should/ might/ could do与将来相反与过去相反did (behad donewould/ should/ might/ could dowould/ should/ might/ could have done例句If we left (leave) now, we should arrive in time.If they hadn’t gone on vacation, their house wouldn’t have been broken (break) into.2.原形虚拟:a.表命令、决定、要求、建议等词语之后的that-分句中,用动词原形。
suggest, demand, advise, propose, order, arrange, insist, command, require, request, desire …… that +(should) do 例如He suggested that we should leave early.My suggestion is that we should tell him.b.It is (was) 形容词/名词that …… (should) do/例如It is absolutely essential that all the facts be examined first.3.一些句型中的虚拟形式:1. It’s (high, about, the first, etc.) time (that) …动词过去时…例如It’s time we left.例如It is time we went to bed.2 would rather/sooner 宁愿as if/ though 好像would rather/sooner 谓语用过去时与现在或者将来相反as if/ though 谓语用过去完成时与过去相反4.练习1.I try it again if I you.A.will;amB. should;amC. would;wereD. would;had been2.If it not for the water,the plants live.A.were;would notB. is;could notC. were;couldD. did;could not3.If I that chance to show my ability, I the president of this school.A.have not had;could not becomeB. had not had;would not have becomeC. did not have;could not becomeD. doesn’t have;will not become4.He by that burglar if you to save him.A.might have been killed;hadn’t comeB. will be killed;didn’t comeC. may be killed;did’t comeD. could be killed;haven’t come5.If it for your help,I that hard time with so little money.A.were not;would not spendB. is not;can not spendC. had not been;would not have spentD. have not been;will not spend6.Where you go if war ?A.will;breaks outB. do;will break outC. would;were to break outD. will;is to break out7.She wishes she that humiliating thing.A.doesn’t doB. didn’t doC. haven’t doneD. hadn’t done8.The chairman suggested that the meeting put off.A.can beB. beC. isD. will be9.It is vital that he immediately.A.should goB. must goC. goesD. went10.It is time we do our homework.A.begin toB. can begin toC. began toD. will begin to答案:1.选C。
语法分析器初步学习——LISP语法分析

语法分析器初步学习——LISP语法分析语法分析器初步学习——LISP语法分析本⽂参考⾃vczh的《》。
LISP的表达式是按照前缀的形式写的,⽐如(1+2)*(3+4)在LISP中会写成(*(+ 1 2)(+ 3 4)),1 + 2会写成(+ 1 2)。
LISP语⾔的语法如下形式:1.Operator = “+” | “-” | “*” | “/”2.Expression = <数字> | ”(”Expression”)” | “(”Operator Expression Expression”)”我们根据以上两条语法规则来写代码:// LISP语法分析器#include <iostream>#include <string>using namespace std;// 检测是否是空⽩符bool IsBlank(char ch){return ch == '' || ch == '\t';}// 检测Text是否是Stream的前缀// 如果是前缀,则返回true,并将pos前移Text.size()个字符// 如果不是前缀,则返回false// 此函数⼀开始会过滤掉Stream开头的空格bool IsPrefix(const string& Stream, int& pos, const string& Text){int read = pos;// 过滤空⽩符while (IsBlank(Stream[read])){++read;}// 不能写为:// while (IsBlank(Stream[read++]));// 因为这样写会导致read⾄少加1if (Stream.substr(read, Text.size()) == Text) // 如果是前缀{pos = read + Text.size();return true;}else{return false;}}// 检测Stream开头是否是操作符+、-、*、/// 是的话,函数返回实际的操作符,并将pos便宜到操作符之后// 否则返回0// 判断语法1:Operator = “+” | “-” | “*” | “/”char IsOperator(const string& Stream, int& pos){if (IsPrefix(Stream, pos, "+")|| IsPrefix(Stream, pos, "-")|| IsPrefix(Stream, pos, "*")|| IsPrefix(Stream, pos, "/")) // 如果开头是操作符{return Stream[pos - 1]; // 如果是的话,pos已经向前偏移了}else{return0;}}// 表达式结构体struct Expression{int Result; // 返回表达式结果string Error; // 返回错误信息,没错误则为空int Start; // 错误发⽣的位置Expression() : Result(0), Start(0) {}};// 检测Stream开头是否是数字,如果是,则将pos便宜到数字之后// 函数返回Expression// 判断语法2中的第⼀部分:Expression = <数字>Expression GetNumber(const string& Stream, int& pos){Expression Result;bool GotNumber = false;int read = pos;// 过滤空⽩符while (IsBlank(Stream[read])){++read;}while (true){// 依次读⼊⼀个字符char ch = Stream[read];if (ch >= '0' && ch <= '9'){Result.Result = Result.Result * 10 + ch - '0';GotNumber = true;++read;}else{break;}}if (GotNumber){pos = read;}else{Result.Error = "这⾥需要数字";Result.Start = read;}return Result;}// 检测Stream开头是否是表达式// 如果是,则将pos前移到表达式后// 实现语法2:Expression = <数字> | “(”Expression“)” | “(”Operator Expression Expression“)”Expression GetExpression(const string& Stream, int& pos){int read = pos;// 检测开头是否是数字// 语法2第⼀部分:Expression = <数字>Expression Result = GetNumber(Stream, read);if (!Result.Error.empty()) // 如果开头不是数字{if (IsPrefix(Stream, read, "(")) // 检测是否"("开头{// 将Result的Error清空Result.Error.clear();char Operator = 0;if ((Operator = IsOperator(Stream, read)) != 0)// 如果是操作符,语法2第三部分:Expression = “(”Operator Expression Expression“)” {// 获取左参数// 递归调⽤Expression left = GetExpression(Stream, read);if (!left.Error.empty()){return left;}// 保持当前readint rightRead = read;// 获取右参数// 递归调⽤Expression right = GetExpression(Stream, read);if (!right.Error.empty()){return right;}// 根据操作符Operator进⾏计算switch (Operator){case'+':Result.Result = left.Result + right.Result;break;case'-':Result.Result = left.Result - right.Result;break;case'*':Result.Result = left.Result * right.Result;break;case'/':if (right.Result == 0) // 除数为0{Result.Error = "除数为0";Result.Start = rightRead;}else{Result.Result = left.Result / right.Result;}break;default: // 这种情况不会发⽣,因为前提是Operator,所以只有+、-、*、/四种情况 Result.Error = "未知的操作符";Result.Start = read;return Result;}}else// 如果不是操作符// 语法2的第⼆部分:Expression = “(”Expression“)”{// 获取表达式Result = GetExpression(Stream, read);// 如果获取失败,则直接返回if (!Result.Error.empty()){return Result;}}// 检测是否有配套的")"if (!IsPrefix(Stream, read, ")")){Result.Error = "此处缺少右括号";Result.Start = read;}}}// 如果没有出错,则更新posif (Result.Error.empty()){pos = read;}// 检测是否有配套")"时,如果不存在,可以直接将Result返回// 这样在后⾯就不⽤检测是否出错了,因为前⾯凡是出错的情况// 都返回了,这样就不⽤检测了,⽽直接更新pos: pos = readreturn Result;}// 测试int main(){while (true){string Stream;cout << "输⼊⼀个LISP表达式" << endl;getline(cin, Stream);int pos = 0;if (IsPrefix(Stream, pos, "exit")){break;}pos = 0;Expression Result = GetExpression(Stream, pos);if (!Result.Error.empty()){cout << "表达式错误" << endl;cout << "位置:" << Result.Start << endl;cout << "错误信息:" << Result.Error << endl;}else{cout << "结果:" << Result.Result << endl;}}return0;}下⾯对程序代码解释如下:数据结构程序中⽤string型的字符串Stream来存储⽤户输⼊的表达式,int型的pos 作为当前扫描的位置。
pda

例5
文法G[S]:
– S → 0S1 | ε
语法树
S
分析过程
– 令输入串α = 0011 – 分析过程即从S开始试 图推导出0011 – S⇒0S1 ⇒00S11 ⇒0011 0 0 S S ε 1 1
5.1.2 基于 基于PDA的分析算法 的分析算法
基本思想
– 利用PDA的栈来存储推导的中间结果。 – 利用PDA的非确定性来“猜测”所有可能的推导。 – 采用最左推导,及时将推导产生出来的最左终结符 与输入匹配
编译原理
Principles of Compiler
5.1 非确定性的自上而下分析
上节内容回顾
– – – – 上下文无关文法(Context Free Grammar) 上下文无关语言(Context Free Language) 下推自动机(Push Down Automata) 下推自动机与上下文无关的等价性
本节内容
– 自上而下的分析方法 – 基于PDA的自上而下分析方法
5.1.1 自上而下的分析方法
一般策略
– 给定一个文法G,判断一个串α是否属于G的语言。 – 自上而下的分析方法试图从文法的开始符号推导出 目标串α,如果成功则认为α属于G的语言。 – 由于该推导过程正好表示对应语法树从上到下的生 成过程,因此称之为自上而下的分析方法。
1 $ 2
0 1 1 $ 2
小结
自上而下分析方法 PDA与上下文无关文法的关系 如果利用PDA分析上下文无关语言 该方法的特点
– 通用性好 – 抽象层次高 – 算法效率低
5.1.2 基于 基于PDA的分析算法 的分析算法
构造思想
– 给定文法G=(VN,VT,P,S),构造PDA M=(Q,Σ,Γ,q0,δ,F),使M恰好接受G的语言。
第三章语法分析

图3-1 句子aabbbb对应的两棵不同语法树
第三章语法分析
第三章 语法分析 因此,文法G[S]为二义文法(对句子abbb也可画出
两棵不同语法树)。 3.4 已知文法G[S]为S→SaS|ε,试证明文法G[S]
为二义文法。 【解答】 由文法G[S]:S→SaS|ε,句子aa的语法
树如图3-2所示。
(4) d
3.2 令文法G[N]为
G[N]: N→D|ND
D→0|1|2|3|4|5|6|7|8|9
(1) G[N]的语言L(G[N])是什么?
(2) 给出句子0127、34和568的最左推导和最右推导。
第三章语法分析
第三章 语法分析
【解答】 (1) G[N]的语言L(G[N])是非负整数。 (2) 最左推导: NNDNDDNDDDDDDD0DDD01DD012D0127 NNDDD3D34 NNDNDDDDD5DD56D568 最右推导: NNDN7ND7N27ND27N127D1270127 NNDN4D434 NNDN8ND8N68D68568
b. 必有ca
c. 必有ba
d. a~c都不一定成立
第三章语法分析
第三章 语法分析
(5) 在规范归约中,用 来刻画可归约串。
a. 直接短语
b. 句柄
c. 最左素短语 d. 素短语
(6) 若a为终结符,则A→α·aβ为 项目。
a. 归约
b. 移进
c. 接受
d. 待约
(7) 若项目集Ik含有A→α· ,则在状态k时,仅 当 面 临 的 输 入 符 号 a∈FOLLOW(A) 时 , 才 采 取
第三章 语法分析
第三章 语法分析
3.1 完成下列选择题:
Part5语法分析

移动归约分析法相关概念
规范归约 文法的最右推导为规范推导, 文法的最右推导为规范推导,自底向上分析是自顶向下最右推导的逆 过程, 过程,叫规范归约 句柄 直观来看:一个符号串的“句柄”是和一个产生式右部匹配的子串, 直观来看:一个符号串的“句柄”是和一个产生式右部匹配的子串, 而且把它归约到该产生式左部的非终结符代表了最右推导逆过程的一 步。 形式定义:右句型(最右推导可得到的句型) 的句柄是一个产生式 的句柄是一个产生式A 形式定义:右句型(最右推导可得到的句型)γ的句柄是一个产生式 →β以及 的一个位置,在该位置可以找到串 ,而且用 代替 可以得到 以及γ的一个位置 代替β可以得到 以及 的一个位置,在该位置可以找到串β,而且用A代替 γ的最右推导的前一个右句型 的最右推导的前一个右句型 对于有二义性的文法而言,由于最右推导不一定,则句柄不一定唯一。 对于有二义性的文法而言,由于最右推导不一定,则句柄不一定唯一。 只有当文法没有二义性时,每个右句型才只有一个句柄。 只有当文法没有二义性时,每个右句型才只有一个句柄。 句柄剪裁 通过“剪裁句柄” 通过“剪裁句柄”可以得到最右推导的逆过程 在归约过程中用到的产生式序列的逆序就是输入串的最右推导
其中, 其中,δ为ε或者B, 或者B 在同一个句柄中,同时被归约, a和b在同一个句柄中,同时被归约,
算符优先关系定义( 算符优先关系定义(续3)
a > b,则存在语法子树如下 ,
A … B b … P … a δ
其中, 其中,δ为ε或者C, 或者C 不在同一个句柄中, a和b不在同一个句柄中,a先被归约
从左端开始扫描串,直到遇到第一个>为止。 为止。 从左端开始扫描串,直到遇到第一个 为止 向左扫描,跳过所有的=,直到遇到一个<为止 为止。 向左扫描,跳过所有的 ,直到遇到一个 为止。 句柄包括从上一步遇到的<右部到第一个 右部到第一个>左部之间的所 句柄包括从上一步遇到的 右部到第一个 左部之间的所 有符号, 有符号,包括介于期间或者两边的非终结符
山东理工大学-编译原理内部课件-第三章:短语直接短语句柄
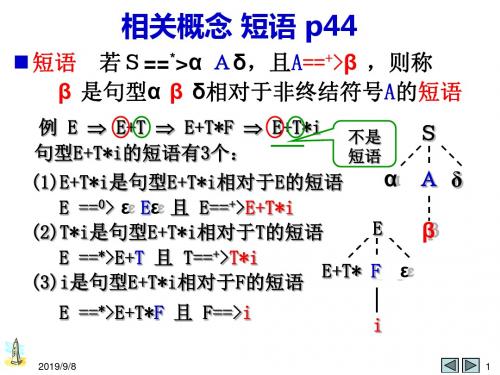
T6 * F7
i3
i2是句型η 相对于F7的短语 i3是句型η 相对于T3,F5的短语
F8
i2
直接短语 3个: i1, i2,i3
i1
句柄:i1
2019/9/8
章节目录
6
2
利用语法树寻找句型的短语、句柄等
寻找方法
句型η 的语法树有:
句型η =E+T*i E①
n个内部节点——n棵子树 n棵子树——n个短语
E + T②
每颗子树的叶结点从左至右排 列组成一个短语
T * F③
m棵直接子树——m个直接短语
i
只有父子两代
3个短语 E+T*i T*i 1个直接短语 i
i
E② + T ③
T+T*F+i 是句型η 相对于E1的短语 T+T*F 是句型η 相对于E2的短语
E ④+ T ⑤ F⑥
T 是句型η 相对于E4的短语
T T*F i
T*F 是句型η 相对于T5的短语
i,i 是句型η 相对于T3,F6的短语 3个直接短语: T ,T*F,i
句柄:T
2019/9/8
5
利用语法树寻找短语、句柄课堂练习
Eβ
E ==*>E+T 且 T==+>T*i (3)i是句型E+T*i相对于F的短语
E+εTE*+ FTE εε
E ==*>E+T*F 且 F==>i
E+TT*i*ii来自2019/9/81
直接短语
直接短语 句柄 p44
若S* α Aδ 且 A β ,则称β 是句型
α β δ 相对于非终结符号A的直接短语
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Example: Goes-To
The previous PA of {0n1n | n > 1} We can describe the sequence of moves by:
(q, 000111, Z0)⊦ (q, 00111, XZ0)⊦ (q, 0111, XXZ0)⊦ (q, 111, XXXZ0)⊦ (p, 11, XXZ0)⊦ (p, 1, XZ0)⊦ (p, ε, Z0)⊦ (f, ε, Z0) (q, 000111, Z0)
29
Proof: L(P) -> N(P’) 直观思考
用P’模拟 P. Idea:
当P接收时,将P'的栈置空. 特殊情况:栈空且没有接收的情况 用一个特殊的栈底标记来表示栈空且没有接
收的情况
30
Proof: L(P) -> N(P’)
P’ 包含P的所有状态、符号、以及迁移, 另外:
1. 栈符号X0 (used to identify the stack bottom against accidental emptying) 2. New start state s and “erase” state e. 3. δ(s, ε, X0) = {(q0, Z0X0)}. Get P started. 4. δ(f, ε, X) = δ(e, ε, X) = {(e, ε)} for any final state f of P and any stack symbol X.
28
Equivalence of Language Definitions
1. For any L(P), there exists a PA P' such that N(P')=L(P). 2. For any N(P'), there exists a PA P'' such that L(P'')=N(P').
1. 2. 3. 4. 5. 6. 7. Q, a finite set of states 与有限状态自动机 Σ, an input alphabet 的区别是什么? 的区别是什么? Γ, a stack alphabet δ, a transition function 栈! q0 in Q, a start state Z0 in Γ, a start stack symbol F ⊆ Q, a set of final states
31
Proof: L(P) -> N(P’)
start
ε, X/ε s q0 ε, X0/Z0X0 P e ε, X/ε ε, X/ε
32
Proof: N(P) -> L(P’’) 直观思考
P” simulates P. P” 通过一个特殊的栈底标志来表示P的 栈为空的情况 If so, P” accepts.
13
Example
迁移:
δ(q, 0, Z0) = {(q, XZ0)}. δ(q, 0, X) = {(q, XX)}. These two rules cause one X to be pushed into the stack for each 0 read from the input. δ(q, 1, X) = {(p, ε)}. When we see a 1, go to state p and pop one X. δ(p, 1, X) = {(p, ε)}. Pop one X per 1. δ(p, ε, Z0) = {(f, Z0)}. Accept at bottom.
1. q, a state in Q 2. a, an input, which is either a symbol in Σ or ε 3. Z, A stack symbol in Γ
函数δ(q, a, Z) 的结果为 a set of actions of the form (p, α)
p is a state; α is a string of stack symbols. 为什么是a set of actions?
*
(f, ε, Z0)
25
What would happen on input 0001111?
Answer
Legal because a PA can use ε input even if input remains. δ(p, ε, Z0) = {(f, Z0)}
(q, 0001111, Z0)⊦(q, 001111, XZ0)⊦ (q, 01111, XXZ0)⊦(q, 1111, XXXZ0)⊦ (p, 111, XXZ0)⊦(p, 11, XZ0)⊦ (p, 1, Z0)⊦(f, 1, Z0) Note the last ID has no move. 0001111 is not accepted, because the input is not completely consumed.
Pushdown Automata 下推自动机
Pushdown Automata
正则语言
正则文法 有限状态自动机
上下文无关语言
上下文无关文法 下推自动机(PA)
2
Pushdown Automata
正则语言
正则文法 NFA = DFA
上下文无关语言
上下文无关文法 NPA (NPA ⊃ DPA)
DPA 仅定义了上下文无关语言一个真子集
6
常用符号
a, b, … 输入符号.
But sometimes we allow ε as a possible value.
…, X, Y, Z 栈符号 …, w, x, y, z 输入符号串 α, β,… 栈符号串
7
迁移函数
表达为: δ(q, a, Z)={(p1, α1), (p2, α2), ...} 函数δ有3个参数:
18
Actions of the Example PA
11
p
X X Z0
19
Actions of the Example PA
1
p
X Z0
20
Actions of the Example PA
p
Z0
21
Actions of the Example PA
f
Z0
22
PA的瞬时描述
瞬时描述(instantaneous description, ID) is a 3-triple (q, w, α) 表达了PA当前的情况:
4
PA的直观思考
在每次迁移中,PA做以下动作:
1. 改变状态 2. 将栈顶符号替换为一个长度可以为0符号序 列
长度为零时 = “pop” 出栈 长度大于0时 = sequence of “pushes”
5
PA 的形式化定义
A PA is defined by a seven tuple (Q, Σ, Γa PA
The common way to define the language of a PA is by final state. If P is a PA, then L(P) is the set of strings w such that (q0, w, Z0) ⊦* (f, ε, α) for final state f and any α.
大部分程序设计语言可以用DPA描述 DPA can model parsers
如果没有特殊说明,本节课中提及的PA一般都是 3 非确定PA
PA的直观思考
下推自动机可以看作是一个具有栈操作 能力的ε-NFA
PA = ε-NFA + 栈(及其操作)
PA迁移取决于:
1. 当前状态 2. 当前输入符号 (可以为 ε) 3. 当前栈顶符号
1. the current state, q. 2. the remaining input, w. 3. stack contents, α (top at the left)
23
The “Goes-To” Relation
Let I and J be two different IDs I⊦J: ID I can become ID J in one move of the PA Formally: (q, aw, Xα)⊦(p, w, βα) for any w and α, if δ(q, a, X) contains (p, β). Extend ⊦ to ⊦*, meaning “zero or more moves” .
0,0/ε 1,1/ε
11
Example
设计一个下推自动机接收语言 {0n1n | n > 1}. 状态: :
q = 初始状态.
• 到目前为止,只看到了0
p = we’ve seen at least one 1 and may now proceed only if the inputs are 1’s. f = final state
9
迁移函数
δ(q, a, Z)={(p1, α1), (p2, α2), ...} a, a1,a2,... a1,a2,...
q
pi
Z,Z1,..
αi, Z1, ...
10
PA的图形表示
是否可以像FSA那样,可以有一个PA的 图形表示?
1,Z0/1 ε,Z0/ε
q3
q1
q2
0,Ζ0/0 1,Ζ0/1
34
Proof: N(P) -> L(P’’)
ε, X0/ε ε, X0/ε s q0 ε, X0/Z0X0 P f ε, X0/ε ε, X/ε
start
35
Aside: FA and PDA Notations
