计算机图形学课程设计-有效边表填充算法的实现
实验三计算机图形学多边形填充算法

实验三计算机图形学多边形填充算法课程名称计算机图形学实验日期 2013-11-7 实验名称多边形填充算法编程成绩实验目的:熟悉多边形填充算法,掌握MFC图形编程的基本方法和调试技巧。
实验条件: 计算机;VS2008;OpenGL实验内容:1(使用MFC技术实现多边形有效边表填充算法,参考界面效果如下:// ChildView.cpp : CChildView 类的实现#include "stdafx.h"#include "demo.h"#include "ChildView.h"#include <math.h>#define Round(d) int(floor(d+0.5))//四舍五入宏定义#ifdef _DEBUG#define new DEBUG_NEW#endif// CChildViewCChildView::CChildView(){}CChildView::~CChildView(){}BEGIN_MESSAGE_MAP(CChildView, CWnd)ON_WM_PAINT()ON_WM_CREATE()ON_COMMAND(ID_DRAW_PIC, &CChildView::OnDrawPic)END_MESSAGE_MAP()// CChildView 消息处理程序BOOL CChildView::PreCreateWindow(CREATESTRUCT& cs) {if (!CWnd::PreCreateWindow(cs))return FALSE;cs.dwExStyle |= WS_EX_CLIENTEDGE;cs.style &= ~WS_BORDER;cs.lpszClass = AfxRegisterWndClass(CS_HREDRAW|CS_VREDRAW|CS_DBLCLKS,::LoadCursor(NULL, IDC_ARROW),reinterpret_cast<HBRUSH>(COLOR_WINDOW+1), NULL);return TRUE;}void CChildView::OnPaint(){CPaintDC dc(this); // 用于绘制的设备上下文// TODO: 在此处添加消息处理程序代码DrawGraph();// 不要为绘制消息而调用CWnd::OnPaint() }void CChildView::ReadPoint() //点表{P[0].x = 50; P[0].y = 100;P[1].x = -150;P[1].y = 300;P[2].x = -250;P[2].y = 50;P[3].x = -150;P[3].y = -250;P[4].x = 0; P[4].y = -50;P[5].x = 100; P[5].y = -250;P[6].x = 300; P[6].y = 150;}void CChildView::DrawPolygon(CDC *pDC) //绘制多边形边界{CLine *line = new CLine;CP2 t;for(int i = 0; i < 7; i++) //绘制多边形{if(i == 0){line->MoveTo(pDC, P[i]);t = P[i];}else{line->LineTo(pDC, P[i]);}}line->LineTo(pDC, t); //闭合多边形delete line;}void CChildView::DrawGraph() //绘制图形 {CRect rect; //定义客户区GetClientRect(&rect); //获得客户区的大小CDC *pDC = GetDC(); //定义设备上下文指针pDC->SetMapMode(MM_ANISOTROPIC); //自定义坐标系pDC->SetWindowExt(rect.Width(), rect.Height()); //设置窗口比例pDC->SetViewportExt(rect.Width(), -rect.Height()); //设置视区比例,且x轴水平向右,y轴垂直向上pDC->SetViewportOrg(rect.Width() / 2, rect.Height() / 2); //设置客户区中心为坐标系原点rect.OffsetRect(-rect.Width() / 2, -rect.Height() / 2); //矩形与客户区重合if(!bFill)DrawPolygon(pDC); //绘制多边形elseFillPolygon(pDC); //填充多边形ReleaseDC(pDC); //释放DC}void CChildView::FillPolygon(CDC *pDC) //填充多边形 {for(int i = 0; i < 7; i++) //转储顶点坐标,y坐标取为整数{P1[i].x = P[i].x;P1[i].y = Round(P[i].y);P1[i].c = CRGB(bRed / 255.0, bGreen / 255.0, bBlue / 255.0);}CFill *fill = new CFill; //动态分配内存fill->SetPoint(P1, 7); //初始化Fill对象fill->CreateBucket(); //建立桶表fill->CreateEdge(); //建立边表fill->Gouraud(pDC); //填充多边形delete fill; //撤销内存 }int CChildView::OnCreate(LPCREATESTRUCT lpCreateStruct) {if (CWnd::OnCreate(lpCreateStruct) == -1)return -1;// TODO: 在此添加您专用的创建代码bFill = FALSE;ReadPoint();return 0;}void CChildView::OnDrawPic(){// TODO: 在此添加命令处理程序代码COLORREF GetClr = RGB(0, 0, 0); //调色板颜色CColorDialog ccd(GetClr, CC_SOLIDCOLOR);if(IDOK == ccd.DoModal()) //调用颜色对话框选取填充色GetClr = ccd.GetColor();elsereturn;bRed = GetRValue(GetClr); //获取红色分量bGreen = GetGValue(GetClr); //获取绿色分量bBlue = GetBValue(GetClr); //获取蓝色分量bFill = TRUE;Invalidate();}2(使用MFC技术实现多边形边缘填充算法,参考界面效果如下:// demoView.cpp : CdemoView 类的实现#include "stdafx.h"#include "demo.h"#include "demoDoc.h"#include "demoView.h"#include <math.h>#define Round(d) int(floor(d+0.5))//四舍五入宏定义 #ifdef _DEBUG #define new DEBUG_NEW#endif// CdemoViewIMPLEMENT_DYNCREATE(CdemoView, CView)BEGIN_MESSAGE_MAP(CdemoView, CView)// 标准打印命令ON_COMMAND(ID_FILE_PRINT, &CView::OnFilePrint)ON_COMMAND(ID_FILE_PRINT_DIRECT, &CView::OnFilePrint)ON_COMMAND(ID_FILE_PRINT_PREVIEW, &CdemoView::OnFilePrintPreview) ON_COMMAND(ID_DRAW_PIC, &CdemoView::OnDrawPic) END_MESSAGE_MAP() // CdemoView 构造/析构CdemoView::CdemoView(){// TODO: 在此处添加构造代码}CdemoView::~CdemoView(){}BOOL CdemoView::PreCreateWindow(CREATESTRUCT& cs) {// TODO: 在此处通过修改// CREATESTRUCT cs 来修改窗口类或样式return CView::PreCreateWindow(cs); }// CdemoView 绘制void CdemoView::OnDraw(CDC* /*pDC*/) {CdemoDoc* pDoc = GetDocument();ASSERT_VALID(pDoc);if (!pDoc)return;// TODO: 在此处为本机数据添加绘制代码DrawGraph();}// CdemoView 打印void CdemoView::OnFilePrintPreview() {AFXPrintPreview(this);}BOOL CdemoView::OnPreparePrinting(CPrintInfo* pInfo){// 默认准备return DoPreparePrinting(pInfo); }void CdemoView::OnBeginPrinting(CDC* /*pDC*/, CPrintInfo* /*pInfo*/) {// TODO: 添加额外的打印前进行的初始化过程 }void CdemoView::OnEndPrinting(CDC* /*pDC*/, CPrintInfo* /*pInfo*/) {// TODO: 添加打印后进行的清理过程 }void CdemoView::OnRButtonUp(UINT nFlags, CPoint point){ClientToScreen(&point);OnContextMenu(this, point);}void CdemoView::OnContextMenu(CWnd* pWnd, CPoint point){theApp.GetContextMenuManager()->ShowPopupMenu(IDR_POPUP_EDIT,point.x, point.y, this, TRUE);}void CdemoView::ReadPoint() //点表 {P[0].x = 50; P[0].y = 100;P[1].x = -150;P[1].y = 300;P[2].x = -250;P[2].y = 50;P[3].x = -150;P[3].y = -250;P[4].x = 0; P[4].y = -50;P[5].x = 100; P[5].y = -250;P[6].x = 300; P[6].y = 150; }void CdemoView::DrawPolygon(CDC *pDC) { for(int i = 0; i < 7; i++) //计算多边形边界{if(P[i].x > MaxX)MaxX = P[i].x;if(P[i].x < MinX)MinX = P[i].x;if(P[i].y > MaxY)MaxY = P[i].y;if(P[i].y < MinY)MinY = P[i].y;}CLine *line = new CLine;CP2 t;for(int i = 0; i < 7; i++) //绘制多边形{if(i == 0){line->MoveTo(pDC, P[i]);t = P[i];}else{line->LineTo(pDC, P[i]);}}line->LineTo(pDC, t); //闭合多边形line->MoveTo(pDC, CP2(MinX, MinY)); //绘制包围盒line->LineTo(pDC, CP2(MinX, MaxY));line->LineTo(pDC, CP2(MaxX, MaxY));line->LineTo(pDC, CP2(MaxX, MinY));line->LineTo(pDC, CP2(MinX, MinY));delete line;}void CdemoView::FillPolygon(CDC *pDC){COLORREF BClr = RGB(255, 255, 255); //背景色COLORREF FClr = GetClr; //填充色int ymin, ymax; //边的最小y值与最大y值double x, y, k; //x,y当前点,k斜率的倒数for(int i = 0; i < 7; i++) //循环多边形所有边{int j = (i + 1) % 7;k = (P[i].x - P[j].x) / (P[i].y - P[j].y); //计算/kif(P[i].y < P[j].y) //得到每条边y的最大值与最小值{ymin = Round(P[i].y);ymax = Round(P[j].y);x = P[i].x; //得到x|ymin}else{ymin = Round(P[j].y);ymax = Round(P[i].y);x = P[j].x;}for(y = ymin; y < ymax; y++) //沿每一条边循环扫描线{for(int m = Round(x); m < MaxX; m++) //对每一条扫描线与边的交点的右侧像素循环{if(FClr == pDC->GetPixel(m, Round(y))) //如果是填充色pDC->SetPixelV(m, Round(y), BClr); //置为背景色elsepDC->SetPixelV(m, Round(y), FClr); //置为填充色}x += k; //计算下一条扫描线的x起点坐标}}}void CdemoView::DrawGraph() //绘制图形 {CRect rect; //定义客户区GetClientRect(&rect); //获得客户区的大小CDC *pDC = GetDC(); //定义设备上下文指针pDC->SetMapMode(MM_ANISOTROPIC); //自定义坐标系pDC->SetWindowExt(rect.Width(), rect.Height()); //设置窗口比例pDC->SetViewportExt(rect.Width(), -rect.Height()); //设置视区比例,且x轴水平向右,y轴垂直向上pDC->SetViewportOrg(rect.Width() / 2, rect.Height() / 2); //设置客户区中心为坐标系原点rect.OffsetRect(-rect.Width() / 2, -rect.Height() / 2); //矩形与客户区重合if(!bFill)DrawPolygon(pDC); //绘制多边形elseFillPolygon(pDC); //填充多边形ReleaseDC(pDC); //释放DC }// CdemoView 诊断#ifdef _DEBUGvoid CdemoView::AssertValid() const{CView::AssertValid();}void CdemoView::Dump(CDumpContext& dc) const{CView::Dump(dc);}CdemoDoc* CdemoView::GetDocument() const // 非调试版本是内联的 { ASSERT(m_pDocument->IsKindOf(RUNTIME_CLASS(CdemoDoc)));return (CdemoDoc*)m_pDocument;}#endif //_DEBUG// CdemoView 消息处理程序void CdemoView::OnInitialUpdate(){CView::OnInitialUpdate();// TODO: 在此添加专用代码和/或调用基类bFill = FALSE;ReadPoint();GetClr = RGB(0,0,0);MinX = MaxX = P[0].x;MinY = MaxY = P[0].y;}void CdemoView::OnDrawPic(){// TODO: 在此添加命令处理程序代码CColorDialog ccd(GetClr, CC_SOLIDCOLOR);if(IDOK == ccd.DoModal()) //调用颜色对话框选取填充色GetClr = ccd.GetColor();elsereturn;bFill = TRUE;Invalidate(FALSE);}3.使用MFC技术实现种子填充算法,参考界面效果如下:// demoView.cpp : CdemoView 类的实现 #include "stdafx.h"#include "demo.h"#include "demoDoc.h"#include "demoView.h"#include <math.h>#define Round(d) int(floor(d+0.5))//四舍五入宏定义 #ifdef _DEBUG #define new DEBUG_NEW#endif// CdemoViewIMPLEMENT_DYNCREATE(CdemoView, CView) BEGIN_MESSAGE_MAP(CdemoView, CView)// 标准打印命令ON_COMMAND(ID_FILE_PRINT, &CView::OnFilePrint)ON_COMMAND(ID_FILE_PRINT_DIRECT, &CView::OnFilePrint)ON_COMMAND(ID_FILE_PRINT_PREVIEW, &CdemoView::OnFilePrintPreview) ON_WM_LBUTTONDOWN()ON_COMMAND(ID_DRAW_PIC, &CdemoView::OnDrawPic)END_MESSAGE_MAP()// CdemoView 构造/析构CdemoView::CdemoView(){// TODO: 在此处添加构造代码bFill = FALSE;SeedClr = RGB(255, 0, 0);}CdemoView::~CdemoView(){}BOOL CdemoView::PreCreateWindow(CREATESTRUCT& cs) { // TODO: 在此处通过修改// CREATESTRUCT cs 来修改窗口类或样式return CView::PreCreateWindow(cs); }// CdemoView 绘制void CdemoView::OnDraw(CDC* /*pDC*/) {CdemoDoc* pDoc = GetDocument();ASSERT_VALID(pDoc);if (!pDoc)return;// TODO: 在此处为本机数据添加绘制代码DrawGraph();}// CdemoView 打印void CdemoView::OnFilePrintPreview() { AFXPrintPreview(this);}BOOL CdemoView::OnPreparePrinting(CPrintInfo* pInfo) {// 默认准备return DoPreparePrinting(pInfo);}void CdemoView::OnBeginPrinting(CDC* /*pDC*/, CPrintInfo* /*pInfo*/) {// TODO: 添加额外的打印前进行的初始化过程}void CdemoView::OnEndPrinting(CDC* /*pDC*/, CPrintInfo* /*pInfo*/) { // TODO: 添加打印后进行的清理过程}void CdemoView::OnRButtonUp(UINT nFlags, CPoint point){ClientToScreen(&point);OnContextMenu(this, point);}void CdemoView::OnContextMenu(CWnd* pWnd, CPoint point) {theApp.GetContextMenuManager()->ShowPopupMenu(IDR_POPUP_EDIT,point.x, point.y, this, TRUE);}// CdemoView 诊断#ifdef _DEBUGvoid CdemoView::AssertValid() const{CView::AssertValid();}void CdemoView::Dump(CDumpContext& dc) const{CView::Dump(dc);}CdemoDoc* CdemoView::GetDocument() const // 非调试版本是内联的 { ASSERT(m_pDocument->IsKindOf(RUNTIME_CLASS(CdemoDoc)));return (CdemoDoc*)m_pDocument;}#endif //_DEBUGvoid CdemoView::DrawGraph()//绘制图形{CDC *pDC = GetDC(); //定义设备上下文指针GetClientRect(&rect); //获得客户区的大小pDC->SetMapMode(MM_ANISOTROPIC); //自定义坐标系pDC->SetWindowExt(rect.Width(), rect.Height()); //设置窗口比例pDC->SetViewportExt(rect.Width(), -rect.Height()); //设置视区比例,且x轴水平向右,y轴垂直向上pDC->SetViewportOrg(rect.Width() / 2, rect.Height() / 2); //设置客户区中心为坐标系原点rect.OffsetRect(-rect.Width() / 2, -rect.Height() / 2); //矩形与客户区重合CDC MemDC;//内存DCCBitmap NewBitmap, *pOldBitmap; //内存中承载图像的位图MemDC.CreateCompatibleDC(pDC); //建立与屏幕pDC兼容的MemDCNewBitmap.LoadBitmap(IDB_BITMAP1); //导入空心汉字位图pOldBitmap = MemDC.SelectObject(&NewBitmap);//将兼容位图选入MemDC MemDC.SetMapMode(MM_ANISOTROPIC); //MemDC自定义坐标系MemDC.SetWindowExt(rect.Width(), rect.Height());MemDC.SetViewportExt(rect.Width(), -rect.Height());MemDC.SetViewportOrg(rect.Width() / 2, rect.Height() / 2);pDC->BitBlt(-rect.Width() / 2, -rect.Height() / 2, rect.Width(), rect.Height(), &MemDC,-rect.Width() / 2, -rect.Height() / 2, SRCCOPY);//将内存位图拷贝到屏幕if(bFill)CharFill(pDC); //填充空心汉字MemDC.SelectObject(pOldBitmap); //恢复位图NewBitmap.DeleteObject(); //删除位图MemDC.DeleteDC(); //删除MemDCReleaseDC(pDC); //释放DC }void CdemoView::CharFill(CDC *pDC) //文字填充函数 {COLORREF BoundaryClr = RGB(0,0,0); //边界色BOOL bSpanFill;pHead = new CStackNode; //建立栈结点pHead->pNext = NULL; //栈头结点的指针域总为空Push(Seed); //种子像素入栈int x, y, x0 = Round(Seed.x), y0 = Round(Seed.y);//x,y用于判断种子与图形的位置关系x = x0 - 1;while(pDC->GetPixel(x, y0) != BoundaryClr && pDC->GetPixel(x, y0) != SeedClr )//左方判断{x--;if(x <= -rect.Width() / 2){MessageBox(L"种子不在图形之内", L"警告");//到达客户区最左端return;}}y = y0 + 1;while(pDC->GetPixel(x0, y) != BoundaryClr && pDC->GetPixel(x0, y) != SeedClr)//上方判断{y++;if(y >= rect.Height() / 2)//到达客户区最上端{MessageBox(L"种子不在图形之内", L"警告");return;}}x = x0 + 1;while(pDC->GetPixel(x, y0) != BoundaryClr && pDC->GetPixel(x, y0) != SeedClr)//右方判断{x++;if(x >= rect.Width() / 2)//到达客户区最右端{MessageBox(L"种子不在图形之内", L"警告");return;}}y = y0 - 1;while(pDC->GetPixel(x0, y) != BoundaryClr && pDC->GetPixel(x0, y) != SeedClr)//下方判断{y--;if(y <= -rect.Height() / 2)//到达客户区最下端{MessageBox(L"种子不在图形之内", L"警告");return;}}double xleft, xright;//区间最左端与最右端像素CP2 PopPoint, PointTemp;while(pHead->pNext != NULL)//如果栈不为空{Pop(PopPoint);if(pDC->GetPixel(Round(PopPoint.x), Round(PopPoint.y)) == SeedClr) continue;// 分别向左和向右填充扫描线PointTemp = PopPoint;while(pDC->GetPixel(Round(PointTemp.x), Round(PointTemp.y)) != BoundaryClr &&pDC->GetPixel(Round(PointTemp.x), Round(PointTemp.y)) != SeedClr) {pDC->SetPixelV(Round(PointTemp.x), Round(PointTemp.y), SeedClr);PointTemp.x++;}xright = PointTemp.x - 1;PointTemp.x = PopPoint.x - 1;while(pDC->GetPixel(Round(PointTemp.x), Round(PointTemp.y)) != BoundaryClr &&pDC->GetPixel(Round(PointTemp.x), Round(PointTemp.y)) != SeedClr) {pDC->SetPixelV(Round(PointTemp.x), Round(PointTemp.y), SeedClr);PointTemp.x--;}xleft=PointTemp.x + 1;//处理上一条扫描线PointTemp.x = xleft;PointTemp.y = PointTemp.y + 1;while(PointTemp.x < xright){bSpanFill = FALSE;while(pDC->GetPixel(Round(PointTemp.x), Round(PointTemp.y)) != BoundaryClr &&pDC->GetPixel(Round(PointTemp.x), Round(PointTemp.y)) != SeedClr) {bSpanFill = TRUE;PointTemp.x++;}if(bSpanFill){if(PointTemp.x == xright && pDC->GetPixel(Round(PointTemp.x),Round(PointTemp.y)) != BoundaryClr && pDC->GetPixel(Round(PointTemp.x), Round(PointTemp.y)) != SeedClr) PopPoint = PointTemp;elsePopPoint.x = PointTemp.x - 1; PopPoint.y = PointTemp.y;Push(PopPoint);bSpanFill = FALSE;}while((pDC->GetPixel(Round(PointTemp.x), Round(PointTemp.y)) == BoundaryClr &&PointTemp.x < xright) || (pDC->GetPixel(Round(PointTemp.x),Round(PointTemp.y)) == SeedClr &&PointTemp.x < xright))PointTemp.x++;}//处理下一条扫描线PointTemp.x = xleft;PointTemp.y = PointTemp.y - 2;while(PointTemp.x < xright){bSpanFill = FALSE;while(pDC->GetPixel(Round(PointTemp.x), Round(PointTemp.y)) != BoundaryClr &&pDC->GetPixel(Round(PointTemp.x), Round(PointTemp.y)) != SeedClr) {bSpanFill = TRUE;PointTemp.x++;}if(bSpanFill){if(PointTemp.x == xright && pDC->GetPixel(Round(PointTemp.x),Round(PointTemp.y)) != BoundaryClr && pDC->GetPixel(Round(PointTemp.x), Round(PointTemp.y)) != SeedClr) PopPoint = PointTemp;elsePopPoint.x = PointTemp.x - 1; PopPoint.y = PointTemp.y;Push(PopPoint);bSpanFill=FALSE;}while((pDC->GetPixel(Round(PointTemp.x), Round(PointTemp.y)) == BoundaryClr &&PointTemp.x < xright) || (pDC->GetPixel(Round(PointTemp.x), Round(PointTemp.y)) == SeedClr &&PointTemp.x < xright))PointTemp.x++;}}delete pHead;pHead = NULL;}void CdemoView::Push(CP2 point)//入栈函数{pTop = new CStackNode;pTop->PixelPoint = point;pTop->pNext = pHead->pNext;pHead->pNext = pTop;}void CdemoView::Pop(CP2 &point) //出栈函数{if(pHead->pNext != NULL){pTop = pHead->pNext;pHead->pNext = pTop->pNext;point = pTop->PixelPoint;delete pTop;}}// CdemoView 消息处理程序void CdemoView::OnLButtonDown(UINT nFlags, CPoint point) {// TODO: 在此添加消息处理程序代码和/或调用默认值Seed = CP2(point.x - rect.Width() / 2, rect.Height() / 2 - point.y); //选择种子位置Invalidate(FALSE);CView::OnLButtonDown(nFlags, point);}void CdemoView::OnDrawPic(){// TODO: 在此添加命令处理程序代码CColorDialog ccd(SeedClr, CC_SOLIDCOLOR);if(IDOK == ccd.DoModal())//调用颜色对话框选取填充色SeedClr = ccd.GetColor();elsereturn;if(IDOK == MessageBox(L"请在空心字体内单击鼠标左键!", L"提示",MB_OKCANCEL))bFill = TRUE;elsereturn;}实验总结:上机做实验主要是看明白程序,现在来说,自己还不会自己编程,还是下载老师的实例程序看代码,然后运行看结果,自己再去琢磨理解程序。
计算机图形学-有效边表填充算法实验报告

实验题目:实验二有效边表填充算法1.实验目的:设计有效边表结点和边表结点数据结构设计有效边表填充算法编程实现有效边表填充算法2.实验描述:下图1 所示多边形覆盖了12 条扫描线,共有7 个顶点和7 条边。
7 个顶点分别为:P0(7,8),P1(3,12),P2(1,7),P3(3,1), P4(6,5), P5(8,1), P6(12,9)。
在1024×768 的显示分辩率下,将多边形顶点放大为P0(500,400),P1(350,600),P2(250,350),P3(350,50), P4(500,250), P5(600,50), P6(800,450)。
请使用有效边表算法填充该多边形。
图1示例多边形图2 屏幕显示多边形3.算法设计:(1)建立AET和BUCKET类;(2)初始化桶,并在建立桶结点时为其表示的扫描线初始化为带头结点的链表;(3)对每个桶结点进行循环,将桶内每个结点的边表合并为有效边表,并进行有效边表循环;(4)按照扫描线从小到大的移动顺序,计算当前扫描线与多边形各边的交点,然后把这些交点按X值递增的顺序进行排序,配对,以确定填充区间;(5)用指定颜色点亮填充区间内的所有像素,即完成填充工作。
4.源程序:1)//AET.hclass AET{AET();virtual ~AET();double x;int yMax;double k;//代替1/kAET *next;};//AET..cppAET::AET(){}AET::~AET(){}2) //Bucket.h#include "AET.h" class Bucket{Bucket();virtual ~Bucket();int ScanLine;AET *p;//桶上的边表指针Bucket *next;};// Bucket.cppBucket::Bucket(){}Bucket::~Bucket(){}3)//TestView.h#include "AET.h"//包含有效边表类#include "Bucket.h"//包含桶类#define Number 7//N为闭合多边形顶点数,顶点存放在整型二维数组Point[N]中class CTestView : public CView{。
计算机图形学课程设计-有效边表填充算法实现

计算机图形学课程设计设计题目改进的有效边表算法对多边形的填充学院名称信息科学与技术学院专业名称计算机科学与技术学生姓名刘柯学生学号201213030112任课教师梅占勇设计(论文)成绩教务处制2015年9 月28 日目录一、设计内容与要求 (3)1.1设计题目 (3)1.2 设计内容 (3)1.3 设计目标 (3)二、总体设计 (3)2.1 多边形的表示 (3)2.2 x-扫描线算法 (4)2.3 改进的有效边表算法 (4)2.3.1 改进的有效边表算法 (4)2.3.2 有效边表 (5)2.3.3 边表 (6)三、详细设计 (8)3.1 改进的有效边表算法的实现 (8)3.2 有效边表算法程序流程图 (9)四、测试结果 (9)五、总结 (15)六、源代码 (15)参考文献 (26)一、设计内容与要求1.1设计题目用改进的有效边表算法实现多边形的填充1.2 设计内容使用OpenGL实现用改进的有效边表算法填充多边形1.3 设计目标参照课本上改进的有效边表算法的思想,实现该算法的C语言代码,并用该算法搭配OpenGL以像素点的方式绘制出给定顶点坐标的多边形。
二、总体设计2.1 多边形的表示在计算机图形学中,多边形有2种重要的表示方法:顶点表示和点阵表示。
顶点表示用多边形的顶点序列来刻画多边形,这种方法直观、几何意义强,占用内存少,应用普遍,但它没有明确指出哪些像素在多边形内,故不能直接用于面着色。
点阵表示用位于多边形内的像素的集合来刻画多边形。
这种表示法虽然失去了许多重要的几何信息,但便于运用帧缓存表示图形,是面着色所需要的图形表示形式。
大多数图形应用系统采用顶点序列表示多边形,而顶点表示又不能直接用于显示,那么就必须有从多边形的顶点表示到点阵表示的转换,这种转换称为多边形的扫描转换或多边形的填充。
即从多边形的顶点信息出发,求出位于其内部的各个像素,并将其颜色值写入帧缓存的相应单元中。
2.2 x-扫描线算法x-扫描线算法的基本思想是,按照扫描线的顺序,计算扫描线与多边形的相交区间,再用要求的颜色显示这些区间的像素,即完成填充工作。
多边形边表桶填充

实验一:改进的有效边表算法一.实验目的用鼠标描绘几个顶点,画出多边形,用边表桶的填充算法实现多边形的填充。
二.算法思想在处理一条扫描线时,仅对与它相交的多边形的边(有效边)求交,其次利用扫描线的连贯性,考虑到当前扫描线与各边的交点顺序与下一条扫描线各边的交点顺序很可能相同或者相似,因此在当前扫描线处理完毕之后,不必为下一条扫描线从头开始构造交点信息;最后利用多边形边的连贯性,认为若某条边与当前扫描线相交,则它很可能也与下一条扫描线相交且其交点与上一次的交点相交。
三.实现过程1.边表的构造1.首先构造一个纵向链表,链表长度为多边形所占有的最大扫描线数,链表的每个结点,称为,称为一个桶,对应多边形覆盖的每一条扫描线。
2.将每条边的信息装入与该边最小Y坐标(Ymin)相对应的桶中,也就是说,若某条边的较低端点为Ymin,则该边就放在相应的Y=Ymin的扫描线桶中。
3.每条边的数据形成一个结点,内容包括该扫描线与该边的初始交点X(即较低端点的X坐标),该边的最大Y 坐标值Ymax,以及边斜率的倒数1/k.4.同一桶中若干条边按x|ymin 由小到大排序,若x|ymin相等,则按照1/k由小到大排序。
2.扫描线的填充算法1.初始化。
构造边表,AET表设置为空。
2.将第一个不空的ET表中的边与AET表合并。
3.由AET表中取出的交点并进行填充,填充时候设置一个布尔量b(初值为假),令指针有效边表中的第一个结点(交点)到最后一个结点遍历一次,每访问一个结点,把b取反一次,若b为真,则把从当前结点的x值开始到下一个结点的x值结束的区间用多边形色填充,填充之后删除y=ymax的边(需注意,填充时同样为避免多边形区域的扩大化,需要多交点进行与x-扫面线算法相同的处理)。
4.y i+1=y i+1,根据x i+1=x i+1/k计算并修改AET表,同时合并ET表中y=y i+1桶中的边,按次序插入到AET 表中形成新的AET表。
实验三计算机图形学多边形填充算法

实验三计算机图形学多边形填充算法课程名称计算机图形学实验日期 2013-11-7 实验名称多边形填充算法编程成绩实验目的:熟悉多边形填充算法,掌握MFC图形编程的基本方法和调试技巧。
实验条件: 计算机;VS2008;OpenGL实验内容:1(使用MFC技术实现多边形有效边表填充算法,参考界面效果如下:// ChildView.cpp : CChildView 类的实现#include "stdafx.h"#include "demo.h"#include "ChildView.h"#include <math.h>#define Round(d) int(floor(d+0.5))//四舍五入宏定义#ifdef _DEBUG#define new DEBUG_NEW#endif// CChildViewCChildView::CChildView(){}CChildView::~CChildView(){}BEGIN_MESSAGE_MAP(CChildView, CWnd)ON_WM_PAINT()ON_WM_CREATE()ON_COMMAND(ID_DRAW_PIC, &CChildView::OnDrawPic)END_MESSAGE_MAP()// CChildView 消息处理程序BOOL CChildView::PreCreateWindow(CREATESTRUCT& cs) {if (!CWnd::PreCreateWindow(cs))return FALSE;cs.dwExStyle |= WS_EX_CLIENTEDGE;cs.style &= ~WS_BORDER;cs.lpszClass = AfxRegisterWndClass(CS_HREDRAW|CS_VREDRAW|CS_DBLCLKS,::LoadCursor(NULL, IDC_ARROW),reinterpret_cast<HBRUSH>(COLOR_WINDOW+1), NULL);return TRUE;}void CChildView::OnPaint(){CPaintDC dc(this); // 用于绘制的设备上下文// TODO: 在此处添加消息处理程序代码DrawGraph();// 不要为绘制消息而调用CWnd::OnPaint() }void CChildView::ReadPoint() //点表{P[0].x = 50; P[0].y = 100;P[1].x = -150;P[1].y = 300;P[2].x = -250;P[2].y = 50;P[3].x = -150;P[3].y = -250;P[4].x = 0; P[4].y = -50;P[5].x = 100; P[5].y = -250;P[6].x = 300; P[6].y = 150;}void CChildView::DrawPolygon(CDC *pDC) //绘制多边形边界{CLine *line = new CLine;CP2 t;for(int i = 0; i < 7; i++) //绘制多边形{if(i == 0){line->MoveTo(pDC, P[i]);t = P[i];}else{line->LineTo(pDC, P[i]);}}line->LineTo(pDC, t); //闭合多边形delete line;}void CChildView::DrawGraph() //绘制图形 {CRect rect; //定义客户区GetClientRect(&rect); //获得客户区的大小CDC *pDC = GetDC(); //定义设备上下文指针pDC->SetMapMode(MM_ANISOTROPIC); //自定义坐标系pDC->SetWindowExt(rect.Width(), rect.Height()); //设置窗口比例pDC->SetViewportExt(rect.Width(), -rect.Height()); //设置视区比例,且x轴水平向右,y轴垂直向上pDC->SetViewportOrg(rect.Width() / 2, rect.Height() / 2); //设置客户区中心为坐标系原点rect.OffsetRect(-rect.Width() / 2, -rect.Height() / 2); //矩形与客户区重合if(!bFill)DrawPolygon(pDC); //绘制多边形elseFillPolygon(pDC); //填充多边形ReleaseDC(pDC); //释放DC}void CChildView::FillPolygon(CDC *pDC) //填充多边形 {for(int i = 0; i < 7; i++) //转储顶点坐标,y坐标取为整数{P1[i].x = P[i].x;P1[i].y = Round(P[i].y);P1[i].c = CRGB(bRed / 255.0, bGreen / 255.0, bBlue / 255.0);}CFill *fill = new CFill; //动态分配内存fill->SetPoint(P1, 7); //初始化Fill对象fill->CreateBucket(); //建立桶表fill->CreateEdge(); //建立边表fill->Gouraud(pDC); //填充多边形delete fill; //撤销内存 }int CChildView::OnCreate(LPCREATESTRUCT lpCreateStruct) {if (CWnd::OnCreate(lpCreateStruct) == -1)return -1;// TODO: 在此添加您专用的创建代码bFill = FALSE;ReadPoint();return 0;}void CChildView::OnDrawPic(){// TODO: 在此添加命令处理程序代码COLORREF GetClr = RGB(0, 0, 0); //调色板颜色CColorDialog ccd(GetClr, CC_SOLIDCOLOR);if(IDOK == ccd.DoModal()) //调用颜色对话框选取填充色GetClr = ccd.GetColor();elsereturn;bRed = GetRValue(GetClr); //获取红色分量bGreen = GetGValue(GetClr); //获取绿色分量bBlue = GetBValue(GetClr); //获取蓝色分量bFill = TRUE;Invalidate();}2(使用MFC技术实现多边形边缘填充算法,参考界面效果如下:// demoView.cpp : CdemoView 类的实现#include "stdafx.h"#include "demo.h"#include "demoDoc.h"#include "demoView.h"#include <math.h>#define Round(d) int(floor(d+0.5))//四舍五入宏定义 #ifdef _DEBUG #define new DEBUG_NEW#endif// CdemoViewIMPLEMENT_DYNCREATE(CdemoView, CView)BEGIN_MESSAGE_MAP(CdemoView, CView)// 标准打印命令ON_COMMAND(ID_FILE_PRINT, &CView::OnFilePrint)ON_COMMAND(ID_FILE_PRINT_DIRECT, &CView::OnFilePrint)ON_COMMAND(ID_FILE_PRINT_PREVIEW, &CdemoView::OnFilePrintPreview) ON_COMMAND(ID_DRAW_PIC, &CdemoView::OnDrawPic) END_MESSAGE_MAP() // CdemoView 构造/析构CdemoView::CdemoView(){// TODO: 在此处添加构造代码}CdemoView::~CdemoView(){}BOOL CdemoView::PreCreateWindow(CREATESTRUCT& cs) {// TODO: 在此处通过修改// CREATESTRUCT cs 来修改窗口类或样式return CView::PreCreateWindow(cs); }// CdemoView 绘制void CdemoView::OnDraw(CDC* /*pDC*/) {CdemoDoc* pDoc = GetDocument();ASSERT_VALID(pDoc);if (!pDoc)return;// TODO: 在此处为本机数据添加绘制代码DrawGraph();}// CdemoView 打印void CdemoView::OnFilePrintPreview() {AFXPrintPreview(this);}BOOL CdemoView::OnPreparePrinting(CPrintInfo* pInfo){// 默认准备return DoPreparePrinting(pInfo); }void CdemoView::OnBeginPrinting(CDC* /*pDC*/, CPrintInfo* /*pInfo*/) {// TODO: 添加额外的打印前进行的初始化过程 }void CdemoView::OnEndPrinting(CDC* /*pDC*/, CPrintInfo* /*pInfo*/) {// TODO: 添加打印后进行的清理过程 }void CdemoView::OnRButtonUp(UINT nFlags, CPoint point){ClientToScreen(&point);OnContextMenu(this, point);}void CdemoView::OnContextMenu(CWnd* pWnd, CPoint point){theApp.GetContextMenuManager()->ShowPopupMenu(IDR_POPUP_EDIT,point.x, point.y, this, TRUE);}void CdemoView::ReadPoint() //点表 {P[0].x = 50; P[0].y = 100;P[1].x = -150;P[1].y = 300;P[2].x = -250;P[2].y = 50;P[3].x = -150;P[3].y = -250;P[4].x = 0; P[4].y = -50;P[5].x = 100; P[5].y = -250;P[6].x = 300; P[6].y = 150; }void CdemoView::DrawPolygon(CDC *pDC) { for(int i = 0; i < 7; i++) //计算多边形边界{if(P[i].x > MaxX)MaxX = P[i].x;if(P[i].x < MinX)MinX = P[i].x;if(P[i].y > MaxY)MaxY = P[i].y;if(P[i].y < MinY)MinY = P[i].y;}CLine *line = new CLine;CP2 t;for(int i = 0; i < 7; i++) //绘制多边形{if(i == 0){line->MoveTo(pDC, P[i]);t = P[i];}else{line->LineTo(pDC, P[i]);}}line->LineTo(pDC, t); //闭合多边形line->MoveTo(pDC, CP2(MinX, MinY)); //绘制包围盒line->LineTo(pDC, CP2(MinX, MaxY));line->LineTo(pDC, CP2(MaxX, MaxY));line->LineTo(pDC, CP2(MaxX, MinY));line->LineTo(pDC, CP2(MinX, MinY));delete line;}void CdemoView::FillPolygon(CDC *pDC){COLORREF BClr = RGB(255, 255, 255); //背景色COLORREF FClr = GetClr; //填充色int ymin, ymax; //边的最小y值与最大y值double x, y, k; //x,y当前点,k斜率的倒数for(int i = 0; i < 7; i++) //循环多边形所有边{int j = (i + 1) % 7;k = (P[i].x - P[j].x) / (P[i].y - P[j].y); //计算/kif(P[i].y < P[j].y) //得到每条边y的最大值与最小值{ymin = Round(P[i].y);ymax = Round(P[j].y);x = P[i].x; //得到x|ymin}else{ymin = Round(P[j].y);ymax = Round(P[i].y);x = P[j].x;}for(y = ymin; y < ymax; y++) //沿每一条边循环扫描线{for(int m = Round(x); m < MaxX; m++) //对每一条扫描线与边的交点的右侧像素循环{if(FClr == pDC->GetPixel(m, Round(y))) //如果是填充色pDC->SetPixelV(m, Round(y), BClr); //置为背景色elsepDC->SetPixelV(m, Round(y), FClr); //置为填充色}x += k; //计算下一条扫描线的x起点坐标}}}void CdemoView::DrawGraph() //绘制图形 {CRect rect; //定义客户区GetClientRect(&rect); //获得客户区的大小CDC *pDC = GetDC(); //定义设备上下文指针pDC->SetMapMode(MM_ANISOTROPIC); //自定义坐标系pDC->SetWindowExt(rect.Width(), rect.Height()); //设置窗口比例pDC->SetViewportExt(rect.Width(), -rect.Height()); //设置视区比例,且x轴水平向右,y轴垂直向上pDC->SetViewportOrg(rect.Width() / 2, rect.Height() / 2); //设置客户区中心为坐标系原点rect.OffsetRect(-rect.Width() / 2, -rect.Height() / 2); //矩形与客户区重合if(!bFill)DrawPolygon(pDC); //绘制多边形elseFillPolygon(pDC); //填充多边形ReleaseDC(pDC); //释放DC }// CdemoView 诊断#ifdef _DEBUGvoid CdemoView::AssertValid() const{CView::AssertValid();}void CdemoView::Dump(CDumpContext& dc) const{CView::Dump(dc);}CdemoDoc* CdemoView::GetDocument() const // 非调试版本是内联的 { ASSERT(m_pDocument->IsKindOf(RUNTIME_CLASS(CdemoDoc)));return (CdemoDoc*)m_pDocument;}#endif //_DEBUG// CdemoView 消息处理程序void CdemoView::OnInitialUpdate(){CView::OnInitialUpdate();// TODO: 在此添加专用代码和/或调用基类bFill = FALSE;ReadPoint();GetClr = RGB(0,0,0);MinX = MaxX = P[0].x;MinY = MaxY = P[0].y;}void CdemoView::OnDrawPic(){// TODO: 在此添加命令处理程序代码CColorDialog ccd(GetClr, CC_SOLIDCOLOR);if(IDOK == ccd.DoModal()) //调用颜色对话框选取填充色GetClr = ccd.GetColor();elsereturn;bFill = TRUE;Invalidate(FALSE);}3.使用MFC技术实现种子填充算法,参考界面效果如下:// demoView.cpp : CdemoView 类的实现 #include "stdafx.h"#include "demo.h"#include "demoDoc.h"#include "demoView.h"#include <math.h>#define Round(d) int(floor(d+0.5))//四舍五入宏定义 #ifdef _DEBUG #define new DEBUG_NEW#endif// CdemoViewIMPLEMENT_DYNCREATE(CdemoView, CView) BEGIN_MESSAGE_MAP(CdemoView, CView)// 标准打印命令ON_COMMAND(ID_FILE_PRINT, &CView::OnFilePrint)ON_COMMAND(ID_FILE_PRINT_DIRECT, &CView::OnFilePrint)ON_COMMAND(ID_FILE_PRINT_PREVIEW, &CdemoView::OnFilePrintPreview) ON_WM_LBUTTONDOWN()ON_COMMAND(ID_DRAW_PIC, &CdemoView::OnDrawPic)END_MESSAGE_MAP()// CdemoView 构造/析构CdemoView::CdemoView(){// TODO: 在此处添加构造代码bFill = FALSE;SeedClr = RGB(255, 0, 0);}CdemoView::~CdemoView(){}BOOL CdemoView::PreCreateWindow(CREATESTRUCT& cs) { // TODO: 在此处通过修改// CREATESTRUCT cs 来修改窗口类或样式return CView::PreCreateWindow(cs); }// CdemoView 绘制void CdemoView::OnDraw(CDC* /*pDC*/) {CdemoDoc* pDoc = GetDocument();ASSERT_VALID(pDoc);if (!pDoc)return;// TODO: 在此处为本机数据添加绘制代码DrawGraph();}// CdemoView 打印void CdemoView::OnFilePrintPreview() { AFXPrintPreview(this);}BOOL CdemoView::OnPreparePrinting(CPrintInfo* pInfo) {// 默认准备return DoPreparePrinting(pInfo);}void CdemoView::OnBeginPrinting(CDC* /*pDC*/, CPrintInfo* /*pInfo*/) {// TODO: 添加额外的打印前进行的初始化过程}void CdemoView::OnEndPrinting(CDC* /*pDC*/, CPrintInfo* /*pInfo*/) { // TODO: 添加打印后进行的清理过程}void CdemoView::OnRButtonUp(UINT nFlags, CPoint point){ClientToScreen(&point);OnContextMenu(this, point);}void CdemoView::OnContextMenu(CWnd* pWnd, CPoint point) {theApp.GetContextMenuManager()->ShowPopupMenu(IDR_POPUP_EDIT,point.x, point.y, this, TRUE);}// CdemoView 诊断#ifdef _DEBUGvoid CdemoView::AssertValid() const{CView::AssertValid();}void CdemoView::Dump(CDumpContext& dc) const{CView::Dump(dc);}CdemoDoc* CdemoView::GetDocument() const // 非调试版本是内联的 { ASSERT(m_pDocument->IsKindOf(RUNTIME_CLASS(CdemoDoc)));return (CdemoDoc*)m_pDocument;}#endif //_DEBUGvoid CdemoView::DrawGraph()//绘制图形{CDC *pDC = GetDC(); //定义设备上下文指针GetClientRect(&rect); //获得客户区的大小pDC->SetMapMode(MM_ANISOTROPIC); //自定义坐标系pDC->SetWindowExt(rect.Width(), rect.Height()); //设置窗口比例pDC->SetViewportExt(rect.Width(), -rect.Height()); //设置视区比例,且x轴水平向右,y轴垂直向上pDC->SetViewportOrg(rect.Width() / 2, rect.Height() / 2); //设置客户区中心为坐标系原点rect.OffsetRect(-rect.Width() / 2, -rect.Height() / 2); //矩形与客户区重合CDC MemDC;//内存DCCBitmap NewBitmap, *pOldBitmap; //内存中承载图像的位图MemDC.CreateCompatibleDC(pDC); //建立与屏幕pDC兼容的MemDCNewBitmap.LoadBitmap(IDB_BITMAP1); //导入空心汉字位图pOldBitmap = MemDC.SelectObject(&NewBitmap);//将兼容位图选入MemDC MemDC.SetMapMode(MM_ANISOTROPIC); //MemDC自定义坐标系MemDC.SetWindowExt(rect.Width(), rect.Height());MemDC.SetViewportExt(rect.Width(), -rect.Height());MemDC.SetViewportOrg(rect.Width() / 2, rect.Height() / 2);pDC->BitBlt(-rect.Width() / 2, -rect.Height() / 2, rect.Width(), rect.Height(), &MemDC,-rect.Width() / 2, -rect.Height() / 2, SRCCOPY);//将内存位图拷贝到屏幕if(bFill)CharFill(pDC); //填充空心汉字MemDC.SelectObject(pOldBitmap); //恢复位图NewBitmap.DeleteObject(); //删除位图MemDC.DeleteDC(); //删除MemDCReleaseDC(pDC); //释放DC }void CdemoView::CharFill(CDC *pDC) //文字填充函数 {COLORREF BoundaryClr = RGB(0,0,0); //边界色BOOL bSpanFill;pHead = new CStackNode; //建立栈结点pHead->pNext = NULL; //栈头结点的指针域总为空Push(Seed); //种子像素入栈int x, y, x0 = Round(Seed.x), y0 = Round(Seed.y);//x,y用于判断种子与图形的位置关系x = x0 - 1;while(pDC->GetPixel(x, y0) != BoundaryClr && pDC->GetPixel(x, y0) != SeedClr )//左方判断{x--;if(x <= -rect.Width() / 2){MessageBox(L"种子不在图形之内", L"警告");//到达客户区最左端return;}}y = y0 + 1;while(pDC->GetPixel(x0, y) != BoundaryClr && pDC->GetPixel(x0, y) != SeedClr)//上方判断{y++;if(y >= rect.Height() / 2)//到达客户区最上端{MessageBox(L"种子不在图形之内", L"警告");return;}}x = x0 + 1;while(pDC->GetPixel(x, y0) != BoundaryClr && pDC->GetPixel(x, y0) != SeedClr)//右方判断{x++;if(x >= rect.Width() / 2)//到达客户区最右端{MessageBox(L"种子不在图形之内", L"警告");return;}}y = y0 - 1;while(pDC->GetPixel(x0, y) != BoundaryClr && pDC->GetPixel(x0, y) != SeedClr)//下方判断{y--;if(y <= -rect.Height() / 2)//到达客户区最下端{MessageBox(L"种子不在图形之内", L"警告");return;}}double xleft, xright;//区间最左端与最右端像素CP2 PopPoint, PointTemp;while(pHead->pNext != NULL)//如果栈不为空{Pop(PopPoint);if(pDC->GetPixel(Round(PopPoint.x), Round(PopPoint.y)) == SeedClr) continue;// 分别向左和向右填充扫描线PointTemp = PopPoint;while(pDC->GetPixel(Round(PointTemp.x), Round(PointTemp.y)) != BoundaryClr &&pDC->GetPixel(Round(PointTemp.x), Round(PointTemp.y)) != SeedClr) {pDC->SetPixelV(Round(PointTemp.x), Round(PointTemp.y), SeedClr);PointTemp.x++;}xright = PointTemp.x - 1;PointTemp.x = PopPoint.x - 1;while(pDC->GetPixel(Round(PointTemp.x), Round(PointTemp.y)) != BoundaryClr &&pDC->GetPixel(Round(PointTemp.x), Round(PointTemp.y)) != SeedClr) {pDC->SetPixelV(Round(PointTemp.x), Round(PointTemp.y), SeedClr);PointTemp.x--;}xleft=PointTemp.x + 1;//处理上一条扫描线PointTemp.x = xleft;PointTemp.y = PointTemp.y + 1;while(PointTemp.x < xright){bSpanFill = FALSE;while(pDC->GetPixel(Round(PointTemp.x), Round(PointTemp.y)) != BoundaryClr &&pDC->GetPixel(Round(PointTemp.x), Round(PointTemp.y)) != SeedClr) {bSpanFill = TRUE;PointTemp.x++;}if(bSpanFill){if(PointTemp.x == xright && pDC->GetPixel(Round(PointTemp.x),Round(PointTemp.y)) != BoundaryClr && pDC->GetPixel(Round(PointTemp.x), Round(PointTemp.y)) != SeedClr) PopPoint = PointTemp;elsePopPoint.x = PointTemp.x - 1; PopPoint.y = PointTemp.y;Push(PopPoint);bSpanFill = FALSE;}while((pDC->GetPixel(Round(PointTemp.x), Round(PointTemp.y)) == BoundaryClr &&PointTemp.x < xright) || (pDC->GetPixel(Round(PointTemp.x),Round(PointTemp.y)) == SeedClr &&PointTemp.x < xright))PointTemp.x++;}//处理下一条扫描线PointTemp.x = xleft;PointTemp.y = PointTemp.y - 2;while(PointTemp.x < xright){bSpanFill = FALSE;while(pDC->GetPixel(Round(PointTemp.x), Round(PointTemp.y)) != BoundaryClr &&pDC->GetPixel(Round(PointTemp.x), Round(PointTemp.y)) != SeedClr) {bSpanFill = TRUE;PointTemp.x++;}if(bSpanFill){if(PointTemp.x == xright && pDC->GetPixel(Round(PointTemp.x),Round(PointTemp.y)) != BoundaryClr && pDC->GetPixel(Round(PointTemp.x), Round(PointTemp.y)) != SeedClr) PopPoint = PointTemp;elsePopPoint.x = PointTemp.x - 1; PopPoint.y = PointTemp.y;Push(PopPoint);bSpanFill=FALSE;}while((pDC->GetPixel(Round(PointTemp.x), Round(PointTemp.y)) == BoundaryClr &&PointTemp.x < xright) || (pDC->GetPixel(Round(PointTemp.x), Round(PointTemp.y)) == SeedClr &&PointTemp.x < xright))PointTemp.x++;}}delete pHead;pHead = NULL;}void CdemoView::Push(CP2 point)//入栈函数{pTop = new CStackNode;pTop->PixelPoint = point;pTop->pNext = pHead->pNext;pHead->pNext = pTop;}void CdemoView::Pop(CP2 &point) //出栈函数{if(pHead->pNext != NULL){pTop = pHead->pNext;pHead->pNext = pTop->pNext;point = pTop->PixelPoint;delete pTop;}}// CdemoView 消息处理程序void CdemoView::OnLButtonDown(UINT nFlags, CPoint point) {// TODO: 在此添加消息处理程序代码和/或调用默认值Seed = CP2(point.x - rect.Width() / 2, rect.Height() / 2 - point.y); //选择种子位置Invalidate(FALSE);CView::OnLButtonDown(nFlags, point);}void CdemoView::OnDrawPic(){// TODO: 在此添加命令处理程序代码CColorDialog ccd(SeedClr, CC_SOLIDCOLOR);if(IDOK == ccd.DoModal())//调用颜色对话框选取填充色SeedClr = ccd.GetColor();elsereturn;if(IDOK == MessageBox(L"请在空心字体内单击鼠标左键!", L"提示",MB_OKCANCEL))bFill = TRUE;elsereturn;}实验总结:上机做实验主要是看明白程序,现在来说,自己还不会自己编程,还是下载老师的实例程序看代码,然后运行看结果,自己再去琢磨理解程序。
计算机图形学教案

装订首页
工业学院教案
课程:计算机图形学
学期:2013/14第一学期
课时:理论52,实验12
教材:计算机图形学基础教程
计算机图形学实践教程
教师:孔令德静丽亚
工业学院教案
工业学院教案
工业学院教案
工业学院教案
工业学院教案
工业学院教案
工业学院教案
工业学院教案
工业学院教案
工业学院教案
工业学院教案
工业学院教案
工业学院教案
工业学院教案
工业学院教案
工业学院教案
工业学院教案
工业学院教案
工业学院教案
工业学院教案
工业学院教案
工业学院教案
工业学院教案
工业学院教案
工业学院教案
工业学院教案
工业学院教案
工业学院教案
工业学院教案
工业学院教案
工业学院教案
工业学院教案。
[VIP专享]计算机图形学 有效边表填充算法实验报告
![[VIP专享]计算机图形学 有效边表填充算法实验报告](https://img.taocdn.com/s3/m/4ea18a9689eb172ded63b7d8.png)
图 2 屏幕显示多边形 3.算法设计: (1)建立 AET 和 BUCKET 类; (2)初始化桶,并在建立桶结点时为其表示的扫描线初始化为带头结点的链表; (3)对每个桶结点进行循环,将桶内每个结点的边表合并为有效边表,并进行有效边表循 环; (4)按照扫描线从小到大的移动顺序,计算当前扫描线与多边形各边的交点,然后把这些 交点按 X 值递增的顺序进行排序,配对,以确定填充区间; (5)用指定颜色点亮填充区间内的所有像素,即完成填充工作。 4.源程序: 1)//AET.h class AET { public:
}
Bucket::~Bucket() {
}
3)//TestView.h #include "AET.h"//包含有效边表类 #include "Bucket.h"//包含桶类 #define Number 7//N 为闭合多边形顶点数,顶点存放在整型二维数组 Point[N]中 class CTestView : public CView { 。。。。。。。。。 public:
COLORREF GetColor;//调色板 CPoint Point[7];//定义多边形 Bucket *HeadB,*CurrentB;//桶的头结点和当前结点 AET E[Number],*HeadE,*CurrentE,*T1,*T2;//有效边表的结点 } (4) TestView.cpp #define ROUND(a) int(a+0.5) //四舍五入 CTestView::CTestView() { //设置多边形的 7 个顶点 Point[0]=CPoint(550,400);//P0 Point[1]=CPoint(350,600);//P1 Point[2]=CPoint(250,350);//P2 Point[3]=CPoint(350,50);//P3 Point[4]=CPoint(500,250);//P4 Point[5]=CPoint(600,50);//P5 Point[6]=CPoint(800,450);//P6 }
有效边表填充算法
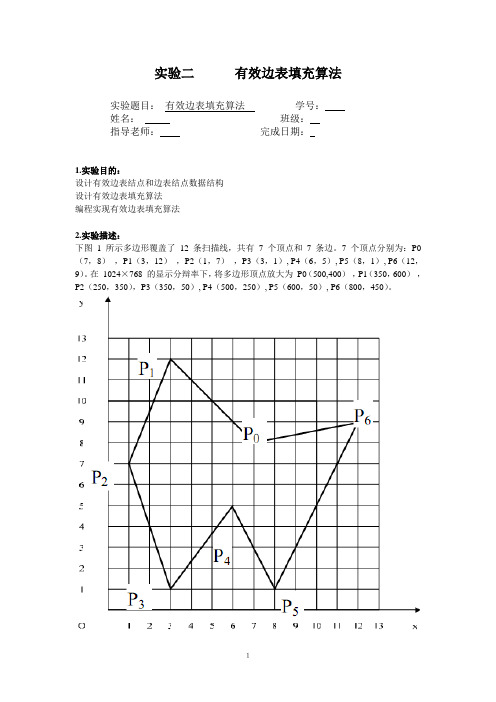
实验二有效边表填充算法实验题目:有效边表填充算法学号:姓名:班级:指导老师:完成日期:1.实验目的:设计有效边表结点和边表结点数据结构设计有效边表填充算法编程实现有效边表填充算法2.实验描述:下图1 所示多边形覆盖了12 条扫描线,共有7 个顶点和7 条边。
7 个顶点分别为:P0(7,8),P1(3,12),P2(1,7),P3(3,1), P4(6,5), P5(8,1), P6(12,9)。
在1024×768 的显示分辩率下,将多边形顶点放大为P0(500,400),P1(350,600),P2(250,350),P3(350,50), P4(500,250), P5(600,50), P6(800,450)。
图1示例多边形图2屏幕显示多边形3.算法设计:多边形的有效边表填充算法的基本原理是按照扫描线从小到大的移动顺序,计算当前扫描线与多边形各边的交点,然后把这些交点按x值递增的顺序进行排序、配对,以确定填充区间,然后用指定颜色点亮填充区间的所有像素,即完成填充工作。
有效边表填充算法通过访问多边形覆盖区间内的每个像素,可以填充凸、凹多边形和环,已成为目前最为有效的多边形填充算法。
4.源程序:1)//AET.h和AET..cppclass AET{public:AET();virtual ~AET();double x;int yMax;double k; //代替1/kAET *next;}2)//Bucket.h和Bucket.cppclass Bucket{public:Bucket();virtual ~Bucket();int ScanLine;AET *p;//桶上的边表指针Bucket *next;}3) // TestView.h#include "AET.h"//包含有效边表类#include "Bucket.h"//包含桶类#define Number 7//N为闭合多边形顶点数,顶点存放在整型二维数组Point[N]中class CTestView : public CView{。
计算机图形学实验及课程设计

实验12 颜色渐变立方体
12.1 实验目的
掌握凸多面体消隐算法。 掌握双线性颜色插值算法。 建立基本三维场景。
实验12 颜色渐变立方体
12.2 实验要求
建立三维坐标系Oxyz,原点位于屏幕客户区中 心,x轴水平向右为正,y轴铅直向上为正,z轴 垂直于屏幕指向观察者。 以原点为体心绘制透视投影立方体,立方体8 个顶点的颜色分别为黑色、白色、红色、绿色、 蓝色、黄色、品红色和青色。背景色为黑色, 如图12-1所示。
实验4 二维几何变换
4.2 实验要求
使用静态切分视图,将窗口分为左右窗格。左窗格为继承于
CFormView类的表单视图类CLeftPortion,右窗格为一般视图
类CTestView。 左窗格提供代表“图形顶点数”(4、8、16和32)、“平移变 换”(x方向和y方向)、“旋转变换”(逆时针和顺时针)和 “比例变换”(放大和缩小)的滑动条,用于控制右窗格内的 图形变化。 右窗格内以屏幕客户区中心为图形的几何中心,绘制图形顶点 数从4变化为8、16和32的正多边形。为了表达图形的旋转,多
实验8 动态三视图
8.3 效果图
多面体动态三视图的效果如图8-1所示。
图8-1 多面体动态三视图的效果图
实验9 动态绘制Bezier曲线
9.1实验目的
掌握直线的参数表示法。 掌握德卡斯特里奥算法的几何意义。 掌握绘制二维Bezier曲线的方法。
实验9 动态绘制Bezier曲线
9.2 实验要求
实验8 动态三视图
8.1实验目的
掌握主视图变换矩阵。 掌握俯视图变换矩阵。 掌握侧视图变换矩阵。 掌握斜等测图绘制方法。
实验8 动态三视图
计算机图形学-填充与裁剪算法的实现资料

- 图形学课程实验报告 -
-5-
}
/* ****************************
第三部分 **********************************
* 求当前扫描线 i 的 AET链表
*/
list<Edge> ET_Structor(RamEdge r[],int n,int i) //i
*(头文件,宏定义,点的结构体 Point ,原始边记录结构体 RamEdg,e边记录类 Edge)*/
#include<algorithm>
#include"graphics.h"
#include<iostream>
#include<stdlib.h>
#include<list> #define MAXSIZE 800 using namespace std;
{
if(p[i].y<=p[i+1].y)
- 图形学课程实验报告 -
-4-
{ r[i].start.x=p[i].x; r[i].start.y=p[i].y; r[i].end.x=p[i+1].x; r[i].end.y=p[i+1].y;
} else {
r[i].start.x=p[i+1].x; r[i].start.y=p[i+1].y; r[i].end.x=p[i].x; r[i].end.y=p[i].y; } } if(p[n-1].y<=p[0].y) { r[n-1].start.x=p[n-1].x; r[n-1].start.y=p[n-1].y; r[n-1].end.x=p[0].x; r[n-1].end.y=p[0].y; } else { r[n-1].start.x=p[0].x; r[n-1].start.y=p[0].y; r[n-1].end.x=p[n-1].x; r[n-1].end.y=p[n-1].y; } return r;
计算机图形学 有效边表填充算法实验报告

实验题目: 实验二有效边表填充算法1.实验目的:设计有效边表结点和边表结点数据结构设计有效边表填充算法编程实现有效边表填充算法2.实验描述:下图 1 所示多边形覆盖了12 条扫描线, 共有7 个顶点和7 条边。
7 个顶点分别为:P0(7, 8), P1(3, 12), P2(1, 7), P3(3, 1), P4(6, 5), P5(8, 1), P6(12, 9)。
在1024×768 的显示分辩率下, 将多边形顶点放大为P0(500,400), P1(350, 600), P2(250, 350), P3(350, 50), P4(500, 250), P5(600, 50), P6(800, 450)。
请使用有效边表算法填充该多边形。
图1示例多边形图2 屏幕显示多边形3.算法设计:(1)建立AET和BUCKET类;(2)初始化桶, 并在建立桶结点时为其表示的扫描线初始化为带头结点的链表;(3)对每个桶结点进行循环, 将桶内每个结点的边表合并为有效边表, 并进行有效边表循环;(4)按照扫描线从小到大的移动顺序, 计算当前扫描线与多边形各边的交点, 然后把这些交点按X值递增的顺序进行排序, 配对, 以确定填充区间;(5)用指定颜色点亮填充区间内的所有像素, 即完成填充工作。
4.源程序:1)//AET.hclass AET{public:AET();virtual ~AET();double x;int yMax;double k;//代替1/kAET *next;};//AET..cppAET::AET(){}AET::~AET(){}2) //Bucket.h#include "AET.h"class Bucket{public:Bucket();virtual ~Bucket();int ScanLine;AET *p;//桶上的边表指针Bucket *next;};// Bucket.cppBucket::Bucket(){}Bucket::~Bucket(){}3)//TestView.h#include "AET.h"//包含有效边表类#include "Bucket.h"//包含桶类#define Number 7//N为闭合多边形顶点数, 顶点存放在整型二维数组Point[N]中class CTestView : public CView{。
《计算机图形学》有序边表填充算法资料讲解

《计算机图形学》有序边表填充算法实验报告一、实验目的1、掌握有序边表算法填充多边形区域;2、理解多边形填充算法的意义;3、增强C语言编程能力。
二、算法原理介绍根据多边形内部点的连续性知:一条扫描线与多边形的交点中,入点和出点之间所有点都是多边形的内部点。
所以,对所有的扫描线填充入点到出点之间所有的点就可填充多边形。
判断扫描线上的点是否在多边形之内,对于一条扫描线,多边形的扫描转换过程可以分为四个步骤:(1)求交:计算扫描线与多边形各边的交点;(2)排序:把所有交点按x值递增顺序排序;(3)配对:第一个与第二个,第三个与第四个等等;每对交点代表扫描线与多边形的一个相交区间;(4)着色:把相交区间内的象素置成多边形颜色,把相交区间外的象素置成背景色。
p1,p3,p4,p5属于局部极值点,要把他们两次存入交点表中。
如扫描线y=7上的交点中,有交点(2,7,13),按常规方法填充不正确,而要把顶点(7,7)两次存入交点表中(2,7,7,13)。
p2,p6为非极值点,则不用如上处理。
为了提高效率,在处理一条扫描线时,仅对与它相交的多边形的边进行求交运算。
把与当前扫描线相交的边称为活性边,并把它们按与扫描线交点x坐标递增的顺序存放在一个链表中,称此链表为活性边表(AET)。
对每一条扫描线都建立一个与它相交的多边形的活性边表(AET)。
每个AET的一个节点代表一条活性边,它包含三项内容1.x -当前扫描线与这条边交点的x坐标;2.Δx -该边与当前扫描线交点到下一条扫描线交点的x增量;3.ymax -该边最高顶点相交的扫描线号。
每条扫描线的活性边表中的活性边节点按照各活性边与扫描线交点的x值递增排序连接在一起。
当扫描线y移动到下一条扫描线y = y+1时,活性边表需要更新,即删去不与新扫描线相交的多边形边,同时增加与新扫描线相交的多边形边,并根据增量法重新计算扫描线与各边的交点x。
当多边形新边表ET构成后,按下列步骤进行:①对每一条扫描线i,初始化ET表的表头指针ET[i];②将ymax = i的边放入ET[i]中;③使y =多边形最低的扫描线号;④初始化活性边表AET为空;⑤循环,直到AET和ET为空。
计算机图形学课程设计报告报告实验报告

《计算机图形学》实验报告班级计算机科学与技术姓名学号2014 年6 月2 日实验一基本图形生成算法一、实验目的:1、掌握中点Bresenham绘制直线的原理;2、设计中点Bresenham算法;3、掌握八分法中点Bresenham算法绘制圆的原理;4、设计八分法绘制圆的中点Bresenham算法;5、掌握绘制1/4椭圆弧的上半部分和下半部分的中点Bresenham算法原理;6、掌握下半部分椭圆偏差判别式的初始值计算方法;7、设计顺时针四分法绘制椭圆的中点Bresenham算法。
二、实验过程:1、实验描述实验1:使用中点Bresenham算法绘制斜率为0<=k<=1的直线。
实验2:使用中点Bresenham算法绘制圆心位于屏幕客户区中心的圆。
实验3:使用中点Bresenham算法绘制圆心位于屏幕客户区中心的椭圆。
2、实验过程1)用MFC(exe)建立一个单文档工程;2)编写对话框,生成相应对象,设置相应变量;3)在类CLineView中声明相应函数,并在相关的cpp文件中实现;4)在OnDraw()函数里调用函数实现绘制直线、圆、椭圆;5)运行程序,输入相应值,绘制出图形。
三、源代码实验1:直线中点Bresenham算法1.// cline.cpp : implementation file// cline dialogcline::cline(CWnd* pParent /*=NULL*/): CDialog(cline::IDD, pParent){//{{AFX_DATA_INIT(cline)m_x0 = 0;m_y0 = 0;m_x1 = 0;m_y1 = 0;//}}AFX_DATA_INIT}void cline::DoDataExchange(CDataExchange* pDX){CDialog::DoDataExchange(pDX);//{{AFX_DATA_MAP(cline)DDX_Text(pDX, IDC_x0, m_x0);DDX_Text(pDX, IDC_y0, m_y0);DDX_Text(pDX, IDC_x1, m_x1);DDX_Text(pDX, IDC_y1, m_y1);//}}AFX_DATA_MAP}BEGIN_MESSAGE_MAP(cline, CDialog)//{{AFX_MSG_MAP(cline)//}}AFX_MSG_MAPEND_MESSAGE_MAP()2、// LineView.hclass CLineView : public CView{public:CLineDoc* GetDocument();..........void Mbline(double,double,double,double); //直线中点Bresenham函数.......}3、// Line.cpp//*******************直线中点Bresenham函数*********************/void CLineView::Mbline(double x0, double y0, double x1, double y1) {CClientDC dc(this);COLORREF rgb=RGB(0,0,255); //定义直线颜色为蓝色double x,y,d,k;x=x0; y=y0; k=(y1-y0)/(x1-x0); d=0.5-k;for(x=x0;x<=x1;x++){dc.SetPixel((int)x,(int)y,rgb);if(d<0){y++;d+=1-k;}elsed-=k;}}4、//LineView.cppvoid CLineView::OnDraw(CDC* pDC){CLineDoc* pDoc = GetDocument();ASSERT_VALID(pDoc);// TODO: add draw code for native data herecline a;a.DoModal();//初始化CLineView::Mbline(a.m_x0,a.m_y0,a.m_x1,a.m_y1); }实验2:圆中点Bresenham算法1、//cricle.cpp// Ccricle dialogCcricle::Ccricle(CWnd* pParent /*=NULL*/): CDialog(Ccricle::IDD, pParent){//{{AFX_DATA_INIT(Ccricle)m_r = 0;//}}AFX_DATA_INIT}void Ccricle::DoDataExchange(CDataExchange* pDX) {CDialog::DoDataExchange(pDX);//{{AFX_DATA_MAP(Ccricle)DDX_Text(pDX, r_EDIT, m_r);//}}AFX_DATA_MAP}2、//CcircleView.hclass CCcircleView : public CView{.......public:CCcircleDoc* GetDocument();void CirclePoint(double,double); //八分法画圆函数void Mbcircle(double); //圆中点Bresenham函数........}3、//CcircleView.cppvoid CCcircleView::OnDraw(CDC* pDC){CCcircleDoc* pDoc = GetDocument();ASSERT_VALID(pDoc);// TODO: add draw code for native data hereCcricle r;r.DoModal();CCcircleView::Mbcircle(r.m_r);//画圆}4、//CcircleView.cpp//*******************八分法画圆*************************************/ void CCcircleView::CirclePoint(double x,double y){CClientDC dc(this);COLORREF rgb=RGB(0,0,255);dc.SetPixel((int)(300+x),(int)(300+y),rgb);dc.SetPixel((int)(300-x),(int)(300+y),rgb);dc.SetPixel((int)(300+x),(int)(300-y),rgb);dc.SetPixel((int)(300-x),(int)(300-y),rgb);dc.SetPixel((int)(300+y),(int)(300+x),rgb);dc.SetPixel((int)(300-y),(int)(300+x),rgb);dc.SetPixel((int)(300+y),(int)(300-x),rgb);dc.SetPixel((int)(300-y),(int)(300-x),rgb);}//**************************圆中点Bresenham函数*********************/ void CCcircleView::Mbcircle(double r){double x,y,d;COLORREF rgb=RGB(0,0,255);d=1.25-r;x=0;y=r;for(x=0;x<y;x++){CirclePoint(x,y); //调用八分法画圆子函数if(d<0)d+=2*x+3;else{d+=2*(x-y)+5;y--;}}}实验3:椭圆中点Bresenham算法1、//ellipse1.cpp// Cellipse dialogCellipse::Cellipse(CWnd* pParent /*=NULL*/) : CDialog(Cellipse::IDD, pParent){//{{AFX_DATA_INIT(Cellipse)m_a = 0;m_b = 0;//}}AFX_DATA_INIT}void Cellipse::DoDataExchange(CDataExchange* pDX) {CDialog::DoDataExchange(pDX);//{{AFX_DATA_MAP(Cellipse)DDX_Text(pDX, IDC_EDIT1, m_a);DDX_Text(pDX, IDC_EDIT2, m_b);//}}AFX_DATA_MAP}2、//EllipseView.hclass CEllipseView : public CView{......................public:CEllipseDoc* GetDocument();void EllipsePoint(double,double); //四分法画椭圆void Mbellipse(double a, double b); //椭圆中点Bresenham函数..................}3、//Ellipse.cpp//*****************四分法画椭圆********************************/void CEllipseView::EllipsePoint(double x,double y){CClientDC dc(this);COLORREF rgb=RGB(0,0,255);dc.SetPixel((int)(300+x),(int)(300+y),rgb);dc.SetPixel((int)(300-x),(int)(300+y),rgb);dc.SetPixel((int)(300+x),(int)(300-y),rgb);dc.SetPixel((int)(300-x),(int)(300-y),rgb);}//************************椭圆中点Bresenham函数*********************/ void CEllipseView::Mbellipse(double a, double b){double x,y,d1,d2;x=0;y=b;d1=b*b+a*a*(-b+0.25);EllipsePoint(x,y);while(b*b*(x+1)<a*a*(y-0.5))//椭圆AC弧段{if(d1<0)d1+=b*b*(2*x+3);else{d1+=b*b*(2*x+3)+a*a*(-2*y+2);y--;}x++;EllipsePoint(x,y);}d2=b*b*(x+0.5)*(x+0.5)+a*a*(y-1)*(y-1)-a*a*b*b;//椭圆CB弧段while(y>0){if(d2<0){d2+=b*b*(2*x+2)+a*a*(-2*y+3);x++;}elsed2+=a*a*(-2*y+3);y--;EllipsePoint(x,y);}}4、//EllipseView.cppvoid CEllipseView::OnDraw(CDC* pDC){CEllipseDoc* pDoc = GetDocument();ASSERT_VALID(pDoc);// TODO: add draw code for native data hereCellipse el;el.DoModal();//初始化CEllipseView::Mbellipse(el.m_a, el.m_b);//画椭圆}四、实结果验实验1:直线中点Bresenham算法实验2:圆中点Bresenham 算法实验3:椭圆中点Bresenham 算法实验二有效边表填充算法一、实验目的:1、设计有效边表结点和边表结点数据结构;2、设计有效边表填充算法;3、编程实现有效边表填充算法。
计算机图形学实验四 区域填充算法的实现

实验四区域填充算法的实现班级 08信计2班学号 20080502082 姓名分数一、实验目的和要求:1、理解区域的表示和类型。
2、能正确区分四连通和八连通的区域3、了解区域填充的实验原理。
4、利用C++实现区域填充的递归算法。
二、实验内容:1假设在多边形内有一像素已知,由此出发利用连通性找到区域内所有像素。
2 取(x,y)为种子点将整个区域填充为新的颜色。
3 进行递归填充。
三、实验结果分析区域填充属性包括填充样式,填充颜色和填充图案的类型。
C语言中定义了某种图形后,即可调用-floodfill函数,对指定区域进行填充. 程序代码#define pi 3.141592#define MAX(a,b) (a>b)? a:b#define MIN(a,b) (a<b)? a:b#include "graphics.h"#include "math.h"struct edge {int ymax;float x;float delat;struct edge * pedge; };struct point{int x;int y;} ;struct et { struct edge * pedge;int n;};struct edge g_aet[10];struct edge dge[10];struct et g_et[10];struct point point1,point2;int ZUO(float x){ if((int)x==x)return (int)x;return (int)x+1;}int YOU(float x){ if((int)x==x)return (int)x-1;return (int)x;}int k=400,l=0;void draw1(){int i,t,j,a,c,p,z; float b;struct edge temp;for(i=k;i<=l;i++){a=0;for(t=0;t<=9;t++){ if(g_et[t].n==i) break;}for(j=0;j<=9;j++){ if(g_aet[j].ymax==0) break;}if(t!=10){ g_aet[j].ymax=g_et[t].pedge->ymax;g_aet[j].x=g_et[t].pedge->x;g_aet[j].delat=g_et[t].pedge->delat;if(g_et[t].pedge->pedge!=0){g_aet[j+1].ymax=g_et[t].pedge->pedge->ymax;g_aet[j+1].x=g_et[t].pedge->pedge->x;g_aet[j+1].delat=g_et[t].pedge->pedge->delat; }}for(j=0;j<=9;j++){ if(g_aet[j].ymax==0) break; }j--;for(t=0;t<=j;t++){ for(z=0;z<=j-1;z++){if(g_aet[z].x>g_aet[z+1].x){ temp.ymax=g_aet[z].ymax;temp.x=g_aet[z].x;temp.delat=g_aet[z].delat;g_aet[z].ymax=g_aet[z+1].ymax;g_aet[z].x=g_aet[z+1].x;g_aet[z].delat=g_aet[z+1].delat;g_aet[z+1].ymax=temp.ymax;g_aet[z+1].x=temp.x;g_aet[z+1].delat=temp.delat;}}}for(j=0;j<=9;j++){ if(g_aet[j].ymax==0) break; }j--;for(p=0;p<=j;p++){ a++;if(a%2!=0)b=g_aet[p].x;else{for(c=ZUO(b);c<=YOU(g_aet[p].x);c++)putpixel(c,i,2);}}for(t=0;t<=j;t++){ if(g_aet[t].ymax==(i+1)){ g_aet[t].ymax=0;g_aet[t].x=0;g_aet[t].delat=0;}g_aet[t].x+=g_aet[t].delat;}for(t=0;t<=j;t++){ for(z=0;z<=j-1;z++){if(g_aet[z].x<g_aet[z+1].x){ temp.ymax=g_aet[z].ymax;temp.x=g_aet[z].x;temp.delat=g_aet[z].delat;g_aet[z].ymax=g_aet[z+1].ymax;g_aet[z].x=g_aet[z+1].x;g_aet[z].delat=g_aet[z+1].delat;g_aet[z+1].ymax=temp.ymax;g_aet[z+1].x=temp.x;g_aet[z+1].delat=temp.delat;}}}}}void generate(){int i,y,n=1,m,q,p;float x;for(i=0;i<=9;i++){if(n==1){ point2.x=point1.x=300;point2.y=point1.y=200;n++;}else{ if(n%2==0){ x=40*cos(i*pi/5)+200;y=40*sin(i*pi/5)+200;}else{ x=100*cos(i*pi/5)+200;y=100*sin(i*pi/5)+200;}if(point1.y==y) { n++; continue;}m=MIN(point1.y,y);if(x==point1.x){ dge[i-1].delat=0;dge[i-1].ymax=MAX(point1.y,y);dge[i-1].x=x;dge[i-1].pedge=0;for(q=0;q<=9;q++){ if(g_et[q].n==m) break;}if(q==10){g_et[i-1].pedge=&dge[i-1];g_et[i-1].n=m;}else{g_et[q].pedge->pedge=&dge[i-1];g_et[i-1].n=0;}}else{dge[i-1].delat=(float)(x-point1.x)/(y-point1.y);dge[i-1].ymax=MAX(point1.y,y);if(point1.y>y) dge[i-1].x=x;else {dge[i-1].x=point1.x; }dge[i-1].pedge=0;for(q=0;q<=9;q++){ if(g_et[q].n==m) break;}if(q==10){ g_et[i-1].pedge=&dge[i-1];g_et[i-1].n=m;}else{g_et[q].pedge->pedge=&dge[i-1];g_et[i-1].n=0;}}p=MAX(point1.y,y);k=MIN(k,m);l=MAX(l,p);point1.x=x;point1.y=y;n++;}}if(point1.y==point2.y) return;else{if(point2.x==point1.x){dge[i-1].delat=0;dge[i-1].ymax=MAX(point1.y,point2.y);dge[i-1].x=point2.x;}else{ dge[i-1].ymax=MAX(point1.y,point2.y);if(point1.y>point2.y) dge[i-1].x=point2.x;else {dge[i-1].x=point1.x;}dge[i-1].delat=(float)(point2.x-point1.x)/(point2.y-point1.y);}}m=MIN(point1.y,point2.y);k=MIN(k,m);l=MAX(l,dge[i-1].ymax);g_et[i-1].n=m;g_et[i-1].pedge=&dge[i-1];}void main(){ int driver=DETECT,mode; int i; registerbgidriver(EGA VGA_driver);initgraph(&driver,&mode,"\\tc");initgraph(&driver,&mode,"\\tc");for(i=0;i<=9;i++){ g_aet[i].ymax=0; g_aet[i].x=0; g_aet[i].delat=0;g_et[i].pedge=0;}generate();draw1();circle(200,200,100); circle(200,200,40);getch();closegraph();}。
《计算机图形学》有序边表填充算法
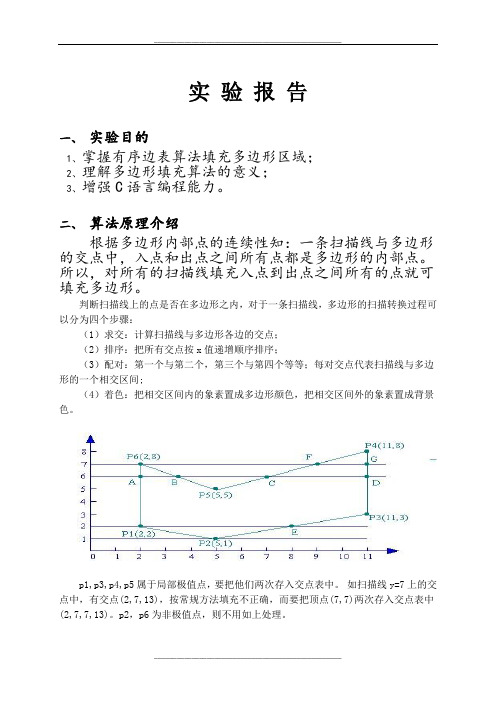
实验报告一、实验目的1、掌握有序边表算法填充多边形区域;2、理解多边形填充算法的意义;3、增强C语言编程能力。
二、算法原理介绍根据多边形内部点的连续性知:一条扫描线与多边形的交点中,入点和出点之间所有点都是多边形的内部点。
所以,对所有的扫描线填充入点到出点之间所有的点就可填充多边形。
判断扫描线上的点是否在多边形之内,对于一条扫描线,多边形的扫描转换过程可以分为四个步骤:(1)求交:计算扫描线与多边形各边的交点;(2)排序:把所有交点按x值递增顺序排序;(3)配对:第一个与第二个,第三个与第四个等等;每对交点代表扫描线与多边形的一个相交区间;(4)着色:把相交区间内的象素置成多边形颜色,把相交区间外的象素置成背景色。
p1,p3,p4,p5属于局部极值点,要把他们两次存入交点表中。
如扫描线y=7上的交点中,有交点(2,7,13),按常规方法填充不正确,而要把顶点(7,7)两次存入交点表中(2,7,7,13)。
p2,p6为非极值点,则不用如上处理。
为了提高效率,在处理一条扫描线时,仅对与它相交的多边形的边进行求交运算。
把与当前扫描线相交的边称为活性边,并把它们按与扫描线交点x坐标递增的顺序存放在一个链表中,称此链表为活性边表(AET)。
对每一条扫描线都建立一个与它相交的多边形的活性边表(AET)。
每个AET的一个节点代表一条活性边,它包含三项内容1.x -当前扫描线与这条边交点的x坐标;2.Δx -该边与当前扫描线交点到下一条扫描线交点的x增量;3.ymax -该边最高顶点相交的扫描线号。
每条扫描线的活性边表中的活性边节点按照各活性边与扫描线交点的x值递增排序连接在一起。
当扫描线y移动到下一条扫描线y = y+1时,活性边表需要更新,即删去不与新扫描线相交的多边形边,同时增加与新扫描线相交的多边形边,并根据增量法重新计算扫描线与各边的交点x。
当多边形新边表ET构成后,按下列步骤进行:①对每一条扫描线i,初始化ET表的表头指针ET[i];②将ymax = i的边放入ET[i]中;③使y =多边形最低的扫描线号;④初始化活性边表AET为空;⑤循环,直到AET和ET为空。
实验二 有效边表填充算法

实验二有效边表填充算法20091104091 计算机科学与技术师范汉班丁仕钰1.实验目的:(1)设计有效边表结点和边表结点数据结构(2)设计有效边表填充算法(3)编程实现有效边表填充算法2.实验描述:下图 1 所示多边形覆盖了12 条扫描线,共有7 个顶点和7 条边。
7 个顶点分别为:P0(7,8),P1(3,12),P2(1,7),P3(3,1), P4(6,5), P5(8,1), P6(12,9)。
在1024×768 的显示分辩率下,将多边形顶点放大为P0(500,400),P1(350,600),P2(250,350),P3(350,50), P4(500,250), P5(600,50), P6(800,450)。
请使用有效边表算法填充该多边形。
图1示例多边形图2 屏幕显示多边形3.算法设计:4.源程序:(1)class AET{public:AET *next;double k;int yMax;double x;AET();virtual ~AET();};(2)#include "AET.h"class Bucket{public:Bucket *next;AET *p;int Scanline;Bucket();virtual ~Bucket();};(3) void CShiyan1View::AddEdge(AET *NewEdge){T1 = HeadE;if(T1 == NULL) //边表为空,将边表置为TempEdge{T1 = NewEdge;HeadE =T1;}else{while(T1->next!=NULL) //边表不为空,将TempEdge连在该边之后{T1 = T1->next;}T1->next = NewEdge;}}(4) void CShiyan1View::PolygonFill(){HeadE = NULL;for(CurrentB = HeadB;CurrentB!=NULL;CurrentB=CurrentB->next) //访问所有的桶节点{for(CurrentE = CurrentB->p;CurrentE!=NULL;CurrentE = CurrentE->next)//桶中所有边节点{AET * TempEdge = new AET;TempEdge->x = CurrentE->x;TempEdge->yMax = CurrentE->yMax;TempEdge->k = CurrentE->k;TempEdge->next = NULL;AddEdge(TempEdge); //将该边插入临时AET表}EdgeOrder(); //边表按照x递增的顺序存放T1 = HeadE; //根据yMax抛弃扫描完的边节点if(T1 == NULL){return;}while(CurrentB->Scanline>=T1->yMax) //放弃该节点,AET表指针后移,下闭上开{T1 = T1->next;HeadE = T1;if(HeadE == NULL){return;}}if(T1->next!=NULL){T2 = T1;T1 = T2->next;}while(T1!=NULL){if(CurrentB->Scanline>=T1->yMax) //跳过一个节点{T2->next = T1->next;T1->next = NULL;T1 = T2->next;}else{T2 = T1;T1 = T2->next;}}bool In =false; //设置一个bool变量In,初始值为假double xb,xe; //扫描线的起点和终点for(T1 = HeadE;T1!=NULL;T1=T1->next) //填充扫描线和多边形相交的区间{if(In == false){xb = T1->x;In =true; //每访问一个节点,把In值取反一次}else //如果In值为真,则填充从当前节点的x值开始到下一个节点的x值结束的区间{xe = T1->x-1; //左闭右开CClientDC dc(this);for(double x = xb;x<=xe;x++)dc.SetPixel(ROUND(x),CurrentB->Scanline,GetColor); //填充Sleep(1); //延时ms,提高填充过程的可视性In = false;}}for(T1 = HeadE;T1!=NULL;T1=T1->next) //边连贯性{T1->x = T1->x+T1->k;}}delete HeadB;delete HeadE;delete CurrentB;delete CurrentE;}(5) void CShiyan1View::EdgeOrder(){AET *F,*T;T1 = HeadE;if(T1 == NULL){return;}if(T1->next== NULL) //如果该边表没有再连接边{return;}else{F =HeadE->next;HeadE->next = NULL;while(F!=NULL){for (T=F, T1=HeadE; ((T1!=NULL) && (T1->x < T->x)); T2=T1, T1=T1->next);F = F->next;if(T1 == HeadE){HeadE = T;}else{T2->next = T;}T->next = T1;}}}(6) void CShiyan1View::Et(){for(int i=0;i<Number;i++) //访问每个顶点{CurrentB = HeadB; //从桶链表的头节点开始循环int j = i+1; //边的第二个顶点,Point[i]和Point[j]构成边if(j==Number) j=0; //保证多边形的闭合if(Point[j].y>Point[i].y) //终点比起点高{while(CurrentB->Scanline!=Point[i].y) //在桶内寻找该边的yMin{CurrentB = CurrentB->next; //移到下一个桶节点}E[i].x = Point[i].x; //计算AET表的值E[i].yMax = Point[j].y;E[i].k = (double(Point[j].x-Point[i].x))/(Point[j].y-Point[i].y);E[i].next = NULL;CurrentE = CurrentB->p; //获得桶上链接边表的地址if(CurrentB->p==NULL) //当前桶节点上没有链接边节点{CurrentE = &E[i]; //赋边的起始地址CurrentB->p=CurrentE; //第一个边节点直接连接到对应的桶中}else{while(CurrentE->next!=NULL) //如果当前边已有边节点{CurrentE = CurrentE->next; //移动指针到当前边的最后一个节点}CurrentE->next = &E[i]; //把当前边接上去}}if(Point[j].y<Point[i].y) //终点比起点低{while(CurrentB->Scanline!=Point[j].y){CurrentB = CurrentB->next;}E[i].x = Point[j].x;E[i].yMax = Point[i].y;E[i].k = (double(Point[i].x-Point[j].x))/(Point[i].y-Point[j].y);E[i].next = NULL;CurrentE = CurrentB->p;if(CurrentE == NULL){CurrentE=&E[i];CurrentB->p = CurrentE;}else{while(CurrentE->next!=NULL){CurrentE = CurrentE->next;}CurrentE->next=&E[i];}}}CurrentB = NULL;CurrentE = NULL;}(7) void CShiyan1View::CreatBucket(){ScanMax = ScanMin = Point[0].y;for(int i=1;i<Number;i++){if(Point[i].y<ScanMin){ScanMin = Point[i].y; //扫描线的最小值}if(Point[i].y>ScanMax){ScanMax = Point[i].y; //扫描线的最大值}}for( i=ScanMin;i<=ScanMax;i++) //建立桶节点{if(ScanMin == i) //桶头结点{HeadB = new Bucket; //建立桶的头结点CurrentB = HeadB; //CurrentB为Bucket当前节点指针CurrentB->Scanline = ScanMin;CurrentB->p = NULL; //没有连接边链表CurrentB->next = NULL;}else{ //建立桶的其他节点CurrentB->next = new Bucket; //新建一个桶节点CurrentB = CurrentB->next; //使CurrentB指向新建的桶节点CurrentB->Scanline = i;CurrentB->p = NULL; //没有连接边链表CurrentB->next = NULL;}}}(8) void CShiyan1View::OnDraw(CDC* pDC){AfxGetMainWnd()->SetWindowText(":有效边表填充算法");CShiyan1Doc* pDc = GetDocument();ASSERT_V ALID(pDc);CShiyan1Doc* pDoc = GetDocument();ASSERT_V ALID(pDoc);// TODO: add draw code for native data here//Cshiyan1Doc *pDoc = GetDocument();ASSERT_V ALID(pDoc);if (!pDoc)return;// TODO: 在此处为本机数据添加绘制代码pDC->Polygon(Point,7); //绘制多边形pDC->TextOut(550,410,_T("P0")); //注意文本的输出pDC->TextOut(350,600,_T("P1"));pDC->TextOut(230,340,_T("P2"));pDC->TextOut(350,30,_T("P3"));pDC->TextOut(490,220,_T("P4"));pDC->TextOut(600,30,_T("P5"));pDC->TextOut(805,450,_T("P6"));}(9) void CShiyan1View::OnTianchong(){// TODO: Add your command handler code hereCColorDialog ccd(GetColor);if(ccd.DoModal() == IDOK){GetColor = ccd.GetColor();}RedrawWindow();CreatBucket();Et();PolygonFill();}5.运行结果:(屏幕截图)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算机图形学课程设计设计题目改进的有效边表算法对多边形的填充学院名称信息科学与技术学院专业名称计算机科学与技术学生姓名刘柯学生学号201213030112任课教师梅占勇设计(论文)成绩教务处制2015年9 月28 日目录一、设计内容与要求 (3)1.1设计题目 (3)1.2 设计内容 (3)1.3 设计目标 (3)二、总体设计 (3)2.1 多边形的表示 (3)2.2 x-扫描线算法 (4)2.3 改进的有效边表算法 (4)2.3.1 改进的有效边表算法 (4)2.3.2 有效边表 (5)2.3.3 边表 (6)三、详细设计 (8)3.1 改进的有效边表算法的实现 (8)3.2 有效边表算法程序流程图 (9)四、测试结果 (9)五、总结 (15)六、源代码 (15)参考文献 (26)一、设计内容与要求1.1设计题目用改进的有效边表算法实现多边形的填充1.2 设计内容使用OpenGL实现用改进的有效边表算法填充多边形1.3 设计目标参照课本上改进的有效边表算法的思想,实现该算法的C语言代码,并用该算法搭配OpenGL以像素点的方式绘制出给定顶点坐标的多边形。
二、总体设计2.1 多边形的表示在计算机图形学中,多边形有2种重要的表示方法:顶点表示和点阵表示。
顶点表示用多边形的顶点序列来刻画多边形,这种方法直观、几何意义强,占用内存少,应用普遍,但它没有明确指出哪些像素在多边形内,故不能直接用于面着色。
点阵表示用位于多边形内的像素的集合来刻画多边形。
这种表示法虽然失去了许多重要的几何信息,但便于运用帧缓存表示图形,是面着色所需要的图形表示形式。
大多数图形应用系统采用顶点序列表示多边形,而顶点表示又不能直接用于显示,那么就必须有从多边形的顶点表示到点阵表示的转换,这种转换称为多边形的扫描转换或多边形的填充。
即从多边形的顶点信息出发,求出位于其内部的各个像素,并将其颜色值写入帧缓存的相应单元中。
2.2 x-扫描线算法x-扫描线算法的基本思想是,按照扫描线的顺序,计算扫描线与多边形的相交区间,再用要求的颜色显示这些区间的像素,即完成填充工作。
区间的端点可以通过计算扫描线与多边形边界线的交点获得。
根据此原理,x-扫描线算法可以填充凸的、凹的或带有孔的多边形区域。
x-扫描线的算法步骤如下:(1)确定多边形顶点的最小和最大y值(y min和y max),得到多边形所占有的最大扫描线数。
(2)从y=y min到y=y max,每次用一条扫描线填充。
每一条扫描线填充的过程分为4个步骤:①求交。
计算扫描线与多边形所有边的交点。
②排序。
把所有交点按x坐标递增的顺序进行排序。
③交点配对。
配对第一与第二、第三与第四个交点等,每对交点代表一个填充区间。
④区间填色。
把这些相交区间内的像素置成不同于背景色的填充色。
x-扫描线算法在处理每条扫描线时,需要与多边形的所有边求交,这样处理效率非常低。
因为一条扫描线往往只与少数几条边相交,甚至与整个多边形都不相交。
因此,有必要对算法进行改进。
2.3 改进的有效边表算法2.3.1 改进的有效边表算法将x-扫描线算法加以改进可以得到改进的有效边表算法,也称y连贯算法。
改进可以从三个方面进行:首先,在处理一条扫描线时,仅对与它相交的多边形的边(有效边)求交;其次,利用扫描线的连贯性,考虑到当前扫描线与各边的交点顺序与下一条扫描线与各边的交点顺序很可能相同或非常相似,因此在当前扫描线处理完毕之后,不必为下一条扫描线从头开始构造交点信息;最后,利用多边形的连贯性,认为若某条边与当前扫描线相交,则它很可能也与下一条扫描线相交且其交点与上一次的交点相关。
如下图所示,设直线的斜率为k,若y=yi 时,x=xi;则当y=yi+1时,有xi+1=xi+1/k。
2.3.2 有效边表有效边(Active Edge)是指与当前扫描线相交的多边形的边,也称活性边。
把有效边按与扫描线交点x坐标递增的顺序存放在一个链表中,此链表称为有效边表(Active Edge Table,AET)。
有效边表的每个结点存放对应边的如下信息:其中,x为当前扫描线与有效边交点的x坐标;y max是有效边所在的最大扫描线值,通过它可以知道何时才能“抛弃”该边;1/k是边斜率的倒数;next是下一个结点的指针。
如下图所示的多边形P0P1P2P3P4P5P6,其顶点表示为:P0(7,8),P1(3,12),P2(1,7),P3(3,1),P4(6,5),P5(8,1),P6(12,9)。
当y=8时的有效边表如下图所示:2.3.3 边表有效边表给出了扫描线和有效边交点坐标的计算方法,但是没有给出新边出现的位置坐标。
为了方便有效边表的建立与更新,就需要构造一个边表(Edge Table,ET),用以存放扫描线上多边形各条边的信息。
由于水平边的1/k为∞,并且水平边本身就是扫描线,所以在建立边表时不予考虑。
边表的构造分为4个步骤:①首先构造一个纵向链表,链表的长度为多边形占有的最大扫描线数,链表的每个结点,称为一个桶,对应多边形覆盖的每一条扫描线。
②将每条边的信息装入与该边最小y坐标(ymin)相对应的桶中。
也就是说,若某边的较低端点为ymin ,则该边就放在相应的y=ymin的扫描线桶中。
③每条边的数据形成一个结点,内容包括该扫描线与该边的初始交点x(即较低端点的x坐标值),该边最大y坐标值ymax,以及斜率的倒数1/k和下一个边结点的指针next:④同一桶中若干条边按x|y min由小到大排列,若x|y min相等,则按1/k由小到大排序。
从上面可以看出,边表是有效边表的特例,有效边表和边表可以使用同一个数据结构来表示。
对于多边形P0P1P2P3P4P5P6,它的边表结构如下图所示:三、详细设计3.1 改进的有效边表算法的实现改进的有效边表算法具体实现过程如下:①初始化边表ET。
为了方便边表的建立,可以定义sort()函数对多边形的边进行排序,保证边表中每个桶中的边是有序的。
同时定义一个creat_edge_table()函数,该函数需要多边形的顶点信息作为参数传入,并返回一个边表指针。
②初始化有效边表AET。
从ET表中取出第一个不为空的桶与AET表合并。
为了初始化AET表,可以定义一个init_active_table()函数,该函数传入边表指针作为形参,返回一个有效边表指针。
③从AET表中取出交点进行填充。
填充时设置一个布尔值b(初值为假),令指针从有效边表的第一个结点(也就是扫描线与有效边的交点)开始遍历。
每访问一个结点,把b取反一次。
若b为真,则把从当前结点的x值开始(设为x1)到下一结点的x值结束(设为x2)的区间[x1, x2]用多边形色填充。
填充时为了避免多边形区域扩大化,需要对区间边界进行如下处理:若x是整数,则按“左闭右开”的原则处理,即左边界上的x(x1)不变,右边界上的x(x2)减1;若x不是整数,左边界上的x(x1)向右取整,右边界上的x(x2)向左取整。
④更新AET表。
设当前AET表中扫描线为y,首先更新扫描线为y=y+1,然后删除AET表中所有ymax =y的边结点;再根据xi+1=xi+1/k计算并修改AET表中各边结点的x坐标,同时合并ET表对应于扫描线y的桶中的边,按次序插入到AET表中,形成新AET表。
此步骤满足多边形的“下闭上开”原则。
此过程用到自定义的函数delete_edge()、add_edge()、update_active_table()。
⑤判断AET表是否为空。
若为空,则结束;否则转到③3.2 有效边表算法程序流程图四、测试结果为了便于观察多边形的填充,本程序将像素点进行放大处理,400 x 300的分辨率投影到20 x 15,并绘制出网格,使用OpenGL画出多边形的边框。
使用了Sleep()函数来延时生成像素点,并且每填充一个像素点刷新一次,给人动态直观的感受。
①在不处理边界的情况下,如下图所示,多边形的区域可能会扩大化。
②对边界进行处理后,结果如下:③为了验证改进的有效边表填充算法,现将本程序的像素大小恢复为1:1,按比例扩大多边形的顶点坐标,测试结果如下:从上图可以看出填充过后的多边形与原多边形P0P1P2P3P4P5P6的形状一致,该算法验证通过。
④测试其他多边形长方形:三角形:五角星:从以上结果来看,该算法基本得到完美实现。
而程序的执行时间来看,生成边表的时间(包括分配内存、对桶中的结点进行排序等)远比填充像素点的时间要长。
因此,该算法的效率虽然很高,但对于表的维护和排序开销太大,它适合软件实现而不适合硬件实现。
五、总结通过本次课程设计,我掌握了多边形的填充算法,了解了OpenGL的运行结构,熟悉了很多OpenGL的函数,对OpenGL编程也产生的浓厚的兴趣。
同时也巩固了对计算机图形学知识的掌握,锻炼了我对手实验的能力,看清了自己的水平,认识到了自己的不足。
在本次课程设计中,存在一些不足之处。
比如对边界的处理,课本上的说法模糊不清,在网上也没有找到相应的解答,我只能根据自己的理解来试着解决;这方面也存在没有及时和老师沟通的原因。
从这一点上,我认识到理论和实践的差别,我们应该多实践才能真正掌握理论。
还有就是完全填充后的多边形,边缘有“锯齿”现象,不知道是我程序的原因还是算法的问题。
或许对于多边形的填充算法还应该处理“锯齿”。
六、源代码//源代码仅包含文件PolygonFilling.cpp#include<stdio.h>#include<malloc.h>#include<gl/glut.h>#include<Windows.h>#define EPSILON 0.000001 //最小浮点数//点结构体struct Point{int x; //x坐标int y; //y坐标};//线结构体struct Line{Point high_point; //高端点Point low_point; //低端点int is_active; //是否为有效边,水平边(0),非水平边(1)double inverse_k; //斜率k的倒数};//边结点struct EdgeNode{double x; //扫描线与边交点的x坐标(边的低端点的x坐标)int y_max; //边的高端点的y坐标ymaxdouble inverse_k; //斜率k的倒数EdgeNode *next; //下一个边结点的指针};//有效边表struct ActiveEdgeTable{int y; //扫描线yEdgeNode *head; //边链表的头指针};//桶结点typedef struct Bucket{int y; //扫描线yEdgeNode *head; //边链表的头指针Bucket *next; //下一个桶的指针} EdgeTable;int compare(Point p1, Point p2);Line* create_lines(Point points[], int n);Point get_lowest_point(Line lines[], int n);Point get_highest_point(Line lines[], int n);void swap(Line &l1, Line &l2);void sort(Line lines[], int n);EdgeTable* create_edge_table(Line lines[], int n);ActiveEdgeTable* init_active_table(EdgeTable *edge_table);void delete_edge(ActiveEdgeTable *active_table, int y_max);void add_edge(ActiveEdgeTable *active_table, EdgeNode edge);ActiveEdgeTable* update_active_table(ActiveEdgeTable *active_table, EdgeTable *edge_table);void DrawPolygon(Point points, int n);void DrawGrid(int x, int y);void Fill(Point points[], int n);void Initial();void Display();int main(int argc, char* argv[]){glutInit(&argc, argv);glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);glutInitWindowSize(400, 300);glutInitWindowPosition(100, 120);glutCreateWindow("Polygon Filling");glutDisplayFunc(Display);Initial();glutMainLoop();return 0;}//比较2个点的高度int compare(Point p1, Point p2){if (p1.y > p2.y)return 1;else if (p1.y == p2.y)return 0;return -1;}//由点数组生成线段数组Line* create_lines(Point points[], int n){Line *lines = (Line*)malloc(n * sizeof(Line));for (int i = 0; i < n; ++i){Point p1 = points[i];Point p2 = points[(i + 1) % n];int result = compare(p1, p2);if (result == 0)lines[i].is_active = 0;elselines[i].is_active = 1;lines[i].high_point = result > 0 ? p1 : p2;lines[i].low_point = result < 0 ? p1 : p2;lines[i].inverse_k = (double)(p2.x - p1.x) / (double)(p2.y - p1.y);}return lines;}//获取线数组中最低的端点Point get_lowest_point(Line lines[], int n){Point lowest_point = lines[0].low_point;for (int i = 1; i < n; ++i){Point low_point = lines[i].low_point;if (compare(lowest_point, low_point) > 0)lowest_point = low_point;}return lowest_point;}//获取线数组中最高的端点Point get_highest_point(Line lines[], int n){Point highest_point = lines[0].high_point;for (int i = 1; i < n; ++i){Point high_point = lines[i].high_point;if (compare(highest_point, high_point) < 0)highest_point = high_point;}return highest_point;}//交换2个Line对象void swap(Line &l1, Line &l2){Line temp = l1;l1=l2;l2= temp;}//对线数组进行排序void sort(Line lines[], int n){//先按低端点的y坐标进行升序排序for (int i = 0; i < n; ++i){int min_index = i;for (int j = i + 1; j < n; ++j){if (lines[j].low_point.y < lines[min_index].low_point.y)min_index = j;}swap(lines[i], lines[min_index]);}//再将有序数组按低端点的x坐标升序排列,若x坐标相等,按inverse_k升序for (int i = 0; i < n; ++i){int min_index = i;for (int j = i + 1; lines[j].low_point.y == lines[i].low_point.y; ++j) {if (lines[j].low_point.x < lines[min_index].low_point.x)min_index = j;}swap(lines[i], lines[min_index]);if (i > 0 && lines[i].low_point.x == lines[i - 1].low_point.x){if (lines[i].is_active == 1 && lines[i - 1].is_active == 1){if (lines[i].inverse_k < lines[i - 1].inverse_k)swap(lines[i], lines[i - 1]);}}}}//创建一个边表EdgeTable* create_edge_table(Line lines[], int n){EdgeTable *edge_table = (EdgeTable*)malloc(sizeof(EdgeTable));edge_table->head = NULL;edge_table->next = NULL;sort(lines, n);Point lowest_point = get_lowest_point(lines, n);Point highest_point = get_highest_point(lines, n);EdgeTable *s = edge_table;for (int i = lowest_point.y; i <= highest_point.y; ++i){Bucket *bucket = (Bucket*)malloc(sizeof(Bucket));bucket->y = i;bucket->next = NULL;bucket->head = (EdgeNode*)malloc(sizeof(EdgeNode));bucket->head->next = NULL;EdgeNode *p = bucket->head;for (int j = 0; j < n; ++j){if (lines[j].is_active == 0)continue;if (lines[j].low_point.y == i){EdgeNode *q = (EdgeNode*)malloc(sizeof(EdgeNode));q->x = lines[j].low_point.x;q->y_max = lines[j].high_point.y;q->inverse_k = lines[j].inverse_k;q->next = NULL;p->next = q;p = q;}}s->next = bucket;s = bucket;}return edge_table;}//从边表中取出第一个不为空的桶初始化有效边表ActiveEdgeTable* init_active_table(EdgeTable *edge_table){ActiveEdgeTable *active_table = (ActiveEdgeTable*)malloc(sizeof(ActiveEdgeTable)); active_table->y = edge_table->next->y;active_table->head = (EdgeNode*)malloc(sizeof(EdgeNode));active_table->head->next = NULL;EdgeNode *p = edge_table->next->head;EdgeNode *q = active_table->head;while (p->next != NULL){EdgeNode *s = (EdgeNode*)malloc(sizeof(EdgeNode));s->x = p->next->x;s->y_max = p->next->y_max;s->inverse_k = p->next->inverse_k;s->next = NULL;q->next = s;q = s;p = p->next;}return active_table;}//从有效边表中删除指定y_max的边结点void delete_edge(ActiveEdgeTable *active_table, int y_max){EdgeNode *p = active_table->head;while (p->next != NULL){EdgeNode *q = p->next;if (q->y_max == y_max){p->next = q->next;free(q);}elsep = p->next;}}//将一个边结点按次序添加到有效边表中void add_edge(ActiveEdgeTable *active_table, EdgeNode edge){EdgeNode *t = (EdgeNode*)malloc(sizeof(EdgeNode));t->x = edge.x;t->y_max = edge.y_max;t->inverse_k = edge.inverse_k;t->next = NULL;EdgeNode *p = active_table->head;while (p->next != NULL){EdgeNode *q = p->next;if ((edge.x < q->x) || (edge.x == q->x && edge.inverse_k < q->inverse_k)){p->next = t;t->next = q;return;}p = p->next;}p->next = t;}//更新有效边表,并与边表中对应的桶合并ActiveEdgeTable* update_active_table(ActiveEdgeTable *active_table, EdgeTable *edge_table) {//更新扫描线y++active_table->y;//删除y=ymax的边delete_edge(active_table, active_table->y);//更新边结点的数据EdgeNode *p = active_table->head->next;while (p != NULL){p->x += p->inverse_k;p = p->next;}//找到边表中对应的桶EdgeTable *q = edge_table;while ((q = q->next) != NULL && q->y != active_table->y);//如果找到,则进行合并if (q != NULL){EdgeNode *s = q->head;while ((s = s->next) != NULL){add_edge(active_table, *s);}}return active_table;}//画出多边形的边框void DrawPolygon(Point points[], int n){glBegin(GL_LINE_LOOP);for (int i = 0; i < n; ++i)glVertex2i(points[i].x, points[i].y);glEnd();}//画出x * y的网格void DrawGrid(int x, int y){glBegin(GL_LINES);//横线for (int i = 0; i <= y; ++i){glVertex2d(0, i);glVertex2d(x, i);}//竖线for (int i = 0; i <= x; ++i){glVertex2d(i, 0);glVertex2d(i, y);}glEnd();}//用指定的像素大小填充多边形void Fill(Point points[], int n){Line *lines = create_lines(points, n);EdgeTable *edge_table = create_edge_table(lines, n);ActiveEdgeTable *active_table = init_active_table(edge_table);while (active_table->head->next != NULL){EdgeNode *p = active_table->head;int b = -1;while (p->next != NULL){if (b > 0){int left = p->x;int right = p->next->x;//如果不是局部最低点,则进行边界处理if (!(p->x - p->next->x >= -EPSILON && p->x - p->next->x <= EPSILON)){//处理左边界if (!(p->x - left >= -EPSILON && p->x - left <= EPSILON))left += 1;//处理右边界if (p->next->x - right >= -EPSILON && p->next->x - right <= EPSILON)right -= 1;}for (int i = left; i <= right; ++i){glBegin(GL_POINTS);glVertex2d(i, active_table->y);glEnd();glFlush();Sleep(50);}}p = p->next;b = -b;}active_table = update_active_table(active_table, edge_table);}}//初始化窗口,x和y指定窗口的坐标大小void Initial(){glClearColor(1.0f, 1.0f, 1.0f, 1.0f);glMatrixMode(GL_PROJECTION);gluOrtho2D(0.0, 20.0, 0.0, 15.0);}//窗口的显示回调函数void Display(){//使用当前背景色填充窗口glClear(GL_COLOR_BUFFER_BIT);//使用灰色画出网格线glColor3f(0.75f, 0.75f, 0.75f);DrawGrid(20, 14);glFlush();//多边形的顶点坐标Point points[] = { { 3, 1 },{ 6, 5 },{ 8, 1 },{ 12, 9 },{ 7, 8 },{ 3, 12 },{ 1, 7 } };//计算顶点个数int n = sizeof(points) / sizeof(Point);//使用黑色画出多边形的边框glColor3f(0.0f, 0.0f, 0.0f);DrawPolygon(points, n);glFlush();//指定点大小glPointSize(6.0f);//使用红色填充多边形glColor3f(1.0f, 0.0f, 1.0f);Fill(points, n);glFlush();}参考文献[1] 陆枫,何云峰. 计算机图形学(第二版). 北京:电子工业出版社,2008.10。
