最小二乘法 (C语言)
最小二乘法c语言实现

最小二乘法c语言实现最小二乘法是一种经典的数据拟合方法,它可以用于求解线性回归问题。
在实际应用中,我们经常需要使用最小二乘法来对一些数据进行拟合,从而得到一个最佳的线性模型。
C语言是一种高效、灵活的编程语言,非常适合进行科学计算和数据处理。
在本文中,我们将介绍如何使用C语言实现最小二乘法,并且给出一个简单的示例程序。
首先,我们需要明确最小二乘法的原理。
其核心思想是寻找一个最佳的线性函数,使得该函数与给定的数据点之间的误差最小。
具体来说,我们可以定义误差函数为:E = Σ(yi - a - bx_i)^2其中,a和b是待求的系数,xi和yi代表第i个数据点的横纵坐标。
我们的目标是寻找a和b的取值,使得E最小。
为了求解这个问题,我们可以采用求导的方法来求得a和b的解析式。
具体来说,我们可以对E关于a和b分别求导,并令其为0,得到如下方程组:Σyi = na + bΣxiΣxiyi = aΣxi + bΣ(x_i)^2其中,n为数据点的数量。
通过解这个方程组,我们可以得到a 和b的解析式:a = (ΣyiΣ(x_i)^2 - ΣxiyiΣxi) / (nΣ(x_i)^2 - (Σxi)^2)b = (nΣxiyi - ΣxiΣyi) / (nΣ(x_i)^2 - (Σxi)^2)有了这个解析式,我们就可以使用C语言来实现最小二乘法。
下面是一个简单的示例程序:#include <stdio.h>int main(){int n = 5; // 数据点的数量double xi[] = {1, 2, 3, 4, 5}; // 横坐标double yi[] = {2.1, 3.9, 6.1, 8.2, 10.2}; // 纵坐标double sum_xi = 0, sum_yi = 0, sum_xi2 = 0, sum_xiyi = 0; for (int i = 0; i < n; i++) {sum_xi += xi[i];sum_yi += yi[i];sum_xi2 += xi[i] * xi[i];sum_xiyi += xi[i] * yi[i];}double a = (sum_yi * sum_xi2 - sum_xi * sum_xiyi) / (n * sum_xi2 - sum_xi * sum_xi);double b = (n * sum_xiyi - sum_xi * sum_yi) / (n * sum_xi2 - sum_xi * sum_xi);printf('a = %.2f, b = %.2f', a, b);return 0;}在这个程序中,我们假设有5个数据点,分别对应横坐标1到5,纵坐标2.1到10.2。
c语言最小二乘法

c语言最小二乘法最小二乘法是一种常用的数学方法,用于拟合数据点的直线或曲线。
在c语言中,最小二乘法可以通过数学库函数来实现。
本文将介绍最小二乘法的原理和c语言中的实现方法。
最小二乘法的原理是通过最小化误差平方和来拟合数据点的直线或曲线。
误差平方和是指每个数据点到拟合直线或曲线的距离的平方和。
最小二乘法的目标是找到一条直线或曲线,使得误差平方和最小。
在c语言中,可以使用数学库函数来实现最小二乘法。
其中,最常用的函数是“lsfit”函数。
该函数的原型如下:int lsfit(double *x, double *y, int n, double *a, double *b, double *r);其中,x和y是数据点的横坐标和纵坐标数组,n是数据点的个数,a和b是拟合直线的斜率和截距,r是相关系数。
该函数的返回值为0表示拟合成功,返回其他值表示拟合失败。
使用“lsfit”函数进行最小二乘法拟合的示例代码如下:#include <stdio.h>#include <math.h>int lsfit(double *x, double *y, int n, double *a, double *b, double *r);int main(){double x[] = {1, 2, 3, 4, 5};double y[] = {2, 4, 6, 8, 10};double a, b, r;int n = 5;int ret = lsfit(x, y, n, &a, &b, &r);if (ret == 0){printf("y = %fx + %f\n", a, b);printf("r = %f\n", r);}else{printf("lsfit failed\n");}return 0;}在上述代码中,我们定义了一个包含5个数据点的数组x和y,然后调用“lsfit”函数进行最小二乘法拟合。
最小二乘法c语言程序

最小二乘法c语言程序最小二乘法是一种用于处理数据拟合问题的方法,它可以通过对数据进行线性回归来找到最佳拟合直线。
在c语言中,我们可以使用以下程序来实现最小二乘法。
首先,我们需要定义一个结构体来存储数据点的坐标信息:```ctypedef struct {double x;double y;} point;```接下来,我们可以定义一个函数来计算最小二乘法的系数:```cvoid least_squares(point *data, int n, double *a, double *b) {double sum_x = 0.0, sum_y = 0.0, sum_xy = 0.0, sum_xx = 0.0; for (int i = 0; i < n; i++) {sum_x += data[i].x;sum_y += data[i].y;sum_xy += data[i].x * data[i].y;sum_xx += data[i].x * data[i].x;}double denom = n * sum_xx - sum_x * sum_x;if (denom == 0) {// handle divide by zero errorreturn;}*a = (n * sum_xy - sum_x * sum_y) / denom;*b = (sum_y - (*a) * sum_x) / n;}```在这个函数中,我们首先计算了数据点的各种和值。
然后,我们使用这些和值来计算最小二乘法的系数。
接下来,我们可以定义一个主函数来读取输入数据,调用最小二乘法函数并输出结果:```cint main() {int n;printf("Enter the number of data points: ");scanf("%d", &n);point *data = malloc(n * sizeof(point));for (int i = 0; i < n; i++) {printf("Enter x and y coordinates of point %d: ", i + 1);scanf("%lf %lf", &(data[i].x), &(data[i].y));}double a, b;least_squares(data, n, &a, &b);printf("The equation of the best fit line is y = %.2lfx + %.2lf\n", a, b);free(data);return 0;}```在这个主函数中,我们首先读取输入数据,并将其存储在一个动态分配的数组中。
最小二乘法C语言的实现

实验三.最小二乘法C语言的实现1.实验目的:进一步熟悉曲线拟合的最小二乘法。
掌握编程语言字符处理程序的设计和调试技术。
2.实验要求:输入:已知点的数目以及各点坐标。
输出:根据最小二乘法原理以及各点坐标求出拟合曲线。
3.程序流程:(1)输入已知点的个数;(2)分别输入已知点的X坐标;(3)分别输入已知点的Y坐标;(4)通过调用函数,求出拟合曲线。
最小二乘法原理如下:根据一组给定的实验数据,求出自变量x与因变量y的函数关系,只要求在给定点上的误差的平方和最小.当时,即(4.4.1)这里是线性无关的函数族,假定在上给出一组数据,以及对应的一组权,这里为权系数,要求使最小,其中(4.4.2)(4.4.2)中实际上是关于的多元函数,求I的最小值就是求多元函数I的极值,由极值必要条件,可得(4.4.3)根据内积定义引入相应带权内积记号(4.4.4)则(4.4.3)可改写为这是关于参数的线性方程组,用矩阵表示为(4.4.5) (4.4.5)称为法方程.当线性无关,且在点集上至多只有n个不同零点,则称在X上满足Haar条件,此时(4.4.5)的解存在唯一。
记(4.4.5)的解为从而得到最小二乘拟合曲线(4.4.6) 可以证明对,有故(4.4.6)得到的即为所求的最小二乘解.它的平方误差为(4.4.7) 均方误差为在最小二乘逼近中,若取,则,表示为(4.4.8)此时关于系数的法方程(4.4.5)是病态方程,通常当n≥3时都不直接取作为基。
程序流程图:开始↓输入已知点个数n↓输入已知点的X坐标↓输入已知点的Y坐标输出结果程序:#include <math.h>#include <stdio.h>#include <stdlib.h>#include<malloc.h>float average(int n,float *x){int i;float av;av=0;for(i=0;i<n;i++)av+=*(x+i);return(av);}//平方和float spfh(int n,float *x){int i;float a,b;a=0;for(i=0;i<n;i++)a+=(*(x+i))*(*(x+i));return(a);}//和平方float shpf(int n,float *x){int i;float a,b;a=0;for(i=0;i<n;i++)a=a+*(x+i);b=a*a/n;return(b);}//两数先相乘,再相加float dcj(int n,float *x,float *y) {int i;float a;a=0;for(i=0;i<n;i++)a+=(*(x+i))*(*(y+i));return(a);}//两数先相加,再相乘float djc(int n,float *x,float *y) {int i;float a=0,b=0;for(i=0;i<n;i++){a=a+*(x+i);b=b+*(y+i);}a=a*b/n;}//系数afloat xsa(int n,float *x,float *y){float a,b,c,d,e;a=spfh(n,x);b=shpf(n,x);c=dcj(n,x,y);d=djc(n,x,y);e=(c-d)/(a-b);//printf("%f %f %f %f",a,b,c,d);return(e);}float he(int n,float *y){int i;float a;a=0;for(i=0;i<n;i++)a=a+*(y+i);return(a);}float xsb(int n,float *x,float *y,float a){ float b,c,d;b=he(n,y);c=he(n,x);d=(b-a*c)/n;return(d);}void main(){ int n,i;float *x,*y,a,b;printf("请输入将要输入的有效数值组数n的值:"); scanf("%d",&n);x=(float*)calloc(n,sizeof(float));if(x==NULL){printf("内存分配失败");exit(1);}y=(float*)calloc(n,sizeof(float));if(y==NULL){printf("内存分配失败");exit(1);}printf("请输入x的值\n");for(i=0;i<n;i++)scanf("%f",x+i);printf("请输入y的值,请注意与x的值一一对应:\n"); for(i=0;i<n;i++)scanf("%f",y+i);for(i=0;i<n;i++){ printf("x[%d]=%3.2f ",i,*(x+i));printf("y[%d]=%3.2f\n",i,*(y+i));}a=xsa(n,x,y);b=xsb(n,x,y,a);printf("经最小二乘法拟合得到的一元线性方程为:\n"); printf("f(x)=%3.2fx+%3.2f\n",a,b);}。
最小二乘法拟合C语言实现

最小二乘法拟合C语言实现实现最小二乘法拟合的思路是首先确定要拟合的函数形式,例如线性函数(y=a*x+b)或二次函数(y=a*x^2+b*x+c)。
然后通过最小化残差平方和来求得最佳拟合函数的参数。
假设我们要拟合的是一个线性函数y=a*x+b,其中x和y是已知的一组数据。
那么最小二乘法的目标是寻找到最逼近这组数据的直线,使得所有数据点到这条直线的距离的平方和最小。
伪代码如下:1.定义数组x和y分别存储输入的x和y值,并知道数据点的个数n。
2. 定义变量sum_x,sum_y,sum_xx,sum_xy,分别用于存储x的和,y的和,x的平方和,x和y的乘积和。
3. 对数组x和y进行累加,计算sum_x,sum_y,sum_xx,sum_xy。
4.计算最小二乘法的参数a和b的值:a = (n * sum_xy - sum_x * sum_y) / (n * sum_xx - sum_x *sum_x)b = (sum_y - a * sum_x) / n5.输出最佳拟合直线的参数a和b。
下面是一个使用C语言实现最小二乘法拟合的示例代码:```c#include <stdio.h>void linearLeastSquaresFit(double x[], double y[], int n, double* a, double* b)double sum_x = 0.0, sum_y = 0.0, sum_xx = 0.0, sum_xy = 0.0;//计算和for (int i = 0; i < n; i++)sum_x += x[i];sum_y += y[i];sum_xx += x[i] * x[i];sum_xy += x[i] * y[i];}//计算最小二乘法参数*a = (n * sum_xy - sum_x * sum_y) / (n * sum_xx - sum_x * sum_x);*b = (sum_y - *a * sum_x) / n;int maidouble x[] = {1.0, 2.0, 3.0, 4.0, 5.0};double y[] = {2.0, 4.0, 6.0, 8.0, 10.0};int n = sizeof(x) / sizeof(x[0]);double a, b;linearLeastSquaresFit(x, y, n, &a, &b);printf("拟合直线的参数:a = %lf, b = %lf\n", a, b);return 0;```在这个示例代码中,给定了一组x和y的数据点(x为1到5,y为2到10),然后使用最小二乘法拟合出一条最佳直线的参数a和b。
最小二乘拟合算法

最小二乘拟合算法最小二乘定义一般情况下,最小二乘问题求的是使某一函数局部最小的向量 x,函数具有平方和的形式,求解可能需要满足一定的约束:信赖域反射最小二乘要理解信赖域优化方法,请考虑无约束最小化问题,最小化 f(x),该函数接受向量参数并返回标量。
假设您现在位于 n 维空间中的点 x 处,并且您要寻求改进,即移至函数值较低的点。
基本思路是用较简单的函数 q 来逼近 f,该函数需能充分反映函数 f 在点 x 的邻域 N 中的行为。
此邻域是信赖域。
试探步 s 是通过在 N 上进行最小化(或近似最小化)来计算的。
以下是信赖域子问题如果f(x + s) < f(x),当前点更新为 x + s;否则,当前点保持不变,信赖域 N 缩小,算法再次计算试探步。
在定义特定信赖域方法以最小化 f(x) 的过程中,关键问题是如何选择和计算逼近 q(在当前点 x 上定义)、如何选择和修改信赖域 N,以及如何准确求解信赖域子问题。
在标准信赖域方法中,二次逼近 q 由 F 在 x 处的泰勒逼近的前两项定义;邻域 N 通常是球形或椭圆形。
以数学语言表述,信赖域子问题通常写作公式2其中,g 是 f 在当前点 x 处的梯度,H 是 Hessian 矩阵(二阶导数的对称矩阵),D 是对角缩放矩阵,Δ是正标量,∥ . ∥是 2-范数。
此类算法通常涉及计算 H 的所有特征值,并将牛顿法应用于以下久期方程它们要耗费与 H 的几个分解成比例的时间,因此,对于信赖域问题,需要采取另一种方法。
Optimization Toolbox 求解器采用的逼近方法是将信赖域子问题限制在二维子空间 S 内。
一旦计算出子空间 S,即使需要完整的特征值/特征向量信息,求解的工作量也不大(因为在子空间中,问题只是二维的)。
现在的主要工作已转移到子空间的确定上。
二维子空间 S 是借助下述预条件共轭梯度法确定的。
求解器将 S 定义为由 s1 和 s2 确定的线性空间,其中 s1 是梯度 g 的方向,s2 是近似牛顿方向,即下式的解或是负曲率的方向,以此种方式选择 S 背后的理念是强制全局收敛(通过最陡下降方向或负曲率方向)并实现快速局部收敛(通过牛顿步,如果它存在)。
最小二乘法一阶线性拟合二阶曲线拟合的C语言程序实现

一、最小二乘法原理与计算方法
对于 m 组测量数据,选取
( x) a0 a1 x a2 x 2
二、1 阶 2 阶拟合功能子函数和计算表达式
通过分析以上系数计算式中各项计算式,写出全部需要用到的子函数:
通过对照系数表达式里各个项的计算表达,写入主函数进行拟合计算。设定输入的数据格式为(x[ i ],y[ i ]) ,用 户输入数据的个数为 c,计算表达式程序代码如下: 1 阶直线拟合:
2 阶曲线拟合:
三、主函数代码
四、用 MATLAB 验证程序的运行结果
第一组:选择 y=x+1 进行线性拟合检验,可见 2 阶拟合对于线性关系,二次项系数为 0
第二组:选择 y=x^2+1入部分的设计参考了[物理实验计算器.
Zhouzb .
zhouzb889@]的部分代码,在此表示感谢。
m n i
当 n=1 时,为 1 阶拟合,又称直线拟合,即系数矩阵是一个 2*2 的矩阵,通过线性方程的求解运 算,求得线性回归方程的系数表达式为:
当 n=2 时,为 2 阶曲线拟合,所得到的系数矩阵是一个 3*3 的矩阵【用 aij(i,j=1,2,……)的 形式表达】 ,通过线性方程的求解运算,求得线性回归方程的系数表达式为:
智能仪器设计作业——最小二乘法——高世浩 1223150078
x
i 1 m
m
i
x
i 1
2 i
x
i 1
m
n 1 i
m x yi 0 i 1 i 1 m m n 1 x x y i 1 i i i 1 i 1 m m n xin yi xi2 n i 1 i 1
最小二乘法 c语言

最小二乘法 c语言最小二乘法是一种常用的数学方法,用于通过已知数据点拟合出一条最佳拟合曲线。
在本文中,我们将讨论如何使用C语言实现最小二乘法。
我们需要明确最小二乘法的基本原理。
最小二乘法的目标是找到一条曲线,使得该曲线上的点到已知数据点的距离之和最小。
具体地,我们假设已知数据点的集合为{(x1, y1), (x2, y2), ..., (xn, yn)},我们需要找到一条曲线y = f(x),使得f(xi)与yi的差的平方和最小。
那么,如何在C语言中实现最小二乘法呢?首先,我们需要定义一个函数来计算拟合曲线上的点f(xi)。
在这个函数中,我们可以使用多项式的形式来表示拟合曲线。
例如,我们可以选择使用一次多项式y = ax + b来拟合数据。
然后,我们可以使用最小二乘法的公式来计算出最优的a和b的值。
接下来,我们需要编写一个函数来计算拟合曲线上每个点f(xi)与已知数据点yi的差的平方和。
通过遍历已知数据点的集合,并计算每个点的差的平方,最后将所有差的平方求和,即可得到拟合曲线的误差。
然后,我们可以使用梯度下降法来最小化误差函数。
梯度下降法是一种优化算法,通过不断迭代来找到误差函数的最小值。
在每次迭代中,我们通过计算误差函数对参数a和b的偏导数,来更新a和b的值。
通过多次迭代,最终可以找到最优的a和b的值,从而得到最佳拟合曲线。
我们可以编写一个主函数来调用以上的函数,并将最终的拟合曲线绘制出来。
在这个主函数中,我们可以读取已知数据点的集合,并调用最小二乘法函数来计算拟合曲线的参数。
然后,我们可以使用绘图库来绘制已知数据点和拟合曲线,并将结果输出到屏幕上。
通过以上的步骤,我们就可以使用C语言实现最小二乘法了。
当然,在实际应用中,我们可能会遇到更复杂的数据和更高阶的多项式拟合。
但是基本的原理和方法是相同的,只是需要做一些适当的调整。
总结一下,最小二乘法是一种常用的数学方法,用于通过已知数据点拟合出一条最佳拟合曲线。
最小二乘法C语言编程

#include <hidef.h> /* common defines and macros */
#include "derivative.h" /* derivative-specific definitions */
x2=x*x*x*x;
x3+=x2;
}
*(pp++)=x3;
}
}
pp=*(b+1);
p=a9;
ppp=a8;
x3=0;
for(i=0;i<10;i++) {
x=*(p++);
x2=*(ppp++);
x3+=x*x2;
}
*pp=x3;
pp=*(b+2);
p=a9;
ppp=a8;
x3=0;
for(i=0;i<10;i++) {
*(p++)=(x1*x5-x2*x4);
p=*(b1+0);
pp=*(b4+0);
for (i=0;i<3;i++) {
for(j=0;j<3;j++){
x1=*(p++);
x=x1*c;
*(pp++)=x;
}
}
//////////////////////////求两矩阵的商//////////////////////////////////////
uwb定位 c语言 最小二乘法

uwb定位 c语言最小二乘法超宽带(UWB)定位是一种高精度定位技术,通常用于室内定位和室外定位。
在UWB定位中,最小二乘法是一种常用的数据处理方法,用于估计目标的位置。
下面是一个简单的C语言程序,使用最小二乘法进行UWB定位:```cinclude <>include <>define MAX_POINTS 100typedef struct {double x;double y;double z;} Point;typedef struct {Point points[MAX_POINTS];int numPoints;} UWB_Data;double distance(Point p1, Point p2) {return sqrt(pow( - , 2) + pow( - , 2) + pow( - , 2)); }Point leastSquares(UWB_Data data) {double sumX = 0, sumY = 0, sumZ = 0;double sumXX = 0, sumYY = 0, sumZZ = 0;double sumXY = 0, sumXZ = 0;int i;Point result;double det, inv[3][3];for (i = 0; i < ; i++) {sumX += [i].x;sumY += [i].y;sumZ += [i].z;sumXX += pow([i].x, 2);sumYY += pow([i].y, 2);sumZZ += pow([i].z, 2);sumXY += [i].x [i].y;sumXZ += [i].x [i].z;}det = (sumXX sumYY - pow(sumXY, 2)) (sumZZ - pow(sumZ, 2)) - (sumXZ sumXZ - pow(sumX, 2) sumZZ);inv[0][0] = (sumYY - pow(sumXY, 2)) / det;inv[1][1] = (sumZZ - pow(sumXZ, 2)) / det;inv[0][1] = inv[1][0] = -sumXY / det;inv[0][2] = inv[2][0] = -sumX / det;inv[1][2] = inv[2][1] = -sumZ / det;inv[2][2] = (sumX sumX - pow(sumXZ, 2)) / det;= inv[0][0] sumX + inv[0][1] sumY + inv[0][2] sumZ;= inv[1][0] sumX + inv[1][1] sumY + inv[1][2] sumZ;= inv[2][0] sumX + inv[2][1] sumY + inv[2][2] sumZ;return result;} ```。
c语言 最小二乘法

c语言最小二乘法最小二乘法是一种数据拟合方法,可以用来找到最优解的参数。
在 C 语言中,可以使用矩阵运算和线性代数的方法来实现最小二乘法。
首先,需要准备好数据集。
假设有一组数据集 (x1, y1), (x2, y2), ..., (xn, yn),我们要拟合的模型是 y = a*x + b。
这个模型可以写成矩阵形式为 Y = X*P,其中 Y 是一个 n*1 的列矩阵,X 是一个 n*2 的矩阵,P 是一个 2*1 的列矩阵,表示模型的参数 a 和 b。
接下来,可以使用矩阵运算来求解 P。
具体地,可以通过求解 X^T * X 的逆矩阵,再乘以 X^T 和 Y,得到 P = (X^T * X)^-1 * X^T * Y。
实现代码如下:```#include <stdio.h>#include <stdlib.h>#include <math.h>#define N 10 // 数据集中的数据个数#define M 2 // 模型中的参数个数// 数据集double x[N] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};double y[N] = {2.1, 4.5, 7.4, 9.5, 12.1, 14.5, 17.3, 19.5, 22.2, 24.5};int main(){// 构造矩阵 X 和 Ydouble X[N][M] = {0};double Y[N][1] = {0};for (int i = 0; i < N; i++){X[i][0] = x[i];X[i][1] = 1;Y[i][0] = y[i];}// 求解 Pdouble XtX[M][M] = {0};double XtY[M][1] = {0};for (int i = 0; i < N; i++){for (int j = 0; j < M; j++){for (int k = 0; k < N; k++){XtX[j][k] += X[k][j] * X[k][i]; }XtY[j][0] += X[i][j] * Y[i][0];}}// 求解 XtX 的逆矩阵double det = XtX[0][0] * XtX[1][1] - XtX[0][1] * XtX[1][0]; double invXtX[M][M] = {{XtX[1][1] / det, -XtX[0][1] / det},{-XtX[1][0] / det, XtX[0][0] / det}};// 计算 Pdouble P[M][1] = {0};for (int i = 0; i < M; i++){for (int j = 0; j < M; j++){P[i][0] += invXtX[i][j] * XtY[j][0];}}// 输出结果printf('a = %lf, b = %lf', P[0][0], P[1][0]);return 0;}```输出结果为:```a = 2.340000,b = -0.300000```表示拟合得到的模型为 y = 2.34*x - 0.3。
最小二乘法一阶线性拟合二阶曲线拟合的C语言程序实现

当 n=1 时,为 1 阶拟合,又称直线拟合,即系数矩阵是一个 2*2 的矩阵,通过线性方程的求解运 算,求得线性回归方程的系数表达式为:
当 n=2 时,为 2 阶曲线拟合,所得到的系数矩阵是一个 3*3 的矩阵【用 aij(i,j=1,2,……)的 形式表达】 ,通过线性方程的求解运算,求得线性回归方程的系数表达式为:
一、最小二乘法原理与计算方法
对于 m 组测量数据,选取
( x) a0 a1 x a2 x 2
an x n 进行 n 阶拟合,按
照残差平方和最小原则,对各个待二乘的法方程为 运算式如下,求解这个线性方程组就可以得出各个系数的值。
二、1 阶 2 阶拟合功能子函数和计算表达式
通过分析以上系数计算式中各项计算式,写出全部需要用到的子函数:
通过对照系数表达式里各个项的计算表达,写入主函数进行拟合计算。设定输入的数据格式为(x[ i ],y[ i ]) ,用 户输入数据的个数为 c,计算表达式程序代码如下: 1 阶直线拟合:
2 阶曲线拟合:
三、主函数代码
四、用 MATLAB 验证程序的运行结果
第一组:选择 y=x+1 进行线性拟合检验,可见 2 阶拟合对于线性关系,二次项系数为 0
第二组:选择 y=x^2+1 进行 2 阶曲线拟合检验
第三组:进行常规数据组检验
数据输入部分的设计参考了[物理实验计算器.
Zhouzb .
zhouzb889@]的部分代码,在此表示感谢。
m 1 i 1 m xi i 1 m x n i i 1
x
i 1 m
m
i
x
i 1
2 i
x
i 1
matlab和C语言实现最小二乘法

matlab和C语⾔实现最⼩⼆乘法Matlab代码:N = 8;x = [12345678 ];y = [6784102120137155172190];subplot(2,1,1);plot(x,y,'*');% 图形的⼀些设置xlabel('时间(秒)');ylabel('位移(⽶)');title('原始数据离散点')grid onsubplot(2,1,2);p = polyfit(x,y,1); %得出P就是线性拟合的系数% 0:0.01:9x1 = 0:1:N; %起始为0,终点为N,步长1y1 = polyval(p,x1);plot(x,y,'*',x1,y1,'r')xlabel('时间(秒)');ylabel('位移(⽶)');title('红线为最⼩⼆乘法拟合')grid onsumxyji =sum(x.*y); %向量内积sumx = sum(x);sumy = sum(y);sumxx = sum(x.*x);k = (N*sumxyji - sumx*sumy)/(N*sumxx-sumx*sumx)b = (sumy-k*sumx)/N效果:⾃⼰C语⾔实现:公式:#include <stdio.h>#include <stdlib.h>//函数功能:进⾏最⼩⼆乘曲线拟合(拟合y=a0+a1*x),计算出对应的系数a//参数说明:// n: 给定数据点的个数// x[]: 存放给定n个数据点的X坐标// y[]: 存放给定n个数据点的Y坐标// k,b: 拟合多项式的系数,表⽰多项式的k,bvoid polyfit(int n,double x[],double y[],double &k,double &b){int i,j;double sumxymultiply = 0.0;double sumx = 0.0;double sumy = 0.0;double sumxx = 0.0;for (i=0;i<n;i++){sumx += x[i];sumy += y[i];sumxymultiply += (x[i]*y[i]);sumxx += (x[i]*x[i]);}k = (n*sumxymultiply - sumx*sumy)/(n*sumxx - sumx*sumx);b = (sumy-k*sumx)/n;}void printArr(double *arr,int n){for(int i=0;i<n;++i)printf("%lf ",arr[i]);printf("\n");}int main(){const int N = 8;double x[N] = {1,2,3, 4,5,6,7,8};double y[N] = {67,84,102,120,137,155,172,190}; double k,b;polyfit(N,x,y,k,b);printf("%lf %lf\n",k,b);return0;}。
最小二乘参数估计的递推算法及其C语言实现
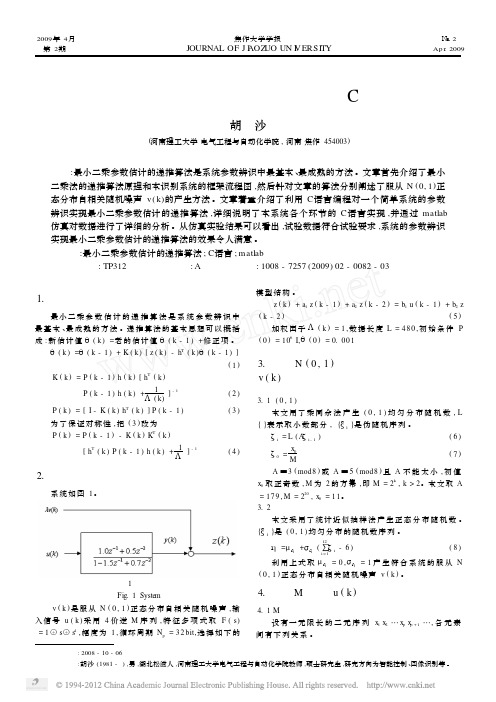
{ 1 } , d [ 2800 ] = { 0 } , k; for ( k = 0 ; k < 2 7 9 9 ; k + + ) { if ( a [ k ] - d [ k ] = = 0 ) a[ k + 1 ] = 1; else a[ k + 1 ] = 0; b[ k +1 ] = a[ k]; c[ k +1 ] = b[ k]; d[ k +1 ] = c[ k];
文章着重介绍了利用c语言编程对一个简单系统的参数辨识实现最小二乘参数估计的递推算法详细说明了本系统各个环节的c语言实现并通过matlab仿真对数据进行了详细的分析
2009年 4月 焦作大学学报 №12 第 2期 JOURNAL O F J IAO ZUO UN IV ERS ITY Ap r. 2009
xi = a1 xi - 1 a2 xi - 2 … ap xi - p
(9)
其 中 , i = p + 1 , p + 2 , …; 系 数 a1, a2, … , ap - 1 取 值 0
或 1 , 系 数 ap 总 为 1 ; 表 示 模 2 和 。
4. 2 逆 M 序 列 的 产 生
设 M ( k ) 是 周 期 为 Np bit元 素 取 值 为 0 或 1 的 M 序 列 , S ( k ) 是 周 期 为 2 bit, 元 素 取 值 为 0 或 1 的 方 波 序
间有下列关系 。
收稿日期 : 2008 - 10 - 06 作者简介 :胡沙 (1981 - ) ,男 ,湖北松滋人 ,河南理工大学电气工程与自动化学院教师 ,硕士研究生 ,研究方向为智能控制 、图像识别等 。
最小二乘法的编程实现

1、最小二乘法:1)(用1TAA方法计算逆矩阵)#include <stdio.h>#include <math.h>#include <stdlib.h>#include<string.h>#include <iostream.h>#define N 200#define n 9void Getdata(double sun[N])//从txt文档中读取数据(小数){char data;char sunpot[10]={0000000000};//为防止结果出现‘烫’字int i=0,j=0;double d;FILE *fp=fopen("新建文本文档.txt","r");if(!fp){printf("can't open file\n");}while(!feof(fp)){data=fgetc(fp);if(data!='\n'){sunpot[i]=data;i++;}else if(data=='\n'){sunpot[i]='\0';//给定结束符d=atof(sunpot);//将字符串转换成浮点数sun[j]=d;j++;i=0;//将i复位}}}void Normal(double sun[N],double sun1[N])//将数据进行标准化{double mean,temp=0,variance=0;int i;for(i=0;i<N;i++)temp=temp+sun[i];mean=temp/N;for(i=0;i<N;i++){sun1[i]=sun[i]-mean;}for(i=0;i<N;i++){variance=variance+sun1[i]*sun1[i];}variance=variance/N;variance=sqrt(variance);for(i=0;i<N;i++){sun1[i]=sun[i]/variance;//减去均值除以均方差进行归一化}}void Matrix(double sun[N],double matrixl[n][n],double matrixr[n])//组建方程的左右两个矩阵{double matrix1[N-n][n];//方程左边系数矩阵double matrix_trans[n][N-n];double matrix2[N-n];//方程右边系数矩阵int i,j,k;double temp;for(i=0;i<N-n;i++)//组建N-nxn维方程矩阵{for(j=0;j<n;j++){matrix1[i][j]=sun[n+i-j-1];//此处与matlab不同,matlab是从1开始的}}for(i=0;i<N-n;i++)matrix2[i]=sun[i+n];for(i=0;i<n;i++)//将N-nxn维矩阵转置{for(j=0;j<N-n;j++){matrix_trans[i][j]=matrix1[j][i];}}for(i=0;i<n;i++)//组建nxn维方阵(A'*A){for(k=0;k<n;k++){temp=0;for(j=0;j<N-n;j++){temp+=matrix_trans[i][j]*matrix1[j][k];}matrixl[i][k]=temp;}}for(i=0;i<n;i++){temp=0;for(j=0;j<N-n;j++){temp+=matrix_trans[i][j]*matrix2[j];}matrixr[i]=temp;}}void ExchangeLine(double a[n][n], int i, int j, int p)//交换矩阵第i行和第j行{int k;double temp;for (k=0;k<=p-1;k++){temp=a[j][k];a[j][k]=a[i][k];a[i][k]=temp;}}void Gauss(double a[n][n],int k,int p)//高斯消元,用第k行消去其他行第一个非零元素{int i,j;double m;for(i=k+1;i<p;i++){if(a[i][k]==0)i++;m = a[i][k] / a[k][k];for (j = k; j < p; j ++){a[i][j] = a[i][j] - m * a[k][j];}}}double Determinant(double a[n][n],int p)//求a的行列式{int k,i,j;double result=1.0;for(k=0;k<p-1;k++)//逐一取对角元素以下矩阵进行消元,n-1是因为最后一个对角元素无需消元{i=k;j=k;while(a[i][j]==0)i++;if((i<p)&&i>k){ExchangeLine(a,k,i,p);result=(-1)*result;//换行之后行列式变号一次}else if(i>=p)//即找不到可以交换的行{result=0;break;}Gauss(a,k,p);//对该列进行消元}for(i=0;i<p;i++){result=result*a[i][i];}return result;}void Adjoint_matrix(double a[n][n],double b[n][n],int p,int i,int j)//求a[i][j]元素的伴随矩阵{double temp[n][n]={{0,0,0},{0,0,0},{0,0,0}};//实际上只要n-1xn-1维,但为了调用方便,此处写为nxn 维int k,m,l,r;b[j][i]=1;for (k = 0, l = 0; k <p-1; k++, l ++)//将原矩阵去除i行j列后复制到temp中{if (l == i) l ++;for (m = 0, r = 0; m <p-1; m ++, r ++){if (r == j) r ++;temp[k][m] = a[l][r];}}b[j][i]=b[j][i]*Determinant(temp,n-1);if ((i + j) % 2 == 1)//(-1)^(i+j)b[j][i]=-b[j][i];}void Inverse(double a[n][n],double b,double c[n][n])//求逆最后一步运算{int i,j;for(i=0;i<n;i++){for(j=0;j<n;j++){c[i][j]=a[i][j]/b;}}}void main(){int p=n,i,j;double sunpot[N],sunpot_normal[N];double fi[n];double matrix[n][n];//要换成返回的方阵double matrixr[n];double adjoint[n][n],inverse[n][n];double determinant,temp;Getdata(sunpot);//从txt文档中读取每年的太阳黑子数据Normal(sunpot,sunpot_normal);//数据归一化Matrix(sunpot_normal,matrix,matrixr);//组建方程for(i=0;i<p;i++){for(j=0;j<p;j++){Adjoint_matrix(matrix,adjoint,p,i,j);}}determinant=Determinant(matrix,p);if (determinant== 0)printf("该矩阵不存在逆矩阵!\n");printf("行列式:\n");printf("%10lf\n",determinant);Inverse(adjoint,determinant,inverse);printf("逆矩阵:\n");for(i=0;i<p;i++){for(j=0;j<p;j++){printf("%12lf",inverse[i][j]);}printf("\n");}printf("fi:\n");for(i=0;i<n;i++){temp=0;for(j=0;j<n;j++){temp+=inverse[i][j]*matrixr[j];}fi[i]=temp;printf("%10lf",fi[i]);}printf("\n");}计算结果:fi:1.327258 -0.622683 0.018571 0.129074 -0.141278 0.103665 -0.046903 0.060403 0.154991下面用matlab进行拟合度计算:clearM=load('太阳黑子数.txt');sunpot=(M(:,2));N=200;n=9;[Y,mu,sigma]=zscore(sunpot);B(1:N-n)=Y(n+1:N);B=B';fi=[1.327258 -0.622683 0.018571 0.129074 -0.141278 0.103665 -0.046903 0.060403 0.154991]; %由C语言计算出的fi值fi=[1;-fi'];ts2=idpoly(fi',[]);B=Y(1:N-n);plot(B);compare(B, ts2, 1);2)用构造矩阵1A I I A-→的方法求逆:(列主元高斯消去法)[;][;]部分主要程序:void BuildMatrix(double a[n][M],double b[n][n]){int i,j;for (i=0;i<n;i++){for (j=0;j<n;j++){a[i][j]=b[i][j];}a[i][i+n]=1.0;}}void ExchangeLine(double a[n][M],int i,int j){int k;double temp;for (k=0;k<M;k++){temp=a[i][k];a[i][k]=a[j][k];a[j][k]=temp;}}void Judge(double a[n][M],int i){int j,m=0;//m=0来表示是否需要换行double temp=a[i][i];for(j=i+1;j<n;j++){if(fabs(a[j][i])>fabs(temp)){temp=a[j][i];m=j;}}if(m)ExchangeLine(a,i,m);}void Gauss(double a[n][M],int k) //高斯消元法,用第k行消去其他行{ { int i,j;double m;for(i=k+1;i<n;i++){if(a[i][k]==0)i++;m = a[i][k] / a[k][k];for (j = k; j < M; j ++){a[i][j] = a[i][j] - m * a[k][j];}}}void Normal(double a[n][M]){int i,j;double temp;for(i=0;i<n;i++){temp=a[i][i];if(temp!=1.0){for(j=i;j<M;j++){a[i][j]=a[i][j]/temp;}}}}void Inverse(double a[n][M]){int i,j,k;double temp;for(i=n-1;i>=0;i--){for(j=i-1;j>=0;j--){temp=a[j][i];for(k=i;k<M;k++){a[j][k]=a[j][k]-temp*a[i][k];}}}}void GetInverse(double a[n][M],double b[n][n]) {int i,j;for(i=0;i<n;i++){for(j=0;j<n;j++){b[i][j]=a[i][j+n];}}}void main(){int i,j;double temp;double sunpot[N];double sunpot_normal[N];double matrixr[n];double matrix1[n][n]={0};//方阵double matrix[n][M]={0};//构造矩阵double inverse[n][n]={0};double fi[n];Getdata(sunpot);//从txt文档中读取每年的太阳黑子数据Normal(sunpot,sunpot_normal);//数据归一化Matrix(sunpot_normal,matrix1,matrixr);//组建方程BuildMatrix(matrix,matrix1);for(i=0;i<n-1;i++){Judge(matrix,i);Gauss(matrix,i);}for(i=0;i<n;i++)//判断是否可逆{if(matrix[i][i]==0){printf("矩阵不可逆!\n");exit(-1);}}Normal(matrix);Inverse(matrix);GetInverse(matrix,inverse);printf("逆矩阵:\n");for(i=0;i<n;i++){for(j=0;j<n;j++){printf("%10lf",inverse[i][j]);}printf("\n");}printf("fi:\n");for(i=0;i<n;i++){temp=0;for(j=0;j<n;j++){temp+=inverse[i][j]*matrixr[j];}fi[i]=temp;printf("%10lf",fi[i]);}}。
最小二乘法 c语言实现

最小二乘法 c语言实现最小二乘法是一种常用的数据拟合方法,它可以通过最小化拟合数据与实际数据之间的平方误差来得到最优的拟合结果。
在实际应用中,最小二乘法广泛应用于数据分析、信号处理、机器学习等领域。
在C语言中,实现最小二乘法需要涉及到矩阵运算和线性代数等基础知识。
以下是一个简单的最小二乘法C语言实现的示例代码:#include <stdio.h>#include <stdlib.h>#include <math.h>#define MAXN 100int main(){int n; // 数据点个数double x[MAXN], y[MAXN]; // 存储数据的数组double sumx = 0.0, sumy = 0.0, sumxy = 0.0, sumx2 = 0.0; // 计算所需的变量double a, b; // 拟合直线的系数printf('Enter number of data points: ');scanf('%d', &n);if (n > MAXN) {printf('Too many data points');}printf('Enter data points:');for (int i = 0; i < n; i++) {scanf('%lf %lf', &x[i], &y[i]);sumx += x[i];sumy += y[i];sumxy += x[i] * y[i];sumx2 += x[i] * x[i];}// 计算拟合直线的系数double denom = n * sumx2 - sumx * sumx; if (fabs(denom) < 1e-10) {printf('Cannot fit a straight line');return 1;}a = (n * sumxy - sumx * sumy) / denom;b = (sumy - a * sumx) / n;printf('Fitted line: y = %g x + %g', a, b);}以上代码通过输入数据点的坐标,计算出最小二乘拟合直线的系数a和b,并输出拟合直线的方程式。
c语言 最小二乘法

c语言最小二乘法最小二乘法是一种经典的线性回归分析方法,广泛应用于数据拟合和趋势线的绘制。
在计算机科学领域中,使用C语言代码来实现最小二乘法,可以快速高效地处理大量数据。
本文将介绍在C语言中实现最小二乘法的步骤和基本原理。
1. 定义输入和输出参数在C语言中,我们需要先定义要输入和输出的参数。
输入参数包括X数组和Y数组,分别表示自变量和因变量的值。
为了便于计算,我们需要定义X的平方和、X乘Y的和、X的和和Y的和。
double X[100], Y[100];double SumX2, SumXY, SumX, SumY;int Count;2. 输入数据利用scanf函数输入数据,可以通过循环操作,一次性输入整个数组。
如果您觉得输入过程繁琐,可以使用文件读取函数读取数据。
printf("请输入X、Y、数据个数: ");scanf("%lf%lf%d", &X[i], &Y[i], &Count);3. 计算和最小二乘法的核心是计算和,利用输入的数据计算出SumX2、SumXY、SumX、SumY四个和数。
这里可以使用循环操作,遍历整个数组并计算值。
for (i = 0; i < Count; i++) {SumX += X[i];SumY += Y[i];SumX2 += (X[i] * X[i]);SumXY += (X[i] * Y[i]);}4. 计算斜率和截距利用计算出来的和,我们可以计算出最小二乘法的斜率和截距。
否则,在调用最小二乘法算法时将无法获得正确的结果。
double Slope = (Count * SumXY - SumX * SumY) / (Count * SumX2 - SumX * SumX);double Intercept = (SumY - Slope * SumX) / Count;5. 输出结果计算出来斜率和截距,就可以使用printf函数输出结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
#include <math.h>
#include <stdio.h>
//////////////////////////////////////////////////////////////////////////// //////////////
//矩阵结构体
struct Matrix
{
int m,n;//m为行数,n为列数
double **pm;//指向矩阵二维数组的指针
};
//初始化矩阵mt,并置矩阵的行为m,列为n
void InitMatrix(struct Matrix *mt,int m,int n)
{
int i;
//指定矩阵的行和列
mt->m=m;
mt->n=n;
//为矩阵分配内存
mt->pm=new double *[m];
for(i=0;i<m;i++)
{
mt->pm[i]=new double[n];
}
}
//用0初始化矩阵mt,并置矩阵的行为m,列为n
void InitMatrix0(struct Matrix *mt,int m,int n)
{
int i,j;
InitMatrix(mt,m,n);
for(i=0;i<m;i++)
for(j=0;j<n;j++) mt->pm[i][j]=0.0;
}
//销毁矩阵mt
void DestroyMatrix(struct Matrix *mt)
{
int i;
//释放矩阵内存
for(i=0;i<mt->m;i++)
{
delete []mt->pm[i];
}
delete []mt->pm;
}
//矩阵相乘mt3=mt1*mt2
//成功返回1,失败返回0
int MatrixMul(Matrix *mt1,Matrix *mt2,Matrix *mt3)
{
int i,j,k;
double s;
//检查行列号是否匹配
if(mt1->n!=mt2->m||mt1->m!=mt3->m||mt2->n!=mt3->n) retu rn 0;
for(i=0;i<mt1->m;i++)
for(j=0;j<mt2->n;j++)
{
s=0.0;
for(k=0;k<mt1->n;k++) s=s+mt1->pm[i][k]*mt2->pm[k][j]; mt3->pm[i][j]=s;
}
return 1;
}
//矩阵转置mt2=T(mt1)
//成功返回1,失败返回0
int MatrixTran(Matrix *mt1,Matrix *mt2)
{
int i,j;
//检查行列号是否匹配
if(mt1->m!=mt2->n||mt1->n!=mt2->m) return 0;
for(i=0;i<mt1->m;i++)
for(j=0;j<mt1->n;j++) mt2->pm[j][i]=mt1->pm[i][j];
return 1;
}
//控制台显示矩阵mt
void ConsoleShowMatrix(Matrix *mt)
{
int i,j;
for(i=0;i<mt->m;i++)
{
printf("\n");
for(j=0;j<mt->n;j++) printf("%2.4f ",mt->pm[i][j]);
}
printf("\n");
}
//////////////////////////////////////////////////////////////////////////// //////////////
//Guass列主元素消元法求解方程Ax=b,a=(A,b)
int Guassl(double **a,double *x,int n)
{
int i,j,k,numl,*h,t;
double *l,max;
l=new double[n];
h=new int[n];
for(i=0;i<n;i++) h[i]=i;//行标
for(i=1;i<n;i++)
{
max=fabs(a[h[i-1]][i-1]);
numl=i-1;
//列元的最大值
for(j=i;j<n;j++)
{
if(fabs(a[h[j]][i-1])>max)
{
numl=h[j];
max=fabs(a[h[j]][i-1]);
}
}
if(max<0.00000000001) return 0;
//交换行号
if(numl>i-1)
{
t=h[i];
h[i]=h[numl];
h[numl]=t;
}
for(j=i;j<n;j++) l[j]=a[h[j]][i-1]/a[h[i-1]][i-1];
for(j=i;j<n;j++)
for(k=i;k<n+1;k++) a[h[j]][k]=a[h[j]][k]-l[j]*a[h[i-1]] [k];
}
for(i=n-1;i>=0;i--)
{
x[i]=a[h[i]][n];
for(j=i+1;j<n;j++) x[i]=x[i]-a[h[i]][j]*x[j];
x[i]=x[i]/a[h[i]][i];
}
//清除临时数组内存
delete []l;
delete []h;
return 1;
}
//////////////////////////////////////////////////////////////////////////// ///////////////
//最小二乘法求解矩阵Ax=b
int MinMul(Matrix A,Matrix b,double *x)
{
int i,j;
if(b.n!=1) return 0;
if(A.m!=b.m) return 0;
Matrix TranA;//定义A的转置
InitMatrix0(&TranA,A.n,A.m);
MatrixTran(&A,&TranA);
Matrix TranA_A;//定义A的转置与A的乘积矩阵
InitMatrix0(&TranA_A,A.n,A.n);
MatrixMul(&TranA,&A,&TranA_A);//A的转置与A的乘积
Matrix TranA_b;//定义A的转置与b的乘积矩阵
InitMatrix0(&TranA_b,A.n,1);
MatrixMul(&TranA,&b,&TranA_b);//A的转置与b的乘积
DestroyMatrix(&TranA);//释放A的转置的内存
Matrix TranA_A_b;//定义增广矩阵
InitMatrix0(&TranA_A_b,TranA_A.m,TranA_A.m+1);
//增广矩阵赋值
for(i=0;i<TranA_A_b.m;i++)
{
for(j=0;j<TranA_A_b.m;j++) TranA_A_b.pm[i][j]=TranA_A.pm[i] [j];
TranA_A_b.pm[i][TranA_A_b.m]=TranA_b.pm[i][0];
}
DestroyMatrix(&TranA_A);
DestroyMatrix(&TranA_b);
//Guass列主消元法求解
Guassl(TranA_A_b.pm,x,TranA_A_b.m);
DestroyMatrix(&TranA_A_b);
return 1;
}
int MinMul(double **A,double *b,int m,int n,double *x)
{
int r,i;
Matrix Al,bl;
Al.pm=new double *[m];
Al.m=m;
Al.n=n;
InitMatrix(&bl,m,1);
for(i=0;i<m;i++)
{
Al.pm[i]=A[i];
bl.pm[i][0]=b[i];
}
r=MinMul(Al,bl,x);
delete []Al.pm;
DestroyMatrix(&bl);
return r;
}。
