2019年高考数学压轴题专题11隐圆问题(原卷版)
专题11定语从句(原卷版)2
第11章 定语从句Part1 中考考点导图定语从句结构图解定语从句 引导词特殊情况 注意事项 先行词是人，用who 先行词非人，用which 宾格whom用that 不用which 的条件 用which 不用that 的条件无引导词：先行词在定从中作宾语，引导词可省略 先行词在定从中作主语，定从谓动单复数由先行词决定 one of+复数名词，作先行词，谓动用复数 the (only) one of, the very/right+复数名词，作先行词，谓动用单数作定语的句子，即“…的”可以作名词或代词的定语 万能钥匙that 定语形容词 介词短语 非谓语动词短语 前置I have a good friend. 后置I want to do something interesting. 后置The boy in white is my friend. 后置I don’t have a house to live in. 修饰名词或代词的成分 常译为“…的” 句子 后置I like students who like English.人主 who 关系代词 引导词人宾 whom 物主/宾 which 人/物主/宾 that 人/物定 whose=of whom 人 =of which 物 时间状 when=in which/ on which=at which 关系副词 地点状 where=in which/ at which 原因 状 why=for which 引导词用that ，不用which 的条件 ①先行词前有最高级修饰；或先行词就是最高级； ②先行词前有序数词修饰；或先行词就是序数词； ③先行词前有the only, the right, the last, just, the same, the very 等词修饰； ④先行词是不定代词all, everything, one 等词；或先行词前有不定代词修饰时； ⑤先行词中既有人又有物； ⑥主句是which 或who 引导的特殊疑问句；⑦There be 句型中 引导词用which ，不用 that 的条件 ①引导词前有介词，如：in which;on which;with whom ②先行词是that, those 不用that 的条件介词后用whom ，which ，不用thatPart2 中考真题精选1．（2021·辽宁营口市·中考真题）I’ll never forget the place ________ we visited together last year.A．which B．what C．who D．whom 2．（2021·黑龙江大庆市·中考真题）I’d like to express my thanks to everyone ________ served the munity.A．which B．who C．where D．when 3．（2021·山东滨州市·中考真题）In my opinion, of all the books, this is the only one ______ is well worth reading.A．who B．that C．whom D．what 4．（2021·湖北黄冈市·中考真题）— What can we do for the lefthome children in the village ________ need help?— We could help them with their study online on weekends.A．which B．whom C．whose D．who 5．（2021·贵州黔东南苗族侗族自治州·中考真题）On December 31, 2020, the New Year speech ________ President Xi Jinping made encouraged us Chinese to work harder for our motherland. A．who B．whose C．which D．what 6．（2021·贵州铜仁市·中考真题）—Do you know the boy ________ hand writing won the first in the petition?—Oh, he is Wang Wei, our monitor.A．who B．whose C．whom D．which 7．（2021·黑龙江绥化市·中考真题）I like smart clothes ________ are made of silk.A．who B．which C．what8．（2021·贵州贵阳市·中考真题）Abing’s Erquan Yingyue is a piece of music _________ has bee one of China’s national treasures.A．who B．which C．whose9．（2021·福建中考真题）We all miss Wu Mengchao ________ saved thousands of lives in his medical work.A．which B．what C．who10．（2021·湖北十堰市·中考真题）This is the first birthday gift _________ I received. I’ve kept it many years.A．which B．that C．who D．what 11．（2021·青海中考真题）Chaka Salt Lake ________ is known as Mirror of the Sky interests more and more tourists.A．where B．which C．who12．（2021·湖南怀化市·中考真题）—Do you know the woman ______ wears a blue skirt? —Oh, she’s my aunt.A．which B．who C．what13．（2021·四川乐山市·中考真题）—Do you like the weekly talk show, The Reader, on CCTV? —Sure. It’s a great TV programme _________ brings the habit of reading back into the public. A．who B．that C．what14．（2021·湖南岳阳市·中考真题）All of the classmates prefer the song Shao Nian ________. A．that they can sing along withB．which can they sing along withC．who they can sing along with15．（2021·四川达州市·中考真题）—Could you tell me ________ kind of movies you like best? —Umm…. I like the movies ________ make me laugh.A．what; which B．what; what C．which; what D．which; where 16．（2021·云南中考真题）Yuan Longping is a great scientist ________ was honored as “The Fathe r of Hybrid Rice”.A．when B．who C．which D．whose 17．（2021·四川成都市·中考真题）Zhang Hong, a Chinese, is the first Asian blind climber________ has reached the top of Qomolangma.A．who B．whose C．which18．（2021·甘肃天水市·中考真题）A true friend is a person ________ reaches for your hand and touches your heart.A．whom B．whose C．who D．which【2020年】1.【2020 •青海省】We’ ll never forget those ________ lost their lives for our country.A. whoB. whichC. whom2.【2020 •福建省】Du Fu is a great Chinese poet ________ has bee popular with many people around the world.A．which B．whom C．who3.【2020 •黑龙江绥化】We all like edies __________ make us relaxed.A. whoB. thatC. whom4.【2020 •吉林省】This is the CD_____________ I bought last year.A. whoB. thatC. whom5.【2020 •盐城市】What our society is like is decided by everyone chooses to behave.A. whereB. whenC. howD. why6.【2020•湖北省恩施州】Mary is my English teacher ________ not only teaches me knowledge but also how to be a good person.A．She B．which C．who7..【2020•湖北省十堰市】—We teenagers should look up to the people ______ have made great achievements to our country, like Yuan Longping.—I think so.A．who B．what C．which D．whose8.【2020•鄂州市】I will remember the important people in my life ________ helped and supported me.A. whoB. whichC. whatD. how9.【2020•黄冈市】—Do you know the girl__ is giving the speech?—Of course. She is my best friend, Meimei.A. whichB. whoC. whomD. what10.【2020•怀化市】—Do you like the song Shao Nian?—Yes. I like the songs ______ I can sing along with.A. thatB. whoC. what11.【2020 •广西北部湾经济区】Our teacher told us a funny story ________ made us laugh.A. whenB. whichC. whoD. whom12.【2020 •黑龙江牡丹江、鸡西地区】The house in ________ Lu Xun used to live is now a museum.A. whichB. whereC. that13.【2020 •黑龙江哈尔滨市中考】—What are they talking about?—They are talking about the greatest inventions ________ have made a big difference to our daily life.A. whichB. whoC. that14.【2020 •山东滨州市中考】—Do you know Li Ziqi?—Of course. She is a beautiful girl________has made many videos to show a traditional Chinese way of life.A. whoseB. whereC. whichD. who15.【2020 •四川省成都市中考】The book ________cover has a beautiful picture is Lily's.A. whichB. whoseC. that16【2020 •甘孜州中考】The nurse _____________ is looking after the old man is Tom’s sister.A. whichB. whoC. what17.【2020 •贵州省安顺市中考】In difficult times, there are always national heroes ________ step up and bring people hope.A. whomB. whichC. who18.【2020 •贵州黔东南州中考】Li Wenliang is a brave doctor ________ is known to millions of Chinese people.A. whoB. whichC. whatD. when【2019年】1. 【2019 • 黑龙江省大庆市】The book __________ I read last night was fantastic.A. thatB. whatC. whoseD. who2. 【2019 • 吉林省中考】Mr. Brown is a teacher __________ is strict with all is students.A. whichB. whoC. where3. 【2019 • 甘肃省天水市】—Have you seen the film The Wandering Earth(流浪地球) ?—Yes. It’s the best one __________ I have ever seen.A. thatB. whichC. whatD. it4. 【2019 • 贵州省贵阳市】Wang Yangming is a great educationalist __________ developedmost of his thoughts in Xiuwen.A. whichB. whatC. who5.【2019 • 四川省内江市】The book __________ was written by him is very interesting.A. whoB. whomC. whichD. /6.【2019 • 四川省遂宁市】My mother doesn’t like stories __________ have sad endings.A. thatB. whoC. whereD. those7. 【2019 • 四川省达州市】—Frank, look! Who are the children under the tree __________waiting in a line?—They are the students from No. 1 Primary School.A. that areB. where areC. which isD. who is8.【2019 • 内蒙古呼和浩特市】Sitting down after a walk is relaxing. But would you like to siton a seat __________ tell you your weight?A. /B. whoC. whomD. that9.【2019 • 湖南省湘潭市】On Monday April 15，2019，the fire __________ broke out in NotreDame Cathedral in Paris shocked the world.A. thatB. whoC. where10.【2019 • 广西玉林市】—Hey, Anna, Would you like to see The White Storm with me?—You mean, the new police story __________ was filmed by Chen Musheng.A. whoB. whatC. whoseD. which11. 【2019 • 甘肃省兰州市】The movie ___________ I have seen twice is The Wandering Earth.A. whoB. whichC. whereD. when12. 【2019 • 四川省乐山市】—What are you looking for?—I’m looking for the storybook ___________ you lent to me last week.A. whoB. whichC. when13.【2019 • 山东省临沂市】Peppa Pig (《小猪佩奇》) is a British cartoon ___________ has beenpopular in China and is much loved by little children and their parents.A. whoB. whichC. /14.【2019 • 四川省眉山市】Success always belongs to those ___________ have tried their bestto make their dreams e true.A. whoB. whomC. whoseD. which15. 【2019 • 湖北省随州市】—What kind of movies do you like?—I prefer movies ___________ give me something to think about.A. whichB. whoC. whatD. when16.【2019 • 甘肃省武威市】I prefer music ___________ has great lyrics.A. whoB. whoseC. thatD. /17.【2019 • 湖南省长沙市】China is getting better at making hitech products ___________ canbe bought in all parts of the world.A. whoB. whichC. what18. 【2019 • 广东省中考】Not all children ___________ watch this video will bee a scientist, butsome may bee interested in science.A. whomB. whichC. whoD. whose19. 【2019 • 湖北省鄂州市】—Do you like the weekly talk show The Readers on CCTV?—Sure. It’s a great TV program ___________ can develop the habit of reading.A. whoB. thatC. whatD. whose20. 【2019 • 福建省中考】Du Fuguo is a hero ___________ is known to millions of Chinese people.A. whoB. whichC. what21. 【2019 • 河南省中考】—Do you know the boy over there?—The one ___________ is holding a ball? Oh, that’s my neighbor Phil.A. whatB. whichC. whoD.不填22.【2019 • 黑龙江省哈尔滨市】—Have you got ready for the soccer game?—Yes. I’ve done everything ___________ I can to win the game.A. whoB. thatC. which【答案】B【解析】本题考查定语从句，不定代词everything作先行词，故定语从句引导词用that。
圆中的重要几何模型-隐圆模型(解析版)精选全文完整版
圆中的重要几何模型-隐圆模型隐圆是各地中考选择题和填空题、甚至解答题中常考题，题目常以动态问题出现，有点、线的运动，或者图形的折叠、旋转等，大部分学生拿到题基本没有思路，更谈不上如何解答。
隐圆常见的有以下四种形式，动点定长、定弦对直角、定弦对定角、四点共圆(对角互补或等弦对等角)，上述四种动态问题的轨迹是圆。
题目具体表现为折叠问题、旋转问题、角度不变问题等，此类问题综合性强，隐蔽性强,很容易造成同学们的丢分。
本专题就隐圆模型的相关问题进行梳理及对应试题分析，方便掌握。
模型1、动点定长模型(圆的定义)若P为动点，但AB=AC=AP，则B、C、P三点共圆，A圆心，AB半径圆的定义：平面内到定点的距离等于定值的所有点构成的集合．寻找隐圆技巧：若动点到平面内某定点的距离始终为定值，则其轨迹是圆或圆弧．例1.(2020·四川中考真题)已知：等腰直角三角形ABC的腰长为4，点M在斜边AB上，点P为该平面内一动点，且满足PC=2，则PM的最小值为()A.2B.22-2C.22+2D.22【答案】B【分析】根据等腰直角三角形的性质得到斜边AB=42，由已知条件得到点P在以C为圆心，PC为半径的圆上，当点P在斜边AB的中线上时，PM的值最小，于是得到结论．【详解】解：∵等腰直角三角形ABC的腰长为4，∴斜边AB=42，∵点P为该平面内一动点，且满足PC=2，∴点P在以C为圆心，PC为半径的圆上，当点P在斜边AB的中线上时，PM的值最小，∵△ABC是等腰直角三角形，∴CM=12AB=22，∵PC=2，∴PM=CM-CP=22-2，故选：B．【点睛】本题考查线段最小值问题，涉及等腰三角形的性质和点到圆的距离，解题的关键是能够画出图形找到取最小值的状态然后求解．例2.(2020·江苏连云港市·中考真题)如图，在平面直角坐标系xOy中，半径为2的eO与x轴的正半轴交于点A，点B是eO上一动点，点C为弦AB的中点，直线y=34x-3与x轴、y轴分别交于点D、E，则△CDE面积的最小值为．【答案】2【分析】如图，连接OB，取OA的中点M，连接CM，过点M作MN⊥DE于N．先证明点C的运动轨迹是以M为圆心，1为半径的⊙M，设⊙M交MN于C′．求出MN，当点C与C′重合时，△C′DE 的面积最小．【详解】解：如图，连接OB，取OA的中点M，连接CM，过点M作MN⊥DE于N．∵AC=CB，AM=OM，∴MC=12OB=1，∴点C的运动轨迹是以M为圆心，1为半径的⊙M，设⊙M交MN于C′．∵直线y=34x-3与x轴、y轴分别交于点D、E，∴D(4，0)，E(0，-3)，∴OD=4，OE=3，∴DE=OE2+OD2=32+42=5，∵∠MDN=∠ODE，∠MND=∠DOE，∴△DNM∽△DOE，∴MNOE=DMDE，∴MN3=35，∴MN=95，当点C与C′重合时，△C′DE的面积最小，△C′DE的面积最小值=12×5×95-1，故答案为2．【点睛】本题考查三角形的中位线定理，三角形的面积，一次函数的性质等知识，解题的关键是学会添加常用辅助线，构造三角形的中位线解决问题，属于中考常考题型．例3.(2022·北京市·九年级专题练习)如图，四边形ABCD中，AE、AF分别是BC，CD的中垂线，∠EAF=80°，∠CBD=30°，则∠ABC=，∠ADC=．【答案】 40°； 60°【分析】连接AC，根据线段垂直平分线的性质可得AB=AC=AD，从而得到B、C、D在以A为圆心，AB为半径的圆上，根据圆周角定理可得∠DAC=2∠DBC=60°，再由等腰三角形的性质可得∠DAF=∠CAF=30°，即可求解．【详解】解：连接AC，∵AE、AF分别是BC、CD的中垂线，∴AB=AC=AD，∴B、C、D在以A为圆心，AB为半径的圆上，∵∠CBD=30°，∴∠DAC=2∠DBC=60°，∵AF⊥CD，CF=DF，∴∠DAF=∠CAF=30°，∴∠ADC=60°，∵AB=AC,BE=CE，∴∠BAE=∠CAE，又∵∠EAC=∠EAF-∠CAF=80°-30°=50°，∴∠ABC=∠ACE=90°-50°=40°．故答案为：40°，60°．【点睛】本题主要考查了圆周角定理，线段垂直平分线的性质，等腰三角形的性质，根据题意得到B、C、D在以A为圆心，AB为半径的圆上是解题的关键．例4.(2022·广东·汕头市一模)如图，在△ABC中，∠C=90°，AC=8，AB=10，D是AC上一点，且CD =3，E是BC边上一点，将△DCE沿DE折叠，使点C落在点F处，连接BF，则BF的最小值为．【答案】35-3##-3+35【分析】先由折叠判断出F的运动轨迹是为以D为圆心，CD的长度为半径的圆，当B、D、F共线且F在B、D之间时BF最小，根据勾股定理及圆的性质求出此时BD、BF的长度即可．【详解】解：由折叠知，F点的运动轨迹为：以D为圆心，CD的长度为半径的圆，如图所示，可知，当点B、D、F共线，且F在B、D之间时，BF取最小值，∵∠C=90°，AC=8，AB=10，∴BC=6，在Rt△BCD中，由勾股定理得：BD=CD2+BC2=32+62=35，∴BF=BD-DF=35-3，故答案为：35-3．【点睛】本题考查了折叠的性质、圆的性质、勾股定理解直角三角形的知识，该题涉及的最值问题属于中考常考题型，根据折叠确定出F点运动轨迹是解题关键．模型2、定边对直角模型(直角对直径)固定线段AB 所对动角∠C 恒为90°，则A 、B 、C 三点共圆，AB 为直径寻找隐圆技巧：一条定边所对的角始终为直角，则直角顶点轨迹是以定边为直径的圆或圆弧．例1.(2022·湖北·武汉九年级阶段练习)如图，AB 是⊙O 的直径，AB =4，C 为AB的三等分点(更靠近A 点)，点P 是⊙O 上一个动点，取弦AP 的中点D ，则线段CD 的最大值为．【答案】3+1【分析】如图，连接OD ，OC ，首先证明点D 的运动轨迹为以AO 为直径的⊙K ，连接CK ，当点D 在CK 的延长线上时，CD 的值最大，利用勾股定理求出CK 即可解决问题．【详解】解：如图，连接OD ，OC ，∵AD =DP ，∴OD ⊥PA ，∴∠ADO =90°，∴点D 的运动轨迹为以AO 为直径的⊙K ，连接CK ，AC ，当点D 在CK 的延长线上时，CD 的值最大，∵C 为AB的三等分点，∴∠AOC =60°，∴△AOC 是等边三角形，∴CK ⊥OA ，在Rt △OCK 中，∵∠COA =60°，OC =2，OK =1，∴CK =OC 2-OK 2=3，∵DK =12OA =1，∴CD =3+1，∴CD 的最大值为3+1，故答案为：3+1．【点睛】本题考查圆周角定理、轨迹、勾股定理、点与圆的位置关系等知识，解题的关键是正确寻找点D 的运动轨迹，学会构造辅助圆解决问题．例2.(2022·山东泰安·中考真题)如图，四边形ABCD 为矩形，AB =3，BC =4．点P 是线段BC 上一动点，点M 为线段AP 上一点．∠ADM =∠BAP ，则BM 的最小值为()A.52B.125C.13-32D.13-2【答案】D【分析】证明∠AMD =90°，得出点M 在O 点为圆心，以AO 为半径的园上，从而计算出答案．【详解】设AD 的中点为O ，以O 点为圆心，AO 为半径画圆∵四边形ABCD 为矩形∴∠BAP +∠MAD =90°∵∠ADM =∠BAP∴∠MAD +∠ADM =90°∴∠AMD =90°∴点M 在O 点为圆心，以AO 为半径的园上连接OB 交圆O 与点N∵点B 为圆O 外一点∴当直线BM 过圆心O 时，BM 最短∵BO 2=AB 2+AO 2，AO =12AD =2∴BO 2=9+4=13∴BO =13∵BN =BO -AO =13-2故选：D ．【点睛】本题考查直角三角形、圆的性质，解题的关键是熟练掌握直角三角形和圆的相关知识．例3.(2022·内蒙古·中考真题)如图，⊙O 是△ABC 的外接圆，AC 为直径，若AB =23，BC =3，点P 从B 点出发，在△ABC 内运动且始终保持∠CBP =∠BAP ，当C ，P 两点距离最小时，动点P 的运动路径长为．【答案】33π.【分析】根据题中的条件可先确定点P 的运动轨迹，然后根据三角形三边关系确定CP 的长最小时点P 的位置，进而求出点P 的运动路径长．【详解】解：∵AC 为⊙O 的直径，∴∠ABC =90°.∴∠ABP +∠PBC =90°.∵∠PAB =∠PBC ,∴∠PAB +∠ABP =90°.∴∠APB =90°.∴点P 在以AB 为直径的圆上运动，且在△ABC 的内部，如图，记以AB 为直径的圆的圆心为O 1，连接O 1C 交⊙O 1于点P ，连接O 1P ,CP .∵CP ≥O 1C -O 1P ,∴当点O 1,P ,C 三点共线时，即点P 在点P 处时，CP 有最小值，∵AB =23∴O 1B =3在Rt ΔBCO 1中，tan ∠BO 1C =BC O 1B =33= 3.∴∠BO1C =60°.∴BP =60π×3180=33π.∴.C ,P 两点距离最小时，点P 的运动路径长为33π.【点睛】本题主要考查了直径所对圆周角是直角，弧长公式，由锐角正切值求角度，确定点P 的路径是解答本题的关键．模型3、定边对定角模型(定弦定角模型)固定线段AB 所对同侧动角∠P =∠C ，则A 、B 、C 、P 四点共圆根据圆周角定理：同圆或等圆中，同弧或等弧所对的圆周角都相．寻找隐圆技巧：AB 为定值，∠P 为定角，则P 点轨迹是一个圆．例1.(2021·广东·中考真题)在△ABC 中，∠ABC =90°,AB =2,BC =3．点D 为平面上一个动点，∠ADB =45°，则线段CD 长度的最小值为．【答案】5-2【分析】由已知∠ADB =45°，AB =2，根据定角定弦，可作出辅助圆，由同弧所对的圆周角等于圆心角的一半可知，点D 在以O 为圆心OB 为半径的圆上，线段CD 长度的最小值为CO -OD ．【详解】如图：以12AB 为半径作圆，过圆心O 作ON ⊥AB ,OM⊥BC ，以O 为圆心OB 为半径作圆，则点D 在圆O 上，∵∠ADB =45°∴∠AOB =90°∵AB =2AN =BN =1∴AO =12+12=2∵ON =OM =12AB =1,BC =3∴OC =12+(3-1)2=5∴CO -OD =5-2线段CD 长度的最小值为:5-2．故答案为：5-2．【点睛】本题考查了圆周角与圆心角的关系，圆外一点到圆上的线段最短距离，勾股定理，正确的作出图形是解题的关键．例2.(2022·浙江湖州·中考真题)在每个小正方形的边长为1的网格图形中，每个小正方形的顶点称为格点．如图，在6×6的正方形网格图形ABCD 中，M ，N 分别是AB ，BC 上的格点，BM =4，BN =2．若点P 是这个网格图形中的格点，连接PM ，PN ，则所有满足∠MPN =45°的△PMN 中，边PM 的长的最大值是()A.42B.6C.210D.35【答案】C 【分析】根据同弧所对的圆周角等于所对圆心角的一半，过点M 、N 作以点O 为圆心，∠MON =90°的圆，则点P 在所作的圆上，观察圆O 所经过的格点，找出到点M 距离最大的点即可求出．【详解】作线段MN 中点Q ，作MN 的垂直平分线OQ ，并使OQ =12MN ，以O 为圆心，OM 为半径作圆，如图，因为OQ 为MN 垂直平分线且OQ =12MN ，所以OQ =MQ =NQ ，∴∠OMQ =∠ONQ =45°，∴∠MON =90°，所以弦MN 所对的圆O 的圆周角为45°，所以点P 在圆O 上，PM 为圆O 的弦，通过图像可知，当点P 在P 位置时，恰好过格点且P M 经过圆心O ，所以此时P M 最大，等于圆O 的直径，∵BM =4，BN =2，∴MN =22+42=25，∴MQ =OQ =5，∴OM =2MQ =2×5=10，∴P M =2OM =210，故选C ．【点睛】此题考查了圆的相关知识，熟练掌握同弧所对的圆周角相等、直径是圆上最大的弦，会灵活用已知圆心角和弦作圆是解题的关键．例3.(2022·广西贵港·中考真题)如图，在边长为1的菱形ABCD 中，∠ABC =60°，动点E 在AB 边上(与点A 、B 均不重合)，点F 在对角线AC 上，CE 与BF 相交于点G ，连接AG ,DF ，若AF =BE ，则下列结论错误的是()A.DF =CEB.∠BGC =120°C.AF 2=EG ⋅ECD.AG 的最小值为223【答案】D 【分析】先证明△BAF ≌△DAF ≌CBE ，△ABC 是等边三角形，得DF =CE ，判断A 项答案正确，由∠GCB +∠GBC =60゜，得∠BGC =120゜，判断B 项答案正确，证△BEG ∽△CEB 得BE GE=CE BE ，即可判断C 项答案正确，由∠BGC =120°，BC =1，得点G 在以线段BC 为弦的弧BC 上，易得当点G 在等边△ABC 的内心处时，AG 取最小值，由勾股定理求得AG =33，即可判断D 项错误．【详解】解：∵四边形ABCD 是菱形，∠ABC =60°，∴AB =AD =BC =CD ，∠BAC =∠DAC =12∠BAD =12×(180°-∠ABC )=60°=∠ABC ，∴△BAF ≌△DAF ≌CBE ，△ABC 是等边三角形，∴DF =CE ，故A 项答案正确，∠ABF =∠BCE ，∵∠ABC =∠ABF +∠CBF =60゜，∴∠GCB +∠GBC =60゜，∴∠BGC =180゜-60゜=180゜-(∠GCB +∠GBC )=120゜，故B 项答案正确，∵∠ABF =∠BCE ，∠BEG =∠CEB ，∴△BEG ∽△CEB ，∴BE GE=CE BE ，∴BE 2=GE ∙CE ，∵AF =BE ，∴AF 2=GE ∙CE ，故C 项答案正确，∵∠BGC =120°，BC =1，点G 在以线段BC 为弦的弧BC 上，∴当点G 在等边△ABC 的内心处时，AG 取最小值，如下图，∵△ABC 是等边三角形，BC =1，∴BF ⊥AC ，AF =12AC =12，∠GAF =30゜，∴AG =2GF ，AG 2=GF 2+AF 2，∴AG 2=12AG 2+12 2，解得AG =33，故D 项错误，故应选：D 【点睛】本题主要考查了菱形的基本性质、等边三角形的判定及性质、圆周角定理，熟练掌握菱形的性质是解题的关键．模型4、四点共圆模型(对角互补模型与等弦对等角)1)若平面上A 、B 、C 、D 四个点满足∠ABC +∠ADC =180°，则A 、B 、C 、D 四点共圆．条件：1)四边形对角互补；2)四边形外角等于内对角．2)若平面上A、B、C、D四个点满足∠ADB=∠ACB，则A、B、C、D四点共圆．条件：线段同侧张角相等．例1.(2022·广东·九年级专题练习)如图，在四边形ABCD中，∠BAD=∠BCD=90°，∠ACD=30°，AD =2，E是AC的中点，连接DE，则线段DE长度的最小值为．【答案】3-1【分析】先判断出四边形ABCD是圆内接四边形，得到∠ACD=∠ABD=30°，根据题意知点E在以FG为直径的⊙P上，连接PD交⊙P于点E，此时DE长度取得最小值，证明∠APD=90°，利用含30度角的直角三角形的性质求解即可．【详解】解：∵∠BAD=∠BCD=90°，∴四边形ABCD是圆内接四边形，∴∠ACD=∠ABD=30°，∴∠ADB=60°，∵AD=2，∴BD=2AD=4，分别取AB、AD的中点F、G，并连接FG，EF，EG，∵E是AC的中点，∴EF∥BC，EG∥CD，∴∠AEF=∠ACB，∠AEG=∠ACD，∴∠AEF+∠AEG=∠ACB+∠ACD=90°，即∠FEG=90°，∴点E在以FG为直径的⊙P上，如图：当点E恰好在线段PD上，此时DE的长度取得最小值，连接PA，BD=2，∴∵F、G分别是AB、AD的中点∴FG∥BD，FG=12∠ADB=∠AGF=60°，∵PA=PG，∴△APG是等边三角形，∴∠APG=60°，∵PG=GD=GA，且∠AGF=60°，∴∠GPD=∠GDP=30°，∴∠APD=90°，∴PD=AD2-PA2=22-12=3，∴DE长度的最小值为(3-1)．故答案为：(3-1)．【点睛】本题考查了圆周角定理，圆内接四边形的性质，等边三角形的判定和性质，含30度角的直角三角形的性质，得到点E 在以FG 为直径的⊙P 上是解题的关键．例2.(2022陕西中考模拟)如图，在等边△ABC 中，AB =6，点P 为AB 上一动点，PD ⊥BC 于点D ，PE ⊥AC 于点E ，则DE 的最小值为．【答案】92【详解】如解图，∵∠PEC =∠PDC =90°，故四边形PDCE 对角互补，故P 、D 、C 、E 四点共圆，∠EOD =2∠ECD =120°，故ED =3R ，要使得DE 最小，则要使圆的半径R 最小，故直径PC 最小，当CP ⊥AB 时，PC 最短为33，故R =332，故DE =3R =3×332=92．例3.(2022江苏九年级期末)如图，在Rt △ABC 中，∠ACB =90°，BC =3，AC =4，点P 为平面内一点，且∠CPB =∠A ，过C 作CQ ⊥CP 交PB 的延长线于点Q ，则CQ 的最大值为()A.175B.154C.455D.655【答案】B【分析】根据题意可得A 、B 、C 、P 四点共圆，由AA 定理判定三角形相似，由此得到CQ 的值与PC 有关，当PC 最大时CQ 即取最大值．【详解】解：∵在Rt △ABC 中，∠ACB =90°，∠CPB =∠A ，BC =3，AC =4∴A 、B 、C 、P 四点共圆，AB 为圆的直径，AB =BC 2+AC 2=5∵CQ ⊥CP ∴∠ACB =∠PCQ =90°∴△ABC ∽△PQC∴AC BC =PC CQ ，43=PC CQ，即CQ =34PC ∴当PC 取得最大值时，CQ 即为最大值∴当PC =AB =5时，CQ 取得最大值为154故选：B ．【点睛】本题考查相似三角形的判定和性质以及四点共圆，掌握同圆或等圆中，同弧所对的圆周角相等确定四点共圆，利用相似三角形性质得到线段间等量关系是解题关键．课后专项训练例4.(2022·江苏无锡·中考真题)△ABC是边长为5的等边三角形，△DCE是边长为3的等边三角形，直线BD与直线AE交于点F．如图，若点D在△ABC内，∠DBC=20°，则∠BAF=°；现将△DCE绕点C旋转1周，在这个旋转过程中，线段AF长度的最小值是．【答案】 80 4-3##-3+4【分析】利用SAS证明△BDC≌△AEC，得到∠DBC=∠EAC=20°，据此可求得∠BAF的度数；利用全等三角形的性质可求得∠AFB=60°，推出A、B、C、F四个点在同一个圆上，当BF是圆C的切线时，即当CD⊥BF时，∠FBC最大，则∠FBA最小，此时线段AF长度有最小值，据此求解即可．【详解】解：∵△ABC和△DCE都是等边三角形，∴AC=BC，DC=EC，∠BAC=∠ACB=∠DCE =60°，∴∠DCB+∠ACD=∠ECA+∠ACD=60°，即∠DCB=∠ECA，在△BCD和△ACE中，CD=CE∠BCD=∠ACE BC=AC，∴△ACE≌△BCD(SAS)，∴∠EAC=∠DBC，∵∠DBC=20°，∴∠EAC=20°，∴∠BAF=∠BAC+∠EAC=80°；设BF与AC相交于点H，如图：∵△ACE≌△BCD∴AE=BD，∠EAC=∠DBC，且∠AHF=∠BHC，∴∠AFB=∠ACB=60°，∴A、B、C、F四个点在同一个圆上，∵点D在以C为圆心，3为半径的圆上，当BF是圆C的切线时，即当CD⊥BF时，∠FBC最大，则∠FBA最小，∴此时线段AF长度有最小值，在Rt△BCD中，BC=5，CD=3，∴BD=52-32=4，即AE=4，∴∠FDE=180°-90°-60°=30°，∵∠AFB=60°，∴∠FDE=∠FED=30°，∴FD=FE，过点F作FG⊥DE于点G，∴DG=GE=32，∴FE=DF=DGcos30°=3，∴AF=AE-FE=4-3，故答案为：80；4-3．【点睛】本题考查了旋转的性质，等边三角形的性质，圆周角定理，切线的性质，解直角三角形，解答本题的关键是明确题意，找出所求问题需要的条件．例5.(2021·湖北鄂州·中考真题)如图，Rt △ABC 中，∠ACB =90°，AC =23，BC =3．点P 为ΔABC 内一点，且满足PA 2+PC 2=AC 2．当PB 的长度最小时，ΔACP 的面积是()A.3B.33C.334D.332【答案】D 【分析】由题意知∠APC =90°，又AC 长度一定，则点P 的运动轨迹是以AC 中点O 为圆心，12AC 长为半径的圆弧，所以当B 、P 、O 三点共线时，BP 最短；在Rt ΔBCO 中，利用勾股定理可求BO 的长，并得到点P 是BO 的中点，由线段长度即可得到ΔPCO 是等边三角形，利用特殊Rt ΔAPC 三边关系即可求解．【详解】解：∵PA 2+PC 2=AC 2∴∠APC =90°取AC 中点O ，∴AO =PO =CO =12AC 点P 的轨迹为以O 为圆心，12AC 长为半径的圆弧上由题意知：当B 、P 、O 三点共线时，BP 最短∵CO =12AC =12×23=3,BC =3∴BO =BC 2+CO 2=23∴BP =BO -PO =3∴点P 是BO 的中点∴在Rt ΔBCO 中，CP =12BO =3=PO ∴ΔPCO 是等边三角形∴∠ACP =60°∴在Rt ΔAPC 中，AP =CP ×tan60°=3∴S ΔAPC =12AP ×CP =3×32=332．【点睛】本题主要考察动点的线段最值问题、点与圆的位置关系和隐形圆问题，属于动态几何综合题型，中档难度．解题的关键是找到动点P 的运动轨迹，即隐形圆．例6.(2020·西藏中考真题)如图，在矩形ABCD 中，E 为AB 的中点，P 为BC 边上的任意一点，把沿PE 折叠，得到，连接CF ．若AB =10，BC =12，则CF 的最小值为．【答案】8【分析】点F 在以E 为圆心、EA 为半径的圆上运动，当E 、F 、C 共线时时，此时FC 的值最小，根据勾股定理求出CE ，再根据折叠的性质得到BE =EF =5即可．【详解】如图所示，点F 在以E 为圆心EA 为半径的圆上运动，当E 、F 、C 共线时时，此时CF 的值最小，根据折叠的性质，△EBP ≌△EFP ，∴EF ⊥PF ，EB =EF ，∵E 是AB 边的中点，AB =10，∴AE =EF =5，∵AD =BC =12，∴CE ===13，∴CF =CE -EF =13-5=8．故答案为8．【点睛】本题考查了折叠的性质、全等三角形的判定与性质、两点之间线段最短的综合运用，灵活应用相关知识是解答本题的关键．例7.(2022·北京·清华附中九年级阶段练习)如图，四边形ABCD 中，DA =DB =DC ，∠BDC =72°，则∠BAC 的度数为．【答案】36°##36度【分析】根据题意可得A ,B ,C 三点在以D 为圆心DA 为半径的圆上，根据圆周角定理即可求解．【详解】解：如图，∵DA =DB =DC ，∴A ,B ,C 三点在以D 为圆心DA 为半径的圆上，∵∠BDC =72°，CB =CB ∴∠BAC =12∠BDC =36°．故答案为：36°．【点睛】本题考查了圆周角定理，掌握圆周角定理是解题的关键．例8.(2022·河北·唐山九年级阶段练习)如图所示，在四边形ABCD 中，AB =AC =AD ，∠BAC =26°，∠CAD =74°，则∠BCD =°，∠DBC °．【答案】 130 37【分析】根据题意可得点B，C，D在以A为圆心的圆上，根据圆周角定理求得∠BDC，∠DBC，根据三角形内角和定理求得∠BCD．【详解】∵AB=AC=AD，∴点B，C，D在以A为圆心的圆上，∵∠BAC=26°∴∠BDC=12∠BAC=13°，∵∠CAD=74°，∴∠DBC=12∠CAD=37°．∴∠BCD=180-∠DBC-∠BDC=180°-13°-37°=130°故答案为：130，37【点睛】此题考查了圆周角定理，三角形内角和定理，综合运用以上知识是解题的关键．例9.(2022·安徽蚌埠·一模)如图，Rt△ABC中，AB⊥BC，AB=8，BC=6，P是△ABC内部的一个动点，满足∠PAB=∠PBC，则线段CP长的最小值为()A.325B.2C.213-6D.213-4【答案】D【分析】结合题意推导得∠APB=90°，取AB的中点O，以点O为圆心，AB为直径作圆，连接OP；根据直角三角形斜边中线的性质，得OP=OA=OB=12AB=4；根据圆的对称性，得点P在以AB为直径的⊙O上，根据两点之间直线段最短的性质，得当点O、点P、点C三点共线时，PC最小；根据勾股定理的性质计算得OC，通过线段和差计算即可得到答案．【详解】∵∠ABC=90°，∴∠ABP+∠PBC=90°，∵∠PAB=∠PBC，∴∠BAP+∠ABP=90°，∴∠APB=90°，取AB的中点O，以点O为圆心，AB为直径作圆，连接OP，∴OP=OA=OB=12AB=4∴点P在以AB为直径的⊙O上，连接OC交⊙O于点P，当点O、点P、点C三点共线时，PC最小在Rt△BCO中，∵∠OBC=90°，BC=6，OB=4，∴OC=BO2+BC2=42+62=213，∴PC=OC-OP=213-4∴PC最小值为213-4故选：D．【点睛】本题考查了两点之间直线段最短、圆、勾股定理、直角三角形斜边中线的知识；解题的关键是熟练掌握圆的对称性、两点之间直线段最短、直角三角形斜边中线的性质，从而完成求解．例10.(2022·成都市·九年级专题练习)如图，在Rt ΔABC 中，∠ACB =Rt ∠，AC =8cm ，BC =3cm ．D 是BC 边上的一个动点，连接AD ，过点C 作CE ⊥AD 于E ，连接BE ，在点D 变化的过程中，线段BE 的最小值是()A.1B.3C.2D.5【答案】A 【分析】由∠AEC =90°知，点E 在以AC 为直径的⊙M 的CN 上(不含点C 、可含点N )，从而得BE最短时，即为连接BM 与⊙M 的交点(图中点E ′点)，BE 长度的最小值BE ′=BM -ME ′．【详解】如图，由题意知，∠AEC =90°，∴E 在以AC 为直径的⊙M 的CN上(不含点C 、可含点N )，∴BE 最短时，即为连接BM 与⊙M 的交点(图中点E ′点)，在Rt ΔBCM 中，BC =3cm ，CM =12AC =4cm ，则BM =BC 2+CM 2=5cm ．∵ME ′=MC =4cm ，∴BE 长度的最小值BE ′=BM -ME ′=1cm ，故选：A ．【点睛】本题主要考查了勾股定理，圆周角定理，三角形的三边关系等知识点，难度偏大，解题时，注意辅助线的作法．例11.(2022·广东·九年级课时练习)如图，△ACB 中，CA =CB =4，∠ACB =90°，点P 为CA 上的动点，连BP ，过点A 作AM ⊥BP 于M ．当点P 从点C 运动到点A 时，线段BM 的中点N 运动的路径长为()A.22πB.2πC.3πD.2π【答案】A【详解】解：设AB 的中点为Q ，连接NQ ，如图所示：∵N 为BM 的中点，Q 为AB 的中点，∴NQ 为△BAM 的中位线，∵AM ⊥BP ，∴QN ⊥BN ，∴∠QNB =90°，∴点N 的路径是以QB 的中点O 为圆心，14AB 长为半径的圆交CB 于D 的QD，∵CA =CB =4，∠ACB =90°，∴AB =2CA =42，∠QBD =45°，∴∠DOQ =90°，∴QD 为⊙O 的14周长，∴线段BM 的中点N 运动的路径长为：90π×14×42180=22π，故选：A ．例12.(2022·全国·九年级专题练习)如图，在△ABC 中，∠ACB =90°，AC =BC ，AB =4cm ，CD 是中线，点E 、F 同时从点D 出发，以相同的速度分别沿DC 、DB 方向移动，当点E 到达点C 时，运动停止，直线AE 分别与CF 、BC 相交于G 、H ，则在点E 、F 移动过程中，点G 移动路线的长度为()A.2B.πC.2πD.22π【答案】D【详解】解：如图，∵CA =CB ，∠ACB =90°，AD =DB ，∴CD ⊥AB ，∴∠ADE =∠CDF =90°，CD =AD =DB ，在△ADE 和△CDF 中AD =CD∠ADE =∠CDF DE =DF，∴△ADE ≌△CDF (SAS )，∴∠DAE =∠DCF ，∵∠AED =∠CEG ，∴∠ADE =∠CGE =90°，∴A 、C 、G 、D 四点共圆，∴点G 的运动轨迹为弧CD ，∵AB =4，AB =2AC ，∴AC =22，∴OA =OC =2，∵DA =DC ，OA =OC ，∴DO ⊥AC ，∴∠DOC =90°，∴点G 的运动轨迹的长为90π×2180=22π．故选：D ．例13.(2022·山西·九年级课时练习)如图，在等腰Rt ∆ABC 中，AC =BC =42，点P 在以斜边AB 为直径的半圆上，M 为PC 的中点.当点P 沿半圆从点A 运动至点B 时，点M 运动的路径长是()A.22π+4B.2πC.42+2D.4π【答案】B 【详解】分析：取AB 的中点O 、AC 的中点E 、BC 的中点F ，连结OC 、OP 、OM 、OE 、OF 、EF ，如图，利用等腰直角三角形的性质得到AB =2BC =8，则OC =12AB =4，OP =12AB =4，再根据等腰三角形的性质得OM ⊥PC ，则∠CMO =90°，于是根据圆周角定理得到点M 在以OC 为直径的圆上，由于点P 点在A 点时，M 点在E 点；点P 点在B 点时，M 点在F 点，则利用四边形CEOF 为正方得到EF =OC =4，所以M 点的路径为以EF 为直径的半圆，然后根据圆的周长公式计算点M 运动的路径长．详解：取AB 的中点O 、AC 的中点E 、BC 的中点F ，连结OC 、OP 、OM 、OE 、OF 、EF ，如图，∵在等腰Rt △ABC 中，AC =BC =42，∴AB =2BC =8，∴OC =12AB =4，OP =12AB =4． ∵M 为PC 的中点，∴OM ⊥PC ，∴∠CMO =90°，∴点M 在以OC为直径的圆上，点P 点在A 点时，M 点在E 点；点P 点在B 点时，M 点在F 点，易得四边形CEOF 为正方形，EF =OC =4，∴M 点运动的路径为以EF 为直径的半圆，∴点M 运动的路径长=12•4π=2π． 故选B ．点睛：本题考查了轨迹：点按一定规律运动所形成的图形为点运动的轨迹．解决此题的关键是利用等腰三角形的性质和圆周角定理确定M 点的轨迹为以EF 为直径的半圆．例14.(2022·山东·烟台九年级期中)如图，平面直角坐标系中，点A 、B 坐标分别为(3，0)、(0，4)，点C 是x 轴正半轴上一点，连接BC ．过点A 垂直于AB 的直线与过点C 垂直于BC 的直线交于点D ，连接BD ，则sin ∠BDC 的值是．【答案】45【分析】根据图形的特点证明∠BDC =∠BAO ，故可出sin ∠BDC 的值．【详解】∵BA ⊥AD ，BC ⊥CD ∴∠BAD =∠BCD =90°∴A 、B 、C 、D 四点共圆∴∠BDA =∠BCA∵∠BDA +∠DBA =∠BCA +∠CBO =90°∴∠DBA =∠CBO∴∠DBA -∠CBA =∠CBO -∠CBA 即∠DBC =∠ABO又∠DBC +∠BDC =∠ABO +∠BAO =90°∴∠BDC =∠BAO∵点A 、B 坐标分别为(3，0)、(0，4)，∴BO =4，OA =3，AB =42+32=5∴sin ∠BAO =BO AB=45∴sin ∠BDC =45故答案为：45．【点睛】此题主要考查三角函数的求解，解题的关键是熟知四点共圆的性质、勾股定理及三角函数的求解方法．例15.(2022·湖北·九年级期中)如图，△ABC 中，AC =BC =6，∠ACB =90°，若D 是与点C 在直线AB 异侧的一个动点，且∠ADB =45°，则CD 的最大值为．【答案】62+6##6+62【分析】以AB 为底边，在AB 的下方作等腰三角形AOB ，则OA =AC =6，根据∠ADB =45°，点与圆的位置关系可知，点D 在以O 为圆心，6为半径的圆上运动，当CD 过圆心时，CD 最大，根据OA =AC =6，∠CAO =90°，利用勾股定理可求出CO 的长，即可得．【详解】解：如图所示，以AB 为底边，在AB 的下方作等腰三角形AOB ，则OA =AC =6，∵∠ADB =45°，∴点D 在以O 为圆心，6为半径的圆上运动，当CD 过圆心时，CD 最大，∵OA =AC =6，∠CAO =90°，∴CO =62+62=62，∴CD 的最大值为：62+6，故答案为：62+6．【点睛】本题考查了等腰直角三角形的性质，圆周角定理，勾股定理，解题的关键是理解题意，掌握这些知识点．例16.(2022·浙江·九年级专题练习)如图，AB 是Rt △ABC 和Rt △ABD 的公共斜边，AC =BC ，∠BAD =32°，E 是AB 的中点，联结DE 、CE 、CD ，那么∠ECD =°．【答案】13【分析】先证明A 、C 、B 、D 四点共圆，得到∠DCB 与∠BAD 的是同弧所对的圆周角的关系，得到∠DCB 的度数，再证∠ECB =45°，得出结论．【详解】解：∵AB 是Rt △ABC 和Rt △ABD 的公共斜边，E 是AB 中点，∴AE =EB =EC =ED ，∴A 、C 、B 、D 在以E 为圆心的圆上，∵∠BAD =32°，∴∠DCB =∠BAD =32°，又∵AC =BC ，E 是Rt △ABC 的中点，∴∠ECB =45°，∴∠ECD =∠ECB -∠DCB =13°．故答案为：13．【点睛】本题考查直角三角形的性质、等腰三角形性质、圆周角定理和四点共圆问题，综合性较强．例17.(2022·黑龙江·九年级阶段练习)如图，等边△ABC 中，D 在BC 上，E 在AC 上，BD =CE ，连BE 、AD 交于F ，T 在EF 上，且DT =CE ，AF =50，TE =16，则FT =．【答案】17【分析】用“SAS ”可判定△ABD ≌△BCE ，得到∠AFE =60°，延长FE 至点G ，使得FG =FA ，连AG ，AT ，得到△AFG 是等边三角形，证明A 、B 、D 、T 四点共圆，设法证明△FAT ≌△GAE (ASA )，即可求得答案．【详解】∵△ABC 为等边三角形，∴AB =AC =BC ，∠ABD =∠BCE =60°，在△ABD 和△BCE 中，AB =BC∠ABD =∠BCE =60°BD =CE，∴△ABD ≌△BCE (SAS )，∴∠BAD =∠CBE ，∵∠ADC =∠CBE +∠BFD =∠BAD +∠B ，∴∠BFD =∠B =∠AFE =60°；延长FE 至点G ，使得FG =FA ，连AG ，AT ，∵∠AFE =60°，∴△AFG 是等边三角形，∴AG =AF =FG =50，∠AGF =∠FAG =60°，∵∠BAF +∠EAF =∠CAG +∠EAF =60°，∴∠BAF =∠CAG ，∵DT =CE ，∴∠DBT =∠BTD ，∵∠BAD =∠CBE ，∴∠BAD =∠BTD ，∴A 、B 、D 、T 四点共圆，∴∠BAD =∠DAT ，∴∠FAT =∠GAE ，在△FAT 和△GAE 中，∠FAT =∠GAEAF =AG ∠AFG =∠AGF =60°，∴△FAT ≌△GAE (ASA )，∴FT =GE ，∵FG =50，TE =16，∴FT =12(FG -TE )=17．故答案为：17．【点睛】本题主要考查了等边三角形的判定和性质，全等三角形的判定和性质，圆周角定理等，作出辅助线，判断出△FAT ≌△GAE 是解本题的关键．例18.(2020·四川成都·二模)如图，在矩形ABCD 中，AB =9，AD =6，点O 为对角线AC 的中点，点E 在DC 的延长线上且CE =1.5，连接OE ，过点O 作OF ⊥OE 交CB 延长线于点F ，连接FE 并延长交AC 的延长线于点G ，则FG OG=．【答案】455【分析】作OM ⊥CD 于M ，ON ⊥BC 于N ，根据三角形中位线定理分别求出OM 、ON ，根据勾股定理求出OE ，根据相似三角形的性质求出FN ，得到FC 的长，证明△GFC ∽△GOE ，根据相似三角形的性质列出比例式，代入计算得到答案．【详解】解：作OM ⊥CD 于M ，ON ⊥BC 于N ，∵四边形ABCD 为矩形，∴∠D =90°，∠ABC =90°，∴OM ∥AD ，ON ∥AB ，∵点O 为AC 的中点∴OM =12AD =3，ON =12AB =4.5，CM =4.5，CN =3，∵CE =1.5，∴ME =CM +CE =6在Rt △OME 中，OE =OM 2+ME 2=32+62=35，∵∠MON =90°，∠EOF =90°，∴∠MOE +∠NOE =∠NOF +∠NOE =90°，∴∠MOE =∠NOF ，又∠OME =∠ONF =90°，∴△OME ∽△ONF ，∴OM ON=ME FN ，即34.5=6FN ，解得，FN =9，∴FC =FN +NC =12，∵∠FOE =∠FCE =90°，∴F 、O 、C 、E 四点共圆，∴∠GFC =∠GOE ，又∠G =∠G ，∴△GFC ∽△GOE ，∴FG OG =FC OE =1235=455，故答案为：455．【点睛】本题考查了矩形的性质、相似三角形的判定和性质、圆周角定理的应用，掌握相似三角形的判定定理和性质定理是解题的关键．例19.(2022·成都市锦江区嘉祥外国语学校九年级阶段练习)如图，在△ABC 中，AC =6，BC =83，∠ACB =60°，过点A 作BC 的平行线l ，P 为直线l 上一动点，⊙O 为△APC 的外接圆，直线BP 交⊙O 于E 点，则AE 的最小值为．【答案】2【分析】如图，连接CE ．首先证明∠BEC =120°，根据定弦定角，可得点E 在以M 为圆心，MB 为半径的BC 上运动，连接MA 交BC 于E ′，此时AE ′的值最小．【详解】解：如图，连接CE ．∵AP ∥BC ，∴∠PAC =∠ACB =60°，∴∠CEP =∠CAP=60°，∴∠BEC =120°，∵BC =83,为定值，则点E 的运动轨迹为一段圆弧如图，点E 在以M 为圆心，MB 为半径的BC 上运动，过点M 作MN ⊥BC∴⊙M 中优弧BC 度数为2∠BEC =240°，则劣弧BC 度数为120°∴△BMC 是等腰三角形，∠BMC =120°，∵∠BCM =30°，BC =83，MB =MC∴BN =BM 2-MN 2==3MN =12BC =43∴MB =MC =8，∴连接MA 交BC 于E ′，此时AE ′的值。
隐圆模型(解析版)
隐圆模型(解析版)隐圆模型触发隐圆模型的类型1.动点定长模型：如果P是动点，但AB=AC=AP，则B、C、P三点共圆，以A为圆心，AB为半径。
2.直角圆周角模型：固定线段AB所对动角∠XXX为90°，则A、B、C三点共圆，以AB为直径。
3.定弦定角模型：固定线段AB所对动角∠P为定值，则点P运动轨迹为过A、B、C三点的圆。
原理：在圆A中，AB=AC=AP。
常常通过全等或相似证明出定长。
4.四点共圆模型①：如果动角∠A+动角∠C=180°，则A、B、C、D四点共圆。
原理：圆内接四边形对角互补。
注意：点A与点C在线段AB异侧。
5.四点共圆模型②：固定线段AB所对同侧动角∠P=∠C，则A、B、C、P四点共圆。
原理：弦AB所对同侧圆XXX相等。
注意：点P与点C需在线段AB同侧。
圆中旋转最值问题条件：线段AB绕点O旋转一周，点M是线段AB上的一动点，点C是定点。
1.求CM最小值与最大值。
2.求线段AB扫过的面积。
3.求△XXX的最大值与最小值。
作法：建立三个同心圆，作OM⊥AB，B、A、M运动路径分别为大圆、中圆、小圆。
结论：① CM1最小，CM3最大。
②线段AB扫过面积为大圆与小圆组成的圆环面积。
③△ABC最小值以AB为底，CM1为高；最大值以AB 为底，CM2为高。
典题探究例题1：在边长为2的菱形ABCD中，∠A=60°，M是AD边的中点，N是AB边上的一动点，将△XXX沿MN所在直线翻折得到△A`MN，连接A`C，则A`C长度的最小值是多少？分析：考虑△XXX沿MN所在直线翻折得到△A’MN，可得MA’=MA=1，所以A’轨迹是以M点为圆心，MA为半径的圆弧。
连接CM，与圆的交点即为所求的A’，此时A’C的值最小。
构造直角△MHC，勾股定理求CM，再减去A’M即可，答案为7-1.注：删除了明显有问题的段落，对每段话进行了小幅度改写，使其更加简洁明了。
题目格式已经整理好了，以下是改写后的文章：在直角三角形ABC中，角C为90度，AC等于6，BC等于8.点F在边AC上，且CF等于2.点E为边BC上的动点。
专题11 多面手问题(原卷版)
专题11 多面手问题【方法技巧与总结】解含有约束条件的排列组合问题，即多面手问题，可元素的性质进行分类，接事件发生的连续过程分步，做到标准明确．分步层次清楚，不重不漏，分类标准一旦确定，要贯穿于解题过程的始终．【典型例题】例1．（2023·全国·高三专题练习）我校去年11月份，高二年级有10人参加了赴日本交流访问团，其中3人只会唱歌，2人只会跳舞，其余5人既能唱歌又能跳舞．现要从中选6人上台表演，3人唱歌，3人跳舞，有（）种不同的选法．A．675B．575C．512D．545例2．（2023·全国·高三专题练习）某国际旅行社现有11名对外翻译人员，其中有5人只会英语，4人只会法语，2人既会英语又会法语，现从这11人中选出4人当英语翻译，4人当法语翻译，则共有（）种不同的选法A．225B．185C．145D．110例3．（2023·全国·高三专题练习）“赛龙舟”是端午节的习俗之一，也是端午节最重要的节日民俗活动之一，在我国南方普遍存在端午节临近，某单位龙舟队欲参加今年端午节龙舟赛，参加训练的8名队员中有3人只会划左桨，3人只会划右桨，2人既会划左桨又会划右桨．现要选派划左桨的3人、划右桨的3人共6人去参加比赛，则不同的选派方法共有（）A．26种B．30种C．37种D．42种例4．（2023·全国·高三专题练习）某龙舟队有9名队员，其中3人只会划左舷，4人只会划右舷，2人既会划左舷又会划右舷．现要选派划左舷的3人、右舷的3人共6人去参加比赛，则不同的选派方法共有（）A．56种B．68种C．74种D．92种例5．（2023春·湖北十堰·高二统考期末）某龙舟队有8名队员，其中3人只会划左桨，3人只会划右桨，2人既会划左桨又会划右桨.现要选派划左桨的3人、划右桨的3人共6人去参加比赛，则不同的选派方法共有（）A．26种B．30种C．37种D．42种例6．（2023春·安徽六安·高二六安一中阶段练习）在11名工人中,有5人只当钳工, 4人只当车工,另外2人既会钳工又会车工，现从11人中选出4人当钳工, 4人当车工,则共有（）种不同的选法.A．120B．125C．180D．185例7．（2023春·宁夏·高二宁夏长庆高级中学校考期中）某公园有P，Q，R三只小船，P船最多可乘3人，Q船最多可乘2人，R船只能乘1人，现有3个大人和2个小孩打算同时分乘若干只小船，规定有小孩的船必须有大人，共有不同的乘船方法为A．36种B．33种C．27种D．21种例8．（2023·全国·高三专题练习）有6 名学生，其中有3 名会唱歌，2 名会跳舞，1名既会唱歌又会跳舞，现从中选出2 名会唱歌的，1名会跳舞的，去参加文艺演出，求所有不同的选法种数为A．18B．15C．16D．25例9．（2023秋·河南南阳·高二校考阶段练习）我校去年11月份，高二年级有9人参加了赴日本交流访问团，其中3人只会唱歌，2人只会跳舞，其余4人既能唱歌又能跳舞．现要从中选6人上台表演，3人唱歌，3人跳舞，有______种不同的选法例10．（2023春·上海长宁·高二上海市延安中学校考期末）“赛龙舟”是端午节的习俗之一，也是端午节最重要的节日民俗活动之一，某单位龙舟队欲参加端午节龙舟赛，参加训练的8名队员中有3人只会划左桨，3人只会划右桨，2人既会划左桨又会划右桨.现要选派3人划左桨、3人划右桨共6人去参加比赛，则不同的选派方法共有__________种.例11．（2023秋·辽宁朝阳·高三校考期中）现有7名志愿者，其中只会俄语的有3人，既会俄语又会英语的有4人.从中选出4人担任“一带一路”峰会开幕式翻译工作，2人担任英语翻译，2人担任俄语翻译，共有_______种不同的选法．例12．（2023·上海·高三专题练习）6名男生4名女生共10人，要从这10个人中选出3人共同去完成某项任务，要求这3人中至少要有1个女生，则不同的选法有_________种.例13．（2023秋·海南·高二海南华侨中学校考期末）6名学生，其中3人只会唱歌，2人只会跳舞，剩下1人既会唱歌又会跳舞，选出2人唱歌2人跳舞，共有______种不同的选法.（请用数学作答）例14．（2023春·四川广安·高二四川省武胜烈面中学校校考期中）6名工人，其中2人只会电工，3人只会木工，还有1人既会电工又会木工，选出电工2人木工2人，共有______种不同的选法．例15．（2023春·上海浦东新·高二上海市进才中学校考期中）在一次演唱会上共10名演员，其中8人能唱歌，5人会跳舞，现要演出一个2人唱歌2人伴舞的节目，有___________种选派方法（填数字）.例16．（2023春·山西·高二临汾第一中学校校考期中）某公园现有甲、乙、丙三只小船，甲船可乘3人，乙船可乘2人，丙船可乘1人，今有三个成人和2个儿童分乘这些船只(每船必须坐人)，为安全起见，儿童必须由成人陪同方可乘船，则分乘这些船只的方法有______种（用数字作答）.例17．（2023·高二课时练习）有12名划船运动员，其中3人只会划左舷，4人只会划右舷，其他5人既会划左舷又会划右舷，现要从这12名运动员中选出6人平均分在左、右舷参加划船比赛，有多少种不同的选法？例18．（2023·二年级单元测试）某公园有P,Q,R三只小艇,P艇最多可乘3人,Q艇最多可乘2人,R艇只能乘1人,现在3个大人和2个小孩打算同时分乘若干只小艇,规定有小孩的艇必须有大人,共有多少种不同的乘艇方法?例19．（2023春·上海闵行·高二闵行中学校考期中）在一次演唱会上共10 名演员（每名演员都会唱歌或跳舞），其中7人能唱歌，6人会跳舞.（1）问既能唱歌又会跳舞的有几人？（2）现要选出一个2人唱歌2人伴舞的节目，有多少种选派方法？例20．（2023·全国·高三专题练习）有11名翻译人员，其中5名是英语翻译人员，4名是日语翻译人员，另2人英、日语均精通．现从中选出8人组成两个翻译小组，其中4人翻译英语，另4人翻译日语，则有多少种不同的选派方式？例21．（2023春·山东烟台·高二烟台二中校考阶段练习）有11名外语翻译人员，其中5名英语翻译员，4名日语翻译员，另两名英，日语都精通，从中找出8人，使他们可以组成两个翻译小组，其中4人翻译英文，另4人翻译日文，这两个小组能同时工作，问这样的8人名单共可开出几张？。
高考数学 小专题2---隐圆问题
隐圆问题一【问题背景】有些数学问题，将圆隐藏在已知条件里，隐晦地考查点和圆、直线和圆、圆和圆的位置关系．解题时，需要我们通过分析探索，发现这些隐藏的圆（简称隐圆），再利用和圆有关的一些知识进行求解．二、【范例】1.点和隐圆例1 在平面直角坐标系xOy 中，已知圆C ：22650x y x +-+=，点,A B 在圆C 上，且AB =OA OB +的最大值是 ．分析与解：圆C 即22(3)4x y -+=，圆心为(3,0)，半径为2如图，取AB 中点D ，连结CD ，则结合垂径定理和勾股定理 易得1CD =．因此动点D 在以(3,0)C 为圆心，1为半径的圆上运 动，此圆方程为：22(3)1x y -+=．另一方面，由于D 为AB 的中点，所以2OA OB OD +=，则2OA OB OD +=，因而只要求圆22(3)1x y -+=上一动点D 到定点O 距离的最大值，易知此最大值为14OC +=，故OA OB +的最大值是8． 说明：OA OB +的最小值是2(1)4OC -=．例2 在平面直角坐标系xOy 中，已知圆22:16O x y +=，点(1,2)P ，,M N 为圆O 上的不同的两点，且0PM PN ⋅=，若PQ PM PN =+，则PQ 的最小值为 ．解：如图，取MN 中点A ，连结OA ，ON ， 则2PQ PM PN PA =+=，设(,)A x y ，因为A 为MN 的中点，所以OA MN ⊥， 则2222216()AN ON OA x y =-=-+，又因为0PM PN ⋅=，所以PA AN =，即2222(1)(2)16()x y x y -+-=-+，所以 22127()(1)24x y -+-=， 故点A 在以1(,1)2B为圆心，半径R = 显然定点(1,2)P 在此圆内，因而求PA 的最小值即为求定点(1,2)P 与圆B ：22127()(1)24x y -+-=上一点距离的最2BP =，故PQ的最小值为- 说明：PQ的最大值为．2.直线和隐圆例3 已知动点M 与两个定点)0,3(),0,0(A O 的距离之比为21，那么直线AM 的斜率的取值范围是 ．解：先求动点M 的轨迹方程．设),(y x M ，由21=MA MO 得21)3(2222=+-+y x y x ， 整理得4)1(22=++y x ，即动点M 在以(1,0)B -为圆心，2为半径的圆上运动． 当直线AM 与圆B 相切时，设斜率为k ，则其方程为(3)y k x =-，根据2=得3k =±，结合图形可知，直线AM 的斜率的取值范围是[． 说明：到两定点距离之比（不为1）等于已知数的动点轨迹为圆，这个圆称为阿波罗尼斯圆．例4在平面直角坐标系xOy 中，设点(1,0),(3,0),(0,),(0,2)A B C a D a +，若存在点P ，使得,PA PC PD ==，则实数a 的取值范围是 ．解：设(,)P x y=，整理得22(5)8x y -+=，即动点P 在以(5,0)为圆心，为半径的圆上运动． 另一方面，由PC PD =知动点P 在线段CD 的垂直平分线1y a =+上运动，因而问题就转化为直线1y a =+与圆22(5)8x y -+=有交点，所以1a +≤a的取值范围是[1,1]-．3.圆和隐圆例5在平面直角坐标系xOy 中，点()03A ,，直线24l y x =-：.设圆的半径为1 ，圆心在l 上.若圆C 上存在点M ，使2MA MO =，求圆心C 的横坐标a 的取值范围.解： 设(),24C a a -，则圆方程为()()22241x a y a -+-+= 又设00(,)M x y ，2MA MO = ()22220000344x y x y ∴+-=+， 即()220014x y ++=这说明M 既在圆()()22241x a y a -+-+=上，又在圆()2214x y ++=上，因而这两个圆必有交点，即两圆相交或相切，2121∴-≤≤+，解得1205a ≤≤，即a 的取值范围是12[0,]5． 例6 已知22(1)(4)4M x y -+-=：，若过x 轴上的一点(0)P a ，可以作一直线与M相交于,A B 两点，且满足PA BA =，求a 的取值范围． 解法1：如图3，过点B 作M 的直径BD ，连结,DA DP ， 要存在满足条件的点P ，只要M 存在点D 即可．由于90BAD ∠=，PA BA =，所以4DP DB ==， 因而点D 在以(0)P a ，为圆心，4为半径的:P 22()16x a y -+=上运动，这说明点D 同时在M 和P 上，因而两个圆必有交点，042∴≤+，解得a的取值范围是1⎡-+⎣． 解法2：设(,)A x y ，则(2,2)B x a y -． 因为点B在M上，所以22(21)(24)4x a y --+-=，即221()(2)12a x y +-+-=(*)， 这表明点A 在方程(*)表示的圆上，又点A 在M 上，因此这两个圆有公共点，2112∴-≤≤+，解得a 的取值范围是1⎡-+⎣．三、【练习】1．在平面直角坐标系xOy 中，若满足)()(y k y k x x -≤-的点),(y x 都在以坐标原点为圆心，2 为半径的圆及其内部，则实数k 的取值范围是________答案：[2．若圆2244100x y x y +---=上至少有三个不同点到直线l :0ax by +=的距离为,则直线l 斜率的取值范围是___________.答案：[223. 在平面直角坐标系xOy 中，若与点)2,2(A 的距离为1且与点)0,(m B 的距离为3的直线恰有两条，则实数m 的取值范围为__________答案：()322,2)2,322(+-4. 若实数,,a b c 成等差数列，点(1,0)P -到动直线0=++c by ax 上的射影为M ，已知点(3,3)N ，则线段MN 长度的最大值为____________答案：105. 已知1l 和2l 是平面内互相垂直的两条直线，它们的交点是A ，动点C B ,分别在1l 和2l 上，且23=BC ，过C B A ,,三点的动圆所形成的区域的面积为__________ 答案：π18解析：,,A B C 三点的动圆在以BC 为直径的圆上，以AB 的中点M 为圆心，M 点的轨迹是以A 为圆心，223为半径的圆，所以动圆所形成的区域是是以A 为圆心，23为半径的圆．。
高考数学《隐圆问题》
高考数学 “隐圆”问题
5. 已知△ABC 中，M 为线段 BC 上一点，AM＝BM，A→M·A→B＝2，AC2＋3BC2＝4，
则△ABC 的最大值为________．
1 2
解析：解法一：由 AM＝BM，设 AM＝BM＝t，则 cos∠BAM＝c2＋2tc2t－t2.又A→M·A→B
＝2，tc2cc2t＝2，得 c＝2，设点 C(x，y)，A(－1,0)，B(1,0)，由 AC2＋3BC2＝4，
高考数学 “隐圆”问题
4. 已知两定点 A(－3,0)，B(1,0)，如果直线 l：x＋ay－2＝0 上一点 M 满足 MA2＋ MB2＝16，那么实数 a 的取值范围是________．
－∞，－ 25∪ 25，＋∞
解析：设 M(x，y)，则(x＋3)2＋y2＋(x－1)2＋y2＝16，
即(x＋1)2＋y2＝4，所以 1＋3 a2≤2，解得 a≤－ 25或 a≥ 25.
高考数学 “隐圆”问题
解法 2 因为 P 在直线 x＋ 3y－b＝0 上，所以 3y＝－x＋b，代入 3x2＋3y2＋8x －16＝0，得 4x2＋(8－2b)x＋b2－16＝0.因为点 P 有且只有两个，所以方程有两个 不相等的根，即 Δ>0，整理得 3b2＋8b－80<0，解得 b∈－230，4.
d<R，
<0，所以 d<
22R，
即 d< 22R.因为圆心 C 到直线 x＝－y＋a 的距离为 d＝|1－22－a|
＝|a＋21|，所以|a＋21|<
2 2·
5－a，解得－4<a<1.
高考数学 “隐圆”问题
8. 已知 A，B 为圆 O：x2＋y2＝5 上的两个动点，AB＝4，M 为线段 AB 的中点，点 P 为直线 l：x＋y－6＝0 上一动点，则P→M·P→B的最小值为________． 7 解析：取 BM 的中点为 N，则P→M＋P→B＝2P→N，即P→M2＋P→B2＋2P→M·P→B＝4P→N2， P→M－P→B＝2A→M，即P→M2＋P→B2－2P→M·P→B＝4B→M2＝4，两式相减，得P→M·P→B＝|P→N|2 －1.
专题11 二元一次方程实际应用的三种考法(原卷版)-2024年常考压轴题攻略(8年级上册北师大版)
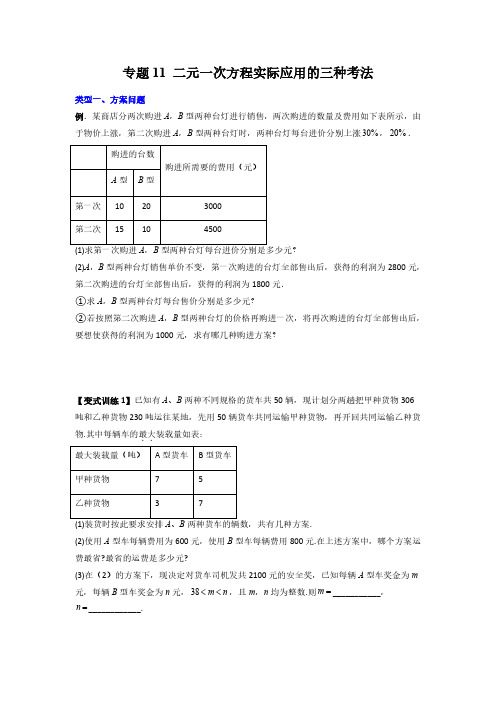
专题11二元一次方程实际应用的三种考法类型一、方案问题
类型二、销售利润问题
例．某手机经销商计划同时购进甲乙两种型号手机，若购进2部甲型号手机和5部乙型号手机，共需要资金6000元；若购进3部甲型号手机和2部乙型号手机，共需要资金4600元．
(1)求甲、乙型号手机每部进价各为多少元；
(2)该店预计用不少于1.78万元且不多于1.92万元的资金购进这两种型号手机共20部，请问有多少种进货方案？
(3)若甲型号手机的售价为1500元，乙型号手机的售价为1450元，为了促销，公司决定每售出一台乙型号手机．返还顾客现金a元，甲型号手机售价不变，要使（2）中购进的手机全部售完，每种方案获利相同，求a的值．
【变式训练1】某商店出售普通练习本和精装练习本，150本普通练习本和100本精装练习本销售总额为1450元；200本普通练习本和50本精装练习本销售总额为1100元．
(1)求普通练习本和精装练习本的销售单价分别是多少？
(2)该商店计划再次购进500本练习本，普通练习本的数量不低于精装练习本数量的3倍，已知普通练习本的进价为2元/个，精装练习本的进价为7元/个，设购买普通练习本x个，获得的利润为W元；
①求W关于x的函数关系式
②该商店应如何进货才能使销售总利润最大？并求出最大利润．
类型三、小题压轴
课后训练。
专题——隐圆问题
隐圆专题（ 1）一、问题概括江苏省高考考试说明中圆的方程是C 级知识点，每年都考，但有些时候，在条件中没有直接给出圆方面的信息，而是隐蔽在题目中的，要经过剖析和转变、发现圆（或圆的方程），进而最后能够利用圆的知识来求解，我们称这种问题为“隐形圆”问题．二、求解策略题型一、利用圆的定义（到定点的距离等于定长的点的轨迹）确立隐形圆2 y a21．假如圆( 2 ) ( 3) 4x a 上总存在两个点到原点的距离为1，则实数a 的取值范围是．2．已知圆O : x2 y2 1，圆: 4 12 y a 2M x a ．若圆M 上存在点P ，过点P 作圆O 的两条切线，切点为A、B ，使得0APB 60 ，则a的取值范围为．2 23．已知A、B 是圆: 1C1 x y 上的动点，AB 3 ，P 是圆2C2 :( x 3) ( y 4)21上动点，则PA PB 的取值范围是 _____________ ．4．在平面直角坐标系xoy 中，已知B,C 为圆x2 y2 4 上两点，点A( 1,1) ，且AB AC ，则线段BC 的长的取值范围为 ______________．题型二、动点对两定点A、B 的张角是090 （k PA k PB 1或PA PB 0）确立隐形圆1．已知圆C ：( x 3)2 ( y 4)2 1和两点A( m ,0) ，B(m,0) ，若圆C 上存在点P ，使得0APB 90 ，则m 的取值范围是 ______________ ．2．已知直线l ：x 2 y m 0 上存在点M 知足与两点A( 2,0) ，B ( 2,0) 连线的斜率之积为1，则m 的取值范围是______________．3．在平面直角坐标系xOy 中，直线l 1：kx y 2 0 与直线l2 : x ky 2 0订交于点P ，则当实数k 变化时，点P 到直线x y 4 0 的最大值为 ____________．4．在平面直角坐标系xOy 中，已知点P( 1,0)，点Q(2,1)，直线l ：ax by c 0，（其中a,b,c 成等差数列），点P 在直线l 上的射影为H ，则线段QH 的取值范围是 ________．题型三、两定点A、B ，动点P 知足PA PB 确立隐形圆1．已知圆C ：( x 3)2 ( y 4)2 1和两点A( m ,0) ，B(m,0) （m 0），若圆C 上存在点P ，使得PA PB 1，则m 的取值范围是___________．2．在平面直角坐标系xOy 中，已知点A( t ,0) （t 0 ），B(t,0)，点C 知足AC BC 8 ，9且点C 到直线l ：3x 4 y 24 0 的最小距离为，则实数t 的值为___________．53．已知点A( 2,3) ，点B(6, 3) ，点P 在直线3x 4 y 3 0 上，若知足等式AP BP 20 的点P 有两个，则实数的取值范围是 ___________ ．题型四两定点A、B ，动点P 知足PA2 PB2 是定值确立隐形圆2 y a 21．在平面直角坐标系xOy 中，已知圆C ：( ) ( 2) 1x a ，点A(0,2)，若圆C2 PO 2 上存在点P ，知足10PA ，则实数a 的取值范围是 ___________ ．2．已知A, B 为直线l : y x 上两动点，且AB 4，圆C：x2 y2 6x 6y 2 0，2 PB 2圆C 上存在点P ，知足10PA ，则线段AB 中点M 的横坐标取值范围为___________．2 b2 c23．在ABC 中，A, B,C 所对的边分别为a, b,c ，若2 8a ，则ABC 面积的最大值为___________．三、加强练习1．已知线段AB 的长为2 , 动点C 知足CA CB （0 ），且点C 总不在以点B 为圆心 , 1为半径的圆内，则负数的最大值是 ___________．22 y 22．在平面中，A( 12,0) ，B (0,6) ，点P 在圆O : 50x 上．若PA PB 20 ，则点P 的横坐标的取值范围是 ________．2 y23．在平面直角坐标系xOy 中，已知点A (0, 2) ，点B (1, 1) ，P 为圆2x 上一动点，P B的最大值是 _________．则PA隐圆专题（ 2）PA策略五两定点A、B 动点P 知足（0 且1）确立隐形圆（阿波罗尼斯圆）PB1．已知O (0,0) ，A( 0,3) ，假如圆C ：( x a)2 ( y 2a 4)2 1上总存在点M 使得MA 2 MO ，则圆心C 的横坐标a 的取值范围是 ___________ ．2 y22．在平面直角坐标系xOy 中，圆1x 交x 轴于A, B 两点，且点A 在点B 左侧，若直线x 3 y m 0 上存在P 使得PA 2 PB ，则实数m 的取值范围为_________．3．在平面直角坐标系xOy 中，已知点A (1，0) ，B(4，0) ，若直线x y m 0上存在点P 1,则实数m 的取值范围是 ___________ ．使得PA PB224．在平面直角坐标系xOy 中，已知圆O : x2 y2 1，4 2 4O1：x y ，动点P 在直线x 3y b 0 上，过点P 作圆O,OA, B ，若知足的两条切线，切点分别为1PB 2 PA 的点P 有且仅有两个，则实数b 的取值范围为 ___________ ．5．在ABC 中，若AB 2 ，AC 2BC ，则S ABC 的最大值为 ___________．6．在ABC 中，BC 2 ，AC 1，以AB 为边作等腰直角三角形ABD （B 为直角极点，C, D 两点在直线AB 的双侧）．当C 变化时，线段CD 长的最大值为 ________ ．7．已知点A (0,1) ，B (1,0) ，C( t,0) ，点D 是直线AC 上的动点，若AD 2 BD 恒建立，则t 的值为_______．最小正整数题型六、有关点法确立隐形圆2 y 2 1．在平面直角坐标系xOy 中，若直线y k( x3 3) 上存在一点P ，圆( 1) 1x 上存在一点Q ，知足OP 3OQ ，则实数k 的最小值为 ___________ ．2 AC22．已知A, B ,C, D 四点共面，BC 2 , AB 20 , CD 3 CA ，则| BD |的最大值为_________．3．已知ABC 是边长为3 的等边三角形 , 点P 是以A 为圆心的单位圆上一动点，点Q 知足AQ2 3 AP 1 3AC ，则 | BQ | 的最小值是 __________ ． 4．在平面直角坐标系xoy 中，已知圆O : x2y 2 16，点P (1,2) ，M , N 为圆O 上两个不一样的点，且PM PN 0, 若PQ PM PN , 则| PQ|的最小值为___________．加强练习1．已知圆2 2 92 2C 1：x y ，与圆C 2：x y 4，定点P (1,0 ) ，动点A, B 分别在圆C 1与圆 C 上，知足2APB 90 ，则线段 AB 的取值范围 ______________ ．2y 2 y a 222．已知圆O ：1 x ( a 为实数 ) ．若圆O 与圆Mx ，圆M ：( a 3) ( 2 ) 1上分别存在点 P,Q ，使得OQP 30 ，则 a 的取值范围是 __________ ．3．设m R ，直线l 1 : x my 0与直线l 2 : mx y 2m 4 0交于P(x 0 , y 0) ，则2 2x0 y 2x 的取值范围 _______.0 04．在平面直角坐标系xOy 中，已知圆C ：( x 1)2 y2 2，点A(2,0)，若圆C 上存在点M 知足MA 2 MO 2 10 ，则点M 的纵坐标的取值范围是 ______________ ．2 y a2 5．在平面直角坐标系xOy 中，已知A, B 为圆C ：( 4) ( ) 16x 上两个动点，且AB 2 11．若直线l ：y 2x 上存在独一的一个点P ，使得PA PB OC ，则实数a 的值为 ______________ ．6．在平面四边形ABCD 中，AB 4 ，AD 2，最小值为______________．DAB 60 ，CA 3CB ，则边CD 长的7．在平面直角坐标系xOy 中，圆 2 2C1 : x 1 y 2，圆2 2 2C1 : x m y m m ，若圆C 上存在点P 知足：过点P 向圆2 C 作两条切线PA, PB, 切点为A, B ，ABP 的面积为11，则正数m 的取值范围是．。
隐圆问题 最值问题 7种题型 知识点+例题+练习(非常好 分类全面)
4、90o的圆周角所对的弦为直径
（动态问题中一般会出现多个直角，往往会有一个直角所对斜边是固定不变的，选取该斜边中点为圆心，斜边中线为半径）
7、寻找特殊点和线段两端点形成特殊角
例1：如图， 为正三角形，做 的外接圆
（1）D为优弧 上一点，则 =
（2）已知线段 和直线 ，请用尺规作图在直线 上找一点 ，使得 .（可改成 ， ）
练习：1、如图， 为正三角形，做 的外接圆
（1）D为劣弧 上一点，则 =
（2）若三角形的3个内角均小于120°，三角形存在一点P，使得PA、PB、PC的夹角均为120°，我们称点P为 的费马点。
A．1B． C． D．5
3、如图，已知△ABC为等腰直角三角形，∠BAC=90∘，AC=2，以点C为圆心，1为半径作圆，点P为⊙C上一动点，连结AP，并绕点A顺时针旋转90∘得到AP′，连结CP′，则CP′的取值范围是____________.
4、如图，在Rt△ABC中，∠ACB=90∘，AC=4，BC=3，点D是平面内的一个动点，且AD=2，M为BD的中点，在D点运动过程中，线段CM长度的取值范围是_________.
例2、平面内有四个点A、O、B、C，其中∠AOB=120°，∠ACB=60°，AO=BO=2，则满足题意的OC长度为整数的值可以是___________
练习、如图，AB为直径，AB=4，C、D为圆上两个动点，N为CD中点，CM⊥AB于M，当C、D在圆上运动时保持∠CMN=30°，则CD的长（ ）
2019年高三数学文科第二轮专题复习：微点深化“解析几何中的隐形圆”问题
微点深化 解析几何中的“隐形圆”问题 高考中圆的方程是C 级知识点，其重要性不言而喻.但在一些题目中，条件没有直接给出圆方面的信息，而是隐藏在题目中，要通过分析和转化，发现圆(或圆的方程)，从而最终可以利用圆的知识求解，我们称此类问题为“隐形圆”问题.【例1】 (1)(2018·南通、泰州调研)在平面直角坐标系xOy 中，已知点A (－4，0)，B (0，4)，从直线AB 上一点P 向圆x 2＋y 2＝4引两条切线PC ，PD ，切点分别为C ，D .设线段CD 的中点为M ，则线段AM 长的最大值为________.(2)已知实数a ，b ，c 满足a 2＋b 2＝c 2，c ≠0，那么b a －2c的取值范围为________. 解析 (1)法一(几何法) 因为直线AB 的方程为y ＝x ＋4，所以可设P (a ，a ＋4), 设C (x 1，y 1)，D (x 2，y 2)，所以PC 方程为x 1x ＋y 1y ＝4，PD ：x 2x ＋y 2y ＝4，将P (a ，a ＋4)分别代入PC ，PD 方程，⎩⎨⎧ax 1＋（a ＋4）y 1＝4，ax 2＋（a ＋4）y 2＝4，则直线CD 的方程为ax ＋(a ＋4)y ＝4，即a (x ＋y )＝4－4y ，所以直线CD 过定点N (－1，1)，又因为OM ⊥CD ，所以点M 在以ON 为直径的圆上(除去原点)，又因为以ON 为直径的圆的方程为⎝ ⎛⎭⎪⎫x ＋122＋⎝ ⎛⎭⎪⎫y －122＝12，所以AM 的最大值为⎝ ⎛⎭⎪⎫－4＋122＋⎝ ⎛⎭⎪⎫122＋22＝3 2. 法二(参数法) 因为直线AB 的方程为y ＝x ＋4，所以可设P (a ，a ＋4)，同法一可知直线CD 的方程为ax ＋(a ＋4)y ＝4，即a (x ＋y )＝4－4y ，得a ＝4－4y x ＋y.又因为O ，P ，M 三点共线，所以ay －(a ＋4)x ＝0，得a ＝4x y －x .因为a ＝4－4y x ＋y ＝4x y －x，所以点M 的轨迹方程为⎝ ⎛⎭⎪⎫x ＋122＋⎝ ⎛⎭⎪⎫y －122＝12(除去原点)，所以AM 的最大值为⎝ ⎛⎭⎪⎫－4＋122＋⎝ ⎛⎭⎪⎫122＋22＝3 2.(2)由已知得⎝ ⎛⎭⎪⎫a c 2＋⎝ ⎛⎭⎪⎫b c 2＝1，设a c ＝x ，b c ＝y ，则x 2＋y 2＝1，b a －2c ＝b ca c －2＝y x －2，问题就转化为求单位圆上的点与点(2，0)连线斜率的取值范围.设直线的方程为y ＝k (x －2)，即kx －y －2k ＝0，由d ＝r ，得|－2k |k 2＋（－1）2＝1，解得k ＝±33，所以所求斜率的取值范围为⎣⎢⎡⎦⎥⎤－33，33，即b a －2c 的取值范围为⎣⎢⎡⎦⎥⎤－33，33. 答案 (1)32 (2)⎣⎢⎡⎦⎥⎤－33，33 【例2】 (1)(2018·南京、盐城一模)在平面直角坐标系xOy 中，若直线y ＝k (x －33)上存在一点P ，圆x 2＋(y －1)2＝1上存在一点Q ，满足OP→＝3OQ →，则实数k 的最小值为________.(2)(2018·南通一调)在平面直角坐标系xOy 中，点A (1，0)，B (4，0).若直线x －y＋m ＝0上存在点P 使得P A ＝12PB ，则实数m 的取值范围是________.解析 (1)设点P (x ，y )，由OP →＝3OQ →可得Q ⎝ ⎛⎭⎪⎫x 3，y 3.又点Q 在圆x 2＋(y －1)2＝1上，可得⎝ ⎛⎭⎪⎫x 32＋⎝ ⎛⎭⎪⎫y 3－12＝1，即x 2＋(y －3)2＝9，所以点P 既在圆x 2＋(y －3)2＝9上，又在直线y ＝k (x －33)上，即直线与圆有交点，所以圆心到直线距离d ＝|－3－33k |1＋k 2≤3，解得－3≤k ≤0. (2)设P (x ，y )，由P A ＝12PB ，得（x －1）2＋y 2＝12（x －4）2＋y 2，化简得x 2＋y 2＝4，问题等价于直线与圆有交点，即d ＝|m |2≤2，解得m ∈[－22，22]. 答案 (1)－3 (2)[－22，22]【例3】 (1)在平面直角坐标系xOy 中，已知圆C ：(x －a )2＋(y －a ＋2)2＝1，点A (0，2)，若圆C 上存在点M ，满足MA 2＋MO 2＝10，则实数a 的取值范围是________.(2)在平面直角坐标系xOy 中，已知圆M ：(x －a )2＋(y ＋a －3)2＝1(a ＞0)，点N为圆M 上任意一点.若以N 为圆心，ON 为半径的圆与圆M 至多有一个公共点，则a 的最小值为________.解析 (1)设点M (x ，y )，由A (0，2)，O (0，0)及MA 2＋MO 2＝10，得x 2＋(y －2)2＋x 2＋y 2＝10，整理得x 2＋(y －1)2＝4，即点M 在圆E ：x 2＋(y －1)2＝4上.若圆C 上存在点M 满足MA 2＋MO 2＝10也就等价于圆E 与圆C 有公共点，所以|2－1|≤CE ≤2＋1，即|2－1|≤a 2＋（a －3）2≤2＋1，整理得1≤2a 2－6a ＋9≤9，解得0≤a ≤3，即实数a 的取值范围是[0，3].(2)圆M 的圆心M (a ，3－a )在直线x ＋y ＝3上，点O 到直线x ＋y －3＝0的距离为322＞2，所以ON ＞2－1＝1.圆M 与圆N 至多有一个公共点，则两圆内含或内切(圆M 在圆N 内)，所以MN ＝1≤ON －1，所以ON ≥2，即(ON )min ≥2，所以OM －1≥2，即a 2＋(3－a )2≥9(a ＞0)，解得a ≥3.故a 的最小值为3.答案 (1)[0，3] (2)3探究提高 (1)如何发现隐形圆(或圆的方程)是关键，常见的有以下五个策略： 策略一：利用圆的定义(到定点的距离等于定长的点的轨迹)确定隐形圆；策略二：动点P 对两定点A ，B 的张角是90°(k P A ·k PB ＝－1或P A →·PB→＝0)确定隐形圆；策略三：两定点A ，B ，动点P 满足P A →·PB→＝λ确定隐形圆； 策略四：两定点A ，B ，动点P 满足P A 2＋PB 2是定值确定隐形圆；策略五：两定点A ，B ，动点P 满足AP ＝λBP (λ＞0，λ≠1)确定隐形圆(阿波罗尼斯圆).(2)“隐形圆”发掘出来以后常考查点和圆、直线和圆、圆和圆的位置关系等相关知识点，例1、例2和例3分别从三个方面作了考查，一般解决思路可从“代数角度”或“几何角度”入手.【训练】 (1)若实数a ，b ，c 成等差数列，点P (－1，0)在动直线ax ＋by ＋c ＝0上的射影为点M ，点N (3，3)，则线段MN 长度的最大值为________.(2)(2016·镇江模拟)已知集合M ＝{(x ，y )|x －3≤y ≤x －1}，N ＝{P |P A ≥2PB ， A (－1，0)，B (1，0)}，则表示M ∩N 的图形面积等于________.解析 (1)由题意，2b ＝a ＋c ，所以动直线的方程为2ax ＋(a ＋c )y ＋2c ＝0，即a (2x＋y)＋c(y＋2)＝0，所以动直线ax＋by＋c＝0过定点A(1，－2).设点M(x，y)，由MP⊥MA可求得点M的轨迹方程为圆Q：x2＋(y＋1)2＝2，故线段MN长度的最大值为QN＋r＝5＋ 2.(2)令P(x，y)，所以(x＋1)2＋y2≥2[(x－1)2＋y2].所以x2－6x＋y2＋1≤0，所以(x－3)2＋y2≤8，所以点P的轨迹为以(3，0)为圆心的圆及圆的内部.表示M∩N的图形如图中阴影部分所示，由于直线y＝x－3过圆心(3，0)，圆心(3，0)到直线y＝x－1的距离为|3－1|2＝2，直线y＝x－1与圆的两个交点所对的圆心角为2π3，所以阴影部分面积为12×(22)2×sin2π3＋12×(22)2×π3＝23＋4π3.答案(1)5＋2(2)23＋4π3。
江苏省2019年高考数学 小专题2---隐圆问题
隐圆问题一【问题背景】有些数学问题，将圆隐藏在已知条件里，隐晦地考查点和圆、直线和圆、圆和圆的位置关系．解题时，需要我们通过分析探索，发现这些隐藏的圆（简称隐圆），再利用和圆有关的一些知识进行求解．二、【范例】1.点和隐圆例1在平面直角坐标系xOy 中，已知圆C ：22650x y x +-+=，点,A B 在圆C 上，且AB =OA OB +的最大值是．分析与解：圆C 即22(3)4x y -+=，圆心为(3,0)，半径为2．如图，取AB 中点D ，连结CD ，则结合垂径定理和勾股定理易得1CD =．因此动点D 在以(3,0)C 为圆心，1为半径的圆上运动，此圆方程为：22(3)1x y -+=．另一方面，由于D 为AB 的中点，所以2OA OB OD +=，则2OA OB OD += ，因而只要求圆22(3)1x y -+=上一动点D 到定点O 距离的最大值，易知此最大值为14OC +=，故OA OB +的最大值是8．说明：OA OB +的最小值是2(1)4OC -=．例2在平面直角坐标系xOy 中，已知圆22:16O x y +=，点(1,2)P ，,M N 为圆O 上的不同的两点，且0PM PN ⋅= ，若PQ PM PN =+ ，则PQ的最小值为．解：如图，取MN 中点A ，连结OA ，ON ，则2PQ PM PN PA =+= ，设(,)A x y ，因为A 为MN 的中点，所以OA MN ⊥，则2222216()AN ON OA x y =-=-+，又因为0PM PN ⋅=，所以PA AN =，即2222(1)(2)16()x y x y -+-=-+，所以22127((1)24x y -+-=，故点A 在以1(,1)2B为圆心，半径R =显然定点(1,2)P 在此圆内，因而求PA 的最小值即为求定点(1,2)P 与圆B ：22127((1)24x y -+-=上一点距离的最2BP -=，故PQ的最小值为说明：PQ的最大值为．2.直线和隐圆例3已知动点M 与两个定点)0,3(),0,0(A O 的距离之比为21，那么直线AM 的斜率的取值范围是．解：先求动点M 的轨迹方程．设),(y x M ，由1=MO 得1)3(2222=+-+y x y x ，整理得4)1(22=++y x ，即动点M 在以(1,0)B -为圆心，2为半径的圆上运动．当直线AM 与圆B 相切时，设斜率为k ，则其方程为(3)y k x =-，根据2=得3k =±，结合图形可知，直线AM 的斜率的取值范围是33[]33-．说明：到两定点距离之比（不为1）等于已知数的动点轨迹为圆，这个圆称为阿波罗尼斯圆．例4在平面直角坐标系xOy 中，设点(1,0),(3,0),(0,),(0,2)A B C a D a +，若存在点P ，使得,PA PC PD ==，则实数a 的取值范围是．解：设(,)P x y=，整理得22(5)8x y -+=，即动点P 在以(5,0)为圆心，为半径的圆上运动．另一方面，由PC PD =知动点P 在线段CD 的垂直平分线1y a =+上运动，因而问题就转化为直线1y a =+与圆22(5)8x y -+=有交点，所以1a +≤a的取值范围是[1,1]--．3.圆和隐圆例5在平面直角坐标系xOy 中，点()03A ,，直线24l y x =-：.设圆的半径为1，圆心在l 上.若圆C 上存在点M ，使2MA MO =，求圆心C 的横坐标a 的取值范围.解：设(),24C a a -，则圆方程为()()22241x a y a -+-+=又设00(,)M x y ，2MA MO = ()22220000344x y x y ∴+-=+，即()220014x y ++=这说明M 既在圆()()22241x a y a -+-+=上，又在圆()2214x y ++=上，因而这两个圆必有交点，即两圆相交或相切，2121∴-≤+，解得1205a ≤≤，即a 的取值范围是12[0,]5．例6已知22(1)(4)4M x y -+-= ：，若过x 轴上的一点(0)P a ，可以作一直线与M 相交于,A B 两点，且满足PA BA =，求a 的取值范围．解法1：如图3，过点B 作M 的直径BD ，连结,DA DP ，要存在满足条件的点P ，只要M 存在点D 即可．由于90BAD ∠=，PA BA =，所以4DP DB ==，因而点D 在以(0)P a ，为圆心，4为半径的:P 22()16x a y -+=上运动，这说明点D 同时在M和P 上，因而两个圆必有交点，042∴≤+，解得a的取值范围是1⎡-+⎣．解法2：设(,)A x y ，则(2,2)B x a y -．因为点B在M上，所以22(21)(24)4x a y --+-=，即221()(2)12a x y +-+-=(*)，这表明点A 在方程(*)表示的圆上，又点A 在M 上，因此这两个圆有公共点，图32112∴-≤+，解得a 的取值范围是1⎡-+⎣．三、【练习】1．在平面直角坐标系xOy 中，若满足)()(y k y k x x -≤-的点),(y x 都在以坐标原点为圆心，2为半径的圆及其内部，则实数k 的取值范围是________答案：[2．若圆2244100x y x y +---=上至少有三个不同点到直线l :0ax by +=的距离为,则直线l 斜率的取值范围是___________.答案：[22+3.在平面直角坐标系xOy 中，若与点)2,2(A 的距离为1且与点)0,(m B 的距离为3的直线恰有两条，则实数m 的取值范围为__________答案：()322,2)2,322(+- 4.若实数,,a b c 成等差数列，点(1,0)P -到动直线0=++c by ax 上的射影为M ，已知点(3,3)N ，则线段MN 长度的最大值为____________答案：105.已知1l 和2l 是平面内互相垂直的两条直线，它们的交点是A ，动点C B ,分别在1l 和2l 上，且23=BC ，过C B A ,,三点的动圆所形成的区域的面积为__________答案：π18解析：,,A B C 三点的动圆在以BC 为直径的圆上，以AB 的中点M 为圆心，M 点的轨迹是以A 为圆心，223为半径的圆，所以动圆所形成的区域是是以A 为圆心，23为半径的圆．。
2019年浙江省高考数学压轴试卷(解析版)
2019年浙江省高考数学压轴试卷一、选择题（本大题共11小题，共44.0分）1.已知全集U={1，2，3，4，5，6}，集合A={1，3，5}，B={1，2}，则A∩（∁U B）（）A. B. C. D.2.已知双曲线（a＞0）的离心率为，则a的值为（）A. B. C. D.3.《九章算术》中，将底面是直角三角形的直三棱柱称之为“堑堵”．已知某“堑堵”的三视图如图所示，俯视图中间的实线平分矩形的面积，则该“堑堵”的表面积为（）A.B. 2C.D.4.若复数z满足：1+（1+2z）i=0（i是虚数单位），则复数z的虚部是（）A. B. C. D.5.函数y=2x2-e|x|在[-2，2]的图象大致为（）A.B.C.D.6.已知平面α与两条不重合的直线a，b，则“a⊥α，且b⊥α”是“a∥b”的（）A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件7.（1-x）4（1+x）5的展开式中x3的系数为（）A. 4B.C. 6D.8.4月23日是“世界读书日”，某中学在此期间开展了一系列的读书教育活动．为了解本校学生课外阅读情况，学校随机抽取了100名学生对其课外阅读时间进行调查．根据调查结果知道，从该校学生中任意抽取1名学生恰为读书迷的概率是．现在从该校大量学生中，用随机抽样的方法每次抽取1人，共抽取3次，记被抽取的3人中的“读书迷”的人数为X．若每次抽取的结果是相互独立的，则期望E（X）和方差D（X）分别是（）A. ，B. ，C. ，D. ，9.已知A，B，C是球O球面上的三点，且，，D为该球面上的动点，球心O到平面ABC的距离为球半径的一半，则三棱锥D-ABC体积的最大值为（）A. B. C. D.10.设S n为等差数列{a n}的前n项和，若a7=5，S5=-55，则nS n的最小值为（）A. B. C. D.11.某校毕业典礼由6个节目组成，考虑整体效果，对节目演出顺序有如下要求：节目甲必须排在前三位，且节目丙、丁必须排在一起，则该校毕业典礼节目演出顺序的编排方案共有（）A. 120种B. 156种C. 188种D. 240种二、填空题（本大题共6小题，共32.0分）12.《九章算术》第七章“盈不足”中第一题：“今有共买物，人出八，盈三钱；人出七，不足四，问人数物价各几何？”借用我们现在的说法可以表述为：有几个人合买一件物品，每人出8元，则付完钱后还多3元；若每人出7元，则还差4元才够付款．问他们的人数和物品价格？答：一共有______人；所合买的物品价格为______元．13.已知x，y满足条件则2x+y的最大值是______，原点到点P（x，y）的距离的最小值是______14.在△ABC中，若b=2，A=120°，三角形的面积S=，则c=______；三角形外接圆的半径为______．15.已知向量、满足||=1，||=2，则|+|+|-|的最小值是______，最大值是______．16.已知实数f（x）=，若关于x的方程f2（x）+f（x）+t=0有三个不同的实根，则t的取值范围为______．17.已知直线y=-x+1与椭圆+=1（a＞b＞0）相交于A，B两点，且OA⊥OB（O为坐标原点），若椭圆的离心率e∈[，]，则a的最大值为______．三、解答题（本大题共5小题，共60.0分）18.设函数f（x）=sin（ωx-）+sin（ωx-），其中0＜ω＜3，已知f（）=0．（Ⅰ）求ω；（Ⅱ）将函数y=f（x）的图象上各点的横坐标伸长为原来的2倍（纵坐标不变），再将得到的图象向左平移个单位，得到函数y=g（x）的图象，求g（x）在[-，]上的最小值．19.已知等差数列{a n}的前n项和为S n，若，，，且∈．（1）求首项a1与m的值；（2）若数列{b n}满足∈，求数列{（a n+6）•b n}的前n项和．20.如图，已知四棱锥P-ABCD，底面ABCD为菱形，AB=2，∠BAD=120°，PA⊥平面ABCD，M，N分别是BC，PC的中点．（1）证明：AM⊥平面PAD；（2）若H为PD上的动点，MH与平面PAD所成最大角的正切值为，求二面角M-AN-C的余弦值．21.已知抛物线C的顶点在原点，焦点在x轴上，且抛物线上有一点P（4，m）到焦点的距离为5．（1）求该抛物线C的方程；（2）已知抛物线上一点M（t，4），过点M作抛物线的两条弦MD和ME，且MD⊥ME，判断直线DE是否过定点？并说明理由．22.已知函数f（x）=-x2+ax-ln x（a∈R）．（1）若函数f（x）是单调递减函数，求实数a的取值范围；（2）若函数f（x）在区间（0，3）上既有极大值又有极小值，求实数a的取值范围．答案和解析1.【答案】D【解析】解：∵U={1，2，3，4，5，6}，B={1，2}，∴∁U B═{3，4，5，6}，又集合A={1，3，5}，∴A∩∁U B={3，5}，故选：D．先由补集的定义求出∁U B，再利用交集的定义求A∩∁U B．本题考查交、并补集的混合运算，解题的关键是熟练掌握交集与补集的定义，计算出所求的集合．2.【答案】B【解析】解：双曲线，可得c=1，双曲线的离心率为：，∴，解得a=．故选：B．直接利用双曲线求出半焦距，利用离心率求出a即可．本题考查双曲线的离心率的求法，双曲线的简单性质的应用．3.【答案】D【解析】解：根据题意和三视图知几何体是一个放倒的直三棱柱ABC-A′B′C′，底面是一个直角三角形，两条直角边分别是、斜边是2，且侧棱与底面垂直，侧棱长是2，∴几何体的表面积S=2×+2×2+2×=6+4，故选：D．根据题意和三视图知几何体是一个放倒的直三棱柱，由三视图求出几何元素的长度，由面积公式求出几何体的表面积．本题考查三视图求几何体的表面积，由三视图正确复原几何体是解题的关键，考查空间想象能力．4.【答案】B【解析】解：由1+（1+2z）i=0，得z=，∴复数z 的虚部是，故选：B．把已知等式变形，再由复数代数形式的乘除运算化简得答案．本题考查复数代数形式的乘除运算，考查复数的基本概念，是基础题．5.【答案】D【解析】解：∵f（x）=y=2x2-e|x|，∴f（-x）=2（-x）2-e|-x|=2x2-e|x|，故函数为偶函数，当x=±2时，y=8-e2∈（0，1），故排除A，B；当x∈[0，2]时，f（x）=y=2x2-e x，∴f′（x）=4x-e x=0有解，故函数y=2x2-e|x|在[0，2]不是单调的，故排除C，故选：D．根据已知中函数的解析式，分析函数的奇偶性，最大值及单调性，利用排除法，可得答案．本题考查的知识点是函数的图象，对于超越函数的图象，一般采用排除法解答．6.【答案】A【解析】解：a⊥α，且b⊥α⇒a∥b，反之不成立．可能a，b分别于α，β斜交．∴“a⊥α，且b⊥α”是“a∥b”的充分不必要条件．故选：A．a⊥α，且b⊥α⇒a∥b，反之不成立．可能a，b分别于α，β斜交．本题考查了空间线面位置关系、简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．7.【答案】B【解析】解：（1-x）4（1+x）5=（1-4x+6x2-4x3+x3）（1+5x+10x2+10x3+5x4+x5），故展开式中x3的系数为10-40+30-4=-4，故选：B．把（1-x）4和（1+x）5按照二项式定理展开，可得展开式中x3的系数．本题主要考查二项式定理的应用，二项展开式的通项公式，二项式系数的性质，属于基础题．8.【答案】B【解析】解：由题意，从该校学生中任意抽取1名学生恰为读书迷的概率．从该校大量学生中，用随机抽样的方法每次抽取1人，共抽取3次，记被抽取的3人中的“读书迷”的人数为X．若每次抽取的结果是相互独立的，所以．X的分布列为均值，方差．故选：B．从该校学生中任意抽取1名学生恰为读书迷的概率．说明每次抽取的结果是相互独立的，推出．得到分布列，然后求解期望即可．本题考查独立重复实验的概率的分布列以及期望的求法，考查转化思想以及计算能力．9.【答案】D【解析】解：如图，在△ABC中，∵AB=AC=3，BC=3，∴由余弦定理可得cosA==-，则A=120°，∴sinA=．设△ABC外接圆的半径为r，则，得r=3．设球的半径为R，则，解得R=2．∵×3×3×=，∴三棱锥D-ABC体积的最大值为=，故选：D．由题意画出图形，求出三角形ABC外接圆的半径，设出球的半径，利用直角三角形中的勾股定理求得球的半径，则三棱锥D-ABC体积的最大值可求．本题主要考查空间几何体的体积等基础知识，考查空间想象能力、推理论证能力、运算求解能力，考查化归与转化思想、数形结合思想等，是中档题．10.【答案】A【解析】解：由题意可得，解可得a1=-19，d=4，∴S n=-19n=2n2-21n，∴nS n=2n3-21n2，设f（x）=2x3-21x2，f′（x）=6x（x-7），当0＜x＜7时，f′（x）＜0；函数是减函数；当x＞7时，f′（x）＞0，函数是增函数；所以n=7时，nS n取得最小值：-343．故选：A．分别利用等差数列的通项公式及求和公式表示已知条件，然后求出得a1，d，在代入求和公式即可求解．本题主要考查了等差数列的通项公式及求和公式的简单应用，属于基础试题．11.【答案】A【解析】解：根据题意，由于节目甲必须排在前三位，分3种情况讨论：①、甲排在第一位，节目丙、丁必须排在一起，则乙丙相邻的位置有4个，考虑两者的顺序，有2种情况，将剩下的3个节目全排列，安排在其他三个位置，有A33=6种安排方法，则此时有4×2×6=48种编排方法；②、甲排在第二位，节目丙、丁必须排在一起，则乙丙相邻的位置有3个，考虑两者的顺序，有2种情况，将剩下的3个节目全排列，安排在其他三个位置，有A33=6种安排方法，则此时有3×2×6=36种编排方法；③、甲排在第三位，节目丙、丁必须排在一起，则乙丙相邻的位置有3个，考虑两者的顺序，有2种情况，将剩下的3个节目全排列，安排在其他三个位置，有A33=6种安排方法，则此时有3×2×6=36种编排方法；则符合题意要求的编排方法有36+36+48=120种；故选：A．根据题意，由于节目甲必须排在前三位，对甲的位置分三种情况讨论，依次分析乙丙的位置以及其他三个节目的安排方法，由分步计数原理可得每种情况的编排方案数目，由加法原理计算可得答案．本题考查排列、组合的应用，注意题目限制条件比较多，需要优先分析受到限制的元素．12.【答案】7 53【解析】解：设人数为x，物品价格为y，则，解得x=7，y=53．故答案为：7，53．列方程组求解．本题考查了方程的应用，属于基础题．13.【答案】6【解析】解：作出x，y满足条件的可行域如图：目标函数z=2x+y在的交点A（2，2）处取最大值为z=2×2+1×2=6．原点到点P（x，y）的距离的最小值是：|OB|=．故答案为：6；；画出约束条件表示的可行域，判断目标函数z=2x+y的位置，求出最大值．利用可行域转化求解距离即可．本题考查简单的线性规划的应用，正确画出可行域，判断目标函数经过的位置是解题的关键．14.【答案】2 2【解析】解：△ABC中，∵b=2，A=120°，三角形的面积S==bc•sinA=c•，∴c=2=b，故B=（180°-A）=30°．再由正弦定理可得=2R==4，∴三角形外接圆的半径R=2，故答案为：2；2由条件求得c=2=b，可得B的值，再由正弦定理求得三角形外接圆的半径R的值．本题主要考查正弦定理的应用，属于基础题．15.【答案】4【解析】解：记∠AOB=α，则0≤α≤π，如图，由余弦定理可得：|+|=，|-|=，令x=，y=，则x2+y2=10（x、y≥1），其图象为一段圆弧MN，如图，令z=x+y，则y=-x+z，则直线y=-x+z过M、N时z最小为z min=1+3=3+1=4，当直线y=-x+z与圆弧MN相切时z最大，由平面几何知识易知z max即为原点到切线的距离的倍，也就是圆弧MN所在圆的半径的倍，所以z max=×=．综上所述，|+|+|-|的最小值是4，最大值是．故答案为：4、．通过记∠AOB=α（0≤α≤π），利用余弦定理可可知|+|=、|-|=，进而换元，转化为线性规划问题，计算即得结论．本题考查函数的最值及其几何意义，考查数形结合能力，考查运算求解能力，涉及余弦定理、线性规划等基础知识，注意解题方法的积累，属于中档题．16.【答案】（-∞，-2]【解析】解：原问题等价于f2（x）+f（x）=-t有三个不同的实根，即y=-t与y=f2（x）+f（x）有三个不同的交点，当x≥0时，y=f2（x）+f（x）=e2x+e x为增函数，在x=0处取得最小值为2，与y=-t只有一个交点．当x＜0时，y=f2（x）+f（x）=lg2（-x）+lg（-x），根据复合函数的单调性，其在（-∞，0）上先减后增．所以，要有三个不同交点，则需-t≥2，解得t≤-2．原问题等价于f2（x）+f（x）=-t有三个不同的实根，即y=-t与y=f2（x）+f（x）有三个不同的交点，然后分x≥0和x＜0两种情况代入解析式可得．本题考查了函数与方程的综合运用，属难题．17.【答案】【解析】解：设A（x1，y1）、B（x2，y2），由，消去y，可得（a2+b2）x2-2a2x+a2（1-b2）=0，∴则x1+x2=，x1x2=，由△=（-2a2）2-4a2（a2+b2）（1-b2）＞0，整理得a2+b2＞1．∴y1y2=（-x1+1）（-x2+1）=x1x2-（x1+x2）+1．∵OA⊥OB（其中O为坐标原点），可得•=0∴x1x2+y1y2=0，即x1x2+（-x1+1）（-x2+1）=0，化简得2x1x2-（x1+x2）+1=0．∴2•-+1=0．整理得a2+b2-2a2b2=0．∵b2=a2-c2=a2-a2e2，∴代入上式，化简得2a2=1+，∴a2=（1+）．∵e∈[，]，平方得≤e2≤，∴≤1-e2≤，可得≤≤4，因此≤2a2=1+≤5，≤a2≤，可得a2的最大值为，满足条件a2+b2＞1，∴当椭圆的离心率e=时，a的最大值为．故答案为：．将直线方程代入椭圆方程，由韦达定理，向量数量积的坐标运算，求得2a2=1+，由离心率的取值范围，即可求得a的最大值．本题考查椭圆的标准方程，直线与椭圆的位置关系，韦达定理，向量数量积的坐标运算，考查计算能力，属于中档题．18.【答案】解：（Ⅰ）函数f（x）=sin（ωx-）+sin（ωx-）=sinωx cos-cosωx sin-sin（-ωx）=sinωx-cosωx=sin（ωx-），又f（）=sin（ω-）=0，∴ω-=kπ，k∈Z，解得ω=6k+2，又0＜ω＜3，∴ω=2；（Ⅱ）由（Ⅰ）知，f（x）=sin（2x-），将函数y=f（x）的图象上各点的横坐标伸长为原来的2倍（纵坐标不变），得到函数y=sin（x-）的图象；再将得到的图象向左平移个单位，得到y=sin（x+-）的图象，∴函数y=g（x）=sin（x-）；当x∈[-，]时，x-∈[-，]，∴sin（x-）∈[-，1]，∴当x=-时，g（x）取得最小值是-×=-．【解析】（Ⅰ）利用三角恒等变换化函数f（x）为正弦型函数，根据f（）=0求出ω的值；（Ⅱ）写出f（x）解析式，利用平移法则写出g（x）的解析式，求出x∈[-，]时g（x）的最小值．本题考查了三角恒等变换与正弦型函数在闭区间上的最值问题，是中档题．19.【答案】解：（1）由已知得a m=S m-S m-1=4，且a m+1+a m+2=S m+2-S m=14，设数列{a n}的公差为d，则有2a m+3d=14，∴d=2…（2分）由S m=0，得，即a1=1-m，∴a m=a1+（m-1）×2=m-1=4∴m=5，a1=-4…（6分）（2）由（1）知a1=-4，d=2，∴a n=2n-6∴n-3=log2b n，得．∴ ．设数列{（a n+b）b n}的前n项和为T n∴ ①②①②，得==∴∈…（12分）【解析】（1）利用a m=S m-S m-1，转化求出数列的公差，然后利用已知条件求解m．（2）化简数列的通项公式，利用错位相减法求和求解即可．本题考查数列的递推关系式的应用，数列求和，考查转化思想以及计算能力．20.【答案】（1）证明：由四边形ABCD为菱形，∠BAD=120°，可得∠ABC=60°，△ABC为正三角形．因为M为BC的中点，所以AM⊥BC．…（2分）又BC∥AD，因此AM⊥AD．因为PA⊥平面ABCD，AM⊂平面ABCD，所以PA⊥AM．而PA∩AD=A，所以AM⊥平面PAD．…（4分）（2）解：AB=2，H为PD上任意一点，连接AH，MH．由（1）知：AM⊥平面PAD，则∠MHA为MH与平面PAD所成的角．在Rt△MAH中，AM=，∴当AH最短时，∠MHA最大，即当AH⊥PD时，∠MHA最大．此时，tan∠MHA==又AD=2，∴∠ADH=45°，∴PA=2．由（1）知AM，AD，AP两两垂直，以A为坐标原点如图建立空间直角坐标系，则A（0，0，0），P（0，0，2），D（0，2，0），，，，，，，，，，则，，，，，，，，，设AC的中点为E，则，，，故就是面PAC的法向量，，，．设平面MAN的法向量为n=（x，y，1），二面角M-AN-C的平面角为θ．⇒⇒，，，，，．＜，＞，∴二面角M-AN-C的余弦值为．…（12分）【解析】（1）利用菱形与等边三角形的性质可得：AM⊥BC，于是AM⊥AD．利用线面垂直的性质可得PA⊥AM．再利用线面垂直的判定与性质定理即可得出；（2）连接AH，MH．由（1）知：AM⊥平面PAD，可得：∠MHA为EH与平面PAD所成的角．在Rt△EAH中，AM=，可知：当AH最短时，∠MHA最大，即当AH⊥PD时，∠MHA最大．利用直角三角形边角关系可得PA=2．由（1）知AM，AD，AP两两垂直，以A为坐标原点，建立如图所示的空间直角坐标系．求出法向量，利用向量夹角求解即可．本题考查了直线与平面垂直的判定．在题中出现了探究性问题，在解题过程中“空间问题平面化的思路”，是立体几何常用的数学思想，属于中档题．21.【答案】解：（1）由题意设抛物线方程为y2=2px，其准线方程为，∵P（4，m）到焦点的距离等于A到其准线的距离，∴，∴p=2．∴抛物线C的方程为y2=4x．（2）由（1）可得点M（4，4），可得直线DE的斜率不为0，设直线DE的方程为：x=my+t，联立，得y2-4my-4t=0，则△=16m2+16t＞0①．设D（x1，y1），E（x2，y2），则y1+y2=4m，y1y2=-4t．∵•=（x1-4，y1-4）•（x2-4，y2-4），=x1x2-4（x1+x2）+16+y1y2-4（y1+y2）+16，=，=，=t2-16m2-12t+32-16m=0即t2-12t+32=16m2+16m，得：（t-6）2=4（2m+1）2，∴t-6=±2（2m+1），即t=4m+8或t=-4m+4，代入①式检验均满足△＞0，∴直线DE的方程为：x=my+4m+8=m（y+4）+8或x=m（y-4）+4．∴直线过定点（8，-4）（定点（4，4）不满足题意，故舍去）．【解析】（1）求出抛物线的焦点坐标，结合题意列关于p的等式求p，则抛物线方程可求；（2）由（1）求出M的坐标，设出直线DE的方程x=my+t，联立直线方程和抛物线方程，化为关于y的一元二次方程后D，E两点纵坐标的和与积，利用⊥得到t与m的关系，进一步得到DE方程，由直线系方程可得直线DE所过定点．本题考查抛物线的简单性质，考查了直线与圆锥曲线位置关系的应用，训练了平面向量在求解圆锥曲线问题中的应用，属中档题．22.【答案】解：（1）＞，∵函数f（x）是单调递减函数，∴f'（x）≤0对（0，+∞）恒成立，（3分）∴-2x2+ax-1≤0对（0，+∞）恒成立，即对，恒成立，∵（当且仅当2x=，即x=时取等号），∴（7分）（2）∵函数f（x）在（0，3）上既有极大值又有极小值．∴在（0，3）上有两个相异实根，即2x2-ax+1=0在（0，3）上有两个相异实根，（9分），则△＞＜＜＞＞，得＜或＞＜＜＜，即＜＜．（12分）【解析】（1）求出导函数，通过f'（x）≤0对（0，+∞）恒成立，分离变量推出a，利用基本不等式求解函数的最小值，得到a的范围．（2）通过函数f（x）在（0，3）上既有极大值又有极小值．说明导函数由两个零点，列出不等式组求解即可．本题考查函数的导数的应用，函数的单调性以及函数的极值的求法，考查转化思想以及计算能力．。
专题11 隐圆问题(解析版)
专题11 隐圆问题直线与圆是高中数学的C 级知识点，是高中数学中数形结合思想的典型体现．但有些时候，在条件中没有直接给出圆方面的信息，而是隐藏在题目中的，要通过分析和转化，发现圆（或圆的方程），从而最终可以利用圆的知识来求解，我们称这类问题为“隐形圆”问题类型一 利用圆的定义（到定点的距离等于定长的点的轨迹）确定隐形圆典例1 如果圆22(2)(3)4x a y a -+--=上总存在两个点到原点的距离为1，则实数a 的取值范围是________【答案】605a -<<【解析】到原点的距离为1的点的轨迹是以原点为圆心的单位圆，转化到此单位圆与已知圆相交求解2121-<<+∴605a -<<类型二 由圆周角的性质确定隐形圆典例 2 已知圆22:5,,O x y A B +=为圆O 上的两个动点，且2,AB M =为弦AB 的中点，()(),2C a D a +.当,A B 在圆O 上运动时，始终有CMD ∠为锐角，则实数a 的取值范围为__________．【答案】()(),20,-∞-⋃+∞【解析】由题意得2OM ==， ∴点M 在以O 为圆心，半径为2的圆上．设CD 的中点为N ，则()1N a +，且2CD =． ∵当,A B 在圆O 上运动时，始终有CMD ∠为锐角，∴以O 为圆心，半径为2的圆与以()1N a +为圆心，半径为1的圆外离．3>，整理得()211a +>， 解得2a <-或0a >．∴实数a 的取值范围为()(),20,-∞-⋃+∞．类型三 两定点A 、B ，动点P 满足(0,1)PAPBλλλ=>≠确定隐形圆（阿波罗尼斯圆） 典例3 一缉私艇巡航至距领海边界线l （一条南北方向的直线）3.8 海里的A 处，发现在其北偏东30°方向相距4 海里的B 处有一走私船正欲逃跑，缉私艇立即追击．已知缉私艇的最大航速是走私船最大航速的3 倍．假设缉私艇和走私船均按直线方向以最大航速航行．（1）若走私船沿正东方向逃离，试确定缉私艇的追击方向，使得用最短时间在领海内拦截成功；（参考数据： sin17 5.7446︒≈≈ ）（2）问：无论走私船沿何方向逃跑，缉私艇是否总能在领海内成功拦截？并说明理由．【答案】（1）略（2）能 【解析】：（1）略 （2）如图乙，以A 为原点，正北方向所在的直线为y 轴建立平面直角坐标系xOy ．则(2,B ，设缉私艇在P (x ，y )处（缉私艇恰好截住走私船的位置）与走私船相遇，则3PAPB=3=,229944x y ⎛⎫⎛-+= ⎪ ⎝⎭⎝因为圆心94⎛⎝到领海边界线l ：x = 3.8的距离为1.55，大于圆半径32所以缉私艇能在领海内截住走私船．1．已知ABC ∆中，AB AC == ABC ∆所在平面内存在点P 使得22233PB PC PA +==，则ABC∆面积的最大值为__________．【解析】设2BC a =，以BC 所在直线为x 轴、其中垂线OA 所在直线为y 轴建立直角坐标系（如图所示），则()()(,0,,0,B a C a A -，设(),P x y ，由22233PB PC PA +==，得222((3{ (1x x yy y x +++=+=，即22222232{31x y a x y a +=-+-+-=，则2722{ 11a y -=≤≤，则()()222323aa --≤≤-+即()()2222272323223232a a a a a ---≤-≤-+-， 解得234a ≤，即2241523233216ABC S a a a a ∆=⨯⨯-=-≤，即ABC ∆面积的最大值为52316.2．在平面直角坐标系xOy 中，已知B ，C 为圆224x y +=上两点， 点A(1,1)，且AB ⊥AC ，则线段BC 的长的取值范围为_______ 【答案】[62,62]-+ 【解析】设BC 的中点为M (x,y)，,因为22222OB OM BM OM AM =+=+，所以22224(1)(1)x y x y =++-+-，化简得22113222x y ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭，所以点M 的轨迹是以11,22⎛⎫⎪⎝⎭32为半径的圆，所以AM 的取值范围是6262-+⎣⎦，所以BC 的取值范围是[62,62]．3．在平面直角坐标系xOy 中，已知圆()(22:161C x y -+-=和两点()(),2,,2A a a B a a ---，且1a >，若圆C 上存在两个不同的点,P Q ，使得90APB AQB ∠=∠=︒，则实数a 的取值范围为__________． 【答案】17117a ≤+【解析】原问题等价于以,A B 为圆心的圆与圆C 有两个交点，AB 中点坐标为()0,0，以,A B 为圆心的圆的半径1R = 且圆C 的圆心为(，半径为21R =，两圆的圆心距为： 5d ==， 结合1a >可得关于实数a 的不等式组：15 15≤≥，求解关于实数a的不等式组可得实数a的取值范围为11a ≤≤4．在平面直角坐标系xOy 中，已知点A （1-，0），B （1，0）均在圆C ： ()()22234x y r -+-=外，且圆C 上存在唯一一点P 满足AP BP ⊥，则半径r 的值为____． 【答案】4【解析】根据题意,点A(−1,0),B(1,0)，若点P 满足AP BP ⊥， 则点P 在以AB 为直径的圆上，设AB 的中点为M,则M 的坐标为 (0,0)， |AB|=2， 则圆M 的方程为221x y +=，若圆C 上存在唯一一点P 满足AP BP ⊥，则圆C 与圆M 只有一个交点，即两圆外切，则有5=，解可得r=4.5．已知等边ABC ∆的边长为2，点P 在线段AC 上，若满足等式•PA PB λ=的点P 有两个，则实数λ的取值范围是_____． 【答案】104λ-<≤ 【解析】以AB 中点为坐标原点，AB 所在直线为x 轴建立直角坐标系，则()()(()10,10,,,A B C P x y -，，，AC：()10y x =-≤≤由•PA PB λ=得221x y λ-+= ，()22111,1010044λλλ∴>-=-≤-+-=∴-<≤⎝⎭6.已知圆O ：x 2＋y 2＝1，圆M ：(x －a)2＋(y －a ＋4)2＝1.若圆M 上存在点P ，过点P 作圆O 的两条切线，切点为A ，B ，使得∠APB＝60°，则实数a 的取值范围为____________． 【答案】⎣⎢⎡⎦⎥⎤2－22，2＋22【解析】设P(x ，y)，sin ∠OPA ＝sin30°＝1x 2＋y2，则x 2＋y 2＝4 ①.又P 在圆M 上，则(x －a)2＋(y －a＋4)2＝1 ②.由①②得1≤a 2＋（a －4）2≤3，所以4－22≤a ≤4＋22.7.在平面直角坐标系xOy 中，已知过原点O 的动直线l 与圆C ：x 2＋y 2－6x ＋5＝0相交于不同的两点A ，B ，若点A 恰为线段OB 的中点，则圆心C 到直线l 的距离为____________．【答案】364【解析】∵ 圆C 1：x 2＋y 2－6x ＋5＝0，整理，得其标准方程为(x －3)2＋y 2＝4，∴ 圆C 1的圆心坐标为(3，0)；设直线l 的方程为y ＝kx ，A(x 1，y 1)，B(x 2，y 2)，联立(x －3)2＋y 2＝4，y ＝kx ，消去y 可得(1＋k 2)x2－6x ＋5＝0，由题知x 1＝12x 2, y 1＝12y 2，由韦达定理化简可得k 2＝35，即k ＝±155，直线l 的方程为y ＝±155x ，由点到直线的距离公式知，所求的距离为364.8.在平面直角坐标系xOy 中，过点P(－2，0)的直线与圆x 2＋y 2＝1相切于点T ，与圆(x －a)2＋(y －3)2＝3相交于点R ，S ，且PT ＝RS ，则正数a 的值为____________． 【答案】4【解析】圆x 2＋y 2＝1半径为1，PO ＝2，则直线PT 的倾斜角为30°，则直线方程为x －3y ＋2＝0，PT ＝3，RS ＝3，圆(x －a)2＋(y －3)2＝3的半径为3，则圆(x －a)2＋(y －3)2＝3的圆心(a ，3)到直线PT 的距离为32，由点到直线距离公式得|a －1|＝3，则正数a ＝4.9.在平面直角坐标系xOy 中，圆M ：(x －a)2＋(y ＋a －3)2＝1(a ＞0)，点N 为圆M 上任意一点．若以N 为圆心，ON 为半径的圆与圆M 至多有一个公共点，则a 的最小值为__________． 【答案】3【解析】根据题意，圆M 与以N 为圆心的圆的位置关系是内切或内含．则d MN ≤d ON －1，即1≤d ON －1.所以d ON ≥2恒成立．因为N 在圆M 上运动，所以d ON 的最小值为d OM －1，即d OM －1≥2，所以a 2＋（3－a ）2≥3，解得a≥3，所以a 的最小值为3.10.已知线段AB 的长为2，动点C 满足CA →·CB →＝λ(λ为常数)，且点C 总不在以点B 为圆心，12为半径的圆内，则实数λ的最大值是__________． 【答案】－34【解析】建立平面直角坐标系，B(0，0)，A(2，0)，设C(x ，y)，则CA →·CB →＝x(x －2)＋y 2＝λ，则(x －1)2＋y 2＝λ＋1，得（x －1）2＋y 2＝λ＋1，点C 的轨迹是以(1，0)为圆心λ＋1为半径的圆且与x 2＋y 2＝14外离或相切．所以λ＋1≤12，λ的最大值为－34. 11.在平面直角坐标系xOy 中，设直线y ＝－x ＋2与圆x 2＋y 2＝r 2(r ＞0)交于A ，B 两点．若圆上存在一点C ，满足OC →＝54OA →＋34OB →，则r 的值为________．【答案】10【解析】OC →2＝⎝ ⎛⎭⎪⎫54OA →＋34OB →2＝2516OA →2＋2·54OA →·34OB →＋916OB →2，即r 2＝2516r 2＋158r 2cos ∠AOB ＋916r 2，整理化简得cos ∠AOB ＝－35，过点O 作AB 的垂线交AB 于D ，则cos ∠AOB ＝2cos 2∠AOD －1＝－35，得cos 2∠AOD ＝15.又圆心到直线的距离为OD ＝22＝2，所以cos 2∠AOD ＝15＝OD 2r 2＝2r 2，所以r 2＝10，r ＝10.12.已知圆M ：(x －1)2＋(y －1)2＝4，直线l ：x ＋y －6＝0，A 为直线l 上一点．若圆M 上存在两点B ，C ，使得∠BAC＝60°，则点A 横坐标的取值范围是__________． 【答案】[1，5]【解析】圆M ：(x －1)2＋(y －1)2＝4上存在两点B ，C ，使得∠BAC＝60°，说明点A(x ，y)到M (1，1)的距离小于等于4，即(x －1)2＋(y －1)2≤16，而y ＝6－x ，得x 2－6x ＋5≤0，即1≤x≤5.点A 横坐标的取值范围为[1，5]．13.已知点A(0，2)为圆M ：x 2＋y 2－2ax －2ay ＝0(a ＞0)外一点，圆M 上存在点T 使得∠MAT＝45°，则实数a 的取值范围是________________． 【答案】3－1≤a＜1【解析】点A(0，2)在圆M ：x 2＋y 2－2ax －2ay ＝0(a ＞0)外，得4－4a ＞0，则a ＜1.圆M 上存在点T 使得∠MAT ＝45°，则AM2≤r ＝2a ，即AM≤2a，(a －2)2＋a 2≤4a 2(a ＞0)，解得3－1≤a.综上，实数a 的取值范围是3－1≤a＜1.14.在平面直角坐标系xOy 中，已知圆O 1，圆O 2均与x 轴相切且圆心O 1，O 2与原点O 共线，O 1，O 2两点的横坐标之积为6，设圆O 1与圆O 2相交于P ，Q 两点，直线l ：2x －y －8＝0，则点P 与直线l 上任意一点M 之间的距离的最小值为____________． 【答案】855－ 6【解析】设圆O 1的方程为(x －a)2＋(y －ka)2＝k 2a 2①，圆O 2的方程为⎝ ⎛⎭⎪⎫x －6a 2＋⎝⎛⎭⎪⎫y －6k a 2＝36k2a 2 ②，②－①，得2ax －12a x ＋2aky －12a ky ＋36a 2－a 2＝0，即2x ＋2y －a －6a ＝0.设P(x 0，y 0)，则(x 0－a)2＋(y 0－ka)2＝k 2a 2，即x 20＋y 20＝2ax 0＋2ay 0－a 2，又2x 0＋2y 0－a －6a＝0，可得2ax 0＋2ay 0－a 2＝6，故x 20＋y 20＝6，即点P 的轨迹是以原点为圆心，半径为6的圆，则点P 与直线l 上任意一点M 之间的距离的最小值为855－ 6.15.已知直线l 过点P(1，2)且与圆C ：x 2＋y 2＝2相交于A ，B 两点，△ABC 的面积为1，则直线l 的方程为________________．【答案】x －1＝0，3x －4y ＋5＝0【解析】由S △ABC ＝12×2×sin ∠ACB ＝1，sin ∠ACB ＝1，∠ACB ＝90°，则点C(0，0)到直线l 的距离为1，设直线l 的方程为y －2＝k(x －1)，利用距离公式可得k ＝34，此时直线l 的方程为3x －4y ＋5＝0，当k 不存在时，x －1＝0满足题意．16.在平面直角坐标系xOy 中，已知圆C ：x 2＋(y －1)2＝5，A 为圆C 与x 轴负半轴的交点，过A 作圆C 的弦AB ，记线段AB 的中点为M.若OA ＝OM ，则直线AB 的斜率为________． 【答案】2【解析】设点B(x 0，y 0)，则M ⎝⎛⎭⎪⎫x 0－22，y 02，圆x 2＋(y －1)2＝5与x 轴负半轴的交点A(－2，0)，OA ＝OM ＝2＝⎝ ⎛⎭⎪⎫x 0－222＋⎝ ⎛⎭⎪⎫y 022，即⎝ ⎛⎭⎪⎫x 0－222＋⎝ ⎛⎭⎪⎫y 022＝4.又 x 20＋(y 0－1)2＝5，两式相减得y 0＝2x 0＋4.而A(－2，0)也满足y 0＝2x 0＋4，即直线AB 的方程为y 0＝2x 0＋4，则直线AB 的斜率为2.17.在平面直角坐标系xOy 中，圆C 1：(x ＋1)2＋(y －6)2＝25，圆C 2：(x －17)2＋(y －30)2＝r 2.若圆C 2上存在一点P ，使得过点P 可作一条射线与圆C 1依次交于点A 、B ，满足PA ＝2AB ，则半径r 的取值范围是______________． 【答案】[5，55]【解析】在圆C 2上任取一点P ，过点P 可作一条射线与圆C 1依次交于点A 、B ，当AB 过圆心时，此时PA 在该点处最小，AB 在该点情况下最大，此时在P 点情况下PAPB 最小，当P ，A ，B 三点共线时，如图1，2，PA 为所有位置最小，且PA AB 是所有位置中最小，所以只要满足PAAB ≤2，即满足题意，错误! 5≤r ≤55.18.直角坐标系xOy 中，圆C 的方程为(x －1)2＋(y －1)2＝9，直线l ：y ＝kx ＋3与圆C 相交于A 、B 两点，M 为弦AB 上一动点，以M 为圆心，2为半径的圆与圆C 总有公共点，则实数k 的取值范围为________．【答案】⎣⎢⎡⎭⎪⎫－34，＋∞ 【解析】以M 为圆心，2为半径的圆与圆C 总有公共点，则C 点到直线l 的距离小于1，即d ＝|k ＋2|k 2＋1≤1，解得k ≤－34.19平面直角坐标系xOy 中，已知圆C ：(x －a)2＋(y －a ＋2)2＝1，点A(0，2)，若圆C 上存在点M ，满足MA 2＋MO 2＝10，则实数a 的取值范围是________． 【答案】[0，3]【解析】设M(x ，y)，由MA 2＋MO 2＝10，A(0，2)，得x 2＋(y －1)2＝4，而(x －a)2＋(y －a ＋2)2＝1，它们有公共点，则1≤a 2＋(a －3)2≤9，解得实数a 的取值范围是[0，3]．20.平面直角坐标系xOy 中，圆C 的方程为(x －1)2＋y 2＝4，P 为圆C 上一点．若存在一个定圆M ，过P 作圆M 的两条切线PA 、PB ，切点分别为A 、B ，当P 在圆C 上运动时，使得∠APB 恒为60°，则圆M 的方程为______________． 【答案】(x －1)2＋y 2＝1【解析】∵ 当P 在圆C 上运动时∠APB 恒为60°，∴ 圆M 与圆C 一定是同心圆，∴ 可设圆M 的方程为(x －1)2＋y 2＝r 2.当点P 坐标是(3，0)时，设直线AB 与x 轴的交点为H ，则MH ＋HP ＝2，MH ＝12r ，AB ＝2×32r ，所以12r ＋2×32r ×32＝2，解得r ＝1，所以所求圆M 的方程为(x －1)2＋y 2＝1.。
专题11 高考新题型(原卷版)
11高考新题型基础知识巩固（建议时间：45分钟）1.定义行列式运算12142334a a a a a a a a =-，将函数()3sin 1cos x f x x=的图像向左平移(0)n n >个单位，所得图像关于y 轴对称，则n 的最小值为（ ）A ． 6πB ． 3πC ． 23πD ． 56π 2．【北京市海淀区2018第一学期期末】已知正方体1111ABCD A B C D -的棱长为42，点M 是棱BC 的中点，点P 在底面ABCD 内，点Q 在线段11A C 上，若1PM =，则PQ 长度的最小值为_____．3.设a ，b ∈R ，定义运算“∧”和“∨”如下：a ∧b ＝,{,a a b b a b ≤>，a ∨b ＝,{ ,b a b a a b ≤>若正数a ，b ，c ，d 满足ab ≥4，c ＋d ≤4，则（ ）A ． a ∧b ≥2，c ∧d ≤2B ． a ∧b ≥2，c ∨d ≥2C ． a ∨b ≥2，c ∧d ≤2D ． a ∨b ≥2，c ∨d ≥24.【江西省抚州市临川区一中2018上学期质检】已知正方体1111ABCD A B C D -的体积为1，点M 在线段BC 上（点M 异于B 、C 两点），点N 为线段1CC 的中点，若平面AMN 截正方体1111ABCD A B C D -所得的截面为四边形，则线段BM 的取值范围为（ ）A ． 10,3⎛⎤ ⎥⎝⎦B ． 10,2⎛⎤ ⎥⎝⎦C ． 2,13⎡⎫⎪⎢⎣⎭D ． 1,12⎡⎫⎪⎢⎣⎭ 5．【湖南师大附中2018上学期月考】狄利克雷函数是高等数学中的一个典型函数，若()1,{ 0,R x Qf x x C Q ∈=∈，则称()f x 为狄利克雷函数．对于狄利克雷函数()f x ，给出下面4个命题：①对任意x R ∈，都有()1f f x ⎡⎤=⎣⎦；②对任意x R ∈，都有()()0f x f x -+=；③对任意1x R ∈，都有2x Q ∈， ()()121f x x f x +=；④对任意(),,0a b ∈-∞，都有(){}(){}x f x a x f x b =．其中所有真命题的序号是（ ）A ． ①④B ． ②③C ． ①②③D ． ①③④6．【北京市朝阳区2019届第一学期期末】如图， PAD ∆为等边三角形，四边形ABCD 为正方形，平面PAD ⊥平面ABCD ．若点M 为平面ABCD 内的一个动点，且满足MP MC =，则点M 在正方形ABCD 及其内部的轨迹为（ ）A ． 椭圆的一部分B ． 双曲线的一部分C ． 一段圆弧D ． 一条线段7.设D 是函数y ＝f (x )定义域内的一个区间，若存在x 0∈D ，使得f (x 0)＝－x 0，则称x 0是f (x )的一个“次不动点”，也称f (x )在区间D 上存在“次不动点”．若函数f (x )＝ax 2－3x －a ＋52在区间[1,4]上存在“次不动点”，则实数a 的取值范围是( )A ．(－∞，0]B.⎝⎛⎭⎫0，12C.⎝⎛⎦⎤－∞，12D.⎣⎡⎭⎫12，＋∞ 8.【北京市石景山区2018届第一学期期末】小明在如图1所示的跑道上匀速跑步，他从点A 出发，沿箭头方向经过点B 跑到点C ，共用时30s ，他的教练选择了一个固定的位置观察小明跑步的过程，设小明跑步的时间为()t s ，他与教练间的距离为()y m ，表示y 与t 的函数关系的图象大致如图2所示，则这个固定位置可能是图1中的（ ）A ． 点MB ． 点NC ． 点PD ． 点Q9.若集合(){,,,04,04,04Εp q r s p s q s r s =<<<≤≤≤≤≤≤，且,,,}p q r s ∈N ，(){},,,04,04,,,F t u v w t u v w t u v w =<<∈N ≤≤≤≤且，用()card Χ表示集合Χ中的元素个数，则()()card card ΕF +=（ ）10．若直角坐标平面内不同两点P，Q满足条件：①P，Q都在函数y＝f(x)的图象上；②P，Q关于原点对称，则称(P，Q)是函数y＝f(x)的一个“伙伴点组”(点组(P，Q)与(Q，P)可看成同一个“伙伴点组”)．已知函数f(x)＝()21,0{1,0k x xx x+<+≥有两个“伙伴点组”，则实数k的取值范围是______________．11．【河南省焦作市2017届高三下学期第二次模拟】《孙子算经》是我国古代内容极其丰富的数学名著，书中有如下问题：“今有圆窖，周五丈四尺，深一丈八尺，问受粟几何？”其意思为：“有圆柱形容器，底面圆周长五丈四尺，高一丈八尺，求此容器能装多少斛米.”则该圆柱形容器能装米__________斛.（古制1丈=10尺，1斛=1.62立方尺，圆周率）12．【黑龙江省哈尔滨市第三中学2017年第一次高考模拟考试】进位制是人们为了计数和运算方便而约定的计数系统，“满几进一”就是几进制，不同进制之间可以相互转化，例如把十进制的89转化为二进制，根据二进制数“满二进一”的原则，可以用2连续去除89得商，然后取余数，具体计算方法如下：把以上各步所得余数从下到上排列，得到这种算法叫做“除二取余法”，上述方法也可以推广为把十进制数化为进制数的方法，称为“除取余法”，那么用“除取余法”把89化为七进制数为__________．13．【广西南宁市2017届高三第一次适应性测试】我国古代数学著作《九章算术》有如下问题：“今有金箠，长五尺.斩本一尺，重四斤．斩末一尺，重二斤．问次一尺各重几何？”意思是：“现有一根金杖，长5尺，一头粗，一头细．在粗的一端截下1尺，重4斤；在细的一端截下1尺，重2斤；问依次每一尺各重多少斤？”设该金杖由细到粗是均匀变化的，其重量为.现将该金杖截成长度相等的10段，记第段的重量为，且，若，则__________．14．【江西省红色七校2017届高三下学期第二次联考】下边程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”，执行该程序框图（图中“m MOD n”表示除以的余数），若输入的m，n分别为485，135，则输出的m=（）A. 0B. 5C. 25D. 45能力提升（建议时间：35分钟）15．【2017届四川省简阳市期末检测数学】齐王与田忌赛马，田忌的上等马优于齐王的中等马，劣于齐王的上等马，田忌的中等马优于齐王的下等马，劣于齐王的中等马，田忌的下等马劣于齐王的下等马，现从双方的马匹中随机选一匹进行一场比赛，则齐王的马获胜概率为（）A. B. C. D.16．【2017届河北省石家庄市第二中学高三下学期模拟联考】在《九章算术》中有一个古典名题“两鼠穿墙”问题：今有垣厚五尺，两鼠对穿.大鼠日一尺，小鼠也日一尺.大鼠日自倍，小鼠日自半，问何日相逢？大意是有厚墙五尺，两只老鼠从墙的两边分别打洞穿墙.大老鼠第一天进一尺，以后每天加倍；小老鼠第一天也进一尺，以后每天减半.问几天后两鼠相遇？（）A. B. C. D.17.如图，正方形ABCD 内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点，则此点取自黑色部分的概率是A ．14B ．π8 C ．12 D ．π4 18.2016年1月14日，国防科工局宣布，嫦娥四号任务已经通过了探月工程重大专项领导小组审议通过，正式开始实施.如图所示，假设“嫦娥四号”卫星将沿地月转移轨道飞向月球后，在月球附近一点P 变轨进入以月球球心F 为一个焦点的椭圆轨道Ⅰ绕月飞行，之后卫星在P 点第二次变轨进入仍以F 为一个焦点的椭圆轨道Ⅱ绕月飞行.若用2c 1和2c 2分别表示椭圆轨道Ⅰ和Ⅱ的焦距，用2a 1和2a 2分别表示椭圆轨道Ⅰ和Ⅱ的长轴长，给出下列式子：①a 1＋c 1＝a 2＋c 2；②a 1－c 1＝a 2－c 2；③c 1a 1<c 2a 2；④c 1a 2>a 1c 2. 其中正确式子的序号是( )A.①③B.①④C.②③D.②④19.某产品进入商场销售，商场第一年免收管理费，因此第一年该产品定价为每件70元，年销售量为11.8万件，从第二年开始，商场对该产品征收销售额的%x 的管理费（即销售100元要征收x 元），于是该产品定价每件比第一年增加了70%1%x x ⋅-元，预计年销售量减少x 万件，要使第二年商场在该产品经营中收取的管理费不少于14万元，则x 的最大值是（ ）A. 2B. 6C. 8.5D. 1020.【2017届河南省安阳市高三第一次模拟考试数学】三国时代吴国数学家赵爽所注《周髀算经》中给出了勾股定理的绝妙证明．下面是赵爽的弦图及注文，弦图是一个以勾股形之弦为边的正方形，其面积称为弦实．图中包含四个全等的勾股形及一个小正方形，分别涂成红（朱）色及黄色，其面积称为朱实、黄实，利用勾股股勾朱实黄实弦实，化简，得勾股弦．设勾股形中勾股比为，若向弦图内随机抛掷1000颗图钉（大小忽略不计），则落在黄色图形内的图钉数大约为（ ）A. 866B. 500C. 300D. 13421. 【2019全国II 理4】2019年1月3日嫦娥四号探测器成功实现人类历史上首次月球背面 软着陆，我国航天事业取得又一重大成就.实现月球背面软着陆需要解决的一个关键技术问 题是地面与探测器的通讯联系．为解决这个问题，发射了嫦娥四号中继星“鹊桥”，鹊桥沿 着围绕地月拉格朗日2L 点的轨道运行．2L 点是平衡点，位于地月连线的延长线上．设地球 质量为M １，月球质量为M ２，地月距离为R ，2L 点到月球的距离为r ，根据牛顿运动定律和 万有引力定律，r 满足方程：121223()()M M M R r R r r R +=++. 设r Rα=，由于α的值很小，因此在近似计算中34532333(1)ααααα++≈+，则r 的近似值为 A 21M R M B 212M R M C 2313M R M D 2313M R M。
专题11 圆的最值问题(隐圆模型)(解析版)-2024年常考压轴题攻略(9年级上册人教版)
专题11圆的最值问题（隐圆模型）【知识点梳理】隐圆模型汇总固定线段AB所对同侧动角∠P=∠C，则A、B、C、P四点共圆若P为动点，但AB=AC=AP，则B、C、P三点共圆，A圆心，AB半径固定线段AB所对动角∠C恒为90°，则A、B、C三点共圆，AB为直径A．1B．作正方形ABCD关于直线BC对称的正方形则点D的对应点是F，连接FO交BC于P，交半圆O于=，根据对称性有：PD PF+=+，则有：PE PD PE PF+的长度最小值，则线段EF的长即为PE PD【答案】634-【分析】取AD 的中点O ，连接OF BC ⊥于F ，交CD 于G 取AD 的中点O ，连接OM ，过点于F ，交CD 于G ，则OM ME + AB CD ，60DAB ∠= ，AD ∴120ADC ∠=︒，AD CD =，【答案】3∴BD＝2，∴11 2BD=．D运动的一个动点，联结EF，将AEF沿EF折叠，点A落在点G处，在运动的过程中，点G运动的路径长为（）A．23πB C．3πD．1【答案】A【详解】解：∵点E 为AB 中点，点F 为AD 边上从A 到D 运动的一个动点，联结EF ，将AEF 沿EF 折叠，∴AE EB EG ==，∴G 点在以E 为圆心，AE 长为半径的圆上运动．当F 与D 点重合时，如图，则G 点运动的路径为 AG ．∵AB ＝2，点E 为AB 中点，∴112AE AB ==，∵矩形ABCD ，∴90EAD ∠=︒，∵1AE =，AD =90EAD ∠=︒，∴tan AD AED AE∠==60AED ∠=︒．∵将AEF 沿EF 折叠，∴60DEG AED ∠=∠=︒，∴120AEG ∠=︒，∵1AE =，∴120223603AG AE ππ=⨯⨯=．故选：A ．3．如图，在Rt ABC 中，90ACB ∠=︒，5AC =，12BC =，D 是以点A 为圆心，3为半径的圆上一点，连接BD ，M 是BD 的中点，则线段CM 长度的最小值为（）A ．3B ．4C ．5D ．6【答案】C 【详解】作AB 的中点E ，连接EM 、CE 、AD ，则有AD =3，∵∠ACB =90°，即在Rt ABC 中，13AB ==，∵E 是Rt ABC 斜边AB 上的中点，∴11322CE AB ==，∵M 是BD 的中点，E 是AB 的中点，∴1322ME AD ==，∴在CEM 中，1331332222CM -+＜＜，即58CM ＜＜；当C 、M 、E 三点共线时有133822CM +==或者133522CM -==；即58CM ≤≤，∴CM 最小值为5，故选：C ．【答案】21022-【分析】由题意可知，AGB ∠圆周角45APB ∠=︒的圆上，（要使。
隐圆专题
皖ICP 备裕安中学电教中心
二、合理发散，注意找根
（一）、找定点，定圆心，找定长，定半径 例1：如图，在矩形中，AB=4，AD=6，E是AB边的中点，F 是线段BC边上的动点，将△EBF沿EF所在直线折叠得到 △EB'F，连接B’D，则B’D的最小值是__2__1_0_- 2
A． 4+4 2 B． 2+4 2
C． 4 2 D．6
皖ICP 备裕安中学电教中心
练习：如图，正方形ABCD中，AB=2，动点E从点 A出发向点D运动，同时动点F从点D出发向点C运 动，点E、F运动的速度相同，当它们到达各自终 点时停止运动，运动过程中线段AF、BE相交于点 P，则线段DP的最小值为___5__1__．
C(0,5),点D在第一象限内,且∠ADB=60∘.则线段CD的最
小值为（
B）
A、2 3 B、2 7 - 2
C、4
D、2 13 - 2
皖ICP 备裕安中学电教中心
【拓展提高】：如图，矩形ABCD中，AB=2，AD=3， 点E、F分别为AD、DC边上的点，且EF=2，点G为EF的 中点，点P为BC上一动点，则PA+PG的最小值为____。
皖ICP 备裕安中学电教中心
三、小结 通过本节课的学习你有哪些收获？
1、圆O外一点A到圆上一点B的最值问题 当O，B，A三点共线， 若点A、B位于点O同侧时，AB取最小值, 若点A、B位于点O两侧时，AB取最大值。
2、口诀：定点定长走圆周，定线定角跑双弧。 直角必有外接圆，对角互补也共圆。
四、作业：完成发的强化练习
用“隐圆”巧解最值问题
专题11 解题技巧专题：勾股定理与面积问题、方程思想压轴题七种模型全攻略(原卷版)
专题11解题技巧专题：勾股定理与面积问题、方程思想压轴题七种模型全攻略【考点导航】目录【典型例题】 (1)【类型一三角形中，利用面积求斜边上的高】 (1)【考点二结合乘法公式巧求面积或长度】 (3)【考点三巧妙割补求面积】 (3)【考点四“勾股树”及其拓展类型求面积】 (5)【考点五几何图形中的方程思想—折叠问题（利用等边建立方程）】 (7)【考点六几何图形中的方程思想—公边问题（利用公边建立方程）】 (9)【考点七实际问题中的方程思想】 (10)【典型例题】【类型一三角形中，利用面积求斜边上的高】A．8013B．【变式训练】1．（2023春·内蒙古鄂尔多斯·八年级统考期末）如图，在22 的方格中，小正方形的边长是1，点A、B、C 都在格点上，则AC边上的高为（）A ．52．（2023春·辽宁朝阳高为（）A ．123．（2022·全国·八年级课时练习）如图，在网格中，每个小正方形的边长均为1．点A 、B ，C 都在格点上，若BD 是△ABC 的高，则BD 的长为__________．4．（2023春·安徽合肥·八年级校考期末）如图所示，在边长为单位1的网格中，ABC 是格点图形，求ABC 中AB 边上的高．5．如图，在Rt ABC △中，90C ∠=︒，8AC =，在ABE △中，DE 是AB 边上的高，12DE =，60ABE S =△．(1)求BC 的长．(2)求斜边AB 边上的高．6．（2023秋·全国·八年级专题练习）在ABC 中，90C ∠=︒，3AC =，4CB =，CD 是斜边AB 上高．(1)求ABC 的面积；(2)求斜边AB ；(3)求高CD ．【类型二结合乘法公式巧求面积或长度】例题：已知在Rt ABC 中，90,,C A B C ∠=︒∠∠∠,所对的边分别为a ，b ，c ，若10cm,8cm a b c +==，则Rt ABC的面积为（）A ．29cm B ．218cm C ．224cm D ．236cm 【变式训练】1．在ABC 中，AD 是BC 边上的高，4,5AD AB AC ===，则ABC 的面积为（）A ．18B ．24C ．18或24D ．18或303．直角ABC 三边长分别是x ，1x +和5，则ABC 的面积为__________．【类型三巧妙割补求面积】例题：（2023春·河南许昌·八年级校考期中）如图，在四边形ABCD 中，已知90B Ð=°，30ACB ∠=︒，6AB =，13AD =，5CD =．是直角三角形；(1)求证：ACD(2)求四边形ABCD的面积．【变式训练】(1)求这个四边形草地的面积；(2)如果清理草地杂草，每平方米需要人工费4．（2022春·重庆綦江·八年级校考阶段练习）计算：如图，每个小正方形的边长都为1．(1)求线段CD 与BC 的长；(2)求四边形ABCD 的面积；(3)求证：90BCD ∠=︒．【类型四“勾股树”及其拓展类型求面积】例题：（2023秋·重庆渝中·八年级重庆巴蜀中学校考期末）如图，所有的四边形都是正方形，所有的三角形都是直角三角形，若正方形A 、B 、C 、D 的面积分别是6、10、4、6，则最大正方形E 的面积是（）A ．20B ．26C ．30D ．52【变式训练】1．（2023·广西柳州·校考一模）如图，90BDE ∠=︒，正方形BEGC 和正方形AFED 的面积分别是289和225，则以BD 为直径的半圆的面积是（）A ．16πB ．8πC ．4πD ．2π2．（2023春·全国·八年级专题练习）如图，以Rt ABC 的三边向外作正方形，其面积分别为123,,S S S 且124,8S S ==，则3S =___________；以Rt ABC 的三边向外作等边三角形，其面积分别为123,,S S S ，则123,,S S S 三者之间的关系为___________．3．（2023春·八年级课时练习）已知：在Rt ABC 中，90C ∠=︒，A ∠、B ∠、C ∠所对的边分别记作a 、b 、c ．如图1，分别以ABC 的三条边为边长向外作正方形，其正方形的面积由小到大分别记作1S 、2S 、3S ，则有123S S S +=，(1)如图2，分别以ABC 的三条边为直径向外作半圆，其半圆的面积由小到大分1S 、2S 、3S ，请问12S S +与3S 有怎样的数量关系，并证明你的结论；(2)分别以直角三角形的三条边为直径作半圆，如图3所示，其面积由小到大分别记作S 1、S 2Sa ，根据（2）中的探索，直接回答12S S +与3S 有怎样的数量关系；(3)若Rt ABC 中，6AC =，8BC =，求出图4中阴影部分的面积．4．（2023春·江西南昌·八年级南昌市第三中学校考期中）勾股定理是人类最伟大的十个科学发现之一，西方国家称之为毕达哥拉斯定理．在我国古书《周髀算经》中就有“若勾三，股四，则弦五”的记载，我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”（如图1），后人称之为“赵爽弦图”，流传至今．(1)①如图2，3，4，以直角三角形的三边为边或直径，分别向外部作正方形、半圆、等边三角形，面积分别为1S ，2S ，3S ，利用勾股定理，判断这3个图形中面积关系满足123S S S +=的有________个．②如图5，分别以直角三角形三边为直径作半圆，设图中两个月牙形图案（图中阴影部分）的面积分别为1S ，2S ，直角三角形面积为3S ，也满足123S S S +=吗？若满足，请证明；若不满足，请求出1S ，2S ，3S 的数量关系．(2)如果以正方形一边为斜边向外作直角三角形，再以该直角三角形的两直角边分别向外作正方形，重复这一过程就可以得到如图6所示的“勾股树”．在如图7所示的“勾股树”的某部分图形中，设大正方形M 的边长为定值m ，四个小正方形A ，B ，C ，D 的边长分别为a ，b ，c ，d ，则2222a b c d +++=__________．【类型五几何图形中的方程思想—折叠问题（利用等边建立方程）】例题：（2023春·河南许昌·八年级统考期中）已知直角三角形纸片ABC 的两直角边长分别为6，8，现将ABC 按如图所示的方式折叠，使点A 与点B 重合，则CE 的长是（）A．54B．74C．15【变式训练】1．（2023春·湖北咸宁·八年级校考阶段练习）如图，有一块直角三角形纸片，A．3 42．（2023春·山东菏泽使点C与AB的中点3．（2023·辽宁葫芦岛·统考二模）如图，在点E是斜边AB上一动点，直角三角形，则AE的长为4．（2022秋·河北张家口·点重合）．将ADE V 沿DE 折叠，点A 落在A '的位置．(1)如图①，当A '与点B 重合且3,5BC AB ==．①直接写出AC 的长；②求BCD △的面积．(2)当37A ∠=︒．①A '与点E 在直线AC 的异侧时．如图②，直接写出A EB A DC ∠-'∠'的大小；②A '与点E 在直线AC 的同侧时，且A DE ' 的一边与BC 平行，直接写出ADE ∠的度数．【类型六几何图形中的方程思想—公边问题（利用公边建立方程）】例题：如图，在△ABC 中，AB ＝10，BC ＝9，AC ＝17，则BC 边上的高为_______．【变式训练】1．已知：如图，在ABC 中，90C AD ∠=︒，是ABC 的角平分线，35CD BD ==，，则AC =____．2．如图，在Rt ABC △和Rt ADE △中，90B D ∠=∠=︒，AC AE =，BC DE =，延长BC ，DE 交于点M ．(1)求证：点A 在M ∠的平分线上；(2)若AC DM ∥，12AB =，18BM =，求BC 的长．【类型七实际问题中的方程思想】例题：（2022·全国·八年级）明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》：“平地秋千未起，踏板一尺离地，送行二步恰竿齐，五尺板高离地……”翻译成现代文为：如图，秋千绳索OA 悬挂于O 点，静止时竖直下垂，A 点为踏板位置，踏板离地高度为一尺（AC ＝1尺）．将它往前推进两步（EB ⊥OC 于点E ，且EB ＝10尺），踏板升高到点B 位置，此时踏板离地五尺（BD ＝CE ＝5尺），则秋千绳索（OA 或OB ）长______尺．【变式训练】1．（2022·全国·八年级课时练习）如图1、2（图2为图1的平面示意图），推开双门，双门间隙CD 的距离为2寸，点C 和点D 距离门槛AB 都为1尺（1尺＝10寸），则AB 的长是（）A ．50.5寸B ．52寸C ．101寸D ．104寸2．（2022·河南·金明中小学八年级期中）《九章算术》是我国古代数学名著，有题译文如下：今有门，不知其高宽；有竿，不知其长短．横放，竿比门宽长出4尺；竖放，竿比门高短2尺；斜放，门对角线长恰好倍．问门高、门宽各为多少？3．（2022·重庆市求精中学校八年级期中）在一条东西走向的河的一侧有一村庄C ，河边原有两个取水点A ，B ，其中AB AC =，由于某种原由C 到A 的路现在已经不通，某村为方便村民取水决定在河边新建一个取水点H （A 、H 、B 在一条直线上），并新修一条路CH ，测得 1.5CB =千米， 1.2CH =千米，0.9HB =千米．(1)问CH 是否为从村庄C 到河边的最近路？请通过计算加以说明．(2)求原来的路线AC 的长．4．（2022·浙江·浦江县实验中学八年级期中）图1是一张可以折叠的小床展开后支撑起来放在地面的示意图，此时点A 、B 、C 在同一直线上，且∠ACD ＝90°，图2是小床支撑脚CD 折叠的示意图，在折叠过程中，△ACD 变形为四边形ABC'D'，最后折叠形成一条线段BD ''．某家装厂设计的折叠床是AB ＝4cm ，BC ＝8cm ，（1）此时CD 为_________cm ；（2）折叠时，当AB ⊥BC′时，四边形ABC′D′的面积为_______cm 2．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1 B 为圆心， 为半径
2
的圆内，则实数λ的最大值是 __________．
11. 在平面直角坐标系 xOy 中，设直线 y＝－ x＋2 与圆 x2＋ y2＝ r2(r ＞ 0) 交于 A， B 两点．若圆上存在
一点 C，满足 O→C＝ 54O→A＋ 34O→B，则 r 的值为 ________． 12. 已知圆 M：(x － 1)2 ＋ (y － 1)2 ＝ 4，直线 l ：x＋ y－6＝ 0，A 为直线 l 上一点． 若圆 M上存在两点 B， C，使得∠ BAC＝ 60°，则点 A 横坐标的取值范围是 __________． 13. 已知点 A(0 ， 2) 为圆 M： x2＋ y2－ 2ax－ 2ay＝ 0(a ＞ 0) 外一点，圆 M上存在点 T 使得∠ MAT＝ 45°， 则实数 a 的取值范围是 ________________ ． 14. 在平面直角坐标系 xOy 中，已知圆 O1，圆 O2 均与 x 轴相切且圆心 O1， O2 与原点 O 共线， O1，O2 两点的横坐标之积为 6，设圆 O1 与圆 O2 相交于 P，Q两点，直线 l ：2x－ y－ 8＝ 0，则点 P与直线 l 上 任意一点 M之间的距离的最小值为 ____________． 15. 已知直线 l 过点 P(1 ，2) 且与圆 C：x2＋ y2＝ 2 相交于 A，B 两点，△ ABC的面积为 1，则直线 l 的方 程为 ________________ ． 16. 在平面直角坐标系 xOy 中，已知圆 C：x2＋ (y －1)2 ＝ 5，A 为圆 C与 x 轴负半轴的交点，过 A 作圆 C 的弦 AB，记线段 AB的中点为 M.若 OA＝ OM，则直线 AB 的斜率为 ________． 17. 在平面直角坐标系 xOy 中，圆 C1： (x ＋ 1)2 ＋ (y － 6)2 ＝ 25，圆 C2：(x － 17)2 ＋ (y － 30)2 ＝ r2. 若圆 C2 上存在一点 P，使得过点 P 可作一条射线与圆 C1 依次交于点 A、 B，满足 PA＝ 2AB，则半径 r 的取值 范围是 ______________． 18. 直角坐标系 xOy 中，圆 C 的方程为 (x － 1)2 ＋ (y － 1)2 ＝ 9，直线 l ： y＝ kx＋ 3 与圆 C 相交于 A、 B 两 点，M为弦 AB上一动点，以 M为圆心，2 为半径的圆与圆 C总有公共点， 则实数 k 的取值范围为 ________． 19 平面直角坐标系 xOy 中，已知圆 C： (x －a)2 ＋ (y － a＋ 2)2 ＝1，点 A(0 ， 2) ，若圆 C 上存在点 M，满 足 MA2＋ MO＝2 10，则实数 a 的取值范围是 ________． 20. 平面直角坐标系 xOy 中，圆 C 的方程为 (x － 1)2 ＋ y2＝ 4，P 为圆 C上一点．若存在一个定圆 M，过 P 作圆 M的两条切线 PA、 PB，切点分别为 A、B，当 P 在圆 C上运动时，使得∠ APB恒为 60°，则圆 M的 方程为 ______________．
专题 11 隐圆问题
直线与圆是高中数学的 C级知识点，是高中数学中数形结合思想的典型体现．但有些时候，在条件 中没有直接给出圆方面的信息，而是隐藏在题目中的，要通过分析和转化，发现圆（或圆的方程）， 从而最终可以利用圆的知识来求解，我们称这类问题为“隐形圆”问题
类型一 典例 1
利用圆的定义（到定点的距离等于定长的点的轨迹）确定隐形圆
BC 的长的取值范围为 _______
2
2
3．在平面直角坐标系 xOy 中，已知圆 C : x 1 y 2 6 1和两点 A a,2 a , B a, a 2 ，
且 a 1 ，若圆 C 上存在两个不同的点 P, Q ，使得 APB AQB 90 ，则实数 a 的取值范围为
__________ ． 4．在平面直角坐标系
B，若点 A恰为线段 OB的中点，则圆心 C到直线 l 的距离为 ____________ ．
8. 在平面直角坐标系 xOy 中，过点 P( －2，0) 的直线与圆 x2 ＋ y2＝ 1 相切于点 T，与圆 (x － a)2 ＋(y － 3)2
＝ 3 相交于点 R， S，且 PT＝RS，则正数 a 的值为 ____________ ．
如果圆 ( x 2a )2 ( y a 3)2 4 上总存在两个点到原点的距离为
1，则实数 a的取值范围是
________
类型二 由圆周角的性质确定隐形圆
典例 2 已知圆 O : x2 y2 5, A, B 为圆 O 上的两个动点，且 AB 2, M 为弦 AB 的中点， C 2 2, a , D 2 2, a 2 . 当 A, B 在圆 O 上运动时，始终有 CMD 为锐角，则实数 a 的取值范围
xOy 中，已知点 A（ 1， 0）， B（ 1， 0）均在圆 C ：
2
x3
2
2
y4 r
外，且圆 C 上存在唯一一点 P 满足 AP BP ，则半径 r 的值为 ____．
5．已知等边 ABC 的边长为 2，点 P 在线段 AC 上，若满足等式 PA ?PB 的点 P 有两个，则实数
的取值范围是 _____． 6. 已知圆 O：x2＋ y2＝1，圆 M： (x － a)2 ＋ (y － a＋ 4)2 ＝ 1. 若圆 M上存在点 P，过点 P 作圆 O的两条切 线，切点为 A， B，使得∠ APB＝ 60°，则实数 a 的取值范围为 ____________． 7. 在平面直角坐标系 xOy 中，已知过原点 O的动直线 l 与圆 C：x2＋ y2－ 6x＋ 5＝ 0 相交于不同的两点 A，
9. 在平面直角坐标系 xOy 中，圆 M：(x － a)2 ＋ (y ＋a－ 3)2 ＝1(a ＞ 0) ，点 N为圆 M上任意一点．若以 N 为圆心， ON为半径的圆与圆 M至多有一个公共点，则 a 的最小值为 __________ ．
10. 已知线段
AB的长为 2，动点 C 满足 C→A·C→B＝λ ( λ为常数 ) ，且点 C 总不在以点
为 __________ ．
类型三 两定点 A、 B，动点 P 满足 PA ( 0, 1) 确定隐形圆（阿波罗尼斯圆） PB
典例 3 一缉私艇巡航至距领海边界线 l （一条南北方向的直线） 3.8 海里的 A 处，发现在其北偏东 30°
方向相距 4 海里的 B 处有一走私船正欲逃跑，缉私艇立即追击．已知缉私艇的最大航速是走私船最大 航速的 3 倍．假设缉私艇和走私船均按直线方向以最大航速航行． （ 1截成功；（参
考数据： sin17
3 , 33 5.7446 ）
6
（ 2）问：无论走私船沿何方向逃跑，缉私艇是否总能在领海内成功拦截？并说明理由．
1．已知 ABC 中， AB AC 3 ， ABC 所在平面内存在点 P 使得 PB 2 PC2 3PA2 3 ，则
ABC 面积的最大值为 __________ ． 2．在平面直角坐标系 xOy 中，已知 B， C 为圆 x2 y 2 4 上两点， 点 A(1,1) ，且 AB⊥ AC，则线段