第一章 磁路
第一章 磁路

Ce--涡流损耗系数,取决于材料的电阻率 Δ--硅钢片厚度. 为减小涡流损耗,电机和变压器铁心 采用含硅量较高的薄硅钢片(0.35~0.5mm)叠成。
43
3. 铁心损耗 铁心损耗为磁滞损耗和涡流损耗之和,即
PFe P h P e (Ch fBm Ce f Bm )V
磁链 Ψ=NФ 按右手螺旋关系确定e与Ф的方向 感应电势正方向:楞次定律
楞次定律:感应电动势趋于产生一个电流,该电流的方向 总是阻止产生此感应电动势的磁通的变化。
13
(3) 电磁力
通电导体在磁场中要受到电磁力的作用 F = Bil (N) 电磁力方向:左手定则
14
图4 电磁力方向(左手定则)
15
③ 铁磁材料磁导率μ不是常数, 且μFe>>μ0 常用铁磁材料μFe=(2000~6000)μ0
8
◆ H与B 的关系与区别
⑴ H代表电流本身产生的磁场的强弱,反应了电流 的励磁能力,与介质的性质无关, H ∝ I ⑵ B代表电流产生的且介质被磁化后的总磁场的强 弱,其大小不仅与电流的大小有关,还与介质的性 质有关。 B=μH 空心线圈: B0=μ0H, 加入铁心BFe=μFeH BFe>>B0 通电线圈中加入铁心可以大大增强磁感应强度B
H2 H1
i
H1>H2
21
(2) 磁路的欧姆定律
Hl Ni
Ni F H l l
H
B
/ A
A
F F F H A A l l / A Rm
22
磁路的欧姆定律
F Rm
磁动势: 磁阻: I=U/R F=Ni--作用在磁路上的安匝数
第一章大学物理磁路

一、简单串联磁路
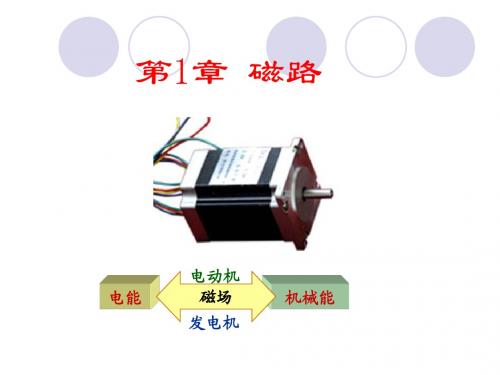
[例1-2] 铁心由铸钢和空气隙构成,截面积AFe=0.0009m2,
磁路平均长度lFe=0.3m,气隙长度δ=5×10-4m,求该磁路获 得磁通量Φ=0.0009Wb时所需的励磁磁动势。
解:铁心内磁通密度为 BFeA Fe0 0..0 00 00 0T9 91T
解 用安培环路定律求解如下
H B / F e50 0 1 4 π 0 1 0 7 0 A /1 m A 59/m
F H 1 l 0 5 . 3 A 9 4 . 7 A 7
iF/N4.7A9.5 410 2A 500
3、磁路的基尔霍夫定律
(1)磁路的基尔霍夫电流定律
1230 或
0
(2)磁路的基尔霍夫电压定律
2、涡流损耗——铁心内部由于涡流在铁心电阻上产生的 热能损耗。
3、铁心损耗——磁滞损耗和涡流损耗之和。
第三节 直流磁路的计算
磁路计算正问题——给定磁通量,计算所需的励磁磁动势 磁路计算逆问题——给定励磁磁势,计算磁路内的磁通量
磁路计算正问题的步骤: 1)将磁路按材料性质和不同截面尺寸分段; 2)计算各段磁路的有效截面积Ak和平均长度lk; 3)计算各段磁路的平均磁通密度Ak ,Bk=Φk/Ak; 4)根据Bk求出对应的Hk; 5)计算各段磁位降Hklk,最后求出 F=∑ Hklk。
第一章 磁路
第一节 磁路的基本定律
电机是进行机电能量转换的装置。
机电能量转换的媒介是磁场,磁通所经过的 路径称为磁路。
在工程中,通常将磁场问题简化为磁路问题。
一. 磁场的几个常用量
磁感应强度(又称磁通密度)B ——表征磁场强弱及 方向的物理量。单位:Wb/m2
第1章磁路
T 1T
从铸钢磁化曲线查得:与BFe对应的HFe=9×102A/m 铁心段的磁位降: H Fe l Fe 9 10 0 . 3 A 270 A
2
空气隙中: B
H
A B
0 . 0009 3 . 05 10
2 4
T 0 . 967 T
4
0 . 967 4 10
电磁力方向:左手定则判断
f
在旋转电机里,作用在转子载流导体上的电磁力将 使转子受到一个力矩,即为电磁力矩。在电机进行 机电能量转换过程中起着重要作用。
上一张下一张
4. 磁路欧姆定律
Φ 铁心中: Bc = u Ac Bc - Φ = Hc = c c Ac 气隙中: B0 = Φ A0 B0 Φ = H0 = 0 0 A0 安培环路定律: ∮H dl = I =F
N I 一定时, 因 Rm0 的存在,使Φ 大大减小; 若要保持 Φ 一定,则需增大磁动势 F。
上一张下一张
5、磁路的基尔霍夫第一定律
任何磁路中,流进节点的磁通代数和为零 A
1
2
3
节点A: 1+ 2+ 3=0
6、磁路的基尔霍夫第二定律 在闭合磁回路中,磁路各段磁压降代数和等于 作用于该磁路上的磁动势之和。 Hl Ni 该定律的本质是全电流定律。
上一张下一张
(3)铁芯损耗
铁芯中的磁滞损耗和涡流损耗之合称为铁芯损耗, 即有:
p Fe p h p w
1 .3
对于一般的电工硅钢片,可以近似写成:
PFe C Fe f
B G
2 m
铁心损耗与频率的1.3次方、磁通密度的平方和 铁心重量成正比。
第1章磁路me

(1)安培环路定律 ——全电流定律
在磁路中,沿任意一闭合路径L,磁场强度H的线积分∮Hdl 恒等于该闭合路径所包围的电流的代数和i ,这就是安培环 路定律或全电流定律。
∮LH dl= i ∮LH dl= -i1+i2-i3
若沿着回路L,H的方向总是沿着 切线方向,大小处处相等,且闭合 回线所包围的总电流是由通有电流 i的N匝线圈所提供
1.4 磁路计算
1.直流磁路的计算
在直流磁路中进行计算时,漏磁通忽略不计,每段磁路中的磁通处处相 等。 对于磁路计算的正问题可按下述步骤进行: (1)按磁路中各部分的材料和截面积进行分段,要求每段磁路的材料 相同,截面积相等。 (2)根据磁路尺寸计算出各段磁路的有效截面积Sk和平均长度l。 在计算用硅钢片叠成的铁芯的有效截面积时,必须除去片间绝缘膜 厚度,一般按下式计算,即
直导线电流的磁场
线圈电流的磁场
某点磁感应强度的大小可以用该点磁场作用于长1m,通过1A电流的导体 上的力来衡量,该导体与磁场方向垂直,即
B
F LI
若磁场内各点的磁感应强度大小相等, 方向也相同,则称该磁场为均匀磁场。 在SI中,B的单位为T,即Wb/m2。
2
Copyright © 2010 电气工程系. All Rights Reserved
1.2 铁磁物质的磁性能
1.铁磁材料的高磁导率
磁性物质内部存在着很多很小的“磁畴”。
磁畴(磁化前)
磁畴(磁化后)
磁性物质的高导磁性被广泛应用于变压器和电机中。
6
Copyright © 2010 电气工程系. All Rights Reserved
1.2 铁磁物质的磁性能
2.铁磁材料的磁饱和性
第一章 磁路基础知识

l1 l2 3l 15 10 2 m 两边磁路长度:
气隙磁位降: B 1.211 2H 2 2 2.5 10 3 A 4818 A 0 4π 10 7
1.211 (2 0.25) 2 B T 1.533T 中间铁心磁位降: 3 4 A 4 10
磁路基础知识
1.2.3涡流与涡流损耗 1、涡流 2、涡流损耗:涡流在铁心中引起的损耗 3、注意:为减小涡流损耗,电机和变压器的铁心都用 含硅量较高的薄硅钢片叠成。 4、铁心损耗:磁滞损耗+涡流损耗
2 pFe f 1.3 BmG
南通大学《电机学》
磁路基础知识
1.3直流磁路的计算
磁路计算正问题——给定磁通量,计算所需的励磁磁动势 磁路计算逆问题——给定励磁磁势,计算磁路内的磁通量 磁路计算正问题的步骤: 1)将磁路按材料性质和不同截面尺寸分段; 2)计算各段磁路的有效截面积Ak和平均长度lk; 3)计算各段磁路的平均磁通密度Ak ,Bk=Φk/Ak; 4)根据Bk求出对应的Hk;
Φ
RmFe
N
F
Rm
i
Φ
串联磁路 南通大学《电机学》 磁路基础知识
模拟电路图
解:铁心内磁通密度为 BFe 0.0009 T 1T
AFe 0.0009
从铸钢磁化曲线查得:与BFe对应的HFe=9×102A/m
H FelFe 9 10 2 0.3A 270 A 铁心段的磁位降:
查磁化曲线:H1 H 2 215 A/m
H1l1 H 2l2 215 15 10 2 A 32.25A
总磁动势和励磁电流为:
Ni 2H H l
3 3
H 1l1
电机学 第一章磁路

起始磁化曲线
oa段
ab段
bc段
cd段
膝点
饱和
铁磁材料 图1-7.
µ Fe = f ( H ) 磁化曲线见示意
� 应用: 设计电机和变压器时,为使主磁路内得 到较大的磁通量而又不过分增大励磁磁动势, 通常把铁心内的工作磁通密度选择在膝。 剩磁:去掉外磁场之后,铁磁材料内仍然保留的 磁通密度 B r 。 矫顽力:要使B值从减小到零,必须加上相应的反 向外磁场,此反向磁场强度Hc称为矫顽力。 磁滞:铁磁材料所具有的这种磁通密度B的变化滞 后于磁场强度H变化的现象。 磁滞现象是铁磁材料的另一个特性。
2.硬磁(永磁)材料 定义:磁滞回线宽、剩磁和矫顽力都很大的铁磁材 料称为硬磁材料,又称为永磁材料。 附图1-11b 磁性能指标 剩磁 矫顽力 最大磁能积
铸造型 铝镍钴
种类示意图
粉末型 铝镍钴
永磁材料 种类
铁氧体
稀土钴
钕铁硼
四、铁心损耗 1.磁滞损耗 定义: 铁磁材料置于交变磁场中时,磁畴相 互间不停地摩擦、消耗能量、造成损耗,这种 损耗称为磁滞损耗。 n 公式: p = C fB V
Hδ lδ = 385A
F = H FelFe + H δ lδ = 432.6 A
返回
2.简单并联磁路 定义:指考虑漏磁影响,或磁回路有两个以上分 支的磁路。 点击书本进入例题1-3
例 题
� [例1—3] 图1—14a所示并联磁路,铁心所 用材料为DR530硅钢片,铁心柱和铁轭的截面 积均为 A = 2 × 2 × 10 −4 m 2 ,磁路段的平均长 −3 度l = 5 ×10−2 m ,气隙长度 δ1 =δ2 = 2.5×10 m 励磁线圈匝数 N 1 = N 2 = 1000 匝。不计漏磁通,试求在气隙内产生 B δ =1.211T的磁通密度时,所需的励磁电流i。
第1章磁路-专业知识讲座

第1章 磁路
交变磁通旳效应: (1).磁通量随时间交变,必然会在激磁线圈内产生
感应电动势; (2).磁通量随时间交变,必然会在铁心中产生铁心
损耗。 (3).磁饱和现象会造成电流、磁通和电动势波形旳
畸变。
支旳磁路。
1
2
N1
1 2N2
L
A
L
L
第1章 磁路
[例1-3] 铁心由DR530硅钢片构成,铁心柱和 铁轭截
面积AFe=0.0004m2,磁路平均长度lFe=0.05m,气隙长 度δ1 =δ2=2.5×10-3m,励磁线圈匝数N1=N2=1000匝。 不计漏磁通,试求在气隙中产生磁通密度Bδ=1.211T时,
然后再逐渐减小H,B值将 沿曲线ab下降。
B Bm
Br
b
当H=0 时,B值并不等于零, 而是Br。这就是剩磁。
a
H
Hm
第1章 磁路
矫顽力——要使
B值为零,必须
B Bm
a
加上相应旳反向
b
B 磁场,此反向磁 r
H
场强度称为矫顽
力Hc。
c Hc
Hm
第1章 磁路
磁滞回线——
B Bm
a
铁磁材料旳磁滞回线
当H在Hm和- Hm之间反复变
真实旳物理量,反应了 该点处旳磁特征
第1章 磁路
2.磁通量Φ —— 垂直穿过某截面积旳磁力线总和。 单位:Wb
磁感应强度旳积分值, 描述了磁场旳总体特征
3.磁场强度H —— 计算磁场时引用旳物理量。 B=μH ,单位:A/m
磁感应强度与该点磁导率旳 乘积,反应了建立该点磁场
旳源
第1章 磁路
4.B、H、Φ之间旳关系
电机学第1章磁路

涡流损耗
铁芯是有阻值的,当磁通交变时,铁芯中就会感应交变的电 势,进而在铁心内引起环流。这些环流通作涡流状流动,称 为涡流涡流引起的损耗,称为涡流损耗。
pw k w f B
2
2 m
思考:如何尽量减小涡流损耗?
• 为减小涡流损耗, 电机和变压器的铁 心都用含硅量较高 的薄硅钢片叠成。
后于磁场强度变化,通常在电机内也可理解为磁通落后于 激磁电流的现象,称为磁滞现象)。
磁滞回线:磁场强度H缓慢地循环变化,B-H曲线封 闭曲线 • 磁滞现象是铁磁材料的另一个特性。
B
Bm
b
a
Br
Hc
c f e
Hc
H
Hm
Hm
d
Bm
图1-7 铁磁材料的磁滞回线
基本磁化曲线:
对同一铁磁材料,选择不同的磁场强度进行反复 磁化,可得一系列大小不同的磁滞回线,再将各 磁滞回线的顶点联接起来,所得的曲线。
2.磁化曲线和磁滞回线
磁化曲线:将一块尚未磁化的铁磁材料进行磁化,当磁 场强度H由零逐渐增大时,磁通密度B将随之增大, 得到曲线B=f(H)。 特性:①具有高的导磁性能;②磁化曲线呈非线性(饱 和特性)它的磁化曲线具有饱和性,磁导率μFe不 是常数,且随H的变化而变化。 磁滞回线在oa段:当H增大→B增大,但B增大速度较慢 在ab段:当H增大→B增大,B增大速度快; 在bc段:B随H增大的速度又较慢; 在cd段:为磁饱和区(又呈直线段)。其中拐弯点b称 为膝点;c点为饱和点。 • 过了饱和点c,铁磁材料的磁导率趋近μ0。
R
k
mk
Fm
• 磁路和电路的比拟仅是一种数学形式上的类似、 而不是物理本质的相似。
电机学第一章 磁路

H
随着磁场强度H的增大,饱和程度增加,μFe减 小,Rm增大,导磁性能降低.
B
c b
B = f ( H)
d
μFe = f ( H )
a
B = μ0 H
H
设计电机和变压器时,为使主磁路内得到较大的 磁通量而又不过分增大励磁磁动势.通常把铁心 内的工作磁通密度选择在膝点附近
B
c b
膝点 饱和点
B = f ( H)
四、铁心损耗
1.磁滞损耗
定义: 铁磁材料置于交变磁场中时,磁畴相 互间不停地摩擦、消耗能量、造成损耗,这种 损耗称为磁滞损耗。 公式: n h h m
p = C fB V
应用:由于硅钢片磁滞回线的面积较 小,故电机和变压器的铁心常用硅钢片叠成。
2.涡流损耗
¾涡流:铁磁材料在交变磁场将 有围绕磁通呈蜗旋状的感应电动 势和电流产生,简称涡流。 ¾涡流损耗:涡流在其流通路径 上的等效电阻中产生的I2R损耗 称为涡流损耗。 ¾涡流损耗与磁场交变频率f, 厚度d和最大磁感应强度Bm的平 方成正比,与材料的电阻率成反 比。 ¾要减小涡流损耗,首先应减小 厚度,其次是增加涡流回路中的 电阻。电工硅钢片中加入适量的 硅,制成硅钢片,显著提高电阻 率
表1.1 磁路和电路对比表 序 号 1 2 3 4 5 6 7 8 9 电 基本物理量 或基本定律 电 流 电 压 电 阻 电 导 电流密度 电导率 基尔霍夫 第一定律 基尔霍夫 第二定律 欧姆定律 路 符号或 定义 I U R=l/(γA) G=1/R J=I/A 单位 A V Ω S A/m2 S/m 磁 路 单 位 Wb A 1/H H Wb/m2(T) H/m 基本物理量或 符号或 基本定律 定义 磁 通 φ F 磁动势 磁 阻 磁 导 磁通密度 磁导率 磁通连续性 原理 Rm=l/(μA)
第一章磁路

第一章 磁路
电力拖动中广泛应用的电机、变压 器及部分控制电机都是依靠电与磁相 互作用而运行的,它们的工作原理既 涉及电路又涉及磁路。
电机学
1.1 1.2 1.3 1.4 1.5
磁场基本物理量 磁性材料 磁路的计算 交流铁心线圈 电磁铁
电机学
1.1 磁场的基本物理量
• 磁感应强度B
描述磁场强弱与方向的物理量 定义:单位正电荷以单位速度向垂直于磁场方向的方 向上运动时所受的机械力。 方向: B与产生磁场的电流方向符合右手螺旋定则。 单位:磁感应强度的单位: T(特斯拉) (高斯)
Φ2 B2
Φ3 B3 S3
2 B2S2 =1 6 10-4 =6 10-4 wb 截面S3中的磁通为: 3 1 2 10 104 6 104 4 104 wb 3 4 104 B3 0.8T 4 S3 5 10
电机学
例4:如图是一个对称磁路,中间柱截面积S3 是两边柱截面积S1或S2的两倍,假使N1I1=N2I2 , 求Φ1 ,Φ2,Φ3的大小关系和B1,B2,B3的大 小关系。
电机学
磁路
电路
磁动势F 磁通Φ 磁感应强度B 磁阻Rm=l/μS 欧姆定律φ=NI/Rm 克希荷夫磁通定律ΣΦk=0 克希荷夫定律磁压定律 ΣIN=Σ(H l)
电动势E 电流I 电流密度J 电阻R=l/rS 欧姆定律I=E/R 克希荷夫定律电流定律ΣI=0 克希荷夫定律电压定律 ΣE =Σ(IR)
1 2 , 3 21 2 2 B 1 =B 2 =B 3
电机学
例1.3.2 已知:l1=l3=60cm,l2=20cm, S2=S3=10cm2 , S1=20cm2 ,Φ3=5*10-4wb,材料为铸钢,求磁动势。
第一章磁路

铁磁物质的磁导率
非铁磁材料的磁导率接近真空磁导率0 ,铁 磁材料的磁导率比非铁磁材料的磁导率大得多, 即 0 。 常用铁磁材料的磁导率 铸钢: ≈1000 0 硅钢片:≈(6000 ~ 7000) 0 玻莫合金: ≈(20000 ~ 200000) 0
二、磁化曲线及磁滞回线
???
F Hl 159 0 .3 A 47 .7 A
励磁电流
iF
N
9.54 10 A
2
磁路的基本定律
磁路的基尔霍夫第一定律
磁路的基尔霍夫第一定律:穿出或进入 任一闭和面的总磁通量恒等于零(或者说, 进入任一闭合面的磁通量恒等于穿出该闭 合面的磁通量),这就是磁通连续性定律。
在电路中有电流时,就有功率损耗 I R ;而在直流磁路中,维持一 定的磁通量 ,铁心中没有功率损耗。
2
在电路中可以认为电流全部在导线中流过,导线外没有电流,在 磁路中,则没有绝对的磁绝缘体,除了铁心中的磁通外,实际上总 有一部分漏磁通散布在周围的空气中。 电路中导体的电阻率 在一定的温度下是不变的,而磁路中铁心 的磁导率 Fe却不是常值,它是随铁心的饱和程度大小而变化的。
2、磁路欧姆定律
对于一个等截面无分支的铁心磁路,如图 由于:Ф =∫BdA=BA H=B/μ F=Ni=Hl=(B/μ )l= Ф l/(μ A) 所以: F= ФRm
Ф i N A
Ф i N 磁路 A
F
磁路
Ф
Rm
相当于电路的欧姆定律: U= RI 模拟电路图如图。
模拟电路图 Ф F
Rm
公式:
- Φ1 Φ2 Φ3 0
Φ 0
Rm2
又称磁路的并联定律。
第一章 磁路
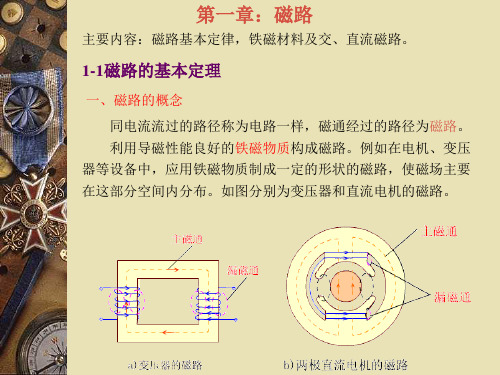
磁路的欧姆定律,在形式上与电路欧姆定律相似。
I Rm R F E
注:由于铁磁材料的磁导率不是常数,所以Rm一般不是常数。 3、磁路的基尔霍夫第一定律 对于有分支磁路,任意取一 闭合面A,由磁通的连续性,穿过 闭合面的磁通的代数和应为零,即
I R F R Rm m F E
2
4
解 :本题可用磁路的欧姆定律或安培环路定律解。 1)用磁路的欧姆定律 磁通量 磁阻
磁动势
BA 1 9 104 9 104 Wb
Rm
L
Fe A
0.3 5.3 104 A / Wb 7 4 5000 4 10 9 10
磁动势
F Rm 9 104 5.3 104 47.7A F 47.7 励磁电流 i 9.54 10 2 A N 500
2)用安培环路定律 磁场强度 H 磁动势
B
Fe
1 159 A/m 7 5000 4 10
F Hl 159 0.3 47.7A
励磁电流 i F 47.7 9.54 10 2 A
N
500
II Rm R m R F E F E
一、铁磁பைடு நூலகம்质的磁化
1 、铁磁物质 铁磁物质的磁导率都很大,一般是 0的几千倍。 金属 铁磁物质 非金属 2、铁磁物质的磁化 将铁磁材料放入磁场后,磁场会显著增强,铁磁材料在磁场中 呈现很强的磁性这一现象,称为铁磁物质的磁化。 原因:铁磁物质中有许多称为磁畴的天然磁化区,当未投入磁场时, 磁畴杂乱无章的排列,磁效应相互抵消对外不显磁性。当放入磁场 后,磁畴按外磁场方向排列起来,形成一附加磁场叠加在外磁场上。 铁、钴、镍: B高,居里温度高。缺点是电阻率 低,涡流耗严重。 铁氧体: 电阻率高,涡流损耗小,抗锈防腐。 缺点是B低,温度稳定性差。
电机学第五版第1章 磁路ppt课件

涡流损耗 涡流在铁心中引起的损耗。 公式:
pe=CeD2f2Bm 2V
应用:C为e — 减小涡涡流流损 损耗耗,系 电机数和变 压器的铁心都用含硅量较高的薄硅钢片 (0.35~0.5mm)叠成。
.
41..铁2心损常耗用的铁磁材料及其特性
磁滞损耗 铁磁材料置于交变磁场中时,材料被反复交变磁化, 与此同时,磁畴相互间不停地摩擦造成损耗,这种损耗称为磁滞损耗。
公式: ph = Ch fBmnV
Ch —磁滞损耗系数
应用:由于硅钢片磁滞回线的面积较小,故电机和变压器的铁心 常用硅钢片叠成。
.
41..铁2心损常耗用的铁磁材料及其特性
图1-17 直流电机的磁化曲线
.
3.永磁磁路的计算特点
(1)气隙内的磁位降Hδδ,是由永磁体内所形成的或者说所提供的,FM=-HMlM; 永磁体内的工作磁场强度HM和长度lM愈大,永磁体提供的磁动势就愈大。 (2)永磁体·的磁场HM总是负值,也就是说,它总是工作在永磁材料磁滞回线 的第二象限这段曲线上,这段曲线通常称为退磁曲线,如图1-19中段所示。 (3)若磁路中没有气隙,δ=0,则HMlM=0,于是HM=0,从退磁曲线可见,此时 永磁体内的磁通密度为剩磁Br,如图1-19中的R点所示。 。
???
图1-14 气隙磁场的边缘效应
.
1.3 磁路的计算
解 用磁路的基尔霍夫第二定律来求解。
铁心内的磁场强度: H F e=m B F F e e=5000创 4 1 p10 -7=159A /m
气隙磁场强度:
Hd=m B0d =41´p´3.130025-27 =77?104A/m
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章磁路电机是一种机电能量转换装置,变压器是一种电能传递装置,它们的工作原理都以电磁感应原理为基础,且以电场或磁场作为其耦合场。
在通常情况下,由于磁场在空气中的储能密度比电场大很多,所以绝大多数电机均以磁场作为耦合扬。
磁场的强弱和分布,不仅关系到电机的性能,而且还将决定电机的体积和重量;所以磁场的分析扣计箅,对于认识电机是十分重要的。
由于电机的结构比校复杂,加上铁磁材料的非线性性质,很难用麦克斯韦方程直接解析求解;因此在实际工作中.常把磁场问题简化成磁路问题来处理。
从工程观点来说,准确度已经足够。
本章先说明磁路的基本定律,然后介绍常用铁磁材料及其性能,最后说明磁路的计算方法。
1-1 磁路的基本定律一、磁路的概念磁通所通过的路径称为磁路。
图1—1表示两种常见的磁路,其中图a为变压器的磁路,图b为两极直流电机的磁路。
在电机和变压器里,常把线圈套装在铁心上。
当线圈内通有电流时、在线圈周围的空间(包括铁心内、外)就会形成磁场。
由于铁心的导磁性能比空气要好得多,所以绝大部分磁通将在铁心内通过,并在能量传递或转换过程中起耦合场的作用,这部分磁通称为主磁通。
围绕裁流线圈、部分铁心和铁心周围的空间,还存在少量分散的磁通,这部分磁通称为漏磁通。
主磁通和漏磁通所通过的路径分别构成主磁路和漏磁路,图1—l中示意地表出了这两种磁路。
用以激励磁路中磁通的载流线圈称为励磁线圈(或称励磁绕组),励磁线圈中的电流称为励磁电流(或激磁电流)。
若励磁电流为直流,磁路中的磁通是恒定的,不随时间而变化,这种磁路称为直流磁路;直流电机的磁路就属于这一类。
若励磁电流为交流(为把交、直流激励区分开,本书中对文流情况以后称为激磁电流),磁路中的磁通随时间交变变化,这种磁路称为交流磁路;交流铁心线圈、变压器和感应电机的磁路都属于这一类。
二、磁路的基本定律进行磁路分析和计算时,往往要用到以下几条定律。
安培环路定律 沿着任何一条闭合回线L ,磁场强度H 的线积分值dlH L∙⎰ 恰好等于该闭合回线所包围的总电流值∑i ,(代数和).这就是安培环路定律(图l —2)。
用公式表示,有idl HL∑=∙⎰ (1—1)式中,若电流的正方向与闭合回线L 的环行方向符合右手螺旋关系时,i 取正号,否则取负号。
例如在图1—2中,i 2的正方向向上,取正号;i 1和i 3的正方向向下,取负号;故有321i i i dl H L-+-=∙⎰.若沿着回线L ,磁场强度H 的方向总在切线方向、其大小处处相等,且闭合回线所包围的总电流是由通有电流i 的N 匝线圈所提供,则式(1—1)可简写成HL=Ni (1—2)磁路的欧姆定律 图l —3a 是一个无分支铁心磁路,铁心上绕有N 匝线圈,线圈中通有电流i ;铁心截面积为A ,磁路的干均长度为l ,材料的磁导率为μ。
若不计漏磁通,并认为各截面上的磁通密度为均匀,并且垂直于各截面,则磁通量Ф将等于磁通密度乘以面 积,即BA A B =∙=Φ⎰ (1—3)考虑到磁场强度等于磁通密度除以磁导率,即H =B /μ,于是式(1—2)可改写成如下形式A ll B Ni μμΦ==(1—4)或Λ==φφm R F (1—5)式中,F =Ni 为作用在铁心磁路上的安匝数,称为磁路的磁动势,单位为A;A lR m μ=为磁路的磁阻,单位为A /Wb ;m R 1=Λ为磁路的磁导,单位为Wb /A 。
式(l —5)表明,作用在磁路上的磁动势F 等于磁路内的磁通量Ф乘以磁阻Rm,此关系与电路中的欧姆定律在形式上十分相似,因此式(l —5)亦称为磁路的欧姆定律。
这里,我们把磁路中的磁动势F 比拟于电路中的电动势E ,磁通量Ф比拟于电流I ,磁阻Rm 和磁导Λ分别比拟于电阻R 和电导G 。
图1—3b 表示相应的模拟电路图。
磁阻Rm 与磁路的平均长度l 成正比,与磁路的截面积A 及构成磁路材料的磁导率μ成反比。
需要注意的是,铁磁材料的磁导率μ不是一个常数,所以由铁磁材料构成的磁路,其磁阻不是常数,而是随着磁路中磁通密度的大小而变化,这种情况称为非线性。
[例1—1] 有一闭合铁心磁路,铁心的截面积A =9XlO -4m 2,磁路的平均长度l =o .3m ,铁心的磁导率5000μμ=Fe ,套装在铁心上的励磁绕组为500匝。
试求在铁心中产生1T 的磁通密度时,所需的励磁磁动势和励磁电流。
解 用安培环路定律来求解。
磁场强度mA m A F BH Fe/159/104500017=⨯⨯==-πμ磁动势 F =HI =159X0.3A =47.7A励磁电流 AA N F i 21054.95007.47-⨯===磁路的基尔霍夫第一定律 如果铁心不是一个简单回路,而是带有并联分支的分支磁路,如图1—4所示,则当中间铁心柱上加有磁动势F 时,磁通的路径将如图中虚线所示。
如令进入闭合面A 的磁通为负,穿出闭合面的磁通为正,从图1—4可见,对闭合面A ,显然有321=Φ+Φ+Φ-或 0=Φ∑ (1—6)式(1—6)表明:穿出(或进入)任一闭和面的总磁通量恒等于零(或者说,进入任一闭合面的磁通量恒等于穿出该闭合面的磁通量),这就是磁通连续性定律.比拟于电路中的基尔霍夫第一定律0=∑i ,该定律亦称为磁路的基尔霍夫第一定律.磁路的基尔霍夫第二定律 电机和变压器的磁路总是由数段不同截面、不同铁磁材料的铁心组成,而且还可能含有气隙。
磁路计算时,总是把整个磁路分成若于段,每段为同一材料、相同截面积,且段内磁通密度处处相等,从而磁场强度亦处处相等。
例如图1—5所示磁路由三段组成,其中两段为截面不同的铁磁材料,第三段为气隙。
若铁心上的励磁磁动势为Ni ,根据安培环路定律(磁路欧姆定律)可得δδδδm m m k kk R R R H l H l H l HNi Φ+Φ+Φ=++==∑=2211221131(1—5)式中,l 1和l 2分别为1、2两段铁心的长度,其截面积备为A 1和A 2;δ为气隙长度;H 1、H 2分别为1、2两段磁路内的磁场强度;H δ为气隙内的磁场强度;Φ1和Φ2为1、2两段铁心内的磁通;Φδ为气隙内磁通;1m R 、2m R 为1、2两段铁心磁路的磁阻;δm R 为气隙磁阻。
由于H k 是单位长度上的磁位降、kk l H 则是一段磁路上的磁位降,Ni 是作用在磁路上的总磁动势,故式<1-7)表明:沿任何闭合磁路的总磁动势恒等于各段磁路磁位降的代数和。
类比于电路中的基尔霍夫第二定律,该定律就称为磁路的基尔霍夫第二定律。
不难看出,此定律实际上是安培环路定律的另一种表达形式。
需要指出,磁路和电路的比拟仅是—种数学形式上的类似、而不是物理本质的相似。
1. 2 常用的铁磁材料及其特性为了在一定的励磁磁动势作用下能激励较强的磁场,电机和变压器的铁心常用磁导率较高的铁磁材料制成。
下面对常用的铁磁材料及其特性作一说明。
一、铁磁物质的磁化铁磁物质包括铁、镍、钻等以及它们的合金。
将这些材料放人磁场后,磁场会显著增强。
铁磁材料在外磁场中呈现很强的磁性,此现象称为铁磁物质的磁化.铁磁物质能被磁化,是因为在它内部存在着许多很小的被称为磁畴的天然磁化区。
在图l-6中磁畴用一些小磁铁来示意地表出。
在铁磁物质未放人磁场之前,这些磁畴杂乱无章地排列着,其磁效应互相抵消,对外部不呈现磁性(图1—6a).一旦将铁磁物质放人磁场,在外磁场的作用下,磁畴的轴线将趋于一致<图1-6b),由此形成一个附加磁场.叠加在外磁场上,使合成磁场大为增强.由于磁畴所产生的附加磁场将比非铁磁物质在同一磁场强度下所激励的磁场强得多,所以铁磁材料的磁导率Fe μ要比非铁磁材料大得多。
非铁磁材料的磁导率接近于真空的磁导率0μ,电机中常用的铁磁材料,其磁导率Fe μ=(2000—6000) 0μ。
磁化是铁磁材料的特性之一。
二、磁化曲线和磁滞回线起始磁化曲线 在非铁磁材料中,磁通密度B 和磁场强度H 之间呈直线关系,直线的斜率就等于μ。
铁磁材料的B 与H之间则为曲线关系。
将一块尚未磁化的铁磁材料进行磁化,当磁场强度H 由零逐渐增大时,磁通密度B 将随之增大,曲线B=f(H)就称为起始磁化曲线,如图1—7所示。
起始磁化曲线基本上可分为四段:开始磁化时,外磁场较弱.磁通密度增加得不快,如图1—7中Oa 段所示。
随着外磁场的增强,材料内部大量磁畴开始转向,趋向于外磁场方向,此时B 值增加得很快,如ab 段所示.若外磁场继续增加,大部分磁畴已趋向外磁场方向,可转向的磁畴越来越少,B 值增加越来越慢,如bc 段所示,这种现象称为饱和。
达到饱和以后,磁化曲线基本上成为与非铁磁材料的HB 0μ=特性相平行的直线,如cd 段所示。
磁化曲线开始拐弯的点(图l —7中的b 点),称为膝点。
由于铁磁材料的磁化曲线不是一条直线,所以HB Fe /=μ也随H 值的变化而变化,图1-7中同时示出了曲线)(H f Fe =μ。
设计电机和变压器时,为使主磁路内得到较大的磁通量而又不过分增大励磁磁动势.通常把铁心内的工作磁通密度选择在膝点附近.磁滞回线若将铁磁材料进行周期性磁化,B和H之间的变化关系就会变成如图l--8中曲线abcdefa所示。
由图可见,当H开始从零增加到H时,B相应地从零增加到Bm;以后m如逐渐减小磁场强度H,B值将沿曲线ab下降。
当H=0时,B值并不等于零,而等于τB,这种去掉外磁场之后,铁磁材料内仍然保留的磁通密度τB,称为剩余磁通密度,简称剩磁.要使B值从τB减小到零,必须加上相应的反向外磁场,此反向磁场强度称为矫顽力,用H c表示。
τB和Hc是铁磁材料的两个重要参数.铁磁材料所具有的这种磁通密度B的变化滞后于磁场强度H变化的现象,叫做磁滞。
呈现磁滞现象的B-H闭合回线,称为磁滞回线,如图1—8中abcdefa所示。
磁滞现象是铁磁材料的另一个特性。
基本磁化曲线对同一铁磁材料,选择不同的磁场强度Hm进行反复磁化,可得一系列大小不同的磁滞回线,如图1-9所示。
再将各磁滞回线的顶点联接起来,所得的曲线称为基本磁化曲线或平均磁化曲线。
基本磁化曲线不是起始磁化曲线,但差别不大。
直流磁路计算时所用的磁化曲线都是基本磁化曲线。
图1—10表示电机中常用的硅钢片、铸铁和铸钢的基本磁化曲线。
三、铁磁材料按照磁滞回线形状的不同,铁磁材料可分为软磁材料和硬磁(永磁)材料两大类,现分述如下。
软磁材料磁滞回线窄、剩磁τB和矫顽力Hc都小的材料,称为软磁材料,如图1—lla所示。
常用的软磁材料有铸铁、铸钢和硅钢片等。
软磁材料的磁导率较高.故用以制造电机和变压器的铁心。
硬磁(永磁)材料磁滞回线宽、τB和Hc都大的铁磁材料称为硬磁材料,如图1—l1b所示。
由于剩磁τB大,可用以制成永久磁铁,因而硬磁材料亦称为永磁材料。
