动态规划练习试题和解答
动态规划练习题(含答案)

动态规划练习题USACO 2.2 Subset Sums题目如下:对于从1到N的连续整集合合,能划分成两个子集合,且保证每个集合的数字和是相等的。
举个例子,如果N=3,对于{1,2,3}能划分成两个子集合,他们每个的所有数字和是相等的:and {1,2}这是唯一一种分发(交换集合位置被认为是同一种划分方案,因此不会增加划分方案总数)如果N=7,有四种方法能划分集合{1,2,3,4,5,6,7},每一种分发的子集合各数字和是相等的:{1,6,7} and {2,3,4,5} {注1+6+7=2+3+4+5}{2,5,7} and {1,3,4,6}{3,4,7} and {1,2,5,6}{1,2,4,7} and {3,5,6}给出N,你的程序应该输出划分方案总数,如果不存在这样的划分方案,则输出0。
程序不能预存结果直接输出。
PROGRAM NAME: subsetINPUT FORMAT输入文件只有一行,且只有一个整数NSAMPLE INPUT (file subset.in)7OUTPUT FORMAT输出划分方案总数,如果不存在则输出0。
SAMPLE OUTPUT (file subset.out)4参考程序如下:#include <fstream>using namespace std;const unsigned int MAX_SUM = 1024;int n;unsigned long long int dyn[MAX_SUM];ifstream fin ("subset.in");ofstream fout ("subset.out");int main() {fin >> n;fin.close();int s = n*(n+1);if (s % 4) {fout << 0 << endl;fout.close ();return ;}s /= 4;int i, j;dyn [0] = 1;for (i = 1; i <= n; i++)for (j = s; j >= i; j--)dyn[j] += dyn[j-i];fout << (dyn[s]/2) << endl;fout.close();return 0;}USACO 2.3 Longest Prefix题目如下:在生物学中,一些生物的结构是用包含其要素的大写字母序列来表示的。
动态规划专项练习题解

另一种方法
• 将原串与原串的倒序做一次LCS—最长公 共子序列,用原串长度减去LCS长度,即 为需要插入字符的个数 • 例如:ab3bd与 db3ba • LCS(‘ab3bd’, ‘db3ba’)=‘b3b’ • 因此, ans=Len(‘ab3bd’)-Len(‘b3b’)=2
LCS的求法
• 最长公共子串(LCS),有三种情况: 1. 公共子串的元素必须相邻. 2. 公共子串的元素可以不相邻 3. 求多个字符串而不是两个字符串的最长公共 子串 • 动归4中,我们讲了求情况2的LCS序列。下面我们 来讨论情况1的做法。
• 任务:对于任意一个字符串,输出将这个字符串 变为回文串需要插入的最少字符个数,比如, ab3bd只需要插入2个字符就可以变为一个回文串. • 0<n<=1992,n为字符串长度。
分析
• ab3bd • 只需变为adb3bda即可,在前面插入d,在 后面插入a; • 我们分几种情况讨论:
– 若A形如 ?A?,(问号代表任意一个相同字符, 下同)则只需将A变为回文串。 – 若A形如?A再在A的后面插入一个”?” – 若A形如A ?再在A的前面插入一个”?”
分析
• 性质:青蛙遍历的路径不会相交。
• 上图中图2的路径比图1要短。 • 证明:图1: D1=d(1,3)+d(2,3)+d(2,4) 图2: D2=d(1,2)+d(2,3)+d(3,4) 要证明D1>D2,只要证明d(1,3) +d(2,4)>d(1,2)+d(3,4) 连接两边,见图3,由三角形的三边关系定理即可证明。
动态规划
• 设f(i,j)为将Ai..Aj变为回文串的最小代价,则
f (i 1, j 1), 若a[i] a[ j ] f (i, j ) min f (i 1, j ) 1, 若a[i] a[ j ],后插一个字符 f (i, j - 1) 1,若a[i] a[ j ],前插一个字符
第五章 动态规划建模与求解作业题解答

2.(2)某公司从事某种商品的经营,现欲制定本年度10月至12月的进货及销售计划。
已知该种商品的初始库存量为2000件,公司库存最多可存放该种商品10000件。
公司拥有的经营资金为80万元,据预测,10月至12月的进货及销售价格如表5.29所示。
若每个月在1号进货1次,且要求年底时商品的库存量达到3000件。
在以上条件下,问如何安排进货及销售计划,使公司获得最大利润?解:(0)阶段划分:按月份划分阶段,阶段变量 k =1,2,3。
(1)条件1:状态及状态变量用k x 表示k 阶段的库存量,12000x =件, 43000x =,最大库存量M =10000件。
0≤k 阶段的库存量≤M, 所以状态可能集:0k x M ≤≤ (2)条件2:决策及决策变量设k u ,k v 是k 阶段的进货量和销售量, 全部流动资金=800000+上一阶段的盈利 =800000元+2,111,11()k k k k P v P u ----- 其中1,1k P -,2,1k P -是k -1阶段的进货价格和销售价格;1k u -,1k v -是k -1阶段的进货量和销售量(000,0u v ==); 1,k P ,2,k P 是k 阶段的进货价格和销售价格(见数据表)。
则:12,1,01,800000()0min{,}k m m m m m k k kP v P u u M x P -=+-≤≤-∑, 0k k k v x u ≤≤+。
(3)条件3:状态转移方程1k k k k x x u v +=+-(k 阶段的库存量+k 阶段的进货量-k 阶段的销售量)(4)阶段效应和目标函数 2,1,k k k k k r P v P u =- 31kk R r==∑(5)动态规划的基本方程2,1,11,44()max{()}()0k kk k k k k k k k u v f x P v P u f x f x ++=-+⎧⎪⎨=⎪⎩2.(4)某公司计划用100万元对其三个分厂进行投资,三个分厂的投资方式各不相同,其投资和收。
动态规划练习题

最小乘车费用 (bus)【问题描述】而任意一辆汽车从不行驶超过1 0公里。
某人想乘车到达n公里远的地方,假设他可以任意次换车,请你帮他找到一种乘车方案,使得总费用最小。
注意:1 0公里的费用比1公里小的情况是允许的。
【输入文件】共两行:第一行为1 0个不超过200的整数,依次表示行驶1~1 0公里的费用,相邻两数间用一个空格隔开:第二行为某人想要乘车的公里数(不超过20000的整数)。
【输出文件】仅一行,包含一个整数,表示到达n公里所需要的最小费用。
【样例输入】12 21 31 40 49 58 69 79 90 10115【样例输出】147船 (ships)【问题描述】PALMIA国家被一条河流分成南北两岸,南北两岸上各有N个村庄。
北岸的每一个村庄有一个唯一的朋友在南岸,且他们的朋友村庄彼此不同。
每一对朋友村庄想要一条船来连接他们,他们向政府提出申请以获得批准。
由于河面上常常有雾,政府决定禁止船只航线相交(如果相交,则很可能导致碰船)。
你的任务是编写一个程序,帮助政府官员决定批准哪些船只航线,使得不相交的航线数目最大。
【输入文件】ships.in输入文件由几组数据组成。
每组数据的第一行有2个整数X,Y,中间有一个空格隔开,X代表PALMIA河的长度(10<=X<=6000),Y代表河的宽度(10<=Y<=100)。
第二行包含整数N,表示分别坐落在南北两岸上的村庄的数目(1<=N<=5000)。
在接下来的N行中,每一行有两个非负整数C,D,由一个空格隔开,分别表示这一对朋友村庄沿河岸与PALMIA 河最西边界的距离(C代表北岸的村庄,D代表南岸的村庄),不存在同岸又同位置的村庄。
最后一组数据的下面仅有一行,是两个0,也被一空格隔开。
【输出文件】ships.out对输入文件的每一组数据,输出文件应在连续的行中表示出最大可能满足上述条件的航线的数目。
【输入样例】30 4722 42 610 315 129 817 174 20 0【输出样例】4DOLLARS (dollars)【问题描述】在以后的若干天里戴维将学习美元与德国马克的汇率。
运筹学动态规划习题

二、某厂有100台机床,能够加工两种零件, 要安排4个月的任务,根据以往经验,用这 些机床加工第一种零件,一个月后损坏率 为1/3;加工第二种零件时,一个月后损坏 率为1/10。又已知机床加工第一种零件时一 个月的受益为10万元,机床加工第二种零 件时一个月的受益为7万元。现安排4个月 的任务,使总收益为最大。
• 首先建立动态规划的模型 • 划分成3个阶段,每个阶段决策一个项目 的投资额,每个阶段决策的投资时可以使 用的资金作为状态变量,利润为阶段的指 标函数。 • 利用基本递推方程从第3阶段开始求解 • 给企业的投资额为 95万元 在城市购买房 地产的投资额为 105万元 • 最大利润为 681万元
三、某公司有资金200万元,打算全部参与三 个方面的投资。(1)参与一个企业投资, 当投资额为X1(万元)时,可得利润为 J1=4X1-2(万元);(2)参与一个电视片 制作,当投资额为X2(万元)时,可得利 润为J2=1/16X2-1/5X2-2(万元);(3)在 城市购买房地产,当投资额为X3(万元) 时,可得利润为J3=3X3-10(万元)。又知 投资额的上限为X1≤95万元;X2≤50万元。 用动态规划法决策使总利润最大?
• 答案: • 设每个月为一个阶段,共4个阶段。每个阶 段可投入生产的机床数为状态变量SK,加 工第一种零件的机床数为决策变量UK,加 工第二种零件的机床数为SK-UK,阶段指标 函数为DK=7SK+3UK,SK+1=9/10SK-7/30UK。 用逆序的递推方法求解:前两月全部加工 第二种零件,后两月全部加工第一种零件。 其最大收益为2680
习题三
一、某工厂购进100台机器,准备生产A、B 两种产品。如生产产品A,每台机器每年可 收入45万元,损坏率为65%;若生产产品B, 每台机器每年可收入35万元,损坏率为 35%;估计三年后有新机器出现,旧的机 器将全部淘汰。试问每年应然后安排生产, 使在三年内收入最多?
动态规划习题答案汇编

2.某公司有资金4百万元向A,B和C3个项目追加投资,各个项目可以有不同的投资额(百万元计),相应的效益如表所示。
问怎样分配资金,使总效益值最大?##表8-47解:设S1-A,B,C项目的总投资额,S2-B、C项目的总投资额S3-C项目的投资额;X k-k项目的投资额;(X1-A项目的投资额,X2-B项目的投资额,X3-C项目的投资额)W k(S k,X k)-对K项目投资X k后的收益:W k(S k,X k)=W k (X k)T k (S k,X k)-S k+1=S k-X kf k (S k)-当K至第3项目允许的投资额为S k时所能获得的最大收益。
为获得最大利润,必须将4百万全部投资,假设有4阶段存在,有S4=0,建立递归方程f4 (S k)=0f k (S k)=max{ W k (X k)+f k +1(S k+1)} k=3,2,1X k∈D k(S k)第一步,K=3f4(S4)=0f3 (S3)=max{W3 (X3)+f4 (S4)}X3∈D3(S3)S4=S3-X3第二步:K=2 f2 (S2)=max{W2 (X2)+f3 (S3)}X2∈D2(S2)S3=S2-X2W2 (X2)+f3 (S2-X2)第三步:K=1 f1 (S1) =max {W1 (X1)+ f2 (S2)}X1∈D1(S1)S2= S1- X1W1 (X1)+ f2 (S1- X1)S1=4 →S2=1 →S3=1↓↓↓X1*=3 X2*=0 X3*=1A投资3百万,B不投资C投资1百万。
总收益164百万元。
3.(最优分配问题)有一个仪表公司打算向它的3个营业区设立6家销售店。
每个营业区至少设一家,所获利润如表。
问设立的6家销售店数应如何分配,可使总利润最大?解:s k——对k#,…,3#营业区允许设立的销售店数x k——对k#营业区设立的销售店数w k (s k,x k)——对k#营业区设立x k销售店后的利润:w k (s k,,x k)= w k (x k)T k (s k, x k)——s k +1= s k - x kf k (s k)——当第k至第3个营业区允许设立的销售店数为s k 时所能获得的最大利润递归方程:f4(s4)=0f k (s k)=max {wk (xk)+ fk+1(sk+1)}, k=3,2,1 xk∈Dk(sk)k=3时,有方程f4 (s4)=0f3(s3)= max {w3(x3)+ f4(s4) }x3∈D3(s3)s3=s2—x2k=2,有方程f2(s2)= max {w2(x2)+ f3(s3) }x2∈D2(s2)s3=s2—x2k=1,有方程f1(s1)= max{w1(x1)+ f2(s2) } x1∈D1(s1) s2=s1—x1s1=6 → s2=3 → s3=2 ↓ ↓ ↓x1*=3 x2*=1 x3*=2分别A1、A2、A3营业区设立3家、1家、2家销售店,最大利润为7704.用动态规划方法求解下列模型:maxf=10X1+4X2+5X3s.t. 3X1+5 X2+4 X3≤150≤X1≤2 0≤X2≤2 X3≥0 ,X j为整数j=1,2,3解:收费C1=10 C2=4 C3=5X1为货物1的装载件数X2为货物2的装载件数X3为货物3的装载件数分3阶段S1为货物1、2、3允许的装载重量(3X1+5 X2+4 X3的允许值)S2为货物2、3允许装载的重量(5 X2+4 X3的允许值)S3 为货物3允许装载的重量(4 X3的允许值)第一步:K=3f4(S4)=0f3(S3)= max{5X3+ f4(S4)| X3∈D3(S3)}S4= S3 -4 X3第二步:K=2f2(S2)= max{4X2+ f3(S3)| X2∈D2(S2)} S3= S2 -5 X2划分点:第三步:K=1f1(S3)= max{10X1+ f2(S2)| X1∈D1(S1)}S2= S1-3 X110X1+ f2(S1-3 X1)顺序追踪:最优策略为S1=15 →S2=9 →S3=9↓↓↓X1*=2 X2*=0 X3*=2最优装载方案为:货物1装2件;货物2不装;货物3装2件装载收费为30元5.用动态规划方法解下列0—1背包问题:Max f =12x1+12x2+9x3+16x4+30x5;s.t. 3x1+4x2+3x3+4x4+6x5≤12;x j=0,1, j=1,……,5解:本问题分为5个阶段。
第9章 动态规划应用举例习题详解习题.doc

第9章动态规划应用举例习题详解(习题)9. 1有一部货车每天沿着公路给四个零售店卸下6箱货物,如果各零售店出售该货物所得利润如表9-1所示,试求在各零售店卸下几箱货物,能使获得总利润最大?其值是多少?9.2设有某种肥料共6个单位重量,准备供给四块粮田用。
其每块田施肥数量与增产粮食数字关系如表9-2所示。
试求对每块田施多少单位重量的肥料,才使总的增产粮食最多。
粮田增肥1234000001202518282424539473605761654756578745857090806907395859.3某公司打算向它的三个营业区增设六个销售店,每个营业区至少增设一个。
从各区赚取的利润(单位为万元)与增设的销售店个数有关,其数据如表9-3所示。
销售店增加数A区利润B区利润C区利润9.4某工厂有100台机器,拟分四个周期使用,在每一周期有两种生产任务。
据经验,把机器q 台投入第一种生产任务,则在一个生产周期中将有;n/3台机器作废;余下的机器全部投入第二种生产任务,则有1/10台机器作废。
如果干第一种生产任务每台机器可收益10, 干第二种生产任务每台机器可收益7。
问怎样分配机器,使总收益最大?9. 5设有三种资源,每单位的成本分别为a、b. co给定的利润函数为n(xi, yi,z),(/ = 1,2,•••,«)现有资金为W,应购买各种资源多少单位分配给"个行业,才能使总利润最大。
试给出动态规划的公式,并写出它的一维递推关系式。
9. 6某厂生产一种产品,估计该产品在未来4个月的销售量分别为400、500、300、200件。
该项产品的生产准备费用每批为500元,每件的生产费用为1元,存储费用每件每月为1 元。
假定1月初的存货为100件,4月底的存货为零。
试求该厂在这4个月内的最优生产计划。
9.7某电视机厂为生产电视机而需生产喇叭,生产以万只为单位。
根据以往记录,一年的四个季度需要喇叭分别是3万、2万、3万、2万只。
动态规划 练习题
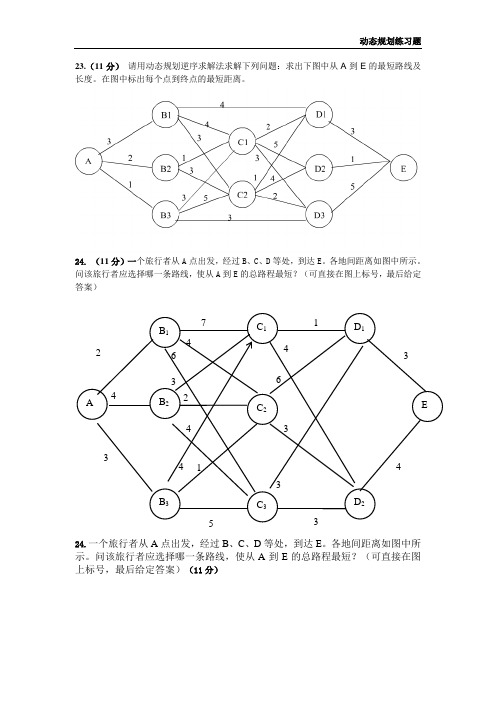
23.(11分)请用动态规划逆序求解法求解下列问题:求出下图中从A到E的最短路线及长度。
在图中标出每个点到终点的最短距离。
24. (11分)一个旅行者从A点出发,经过B、C、D等处,到达E。
各地间距离如图中所示。
问该旅行者应选择哪一条路线,使从A到E的总路程最短?(可直接在图上标号,最后给定答案)
24.一个旅行者从A点出发,经过B、C、D等处,到达E。
各地间距离如图中所示。
问该旅行者应选择哪一条路线,使从A到E的总路程最短?(可直接在图上标号,最后给定答案)(11分)
解:此为动态规划之“最短路问题”,可用逆向追踪“图上标号法”解决如下:
最佳策略为:A →B 2→C 1→D 1→E 或A →B 3→C 1→D 1→E 此时从A 到E 的总路程的最短距离都是11
23. 请用动态规划逆序求解法求解下列问题:
各点标号依次为:A:8, B1:7,B2:6, B3:8, C1:5, C2:4,D1:3,D2:1,D3:5.
25. 某厂生产C B A ,,三种产品,其所需劳动力、材料等有关数据见下表。
要求:建立模型,并用单纯形法计算,确定获利最大的产品生产计划。
解:(1)设C B A ,,
各生产321,,x x x 件。
有
32143min x x x z ++=
st.⎪⎩⎪
⎨⎧=≥≤++≤++)3,2,1(,03054345
536321321j x x x x x x x j
(4分)
获利最大的生产计划是C B A ,,各生产5件、0件、3件,最大利润为273453=⨯+⨯=z 元。
(15分)。
运筹学 动态规划-作业及答案
1
第五章 动态规划作业题及答案
1.用动态规划法求解求最短路径
从起点A 到终点E 之间各点的距离如图所示。
求A 到E 的最短路径。
B A
C B
D B C D E
C 21
23
12
31
2
5
11214
10610
41312113
96
5810
5
2
2.用动态规划法求解资源分配问题
有资金4万元,投资A 、B 、C 三个项目,每个项目的投资效益与投入该项目的资金有关。
三个项目A 、B 、C 的投资效益(万吨)和投入资金(万元)的关系见下表:
用动态规划法求解对三个项目的最优投资分配,使总投资效益最大。
3.用动态规划法求解生产库存问题
一个工厂生产某种产品,1~7月份生产成本和产品需求量的变化情况如下表:
为了调节生产生产和需求,工厂设有一个产品仓库,库容量H=9。
已知期初库存量为2,要求期末(七月低)库存量为0。
每个月生产的产品在月末入库,月初根据当月需求发货。
求七个月的生产量,能满足各月的需求,并使生产成本最低。
4.用动态规划法求解背包问题
第i 种每件价值c 1=65,c 2=85,c 3=40元; 第i 种物品每件重量为:w 1=2,w 2=3,w 3=1公斤;现有一只可装载重量为5公斤的背包,求各种物品应各取多少件放入背包,使背包中物品的价值最高。
动态规划作业完整

动态规划作业1、1、设某工厂自国外进口一部精密机器,由机器制造厂至出口港有三个港口可供选择,而进口港又有三个可供选择,进口后可经由两个城市到达目的地,其间的运输成本如图中所标的数字,试求运费最低的路线?把A看作终点,该问题可分为4个阶段f k(S k)表示从第K阶段点S k到终点A的最短距离f4(B i)=20, f4(B2)=40, f4(B3)=30f3(C i)=min[d 3(C i, B i)+ f4(B i), d3(C i, B2)+ f4(B2), d3(C i, B3)+ f4(B3)]=70,U3(C l)= B2 或B3f3(C2)=40,U3(C2)= B3f3(C3)=80,U3(C3)= B l 或B2 或B3以D i)=80,U2(D I)=C If2(D2)=70,U2(D2)= C2f i(E)=110,U i(E)= D i 或D2所以可以得到以下最短路线,E T D I^C I^B 2 / B3^AE TD 2^C 2TB 3—A2、习题4 — 2解:1)将问题按地区分为三个阶段,三个地区的编号分别为1、2、3;2)设Sk表示为分配给第k个地区到第n个地区的销售点数,Xk表示为分配给第k个地区的销售点数,S k +1 = S k —X kPk(Xk)表示为Xk个销售点分到第k个地区所得的利润值fk(Sk)表示为Sk个销售点分配给第k个地区到第n个地区的最大利润值3)递推关系式:fk(Sk) = max[ Pk(Xk)+ f k+i(S k —X k) ] k=3,2,1f4(S4) = 04)从最后一个阶段开始向前逆推计算第三阶段:设将S3个销售点(S3= 0,1,2,3,4)全部分配给第三个地区时,最大利润值为:f3(S3)= max[P3(X3)] 其中X3 = S3= 0,1,2,3,4表1第二阶段:设将S2个销售点(S2= 0,1,2,3,4)分配给乙丙两个地区时,对每一个S2值,都有一种最优分配方案,使得最大盈利值为: f2(S2)= max[ P2(X2)+ f3(S2 —X2)]其中,X2= 0,1,2,3,42第一阶段:设将S1个销售点(S1 = 4)分配给三个地区时,则最大利润值为: f1(S1)= max[ P1(X1)+ f2(4 —X1)]其中,X1 = 0,1,2,3,4表3然后按计算表格的顺序反推,可知最优分配方案有两个:最大总利润为531)由X1* = 2, X2* = 1, X3* = 1。
动态规划习题答案

2.某公司有资金4百万元向A,B和C3个项目追加投资,各个项目可以有不同的投资额(百万元计),相应的效益如表所示。
问怎样分配资金,使总效益值最大?##表8-47W k (X k)投资额(项目k#012341#(A)-414860662#(B )40425060-3#(C)-64687884解:设S1-A,B,C项目的总投资额,S2-B、C项目的总投资额S3-C项目的投资额;X k-k项目的投资额;(X1-A项目的投资额,X2-B项目的投资额,X3-C项目的投资额)W k(S k,X k)-对K项目投资X k后的收益:W k(S k,X k)=W k (X k)T k (S k,X k)-S k+1=S k-X kf k (S k)-当K至第3项目允许的投资额为S k时所能获得的最大收益。
为获得最大利润,必须将4百万全部投资,假设有4阶段存在,有S4=0,建立递归方程f4 (S k)=0f k (S k)=max{ W k (X k)+f k +1(S k+1)} k=3,2,1X k∈D k(S k)第一步,K=3f4(S4)=0f3 (S3)=max{W3 (X3)+f4 (S4)}X3∈D3(S3)S4=S3-X3S3f3 (S3)X3* 1641268237834844第二步:K=2 f2 (S2)=max{W2 (X2)+f3 (S3)}X2∈D2(S2)S3=S2-X2W2 (X2)+f3 (S2-X2)S2X2 =0X2 =1X2 =2X2 =3f2 (S2)X2 * 140+64---1040 240+6842+64--1080 340+7842+6850+64-1180 440+8442+7850+6860+641240,3第三步:K=1 f1 (S1) =max {W1 (X1)+ f2 (S2)}X1∈D1(S1)S2= S1- X1W1 (X1)+ f2 (S1- X1)S1X1=0X1=1X1=2X1=3f1 (S1)X1 * 4-41+118 48+10860+1041643S1=4 →S2=1 →S3=1↓↓↓X1*=3 X2*=0 X3*=1A投资3百万,B不投资C投资1百万。
动态规划练习解答

Var a:array[1..1000000] of longint; c,p:array[1..100] of longint; k,n,tmp,s,min,i:longint; begin assign(input,'panda.in'); assign(output,'panda.out'); reset(input); rewrite(output); readln(k, n); inc(n); for i:=1 to k do read(c[i]); i-1; end; for i:=1 to n do if k[i]>0 then writeln(i,' ',k[i]); close(input); close(output); end.
2、最小乘车费用(work.pas) 、最小乘车费用( ) 假设某条街上每一公里就有一个公共汽车站, 假设某条街上每一公里就有一个公共汽车站,并 且乘车费用如下表: 且乘车费用如下表:
For i:=1 to 10 do read(a[i]); readln(n); fillchar(b,sizeof(b),0); for i:=1 to n do begin max:=maxlongint; for j:=1 to 10 do if (i-j>=0) and (a[j]+b[i-j]<max) then max:=a[j]+b[i-j]; b[i]:=max; end; writeln(b[n]); close(input); close(output); end.
输入: 输入:panda.in 行有2个数 代表质因数的个数, 代表那个宇宙系数 第1行有 个数 行有 个数n,k,n代表质因数的个数,k代表那个宇宙系数 代表质因数的个数 (1<=n<=100,1<=k<=1e5) ) 行有n个数 个质因数。(每个均小于1000,且 第2行有 个数,代表这 个质因数。(每个均小于 行有 个数,代表这n个质因数。(每个均小于 , 不相同) 不相同) 输出: 输出:panda.out 个质因数的数中第k小的数 仅1行,即至多只包含这 个质因数的数中第 小的数。 行 即至多只包含这n个质因数的数中第 小的数。 这个数不会超过2e9) (这个数不会超过 ) 输入样例 27 35 输出样例 45(前6个分别是 个分别是3,5,9,15,25,27) ( 个分别是 )
动态规划模拟试卷及答案

动态规划模拟试卷及答案模拟试卷——第三章动态规划一、填空题(每小题4分,共20分)1、动态规划算法的基本要素是()和()。
2、()是动态规划法的变形。
3、()是最大子段和问题想二维的推广。
4、矩阵连乘问题的算法可由()设计实现。
5、动态规划算法中,通常不同子问题的个数随问题大小呈()增长。
二、简答题(每小题6分,共30分)1、写出设计动态规划算法的主要步骤。
2、简述什么是备忘录方法。
3、简述备忘录法与动态规划法的异同。
4、简述动态规划算法的基本思想。
5. 写出最长公共子序列问题具有的性质。
三、综合题(每小题25分,共50分)1、用动态规划算法实现最长公共子序列问题。
2、用动态规划算法实现下列问题:设A和B是两个字符串。
我们要用最少的字符操作将字符串A转换为字符串B,这里所说的字符操作包括:(1)删除一个字符;(2)插入一个字符;(3)将一个字符改为另一个字符。
将字符串A变换为字符串B所用的最少字符操作数称为字符串A 到B的编辑距离,记为d(A,B)。
试设计一个有效算法,对任给的两个字符串A和B,计算出它们的编辑距离d(A,B)。
答案一、填空题1、最优子结构、子问题重叠2、备忘录方法3、最大子矩阵的问题4、动态规划法5、多项式二、简答题1、(1)找出最优解的性质,并刻画其结构特征;(2)递归地定义最优解;(3)以自底向上的方法计算出最优值;(4)根据计算最优值时得到的信息,构造最优解。
2、备忘录方法是动态规划算法的变形。
备忘录方法的控制结构与直接递归方法的控制结构相同,区别在于备忘录方法为每个解过的子问题建立了备忘录以备需要时查看,避免了相同子问题的重复求解。
3、与动态规划算法一样,备忘录方法用表格保存已解决的子问题的答案,在下次需要解此子问题时,只要简单地查看该子问题的解答,而不必重新计算。
与动态规划算法不同的是,备忘录方法的递归方式是自顶向下的,而动态规划算法则是自底向上递归的。
4、动态规划算法的基本思想是将待求解问题分解成若干子问题,先求解子问题,然后从这些子问题的解得到原问题的解。
《运筹学》 第五章习题及 答案
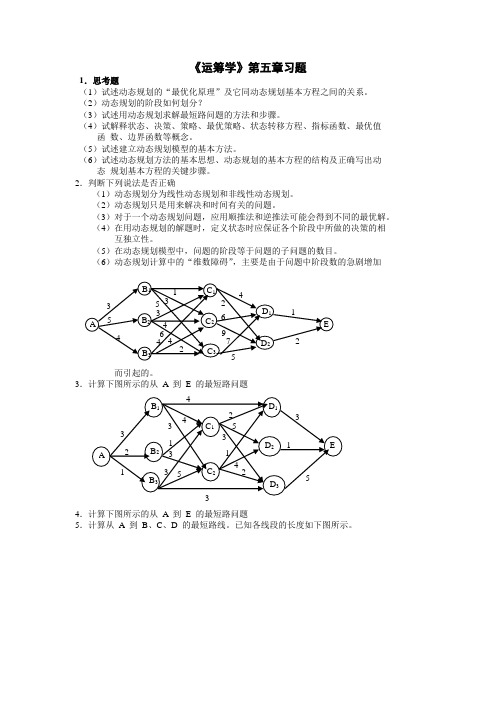
《运筹学》第五章习题1.思考题(1)试述动态规划的“最优化原理”及它同动态规划基本方程之间的关系。
(2)动态规划的阶段如何划分?(3)试述用动态规划求解最短路问题的方法和步骤。
(4)试解释状态、决策、策略、最优策略、状态转移方程、指标函数、最优值函数、边界函数等概念。
(5)试述建立动态规划模型的基本方法。
(6)试述动态规划方法的基本思想、动态规划的基本方程的结构及正确写出动态规划基本方程的关键步骤。
2.判断下列说法是否正确(1)动态规划分为线性动态规划和非线性动态规划。
(2)动态规划只是用来解决和时间有关的问题。
(3)对于一个动态规划问题,应用顺推法和逆推法可能会得到不同的最优解。
(4)在用动态规划的解题时,定义状态时应保证各个阶段中所做的决策的相互独立性。
(5)在动态规划模型中,问题的阶段等于问题的子问题的数目。
(6)动态规划计算中的“维数障碍”,主要是由于问题中阶段数的急剧增加而引起的。
3.计算下图所示的从A 到E 的最短路问题4.计算下图所示的从A 到E 的最短路问题5.计算从A 到B、C、D 的最短路线。
已知各线段的长度如下图所示。
6.设某油田要向一炼油厂用管道供应油料,管道铺设途中要经过八个城镇,各城镇间的路程如下图所示,选择怎样的路线铺设,才使总路程最短?7.用动态规划求解下列各题(1).222211295max x x x x z -+-=;⎩⎨⎧≥≤+0,52121x x x x ;(2).33221max x x x z =⎩⎨⎧≥≤++0,,6321321x x x x x x ;8.某人外出旅游,需将3种物品装入背包,但背包重量有限制,总重量不超过10千克。
物品重量及其价值等数据见下表。
试问每种物品装多少件,使整个 背包的价值最大?913 千克。
物品重量及其价值的关系如表所示。
试问如何装这些物品,使整个背包 价值最大?10 量和相应单位价值如下表所示,应如何装载可使总价值最大?303011 底交货量,该厂的生产能力为每月600件,该厂仓库的存货能力为300件,又 每生产100件产品的费用为1000元。
动态规划习题集全

动态规划专题训练护卫队【问题描述】护卫车队在一条单行的街道前排成一队,前面河上是一座单行的桥。
因为街道是一条单行道,所以任何车辆都不能超车。
桥能承受一个给定的最大承载量。
为了控制桥上的交通,桥两边各站一个指挥员。
护卫车队被分成几个组,每组中的车辆都能同时通过该桥。
当一组车队到达了桥的另一端,该端的指挥员就用电话通知另一端的指挥员,这样下一组车队才能开始通过该桥。
每辆车的重量是已知的。
任何一组车队的重量之和不能超过桥的最大承重量。
被分在同一组的每一辆车都以其最快的速度通过该桥。
一组车队通过该桥的时间是用该车队中速度最慢的车通过该桥所需的时间来表示的。
问题要求计算出全部护卫车队通过该桥所需的最短时间值。
【输入格式】输入文件中的第一行包含三个正整数(用空格隔开),第一个整数表示该桥所能承受的最大载重量(用吨表示),第二个整数表示该桥的长度(用千米表示),第三个整数表示该护卫队中车辆的总数(n<1000)。
接下来的几行中,每行包含两个正整数W和S(用空格隔开),W表示该车的重量(用吨表示),S表示该车过桥能达到的最快速度(用千米/小时表示)。
车子的重量和速度是按车子排队等候时的顺序给出的。
【输出格式】输出文件中应该是一个实数,四舍五入精确到小数点后1位,表示整个护卫车队通过该桥所需的最短时间(用分钟表示)。
【输入输出样例】输入:100 5 1040 2550 2050 2070 1012 509 7049 3038 2527 5019 70输入:75.0DOLLARS【问题描述】在以后的若干天里戴维将学习美元与德国马克的汇率。
编写程序帮助戴维何时应买或卖马克或美元,使他从100美元开始,最后能获得最高可能的价值。
【输入格式】输入文件中的第一行是一个自然数N(1<=N<=100),表示戴维学习汇率的天数。
接下来的N行中每行是一个自然数A(1<=A<=1000)。
第i+1行的A表示预先知道的第i+1天的平均汇率,在这一天中,戴维既能用100美元买A马克也能用A马克购买100美元。
动态规划算法题(5题)

动态规划算法题(5题)1、题⽬描述(⽹易)有 n 个学⽣站成⼀排,每个学⽣有⼀个能⼒值,⽜⽜想从这 n 个学⽣中按照顺序选取 k 名学⽣,要求相邻两个学⽣的位置编号的差不超过d,使得这 k 个学⽣的能⼒值的乘积最⼤,你能返回最⼤的乘积吗?输⼊描述:每个输⼊包含 1 个测试⽤例。
每个测试数据的第⼀⾏包含⼀个整数 n (1 <= n <= 50),表⽰学⽣的个数,接下来的⼀⾏,包含 n 个整数,按顺序表⽰每个学⽣的能⼒值 ai(-50 <= ai <= 50)。
接下来的⼀⾏包含两个整数,k 和 d (1 <= k <= 10, 1 <= d <= 50)。
输出描述:输出⼀⾏表⽰最⼤的乘积。
试题分析:本题要使⽤动态规划来解,动态规划的特点:1.求解的是最优化问题;2.可以分解为最优⼦结构本题可以先求解在第i个学⽣的位置下,j(j<K)个学⽣的能⼒值的最⼤值,得到所有学⽣位置下j个学⽣的能⼒值的最⼤值;在j个学⽣的情况下,得到j+1个学⽣的最⼤值,样例输出: 10 8 7 2 -7 9 5 4 10 -7 1 3 3输出: 630如上,第⼀步先计算k=2的情况:7:在d=3的情况下,最⼤最⼩值都为562:在d=3的情况下,最⼤值为16,最⼩值为14-7:在d=3的情况下,最⼤值为-14,最⼩值为-56......得到第⼀趟的结果k=3的情况下(这⾥以第⼀趟的结果为基础,只有这样就不需要考虑第⼀趟中d=3的限制):2:在d=3的情况下,最⼤最⼩值都为112(56*2)-7:在d=3的情况下,最⼤值为-98(14*-7)最⼩值为-392(56*-7)9:在d=3的情况下,最⼤值为504(56*9)最⼩值为-504(-56*9)......得到第⼆趟的结果返回最⼤值就是最后的结果#-*- coding:utf-8 -*-n=input()array=[int(i) for i in raw_input().split()]k,d=[int(i) for i in raw_input().split()]# n=36array_max=array_min=array#轮询k-1趟即可for i in range(0,k-1):_max=[-float('inf')]*n#将最⼤值的数组赋值⽆穷⼩_min=[float('inf')]*n#将最⼩值的数组赋值⽆穷⼤for j in range(i+1,n):if j<=d+i:#下⾯对应的min、max都是考虑到array[j]为负值的情况下temp_max = max(max(ii*array[j] for ii in array_max[i:j]),max(ii*array[j] for ii in array_min[i:j]))temp_min = min(min(ii*array[j] for ii in array_max[i:j]),min(ii*array[j] for ii in array_min[i:j]))else:temp_max = max(max(ii*array[j] for ii in array_max[j-d:j]),max(ii*array[j] for ii in array_min[j-d:j]))temp_min = min(min(ii*array[j] for ii in array_max[j-d:j]),min(ii*array[j] for ii in array_min[j-d:j]))_max[j]=temp_max_min[j]=temp_minarray_max=_maxarray_min=_minprint array_maxprint array_minprint max(array_max)2、题⽬描述(腾讯):腾讯⼤厦有39层,你⼿⾥有两颗⼀抹⼀眼的玻璃珠。
动态规划模拟题及答案

动态规划测试题一:填空题(每空2分,共20分)1.动态规划算法的步骤是(找出最优解的性质,并刻画其结构特征)、(递归地定义最优值)(以自底向上的方式计算最优值)、(根据计算最优值时得到的信息构造最优解)。
2.为方便起见、将矩阵连乘积A i A i+1……A j简记为(A[i:j] )。
3.动态规划算法的两个基本要素是(最优子结构性质)和(重叠子问题性质)。
4.矩阵连乘问题的算法可由(递归)设计实现。
5.对于矩阵连乘问题、设计算A[i:j]、1≤i≤j≤n,所需要的最少数乘次数为m[i][j],则原则问题的最优值为(m[1][n] )。
6. 动态规划算法的基本思想是将待求解问题分解成若干(子问题),先求解(子问题),然后从这些(子问题)的解得到原问题的解。
二:综合题(第一题5分其余各题15分,共50分)1.补充下面的最大子段和动态规划算法。
int MaxSum(int n,int *a){int sum=0,b=0;for(int i=1;i<=n;i++){if(b>0){b+=a[i];besti=1;}else b=a[i];if(b>sum){sum=b;bestj=i;}}return sum;}2. 0—1背包问题:有5种物品,背包的容量为c=10,物品i的重量为wi,其价值为vi:(w1,v1)=(2,6) (w2,v2)=(2,3) (w3,v3)=(6,5) (w4、v4)=(5,4)(w5,v5)=(4,6), 求最优解及最优值。
解∵p[5+1]={(0,0)}又∵(w5,w5)=(4,6)∴q[5+1]=p[5+1]○+(4,6)={(4,6)}则p[5]=m5j-其中的受控点={(0,0),(4,6)}又∵(w4,v4)=(5,4)∴q[5]○+(w4,v4)={(0,0),(4,6)}○+(5,4)={(5,4),(9,10)}∴w4j=p[5]∨q[5]={(0,0),(4,6),(5,4),(9,10)}又∵(w3,v3)=(6,5)∴q[4]=p[4]○+(w3,v3)={(6,5),(10,11)}∴m3j=p[4]∨q[4]={(0,0),(4,6),(6,5),(9,10),(10,11)} 则p[3]=m3j-其中的受控点={(0,0),(4,6),(9,10),(10,11)}又∵(w2,v2)=(2,3)∴q[3]=p[3]○+(w2,v2)={(2,3),(6,9)}∴m2j={(0,0),(2,3),(4,6), (6,9),(9,10),(10,11) } p[2]=m2j-其中的受控点={(0,0),(2,3),(4,6),(6,9),(9,10),(10,11)}又∵(w1,v1)=(2,6)∴q[2]=p[2]○+(w2,v2)={(2,6),(4,9),(6,12),(8,15)}∴m1j={(0,0),92,3},(2,6),(4,6),(4,9),(6,9),(6,12),(8,15),(9,10),(10,11)}∴p[1]={(0,0),(2,6),(4,9),(6,12),(8,15)}∴此0—1问题的最优值15.最优解为p[1]={(0,0),(2,6),(4,9)(6,12),(8,15)}3.设n=4,(a1,a2,a3,a4)=(3,4,8.10),(b1,b2,b3,b4)=(6,2,9,15),求作业中的一种最优调度方案并计算其最优值。
动态规划训练题目

动态规划题目【引例1、上楼梯】一个含有n阶的楼梯,一次可以走1阶或2阶,从底走到顶一共有几种走法?n<=90。
【引例2、数字三角形】a1有一个数字三角形,编程求从最顶层到最底层的一条路所经过位置上数字之和的最大值。
每一步只能向左下或右下方向走。
下图数据的路应为7->3->8->7->5,和为30。
输入:文件输入(从键盘读入文件名),文件格式:第一行:R(1<=R<=10000),数字三角形共有R行;以下R行:依次表示数字三角形中每行中的数字。
每个数都是非负的,且<=100.输出:一个正整数,路径上数字之和的最大值。
输入样例:573 88 1 02 7 4 44 5 2 6 5输出样例:30【引例3、求最大连续子序列的和。
】a2输入:第一行:n(N<500)第二行:n个整数(-3000,3000)。
输出:最大连续子序列的和。
样例:输入:7-6 4 -1 3 2 -3 2输出:81、最长递增序列b1设有整数序列b1,b2,b3,…,bm,若存在i1<i2<i3<…<in,且bi1<bi2<bi3<…<bin,则称b1,b2,b3,…,bm 中有长度为n的递增序列bi1,bi2,bi3,…,bin。
求序列b1,b2,b3,…,bm中最大递增序列长度(n)。
输入:m(<1000),整数序列输出:最大长度n样例:输入:7-6 4 -1 3 8 -3 2输出:42、背包问题b2设有n种物品,每种物品有一个重量及一个价值。
同时有一个背包,最大载重量为W,今从n种物品中选取若干件,使其重量的和小于等于W,而价值的和为最大。
输入数据:第一行两个数:物品总数N(<100),背包载重量W(<100);两个数用空格分隔;第二行N个数,为N种物品重量Wi;两个数用空格分隔;第三行N个数,为N种物品价值Vi; 两个数用空格分隔;输出数据:第一行总价值;输入样例:4 103 4 5 77 15 20 25输出样例:353、迷宫寻宝b3一个n行m列的迷宫(1<=n,m<=50),入口在左上角,规定只能向下或向右走。
运筹学习题解答(chap8 动态规划)
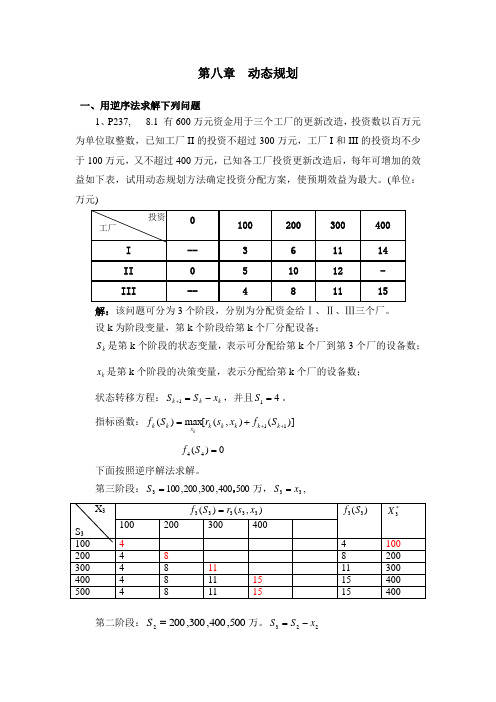
第八章 动态规划一、用逆序法求解下列问题1、P237, 8.1 有600万元资金用于三个工厂的更新改造,投资数以百万元为单位取整数,已知工厂II 的投资不超过300万元,工厂I 和III 的投资均不少于100万元,又不超过400万元,已知各工厂投资更新改造后,每年可增加的效益如下表,试用动态规划方法确定投资分配方案,使预期效益为最大。
(单位:万元)解:该问题可分为3个阶段,分别为分配资金给Ⅰ、Ⅱ、Ⅲ三个厂。
设k 为阶段变量,第k 个阶段给第k 个厂分配设备;k S 是第k 个阶段的状态变量,表示可分配给第k 个厂到第3个厂的设备数;k x 是第k 个阶段的决策变量,表示分配给第k 个厂的设备数;状态转移方程:k k k x S S -=+1,并且41=S 。
指标函数:)](),([max )(11+++=k k k k k x k k S f x s r S f k0)(44=S f下面按照逆序解法求解。
第三阶段:500400,300,200,1003,=S 万,33x S =, 第二阶段:500,400,300,2002=S 万。
223x S S -=第1阶段:6001=S 万。
112x S S -=按照与计算相反的顺序可推知有一个最优解:3001=*X ,2002=*X ,1003=*X ,最大利润为25万。
2、P237, 8.2 如图,要铺设一条从A 到E 的输油管线,箭线旁数字为各点间相应距离(km )一个运筹学小组正研究讨论线路选择,使得总距离为最短。
甲提出用求最短距离的Dijkstra 算法求解;乙认为这个问题也可用动态规划方法求解,但丙丁认为从A 到E 经B1、D1的线路,与经B2、C1、D2的线路阶段数不等,故动态规划行不通;丙提出建立整数规划模型求解,甲乙对此持怀疑的态度;丁设想用破圈法或避圈法找出图中最小部分树,树图中A-E 的唯一链即为A 至E 铺设管道的最佳选择,对此甲和乙不同意。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
动态规划练习题[题1] 多米诺骨牌(DOMINO)问题描述:有一种多米诺骨牌是平面的,其正面被分成上下两部分,每一部分的表面或者为空,或者被标上1至6个点。
现有一行排列在桌面上:顶行骨牌的点数之和为6+1+1+1=9;底行骨牌点数之和为1+5+3+2=11。
顶行和底行的差值是2。
这个差值是两行点数之和的差的绝对值。
每个多米诺骨牌都可以上下倒置转换,即上部变为下部,下部变为上部。
现在的任务是,以最少的翻转次数,使得顶行和底行之间的差值最小。
对于上面这个例子,我们只需翻转最后一个骨牌,就可以使得顶行和底行的差值为0,所以例子的答案为1。
输入格式:文件的第一行是一个整数n(1〈=n〈=1000〉,表示有n个多米诺骨牌在桌面上排成一行。
接下来共有n行,每行包含两个整数a、b(0〈=a、b〈=6,中间用空格分开〉。
第I+1行的a、b分别表示第I个多米诺骨牌的上部与下部的点数(0表示空)。
输出格式:只有一个整数在文件的第一行。
这个整数表示翻动骨牌的最少次数,从而使得顶行和底行的差值最小。
[题2] Perform巡回演出题目描述:Flute市的Phlharmoniker乐团2000年准备到Harp市做一次大型演出,本着普及古典音乐的目的,乐团指挥L.Y.M准备在到达Harp市之前先在周围一些小城市作一段时间的巡回演出,此后的几天里,音乐家们将每天搭乘一个航班从一个城市飞到另一个城市,最后才到达目的地Harp市(乐团可多次在同一城市演出).由于航线的费用和班次每天都在变,城市和城市之间都有一份循环的航班表,每一时间,每一方向,航班表循环的周期都可能不同.现要求寻找一张花费费用最小的演出表.输入: 输入文件包括若干个场景.每个场景的描述由一对整数n(2<=n<=10)和k(1<=k<=1000)开始,音乐家们要在这n个城市作巡回演出,城市用1..n标号,其中1是起点Flute市,n是终点Harp市,接下来有n*(n-1)份航班表,一份航班表一行,描述每对城市之间的航线和价格,第一组n-1份航班表对应从城市1到其他城市(2,3,...n)的航班,接下的n-1行是从城市2到其他城市(1,3,4...n)的航班,如此下去.每份航班又一个整数d(1<=d<=30)开始,表示航班表循环的周期,接下来的d个非负整数表示1,2...d天对应的两个城市的航班的价格,价格为零表示那天两个城市之间没有航班.例如"3 75 0 80"表示第一天机票价格是75KOI,第二天没有航班,第三天的机票是80KOI,然后循环:第四天又是75KOI,第五天没有航班,如此循环.输入文件由n=k=0的场景结束.输出:对每个场景如果乐团可能从城市1出发,每天都要飞往另一个城市,最后(经过k天)抵达城市n,则输出这k个航班价格之和的最小值.如果不可能存在这样的巡回演出路线,输出0.样例输入: 样例输出:3 6 4602 130 150 03 75 0 807 120 110 0 100 110 120 04 60 70 60 503 0 135 1402 70 802 32 0 701 800 0[题3] 复制书稿(BOOKS)问题描述:假设有M本书(编号为1,2,…M),想将每本复制一份,M本书的页数可能不同(分别是P1,P2,…PM)。
任务时将这M本书分给K个抄写员(K 〈=M〉,每本书只能分配给一个抄写员进行复制,而每个抄写员所分配到的书必须是连续顺序的。
意思是说,存在一个连续升序数列0=bo〈b1〈b2〈…<bk-1 <bk=m,这样,第I号抄写员得到的书稿是从bi-1+1到第bi本书。
复制工作是同时开始进行的,并且每个抄写员复制的速度都是一样的。
所以,复制完所有书稿所需时间取决于分配得到最多工作的那个抄写员的复制时间。
试找一个最优分配方案,使分配给每一个抄写员的页数的最大值尽可能小(如存在多个最优方案,只输出其中一种)。
输入格式:文件的第一行是两个整数m和k (1〈=k〈=m〈=500)。
第二行有m个整数P1,P2,…,Pm,这m个整数均为正整数且都不超过1000000。
每两个整数之间用空格分开。
输出格式:文件有k行,每行有两个正整数。
整数之间用空格分开。
第I行的两个整数ai和bi,表示第I号抄写员所分配得到的书稿的起始编号与终止编号。
动态规划题参考程序:题1:解决问题:例子的上下部分之差是6+1+1+1-(1+5+3+2)=(6-1)+(1-5)+(1-3)+(1-2)=-2,而翻转最后一个骨牌后,上下之差变为(6-1)+(1-5)+(1-3)+(2-1)=0。
由此看出,一个骨牌对翻转策略造成影响的是上下两数之差,骨牌上的数则是次要的了。
这么一来,便把骨牌的放置状态由8个数字变为4个: 5 -4 -2 -1,翻转时只需取该位数字的相反数就行了。
在本题中,因为各骨牌的翻转顺序没有限定,所以不能按骨牌编号作为阶段来划分。
怎么办呢?考虑到隐含阶段类型的问题可以按状态最优值的大小来划分阶段。
于是,我们以骨牌序列上下两部分的差值I作为状态,把达到这一状态的翻转步数作为状态值,记为f(I)。
便有f(I)=min{f(I+j)+1} (-12〈=j<=12,j 为偶数,且要求当前状态有差值为j/2的骨牌)。
这里,I不是无限增大或减小,其范围取决于初始骨牌序列的数字差的和的大小。
具体动态规划时,如例题,我们以f(-2)=0起步,根据骨牌状态,进行一次翻转,可得到f(-12)=1,f(6)=1,f(2)=1,f(0)=1,由于出现了f (0),因此程序便可以结束,否则将根据四个新状态继续扩展,直至出现f(0)或者无法生成新状态为止。
注意:在各状态,除记录最少步数外,还需记录到达这一状态时各骨牌的放置情况;而当到达某一状态发现已记录有一种翻转策略时,则取步数较小的一种。
程序如下:program domino;type tp=array[1..6] of integer;var t:array[1..6000] of ^tp;{记录骨牌摆放状态}f:array[-6000..6000] of integer;{记录达到某个差值的最少步数}l:array[1..6000] of integer;{扩展队列}tt:tp;i,j,n,m,x,y,ft,re:integer;f1,f2:text;procedure init;{程序初始化}beginassign(f1,'domino.dat');reset(f1);assign(f2,'domino.out');rewrite(f2);m:=0;ft:=0;re:=1;new(t[1]);fillchar(t[1]^,sizeof(t[1]^),0);fillchar(f,sizeof(f),0);fillchar(tt,sizeof(tt),0);readln(f1,n);for i:=1 to n dobeginreadln(f1,x,y);if x<>y thenbeginx:=x-y;inc(m,x);inc(tt[abs(x)]);if x>0 then inc(t[1]^[x]);end;end;if m=0 thenbeginwriteln(f2,0);close(f2);halt;end;{处理步数为零的情况}l[1]:=m;f[m]:=1;end;procedure main;{主过程}beginrepeatfor ft:=ft+1 to re do{以步数为阶段扩展状态}beginx:=l[ft];for i:=1 to 6 do{不同差值的六种情况}beginif x<6 thenif (t[ft]^[i]<tt[i])and(f[x+i*2]=0) then begininc(re);l[re]:=x+i*2;f[l[re]]:=f[x]+1;if l[re]=0 then{找到解便打印}beginwriteln(f2,f[l[re]]-1);close(f2);halt;end;new(t[re]);t[re]^:=t[ft]^;inc(t[re]^[i]);end;{差值增加}if x>-6 thenif (t[ft]^[i]>0)and(f[x-i*2]=0) thenbegininc(re);l[re]:=x-i*2;f[l[re]]:=f[x]+1;if l[re]=0 then{找到解便打印}beginwriteln(f2,f[l[re]]-1);close(f2);halt;end;new(t[re]);t[re]^:=t[ft]^;dec(t[re]^[i]);end;{差值减少}end;end;until ft=re;for i:=1 to 6 doif (f[i]>0)or(f[-i]>0) thenbeginif (f[-i]>0)and((f[i]=0)or(f[-i]<f[i])) then x:=f[-i]else x:=f[i];writeln(f2,x-1);i:=6;end;close(f2);{骨牌上下两行点数之和的绝对值不为零}end;begininit;main;end.题2:初看这道题,很容易便可以想到动态规划,因为第x天在第y个地方的最优值只与第x-1天有关,符合动态规划的无后效性原则,即只与上一个状态相关联,而某一天x航班价格不难求出S=C[(x-1) mod m +1].我们用天数和地点来规划用一个数组A[1..1000,1..10]来存储,A[i,j]表示第i天到达第j个城市的最优值,C[i,j,l]表示i 城市与j城市间第l天航班价格,则A[i,j]=Min{A[i-1,l]+C[l,j,i] (l=1..n且C[l,j,i]<>0)},动态规划方程一出,尽可以放怀大笑了.示范程序:program perform_hh;varf,fout:text;p,l,i,j,n,k:integer;a:array [1..1000,1..10] of integer; {动态规划数组}c:array [1..10,1..10] of record {航班价格数组}num:integer;t:array [1..30] of integer;end;e:array [1..1000] of integer;procedure work;begin{人工赋第一天各城市最优值}for i:=1 to n dobeginif c[1,i].t[1]<>0then a[1,i]:=c[1,i].t[1];end;for i:=2 to k dobeginfor j:=1 to n dobeginfor l:=1 to n dobeginif (j<>l)and (c[l,j].t[(i-1) mod c[l,j].num+1]<>0) {判断存在航班}and ((a[i,j]=0) or (a[i-1,l]+c[l,j].t[(i-1) mod c[l,j].num+1]<a[i,j])) {判断比当前解优}then a[i,j]:=a[i-1,l]+c[l,j].t[(i-1) mod c[l,j].num+1]; {赋值}end;end;end;e[p]:=a[k,n]; {第p个场景的最优值}end;procedure readfile; {读文件}beginassign(f,'PERFORM.DAT'); reset(f);assign(fout,'PERFORM.OUT'); rewrite(fout);readln(f,n,k); p:=0;while (n<>0) and (k<>0) dobeginp:=p+1;fillchar(c,sizeof(c),0);fillchar(a,sizeof(a),0);for i:=1 to n dobeginfor j:=1 to i-1 dobeginread(f,c[i,j].num);for l:=1 to c[i,j].num doread(f,c[i,j].t[l]);end;for j:=i+1 to n dobeginread(f,c[i,j].num);for l:=1 to c[i,j].num doread(f,c[i,j].t[l]);end;end;work;readln(f,n,k);end;{输出各个场景的解}for i:=1 to p-1 dowriteln(fout,e[i]);write(fout,e[p]);close(f);close(fout);end;beginreadfile;end.[题3:]解决问题:该题中M本书是顺序排列的,K个抄写员选择数也是顺序且连续的。
