正态分布图程序
正态概率图(normal probability plot)
正态概率图(normal probability plot)方法演变:概率图,分位数-分位数图( Q- Q)➢概述正态概率图用于检查一组数据是否服从正态分布。
是实数与正态分布数据之间函数关系的散点图。
如果这组实数服从正态分布,正态概率图将是一条直线。
通常,概率图也可以用于确定一组数据是否服从任一已知分布,如二项分布或泊松分布。
➢适用场合·当你采用的工具或方法需要使用服从正态分布的数据时;·当有50个或更多的数据点,为了获得更好的结果时。
例如:·确定一个样本图是否适用于该数据;·当选择作X和R图的样本容量,以确定样本容量是否足够大到样本均值服从正态分布时;·在计算过程能力指数Cp或者Cpk之前;·在选择一种只对正态分布有效的假设检验之前。
➢实施步骤通常,我们只需简单地把数据输入绘图的软件,就会产生需要的图。
下面将详述计算过程,这样就可以知道计算机程序是怎么来编译的了,并且我们也可以自己画简单的图。
1将数据从小到大排列,并从1~n标号。
2计算每个值的分位数。
i是序号:分位数=(i-0.5)/n3找与每个分位数匹配的正态分布值。
把分位数记到正态分布概率表下面的表A.1里面。
然后在表的左边和顶部找到对应的z值。
4根据散点图中的每对数据值作图:每列数据值对应个z值。
数据值对应于y轴,正态分位数z值对应于x轴。
将在平面图上得到n个点。
5画一条拟合大多数点的直线。
如果数据严格意义上服从正态分布,点将形或一条直线。
将点形成的图形与画的直线相比较,判断数据拟合正态分布的好坏。
请参阅注意事项中的典型图形。
可以计算相关系数来判断这条直线和点拟合的好坏。
➢示例为了便于下面的计算,我们仅采用20个数据。
表5. 12中有按次序排好的20个值,列上标明“过程数据”。
下一步将计算分位数。
如第一个值9,计算如下:分位数=(i-0.5)/n=(1-0.5)/20=0.5/20=0.025同理,第2个值,计算如下:分位数=(i-0.5)/n=(2-0.5)/20=1.5/20=0.075可以按下面的模式去计算:第3个分位数=2.5÷20,第4个分位数=3 5÷20以此类推直到最后1个分位数=19. 5÷20。
正态分布

正态分布维基百科,自由的百科全书跳转到:导航, 搜索此条目或章节需要精通或熟悉本主题的专家参与编辑请协助邀请适合的人士,或参照相关专业文献,自行改善这篇条目。
更多的细节与详情请参见条目讨论页。
汉漢▼正态分布概率密度函数绿线代表标准正态分布累积分布函数颜色与概率密度函数同参数μlocation(real)σ2 > 0 squared scale(real)支撑集概率密度函數累积分布函数期望值μ中位数μ众数μ方差σ2偏度0峰度 3信息熵动差生成函数特性函数正态分布(Normal distribution)又名高斯分布(Gaussian distribution),是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。
若随机变量X服从一个数学期望为μ、标准方差为σ2的高斯分布,记为:X∼N(μ,σ2),则其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。
因其曲线呈钟形,因此人们又经常称之为钟形曲线。
我们通常所说的标准正态分布是μ = 0,σ = 1的正态分布(见右图中绿色曲线)。
目录• 1 概要o 1.1 历史• 2 正态分布的定义o 2.1 概率密度函数o 2.2 累积分布函数o 2.3 生成函数▪ 2.3.1 动差生成函数▪ 2.3.2 特征函数• 3 性质o 3.1 标准化正态随机变量o 3.2 矩(英文:moment)o 3.3 生成正态随机变量o 3.4 中心极限定理o 3.5 无限可分性o 3.6 稳定性o 3.7 标准偏差• 4 正态测试• 5 相关分布• 6 参量估计o 6.1 参数的极大似然估计▪ 6.1.1 概念一般化o 6.2 参数的矩估计•7 常见实例o7.1 光子计数o7.2 计量误差o7.3 生物标本的物理特性o7.4 金融变量o7.5 寿命o7.6 测试和智力分布•8 计算统计应用o8.1 生成正态分布随机变量•9 参见•10 引用条目•11 外部连接[编辑]概要正态分布是自然科学与行为科学中的定量现象的一个方便模型。
平均分布,正态分布,一阶滑动和,一阶线性回归 C语言编程

#include <stdlib.h>#include <stdio.h>#include <time.h>#include <math.h>#include<string.h># define pi 3.1415926# define sqr 0.707106781//在一阶线性回归出现了参数adouble uni[2000]={0};//程序中出现大数组时,很可能导致堆栈溢出,为了避免double nor[2000]={0};//这个问题,把数组声明为全局变量,double ovlap[1000];double linreg[1000];double nor_num[10];double nor_num_theory[10]={0.0};double mean( double a[]){ int i;double ever=0.0;for(i=0;i<2000;i++)ever+=a[i]/2000.0;return ever;}double std(double a[],double mean){ int i;double stda=0.0;for(i=0;i<2000;i++)stda+=(a[i]-mean)*(a[i]-mean)/2000.0;return stda;}double integral(double a,double b){double i,num=0.0;for(i=a;i<b;i+=0.0001){num+=1/sqrt(2*pi)*exp(-i*i/2)*0.0001;}num=2000*num;return num;}//double B_rela(double a)void main( ){FILE *fp1=fopen("D:\\data1.txt","w");//用于存放平均分布的相关函数FILE *fp2=fopen("D:\\data2.txt","w");//用于存放正态分布的相关函数FILE *fp3=fopen("D:\\data3.txt","w");//用于存放一阶滑动序列的相关函数FILE *fp4=fopen("D:\\data4.txt","w");//用于存放一阶线性回归的相关函数FILE *fp=fopen("D:\\data.txt","w");int i,j,k=0,uni_num[10]={0};//检验平均分布double uni_mean,uni_std; //均匀分布double nor_mean,nor_std;//正态分布double ovlap_mean,ovlap_ju,ovlap_std;//一阶滑动序列的平均数,矩,方差double linreg_mean,linreg_ju,linreg_std;// 一阶线性回归的平均数,矩,方差double uni_B[21],nor_B[21], ovlap_B[21],linreg_B[21];//相关函数srand( (unsigned)time( NULL ) );fprintf(fp,"the following are contents of uniform distribution:\n");for( i=0;i<2011;i++ )uni[i]=rand()/32767.0 ;for(j=0;j<=9;j++){if(i<2000&&(uni[i]>=j*0.1)&&(uni[i]<(j+1)*0.1))uni_num[j]++ ;}if(i<50)fprintf( fp,"%6.4f\t", uni[i]);}fprintf(fp,"\n\n");uni_mean=mean(uni);fprintf(fp,"the average number of the uniform distribution is:%6.4f\n",uni_mean);//打印平均分布的平均数uni_std=std(uni,uni_mean);fprintf(fp,"the variance of the uniform distribution is :%6.4f\n",uni_std);//打印平均分布的方差fprintf(fp,"the following are numbers in each erea \n\n");for(j=0;j<=9;j++) fprintf(fp,"%d\t",uni_num[j]);fprintf(fp,"\n\n");fprintf(fp,"the followings are correlation function value\n\n");double sum1;int B_j=-10;for(i=0;i<=20;i++){ sum1=0.0;for(j=0;j<1000-abs(B_j);j++){sum1+=(uni[j+abs(B_j)]-uni_mean)*(uni[j]-uni_mean);}uni_B[i]=sum1/1000.0;fprintf(fp,"%f\n",uni_B[i]);fprintf(fp1,"%f\n",uni_B[i]);B_j++;fclose(fp1);fprintf(fp,"\n\nthe following are the contents of normal distribution:\n"); memset(nor_num,0,sizeof(nor_num));memset(nor_num,0,sizeof(nor_num));//将数组置零,避免堆栈的叠加double index1,index2;srand( (unsigned)time( NULL ) );for(i=0;i<2000;i++){do{index1=rand()/32767.0 ;index2=rand()/32767.0;}while(index1==0);nor[i]=sqrt(-2*log(index1))*cos(2*pi*index2);if(i<50){fprintf(fp,"%f\t",nor[i]);}if(nor[i]>=-2.0 && nor[i]<-1.6) nor_num[0]++;if(nor[i]>=-1.6 && nor[i]<-1.2) nor_num[1]++;if(nor[i]>=-1.2 && nor[i]<-0.8) nor_num[2]++;if(nor[i]>=-0.8 && nor[i]<-0.4) nor_num[3]++;if(nor[i]>=-0.4 && nor[i]<0.0) nor_num[4]++;if(nor[i]>=0.0 && nor[i]<0.4) nor_num[5]++;if(nor[i]>=0.4 && nor[i]<0.8) nor_num[6]++;if(nor[i]>=0.8 && nor[i]<1.2) nor_num[7]++;if(nor[i]>=1.2 && nor[i]<1.6) nor_num[8]++;if(nor[i]>=1.6 && nor[i]<2.0) nor_num[9]++;}nor_mean=mean(nor);fprintf(fp,"the average number of normal distribution is:%6.4f\n",nor_mean); //正态分布的平均数nor_std=std(nor,nor_mean);fprintf(fp,"the variance of normal distribution is %6.4f\n",nor_std);//正态分布的方差fprintf(fp," the following outputs showed numbers of random number in determined zone\n"); fprintf(fp,"the former number is calculated in theory,the latter one is actual quantity\n");fprintf(fp," theoretical\t\t\tactual\n");for(i=-5;i<5;i++){nor_num_theory[i+5]=integral(0.4*i,0.4*i+0.4);fprintf(fp,"%f\t\t\t",nor_num_theory[i+5]);fprintf(fp,"%f\n",nor_num[i+5]);}//在求相关函数的过程中,会用到中间量fprintf(fp,"\n\n\n");fprintf(fp,"the followings are values of correlation functions\n\n ");B_j=-10;for(i=0;i<=20;i++){ sum1=0.0;for(j=0;j<1000-abs(B_j);j++){sum1+=(nor[j+abs(B_j)]-nor_mean)*(nor[j]-nor_mean);}nor_B[i]=sum1/1000.0;fprintf(fp,"%f\n",nor_B[i]);fprintf(fp2,"%f\n",nor_B[i]);B_j++;}fprintf(fp,"\n\n");fclose(fp2);// 以下部分为关于一阶滑动和序列的内容fprintf(fp,"the follwings are contents of overlap \n\n\n");memset(ovlap,0,sizeof(ovlap));ovlap_mean=0;ovlap_ju=0;ovlap_std=0;double ov_sum2=0.0,ov_sum3=0.0;for(i=0;i<1100;i++){ovlap[i]=nor[i+1]+4*nor[i];if(i<50)fprintf(fp,"%f\t",ovlap[i]);ov_sum2+=ovlap[i]; //ov_sum3+=ovlap[i]*ovlap[i];}ovlap_mean=ov_sum2/1000.0;//求平均数ovlap_ju=ov_sum3/1000.0;//求二阶距ovlap_std=ovlap_ju-ovlap_mean*ovlap_mean;//求方差fprintf(fp,"\n\naverage:%f\nju:%f\nstandard:%f\n",ovlap_mean,ovlap_ju,ovlap_std); fprintf(fp,"\n\n\n");/////123fprintf(fp,"the following are correlation function value\n\n");B_j=-10;for(i=0;i<=20;i++){ sum1=0.0;for(j=0;j<1000-abs(B_j);j++){sum1+=(ovlap[j+abs(B_j)]-ovlap_mean)*(ovlap[j]-ovlap_mean);}ovlap_B[i]=sum1/1000.0;fprintf(fp,"%f\n",ovlap_B[i]);fprintf(fp3,"%f\n",ovlap_B[i]);B_j++;}fprintf(fp,"\n\n");fclose(fp3);//一下为关于一阶线性回归的内容memset(linreg,0,sizeof(linreg));fprintf(fp,"the following are contents about linear regression\n\n ");linreg_mean=0;linreg_ju=0;linreg_std=0;linreg[0]=0.5;//get the value of each memberdouble li_sum1,li_sum2;li_sum1=0;li_sum2=0;for(i=1;i<=1000;i++){linreg[i]=nor[i]-sqr*linreg[i-1];if(i<50){fprintf(fp,"%f\t",linreg[i]);}if(i>100){li_sum1+=linreg[i];li_sum2+=pow(linreg[i],2);}}linreg_mean=li_sum1/900; //求平均数linreg_ju=li_sum2/900; //求二阶原点矩linreg_std=linreg_ju-pow(linreg_mean,2); //求方差fprintf(fp,"\n\naverage:%f\nju:%f\nstandard:%f\n\n",linreg_mean,linreg_ju,linreg_std);fprintf(fp,"the following are correlation function value\n\n");B_j=-10;for(i=0;i<=20;i++){ sum1=0.0;for(j=100;j<1000-abs(B_j);j++){sum1+=(linreg[j+abs(B_j)]-linreg_mean)*(linreg[j]-linreg_mean);}linreg_B[i]=sum1/900;fprintf(fp,"%f\n",linreg_B[i]);fprintf(fp4,"%f\n",ovlap_B[i]);B_j++;}fprintf(fp,"\n\n");fclose(fp4);fclose(fp);getchar();}以下为程序生成的数据:the following are contents of uniform distribution:0.0949 0.2003 0.1722 0.7819 0.7060 0.1859 0.9555 0.6196 0.4057 0.12170.0213 0.8671 0.1353 0.0969 0.8642 0.2540 0.5656 0.0188 0.50070.0146 0.6431 0.6016 0.6290 0.0331 0.2777 0.9265 0.0720 0.14010.5796 0.3563 0.1599 0.5901 0.5519 0.0843 0.2079 0.2519 0.64290.0991 0.7468 0.5435 0.0682 0.8469 0.6612 0.6420 0.3045 0.37220.8919 0.0005 0.6651 0.2186the average number of the uniform distribution is:0.5050the variance of the uniform distribution is :0.0851the following are numbers in each erea206 189 214 182 184 209 199 200 211 206the followings are correlation function value0.0030370.0000780.0015480.0030860.0008270.0012770.001035-0.001017-0.003483-0.0065300.087185-0.006530-0.003483-0.0010170.0010350.0012770.0008270.0030860.0015480.0000780.003037the following are the contents of normal distribution:0.667303 0.372894 0.326978 -0.220477 0.969196 1.862360 1.640884 -0.0137021.060122 1.171379 -0.754567 0.942319 1.433209 1.461014 -0.646995 -1.6161470.940878 -0.021497 0.763536 -0.735703 1.325226 -0.570759 -1.0710600.478394 0.177006 -0.160915 0.977499 -0.633792 0.310996 -0.881002-0.847941 -0.221102 -1.514981 0.270405 -0.919251 0.421879 -1.2492052.062010 -0.070496 0.538043 2.382505 0.088082 -0.374721 -1.116906-2.267095 1.570966 -0.136206 -0.417198 0.960820 0.078101 the average number of normal distribution is:-0.0052the variance of normal distribution is 1.0091the following outputs showed numbers of random number in determined zonethe former number is calculated in theory,the latter one is actual quantitytheoretical actual64.114811 71.000000120.571269 132.000000193.619846 202.000000265.511518 269.000000310.920207 317.000000310.920207 298.000000265.511518 237.000000193.619846 196.000000120.571269 120.00000064.114811 81.000000the followings are values of correlation functions0.005019-0.000179-0.0239050.022543-0.0009890.024601-0.0068160.028706-0.0051880.0249710.9695730.024971-0.0051880.0287060.024601-0.0009890.022543-0.023905-0.0001790.005019the follwings are contents of overlap3.042107 1.818552 1.087433 0.087288 5.739144 9.090323 6.5498351.005315 5.411866 3.930947 -2.075949 5.202484 7. 193850 5.197061-4.204127 -5.523712 3.742015 0.677548 2.318441 -1.617586 4.730147 -3.354095 -3.805846 2.090581 0.547111 0.333840 3.276205 -2.2241700.362982 -4.371949 -3.612864 -2.399387 -5.789518 0.162370 - 3.2551270.438311 -2.934810 8.177543 0.256058 4.534676 9.618101 -0.022393-2.615791 -6.734720 -7.497414 6.147657 -0.962023 -0.7079743.921381 0.589083average:0.111364ju:18.264297standard:18.251895the following are correlation function value0.105750-0.109536-0.3461690.2506860.1354860.3537250.0650560.4082470.0942794.24996516.6526394.2499650.0942790.4082470.0650560.1354860.250686-0.346169-0.1095360.105750the following are contents about linear regression0.019340 0.313302 -0.442015 1.281748 0.956027 0.964871 -0.695969 1.5522460.073775 -0.806734 1.512766 0.363522 1.203965 -1.498327 -0.5566711.334504 -0.965134 1.445989 -1.7581712.568441 -2.386921 0.6167480.042287 0.147105 -0.264934 1.164835 -1.457455 1.341572 -1.8296370.445808 -0.536335 -1.135735 1.073491 -1.678324 1.608633 -2.3866803.749648 -2.721897 2.462715 0.641102 -0.365246 -0.116453 -1.034561-1.535550 2.656763 -2.014821 1.007495 0.248413 -0.097553average:0.018926ju:1.770050standard:1.769692the following are correlation function value0.018228-0.000412-0.007155-0.0265130.100574-0.1809430.310911-0.5030500.804904-1.2063651.777504-1.2063650.804904-0.5030500.310911-0.1809430.100574-0.026513-0.007155-0.000412平均分布图:正态数列分布图:相关函数图:。
2012-05-07 简单易学 图文并茂 Excel VBA 制作正态分布曲线

<简单易学> <图文并茂>Excel VBA 制作正态分布曲线简介正态分布与Excel测量数据的正态分布,对相关工作有很重要的判定意义;特别是直观的分布曲线,让人对数据质量一目了然。
/view/45379.htm?wtp=tt参看不少文档,没有见到Excel有直接绘制正态分布曲线的函数,故考虑使用VBA编程的方法,实现从测量数据自动生成正态分布曲线的功能。
约定和程序假设有Excel数据表,把测试数据放在第一张表的第一列中:在VBA编辑器中新建一个模块,名字默认,输入如下代码(代码已经包含注释,请自行参看):'*****************************************************Public Sub myDistrib()Dim Aver As Double '平均数Dim Std As Double '标准差Dim Max As Double '最大值Dim Min As Double '最小值Dim Limit As Double '极限值Aver = Application.WorksheetFunction.Average(Selection)Std = Application.WorksheetFunction.StDev(Selection)Max = Application.WorksheetFunction.Max(Selection)Min = Application.WorksheetFunction.Min(Selection)'取极值的三倍作为今后绘图的上下限Limit = Application.WorksheetFunction.Max(Max - Aver, Aver - Min) * 2'在上下限间创建100个单点值step = Limit * 2 / 100Selection.Copy'创建一个新的表生成需要的数据'这是绘制分布曲线需要的数据Worksheets.Add , Worksheets(Worksheets.Count), 1Worksheets(Worksheets.Count).Name = "【正态分布】" & Trim(Str(Sheets.Count)) Range("A1").SelectActiveSheet.Paste[C1] = "平均值"[D1] = Round(Aver, 2)[C2] = "标准差"[D2] = Round(Std, 2)[C3] = "绘图上限(X2)"[D3] = Round(Aver + Limit, 2)[C4] = "绘图下限(X2)"[D4] = Round(Aver - Limit, 2)For I = 1 To 100Cells(I, 6).Value = (I - 1) * step + (Aver - Limit)Cells(I, 7).Value = Application.WorksheetFunction.NormDist(Cells(I, 6).Value, Aver, Std, 0)Next I'这是绘制上下标识和平均值需要的数据[C6] = "最大值"[D6] = Max[E6] = Max[D7] = 0[E7] = [G51][C9] = "最小值"[D9] = Min[E9] = Min[C10] = "绘图上标值"[D10] = 0[E10] = [G51][C12] = "平均值"[D12] = Aver[E12] = Aver[C13] = "绘图上标值"[D13] = 0[E13] = [G51]Columns.AutoFit'绘制图形ActiveSheet.Shapes.AddChart.SelectActiveChart.ChartType = xlXYScatterSmoothNoMarkersActiveChart.SeriesCollection.NewSeriesActiveChart.SeriesCollection(1).XValues = "='【正态分布】4'!$F$1:$F$100" ActiveChart.SeriesCollection(1).Values = "='【正态分布】4'!$G$1:$G$100" ActiveChart.SeriesCollection(1).Name = "=""分布曲线"""ActiveChart.SeriesCollection(2).DeleteActiveChart.SeriesCollection.NewSeriesActiveChart.SeriesCollection(2).XValues = "='【正态分布】4'!$D$6:$E$6" ActiveChart.SeriesCollection(2).Values = "='【正态分布】4'!$D$7:$E$7"ActiveChart.SeriesCollection(2).Name = "=""最大值"""ActiveChart.SeriesCollection.NewSeriesActiveChart.SeriesCollection(3).XValues = "='【正态分布】4'!$D$9:$E$9"ActiveChart.SeriesCollection(3).Values = "='【正态分布】4'!$D$10:$E$10"ActiveChart.SeriesCollection(3).Name = "=""最小值"""ActiveChart.SeriesCollection.NewSeriesActiveChart.SeriesCollection(4).XValues = "='【正态分布】4'!$D$12:$E$12"ActiveChart.SeriesCollection(4).Values = "='【正态分布】4'!$D$13:$E$13"ActiveChart.SeriesCollection(4).Name = "=""平均值"""'调整图形的位置ActiveSheet.Shapes(1).IncrementLeft 185ActiveSheet.Shapes(1).IncrementTop -93.75End Sub'*****************************************************使用方法为:选择Sheet1上,第一列的原始数据;按Alt+F8。
正态分布讲解(含标准表)
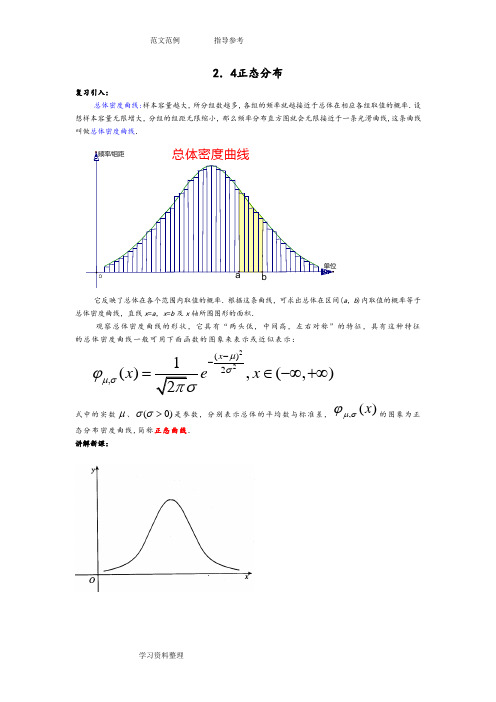
2.4正态分布复习引入:总体密度曲线:样本容量越大,所分组数越多,各组的频率就越接近于总体在相应各组取值的概率.设想样本容量无限增大,分组的组距无限缩小,那么频率分布直方图就会无限接近于一条光滑曲线,这条曲线叫做总体密度曲线. 总体密度曲线b 单位O 频率/组距a它反映了总体在各个范围内取值的概率.根据这条曲线,可求出总体在区间(a ,b )内取值的概率等于总体密度曲线,直线x =a ,x =b 及x 轴所围图形的面积.观察总体密度曲线的形状,它具有“两头低,中间高,左右对称”的特征,具有这种特征的总体密度曲线一般可用下面函数的图象来表示或近似表示:22()2,1(),(,)2x x e x μσμσϕπσ--=∈-∞+∞ 式中的实数μ、)0(>σσ是参数,分别表示总体的平均数与标准差,,()x μσϕ的图象为正态分布密度曲线,简称正态曲线.讲解新课:一般地,如果对于任何实数a b <,随机变量X 满足,()()b aP a X B x dx μσϕ<≤=⎰, 则称 X 的分布为正态分布(normal distribution ) .正态分布完全由参数μ和σ确定,因此正态分布常记作),(2σμN .如果随机变量 X 服从正态分布,则记为X ~),(2σμN .经验表明,一个随机变量如果是众多的、互不相干的、不分主次的偶然因素作用结果之和,它就服从或近似服从正态分布.例如,高尔顿板试验中,小球在下落过程中要与众多小木块发生碰撞,每次碰撞的结果使得小球随机地向左或向右下落,因此小球第1次与高尔顿板底部接触时的坐标 X 是众多随机碰撞的结果,所以它近似服从正态分布.在现实生活中,很多随机变量都服从或近似地服从正态分布.例如长度测量误差;某一地区同年龄人群的身高、体重、肺活量等;一定条件下生长的小麦的株高、穗长、单位面积产量等;正常生产条件下各种产品的质量指标(如零件的尺寸、纤维的纤度、电容器的电容量、电子管的使用寿命等);某地每年七月份的平均气温、平均湿度、降雨量等;一般都服从正态分布.因此,正态分布广泛存在于自然现象、生产和生活实际之中.正态分布在概率和统计中占有重要的地位.说明:1参数μ是反映随机变量取值的平均水平的特征数,可以用样本均值去佑计;σ是衡量随机变量总体波动大小的特征数,可以用样本标准差去估计.2.早在 1733 年,法国数学家棣莫弗就用n !的近似公式得到了正态分布.之后,德国数学家高斯在研究测量误差时从另一个角度导出了它,并研究了它的性质,因此,人们也称正态分布为高斯分布.2.正态分布),(2σμN )是由均值μ和标准差σ唯一决定的分布 通过固定其中一个值,讨论均值与标准差对于正态曲线的影响3.通过对三组正态曲线分析,得出正态曲线具有的基本特征是两头底、中间高、左右对称 正态曲线的作图,书中没有做要求,教师也不必补上 讲课时教师可以应用几何画板,形象、美观地画出三条正态曲线的图形,结合前面均值与标准差对图形的影响,引导学生观察总结正态曲线的性质4.正态曲线的性质:(1)曲线在x 轴的上方,与x 轴不相交(2)曲线关于直线x=μ对称(3)当x=μ时,曲线位于最高点(4)当x <μ时,曲线上升(增函数);当x >μ时,曲线下降(减函数) 并且当曲线向左、右两边无限延伸时,以x 轴为渐近线,向它无限靠近(5)μ一定时,曲线的形状由σ确定σ越大,曲线越“矮胖”,总体分布越分散;σ越小.曲线越“瘦高”.总体分布越集中:五条性质中前三条学生较易掌握,后两条较难理解,因此在讲授时应运用数形结合的原则,采用对比教学5.标准正态曲线:当μ=0、σ=l 时,正态总体称为标准正态总体,其相应的函数表示式是2221)(x e x f -=π,(-∞<x <+∞)其相应的曲线称为标准正态曲线标准正态总体N (0,1)在正态总体的研究中占有重要的地位 任何正态分布的概率问题均可转化成标准正态分布的概率问题讲解范例:例1.给出下列三个正态总体的函数表达式,请找出其均值μ和标准差σ (1)),(,21)(22+∞-∞∈=-x e x f x π(2)),(,221)(8)1(2+∞-∞∈=--x e x f x π (3)22(1)2(),(,)2x f x e x π-+=∈-∞+∞ 答案:(1)0,1;(2)1,2;(3)-1,0.5例2求标准正态总体在(-1,2)内取值的概率.解:利用等式)()(12x x p Φ-Φ=有)([]}{11)2()1()2(--Φ--Φ=-Φ-Φ=p=1)1()2(-Φ+Φ=0.9772+0.8413-1=0.8151.1.标准正态总体的概率问题: xy对于标准正态总体N (0,1),)(0x Φ是总体取值小于0x 的概率,即 )()(00x x P x <=Φ, 其中00>x ,图中阴影部分的面积表示为概率0()P x x < 只要有标准正态分布表即可查表解决.从图中不难发现:当00<x 时,)(1)(00x x -Φ-=Φ;而当00=x 时,Φ(0)=0.5 2.标准正态分布表标准正态总体)1,0(N 在正态总体的研究中有非常重要的地位,为此专门制作了“标准正态分布表”.在这个表中,对应于0x 的值)(0x Φ是指总体取值小于0x 的概率,即)()(00x x P x <=Φ,)0(0≥x .若00<x ,则)(1)(00x x -Φ-=Φ.利用标准正态分布表,可以求出标准正态总体在任意区间),(21x x 内取值的概率,即直线1x x =,2x x =与正态曲线、x 轴所围成的曲边梯形的面积1221()()()P x x x x x <<=Φ-Φ. 3.非标准正态总体在某区间内取值的概率:可以通过)()(σμ-Φ=x x F 转化成标准正态总体,然后查标准正态分布表即可 在这里重点掌握如何转化 首先要掌握正态总体的均值和标准差,然后进行相应的转化4.小概率事件的含义发生概率一般不超过5%的事件,即事件在一次试验中几乎不可能发生假设检验方法的基本思想:首先,假设总体应是或近似为正态总体,然后,依照小概率事件几乎不可能在一次试验中发生的原理对试验结果进行分析假设检验方法的操作程序,即“三步曲”一是提出统计假设,教科书中的统计假设总体是正态总体;二是确定一次试验中的a 值是否落入(μ-3σ,μ+3σ);三是作出判断讲解范例:例1. 若x ~N (0,1),求(l)P (-2.32<x <1.2);(2)P (x >2).解:(1)P (-2.32<x <1.2)=Φ(1.2)-Φ(-2.32)=Φ(1.2)-[1-Φ(2.32)]=0.8849-(1-0.9898)=0.8747.(2)P (x >2)=1-P (x <2)=1-Φ(2)=l-0.9772=0.0228.例2.利用标准正态分布表,求标准正态总体在下面区间取值的概率:(1)在N(1,4)下,求)3(F(2)在N (μ,σ2)下,求F(μ-σ,μ+σ);F(μ-1.84σ,μ+1.84σ);F(μ-2σ,μ+2σ);F(μ-3σ,μ+3σ) 解:(1))3(F =)213(-Φ=Φ(1)=0.8413 (2)F(μ+σ)=)(σμσμ-+Φ=Φ(1)=0.8413 F(μ-σ)=)(σμσμ--Φ=Φ(-1)=1-Φ(1)=1-0.8413=0.1587 F(μ-σ,μ+σ)=F(μ+σ)-F(μ-σ)=0.8413-0.1587=0.6826F(μ-1.84σ,μ+1.84σ)=F(μ+1.84σ)-F(μ-1.84σ)=0.9342F(μ-2σ,μ+2σ)=F(μ+2σ)-F(μ-2σ)=0.954F(μ-3σ,μ+3σ)=F(μ+3σ)-F(μ-3σ)=0.997对于正态总体),(2σμN 取值的概率:68.3%2σx 95.4%4σx 99.7%6σx在区间(μ-σ,μ+σ)、(μ-2σ,μ+2σ)、(μ-3σ,μ+3σ)内取值的概率分别为68.3%、95.4%、99.7% 因此我们时常只在区间(μ-3σ,μ+3σ)内研究正态总体分布情况,而忽略其中很小的一部分 例3.某正态总体函数的概率密度函数是偶函数,而且该函数的最大值为π21,求总体落入区间(-1.2,0.2)之间的概率解:正态分布的概率密度函数是),(,21)(222)(+∞-∞∈=--x e x f x σμσπ,它是偶函数,说明μ=0,)(x f 的最大值为)(μf =σπ21,所以σ=1,这个正态分布就是标准正态分布( 1.20.2)(0.2)( 1.2)(0.2)[1(1.2)](0.2)(1.2)1P x -<<=Φ-Φ-=Φ--Φ=Φ+Φ- 教学反思:1.在实际遇到的许多随机现象都服从或近似服从正态分布 在上一节课我们研究了当样本容量无限增大时,频率分布直方图就无限接近于一条总体密度曲线,总体密度曲线较科学地反映了总体分布 但总体密度曲线的相关知识较为抽象,学生不易理解,因此在总体分布研究中我们选择正态分布作为研究的突破口 正态分布在统计学中是最基本、最重要的一种分布 2.正态分布是可以用函数形式来表述的 其密度函数可写成:22()21(),(,)2x f x e x μσπσ--=∈-∞+∞, (σ>0)由此可见,正态分布是由它的平均数μ和标准差σ唯一决定的 常把它记为),(2σμN 3.从形态上看,正态分布是一条单峰、对称呈钟形的曲线,其对称轴为x=μ,并在x=μ时取最大值 从x=μ点开始,曲线向正负两个方向递减延伸,不断逼近x 轴,但永不与x 轴相交,因此说曲线在正负两个方向都是以x 轴为渐近线的4.通过三组正态分布的曲线,可知正态曲线具有两头低、中间高、左右对称的基本特征。
monte carlo计算正态分布概率matlab程序

monte carlo计算正态分布概率matlab程序
"Monte Carlo 计算正态分布概率Matlab 程序" 这句话的意思是使用Matlab 编程语言编写一个程序,该程序使用 Monte Carlo 方法来估计正态分布的概率。
Monte Carlo 方法是一种统计模拟技术,通过随机抽样来近似求解数学问题。
在计算正态分布概率的情境下,Monte Carlo 方法可以用来估计给定区间内正态分布的累积分布函数 (CDF) 值。
一个简单的 Matlab 程序示例,使用 Monte Carlo 方法计算正态分布的概率,可能包括以下步骤:
1.设置正态分布的均值(μ)和标准差(σ)。
2.确定要估计的概率值,例如 P(X < x),其中 X 是正态分布的随机变量,x 是
一个给定的值。
3.生成大量来自正态分布的随机样本。
4.统计这些样本中满足 P(X < x) 的数量。
5.将统计的数量除以总的样本数量,得到近似的概率值。
通过重复上述过程多次,可以得到一系列近似概率值,并对这些值进行统计处理(如计算平均值和置信区间)以获得更精确的结果。
总结:"Monte Carlo 计算正态分布概率 Matlab 程序" 是指使用 Matlab 编程语言编写的程序,该程序应用 Monte Carlo 方法来估计正态分布的概率。
通过随机抽样和统计处理,程序可以近似计算给定区间内正态分布的概率值。
这种方法的优点是可以在缺乏精确解析解的情况下得到近似结果,并且可以通过增加样本数量来提高近似精度。
直方图和正态分布图

直方图和正态分布图
直方图(Historgram)是将某期间所收集的计量值数据经分组整理成次数统计表,并使用柱形予以图形化,以掌握这些数据的分布状况。
直方图的应用
制造---加工尺寸的分布
经济---收入支出的分布
教育---考试成绩的分布……
●直方图是反映分组数据频数的柱形图
●正态分布图是一条单峰、对称成钟形的曲线。
Frequency函数
●以一个垂直数组返回某个区域中数据的频率分布
●由于函数frequency返回返回一个数组,所以必须以数组公式的形式输入
Frequency(data_array,bins_array):
data_array为一数组或对一组数值的引用,用来计算频率。
Bins_array 为间隔的数组或对间隔的引用,该间隔用于对data_array中的数值进行分组
Normdist函数
返回指定平均值和标准偏差的正态分布函数
Normdist (x,mean,standard_dev,cumulative)
其中x为需要计算其分布的数值
Mean 分布的算术平均数
Standard_dev 分布的标准偏差
Cumulative 如果为false,则返回概率密度函数
正态分布图的差异:中心偏移,分布不同
分析工具库-安装加载宏:制作直方图
VBA:全称Visual Basic for Application, 它是Visual Basic 的应用程序版本,是面向对象的编程语言。
VBA也可应用于AutoCAD
VBA的应用
●自动执行重复的操作
●进行“智能化”处理
●Office二次开发的平台。
正态分布图0321版

图形设定TRUE起点0操作步骤及说明:1. 在Excel、Word等电子文档的表格内复制源数据,不限排列方式,但不得含有其它无关数据;然后点击本页面的“更新数据”按钮,源数据即被调入本文件;2. 在本页面黄色区域内填写相关信息和测试标准,然后点击“重新绘图”按钮,则生成相关图片;3. 当复制的所有数据完全相等,或者所复制的内容、数据为文字格式时,本程式无法绘图。
4. 本图表可以自定义图形的组距和组界,其中组界是通过设定 X 起点的方式实现;图形实际显示的范围比 X 起点和 X 终点都要多出半个组距,如例图,如果起点设定为2.72,组距设定为 0.04,那么当把下限设定为2.7时,红色的规格线2.7也将出现在图形上。
5. 图形的复制和保存的默认路径在本程序所在的文件夹下,如果点击“另存打开”,则复制后得到的图形文件呈打开状态,点击“另存关闭”,则所复制得到图形文件直接保存并关闭。
6. 首次使用VBA程序时,应首先将EXCEL中的安全性设定为“中” (具体设定位置在“工具” → “宏” →“安全性”),然后关闭本文件,再次打开这个文件,在打开文件时遇到的第一个对话框上选择“启用宏”。
如果您觉得这个小程序非常好用,别忘了转发给需要的朋友,谢谢!可到以下链接下载最新版本:下载地址:http://58.211.3.23/downloads/download.asp Lijiuqinn@ 版 本 号:V070321A 2007-3-21(excellent)软件感谢感谢您使用这个小程序,同时,为向您发布下面的小广告而诚挚道歉,并期待您的谅解。
也许您比较讨厌这个小广告,那么,您只要点击上面的“清除广告”按钮,或者在您电C:\Documents and Settings\All users\Application Data\”文件夹,并在其下建立一个文Normalschoolchart”的文本文件,那么这些文字和小广告将不再出现。
离散型随机变量均值(正态分布)
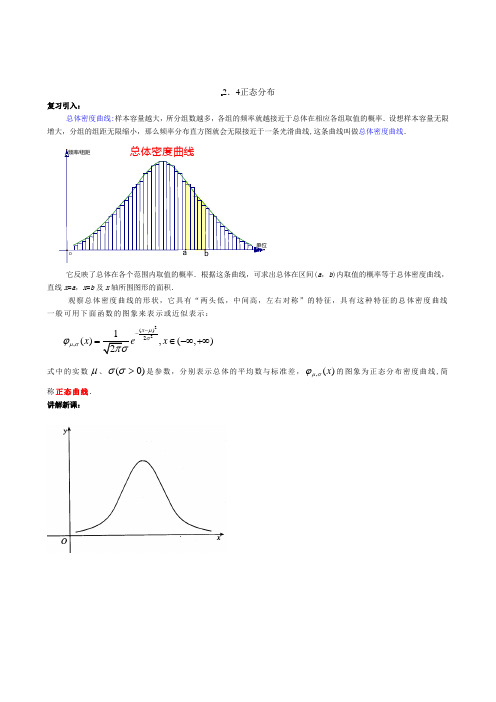
2.4正态分布复习引入:总体密度曲线:样本容量越大,所分组数越多,各组的频率就越接近于总体在相应各组取值的概率.设想样本容量无限增大,分组的组距无限缩小,那么频率分布直方图就会无限接近于一条光滑曲线,这条曲线叫做总体密度曲线.它反映了总体在各个范围内取值的概率.根据这条曲线,可求出总体在区间(a ,b )内取值的概率等于总体密度曲线,直线x =a ,x=b 及x 轴所围图形的面积.观察总体密度曲线的形状,它具有“两头低,中间高,左右对称”的特征,具有这种特征的总体密度曲线一般可用下面函数的图象来表示或近似表示:22()2,(),(,)x x x μσμσϕ--=∈-∞+∞式中的实数μ、)0(>σσ是参数,分别表示总体的平均数与标准差,,()xμσϕ的图象为正态分布密度曲线,简称正态曲线. 讲解新课:一般地,如果对于任何实数a b <,随机变量X 满足,()()baP a X B x dx μσϕ<≤=⎰,则称 X 的分布为正态分布(normal distribution ) .正态分布完全由参数μ和σ确定,因此正态分布常记作),(2σμN .如果随机变量 X 服从正态分布,则记为X ~),(2σμN .经验表明,一个随机变量如果是众多的、互不相干的、不分主次的偶然因素作用结果之和,它就服从或近似服从正态分布.例如,高尔顿板试验中,小球在下落过程中要与众多小木块发生碰撞,每次碰撞的结果使得小球随机地向左或向右下落,因此小球第1次与高尔顿板底部接触时的坐标 X 是众多随机碰撞的结果,所以它近似服从正态分布.在现实生活中,很多随机变量都服从或近似地服从正态分布.例如长度测量误差;某一地区同年龄人群的身高、体重、肺活量等;一定条件下生长的小麦的株高、穗长、单位面积产量等;正常生产条件下各种产品的质量指标(如零件的尺寸、纤维的纤度、电容器的电容量、电子管的使用寿命等);某地每年七月份的平均气温、平均湿度、降雨量等;一般都服从正态分布.因此,正态分布广泛存在于自然现象、生产和生活实际之中.正态分布在概率和统计中占有重要的地位.说明:1参数μ是反映随机变量取值的平均水平的特征数,可以用样本均值去佑计;σ是衡量随机变量总体波动大小的特征数,可以用样本标准差去估计.2.早在 1733 年,法国数学家棣莫弗就用n !的近似公式得到了正态分布.之后,德国数学家高斯在研究测量误差时从另一个角度导出了它,并研究了它的性质,因此,人们也称正态分布为高斯分布. 2.正态分布),(2σμN )是由均值μ和标准差σ唯一决定的分布通过固定其中一个值,讨论均值与标准差对于正态曲线的影响3.通过对三组正态曲线分析,得出正态曲线具有的基本特征是两头底、中间高、左右对称 正态曲线的作图,书中没有做要求,教师也不必补上 讲课时教师可以应用几何画板,形象、美观地画出三条正态曲线的图形,结合前面均值与标准差对图形的影响,引导学生观察总结正态曲线的性质4.正态曲线的性质:(1)曲线在x 轴的上方,与x 轴不相交(2)曲线关于直线x=μ对称(3)当x=μ时,曲线位于最高点(4)当x <μ时,曲线上升(增函数);当x >μ时,曲线下降(减函数)并且当曲线向左、右两边无限延伸时,以x轴为渐近线,向它无限靠近(5)μ一定时,曲线的形状由σ确定σ越大,曲线越“矮胖”,总体分布越分散; σ越小.曲线越“瘦高”.总体分布越集中:五条性质中前三条学生较易掌握,后两条较难理解,因此在讲授时应运用数形结合的原则,采用对比教学5.标准正态曲线:当μ=0、σ=l 时,正态总体称为标准正态总体,其相应的函数表示式是2221)(x ex f -=π,(-∞<x <+∞)其相应的曲线称为标准正态曲线标准正态总体N (0,1)在正态总体的研究中占有重要的地位任何正态分布的概率问题均可转化成标准正态分布的概率问题讲解范例:例1.给出下列三个正态总体的函数表达式,请找出其均值μ和标准差σ(1)),(,21)(22+∞-∞∈=-x ex f x π(2)),(,221)(8)1(2+∞-∞∈=--x ex f x π(3)22(1)(),(,)x f x x -+=∈-∞+∞例2求标准正态总体在(-1,2)内取值的概率.1.标准正态总体的概率问题:对于标准正态总体N (0,1),)(0x Φ是总体取值小于0x 的概率, 即 )()(00x x P x <=Φ,其中00>x ,图中阴影部分的面积表示为概率0()P x x <只要有标准正态分布表即可查表解决.从图中不难发现:当00<x 时,)(1)(00x x -Φ-=Φ;而当00=x 时,Φ(0)=0.52.标准正态分布表 标准正态总体)1,0(N 在正态总体的研究中有非常重要的地位,为此专门制作了“标准正态分布表”.在这个表中,对应于0x 的值)(0x Φ是指总体取值小于0x 的概率,即 )()(00x x P x <=Φ,)0(0≥x .若00<x ,则)(1)(00x x -Φ-=Φ.利用标准正态分布表,可以求出标准正态总体在任意区间),(21x x 内取值的概率,即直线1x x =,2x x =与正态曲线、x 轴所围成的曲边梯形的面积1221()()()P x x x x x <<=Φ-Φ.3.非标准正态总体在某区间内取值的概率:可以通过)()(σμ-Φ=x x F 转化成标准正态总体,然后查标准正态分布表即可 在这里重点掌握如何转化 首先要掌握正态总体的均值和标准差,然后进行相应的转化4.小概率事件的含义发生概率一般不超过5%的事件,即事件在一次试验中几乎不可能发生假设检验方法的基本思想:首先,假设总体应是或近似为正态总体,然后,依照小概率事件几乎不可能在一次试验中发生的原理对试验结果进行分析假设检验方法的操作程序,即“三步曲”一是提出统计假设,教科书中的统计假设总体是正态总体;二是确定一次试验中的a 值是否落入(μ-3σ,μ+3σ); 三是作出判断讲解范例:例1. 若x ~N (0,1),求(l)P (-2.32<x <1.2);(2)P (x >2).例2.利用标准正态分布表,求标准正态总体在下面区间取值的概率: (1)在N(1,4)下,求)3(F(2)在N (μ,σ2)下,求F(μ-σ,μ+σ); F(μ-1.84σ,μ+1.84σ);F(μ-2σ,μ+2σ); F(μ-3σ,μ+3σ)对于正态总体),(2σμN 取值的概率:在区间(μ-σ,μ+σ)、(μ-2σ,μ+2σ)、(μ-3σ,μ+3σ)内取值的概率分别为68.3%、95.4%、99.7% 因此我们时常只在区间(μ-3σ,μ+3σ)内研究正态总体分布情况,而忽略其中很小的一部分例3.某正态总体函数的概率密度函数是偶函数,而且该函数的最大值为π21,求总体落入区间(-1.2,0.2)之间的概率巩固练习:书本第74页 1,2,3课后作业: 书本第75页 习题2. 4 A 组 1 , 2 B 组1 , 2教学反思:1.在实际遇到的许多随机现象都服从或近似服从正态分布在上一节课我们研究了当样本容量无限增大时,频率分布直方图就无限接近于一条总体密度曲线,总体密度曲线较科学地反映了总体分布但总体密度曲线的相关知识较为抽象,学生不易理解,因此在总体分布研究中我们选择正态分布作为研究的突破口正态分布在统计学中是最基本、最重要的一种分布2.正态分布是可以用函数形式来表述的其密度函数可写成:22()2(),(,)xf x xμσ--=∈-∞+∞,(σ>0)由此可见,正态分布是由它的平均数μ和标准差σ唯一决定的常把它记为),(2σμN3.从形态上看,正态分布是一条单峰、对称呈钟形的曲线,其对称轴为x=μ,并在x=μ时取最大值从x=μ点开始,曲线向正负两个方向递减延伸,不断逼近x轴,但永不与x轴相交,因此说曲线在正负两个方向都是以x轴为渐近线的4.通过三组正态分布的曲线,可知正态曲线具有两头低、中间高、左右对称的基本特征。
数据的正态分布

数据的正态性检验汇总2012-11-21 00:01:04| 分类:统计学习|字号订阅如何在spss中进行正态分布检验一、图示法1、P-P图以样本的累计频率作为横坐标,以安装正态分布计算的相应累计概率作为纵坐标,把样本值表现为直角坐标系中的散点。
如果资料服从整体分布,则样本点应围绕第一象限的对角线分布。
2、Q-Q图以样本的分位数作为横坐标,以按照正态分布计算的相应分位点作为纵坐标,把样本表现为指教坐标系的散点。
如果资料服从正态分布,则样本点应该呈一条围绕第一象限对角线的直线。
以上两种方法以Q-Q图为佳,效率较高。
3、直方图判断方法:是否以钟形分布,同时可以选择输出正态性曲线。
4、箱式图判断方法:观测离群值和中位数。
5、茎叶图类似与直方图,但实质不同。
二、计算法1、偏度系数(Skewness)和峰度系数(Kurtosis)计算公式:g1表示偏度,g2表示峰度,通过计算g1和g2及其标准误σg1及σg2然后作U检验。
两种检验同时得出U<U0.05=1.96,即p>0.05的结论时,才可以认为该组资料服从正态分布。
由公式可见,部分文献中所说的"偏度和峰度都接近0……可以认为……近似服从正态分布"并不严谨。
2、非参数检验方法非参数检验方法包括Kolmogorov-Smirnov检验(D检验)和Shapiro- Wilk(W检验)。
SAS中规定:当样本含量n≤2000时,结果以Shapiro – Wilk(W检验)为准,当样本含量n >2000时,结果以Kolmogorov – Smirnov(D检验)为准。
SPSS中则这样规定:(1)如果指定的是非整数权重,则在加权样本大小位于3和50之间时,计算Shapiro-Wilk统计量。
对于无权重或整数权重,在加权样本大小位于3 和 5000 之间时,计算该统计量。
由此可见,部分SPSS教材里面关于"Shapiro – Wilk 适用于样本量3-50之间的数据"的说法实在是理解片面,误人子弟。
正态抽样及概率分布的EXCEL模拟演示

正态抽样及概率分布的EXCEL模拟演⽰正态抽样及概率分布的EXCEL模拟张庆远1[摘要] 利⽤EXCEL办公软件的函数及VBA功能,编制正态分布抽样的演⽰程序,并根据所抽到的样本数据⾃动进⾏相应的统计分析,通过理论分布频数与计算出的实际分布频数⽐较,帮助学⽣加深理解正态分布的概率分布规律,辅助于医学统计学教学;该⽅法具有直观、形象、易⽤且快速得到结果等特点,使复杂的抽象理论变得形象⽽具体,极⼤提⾼了课堂教学效果。
[关键词] EXCEL 正态分布统计教学演⽰在医学统计学教学过程中,正态分布规律是⼀个教学重点,也是统计学习所遇到的第⼀个概率分布规律。
曾有⽼师以实际调查的⽅式指导学⽣对某校⼊学新⽣的相应体检指标数据进⾏统计分析[1],以达到帮助学⽣来加深对正态分布规律的认识和理解,但这种⽅法效率低,⼿⼯计算⼯作量⼤,在实际操作中会存在⼀定难度。
也有以EXCEL制作简单的动态正态分布曲线的⽅式来进⾏课件展⽰[2],感觉也仅是将⼿⼯画正态分布曲线改为⽤多媒体来制作,少了抽样模拟的效果。
在借鉴他⼈经验的基础上[3],本⼈利⽤EXCEL的相关函数及VBA 功能,编制程序,模拟正态分布的抽样,并利⽤表格中的关联计算,即时完成对所抽到样本数据的统计描述分析,随时了解查看不同u值下样本数据的频数分布情况。
1、设计思路给出⼀个假设已知其总体均数和总体标准差的正态分布总体,在要求的样本含量及精度的情况下,利⽤相应函数从中随机进⾏单个数据抽取,每抽出⼀个数据便依次写在相应列中,抽完后,做出该批样本数据的频数分布表,并⾃动绘出频数分布直⽅图,最后按照所给的不同标准正态分布u值,计算并⽐较相应理论频数分布与实际概率分布的吻合程度。
2 具体操作⾸先⽤EXCEL新建⼀个⽂件,保存并命名为“正态抽样及概率分布的EXCEL演⽰”,接着在此⽂件SHEET1⼯作薄中相应单元格输⼊如下⽂字、公式代码或数值。
2.1 完成假设已知总体的总体均数及总体标准差的设置,见图1,其中B1、B2、B3、B4格⼦中可以⾃⾏设置已知总体的总体均数,总体标准差,欲抽样本含量值,及抽出样本值欲保留的⼩数位数;B5格中所输⼊公式可以完成以假设已知总体的相应参数为基础的⼀次正态抽样,抽出⼀个样本值显⽰在B5格中,通过编制相应程序,可以做到当抽样时,每抽出⼀个样本值后,便依次将其数值写在D列中保存,B7、B8、B9、B10、B11格中为即时根据所抽样本计算出的相应统计量值,以备下⾯进⾏频数表编制时组距的计算和组段的划分引⽤。
excel正态分布

正态分布函数的语法是NORMDIST(x,mean,standard_dev,cumulative)cumulative为一逻辑值,如果为0则是密度函数,如果为1则是累积分布函数。
如果画正态分布图,则为0。
例如均值10%,标准值为20%的正态分布,先在A1中敲入一个变量,假定-50,选中A列,点编辑-填充-序列,选择列,等差序列,步长值10,终止值70。
然后在B1中敲入NORMDIST (A1,10,20,0),返回值为0.000222,选中B1,当鼠标在右下角变成黑十字时,下拉至B13,选中A1B13区域,点击工具栏上的图表向导-散点图,选中第一排第二个图,点下一步,默认设置,下一步,标题自己写,网格线中的勾去掉,图例中的勾去掉,点下一步,完成。
图就初步完成了。
下面是微调把鼠标在图的坐标轴上点右键,选坐标轴格式,在刻度中填入你想要的最小值,最大值,主要刻度单位(x轴上的数值间隔),y轴交叉于(y 为0时,x多少)等等。
确定后,正态分布图就大功告成了。
PS:标准正态分布的语法为NORMSDIST(z),正态分布(一)NORMDIST函数的数学基础利用Excel计算正态分布,可以使用函数。
格式如下:变量,均值,标准差,累积,其中:变量:为分布要计算的值;均值:分布的均值;标准差:分布的标准差;累积:若1,则为分布函数;若0,则为概率密度函数。
当均值为0,标准差为1时,正态分布函数即为标准正态分布函数。
例3已知考试成绩服从正态分布,,,求考试成绩低于500分的概率。
解在Excel中单击任意单元格,输入公式:“ 500,600,100,1 ”,得到的结果为0.158655,即,表示成绩低于500分者占总人数的15.8655%。
例4假设参加某次考试的考生共有2000人,考试科目为5门,现已知考生总分的算术平均值为360,标准差为40分,试估计总分在400分以上的学生人数。
假设5门成绩总分近似服从正态分布。
使用Python绘制直方图和正态分布曲线
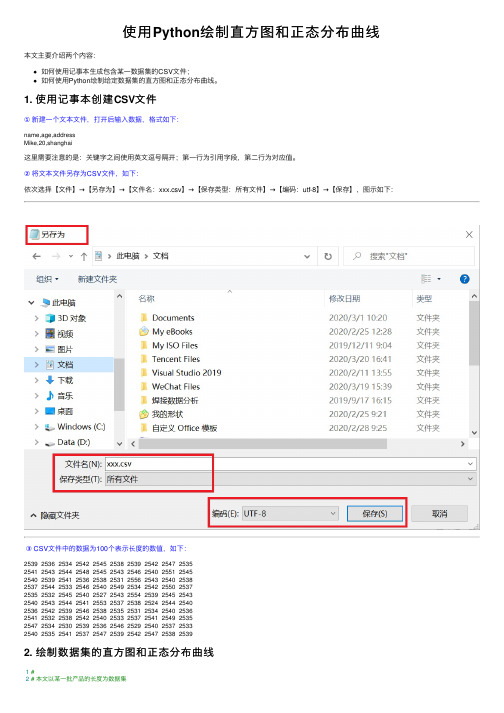
使⽤Python绘制直⽅图和正态分布曲线本⽂主要介绍两个内容:如何使⽤记事本⽣成包含某⼀数据集的CSV⽂件;如何使⽤Python绘制给定数据集的直⽅图和正态分布曲线。
1. 使⽤记事本创建CSV⽂件①新建⼀个⽂本⽂件,打开后输⼊数据,格式如下:name,age,addressMike,20,shanghai这⾥需要注意的是:关键字之间使⽤英⽂逗号隔开;第⼀⾏为引⽤字段,第⼆⾏为对应值。
②将⽂本⽂件另存为CSV⽂件,如下:依次选择【⽂件】→【另存为】→【⽂件名:xxx.csv】→【保存类型:所有⽂件】→【编码:utf-8】→【保存】,图⽰如下:③ CSV⽂件中的数据为100个表⽰长度的数值,如下:2539 2536 2534 2542 2545 2538 2539 2542 2547 25352541 2543 2544 2548 2545 2543 2546 2540 2551 25452540 2539 2541 2536 2538 2531 2556 2543 2540 25382537 2544 2533 2546 2540 2549 2534 2542 2550 25372535 2532 2545 2540 2527 2543 2554 2539 2545 25432540 2543 2544 2541 2553 2537 2538 2524 2544 25402536 2542 2539 2546 2538 2535 2531 2534 2540 25362541 2532 2538 2542 2540 2533 2537 2541 2549 25352547 2534 2530 2539 2536 2546 2529 2540 2537 25332540 2535 2541 2537 2547 2539 2542 2547 2538 25392. 绘制数据集的直⽅图和正态分布曲线1#2# 本⽂以某⼀批产品的长度为数据集3# 在此数据集的基础上绘制直⽅图和正态分布曲线4#56import pandas as pd # pandas是⼀个强⼤的分析结构化数据的⼯具集7import numpy as np # numpy是Python中科学计算的核⼼库8import matplotlib.pyplot as plt # matplotlib数据可视化神器910# 正态分布的概率密度函数11# x 数据集中的某⼀具体测量值12# mu 数据集的平均值,反映测量值分布的集中趋势13# sigma 数据集的标准差,反映测量值分布的分散程度14def normfun(x, mu, sigma):15 pdf = np.exp(-((x - mu) ** 2) / (2 * sigma ** 2)) / (sigma * np.sqrt(2 * np.pi)) 16return pdf1718if__name__ == '__main__':1920 data = pd.read_csv('length.csv') # 载⼊数据⽂件21 length = data['length'] # 获得长度数据集22 mean = length.mean() # 获得数据集的平均值23 std = length.std() # 获得数据集的标准差2425# 设定X轴:前两个数字是X轴的起⽌范围,第三个数字表⽰步长26# 步长设定得越⼩,画出来的正态分布曲线越平滑27 x = np.arange(2524, 2556, 0.1)28# 设定Y轴,载⼊刚才定义的正态分布函数29 y = normfun(x, mean, std)30# 绘制数据集的正态分布曲线31 plt.plot(x, y)3233# 绘制数据集的直⽅图34 plt.hist(length, bins=12, rwidth=0.9, density=True)35 plt.title('Length distribution')36 plt.xlabel('Length')37 plt.ylabel('Probability')3839# 输出正态分布曲线和直⽅图40 plt.show()程序执⾏结果如下:。
变换抽样法产生正态分布随机数的程序

编制变换抽样法产生正态分布随机数的程序并进行验证分析;设y1,y2是相互独立的均匀分布的随机变量,则新变量x1=(−2log y1)12cos(2πy2)x2=(−2log y1)12sin(2πy2)也是相互独立的,而且服从正态分布。
程序及结果如下:N=5000;%初始化数据长度for i=1:Ny1=rand;%生成均匀分布的随机数y2=rand;%生成均匀分布的随机数x1(i)=sqrt((-2)*log(y1))*cos(2*pi*y2);%用变换抽样法产生正态分布随机数x2(i)=sqrt((-2)*log(y1))*sin(2*pi*y2);%用变换抽样法产生正态分布随机数endu1=mean(x1);%计算出x1的平均值v1=std(x1);%计算出x1的标准差u2=mean(x1);%计算出x2的平均值v2=std(x1);%计算出x2的标准差subplot(1,2,1);histfit(x1);%绘制带有正态密度曲线的直方图hold onxlabel('随机数');ylabel('x1');title('均值为u1,标准差为v1');subplot(1,2,2);histfit(x2);%绘制带有正态密度曲线的直方图hold onxlabel('随机数');ylabel('x2');title('均值为u2,标准差为v2');>> u1u1 =0.0167 >> v1v1 =1.0020 >> u2u2 =0.0167 >> v2v2 =1.0020。
验证数据是否满足正态分布——Q-Q图和P-P图

验证数据是否满⾜正态分布——Q-Q图和P-P图Q-Q图 Q-Q图是⼀种散点图,对应于正态分布的Q-Q图,就是由标准正态分布的分位数为横坐标,样本值为纵坐标的散点图. 要利⽤QQ图鉴别样本数据是否近似于正态分布,只需看QQ图上的点是否近似地在⼀条直线附近,⽽且该直线的斜率为标准差,截距为均值. ⽤QQ图还可获得样本偏度和峰度的粗略信息. Q-Q图可以⽤于检验数据的分布,所不同的是,Q-Q图是⽤变量数据分布的分位数与所指定分布的分位数之间的关系曲线来进⾏检验的。
P-P图和Q-Q图的⽤途完全相同,只是检验⽅法存在差异 由于P-P图和Q-Q图的⽤途完全相同,只是检验⽅法存在差异。
要利⽤QQ图鉴别样本数据是否近似于正态分布,只需看QQ图上的点是否近似地在⼀条直线附近,⽽且该直线的斜率为标准差,截距为均值. ⽤QQ图还可获得样本偏度和峰度的粗略信息.这篇⽂章是关于Q-Q图的程序设计:有个关于Q-Q图和P-P图的R语⾔例⼦:n=100a=rnorm(n) #产⽣100个正态随机变量p=pnorm(a) #求正态分布函数值(正态累积概率)t=rank(a)/n#求观察累积概率q=qnorm(t) #求分位数值plot(p,t)#画P-P图plot(a,q) #画Q-Q图有关分位数的概念:分位数 quantile fractile 分位数⼜称百分位点,或者下侧分位数。
定义 设连续随机变量X的为F(X),密度函数为p(x)。
那么,对任意0<p<1的p,称F(X)=p的x为此分布的分位数,或者下侧分位数。
简单的说,分位数指的就是连续分布函数中的⼀个点,这个点对应概率p。
其他定义 若概率0<p<1,随机变量X或它的概率分布的分位数Za。
是指满⾜条件p(X>Za)=α的实数。
分位数有三种不同的称呼,即α分位数、上侧α分位数与双侧α分位数,它们的定义如下: 当随机变量X的分布函数为 F(x),实数α满⾜0 <α<1 时,α分位数是使P{X< xα}=F(xα)=α的数xα, 上侧α分位数是使P{X >λ}=1-F(λ)=α的数λ, 双侧α分位数是使P{X<λ1}=F(λ1)=0.5α的数λ1、使 P{X>λ2}=1-F(λ2)=0.5α的数λ2 如t分布的分位数表,⾃由度f=20和α=0.10时的双侧分位数为正负1.7247。
正态分布图程序

正态分布图程序操作步骤及说明:1. 在Excel 、Word 等电⼦⽂档的表格内复制源数据,不限排列⽅式,但不得含有其它⽆关数据;然后点击本页⾯的“更新数据”按钮,源数据即被调⼊本⽂件;2. 在本页⾯黄⾊区域内填写相关信息和测试标准,然后点击“重新绘图”按钮,⽣成相关图⽚;3. 本图表可以⾃定义图形的组距和组界,其中组界是通过设定 X 起点的⽅式实现;4. 挪动单元格位置或者改变图表的设置可能会导致本⽂件⽆法使⽤。
⼏个重要的⼩技巧:1. 更新数据之前,先填写规格和⽬标值,再复制、更新数据可直接得到漂亮的图形;由默认图形改变为⾃定义图形之前,先填写⾃定义参数,再点选“⾃定义”按钮,可⽴即⽣成⾃定义图形。
否则,在改变相应的参数后,需要点击“重新绘图”才可以看到更新设定后的图形。
2. 图形实际显⽰的范围⽐ X 起点和 X 终点都要多出半个组距,如例图,如果起点设定为2.63,组距设定为0.05,那么当把下限设定为2.61时,红⾊的规格线2.61也将出现在图形上。
3. ⼀般情况下,在⾃定义时宜先填写组距,接着填写 X 终点,最后填写 X 起点。
设定组距时,宜参照默认组距,或者⽐默认组距略⼩。
当复制的所有数据完全相等时,本程式⽆法绘图。
4. 填写 X 起点时有⼀个很重要的技巧:⼀般来说,平均值在图形正中的图是最漂亮的。
如何让平均值出现在图形的正中呢?最佳⽅案是变更 X 起点值,可以使⾃定义“正中组”的值等于默认“正中组”的数值,另⼀种⽅式是变更 X 起点值,使“正中组”的值等于“平均值”±半个组距。
5. ⾸次使⽤VBA 程序时,应⾸先将EXCEL 中的安全性设定为“中” (具体设定位置在“⼯具” → “宏” →“安全性”),然后关闭本⽂件,再次打开这个⽂件,在打开⽂件时遇到的第⼀个对话框上选择“启⽤宏”。
正态分布图6. 其中图⽚的复制⽅法如下:如果希望将图⽚复制到Word⽂档中,请先⽤⿏标选定图表,然后点击“复制”,打开相应的Word⽂档,如果希望将图⽚复制到其它Excel⽂档中,请先将图⽚粘贴到Word中,然后再复制、粘贴到Excel中即可如果您觉得这个⼩程序⾮常好⽤,别忘了转发给需要的朋友,谢谢!下载地址:http://222.73.15.32/downloads/download.aspLijiuqinn@/doc/11e8c8d76529647d26285245.html版本号:V061110A2006-11-1Test Item = 组界上限LSL = -7组界下限Target = 极差UCL = 7数据精度Max = -2.53数据精度Min = -7.79每组宽幅Ave = -5.712Std = 0.91⽬标Ave+3σ = -2.981下限-7Ave-3σ = -8.442上限7Sample Size = 200-8.44243Defect Ratio = 7.9%-2.98127Ca = 81.6%CpU = 4.66CpL = 0.47Cp = 2.56Cpk = 0.47Skewness = 0.224Kurtosis = 0.069图形设定TRUE FALSE Programmer: Lijiuqinn@/doc/11e8c8d76529647d26285245.html 起点-9⽅式实现;漂亮的图形;由默认图,可⽴即⽣成⾃定义图新设定后的图形。
matlab对数正态分布

matlab对数正态分布
MATLAB是一种多用途的科学计算语言,用于编写数值、统计和图形处理程序。
它拥有几乎无穷的用途,从处理大量数据,建模系统与过程,分析信号以及对图像进行处理等等。
MATLAB可以以多种方式建模特定的数据,其中之一就是使用对数正态分布(LOGN)。
所谓的“对数正态分布”是指其变量x的概率密度函数为:
P(x)=1/(σsqrt(2π)) e^(-((ln(x)-μ)^2 / (2σ^2)))
其中μ为均值,σ为标准差。
该分布也被称为双曲正态分布,因为对其密度函数取
对数之后得到的变量为正态分布。
因此,使用该分布可以更好地拟合某些数据点,特别是
当出现正态分布的一极左或一极右状态时。
MATLAB可以用来计算特定数据点的对数正态分布,并可以根据用户指定的参数计算该分布的概率密度函数。
只需使用“lognpdf”函数,并输入变量x、均值μ及标准差σ,
就可以实现快速方便地求得该分布的概率值。
此外,也可以使用“lognfit”函数手动拟
合数据,得出最佳的拟合模型,并输出此模型所需的参数。
凭借其计算速度和高效性,MATLAB在数学和科学运算领域受到广泛的应用。
尤其是在对数正态分布的运算中,可以利用MATLAB来快速精确地拟合和处理数据,从而获得准确
有效的结果。
卡西欧计算正态分布

卡西欧计算正态分布
卡西欧计算器可以用来计算正态分布。
以卡西欧fx-991es为例,操作步骤如下:
1. 进入单一变量统计模式Mode 3。
2. 按1 ACb,进入正态分布模式。
3. 按shift 1,接着按7,再按3,输入数据0.3(表示要求的概率值)。
4. 按等号键,计算器会显示对应的正态分布概率值。
需要注意的是,卡西欧计算器在计算正态分布时,可能无法直接计算累积分布函数。
在这种情况下,可以查找数学表格或使用其他计算工具来计算累积分布函数。
此外,卡西欧计算器还支持其他功能,如三角函数、微积分、统计等。
高级的现代计算器甚至可以显示图形,包含计算机代数系统,可以编写程序等。
这些功能可以帮助用户解决更复杂的问题。
标准正态分布表的程序设计

标准正态分布表的程序设计
吴之敏;韩忠义
【期刊名称】《地质与勘探》
【年(卷),期】1990(26)6
【摘要】本文设计的标准正态分布表程序,从分布函数出发,采用一定的计算方法,可在限定的精度范围内,进行制表或计算.所得结果与原表相比偏差很小(当u>3时,最大绝对误差为0.001),且具有程序占用内存少(约197字节),检索速度快(计算1~6秒、制表平均3秒)等优点.现介绍如下.
【总页数】2页(P36-37)
【关键词】正态分布表;程序;设计
【作者】吴之敏;韩忠义
【作者单位】安徽省地矿局三二七地质队
【正文语种】中文
【中图分类】P628.5
【相关文献】
1.杨辉标准正态分布几何量数学模型和函数表——以古代科举“五级百分”计量标准理论为基础 [J], 刘立云;干有成;赵霖;黄裕泉
2.正态分布的子样标准差过低估计了总体标准差 [J], 樊顺厚
3.标准正态分布表的应用 [J], 薛振峰
4.论标准正态分布在考试分数标准化中的应用 [J], 陈亚丽
5.标准正态分布表的一种简便编程方法 [J], 赵玉琛
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
操作步骤及说明:1. 在Excel 、Word 等电子文档的表格内复制源数据,不限排列方式,
但不得含有其它无关数据;然后点击本页面的“更新数据”按钮,源数据即被调入本文件;2. 在本页面黄色区域内填写相关信息和测试标准,然后点击“重新绘图”按钮,生成相关图片;3. 本图表可以自定义图形的组距和组界,其中组界是通过设定 X 起点的方式实现;4. 挪动单元格位置或者改变图表的设置可能会导致本文件无法使用。
几个重要的小技巧:
1. 更新数据之前,先填写规格和目标值,再复制、更新数据可直接得到漂亮的图形;由默认图 形改变为自定义图形之前,先填写自定义参数,再点选“自定义”按钮,可立即生成自定义图 形。
否则,在改变相应的参数后,需要点击“重新绘图”才可以看到更新设定后的图形。
2. 图形实际显示的范围比 X 起点和 X 终点都要多出半个组距,如例图,如果起点设定为2.63, 组距设定为0.05,那么当把下限设定为2.61时,红色的规格线2.61也将出现在图形上。
3. 一般情况下,在自定义时宜先填写组距,接着填写 X 终点,最后填写 X 起点。
设定组距时, 宜参照默认组距,或者比默认组距略小。
当复制的所有数据完全相等时,本程式无法绘图。
4. 填写 X 起点时有一个很重要的技巧:一般来说,平均值在图形正中的图是最漂亮的。
如何让 平均值出现在图形的正中呢?最佳方案是变更 X 起点值,可以使自定义“正中组”的值等于默 认“正中组”的数值,另一种方式是变更 X 起点值,使“正中组”的值等于“平均值”±半个组距。
5. 首次使用VBA 程序时,应首先将EXCEL 中的安全性设定为“中” (具体设定位置在“工具” → “宏” →“安全性”),然后关闭本文件,再次打开这个文件,在打开文件时遇到的第一个对话框上选 择“启用宏”。
正态分布图
6. 其中图片的复制方法如下:
如果希望将图片复制到Word文档中,请先用鼠标选定图表,然后点击“复制”,打开相应的Word文档,如果希望将图片复制到其它Excel文档中,请先将图片粘贴到Word中,然后再复制、粘贴到Excel中即可如果您觉得这个小程序非常好用,别忘了转发给需要的朋友,谢谢!
下载地址:http://222.73.15.32/downloads/download.asp Lijiuqinn@
版 本 号:V061110A2006-11-1
Test Item = 组界上限LSL = -7组界下限Target = 极差
UCL = 7数据精度
Max = -2.53数据精度
Min = -7.79每组宽幅
Ave = -5.712
Std = 0.91目标
Ave+3σ = -2.981下限-7
Ave-3σ = -8.442上限7
Sample Size = 200-8.44243
Defect Ratio = 7.9%-2.98127
Ca = 81.6%
CpU = 4.66
CpL = 0.47
Cp = 2.56
Cpk = 0.47
Skewness = 0.224
Kurtosis = 0.069
图形设定TRUE FALSE Programmer: Lijiuqinn@
起点-9
方式实现;
漂亮的图形;由默认图
,可立即生成自定义图
新设定后的图形。
如果起点设定为2.63,
出现在图形上。
X 起点。
设定组距时,
时,本程式无法绘图。
图是最漂亮的。
如何让
义“正中组”的值等于默
于“平均值”±半个组距。
设定位置在“工具” → “宏”
到的第一个对话框上选
“复制”,打开相应的Word文档,“粘贴”。
,然后再复制、粘贴到Excel中即可。
7组名组界数据个数正态曲线-10.2-9-9.4500.110316455
17.2-8.1-8.551 2.439379611
0-7.2-7.652420.29063365
-1-6.3-6.756263.48760717
0.9-5.4-5.857874.72388398
-4.5-4.952933.08316455
85.8-3.6-4.055 5.509748583
81.51-2.7-3.1510.345170481
81.51-1.8-2.2500.008134159
57.057-0.9-1.3507.21056E-05
57.057 1.55E-15-0.450 2.40437E-07
0.90.450 3.01587E-10
-2.53 1.8 1.350 1.42298E-13
-7.79 2.7 2.250 2.5256E-17 -5.71185 3.6 3.150 1.68619E-21
0.910192 4.5 4.050 4.23473E-26
-2.98127 5.4 4.950 4.00056E-31
-8.44243 6.3 5.850 1.42166E-36
7.2 6.750 1.9004E-42 er: Lijiuqinn@8.17.6509.55591E-49
98.550 1.80749E-55
9.99.450 1.28605E-62
10.810.350 3.44205E-70
11.711.250 3.4654E-78
12.612.150 1.3124E-86
13.513.050 1.86963E-95
14.413.950 1.0019E-104
15.314.850 2.0196E-114
16.215.750 1.5314E-124
17.116.650 4.3681E-135
1817.550 4.6867E-146
18.918.450 1.8915E-157
19.819.350 2.8718E-169
20.720.250 1.64E-181
21.621.150 3.5232E-194
22.522.050 2.8471E-207
23.422.9508.6544E-221
24.323.8509.8959E-235
25.224.750 4.2565E-249
26.125.650 6.8868E-264
2726.550 4.1915E-279
27.927.4509.596E-295
28.828.3500
29.729.2500
30.630.1500
31.531.0500
32.431.9500
33.332.8500
34.233.7500
35.134.6500 3635.5500
36.936.4500
37.837.3500
38.738.2500
39.639.1500
40.540.05。
