第五讲 正交试验设计(二)
正交试验设计方法(详细步骤) 共67页共69页文档

正交试验设计方法(详细步骤) 共67页
1、合法而稳定的失去温厚善良的美 德。— —伯克
3、最大限度地行使权力总是令人反感 ;权力 不易确 定之处 始终存 在着危 险。— —塞·约翰逊 4、权力会奴化一切。——塔西佗
5、虽然权力是一头固执的熊,可是金 子可以 拉着它 的鼻子 走。— —莎士 比
46、我们若已接受最坏的,就再没有什么损失。——卡耐基 47、书到用时方恨少、事非经过不知难。——陆游 48、书籍把我们引入最美好的社会,使我们认识各个时代的伟大智者。——史美尔斯 49、熟读唐诗三百首,不会作诗也会吟。——孙洙 50、谁和我一样用功,谁就会和我一样成功。——莫扎特
正交试验设计讲义

河南工业大学
shiyanshujuchulishiyongfangfa
二、正交试验设计法 正交设计方法主要讨论: (1) 如何合理地安排试验,确定试验数据收集的方法 (2) 如何对试验中所得的试验数据进行分析与处理 可达到的目的: (1) 因素的主次,即各因素对所考察指标影响 的大小 顺序; (2) 因素与指标的关系,即每个因素水平不同 时,指
整齐可比性-----正交表中任意两列,把同行的两
个数字看成有序数对时,所有可能的数对出现的次数 相同;
表示:任意两因素的各种水
平的搭配在所选试验中出现的
次数相等。
设计正交试验表 的基本准则
河南工业大学
2. 混合水平正交表
shiyanshujuchulishiyongfangfa
在试验中,由于条件的限制,会出现个别因素不能多
试验号 1 1 2 3 4 5 6 7 8 1 1 2 2 3 3 4 4
列
1列),4 个是 2水
平因素(位于第2 ~ 5 列)。
河南工业大学
shiyanshujuchulishiyongfangfa
第二节 正交设计的基本方法
正交试验设计一般来说包括两部分:
一是,试验设计,也即方案的选择与确定。
二是,数据处理,进行统计推断。
如三因素四水平43并包括第一二个因素的交互作用的正交试验至少应安排的试验次数为?????34141??????34141???3342?又如安排的混合水平的正交试验至少应安排??4141?111919????所以一般地有1iijiij?ndfdf?????若再加上包括第一五个因素的交互作用的正交试验则至少应安排的试验次数为?????????4341321121?161??????????341321113?????次以上的试验
正交试验设计

4
上一张 下一张 主 页 退 出
表5-1
5
上一张 下一张 主 页 退 出
注:任意两列旳交互作用列为另外两 列
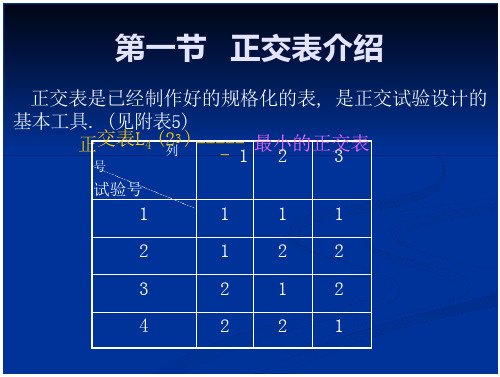
附:正交表L9(34)
试验号
列号
1
2
3
4
1
1
1
1
1
2
1
2
2
2
3
1
3
3
3
4
2
1
2
3
5
2
2
3
1
6
2
3
1
2
7
3
1ห้องสมุดไป่ตู้
3
2
8
3
2
1
3
9
3
3
2
1
6
3
上一张 下一张 主 页 退 出
1.2 正交设计旳基本特点
❖ 用部分试验来替代全方面试验,经过对部分 试验成果旳分析,了解全方面试验旳情况。
❖ 当交互作用存在时,有可能出现交互作用旳 混杂。即忽视了部分交互作用来降低试验次 数。
如对于上述3原因3水平试验,若不考虑交
互作用,可利用正交表L9(34)安排,试验方
代表正交表;
❖ L右下角旳数字“8”表达有8行,用这张正交 表安排试验包括8个处理(水平组合);
❖ 括号内旳底数“2” 表达原因旳水平数,括 号内2旳指数“7”表达有7列,
❖ 用这张正交表最多能够安排7个2水平原因。 8
上一张 下一张 主 页 退 出
表5-2
9
上一张 下一张 主 页 退 出
L8(27)二列间交互作用列表
第五章 正交试验设计
第五讲--正交实验设计与数据处理PPT课件

其它如L18(21×37),L32(81×46×26)等等,都有 类似的含义。
-
20
交互作用表
需要考虑因素的交互作用时,许多正交表都配有一张交 互作用表
常常用来解决二水平或三水平或二、三水混合 水平的多因素设计问题;
适用于需要考察的交互作用不多、也不太复杂 的多因素试验研究的场合;
通过方差分析鉴别各因素对试验指标的影响。
-
22
正交试验设计步骤
首先要根据试验目的,确定要观察的因素 确定每个因素的水平 然后选用适当的正交表安排试验。
-
23
安排试验是一种较好的方法,在实践中已得到 广泛的应用 正交试验设计是用一套规格化的表格来安排试 验,这种表格叫做正交表
-
12
正交表简介
是一种特制的表格,每个表都有一个记号,如L9(34), L8(27),就是两个最常用的正交表;
符号说明: L——正交表 L下角的9、8——正交表的行数
括号里的3、2——因素所取的水平数, 指数4、7——正交表的列数
表内的数字1、2、3——因素的水平
-
13
二水平的正交表还有L16(215)、L12(211), 三水平的正交表还有L18(37),L27(313), 四水平的正交表还有L16(45)等等。
-
14
正交表L9(34)
-
15
正交表记法
一般正交表记为Ln(mk), n——是表的行数,是要安排的试验次数; k——表中列数,表示因素的个数; m——是各因素的水平数。
SB——反映了因素B各水平效应引起的差异,它正好 等于正交表L9(34)中第二列各水平的偏差平方和S2;
第五章 正交试验设计

0.18
0.30 0.50 0.80
C A B
优方案
C1A3B1
隶属度计算方法:
指标隶属度 指标值 - 指标最小值 指标最大值- 指标最小值
若两个指标的重要性不一样,取代度和酯化率 的权重分别为0.4和0.6,每号试验的综合分数 =取代度隶属度×0.4+酯化率隶属度×0.6,满 分为1.00。
2
3 4 5
1
1 2 2
2
3 1 2
2
3 2 3
2
3 3 1
2.18
2.45 2.70 2.49
40.36
54.31 41.09 56.29
0.00
0.35 0.67 0.40
0.00
0.55 0.03 0.63
0.00
0.47 0.29 0.54
6
7 8 9 K1 K2 K3 极差R 因素主次
2
3 3 3 1.47 1.01 1.60 0.59
5.1.3 正交试验设计的基本步骤
(1)明确试验目的,确定评价指标
任何一个试验都是为了解决某一个(或某些)问题,或为 了得到某些结论而进行的,所以任何一个正交试验都应该 有一个明确的目的,这是正交试验设计的基础。 挑选的因素不易过多,一般以3~7个为宜; 确定因素的水平数时,一般重要的因素可多取一些水平, 各水平的数值应适当拉开,以利于试验结果的分析。当因 素的水平数相等时,可方便试验数据处理。
第五章 正交试验设计
任课教师:王凤花 现代农业工程学院
第五章 正交试验设计
5.1 概述 5.2 正交试验设计结果的直观分析法 5.3 正交试验设计结果的方差分析法 5.4 本章习题
正交试验2

什么是正交试验设计正交试验设计(Orthogonal experimental design)是研究多因素多水平的又一种设计方法,它是根据正交性从全面试验中挑选出部分有代表性的点进行试验,这些有代表性的点具备了“均匀分散,齐整可比”的特点,正交试验设计是分析因式设计的主要方法。
是一种高效率、快速、经济的实验设计方法。
日本著名的统计学家田口玄一将正交试验选择的水平组合列成表格,称为正交表。
例如作一个三因素三水平的实验,按全面实验要求,须进行3^3 = 27种组合的实验,且尚未考虑每一组合的重复数。
若按L9(3)正交表安排实验,只需作9次,按L18(3)正交表进行18次实验,显然大大减少了工作量。
因而正交实验设计在很多领域的研究中已经得到广泛应用。
正交表是一整套规则的设计表格,用L为正交表的代号,n为试验的次数,t为水平数,c为列数,也就是可能安排最多的因素个数。
例如L9(3),它表示需作9次实验,最多可观察4个因素,每个因素均为3水平。
一个正交表中也可以各列的水平数不相等,我们称它为混合型正交表,如L8(4×2),此表的5列中,有1列为4水平,4列为2水平。
正交试验设计表[1]正交试验因素水平表正交试验设计方案及试验结果极差分析表(或指标与因素关系图) 方差分析表(简单分析时可无)正交表的性质(1)每一列中,不同的数字出现的次数相等。
例如在两水平正交表中,任何一列都有数码“1”与“2”,且任何一列中它们出现的次数是相等的;如在三水平正交表中,任何一列都有“1”、“2”、“3”,且在任一列的出现数均相等。
(2)任意两列中数字的排列方式齐全而且均衡。
例如在两水平正交表中,任何两列(同一横行内)有序对子共有4种:(1,1)、(1,2)、(2,1)、(2,2)。
每种对数出现次数相等。
在三水平情况下,任何两列(同一横行内)有序对共有9种,1.1、1.2、 1.3、2.1、2.2、2.3、3.1、3.2、3.3,且每对出现数也均相等。
正交试验设计方法详细步骤

正交试验设计方法详细步骤正交试验设计是一种高效、经济的多因素试验设计方法,它能够通过合理安排试验,有效地分析各因素对试验结果的影响,从而找到最优的试验条件。
下面我们来详细了解一下正交试验设计的步骤。
一、明确试验目的和确定试验指标首先,要明确为什么要进行这个试验,是为了提高产品质量、降低成本,还是优化工艺参数等。
然后,根据试验目的确定一个或多个能够衡量试验效果的指标,这些指标可以是定量的,如产量、纯度、强度等;也可以是定性的,如颜色、外观、口感等。
例如,在研究某种新材料的制备工艺时,试验目的可能是提高材料的强度,那么强度就是试验指标。
二、挑选因素和确定水平因素是指对试验指标可能产生影响的变量,水平则是因素的不同取值。
在挑选因素时,要结合专业知识和实际经验,选择那些可能对试验指标有重要影响的因素。
假设我们在研究某个化学反应,可能的因素有反应温度、反应时间、反应物浓度等。
每个因素通常选取 2 5 个水平。
比如,反应温度可以选择 50℃、60℃、70℃三个水平。
三、选择合适的正交表正交表是一种已经标准化的表格,它能够保证试验点在因素空间上均匀分布,从而使试验具有代表性和可比性。
选择正交表时,要根据因素的个数和水平数来确定。
常见的正交表有 L4(2³)、L8(2⁷)、L9(3⁴) 等。
其中,L 表示正交表,数字 4、8、9 表示试验次数,括号中的指数表示因素的个数和每个因素的水平数。
如果有 3 个因素,每个因素有 3 个水平,那么可以选择 L9(3⁴) 正交表。
四、进行表头设计表头设计就是将选定的因素安排到正交表的列中。
原则上,任意一列都可以安排任意一个因素,但为了减少试验误差,通常要遵循一些规则,比如尽量避免将交互作用明显的因素安排在相邻的列。
五、编写试验方案根据表头设计,确定每个试验的具体条件,即每个因素在每个试验中的水平组合。
这样就得到了完整的试验方案。
例如,第一个试验中,因素 A 取水平 1,因素 B 取水平 2,因素 C取水平 3,以此类推。
正交试验设计方法详细步骤

正交试验设计方法详细步骤正交试验设计是研究多因素多水平的一种设计方法,它是根据正交性从全面试验中挑选出部分有代表性的点进行试验,这些有代表性的点具备了“均匀分散,齐整可比”的特点。
下面为您详细介绍正交试验设计的步骤。
一、明确试验目的和确定试验指标首先要清楚为什么要进行这个试验,是为了提高产品质量、降低成本,还是为了优化某个工艺过程等。
然后根据试验目的确定一个或多个能够衡量试验结果好坏的指标,这些指标可以是定量的,如产量、纯度、强度等;也可以是定性的,如外观、色泽、口感等。
需要注意的是,试验指标要尽量具体、明确、可测量。
二、挑选因素和确定水平因素就是影响试验指标的各种条件,比如温度、压力、时间、浓度等。
在挑选因素时,要综合考虑实际情况和专业知识,找出那些对试验指标可能有较大影响的因素。
每个因素又有不同的取值,这些取值就称为水平。
水平的设置要合理,既要有一定的范围,又不能过于宽泛或狭窄。
例如,在研究某个化学反应时,我们可能会选择反应温度、反应时间和反应物浓度作为因素。
假设反应温度的水平设定为 60℃、70℃和80℃;反应时间的水平设定为 1 小时、2 小时和 3 小时;反应物浓度的水平设定为 10%、20%和 30%。
三、选择合适的正交表正交表是一种已经标准化的表格,它能够保证试验点的均匀分散和齐整可比。
选择正交表时,要根据因素的个数和水平数来确定。
通常,我们可以参考现成的正交表手册,或者使用相关的软件来帮助选择。
在选择正交表时,需要遵循以下两个原则:一是正交表的列数要大于或等于因素的个数;二是正交表能够安排下所有因素的水平。
例如,如果有 3 个因素,每个因素有 3 个水平,那么可以选择 L9(3^4)正交表。
四、表头设计表头设计就是将因素安排到正交表的列中。
一般来说,可以随机安排因素的位置,但为了方便分析试验结果,有时也会根据因素的重要性或主次顺序进行安排。
比如,将上述的 3 个因素(反应温度、反应时间、反应物浓度)分别安排到 L9(3^4)正交表的前 3 列。
试验设计与数据处理第五章--正交试验设计
2. 利用正交表,确定试验方案 •3. 试验结果----- 这批四个试验基本都消除了应力.
利用SAS进行方差分析
■正交试验采用极差分析或方差分析都可以, 两 者没有本质区别只是前者较方便而后者分析更 精确, 以下见例5.3.1用SAS进行方差方析 (E531). 一、利用菜单系统对每个因素进行单因素 方差分析, 模型的平方和即该因素的平方和 在正交试验的分析中与极差作用类似. 亦可 用因素的原始数据值(xa xb xc)求水平趋势 图(plot选项中选取均值图)
(2) 任意两个纵列,其横方向形成的四个数字对中,恰 好(1,1)、(1,2)、(2,1)和(2,2)各出现一次. 这说 对于任意两个纵列,数码“1”、“2”间的搭配是
均衡 的. 2. L成8(2. 7它)有8个横行和7个纵列,由数码“1”和“2”组 有两个特点: (1) 每纵列恰有四个“1”和四个“2”;
考核指标: 应力(度)
第一批撒大网
1. 挑因素、选水平,制定因素水平表( 略) 2. 利用正交表,确定试验方案
•3. 试验结果分析 (1)直观分析 第5号试验最好, 第7号试验次之. (2)极差分析 A2B2C1D3称为全体水平组合关于应力的可能 好的水平组合.
本例因素的主次顺序为: 升温速度A(极差21.5) →恒温时间C(极差14) →恒温速度B(极差12.5) →降温速度D(极差11.5
=每个平面上红点数 :每个平面上交叉点数 =每条棱上红点数 :每条棱上交叉点数 即 9/27=3/9=1/3 (三因素三水平场合)
2. 整齐可比性: 使正交表的同一列可比较产生” 好
水平”. 上图说明A1的三次试验(红点)中因素B的三个水 平和因素C的三个水平各出现一次,A2和A3有同 样情况,就是说,对因素A的三个不同水平,受
第二章 正交实验设计

第二章 正交实验设计1.概述任何实验工作,为达到预期目的和效果都必须恰当地进行实验安排,力求通过次数不多的实验掌握实验的基本规律并取得满意的结果。
为了拟定一个正确而简便的实验流程,必然要研究影响实验结果的种种条件,诸如原料的配比、反应温度、反应时间以及各实验条件之间的相互影响等等。
同时,对于影响实验结果的每一种条件,还应通过试验选择合理的范围。
在这里,我们把实验研究的目的叫做指标;把实验中要研究的条件叫做因素;把每种条件在实验范围内的取值叫做该条件的水平。
这就是说我们实验过程中遇到的问题可能包括多种因素,各种因素又有不同的水平,每种因素可能对实验结果产生各自的影响,也可能彼此交织在一起影响实验结果。
正交试验设计(Orthogonal experimental design)就是用于安排多因素实验并考察各因素影响大小的一种科学设计方法。
它始于1942年,之后在各个领域里都得到很快的发展和广泛应用。
这种科学设计方法是应用一套已规格化的表格——正交表来安排实验工作,其优点是适合于多种因素的实验设计,便于同时考查多种因素、各种水平对指标的影响,通过较少的实验次数,选出最佳的实验条件。
2. 正交试验设计的基本方法2.1 全面试验法例1: 某实验中为了提高石膏产品的抗压强度,对实验中三个主要因素各按三个水平进行试验(见表2-1),试验的目的是寻求最适宜的成分配比。
表2.1 因素水平对此实例进行全面试验法方案(如图2.1所示),此方案数据点分布的均匀性极好,因素和水平的搭配十分全面,唯一的缺点是实验次数多达33=27次(指数3代表3个因素,底数3代表每因素有3个水平)。
图2.1全面试验法方案2.2 比较实验法W 2 W 2 W 2 R 3 R 2 R 1W 3W 1 W 3 W 1 W 3 W 1S 1 R 3 R 2 R 1S 2W 1 W 2 W 3 W 1 W 2 W 3 W 1 W 2 W 3R 2R 3W 2 W 2 W 3W 1 W 3 W 1 W 3 W 1 W 2 R 1S 3从例1可看出,采用全面试验法方案,需做27次实验,采用比较法方案见图2.2.(1) (2) (3)图2.2比较法方案先固定S 1和R 1,只改变W ,观察因素W 不同水平的影响,做了如图2.2(1)所示的三次实验,发现W =W 2时的实验效果最好(好的用□表示),石膏强度最高,因此认为在后面的实验中因素W 应取W 2水平。
正交试验法的设计步骤

正交试验法的设计步骤正交试验法(Orthogonal Experimental Design)是一种有效的实验设计方法,用于在有限的实验次数下,系统地研究多个因素对结果的影响,并确定各个因素的最佳水平组合。
下面是正交试验法的设计步骤:1.确定实验目的和研究问题:首先明确实验目的和研究问题,确定需要研究的因素和其水平。
2.确定因素和水平:根据实验目的和研究问题,确定需要考察的因素和其水平。
每个因素可以有不同的水平,每个因素至少有两个水平。
3.确定正交表的类型和级数:根据因素的个数和水平的个数,选择适当的正交表。
正交表是一张具有特定性质的矩阵,具有均衡、方便的性质,可以有效地减少试验次数。
4.指定正交表中的试验方案:根据所选择的正交表,将各个水平对应的实验条件填入正交表中。
5.进行试验:按照正交表中的试验方案进行实验,记录实验结果。
6.数据分析:根据实验结果,进行统计分析,包括方差分析、回归分析等方法。
分析结果可以帮助确定各个因素对结果的影响程度以及最佳的因素水平组合。
7.结果解释和优化:根据数据分析结果,解释各个因素的影响程度,找出最佳的因素水平组合。
如果存在交互作用,进一步考虑因素之间的相互影响,并对结果进行优化。
8.实验验证:根据最佳因素水平组合进行进一步的试验验证,确保最佳组合具有良好的稳定性和可复制性。
9.结果总结和报告:对实验结果进行总结,撰写报告并给出适当的建议。
需要注意的是,设计正交试验时应尽可能选择与实际问题相关的因素和水平,并合理安排试验次序。
此外,正交试验不宜过多因素和水平,一般建议每个因素不超过5个水平。
如果需要考察多个因素和水平,可以采用逐步设计、交叉设计等方法进行扩展。
正交试验设计方法详细步骤

正交试验设计方法详细步骤正交试验设计方法(Orthogonal Experimental Design)是一种通过系统地变化每个试验因素的水平,来确定各个试验因素对结果的影响的实验设计方法。
它可以帮助研究者有效地评估各个试验因素对结果的影响程度,并找到最佳的组合方案。
本文将详细介绍正交试验设计方法的步骤。
一、确定试验因素和水平首先,我们需要确定参与实验的各个试验因素及其可能的水平。
试验因素是指影响结果的各个因素,而水平则是试验因素可能的取值。
在确定试验因素和水平时,要考虑到实验目的和实际情况,确保涵盖了可能的影响因素。
二、建立正交表正交表是正交试验设计的核心工具,它是由行和列组成的表格,用于指导实验的进行。
根据试验因素的个数和水平数量,选择适当的正交表。
常用的正交表包括L8、L16、L32等。
三、确定试验方案根据正交表,确定实验方案。
将正交表的行用于标识试验次数,将列用于表示各个试验因素及其水平的组合。
在确定试验方案时,要保证各个水平和因素的组合均匀且全面。
四、进行实验按照试验方案,进行实验。
根据正交表的设计原理,每个试验因素的水平都会被均匀地应用到各个试验中,从而使得各个试验的结果具有可比性。
五、收集数据在实验进行过程中,要准确地记录各个试验的结果数据。
根据实验目的和需要,可以选择合适的数据收集方法和工具,如测量仪器、问卷调查等。
六、数据分析与解释对收集到的数据进行分析和解释,评估各个试验因素对结果的影响程度。
常用的数据分析方法包括方差分析、回归分析等。
通过数据分析,可以得出各个试验因素的影响大小和统计显著性,为进一步优化和改进提供依据。
七、优化和改进根据数据分析的结果,可以进一步优化和改进设计方案。
针对影响较大的试验因素,可以考虑调整其水平,或者进行二次试验以进一步验证结果。
八、总结报告最后,根据实验结果和分析,撰写总结报告。
总结报告应包括实验目的、方法、结果和结论等内容,以便他人理解和参考。
《正交试验设计》 (2)幻灯片

试验设计与方差分析
试验设计
完全随机化 设计
单因素 方差分析
随机化 区组设计
因子 设计
无重复双因素 方差分析
可重复双因素 方差分析
3
完全随机化设计
➢ “处理〞被随机地指派给试验单元的一种设计 ➢ “处理〞是指可控制的因素的各个水平 ➢ “试验单元(experiment unit)〞是承受“处理
〞的对象或实体 ➢ 在试验性研究中,感兴趣的变量是明确规定的,
➢ 正交试验设计能既方便,又有效地解决多个多 水平的因子的试验设计问题
15
什么是正交试验设计
➢ 研究多因素多水平的又一种设计方法,并进 一步分析对所研究对象的指标的影响程度
➢ 它是根据正交性从全面试验中挑选出局部有 代表性的点进展试验
➢ 是一种高效率、快速、经济的实验设计方法, 并可以得到根本令人满意的结果
➢ 一个正交表中也可以各列的水平数不相等,我们称它为混合型 正交表
18
L9(34)正交表安排三因子三水平试验选点示意图
3 6
B3 9
2
5
B2
8 7 B1
C3
1 A1
4 A2
C2 A C1
3
19
正交表的特点
➢ 每个因素的每个水平与另一个因素各水平各碰一次, 这就是正交性
➢ 每一列中,不同数字出现的次数相等---均匀分散性 ➢ 任意两列中,将同一横行的两个数字看成有序数对
时,每种数对出现的次数相等---综合可比性 ➢ 将正交表中的任两行交换,或任两列交换,仍然还
是正交表 ➢ 将某一列中的各数码作对换或轮换,结果仍然是正
交表
20
正交表的表头设计原那么
➢ 选定正交表后,把因子放到正交表的列上 去,称为表头设计
正交试验实验设计2

试验设计方法讲稿绪言课程度的性质:试验设计方法是一项通用技术,是当代科技和工程技术人员必须掌握的技术方法。
课程的任务:让学生熟悉并掌握近代最常用、最有效的几种优化试验设计方法的基本原理及其应用。
什么叫做(优化)试验设计方法?把数学上优化理论、技术应用于试验设计中,科学的安排试验、处理试验结果的方法。
采用科学的方法去安排试验,处理试验结果,以最少的人力和物力消费,在最短的时间内取得更多、更好的生产和科研成果的最有效的技术方法。
优化试验设计方法起源⏹上世纪30年代,由于农业试验的需要,费歇(R.A.Fisher)在试验设计和统计分析方面做出了一系列先驱工作,从此试验设计成为统计科学的一个分支。
⏹上世纪40年代,在二次世界大战期间,美国军方大量应用试验设计方法。
⏹随后,F.Yates,R.C.Bose,O.Kempthome,W.G.Cochran,D.R.Cox和G.E.P.Box对试验设计都作出了杰出的贡献,使该分支在理论上日趋完善,在应用上日趋广泛。
⏹50年代,日本统计学家田口玄一将试验设计中应用最广的正交设计表格化,在方法解说方面深入浅出为试验设计的更广泛使用作出了众所周知的贡献。
我国优化试验设计方法⏹60末期代,华罗庚教授在我国倡导与普及的“优选法”,如黄金分割法、分数法和斐波那契数列法等。
⏹数理统计学者在工业部门中普及“正交设计”法。
⏹70年代中期,优选法在全国各行各业取得明显成效。
⏹1978年,七机部由于导弹设计的要求,提出了一个五因素的试验,希望每个因素的水平数要多于10,而试验总数又不超过50,显然优选法和正交设计都不能用,随后,方开泰教授(中国科学院应用数学研究所)和王元院士提出“均匀设计”法,这一方法在导弹设计中取得了成效。
优化试验设计试验设计在科学研究中的地位与意义:1.试验设计方法是一项通用技术,是当代科技和工程技术人员必须掌握的技术方法。
2.科学地安排实验,以最少的人力和物力消费,在最短的时间内取得更多、更好的生产和科研成果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考虑交互作用CE,则例22-4的表头可设计为
列号 因子 1 A 2 B 3 C 4 D 5 E 6 CE 7
2014年9月1日
(3)安排实验
水 列 平 号 试验号
A 1
B 2
C 3
D 4
E 5
C*E 6
X 7
试验 结果
1
2
1
1
1
1
1
1
1
2
1
2
1
提高乙醇胺本的收率,试验的因素和水 平见下表1; 选用正交表 L8 2 7 。实验安排及结果如 表2; 使用方差分析法对实验结果进行统计分 析,找出提高乙醇胺本收率的最佳工艺 。
2014年9月1日
表1
乙醇胺本反应试验的因素与水平 水平1 5度 1小时 17% 搅拌 水平2 7度 2小时 27% 不搅拌
2014年9月1日
按正交表及试验结果输入数据。
2014年9月1日
2. spss操作过程
在spss中调出数据文件Li22-4.sav (1) 从菜单选择 Analyze→ General Linear Models (一般线性模型)→ Univariate(单变量分析) Dependent Variables:y Fixed Factors (固定因素): a、b、c、d 、e、ce、x 击Model(模型)按钮,选Custom Model(模型): a、b、c、d、e、ce
在spss中调出数据文件Li22-4.sav (1) 从菜单选择 Analyze→ General Linear Models (一般线性模型)→ Univariate(单变量分析) Dependent Variables:y Fixed Factors (固定因素): 重复试验、a 、 b、 c、 x 击Model(模型)按钮,选Custom Model(模型):重复试验、 a、b、c
2 2 2 2 1 1
1 2 1 2 1 2
1 2 2 1 2 1
2 1 1 2 2 1
2 1 2 1 1 2
71 73 70 73 62 67
2014年9月1日
2014年9月1日
击Options(选项)按钮: Display Means for: a、b、c 在Display框:选择Descriptive statistics (描述统计量)
2014年9月1日
方差分析表
2014年9月1日
结果分析
模型检验:F=32.375,P=0.000<0.05,所 选模型有统计学意义。 重复试验的P=0.844>0.05,无统计学意义, 可认为重复试验间无差异。因素A、C的 P=0.000<0.05,有统计学意义,表示A、C均 为主要因素,因素B的P=0.828>0.05,无统计 学意义,为次要因素。
2014年9月1日
因素
A B
水平1
甘草、桑寄生 丹参
水平2
0 丹参、黄精、 首乌、葛根 0 明胶除杂
C
D
吐温-80
调pH除杂
E
乙醇渗漉
水煎煮
选用5因素2水平,考虑交互作用C×E的正交试验分析 2014年9月1日
(1)选择正交表
n 5( 2 1) ( 2 1)( 2 1) 1 7
2014年9月1日
方差分析表-1
2014年9月1日
第一次结果分析
模型检验:F=5.705,P=0.310>0.05,所 选模型无统计学意义。 因素a、e的平方和小于误差Error平方和 (F<1) 表示该因素的影响力比试验误差更小, 去掉这些因素,将它们造成的微小差异归到试 验误差中,则可突显其它因素的影响。 (2) 从Model框删除a、e,进行第二次操 作 2014年9月1日
2014年9月1日
比较主要因素的水平均值,确定最佳方案
指标为产率, 越大越好,故 因素A取A1
因素C 取选C2
2014年9月1日
因素B为次要因素, 本着节约的原则因素B取B3
最佳试验方案:
A 1B 3C 2
即提取时间为4小时,加7倍水,煎煮2次。
2014年9月1日
练习2
乙醇胺本磺化反应试验,试验目的在于
同时选定c、e,把c×e选入Model框 击Options(选项)按钮: Display Means for:b、d、c×e 在Display框:选择Descriptive statistics (描述统计量)
2014年9月1日
比较主要因素的水平均值,确定最佳方案
指标为分数, 越大越好,故 因素B取B2
因素 A:反应温度 B:反应时间 C:硫酸浓度 D:操作方法
2014年9月1日
表2
水 列 平 号 试验号
试验安排及实验数据
A B AXB C AXC x D 试验 结果 65 74
1
1 1
2
1 1
3
1 1
4
1 2
5
1 2
6
1 2
7
1 2
1 2
3 4 5 6 7 8
1 1 2 2 2 2
2 2 1 1 2 2
第四步
分析正交试验结果
正交试验结果分析要解决的问题: (1)确定因素各水平的优劣
(2)分析因素的主次
(3)选择交互作用的搭配 (4)预测最佳试验结果方案
2014年9月1日
(1)无重复正交试验结果的分析
方差分析的基本思想与双因素方差分析方法一致: 将总的离均差平方和分解成各因素及各交互作用 的离差平方和,构造F统计量,对各因素是否对 试验指标具有影响,作F检验。
因素D 取选D2
2014年9月1日
C×E取搭配C1E2, 本着节约的原则因素A取A2
最佳试验方案:
A2B2C1D2E2
即以丹参、首乌、黄精、葛根为最佳配方,用 水煎煮,用明胶除杂,加吐温-80助溶。 2014年9月1日
(2)有重复正交试验结果的分析
例22-5 还春口服液提取工艺探讨(见黑龙江 医药2004年第17卷第一期)。淫羊藿苷提取工 艺中,试验指标为产率,考察因素有3个,每个 因素均有3个水平,见表22-12. 不考虑交互作用,用 L9 34 可任意安排实验。 前3列安排A、B、C,第4列为空白(记为x), 作3次重复试验,结果见表22-13,进行有重复 正交试验结果的方差分析
2014年9月1日
例22-4 临床用复方丹参汤由丹参、葛根、桑 寄生、黄精、首乌和甘草组成,治疗冠心病有明 显疗效。为将其改制成注射液,指标采用兼顾冠 脉血流量和毒性评出的分数Y(越大越好)。需考 察①组方是否合理,能否减少几味药?②用水煎 煮,还是用乙醇渗漉?③用调pH除杂,还是用明 胶除杂?④是否加吐温-80助溶?
方差分析表-2
2014年9月1日
第二次结果分析
模型检验:F=22.676,P=0.014<0.05,所 选模型有统计学意义。 因素B、C、D 、 C×E的P<0.05,有统计 学意义,表示B、C、D均为主要因素,C与E 有交互作用。 (3)为确定因素B、D水平的优劣以及交互作 用C×E的最优搭配,从Model框删除c、ce, 进行第三次操作。 2014年9月1日
2
1
2
4.0
8.7
3
4 5 6 7 8
1
1 2 2 2 2
2
2 1 1 2 2
2
2 2 2 1 1
1
2 1 2 ቤተ መጻሕፍቲ ባይዱ 2
1
2 2 1 2 1
2
1 1 2 2 1
2
1 2 1 1 2
8.6
9.9 0.3 6.7 12.7 10.7
2014年9月1日
1.建立数据文件
在SPSS数据编辑窗,建立数据文件Li224.sav。 分组变量:a、b、c、d、e、ce、x 应变量:y
0.191 0.201 0.210
8
9
3
3
2
3
1
2
3
1
0.196 0.210 0.201
0.347 0.351 0.336
2014年9月1日
1.建立数据文件
在SPSS数据编辑窗,建立数据文件Li225.sav。 分组变量:重复试验、a、b、c、x 应变量:y
2014年9月1日
2. spss操作过程
2 3 1 2
3 1
2 3 2 3
4 1
2 3 3 1
3次重复试验结果 y1 y2 y3 0.287 0.294 0.285 0.361 0.359 0.369 0.257 0.271 0.249 0.374 0.351 0.369 0.271 0.280 0.269
6
7
2
3
3
1
1
3
2
2
0.241 0.253 0.249
2014年9月1日
例22-5 淫羊藿苷提取工艺的3因素3水平
水平
1 2
A(提取时间) (h)
4 3
B(加水量) (倍) 12
10
C(煎煮次数) (次) 3
2
3
2
7
1
2014年9月1日
表22-13 淫羊藿苷提取工艺的正交设计
A 试验号 1 2 3 4 5 B C x
1 1
1 1 2 2
2 1
