初中中考反比例函数应用题

合集下载

专题11 反比例函数及其应用(共65题)(学生版)

专题11反比例函数及其应用(65题)一、单选题1(2023·浙江·统考中考真题)如果100N的压力F作用于物体上，产生的压强P要大于1000Pa，则下列关于物体受力面积S m2的说法正确的是()A.S小于0.1m2B.S大于0.1m2C.S小于10m2D.S大于10m22(2023·内蒙古通辽·统考中考真题)已知点A x1,y1,B x2,y2在反比例函数y=-2x的图像上，且x1<0<x2，则下列结论一定正确的是()A.y1+y2<0B.y1+y2>0C.y1-y2<0D.y1-y2>03(2023·湖北宜昌·统考中考真题)某反比例函数图象上四个点的坐标分别为-3,y1,-2,3,1,y2, 2,y3，则，y1,y2,y3的大小关系为()A.y2<y1<y3B.y3<y2<y1C.y2<y3<y1D.y1<y3<y24(2023·浙江嘉兴·统考中考真题)已知点A-2,y1,B-1,y2,C1,y3均在反比例函数y=3x的图象上，则y1,y2,y3的大小关系是()A.y1<y2<y3B.y2<y1<y3C.y3<y1<y2D.y3<y2<y15(2023·云南·统考中考真题)若点A1,3是反比例函数y=kx(k≠0)图象上一点，则常数k的值为()A.3B.-3C.32D.-326(2023·湖南永州·统考中考真题)已知点M2,a在反比例函数y=kx的图象上，其中a，k为常数，且k>0﹐则点M一定在()A.第一象限B.第二象限C.第三象限D.第四象限7(2023·天津·统考中考真题)若点A x1,-2,B x2,1,C(x3,2)都在反比例函数y=-2x的图象上，则x1,x2,x3的大小关系是()A.x3<x2<x1B.x2<x1<x3C.x1<x3<x2D.x2<x3<x18(2023·湖北随州·统考中考真题)已知蓄电池的电压为定值，使用某蓄电池时，电流I(单位：A)与电阻R(单位：Ω)是反比例函数关系，它的图象如图所示，则当电阻为6Ω时，电流为()A.3AB.4AC.6AD.8A9(2023·山西·统考中考真题)已知A(-2,a),B(-1,b),C(3,c)都在反比例函数y=4x的图象上，则a、b、c的关系是()A.a<b<cB.b<a<cC.c<b<aD.c<a<b10(2023·吉林长春·统考中考真题)如图，在平面直角坐标系中，点A、B在函数y=kx(k>0,x>0)的图象上，分别以A、B为圆心，1为半径作圆，当⊙A与x轴相切、⊙B与y轴相切时，连结AB，AB= 32，则k的值为()A.3B.32C.4D.611(2023·湖北·统考中考真题)在反比例函数y=4-kx的图象上有两点A x1,y1,B x2,y2，当x1<0<x2时，有y1<y2，则k的取值范围是()A.k<0B.k>0C.k<4D.k>412(2023·湖南·统考中考真题)如图，平面直角坐标系中，O是坐标原点，点A是反比例函数y=k xk≠0图像上的一点，过点A分别作AM⊥x轴于点M，AN⊥y轴于直N，若四边形AMON的面积为2．则k的值是()A.2B.-2C.1D.-113(2023·内蒙古·统考中考真题)如图，在平面直角坐标系中，△OAB三个顶点的坐标分别为O(0,0), A(23,0),B(3,1),△OA B与△OAB关于直线OB对称，反比例函数y=kx(k>0,x>0)的图象与A B 交于点C．若A C=BC，则k的值为()A.23B.332C.3D.3214(2023·湖南怀化·统考中考真题)如图，反比例函数y =kx(k >0)的图象与过点(-1,0)的直线AB 相交于A 、B 两点．已知点A 的坐标为(1,3)，点C 为x 轴上任意一点．如果S △ABC =9，那么点C 的坐标为()A.(-3,0)B.(5,0)C.(-3,0)或(5,0)D.(3,0)或(-5,0)15(2023·湖南·统考中考真题)如图，矩形OABC 的顶点B 和正方形ADEF 的顶点E 都在反比例函数y =kxk ≠0 的图像上，点B 的坐标为2,4 ，则点E 的坐标为()A.4,4B.2,2C.2,4D.4,216(2023·广西·统考中考真题)如图，过y =kx(x >0)的图象上点A ，分别作x 轴，y 轴的平行线交y =-1x的图象于B ，D 两点，以AB ，AD 为邻边的矩形ABCD 被坐标轴分割成四个小矩形，面积分别记为S 1，S 2，S 3，S 4，若S 2+S 3+S 4=52，则k 的值为()A.4B.3C.2D.117(2023·福建·统考中考真题)如图，正方形四个顶点分别位于两个反比例函数y=3x和y=nx的图象的四个分支上，则实数n的值为()A.-3B.-13C.13D.318(2023·湖南张家界·统考中考真题)如图，矩形OABC的顶点A，C分别在y轴、x轴的正半轴上，点D在AB上，且AD=14AB，反比例函数y=kxk>0的图象经过点D及矩形OABC的对称中心M，连接OD,OM,DM．若△ODM的面积为3，则k的值为()A.2B.3C.4D.519(2023·黑龙江·统考中考真题)如图，△ABC是等腰三角形，AB过原点O，底边BC∥x轴，双曲线y=kx过A,B两点，过点C作CD∥y轴交双曲线于点D，若S△BCD=12，则k的值是()A.-6B.-12C.-92D.-920(2023·黑龙江绥化·统考中考真题)在平面直角坐标系中，点A 在y 轴的正半轴上，AC 平行于x 轴，点B ，C 的横坐标都是3，BC =2，点D 在AC 上，且其横坐标为1，若反比例函数y =kx(x >0)的图像经过点B ，D ，则k 的值是()A.1B.2C.3D.3221(2023·四川宜宾·统考中考真题)如图，在平面直角坐标系xOy 中，点A 、B 分别在y ，x 轴上，BC ⊥x 轴．点M 、N 分别在线段BC 、AC 上，BM =CM ，NC =2AN ，反比例函数y =kxx >0 的图象经过M 、N 两点，P 为x 正半轴上一点，且OP :BP =1:4，△APN 的面积为3，则k 的值为()A.454B.458C.14425D.7225二、填空题22(2023·广东·统考中考真题)某蓄电池的电压为48V ，使用此蓄电池时，电流I (单位：A )与电阻R (单位：Ω)的函数表达式为I =48R，当R =12Ω时，I 的值为A ．23(2023·四川成都·统考中考真题)若点A -3,y 1 ,B -1,y 2 都在反比例函数y =6x的图象上，则y 1y 2(填“>”或“<”)．24(2023·浙江温州·统考中考真题)在温度不变的条件下，通过一次又一次地对汽缸顶部的活塞加压，加压后气体对汽缸壁所产生的压强P (kPa )与汽缸内气体的体积V (mL )成反比例，P 关于V 的函数图象如图所示．若压强由75kPa 加压到100kPa ，则气体体积压缩了mL ．25(2023·河北·统考中考真题)如图，已知点A (3,3),B (3,1)，反比例函数y =kx(k ≠0)图像的一支与线段AB 有交点，写出一个符合条件的k 的数值：．26(2023·湖北鄂州·统考中考真题)如图，在平面直角坐标系中，直线y 1=k 1x +b 与双曲线y 2=k 2x(其中k 1⋅k 2≠0)相交于A -2,3 ，B m ,-2 两点，过点B 作BP ∥x 轴，交y 轴于点P ，则△ABP 的面积是．27(2023·新疆·统考中考真题)如图，在平面直角坐标系中，△OAB 为直角三角形，∠A =90°，∠AOB =30°，OB =4．若反比例函数y =kxk ≠0 的图象经过OA 的中点C ，交AB 于点D ，则k =．28(2023·浙江绍兴·统考中考真题)如图，在平面直角坐标系xOy 中，函数y =kx(k 为大于0的常数，x >0)图象上的两点A x 1,y 1 ,B x 2,y 2 ，满足x 2=2x 1．△ABC 的边AC ∥x 轴，边BC ∥y 轴，若△OAB 的面积为6，则△ABC 的面积是．29(2023·山东烟台·统考中考真题)如图，在直角坐标系中，⊙A 与x 轴相切于点B ,CB 为⊙A 的直径，点C 在函数y =kx(k >0,x >0)的图象上，D 为y 轴上一点，△ACD 的面积为6，则k 的值为．30(2023·山东枣庄·统考中考真题)如图，在反比例函数y =8x(x >0)的图象上有P 1,P 2,P 3,⋯P 2024等点，它们的横坐标依次为1，2，3，⋯，2024，分别过这些点作x 轴与y 轴的垂线，图中所构成的阴影部分的面积从左到右依次为S 1,S 2,S 3,⋯,S 2023，则S 1+S 2+S 3+⋯+S 2023=．31(2023·四川内江·统考中考真题)如图，在平面直角坐标系中，O 为坐标原点，MN 垂直于x 轴，以MN 为对称轴作△ODE 的轴对称图形，对称轴MN 与线段DE 相交于点F ，点D 的对应点B 恰好落在反比例函数y =kx(x <0)的图象上，点O 、E 的对应点分别是点C 、A ．若点A 为OE 的中点，且S △EAF =14，则k 的值为．32(2023·黑龙江齐齐哈尔·统考中考真题)如图，点A 在反比例函数y =kxk ≠0 图像的一支上，点B 在反比例函数y =-k2x图像的一支上，点C ，D 在x 轴上，若四边形ABCD 是面积为9的正方形，则实数k 的值为．33(2023·广东深圳·统考中考真题)如图，Rt △OAB 与Rt △OBC 位于平面直角坐标系中，∠AOB =∠BOC =30°，BA ⊥OA ，CB ⊥OB ，若AB =3，反比例函数y =kxk ≠0 恰好经过点C ，则k =．34(2023·江苏连云港·统考中考真题)如图，矩形OABC 的顶点A 在反比例函数y =kx(x <0)的图像上，顶点B 、C 在第一象限，对角线AC ∥x 轴，交y 轴于点D ．若矩形OABC 的面积是6，cos ∠OAC =23，则k =．35(2023·浙江宁波·统考中考真题)如图，点A，B分别在函数y=ax(a>0)图象的两支上(A在第一象限)，连接AB交x轴于点C．点D，E在函数y=bx(b<0,x<0)图象上，AE∥x轴，BD∥y轴，连接DE,BE．若AC=2BC，△ABE的面积为9，四边形ABDE的面积为14，则a-b的值为，a的值为．36(2023·湖北荆州·统考中考真题)如图，点A2,2在双曲线y=kx(x>0)上，将直线OA向上平移若干个单位长度交y轴于点B，交双曲线于点C．若BC=2，则点C的坐标是．三、解答题37(2023·浙江杭州·统考中考真题)在直角坐标系中，已知k1k2≠0，设函数y1=k1x与函数y2=k2x-2+5的图象交于点A和点B．已知点A的横坐标是2，点B的纵坐标是-4．(1)求k1,k2的值．(2)过点A作y轴的垂线，过点B作x轴的垂线，在第二象限交于点C；过点A作x轴的垂线，过点B作y 轴的垂线，在第四象限交于点D．求证：直线CD经过原点．38(2023·湖南常德·统考中考真题)如图所示，一次函数y1=-x+m与反比例函数y2=kx相交于点A和点B3,-1．(1)求m的值和反比例函数解析式；(2)当y1>y2时，求x的取值范围．39(2023·湖南·统考中考真题)如图，点A的坐标是-3,0，点B的坐标是(0,4)，点C为OB中点，将△ABC绕着点B逆时针旋转90°得到△A BC ．(1)反比例函数y=kx的图像经过点C，求该反比例函数的表达式；(2)一次函数图像经过A、A 两点，求该一次函数的表达式．40(2023·四川自贡·统考中考真题)如图，点A 2，4 在反比例函数y 1=mx图象上．一次函数y 2=kx +b 的图象经过点A ，分别交x 轴，y 轴于点B ，C ，且△OAC 与△OBC 的面积比为2:1．(1)求反比例函数和一次函数的解析式；(2)请直接写出y 1≥y 2时，x 的取值范围．41(2023·四川泸州·统考中考真题)如图，在平面直角坐标系xOy 中，直线l :y =kx +2与x ，y 轴分别相交于点A ，B ，与反比例函数y =mxx >0 的图象相交于点C ，已知OA =1，点C 的横坐标为2．(1)求k ，m 的值；(2)平行于y 轴的动直线与l 和反比例函数的图象分别交于点D ，E ，若以B ，D ，E ，O 为顶点的四边形为平行四边形，求点D 的坐标．42(2023·四川南充·统考中考真题)如图，一次函数图象与反比例函数图象交于点A-1，6，B3a ,a-3，与x轴交于点C，与y轴交于点D．(1)求反比例函数与一次函数的解析式；(2)点M在x轴上，若S△OAM=S△OAB，求点M的坐标．43(2023·四川宜宾·统考中考真题)如图，在平面直角坐标系xOy中，等腰直角三角形ABC的直角顶点C3，0，顶点A、B6，m恰好落在反比例函数y=kx第一象限的图象上．(1)分别求反比例函数的表达式和直线AB所对应的一次函数的表达式；(2)在x轴上是否存在一点P，使△ABP周长的值最小．若存在，求出最小值；若不存在，请说明理由．44(2023·四川广安·统考中考真题)如图，一次函数y =kx +94(k 为常数，k ≠0)的图象与反比例函数y =mx(m 为常数，m ≠0)的图象在第一象限交于点A 1,n ，与x 轴交于点B -3,0 ．(1)求一次函数和反比例函数的解析式．(2)点P 在x 轴上，△ABP 是以AB 为腰的等腰三角形，请直接写出点P 的坐标．45(2023·四川遂宁·统考中考真题)如图，一次函数y =k 1x +b 的图像与反比例函数y =k 2x的图像交于A -4，1 ，B m ，4 两点．(k 1，k 2，b 为常数)(1)求一次函数和反比例函数的解析式；(2)根据图像直接写出不等式k 1x +b >k2x的解集；(3)P 为y 轴上一点，若△PAB 的面积为3，求P 点的坐标．46(2023·四川眉山·统考中考真题)如图，在平面直角坐标系xOy中，直线y=kx+b与x轴交于点A4,0，与y轴交于点B0,2，与反比例函数y=mx在第四象限内的图象交于点C6,a．(1)求反比例函数的表达式：(2)当kx+b>mx时，直接写出x的取值范围；(3)在双曲线y=mx上是否存在点P，使△ABP是以点A为直角顶点的直角三角形？若存在，求出点P 的坐标；若不存在，请说明理由．47(2023·江西·统考中考真题)如图，已知直线y=x+b与反比例函数y=kx(x>0)的图象交于点A(2,3)，与y轴交于点B，过点B作x轴的平行线交反比例函数y=kx(x>0)的图象于点C．(1)求直线AB和反比例函数图象的表达式；(2)求△ABC的面积．48(2023·四川乐山·统考中考真题)如图，一次函数y=kx+b的图象与反比例函数y=4x的图象交于点A m,4，与x轴交于点B，与y轴交于点C0,3．(1)求m的值和一次函数的表达式；(2)已知P为反比例函数y=4x图象上的一点，S△OBP=2S△OAC，求点P的坐标．49(2023·湖南岳阳·统考中考真题)如图，反比例函数y=kx(k为常数，k≠0)与正比例函数y=mx(m为常数，m≠0)的图像交于A1,2,B两点．(1)求反比例函数和正比例函数的表达式；(2)若y轴上有一点C0,n,△ABC的面积为4，求点C的坐标．3x相交于点A．(1)求点A的坐标．(2)分别以点O、A为圆心，大于OA一半的长为半径作圆弧，两弧相交于点B和点C，作直线BC，交x轴于点D．求线段OD的长．x交于点A4,n．将点A沿x轴正方向平移m个单位长度得到点B,D为x轴正半轴上的点，点B的横坐标大于点D的横坐标，连接BD,BD的中点C在反比例函数y=kx(x>0)的图象上．(1)求n,k的值；(2)当m为何值时，AB⋅OD的值最大?最大值是多少?52(2023·山东东营·统考中考真题)如图，在平面直角坐标系中，一次函数y=ax+b a<0与反比例函数y=kxk≠0交于A-m,3m，B4,-3两点，与y轴交于点C，连接OA，OB．(1)求反比例函数和一次函数的表达式；(2)求△AOB的面积；(3)请根据图象直接写出不等式kx<ax+b的解集．53(2023·山东枣庄·统考中考真题)如图，一次函数y=kx+b(k≠0)的图象与反比例函数y=4x的图象交于A(m,1),B(-2,n)两点．(1)求一次函数的表达式，并在所给的平面直角坐标系中画出这个一次函数的图象；(2)观察图象，直接写出不等式kx+b<4x的解集；(3)设直线AB与x轴交于点C，若P(0,a)为y轴上的一动点，连接AP,CP，当△APC的面积为52时，求点P的坐标．54(2023·山东滨州·统考中考真题)如图，直线y =kx +b (k ,b 为常数)与双曲线y =m x(m 为常数)相交于A 2,a ，B -1,2 两点．(1)求直线y =kx +b 的解析式；(2)在双曲线y =m x上任取两点M x 1,y 1 和N x 2,y 2 ，若x 1<x 2，试确定y 1和y 2的大小关系，并写出判断过程；(3)请直接写出关于x 的不等式kx +b >m x的解集．55(2023·四川内江·统考中考真题)如图，在平面直角坐标系中，一次函数y =mx +n 与反比例函数y =k x的图象在第一象限内交于A a ,4 和B 4,2 两点，直线AB 与x 轴相交于点C ，连接OA ．(1)求一次函数与反比例函数的表达式；(2)当x >0时，请结合函数图象，直接写出关于x 的不等式mx +n ≥k x的解集；(3)过点B 作BD 平行于x 轴，交OA 于点D ，求梯形OCBD 的面积．56(2023·湖南·统考中考真题)如图所示，在平面直角坐标系xOy中，四边形OABC为正方形，其中点A、C分别在x轴负半轴，y轴负半轴上，点B在第三象限内，点A t,0，点P1,2在函数y=k xk>0，x>0的图像上(1)求k的值；(2)连接BP、CP，记△BCP的面积为S，设T=2S-2t2，求T的最大值．57(2023·湖北十堰·统考中考真题)函数y=kx+a的图象可以由函数y=kx的图象左右平移得到．(1)将函数y=1x的图象向右平移4个单位得到函数y=1x+a的图象，则a=；(2)下列关于函数y=1x+a的性质：①图象关于点-a,0对称；②y随x的增大而减小；③图象关于直线y=-x+a对称；④y的取值范围为y≠0．其中说法正确的是(填写序号)；(3)根据(1)中a的值，写出不等式1x+a >1x的解集：．58(2023·甘肃兰州·统考中考真题)如图，反比例函数y=kxx<0与一次函数y=-2x+m的图象交于点A-1,4，BC⊥y轴于点D，分别交反比例函数与一次函数的图象于点B，C．(1)求反比例函数y=kx与一次函数y=-2x+m的表达式；(2)当OD=1时，求线段BC的长．59(2023·湖北黄冈·统考中考真题)如图，一次函数y1=kx+b(k≠0)与函数为y2=mx(x>0)的图象交于A(4,1),B12,a两点．(1)求这两个函数的解析式；(2)根据图象，直接写出满足y1-y2>0时x的取值范围；(3)点P在线段AB上，过点P作x轴的垂线，垂足为M，交函数y2的图象于点Q，若△POQ面积为3，求点P的坐标．60(2023·四川·统考中考真题)如图，已知一次函数y=kx+6的图象与反比例函数y=mxm>0的图象交于A3，4，B两点，与x轴交于点C，将直线AB沿y轴向上平移3个单位长度后与反比例函数图象交于点D，E．(1)求k，m的值及C点坐标；(2)连接AD，CD，求△ACD的面积．61(2023·山东聊城·统考中考真题)如图，一次函数y=kx+b的图像与反比例函数y=mx的图像相交于A-1,4，B a,-1两点．(1)求反比例函数和一次函数的表达式；(2)点P n,0在x轴负半轴上，连接AP，过点B作BQ∥AP，交y=mx的图像于点Q，连接PQ．当BQ=AP时，若四边形APQB的面积为36，求n的值．62(2023·山东·统考中考真题)如图，正比例函数y1=12x和反比例函数y2=kx(x>0)的图像交于点A m,2．(1)求反比例函数的解析式；(2)将直线OA向上平移3个单位后，与y轴交于点B，与y2=kx(x>0)的图像交于点C，连接AB，AC，求△ABC的面积．63(2023·山东·统考中考真题)如图，已知坐标轴上两点A0,4，连接AB，过点B作BC⊥,B2,0AB，交反比例函数y=kx在第一象限的图象于点C(a,1)．(1)求反比例函数y=kx和直线OC的表达式；(2)将直线OC向上平移32个单位，得到直线l，求直线l与反比例函数图象的交点坐标．64(2023·河南·统考中考真题)小军借助反比例函数图象设计“鱼形”图案，如图，在平面直角坐标系中，以反比例函数y =k x 图象上的点A 3,1 和点B 为顶点，分别作菱形AOCD 和菱形OBEF ，点D ，E 在x 轴上，以点O 为圆心，OA 长为半径作AC ，连接BF ．(1)求k 的值；(2)求扇形AOC 的半径及圆心角的度数；(3)请直接写出图中阴影部分面积之和．65(2023·四川成都·统考中考真题)如图，在平面直角坐标系xOy中，直线y=-x+5与y轴交于点A，与反比例函数y=kx的图象的一个交点为B(a,4)，过点B作AB的垂线l．(1)求点A的坐标及反比例函数的表达式；(2)若点C在直线l上，且△ABC的面积为5，求点C的坐标；(3)P是直线l上一点，连接PA，以P为位似中心画△PDE，使它与△PAB位似，相似比为m．若点D，E 恰好都落在反比例函数图象上，求点P的坐标及m的值．·31·。

初中中考反比例函数应用题

初中中考反比例函数应用(Yong)题一(Yi)、选择1．已知反比例(Li)函数的图象经(Jing)过点(Dian)P(一(Yi)l ，2)，则这(Zhe)个函数的图象位于A ．第(Di)二、三象限B ．第一、三象限C ．第三、四象限D ．第二、四象限2.反比例函数x k y =在第一象限的图象如图所示，则x k y =的值可能是（） A ．1B ．2C ．3D ．43．如图5，A 、B 是函数x ky =的图象上关于原点对称的任意两点， BC ∥x k y =轴，AC ∥x k y =轴，△ABC 的面积记为x k y =，则（） A ．x k y = B ． x k y = C ．x k y = D ．x k y =4．市一小数学课外兴趣小组的同学每人制作一个面积为200cm 2的矩形学具进行展示. 设矩形的宽为x cm ，长为y cm ，那么这些同学所制作的矩形长y （cm ）与宽x （cm ）之间的函数关系的图象大致是 ( )【关键词】反比例函数5．一次函数y =kx +b 与反比例函数y =kx 的图象如图5所示，则下列说法正确的是（）A ．它们的函数值y 随着x 的增大而增大B ．它们的函数值y 随着x 的增大而减小C ．k ＜0D ．它们的自变量x 的取值为全体实数6．如(Ru)图，点(Dian)x k y =在反比(Bi)例函数x ky =(x > 0)的(De)图(Tu)象上，且横坐标为(Wei)2. 若(Ruo)将点x ky =先(Xian)向右平移两个单位，再向上平移一个单位后所得的像为点x k y =.则在第一象限内，经过点x k y =的反比例函数图象的解析式是 A ．x k y = B .x k y = C . x k y = D . x k y =7．一张正方形的纸片，剪去两个一样的小矩形得到一个“x ky =”图案，如图所示，设小矩形的长和宽分别为x k y =、x k y =，剪去部分的面积为20，若x k y =，则x k y =与x k y =的函数图象是（）8．在反比例函数x k y =的图象的每一条曲线上，x k y =的增大而增大，则x k y =的值可以是（）A ．x k y =B ．0C ．1D ．2 【关键词】反比例函数9．如图，直线y=mx 与双曲线y=x ky =交于A 、B 两点，过点A 作AM ⊥x 轴，垂足为M ，连结BM,若x k y ==2，则k 的值是（） A ．2 B 、m-2 C 、m D 、4【关键词】一次函数与反比例函数的综合应用10．如图，双曲(Qu)线x ky =经(Jing)过矩形(Xing)QABC 的(De)边(Bian)BC 的(De)中点(Dian)E ，交(Jiao)AB 于点D 。

(中考)反比例函数综合应用题

反比例函数综合应用题如图，A 、B 两点在函数()0m y x x=>的图象上.（1）求m 的值及直线AB 的解析式；（2）如果一个点的横、纵坐标均为整数，那么我们称这个点是格点.请直接写出图中阴影部分（不包括边界）所含格点的个数。

2、如图，点P 是双曲线11(00)k y k x x=<<，上一动点，过点P 作x 轴、y 轴的垂线，分别交x 轴、y 轴于A 、B 两点，交双曲线y =xk 2（0＜k 2＜|k 1|）于E 、F 两点．（1）图1中，四边形PEOF 的面积S 1= (用含k 1、k 2的式子表示)；（3分）（2）图2中，设P 点坐标为（－4，3）．①判断EF 与AB 的位置关系，并证明你的结论；（4分） ②记2PEF OEF S S S ∆∆=-，S 2是否有最小值？若有，求出其最小值；若没有，请说明理由．（5分）3、如图11，已知正比例函数和反比例函数的图像都经过点M （－2，1-），且P （1-，－2）为双曲线上的一点，Q 为坐标平面上一动点，P A 垂直于x 轴，QB 垂直于y 轴，垂足分别是A 、B ．（1）写出正比例函数和反比例函数的关系式；（2）当点Q 在直线MO 上运动时，直线MO 上是否存在这样的点Q ，使得△OBQ 与△OAP 面积相等？如果存在，请求出点的坐标，如果不存在，请说明理由；（3）如图12，当点Q 在第一象限中的双曲线上运动时，作以OP 、OQ 为邻边的平行四边形OPCQ ，求平行四边形OPCQ 周长的最小值．4、已知：如图，正比例函数y ax =的图象与反比例函数k y x=的图象交于点()32A ，．（1）试确定上述正比例函数和反比例函数的表达式；（2）根据图象回答，在第一象限内，当x 取何值时，反比例函数的值大于正比例函数的值？（3）()M m n ，是反比例函数图象上的一动点，其中03m <<，过点M 作直线MN x ∥轴，交y 轴于点B ；过点A 作直线AC y ∥轴(第7题图)交x 轴于点C ，交直线MB 于点D ．当四边形OADM 的面积为6时，请判断线段BM 与DM 的大小关系，并说明理由．一次函数y ax b =+的图象分别与x 轴、y 轴交于点,M N ，与反比例函数k y x=的图象相交于点,A B ．过点A 分别作AC x ⊥轴，AE y ⊥轴，垂足分别为,C E ；过点B 分别作BF x ⊥轴，，与交于点，连接．（1）若点A B ，在反比例函数ky x=的图象的同一分支上，如图1，试证明： ①AEDK CFBK S S =四边形四边形；②AN BM =．（2）若点A B ，分别在反比例函数ky x =6已知点A 、B 分别是x 轴、y 轴上的动点，点C 、D 是某个函数图像上的点，当四边形ABCD （A 、B 、C 、D 各点依次排列）为正方形时，称这个正方形为此函数图像的伴侣正方形。

中考数学中反比例函数100题(教师版)

1.如图1.1所示，矩形ABCO 中的顶点O 与坐标原点重合，点A 在x 轴上，点C 在y 轴上，反比例函数ky x （x ≠0）的图像分布与BC 、AB 交于点E 、F 两点，连接AC . 证明：（1）AC ∥EF ；（2）GE =FH1.证（1）设E (,)k m m ，F (,)k n n，则B (,)kn m ，如图2.1所示，∴CE =m ，AF =k n ，BC =n ，AB =km，∴CE m BC n ，kAF m n k AB n m∴CE AFBC AB ∴AC ∥EF（2）由（1）得AC ∥EF又AB ∥y 轴，BC ∥x 轴， ∴四边形GCAF 、ECAH 都是平行四边形， ∴GF =AC =EH∵GE =GF -EF ，FH =EH -EF ， ∴GE =FH2.如图1.2所示，矩形ABCO 中的顶点O 与坐标原点重合，点A 在x 轴上，点C 在y 轴上，反比例函数ky x （x ≠0）的图像分布与BC 、BA 的延长线交于点E 、F 两点，连接AC . 证明：（1）AC ∥EF ；（2）GE =FH .2.证（1）设E (,)k m m ，F (,)k n n，则B (,)kn m ，如图2.2所示，∴CE =m ，AF =k n ，BC =-n ，AB =km，图1.2∴CE m BC n，kAF m n k AB nm∴CE AFBC AB∴AC ∥EF（2）由（1）得AC ∥EF 又AB ∥y 轴，BC ∥x 轴，∴四边形GCAF 、ECAH 都是平行四边形， ∴GF =AC =EH∵GE = EF -GF ，FH = EF -EH ， ∴GE =FH3.如图1.3所示，A 、B 是反比例函数1k y x第一象限图像上任意两点，射线OA 、OB 分别交反比例函数2k y x的图像于C 、D 两点. 证明：（1）12k OAOC k ；（2）AB ∥CD .3.证（1）作AE ⊥x 轴于点E ，CF ⊥x 轴于点F ，如图2.3所示.设A 111(,)k x x ，C 222(,)kx x ，则E 1(,0)x ，F 2(,0)x∴OE =1x ，OF =2x ，11k AE x ，22k CF x∵AE ∥CF ，∴△AOE ∽△COF ， ∴OA OE AE OC OF CF， ∴1111222212k x x k x OA k OC x k x x∴1122x k OA OCx k （2）由（1）得12k OB OAODk OC， ∴AB ∥CD 此外，当2k yx的图像在第三象限时，如图2.4所示，此结论依然成立.4.如图1.4所示，平行四边形ABCD 的顶点A 、B 位于反比例函数ky x第一象限的图像上，点C 、D 位于x 轴正半轴和y 轴正半轴上. 证明：（1）∠1=∠2，∠3=∠4.4.证作CK ∥y 轴交EF 于点K ，如图2.5所示， ∴四边形CDEK 是平行四边形，CK ⊥x 轴， ∴EK =CD =AB ， ∴EA +AK =AK +BK ， ∴EA =BK .由题1的结论（2）可得EA =BF +BK ， ∴BC =BF ，所以∠1=∠5=∠2. 同理，∠3=∠4.5.如图1.5所示，平行四边形ABCD 的顶点A 、B 位于反比例函数k yx第一象限的图像上，点别位于y 轴负半轴和x 轴负半轴上，AD 交y 轴于点H ，BC 交x 轴于点G . 证明：（1）∠1=∠2，∠3=∠4；（2）四边形CDHG 是菱形.5.证明（1）延长直线AB ，分别交y 轴、x轴于点E 、F ，过点C 做y 图2.6所示. ∵四边ABCD 是平行四边形， ∴EI ∥CD ，AB =DC∵CI ∥DF ，∴四边形CDFI 是平行四边形，∴FI =CD =AB .由题1的结论（2）得AE =BF ， ∴AE +AB =BF +FI ，∴BE=BI=BC，∴∠5=∠2.∵AB∥CD，∴∠1=∠5=∠2.∵∠1+∠4=∠2+∠6=90°，∴∠4=∠6.∵AD∥BC，∴∠3=∠6=∠4（2）连接HG，如图2.7所示.由（1）得∠1=∠2，∠4=∠6，∴CD=CG.又CO⊥DG于点O，∴OD=OG.同理OH=OC.∴四边形CDHG是平行四边形.∵HC⊥DG，∴四边形CDHG是菱形.6．如图1.6所示，A、B为反比例函数kyx第一象限图像上任意两点，连接AO并延长交反比例函数图像另一支于点C，连接BC交x轴于点G、交y轴于点F，连接AB并向两侧延长分别交x轴于点E、交y轴于点D．证明：∠1＝∠2，∠3＝∠4．证明：取DE得中点M，连接OM，如图2.8所示，∴MD＝ME∵∠EOD＝90°∴OM＝MD＝ME∴∠5＝∠2，∠4＝∠6由题1的结论（2）得AD＝BE∴DM－AD＝EM－BE∴AM＝BM由反比例的对称性知OA＝OC∴OM∥BC∴∠5＝∠1＝∠2，∠3＝∠6＝∠4思路点拨（1）构造DE 的中点M ，结合题1的结论（2）得AD ＝BE ，进而得AM ＝BM ，∴M 为“双中点”．（2）进一步地，结合反比例函数图像的对称性可知OA ＝OC ，从而可用中位线定理和斜边中线定理，进而导角．7．如图1.7所示，在平面直角坐标系xOy 中，点A 、B 在反比例函数4y x=(x ＞0)的图像上，延长AB 交x轴于点C ，且12BC AB =，连接OA 交反比例函数1y x=(x ＞0)的图像于点D ，则ABD S △＝．解：延长CA 交y 轴于点E ，作AF ⊥y 轴于点F ，BK ⊥x 轴于点K ，如图2.9所示由题1的结论（2）得AE ＝BC ∴1=4AE EF EC OE =，1=4CK BC OC EC = ∵OBK S △＝OAF S △＝12×4＝2∴BCK S △＝AEF S △＝13OBK S △＝13×2＝23∴OBC S △＝OBK S △＋BCK S △＝83∴OAB S △＝2OBC S△＝163由题3的结论（1）得12OD OA = ∴1=2AD OA ∴ABD S △＝2OAB S △＝83思路点拨（1）由题1的结论（2）得AE ＝BC ，结合12BC AB =，可知1=4AE EF EC OE =，1=4CK BC OC EC =，从而得到喇叭三角形△AOB 与△OBC 的面积比例．（2）进一步地，利用题3的结论（1）得12OD OA =，由△ABD 与△AOB 共边可知=ABD AOB S AD S OA△△．8．如图1.8所示，双曲线4y x=(x ＞0)与直线EF 交于点A 、B ，且AE ＝AB ＝BF ，线段AO 、BO 分别与双曲线2y x=(x ＞0)交于点C 、D ，则：（1）AB 与CD 的位置关系是；（2）四边形ABDC 的面积为．解：（1）由题3的结论（2）得AB ∥CD（2）作BM ⊥x 轴于点M ，AN ⊥y 轴于点N ，如图2．10所示 ∵AE ＝AB ＝BF ∴1=3AE BF EF EF = ∴1=3FM BF OF EF = ∴BFM S △＝AEN S △＝12OBM S △＝12×12×4＝1∴OBF S △＝OBM S △＋BFM S △＝2＋1＝3 ∴AOB S △＝BOF S △＝3 由题3的结论（1）得OC OA =∴21=2COD AOB S OC S OA ⎛⎫= ⎪⎝⎭△△ ∴1322AOB ABDC S S ==△四边形思路点拨（1）由题3的结论（2）得到AB ∥CD ，从而得到21=2COD AOB S OC S OA ⎛⎫= ⎪⎝⎭△△（2）作BM ⊥x 轴于点M ，AN ⊥y 轴于点N ，便于将AE ＝AB ＝BF 这一等量关系转化为1=3FM BF OF EF =．（3）进一步得OBM S △＝2BFM S △，则OBF S △＝OBM S △＋BFMS △＝2＋1＝3，从而AOB S △＝3，最后不难得出1322AOB ABDC S S ==△四边形9．如图1.9所示，直线y ＝－x 与反比例函数ky x=的图像交于A 、B 两点，过点B 作BD ∥x 轴，交y 轴于点D ，延长AD 交反比例函数k y x =的图像于另一点C ，则BCAC的值为．解：设AD 交x 轴于点E ，由题2的结论（2）得AE ＝CD 由反比例函数图像的中心对称性得OA ＝OB ∵OE ∥BD ∴=1AE OA DE OB = ∴CD ＝DE ＝AE ∴13CD AC = 过点C 作CF ⊥BD 于点F ，如图2．11所示易证△CDF ≌△DEO∴FD ＝OE ＝12BD ＝BF∴BC ＝CD ∴13BC AC =思路点拨（1）运用题2的结论（2）得AE ＝CD ，并根据反比例函数图像的中心对称性知OA ＝OB（2）由题意知OE ∥BD ，则=1AE OADE OB=（3）关键还要求出BC 和CD 的关系，可通过CF 垂直平分BD 得到．10．如图1.10所示，已知四边形ABCD 是平行四边形，BC ＝2AB ，A 、B 两点的坐标分别是(－1，0)和(0，2)，C 、D 两点在反比例函数ky x=的图像上，则k ＝．解：作CE ⊥y 轴于点E ，如图2．12所示，由题4的等角模型得∠CBE ＝∠ABO ，又∠CEB ＝∠AOB ＝90° ∴△AOB ∽△CEB (AA ) ∴==2CE BE BC OA OB AB= ∴CE ＝2OA ＝2，BE ＝2OB ＝4 ∴C (－2，6)∴k ＝－2×6＝－12思路点拨（1）根据题4的等角模型得∠CBE ＝∠ABO ，作CE ⊥y 轴，目的在于构造相似三角形，得==2CE BE BCOA OB AB= （2）进一步可导出C (－2，6)，从而求出k11.如图1.11所示，□ABCD 的顶点A 、B 的坐标分别是A （－1，0）、B （0，－2），顶点C 、D 在双曲线y =kx 上，边AD 交y 轴于点E ，且四边形BCDE 的面积是△ABE 的面积的5倍，则k = ；解答：作DF ⊥y 轴于点F ，连接BD ，如图2.13所示；∵S △ACB =12OA OB =1∴由题5的等角模型可得：AE =AB ，OE =OB ， ∴S △ABO =S △ACB =1∵S △ABC S 四边形BCDE=15，S △ABD =S △BCD ，∴S △ABCS △DBE=12，∴AE DE =OE EF =12 易证△AEO ∽△DEF∴S △DEFS△AEO=(DE AE )2=4∴S △DEF =4S △ABD =4，∴S △CDF =OF EF S △DEF =32×4=6=k2 ∴k =12 思路点拨：（1）通过点、的坐标计算出S △ACB =1，由题5的等角模型得S △ABO =S △ACB =1，进而计算S △ACE 的比值，图1.11图2.13得到AEDE =12（2）由于△AEO∽△DEF，故S△DEFS△AEO =(DEAE)2=4，再S△CDF=OFEFS△DEF由得S△CDF=k2=6，则k=12；12.如图1.12所示；A、B为反比例函数y=kx 第一象限图像上任意两点，连接BO并延长交反比例函数图像另一支于点C，连接AC交x轴于点F、交y轴于点G，连接BG，连接AB并向外两侧延长分别交x轴于点E、交y轴于点D；已知BEAB =12，S△GBO=1，则k= ；解答：由题1的结论（2）可得BE=AD；由题5的等角模型得∠1=∠2，∠3=∠4；∴AD=AG=BE作AH⊥x轴于点H，BK⊥y轴于点K，如图2.14所示；∴AH∥BK∥x轴∴DH:HK:OK=AD:AB:BE=1:2:1，∴DH=OK=HG=12HK=GK，∴S△GBK=12S△OBG=12=K2∴k=1思路点拨：（1）根据题5的等角模型的特征得∠1=∠2，∠3=∠4，则AD=AG；作AH⊥y轴于点，BK⊥y轴于点，进而得DH=HG；（2）根据题1的结论（2）得到BE=AD，推出AD:AB:BE=1:2:1，，根据平分线段成比例定理得DH: HK :OK= 1:2:1，，则DH=OK=HG=GK；（3）由S△GBK=12S△OBG=12=K2推出k=1图1.12图2.1413. 如图1.13所示；在平面直角坐标系xOy 中，A （1，m ）、B （n ，a ）在反比例函数y =kx （k ＞0，x ＞0）的图像上，∠AOB =45°；（1）若a =12，已知∠AOB =∠OBA ，求k ；（2）若a =√63，求k解答：（1）如图2.15所示；连接AB ，分别过点A 作AC ⊥y 轴于点C ，AC ⊥x 轴于点E ，且延长CA 、EB 交于点D ；∵∠AOB =∠OBA =45°，∴OA =AB ，∠OAB =90°， ∵∠CAO +∠COA =90°，∠DAB +∠CAO =90°， ∴∠COA =∠DAB ∵在△CAO 和△DBA{∠ACO =∠ADB =90°∠COA =∠DAB OA =AB∴△CAO ≌△DBA (AAS ) ∴CO =AD ，∴CD =CA +AD =CA +CO =1+m∵a =12，∴B （1+m ，12）将A （1，m ）、B （1+m ，12）代入y =k x 得k =m =12（1+m ），∴k =1 （2）如图2.16所示；作GA ⊥OA 交OB 的延长线于点G ；图1.13图2.15类似（1），可得△CAO ≌△EGA （AAS ）∴CO =AE ，CA =EG ，∴CE =AE +CA =CA ＋CO =1+m ，GD =ED －EG =CO －CA =m －1， ∴G （1＋m ，m －1）， ∵a =√63，∴B （n ，√63）将A （1，m ）、B （n ，√63）代入y =kx得k =m = a =√63n ， ∴n =√62m ，∴B （√62m ，√63）∵BF ∥GD ，∴OFBF =ODGD ，∴√62m √63=1+mm−1∴3m 2－5m －2=0，∴m =2（负值舍去） ∴k =m =2 思路点拨：（1）保留特殊角，利用垂直模型构造出全等三角形或相似三角形，如图2.17（a ）、（b ）所示，求出对应点的坐标；（2）结合题目条件，通过将点的坐标代入反比例函数得到数量关系，并利用平行判定法建立相似比例式；（3）解方程求出k14. 如图1.14所示；已知点A 、B 分别在反比例函数y =k x （x ＞0）和y =−4x （x ＞0）的图像上，且OA ⊥OB ，则OBOA 的值为；图2.16（a ）（b ）解答：作AC ⊥y 轴于点C ，BD ⊥y 轴于点D ，如图2.18所示；∵∠AOC +∠OAC =∠AOC +∠BOD =90°， ∴∠OAC =∠BOD ，又∠ACO =∠ODB =90°，∴△ACO ∽△ODB （AA ），∴DB CD =OD CA =OBOA 设DBCD =OD CA=OBOA =m ，A （a ，b ），则ab =1，∴OD =m ⋅CA =ma ，DB =m ⋅OC =mb ， ∴B （mb ，－ma ）将点B 的坐标代入y =−4x （x ＞0）得m 2ab =4， ∴m =2（负值舍去） ∴OB OA =2思路点拨：具体参见题13中直角的构造方式15. 如图1.15所示；已知点A （2，3）和点B （0，2），点A 在反比例函数y =kx 的图像上，作AB ，再将射线AB 绕点A 按逆时针方向旋转45°，交反比例函数的图像于点C ，则点C 的坐标为；图1.14图2.18解答：作BE ⊥AB 交AC 于点E ，AD ⊥y 轴于点D ，如图2.19所示，易证：△ABD ≌△BEO （AAS ），∴BO =AD =2，EO =BD =1， ∴E （1，0）∵A （2，3），E （1，0）∴直线AE 的解析式为y =3x −3, 反比例函数为y =6x， ∴x 2－x －2=0，∴x 1=－1，x 2=2（舍） ∴将x C =－1代入y =6x 得C （－1，－6）思路点拨：（1）出现45°角时通常构造等腰直角三角形进行求解，选取的垂足尽量在坐标轴上，方便计算；例如，本题中垂足选取坐标轴上的点B ，构造等腰Rt △ABE ，进而求得点E 的坐标；（2）利用点A 、E 的坐标求出直线AE 解析式，联立反比例函数，即可求出点C 的坐标21、如图1.21所示，点A 是双曲线xy 9-=第二象限分支上的一个动点，连接AO 并延长交另一分支于点B ，以AB 为底作等腰△ABC ，且∠ACB=1200，点C 在第一象限，随着点A 的运动，点C 的位置也不断变化，但点C 始终在双曲线xky =上运动，则k 的值为___________。

中考总复习反比例函数专项练习(含解析)

教育选轻轻·家长更放心页 1 第62讲反比例函数微课反比例函数的概念题一：当m 取什么值时，函数22(1)m y m x -=+是反比例函数？题二：当m 取什么值时，函数23m m y x --=是反比例函数？第63讲反比例函数微课反比例函数的图象及性质题一：已知反比例函数210(2)m y m x -=-的图象在第二、四象限，求m 值，并指出在每个象限内y 随x 的变化情况？教育选轻轻·家长更放心页 2 题二：已知反比例函数25(1)m y m x -=-的图象在第一、三象限，求m 值，并指出在每个象限内y随x 的变化情况？题三：已知反比例函数1y x=，当x =1时，y 的值是多少；当x ＞1时，y 的取值范围是多少；当x ＜1时，y 的取值范围是多少．题四：已知反比例函数3y x=，当y =3时，x 的值是多少；；当y ＞3时，x 的取值范围是多少；当y ＜3时，x 的取值范围是多少．教育选轻轻·家长更放心页 3第64讲反比例函数微课反比例函数的几何意义题一：如图，过点O 作直线与双曲线k y x=(k ≠0)交于A 、B 两点，过点B 作BC ⊥x 轴于点C ，作BD ⊥y 轴于点D ．在x 轴上分别取点E 、F ，使点A 、E 、F 在同一条直线上，且AE =AF ．设图中矩形ODBC 的面积为S 1，△EOF 的面积为S 2，则S 1、S 2的数量关系是( )A ．S 1=S 2B ．2S 1=S 2C ．3S 1=S 2D ．4S 1=S 2题二：如图，A 、B 是反比例函数2y x=(x ＞0)图象上的两点，AC ⊥y 轴于点C ，BD ⊥y 轴于点D ，OB 与AC 相交于点E ，记△AOE 的面积为S 1，四边形BDCE 的面积为S 2，则S 1、S 2的大小关系是( )A ．S 1=S 2B ．S 1＜S 2C ．S 1＞S 2D ．不能确定教育选轻轻·家长更放心页 4 题三：如图，过点P (2，3)分别作PC ⊥x 轴于点C ，PD ⊥y 轴于点D ，PC 、PD 分别交反比例函数2y x=(x ＞0)的图象于点A 、B ，则图中阴影部分的面积为________．题四：如图，双曲线k y x=(k ＞0)与⊙O 在第一象限内交于P ，Q 两点，分别过P ，Q 两点向x 轴、y 轴作垂线，已知点P 坐标为(1，3)，则图中阴影部分的面积为________．第65讲反比例函数微课反比例函数与一次函数综合题一：已知在一、三或二、四象限内，正比例函数y = kx (k ≠0)和反比例函数b y x=(b ≠0)的函数值都随x 的增大而增大，则这两个函数在同一坐标系中的大致图象是( ) A ． B ．C ．D ．教育选轻轻·家长更放心页 5题二：若ab ＞0，则一次函数y =ax +b 与反比例函数ab y x=在同一坐标系数中的大致图象是( ) A ． B ．C ．D ．题三：如图，一次函数y = kx +b 的图象与反比例函数m y x=的图象相交于A (1，2)、B (-2，-1)两点． (1) 利用图中条件，求反比例函数和一次函数的解析式；(2) 根据图象写出使一次函数的值大于反比例函数的值x 的取值范围．教育选轻轻·家长更放心页 6题四：已知如图，一次函数y =kx +b 的图象与反比例函数m y x的图象相交于A 、B 两点． (1) 利用图中条件，求反比例函数和一次函数的解析式； (2) 根据图象写出使一次函数的值大于反比例函数的值x 的取值范围．第66讲反比例函数微课反比例函数的应用题一：你吃过拉面吗？实际上在做拉面的过程中就渗透着数学知识：一定体积的面团做成拉面，面条的总长度y (m)是面条的粗细(横截面积)x (mm 2)的反比例函数，其图象如图所示．(1)写出y 与x 的函数关系式；(2)求当面条粗1.6mm 2时，面条的总长度是多少米？教育选轻轻·家长更放心页 7题二：某汽车的功率P 为一定值，汽车行驶时的速度v (米/秒)与它所受的牵引力F (牛)之间的函数关系如下图所示：(1)这辆汽车的功率是多少瓦？请写出这一函数的表达式；(2)当它所受牵引力为1200牛时，汽车的速度为多少千米/时？(3)如果限定汽车的速度不超过30米/秒，那么它所受的牵引力F 应不小于多少牛？第67讲反比例函数微课反比例函数综合题一：如图，在直角坐标系中，正方形OABC 是由四个边长为1的小正方形组成的，反比例函数11k y x =(x ＞0)过正方形OABC 的中心E ，反比例函数22k y x=(x ＞0)过AB 的中点D ，两个函数分别交BC 于点N ，M ，有下列四个结论： ①双曲线y 1的解析式为11y x =(x ＞0)； ②两个函数图象在第一象限内一定会有交点；③MC =2NC ；④反比例函数y 2的图象可以是看成是由反比例函数y 1的图象向上平移一个单位得到．其中正确的结论是________．教育选轻轻·家长更放心页8题二：如图，OABC 是平行四边形，对角线OB 在y 轴正半轴上，位于第一象限的点A 和第二象限的点C 分别在双曲线11k y x =和22k y x =的一支上，分别过点A 、C 作x 轴的垂线，垂足分别为M 和N ，则有以下的结论：①12k AM CN k =；②阴影部分面积是12(k 1+k 2)； ③当∠AOC =90°时，|k 1|=|k 2|；④若OABC 是菱形，则两双曲线既关于x 轴对称，也关于y 轴对称．其中正确的结论是____________．第68讲二次函数微课描点法画函数图象题一：观察函数y = -2x 2与y =12x 2的图像，回答：抛物线的开口方向，对称轴，顶点坐标及函数的单调性．题二：观察函数y = 3x2与y = 3x2的图像，回答：抛物线的开口方向，对称轴，顶点坐标及函数的单调性．教育选轻轻·家长更放心页9教育选轻轻·家长更放心页 10 第62讲反比例函数微课反比例函数的概念题一：1．详解：∵22(1)m y m x -=+是反比例函数，∴22110m m ⎧-=-⎪⎨+≠⎪⎩，解得m =1．题二：－3．详解：∵23m m y x --=是反比例函数，∴2130m m ⎧-=⎪⎨-≠⎪⎩，解得m =－3．第63讲反比例函数微课反比例函数的图象及性质题一：－3，该函数图象在每个象限内y 随x 的增大而减小．详解：∵210(2)m y m x -=-是反比例函数，∴m 2－10=－1，解得m =3或－3，又∵函数的图象在第二、四象限，∴m －2＜0，解得m ＜2，综上所述，m =－3，且该函数图象在每个象限内y 随x 的增大而增大．题二：2；该函数图象在每个象限内y 随x 的增大而减小．详解：依题意有m 2－5=－1，解得m =2或－2，又∵函数的图象在第一、三象限，∴m －1＞0，解得m ＞1，综上所述，m =2，且该函数图象在每个象限内y 随x 的增大而减小．题三：1；0＜y ＜1；y ＜0或y ＞1．详解：∵反比例函数1y x=中，k =1＞0， ∴此函数图象的两个分支位于一、三象限，且在每一象限内y 随x 的增大而减小，如图所示，当x =1时，y =1；当x ＞1时，0＜y ＜1；当x ＜1时，y ＜0或y ＞1．教育选轻轻·家长更放心页 11题四：x =1；0＜x ＜1；x ＜0或x ＞1．详解：∵反比例函数3y x=中，k =3＞0， ∴此函数图象的两个分支位于一、三象限，且在每一象限内y 随x 的增大而减小，如图所示，当y =3时，x =1；当y ＞3时，0＜x ＜1；当y ＜3时，x ＜0或x ＞1．第64讲反比例函数微课反比例函数的几何意义题一：B ．详解：设A 点坐标为(m ，－n )，过点O 的直线与双曲线k y x =交于A 、B 两点，则A 、B 两点关于原点对称，则B 的坐标为(－m ，n )；矩形OCBD 中，易得OD =n ，OC =m ；则S 1=mn ；在Rt △EOF 中，AE =AF ，故A 为EF 中点，由中位线的性质可得OF =2n ，OE =2m ；则S 2=12×OF ×OE =2mn ；故2S 1=S 2．故选B ．题二：A．详解：设点A的坐标为(x A，y A)，点B的坐标为(x B，y B)，∵A、B在反比例函数2yx=上，∴x A y A=2，x B y B=2，∴S△AOC=12x A y A=1；S△OBD=12x B y B=1．∴S△AOC=S△OBD，∴S△AOC－S△OCE=S△OBD－S△OCE，∴S△AOE=S梯形ECDB；又∵△AOE与梯形ECDB的面积分别为S1、S2，∴S1=S2．故选A．题三：4．详解：∵B、A两点在反比例函数2yx=(x＞0)的图象上，∴S△DBO=S△AOC=12×2=1，∵P(2，3)，∴四边形DPCO的面积为2×3=6，∴图中阴影部分的面积为6－1－1= 4．题四：4．详解：∵双曲线kyx=(k＞0)与⊙O在第一象限内交于P，Q两点，∴点P与点Q关于直线y=x对称，∴Q点坐标为(3，1)，∴图中阴影部分的面积为2×1×3－2×1×1= 4．第65讲反比例函数微课反比例函数与一次函数综合题一：C．详解：∵正比例函数的函数值随x的增大而增大，∴正比例函数应过一、三象限，排除A、D；又∵反比例函数的函数值随x的增大而增大，∴反比例函数应过二、四象限，B、C两选项中只有C符合．故选C．题二：A．教育选轻轻·家长更放心页12详解：A、根据一次函数可判断a＞0，b＞0，根据反比例函数可判断ab＞0，故符合题意，本选项正确；B、根据一次函数可判断a＜0，b＜0，根据反比例函数可判断ab＜0，故不符合题意，本选项错误；C、根据一次函数可判断a＜0，b＞0，根据反比例函数可判断ab＞0，故不符合题意，本选项错误；D、根据一次函数可判断a＞0，b＞0，根据反比例函数可判断ab＜0，故不符合题意，本选项错误；故选A．题三：(1)2yx=，y=x+1．(2) -2＜x＜0或x＞1．详解：(1) 把A(1，2)代入反比例函数myx=得m=2，即反比例函数的解析式是2yx=；把A(1，2)、B(-2，-1)代入一次函数y=kx+b得：2= k+b 且−1= −2k+b，所以k=1，b=1，即一次函数的解析式是y= x+1．(2)∵A(1，2)、B(-2，-1)，∴一次函数的值大于反比例函数的值的x的取值范围是-2＜x＜0或x＞1．题四：(1) y=2x-，y= -x-1．(2) x＜-2或0＜x＜1．详解：(1)据题意，反比例函数myx=的图象经过点A(-2，1)∴有m = xy = -2∴反比例函数解析式为y=2x -，又反比例函数的图象经过点B(1，n)∴n= -2，∴B(1，-2)将A、B两点代入y=kx+b有− 2k + b = 1，k + b = −2，解得k= −1，b= −1，∴一次函数的解析式为y= -x-1，(2)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围为：教育选轻轻·家长更放心页13x取相同值，一次函数图象在反比例函数上方即一次函数大于反比例函数，∴x＜-2或0＜x＜1．第66讲反比例函数微课反比例函数的应用题一：y=128x；80．详解：(1)设y与x的函数关系式为kyx =，将x=4，y=32代入kyx=，得k=4×32=128，∴y=128x，答：y与x的函数关系式y=128x；(2)当x=1.6时，y=1281.6=80，答：当面条粗1.6mm2时，面条的总长度是80米．题二：60000，v=60000F；180；2000．详解：(1)设v与F之间的函数关系式为v=PF，把(3000，20)代入v=PF，得P=60000，∴这辆汽车的功率是60000瓦，这一函数的表达式为v=60000F；(2)把F=1200牛代入v=60000F=600001200=50(米/秒)；∴v的速度是3600×50÷1000=180(千米/时)；(3)把v≤30代入v=60000F，得F≥2000，∴它所受的牵引力F应不小于2000牛．第67讲反比例函数微课反比例函数综合题一：①③．教育选轻轻·家长更放心页14详解：①点E的坐标是(1，1)，代入11kyx=，解得k1=1，则双曲线y1的解析式为11yx=(x＞0)，故①正确；②点D的坐标是(1，2)，代入22kyx=得k2=2，则解析式是22yx=(x＞0)，方程12x x=无解，故两个函数图象在第一象限内一定不会有交点，故②错误；③在11yx=中，令x=2，解得y=12，则NC=12，在22yx=中，令x=2，解得y=1，则MC=1，故MC=2NC，故③正确；④函数y1的图象向上平移一个单位长度得到的函数解析式是y=1x+1，故④错误．故答案为①③．题二：①④．详解：作AE⊥y轴于E，CF⊥y轴于F，如图，∵四边形OABC是平行四边形，∴S△AOB=S△COB，∴AE=CF，∴OM=ON，∵S△AOM=12|k1|=12OM•AM，S△CON=12|k2|=12ON•CN，∴12kAMCN k=，故①正确；∵S△AOM=12|k1|，S△CON=12|k2|，教育选轻轻·家长更放心页15∴S阴影部分=S△AOM+S△CON=12(|k1|+|k2|)，而k1＞0，k2＜0，∴S阴影部分=12(k1－k2)，故②错误；当∠AOC=90°，∴四边形OABC是矩形，∴不能确定OA与OC相等，而OM=ON，∴不能判断△AOM≌△CON，∴不能判断AM=CN，∴不能确定|k1|=|k2|，故③错误；若OABC是菱形，则OA=OC，而OM=ON，∴Rt△AOM≌Rt△CON，∴AM=CN，∴|k1|=|k2|，∴k1=－k2，∴两双曲线既关于x轴对称，也关于y轴对称，故④正确．故答案为①④．第68讲二次函数微课描点法画函数图象题一：见详解．详解：（1）抛物线y =12x2的开口方向是向上，对称轴是y轴，顶点坐标是（0，0），当x≠0时，抛物线上的点都在x轴上方；当x＞0时，曲线自左向右逐渐上升，当x＜0时，曲线自左向右逐渐下降；二次函数y = -2x2的开口方向是向下，对称轴是y轴，顶点坐标是（0，0），当x≠0时，抛物线上的点都在x轴下方；当x＞0时，曲线自左向右逐渐下降，当x＜0时，曲线自左向右逐渐上升．题二：见详解．详解：（1）抛物线y = 3x2的开口方向是向上，对称轴是y轴，顶点坐标是（0，0），当x≠0时，抛物线上的点都在x轴上方；当x＞0时，曲线自左向右逐渐上升，当x＜0时，曲线自左向右逐渐下降；二次函数y = - 3x2的开口方向是向下，对称轴是y轴，顶点坐标是（0，0），当x≠0时，抛物线上的点都在x轴下方；当x＞0时，曲线自左向右逐渐下降，当x＜0时，曲线自左向右逐渐上升．教育选轻轻·家长更放心页16。

2024年人教版九年级数学中考专题训练：反比例函数(含解析)

2024年人教版九年级数学中考专题训练：反比例函数1．如图，在平面直角坐标系中，一次函数y ＝﹣x+m 的图象与反比例函数y＝（x ＞0）的图象交于A 、B 两点，已知A （1，2）（1）求一次函数和反比例函数的解析式；（2）连接AO 、BO ，求△AOB 的面积．2．某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压是气体体积的反比例函数.已知当时，.（1）求出这个函数的表达式；（2）当气球内的气压大于时，气球将爆炸，为了安全起见，气球的体积应不小于多少立方米？3．如图，反比例函数与一次函数的图像在第一象限交于、两点．（1）则，　　，　（2）观察图像，请直接写出满足的取值范围．（3）若Q 为y 轴上的一点，使最小，求点Q 的坐标．4．如图，在平面直角坐标系中，一次函数的图象分别交x 轴，y 轴正半轴于点A ，B ，内切于，反比例函数的图象经过点P ，交直线于点C ，D （C 在点D 的左侧）.kx()P kPa ()3mV 30.8m V =120kPa P =128kPa ()10ky k x=≠2y x b =-+()13A ，()3B n ，k =b =n =12y y ≥QA QB +364y x =-+P ABO ()0ky x x=>AB（1）求反比例函数的解析式；（2）过点C ，D 分别作x 轴，y 轴的平行线交于点E ，求的面积.5．如图1，点A （1，0），B （0，m ）都在直线y ＝﹣2x+b 上，四边形ABCD 为平行四边形，点D 在x轴上，AD=3，反比例函数（x>0）的图象经过点C ．（1）求k 的值；（2）将图1的线段CD 向右平移n 个单位长度（n≥0），得到对应线段EF ，线段EF 和反比例函数（x>0）的图象交于点M ．①在平移过程中，如图2，若点M 为EF 的中点，求△ACM 的面积；②在平移过程中，如图3，若AM ⊥EF ，求n 的值．6．如图，点A 是反比例函数图象上的点，AB 平行于y 轴，且交x 轴于点，点C 的坐标为，AC 交y 轴于点D ，连接BD ，（1）求反比例函数的表达式；（2）设点P 是反比例函数图象上一点，点Q 是直线AC 上一点，若以点O ，P ，D ，Q CDE ky x=ky x=()0ky k x=>()10B ，()10-，AD =()0ky x x=>为顶点的四边形是平行四边形，求点Q 的坐标；（3）若点是该反比例函数图象上的点，且满足∠MDB>∠BDC ，请直接写a 的取值范围.7．某种商品上市之初采用了大量的广告宣传，其销售量与上市的天数之间成正比，当广告停止后，销售量与上市的天数之间成反比（如图），现已知上市30天时，当日销售量为120万件．（1）写出该商品上市以后销售量y （万件）与时间x （天数）之间的表达式；（2）求上市至第100天（含第100天），日销售量在36万件以下（不含36万件）的天数；（3）广告合同约定，当销售量不低于100万件，并且持续天数不少于12天时，广告设计师就可以拿到“特殊贡献奖”，那么本次广告策划，设计师能否拿到“特殊贡献奖”？8．在学习反比例函数后，小华在同一个平面直角坐标系中画出了（x>0）和的图象，两个函数图象交于A （x 1，y 2），B （x 2，y 2）两点，在线段AB 上选取一点P ，过点P 作y 轴的平行线交反比例函数图象于点 O （如图1）.在点P 移动的过程中，发现PO 的长度随着点P 的运动而变化.为了进一步研究 PO 的长度与点P 的横坐标之间的关系，小华提出了下列问题∶（1）设点P 的横坐标为x ，PQ 的长度为y ，则y 与x 之间的函数关系式为（x 1<x<x 2）；（2）为了进一步的研究（1）中的函数关系，决定运用列表，描点，连线的方法绘制函数的图象；①列表∶()M a b ，ky x=1y x=5y x =-+x 1234ym3n表中 m ＝，n ＝；②描点∶根据上表中的数据，在图2中描出各点；③连线∶请在图2中画出该函数的图象.观察函数图象，当x ＝时，y 的最大值为；（3）应用∶已知某矩形的一组邻边长分别为m ，n ，且该矩形的周长 W 与n 存在函数关系，求 m 取最大值时矩形的对角线长.9．如图，点P 为函数与函数图象的交点，点P 的纵坐标为4，轴，垂足为点B ．（1）求m 的值；（2）点M 是函数图象上一动点，过点M 作于点D ，若，求点M 的坐标．10．若关于x 的函数y ，当时，函数y 的最大值为M ，最小值为N ，令函数，我们不妨把函数h 称之为函数y 的“共同体函数”.（1）①若函数，当时，求函数y 的“共同体函数”h 的值；②若函数（，k ，b 为常数），求函数y 的“共同体函数”h 的解析式；（2）若函数，求函数y 的“共同体函数”h 的最大值；（3）若函数，是否存在实数k ，使得函数y 的最大值等于函数y 的“共同体函数”h 的最小值.若存在，求出k 的值；若不存在，请说明理由.11．已知一块矩形草坪的两边长分别是2米与3米，现在要把这个矩形按照如图1的方式扩大到面积为1x 13122x 535234220W n=-+1y x =+()0my x x=>PB x ⊥()0m y x x =>MD BP ⊥12tan PMD ∠=1122t x t -≤≤+2M Nh -=4044y x =1t =y kx b =+0k ≠21y x x=≥（）24y x x k =-++原来的2倍，设原矩形的一边加长a 米，另一边长加长b 米，可得a 与b 之间的函数关系式b＝﹣2．某班“数学兴趣小组”对此函数进一步推广，得到更一般的函数y ＝﹣2，现对这个函数的图象和性质进行了探究，研究过程如下，请补充完整：（1）类比反比例函数可知，函数y ＝﹣2的自变量x 的取值范围是，这个函数值y 的取值范围是　　．（2）“数学兴趣小组”进一步思考函数y ＝|﹣2|的图象和性质，请根据函数y ＝﹣2的图象，画出函数y ＝|﹣2|的图象；（3）结合函数y ＝|﹣2|的图象解答下列问题：①求出方程|﹣2|＝0的根；②如果方程|﹣2|＝a 有2个实数根，请直接写出a 的取值范围．12．如图，抛物线与x 轴交于两点（在的左边），与y 轴交于C ，；双曲线经过抛物线的顶点，点的横坐标为1．123a +123x +123x +123x +123x +123x +123x +123x +123x +23y ax bx =++A B 、A B 3tan CAB ∠=(0)ky k x=≠23y ax bx =++D D（1）求抛物线和双曲线的解析式．（2）点P 为抛物线上一动点，且在第一象限，连接，求当四边形取得最大值时，点P 的坐标，并求出这个最大值．（3）若在此抛物线和双曲线上存在点Q ，使得，请求出点Q 的坐标．13．如图，在平面直角坐标系中，一次函数的图象与反比例函数的图象相交于，两点．（1）分别求一次函数及反比例函数的表达式；（2）在第三象限内的B 点右侧的反比例函数图象上取一点P ，连接且满足．i ）求点P 的坐标；ii ）过点A 作直线，在直线l 上取一点Q ，且点Q 位于点A 的左侧，连接，试问：能否与相似？若能，求出此时点Q 的坐标；若不能，请说明理由．14．定义：函数图象上到两坐标轴的距离都不大于的点叫做这个函数图象的“n 阶方点”．例如，点是函数图像的“阶方点”；点是函数图像的“2阶方点”．（1）在①；②；③三点中，是反比例函数图像的“1阶方点”的有（填序号）；（2）若y 关于x 的一次函数图像的“2阶方点”有且只有一个，求a 的值；（3）若y 关于x 的二次函数图像的“n 阶方点”一定存在，请直接写出n 的取值范围．15．如图1，已知反比例函数的图象与一次函数的图象相交于A （2，a ），B 两点.BP CP 、ABPC QB QC =xOy y kx b =+my x=(14)A ，(4)B n -，PA PB ，15PAB S = l PB BQ QAB ABP (0)n n ≥1133⎛⎫⎪⎝⎭，y x =12(21)，2y x =122⎛⎫-- ⎪⎝⎭，(11)--，(11)，1y x=31y ax a =-+2()21y x n n =---+(0)ky k x=≠1y x =-（1）求反比例函数的表达式及A ，B 两点的坐标；（2）M 是x 轴上一点，N 是y 轴上一点，若以A ，B ，M ，N 为顶点的四边形是以为边的平行四边形，求点M 的坐标；（3）如图2，反比例函数的图象上有P ，Q 两点，点P 的横坐标为，点Q 的横坐标与点P 的横坐标互为相反数，连接，，，.若的面积是的面积的3倍，求m 的值.16．如图，直线AC 与双曲线交于A （m ，6），B （3，n ）两点，与x 轴交于点C ，直线AD 与x 轴交于点D （－11，0），（1）请直接写出m ，n 的值；（2）若点E 在x 轴上，若点F 在y 轴上，求的最小值；（3）P 是直线AD 上一点，Q 是双曲线上一点，是否存在点P ，Q ，使得四边形ACQP 是正方形？若存在，求出点P ，Q 的坐标；若不存在，请说明理由．17．在平面直角坐标系中，将一点（横坐标与纵坐标不相等）横坐标与纵坐标互换后得到的点叫这一点的“H 点”，如（2，-3）与（-3，2）是一对“H 点”.（1）点和它的“H 点”均在直线上，求k 的值；AB ky x=(2)m m >AP AQ BP BQ ABQ ABP ()60y k x=≠AF EF BE ++()m n ，y kx a =+（2）若直线经过的A ，B 两点恰好是一对“H 点”，其中点A 还在反比例函数的图象上，一条抛物线也经过A ，B 两点，求该抛物线的解析式；（3）已知，B 为抛物线上的一对“H 点”，且满足：，，点P 为抛物线上一动点，若该抛物线上有且仅存在3个点P 满足△PAB 的面积为16，求的值.18．已知：如图，一次函数y ＝-2x+10的图象与反比例函数y＝的图象相交于A 、B 两点（A 在B 的右侧），点A 横坐标为4.（1）求反比例函数解析式及点B 的坐标；（2）观察图象，直接写出关于x 的不等式-2x+10-＞0的解集；（3）反比例函数图象的另一支上是否存在一点P ，使△PAB 是以AB 为直角边的直角三角形？若存在，求出所有符合条件的点P 的坐标；若不存在，请说明理由.19．如图，反比例函数与一次函数相交于点A （1，4）和点B （4，1），直线的图象与y 轴和x 轴分别相交于点C 和点D ；（1）请直接写出当时自变量x 的取值范围；（2）将一次函数向下平移8个单位长度得到直线EF ，直线EF 与x 和y 轴分别交于点E 和点F ，抛物线过点A 、D 、E 三点，求该抛物线的函数解析式（也称函数表达式）；3y kx =+2y x=2y x bx c =++()()A m n m n <，()20y ax bx c a =++≠2m n +=3mn =-a b c ++kxkx()110k y x x=>22y k x n =+2y 12y y ≥22y k x n =+2y ax bx c =++（3）在（2）抛物线的对称轴上是否存在一点P ，使得△PBF 是以BF 为斜边的直角三角形，若存在，请用尺规作图（圆规和无刻度直尺）画出点P 所在位置，保留作图痕迹，并直接写出点P 的坐标；若不存在，请说明理由．20．如图1，平面直角坐标系中，，反比例函数的图象分别交矩形的两边、于E 、F （E 、F 不与A 重合），沿着将矩形折叠使A 、D 重合．（1）当点E 为中点时，求点F 的坐标，并直接写出与对角线的关系；（2）如图2，连接．①的周长是否有最小值，若有，请求出最小值；若没有，请说明理由；②当平分时，直接写出k 的值．21．如图1，四边形为正方形，点A 在y 轴上，点B 在x 轴上，且，，反比例函数在第一象限的图象经过正方形的顶点C ．（1）求点C 的坐标和反比例函数的关系式；（2）如图，将正方形沿x 轴向右平移m 个单位长度得到正方形A ′B ′C ′D ′，点A ′恰好落在反比例函数的图象上，求n 值．（3）在（2）的条件下，坐标系内是否存在点P ，使以点O ，A ′，B ′，P 为顶点的四边形为平行四边形，若存在，请直接写出点P的坐标，若不存在，请说明理由．xOy (43)A -，(0)ky k x=<ABOC AC AB EF ABOC AC EF BC CD CDE CD ACO ∠ABCD 4OA =2OB =()0ky k x=≠2ABCD22．如图，在平面直角坐标系中，A （8，0）、B （0，6）是矩形OACB 的两个顶点，双曲线y＝（k≠0，x ＞0）经过AC 的中点D ，点E 是矩形OACB 与双曲线y ＝的另一个交点．（1）点D 的坐标为，点E 的坐标为；（2）动点P 在第一象限内，且满足S △PBO ＝S △ODE ．①若点P 在这个反比例函数的图象上，求点P 的坐标；②若点Q 是平面内一点，使得以A 、C 、P 、Q 为顶点的四边形是菱形，请你直接写出满足条件的所有点Q 的坐标．23．如图，一次函数的图像与反比例函数的图像交于，两点．（，，为常数）（1）求一次函数和反比例函数的解析式；（2）将一次函数向下平移个单位后与反比例函数的图像有且只有一个公共点，求的值；（3）为轴上一点，若的面积为，求点的坐标．24．如图，一次函数的图象与反比例函数（k 为常数且）的图象交于A ，B 两点，其中，直线与y 轴、x 轴分别交于C ，D 两点．kxkx561y k x b =+2k y x=()41A -，()4B m ，1k 2k b 1y k x b =+m 2k y x=m P y PAB 3P 4y x =+ky x=0k ≠()13A -，4y x =+（1）求反比例函数的表达式；（2）在x 轴上找一点P ，使的值最小，并求满足条件的点P 的坐标；（3）在坐标平面中是否存在点Q ，使得以Q ，A ，B 为顶点的三角形与相似？如果存在，请直接写出所有满足条件的点Q的坐标．PA PB COD答案解析部分1．【答案】（1）解：把点A （1，2）代入y ＝-x+m ，得-1+m ＝2，∴m ＝3，∴一次函数解析式为y ＝﹣x+3；把点A （1，2）代入y ＝，∴k ＝1×2＝2，∴反比例函数解析式为y ＝；（2）解：联立方程组{y ＝−x +3y ＝2x ，解得或，∴B （2，1），设直线y ＝﹣x+3与y 轴的交点为C ，∴C （0，3），∴S △AOB =S △COB -S △COA =×3×2-×3×1=1.5.【解析】【分析】（1）利用待定系数法求出一次函数的解析式和反比例函数的解析式即可；（2）先求出点B 的坐标，再求出直线与y 轴的交点C 的坐标，再利用S △AOB =S △COB -S △COA ，根据三角形的面积公式进行计算即可.2．【答案】（1）解：设P 与V 之间的函数表达式为，当时，，所以，∴，∴P 与V 之间的函数表达式为；（2）解：当时，，∴，∴为确保气球不爆炸，气球的体积应不小于.【解析】【分析】（1）由题意可设，把V=0.8，P=120代入解析式计算可求得F 的值，则解析式可k x 2x12x y =⎧⎨=⎩21x y =⎧⎨=⎩1212F P V=0.8V =120P =1200.8F =96F =96P V =128P ≤96128V ≤0.75V ≥30.75m F P V=求解；（2）由题意可得关于V 的不等式，解这个不等式可求解.3．【答案】（1）3；4；1（2）解：0＜x≤1或x≥3（3）解：作A 关于y 轴的对称点，连接，如图，∵，∴A 关于y 轴的对称点A ′(−1，3)．设直线的解析式为，将A ′(−1，3)，代入可得：∴，解得：．∴直线的解析式为，令，则，∴．【解析】【解答】（1）解：∵反比例函数与一次函数的图像在第一象限交于、两点，∴，，∴，，∴反比例函数和一次函数的表达式分别为：，；将点代入得；故答案为：3，4，1（2）解：由图像可得：满足的取值范围是或；A 'A B '()13A ，A B 'y ax c =+()31B ，331a c a c -+=⎧⎨+=⎩1252a c ⎧=-⎪⎪⎨⎪=⎪⎩A B '1522y x =-+0x =52y =502Q ⎛⎫ ⎪⎝⎭，()10k y k x=≠2y x b =-+()13A ，()3B n ，3k =31b =-+3k =4b =13y x =24y x =-+()3B n ，13y x=1n =12y y ≥01x <≤3x ≥【分析】（1）将点A 、B 的坐标代入求出k 、n 的值，再将点A 的坐标代入求出b 的值即可；（2）结合函数图象，利用函数值大的图象在上方的原则求解即可；（3）作A 关于y 轴的对称点，连接，利用待定系数法求出直线的解析式，再将代入解析式求出y 的值，可得点Q 的坐标。

反比例函数及其应用(26题)(解析版)—2024年中考数学真题分类汇编(全国通用)

反比例函数及其应用（26题）一、单选题1．（2024·黑龙江大庆·中考真题）在同一平面直角坐标系中，函数()0y kx k k =-¹与ky x=的大致图象为（）A ．B ．C ．D ．2．（2024·山东济宁·中考真题）已知点()()()1232,,1,,3,A y B y C y --在反比例函数(0)ky k x=<的图象上，则123,,y y y 的大小关系是（）A ．123y y y <上，将正六边形ABCDEF D 恰好落在双曲线上，则k 的值为（）A ．B ．C ．D ．3二、填空题4．（2024·江苏无锡·中考真题）某个函数的图象关于原点对称，且当0x >时，y 随x 的增大而增大．请写出一个符合上述条件的函数表达式：．5．（2024·江苏连云港·中考真题）杠杆平衡时，“阻力´阻力臂=动力´动力臂”．已知阻力和阻力臂分别为1600N 和0.5m ，动力为(N)F ，动力臂为(m)l ．则动力F 关于动力臂l 的函数表达式为．6．（2024·江苏无锡·中考真题）在探究“反比例函数的图象与性质”时，小明先将直角边长为5个单位长度的等腰直角三角板ABC摆放在平面直角坐标系中，使其两条直角边AC BC，分别落在x轴负半轴、y轴正半轴上（如图所示），然后将三角板向右平移a个单位长度，再向下平移a个单位长度后，小明发现A B，两点恰好都落在函数6yx=的图象上，则a的值为．故答案为：2或3．7．（2024·福建·中考真题）如图，在平面直角坐标系xOy 中，反比例函数ky x=的图象与O e 交于,A B 两点，且点,A B 都在第一象限．若()1,2A ，则点B 的坐标为．∵反比例函数ky x=的图象与∴221kk ==，设()B n m ，，则2nm k ==∵22215OB OA ==+=三、解答题8．（2024·江苏常州·中考真题）如图，在平面直角坐标系xOy 中，一次函数y kx b =+的图像与反比例函数my x=的图像相交于点()1,A n -、()2,1B ．(1)求一次函数、反比例函数的表达式；(2)连接OA OB 、，求OAB V 的面积．∵1y x =-，∴当0x =时，1y =-，∴()0,1C -，∴OAB V 的面积12OC x =×9．（2024·四川内江·中考真题）如图，一次函数y ax b =+的图象与反比例函数ky x=的图象相交于A 、B 两点，其中点A 的坐标为()2,3-，点B 的坐标为()3,n(1)求这两个函数的表达式；(2)根据图象，直接写出关于x 的不等式kax b x+<的解集10．（2024·四川资阳·中考真题）如图，已知平面直角坐标系中，O 为坐标原点，一次函数y kx b =+（0k ¹）的图象与反比例函数4y x=的图象相交于(),4A m ，()4,B n 两点．(1)求一次函数的解析式；C t t在一次函数的图象上，直线CO与反比例函数的图象在第三象限内交于点D，求点D的坐标，(2)若点(),并写出直线CD在图中的一个特征．11．（2024·黑龙江大庆·中考真题）如图1，在平面直角坐标系中，O 为坐标原点，点A 在x 轴的正半轴上，点B ，C 在第一象限，四边形OABC 是平行四边形，点C 在反比例函数ky x=的图象上，点C 的横坐标为2，点B 的纵坐标为3．提示：在平面直角坐标系中，若两点分别为()111,P x y ，()222,P x y ，则12PP 中点坐标为1212,22x x y y ++⎛⎫⎪⎝⎭．(1)求反比例函数的表达式；(2)如图2，点D 是AB 边的中点，且在反比例函数ky x=图象上，求平行四边形OABC 的面积；(3)如图3，将直线13:4l y x =-向上平移6个单位得到直线2l ，直线2l 与函数()0ky x x =>图象交于1M ，2M 两点，点P 为12M M 的中点，过点1M 作11M N l ⊥于点N ．请直接写出P 点坐标和1M NOP的值．【点睛】本题考查平行四边形的性质、中点坐标公式、一次函数的平移规律、一次函数与反比例函数的交点问题、锐角三角函数、平行线定理、一次函数与坐标轴的交点问题、勾股定理、一元二次方程的根与系数的关系、用待定系数法求反比例函数解析式，熟练掌握相关知识是解题的关键．12．（2024·四川巴中·中考真题）如图，在平面直角坐标系中，直线2y x =+与反比例函数()0ky k x=¹的图象交于AB 、两点，点A 的横坐标为1．(1)求k 的值及点B 的坐标．(2)点P 是线段AB 上一点，点M 在直线OB 上运动，当12BPO ABO S S =△△时，求PM 的最小值．∴222210510BP OP PM OB ×´===【点睛】本题考查的是一次函数与反比例函数的综合，求解函数解析式，一元二次方程的解法，勾股定理的应用，等腰三角形的性质，理解题意是解本题的关键13．（2024·四川·中考真题）如图，在平面直角坐标系xOy 中，已知()()2,3,,2A B m -两点在反比例函数ky x=的图象上．(1)求k 与m 的值；(2)连接BO ，并延长交反比例函数ky x=的图象于点C ．若一次函数的图象经过A ，C 两点，求这个一次函数的解析式．14．（2024·江西·中考真题）如图，AOB V 是等腰直角三角形，90Ð=°ABO ，双曲线()0,0ky k x x=>>经过点B ，过点()4,0A 作x 轴的垂线交双曲线于点C ，连接BC ．(1)点B 的坐标为______；(2)求BC 所在直线的解析式．∵AOB V 是等腰直角三角形，90Ð=ABO ∴4OA =，∴2BD OD AD ===，∴()2,2B ，15．（2024·山东泰安·中考真题）直线()10y kx b k =+¹与反比例函数28y x=-的图象相交于点()2,A m -，(),1B n -，与y 轴交于点C ．(1)求直线1y 的表达式；(2)若12y y >，请直接写出满足条件的x 的取值范围；(3)过C 点作x 轴的平行线交反比例函数的图象于点D ，求ACD V 的面积．16．（2024·四川泸州·中考真题）如图，在平面直角坐标系xOy 中，一次函数y kx b =+与x 轴相交于点()2,0A -，与反比例函数ay x=的图象相交于点()2,3B ．(1)求一次函数和反比例函数的解析式；(2)直线()2x m m =>与反比例函数()0a y x x =>和()20y x x=->的图象分别交于点C ，D ，且2OBC OCD S S =△△，求点C 的坐标．【分析】本题主要考查了一次函数与反比例函数综合，反比例函数与几何综合：17．（2024·四川广安·中考真题）如图，一次函数y ax b =+（a ，b 为常数，0a ¹）的图象与反比例函数ky x=（k 为常数，0k ¹）的图象交于(2,4)A ，(,2)B n -两点．(1)求一次函数和反比例函数的解析式．(2)直线AB 与x 轴交于点C ，点(,0)P m 是x 轴上的点，若PAC △的面积大于12，请直接写出m 的取值范围．对于2y x =+，当20y x =+=，解得∴()2,0C -，∵(,0)P m ，∴2CP m =+，18．（2024·江苏连云港·中考真题）如图1，在平面直角坐标系xOy 中，一次函数1(0)y kx k =+¹的图像与反比例函数6y x=的图像交于点A 、B ，与y 轴交于点C ，点A 的横坐标为2．(1)求k 的值；(2)利用图像直接写出61kx x+<时x 的取值范围；(3)如图2，将直线AB 沿y 轴向下平移4个单位，与函数6(0)y x x =>的图像交于点D ，与y 轴交于点E ，再将函数6(0)y x x=>的图像沿AB 平移，使点A 、D 分别平移到点C 、F 处，求图中阴影部分的面积．19．（2024·上海·中考真题）在平面直角坐标系xOy 中，反比例函数k y x=（k 为常数且0k ¹）上有一点()3,A m -，且与直线24y x =-+交于另一点(),6B n ．(1)求k 与m 的值；(2)过点A 作直线l x ∥轴与直线24y x =+交于点C ，求sin OCA Ð的值．∵l x ∥轴，x 轴y ⊥轴，∴A 、C 、D 的纵坐标相同，均为把2y =代入24y x =-+解得1x =，∴()1,2C ，20．（2024·江苏盐城·中考真题）小明在草稿纸上画了某反比例函数在第二象限内的图像，并把矩形直尺放在上面，如图．请根据图中信息，求：(1)反比例函数表达式；(2)点C 坐标．由图可得3AD =，2OD =，设点C 的坐标为6,m m ⎛⎫- ⎪⎝⎭，则CE \63BE OE OB m=-=--，Q 矩形直尺对边平行，21．（2024·四川达州·中考真题）如图，一次函数y kx b =+（k 、b 为常数，0k ¹）的图象与反比例函数m y x=（m 为常数，0m ¹）的图象交于点()2,3A ，(),2B a -．(1)求反比例函数和一次函数的解析式；(2)若点C 是x 轴正半轴上的一点．且90BCA Ð=°．求点C 的坐标．90BCA Ð=°Q NCB ACM \Ð+Ð=MAC ACM Ð+Ð=Q NCB MAC\Ð=Ðtan tan NCB MAC\Ð=Ð即NB MC NC AM=22．（2024·四川遂宁·中考真题）如图，一次函数()10y kx b k =+¹的图象与反比例函数()20m y m x=¹的图象相交于()()1,3,1A B n -，两点．(1)求一次函数和反比例函数的表达式；(2)根据图象直接写出12y y >时，x 的取值范围；V的面积．(3)过点B作直线OB，交反比例函数图象于点C，连结AC，求ABC∵点B C 、关于原点对称，∴()3,1C ，∴312MN =-=，1CN =，ON ∴ABC BOD ADOM S S S S =++V V 梯形梯形()(11123．（2024·四川宜宾·中考真题）如图，一次函数．()0y ax b a =+¹的图象与反比例函数()0k y k x=¹的图象交于点()()1,4,1A B n -、．(1)求反比例函数和一次函数的表达式；(2)利用图象，直接写出不等式k ax b x+<的解集；(3)已知点D 在x 轴上，点C 在反比例函数图象上．若以A 、B 、C 、D 为顶点的四边形是平行四边形，求点C 的坐标．24．（2024·四川德阳·中考真题）如图，一次函数22y x =-+与反比例函数(0)k y x x=<的图象交于点()1,A m -．(1)求m 的值和反比例函数k y x=的解析式；(2)将直线22y x =-+向下平移h 个单位长度(0)h >后得直线y ax b =+，若直线y ax b =+与反比例函数(0)k y x x =<的图象的交点为(),2B n ，求h 的值，并结合图象求不等式k ax b x<+的解集．25．（2024·山东潍坊·中考真题）如图，正比例函数y =的图象与反比例函数k y x =的图象的一个交点是(A m ．点()P n 在直线y =上，过点P 作y 轴的平行线，交k y x =的图象于点Q ．(1)求这个反比例函数的表达式；(2)求OPQ △的面积．26．（2024·四川雅安·中考真题）如图，在平面直角坐标系中，一次函数的图象l 与反比例函数k y x =的图象交于1,42M ⎛⎫ ⎪⎝⎭，(),1N n 两点．(1)求反比例函数及一次函数的表达式；(2)求OMN V 的面积；(3)若点P 是y 轴上一动点，连接PM PN ，．当PM PN +的值最小时，求点P 的坐标．又直线l 为25y x =-+，∴5,02A ⎛⎫ ⎪⎝⎭，()0,5B ．∴52OA =，5OB =，∴12OMN AOB AON BOM S S S S =--=´△△△△轴于点∵1,42M ⎛⎫ ⎪⎝⎭与M ¢关于y 轴对称，∴M ¢为1,42⎛⎫- ⎪⎝⎭．又()2,1N ，设M N ¢的解析式为则14221c d c d ì-+=ïíï+=î，解得65175c d ì=-ïïíï=ïî。

中考数学反比例函数综合经典题及答案

中考数学反比例函数综合经典题及答案一、反比例函数1．已知一次函数y=kx+b与反比例函数y= 交于A（﹣1，2），B（2，n），与y轴交于C 点．（1）求反比例函数和一次函数解析式；（2）如图1，若将y=kx+b向下平移，使平移后的直线与y轴交于F点，与双曲线交于D，E两点，若S△ABD=3，求D，E的坐标．（3）如图2，P为直线y=2上的一个动点，过点P作PQ∥y轴交直线AB于Q，交双曲线于R，若QR=2QP，求P点坐标．【答案】（1）解：点A（﹣1，2）在反比例函数y= 的图象上，∴m=（﹣1）×2=﹣2，∴反比例函数的表达式为y=﹣，∵点B（2，n）也在反比例函数的y=﹣图象上，∴n=﹣1，即B（2，﹣1）把点A（﹣1，2），点B（2，﹣1）代入一次函数y=kx+b中，得，解得：k=﹣1，b=1，∴一次函数的表达式为y=﹣x+1，答：反比例函数的表达式是y=﹣，一次函数的表达式是y=﹣x+1；（2）解：如图1，连接AF，BF，∵DE∥AB，∴S△ABF=S△ABD=3（同底等高的两三角形面积相等），∵直线AB的解析式为y=﹣x+1，∴C（0，1），设点F（0，m），∴AF=1﹣m，∴S△ABF=S△ACF+S△BCF= CF×|x A|+ CF×|x B|= （1﹣m）×（1+2）=3，∴m=﹣1，∴F（0，﹣1），∵直线DE的解析式为y=﹣x+1，且DE∥AB，∴直线DE的解析式为y=﹣x﹣1①．∵反比例函数的表达式为y=﹣②，联立①②解得，或∴D（﹣2，1），E（1，﹣2）；（3）解：如图2由（1）知，直线AB的解析式为y=﹣x﹣1，双曲线的解析式为y=﹣，设点P（p，2），∴Q（p，﹣p﹣1），R（p，﹣），PQ=|2+p+1|，QR=|﹣p﹣1+ |，∵QR=2QP，∴|﹣p﹣1+ |=2|2+p+1|，解得，p= 或p= ，∴P（，2）或（，2）或（，2）或（，2）．【解析】【分析】（1）把A的坐标代入反比例函数的解析式可求得m的值，从而可得到反比例函数的解析式；把点A和点B的坐标代入一次函数的解析式可求得一次函数的解析式；（2）依据同底等高的两个三角形的面积相等可得到S△ABF=S△ABD=3，再利用三角形的面积公式可求得点F的坐标，即可得出直线DE的解析式，即可求出交点坐标；（3）设点P（p，2），则Q（p，﹣p﹣1），R（p，﹣），然后可表示出PQ与QR的长度，最后依据QR=2QP，可得到关于p的方程，从而可求得p的值，从而可得到点P的坐标.2．如图，一次函数y=kx+b的图象分别与反比例函数y= 的图象在第一象限交于点A（4，3），与y轴的负半轴交于点B，且OA=OB．（1）求函数y=kx+b和y= 的表达式；（2）已知点C（0，5），试在该一次函数图象上确定一点M，使得MB=MC，求此时点M 的坐标．【答案】（1）解：把点A（4，3）代入函数y= 得：a=3×4=12，∴y= ．OA= =5，∵OA=OB，∴OB=5，∴点B的坐标为（0，﹣5），把B（0，﹣5），A（4，3）代入y=kx+b得：解得：∴y=2x﹣5．（2）解：∵点M在一次函数y=2x﹣5上，∴设点M的坐标为（x，2x﹣5），∵MB=MC，∴解得：x=2.5，∴点M的坐标为（2.5，0）．【解析】【分析】（1）先求反比例函数关系式，由OA=OB，可求出B坐标，再代入一次函数解析式中求出解析式；（2）M点的纵坐标可用x 的式子表示出来，可套两点间距离公式，表示出MB、MC，令二者相等，可求出x .3．如图1，已知直线y=x+3与x轴交于点A，与y轴交于点B，将直线在x轴下方的部分沿x轴翻折，得到一个新函数的图象（图中的“V形折现”）（1）类比研究函数图象的方法，请列举新函数的两条性质，并求新函数的解析式；（2）如图2，双曲线y= 与新函数的图象交于点C(1，a)，点D是线段AC上一动点(不包括端点)，过点D作x轴的平行线，与新函数图象交于另一点E，与双曲线交于点P．①试求△PAD的面积的最大值；②探索：在点D运动的过程中，四边形PAEC能否为平行四边形?若能，求出此时点D的坐标；若不能，请说明理由．【答案】（1）解：如图1，新函数的性质：1.函数的最小值为0；2.函数图象的对称轴为直线x=3.由题意得，点A的坐标为（-3，0），分两种情况：①当x-3时，y=x+3；②当x<-3时，设函数解析式为y=kx+b，在直线y=x+3中，当x=-4时，y=-1，则点（-4，-1）关于x轴的对称点为（-4，1），把点（-4，1），（-3，0），代入y=kx+b中，得：，解得：，∴y=-x-3.综上，新函数的解析式为y=.（2）解：如图2，①∵点C（1，a）在直线y=x+3上，∴a=4，∵点C（1，4）在反比例函数y=上，∴k=4，∴反比例函数的解析式为y=.∵点D是线段AC上一动点，∴设点D的坐标为（m，m+3），且-3<m<1，∵DP∥x轴，且点P在双曲线上，∴点P的坐标为（，m+3），∴PD=-m，∴S△PAD=（-m）（m+3）=m2-m+2=（m+）2+，∵a=<0，∴当m=时，S有最大值，最大值为，又∵-3<<1，∴△PAD的面积的最大值为.②在点D的运动的过程中，四边形PAEC不能为平行四边形，理由如下：当点D为AC的中点时，其坐标为（-1，2），此时点P的坐标为（2，2），点E的坐标为（-5，2），∵DP=3，DE=4，∴EP与AC不能互相平分，∴四边形PAEC不能为平行四边形.【解析】【分析】（1）根据一次函数的性质，结合函数图象写出新函数的两条性质；利用待定系数法求新函数解析式，注意分两种情况讨论；（2）①先求出点C的坐标，再利用待定系数法求出反比例函数解析式，设出点D的坐标，进而得到点P的坐标，再根据三角形的面积公式得出函数解析式，利用二次函数的性质求解即可；②先求出A的中点D的坐标，再计算DP、DE的长度，如果对角线互相平分，则能成为平行四边形，如若对角线不互相平分，则不能成为平行四边形.4．如图，一次函数y=﹣x+3的图象与反比例y= （k为常数，且k≠0）的图象交于A（1，a），B两点．（1）求反比例函数的表达式及点B的坐标；（2）在x轴上找一点P，使PA+PB的值最小，求满足条件的点P的坐标．【答案】（1）解：∵点A（1，a）在一次函数y=﹣x+3的图象上，∴a=﹣1+3=2，∴点A（1，2）．∵点A（1，2）在反比例y= （k为常数，且k≠0）的图象上，∴k=1×2=2，∴反比例函数的表达式为y= ．联立一次函数与反比例函数关系式成方程组，得：，解得：，，∴点B（2，1）（2）解：作B点关于x轴的对称点B′（2，﹣1），连接AB’，交x轴于点P，连接PB，如图所示．∵点B、B′关于x轴对称，∴PB=PB′．∵点A、P、B′三点共线，∴此时PA+PB取最小值．设直线AB′的函数表达式为y=mx+n（m≠0），将A（1，2）、B（2，﹣1）代入y=mx+n，，解得：，∴直线AB′的函数表达式为y=﹣3x+5．当y=﹣3x+5=0时，x= ，∴满足条件的点P的坐标为（，0）．【解析】【分析】（1）将x=1代入直线AB的函数表达式中即可求出点A的坐标，由点A 的坐标利用反比例函数图象上点的坐标特征即可求出反比例函数的表达式，联立两函数表达式成方程组，通过解方程组即可求出点B的坐标；（2）作B点关于x轴的对称点B′（2，﹣1），连接AB’，交x轴于点P，连接PB，由两点之间线段最短可得出此时PA+PB 取最小值，根据点A、B′的坐标利用待定系数法可求出直线AB′的函数表达式，再利用一次函数图象上点的坐标特征即可求出点P的坐标．5．【阅读理解】我们知道，当a＞0且b＞0时，（﹣）2≥0，所以a﹣2 +≥0，从而a+b≥2 （当a=b时取等号），【获得结论】设函数y=x+ （a＞0，x＞0），由上述结论可知：当x= 即x= 时，函数y有最小值为2（1）【直接应用】若y1=x（x＞0）与y2= （x＞0），则当x=________时，y1+y2取得最小值为________．（2）【变形应用】若y1=x+1（x＞﹣1）与y2=（x+1）2+4（x＞﹣1），则的最小值是________（3）【探索应用】在平面直角坐标系中，点A（﹣3，0），点B（0，﹣2），点P是函数y= 在第一象限内图象上的一个动点，过P点作PC⊥x轴于点C，PD⊥y轴于点D，设点P的横坐标为x，四边形ABCD的面积为S①求S与x之间的函数关系式；②求S的最小值，判断取得最小值时的四边形ABCD的形状，并说明理由．【答案】（1）1；2（2）4（3）解：①设P（x，），则C（x，0），D（0，），∴AC=x+3，BD= +2，∴S= AC•BD= （x+3）（ +2）=6+x+ ；②∵x＞0，∴x+ ≥2 =6，∴当x= 时，即x=3时，x+ 有最小值6，∴此时S=6+x+ 有最小值12，∵x=3，∴P（3，2），C（3，0），D（0，2），∴A、C关于x轴对称，D、B关于y轴对称，即四边形ABCD的对角线互相垂直平分，∴四边形ABCD为菱形．【解析】【解答】解：（1）∵x＞0，∴y1+y2=x+ ≥2 =2，∴当x= 时，即x=1时，y1+y2有最小值2，故答案为：1；2；（2）∵x＞﹣1，∴x+1＞0，∴ = =（x+1）+ ≥2 =4，∴当x+1= 时，即x=1时，有最小值4，故答案为：4；【分析】（1）直接由结论可求得其取得最小值，及其对应的x的值；（2）可把x+1看成一个整体，再利用结论可求得答案；（3）①可设P（x，），则可表示出C、D的坐标，从而可表示出AC和BD，再利用面积公式可表示出四边形ABCD的面积，从而可得到S 与x的函数关系式；②再利用结论可求得其最得最小值时对应的x的值，则可得到P、C、D的坐标，可判断A、C关于x轴对称，B、D关于y轴对称，可判断四边形ABCD为菱形．6．如图，过原点的直线y=k1x和y=k2x与反比例函数y= 的图象分别交于两点A，C和B，D，连接AB，BC，CD，DA．（1）四边形ABCD一定是________四边形；（直接填写结果）（2）四边形ABCD可能是矩形吗？若可能，试求此时k1，k2之间的关系式；若不能，说明理由；（3）设P（x1，y1），Q（x2，y2）（x2＞x1＞0）是函数y= 图象上的任意两点，a=，b= ，试判断a，b的大小关系，并说明理由．【答案】（1）平行（2）解：∵正比例函数y=k1x（k1＞0）与反比例函数y= 的图象在第一象限相交于A，∴k1x= ，解得x= （因为交于第一象限，所以负根舍去，只保留正根）将x= 带入y=k1x得y= ，故A点的坐标为（，）同理则B点坐标为（，），又∵OA=OB，∴ = ，两边平方得： +k1= +k2，整理后得（k1﹣k2）（k1k2﹣1）=0，∵k1≠k2，所以k1k2﹣1=0，即k1k2=1；（3）解：∵P（x1， y1），Q（x2， y2）（x2＞x1＞0）是函数y= 图象上的任意两点，∴y1= ，y2= ，∴a= = = ，∴a﹣b= ﹣ = = ，∵x2＞x1＞0，∴＞0，x1x2＞0，（x1+x2）＞0，∴＞0，∴a﹣b＞0，∴a＞b．【解析】【解答】解：（1）∵直线y=k1x和y=k2x与反比例函数y= 的图象关于原点对称，∴OA=OC，OB=OD，∴四边形ABCD 是平行四边形；故答案为：平行；【分析】（1）由直线y=k1x和y=k2x与反比例函数y= 的图象关于原点对称，即可得到结论．（2）联立方程求得A、B点的坐标，然后根据OA=OB，依据勾股定理得出 = ，两边平分得 +k1= +k2，整理后得（k1﹣k2）（k1k2﹣1）=0，根据k1≠k2，则k1k2﹣1=0，即可求得；（3）由P（x1，y1），Q（x2，y2）（x2＞x1＞0）是函数y= 图象上的任意两点，得到y1= ，y2= ，求出a= = = ，得到a﹣b= ﹣ = = ＞0，即可得到结果．7．如图所示，在平面直角坐标系xoy中，直线y= x+ 交x轴于点B，交y轴于点A，过点C（1，0）作x轴的垂线l，将直线l绕点C按逆时针方向旋转，旋转角为α（0°＜α＜180°）.（1）当直线l与直线y= x+ 平行时，求出直线l的解析式；（2）若直线l经过点A，①求线段AC的长；②直接写出旋转角α的度数；（3）若直线l在旋转过程中与y轴交于D点，当△ABD、△ACD、△BCD均为等腰三角形时，直接写出符合条件的旋转角α的度数.【答案】（1）解：当直线l与直线y＝ x＋平行时，设直线l的解析式为y＝ x ＋b，∵直线l经过点C（1，0），∴0＝＋b，∴b＝，∴直线l的解析式为y＝x−（2）解：①对于直线y＝ x＋，令x＝0得y＝，令y＝0得x＝−1，∴A（0，），B（−1，0），∵C（1，0），∴AC＝，②如图1中，作CE∥OA，∴∠ACE＝∠OAC，∵tan∠OAC＝，∴∠OAC＝30°，∴∠ACE＝30°，∴α＝30°（3）解：①如图2中，当α＝15°时，∵CE∥OD，∴∠ODC＝15°，∵∠OAC＝30°，∴∠ACD＝∠ADC＝15°，∴AD＝AC＝AB，∴△ADB，△ADC是等腰三角形，∵OD垂直平分BC，∴DB＝DC，∴△DBC是等腰三角形；②当α＝60°时，易知∠DAC＝∠DCA＝30°，∴DA＝DC＝DB，∴△ABD、△ACD、△BCD均为等腰三角形；③当α＝105°时，易知∠ABD＝∠ADB＝∠ADC＝∠ACD＝75°，∠DBC＝∠DCB＝15°，∴△ABD、△ACD、△BCD均为等腰三角形；④当α＝150°时，易知△BDC是等边三角形，∴AB＝BD＝DC＝AC，∴△ABD、△ACD、△BCD均为等腰三角形，综上所述：当α＝15°或60°或105°或150°时，△ABD、△ACD、△BCD均为等腰三角形.【解析】【分析】（1）设直线l的解析式为y＝ x＋b，把点C（1，0）代入求出b即可；（2）①求出点A的坐标，利用两点间距离公式即可求出AC的长；②如图1中，由CE∥OA，推出∠ACE＝∠OAC，由tan∠OAC＝，推出∠OAC＝30°，即可解决问题；（3）根据等腰三角形的判定和性质，分情况作出图形，进行求解即可.8．综合实践问题情景：某综合实践小组进行废物再利用的环保小卫士行动. 他们准备用废弃的宣传单制作装垃圾的无盖纸盒.操作探究：（1）若准备制作一个无盖的正方体形纸盒，如图1，下面的哪个图形经过折叠能围成无盖正方体形纸盒？（2）如图2是小明的设计图，把它折成无盖正方体形纸盒后与“保”字相对的是哪个字？（3）如图3，有一张边长为20cm的正方形废弃宣传单，小华准备将其四角各剪去一个小正方形，折成无盖长方体形纸盒.①请你在图3中画出示意图，用实线表示剪切线，虚线表示折痕.②若四角各剪去了一个边长为xcm的小正方形，用含x的代数式表示这个纸盒的高为________cm，底面积为________cm2，当小正方形边长为4cm时，纸盒的容积为________cm3.【答案】（1）解：A．有田字，故A不能折叠成无盖正方体；B．只有4个小正方形，无盖的应该有5个小正方形，不能折叠成无盖正方体；C．可以折叠成无盖正方体；D．有6个小正方形，无盖的应该有5个小正方形，不能折叠成无盖正方体．故答案为：C．（2）解：正方体的平面展开图中，相对面的特点是中间必须间隔一个正方形，所以与“保”字相对的字是“卫”（3）x；（20﹣2x）2；576【解析】【解答】（3）解：①如图，②设剪去的小正方形的边长为x（cm），用含字母x的式子表示这个盒子的高为xcm，底面积为（20﹣2x）2cm2，当小正方形边长为4cm时，纸盒的容积为=x（20﹣2x）2=4×（20﹣2×4）2=576（cm3）．故答案为：x，（20﹣2x）2， 576【分析】（1）由平面图形的折叠及正方体的展开图解答本题；（2）正方体的平面展开图中，相对面的特点是中间必须间隔一个正方形，据此作答；（3）①根据题意，画出图形即可；②根据正方体底面积、体积，即可解答．9．请完成下面题目的证明．如图,AB为⊙O的直径,AB=8,点C和点D是⊙O上关于直线AB 对称的两个点,连接OC,AC,且∠BOC<90°,直线BC与直线AD相交于点E,过点C作直线CG与线段AB的延长线相交于点F,与直线AD相交于点G,且∠GAF=∠GCE（1）求证:直线CG为⊙O的切线；（2）若点H为线段OB上一点,连接CH,满足CB=CH；①求证:△CBH∽△OBC；②求OH+HC的最大值.【答案】（1）证明：由题意可知：∠CAB=∠GAF，∵AB是⊙O的直径，∴∠ACB=90°∵OA=OC，∴∠CAB=∠OCA，∴∠OCA+∠OCB=90°，∵∠GAF=∠GCE，∴∠GCE+∠OCB=∠OCA+∠OCB=90°，∵OC是⊙O的半径，∴直线CG是⊙O的切线；（2）证明：①∵CB=CH，∴∠CBH=∠CHB，∵OB=OC，∴∠CBH=∠OCB，∴△CBH∽△OBC解：②由△CBH∽△OBC可知：∵AB=8，∴BC2=HB•OC=4HB，∴HB= ，∴OH=OB-HB=∵CB=CH，∴OH+HC=当∠BOC=90°，此时BC=∵∠BOC＜90°，∴0＜BC＜令BC=x∴OH+HC= = =当x=2时，∴OH+HC可取得最大值，最大值为5【解析】【分析】（1）由题意可知：∠CAB=∠GAF，∠GAF=∠GCE，由圆的性质可知：∠CAB=∠OCA，所以∠OCA=∠GCE，从而可证明直线CG是⊙O的切线；（2）①由于CB=CH，所以∠CBH=∠CHB，易证∠CBH=∠OCB，从而可证明△CBH∽△OBC；②由△CBH∽△OBC可知：，所以HB= ，由于BC=HC，所以OH+HC=利用二次函数的性质即可求出OH+HC的最大值．10．如图1，抛物线y＝ax2+bx﹣3经过点A，B，C，已知点A（﹣1，0），点B（3，0）（1）求抛物线的解析式（2）点D为抛物线的顶点，DE⊥x轴于点E，点N是线段DE上一动点①当点N在何处时，△CAN的周长最小？②若点M（m，0）是x轴上一个动点，且∠MNC＝90°，求m的取值范围．【答案】（1）解：函数的表达式为：y=a（x+1）（x﹣3）=a（x2﹣2x﹣3），故﹣3a=﹣3，解得：a=1，故函数的表达式为：y=x2﹣2x﹣3（2）解：①过点C作x轴的平行线交抛物线于点C'（2，﹣3），连接AC'交DE于点N，则此时△CAN的周长最小．设过点A、C'的一次函数表达式为y=kx+b，则：，解得：，故直线AC'的表达式为：y=﹣x﹣1，当x=1时，y=﹣2，故点N（1，﹣2）；②如图2，过点C作CG⊥ED于点G．设NG=n，则NE=3﹣n．∵∠CNG+∠GCN=90°，∠CNG+∠MNE=90°，∴∠NCG=∠MNE，则tan∠NCG=n=tan∠MNE，故ME=﹣n2+3n，∴﹣1＜0，故ME有最大值，当n时，ME，则m的最小值为：；如下图所示，当点N与点D重合时，m取得最大值．过C作CG⊥ED于G．∵y=x2﹣2x﹣3= y=（x－1）2﹣4，∴D（1，－4），∴CG=OE=1．∵EG=OC=3∴GD=4－3=1，∴CG=DG=1，∴∠CDG=45°．∵∠CDM=90°，∴∠EDM=45°，∴△EDM是等腰直角三角形，∴EM=ED=4，∴OM=OE+EM=1+4=5，∴m=5．故：m≤5．【解析】【分析】（1）函数的表达式为：y=a（x+1）（x﹣3）=a（x2﹣2x﹣3），即可求解；（2）①过点C作x轴的平行线交抛物线于点C'（2，﹣3），连接AC'交DE于点N，则此时△CAN的周长最小，即可求解；②如图2，ME=﹣n2+3n，求出ME最大值，则可求出m的最小值；当点N与点D处时，m取得最大值，求解即可．11．已知：如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB＝90°，点A，C的坐标分别为A（﹣3，0），C（1，0），BC＝AC．（1）在x轴上找一点D，连接DB，使得△ADB与△ABC相似（不包括全等），并求点D的坐标；（2）在（1）的条件下，如P，Q分别是AB和AD上的动点，连接PQ，设AP＝DQ＝m，问是否存在这样的m，使得△APQ与△ADB相似？如存在，请求出m的值；如不存在，请说明理由．【答案】（1）解：如图1，过点B作BD⊥AB，交x轴于点D，∵∠A＝∠A，∠ACB＝∠ABD＝90°，∴△ABC∽△ADB，∴∠ABC＝∠ADB，且∠ACB＝∠BCD＝90°，∴△ABC∽△BDC，∴∵A（﹣3，0），C（1，0），∴AC＝4，∵BC＝AC．∴BC＝3，∴AB＝＝＝5，∵，∴，∴CD＝，∴AD＝AC+CD＝4+ ＝，∴OD＝AD﹣AO＝，∴点D的坐标为：（，0）；（2）解：如图2，当∠APC＝∠ABD＝90°时，∵∠APC＝∠ABD＝90°，∠BAD＝∠PAQ，∴△APQ∽△ABD，∴，∴∴m＝，如图3，当∠AQP＝∠ABD＝90°时，∵∠AQP＝∠ABD＝90°，∠PAQ＝∠BAD，∴△APQ∽△ADB，∴，∴∴m＝；综上所述：当m＝或时，△APQ与△ADB相似．【解析】【分析】（1）如图1，过点B作BD⊥AB，交x轴于点D，可证△ABC∽△ADB，可得∠ABC＝∠ADB，可证△ABC∽△BDC，可得，可求CD 的长，即可求点D坐标；（2）分两种情况讨论，由相似三角形的性质可求解．12．在平面直角坐标系xOy中，抛物线y=mx2－2mx＋m－1（m＞0）与x轴的交点为A，B．（1）求抛物线的顶点坐标；（2）横、纵坐标都是整数的点叫做整点．①当m=1时，求线段AB上整点的个数；②若抛物线在点A，B之间的部分与线段AB所围成的区域内（包括边界）恰有6个整点，结合函数的图象，求m的取值范围．【答案】（1）解：将抛物线表达式变为顶点式，则抛物线顶点坐标为（1，-1）；（2）解：①m=1时，抛物线表达式为，因此A、B的坐标分别为（0，0）和（2，0），则线段AB上的整点有（0，0），（1，0），（2，0）共3个；②抛物线顶点为（1，-1），则由线段AB之间的部分及线段AB所围成的区域的整点的纵坐标只能为-1或者0，所以即要求AB线段上（含AB两点）必须有5个整点；又有抛物线表达式，令y=0，则，得到A、B两点坐标分别为（，0），（，0），即5个整点是以（1，0）为中心向两侧分散，进而得到，∴．【解析】【分析】（1）将抛物线表达式变为顶点式，即可得到顶点坐标；（2）①m=1时，抛物线表达式为，即可得到A、B的坐标，可得到线段AB上的整点个数；②抛物线顶点为（1，-1），则由线段AB之间的部分及线段AB所围成的区域的整点的纵坐标只能为-1或者0，所以即要求AB线段上（含AB两点）必须有5个整点；令y=0，则，解方程可得到A、B两点坐标分别为（，0），（，0），即5个整点是以（1，0）为中心向两侧分散，进而得到，即可得到结论．。

反比例函数应用题

反比例函数应用题
1. 如果8个工人需要10天完成某项工作，那么需要多少天才能由6个工人完成同样的工作？
2. 一辆汽车以每小时60公里的速度行驶，那么行驶120公里需要多长时间？
3. 一箱苹果卖出去总共收入300元，如果每箱销售的数量减少1/3，那么平均每箱的售价是多少？
4. 某种商品的价格每降低10%，销量就增加20%，如果原价是100元，降价后的售价是多少？
5. 一辆自行车以每分钟30米的速度行驶，那么行驶150米需要多长时间？
6. 一个水库的水位下降速度是每小时2米，如果继续以相同速度下降，需要多少小时水位下降10米？
7. 一根铁丝长80米，如果每段长度增加4米，那么可以分成多少段？
8. 某种药物的剂量与患者体重成反比，如果一个50公斤的患者需要100毫升的药物，那么一个60公斤的患者需要多少毫升？
9. 一根绳子每天缩短长度为原来的1/5，如果第一天长度为100米，那么第6天的长度是多少？
10. 一支笔每经过1小时，墨水消耗原来的1/3，如果一开始有完整的墨水，那么经过3个小时后，还剩下多少的墨水？。

中考数学《反比例函数》专项练习题(附带答案)

中考数学《反比例函数》专项练习题(附带答案)一、单选题1．如图，反比例函数y= 2x的图象经过矩形OABC的边AB的中点D，则矩形OABC的面积为（）A．2B．4C．5D．82．小兰画了一个函数y= ax−1的图象如图，那么关于x的分式方程ax−1=2的解是（）A．x=1B．x=2C．x=3D．x=43．若A(a1，b1)，B(a2，b2)是反比例函数y = –√2x图象上的两点，且a1＜a2，则b1与b2的大小关系是（）A．b1＜b2B．b1 = b2C．b1＞b2D．不能确定4．某公司计划新建一个容积V（m3）一定的长方体污水处理池，池的底面积S（m2）与其深度h（m）之间的函数关系式为S=Vℎ(ℎ≠0)，这个函数的图象大致是（）A．B．C．D．5．若反比例函数y＝k x（k为常数，且k≠0）的图象过点（3，－4），则下列各点在该图象上的是（）A．（6，－8）B．(－6，8)C．（－3，4）D．(－3，－4)6．已知反比例函数y=k x（k＞0）的图象与直线y=﹣x+6相交于第一象限A、B的两点．如图所示，过A、B两点分别作x、y轴的垂线，线段AC、BD相交与P，给出以下结论：①OA=OB；②四边形OCPD 是正方形；③若k=5．则△ABP的面积是8；④P点一定在直线y=x上，其中正确命题的个数是几个（）A．4B．3C．2D．17．已知点P(3，2)在反比例函数y=k x(k≠0)图象上，则下列各点中在此反比例函数图象上的是（）A．(−3，−2)B．(3，−2)C．(−2，3)D．(2，−3)8．下列函数：①y=−x；②y=−1x；③y=√2x；④y=120x2+240x+3(x<0)中，y随x的增大而减小的函数有（）A．1个B．2个C．3个D．4个9．如图，在平面直角坐标系中，菱形OABC的顶点A在x轴的正半轴上，顶点B在函数y＝k x（x ＞0）的图象上，若△C＝60°，AB＝2，则k的值为（）A．√2B．√3C．1D．2 10．对于反比例函数y=﹣1x，下列说法正确的是（）A．图象经过点（1，1）B．图象位于第一、三象限C．图象是中心对称图形D．当x＜0时，y随x的增大而减小11．一次函数y=ax+a与反比例函数y=−ax(a≠0)在同一平面直角坐标系中的图象可能是（）A．B．C．D．12．面积为2的△ABC，一边长为x，这边上的高为y，则y与x的变化规律用图象表示大致是() A．B．C．D．二、填空题13．如图，在平面直角坐标系中，菱形ABCD的顶点A与D在函数y=k x（x>0）的图象上，AC⊥x轴，垂足为C，∠BCO=30°，点B的坐标为(0,1)，则k的值为．14．如图，反比例函数y=6x在第一象限的图象上有两点A，B，它们的横坐标分别是2，6，则△AOB 的面积是．15．反比例函数y=7x图象与正比例函数y=kx图象交于A(x1，y1)，B(x2，y2)，则x1y2+x2y1的值为.16．如图，正比例函数y1=ax(a≠0)与反比例函数y2=k x(k≠0)的图象相交于A，B两点，其中点A的坐标为(1，3).当y1<y2时，x的取值范围是.17．如图，在平面直角坐标系中，O为坐标原点，平行四边形ABCD的边AB在x轴上、顶点D在y 轴的正半轴上，点C在第二象限，将△AOD沿y轴翻折，使点A落在x轴上的点E处、点B恰好为OE的中点.DE与BC交于点F.若y=kx(k≠0)图象经过点C，且S△BEF=12，则k的值为.18．如图，一次函数y＝x+k（k＞0）的图象与x轴和y轴分别交于点M，N，与反比例函数y=kx的图象在第一象限内交于点B，过点B作BA△x轴，BC△y轴．垂足分别为点A，C．当矩形OABC与△OMN 的面积相等时，点B的坐标为．三、综合题19．如图，双曲线y1＝k x（k为常数，且k≠0）与直线y2＝﹣13x+b交于点A（﹣2，a）和B（3c，2﹣c）.（1）求k，b的值；（2）求直线与x轴的交点坐标.20．如图，已知一次函数y=2x+2的图象与y轴交于点B，与反比例函数y= k1x的图象的一个交点为A（1，m）．过点B作AB的垂线BD，与反比例函数y= k2x（x＞0）的图象交于点D（n，﹣2）．（1）求k1和k2的值；（2）若直线AB、BD分别交x轴于点C、E，试问在y轴上是否存在一个点F，使得△BDF△△ACE？若存在，求出点F的坐标；若不存在，请说明理由．21．如图，直线y＝2x+1与双曲线相交于点A（m，32）与x轴交于点B.（1）求双曲线的函数表达式：（2）点P在x轴上，如果△ABP的面积为6，求点P坐标.22．在初中阶段的函数学习中，我们经历了列表、描点、连线画函数图象，观察分析函数特征，概括函数性质的过程，已知函数y＝﹣2|x−2|x−1上，结合已有的学习经验，完成下列各小题．（1）请在表格中空白处填入恰当的数据：x…﹣3﹣2﹣101243322345…y (5)2834﹣40﹣1﹣43…（2）根据表中的数据，在所给的平面直角坐标系中画出函数y＝﹣2|x−2|x−1的图象；（3）根据函数图象，写出该函数的一条性质：；（4）结合所画函数图象，直接写出不等式﹣2|x−2|x−1＜﹣53x+5的解集为：.（保留1位小数，误差不超过0.2）23．在平面直角坐标系xOy中，点A(x1，y1)，B(x2，y2)在抛物线y=−x2+2ax−a2−a+2(a 是常数)上.（1）若该二次函数图象的顶点在第二象限时，求a的取值范围；（2）若抛物线的顶点在反比例函数y=−8x(x<0)的图象上，且y1=y2，求x1+x2的值；（3）若当1<x1<x2时，都有y2<y1<1，求a的取值范围.24．如图，点A（m，m+1），B（m+3，m﹣1）是反比例函数y=k x（x＞0）与一次函数y＝ax+b的交点．求：（1）反比例函数与一次函数的解析式；（2）根据图象直接写出当反比例函数的函数值大于一次函数的函数值时x的取值范围．参考答案1．【答案】B2．【答案】A3．【答案】D4．【答案】C5．【答案】C6．【答案】A7．【答案】A8．【答案】A9．【答案】B10．【答案】C11．【答案】A12．【答案】B13．【答案】2√314．【答案】815．【答案】－1416．【答案】x＜-1或0＜x＜117．【答案】-1218．【答案】(−1+√3，1+√3)19．【答案】（1）解：∵点B（3c，2﹣c）在直线y2＝﹣13x+b的图象上∴−13×3c+b=2−c解得：b=2∴直线解析式为y2＝﹣13x+2∵点A（﹣2，a）在直线y2＝﹣13x+2的图象上∴a=−13×(−2)+2=83∴点A坐标为（-2，8 3）∵点A（-2，83）在y1＝kx图象上∴83=k−2解得：k=−16 3 .（2）解：∵直线解析式为y2＝﹣13x+2∴当y2=0时，x=6∴直线与x轴的交点坐标为（6，0）.20．【答案】（1）解：将A（1，m）代入一次函数y=2x+2中，得：m=2+2=4，即A（1，4）将A（1，4）代入反比例解析式y= k1x得：k1=4；过A作AM△y轴，过D作DN△y轴∴△AMB=△DNB=90°∴△BAM+△ABM=90°∵AC△BD，即△ABD=90°∴△ABM+△DBN=90°∴△BAM=△DBN∴△ABM△△BDN∴AMBN=BMDN，即14=2DN∴DN=8∴D（8，﹣2）将D坐标代入y= k2x得：k2=﹣16（2）解：符合条件的F坐标为（0，﹣8），理由为：由y=2x+2，求出C坐标为（﹣1，0）∵OB=ON=2，DN=8∴OE=4可得AE=5，CE=5，AC=2 √5，BD=4 √5，△EBO=△ACE=△EAC若△BDF△△ACE，则BDAC=BFAE，即√52√5=BF5解得：BF=10则F（0，﹣8）．综上所述：F点坐标为（0，﹣8）时，△BDF△△ACE．21．【答案】（1）解：把A（m，32）代入直线y＝2x+1得：32＝2m+1，即m＝14∴A（14，32）∵点A（14，32）为直线与反比例函数y=kx的交点把A点坐标代入y=k x，得k＝14× 32＝38则双曲线解析式为y=38x；（2）解：对于直线y＝2x+1，令y＝0，得到x＝−12，即B（−12，0）设P（x，0），可得PB＝|x+1 2|∵△ABP面积为6∴12×|x+12|×32=6，即|x+12|＝8解得：x＝7.5或x＝﹣8.5则P坐标为（7.5，0）或（﹣8.5，0）. 22．【答案】（1）解：如下表所示：x…﹣3﹣2﹣101243322345…y (5)283346﹣4-20﹣1﹣43-32…（3）当x<1时，y随x的增大而增大（4）x<0.3或1<x<3.723．【答案】（1）解：∵y=−x2+2ax−a2−a+2=−(x−a)2−a+2第 11 页共 11 页 ∴ 抛物线 y =−x 2+2ax −a 2−a +2 的顶点为 (a ，−a +2) ∵ 抛物线的顶点在第二象限∴{a <0−a +2>0解得 2<a <0 ；（2）解： ∵ 抛物线 y =−x 2+2ax −a 2−a +2 的顶点在反比例函数 y =−8x(x <0) 的图象上 ∴a(−a +2)=−8解得 a =4 或 a =−2∵a <0∴a =−2∴ 顶点为 (−2，4)∵y 1=y 2∴ 点 A(x 1，y 1) ， B(x 2，y 2) 关于直线 x =−2 对称∴x 1+x22=−2∴x 1+x 2=−4 ；（3）解： ∵ 当 1<x 1<x 2 时，都有 y 2<y 1<1∴ 抛物线的对称轴 x =a <1 ，经过点为 (1，1)∴{a <1−1+2a −a 2−a +2=1解得 a =0 或 a =−3故 a 的取为0或-3.24．【答案】（1）解：由题意可知，m （m+1）=（m+3）（m ﹣1）．解得m=3．∴A （3，4），B （6，2）； ∴k=4×3=12， ∴y =12x∵A 点坐标为（3，4），B 点坐标为（6，2）， ∴{3a +b =46a +b =2 ， ∴{a =−23b =6 ，∴y=﹣ 23 x+6 （2）解：根据图象得x 的取值范围：0＜x ＜3或x ＞6．。

2024年中考数学《反比例函数及其应用》真题含解析

专题反比例函数及其应用(41题)一、单选题1.(2024·安徽·中考真题)已知反比例函数y=kxk≠0与一次函数y=2-x的图象的一个交点的横坐标为3，则k的值为()A.-3B.-1C.1D.3【答案】A【分析】题目主要考查一次函数与反比例函数的交点问题，根据题意得出y=2-3=-1，代入反比例函数求解即可【详解】解：∵反比例函数y=kxk≠0与一次函数y=2-x的图象的一个交点的横坐标为3，∴y=2-3=-1，∴-1=k3，∴k=-3，故选：A2.(2024·重庆·中考真题)反比例函数y=-10x的图象一定经过的点是()A.1,10B.-2,5C.2,5D.2,8【答案】B【分析】本题考查了求反比例函数值．熟练掌握求反比例函数值是解题的关键．分别将各选项的点坐标的横坐标代入，求纵坐标，然后判断作答即可．【详解】解：解：当x=1时，y=-101=-10，图象不经过1,10，故A不符合要求；当x=-2时，y=-10-2=5，图象一定经过-2,5，故B符合要求；当x=2时，y=-102=-5，图象不经过2,5，故C不符合要求；当x=2时，y=-102=-5，图象不经过2,8，故D不符合要求；故选：B．3.(2024·天津·中考真题)若点A x1,-1,B x2,1,C x3,5都在反比例函数y=5x的图象上，则x1,x2,x3的大小关系是()A.x1<x2<x3B.x1<x3<x2C.x3<x2<x1D.x2<x1<x3【答案】B【分析】本题主要考查了比较反比例函数值的大小，根据反比例函数性质即可判断．【详解】解：∵k=5>0，∴反比例函数y =5x的图象分布在第一、三象限，在每一象限y 随x 的增大而减小，∵点B x 2,1 ,C x 3,5 ，都在反比例函数y =5x的图象上，1<5，∴x 2>x 3>0．∵-1<0，A x 1,-1 在反比例函数y =5x的图象上，∴x 1<0，∴x 1<x 3<x 2.故选：B ．4.(2024·广西·中考真题)已知点M x 1,y 1 ，N x 2,y 2 在反比例函数y =2x的图象上，若x 1<0<x 2，则有()A.y 1<0<y 2B.y 2<0<y 1C.y 1<y 2<0D.0<y 1<y 2【答案】A【分析】本题考查了反比例函数的图象，熟练掌握反比例函数图象上点的坐标特征是解题的关键．根据点M x 1,y 1 ，N x 2,y 2 在反比例函数图象上，则满足关系式y =2x，横纵坐标的积等于2，结合x 1<0<x 2即可得出答案．【详解】解：∵点M x 1,y 1 ，N x 2,y 2 在反比例函数y =2x的图象上，∴x 1y 1=2，x 2y 2=2，∵x 1<0<x 2，∴y 1<0，y 2>0，∴y 1<0<y 2．故选：A ．5.(2024·浙江·中考真题)反比例函数y =4x的图象上有P t ,y 1 ，Q t +4,y 2 两点．下列正确的选项是()A.当t <-4时，y 2<y 1<0B.当-4<t <0时，y 2<y 1<0C.当-4<t <0时，0<y 1<y 2D.当t >0时，0<y 1<y 2【答案】A【分析】本题考查了反比例函数图象上的点的坐标特征，由于反比例函数y =4x，可知函数位于一、三象限，分情况讨论，根据反比例函数的增减性判断出y 1与y 2的大小．【详解】解：根据反比例函数y =4x，可知函数图象位于一、三象限，且在每个象限中，y 都是随着x 的增大而减小，反比例函数y =4x的图象上有P t ,y 1 ，Q t +4,y 2 两点，当t<t+4<0，即t<-4时，0>y1>y2；当t<0<t+4，即-4<t<0时，y1<0<y2；当0<t<t+4，即t>0时，y1>y2>0；故选：A．6.(2024·河北·中考真题)节能环保已成为人们的共识．淇淇家计划购买500度电，若平均每天用电x度，则能使用y天．下列说法错误的是()A.若x=5，则y=100B.若y=125，则x=4C.若x减小，则y也减小D.若x减小一半，则y增大一倍【答案】C【分析】本题考查的是反比例函数的实际应用，先确定反比例函数的解析式，再逐一分析判断即可．【详解】解：∵淇淇家计划购买500度电，平均每天用电x度，能使用y天．∴xy=500，∴y=500x，当x=5时，y=100，故A不符合题意；当y=125时，x=500125=4，故B不符合题意；∵x>0，y>0，∴当x减小，则y增大，故C符合题意；若x减小一半，则y增大一倍，表述正确，故D不符合题意；故选：C．7.(2024·四川泸州·中考真题)已知关于x的一元二次方程x2+2x+1-k=0无实数根，则函数y=kx与函数y=2x的图象交点个数为()A.0B.1C.2D.3【答案】A【分析】本题考查了根的判别式及一次函数和反比例函数的图象．首先根据一元二次方程无实数根确定k 的取值范围，然后根据一次函数和反比例函数的性质确定其图象的位置．【详解】解：∵方程x2+2x+1-k=0无实数根，∴Δ=4-41-k<0，解得：k<0，则函数y=kx的图象过二，四象限，而函数y=2x的图象过一，三象限，∴函数y=kx与函数y=2x的图象不会相交，则交点个数为0，故选：A．8.(2024·重庆·中考真题)已知点-3,2 在反比例函数y =kxk ≠0 的图象上，则k 的值为()A.-3B.3C.-6D.6【答案】C【分析】本题考查了待定系数法求反比例解析式，把-3,2 代入y =kxk ≠0 求解即可．【详解】解：把-3,2 代入y =kxk ≠0 ，得k =-3×2=-6．故选C ．9.(2024·黑龙江牡丹江·中考真题)矩形OBAC 在平面直角坐标系中的位置如图所示，反比例函数y =kx的图象与AB 边交于点D ，与AC 边交于点F ，与OA 交于点E ，OE =2AE ，若四边形ODAF 的面积为2，则k 的值是()A.25B.35C.45D.85【答案】D【分析】本题考查了矩形的性质、三角形面积的计算、反比例函数的图象和性质、相似三角形的判定和性质；熟练掌握矩形的性质和反比例函数的性质是解决问题的关键．过点E 作EM ⊥OC ，则EM ∥AC ，设E a ，k a ，由△OME ∽△OCA ，可得OC =32a ，AC =32⋅ka，再由S 矩形OBAC =S △OBD +S △OCF +S 四边形ODAF ，列方程，即可得出k 的值．【详解】过点E 作EM ⊥OC ，则EM ∥AC ，∴△OME ∽△OCA ，∴OM OC =EM AC =OEOA设E a ，k a ，∵OE =2AE ∴OM OC =EM AC=23，∴OC =32a ，AC =32⋅ka∴S 矩形OBAC =S △OBD +S △OCF +S 四边形ODAF =32a ⋅32⋅ka即k 2+k 2+2=32a ⋅32⋅k a ，解得：k =85故选D10.(2024·黑龙江大兴安岭地·中考真题)如图，双曲线y =12xx >0 经过A 、B 两点，连接OA 、AB ，过点B 作BD ⊥y 轴，垂足为D ，BD 交OA 于点E ，且E 为AO 的中点，则△AEB 的面积是()A.4.5B.3.5C.3D.2.5【答案】A【分析】本题考查了反比例函数，相似三角形的判定与性质等知识，过点A 作AF ⊥BD ，垂足为F ，设A a ,12a ，证明△AFE ∽△ODE ，有AF OD =AE OE=EF DE ，根据E 为AO 的中点，可得AF =OD ，EF =DE ，进而有EF =DE =12DF =12a ，AF =OD =12y A =6a ，可得y B =OD =6a ，x B=2a ，则有BE =BD -DE=32a ，问题随之得解．【详解】如图，过点A 作AF ⊥BD ，垂足为F ，设A a ,12a，a >0，∵BD ⊥y 轴，AF ⊥BD ，∴AF ∥y 轴，DF =a ，∴△AFE ∽△ODE ，∴AF OD =AE OE=EFDE ，∵E 为AO 的中点，∴AE =OE ，∴AF OD =AE OE=EFDE =1，∴AF =OD ，EF =DE ∴EF =DE =12DF =12a ，AF =OD =12y A =6a，∵OD =y B ，∴y B =OD =6a，∴xB =2a ，∴BD=x B=2a，∴BE=BD-DE=32a，∴S△ABE=12×AF×BE=12×6a×32a=92=4.5，故选：A．11.(2024·江苏扬州·中考真题)在平面直角坐标系中，函数y=4x+2的图像与坐标轴的交点个数是()A.0B.1C.2D.4【答案】B【分析】根据函数表达式计算当x=0时y的值，可得图像与y轴的交点坐标；由于4x+2的值不可能为0，即y≠0，因此图像与x轴没有交点，由此即可得解．本题主要考查了函数图像与坐标轴交点个数，掌握求函数图像与坐标轴交点的计算方法是解题的关键．【详解】当x=0时，y=42=2，∴y=4x+2与y轴的交点为0,2；由于4x+2是分式，且当x≠-2时，4x+2≠0，即y≠0，∴y=4x+2与x轴没有交点．∴函数y=4x+2的图像与坐标轴的交点个数是1个，故选：B．12.(2024·吉林长春·中考真题)如图，在平面直角坐标系中，点O是坐标原点，点A4,2在函数y=k xk>0,x>0的图象上．将直线OA沿y轴向上平移，平移后的直线与y轴交于点B，与函数y=k xk>0,x>0的图象交于点C．若BC=5，则点B的坐标是()A.0,5B.0,3C.0,4D.0,25【答案】B【分析】本题主要考查反比例函数、解直角三角形、平移的性质等知识点，掌握数形结合思想成为解题的关键．如图：过点A作x轴的垂线交x轴于点E，过点C作y轴的垂线交y轴于点D，先根据点A坐标计算出sin∠OAE、k值，再根据平移、平行线的性质证明∠DBC=∠OAE，进而根据sin∠DBC=CDBC=sin∠OAE求出CD，最后代入反比例函数解析式取得点C的坐标，进而确定CD=2,OD=4，再运用勾股定理求得BD，进而求得OB即可解答．【详解】解：如图，过点A作x轴的垂线交x轴于点E，过点C作y轴的垂线交y轴于点D，则AE∥y轴，∵A4,2，∴OE=4，OA=22+42=25，∴sin∠OAE=OEOA =425=255．∵A4,2在反比例函数的图象上，∴k=4×2=8．∴将直线OA向上平移若干个单位长度后得到直线BC，∴OA∥BC，∴∠OAE=∠BOA，∵AE∥y轴，∴∠DBC=∠BOA，∴∠DBC=∠OAE，∴sin∠DBC=CDBC =sin∠OAE=255，∴CD5=255，解得：CD=2，即点C的横坐标为2，将x=2代入y=8x，得y=4，∴C点的坐标为2,4，∴CD=2,OD=4，∴BD=BC2-CD2=1，∴OB=OD-BD=4-1=3,∴B0,3故选：B．13.(2024·四川宜宾·中考真题)如图，等腰三角形ABC中，AB=AC，反比例函数y=kxk≠0的图象经过点A、B及AC的中点M，BC∥x轴，AB与y轴交于点N．则ANAB的值为()A.13B.14C.15D.25【答案】B【分析】本题考查反比例函数的性质，平行线分线段成比例定理，等腰三角形的性质等知识，找到坐标之间的关系是解题的关键．作辅助线如图，利用函数表达式设出A 、B 两点的坐标，利用D ，M 是中点，找到坐标之间的关系，利用平行线分线段成比例定理即可求得结果．【详解】解：作过A 作BC 的垂线垂足为D ，BC 与y 轴交于E 点，如图，在等腰三角形ABC 中，AD ⊥BC ，D 是BC 中点，设A a ,k a，B b ,kb ，由BC 中点为D ，AB =AC ，故等腰三角形ABC 中，∴BD =DC =a -b ，∴C 2a -b ,kb，∵AC 的中点为M ，∴M 3a -b 2,ka +kb 2 ，即3a -b 2,k a +b 2ab，由M 在反比例函数上得M 3a -b 2,k 3a -b2，∴k a +b 2ab=k3a -b 2，解得：b =-3a ，由题可知，AD ∥NE ，∴AN AB=DE BD =a a -b =a a +3a =14．故选：B ．二、填空题14.(2024·北京·中考真题)在平面直角坐标系xOy 中，若函数y =kxk ≠0 的图象经过点3,y 1 和-3,y 2 ，则y1+y2的值是.【答案】0【分析】本题考查了反比例函数图象上点的坐标特征，已知自变量求函数值，熟练掌握反比例函数的性质是解题的关键．将点3,y1和-3,y2代入y=kxk≠0，求得y1和y2，再相加即可．【详解】解：∵函数y=kxk≠0的图象经过点3,y1和-3,y2，∴有y1=k3,y2=-k3，∴y1+y2=k3-k3=0，故答案为：0．15.(2024·云南·中考真题)已知点P2,n在反比例函数y=10x的图象上，则n=．【答案】5【分析】本题考查反比例函数图象上点的坐标特征，将点P2,n代入y=10x求值，即可解题．【详解】解：∵点P2,n在反比例函数y=10x的图象上，∴n=102=5，故答案为：5．16.(2024·山东威海·中考真题)如图，在平面直角坐标系中，直线y1=ax+b a≠0与双曲线y2=kxk≠0交于点A-1,m，B2,-1．则满足y1≤y2的x的取值范围．【答案】-1≤x<0或x≥2【分析】本题考查了一次函数与反比例函数的交点问题，根据图象解答即可求解，利用数形结合思想解答是解题的关键．【详解】解：由图象可得，当-1≤x<0或x≥2时，y1≤y2，∴满足y1≤y2的x的取值范围为-1≤x<0或x≥2，故答案为：-1≤x<0或x≥2．17.(2024·湖南·中考真题)在一定条件下，乐器中弦振动的频率f与弦长l成反比例关系，即f=kl(k为常数．k≠0)，若某乐器的弦长l为0.9米，振动频率f为200赫兹，则k的值为．【答案】180【分析】本题考查了待定系数法求反比例函数解析式，把l=0.9，f=200代入f=kl求解即可．【详解】解：把l=0.9，f=200代入f=kl，得200=k0.9，解得k=180，故答案为：180．18.(2024·陕西·中考真题)已知点A-2,y1和点B m,y2均在反比例函数y=-5x的图象上，若0<m<1，则y1+y20．【答案】</小于【分析】本题主要考查了反比例函数的性质，先求出y1=52，y2=-5m，再根据0<m<1，得出y2<-5，最后求出y1+y2<0即可．【详解】解：∵点A-2,y1和点B m,y2均在反比例函数y=-5x的图象上，∴y1=52，y2=-5m，∵0<m<1，∴y2<-5，∴y1+y2<0．故答案为：<．19.(2024·湖北武汉·中考真题)某反比例函数y=kx具有下列性质：当x>0时，y随x的增大而减小，写出一个满足条件的k的值是．【答案】1(答案不唯一)【分析】本题考查的是反比例函数的性质，反比例函数的图象是双曲线，当k>0，双曲线的两支分别位于第一、第三象限，在每一象限内y随x的增大而减小，当k<0，双曲线的两支分别位于第二、第四象限，在每一象限内y随x的增大而增大．直接根据反比例函数的性质写出符合条件的的值即可．【详解】解：∵当x>0时，y随x的增大而减小，∴k>0故答案为：1(答案不唯一)．20.(2024·黑龙江齐齐哈尔·中考真题)如图，反比例函数y=kx(x<0)的图象经过平行四边形ABCO的顶点A，OC在x轴上，若点B-1,3，S▱ABCO=3，则实数k的值为．【答案】-6【分析】本题考查了反比例函数，根据A ,B 的纵坐标相同以及点A 在反比例函数上得到A 的坐标，进而用代数式表达AB 的长度，然后根据S ▱ABCO =3列出一元一次方程求解即可．【详解】∵ABCO 是平行四边形∴A ,B 纵坐标相同∵B -1,3∴A 的纵坐标是3∵A 在反比例函数图象上∴将y =3代入函数中，得到x =k 3∴A k 3,3∴AB =-1-k 3∵S ▱ABCO =3,B 的纵坐标为3∴AB ×3=3即：-1-k 3×3=3解得：k =-6故答案为：-6．21.(2024·内蒙古包头·中考真题)若反比例函数y 1=2x ，y 2=-3x，当1≤x ≤3时，函数y 1的最大值是a ，函数y 2的最大值是b ，则a b =．【答案】12/0.5【分析】此题主要考查了反比例函数的性质，负整数指数幂，正确得出a 与b 的关系是解题关键．直接利用反比例函数的性质分别得出a 与b ，再代入a b 进而得出答案．【详解】解：∵函数y 1=2x，当1≤x ≤3时，函数y 1随x 的增大而减小，最大值为a ，∴x =1时，y 1=2=a ，∵y 2=-3x ，当1≤x ≤3时，函数y 2随x 的增大而减大，函数y 2的最大值为y 2=-1=b ，∴a b =2-1=12．故答案为：12．22.(2024·四川遂宁·中考真题)反比例函数y =k -1x 的图象在第一、三象限，则点k ,-3 在第象限．【答案】四/4【分析】本题考查了反比例函数的性质，点所在的象限，根据反比例函数的性质得出k >1，进而即可求解．【详解】解：∵反比例函数y =k -1x的图象在第一、三象限，∴k -1>0∴k >1∴点k ,-3 在第四象限，故答案为：四．23.(2024·江苏扬州·中考真题)如图，在平面直角坐标系中，点A 的坐标为(1,0)，点B 在反比例函数y =k x (x >0)的图像上，BC ⊥x 轴于点C ，∠BAC =30°，将△ABC 沿AB 翻折，若点C 的对应点D 落在该反比例函数的图像上，则k 的值为．【答案】23【分析】本题考查了反比例函数k 的几何意义，掌握求解的方法是解题的关键．如图，过点D 作DE ⊥x 轴于点E ．根据∠BAC =30°，BC ⊥x ，设BC =a ，则AD =AC =3a ，由对称可知AC =AD ，∠DAB =∠BAC =30°，即可得AE =32a ，DE =32a ，解得B (1+3a ,a ),D 1+32a ,32a ，根据点B 的对应点D 落在该反比例函数的图像上，即可列方程求解；【详解】解：如图，过点D 作DE ⊥x 轴于点E ．∵点A 的坐标为(1,0)，∴OA =1，∵∠BAC =30°，BC ⊥x 轴，设BC =a ，则AD =AC =BC tan30°=3a ，由对称可知AC =AD ，∠DAB =∠BAC =30°，∴∠DAC =60°,∠ADE =30°，∴AE =32a ，DE =AD ·sin60°=32a ，∴B (1+3a ,a ),D 1+32a ,32a ，∵点B 的对应点D 落在该反比例函数的图像上，∴k =a 1+3a =32a ⋅1+32a，解得：a =233，∵反比例函数图象在第一象限，∴k =2331+233×3 =23，故答案为：23．24.(2024·内蒙古呼伦贝尔·中考真题)如图，在平面直角坐标系中，点A ，B 的坐标分别为5,0 ，2,6 ，过点B 作BC ∥x 轴交y 轴于点C ，点D 为线段AB 上的一点，且BD =2AD ．反比例函数y =k x(x >0)的图象经过点D 交线段BC 于点E ，则四边形ODBE 的面积是．【答案】12【分析】本题主要考查了反比例函数的图象与性质，反比例函数图象上点的坐标特征，反比例函数k 的几何意义，作BM ⊥x 轴于M ，作DN ⊥x 轴于N ，则DN ∥BM ，由点A ，B 的坐标分别为5,0 ，2,6 得BC =OM =2，BM =OC =6，AM =3，然后证明△ADN ∽△ABM 得DN BM =AN AM =AD AB ，求出DN =2，则ON =OA -AN =4，故有D 点坐标为4,2 ，求出反比例函数解析式y =8x ，再求出E 43,6 ，最后根据S 四边形ODBE =S 梯形OABC -S △OCE -S △OAD 即可求解，熟练掌握知识点的应用是解题的关键．【详解】如图，作BM ⊥x 轴于M ，作DN ⊥x 轴于N ，则DN ∥BM ，∵点A ，B 的坐标分别为5,0 ，2,6 ，∴BC =OM =2，BM =OC =6，AM =3，∵DN ∥BM ，∴△ADN ∽△ABM ，∴DN BM =AN AM =AD AB，∵BD =2AD ，∴DN 6=AN 3=13，∴DN =2，AN =1，∴ON =OA -AN =4，∴D 点坐标为4,2 ，代入y =k x 得，k =2×4=8，∴反比例函数解析式为y =8x，∵BC ∥x 轴，∴点E 与点B 纵坐标相等，且E 在反比例函数图象上，∴E 43,6，∴CE =43，∴S 四边形ODBE =S 梯形OABC -S △OCE -S △OAD =12×2+5 ×6-12×6×43-12×5×2=12，故答案为：12．25.(2024·四川广元·中考真题)已知y =3x 与y =k x x >0 的图象交于点A 2,m ，点B 为y 轴上一点，将△OAB 沿OA 翻折，使点B 恰好落在y =k x x >0 上点C 处，则B 点坐标为．【答案】0,4【分析】本题考查了反比例函数的几何综合，折叠性质，解直角三角形的性质，勾股定理，正确掌握相关性质内容是解题的关键．先得出A 2,23 以及y =43xx >0 ，根据解直角三角形得∠1=30°，根据折叠性质，∠3=30°，然后根据勾股定理进行列式，即OB =OC =23 2+22=4．【详解】解：如图所示：过点A 作AH ⊥y 轴，过点C 作CD ⊥x 轴，∵y =3x 与y =k xx >0 的图象交于点A 2,m ，∴把A 2,m 代入y =3x ，得出m =3×2=23，∴A 2,23 ，把A 2,23 代入y =k xx >0 ，解得k =2×23=43，∴y =43xx >0 ，设C m ，43m，在Rt △AHO ，tan ∠1=AH OH =223=33，∴∠1=30°，∵点B 为y 轴上一点，将△OAB 沿OA 翻折，∴∠2=∠1=30°，OC =OB ，∴∠3=90°-∠1-∠2=30°，则CD OD=tan ∠3=33=43m m ，解得m =23(负值已舍去)，∴C 23，2 ，∴OB =OC =23 2+22=4，∴点B 的坐标为0，4 ，故答案为：0，4 ．26.(2024·广东深圳·中考真题)如图，在平面直角坐标系中，四边形AOCB 为菱形，tan ∠AOC =43，且点A 落在反比例函数y =3x 上，点B 落在反比例函数y =k x k ≠0 上，则k =．【答案】8【分析】本题主要考查反比例函数与几何的综合及三角函数；过点A 、B 作x 轴的垂线，垂足分别为D 、E ，然后根据特殊三角函数值结合勾股定理求得A 32，2 ，OA =52，再求得点B 4，2 ，利用待定系数法求解即可．【详解】解：过点A 、B 作x 轴的垂线，垂足分别为D 、E ，如图，∵tan ∠AOC =43，∴AD OD =43，∴设AD =4a ，则OD =3a ，∴点A 3a ，4a，∵点A 在反比例函数y =3x 上，∴3a ⋅4a =3，∴a =12(负值已舍)，则点A 32，2，∴AD =2，OD =32，∴OA =OD 2+AD 2=52，∵四边形AOCB 为菱形，∴AB =OA =52，AB ∥CO ，∴点B 4，2 ，∵点B 落在反比例函数y =k x k ≠0 上，∴k =4×2=8，故答案为：8．27.(2024·广东广州·中考真题)如图，平面直角坐标系xOy 中，矩形OABC 的顶点B 在函数y =k x(x >0)的图象上，A (1,0)，C (0,2)．将线段AB 沿x 轴正方向平移得线段A B (点A 平移后的对应点为A )，A B 交函数y =k x (x >0)的图象于点D ，过点D 作DE ⊥y 轴于点E ，则下列结论：①k =2；②△OBD 的面积等于四边形ABDA 的面积；③A E 的最小值是2；④∠B BD =∠BB O ．其中正确的结论有．(填写所有正确结论的序号)【答案】①②④【分析】由B 1,2 ，可得k =1×2=2，故①符合题意；如图，连接OB ，OD ，BD ，OD 与AB 的交点为K ，利用k 的几何意义可得△OBD 的面积等于四边形ABDA 的面积；故②符合题意；如图，连接A E ，证明四边形A DEO 为矩形，可得当OD 最小，则A E 最小，设D x ,2xx >0 ，可得A E 的最小值为2，故③不符合题意；如图，设平移距离为n ，可得B n +1,2 ，证明△B BD ∽△A OB ，可得∠B BD =∠B OA ，再进一步可得答案．【详解】解：∵A (1,0)，C (0,2)，四边形OABC 是矩形；∴B 1,2 ，∴k =1×2=2，故①符合题意；2如图，连接OB ，OD ，BD ，OD 与AB 的交点为K ，05∵S △AOB =S △A OD =12×2=1，∴S △BOK =S 四边形AKDA，∴S △BOK +S △BKD =S 四边形AKDA+S △BKD ，∴△OBD 的面积等于四边形ABDA 的面积；故②符合题意；如图，连接A E ，∵DE ⊥y 轴，∠DA O =∠EOA =90°，∴四边形A DEO 为矩形，∴A E =OD ，∴当OD 最小，则A E 最小，设D x ,2x x >0 ，∴OD 2=x 2+4x 2≥2⋅x ⋅2x =4，∴OD ≥2，∴A E 的最小值为2，故③不符合题意；如图，设平移距离为n ，∴B n +1,2 ，∵反比例函数为y =2x，四边形A B CO 为矩形，∴∠BB D =∠OA B =90°，D n +1,2n +1 ，∴BB =n ，OA =n +1，B D =2-2n +1=2n n +1，A B =2，∴BB OA =n n +1=2n n +12=B D A B，∴△B BD ∽△A OB ，∴∠B BD =∠B OA ，∵B C ∥A O ，∴∠CB O =∠A OB ，∴∠B BD =∠BB O ，故④符合题意；故答案为：①②④【点睛】本题考查的是反比例函数的图象与性质，平移的性质，矩形的判定与性质，相似三角形的判定与性质，勾股定理的应用，作出合适的辅助线是解本题的关键．28.(2024·四川乐山·中考真题)定义：函数图象上到两坐标轴的距离都小于或等于1的点叫做这个函数图象的“近轴点”．例如，点0,1 是函数y =x +1图象的“近轴点”．(1)下列三个函数的图象上存在“近轴点”的是(填序号)；①y =-x +3；②y =2x；③y =-x 2+2x -1．(2)若一次函数y =mx -3m 图象上存在“近轴点”，则m 的取值范围为．【答案】③-12≤m <0或0<m ≤12【分析】本题主要考查了新定义--“近轴点”．正确理解新定义，熟练掌握一次函数，反比例函数，二次函数图象上点的坐标特点，是解决问题的关键．(1)①y =-x +3中，取x =y =1.5，不存在“近轴点”；②y =2x，由对称性，取x =y =±2，不存在“近轴点”；③y =-x 2+2x -1=-x -1 2，取x =1时，y =0，得到1,0 是y =-x 2+2x -1的“近轴点”；(2)y =mx -3m =m x -3 图象恒过点3,0 ，当直线过1,-1 时，m =12，得到0<m ≤12；当直线过1,1 时，m =-12，得到-12≤m <0．【详解】(1)①y =-x +3中，x =1.5时，y =1.5，不存在“近轴点”；②y =2x，由对称性，当x =y 时，x =y =±2，不存在“近轴点”；③y =-x 2+2x -1=-x -1 2，x =1时，y =0，∴1,0 是y =-x 2+2x -1的“近轴点”；∴上面三个函数的图象上存在“近轴点”的是③故答案为：③；(2)y =mx -3m =m x -3 中，x =3时，y =0，∴图象恒过点3,0 ，当直线过1,-1 时，-1=m 1-3 ，∴m =12，∴0<m ≤12；当直线过1,1 时，1=m 1-3 ，∴m =-12，∴-12≤m <0；∴m 的取值范围为-12≤m <0或0<m ≤12．故答案为：-12≤m <0或0<m ≤12．三、解答题29.(2024·甘肃·中考真题)如图，在平面直角坐标系中，将函数y =ax 的图象向上平移3个单位长度，得到一次函数y =ax +b 的图象，与反比例函数y =k x x >0 的图象交于点A 2，4 ．过点B 0，2 作x 轴的平行线分别交y =ax +b 与y =k xx >0 的图象于C ，D 两点．(1)求一次函数y =ax +b 和反比例函数y =k x的表达式；(2)连接AD ，求△ACD 的面积．【答案】(1)一次函数y =ax +b 的解析式为y =12x +3；反比例函数y =k x x >0 的解析式为y =8xx >0 ；(2)6【分析】本题主要考查了一次函数与反比例函数综合：(1)先根据一次函数图象的平移规律y =ax +b =ax +3，再把点A 的坐标分别代入对应的一次函数解析式和反比例函数解析式中，利用待定系数法求解即可；(2)先分别求出C 、D 的坐标，进而求出CD 的长，再根据三角形面积计算公式求解即可．【详解】(1)解：∵将函数y =ax 的图象向上平移3个单位长度，得到一次函数y =ax +b 的图象，∴y =ax +b =ax +3，把A 2，4 代入y =ax +3中得：2a +3=4，解得a =12，∴一次函数y =ax +b 的解析式为y =12x +3；把A 2，4 代入y =k x x >0 中得：4=k 2x >0 ，解得k =8，∴反比例函数y =k x x >0 的解析式为y =8xx >0 ；(2)解：∵BC ∥x 轴，B 0，2 ，∴点C 和点D 的纵坐标都为2，在y =12x +3中，当y =12x +3=2时，x =-2，即C -2，2 ；在y =8x x >0 中，当y =8x =2时，x =4，即D 4，2 ；∴CD =4--2 =6，∵A 2，4 ，∴S △ACD =12CD ⋅y A -y C =12×6×4-2 =6．30.(2024·青海·中考真题)如图，在同一直角坐标系中，一次函数y =-x +b 和反比例函数y =9x 的图象相交于点A 1,m ，B n ,1 ．(1)求点A ，点B 的坐标及一次函数的解析式；(2)根据图象，直接写出不等式-x +b >9x的解集．【答案】(1)A 1,9 ，B 9,1 ，y =-x +10(2)x <0或1<x <9【分析】本题主要考查了一次函数与反比函数的交点问题：(1)分别把点A 1,m ，点B n ,1 代入y =9x，可求出点A ，B 的坐标，即可求解；(2)直接观察图象，即可求解．【详解】(1)解：把点A 1,m 代入y =9x 中，得：m =91=9，∴点A 的坐标为1,9 ，把点B n ,1 代入y =9x 中，得：n =91=9，∴点B 的坐标为9,1 ，把x =1，y =9代入y =-x +b 中得：-1+b =9，∴b =10，∴一次函数的解析式为y =-x +10，(2)解：根据一次函数和反比例函数图象，得：当x <0或1<x <9时，一次函数y =-x +b 的图象位于反比例函数y =9x的图象的上方，∴-x +b >9x的解集为x <0或1<x <9．31.(2024·吉林·中考真题)已知蓄电池的电压为定值，使用蓄电池时，电流I (单位：A )与电阻R (单位：Ω)是反比例函数关系，它的图象如图所示．(1)求这个反比例函数的解析式(不要求写出自变量R 的取值范围)．(2)当电阻R 为3Ω时，求此时的电流I ．【答案】(1)I =36R(2)12A【分析】本题主要考查了反比例函数的实际应用：(1)直接利用待定系数法求解即可；(2)根据(1)所求求出当R =3Ω时I 的值即可得到答案．【详解】(1)解：设这个反比例函数的解析式为I =URU ≠0 ，把9，4 代入I =U RU ≠0 中得：4=U9U ≠0 ，解得U =36，∴这个反比例函数的解析式为I =36R；(2)解：在I =36R中，当R =3Ω时，I =363=12A ，∴此时的电流I 为12A ．32.(2024·山东·中考真题)列表法、表达式法、图像法是三种表示函数的方法，它们从不同角度反映了自变量与函数值之间的对应关系．下表是函数y =2x +b 与y =kx部分自变量与函数值的对应关系：x -72a12x +ba1________kx________________7(1)求a、b的值，并补全表格；(2)结合表格，当y=2x+b的图像在y=kx的图像上方时，直接写出x的取值范围．【答案】(1)a=-2b=5，补全表格见解析(2)x的取值范围为-72<x<0或x>1；【分析】本题考查的是一次函数与反比例函数的综合，利用图像法写自变量的取值范围；(1)根据表格信息建立方程组求解a,b的值，再求解k的值，再补全表格即可；(2)由表格信息可得两个函数的交点坐标，再结合函数图像可得答案.【详解】(1)解：当x=-72时，2x+b=a，即-7+b=a，当x=a时，2x+b=1，即2a+b=1，∴a-b=-72a+b=1，解得：a=-2b=5，∴一次函数为y=2x+5，当x=1时，y=7，∵当x=1时，y=kx=7，即k=7，∴反比例函数为：y=7x，当x=-72时，y=7÷-72=-2，当y=1时，x=a=-2，当x=-2时，y=-7 2，补全表格如下：x-72-212x+b-217kx-2-7 27(2)由表格信息可得：两个函数的交点坐标分别为-72,-2，1,7 ，∴当y=2x+b的图像在y=kx的图像上方时，x的取值范围为-72<x<0或x>1；33.(2024·湖北·中考真题)一次函数y=x+m经过点A-3,0，交反比例函数y=kx于点B n,4．(1)求m，n，k；(2)点C在反比例函数y=kx第一象限的图象上，若S△AOC<S△AOB，直接写出C的横坐标a的取值范围．【答案】(1)m=3，n=1，k=4；(2)a>1．【分析】本题主要考查了一次函数和反比例函数的综合，求反比例函数解析式，解题的关键是熟练掌握数形结合的思想．(1)利用一次函数y=x+m经过点A-3,0，点B n,4，列式计算求得m=3，n=1，得到点B1,4，再利用待定系数法求解即可；(2)利用三角形面积公式求得S△AOB=6，得到32y C<6，据此求解即可．【详解】(1)解：∵一次函数y=x+m经过点A-3,0，点B n,4，∴-3+m=0 n+m=4 ，解得m=3 n=1 ，∴点B1,4，∵反比例函数y=kx经过点B1,4，∴k=1×4=4；(2)解：∵点A-3,0，点B1,4，∴AO =3，∴S △AOB =12AO ×y B =12×3×4=6，S △AOC =12AO ×y C =32y C ，由题意得32y C<6，∴y C <4，∴x C >1，∴C 的横坐标a 的取值范围为a >1．34.(2024·四川凉山·中考真题)如图，正比例函数y 1=12x 与反比例函数y 2=kxx >0 的图象交于点A m ，2 ．(1)求反比例函数的解析式；(2)把直线y 1=12x 向上平移3个单位长度与y 2=kxx >0 的图象交于点B ，连接AB ,OB ，求△AOB 的面积．【答案】(1)y 2=8x(2)6【分析】本题考查了一次函数与反比例函数的交点问题，待定系数法求函数解析式，一次函数的平移等知识，熟练掌握函数的平移法则是关键．(1)待定系数法求出反比例函数解析式即可；(2)先得到平移后直线解析式，联立方程组求出点B 坐标，根据平行线间的距离可得S △AOB =S △ADO ，代入数据计算即可．【详解】(1)解：∵点A (m ,2)在正比例函数图象上，∴2=12m ，解得m =4，∴A (4,2)，∵A (4,2)在反比例函数图象上，∴k =8，∴反比例函数解析式为y 2=8x．(2)解：把直线y 1=12x 向上平移3个单位得到解析式为y =12x +3，令x =0，则y =3，∴记直线与y 轴交点坐标为D (0,3)，连接AD ，联立方程组y =8xy =12x +3，解得x =2y =4，x =-8y =-1 (舍去)，∴B (2,4)，由题意得：BD ∥AO ，∴△AOB ,△AOD 同底等高，∴S △AOB =S △ADO =12OD ⋅x A =12×3×4=6．35.(2024·贵州·中考真题)已知点1,3 在反比例函数y =kx的图象上．(1)求反比例函数的表达式；(2)点-3,a ，1,b ，3,c 都在反比例函数的图象上，比较a ，b ，c 的大小，并说明理由．【答案】(1)y =3x(2)a <c <b ，理由见解析【分析】本题主要考查了反比例函数的性质，以及函数图象上点的坐标特点，待定系数法求反比例函数解析式，关键是掌握凡是函数图象经过的点必能满足解析式．(1)把点1,3 代入y =kx可得k 的值，进而可得函数的解析式；(2)根据反比例函数表达式可得函数图象位于第一、三象限，再根据点A 、点B 和点C 的横坐标即可比较大小．【详解】(1)解：把1,3 代入y =k x ，得3=k 1，∴k =3，∴反比例函数的表达式为y =3x；(2)解：∵k =3>0，∴函数图象位于第一、三象限，∵点-3,a ，1,b ，3,c 都在反比例函数的图象上，-3<0<1<3，∴a <0<c 0 的图象经过点A ．(1)求这个反比例函数的表达式．(2)请先描出这个反比例函数图象上不同于点A 的三个格点，再画出反比例函数的图象．(3)将矩形ABCD 向左平移，当点E 落在这个反比例函数的图象上时，平移的距离为．【答案】(1)y =6x(2)见解析(3)92【分析】本题考查了待定系数法求反比例函数解析，画反比例函数图象，平移的性质等知识，解题的关键是：(1)利用待定系数法求解即可；(2)分别求出x =1，x =2，x =6对应的函数值，然后描点、连线画出函数图象即可；(3)求出平移后点E 对应点的坐标，利用平移前后对应点的横坐标相减即可求解．【详解】(1)解：反比例函数y =kx的图象经过点A 3,2 ，∴2=k3，∴k =6，∴这个反比例函数的表达式为y =6x；(2)解：当x =1时，y =6，当x =2时，y =3，当x =6时，y =1，∴反比例函数y =6x的图象经过1,6 ，2,3 ，6,1 ，画图如下：(3)解：∵E 6,4 向左平移后，E 在反比例函数的图象上，∴平移后点E 对应点的纵坐标为4，当y =4时，4=6x，解得x =32，∴平移距离为6-32=92．故答案为：92．37.(2024·四川乐山·中考真题)如图，已知点A 1,m 、B n ,1 在反比例函数y =3xx >0 的图象上，过点A 的一次函数y =kx +b 的图象与y 轴交于点C 0,1 ．(1)求m 、n 的值和一次函数的表达式；(2)连接AB ，求点C 到线段AB 的距离．【答案】(1)m =3，n =3，y =2x +1(2)点C 到线段AB 的距离为322【分析】(1)根据点A 1,m 、B n ,1 在反比例函数y =3x图象上，代入即可求得m 、n 的值；根据一次函数y =kx +b 过点A 1,3 ，C 0,1 ，代入求得k ，b ，即可得到表达式；(2)连接BC ，过点A 作AD ⊥BC ，垂足为点D ，过点C 作CE ⊥AB ，垂足为点E ，可推出BC ∥x 轴，BC 、AD 、DB 的长度，然后利用勾股定理计算出AB 的长度，最后根据S △ABC =12BC ⋅AD =12AB ⋅CE ，计算得CE 的长度，即为点C 到线段AB 的距离．【详解】(1)∵点A 1,m 、B n ,1 在反比例函数y =3x图象上。

初三数学反比例函数试题答案及解析

初三数学反比例函数试题答案及解析1.如图，Rt△ABC的顶点B在反比例函数的图象上，AC边在x轴上，已知∠ACB=90°，∠A=30°，BC=4，则图中阴影部分的面积是（）A．12B．C．D．【答案】D．【解析】先由∠ACB=90°，BC=4，得出B点纵坐标为4，根据点B在反比例函数的图象上，求出B点坐标为（3，4），则OC=3，再解Rt△ABC，得出AC=，则OA=。

设AB与y轴交于点D，由OD∥BC，根据平行线分线段成比例定理得出，求得OD=，最后根据梯形的面积公式即可求出阴影部分的面积。

∵∠ACB=90°，BC=4，∴B点纵坐标为4，∵点B在反比例函数的图象上，∴当y=4时，x=3，即B点坐标为（3，4），∴OC=3。

在Rt△ABC中，∠ACB=90°，∠A=30°，BC=4，∴AB=2BC=8，，OA=AC﹣OC=。

设AB与y轴交于点D．∵OD∥BC，∴，即，解得OD=，∴阴影部分的面积是：。

故选：D．【考点】1.反比例函数系数k的几何意义；2.含30度角的直角三角形；3.勾股定理。

2.如图，矩形ABCD的顶点A在第一象限，AB∥x轴，AD∥y轴，且对角线的交点与原点重合，在边AB从小于AD到大于AD的变化过程中，若矩形ABCD的周长始终保持不变，则经过动点A的反比例函数中，k的值的变化情况是（）A．一直增大B．一直减小C．先增大后减小D．先减小后增大【答案】C．【解析】设矩形ABCD中，AB=2a，AD=2b．∵矩形ABCD的周长始终保持不变，∴2（2a+2b）=4（a+b）为定值.∴a+b为定值．设（定值），则∵矩形对角线的交点与原点O重合, ∴k=AB•AD=ab=.∴k是a的二次函数，它的图象开口向下，当时，有最大值.∴在边AB从小于AD到大于AD的变化过程中，k的值先增大后减小．故选C．【考点】1.单动点问题；2.曲线上点的坐标与方程的关系；3.矩形的性质；4.二次函数的性质. 3.矩形的面积一定，则它的长和宽的关系是（）A．正比例函数B．一次函数C．反比例函数D．二次函数【答案】C.【解析】设某矩形的面积为S，相邻的两条边长分别为x和y．那么当S一定时，x与y的函数关系式是y=，由于S≠0，且是常数，因而这个函数是:y是x的反比例函数．故选C.考点: 1.反比例函数的定义；2.正比例函数的定义．4.如图，△ABC的三个顶点分别为A（1，2），B（2，5），C（6，1）.若函数在第一象限内的图像与△ABC有交点，则的取值范围是A．2≤≤B．6≤≤10C．2≤≤6D．2≤≤【答案】A．【解析】把A点的坐标代入即可求出k的最小值；当反比例函数和直线BC相交时，求出b2﹣4ac的值，得出k的最大值．把点A（1，2）代入得：k=2；C的坐标是（6，1），B的坐标是（2，5），设直线BC的解析式是y=kx+b，则，解得：，则函数的解析式是： y=﹣x+7，根据题意，得：=﹣x+7，即x2﹣7x+k=0，△=49﹣4k≥0，解得：k≤．则k的范围是：2≤k≤．故选A．【考点】反比例函数综合题．5.如图，在平面直角坐标系中，正方形的边长为2．写出一个函数，使它的图象与正方形有公共点，这个函数的表达式为．【答案】(答案不唯一）【解析】由图象可知过B点时图象与正方形只有一个公共点，此时k值最大∵正方形OABC的边长为2，∴B点坐标为（2，2），当函数y=（k≠0）过B点时，k=2×2=4，∴满足条件的一个反比例函数解析式为y=．故答案为：y=，y=（0＜k≤4）（答案不唯一）【考点】1、反比例函数；2、正方形6.反比例函数的图象在第象限．【答案】二、四【解析】反比例函数y=的图像是双曲线，当k＞0时，x,y 同号，所以图像在第一、三象限；当k<0时，x,y 异号，所以图像在第二、四象限．∴,因为k=-2<0,图像在二、四象限.【考点】反比例函数图像与k的关系.7.点A在双曲线上，AB⊥x轴于B，且△AOB的面积为3，则k=（）A．3B．6C．±3D．±6【答案】D.【解析】∴S△AOB =3，∴|k|=6，∴k=±6．故选D．考点: 反比例函数系数k的几何意义．8.如图，矩形OABC的顶点A，C分别在x，y轴的正半轴上，点D为对角线OB的中点，点E(4，n)在边AB上，反比例函数y＝(k≠0)在第一象限内的图象经过点D，E，且tan∠BOA＝.(1)求边AB的长；(2)求反比例函数的解析式和n的值；(3)若反比例函数的图象与矩形的边BC交于点F，将矩形折叠，使点O与点F重合，折痕分别与x，y轴正半轴交于点H，G，求线段OG的长．【答案】(1)2 (2)y＝ n＝ (3)【解析】解：(1)在Rt△BOA中，∵OA＝4，tan∠BOA＝，∴AB＝OA×tan∠BOA＝2.(2)∵点D为OB的中点，点B(4，2)，∴点D(2，1)，又∵点D在y＝的图象上，∴1＝，∴k＝2，∴y＝.又∵点E在y＝图象上，∴4n＝2，∴n＝.(3)设点F(a，2)，∴2a＝2，∴CF＝a＝1，连接FG，设OG＝t，则OG＝FG＝t，CG＝2－t，在Rt△CGF中，GF2＝CF2＋CG2，∴t2＝(2－t)2＋12，解得t＝，∴OG＝t＝.9.反比例函数y=过点(2,3),则k=_____________________;反比例函数y=过点(-2,3),则k=_________________.【答案】6 -5【解析】点在函数图象上，则点的坐标满足函数关系式，把点的坐标值代入解析式求k的值.3= ,k=6;=3,k-1=-6,k=-5.10.如图，已知点A在反比例函数的图象上，点B在反比例函数的图象上，AB∥x轴，分别过点A、B作x轴作垂线，垂足分别为C、D，若，则k的值为_________．【答案】12.【解析】设A（a，b），∵点A在反比例函数y=的图象上，∴ab=4，∵OC=a，OC=OD，∴OD=3a，∴B（3a，b），∵点B在反比例函数y=(k≠0)的图象上，∴k=3ab=3×4=12，考点: 反比例函数综合题．11.已知点（﹣1,y1）,（2,y2）,（3,y3）在反比例函数的图象上．下列结论中正确的是（）A．y1＞y2＞y3B．y1＞y3＞y2C．y3＞y1＞y2D．y2＞y3＞y1【答案】B．【解析】∵k2≥0,∴﹣k2≤0,﹣k2﹣1＜0,∴反比例函数的图象在二、四象限,∵点（﹣1,y1）的横坐标为﹣1＜0,∴此点在第二象限,y1＞0;∵（2,y2）,（3,y3）的横坐标3＞2＞0,∴两点均在第四象限y2＜0,y3＜0,∵在第四象限内y随x的增大而增大,∴0＞y3＞y2,∴y1＞y3＞y2．故选B．【考点】反比例函数图象上点的坐标特征．12.如图，直线y=2x与双曲线交于点A．将直线y=2x向右平移3个单位后，与双曲线交于点B，与x轴交于点C，若，则k= .【答案】8．【解析】根据直线平移的规律，即可得出直线BC的解析式；根据反比例函数的性质得出A，B 两点的坐标，根据xy=k即可得出k的值．试题解析：∵将直线y=2x向右平移3个单位后，得到的直线是BC，∴直线BC的解析式是：y=2（x-3）；过点A作AD⊥x轴于点D，BE⊥x轴于点E，∵直线BC是由直线OA平移得到的，∴，∵，∴，∴AD=2BE，又∵直线BC的解析式是：y=2（x-3），∴设B点的横坐标为3+x，∴B点的纵坐标为：y=2（x+3-3）=2x，∴BE=2x，∵AD=2BE，∴AD=4x，∵y=2x，∴，∴，∴A点的纵坐标为4x，根据A，B都在反比例函数图象上得出：∴2x×4x=（3+x）×2x，x=1，∴k的值为：2×1×4×1=8．考点: 反比例函数综合题．13.如图，双曲线经过的两个顶点、轴，连接，将沿翻折后得到，点刚好落在线段上，连接，恰好平分与轴负半轴的夹角，若的面积为3，则的值为。

反比例函数及其应用(共35道)—2023年中考数学真题(全国通用)(解析版)

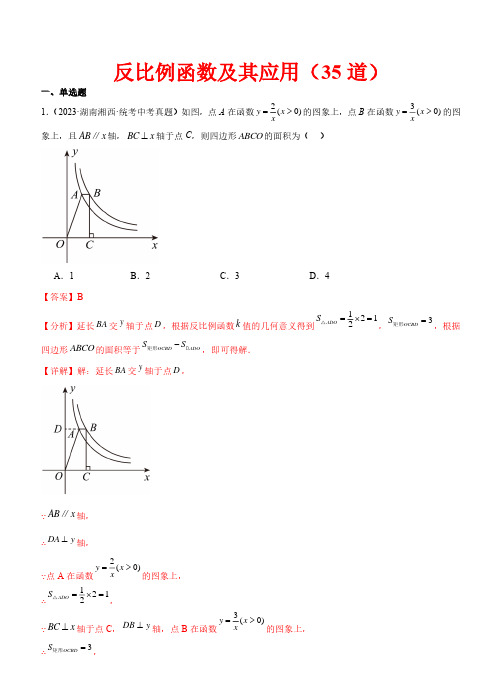
反比例函数及其应用（35道）一、单选题A ．1B ．2C ．3D ．4【答案】B【分析】延长BA 交y 轴于点D ，根据反比例函数k 值的几何意义得到1212ADO S =⨯=△，3OCBD S =矩形，根据四边形ABCO 的面积等于ADOOCBD S S−矩形，即可得解．【详解】解：延长BA 交y 轴于点D ，∵AB x ∥轴， ∴DA y ⊥轴，∵点A 在函数2(0)y x x =>的图象上，∴1212ADO S =⨯=△，∵BC x ⊥轴于点C ，DB y ⊥轴，点B 在函数3(0)y x x =>的图象上，∴3OCBD S =矩形，∴四边形ABCO 的面积等于312ADOOCBD S S−=−=矩形；故选B ．【点睛】本题考查反比例函数与几何图形的综合应用．熟练掌握反比例函数中k 的几何意义，是解题的关键．A ．321y y y <，20y >，函数图象在第二象限内为增函数，420−<−<， 120y y ∴<<．30>，3(3,)C y ∴点在第四象限，30y \<，1y ∴，2y ，3y 的大小关系为312y y y <<．故选：C ．【点睛】此题考查的是反比例函数图象上点的坐标特点及平面直角坐标系中各象限内点的坐标特点，比较简单．A ．当3x >时，12y y D ．当10x −<<时，12y y <【答案】B【分析】结合一次函数与反比例函数的图象，逐项判断即可得．【详解】解：A 、当3x >时，12y y >，则此项错误，不符合题意； B 、当1x <−时，12y y <，则此项正确，符合题意； C 、当03x <<时，12y y <，则此项错误，不符合题意； D 、当10x −<<时，12y y >，则此项错误，不符合题意；故选：B ．【点睛】本题考查了一次函数与反比例函数的图象，熟练掌握函数图象法是解题关键．A ．123y y y <，∴图象在一、三象限，且在每个象限内y 随x 的增大而减小， ∵2101−<−<<， ∴2130y y y <<<．故选：C ．【点睛】本题考查了反比例函数的图象与性质，反比例函数ky x =(k 是常数，0k ≠)的图象是双曲线，当0k >，反比例函数图象的两个分支在第一、三象限，在每一象限内，y 随x 的增大而减小；当 0k <，反比例函数图象的两个分支在第二、四象限，在每一象限内，y 随x 的增大而增大．【答案】A【分析】连接四边形ABCD 的对角线AC BD 、，过D 作DE x ⊥轴，过C 作CF x ⊥轴，直线1y x =−与x 轴交于点M ，如图所示，根据函数图像交点的对称性判断四边形ABCD 是平行四边形，由平行四边形性质及平面直角坐标系中三角形面积求法，确定()11142四边形△ABC COD D S S OM DE CF ===⋅+，再求出直线1y x =−与x 轴交于点()1,0M ，通过联立1y x k y x =−⎧⎪⎨=⎪⎩求出C D 、纵坐标，代入方程求解即可得到答案．【详解】解：连接四边形ABCD 的对角线AC BD 、，过D 作DE x ⊥轴，过C 作CF x ⊥轴，直线1y x =−与x 轴交于点M ，如图所示：根据直线1y x =+、1y x =−与双曲线()0ky k x =>交点的对称性可得四边形ABCD 是平行四边形，()11142四边形△ABC O D C D S S OM DE CF ∴===⋅+，直线1y x =−与x 轴交于点M ， ∴当0y =时，1x =，即()1,0M ，1y x =−与双曲线()0ky k x =>分别相交于点C D 、，∴联立1y x k y x =−⎧⎪⎨=⎪⎩，即1k y y =−，则20y y k +−=，由0k >，解得y =，∴1112⎤⨯⨯−=⎥⎢⎥⎝⎭⎣⎦2=，解得34k =，故选：A ．【点睛】本题考查一次函数与反比例函数综合，涉及平行四边形的判定与性质，熟练掌握平面直角坐标系中三角形面积求法是解决问题的关键．A ．2:3:6B ．6:3:2C ．1:2:3D ．3:2:1【答案】A【分析】首先根据长方体的性质，得出相对面的面积相等，再根据物体的压力不变，结合反比例函数的性质进行分析，即可得出答案．【详解】解：∵长方体物体的一顶点所在A 、B 、C 三个面的面积比是3:2:1， ∴长方体物体的A 、B 、C 三面所对的与水平地面接触的面积比也为3:2:1， ∵FP S =，0F >，且F 一定，∴P 随S 的增大而减小， ∴111::::2:3:6321A B C P P P ==．故选：A ．【点睛】本题考查了反比例函数的性质，解本题的关键在熟练掌握反比例函数的性质．A ．B ．C ．D ．【答案】D【分析】先根据一次函数图象确定a 、b 的符号，进而求出ab 的符号，由此可以确定反比例函数图象所在的象限，看是否一致即可．【详解】解：A 、∵一次函数图象经过第一、二、三象限， ∴00a b >>，， ∴0ab >，∴反比例函数aby x =的图象见过第一、三象限，这与图形不符合，故A 不符合题意；B 、∵一次函数图象经过第一、二、四象限， ∴00a b <>，， ∴0ab <， ∴反比例函数aby x =的图象见过第二、四象限，这与图形不符合，故B 不符合题意；C 、∵一次函数图象经过第一、三、四象限， ∴00a b ><，， ∴0ab <， ∴反比例函数aby x =的图象见过第二、四象限，这与图形不符合，故C 不符合题意；D 、∵一次函数图象经过第一、二、四象限， ∴00a b <>，， ∴0ab <， ∴反比例函数aby x =的图象见过第二、四象限，这与图形符合，故D 符合题意；故选D ．【点睛】本题主要考查了一次函数与反比例函数图象和性质，熟练掌握相关性质与函数图象的关系是解决本题的关键．A ．B ．C ．D ．【答案】B 【分析】根据题意11FL F L =代入数据求得245F L =，即可求解．【详解】解：∵11FL F L =，125cm L =，19.8NF =，∴259.8245FL =⨯=， ∴245F L =，函数为反比例函数，当35cm L =时，245735F ==，即245F L =函数图象经过点()35,7．故选：B ．【点睛】本题考查了反比例函数的应用以及函数图象，根据题意求出函数关系式是解题的关键．A ．3B ．4C ．5D ．6【答案】B【分析】由正方形的性质得2BC AB ==，可设2,2k C ⎛⎫ ⎪⎝⎭，1,22k E ⎛⎫+ ⎪⎝⎭，根据21222k k ⎛⎫⨯=⨯+ ⎪⎝⎭可求出k 的值．【详解】解：∵四边形ABCD 是正方形， ∵2,AB BC CD AD ==== ∵点E 为AD 的中点， ∴11,2AE AD ==设点C 的坐标为2,2k ⎛⎫ ⎪⎝⎭，则,222k kBO AO AB BO ==+=+, ∴1,22k E ⎛⎫+ ⎪⎝⎭， ∵点C ，E 在反比例函数ky x =的图象上，∴21222k k ⎛⎫⨯=⨯+ ⎪⎝⎭，解得，4k =，故选：B ．【点睛】本题考查了反比例函数图象上点的坐标特征：反比例函数ky x =（k 为常数，0k ≠）的图象是双曲线，图象上的点()x y ，的横纵坐标的积是定值k ，即xy k =．为半径作圆，当A 与x 轴相切、B 与y 轴相切时，连结【答案】C【分析】过点,A B 分别作,y x 轴的垂线，垂足分别为,E D ，,AE BD 交于点C ，得出B 的横坐标为1，A 的纵坐标为1，设(),1A k ，()1,B k ，则1,1AC k BC k =−=−，根据AB =【详解】解：如图所示，过点A B ，分别作y x ，轴的垂线，垂足分别为E D ，，AE BD ，交于点C ，依题意，B 的横坐标为1，A 的纵坐标为1，设(),1A k ，()1,B k∴()1,1C ，则1,1AC k BC k =−=−，又∵90ACB ∠=︒，AB =∴()()(22211k k −+−=∴13k −=（负值已舍去）解得：4k =，故选：C ．【点睛】本题考查了切线的性质，反比例函数的性质，勾股定理，掌握以上知识是解题的关键．统考中考真题）如图，在平面直角坐标系中，OAB 三个顶点的坐标分别为与OAB 关于直线 A ．23 【答案】A【分析】过点B 作BD x ⊥轴，根据题意得出1,BD OD ==和性质得出2OB AB ==，30BOA BAO ∠∠==︒，利用各角之间的关系180OBA OBD '∠+∠=︒，确定A '，B ，D 三点共线，结合图形确定)2C，然后代入反比例函数解析式即可．【详解】解：如图所示，过点B 作BD x ⊥轴，∵(0,0),O A B ，∴1,BD OD ==∴AD OD =tan BD BOA OD ∠==，∴2OB AB ==，30BOA BAO ∠∠==︒，∴60OBD ABD ∠∠==︒，120OBA ∠=︒， ∵OA B '与OAB 关于直线OB 对称， ∴120OBA '∠=︒， ∴180OBA OBD '∠+∠=︒， ∴A '，B ，D 三点共线， ∴2A B AB '==， ∵A C BC '=， ∴1BC =， ∴2CD =，∴)2C，将其代入(0,0)ky k x x =>>得：k =故选：A ．【点睛】题目主要考查等腰三角形的判定和性质，特殊角的三角函数及反比例函数的确定，理解题意，综合运用这些知识点是解题关键．A ．2B ．2−C ．1D ．1−【答案】A【分析】证明四边形ANOM 是矩形，根据反比例函数的k 值的几何意义，即可解答．【详解】解：AM x ⊥轴于点M ，AN y ⊥轴于直N ，90MON ∠=︒，∴四边形AMON 是矩形，四边形AMON 的面积为2， 2k ∴=，反比例函数在第一、三象限，2k ∴=，故选：A ．【点睛】本题考查了矩形的判定，反比例函数的k 值的几何意义，熟知在一个反比例函数图像上任取一点，过点分别作x 轴，y 轴的垂线段，与坐标轴围成的矩形面积为k是解题的关键．二、填空题【答案】63y x =−【分析】函数图象的平移规则为：上加下减，左加右减，根据平移规则可得答案．【详解】解：将反比例函数6y x =的图象向下平移3个单位可得平移后的解析式为：63y x =−，故答案为：63y x =−．【点睛】本题考查的是函数图象的平移，解题的关键是理解并熟记函数图象的平移规则为：上加下减，左加右减．14．（2023·陕西·统考中考真题）如图，在矩形OABC 和正方形CDEF 中，点A 在y 轴正半轴上，点C ，F 均在x 轴正半轴上，点D 在边BC 上，2BC CD =，3AB =．若点B ，E 在同一个反比例函数的图象上，则这个反比例函数的表达式是．【答案】18y x =【分析】设正方形CDEF 的边长为m ，根据2BC CD =，3AB =，得到()3,2B m ，根据矩形对边相等得到3OC =，推出()3,E m m +，根据点B ，E 在同一个反比例函数的图象上，得到()323m m m⨯=+，得到3m =，推出18y x =．【详解】解：∵四边形OABC 是矩形， ∴3OC AB ==，设正方形CDEF 的边长为m ， ∴CD CF EF m ===， ∵2BC CD =， ∴2BC m =， ∴()3,2B m ，()3,E m m +，设反比例函数的表达式为ky x =，∴()323m m m⨯=+，解得3m =或0m =（不合题意，舍去）， ∴()3,6B ，∴3618=⨯=k ，∴这个反比例函数的表达式是18y x =，故答案为：18y x =．【点睛】本题主要考查了反比例函数，解决问题的关键是熟练掌握矩形性质，正方形性质，反比例函数性质，k 的几何意义．统考中考真题）如图，在平面直角坐标系中，AOC 的边两点．若AOC 的面积是【答案】4【分析】过B ，C 两点分别作y 轴的垂线，垂足分别为D ，E ，设B 点坐标为k m m ⎛⎫ ⎪⎝⎭，，则BD m =，由点B 为AC 的中点，推出C 点坐标为22k m m ⎛⎫ ⎪⎝⎭，，求得直线BC 的解析式，得到A 点坐标，根据AOC 的面积是6，列式计算即可求解．【详解】解：过B ，C 两点分别作y 轴的垂线，垂足分别为D ，E ，∴BD CE ∥， ∴ABD ACE ∽，∴BD ABCE AC =，设B 点坐标为k m m ⎛⎫ ⎪⎝⎭，，则BD m =， ∵点B 为AC 的中点， ∴12BD AB CE AC ==， ∴22CE BD m ==，∴C 点坐标为22k m m ⎛⎫ ⎪⎝⎭，，设直线BC 的解析式为y ax b =+， ∴22k ma b mk ma b m ⎧+=⎪⎪⎨⎪+=⎪⎩，解得2232k a m k b m ⎧=−⎪⎪⎨⎪=⎪⎩， ∴直线BC 的解析式为2322k k y x m m =−+，当0x =时，32ky m =，∴A 点坐标为302k m ⎛⎫ ⎪⎝⎭，，根据题意得132622k m m ⋅⋅=，解得4k =，故答案为：4．【点睛】本题考查了反比例函数的性质、相似三角形的判定及性质、求一次函数解析式、坐标与图形，解题关键是熟练掌握反比例函数的性质及相似三角形的性质．【答案】33【分析】过点B 作BC y ⊥轴于点C ，由旋转的性质得，AO AB =，120OAB ∠=︒，在Rt ABC 中求出BC 、AC 的长，即可得出点B 的坐标，代入反比例函数解析式即可求出k 的值．【详解】解∶过点B 作BC y ⊥轴于点C ，由旋转的性质得，AO AB =，120OAB ∠=︒， ∵点A 的坐标为(0，2)， ∴2AO AB ==， ∵120OAB ∠=︒，∴180********BAC OAB ∠∠=︒−=︒−︒=︒， ∴9030ABC BAC ∠∠=︒−=︒， ∴AC =12AB =1221⨯=，由勾股定理得BC ==∴213OC AO AC =+=+=，∴点B 的坐标为(3)， ∵点B 恰好落在反比例函数ky x =的图象上，∴3k =故答案为∶3【点睛】本题考查了反比例函数图象上点的坐标特征，坐标与图形的变化之旋转，解答本题的关键是求出点B 的坐标．【答案】>【分析】把2x =−和=1x −分别代入反比例函数2y x =中计算y 的值，即可做出判断．【详解】解：∵点()12,A y −和点()21,B y −都在反比例函数2y x =的图象上，∴令2x =−，则1212y ==−−；令=1x −，则2221y ==−−，12−>−，12y y ∴>，故答案为：>．【点睛】本题考查了反比例函数图像上点的坐标特征，计算y 的值是解题的关键．若OAB 的面积为【答案】196/136【分析】由k 的几何意义可得19212k =，从而可求出k 的值．【详解】解：AOB 的面积为||192212k k ==，所以k =196．故答案为：196．【点睛】本题主要考查了k 的几何意义．用k 表示三角形AOB 的面积是本题的解题关键．【答案】3【分析】先把点A 坐标代入求出反比例函数解析式，再把点B 代入即可求出m 的值．【详解】解：∵函数()0ky k x =≠的图象经过点()3,2A −和(),2B m −∴把点()3,2A −代入得326k =−⨯=−，∴反比例函数解析式为6y x −=，把点(),2B m −代入得：62m −−=，解得：3m =，故答案为：3．【点睛】本题考查了待定系数法求反比例函数解析式，反比例函数图象上点的坐标特征，熟知反比例函数图象上的点的坐标一定满足函数解析式是解题的关键．【答案】1.5（满足12k <<都可以）【分析】先判断出一次函数7y x b =−+的图象必定经过第二、四象限，再根据120x x ⋅>判断出反比例函数图象和一次函数图象的两个交点在同一象限，从而可以得到反比例函数的图象经过第二、四象限，即630k −<，最终选取一个满足条件的值即可．【详解】解：70−<，∴一次函数7y x b =−+的图象必定经过第二、四象限，120x x ⋅>，∴反比例函数图象和一次函数图象的两个交点在同一象限， ∴反比例函数63ky x −=（1k >且2k ≠）的函数图象经过第一、三象限，∴630k −>，∴2k <， ∵1k >， ∴12k <<，∴满足条件的k 值可以为1.5，故答案为：1.5（满足12k <<都可以）．【点睛】本题考查一次函数和反比例函数的图形性质，解题的关键是根据120x x ⋅>判断出反比例函数图象和一次函数图象的两个交点在同一象限．的正ABC 的顶点，现将ABC 绕原点【答案】6【分析】画出变换后的图像即可（画AOB 即可），当点A 在y 轴上，点B 、C 在x 轴上时，根据ABC 为等边三角形且AO BC ⊥，可得OB OA=A 、B 分别作x 轴垂线构造相似，则BFO OEA ∽，根据相似三角形的性质得出3AOE S =△，进而根据反比例函数k 的几何意义，即可求解．【详解】当点A 在y 轴上，点B 、C 在x 轴上时，连接AO ，ABC 为等边三角形且AO BC ⊥，则30BAO ∠=︒，∴tan tan30BAO ∠=︒=OB OA=，如图所示，过点,A B 分别作x 轴的垂线，交x 轴分别于点,E F ，AO BO ⊥，90BFO AEO AOB ∠=∠=∠=︒，∴90BOF AOE EAO ∠=︒−∠=∠， ∴BFO OEA ∽，∴213BFO AOES OB S OA ⎛⎫== ⎪⎝⎭， ∴212BFOS−==，∴3AOE S =△， ∴6k =．【点睛】本题考查了反比例函数的性质，k 的几何意义，相似三角形的性质与判定，正确作出辅助线构造相似三角形是解题关键．【答案】2/2−+【分析】过点A 作CD y ⊥轴于点D ，过点B 作BC CD ⊥于点C ，证明DAO CBA ≌，进而根据全等三角形的性质得出,DA CB AC OD ==，根据点(),2A m ，进而得出()2,2B m m +−，根据点,A B 在反比例函数(0)ky x x =>的图象上．列出方程，求得m 的值，进而即可求解．【详解】解：如图所示，过点A 作CD y ⊥轴于点D ，过点B 作BC CD ⊥于点C ，∴90C CDO ∠=∠=︒， ∵,90OA AB OAB =∠=︒， ∴90DAO CAB CBA ∠=︒−∠=∠ ∴DAO CBA ≌ ∴,DA CB AC OD == ∵点A 的坐标为()m,2．∴2AC OD ==，AD BC m == ∴()2,2B m m +−∵,A B 在反比例函数(0)ky x x =>的图象上，∴()()222m m m =+−解得：1m =或1m =（舍去）∴22k m ==故答案为：2．【点睛】本题考查了反比例函数的图象和性质，全等三角形的判定和性质，求得点B 的坐标是解题的关键．【答案】4【分析】根据题意可设点P 的坐标为()22m m ，，则()2D m m ，，把()2D m m ，代入一次函数解析式中求出m 的值进而求出点P 的坐标，再求出k 的值即可．【详解】解：∵PA x ⊥轴于点,A PB y ⊥轴于点,B PA PB =， ∴点P 的横纵坐标相同， ∴可设点P 的坐标为()22m m ，，∵D 为PB 的中点， ∴()2D m m ，，∵()2D m m ，在直线1y x =+上，∴12m m +=， ∴1m =， ∴()22P ，，∵点P 在反比例函数()0ky k x =>的图象上，∴224k =⨯=，故答案为：4．【点睛】本题主要考查了一次函数与反比例函数综合，正确求出点P 的坐标是解题的关键．【答案】6【分析】延长CD 交x 轴于点F ，设,k D a a ⎛⎫ ⎪⎝⎭，利用相似三角形的判定与性质可求得矩形的长与宽，再由矩形的面积即可求和k 的值．【详解】解：延长CD 交x 轴于点F ，如图，由点D 在反比例函数()0k y x x =>的图象上，则设,k D a a ⎛⎫ ⎪⎝⎭，∵矩形ABCD 的边AB 平行于x 轴，AB CD ∥，AD CD ⊥， ∴CD y ⊥轴，AD OF ∥，则kDF a OF a ==，，∵AD OF ∥， ∴CDA CFO △∽△， ∴CD AD ACCF OF OC ==， ∵2AC AO =，∴23AC OC =， ∴2223CD CF DF a ===，2233k AD OF a ==， ∵8AD CD ⋅=，即2283k a a ⨯=，∴6k =，故答案为：6．【点睛】本题考查了相似三角形的判定与性质，反比例函数图象上点的坐标特征，其中相似三角形的判定与性质是关键．则ABP 的面积是【答案】152【分析】把()2,3A −代入到22k y x =可求得2k 的值，再把(),2Bm −代入双曲线函数的表达式中，可求得m 的值，进而利用三角形的面积公式进行求解即可．【详解】∵直线11y k x b =+与双曲线22k y x =（其中120k k ⋅≠）相交于()2,3A−，(),2B m −两点，∴2232k m =−⨯=−∴263k m =−=，，∴双曲线的表达式为：26y x =−，()3,2B −，∵过点B 作BP x ∥轴，交y 轴于点P ， ∴3BP =， ∴1153(32)22ABPS=⨯⨯+=，故答案为152．【点睛】本题是一次函数与反比例函数的交点问题，考查了待定系数法求反比例函数，反比例函数图象上点的坐标特征，三角形的面积，数形结合是解答此题的关键．三、解答题26．（2023·四川绵阳·统考中考真题）如图，设反比例函数的解析式为（k ＞0）．（1）若该反比例函数与正比例函数y=2x 的图象有一个交点的纵坐标为2，求k 的值；（2）若该反比例函数与过点M （﹣2，0）的直线l ：y=kx+b 的图象交于A ，B 两点，如图所示，当△ABO 的面积为时，求直线l 的解析式．【答案】（1）；（2）．【详解】试题分析：（1）由题意可得A（1，2），利用待定系数法即可解决问题；（2）把M（﹣2，0）代入y=kx+b，可得b=2k，可得y=kx+2k，由消去y得到，解得x=﹣3或1，推出B（﹣3，﹣k），A（1，3k），根据△ABO的面积为，可得•23k+•2k=，解方程即可解决问题；试题解析：（1）由题意A（1，2），把A（1，2）代入，得到3k=2，∴．（2）把M（﹣2，0）代入y=kx+b，可得b=2k，∴y=kx+2k，由消去y得到，解得x=﹣3或1，∴B（﹣3，﹣k），A（1，3k），∵△ABO的面积为，∴×2×3k+•2k=，解得k=，∴直线l 的解析式为．考点：反比例函数与一次函数的交点问题．(1)2m =，4a =，求函数3y 的表达式及(2)当a 、m 在满足0a m >>的条件下任意变化时，(3)试判断直线PH 与BC 边的交点是否在函数【答案】(1)函数3y 的表达式为325y x =−+，PGH △的面积为12(2)不变，理由见解析 (3)在，理由见解析【分析】（1）由2m =，4a =，可得(20)A ，，()20B −，，12y x=，22y x −=，则4AB =，当2x =，1212y ==，则()21E ，；当14y =，24x =，解得12x =，则142G ⎛⎫ ⎪⎝⎭，；当24y =，24x −=，解得12x =−，则142H ⎛⎫− ⎪⎝⎭，；待定系数法求一次函数3y 的解析式为325y x =−+，当0x =，35y =，则()05P ，，根据()11154222PGH S ⎡⎤⎛⎫=⨯−−⨯− ⎪⎢⎥⎝⎭⎣⎦△，计算求解即可；（2）求解过程同（1）；（3）设直线PH 的解析式为22y k x b =+，将()01P a +，，m a H a a −⎛⎫⎪⎝⎭，，代入22y k x b =+得，2221b am a k b a a =+⎧⎪−⎨+=⎪⎩，解得221b aa k a m =+⎧⎪⎨=⎪−⎩，即1a x a a m y +−=+，当x m a =−，()11y a m a a a m ⨯+=−+=−，则直线PH 与BC 边的交点坐标为()1m a −，，当x m a =−，21m ay m a −=−=，进而可得结论．【详解】（1）解：∵2m =，4a =，∴(20)A ，，()20B −，，12y x=，22y x −=，∴4AB =，当2x =，1212y ==，则()21E ，；当14y =，24x =，解得12x =，则142G ⎛⎫ ⎪⎝⎭，；当24y =，24x −=，解得12x =−，则142H ⎛⎫− ⎪⎝⎭，；设一次函数3y 的解析式为3y kx b =+，将()21E ，，142G ⎛⎫⎪⎝⎭，，代入3y kx b =+得，21142k b k b +=⎧⎪⎨+=⎪⎩，解得25k b =−⎧⎨=⎩，∴325y x =−+，当0x =，35y =，则()05P ，，∴()1111542222PGH S ⎡⎤⎛⎫=⨯−−⨯−=⎪⎢⎥⎝⎭⎣⎦△； ∴函数3y 的表达式为325y x =−+，PGH △的面积为12；（2）解：PGH △的面积不变，理由如下：∵(0)A m ，，(0)B m a −，，1m y x =，2m ay x −=，∴AB a =，当x m =，11m y m ==，则()1E m ，；当1y a =，m a x =，解得m x a =，则m G a a ⎛⎫⎪⎝⎭，；当2y a =，m a a x −=，解得m a x a −=，则m a H a a−⎛⎫ ⎪⎝⎭，；设一次函数3y 的解析式为113k x b y =+，将()1E m ，，m G a a ⎛⎫ ⎪⎝⎭，，代入113k x b y =+得，11111mk b m k b a a +=⎧⎪⎨+=⎪⎩，解得111a k m b a ⎧=−⎪⎨⎪=+⎩，∴31ax a m y =−++，当0x =，31y a =+，则()01P a +，，∴()11122PGH m m a S a a a a ⎡−⎤⎛⎫=⨯−⨯+−= ⎪⎢⎥⎝⎭⎣⎦△； ∴PGH △的面积不变；（3）解：直线PH 与BC 边的交点在函数2y 的图像上，理由如下：设直线PH 的解析式为22y k x b =+，将()01P a +，，m a H a a −⎛⎫⎪⎝⎭，，代入22y k x b =+得，2221b a m a k b a a =+⎧⎪−⎨+=⎪⎩，解得221b aa k a m =+⎧⎪⎨=⎪−⎩， ∴1ax a a m y +−=+，当x m a =−，()11y am a a a m ⨯+=−+=−，∴直线PH 与BC 边的交点坐标为()1m a −，，当x m a =−，21m ay m a −=−=，∴直线PH 与BC 边的交点在函数2y 的图像上．【点睛】本题考查了正方形的性质，一次函数解析式，反比例函数解析式，交点坐标．解题的关键在于对知识的熟练掌握与灵活运用．(1)求一次函数和反比例函数的表达式； (2)求OAB 的面积；(3)过动点()0T t ，作x 轴的垂线l ，l 与一次函数y x m =−+和反比例函数ky x=的图象分别交于当M 在N 的上方时，请直接写出t 的取值范围．【答案】(1)一次函数的解析式为3y x =−+，反比例函数的解析式为2y x =(2)32(3)0t <或12t << 【分析】（1）把()1，2A 分别代入一次函数和反比例函数求出m k 、的值即可得到答案；（2）联立32y x y x =−+⎧⎪⎨=⎪⎩求出点B 的坐标，令直线AB 与x 交于点C ，由直线AB 求出点C 的坐标，最后由1122AOBAOCBOCA B SSSOC y OC y =−=⋅⋅−⋅⋅，进行计算即可得到答案；（3）直接由函数图象即可得到答案．【详解】（1）解：把()1，2A 代入一次函数y x m =−+，得12m −+=，解得：3m =，∴一次函数的解析式为：3y x =−+，把()1，2A 代入反比例函数ky x =，得21k =，解得：2k =，∴反比例函数的解析式为：2y x =；（2）解：联立32y x y x =−+⎧⎪⎨=⎪⎩，解得：12x y =⎧⎨=⎩或21x y =⎧⎨=⎩，()21B ∴，，令直线AB 与x 交于点C ，如图，，当0y =时，30x −+=，解得：3x =， ()30C ∴，，11113323122222AOBAOCBOCA B SS SOC y OC y ∴=−=⋅⋅−⋅⋅=⨯⨯−⨯⨯=（3）解：由图象可得：，当M 在N 的上方时，t 的取值范围为：0t <或12x <<．【点睛】本题考查了求反比例函数的解析式、求一次函数的解析式、反比例函数与一次函数的交点问题，熟练掌握反比例函数和一次函数的图象与性质，是解题的关键．(1)当气球内的气压超过150KPa 少时气球不会爆炸（球体的体积公式(2)请你利用p 与V 的关系试解释为什么超载的车辆容易爆胎．【答案】(1)气球的半径至少为0.2m 时，气球不会爆炸； (2)由于车辆超载，轮胎体积变小，胎内气压增大导致爆胎【分析】（1）设函数关系式为k p =，用待定系数法可得 4.8p V =，即可得当150p =时， 4.80.032150V ==，从而求出0.2r =；（2）由于车辆超载，轮胎体积变小，胎内气压增大导致爆胎．【详解】（1）设函数关系式为kp V =，根据图象可得：1200.04 4.8k pV ==⨯=， ∴4.8p V =，∴当150p =时，4.80.032150V ==，∴3430.0323r ⨯=，解得：0.2r =，4.80k =>，p ∴随V 的增大而减小，∴要使气球不会爆炸，0.032V ≥，此时0.2r ≥， ∴气球的半径至少为0.2m 时，气球不会爆炸；（2）由于车辆超载，轮胎体积变小，胎内气压增大导致爆胎．【点睛】本题考查反比例函数的应用，涉及立方根等知识，解题的关键是读懂题意，掌握待定系数法求出反比例函数的解析式．轴的对称点，OAC 的面积是【答案】(1)y x =(2)(2P −++或(2P −−−【分析】（1）设,k A m m ⎛⎫ ⎪⎝⎭，可得,k C m m ⎛⎫− ⎪⎝⎭，结合OAC 的面积是8．可得()182k m m m +=，从而可得答案；（2）先求解()2,4A ，()2,4C −，可得直线为28y x =+，联立828y x y x ⎧=⎪⎨⎪=+⎩，再解方程组即可．【详解】（1）解：∵点A 在反比例函数(0)ky k x =≠的图象上，∴设,k A m m ⎛⎫⎪⎝⎭，∵点C 是点A 关于y 轴的对称点，∴,k C m m ⎛⎫− ⎪⎝⎭， ∵OAC 的面积是8．∴()182k m m m +=，解得：8k =；∴反比例函数解析式为：8y x =；（2）∵点A 的横坐标为2时， ∴842A y ==，即()2,4A ，则()2,4C −，∵直线2y x b =+过点C ， ∴44b −+=， ∴8b =，∴直线为28y x =+， ∴828y x y x ⎧=⎪⎨⎪=+⎩，解得：24x y ⎧=−+⎪⎨=+⎪⎩或24x y ⎧=−−⎪⎨=−⎪⎩，经检验，符合题意；∴(2P −++或(2P −−−．【点睛】本题考查的是一次函数与反比例函数的综合应用，轴对称的性质，一元二次方程的解法，熟练的利用图形面积建立方程求解是解本题的关键．(1)求反比例函数的表达式；(2)点D 在反比例函数图象上，且横坐标大于3OBDS=【答案】(1)4y x =(2)132y x =−+【分析】（1）根据四边形OABC 是边长为2的正方形求出点B 的坐标，代入ky x =求出k ；（2）设4,D a a ⎛⎫ ⎪⎝⎭，过点D 作DH x ⊥轴，根据OBD OBH BHD ODH S S S S =+−V V V V 面积列方程，求出点D 坐标，再由待定系数法求出直线BD 的函数表达式．【详解】（1）解：四边形OABC 是边长为2的正方形， ∴4OABC S xy ==正方形， ∴4k =；即反比例函数的表达式为4y x =．（2）解：设4,D a a ⎛⎫ ⎪⎝⎭，过点D 作DH x ⊥轴，点()2,2B ，4,D a a ⎛⎫ ⎪⎝⎭，(),0H a ，∴12OBH S OH AB a=⋅=V 1144(2)(2)222BHD a S DH AH a a a −=⋅=⋅⋅−=V ，122ODH S OH DH =⋅=V3OBD OBH BHD ODH S S S S =+−=V V V V∴4(2)232a a a −+−=，解得：14a =，21a =−，经检验4a =，是符合题意的根，即点()4,1D ，设直线BD 的函数解析式为y kx b =+，得∶ 2241k b k b +=⎧⎨+=⎩，解得：123k b ⎧=−⎪⎨⎪=⎩，即：直线BD 的函数解析式为132y x =−+．【点睛】本题考查了反比例函数的几何意义和待定系数法求一次函数解析式，反比例函数ky x =图象上任意一点做x 轴、y 轴的垂线，组成的长方形的面积等于k，灵活运用几何意义是解题关键．2(1)求反比例函数的解析式；(2)点C 在这个反比例函数图象上，连接【答案】(1)8y x =(2)()4,2C【分析】（1）利用正切值，求出4OB =，进而得到()2,4A ，即可求出反比例函数的解析式；（2）过点A 作AE x ⊥轴于点E ，易证四边形ABOE 是矩形，得到2OE =，4AE =，再证明AED △是等腰直角三角形，得到4DE =，进而得到()6,0D ，然后利用待定系数法求出直线AD 的解析式为6y x =−+，联立反比例函数和一次函数，即可求出点C 的坐标．【详解】（1）解：AB y ⊥轴，90ABO ∴∠=︒，1tan 2AOB =∠，12AB OB ∴=，2AB =，4OB ∴=，()2,4A ∴，点A 在反比例函数()0ky x x =>的图象上，248k ∴=⨯=，∴反比例函数的解析式为8y x =；（2）解：如图，过点A 作AE x ⊥轴于点E ，90ABO BOE AEO ∠=∠=∠=︒，∴四边形ABOE 是矩形，2OE AB ∴==，4OB AE ==，45ADO ∠=︒，AED ∴是等腰直角三角形， 4DE AE ∴==，246OD OE DE ∴=+=+=，()6,0D ∴，设直线AD 的解析式为y kx b =+，2460k b k b +=⎧∴⎨+=⎩，解得：16k b =−⎧⎨=⎩， ∴直线AD 的解析式为6y x =−+，点A 、C 是反比例函数8y x =和一次函数6y x =−+的交点，联立86y x y x ⎧=⎪⎨⎪=−+⎩，解得：24x y =⎧⎨=⎩或42x y =⎧⎨=⎩，()2,4A ， ()4,2C ∴．【点睛】本题是反比例函数综合题，考查了锐角三角函数值，矩形的判定和性质，待定系数法求函数解析式，反比例函数和一次函数交点问题等知识，求出直线AD 的解析式是解题关键．(1)求反比例函数的表达式和点E 的坐标；(2)若一次函数y x m =+与反比例函数的部分时（点M 可与点,D E 重合）【答案】(1)反比例函数解析式为y x =，()22E ，(2)30m −≤≤【分析】（1）根据矩形的性质得到BC OAAB OA ∥，⊥，再由()4,1D 是AB 的中点得到()42B ，，从而得到点E的纵坐标为2，利用待定系数法求出反比例函数解析式，进而求出点E 的坐标即可；（2）求出直线y x m =+恰好经过D 和恰好经过E 时m 的值，即可得到答案．【详解】（1）解：∵四边形OABC 是矩形，∴BC OAAB OA ∥，⊥， ∵()4,1D 是AB 的中点， ∴()42B ，，∴点E 的纵坐标为2，∵反比例函数()0ky x x =>的图象分别与,AB BC 交于点()4,1D 和点E ，∴14k =，∴4k =，∴反比例函数解析式为4y x =，在4y x =中，当42y x ==时，2x =， ∴()22E ，；（2）解：当直线 y x m =+经过点()22E ，时，则22m +=，解得0m =；当直线 y x m =+经过点()41D ，时，则41m +=，解得3m =−；∵一次函数y x m =+与反比例函数()0ky x x =>的图象相交于点M ，当点M 在反比例函数图象上,D E 之间的部分时（点M 可与点,D E 重合）， ∴30m −≤≤．【点睛】本题主要考查了求一次函数解析式，一次函数与反比例函数综合，矩形的性质等等，灵活运用所学知识是解题的关键．【答案】(1)反比例函数的表达式为y x =−；一次函数的表达式为22y x =−+(2)142BC =【分析】（1）利用待定系数法即可求解；（2）先求得直线BC 的表达式为1y =，再分别求得B C 、的坐标，据此即可求解．【详解】（1）解：∵反比例函数()0ky x x =<的图象经过点()1,4A −，∴144k =−⨯=−， ∴反比例函数的表达式为4y x =−；∵一次函数2y x m =−+的图象经过点()1,4A −，∴()421m=−⨯−+，∴2m =，∴一次函数的表达式为22y x =−+；（2）解：∵1OD =， ∴()01D ，，∴直线BC 的表达式为1y =， ∵1y =时，14x =−，解得4x =−，则()41B −，，∵1y =时，122x =−+，解得12x =，则112C ⎛⎫ ⎪⎝⎭，，∴()114422BC =−−=．【点睛】本题考查一次函数、反比例函数图象上点的坐标特征，待定系数法是求函数解析式的基本方法．(1)求反比例函数和一次函数的表达式；(2)求AOB 的面积； (3)请根据图象直接写出不等式【答案】(1)12y x =−，32y x =−+(2)9(3)<2x −或04x <<【分析】（1）把点B 代入反比例函数()0ky k x =≠，即可得到反比例函数的解析式；把点A 代入反比例函数，即可求得点A 的坐标；把点A 、B 的坐标代入一次函数一次函数()0y ax b a =+<即可求得a 、b 的值，从而得到一次函数的解析式；（2）AOB 的面积是AOC 和BOC 的面积之和，利用面积公式求解即可；（3）利用图象，找到反比例函数图象在一次函数图象下方所对应的x 的范围，直接得出结论．【详解】（1）∵点()4,3B −在反比例函数ky x =的图象上，∴34k −=，解得：12k =− ∴反比例函数的表达式为12y x =−．∵(),3A m m −在反比例函数12y x =−的图象上，∴123m m =−−，解得12m =，22m =−（舍去）．∴点A 的坐标为()2,6−．∵点A ，B 在一次函数y ax b =+的图象上，把点()2,6A −，()4,3B −分别代入，得2643a b a b −+=⎧⎨+=−⎩，解得323a b ⎧=−⎪⎨⎪=⎩，∴一次函数的表达式为332y x =−+；（2）∵点C 为直线AB 与y 轴的交点，∴把0x =代入函数332y x =−+，得3y = ∴点C 的坐标为()0,3 ∴3OC =，∴AOB AOC BOC SS S =+ 1122A B OC x OC x =⋅⋅+⋅⋅11323422=⨯⨯+⨯⨯9=．（3）由图象可得，不等式k ax b x <+的解集是<2x −或04x <<．【点睛】此题是反比例函数与一次函数的交点问题，考查了待定系数法求函数的解析式，三角形面积，函数与不等式的关系，求出两个函数解析式是解本题的关键．。

2022年中考复习《反比例函数应用题》专项练习附答案

反比例函数应用题1、〔2021•曲靖〕某地资源总量Q 一定，该地人均资源享有量与人口数n的函数关系图象是〔〕A．B．C．D．考点：反比例函数的应用；反比例函数的图象．分析：根据题意有：=；故y与x 之间的函数图象双曲线，且根据，n 的实际意义，n 应大于0；其图象在第一象限．解答：解：∵由题意，得Q=n，∴=，∵Q为一定值，∴是n的反比例函数，其图象为双曲线，又∵＞0，n＞0，∴图象在第一象限．应选B．点评：此题考查了反比例函数在实际生活中的应用，现实生活中存在大量成反比例函数的两个变量，解答该类问题的关键是确定两个变量之间的函数关系，然后利用实际意义确定其所在的象限．2、〔2021•绍兴〕教室里的饮水机接通电源就进入自动程序，开机加热时每分钟上升10℃，加热到100℃，停止加热，水温开始下降，此时水温〔℃〕与开机后用时〔min〕成反比例关系．直至水温降至30℃，饮水机关机．饮水机关机后即刻自动开机，重复上述自动程序．假设在水温为30℃时，接通电源后，水温y〔℃〕和时间〔min〕的关系如图，为了在上午第一节下课时〔8：45〕能喝到不超过50℃的水，那么接通电源的时间可以是当天上午的〔〕A．7：20 B．7：30 C．7：45 D．7：50考反比例函数的应用．点：分析：第1步：求出两个函数的解析式；第2步：求出饮水机完成一个循环周期所需要的时间；第3步：求出每一个循环周期内，水温不超过50℃的时间段；第4步：结合4个选择项，逐一进行分析计算，得出结论．解答：解：∵开机加热时每分钟上升10℃，∴从30℃到100℃需要7分钟，设一次函数关系式为：y=k1x+b，将〔0，30〕，〔7，100〕代入y=k1x+b得k1=10，b=30∴y=10x+30〔0≤x≤7〕，令y=50，解得x=2；设反比例函数关系式为：y=，将〔7，100〕代入y=得k=700，∴y=，将y=30代入y=，解得x=；∴y=〔7≤x≤〕，令y=50，解得x=14．所以，饮水机的一个循环周期为分钟．每一个循环周期内，在0≤x≤2及14≤x≤时间段内，水温不超过50℃．逐一分析如下：选项A：7：20至8：45之间有85分钟．85﹣×3=15，位于14≤x≤时间段内，故可行；选项B：7：30至8：45之间有75分钟．75﹣×3=5，不在0≤x≤2及14≤x≤时间段内，故不可行；选项C：7：45至8：45之间有60分钟．60﹣×2=≈13.3，不在0≤x≤2及14≤x≤时间段内，故不可行；选项D：7：50至8：45之间有55分钟．55﹣×2=≈8.3，不在0≤x≤2及14≤x≤时间段内，故不可行．综上所述，四个选项中，唯有7：20符合题意．应选A．点评：此题主要考查了一次函数及反比例函数的应用题，还有时间的讨论问题．同学们在解答时要读懂题意，才不易出错．3、〔2021•玉林〕工匠制作某种金属工具要进行材料煅烧和锻造两个工序，即需要将材料烧到800℃，然后停止煅烧进行锻造操作，经过8min时，材料温度降为600℃．煅烧时温度y 〔℃〕与时间x〔min〕成一次函数关系；锻造时，温度y〔℃〕与时间x〔min〕成反比例函数关系〔如图〕．该材料初始温度是32℃．〔1〕分别求出材料煅烧和锻造时y与x的函数关系式，并且写出自变量x的取值范围；〔2〕根据工艺要求，当材料温度低于480℃时，须停止操作．那么锻造的操作时间有多长？考点：反比例函数的应用；一次函数的应用．分析：〔1〕首先根据题意，材料加热时，温度y与时间x成一次函数关系；停止加热进行操作时，温度y与时间x成反比例关系；将题中数据代入用待定系数法可得两个函数的关系式；〔2〕把y=480代入y=中，进一步求解可得答案．解答：解：〔1〕停止加热时，设y=〔k≠0〕，由题意得600=，解得k=4800，当y=800时，解得x=6，∴点B的坐标为〔6，800〕材料加热时，设y=ax+32〔a≠0〕，由题意得800=6a+32，解得a=128，∴材料加热时，y与x的函数关系式为y=128x+32〔0≤x≤5〕．∴停止加热进行操作时y与x的函数关系式为y=〔5＜x≤20〕；〔2〕把y=480代入y=，得x=10，故从开始加热到停止操作，共经历了10分钟．答：从开始加热到停止操作，共经历了10分钟．点评：考查了反比例函数和一次函数的应用，现实生活中存在大量成反比例函数的两个变量，解答该类问题的关键是确定两个变量之间的函数关系，然后利用待定系数法求出它们的关系式。

九年级数学反比例函数综合应用题

（1）求k的值及点E的坐标；
（2）若点F是OC边上一点，且△FBC∽△DEB，求直线FB的解析式．
九年级数学反比例函数综合应用题
1．如图，一次函数y=kx+b的图象l与坐标轴分别交于点E、F，与双曲线y=- （x＜0）交于点P（-1，n），且F是PE的中点．（1）求直线l的解析式；（2）若直线x=a与l交于点A，与双曲线交于点B（不同于A），问a为何值时，PA=PB？
2．如图，已知反比例函数y= 的图象与正比例函数y=kx的图象交于点A（m，-2）．（1）求正比例函数的解析式及两函数图象另一个交点B的坐标；（2）试根据图象写出不等式的解集；（3）在反比例函数图象上是否存在点C，使△OAC为等边三角形？若存在，求出点C的坐标；若不存在，请说明理由．
（2）若将矩形只向下平移，矩形的两个顶点恰好同时落在反比例函数的图象上，求反比例函数的解析式和此时直线AC的解析式y=mx+n．并直接写出满足 <mx+n的x取值范围．
9．已知直线y=4-x与x轴、y轴分别相交于C、D两点，有反比例函数y= （m＞0，x＞0）的图象与之在同一坐标系．（1）若直线y=4-x与反比例函数图象相切，求m的值；（2）如图1，若两图象相交于A、B两点，其中点A的横坐标为1，利用函数图象求关于x的不等式4-x＜的解集；
7．已知直线OA：y1=k1x与双曲线y2= 交于第一象限于点A（2，2）
（1）求直线和双曲线的解析式；
（2）将直线OA沿y轴向下平移，交y轴于点C，交双曲线于点B，直线BA交y轴于点D，若O恰好是CD的中点，求平移后直线BC的解析式．
8．如图，在平面直角坐标系中，反比例函数y= 的图象和矩形ABCD在第二象限，AD平行于x轴，且AB=2，AD=4，点C的坐标为（-2，4）．（1）直接写出A、B、D三点的坐标；

中考数学《反比例函数》专项练习(附答案解析)

中考数学《反比例函数》专项练习（附答案解析）一、综合题1．已知：如图1，函数y1=kx 和y2=xk(k>1)的图象相交于点A和点B .（1）求点A和点B的坐标（用含k的式子表示）；（2）如图2，点C的坐标为(1，k)，点D是第一象限内函数y1的图象上的动点，且在点A的右侧，直线AC、BC、AD、BD分别与x轴相交于点E、F、G、H .①判定△CEF的形状，并说明理由；②点D在运动的过程中，∠CAD和∠CBD的度数和是否变化？如果变化，说明理由；如果不变，求出∠CAD和∠CBD的度数和.2．在平面直角坐标系中，我们把横坐标和纵坐标相等的点叫“梦之点”，例如点（1，1），（－2，－2），（√2，√2），…都是“梦之点”，显然“梦之点”有无数个.（1）若点P（2，m）是反比例函数y=nx（n为常数，n≠0）的图象上的“梦之点”，求这个反比例函数的解析式；（2）函数y＝3kx＋s－1（k，s为常数）的图象上存在“梦之点”吗？若存在，请求出“梦之点”的坐标，若不存在，说明理由.3．如图，点A是坐标原点，点D是反比例函数y=6x(x>0)图象上一点，点B在x轴上，AD=BD，四边形ABCD是平行四边形，BC交反比例函数y=6x(x>0)图象于点E.（1）平行四边形BCD 的面积等于；（2）设D 点横坐标为m ，试用m 表示点E 的坐标；（要有推理和计算过程）（3）求 CE:EB 的值；（4）求 EB 的最小值.4．如图，一次函数y=kx+b 的图象与反比例函数y= mx 的图象交于点A （﹣3，m+8），B （n ，﹣6）两点．（1）求一次函数与反比例函数的解析式；（2）求△AOB 的面积．5．已知双曲线y=1x （x ＞0），直线l 1：y ﹣√2=k （x ﹣√2）（k ＜0）过定点F 且与双曲线交于A ，B 两点，设A （x 1，y 1），B （x 2，y 2）（x 1＜x 2），直线l 2：y=﹣x+√2．（1）若k=﹣1，求△OAB 的面积S ；（2）若AB=52√2，求k 的值；（3）设N （0，2√2），P 在双曲线上，M 在直线l 2上且PM ∥x 轴，求PM+PN 最小值，并求PM+PN 取得最小值时P 的坐标．（参考公式：在平面直角坐标系中，若A （x 1，y 1），B （x 2，y 2）则A ，B 两点间的距离为AB=√(x 1−x 2)2+(y 1−y 2)2）6．已知反比例函数y=1−2mx( m为常数)的图象在一、三象限.（1）求m的取值范围.（2）如图，若该反比例函数的图象经过▱ ABCD的顶点D，点A，B的坐标分别为(0，3)，(-2，0).①求出反比例函数表达式；②设点P是该反比例函数图象上的一点，若OD=OP，则P点的坐标为▲ .若以D，O，P为顶点的三角形是等腰三角形，则满足条件的点P的个数为▲ .7．绘制函数y=x+1x的图象，我们经历了如下过程：确定自变量x的取值范围是x≠0；列表﹣﹣描点﹣﹣连线，得到该函数的图象如图所示．x …-4 -3 -2 -1 −12−13−141413121 2 3 4 …y …−414−313−212−2−212−313−4144143132122 212313414…观察函数图象，回答下列问题：（1）函数图象在第象限；（2）函数图象的对称性是A．既是轴对称图形，又是中心对称图形B．只是轴对称图形，不是中心对称图形C．不是轴对称图形，而是中心对称图形D．既不是轴对称图形，也不是中心对称图形（3）在x＞0时，当x＝时，函数y有最（大，小）值，且这个最值等于；在x＜0时，当x＝时，函数y有最（大，小）值，且这个最值等于；=−2x+1是否有实数解？说明理由．（4）方程x+1x8．菱形ABCD在平面直角坐标系中的位置如图所示，对角线AC与BD的交点E恰好在y轴上，过点D和BC的中点H的直线交AC于点F，线段DE，CD的长是方程x2﹣9x+18=0的两根，请解答下列问题：（1）求点D的坐标；（k≠0）的图象经过点H，则k= ；（2）若反比例函数y= kx（3）点Q在直线BD上，在直线DH上是否存在点P，使以点F，C，P，Q为顶点的四边形是平行四边形？若存在，请直接写出点P的坐标；若不存在，请说明理由．9．设P(x,0)是x轴上的一个动点，它与原点的距离为y1．（1）求y1关于x的函数解析式，并画出这个函数的图象；的图象与函数y1的图象相交于点A，且点A的纵坐标为2．（2）若反比例函数y2=kx①求k的值；②结合图象，当y1>y2时，写出x的取值范围．10．受新冠肺炎疫情的影响，运城市某化工厂从2020年1月开始产量下降．借此机会，为了贯彻“发展循环经济，提高工厂效益”的绿色发展理念；管理人员对生产线进行为期5个月的升级改造，改造期间的月利润与时间成反比例函数；到5月底开始恢复全面生产后，工厂每月的利润都比前一个月增加10万元．设2020年1月为第1个月，第x个月的利润为y万元，其图象如图所示，试解决下列问题：（1）分别写出该化工厂对生产线进行升级改造前后，y与x的函数表达式．（2）到第几个月时，该化工厂月利润才能再次达到100万元？（3）当月利润少于50万元时，为该化工厂的资金紧张期，问该化工厂资金紧张期共有几个月？11．（如图，四边形ABCD在平面直角坐标系的第一象限内，其四个顶点分别在反比例函数y1＝nx 与y2＝4nx的图象上，对角线AC⊥BD于点P，AC⊥x轴于点N（2，0）（1）若CN＝12，试求n的值；（2）当n＝2，点P是线段AC的中点时，试判断四边形ABCD的形状，并说明理由；（3）直线AB与y轴相交于E点．当四边形ABCD为正方形时，请求出OE的长度．12．如图点A、B分别在x，y轴上，点D在第一象限内，DC⊥x轴于点C，AO=CD=2，AB=DA= √5，反比例函数y= kx（k＞0）的图象过CD的中点E．（1）求证：△AOB≌△DCA；（2）求k的值；（3）△BFG和△DCA关于某点成中心对称，其中点F在y轴上，试判断点G是否在反比例函数的图象上，并说明理由．13．如图所示，一次函数y=kx+b的图象与x轴、y轴分别交于点A、B，且与反比例函数y=m的图象在第二象限交于点C，CD⊥x轴，垂足为点D.若OB=2OA=3OD= x12 .（1）求一次函数与反比例函数的解析式；（2）若两函数图象的另一个交点为E，连结DE，求△CDE的面积；（3）直接写出不等式kx+b≤m的解集.x与y2= 14．某校九年级数学小组在课外活动中，研究了同一坐标系中两个反比例函数y1=k1xk2(k2>k1>0)在第一象限图象的性质，经历了如下探究过程：x操作猜想：（1）如图①，当k1=2，k2=6时，在y轴的正方向上取一点A作x轴的平行线交y1于点B，交y2于点C .当OA=1时，AB=，BC=，BC AB =；当OA=3时，AB=，BC=，BCAB=；当OA=a时，猜想BCAB=（2）在y轴的正方向上任意取点A作x轴的平行线，交y1于点B、交y2于点C，请用含k1、k2的式子表示BCAB的值，并利用图②加以证明.（3）如图③，若k2=12，BCAB =12，在y轴的正方向上分别取点A、D(OD>OA)作x轴的平行线，交y1于点B、E，交y2于点C、F，是否存在四边形ADFB是正方形？如果存在，求OA的长和点B的坐标；如果不存在，请说明理由.15．如图，直线y＝2x+2与y轴交于A点，与反比例函数y＝kx（x＞0）的图象交于点M，过M作MH⊥x轴于点H，且tan∠AHO＝2．（1）求H点的坐标及k的值；（2）点P在y轴上，使△AMP是以AM为腰的等腰三角形，请直接写出所有满足条件的P 点坐标；（3）点N（a，1）是反比例函数y＝kx（x＞0）图象上的点，点Q（m，0）是x轴上的动点，当△MNQ的面积为3时，请求出所有满足条件的m的值．16．如图，双曲线y1＝k1x与直线y2＝xk2的图象交于A、B两点．已知点A的坐标为（4，1），点P（a，b）是双曲线y1＝k1x上的任意一点，且0＜a＜4．（1）分别求出y1、y2的函数表达式；（2）连接PA、PB，得到△PAB，若4a＝b，求三角形ABP的面积；（3）当点P在双曲线y1＝k1x上运动时，设PB交x轴于点E，延长PA交x轴于点F，判断PE与PF的大小关系，并说明理由．参考答案与解析1．【答案】（1）解：由题意，联立{y=kxy=xk，解得{x=ky=1或{x=−ky=−1，∵点A在第一象限，点B在第二象限，且k>1，∴A(k，1)，B(−k，−1)（2）解：①△CEF是等腰直角三角形，理由如下：设直线BC的解析式为y=k0x+b0，将点B(−k，−1)，C(1，k)代入得：{−kk0+b0=−1k0+b0=k，解得{k0=1b0=k−1，则直线BC的解析式为y=x+k−1，当y=0时，x+k−1=0，解得x=1−k，即F(1−k，0)，同理可得：点E的坐标为E(1+k，0)，∴CF=√(1−k−1)2+(0−k)2=√2k，CE=√(1+k−1)2+(0−k)2=√2k，EF=1+k−(1−k)=2k，∴CE=CF，CE2+CF2=4k2=EF2，∴△CEF是等腰直角三角形；②由题意，设点D的坐标为D(m，km)，则m>k>1，∵△CEF是等腰直角三角形，∴∠CFE=∠CEF=45°，∴∠BFH=∠AEG=135°，设直线BD的解析式为y=k1x+b1，将点B(−k，−1)，D(m，km )代入得：{−kk1+b1=−1mk1+b1=km，解得{k1=1mb1=k−mm，则直线BD的解析式为y=1m x+k−mm，当y=0时，1m x+k−mm=0，解得x=m−k，即H(m−k，0)，同理可得：点G的坐标为G(k+m，0)，∴DH=√(m−k−m)2+(0−km )2=km√1+m2，DG=√(k+m−m)2+(0−km )2=km√1+m2，∴DH=DG，∴∠DHG=∠DGH，∵∠DHG=∠BHF，∴∠DGH=∠BHF，∴∠CAD+∠CBD=∠AEG+∠DGH+∠CBD，=∠BFH+∠BHF+∠CBD，=180°，即∠CAD与∠CBD的度数和不变，度数和为180°2．【答案】（1）解：根据题意，“梦之点”就是有关函数图象与直线y=x的交点，其坐标就是对应的方程组的解.由题意可得：m=2由点P(2， 2)在反比例函数y=nx图象上，可得n=2×2=4故所求的反比例函数的解析式为y=4x（2）解：由题意可得：（Ⅰ）当k=0时，y=s−1，此时“梦之点”的坐标为(s−1， s−1 ) . （Ⅱ）当k≠0 时， (3k−1)x=1−s显然，此方程的解的情况决定函数y=3kx+s−1的图象上“梦之点”的存在情况，当k=13， s≠1时，方程无解，不存在“梦之点”；当k=13， s=1时，方程有无数个解，此时存在无数个“梦之点”，“梦之点”的坐标可表示为(ℎ，ℎ)（ℎ为任意实数）；当k≠13时，得{x=1−s3k−1y=1−s3k−1，即“梦之点”的坐标为(1−s3k−1， 1−s3k−1)3．【答案】（1）12（2）解：由题意D(m,6m)，由（1）可知AB=2m，∵四边形ABCD是平行四边形，∴CD=AB=2m，∴C(3m,6m) .∵B(2m,0)，C(3m,6m)，∴直线BC的解析式为y=6m2x−12m，由{y=6xy=6m2x−12m，解得{x=(√2+1)my=6√2−6m或{x=(1−√2)my=6(1+√2)m（舍弃），∴E((√2+1)m,6√2−6m)；（3）解：作EF⊥x轴于F，CG⊥x轴于G . ∵EF//CG，∴CE BE=FG BF=√2+1)m (√2+1)m−2m =√2√2−1=√2 ；（4）解：∵CEBE =√2 ∴BE =√2+1 ，要使得 BE 最小，只要 AD 最小， ∵AD =√m 2+36m 2=√(m −6m )2+12 ，∴AD 的最小值为 2√3 ， ∴BE 的最小值为√3√2+1=2√6−2√3 .4．【答案】（1）解：将A （﹣3，m+8）代入反比例函数y= mx 得，m −3=m+8，解得m=﹣6， m+8=﹣6+8=2，所以，点A 的坐标为（﹣3，2），反比例函数解析式为y=﹣ 6x ，将点B （n ，﹣6）代入y=﹣ 6x 得，﹣ 6n =﹣6，解得n=1，所以，点B 的坐标为（1，﹣6），将点A （﹣3，2），B （1，﹣6）代入y=kx+b 得， {−3k +b =2k +b =−6 ，解得 {k =−2b =−4，所以，一次函数解析式为y=﹣2x ﹣4；（2）解：设AB 与x 轴相交于点C ，令﹣2x ﹣4=0解得x=﹣2，所以，点C 的坐标为（﹣2，0），所以，OC=2， S △AOB =S △AOC +S △BOC ， = 12 ×2×3+ 12 ×2×1，=3+1， =4．5．【答案】（1）解：当k=-1时，l 1：y=﹣x+2√2，联立得，{y =−x +2√2y =1x ，化简得x 2﹣2√2x+1=0，解得：x 1=√2﹣1，x 2=√2+1，设直线l 1与y 轴交于点C ，则C （0，2√2）． S △OAB =S △AOC ﹣S △BOC =12•2√2•（x 2﹣x 1）=2√2；（2）解：根据题意得：{y −√2=k(x −√2)y =1x 整理得：kx 2+√2（1﹣k ）x ﹣1=0（k ＜0）， ∵△=[√2（1﹣k ）]2﹣4×k ×（﹣1）=2（1+k 2）＞0， ∴x 1、x 2 是方程的两根， ∴{x 1+x 2=√2(k−1)k x 1·x 2=−1k①， ∴AB=√(x 1−x 2)2+(y 1−y 2)2=√(x 1−x 2)2+(1x 1−1x 2)2=√(x 1−x 2)2(1+1x 12·x 22)=√[(x 1+x 2)2−4x 1x 2](1+1x 12·x 22)，将①代入得，AB=√2(k 2+1)2k 2=√2(k 2+1)−k （k ＜0），∴√2(k 2+1)−k =5√22，整理得：2k2+5k+2=0，解得：k=﹣2，或 k=12；（3）解：∵直线l1：y﹣√2=k（x﹣√2）（k＜0）过定点F, ∴ F（√2，√2）.如图：设P（x，1x ），则M（﹣1x+√2，1x），则PM=x+1x ﹣√2=√(x+1x−√2)2=√x2+1x2−2√2(x+1x)+4，∵PF=√(x−√2)2+(1x −√2)2=√x2+1x2−2√2(x+1x)+4，∴PM=PF．∴PM+PN=PF+PN≥NF=2，当点P在NF上时等号成立，此时NF的方程为y=﹣x+2√2，由（1）知P（√2﹣1，√2+1），∴当P（√2﹣1，√2+1）时，PM+PN最小值是2．6．【答案】（1）解：根据题意，得1−2m>0，解得m<12，∴m的取值范围是m<12.（2）解：①∵四边形ABCD是平行四边形，A(0，3)，B(−2，0)，∴D(2，3) .把D(2，3)代入y=1−2mx ，得3=1−2m2，∴1−2m=6 .∴反比例函数表达式为y=6x；②(3，2)或(-2，-3)或(-3，-2)；4 7．【答案】（1）一、三（2）C（3）1；小；2；−1；大；−2（4）解：方程x ＋ 1x ＝﹣2x ＋1没有实数解，理由为：y ＝x ＋ 1x 与y ＝﹣2x ＋1在同一直角坐标系中无交点．8．【答案】（1）解：x 2﹣9x+18=0，（x ﹣3）（x ﹣6）=0， x=3或6， ∵CD ＞DE ， ∴CD=6，DE=3， ∵四边形ABCD 是菱形，∴AC ⊥BD ，AE=EC= √62−32 =3 √3 ， ∴∠DCA=30°，∠EDC=60°， Rt △DEM 中，∠DEM=30°， ∴DM= 12 DE= 32 ， ∵OM ⊥AB ，∴S 菱形ABCD = 12 AC •BD=CD •OM ， ∴12×6√3×6 =6OM ，OM=3 √3 ， ∴D （﹣ 32 ，3 √3 ）（2）解：（3）解：如图1，①∵DC=BC ，∠DCB=60°， ∴△DCB 是等边三角形， ∵H 是BC 的中点，∴DH⊥BC，∴当Q与B重合时，如图1，四边形CFQP是平行四边形，∵FC=FB，∴∠FCB=∠FBC=30°，∴∠ABF=∠ABC﹣∠CBF=120°﹣30°=90°，∴AB⊥BF，CP⊥AB，Rt△ABF中，∠FAB=30°，AB=6，∴FB=2 √3 =CP，，√3）；∴P（92②如图2，∵四边形QPFC是平行四边形，∴CQ∥PH，由①知：PH⊥BC，∴CQ⊥BC，Rt△QBC中，BC=6，∠QBC=60°，∴∠BQC=30°，∴CQ=6 √3，连接QA，∵AE=EC，QE⊥AC，∴QA=QC=6 √3，∴∠QAC=∠QCA=60°，∠CAB=30°，∴∠QAB=90°，∴Q（﹣92，6 √3），由①知：F（32，2 √3），由F到C的平移规律可得P到Q的平移规律，则P（﹣92﹣3，6 √3﹣√3），即P（﹣152，5 √3）；③如图3，四边形CQFP是平行四边形，同理知：Q（﹣92，6 √3），F（32，2 √3），C（92，3 √3），∴P（212，﹣√3）；综上所述，点P的坐标为：（92，√3）或（﹣152，5 √3）或（212，﹣√3）．9．【答案】（1）解：由题意y1=|x|．函数图象如图所示：（2）解：①当点A在第一象限时，由题意A(2,2)，∴2=k2，∴k=4．同法当点A在第二象限时，k=−4，②观察图象可知：当k>0时，x>2时，y1>y2或x<0时，y1>y2．当k<0时，x<−2时，y1>y2或x>0时，y1>y2．10．【答案】（1）解：由题意得，设前5个月中y= kx，把x=1，y=100代入得，k=100，∴y与x之间的函数关系式为y= 100x（0<x<5，且x为整数），把x=5代入，得y=20，由题意设5月份以后y与x的函数关系式为y=10x+b，把x=5，y=20代入得，20=10×5+b，解得：b=-30，∴y与x之间的函数关系式为y=10x-30（x>5且x为整数）；（2）解：在函数y=10x−30中，令y=100，得10x−30=100解得：x=13答：到第13个月时，该化工厂月利润再次达到100万元．（3）解：在函数y=100x中，当y=50时，x=2，∵100>0，y随x的增大而减小，∴当y<50时，x>2在函数y=10x−30中，当y<50时，得10x−30<50解得：x<8∴2<x<8且x为整数；∴x可取3，4，5，6，7；共5个月．答：该化工厂资金紧张期共有5个月．11．【答案】（1）解：∵点N的坐标为（2，0），CN⊥x轴，且CN＝12，∴点C的坐标为（2，12）．∵点C在反比例函数y1＝nx的图象上，∴n＝2×12＝1．（2）解：四边形ABCD为菱形，理由如下：当n＝2时，y1＝nx＝2x，y2＝4nx＝8x．当x＝2时，y1＝2x＝1，y2＝8x＝4，∴点C的坐标为（2，1），点A的坐标为（2，4）．∵点P是线段AC的中点，∴点P 的坐标为（2， 52 ）．当y ＝ 52 时， 2x ＝ 52 ， 8x ＝ 52 ，解得：x ＝ 45 ，x ＝ 165 ，∴点B 的坐标为（ 45 ， 52 ），点D 的坐标为（ 165 ， 52 ）， ∴BP ＝2﹣ 45 ＝ 65 ，DP ＝ 165 ﹣2＝ 65 ， ∴BP ＝DP ．又∵AP ＝CP ，AC ⊥BD ， ∴四边形ABCD 为菱形．（3）解：∵四边形ABCD 为正方形， ∴AC ＝BD ，且点P 为线段AC 及BD 的中点．当x ＝2时，y 1＝ 12 n ，y 2＝2n ，∴点A 的坐标为（2，2n ），点C 的坐标为（2， 12 n ），AC ＝ 32 n ， ∴点P 的坐标为（2， 54 n ）．同理，点B 的坐标为（ 45 ， 54 n ），点D 的坐标为（ 165 ， 54 n ），BD ＝ 125 ． ∵AC ＝BD ， ∴32 n ＝ 125 ， ∴n ＝ 85 ，∴点A 的坐标为（2， 165 ），点B 的坐标为（ 45 ，2）．设直线AB 的解析式为y ＝kx+b （k ≠0），将A （2， 165 ），B （ 45 ，2）代入y ＝kx+b ，得： {2k +b =16545k +b =2 ，解得： {b =65k =1 ，∴直线AB 的解析式为y ＝x+ 65 ．当x ＝0时，y ＝x+ 65 ＝ 65 ， ∴点E 的坐标为（0， 65 ），∴当四边形ABCD为正方形时，OE的长度为6．512．【答案】（1）证明：∵点A、B分别在x，y轴上，点D在第一象限内，DC⊥x轴，∴∠AOB=∠DCA=90°，在Rt△AOB和Rt△DCA中，AO=CD，AB=DA∴Rt△AOB≌Rt△DCA（HL）（2）解：在Rt△ACD中，CD=2，AD= √5，∴AC= =1，∴OC=OA+AC=2+1=3，∴D点坐标为（3，2），∵点E为CD的中点，∴点E的坐标为（3，1），k=3×1=3（3）解：点G在反比例函数的图象上．理由如下：∵△BFG和△DCA关于某点成中心对称，∴△BFG≌△DCA，∴FG=CA=1，BF=DC=2，∠BFG=∠DCA=90°，而OB=AC=1，∴OF=OB+BF=1+2=3，∴G点坐标为（1，3），∵1×3=3，∴G（1，3）在反比例函数y= 的图象上13．【答案】（1）解：∵OB =2OA =3OD =12 ∴OA =6,OD =4 ∴A(6,0),B(0,12)把 A(6,0),B(0,12) 分别代入 y =kx +b 得： {6k +b =0b =12 ，解之得： m =−4×20=−80 ∴一次函数的解析式为 y =−2x +12 令 x =−4 ，则 y =20 ∴C(−4,20)把 C(−4,20) 代入 y =mx 得：m =−4×20=−80∴反比例函数的解析式为 y =−80x ；（2）解：解方程组 {y =−2x +12y =−80x 得： {x 1=−4y 1=20,{x 2=10y 2=−8∴E(10,−8)∴S ΔCDE =S ΔADC +S ΔADE=12AD ⋅(CD +|y E |)=12×(4+6)×(20+8) =140（3）解：如图：当x ＜-4时， y =mx 的图象在 y =kx +b 的下方，即 kx +b ＞ mx ；当 −4 ≤ x <0 时， y =mx 的图象在 y =kx +b 的上方，即 kx +b ≤ mx ；当0＜x ＜10时， y =mx 的图象在 y =kx +b 的下方，即 kx +b ＞ mx ；当 x ≥10时， y =mx 的图象在 y =kx +b 的上方，即 kx +b ≤ mx ；综上可得，不等式 kx +b ≤ mx 的解集为 −4 ≤ x <0 或 x ≥10. 14．【答案】（1）2；4；2；23；43；2；2 数学思考：（2）BCAB =k 2−k 1k 1证明：∵AB ·OA =k 1 ， AC ·OA =k 2 ， ∴AC ·OA −AB ·OA =BC ·OA =k 2−k 1 ，∴BCAB =BC·OAAB·OA=k2−k1k1.推广应用：（3）解：若四边形ADFB是正方形，设点B的坐标为(a,b)（a>0，b>0），则有DF=DA=AB=a，OA=b，OD=a+b，∴点F的坐标为(a,a+b) .∵k2=12，BCAB =k2−k1k1=12，∴12−k1k1=12，解得：k1=8 .∵点B在y=8x 图象上，点F在y=12x图象上，∴ab=8，a (a+b)=12，∴a2=12−8=4，∴a=2，∴b=4，∴OA=4，点B的坐标为(2,4) .15．【答案】（1）解：由y＝2x+2可知A（0，2），即OA＝2，∵tan∠AHO＝2，∴OH＝1，∴H（1，0），∵MH⊥x轴，∴点M的横坐标为1，∵点M在直线y＝2x+2上，∴点M的纵坐标为4，即M（1，4），∵点M在y＝kx上，∴k＝1×4＝4；（2）解：①当AM＝AP时，∵A（0，2），M（1，4），∴AM＝√5，则AP＝AM＝√5，∴此时点P的坐标为（0，2﹣√5）或（0，2+ √5）；②若AM＝PM时，设P（0，y），则PM＝√(1−0)2+(4−y)2，∴√(1−0)2+(4−y)2＝√5，解得y＝2（舍）或y＝6，此时点P的坐标为（0，6），综上所述，点P的坐标为（0，6）或（0，2+ √5），或（0，2﹣√5）；（3）解：∵点N（a，1）在反比例函数y＝4x（x＞0）图象上，∴a＝4，∴点N（4，1），延长MN交x轴于点C，设直线MN的解析式为y＝mx+n，则有{m+n＝44m+n＝1,，解得{m＝−1n＝5，∴直线MN的解析式为y＝﹣x+5．∵点C是直线y＝﹣x+5与x轴的交点，∴点C的坐标为（5，0），OC＝5，∵S△MNQ＝3，∴S△MNQ ＝S△MQC﹣S△NQC＝12×QC×4﹣12×QC×1＝32QC＝3，∴QC＝2，∵C（5，0），Q（m，0），∴|m﹣5|＝2，∴m＝7或3，故答案为7或3．16．【答案】（1）解：把点A（4，1）代入双曲线y1=k1x得k1=4，∴双曲线的解析式为y1=4x；把点A（4，1）代入直线y2=x k2得k2=4，∴直线的解析式为y2=14x（2）解：∵点P（a，b）在y1=4x的图象上，∴ab=4，∵4a=b，∴4a2=4，则a=±1，∵0<a<4，∴a=1，∴点P的坐标为（1，4），又∵双曲线y1=4x 与直线y2=14x的图象交于A、B两点，且点A的坐标为（4，1），∴点B的坐标为（−4，−1），过点P作PG∥y轴交AB于点G，如图所示，把x=1代入y2=14x，得到y=14，∴点G的坐标为（1，14），∴PG =4−14=154 ， ∴S △ABP =12 PG （ x A −x B )=12×154×8=15 （3）解：PE=PF ．理由如下：∵点P （ a ， b ）在 y 1=4x 的图象上，∴b =4a ，∵点B 的坐标为（ −4 ， −1 ），设直线PB 的表达式为 y =mx +n ， ∴{am +n =4a −4m +n =−1， ∴{m =1a n =4a −1， ∴直线PB 的表达式为 y =1a x +4a −1 ，当 y =0 时， x =a −4 ，∴E 点的坐标为（ a −4 ，0），同理：直线PA 的表达式为 y =−1a x +4a +1 ，当 y =0 时， x =a +4 ，∴F 点的坐标为（ a +4 ，0），过点P 作PH ⊥x 轴于H ，如图所示，∵P 点坐标为（，∴H 点的坐标为（ a ，0），∴EH =x H −x E =a −(a −4)=4 ， FH =x F −x H =a +4−a =4 ， ∴EH=FH ，∴PE=PF ．。

中考数学反比例函数及其应用专题训练(含答案)

中考数学反比例函数及其应用专题训练一、选择题1. 姜老师给出一个函数表达式，甲、乙、丙三位同学分别正确指出了这个函数的一个性质．甲：函数图象经过第一象限；乙：函数图象经过第三象限；丙：在每一个象限内，y值随x值的增大而减小．根据他们的叙述，姜老师给出的这个函数表达式可能是()A. y＝3xB. y＝3 xC. y＝－1x D. y＝x22.若点（1，y1），（2，y2），（3，y3）在反比例函数y=kx（k<0）的图象上，则y1，y2，y3的大小关系是A．y1＞y2＞y3B．y3＞y2＞y1 C．y1＞y3＞y2D．y2＞y3＞y13.反比例函数y=kx经过点(2，1) ，则下列说法错误．．的是（）A. k=2B.函数图象分布在第一、三象限C.当x>0时，随x的增大而增大D.当x>0时，y随x的增大而减小4. 如图，过反比例函数y＝kx(k＞0)的图象上一点A作AB⊥x轴于点B，连接AO，若S△AOB＝2，则k的值为() A. 2 B. 3 C. 4 D. 55.如图，函数(0)y kx b k =+≠与my (m 0)x=≠的图象相交于点(2,3),(1,6)A B --两点，则不等式mkx b x+>的解集为（）A. 2x >-B. 20x -<<或1x >C. 1x >D. 2x <-或01x <<6. 如图，O 为坐标原点，四边形OACB 是菱形，OB 在x 轴的正半轴上，sin ∠AOB＝45，反比例函数y ＝48x 在第一象限内的图象经过点A ，与BC 交于点F ，则△AOF 的面积等于( )A. 60B. 80C. 30D. 407.如图，在平面直角坐标系中，△OAB的边OA 在x 轴正半轴上，其中∠OAB =90°，AO =AB ，点C 为斜边OB 的中点，反比例函数y =kx（k ＞0，x ＞0）的图象过点C ，且交线段AB 于点D ，连结CD ，OD ，若S △OCD =32，则k 的值为（）D CBAxyOA ．3B ．52C ．2D ．18.如图，函数y =1(0)1(0)x xx x⎧>⎪⎪⎨⎪-<⎪⎩的图象所在坐标系的原点是（）A ．点MB ．点NC ．点PD ．点Q二、填空题9. 若点(3，5)在反比例函数y=(k ≠0)的图象上，则k= .10. 已知函数y ＝－1x ，当自变量的取值为－1＜x ＜0或x ≥2，函数值y 的取值____________．11. 我们把直角坐标系中横坐标与纵坐标都是整数的点称为整点．反比例函数y＝－3x 的图象上有一些整点，请写出其中一个整点的坐标________．12. 已知反比例函数y ＝kx (k ≠0)的图象如图所示，则k 的值可能是________(写一个即可)．13. 如图，过原点O 的直线与反比例函数y 1、y 2的图象在第一象限内分别交于点A 、B ，且A 为OB 的中点．若函数y 1＝1x ，则y 2与x 的函数表达式是________．14. 双曲线y ＝m －1x 在每个象限内，函数值y 随x 的增大而增大，则m 的取值范围是________．15. 如图，直线y 1＝kx (k ≠0)与双曲线y 2＝2x (x >0)交于点A (1，a )，则y 1>y 2的解集为________．16. 如图，直线l ⊥x 轴于点P ，且与反比例函数y 1＝k 1x (x ＞0)及y 2＝k 2x (x ＞0)的图象分别交于点A ，B ，连接OA ，OB ，已知△OAB 的面积为2，则k 1－k 2＝__________．三、解答题17. 如图，已知反比例函数y=(x>0)的图象与一次函数y=-x+4的图象交于A和B(6，n)两点.(1)求k和n的值;(2)若点C(x，y)也在反比例函数y=(x>0)的图象上，求当2≤x≤6时，函数值y的取值范围.18. 如图，在平面直角坐标系中，点O为坐标原点，菱形OABC的顶点A在x轴的正半轴上，顶点C的坐标为(1，3)．(1)求图象过点B的反比例函数的解析式；(2)求图象过点A、B的一次函数的解析式；(3)在第一象限内，当以上所求一次函数的图象在所求反比例函数的图象下方时，请直接写出自变量x的取值范围．19. 如图，在直角坐标系中，直线y＝－12x与反比例函数y＝kx的图象交于关于原点对称的A，B两点，已知A点的纵坐标是3.(1)求反比例函数的表达式；(2)将直线y＝－12x向上平移后与反比例函数在第二象限内交于点C，如果△ABC的面积为48，求平移后的直线的函数表达式．20. 如图，在平面直角坐标系中，一次函数的图象与反比例函数的图象交于第二、四象限内的A，B两点，与x轴交于点C，与y轴交于点D，点B的坐标是(m，－4)，连接AO，AO＝5，sin∠AOC＝35.(1)求反比例函数的解析式；(2)连接OB，求△AOB的面积．21.如图，在直角坐标系中，已知点B(4，0)，等边三角形OAB的顶点A在反比例函数y k的图象上．x(1)求反比例函数的表达式．(2)把△OAB向右平移a个单位长度，对应得到△O'A'B'，当这个函数图象经过△O'A'B'一边的中点时，求a的值．答案一、选择题1. 【答案】B【解析】图象经过一，三象限，则它可能是正比例函数或反比例函数；在每一个象限内，y随x的增大而减小，则它是反比例函数，并且反比例函数中的比例系数大于0，故本题选B.2. 【答案】C【解析】∵k<0，∴在每个象限内，y随x值的增大而增大，∴当x=–1时，y1＞0，∵2<3，∴y2<y3<y1，故选C．3. 【答案】C【解析】本题考查了反比例函数图象上点的坐标特征与反比例函数的性质，因为反比例函数y=kx经过点(2，1) ，∴1=2k，∴k=2，故A选项正确；∵反比例函数的解析式为y=2x，k=2>0，∴图象分布在第一、三象限，故B选项正确；∵k=2>0，∴当x＞0时，y随x的增大而减小，故C选项错误；∵k=2>0，∴当x<0时，y 随x的增大而减小，故D选项正确，故选C．4. 【答案】C【解析】∵点A在反比例函数y＝kx的图象上，且AB⊥x轴于点B，设点A坐标为(x，y)，∴k＝xy，∵点A在第一象限，∴x、y都是正数，∴S△AOB＝12OB·AB＝12xy，∵S△AOB＝2，∴k＝xy＝4.5. 【答案】【答案】D【解析】本题是数形结合题，通过观察反比例函数与一次函数的图像解决问题.通过图像观察，可知，当2x<-或01x<<时，一次函数的图像在反比例函数图像的上方.故选D.6. 【答案】D【解析】如解图所示，过点A作AG⊥OB，垂足为G，设A点纵坐标为4m，∵sin∠AOB＝45，∴OA＝5m，根据勾股定理可得OG＝3m，又∵点A在反比例函数y＝48x上，∴3m×4m＝48，∴m1＝2，m2＝－2(不合题意，舍去)，∴AG＝8，OG＝6，OA＝OB＝10，∵四边形OBCA是菱形，∴BC∥OA，∴S△AOF＝12S菱形OBCA＝12×AG×OB＝12×8×10＝40.故选D.7. 【答案】C【解析】如图，作CE⊥x轴于点E，∵点C，D均在反比例函数y=kx的图象上，∴S △COE= S △AOD=2k，∵S 四边形OADC=S △COE +S 梯形ADCE=S △AOD+S △OCD ，∴S 梯形ADCE= S △OCD=32，不妨设OA=AB=a ，∵∠OAB=90°，∴点A （a ，0），B （a ，a ），∵点C 为斜边OB 的中点，∴C （12a ，12a ）∴k =12a ×12a =14a 2，∵点D 的横坐标是a ，∴点D 的纵坐标是14a ，即D （a ，14a ）．∵S 梯形ADCE=12（AD+CE ）·AE=32，∴12×（14a +12a ）×（a －12a ）=32，得：a 2=8，∴k =14a 2=14×8=2．ED CBAxyO8. 【答案】A【解析】由已知可知函数y =1(0)1(0)x xx x⎧>⎪⎪⎨⎪-<⎪⎩关于y 轴对称，所以点M 是原点；故选A ．二、填空题9. 【答案】15[解析]把点(3，5)的坐标代入反比例函数y=，得k=3×5=15，故答案为15.10. 【答案】y ＞1或－12≤y ＜0 【解析】∵函数y ＝－1x ，∴该反比例函数图象在二、四象限，且在二、四象限都随x 的增大而增大，画出草图如解图，当－1＜x ＜0时，y ＞1；当x≥2时，－12≤y ＜0，∴函数值y 的取值为y ＞1或－12≤y ＜0.11. 【答案】(1，－3)(答案不唯一，合理即可)【解析】对于y ＝－3x ，依题意，说明只要x 是3的约数即可，如(1，－3)，(－1，3)．12. 【答案】－2(答案不唯一)【解析】根据反比例函数的图象在二、四象限，则k ＜0，如k ＝－2(答案不唯一)．13. 【答案】y 2＝4x 【解析】设y 2与x 的函数关系式为y 2＝k x ，A 点坐标为(a ，b)，则ab ＝1.又A 点为OB 的中点，因此，点B 的坐标为(2a ，2b)，则k ＝2a·2b ＝4ab ＝4，所以y 2与x 的函数关系式为y 2＝4x .14. 【答案】m ＜1【解析】∵在每个象限内，函数值y 随x 的增大而增大，∴双曲线在二、四象限内，∴在函数y ＝m －1x 中，m －1＜0，即m ＜1.15. 【答案】x ＞1【解析】当x ＞1时，直线的图象在双曲线图象的上方，即y 1＞y 2.因此，y 1＞y 2的解集为x ＞1.16. 【答案】4【解析】∵反比例函数y 1＝k 1x (x ＞0)及y 2＝k 2x (x ＞0)的图象均在第一象限内，∴k 1＞0，k 2＞0，∵AP ⊥x 轴，∴S △OAP ＝12k 1，S △OBP ＝12k 2，∴S △OAB ＝S △OAP －S △OBP＝12(k1－k2)＝2，解得k1－k2＝4.三、解答题17. 【答案】解:(1)把B(6，n)代入一次函数y=-x+4中，可得n=-×6+4=1，所以B点的坐标为(6，1).又B在反比例函数y=(x>0)的图象上，所以k=xy=1×6=6，所以k的值为6，n的值为1.(2)由(1)知反比例函数的解析式为y=.当x=2时，y==3;当x=6时，y==1，由函数图象可知，当2≤x≤6时函数值y的取值范围是1≤y≤3.18. 【答案】(1)如解图，过点C作CD⊥OA于点D，则OD＝1，CD＝3，在Rt△OCD中，由勾股定理得OC＝OD2＋CD2＝2，∵四边形OABC为菱形，∴BC＝AB＝OA＝OC＝2，则点B的坐标为(3，3)，设反比例函数的解析式为y＝kx(k≠0)，∵其图象经过点B，∴将B(3，3)代入，得3＝k3，解得k ＝33， ∴该反比例函数的解析式为y ＝33x ；(2)∵OA ＝2，∴点A 的坐标为(2，0)，由(1)得B (3，3)，设图象经过点A 、B 的一次函数的解析式为y ＝k ′x ＋b (k ′≠0)，将A (2，0)，B (3，3)分别代入，得⎩⎪⎨⎪⎧2k ′＋b ＝03k ′＋b ＝3，解得⎩⎪⎨⎪⎧k ′＝3b ＝－23， ∴该一次函数的解析式为y ＝3x －23；(3)由图象可得，满足条件的自变量x 的取值范围是2＜x ＜3.19. 【答案】解：(1)∵点A 的纵坐标是3，当y ＝3时，3＝－12x, 解得x ＝－6，∴点A 的坐标为(－6，3)，(1分)把A(－6，3)代入y ＝k x ，得3＝k －6，解得k ＝－18，∴反比例函数的解析式为y ＝－18x .(3分)解图(2)如解图，连接CO ，∵A ，B 关于原点对称，∴AO ＝BO ，∴S △AOC ＝12S △ABC ＝24.(4分)作CF ⊥x 轴于点F ，AE ⊥x 轴于点E ，则S △CFO ＝S △AEO ＝12AE·EO ＝12×3×6＝9，S △AOC ＝S 梯形AEFC ＝24.设C(x ，－18x )，则有（3－18x ）（x ＋6）2＝24，(5分) 整理得x 2－16x －36＝0，∴x 1＝－2，x 2＝18(舍去)，∴C(－2，9)，(7分)设y ＝－12x 平移后的解析式为y ＝－12x ＋b ，把C(－2，9)代入上式得，9＝1＋b ，解得b ＝8，∴平移后的直线的函数表达式为y ＝－12x ＋8.(8分)20. 【答案】(1)【思路分析】如解图，过点A 作AE ⊥x 轴于点E ，由三角函数求出点A 坐标，再用待定系数法求出反比例函数的解析式便可．解：如解图过点A 作AE ⊥x 轴于点E ，∵OA ＝5，sin ∠AOC ＝35，∴AE ＝OA·sin ∠AOC ＝5×35＝3，OE ＝OA 2－AE 2＝4，∴A(－4，3)，(3分)设反比例函数的解析式为y ＝k x (k≠0)，把A(－4，3)代入解析式，得k ＝－12，∴反比例函数的解析式为y ＝－12x .(5分)(2)【思路分析】先把B 点坐标代入所求出的反比例函数解析式，求出m 的值，进而求出直线AB 的解析式，再求出点D 的坐标，便可求△AOD 与△BOD 的面积之和，即△AOB 的面积．解：把B(m ，－4)代入y ＝－12x 中，得m ＝3，∴B(3，－4)．设直线AB 的解析式为y ＝kx ＋b ，把A(－4，3)和B(3，－4)代入得， ⎩⎪⎨⎪⎧－4k ＋b ＝33k ＋b ＝－4，解得⎩⎪⎨⎪⎧k ＝－1b ＝－1，(7分) ∴直线AB 的解析式为y ＝－x －1，(8分)则AB 与y 轴的交点D(0，－1)，∴S △AOB ＝S △AOD ＋S △BOD ＝12×1×4＋12×1×3＝3.5.(10分)21. 【答案】(1)反比例函数的解析式为y =；(2)a 的值为1或3．【解析】(1)如图1，过点A 作AC ⊥OB 于点C ，∵△OAB 是等边三角形，∴∠AOB =60°，OC 12=OB ， ∵B (4，0)，∴OB =OA =4，∴OC=2，AC=23．把点A(2，23)代入y kx=，解得k=43．∴反比例函数的解析式为y43x =；(2)分两种情况讨论：①当点D是A′B′的中点，如图2，过点D作DE⊥x轴于点E．由题意得A′B′=4，∠A′B′E=60°，在Rt△DEB′中，B′D=2，DE=3，B′E=1．∴O′E=3，把y3=代入y43=，得x=4，∴OE=4，∴a=OO′=1；②如图3，点F是A′O′的中点，过点F作FH⊥x轴于点H．由题意得A′O′=4，∠A′O′B′=60°，在Rt△FO′H中，FH3=O′H=1．把y=y=，得x=4，x∴OH=4，∴a=OO′=3，综上所述，a的值为1或3．。