六年级奥数 图形综合(一)
六年级下册奥数试题-几何专题 全国通用(含答案) (1)

小学奥数几何专题1、(★★)如图,已知四边形ABCD 中,AB=13,BC=3,CD=4,DA=12,并且BD 与AD 垂直,则四边形的面积等于多少?[思 路]:显然四边形ABCD 的面积将由三角形ABD 与三角形BCD 的面积求和得到.三角形ABD 是直角三角形,底AD 已知,高BD 是未知的,但可以通过勾股定理求出,进而可以判定三角形BCD 的形状,然后求其面积.这样看来,BD 的长度是求解本题的关键.解:由于BD 垂直于AD ,所以三角形ABD 是直角三角形.而AB=13,DA=12,由勾股定理,BD 2=AB 2-AD 2=132—122=25=52,所以BD=5.三角形BCD 中BD=5,BC=3,CD=4,又32十42=52,故三角形BCD 是以BD 为斜边的直角三角形,BC 与CD 垂直.那么:ABCD S 四边形=ABD S ∆+BCD S∆=12×5÷2+4×3÷2=36.. 即四边形ABCD 的面积是36. 2、(★★)如图四边形土地的总面积是48平方米,三条线把它分成了4个小三角形,其中2个小三角形的面积分别是7平方米和9平方米.那么最大的一个三角形的面积是________平方米;[分析]:剩下两个三角形的面积和是 48-7-9=32 ,是右侧两个三角形面积和的2 倍,故左侧三角形面积是右侧对应三角形面积的2倍,最大三角形面积是 9×2=18。
3.(★★)将下图中的三角形纸片沿虚线折叠得到右图,其中的粗实线图形面积与原三角形面积之比为2:3。
已知右图中3个阴影的三角形面积之和为1,那么重叠部分的面积为多少?[思 路]:小升初中常把分数,百分数,比例问题处理成份数问题,这个思想一定要养成。
解:粗线面积:黄面积=2:3绿色面积是折叠后的重叠部分,减少的部分就是因为重叠才变少的,这样可以设总共3份,后来粗线变2份,减少的绿色部分为1份,所以阴影部分为2-1=1份,7 94、(★★)求下图中阴影部分的面积:【解】如左下图所示,将左下角的阴影部分分为两部分,然后按照右下图所示,将这两部分分别拼补在阴影位置。
六年级奥数题-圆及组合图形含分析答案解析
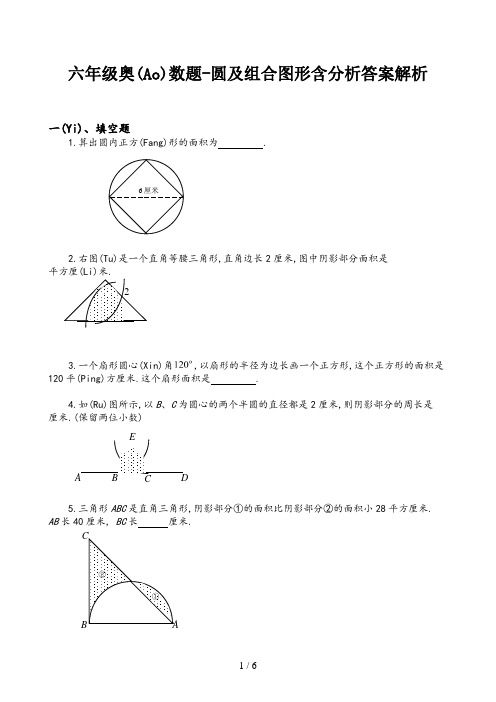
ED C B A 六年级奥(Ao)数题-圆及组合图形含分析答案解析一(Yi)、填空题1.算出圆内正方(Fang)形的面积为 .2.右图(Tu)是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是 平方厘(Li)米.3.一个扇形圆心(Xin)角,以扇形的半径为边长画一个正方形,这个正方形的面积是120平(Ping)方厘米.这个扇形面积是 .4.如(Ru)图所示,以B 、C 为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是 厘米.(保留两位小数)5.三角形ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米. AB 长40厘米, BC 长 厘米.6厘米2C ② ① A B6.如右图,阴影部分的面积为(Wei)2平方厘米,等腰直角三角形的面积为 .7.扇形的面积是31.4平方厘米,它所在圆的面积是157平方厘米,这个(Ge)扇形的圆心角是 度(Du).8.图中(Zhong)扇形的半径OA =OB =6厘(Li)米., AC 垂(Chui)直OB 于(Yu)C ,那么图(Tu)中阴影部分的面积是 平方厘米.9.右图中正方形周长是20厘米.图形的总面积是 平方厘米.10.在右图中(单位:厘米),两个阴影部分面积的和是 平方厘米.二、解答题6CB AO 4512 15 2011. ABC 是等腰直角(Jiao)三角形. D 是半圆周(Zhou)的中点, BC 是半圆的直径,已(Yi)知:AB =BC =10,那么阴影部分的面积(Ji)是多少?(圆周率)12.如(Ru)图,半圆S 1的面积是14.13平方厘米(Mi),圆S 2的(De)面积是19.625平方厘米.那么长方形(阴影部分的面积)是多少平方厘米?13.如图,已知圆心(Xin)是O ,半径r =9厘米,,那么阴影部分的面积是多少平方厘米?14.右图中4个圆的圆心是正方形的4个顶点,它们的公共点是该正方形的中心.如果每个圆的半径都是1厘米,那么阴影部分的总面积是多少平方厘米?S 2S 1 CB A0 1 2 A10 DC B———————————————答(Da) 案——————————————————————1. 18平方(Fang)厘米.由图示可知,正方形两条对角线(Xian)的长都是6厘米,正方形由两个面积相等的三角形构成.三角形底为6厘米,高为3厘米,故正方形面积为(平(Ping)方厘米).2. 1.14平(Ping)方厘米.由图示可知,图中阴影部分(Fen)面积为两个圆心角为的扇形(Xing)面积减去直角三角形的面积.即(平方(Fang)厘米).3. 125.6平方厘米.由已知条件可知圆的半径的平方为120平方厘米.故扇形面积为(平方厘米).4. 3.09厘米.边结BE 、CE ,则BE=CE=BC=1(厘米),故三角形BCE 为等边三角形.于是.BE=CE=(厘米).于是阴影部分周长为(厘米).5. 32.8厘米.从图中可以看出阴影部分①加上空白部分的面积是半圆的面积,阴影部分②加上空白部分的面积是三角形ABC 的面积.又已知①的面积比②的面积小28平方厘米,故半圆面积比三角形ABC 的面积小28平方厘米.⌒⌒A 10DCB O E 半圆面积(Ji)为(平方厘米),三(San)角形ABC 的(De)面积为628+28=656(平方厘米).BC 的(De)长为(厘(Li)米).6.平方厘(Li)米.将等腰直角三角形(Xing)补成一个正方形,设正方形边长为x 厘(Li)米,则圆的半径为厘米.图中阴影部分面积是正方形与圆的面积之差的,于是有,解得.故等腰直角三角形的面积为(平方厘米).7..扇形面积是圆面积的,故扇形圆心角为的即72.8. 5.13.三角形ACO 是一个等腰直角三角形,将AO 看作底边,AO 边上的高为(厘米),故三角形ACO 的面积为(平方厘米).而扇形面积为(平方厘米),从而阴影部分面积为14.13-9=5.13(平方厘米).9. 142.75.由正方形周长是20厘米,可得正方形边长也就是圆的半径为(厘米).图形总面积为两个圆面积加上正方形的面积,即(平方厘米).10. 90平方厘米.图中阴影部分的面积是从两个以直角三角形直角边为直径的半圆及一个直角三角的面积和中减去一个以直角三角形斜边为直径的半圆的面积即(平方厘米). 11. 如图作出辅助线,则阴影部分的面(Mian)积为三角形AED 的面(Mian)积减去正方形BEDO 的面(Mian)积再加上圆面积的.三角(Jiao)形AED 的面积(Ji)是;正方形面积(Ji)是,圆(Yuan)面积的41是(Shi),故阴影部分面积为:(平方厘米).12. 由已知半圆S 1的面积是14.13平方厘米得半径的平方为(平方厘米),故半径为3厘米,直径为6厘米.又因圆S 2的面积为19.625平方厘米,所以S 2半径的平方为(平方厘米),于是它的半径为2.5厘米,直径为5厘米. 阴影部分面积为(平方厘米).13. 因OA=OB ,故三角形OAB 为等腰三角形,即 , 同理,于是.扇形面积为:(平方厘米).14. 正方形可以分割成两个底为2,高为1的三角形,其面积为(平方厘米).正方形内空白部分面积为4个41圆即一个圆的面积与正方形面积之差,即 (平方厘米),所有空白部分面积为平方厘米. 故阴影部分面积为四个圆面积之和与两个空白面积之和的差,即为 (平方厘米).。
小学奥数 数论 数字谜综合 数阵图(一).题库版

1.了解数阵图的种类2. 学会一些解决数阵图的解题方法3. 能够解决和数论相关的数阵图问题.一、数阵图定义及分类:1. 定义:把一些数字按照一定的要求,排成各种各样的图形,这类问题叫数阵图.2. 数阵是一种由幻方演变而来的数字图.数阵图的种类繁多,这里只向大家介绍三种数阵图:即封闭型数阵图、辐射型数阵图和复合型数阵图.3.二、解题方法:解决数阵类问题可以采取从局部到整体再到局部的方法入手: 第一步:区分数阵图中的普通点(或方格)和关键点(或方格);第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算这些关键点与相关点的数量关系,得到关键点上所填数的范围;第三步:运用已经得到的信息进行尝试.这个步骤并不是对所有数阵题都适用,很多数阵题更需要对数学方法的综合运用.模块一、封闭型数阵图【例 1】 把1~8的数填到下图中,使每个四边形中顶点的数字和相等。
【考点】复合型数阵图 【难度】3星 【题型】填空 【关键词】2010年,学而思杯,3年级,第6题 【解析】例题精讲知识点拨教学目标5-1-3-1.数阵图87654321【答案】87654321【例 2】 将1~8这八个自然数分别填入下图中的八个○内,使四边形每条边上的三个数之和都等于14,且数字1出现在四边形的一个顶点上.应如何填?(1)【考点】封闭型数阵图 【难度】2星 【题型】填空【解析】 为了叙述方便,先在各圆圈内填上字母,如下图(2).由条件得出以下四个算式:(2)h gf ed c baa+b+c=14(1)c+d+e=14 (2) e+f+g=14 (3)a+h+g=14 (4)由(1)+(3),得:a+b+c+e+f+g=28,(a+b+c+d+e+f+g+h )-(d+h )=28,d+h=(1+2+3+4+5+6+7+8)-28=8,由(2)+(4),同样可得b+f=8, 又1,2,3,4,5,6,7,8中有1+7=2+6=3+5=8.又1要出现在顶点上,d+h 与b+f 只能有2+6和3+5两种填法. 又由对称性,不妨设b=2,f=6,d=3,h=5. a ,c ,e ,g 可取到1,4,7,8若a=1,则c=14-(1+2)=11,不在1,4,7,8中,不行.若c=1,则a=14-(1+2)=11,不行. 若e=1,则c=14-(1+3)=10,不行. 若g=1,则a=8,c=4,e=7.说明:例题为封闭型数阵,由它的分析思考过程可以看出,确定各边顶点所应填的数为封闭型数阵的解题突破口.【答案】【例 3】 在如图6所示的○内填入不同的数,使得三条边上的三个数的和都是12,若A 、B 、C 的和为18,则三个顶点上的三个数的和是 。
小学数学六年级奥数《立体图形(1)》练习题(含答案)

小学数学六年级奥数《立体图形(1)》练习题(含答案)一、填空题1.一个正方体的表面积是384平方分米,体积是512立方分米,这个正方体棱长的总和是 .2.如图,在一块平坦的水泥地上,用砖和水泥砌成一个长方体的水泥池,墙厚为10厘米(底面利用原有的水泥地).这个水泥池的体积是 .3.一个边长为4分米的正方形,以它的一条边为轴,把正方形旋转一周后,得到一个 ,这个形体的体积是 .4.把19个边长为2厘米的正方体重叠起来堆成如右图所示的立方体,这个立方体的表面积是 平方厘米.5.图中是一个圆柱和一个圆锥(尺寸如图).问:柱锥V V 等于 .6.一个长方体的表面积是67.92平方分米.底面的面积是19平方分米.底面周长是17.6分米,这个长方体的体积是 .2 单位:米7.一块长方体木块长2.7米,宽1.8分米,高1.5分米.要把它裁成大小相等的正方体小木块,不许有剩余,小正方体的棱长最大是 分米.8.王师傅将木方刨成横截面如右图(单位:厘米)那样高40厘米的一根棱柱.虚线把横截面分成大小两部分,较大的那部分的面积占整个底面的60%.这个棱柱的体积是 立方厘米.9.小玲有两种不同形状的纸板.一种是正方形的,一种是长方形的(如下图).正方形纸板的总数与长方形纸板的总数之比是1:2.她用这些纸板做成一些竖式和横式的无盖纸盒,正好将纸板用完.在小玲所做的纸盒中,坚式纸盒的总数与横式纸盒的总数之比是 .10.在桌面上摆有一些大小一样的正方体木块,从正南方向看如下图(1),从正东方向看如下图(2),要摆出这样的图形至多能用 块正方体木块,至少需要 块正方体木块.二、解答题11.一个长方形水箱,从里面量长40厘米,宽30厘米,深35厘米.原来水深10厘米,放进一个棱长20厘米的正方形铁块后,铁块的顶面仍然高于水面,这时水面高多少厘米?12.如图表示一个正方体,它的棱长为4厘米,在它的上下、前后、左右的正中位置各挖去一个棱长为1厘米的正方体,问此图的表面积是多少?8 28 2412(图1)(图2)13.下图是正方体,四边形APQC 是表示用平面截正方体的截面,截面的线表现在展开图的哪里呢?把大致的图形在右面展开图里画出来.14.雨哗哗地不停地下着,如在雨地里放一个如图1那样的长方形的容器,雨水将它下满要用1小时.有下列(A )-(E )不同的容器(图2),雨水下满各需多少时间(注面是朝上的敞口部分.)PF2cm 2cm (A ) (B ) (C ) (D ) (E ) 雨———————————————答 案——————————————————————1. 96分米.正方体的底面积为384÷6=64(平方分米).故它的棱长为512÷64=8(分米),棱长的总和为8×12=96(分米).2. 8.96立方米.(3-0.1×2)×(1.8-0.1×2)×2=8.96(立米米).3. 圆柱体,200.96立方分米.(3.14×42)×4=200.96(立方分米).4. 216.这个立方体的表面由3×3×2+8×2+10×2=54个小正方形组成,故表面积为4×54=216(平方厘米).5. 241. ππππ816828,3164243122⨯=⨯⎪⎭⎫ ⎝⎛⨯==⨯⎪⎭⎫ ⎝⎛⨯⨯=柱锥V V ,故241=柱锥V V .6. 32.3立方分米.长方体的侧面积是67.92-19×2=29.92(平方分米),长方体的高为29.92÷17.6=1.7(分米),故长方体的体积为19×1.7=32.3(立方分米).7. 0.3长、宽、高分别是270厘米、18厘米和15厘米,而270、18和15的最大公约数为3(厘米),这就是小正方体棱长的最大值.8. 17200.设较大部分梯形高为x 厘米,则较小部分高为(28- x )厘米.依题意有: 4:6)28()824(21:)2412(21=⎥⎦⎤⎢⎣⎡-⨯+⨯⎥⎦⎤⎢⎣⎡+⨯x x 解得x =16,故这棱柱的体积为 1920040)1628()824(2116)2412(21=⨯⎥⎦⎤⎢⎣⎡-⨯+⨯+⨯+⨯(立方厘米).9. 3:1.一个竖式的无盖纸盒要用一个正方形纸板和4个长方形纸板,一个横式的无盖纸盒要用2个正方形纸板和3个长方形纸板.设小玲做的纸盒中,有x 个竖式的, y 个横式的,则共用正方形纸板(x +2 y )个,用长方形纸板(4 x +3 y )个,依题意有: (x +2 y ):(4 x +3 y )=1:3.解得x : y =3:1.10. 20,6.至多要20块(左下图),至少需要6块(右下图).11. 若铁块完全浸入水中,则水面将提高326)3040(203=⨯÷(厘米).此时水面的高小于20厘米,与铁块完全浸入水中矛盾,所以铁块顶面仍然高于水面.设放入铁块后,水深为x 厘米.因水深与容器底面积的乘积应等于原有水体积与铁块浸入水中体积之和,故有:x x 20201030403040⨯+⨯⨯=⨯解得x =15,即放进铁块后,水深15厘米.12. 大正方体的表面还剩的面积为()9014622=-⨯(厘米2),六个小孔的表面积为()305162=⨯⨯(厘米2),因此所求的表面积为90+30=120(厘米2).13. 截面的线在展开图中如右图的A -C -Q -P -A .14. 在例图所示的容器中,容积:按水面积=(10×10×30):(10×30)=10:1,需1小时接满,所以容器(A):容积:接水面积=(10×10×10):(10×10)=10:1,需1小时接满; 容器(B):容积:接水面积=(10×10×30):(10×10)=30:1,需3小时接满; 容器(C):容积:接水面积=(20×20×10-10×10×10):(10×10)=30:1,需32 1 2 1 2 2 1 2 1 1 1 1 1 1 1 1 1 2 1 1A小时接满;容器(D):容积:接水面积=(20×20×10-10×10×10):(20×10)=15:1,需1.5小时接满;容器(E):容积:接水面积=20×S:S=20:1(S为底面积),接水时间为2小时.。
六年级图形问题综合(奥数)含答案

平面图形计算(一)经典图形:1. 任意三角形ABC 中,CD=31AC ,EC=43BC ,则三角形CDE 的面积占总面积的31⨯43=41(为什么?)2. 任意平行四边形中任意一点,分别连接四个顶点,构成的四个三角形中,上下两个三角形面积之和等于左右两个三角形面积之和。
(为什么?)3. 任意梯形,连接对角线,构成四个三角形。
(1)腰上的两个三角形面积相等;(2)上下两个三角形面积之积等于左右两个三角形面积之积。
(为什么?)4. 正方形的面积等于边长的平方,或者等于对角线的平方÷2.等腰直角三角形面积等于直角边的平方÷2,或者等于斜边的平方÷4.(为什么?)例题: 例1. 如右图,三角形ABC 的面积是10,BE=2AB ,CD=3BC ,求三角形BDE 的面积。
例2. 如图,已知三角形ABC 的面积是1,延长AB 至D ,使BD=AB ,延长BC 至E ,使CE=2BC ,延长CA 至F ,使AF=3AC ,求三角形DEF 的面积。
例3.如图,三角形ABC的面积是180平方厘米,D是BC的中点,AE=ED,EF=2BF,求AEF的面积。
例4.如图,ABCD是个长方形,DEFG是个平行四边形,E点在BC边上,FG过A点,已知,三角形AKF与三角形ADG面积之和等于5平方厘米,DC=CE=3厘米。
求三角形BEK的面积。
FKB E CDGA例5.如图,三角形ABC的AB和AC两条边分别被分成5等分。
三角形ABC面积是500,求图中阴影部分的面积?例6.如图,设正方形ABCD的面积为120,E、F分别为边AB、AD的中点,FC=3GC,则阴影部分的面积是多少?AB CDFEG例7.在如图所示的三角形AGH中,三角形ABC,BCD,CDE,DEF,EFG,FGH的面积分别是1,2,3,4,5,6平方厘米,那么三角形EFH的面积是多少平方厘米?ABCDEFGH例8.如图,在平行四边形ABCD中,AC为对角线,EF平行于AC,如果三角形AED的面积为12平方厘米,,求三角形DCF的面积。
六年级奥数举一反三-组合图形面积计算小学

六年级奥数举⼀反三-组合图形⾯积计算⼩学组合图形⾯积计算(⼀)⼀、知识要点在进⾏组合图形的⾯积计算时,要仔细观察,认真思考,看清组合图形是由⼏个基本单位组成的,还要找出图中的隐蔽条件与已知条件和要求的问题间的关系。
⼆、精讲精练【例题1】求图中阴影部分的⾯积(单位:厘⽶)。
圆的⾯积。
【思路导航】如图所⽰的特点,阴影部分的⾯积可以拼成14=28.26(平⽅厘⽶)62×3.14×14答:阴影部分的⾯积是28.26平⽅厘⽶。
练习1:1.求下⾯各个图形中阴影部分的⾯积(单位:厘⽶)。
2.求下⾯各个图形中阴影部分的⾯积(单位:厘⽶)。
3.求下⾯各个图形中阴影部分的⾯积(单位:厘⽶)。
【例题2】求图中阴影部分的⾯积(单位:厘⽶)。
【思路导航】阴影部分通过翻折移动位置后,构成了⼀个新的图形(如图所⽰)。
从图中可以看出阴影部分的⾯积等于⼤扇形的⾯积减去⼤三⾓形⾯积的⼀半。
3.14×2144-4×4÷2÷2=8.56(平⽅厘⽶)答:阴影部分的⾯积是8.56平⽅厘⽶。
练习2:1.计算下⾯图形中阴影部分的⾯积(单位:厘⽶)。
2.计算下⾯图形中阴影部分的⾯积(单位:厘⽶,正⽅形边长4)。
3.计算下⾯图形中阴影部分的⾯积(单位:厘⽶,正⽅形边长4)。
【例题3】如图19-10所⽰,两圆半径都是1厘⽶,且图中两个阴影部分的⾯积相等。
求长⽅形ABO1O的⾯积。
【思路导航】因为两圆的半径相等,所以两个扇形中的空⽩部分相等。
⼜因为图中两个阴影部分的⾯积相等,所以扇形的⾯积等于长⽅形⾯积的⼀半(如图19-10右图所⽰)。
所以3.14×12×1/4×2=1.57(平⽅厘⽶)答:长⽅形长⽅形ABO1O的⾯积是1.57平⽅厘⽶。
练习3:1.如图所⽰,圆的周长为12.56厘⽶,AC两点把圆分成相等的两段弧,阴影部分(1)的⾯积与阴影部分(2)的⾯积相等,求平⾏四边形ABCD的⾯积。
六年级图形问题综合(奥数)含答案

平面图形计算(一)经典图形:1. 任意三角形ABC 中,CD=31AC ,EC=43BC ,则三角形CDE 的面积占总面积的31⨯43=41(为什么?)2. 任意平行四边形中任意一点,分别连接四个顶点,构成的四个三角形中,上下两个三角形面积之和等于左右两个三角形面积之和。
(为什么?)3. 任意梯形,连接对角线,构成四个三角形。
(1)腰上的两个三角形面积相等;(2)上下两个三角形面积之积等于左右两个三角形面积之积。
(为什么?)4. 正方形的面积等于边长的平方,或者等于对角线的平方÷2.等腰直角三角形面积等于直角边的平方÷2,或者等于斜边的平方÷4.(为什么?)例题: 例1. 如右图,三角形ABC 的面积是10,BE=2AB ,CD=3BC ,求三角形BDE 的面积。
例2. 如图,已知三角形ABC 的面积是1,延长AB 至D ,使BD=AB ,延长BC 至E ,使CE=2BC ,延长CA 至F ,使AF=3AC ,求三角形DEF 的面积。
例3. 如图,三角形ABC 的面积是180平方厘米,D 是BC 的中点,AE=ED ,EF=2BF ,求AEF 的面积。
例4. 如图,ABCD 是个长方形,DEFG 是个平行四边形,E 点在BC 边上,FG 过A 点,已知,三角形AKF 与三角形ADG 面积之和等于5平方厘米,DC=CE=3厘米。
求三角形BEK 的面积。
FK BEC DGA例5. 如图,三角形ABC 的AB 和AC 两条边分别被分成5等分。
三角形ABC 面积是500,求图中阴影部分的面积?例6. 如图,设正方形ABCD 的面积为120,E 、F 分别为边AB 、AD 的中点,FC=3GC ,则阴影部分的面积是多少?ABC DFEG例7. 在如图所示的三角形AGH 中,三角形ABC ,BCD ,CDE ,DEF,EFG ,FGH 的面积分别是1,2,3,4,5,6平方厘米,那么三角形EFH 的面积是多少平方厘米?ABCD EFG H例8. 如图,在平行四边形ABCD 中,AC 为对角线,EF 平行于AC ,如果三角形AED 的面积为12平方厘米,,求三角形DCF 的面积。
6年级奥数几何综合问题(上)例题解析

【内容概述】勾股定理,多边形的内角和,两直线平行的判别准则,由平行线形成的相似三角形中对应线段和面积所满足的比例关系.与上述知识相关的几何计算问题.各种具有相当难度的几何综合题. 【例题】1.如图16-1,已知四边形ABCD 中,AB=13,BC=3,CD=4,DA=12,并且BD 与AD 垂直,则四边形ABCD 的面积等于多少?[分析与解] 因为∠ADB =90°,所以在△ABD 中有AB 2=AD 2+BD 2,即BD 2=AB 2-AD 2=132-122=25,所以BD =5.△ABD 的面积为12×BD ×AD =30.而在△BCD 中有32+42=52,即BC 2+CD 2=BD 2,所以有△BCD 为直角三角形.△BCD 的面积为12×BC ×CD =6.而四边形ABCD 的面积为△ABD 、△BCD 的面积和,即为30+6=36.2.如图16-2,已知四边形ABCD 和CEFG 都是正方形,且正方形ABCD 的边长为10厘米,那么图中阴影三角形BFD 的面积为多少平方厘米?[分析与解] 因为CEFG 的边长题中未给出,那么显然阴影部分的面积与其无关. 设正方形CEFG 的边长为x ,有:S 正方形ABCD =10×10=100,S 正方形CEFG =x 2,S △BGF =12DG ×GF =12(10-x)x =.又S △ABD =12×10×10=50,S △BEF =12(10+x)x =.阴影部分的面积为:S 正方形ABCD +S 正方形CEFG +S △BGF -S △ABD -S △BEF =100+x 2+-50-=50(平方厘米).解法二:连接FC ,有FC 平行与DB ,则四边形BCFD 为梯形.有△DFB 、△DBC 共底DB ,等高,所以这两个三角形的面积相等,显然△DBC 的面积为12×10×10=50(平方厘米).阴影部分△DFB 的面积为50平方厘米.3.如图16-3,在平行四边形ABCD 中,AB=16,AD=10,BE=4,那么FC 的长度是多少?[分析与解]因为有CB平行与DA,有=,有FB=×DA=×10=2,所以CF=CB-FB=10-2=8.解法二:如下图所示,连接DB,CE,有DC:BE=4:1,所以△DFC与△FBE的面积比为16:1,有S△DCF ×S△FBE=S△DBF×S△CEF ,又S△DFB=S△CFE.所以△DCF,△FBE,△DBF,△CEF的面积比为16:1:4:1,即S△DCF :S△DFB=16:4=4:1.有△DCF,△DFB同高,面积比为底的比,即CF:BF=4:1,而CF,BF的长度和为10,有FC=×BC=8.4.如图16-4,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I等于多少度?[分析与解]为了方便所述,如下图所示,标上数字,有∠I=180°-(∠1+∠2),而∠1=180°-∠3,∠2=180°-∠4,有∠I=∠3+∠4-180°.同理有∠H=∠4+∠5-180°,∠G=∠5+∠6-180°,∠F=∠6+∠7-180°,∠E=∠7+∠8-180°,∠D=∠8+∠9-180°,∠C=∠9+∠10-180°,∠B=∠10+∠11-180°,∠A=∠11+∠3-180°.则∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I=2×(∠3+∠4+∠5+∠6+∠7+∠8+∠9+∠10+∠11)-9×180°.而∠3+∠4+∠5+∠6+∠7+∠8+∠9+∠10+∠11正是9边形的内角和为(9-2)×180°=1260°.所以∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I=2×1260°-9×180°=900°.5.如图16-5,设正方形ABCD的面积为l,E,F分别为边AB,AD的中点,FC=3GC,则阴影部分的面积是多少?[分析与解]过G作线段PQ垂直于AB,分别交AB、DC于P、Q两点:有G为FC三等分点,且GQ平行与FD,所以GQ=FD=.=×EB×PG=××=.则PG=PQ-GQ=,有S△EBG6.长边和短边的比例是2:1的长方形称为基本长方形.考虑用短边互不相同的基本长方形拼图,要求任意两个基本长方形之间既没有重叠,也没有空隙.现在要用短边互不相同且最小短边长为1的5个基本长方形拼接成一个更大的长方形.例如,短边长分别是1,2,5,6,12的基本长方形能拼接成大长方形,具体方案如图16-6所示.请给出这5个基本长方形所有可能的选择方式.设a1=1<a2<a3<a4<a5分别为5条短边的长度,则我们将这种选择方式记为(al,a2,a3,a4,a5),这里无需考虑5个基本长方形的拼图方案是否惟一.共有16组解,它们是:(1,2,2.5,5,7.25),(1,2,2.5,5,14.5),(1,2,2.25,2.5,3.625),(1,2,2.25,2.5,7.25),(1,2,5,5.5,6),(1,2,5,6,11),(1,2,2.5,4.5,7),(1,2,2.5,4.5,14),(1,2,5,12,14.5),(1,2,5,12,29),(1,2,2.25,2.5,4.5),(1,2,5,6,12),(1,,2,,),(1,2,2.4,4.8,5),(1,,,,),(1,,,,).7.如图16-7,ABCG是4×7的长方形,DEFG是2×10的长方形.那么,三角形BCM的面积与三角形DEM的面积之差是多少?[分析与解]如下图所示,连接BD,CE.四边形BCED的面积为△BCD与△CDE的面积和,S△BCD=×BC×CD=×4×(10-7)=6,S△CDE=×CD×DE=×(10-7)×2=3.所以S四边形BCED =S△BCD+S△CDE=6+3=9.有BC平行与DE,所以四边形BCED为梯形,有BC=4,DE=2,则BC:DE=4:2=2:1.则S△BCM :S△EDM=BC2:DE2=4:1,S△BCM×S△EDM=S△BMD×S△EMC,又有S△BMD=S△EMC,所以S△BMD =2S△EDM.即△BCM,△EDM,△BMD,△EMC的面积比为4:1:2:2,且这四个三角形组成梯形BCED.8.如图16-8,ABCD是平行四边形,面积为72平方厘米,E,F分别为边AB,BC的中点.则图形中阴影部分的面积为多少平方厘米?[分析与解]如下图所示,连接EC,并在某些点处标上字母,因为AE平行与DC,所以四边形AECD为梯形,有AE:DC=1:2,所以S△AEG :S△DCG =1:4,S△AGD×S△ECG=S△AEG×S△DCG,且有S△AGD=S△ECG,所以S△AEG:S△ADG=1:2,而这两个三角形高相同,面积比为底的比,即EG:GD=1:2,同理FH:HD=1:2.有S△AED =S△AEG+S△AGD,而S△AED=×S平行四边形ABCD=18(平方厘米).有EG:GD=S△AEG :S△AGB,所以S△AEG=×S△AED=6(平方厘米),S△AGD=×S△AED=12(平方厘米).同理可得S△HFC =6(平方厘米),S△DCH=12(平方厘米).而S△DCG =4S△AEG=4×6=24(平方厘米),又S△GHD=S△DCG-S△DCH=24-12=12(平方厘米),所以原题平行四边形中空白部分的面积为6+6+12=24(平方厘米),所以剩下的阴影部分面积为72-24=48(平方厘米).9.在图16-9中,AE:EC=l:2,CD:DB=l:4,BF:FA=1:3,三角形ABC的面积等于1.那么四边形AFHG的面积是多少?[分析与解]如下图所示,我们分别求出BFH、CDI的面积问题也就解决.①如上左图,我们设S△BFH =x,则S△AFH=3x;设S△AHE=y,则S△CEH=2y.10.图16-10是一个正方形,其中所标数值的单位是厘米.问:阴影部分的面积是多少平方厘米?[分析与解]如下图所示,为了方便所叙,将某些点标上字母,并连接BG.设△AEG 的面积为x ,显然△EBG 、△BFG 、△FCG 的面积均为x ,则△ABF 的面积为3x ,S △ABF =12×20×10=100,即x =1003,那么正方形内空白部分的面积为4x=4003.所以原题中阴影部分面积为20×20-4003=8003(平方厘米).11.如图16-11,ABCD 是一个长方形,AC 是对角线.试比较两块阴影区域的面积与是的大小.[分析与解] 在长方形AEOH 中,被对角线AO 平分的两块三角形面积相等,有S △AHO =S △AEO .同理在长方形OGCF 中,S △OGC =S △OFC ;在长方形ABCD 中,S △ADC =S △ABC . 所以有S △ADC -S △AHO -S △OGC =S △ABC -S △AEO -S △OFC ,即S HDGO =S EOFB . 将PJCI 视为ABCD ,同理有S KJGO =S LOFI .有S HDGO -S KJGO =S LOFI -S EOFB ,即S 1=S 2.12.如图16-12,若图中的圆和半圆都两两相切,两个小圆和三个半圆的半径长都是1.求阴影部分的面积.[分析与解]如下图所示,左图中的3个阴影部分面积相等,右图中的3个阴影部分的面积也相等.我们把下左图中的阴影称为A,下右图中的阴影称为B.13.如图16-13所示,一块半径为2厘米的圆板,从平面上标有1号位置起始,沿线段AB,BC,CD滚到2号位置.如果AB,BC,CD的长都是20厘米,那么圆板经过区域的面积是多少平方厘米?(π取3.14,答案保留两位小数.)[分析与解]如下图所示,我们将小圆板经过的区域分成4个部分,其中第1部分是半径为2厘米的半圆;其中第2部分是长为(20-2=)18厘米,宽4厘米的长方形;其中第3部分是半径为2×2=4厘米,圆心角为(360°-90°-90°-120°)=60°的扇形;其中第4部分是半径为(20-2=)18厘米,宽4厘米的长方形;其中第5部分是半径为(20-2-2=)16厘米,宽4厘米的长方形;注意第4、5部分有重叠,为边长是2的正方形;其中第6部分是半径为2厘米的14圆;其中第7部分是半径为2厘米的半圆.这4部分的面积和为+18×4++18×4+16×4-2×2+ +=204+≈208.07(平方厘米).14.如图16-14,将长方形ABCD绕顶点C顺时针旋转90度,若AB=4,BC=3,AC=5,求AD边扫过部分的面积.(π取3.14.)[分析与解]如下图所示,如上中图所示,端点A扫过的轨迹为AA″A′,端点D扫过轨迹为DD″D′,而AD之间的点,扫过的轨迹在以A、D轨迹,AD,A′D′所形成的封闭图形内,且这个封闭图形的每一点都有线段AD上某点扫过,所以AD边扫过的图形为阴影部分.显然有阴影部分面积为S直角△A′D′C +S扇形ACA′-S直角△ACD-S扇形CD′D,而直角三角形A′D′C、ACD面积相等.所以S直角△A′D′C +S扇形ACA′-S直角△ACD-S扇形CD′D=S扇形ACA′-S扇形CD′D=-=(52-42)==7.065(平方厘米).即AD边扫过部分的面积为7.065平方厘米.15.在图16-15中有分别标记为①,②,③,④的4个平面图形.(1)数一数每个图中有多少个顶点、多少条边,这些边围出了多少块区域,将结果填入图16-16的表中.这里①号图形的有关数据已经填好.(2)观察上表,推断一个平面图的顶点数、边数、区域数之间存在的关系.(3)已知某一平面图有999个顶点,且围成了999块区域.试根据上一小题中推断出的关系,确定出这个图有多少条边?[分析与解](1)如下表,将题中各个图形中的顶点数、边数、区域数一一标在下表.(2)由上表不难得知顶点数+区域数=边数+1.(3)当顶点数=999,区域数=999时,有边数=999+999-1=1997.。
六年级奥数题及答案(高等难度)

六年级奥数题及答案:图形(高等难度)1 图形:(高等难度)如图,长方形ABCD中,E为的AD中点,AF与BE、BD 分别交于G、H,OE垂直AD于E,交AF于O,已知AH=5cm,HF=3cm,求AG.图形答案:2图形面积:(高等难度)直角三角形ABC的两直角边AC=8cm,BC=6cm,以AC、B C为边向形外分别作正方形ACDE与BCFG,再以AB为边向上作正方形ABMN,其中N点落在DE上,BM交CF于点T.问:图中阴影部分(与梯形BTFG)的总面积等于多少?图形面积答案:3 应用题:(高等难度)我国某城市煤气收费规定:每月用量在8立方米或8立方米以下都一律收6.9元,用量超过8立方米的除交6.9元外,超过部分每立方米按一定费用交费,某饭店1月份煤气费是82.26元,8月份煤气费是40.02元,又知道8月份煤气用量相当于1月份的,那么超过8立方米后,每立方米煤气应收多少元?应用题答案:4 乒乓球训练(逻辑):(高等难度)甲、乙、丙三人用擂台赛形式进行乒乓球训练,每局2人进行比赛,另1人当裁判.每一局的输方去当下一局的裁判,而由原来的裁判向胜者挑战.半天训练结束时,发现甲共打了15局,乙共打了21局,而丙共当裁判5局.那么整个训练中的第3局当裁判的是_______.乒乓球训练(逻辑)答案:本题是一道逻辑推理要求较高的试题.首先应该确定比赛是在甲乙、乙丙、甲丙之间进行的.那么可以根据题目中三人打的总局数求出甲乙、乙丙、甲丙之间的比赛进行的局数.⑴丙当了5局裁判,则甲乙进行了5局;⑵甲一共打了15局,则甲丙之间进行了15-5=10局;⑶乙一共打了21局,则乙丙之间进行了21-5=16局;所以一共打的比赛是5+10+6=31局.此时根据已知条件无法求得第三局的裁判.但是,由于每局都有胜负,所以任意连续两局之间不可能是同样的对手搭配,就是说不可能出现上一局是甲乙,接下来的一局还是甲乙的情况,必然被别的对阵隔开.而总共31局比赛中,乙丙就进行了16局,剩下的甲乙、甲丙共进行了15局,所以类似于植树问题,一定是开始和结尾的两局都是乙丙,中间被甲乙、甲丙隔开.所以可以知道第奇数局(第1、3、5、……局)的比赛是在乙丙之间进行的.那么,第三局的裁判应该是甲.5唐老鸭和米老师赛跑:(高等难度)唐老鸭与米老鼠进行一万米赛跑,米老鼠的速度是每分钟125米,唐老鸭的速度是每分钟100米。
六年级图形问题综合(奥数)含答案解析-精选.pdf

3. 任意梯形,连接对角线,构成四个三角形。 (1)腰上的两个三角形面积相等; ( 2)上下两个三角形 面积之积等于左右两个三角形面积之积。 (为什么?)
4. 正方形的面积等于边长的平方,或者等于对角线的平方 2,或者等于斜边的平方 4.(为什么?)
2.等腰直角三角形面积等于直角边的平方
例题: 例 1. 如 右图,三角形 ABC 的面积是 10,BE=2AB , CD=3BC ,求三角形 BDE 的面积。
6. 下图正方形 ABCD 边长是 10 厘米 , 长方形 EFGH 的长为 8 厘米 , 宽为 5 厘米 . 阴影部分甲与阴影部分乙
的面积差是 ______平方厘米 .
7. 如图所示 , 一个矩形被分成 A 、 B 、C 、 D 四个矩形 . 现知 A 的面积是 2cm2, B 的面积是 4cm2, C 的面积
H
F
D
B
ACE
G
例 8. 如 图,在平行四边形 ABCD中,AC为对角线, EF平行于 AC,如果三角形 AED的面积为 12 平方厘米,,
求三角形 DCF的面积。
专业 知识分享
D
C
完美 WORD 格式
F
A
E
B
练习:
1. 已知正方形 ABCD 的边长是 5cm,又 EF=FG , FD=DG ,求三角形 ECG 的面积。
B
A
8 平方厘米,三角形 COD
O
C
D
专业 知识分享
完美 WORD 格式
图形与面积 ( 一 ) 一、填空题
1. 如下图 , 把三角形 ABC 的一条边 AB 延长 1 倍到 D , 把它的另一边 AC 延长 2 倍到 E , 得到一个较大 的三角形 ADE , 三角形 ADE 的面积是三角形 ABC 面积的 ______倍 .
六年级奥数专题 平面几何综合(学生版)

学科培优数学“平面几何综合”学生姓名授课日期教师姓名授课时长知识定位本讲复习以前所学过的有关平面几何方面的知识,包括直线型图形的五大模型以及圆与扇形方面的知识,旨在提高学生对该部分知识的综合运用能力。
知识梳理直线型图形五大模型模型一:同一三角形中,相应面积与底的正比关系:即:两个三角形高相等,面积之比等于对应底边之比。
S1︰S2=a︰b ;模型一的拓展:等分点结论(“鸟头定理”)如图,三角形AED占三角形ABC面积的23×14=16模型二:任意四边形中的比例关系(“蝴蝶定理”)①S1︰S2=S4︰S3或者S1×S3=S2×S4②②AO︰OC=(S1+S2)︰(S4+S3)模型三:梯形中比例关系(“梯形蝴蝶定理”)①S1︰S3=a2︰b2S4S3s2s1babs2s1S4S3s2s1ODCBA②S 1︰S 3︰S 2︰S 4= a 2︰b 2︰ab ︰ab ; ③S 的对应份数为(a+b )2模型四:相似三角形性质①a b c hA B C H=== ; ②S 1︰S 2=a 2︰A 2模型五:燕尾定理S △ABG :S △AGC =S △BGE :S △GEC =BE :EC ; S △BGA :S △BGC =S △AGF :S △GFC =AF :FC ; S △AGC :S △BCG =S △ADG :S △DGB =AD :DB ;【重点难点解析】1. 三角形的相似问题2. 四边形中的蝴蝶定理3. 三角形中燕尾定理的运用【竞赛考点挖掘】1. 三角形或四边形中的部分面积求解2. 相似形的相关性质3. 多边形内角和4. 圆与圆弧的相关图形面积和周长求解hh H cb a CB Aac b HC BAF ED CBA例题精讲【试题来源】【题目】如图,长方形ABCD中,阴影部分是直角三角形且面积为54,OD的长是16,OB的长是9.那么四边形OECD的面积是_____.【试题来源】【题目】如下左图.将三角形ABC的BA边延长1倍到D,CB边延长2倍到E,AC边延长3倍到F.如果三角形ABC的面积等于l,那么三角形DEF的面积是_____.【试题来源】【题目】如图,三角形ABC的面积是1平方厘米,且BE=2EC,F是CD的中点.那么阴影部分的面积是( )平方厘米.【试题来源】【题目】如图,已知AE=15AC,CD=14BC,BF=16AB,那么DEF=____ABC三角形的面积三角形的面积【试题来源】【题目】如图,BD是梯形ABCD的一条对角线,线段AE与梯形的一条腰DC平行,AE与BD相交于O点.已知三角形BOE的面积比三角形AOD的面积大4平方米,并且EC=25BC.求梯形ABCD的面积.【试题来源】【题目】如图,平行四边形的花池边长分别为60米与30米.小明和小华同时从A点出发,沿着平行四边形的边由A→B→C→D→A…顺序走下去.小明每分钟走50米,小华每分钟走20米,出发5分钟后小明走到E点,小华走到F点.连结AE、AF,则四边形AECF的面积与平行四边形ABCD的面积的比是______.【试题来源】【题目】图中正方形周长是20厘米.那么图形的总面积是_____平方厘米.习题演练【试题来源】【题目】如图中,阴影部分的面积是5.7平方厘米,三角形ABC的面积是____平方厘米.(π取3.14)15,那么阴影部分的面积是_____平方【题目】图中,已知圆心是○,半径r=9厘米,∠1=∠2=0厘米.π(≈3.14)【试题来源】【题目】图中阴影部分的面积是____平方厘米.(π≈3.14)【试题来源】【题目】图中两个阴影部分面积的和是多少平方厘米?【试题来源】【题目】如右图,ABCD是正方形.E是BC边的中点,三角形ECF与三角形ADF面积一样大,那么三角形AEF(阴影部分)的面积是正方形ABCD面积的百分之____.(结果保留小数点后两位)【试题来源】【题目】图中ABCD是直角梯形,其中,AD=12厘米,AB=8厘米,BC=15厘米.且三角形ADE、四边形DEBF、三角形CDF的面积相等.那么三角形EBF的面积是______平方厘米.【试题来源】【题目】正方形ABCD的面积是160平方厘米,连接这个正方形4条边的中点,又得到一个正方形EFGH.像这样重复几次后得到下图,图中涂黑色部分的面积是____平方厘米.【试题来源】【题目】如图,三个一样大小的正方形放在一个长方形的盒内,A和B是两个正方形的重叠部分,C、D、E是空出的部分,每一部分都是矩形,它们的面积比是A:B:C:D:E=1:2:3:4:5,那么这个长方形的长与宽之比是________.【试题来源】【题目】已知四边形ABCD是直角梯形,上底AD=8厘米,下底BC=10厘米,直角腰CD=6厘米,E是AD的中点,F是BC上的点,BF=23BC,G为DC上的点,三角形DEG的面积与三角形CFG的面积相等.那么,三角形ABG的面积是_____平方厘米.。
(完整版)六年级奥数图形问题精选
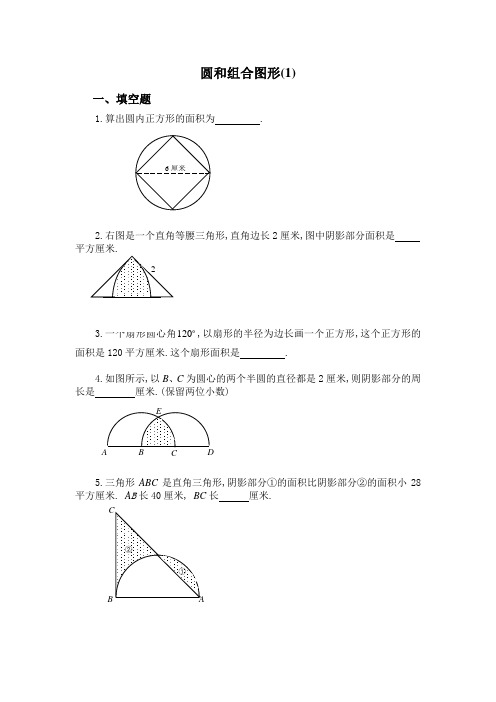
圆和组合图形(1)一、填空题1.算出圆内正方形的面积为 .2.右图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是 平方厘米.120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是 .4.如图所示,以B 、C 为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是 厘米.(保留两位小数)5.三角形ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小28长 厘米.6.如右图,阴影部分的面积为2平方厘米,等腰直角三角形的面积7.扇形的面积是31.4平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是 度.8.图中扇形的半径OA =OB =6厘米.45=∠AOB , AC 垂直OB 于C ,那么图中阴影部分的面积是 平方厘米.)14.3(=π9.右图中正方形周长是20厘米.图形的总面积是 平方厘米.10.在右图中(单位:厘米),两个阴影部分面积的和是 平方厘米.45二、解答题11. ABC 是等腰直角三角形. D 是半圆周的中点, BC 是半圆的直径,已知: AB =BC =10,那么阴影部分的面积是多少?(圆周率14.3=π)12.如图,半圆S 1的面积是14.13平方厘米,圆S 2的面积是19.625平方厘米.那么长方形(阴影部分的面积)是多少平方厘米?13.如图,已知圆心是O ,半径r =9厘米,1521=∠=∠,那么阴影部分的面积是多少平方厘米?)14.3(≈π14.右图中4个圆的圆心是正方形的4个顶点,它们的公共点是该正方形的中心.如果每个圆的半径都是1厘米,那么阴影部分的总面积是多少平方厘米?———————————————答 案——————————————————————1. 18平方厘米.由图示可知,正方形两条对角线的长都是6厘米,正方形由两个面积相等的三角形构成.三角形底为6厘米,高为3厘米,故正方形面积为1822136=⨯⨯⨯(平方厘米).2. 1.14平方厘米.由图示可知,图中阴影部分面积为两个圆心角为45的扇形面积减去直角三角形的面积.即14.12122236045214.32=⨯⨯-⨯⨯⨯(平方厘米).3. 125.6平方厘米.由已知条件可知圆的半径的平方为120平方厘米.故扇形面积为6.12536012012014.3=⨯⨯(平方厘米).4. 3.09厘米.边结BE 、CE ,则BE=CE=BC=1(厘米),故三角形BCE 为等边三角形.于是60=∠=∠BCE EBC .BE=CE=045.136060214.3=⨯⨯(厘米).于是阴影部分周长为09.312045.1=+⨯(厘米).5. 32.8厘米.从图中可以看出阴影部分①加上空白部分的面积是半圆的面积,阴影部分②加上空白部分的面积是三角形ABC 的面积.又已知①的面积比②的面积小28平方厘米,故半圆面积比三角形ABC 的面积小28平方厘米.半圆面积为6282124014.32=⨯⎪⎭⎫ ⎝⎛⨯(平方厘米),三角形ABC 的面积为628+28=656(平方厘米).BC 的长为8.32402656=÷⨯(厘米).6. 13937平方厘米.将等腰直角三角形补成一个正方形,设正方形边长为x 厘米,则圆的半径为2x 厘米.图中阴影部分面积是正方形与圆的面积之差的81,于是有282114.322⨯=⎪⎭⎫⎝⎛⨯-x x ,解得1332002=x .故等腰直角三角形的面积为1393721133200=⨯(平方厘米). ⌒⌒7. 72.扇形面积是圆面积的511574.31=÷,故扇形圆心角为360的51即72.8. 5.13.三角形ACO 是一个等腰直角三角形,将AO 看作底边,AO 边上的高为3262=÷=÷AO (厘米),故三角形ACO 的面积为93621=⨯⨯(平方厘米).而扇形面积为13.1436045614.32=⨯⨯(平方厘米),从而阴影部分面积为14.13-9=5.13(平方厘米).9. 142.75.由正方形周长是20厘米,可得正方形边长也就是圆的半径为5420=÷(厘米).图形总面积为两个43圆面积加上正方形的面积,即75.1425243514.322=+⨯⨯⨯(平方厘米).10. 90平方厘米.图中阴影部分的面积是从两个以直角三角形直角边为直径的半圆及一个直角三角的面积和中减去一个以直角三角形斜边为直径的半圆的面积即()902114.3)220(2115122114.3)216(2114.3212222=⨯⨯÷-⨯⨯+⨯⨯÷+⨯⨯÷(平方厘米).11. 如图作出辅助线,则阴影部分的面积为三角形AED 的面积减去正方形BEDO 三角形AED 的面积是21)210()21010(⨯÷⨯÷+;积是2)210(÷,圆面积的41是2)210(14.341÷⨯⨯,故阴影部分面积为:22)210(14.341)210(21)210()21010(÷⨯⨯+÷-⨯÷⨯÷+125.32625.19255.37=+-=(平方厘米).12. 由已知半圆S 1的面积是14.13平方厘米得半径的平方为914.3213.14=÷⨯(平方厘米),故半径为3厘米,直径为6厘米. 又因圆S 2的面积为19.625平方厘米,所以S 2半径的平方为25.614.3625.19=÷(平方厘米),于是它的半径为2.5厘米,直径为5厘米. 阴影部分面积为55)56(=⨯-(平方厘米).13. 因OA=OB ,故三角形OAB 为等腰三角形,即 150215180,151=⨯-=∠=∠=∠AOB OBA , 同理150=∠AOC ,于是602150360=⨯-=∠BOC . 扇形面积为:39.42914.3360602=⨯⨯(平方厘米).14. 正方形可以分割成两个底为2,高为1的三角形,其面积为221221=⨯⨯⨯(平方厘米).正方形内空白部分面积为4个41圆即一个圆的面积与正方形面积之差,即2212-=-⨯ππ(平方厘米),所有空白部分面积为)2(2-π平方厘米. 故阴影部分面积为四个圆面积之和与两个空白面积之和的差,即为 8)2(22412=-⨯-⨯⨯ππ(平方厘米).十二、圆和组合图形(2)一、填空题1.如图,阴影部分的面积是 .2.大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面积比小圆的面积大 平方厘米.3.在一个半径是4.5厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是 平方厘米.(π取3.14,结果精确到1平方厘米)4.右图中三角形是等腰直角三角形,阴影部分的面积是 (平方厘米).5.如图所求,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是 厘米.)14.3(=π6.如图,151=∠的圆的周长为62.8厘米,平行四边形的面积为100平方厘米.阴影部分的面积是 .2 1 27.有八个半径为1厘米的小圆,用它们的圆周的一部分连成一个花瓣图形(如图).图中黑点是这些圆的圆心.如果圆周率1416.3=π,那么花瓣图形的面积是 平方厘米.8.已知:ABC D 是正方形, ED =DA =AF =2厘米,阴影部分的面积是 .9.图中,扇形BAC 的面积是半圆ADB 的面积的311倍,那么,CAB ∠是 度.10.右图中的正方形的边长是2厘米,以圆弧为分界线的甲、乙两部分的面积差(大减小)是 平方厘米.(π取3.14)二、解1.如图:阴影部分的面积是多少?四分之一大圆的半径为r .(计算时圆周率取722)12.已知右图中大正方形边长是6厘米,中间小正方形边长是4厘米.求阴影部分的面积.13.有三个面积都是S 的圆放在桌上,桌面被圆覆盖的面积是2S +2,并且重合的两块是等面积的,直线a 过两个圆心A 、B , 如果直线a 下方被圆覆盖的面积是9,求圆面积S 的值.14.如图所示,1的位置沿线段AB 、BC 、CD 滚到2的位置,如果AB 、BC 、C D 的长都是20厘米,那么圆板的正面滚过的面积是多少平方厘米?———————————————答 案——————————————————————1. 6.两个扇形面积相等,故阴影部分面积等于一个长为3,宽为2的长方形面积,为6个平方单位.2. 188.4.小圆的半径为2)14(6=-÷(厘米),大圆的半径为842=⨯(厘米).大圆的面积比小圆的面积大4.18814.3)28(22=⨯-(平方厘米).3. 57.305.57214.3)22(14.35.422=⨯⨯÷-⨯(平方厘米)≈57(平方厘米).4. 10.26.从圆中可以看出,阴影部分的面积是两个半圆的面积与三角形面积之差,即26.10621)26(14.322=⨯-÷⨯(平方厘米).5. 20.5.设圆的半径为r ,则圆面积即长方形面积为2r π,故长方形的长为r DC π=.阴影部分周长r r r r r r AD BA BC DC ππππ245241)(⨯=⨯+-++=+++=5.204.1645=⨯=(厘米).6. 6548(平方厘米).如图,连结OA 、AC ,过A 点作CD 的垂线交CD 于E .三角形ACD 的面积为502100=÷(平方厘米).又圆半径为10)214.3(28.6=⨯÷(厘米),因为151=∠又OA=OD ,故30215=⨯=∠AOC ,扇形AOC 的面积为61261014.3360302=⨯⨯(平方厘米).三角形AOC 的面积为25250=÷(平方厘米).方形面积为611256126=-(平方厘米),从而阴影部分的面积为654861150=-(平方厘米).7. 19.1416.⌒花瓣图形的结构是正方形的面积,加上四个43圆面积后,再割去四个半圆的面积.圆的半径为1厘米,正方形边长为4厘米.故花瓣图形的面积是1416.1916421144314222=+=⨯⨯⨯-⨯⨯⨯+πππ(平方厘米).8. 2.43平方厘米.如图,将①移到②得:阴影部分面积等于梯形CEFB 的 面积减去三角形CED 、三角形CDA 、扇形AFG 的面积,即43.236045214.32122122212)322(22=⨯⨯-⨯-⨯⨯-⨯⨯⨯+(平方厘米).9. 60.设扇形ABC 圆心角的度数是x ,半圆的半径OA=r ,有2221311)2(360r r x⨯⨯⨯=⨯⨯ππ,解得x=60.10. 0.14.扇形面积为14.341214.32=⨯⨯(平方厘米),甲部分面积为43.0214.32122=÷-⨯(平方厘米),乙部分面积为57.04122214.3=⨯⨯-÷(平方厘米),甲乙两部分面积差为14.043.057.0=-(平方厘米11. 如图,小正方形的边长为2r,则①的面积为:72227224122r rr r =⨯-⎪⎭⎫ ⎝⎛⨯⨯, ②的面积为222417272221r r r =-⎪⎭⎫ ⎝⎛⨯⨯,2227224172241r r r =⨯⨯-⨯⨯.即阴影部分面积为272r .12. 将阴影部分旋转后,可以看出所求阴影部分面积为大正方形面积的一半减去小正形的一半,即阴影部分面积等于10242622=÷-÷(平方厘米).13. 设一个阴影部分的面积为x ,则有:2223+=-S x S ,于是22+=x S (1)又9232=-x S ,于是有23184+-=Sx ,解得S=6.D14. 圆板的正面滚过的部分如右图阴影部分所求,它的面积为: )420(4614)220(22122-+⨯⨯+⨯-+⨯⨯ππ 07.228323204221)24(414)220(4222≈+=⨯⨯+⨯-⨯-⨯-+⨯πππ(平方厘米).面积计算(三)专题简析:对于一些比较复杂的组合图形,有时直接分解有一定的困难,这时,可以通过把其中的部分图形进行平移、翻折或旋转,化难为易。
6年级奥数数论综合问题(1)例题解析

【内容概述】进位制的概念、四则运算法则及整数在不同进位制之间的转化,利用恰当的进位制解数论问题.取整符号[]与取小数部分符号{}的定义与基本性质,包含这两种符号的算式与方程的求解.两次与分式不定方程,不便直接转化为不定方程的数论问题.各种数论证明题.【例题】1.用a,b,c,d,e分别代表五进制中五个互不相同的数字,如果(ade)5,(adc)5,(aab)5是由小到大排列的连续正整数,那么(cde)5所表示的整数写成十进制的表示是多少?[分析与解]注意(adc)5+(1)5=(aab)5,第二位改变了,也就是说求和过程个位有进位,则b=0,而c=(10)5-(1)5=(4)5,则c=4.而(ade)5+(1)5=(adc)5,所以e+1=c,则e=3.又d+1=a,所以d=1,a=2.那么,(cde)5为(413)5=4×52+1×5+3=108.即(cde)5所表示的整数写成十进制的表示是108.批注:二进制中是逢二进一,五进制中是逢五进一。
2.算式1534×25=43214是几进位制数的乘法?[分析与解]注意到尾数,在足够大的进位制中有乘积的个位数字为4×5=20,但是现在为4,说明进走20-4=16,所以进位制为16的约数:16、8、4、2.因为原式中有数字5,所以不可能为4、2进位,而在十进制中有1534×25=38350<43214,所以在原式中不到10就有进位,即进位制小于10,于是原式为8进制.3.设l,3,9,27,81,243是6个给定的数,从这6个数中取出若干个数,每个数至多取一次,然后将取出的数相加得到一个和数,这样共可得到63个不同的和数.把这些数从小到大排列起来依次是1,3,4,9,l0,12,…,那么其中第39个数是多少?[分析与解]我们知道1,3,9,27,81,243都是3的若干次幂,写成3进制依次为:(1)3,(10)3,(100)3,(1000)3,(10000)3,(100000)3,则从中任意选取若干数,且不重复,那么它们的和在3进制中都只是由1和0组成.但是在3进制中,并不是所有的数字都是只由0,1组成,这就给计数造成了困难.而2进制中所有的数字都是只由1和0组成.于是,我们想到使用2进制,在2进制中第39个非零自然数,即39应记为:(100111)2.在3进制中,只用1和0表示的数,第39个也是100111,有(100111)3=1×35+1×32+1×3+1=256.即其中第39个数是256.评注:这道题我们不厌其烦的详细说明这些,只是想帮助大家复习进位制中的n进制与十进制的互相转化.此63个数的范围在3进制中的范围是(1)3~(111111)3而且不会有进位产生,也就是都是由0和1这两个数字组成的,所以我们可以把其想象为二进制,中的第39个数是什么?4.求方程19[x]-96{x}=0的解的个数.[分析与解]有{x}为一个数的小数部分,显然小于1,则96{x}小于96,而19[x]=96{x},所以19[x]小于96,即[x]小于,又[x]为整数,所以[x]可以取0,1,2,3,4,5,对应有6组解.进一步计算有0,,,,,为原方程的解.批注;解决此类问题的方法就是要销去一个定义符号,然后用不等式的方法来解答。
六年级上册秋季奥数培优讲义——6-02-组合图形(一)3-讲义-学生

第2讲组合图形求面积(一)【学习目标】1、复习圆的面积计算;2、熟练掌握组合图形的面积计算。
【知识梳理】1、拼接法:把不规则的图形拼接成规则的可以直接计算的图形;2、大减小:用大图的面积减去其他部分的面积;3、整体法:在计算过程中把某一个中间数(如半径的平方)当做一个整体来求解。
【典例精析】【例1】如图,正方形的面积是12平方厘米,求图中阴影部分的面积。
【趁热打铁-1】下图中圆的面积是125.6cm²,正方形的面积是多少平方厘米?【例2】如图,阴影部分的面积是25m²。
圆环的面积是多少?【趁热打铁-2】图中阴影部分的面积是50平方厘米,求环形的面积。
【例3】如图4个大小相同的圆的直径都是10厘米,求阴影部分的面积和周长。
【趁热打铁-3】如图个圆半径都是2厘米,求阴影部分的面积。
(图中三角形是直角三角形)【例4】如果,图中三个圆的周长都是25.12厘米圆心恰在直角梯形的三个顶点处,则圆与梯形重叠部分的面积是平方厘米。
(π取3.14)【趁热打铁-4】图中三个圆的周长都是25.12厘米,圆心恰好在直角梯形的三个顶点处,则圆与梯形重叠部分的面积是平方厘米。
(π取3.14)【例5】下图是由一个平行四边形和个半圆组成的图形,已知半圆的半径是10厘米,计算图中阴影部分的面积。
【趁热打铁-5】下图由半圆和等腰直角三角形重叠而成。
已知等腰直角三角形的直角边长为4厘米,求图中阴影部分的面积。
【例6】下图中长方形的宽是4厘米,图中阴影部分的面积是平方厘米。
【趁热打铁-6】如图,正方形的边长是4厘米,则阴影部分的面积为________平方厘米。
【例7】下图中阴影部分的面积为________平方厘米。
(单位:厘米)【趁热打铁-7】下图中阴影部分的面积为________平方厘米。
(单位:厘米)【例8】在长方形ABCD中,AB长8厘米,BC长6厘米,AC长10厘米.如果把这个长方形绕顶点C旋转90°(如图),那么AD边所扫过部分(阴影部分)的面积是多少平方厘米?【趁热打铁-8】如图,圆0的直径AB与CD互相垂直,AB=20厘米,以C为圆心,CA为半径画弧AB,则阴影部分面积是____平方厘米.【例9】如图所示,求图中阴影部分的面积。
六年级奥数题及答案(高等难度)

六年级奥数题及答案(⾼等难度)六年级奥数题及答案:图形(⾼等难度)1 图形:(⾼等难度)如图,长⽅形ABCD中,E为的AD中点,AF与BE、BD 分别交于G、H,OE垂直AD于E,交AF于O,已知AH=5cm,HF=3cm,求AG.图形答案:2图形⾯积:(⾼等难度)直⾓三⾓形ABC的两直⾓边AC=8cm,BC=6cm,以AC、B C为边向形外分别作正⽅形ACDE与BCFG,再以AB为边向上作正⽅形ABMN,其中N点落在DE上,BM交CF于点T.问:图中阴影部分(与梯形BTFG)的总⾯积等于多少?图形⾯积答案:3 应⽤题:(⾼等难度)我国某城市煤⽓收费规定:每⽉⽤量在8⽴⽅⽶或8⽴⽅⽶以下都⼀律收6.9元,⽤量超过8⽴⽅⽶的除交6.9元外,超过部分每⽴⽅⽶按⼀定费⽤交费,某饭店1⽉份煤⽓费是82.26元,8⽉份煤⽓费是40.02元,⼜知道8⽉份煤⽓⽤量相当于1⽉份的,那么超过8⽴⽅⽶后,每⽴⽅⽶煤⽓应收多少元?应⽤题答案:4 乒乓球训练(逻辑):(⾼等难度)甲、⼄、丙三⼈⽤擂台赛形式进⾏乒乓球训练,每局2⼈进⾏⽐赛,另1⼈当裁判.每⼀局的输⽅去当下⼀局的裁判,⽽由原来的裁判向胜者挑战.半天训练结束时,发现甲共打了15局,⼄共打了21局,⽽丙共当裁判5局.那么整个训练中的第3局当裁判的是_______.乒乓球训练(逻辑)答案:本题是⼀道逻辑推理要求较⾼的试题.⾸先应该确定⽐赛是在甲⼄、⼄丙、甲丙之间进⾏的.那么可以根据题⽬中三⼈打的总局数求出甲⼄、⼄丙、甲丙之间的⽐赛进⾏的局数.⑴丙当了5局裁判,则甲⼄进⾏了5局;⑵甲⼀共打了15局,则甲丙之间进⾏了15-5=10局;⑶⼄⼀共打了21局,则⼄丙之间进⾏了21-5=16局;所以⼀共打的⽐赛是5+10+6=31局.此时根据已知条件⽆法求得第三局的裁判.但是,由于每局都有胜负,所以任意连续两局之间不可能是同样的对⼿搭配,就是说不可能出现上⼀局是甲⼄,接下来的⼀局还是甲⼄的情况,必然被别的对阵隔开.⽽总共31局⽐赛中,⼄丙就进⾏了16局,剩下的甲⼄、甲丙共进⾏了15局,所以类似于植树问题,⼀定是开始和结尾的两局都是⼄丙,中间被甲⼄、甲丙隔开.所以可以知道第奇数局(第1、3、5、……局)的⽐赛是在⼄丙之间进⾏的.那么,第三局的裁判应该是甲.5唐⽼鸭和⽶⽼师赛跑:(⾼等难度)唐⽼鸭与⽶⽼⿏进⾏⼀万⽶赛跑,⽶⽼⿏的速度是每分钟125⽶,唐⽼鸭的速度是每分钟100⽶。
2018六年级奥数数学几何综合训练一

2017年六年级外冲班数学几何综合训练一一、兴趣篇1.图中八条边的长度正好分别是1、2、3、4、5、6、7、8厘米.已知a=2厘米,b=4厘米,c=5厘米,求图形的面积.2.如图所示,∠1+∠2+∠3+∠4+∠5+∠6等于度.3.平行四边形ABCD周长为75厘米,以BC为底时高是14厘米(如图);以CD 为底时高是16厘米.求:平行四边形ABCD的面积.4.如图,一个边长为1米的正方形被分成4个小长方形,它们的面积分别是平方米、平方米、平方米和平方米.已知图中的阴影部分是正方形,那么它的面积是多少平方米?5.如图,红、黄、绿三块大小一样的正方形纸片,放在一个正方形盒内,它们之间互相叠合.已知露在外面的部分中,红色的面积是20,黄色的面积是14,绿色的面积是lO.那么,正方形盒子的底面积是多少?6.如图,在三角形ABC中,IF和BC平行,GD和AB平行,HE和AC平行.已知AG:GF:FC=4:3:2,那么AH:HI:IB和BD:DE:EC分别是多少?7.如图,已知三角形ABC的面积为60平方厘米,D、E分别是AB、AC边的中点,求三角形OBC的面积.8.在如图的正方形中,A、B、C分别是ED、EG、GF的中点.请问:三角形CDO 的面积是三角形ABO面积的几倍?9.如图,ABCD是平行四边形,面积为72平方厘米,E,F分别为AB,BC的中点,则图中阴影部分的面积为平方厘米.10.如图,在三角形ABC中,CE=2AE,F是AD的中点,三角形ABC的面积是1,那么阴影部分的面积是多少?二、拓展篇11.如图,A、B是两个大小完全一样的长方形,已知这两个长方形的长比宽长8厘米,图中的字母表示相应部分的长度.问:A、B 中阴影部分的周长哪个长?长多少?12.如图,ABCDE是正五边形,CDF是正三角形,∠BFE等于多少度?13.一个各条边分别为5厘米、12厘米、13厘米的直角三角形,将它的短直角边对折到斜边上去与斜边相重合,如图所示.问:图中的阴影部分(即折叠的部分)的面积是多少平方厘米?14.图中大长方形被分成四个小长方形,面积分别为12、24、36、48.请问:图中阴影部分的面积是多少?15.三个面积都是12的正方形放在一个长方形的盒子里面,如图,盒中空白部分的面积已经标出,求图中大长方形的面积.16.如图,三角形ABC的面积为1,D、E分别为AB、AC的中点,F、G是BC边上的三等分点.求三角形DEF和三角形DOE的面积.17.如图,梯形ABCD的上底AD长10厘米,下底BC长15厘米.如果EF与上、下底平行,那么EF的长度为多少?18.如图,正六边形的面积为6,那么阴影部分的面积是多少?19.两盏4米高的路灯相距10米,有一个身高1.5米的同学行走在这两盏路灯之间,那么他的两个影子总长度是多少米?20.如图,D是长方形ABCD一条对角线的中点,图中已经标出两个三角形的面积为3和4,那么阴影直角三角形的面积是多少?21.如图,在三角形ABC中,AE=ED,D点是BC的四等分点,阴影部分的面积占三角形ABC面积的几分之几?22.如图,在三角形ABC中,三角形AEO的面积是1,三角形ABO的面积是2,三角形BOD的面积是3,则四边形DCEO的面积是多少?三、超越篇23.如图,长方形的面积是60平方厘米,其内3条长度相等且两两夹角为120°的线段将长方形分成了两个梯形和一个三角形.请问:一个梯形的面积是多少平方厘米?24.如图,P是三角形ABC内一点,DE平行于AB,FG平行于BC,HI平行于CA,四边形AIPD的面积是12,四边形PGCH的面积是15,四边形BEPF的面积是20.请问:三角形ABC的面积是多少?25.如图所示,正方形ABCD的面积为1.E、F分别是BC和DC的中点,DE与BF 交于M点,DE与AF交于N点,那么阴影三角形MFN的面积为多少?26.如图,三角形ABC的面积为1,D、E、F分别是三条边上的三等分点,求阴影三角形的面积.27.如图,小悦测出家里瓷砖的长为24厘米,宽为10厘米,而且还测出了边上的中间线段均为4厘米,那么中间菱形的面积是多少平方厘米?28.如图,ED垂直于等腰梯形ABCD的上底AD,并交BC于G,AE平行于BD,∠DCB=45°,且三角形ABD和三角形EDC的面积分别为75、45,那么三角形AED的面积是多少?29.在长方形ABCD中,E、F、G、H分别是边AB、BC、CD、DA上的点,将长方形的四个角分别沿着HE、EF、FG、GH对折后,A点与B点重合,C点与D点重合.已知EH=3,EF=4,求线段AD与AB的长度比.30.如图,在长方形ABCD中,AE:ED=AF:AB=BG:GC.已知△EFC的面积为20,△FGD的面积为16,那么长方形ABCD的面积是多少?2017年六年级外冲班数学几何综合训练一参考答案与试题解析一、兴趣篇1.图中八条边的长度正好分别是1、2、3、4、5、6、7、8厘米.已知a=2厘米,b=4厘米,c=5厘米,求图形的面积.【解答】解:如图所示,图形的面积为:7×2+5×(7﹣4)+6×1=14+15+6=35(平方厘米)答:图形的面积是35平方厘米.2.如图所示,∠1+∠2+∠3+∠4+∠5+∠6等于360 度.【解答】解:∠3=∠7,所以∠2+∠3=180°﹣∠A;同理,∠6=∠8,所以∠1+∠6=180°﹣∠C;∠4+∠5=180°﹣∠B;则∠1+∠2+∠3+∠4+∠5+∠6,=180°×3﹣(∠A+∠B+∠C),=540°﹣180°,=360°,答:∠1+∠2+∠3+∠4+∠5+∠6=360°.故答案为:360.3.平行四边形ABCD周长为75厘米,以BC为底时高是14厘米(如图);以CD 为底时高是16厘米.求:平行四边形ABCD的面积.【解答】解:由平行四边形面积公式知14×BC=16×CD,即14BC=16CD,则BC:CD=16:14=8:7,BC=CD,又2×(BC+CD)=75,则BC+CD=37.5(厘米),CD+CD=37.5(厘米),CD=17.5(厘米),因此,平行四边形ABCD的面积为:16×17.5=280(平方厘米);答:平行四边形ABCD的面积为280平方厘米.4.如图,一个边长为1米的正方形被分成4个小长方形,它们的面积分别是平方米、平方米、平方米和平方米.已知图中的阴影部分是正方形,那么它的面积是多少平方米?【解答】解:如图所示:+++=1(平方米);大正方形的边长就是1米;(FE×AE):(FE×EB)=:,即:AE:EB=3:4;AE就是大正方形边长的;1×=(米);(CH×HG):(HG×HD)=:;BE:EC=2:1;CH是大正方形边长的;1×=(米);FG=﹣=(米);×=(平方米);答:阴影部分的面积是平方米.5.如图,红、黄、绿三块大小一样的正方形纸片,放在一个正方形盒内,它们之间互相叠合.已知露在外面的部分中,红色的面积是20,黄色的面积是14,绿色的面积是lO.那么,正方形盒子的底面积是多少?【解答】解:把黄块向左移动就会发现,黄色减少的面积等于绿色增加的面积,从而得出黄+绿=24,黄和绿各是24÷2=12,即两个长方形的面积都是12,设红块边长是b,与红色并排的绿边是a,则根据正方形的面积公式,得大正方形面积b2=20,两个长方形的面积ab=12,小正方形的面积a2=(ab)2÷b2=12×12÷20=144÷20,=7.2;底面积:20+12×2+7.2=51.2;答:正方形盒子的底面积是51.2.6.如图,在三角形ABC中,IF和BC平行,GD和AB平行,HE和AC平行.已知AG:GF:FC=4:3:2,那么AH:HI:IB和BD:DE:EC分别是多少?【解答】解:AG:GF:FC=4:3:2,则(AG+GF):FC=(4+3):2,即AF:FC=7:2;因为IF和BC平行,所以△AIF∽△ABC,则AI:IB=AF:FC=7:2;因为GD和AB平行,所以△FGO∽△FAI,则FO:OI=FG:GA=3:4;因为HE和AC平行,所以△IHO∽△IAF,则HI:AH=OI:FO=4:3;所以AH:HI:IB=3:4:2同理可证:BD:DE:EC=4:2:3答:AH:HI:IB=3:4:2;BD:DE:EC=4:2:3.7.如图,已知三角形ABC的面积为60平方厘米,D、E分别是AB、AC边的中点,求三角形OBC的面积.【解答】解:由题意可知AE=CE,AD=BD,根据等底同高的三角形的面积相等得:S△ADC=S△BDC=60÷2=30平方厘米,S△AEB=S△CBE=30(平方厘米),所以S△ADC=S△AEB=30(平方厘米),则S△BOD=S△COE再根据等底同高的三角形的面积相等得:S△AOE=S△COE,S△AOD=S△BOD,所以S△AOE=S△COE=S△AOD=S△BOD,S△ADC=S△AOE+S△COE+S△AOD=30(平方厘米),所以S△COE=30÷3=10(平方厘米),所以S△BOC是:30﹣10=20(平方厘米),答:S△BOC是20平方厘米.8.在如图的正方形中,A、B、C分别是ED、EG、GF的中点.请问:三角形CDO 的面积是三角形ABO面积的几倍?【解答】解:因为四边形是正方形且A、B、C分别是ED、EG、GF的中点.所以:AD=DE=CE=BE=DE,线段AO=BE所以:S△BED=S△CAD,S△AOD=S△BED=S△CAD,S△ABD=S△CAD所以:S△AOB=S△BAD﹣S△AOD=S△CAD﹣S△CAD=S△CADS△COD=S△CAD﹣S△AOD=S△CAD﹣S△CAD=S△CADS△CDO÷S△ABO=S△CAD÷S△CAD=3答:三角形CDO的面积是三角形ABO面积的3倍.9.如图,ABCD是平行四边形,面积为72平方厘米,E,F分别为AB,BC的中点,则图中阴影部分的面积为48 平方厘米.【解答】解:DE、DF分别于AC交于点M、N,M、N是AC的三等分点因为平行四边形的面积=72平方厘米,则S△ADC=72÷2=36(平方厘米),S△ADM=S△DMN=S△DNC=S△ADC=×36=12(平方厘米),S△AEM=S△NFC=S△ADM=×12=6(平方厘米),所以阴影部分的面积=72﹣12﹣6﹣6=60﹣12,=48(平方厘米);答:阴影部分的面积是48平方厘米.故答案为:48.10.如图,在三角形ABC中,CE=2AE,F是AD的中点,三角形ABC的面积是1,那么阴影部分的面积是多少?【解答】解:连接CF,因为CE=2AE,根据燕尾定理,所以==,同理,=,设S△AEF=1份,那么S△CEF=2份,因为F是AD的中点,S△CFD=S△ACF=S△AEF+S△CEF=1+2=3份,同理,,又因为==,所以,所以S△BDF=S△ABF=3份,这样S△ABC=1+2+3+3+3=12份,阴影部分的份数是:2+3=5份,5÷12=,即1×=.二、拓展篇11.如图,A、B是两个大小完全一样的长方形,已知这两个长方形的长比宽长8厘米,图中的字母表示相应部分的长度.问:A、B 中阴影部分的周长哪个长?长多少?【解答】解:图形A中阴影部分的周长是:2(a+a﹣b)+2(b+2b)=4a+4b,图形B中阴影部分的周长是:2(a+2b+a+b)=4a+6b,4a+6b﹣(4a+4b)=2b,又因为大长方形的长比宽长8厘米,即a+2b﹣(a+b)=8,可得b=8厘米,所以2b=2×8=16(厘米),答:图形B中的阴影部分的周长较长,比图形A中的阴影部分的周长长16厘米.12.如图,ABCDE是正五边形,CDF是正三角形,∠BFE等于多少度?【解答】解:∠BCF=∠EDF=108°﹣60°=48°,因为BC=CF,DF=DE,所以∠BFC=∠EFD=(180°﹣48°)÷2=66°,因此∠BFE=360°﹣66°×2﹣60°=168°.答:∠BFE等于168度.13.一个各条边分别为5厘米、12厘米、13厘米的直角三角形,将它的短直角边对折到斜边上去与斜边相重合,如图所示.问:图中的阴影部分(即折叠的部分)的面积是多少平方厘米?【解答】解:见下图:×13×DC=×(12﹣DC)×5,13×DC=60﹣DC×5,DC=(厘米);△ADC=△AEC=××5=(平方厘米).答:图中的阴影部分(即折叠的部分)的面积是平方厘米.14.图中大长方形被分成四个小长方形,面积分别为12、24、36、48.请问:图中阴影部分的面积是多少?【解答】解:如图,阴影部分面积为:是EF×AJ,设大长方形的长为a,宽为b,则EF=a﹣a=a,因此,阴影部分面积为×a×b,=×(a×b)=×(12+24+36+48)=×120=答:图中阴影部分的面积.故答案为:.15.三个面积都是12的正方形放在一个长方形的盒子里面,如图,盒中空白部分的面积已经标出,求图中大长方形的面积.【解答】解:由分析可知,小长方形3的面积=(大长方形的底边﹣2倍的正方形边长)×(大长方形宽﹣正方形边长)=3,小长方形4+小长方形5的面积=(大长方形底边﹣正方形边长)×(大长方形宽﹣正方形边长)=9,(大长方形底边﹣正方形边长)÷(大长方形的底边﹣2倍的正方形边长)=3,大长方形底边﹣正方形边长=3倍大长方形的底边﹣6倍的正方形边长,2倍大长方形的底边=5倍的正方形边长,大长方形的底边=2.5倍的正方形边长,则大长方形的宽=1.5倍正方形边长,大长方形面积=大长方形的底边×大长方形的宽=2.5倍正方形边长×1.5倍正方形边长=2.5×1.5倍的正方形面积=2.5×1.5×12=45.答:大长方形的面积是45.16.如图,三角形ABC的面积为1,D、E分别为AB、AC的中点,F、G是BC边上的三等分点.求三角形DEF和三角形DOE的面积.【解答】解:①过点A作线段BC的垂线,垂足为Q,过点D作线段BC的垂线,垂足为M,所以线段DM=AQ那么三角形ABC的面积是:BC×AQ÷2=1所以:BC×AQ=2因为D、E分别为AB、AC的中点,所以线段DE=BC,所以三角形DEF的面积:DE×DM÷2=×BC××AQ÷2=×2÷2=②又因为DE=,FG=,所以=,所以三角形DOE面积为:三角形DEF面积×3÷(3+2)=×3÷5=.答:三角形DEF的面积是,三角形DOE的面积.17.如图,梯形ABCD的上底AD长10厘米,下底BC长15厘米.如果EF与上、下底平行,那么EF的长度为多少?【解答】解:∵AD∥BC,EF∥BC,∴===,又==,==∴OE=BC=×15=6(厘米),OF=AD=×10=6(厘米)∴EF=OE+OF=6+6=12(厘米)答:EF的长度为12厘米.18.如图,正六边形的面积为6,那么阴影部分的面积是多少?【解答】解:如图,连结AC、BF、CE、DF,根据六正边形的特征及蝴蝶定理,阴影部分面积:×6=×6=答:阴影部分的面积是.故答案为:.19.两盏4米高的路灯相距10米,有一个身高1.5米的同学行走在这两盏路灯之间,那么他的两个影子总长度是多少米?【解答】解:如图所示:CD、EF为路灯高度,AB为该人高度,BM、BN为该人前后的两个影子.由题意得:b=4米,a=1.5米,DF=10米,∵AB∥CD,∴==,∴==即MB=DB同理BN=FB∴MB+BN=(DB+FB)=0.6×10=6(米)答:他的两个影子总长度是6米.20.如图,D是长方形ABCD一条对角线的中点,图中已经标出两个三角形的面积为3和4,那么阴影直角三角形的面积是多少?【解答】解:如图:设BC=x,阴影部分三角形的高为h,DC=y因为四边形ABCD是长方形,点O是对角线的中点,所以S△ABC=2×4=8,S△BCD=8所以:S△BWC=8﹣3=5即为:xh÷2=5xh=10所以S长方形ABCD=xy=4×4=16xh:xy=10:16即为:h:y=5:8所以:==所以:=S△BQW=×5=答:阴影直角三角形的面积是.21.如图,在三角形ABC中,AE=ED,D点是BC的四等分点,阴影部分的面积占三角形ABC面积的几分之几?【解答】解:连接CE,设S△CDE=1,因为AE=ED,S△ACE=1,D点是BC的四等分点,根据燕尾模型可得:S△BDE=S△ABE=3,则,所以,S△AEF=,.22.如图,在三角形ABC中,三角形AEO的面积是1,三角形ABO的面积是2,三角形BOD的面积是3,则四边形DCEO的面积是多少?【解答】解:如图:过点O作线段OF∥BC交AC于点F,因为三角形AEO的面积是1,三角形ABO的面积是2,三角形BOD的面积是3,所以==,==所以:S△EOF:S△EBC=,S△AOF:S△ADC=设S△EOF=x,S四边形EODF=y所以x:(3+y+x)=1:9①(1+x):(1+x+y)=4:25②由①②解得:x=3,y=21所以四边形DCEO的面积是:3+21=24答:四边形DCEO的面积是24.三、超越篇23.如图,长方形的面积是60平方厘米,其内3条长度相等且两两夹角为120°的线段将长方形分成了两个梯形和一个三角形.请问:一个梯形的面积是多少平方厘米?【解答】解:过F点作FG⊥BC于G.因为∠BFC=120°,BF=CF=EF,所以∠FBG=30°,所以EF=BF=2FG,所以FG=EG,所以△BFC=长方形的面积×=10(平方厘米)(60﹣10)÷2=50÷2=25(平方厘米).答:一个梯形的面积是25平方厘米.24.如图,P是三角形ABC内一点,DE平行于AB,FG平行于BC,HI平行于CA,四边形AIPD的面积是12,四边形PGCH的面积是15,四边形BEPF的面积是20.请问:三角形ABC的面积是多少?【解答】解:DE平行于AB,FG平行于BC,HI平行于CA,四边形AIPD的面积是12,四边形PGCH的面积是15,四边形BEPF的面积是20.又因为四边形AIPD和四边形BEPF的高相等,所以DP:PE=12:20=3:5;则DG:GC=3:5,又因为三角形PDG与平行四边形PHCG高相等,所以三角形PDG的面积与四边形PHCG的面积的一半的比是3:5,所以三角形PDG的面积是:(15÷2)×3÷5=4.5,同理:三角形PEH的面积与平行四边形PFBE的面积的一半的比是:5:4,所以三角形PEH的面积是:(20÷2)×5÷4=12.5,同理三角形PIF的面积与四边形PEBF的面积的一半的比是4:5,所以三角形PIF的面积是:(20÷2)×4÷5=8,12+20+15+4.5+12.5+8=72.答:三角形ABC的面积是72.25.如图所示,正方形ABCD的面积为1.E、F分别是BC和DC的中点,DE与BF 交于M点,DE与AF交于N点,那么阴影三角形MFN的面积为多少?【解答】解:连接CM、EF和AE,因为E、F是中点,所以S△BEM=S△CEM=S△CMF=1÷4÷3=,因为F是CD的中点,所以S△DEF=1÷4÷2=,AN:FN=S△ADE:S△DEF=(1÷2):=1:4所以S△DFN=1÷4÷(1+4)=,所以S△MFN=S△DEC﹣S△CME﹣S△CMF﹣S△DFN=﹣﹣﹣=.答:阴影三角形MFN的面积为.26.如图,三角形ABC的面积为1,D、E、F分别是三条边上的三等分点,求阴影三角形的面积.【解答】解:1×××=××=×=.答:阴影三角形的面积是.27.如图,小悦测出家里瓷砖的长为24厘米,宽为10厘米,而且还测出了边上的中间线段均为4厘米,那么中间菱形的面积是多少平方厘米?【解答】解:左右两边三角形的高为:(10+4)×2÷7=4(厘米)上下两个三角形的高为:(3+4)×2÷14=1(厘米)四个小三角形的面积和为:(4×4÷2+4×1÷2)=20(平方厘米)大直角三角形的面积为:7×14÷2=49(平方厘米)空白部分面积为:49×4﹣20=176(平方厘米)中间大菱形面积为:24×10﹣176=64(平方厘米)答:中间菱形的面积为64平方厘米.28.如图,ED垂直于等腰梯形ABCD的上底AD,并交BC于G,AE平行于BD,∠DCB=45°,且三角形ABD和三角形EDC的面积分别为75、45,那么三角形AED的面积是多少?【解答】解:过A作AH⊥BC,垂足为H,AH交BD于F,则AH∥EG.因为四边形ABCD是等腰梯形,AD∥BC,∠DCB=45°,所以∠ABC=45°,AH=DG=GC=BH,又因为AE∥BD,所以四边形AFDE是平行四边形,DE=AF,S△AED=S△AFD,因为S△DEC=DE•GC=45,S△ABD=S△AFD+S△AFB=75,其中S△AFD=S△AED,S△AFB=AF•BH=DE•GC=S△DEC=45,这样S△AED=S△ABD﹣S△AFB=75﹣45=30.答:三角形AED的面积是30.29.在长方形ABCD中,E、F、G、H分别是边AB、BC、CD、DA上的点,将长方形的四个角分别沿着HE、EF、FG、GH对折后,A点与B点重合,C点与D点重合.已知EH=3,EF=4,求线段AD与AB的长度比.【解答】解:由对称性得:∠AEH=∠A'EH,∠BEF=∠B'EF,∠AEH+∠A'EH+∠BEF+∠B'EF=180°,∠A'EH+∠B'EF=90°,∠HEF=90°.根据勾股定理得:HF=5,HF×EA'=HE×EF=3×4=12,EA'=2.4.由对称性得:AE=A'E BE=B'E A'E=B'E 所以AE=BE AE=BE=2.4,AB=4.8.由对称性得:AH=A'H BF=B'F DH=D'H CF=C'F A'H+B'F+D'H+C'F=2HF=10AH+BF+DH+CF=10AD+BC=10AD=5AD:AB=5:4.8=25:24答:线段AD与AB的长度比为25:24.30.如图,在长方形ABCD中,AE:ED=AF:AB=BG:GC.已知△EFC的面积为20,△FGD的面积为16,那么长方形ABCD的面积是多少?【解答】解:设矩形ABCD的对边AB=CD=a,AD=BC=b,再设题中的比例常数AE:ED=AF:AB=BG:GC=k,把这个表达式变换成k和矩形ABCD边长a、b的表达式,则有:AE=BG=kb:(k+1)ED=GC=AF=ka,FB=(1﹣k)aS(矩形ABCD)=ab=S(Rt△AFE)+S(△FEC)+S( Rt△EDC)+S(Rt△FBC)=×AF×AE+20+×ED×CD+×FB×BC=×ka×kb:(k+1)+20+×b:(k+1)×a+×(1﹣k)a×b=×ab+20解ab,得:ab=(1)同理S(矩形ABCD)=ab=S(Rt△FBG)+S(△FGD)+S( Rt△GDC)+S(Rt△AFD)=FB×BG+16+GC×CD+AF×AD=(1﹣k)a×+16++b×a+ka×b=×ab+16解ab,得:ab=32(k+1)(2)根据(1)(2),解得k=,代入(1)或(2),得到S(矩形ABCD)=ab=52cm。
小学六年级奥数--立体几何综合

学科培优 数学立体几何综合学生姓名 授课日期 教师姓名授课时长知识定位本讲复习已经学过的立体图形的相关知识和解题技巧,主要有:长方体、立方体、圆柱、圆锥的体积及表面积求解,立体几何计数及多面体顶点与棱以及表面的关系。
重难点在于:1.不规则立体图形的表面积或体积求解2.多面体的顶点与棱数计数 3.体积的等量代换主要的考点:1.规则立体图形的表面积(侧面积)与体积计算2.不规则立体图形的表面积与体积计算 3.染色问题4.立体图形的三视图与展开图知识梳理主要知识点 立体几何⑴规则立体图形的表面积和体积公式长方体:体积:长宽高 表面积:(长宽+宽高+长高) 立方体:体积:棱长的立方 表面积:棱长的平方6 圆柱: 体积:2r h π 侧面积:2rh π 圆锥: 体积:213r h π⑵不规则立体图形的表面积整体观照法⑶体积的等积变形①水中浸放物体:V 升水=V 物 ②测啤酒瓶容积:V=V 空气+V 水⑷三视图与展开图最短线路与展开图形状问题⑸染色问题几面染色的块数与“芯”、棱长、顶点、面数的关系。
例题精讲【试题来源】【题目】一个长方体的表面积是33.66平方分米,其中一个面的长是2.3分米,宽是2.1分米,它的体积是_____立方分米.【试题来源】 【题目】右图是一个棱长为2厘米的正方体,在正方体上面的正中向下挖一个棱长为1厘米的正方形小洞;接着在小洞的底面正中再挖一个棱长为21厘米的小洞;第三个小洞的挖法与前两个相同,棱长为41厘米.那么最后得到的立体图形的表面积是 平方厘米【试题来源】【题目】把一个长25厘米,宽10厘米,高4厘米的长方体木块锯成若干个大小相等的正方体,然后拼成一个大的正方体.这个大正方体的表面积是_____平方厘米。
【试题来源】【题目】右图是3层没有缝隙的小立方块组成的.如果它的外表面(包括底面)全都被涂成红色,那么把它们再分开成一个个小立方块时,有多少个小立方块恰有三面是红色的?【试题来源】【题目】一个正方体木块,棱长是15.从它的八个顶点处各截去棱长分别是1、2、3、4、5、6、7、8的小正方体.这个木块剩下部分的表面积最少是( ).【试题来源】【题目】把一根长2.4米的长方体木料锯成5段(如图),表面积比原来增加了96平方厘米.这根木料原来的体积是_____立方厘米.【试题来源】【题目】用棱长是1厘米的立方体拼成右图所示的立体图形.求这个立体图形的表面积.【试题来源】【题目】把1个棱长是3厘米的正方体分割成若干个小的正方体,这些小正方体的棱长必须是整厘米数.如果这些小正方体的体积不要求都相等,那么最少可分割成个小正方体.【试题来源】【题目】用10块长7厘米,宽5厘米,高3厘米的长方体积木堆成一个长方体,这个长方体的表面积最小是多少?【试题来源】【题目】一个盛有水的圆柱形容器,底面内半径为5厘米,深20厘米,水深15厘米.今将一个底面半径为2厘米,高为17厘米的铁圆柱垂直放人容器中.求这时容器的水深是多少厘米?【试题来源】【题目】有甲、乙两只圆柱形玻璃杯,其内直径依次是10厘米、20厘米,杯中盛有适量的水.甲杯中沉没着一铁块,当取出此铁块后,甲杯中的水位下降了2厘米;然后将铁块沉没于乙杯,且乙杯中的水未外溢.问:这时乙杯中的水位上升了多少厘米?【试题来源】【题目】将高都是1米,底面半径分别为1.5米、1米和0.5米的三个圆柱组成一个物体.求这个物体的表面积.【试题来源】【题目】这里有一个圆柱和一个圆锥(下图),它们的高和底面直径都标在图上,单位是厘米.请回答:圆锥体积与圆柱体积的比是多少?【试题来源】【题目】一个长、宽、高分别为21厘米、15厘米、12厘米的长方体.现从它的上面尽可能大的切下一个正方体.然后从剩余的部分再尽可能大的切下一个正方体.最后再从第二次剩余的部分尽可能大的切下一个正方体.剩下的体积是平方厘米.【试题来源】【题目】一个圆柱形玻璃杯内盛有水,水面高2.5厘米,玻璃杯内侧的底面积是72平方厘米.在这个杯中放进棱长6厘米的正方体铁块后,水面没有淹没铁块.这时水面高多少厘米?【试题来源】【题目】图1是下面的表面展开图①甲正方体;②乙正方体;③丙正方体;④甲正方体或丙正方体.【试题来源】【题目】如图,剪一块硬纸片可以做成一个多面体的纸模型(沿虚线折,沿实线粘).这个多面体的面数、顶点数和棱数的总和是多少?【试题来源】【题目】下面是一辆汽车模型纸工平面展开图,中轴线上面的一半标出了尺寸.将该图剪下折叠粘合(相同字母标记处粘合在一起)做成汽车模型的体积为V .请回答:①403<v<445②473<V<500,哪一个正确,为什么?【试题来源】【题目】现有一张长40厘米、宽20厘米的长方形铁皮,请你用它做一只深是5厘米的长方体无盖铁皮盒(焊接处及铁皮厚度不计,容积越大越好),你做出的铁皮盒容积是多少立方厘米?【试题来源】【题目】如图,在一个立方体的两对侧面的中心各打通一个长方体的洞在上下侧面的中心打通一个圆柱形的洞,已知立方体边长为10厘米,侧面上的洞口是边长为4厘米的正方形,上下侧面的洞口是直径为4厘米的圆,求该立方体的表面积和体积(取 =3.14).【试题来源】【题目】用大小相等的无色透明玻璃小正方体和红色玻璃小正方体拼成一个大正方体ABCD —1A 1B 1C 1D (如图),大正方体内的对角线A 1C ,B 1D ,C 1A ,D 1B 所穿的小正方体都是红色玻璃小正方体,其它部分都是无色透明玻璃小正方体,小红正方体共用了401个,问:无色透明小正方体用了多少个?习题演练【试题来源】【题目】一个长方体的各条棱长的和是48厘米,并且它的长是宽的2倍,高与宽相等,那么这个长方体的体积是______ 立方厘米【试题来源】【题目】右图是一个表面被涂上红色的棱长为lO厘米的正方体木块,如果把它沿虚线切成8个正方体,这些小正方体中没有被涂上红色的所有表面的面积和是_____平方厘米【试题来源】【题目】张大爷去年用长2米、宽1米的长方形苇席围成容积最大的圆柱形粮囤.今年改用了长3米、宽2米的长方形苇席围成容积最大的圆柱形粮囤.问:今年粮囤的容积是去年粮囤容积的多少倍?【试题来源】【题目】把一个大长方体木块表面上涂满红色后,分割成若干个同样大小的小长方体,其中只有两个面涂上红色的小长方体恰好是12块.那么至少要把这个大长方体分割成个小长方体.【试题来源】【题目】六个立方体A、B、C、D、E、F的可见部分如下图,下边是其中一个立体的侧面展开图,那么它是立方体____的侧面展开图.2。
六年级奥数图形问题精选

圆和组合图形(1)一、填空题1.算出圆内正方形的面积为 .2.右图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是 平方厘米.120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是 .4.如图所示,以B 、C 为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是厘米.(保留两位小数)5.三角形ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小28长 厘米.6.如右图,阴影部分的面积为2平方厘米,等腰直角三角形的面积7.扇形的面积是31.4平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是 度.8.图中扇形的半径OA =OB =6厘米.45=∠AOB , AC 垂直OB 于C ,那么图中阴影部分的面积是 平方厘米.)14.3(=π9.右图中正方形周长是20厘米.图形的总面积是 平方厘米.10.在右图中(单位:厘米),两个阴影部分面积的和是 平方厘米.45二、解答题11. ABC 是等腰直角三角形. D 是半圆周的中点, BC 是半圆的直径,已知: AB =BC =10,那么阴影部分的面积是多少?(圆周率14.3=π)12.如图,半圆S 1的面积是14.13平方厘米,圆S 2的面积是19.625平方厘米.那么长方形(阴影部分的面积)是多少平方厘米?13.如图,已知圆心是O ,半径r =9厘米,1521=∠=∠,那么阴影部分的面积是多少平方厘米?)14.3(≈π14.右图中4个圆的圆心是正方形的4个顶点,它们的公共点是该正方形的中心.如果每个圆的半径都是1厘米,那么阴影部分的总面积是多少平方厘米?———————————————答 案——————————————————————1. 18平方厘米.由图示可知,正方形两条对角线的长都是6厘米,正方形由两个面积相等的三角形构成.三角形底为6厘米,高为3厘米,故正方形面积为1822136=⨯⨯⨯(平方厘米).2. 1.14平方厘米.由图示可知,图中阴影部分面积为两个圆心角为45的扇形面积减去直角三角形的面积.即14.12122236045214.32=⨯⨯-⨯⨯⨯(平方厘米).3. 125.6平方厘米.由已知条件可知圆的半径的平方为120平方厘米.故扇形面积为6.12536012012014.3=⨯⨯(平方厘米).4. 3.09厘米.边结BE 、CE ,则BE=CE=BC=1(厘米),故三角形BCE 为等边三角形.于是60=∠=∠BCE EBC .BE=CE=045.136060214.3=⨯⨯(厘米).于是阴影部分周长为09.312045.1=+⨯(厘米).5. 32.8厘米.从图中可以看出阴影部分①加上空白部分的面积是半圆的面积,阴影部分②加上空白部分的面积是三角形ABC 的面积.又已知①的面积比②的面积小28平方厘米,故半圆面积比三角形ABC 的面积小28平方厘米.半圆面积为6282124014.32=⨯⎪⎭⎫ ⎝⎛⨯(平方厘米),三角形ABC 的面积为628+28=656(平方厘米).BC 的长为8.32402656=÷⨯(厘米).6. 13937平方厘米.将等腰直角三角形补成一个正方形,设正方形边长为x 厘米,则圆的半径为2x 厘米.图中阴影部分面积是正方形与圆的面积之差的81,于是有282114.322⨯=⎪⎭⎫⎝⎛⨯-x x ,解得1332002=x .故等腰直角三角形的面积为1393721133200=⨯(平方厘米). ⌒⌒7. 72.扇形面积是圆面积的511574.31=÷,故扇形圆心角为360的51即72.8. 5.13.三角形ACO 是一个等腰直角三角形,将AO 看作底边,AO 边上的高为3262=÷=÷AO (厘米),故三角形ACO 的面积为93621=⨯⨯(平方厘米).而扇形面积为13.1436045614.32=⨯⨯(平方厘米),从而阴影部分面积为14.13-9=5.13(平方厘米).9. 142.75.由正方形周长是20厘米,可得正方形边长也就是圆的半径为5420=÷(厘米).图形总面积为两个43圆面积加上正方形的面积,即75.1425243514.322=+⨯⨯⨯(平方厘米).10. 90平方厘米.图中阴影部分的面积是从两个以直角三角形直角边为直径的半圆及一个直角三角的面积和中减去一个以直角三角形斜边为直径的半圆的面积即()902114.3)220(2115122114.3)216(2114.3212222=⨯⨯÷-⨯⨯+⨯⨯÷+⨯⨯÷(平方厘米).11. 如图作出辅助线,则阴影部分的面积为三角形AED 的面积减去正方形BEDO 三角形AED 的面积是21)210()21010(⨯÷⨯÷+;积是2)210(÷,圆面积的41是2)210(14.341÷⨯⨯,故阴影部分面积为:22)210(14.341)210(21)210()21010(÷⨯⨯+÷-⨯÷⨯÷+125.32625.19255.37=+-=(平方厘米).12. 由已知半圆S 1的面积是14.13平方厘米得半径的平方为914.3213.14=÷⨯(平方厘米),故半径为3厘米,直径为6厘米. 又因圆S 2的面积为19.625平方厘米,所以S 2半径的平方为25.614.3625.19=÷(平方厘米),于是它的半径为2.5厘米,直径为5厘米. 阴影部分面积为55)56(=⨯-(平方厘米).13. 因OA=OB ,故三角形OAB 为等腰三角形,即 150215180,151=⨯-=∠=∠=∠AOB OBA , 同理150=∠AOC ,于是602150360=⨯-=∠BOC . 扇形面积为:39.42914.3360602=⨯⨯(平方厘米).14. 正方形可以分割成两个底为2,高为1的三角形,其面积为221221=⨯⨯⨯(平方厘米).正方形内空白部分面积为4个41圆即一个圆的面积与正方形面积之差,即2212-=-⨯ππ(平方厘米),所有空白部分面积为)2(2-π平方厘米. 故阴影部分面积为四个圆面积之和与两个空白面积之和的差,即为 8)2(22412=-⨯-⨯⨯ππ(平方厘米).十二、圆和组合图形(2)一、填空题1.如图,阴影部分的面积是 .2.大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面积比小圆的面积大 平方厘米.3.在一个半径是4.5厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是 平方厘米.(π取3.14,结果精确到1平方厘米)4.右图中三角形是等腰直角三角形,阴影部分的面积是 (平方厘米).5.如图所求,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是 厘米.)14.3(=π6.如图,151=∠的圆的周长为62.8厘米,平行四边形的面积为100平方厘米.阴影部分的面积是 .7.有八个半径为1厘米的小圆,用它们的圆周的一部分连成一个花瓣图形(如图).图中黑点是这些圆的圆心.如果圆周率1416.3=π,那么花瓣图形的面积是 平方厘米.8.已知:ABC D 是正方形, ED =DA =AF =2厘米,阴影部分的面积是 .9.图中,扇形BAC 的面积是半圆ADB 的面积的311倍,那么,CAB ∠是 度.10.右图中的正方形的边长是2厘米,以圆弧为分界线的甲、乙两部分的面积差(大减小)是 平方厘米.(π取3.14)2二、解答题11.如图:阴影部分的面积是多少?四分之一大圆的半径为r .(计算时圆周率22)取12.已知右图中大正方形边长是6厘米,中间小正方形边长是4厘米.求阴影部分的面积.13.有三个面积都是S 的圆放在桌上,桌面被圆覆盖的面积是2S +2,并且重合的两块是等面积的,直线a 过两个圆心A 、B , 如果直线a 下方被圆覆盖的面积是9,求圆面积S 的值.14.如图所示,1的位置沿线段AB 、BC 、CD 滚到2的位置,如果AB 、BC 、C D 的长都是20厘米,那么圆板的正面滚过的面积是多少平方厘米?———————————————答 案——————————————————————1. 6.两个扇形面积相等,故阴影部分面积等于一个长为3,宽为2的长方形面积,为6个平方单位.2. 188.4.小圆的半径为2)14(6=-÷(厘米),大圆的半径为842=⨯(厘米).大圆的面积比小圆的面积大4.18814.3)28(22=⨯-(平方厘米).3. 57.305.57214.3)22(14.35.422=⨯⨯÷-⨯(平方厘米)≈57(平方厘米).4. 10.26.从圆中可以看出,阴影部分的面积是两个半圆的面积与三角形面积之差,即26.10621)26(14.322=⨯-÷⨯(平方厘米).5. 20.5.设圆的半径为r ,则圆面积即长方形面积为2r π,故长方形的长为r DC π=.阴影部分周长r r r r r r AD BA BC DC ππππ245241)(⨯=⨯+-++=+++=5.204.1645=⨯=(厘米).6. 6548(平方厘米).如图,连结OA 、AC ,过A 点作CD 的垂线交CD 于E .三角形ACD 的面积为502100=÷(平方厘米).又圆半径为10)214.3(28.6=⨯÷(厘米),因为151=∠又OA=OD ,故30215=⨯=∠AOC ,扇形AOC 的面积为61261014.3360302=⨯⨯(平方厘米).三角形AOC 的面积为25250=÷(平方厘米).方形面积为611256126=-(平方厘米),从而阴影部分的面积为654861150=-(平⌒方厘米).7. 19.1416.花瓣图形的结构是正方形的面积,加上四个43圆面积后,再割去四个半圆的面积.圆的半径为1厘米,正方形边长为4厘米.故花瓣图形的面积是1416.1916421144314222=+=⨯⨯⨯-⨯⨯⨯+πππ(平方厘米). 8. 2.43平方厘米. 如图,将①移到②得:阴影部分面积等于梯形CEFB 的面积减去三角形CED 、三角形CDA 、扇形AFG 的面积,即 43.236045214.32122122212)322(22=⨯⨯-⨯-⨯⨯-⨯⨯⨯+(平方厘米).9. 60.设扇形ABC 圆心角的度数是x ,半圆的半径OA=r ,有2221311)2(360r r x ⨯⨯⨯=⨯⨯ππ, 解得x=60.10. 0.14.扇形面积为14.341214.32=⨯⨯(平方厘米),甲部分面积为43.0214.32122=÷-⨯(平方厘米),乙部分面积为57.04122214.3=⨯⨯-÷(平方厘米),甲乙两部分面积差为14.043.057.0=-(平方厘米11. 如图,小正方形的边长为2r ,则①的面积为: 72227224122r r r r =⨯-⎪⎭⎫ ⎝⎛⨯⨯, ②的面积为222417272221r r r =-⎪⎭⎫ ⎝⎛⨯⨯,2227224172241r r r =⨯⨯-⨯⨯.即阴影部分面积为272r .12. 将阴影部分旋转后,可以看出所求阴影部分面积为大正方形面积的一半减去小正形的一半,即阴影部分面积等于10242622=÷-÷(平方厘米).13. 设一个阴影部分的面积为x ,则有:2223+=-S x S ,于是22+=x S (1) 又9232=-x S ,于是有23184+-=S x ,解得S=6.14. 圆板的正面滚过的部分如右图阴影部分所求,它的面积为: )420(4614)220(22122-+⨯⨯+⨯-+⨯⨯ππ 07.228323204221)24(414)220(4222≈+=⨯⨯+⨯-⨯-⨯-+⨯πππ(平方厘米).D面积计算(三)专题简析:对于一些比较复杂的组合图形,有时直接分解有一定的困难,这时,可以通过把其中的部分图形进行平移、翻折或旋转,化难为易。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
B
2 201212
图形综合(一)
姓名 日期 成绩
【基础篇】
1.如下图中,那么:∠1+∠2+∠3+∠4+∠5= 度。
3.一个长方形的周长是70厘米,长比宽多5厘米,现在要同时减少长和宽,减少以后的长方形面积是原来长方形面积的一半。
如果长减少5厘米,宽应该减少多少厘米?
4.已知大正方形比小正方形边长多2厘米,大正方形比小正方形的面积大40平方厘米。
求大、小正方形的面积各是多少平方厘米?
5.如图,在一个边长不超过8厘米的大正方形中用三张面积均为20平方厘米的正方形
纸片盖住大正方形内一部分,总面积是44平方厘米,问大正方形的面积是多少平方厘米?
6.图由8个边长都是2厘米的正方形组成,求这个图形的周长。
7.一条白色的正方形手帕,它的边长是18厘米,手帕上横竖各有二道红条,如下左图阴影所示部分,红条宽都是2厘米。
问:这条手手帕白色部分的面积是多少?
1 2 3
4
5
8.边长分别为10厘米和7厘米的正方形,部分重叠成下图所示。
图中两个阴影部分的面积相差 平方厘米。
【提高篇】
1.下图中,小于180°的角有多少个?如果∠2+∠3=∠1+∠4,那么当∠AOB 等于多少度时,图中所有角的和等于360°。
2.正方形ABCD 的边长是6厘米,在正方形内的任意画四条直线,可把正方形分成9个
小长方形。
这9个小长方形的周长之和是多少厘米?
3.一块正方形木版,一边截去15厘米,一边截去9厘米,剩下的面积比原来少了1665平方厘米。
求原来正方形的面积。
4.从一块正方形木板上锯下宽5cm 的一个木条后,剩下的面积是750cm 2。
问:锯下的木条面积是。
7.一队战士排成一个实心正方形队伍(排与队的人数相等),还多12人,如果横竖各增加一排,成为大一点的正方形则差19人。
那么这队战士的人数是 。
8.□ABCD 的周长为75厘米,以BC 为底时高为14厘米,以CD 为底时高为16厘米,求□ABCD 的面积。
A
O
B
1 2 3
4
9.如图,在△ABC 中,AD 垂直于BC ,CE 垂直于AB ,AD=8厘米,CE=7厘米,AB +BC=21厘米,求△
ABC 的面积。
10.从一个正方形一边上截一条宽为
21的长方条,剩下部分的矩形面积为18
65
,问:截下的长方条的面积是多少?
11.有一个正方形的纸盒底内放有三块同样大小的A 、B 、C 正方形纸片,如图所示,已知露在外面的部分A 块的面积是40平方厘米,B 块的面积是28平方厘米,C 块的面积是20平方厘米,那么正方形盒子的底面积是多少平方厘米?
12.如图,求A 的面积单位(cm 2
)
13.右图中,AFCD 是一个长方形,AB=10厘米,AD=4厘米,E 、F 分别是BC 、AD 的中点,G 是线段CD 上任意一点。
阴影部分的面积是多少平方厘米?
14.如图,在长方形ABCD 中,AB 长8厘米,BC 长15厘米,四边形EFGH
阴影部分面积的和是 平方厘米。
B A
B
C
D
15.如图,长方形ABCD的AB长16厘米,BC长20厘米,M是BC边上的中点,在AB边上取一点P,使三角形PMD的面积为100平方厘米,P点应取在距离A点厘米处。
16.在一张正方形大纸片上覆盖着A、B两张面积相等的小正方形纸片(如下图)。
已知A与B重叠的小正方形面积是5平方厘米,且两个空白部分的面积之和是40平方厘米,求大正方形的面积?
17.如图所示,在正方形ABCD中,红色、绿色正方形的面积分别是27和12,且红、绿两个正方形有一个顶点重合,黄色正方形的两个对顶点位于红、绿正方形的中心,求黄色正方形的面积。
D
C
B
黄
红
绿。
