MATLAB练习题及求解
matlab习题及答案

习题:1, 计算⎥⎦⎤⎢⎣⎡=572396a 与⎥⎦⎤⎢⎣⎡=864142b 的数组乘积。
2, 对于B AX =,如果⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=753467294A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=282637B ,求解X 。
3, 已知:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321a ,分别计算a 的数组平方和矩阵平方,并观察其结果。
4, 角度[]604530=x ,求x 的正弦、余弦、正切和余切。
(应用sin,cos,tan.cot)5, 将矩阵⎥⎦⎤⎢⎣⎡=7524a 、⎥⎦⎤⎢⎣⎡=3817b 和⎥⎦⎤⎢⎣⎡=2695c 组合成两个新矩阵: (1)组合成一个4⨯3的矩阵,第一列为按列顺序排列的a 矩阵元素,第二列为按列顺序排列的b 矩阵元素,第三列为按列顺序排列的c 矩阵元素,即 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡237912685574(2)按照a 、b 、c 的列顺序组合成一个行矢量,即 []2965318772546, 将(x -6)(x -3)(x -8)展开为系数多项式的形式。
(应用poly,polyvalm)7, 求解多项式x 3-7x 2+2x +40的根。
(应用roots)8, 求解在x =8时多项式(x -1)(x -2) (x -3)(x -4)的值。
(应用poly,polyvalm)9, 计算多项式9514124234++--x x x x 的微分和积分。
(应用polyder,polyint ,poly2sym)10, 解方程组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡66136221143092x 。
(应用x=a\b)11, 求欠定方程组⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡5865394742x 的最小范数解。
(应用pinv) 12, 矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=943457624a ,计算a 的行列式和逆矩阵。
(应用det,inv)13, y =sin(x ),x 从0到2π,∆x =0.02π,求y 的最大值、最小值、均值和标准差。
MATLAB习题及参考答案经典.doc

习题:1, 计算⎥⎦⎤⎢⎣⎡=572396a 与⎥⎦⎤⎢⎣⎡=864142b 的数组乘积。
2, 对于B AX =,如果⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=753467294A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=282637B ,求解X 。
3, 已知:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321a ,分别计算a 的数组平方和矩阵平方,并观察其结果。
4, 角度[]604530=x ,求x 的正弦、余弦、正切和余切。
(应用sin,cos,tan.cot)5, 将矩阵⎥⎦⎤⎢⎣⎡=7524a 、⎥⎦⎤⎢⎣⎡=3817b 和⎥⎦⎤⎢⎣⎡=2695c 组合成两个新矩阵: (1)组合成一个4⨯3的矩阵,第一列为按列顺序排列的a 矩阵元素,第二列为按列顺序排列的b 矩阵元素,第三列为按列顺序排列的c 矩阵元素,即 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡237912685574(2)按照a 、b 、c 的列顺序组合成一个行矢量,即 []2965318772546, 将(x -6)(x -3)(x -8)展开为系数多项式的形式。
(应用poly,polyvalm)7, 求解多项式x 3-7x 2+2x +40的根。
(应用roots)8, 求解在x =8时多项式(x -1)(x -2) (x -3)(x -4)的值。
(应用poly,polyvalm)9, 计算多项式9514124234++--x x x x 的微分和积分。
(应用polyder,polyint ,poly2sym)10, 解方程组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡66136221143092x 。
(应用x=a\b)11, 求欠定方程组⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡5865394742x 的最小范数解。
(应用pinv) 12, 矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=943457624a ,计算a 的行列式和逆矩阵。
(应用det,inv)13, y =sin(x ),x 从0到2π,∆x =0.02π,求y 的最大值、最小值、均值和标准差。
matlab习题及答案

matlab习题及答案2. ⽤MATLAB 语句输⼊矩阵A 和B3.假设已知矩阵A ,试给出相应的MATLAB 命令,将其全部偶数⾏提取出来,赋给B 矩阵,⽤magic(8)A =命令⽣成A 矩阵,⽤上述命令检验⼀下结果是不是正确。
4.⽤数值⽅法可以求出∑=++++++==6363622284212i i S ,试不采⽤循环的形式求出和式的数值解。
由于数值⽅法是采⽤double 形式进⾏计算的,难以保证有效位数字,所以结果不⼀定精确。
试采⽤运算的⽅法求该和式的精确值。
5.选择合适的步距绘制出下⾯的图形。
(1))/1sin(t ,其中)1,1(-∈t ;(2))tan(sin )sin(tan t t -,其中),(ππ-∈t6. 试绘制出⼆元函数2222)1(1)1(1),(yx yx y x f z ++++-==的三维图和三视图7. 试求出如下极限。
(1)xxxx 1)93(lim +∞→;(2)11lim0-+→→xy xy y x ;(3)22)()cos(1lim222200y x y x ey x y x +→→++-8. 已知参数⽅程-==tt t y t x sin cos cos ln ,试求出x y d d 和3/22d d π=t x y9. 假设?-=xyt t e y x f 0d ),(2,试求222222y fy x f x f y x ??+-?? 10. 试求出下⾯的极限。
(1)-++-+-+-∞→1)2(1161141121lim 2222n n ;(2))131211(lim 2222ππππn n n n n n n ++++++++∞→ 11. 试求出以下的曲线积分。
(1)?+ls y x d )(22,l 为曲线)sin (cos t t t a x +=,)cos (sin t t t a y -=,)20(π≤≤t 。
(2)?-+++ly y y xe x e yx )dy 2(xy d )(33,其中l 为22222c y b x a =+正向上半椭圆。
MATLAB实验练习题(计算机)-南邮-MATLAB-数学实验大作业答案
“MATLAB”练习题要求:抄题、写出操作命令、运行结果,并根据要求,贴上运行图。
1、求230x e x -=的所有根.(先画图后求解)(要求贴图)>> solve('exp(x)—3*x^2',0)ans =—2*lambertw (—1/6*3^(1/2))-2*lambertw(—1,—1/6*3^(1/2))—2*lambertw (1/6*3^(1/2))3、求解下列各题:1)30sin lim x x x x ->->> sym x ;〉> limit((x-sin (x))/x^3)ans =1/62) (10)cos ,x y e x y =求>> sym x;>> diff (exp(x )*cos(x),10)ans =(-32)*exp(x)*sin (x)3)21/20(17x e dx ⎰精确到位有效数字)〉〉 sym x;〉〉 vpa((int(exp(x^2),x,0,1/2)),17)ans =0.544987104183622224)42254x dx x+⎰〉> sym x ;>〉 int (x^4/(25+x^2),x)ans =125*atan (x/5) - 25*x + x^3/35)求由参数方程arctan x y t⎧⎪=⎨=⎪⎩dy dx 与二阶导数22d y dx 。
〉> sym t;>> x=log(sqrt (1+t^2));y=atan(t);〉> diff (y ,t )/diff (x ,t)ans =1/t6)设函数y =f (x )由方程xy +e y = e 所确定,求y ′(x ).>> syms x y ;f=x *y+exp(y )—exp (1);〉> -diff(f,x )/diff (f,y)ans =-y/(x + exp (y))7)0sin 2x e xdx +∞-⎰>〉 syms x ;>〉 y=exp(-x)*sin(2*x );〉> int(y ,0,inf )ans =2/58) 08x =展开(最高次幂为)〉> syms xf=sqrt(1+x);taylor(f,0,9)ans =— (429*x^8)/32768 + (33*x^7)/2048 — (21*x^6)/1024 +(7*x^5)/256 - (5*x^4)/128 + x^3/16 - x^2/8 + x/2 + 19) 1sin (3)(2)x y e y =求〉> syms x y ;>〉 y=exp(sin (1/x));>〉 dy=subs (diff(y,3),x ,2)dy =—0.582610)求变上限函数2x x ⎰对变量x 的导数.>> syms a t ;>〉 diff (int(sqrt(a+t),t,x ,x^2))Warning: Explicit integral could not be found 。
matlab期末考试题目及答案

matlab期末考试题目及答案1. 题目:编写一个MATLAB函数,实现矩阵的转置操作。
答案:可以使用`transpose`函数或`.'`操作符来实现矩阵的转置。
例如,对于一个矩阵`A`,其转置可以通过`A'`或`transpose(A)`来获得。
2. 题目:使用MATLAB求解线性方程组Ax=b,其中A是一个3x3的矩阵,b是一个3x1的向量。
答案:可以使用MATLAB内置的`\`操作符来求解线性方程组。
例如,如果`A`和`b`已经定义,求解方程组的代码为`x = A\b`。
3. 题目:编写MATLAB代码,计算并绘制函数f(x) = sin(x)在区间[0, 2π]上的图像。
答案:首先定义x的范围,然后计算对应的函数值,并使用`plot`函数绘制图像。
代码示例如下:```matlabx = linspace(0, 2*pi, 100); % 定义x的范围y = sin(x); % 计算函数值plot(x, y); % 绘制图像xlabel('x'); % x轴标签ylabel('sin(x)'); % y轴标签title('Plot of sin(x)'); % 图像标题```4. 题目:使用MATLAB编写一个脚本,实现对一个给定的二维数组进行排序,并输出排序后的结果。
答案:可以使用`sort`函数对数组进行排序。
如果需要对整个数组进行排序,可以使用`sort`函数的两个输出参数来获取排序后的索引和值。
代码示例如下:```matlabA = [3, 1, 4; 1, 5, 9; 2, 6, 5]; % 给定的二维数组[sortedValues, sortedIndices] = sort(A(:)); % 对数组进行排序sortedMatrix = reshape(sortedValues, size(A)); % 将排序后的值重新构造成矩阵disp(sortedMatrix); % 显示排序后的结果```5. 题目:编写MATLAB代码,实现对一个字符串进行加密,加密规则为将每个字符的ASCII码值增加3。
matlab习题及答案

matlab习题及答案Matlab习题及答案Matlab是一种强大的数学计算软件,被广泛应用于科学计算、数据分析和工程设计等领域。
在学习和使用Matlab的过程中,习题是一种非常有效的学习方式。
本文将给出一些常见的Matlab习题及其答案,帮助读者更好地掌握Matlab的使用技巧。
一、基础习题1. 计算1到100之间所有奇数的和。
解答:```matlabsum = 0;for i = 1:2:100sum = sum + i;enddisp(sum);```2. 编写一个函数,计算任意两个数的最大公约数。
解答:```matlabfunction gcd = computeGCD(a, b)while b ~= 0temp = b;a = temp;endgcd = a;end```3. 编写一个程序,生成一个5×5的随机矩阵,并计算矩阵的行和列的平均值。
解答:```matlabmatrix = rand(5);row_average = mean(matrix, 2);col_average = mean(matrix);disp(row_average);disp(col_average);```二、进阶习题1. 编写一个程序,实现插入排序算法。
解答:```matlabfunction sorted_array = insertionSort(array)n = length(array);for i = 2:nj = i - 1;while j > 0 && array(j) > keyarray(j+1) = array(j);j = j - 1;endarray(j+1) = key;endsorted_array = array;end```2. 编写一个程序,实现矩阵的转置。
解答:```matlabfunction transposed_matrix = transposeMatrix(matrix) [m, n] = size(matrix);transposed_matrix = zeros(n, m);for i = 1:mfor j = 1:ntransposed_matrix(j, i) = matrix(i, j);endendend```3. 编写一个程序,实现二分查找算法。
matLAB经典例题及答案
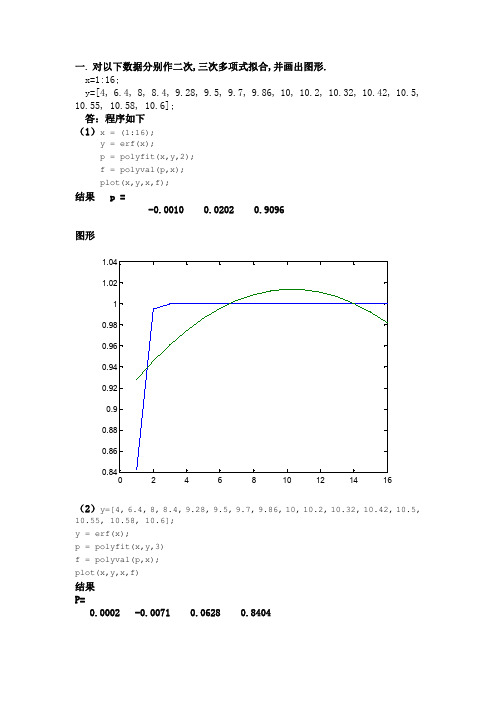
一.对以下数据分别作二次,三次多项式拟合,并画出图形.x=1:16;y=[4,6.4,8,8.4,9.28,9.5,9.7,9.86,10,10.2,10.32,10.42,10.5, 10.55,10.58,10.6];答:程序如下(1)x=(1:16);y=erf(x);p=polyfit(x,y,2);f=polyval(p,x);plot(x,y,x,f);结果p=-0.00100.02020.9096(2)y=[4,6.4,8,8.4,9.28,9.5,9.7,9.86,10,10.2,10.32,10.42,10.5, 10.55,10.58,10.6];y=erf(x);p=polyfit(x,y,3)f=polyval(p,x);plot(x,y,x,f)结果P=0.0002-0.00710.06280.8404二.在[0,4pi]画sin(x),cos(x)(在同一个图象中);其中cos(x)图象用红色小圆圈画.并在函数图上标注“y=sin(x)”,“y=cos(x)”,x轴,y轴,标题为“正弦余弦函数图象”.答:程序如下x=[0:720]*pi/180;plot(x,sin(x),x,cos(x),'ro');x=[2.5;7];y=[0;0];s=['y=sin(x)';'y=cos(x)'];text(x,y,s);xlabel('正弦余弦函数图象'),ylabel('正弦余弦函数图象')图形如下三.选择一个单自由度线性振动系统模型,自定质量、弹簧刚度、阻尼、激振力等一组参数,分别编程(m 文件)计算自由和强迫振动时的响应,并画出振动曲线图。
(要求画出该单自由度线性振动系统模型图)其中质量为m=1000kg,弹性刚度k=48020N/m,阻尼c=1960N.s/m,激振力f(t)=0.阻尼比ζ的程序p=1960/(2*sqrt(48020*1000))求得p=0.1414而p为阻尼比ζ强迫振动时的响应程序g =tf([-101],[48020048020*1.9848020]);bode(g)图形g =tf([001],[0001]);bode(g)振动曲线图程序:函数文件function dx =rigid(t,x)dx =zeros(2,1);dx(1)=x(2);dx(2)=(-48020*x(1)-1960*x(2))/1000;命令文件options =odeset('RelTol',1e-4,'AbsTol',[1e-41e-4]);[T,X]=ode45(@rigid,[012],[11],options);plot(T,X(:,1),'-')其图形如下024681012-6-5-4-3-2-11234单自由度线性强迫振动系统模型图其中质量为m=1000kg,弹性刚度k=48020N/m,阻尼c=1960N.s/m,f(t)=cos(3*pi*t)振动曲线图程序:函数文件function dx=rigid(t,x)dx=zeros(2,1);dx(1)=x(2);dx(2)=(-48020*x(1)-1960*x(2))/1000+cos(3*pi*t);命令文件options=odeset('RelTol',1e-4,'AbsTol',[1e-41e-4]);[T,X]=ode45(@rigid,[020],[11],options);plot(T,X(:,1),'-')力等一组参数,建立Simulink仿真模型框图进行仿真分析。
matlab习题及答案

matlab习题及答案《Matlab习题及答案:提升编程技能,解决实际问题》Matlab是一种强大的数值计算和数据分析工具,它被广泛应用于工程、科学和其他领域的计算和模拟。
为了帮助大家提升编程技能,解决实际问题,我们为大家准备了一些Matlab习题及答案,希望能够帮助大家更好地掌握Matlab的使用。
1. 习题一:编写一个Matlab程序,计算斐波那契数列的前20个数字,并将结果打印出来。
答案:下面是一个简单的Matlab程序,用于计算斐波那契数列的前20个数字。
```matlaba = 0;b = 1;fib = zeros(1, 20);fib(1) = a;fib(2) = b;for i = 3:20fib(i) = fib(i-1) + fib(i-2);enddisp(fib);```2. 习题二:编写一个Matlab程序,求解一个二次方程ax^2 + bx + c = 0的根。
答案:下面是一个简单的Matlab程序,用于求解二次方程的根。
```matlaba = 1;b = -3;c = 2;delta = b^2 - 4*a*c;if delta > 0x1 = (-b + sqrt(delta))/(2*a);x2 = (-b - sqrt(delta))/(2*a);disp(['The roots are ', num2str(x1), ' and ', num2str(x2)]);elseif delta == 0x = -b/(2*a);disp(['The root is ', num2str(x)]);elsedisp('The equation has no real roots');end```通过以上两个习题及答案的示例,我们可以看到Matlab的强大功能和灵活性。
通过练习这些习题,我们可以更好地掌握Matlab的基本语法和常用函数,从而在实际问题中更快更准确地解决数值计算和数据分析的挑战。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
建立模型并求解
练习1:如图, P, Q 到河岸的距离分别为10,8,试选一点R,使得R 到河岸的距离及RP,RQ 的和最小.
解:设点R 的坐标为(
x ,y )则有:
min ()x R
f x ∈在lingo 中输入:
RP=@sqrt((x)^2+(10-y)^2);
RY=y;
RQ=@sqrt((x-6)^2+(y-8)^2);
min= RP+RY+RQ;
则可得到结果:
Local optimal solution found.
Objective value: 14.19615
Infeasibilities: 0.3330669E-14
Extended solver steps: 5
Total solver iterations: 200
Variable Value Reduced Cost
RP 5.464102 0.000000
X 4.732051 -0.2154924E-07
Y 7.267949 0.000000
RY 7.267949 0.000000
RQ 1.464102 0.000000
Row Slack or Surplus Dual Price
1 0.000000 -1.000000
2 0.000000 -1.000000
3 0.000000 -1.000000
4 14.1961
5 -1.000000
所以R (4.732,7.268)。
()PR R y y RQ ⎧=⎪⎪=⎨⎪=⎪⎩
练习2:要把7种规格的包装箱装到两辆铁路平板车上去,箱子宽、高相同,而厚度和重量不同,下表给出了它们的厚度、重量和数量。
c1c2c3c4c5c6c7
厚度t(厘米)重量w(千克) 数量n 48.7
2000
8
52.0
3000
7
61.3
1000
9
72.0
500
6
48.7
4000
6
52.0
2000
4
64.0
1000
8
每辆平板车有10.2米长的地方用于装箱(像面包片那样),载重40吨。
由于货运限制,对c5,c6,c7三种包装箱的装载有如下特殊约束:它们所占的空间(厚度)不得超过302.7厘米。
试把包装箱装到平板车上,使浪费的空间最小。
解:
程序为:
min=2040-x11*48.7-x21*48.7-(x12+x22)*52-(x13+x23)*61.3-(x14+x24)*72-(
x15+x25)*48.7-(x16+x26)*52-(x17+x27)*64;
x11+x21<=8;
x12+x22<=7;
x13+x23<=9;
x14+x24<=6;
x15+x25<=6;
x16+x26<=4;
x17+x27<=8;
x11*48.7+x12*52+x13*61.3+x14*72+x15*48.7+x16*52+x17*64<=1020;
x21*48.7+x22*52+x23*61.3+x24*72+x25*48.7+x26*52+x27*64<=1020;
x15*47.8+x16*52+x17*64<=302.7;
x25*47.8+x26*52+x27*64<=302.7;
x11*2+x12*3+x13*1+x14*0.5+x15*4+x16*2+x17*1<=40;
x21*2+x22*3+x23*1+x24*0.5+x25*4+x26*2+x27*1<=40;
@gin(x11);@gin(x12);@gin(x13);@gin(x14);@gin(x15);@gin(x16);
@gin(x17);@gin(x21);@gin(x22);@gin(x23);@gin(x24);@gin(x25);
@gin(x26);@gin(x27);
运行结果:
Global optimal solution found.
Objective value: 0.000000
Objective bound: 0.000000
Infeasibilities: 0.1154632E-12
Extended solver steps: 140191
Total solver iterations: 262446
Variable Value Reduced Cost
X11 0.000000 -48.70000
X21 6.000000 -48.70000
X12 5.000000 -52.00000
X22 2.000000 -52.00000
X13 2.000000 -61.30000
X23 6.000000 -61.30000
X14 5.000000 -72.00000
X24 0.000000 -72.00000
X15 2.000000 -48.70000
X25 0.000000 -48.70000
X16 1.000000 -52.00000
X26 0.000000 -52.00000
X17 2.000000 -64.00000
X27 4.000000 -64.00000
Row Slack or Surplus Dual Price
1 0.000000 -1.000000
2 2.000000 0.000000
3 0.000000 0.000000
4 1.000000 0.000000
5 1.000000 0.000000
6 4.000000 0.000000
7 3.000000 0.000000
8 2.000000 0.000000
9 0.000000 0.000000
10 0.000000 0.000000
11 27.10000 0.000000
12 46.70000 0.000000
13 8.500000 0.000000
14 12.00000 0.000000
结论:第一辆车中装有c1:0,c2:5,c3:2,c4:5,c5:2,c6:1,c7:2
第二辆车中装有c1:6,c2:2,c3:6,c4:0,c5:0,c6:0,c7:4
练习3:某工厂向用户提供一种产品,按合同规定,其交货数量和日期是:第一季度末交40吨,第二季度末交60吨,第三季度末交80吨。
工厂的最大生产能力为每季度100吨,每季度的生产费用是2
2.050)(x x x f +=(元),其中x 为该季度生产该产品的吨数。
若工厂生产的多,多余的产品可移到下季度向用户交货,这样,工厂就要支付存储费,每吨该产品每季度的存储费为4元。
问该厂每季度应生产多少吨该产品,才能既满足交货合同,又使工厂所花的费用最少(假设第一季度开始时该产品无存货)。
解:设xi 为第i 季度分别生产的产品数。
分析:所花的费用为生产费用加上存贮费用:
min=50*x1+0.2*x1^2+(x1-40)*4+50*x2+0.2*x2^2+(x1+x2-100)*4+50*x3+0.2*x3^2; x1>=40;x1+x2>=100;x1+x2+x3>=180;
x1<=100;x2<=100;x3<=100;
运行可得:
Local optimal solution found.
Objective value: 11280.00
Infeasibilities: 0.000000
Extended solver steps: 5
Total solver iterations: 53
Variable Value Reduced Cost X1 50.00000 0.000000 X2 60.00000 0.000000 X3 70.00000 0.000000
Row Slack or Surplus Dual Price
1 11280.00 -1.000000
2 10.00000 0.000000
3 10.00000 0.000000
4 0.000000 -78.00000
5 50.00000 0.000000
6 40.00000 0.000000
7 30.00000 0.000000
则为每季度都生产50,60,70吨。
