c++求解非线性方程组的牛顿顿迭代法(可编辑修改版).
c语言计算机编程三种方法求解非线性方程

本科专业学年论文题目:非线性方程求解比较姓名:何娟专业:计算机科学技术系班级:08级本科(2)班指导老师:刘晓娜完成日期:2010年11 月21 日题 目:非线性方程求解比较摘 要本文给出了三种求解非线性方程的方法,分别是二分法,牛顿迭代法,割弦法。
二分法巧妙地利用插值得到的点以及有根区间中点这两点处的函数值,缩小隔根区间,以期望得到更快的收敛速度。
牛顿迭代法是非线性方程根的一种常见的数值方法,对于非线性方程的单重零点来说,牛顿迭代法一般具有局部二阶收敛性,但是当所求的根X*是F(X)的M 重根时,M 是大于等于2的整数,此时牛顿迭代法只有一阶收敛性。
弦截法是将牛顿迭代公式中用差商F(k x )-F(1-k x )/ (k x - 1-k x )代替导数'()k F x 。
本文给出了算法改进的具体步骤及算法流程图相关的数值结果也说明了方法的有效性。
关 键 词 : 二分法;牛顿迭代法;割弦法;非线性方程目录第一章绪论- 3 -第二章求解非线性方程的三种常见算法……………………………- 4-2.1 二分法………………………………………………………-4 -2.2 牛顿迭代法……………………………………………………- 5 -2.3 割弦法- 6 -第三章求解非线性方程的三种算法比较- 8 -3.1 二分法求解方法- 8 -3.2 牛顿迭代法求解- 10 -3.3 割弦法求解- 11 -参考文献- 14 -第一章绪论在科技飞速发展的今天,计算机已经成为我们生活中不可缺少的一部分了,在我们生活与生产中扮演越来越重要的角色,而科学计算已经成为科学计算的重要方法之一,其应用范围已渗透到所有科学领域,作为科学与工程计算的数学工具,计算方法已成为高等院校数学与应用数学,信息与计算科学,应用物理学等必修课。
在永恒变化发展的自然界与人类社会中,在研究其内部规律的各个科学领域中,更深刻、更精确地描述其内部规律的数学工具之一,就是非线性方程。
牛顿迭代法解非线性方程(组)

牛顿迭代法解非线性方程(组)在辨识工作中,常常需要对辨识准则或者判据进行求极值,这往往涉及到求非线性方程(组)的解问题。
牛顿迭代法是一种常用方法。
下面把自己对牛顿迭代法的学习和理解做个总结。
1.一元非线性方程的牛顿迭代公式和原理以一元非线性方程 f(x)=0 为例,对函数 f(x)进行Taylor级数展开(只展开至线性项)得f(x) = f(x0)+f'(x0)(x-x0)所以方程可写成f(x0)+f'(x0)(x-x0) = 0其中x0是给定的已知值,则不难推导出方程的解(当然,只是近似解,毕竟Taylor展开过程中只取了线性项)x = x0 - f(x0) / f'(x0)其中x不是真实解,但是相比之前的x0更靠近真实解了,因此可以多重复几次上述过程,从而使得到的解非常接近准确值。
所以,对于一元非线性方程,牛顿拉夫逊迭代公式为:x(k+1) = x(k) - f(x(k)) / f'(x(k))根据Taylor级数的几何意义我们可以从几何上形象的看牛顿迭代法的求解f(x)=0的过程。
第一次迭代x1 = x0 - f(x0) / f'(x0),其中f(x0) / f'(x0)的几何意义很明显,就是x0到x1的线段长度(这可以从直角三角形的知识得到)。
第二次迭代x2 = x1 - f(x1) / f'(x1),其中f(x1) / f'(x1)的几何意义很明显,就是x1到x2的线段长度。
同理可以进行第三次迭代第四次迭代,可以明显的看出x的取值在不断逼近真实解x*。
可能有人问,迭代求得的结果会不会不收敛,也就是x会不会偏离x*。
由于x0是在x*附近区域取值的,因此x0到x1这段曲线应该认为是平滑的没有转折的,因此切线与x轴的交点只会越来越接近真实解x*。
但是如果x0的取值离x*比较远的话,那么x0到x1这段曲线上可能有“转折”,这样就可能引起迭代的不收敛。
非线性方程求根—牛顿迭代法(新)

非线性方程求根——牛顿迭代法一、牛顿迭代法的基本思想基本思想:将非线性方程逐步归结为某种线性方程求解。
设方程f (x )=0有近似根x k (f `(x k )≠0),将f (x )在x k 展开:(ξ在x 和x k 之间)2()()()()()()2!k k k k f f x f x f x x x x x ξ'''=+-+-()()()()k k k f x f x f x x x '≈+-可设记该线性方程的根为x k +1,则()()()0k k k f x f x x x '+-=1()()k k k k f x x x f x +=-'故f (x )=0可近似表示为即为Newton 法迭代格式。
(k =0,1,……)例:用Newton 迭代法求方程310x x --=在x 0=1.5附近的近似实根。
解:32()1,()31f x x x f x x '=--=-迭代公式为312131kk k k k x x x x x +--=--计算步骤如下:(1)取初值x 0=1.5;(2)按照迭代公式计算x 1;(3)若|x 1-x 0|<=0.00001,终止迭代;否则,x 0=x 1;转(2);(4)输出迭代次数和近似根.二、牛顿迭代法的实现MATLAB求解程序设计:方程及一阶导数函数:function[fun,dfun]=fun0(x)fun=x^3-x-1;%求原函数的值dfun=3*x^2-1;%求一阶导数的值计算主程序:clearx0=1.5;[fun,dfun]=fun0(x0);x1=x0-fun/dfun;i=1;while abs(x1-x0)>1e-5x0=x1;[fun,dfun]=fun0(x0);x1=x0-fun/dfun;i=i+1;enddisp('the solution is x1=')x1disp('the iter time is ')i计算结果为:the solution is x1=x1 =1.3247the iter time isi =4可见经过4次迭代即到达要求的精度,原方程的一个近似实数根为1.3247.三、牛顿迭代法的收敛性牛顿迭代法的迭代函数:)()()(x f x f x x '-=ϕ222)]([)()()]([)()()]([1)(x f x f x f x f x f x f x f x '''='''-'-='ϕ设f (x *)=0,f `(x *)≠0,则ϕ`(x *)=0,故Newton 迭代法在x *附近至少平方收敛。
c++ 牛顿迭代法解方程组

c++ 牛顿迭代法解方程组牛顿迭代法(Newton's Method)是一种用于解方程的迭代算法,可以用于解非线性方程组。
下面是使用 C++ 实现牛顿迭代法解方程组的示例:#include <iostream>#include <cmath>// 定义方程组中的函数double f1(double x, double y) {return x * x + y * y - 1;}double f2(double x, double y) {return x - y * y;}// 定义方程组中的偏导数double df1_dx(double x, double y) {return 2 * x;}double df1_dy(double x, double y) {return 2 * y;}double df2_dx(double x, double y) {return 1;}double df2_dy(double x, double y) {return -2 * y;}// 牛顿迭代法解方程组void newtonIteration(double x0, double y0, int maxIterations) { double epsilon = 1e-6; // 迭代精度double x = x0;double y = y0;for (int i = 0; i < maxIterations; i++) {double det = df1_dx(x, y) * df2_dy(x, y) - df1_dy(x, y) * df2_dx(x, y);double dx = (-f1(x, y) * df2_dy(x, y) + f2(x, y) * df1_dy(x, y)) / det;double dy = (f1(x, y) * df2_dx(x, y) - f2(x, y) * df1_dx(x, y)) / det;x += dx;y += dy;if (std::abs(dx) < epsilon && std::abs(dy) < epsilon) { std::cout << "Converged to solution: x = " << x << ", y = " << y << std::endl;return;}}std::cout << "Iteration did not converge to a solution" << std::endl;}int main() {double initialX = 0.5;double initialY = 0.5;int maxIterations = 100;newtonIteration(initialX, initialY, maxIterations);return 0;}在上述示例中,我们定义了一个方程组,包含两个方程 f1(x, y) = x^2 + y^2 - 1和f2(x, y) = x - y^2。
非线性方程的牛顿法

求函数 f x x 10 x 精度要求: 106
3
例题2
2
19.68x 10.944 的正实根
用Matlab画图,查看根的分布情形
从图形中我们可 以看出: 在x=7和x=8 之 间有一单根; 在x=1和x=2 之 间有一重根。
初值x0=8.0 时,计算的是单根, The iterative number is 28,The numerical solution is 7.600001481 初值x0=1.0 ,计算的是重根, The iterative number is 1356,The numerical solution is 1.198631981
重复上述过程
xk 1
f ( xk ) xk f ( xk )
牛顿法的几何意义
Tangent line : y f ( x0 ) f ( x0 )( x x0 )
y
f ( x0 ) x1 x0 f ( x0 )
x*
x2
x
x1 x0
牛顿法也称为切线法
f ( x1 ) x2 x1 f ( x1 )
例3:设C为正实数,导出用牛顿法求 C 的公式,并证明 2 en 迭代序列的误差 en xn C 满足 en 1 2 xn 2 x C 解:设 x C ,则 于是有
f ( x) x 2 C, f ' ( x) 2x, f ' ' ( x) 2
由于 f (0) C, f ( C 1) 2 C 1 0 ], 所以在 [0,1 C ] 内有一正根.又在 [0,1 C 内 f ' ( x) 0, f ' ' ( x) 0根据定理得牛顿迭代格式为:
非线性方程组的牛顿迭代法-最速下降法
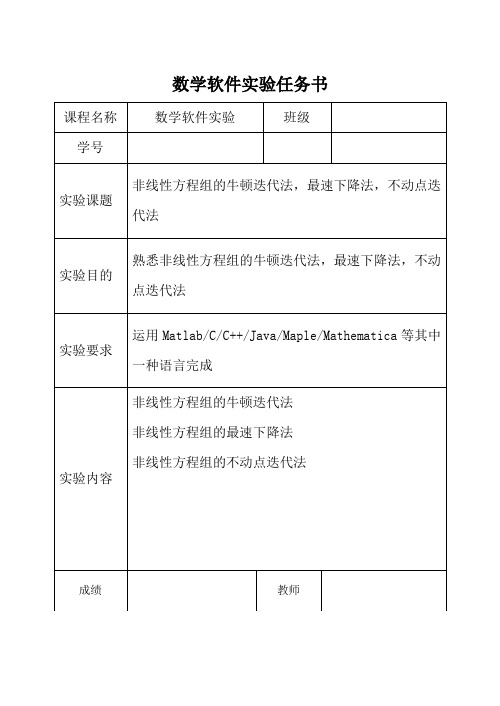
数学软件实验任务书实验一 非线性方程组的牛顿迭代法 1 实验原理对于非线性方程11221212(,,,)(,,,)(,,,)n n n n f x x x f x x x f f x x x ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭ 在x (k )处按照多元函数的泰勒展开,并取线性项得到 ()()()()(1)()1111()()()()(1)()()122()()()()(1)()1(,,,)(,,,)()0(,,,)k k k k k k n n k k k k k k k n n n k k k k k k n n n nn f x x x x x f x x x x x f x f x x x x x +++⎛⎫⎛⎫- ⎪ ⎪- ⎪ ⎪'+= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭ 其中1111()n n n n f f x x f x f f x x ∂∂⎛⎫ ⎪∂∂ ⎪' ⎪= ⎪∂∂ ⎪ ⎪∂∂⎝⎭(1)()()()()()1111(1)()()()()()()1221(1)()()()()()1(,,,)(,,,)[()](,,,)k k k k k k n n k k k k k k k n n n k k k k k k n n n n n x x f x x x x x f x x x f x x x f x x x ++-+⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪'=- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 2 数据来源计算非线性方程组22220.50440x x y x y ⎧--+=⎨+-=⎩ 初值取11x y ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦3 实验步骤步骤一:编写牛顿迭代法的基本程序。
打开Editor 编辑器,输入以下语句:function [x,n,data]=new_ton(x0,tol)if nargin==1tol=1e-10;endx1=x0-f1(x0)/df1(x0);MATLAB 241 数值分析与应用n=1;%迭代过程while (norm(x1-x0)>tol)x0=x1;x1=x0-f1(x0)/df1(x0);n=n+1;%data 用来存放中间数据data(:,n)=x1;endx=x1;以文件名new_ton.m保存。
C语言编程 牛顿迭代法求方程1

牛顿迭代公式设r 是f(x) = 0的根,选取x0作为r 初始近似值,过点(x0,f(x0))的切线L ,L 的方程为y = f(x0)+f'(x0)(x-x0),求出L 与x 轴交点的横坐标 x1 = x0-f(x0)/f'(x0),称x1为r 的一次近似值。
过点(x1,f(x1))做曲线y = f(x)的切线,并求该切线与x 轴交点的横坐标 x2 = x1-f(x1)/f'(x1),称x2为r 的二次近似值。
重复以上过程,得r 的近似值序列,其中x(n+1)=x(n)-f(x(n))/f'(x(n)),称为r 的n+1次近似值,上式称为牛顿迭代公式。
解非线性方程f(x)=0似方法。
把f(x)在x0 f(x) = f(x0)+(x -x0)f'(x0)+(x -x0)^2*f''(x0)/2! +… 取其线性部分,作为非线性方程f(x) = 0的近似方程,即泰勒展开的前两项,则有f(x0)+f'(x0)(x -x0)-f(x)=0 设f'(x0)≠0则其解为x1=x0-f(x0)/f'(x0) 这样,得到牛顿法的一个迭代序列:x(n+1)=x(n)-f(x(n))/f'(x(n))。
牛顿迭代法又称牛顿切线法,它采用以下方法求根:先任意设定一个与真实的根接近的值x 0作为第一个近似根,由x 0求出f(x 0),过(x 0,f(x 0))点做f(x)的切线,交x 轴于x 1,把它作为第二次近似根,再由x 1求出f(x 1),再过(x 1,f(x 1))点做f(x)的切线,交x 轴于x 2,再求出f(x 2),再作切线……如此继续下去,直到足够接近真正的x *为止。
)()()()(0'0010100'x f x f x x x x x f x f -=-=因此, 就是牛顿迭代公式。
例1 用牛顿迭代法求方程2x 3-4x 2+3x-6=0在1.5附近的根。
求解非线性方程的三种新的迭代法

求解非线性方程的三种新的迭代法【摘要】本文介绍了三种新的迭代法用于求解非线性方程,分别是Newton法,拟牛顿法和Levenberg-Marquardt算法。
在首先介绍了非线性方程及其求解的重要性,然后简要介绍了传统的迭代法。
在详细讨论了这三种新的迭代法的原理和应用情况。
在总结了三种新的迭代法的特点和适用范围,并展望了非线性方程求解方法的未来发展方向。
这些新的迭代法为解决复杂的非线性方程提供了新的思路和方法,有望在实际应用中取得更好的效果。
【关键词】非线性方程、求解方法、迭代法、Newton法、拟牛顿法、Levenberg-Marquardt算法、特点、适用范围、未来发展1. 引言1.1 介绍非线性方程及其求解的重要性非线性方程在数学和工程领域中无处不在,其求解具有广泛的应用价值和意义。
非线性方程是指未知数与未知数的各项之间存在着非线性关系的方程,与线性方程相比,非线性方程的求解更加困难。
非线性方程可以描述许多复杂的现实问题,如物理学中的非线性波动方程、工程学中的非线性力学问题等,因此求解非线性方程是科学研究和工程设计中的一个重要任务。
传统的迭代法是求解非线性方程的常用方法之一,其基本思想是通过不断迭代更新初始猜测值,直至满足一定的收敛条件为止。
传统的迭代法在求解复杂的非线性方程时存在收敛速度慢、计算量大等问题,因此需要更加高效和精确的迭代法来解决这些困难。
本文将介绍三种新的迭代法:Newton法、拟牛顿法和Levenberg-Marquardt算法,这些方法在求解非线性方程中具有独特的优势和应用价值。
通过对这些新的迭代法的研究和应用,可以提高非线性方程的求解效率和精度,推动非线性方程求解方法的发展和应用。
1.2 简要介绍传统的迭代法传统的迭代法是解决非线性方程的常见方法之一,它通过不断迭代逼近函数的根,直至满足一定的精度要求。
最常见的传统迭代法包括二分法、试位法和弦截法等。
二分法是一种简单但有效的方法,通过不断缩小根所在的区间来逼近根的位置;试位法则是通过选择一个适当的初始点,然后通过不断调整该点的位置来逼近根;弦截法则是通过连接两个不同点所在的直线,找到直线与横轴的交点,进而更新两个点的位置。
解非线性方程组的牛顿迭代法

3 x3 1.425497619 1.414213562 1.414213562
19
计算三步,方法(2)及(3)均达到10位有效数字, 而用牛顿法只有线性收敛,要达到同样精度需迭代30次.
20
7.5 弦截法与抛物线法
用牛顿法求方程(1.1)的根,每步除计算 f (xk ) 外 还要算 f (xk ),当函数 f (x)比较复杂时,计算 f (x) 往 往较困难,为此可以利用已求函数值 f (xk ), f (xk1), 来回避导数值 f (xk ) 的计算.
的导数为
(x) x f (x)
f (x)
(x*) 1 1 0
m
且 (x*) 1,所以牛顿法求重根只是线性收敛. 若取
16
(x) x m f (x) ,
f (x)
则 (x*) 0
. 用迭代法
xk 1
xk
m
f ( xk ) f (xk )
(k 0,1,)
7.5.1 弦截法
设 xk , xk 1是 f (x) 0的近似根,利用 f (xk ), f (xk1) 构造一次插值多项式 p1(x),并用 p1(x) 0的根作为新的 近似根 xk 1 . 由于
p1(x)
f (xk )
f
( xk ) xk
f xk 1
xk 1
10
在(4.7)中取C 1 ,则称为简化牛顿法,这
f ( x0 )
类方法计算量省,但只有线性收敛,其几何意义是用平行 弦与 x轴交点作为 x *的近似. 如图7-4所示.
图7-4
11
(2) 牛顿下山法.
牛顿法收敛性依赖初值 x0的选取. 如果x0 偏离所求根 x *较远,则牛顿法可能发散.
求解非线性方程的三种新的迭代法

求解非线性方程的三种新的迭代法随着现代科学技术的发展,非线性方程在数学、物理、化学、工程等领域中应用广泛,因此求解非线性方程成为一个重要课题。
传统的求解非线性方程的方法包括二分法、牛顿法、割线法等,但这些方法在一些实际问题中效率不高,甚至可能无法求解出解。
研究人员不断提出新的迭代方法来解决这一问题。
本文将介绍三种新的迭代方法,分别为拟牛顿法、弦截法和混合迭代法。
拟牛顿法是一种经典的非线性方程迭代方法,它是基于牛顿法的改进版本。
牛顿法的迭代公式为:\[x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}\]\(f(x)\)是非线性方程的函数,\(f'(x)\)是\(f(x)\)的导数,\(x_n\)是第n次迭代的解。
拟牛顿法的迭代公式为:\[x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}+\frac{f(x_n)}{f'(x_n)}\]拟牛顿法相比牛顿法的优势在于不需要计算导数,而是通过近似导数的方式进行迭代。
这样可以减少计算量,提高求解效率。
但是拟牛顿法的收敛性和稳定性需要根据具体问题进行验证,因为在某些情况下可能会出现收敛不到解的情况。
弦截法的思路是通过连接两个不同点的切线来逼近方程的解,它不需要计算导数,而是通过两个不同点的函数值来逼近导数,因此也可以减少计算量。
但是弦截法需要使用两个初值进行迭代,初始值的选择对迭代的效果有很大影响。
在一些情况下,弦截法可能会出现跳过解的情况,因此需要谨慎选择初始值。
混合迭代法是将不同的迭代方法结合起来的一种求解非线性方程的方法。
混合迭代法的思路是通过将不同的迭代方法进行交替使用,来提高收敛速度和稳定性。
例如可以将牛顿法和弦截法结合起来,每次迭代使用不同的方法来求解方程。
混合迭代法的好处是可以充分利用不同迭代方法的优势,提高求解效率。
但是需要注意的是,混合迭代法需要根据具体问题来进行调整,选取合适的迭代策略来保证收敛性和稳定性。
Newton迭代法求解非线性方程

Newton迭代法求解非线性方程Newton迭代法求解非线性方程一、 Newton 迭代法概述构造迭代函数的一条重要途径是用近似方程来代替原方程去求根。
因此,如果能将非线性方程f (x )=0用线性方程去代替,那么,求近似根问题就很容易解决,而且十分方便。
牛顿(Newton)法就是一种将非线性方程线化的一种方法。
设k x 是方程f (x )=0的一个近似根,把如果)(x f 在k x 处作一阶Taylor 展开,即:)x x )(x ('f )x (f )x (f k k k -+≈ (1-1)于是我们得到如下近似方程:0)x x )(x ('f )x (f k k k =-+ (1-2)设0)('≠k x f ,则方程的解为:x ?=x k +f (x k )f (x k )?(1-3)取x ~作为原方程的新近似根1+k x ,即令: )x ('f )x (f x x k k k 1k -=+, k=0,1,2,…(1-4)上式称为牛顿迭代格式。
用牛顿迭代格式求方程的根的方法就称为牛顿迭代法,简称牛顿法。
牛顿法具有明显的几何意义。
方程:)x x )(x ('f )x (f y k k k -+= (1-5)是曲线)x (f y =上点))x (f ,x (k k 处的切线方程。
迭代格式(1-4)就是用切线式(1-5)的零点来代替曲线的零点。
正因为如此,牛顿法也称为切线法。
牛顿迭代法对单根至少是二阶局部收敛的,而对于重根是一阶局部收敛的。
一般来说,牛顿法对初值0x 的要求较高,初值足够靠近*x时才能保证收敛。
若要保证初值在较大范围内收敛,则需对)x (f 加一些条件。
如果所加的条件不满足,而导致牛顿法不收敛时,则需对牛顿法作一些改时,即可以采用下面的迭代格式:)x ('f )x (f x x k k k 1k λ-=+,=,2,1,0k (1-6)上式中,10<λ<,称为下山因子。
解非线性方程组的牛顿法

考虑非线性方程组
f1(x1, x2, , xn ) 0,
f2(x1, x2, , xn ) 0,
fn (x1, x2, , xn ) 0. 利用向量记号写为
F (X ) O. 这里F (X )是定义在某区域D Rn上向量值函数. 若存在 X* D, 使得F (X*) O, 则称X*为非线性方程组的解.
.
逐次迭代得结果.
Step 5 Set x x y
Step 6 If y TOL then OUTPUT(x)
Step7 Set k k 1
STOP.
Step8 OUTPUT (‘Maximum number of iterations exceeded’) STOP.
为了说明上述算法,我们可以看看下面的例子。设
s1
145 272
,
145 272
T
.
x2 x1 s1 0.092,3.092 T .
显然,我们只经过两步计算,所得到的 x2就已经非常靠近 解 0,3T .
例1 用牛顿法求解方程组
k x (k) 0 (1.5, 1.0)T
f1( f2(
x1 x1
,x2 ,x2
) )
x1 2 x12
定理 2 设G : D Rn Rn在D内有一不动点X *且G在X *可导,
(G(X*)) 1, 则存在开球 S S( X*, ) D, 对X (0) S, 迭代序列{X (k)}
收敛于X *.
牛顿迭代公式:
X (k1) X (k) F( X (k) ) 1 F ( X (k) ),
其中
f1
F
(
X
(k
)
)
c语言牛顿迭代法

c语言牛顿迭代法牛顿迭代法(Newton-Raphson法)是一种求解方程近似解的方法,它是利用泰勒级数展开函数在某点的值,然后用一阶泰勒展开式的根近似表示函数的零点,因此也被称为牛顿拉弗森法。
它可以高效地解决复杂的非线性方程组,是科学计算领域中最为常用和基础的方法之一。
牛顿迭代法的基本思想是:在第k次迭代时,求出曲线f(x)在点xk的一次导数斜率,以此确定x轴上的一个点xk+1,和该点处曲线的一次切线。
这条切线和x轴交点的横坐标就是极值点的估计值。
这个过程可以迭代多次,直到达到满足一定的误差精度或者迭代次数的要求。
C语言实现牛顿迭代法需要先定义一个函数,这个函数就是需要求解方程的函数。
定义完函数之后,需要实现牛顿迭代公式来求出下一次迭代的估计值,然后不断迭代。
具体实现过程如下:1. 定义函数f(x),即需要求解方程的函数。
2. 定义函数f_prime(x),即f(x)的一次导数。
3. 定义变量x和x_next,初始化它们的值。
4. 在循环中,首先计算f(x)和f_prime(x),然后计算下一个迭代点的估计值x_next = x - f(x) / f_prime(x)。
5. 如果x_next和x的差异满足预设的精度要求,则退出循环。
6. 否则,将x_next的值赋值给x,并重复执行第4步。
C语言实现牛顿迭代法的代码如下:#include <stdio.h>#include <math.h>定义函数f(x)double f(double x) {return x * x - 2;}定义函数f_prime(x)double f_prime(double x) {return 2 * x;}int main() {定义变量double x, x_next, epsilon;int iter;初始化变量x = 1.0;epsilon = 1e-6;iter = 0;迭代求解do {x_next = x - f(x) / f_prime(x);iter++;printf("Iteration %d: x = %lf\n", iter, x_next);x = x_next;} while (fabs(x_next - x) >= epsilon);输出结果printf("Final result: x = %lf\n", x);return 0;}在这个代码中,我们使用了do-while循环来不断执行迭代过程,直到达到预设的精度要求。
C语言实现牛顿迭代法解方程详解

C语⾔实现⽜顿迭代法解⽅程详解C语⾔实现⽜顿迭代法解⽅程详解利⽤迭代算法解决问题,需要做好以下三个⽅⾯的⼯作:⼀、确定迭代变量在可以⽤迭代算法解决的问题中,我们可以确定⾄少存在⼀个可直接或间接地不断由旧值递推出新值的变量,这个变量就是迭代变量。
⼆、建⽴迭代关系式所谓迭代关系式,指如何从变量的前⼀个值推出其下⼀个值的公式(或关系)。
迭代关系式的建⽴是解决迭代问题的关键,通常可以使⽤递推或倒推的⽅法来完成。
三、对迭代过程进⾏控制在什么时候结束迭代过程?这是编写迭代程序必须考虑的问题。
不能让迭代过程⽆休⽌地执⾏下去。
迭代过程的控制通常可分为两种情况:⼀种是所需的迭代次数是个确定的值,可以计算出来;另⼀种是所需的迭代次数⽆法确定。
对于前⼀种情况,可以构建⼀个固定次数的循环来实现对迭代过程的控制;对于后⼀种情况,需要进⼀步分析得出可⽤来结束迭代过程的条件。
接下来,我介绍⼀种迭代算法的典型案例----⽜顿-拉夫逊(拉弗森)⽅法⽜顿-拉夫逊(拉弗森)⽅法,⼜称⽜顿迭代法,也称⽜顿切线法:先任意设定⼀个与真实的根接近的值x0作为第⼀次近似根,由x0求出f(x0),过(x0,f(x0))点做f(x)的切线,交x轴于x1,把它作为第⼆次近似根,再由x1求出f(x1),过(x1,f(x1))点做f(x)的切线,交x轴于x2,……如此继续下去,直到⾜够接近(⽐如|x- x0|<1e-6时)真正的根x*为⽌。
⽽f '(x0)=f(x0)/( x1- x0)所以 x1= x0- f(x0)/ f ' (x0)。
我们来看⼀副从⽹上找到的图:接下来,我们来看⼀个例⼦:我们还是直接上代码:例⼦:⽤⽜顿迭代法求下列⽅程在值等于2.0附近的根:2x3-4x2+3x-6=0。
#include <stdio.h>#include <math.h>int main(void){float x,x0,f,f1;x = 2.0;do{x0=x;f=2*x0*x0*x0-4*x0*x0+3*x0-6;f1=6*x0*x0-8*x0+3;x=x0-f/f1;//函数fabs:求浮点数x的绝对值//说明:计算|x|, 当x不为负时返回 x,否则返回 -x}while(fabs(x-x0)>=1e-5);printf ("%f\n",x);return 0 ;}执⾏结果:当x=1.5时,⽅程2x3-4x2+3x-6=0。
求解非线性方程的牛顿迭代法

求方程的近似根"一般要考虑如下几个问题!
)$* 根的存在性问题"即方程有没有实根"有几个根#
))*有根区间的确定# 本文介绍的算法通常是假设有根
的前提下给出求近似根的方法"一般需要以别的辅助工具先
确定有根区间#
)(* 求出足够近似的根"即在制定精度下缩小有根区间"
或通过某些判别条件断定近似根的精度#
科教论坛
到方程))&(* 的等价形式为 "Q"g$) "* &此式被称为牛顿迭 $*) "*
代式# 在区间% ("#& 上取一个初值 "% "就可以得到牛顿迭代 格式 "/V$ Q"/ g$$*))""//** #
三345678迭代法局部收敛性分析
定 义 (&$! ) 局 部 收 敛 * 若 存 在 "! 的 某 邻 域 0Q
{"i"g"! h%} "对任意的 "% #0"由 ")V$ Q!) ")* 所产生的点 列收敛"则称 ")V$ Q!) ")* 在 0上收敛于 "! #
定理 (&$ ) 局 部 收 敛 判 别 定 理 * 设 ")V$ Q!) ")* " 0Q {"i"g"! h%} "若 !) "* 满足!
)$* !*) "* 在 0内连续+))* !*) "! * 1h$"
一元非线性方程的求解问题有如下形式!
给定函数 $"寻找 ") 实的或复的* "使得 $) "*Q%# 若存在
6.解非线性方程组的牛顿迭代法

eN TN (1 hL) eN 1
TN (1 hL) TN 1 (1 hL) eN 2
TN (1 hL) TN 1
(1 hL)2 TN 2 (1 hL)N 1 T1
N 1 k 0
(1
function f=myfun syms x; syms y f=[x^2+y^2-1;x^3-y]; x0=[0.8;0.6];
>> newton (myfun,x0,1e-6) n=
4 ans =
0.8260 0.5636
7. 最速下降法
f1( x, f2 (x,
y) y)
f1 y f2 y
y1
y0
1 J0
f1 f2
f1 f2 ( x0 , y0 ) f1x f2x
(**)
例: x 2 ( x
y2 5 0 1) y (3x
1)
0
求
(1,1) 附近的解
f1x
f2x
f1 y f2 y
2x y3
Tn1 y( xn1 ) yn1 一步产生的误差
其中是由公式根据前一步的准确值获得的。
y( xn1 ) y( xn h)
y( xn ) hf ( xn ,
y(xn ))
h2 2
y( )
xn xn!
yn1 y( xn ) hf (xn , y( xn )) (Euler方法)
f
(x,
y ( x))dx
Newton迭代法-数值分析非线性方程组数值解法

实验七、Newton 迭代法一、实验目的了解非线性方程与方程组的数值解法;深入理解Newton 迭代法,并用C++实现计算结果。
二、计算公式()())2(),1,0(1 ='-=+n x f x f x x n n n n它对应的迭代方程为显然是f(x)=0的同解方程,故其迭代函数为在 f(x)=0的根x*的某个邻域内,在x*的邻域R 内,对任意初值,应用公式(2)来解方程三、程序代码#include<stdio.h>#include<math.h>#include<conio.h>double f(double x);doubleft(double x);main(){double X0,X1,tol;int n;int count=0;printf("请输入初始值:\n");将f(x)在点x n 作Taylor 展开:)()(')()()(!2)()()(')()(2n n n n n n n n x x x f x f x f x x x f x x x f x f x f -+≈+-''+-+= ——Taylor 展开线性化f(x)=0近似于f(x n )+ f ′(x n )(x-x n )=0 (1)从(1)解出x,记为x n+1 ,则 )()(x f x f x x '-=)()()(x f x f x x '-=ϕ)0)((≠'x f )(δα≤-x R 0)(≈x f 1)()()()(2<≤'∙''=ϕ'L x f x f x f x 0xscanf("%lf",&X0);printf("请输入精度:\n");scanf("%lf",&tol);printf("请输入最大循环次数\n");scanf("%d",&n);X1=X0-f(X0)/ft(X0);while(fabs(X1-X0)>=tol)/*在没有达到精度要求情况下就循环*/ {X0=X1;X1=X0-f(X0)/ft(X0);count++;/*循环次数计数*//*如果循环次数到用户输入的最大循环次数就退出,可以适当修改*/ if(count==n){break;}}printf("方程的根为:%f\n",X1);getch();}/*************************函数功能:用于求f(x)的值**************************/double f(double x){double y;y=x*x*x+2*x*x+10*x-20;return y;}/*************************函数功能:用于求f(x)的导数值**************************/doubleft(double x){double y;y=3*x*x+4*x+10;return y;}四、例题用Newton 迭代法求下面方程的一个正根,计算结果精确到7位小数.02010223=-++x x x []得取初值,2,020∈=x。
(完整word版)c++求解非线性方程组的牛顿顿迭代法

void inv_jacobian(float yy[N][N],float inv[N][N])
{float aug[N][N2],L;
int i,j,k;
cout<<"开始计算雅克比矩阵的逆矩阵:"<<endl;
for (i=0;i<N;i++)
{ for(j=0;j<N;j++)
aug[i][j]=yy[i][j];
ff(x0,y0);//计算雅克比矩阵jacobian
ffjacobian(x0,jacobian);//计算雅克比矩阵的逆矩阵invjacobian
inv_jacobian(jacobian,invjacobian);//由近似解向量x0计算近似解向量x1
newdundiedai(x0, invjacobian,y0,x1);//计算差向量的1范数errornorm
yy[0][0]=2*x-2;
yy[0][1]=-1;
yy[1][0]=2*x;
yy[1][1]=8*y;
cout<<"雅克比矩阵是:"<<endl;
for( i=0;i<N;i++)
{for(j=0;j<N;j++)
cout<<yy[i][j]<<" ";
cout<<endl;
}
cout<<endl;
{ for(j=0;j<N2;j++)
cout<<aug[i][j]<<" ";
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
for (i=0;i<N;i++) x0[i]=x1[i];
} while (iter<Max);
return 0; }
void ff(float xx[N],float yy[N]) {float x,y; int i;
//调用函数
x=xx[0]; y=xx[1]; yy[0]=x*x-2*x-y+0.5; yy[1]=x*x+4*y*y-4;
newdundiedai(x0, invjacobian,y0,x1); errornorm=0; for (i=0;i<N;i++) errornorm=errornorm+fabs(x1[i]-x0[i]); if (errornorm<Epsilon) break;
//计算差向量的 1 范数 errornorm
计算近似解向量 x1
float x0[N]={2.0,0.25},y0[N],jacobian[N][N],invjacobian[N][N],x1[N],errornorm; int i,j,iter=0;
for( i=0;i<N;i++) cin>>x0[i];
//如果取消对 x0 的初始化,撤销下面两行的注释 符, 就可以由键盘向 x0 读入初始近似解向量
void inv_jacobian(float yy[N][N],float inv[N][N]); //计算雅克比矩阵的逆矩阵 inv
void newdundiedai(float x0[N], float inv[N][N],float y0[N],float x1[N]); //由近似解向量 x0
//计算雅克比矩阵 jacobian
The shortest way to do many things is
ffjacobian(x0,jacobian);
//计算雅克比矩阵的逆矩阵 invjacobian
inv_jacobian(jacobian,invjacobian);
//由近似解向量 x0 计算近似解向量 x1
cout<<"雅克比矩阵的逆矩阵: "<<endl; for (i=0;i<N;i++)
{ for(j=0;j<N;j++) cout<<inv[i][j]<<" ";
cout<<endl; } cout<<endl;
}
void newdundiedai(float x0[N], float inv[N][N],float y0[N],float x1[N]) {
The顿迭代法 c++程序设计
求解
0=x*x-2*x-y+0.5;
0=x*x+4*y*y-4;的方程
#include<iostream>
#include<cmath>
#define N 2
// 非线性方程组中方程个数、未知量个数
#define Epsilon 0.0001
cout<<endl;
for (i=0;i<N;i++) { for (k=i+1;k<N;k++) {L=-aug[k][i]/aug[i][i]; for(j=i;j<N2;j++) aug[k][j]=aug[k][j]+L*aug[i][j]; } }
The shortest way to do many things is
int i,j; float sum=0;
for(i=0;i<N;i++) { sum=0;
for(j=0;j<N;j++) sum=sum+inv[i][j]*y0[j]; x1[i]=x0[i]-sum;
}
cout<<"近似解向量:"<<endl; for (i=0;i<N;i++) cout<<x1[i]<<" "; cout<<endl;cout<<endl;
for (i=0;i<N;i++) { for(j=0;j<N2;j++) cout<<aug[i][j]<<" "; cout<<endl; }
cout<<endl;
for (i=N-1;i>=0;i--) for(j=N2-1;j>=0;j--) aug[i][j]=aug[i][j]/aug[i][i];
for (i=0;i<N;i++) { for(j=0;j<N2;j++) cout<<aug[i][j]<<" "; cout<<endl; for(j=N;j<N2;j++) inv[i][j-N]=aug[i][j]; }
cout<<endl;
The shortest way to do many things is
// 差向量 1 范数的上限
#define Max 100
//最大迭代次数
using namespace std;
const int N2=2*N;
int main()
{
void ff(float xx[N],float yy[N]);
//计算向量函数的因变量向量 yy[N]
void ffjacobian(float xx[N],float yy[N][N]);/ /计算雅克比矩阵 yy[N][N]
for (i=0;i<N;i++) { for(j=0;j<N2;j++) cout<<aug[i][j]<<" "; cout<<endl; }
cout<<endl;
for (i=N-1;i>0;i--) { for (k=i-1;k>=0;k--) {L=-aug[k][i]/aug[i][i]; for(j=N2-1;j>=0;j--) aug[k][j]=aug[k][j]+L*aug[i][j]; } }
x=xx[0]; y=xx[1]; //jacobian have n*n element yy[0][0]=2*x-2;
//计算函数雅克比的值
The shortest way to do many things is
yy[0][1]=-1; yy[1][0]=2*x; yy[1][1]=8*y;
cout<<"开始计算雅克比矩阵的逆矩阵 :"<<endl; for (i=0;i<N;i++)
{ for(j=0;j<N;j++) aug[i][j]=yy[i][j];
for(j=N;j<N2;j++) if(j==i+N) aug[i][j]=1; else aug[i][j]=0; }
for (i=0;i<N;i++) { for(j=0;j<N2;j++) cout<<aug[i][j]<<" "; cout<<endl; }
cout<<"雅克比矩阵是: "<<endl; for( i=0;i<N;i++) {for(j=0;j<N;j++)
cout<<yy[i][j]<<" "; cout<<endl; } cout<<endl; }
void inv_jacobian(float yy[N][N],float inv[N][N]) {float aug[N][N2],L; int i,j,k;
cout<<"初始近似解向量:"<<endl; for (i=0;i<N;i++)
cout<<x0[i]<<" "; cout<<endl;cout<<endl;
do {
iter=iter+1; cout<<"第 "<<iter<<" 次迭代开始"<<endl;
//计算向量函数的因变量向量 y0
ff(x0,y0);
}
//计算初值位置的值
cout<<"向量函数的因变量向量是: "<<endl; for( i=0;i<N;i++)
cout<<yy[i]<<" "; cout<<endl; cout<<endl;
}
void ffjacobian(float xx[N],float yy[N][N]) {
float x,y; int i,j;
