c++求解非线性方程组的牛顿顿迭代法
牛顿迭代法解非线性方程(组)

牛顿迭代法解非线性方程(组)在辨识工作中,常常需要对辨识准则或者判据进行求极值,这往往涉及到求非线性方程(组)的解问题。
牛顿迭代法是一种常用方法。
下面把自己对牛顿迭代法的学习和理解做个总结。
1.一元非线性方程的牛顿迭代公式和原理以一元非线性方程 f(x)=0 为例,对函数 f(x)进行Taylor级数展开(只展开至线性项)得f(x) = f(x0)+f'(x0)(x-x0)所以方程可写成f(x0)+f'(x0)(x-x0) = 0其中x0是给定的已知值,则不难推导出方程的解(当然,只是近似解,毕竟Taylor展开过程中只取了线性项)x = x0 - f(x0) / f'(x0)其中x不是真实解,但是相比之前的x0更靠近真实解了,因此可以多重复几次上述过程,从而使得到的解非常接近准确值。
所以,对于一元非线性方程,牛顿拉夫逊迭代公式为:x(k+1) = x(k) - f(x(k)) / f'(x(k))根据Taylor级数的几何意义我们可以从几何上形象的看牛顿迭代法的求解f(x)=0的过程。
第一次迭代x1 = x0 - f(x0) / f'(x0),其中f(x0) / f'(x0)的几何意义很明显,就是x0到x1的线段长度(这可以从直角三角形的知识得到)。
第二次迭代x2 = x1 - f(x1) / f'(x1),其中f(x1) / f'(x1)的几何意义很明显,就是x1到x2的线段长度。
同理可以进行第三次迭代第四次迭代,可以明显的看出x的取值在不断逼近真实解x*。
可能有人问,迭代求得的结果会不会不收敛,也就是x会不会偏离x*。
由于x0是在x*附近区域取值的,因此x0到x1这段曲线应该认为是平滑的没有转折的,因此切线与x轴的交点只会越来越接近真实解x*。
但是如果x0的取值离x*比较远的话,那么x0到x1这段曲线上可能有“转折”,这样就可能引起迭代的不收敛。
求解非线性方程的三种新的迭代法

求解非线性方程的三种新的迭代法
迭代法是一种通过迭代逼近的方式来求解方程的方法。
它的基本思想是通过不断逼近
方程的解,使得逼近值与真实解的差距越来越小,最终得到方程的解。
下面介绍三种新的迭代法:牛顿迭代法,弦截法和切线法。
一、牛顿迭代法
牛顿迭代法是一种通过利用函数导数的信息来逼近方程解的方法。
它的迭代公式为:
x_(n+1) = x_n - f(x_n)/f'(x_n)
x_n表示第n次迭代得到的逼近解,f(x_n)表示在x_n处的函数值,f'(x_n)表示在x_n 处的导数值。
牛顿迭代法的优点是收敛速度快,通常是二阶收敛,但其缺点是需要计算函数的导数,如果导数计算困难或者导数为零的情况下,该方法可能不适用。
二、弦截法
三、切线法
切线法的优点和牛顿迭代法类似,但其缺点是需要计算函数的导数,且对于初始逼近
解的选择比较敏感。
牛顿迭代法、弦截法和切线法都是三种常用的非线性方程迭代法。
它们各自有着优点
和缺点,适用的领域和条件也不尽相同。
在实际问题中,需要根据具体情况选择合适的方
法来求解非线性方程。
数值分析求解非线性方程根的二分法简单迭代法和牛顿迭代法

实验报告一:实验题目一、 实验目的掌握求解非线性方程根的二分法、简单迭代法和牛顿迭代法,并通过数值实验比较两种方法的收敛速度。
二、 实验内容1、编写二分法、并使用这两个程序计算02)(=-+=x e x x f 在[0, 1]区间的解,要求误差小于 410- ,比较两种方法收敛速度。
2、在利率问题中,若贷款额为20万元,月还款额为2160元,还期为10年,则年利率为多少?请使用牛顿迭代法求解。
3、由中子迁移理论,燃料棒的临界长度为下面方程的根,用牛顿迭代法求这个方程的最小正根。
4、用牛顿法求方程的根,精确至8位有效数字。
比较牛顿迭代法算单根和重根的收敛速度,并用改进的牛顿迭代法计算重根。
第1题:02)(=-+=x e x x f 区间[0,1] 函数画图可得函数零点约为0.5。
画图函数:function Test1()% f(x) 示意图, f(x) = x + exp(x) - 2; f(x) = 0r = 0:0.01:1;y = r + exp(r) - 2plot(r, y);grid on 二分法程序:计算调用函数:[c,num]=bisect(0,1,1e-4)function [c,num]=bisect(a,b,delta)%Input –a,b 是取值区间范围% -delta 是允许误差%Output -c 牛顿迭代法最后计算所得零点值% -num 是迭代次数ya = a + exp(a) - 2;yb = b + exp(b) - 2;if ya * yb>0return;endfor k=1:100c=(a+b)/2;yc= c + exp(c) - 2;if abs(yc)<=deltaa=c;b=c;elseif yb*yc>0b=c;yb=yc;elsea=c;ya=yc;endif abs(b-a)<deltanum=k; %num为迭代次数break;endendc=(a+b)/2;err=abs(b-a);yc = c + exp(c) - 2;牛顿迭代法程序:计算调用函数:[c,num]=newton(@func1,0.5,1e-4) 调用函数:function [y] = func1(x)y = x + exp(x) - 2;end迭代算法:function[c,num]=newton(func,p0,delta)%Input -func是运算公式% -p0是零点值% -delta是允许误差%Output -c牛顿迭代法最后计算所得零点值% -num是迭代次数num=-1;for k=1:1000y0=func(p0);dy0=diff(func([p0 p0+1e-8]))/1e-8;p1=p0-y0/dy0;err=abs(p1-p0);p0=p1;if(err<delta)num=k;%num为迭代次数break;endendc=p0;第2题:由题意得到算式:计算调用函数:[c,num]=newton(@func2,0.02,1e-8)程序:先用画图法估计出大概零点位置在0.02附近。
非线性方程求根—牛顿迭代法(新)

非线性方程求根——牛顿迭代法一、牛顿迭代法的基本思想基本思想:将非线性方程逐步归结为某种线性方程求解。
设方程f (x )=0有近似根x k (f `(x k )≠0),将f (x )在x k 展开:(ξ在x 和x k 之间)2()()()()()()2!k k k k f f x f x f x x x x x ξ'''=+-+-()()()()k k k f x f x f x x x '≈+-可设记该线性方程的根为x k +1,则()()()0k k k f x f x x x '+-=1()()k k k k f x x x f x +=-'故f (x )=0可近似表示为即为Newton 法迭代格式。
(k =0,1,……)例:用Newton 迭代法求方程310x x --=在x 0=1.5附近的近似实根。
解:32()1,()31f x x x f x x '=--=-迭代公式为312131kk k k k x x x x x +--=--计算步骤如下:(1)取初值x 0=1.5;(2)按照迭代公式计算x 1;(3)若|x 1-x 0|<=0.00001,终止迭代;否则,x 0=x 1;转(2);(4)输出迭代次数和近似根.二、牛顿迭代法的实现MATLAB求解程序设计:方程及一阶导数函数:function[fun,dfun]=fun0(x)fun=x^3-x-1;%求原函数的值dfun=3*x^2-1;%求一阶导数的值计算主程序:clearx0=1.5;[fun,dfun]=fun0(x0);x1=x0-fun/dfun;i=1;while abs(x1-x0)>1e-5x0=x1;[fun,dfun]=fun0(x0);x1=x0-fun/dfun;i=i+1;enddisp('the solution is x1=')x1disp('the iter time is ')i计算结果为:the solution is x1=x1 =1.3247the iter time isi =4可见经过4次迭代即到达要求的精度,原方程的一个近似实数根为1.3247.三、牛顿迭代法的收敛性牛顿迭代法的迭代函数:)()()(x f x f x x '-=ϕ222)]([)()()]([)()()]([1)(x f x f x f x f x f x f x f x '''='''-'-='ϕ设f (x *)=0,f `(x *)≠0,则ϕ`(x *)=0,故Newton 迭代法在x *附近至少平方收敛。
解非线性方程的牛顿迭代法及其应用

解非线性方程的牛顿迭代法及其应用一、本文概述非线性方程是数学领域中的一个重要研究对象,其在实际应用中广泛存在,如物理学、工程学、经济学等领域。
求解非线性方程是一个具有挑战性的问题,因为这类方程往往没有简单的解析解,需要通过数值方法进行求解。
牛顿迭代法作为一种古老而有效的数值求解方法,对于求解非线性方程具有重要的应用价值。
本文旨在介绍牛顿迭代法的基本原理、实现步骤以及在实际问题中的应用。
我们将详细阐述牛顿迭代法的基本思想,包括其历史背景、数学原理以及收敛性分析。
我们将通过具体实例,展示牛顿迭代法的计算步骤和实际操作过程,以便读者能够更好地理解和掌握该方法。
我们将探讨牛顿迭代法在各个领域中的实际应用,包括其在物理学、工程学、经济学等领域中的典型应用案例,以及在实际应用中可能遇到的问题和解决方法。
通过本文的介绍,读者可以深入了解牛顿迭代法的基本原理和应用技巧,掌握其在求解非线性方程中的实际应用方法,为进一步的研究和应用提供有力支持。
二、牛顿迭代法的基本原理牛顿迭代法,又称为牛顿-拉夫森方法,是一种在实数或复数域上近似求解方程的方法。
其基本原理是利用泰勒级数的前几项来寻找方程的根。
如果函数f(x)在x0点的导数f'(x0)不为零,那么函数f(x)在x0点附近可以用一阶泰勒级数来近似表示,即:这就是牛顿迭代法的基本迭代公式。
给定一个初始值x0,我们可以通过不断迭代这个公式来逼近f(x)的根。
每次迭代,我们都用当前的近似值x0来更新x0,即:这个过程一直持续到满足某个停止条件,例如迭代次数达到预设的上限,或者连续两次迭代的结果之间的差小于某个预设的阈值。
牛顿迭代法的收敛速度通常比线性搜索方法快,因为它利用了函数的导数信息。
然而,这种方法也有其局限性。
它要求函数在其迭代点处可导,且导数不为零。
牛顿迭代法可能不收敛,如果初始点选择不当,或者函数有多个根,或者根是重根。
因此,在使用牛顿迭代法时,需要谨慎选择初始点,并对迭代过程进行适当的监控和调整。
非线性方程的数值求法牛顿迭代法和弦截法PPT课件

26
Newton下山法
原理:若由 xk 得到的 xk+1 不能使 | f | 减小,则在 xk 和 xk+1 之 间找一个更好的点 xk1,使得 f ( xk1) f ( xk ) 。
xk
xk+1
xk1 (1 )xk , [0, 1]
xk 1
[xk
)g( xn
)
n1
n
mng(xn ) mg( xn ) n g(
xn
)
n2 g( xn )
mg( xn ) n g( xn )
n1
2 n
g( xn )
mg( xn ) n g( xn )
若 xn 收敛,即
n 0 (n ),
没有具体的描述,而且若x0 的值没有取好,有可 能得不到收敛的结果。
以下定理,给出了 f x 满足一定的条件时,要使得牛顿
迭代法收敛,x0 应满足什么条件。
又 f ( ) 0
( ) 0 1,
牛顿迭代法局部收敛于
又 ( ) 0
即有:牛顿迭代法具有二阶(平方)收敛速度。
注. 定理要求 x0 充分接近 (局部收敛),充分的程度
没有具体的描述,而且若x0 的值没有取好,有可 能得不到收敛的结果。
以下定理,给出了 f x 满足一定的条件时,要使得牛顿
迭代法收敛,x0 应满足什么条件。
定理 设 f x 在区间 a,b 上的二阶导数存在,且满足: ① f (a) f (b) 0; (保证 a, b中至少存在一个根)
若 xn 收敛,即 n 0 (n )
lim n1 lim[1
C语言编程 牛顿迭代法求方程1

牛顿迭代公式设r 是f(x) = 0的根,选取x0作为r 初始近似值,过点(x0,f(x0))的切线L ,L 的方程为y = f(x0)+f'(x0)(x-x0),求出L 与x 轴交点的横坐标 x1 = x0-f(x0)/f'(x0),称x1为r 的一次近似值。
过点(x1,f(x1))做曲线y = f(x)的切线,并求该切线与x 轴交点的横坐标 x2 = x1-f(x1)/f'(x1),称x2为r 的二次近似值。
重复以上过程,得r 的近似值序列,其中x(n+1)=x(n)-f(x(n))/f'(x(n)),称为r 的n+1次近似值,上式称为牛顿迭代公式。
解非线性方程f(x)=0似方法。
把f(x)在x0 f(x) = f(x0)+(x -x0)f'(x0)+(x -x0)^2*f''(x0)/2! +… 取其线性部分,作为非线性方程f(x) = 0的近似方程,即泰勒展开的前两项,则有f(x0)+f'(x0)(x -x0)-f(x)=0 设f'(x0)≠0则其解为x1=x0-f(x0)/f'(x0) 这样,得到牛顿法的一个迭代序列:x(n+1)=x(n)-f(x(n))/f'(x(n))。
牛顿迭代法又称牛顿切线法,它采用以下方法求根:先任意设定一个与真实的根接近的值x 0作为第一个近似根,由x 0求出f(x 0),过(x 0,f(x 0))点做f(x)的切线,交x 轴于x 1,把它作为第二次近似根,再由x 1求出f(x 1),再过(x 1,f(x 1))点做f(x)的切线,交x 轴于x 2,再求出f(x 2),再作切线……如此继续下去,直到足够接近真正的x *为止。
)()()()(0'0010100'x f x f x x x x x f x f -=-=因此, 就是牛顿迭代公式。
例1 用牛顿迭代法求方程2x 3-4x 2+3x-6=0在1.5附近的根。
解非线性方程组的牛顿迭代法

为克服这两个缺点,通常可用下述方法.
(1) 简化牛顿法,也称平行弦法.
xk 1 xk Cf ( xk )
其迭代公式为 (4.7)
C 0,1 ,.
迭代函数 ( x) x Cf ( x).
若在根 x * 附近成立 ( x) 1 Cf ( x) 1 ,即取 0 Cf ( x) 2,则迭代法(4.7)局部收敛.
8
xk
C 2 C
q2
k
1 q
2k
.
对任意 x0 0,总有 q 1,故由上式推知,当 k 时 xk C ,即迭代过程恒收敛. 例8 解 求 115 .
表7 6 计算结果 k 0 1 2 3 4 xk 10 10.750000 10.723837 10.723805 10.723805
f ( x) , f ( x)
由于
( x)
f ( x) f ( x) . 2 [ f ( x)]
假定 x *是 f ( x) 的一个单根,即 f ( x*) 0, f ( x*) 0 , 则由上式知 ( x*) 0 ,于是依据定理4可以断定,牛顿法 在根 x *的邻近是平方收敛的.
准备 迭代
x0 ,计算 f 0 f ( x0 ), 选定初始近似值
步骤2
按公式
x1 x0 f 0 / f 0
迭代一次,得新的近似值 x1,计算 f1 f ( x1 ), f1 f ( x1 ). 步骤3 控制
x1 满足 1 如果
f1 2 ,则终 或
5
止迭代,以 x1作为所求的根;否则转步骤4. 允许误差,而
3
又因
( x*)
f ( x*) , f ( x*)
C语言求解非线性方程、线性方程组代码

本文档提供了牛顿法、列主元素消去法、LU分解法三类求解方程的代码,对应非线性方程及线性方程组。
利用C语言编写,采用txt文件输入、输出方式。
/*牛顿法求解非线性方程*/#include<stdio.h>#include<math.h>#include<stdlib.h>float f(float x) /* 定义函数f(x) */{ return 2*x*x+2*x+1-exp(2*x); }float f1(float x) /* 定义函数f(x)的导数f1(x) */{ return 4*x+2-2*exp(2*x); }main(){float x0,x1,eps; /*定义初值和迭代精度*/FILE *fp1,*fp2;if((fp1=fopen("in.txt","r"))==NULL){printf("Can't open this file!\n");exit(0);}fscanf(fp1,"%f %f",&x1,&eps);do{x0=x1;if(fabs(f(x0))<=eps) x1=x0;elsex1=x0-f(x0)/f1(x0); /*牛顿迭代*/}while(fabs(f(x1))>eps); /*循环条件*/fp2=fopen("out.txt","w");fprintf(fp2,"%e",x1);fclose(fp1);fclose(fp2);}/*列主元素消去法求解线性方程组*/#include<stdio.h>#include<math.h>#include<stdlib.h>#define N 3void main(){ int i,j,k,mi; /*定义变量类型*/ float max,temp;float a[N][N],b[N],x[N],r[N][N+1];FILE *fp1; /*输入系数矩阵及列向量b*/ if((fp1=fopen("in.txt","r"))==NULL){printf("Can't open this file!\n");exit(0);}for(i=0;i<N;i++)for(j=0;j<N+1;j++)fscanf(fp1,"%f",&r[i][j]);fclose(fp1);for(i=0;i<N;i++)for(j=0;j<N;j++)a[i][j]=r[i][j];for(i=0;i<N;i++)b[i]=r[i][N];for(j=0;j<N-1;j++) /*找出列主元素并交换*/{for(i=j+1,mi=j,max=fabs(a[j][j]);i<N;i++)if(fabs(a[i][j])>max){mi=i;max=fabs(a[i][j]);}if(j<mi){temp=b[j];b[j]=b[mi];b[mi]=temp;for(k=j;k<N;k++){temp=a[j][k];a[j][k]=a[mi][k];a[mi][k]=temp;}}for(i=j+1;i<N;i++){temp=-a[i][j]/a[j][j];b[i]+=b[j]*temp;for(k=j;k<N;k++)a[i][k]+=a[j][k]*temp;}}x[N-1]=b[N-1]/a[N-1][N-1]; /*消去求解*/ for(i=N-2;i>=0;i--){x[i]=b[i];for(j=i+1;j<N;j++)x[i]-=a[i][j]*x[j];x[i]/=a[i][i];}FILE *fp2;fp2=fopen("out.txt","w");for(i=0;i<N;i++)fprintf(fp2,"x[%d]=%f\n",i+1,x[i]);fclose(fp2);}/*线性方程组的LU分解法*/#include<stdio.h>#include<math.h>#include<stdlib.h>#define N 3void main(){ int i,j,k,n;float temp;float a[N][N],b[N],x[N],y[N],L[N][N],U[N][N],r[N][N+1];FILE *fp1;if((fp1=fopen("in.txt","r"))==NULL){printf("Can't open this file!\n");exit(0);}for(i=0;i<N;i++)for(j=0;j<N+1;j++)fscanf(fp1,"%f",&r[i][j]);fclose(fp1);for(i=0;i<N;i++)for(j=0;j<N;j++)a[i][j]=r[i][j];for(i=0;i<N;i++)b[i]=r[i][N];for(i=0;i<N;i++) /*矩阵分解*/{U[0][i]=a[0][i];L[i][i]=1.0;L[i][0]=a[i][0]/a[0][0];for(j=i+1;j<N;j++){ L[i][j]=0;U[j][i]=0;}}for(i=1;i<N;i++){for(j=i;j<N;j++){temp=0;for(k=0;k<i;k++)temp=temp+L[i][k]*U[k][j];U[i][j]=a[i][j]-temp;}for(j=i;j<N;j++){temp=0;for(k=0;k<i;k++)temp=temp+L[j][k]*U[k][i];L[j][i]=(a[j][i]-temp)/U[i][i];}}y[0]=b[0]; /*解该线性方程组*/ for(i=1;i<N;i++){temp=0;for(j=0;j<i;j++)temp=temp+L[i][j]*y[j];y[i]=b[i]-temp;}x[N-1]=y[N-1]/U[N-1][N-1];for(i=N-2;i>=0;i--){x[i]=y[i];for(j=i+1;j<N;j++)x[i]-=U[i][j]*x[j];x[i]/=U[i][i];}FILE *fp2;fp2=fopen("out.txt","w");for(i=0;i<N;i++)fprintf(fp2,"x[%d]=%f\n",i+1,x[i]);fclose(fp2);}。
Newton迭代法求解非线性方程

Newton迭代法求解非线性方程Newton迭代法求解非线性方程一、 Newton 迭代法概述构造迭代函数的一条重要途径是用近似方程来代替原方程去求根。
因此,如果能将非线性方程f (x )=0用线性方程去代替,那么,求近似根问题就很容易解决,而且十分方便。
牛顿(Newton)法就是一种将非线性方程线化的一种方法。
设k x 是方程f (x )=0的一个近似根,把如果)(x f 在k x 处作一阶Taylor 展开,即:)x x )(x ('f )x (f )x (f k k k -+≈ (1-1)于是我们得到如下近似方程:0)x x )(x ('f )x (f k k k =-+ (1-2)设0)('≠k x f ,则方程的解为:x ?=x k +f (x k )f (x k )?(1-3)取x ~作为原方程的新近似根1+k x ,即令: )x ('f )x (f x x k k k 1k -=+, k=0,1,2,…(1-4)上式称为牛顿迭代格式。
用牛顿迭代格式求方程的根的方法就称为牛顿迭代法,简称牛顿法。
牛顿法具有明显的几何意义。
方程:)x x )(x ('f )x (f y k k k -+= (1-5)是曲线)x (f y =上点))x (f ,x (k k 处的切线方程。
迭代格式(1-4)就是用切线式(1-5)的零点来代替曲线的零点。
正因为如此,牛顿法也称为切线法。
牛顿迭代法对单根至少是二阶局部收敛的,而对于重根是一阶局部收敛的。
一般来说,牛顿法对初值0x 的要求较高,初值足够靠近*x时才能保证收敛。
若要保证初值在较大范围内收敛,则需对)x (f 加一些条件。
如果所加的条件不满足,而导致牛顿法不收敛时,则需对牛顿法作一些改时,即可以采用下面的迭代格式:)x ('f )x (f x x k k k 1k λ-=+,=,2,1,0k (1-6)上式中,10<λ<,称为下山因子。
牛顿迭代法求根c语言

牛顿迭代法求根c语言牛顿迭代法是一种常用的数值计算方法,其可以用来求解非线性方程的根。
本文将介绍牛顿迭代法的基本原理和实现方法,并提供一些使用C语言实现牛顿迭代法求根的示例代码。
一、牛顿迭代法的原理在介绍牛顿迭代法的原理之前,我们先来看一个简单的例子。
假设我们要求解方程f(x) = 0的近似根,其中f(x)是一个可导函数。
我们可以通过利用切线来逼近方程f(x) = 0的根。
具体地,我们可以选择一个起始点x0,然后在x0处取得f(x0)的切线,将其延长到x轴上的交点x1,那么x1就是f(x) = 0的一个近似根。
可以通过数学方法得到x1的表达式:x1 = x0 - f(x0) / f'(x0)其中f'(x0)表示函数f(x)在x0处的导数。
换句话说,我们使用f(x)在x0处的切线来近似替代f(x)的图形,直到得到f(x) = 0的一个近似根为止。
这就是牛顿迭代法的基本思想。
牛顿迭代法的具体步骤如下:1. 选择一个起始点x0;2. 使用f(x)在x0处的切线来近似替代f(x)的图形;3. 在切线上取得x轴的交点x1; 4. 将x1作为新的起始点,重复步骤2和3,直到得到近似根。
二、牛顿迭代法的实现牛顿迭代法的实现过程比较简单,但需要注意一些细节。
具体实现可以分为以下几个步骤:1. 定义一个函数f(x),表示待求解的方程;2. 定义一个函数f_prime(x),表示函数f(x)在x处的导数;3. 定义一个起始点x0;4. 通过牛顿迭代公式计算出x1; 5. 将x1作为新的起始点,重复步骤4,直到满足精度要求为止。
下面,我们提供一段使用C语言实现牛顿迭代法求根的代码示例:```c #include<stdio.h> #include<math.h>#define EPSILON 0.0001double f(double x) { // 表示待求解的非线性方程 return x*x*x - x*x + 2; }double f_prime(double x) { // 表示f(x)在x 处的导数 return 3*x*x - 2*x; }double newton_raphson(double x) { // 牛顿迭代法求根 double x0 = x;while (1) { double x1 = x0 - f(x0) / f_prime(x0);if (fabs(x1 - x0) < EPSILON) return x1;x0 = x1; } }int main() { double x = 0;printf("The root is: %lf\n",newton_raphson(x));return 0; } ```代码中,定义了非线性方程f(x)和它在x处的导数f_prime(x),然后利用牛顿迭代法计算出方程的近似根。
解非线性方程组的牛顿法

考虑非线性方程组
f1(x1, x2, , xn ) 0,
f2(x1, x2, , xn ) 0,
fn (x1, x2, , xn ) 0. 利用向量记号写为
F (X ) O. 这里F (X )是定义在某区域D Rn上向量值函数. 若存在 X* D, 使得F (X*) O, 则称X*为非线性方程组的解.
.
逐次迭代得结果.
Step 5 Set x x y
Step 6 If y TOL then OUTPUT(x)
Step7 Set k k 1
STOP.
Step8 OUTPUT (‘Maximum number of iterations exceeded’) STOP.
为了说明上述算法,我们可以看看下面的例子。设
s1
145 272
,
145 272
T
.
x2 x1 s1 0.092,3.092 T .
显然,我们只经过两步计算,所得到的 x2就已经非常靠近 解 0,3T .
例1 用牛顿法求解方程组
k x (k) 0 (1.5, 1.0)T
f1( f2(
x1 x1
,x2 ,x2
) )
x1 2 x12
定理 2 设G : D Rn Rn在D内有一不动点X *且G在X *可导,
(G(X*)) 1, 则存在开球 S S( X*, ) D, 对X (0) S, 迭代序列{X (k)}
收敛于X *.
牛顿迭代公式:
X (k1) X (k) F( X (k) ) 1 F ( X (k) ),
其中
f1
F
(
X
(k
)
)
[新版]c++求解非线性方程组的牛顿顿迭代法
![[新版]c++求解非线性方程组的牛顿顿迭代法](https://img.taocdn.com/s3/m/3c86bf0f2379168884868762caaedd3383c4b527.png)
牛顿迭代法c++程序设计00000求解0=x*x-2*x-y+0.5; 0=x*x+4*y*y-4;的方程00000#include<iostream>00000#include<cmath>00000#define N 2 // 非线性方程组中方程个数、未知量个数000000#define Epsilon 0.0001 // 差向量1范数的上限00000#define Max 100 //最大迭代次数000000using namespace std;00000const int N2=2*N;00000int main()00000{00000void ff(float xx[N],float yy[N]); //计算向量函数的因变量向量yy[N]00000void ffjacobian(float xx[N],float yy[N][N]);/ /计算雅克比矩阵yy[N][N]00000void inv_jacobian(float yy[N][N],float inv[N][N]); //计算雅克比矩阵的逆矩阵i nv000 00void newdundiedai(float x0[N], float inv[N][N],float y0[N],float x1[N]); //由近似解向量x0计算近似解向量x100000float x0[N]={2.0,0.25},y0[N],jacobian[N][N],invjacobian[N][N],x1[N],errornorm;00000int i,j,iter=0;000000//如果取消对x0的初始化,撤销下面两行的注释符,就可以由键盘向x0读入初始近似解向量00000for( i=0;i<N;i++)00000cin>>x0[i];00000cout<<"初始近似解向量:"<<endl;00000for (i=0;i<N;i++)00000cout<<x0[i]<<" ";00000cout<<endl;cout<<endl;00000do00000{00000iter=iter+1;00000cout<<"第"<<iter<<" 次迭代开始"<<endl; //计算向量函数的因变量向量y0000 00ff(x0,y0); //计算雅克比矩阵jacobian00000ffjacobian(x0,jacobian); //计算雅克比矩阵的逆矩阵invjacobian 00000inv_jacobian(jacobian,invjacobian); //由近似解向量x0 计算近似解向量x1 00000newdundiedai(x0, invjacobian,y0,x1); //计算差向量的1范数errornorm000 00errornorm=0;000000for (i=0;i<N;i++)00000errornorm=errornorm+fabs(x1[i]-x0[i]);00000if (errornorm<Epsilon) break;00000for (i=0;i<N;i++)00000x0[i]=x1[i];00000} while (iter<Max);00000return 0;00000}00000void ff(float xx[N],float yy[N]) //调用函数00000{float x,y;00000int i;00000x=xx[0];00000y=xx[1];00000yy[0]=x*x-2*x-y+0.5; 00000yy[1]=x*x+4*y*y-4; //计算初值位置的值00000cout<<"向量函数的因变量向量是:"<<endl;00000for( i=0;i<N;i++)00000cout<<yy[i]<<" ";00000cout<<endl;00000cout<<endl;00000}00000void ffjacobian(float xx[N],float yy[N][N])000000{00000float x,y;000000int i,j;000000x=xx[0];00000y=xx[1];00000//jacobian have n*n element //计算函数雅克比的值00000yy[0][0]=2*x-2;00000yy[0][1]=-1;00000yy[1][0]=2*x;000000yy[1][1]=8*y;000000cout<<"雅克比矩阵是:"<<endl;00000for( i=0;i<N;i++)00000{for(j=0;j<N;j++)000000cout<<yy[i][j]<<" ";000000cout<<endl;00000}00000cout<<endl;00000}00000void inv_jacobian(float yy[N][N],float inv[N][N])00000{float aug[N][N2],L;00000int i,j,k;00000cout<<"开始计算雅克比矩阵的逆矩阵:"<<endl;00000for (i=0;i<N;i++)00000{ for(j=0;j<N;j++)000000aug[i][j]=yy[i][j];00000for(j=N;j<N2;j++)00000if(j==i+N) aug[i][j]=1;000000else aug[i][j]=0;00000}00000for (i=0;i<N;i++)00000{ for(j=0;j<N2;j++)000000cout<<aug[i][j]<<" ";00000cout<<endl;00000}00000cout<<endl;00000for (i=0;i<N;i++)00000{00000for (k=i+1;k<N;k++)000000{L=-aug[k][i]/aug[i][i];00000for(j=i;j<N2;j++)00000aug[k][j]=aug[k][j]+L*aug[i][j];000000 }00000}00000for (i=0;i<N;i++)00000{ for(j=0;j<N2;j++)000000cout<<aug[i][j]<<" ";00000cout<<endl;00000}00000cout<<endl; 00000for (i=N-1;i>0;i--)000000{ 00000for (k=i-1;k>=0;k--)000000{L=-aug[k][i]/aug[i][i];00000for(j=N2-1;j>=0;j--)00000aug[k][j]=aug[k][j]+L*aug[i][j];000000 }00000}00000for (i=0;i<N;i++)00000{ for(j=0;j<N2;j++)000000cout<<aug[i][j]<<" ";00000cout<<endl;00000}00000cout<<endl;00000for (i=N-1;i>=0;i--)000000for(j=N2-1;j>=0;j--)00000aug[i][j]=aug[i][j]/aug[i][i];00000for (i=0;i<N;i++)00000{ for(j=0;j<N2;j++)000000cout<<aug[i][j]<<" ";00000cout<<endl; 000000for(j=N;j<N2;j++)00000inv[i][j-N]=aug[i][j];000000}00000cout<<endl;00000cout<<"雅克比矩阵的逆矩阵:"<<endl;00000for (i=0;i<N;i++)00000{ for(j=0;j<N;j++)000000cout<<inv[i][j]<<" ";00000cout<<endl;00000}00000cout<<endl;00000}00000void newdundiedai(float x0[N], float inv[N][N],float y0[N],float x1[N])00000 {00000int i,j;000000float sum=0;00000for(i=0;i<N;i++)00000{ sum=0;00000for(j=0;j<N;j++)00000sum=sum+inv[i][j]*y0[j];00000x1[i]=x0[i]-sum;00000}00000cout<<"近似解向量:"<<endl;00000for (i=0;i<N;i++)00000cout<<x1[i]<<" ";00000cout<<endl;cout<<endl;00000。
c语言牛顿迭代法

c语言牛顿迭代法牛顿迭代法(Newton-Raphson法)是一种求解方程近似解的方法,它是利用泰勒级数展开函数在某点的值,然后用一阶泰勒展开式的根近似表示函数的零点,因此也被称为牛顿拉弗森法。
它可以高效地解决复杂的非线性方程组,是科学计算领域中最为常用和基础的方法之一。
牛顿迭代法的基本思想是:在第k次迭代时,求出曲线f(x)在点xk的一次导数斜率,以此确定x轴上的一个点xk+1,和该点处曲线的一次切线。
这条切线和x轴交点的横坐标就是极值点的估计值。
这个过程可以迭代多次,直到达到满足一定的误差精度或者迭代次数的要求。
C语言实现牛顿迭代法需要先定义一个函数,这个函数就是需要求解方程的函数。
定义完函数之后,需要实现牛顿迭代公式来求出下一次迭代的估计值,然后不断迭代。
具体实现过程如下:1. 定义函数f(x),即需要求解方程的函数。
2. 定义函数f_prime(x),即f(x)的一次导数。
3. 定义变量x和x_next,初始化它们的值。
4. 在循环中,首先计算f(x)和f_prime(x),然后计算下一个迭代点的估计值x_next = x - f(x) / f_prime(x)。
5. 如果x_next和x的差异满足预设的精度要求,则退出循环。
6. 否则,将x_next的值赋值给x,并重复执行第4步。
C语言实现牛顿迭代法的代码如下:#include <stdio.h>#include <math.h>定义函数f(x)double f(double x) {return x * x - 2;}定义函数f_prime(x)double f_prime(double x) {return 2 * x;}int main() {定义变量double x, x_next, epsilon;int iter;初始化变量x = 1.0;epsilon = 1e-6;iter = 0;迭代求解do {x_next = x - f(x) / f_prime(x);iter++;printf("Iteration %d: x = %lf\n", iter, x_next);x = x_next;} while (fabs(x_next - x) >= epsilon);输出结果printf("Final result: x = %lf\n", x);return 0;}在这个代码中,我们使用了do-while循环来不断执行迭代过程,直到达到预设的精度要求。
C语言实现牛顿迭代法解方程详解

C语⾔实现⽜顿迭代法解⽅程详解C语⾔实现⽜顿迭代法解⽅程详解利⽤迭代算法解决问题,需要做好以下三个⽅⾯的⼯作:⼀、确定迭代变量在可以⽤迭代算法解决的问题中,我们可以确定⾄少存在⼀个可直接或间接地不断由旧值递推出新值的变量,这个变量就是迭代变量。
⼆、建⽴迭代关系式所谓迭代关系式,指如何从变量的前⼀个值推出其下⼀个值的公式(或关系)。
迭代关系式的建⽴是解决迭代问题的关键,通常可以使⽤递推或倒推的⽅法来完成。
三、对迭代过程进⾏控制在什么时候结束迭代过程?这是编写迭代程序必须考虑的问题。
不能让迭代过程⽆休⽌地执⾏下去。
迭代过程的控制通常可分为两种情况:⼀种是所需的迭代次数是个确定的值,可以计算出来;另⼀种是所需的迭代次数⽆法确定。
对于前⼀种情况,可以构建⼀个固定次数的循环来实现对迭代过程的控制;对于后⼀种情况,需要进⼀步分析得出可⽤来结束迭代过程的条件。
接下来,我介绍⼀种迭代算法的典型案例----⽜顿-拉夫逊(拉弗森)⽅法⽜顿-拉夫逊(拉弗森)⽅法,⼜称⽜顿迭代法,也称⽜顿切线法:先任意设定⼀个与真实的根接近的值x0作为第⼀次近似根,由x0求出f(x0),过(x0,f(x0))点做f(x)的切线,交x轴于x1,把它作为第⼆次近似根,再由x1求出f(x1),过(x1,f(x1))点做f(x)的切线,交x轴于x2,……如此继续下去,直到⾜够接近(⽐如|x- x0|<1e-6时)真正的根x*为⽌。
⽽f '(x0)=f(x0)/( x1- x0)所以 x1= x0- f(x0)/ f ' (x0)。
我们来看⼀副从⽹上找到的图:接下来,我们来看⼀个例⼦:我们还是直接上代码:例⼦:⽤⽜顿迭代法求下列⽅程在值等于2.0附近的根:2x3-4x2+3x-6=0。
#include <stdio.h>#include <math.h>int main(void){float x,x0,f,f1;x = 2.0;do{x0=x;f=2*x0*x0*x0-4*x0*x0+3*x0-6;f1=6*x0*x0-8*x0+3;x=x0-f/f1;//函数fabs:求浮点数x的绝对值//说明:计算|x|, 当x不为负时返回 x,否则返回 -x}while(fabs(x-x0)>=1e-5);printf ("%f\n",x);return 0 ;}执⾏结果:当x=1.5时,⽅程2x3-4x2+3x-6=0。
非线性方程组的Newton法与拟Newton法
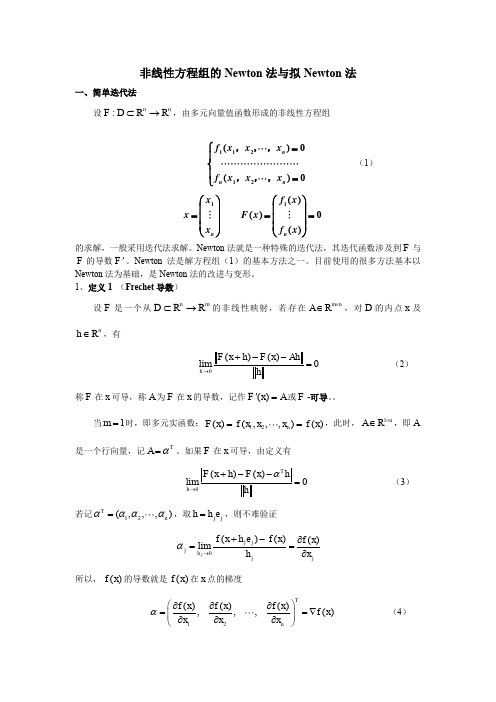
非线性方程组的Newton 法与拟Newton 法一、简单迭代法设:nnF D R R ⊂→,由多元向量值函数形成的非线性方程组11212()0()0n n n f x x x f x x x ⎧=⎪⎨⎪=⎩,,,,,, (1) 11()()0()n n x f x x F x x f x ⎛⎫⎛⎫ ⎪ ⎪=== ⎪⎪ ⎪ ⎪⎝⎭⎝⎭的求解,一般采用迭代法求解。
Newton 法就是一种特殊的迭代法,其迭代函数涉及到F 与F 的导数F '。
Newton 法是解方程组(1)的基本方法之一。
目前使用的很多方法基本以Newton 法为基础,是Newton 法的改进与变形。
1、定义1 (Frechet 导数)设F 是一个从nmD R R ⊂→的非线性映射,若存在m nA R⨯∈,对D 的内点x 及n h R ∈,有()()lim0h F x h F x Ahh→+--= (2)称F 在x 可导,称A 为F 在x 的导数,记作()F x A '=或F -可导。
当1m =时,即多元实函数:12()(,,,)()n F x f x x x f x ==,此时,1n A R ⨯∈,即A是一个行向量,记TA α=。
如果F 在x 可导,由定义有()()lim0T h F x h F x hhα→+--= (3)若记12(,,,)Tn αααα=,取j j h h e =,则不难验证()()()limj j j j h jjf x h e f x f x h x α→+-∂==∂ 所以,()f x 的导数就是()f x 在x 点的梯度12()()(),,,()Tn f x f x f x f x x x x α⎛⎫∂∂∂==∇ ⎪∂∂∂⎝⎭(4)对于一般情形,F :n m D R R ⊂→,记A 的第i 行为Ti α,导数的定义可以写成等价形式0()()lim 0T i i i h f x h f x h hα→+--=,1,2,,i m =所以,可以得到()i i f x α=∇,1,2,,i m = (5)因此,得到多元向量值函数()F x 的导数'F x (),:nnF D R R ⊂→,有111122221212()()()()()()'()()()n n n n n n n n f x f x f x xx x f x f x f x x x x F x DF x R f x f x f x x x x ⨯∂∂∂⎡⎤⎢⎥∂∂∂⎢⎥∂∂∂⎢⎥⎢⎥∂∂∂∈⎢⎥⎢⎥⎢⎥∂∂∂⎢⎥⎢⎥∂∂∂⎣⎦()=()= (6)称()DF x 为()F x 在点x 的Jacobi (雅克比)矩阵。
求解非线性方程的牛顿迭代法

求解非线性方程的牛顿迭代法作者:李晓辉任伟和程长胜来源:《科技风》2021年第14期摘要:本文主要讲了求解非线性方程的牛顿迭代法。
文章首先引入牛顿迭代法的公式、迭代函数。
紧接着文章又介绍了牛顿迭代法的局部收敛性以及它的收敛速度,并通过数值实验验证了牛顿迭代法求解非线性方程的有效性。
关键词:牛顿迭代法;局部收敛;收敛速度中图分类号:O010224文献标识码:A一、绪论类似于线性方程组Ax=b求解的问题,非线性方程的一般问题可化为f(x)=y,即“对于什么样的x的值,函数f取值为y”,这里可以暂且先把f当成单变量函数,通常把y移项并吸收进f,从而一般形式可记为f(x)=0,因此,一个一般的一元非线性方程的求解问题有如下形式:给定函数f,寻找x(实的或复的),使得f(x)=0。
若存在一点x*满足该性质,称x*是方程f(x)=0的根或函数的零点。
这类问题称为求根问题或求零点问题。
此外,方程的根的情况可分为单根和重根。
一般的非线性方程的重数可以定义如下:若f(x)=(x-x*)m·g(x)且g(x)≠0,其中,m为自然数,称x*为f(x)的m重根,m=1时也称单根。
若区间[a,b]上有方程的一个实根,称该区间为方程的一个有根区间,如果能把方程的有根区间的长度缩短到一定的范围内,那么就求到了一个近似根,通常采用的都是数值求解的办法,因此若假设要求有根区间长度为0(即求到精确解),这些数值求解的办法通常都会产生一个逐渐逼近根的一个无穷序列。
求方程的近似根,一般要考虑如下几个问题:(1)根的存在性问题,即方程有没有实根,有几个根。
(2)有根区间的确定。
本文介绍的算法通常是假设有根的前提下给出求近似根的方法,一般需要以别的辅助工具先确定有根区间。
(3)求出足够近似的根,即在制定精度下缩小有根区间,或通过某些判别条件断定近似根的精度。
二、Newton迭代公式的构造简单迭代是将非线性方程f(x)=0通过代数恒等变形,将原方程化成等价方程x=φ(x),从而形成迭代式xk+1=φ(xk)。
(完整word版)c++求解非线性方程组的牛顿顿迭代法

void inv_jacobian(float yy[N][N],float inv[N][N])
{float aug[N][N2],L;
int i,j,k;
cout<<"开始计算雅克比矩阵的逆矩阵:"<<endl;
for (i=0;i<N;i++)
{ for(j=0;j<N;j++)
aug[i][j]=yy[i][j];
ff(x0,y0);//计算雅克比矩阵jacobian
ffjacobian(x0,jacobian);//计算雅克比矩阵的逆矩阵invjacobian
inv_jacobian(jacobian,invjacobian);//由近似解向量x0计算近似解向量x1
newdundiedai(x0, invjacobian,y0,x1);//计算差向量的1范数errornorm
yy[0][0]=2*x-2;
yy[0][1]=-1;
yy[1][0]=2*x;
yy[1][1]=8*y;
cout<<"雅克比矩阵是:"<<endl;
for( i=0;i<N;i++)
{for(j=0;j<N;j++)
cout<<yy[i][j]<<" ";
cout<<endl;
}
cout<<endl;
{ for(j=0;j<N2;j++)
cout<<aug[i][j]<<" ";
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
牛顿迭代法c++程序设计
求解0=x*x-2*x-y+0.5; 0=x*x+4*y*y-4;的方程
#include<iostream>
#include<cmath>
#define N 2 // 非线性方程组中方程个数、未知量个数
#define Epsilon 0.0001 // 差向量1范数的上限
#define Max 100 //最大迭代次数
using namespace std;
const int N2=2*N;
int main()
{
void ff(float xx[N],float yy[N]); //计算向量函数的因变量向量yy[N]
void ffjacobian(float xx[N],float yy[N][N]);/ /计算雅克比矩阵yy[N][N]
void inv_jacobian(float yy[N][N],float inv[N][N]); //计算雅克比矩阵的逆矩阵inv
void newdundiedai(float x0[N], float inv[N][N],float y0[N],float x1[N]); //由近似解向量x0
计算近似解向量x1
float x0[N]={2.0,0.25},y0[N],jacobian[N][N],invjacobian[N][N],x1[N],errornorm;
int i,j,iter=0;
//如果取消对x0的初始化,撤销下面两行的注释
符,就可以由键盘向x0读入初始近似解向量
for( i=0;i<N;i++)
cin>>x0[i];
cout<<"初始近似解向量:"<<endl;
for (i=0;i<N;i++)
cout<<x0[i]<<" ";
cout<<endl;cout<<endl;
do
{
iter=iter+1;
cout<<"第"<<iter<<" 次迭代开始"<<endl; //计算向量函数的因变量向量y0
ff(x0,y0); //计算雅克比矩阵jacobian
ffjacobian(x0,jacobian); //计算雅克比矩阵的逆矩阵invjacobian
inv_jacobian(jacobian,invjacobian); //由近似解向量x0 计算近似解向量x1
newdundiedai(x0, invjacobian,y0,x1); //计算差向量的1范数errornorm errornorm=0;
for (i=0;i<N;i++)
errornorm=errornorm+fabs(x1[i]-x0[i]);
if (errornorm<Epsilon) break;
for (i=0;i<N;i++)
x0[i]=x1[i];
} while (iter<Max);
return 0;
}
void ff(float xx[N],float yy[N]) //调用函数
{float x,y;
int i;
x=xx[0];
y=xx[1];
yy[0]=x*x-2*x-y+0.5;
yy[1]=x*x+4*y*y-4; //计算初值位置的值
cout<<"向量函数的因变量向量是:"<<endl;
for( i=0;i<N;i++)
cout<<yy[i]<<" ";
cout<<endl;
cout<<endl;
}
void ffjacobian(float xx[N],float yy[N][N])
{
float x,y;
int i,j;
x=xx[0];
y=xx[1];
//jacobian have n*n element //计算函数雅克比的值
yy[0][0]=2*x-2;
yy[0][1]=-1;
yy[1][0]=2*x;
yy[1][1]=8*y;
cout<<"雅克比矩阵是:"<<endl;
for( i=0;i<N;i++)
{for(j=0;j<N;j++)
cout<<yy[i][j]<<" ";
cout<<endl;
}
cout<<endl;
}
void inv_jacobian(float yy[N][N],float inv[N][N]) {float aug[N][N2],L;
int i,j,k;
cout<<"开始计算雅克比矩阵的逆矩阵:"<<endl; for (i=0;i<N;i++)
{ for(j=0;j<N;j++)
aug[i][j]=yy[i][j];
for(j=N;j<N2;j++)
if(j==i+N) aug[i][j]=1;
else aug[i][j]=0;
}
for (i=0;i<N;i++)
{ for(j=0;j<N2;j++)
cout<<aug[i][j]<<" ";
cout<<endl;
}
cout<<endl;
for (i=0;i<N;i++)
{
for (k=i+1;k<N;k++)
{L=-aug[k][i]/aug[i][i];
for(j=i;j<N2;j++)
aug[k][j]=aug[k][j]+L*aug[i][j];
}
}
for (i=0;i<N;i++)
{ for(j=0;j<N2;j++)
cout<<aug[i][j]<<" ";
cout<<endl;
}
cout<<endl;
for (i=N-1;i>0;i--)
{
for (k=i-1;k>=0;k--)
{L=-aug[k][i]/aug[i][i];
for(j=N2-1;j>=0;j--)
aug[k][j]=aug[k][j]+L*aug[i][j];
}
}
for (i=0;i<N;i++)
{ for(j=0;j<N2;j++)
cout<<aug[i][j]<<" ";
cout<<endl;
}
cout<<endl;
for (i=N-1;i>=0;i--)
for(j=N2-1;j>=0;j--)
aug[i][j]=aug[i][j]/aug[i][i];
for (i=0;i<N;i++)
{ for(j=0;j<N2;j++)
cout<<aug[i][j]<<" ";
cout<<endl;
for(j=N;j<N2;j++)
inv[i][j-N]=aug[i][j];
}
cout<<endl;
cout<<"雅克比矩阵的逆矩阵:"<<endl;
for (i=0;i<N;i++)
{ for(j=0;j<N;j++)
cout<<inv[i][j]<<" ";
cout<<endl;
}
cout<<endl;
}
void newdundiedai(float x0[N], float inv[N][N],float y0[N],float x1[N]) {
int i,j;
float sum=0;
for(i=0;i<N;i++)
{ sum=0;
for(j=0;j<N;j++)
sum=sum+inv[i][j]*y0[j];
x1[i]=x0[i]-sum;
}
cout<<"近似解向量:"<<endl;
for (i=0;i<N;i++)
cout<<x1[i]<<" ";
cout<<endl;cout<<endl;
}。
