第五章-定子磁场定向矢量控制
永磁同步电机的矢量控制系统

永磁同步电机的矢量控制系统一、本文概述随着科技的不断进步和工业的快速发展,电机作为核心动力设备,在各种机械设备和工业自动化系统中扮演着至关重要的角色。
其中,永磁同步电机(Permanent Magnet Synchronous Motor,简称PMSM)因其高效率、高功率密度和优良的控制性能等优点,被广泛应用于电动汽车、风力发电、机床设备等领域。
为了实现永磁同步电机的精确控制,提高其运行效率和稳定性,矢量控制(Vector Control)技术被引入到永磁同步电机的控制系统中。
本文将对永磁同步电机的矢量控制系统进行深入探讨。
文章将简要介绍永磁同步电机的基本结构和运行原理,为后续的矢量控制理论奠定基础。
接着,文章将重点阐述矢量控制的基本原理和实现方法,包括坐标变换、空间矢量脉宽调制(SVPWM)等关键技术。
文章还将分析矢量控制系统中的传感器选择、参数辨识以及控制策略优化等问题,以提高系统的控制精度和鲁棒性。
通过本文的研究,读者可以对永磁同步电机的矢量控制系统有一个全面而深入的了解,为实际应用中提高永磁同步电机的控制性能提供理论支持和指导。
本文还将探讨未来永磁同步电机矢量控制系统的发展趋势和挑战,为相关领域的研究者和工程师提供有价值的参考信息。
二、永磁同步电机的基本原理永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)是一种高效、高性能的电机类型,其工作原理基于电磁感应和磁场相互作用。
PMSM的核心组成部分包括定子、转子和永磁体。
定子通常由三相绕组构成,负责产生旋转磁场;转子则装有永磁体,这些永磁体在定子产生的旋转磁场作用下,产生转矩从而驱动电机旋转。
PMSM的工作原理可以简要概括为:当定子三相绕组通入三相交流电时,会在定子内部形成旋转磁场。
由于转子上的永磁体具有固定的磁极,它们在旋转磁场的作用下会受到力矩的作用,从而使转子跟随定子磁场的旋转而旋转。
通过控制定子电流的相位和幅值,可以精确控制旋转磁场的转速和转向,从而实现对PMSM的精确控制。
矢量控制

70年代初西门子工程师F.Blaaschke在读博士期间,其导师给他出了一个课题,就是如何通过运算来实现交流电机的直流化控制。
(因为直流电机的励磁和电枢部分单独实现调节,在励磁恒定的情况下,只需控制直流电机的电枢电流即可实现对电机转矩的控制,而交流电动机则不同。
根据公式3可知。
)交流电动机的磁通和电流是耦合在一起的,改变磁通的同时会同时引起电流的变化。
F.Blaaschke想出一个非常天才的想法,即通过坐标变换先将电动机的三相系统等效为两相系统,再经过按转子磁场定向的同步旋转变换实现定子电流励磁分量与转矩分量之间的解耦,从而达到对交流电机的磁通和电流分别控制的目的,这样就可以将一台三相异步电机等效为直流电机来控制,因而获得与直流调速系统同样的静、动态性能,一举打破了直流调速系统一统天下的局面。
七十年代初期,西门子公司的FBlaschke和WFlotor提出了“感应电机磁场定向的控制原理”,通过矢量旋转变换和转子磁场定向,将定子电流按转子磁链空间方向分解成为励磁分量和转矩分量,得到类似于直流电机的数学模型。
1980年,日本ANabas教授和山村昌教授提出转差矢量控制系统。
直到现在,科学家仍在进行着不懈的研究。
仿真分析是解决矢量控制系统复杂性问题的有力手段,为此,本文根据矢量控制系统的构成框图,建立了面向结构图的电流滞环型矢量控制交流调速系统的一体化仿真模型,并用MATLAB的Simulink语言,直接进行仿真,得到了良好的效果。
同时,该仿真模型可以直接作为平台对调速系统的控制器、电流变换和磁链观测器、电流控制变频器及异步电动机等模块进行检验和比较,具有很好的通用性。
1 系统的组成本文所用的仿真系统为转速、磁链闭环电流滞环型PWM变频调速系统,为了提高系统的快速性和限流的必要性,电流调节器采用传统的PI调节器。
同时为了保持系统的通用性,转速和转矩调节器亦采用PI调节器,系统的原理框图如图1所示。
图1 转速、磁链闭环电流滞环型PWM变频调速系统ASR-速度调节器;ATR-转矩调节器;AΨR-磁链调节器;BRT-速度传感器转速、磁链闭环电流滞环型调速系统其简化构成框图如图2所示。
第5章三相永磁同步电动机直接转矩控制

第5章 三相永磁同步电动机直接转矩控制
te p
1 f s sin sf Ls
(5-5)
式(5-5)中, 转子磁链矢量 ψ f 的幅值不变, 若能控制定子磁链矢量 ψ s 的 幅值为常值,电磁转矩就仅与 sf 有关, sf 称负载角,通过控制 sf 可 以控制电磁转矩,这就是 PMSM 直接转矩控制基本原理。 在 ABC 轴系中,定子电压矢量方程为
便成为式(5-5)的形式。虽然插入式和内装式 PMSM 产生了磁阻转矩,但是两者直 接转矩控制原理相同。 电动机电磁功率可表示为
p e t e Ωs
(5-23)
式中, Ωs 为机械角速度, Ωs ωs p 。
13
现代电机控制技术
第5章 三相永磁同步电动机直接转矩控制
在正弦稳态下, ωr ωs , e0 ωs f ;在忽略定子电阻 Rs 情况下,
第5章 三相永磁同步电动机直接转矩控制
5.1 控制原理与控制方式
5.1.1 转矩生成与控制 5.1.2 滞环比较控制与控制系统 5.1.3 磁链和转矩估计 5.1.4 电机参数和转速影响 5.1.5 预期电压直接转矩控制
3
现代电机控制技术
第5章 三相永磁同步电动机直接转矩控制
5.1.1 转矩生成与控制
δsr 为定子磁链矢量 ψ s 与转子磁链矢量 ψ r 间的相位差。
10
现代电机控制技术
第5章 三相永磁同步电动机直接转矩控制
2. 插入式和内装式 PMSM
对于插入式和内装式 PMSM,由式(3-57)已知,电磁转矩方程为
t e p[ f iq ( Ld Lq )id iq ]
(5-15)
(5-16) (5-17)
矢量控制FOC基本原理
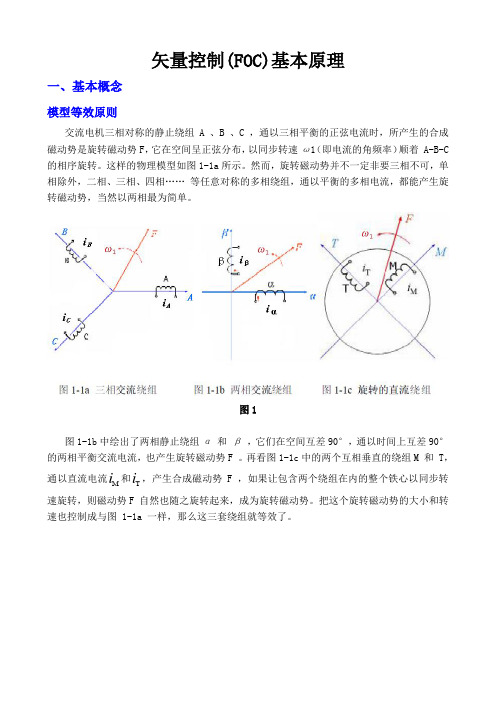
矢量控制(FOC)基本原理一、基本概念模型等效原则交流电机三相对称的静止绕组 A 、B 、C ,通以三相平衡的正弦电流时,所产生的合成磁动势是旋转磁动势F ,它在空间呈正弦分布,以同步转速ω1(即电流的角频率)顺着 A-B-C 的相序旋转。
这样的物理模型如图1-1a 所示。
然而,旋转磁动势并不一定非要三相不可,单相除外,二相、三相、四相…… 等任意对称的多相绕组,通以平衡的多相电流,都能产生旋转磁动势,当然以两相最为简单。
图1图1-1b 中绘出了两相静止绕组α 和 β ,它们在空间互差90°,通以时间上互差90°的两相平衡交流电流,也产生旋转磁动势F 。
再看图1-1c 中的两个互相垂直的绕组M 和 T ,通以直流电流M i 和T i ,产生合成磁动势F ,如果让包含两个绕组在内的整个铁心以同步转速旋转,则磁动势F 自然也随之旋转起来,成为旋转磁动势。
把这个旋转磁动势的大小和转速也控制成与图 1-1a 一样,那么这三套绕组就等效了。
三相--两相变换(3S/2S 变换)在三相静止绕组A 、B 、C 和两相静止绕组α、β之间的变换,简称3S/2S 变换。
其电流关系为111221022A B C ii i i i αβ⎡⎤⎡⎤--⎢⎥⎡⎤⎢⎥⎢=⎢⎥⎢⎥⎢⎣⎦⎢⎥-⎣⎦⎢⎦⎣() 两相—两相旋转变换(2S/2R 变换)同步旋转坐标系中(M 、T 坐标系中)轴向电流分量与α、β坐标系中轴向电流分量的转换关系为cos sin 2sin cos M T i i i i αβϕϕϕϕ⎡⎤⎡⎡⎤⎤=⎢⎥⎢⎢⎥⎥-⎦⎣⎦⎣⎣⎦ ()矢量控制简介矢量控制是指“定子三相电流矢量控制”。
矢量控制理论最早为解决三相异步电机的调速问题而提出。
交流矢量的直流标量化可以使三相异步电机获得和直流电机一样优越的调速性能。
将交流矢量变换为两相直流标量的过程见图2。
图2图2的上图为静止坐标系下的定子三相交流矢量 图2的中图为静止坐标系下的等效两相交流矢量 图2的下图为旋转坐标系下的等效两相直流标量,T i 是转矩电流,M i 是励磁电流。
异步电机定子磁链定向矢量控制系统的设计与研究的开题报告

异步电机定子磁链定向矢量控制系统的设计与研究的开题报告一、选题背景及意义随着电力电子技术的快速发展,异步电机磁链定向矢量控制技术也日趋成熟,已成为现代工业中普遍采用的控制方式。
在电力驱动系统中,异步电机具有结构简单、制造成本低、运行可靠等优点,在机床、风力发电、轨道交通等领域的应用越来越广泛。
磁链定向矢量控制技术是通过对异步电机定子和转子电流的控制,实现电机高效、高精度的转矩控制和速度调节。
电机控制系统设计的好坏,直接决定了电机的效率、动态性能和稳定性能。
因此,对异步电机定子磁链定向矢量控制系统的设计与研究,具有重要的理论和实际意义。
二、选题内容和研究方法本课题旨在研究异步电机定子磁链定向矢量控制系统的设计与优化,主要包括以下内容:(1)基于Matlab/Simulink平台,建立异步电机磁链定向矢量控制系统的仿真模型,分析系统的动态性能和稳态性能。
(2)通过分析电机运行特性、控制要求和控制器结构,设计异步电机磁链定向矢量控制系统的控制器。
(3)基于DSP技术,实现异步电机磁链定向矢量控制系统的硬件控制器设计,完成控制算法的编写和调试。
(4)在实验室进行实验验证,测试系统的控制性能,比较实验结果与仿真模型结果,分析系统的优化空间和改进方向。
研究方法主要包括理论分析、仿真模拟和实验验证。
三、预期结果和创新性本课题的预期结果是成功设计出异步电机定子磁链定向矢量控制系统,并通过实验验证系统的性能优异,系统稳定可靠,具有一定的创新性。
同时,本课题还具有以下的创新性:(1)采用DSP技术和Matlab/Simulink平台相结合的方法,提高了研究的效率和准确性。
(2)提出了一种新的控制器结构,通过优化控制算法,控制器具有更好的控制精度和抗扰性能。
(3)探索了异步电机磁链定向矢量控制系统在工业应用中的实际情况和应用效果,为异步电机的磁链定向矢量控制系统研究提供了新的思路和方法。
四、研究目标和任务本课题的研究目标是设计一种高效、高精度、高稳定性的异步电机定子磁链定向矢量控制系统,并通过实验验证其性能优异。
矢量控制

矢量控制技术通过坐标变换,将三相系统等效变换为M-T两相系统,将交流电机定子电流矢量分解成两个直流分量(即磁通分量和转矩分量),从而达到分别控制交流电动机的磁通和转矩的目的,因而可获得与直流调速系统同样好的控制效果。
矢量控制系统采用双闭环控制系统,图1是其矢量控制系统框图。
采用矢量控制方式的通用变频器不仅可在调速范围上与直流电动机相匹配,而且可以控制异步电动机产生的转矩。由于矢量控制方式所依据的是准确的被控异步电动机的参数,有的通用变频器在使用时需要准确地输入异步电动机的参数,有的通用变频器需要使用速度传感器和编码器。鉴于电机参数有可能发生变化,会影响变频器对电机的控制性能,目前新型矢量控制通用变频器中已经具备异步电动机参数自动检测、自动辨识、自适应功能,带有这种功能的通用变频器在驱动异步电动机进行正常运转之前可以自动地对异步电动机的参数进行辨识,并根据辨识结果调整控制算法中的有关参数,从而对普通的异步电动机进行有效的矢量控制。
1 引言
交流电机矢量控制理论是德国学者K Hass和FBlaschke建立起来的,作为交流异步电机控制的一种方式,矢量控制技术已成为高性能变频调速系统的首选方案。
交流电机的矢量控制技术是基于交流电机的动态模型,通过建立交流电机的空间矢量图,采用磁场定向的方法将定子电流分解为与磁场方向一致的励磁分量和与磁场方向正交的转矩分量,并分别对磁通和力矩进行控制,而使异步电机可以像他励直流电机一样控制。随着计算机技术飞速发展,功能强大的数字信号处理器(DSP)的广泛应用使得矢量控制逐渐走向了实用化。
6 结论
由上述结果可得出以下结论:
(1)本文所设计的双DSP结构矢量控制系统中各子系统分工明确,能可靠完成各自功能,且设计合理。
矢量控制(FOC)基本原理

矢量控制(FOC)基本原理一、基本概念1.1模型等效原则交流电机三相对称的静止绕组 A 、B 、C ,通以三相平衡的正弦电流时,所产生的合成磁动势是旋转磁动势F ,它在空间呈正弦分布,以同步转速ω1(即电流的角频率)顺着 A-B-C 的相序旋转。
这样的物理模型如图1-1a 所示。
然而,旋转磁动势并不一定非要三相不可,单相除外,二相、三相、四相…… 等任意对称的多相绕组,通以平衡的多相电流,都能产生旋转磁动势,当然以两相最为简单。
图1图1-1b 中绘出了两相静止绕组α 和 β ,它们在空间互差90°,通以时间上互差90°的两相平衡交流电流,也产生旋转磁动势F 。
再看图1-1c 中的两个互相垂直的绕组M 和 T ,通以直流电流M i 和T i ,产生合成磁动势F ,如果让包含两个绕组在内的整个铁心以同步转速旋转,则磁动势F 自然也随之旋转起来,成为旋转磁动势。
把这个旋转磁动势的大小和转速也控制成与图 1-1a 一样,那么这三套绕组就等效了。
三相--两相变换(3S/2S 变换)在三相静止绕组A 、B 、C 和两相静止绕组α、β之间的变换,简称3S/2S 变换。
其电流关系为111221022A B C i i i i i αβ⎡⎤⎡⎤--⎢⎥⎡⎤⎢⎥⎢=⎢⎥⎢⎥⎢⎣⎦⎢⎥-⎣⎦⎢⎦⎣() 两相—两相旋转变换(2S/2R 变换) 同步旋转坐标系中(M 、T 坐标系中)轴向电流分量与α、β坐标系中轴向电流分量的转换关系为cos sin 2sin cos M T i i i i αβϕϕϕϕ⎡⎤⎡⎡⎤⎤=⎢⎥⎢⎢⎥⎥-⎦⎣⎦⎣⎣⎦ ()1.2矢量控制简介矢量控制是指“定子三相电流矢量控制”。
矢量控制理论最早为解决三相异步电机的调速问题而提出。
交流矢量的直流标量化可以使三相异步电机获得和直流电机一样优越的调速性能。
将交流矢量变换为两相直流标量的过程见图2。
图2图2的上图为静止坐标系下的定子三相交流矢量图2的中图为静止坐标系下的等效两相交流矢量图2的下图为旋转坐标系下的等效两相直流标量,T i 是转矩电流,M i 是励磁电流。
永磁同步电机及转子磁场定向矢量控制

12 伺服系统概述
船舶电力推进领域 推进电机是船舶综合电力系统的重要组成部分、永磁同步推进电 机具有体积小、重量轻、效率高、噪声低、易于实现集中遥控、可靠 性高、可维护性好等优点,是船舶推进电机的理想选择。
12 伺服系统概述
3. 永磁同步电机的数学模型
3.1 在静止坐标系下的数学模型
电机的数学模型中含有时变参数,给分析和计算带来困难。为了简 化永磁同步电机的数学模型,首先对电机做如下假设: 1)忽略铁心饱和; 2)忽略电机绕组漏感; 3)转子上没有阻尼绕组; 4)永磁材料的电导率为零; 5)不计涡流和磁滞损耗; 6) 定子相绕组的感应电动势波为正弦型的,定子绕组的电流在气 隙中只产生正弦分布的磁势,忽略磁场的高次谐波。
12 伺服系统概述
为了使得永磁同步电动机具有正弦波感应电动势波形,其转子磁钢形 状呈抛物线状,使其气隙中产生的磁通密度尽量呈正弦分布。定子电枢采 用短距分布式绕组,能最大限度地消除谐波磁动势。
图1-2 旋转磁动势波形图
12 伺服系统概述
2. 永磁同步电机的优势与应用
2.1 永磁同步电动机的优势
我国电动机保有量大,消耗电能大,设备老化,效率较低。永 磁同步电动机(PMSM)具有体积小、效率高、功率因数高、起动力矩 大、力能指标好、温升低等特点。
12 伺服系统概述
三相永磁同步电机在定子静止三相坐标系下的电压方程为:
式中: uA、uB、uC——定子相电压; r ——定子绕组每相电阻; iA、iB、iC——定子相电流。 由永磁同步电机的电磁关系可知,其磁链方程和电压方程是一组变系 数微分方程,微分方程的系数随着定转子的相对位置变化而变化,是时间 的函数。
12 伺服系统概述
5. PMSM的矢量控制
三种磁场定向矢量控制技术的比较

三种磁场定向矢量控制技术的比较磁场定向矢量控制技术是一种利用磁场控制机械运动的新技术,其应用范围广泛,包括磁悬浮列车、磁共振成像、磁力驱动机械装置等领域。
本文将介绍三种磁场定向矢量控制技术:PID算法控制、模糊控制和神经网络控制,并对其进行比较分析。
1. PID算法控制PID算法控制是磁场定向矢量控制技术中最常用的一种。
PID算法通过对磁场定向矢量的大小和方向进行控制,来实现机械运动的精确控制。
PID控制器由三个部分组成:比例部分、积分部分和微分部分。
比例部分控制机械的位置,积分部分控制机械位置的变化率,微分部分控制机械位置变化率的变化率。
PID算法控制具有响应速度快、控制精度高、易于实现等优点。
2. 模糊控制模糊控制是一种以模糊逻辑为基础的控制方法,其特点是通过定义一系列模糊规则来实现机械运动的控制。
模糊控制可以适应各种不确定因素,能够有效地处理机械系统中的误差和干扰,具有很好的鲁棒性。
同时,模糊控制能够处理复杂系统,并且不需要过多的数学模型,因此能够快速实现机械运动的控制。
3. 神经网络控制神经网络控制是一种利用神经网络方法,通过对输入信号进行加权和处理,得到输出信号,来实现机械运动的控制。
神经网络控制具有非线性、自适应、强鲁棒性的特点,能够处理复杂系统和多变量系统。
神经网络控制需要大量的训练数据和时间,在实际应用中需要对系统进行控制分析和建模。
4. 比较分析三种磁场定向矢量控制技术各有优劣,具体比较如下:1.控制精度方面:PID算法控制精度最高,模糊控制次之,神经网络控制较差。
2.响应速度方面:PID算法控制响应速度最快,神经网络控制次之,模糊控制最慢。
3.鲁棒性方面:模糊控制和神经网络控制具有良好的鲁棒性,PID控制较差。
4.实现难度方面:PID算法控制易于实现,模糊控制稍显复杂,神经网络控制非常复杂。
综合考虑,根据具体应用场景选择合适的磁场定向矢量控制技术是非常重要的。
在控制精度要求较高的场合,建议使用PID算法控制;在对控制精度要求相对较低,但需要处理不确定因素的场合,建议使用模糊控制;在对非线性系统进行控制,处理复杂系统的场合,建议使用神经网络控制。
磁场定向控制

利用一个ARM7处理器对无刷电机实施磁场定向控制电机驱动能效不论提高多少,都会节省大量的电能,这就是市场对先进的电机控制算法的兴趣日浓的部分原因。
三相无刷电机主要指是交流感应异步电机和永磁同步电机。
这些电机以能效高、可靠性高、维护成本低、产品成本低和静音工作而著称。
感应电机已在水泵或风扇等工业应用中得到广泛应用,并正在与永磁同步电机一起充斥家电、空调、汽车或伺服驱动器等市场。
推动三相无刷电机发展的主要原因有:电子元器件的价格降低,实现复杂的控制策略以克服本身较差的动态性能成为可能。
以异步电机为例。
简单的设计需要给定子施加三个120°相移的正弦波电压,这些绕组的排列方式能够产生一种旋转磁通量。
利用变压器效应,这个磁通量在转子笼内感应出一股电流,然后产生转子磁通量。
就是这两种磁通量相互作用产生电磁力矩,使电机旋转。
在转子上感应出电流的条件是,确保转子的转速与定子的磁通量频率不同;如果相同,转子只经历一个恒定的磁通量,不会有感应电流产生(楞次定律)。
通电频率和其产生的机械频率之间的微小差异是异步电机命名的原因。
一个三相交流电机实现转速可调操作的最简单方式是,实现一个所谓的电压/频率控制(或者叫做标量控制),其工作原理是在频率与电机通电电压之间保持恒比。
这种方法产生一个恒定的定子磁通量,然后在转子主轴上得到额定的电机力矩。
对于应用负载特性被大家了解的低成本驱动器,以及控制带宽要求不是很高的驱动器,如数量很少的HP泵和风扇、洗衣机等,这是一个很受欢迎的控制方法。
一个MIPS 不是很高并带有合理的外设接口的8位单片机如ST7MC,即可满足这种应用需求,同时编程也很简单。
这种方法无法在瞬间工作过程中保证最佳的电机特性(力矩、能效)。
而且为防止电机出现临时消磁现象,还必须限制驱动器反作用力的时间。
为了克服这些限制条件,考虑到电机的动态特性,市场上出现了其他的控制策略。
磁场定向控制(也称矢量控制)是应用最广泛的控制算法,目标应用包括带式传输机、大功率水泵、汽车废气排放、工厂自动化。
永磁同步电机及转子磁场定向矢量控制

电气工程
王俊鹏
12 伺服系统概述
永磁同步电机结构和工作原理 永磁同步电机的优势与应用 永磁同步电机的数学模型 永磁同步电机的控制方式 PMSM的转子磁场定向矢量控制
总结
12 伺服系统概述
1. 永磁同步电机的结构和工作原理
1.1 永磁同步电机(PermanentMagneticSynchronousMachine)的结构
12 伺服系统概述
船舶电力推进领域 推进电机是船舶综合电力系统的重要组成部分、永磁同步推进电 机具有体积小、重量轻、效率高、噪声低、易于实现集中遥控、可靠 性高、可维护性好等优点,是船舶推进电机的理想选择。
12 伺服系统概述
3. 永磁同步电机的数学模型
3.1 在静止坐标系下的数学模型
电机的数学模型中含有时变参数,给分析和计算带来困难。为了简 化永磁同步电机的数学模型,首先对电机做如下假设: 1)忽略铁心饱和; 2)忽略电机绕组漏感; 3)转子上没有阻尼绕组; 4)永磁材料的电导率为零; 5)不计涡流和磁滞损耗; 6) 定子相绕组的感应电动势波为正弦型的,定子绕组的电流在气 隙中只产生正弦分布的磁势,忽略磁场的高次谐波。
12 伺服系统概述
3.2 PMSM在 dq0 坐标系下的数学模型
二十世纪年代,由采用坐标变换将同步电机定子坐标系下的各个变量 等效变换为转子坐标系下的变量,消除了同步电机数学模型中的时变系数, 建立了著名的Park方程,从而为研究和分析永磁同步电机提供了理论基础。 转子磁场定向控制实际上是将 dq0 同步旋转坐标系放在转子上随转 子同步旋转。其d 轴与转子的磁场方向重合(定向),q 轴逆时针超前d 轴 90o电角度如图所示定子 ABC 坐标系与转子dq0坐标步电机相比交流异步电机优势: (1)效率高、更加省电。由于永磁同步电机的磁场是由永磁 体产生的,从而避免通过励磁电流来产生磁场而导致的励磁损耗。 永磁同步电机的外特性效率曲线相比异步电机,其在轻载时效 率值要高很多,这是永磁同步电机在节能方面,相比异步电机最 大的一个优势。 由于永磁同步电机功率因数高,这样相比异步电机其电机电流 更小,相应地电机的定子铜耗更小,效率也更高。 永磁电机参数,不受电机极数的影响,因此便于设计成多极电 机,这样对于传统需要通过减速箱来驱动负载电机,可以做成直 接用永磁同步电机驱动的直驱系统,从而省去了减速箱,提高了 传动效率。
定子磁场定向控制方法报告

异步电机定子磁场定向控制方法目前应用广泛的高动态性能的交流调速系统控制方法有矢量控制和直接转矩控制,这两种控制方法各有所长,但也存在着一些缺点。
矢量控制采用转子磁场定向的方法,实现定子电流的励磁分量与转矩分量的动态解耦,采用PI连续调节方式,实现转矩与转子磁场的控制。
但是其解耦性能取决于转子磁场的精确定向,由于转子磁链的观测或计算是在电机模型的基础上进行的,因而转子磁场的定向受到电机参数特别是易于变化的转子电阻的影响。
直接转矩控制是根据转矩及定子磁链的偏差,分别采用砰砰控制的方法,根据定子磁链所在的扇区,直接产生PWM驱动信号,系统结构简单,对转子参数不敏感,但砰砰控制决定了转矩脉动不可避免,虽然增加电压综合矢量个数可以降低转矩脉动,但不能消除,本报告中的定子磁场定向控制方法是在两种系统的基础上,取长补短的一种新方法。
异步电机定子磁场定向控制方法有两个特点:1、定子磁链用电压模型计算,采用连续的闭环控制,在补偿定子电阻压降的基础上直接控制定子磁链的变化率;2、转速控制采用与矢量控制相仿的三环结构,内环为定子电流转矩分量控制,实现了转矩电流的快速跟随,第二环是转矩闭环控制,用以抑制定子磁链对转矩的扰动,最外环为转速闭环。
这种控制方法克服了矢量控制对转子电阻的直接依赖性,同时采用连续的控制方法克服了砰砰控制带来的转矩脉动。
为了研究异步电机定子磁场定向控制方法,我们要建立异步电机按定子磁场定向的动态模型。
根据定子磁场定向的定义可知,在d-q坐标系中,规定d轴与定子磁链矢量ψ的方向重合,q轴与ψ的方向垂直。
因此,在d-q坐标系中,A相的电流、电压、磁链可以表示为:)sin cos (32)sin cos (32)sin cos (32s sq s sd A s sq s sd A s sq s sd A u u u i i i θψθψψθθθθ-=-=-= 将上式代入A 相电压方程:dtd i R u AA s A ψ+= 对于任意s θ都成立,因此可得d-q 坐标系中的定子电压方程:dtd dt d i R u dt d dt d i R u s sdsqsq s sq s sq sdsd s sd θψψθψψ++=-+= 同理可得d-q 坐标系中的转子电压方程:dt d dt d i R u dtd dt d i R u slrs rq rq r rq sl rq rd rd r rd θψψθψψ++=-+=综上可得同步旋转的d-q 坐标变换后的电压方程为:)()(r s rd rqrq r rq r s rq rdrd r rd ssd sqsq s sq s sq sdsd s sd dt d i R u dt d i R u dtd i R u dt d i R u ωωψψωωψψωψψωψψ-++=--+=++=-+=而磁链方程为:sqm rq r rq sd m rd r rd rq m sq s sq rd m sd s sd i L i L i L i L i L i L i L i L +=+=+=+=ψψψψ由上述磁链方程可得定转子磁链的关系:sq rmr s rq r m rsqm rq m sq s sq i L L L L L L L i L L i L 2-+=-⋅+=ψψψ··········(1) 同理可得:sd r mr s rd r m r sdm rd m sd s sd i L L L L L L L i L L i L 2-+=-⋅+=ψψψ··········(2) sd m s r m sd m r msds sd r sd m rd i L L L L L LL i L L i L -+=-⋅+=2ψψψ··········(3) sq ms r m sq m r msqs sq r sq m rq i L L L L L LL i L L i L -+=-⋅+=2ψψψ· (4)考虑鼠笼型异步电机0==rq rd u u ,则由转子电压方程可得:rd r rq r s rdi R dtd --=ψωωψ)( 又由第三个磁链方程可得:rsdm rd rd L i L i -=ψ代入上式转子电压方程可得:sd rmrrdrq r s r sdm rd r rq r s rd i T L T L i L R dt d +--=-⋅--=ψψωωψψωωψ)()( (5)同理,将第四个磁链方程代入第四个电压方程可得:sq rmrrqrq r s rsqm rq r rd r s rq i T L T L i L R dtd +---=-⋅---=ψψωωψψωωψ)()( (6)将磁链方程代入电压方程可得:)(0)(0r s rd sqm rq r rq r r s rq sd m rd r rd r ssd rqm sq s sq s sq s sq rd m sd ssd s sd dt di L dt di L i R dt diL dt di L i R dtdi L dt di L i R u dt diL dt di L i R u ωωψωωψωψωψ-+++=--++=+++=-++= (7)将(7)中第三个式子的dtdi rd代入(7)中第一个式子,并将代入式(5)和(1)可得:s sq sd m sd r m r rd r s rq r m sd s sd s sd dt di L i T L T L L dt di L i R u ωψψωωψ-⎥⎦⎤⎢⎣⎡++--++=)(移项整理可得:ssdsq s sd r s m r r s rq r r s m rd r r s m sd L u i i L L L R L R L L L T L L L dt di σωσψωσψσ+++-+=222·······(8) 其中sr m L L L21-=σ为漏磁系数,r r r R L T =为电磁时间常数。
矢量控制

转子磁链定向矢量控制策略转子磁场定向的矢量控制方式目前应用较普遍。
将转子磁链的方向定义为m 轴的方向,垂直于m 轴的方向定义为t 轴方向。
这时,将以转子磁场进行定向时的m 轴也称为d 轴,t 轴称为q 轴。
在异步电机运行过程中假如保持励磁电流恒定,则输出的转矩仅与转矩电流成正比。
它的优点是解耦了磁链与转矩,使得控制上较为接近于直流电机的控制,实现了人们最初的设想。
矢量控制的磁链取得方法有间接或直接,也称间接磁场定向和直接磁场定向,它们的区别在于:①间接磁场定向间接磁场定向的矢量控制是根据异步电机的数学模型,及各个坐标系下的电机方程,通过计算得到其固有关系式,引入电机参数进行计算,估计磁链的幅值与相角,其缺点是受电机参数的准确性影响较大,且在电机运行过程中,电机参数发生变化需要进行相应的调整,其优点是不需要受到特殊硬件检测设备的制约,节约成本,提高应用性。
②直接磁场定向直接磁场定向的矢量控制是运用直接方式,获取磁链的位置、幅值,需安装磁链传感器,而在一些场合,安装磁链传感器很难做到。
随着DSP 不断更新升级,使在较短时间内完成运算估算磁链已越来越可行,因此直接磁链观测器越来越多地受到人们重视。
其缺点是对仪器的精度要求很高,优点是基本不受转子时间常数影响。
如果观测的精度足够高,那么进行矢量控制的准确度就会极为简便。
1.三相异步电动机动态数学模型在以转子磁场定向的同步旋转坐标系dq 轴下,异步电动机的动态数学模型为 (1) 电压方程为sd sd s s e sm e m sq sq e s s s e m m rd rd m s m r r s rq rq s m m s r r r u i R L p L L p L u i L R L p L L p u i L p L R L p L u i L L p L R ωωωωωωωω+--⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥+⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥-+-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦(1-1) 式中,u sd 、u sq 、u rd 、u rq 、i sd 、i sq 、i rd 、i rq 分别为定子电压、转子电压、定子电流、转子电流、在dq 轴上的分量;ωs 为转差角速度,即ωs =ωe -ωr ;ωe 为同步角速度;ωr 为转子角速度。
矢量变换控制变频调速系统

2.异步电机产生转矩的原理
IT1
I1(F1) m
Im (Fm )
2s
IM1
2
因此,如果能够检测出每个瞬间2在空间的位置,I即2 它(F对2 )定子绕
组的相位角,就可以通过坐标的旋转变换将其变换到静止坐标,
控制iM1
和i(T1 通过iT1
控制I
),象控制直流电机一样来控制异步电
2
动机的转速和转矩。
这就是交流电动机模拟成直流电动机的控制原理。这种以2 为基准分解,变换矢量来控制交流异步电动机转速与转矩的控制
然后可以列出由电压方程组,磁链方程组,转矩方程组和运动方 程组组成的异步电动机的数学模型.
2.模型简化
上面讲解的是矢量控制的基本概念以及矢量变换规律表明:三相异步电动机 可以等效地变换成类似直流电动机的模式,这样就可以模仿直流电动机去进 行控制.
m
I
2
(F2 )
一组通过电流IT1
与产生转矩的转子电流I
2相平衡,而I
,I M1
T1
和
2都以同步速度1在空间旋转。而直流电动机的电流及磁通在
空间是静止的。
如果站在
2的轴线上跟
2旋转,再观察I
M
,I 1
T1
等量,
则这些量就如同直流电动机一样是相对静止的,其效果和
通以直流电流iM
,i 1
T1
所产生的结果是一样的。
图6-26(c)
三.矢量变换控制原理分析
1.直流电机产生转矩的原理
mm等效励磁绕组,产生主磁通,相应磁动势Fm与mm绕组平面垂直;aa等效
电枢绕组,产生电枢磁通,相应磁动势Fa与Fm相差90度,并且在空间保持不变。
通俗地解释转子磁链和矢量控制

6通过霍尔元件检测三相定子电流以转子磁场与a相轴线之间的偏差角度作为算子相当于观察者与转子磁场同步旋转通过坐标变换分解出定子旋转磁场中与转子磁极对齐的分量直轴电流id产生转矩的分量交轴电流iq
通俗地解释转子磁链和矢量控制
关于矢量控制,通俗理解是: 1. 先把电机想像成2块飞速旋转磁铁,定子磁铁和转子磁铁。进一步可以引申为定子磁场和转子磁场。 2. 电机的电磁转矩与定子磁场强度、转子磁场强度、2块磁铁之间的夹角的正弦成正比。关于这一点不难理解,两块磁铁对齐的时候(0 度,sin0=0;),不存在电磁转矩;两块磁铁相差90度的时候(sin90=1;),电磁转矩达到顶峰; 3. 接下来控制的目标就是: 1)稳定其中的一个旋转磁场的强度(恒定磁场); 2)控制磁铁之间角度为90度(磁场定向FOC); 3)控制另一个磁场(受控磁场)的强度以达到控制电磁转矩大小(力矩控制)。 4. 关于坐标变换的物理意义(以同步电机为例): 1)在电机不失步的情况下,可以认为两个磁极之间相对静止,最多在夹角0~90度之间移动。 2)既然交流电产生的是一个旋转磁场,那么 自然可以把它想像成一个直流电产生的恒磁场,只不过这个恒磁场处于旋转当中。 3)如果恒磁场对应的直流电流产生的磁场强度,与对应交流电产生的磁场强度相等,就可以认为两者等同。 4)坐标变换基于以上认知,首先认为观察者站在恒定定磁场上并随之运转,观察被控磁场的直流电线圈电流及两个磁场之间的夹角。 5)实际的坐标变化计算出的结果有两个,直轴电流Id和交轴电流Iq。通过Id和Iq可以算出两者的矢量和(总电流),及两个磁场之间的夹 角。 6)直轴电流Id是不出力的,交轴电流Iq是产生电磁转矩关键因素。 5. 对于交流同步隐极电动机: 1)其转子磁场是恒定的。 2)转子的当前磁极位置用旋转编码器实时检测。 3)定子磁极(旋转磁场)的位置从A相轴线为起点,由变频器所发的正弦波来决定。 4)实际上先有定子磁场的旋转,然后才有转子磁场试图与之对齐而产生的跟随。 5)计算出转子磁场与A相轴线之间的偏差角度。 6)通过霍尔元件检测三相定子电流,以转子磁场与A相轴线之间的偏差角度作为算子(相当于观察者与转子磁场同步旋转),通过坐标变 换分解出定子旋转磁场中与转子磁极对齐的分量(直轴电流Id),产生转矩的分量(交轴电流Iq)。 7)定子电流所产生旋转磁场与观察者基本同步,最多在夹角0~90度之间移动。移动量是多少,会体现在直轴电流Id、交轴电流Iq的数值对 比上。 8)驱动器通过前面的速度环的输出产生电流环的给定,通过第6)条引入电流环的反馈Iq,通过PI控制产生Iq输出。 9)设定Id=0。这一点不难理解,使两个磁极对齐的电流我们是不需要的。通过这一点,我们实现了磁场定向FOC(控制磁铁之间角度为90 度)。 10)计算出了Iq, Id=0。引入偏差角度算子通过坐标反变换变换产生了三相电流的输出。 11) 当Iq>0, 定子旋转磁场对转子磁场的超前90 度,电磁转矩依靠两个磁场之间异性相吸的原理来产生,这时候电磁转矩起到加速的作用。 12)当Iq<0, 定子旋转磁场对转子磁场的仍然超前90度,但是定子磁场的N、S极调换了一下,电磁转矩依靠两个磁场之间同性相排斥的原 理来产生,这时候电磁转矩起到减速制动的作用。 13)从本质上讲,我们是依靠控制定子旋转磁场对转子磁场的超前角度及该磁场的强度来实现矢量控制的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章 定子磁场定向矢量控制
5.1 转子电流控制
在双馈电机定子磁场定向的矢量控制策略中,通常将同步旋转坐标系的d 轴与双馈电机定子磁场相重合,逆时针旋转90度的方向作为q 轴方向,即在同步旋转dq 坐标系中定子磁链可表述为:
⎩⎨⎧ψ=ψ=ψs
sd sq 0 (5-1) 其中,s ψ为定子磁链的幅值。
由此,在定子磁链定向的情况下,重写双馈电机在同步旋转坐标系中的定转子电压方程、磁链方程:
⎪⎪⎪⎪⎩
⎪⎪⎪⎪⎨⎧++=+-=+-=+-=qr dr s qr r qr dr qr s dr r dr ds qs s qs ds ds s ds dt d i r u dt d i r u i r u dt d i r u ψψωψψωψωψ1 (5-2) ⎪⎪⎩
⎪⎪⎨⎧+-=ψ+-=ψ+-=+-=ψqr r qs m qr dr r ds m dr
qr m qs s dr m ds s s i L i L i L i L i L i L i L i L 0 (5-3) 求解后,得: qr s m qs i L L i =、()ms dr s m ds i i L L i -= (5-4)
其中:m
s ms L i ψ=,称为通用励磁电流 计算转子磁链如下: ⎪⎪⎩⎪⎪⎨⎧⎪⎪⎭⎫ ⎝⎛+-=ψ⎪⎪⎭⎫ ⎝⎛+-+=ψqr r s m qr dr r s m ms s m dr i L L L i L L L i L L 222 (5-5) 设⎪⎪⎭
⎫ ⎝⎛-=s m r s L L L L 2σ为漏磁系数,则5-5式又可表示为: ⎪⎩⎪⎨⎧=ψ+=ψqr r qr dr r ms s m dr i L i L i L L σσ2 (5-6) 利用式5-2计算转子电压如下:
⎪⎪⎩⎪⎪⎨⎧+⎪⎪⎭⎫ ⎝⎛++=+-=qr r dr r ms s m s qr r qr dr r qr r s dr r dr i dt d L i L i L L i r u i dt d L i L i r u σσωσσω2 (5-7)
式5-7便是采用电压源变流器对双馈电机转子电流控制的理论依据,式中ms s
m s i L L 2
ω为双馈电机反电势所引起的扰动项,dr r s i L σω与qr r s i L σω-为旋转电势所引起的交叉耦合扰动项,扰动项和耦合项给调节器的设计造成一定的困难。
为此可采用前馈补偿控制策略,把反电动势引起的扰动项和旋转电动势引起的交叉耦合项等扰动项前馈解耦后,双馈电机转子d 轴电流直接由转子侧d 轴端电压dr u 控制,转子q 轴电流直接由转子侧q 轴端电压qr u 控制。
此时,当双馈电机转子电流采用PI 调节器,并以PI 调节器的输出来控制式5-7中的转子电流动态项时,则转子电压dr u 和qr u 的控制方程如下:
()()
⎪⎪⎩
⎪⎪⎨⎧⎪⎪⎭⎫ ⎝⎛++-⎪⎭⎫ ⎝⎛+=--⎪⎭⎫ ⎝⎛+=dr r ms s m s qr qr irI irP qr qr r s dr dr irI irP dr i L i L L i i s K K u i L i i s K K u σωσω2** (5-8) 其中,irP K 、irI K 为转子电流内环比例系数和积分系数,*dr i 、*qr i 分别为转子电流d 轴、q 轴分量的指令值。
5.2转子电流指令
根据电磁转矩方程4-6,以及式5-4、式5-6可得在定子磁场定向同步旋转坐标系下双馈电机电磁转矩表达式为:
()qr ms s
m p qs ms m p qs ds p ds qs qs ds p e i i L L n i i L n i n i i n T 2==ψ=ψ-ψ= (5-9) 上式表明,双馈电机在定子磁场不变,即ms i 恒定的情况下,双馈电机的电磁转矩的大小与双馈电机转子电流的q 轴分量成正比。
根据式4-7、式5-4,并在忽略定子电阻的情况下,可得:
⎪⎩⎪⎨⎧-=+=qs ds ds qs qs qs ds ds i u i u Q i u i u P 11 =〉()⎪⎪⎩
⎪⎪⎨⎧-==ms dr s m qs qr s m qs i i L L u Q i L L u P 11 (5-10) 上式表明,在利用转子电流q 轴分量qr i 控制双馈电机电磁转矩的同时,也控制了其定子侧有功
功率,而定子侧无功功率的调节可通过转子电流的d 轴分量dr i 进行控制,而相应的dr i 的指令值*dr i 取
决于具体的控制要求,如无功功率控制、定子电压控制、功率因数控制等。
当双馈电机采用速度全控型控制策略时,双馈电机控制的外环为速度环,而转子q 轴电流的指令值由速度环决定。
由双馈电机的运动方程可知,若速度外环采用PI 调节器,则双馈电机的电磁转矩的控制方程可表述为:
))((**n n s
K K T nI nP e -+= (5-11(a)) 其中,nP K 、nI K 分别为速度外环的比例系数和积分系数;*n 为双馈电机的转速指令值。
或将其表述为电流指令的形式,即:
))((*2*n n s K K i L n L i nI nP ms m p s qr -+= (5-11(b))
5.3 定子磁链检测
由于双馈电机的特殊结构,使其定子电气量和转子电气量均可以被直接检测,所以双馈电机定子磁链有几种不同的检测方法。
其中较为典型的有定子电压模型与定转子电流模型两种。
5.3.1 定子电压模型
对于定子电压模型法,即将检测到的定子电压、定子电流经三相静止到两相静止的Clark 变换,再运用双馈电机两相静止坐标系下定子电压方程,即可求出两相静止αβ坐标系中定子磁链的α分量和β分量,如式5-12所示
⎪⎩⎪⎨⎧+=ψ+=ψ⎰⎰dt i r u dt i r u s s s s sa s sa s )()(β
ββα (5-12) 在实际控制中,上式中的积分运算通常采用0.5Hz 到1Hz 的带通滤波器获得,以克服其直流偏置的影响。
5.3.2 定转子电流模型
对于定转子电流模型,即将检测出的定子电流、转子电流经三相静止到两相静止的Clark 变换,再运用双馈电机的磁链方程求的两相静止αβ坐标系中定子磁链的α分量和β分量,如式5-13所示
⎩⎨⎧+-=ψ+-=ψβββ
αααr m s s s r m s s s i L i L i L i L (5-13) 于是,有
22βαs s s ψ+ψ=ψ、⎪⎪⎭
⎫ ⎝⎛ψψ=-βαθs s s 1tan (5-14) 相对于定子电压模型而言,定转子电流模型法可以避免积分或准积分运算,但定转子电流模型也有其自身的缺陷;一方面观测的准确性受双馈电机参数的影响,而双馈电机的参数在运行过程中因磁化曲线的非线性(如磁饱和作用)使得这些参数较易发生改变,从而影响观测精度;另一方面,由于不能直接与电网同步,不利于软并网策略的实施。
因此定子磁场的观测通常可以采用准积分电压模型进行观测,其准积分模型的表达式为:
2
223)(ππ++=s s s s G bp (5-15) 上式所表达的准积分环节与纯积分环节的特性相比,如图5-1所示:
图5-1 准积分环节与纯积分环节性能对比(a:频域对比;b:时域对比)
由图5-1不难看出,准积分环节对高频交流部分具有与纯积分环节相同的特性,而对于低频部分,尤其是直流环节,准积分滤波器具有滤除直流偏置的作用。
图5-1(b)同时给出了纯积分环节和准积分环节对一个初相为0的正弦信号的积分作用,由该图不难看出纯积分环节含有较大的直流分量,而准积分环节在稳态后没有明显的直流偏置。
5.4 控制结构图
图5-2 定子磁链矢量定向控制结构图。
