个体遗传评定优秀课件
合集下载
第五章 个体遗传评定-2010课件

遗传进展是如何获得?▬生产水平的长期、不断提高主要依赖于遗传进展▬遗传进展的重要手段是选择▬选择优秀种畜▬获得更多优秀后代、获得遗传进展如何选择优秀种畜?第5章个体遗传评定Genetic Evaluation留哪些个体?个体遗传评定的意义Gt =Δ遗传评定方法的发展▬通过表型观察▬采用统计学方法数学模型;计算机技术发展▬联合育种:国内国际▬分子标记辅助育种:遗传标记;QTL/QTN ▬基因组选择(genomic selection)个体遗传评定的意义▬遗传评定是畜禽育种工作的中心任务▬遗传价值越高的个体种用价值越高▬遗传评定(genetic evaluation):评估畜禽传价值的高低,以此作为衡量指标来选择优秀的个体作为种畜遗传评定的实质内容即育种值估计;按照估计的个体育种值选择排名在前的优秀个体个体育种值概念(breeding value)个体育种值(breeding value )(不能被观测,只能根据表型信息(表型值表型值)经统计分析,估计而得数量性状(目的:预测个体遗传价值,选择遗传价值高的个体作为亲本,使其后代生产性能获得较大改进衡量种用价值高低的指标即个体作为亲本的种用价值(对后代的遗传贡献)个体育种值(breeding value)(加性遗传效应可以由亲代传递给后代的遗传组分,即为个体的育种值▬个体加性效应的高低反映了它在育种上的贡献大小,因此称为育种值举例(estimated transmission ability,ETA)利用个体各种来源的*hr rA P=统计方法估计加性效应准确性r。
畜牧业课件Chapter06个体遗传评定

第三节 同胞测定
1.概念:同胞分全同胞和半同胞。同胞测定,就 是根据其同胞的成绩,来对一个个体本身作出 种用价值的评定。
2.全同胞:同父同母的子女之间为全同胞。
半同胞:同父异母或异父同母的子女之间为半 同胞。
“全同胞-半同胞”混合家系:“一公畜家系”
3.同胞测定的应用:限性性状,活体难以度量的 性状(胴体性状)
选择
10月 64月龄
9月 27月龄
女儿
9月
分娩 54月龄
18月 45 月 龄
女儿配种
2)耗资大 3)留种率增大
留种率=留种数/供选个体数100%,故使留种率增大。 3. 应用:主要用于公畜。 (1)公畜本身不能度量的性状; (2)限性性状; (3)遗传力低的性状。
二、后裔测定应注意事项: 1. 后代的品质是由父母双方共同决定的,尽可能减少母畜
2. 系谱的形式:竖式系谱和横式系谱; 结构式系谱和畜群 系谱
M MM
种畜的畜号与名字
F
MF
FM
FF
MMM MMF MFM MFF FMM FMF FFM FFF 竖式系谱
被鉴定种畜
FF F
FM
MF M
MM 横式系谱
FFF FFM FMF FMM
MFF MFM MMF MMM
3. 系谱测定的运用 系谱测定:通过查阅和分析各代祖先的生产性能、发育表 现以及其他材料,来估计该种畜的近似种用价值,同时了 解该种畜祖先的情况。 方法:进行同代比较,首先注意父母代,然后祖父母代。 单独用系谱选择,对改良畜群的作用不大,应结合其他一 些方法来使用。
Yijkl hi g j s jk eijkl
式中,Yijkl=第i场第j组公牛第k头公牛的第l头女儿的观察值; n-1
遗传算法的实例ppt课件.ppt

上述操作反复执行,个体逐渐优化
病 原 体 侵 入 机体, 消弱机 体防御 机能, 破坏机 体内环 境的相 对稳定 性,且 在一定 部位生 长繁殖 ,引起 不同程 度的病 理生理 过程
遗传算法的手工模拟计算示例
为更好地理解遗传算法的运算过程,下面用手工计算来简单地模拟遗传算法的各 个主要执行步骤。
例:求下述二元函数的最大值:
个体
A
B
C
D
病 原 体 侵 入 机体, 消弱机 体防御 机能, 破坏机 体内环 境的相 对稳定 性,且 在一定 部位生 长繁殖 ,引起 不同程 度的病 理生理 过程
步骤三:交叉
• 选中的优势个体进行交叉 ----- 由父个体生成子个体
相同的两个父个体生成相同的两个子个体
病 原 体 侵 入 机体, 消弱机 体防御 机能, 破坏机 体内环 境的相 对稳定 性,且 在一定 部位生 长繁殖 ,引起 不同程 度的病 理生理 过程
• 程序结束时,最优个体即为所求解 • 程序结束的判定
根据循环次数 根据最大适应度 根据种群中相同个体数与总个体数的比值
病 原 体 侵 入 机体, 消弱机 体防御 机能, 破坏机 体内环 境的相 对稳定 性,且 在一定 部位生 长繁殖 ,引起 不同程 度的病 理生理 过程
遗传算法各步骤的评价
• 选择 --- 优胜劣汰
011101 111001 101011 111001
配对情况 交叉点位置
1-2
1-2:2
3-4
3-4:4
交叉结果
011001 111101 101001 111011
变异点 变异结果
4 011101 5 111111 2 111001 6 111010
子代群体p(1) x1 x2
病 原 体 侵 入 机体, 消弱机 体防御 机能, 破坏机 体内环 境的相 对稳定 性,且 在一定 部位生 长繁殖 ,引起 不同程 度的病 理生理 过程
遗传算法的手工模拟计算示例
为更好地理解遗传算法的运算过程,下面用手工计算来简单地模拟遗传算法的各 个主要执行步骤。
例:求下述二元函数的最大值:
个体
A
B
C
D
病 原 体 侵 入 机体, 消弱机 体防御 机能, 破坏机 体内环 境的相 对稳定 性,且 在一定 部位生 长繁殖 ,引起 不同程 度的病 理生理 过程
步骤三:交叉
• 选中的优势个体进行交叉 ----- 由父个体生成子个体
相同的两个父个体生成相同的两个子个体
病 原 体 侵 入 机体, 消弱机 体防御 机能, 破坏机 体内环 境的相 对稳定 性,且 在一定 部位生 长繁殖 ,引起 不同程 度的病 理生理 过程
• 程序结束时,最优个体即为所求解 • 程序结束的判定
根据循环次数 根据最大适应度 根据种群中相同个体数与总个体数的比值
病 原 体 侵 入 机体, 消弱机 体防御 机能, 破坏机 体内环 境的相 对稳定 性,且 在一定 部位生 长繁殖 ,引起 不同程 度的病 理生理 过程
遗传算法各步骤的评价
• 选择 --- 优胜劣汰
011101 111001 101011 111001
配对情况 交叉点位置
1-2
1-2:2
3-4
3-4:4
交叉结果
011001 111101 101001 111011
变异点 变异结果
4 011101 5 111111 2 111001 6 111010
子代群体p(1) x1 x2
遗传的基本规律PPT课件精选全文完整版
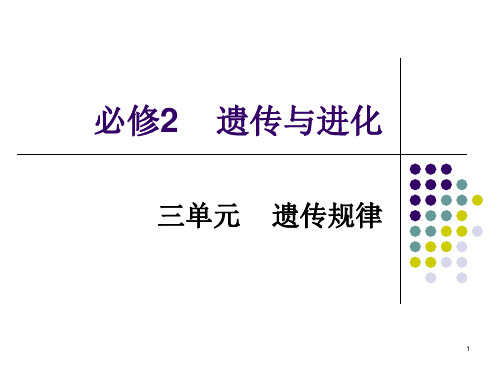
则双亲至少有一方为显性纯合体, 即AA×aa(AA、Aa ) → 全部A_
若后代只有隐性性状, 则双亲一定是隐性纯合体,即aa×aa → 全部aa
17
方法三:根据性状遗传规律解题(群体中)
相同性状个体杂交,后代出现性状分离 则亲本中有杂合子,亲本性状为显性,子代新出现性 状为隐性,即有Aa×Aa→3A_ :1aa
24
性别决定
1.定义:雌雄异体的生物决定性别的方式。 常染色体: 与性别决定无关。
2.染色体 性染色体: 决定性别。
3.方式
XY型: ♀ XX ♂ XY
例:人: 44+XX; 44+XY (体细胞中染色体组成) 果蝇:6+XX; 6+XY
普遍存在:人、哺乳、昆虫、雌雄异株的植物……
ZW型: ♀ ZW ♂ ZZ 鸟类、蛾蝶类 25
20
P
YY
yy
RR
╳
rr
黄色 圆粒
绿色 皱粒
对
自 配子
由
组
合
F1
减数 分裂 YR
受精
Yy Rr 黄色 圆粒
减数 分裂 yr
现
减数 分裂
象 的
F 1 配子
YR yR
Yr
yr
解
YR YY
Yy
YY Yy
RR RR
Rr Rr
释
yR
Yy
yy
Yy yy
F2
RR RR
Rr Rr
YY
Yy
YY Yy
Yr
Rr
Rr
rr
②配子形成时,成双的基因分开, 分别进入不同的配子。
③当雌雄配子结合完成受精后,基 因又恢复成对。显性基因(D)对隐 性基因(d)有显性作用,所以F1表 现显性性状。
若后代只有隐性性状, 则双亲一定是隐性纯合体,即aa×aa → 全部aa
17
方法三:根据性状遗传规律解题(群体中)
相同性状个体杂交,后代出现性状分离 则亲本中有杂合子,亲本性状为显性,子代新出现性 状为隐性,即有Aa×Aa→3A_ :1aa
24
性别决定
1.定义:雌雄异体的生物决定性别的方式。 常染色体: 与性别决定无关。
2.染色体 性染色体: 决定性别。
3.方式
XY型: ♀ XX ♂ XY
例:人: 44+XX; 44+XY (体细胞中染色体组成) 果蝇:6+XX; 6+XY
普遍存在:人、哺乳、昆虫、雌雄异株的植物……
ZW型: ♀ ZW ♂ ZZ 鸟类、蛾蝶类 25
20
P
YY
yy
RR
╳
rr
黄色 圆粒
绿色 皱粒
对
自 配子
由
组
合
F1
减数 分裂 YR
受精
Yy Rr 黄色 圆粒
减数 分裂 yr
现
减数 分裂
象 的
F 1 配子
YR yR
Yr
yr
解
YR YY
Yy
YY Yy
RR RR
Rr Rr
释
yR
Yy
yy
Yy yy
F2
RR RR
Rr Rr
YY
Yy
YY Yy
Yr
Rr
Rr
rr
②配子形成时,成双的基因分开, 分别进入不同的配子。
③当雌雄配子结合完成受精后,基 因又恢复成对。显性基因(D)对隐 性基因(d)有显性作用,所以F1表 现显性性状。
《遗传与个体发育》PPT课件

和生殖核的分化,不能进行第二次孢子有丝分裂 不
能发育为成熟的花粉粒。
10
第一节 (细胞核与)细胞质在遗传中的作用 P254
卵细胞的发育也是如此,远离珠孔一极的细胞质较多, 靠近珠孔一极的细胞质较少。
大孢母细胞经过减数分裂形成的四个大孢子中 远离 珠孔的一个子细胞能继续分裂和发育为胚囊,其余3个最 终退化 说明细胞质的不同部位对卵细胞的分化会产生不 同的影响。
其中细胞质不等分裂起着重要作用;细胞质的等分裂 细胞的分化。
海胆受精卵和植物小孢子分裂 后的分化可以说明这一点。
19
第一节 (细胞核与)细胞质在遗传中的作用 P254
例如,叶绿体DuBp羧化酶的8个小亚基和8个大 亚基,虽然分别由核基因和叶绿体基因编码合成,但 叶绿体的形成却是在核基因的控制之下的。
这个试验结果,肯定了核在伞藻个体发育中的主导作用。
17
第一节 (细胞核与)细胞质在遗传中的作用 P254
三、细胞核和细胞质在个体发育中的相互依存: 在个体发育过程中,细胞核和细胞质相互依存、不可分
割,细胞核起主导作用。 细胞核内的“遗传信息” 个体发育方向和模式 为蛋
白质(包括酶)合成提供模板(mRNA) 各种RNA 控制 细胞代谢方式和分化程序。
①海胆受精卵第一、二次分裂,顺着对称轴方向进行。 ②如果将四个卵裂细胞分开 每一个卵裂细胞都能发育成
小幼虫 说明各个卵裂细胞中细胞质是完全相同的。 ③第三次卵裂方向与对称轴垂直 分裂的8个卵裂细胞分
开后,就不能发育成小幼虫。
7
第一节 (细胞核与)细胞质在遗传中的作用 P254
海胆切割实验
植物极
动物极
20
第一节 (细胞核与)细胞质在遗传中的作用 P254
06个体遗传评定

ˆ (P P)h2 P AX HS HS
根据半同胞兄妹信息计算半同胞加权遗传力:
2 hHS
0.25nh2 0.25 116 0.2 0.8593 2 1 (n 1)0.25h 1 (116 1)0.25 0.2
P rAA rAP bAP ˆ A
rA
*
nh2 1 (n 1)rp
(6 5)
证明: 由公式(2-14)
2 P*
1 (n 1)rp n
2 P
n :个体本身度量次数或同类亲属个体数 2 P :性状的表形方差 rp :多个表型值之间的相关(同一个体多次度量时为重复 率)且有如下关系:
表6-1 4头种公羊及其有关亲属的剪毛量(Kg)记录,试计算各个公羊的育种值。 半同胞兄妹 公羊号 本身 父亲 母亲 祖父 祖母 外祖父 外祖母 N 116 116 64 75 均值 5.73 5.73 5.32 5.61 半同胞子女 N 15 25 17 15 均值 6.08 5.75 5.42 5.54
rp rA* h2
用通经系数法证明该式
由通经分析的原理可知
rp rA* hh rA* h2
rA* :为同类个体间的亲缘系数;
* * 2 (∵ Cov( A, P ) Cov( A, A ) rA A
)
将公式(2-14)带入 公式(6-4)得:
bAP*
Cov( A, P* )
4、综合育种值(total breeding value):
对多性状选择时,综合考虑各个性状的遗传特征,各性状 间的遗传相关和经济重要性,制定一个综合选择指数,称该选 择指数为综合育种值(total breeding value)。
《遗传13个体发育》课件

基因的表达与调控
01
基因表达
基因表达是指基因经过转录和翻译过程合成蛋白质的过程,是生物体实
现其生命活动所必需的。
02
基因调控
基因表达受到多种因素的调控,包括DNA甲基化、组蛋白修饰、非编
码RNA等,这些调控方式可以影响基因的表达水平。
03
表观遗传学
表观遗传学研究基因型未发生变化的情况下,基因的表达却发生了可遗
持。
谢谢聆听
现新的基因和基因变异。
基因表达分析
利用分子生物学技术,检测生物 体在不同生理或病理状态下基因 的表达水平,以了解基因的功能
和调控机制。
基因组注释
对基因组数据进行注释,包括基 因预测、转录本预测、功能注释 等,以揭示基因组的生物学意义
。
蛋白质组学的研究方法
蛋白质分离与鉴定
利用色谱、质谱等技术分离和鉴定生物体内的蛋白质,了解蛋白 质的组成和结构。
传的改变,如DNA甲基化、组蛋白乙酰化等。这些变化可导致基因表
达的差异,进而影响生物体的性状。
03 个体发育的过程
胚胎发育的过程
受精卵形成
受精卵由精子和卵子结 合形成,标志着新生命 的开始。
卵裂与囊胚形成
受精卵经过多次分裂形 成卵裂球,最终形成囊 胚。
胚胎植入
囊胚通过植入过程进入 子宫内膜,与母体建立 营养联系。
蛋白质相互作用研究
通过酵母双杂交、免疫共沉淀等技术,研究蛋白质之间的相互作 用,揭示蛋白质的功能和调控机制。
蛋白质修饰研究
研究蛋白质的磷酸化、乙酰化、糖基化等修饰,了解蛋白质的活 化和调控方式。
生物信息学的研究方法
1 2 3
数据库建设与维护
建立和维护生物信息学数据库,包括基因组数据 库、蛋白质数据库等,提供数据存储、检索和分 析服务。
第五章 个体遗传评定-2010课件

牛场
南口2队 南口3队 中以示范(原名:德任务) 渠头 半截河 三垡 朝阳北 朝阳南 草厂 小务
总计:21个场
举例:2头种公羊及其亲属的剪毛量(kg)记录
半同胞兄妹 半同胞子女 n 9-781 8.2 13.6 5.6 10.4 7.6 10.7 4.3 9-752 7.4 14.5 7.3 6.0 6.8 8.7 4.6 均值 n 15 15 均值 6.08 5.54
ˆ A = h 2 ( P * − P ) = 0.2 × (8.2 − 5.0) = 0.64(kg )
rAA = rAP = rA ˆ nh 2 = rA h = h = 0.2 = 0.447 1 + (n − 1)rP
9-752号公羊: ˆ A = h 2 ( P * − P ) = 0.2 × (7.4 − 5.0) = 0.48( kg )
rAA = rAP = h = 0.2 = 0.447 ˆ
2、根据半同胞兄妹记录 9-781号公羊:
bAP 0.25 ×116 × 0.2 rA nh 2 rA nh 2 = 0.8593 = = = 2 1 + (n − 1)rP 1 + (n − 1)r( HS ) h 1 + (116 − 1) × 0.25 × 0.2
ˆ A = bAP ( P * − P ) = 0.8824 × (6.08 − 5.0) = 0.9530( kg )
rAA = rA ˆ nh 2 15 × 0.2 = 0.5 = 0.664 2 1 + (n − 1)r( HS ) h 1 + (15 − 1) × 0.25 × 0.2
注意分子与分母的亲缘相关系数取值不同
配;遗传缺陷
课件:第十章 遗传与个体发育

• 异固缩、巴氏小体 • 在哺乳动物雌性个体的两条X染色体中,有
一条X在个体发育早期(受精卵细胞增殖到 5000-6000细胞,植入子宫壁时)异染色质化, 这条X上的基因随之处于失活状态,即所谓 莱昂化(lyonization) • 随机性、恒定性
• 哺乳动物的雌性在X连锁的基因上是嵌合体。
证据一
裂缘伞藻(A. crenulate),子实体边缘裂 成分瓣形。
• 原因:控制子实体形态的物质是mRNA →它在 核内形成后迅速向藻体上部移动→编码决定子 实体形态的特殊蛋白质合成。
• 该试验肯定了核在伞藻个体发育中的主导作用。
本章重点
• 果蝇胚胎发育中各类基因的作用 • X染色体剂量补偿效应的机制
• 裂隙基因的表达受到母体效应基因的严格调控。 两者协同作用可以将胚胎分成独立的区域,为 下一阶段的发育提供位置信息。
四、成对规则基因(Pair-rule gene)
• 裂隙基因的蛋白质产物进一步调控成对规则 基因在间隔体节中转录,使得裂隙基因规划 的宽阔的体节范围被进一步细分成垂直于头 尾轴的7个带区
五、细胞分化(cell differentiation)
在细胞分化时期,在图式形成阶段已经特化成各个 胚层的细胞向着既定的命运走上分化的道路。 中胚层细胞:分化为脊索、肌肉、心脏、肾和造血组 织等; 外胚层细胞:形成表皮和神经系统; 内胚层细胞:形成肠和肺。
• 从遗传的角度讲,细胞分化是基因组内的遗传信 息在特定发育阶段、特定组织部位、特定细胞类型中 选择性表达的结果;其结果是,携带完全相同的遗传 物质的细胞在形态、结构和生理功能上各不相同。
人类的Hox基因可分成4个群集, HOX A、 HOX B、HOX C与HOX D,分别位于7、17、 12与2号染色体上。此外,这些基因可分成13个 平行同源家族,以数字表示,如HOX A4, HOX B4,HOX C4与HOX D4。这些家族成员 的DNA序列与编码的蛋白质序列都很类似。
《个体遗传评定》PPT课件

29
▪ MBLUP法
❖ 二十世纪九十年代以来,随着分子生物学技术的快速发展,涌现了大 量分子遗传标记
❖ 将分子遗传标记提供的信息引入到BLUP方法中,形成标记辅助BLUP
(MBLUP)方法
y X Za e
❖ MBLUP法将表型信息和分子遗传标记信息有机结合起来,从分子水平对 产生个体间表型差异的原因进行精细剖分
BLUP法获得的个体育种值具有最佳线性无偏性:具有估计值方差最小、估
计值无偏、可消除因选择和淘汰等原因造成的偏差等特性,精确性较高
BLUP法是目前世界上主要的育种值估计方法
28
Genetic Evaluation
▪BLUP法在应用中受到的制约因 素:
收集表型信息花时较长,遗传评 定结果滞后于育种需求 表型信息易受环境影响,遗传评 定的准确性有限
三、育种值估计方法概述
▪ 估计育种值是选择种用畜禽的主要依据,育种值估计的精确与否影响着畜 禽育种效果的好坏
▪ 育种值估计方法在不断改进和发展:
选择指数法(selection index,I) 最佳线性无偏预测法(best linear unbiased prediction,BLUP) 标记辅助BLUP法(marker-assisted BLUP, MBLUP)等
Sy= 3.16
X = [1, 2, 3, 4,co5v](xS,yS)x=52.5,
Sx =c1o.v5(8x,y)
r
1
b cov (x,y) 2
sx s y
SS x
表示变量x每改变一个标准 表示变量x每改变一个
差,Y也改变一个标准差
单位,y改变2个单位
个体遗传评定
遗传评定概述 单性状育种值估计 多性状综合遗传评定
▪ MBLUP法
❖ 二十世纪九十年代以来,随着分子生物学技术的快速发展,涌现了大 量分子遗传标记
❖ 将分子遗传标记提供的信息引入到BLUP方法中,形成标记辅助BLUP
(MBLUP)方法
y X Za e
❖ MBLUP法将表型信息和分子遗传标记信息有机结合起来,从分子水平对 产生个体间表型差异的原因进行精细剖分
BLUP法获得的个体育种值具有最佳线性无偏性:具有估计值方差最小、估
计值无偏、可消除因选择和淘汰等原因造成的偏差等特性,精确性较高
BLUP法是目前世界上主要的育种值估计方法
28
Genetic Evaluation
▪BLUP法在应用中受到的制约因 素:
收集表型信息花时较长,遗传评 定结果滞后于育种需求 表型信息易受环境影响,遗传评 定的准确性有限
三、育种值估计方法概述
▪ 估计育种值是选择种用畜禽的主要依据,育种值估计的精确与否影响着畜 禽育种效果的好坏
▪ 育种值估计方法在不断改进和发展:
选择指数法(selection index,I) 最佳线性无偏预测法(best linear unbiased prediction,BLUP) 标记辅助BLUP法(marker-assisted BLUP, MBLUP)等
Sy= 3.16
X = [1, 2, 3, 4,co5v](xS,yS)x=52.5,
Sx =c1o.v5(8x,y)
r
1
b cov (x,y) 2
sx s y
SS x
表示变量x每改变一个标准 表示变量x每改变一个
差,Y也改变一个标准差
单位,y改变2个单位
个体遗传评定
遗传评定概述 单性状育种值估计 多性状综合遗传评定
《遗传评估过程》幻灯片PPT

方程组的解为:
1.3 43 1 2 .2 3 59 2 0 2 .1 16 3 5 .62 2 1 4 .4 56 1 1 .0 29 3 4 .51 0
h ˆ 1h ˆ 2a ˆ 1a ˆ 2a ˆ 3a ˆ 4a ˆ 5
27
BLUP育种值估计软件
PEST PEST是由美国Illinois大学的Groeneveld、Kovac和 Wang〔1990〕开发研制的多性状遗传评估软件, 其英文全文名为〔Multivariate Prediction and ESTimation,目前已在世界各国广泛应用。 根据性能测定和生产数据,PEST提供了基于30多 种数学模型的单性状或多性状BLUP育种值的计算 ,包括固定模型、个体动物模型、公畜模型、公 畜—母畜模型和外祖父模型等 。为了满足实际28育
是随机残1差401 0
1 0 0 0 0a1 e11
用矩阵形y式1 1 1表5 3 4示 2 5 3,0 1 1那0 0 1么h h对2 1 于0 0 0该0 0 1 资料0 0 1 有0 0 1:0 0 0a a a4 2 3e e e1 1 22 3 4
1600 1
0 0 0 0 1a5 e25
29
A = b(P-m) A = .206 ( 12 - 10 )
= .41
10
遗传评估过程
后裔纪录
A=b(P-m) b = 2ph2 / [ 4 + (p-1) h2]
A = 育种值 p = 后裔数 h2= 遗传力 P = 表型值 m = 同龄组均值
11
遗传评估过程
后裔纪录
一公猪有五后裔 平均日龄 140 天
预测
一个体将来作为亲本的预测育种值
16
遗传学-第14章 遗传与个体发育-修改1 18页PPT文档

第十四章 遗传与个体发育 P25在遗传中的作用 细胞分化的可逆性 基因表达的调控
1
2
3
第一节 (细胞核与)细胞质在遗传中的作用 P254
4
第一节 (细胞核与)细胞质在遗传中的作用 P254
正 常 发 育
5
第一节 (细胞核与)细胞质在遗传中的作用 P254
不 正 常 发 育
6
第二节 细胞分化的可逆性(细胞的全能性) P263
7
第二节 细胞分化的可逆性(细胞的全能性) P263
8
第二节 细胞分化的可逆性(细胞的全能性) P263
1958年斯蒂伍德用野生胡萝卜根的韧皮部细胞进行离体培养, 成功地长出了幼株。
9
第二节 细胞分化的可逆性(细胞的全能性) P263
10
第二节 细胞分化的可逆性(细胞的全能性) P263
11
第三节 基因表达的调控
12
13
14
15
16
17
Thank you
1
2
3
第一节 (细胞核与)细胞质在遗传中的作用 P254
4
第一节 (细胞核与)细胞质在遗传中的作用 P254
正 常 发 育
5
第一节 (细胞核与)细胞质在遗传中的作用 P254
不 正 常 发 育
6
第二节 细胞分化的可逆性(细胞的全能性) P263
7
第二节 细胞分化的可逆性(细胞的全能性) P263
8
第二节 细胞分化的可逆性(细胞的全能性) P263
1958年斯蒂伍德用野生胡萝卜根的韧皮部细胞进行离体培养, 成功地长出了幼株。
9
第二节 细胞分化的可逆性(细胞的全能性) P263
10
第二节 细胞分化的可逆性(细胞的全能性) P263
11
第三节 基因表达的调控
12
13
14
15
16
17
Thank you
遗传ppt课件
例题:
1. 下列疾病中,不属于遗传病的是
()
A. 色盲
B. 后天性聋哑 C. 先天性愚型 D. 血友病
2.预防遗传病发生的最简单有效的措施是
()
A.遗传咨询
B.产前诊断 C.提倡“适龄生育” D.禁止近亲结婚
B
D
;.
10
二十八.生物变异——可以遗传、不可以遗传的常见例子。 类型:可遗传变异(如镰刀型红细胞贫血)和不可遗传变异(如双胞胎肤色)
下表为小李同学对自己家庭进行的遗传调查记录请你帮着分析家庭成员调查项目父亲母亲小李单双眼皮单单单有无耳垂有有无能否卷舌能否能所调查的眼皮耳垂等特征项目在遗传上称为而眼皮的单双能否卷舌在遗传学则叫做相对性状父母是单眼皮小李也是单眼皮这一现象叫遗传父母有耳垂而小李无耳垂这一现象叫变异如果能卷舌的控制基因是b不能卷舌的控制基因是b父亲的基因组成是bb或bb
。
③如果能卷舌的控制基因是B,不能卷舌的控制基因是b,
父亲的基因组成是
。母亲的基因组成是 。小李的基因组成是 。
④根据计划生育的有关条例,如果小李的父母可以再生育一胎,
则这一胎能否生出一个有耳垂的孩子? ,所占比例为 ,
能否生出一个无耳垂的孩子?
,所占比例为: ,
生女孩的可能性是 。
在生二胎之前,小李的母亲去做了割双眼皮的美容手术,希望将来孩子也跟她一样是双眼皮,
在生二胎之前,小李的母亲去做了割双眼皮的美容手术,希望将来孩子也跟她一样是双眼皮, 你觉得她的愿望能实现吗?不能 原因是: 遗传物质没有改变
;.
9
二十七.遗传病——常见例子、近亲结婚的危害、优生优育具体措施。
1、遗传病:由遗传物质改变或致病基因控制的病症(如:色盲、血友病、白化病、先天愚形等) 2、近亲结婚是导致遗传病发病率高的主要原因,因为近亲间携带相同致病基因的可能性比较大。 3、优生优育的措施有:禁止近亲结婚,遗传咨询,产前诊断。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
tr aq tr qa qa
✓ 范数 (norm):矩阵与其转置矩阵乘积的迹的 平方根,即:
0.5
Α trΑΑ 0.5 i j ai2j
范数的性质: • ||A|| > 0,除非A = 0; ||A|| = 0 ⇐⇒ A=0 • ||kA|| = |k| ||A||(k为一纯量); • ||A+B||≤||A||+||B|| • ||AB||≤||A|| ||B||
✓ 逆矩阵 (inverse matrix):对于一方阵A,若
个体遗传评定
第一节 有关基础知识
矩阵代数基础
➢ 纯量、矩阵和向量 ✓ 纯量(scalar)
• 只有大小的一个数值,也称为标量、数量 或元向量。 • 用数字或经定义的拉丁字母斜体、小写表 示。 • 如a、r和k。
✓ 矩阵(matrix)
• 由一定行数和一定列数的纯量,按一定顺序排 列的表。 • 一般用大写粗体字母表示。 • 矩阵的阶数 (order) 或维数(dimension)是指 矩阵的行数 (m) 和列数 (n) ,表示为m n。 • 例如:
✓ 乘法 (multiplication) 纯量与矩阵相乘:一个纯量 与一个矩阵 A 的乘积是用 去乘 A 的每个元素,表示为A。
A Aij
对于m n 阶矩阵 A 和 B 以及纯量 和 ,
具有如下性质:
• 闭 合 性: A 仍然是一个 m n 阶矩阵; • 结 合 性:() A = (A); • 分 配 性: (A+B) =A+B;
00
ann
• 下三角阵:主对角线以 上元素全部为0,即当 j
a11 0 a21 a22
0 0
> i 时, aij = 0 (i < j)
an1 an2
ann
✓ 对角阵 (diagonal matrix):除 i=j 时的元素
(主对角线元素)外,其它元素均为零的方阵, 即aij = 0 (j i 时)。通常可以用Diag {aj }表示, 其中aj 为该阵的第 i 个对角线元素。
2 1 1 0 1
1 2 2 3 A 0 0 1 0
0 0 0 1
0 0 0
A1 O
A2 I 1
0 0 0 0 1
0 0 1 0 0
2 1
1 2
A1,
1 2
0 2
1 0
A2 ,
0 0
0 O, 0 0 0
1 0
0 I 1
✓ 分块对角阵 (block diagonal matrix):主对角线 上的子阵都为方阵,其余子阵都是零阵的分块阵。 如:
1 a 2
3
a1 2ix):行数与列数相等的矩
阵,如An×n。其他矩阵称为直角阵(rectangular
matrices) 。 a b c
A c a b b c a
✓ 对称阵 (symmetric matrix):元素间满足 aij =
aji 的方阵。
a b c A b a b
c b a
1 0.5 0.8 B 0.5 1 0.2
0.8 0.2 1
✓ 三角阵(triangular matrix): a11 a12
a1n
• 上三角阵:主对角线以 0 a 22
a2n
下元素全部为0,即当 j <
i 时, aij = 0 (j < i)
A
4 6
5 0
3 2
B
1 3
0 4
2 1
A
B
4 1 6 3
50 04
3 2 2 1
5 9
5 4
5 3
B
A
对于 m n 阶矩阵 A、 B和 C,具有如下性质: • 闭 合 性:A + B 仍然是一个 m n 阶矩阵; • 结 合 性:(A + B) + C = A + (B + C); • 交 换 性:A + B = B + A; • 加性等同:A + 0 = A; • 加 性 逆: A + (−A) = 0 。
a11 0
0
0 a22
0
0 0
ann
✓ 单位矩阵(identity matrix):所有对角线元素为1,
其他元素均为0的矩阵。
1 0
0
0 1
0
0 0
1
✓ 分块矩阵(block matrix):用水平和垂直虚线将
矩阵分为若干小块,此时的矩阵称为分块矩阵。 其中的小块称为子阵(sub-matrix)。
✓ 矩阵的迹 (trace):一个方阵的迹为其对角线元
素之和,表示为:
tr Α aii i
0.51 0.32 0.19 设: A 0.28 0.46 0.14
则
0.21 0.16 0.33
tr Α 0.51 0.46 0.33 1.30
迹的运算性质:
tr ΑΒ tr ΒΑ tr ABC tr BCA tr CAB
(+) A=A+A;
• 等 同 性:1A = A。
矩阵相乘:当矩阵A的列数与矩阵B的行数相等 时,A与B可乘,即
Arcc Bcl Crl cij
其中, cij aikbkj k
例如:
矩阵乘法具有如下性质: • AB BA • (AB)C = A(BC) • (A + B)C = AC + BC;C(A + B) = CA + CB
✓ 转置(transposition):矩阵的行与列对调,用A´ 或AT表示,即:
Αmn aij Αnm aji
矩阵的转置有如下性质: • 当A为对称方阵时, A´ = A; • (A´) ´ = A • (AB) ´ = B ´A ´ • (AB ´ C) ´ = C ´BA ´ • (A + B + C) ´= A ´ + B ´ + C ´
Α11 0
Α
0
Α22
0 0
0 0
Αkk
✓ 稀疏矩阵 (sparse matrix):设矩阵Amn中有 s 个非零元素,若 s 远远小于矩阵元素的总数 (即
s<<m×n),则称A为稀疏矩阵。
➢ 矩阵的运算
✓ 加法(addition):当矩阵A和B同阶时,有:
A B aij bij
例如:
✓ 向量 (Vector)
• 仅有一列或一行的矩阵,前者称为列向量 (column vector),后者称为行向量(row vector)。
• 通常用小写粗体字母表示。
• 为区别行向量和列向量,通常在字母的右上 角加一撇表示行向量,不加撇表示列向量。
• 行向量的阶数为1j,列向量的阶数为j1。
• 例如:
✓ 范数 (norm):矩阵与其转置矩阵乘积的迹的 平方根,即:
0.5
Α trΑΑ 0.5 i j ai2j
范数的性质: • ||A|| > 0,除非A = 0; ||A|| = 0 ⇐⇒ A=0 • ||kA|| = |k| ||A||(k为一纯量); • ||A+B||≤||A||+||B|| • ||AB||≤||A|| ||B||
✓ 逆矩阵 (inverse matrix):对于一方阵A,若
个体遗传评定
第一节 有关基础知识
矩阵代数基础
➢ 纯量、矩阵和向量 ✓ 纯量(scalar)
• 只有大小的一个数值,也称为标量、数量 或元向量。 • 用数字或经定义的拉丁字母斜体、小写表 示。 • 如a、r和k。
✓ 矩阵(matrix)
• 由一定行数和一定列数的纯量,按一定顺序排 列的表。 • 一般用大写粗体字母表示。 • 矩阵的阶数 (order) 或维数(dimension)是指 矩阵的行数 (m) 和列数 (n) ,表示为m n。 • 例如:
✓ 乘法 (multiplication) 纯量与矩阵相乘:一个纯量 与一个矩阵 A 的乘积是用 去乘 A 的每个元素,表示为A。
A Aij
对于m n 阶矩阵 A 和 B 以及纯量 和 ,
具有如下性质:
• 闭 合 性: A 仍然是一个 m n 阶矩阵; • 结 合 性:() A = (A); • 分 配 性: (A+B) =A+B;
00
ann
• 下三角阵:主对角线以 上元素全部为0,即当 j
a11 0 a21 a22
0 0
> i 时, aij = 0 (i < j)
an1 an2
ann
✓ 对角阵 (diagonal matrix):除 i=j 时的元素
(主对角线元素)外,其它元素均为零的方阵, 即aij = 0 (j i 时)。通常可以用Diag {aj }表示, 其中aj 为该阵的第 i 个对角线元素。
2 1 1 0 1
1 2 2 3 A 0 0 1 0
0 0 0 1
0 0 0
A1 O
A2 I 1
0 0 0 0 1
0 0 1 0 0
2 1
1 2
A1,
1 2
0 2
1 0
A2 ,
0 0
0 O, 0 0 0
1 0
0 I 1
✓ 分块对角阵 (block diagonal matrix):主对角线 上的子阵都为方阵,其余子阵都是零阵的分块阵。 如:
1 a 2
3
a1 2ix):行数与列数相等的矩
阵,如An×n。其他矩阵称为直角阵(rectangular
matrices) 。 a b c
A c a b b c a
✓ 对称阵 (symmetric matrix):元素间满足 aij =
aji 的方阵。
a b c A b a b
c b a
1 0.5 0.8 B 0.5 1 0.2
0.8 0.2 1
✓ 三角阵(triangular matrix): a11 a12
a1n
• 上三角阵:主对角线以 0 a 22
a2n
下元素全部为0,即当 j <
i 时, aij = 0 (j < i)
A
4 6
5 0
3 2
B
1 3
0 4
2 1
A
B
4 1 6 3
50 04
3 2 2 1
5 9
5 4
5 3
B
A
对于 m n 阶矩阵 A、 B和 C,具有如下性质: • 闭 合 性:A + B 仍然是一个 m n 阶矩阵; • 结 合 性:(A + B) + C = A + (B + C); • 交 换 性:A + B = B + A; • 加性等同:A + 0 = A; • 加 性 逆: A + (−A) = 0 。
a11 0
0
0 a22
0
0 0
ann
✓ 单位矩阵(identity matrix):所有对角线元素为1,
其他元素均为0的矩阵。
1 0
0
0 1
0
0 0
1
✓ 分块矩阵(block matrix):用水平和垂直虚线将
矩阵分为若干小块,此时的矩阵称为分块矩阵。 其中的小块称为子阵(sub-matrix)。
✓ 矩阵的迹 (trace):一个方阵的迹为其对角线元
素之和,表示为:
tr Α aii i
0.51 0.32 0.19 设: A 0.28 0.46 0.14
则
0.21 0.16 0.33
tr Α 0.51 0.46 0.33 1.30
迹的运算性质:
tr ΑΒ tr ΒΑ tr ABC tr BCA tr CAB
(+) A=A+A;
• 等 同 性:1A = A。
矩阵相乘:当矩阵A的列数与矩阵B的行数相等 时,A与B可乘,即
Arcc Bcl Crl cij
其中, cij aikbkj k
例如:
矩阵乘法具有如下性质: • AB BA • (AB)C = A(BC) • (A + B)C = AC + BC;C(A + B) = CA + CB
✓ 转置(transposition):矩阵的行与列对调,用A´ 或AT表示,即:
Αmn aij Αnm aji
矩阵的转置有如下性质: • 当A为对称方阵时, A´ = A; • (A´) ´ = A • (AB) ´ = B ´A ´ • (AB ´ C) ´ = C ´BA ´ • (A + B + C) ´= A ´ + B ´ + C ´
Α11 0
Α
0
Α22
0 0
0 0
Αkk
✓ 稀疏矩阵 (sparse matrix):设矩阵Amn中有 s 个非零元素,若 s 远远小于矩阵元素的总数 (即
s<<m×n),则称A为稀疏矩阵。
➢ 矩阵的运算
✓ 加法(addition):当矩阵A和B同阶时,有:
A B aij bij
例如:
✓ 向量 (Vector)
• 仅有一列或一行的矩阵,前者称为列向量 (column vector),后者称为行向量(row vector)。
• 通常用小写粗体字母表示。
• 为区别行向量和列向量,通常在字母的右上 角加一撇表示行向量,不加撇表示列向量。
• 行向量的阶数为1j,列向量的阶数为j1。
• 例如:
