5.多项式乘以多项式练习题

合集下载

多项式乘以多项式训练题

五、解答题 1．证明 (a-1)(a 2-3)+a 2(a+1)-2(a 3-2a-4)-a 的值与 a 无关．
2．已知多项式 (x 2＋ px＋q)(x 2－ 3x＋2) 的结果中不含 x3 项和 x2 项，求 p 和 q 的值．
3. 若 (x 2＋ ax－ b)(2x 2－ 3x＋1) 的积中， x 3 的系数为 5， x2 的系数为－ 6，求 a， b．
3. 当 k＝ __________ 时，多项式 x－ 1 与 2－ kx 的乘积不含一次项．
4. 在长为 (3a ＋2) 、宽为 (2a ＋ 3) 的长方形铁皮上剪去一个边长为 (a － 1) 的小正方形，则剩余部
分的面积为 ___________．
5．已知 ( x y) 2 1 , ( x y) 2 49 ，则 x 2 y2 =
三、计算题
1． (3m-n)(m-2n) ．
2
． (x+2y)(5a+3b) ．
3． (x+y)(x 2-xy+y 2) ．
4
． (x+3y+4)(2x-y) ．
四、化简求值
1. m 2(m＋ 4) ＋ 2m(m2－1) － 3m(m2＋ m－ 1) ，其中 m＝ 2 5
2．（ a－ 2）（ a＋ 2）＋ 3（ a＋ 2）２－6a（ a＋2） , 其中 a＝ 5.
3. x(x 2－ 4) －(x ＋ 3)(x 2－3x＋ 2) －2x(x － 2) ，其中 x ＝ 3 ． 2
4. (x-2)(x-3)+2(x+6)(x-5)-3(x
2-7x+13) ，其中 x= 3 1 2
5. y n(y n+9y-12)-3(3y n+1-4y n) ，其中 y=-3 ， n=2．

多项式与多项式的乘法

（a+b)(m+n)=am+an+bm+bn
实质上是转化为单项式×多项式的运算
不要漏乘；正确确定各符号；结果要最简
(x-1)2在一般情况下不等于x2-12.
[义务教育教科书]( R J ) 八上数学课件
第十四章整式的乘法与因式分解
14.1.4 整式的乘法
第3课时整式的除法
导入新课
例2 已知am＝12，an＝2，a＝3，求am－n－1的值．解：∵am＝12，an＝2，a＝3， ∴am－n－1＝am÷an÷a＝12÷2÷3＝2.
方法总结：解此题的关键是逆用同底数幂的除法，对am－n－1进行变形，再代入数值进行计算．
解：去括号，得40x－8x2=34－8x2+6x，移项，得40x－6x=34，合并同类项，得34x=34，解得 x=1.
拓展提升
8.某同学在计算一个多项式乘以－3x2时，算成了加
上－3x2，得到的答案是x2－2x＋1，那么正确
的计算结果是多少？解：设这个多项式为A，则
A＋(－3x2)＝x2－2x＋1， ∴A＝4x2－2x＋1.
am ÷an=am-n
验证：因为am-n ·an=am-n+n=am,所以am ÷an=am-n.
知识要点同底数幂的除法
一般地，我们有
am ÷an=am-n (a ≠0,m,n都是正整数，且m>n)
即同底数幂相除，底数不变，指数相减.
想一想：am÷am=? (a≠0) 答：am÷am=1，根据同底数幂的除法法则可得am÷am=a0.
3.如果(x+a)(x+b)的结果中不含x的一次项，那么a、b
满足（ C ）

多项式乘多项式专项练习30题选择解答(有答案)ok

多项式乘多项式专项练习30题选择解答(有答案)ok1.若 $(x-1)(x+3)=x+mx+n$，则 $m$，$n$ 的值分别为（）。

A。

$m=1$，$n=3$ B。

$m=4$，$n=5$ C。

$m=2$，$n=-3$ D。

$m=-2$，$n=3$2.下列各式中，计算结果是 $x+7x-18$ 的是（）。

A。

$(x-1)(x+18)$ B。

$(x+2)(x+9)$ C。

$(x-3)(x+6)$ D。

$(x-2)(x+9)$3.若 $(x-a)(x+2)$ 的展开项中不含 $x$ 的一次项，则$a$ 的值为（）。

A。

$a=-2$ B。

$a=2$ C。

无法确定4.如果 $(x-3)(2x+4)=2x-mx+n$，那么 $m$，$n$ 的值分别是（）。

A。

$m=2$，$n=12$ B。

$m=-2$，$n=12$ C。

$m=2$，$n=-12$ D。

$m=-2$，$n=-12$5.已知$m+n=2$，$mn=-2$，则$(1-m)(1-n)$ 的值为（）。

A。

$1-3$ B。

$-1$ C。

$5$6.先化简，再求值：$5(3xy-xy)-4(-xy+3xy)$，其中$x=-2$，$y=3$。

7.计算：1）$3-2+(-3)-(\frac{3}{2})$2）$(-2ab)+(-a)\cdot(2b)$3）$x(2x+1)(1-2x)-4x(x-1)(1-x)$4）$(2a-b+3)(2a+b-3)$5）$\frac{x^2-1}{2}(2x+1)$8.计算：1）$(-7x-8y)\cdot(-x+3y)$2）$(3x-2y)(y-3x)-(2x-y)(3x+y)$9.计算：$a(a+2)(a-3)$10.计算：$(a+b)(a-ab+b)$11.计算：$(2x-3y)(x+4y)$12.计算：1）$(2x+3y)(3y-4x)$2）$(-4x-3y)(3y-4x)$13.计算：$(2x+5y)(3x-2y)-2x(x-3y)$14.$5x-(x-2)(3x+1)-2(x+1)(x-5)$15.已知多项式$6x-7xy-3y+14x+y+a=(2x-3y+b)(3x+y+c)$，试确定 $a$，$b$，$c$ 的值。

多项式乘多项式试题附答案

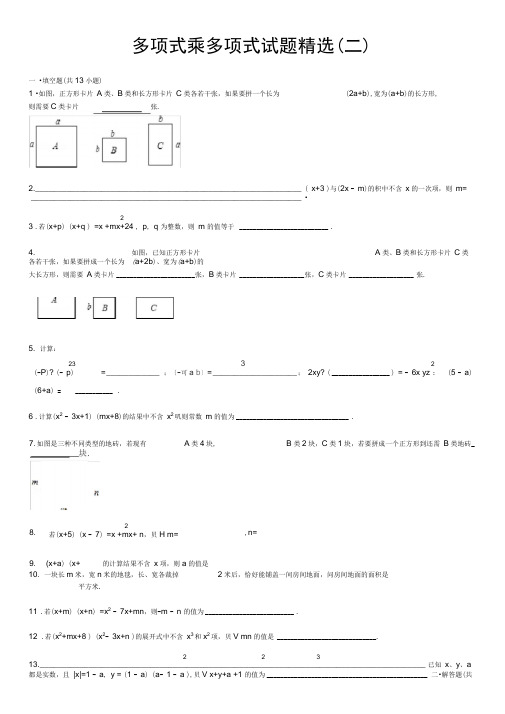
多项式乘多项式试题精选（二）一．填空题（共13小题）1．如图，正方形卡片A类、B类和长方形卡片C类各若干张，如果要拼一个长为（2a+b），宽为（a+b）的长方形，则需要C类卡片_________张．2．（x+3）与（2x﹣m）的积中不含x的一次项，则m=_________．3．若（x+p）（x+q）=x2+mx+24，p，q为整数，则m的值等于_________．4．如图，已知正方形卡片A类、B类和长方形卡片C类各若干张，如果要拼成一个长为（a+2b）、宽为（a+b）的大长方形，则需要A类卡片_________张，B类卡片_________张，C类卡片_________张．5．计算：（﹣p）2?（﹣p）3=_________；=_________；2xy?（_________）=﹣6x2yz；（5﹣a）（6+a）=_________．6．计算（x2﹣3x+1）（mx+8）的结果中不含x2项，则常数m的值为_________．7．如图是三种不同类型的地砖，若现有A类4块，B类2块，C类1块，若要拼成一个正方形到还需B类地砖_________块．8．若（x+5）（x﹣7）=x2+mx+n，则m=_________，n=_________．9．（x+a）（x+）的计算结果不含x项，则a的值是_________．10．一块长m米，宽n米的地毯，长、宽各裁掉2米后，恰好能铺盖一间房间地面，问房间地面的面积是_________平方米．11．若（x+m）（x+n）=x2﹣7x+mn，则﹣m﹣n的值为_________．12．若（x2+mx+8）（x2﹣3x+n）的展开式中不含x3和x2项，则mn的值是_________．13．已知x、y、a都是实数，且|x|=1﹣a，y2=（1﹣a）（a﹣1﹣a2），则x+y+a3+1的值为_________．二．解答题（共17小题）14．若（x2+2nx+3）（x2﹣5x+m）中不含奇次项，求m、n的值．15．化简下列各式：（1）（3x+2y）（9x2﹣6xy+4y2）；（2）（2x﹣3）（4x2+6xy+9）；（3）（m﹣）（m2+m+）；（4）（a+b）（a2﹣ab+b2）（a﹣b）（a2+ab+b2）．16．计算：（1）（2x﹣3）（x﹣5）；（2）（a2﹣b3）（a2+b3）17．计算：（1）﹣（2a﹣b）+[a﹣（3a+4b）]（2）（a+b）（a2﹣ab+b2）18．（x+7）（x﹣6）﹣（x﹣2）（x+1）19．计算：（3a+1）（2a﹣3）﹣（6a﹣5）（a﹣4）．20．计算：（a﹣b）（a2+ab+b2）21．若（x2+px﹣）（x2﹣3x+q）的积中不含x项与x3项，（1）求p、q的值；（2）求代数式（﹣2p2q）2+（3pq）﹣1+p2012q2014的值．22．先化简，再求值：5（3x2y﹣xy2）﹣4（﹣xy2+3x2y），其中x=﹣2，y=3．23．若（x﹣1）（x2+mx+n）=x3﹣6x2+11x﹣6，求m，n的值．24．如图，有多个长方形和正方形的卡片，图甲是选取了2块不同的卡片，拼成的一个图形，借助图中阴影部分面积的不同表示可以用来验证等式a（a+b）=a2+ab成立．（1）根据图乙，利用面积的不同表示方法，写出一个代数恒等式_________；（2）试写出一个与（1）中代数恒等式类似的等式，并用上述拼图的方法说明它的正确性．25．小明想把一长为60cm，宽为40cm的长方形硬纸片做成一个无盖的长方体盒子，于是在长方形纸片的四个角各剪去一个相同的小正方形．（1）若设小正方形的边长为xcm，求图中阴影部分的面积；（2）当x=5时，求这个盒子的体积．26．（x﹣1）（x﹣2）=（x+3）（x﹣4）+20．27．若（x﹣3）（x+m）=x2+nx﹣15，求的值．28．小明在进行两个多项式的乘法运算时（其中的一个多项式是b﹣1），把“乘以（b﹣1）”错看成“除以（b﹣1）”，结果得到（2a﹣b），请你帮小明算算，另一个多项式是多少？29．有足够多的长方形和正方形的卡片如图．如果选取1号、2号、3号卡片分别为1张、2张、3张，可拼成一个长方形（不重叠无缝隙）．请画出这个长方形的草图，并运用拼图前后面积之间的关系说明这个长方形的代数意义．30．（1）填空：（a﹣1）（a+1）=_________（a﹣1）（a2+a+1）=_________（a﹣1）（a3+a2+a+1）=_________（2）你发现规律了吗？请你用你发现的规律填空：（a﹣1）（a n+a n﹣1+…+a2+a+1）=_________（3）根据上述规律，请你求42012+42011+42010+…+4+1的值．_________．多项式乘单项式试题精选（二）参考答案与试题解析一．填空题（共13小题）1．如图，正方形卡片A类、B类和长方形卡片C类各若干张，如果要拼一个长为（2a+b），宽为（a+b）的长方形，则需要C类卡片3张．考点：多项式乘多项式．分析：根据长方形的面积等于长乘以宽列式，再根据多项式的乘法法则计算，然后结合卡片的面积即可作出判断．解答：解：长为2a+b，宽为a+b的矩形面积为（2a+b）（a+b）=2a2+3ab+b2，A图形面积为a2，B图形面积为b2，C图形面积为ab，则可知需要A类卡片2张，B类卡片1张，C类卡片3张．故答案为：3．点评：此题主要考查了多项式乘多项式，掌握多项式乘以多项式的法则是本题的关键．注意不要漏项，漏字母，有同类项的合并同类项．2．（x+3）与（2x﹣m）的积中不含x的一次项，则m=6．考点：多项式乘多项式．专题：计算题．分析：先求出（x+3）与（2x﹣m）的积，再令x的一次项为0即可得到关于m的一元一次方程，求出m的值即可．解答：解：∵（x+3）（2x﹣m）=2x2+（6﹣m）x﹣3m，∴6﹣m=0，解得m=6．故答案为：6．点评：本题考查的是多项式乘以多项式的法则，即先用一个多项式的每一项乘另外一个多项式的每一项，再把所得的积相加．3．若（x+p）（x+q）=x2+mx+24，p，q为整数，则m的值等于10，11，14，25．考点：多项式乘多项式．分析：根据多项式的乘法法则，可得一个多项式，根据多项式相等，可得对应项相等，由p?q=24，p，q为整数，可得p，q的值，再根据p+q=m，可得m的值．解答：解：∵（x+p）（x+q）=x2+mx+24，∴p=24，q=1；p=12，q=2；p=8，q=3；p=6，q=4，∵当p=24，q=1时，m=p+q=25，当p=12，q=2时，m=p+q=14，当p=8，q=3时，m=p+q=11，当p=6，q=4时，m=p+q=10，故答案为：10，11，14，25．点评：本题考察了多项式，先根据多项式的乘法法则计算，分类讨论p，q是解题关键．4．如图，已知正方形卡片A类、B类和长方形卡片C类各若干张，如果要拼成一个长为（a+2b）、宽为（a+b）的大长方形，则需要A类卡片1张，B类卡片2张，C类卡片3张．考点：多项式乘多项式．分析：根据边长组成图形．数出需要A类卡片1张，B类卡片2张，C类卡片3张．解答：解：如图，要拼成一个长为（a+2b）、宽为（a+b）的大长方形，则需要A类卡片1张，B类卡片2张，C 类卡片3张．点评：本题主要考查了多项式乘多项式，解题的关键是根据边长组成图形．5．计算：（﹣p）2?（﹣p）3=﹣p5；=﹣a6b3；2xy?（﹣3xz）=﹣6x2yz；（5﹣a）（6+a）=﹣a2﹣a+30．考点：多项式乘多项式；同底数幂的乘法；幂的乘方与积的乘方；单项式乘单项式．分析：根据同底数幂的乘法、积的乘方和幂的乘方、单项式除以单项式法则、多项式乘以多项式法则求出每个式子的值即可．解答：解：（﹣p）2?（﹣p）3=（﹣p）5=﹣p5，（﹣a2b）3=（﹣）3?（a2）3b3=﹣a6b3，∵﹣6x2yz÷2xy=﹣3xz，∴2xy?（﹣3xz）=﹣6x2yz，（5﹣a）（6+a）=30+5a﹣6a﹣a2=30﹣a﹣a2=﹣a2﹣a+30，故答案为：﹣p5，﹣a6b3，﹣3xz，﹣a2﹣a+30．点评：本题考查了同底数幂的乘法、积的乘方和幂的乘方、单项式除以单项式法则、多项式乘以多项式法则的应用．6．计算（x2﹣3x+1）（mx+8）的结果中不含x2项，则常数m的值为．考点：多项式乘多项式．分析：把式子展开，找到所有x2项的所有系数，令其为0，可求出m的值．解答：解：∵（x2﹣3x+1）（mx+8）=mx4+8x2﹣3mx2﹣24x+mx+8．又∵结果中不含x2的项，∴8﹣3m=0，解得m=．故答案为：．点评：本题主要考查了多项式乘多项式的运算，注意当要求多项式中不含有哪一项时，应让这一项的系数为0．7．如图是三种不同类型的地砖，若现有A类4块，B类2块，C类1块，若要拼成一个正方形到还需B类地砖2块．考点：多项式乘多项式．分析：分别计算出4块A的面积和2块B的面积、1块C的面积，再计算这三种类型的砖的总面积，用完全平方公式化简后，即可得出少了哪种类型的地砖．解答：解：4块A的面积为：4×m×m=4m2；2块B的面积为：2×m×n=2mn；1块C的面积为n×n=n2；那么这三种类型的砖的总面积应该是：4m2+2mn+n2=4m2+4mn+n2﹣2mn=（2m+n）2﹣2mn，因此，少2块B型地砖，故答案为：2．点评：本题考查了完全平方公式的几何意义，立意较新颖，注意面积的不同求解是解题的关键，对此类问题要深入理解．8．若（x+5）（x﹣7）=x2+mx+n，则m=﹣2，n=﹣35．考点：多项式乘多项式．分析：已知等式左边利用多项式乘以多项式法则计算，利用多项式相等的条件即可求出m与n的值．解答：解：（x+5）（x﹣7）=x2﹣2x﹣35=x2+mx+n，则m=﹣2，n=﹣35．故答案为：﹣2，﹣35．点评：此题考查了多项式乘以多项式，熟练掌握运算法则是解本题的关键．9．（x+a）（x+）的计算结果不含x项，则a的值是．考点：多项式乘多项式．分析：多项式乘多项式法则，先用一个多项式的每一项乘以另一个多项式的每一项，再把所得的积相加，依据法则运算，展开式不含关于字母x的一次项，那么一次项的系数为0，就可求a的值．解答：解：∵（x+a）（x+）=又∵不含关于字母x的一次项，∴，解得a=．点评：本题考查了多项式乘多项式法则，相乘后不含哪一项，就让这一项的系数等于0，难度适中．10．一块长m米，宽n米的地毯，长、宽各裁掉2米后，恰好能铺盖一间房间地面，问房间地面的面积是（m﹣2）（n﹣2）或（mn﹣2m﹣2n+4）平方米．考点：多项式乘多项式．分析：根据题意得出算式是（m﹣2）（n﹣2），即可得出答案．解答：解：根据题意得出房间地面的面积是（m﹣2）（n﹣2）；（m﹣2）（n﹣2）=mn﹣2m﹣2n+4．故答案为：（m﹣2）（n﹣2）或（mn﹣2m﹣2n+4）点评：本题考查了多项式乘多项式的应用，关键是能根据题意得出算式，题目比较好，难度适中．11．若（x+m）（x+n）=x2﹣7x+mn，则﹣m﹣n的值为7．考点：多项式乘多项式．专题：计算题．分析：按照多项式的乘法法则展开运算后解答：解：∵（x+m）（x+n）=x2+（m+n）x+mn=x2﹣7x+mn，∴m+n=﹣7，∴﹣m﹣n=7，故答案为：7．点评：本题考查了多项式的乘法，解题的关键是牢记多项式乘以多项式的乘法法则，属于基础题，比较简单．12．若（x2+mx+8）（x2﹣3x+n）的展开式中不含x3和x2项，则mn的值是3．考点：多项式乘多项式．专题：计算题．分析：利用多项式乘以多项式法则计算得到结果，根据展开式中不含x2和x3项列出关于m与n的方程组，求出方程组的解即可得到m与n的值．解答：解：原式=x4+（m﹣3）x3+（n﹣3m+8）x2+（mn﹣24）x+8n，（x2+mx﹣8）（x2﹣3x+n）根据展开式中不含x2和x3项得：，解得：，∴mn=3，故答案为：3．点评：此题考查了多项式乘以多项式，熟练掌握运算法则是解本题的关键．13．已知x、y、a都是实数，且|x|=1﹣a，y2=（1﹣a）（a﹣1﹣a2），则x+y+a3+1的值为2．考点：代数式求值；绝对值；多项式乘多项式．专题：计算题．分析：根据绝对值非负数，平方数非负数的性质可得1﹣a=0，从而得到a的值，然后代入求出x、y的值，再把a、x、y的值代入代数式进行计算即可求解．解答：解：∵|x|=1﹣a≥0，∴a﹣1≤0，﹣a2≤0，∴a﹣1﹣a2≤0，又y2=（1﹣a）（a﹣1﹣a2）≥0，∴1﹣a=0，解得a=1，∴|x|=1﹣1=0，x=0，y2=（1﹣a）（﹣1﹣a2）=0，∴x+y+a3+1=0+0+1+1=2．故答案为：2．点评：本题主要考查了代数式求值问题，把y2的多项式整理，然后根据非负数的性质求出a的值是解题的关键，也是解决本题的突破口，本题灵活性较强．二．解答题（共17小题）14．若（x2+2nx+3）（x2﹣5x+m）中不含奇次项，求m、n的值．考点：多项式乘多项式．分析：把式子展开，让x4的系数，x2的系数为0，得到m，n的值．解答：解：（x2+2nx+3）（x2﹣5x+m）=x4﹣5x3+mx2+2nx3﹣10nx2+2mnx+3x2﹣15x+3m=x4+（2n﹣5）x3+（m﹣10n+3）x2+（2mn﹣15）x+3m，∵结果中不含奇次项，∴2n﹣5=0，2mn﹣15=0，解得m=3，n=．点评：本题主要考查了多项式乘多项式的运算，注意当要求多项式中不含有哪一项时，应让这一项的系数为0．15．化简下列各式：（1）（3x+2y）（9x2﹣6xy+4y2）；（2）（2x﹣3）（4x2+6xy+9）；（3）（m﹣）（m2+m+）；（4）（a+b）（a2﹣ab+b2）（a﹣b）（a2+ab+b2）．考点：多项式乘多项式．分析：根据立方和与立方差公式解答即可．解答：解：（1）（3x+2y）（9x2﹣6xy+4y2）=（3x）3+（2y）3=27x3+8y3；（2）（2x﹣3）（4x2+6xy+9）=（2x）3﹣33=8x3﹣27；（3）（m﹣）（m2+m+）=﹣=﹣；（4）（a+b）（a2﹣ab+b2）（a﹣b）（a2+ab+b2）=（a3+b3）（a3﹣b3）=a6﹣b6．点评：本题考查了立方和与立方差公式，熟练记忆公式是解题的关键．16．计算：（1）（2x﹣3）（x﹣5）；（2）（a2﹣b3）（a2+b3）考点：多项式乘多项式．分析：（1）根据多项式乘以多项式的法则，可表示为（a+b）（m+n）=am+an+bm+bn，计算即可；（2）根据平方差公式计算即可．解答：解：（1）（2x﹣3）（x﹣5）=2x2﹣10x﹣3x+15=2x2﹣13x+15；（2）（a2﹣b3）（a2+b3）=a4﹣b6．点评：本题考查了多项式乘以多项式的法则以及平方差公式．注意不要漏项，漏字母，有同类项的合并同类项．17．计算：（1）﹣（2a﹣b）+[a﹣（3a+4b）]（2）（a+b）（a2﹣ab+b2）考点：多项式乘多项式；整式的加减．专题：计算题．分析：（1）先去小括号，再去大括号，最后按照整式加减混合运算规则进行计算即可；（2）根据多项式乘以多项式的法则，可表示为（a+b）（m+n）=am+an+bm+bn，计算即可．解答：解：（1）原式=﹣2a+b+[a﹣3a﹣4b]，=﹣2a+b+a﹣3a﹣4b，=﹣4a﹣3b；（2）原式=a3﹣a2b+ab2+a2b﹣ab2+b3，=a3+b3．点评：本题主要考查多项式乘以多项式的法则．注意不要漏项，漏字母，有同类项的合并同类项．18．（x+7）（x﹣6）﹣（x﹣2）（x+1）考点：多项式乘多项式．分析：依据多项式乘多项式法则运算．解答：解：（x+7）（x﹣6）﹣（x﹣2）（x+1）=x2﹣6x+7x﹣42﹣x2﹣x+2x+2=2x﹣40．点评：本题考查了多项式乘多项式法则，先用一个多项式的每一项乘以另一个多项式的每一项，再把所得的积相加．关键是不能漏项．19．计算：（3a+1）（2a﹣3）﹣（6a﹣5）（a﹣4）．考点：多项式乘多项式．分析：根据整式混合运算的顺序和法则分别进行计算，再把所得结果合并即可．解答：解：（3a+1）（2a﹣3）+（6a﹣5）（a﹣4）=6a2﹣9a+2a﹣3+6a2﹣24a﹣5a+20=12a2﹣36a+17．点评：此题考查了整式的混合运算，在计算时要注意混合运算的顺序和法则以及运算结果的符号，是一道基础题．20．计算：（a﹣b）（a2+ab+b2）考点：多项式乘多项式；单项式乘单项式．专题：计算题．分析：根据多项式乘以多项式的法则和单项式乘单项式的法则进行计算即可．解答：解：原式=a3+a2b+ab2﹣a2b﹣ab2﹣b3=a3﹣b3．点评：本题主要考查对多项式乘以多项式的法则和单项式乘单项式的法则得理解和掌握，能熟练地运用法则进行计算是解此题的关键．21．若（x2+px﹣）（x2﹣3x+q）的积中不含x项与x3项，（1）求p、q的值；（2）求代数式（﹣2p2q）2+（3pq）﹣1+p2012q2014的值．考点：多项式乘多项式．分析：（1）形开式子，找出x项与x3令其系数等于0求解．（2）把p，q的值入求解．解答：解：（1）（x2+px﹣）（x2﹣3x+q）=x4+（p﹣3）x3+（9﹣3p﹣）x2+（qp+1）x+q，∵积中不含x项与x3项，∴P﹣3=0，qp+1=0∴p=3，q=﹣，（2）（﹣2p2q）2+（3pq）﹣1+p2012q2014=[﹣2×32×（﹣）]2++×32=36﹣+9=44．点评：本题主要考查了多项式乘多项式，解题的关键是正确求出p，q的值22．先化简，再求值：5（3x2y﹣xy2）﹣4（﹣xy2+3x2y），其中x=﹣2，y=3．考点：整式的加减—化简求值；合并同类项；多项式乘多项式．专题：计算题．分析：根据单项式乘多项式的法则展开，再合并同类项，把x y的值代入求出即可．解答：解：原式=15x2y﹣5xy2+4xy2﹣12x2y=3x2y﹣xy2，当x=﹣2，y=3时，原式=3×（﹣2）2×3﹣（﹣2）×32=36+18=54．点评：本题考查了对整式的加减，合并同类项，单项式乘多项式等知识点的理解和掌握，注意展开时不要漏乘，同时要注意结果的符号，代入﹣2时应用括号．23．若（x﹣1）（x2+mx+n）=x3﹣6x2+11x﹣6，求m，n的值．考点：多项式乘多项式．专题：计算题．分析：把（x﹣1）（x2+mx+n）展开后，每项的系数与x3﹣6x2+11x﹣6中的项的系数对应，可求得m、n的值．解答：解：∵（x﹣1）（x2+mx+n）=x3+（m﹣1）x2+（n﹣m）x﹣n=x3﹣6x2+11x﹣6∴m﹣1=﹣6，﹣n=﹣6，解得m=﹣5，n=6．点评：本题主要考查了多项式乘多项式的法则，注意不要漏项，漏字母，有同类项的合并同类项．根据对应项系数相等列式求解m、n是解题的关键．24．如图，有多个长方形和正方形的卡片，图甲是选取了2块不同的卡片，拼成的一个图形，借助图中阴影部分面积的不同表示可以用来验证等式a（a+b）=a2+ab成立．（1）根据图乙，利用面积的不同表示方法，写出一个代数恒等式（a+2b）（a+b）=a2+3ab+2b2；（2）试写出一个与（1）中代数恒等式类似的等式，并用上述拼图的方法说明它的正确性．考点：多项式乘多项式．专题：计算题．分析：（1）根据图形是一个长方形求出长和宽，相乘即可；（2）正方形的面积是2个长方形的面积加上2个正方形的面积，代入求出即可．解答：解：（1）观察图乙得知：长方形的长为：a+2b，宽为a+b，∴面积为：（a+2b）（a+b）=a2+3ab+2b2；（2）如图所示：恒等式是，（a+b）（a+b）=a2+2ab+b2．答：恒等式是a+b）（a+b）=a2+2ab+b2．点评：本题主要考查对多项式乘多项式的理解和掌握，能表示各部分的面积是解此题的关键．25．小明想把一长为60cm，宽为40cm的长方形硬纸片做成一个无盖的长方体盒子，于是在长方形纸片的四个角各剪去一个相同的小正方形．（1）若设小正方形的边长为xcm，求图中阴影部分的面积；（2）当x=5时，求这个盒子的体积．考点：多项式乘多项式；代数式求值．分析：（1）剩余部分的面积即是边长为60﹣2x，40﹣2x的长方形的面积；（2）利用长方体的体积公式先表示出长方形的体积，再把x=5，代入即可．解答：解：（1）（60﹣2x）（40﹣2x）=4x2﹣200x+2400，答：阴影部分的面积为（4x2﹣200x+2400）cm2；（2）当x=5时，4x2﹣200x+2400=1500（cm2），这个盒子的体积为：1500×5=7500（cm3），答：这个盒子的体积为7500cm3．点评：此题主要考查用代数式表示正方形、矩形的面积和体积，需熟记公式，且认真观察图形，得出等量关系．26．（x﹣1）（x﹣2）=（x+3）（x﹣4）+20．考点：多项式乘多项式；解一元一次方程．分析：将方程的两边利用多项式的乘法展开后整理成方程的一般形式求解即可．解答：解：原方程变形为：x2﹣3x+2=x2﹣x﹣12+20整理得：﹣2x﹣6=0，解得：x=﹣3．点评：本题考查了多项式乘多项式及解一元二次方程的知识，解题的关键是利用多项式的乘法对方程进行化简．27．若（x﹣3）（x+m）=x2+nx﹣15，求的值．考点：多项式乘多项式．分析：首先把）（x﹣3）（x+m）利用多项式的乘法公式展开，然后根据多项式相等的条件：对应项的系数相同即可得到m、n的值，从而求解．解答：解：（x﹣3）（x+m）=x2+（m﹣3）x﹣3m=x2+nx﹣15，则解得：．=．点评：本题考查了多项式的乘法法则以及多项式相等的条件，理解多项式的乘法法则是关键．28．小明在进行两个多项式的乘法运算时（其中的一个多项式是b﹣1），把“乘以（b﹣1）”错看成“除以（b﹣1）”，结果得到（2a﹣b），请你帮小明算算，另一个多项式是多少？考点：多项式乘多项式．分析：根据被除式=商×除式，所求多项式是（2a﹣b）（b﹣1），根据多项式乘多项式的法则计算即可．解答：解：设所求的多项式是M，则M=（2a﹣b）（b﹣1）=2ab﹣2a﹣b2+b．点评：本题考查了多项式乘多项式法则，根据被除式、除式、商三者之间的关系列出等式是解题的关键，熟练掌握运算法则也很重要．29．有足够多的长方形和正方形的卡片如图．如果选取1号、2号、3号卡片分别为1张、2张、3张，可拼成一个长方形（不重叠无缝隙）．请画出这个长方形的草图，并运用拼图前后面积之间的关系说明这个长方形的代数意义．考点：多项式乘多项式．分析：先根据题意画出图形，然后求出长方形的长和宽，长为a+2b，宽为a+b，从而求出长方形的面积．解答：解：如图：或a2+3ab+2b2=（a+b）（a+2b）．点评：考查多项式与多项式相乘问题；根据面积的不同表示方法得到相应的等式是解决本题的关键．30．（1）填空：（a﹣1）（a+1）=a2﹣1（a﹣1）（a2+a+1）=a3﹣1（a﹣1）（a3+a2+a+1）=a4﹣1（2）你发现规律了吗？请你用你发现的规律填空：（a﹣1）（a n+a n﹣1+…+a2+a+1）=a n+1﹣1（3）根据上述规律，请你求42012+42011+42010+…+4+1的值．（42013﹣1）．考点：多项式乘多项式．专题：规律型．分析：（1）根据平方差公式和立方差公式可得前2个式子的结果，利用多项式乘以多项式的方法可得出第3个式子的结果；（2）从而总结出规律是：（a﹣1）（a n+a n﹣1+…+a2+a+1）=a n+1﹣1；（3）根据上述结论计算下列式子即可．解答：解：根据题意：（1）（a﹣1）（a+1）=a2﹣1；（a﹣1）（a2+a+1）=a3﹣1；（a﹣1）（a3+a2+a+1）=a4﹣1；（2）（a﹣1）（a n+a n﹣1+a n﹣2+…+a2+a+1）=a n+1﹣1．（3）根据以上分析（1）42012+42011+42010+…+4+1299+298+297+…+2+1，=（4﹣1）（42012+42011+42010+…+4+1），=（42013﹣1）．故答案为：（1）a2﹣1，a3﹣1，a4﹣1；（2）a n+1﹣1；（3）（42013﹣1）．点评：主要考查了学生的分析、总结、归纳能力，规律型的习题一般是从所给的数据和运算方法进行分析，从特殊值的规律上总结出一般性的规律．。

湘教版数学七年级下册_《多项式的乘法》提高训练

《多项式的乘法》提高训练一、选择题1．已知多项式（x2+mx+8）和（x2﹣3x+n）的乘积中不含x2和x3的项，则m、n 的值为（）A．m=﹣1，n=1B．m=2，n=﹣1C．m=2，n=3D．m=3，n=1 2．已知a+b+c=0可得：a+b=﹣c，则代数式（a+b）（b+c）（c+a）+abc的值为（）A．a+b+c B．abc C．2abc D．03．下列各式中，计算正确的是（）A．（﹣5a n+1b）•（﹣2a）=10a n+1bB．（﹣4a2b）•（﹣a2b2）•cC．（﹣3xy）•（﹣x2z）•6xy2=3x3y3zD．4．观察下列两个多项式相乘的运算过程：根据你发现的规律，若（x+a）（x+b）=x2﹣7x+12，则a，b的值可能分别是（）A．﹣3，﹣4B．﹣3，4C．3，﹣4D．3，45．如果（x+a）（5x+1）的乘积中，x的一次项系数为3，则a的值为（）A．2B．﹣2C．D．﹣二、填空题6．若（x+2）（x﹣a）=x2+bx﹣10，则b的值为7．若多项式与单项式2a2b的积是6a3b﹣2a2b2，则该多项式为．8．设A=（x﹣3）（x﹣7），B=（x﹣2）（x﹣8），则A、B的大小关系为．9．已知：a+b=﹣1，ab=1，化简（a﹣2）（b﹣2）的结果是．10．若（x2﹣mx+1）（x﹣2018）的积中，x的二次项系数为零，则m的值是．三、解答题11．计算（1）（﹣2a2）（3ab2﹣5ab3）（2）（5x+2y）•（3x﹣2y）12．已知x﹣y=3，xy=2，求下列代数式的值：（1）（x﹣2）（y+2）（2）x3y﹣2x2y2+xy313．已知多项式A=（x+5）2﹣（2﹣x）（3+x）﹣4．（1）请化简多项式A；（2）若（x+3）2=16，且x＞0，试求A的值．14．若（x2+px﹣）（x2﹣3x+q）的积中不含x项与x3项，求p、q的值；15．已知（x+a）（x2﹣x+c）的乘积中不含x2和x项，求a，c的值．《多项式的乘法》提高训练参考答案与试题解析一、选择题1．已知多项式（x2+mx+8）和（x2﹣3x+n）的乘积中不含x2和x3的项，则m、n 的值为（）A．m=﹣1，n=1B．m=2，n=﹣1C．m=2，n=3D．m=3，n=1【分析】本题需先根据多项式乘多项式的运算法则进行计算，再根据不含x2和x3的项，即可求出答案【解答】解：（x2+mx+8）（x2﹣3x+n）=x4+mx3+8x2﹣3x3﹣3mx2﹣24x+nx2+nmx+8n=x4+（m﹣3）x3+（8﹣3m+n）x2﹣24x+8n，∵不含x2和x3的项，∴m﹣3=0，∴m=3．∴8﹣3m+n=0，∴n=1．故选：D．【点评】本题主要考查了多项式乘多项式，在解题时要根据多项式乘多项式的运算法则进行计算是本题的关键．2．已知a+b+c=0可得：a+b=﹣c，则代数式（a+b）（b+c）（c+a）+abc的值为（）A．a+b+c B．abc C．2abc D．0【分析】直接利用已知得出a+b=﹣c，b+c=﹣a，a+c=﹣b，进而代入求出答案．【解答】解：∵a+b+c=0，∴a+b=﹣c，a+c=﹣b，b+c=﹣a，则原式=（﹣c）×（﹣a）×（﹣b）+abc=﹣abc+abc=0，故选：D．【点评】此题主要考查了多项式乘多项式，正确将原式变形是解题关键．3．下列各式中，计算正确的是（）A．（﹣5a n+1b）•（﹣2a）=10a n+1bB．（﹣4a2b）•（﹣a2b2）•cC．（﹣3xy）•（﹣x2z）•6xy2=3x3y3zD．【分析】单项式与单项式相乘，把它们的系数，相同字母分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式．单项式与多项式相乘，就是用单项式去乘多项式的每一项，再把所得的积相加．依此即可求解．【解答】解：A、（﹣5a n+1b）•（﹣2a）=10a n+2b，此选项错误；B、（﹣4a2b）•（﹣a2b2）•c，此选项正确；C、（﹣3xy）•（﹣x2z）•6xy2=18x4y3z，此选项错误；D、（2a n b3）（﹣ab n﹣1）=﹣a n+1b n+2，此选项错误．故选：B．【点评】考查了单项式乘单项式，单项式乘多项式，关键是熟练掌握计算法则正确进行计算．4．观察下列两个多项式相乘的运算过程：根据你发现的规律，若（x+a）（x+b）=x2﹣7x+12，则a，b的值可能分别是（）A．﹣3，﹣4B．﹣3，4C．3，﹣4D．3，4【分析】根据题意，即可得出a+b=﹣7，ab=12，进而得到a，b的值可能分别是﹣3，﹣4．【解答】解：根据题意，知：a+b=﹣7，ab=12，∴a，b的值可能分别是﹣3，﹣4，故选：A．【点评】本题主要考查完了多项式乘多项式的法则的运用，多项式与多项式相乘，先用一个多项式的每一项乘另外一个多项式的每一项，再把所得的积相加．5．如果（x+a）（5x+1）的乘积中，x的一次项系数为3，则a的值为（）A．2B．﹣2C．D．﹣【分析】根据多项式与多项式相乘的法则把原式变形，根据得出关于a的方程，解之可得．【解答】解：∵（x+a）（5x+1）=5x2+x+5ax+a=5x2+（1+5a）x+a，∴1+5a=3，解得：a=，故选：C．【点评】本题考查的是多项式与多项式相乘的法则，掌握多项式与多项式相乘，先用一个多项式的每一项乘另外一个多项式的每一项，再把所得的积相加是解题的关键．二、填空题6．若（x+2）（x﹣a）=x2+bx﹣10，则b的值为﹣3【分析】由多项式乘以多项式的运算法则求解可求得原式=x2+（2﹣a）x﹣2a，继而可得2﹣a=b，﹣2a=﹣10，则可求得答案．【解答】解：∵（x+2）（x﹣a）=x2+b﹣ax+2x﹣2a=x2+（2﹣a）x﹣2a=x2+bx﹣10，∴2﹣a=b，﹣2a=﹣10，解得：a=5，b=﹣3．故答案为：﹣3．【点评】此题考查了多项式乘多项式的知识．注意熟记多项式乘以多项式的运算法则是关键．7．若多项式与单项式2a2b的积是6a3b﹣2a2b2，则该多项式为3a﹣b．【分析】直接利用整式的除法运算法则计算得出答案．【解答】解：∵多项式与单项式2a2b的积是6a3b﹣2a2b2，∴该多项式为：（6a3b﹣2a2b2）÷2a2b=3a﹣b．故答案为：3a﹣b．【点评】此题主要考查了单项式乘以多项式，正确掌握运算法则是解题关键．8．设A=（x﹣3）（x﹣7），B=（x﹣2）（x﹣8），则A、B的大小关系为A＞B．【分析】根据多项式乘以多项式的法则，先把A、B进行整理，然后比较即可得出答案．【解答】解：∵A=（x﹣3）（x﹣7）=x2﹣10x+21，B=（x﹣2）（x﹣8）=x2﹣10x+16，∴A﹣B=x2﹣10x+21﹣（x2﹣10x+16）=5＞0，∴A＞B，故答案为：A＞B．【点评】本题主要考查多项式乘以多项式的法则，注意不要漏项，漏字母，有同类项的合并同类项．9．已知：a+b=﹣1，ab=1，化简（a﹣2）（b﹣2）的结果是7．【分析】将a+b、ab的值代入到原式=ab﹣2a﹣2b+4=ab﹣2（a+b）+4，计算可得．【解答】解：当a+b=﹣1，ab=1时，原式=ab﹣2a﹣2b+4=ab﹣2（a+b）+4=1﹣2×（﹣1）+4=1+2+4=7，故答案为：7．【点评】本题主要考查多项式乘多项式，解题的关键是掌握多项式乘多项式的运算法则及整体代入思想的运用．10．若（x2﹣mx+1）（x﹣2018）的积中，x的二次项系数为零，则m的值是﹣2018．【分析】直接利用多项式乘以多项式运算法则计算得出答案．【解答】解：∵（x2﹣mx+1）（x﹣2018）的积中，x的二次项系数为零，∴原式=x3﹣2018x2﹣mx2+2018mx+x﹣2018=x2﹣（2018+m）x2+（1+2018m）x﹣2018，∴2018+m=0，解得：m=﹣2018．故答案为：﹣2018．【点评】此题主要考查了多项式乘以多项式，正确掌握运算法则是解题关键．三、解答题11．计算（1）（﹣2a2）（3ab2﹣5ab3）（2）（5x+2y）•（3x﹣2y）【分析】（1）根据单项式乘多项式的计算法则计算即可求解；（2）根据多项式乘多项式的计算法则计算即可求解．【解答】解：（1）（﹣2a2）（3ab2﹣5ab3）=﹣6a3b2+10a3b3；（2）（5x+2y）•（3x﹣2y）=15x2﹣10xy+6xy﹣4y2）=15x2﹣4xy﹣4y2．【点评】考查了单项式乘多项式，多项式乘多项式，关键是熟练掌握计算法则正确进行计算．12．已知x﹣y=3，xy=2，求下列代数式的值：（1）（x﹣2）（y+2）（2）x3y﹣2x2y2+xy3【分析】（1）按照多项式乘以多项式的运算法则进行计算后代入即可求得答案；（2）首先提取公因式xy，然后利用完全平方公式因式分解后代入即可求得答案．【解答】解：（1）原式=xy+2（x﹣y）﹣4=2+6﹣4=4；（2）原式=xy（x2﹣2xy+y2）=xy（x﹣y）2=2×9=18；【点评】本题考查了多项式乘以多项式及因式分解的知识，解题的关键是对算式进行变形，难度不大．13．已知多项式A=（x+5）2﹣（2﹣x）（3+x）﹣4．（1）请化简多项式A；（2）若（x+3）2=16，且x＞0，试求A的值．【分析】（1）原式利用完全平方公式，多项式乘以多项式法则计算，去括号合并即可得到结果；（2）根据题意确定出x的值，代入计算即可求出A的值．【解答】解：（1）A=x2+10x+25﹣6+x+x2﹣4=2x2+11x+15；（2）∵（x+3）2=16，且x＞0，∴x+3=4或x+3=﹣4，∴x=1或x=﹣7（舍去），把x=1代入代数式A中，得：A=28．【点评】此题考查了整式的加减﹣化简求值，熟练掌握运算法则是解本题的关键．14．若（x2+px﹣）（x2﹣3x+q）的积中不含x项与x3项，求p、q的值；【分析】利用多项式乘多项式法则及合并同类项法则化简式子，找出x项与x3令其系数等于0求解．【解答】解：（x2+px﹣）（x2﹣3x+q）=x4+（p﹣3）x3+（q﹣3p﹣）x2+（qp+1）x+q，∵积中不含x项与x3项，∴p﹣3=0，qp+1=0，∴p=3，q=﹣．【点评】本题主要考查了多项式乘多项式，解题的关键是熟练掌握多项式乘多项式法则及合并同类项法则．15．已知（x+a）（x2﹣x+c）的乘积中不含x2和x项，求a，c的值．【分析】根据多项式乘多项式的法则计算，让x2项和x项的系数为0，即可求得a，c的值．【解答】解：（x+a）（x2﹣x+c）=x3﹣x2+cx+ax2﹣ax+ac=x3+（a﹣1）x2+（c﹣a）x+ac，∵（x+a）（x2﹣x+c）的乘积中不含x2和x项，∴a﹣1=0且c﹣a=0，则a=c=1．【点评】本题考查了多项式乘以多项式，注意当要求多项式中不含有哪一项时，应让这一项的系数为0．。

多项式乘多项式基础题30道填空题附详细答案

9.3 多项式乘多项式基础题汇编（2）一．填空题（共30小题）1．（2014•润州区校级模拟）计算：（a+2）（2a﹣3）=．2．（2014秋•花垣县期末）计算：（2x﹣1）2=；（2x﹣2）（3x+2）=．3．（2014秋•花垣县期末）计算：（x﹣2）（x+3）=；（﹣2x﹣3）（﹣2x+3）=．4．（2014春•富宁县校级期末）已知（x+a）（x+b）=x2+5x+ab，则a+b=．5．（2014秋•蓟县期末）若（x+2）（x﹣m）=x2﹣3x﹣n，则m=，n=．6．（2013秋•东城区期末）计算：（m+2）（m﹣2）﹣（m﹣1）（m+5）=．7．（2013秋•孟津县期末）要使（x2+ax+1）（3x2+3x+1）的展开式中不含x3项，则a=．8．（2014春•北仑区校级期中）已知m+n=2，mn=﹣2，则（1+m）（1+n）的值为．9．（2014春•东营区校级期中）已知：（x+3）（x+p）=x2+mx+36，则p=，m=．10．（2014春•贺兰县校级期中）若（y+3）（y﹣2）=y2+my+n，则m、n的值分别为．11．（2014春•雁塔区校级期中）如图：有足够的长方形和正方形卡片，如果拼成的长方形（不重叠无缝隙）的长和宽分别是2a+b和a+b，若应选取1号卡片x张、2号卡片y张、3号卡片z张，则x+y+z=．12．（2014秋•宜宾校级期中）如果（x+m）与（x+）的乘积中不含关于x的一次项，则m=．13．（2014秋•如皋市校级期中）若多项式x2+ax+b是（x+1）与（x﹣2）乘积的结果，则a+b的值为．14．（2014春•崇州市校级期中）若（x2+kx+5）（x3+2x+3）的展开式中不含x2的项，则k的值为．15．（2014春•阜宁县期中）（x2+mx﹣1）与（x﹣2）的积中不含x2项，则m的值是．16．（2014秋•启东市校级月考）已知（x﹣4）（x+9）=x2+mx+n，则m+n=．17．（2014秋•常州校级月考）①用甲图所示的大小正方形和长方形卡片若干张，拼成一个长为2a+b，宽为a+b的矩形，需要A类卡片张，B类卡片张，C类卡片张．②现有长为a+3b，宽为a+b的长方形（如乙图），你能用上属三类卡片拼出这个长方形吗？试试看！18．（2013春•桐乡市期末）观察下列各式的计算结果与相乘的两个多项式之间的关系：（x+1）（x2﹣x+1）=x3+1；（x+2）（x2﹣2x+4）=x3+8；（x+3）（x2﹣3x+9）=x3+27．请根据以上规律填空：（x+y）（x2﹣xy+y2）=．19．（2012秋•越秀区校级期末）若（x﹣2）（x+m）=x2+nx﹣6，则m=n=．20．（2013秋•万州区校级期中）（x+a）与5（x+2）的乘积中不含x的一次项，则a=．21．（2013秋•东安县校级期中）在（ax2+bx﹣3）（x2﹣x+8）的结果中不含x3和x项，则a=，b=．22．（2013秋•川汇区校级月考）若（x2﹣mx+1）（x+2）的积中x的二次项系数为零，则m的值为．23．（2013春•西湖区校级月考）若（x+m）（x﹣3）=x2+nx﹣15，则m=，n=．24．（2012•润州区校级模拟）计算：﹣3x2y3•x2y2=，（x+1）（x﹣3）=．25．（2012•思明区校级模拟）已知a﹣b=2，（a﹣1）（b+2）＜ab，则a的取值范围是．26．（2012秋•南陵县期末）若（x+2）（x﹣2）=x2﹣mx﹣n，则m=，n=．27．（2012春•姜堰市期末）若干张如图所示的A类，B类正方形卡片和C类长方形卡片，如果要拼成一个长为（2a+b）宽为（a+b）的大长方形，则需要C类卡片张．28．（2012春•金阊区校级期中）计算的结果不含关于字母x的一次项，那么m等于．29．（2012秋•简阳市校级期中）若多项式x2+ax﹣b=（x﹣2）（x+1），则a b=．30．（2012春•江阴市校级期中）计算：（﹣p）2•（﹣p）3=；=；2xy•（）=﹣6x2yz；（5﹣a）（6+a）=．9.3 多项式乘多项式基础题汇编（2）参考答案与试题解析一．填空题（共30小题）1．（2014•润州区校级模拟）计算：（a+2）（2a﹣3）=2a2+a﹣6．考点：多项式乘多项式．分析：根据多项式乘以多项式的法则，可表示为（a+b）（m+n）=am+an+bm+bn，计算即可．解答：解：（a+2）（2a﹣3）=2a2﹣3a+4a﹣6=2a2+a﹣6．故答案为：2a2+a﹣6．点评：本题主要考查多项式乘以多项式的法则．注意不要漏项，漏字母，有同类项的合并同类项．2．（2014秋•花垣县期末）计算：（2x﹣1）2=4x2﹣4x+1；（2x﹣2）（3x+2）=6x2﹣2x﹣4．考点：多项式乘多项式；完全平方公式．分析：根据根据完全平方公式和多项式乘多项式的法则分别进行计算即可求出答案．解答：解：（2x﹣1）2=4x2﹣4x+1；（2x﹣2）（3x+2）=6x2+4x﹣6x﹣4=6x2﹣2x﹣4；故答案为：4x2﹣4x+1，6x2﹣2x﹣4．点评：本题主要考查了多项式乘多项式和完全平方公式，熟记公式结构和多项式乘多项式的法则是解题的关键．3．（2014秋•花垣县期末）计算：（x﹣2）（x+3）=x2+x﹣6；（﹣2x﹣3）（﹣2x+3）=4x2﹣9．考点：多项式乘多项式；平方差公式．分析：（x﹣2）（x+3）根据多项式乘以多项式的法则，可表示为（a+b）（m+n）=am+an+bm+bn，计算即可；（﹣2x﹣3）（﹣2x+3）根据平方差公式计算即可．解答：解：（x﹣2）（x+3）=x2+3x﹣2x﹣6=x2+x﹣6；（﹣2x﹣3）（﹣2x+3）=（2x+3）（2x﹣3）=4x2﹣9．故答案为：x2+x﹣6；4x2﹣9．点评：本题主要考查多项式乘以多项式的法则．注意不要漏项，漏字母，有同类项的合并同类项．同时考查了平方差公式：两个数的和与这两个数的差相乘，等于这两个数的平方差．即（a+b）（a﹣b）=a2﹣b2．4．（2014春•富宁县校级期末）已知（x+a）（x+b）=x2+5x+ab，则a+b=5．考点：多项式乘多项式．专题：计算题．分析：将等式的左边展开，由对应相等得答案．解答：解：∵（x+a）（x+b）=x2+5x+ab，∴x2+（a+b）x+ab=x2+5x+ab，∴a+b=5，故答案为5．点评：本题考查了多项式乘以多项式，是基础知识要熟练掌握．5．（2014秋•蓟县期末）若（x+2）（x﹣m）=x2﹣3x﹣n，则m=5，n=10．考点：多项式乘多项式．分析：根据多项式乘以多项式的法则，可表示为（a+b）（m+n）=am+an+bm+bn，计算即可．解答：解：∵（x+2）（x﹣m）=x2﹣mx+2x﹣2m=x2+（﹣m+2）x﹣2m=x2﹣3x﹣n，∴﹣m+2=﹣3，n=2m，∴m=5，n=10；故答案为：5，10．点评：本题主要考查多项式乘以多项式的法则．注意不要漏项，漏字母，有同类项的合并同类项．6．（2013秋•东城区期末）计算：（m+2）（m﹣2）﹣（m﹣1）（m+5）=1﹣4m．考点：多项式乘多项式；平方差公式．分析：先运用平方差公式和多项式乘多项式的法则进行计算，再合并同类项．解答：解：（m+2）（m﹣2）﹣（m﹣1）（m+5）=m2﹣4﹣m2﹣4m+5=1﹣4m．故答案为：1﹣4m．点评：本题主要考查了平方差公式和多项式乘多项式．运用平方差公式计算时，关键要找相同项和相反项，其结果是相同项的平方减去相反项的平方．7．（2013秋•孟津县期末）要使（x2+ax+1）（3x2+3x+1）的展开式中不含x3项，则a=﹣1．考点：多项式乘多项式．分析：先展开式子，找出所有x3项的系数，令其为0，即可求a的值．解答：解：∵（x2+ax+1）（3x2+3x+1）=4x4+3x3+x2+3ax3+3ax2+ax+3x2+3x+1，=4x4+（3a+3）x3+（1+3a+3）x2+（a+3）x+1，又∵展开式中不含x3项∴3a+3=0，解得：a=﹣1．故答案为：﹣1．点评：本题主要考查了多项式乘多项式的运算，注意当要求多项式中不含有哪一项时，应让这一项的系数为0，注意各项符号的处理．8．（2014春•北仑区校级期中）已知m+n=2，mn=﹣2，则（1+m）（1+n）的值为1．考点：多项式乘多项式．分析：根据多项式乘以多项式的法则，可表示为（a+b）（m+n）=am+an+bm+bn，再代入计算即可．解答：解：∵m+n=2，mn=﹣2，∴（1+m）（1+n）=1+n+m+mn=1+2﹣2=1；故答案为：1．点评：本题主要考查多项式乘以多项式，掌握多项式乘以多项式的法则是本题的关键．注意不要漏项，漏字母，有同类项的合并同类项．9．（2014春•东营区校级期中）已知：（x+3）（x+p）=x2+mx+36，则p=12，m=15．考点：多项式乘多项式．分析：利用多项式乘以多项式法则，直接去括号，进而让各项系数相等求出即可．解答：解：∵（x+3）（x+p）=x2+mx+36，∴x2+（p+3）x+3p=x2+mx+36，∴3p=36，p+3=m，解得：p=12，m=15，故答案为：12，15．点评：此题主要考查了多项式乘以多项式，正确计算得出对应系数相等是解题关键．10．（2014春•贺兰县校级期中）若（y+3）（y﹣2）=y2+my+n，则m、n的值分别为1、6．考点：多项式乘多项式．分析：先根据多项式乘以多项式的法则计算（y+3）（y﹣2），再根据多项式相等的条件即可求出m、n的值．解答：解：∵（y+3）（y﹣2）=y2﹣2y+3y﹣6=y2+y﹣6，∵（y+3）（y﹣2）=y2+my+n，∴y2+my+n=y2+y﹣6，∴m=1，n=﹣6．故答案为：1、6．点评：本题主要考查多项式乘以多项式的法则：（a+b）（m+n）=am+an+bm+bn．注意不要漏项，漏字母，有同类项的合并同类项．11．（2014春•雁塔区校级期中）如图：有足够的长方形和正方形卡片，如果拼成的长方形（不重叠无缝隙）的长和宽分别是2a+b和a+b，若应选取1号卡片x张、2号卡片y张、3号卡片z张，则x+y+z=6．考点：多项式乘多项式．分析：根据多项式乘多项式的法则得出需要用的卡片数，再把它们相加即可得出答案．解答：解：∵（2a+b）（a+b）=2a2+3ab+b2，∴需要用1号卡2张，2号卡1张，3号卡3张，∴x+y+z=2+1+3=6；故答案为：6．点评：此题考查了多项式乘以多项式，掌握多项式乘多项式的法则是本题的关键，多项式乘以多项式的法则，可表示为（a+b）（m+n）=am+an+bm+bn．12．（2014秋•宜宾校级期中）如果（x+m）与（x+）的乘积中不含关于x的一次项，则m=﹣．考点：多项式乘多项式．专题：计算题．分析：原式利用多项式乘多项式法则计算，根据乘积中不含x的一次项，求出m的值即可．解答：解：原式=x2+（m+）x+m，由结果不含x的一次项，得到m+=0，解得：m=﹣，故答案为：﹣点评：此题考查了多项式乘多项式，熟练掌握运算法则是解本题的关键．13．（2014秋•如皋市校级期中）若多项式x2+ax+b是（x+1）与（x﹣2）乘积的结果，则a+b的值为﹣3．考点：多项式乘多项式．分析：直接利用多项式乘以多项式运算法则求出a，b的值，进而得出答案．解答：解：∵x2+ax+b=（x+1）（x﹣2），∴x2+ax+b=x2﹣x﹣2，∴a=﹣1，b=﹣2，∴a+b=﹣3．故答案为：﹣3．点评：此题主要考查了多项式乘以多项式，正确掌握运算法则是解题关键．14．（2014春•崇州市校级期中）若（x2+kx+5）（x3+2x+3）的展开式中不含x2的项，则k的值为﹣1.5．考点：多项式乘多项式．分析：先展开式子，找出所有x2项的系数，令其为0，即可求k的值．解答：解：∵（x2+kx+5）（x3+2x+3）=x5+2x3+3x2+kx4+2kx2+3kx+5x3+10x+15，=x5+kx4+7x3+（3+2k）x2+（3k+10）x+15，又∵展开式中不含x2项，∴3+2k=0，解得：k=﹣1.5．故答案为：﹣1.5．点评：本题主要考查了多项式乘多项式的运算，注意当要求多项式中不含有哪一项时，应让这一项的系数为0，注意各项符号的处理．15．（2014春•阜宁县期中）（x2+mx﹣1）与（x﹣2）的积中不含x2项，则m的值是2．考点：多项式乘多项式．分析：先根据多项式乘多项式的运算法则（a+b）（m+n）=am+an+bm+bn，先展开，再根据题意，二次项的系数等于0列式求解即可．解答：解：（x2+mx﹣1）（x﹣2）=x3+（﹣2+m）x2+（﹣1﹣2m）x+2，∵不含x2项，∴﹣2+m=0，解得m=2．故答案为：2．点评：本题主要考查单项式与多项式的乘法，掌握运算法则和不含某一项就让这一项的系数等于0是解题的关键．16．（2014秋•启东市校级月考）已知（x﹣4）（x+9）=x2+mx+n，则m+n=﹣31．考点：多项式乘多项式．专题：计算题．分析：已知等式左边利用多项式乘以多项式法则计算，再利用多项式相等的条件求出m与n的值，即可求出m+n的值．解答：解：∵（x﹣4）（x+9）=x2+5x﹣36=x2+mx+n，∴m=5，n=﹣36，则m+n=5﹣36=﹣31．故答案为：﹣31．点评：此题考查了多项式乘以多项式，熟练掌握运算法则是解本题的关键．17．（2014秋•常州校级月考）①用甲图所示的大小正方形和长方形卡片若干张，拼成一个长为2a+b，宽为a+b的矩形，需要A类卡片2张，B类卡片3张，C类卡片1张．②现有长为a+3b，宽为a+b的长方形（如乙图），你能用上属三类卡片拼出这个长方形吗？试试看！考点：多项式乘多项式．专题：计算题．分析：①利用多项式乘以多项式法则计算（2a+b）（a+b），得到结果，即可做出判断；②利用多项式乘以多项式法则计算（a+3b）（a+b），得到结果，即可做出判断．解答：解：①长为2a+b，宽为a+b的矩形面积为（2a+b）（a+b）=2a2+3ab+b2，A图形面积为a2，B图形面积为ab，C图形面积为b2，则可知需要A类卡片2张，B类卡片3张，C类卡片1张．故本题答案为：2；3；1；②∵现有长为a+3b，宽为a+b的长方形，∴（a+3b）（a+b）=a2+4ab+3b2，∵A图形面积为a2，B图形面积为ab，C图形面积为b2，∴可知需要A类卡片1张，B类卡片4张，C类卡片3张；（2a+b）（a+b）=2a2+3ab+b2，则拼成一个长为2a+b，宽为a+b的矩形，需要A类卡片2张，B类卡片3张，C类卡片1张．点评：此题考查了多项式乘多项式，熟练掌握运算法则是解本题的关键．18．（2013春•桐乡市期末）观察下列各式的计算结果与相乘的两个多项式之间的关系：（x+1）（x2﹣x+1）=x3+1；（x+2）（x2﹣2x+4）=x3+8；（x+3）（x2﹣3x+9）=x3+27．请根据以上规律填空：（x+y）（x2﹣xy+y2）=x3+y3．考点：多项式乘多项式．专题：规律型．分析：根据所给的多项式乘多项式的运算法则以及得出的规律，即可得出（x+y）（x2﹣xy+y2）=x3+y3．解答：解：∵（x+1）（x2﹣x+1）=x3+1；（x+2）（x2﹣2x+4）=x3+8；（x+3）（x2﹣3x+9）=x3+27，∴（x+y）（x2﹣xy+y2）=x3+y3；故答案为：x3+y3；点评：此题考查了多项式乘多项式，掌握多项式乘多项式的法则和得出的规律是本题的关键，注意不要漏项，漏字母，有同类项的合并同类项．19．（2012秋•越秀区校级期末）若（x﹣2）（x+m）=x2+nx﹣6，则m=3n=1．考点：多项式乘多项式．分析：先把原式进行变形为x2+（m﹣2）x﹣2m，再根据原式等于x2+nx﹣6，求出m的值，从而求出n的值．解答：解：∵（x﹣2）（x+m）=x2+mx﹣2x﹣2m=x2+（m﹣2）x﹣2m又∵（x﹣2）（x+m）=x2+nx﹣6，∴x2+（m﹣2）x﹣2m=x2+nx﹣6，∴m﹣2=n，2m=6，解得：m=3，n=1．故答案为：3，1．点评：此题考查了多项式乘多项式，根据项式乘多项式的运算法则先把原式进行变形是解题的关键，注意不要漏项，漏字母．20．（2013秋•万州区校级期中）（x+a）与5（x+2）的乘积中不含x的一次项，则a=﹣2．考点：多项式乘多项式．分析：把式子展开，找到所有x项的系数，令其和为0，求解即可．解答：解：∵5（x+a）（x+2）=5（x2+ax+2x+2a）=5x2+5（a+2）x+5a，又∵乘积中不含x一次项，∴a+2=0，解得a=﹣2．故答案为：﹣2．点评：本题主要考查了多项式乘多项式，注意当要求多项式中不含有哪一项时，应让这一项的系数为0．21．（2013秋•东安县校级期中）在（ax2+bx﹣3）（x2﹣x+8）的结果中不含x3和x项，则a=﹣，b=﹣．考点：多项式乘多项式．分析：首先利用多项式乘法法则计算出（ax2+bx﹣3）（x2﹣x+8），再根据积不含x3和x项，可得含x3的项和含x的项的系数等于零，即可求出a与b的值．解答：解：（ax2+bx﹣3）（x2﹣x+8）=ax4﹣ax3+8ax2+bx3﹣bx2+8bx﹣3x2+x﹣24=ax4+（﹣a+b）x3+（8a﹣b﹣3）x2+（8b+）x﹣24，∵积不含x3的项，也不含x的项，∴﹣a+b=0，8b+=0，解得：b=﹣，a=﹣，故答案为：﹣，﹣．点评：此题主要考查了多项式乘以多项式，关键是掌握多项式与多项式相乘的法则：多项式与多项式相乘，先用一个多项式的每一项乘另外一个多项式的每一项，再把所得的积相加．22．（2013秋•川汇区校级月考）若（x2﹣mx+1）（x+2）的积中x的二次项系数为零，则m的值为2．考点：多项式乘多项式．专题：计算题．分析：原式利用多项式乘以多项式法则计算，根据结果中x的二次项系数为零，求出m的值即可．解答：解：原式=x3+（2﹣m）x2﹣（2m﹣1）x+2，由结果中x的二次项系数为0，得到2﹣m=0，解得：m=2，故答案为：2点评：此题考查了多项式乘多项式，熟练掌握运算法则是解本题的关键．23．（2013春•西湖区校级月考）若（x+m）（x﹣3）=x2+nx﹣15，则m=5，n=2．考点：多项式乘多项式．分析：首先把（x+m）（x﹣3）利用多项式的乘法公式展开，然后根据多项式相等的条件：对应项的系数相同即可得到关于m、n的方程，从而求解．解答：解：（x+m）（x﹣3）=x2+（m﹣3）x﹣3m，则，解得：．故答案是：5，2．点评：本题考查了多项式的乘法法则以及多项式相等的条件，理解多项式的乘法法则是关键．24．（2012•润州区校级模拟）计算：﹣3x2y3•x2y2=﹣3x4y5，（x+1）（x﹣3）=x2﹣2x﹣3．考点：多项式乘多项式；单项式乘单项式．分析：分别利用单项式乘以单项式、多项式乘以多项式的运算法则进行计算即可．解答：解：﹣3x2y3•x2y2=﹣3x2+2y3+2=﹣3x4y5（x+1）（x﹣3）=x2﹣3x+x﹣3=x2﹣2x﹣3 故答案为：﹣3x4y5，x2﹣2x﹣3点评：本题考查了整式的有关运算，单项式乘以单项式时，系数和系数相乘作为结果的系数，相同字母和相同字母按同底数幂的乘法计算即可．25．（2012•思明区校级模拟）已知a﹣b=2，（a﹣1）（b+2）＜ab，则a的取值范围是a＜0．考点：多项式乘多项式；解一元一次不等式．分析：先将条件变形为b=a﹣2，然后代入不等式，最后解一个关于a的不等式就可以得出结论．解答：解：∵a﹣b=2，∴b=a﹣2，∴（a﹣1）（a﹣2+2）＜a（a﹣2），∴a2﹣a＜a2﹣2a，∴a＜0．故答案为：a＜0点评：本题考查了单项式乘以多项式的运用，一元一次不等式的解法的运用，在解答过程中对不等式的性质3要正确理解．26．（2012秋•南陵县期末）若（x+2）（x﹣2）=x2﹣mx﹣n，则m=0，n=4．考点：多项式乘多项式．分析：首先利用平方差公式计算（x+2）（x﹣2），然后根据对应项的系数相同即可求得m、n的值．解答：解：（x+2）（x﹣2）=x2﹣4=x2﹣mx﹣n，则m=0，n=4．故答案是：0，4．点评：本题考查了平方差公式，理解多项式相等的条件是关键．27．（2012春•姜堰市期末）若干张如图所示的A类，B类正方形卡片和C类长方形卡片，如果要拼成一个长为（2a+b）宽为（a+b）的大长方形，则需要C类卡片3张．考点：多项式乘多项式．专题：计算题．分析：根据长乘以宽表示出大长方形的面积，即可确定出C类卡片的张数．解答：解：根据题意得：（2a+b）（a+b）=2a2+3ab+b2，∵一张C类卡片面积为ab，∴需要C类卡片3张．故答案为：3．点评：此题考查了多项式乘多项式，弄清题意是解本题的关键．28．（2012春•金阊区校级期中）计算的结果不含关于字母x的一次项，那么m等于．考点：多项式乘多项式．专题：计算题．分析：根据乘法公式：（x+a）（x+b）=x2+（a+b）x+ab得到（x+m）（x+）=x2+（m+）x+m，然后根据题意得到m+=0，解方程即可得到m的值．解答：解：（x+m）（x+）=x2+（m+）x+m，∵的结果不含关于字母x的一次项，∴m+=0，∴m=﹣．故答案为﹣．点评：本题考查了多项式乘多项式：把一个多项式的每一项与另一多项式相乘，即多项式乘多项式转化为单项式乘多项式，再进行单项式乘多项式，然后进行合并同类项；记住乘法公式：（x+a）（x+b）=x2+（a+b）x+ab．29．（2012秋•简阳市校级期中）若多项式x2+ax﹣b=（x﹣2）（x+1），则a b=1．考点：多项式乘多项式．分析：先根据多项式乘以多项式的法则计算（x﹣2）（x+1），再比较等式两边，得出x的一次项系数为a，常数项为﹣b，然后将a，b的值代入计算即可．解答：解：∵（x﹣2）（x+1）=x2﹣x﹣2，∴x2+ax﹣b=x2﹣x﹣2．比较两边系数，得a=﹣1，b=2，∴a b=（﹣1）2=1．故答案为1．点评：本题考查了多项式乘以多项式的法则，用到的知识点为：（x+a）（x+b）=x2+（a+b）x+ab．30．（2012春•江阴市校级期中）计算：（﹣p）2•（﹣p）3=﹣p5；=﹣a6b3；2xy•（﹣3xz）=﹣6x2yz；（5﹣a）（6+a）=﹣a2﹣a+30．考点：多项式乘多项式；同底数幂的乘法；幂的乘方与积的乘方；单项式乘单项式．分析：根据同底数幂的乘法、积的乘方和幂的乘方、单项式除以单项式法则、多项式乘以多项式法则求出每个式子的值即可．解答：解：（﹣p）2•（﹣p）3=（﹣p）5=﹣p5，（﹣a2b）3=（﹣）3•（a2）3b3=﹣a6b3，∵﹣6x2yz÷2xy=﹣3xz，∴2xy•（﹣3xz）=﹣6x2yz，（5﹣a）（6+a）=30+5a﹣6a﹣a2=30﹣a﹣a2=﹣a2﹣a+30，故答案为：﹣p5，﹣a6b3，﹣3xz，﹣a2﹣a+30．点评：本题考查了同底数幂的乘法、积的乘方和幂的乘方、单项式除以单项式法则、多项式乘以多项式法则的应用．。

多项式乘多项式试题附答案

多项式乘多项式试题精选(二)一 •填空题(共13小题)1 •如图，正方形卡片 A 类、B 类和长方形卡片 C 类各若干张，如果要拼一个长为(2a+b ),宽为(a+b )的长方形,则需要C 类卡片张.2. ____________________________________________________________ ( x+3 )与(2x - m )的积中不含 x 的一次项，则 m= _____________________________________________________________ •23 .若(x+p ) (x+q ) =x +mx+24 , p , q 为整数，则 m 的值等于 __________________________ .4. 如图，已知正方形卡片A 类、B 类和长方形卡片C 类各若干张，如果要拼成一个长为 (a+2b )、宽为(a+b )的大长方形，则需要 A 类卡片 _______________________ 张，B 类卡片 ___________________ 张，C 类卡片 ___________________ 张.5. 计算：233 2 (-P )? (- p )= ____________ ；〔-可a b 〕= ___________________ ； 2xy? ( _________________ ) = - 6x yz ; (5 - a ) (6+a ) = ___________ .6 .计算(x 2 - 3x+1) (mx+8)的结果中不含 x 2叽则常数 m 的值为 _________________________________ .B 类2块，C 类1块，若要拼成一个正方形到还需 B 类地砖_10. 一块长m 米，宽n 米的地毯，长、宽各裁掉 2米后，恰好能铺盖一间房间地面，问房间地面的面积是平方米.11 .若(x+m ) (x+n ) =x 2 - 7x+mn ，则-m - n 的值为 __________________________ .12 .若(x 2+mx+8 ) (x 2- 3x+n )的展开式中不含 x 3和x 2项，贝V mn 的值是 _____________________________ .2 2 313. _______________________________________________________________________________________ 已知 x 、y 、a 都是实数，且 |x|=1 - a , y = (1 - a ) (a - 1 - a ),贝V x+y+a +1 的值为 _______________________________________________ 二•解答题(共7.如图是三种不同类型的地砖，若现有 A 类4块, 8. 2 若(x+5) (x - 7) =x +mx+ n ，贝H m= ,n=9. (x+a ) (x+ 的计算结果不含 x 项，则a 的值是17小题)14. 若(X2+2nx+3 ) (x2-5x+m )中不含奇次项，求m、n的值.15. 化简下列各式：(1)(3x+2y) ( 9X2- 6xy+4y2);(2)( 2X - 3) (4x2+6xy+9 );(3)(3m-丄)(丄m2+2m+丄)；2 3 4 6 9(4)(a+b) (a2- ab+b2) (a- b) (X+ab+b2)16. 计算:(1)( 2X - 3) ( X - 5);(2)(a2-b3) ( a2+b3)17 .计算：(1)-( 2a- b) +[a -( 3a+4b)](2) (a+b) (a2- ab+b2)18. (X+7) (X - 6)-( X - 2) (X+1 )19. 计算：(3a+1) (2a- 3)-( 6a- 5) (a- 4)2 220 .计算：(a - b) (a+ab+b )21.若(x2+px --) (x2- 3x+q)的积中不含x项与x3项,3(1)求p、q的值；(2)求代数式(-2p2q) 2+ (3pq) -1+p2012q2014的值.22 .先化简，再求值：5 ( 3x2y- xy2)- 4( - xy2+3x2y)，其中x= - 2, y=3 .23 .若(x - 1) (x2+mx+n) =x3- 6x2+11x- 6，求m, n 的值.24.如图，有多个长方形和正方形的卡片，图甲是选取了2块不同的卡片，拼成的一个图形，借助图中阴影部分面积的不同表示可以用来验证等式 a (a+b) =a2+ab成立.(1)根据图乙，利用面积的不同表示方法，写出一个代数恒等式;(2)试写出一个与(1)中代数恒等式类似的等式，并用上述拼图的方法说明它的正确性.25.小明想把一长为60cm,宽为40cm的长方形硬纸片做成一个无盖的长方体盒子，于是在长方形纸片的四个角各剪去一个相同的小正方形.(1)若设小正方形的边长为xcm，求图中阴影部分的面积；(2)当x=5时，求这个盒子的体积.26.( x—1) (x—2) = (x+3) ( x—4) +20 .2 - 227.若(x-3)( x+m)=x2+nx - 15,求的值.28•小明在进行两个多项式的乘法运算时（其中的一个多项式是b—1），把乘以（b- 1）”错看成除以（b- 1）结果得到（2a—b），请你帮小明算算，另一个多项式是多少？29. 有足够多的长方形和正方形的卡片如图.如果选取1号、2号、3号卡片分别为1张、2张、3张，可拼成一个长方形（不重叠无缝隙）•请画出这个长方形的草图，并运用拼图前后面积之间的关系说明这个长方形的代数意义.多项式乘单项式试题精选（二）参考答案与试题解析一•填空题（共13小题）1 •如图，正方形卡片A类、B类和长方形卡片C类各若干张，如果要拼一个长为（2a+b）,宽为（a+b）的长方形, 则需要C类卡片3张.考点：多项式乘多项式.分析：根据长方形的面积等于长乘以宽列式，再根据多项式的乘法法则计算，然后结合卡片的面积即可作出判断.解答：解：长为2a+b，宽为a+b的矩形面积为（2a+b）（a+b）=2a2+3ab+b2，A图形面积为a2，B图形面积为b2，C图形面积为ab，则可知需要A类卡片2张，B类卡片1张，C类卡片3张.故答案为：3 •点评：此题主要考查了多项式乘多项式，掌握多项式乘以多项式的法则是本题的关键.注意不要漏项，漏字母, 有同类项的合并同类项.2.（x+3 ）与（2x - m）的积中不含x的一次项，则m= 6考点：多项式乘多项式.专题：计算题.分析：先求出（x+3 ）与（2x m）的积，再令x的一次项为0即可得到关于m的一兀一次方程，求出m的值即可.解答：解：•/ (x+3) ( 2x - m) =2x2+ (6- m) x- 3m , ••• 6 - m=0，解得m=6 .故答案为：6.点评：本题考查的是多项式乘以多项式的法则，即先用一个多项式的每一项乘另外一个多项式的每一项，再把所得的积相加.23. 若(x+p) (x+q ) =x +mx+24 , p, q 为整数，则m 的值等于10, 11, 14, 25考点：多项式乘多项式.分析：根据多项式的乘法法则，可得一个多项式，根据多项式相等，可得对应项相等，由P?q-24, p, q为整数,可得p, q的值，再根据p+q-m，可得m的值.解答：2解：•/ (x+p) ( x+q) -x +mx+24 ,• p-24, q-1; p-12, q-2; p-8, q-3; p-6, q-4, ■/ 当p-24, q-1 时，m-p+q-25 ,当p-12 , q-2 时，m-p+q-14 ,当p-8, q-3 时，m-p+q-11 ,当p-6 , q-4 时，m-p+q-10 ,故答案为：10, 11, 14, 25.点评：本题考察了多项式，先根据多项式的乘法法则计算，分类讨论p, q是解题关键.4. 如图，已知正方形卡片 A 类、B 类和长方形卡片 C 类各若干张，如果要拼成一个长为 (a+2b )、宽为(a+b )的大长方形，则需要 A 类卡片 1张，B 类卡片 2张，C 类卡片 3张.考点：多项式乘多项式.解：如图，要拼成一个长为(a+2b )、宽为(a+b )的大长方形，则需要 A 类卡片1张，B 类卡片2张，C 类卡片3张.点评：本题主要考查了多项式乘多项式，解题的关键是根据边长组成图形.5. 计算：(-P )2? (- p ) 3= - p 5；(一占)汇 ~~r a 6b 3 ； 2xy? ( - 3xz ) = - 6x 2yz ；(5 - a ) (6+a )= - 2 82a - a+30 .考点：多项式乘多项式；同底数幕的乘法；幕的乘方与积的乘方；单项式乘单项式.分析：根据同底数幕的乘法、积的乘方和幕的乘方、单项式除以单项式法则、多项式乘以多项式法则求出每个式子的值即可.解答：解：(-p ) 2? (- p ) 3= (- p ) 5= - p 5,(-抄)3=(-丄)3? (a 2) 3b 3= -Aa 6b 3,2 T - 6x yz 吃xy= - 3xz ,2••• 2xy? (- 3xz ) = - 6x yz ,2 2 2 (5- a ) ( 6+a ) =30+5a - 6a - a 2=30 - a - a 2= - a 2- a+30, 故答案为：-p 5,-丄a 6b 3,- 3xz ，- ai 2- a+30.点评：本题考查了同底数幕的乘法、积的乘方和幕的乘方、单项式除以单项式法则、多项式乘以多项式法则的应用.6 .计算(x 2 - 3x+1) (mx+8)的结果中不含考点：多项式乘多项式. 分析：把式子展开，找到所有 x 2项的所有系数，令其为 0，可求出m 的值. 解答：解：■/ (x 2- 3x+1 ) ( mx+8 ) =mx 4+8x 2- 3mx 2- 24x+mx+8 . 又•••结果中不含x 2的项，g• 8 - 3m=0，解得 mn-2.分析: 解答: 根据边长组成图形•数出需要A 类卡片1张，B 类卡片2张，C 类卡片3张.x 2叽则常数m 的值为故答案为：」•3点评：本题主要考查了多项式乘多项式的运算，注意当要求多项式中不含有哪一项时，应让这一项的系数为 o .考点：多项式乘多项式.分析：分别计算出4块A 的面积和2块B 的面积、1块C 的面积，再计算这三种类型的砖的总面积，用完全平方公式化简后，即可得出少了哪种类型的地砖.解答：解：4块A 的面积为：4>m>m=4m 2;2块B 的面积为：2 X m >n=2mn ;1块C 的面积为n>h=n 2；那么这三种类型的砖的总面积应该是：2 2 2 2 24m +2mn+n =4m +4mn+n — 2mn= (2m+n )- 2mn ,因此，少2块B 型地砖，故答案为：2 • 点评：本题考查了完全平方公式的几何意义，立意较新颖，注意面积的不同求解是解题的关键，对此类问题要深入理解.28 .若(x+5) (x - 7) =x +mx+ n ，贝U m= -2, n= - 35 •考点：多项式乘多项式. 分析：已知等式左边利用多项式乘以多项式法则计算，利用多项式相等的条件即可求出m 与n 的值.解答：解：(x+5) (x - 7) =x 2 - 2x - 35=x 2+mx+n ,贝U m= - 2, n= - 35.故答案为：-2, - 35.点评：此题考查了多项式乘以多项式，熟练掌握运算法则是解本题的关键. 9.( x+a ) (x+〒)的计算结果不含 x 项，则a 的值是—丄_.考点：多项式乘多项式.分析：多项式乘多项式法则，先用一个多项式的每一项乘以另一个多项式的每一项，再把所得的积相加，依据法则运算，展开式不含关于字母 x的一次项，那么一次项的系数为 0,就可求a 的值.又•••不含关于字母x 的一次项，—,解得a= -丄.点评：本题考查了多项式乘多项式法则，相乘后不含哪一项，就让这一项的系数等于 0,难度适中.7•如图是三种不同类型的地砖，若现有 A 类4块, B 类2块，C 类1块，若要拼成一个正方形到还需B 类地砖 210. 一块长m米，宽n米的地毯，长、宽各裁掉2米后，恰好能铺盖一间房间地面，问房间地面的面积是(m 2) (n - 2)或(mn - 2m - 2n+4) 平方米.考点：多项式乘多项式.分析：根据题意得出算式是(m-2) ( n- 2),即可得出答案.解答：解：根据题意得出房间地面的面积是( m - 2) ( n- 2);(m- 2) (n- 2) =mn - 2m - 2n+4.故答案为：(m - 2) ( n- 2)或(mn - 2m - 2n+4)点评：本题考查了多项式乘多项式的应用，关键是能根据题意得出算式，题目比较好，难度适中.11.若(x+m ) (x+n) =x2- 7x+m n，则- m - n 的值为7 .考点：多项式乘多项式.专题：计算题.分析：按照多项式的乘法法则展开运算后解答：解：I (x+m) (x+n) =x2+ (m+n) x+mn=x2- 7x+mn，/• m+n= —7，/• - m - n=7，故答案为：7.点评：本题考查了多项式的乘法，解题的关键是牢记多项式乘以多项式的乘法法则，属于基础题，比较简单.12.若(x2+mx+8 ) (x2- 3x+n )的展开式中不含x3和x2项，贝V mn的值是3 .考点：多项式乘多项式.专题：计算题.x2和x3项列出关于m与n的方程组，求出分析：利用多项式乘以多项式法则计算得到结果，根据展开式中不含方程组的解即可得到m与n的值.解答：43 2 2 2解：原式=x + ( m- 3) x + (n - 3m+8) x + ( mn - 24) x+8 n，( x +mx - 8) (x - 3x+n)2 3- 3-0根据展开式中不含x2和x3项得：，，n - 3ini-8=0解得：胃，mn=3，故答案为：3.点评：此题考查了多项式乘以多项式，熟练掌握运算法则是解本题的关键.2 2 313.已知x、y、a 都是实数，且|x|=1 - a, y2= (1 - a) (a- 1 - a2),贝V x+y+a3+i 的值为2考点：代数式求值；绝对值；多项式乘多项式.专题：计算题.分析：根据绝对值非负数，平方数非负数的性质可得1-a=0，从而得到a的值，然后代入求出x、y的值，再把a、x、y的值代入代数式进行计算即可求解.解答：解：■/ |x|=1 - a%，2皿.a- 1 包)，-a 切，2.a- 1 - a 切，2 2又y = (1 - a) ( a- 1 - a )为，1 —a=0，解得a=1,••• |x|=1 - 1=0,x=0 ,2 2y = (1 - a) (- 1 - a ) =0,3•x+y+a +1=0+0+1+1=2 .故答案为：2.点评：本题主要考查了代数式求值问题，把y2的多项式整理，然后根据非负数的性质求出a的值是解题的关键，也是解决本题的突破口，本题灵活性较强.二.解答题(共17小题)2 214 .若(x +2nx+3 ) (x - 5x+m )中不含奇次项，求m、n的值.考点：多项式乘多项式.分析：把式子展开，让x4的系数，x2的系数为0,得到m, n的值.2 2解答：解：(x +2nx+3) (x - 5x+m )4 3 2 3=x - 5x +mx +2nx - 10nx +2mnx+3x - 15x+3m4 3 2=x + (2n - 5) x + ( m - 10n+3) x + (2mn - 15) x+3m ,•••结果中不含奇次项，•2n - 5=0, 2mn - 15=0,解得m=3, n=—2点评：本题主要考查了多项式乘多项式的运算，注意当要求多项式中不含有哪一项时，应让这一项的系数为0.15.化简下列各式：(1)(3x+2y) ( 9x2- 6xy+4y2);2(2)(2x - 3) (4x +6xy+9 );(3)(新弓中MH寺；(4)(a+b) (a2- ab+b2) (a- b) (s F+ab+b2)考点：多项式乘多项式.分析：根据立方和与立方差公式解答即可.解答：解：(1) (3x+2y) (9x2- 6xy+4y 2)3 3=(3x) 3+ (2y) 33 3=27x +8y ；(2) (2x - 3) (4x2+6xy+9 )3 小3=(2x) - 3=8x3- 27;(3) (*m -4 (a+b) (a2- ab+b2) (a- b) (X+ab+b2) =(a3+b3) ( a3- b3)6- b6．=a点评：本题考查了立方和与立方差公式，熟练记忆公式是解题的关键．16．计算：(1)(2x - 3) (x - 5);(2)(a2-b3) ( a2+b3)考点：多项式乘多项式．分析：( 1)根据多项式乘以多项式的法则，可表示为( a+b)( m+n) =am+an+bm+bn ，计算即可；( 2)根据平方差公式计算即可．解答：解：( 1)(2x- 3)(x- 5)=2x2- 10x- 3x+1522- 13x+15；=2x( 2)(a2- b3)( a2+b3)=a4- b6．点评：本题考查了多项式乘以多项式的法则以及平方差公式．注意不要漏项，漏字母，有同类项的合并同类项．17．计算：( 1 )-( 2a- b) +[a -( 3a+4b) ]( 2)( a+b)( a2- ab+b2)考点：多项式乘多项式；整式的加减．专题：计算题．分析：( 1 )先去小括号，再去大括号，最后按照整式加减混合运算规则进行计算即可；( 2)根据多项式乘以多项式的法则，可表示为( a+b)( m+n) =am+an+bm+bn ，计算即可．解答：解：( 1 )原式=- 2a+b+[a- 3a- 4b]，=- 2a+b+a- 3a- 4b，=- 4a- 3b；( 2)原式=a3- a2b+ab2+a2b- ab2+b3，33=a +b ．点评：本题主要考查多项式乘以多项式的法则．注意不要漏项，漏字母，有同类项的合并同类项．18．( x+7)(x- 6)-( x- 2)(x+1 )考点：多项式乘多项式．分析：依据多项式乘多项式法则运算．解答：解：( x+7)( x- 6)-( x- 2)( x+1 )22=x2- 6x+7x- 42- x2- x+2x+2=2x- 40．点评：本题考查了多项式乘多项式法则，先用一个多项式的每一项乘以另一个多项式的每一项，再把所得的积相加．关键是不能漏项．19．计算：( 3a+1)(2a- 3)-( 6a- 5)(a- 4)考点：多项式乘多项式．分析：根据整式混合运算的顺序和法则分别进行计算，再把所得结果合并即可．解答：解：( 3a+1)(2a- 3) +( 6a- 5)(a- 4)22=6a2- 9a+2a- 3+6a2- 24a- 5a+202 =12a - 36a+17.点评：此题考查了整式的混合运算，在计算时要注意混合运算的顺序和法则以及运算结果的符号，是一道基础题.20.计算：(a - b ) (a 2+ab+b 2) 考点：多项式乘多项式；单项式乘单项式.专题：计算题.分析：根据多项式乘以多项式的法则和单项式乘单项式的法则进行计算即可.解答：解：原式=a 3+a 2b+ab 2 - a 2b - ab 2- b 33 .3=a - b .点评：本题主要考查对多项式乘以多项式的法则和单项式乘单项式的法则得理解和掌握，能熟练地运用法则进行计算是解此题的关键.21.若 (x 2+px - —) (x 2 - 3x+q )的积中不含x 项与x 3项，^5(1) 求p 、q 的值；(2) 求代数式(-2p 2q ) 2+ (3pq ) -1+p 2012q 2014 的值. 考点：多项式乘多项式.分析： (1) 形开式子，找出 x 项与x 3令其系数等于0求解.(2) 把p , q 的值入求解.解答：解：(1 (x 2+px 遗)(x 2-3x+q ) =X 4+ (p -3) x3+ (9 - 3p 弓)x2+ (qp+1) x+q ，•/积中不含x 项与x 3项，••• P - 3=0, qp+1=0二 p=3, q=-g,(2) (- 2p 2q ) 2+ ( 3pq ) -1+p 2012q 2014- i -1 1 Z012=[-2 >32 X ( J)『+13X3X (-(•可)]>32 =369=4错- 点评：本题主要考查了多项式乘多项式，解题的关键是正确求出 p , q 的值2 2 2 2 22 .先化简，再求值： 5 ( 3x y - xy )- 4( - xy +3x y )，其中 x= - 2, y=3 .考点：整式的加减一化简求值；合并冋类项；多项式乘多项式.专题：计算题.分析：根据单项式乘多项式的法则展开，再合并冋类项，把xy 的值代入求出即可.解答：解：原式=15x 2y - 5xy 2+4xy 2- 12x 2y c 2 2 =3x y - xy ,当 x= - 2, y=3 时，原式=3 X (- 2) 2X 3-( - 2) X 32=36+18=54 .点评：本题考查了对整式的加减，合并同类项，单项式乘多项式等知识点的理解和掌握，注意展开时不要漏乘，同时要注意结果的符号，代入-2时应用括号.2 3 223. 若(x- 1) (x +mx+ n) =x - 6x +iix- 6，求m, n 的值.考点：多项式乘多项式.专题：计算题.2 3 2分析：把(x - 1) (x +mx+ n )展开后，每项的系数与x - 6x +iix - 6中的项的系数对应，可求得m、n的值. 解答：解：T (x - 1)(x2+mx+n)=x + (m - 1) x + (n - m) x - n3 2=x - 6x +11x - 6m - 1= - 6, - n= - 6, 解得m= - 5, n=6.点评：本题主要考查了多项式乘多项式的法则，注意不要漏项，漏字母，有同类项的合并同类项.根据对应项系数相等列式求解m、n是解题的关键.24. 如图，有多个长方形和正方形的卡片，图甲是选取了2块不同的卡片，拼成的一个图形，借助图中阴影部分面积的不同表示可以用来验证等式 a (a+b) =a2+ab成立.(1)根据图乙，利用面积的不同表示方法，写出一个代数恒等式(a+2b) (a+b) =a2+3ab+2b2;(2)试写出一个与(1)中代数恒等式类似的等式，并用上述拼图的方法说明它的正确性.考点：多项式乘多项式.专题：计算题.分析：(1)根据图形是一个长方形求出长和宽，相乘即可；(2)正方形的面积是2个长方形的面积加上2个正方形的面积，代入求出即可.解答：解：(1)观察图乙得知：长方形的长为：a+2b,宽为a+b,•••面积为：(a+2b) (a+b) =a +3ab+2b ；点评：本题主要考查对多项式乘多项式的理解和掌握，能表示各部分的面积是解此题的关键.25. 小明想把一长为60cm,宽为40cm的长方形硬纸片做成一个无盖的长方体盒子，于是在长方形纸片的四个角各剪去一个相同的小正方形.(2)如图所示：恒等式是，答：恒等式是a+b) (a+b)2 2 ( a+b) (a+b) =a +2ab+b .2 2=a +2ab+b .(1) 若设小正方形的边长为 xcm ，求图中阴影部分的面积;(2) 当x=5时，求这个盒子的体积.考点：多项式乘多项式；代数式求值.分析：(1)剩余部分的面积即是边长为 60 - 2x , 40 - 2x 的长方形的面积；(2)利用长方体的体积公式先表示出长方形的体积，再把x=5，代入即可. 解答：解：(1) (60 - 2x ) (40 - 2x ) =4x 2- 200X+2400,答：阴影部分的面积为(4x 2 - 200X+2400) cm 2;(2)当 x=5 时，4x 2- 200x+2400=1500 (cm 2),这个盒子的体积为：1500拓=7500 (cm 3), 答：这个盒子的体积为 7500cm 3.点评：此题主要考查用代数式表示正方形、矩形的面积和体积，需熟记公式，且认真观察图形，得出等量关系.26. ( x - 1) (x - 2) = (x+3) ( x - 4) +20 .考点：多项式乘多项式；解一元一次方程.分析：将方程的两边利用多项式的乘法展开后整理成方程的一般形式求解即可.解答：解：原方程变形为： x 2 - 3x+2=x 2 - x - 12+20整理得：-2x - 6=0,解得：x= - 3.点评：本题考查了多项式乘多项式及解一元二次方程的知识，解题的关键是利用多项式的乘法对方程进行化简.2 _ 227. 若(x - 3) (x+m ) =x 2+nx - 15,求的值.8n+5 考点：多项式乘多项式.分析：首先把)(x - 3) (x+m )利用多项式的乘法公式展开，然后根据多项式相等的条件：对应项的系数相同即可得到m 、n 的值，从而求解. 解答：解：(x - 3) (x+m )2 =x + ( m - 3) x - 3m2 =x +nx - 15,贝叽[-如-15解得:点评：本题考查了多项式的乘法法则以及多项式相等的条件，理解多项式的乘法法则是关键.28.小明在进行两个多项式的乘法运算时 (其中的一个多项式是 b - 1)，把乘以(b - 1) ”错看成除以(b - 1) 结果得到(2a - b )，请你帮小明算算，另一个多项式是多少？ _ 28n+5 8X2+5考点：多项式乘多项式.分析：根据被除式=商＞除式，所求多项式是(2a- b) (b - 1)，根据多项式乘多项式的法则计算即可.解答：解：设所求的多项式是M,则M= (2a-b) (b- 1)2=2ab - 2a- b +b.点评：本题考查了多项式乘多项式法则，根据被除式、除式、商三者之间的关系列出等式是解题的关键，熟练掌握运算法则也很重要.29. 有足够多的长方形和正方形的卡片如图.如果选取1号、2号、3号卡片分别为1张、2张、3张，可拼成一个长方形(不重叠无缝隙)•请画出这个长方形的草图，并运用拼图前后面积之间的关系说明这个长方形的代数意义.考点：多项式乘多项式.分析：先根据题意画出图形，然后求出长方形的长和宽，长为a+2b,宽为a+b,从而求出长方形的面积.解答：解：如图：2 2a +3ab+2b = (a+b) (a+2b).点评：考查多项式与多项式相乘问题；根据面积的不同表示方法得到相应的等式是解决本题的关键.2 23 3 2 430. ( 1)填空：(a- 1) (a+1) = a ~ 1 (a- 1) ( a +a+1) = a ~ 1 (a- 1) (a +a +a+1) = a ~ 1 (2)你发现规律了吗？请你用你发现的规律填空：( a- 1) (a n+a n 1+ --+a2+a+1) = a n+1- 1(3)根据上述规律，请你求42012+42011+42010+ ••+4+1 的值.—(42013- 1 ).一3考点：多项式乘多项式.专题：规律型.分析：(1)根据平方差公式和立方差公式可得前2个式子的结果，利用多项式乘以多项式的方法可得出第3个式子的结果；(2)从而总结出规律是：(a- 1) (a n+a n 1+ --+a2+a+1) =a n+1- 1;(3)根据上述结论计算下列式子即可.解答：解：根据题意：(1) (a- 1) (a+1) =a2- 1;(a- 1) ( ai2+a+1) =a3- 1;(a- 1) ( a3+a2+a+1) =a4- 1;(2) (a- 1) (a +a +a + --+a +a+1) =a - 1.(3 )根据以上分析(1) 42012+42011+42010+ -- +4+12 99+298+297+ - +2+1 ,2012 2011 2010 、「(4 - 1) (4 +4 +4 +—+4+1 ),1 Zyl2013 1)「(4 - 1)•故答案为：(1) a2- 1, a3- 1, a4- 1;( 2) a n+1- 1;( 3)丄(42013- 1 ).点评：主要考查了学生的分析、总结、归纳能力，规律型的习题一般是从所给的数据和运算方法进行分析，从特殊值的规律上总结出一般性的规律.2 3 230. (1)填空：(a—1)(a+1)= _ _ (a—1)( a+a+1) = _ _ (a—1)(a +a +a+1) = _ - (2)你发现规律了吗？请你用你发现的规律填空：( a—1) (a n+a n —1 + --+a2+a+1) = _ _(3)根据上述规律，请你求42012+42011+4201°+ --+4+1的值. _ _ .。

2022-2023学年初一数学第二学期培优专题训练17 多项式乘多项式

专题17 多乘多不含某字母【例题讲解】已知多项式()()2232x px q x x ++-+的结果中不含3 x 项和2x 项，求p 和q 的值．【答案】3p =，7q = 【分析】首先利用多项式乘法去括号，进而利用多项式（x 2+px +q ）（x 2﹣3x +2）的结果中不含x 3项和x 2项，进而得出两项的系数为0，进而得出答案．【解答】解：∵()()2232x px q x x ++-+432322323232x x x px px px qx qx q =-++-+++﹣()()432323232x p x p q x px qx q =--+-++-+由多项式()()2232x px q x x ++-+的结果中不含3x 项和2x 项，∴30p -=，230p q -+=，解得：3p =，7q =．故答案为：3p =，7q =．【点评】此题主要考查了多项式乘法，正确利用多项式乘法去括号得出是解题关键．【综合解答】1．如()x m +与(3)x +的乘积中不含x 的一次项，则m 的值为（）A ．3-B ．3C ．0D ．12．如果()()x a x b ++的结果中不含x 的一次项，那么a 、b 应满足（）A ．a b =B ．0a =C ．1ab =D ．0a b +=3．关于字母x 的整式（x +1）（x 2+mx ﹣2）化简后的结果中二次项系数为0，则（）A ．m ＝2B ．m ＝﹣2C ．m ＝1D ．m ＝﹣14．已知多项式2(1)(2)x mx x -+-的积中x 的一次项系数为零，则m 的值是（）A ．1B ．–1C ．–2D ．12- 5．已知多项式2(1)(2)x mx x -+-的积中不含x 2项，则m 的值是 ( )A ．－2B ．－1C ．1D ．26．若（x +k ）（x ﹣5）的积中不含有 x 的一次项，则 k 的值是（）A ．0B ．5C ．﹣5D ．﹣5 或 57．若关于x 的多项式(1)(2)ax x -+展开后不含x 的一次项，则=a _______．8．若关于x 的多项式()287()x x x m -++的计算结果中不存在2x 项，则m =______．9．若()()21x a x -+的积中不含x 的一次项，则a 的值为______．10．若（x+2）（x 2-ax+3）的乘积中不含x 的一次项，则a=____11．若()()5x a x ++的结果中不含关于字母x 的一次项，则=a ___________．12．若计算(x ＋2)(3x ＋m)的结果中不含关于字母x 的一次项，则m 的值为____________．13．若：（x²+mx+n ）（x+1）的结果中不含x 2的项和x 的项，则mn=__________．14．如果2(2)(51)x x ax +-+的乘积中不含2x 项，则a 为______．15．若(42)(3)x m x -+的乘积中不含x 的一次项，则常数m =_________．16．若多项式 x + m 与 x - 5 的乘积中不含 x 的一次项，则 m 的值为_____．17．多项式223368x mxy y xy --+-中不含xy 项，则常数m 的值是___．18．若 (x +2)( x 2+mx +4) 的展开式中不含有 x 的二次项，则 m 的值为_________．19．若（x2﹣mx+1）（x ﹣1）的积中x 的二次项系数为零，则m 的值是__________________.20．已知22()(21)x px x x ---的结果中不含x 3项，则p=___________.21．如果多项式x2+5ab+b2+kab ﹣1不含ab 项，则k 的值为_________-22．若多项式没有二次项，则m 的值是________．23．要使（x 2+ax+1）•（﹣6x 3）的展开式中不含x 4项，则a=___________．24．若()()2282x mx x x n +--+的展开式中不含2x 和3x 项，求m +n 的值. 25．若21(3)3x m x x n ⎛⎫--+- ⎪⎝⎭的计算结果中不含x 2与x 项． (1)求m 、n 的值；(2)求代数式（3m －n ）2＋m 2020·n 2021的值．26．若()2(2)x x ax b -++的积中不含x 的二次项和一次项，求2(32)2a b ab -+的值．27．若()2133x p x x q ⎛⎫+-+ ⎪⎝⎭的积中不含x 项与2x 项（1）求p 、q 的值；（2）求代数式20192020p q 的值28．若（x 2+nx ）(x 2-3x+m)的乘积中不含x 2和x 3项，求m 和n 的值．29．先化简，再求值：已知代数式2(3)(24)-+--ax x x b 化简后，不含有x 2项和常数项.（1）求a、b的值；（2）求2---+---+的值.()()()(2)b a a b a b a a b专题17 多乘多不含某字母【例题讲解】已知多项式()()2232x px q x x ++-+的结果中不含3 x 项和2x 项，求p 和q 的值．【答案】3p =，7q = 【分析】首先利用多项式乘法去括号，进而利用多项式（x 2+px +q ）（x 2﹣3x +2）的结果中不含x 3项和x 2项，进而得出两项的系数为0，进而得出答案．【解答】解：∵()()2232x px q x x ++-+432322323232x x x px px px qx qx q =-++-+++﹣()()432323232x p x p q x px qx q =--+-++-+由多项式()()2232x px q x x ++-+的结果中不含3x 项和2x 项，∴30p -=，230p q -+=，解得：3p =，7q =．故答案为：3p =，7q =．【点评】此题主要考查了多项式乘法，正确利用多项式乘法去括号得出是解题关键．【综合解答】1．如()x m +与(3)x +的乘积中不含x 的一次项，则m 的值为（）A ．3-B ．3C ．0D ．1【答案】A【分析】先用多项式乘以多项式的运算法则展开求它们的积，并且把m 看作常数合并关于x 的同类项，令x 的系数为0，得出关于m 的方程，求出m 的值．【解答】解：22()(3)33(3)3x m x x x mx m x m x m ++=+++=+++，又()x m +与(3)x +的乘积中不含x 的一次项，30m ∴+=，解得3m =-．故选：A ．【点评】本题主要考查了多项式乘多项式的运算，根据乘积中不含哪一项，则哪一项的系数等于0列式是解题的关键．2．如果()()x a x b ++的结果中不含x 的一次项，那么a 、b 应满足（）A ．a b =B ．0a =C ．1ab =D ．0a b += 【答案】D 【分析】先根据多项式乘以多项式法则展开，合并后即可得出选项．【解答】解：()()x a x b ++()2x a b x ab =+++ ，∵()()x a x b ++的结果中不含x 的一次项，∴0a b +=，故选：D ．【点评】本题考查了多项式乘以多项式法则的应用，能正确根据多项式乘以多项式法则展开是解此题的关键．3．关于字母x 的整式（x +1）（x 2+mx ﹣2）化简后的结果中二次项系数为0，则（）A ．m ＝2B ．m ＝﹣2C ．m ＝1D ．m ＝﹣1 【答案】D【分析】先根据多项式乘以多项式的法则计算，由二次项系数为0得关于m 的方程，解方程即得结果.【解答】解：∵关于字母x 的整式（x +1）（x 2+mx ﹣2）化简后的结果中二次项系数为0，∴（x +1）（x 2+mx ﹣2）＝x 3+mx 2﹣2x +x 2+mx ﹣2＝x 3+（m +1）x 2+（m ﹣2）x ﹣2，故m +1＝0，解得：m ＝﹣1．故选D ．【点评】本题考查了多项式的有关概念和多项式的乘法运算，正确的进行多项式的乘法运算是解题的关键. 4．已知多项式2(1)(2)x mx x -+-的积中x 的一次项系数为零，则m 的值是（）A ．1B ．–1C ．–2D ．12-5．已知多项式2(1)(2)x mx x -+-的积中不含x2项，则m 的值是 ( )A ．－2B ．－1C ．1D ．2 【答案】A【解答】展开后，x2项为2(2)m x -- ，则20,2m m --==- ，故选A.6．若（x +k ）（x ﹣5）的积中不含有 x 的一次项，则 k 的值是（）A ．0B ．5C ．﹣5D ．﹣5 或 5 【答案】B【解答】试题分析：根据多项式乘多项式的运算法则，展开后令x 的一次项的系数为0，列式求解即可．解：（x+k ）（x ﹣5）=x 2﹣5x+kx ﹣5k=x 2+（k ﹣5）x ﹣5k ，∵不含有x 的一次项，∴k ﹣5=0，解得k=5．故选B ．考点：多项式乘多项式．7．若关于x 的多项式(1)(2)ax x -+展开后不含x 的一次项，则=a _____________．【答案】12##0.5【分析】先运用多项式乘以多项式法则展开，再按字母x 合并同类项，然后根据展开后不含x 的一次项，8．若关于x 的多项式()287()x x x m -++的计算结果中不存在2x 项，则m =______．【答案】8【分析】根据多项式乘以多项式展开，合并同类项，令2x 的系数为0即可【解答】∵()287()x x x m -++=3228787x x x mx mx m -++-+=()()328787x m x m x m +-+-+，且结果中不存在2x 项，∴m -8=0,∴m =8,故答案为：8【点评】本题考查了多项式乘以多项式，不含项的条件，熟练进行多项式的乘法，清楚不含有项的条件是系数为0是解题的关键．9．若()()21x a x -+的积中不含x 的一次项，则a 的值为______．【答案】2【分析】先运用多项式的乘法法则计算，再合并同类项，因积中不含x 的一次项，所以让一次项的系数等于0，得a 的等式，再求解．【解答】解：（2x-a ）（x+1）=2x 2+（2-a ）x-a ，∵积中不含x 的一次项，∴2-a=0，∴a=2，故答案为：2．【点评】本题考查了多项式乘多项式法则，注意当要求多项式中不含有哪一项时，应让这一项的系数为0．10．若（x+2）（x 2-ax+3）的乘积中不含x 的一次项，则a=____11．若()()5x a x ++的结果中不含关于字母x 的一次项，则=a ___________．【答案】-5【分析】根据整式的运算法则即可求出答案．【解答】解：（x +a ）（x +5）＝x 2+（5+a ）x +5a ，由于结果中不含关于字母x 的一次项，故5+a ＝0，∴a ＝﹣5，故答案为：﹣5【点评】本题考查整式的运算，解题的关键是熟练运用整式的运算法则，本题属于基础题型．12．若计算(x ＋2)(3x ＋m)的结果中不含关于字母x 的一次项，则m 的值为____________．【答案】-6【分析】原式利用多项式乘多项式法则计算，根据结果不含x 的一次项，确定出m 的值即可．【解答】解：原式23(6)2x m x m ，由结果不含x 的一次项，得到60+=m ，解得：6m =-，故答案为：-6【点评】此题考查了多项式乘多项式，熟练掌握运算法则是解本题的关键．13．若：（x²+mx+n ）（x+1）的结果中不含x 2的项和x 的项，则mn=__________．【答案】-1【分析】先计算整式乘法，根据所不含的项得到系数为0求出答案.【解答】232()(1)(1)()x mx n x x m x m n x n +++=+++++，∵计算结果中不含x 2的项和x 的项，∴m+1=0，m+n=0，∴m=-1，n=1，∴mn=-1，故答案为：-1.【点评】此题考查整式的乘法计算，多项式中不含问题，正确计算是解题的关键.14．如果2(2)(51)x x ax +-+的乘积中不含2x 项，则a 为______．结果不含15．若(42)(3)x m x -+的乘积中不含x 的一次项，则常数m =_________．【答案】6【分析】直接利用多项式乘法去括号，进而得出一次项系数为0，求解即可．【解答】∵(42)(3)x m x -+的乘积中不含x 的一次项，∴(42)(3)x m x -+=24(122)6x m x m +--中1220m -=∴6m =故答案为：6．【点评】本题主要考查了多项式乘多项式，解答本题的关键在于正确去括号并计算．16．若多项式 x + m 与 x - 5 的乘积中不含 x 的一次项，则 m 的值为_____．【答案】5【分析】先根据多项式乘以多项式法则求出(x+m)(x-5)=x 2 +(m-5)x-5m,根据已知得出m-5=0,求出即可.【解答】解: (x+m)(x-5)=x 2 +(m-5)x-5m∵x+m 与x-5的乘积中不含x 的一次项∴m-5=0∴m=5故答案为5.【点评】该题考查了多项式乘以多项式和解一元一次方程，能正确根据多项式乘以多项式法则进行计算是解该题的关键.17．多项式223368x mxy y xy --+-中不含xy 项，则常数m 的值是___．【答案】2【分析】先将多项式合并同类项，再根据多项式不含xy 项得630m -=，即可解出m.【解答】整理原式22223368(63)38x mxy y xy x m xy y ，∵该多项式不含xy 项，∴630m -=，得m=2.故填：2.【点评】此题考查多项式的意义，多项式中不含有某一项，需先将多项式化简，确定不含有的项的系数为0，由此解得某一未知数的值.18．若 (x +2)( x 2+mx +4) 的展开式中不含有 x 的二次项，则 m 的值为_________．【答案】m=-2.【分析】原式利用多项式乘以多项式法则计算，合并后根据结果不含x 2项，求出m 的值．【解答】()()()()232242248x x mx x m x m x +++=+++++，由展开式中不含2x 项，得到m +2=0，则m =−2.故答案为−2.【点评】本题主要考查多项式乘以多项式法则，熟悉掌握法则是关键.19．若（x2﹣mx+1）（x ﹣1）的积中x 的二次项系数为零，则m 的值是__________________.【答案】-1【分析】直接利用多项式乘法运算法则去括号，进而得出二次项的系数为零，求出答案．【解答】∵（x 2-mx+1）（x-1）的积中x 的二次项系数为零，∴x 3-x 2-mx 2+mx+x-1=x 3-（1+m ）x 2+（1+m ）x-1，则1+m=0，解得：m=-1．故答案为-1【点评】此题主要考查了多项式乘以多项式，正确掌握多项式乘法运算法则是解题关键．20．已知22()(21)x px x x ---的结果中不含x 3项，则p=___________.【答案】-2【解答】分析：先根据多项式乘以多项式法则展开，合并后即可得出方程，求出方程的解即可．解答：（x2-px）•（x2-2x-1）=x4-2x3-x2-px3+2px2+px=x4-（2+p）x3+（2p-1）x2+px，∵（x2-px）•（x2-2x-1）的结果中不含x3项，∴2+p=0，解得：p=-2，故答案为-2．点评：本题考查了多项式乘以多项式法则的应用，能正确根据多项式乘以多项式法则展开是解此题的关键．21．如果多项式x2+5ab+b2+kab﹣1不含ab项，则k的值为_________-【答案】-5【解答】∵不含ab项，∴5+k=0，k=−5，故答案为−5.22．若多项式没有二次项，则m的值是________．【答案】-1【解答】试题分析：因为多项式没有二次项，所以m+1=0，所以m=-1．考点：多项式．23．要使（x2+ax+1）•（﹣6x3）的展开式中不含x4项，则a=___________．【答案】0【解答】试题分析：根据单项式与多项式相乘的法则展开，然后让x4项的系数等于0，列式求解即可．解：（x2+ax+1）•（﹣6x3）=﹣6x5﹣6ax4﹣6x3，∵展开式中不含x4项，∴﹣6a=0，解得a=0．考点：单项式乘多项式．点评：本题考查了单项式与多项式相乘，不含某一项就是让这一项的系数等于0．24．若()()2282x mx x x n +--+的展开式中不含2x 和3x 项，求m +n 的值. 【答案】14【分析】首先根据多项式的乘法法则将多项式进行展开，然后进行合并同类项．根据不含哪一项，则哪一项的系数为零列出方程组，从而得出答案．【解答】解：()()2282x mx x x n +--+ 432322822168x mx x x mx x nx mnx n =+---+++-()()()432228168x m x n m x mn x n =+-+--++-，∵()()2282x mx x x n +--+的展开式中不含2x 和3x 项， ∴20280m n m -=⎧⎨--=⎩，解得：212m n =⎧⎨=⎩， ∴14m n +=．【点评】本题主要考查多项式的乘法计算法则，代数式求值，解二元一次方程组，属于中等难度的题型．能够进行合并同类项是解决这个问题的关键．25．若21(3)3x m x x n ⎛⎫--+- ⎪⎝⎭的计算结果中不含x 2与x 项． (1)求m 、n 的值；(2)求代数式（3m －n ）2＋m 2020·n 2021的值．26．若()2(2)x x ax b -++的积中不含x 的二次项和一次项，求2(32)2a b ab -+的值．【答案】20【分析】原式利用多项式乘多项式法则计算，由积中不含x 的二次项和一次项，求出a 与b 的值，再把a 、b 的值代入计算可得．【解答】解：（x -2）（x 2+ax +b ）=x 3+ax 2+bx -2x 2-2ax -2b =x 3+（a -2）x 2+（b -2a ）x -2b ，∵（x -2）（x 2+ax +b ）的积中不含x 的二次项和一次项，∴a -2=0且b -2a =0，解得：a =2、b =4，将a =2、b =4代入2(32)2a b ab -+=2(3224)224⨯-⨯+⨯⨯=4+16=20．【点评】本题主要考查整式的化简求值，解题的关键是熟练掌握整式的混合运算顺序和运算法则．27．若()2133x p x x q ⎛⎫+-+ ⎪⎝⎭的积中不含x 项与2x 项（1）求p 、q 的值；（2）求代数式20192020p q 的值201920191)(3)3p q q =⨯【点评】本题主要考查了多项式乘多项式的运算，注意当要求多项式中不含有哪一项时，应让这一项的28．若（x 2+nx ）(x 2-3x+m)的乘积中不含x 2和x 3项，求m 和n 的值．【答案】9m =，3n =【分析】将已知的式子利用多项式乘以多项式的法则变形，合并后根据乘积中不含x 2和x 3项，得到这两项系数为0，列出关于m 与n 的方程，求出方程的解即可得到m 与n 的值．【解答】解：22()(3)x nx x x m +-+=4323233x x mx nx nx mnx -++-+=432(3)(3)x n x m n x mnx --+-+；∵乘积中不含x 2和x 3项，∴(3)030n m n --=⎧⎨-=⎩，解得：93m n =⎧⎨=⎩； ∴9m =，3n =；【点评】此题考查了整式的混合运算，涉及的知识有：多项式乘以多项式的法则，合并同类项法则，解二元一次方程组，熟练掌握法则是解本题的关键．29．先化简，再求值：已知代数式2(3)(24)-+--ax x x b 化简后，不含有x 2项和常数项.（1）求a 、b 的值；（2）求2()()()(2)b a a b a b a a b ---+---+的值.。

多项式的运算练习题及解析

多项式的运算练习题及解析一、综合练习题1. 计算多项式 P(x) = 3x^3 - 2x^2 + 5x - 1 在 x = 2 时的值。

解析：将 x = 2 代入多项式 P(x) 中，得到：P(2) = 3(2)^3 - 2(2)^2 + 5(2) - 1= 3(8) - 2(4) + 10 - 1= 24 - 8 + 10 - 1= 25因此，在 x = 2 时，多项式 P(x) 的值为 25。

2. 将多项式 P(x) = 2x^4 + 3x^3 - 5x^2 + x + 6 与多项式 Q(x) = x^3 - 2x + 5 相加，并将结果化简。

解析：将 P(x) 和 Q(x) 相加，得到：P(x) + Q(x) = (2x^4 + 3x^3 - 5x^2 + x + 6) + (x^3 - 2x + 5)= 2x^4 + 3x^3 + x^3 - 5x^2 - 2x + x + 6 + 5= 2x^4 + 4x^3 - 5x^2 - 2x + 11因此，将多项式 P(x) 和 Q(x) 相加后化简后得到 2x^4 + 4x^3 - 5x^2 - 2x + 11。

3. 将多项式 P(x) = 4x^5 - 6x^4 + 2x^3 - x^2 + 8x - 3 与多项式 Q(x) = 2x^3 - 3x^2 + 5 相乘，并将结果化简。

解析：将 P(x) 和 Q(x) 相乘，得到：P(x) * Q(x) = (4x^5 - 6x^4 + 2x^3 - x^2 + 8x - 3) * (2x^3 - 3x^2 + 5)= 8x^8 - 12x^7 + 4x^6 - 2x^5 + 16x^4 - 6x^3 - 3x^5 + 4x^4 -x^3 + 5x^2 + 8x - 3化简后，将同类项合并得：P(x) * Q(x) = 8x^8 - 12x^7 + 4x^6 - 5x^5 + 20x^4 - 7x^3 + 5x^2 + 8x - 3因此，将多项式 P(x) 和 Q(x) 相乘并化简后得到 8x^8 - 12x^7 + 4x^6 - 5x^5 + 20x^4 - 7x^3 + 5x^2 + 8x - 3。

多项式的乘法同步练习（原卷解析卷）

3.3多项式的乘法同步练习参考答案与试题解析一．选择题（共8小题）1．已知ab2＝﹣1，则﹣ab（a2b5﹣ab3﹣b）的值等于（）A．﹣1B．0C．1D．无法确定解：∵ab2＝﹣1，∴原式＝﹣（ab2）3+（ab2）2+ab2＝1+1﹣1＝1，故选：C．2．若a2﹣2a﹣3＝0，代数式×的值是（）A．0B．﹣C．2D．﹣解：∵a2﹣2a﹣3＝0，∴a2﹣2a＝3，则原式＝＝＝﹣．故选：D．3．若（x+4）（x﹣2）＝x2+mx+n，则m、n的值分别是（）A．2，8B．﹣2，﹣8C．2，﹣8D．﹣2，8解：∵（x+4）（x﹣2）＝x2+2x﹣8，∴x2+2x﹣8＝x2+mx+n，∴m＝2，n＝﹣8．故选：C．4．已知A＝﹣4x2，B是多项式，在计算B+A时，小马虎同学把B+A看成了B•A，结果得32x5﹣16x4，则B+A为（）A．﹣8x3+4x2B．﹣8x3+8x2C．﹣8x3D．8x3解：由题意可知：﹣4x2•B＝32x5﹣16x4，∴B＝﹣8x3+4x2∴A+B＝﹣8x3+4x2+（﹣4x2）＝﹣8x3故选：C．5．如（x+a）与（x+3）的乘积中不含x的一次项，则a的值为（）A．3B．﹣3C．1D．﹣1解：原式＝x2+（a+3）x+3a，由结果不含x的一次项，得到a+3＝0，解得：a＝﹣3，故选：B．6．通过计算几何图形的面积可表示一些代数恒等式，如图可表示的代数恒等式是（）A．（a﹣b）2＝a2﹣2ab+b2B．（a+b）2＝a2+2ab+b2C．2a（a+b）＝2a2+2ab D．（a+b）（a﹣b）＝a2﹣b2解：长方形的面积等于：2a（a+b），也等于四个小图形的面积之和：a2+a2+ab+ab＝2a2+2ab，即2a（a+b）＝2a2+2ab．故选：C．7．已知多项式（x2+mx+8）和（x2﹣3x+n）的乘积中不含x2和x3的项，则m、n的值为（）A．m＝﹣1，n＝1B．m＝2，n＝﹣1C．m＝2，n＝3D．m＝3，n＝1解：（x2+mx+8）（x2﹣3x+n）＝x4+mx3+8x2﹣3x3﹣3mx2﹣24x+nx2+nmx+8n＝x4+（m﹣3）x3+（8﹣3m+n）x2﹣24x+8n，∵不含x2和x3的项，∴m﹣3＝0，∴m＝3．∴8﹣3m+n＝0，∴n＝1．故选：D．8．已知a+b+c＝0可得：a+b＝﹣c，则代数式（a+b）（b+c）（c+a）+abc的值为（）A．a+b+c B．abc C．2abc D．0解：∵a+b+c＝0，∴a+b＝﹣c，a+c＝﹣b，b+c＝﹣a，则原式＝（﹣c）×（﹣a）×（﹣b）+abc＝﹣abc+abc＝0，故选：D．二．填空题（共6小题）9．计算：（4a3﹣a3）•a2＝3a5．解：原式＝4a5﹣a5，＝3a5，故答案为：3a510．如果长方体的长为3a﹣4，宽为2a，高为2a，则它的体积是12a3﹣16a2．解：根据题意知，它的体积是（3a﹣4）×2a×2a＝（3a﹣4）×4a2＝12a3﹣16a2，故答案为：12a3﹣16a2．11．若多项式与单项式2a2b的积是6a3b﹣2a2b2，则该多项式为3a﹣b．解：∵多项式与单项式2a2b的积是6a3b﹣2a2b2，∴该多项式为：（6a3b﹣2a2b2）÷2a2b＝3a﹣b．故答案为：3a﹣b．12．不等式（3x+4）（3x﹣4）＜9（x﹣2）（x+3）的解集为x＞．解：（3x+4）（3x﹣4）＜9（x﹣2）（x+3），9x2﹣16＜9（x2+x﹣6），9x2﹣16＜9x2+9x﹣54，移项，得9x2﹣9x2﹣9x＜﹣54+16，合并同类项，得﹣9x＜﹣38，系数化为1得x＞．故答案为：x＞．13．多项式（mx+8）（2﹣3x）展开后不含x项，则m＝12．解：（mx+8）（2﹣3x）＝2mx﹣3mx2+16﹣24x＝﹣3mx2+（2m﹣24）x+16，∵多项式（mx+8）（2﹣3x）展开后不含x项，∴2m﹣24＝0，解得：m＝12，故答案为：12．14．若（x+3）（x﹣p）＝x2+mx﹣27，则m+p的值是3．解：（x+3）（x﹣p）＝x2+3x﹣px﹣3p＝x2+（3﹣p）x﹣3p，则3﹣p＝m，﹣3p＝﹣27，解得，p＝9，m＝﹣6，则m+p＝﹣6+9＝3，故答案为3．三．解答题（共4小题）15．计算：解：原式＝a2b2（﹣a2b﹣12ab+b2）＝﹣8a4b3﹣a3b3+a2b4．16．试说明：对于任意自然数n，代数式n（n+7）﹣n（n﹣5）+6的值都能被6整除．解：∵n（n+7）﹣n（n﹣5）+6＝n2+7n﹣n2+5n+6＝12n+6＝6（2n+1），所以，对于任意自然数n，代数式n（n+7）﹣n（n﹣5）+6的值都能被6整除．17．如图，某市有一块长为（3a+b）米、宽为（2a+b）米的长方形地块，中间是边长为（a+b）米的正方形，规划部门计划将在中间的正方形修建一座雕像，四周的阴影部分进行绿化．（1）绿化的面积是多少平方米？（用含字母a、b的式子表示）（2）求出当a＝10，b＝12时的绿化面积．解：（1）依题意得：（3a+b）（2a+b）﹣（a+b）2＝6a2+3ab+2ab+b2﹣a2﹣2ab﹣b2＝（5a2+3ab）平方米．答：绿化面积是（5a2+3ab）平方米；（2）当a＝10，b＝12时，原式＝500+360＝860（平方米）．答：绿化面积是860平方米．18．甲、乙两人共同计算一道整式乘法题：（2x+a）（3x+b）．甲由于把第一个多项式中的“+a”看成了“﹣a”，得到的结果为6x2+11x﹣10；乙由于漏抄了第二个多项式中x的系数，得到的结果为2x2﹣9x+10．（1）求正确的a、b的值．（2）计算这道乘法题的正确结果．解：（1）（2x﹣a）（3x+b）＝6x2+2bx﹣3ax﹣ab＝6x2+（2b﹣3a）x﹣ab＝6x2+11x﹣10．（2x+a）（x+b）＝2x2+2bx+ax+ab＝2x2+（2b+a）x+ab＝2x2﹣9x+10．∴，∴；（2）（2x﹣5）（3x﹣2）＝6x2﹣4x﹣15x+10＝6x2﹣19x+10．。

专题1.6整式的乘法(3)多项式乘多项式

2020-2021学年七年级数学下册尖子生同步培优题典【北师大版】专题1.6整式的乘法(3)多项式乘多项式姓名：__________________ 班级：______________ 得分：_________________注意事项：本试卷满分100分，试题共24题，选择10道、填空8道、解答6道．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．一、选择题(本大题共10小题，每小题3分，共30分)在每小题所给出的四个选项中，只有一项是符合题目要求的．1．(2020秋•南关区校级期中)计算(a+3)(﹣a+1)的结果是()A．﹣a2﹣2a+3B．﹣a2+4a+3C．﹣a2+4a﹣3D．a2﹣2a﹣3【分析】运用多项式乘以多项式法则，直接计算即可．解析(a+3)(﹣a+1)＝﹣a2﹣3a+a+3＝﹣a2﹣2a+3．故选：A．2．(2020秋•朝阳区期中)若(x﹣3)(2x+1)＝2x2+ax﹣3，则a的值为()A．﹣7B．﹣5C．5D．7【分析】将题中所给等式左边利用多项式乘多项式的运算法则进行计算，再与等式右边比较即可得出答案．解析(x﹣3)(2x+1)＝2x2+x﹣6x﹣3＝2x2﹣5x﹣3，∵(x﹣3)(2x+1)＝2x2+ax﹣3，∴a＝﹣5．故选：B．3．(2020秋•偃师市期中)若(x2+px+8)(x2﹣3x+1)乘积中不含x2项，则p的值为() A．p＝0B．p＝3C．p＝﹣3D．p＝﹣1【分析】先利用多项式乘多项式法则，把(x2+px+8)(x2﹣3x+1)展开合并，根据积不含x2的项，得关于p 的方程，求解即可．解析(x2+px+8)(x2﹣3x+1)＝x4+px3+8x2﹣3x3﹣3px2﹣24x+x2+px+8＝x4+(p﹣3)x3+(9﹣3p)x2+(p﹣24)x+8．∵(x2+px+8)(x2﹣3x+1)乘积中不含x2项，∴9﹣3p＝0．∴p＝3．故选：B．4．(2020秋•射洪市期中)如果(x﹣3)(3x+m)的积中不含x的一次项，则m的值为() A．7B．8C．9D．10【分析】先根据多项式乘以多项式法则展开，再合并同类项，根据已知得出m﹣9＝0，求出即可．解析(x﹣3)(3x+m)＝3x2+mx﹣9x﹣3m＝3x2+(m﹣9)x﹣3m，∵(x﹣3)(3x+m)的积中不含x的一次项，∴m﹣9＝0，解得：m＝9，故选：C．5．(2020秋•房县期中)若x+y＝1且xy＝﹣2，则代数式(1﹣x)(1﹣y)的值等于() A．﹣2B．0C．1D．2【分析】先根据多项式乘以多项式法则进行计算，再变形，最后求出答案即可．解析∵x+y＝1，xy＝﹣2，∴(1﹣x)(1﹣y)＝1﹣y﹣x+xy＝1﹣(x+y)+xy＝1﹣1+(﹣2)＝﹣2，故选：A．6．(2020秋•西陵区校级期中)以下表示图中阴影部分面积的式子，不正确的是()A．x(x+5)+15B．x2+5(x+3)C．(x+3)(x+5)﹣3x D．x2+8x【分析】根据长方形和正方形的面积公式得出各个部分的面积，再逐个判断即可．解析阴影部分的面积为x(x+5)+3×5＝x(x+5)+15或x2+5(x+3)或(x+3)(x+5)﹣3x，即选项A、B、C不符合题意，选项D符合题意，故选：D．7．(2020秋•路南区期中)若关于x的多项式(2x﹣m)与(3x+5)的乘积中，一次项系数为25，则m的值() A．5B．﹣5C．3D．﹣3【分析】先求出两个多项式的积，再根据一次项系数为25，得到关于m的一次方程，求解即可．解析(2x﹣m)(3x+5)＝6x2﹣3mx+10x﹣5m＝6x2+(10﹣3m)x﹣5m．∵积的一次项系数为25，∴10﹣3m＝25．解得m＝﹣5．故选：B．8．(2020秋•思明区校级期中)如图是一所楼房的平面图，下列式子中不能表示它的面积的是()A．x2+3x+6B．(x+3)(x+2)﹣2xC．x(x+3)+6D．x(x+2)+x2【分析】把楼房的平面图转化为三个矩形，求出三个矩形的面积和即可．解析S楼房的面积＝S矩形ABCD+S矩形DEFC+S矩形CFHG＝AD•AB+DC•DE+CF•FH．∵AB＝DC＝AD＝x，DE＝CF＝3，FH＝2，∴S楼房的面积＝x2+3x+6．故选：D．9．(2021•宁波模拟)已知a、b、c三个数中有两个奇数，一个偶数，n是整数，如果S＝(a+n+1)+(b+2n+2)+(c+3n+3)，那么()A．S是偶数B．S是奇数C．S的奇偶性与n的奇偶性相同D．S的奇偶不能确定【分析】弄清a+n+1，b+2n+2，c+3n+3的奇偶性即可．可将3数相加，可知和为偶数，再根据三数和为偶数必有一数为偶数的性质可得积也为偶数．解析(a+n+1)+(b+2n+2)+(c+3n+3)＝a+b+c+6(n+1)．∵a+b+c为偶数，6(n+1)为偶数，∴a+b+c+6(n+1)为偶数∴S是偶数．故选：A．10．(2020秋•沙河口区期末)若(x+a)(x+b)＝x2+4x+3，则a+b的值为()A．3B．﹣3C．4D．﹣4【分析】直接利用多项式乘以多项式运算法则去括号，进而得出a+b的值．解析∵(x+a)(x+b)＝x2+4x+3，∴x2+(a+b)x+ab＝x2+4x+3，∴a+b＝4．故选：C．二、填空题(本大题共8小题，每小题3分，共24分)请把答案直接填写在横线上11．(2020秋•浦东新区期中)计算：(3x+2)(2x﹣3)＝6x2﹣5x﹣6．【分析】运用多项式乘多项式的法则计算即可．解析原式＝6x2﹣9x+4x﹣6＝6x2﹣5x﹣6．故答案为：6x2﹣5x﹣6．12．(2020秋•香坊区校级期中)已知a﹣b＝6，ab＝5，则(a+1)(b﹣1)＝﹣2．【分析】原式利用多项式乘以多项式法则计算，整理后将已知等式代入计算即可求出值．解析∵a﹣b＝6，ab＝5，∴(a+1)(b﹣1)＝ab﹣a+b﹣1＝ab﹣(a﹣b)﹣1＝5﹣6﹣1＝﹣2；故答案为：﹣2．13．(2020秋•浦东新区期中)将关于x的多项式x2+2x+3与2x+b相乘，若积中不出现一次项，则b＝﹣3．【分析】根据题意，利用多项式乘多项式法则计算，确定出b的值即可．解析根据题意得：(x2+2x+3)(2x+b)＝2x3+(4+b)x2+(6+2b)x+3b，由积中不出现一次项，得到6+2b＝0，解得：b＝﹣3．故答案为：﹣3．14．(2020秋•朝阳区期中)如图，现有A类、B类正方形卡片和C类长方形卡片各若干张，若要拼一个长为(3a+b)，宽为(a+2b)的大长方形，则需要7张C类卡片．【分析】用长乘以宽，列出算式，根据多项式乘以多项式的运算法则展开，然后根据A、B、C类卡片的形状可得答案．解析∵(3a+b)(a+2b)＝3a2+6ab+ab+2b2＝3a2+7ab+2b2，∴若要拼一个长为(3a+b)，宽为(a+2b)的大长方形，则需要A类3张，B类2张，C类7张．故答案为：7．15．(2020秋•沙坪坝区校级期中)已知x﹣y＝7，xy＝5，则(2﹣x)(y+2)的值为﹣15．【分析】认真观察题目的特点，易发现(2﹣x)(y+2)化简后会出现，x﹣y，xy，可以进行整体代入即可求得答案．解析(2﹣x)(y+2)＝2y+4﹣xy﹣2x＝﹣xy﹣2(x﹣y)+4，把x﹣y＝7，xy＝5代入，原式＝﹣5﹣2×7+4＝﹣15．故答案为：﹣15．16．(2020秋•九龙坡区校级期中)已知(x﹣2)(x2+mx+n)的乘积项中不含x2和x项，则m+n＝6．【分析】直接利用多项式乘多项式计算，再得出m，n的值，即可得出答案．解析(x﹣2)(x2+mx+n)＝x3+mx2+nx﹣2x2﹣2mx﹣2n＝x3+(m﹣2)x2+(n﹣2m)x﹣2n∵(x﹣2)(x2+mx+n)的乘积项中不含x2和x项，∴m﹣2＝0，n﹣2m＝0，解得：m＝2，n＝4，∴m+n＝6．故答案为：6．17．(2020秋•崇川区校级期中)如果(m2+n2+1)与(m2+n2﹣1)的乘积为15，那么m2+n2的值为4．【分析】根据题意列出等式，再根据平方差公式进行计算，最后求出答案即可．解析解；∵(m2+n2+1)与(m2+n2﹣1)的乘积为15，∴(m2+n2+1)(m2+n2﹣1)＝15，∴(m2+n2)2﹣1＝15，即(m2+n2)2＝16，解得：m2+n2＝4(负数舍去)，故答案为：4．18．(2020秋•西峰区期末)若(x+m)(x+n)＝x2﹣7x+mn，则﹣m﹣n的值为7．【分析】按照多项式的乘法法则展开运算后解析∵(x+m)(x+n)＝x2+(m+n)x+mn＝x2﹣7x+mn，∴m+n＝﹣7，∴﹣m﹣n＝7，故答案为：7．三、解答题(本大题共6小题，共46分．解答时应写出文字说明、证明过程或演算步骤) 19．(2020秋•南岗区期末)化简：(1)(2x)3(﹣5xy2)；(2)(3x+2)(x+2)．【分析】(1)先算积的乘方，然后再利用单项式乘以单项式计算法则进行计算即可；(2)根据多项式乘以多项式的计算法则进行计算即可．解析(1)原式＝8x3•(﹣5xy2)＝﹣8x3•5xy2＝﹣40x4y2；(2)原式＝3x2+6x+2x+4＝3x2+8x+4．20．(2020秋•淅川县期末)已知(x2+mx+n)(x﹣1)的结果中不含x2项和x项，求m、n的值．【分析】把式子展开，合并同类项后找到x2项和x项的系数，令其为0，可求出m和n的值．解析(x2+mx+n)(x﹣1)＝x3+(m﹣1)x2+(n﹣m)x﹣n．∵结果中不含x2的项和x项，∴m﹣1＝0且n﹣m＝0，解得：m＝1，n＝1．21．计算：(1)(2a﹣1)(a﹣4)﹣(a+3)(a﹣1)；(2)t2﹣(t+1)(t﹣5)；(3)(x+1)(x2+x+1)；(4)(2x+3)(x2﹣x+1)．【分析】(1)根据多项式的乘法和合并同类项解答即可；(2)根据多项式的乘法和合并同类项解答即可；(3)根据多项式的乘法和合并同类项解答即可；(4)根据多项式的乘法和合并同类项解答即可．解析(1)(2a﹣1)(a﹣4)﹣(a+3)(a﹣1)＝2a2﹣8a﹣a+4﹣a2+a﹣3a+3＝a2﹣11a+7；(2)t2﹣(t+1)(t﹣5)＝t2﹣t2+5t﹣t+5＝4t+5；(3)(x+1)(x2+x+1)；＝x3+x2+x+x2+x+1＝x3+2x2+2x+1；(4)(2x+3)(x2﹣x+1)＝2x3﹣2x2+2x+3x2﹣3x+3＝2x3+x2﹣x+3．22．(2020秋•新宾县期末)如图，某市有一块长(3a+b)米，宽为(2a+b)米的长方形地块，规划部门计划将阴影部分进行绿化，中间空白处将修建一座雕像．(1)求绿化的面积是多少平方米．(2)当a＝2，b＝1时求绿化面积．【分析】(1)绿化面积＝长方形的面积﹣正方形的面积；(2)把a＝2，b＝1代入(1)求出绿化面积．解析(1)S绿化面积＝(3a+b)(2a+b)﹣(a+b)2＝6a2+5ab+b2﹣a2﹣2ab﹣b2＝5a2+3ab；答：绿化的面积是(5a2+3ab)平方米；(2)当a＝2，b＝1时，绿化面积＝5×22+3×2×1＝20+6＝26．答：当a＝2，b＝1时，绿化面积为26平方米．23．如图1，长方形的两边分别是m+8，m+4．如图2的长方形的两边为m+13，m+3(其中m为正整数)．(1)求出两个长方形的面积S1、S2，并比较S1、S2的大小；(2)现有一个正方形，它的周长与图1的长方形的周长相等，试证明该正方形的面积与图1的长方形的面积的差是一个常数，并求出这个常数．【分析】(1)利用长方形的面积＝长×宽易得S1，S2的大小，并用作差的方法进行比较；(2)利用正方形的周长与图1中的长方形的周长相等易得正方形的边长，从而得正方形的面积，再作差去解决问题．解析(1)∵S1＝(m+8)(m+4)＝m2+12m+32，S2＝(m+13)(m+3)＝m2+16m+39，m为正整数，∴S1﹣S2＝m2+12m+32﹣(m2+16m+39)＝﹣4m﹣7＜0，∴S1＜S2；(2)∵一个正方形的周长与图1中的长方形的周长相等，∴正方形的边长为2(m+8+m+4)÷4＝m+6，正方形的面积为(m+6)2＝m2+12m+36，∴m2+12m+36﹣(m2+12m+32)＝m2+12m+36﹣m2﹣12m﹣32＝4，∴该正方形的面积与图1的长方形的面积的差是一个常数4．24．(2020秋•岳麓区校级月考)定义：L(A)是多项式A化简后的项数．例如多项式A＝x2+2x﹣3，则L(A)＝3．一个多项式A乘以多项式B，化简得到多项式C(即C＝A×B)，如果L(A)≤L(C)≤L(A)+1，则称B是A的“郡园多项式”；如果L(A)＝L(C)，则称B是A的“郡园志勤多项式”．(1)若A＝x﹣2，B＝x+3；那么B是不是A的“郡园多项式”，说明理由；(2)若A＝x﹣2，B＝x2+ax+4是关于x的多项式且B是A的“郡园志勤多项式”，求a的值？(3)若A＝x2﹣x+3m，B＝x2+x+m是关于x的多项式且B是A的“郡园志勤多项式”，求m的值？【分析】(1)根据多项式乘多项式的法则计算，根据“郡园多项式”的定义判断；(2)根据多项式乘多项式的法则计算，根据“郡园志勤多项式”，得到关于a的方程，解方程即可求解；(3)根据多项式乘多项式的法则计算，根据“郡园志勤多项式”，得到关于m的方程，解方程即可求解．解析(1)B是A的“郡园多项式”，理由如下：(x﹣2)(x+3)＝x2﹣2x+3x﹣6＝x2+x﹣6，x2+x﹣6的项数比A的项数多1项，则B是A的“郡园多项式”；(2)(x﹣2)(x2+ax+4)＝x3+ax2+4x﹣2x2﹣2ax﹣8＝x3+(a﹣2)x2+(4﹣2a)x﹣8，∵B是A的“郡园志勤多项式”，∴a﹣2＝0且4﹣2a＝0，解得a＝2．∴a的值是2；(3)(x2﹣x+3m)(x2+x+m)＝x4+x3+mx2﹣x3﹣2x2﹣mx+3mx2+3mx+3m2＝x4+(4m+1)x2+2mx+3m2，∵B是A的“郡园志勤多项式”，∴4m+1＝0或m＝0，解得m=−14或0．∴m的值是−14或0．。

多项式乘法计算题

多项式乘法练习题一、计算题（本大题共12小题，共72.0分）1.计算：(a−1)(a+4)−(a−2)22.计算：(1)(x+5)(x−2)−2(x+1)(x−2);(2)(x+2)2−(x−1)(x+1);3.解方程：(2−x)(3−x)+2(x+6)(x−5)=(3x−1)(x+5)．4.计算：(2)8x2−(x−2)(3x+1)−2(x+1)(x−5)．(4)3a(a2+4a+4)−a(a−3)(3a+4)．5.3(x+5)(x−3)−5(x−2)(x+3)6.计算(2)(−2x−1)2−4(x−1)(x+2)7.计算：(4)(x+2)2−(x−3)(2x+1)．8.计算：(4)(2a+3b)2−2(2a+3b)(a−2b)+(−a+2b)2；计算(2x−1)2−(3x−1)(x+1)+5x(x−1)9.计算(3)2(2x−1)(2x+1)−5x(−x+3y)+4x(−4x2−5y)，其中x=−1，y=2.210.化简：(1)2(a+1)2+(a+1)(1−2a)11.化简下列各式：(1)3(x−1)2+(x+2)(1−2x)答案和解析1.【答案】解：原式=a2+3a−4−(a2−4a+4)=7a−8．【解析】本题考查了整式运算，涉及到完全平方公式、多项式乘多项式，属于基础题.解题时直接用公式，可以得到结果．2.【答案】解：(1)原式=x2+3x−10−2(x2−x−2)=x2+3x−10−2x2+2x+4=−x2+5x−6;(2)原式=x2+4x+4−(x2−1)=x2+4x+4−x2+1=4x+5；(3)原式=(a2−9)(a2+9)=a4−81；(4)原式=−(3x−4y)2=−9x2+24xy−16y2；(5)原式=[(m−n)−3]2=(m−n)2−6(m−n)+9=m2−2mn+n2−6m+6n+9；(6)原式=[m−(2n−3)][m+(2n−3)]=m2−(2n−3)2=m2−4n2+12n−9．【解析】本题主要考查了多项式的混合运算，其中涉及了多项式乘以多项式，平方差公式及完全平方公式，整式加减，解题的关键是熟练掌握它们的运算法则．(1)首先分别进行多项式乘以多项式的运算，然后再进行加减运算即可；(2)首先分别利用平方差公式及完全平方公式进行乘法运算，然后再进行加减运算即可；(3)连续运用平方差公式计算即可；(4)提取负号，再利用完全平方公式计算即可；(5)将原式变形为[(m−n)−3]2，再用完全平方公式计算即可；(6)将原式变形为[m−(2n−3)][m+(2n−3)]，然后依次用平方差公式及完全平方公式计算即可．3.【答案】解：(2−x)(3−x)+2(x+6)(x−5)=(3x−1)(x+5)，整理可得−17x=49，．解得x=−4917【解析】本题考查解方程，掌握多项式与多项式的乘法法则是解题关键.先利用多项式与多项式的乘法法则计算，再去括号，合并同类项，然后解方程求出x的值即可．4.【答案】解：=3x 2+13x +12=a 4−4a 2−5=3a 3+12a 2+12a −3a 3+5a 2+12a=17a 2+24a【解析】本题考查了多项式乘多项式及单项式乘多项式的：先把各多项式乘多项式及单项式乘多项式的积展开，然后进行同类项合并即可．(1)将多项式与多项式的积展开；(2)将多项式与多项式的积展开，同类项合并；(3)将多项式与多项式的积展开，同类项合并；(4)将单项式与多项式的积及多项式与多项式的积展开，同类项合并。

(完整版)多项式乘多项式试题精选(二)附答案

多项式乘多项式试题精选（二）一．填空题（共13小题）1．如图，正方形卡片A类、B类和长方形卡片C类各若干张，如果要拼一个长为（2a+b），宽为（a+b）的长方形，则需要C类卡片_________张．2．（x+3）与（2x﹣m）的积中不含x的一次项，则m=_________．3．若（x+p）（x+q）=x2+mx+24，p，q为整数，则m的值等于_________．4．如图，已知正方形卡片A类、B类和长方形卡片C类各若干张，如果要拼成一个长为（a+2b）、宽为（a+b）的大长方形，则需要A类卡片_________张，B类卡片_________张，C类卡片_________张．5．计算：（﹣p）2•（﹣p）3=_________；=_________；2xy•（_________）=﹣6x2yz；（5﹣a）（6+a）=_________．6．计算（x2﹣3x+1）（mx+8）的结果中不含x2项，则常数m的值为_________．7．如图是三种不同类型的地砖，若现有A类4块，B类2块，C类1块，若要拼成一个正方形到还需B类地砖_________块．8．若（x+5）（x﹣7）=x2+mx+n，则m=_________，n=_________．9．（x+a）（x+）的计算结果不含x项，则a的值是_________．10．一块长m米，宽n米的地毯，长、宽各裁掉2米后，恰好能铺盖一间房间地面，问房间地面的面积是_________平方米．11．若（x+m）（x+n）=x2﹣7x+mn，则﹣m﹣n的值为_________．12．若（x2+mx+8）（x2﹣3x+n）的展开式中不含x3和x2项，则mn的值是_________．13．已知x、y、a都是实数，且|x|=1﹣a，y2=（1﹣a）（a﹣1﹣a2），则x+y+a3+1的值为_________．二．解答题（共17小题）14．若（x2+2nx+3）（x2﹣5x+m）中不含奇次项，求m、n的值．15．化简下列各式：（1）（3x+2y）（9x2﹣6xy+4y2）；（2）（2x﹣3）（4x2+6xy+9）；（3）（m﹣）（m2+m+）；（4）（a+b）（a2﹣ab+b2）（a﹣b）（a2+ab+b2）．16．计算：（1）（2x﹣3）（x﹣5）；（2）（a2﹣b3）（a2+b3）17．计算：（1）﹣（2a﹣b）+[a﹣（3a+4b）]（2）（a+b）（a2﹣ab+b2）18．（x+7）（x﹣6）﹣（x﹣2）（x+1）19．计算：（3a+1）（2a﹣3）﹣（6a﹣5）（a﹣4）．20．计算：（a﹣b）（a2+ab+b2）21．若（x2+px﹣）（x2﹣3x+q）的积中不含x项与x3项，（1）求p、q的值；（2）求代数式（﹣2p2q）2+（3pq）﹣1+p2012q2014的值．22．先化简，再求值：5（3x2y﹣xy2）﹣4（﹣xy2+3x2y），其中x=﹣2，y=3．23．若（x﹣1）（x2+mx+n）=x3﹣6x2+11x﹣6，求m，n的值．24．如图，有多个长方形和正方形的卡片，图甲是选取了2块不同的卡片，拼成的一个图形，借助图中阴影部分面积的不同表示可以用来验证等式a（a+b）=a2+ab成立．（1）根据图乙，利用面积的不同表示方法，写出一个代数恒等式_________；（2）试写出一个与（1）中代数恒等式类似的等式，并用上述拼图的方法说明它的正确性．25．小明想把一长为60cm，宽为40cm的长方形硬纸片做成一个无盖的长方体盒子，于是在长方形纸片的四个角各剪去一个相同的小正方形．（1）若设小正方形的边长为xcm，求图中阴影部分的面积；（2）当x=5时，求这个盒子的体积．26．（x﹣1）（x﹣2）=（x+3）（x﹣4）+20．27．若（x﹣3）（x+m）=x2+nx﹣15，求的值．28．小明在进行两个多项式的乘法运算时（其中的一个多项式是b﹣1），把“乘以（b﹣1）”错看成“除以（b﹣1）”，结果得到（2a﹣b），请你帮小明算算，另一个多项式是多少？29．有足够多的长方形和正方形的卡片如图．如果选取1号、2号、3号卡片分别为1张、2张、3张，可拼成一个长方形（不重叠无缝隙）．请画出这个长方形的草图，并运用拼图前后面积之间的关系说明这个长方形的代数意义．30．（1）填空：（a﹣1）（a+1）=_________（a﹣1）（a2+a+1）=_________（a﹣1）（a3+a2+a+1）=_________（2）你发现规律了吗？请你用你发现的规律填空：（a﹣1）（a n+a n﹣1+…+a2+a+1）=_________（3）根据上述规律，请你求42012+42011+42010+…+4+1的值．_________．多项式乘单项式试题精选（二）参考答案与试题解析一．填空题（共13小题）1．如图，正方形卡片A类、B类和长方形卡片C类各若干张，如果要拼一个长为（2a+b），宽为（a+b）的长方形，则需要C类卡片3张．考点：多项式乘多项式．分析：根据长方形的面积等于长乘以宽列式，再根据多项式的乘法法则计算，然后结合卡片的面积即可作出判断．解答：解：长为2a+b，宽为a+b的矩形面积为（2a+b）（a+b）=2a2+3ab+b2，A图形面积为a2，B图形面积为b2，C图形面积为ab，则可知需要A类卡片2张，B类卡片1张，C类卡片3张．故答案为：3．点评：此题主要考查了多项式乘多项式，掌握多项式乘以多项式的法则是本题的关键．注意不要漏项，漏字母，有同类项的合并同类项．2．（x+3）与（2x﹣m）的积中不含x的一次项，则m=6．考点：多项式乘多项式．专题：计算题．分析：先求出（x+3）与（2x﹣m）的积，再令x的一次项为0即可得到关于m的一元一次方程，求出m的值即可．解答：解：∵（x+3）（2x﹣m）=2x2+（6﹣m）x﹣3m，∴6﹣m=0，解得m=6．故答案为：6．点评：本题考查的是多项式乘以多项式的法则，即先用一个多项式的每一项乘另外一个多项式的每一项，再把所得的积相加．3．若（x+p）（x+q）=x2+mx+24，p，q为整数，则m的值等于10，11，14，25．考点：多项式乘多项式．分析：根据多项式的乘法法则，可得一个多项式，根据多项式相等，可得对应项相等，由p•q=24，p，q为整数，可得p，q的值，再根据p+q=m，可得m的值．解答：解：∵（x+p）（x+q）=x2+mx+24，∴p=24，q=1；p=12，q=2；p=8，q=3；p=6，q=4，∵当p=24，q=1时，m=p+q=25，当p=12，q=2时，m=p+q=14，当p=8，q=3时，m=p+q=11，当p=6，q=4时，m=p+q=10，故答案为：10，11，14，25．点评：本题考察了多项式，先根据多项式的乘法法则计算，分类讨论p，q是解题关键．4．如图，已知正方形卡片A类、B类和长方形卡片C类各若干张，如果要拼成一个长为（a+2b）、宽为（a+b）的大长方形，则需要A类卡片1张，B类卡片2张，C类卡片3张．考点：多项式乘多项式．分析：根据边长组成图形．数出需要A类卡片1张，B类卡片2张，C类卡片3张．解答：解：如图，要拼成一个长为（a+2b）、宽为（a+b）的大长方形，则需要A类卡片1张，B类卡片2张，C 类卡片3张．点评：本题主要考查了多项式乘多项式，解题的关键是根据边长组成图形．5．计算：（﹣p）2•（﹣p）3=﹣p5；=﹣a6b3；2xy•（﹣3xz）=﹣6x2yz；（5﹣a）（6+a）=﹣a2﹣a+30．考点：多项式乘多项式；同底数幂的乘法；幂的乘方与积的乘方；单项式乘单项式．分析：根据同底数幂的乘法、积的乘方和幂的乘方、单项式除以单项式法则、多项式乘以多项式法则求出每个式子的值即可．解答：解：（﹣p）2•（﹣p）3=（﹣p）5=﹣p5，（﹣a2b）3=（﹣）3•（a2）3b3=﹣a6b3，∵﹣6x2yz÷2xy=﹣3xz，∴2xy•（﹣3xz）=﹣6x2yz，（5﹣a）（6+a）=30+5a﹣6a﹣a2=30﹣a﹣a2=﹣a2﹣a+30，故答案为：﹣p5，﹣a6b3，﹣3xz，﹣a2﹣a+30．点评：本题考查了同底数幂的乘法、积的乘方和幂的乘方、单项式除以单项式法则、多项式乘以多项式法则的应用．6．计算（x2﹣3x+1）（mx+8）的结果中不含x2项，则常数m的值为．考点：多项式乘多项式．分析：把式子展开，找到所有x2项的所有系数，令其为0，可求出m的值．解答：解：∵（x2﹣3x+1）（mx+8）=mx4+8x2﹣3mx2﹣24x+mx+8．又∵结果中不含x2的项，∴8﹣3m=0，解得m=．故答案为：．点评：本题主要考查了多项式乘多项式的运算，注意当要求多项式中不含有哪一项时，应让这一项的系数为0．7．如图是三种不同类型的地砖，若现有A类4块，B类2块，C类1块，若要拼成一个正方形到还需B类地砖2块．考点：多项式乘多项式．分析：分别计算出4块A的面积和2块B的面积、1块C的面积，再计算这三种类型的砖的总面积，用完全平方公式化简后，即可得出少了哪种类型的地砖．解答：解：4块A的面积为：4×m×m=4m2；2块B的面积为：2×m×n=2mn；1块C的面积为n×n=n2；那么这三种类型的砖的总面积应该是：4m2+2mn+n2=4m2+4mn+n2﹣2mn=（2m+n）2﹣2mn，因此，少2块B型地砖，故答案为：2．点评：本题考查了完全平方公式的几何意义，立意较新颖，注意面积的不同求解是解题的关键，对此类问题要深入理解．8．若（x+5）（x﹣7）=x2+mx+n，则m=﹣2，n=﹣35．考点：多项式乘多项式．分析：已知等式左边利用多项式乘以多项式法则计算，利用多项式相等的条件即可求出m与n的值．解答：解：（x+5）（x﹣7）=x2﹣2x﹣35=x2+mx+n，则m=﹣2，n=﹣35．故答案为：﹣2，﹣35．点评：此题考查了多项式乘以多项式，熟练掌握运算法则是解本题的关键．9．（x+a）（x+）的计算结果不含x项，则a的值是．考点：多项式乘多项式．分析：多项式乘多项式法则，先用一个多项式的每一项乘以另一个多项式的每一项，再把所得的积相加，依据法则运算，展开式不含关于字母x的一次项，那么一次项的系数为0，就可求a的值．解答：解：∵（x+a）（x+）=又∵不含关于字母x的一次项，∴，解得a=．点评：本题考查了多项式乘多项式法则，相乘后不含哪一项，就让这一项的系数等于0，难度适中．10．一块长m米，宽n米的地毯，长、宽各裁掉2米后，恰好能铺盖一间房间地面，问房间地面的面积是（m﹣2）（n﹣2）或（mn﹣2m﹣2n+4）平方米．考点：多项式乘多项式．分析：根据题意得出算式是（m﹣2）（n﹣2），即可得出答案．解答：解：根据题意得出房间地面的面积是（m﹣2）（n﹣2）；（m﹣2）（n﹣2）=mn﹣2m﹣2n+4．故答案为：（m﹣2）（n﹣2）或（mn﹣2m﹣2n+4）点评：本题考查了多项式乘多项式的应用，关键是能根据题意得出算式，题目比较好，难度适中．11．若（x+m）（x+n）=x2﹣7x+mn，则﹣m﹣n的值为7．考点：多项式乘多项式．专题：计算题．分析：按照多项式的乘法法则展开运算后解答：解：∵（x+m）（x+n）=x2+（m+n）x+mn=x2﹣7x+mn，∴m+n=﹣7，∴﹣m﹣n=7，故答案为：7．点评：本题考查了多项式的乘法，解题的关键是牢记多项式乘以多项式的乘法法则，属于基础题，比较简单．12．若（x2+mx+8）（x2﹣3x+n）的展开式中不含x3和x2项，则mn的值是3．考点：多项式乘多项式．专题：计算题．分析：利用多项式乘以多项式法则计算得到结果，根据展开式中不含x2和x3项列出关于m与n的方程组，求出方程组的解即可得到m与n的值．解答：解：原式=x4+（m﹣3）x3+（n﹣3m+8）x2+（mn﹣24）x+8n，（x2+mx﹣8）（x2﹣3x+n）根据展开式中不含x2和x3项得：，解得：，∴mn=3，故答案为：3．点评：此题考查了多项式乘以多项式，熟练掌握运算法则是解本题的关键．13．已知x、y、a都是实数，且|x|=1﹣a，y2=（1﹣a）（a﹣1﹣a2），则x+y+a3+1的值为2．考点：代数式求值；绝对值；多项式乘多项式．专题：计算题．分析：根据绝对值非负数，平方数非负数的性质可得1﹣a=0，从而得到a的值，然后代入求出x、y的值，再把a、x、y的值代入代数式进行计算即可求解．解答：解：∵|x|=1﹣a≥0，∴a﹣1≤0，﹣a2≤0，∴a﹣1﹣a2≤0，又y2=（1﹣a）（a﹣1﹣a2）≥0，∴1﹣a=0，解得a=1，∴|x|=1﹣1=0，x=0，y2=（1﹣a）（﹣1﹣a2）=0，∴x+y+a3+1=0+0+1+1=2．故答案为：2．点评：本题主要考查了代数式求值问题，把y2的多项式整理，然后根据非负数的性质求出a的值是解题的关键，也是解决本题的突破口，本题灵活性较强．二．解答题（共17小题）14．若（x2+2nx+3）（x2﹣5x+m）中不含奇次项，求m、n的值．考点：多项式乘多项式．分析：把式子展开，让x4的系数，x2的系数为0，得到m，n的值．解答：解：（x2+2nx+3）（x2﹣5x+m）=x4﹣5x3+mx2+2nx3﹣10nx2+2mnx+3x2﹣15x+3m=x4+（2n﹣5）x3+（m﹣10n+3）x2+（2mn﹣15）x+3m，∵结果中不含奇次项，∴2n﹣5=0，2mn﹣15=0，解得m=3，n=．点评：本题主要考查了多项式乘多项式的运算，注意当要求多项式中不含有哪一项时，应让这一项的系数为0．15．化简下列各式：（1）（3x+2y）（9x2﹣6xy+4y2）；（2）（2x﹣3）（4x2+6xy+9）；（3）（m﹣）（m2+m+）；（4）（a+b）（a2﹣ab+b2）（a﹣b）（a2+ab+b2）．考点：多项式乘多项式．分析：根据立方和与立方差公式解答即可．解答：解：（1）（3x+2y）（9x2﹣6xy+4y2）=（3x）3+（2y）3=27x3+8y3；（2）（2x﹣3）（4x2+6xy+9）=（2x）3﹣33=8x3﹣27；（3）（m﹣）（m2+m+）=﹣=﹣；（4）（a+b）（a2﹣ab+b2）（a﹣b）（a2+ab+b2）=（a3+b3）（a3﹣b3）=a6﹣b6．点评：本题考查了立方和与立方差公式，熟练记忆公式是解题的关键．16．计算：（1）（2x﹣3）（x﹣5）；（2）（a2﹣b3）（a2+b3）考点：多项式乘多项式．分析：（1）根据多项式乘以多项式的法则，可表示为（a+b）（m+n）=am+an+bm+bn，计算即可；（2）根据平方差公式计算即可．解答：解：（1）（2x﹣3）（x﹣5）=2x2﹣10x﹣3x+15=2x2﹣13x+15；（2）（a2﹣b3）（a2+b3）=a4﹣b6．点评：本题考查了多项式乘以多项式的法则以及平方差公式．注意不要漏项，漏字母，有同类项的合并同类项．17．计算：（1）﹣（2a﹣b）+[a﹣（3a+4b）]（2）（a+b）（a2﹣ab+b2）考点：多项式乘多项式；整式的加减．专题：计算题．分析：（1）先去小括号，再去大括号，最后按照整式加减混合运算规则进行计算即可；（2）根据多项式乘以多项式的法则，可表示为（a+b）（m+n）=am+an+bm+bn，计算即可．解答：解：（1）原式=﹣2a+b+[a﹣3a﹣4b]，=﹣2a+b+a﹣3a﹣4b，=﹣4a﹣3b；（2）原式=a3﹣a2b+ab2+a2b﹣ab2+b3，=a3+b3．点评：本题主要考查多项式乘以多项式的法则．注意不要漏项，漏字母，有同类项的合并同类项．18．（x+7）（x﹣6）﹣（x﹣2）（x+1）考点：多项式乘多项式．分析：依据多项式乘多项式法则运算．解答：解：（x+7）（x﹣6）﹣（x﹣2）（x+1）=x2﹣6x+7x﹣42﹣x2﹣x+2x+2=2x﹣40．点评：本题考查了多项式乘多项式法则，先用一个多项式的每一项乘以另一个多项式的每一项，再把所得的积相加．关键是不能漏项．19．计算：（3a+1）（2a﹣3）﹣（6a﹣5）（a﹣4）．考点：多项式乘多项式．分析：根据整式混合运算的顺序和法则分别进行计算，再把所得结果合并即可．解答：解：（3a+1）（2a﹣3）+（6a﹣5）（a﹣4）=6a2﹣9a+2a﹣3+6a2﹣24a﹣5a+20=12a2﹣36a+17．点评：此题考查了整式的混合运算，在计算时要注意混合运算的顺序和法则以及运算结果的符号，是一道基础题．20．计算：（a﹣b）（a2+ab+b2）考点：多项式乘多项式；单项式乘单项式．专题：计算题．分析：根据多项式乘以多项式的法则和单项式乘单项式的法则进行计算即可．解答：解：原式=a3+a2b+ab2﹣a2b﹣ab2﹣b3=a3﹣b3．点评：本题主要考查对多项式乘以多项式的法则和单项式乘单项式的法则得理解和掌握，能熟练地运用法则进行计算是解此题的关键．21．若（x2+px﹣）（x2﹣3x+q）的积中不含x项与x3项，（1）求p、q的值；（2）求代数式（﹣2p2q）2+（3pq）﹣1+p2012q2014的值．考点：多项式乘多项式．分析：（1）形开式子，找出x项与x3令其系数等于0求解．（2）把p，q的值入求解．解答：解：（1）（x2+px﹣）（x2﹣3x+q）=x4+（p﹣3）x3+（9﹣3p﹣）x2+（qp+1）x+q，∵积中不含x项与x3项，∴P﹣3=0，qp+1=0∴p=3，q=﹣，（2）（﹣2p2q）2+（3pq）﹣1+p2012q2014=[﹣2×32×（﹣）]2++×32=36﹣+9=44．点评：本题主要考查了多项式乘多项式，解题的关键是正确求出p，q的值22．先化简，再求值：5（3x2y﹣xy2）﹣4（﹣xy2+3x2y），其中x=﹣2，y=3．考点：整式的加减—化简求值；合并同类项；多项式乘多项式．专题：计算题．分析：根据单项式乘多项式的法则展开，再合并同类项，把x y的值代入求出即可．解答：解：原式=15x2y﹣5xy2+4xy2﹣12x2y=3x2y﹣xy2，当x=﹣2，y=3时，原式=3×（﹣2）2×3﹣（﹣2）×32=36+18=54．点评：本题考查了对整式的加减，合并同类项，单项式乘多项式等知识点的理解和掌握，注意展开时不要漏乘，同时要注意结果的符号，代入﹣2时应用括号．23．若（x﹣1）（x2+mx+n）=x3﹣6x2+11x﹣6，求m，n的值．考点：多项式乘多项式．专题：计算题．分析：把（x﹣1）（x2+mx+n）展开后，每项的系数与x3﹣6x2+11x﹣6中的项的系数对应，可求得m、n的值．解答：解：∵（x﹣1）（x2+mx+n）=x3+（m﹣1）x2+（n﹣m）x﹣n=x3﹣6x2+11x﹣6∴m﹣1=﹣6，﹣n=﹣6，解得m=﹣5，n=6．点评：本题主要考查了多项式乘多项式的法则，注意不要漏项，漏字母，有同类项的合并同类项．根据对应项系数相等列式求解m、n是解题的关键．24．如图，有多个长方形和正方形的卡片，图甲是选取了2块不同的卡片，拼成的一个图形，借助图中阴影部分面积的不同表示可以用来验证等式a（a+b）=a2+ab成立．（1）根据图乙，利用面积的不同表示方法，写出一个代数恒等式（a+2b）（a+b）=a2+3ab+2b2；（2）试写出一个与（1）中代数恒等式类似的等式，并用上述拼图的方法说明它的正确性．考点：多项式乘多项式．专题：计算题．分析：（1）根据图形是一个长方形求出长和宽，相乘即可；（2）正方形的面积是2个长方形的面积加上2个正方形的面积，代入求出即可．解答：解：（1）观察图乙得知：长方形的长为：a+2b，宽为a+b，∴面积为：（a+2b）（a+b）=a2+3ab+2b2；（2）如图所示：恒等式是，（a+b）（a+b）=a2+2ab+b2．答：恒等式是a+b）（a+b）=a2+2ab+b2．点评：本题主要考查对多项式乘多项式的理解和掌握，能表示各部分的面积是解此题的关键．25．小明想把一长为60cm，宽为40cm的长方形硬纸片做成一个无盖的长方体盒子，于是在长方形纸片的四个角各剪去一个相同的小正方形．（1）若设小正方形的边长为xcm，求图中阴影部分的面积；（2）当x=5时，求这个盒子的体积．考点：多项式乘多项式；代数式求值．分析：（1）剩余部分的面积即是边长为60﹣2x，40﹣2x的长方形的面积；（2）利用长方体的体积公式先表示出长方形的体积，再把x=5，代入即可．解答：解：（1）（60﹣2x）（40﹣2x）=4x2﹣200x+2400，答：阴影部分的面积为（4x2﹣200x+2400）cm2；（2）当x=5时，4x2﹣200x+2400=1500（cm2），这个盒子的体积为：1500×5=7500（cm3），答：这个盒子的体积为7500cm3．点评：此题主要考查用代数式表示正方形、矩形的面积和体积，需熟记公式，且认真观察图形，得出等量关系．26．（x﹣1）（x﹣2）=（x+3）（x﹣4）+20．考点：多项式乘多项式；解一元一次方程．分析：将方程的两边利用多项式的乘法展开后整理成方程的一般形式求解即可．解答：解：原方程变形为：x2﹣3x+2=x2﹣x﹣12+20整理得：﹣2x﹣6=0，解得：x=﹣3．点评：本题考查了多项式乘多项式及解一元二次方程的知识，解题的关键是利用多项式的乘法对方程进行化简．27．若（x﹣3）（x+m）=x2+nx﹣15，求的值．考点：多项式乘多项式．分析：首先把）（x﹣3）（x+m）利用多项式的乘法公式展开，然后根据多项式相等的条件：对应项的系数相同即可得到m、n的值，从而求解．解答：解：（x﹣3）（x+m）=x2+（m﹣3）x﹣3m=x2+nx﹣15，则解得：．=．点评：本题考查了多项式的乘法法则以及多项式相等的条件，理解多项式的乘法法则是关键．28．小明在进行两个多项式的乘法运算时（其中的一个多项式是b﹣1），把“乘以（b﹣1）”错看成“除以（b﹣1）”，结果得到（2a﹣b），请你帮小明算算，另一个多项式是多少？考点：多项式乘多项式．分析：根据被除式=商×除式，所求多项式是（2a﹣b）（b﹣1），根据多项式乘多项式的法则计算即可．解答：解：设所求的多项式是M，则M=（2a﹣b）（b﹣1）=2ab﹣2a﹣b2+b．点评：本题考查了多项式乘多项式法则，根据被除式、除式、商三者之间的关系列出等式是解题的关键，熟练掌握运算法则也很重要．29．有足够多的长方形和正方形的卡片如图．如果选取1号、2号、3号卡片分别为1张、2张、3张，可拼成一个长方形（不重叠无缝隙）．请画出这个长方形的草图，并运用拼图前后面积之间的关系说明这个长方形的代数意义．考点：多项式乘多项式．分析：先根据题意画出图形，然后求出长方形的长和宽，长为a+2b，宽为a+b，从而求出长方形的面积．解答：解：如图：或a2+3ab+2b2=（a+b）（a+2b）．点评：考查多项式与多项式相乘问题；根据面积的不同表示方法得到相应的等式是解决本题的关键．30．（1）填空：（a﹣1）（a+1）=a2﹣1（a﹣1）（a2+a+1）=a3﹣1（a﹣1）（a3+a2+a+1）=a4﹣1（2）你发现规律了吗？请你用你发现的规律填空：（a﹣1）（a n+a n﹣1+…+a2+a+1）=a n+1﹣1（3）根据上述规律，请你求42012+42011+42010+…+4+1的值．（42013﹣1）．考点：多项式乘多项式．专题：规律型．分析：（1）根据平方差公式和立方差公式可得前2个式子的结果，利用多项式乘以多项式的方法可得出第3个式子的结果；（2）从而总结出规律是：（a﹣1）（a n+a n﹣1+…+a2+a+1）=a n+1﹣1；（3）根据上述结论计算下列式子即可．解答：解：根据题意：（1）（a﹣1）（a+1）=a2﹣1；（a﹣1）（a2+a+1）=a3﹣1；（a﹣1）（a3+a2+a+1）=a4﹣1；（2）（a﹣1）（a n+a n﹣1+a n﹣2+…+a2+a+1）=a n+1﹣1．（3）根据以上分析（1）42012+42011+42010+…+4+1299+298+297+…+2+1，=（4﹣1）（42012+42011+42010+…+4+1），=（42013﹣1）．故答案为：（1）a2﹣1，a3﹣1，a4﹣1；（2）a n+1﹣1；（3）（42013﹣1）．点评：主要考查了学生的分析、总结、归纳能力，规律型的习题一般是从所给的数据和运算方法进行分析，从特殊值的规律上总结出一般性的规律．。

多项式乘多项式试题精选(一)附答案

多项式乘多项式试题精选（一）一．选择题（共25小题）1．计算：（x+1）（x﹣2）=（）A．x2﹣x﹣2 B．x2+x﹣2 C．x2﹣x+2 D．x2+x+2 2．（2002•潍坊）计算（a+m）（a+）的结果中不含关于字母a的一次项，则m等于（）A．2B．﹣2 C．D．﹣3．若（x﹣1）（x+3）=x2+mx+n，那么m，n的值分别是（）A．m=1，n=3 B．m=4，n=5 C．m=2，n=﹣3 D．m=﹣2，n=34．已知m+n=2，mn=﹣2，则（1﹣m）（1﹣n）的值为（）A．﹣3 B．﹣1 C．1D．55．下列多项式相乘的结果是a2﹣3a﹣4的是（）A．（a﹣2）（a+2）B．（a+1）（a﹣4）C．（a﹣1）（a+4）D．（a+2）（a+2）6．如果（x+a）（x+b）的结果中不含x的一次项，那么a、b满足（）A．a=b B．a=0 C．a=﹣b D．b=07．计算（x+y）（x2﹣xy+y2）的结果是（）A．x3﹣y3B．x3+y3C．x3+2xy+y3D．x3﹣2xy+y38．若（x﹣1）（x+2）=x2+px﹣2，则p的值是（）A．1B．﹣1 C．2D．39．如果（x+1）（x2﹣5ax+a）的乘积中不含x2项，则a为（）A．B．﹣C．﹣5 D．510．（x2﹣mx+3）（3x﹣2）的积中不含x的二次项，则m的值是（）A．0B．C．﹣D．﹣11．已知（5﹣3x+mx2﹣6x3）（1﹣2x）的计算结果中不含x3的项，则m的值为（）A．3B．﹣3 C．﹣D．012．多项式（mx+4）（2﹣3x）展开后不含x项，则m的值为（）A．2B．4C．﹣6 D．613．若（x+4）（x﹣3）=x2+mx﹣n，则（）A．m=﹣1，n=12 B．m=﹣1，n=﹣12 C．m=1，n=﹣12 D．m=1，n=1214．计算（y+1）（y2﹣1）的结果正确的是（）A．y3﹣y+y2﹣1 B．y3﹣y﹣y2﹣1 C．y3+y+y2﹣1 D．y3+y+y2+115．要使（4x﹣a）（x+1）的积中不含有x的一次项，则a等于（）A．﹣4 B．2C．3D．416．若（x2+px+q）（x2+7）的计算结果中，不含x2项，则q的值是（）A．0B．7C．﹣7 D．±717．若（x2+x﹣1）（px+2）的乘积中，不含x2项，则p的值是（）A．1B．0C．﹣1 D．﹣218．若（x2+px﹣q）（x2+3x+1）的结果中不含x2和x3项，则p﹣q的值为（）A．11 B．5C．﹣11 D．﹣1419．计算（2a﹣3b）（2b+3a）的结果是（）A．4a2﹣9b2B．6a2﹣5ab﹣6b2C．6a2﹣5ab+6b2D．6a2﹣15ab+6b220．若（x+k）（x﹣5）的积中不含有x的一次项，则k的值是（）A．0B．5C．﹣5 D．﹣5或521．利用形如a（b+c）=ab+ac的分配性质，求（3x+2）（x﹣5）的积的第一步骤是（）A．（3x+2）x+（3x+2）（﹣5）B．3x（x﹣5）+2（x﹣5）C．3x2﹣13x﹣10 D．3x2﹣17x﹣1022．如果多项式4a4﹣（b﹣c）2=M（2a2﹣b+c），则M表示的多项式是（）A．2a2﹣b+c B．2a2﹣b﹣c C．2a2+b﹣c D．2a2+b+c23．下面的计算结果为3x2+13x﹣10的是（）A．（3x+2）（x+5）B．（3x﹣2）（x﹣5）C．（3x﹣2）（x+5）D．（x﹣2）（3x+5）24．下列运算中，正确的是（）A．2ac（5b2+3c）=10b2c+6ac2B．（a﹣b）2（a﹣b+1）=（a﹣b）3﹣（b﹣a）2C．（b+c﹣a）（x+y+1）=x（b+c﹣a）﹣y（a﹣b﹣c）﹣a+b﹣c D．（a﹣2b）（11b﹣2a）=（a﹣2b）（3a+b）﹣5（2b﹣a）225．根据需要将一块边长为x的正方形铁皮按如图的方法截去一部分后．制成的长方形铁皮（阴影部分）的面积是多少？几名同学经过讨论给出了不同的答案，其中正确的是（）①（x﹣5）（x﹣6）；②x2﹣5x﹣6（x﹣5）；③x2﹣6x﹣5x；④x2﹣6x﹣5（x﹣6）A．①②④B．①②③④C．①D．②④二．填空题（共5小题）26．（2014•江西样卷）已知（x+5）（x+n）=x2+mx﹣5，则m+n=_________．27．（2011•翔安区质检）若x2﹣2x﹣15=（x+3）（x+m），则m=_________．28．已知a2﹣a+5=0，则（a﹣3）（a+2）的值是_________．29．如果（x+1）（x2﹣5ax+a）的乘积中不含x2项，则a为_________．30．若（x+2）（x2+px+4）的化简结果不含x2和x项，则p=_________．多项式乘多项式试题精选（一）附答案参考答案与试题解析一．选择题（共25小题）1．计算：（x+1）（x﹣2）=（）A．x2﹣x﹣2 B．x2+x﹣2 C．x2﹣x+2 D．x2+x+2考点：多项式乘多项式．分析：运用多项式乘多项式展开求解．解答：解：（x+1）（x﹣2）=x2﹣x﹣2，故选：A．点评：本题主要考查了多项式乘多项式，熟练掌握运算法则是解题的关键．2．（2002•潍坊）计算（a+m）（a+）的结果中不含关于字母a的一次项，则m等于（）A．2B．﹣2 C．D．﹣考点：多项式乘多项式．分析：多项式乘多项式法则，先用一个多项式的每一项乘以另一个多项式的每一项，再把所得的积相加．依据法则运算，展开式不含关于字母a的一次项，那么一次项的系数为0，就可求m的值．解答：解：∵（a+m）（a+）=a2+（m+）a+m，又∵不含关于字母a的一次项，∴m+=0，∴m=﹣．故选D．点评：本题考查了多项式乘多项式法则，相乘后不含哪一项，就让这一项的系数等于0．3．若（x﹣1）（x+3）=x2+mx+n，那么m，n的值分别是（）A．m=1，n=3 B．m=4，n=5 C．m=2，n=﹣3 D．m=﹣2，n=3考点：多项式乘多项式．分析：运用多项式与多项式相乘的法则将等式左边展开，通过比较左右两边的对应项系数，将问题转化为关于m，n的方程来确定m，n的值．解答：解：∵（x﹣1）（x+3）=x2+2x﹣3=x2+mx+n，∴m=2，n=﹣3．故选C．点评：本题考查了多项式乘多项式，运算法则需要熟练掌握，利用对应项系数相等求解是解题的关键．4．已知m+n=2，mn=﹣2，则（1﹣m）（1﹣n）的值为（）A．﹣3 B．﹣1 C．1D．5考点：多项式乘多项式．分析：多项式乘多项式法则，先用一个多项式的每一项乘以另一个多项式的每一项，再把所得的积转换成以m+n，mn为整体相加的形式，代入求值．解答：解：∵m+n=2，mn=﹣2，∴（1﹣m）（1﹣n），=1﹣（m+n）+mn，=1﹣2﹣2，=﹣3．故选A．点评：本题考查了多项式乘多项式法则，合并同类项时要注意项中的指数及字母是否相同．5．下列多项式相乘的结果是a2﹣3a﹣4的是（）A．（a﹣2）（a+2）B．（a+1）（a﹣4）C．（a﹣1）（a+4）D．（a+2）（a+2）考点：多项式乘多项式．分析：首先根据多项式乘多项式的法则分别对各选项计算，然后比较即可．解答：解：A、（a﹣2）（a+2）=a2﹣4，不符合题意；B、（a+1）（a﹣4）=a2﹣3a﹣4，符合题意；C、（a﹣1）（a+4）=a2+3a﹣4，不符合题意；D、（a+2）（a+2）=a2+4a+4，不符合题意．故选B．点评：本题考查多项式乘多项式法则：先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加．要求学生熟练掌握．本题还可以直接将a2﹣3a﹣4进行因式分解，得出结果．6．如果（x+a）（x+b）的结果中不含x的一次项，那么a、b满足（）A．a=b B．a=0 C．a=﹣b D．b=0考点：多项式乘多项式．分析：把式子展开，找到所有x项的所有系数，令其为0，可求出m的值．解答：解：∵（x+a）（x+b）=x2+ax+bx+ab=x2+（a+b）x+ab．又∵结果中不含x的一次项，∴a+b=0，即a=﹣b．故选C．点评：本题主要考查了多项式乘多项式的运算，注意当要求多项式中不含有哪一项时，应让这一项的系数为0．7．计算（x+y）（x2﹣xy+y2）的结果是（）A．x3﹣y3B．x3+y3C．x3+2xy+y3D．x3﹣2xy+y3考点：多项式乘多项式．专题：计算题．分析：直接利用立方和公式即可得到答案．解答：解：由立方和公式得：（x+y）（x2﹣xy+y2）=x3+y3，故选B．点评：本题考查了立方和公式，也可以利用多项式的乘法进行计算．8．若（x﹣1）（x+2）=x2+px﹣2，则p的值是（）A．1B．﹣1 C．2D．3考点：多项式乘多项式．分析：将等式左边根据多项式乘以多项式的法则，可表示为（a+b）（m+n）=am+an+bm+bn，再根据等式左右两边对应项的系数相等计算即可．解答：解：∵（x﹣1）（x+2）=x2+x﹣2，且（x﹣1）（x+2）=x2+px﹣2，∴x2+x﹣2=x2+px﹣2，根据对应项系数相等得p=1．故答案选A．点评：本题主要考查多项式乘以多项式的法则．注意不要漏项，漏字母，有同类项的合并同类项．同时也考查了恒等式的性质．9．如果（x+1）（x2﹣5ax+a）的乘积中不含x2项，则a为（）A．B．﹣C．﹣5 D．5考点：多项式乘多项式．分析：先根据多项式乘以多项式的法则展开，再合并同类项，根据已知得出方程﹣5a+1=0，求出即可．解答：解：（x+1）（x2﹣5ax+a）=x3﹣5ax2+ax+x2﹣5ax+a=x3+（﹣5a+1）x2+ax+a，∵（x+1）（x2﹣5ax+a）的乘积中不含x2项，∴﹣5a+1=0，a=，故选A．点评：本题考查了多项式乘以多项式的法则，关键是能根据题意得出关于a的方程．10．（x2﹣mx+3）（3x﹣2）的积中不含x的二次项，则m的值是（）A．0B．C．﹣D．﹣考点：多项式乘多项式．专题：计算题．分析：根据多项式乘多项式的法则先把原式展开得出3x3+（﹣2﹣3m）x2+（2m+9）x﹣6，根据已知积中不含x 的二次项得出方程﹣2﹣3m=0，求出方程的解即可．解答：解：（x2﹣mx+3）（3x﹣2）=3x3﹣2x2﹣3mx2+2mx+9x﹣6=3x3+（﹣2﹣3m）x2+（2m+9）x﹣6，∵（x2﹣mx+3）（3x﹣2）的积中不含x的二次项，∴﹣2﹣3m=0，解得：m=﹣．故选：C．点评：本题考查了多项式乘多项式和解一元一次方程的应用，关键是根据题意得出方程﹣2﹣3m=0，题型较好，主要培养学生的理解能力和计算能力．11．已知（5﹣3x+mx2﹣6x3）（1﹣2x）的计算结果中不含x3的项，则m的值为（）A．3B．﹣3 C．﹣D．0考点：多项式乘多项式．分析：把式子展开，找到所有x3项的所有系数，令其为0，可求出m的值．解答：解：∵（5﹣3x+mx2﹣6x3）（1﹣2x）=5﹣13x+（m+6）x2+（﹣6﹣2m）x3+12x4．又∵结果中不含x3的项，∴﹣2m﹣6=0，解得m=﹣3．故选B．点评：本题主要考查了多项式乘多项式的运算，注意当要求多项式中不含有哪一项时，应让这一项的系数为0．12．多项式（mx+4）（2﹣3x）展开后不含x项，则m的值为（）A．2B．4C．﹣6 D．6考点：多项式乘多项式．分析：根据多项式乘以多项式法则展开后，根据x项的系数相等0可得出m的值．解答：解：（mx+4）（2﹣3x）=2mx﹣3mx2+8﹣12x=（2m﹣12）x﹣3mx2+8∵展开后不含x项，∴2m﹣12=0∴m=6．故选：D．点评：本题考查了多项式乘以多项式的法则的应用，主要考查学生的化简能力．13．若（x+4）（x﹣3）=x2+mx﹣n，则（）A．m=﹣1，n=12 B．m=﹣1，n=﹣12 C．m=1，n=﹣12 D．m=1，n=12考点：多项式乘多项式．分析：首先根据多项式乘法法则展开（x+4）（x﹣3），然后根据多项式各项系数即可确定m、n的值．解答：解：∵（x+4）（x﹣3）=x2+x﹣12，而（x+4）（x﹣3）=x2+mx﹣n，∴x2+x﹣12=x2+mx﹣n，∴m=1，n=12．故选D．点评：此题主要考查了多项式的定义和乘法法则，首先利用多项式乘法法则展开，再根据多项式的定义确定m、n 的值．14．计算（y+1）（y2﹣1）的结果正确的是（）A．y3﹣y+y2﹣1 B．y3﹣y﹣y2﹣1 C．y3+y+y2﹣1 D．y3+y+y2+1考点：多项式乘多项式．分析：根据多项式乘以多项式的法则，可表示为（a+b）（m+n）=am+an+bm+bn，计算即可．解答：解：（y+1）（y2﹣1）=y3﹣y+y2﹣1，故选：A．点评：本题主要考查多项式乘以多项式的法则．注意不要漏项，漏字母，有同类项的合并同类项．15．要使（4x﹣a）（x+1）的积中不含有x的一次项，则a等于（）A．﹣4 B．2C．3D．4考点：多项式乘多项式．分析：先运用多项式的乘法法则计算，再合并同类项，因积中不含x的一次项，所以让一次项的系数等于0，得a 的等式，再求解．解答：解：（4x﹣a）（x+1），=4x2+4x﹣ax﹣a，=4x2+（4﹣a）x﹣a，∵积中不含x的一次项，∴4﹣a=0，解得a=4．故选：D．点评：本题考查了多项式乘多项式法则，注意当要求多项式中不含有哪一项时，应让这一项的系数为0．16．若（x2+px+q）（x2+7）的计算结果中，不含x2项，则q的值是（）A．0B．7C．﹣7 D．±7考点：多项式乘多项式．分析：把式子展开，找到所有x2项的系数，令它的系数分别为0，列式求解即可．解答：解：∵（x2+px+q）（x2+7）=x4+7x2+px3+7px+qx2+7q=x4+px3+（7+q）x2+7px+7q．∵乘积中不含x2项，∴7+p=0，∴q=﹣7．故选：C．点评：考查了多项式乘多项式，灵活掌握多项式乘以多项式的法则，注意各项符号的处理．17．若（x2+x﹣1）（px+2）的乘积中，不含x2项，则p的值是（）A．1B．0C．﹣1 D．﹣2考点：多项式乘多项式．分析：根据多项式乘以多项式法则展开，合并后根据对应的x2的系数相等得出2+p=0，求出即可．解答：解：（x2+x﹣1）（px+2）=px3+2x2+px2+2x﹣px﹣2=px3+（2+p）x2+（2﹣p）x﹣2，∵（x2+x﹣1）（px+2）的乘积中，不含x2项，∴2+p=0，p=﹣2，故选D．点评：本题考查了多项式乘以多项式法则的应用．18．若（x2+px﹣q）（x2+3x+1）的结果中不含x2和x3项，则p﹣q的值为（）A．11 B．5C．﹣11 D．﹣14考点：多项式乘多项式．分析：把式子展开，找到所有x2和x3项的系数，令它们的系数分别为0，列式求解即可．解答：解：∵（x2+px﹣q）（x2+3x+1）=x4+3x3+x2+px3+3px2+px﹣qx2﹣3qx﹣q=x4+（3+p）x3+（1+3p﹣q）x2+（p﹣3q）x﹣q．∵乘积中不含x2与x3项，∴3+p=0，1+3p﹣q=0，∴p=﹣3，q=﹣8．∴p﹣q=﹣3﹣（﹣8）=5．故选：B．点评：查了多项式乘多项式，灵活掌握多项式乘以多项式的法则，注意各项符号的处理．19．计算（2a﹣3b）（2b+3a）的结果是（）A．4a2﹣9b2B．6a2﹣5ab﹣6b2C．6a2﹣5ab+6b2D．6a2﹣15ab+6b2考点：多项式乘多项式．专题：计算题．分析：按照多项式的乘法法则展开运算即可．解答：解：（2a﹣3b）（2b+3a）=4ab+6a2﹣6b2﹣9ab，=6a2﹣6b2﹣5ab故选B．点评：考查了多项式的乘以多项式的知识，解题的关键是牢记运算法则，符号容易出错．20．若（x+k）（x﹣5）的积中不含有x的一次项，则k的值是（）A．0B．5C．﹣5 D．﹣5或5考点：多项式乘多项式．分析：根据多项式乘多项式的运算法则，展开后令x的一次项的系数为0，列式求解即可．解答：解：（x+k）（x﹣5）=x2﹣5x+kx﹣5k=x2+（k﹣5）x﹣5k，∵不含有x的一次项，∴k﹣5=0，解得k=5．故选B．点评：本题考查了多项式乘多项式的运算法则，注意当要求多项式中不含有哪一项时，应让这一项的系数为0．21．利用形如a（b+c）=ab+ac的分配性质，求（3x+2）（x﹣5）的积的第一步骤是（）A．（3x+2）x+（3x+2）（﹣5）B．3x（x﹣5）+2（x﹣5）C．3x2﹣13x﹣10 D．3x2﹣17x﹣10考点：多项式乘多项式．分析：把3x+2看成一整体，再根据乘法分配律计算即可．解答：解：（3x+2）（x﹣5）的积的第一步骤是（3x+2）x+（3x+2）（﹣5）．故选A．点评：本题主要考查了多项式乘多项式的运算，把3x+2看成一整体是关键，注意根据题意不要把x﹣5看成一整体．22．如果多项式4a4﹣（b﹣c）2=M（2a2﹣b+c），则M表示的多项式是（）A．2a2﹣b+c B．2a2﹣b﹣c C．2a2+b﹣c D．2a2+b+c考点：多项式乘多项式．分析：首先将多项式4a4﹣（b﹣c）2分解成两个因式的乘积，然后与M（2a2﹣b+c）进行比较，得出结果．解答：解：∵4a4﹣（b﹣c）2，=（2a2+b﹣c）（2a2﹣b+c），=M（2a2﹣b+c），∴M=2a2+b﹣c．故选C．点评：本题主要考查了多项式乘多项式的运算，灵活应用平方差公式a2﹣b2=（a+b）（a﹣b），将多项式4a4﹣（b﹣c）2分解成两个因式的乘积，是解本题的关键．23．下面的计算结果为3x2+13x﹣10的是（）A．（3x+2）（x+5）B．（3x﹣2）（x﹣5）C．（3x﹣2）（x+5）D．（x﹣2）（3x+5）考点：多项式乘多项式．分析：依据多项式乘以多项式的法则分别计算，然后比较．解答：解：A、（3x+2）（x+5）=3x2+17x+10；B、（3x﹣2）（x﹣5）=3x2﹣17x+10；C、（3x﹣2）（x+5）=3x2+13x﹣10；D、（x﹣2）（3x+5）=3x2﹣x﹣10．故选C．点评：主要考查多项式乘以多项式的运算法则，可表示为（a+b）（m+n）=am+an+bm+bn，熟练掌握运算法则是解题的关键．24．下列运算中，正确的是（）A．2ac（5b2+3c）=10b2c+6ac2B．（a﹣b）2（a﹣b+1）=（a﹣b）3﹣（b﹣a）2C．（b+c﹣a）（x+y+1）=x（b+c﹣a）﹣y（a﹣b﹣c）﹣a+b﹣c D．（a﹣2b）（11b﹣2a）=（a﹣2b）（3a+b）﹣5（2b﹣a）2考点：多项式乘多项式；单项式乘多项式．分析：根据多项式乘以多项式的法则．多项式与多项式相乘，先用一个多项式的每一项乘另外一个多项式的每一项，再把所得的积相加．解答：解：A、应为2ac（5b2+3c）=10ab2c+6ac2，故本选项错误；B、应为（a﹣b）2（a﹣b+1）=（a﹣b）3+（b﹣a）2，故本选项错误；C、应为（b+c﹣a）（x+y+1）=x（b+c﹣a）﹣y（a﹣b﹣c）﹣a﹣b﹣c，故本选项错误；D、（a﹣2b）（11b﹣2a）=（a﹣2b）（3a+b）﹣5（2b﹣a）2．故选D．点评：本题主要考查了多项式乘多项式的运算，熟练掌握运算法则是解题的关键，注意各项符号的处理．25．根据需要将一块边长为x的正方形铁皮按如图的方法截去一部分后．制成的长方形铁皮（阴影部分）的面积是多少？几名同学经过讨论给出了不同的答案，其中正确的是（）①（x﹣5）（x﹣6）；②x2﹣5x﹣6（x﹣5）；③x2﹣6x﹣5x；④x2﹣6x﹣5（x﹣6）A．①②④B．①②③④C．①D．②④考点：多项式乘多项式．分析：因为正方形的边长为x，一边截去宽5的一条，另一边截去宽6的一条，所以阴影部分长方形的长和宽分别为x﹣5与x﹣6．然后根据长方形面积计算公式进行计算．解答：解：①由题意得：阴影部分长方形的长和宽分别为x﹣5、x﹣6，则阴影的面积=（x﹣5）（x﹣6）=x2﹣11x+30．故该项正确；②如图所示：阴影部分的面积=x2﹣5x﹣6（x﹣5），故该项正确；④如图所示：阴影部分的面积=x2﹣6x﹣5（x﹣6），故该项正确；③由④知本项错误．故选：A．点评：本题主要考查了整式的乘除运算﹣多项式乘多项式．实际上也是去括号、合并同类项，这是各地中考的常考点．二．填空题（共5小题）26．（2014•江西样卷）已知（x+5）（x+n）=x2+mx﹣5，则m+n=3．考点：多项式乘多项式．分析：把式子展开，根据对应项系数相等，列式求解即可得到m、n的值．解答：解：展开（x+5）（x+n）=x2+（5+n）x+5n∵（x+5）（x+n）=x2+mx﹣5，∴5+n=m，5n=﹣5，∴n=﹣1，m=4．∴m+n=4﹣1=3．故答案为：3点评：此题主要考查了多项式乘多项式，根据对应项系数相等求解是解本题的关键．27．（2011•翔安区质检）若x2﹣2x﹣15=（x+3）（x+m），则m=﹣5．考点：多项式乘多项式．专题：计算题．分析：根据多项式的乘法将（x+3）（x+m），展开，然后根据对应项系数相等列式求解即可．解答：解：∵x2﹣2x﹣15=（x+3）（x+m）=x2+（3+m）x+3m，∴3m=﹣15解得：m=﹣5．故答案为：﹣5．点评：本题主要考查多项式的乘法，根据对应项系数相等列出等式是求解的关键．28．已知a2﹣a+5=0，则（a﹣3）（a+2）的值是﹣11．考点：多项式乘多项式．分析：先把所求代数式展开后，利用条件得到a2﹣a=﹣5，整体代入即可求解．解答：解：（a﹣3）（a+2）=a2﹣a﹣6，∵a2﹣a+5=0，∴a2﹣a=﹣5，∴原式=﹣5﹣6=﹣11．点评：本题考查多项式乘以多项式的法则和整体代入思想，熟练掌握运算法则是解题的关键．29．如果（x+1）（x2﹣5ax+a）的乘积中不含x2项，则a为．考点：多项式乘多项式．分析：先用多项式乘以多项式的运算法则展开求它们的积，并且把a看作常数合并关于x2的同类项，令x2的系数为0，求出a的值．解答：解：原式=x3﹣5ax2+ax+x2﹣5ax+a，=x3+（1﹣5a）x2﹣4ax+a，∵不含x2项，∴1﹣5a=0，解得a=．点评：本题考查了多项式乘多项式法则，并利用不含某一项，就是让这一项的系数等于0求解．30．若（x+2）（x2+px+4）的化简结果不含x2和x项，则p=﹣2．考点：多项式乘多项式．分析：把式子展开，找到所有不含x2和x项，项的系数，令它的系数分别为0，列式求解即可．解答：解：（x+2）（x2+px+4）=x3+（p+2）x2+（4+2p）x+8∵乘积中不含x2项x项，∴p+2=0，4+2p=0∴p=﹣2．故答案为：﹣2．点评：考查了多项式乘多项式，灵活掌握多项式乘以多项式的法则，注意各项符号的处理．。

多项式乘多项式试题精选附答案

多项式乘多项式试题精选（二）一．填空题（共13小题）1．如图，正方形卡片A类、B类和长方形卡片C类各若干张，如果要拼一个长为（2a+b），宽为（a+b）的长方形，则需要C类卡片_________ 张．2．（x+3）与（2x﹣m）的积中不含x的一次项，则m= _________ ．3．若（x+p）（x+q）=x2+mx+24，p，q为整数，则m的值等于_________ ．4．如图，已知正方形卡片A类、B类和长方形卡片C类各若干张，如果要拼成一个长为（a+2b）、宽为（a+b）的大长方形，则需要A类卡片_________ 张，B类卡片_________ 张，C类卡片_________ 张．5．计算：（﹣p）2•（﹣p）3= _________ ；= _________ ；2xy•（_________ ）=﹣6x2yz；（5﹣a）（6+a）= _________ ．6．计算（x2﹣3x+1）（mx+8）的结果中不含x2项，则常数m的值为_________ ．7．如图是三种不同类型的地砖，若现有A类4块，B类2块，C类1块，若要拼成一个正方形到还需B类地砖_________ 块．8．若（x+5）（x﹣7）=x2+mx+n，则m= _________ ，n= _________ ．9．（x+a）（x+）的计算结果不含x项，则a的值是_________ ．10．一块长m米，宽n米的地毯，长、宽各裁掉2米后，恰好能铺盖一间房间地面，问房间地面的面积是_________ 平方米．11．若（x+m）（x+n）=x2﹣7x+mn，则﹣m﹣n的值为_________ ．12．若（x2+mx+8）（x2﹣3x+n）的展开式中不含x3和x2项，则mn的值是_________ ．13．已知x、y、a都是实数，且|x|=1﹣a，y2=（1﹣a）（a﹣1﹣a2），则x+y+a3+1的值为_________ ．二．解答题（共17小题）14．若（x2+2nx+3）（x2﹣5x+m）中不含奇次项，求m、n的值．15．化简下列各式：（1）（3x+2y）（9x2﹣6xy+4y2）；（2）（2x﹣3）（4x2+6xy+9）；16．计算：（1）（2x﹣3）（x﹣5）；（2）（a2﹣b3）（a2+b3）17．计算：（1）﹣（2a﹣b）+[a﹣（3a+4b）]（2）（a+b）（a2﹣ab+b2）18．（x+7）（x﹣6）﹣（x﹣2）（x+1）19．计算：（3a+1）（2a﹣3）﹣（6a﹣5）（a﹣4）．20．计算：（a﹣b）（a2+ab+b2）21．若（x2+px﹣）（x2﹣3x+q）的积中不含x项与x3项，（1）求p、q的值；（2）求代数式（﹣2p2q）2+（3pq）﹣1+p2012q2014的值．22．先化简，再求值：5（3x2y﹣xy2）﹣4（﹣xy2+3x2y），其中x=﹣2，y=3．23．若（x﹣1）（x2+mx+n）=x3﹣6x2+11x﹣6，求m，n的值．24．如图，有多个长方形和正方形的卡片，图甲是选取了2块不同的卡片，拼成的一个图形，借助图中阴影部分面积的不同表示可以用来验证等式a（a+b）=a2+ab成立．（1）根据图乙，利用面积的不同表示方法，写出一个代数恒等式_________ ；（2）试写出一个与（1）中代数恒等式类似的等式，并用上述拼图的方法说明它的正确性．25．小明想把一长为60cm，宽为40cm的长方形硬纸片做成一个无盖的长方体盒子，于是在长方形纸片的四个角各剪去一个相同的小正方形．（1）若设小正方形的边长为xcm，求图中阴影部分的面积；（2）当x=5时，求这个盒子的体积．26．（x﹣1）（x﹣2）=（x+3）（x﹣4）+20．27．若（x﹣3）（x+m）=x2+nx﹣15，求的值．28．小明在进行两个多项式的乘法运算时（其中的一个多项式是b﹣1），把“乘以（b﹣1）”错看成“除以（b﹣1）”，结果得到（2a﹣b），请你帮小明算算，另一个多项式是多少29．有足够多的长方形和正方形的卡片如图．如果选取1号、2号、3号卡片分别为1张、2张、3张，可拼成一个长方形（不重叠无缝隙）．请画出这个长方形的草图，并运用拼图前后面积之间的关系说明这个长方形的代数意义．30．（1）填空：（a﹣1）（a+1）= _________ （a﹣1）（a2+a+1）= _________ （a﹣1）（a3+a2+a+1）= _________ （2）你发现规律了吗请你用你发现的规律填空：（a﹣1）（a n+a n﹣1+…+a2+a+1）= _________（3）根据上述规律，请你求42012+42011+42010+…+4+1的值．_________ ．多项式乘单项式试题精选（二）参考答案与试题解析一．填空题（共13小题）1．如图，正方形卡片A类、B类和长方形卡片C类各若干张，如果要拼一个长为（2a+b），宽为（a+b）的长方形，则需要C类卡片 3 张．考点：多项式乘多项式．分析：根据长方形的面积等于长乘以宽列式，再根据多项式的乘法法则计算，然后结合卡片的面积即可作出判断．解答：解：长为2a+b，宽为a+b的矩形面积为（2a+b）（a+b）=2a2+3ab+b2，A图形面积为a2，B图形面积为b2，C图形面积为ab，则可知需要A类卡片2张，B类卡片1张，C类卡片3张．故答案为：3．点评：此题主要考查了多项式乘多项式，掌握多项式乘以多项式的法则是本题的关键．注意不要漏项，漏字母，有同类项的合并同类项．2．（x+3）与（2x﹣m）的积中不含x的一次项，则m= 6 ．考点：多项式乘多项式．专题：计算题．分析：先求出（x+3）与（2x﹣m）的积，再令x的一次项为0即可得到关于m的一元一次方程，求出m的值即可．解答：解：∵（x+3）（2x﹣m）=2x2+（6﹣m）x﹣3m，∴6﹣m=0，解得m=6．故答案为：6．点评：本题考查的是多项式乘以多项式的法则，即先用一个多项式的每一项乘另外一个多项式的每一项，再把所得的积相加．3．若（x+p）（x+q）=x2+mx+24，p，q为整数，则m的值等于10，11，14，25 ．考点：多项式乘多项式．分析：根据多项式的乘法法则，可得一个多项式，根据多项式相等，可得对应项相等，由p•q=24，p，q为整数，可得p，q的值，再根据p+q=m，可得m的值．解答：解：∵（x+p）（x+q）=x2+mx+24，∴p=24，q=1；p=12，q=2；p=8，q=3；p=6，q=4，∵当p=24，q=1时，m=p+q=25，当p=12，q=2时，m=p+q=14，当p=8，q=3时，m=p+q=11，当p=6，q=4时，m=p+q=10，故答案为：10，11，14，25．点评：本题考察了多项式，先根据多项式的乘法法则计算，分类讨论p，q是解题关键．4．如图，已知正方形卡片A类、B类和长方形卡片C类各若干张，如果要拼成一个长为（a+2b）、宽为（a+b）的大长方形，则需要A类卡片 1 张，B类卡片 2 张，C类卡片 3 张．分析：根据边长组成图形．数出需要A类卡片1张，B类卡片2张，C类卡片3张．解答：解：如图，要拼成一个长为（a+2b）、宽为（a+b）的大长方形，则需要A类卡片1张，B类卡片2张，C类卡片3张．点评：本题主要考查了多项式乘多项式，解题的关键是根据边长组成图形．5．计算：（﹣p）2•（﹣p）3= ﹣p5；= ﹣a6b3；2xy•（﹣3xz ）=﹣6x2yz；（5﹣a）（6+a）= ﹣a2﹣a+30 ．考点：多项式乘多项式；同底数幂的乘法；幂的乘方与积的乘方；单项式乘单项式．分析：根据同底数幂的乘法、积的乘方和幂的乘方、单项式除以单项式法则、多项式乘以多项式法则求出每个式子的值即可．解答：解：（﹣p）2•（﹣p）3=（﹣p）5=﹣p5，（﹣a2b）3=（﹣）3•（a2）3b3=﹣a6b3，∵﹣6x2yz÷2xy=﹣3xz，∴2xy•（﹣3xz）=﹣6x2yz，（5﹣a）（6+a）=30+5a﹣6a﹣a2=30﹣a﹣a2=﹣a2﹣a+30，故答案为：﹣p5，﹣a6b3，﹣3xz，﹣a2﹣a+30．点评：本题考查了同底数幂的乘法、积的乘方和幂的乘方、单项式除以单项式法则、多项式乘以多项式法则的应用．6．计算（x2﹣3x+1）（mx+8）的结果中不含x2项，则常数m的值为．考点：多项式乘多项式．分析：把式子展开，找到所有x2项的所有系数，令其为0，可求出m的值．解答：解：∵（x2﹣3x+1）（mx+8）=mx4+8x2﹣3mx2﹣24x+mx+8．又∵结果中不含x2的项，∴8﹣3m=0，解得m=．故答案为：．点评：本题主要考查了多项式乘多项式的运算，注意当要求多项式中不含有哪一项时，应让这一项的系数为0．7．如图是三种不同类型的地砖，若现有A类4块，B类2块，C类1块，若要拼成一个正方形到还需B类地砖 2 块．考点：多项式乘多项式．分析：分别计算出4块A的面积和2块B的面积、1块C的面积，再计算这三种类型的砖的总面积，用完全平方公式化简后，即可得出少了哪种类型的地砖．解答：解：4块A的面积为：4×m×m=4m2；2块B的面积为：2×m×n=2mn；1块C的面积为n×n=n2；那么这三种类型的砖的总面积应该是：4m2+2mn+n2=4m2+4mn+n2﹣2mn=（2m+n）2﹣2mn，因此，少2块B型地砖，故答案为：2．点评：本题考查了完全平方公式的几何意义，立意较新颖，注意面积的不同求解是解题的关键，对此类问题要深入理解．考点：多项式乘多项式．分析：已知等式左边利用多项式乘以多项式法则计算，利用多项式相等的条件即可求出m与n的值．解答：解：（x+5）（x﹣7）=x2﹣2x﹣35=x2+mx+n，则m=﹣2，n=﹣35．故答案为：﹣2，﹣35．点评：此题考查了多项式乘以多项式，熟练掌握运算法则是解本题的关键．9．（x+a）（x+）的计算结果不含x项，则a的值是．考点：多项式乘多项式．分析：多项式乘多项式法则，先用一个多项式的每一项乘以另一个多项式的每一项，再把所得的积相加，依据法则运算，展开式不含关于字母x的一次项，那么一次项的系数为0，就可求a的值．解答：解：∵（x+a）（x+）=又∵不含关于字母x的一次项，∴，解得a=．点评：本题考查了多项式乘多项式法则，相乘后不含哪一项，就让这一项的系数等于0，难度适中．10．一块长m米，宽n米的地毯，长、宽各裁掉2米后，恰好能铺盖一间房间地面，问房间地面的面积是（m﹣2）（n﹣2）或（mn﹣2m﹣2n+4）平方米．考点：多项式乘多项式．分析：根据题意得出算式是（m﹣2）（n﹣2），即可得出答案．解答：解：根据题意得出房间地面的面积是（m﹣2）（n﹣2）；（m﹣2）（n﹣2）=mn﹣2m﹣2n+4．故答案为：（m﹣2）（n﹣2）或（mn﹣2m﹣2n+4）点评：本题考查了多项式乘多项式的应用，关键是能根据题意得出算式，题目比较好，难度适中．11．若（x+m）（x+n）=x2﹣7x+mn，则﹣m﹣n的值为7 ．考点：多项式乘多项式．专题：计算题．分析：按照多项式的乘法法则展开运算后解答：解：∵（x+m）（x+n）=x2+（m+n）x+mn=x2﹣7x+mn，∴m+n=﹣7，∴﹣m﹣n=7，故答案为：7．点评：本题考查了多项式的乘法，解题的关键是牢记多项式乘以多项式的乘法法则，属于基础题，比较简单．12．若（x2+mx+8）（x2﹣3x+n）的展开式中不含x3和x2项，则mn的值是 3 ．考点：多项式乘多项式．专题：计算题．分析：利用多项式乘以多项式法则计算得到结果，根据展开式中不含x2和x3项列出关于m与n的方程组，求出方程组的解即可得到m与n的值．解得：，∴mn=3，故答案为：3．点评：此题考查了多项式乘以多项式，熟练掌握运算法则是解本题的关键．13．已知x、y、a都是实数，且|x|=1﹣a，y2=（1﹣a）（a﹣1﹣a2），则x+y+a3+1的值为 2 ．考点：代数式求值；绝对值；多项式乘多项式．专题：计算题．分析：根据绝对值非负数，平方数非负数的性质可得1﹣a=0，从而得到a的值，然后代入求出x、y的值，再把a、x、y的值代入代数式进行计算即可求解．解答：解：∵|x|=1﹣a≥0，∴a﹣1≤0，﹣a2≤0，∴a﹣1﹣a2≤0，又y2=（1﹣a）（a﹣1﹣a2）≥0，∴1﹣a=0，解得a=1，∴|x|=1﹣1=0，x=0，y2=（1﹣a）（﹣1﹣a2）=0，∴x+y+a3+1=0+0+1+1=2．故答案为：2．点评：本题主要考查了代数式求值问题，把y2的多项式整理，然后根据非负数的性质求出a的值是解题的关键，也是解决本题的突破口，本题灵活性较强．二．解答题（共17小题）14．若（x2+2nx+3）（x2﹣5x+m）中不含奇次项，求m、n的值．考点：多项式乘多项式．分析：把式子展开，让x4的系数，x2的系数为0，得到m，n的值．解答：解：（x2+2nx+3）（x2﹣5x+m）=x4﹣5x3+mx2+2nx3﹣10nx2+2mnx+3x2﹣15x+3m=x4+（2n﹣5）x3+（m﹣10n+3）x2+（2mn﹣15）x+3m，∵结果中不含奇次项，∴2n﹣5=0，2mn﹣15=0，解得m=3，n=．点评：本题主要考查了多项式乘多项式的运算，注意当要求多项式中不含有哪一项时，应让这一项的系数为0．15．化简下列各式：（1）（3x+2y）（9x2﹣6xy+4y2）；（2）（2x﹣3）（4x2+6xy+9）；（3）（m﹣）（m2+m+）；（4）（a+b）（a2﹣ab+b2）（a﹣b）（a2+ab+b2）．考点：多项式乘多项式．分析：根据立方和与立方差公式解答即可．解答：解：（1）（3x+2y）（9x2﹣6xy+4y2）（2）（2x﹣3）（4x2+6xy+9）=（2x）3﹣33=8x3﹣27；（3）（m﹣）（m2+m+）=﹣=﹣；（4）（a+b）（a2﹣ab+b2）（a﹣b）（a2+ab+b2）=（a3+b3）（a3﹣b3）=a6﹣b6．点评：本题考查了立方和与立方差公式，熟练记忆公式是解题的关键．16．计算：（1）（2x﹣3）（x﹣5）；（2）（a2﹣b3）（a2+b3）考点：多项式乘多项式．分析：（1）根据多项式乘以多项式的法则，可表示为（a+b）（m+n）=am+an+bm+bn，计算即可；（2）根据平方差公式计算即可．解答：解：（1）（2x﹣3）（x﹣5）=2x2﹣10x﹣3x+15=2x2﹣13x+15；（2）（a2﹣b3）（a2+b3）=a4﹣b6．点评：本题考查了多项式乘以多项式的法则以及平方差公式．注意不要漏项，漏字母，有同类项的合并同类项．17．计算：（1）﹣（2a﹣b）+[a﹣（3a+4b）]（2）（a+b）（a2﹣ab+b2）考点：多项式乘多项式；整式的加减．专题：计算题．分析：（1）先去小括号，再去大括号，最后按照整式加减混合运算规则进行计算即可；（2）根据多项式乘以多项式的法则，可表示为（a+b）（m+n）=am+an+bm+bn，计算即可．解答：解：（1）原式=﹣2a+b+[a﹣3a﹣4b]，=﹣2a+b+a﹣3a﹣4b，=﹣4a﹣3b；（2）原式=a3﹣a2b+ab2+a2b﹣ab2+b3，=a3+b3．点评：本题主要考查多项式乘以多项式的法则．注意不要漏项，漏字母，有同类项的合并同类项．18．（x+7）（x﹣6）﹣（x﹣2）（x+1）考点：多项式乘多项式．=x2﹣6x+7x﹣42﹣x2﹣x+2x+2=2x﹣40．点评：本题考查了多项式乘多项式法则，先用一个多项式的每一项乘以另一个多项式的每一项，再把所得的积相加．关键是不能漏项．19．计算：（3a+1）（2a﹣3）﹣（6a﹣5）（a﹣4）．考点：多项式乘多项式．分析：根据整式混合运算的顺序和法则分别进行计算，再把所得结果合并即可．解答：解：（3a+1）（2a﹣3）+（6a﹣5）（a﹣4）=6a2﹣9a+2a﹣3+6a2﹣24a﹣5a+20=12a2﹣36a+17．点评：此题考查了整式的混合运算，在计算时要注意混合运算的顺序和法则以及运算结果的符号，是一道基础题．20．计算：（a﹣b）（a2+ab+b2）考点：多项式乘多项式；单项式乘单项式．专题：计算题．分析：根据多项式乘以多项式的法则和单项式乘单项式的法则进行计算即可．解答：解：原式=a3+a2b+ab2﹣a2b﹣ab2﹣b3=a3﹣b3．点评：本题主要考查对多项式乘以多项式的法则和单项式乘单项式的法则得理解和掌握，能熟练地运用法则进行计算是解此题的关键．21．若（x2+px﹣）（x2﹣3x+q）的积中不含x项与x3项，（1）求p、q的值；（2）求代数式（﹣2p2q）2+（3pq）﹣1+p2012q2014的值．考点：多项式乘多项式．分析：（1）形开式子，找出x项与x3令其系数等于0求解．（2）把p，q的值入求解．解答：解：（1）（x2+px﹣）（x2﹣3x+q）=x4+（p﹣3）x3+（9﹣3p﹣）x2+（qp+1）x+q，∵积中不含x项与x3项，∴P﹣3=0，qp+1=0∴p=3，q=﹣，（2）（﹣2p2q）2+（3pq）﹣1+p2012q2014=[﹣2×32×（﹣）]2++×32=36﹣+9=44．点评：本题主要考查了多项式乘多项式，解题的关键是正确求出p，q的值22．先化简，再求值：5（3x2y﹣xy2）﹣4（﹣xy2+3x2y），其中x=﹣2，y=3．考点：整式的加减—化简求值；合并同类项；多项式乘多项式．专题：计算题．分析：根据单项式乘多项式的法则展开，再合并同类项，把x y的值代入求出即可．解答：解：原式=15x2y﹣5xy2+4xy2﹣12x2y原式=3×（﹣2）2×3﹣（﹣2）×32=36+18=54．点评：本题考查了对整式的加减，合并同类项，单项式乘多项式等知识点的理解和掌握，注意展开时不要漏乘，同时要注意结果的符号，代入﹣2时应用括号．23．若（x﹣1）（x2+mx+n）=x3﹣6x2+11x﹣6，求m，n的值．考点：多项式乘多项式．专题：计算题．分析：把（x﹣1）（x2+mx+n）展开后，每项的系数与x3﹣6x2+11x﹣6中的项的系数对应，可求得m、n的值．解答：解：∵（x﹣1）（x2+mx+n）=x3+（m﹣1）x2+（n﹣m）x﹣n=x3﹣6x2+11x﹣6∴m﹣1=﹣6，﹣n=﹣6，解得m=﹣5，n=6．点评：本题主要考查了多项式乘多项式的法则，注意不要漏项，漏字母，有同类项的合并同类项．根据对应项系数相等列式求解m、n是解题的关键．24．如图，有多个长方形和正方形的卡片，图甲是选取了2块不同的卡片，拼成的一个图形，借助图中阴影部分面积的不同表示可以用来验证等式a（a+b）=a2+ab成立．（1）根据图乙，利用面积的不同表示方法，写出一个代数恒等式（a+2b）（a+b）=a2+3ab+2b2；（2）试写出一个与（1）中代数恒等式类似的等式，并用上述拼图的方法说明它的正确性．考点：多项式乘多项式．专题：计算题．分析：（1）根据图形是一个长方形求出长和宽，相乘即可；（2）正方形的面积是2个长方形的面积加上2个正方形的面积，代入求出即可．解答：解：（1）观察图乙得知：长方形的长为：a+2b，宽为a+b，∴面积为：（a+2b）（a+b）=a2+3ab+2b2；（2）如图所示：恒等式是，（a+b）（a+b）=a2+2ab+b2．答：恒等式是a+b）（a+b）=a2+2ab+b2．点评：本题主要考查对多项式乘多项式的理解和掌握，能表示各部分的面积是解此题的关键．25．小明想把一长为60cm，宽为40cm的长方形硬纸片做成一个无盖的长方体盒子，于是在长方形纸片的四个角各剪去一个相同的小正方形．（1）若设小正方形的边长为xcm，求图中阴影部分的面积；（2）当x=5时，求这个盒子的体积．考点：多项式乘多项式；代数式求值．分析：（1）剩余部分的面积即是边长为60﹣2x，40﹣2x的长方形的面积；（2）利用长方体的体积公式先表示出长方形的体积，再把x=5，代入即可．解答：解：（1）（60﹣2x）（40﹣2x）=4x2﹣200x+2400，答：阴影部分的面积为（4x2﹣200x+2400）cm2；（2）当x=5时，4x2﹣200x+2400=1500（cm2），这个盒子的体积为：1500×5=7500（cm3），答：这个盒子的体积为7500cm3．点评：此题主要考查用代数式表示正方形、矩形的面积和体积，需熟记公式，且认真观察图形，得出等量关系．26．（x﹣1）（x﹣2）=（x+3）（x﹣4）+20．考点：多项式乘多项式；解一元一次方程．分析：将方程的两边利用多项式的乘法展开后整理成方程的一般形式求解即可．解答：解：原方程变形为：x2﹣3x+2=x2﹣x﹣12+20整理得：﹣2x﹣6=0，解得：x=﹣3．点评：本题考查了多项式乘多项式及解一元二次方程的知识，解题的关键是利用多项式的乘法对方程进行化简．27．若（x﹣3）（x+m）=x2+nx﹣15，求的值．考点：多项式乘多项式．分析：首先把）（x﹣3）（x+m）利用多项式的乘法公式展开，然后根据多项式相等的条件：对应项的系数相同即可得到m、n的值，从而求解．解答：解：（x﹣3）（x+m）=x2+（m﹣3）x﹣3m=x2+nx﹣15，则解得：．=．点评：本题考查了多项式的乘法法则以及多项式相等的条件，理解多项式的乘法法则是关键．28．小明在进行两个多项式的乘法运算时（其中的一个多项式是b﹣1），把“乘以（b﹣1）”错看成“除以（b﹣1）”，结果得到（2a﹣b），请你帮小明算算，另一个多项式是多少考点：多项式乘多项式．分析：根据被除式=商×除式，所求多项式是（2a﹣b）（b﹣1），根据多项式乘多项式的法则计算即可．解答：解：设所求的多项式是M，则M=（2a﹣b）（b﹣1）=2ab﹣2a﹣b2+b．点评：本题考查了多项式乘多项式法则，根据被除式、除式、商三者之间的关系列出等式是解题的关键，熟练掌握运算法则也很重要．29．有足够多的长方形和正方形的卡片如图．如果选取1号、2号、3号卡片分别为1张、2张、3张，可拼成一个长方形（不重叠无缝隙）．请画出这个长方形的草图，并运用拼图前后面积之间的关系说明这个长方形的代数意义．考点：多项式乘多项式．分析：先根据题意画出图形，然后求出长方形的长和宽，长为a+2b，宽为a+b，从而求出长方形的面积．解答：解：如图：或a2+3ab+2b2=（a+b）（a+2b）．点评：考查多项式与多项式相乘问题；根据面积的不同表示方法得到相应的等式是解决本题的关键．30．（1）填空：（a﹣1）（a+1）= a2﹣1 （a﹣1）（a2+a+1）= a3﹣1 （a﹣1）（a3+a2+a+1）= a4﹣1 （2）你发现规律了吗请你用你发现的规律填空：（a﹣1）（a n+a n﹣1+…+a2+a+1）= a n+1﹣1（3）根据上述规律，请你求42012+42011+42010+…+4+1的值．（42013﹣1）．考点：多项式乘多项式．专题：规律型．分析：（1）根据平方差公式和立方差公式可得前2个式子的结果，利用多项式乘以多项式的方法可得出第3个式子的结果；（2）从而总结出规律是：（a﹣1）（a n+a n﹣1+…+a2+a+1）=a n+1﹣1；（3）根据上述结论计算下列式子即可．解答：解：根据题意：（1）（a﹣1）（a+1）=a2﹣1；（a﹣1）（a2+a+1）=a3﹣1；（a﹣1）（a3+a2+a+1）=a4﹣1；（2）（a﹣1）（a n+a n﹣1+a n﹣2+…+a2+a+1）=a n+1﹣1．（3）根据以上分析（1）42012+42011+42010+…+4+1299+298+297+…+2+1，=（4﹣1）（42012+42011+42010+…+4+1），=（42013﹣1）．故答案为：（1）a2﹣1，a3﹣1，a4﹣1；（2）a n+1﹣1；（3）（42013﹣1）．点评：主要考查了学生的分析、总结、归纳能力，规律型的习题一般是从所给的数据和运算方法进行分析，从特殊值的规律上总结出一般性的规律．。

多项式计算题

多项式计算题一、多项式加法与减法1.计算多项式 3x2+2x−5 与 4x2−3x+7 的和。

2.计算多项式 6x3−4x2+5x−1 与−2x3+3x2−x+4 的差。

二、多项式乘法3.计算多项式 (2x+3)(x−4)。

4.计算多项式 (x2−2x+1)(x+3)。

5.展开多项式 (2x−y)2。

三、多项式除法6.将多项式 6x3−11x2−x+5 除以 3x+1，并求出商和余数。

7.将多项式x4−3x3+2x2−x+1 除以x−1，并判断是否能整除。

四、多项式因式分解8.因式分解多项式x2−9。

9.因式分解多项式 2x2−5x−3。

10.因式分解多项式x4−16。

五、多项式求值11.当x=2 时，求多项式 3x2−4x+1 的值。

12.当x=−1，y=2 时，求多项式 2x2+3xy−y2 的值。

六、综合题13.已知多项式f(x)=x3−6x2+11x−6，求：a) f(x)的所有因式；b) f(x)在x=3时的值。

解答示例（部分）1.多项式加法：(3x2+2x−5)+(4x2−3x+7)=7x2−x+22.多项式减法：(6x3−4x2+5x−1)−(−2x3+3x2−x+4)=8x3−7x2+6x−53.多项式乘法：(2x+3)(x−4)=2x2−8x+3x−12=2x2−5x−124.多项式乘法：(x2−2x+1)(x+3)=x3+3x2−2x2−6x+x+3=x3+x2−5x+35.多项式平方：(2x−y)2=4x2−4xy+y26.多项式除法（示例，具体计算需使用长除法或综合除法）：商为 2x2−5x+2，余数为−7（注意：这里仅为示例，实际计算可能不同）7.多项式除法（判断整除）：因为x−1 是x4−3x3+2x2−x+1 的一个因式（可通过长除法验证），所以多项式能被x−1 整除。

8.因式分解：x2−9=(x+3)(x−3)9.因式分解（需使用十字相乘法或求根公式）：2x2−5x−3=(2x+1)(x−3)10.因式分解：x4−16=(x2+4)(x2−4)=(x2+4)(x+2)(x−2)。

八年级数学上册多项式乘以多项式同步训练(含解析)

多项式乘以多项式·一．选择题;;1．（2015•镇江模拟）学校买来钢笔若干枝，可以平均分给（x﹣1）名同学，也可分给（x﹣2）名同学（x为正整数）．用代数式表示钢笔的数量不可能的是（）A．x2+3x+2 B．3（x﹣1）（x﹣2） C．x2﹣3x+2 D．x3﹣3x2+2x2．（2015•佛山）若（x+2）（x﹣1）=x2+mx+n，则m+n=（）;A．1 B．﹣2 C．﹣1 D．23．（2015春•岱岳区期末）若（x+a）（x+b）=x2﹣kx+ab，则k的值为（）;;A．a+b B．﹣a﹣b C．a﹣b D．b﹣a4．（2015春•莘县期末）已知m+n=2，mn=﹣2，则（1﹣m）（1﹣n）的值为（）A．﹣3 B．﹣1 C．1 D．55．（2015春•张家港市期末）如果的积中不含x项，则q等于（）A．B．5 C． D．﹣56．（2015春•乐平市期中）如图，甲、乙、丙、丁四位同学给出了四种表示该长方形面积的多项式：①（2a+b）（m+n）；②2a（m+n）+b（m+n）；③m（2a+b）+n（2a+b）；④2am+2an+bm+bn，你认为其中正确的有（）A．①② B．③④ C．①②③D．①②③④7．（2015春•西安校级月考）如果（x+a）（x+b）的积中不含x的一次项，那么a，b一定（）A．互为倒数 B．互为相反数C．a=b且b=0 D．ab=08．（2014•溧水县校级模拟）把三张大小相同的矩形卡片A，B，C叠放在一个底面为矩形的盒底上，底面未被卡片覆盖的部分用阴影表示．若按图1摆放时，阴影部分的面积为S1；若按图2摆放时，阴影部分的面积为S2，则（）A．S1＞S2B．S1=S2 C．S1＜S2D．无法确定二．填空题9．（2015•徐州校级模拟）计算：（2x+1）（x﹣1）= ．10．（2015春•嵊州市期末）如果（x+3）（x+a）=x2﹣2x﹣15，则a= ．11．（2015春•兴化市校级期末）在（x+1）（2x2﹣ax+1）的运算结果中x2的系数是﹣6，那么a的值是．12．（2015春•肥城市期末）若（ax﹣b）（3x+4）=bx2+cx+72，则a+b+c的值为．13．（2015春•苏州校级期末）现有若干张边长为a的正方形A型纸片，边长为b的正方形B型纸片，长宽为a、b的长方形C型纸片，小明同学选取了2张A型纸片，7张B型纸片，3张C型纸片拼成了一个四边形，则此四边形的周长为．（用a、b代数式表示）三．解答题14．（2015春•莘县期末）计算（1）﹣12+（π﹣3.14）0﹣3﹣2（2）（2m﹣n）（m﹣2n）15．（2015春•成都校级月考）若x2+5y2﹣4（xy﹣y﹣1）=0，且（2x+m）（x+1）的展开式中不含x的一次项，求代数式（x﹣y）m的值．16．（2014春•成都校级月考）已知将（x2+nx+3）（x2﹣2x﹣m）乘开的结果不含x3和x2项．（1）求m、n的值；（2）当m、n取第（1）小题的值时，求（m﹣n）（m2+mn+n2）的值．17．（2015春•宿州期末）观察下列各式（x﹣1）（x+1）=x2﹣1（x﹣1）（x2+x+1）=x3﹣1（x﹣1）（x3+x2+x+1）=x4﹣1…①根据以上规律，则（x﹣1）（x6+x5+x4+x3+x2+x+1）= ．②你能否由此归纳出一般性规律：（x﹣1）（x n+x n﹣1+…+x+1）= ．③根据②求出：1+2+22+…+234+235的结果．人教版八年级数学上册《14.1.4.3多项式乘以多项式》同步训练习题（教师版）一．选择题1．（2015•镇江模拟）学校买来钢笔若干枝，可以平均分给（x﹣1）名同学，也可分给（x﹣2）名同学（x为正整数）．用代数式表示钢笔的数量不可能的是（）A．x2+3x+2 B．3（x﹣1）（x﹣2） C．x2﹣3x+2 D．x3﹣3x2+2x考点：多项式乘多项式．专题：计算题．分析：根据题意列出算式，利用多项式乘以多项式法则计算，即可做出判断．解答：解：根据题意得：（x﹣1）（x﹣2）=x2﹣3x+2，则钢笔的数量不可能的是x2+3x+2，故选A点评：此题考查了多项式乘以多项式，熟练掌握运算法则是解本题的关键．2．（2015•佛山）若（x+2）（x﹣1）=x2+mx+n，则m+n=（）A．1 B．﹣2 C．﹣1 D．2考点：多项式乘多项式．分析：依据多项式乘以多项式的法则，进行计算，然后对照各项的系数即可求出m，n的值．解答：解：∵原式=x2+x﹣2=x2+mx+n，∴m=1，n=﹣2．∴m+n=1﹣2=﹣1．故选：C．点评：本题考查了多项式的乘法，熟练掌握多项式乘以多项式的法则是解题的关键．3．（2015春•岱岳区期末）若（x+a）（x+b）=x2﹣kx+ab，则k的值为（）A．a+b B．﹣a﹣b C．a﹣b D．b﹣a考点：多项式乘多项式．分析：已知等式左边利用多项式乘以多项式法则计算，利用多项式相等的条件即可求出k．解答：解：（x+a）（x+b）=x2+（a+b）x+ab=x2﹣kx+ab，得到a+b=﹣k，则k=﹣a﹣b．故选：B．点评：此题考查了多项式乘多项式，熟练掌握运算法则是解本题的关键．4．（2015春•莘县期末）已知m+n=2，mn=﹣2，则（1﹣m）（1﹣n）的值为（）A．﹣3 B．﹣1 C．1 D．5考点：多项式乘多项式．分析：多项式乘多项式法则，先用一个多项式的每一项乘以另一个多项式的每一项，再把所得的积转换成以m+n，mn为整体相加的形式，代入求值．解答：解：∵m+n=2，mn=﹣2，∴（1﹣m）（1﹣n），=1﹣（m+n）+mn，=1﹣2﹣2，=﹣3．故选：A．点评：本题考查了多项式乘多项式法则，合并同类项时要注意项中的指数及字母是否相同．5．（2015春•张家港市期末）如果的积中不含x项，则q等于（）A．B．5 C． D．﹣5考点：多项式乘多项式．分析：把式子展开，找出所有x的系数，令其为0，解即可．解答：解：∵=x2+（q+）x+q，又∵积中不含x项，则q+=0，q=﹣．故选C．点评：本题主要考查了多项式乘多项式的运算，注意当要求多项式中不含有哪一项时，应让这一项的系数为0．6．（2015春•乐平市期中）如图，甲、乙、丙、丁四位同学给出了四种表示该长方形面积的多项式：①（2a+b）（m+n）；②2a（m+n）+b（m+n）；③m（2a+b）+n（2a+b）；④2am+2an+bm+bn，你认为其中正确的有（）A．①② B．③④ C．①②③D．①②③④考点：多项式乘多项式．专题：计算题．分析：①大长方形的长为2a+b，宽为m+n，利用长方形的面积公式，表示即可；②长方形的面积等于左边，中间及右边的长方形面积之和，表示即可；③长方形的面积等于上下两个长方形面积之和，表示即可；④长方形的面积由6个长方形的面积之和，表示即可．解答：解：①（2a+b）（m+n），本选项正确；②2a（m+n）+b（m+n），本选项正确；③m（2a+b）+n（2a+b），本选项正确；④2am+2an+bm+bn，本选项正确，则正确的有①②③④．故选D．点评：此题考查了多项式乘以多项式，熟练掌握运算法则是解本题的关键．7．（2015春•西安校级月考）如果（x+a）（x+b）的积中不含x的一次项，那么a，b一定（）A．互为倒数 B．互为相反数C．a=b且b=0 D．ab=0考点：多项式乘多项式．专题：计算题．分析：原式利用多项式乘以多项式法则计算，根据结果中不含x的一次项求出a与b的值即可．解答：解：原式=x2+（a+b）x+ab，由结果中不含x的一次项，得到a+b=0，则a，b一定互为相反数，故选B．点评：此题考查了多项式乘以多项式，熟练掌握运算法则是解本题的关键．8．（2014•溧水县校级模拟）把三张大小相同的矩形卡片A，B，C叠放在一个底面为矩形的盒底上，底面未被卡片覆盖的部分用阴影表示．若按图1摆放时，阴影部分的面积为S1；若按图2摆放时，阴影部分的面积为S2，则（）A．S1＞S2B．S1=S2 C．S1＜S2D．无法确定考点：多项式乘多项式．专题：计算题．分析：根据矩形的性质，可以把两块阴影部分合并后计算面积，然后，比较S1和S2的大小．解答：解：设底面的矩形的长为a，宽为b，矩形卡片A，B，C的长为m，宽为n，由图1，得S1=（b﹣n）（a﹣m）=ab﹣bm﹣an+mn，由图2，得S2=（b﹣n）（a﹣m）=ab﹣bm﹣an+mn，则S1=S2．故选B．点评：此题考查了多项式乘多项式，熟练掌握运算法则解本题的关键．二．填空题9．（2015•徐州校级模拟）计算：（2x+1）（x﹣1）= 2x2﹣x﹣1 ．考点：多项式乘多项式．分析：根据多项式乘以多项式的法则，可表示为（a+b）（m+n）=am+an+bm+bn，计算即可．解答：解：（2x+1）（x﹣1）=2x2﹣2x+x﹣1=2x2﹣x﹣1．故答案为：2x2﹣x﹣1．点评：本题主要考查多项式乘以多项式的法则．注意不要漏项，漏字母，有同类项的合并同类项．10．（2015春•嵊州市期末）如果（x+3）（x+a）=x2﹣2x﹣15，则a= ﹣5 ．考点：多项式乘多项式．分析：已知等式左边利用多项式乘多项式法则计算，合并后利用多项式相等的条件即可求出a的值．解答：解：（x+3）（x+a）=x2+（a+3）x+3a=x2﹣2x﹣15，可得a+3=﹣2，解得：a=﹣5．故答案为：﹣5．点评：此题考查了多项式乘多项式，熟练掌握运算法则是解本题的关键．11．（2015春•兴化市校级期末）在（x+1）（2x2﹣ax+1）的运算结果中x2的系数是﹣6，那么a的值是8 ．考点：多项式乘多项式．分析：先运用多项式的乘法法则进行计算，再根据运算结果中x2的系数是﹣6，列出关于a的等式求解即可．解答：解：（x+1）（2x2﹣ax+1）=2x3﹣ax2+x+2x2﹣ax+1=2x3+（﹣a+2）x2+（1﹣a）x+1；∵运算结果中x2的系数是﹣6，∴﹣a+2=﹣6，解得a=8，故答案为：8．点评：本题考查了多项式的乘法，注意运用运算结果中x2的系数是﹣6，列方程求解．12．（2015春•肥城市期末）若（ax﹣b）（3x+4）=bx2+cx+72，则a+b+c的值为 6 ．考点：多项式乘多项式．专题：计算题．分析：已知等式左边利用多项式乘以多项式法则计算，利用多项式相等的条件求出a，b，c的值，即可求出a+b+c 的值．解答：解：∵（ax﹣b）（3x+4）=3ax2+（4a﹣3b）x﹣4b=bx2+cx+72，∴3a=b，4a﹣3b=c，﹣4b=72，解得：a=﹣6，b=﹣18，c=30，则a+b+c=﹣6﹣18+30=6．故答案为：6点评：此题考查了多项式乘多项式，熟练掌握运算法则是解本题的关键．13．（2015春•苏州校级期末）现有若干张边长为a的正方形A型纸片，边长为b的正方形B型纸片，长宽为a、b的长方形C型纸片，小明同学选取了2张A型纸片，7张B型纸片，3张C型纸片拼成了一个四边形，则此四边形的周长为6a+8b ．（用a、b代数式表示）考点：多项式乘多项式．分析：首先求出四边形的面积将原式分解因式进而得出其边长求出即可．解答：解：根据题意得：2a2+7b2+3ab=（a+3b）（2a+b），故四边形的边长为：a+3b，2a+b，则此四边形的周长为：2（a+3b+2a+b）=6a+8b．故答案为：6a+8b．点评：此题考查了十字相乘法因式分解，正确掌握十字相乘法分解因式是解题关键．三．解答题14．（2015春•莘县期末）计算（1）﹣12+（π﹣3.14）0﹣3﹣2（2）（2m﹣n）（m﹣2n）考点：多项式乘多项式；零指数幂；负整数指数幂．分析：（1）直接利用零指数幂的性质以及负整数指数幂的性质化简进而求出即可；（2）利用多项式乘以多项式运算法则化简求出即可．解答：解：（1））﹣12+（π﹣3.14）0﹣3﹣2=﹣1+1﹣=﹣；（2）（2m﹣n）（m﹣2n）=2m2﹣4mn﹣mn+2n2，=2m2﹣5mn+2n2．点评：此题主要考查了多项式乘以多项式以及实数运算，正确掌握运算法则是解题关键．15．（2015春•成都校级月考）若x2+5y2﹣4（xy﹣y﹣1）=0，且（2x+m）（x+1）的展开式中不含x的一次项，求代数式（x﹣y）m的值．考点：多项式乘多项式．专题：计算题．分析：已知等式整理后，利用完全平方公式化简，利用非负数的性质求出x与y的值，再利用多项式乘以多项式法则化简（2x+m）（x+1），求出m的值，即可确定出原式的值．解答：解：x2+5y2﹣4（xy﹣y﹣1）=0，整理得：x2﹣4xy+4y2+y2+4y+4=0，即（x﹣2y）2+（y+2）2=0，∴x+2y=0，y+2=0，解得：x=4，x=﹣2，∵（2x+m）（x+1）=2x2+（m+2）x+m中不含x的一次项，∴m+2=0，即m=﹣2，则原式=．点评：此题考查了多项式乘以多项式，熟练掌握运算法则是解本题的关键．16．（2014春•成都校级月考）已知将（x2+nx+3）（x2﹣2x﹣m）乘开的结果不含x3和x2项．（1）求m、n的值；（2）当m、n取第（1）小题的值时，求（m﹣n）（m2+mn+n2）的值．考点：多项式乘多项式．专题：计算题．分析：（1）原式利用多项式乘以多项式法则计算，合并后根据乘开的结果不含x3和x2项，求出m与n的值即可；（2）原式利用多项式乘以多项式法则计算，把m与n的值代入计算即可求出值．解答：解：（1）原式=x4﹣2x3﹣mx2+nx3﹣2nx2﹣mnx+3x2﹣6x﹣3m=x4+（n﹣2）x3+（3﹣m﹣2n）x2+（mn+6）x﹣3m，由乘开的结果不含x3和x2项，得到n﹣2=0，3﹣m﹣2n=0，解得：m=﹣1，n=2；（2）当m=﹣1，n=2时，原式=m3+m2n+mn2﹣m2n﹣mn2﹣n3=m3﹣n3=﹣1﹣8=﹣9．点评：此题考查了多项式乘以多项式，熟练掌握运算法则是解本题的关键．17．（2015春•宿州期末）观察下列各式（x﹣1）（x+1）=x2﹣1（x﹣1）（x2+x+1）=x3﹣1（x﹣1）（x3+x2+x+1）=x4﹣1…①根据以上规律，则（x﹣1）（x6+x5+x4+x3+x2+x+1）= x7﹣1 ．②你能否由此归纳出一般性规律：（x﹣1）（x n+x n﹣1+…+x+1）= x n+1﹣1 ．③根据②求出：1+2+22+…+234+235的结果．考点：多项式乘多项式．专题：规律型．分析：①观察已知各式，得到一般性规律，化简原式即可；②原式利用得出的规律化简即可得到结果；③原式变形后，利用得出的规律化简即可得到结果．解答：解：①根据题意得：（x﹣1）（x6+x5+x4+x3+x2+x+1）=x7﹣1；②根据题意得：（x﹣1）（x n+x n﹣1+…+x+1）=x n+1﹣1；③原式=（2﹣1）（1+2+22+…+234+235）=236﹣1．故答案为：①x7﹣1；②x n+1﹣1；③236﹣1点评：此题考查了多项式乘以多项式，弄清题中的规律是解本题的关键．。