4因素3水平Excel计算表.xls
四等水准观测记录计算表_Microsoft_Excel_校核成果用

四等水准观测记录、计算表 第 6页 共 页
四等水准观测记录、计算表 第 7 页 共 页
四等水准观测记录、计算表 第 8 页 共 页
四等水准观测记录、计算表 第 9 页 共 页
四等水准观测记录、计算表 第 10 页 共 页
四等水准观测记录、计算表 第 11 页 共 页
编号
及
尺号
减红
四等水准观测记录、计算表 第 12 页 共 页
尺号
方向
+Array
四等水准观测记录、计算表 第 13 页 共 页
1
四等水准观测记录、计算表 第 14 页 共 页
四等水准观测记录、计算表 第 15 页 共 页
四等水准观测记录、计算表 第 16 页 共 页
四等水准观测记录、计算表 第 17 页 共 页
四等水准观测记录、计算表 第 18 页 共 页
四等水准观测记录、计算表 第 19 页 共 页
四等水准观测记录、计算表 第 20 页 共 页
四等水准观测记录、计算表 第 21 页 共 页
3
四等水准观测记录、计算表 第 22 页 共 页
四等水准观测记录、计算表 第 23 页 共 页
四等水准观测记录、计算表 第 24 页 共 页
四等水准观测记录、计算表 第 25 页 共 页
四等水准观测记录、计算表 第 26 页 共 页。
Excel模拟运算表(数据分析)

Excel高级使用技巧17默认文件夹在使用打开或保存命令时会发现Excel自动把“我的文档”作为默认的保存和打开文件夹,如果我们平时的工作成果并不在这个文件夹中,这样是很不方便的,不过我们可以设置这个默认的文件夹:打开“工具”菜单,选择“选项”命令,打开“选项”对话框;单击“常规”选项卡;在“默认工作目录”输入框中输入文件夹的路径名,然后单击“确定”按钮就可以了。
默认字体在默认情况下,Excel 工作表使用10 磅的Arial 字体;我们也可以将这个默认的设置改变:选择“工具”菜单的“选项”命令,打开“选项”对话框,从“常规”选项卡的“标准字体”下拉列表框中选择一种字体,从“大小”下拉列表框中选择字体的大小,单击“确定”按钮;Excel会弹出对话框提示我们要重新启动Excel,重新启动Excel后Excel就会以设置的字体显示了。
单变量求解(数据分析)用Excel可以进行比较复杂的数值计算,比如算式z=3x+4y+1,我们要求当z=20、y=2时x的值,就可以使用单变量求解功能:首先按一般的样子将公式建立起来,然后打开“工具”菜单,单击“单变量求解”命令(如图15),打开“单变量求解”对话框(如图16),拾取“目标”为公式所在的单元格,在“目标值”输入框中输入期望的值20,然后将“可变单元格”定位为x的数值所在单元格,单击“确定”按钮,在单元格中可以看到计算的结果;同时界面中出现了“单元格求解状态”对话框,此时单击“确定”可以接受通过计算导致单元格数值的改变,而单击“取消”按钮就可以撤消改变了。
图15 图16模拟运算表(数据分析)Excel作为一个电子表格其作用不仅仅是数据的电子化存储及排序和检索,它还有另外一项很重要的功能,那就是数据分析功能,这里用得最多的就是模拟运算表:用一个简单的算式z=3x+4y+1来看:要求当x等于从1到4间的所有整数,而y为1到7间所有整数时所有z的值,用模拟运算表做:首先排好x与y的位置,然后在下面的单元格中建立一个公式,在公式所在行的右边和下面分别输入两个变量的变化值,这里我们在行上为x,列上为y,然后选中这个方形的区域,选择“数据”菜单中的“模拟运算表”命令,打开“模拟运算表”对话框(如图17),将“输入引用行的单元格”选择为公式中x的数值所在单元格,“输入引用列的单元格”选择为公式中y的数值所在的单元格。
用电子表格(Excel)实现层次分析法(AHP)的简捷计算

经济效益 松树 杉木 松树 1 杉木 1/2 桉树 7
桉树 2 1 4
社会效益 松树 松树 1 杉木 2 桉树 5
杉木 1/2 1 3
桉树
方案层对于生态效益准则的判断矩阵及单排序和一致性检验 生态效益 松树 杉木 桉树 按行相乘开n次方 权重Wi Awi AWi/Wi 松树 1 2 3 6 1.817121 0.5278 1.6118118 3.0536216 杉木 1/2 1 3 1.5 1.144714 0.3325 1.0153778 3.0536216 桉树 1/3 1/3 1 0.11111 0.48075 0.1396 0.4264320 3.0536216 3.442585 3.0536216 方案层对于技术要求准则的判断矩阵及单排序和一致性检验 按行相乘开n次方 权重Wi Awi AWi/Wi 3 1.44225 0.3806 1.1935647 3.1356108 8 2 0.5279 1.6551431 3.1356108 1 0.04167 0.346681 0.0915 0.2869030 3.1356108 3.78893 3.1356108
一致性检验 CI=(入-n) /(n-1) CR=CI/R I
0.001847299 0.00359
一致性检验 CI=(入-n) /(n-1) CR=CI/R I
0.0பைடு நூலகம்6810788 0.05207
一致性检验 CI=(入-n) /(n-1) CR=CI/R I
0.067805422 0.13169
桉树 CIi RIi Cri
0.7238 0.648329 0.139648
0.0915 层次总排序一致性检验 0.0885 0.001847 0.026811 0.06781 CI=∑aiCIi RI=∑aiRIi CR=CI/RI 0.5149 0.5149 0.5149 0.5149 #DIV/0! 0.1701 0.003588 0.05207 0.13169 0.117885599
常用正交表IQ

各种正交实验表说实在的,我对正交表也是一知半解,弄得不很清楚。
其数理统计原理更是摸不着火门。
好在本人收集了一系列的常用正交表,对付一般的正交试验应该没问题。
开始对正交表接触是在上《化工过程开发》那门课的时候,因为是考察科目,当时也没在意听。
现在觉得很后悔。
我搜集了很久,找了了这些常用的正交表,目的是想忠告那些与我一样上课没听的同学,好好把握来之不易上课时光。
现在大四了,成天在实验室做实验,写毕业论文,那还有闲心来看书。
我想以后工作了更是时间紧迫。
希望我搜集的这些常用正交表对你有所帮助。
至少给你一些启发。
废话不多说,转如正体。
由于博客系统自身的问题,上标和下标不能正常显示,采用字体颜色区分上标和下标。
红色为下标,蓝色为上标,请注意区分。
1、L4(23)序号 1 2 31 1 1 12 1 2 23 2 1 24 2 2 12、L8(27)序号 1 2 3 4 5 6 71 1 1 1 1 1 1 12 1 1 1 2 2 2 23 1 2 2 1 1 2 24 1 2 2 2 2 1 15 2 1 2 1 2 1 26 2 1 2 2 1 2 17 2 2 1 1 2 2 18 2 2 1 2 1 1 23、L12(211)序号 1 2 3 4 5 6 7 8 9 10 111 1 1 1 1 1 1 1 1 1 1 12 1 1 1 1 1 2 2 2 2 2 23 1 1 2 2 2 1 1 1 2 2 24 1 2 1 2 2 1 2 2 1 1 25 1 2 2 1 2 2 1 2 1 2 16 1 2 2 2 1 2 2 1 2 1 17 2 1 2 2 1 1 2 2 1 2 18 2 1 2 1 2 2 2 1 1 1 29 2 1 1 2 2 2 1 2 2 1 110 2 2 2 1 1 1 1 2 2 1 211 2 2 1 2 1 2 1 1 1 2 212 2 2 1 1 2 1 2 1 2 2 14、L9(34)序号 1 2 3 41 1 1 1 12 1 2 2 23 1 3 3 34 2 1 2 35 2 2 3 16 2 3 1 27 3 1 3 28 3 2 1 39 3 3 2 15、L16(45)序号 1 2 3 4 51 1 1 1 1 12 1 2 2 2 23 1 3 3 3 34 1 4 4 4 45 2 1 2 3 46 2 2 1 4 310 3 2 4 3 111 3 3 1 2 412 3 4 2 1 313 4 1 4 2 314 4 2 3 1 415 4 3 2 4 116 4 4 1 3 26、L25(56)序号 1 2 3 4 5 61 1 1 1 1 1 12 1 2 2 2 2 23 1 3 3 3 3 34 1 4 4 4 4 45 1 5 5 5 5 56 2 1 2 3 4 57 2 2 3 4 5 18 2 3 4 5 1 29 2 4 5 1 2 310 2 5 1 2 3 411 3 1 3 5 2 412 3 2 4 1 3 513 3 3 5 2 4 114 3 4 1 3 5 215 3 5 2 4 1 316 4 1 4 2 5 317 4 2 5 3 1 418 4 3 1 4 2 519 4 4 2 5 3 120 4 5 3 1 4 221 5 1 5 4 3 222 5 2 1 5 4 323 5 3 2 1 5 424 5 4 3 2 1 525 5 5 4 3 2 1混合水平正交表7、L8(41×24)序号 1 2 3 4 51 1 1 1 1 12 1 2 2 2 23 2 1 1 2 24 2 2 2 1 15 3 1 2 1 26 3 2 1 2 17 4 1 2 2 18 4 2 1 1 28、L12(31×24)序号 1 2 3 4 51 1 1 1 1 12 1 1 1 2 23 1 2 2 1 24 1 2 2 2 15 2 1 2 1 16 2 1 2 2 27 2 2 1 2 28 2 2 1 2 29 3 1 2 1 29、L16(44×23)序号 1 2 3 4 5 6 71 1 1 1 1 1 1 12 1 2 2 2 1 2 23 1 3 3 3 2 1 24 1 4 4 4 2 2 15 2 1 2 3 2 2 16 2 2 1 4 2 1 27 2 3 4 1 1 2 28 2 4 3 2 1 1 19 3 1 3 4 1 2 210 3 2 4 3 1 1 111 3 3 1 2 2 2 112 3 4 2 1 2 1 213 4 1 4 2 2 1 214 4 2 3 1 2 2 115 4 3 2 4 1 1 116 4 4 1 3 1 2 2附录1:常用正交表(1)L4(23)列号 1 2 3试验号1 1 1 12 1 2 23 2 1 24 2 2 1(2)L8(27)列号 1 2 3 4 5 6 7试验号1 1 1 1 1 1 1 12 1 1 1 2 2 2 23 1 2 2 1 1 2 24 1 2 2 2 2 1 15 2 1 2 1 2 1 26 2 1 2 2 1 2 17 2 2 1 1 2 2 18 2 2 1 2 1 1 2(3)L12(211)列号 1 2 3 4 5 6 7 8 9 10 11 试验号1 1 1 1 1 1 1 1 1 1 1 12 1 1 1 1 1 2 2 2 2 2 23 1 1 2 2 2 1 1 1 2 2 24 1 2 1 2 2 1 2 2 1 1 25 1 2 2 1 2 2 1 2 1 2 16 1 2 2 2 1 2 2 1 2 1 17 2 1 2 2 1 1 2 2 1 2 18 2 1 2 1 2 2 2 1 1 1 29 2 1 1 2 2 2 1 2 2 1 110 2 2 2 1 1 1 1 2 2 1 211 2 2 1 2 1 2 1 1 1 2 212 2 2 1 1 2 1 2 1 2 2 1列号 1 2 3 4试验号1 1 1 1 12 1 2 2 23 1 3 3 34 2 1 2 35 2 2 3 16 2 3 1 27 3 1 3 28 3 2 1 39 3 3 2 1 (5)L16(45)列号 1 2 3 4 5试验号1 1 1 1 1 12 1 2 2 2 23 1 3 3 3 34 1 4 4 4 45 2 1 2 3 46 2 2 1 4 37 2 3 4 1 28 2 4 3 2 19 3 1 3 4 210 3 2 4 3 111 3 3 1 2 412 3 4 2 1 313 4 1 4 2 314 4 2 3 1 415 4 3 2 4 116 4 4 1 3 2 (6)L25(56)列号 1 2 3 4 5 6 试验号1 1 1 1 1 1 12 1 2 2 2 2 23 1 3 3 3 3 34 1 4 4 4 4 45 1 5 5 5 5 56 2 1 2 3 4 57 2 2 3 4 5 18 2 3 4 5 1 29 2 4 5 1 2 310 2 5 1 2 3 411 3 1 3 5 2 412 3 2 4 1 3 513 3 3 5 2 4 114 3 4 1 3 5 215 3 5 2 4 1 316 4 1 4 2 5 317 4 2 5 3 1 418 4 3 1 4 2 519 4 4 2 5 3 120 4 5 3 1 4 221 5 1 5 4 3 222 5 2 1 5 4 323 5 3 2 1 5 424 5 4 3 2 1 525 5 5 4 3 2 1 (7)L8(4×24)1 1 1 1 1 12 1 2 2 2 23 2 1 1 2 24 2 2 2 1 15 3 1 2 1 26 3 2 1 2 17 4 1 2 2 18 4 2 1 1 2 (8)L12(3×24)列号 1 2 3 4 5试验号1 1 1 1 1 12 1 1 1 2 23 1 2 2 1 24 1 2 2 2 15 2 1 2 1 16 2 1 2 2 27 2 2 1 2 28 2 2 1 2 29 3 1 2 1 210 3 1 1 2 111 3 2 1 1 212 3 2 2 2 1 (9)L16(44×23)列号 1 2 3 4 5 6 7 试验号1 1 1 1 1 1 1 12 1 2 2 2 1 2 23 1 3 3 3 2 1 24 1 4 4 4 2 2 15 2 1 2 3 2 2 16 2 2 1 4 2 1 27 2 3 4 1 1 2 28 2 4 3 2 1 1 19 3 1 3 4 1 2 210 3 2 4 3 1 1 111 3 3 1 2 2 2 112 3 4 2 1 2 1 213 4 1 4 2 2 1 214 4 2 3 1 2 2 115 4 3 2 4 1 1 116 4 4 1 3 1 2 2Excel表格在L9(34)正交试验数据处理中的应用L9(34)正交试验是医药工作中常用的实验方法之一。
SPC_CPK分析Excel版_表格类模板_表格模板_实用文档

NO
测定 D A T A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16Байду номын сангаас
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
1 -0.3=SL
1
0 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
基准表 ★ 工程能力的有无是按照如下基准来判断 A+▶ 2.0 > Cpk ≥ 1.67 : 优,应当保持 A▶ 1.67 > Cpk ≥ 1.33 : 能力良好,状态稳定,但应尽力提升为 B ▶ 1.33 > Cpk ≥ 1.00 : 状态一般,制程因素稍有变异即有产 C▶ 1.00 > Cpk ≥ 0.67 : 差 制程不良较多,必须提升其能力 D ▶ 0.67 > Cpk : 不可接受,其能力太差,应考虑重新整改设计
#DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0!
4因素3水平和3因素3水平讲课讲稿
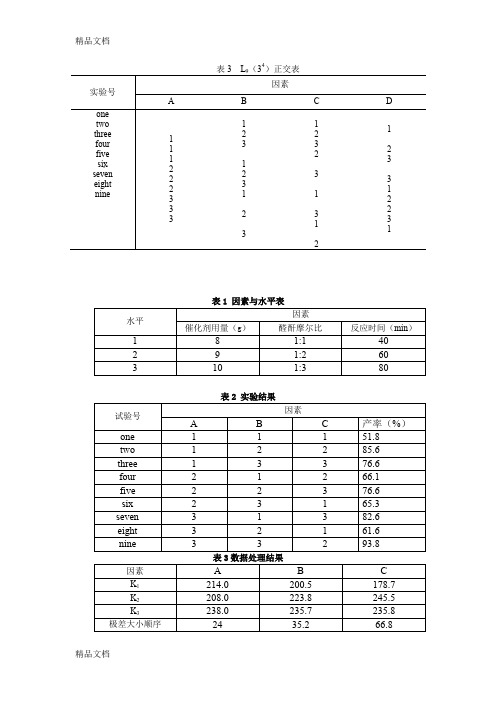
实验号
因素
A
B
C
D
one
two
three
four
five
six
seven
eight
nine
1
1
1
2
2
2
3
3
3
1
2
3
中式饰品风格的饰品绝对不拒绝采用金属,而且珠子的种类也更加多样。五光十色的水晶珠、仿古雅致的嵌丝珐琅珠、充满贵族气息的景泰蓝珠、粗糙前卫的金属字母珠片的材质也多种多样。1
3
标题:大学生“负债消费“成潮流2004年3月18日3
1
2
2
3
1
表1因素与水平表
水平
因素
催化剂用量(g)
醛酐摩尔比
反应时间(min)
1
8
1:1
40
2
9
1:2
60
3
10
1:3
80
表2实验结果
试验号
因素
A
B
C
产率(%)
one
1
1
1
51.8
two
1
2
2
85.6
three
1
3
3
76.6
four
2ห้องสมุดไป่ตู้
1
2
66.1
five
2
2
3
76.6
six
2
3
1
65.3
seven
3
1
3
82.6
eight
3
2
1
61.6
nine
3
3
Excel表1——水平分析法

四,利润总额(亏损以“-”号填列) 减:所得税费用
五,净利润(净亏损以“-”号填列) 归属于母公司所有者的净利润 少数股东权益
六,每股权益: (一)基本每股收益 (二)稀释每股权益
七,其他综合收益 八,综合收益总额
上期金额 2,697,881,265.06 2,697,881,265.06
2,934,663,235.02 2,546,542,688.51
水平分析法 0.023904137 0.023904137
0.108319092 0.082116187
13,954,393.27 131,027,964.53 159,716,146.04
归属于母公司所有者的综合收益总额 归属于少数股东的综合收益总额
五,30
附注
五,30
五,31 五,32 五,33 五,34 五,36
五,35
五,37 五,38
五,39
合并利
合并利润表 本期金额 2,762,371,787.09 2,762,371,787.09
3,252,543,291.64 2,755,655,064.98
-234,098,912.57 266,159,354.64
9,885,191.87 4,404,312.67 22,175,250.20
22,175,250.20 17,584,517.58 4,590,732.62
0.0166 0.0166
22,175,250.20 17,584,517.58 4,590,732.62
-27.03614458 -27.03614458
-21.84055946 84 -1.681406106
3因素4水平正交试验设计

3因素4水平正交试验设计
正交试验设计是一种有效的实验方法,可以通过少量试验来研究多个因素对指标的影响。
3因素4水平正交试验设计是指实验涉及3个因素,每个因素有4个水平。
1. 因素及水平
假设3个因素分别为、、,每个因素的4个水平分别编码为1、2、3、4。
因素: 1、2、3、4
因素: 1、2、3、4
因素: 1、2、3、4
2. 正交表的选择
对于3因素4水平的正交试验,需要选择适当的正交表。
常用的正交表有16(4^3)、16(4^5)等。
本例中,我们选择16(4^3)正交表。
3. 试验设计
16(4^3)正交表包含16个试验组合,每个试验组合对应不同的因素水平组合。
下表展示了该正交表的试验设计:
试验号
1 1 1 1
2 1 2 2
3 1 3 3
4 1 4 4
5 2 1 2
6 2 2 1
7 2 3 4
8 2 4 3
9 3 1 3
10 3 2 4
11 3 3 1
12 3 4 2
13 4 1 4
14 4 2 3
15 4 3 2
16 4 4 1
4. 数据分析
根据上述试验设计,进行16次试验,收集相应的数据。
然后,对数据进行统计分析,计算各因素对指标的影响,确定最优水平组合。
需要注意的是,正交试验设计适用于初步筛选重要因素,了解各因素对指标的影响程度。
如果需要进一步研究因素之间的交互作用,可以考虑增加试验次数或采用其他实验设计方法。
实验四 用EXCEL实现方差分析

壤种 B2(二合)
13.0 13.7 12.0 14.2 13.6 13.3
类 B3(黏土)
13.3 14.0 13.9 12.0 14.6 14.0
得其产量结果
1 21.4 19.6 17.6
(g)于表4.4,试 A3 2 21.2 18.8 16.6
作分析。
3 20.1 16.4 17.5
1 15.3 13.1 14.5
A因素 B因素
第三步: 获得F测验结 果,可以看出, A因素有极显 著差异,B因 素无显著差异。
F0.05值
为了下面的方便,注意 此处临界值的排列方向
第五步:多重比较 先计算标准误SE ,再手 工输入SSRα值,然后编 辑公式计算LSRα值,如 图。
“=$B39+C$38”, 然后用填充柄向右 和向下填充,然后 清除无效数据
差异显著性。
▼注意修正公式中的单元 格引用,使每一处理所在 行的最后一个差数均与 p=2时的LSRα值比较。
“=IF(D36>=D$32,FIXED(D36,1)&”**”,IF(D36>=D$31,FIXED(D 36,1)&”*”,FIXED(D36,1)))”,同理按住填充柄向左填充
▼注意修正公式中的单元 格引用,使每一处理所在 行的最后一个差数均与 p=2时的LSRα值比较。
分析。
D 25 26 21 27 22
第一步:打开一张工作表,并输入相应的数据, 如A2:F6。
第二步:单击“工具”菜单→“数据分析”命令 →选中“方差分析:单因素方差分析”命令,然 后单击“确定”按钮,如图。
输入区域:“$A$3:$F$6”
分组方式:“行”
选中“标志位于第一列”选 项 α(A):“0.05”
CPK分析Excel版

5.20 5.24 5.36 5.24 5.38 5.39 5.24 5.38 5.39 5.42 5.28 5.38 5.39 5.42 5.28 5.45 5.31 5.39 5.42 5.37
测定 D A T A
5.35
5.37
5.20
5.31
5.37
5.34
5.28
5.37
5.45
5.24
5.31
0.000 4.000 14.000 8.000 16.000 13.000 17.000 14.000 5.000 9.000 0.000 0.000
결 작성
담당
팀장
재
0.010
치수 4.610 4.620 4.630 4.640 4.650 4.660 4.670 4.680 4.690 4.700 4.710 4.720 4.730 4.740 4.750 4.760 4.770 4.780 4.790 4.800 4.810 4.820 4.830 4.840 4.850 4.860 4.870 4.880 4.890 4.900 4.910 4.920
6.283
2.507
6.283
2.507
함수값
0.399
0.000
0.399
0.000
0.399
0.000
0.399
0.000
0.399
0.000
0.399
0.000
0.399
0.000
0.399
0.000
0.399
0.000
0.399
0.000
0.399
0.000
0.399
0.000
0.399
三因素析因实验计算表

表1:三因素析因实验ABCN计算表一、平方和的计算: ()93.5925333480022=⨯⨯⨯==∑∑∑∑npqrX G ijrk07.66893.592565942=-=-=∑∑∑∑G X SS ijrkt()90.28693.59253343342751912222=-⨯⨯++=-=∑∑∑∑∙G nqrXSSpjrkA()07.893.59253342542682782222=-⨯⨯++=-=∑∑∑∑∙G nprXSSqrki B()24.15093.59253343192152662222=-⨯⨯++=-=∑∑∑∑∙G npqXSS kij rC()G SSSSnrXSSABpqrkAB---=∑∑∑∑∙∙293.193.592590.28607.834110110114869297586667222222222=---⨯++++++++=()G SSSS nqXSSAC prkq AC---=∑∑∑∑∙∙226.893.592590.28624.15034131103859577431089563222222222=---⨯++++++++=()G SS SS npXSS B C qrki BC ---=∑∑∑∑∙∙293.693.592507.824.15034106103110637379859289222222222=---⨯++++++++=()G SS SSSSSSSSSSnX SSC BABCACABpqrkABC-------=∑∑∑∑∙∙∙274.793.592524.15007.890.28693.626.893.16396=-------=()1986396659422=-=-=∑∑∑∑∑∑∑∑∙∙∙nXXSS kijrke二、不同效应模型F 值的计算1. 固定效应模型eA A MSMS F =eB B MSMS F =eC C MSMS F =eABAB MS MSF =eBCBC MS MSF =eAC AC MSMS F =eABC ABC MSMSF =2. 随机效应模型 )(ABCABACAABACABC A A MSMS MSMSorMS MS MSMS F -+++=')(ABCABBCBABBCABC B B MSMSMSMSorMS MS MSMS F -+++=')(ABCBCACCBCACABC C C MSMSMSMSorMSMSMSMS F -+++='ABCAB AB MSMS F =ABCBC BC MSMS F =A B CAC AC MSMS F =eA B C A B C MSMSF =3. 混合效应模型(1) A 固定,B 、C 随机 )('ABCACABAACABABC A A MSMSMSMSorMSMSMSMS F -+++=BCBB MSMSF /= BC C C MS MS F /= ABCABAB MSMSF /=ABCACAC MSMSF /= e BC BC MS MS F /= e A B CA B C MS MSF /=(2) B 固定,A 、C 随机ACA A MSMSF /= )('A B CBCABBBCABABC B B MSMSMSMSorMSMSMSMS F -+++=ACC C MS MS F /= ABCABAB MSMSF /= e ACAC MS MSF /=ABCBCBC MSMSF /= e A B CA B C MS MSF /=(3)C 固定,A 、B 随机 ABAA MSMS F /= ABBB MS MS F /=)('ABCBCACCBCACABC C C MSMSMSMSorMSMSMSMS F -+++=eABAB MSMSF /=A B CAC AC MSMSF /= A B CBC BC MSMS F /= e A B CA B C MS MSF /=(4)A 、B 固定,C 随机ACAA MSMSF /=BCBB MSMS F /=e C C MS MS F /= ABC ABAB MSMS F /=eACAC MS MSF /=e BC BC MS MS F /=e A B CA B C MS MSF /=(5)A 、C 固定,B 随机 ABAA MSMSF /=eBB MS MS F /= BCCC MSMSF /=e ABAB MSMSF /=ABCAC AC MSMSF /=e BC BC MS MS F /=e A B CA B C MS MSF /=(6)B 、C 固定,A 随机eAA MSMSF /=ABBB MSMSF /=ACCC MS MS F /= e ABAB MSMSF /=eACAC MS MSF /=ABCBC BC MSMSF /=e A B CA B C MS MSF /=三、方差分析表表2:三因素析因实验的方差分析表四、SPSS 运算结果在SPSS 中执行如下操作,可以完成上述三因素析因实验设计数据的分析 1.固定效应方差分析ANALYSIS ——GENERAL LINEAR MODEL ——UNIV ARIA TE 将A 、B 、C 三个因素都定义为固定因素,得到分析结果如下:Tests of Between-Subjects Effects Dependent Variable: X88.496.301.05.)81,2(=F 56.348.201.05.)81,4(=F 65.846.401.05.)8,2(=Fa R Squared = .970 (Adjusted R Squared = .960)2.随机效应方差分析将A、B、C都定义为随机效应,得到结果如下:Tests of Between-Subjects EffectsDependent Variable: Xa MS(A * B) + MS(A * C) - MS(A * B * C)b MS(A * B) + MS(B * C) - 1.000 MS(A * B * C)c MS(A * C) + MS(B * C) - 1.000 MS(A * B * C) + 7.216E-15 MS(Error)d MS(A * B * C)e MS(Error)3.混合效应模型(1)A、B固定,C随机将A、B定义为固定因素,C定义为随机因素,得到的计算结果如下:Tests of Between-Subjects Effectsa MS(A * C)b MS(B * C)c MS(A * C) + MS(B * C) - 1.000 MS(A * B * C) + 7.327E-15 MS(Error)d MS(A * B * C)e MS(Error)(2)A固定,B、C随机Tests of Between-Subjects Effectsa MS(A * B) + MS(A * C) - MS(A * B * C)b MS(A * B) + MS(B * C) - 1.000 MS(A * B * C)c MS(A * C) + MS(B * C) - 1.000 MS(A * B * C) + 7.216E-15 MS(Error)d MS(A * B * C)e MS(Error)结论:从上面模型检验结果可以看出,A、C的主效应显著。
4因素3水平Excel计算表xls

4因素3水平Excel计算表.xls
假设每个因素的权重是相等的,即每个因素都占据了相同的比重。
为了计算总得分,我们可以在每个单元格中添加相应的权重值。
例如,对于第一行“因素1”,我们有以下三个水平的得分:
•水平1得分: 10 x 1/3 = 3.33
•水平2得分: 15 x 1/3 = 5.00
•水平3得分: 20 x 1/3 = 6.67
我们可以将这三个得分相加得到该行的总得分:3.33 + 5.00 + 6.67 =
15.00。
同样地,我们可以为其他三个因素计算总得分。
最后,我们可以将这四个因素的总得分相加得到最终的总得分。
这种方法可以帮助我们评估每个因素在不同水平下的表现,并最终得出一个综合得分。
请注意,权重值的设置可以根据具体情况进行调整,以满足特定的评估需求。
此外,此示例仅包含了四个因素和三个水平,实际应用中可能需要根据具体情况进行扩展或缩减。
单因素三水平表

单因素三水平表### 文档标题:如何有效提高学习效率学习是每个人成长过程中必不可少的环节,因此如何提高学习效率对于每个人来说都是非常重要的。
本文将介绍一些有效的方法来提高学习效率,让你在学习过程中更加高效和有效地获取知识。
#### 一、制定合理的学习计划制定合理的学习计划是提高学习效率的第一步。
合理的学习计划应包括以下几个方面:1. 设定明确的学习目标:明确自己想要学习的内容和目标,确保目标清晰明确。
将大的学习目标分解为小的任务,有针对性地进行学习。
2. 安排合理的学习时间:根据自己的日程和生活习惯,合理安排每天的学习时间。
避免时间浪费和学习疲劳,根据自身情况调整学习时间的长度和间隔。
3. 制定学习计划表:将学习任务和时间表格化,制定每天、每周的学习计划。
明确每天需要完成的任务,确保学习进度的可控性和可执行性。
#### 二、培养良好的学习习惯良好的学习习惯对于提高学习效率起着至关重要的作用。
以下是一些可以帮助你培养良好学习习惯的建议:1. 高效利用碎片时间:比如在排队、坐车等等空闲时间,可以进行一些简单的复习或者阅读,充分利用碎片时间提高学习效率。
2. 分清主次任务:根据学习计划将学习任务分清主次,优先完成重要的任务。
不要让琐碎的任务耽误了重要的学习内容。
3. 避免拖延症:制定学习计划后,要严格按时执行,避免拖延症的产生。
及时完成任务,不要等到最后一刻才开始。
#### 三、优化学习环境良好的学习环境可以提高学习效率和品质。
以下是一些建议来优化学习环境:1. 安静、整洁的学习空间:选择一个安静、整洁的学习环境,避免嘈杂的音乐和喧闹的场所。
整理好书桌和学习用品,确保学习环境舒适。
2. 远离干扰:尽量远离手机、电视、社交媒体等可能干扰学习的因素。
保持专注和集中注意力,提高学习效率。
3. 合理利用辅助工具:根据自己的学习需求,合理选择和使用辅助工具,如电子书、学习软件等,提高学习效率和便捷性。
#### 四、合理安排休息时间学习效率高并不意味着一直处于紧张的学习状态,合理安排休息时间对于保持学习效率也很重要。
