参考椭球定位和不同坐标系之间的转换-Read
GPS测量中坐标系之间的转换

GPS测量中的坐标系转换第一章绪论1.1概述坐标转化并不是一个新的课题,随着测绘事业的发展,全球一体化的形成,越来越要求全球测绘资料的统一。
尤其是在坐标系统的统一方面.原始的大地测量工作主要是依靠光学仪器进行,这样不免受到近地面大气的影响,同时受地球曲率的影响很大,在通视条件上受到很大的限制,从而对全球测绘资料的一体化产生巨大的约束性。
另外由于每一个国家的大地坐标系的建立和发展具有一定的历史特性,仅常用的大地坐标系就有150余个。
在同一个国家,在不同的历史时期由于习惯的改变或经济的发展变化也会采用不同的坐标系统。
例如:在我国建国之后,为了尽快搞好基础建设,我国采用了应用克氏椭球与我国实际相结合的北京54坐标系;随着经济的发展北京54坐标系的缺陷也随之被表露的越来越明显,特别是对我国经济较发达的东南沿海地区的影响表现得更为明显,进而我国开始研究并使用国家80坐标系。
在实际生活中,在一些地区由于国家建设的急需,来不及布设国家统一的大地控制网,而建立局部的独立坐标系。
而后,再将其转换到国家统一的大地控制网中,这些坐标系的变换都离不开坐标值的转化.在国际上,随着1964年美国海军武器实验室对第一代卫星导航系统─NNSS的研制成功,为测绘资料的全球一体化提供了可能。
到1972年,经过美国国防部的批准,开始了第二代卫星导航系统的开发研究工作,即为现在所说的GPS。
此套卫星导航系统满足了全球范围、全天候、连续实时以及三维导航和定位的要求.正是由于GPS卫星的这些特性,这种技术就很快被广大测绘工作者接受。
是由于坐标系统的不同,对GPS技术的推广使用造成了一定的障碍。
这样坐标转换的问题再一次被提到了重要的位置。
为了描述卫星运动,处理观测数据和表示测站位置,需要建立与之相应的坐标系统。
在GPS测量中,通常采用两种坐标系统,即协议天球坐标系和协议地球坐标系。
其中协议地球坐标系采用的是1984年世界大地坐标系(Word Geodetic System 1984─WGS-84)其主要参数为:长半轴 a=6378137; 扁率 f=1:298.257223563.而我国采用的坐标系并不是WGS-84坐标系而是BJ-54坐标系,这个坐标系是与前苏联的1942年普耳科沃坐标系有关的,其主要参数为: 长半轴 a=6378245; 扁率 f=1:298.3.这就使得同一点在不同的坐标系下有不同的坐标值,这样使测绘资料的使用范围受到很大的限制,并且对GPS系统在我国的广泛使用造成了一定的约束性,对我国的测绘事业的发展不利。
2000坐标系转化椭球84

2000坐标系转化椭球84全文共四篇示例,供读者参考第一篇示例:2000坐标系转化椭球84,是指将地图上的坐标点在地球上的位置转化为相应的经纬度坐标,并且使用椭球84参考系统。
为了更准确地定位地球上的点,地图制图者使用这种转化方法来进行精确的测量和定位。
在进行坐标转化的过程中,地图制图者需要将地图上的坐标点转化为经纬度坐标。
经度是指地球表面上一个点相对于本初子午线的位置,而纬度是指地球表面上一个点相对于赤道的位置。
通过将地图上的坐标点转化为经纬度坐标,我们可以更准确地确定地球上不同位置之间的距离和方向。
2000坐标系转化椭球84在地图制图和地理信息系统中有着广泛的应用。
通过这种转化方法,地图制图者可以更准确地绘制地图,并且可以在地图上标注出精确的地理位置信息。
这对于土地利用规划、自然资源管理、城市规划等领域都具有重要的意义。
2000坐标系转化椭球84是一种非常重要的地理信息处理方法。
通过这种方法,我们可以更准确地测量和定位地球上的位置,并且可以为地图制图、导航服务、资源管理等领域提供更精确的数据支持。
希望我国在地理信息领域的发展能够进一步提升,为社会的发展和进步提供更加精确的地理信息数据。
【字数达到要求,文章结束】。
第二篇示例:2000坐标系转化椭球84是一种用于地理信息系统和测绘领域的坐标系转换方法。
在地球上的任意一点,我们都可以通过经纬度坐标来表示,其中经度表示在东西方向上的位置,纬度表示在南北方向上的位置。
不同的国家和地区可能使用不同的坐标系统,为了在不同系统之间进行坐标转换,就需要使用一些数学模型和算法。
椭球84是一种地球椭球体模型,它与地球的椭球体形状非常接近,并且被广泛用于地理信息系统和测绘领域。
2000坐标系转化是指将其他坐标系下的经纬度坐标转换为椭球84坐标系下的经纬度坐标,或将椭球84坐标系下的经纬度坐标转换为其他坐标系下的经纬度坐标。
为什么要进行坐标系转化呢?在实际应用中,不同的地图、测绘数据、卫星导航系统等可能使用不同的坐标系,如果我们想要将这些数据整合在一起或进行空间分析,就需要将它们统一到同一个坐标系下。
2000国家大地坐标系转换的指南

2000国家大地坐标系转换的指南2000国家大地坐标系是中国大陆地区的统一坐标系统,用于测量和定位地理空间信息。
在进行地理空间数据处理、制图、测绘等工作中,常常需要将其他坐标系的数据转换为2000国家大地坐标系。
本文将为大家介绍2000国家大地坐标系转换的指南。
首先,要进行2000国家大地坐标系转换,需要了解基本的理论知识。
2000国家大地坐标系采用了CGCS2000(China Geodetic Coordinate System 2000)参考椭球面模型,采用Lambert投影。
对于需要进行坐标系转换的数据,我们要了解原始坐标系的参数,包括椭球长半轴、扁率、投影中央子午线经度等。
其次,要转换坐标系,需要使用专业的坐标转换软件。
目前市面上有许多专业测绘软件、地理信息系统(GIS)软件能够进行坐标系转换,例如SuperMap、ArcGIS等。
这些软件提供了丰富的转换算法和工具,能够满足不同数据源的转换需求。
常见的2000国家大地坐标系转换方法包括参数法和格网法。
参数法是根据原始坐标系的参数设置进行转换,通过坐标点的位移、旋转和缩放来完成转换。
参数法适用于少量坐标点的转换,可以保证转换的准确性。
格网法是基于已经建立好的2000国家大地坐标系格网,通过查表或插值等方式进行转换。
格网法适用于大量的坐标点的转换,效率较高。
在进行坐标系转换时,还需要注意一些常见的问题。
首先,要注意转换结果的精度损失问题。
由于不同坐标系的误差和精度不同,转换过程中可能会引入一定的误差。
因此,在进行精确测量和定位时,需要考虑坐标系转换引入的误差。
其次,要注意数据投影带的选择。
2000国家大地坐标系采用了Lambert投影,根据不同区域选择不同的投影带可以提高数据的精度和准确性。
最后,要进行坐标系转换后,还需要进行后续的数据处理和分析工作。
转换为2000国家大地坐标系后的数据可以与其他地理数据进行叠加、分析和可视化。
通过使用专业的地理信息系统软件,可以进行空间查询、地图制图、空间分析等各种功能操作,以满足不同领域的需求。
浅析几种常用坐标系和坐标转换

浅析⼏种常⽤坐标系和坐标转换⼀般来讲,GPS直接提供的坐标(B,L,H)是1984年世界⼤地坐标系(Word Geodetic System 1984即WGS-84)的坐标,其中B为纬度,L为经度,H为⼤地⾼即是到WGS-84椭球⾯的⾼度。
⽽在实际应⽤中,我国地图采⽤的是1954北京坐标系或者1980西安坐标系下的⾼斯投影坐标(x,y,),不过也有⼀些电⼦地图采⽤1954北京坐标系或者1980西安坐标系下的经纬度坐标(B,L),⾼程⼀般为海拔⾼度h。
GPS的测量结果与我国的54系或80系坐标相差⼏⼗⽶⾄⼀百多⽶,随区域不同,差别也不同,经粗落统计,我国西部相差70⽶左右,东北部140⽶左右,南部75⽶左右,中部45⽶左右。
现就上述⼏种坐标系进⾏简单介绍,供⼤家参阅,并提供各坐标系的基本参数,以便⼤家在使⽤过程中⾃定义坐标系。
1、1984世界⼤地坐标系WGS-84坐标系是美国国防部研制确定的⼤地坐标系,是⼀种协议地球坐标系。
WGS-84坐标系的定义是:原点是地球的质⼼,空间直⾓坐标系的Z轴指向BIH(1984.0)定义的地极(CTP)⽅向,即国际协议原点CIO,它由IAU和IUGG共同推荐。
X轴指向BIH定义的零度⼦午⾯和CTP⾚道的交点,Y轴和Z,X轴构成右⼿坐标系。
WGS-84椭球采⽤国际⼤地测量与地球物理联合会第17届⼤会测量常数推荐值,采⽤的两个常⽤基本⼏何参数:长半轴a=6378137m;扁率f=1:298.2572235632、1954北京坐标系1954北京坐标系是将我国⼤地控制⽹与前苏联1942年普尔科沃⼤地坐标系相联结后建⽴的我国过渡性⼤地坐标系。
属于参⼼⼤地坐标系,采⽤了前苏联的克拉索夫斯基椭球体。
其长半轴 a=6378245,扁率 f=1/298.3。
1954年北京坐标系虽然是苏联1942年坐标系的延伸,但也还不能说它们完全相同。
3、1980西安坐标系1978年,我国决定建⽴新的国家⼤地坐标系统,并且在新的⼤地坐标系统中进⾏全国天⽂⼤地⽹的整体平差,这个坐标系统定名为1980年西安坐标系。
测量学中的坐标系和他们之间相互转换
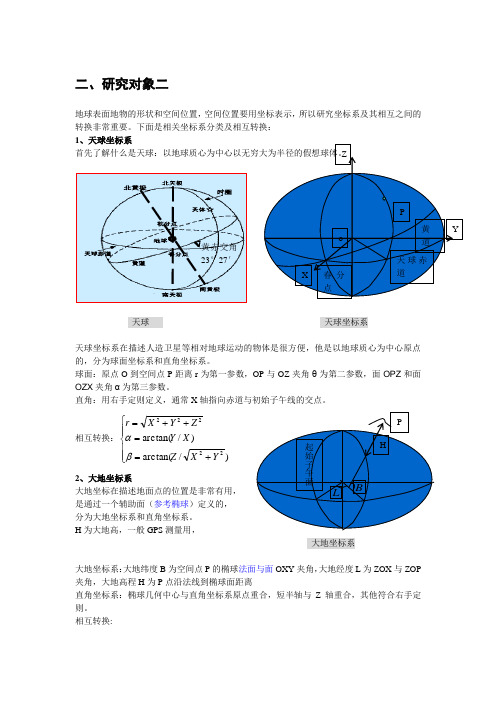
二、研究对象二地球表面地物的形状和空间位置,空间位置要用坐标表示,所以研究坐标系及其相互之间的转换非常重要。
下面是相关坐标系分类及相互转换: 1、天球坐标系首先了解什么是天球:以地球质心为中心以无穷大为半径的假想球体。
天球 天球坐标系天球坐标系在描述人造卫星等相对地球运动的物体是很方便,他是以地球质心为中心原点的,分为球面坐标系和直角坐标系。
球面:原点O 到空间点P 距离r 为第一参数,OP 与OZ 夹角θ为第二参数,面OPZ 和面OZX 夹角α为第三参数。
直角:用右手定则定义,通常X 轴指向赤道与初始子午线的交点。
相互转换:⎪⎪⎩⎪⎪⎨⎧+==++=)/arctan()/arctan(22222Y X Z X Y Z Y X r βα 2、大地坐标系大地坐标在描述地面点的位置是非常有用, 是通过一个辅助面(参考椭球)定义的, 分为大地坐标系和直角坐标系。
H 为大地高,一般GPS 测量用,大地坐标系大地坐标系:大地纬度B 为空间点P 的椭球法面与面OXY 夹角,大地经度L 为ZOX 与ZOP 夹角,大地高程H 为P 点沿法线到椭球面距离直角坐标系:椭球几何中心与直角坐标系原点重合,短半轴与Z 轴重合,其他符合右手定则。
相互转换:黄赤交角23°27′X YZ oP春分点黄道 天球赤道 起始子午面L B PH[]⎪⎩⎪⎨⎧+=+=-=+-=L B H N X L B H N Y B e a N B H e N Z cos cos )(sin cos )(e ,2sin 21/ sin )21(为第一扁率卯酉全曲率半径,其中3、惯性坐标系(CIS )与协议天球坐标系① 惯性坐标系(CIS ):在空间不动或做匀速直线运动的坐标系.② 协议天球坐标系:以某一约定时刻t0作为参考历元,把该时刻对应的瞬时自转轴经岁差和章动改正后作为Z 轴,以对应的春分点为X 轴的指向点,以XOZ 的垂直方向为Y 轴方向建立的天球坐标系。
坐标系转换步骤以及公式

一、各坐标系下椭球参数WGS84大地参数北京54大地参数西安80大地参数参考椭球体:WGS 84 长半轴:6378137短半轴:6356752.3142 扁率:1/298.257224 参考椭球体:Krasovsky_1940长半轴:6378245短半轴:6356863.0188扁率:1/298.3参考椭球体:IAG 75长半轴:6378140短半轴:6356755.2882扁率:1/298.257000二、WGS84转北京54一般步骤(转80一样,只是椭球参数不同)前期工作:收集测区高等级控制点资料。
在应用手持GPS接收机观测的区域内找出三个以上分布均匀的等级点(精度越高越好)或GPS“B”级网网点,点位最好是周围无电磁波干扰,视野开阔,卫星信号强。
并到测绘管理部门抄取这些点的54北京坐标系的高斯平面直角坐标(x、y),大地经纬度(B、L),高程h ,高程异常值ξ和WGS-84坐标系的大地经纬度(B、L),大地高H。
如果没有收集到WGS-84下的大地坐标,则直接用手持GPS测定已知点B、L、H值。
转换步骤:1、把从GPS中接收到84坐标系下的大地坐标(经纬度高程B、L, H,其中B为纬度,L为经度,H为高程),使用84坐标系的椭球参数转换为84坐标系下的地心直角坐标(空间坐标):式中,N为法线长度,为椭球长半径,b为椭球短半径,为第一偏心率。
2、使用七参数转换为54坐标系下的地心直角坐标(x,y,z):x = △x + k*X- β*Z+ γ*Y+ Xy = △y + k*Y + α*Z - γ*X + Yz = △z + k*Z - α*Y + β*X + Z其中,△x,△y,△z为三个坐标方向的平移参数;α,β,γ为三个方向的旋转角参数;k为尺度参数。
(采用收集到的控制点计算转换参数,并需要验证参数)在小范围内可使用七参数的特殊形式即三参数,即k、α、β、γ都等于0,变成:x = △x+ Xy = △y+ Yz = △z + Z3、根据54下的椭球参数,将第二步得到的地心坐标转换为大地坐标(B54,L54,H54)计算B时要采用迭代,推荐迭代算法为:4、根据工程需要以及各种投影(如高斯克吕格)规则进行投影得到对应的投影坐标,即平面直角坐标。
坐标系转换问题及转换参数的计算方法

坐标系转换问题及转换参数的计算方法对于坐标系的转换,给很多GPS的使用者造成一些迷惑,尤其是对于刚刚接触的人,搞不明白到底是怎么一回事。
我对坐标系的转换问题,也是一知半解,对于没学过测量专业的人来说,各种参数的搞来搞去实在让人迷糊。
在我有限的理解范围内,我想在这里简单介绍一下,主要是抛砖引玉,希望能引出更多的高手来指点迷津。
我们常见的坐标转换问题,多数为WGS84转换成北京54或西安80坐标系。
其中WGS84坐标系属于大地坐标,就是我们常说的经纬度坐标,而北京54或者西安80属于平面直角坐标。
对于什么是大地坐标,什么是平面直角坐标,以及他们如何建立,我们可以另外讨论。
这里不多罗嗦。
那么,为什么要做这样的坐标转换呢?因为GPS卫星星历是以WGS84坐标系为根据而建立的,我国目前应用的地形图却属于1954年北京坐标系或1980年国家大地坐标系;因为不同坐标系之间存在着平移和旋转关系(WGS84坐标系与我国应用的坐标系之间的误差约为80),所以在我国应用GPS进行绝对定位必须进行坐标转换,转换后的绝对定位精度可由80提高到5-10米。
简单的来说,就一句话,减小误差,提高精度。
下面要说到的,才是我们要讨论的根本问题:如何在WGS84坐标系和北京54坐标系之间进行转换。
说到坐标系转换,还要罗嗦两句,就是上面提到过的椭球模型。
我们都知道,地球是一个近似的椭球体。
因此为了研究方便,科学家们根据各自的理论建立了不同的椭球模型来模拟地球的形状。
而且我们刚才讨论了半天的各种坐标系也是建立在这些椭球基准之上的。
比如北京54坐标系采用的就是克拉索夫斯基椭球模型。
而对应于WGS84坐标系有一个WGS84椭球,其常数采用IUGG第17届大会大地测量常数的推荐值。
WGS84椭球两个最常用的几何常数:长半轴:6378137±2(m);扁率:1:298.257223563之所以说到半长轴和扁率倒数是因为要在不同的坐标系之间转换,就需要转换不同的椭球基准。
CORS环境下GPS RTK测量时的坐标系统及相互转换

CORS环境下GPS RTK测量时的坐标系统及相互转换袁斌【摘要】GPS定位技术已经被广泛地运用并发展成为一个真正的三维测量工具.GPS CORS系统是GPS的连续运行参考站,是在一个城市、一个地区、或一个国家范围内,根据要求按一定距离间隔,建立常年连续运行的若干个固定GNSS参考站,组成的网络系统.本文通过对GPSRTK测量中遇到的不同坐标系统的分析,阐明了不同坐标系统之间数据转换的本质.结合在生产中使用的GPSRTK设备,说明了WGS-84坐标系向地方坐标系转换的一般过程和注意事项;对GPSRTK测量中遇到的不同坐标系统,进行理论上和实践上的研究,达到了预期效果,掌握了中海达V8 GNSS RTK接收机在GPSRTK测量中的使用问题.【期刊名称】《北京测绘》【年(卷),期】2014(000)001【总页数】4页(P84-87)【关键词】CORS;GPS;测量;坐标系统;转换【作者】袁斌【作者单位】江西荡坪钨业有限公司,江西大余341500【正文语种】中文【中图分类】P228.4由于历史的原因,我国的国家坐标系,经历了从1954年北京坐标系、1980西安坐标系和2000国家大地坐标系。
按所采用的参考椭球来分,主要为基于克拉索夫斯基椭球的1954年北京坐标系和基于IAG 75地球椭球的1980西安坐标系;根据《中华人民共和国测绘法》[1]、,经国务院批准,我国自2008年7月1日起,启用2000国家大地坐标系。
而GPS测量所采用的坐标系统是WGS-84坐标系,WGS-84坐标向地方坐标转换的本质是 WGS-84坐标向1954年北京坐标系或1980西安坐标系的转换。
因此在实际工作中我们经常会遇到上述三个坐标系之间的转换问题,搞清楚它们之间的转换关系是对GPS测量人员的基本要求,也是能够得到GPS准确测量结果的前题。
GPS CORS系统是GPS的连续运行参考站,是在一个城市、一个地区、或一个国家范围内,根据要求按一定距离间隔,建立常年连续运行的若干个固定GNSS参考站,组成的网络系统。
参考系坐标系及转换讲解

1 天球坐标系、地球坐标系和卫星测量中常用的坐标系的建立方法。
天球直角坐标系天球坐标系天球球面坐标系坐标系地球直角坐标系地球坐标系地球大地坐标系常用的天球坐标系:天球赤道坐标系、天球地平坐标系和天文坐标系。
在天球坐标系中,天体的空间位置可用天球空间直角坐标系或天球球面坐标系两种方式来描述。
1 天球空间直角坐标系的定义地球质心O为坐标原点,Z轴指向天球北极,X轴指向春分点,Y轴垂直于XOZ 平面,与X轴和Z轴构成右手坐标系。
则在此坐标系下,空间点的位置由坐标(X,Y,Z)来描述。
春分点:当太阳在地球的黄道上由天球南半球进入北半球,黄道与赤道的交点)2 天球球面坐标系的定义地球质心O为坐标原点,春分点轴与天轴(天轴:地球自转的轴)所在平面为天球经度(赤经)测量基准——基准子午面,赤道为天球纬度测量基准而建立球面坐标。
空间点的位置在天球坐标系下的表述为(r,α,δ)。
天球空间直角坐标系与天球球面坐标系的关系可用图2-1表示:岁差和章动的影响岁差:地球实际上不是一个理想的球体,地球自转轴方向不再保持不变,这使春分点在黄道上产生缓慢的西移,这种现象在天文学中称为岁差。
章动:在日月引力等因素的影响下,瞬时北天极将绕瞬时平北天极旋转,大致呈椭圆,这种现象称为章动。
极移:地球自转轴相对地球体的位置并不是固定的,因而,地极点在地球表面上的位置,是随时间而变化的,这种现象称为极移。
地球的自转轴不仅受日、月引力作用而使其在空间变化,而且还受地球内部质量不均匀影响在地球内部运动。
前者导致岁差和章动,后者导致极移。
协议天球坐标系:为了建立一个与惯性坐标系统相接近的坐标系,人们通常选择某一时刻,作为标准历元,并将此刻地球的瞬时自转轴(指向北极)和地心至瞬时春分点的方向,经过瞬时的岁差和章动改正后,分别作为X轴和Z轴的指向,由此建立的坐标系称为协议天球坐标系。
3 地球坐标系地球直角坐标系和地球大地坐标系的转换其中:过椭球面上一点的法线,可作无限个法截面,其中一个与该点子午面相垂直的法截面同椭球面相截形成的闭合的圈称为卯酉圈。
参考椭球定位与不同坐标系间换算

参考椭球定位和不同坐标系间的换算
10.2(地球)参心坐标系
10.2.1参考椭球定位与定向的实现方法 建立(地球)参心坐标系,需进行下面几个工作: ①选择或求定椭球的几何参数(长短半径);②确定椭球中心位置 (定位);③确定椭球短轴的指向(定向);④建立大地原点。 椭球的几何参数一般可选IUGG推荐值,下面主要讨论参考椭球的定位
10.1.2坐标系的类型
以参考椭球为基准的坐标系,叫做参心坐标系;以总地球椭球为基准的
坐标系叫做地心坐标系。无论参心坐标系还是地心坐标系均可分为空 间直角坐标系和大地坐标系两种,它们都与地球体固连在一起,与地球
同步运动因而又称为地固坐标系,以地心为原点的地固坐标系则称地
心地固坐标系,主要用于描述地面点的相对位置;另一类是空间固定 坐标系与地球自转无关,称为天文坐标系或天球坐标系或惯性坐标系, 主要用于描述卫星和地球的运行位置和状态。在这里,我们研究地固 坐标系。
LK K K sec K ( y sin K x cosK )tg K z
AK K K tg K ( y sin K x cosK ) sec K H K H正 K N K ( y cosK x sin K ) N K e 2 sin K cos K
一点定位 在天文大地测量工作的初期,由于缺乏必要的资料确定 通常只能简单地取
K , K , N 值, K
K 0, K 0, N K 0
即表明在大地原点K处,椭球的法线方向和铅垂线方向重合,椭球面 和大地水准面相切。这时由(10-4)和(10-5)式得
参考椭球定位和不同坐标系间的换算
LK K , BK K , AK K H K H 正K
参考椭球坐标系统转换

参考椭球坐标系统转换不同参考系坐标转化需进行如下处理:1、高斯投影平面坐标求大地坐标2、正常高到大地高换算3、大地坐标求地心坐标4、参考椭球间的转化5、地心坐标求大地坐标6、大地坐标求高斯投影平面坐标7、大地高到正常高换算一.高斯投影平面到大地坐标系的换算直接求解公式:{(4-1)式中,B f为底点纬度,下标“f”表示与B f有关的量。
,,,二.大地高与正常高之间的换算高斯投影平面坐标和摄影测量坐标一般采用正常高,而GPS等导航设备获取的是大地高。
如图1-1所示。
大地高与正常高之间的转换需要知道该点的垂线偏差ε和似大地水准面与椭球面之间的差异N’。
理论表达式为:在摄影测量中,一般示垂线偏差ε为0,故可取:N’在不同的地区有不同的数据,可由大地测量成果中获得。
在摄影测量中,在单个测区内,一般认为它为常数。
三.大地坐标系到地理坐标系的换算直接求解公式:{(2-1)式中:四.三维转换模型(布尔沙模型)三维转换模型的实质是引入平移、旋转和缩放三组参数,进行空间三维相似变换。
以WGS84到西安80的转换为例予以说明。
设任意点在WGS84和西安80两个地理参考中的地心直角坐标分别为:(X84i,Y84i,Z84i)和(X80i,Y80i,Z80i),则两者满足以下模型:(7-1)式中,∆X,∆Y,∆Z为平移参数;εX,εY,εZ为旋转参数;λ为尺度变化参数。
如果至少有三个点,既有WGS84坐标,也有西安80坐标系下的坐标,就可以利用最小二乘的原理,求出上述模型中的七个参数。
从而实现WGS84到西安80坐标的转换。
在上述公式中,可以看到坐标系统间有一个坐标偏移值。
因此不同坐标系统之间进行坐标转换,高程值转换前后是不相同的。
五.根据地心坐标求大地坐标直接求解公式:{(1-1)式中:,六.根据大地坐标求高斯投影平面坐标直接求解公式:{(3-1)式中:X0为该点到赤道间的中央子午线弧长。
,,。
在测绘过程中如何处理不同坐标系统的转换

在测绘过程中如何处理不同坐标系统的转换在测绘过程中,不同坐标系统的转换是一个非常重要和复杂的问题。
由于地球是一个三维的椭球体,而测量时通常是在二维平面上进行,因此需要将地球表面的三维坐标转换为平面上的二维坐标。
而不同的国家和地区使用的测量标准也不尽相同,导致了不同的坐标系统。
首先,我们来了解一下什么是坐标系统。
坐标系统是一种用于描述和定位地理空间位置的方式。
它由坐标轴、坐标原点和度量单位组成。
在测绘中常用的坐标系统有经纬度坐标系统和投影坐标系统。
经纬度坐标系统是一种描述地球表面位置的方式。
它以地球的赤道为基准,将地球表面分为纬度和经度两个坐标轴。
纬度表示地点距离赤道的远近,经度表示地点距离本初子午线的东西方向。
经纬度坐标系统在全球范围内使用广泛,但是由于地球是一个椭球体,因此在进行计算和测绘时会存在一定的误差。
为了解决地球椭球体带来的误差,人们引入了投影坐标系统。
投影坐标系统是将地球表面的三维坐标投影到平面上的二维坐标系统。
常见的投影坐标系统有UTM投影坐标系统和高斯-克吕格投影坐标系统。
UTM投影坐标系统是一种面积坐标系统,适用于全球大部分地区。
它将地球分为60个纵向的投影带,每个投影带都有一个中央子午线作为基准。
UTM坐标系统通过将地球上每个投影带投影到一个独立的平面上,来减小地球椭球体带来的误差。
与UTM坐标系统相似,高斯-克吕格投影坐标系统也是一种投影坐标系统,适用于中国的测绘工作。
它将地球表面分为了以某一纬度为标准的若干带状投影带。
在高斯-克吕格投影中,地球上每个投影带是用高斯正轴投影系统进行投影的,能够较好地保留山脉、河流等地形图上的形状。
不同坐标系统之间的转换是进行测绘工作时必不可少的环节。
在进行坐标转换时,一个常用的方法是通过共椭球参数和转换公式进行计算。
共椭球参数指的是在多个坐标系统中共同使用的椭球体参数,例如椭球体的长半轴、短半轴、扁率等。
通过共椭球参数,将不同坐标系统中的坐标转换为统一的椭球体上的坐标,再进行转换到目标坐标系统。
3 参考椭球定位与坐标转换

(一)建立大地坐标系的基本原理(重点)
1、椭球定位、定向的概念
大地坐标系是建立在一定的大地基准上的用于表达地球表面 空间位置及其相对关系的数学参照系,这里所说的大地基准 是指能够最佳拟合地球形状的地球椭球的参数及椭球定位和 定向。 椭球定位是指确定椭球中心的位置,可分为两类:局部定位和 地心定位。局部定位要求在一定范围内椭球面与大地水准面 有最佳的符合,而对椭球的中心位置无特殊要求;地心定位要 求在全球范围内椭球面与大地水准面有最佳的符合,同时要求 椭球中心与地球质心一致或最为接近。
向,从而建立新的参心大地坐标系。按这种方法进行参考椭 球的定位和定向,由于包含了许多拉普拉斯点,因此通常称 为多点定位法。
多点定位的结果使椭球面在大地原点不再同大地水准面相 切,但在所使用的天文大地网资料的范围内,椭球面与大 地水准面有最佳的密合。
3 参考椭球定位与坐标转换
(二)大地原点和大地起算数据
椭球定向是指确定椭球旋转轴的方向,不论是局部定位还是 地心定位,都应满足两个平行条件:
①椭球短轴平行于地球自转轴; ②大地起始子午面平行于天文起始子午面
3 参考椭球定位与坐标转换
要正确区分的两个概念
▪ 具有确定参数(长半径a和扁率α),经过局部 定位和定向,同某一地区大地水准面最佳拟
合的地球球,叫做参考椭球。
▪ BJ54坐标系的缺点:
▪ ①椭球参数有较大误差。与现代精确的椭球参数相比,长半轴约大109m; ▪ ②参考椭球面与我国大地水准面存在着自西向东明显的系统性的倾斜,东部
地区大地水准面差距最大+68m。使得大比例尺地图反映地面的精度受到影 响,也对观测元素的归算提出了严格要求; ▪ ③几何大地测量和物理大地测量应用的参考面不统一。我国在处理重力数据 时采用赫尔默特1900年—1909年正常重力公式,与这个公式相应的赫尔默 特扁球不是旋转椭球,它与克拉索夫斯基椭球不一致,给实际工作带来麻烦; ▪ ④定向不明确。椭球短轴的指向既不是国际上较普遍采用的国际协议(习用) 原点CIO(Conventional International Origin),也不是我国地极原点;起 始大地子午面也不是国际时间局BIH所定义的格林尼治平均天文台子午面, 从而给坐标换算带来一些不便和误差。 ▪ 另外,监于该坐标系是按局部平差逐步提供大地点成果的,因而不可避免地 出现一些矛盾和不够合理的地方。
精品毕业论文-浅谈我国几种坐标系的坐标转换

浅谈我国几种坐标系的坐标转换摘要:如今测量当中,我们大部分应用的是GPS测量技术,而GPS测量得到的是WGS-84坐标,所以我们要对其进行坐标转换,转换成我国的平面坐标。
本文详细介绍了几种转换的方法,进而很容易的实现了不同坐标系之间的转换。
关键词:坐标系统;坐标转换;高程拟合中图分类号:{P286+.1} 文献标识码:A 文章编号:1 坐标系统的介绍1.1 WGS—84坐标系统WGS—84坐标系是目前GPS所采用的坐标系统。
坐标原点位于地球的质心,Z 轴指向BIHl984.0定义的协议地球极方向,X轴指向BIHl984.0的起始子午面和赤道的交点,Y轴与X轴和Z轴构成右手系。
WGS—84系所采用椭球参数为:a=6378138m;f=1/298.257223563。
1.2 1954年北京坐标系1954年北京坐标系是我国目前广泛采用的大地测量坐标系。
该坐标系源自于原苏联采用过的1942年普尔科夫坐标系。
该坐标采用的参考椭球是克拉索夫斯基椭球,该椭球的参数为:a=6378245m;f=1/298.3。
该椭球并未依据当时我国的天文观测资料进行重新定位。
而是由前苏联西伯利亚地区的一等锁,经我国的东北地区传算过来的,该坐标的高程异常是以前苏联1955年大地水准面重新平差的结果为起算值,按我国天文水准路线推算出来的,而高程又是以1956年青岛验潮站的黄海平均海水面为基准。
1.3 1980年西安坐标系1980年西安坐标系的原点位于我国的中部,陕西西安市的附近。
椭球的短轴平行于由地球质心指向我国地极原点JYD1968。
0的方向,起始大地子午面平行与我国起始天文子午面。
大地点的高程是1956年青岛验潮站的黄海平均海水面为基准。
2.坐标转换既然不同的坐标系,就存在坐标转换的问题。
关于坐标转换,首先要搞清楚转换的严密性问题,即在同一个椭球里的坐标转换都是严密的,而在不同的椭球之间的转换这时不严密的。
例如,由1954北京坐标系的大地坐标转换到1954北京坐标系的高斯平面直角坐标是在同一参考椭球体范畴内的坐标转换,其转换过程是严密的。
了解测绘坐标系及其转换方法

了解测绘坐标系及其转换方法测绘坐标系是地理测量中应用的重要概念和工具,它是区域内地理位置的唯一标识。
在现代测绘工作中,了解测绘坐标系及其转换方法是非常重要的,因为它涉及到地图制作、导航定位以及地理信息系统等方面。
本文将简要介绍测绘坐标系的基本概念,然后重点讨论常见的坐标系转换方法。
一、测绘坐标系的基本概念测绘坐标系是一种用于定位地理位置的坐标系统,它是地球表面上无限多个点的坐标集合。
通常情况下,我们使用直角坐标系或大地坐标系来表示地理位置。
直角坐标系是由水平的X轴、Y轴和垂直的Z轴组成,通过三个坐标值来表示地理位置。
大地坐标系则是基于地球的椭球形状和地球参考椭球体模型,通过纬度、经度和高程来表示地理位置。
不同国家和地区使用不同的测绘坐标系,常见的坐标系包括WGS84(世界大地坐标系)、UTM(通用横轴墨卡托坐标系)等。
这些坐标系在取样方法、椭球模型和精度要求上有所不同。
因此,在进行测绘工作时,需要根据具体情况选择相应的坐标系。
二、坐标系转换方法坐标系转换是指将一个坐标系中的坐标数据转换到另一个坐标系中的过程。
由于不同坐标系具有不同的基准和度量标准,所以在不同坐标系之间进行转换是必要的。
下面介绍几种常见的坐标系转换方法。
1.七参数转换法七参数转换法是一种常见的坐标系转换方法,它通过平移、旋转和尺度变换来实现坐标系之间的转换。
这种方法适用于相对较小区域的测绘工作,如城市测绘和局部地图制作。
通过测量控制点的坐标,可以求解出七个参数,并将输入坐标转换为目标坐标。
2.Molodensky-Badekas转换法Molodensky-Badekas转换法是一种用于大范围坐标系转换的方法,它通过对于物体的三维坐标进行扭曲和伸缩,以适应两个坐标系之间的差异。
这种方法适用于全球范围的坐标转换,如GPS导航和地球物理研究。
3.坐标系四参数转换法坐标系四参数转换法是一种用于平面直角坐标系转换的简单方法,它通过平移和尺度变换来实现坐标系之间的转换。
utm坐标系和wgs84坐标转换规则的概述

utm坐标系和wgs84坐标转换规则的概述utm坐标系和wgs84坐标转换规则的概述引言:UTM坐标系(Universal Transverse Mercator)和WGS84坐标系(World Geodetic System 1984)是地理信息系统(GIS)中常用的坐标系统。
它们以不同的方式定位地球表面上的点,且在不同的地理应用中具有重要的作用。
本文将对UTM坐标系和WGS84坐标系进行概述,并探讨它们之间的转换规则。
一、UTM坐标系1. UTM坐标系的定义UTM坐标系是一种平面直角坐标系,将地球表面划分为多个横切的投影带,每个投影带的宽度为6度。
每个投影带都以中央子午线为基准线,并使用横轴为东西方向、纵轴为南北方向的坐标系统来描述地球上的点位置。
2. UTM坐标系的特点- UTM坐标系是基于高斯-克吕格投影(Transverse Mercator Projection)而建立的。
- UTM坐标系有多个投影带,每个投影带的中央子午线都位于该带的中央。
- UTM坐标系适用于大部分地区的小到中等范围地理应用,尤其是陆地表面的测量和制图。
3. UTM坐标的表示方法UTM坐标使用两个值来表示一个点的位置,分别是东偏移和北偏移。
其中东偏移指的是距离中央子午线的偏移量,北偏移指的是距离赤道的偏移量。
二、WGS84坐标系1. WGS84坐标系的定义WGS84坐标系是一个全球的地理坐标系统,它是由美国国家测绘局(National Geospatial-Intelligence Agency)和国防部联合制定的。
WGS84坐标系采用椭球体来近似地球形状,并将地球表面划分为经度和纬度。
2. WGS84坐标系的特点- WGS84坐标系是一个大地坐标系统,用于确定地球表面上的点的经度、纬度和海拔。
- WGS84坐标系在全球范围内被广泛应用,特别是用于GPS定位和导航系统。
3. WGS84坐标的表示方法WGS84坐标使用经度和纬度来表示一个点的位置。
GPS测量常用坐标系统及相互转换

GPS测量常用坐标系统及坐标转换摘要:本文GPS测量常用坐标系统,以及GPS静态、动态测量中坐标变换的参数和方法。
关键词:GPS;坐标系统;坐标转换GPS(Global Positioning System)即全球定位系统,是由美国建立的一个卫星导航定位系统。
它具有全球性、全天候、连续性和实时性的精密三维导航与定位功能,现已广泛用于大地测量、工程测量、航空摄影测量以及地形测量等各个方面。
相对于常规测量来说,GPS 测量具有测量精度高、测站间无需通视、观测时间短、仪器操作简便、全天候作业、可提供三维坐标等特点。
大大地提高了测量效率和精度。
但是由于坐标系统的不同,面临着大量的坐标转换问题。
对GPS技术的推广使用造成了一定的障碍。
本文就GPS测量常用坐标系统及坐标转换的原理和方法,根据作者的理解介绍如下。
一、GPS测量常用坐标系统及投影一个完整的坐标系统是由坐标系和基准两方面要素所构成的。
坐标系指的是描述空间位置的表达形式,而基准指的是为描述空间位置而定义的一系列点、线、面。
在大地测量中的基准一般是指为确定点在空间中的位置,而采用的地球椭球或参考椭球的几何参数和物理参数,及其在空间的定位、定向方式,以及在描述空间位置时所采用的单位长度的定义。
大地基准面是利用特定椭球体对特定地区地球表面的逼近,每个国家或地区均有各自的大地基准面,因此相对同一地理位置,不同的大地基准面,它们的经纬度坐标是有差异的。
基准面是在椭球体基础上建立的,但椭球体不能代表基准面,同样的椭球体能定义不同的基准面。
1、坐标系统的分类1.1、空间直角坐标系空间直角坐标系的坐标系原点位于参考椭球的中心,Z轴指向参考椭球的北极,X轴指向起始子午面与赤道的交点,Y轴位于赤道面上,且按右手系与X轴呈90 夹角。
某点在空间中的坐标可用该点在此坐标系的各个坐标轴上的投影来表示。
1.2、空间大地坐标系空间大地坐标系是采用大地经度(L)、大地纬度(B)和大地高(H)来描述空间位置的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
10.2.2大地原点和大地起算数据
大地测量基准,也叫 大地测量起算数据
一定的参考椭球和一定的大地原点起算数据, 确定了一定的坐标系。通常就是用参考椭球 和大地原点上的起算数据的确立作为一个参 心大地坐标系建成的标志。
§10.3我国大地坐标系
1954年北京坐标系
建国初期,为了迅速开展我国的测绘事业,鉴于当时的实际 情况,将我国一等锁与原苏联远东一等锁相连接,然后以连接处 呼玛、吉拉宁、东宁基线网扩大边端点的原苏联1942年普尔科沃 坐标系的坐标为起算数据,平差我国东北及东部区一等锁,这样 传算过来的坐标系就定名为1954年北京坐标系。因此,P54可归 结为: a.属参心大地坐标系; b.采用克拉索夫斯基椭球的两个几何参数; c. 大地原点在原苏联的普尔科沃; d.采用多点定位法进行椭球定位; e.高程基准为 1956年青岛验潮站求出的黄海平均海水面; f.高程异常以原苏联 1955年大地水准面重新平差结果为起 算数据。按我国天文水准路线推算而得 。
2、坐标系的类型
参心坐标系:以参考椭球为基准的坐标系 地心坐标系:以总地球椭球为基准的坐标系。 无论参心坐标系还是地心坐标系均可分为空间 直角坐标系和大地坐标系两种,它们都与地球体固连 在一起,与地球同步运动,因而又称为地固坐标系,以 地心为原点的地固坐标系则称地心地固坐标系,主 要用于描述地面点的相对位置;另一类是空间固定 坐标系与地球自转无关,称为天文坐标系或天球坐 标系或惯性坐标系,主要用于描述卫星和地球的运 行位置和状态。在这里,我们研究地固坐标系。
10.1建立大地坐标系的基本原理(重点)
1、椭球定位、定向的概念 大地坐标系是建立在一定的大地基准上的用于表达地球表面 空间位置及其相对关系的数学参照系,这里所说的大地基准 是指能够最佳拟合地球形状的地球椭球的参数及椭球定位和 定向。 椭球定位是指确定椭球中心的位置,可分为两类:局部定位和 地心定位。局部定位要求在一定范围内椭球面与大地水准面 有最佳的符合,而对椭球的中心位置无特殊要求;地心定位要 求在全球范围内椭球面与大地水准面有最佳的符合,同时要求 椭球中心与地球质心一致或最为接近。
O1 X1Y1Z1
X 0 , Y0 , Z0
x , y , z
O X YZ
参考椭球定位定向方法
选定某一适宜的点K作为大地原点,在该点上实施精密的天文 测量和高程测量,由此得到该点的天文经度K ,天文纬度 , K K 至某一相邻点的天文方位角 和正高 H正
K
大地原点垂线偏差的 子午圈分量和卯酉 圈分量及该点的大地 水准面差距
BJ54坐标系的缺点:
①椭球参数有较大误差。与现代精确的椭球参数相比,长半轴约大109m; ②参考椭球面与我国大地水准面存在着自西向东明显的系统性的倾斜,东部 地区大地水准面差距最大+68m。使得大比例尺地图反映地面的精度受到影 响,也对观测元素的归算提出了严格要求; ③几何大地测量和物理大地测量应用的参考面不统一。我国在处理重力数据 时采用赫尔默特1900年—1909年正常重力公式,与这个公式相应的赫尔默 特扁球不是旋转椭球,它与克拉索夫斯基椭球不一致,给实际工作带来麻烦; ④定向不明确。椭球短轴的指向既不是国际上较普遍采用的国际协议(习用) 原点CIO(Conventional International Origin),也不是我国地极原点;起 始大地子午面也不是国际时间局BIH所定义的格林尼治平均天文台子午面, 从而给坐标换算带来一些不便和误差。 另外,监于该坐标系是按局部平差逐步提供大地点成果的,因而不可避免地 出现一些矛盾和不够合理的地方。
x y z 0
确定椭球的定位 和定向
多点定位
一点定位的结果在较大范围内往往难以使椭球面与大地水准 面有较好的密合。所以在国家或地区的天文大地测量工作进 行到一定的时候或基本完成后,利用许多拉普拉斯点(即测 定了天文经度、天文纬度和天文方位角的大地点)的测量成 果和已有的椭球参数,按照广义弧度测量方程按 N 2 =最小 2 (或 =最小)这一条件,通过计算进行新的定位和定 向,从而建立新的参心大地坐标系。按这种方法进行参考椭 球的定位和定向,由于包含了许多拉普拉斯点,因此通常称 为多点定位法。 多点定位的结果使椭球面在大地原点不再同大地水准面相 切,但在所使用的天文大地网资料的范围内,椭球面与大 地水准面有最佳的密合。
椭球定向是指确定椭球旋转轴的方向,不论是局部定位还是 地心定位,都应满足两个平行条件: ①椭球短轴平行于地球自转轴; ②大地起始子午面平行于天文起始子午面
具有确定参数(长半径a和扁率α),经过局部 定位和定向,同某一地区大地水准面最佳拟 合时能使它在全球范围内与大地体 最密合的地球椭球,叫做总地球椭球。
K ,K , NK
x , y , z
天文坐标
大地坐标
得到K点相应的大地经度 LK ,大地纬度 BK ,至某一 相邻点的大地方位角 AK 和大地高 H K
LK K K sec K BK K K AK K K tgK H K H正K N K
一点定位
LK K K sec K BK K K AK K K tgK H K H正K N K
表明在大地原点K 处,椭球的法线方 向和铅垂线方向重 合,椭球面和大地 水准面相切
K 0, K 0, N K 0
LK K , BK K , AK K H K H 正K
§10.2(地球)参心坐标系(了解)
10.2.1参考椭球定位与定向的实现方法
建立(地球)参心坐标系,需进行下面几个工作: ①选择或求定椭球的几何参数(长短半径); ②确定椭球中心位置(定位); ③确定椭球短轴的指向(定向); ④建立大地原点。
参考椭球的定位与定向
椭球中 心 O相 对于地 心的平 移参数 三个绕坐标 轴的旋转参 数(表示参 考椭球定向)
