材料力学(张功学)-第11章
《材料力学 第2版》_顾晓勤第11章第1节 惯性力问题

21.9
MPa
d max Kd st max 26.3 MPa
OB
al
A m
第 1 节 惯性力问题
第十一章 动载荷和疲劳
二、杆件作匀速转动时的应力计算
在设计飞轮时,要求用料少而惯性大,所以常把 飞轮设计成轮缘厚、中间薄的样式。若不考虑轮辐的 影响,可以近似地认为飞轮的质量绝大部分集中在轮 缘上,将飞轮简化为一个绕中心旋转的圆环。
16
第 1 节 惯性力问题
第十一章 动载荷和疲劳
例 11-4 钢质飞轮匀角速转动如图所示,轮缘外径
D 1.8 m,内径 d 1.4 m ,材料密度 7.85 103 kg/m3。 要求轮缘内的应力不得超过许用应力 [ ] 60 MPa,轮
辐影响不计。试计算飞轮的极限转速 n 。
解:由强度条件,得到 轮缘允许的线速度
解:由附表 4 查得 32a 工字钢:
10 a
2m
8m
2m
= 52.717kg/m;加速度 a = 0 时,
每根钢绳的拉力 Fst = mg /2,应力 32a 号工字钢
st
Fst πd 2 / 4
39.5106 N/m2
39.5 MPa
动荷系数:
Kd
1
a g
1
6 9.8
1.612
d Kd st 1.612 39.5 MPa 63.6 MPa
第 1 节 惯性力问第题十一章 动载荷和疲第劳十一章 动载荷和疲劳
静载荷:所加载荷的特点是由零缓慢地增加到某一 数值,以后保持不变,即是静载荷。由静载荷产生 的应力,称为静应力。
动载荷:主要是指随时间而变化的载荷,特别是冲 击载荷。 动应力:凡是由动载荷引起的构件的应力。
材料力学第十一章

2F 2 ⋅ 3l 8
2F 2 ⋅ l
×2+
4=
7lF 2
2EAi π E(2d )2
π Ed 2 8π Ed 2
(c)取 d x 长的微段(如右图),在均布轴力 f 的作用下,它具有的应变能
dVε
=
1 2
FN (x)dΔ
式中
FN (x)
=
F l
x,
dΔ = FN (x)dx = Fx dx EA EAl
=
Vε
(F
)
+
Vε
(M
)
+
1 2
(Mθ
+
Fwmax
)
。
11-2 图示简支梁中点只承受集中力 F 时,梁的最大转角为θ max ,应变能为Vε (F ) ;中 点只承受集中力偶 M 时,最大挠度为 wmax ,梁的应变能为Vε (M ) 。当同时在中点施加 F
和 M 时,梁的应变能为多少?
解 对于线性结构简支梁,先加 F 时梁贮存的应变能
(顺)
(二)单位载荷法解(a)
(a3)
(a4)
(a5)
149
解 图(b)
FA
=
FB
=
Me 2a
AD 段
M (x1 ) =
Me 2a
x1 , M 1(x1 ) =
x1 , M
2 (x1 ) =
− x1 2a
DC 段
M (x2 ) = M e , M 1(x2 ) = 2a − x2 , M 2 (x2 ) = −1
11-5 超静定问题有哪几类?怎样确定超静定问题的次数?什么是相当系统?什么是静 定基?静定基是否唯一?
答 超静定问题有外约束超静定、内约束超静定及外约束超静定加内约束超静定混合。 全部未知力个数与全部独立平衡方程数的差就是超静定问题的次数。 拆去多余内、外约束,用相应的约束力代替其作用,使之成为静定形式的结构,它就 是原结构的相当系统(相当系统加上变形协调条件称为原超静定结构的等效系统)。 解除约束后的不包括外载荷的静定结构称为原结构的静定基。 静定基不唯一。
第十一章材料力学课程课件PPT

2.18
BC
第11章
表达式为
变 型能法
11.3 卡 氏 定 理
δ1 =
证明如下: 设 FP1 , FP 2 , , FPn 作用于弹性体上(图11.6),这些力产生的相应位移 为 δ1 , δ 2 ,δ n ,在变形过程中,外力所做的功等于弹性体的变形能,于 是变形能 U 为 FP1 , FP 2 , , FPn 的函数.
M θB W = 0 ,而外力 2
偶所做的功为 M0
M 02 l U = ,由 2 EI
W =可得 U
M 0θ B M 02l = 2 2 EI
θB =
M 0l EI
2.17
第11章
变 型能法
11.3 卡 氏 定 理
其结果与梁的变形一章中计算结果一致.从上面的计算可以看出,由于 变形能为力的函数,若将变形能对力求偏导数,则
与集中力对应的是线位移,与集中力偶对应的是角位移.在线弹性体的 情况下,广义力和广义位移是线性关系,运用胡克定理,上式还可以写 成: FP2 l Cδ 2 U= = (11.11) 2C 2l 式中,C是杆的刚度,从上式可以看出,弹性变形能是广义力或广义位 移的二次函数.
2.13
第11章
变 型能法
(a) (b) 图11.1 轴向受拉杆外力的功 (a) 受拉直杆;(b) 与关系
2.4
P
第11章
W=
变 型能法
1 FP l 2
11.2 变形能的计算
(11.2)
根据式(11.1)可知,受拉杆的弹性变形能为
U =W = 1 FP l 2
因,上式可写成
l = FP l EA
(11.3)
2.5
第11章
工程力学 材料力学 第11章

0
3 Px 2 PL dx EI 3EI
求转角 A
没有与A向相对应的力(广义力),加之。 P A
MA
①求内力
M ( x ) xP M
A
②将内力对MA求偏导后,令M A=0
M ( x ) 1 M A M 0
A
L
x
O
③求变形( 注意:M A=0)
A
A
O f
④变形
fC
U RC
L
M ( x ) M ( x ) dx EI RC
RC ( L x ) d x 0
2 L
0 .5 L 1 P ( 0 . 5 L x ) ( L x ) d x EI 0
1 5 PL 3 R C L3 ( )0 EI 48 3
M
AB
( x1 ) P ( L x1 ) Px ( x x1 )
M BC ( x1 ) P ( L x1 )
②将内力对Px 求偏导后,令Px=0
M AB ( x ) Px
P x 0 x1 x
M
BC
(x)
Px
Px 0 0
③变形( 注意:Px=0)
,
,
其中
16
代入上式并积分,得组合变形 杆件的变形能一般表达式:
细长杆,剪力引起的变形能可忽略不计:
2 N 2 ( x) Mn ( x) M 2 ( x) U dx dx dx L 2 EA L 2GI L 2 EI P
17
功互等定理与位移互等定理
U 11
P 1
1
△ 11
材料力学答案第十一章
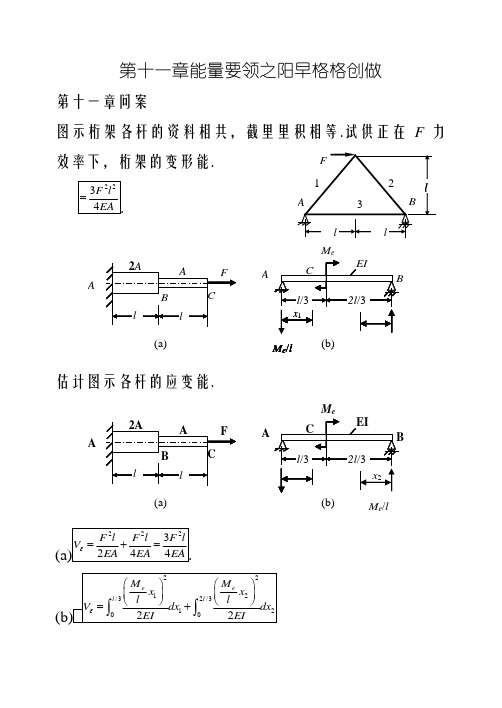
第十一章能量要领之阳早格格创做第十一章问案图示桁架各杆的资料相共,截里里积相等.试供正在F 力效率下,桁架的变形能.估计图示各杆的应变能.传动轴受力情况如图所示.轴的直径为40mm ,资料为45钢,E = 210GPa ,G = 80GPa.由扭转引起的应变能: 由蜿蜒引起的应变能:估计图示梁的应变能,并证明是可谦脚叠加本理及其本果.而没有谦脚叠加本理,果为应变能取内力的闭系没有是线性的.借帮于附录E ,供跨度中面(睹课本下册p40例12-4)11.6 图示刚刚架的各杆的EI 皆相等,试供截里A 、B 的位移战截里C 的转角.(a)A 面:正在A 面加一个背下的单位力.M (x 1)=0, M (x 2)=Fx 2, M (x 3)=FbC 面:正在C 加一个顺时针的力奇矩为1的单位力奇(b) A 面:正在A面加一个背下的单位力B 面:正在B 面加一个背左的单位力图示桁架各杆的资料相共,截里里积相等C 处的火仄位移战笔直位移.CF BAR火仄位移:(122) 3.828Fl FlEA EA +=-=-.笔直位移:Fl EA ∆=-.2,E 索 = 177GPa.F = 20kN ,(a)假设横梁ABCD 为刚刚体,供C 面的笔直位移.(2)若没有把ABCD 假设为刚刚体,且已知其抗直刚刚度为EI 2,试再供C 面的笔直位移.(1)42110.87.891033F EA -⎛⎫∆=⨯=⨯ ⎪⎝⎭m.(2)20.44047.89102Fx dx EI -∆=⨯+⎰4447.8910 1.48109.3710---=⨯+⨯=⨯m.11.9 等截里直杆BC 的轴线为四分之三的圆周.若AB 杆可视为刚刚性杆,试供正在F 力效率下,截里B 的火仄位移及笔直位移.火仄位移:M ()=FR cos, ()sin M R θθ=33320sin cos 2FR FRd EI EI πθθθ∆==⎰.D CFAB60 ° 60 ° 800 400400RFO B BF ORA F笔直位移:()(1cos )M R θθ=--33.36FR EI =.11.10 图示圆弧形小直率杆,仄衡半径为R .力F笔直于圆环中线地圆的仄里.试供二个F 力效率面的相对于线位移.M ()=FR sin, ()sin M R θθ= T ()=FR (1-cos), ()(1cos )T R θθ=-333pFR FR EI GI ππ=+.11.11图示圆弧形小直率杆,仄衡半径为R .正在横截里A 取B 处受一对于集结力F 效率.力F 正在圆环中线地圆的仄里内.试供二个F 力效率面的相对于线位移. M ()=FR sin,()sin M R θθ=32320sin FR FRd EI EI πθπθ∆==⎰.11.12图示轴线为火仄里内四分之一圆周的直杆,正在自由端B 效率笔直荷载F ,设EI 战GI P 为已知,试供正在F 力效率下端里B 的笔直位移.F O O Rθ B F AM ()=FR sin, ()sin M R θθ= T ()=FR (1-cos), ()(1cos )T R θθ=- 33(38)44pFR FR EI GI ππ-=+.。
《材料力学》第11章典型习题解析

第11章典型习题解析1.用卡氏第二定理求图12.3所示刚架A 截面的位移和B 截面的转角。
略去剪力Q 和轴力N 的影响,E Ⅰ为已知.解:(1)A 截面的位移AB 段弯矩:M(x)=-Px (0≤x ≤l ) ∂M(x) /∂P=-x在A 处虚加一水平力向右的力Q,之后,再令其为0.那么,BC 段弯矩:M(y)=-2P l - Q l +(P+Q)y∂M(y) /∂P=-2l +y ∂M(y) /∂ Q=-l +yA 截面的竖直位移:Y A ==∂∂∑⎰EI P Mdx ML 0 ()()()()⎰⎰+-+-+--L LEIdy y L Py PL EI dx x Px 00222 =EIPL 223A 截面的水平位移: X A =EI Q M M L ∂∂∑⎰0dx=()()EI dy y L Qy Py QL PL L 200+-++--⎰ 积分,令Q=0得 ()()EIPL EI dy y L Py PL XA L 1252230=+-+-=⎰(2)B 截面的转角在B 处虚加一力偶M B,AB 段弯矩:M(x)=-Px (0≤x<l )BC 段弯矩:M(y)=-2P l -B M +Py (0<y<l )∂M(x) /∂MB=0 ∂M(y) /∂MB =-1 ∑⎰∂∂=L B B EI dx M M M 0θ =()()⎰-+--L B EI dxPy M PL 0212 EIPL 432= 2.用卡氏第二定理求图示的A 截面的位移和B 截面的转角。
略去剪力Q 和轴力N 的影响,E Ⅰ为已知。
解:(1)A 截面的位移在A 点虚加一向下的力F ,支反力2qL F P Y B ++= (L 为AB 和AD 的长度) P X qL P Y C C -=--=,2AB 段弯矩: M1=0∂ M1 /∂F=0AD 段弯矩:M2(x)=2qL P F qx 2++⋅1()x-2∂M2(x) /∂F=xCD 段弯矩:M3(y)=PyaⅠⅠ2ⅠC DA 截面的竖直位移:∑⎰∂∂=L A EIdx F M M Y 0=⎰⋅⎥⎦⎤⎢⎣⎡-⋅⎪⎭⎫ ⎝⎛++L EI xdx qx x F qL P 02222 积分,令F=0得34A PL qL Y 6EI 24EI =+求A 截面的水平位移时, 在A 处虚加一水平力向右的力Q, 再令其为0.那么, 支反力B qL Y P Q 2=++ (L 为AB 和AD 的长度)C C qL Y P Q X P Q 2=-+=-+()+,() AB 段弯矩: M1=0∂ M1 /∂Q=0AD 段弯矩:M2(x)=(P+Q)x ⋅∂M2(x) /∂Q=xCD 段弯矩:M3(y)=(P+Q )y∂M3(y) /∂Q=yA 截面的水平位移∑⎰∂∂=L A EI dx Q M M X 0=()⎰⋅+L EIdx x Q P 022=()⎰⋅+L EI ydy y Q P 0积分,令Q=0得 EIPL X A 23= (2) B 截面的转角在B 处虚加一顺时针的力偶M B, 积分,并令其为零。
材料力学 第11章 能量法讲解

A
l FAy
B FBy
(1) 应变能计算
梁的约束力
FA
FB
Me l
梁的弯矩方程
代入应变能公式
M (x)
FA x M e
x Me(l
1)
Vε
M 2(x) dx
l 2EI
1 2EI
l 0
M
2 e
(
x l
1)2 dx
M e2l 6EI
15/65
11.1 外力功与应变能 【例11-1】解
10/65
11.1 外力功与应变能
11.1.3 克拉贝依隆原理
F1Δ12 F2 Δ21
W
1 2
F1 Δ11
1 2
F2 Δ22
F1 Δ12
上式可推广到有多个广义力共同作用于线性弹性体的情况 Vε W
Vε
W
1 2
Fi Δi
上式称为克拉贝依隆原理。
式中为全部外力(F1,F2,…,Fi,…,Fn)在广义力Fi处
l GI p
M xdq
2
w M EI
12/65
11.1 外力功与应变能
M(x)
T(x) FN(x) FN(x)
11.1.4 杆件的应变能
dq
T(x) M(x)
dj
dx
dx dd
dx
dx
dVε
FN2 (x)dx 2EA
T 2 (x)dx 2GIp
M 2 (x)dx 2EI
则整个圆截面杆的应变能 Vε
FN2 (x) dx l 2EA
材料力学课后习题答案11章

S z (η2 ) = 2.5 × 10 − 5 + (0.010η2 )(0.050 −
S z ,max (η 2 ) = 3.75 × 10 −5 m 3
η2
2
)
τ1 =
FSy S z , max (η1 ) 5 × 103 × 2.5 × 10 −5 N = = 3.75 × 106 Pa = 3.75MPa I zδ 3.333 × 10 − 6 × 0.010m 2 FSy S z , max (η2 ) I zδ 5 × 103 × 3.75 × 10 −5 N = = 5.63 × 106 Pa = 5.63MPa −6 2 3.333 × 10 × 0.010m
2 = 2.5 × 10 −5 + 2.5 × 10 −4 η 2 − 5 × 10 −3 η 2
τ 1, max =
FSy S z , max (η1 ) I zδ 1
=
5 × 103 × 1.25 × 10 −5 N = 3.00 ×106 Pa = 3.00MPa 2.08 × 10 − 6 × 0.010m 2
S z , A (ω ) =
δ
2 yA =
0.010 × 0.050 2 m 3 = 1.25 × 10 − 5 m 3 2
= 1.875 × 10 −4 m 3
据公式
τ (η ) =
得
FS S z (ω ) I zδ
40 × 10 3 × 1.25 × 10 −5 N τA = = 1.499 × 10 6 Pa = 1.499MPa −5 2 3.335 × 10 × 0.010m
[
]
11-6
试指出图示截面的剪心位置。
题 11-6 图 解: (a)双对称截面,剪心与形心重合; (b)角钢形截面,剪心在二边条中心线相交处; (c)T 形截面,剪心在翼缘中心线与腹板中心线相交处。
材料力学第十一章

解超静定梁的基本步骤如下。 (1)判断超静定次数,去掉多余约束,得到静定基。 (2)用未知的多余约束力代替去掉的多余约束加到静定基上(即得到相 当系统)。 (3)根据多余约束处的变形条件及其相应的物理条件建立补充方程,解 出多余未知约束力。 (4)由静定基的平衡条件求出其他约束力,画出内力图,并作强度或刚度 计算。
Fl2 M Al 0 16EI 3EI
所以
MA
3Fl 16
(
)
这里与按图 11-5(b)所示的静定基求得的结果相同(负号表明 MA 实际方 向与图上所设方向相反)。
多余约束力求出后,可对超静定梁进行强度或刚度计算。一般在静定基
上进行。如图
11-5(b)所示的悬臂梁,在
F
和
FB(
FB
5 16
图 11-5(a)所示的梁,也可选 MA 作为多余约束力,即去掉 A 处的 转角约束,使 A 处变成固定铰支座,其静定基将变成简支梁 AB ,如图 116(a)所示,上面作用有载荷 F 和多余约束力矩 MA 。
(a)
(b) (c)
图11-6
A 处的变形协调条件可由叠加法写出,可得
θAF θAM A 0 式中, θAF 和 θAM A 分别为 F 和 MA 单独作用时 A 处的转角,如图 11-6(b)、(c) 所示。再由物理条件,代入式(a),得补充方程为
材料力学
第十一章 超静定系统
一
超静定系统的概念
二 弯曲超静定问题
三
力法解超静定系统
四
对称及反对称性质的应用
五
连续梁及三弯矩方程
第一节 超静定系统的概念
在图 11-1(a)中,将被车削的工件简化成悬臂梁。当车削力 F 作用时, 固定端(卡盘)有三个未知约束力 FAx , FAy 和 MA ,如图 11-1(b)所示。独 立的静力平衡方程式也有三个,即
材料力学

§11-4 图形互乘法
在应用莫尔定理求位移时,需计算下列形式的积分: 在应用莫尔定理求位移时,需计算下列形式的积分:
M ( x) M 0 ( x) =∫ dx EI l
对于等直杆,EI=const,可以 对于等直杆, , 提到积分号外,故只需计算积分。 提到积分号外,故只需计算积分。 直杆的M 直杆的 0(x)图必定是直线或折 图必定是直线或折 线。
U
1
= U
′
1
f =
∫
M
L
( x )M 0 ( x )
EI
Z
dx
——计算挠度的莫尔定理 计算挠度的莫尔定理
5.推论:同样的道理,如果我们要求截面的转角,也只需在 推论:同样的道理,如果我们要求截面的转角, 推论 C截面上施加一个单位力偶,用上述同样的方法可求出: 截面上施加一个单位力偶, 截面上施加一个单位力偶 用上述同样的方法可求出:
1.能量法的概念 1.能量法的概念 2.杆件变形能的计算 杆件变形能的计算 3.莫尔定理 莫尔定理—— 一种具体的能量方法(本节课的中心内容) 一种具体的能量方法(本节课的中心内容) 莫尔定理
材料力学
基本概念: 三.基本概念: 基本概念
1. 功能原理 功能原理——W=U 物理意义: 物理意义:弹性体在变形的过程中,外力所做的功全部 转化为储存于弹性体内部的变形能。 2. 能量法 能量法——从能量的角度出发,利用功能原理来求解弹 性体变形的方法,即:
=U 能量 W → 变形
材料力学
目录
(1) 由于本课位于第二册之首,因此在学习之前对上册进 由于本课位于第二册之首, 行简单总结,同时,在总结过程中可自然地引出该章内容。 行简单总结,同时,在总结过程中可自然地引出该章内容。
工程力学-材料力学-第11章--动量定理

1
质点系内各质点动量的矢量和称为质点系的动量,即
n
p mivi i 1
(11-2)
式中的 为质点系内的质点数, 为质点系内第个 质点的质量, 为该质点的速度。
例11-1 三物块用绳相连如图11-1所示,其质量分别
为
,如绳的质量和变形忽略不计,且
pBD pB pD 2(m1 m2 )vA 2(m1 m2 )l
其方向同A点的速度方向一致,如图(b)所示。再将求得的动量 计算矢量和,可知系统的动量大小为
p
1 2
m1l
2(m1
m2 )l
1 2
(5m1
4m2
)l
方向同A点和E点的速度方向一致。
6
2.冲量
力对物体作用的运动效应不仅取决于力的大小和方向,而且 和该力所作用的时间有关,因此将力在一段时间间隔内的累积效 应称为力的冲量。
dt
Fx e
dpy
dt
Fy e
dpz
dt
Fz e
(11-12)
11
将(11-11)的两边同乘以 ,并在时间间隔 到 内积分, 可得
p2 p1
t2 t1
Fi e dt
I
e i
(11-13)
即质点系的动量在任一时间间隔内的变化,等于在同一时间间隔 内作用在该质点系衫所有外力的冲量的矢量和,这就是积分形式 的质点系动量定理,又称冲量定理。
内力的矢量和(内力系的主矢) 恒等于零,即
Fii 0
于是上式简化为
dp d
dt dt
mivi
Fie
(11-11)
即质点系的动量对时间的一阶导数等于作用在该质点系上 所有外力的矢量和(外力的主矢),这就是微分形式的质点系 动量定理。在具体计算时,常采用其投影式。如投影到直 角坐标轴上有
材料力学第11章能量方法

M ( x) M ( x) U P0 U P x) dx l EI
莫尔积分
其中:M(x):只在实际载荷作用下的弯矩方程 : )x ( M 只在在单位力作用下的弯矩方程
单独产生的变形
1 1 1 dU N ( x)d (l ) M ( x)d T ( x)d 2 2 2
N 2 ( x)dx M 2 ( x)dx T 2 ( x)dx U l l l 2GI 2EA 2EI P
计算变形能的方法:(1)求内力
例题
(2)利用公式
21
§11.4 互等定理
例:轴向拉压杆 外力作的功:
dw=P· d(Δl)
W P d (l )
0
l
4
W P d (l )
1 P l 2
在线弹性范围内
0
l
1 U W P l 2
当:
Pl l EA
2
N l U 2 EA
5 变形比能:
dU u dV 1 dU u d 0 dV
63 例:用能量法的方法求图示刚架B点水平位移。EI=常 数,略去轴力、剪力对变形的影响。 解: ⑴在真实载荷作用下 求支反力
R A RB
列内力方程:
m a
BC:
AC:
m M ( x1 ) x1 a
M ( x2 ) 0
64 ⑵B点加一水平单位力 求支反力 R A RB 3 2 列内力方程:
n
2 i i
变形比能
1 u 2 2.剪切:
变形比能
材料力学第十一章

F3
F2
3
' 3
V1 V2
Fδ Fδ Fδ Fδ
' 1 1 ' 2 2
4
' 4
1
26
功的互等定理 第一组力在第二组力引起的位移上所作的功,
等于第二组力在第一组力引起的位移上所作的功.
二、位移互等定理
若第一组力 F1,第二组力只有 F3,则
' F1δ1 F3δ'3
如果 F1= F3 ,则有
30
2、梁的应变能
任意截面的弯矩: M ( x ) M ( x )
变形能:
[ M ( x ) M ( x )] 2 V dx L 2 EI
W总 V
1 Fi i [ M ( x ) M ( x )] 1 fA dx l 2 2 2 EI i 1
n
2 Ni
当轴力或截面连续变化时:
7
应变能密度 : 单位体积的应变能. 记作
▼
1 FΔl 1 V 2 ζε V Al 2
ζ Eε
1 ζ Eε ζε 2 2E 2
2
2
(单位 J/m3)
8
2、扭转杆内的变形能
Me
Me
Me
l
2
2
1 1 M el M e l Tl V W M e Δ M e 2 2 GI p 2GI p 2GI p
25
若按先加 F3 ,F4 后加 F1 , F2 的次序加力,又可求得结构的
应变能为
1 1 1 1 V2 F1δ1 F2 δ2 F3 δ3 F4 δ4 F3 δ3' F4 δ4' 2 2 2 2
北航材料力学-第十一章1-能量法(一)

dW T ( x)d
2 T 2 ( x)dx
2GI t
dW M ( x)d
2 M 2 ( x)dx
2EI
Page16
MECHANICS OF MATERIALS
3、通过计算微体的应变能: 最一般的方法,适用于任意形状、任意受力的情况
三向应力状态下的应变能:
2 dz
1 dy
3
dx
dV
1 2
F2
22
F112
若F1=F2
F221 F112 功的互等定理
ij —— i 代表位置,j 代表载荷
21 12 位移互等定理
Page20
MECHANICS OF MATERIALS
➢ 有关位移互等定理的讨论:
在梁变形实验中的应用:
F
A
B
DA
F
B
D
其它情况:
F
A
B
C
A
F
B
C
只要克拉比隆定理成立
Md
W
0
Td
材料力学主要研究线弹性体
1、材料服从虎克定律 2、小变形 3、可按结构的原有几何尺寸来分析内力、
应力和位移
Page7
MECHANICS OF MATERIALS
➢ 克拉比隆定理:(线弹性体上作用有多个广义力的情况)
F1
A
B
1
D
W 2 F11
1
F1
F2
A
B
C
D
1
2
F1
A
B
D
11
F2
A
为B。试计算当在B截面作用力偶矩M时,截面C的挠 度。梁的弯曲刚度为EI。
材料力学答案第十一章

第十一章 能量方法第十一章答案11.1 图示桁架各杆的材料相同,截面面积相等。
试求在F 力作用下,桁架的变形能。
12,2N N F F F ==32N F F =222222()2222N F l l F x V dx EA EA EAε⎫⎛⎫⎪ ⎪⎝⎭⎝⎭==+⎰2234F l EA=.11.2计算图示各杆的应变能。
(a) 2223244F l F l F lV EA EA EAε=+=. (b) 2212/32/3120022e e l l M M x x l l V dx dx EI EIε⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭=+⎰⎰ /32/322221220023318l l e e M M l x x EIl EI⎛⎫⎛⎫⎛⎫ ⎪=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.11.3 传动轴受力情况如图所示。
轴的直径为40mm ,材料为45钢,E = 210GPa ,G = 80GPa 。
试计算轴的应变能。
由扭转引起的应变能:20.220800.0322pV dx GI ε==⎰由弯曲引起的应变能:20.210(531.4)20.0292x V dx EIε==⎰120.061J V V V εεε=+=.11.4 计算图示梁的应变能,并说明是否满足叠加原理及其原因。
2230()26lFl Fx F l V dx EI EIε-==⎰而22310()22lFl F lV dx EI EIε==⎰22320()26lFx F l V dx EI EIε-==⎰.不满足叠加原理,因为应变能与内力的关系不是线性的。
11.5在外伸梁的自由端作用力偶矩跨度中点C 的挠度w c 。
(见课本下册p40例12-4)11.6 图示刚架的各杆的EI 皆相等,试求截面A 、B 的位移和截面C 的转角。
(a) A 点:在A 点加一个向下的单位力。
M (x 1)=0, M (x 2)=Fx 2, M (x 3)=Fb11()M x x =,22()M x Fx =,3()0M x = 3330()()hM x M x Fabhdx EI EI∆==-⎰.C 点:在C 加一个逆时针的力偶矩为1的单位力偶。
材料力学11-1

U
N 2(x)dx
M
2 n
(
x)dx
M 2(x)dx
L 2EA
L 2GIP
L 2EI
L
S
Q2(x) 2EA
dx
S 剪切挠度因子
细长杆,剪力引起的变形能可忽略不计。
U
N 2(x)dx
M
2 n
(
x)dx
M 2(x)dx
L 2EA
L 2GIP
L 2EI
四、变形能的特点:
1.产生同一种基本变形的一组外力在杆内所产生的变形 能,不等于各力分别作用时产生的变形能之和。
L x1
O
x
①求内力 M AB ( x1) P(L x1) Px ( x x1)
f
M BC ( x1) P(L x1)
②将内力对Px 求偏导后,令Px=0
M AB ( x) Px
Px 0 x1x
M BC ( x) Px
Px 0 0
21
③变形( 注意:Px=0)
f ( x) U M ( x) M ( x) dx
38
2. 试求图示刚架截面A的转角和截面C的铅垂位移。EI为已知 常数。
39
3. 试求图示刚架C点两侧截面的相对转角。EI已知。
40
4. 由杆系及梁组成的混合结构如图所示。设FP、a、E、A、I均 为已知。试求C点的垂直位移。
41
5. 半圆形小曲率曲杆的A端固定,在自由端作用扭转力偶矩Me 。曲杆横截面为圆形,其直径为d。试求B端的扭转角。
U PA
L
M ( x) M ( x) dx EI PA
L Px2 dx
0 EI
PL3 3EI
()
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
若轴力FN沿杆件轴线为一变量FN(x),则应变能的一般表达式为
V
l
FN2
x
dx
2EA
(11-4)
第11章 能 量 法 若结构是由n根直杆组成的桁架,整个结构内的应变能为
V
n i 1
FN2 i li 2Ei Ai
(11-5)
式中FNi、li、Ei和Ai分别为桁架中第i根杆的轴力、长度、弹性 模量和横截面面积。
忽略剪力影响的情况下,由功能原理与克拉比隆定理可得,微
段dx的应变能为
dV
dW
FN xd
2
T xd
2
M xd
2
FN2xdx T 2xdx M 2xdx
2EA 2GIP
2EI
而整个杆或杆系结构的应变能为
V
l
FN2 x dx
2EA
l
T 2x
dx 2GI P
l
M 2x
dx 2EI
(11-9)
第11章 能 量 法
11.1.3 互等定理 当线性弹性体上作用几个外力时,外力所做之总功或弹性
体的应变能与外力的加载次序无关。据此,可以建立两个重要 的定理——
图11-6(a)、(b)所示为同一线性弹性体(以简支梁为例) 的两种受力变形状态。规定广义位移Δij表示作用在点j的载 荷Fj引起的点i沿Fi方向的位移。在第一种受力状态 (见图11-6(a))下,则点1、点2的位移分别为Δ11、Δ21; 在第二种受力状态(见图11-6 (b))下,则点1、点2的位 移分别为Δ12、Δ22。
上式只适用于圆截面杆。对于非圆截面等一般杆件,则有
V
l
FN2 x dx
2EA
l
T 2x
dx 2GIt
l
M
2 y
x
dx
2EIy
l
M
2 z
x
dx
2EIz
(11-10)
第11章 能 量 法
例11-1 图11-5所示悬臂梁,在自由端承受集中力F与
矩为Me的集中力偶作用。试计算外力所做之总功。设梁的抗弯 刚度EI为常数。
3.梁弯曲时的应变能 在一般情况下(见图11-3(a)),梁的弯矩和剪力均沿 轴线变化,因此,梁的应变能应从微段dx入手进行计算(见图 11-3(b))。 在弯矩M(x)作用下,微段两端横截面作相对转动(见图 11-3(c)),且
d dx M x dx
EI
第11章 能 量 法
在剪力FS(x)作用下,微段产生剪切变形(见图11-3(d))。 所以,横力弯曲时,弯矩仅在相应的弯曲变形上做功;剪力仅 在相应的剪切变形上做功。但是,对于细长梁,剪力所做的功 远小于弯矩所做的功,通常可忽略不计。所以,梁微段dx的应 变能为
解 对于线性弹性体,根据叠加原理,截面A的挠度与转
角分别为
wA
wAF
wAM e
Fl 3 3EI
M el 2 2EI
(↑)
A
F A
M A
e
Fl 2 2EI
M el EI
第11章 能 量 法 图11-5
第11章 能 量 法
根据式(11-3)可知,载荷F与Me所做之总功为
W FwA M e A F 2l 3 FM el 2 M e2l
2
2 6EI 2EI 2EI
讨论:若载荷F与Me分别单独作用在该悬臂梁时,他们所 做功的和为
WF
WMe
Fw
F A
2
M Me eA
2
F 2l3 6EI
M
Байду номын сангаас2 e
l
2EI
W
即载荷所做之总功不能利用叠加原理进行计算。因为在一般情
况下,各载荷所做之功并非仅与该载荷引起的位移有关,而且
与其他载荷在该点处引起的位移也有关。
W 1 F
(11-2)
2
式(11-2)是计算线性弹性体外力功的基本公式。应该指出,
式中的F为广义力,即或为集中力,或为集中力偶,或为一对大
小相等、方向相反的力或力偶等;式中的Δ则为相应的广义位
移,与集中力相应的位移为线位移,与集中力偶相应的位移为
角位移,与一对大小相等、方向相反的力相应的位移为相对线
dV
dW
M xd
2
M 2 xdx
2EI
而整个梁的变形能则为
Vε
M 2 x dx
l 2EI
(11-8)
第11章 能 量 法 图11-3
第11章 能 量 法 4. 组合变形时,圆截面杆微段受力的一般形式如图11-4(a)
所示。
图11-4
第11章 能 量 法
由于小变形的情况下各内力分量引起的应变互不耦合,在
第11章 能 量 法
第11章 能 量 法
11.1 外力功与应变能的一般表达式 11.2 变形体虚功原理 11.3 单位载荷法 11.4 冲击应力分析 11.5 构件加速运动时的动应力分析
第11章 能 量 法
11.1 外力功与应变能的一般表达式
11.1.1 外力功的计算 在外力作用下,弹性体发生变形,载荷作用点随之产生位
移。载荷作用点在载荷作用方向的位移分量,称为该载荷的相
对于由零缓慢增加到最终值的静载荷f,若其相应位移为 Δ(见图11-1(a)),则此力的功为
W 0 f d
(11-1)
第11章 能 量 法 如果材料服从胡克定律,而且构件或结构的变形很小,则
构件或结构的位移与载荷成正比(见图11-1 (b) ),此 时研究对象为线性弹性体,显然此时外力的功为
W n Fi i
i1 2
(11-3)
上述关系称为克拉比隆定理。
第11章 能 量 法
11.1.2 应变能的计算
根据功能原理,存储在构件内的应变能等于外力所做之功,
对于线性弹性体
V
W
n i 1
Fi i
2
1.轴向拉压时的应变能
在前面已经讨论过,当杆件处于轴向拉伸或压缩时,其应变能为
V
W
FN2l 2EA
位移,与一对大小相等、方向相反的集中力偶对应的相应位移
为相对角位移。总之,广义力在相应广义位移上做功。
第11章 能 量 法 图11-1
第11章 能 量 法
另外可以证明,当线性弹性体上同时作用几个载荷F1、 F2、…、Fn时,不论按何种方法加载,广义力在相应广义位移 Δ1、Δ2、…、Δn上所做之总功恒为
第11章 能 量 法
2.圆轴扭转时的应变能 圆轴受扭时(见图11-2),扭转角为
其应变能为
Tl
GI p
T T 2l
V
2
2GI p
(11-6)
若扭矩T沿轴线为一变量T(x),则应变能的一般表达式为
T 2x
V
l
dx 2GIP
(11-7)
第11章 能 量 法 图11-2
第11章 能 量 法
第11章 能 量 法 图11-6
第11章 能 量 法
考虑两种加载方式。一是先加F1、然后再加F2(见图11- 6 (c)),则外力所做总功为
W1
1 2
F111
1 2
F2 22
F112
