整数四则运算总结与练习

小学五年级四则运算法则,公式,题汇

四则运算法则汇编一、整数四则运算法则。

整数加法计算法则：1）要把相同数位对齐，再把相同计数单位上的数相加；2）哪一位满十就向前一位进。

整数减法计算法则：1）要把相同数位对齐，再把相同计数单位上的数相减；2）哪一位不够减就向前一位退一作十。

整数乘法计算法则：1）从右起，依次用第二个因数每位上的数去乘第一个因数，乘到哪一位，得数的末尾就和第二个因数的哪一位对个因数的哪一位对齐；2）然后把几次乘得的数加起来。

（整数末尾有0的乘法：可以先把0前面的数相乘，然后看各因数的末尾一共有几个0，就在乘得的数的末尾添写几个0。

）整数的除法计算法则1）从被除数的高位起，先看除数有几位，再用除数试除被除数的前几位，如果它比除数小，再试除多一位数；2）除到被除数的哪一位，就在那一位上面写上商；（如果哪一位不够商“1”，就在哪一位上商“0 ”。

）3）每次除后余下的数必须比除数小。

二、小数四则运算法则。

（一）小数加、减法的计算法则：1）计算小数加、减法，先把各数的小数点对齐（也就是把相同数位上的数对齐），2）再按照整数加、减法的法则进行计算，最后在得数里对齐横线上的小数点，点上小数点。

（得数的小数部分末尾有0，一般要把0去掉。

）（二）小数乘法法则：先按照整数乘法法则算出积，再看因数中一共有几位小数，就从积的右边向左数出几位，点上小数点。

例：23.5×1.3=30.5523.5×1.3———70 52 35———3 0.55（三）小数的除法运算法则。

（1）除数是整数的小数的除法除数是整数的小数除法，可按照以下步骤进行计算：①先按照整数除法的法则去除；②商的小数点要和被除数的小数点对齐；③除到被除数的末尾仍有余数时，就在余数后面添0，再继续除。

例1：117÷36=3. 25（2）除数是小数的小数除法除数是小数的小数除法，可按照以下步骤进行计算：①先把除数的小数点去掉使它变成整数；②看除数原来有几位小数，就把被除数小数点向右移动相同的几位（位数不够时补0占位）；③按照除数是整数的除法进行计算。

二、整数、小数四则混合运算和应用题

二、整数、小数四则混合运算和应用题教学要求：1、使学生掌握整数、小数四则混合运算顺序，认识中括号，能够比较熟练地计算整数、小数四则混合运算式题。

2、使学生掌握解答应用题的一般方法和步骤，会列综合算式解答两步和比较容易的三步计算的应用题，进一步提高学生解答应用题的能力。

3、使学生初步掌握两个物体运动中，速度、时间和路程的数量关系，会解答一些比较容易的行程应用题。

教学重、难点：重点：认识中括号，能够比较熟练地计算整数、小数四则混合运算式题，掌握应用题的解答方法。

难点：使学生初步掌握两个物体在运动中，速度、时间和路程的数量关系，会解答一些比较容易的行程应用题。

课时安排：（总29课时）1、整数、小数四则混合运算。

5课时2、应用题。

20课时整理和复习4课时1、整数、小数四则混合运算教学内容：进行四则混合运算的顺序总结，教学例1，例2。

完成相应的“做一做”及练习六的第1——2题。

教学目的：使学生进一步掌握整数、小数四则混合运算的运算顺序，能够正确地计算整数、小数四则混合运算顺序。

教学重点：使学生能够正确地计算整数、小数四则混合运算式题。

教具准备：复习用的卡片教学过程：一、复习：出示卡片，指名学生回答。

5.14+3.26-2.14 15.6-7.9-2.17.5×0.25×4 0.7÷0.35÷0.5完成以后，再让学生说一说小数四则运算的运算顺序。

二、导入新课：教师提问：我们以前学过哪些计算方法？（加、减、乘、除）教师：我们学过的加、减、乘、除运算，统称为四则运算。

今天我们就来总结一下整数和小数四则混合运算的顺序。

然后板书课题：整数、小数四则混合运算。

三、新授：1、教学例1。

出示例1：下面的算式里有哪些运算？运算的顺序怎样？13.7-2.5+4.6 3.6×6÷0.9提问：这两算式里各有哪些运算？学生回答，教师说明：在数学里，加、减法叫第一级运算，乘、除法叫第二级运算。

小学数学：整数四则运算法则

小学数学：整数四则运算法则
1、整数加法：
把两个数合并成一个数的运算叫做加法。

在加法里，相加的数叫做加数，加得的数叫做和。

加数是部分数，和是总数。

加数+加数=和一个加数=和－另一个加数
2、整数减法：
已知两个加数的和与其中的一个加数，求另一个加数的运算叫做减法。

在减法里，已知的和叫做被减数，已知的加数叫做减数，未知的加数叫做差。

被减数是总数，减数和差分别是部分数。

加法和减法互为逆运算。

3、整数乘法：
求几个相同加数的和的简便运算叫做乘法。

在乘法里，相同的加数和相同加数的个数都叫做因数。

相同加数的和叫做积。

在乘法里，0和任何数相乘都得0. 1和任何数相乘都的任何数。

一个因数×一个因数 =积一个因数=积÷另一个因数
4、整数除法：
已知两个因数的积与其中一个因数，求另一个因数的运算叫做除法。

在除法里，已知的积叫做被除数，已知的一个因数叫做除数，所求的因数叫做商。

乘法和除法互为逆运算。

在除法里，0不能做除数。

因为0和任何数相乘都得0，所以任何一个数除以0，均得不到一个确定的商。

被除数÷除数=商除数=被除数÷商被除数=商×除数
5、乘方:
求几个相同因数的积的运算叫做乘方。

小学数学第 1 页共1 页。

四年级数学上册《整数四则混合运算》整理与复习

四年级数学上册整数四则混合运算整理与复习【知识点拨】1.四则混合运算的顺序：①在没有括号的算式里，只有加法和减法，或者只有乘法和除法，要从左到右依次计算；既有加减法，又有乘除法，要先算乘除，后算加减。

②在有括号的算式里，要先算括号里面的，再算括号外面的。

改变算式的运算顺序，可以使用小括号。

2.四则混合运算方法一看、(看数字，运算符号，想想运算顺序是什么。

)二画、(画线，哪一步先算，就在哪一步的下面画一条横线，没有计算的要照抄下来。

)三算、(按照运算顺序计算)四检验、(检验运算顺序是否错误，计算是否算错。

)* 混合运算顺序歌通览全题定方案，细看是否能简便；明确顺序是关键，同级只要依次算；异级出现仔细看，先乘除来后加减；遇到括号别慌张，先小后大依次算；每算一步都检验，又对又快喜心间。

【解题技巧】解答式题技巧(一)“看”。

“看”，就是先看一看题目里有几个什么数。

会有几种运算符号;再看一看运算符号和数据有什么特点，有什么内在联系。

如405×(3076-2980)+2136÷89。

看的结果应是：①有5个数;②有4种运算;③含有小括号;④是一道带有小括号的整数四则混合运算题。

又如3.68×[1÷(2.1-2.09)]+0.6。

看的结果应是①含有5个数;②有4种运算;③含有中括号;④是一道带有中括号的小数四则混合式题。

这是小学数学的计算题的答题技巧之一。

(二)“定”。

“定”，就是对题目整体观察后，确定运算顺序。

即先算什么，再算什么，后算什么。

可采用画线标序的方法，如：405×(3076-2980)+2136÷89└──┬─┘①└─┬─┘└──┬──┘②②└──────┘③(三)“想”。

“想”，就是分析题中的数值特征和运算间的联系，联想到有关运算定律、运算性质，然后进行运算。

如：405×(3076-2980)+2136÷89。

这道题虽不存在简算问题，但括号部分与除法可同时计算，即同时算出3076-2980的差与2136÷89的商。

【沪教版五年制】四年级上册一课一练-整数的四则运算(含答案)

【沪教版五年制】四年级上册一课一练-整数的四则运算【题目】直接写出得数。

1055×2＋3= (1055×2)＋3= 52＋25＝1055×(2＋3)= 5×24＋3= 100+100×0=50+90÷(2×3)=(50+90)÷2×3=50+90÷2×3=(50+90÷2)×3=72÷9×48÷8=64÷64×7=【答案】2113、2113、775275、123、10065、210、185285、48、7【解析】准确计算【知识点】整数的四则运算【适用场合】练习题【难度系数】1【试题来源】【题目】把下面几个分步式改写成综合算式．（1）960÷15=64 64－28=36 综合算式_____________________________. （2）75×24=1800 9000－1800=7200 综合算式____________________________ （3）810-19=791 791×2=1582 1582+216=1798 综合算式___________________ （4）96×5=480 480+20=500 500÷4=125 综合算式____________________ 【答案】（1）960÷15－28=36；（2）9000－75×24=7200；（3）（810－19）×2+216=1798；（4）（96×5+20）÷4=125【解析】根据运算的先后顺序，确定算式。

【知识点】整数的四则运算【适用场合】练习题【难度系数】2【试题来源】【题目】判断(正确的括号中划“√”，错误的在括号中划“×”并改正)。

初一数学上册综合算式专项练习题整数四则运算

初一数学上册综合算式专项练习题整数四则运算整数是我们数学中的一个重要概念，它包含了正整数、负整数和零。

为了掌握整数的四则运算规则，我们需要进行大量的练习。

本文将围绕初一数学上册综合算式专项练习题展开讨论，通过详细解析来帮助大家更好地理解和掌握整数的四则运算。

一、加法运算整数加法的运算规则很简单，同号相加保留符号，异号相加取两数的差的符号。

下面我们通过实例来说明：1. 计算：7 + (-3)解析：由于两数符号不同，需要取两数的差的符号。

绝对值上，7比3大，所以结果的符号是正号。

所以，7 + (-3) = 4。

2. 计算：(-9) + 5解析：由于两数的符号不同，需要取两数的差的符号。

绝对值上，9比5大，所以结果的符号是负号。

所以，(-9) + 5 = -4。

通过这些实例，我们可以总结出整数加法的规律：同号相加，符号不变；异号相加，去绝对值较大数的符号。

二、减法运算整数减法的规则与加法类似，我们仍然通过实例来说明：1. 计算：(-8) - (-2)解析：减法可以转化为加法运算，即(-8) + 2。

由于两数的符号不同，需要取两数的差的符号。

绝对值上，8比2大，所以结果的符号是负号。

所以，(-8) - (-2) = -6。

2. 计算：3 - (-7)解析：减法可以转化为加法运算，即3 + 7。

由于两数符号不同，需要取两数的差的符号。

绝对值上，7比3大，所以结果的符号是正号。

所以，3 - (-7) = 10。

通过这些实例，我们可以总结出整数减法的规律：减法可以转化为加法，负号与减号相连变为加号。

三、乘法运算整数乘法的规则也要根据正负号的情况进行判断。

让我们来看几个例子：1. 计算：(-4) × 6解析：由于两数的符号不同，结果的符号是负号。

绝对值上，4乘以6等于24。

所以，(-4) × 6 = -24。

2. 计算：(-3) × (-5)解析：由于两数的符号相同，结果的符号是正号。

整数的加减乘除法(知识点+练习)

一、整数四则运算定律1、加法交换律：a b b a+=+2、加法结合律：()()++=++a b c a b c3、乘法交换律：a b b a⨯=⨯4、乘法结合律：()()⨯⨯=⨯⨯a b c a b c5、乘法分配律：()b c a b a c a+⨯=⨯+⨯⨯+=⨯+⨯；()a b c a b a c6、减法的性质：()--=-+a b c a b c7、除法的性质：()÷⨯=÷÷；a b c a b c8、除法的“左”分配律：()-÷=÷-÷，a b c a c b c+÷=÷+÷；()a b c a c b c这里尤其要注意，除法是没有“右”分配律的，即()÷+=÷+÷是不成立的！c a b c a c b注：上面的这些运算律，既可以从左到右顺着用，又可以从右到左逆着用。

二、加减法中的速算与巧算1、补数的定义：“补数”就是两个数相加，如果恰好凑成整十、整百、整千……，就把其中的一个数叫做另一个数的“补数”。

2、凑整法：a、分组凑整法：把几个互为“补数”的减数先加起来，再从被减数中减去，或先减去那些与被减数有相同尾数的减数。

b、加补凑整法：有些算式中直接凑整不明显，这时可“借数”或“拆数”凑整。

三、乘法凑整先把能凑成整十、整百、整千的几个乘数结合在一起，最后再与前面的数相乘，使得运算简便。

例如：425100⨯=⨯=，81251000⨯=，520100乘法交换律：a×b=b×a乘法结合律：(a×b) ×c=a×(b×c)乘法分配律：(a+b) ×c=a×c+b×c积不变规律：a×b=(a×c) ×(b÷c)=(a÷c) ×(b×c)四、乘、除法混合运算的性质1、商不变性质：被除数和除数乘（或除）以同一个非零数，其商不变．即：()()()()0a b a n b n a m b m m ÷=⨯÷⨯=÷÷÷≠ ，0n ≠2、在连除时，可以交换除数的位置，商不变．即：a b c a c b ÷÷=÷÷3、在乘、除混合运算中，被乘数、乘数或除数可以连同运算符号一起交换位置（即带着符号搬家）．a b c a c b b c a ⨯÷=÷⨯=÷⨯4、在乘、除混合运算中，去掉或添加括号的规则去括号：①括号前是“×”时，去括号后，括号内的乘、除符号不变．即()()a b c a b c a b c a b c ⨯⨯=⨯⨯⨯÷=⨯÷ ①括号前是“÷”时，去括号后，括号内的“×”变为“÷”，“÷”变为“×”．即()()a b c a b c a b c a b c ÷⨯=÷÷÷÷=÷⨯ 添括号：加括号时，括号前是“×”时，原符号不变；括号前是“÷”时，原符号“×”变为“÷”，“÷”变为“×”．()()()()a b c a b c a b c a b c a b c a b c a b c a b c ⨯⨯=⨯⨯⨯÷=⨯÷÷÷=÷⨯÷⨯=÷÷ ①两个数之积除以两个数之积，可以分别相除后再相乘．即()()()()()()a b c d a c b d a d b c ⨯÷⨯=÷⨯÷=÷⨯÷一、加法【例1】：278+463+22+37 732+580+268二、减法【例2】：2871-299 968-599举一反三：（1）157-99 （2）363-199三、连减（5种）【例3】：528－53－47 545－167－133举一反三：（1）489－134－76 （2）470－254－46【例4】：496－（296＋144）354－（154＋77）举一反三：（1）675－（175＋89）（2）466－（66＋125）【例5】：496－（144＋296）354－（77＋154）举一反三：（1）675－（89＋175）（2）466－（125＋66）【例6】：528－72－28 545－167－145举一反三：（1）489－77－389 （2）465－267－65【例7】：824－224－176－124 545－167－145举一反三：（1）643－164－133－243（2）487－187－139－61四、乘法分配律（8种）【例8】：计算：125×（80＋32）（24＋40）×25举一反三：（1）125×（64＋80）（2）（80＋32）×125（3）（16＋32）×25【例9】：125×（100－8）（125－40）×8举一反三：（1）125×（100－48）（2）（100－16）×25【例10】：（1）117×56＋117×44126×72＋126×12＋126×16举一反三：（1）269×26＋74×269 （2）521×65＋35×521【例11】：125×69－125×61 137×97－44×137－137×43举一反三：（1）25×127－25×119（2）365×251－365×151（3）156×59－156×27－156×22【例12】：45×102举一反三：（1）25×44 （2）125×168 （3）125×18【例13】：36×99举一反三：（1）45×98（2）125×92 （3）35×99【例14】：（1）81＋9×391 （2）9＋9×999 （3）99＋9×99【例15】：（1）9×107－63（2）6×108－48 （3）134×101－134五、连除（2种）【例16】：1250÷25÷5举一反三：（1）2000÷125÷8（2）1280÷16÷8 （3）1300÷5÷20（4）840÷5÷8（5）1700÷25÷4 （6）4800÷50÷2【例17】：630÷（63×5）举一反三：（1）780÷（78×2）（2）1250÷（125×5）（3）6300÷（63×5）。

小学奥数--整数四则混合运算练习（学生版）

1 奥数-------整数四则混合运算练习一、运算定律⑴加法交换律：a b b a +=+的等比数列求和⑵加法结合律：()()a b c a b c ++=++⑶乘法交换律：a b b a´=´⑷乘法结合律：()()a b c a b c ´´=´´⑸乘法分配律：()a b c a b a c ´+=´+´（反过来就是提取公因数）⑹减法的性质：()a b c a b c --=-+⑺除法的性质：()a b c a b c ¸´=¸¸()a b c a c b c +¸=¸+¸()a b c a c b c -¸=¸-¸上面的这些运算律，既可以从左到右顺着用，又可以从右到左逆着用．例1、计算：315325335345¸+¸+¸+¸．巩固练习计算：⑴36196419´+´⑵361964144´+´例2、计算：234432483305+-´+¸=。

例3、9000－9＝×9巩固练习900000－9＝________×99999。

例4、123(45)6+´¸+´=例5、23422640´+´=（）。

例6、20082006200720052007200620082005´+´-´-´巩固练习2000 × 1999－1999 × 1998 ＋1998 × 1997－1997 × 1996＋1996 × 1995－1995 × 1994 例7、求777777777777777777777+++++的和的万位数字是___________.例8、计算：11353715´-´【巩固】计算：99666667818´+´35207035´++´8019953990199522´-+´例9、计算：343535353434´-´． 345345788690105606´+´= 计算：123452345246938275´+´ 88225573444433´+´-´-´= ．3334343535363637´+´+´+´=【巩固】计算：64444222233335555´´+´的得数中有个数字是奇数。

四年级数学上册《整数四则混合运算》整理与复习

四年级数学上册《整数四则混合运算》整理与复习《四则混合运算》整理与复习【知识点拨】1.四则混合运算的顺序：①在没有括号的算式里，只有加法和减法，或者只有乘法和除法，要从左往右依次计算；既有加减法，又有乘除法，要先算乘除，后算加减。

②在有括号的算式里，要先算括号里面的，再算括号外面的。

改变算式的运算顺序，可以使用小括号。

2.四则混合运算方法一看、(看数字，运算符号，想想运算顺序是什么。

)二画、(画线，哪一步先算，就在哪一步的下面画一条横线，没有计算的要照抄下来。

) 三算、(按照运算顺序计算)四检验、(检验运算顺序是否错误，计算是否算错。

)* 混合运算顺序歌通览全题定方案，细看是否能简便；明确顺序是关键，同级只要依次算；异级出现仔细看，先乘除来后加减；遇到括号别慌张，先小后大依次算；每算一步都检验，又对又快喜心间。

【解题技巧】解答式题技巧(一)“看”。

“看”，就是先看一看题目里有几个什么数。

会有几种运算符号;再看一看运算符号和数据有什么特点，有什么内在联系。

如405×(3076-2980)+2136÷89。

看的结果应是：①有5个数;②有4种运算;③含有小括号;④是一道带有小括号的整数四则混合运算题。

又如3.68×[1÷(2.1-2.09)]+0.6。

看的结果应是①含有5个数;②有4种运算;③含有中括号;④是一道带有中括号的小数四则混合式题。

这是小学数学的计算题的答题技巧之一。

(二)“定”。

“定”，就是对题目整体观察后，确定运算顺序。

即先算什么，再算什么，后算什么。

可采用画线标序的方法，如：405×(3076-2980)+2136÷89└──┬─┘①└─┬─┘└──┬──┘└──────┘③(三)“想”。

“想”，就是分析题中的数值特征和运算间的联系，联想到有关运算定律、运算性质，然后进行运算。

如：405×(3076-2980)+2136÷89。

整数混合运算

整数四则混合运算一、加减混合运算加法交换律：两个数相加，交换加数的位置，他们的和不变。

即：a ＋b ＝b ＋a加法结合律：三个数相加，先把前两个数相加，再加上第三个数；或者先把后两个数相加，再与第一个数相加，他们的和不变。

即：a ＋b ＋c ＝〔a ＋b 〕＋c ＝a ＋〔b ＋c 〕a －b －c ＝a －c －b ，a －b ＋c ＝a ＋c －b ，例1、计算〔1〕368764++〔2〕99136101++〔3〕136197263928+++ 〔4〕93+48+47+12+24+57+16 〔5〕273+826+37+453+344+81练习1. 计算57911131517192123+++++++++= ．2. 42734750623368++++++3. 427347230506368321474++++++在加减法混合运算中，去括号时：如果括号前面是“＋”号，那么去掉括号后，括号内的数的运算符号不变； a ＋〔b －c 〕＝a ＋b －c如果括号前面是“－”号，那么去掉括号后，括号内的数的运算符号“＋”变为“－”，“－”变为“＋”．a －〔b ＋c 〕＝a －b －ca －〔b －c 〕＝a －b ＋c例2、（1）〔1350＋249＋468〕＋〔251＋332＋1650〕〔2〕 433845556257+++++（）（）〔3〕 1350496851321650+++++（）（）(4) 832一(454+332)+654；(5) 1 928一(267—72)一33；〔6〕 2187一(1432—3113)；(7) 30000一(1596+10000)；〔8〕(135799)(24698)++++⋅⋅⋅+-+++⋅⋅⋅+〔9〕〔2＋4＋6＋……＋2006〕－〔1＋3＋5+7+……2005〕＝〔10〕(20001)(19992)(19983)(1002999)(10011000)-+-+-+⋅⋅⋅+-+-练习1. 计算：(1) 196一(96+75)；(2) 753一(743—60)．〔3〕计算：162—〔162—135〕—〔35—19〕；〔4〕计算：163—〔50—18〕—〔153—76〕+〔124—18〕。

初中整数四则混合运算练习精选

初中整数四则混合运算练习精选1. 加减乘除练
问题一：
求解: 20 - 5 × 3 + 10 ÷ 5。

将乘法和除法先进行运算：20 - 15 + 2。

然后进行加法和减法运算：20 - 15 + 2 = 7。

问题二：
求解: 3 × (4 + 2) ÷ 2 - 5。

将括号里的加法先进行运算：3 × 6 ÷ 2 - 5。

然后进行乘法和除法运算：18 ÷ 2 - 5。

最后进行减法运算：9 - 5 = 4。

2. 混合运算练
问题一：
求解: (20 - 3) × 2 + 10 ÷ 5。

将括号里的减法先进行运算：17 × 2 + 10 ÷ 5。

然后进行乘法和除法运算：34 + 2。

最后进行加法运算：36。

问题二：
求解: 4 + (6 - 2) × 3 ÷ 2。

将括号里的减法先进行运算：4 + 4 × 3 ÷ 2。

然后进行乘法和除法运算：4 + 12 ÷ 2。

最后进行加法运算：4 + 6 = 10。

这些练习可以帮助学生熟练掌握整数的四则混合运算，提高他们的计算能力和思维能力。

每个问题都需要按照运算法则依次进行
运算，注意运算的优先级和顺序。

通过大量的练习，学生们能够更加熟练地运用整数的四则混合运算解决实际问题。

整数分数小数四则运算的速算与巧算(小升初)

第1讲整数、小数四则运算的速算与巧算1、四则运算基础知识一、解题的四大步骤：看陷阱、找相似、定技巧、查错误1、看陷阱：减法、除法、括号中陷阱最多。

计算次序（优先级）、去（添）括号（负号变号，有乘积因数要遍乘）。

2、看相似：发现数据特点，找到相似的数据，确定解题技巧。

3、定技巧：活用公式、提公因数、组合配对、拆解凑整、裂项消项。

（1）)11(1)(1k n n k k n n +-=+ （2）nm n m n m 11+=⨯+ 4、查错误：每一步都要检查一下，上下比对、检查，有没有明显错误。

二、四则运算的常见问题1、计算错误。

书写不规范；数字次序错误；加法或乘法计算错误，约分未完；对位、进位、借位时错误。

2、错用公式。

，加法或乘法的交换律、结合律、分配律不熟悉，出现乱用、错用引起错误。

3、观察不周。

计算时没有找到简便、合理的方法导致计算过程复杂，出现错误。

4、去括号、计算次序错误。

括号前有负号，打开后没变号；添括号，前面有负号没有变号；括号前有乘积因数，没有将乘积因数乘以所有项；漏写某些项；漏写括号，导致计算次序错误。

在减法、除法和乘除与加减的混合题中。

优先级从高到低：括号（小、中、大）、乘方、乘除、加减。

同级时按次序。

三、注意事项：1、有一定规律且运算的项多时，必有简便方法。

2、尽可能化小数为分数。

3、小数和分数混合，先看小数和分数的分母能否先约分。

4、数序复杂的可先不计算，以便后面统一消项或约分。

5、有多个乘除项时，把分母或分子放在一起，并分别放在分数线的上边和下边，避免约分未完或出现遗漏。

6、带分数乘法时，有时可不通分或化为假分数，直接将带分数表示为整数+分数，用乘法分配律计算。

7、注意题目有意设置的简便运算的陷阱。

如3.46 + 5.64，很多人很容易得到10或9的结论。

8、计算结果应是不可再约分的真分数、带分数，小数或不能化为小数的假分数。

9、计算题要求过程，有过程得分，而填空只要结果。

整数混合运算

整数四则混合运算一、加减混合运算加法交换律：两个数相加，交换加数的位置，他们的和不变。

即：a ＋b ＝b ＋a加法结合律：三个数相加，先把前两个数相加，再加上第三个数；或者先把后两个数相加，再与第一个数相加，他们的和不变。

即：a ＋b ＋c ＝（a ＋b ）＋c ＝a ＋（b ＋c ）a －b －c ＝a －c －b ，a －b ＋c ＝a ＋c －b ，例1、计算（1）368764++ （2）99136101++（3）136197263928+++（4）93+48+47+12+24+57+16 （5）273+826+37+453+344+81 练习1. 计算57911131517192123+++++++++= ．2. 42734750623368++++++3. 427347230506368321474++++++在加减法混合运算中，去括号时：如果括号前面是“＋”号，那么去掉括号后，括号内的数的运算符号不变； a ＋（b －c ）＝a ＋b －c如果括号前面是“－”号，那么去掉括号后，括号内的数的运算符号“＋”变为“－”，“－”变为“＋”．a －（b ＋c ）＝a －b －ca －（b －c ）＝a －b ＋c例2、（1）（1350＋249＋468）＋（251＋332＋1650）（2） 433845556257+++++（）（）（3） 1350496851321650+++++（）（）(4) 832一(454+332)+654；(5) 1 928一(267—72)一33；（6） 2187一(1432—3113)；(7) 30000一(1596+10000)；（8）(135799)(24698)++++⋅⋅⋅+-+++⋅⋅⋅+（9）（2＋4＋6＋……＋2006）－（1＋3＋5+7+……2005）＝（10）(20001)(19992)(19983)(1002999)(10011000)-+-+-+⋅⋅⋅+-+-练习1.计算：(1) 196一(96+75)；(2) 753一(743—60)．（3）计算：162—（162—135）—（35—19）；（4）计算：163—（50—18）—（153—76）+（124—18）。

四年级下册数学试题-四则运算(含答案)人教版

四则运算一、知识点归纳1.加、减、乘、除四种运算统称四则运算．2.加法的意义：把两个（或几个）数合并成一个数的运算叫做加法．3. 减法的意义：已知两个加数的和与其中的一个加数求另一个加数的运算叫做减法．减法中，已知的两个加数的和叫做被减数，其中一个加数叫做减数，求出的另一个加数叫差．4. 乘法的意义：一个数乘以整数，是求几个相同加数的和的简便运算，或是求这个数的几倍是多少．5.除法的意义：已知两个因数的积与其中一个因数求另一个因数的运算叫做除法．在除法中，已知的两个因数的积叫做被除数，其中一个因数叫做除数，求出的另一个因数叫商．二、四则运算各部分之间的关系1.加数+加数=和；和- 一个加数=另一个加数；和-另一个加数=一个加数；2.被减数-减数=差；被减数-差=减数；减数+差=被减数；3.因数×因数=积；积÷一个因数=另一个因数；4.被除数÷除数=商；被除数÷商=除数；被除数=除数×商；被除数=除数×商+余数（余数不为0）；5.除法是乘法的逆运算；6.四则运算分为二级，加减法叫做第一级运算，乘除法叫做第二级运算．三、四则混合运算顺序1、在没有括号的算式里，如果只有加、减法或者只有乘、除法，都要从左往右按顺序计算。

2、在没有括号的算式里，有乘、除法和加、减法、要先算乘除法，再算加减法。

3、算式有括号，要先算括号里面的，再算括号外面的；括号里面的算式计算顺序遵循以上的计算顺序。

四、注意事项1、0的运算“0”不能做除数；字母表示：a÷0错误一个数加上0还得原数；字母表示：a＋0= a一个数减去0还得原数；字母表示：a－0= a被减数等于减数，差是0；字母表示：a－a = 0一个数和0相乘，仍得0；字母表示：a×0= 00除以任何非0的数，还得0；字母表示：0÷a（a≠0）= 02、“除”与“除以”的区别。

36÷6可以读作：36除以6，也可以读作：6除36；总结：a除以b，即a÷b; 也可以读作：b除a，即a÷b。

苏教版小学数学四年级上册第七单元《整数四则混合运算》练习试题共三套

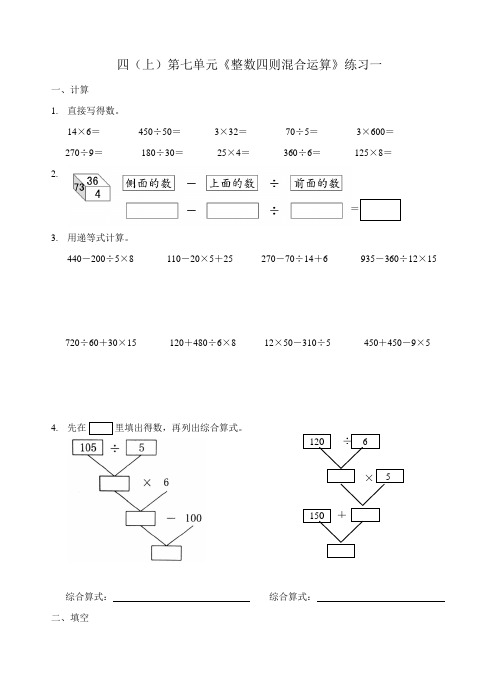
四（上）第七单元《整数四则混合运算》练习一一、计算 1. 直接写得数。

14×6＝ 450÷50＝ 3×32＝ 70÷5＝ 3×600＝ 270÷9＝ 180÷30＝ 25×4＝ 360÷6＝ 125×8＝ 2.3. 用递等式计算。

440－200÷5×8 110－20×5＋25 270－70÷14＋6 935－360÷12×15720÷60＋30×15 120＋480÷6×8 12×50－310÷5 450＋450－9×54. 先在综合算式：综合算式：二、填空150 ＋1.在没有括号的算式里，有乘、除法和加、减法，要先算（）法，后算（）法。

2.把下面每组算式合并成一道综合算式。

240÷6＝40，2×17＝34，40－34＝6. 综合算式：36÷3＝12，51－12＝39，39＋25＝64. 综合算式：3.28＋132×4÷6的运算顺序是：先算（）法，再算（）法，最后算（）法，结果是（）。

4.34＋147÷7－10的运算顺序是：先算（）法，再算（）法，最后算（）法，结果是（）。

5.6本《新华字典》摞在一起高168毫米，15本这样的字典摞在一起的高度是（）毫米；（）本这样的字典摞在一起的高度是504毫米。

6.学校栽了一些盆花，如果每个教室放3盆，可以放24个教室。

如果每个教室放4盆，可以放（）个教室。

7.小东在计算□－40÷4时，先算减法，后算除法，得到的结果是5，那么正确的结果应该是（）。

8.根据下面的算式在横线上补上问题。

甲、乙两城相距630千米，一列火车以平均每小时90千米的速度从甲城开往乙城，已经行驶了5小时，？算式：630÷90－5三、选择1.下列算式计算正确的是（）.A. 44＋26÷2－25B. 186－5×16－80C. 780－78×10÷780＝70÷2－25 ＝186－80－80 ＝780－780÷780＝35－25 ＝186－0 ＝780－1＝10 ＝186 ＝7792.15×2÷15×2的结果是（）.A. 1B. 4C. 2253.计算82×3－95＋5时，最后一步算（）.A. 加法B. 减法C. 乘法1. 兵兵家有3口人，原来居住面积是75平方米，搬入新居后，居住面积是120平方米。

数的运算知识点+例题+提高习题

数的运算知识要点1、四则运算的意义和法则12、四则运算的法则（1）加、减法整数、小数加减法：相同数位上的数对齐（小数点对齐），从低位算起，哪一位上的数相加满十（哪一位上的数不够减），向前一位进一（从前一位退一，当十再减）。

分数加减法：同分母分数相加减，用分子相加减，分母不变；异分母分数相加减，先通分，然后按照同分母分数加减法则进行计算。

（2）乘法整数乘法：先用一个因数每一位上的数分别去乘另一个因数。

用因数哪一位上的数去乘，乘得的数的末尾就要和哪一位对齐，再把几次乘得的数加起来。

小数乘法：先按照整数乘法的法则计算出积，再看因数中一共有几位小数，就从积的右边起数出几位点上小数点。

分数乘法：用分子相乘的积作分子，分母相乘的积作分母，计算过程中能约分的先要约分。

（3）除法整数除法：除数有几位，就看被除数的前几位，不够除就多看一位，除到被除数的哪一位，商就写在哪一位数上面，每次除后余下的数必须比除数小。

小数除法：先移动除数的小数点，使它变成整数；除数的小数点向右移动几位，被除数的小数点也要向右移动几位（位数不够时，在被除数的末尾用“0”补足），然后按照除数是整数的除法进行计算。

分数除法：甲数除以乙数（0除外），等于甲数乘乙数的倒数。

（4）各部分之间的关系①加、减法加数＋加数=和一个加数=和-另一个加数减数=被减数-差减数－减数=差被减数=差+减数②乘、除法因数×因数=积一个因数=积÷另一个因数被除数=商×除数被除数÷除数=商除数=被除数÷商23、四则混合运算1、四则混合运算的顺序在没有括号的算式里，如果只含有同一级运算，要按照从左到右的顺序计算；如果含有两级运算，要先算第二级运算，再算第一级运算。

在有括号的算式里，要先算小括号里面的，再算中括号里面的。

2、几种常用的简算方法（1）拆项法：这是对分配律的逆向运用，常用的方法是分数拆项，主要有以下几种形式：①分子、分母分别为两个相邻自然数的和与积时： n+(n+1)nx(n+1) =1n +1n+1②分母为两个相邻自然数的积时：1n(n+1) =1n -1n+1③分母是差为a(a ≠0)的两个自然数的积时：1n(n+a) =(1n -1n+a )×1a④分母为三个相邻自然数的积时：1n(n+1)(n+2) =12 【1n(n+1) -1(n+1)(n+2)】（2）数字变形法：这是一种从数字特点出发，创新变形，巧妙地运用运算性质，规律达到简算目的的方法，如：19971998 较接近1，可将其转化为（1-11998），然后根据情况运用适当的方法。

小学数学四则混合运算知识总结(附练习)

知识点一：四则运算的概念和运算顺序1、加法、减法、乘法和除法统称四则运算。

2、在没有括号的算式里，如果只有加、减法或者只有乘、除法，都要从左往右按顺序计算。

3、在没有括号的算式里，既有乘、除法又有加、减法的，要先算乘除法，再算加减法。

4、算式有括号，要先算括号里面的，再算括号外面的；大、中、小括号的计算顺序为小→中→大。

括号里面的计算顺序遵循以上1、2、3条的计算顺序。

知识点二：0的运算1、0不能做除数；字母表示：无，a÷0是错误的表达2、一个数加上0还得原数；字母表示：a＋0 = a3、一个数减去0还得原数；字母表示：a－0 = a4、一个数减去它本身，差是0；字母表示：a－a =05、一个数和0相乘，仍得0；字母表示：a×0 =06、0除以任何非0的数，还得0；字母表示：0÷a =0(a≠0)知识点三：运算定律1、加法交换律：在两个数的加法运算中，交换两个加数的位置，和不变。

字母表示：a＋b＝b＋a2、加法结合律：三个数相加，先把前两个数相加，再加另一个加数；或者先把后两个数相加，再加另一个加数,和不变。

字母表示：(a＋b)＋c＝a＋(b＋c)3、乘法交换律：两个数相乘的乘法运算中，交换两个乘数的位置，积不变。

字母表示：a×b＝b×a4、乘法结合律：三个数相乘，先把前两个数相乘，或先把后两个数相乘，积不变。

字母表示：(a×b)×c＝a×(b×c)5、乘法分配律：两个数相加(或相减)再乘另一个数,等于把这个数分别同两个加数（减数）相乘,再把两个积相加（相减）,得数不变。

字母表示：①(a＋b)×c＝a×c＋b×c；a×c＋b×c＝(a＋b)×c；②a×(b—c)＝a×b—a×c；a×b—a×c＝a×(b—c)6、连减定律：①一个数连续减两个数, 等于这个数减后两个数的和，得数不变；字母表示：a—b—c＝a—(b＋c)；a—(b＋c)＝a—b—c；②在三个数的加减法运算中，交换后两个数的位置，得数不变。

初中数学《整数四则混合运算综合》讲义及练习

本讲主要是通过一些速算技巧，培养学生的数感，并通过一些大数运算转化为简单运算，让学生感受学习的成就感，进而激发学生的学习兴趣一、运算定律 ⑴加法交换律：a b b a +=+的等比数列求和⑵加法结合律：()()a b c a b c ++=++⑶乘法交换律：a b b a ⨯=⨯⑷乘法结合律：()()a b c a b c ⨯⨯=⨯⨯⑸乘法分配律：()a b c a b a c ⨯+=⨯+⨯（反过来就是提取公因数）⑹减法的性质：()a b c a b c --=-+⑺除法的性质：()a b c a b c ÷⨯=÷÷()a b c a c b c +÷=÷+÷()a b c a c b c -÷=÷-÷上面的这些运算律，既可以从左到右顺着用，又可以从右到左逆着用．二、要注意添括号或者去括号对运算符号的影响⑴在“+”号后面添括号或者去括号，括号内的“+”、“-”号都不变；⑵在“-”号后面添括号或者去括号，括号内的“+”、“-”号都改变，其中“+”号变成“-”号，“-”号变成“+”号；⑶在“⨯”号后面添括号或者去括号，括号内的“⨯”、“÷”号都不变，但此时括号内不能有加减运算，只能有乘除运算；⑷在“÷”号后面添括号或者去括号，括号内的“⨯”、“÷”号都改变，其中“⨯”号变成“÷”号，“÷”号变成“⨯”号，但此时括号内不能有加减运算，只能有乘除运算．【例 1】计算：315325335345÷+÷+÷+÷．【考点】四则混合运算之提取公因数【难度】1星【题型】计算【关键词】第二届，希望杯，四年级，第二试【解析】原式313233345=+++÷（） 130526=÷= 【答案】26【巩固】计算：⑴ 36196419⨯+⨯⑵ 361964144⨯+⨯【考点】四则混合运算之提取公因数【难度】2星【题型】计算【解析】 ⑴原式3664191900=+⨯=（）例题精讲知识点拨教学目标整数四则混合运算⑵原式36196419125=⨯+⨯+（）36641964125190088125190080009900=+⨯+⨯=+⨯⨯=+=（）【答案】⑴1900 ⑵9900【例 2】计算：。

整数的四则运算练习题

整数的四则运算练习题整数的四则运算练一：1.计算下面各题：a) 630 ÷ (21 - 12) × 16b) (420 - 42 × 7) ÷ 65c) 30 + 54 × 4 ÷ 8d) 186 - 900 ÷ (100 - 95)e) (630 ÷ 9 - 23) × 25f) 168 - 48 × 16 ÷ 82.解决问题：a) 果园里的苹果树和桃树共有840棵，其中苹果树有15行，每行24棵。

如果桃树有8行，平均每行多少棵？b) XXX用3小时加工了105个零件。

照这样计算，XXX 再工作5小时一共可以加工多少个零件？c) 一把椅子售价55元，一张桌子的售价比椅子的2倍还多30元。

买一套这样的桌椅需要多少元？d) 一把椅子售价55元，一张沙发的售价比椅子的7倍还多5元。

一把椅子的售价比一张沙发便宜多少元？e) 一条裤子108元，一件上衣比裤子贵67元，买3套这样的衣服需要多少元？f) 给一个房间的地面贴地砖。

如果用长3米，宽2米的长方形地砖，160块正好贴满。

如果改用边长是4米的正方形地砖，需要多少块？练二：1.a) 1120 - (280 - 96 ÷ 8)b) (42 + 38) ÷ (473 - 468)c) 100 × [(48 - 15) ÷ 5]d) [(125 - 25 × 5) + 35] × 60e) 200 ÷ 10 + 120 × 11f) 516 - (320 + 320 ÷ 5)g) 2500 - 791 ÷ 7 × 82.a) “希望小学”三年级捐152本书，四年级捐的是三年级的2倍少12本，五年级捐的是三、四年级总和的2倍少12本，五年级捐书多少本？b) 公园里有菊花100盆，比月季花少35盆，郁金香是菊花和月季花总数的3倍还多15盆。

整数四则运算总结与练习

小学五年级四则运算法则,公式,题汇

二、整数、小数四则混合运算和应用题

小学数学：整数四则运算法则

四年级数学上册《整数四则混合运算》整理与复习

【沪教版五年制】四年级上册一课一练-整数的四则运算(含答案)

初一数学上册综合算式专项练习题整数四则运算

整数的加减乘除法(知识点+练习)

小学奥数--整数四则混合运算练习（学生版）

四年级数学上册《整数四则混合运算》整理与复习

整数混合运算

初中整数四则混合运算练习精选

整数分数小数 四则运算的速算与巧算(小升初)

整数混合运算

四年级下册数学试题-四则运算(含答案)人教版

苏教版小学数学四年级上册第七单元《整数四则混合运算》练习试题共三套

数的运算知识点+例题+提高习题

小学数学四则混合运算知识总结(附练习)

初中数学《整数四则混合运算综合》讲义及练习

整数的四则运算练习题

整数分数小数四则运算的速算与巧算(小升初)