2019-2020年初三第一学期期末考试及答案
人教版2019--2020学年度第一学期九年级数学上册期末考试题及答案

人教版2019—2020学年度第一学期九年级数学期末试卷及答案(满分:120分 答题时间:120分钟)一、选择题:(本大题共10个小题,每小题3分,共30分)在每小题给出的四个选项中,只有一项是符合题目要求的,请将其序号在题后括号内. 1. 在平面直角坐标系中,点A )7,6(-关于原点对称的点的坐标为( ) A.)7,6(-- B.)7,6( C.)7,6(- D.)7,6(- 2. 一元二次方程02=x 的根的情况是( ) A.有两个相等的实数根 B.有两个不相等的实数根 C.只有一个实数根 D.没有实数根 3. 已知抛物线82++=bx ax y 经过点)2,3(,则代数式83++b a 的值为( ) A.6 B.6- C.10 D.10- 4. 如图,在半径为5的⊙O 中,AB,CD 是互相垂直的两条弦,垂足为P,若AB=CD=4,则OP 的长为( ) A.1 B.2 C.2 D.225. 若双曲线xk y 1-=位于第二、四象限,则k 的取值范围是( )A.1<kB.1≥kC.1>kD.1≠k6. 从6,722,,0,2π这五个数中随机抽取一个数,抽到有理数的概率是( )A.51B.52C.53D.54 7. 如图,在△ABC 中,DE ∥BC,分别交AB,AC 于点D,E.若AD=1,DB=2,则△ADE 的面积与△ABC 的面积的比等于( )A.21B.41C.81D.918.在平面直角坐标系中,二次函数)0()(2≠-=a h x a y 的图象可能是( )A. B. C. D.9.如图,AB 是⊙O 的直径,点E 为BC 的中点,AB=4,∠BED=120°,则图中阴影部分的面积之和是( ) A.3 B.32 C.23D.1 10. 如图,已知△ABC,任取一点O,连接AO,BO,CO,并取它们的中点D,E,F,得△DEF,则下列说法正确的个数是( ) ①△ABC 与△DEF 是位似图形; ②△ABC 与△DEF 是相似图形; ③△ABC 与△DEF 的周长比为1:2;④若△ABC 的面积为4,则△DEF 的面积为1. A.个1 B.个2 C.个3 D.个4 二、填空题:(本大题共6个小题,每小题3分,共18分) 11. 都相同,如果摸到红球的概率是41,那么口袋中有白球__________个.12. 在一个不透明的口袋中,装有4个红球和若干个白球,这些球除颜色外其余用配方法把二次函数1322+-=x x y 写成k h x a y +-=2)(的形式为_____________.13. 关于x 的一元二次方程0)9()3(22=-++-m x x m 的一个根是0,则m 的值是______.14.如图,已知点O 是△ABC 的内切圆的圆心.若∠BAC=58°,则∠BOC=__________. 15.如图所示,点A 在双曲线x ky =上,点A的坐标为)3,31(,点B 在双曲线x y 3=上,且AB ∥x 轴,C,D 在x 轴上,若四边形ABCD 为矩形,则它的面积是_______. 16. 如图,在△ABC 中,∠ACB=90°,BC=16cm,AC=12cm,点P 从点B 出发,以2cm/秒的速度向点C 移动,同时点Q 从点C 出发,以1cm/秒的速度向点A 移动,设运动时间为t 秒,当t =__________秒时,△CPQ 与△ABC 相似. 三、解答题:(本大题共9个小题,共72分)解答应写出文字说明、证明过程或演算步骤.17. (本小题满分6分)某服装店现有A,B,C 三种品牌的衣服和D,E 两种品牌的裤子,小明家现要从该服装店选购一种品牌的衣服与一种品牌的裤子.(1) 写出所有选购方案(利用树状图或列表法表示);(2) 如果(1)中各种选购方案被选中的可能性相同,那么A 品牌衣服被选中的概率是多少?18. 先化简,再求值:21)11(y xy y x y x +÷-++,其中25,25-=+=y x . 19. (本小题满分6分)(本小题满分8分)如图, 在△ABC 中,∠ABC=80°, ∠BAC=40°,AB 的垂直平分线分别与AC,AB 相交于点D,E,连接BD.求证:△ABC ∽△BDC.第19题图 第20题图 第21题图20. (本小题满分8分) 如图,已知A )2,(-n ,B )4,1(是一次函数b kx y +=的图象与反比例函数xm y =的图象的两个交点,直线AB 与y 轴交于点C.(1)求反比例函数和一次函数的解析式; (2)求△AOC 的面积.21. (本小题满分6分)如图,要设计一副宽20cm,长30cm 的图案,其中有一横一竖的彩条,横竖彩条的宽度之比为2:3.如果彩条所占面积是图案面积的19%,求横,竖彩条的宽度各为多少cm?22. (本小题满分8分)为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.莫小贝按照政策投资销售本市生产的一种品牌衬衫.已知这种品牌衬衫的成本价为每件120元,出厂价为每件165元,每月销售量y (件)与销售单价x (元)之间的关系近似满足一次函数:9003+-=x y .(1)莫小贝在开始创业的第1个月将销售单价定为180元,那么政府这个月为他承担的总差价是多少元?(2)设莫小贝获得的利润为w (元),当销售单价为多少元时,每月可获得最大利润?(3)物价部门规定,这种品牌衬衫的销售单价不得高于250元.如果莫小贝想要每月获得的利润不低于19500元,那么政府每个月为他承担的总差价最少为多少元?23. (本小题满分10分)如图,在Rt△ABC中,∠BAC=90°, BD是角平分线,以点D为圆心,DA为半径的⊙D与AC相交于点E.(1)求证:BC是⊙D的切线;(2)若AB=5,BC=13,求CE的长.24.(本小题满分10分)如图,已知:抛物线42-+=bxaxy与x轴交于A)0,1(-、B)0,4(两点,过点A的直线1-=kxy与该抛物线交于点C.点P是该抛物线上不与A,B 重合的动点,过点P作PD⊥x轴于D,交直线AC于点E.(1)求抛物线的解析式;(2)当PE=2DE时,求点P坐标;(3)是否存在点P使得△BEC为等腰三角形,若存在请直接写出点P的坐标,若不存在,请说明你的理由.25.(本小题满分10分)如图,在△ABC中,AB=AC=5,BC=6,点D是BC边上的动点(不与B,C重合),点E是AC上的某点并且满足∠ADE=∠C.(1)求证:△ABD∽△DCE;(2)若BD的长为x,请用含x的代数式表示AE的长;(3)当(2)中的AE最短时,求△ADE的面积. 2019-2020学年度上学期期末测试九年级数学试题参考答案一.选择题二.填空题11. 2312()48y x=-- 12. 3- 13. 12 14.119° 15. 2 16.1164524或(第16题只填一种情况并且对了的,给2分;若填了两种情况,但有一种错误的,给0分)三.解答题17. 解:(1)根据题意,可以画出如下树状图:.....…………………3分(2)由树状图可以看出,所有可能出现的情况共有6种,它们被选中的可能性相同,其中A品牌衣服被选中的情况有2种,所以......……………...............................................……4分3162)(==A P......................................................…………………6分18. 解:原式=)())((yxyyxyxyxyx+⋅-+++-……….........................…………………1分=yxxy-2………........................................................3分∵25,25-=+=yx∴1452)5()25)(25(22=-=-=-+=xy………....…..……4分42525)25()25(=+-+=--+=-yx……….............5分∴原式=21412=⨯………..................................6分裤子衣服EDD EEDCBA19. 解: (1)将B )4,1(代入xmy =得4=m ......................................……1分 ∴反比例函数的解析式为: xy 4=..............................……2分将A )2,(-n 代入上式得2-=n 将A )2,2(--,B )4,1(代入b kx y +=得⎩⎨⎧+=+-=-b k b k 422 解得⎩⎨⎧==22b k .....................................……3分∴一次函数的解析式为:22+=x y .............................……4分(2)在22+=x y 中当0=x 时,2=y 即点C 的坐标为)2,0(........……5分∴OC=2......................................................……6分∴22221||21=⨯⨯=⋅⋅=∆A AOC x OC S ...................……8分20.证明:∵DE 垂直平分AB∴DA=DB..…………..............................................……1分 ∴∠DBA =∠BAC =40º ..…………..........................……2分 ∴︒=︒-︒=∠-∠=∠404080DBA ABC DBC ..……...……5分 ∴BAC DBC ∠=∠..…………......................……6分又∵C C ∠=∠..…………...........................................……7分∴ABC ∆∽BDC ∆..…………..........................................……8分 21. 解:设横彩条的宽度为x 2cm,则竖彩条的宽度为x 3cm,那么………...............……1分 %)191(3020)330)(220(-⨯⨯=--x x ……..................…..……3分 解得:1=x 或19=x (不合题意,舍去)……….........................……4分∴33,22==x x ………....................……5分答:横,竖彩条的宽度分别为2cm 与3cm.…….........……6分 22. (1)在9003+-=x y 中,当180=x 时,360=y ……1分16200360)120165(=⨯-............................……2分 答:政府这个月为他承担的总差价是16200元................……3分(2)由题意得)9003)(120(+--=x x W ...............……4分108000126032-+-=x x24300)210(32+--=x∵03<-=a ,抛物线开口向下∴当210=x 时,W 有最大值24300.............……5分 即当销售单价为210元时,每月可获得最大利润. (3)当19500=W ,即19500)9003)(120(=+--x x 时解得170=x 或250=x ..........................……6分 ∵ 在9003+-=x y 中,y 随x 的增大而减小 即销售量随着销售单价的提高而减少∴当250=x 时,销售量最低,此时1509002503=+⨯-=y6750150)120165(=⨯-...................................……7分答:政府每个月为他承担的总差价最少为6750........................……8分元23.解: (1)证明:过点D 作DF ⊥BC 于F ∵∠BAC=90°∴DA分 又 ∵BD 是角平分线,DF ∴DA=DF,DA 是⊙D ∴BC 是⊙D (2)由(1)知BA,BC 均是⊙D 的切线 ∴BF=BA=5∴8513=-=-=BA BC CF 125132222=-=-=BA BC CA ...........................……7分 ∵ DF ⊥BC∴∠DFC=∠BAC=90°又∵∠C=∠C∴CFD ∆∽CAB ∆.........................……8分∴ABCA FD CF =即......................................……9分∴3202==FD AE ..............……10分24. 解:(1)将A )0,1(-,B )0,4(代入42-+=bx ax y 得⎩⎨⎧=-+=--0441604b a b a ..........................................…1分解得⎩⎨⎧-==31b a ...........................…2分所以抛物线的解析式为432--=x x y .......................…3分 (2)将A )0,1(-代入1-=kx y 得1-=k 即AC 所在直线为1--=x y设点P 坐标为)43,(2--m m m 则点E 坐标为)1,(--m m ..............…4分 ①当点P 在点E 的下方时32)43(122++-=-----=m m m m m PE 1)1(0+=---=m m DE当DE PE 2=,即)1(2322+=++-m m m 时 解得11-==m m 或(不合题意舍去)此时点P 的坐标为)6,1(-.......................…5分 ②当点P 在点D 的上方时32)1()43(22--=-----=m m m m m PE 1)1(0+=---=m m DE当DE PE 2=,即)1(2322+=--m m m 时 解得15-==m m 或(不合题意舍去)此时点P 的坐标为)6,5(........................................…6分 综上所述当DE PE 2=时,点P 的坐标为)6,1(-或)6,5(................…7分(3)当BE BC =时,点P 坐标为)4,0(-;..........................…8分 当CE CB =时,点P 坐标为)2349,2346(±±;................…9分 当BE BC =时,点P 坐标为)36161,61(-.......................…10分25. (1)证明: ∵AB=AC ∴C B ∠=∠..............................................................……1分又∵C ADE ∠=∠ ∴B ADE ∠=∠∵DAB B EDC ADE ADC ∠+∠=∠+∠=∠∴EDC DAB ∠=∠..................................................……2分 ∴△ABD ∽△DCE.....................................................……3分(2)解:∵△ABD ∽△DCE∴CE CDBD AB =...........................................……4分 即CExx -=65∴x x x x CE 56515)6(2+-=-=..................……5分∴55651)5651(522+-=+--=-=x x x x CE AC AE ............…6分(3) ∵516)3(515565122+-=+-=x x x AE∴当3=x 时,AE 最短为516即BD=3时,AE分又∵BD=3=21BC ∴此时点D 恰好为BC 中点 ∴AD ⊥BC∴︒=∠90ADB ..................................................……8分 ∵△ABD ∽△DCE∴︒=∠=∠90ADB DEC∴︒=︒-︒=∠-︒=∠9090180180DEC AED∴当AE 最短时,ADE ∆是直角三角形.........................….…9分∵595)36(35)6(=-⨯=-=x x CE∴51222=-=CE CD DE∴25965125162121=⨯⨯=⋅=∆DE AE S ADE .....................…10分。
2019--2020年九年级上学期期末试卷及答案【数学】(A)

年九年级上学期期末考试 数学试卷考生注意:1.考试时间120分钟2.全卷共三道大题,总分120分题号一二三2122232425262728总分得分得分评卷人一㊁填空题(每题3分,满分30分)1.已知一元二次方程x 2-k x -3=0有一个根为1,则k 的值为.2.抛物线y =x 2-2x -3的顶点坐标是.3.如图,在әA B C 中,øB =40ʎ,将әA B C 绕点A 逆时针方向旋转到әA D E 的位置,使得A D ʅB C ,则øC A E =度.4.在一个不透明的布袋里装有3个红球㊁5个黑球,它们除颜色外其余都相同.从袋中任意摸出1个球,是红球的概率为.5.智能音箱是市场上最火热的智能产品之一,某商户一月份销售了100个智能音箱,三月比一月多销售44个.设该公司二㊁三两个月销量的月平均增长率为x ,则可列方程为.6.如图,C D 是☉O 的直径,A ,B 是☉O 上的两点,若øA D C =65ʎ,则øA B D 的度数为.7.一个圆锥形漏斗模型的底面圆的周长为8πc m ,圆锥的高为3c m ,则这个圆锥漏斗的侧面积是c m 2.8.如图,A B 是☉O 的直径,C ,D 是☉O 上的两点,过点C 作C E ʅA B 于点E ,过点D 作D F ʅA B于点F ,H 为E F 上任意一点.若A B =10,C E =4,D F =3,则C H +D H 的最小值是.9.☉O 的半径为4,一条弦A B =42,则此弦A B所对的圆周角的度数为.10.如图,矩形A B C D 中,A B =6,C =8,矩形在直线l 上绕其右下角的顶点C 向右做无滑动的连续翻转,每次翻转90ʎ,经过2018次翻转之后,点B 在整个旋转过程中所经过的路程之第3题图第6题图第8题图第10题图得分评卷人二㊁选择题(每题3分,满分30分)11.下列图案中,既是轴对称图形,又是中心对称图形的是( )029201-2012.已知反比例函数y=-3x,下列结论不正确的是()A.图象经过点(-3,1)B.图象在第二㊁四象限C.当x<0时,y随着x的增大而增大D.当x>-1时,y>313.如果关于x的一元二次方程k x2+2x-1=0有两个实数根,那么k的取值范围是()A.kȡ-1且kʂ0B.k>-1且kʂ0C.kȡ1D.k>114.如图,A D,B C是☉O的两条互相垂直的直径,点P从点O出发,沿OңCңDңO的路线匀速运动,设øA P B=y(单位:度),那么y与点P运动的时间x(单位:秒)的关系的图象大致是)第14题图15.在一次公司小型酒会上,每两名员工都只碰杯一次,如果一共碰杯45次,则参加酒会的人数为()A.9人B.10人C.11人D.12人16.抛物线y=(x-3)2+2经过平移得到y=x2,平移方法是()A.向右平移3个单位长度,再向下平移2个单位长度B.向右平移3个单位长度,再向上平移2个单位长度C.向左平移3个单位长度,再向下平移2个单位长度D.向左平移3个单位长度,再向上平移2个单位长度17.如图,在方格纸上建立的平面直角坐标系中,将R tәA B C绕原点O按顺时针方向旋转90ʎ,得到R tәF E D,则点A的对应点F的坐标是()A.(1,1)B.(1,2)C.(2,1)D.(-1,-2)18.如图,A,B是双曲线y=k x上的两点,连接O A,O B,过点A作A Cʅx轴,垂足为C,交O B 于点D.若әA C O的面积为2,D为O B的中点,则әC O D的面积为()A.12B.23C.43D.119. 双11 促销活动中,小芳的妈妈计划用1000元在唯品会购买价格分别为80元和120元的两种商品,则可供小芳妈妈选择的购买方案有()A.4种B.5种C.6种D.7种20.小刚从如图所示的二次函数y=a x2+b x+c的图象中,观察得出了下面四条信息:①b2-4a c>0;②c>1;③a b>0;④a+b+c<0;⑤2a-b>0.其中错误信息的个数有().3个C.4个 D.5个第17题图第18题图第20题图三㊁解答题(满分60分)得分评卷人21.(本题满分5分)先化简,再求值:a +3a 2-2a ːa +2-5a -2æèçöø÷,其中a 是方程x 2-3x -4=0的根.得分评卷人22.(本题满分6分)如图,在平面直角坐标系中,已知әA B C 的三个顶点的坐标分别为A (-3,5),B (-2,1),C (-1,3).(1)画出әA B C 关于原点O 对称的әA 1B 1C 1;(2)画出将әA B C 绕点O 顺时针方向旋转90ʎ得到的әA 2B 2C 2;(3)在(2)的旋转变换中,求线段B C 扫过的图形区域面积(结果保留.第22题图如图,二次函数y=-x2+b x+c的图象过点A(3,0),与y轴交于点B,对称轴为x=1.(1)求二次函数的解析式;(2)连接A B,P是抛物线上一点,直线O P把әA O B的周长分成相等的两部分,求点P的坐标.第23题图得分评卷人24.(本题满分7分)如图,直线P A交☉O于A,E两点,P A的垂线D C切☉O于点C,过点A作☉O的直径A B.(1)求证:A C平分øD A B;(2)若D C=4,D A=2,求☉O的直径.第24题图如图,矩形A B C D在平面直角坐标系中,A B,B C的长是一元二次方程x2-20x+96=0的两个根(A B>B C).点E,F,G分别从点A,B,C三点同时出发,沿矩形的边按逆时针方向移动,点E,G的速度均为2c m/s,点F的速度为4c m/s,当点F追上点G(即点F与点G重合)时,三个点随之停止移动.设移动开始后第t s时,әE F G的面积为S c m2.(1)求点D的坐标;(2)写出S和t之间的函数解析式,并指出自变量t的取值范围.第25题图在正方形A B C D中,M为A B的中点,E为直线A B上任意一点,将线段M E绕点M逆时针旋转90ʎ得到线段M F,连接E F,B F,过点F作F GʅB F,交直线A C于点G. (1)当点E在线段MB上时,如图①,易证F B=F G(不需证明);(2)当点E在射线MB上时,如图②;当点E在射线MA上时,如图③,猜想线段F B和F G有怎样的数量关系?请写出你对图的猜想,并选择一种情况给予证明.第26题图以区块链技术为支撑的某网络虚拟货币 M币 最近走出一波有趣的行情,其在第x(1ɤxɤ50)天的售价与销量的相关信息如下表:时间x/天1ɤxɤ50售价/(元/M币)x+40每天销量/个200-2x已知某交易商的进价为每个 M币 30元,设销售该 M币 的每天利润为y元.(1)求出y与x的函数关系式;(2)问销售该 M币 第几天时,当天销售利润最大?最大利润是多少?(3)该 M币 在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.如图,在平面直角坐标系中,直线A B与x轴㊁y轴分别交于A,B两点,且O A,O B的长分别是方程x2-14x+48=0的两根(O A<O B),A C平分øB A O交y轴于点C,过点C作A B 的垂线,垂足为D,交x轴于点E.(1)求线段A B的长;(2)求直线A C的解析式;(3)P是y轴上一点,在坐标平面内是否存在一点Q,使以A,B,P,Q为顶点的四边形为矩形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.第28题图年九年级上学期期末考试数学试卷参考答案及评分标准一㊁填空题(每题3分,满分30分)1.-22.(1,-4)3.504.385.100(1+x )2=100+44 6.25ʎ 7.20π8.72 9.45ʎ或135ʎ 10.6057π二㊁选择题(每题3分,满分30分)11.C 12.D 13.A 14.B 15.B 16.C 17.B 18.A 19.A 20.A 三㊁解答题(满分60分)21.(本题满分5分)解:原式=a +3a (a -2)ːa 2-9a -2(1分) =a +3a (a -2)㊃a -2(a +3)(a -3)(1分) =1a 2-3a .(1分) ȵa 是方程x 2-3x -4=0的根,ʑa 2-3a -4=0.ʑa 2-3a =4.(1分) ʑ原式=14.(1分) 22.(本题满分6分)解:(1)әA 1B 1C 1如图所示.(2分) (2)әA 2B 2C 2如图所示.(2分)(3)ȵO C =10,O B =5,øB O B 2=øC O C 2=90ʎ,ʑ在旋转过程中,B C 所扫过的面积为S 扇形C O C 2-S 扇形B O B 2=90π(10)2-90π(5)2360=54π.(2分) 029201-2023.(本题满分6分)解:(1)由点A (3,0),对称轴为x =1,可得-9+3b +c =0,b 2=1.ìîíïïï(1分)解得b =2,c =3.{(1分)ʑ解析式为y =-x 2+2x +3.(1分)(2)如图,设A B 与直线O P 相交于点C .当x =0时,y =3.ʑB (0,3).ȵA (3,0),ʑәA O B 为等腰直角三角形.ʑO P 经过A B 的中点C .ʑC 32,32æèçöø÷.ʑ直线O P 的解析式为y =x .(1分) 代入抛物线解析式,解得x =1ʃ132.ʑ点P 的坐标为1+132,1+132æèçöø÷或1-132,1-132æèçöø÷.(2分)24.(本题满分7分)解:(1)如图,连接O C .ȵC D 为切线,ʑO C ʅC D .(1分)ȵC D ʅP A ,ʑøP D C =øO C D =90ʎ.ʑO C ʊP A .ʑøD A C =øO C A .(1分) ȵO A =O C ,ʑøO A C =øO C A .(1分) ʑøO A C =øD A C .ʑA C 平分øD A B .(1分)(2)如图,过点O 作O F ʅA E 于点F ,则四边形O C D F 是矩形.ʑO F =C D =4,O C =D F .(1分)在R t әO F A 中,O A 2=O F 2+(O C -D A )2.(1分)即O C 2=42+(O C -2)2.解得O C =5.ʑ☉O 的直径为10.(1分)25.(本题满分8分)解:(1)解方程x 2-20x +96=0,得x 1=12,x 2=8.(2分)ȵA B >B C ,ʑA B =12,B C =8.ʑ点D 的坐标为(8,12).(2分)(2)当0ɤt ɤ2时,点E ,F ,G 分别在A B ,B C ,C D 上移动,此时A E =C G =2t ,E B =12-2t ,B F =4t ,F C =8-4t ,(1分)S =S 梯形E B C G -S әE B F -S әF C G =8t 2-32t +48(0ɤt ɤ2);(1分) 当点F 追上点G 时,4t =2t +8,解得t =4.当2<t ɤ4时,C F =4t -8,C G =2t ,F G =C G -C F =8-2t ,(1分)即S =-8t +32(2<t ɤ4).(1分)26.(本题满分8分)解:图②的结论是:F B =F G .(2分)图③的结论是:F B =F G .(2分)图②的结论证明如下:如图②,设M F 交A G 于点H .由题意可知,M E =M F ,M H ʊB C ,M H ʅA B ,M H =M B =M A ,øE =øF H G =45ʎ,(1分) ʑB E =F H .(1分) ȵøE B F =øB MF +øM F B =90ʎ+øM F B ,F G ʅB F ,)( )页4共(页3第案答学数ʑøH F G =øB F G +øM F B =90ʎ+øM F B .ʑøE B F =øH F G .(1分)ʑәE B F ɸәH F G .ʑF B =F G .(1分) 27.(本题满分10分)解:(1)当1ɤx ɤ50时,y =(200-2x )(x +40-30)=-2x 2+180x +2000.(3分)(2)当1ɤx ɤ50时,二次函数开口下,对称轴为x =45,(1分)当x =45时,y 最大=-2ˑ452+180ˑ45+2000=6050,(2分) ʑ在销售第45天时,当天销售利润最大,最大利润是6050元.(1分)(3)31天.(3分) 28.(本题满分10分)解:(1)解方程x 2-14x +48=0,得x 1=6,x 2=8.(1分)ȵO A <O B ,ʑO A =6,O B =8.(1分) ʑA B =O A 2+O B 2=62+82=10.(1分) (2)ȵA C 平分øB A O ,O C ʅO A ,C D ʅA B ,ʑO C =C D ,A D =O A =6.ʑB D =A B -A D =10-6=4.(1分) 在R t әB C D 中,C D 2+B D 2=C B 2,即O C 2+42=(8-O C )2.解得O C =3.(1分)ʑ点C (0,3).设直线A C 的解析式为y =k x +b (k ʂ0).把点A ,C 的坐标代入,得6k +b =0,b =3.{(1分) 解得k =-12,b =3.ìîíïïï(1分) ʑ直线A C 的解析式为y =-12x +3.(1分) (3)存在.Q 1(6,8),Q 2-6,72æèçöø÷.(2分) ) ( )页4共(页4第案答学数。
2019-2020学年度第一学期九年级数学期末试卷试题(含答案)

2019~2020学年度第一学期期末检测九年级数学评分标准(其他解法参照给分)一、选择题(本大题共8小题,每小题3分,共24分.)二、填空题(本大题共10小题,每小题3分,共30分)9.12; 10.1:4; 11.2; 12.>; 13.110;14.不具有; 15. 16.4; 17.16; 18.2+三、解答题(本大题共10小题,共86分.)19.(本题共2小题,每题5分,共10分)(1)(1)计算:1032sin302020-+︒-解:原式11=2132+⨯-…………………………………………………3分 1113=+-……………………………………………………4分 13=…………………………………………………………5分 (2)解方程:2340x x +-=(解法不唯一)解:()()410x x +-=,……………………………………………………7分40x +=,10x -=…………………………………………………9分 1241x x =-=,………………………………………………………10分20.(本小题7分)解:………………………………………………………………………………………5分 P (两次取球得分的总分不小于5分)=13…………………………………………7分21.(本小题7分)(1)816%=50÷,5010148612m =----=;…………………………2分(2)本次抽查的学生文章阅读篇数的中位数为5,众数为4;………………4分(3)14120033650⨯=,………………………………………………………6分 答:估计该校学生在这一周内文章阅读的篇数为4篇的人数为336人.………7分22.(本小题8分)(1)△ABC 的面积是 12 ;…2分(2)如图所示………6分(3)若P (a ,b )为线段BC 上的任一 点,则变换后点P 的对应点'P 的坐标为 (,)22a b .………8分23.(本小题8分)解:设市政府从2017年到2019年对校舍建设投入资金的年平均增长率为x .…1分 根据题意得,28(1)11.52x +=.…………………………………………………4分解这个方程,得 1220% 2.2x x ==-,(不合题意,舍去)……………………7分答:市政府从2017年到2019年对校舍建设投入资金的年平均增长率为20%…8分24.(本小题8分)解:(1)分别过点E 作EF ⊥AC ,EG ⊥AO,垂足为F 、G.∵至DE 处,测得顶点A 的仰角为75°, ∴∠AEG=75°……………1分∵在BC 处测得直立于地面的AO 顶点A 的仰角为30°,∴∠ACE=30°, ……2分 ∴∠CAE=∠AEG -∠ACE=45°……………………………………………3分(2)在Rt △CFE 中,CE=40,∴1sin 3040202EF CE =︒=⨯=………4分 在Rt △AFE 中,∠CAE =45°,AF=FE=20………5分∴sin 452EF AE ===︒…………………………………………6分(第24题)(3)20AC AF CF =+=在Rt △AFE 中,1sin 3020272AG AC =︒=⨯≈()……7分 ∴27 1.529AO AG OG =+=+≈……………………………8分25.(本小题9分)26.(本小题9分)m.…1分解:(1)设矩形生物园的长为xm,则宽为(8-x)m,小兔的活动范围的面积为y227.(本小题10分)(1)证明:如图1中,AE AD ⊥ ,90DAE ∴∠=︒,90E ADE ∠=︒-∠,…………1分AD 平分BAC ∠,12BAD BAC ∴∠=∠,同理12ABD ABC ∠=∠,…………………2分 ADE BAD DBA ∠=∠+∠ ,180BAC ABC C ∠+∠=︒-∠,11()9022ADE ABC BAC C ∴∠=∠+∠=︒-∠,(2)延长AD 交BC 于点F .AB AE = ,ABE E ∴∠=∠,BE 平分ABC ∠,ABE EBC ∴∠=∠,………………………4分E CBE ∴∠=∠,//AE BC ∴,……………………………………5分90AFB EAD ∴∠=∠=︒,BF BD AF DE=, :2:3BD DE = ,(3)ABC 与ADE 相似,90DAE ∠=︒,ABC ∴∠中必有一个内角为90︒ABC ∠ 是锐角,90ABC ∴∠≠︒.………………………………………………………7分 ①当90BAC DAE ∠=∠=︒时,12E C ∠=∠ , 12ABC E C ∴∠=∠=∠, 90ABC C ∠+∠=︒ ,30ABC ∴∠=︒,此时2ABC ADES S =V V .………………………………………8分 ②当90C DAE ∠=∠=︒时,1452E C ∠=∠=︒, 45EDA ∴∠=︒,ABC 与ADE 相似,45ABC ∴∠=︒,此时ABC ADE S S =V V .………………………………………9分28.(本小题10分) 解:(1)由抛物线2y ax bx c =++交x 轴于A 、B 两点,OA =1,OB =3,得点A 坐标为(1,0)-,点B 的坐标为(3,0);…………………………………2分 Q。
2019--2020学年第一学期期末考试试卷及答案
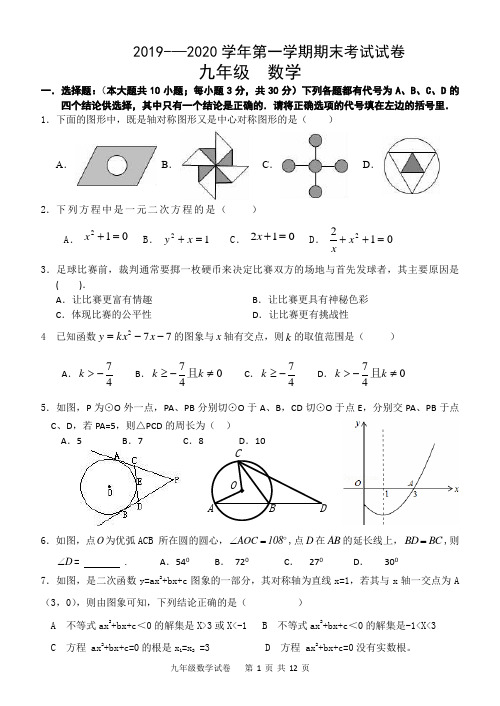
2019-—2020学年第一学期期末考试试卷九年级 数学一.选择题:(本大题共10小题;每小题3分,共30分)下列各题都有代号为A 、B 、C 、D 的四个结论供选择,其中只有一个结论是正确的.请将正确选项的代号填在左边的括号里. 1.下面的图形中,既是轴对称图形又是中心对称图形的是( )A .B .C .D .2.下列方程中是一元二次方程的是( )A .B .C .D .3.足球比赛前,裁判通常要掷一枚硬币来决定比赛双方的场地与首先发球者,其主要原因是( ).A .让比赛更富有情趣B .让比赛更具有神秘色彩C .体现比赛的公平性D .让比赛更有挑战性 4 已知函数772--=x kx y 的图象与x 轴有交点,则k 的取值范围是( )A .47->k B .047≠-≥k k 且 C .47-≥k D .047≠->k k 且 5.如图,P 为⊙O 外一点,PA 、PB 分别切⊙O 于A 、B ,CD 切⊙O 于点E ,分别交PA 、PB 于点C 、D ,若PA=5,则△PCD 的周长为( )A .5B .7C .8D .106.如图,点O 为优弧ACB 所在圆的圆心,AOC 108∠=,点D 在AB 的延长线上,BD BC =,则D ∠= . A .540 B . 720 C . 270 D . 3007.如图,是二次函数y=ax 2+bx+c 图象的一部分,其对称轴为直线x=1,若其与x 轴一交点为A (3,0),则由图象可知,下列结论正确的是( )A 不等式ax 2+bx+c <0的解集是X>3或X<-1 B 不等式ax 2+bx+c <0的解集是-1<X<3 012=+x 12=+x y 012=+x 0122=++x xDB A O8.已知实数a ,b 分别满足,,且,则的值是( )A . 11B . -7C . 7D . -119.在学校组织的实践活动中,小新同学用纸板制作了一个圆锥模型,它的底面半径为1,高为2,则这个圆锥的侧面积是( ) A. 4πB. 3πC. 2πD. 2π10. 已知二次函数()的图象如图所示,有下列4个结论:①②;③;④;其中正确的结论有( )A .1个B .2个C .3个D .4个二.填空题:(本题共8小题;每小题4分,共32分,不需写解答过程,请把结果填在横线上。
2019-2020学年度人教版九年级数学第一学期期末测试题含答案
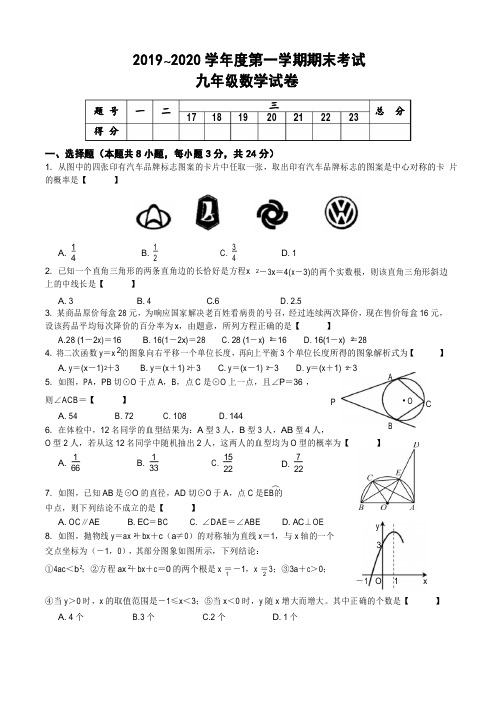
2019~2020 学年度第一学期期末考试九年级数学试卷题 号一二17 18 19三 2021 22 23总分得 分一、选择题(本题共 8 小题,每小题 3 分,共 24 分)1.从图中的四张印有汽车品牌标志图案的卡片中任取一张,取出印有汽车品牌标志的图案是中心对称的卡 片的概率是【 】A.14B.1 2C.3 4D. 12.已知一个直角三角形的两条直角边的长恰好是方程x 上的中线长是【 】-3x =4(x -3)的两个实数根,则该直角三角形斜边A. 3B. 4C.6D. 2.53.某商品原价每盒 28 元,为响应国家解决老百姓看病贵的号召,经过连续两次降价,现在售价每盒 16 元, 设该药品平均每次降价的百分率为 x ,由题意,所列方程正确的是【 】A.28 (1-2x )=16B. 16(1-2x )=28C. 28 (1-x ) =16D. 16(1-x ) =28 4.将二次函数 y =x 的图象向右平移一个单位长度,再向上平衡 3 个单位长度所得的图象解析式为【 】A. y =(x -1)+3 B. y =(x +1) +3 C. y =(x -1) -3 D. y =(x +1) -3 5.如图,PA ,PB 切⊙O 于点 A ,B ,点 C 是⊙O 上一点,且∠P =36°,则∠ACB =【 】 PA. 54°B. 72°C. 108°D. 144°6.在体检中,12 名同学的血型结果为:A 型 3 人,B 型 3 人,AB 型 4 人,AB·OCO 型 2 人,若从这 12 名同学中随机抽出 2 人,这两人的血型均为 O 型的概率为【】A.1 66B.1 33C.15 7 D.22 22︵7.如图,已知 AB 是⊙O 的直径,AD 切⊙O 于 A ,点 C 是E B 的中点,则下列结论不成立的是【 】A. OC ∥AEB. EC =BCC. ∠DAE =∠ABED. AC ⊥OE8.如图,抛物线 y =ax +bx +c (a ≠0)的对称轴为直线 x =1,与 x 轴的一个 交点坐标为(-1,0),其部分图象如图所示,下列结论:①4ac <b ;②方程 ax +bx +c =0 的两个根是 x =-1,x =3;③3a +c >0; 12y3-1 O1 x④当 y >0 时,x 的取值范围是-1≤x <3;⑤当 x <0 时,y 随 x 增大而增大。
【期末试卷】2019-2020学年度第一学期期末九年级质量检测数学试卷及答案

2019-2020学年度第一学期期末九年级质量检测数 学 试 题(满分:150分;考试时间:120分钟)友情提示:1.所有答案都必须填在答题卡相应的位置上,答在本试卷上一律无效.2.参考公式:抛物线2y ax bx c =++(0a ≠)的顶点是(2b a-,244ac b a -).一、选择题(本大题共10小题,每小题4分,共40分.每小题只有一个正确的选项,请在答题卡的相应位置填涂) 1.若∠A 为锐角,cos A =22,则∠A 的度数为( ) A .75°B .60°C .45°D .30°2.如图所示几何体的左视图是( )A B C D 3.由下列光源产生的投影,是平行投影的是( )A .太阳B .路灯C .手电筒D .台灯4.已知Rt △ABC 中,∠ACB=90º,∠B=54º,CD 是斜边AB上的中线,则∠ACD 的度数是( ) A .18 º B .36 º C .54 ºD .72 º5.二次函数2(1)2y x =--图象的对称轴是( )A .直线1x =B .直线1x =-C .直线2x =D .直线2x =-6.下列方程中,没有实数根的是( )A .2690x x -+=B .2230x x -+=C .20x x -=D .(2)(1)0x x +-=C BAD第2题图第4题图7.如图,以点O为位似中心,将△ABC缩小后得到△DEF,已知OD=1,OA=3.若△DEF的面积为S,则△ABC的面积为()A.2S B.3SC.4S D.9S8.口袋中有若干个形状大小完全相同的白球,为估计袋中白球的个数,现往口袋中放入10个形状大小与白球相同的红球.混匀后从口袋中随机摸出40个球,发现其中有3个红球.设袋中有白球x个,则可用于估计袋中白球个数的方程是()A.10340x=B.10140x=C.1013x=D.1031040x=+9.如图,方格纸中的每个小方格都是边长为1的正方形,△ABC的顶点都在格点上,则sin∠ACB的值为()A.24B.13C.1010D.3101010.如图,已知动点A,B分别在x轴,y轴正半轴上,动点P在反比例函数6(0)y xx=>图象上,P A⊥x轴,△P AB是以P A为底边的等腰三角形.当点A的横坐标逐渐增大时,△P AB的面积将会()A.越来越小B.越来越大C.不变D.先变大后变小二、填空题(本大题共6小题,每小题4分,共24分.请将答案填入答题卡的相应位置)11.已知C是线段AB上一点,若23ACBC=,则ABBC=.12.已知二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,则当0x<时,y随x的增大而.(填“增大”或“减小”)AFEDOCB第7题图第9题图第10题图CAB第12题图xyOA xyOPB13.如图一组平行线,每相邻两条平行线间的距离都相等,△ABC 的三个顶点都在平行线上,则图中一定等于14BC的线段是 .14.如图是某超市楼梯示意图,若BA 与CA 的夹角为α,∠C=90︒,AC =6米,则楼梯高度BC 为 米.15.二次函数2y ax bx c =++(a ,b ,c 为常数且a ≠0)中的x 与y 的部分对应值如下表:已知表中有且只有一组数据错误,则这组错误数据中的x 值是 . 16.如图,1ABB △,112A B B △,…,221n n n A B B ---△,11n n n A B B --△是n 个全等的等腰三角形,其中2AB =,11BB =,底边1BB ,12B B ,…,21n n B B --,1n n B B -在同一条直线上,连接n AB 交21n n A B --于点P ,则1n PB -的值为 .三、解答题(本大题有9小题,共86分.请在答题卡的相应位置作答) 17.(本题满分8分)已知点P (-2,3)在反比例函数ky x=(k 为常数,且0k ≠)的图象上. (1)求这个函数的解析式;(2)判断该反比例函数图象是否经过点A (-1,-3),并说明理由.18.(本题满分8分)小明同学解一元二次方程2410x x --=的过程如图所示, (1)小明解方程的方法是 ,他的求解过程从第 步开始出现错误,这一步的运算依据应该是 ;(2)解这个方程.x … -1 0 1 2 3 … y…-3-41…解:241x x -=……① 2441x x -+= ……② 2(2)1x -=……③ 21x -=± ……④ 123,1x x ==……⑤A BCD E FG HI 第13题图 ABA 1A n-1B 1B 2B n -2 B n-1B nP A n-2第16题图第14题图BC Aα19.(本题满分8分)如图,将矩形纸片ABCD 沿对角线BD 折叠,点C 的对应点为E ,BE 交AD 于点F .求证:△ABF ≌△EDF .20.(本题满分8分)如图,四边形ABCD 是平行四边形,E 为边CD 延长线上一点,连接BE 交边AD 于点F .请找出一对相似三角形,并加以证明.21.(本题满分8分)如图所示,有4张除了正面图案不同,其余都相同的图片.(1)以上四张图片所示的立体图形中,主视图是矩形的有 ;(填字母序号) (2)将这四张图片背面朝上混匀,从中随机抽出一张后放回,混匀后再随机抽出一张.求两次抽出的图片所示的立体图形中,主视图都是矩形的概率. 22.(本题满分10分)某商城将每件成本为50元的工艺品,以60元的单价出售时,每天的销售量是400件.已知在每件涨价幅度不超过15元的情况下,若每件涨价1元,则每天就会少售出10件.设每件工艺品涨了x 元.(1)小明根据题中的数量关系列出代数式(6050)x -+和(40010)x -,其中代数式(6050)x -+表示 ,代数式(40010)x -错误!未找到引用源。
2019-2020学年第一学期九年级期末考试试题

2019~2020学年度第一学期九年级期末考试数学试题本试题分第I 卷(选择题)和第II 卷(非选择题)两部分.第I 卷共2页,满分为48分;第II 卷共4页,满分为102分.本试题共6页,满分为150分.考试时间为120分钟.答卷前,请考生务必将自己的学校、班级、姓名和准考证号填写在答题卡上,并同时将学校、姓名、准考证号填写在试卷规定的位置上.考试结束后,将本试卷和答题卡一并交回.本考试不允许使用计算器.第I 卷(选择题共48分)注意事项:第I 卷为选择题,每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号.答案写在试卷上无效.一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.下面几个几何体,左视图是圆的是A B C D2.一元二次方程x 2=1的解是A .x 1=x 2=1B .x 1=x 2=-1C .x 1=1,x 2=﹣1D .x 1=1,x 2=03.做抛掷同一枚啤酒瓶盖的重复实验,经过统计得“凸面朝上”的频率为0.44,则可以估计抛 掷这枚啤酒瓶盖出现“凸面朝上”的概率约为 A .22%B .44%C .50%D .56%4.小兵身高1.4m ,他的影长是2.1m ,若此时学校旗杆的影长是12m ,那么旗杆的高度为 A .4.5m B .6mC .7.2mD .8m5.若m n =38,则m n n 值为A .118B .811C .113D .3116.如图,⊙O 是△ABC 的外接圆,连接OB ,OC ,若OB =BC , 则∠BAC 等于A.60°B.45°C.30°D.20°7.函数y=﹣2x2先向右平移1个单位,再向下平移2个单位,所得函数解析式是A.y=﹣2(x﹣1)2+2 B.y=﹣2(x﹣1)2﹣2C.y=﹣2(x+1)2+2 D.y=﹣2(x+1)2﹣28.一元二次方程x2﹣2x+m=0没有实数根,则m应满足的条件是A.m>1 B.m=1 C.m<1 D.m≤19.如图,在平行四边形ABCD中,E是DC上的点,DE:EC=2:1,连接AE交BD于点F,则△DEF与△BAF的面积之比为A.2:3 B.3:2 C.9:4 D.4:910.如图,点C在反比例函数kyx(x>0)的图象上,过点C的直线与x轴,y轴分别交于点A,B,且AB=BC,△AOB的面积为1,则k的值为A.1B.2 C.3 D.411.如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB,BD 于M,N两点.若AM,则线段BN的长为()A.1 B C.2D12.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b=0;③m为任意实数,则a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2.其中正确的有A.①②③B.②④C.②⑤D.②③⑤第11题图M BA第9题图A BBC第6题图第II 卷(非选择题共102分)注意事项:1.第II 卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效.2.填空题请直接填写答案,解答题应写出文字说明、证明过程或演算步骤. 二、填空题:(本大题共6个小题,每小题4分,共24分.) 13.如果点(3,﹣4)在反比例函数ky x=的图象上,则k = . 14.如图,在8×4的矩形网格中,每格小正方形的边长都是1,若△ABC 的三个顶点在图中 相应的格点上,则tan ∠ACB 的值为 .15.如图,点D ,E 分别在△ABC 的边AB ,AC 上,DE ∥BC ,AD =4 cm ,BD =2cm ,AC = 4.5 cm ,则CE 的长为______.16.如图,AB 为⊙O 的直径,点C 在⊙O 上,若∠OCA =50°,AB =4,则BC 的长为______. 17.如图,在矩形ABCD 中,AB =3,对角线AC ,BD 相交于点O ,AE 垂直平分OB 于点E , 则AD 的长为______.18.如图,四边形OACB 为平行四边形,B 在x 轴上,且∠AOB =60°,反比例函数ky x =(k >0)在第一象限内过点A ,且与BC 交于点F .当F 为BC 的中点,且S △AOF OA 的长为 .第15题图第14题图x三、解答题(本大题9个小题,共78分.解答应写出文字说明、证明过程或演算步骤.) 19.(本小题满分5分)解方程:x 2﹣2x ﹣3=020.(本小题满分6分)计算:3tan30°﹣2sin60°+cos 245°.21.(本小题满分7分)如图,在△ABC 中,∠B =45°,AB AC =5,求边BC 22.(本小题满分8分)如图所示,某学校有一道长为12米的墙,计划用26米长的围栏靠墙围成一个面积为80平方米的矩形草坪ABCD .求该矩形草坪BC 边的长.23.(本小题满分8分)一个不透明的口袋里装有红、白、黄三种颜色的乒乓球(除颜色外其余都相同),其中有白球2个,黄球1个.若从中任意摸出一个球,这个球是白球的概率为0.5. (1)求口袋中红球的个数.(2)从袋中任意摸出一球,放回摇匀后,再摸出一球,则两次都摸到白球的概率是多少?请你用列表或画树状图的方法说明理由.24.(本小题满分10分)如图,CD 是⊙O 的切线,点C 在直径AB (1)求证:∠CAD =∠BDC ;(2)若BC =2,CD =3,求⊙O 的半径.第22题图A25. (本小题满分10分)如图1,正比例函数y=kx 的图象与反比例函数xmy (x >0)的图象都经过点A (2,2). (1)分别求这两个函数的表达式;(2)如图2,将直线OA 向下平移n 个单位长度后与y 轴交于点B ,与x 轴交于点C ,与反比例函数图象在第一象限内的交点为D ,连接OD ,tan ∠COD =14. ①求n 的值.②连接AB ,AD ,求△ABD 的面积.26.(本小题满分12分)在△ABC 中,AB =AC ,点D 为直线BC 上一动点(点D 不与B ,C 重合),以AD 为边在AD 右侧作菱形ADEF ,使∠DAF =∠BAC ,连接CF . (1)如图1,当点D 在线段BC 上时,求证:BD =CF ; (2)如图2,当点D 在线段BC 的延长线上,且∠BAC =90°时,①问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,说明理由;②延长BA 交CF 于点G ,连接GE .若AB=CD =BC ,请求出GE 的长.第26题图1第26题图2FEDCBAGFED CBA27.(本小题满分12分)如图1,抛物线的顶点A 的坐标为(1,4),抛物线与x 轴相交于B ,C 两点,与y 轴交于点D (0,3).(1)求抛物线的表达式以及点B 的坐标;(2)在抛物线的对称轴上是否存在一点P ,使得DP +CP 最小,如果存在,求出点P 的坐标;如果不存在,请说明理由.(3)点Q 是线段BD 上方抛物线上的一个动点.过点Q 作x 轴的垂线,交线段BD 于点E ,再过点Q 作QF ∥x 轴交抛物线于点F ,连结EF ,请问是否存在点Q 使△QEF 为等腰直角三角形?若存在,求出点Q 的坐标;若不存在,说明理由.第27题图1第27题备用图数学试题参考答案一、选择题二、填空题: 13. 14.13 15. 1.5 16.109π17.18. 8三、解答题19.法一解:因式分解,得·······································2分或 ·······································3分 ············································5分20.解:3tan30°﹣2sin60°+cos 245° =3×﹣2×+()2 ·······································3分=﹣+ ·······································5分=.·································6分21.解:作AH ⊥BC , ··················1分 在Rt △ACH 中,∠B=45°,AB= ∴AH =AB sinB=32=,·······································3分 BH =AH =3 ·······································4分∵AC =5∴在Rt △ACH 中,,CH4=······································6分 ∴BC = BH +AH =3+4=7. ···········································7分22. 解:设矩形草坪AB 边的长为x 米,则BC 边的长为(26﹣2x )米,············1分 根据题意得:x (26﹣2x )=80,············································4分整理得:x 2﹣13x +40=0,解得:x 1=5,x 2=8. ·······································6分 当x =5时,26﹣2x=16>12(舍), 当x =8时,26﹣2x =10.·······································7分 答:该矩形草坪BC 边的长为10米.······································8分 23. (1)20.5211÷--=答:口袋中红球有1个.······································2分 (2)············································5分共有16种等可能结果,两次都摸到白球有4种············································7分 所以41164P ==(两次白球).············································8分24. (1)如图,连接OD .··················1分 ∵CD 是⊙O 的切线,∴∠ODC =90°, ∴∠ODB+∠BDC=90°,··················2分∵AB 是 的直径,D 为 上一点,∴∠ADB =90°,··················3分 ∴∠ABD+∠BAD=90°,·················4分∵OB=OD ,∴∠ODB=∠ABD ·················5分 ∴∠CAD =∠BDC ; ·················6分(2)设半径为r ,OB=OD=r ,∵BC =2,CD =3, ∴222(2)3r r +=+ ···········································8分 解得:54r =············································10分(亦可用相似,酌情给分)25.解:(1)∵y=kx ,xmy =(x >0)过点A (2,2) ∴将A (2,2)代入y=kx ,得22k =解得: 1.k = ∴正比例函数的解析式为:y=x ··················2分∴将A (2,2)代入x my =,得22m =∴ 4.m =∴4y x=········(2)过D 作DE ⊥x 轴,∵tan ∠COD =14,即DE OE =14,又∵D 在4y x=上,∴D (4,1);··················5分 ∵BD ∥OA ,∴设BD 表达式为:y=x+b ··················6分 ∵过D (4,1);∴1=4+b ,b=-3,y=x ﹣3, B 的坐标是(0,﹣3)n =3.··················7分(3)∵OA ∥BC ,∴S △ABD =S △OBD =×BO ×x D =×3×4=6.··················10分 26. 解:(1)证明:菱形ADEF 中,AD=AF ,……………………………..1分∵∠BAC=∠DAF ,∴∠BAC-∠DAC=∠DAF-∠DAC 即∠BAD=∠CAF …………………..2分 ∵AB=AC,∴△DAB ≌△FAC ,………………………………………..……..3分 ∴BD=CF ……………………………………………………………..… ..4分(2)解:①(1)中的结论仍然成立…………………………………………………………………..5分 证明:∵∠BAC=∠DAF=90°,∴∠BAC+∠DAC=∠DAF+∠DAC即∠BAD=∠CAF ………………………………………………………………………………………..6分∵AB=AC,AD=AF ,∴△DAB ≌△FAC ,………………………………………………………………..7分 ∴BD=CF …………………………………………………………..8分②解:过A 作AH ⊥BC 于H ,过E 作EM ⊥BD 于M ,EN ⊥CF 于N , ∵∠BAC=90°,AB=AC ,∴AB=4,AH=BH=HC=2,∴CD=BC=4, ∴DH=6,CF=BD=8,………………………………….……..………9分 ∵四边形ADEF 是正方形,∴AD=DE ,∠ADE=90°, ∵BC ⊥CF ,EM ⊥BD ,EN ⊥CF ,∴四边形CMEN 是矩形, ∴NE=CM ,EM=CN ,∵∠AHD=∠ADE=∠EMD=90°,∴∠ADH+∠EDM=∠EDM+∠DEM=90°,∴∠ADH=∠DEM , ∴△ADH ≌△DEM ,∴EM=DH=6,DM=AH=2, ∴CN=EM=6,EN=CM=6,…………………………………………10分∵∠ABC=45°,∴∠BGC=45°,∴△BCG 是等腰直角三角形,∴CG=BC=4,∴GN=2,……………………………………………………….…………..……11分 ∴………………………………………12分其它解法酌情给分27. 解:(1)∵抛物线的顶点A 的坐标为(1,4),∴设抛物线的表达式为:y =a (x ﹣1)2+4,···········································1分把(0,3)代入得:3=a (0﹣1)2+4,a =-1 ························2分∴抛物线的表达式为:y =﹣(x ﹣1)2+4=﹣x 2+2x +3;·····································3分 令y =0,﹣(x ﹣1)2+4=0,解得x 1=3,x 2=﹣1, ∴B 的坐标是(3,0),C 的坐标是(-1,0)·································4分 (2)存在 ···········································5分如图1,因为B ,C 关于对称轴对称,连接BD 交对称轴于P ,此时DP +CP 的值最小,······6 分∵D (0,3),B (3,0),易得BD 的解析式为:y =﹣x +3···································7分 当x =1时,y=﹣1+3=2,∴P 的坐标是(1,2)····························8分 (3)存在点Q 使△QEF 为等腰直角三角形,且点Q 的坐标为(2,3)或(,).设Q (n ,﹣n 2+2n +3),则E (n ,﹣n +3),F (﹣n +2,﹣n 2+2n +3),··················9分 ∴QE =﹣n 2+3n ,QF =|2n ﹣2|,···········································10分 ∵QE ∥x 轴、QD ⊥x 轴,∴∠EQF =90°,∴当QE =QF 时,△QEF 为等腰直角三角形,即:﹣n 2+3n =|2n ﹣2|, ①﹣n 2+3n =2n ﹣2,解得:n 1=﹣1(不合题意,舍去), n 2=2,则Q (2,3);·················11分 ②﹣n 2+3n =﹣2n +2,解得:n 1=>3(不合题意,舍去),n 2=,则Q(,).·················12分数学试题第11页(共6页)。
2019-2020学年度第一学期九年级数学期末试题附答案答案

我爱美丽靓湖2019-2020学年度第一学期九年级数学期末试题答案一、选择题(本大题10小题,共30分)1. 如图是一个小正方体的展开图,把展开图折叠成小正方体后,“爱”字一面的相对面上的字是( )A. 美B. 丽C. 靓D. 湖【答案】C【解析】解:∵正方体的表面展开图,相对的面之间一定相隔一个正方形, ∴有“爱”字一面的相对面上的字是靓.故选C .正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答. 本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.2.当0<x <-1时,x ,1x,x 2的大小顺序是( ) A.1x <x <x 2 B .x <x 2<1x C .x 2<x <1x D.1x<x 2<x 【答案】A3.2018年5月3日,中国科学院在上海发布了中国首款人工智能芯片:寒武纪(MLU100),该芯片在平衡模式下的等效理论峰值速度达每秒128 000 000 000 000次定点运算,将数128 000 000 000 000用科学记数法表示为( )A .1.28×1014B .1.28×10﹣14C .128×1012D .0.128×1011【分析】科学记数法的表示形式为a ×10n 的形式,其中1≤|a|<10,n 为整数.确定n的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>1时,n 是正数;当原数的绝对值<1时,n 是负数.【解答】解:将128 000 000 000 000用科学记数法表示为:1.28×1014. 故选:A .【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a ×10n 的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a 的值以及n 的值.4.如图,直线a ,b 被直线c 所截,a ∥b ,∠1=60°,则∠2的度数是( )A .120°B .60°C .45°D .30°【分析】利用两直线平行,同位角相等就可求出.【解答】解:∵直线被直线a 、b 被直线c 所截,且a ∥b ,∠1=60°∴∠2=∠1=60°.故选:B .【点评】本题考查了平行线的性质,应用的知识为两直线平行,同位角相等.5.若a +b =1,则a 2−b 2+2b 的值为( )A. 4B. 3C. 1D. 0【答案】C【解析】解:∵a +b =1,∴a 2−b 2+2b =(a +b)(a −b)+2b =a −b +2b =a +b =1.故选:C .首先利用平方差公式,求得a 2−b 2+2b =(a +b)(a −b)+2b ,继而求得答案. 此题考查了平方差公式的应用.注意利用平方差公式将原式变形是关键.6.为估计鱼塘中的鱼的数量,可以先从鱼塘中随机打捞50条鱼,在每条鱼身上做上记号后,把这些鱼放归鱼塘,经过一段时间,等这些鱼完全混合于鱼群后,再从鱼塘中随机打捞50条鱼,发现只有2条鱼是前面做好记号的,那么可以估计这个鱼塘鱼的数量约为( )A. 1250条B. 1750条C. 2500条D. 5000条【答案】A【解析】解:由题意可得:50÷250=1250(条).故选:A .首先求出有记号的2条鱼在50条鱼中所占的比例,然后根据用样本中有记号的鱼所占的比例等于鱼塘中有记号的鱼所占的比例,即可求得鱼的总条数.本题考查了统计中用样本估计总体,表示出带记号的鱼所占比例是解题关键.7.若不等式组{x >a x −3≤0,只有三个正整数解,则a 的取值范围为( ) A. 0≤a <1B. 0<a <1C. 0<a ≤1D. 0≤a ≤1 【答案】A【解析】解:{x >a ①x −3≤0 ②∵解不等式①得:x ≤3,又∵不等式组{x >a x −3≤0只有三个正整数解, ∴0≤a <1,故选:A .先确定不等式组的整数解,再求出a 的范围即可.本题考查了一元一次不等式组的整数解的应用,能根据已知不等式组的解集和整数解确定a 的取值范围是解此题的关键.8.方程(x+1)2=9的根是( )A .x =2B .x =-4C .x 1=2 x 2=-4D .x 1=4 x 2=-2解析: 把x=2、-2、4、-4分别代入方程(x+1)2=9中发现只有x =2和x =-4能使方程左右两边相等,所以选择答案C9.如图,在△ABC 中,D 、E 分别是AB 、AC 的中点,下列说法中不正确的是( )A. DE =12BCB. AD AB =AE ACC. △ADE∽△ABCD. S △ADE :S △ABC =1:2【答案】D【解析】解:∵D 、E 分别是AB 、AC 的中点,∴DE//BC ,DE =12BC ,∴ADAB =AEAC =DEBC =12,△ADE∽△ABC , ∴S △ADE :S △ABC =(AD AB )2=14, ∴A ,B ,C 正确,D 错误;故选:D .根据中位线的性质定理得到DE//BC ,DE =12BC ,再根据平行线分线段成比例定理和相似三角形的性质即可判定.该题主要考查了平行线分线段成比例定理和相似三角形的性质即可判定;解题的关键是正确找出对应线段,准确列出比例式求解、计算、判断或证明.10.如图,抛物线y =ax 2+bx +c(a ≠0)过点(1,0)和点(0,−2),且顶点在第三象限,设P =a −b +c ,则P 的取值范围是( )A. −4<P <0B. −4<P <−2C. −2<P <0D. −1<P <0【答案】A【解析】解:经过点(1,0)和(0,−2)的直线解析式为y =2x −2,当x =−1时,y =2x −2=−4,而x =−1时,y =ax 2+bx +c =a −b +c ,∴−4<a −b +c <0,即−4<P <0,故选:A .先利用待定系数法求出经过点(1,0)和(0,−2)的直线解析式为y =2x −2,则当x =−1时,y =2x −2=−4,再利用抛物线的顶点在第三象限,从而得到所以−4<a −b +c <0,根据顶点的纵坐标和与y 轴的交点坐标即可得出答案.本题考查了二次函数图象与系数的关系:二次项系数a 决定抛物线的开口方向和大小.当a >0时,抛物线向上开口;当a <0时,抛物线向下开口;一次项系数b 和二次项系数a 共同决定对称轴的位置:当a 与b 同号时,对称轴在y 轴左;当a 与b 异号时,对称轴在y 轴右.常数项c 决定抛物线与y 轴交点:抛物线与y 轴交于(0,c).抛物线与x 轴交点个数由判别式确定:△=b 2−4ac >0时,抛物线与x 轴有2个交点;△=b 2−4ac =0时,抛物线与x 轴有1个交点;△=b 2−4ac <0时,抛物线与x 轴没有交点二.填空题(本题共8小题,共计24分)11.函数y =√x+3x−1中自变量x 的取值范围是答案: x ≥−3且x ≠1【解析】【分析】本题考查了函数自变量的取值范围,要注意几点:①被开方数为非负数;②分母不为0;③a 0中a ≠0.根据被开方数为非负数和分母不为0列不等式计算.【解答】解:根据题意得:{x +3≥0x −1≠0, 解得:x ≥−3且x ≠1.12.因式分解:16a 2−16a +4= ______ .【答案】4(2a −1)2【解析】解:原式=4(4a 2−4a +1)=4(2a −1)2,故答案为:4(2a −1)2.首先提取公因式4,再利用完全平方公式进行二次分解即可.本题考查了提公因式法与公式法分解因式,要求灵活使用各种方法对多项式进行因式分解,一般来说,如果可以先提取公因式的要先提取公因式,再考虑运用公式法分解.13.一组数据2,4,a ,7,7的平均数x =5,则方差S 2=________.【答案】3.6【解析】解:∵数据2,4,a ,7,7的平均数x =5,∴2+4+a +7+7=25,解得a =5,∴方差s 2=15[(2−5)2+(4−5)2+(5−5)2+(7−5)2+(7−5)2]=3.6;故答案为:3.6.根据平均数的计算公式:x=x1+x2+⋯+x nn ,先求出a的值,再代入方差公式S2=1n[(x1−x)2+(x2−x)2+⋯+(x n−x)2]进行计算即可.本题主要考查的是平均数和方差的求法,一般地设n个数据,x1,x2,…x n的平均数为x,则方差S2=1n[(x1−x)2+(x2−x)2+⋯+(x n−x)2].14.若x1,x2是一元二次方程x2+3x−5=0的两个根,则x12x2+x1x22的值是______.【答案】15【解析】解:∵x1,x2是一元二次方程x2+3x−5=0的两个根,∴x1+x2=−3,x1x2=−5,∴x12x2+x1x22=x1x2(x1+x2)=−5×(−3)=15,故答案为:15.由根与系数的关系可求得(x1+x2)与x1x2的值,代入计算即可.本题主要考查根与系数的关系,由根与系数的关系求得(x1+x2)与x1x2的值是解题的关键.15.如图,在⊙O中,C是弦AB上一点,AC=2,CB=4.连接OC,过点C作DC⊥OC,与⊙O交于点D,DC的长为______.【答案】2√2【解析】解:延长DC交⊙O于点E.∵OC⊥DE,∴DC=CE,∵AC⋅CB=DC⋅EC(相交弦定理,可以证明△ADC∽△EBC得到),∴DC2=2×4=8,∵DC>0,∴DC=2√2,故答案为2√2.延长DC交⊙O于点E.由相交弦定理构建方程即可解决问题.本题考查垂径定理,相交弦定理等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题.16.如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为30°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为90米,那么该建筑物的高度BC约为______米.(精确到1米,参考数据:√3≈1.73)【答案】208【解析】解:由题意可得:tan30°=BDAD =BD90=√33,解得:BD=30√3,tan60°=DCAD =DC90=√3,解得:DC=90√3,故该建筑物的高度为:BC=BD+DC=120√3≈208(m),故答案为:208.分别利用锐角三角函数关系得出BD,DC的长,进而求出该建筑物的高度.此题主要考查了解直角三角形的应用,熟练应用锐角三角函数关系是解题关键.17.如图,三角形ABC是边长为1的正三角形,与所对的圆心角均为120°,则图中阴影部分的面积为.考点:扇形面积的计算;等边三角形的性质.分析:设与相交于点O,连OA,OB,OC,线段OA将阴影的上方部分分成两个弓形,将这两个弓形分别按顺时针及逆时针方向绕点O旋转120°后,阴影部分便合并成△OBC,得到它的面积等于△ABC面积的三分之一,利用等边三角形的面积公式:×边长2,即可求得阴影部分的面积.解答:解:如图,设与相交于点O,连接OA,OB,OC,线段OA将阴影的上方部分分成两个弓形,将这两个弓形分别按顺时针及反时针绕点O旋转120°后,阴影部分便合并成△OBC,它的面积等于△ABC面积的三分之一,∴S阴影部分=××12=.故答案为:.点评:本题考查了旋转的性质:旋转前后两图形全等,对应点到旋转中心的距离相等,对应点与旋转中心的连线段所夹的角等于旋转角.也考查了等边三角形的面积公式:×边长2.x2−4与x轴交于A、B两点,P是以点C(0,3)18.如图,抛物线y=14为圆心,2为半径的圆上的动点,Q是线段PA的中点,连结OQ.则线段OQ的最大值是【答案】72【解析】解:连接BP,如图,x2−4=0,解得x1=4,x2=−4,则A(−4,0),当y=0时,14B(4,0),∵Q是线段PA的中点,∴OQ为△ABP的中位线,BP,∴OQ=12当BP最大时,OQ最大,而BP过圆心C时,PB最大,如图,点P运动到P′位置时,BP最大,∵BC=√32+42=5,∴BP′=5+2=7,∴线段OQ的最大值是7.2x2−4=0得A(−4,0),B(4,0),再判断OQ为△ABP的中位线连接BP,如图,先解方程14BP,利用点与圆的位置关系,BP过圆心C时,PB最大,如图,点P运动到得到OQ=12P′位置时,BP最大,然后计算出BP′即可得到线段OQ的最大值.本题考查了点与圆的位置关系:点的位置可以确定该点到圆心距离与半径的关系,反过来已知点到圆心距离与半径的关系可以确定该点与圆的位置关系.也考查了三角形中位线.三、解答题(本题共计10个小题,共计66分)19.(本题满分4分)计算:+(﹣3)0﹣6cos45°+()﹣1.【分析】本题涉及零指数幂、负指数幂、二次根式化简和特殊角的三角函数值4个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.【解答】解:原式=3+1﹣6×+2=3+1﹣3+2=3.【点评】本题主要考查了实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握负整数指数幂、零指数幂、二次根式、绝对值等考点的运算.20.(本题满分4分)解不等式<x+1,并把它的解集在数轴上表示出来.【分析】根据解一元一次不等式的步骤:①去分母;②去括号;③移项;④合并同类项;⑤化系数为1.依次计算可得.【解答】解:去分母,得:5x﹣1<3x+3,移项,得:5x﹣3x<3+1,合并同类项,得:2x<4,系数化为1,得:x<2,将不等式的解集表示在数轴上如下:【点评】本题主要考查解一元一次不等式,解题的关键是掌握解不等式的步骤:①去分母;②去括号;③移项;④合并同类项;⑤化系数为1.21.(本题满分5分)关于x的分式方程﹣=总无解,求a的值.【分析】分式方程去分母转化为整式方程,分类讨论a的值,使分式方程无解即可.【解答】解:去分母得:3﹣x﹣a(x﹣2)=﹣2,即(a+1)x=2a+5,当a=﹣1时,显然方程无解;当a≠﹣1时,x=,当x=2时,a不存在;当x=3时,a=2,综上,a的值为﹣1,2.【点评】本题考查了分式方程无解的条件,分式方程无解的条件是:去分母后所得整式方程无解,或解这个整式方程得到的解使原方程的分母等于0.22.(本题满分8分)某中学艺术节期间,学校向学生征集书画作品,杨老师从全校30个班中随机抽取了4个班(用A,B,C,D表示),对征集到的作品的数量进行了分析统计,制作了两幅不完整的统计图.请根据以上信息,回答下列问题:(1)杨老师采用的调查方式是(填“普查”或“抽样调查”);(2)请你将条形统计图补充完整,并估计全校共征集多少件作品?(3)如果全校征集的作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生,现要在获得一等奖的作者中选取两人参加表彰座谈会,请你用列表或树状图的方法,求恰好选取的两名学生性别相同的概率.【分析】(1)杨老师从全校30个班中随机抽取了4个班,属于抽样调查.(2)由题意得:所调查的4个班征集到的作品数为:6÷=24(件),C班作品的件数为:24﹣4﹣6﹣4=10(件);继而可补全条形统计图;(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与恰好抽中两名学生性别相同的情况,再利用概率公式即可求得答案.【解答】解:(1)杨老师从全校30个班中随机抽取了4个班,属于抽样调查.故答案为抽样调查.(2)所调查的4个班征集到的作品数为:6÷=24件,平均每个班=6件,C班有10件,∴估计全校共征集作品6×30=180件.条形图如图所示,(3)画树状图得:∵共有20种等可能的结果,两名学生性别相同的有8种情况,∴恰好抽中两名学生性别相同的概率为:=.【点评】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.同时考查了概率公式.23.(本题满分6分)如图,在△ABC中,DE分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连CF(1)求证:四边形BCFE是菱形;(2)若CE=6,∠BEF=120°,求菱形BCFE的面积.【分析】(1)从所给的条件可知,DE是△ABC中位线,所以DE∥BC且2DE=BC,所以BC和EF平行且相等,所以四边形BCFE是平行四边形,又因为BE=FE,所以是菱形;(2)由∠BEF是120°,可得∠EBC为60°,即可得△BEC是等边三角形,求得BE=BC=CE=6,再过点E作EG⊥BC于点G,求的高EG的长,即可求得答案.【解答】(1)证明:∵D、E分别是AB、AC的中点,∴DE∥BC且2DE=BC,又∵BE=2DE,EF=BE,∴EF=BC,EF∥BC,∴四边形BCFE是平行四边形,又∵BE=EF,∴四边形BCFE是菱形;(2)解:∵∠BEF=120°,∴∠EBC=60°,∴△EBC是等边三角形,∴BE=BC=CE=6,过点E作EG⊥BC于点G,∴EG=BE•sin60°=6×=3,∴S菱形BCFE=BC•EG=6×3=18.【点评】本题考查菱形的判定和性质以及三角形中位线定理,以及菱形的面积的计算等知识点.注意证得△BEC是等边三角形是关键.24.(本题满分7分)快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣.已知购买甲型机器人1台,乙型机器人2台,共需14万元;购买甲型机器人2台,乙型机器人3台,共需24万元.(1)求甲、乙两种型号的机器人每台的价格各是多少万元;(2)已知甲型和乙型机器人每台每小时分拣快递分别是1200件和1000件,该公司计划购买这两种型号的机器人共8台,总费用不超过41万元,并且使这8台机器人每小时分拣快递件数总和不少于8300件,则该公司有哪几种购买方案?【答案】解:(1)设甲型机器人每台价格是x 万元,乙型机器人每台价格是y 万元,根据题意得{x +2y =142x +3y =24解这个方程组得:{x =6y =4答:甲、乙两种型号的机器人每台价格分别是6万元、4万元.(2)设该公可购买甲型机器人a 台,乙型机器人(8−a)台,根据题意得{6a +4(8−a)≤411200a +1000(8−a)≥8300解这个不等式组得32≤a ≤92∵a 为正整数∴a 的取值为2,3,4,∴该公司有3种购买方案,分别是购买甲型机器人2台,乙型机器人6台购买甲型机器人3台,乙型机器人5台购买甲型机器人4台,乙型机器人4台26.(本题满分7分)如图,已知一次函数与反比例函数的图象相交于点A (4,n ),与x 轴相交于点B .(1)填空:n 的值为 ,k 的值为 ; (2)以AB 为边作菱形ABCD ,使点C 在x 轴正半轴上,点D 在第一象限,求点D 的坐标;(3)考察反比函数的图象,当时,请直接写出自变量x 的取值范围.(1)3,1226.(本题满分7分)如图①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,28s时注满水槽.水槽内水面的高度y(cm)与注水时间x(s)之间的函数图象如图②所示.(1)正方体的棱长为cm;(2)求线段AB对应的函数解析式,并写出自变量x的取值范围;(3)如果将正方体铁块取出,又经过t(s)恰好将此水槽注满,直接写出t的值.【解答】解:(1)由题意可得:12秒时,水槽内水面的高度为10cm,12秒后水槽内高度变化趋势改变,故正方体的棱长为10cm;故答案为:10;(2)设线段AB对应的函数解析式为:y=kx+b,∵图象过A(12,10),B(28,20),∴,解得:,∴线段AB对应的解析式为:y=x+(12≤x≤28);(3)∵28﹣12=16(s),∴没有立方体时,水面上升10cm,所用时间为:16秒,∵前12秒由立方体的存在,导致水面上升速度加快了4秒,∴将正方体铁块取出,经过4秒恰好将此水槽注满.27.(本题满分9分)如图,△ABC内接于⊙O,CD平分∠ACB交⊙O于D,过点D作PQ//AB 分别交CA、CB延长线于P、Q,连接BD.(1)求证:PQ是⊙O的切线;(2)求证:BD2=AC⋅BQ;(3)若AC、BQ的长是关于x的方程x+4x =m的两实根,且tan∠PCD=13,求⊙O的半径.(x−ℎ)2−2与x轴交于A,B两点(点A在点28.(本题满分9分)如图,抛物线l:y=12B的左侧),将抛物线l在x轴下方部分沿轴翻折,x轴上方的图象保持不变,就组成了函数f的图象.(1)若点A的坐标为(1,0).①求抛物线l的表达式,并直接写出当x为何值时,函数f的值y随x的增大而增大;②如图2,若过A点的直线交函数f的图象于另外两点P,Q,且S△ABQ=2S△ABP,求点P 的坐标;(2)当2<x<3时,若函数f的值随x的增大而增大,直接写出h的取值范围.4.【答案】解:(1)①把A(1,0)代入抛物线y=12(x−ℎ)2−2中得:12(x−ℎ)2−2=0,解得:ℎ=3或ℎ=−1,∵点A在点B的左侧,∴ℎ>0,∴ℎ=3,∴抛物线l的表达式为:y=12(x−3)2−2,∴抛物线的对称轴是:直线x=3,由对称性得:B(5,0),由图象可知:当1<x<3或x>5时,函数f的值y随x的增大而增大;②如图2,作PD⊥x轴于点D,延长PD交抛物线l于点F,作QE⊥x轴于E,则PD//QE,由对称性得:DF=PD,∵S△ABQ=2S△ABP,∴12AB⋅QE=2×12AB⋅PD,∴QE=2PD,∵PD//QE,∴△PAD∽△QAE,∴AEAD =QEPD,∴AE=2AD,设AD=a,则OD=1+a,OE=1+2a,P(1+a,−[12(1+ a−3)2−2]),∵点F、Q在抛物线l上,∴PD=DF=−[12(1+a−3)2−2],QE =12(1+2a −3)2−2, ∴12(1+2a −3)2−2=−2[12(1+a −3)2−2], 解得:a =83或a =0(舍),∴P(113,169); (2)当y =0时,12(x −ℎ)2−2=0,解得:x =ℎ+2或ℎ−2,∵点A 在点B 的左侧,∴A(ℎ−2,0),B(ℎ+2,0),如图3,作抛物线的对称轴交抛物线于点C ,分两种情况:①由图象可知:图象f 在AC 段时,函数f 的值随x 的增大而增大,则{ℎ−2≤2ℎ≥3, ∴3≤ℎ≤4,②由图象可知:图象f 点B 的右侧时,函数f 的值随x 的增大而增大,即:ℎ+2≤2,ℎ≤0,综上所述,当3≤ℎ≤4或ℎ≤0时,函数f 的值随x 的增大而增大.【解析】(1)①利用待定系数法求抛物线的解析式,由对称性求点B 的坐标,根据图象写出函数f 的值y 随x 的增大而增大(即呈上升趋势)的x 的取值;②如图2,作辅助线,构建对称点F 和直角角三角形AQE ,根据S △ABQ =2S △ABP ,得QE =2PD ,证明△PAD∽△QAE ,则AE AD =QE PD ,得AE =2AD ,设AD =a ,根据QE =2FD 列方程可求得a的值,并计算P 的坐标;(2)先令y =0求抛物线与x 轴的两个交点坐标,根据图象中呈上升趋势的部分,有两部分:分别讨论,并列不等式或不等式组可得h 的取值.本题是二次函数的综合题,考查了利用待定系数法求二次函数的解析式、二次函数的增减性问题、三角形相似的性质和判定,与方程相结合,找等量关系,第二问还运用了数形结合的思想解决问题.。
2019-2020学年人教部编版初三语文上册期末考试试卷(含答案)

2019-2020学年九年级语文上册期末考试试题时间:150分钟总分:150分一、积累与运用(32分)1.下面加点的字,每对读音都不相同的一组是( ) (2分)A.玄虚/弓弦啼叫/根深蒂固喏喏连声/惹火烧身B.颠倒/倒叙舟楫/开门揖盗自暴自弃/一曝十寒C.灌溉/气概仿佛/求神拜佛顿开茅塞/敷衍塞责D.着意/着急桑梓/莘莘学子容光焕发/涣然冰释2.下列词语没有错别字的一项是( )(2分)A.拜谒羞赧停滞画龙点睛箪食壶浆B.豢养懦夫压榨轻而一举孜孜不倦C.麻醉摧残儒养怀古伤今走投无路D.诓骗虚忘墨守前扑后继行之有效3.下列加横线的词语使用有误的一项是( ) (2分)A.博物馆里陈列着大量有艺术价值的美术作品,画上的花鸟虫兽栩栩如生,美轮美奂。
B.我们坚信教育可以成为一件美好的、慢的、自然而然发生的,不再是急功近利追求结果的事情。
C.家中的相册里,总有一些年代久远、发黄褪色的老照片。
这些照片的背后,往往隐藏着一些鲜为人知的故事。
D.这些正值豆蔻年华的小姑娘,站在阳光下,浑身散发着青春的气息。
4.下列句子没有语病的一项是( ) (2分)A.贵州一乡镇教师公寓发生重大火灾,为了防止此类事故不在发生,相关部门采取了强有力的应对措施。
B.理论再好,只有被我们掌握、接受和理解,才能成为自觉遵守和奉行的准则。
C.贵州新一轮招商引资工作取得了阶段性成果,但仍然存在产业项目不多、项目转化速度不快。
D.二千多年前,我们的先辈穿越草原沙漠,开辟出联通亚欧非的陆上丝绸之路。
5.下列有关语法的表述有误的一项是( )A.旗鼓相当不动声色故弄玄虚前仆后继,短语类型各不相同.B.“无论植树还是种草,土壤中必须有充足的水分”是条件关系复句.C.“我却怎么也笑不出,陷入了迷茫的沉思”一句中“沉思”是名词D.“翻开有关西域的书籍,你会惊讶于罗布泊的热闹繁华. ”画线部分是补语.6.下列句中标点符号使用有误的一项是( ) (2分)A.“惠水的好花红真美啊!”他说,“有机会一定再来看看。
20192020学年人教版初三上期末数学试卷含

2019-2020 学年人教版初三上期末数学试卷含答案 九年级数学(人教版)上学期期末考试一试卷一、选择题(本大题共10 小题,每题4 分,共 40 分)1.一个直角三角形的两条直角边分别为a=2 3 , b=36 ,那么这个直角三角形的面积是( C )A .8 2B. 7 21) C . 9 2D. 2,则 m 的值等 2.若对于 x 的一元二次方程 (m x 2 5 x m 2 3 m20 的常数项为于( B )A . 1B . 2C .1 或 2D . 03.三角形的两边长分别为 3 和 6,第三边的长是方程 x 26 x 8 0的一个根,则这个三角形的周长是 ( C)A. 9B. 11C. 13D 、144.过⊙ O 内一点 M 的最长弦长为 10cm,最短弦长为 8cm,那么 OM 的长为 ( A )C.41 cm5.图中∠ BOD 的度数是 ( B )A . 55° B. 110°C.125° D . 150°6.如图,⊙ O 是△ ABC 的内切圆,切点分别是D 、E 、F ,已知∠ A=100°,∠ C=30°,则∠ DFE 的度数是 ( C )A.55 °°°°( 第 5 题 ) ( 第 6 题 )7.有一个不透明的布袋中,红色、黑色、白色的玻璃球共有40 个,除颜色外其余完整相同。
小李经过多次摸球试验后发现此中摸到红色、黑色球的频次稳固在 15%和 45%,则口袋中白色球的个数很可能是 ( B )A . 6B . 16C .18D . 248.如图,四边形 ABCD 内接于⊙ O , BC 是直径, AD = DC ,∠ ADB =20o ,则∠ ACB ,∠ DBC 分 别为( B )A . 15o 与 30oB . 20o 与 35oC . 20o 与 40oD . 30o 与 35o9.以下图,小华从一个圆形场所的A 点出发,沿着与半径 OA 夹角为 α 的方向行走,走出席所边沿 B 后,再沿着与半径 OB 夹角为 α 的方向行走。
2019-2020学年度第一学期期末检测九年级数学试题(人教版 含参考答)

2019-2020学年度第一学期期末检测九年级数学试题第I 卷(选择题 共30分)一、选择题(本大题共10个,每小题3分,共30分。
在每小题给出的四个选项中只有一个符合要求)1.下列图形中,既是轴对称图形又是中心对称图形的是A. 等边三角形B. 平行四边形C. 矩形D. 正五边形2.下列事件中,必然事件是A. 某射击运动射击一次,命中靶心B. 通常情况下,水加热到100℃时沸腾C. 掷一次骰子,向上的一面是6点D. 抛一枚硬币,落地后正面朝上3.已知关于x 的一元二次方程x 2+2kx+(k-1)2=0有两个不相等的实数根,则K 的取值范围为 A. K >12 B. K >-12 C. K >18 D. K <124.如图,电线杆CD 的高度为h ,两根拉线AC 与BC 相互垂直,∠CAB=θ,则拉线BC 的长度为(A ,D ,B 在同一条直线上)A cos θ5.已知点A (1x ,1y ),B (2x ,2y )为反比例函数y=6x图象上的两点,当1x >2x >0时,下列结论正确的是A. 0 <1y <2y B. 0 <2y <1yB. C.1y<2y <0 D.2y<1y<06.将二次函数y=12x2-2x+5化成y=a(x-h)2+k的形式为A.Y=12(x-4)2+3 B. Y=12(x-4)2+1C. Y=12(x-2)2+3 D. Y=12(x-2)2+17.如图,AB是⊙O的直径,BC=1,C,D是圆周上的点,且∠CDB=30°,则图中阴影部分的面积为A.8.如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC相似的是A. B. C. D.点,其横坐标为1,则一次函数的图象可能是....10.在平面直角坐标系中,正方形A1B1C1D1,D1E1F1B2,A2B2C2D2,D2E3E4B3,A3B3C3D3,…,按如图所示的方式放置,其中点B1在y轴上,点C1,E1,E2,C2,E3,E4,C3,…在x轴上,已知正方形A1B1C1D1的边长为1,∠OB1C1=30°,B1C1∥B2C2∥B3C3…,则正方形A n B n C n D n的边长是第II卷(非选择题共70分)二、填空题(本大题共5个小题,每小题3分,共15分)12.将抛物线y=2x2向上平移3个单位,得到的抛物线的解析式是___________。
2019-2020年初三数学第一学期期末考试参考答案

2019-2020年初三数学第一学期期末考试参考答案阅卷说明:本试卷72分及格,102分优秀. 一、选择题:(本题共30分,每小题3分)二、填空题(本题共18分, 每小题3分)三、计算题:(本题共72分,第17—26题,每小题5分,第27题7分,第28题7分, 第29题8分)17. 4sin 304560︒︒︒.解:原式=33222214⨯+⨯-⨯--------------------- 4分 =2-1+3 =4--------------------- 5分18. 解:∵在Rt △ABC 中,∠C =90°,∠B =60°∵∠A=90°-∠B =30°--------------------- 1分∴AB==16--------------------- 3分∴AC=BCtanB=8.--------------------- 5分19. 解:(1)∵反比例函数图象两支分别位于第一、三象限,∴k ﹣1>0,解得:k >1;---------------- 2分(2)取k=3,∴反比例函数表达式为x2y = ---------------- 4分 当x=﹣6时,3162x 2y -=-==;--------------------- 5分 (答案不唯一)20. 解: 如图:连接OB,过O 点作OD ⊥BC 于点D ---------------- 1分B在Rt △OBD 中,∵∠BOD =︒︒=606360---------------- 2分 ∵ BD=OD ·tan60°---------------- 3分 =23---------------- 4分 ∴BC=2BD=43∴三角形的边长为43 cm ---------------- 5分 21.证明∵△ABC ∽△ADE ,∴∠BAC =∠DAE ,∠C =∠E ,---------------- 1分 ∴∠BAC -∠DAC =∠DAE -∠DAC ,∴∠1=∠3, ------------------------------ 2分 又∵∠C =∠E ,∠DOC =∠AOE ,∴△DOC ∽△AOE ,----------------------------3分 ∴∠2=∠3 , ----------------------------4分 ∴∠1=∠2=∠3. ----------------------------5分22. 解:过P 作PD ⊥AB 于D ,---------------- 1分在Rt △PBD 中,∠BDP =90°,∠B =45°, ∴BD =PD . ---------------- 2分在Rt △P AD 中,∠ADP =90°,∠A =30°, ∴AD =PD =PD=3PD ,--------------------3分 ∴PD =13100+≈36.6>35, 故计划修筑的高速公路不会穿过保护区.----------------------------5分23.解:(1)不同类型的正确结论有:①BE=CE ;②BD=CD ;③∠BED=90°;④∠BOD=∠A ;⑤AC//OD ;⑥AC ⊥BC ;⑦222OE +BE =OB ;⑧OE BC S ABC ∙=∆;⑨△BOD 是等腰三角形;⑩ΔBOE ΔBAC ~;等等。
2019-2020学年度第一学期期末考试

2019-2020学年度第一学期期末考试 九年级数学(上)试卷(附答案)一、选择题(本大题有10小题,每小题3分,共30分.请选出各题中一个符合题意的正确选项填在相应的答案栏内,不选、多选、错选均不给分.)1.一元二次方程x (x -1)=0的解是( C )A .x =0B .x =1C .x =0或x =1D .x =0或x =-12.在⊿ABC 中,∠A =α,O 为⊿ABC 的内心,则∠BOC 的度数是( A )。
A.90°+α21B.90°-α21C.180°-αD.180°-α213.关于x 的一元二次方程(k-1)x 2-2x +3=0有两相异实根,则k 的取值范围是(B )。
A.k<34 B.k<34 且k ≠1 C.0<k<34D.k ≠1 4.、当钟表上的分针旋转120°时,时针旋转( C )。
A.20°B.12°C.10°D.60° 5.二次函数23(2)1y x =--+的图象的顶点坐标是( B ) A.(2-,)B.(2,)C.(2-,1-) D .(2,1-)6.在一个不透明的盒子中装有8个白球,若干个黄球,除颜色不同外,其余均相同.若从中随机摸出一个球,它是白球的概率为23,则黄球的个数为( B ) A. 2B . 4 C. 12 D. 16 7.二次函数2y ax bx c =++的图象如图所示,则反比例函数ay x=与一次函数 y bx c =+在同一坐标系中的大致图象是( D )8.在半径为 5 cm 的圆中,弦 AB 的长等于 5 cm ,那么弦AB 所对的圆周角为( D ) A.30° B.60° C.150° D.30°或150° 二、填空题(本大题有6小题,每小题4分,共24分.)9.某小区2011年绿化面积为2000平方米,计划2013年底绿化面积要达到2880平方米.如果每年的增长率相同,那么这个增长率是____20%.10.用配方法解方程3x2+6x ―5=0时,原方程应变形为____(x + 1)2 = 3811. 若一个边长为a 的正多边形的内角和等于720,则这个正多边形的外接圆与内切圆的面积的比是 4:3 .12.如图,半径为10的⊙O 中,弦AB 的长为16,则这条弦的弦心距为 6; .13.如图,AB 是⊙O 的直径,点C ,D 都在⊙O 上,连结CA ,CB ,DC ,DB .已 知∠D=30°,BC =3,则AB 的长是 6; .14.如图,已知在Rt △ABC 中, ∠C=90°, AC=3,BC=4,若以点C 为圆心,r 为半径所画的圆与斜边只有一个交点,则r 的取值范围是43512≤<=r r 或 ;15.某种传染病,若有一人感染,经过两轮传染后将共有49人感染.设这种传染病每轮传染中平均一个人传染了x 个人,列出方程为 __比如x (x+1)+x+1=49或2x 149+=()都可以;.16.小明把如图所示的矩形纸板挂在墙上,玩 飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是 ___41___ . 三、解答题(共66分. 请将正确答案及解答过程写在答题纸相应位置)17.(6分)四张小卡片上分别写有数字1、2、3、4.它们除数字外没有任何区别, 现将它们放在盒子里搅匀.第13题第12题第14题AC B(1)随机地从盒子里抽取一张,求抽到数字2的概率;(2)随机地从盒子里抽取一张,不放回再抽取第二张.请你用画树状图或列表的方法表示所有等可能的结果,并求抽到的数字之和为5的概率.解:(1)P (抽到数字2)= 14…………………2分(2)画树状图:从图可知,两次抽取小卡片抽到的数字之和共有12种等可能的结果, 其中抽到的数字之和为5的有4种,∴P (抽到的数字之和为5)=41123=。
人教版2019--2020学年度第一学期九年级数学上册期末考试题及答案

人教版2019—2020学年度第一学期九年级数学期末试卷及答案(满分:120分答题时间:120分钟)一、选择题(共8小题,每小题3分,满分24分)1.下列事件中,必然事件是()A.抛出一枚硬币,落地后正面向上B.打开电视,正在播放广告C.篮球队员在罚球线投篮一次,未投中D.实心铁球投入水中会沉入水底2.如图,点A,B,C,D都在⊙O上,AC,BD相交于点E,则∠ABD=()A.∠ACD B.∠ADB C.∠AED D.∠ACB3.已知四条线段满足,将它改写成为比例式,下面正确的是()A.B.C.D.4.二次函数y=﹣2(x﹣1)2+3的图象的顶点坐标是()A.(1,3)B.(﹣1,3) C.(1,﹣3) D.(﹣1,﹣3)5.已知函数y=x2+2x﹣3,当x=m时,y<0,则m的值可能是()A.﹣4 B.0 C.2 D.36.一个圆锥的高为4cm,底面圆的半径为3cm,则这个圆锥的侧面积为()A.12πcm2B.15πcm2C.20πcm2D.30πcm27.用配方法解一元二次方程x2﹣4x=5时,此方程可变形为()A.(x+2)2=1 B.(x﹣2)2=1 C.(x+2)2=9 D.(x﹣2)2=98.若△ABC∽△A′B′C′,相似比为1:2,则△ABC与△A′B′C′的面积的比为()A.1:2 B.2:1 C.1:4 D.4:1二、填空题(本大题共有8小题,每小题3分,共24分)9.如图,在直角△OAB中,∠AOB=30°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB= °.10.抽屉里放着黑白两种颜色的袜子各1双(除颜色外其余都相同),在看不见的情况下随机摸出两只袜子,它们恰好同色的概率是.11.方程x2﹣4x+c=0有两个不相等的实数根,则c的取值范围是.12.在某一时刻,测得一根高为 1.8m的竹竿的影长为3m,同时测得一根旗杆的影长为25m,那么这根旗杆的高度为m.题号一二三总分得分13.如图,要使△ABC与△DBA相似,则只需添加一个适当的条件是(填一个即可)14.二次函数y=ax2+bx+c的图象如图所示,其对称轴与x轴交于点(﹣1,0),图象上有三个点分别为(2,y1),(﹣3,y2),(0,y3),则y1、y2、y3的大小关系是(用“>”“<”或“=”连接).15.一元二次方程x2+px﹣2=0的一个根为2,则p的值.16.如图,在⊙O中,已知半径为5,弦AB的长为8,那么圆心O到AB的距离为.三、解答题(本大题共有4小题,共24分)17.(6分)解方程:(1)x(x﹣2)+x﹣2=0.(2)x2﹣4x+1=0;18.(6分)一只不透明的箱子里共有3个球,把它们的分别编号为1,2,3,这些球除编号不同外其余都相同,从箱子中随机摸出一个球,记录下编号后将它放回箱子,搅匀后再摸出一个球并记录下编号.(1)用树状图或列表法举出所有可能出现的结果;(2)求两次摸出的球都是编号为3的球的概率.19.(6分)如图,△ABC的三个顶点都在格点上,每个小方格边长均为1个单位长度.(1)请你作出△ABC关于点O成中心对称的△A1B1C1(其中A的对称点是A1,B的对称点是B1,C的对称点是C1);(2)直接写出点B1、C1的坐标.20.(6分)如图,四边形ABCD内接于⊙O,E为AB延长线上一点,若∠AOC=140°.求∠EBC的度数.四、解答题(本大题共有4小题,共28分)21.(7分)如图,AB是⊙O的直径,点C、D在⊙O上,且AC平分∠BAD,点E 为AB的延长线上一点,且∠ECB=∠CAD.(1)①填空:∠ACB= ,理由是;②求证:CE与⊙O相切;(2)若AB=6,CE=4,求AD的长.22.如图1,在△ABC中,∠A=120°,AB=AC,点P、Q同时从点B出发,以相同的速度分别沿折线B→A→C、射线BC运动,连接PQ.当点P到达点C时,点P、Q同时停止运动.设BQ=x,△BPQ与△ABC重叠部分的面积为S.如图2是S 关于x的函数图象(其中0≤x≤8,8<x≤m,m<x≤16时,函数的解析式不同).(1)填空:m的值为;(2)求S关于x的函数关系式,并写出x的取值范围;(3)请直接写出△PCQ为等腰三角形时x的值.23.(7分)如图,Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB于D.(1)求证:△ACB∽△ADE;(2)求AD的长度.24.(7分)如图,进行绿地的长、宽各增加xm.(1)写出扩充后的绿地的面积y(m2)与x(m)之间的函数关系式;(2)若扩充后的绿地面积y是原矩形面积的2倍,求x的值.五、解答题(本大题共有2小题,共20分)25.如图,抛物线y=a(x﹣m)2﹣m(其中m>1)与其对称轴l相交于点P,与y轴相交于点A(0,m).点A关于直线l的对称点为B,作BC⊥x轴于点C,连接PC、PB,与抛物线、x轴分别相交于点D、E,连接DE.将△PBC沿直线PB 翻折,得到△PBC′.(1)该抛物线的解析式为(用含m的式子表示);(2)探究线段DE、BC的关系,并证明你的结论;(3)直接写出C′点的坐标(用含m的式子表示).26.如图(1),将线段AB绕点A逆时针旋转2α(0°<α<90°)至AC,P 是过A,B,C的三点圆上任意一点.(1)当α=30°时,如图(1),求证:PC=PA+PB;(2)当α=45°时,如图(2),PA,PB,PC三条线段间是否还具有上述数量关系?若有,请说明理由;若不具有,请探索它们的数量关系.2019-2020学年九年级(上)期末数学试卷参考答案一、选择题(共8小题,每小题3分,满分24分)1.D.2. A.3.C.4. A.5.B.6.B.7.D.8.C.二、填空题(本大题共有8小题,每小题3分,共24分)9.70.10..11.c<4.12.15.13.∠C=∠BAD.14.y3<y2<y.15.﹣1.16.3 三、解答题(本大题共有4小题,共24分)17.解:(1)(x+1)(x﹣2)=0,(x+1)(x﹣2)=0,解得x1=﹣1,x2=2;(2)方程变形得:x2﹣4x=﹣1,配方得:x2﹣4x+4=3,即(x﹣2)2=3,开方得:x﹣2=±,则x1=2+,x2=2﹣.18.解:(1)画树状图如下:由树状图可知所有可能出现的结果共9种;(2)由(1)中考共有9种等可能的结果,两次摸出的球都是编号为3的球的情况数是1种,所以其概率为.19.解:(1)如图所示:.(2)根据上图可知,B1(2,2),C1(5,﹣1).20.解:由圆周角定理得,∠D=∠AOC=70°,由圆内接四边形的性质得,∠EBC=∠D=70°.四、解答题(本大题共有4小题,共28分)21.解:①∵AB为⊙O的直径,∴∠ACB=90°,故答案为90°,直径所对的圆周角是直角;②连接OC,则∠CAO=∠ACO,∵AC平分∠BAB,∴∠BAC=∠CAD,∵∠ECB=∠CAD.∴∠BAC=∠ECB.∴∠ECB=∠ACO,∵∠ACO+∠OCB=90°,∴∠ECB+∠OCB=90°,即CE⊥OC.∴CE与⊙O相切;(2)∵CE与⊙O相切,∴CE2=BE?AE,∵AB=6,CE=4,∴42=BE(BE+6),∴BE=2,∴AE=6+2=8,∵△ACE∽△CBE,∴=,即=,∴AC=4,∴AC=CE=4,∴∠CAB=∠E,∴∠ECB=∠E,∴∠ABC=2∠ECB=2∠BAC,BC=BE=2,∴∠DAB=∠ABC,∴AD=BC=2.22.解:(1)如图1中,作AM⊥BC,PN⊥BC,垂足分别为M,N.由题意AB=AC=8,∠A=120°,∴∠BAM=∠CAM=60°,∠B=∠C=30°,∴AM=AB=4,BM=CM=4,∴BC=8,∴m=BC=8,故答案为8.(2)①当0≤m≤8时,如图1中,在RT△PBN中,∵∠PNB=90°,∠B=30°,PB=x,∴PN=x.s=?BQ?PN=?x??x=x2.②当8<x≤16,如图2中,在RT△PBN中,∵PC=16﹣x,∠PNC=90°,∠C=30°,∴PN=PC=8﹣x,∴s=?BQ?PN=?x?(8﹣x)=﹣x2+4x.③当8<x≤16时,s=?8?(8﹣?x)=﹣2x+32.(3)①当点P在AB上,点Q在BC上时,△PQC不可能是等腰三角形.②当点P在AC上,点Q在BC上时,PQ=QC,∵PC=QC,∴16﹣x=(8﹣x),∴x=4+4.③当点P在AC上,点Q在BC的延长线时,PC=CQ,即16﹣x=x﹣8,∴x=8+4.∴△PCQ为等腰三角形时x的值为4+4或8+4.23.(1)证明:∵DE⊥AB,∠C=90°,∴∠EDA=∠C=90°,∵∠A=∠A,∴△ACB∽△ADE;(2)解:∵△ACB∽△ADE,∴=,∴=,∴AD=4.24. 解:(1)由图可得,扩充后的绿地的面积y(m2)与x(m)之间的函数关系式是:y=(30xm+m)(20xm+m)=600x2m2+50xm2+m2,即扩充后的绿地的面积y(m2)与x(m)之间的函数关系式是:y=600x2m2+50xm2+m2;(2)∵扩充后的绿地面积y是原矩形面积的2倍,∴600x2m2+50xm2+m2=2×30xm×20xm,解得(舍去),即扩充后的绿地面积y是原矩形面积的2倍,x的值是.五、解答题(本大题共有2小题,共20分)25.解:(1)把点A(0,m)代入y=,得:2am2﹣m=m,am﹣1=0,∵am>1,∴a=,∴y=,故答案为:y=;(2)DE=BC.理由:又抛物线y=,可得抛物线的顶点坐标P(m,﹣m),由l:x=m,可得:点B(2m,m),∴点C(2m,0).设直线BP的解析式为y=kx+b,点P(m,﹣m)和点B(2m,m)在这条直线上,得:,解得:,∴直线BP的解析式为:y=x﹣3m,令y=0, x﹣3m=0,解得:x=,∴点D(,0);设直线CP的解析式为y=k1x+b1,点P(m,﹣m)和点C(2m,0)在这条直线上,得:,解得:,∴直线CP的解析式为:y=x﹣2m;抛物线与直线CP相交于点E,可得:,解得:,(舍去),∴点E(,﹣);∵x D=x E,∴DE⊥x轴,∴DE=y D﹣y E=,BC=y B﹣y C=m=2DE,即DE=BC;(3)C′(,).连接CC′,交直线BP于点F,∵BC′=BC,∠C′BF=∠CBF,∴CC′⊥BP,CF=C′F,设直线BP的解析式为y=kx+b,点B(2m,m),P(m,﹣m)在直线上,∴,解得:,∴直线BP的解析式为:y=x﹣3m,∵CC′⊥BP,∴设直线CC′的解析式为:y=x+b1,∴,解得:b1=2m,联立①②,得:,解得:,∴点F(,),∴CF==,设点C′的坐标为(a,),∴C′F==,解得:a=,∴,∴C′(,).26.证明:(1)如图(1),在PA上截取PD=PA,∵AB=AC,∠CAB=60°,∴△ABC为等边三角形,∴∠APC=∠CPB=60°,∴△APD为等边三角形,∴AP=AD=PD,∴∠ADC=∠APB=120°,在△ACD和△ABP中,,∴△ACD≌△ABP(AAS),∴CD=PB,∵PC=PD+DC,∴PC=PA+PB;(2)PC=PA+PB,如图(2),作AD⊥AP与PC交于一点D,∵∠BAC=90°,∴∠CAD=∠BAP,在△ACD和△ABP中,,∴△ACD≌△ABP,∴CD=PB,AD=AP,根据勾股定理PD=PA,∴PC=PD+CD=PA+PB.。
2019-2020年九年级上册期末试卷附参考答案

2019-2020年九年级上册期末试卷附参考答案( )1. Mr. Green gave us on how to learn English well.A. some advicesB. many adviceC. some adviceD. an advice( )2.—Alice, you on the phone.—I’m coming. Thanks.A. wantB. are wantedC. are wantingD. have wanted( )3.—will Mr Green be back?—In a week, I think.A. How oftenB. How manyC. How longD. How soon( )4. At times they go to the cinema. In this sentence “At times”means .A. all the timeB. usuallyC. on timeD. something( )5. The sign “@” in tzjoy “@” means .A. aB. toC. atD. on( )6. The writing brushes(毛笔) bamboo and animal’s hair.A. are made ofB. is made fromC. is made ofD. are made from( )7.—Do you need more time to finish the work?—Yes, another ten days enough.A. areB. isC. wereD. was( )8. We all how he made such great progress in a short time.A. believedB. thoughtC. wonderedD. decided( )9. Tell me next.A. to do whatB. how to doC. what to doD. to go where( )10. We’ll never give up working on the experiment, difficult it is.A. no matter howB. no matter whenC. no matter whatD. no matter where( )11.—It’s a secret between us. Don’t tell any body else.—Sure, .A. I doB. d don’tC. I willD. I won’t( )12. They have no problems out the maths problem.A. workB. workingC. worksD. to work( )13.—Merry Christmas and best wishes for the New Year!—.A. You are happyB. Happy birthday to youC. The same to youD. Good luck( )14. The letter is in French, I can’t read it.A. writingB. writtenC. wroteD. writes( )15. We’ll do all we could our friends.A. helpB. to helpC. helpsD. helping( )16.—My car has broken down. Can I borrow .—Sorry, they are all out.A. anyone’sB. someone’sC. anyone else’sD. someone else( )17. She can’t the difference between the two words.A. sayB. speakC. talkD. tell( )18.—We have worked for a long time, so we a rest.—Sound good!A. stopped to haveB. stopped havingC. stop havingD. stop to have( )19. Are you fond staying here?A. aboutB. toC. ofD. with( )20. Everyone knows that paper is made wood and books are made paper.A. of; ofB. from; ofC. from; fromD. of; fromⅡ. 完形填空You may think that English dictionaries have been used for many, many centuries. In fact, an English dictionary you 1 today wasn’t made until the Qin Dynasty. They spent most of the important 2 work on dictionaries.They spent nearly all their lives trying to 3 words for their dictionaries. For them, it was a wonderful journey. The largest dictionary in the world is Oxford English Dictionary(牛津字典). The 4 for this dictionary came from an important meeting in Britain in 1857. twenty-two years later, Oxford University asked James Murray to be the editor(编者)of its new dictionary.Murray had never been to 5 . At the age of fourteen, he left his village school in Scotland and taught himself while working in bank. 6 he became a great teacher. After Oxford gave him the job. Murray had a small house 7 in his garden to do the work. Every morning, Murray got out of bed at five o’clock and 8 in the small house several hours before breakfast. Often he would work into the night. Murray hoped to finish the new dictionary in ten years but after five year, he was 9 adding(增加)words for the letter “A”!He worked on the dictionary 10 he was very old. Forty-four years later, in 1928, other editors finished the dictionary.( )1. A. use B. write C. copy D. miss( )2. A. easy B. boring C. early D. dangerous( )3. A. spell B. invent C. collect D. make( )4. A. way B. idea C. use D. prize( )5. A. school B. cinema C. village D. collage( )6. A. Later B. Longer before C. So far D. Ever since( )7. A. sold B. built C. broken D. drawn( )8. A. read B. wrote C. worked D. thought( )9. A. already B. still C. usually D. always( )10. A. if B. because C. until D. sinceⅢ. 阅读理解(A)Which is the best way to learn a language? We know that we all learnt our own language well when we were children, if we learn a second language in the same way, it won’t seem so difficult. How does a small child do? It listens to what people say, and it tries to guess what it hears. When it wants something, ithas to ask for it. It’s using the language, thinking in it and talking in it all the time. If people use a second language all the time, they will learn it quickly.In school, you learn to read, to write, to hear and to speak. It is the best way to learn all new words through the car. You can read them, spell them, and write them later. ( )1. When we were very young .A. it’s difficult for us to understand peopleB. we learnt our language through our earsC. we could not guess what people sayD. we could hear our own language but couldn’t understand it( )2. A small child can learn his own language very well because .A. he’s cleverB. his parents took good care of itC. he keeps on using itD. he often tries to guess what he hears( )3. According to the text, it is the best way to learn a second language, .A. remembering as many words as we canB. writing all the timeC. using out ears firstD. looking up the words in the dictionary when we don’t know theirmeanings.( )4. In school, when we learn a second language, we must .A. do nothing but listen to our teachersB. often listen, speak, read and writeC. learn it by heart all the timeD. translate it into our own language all the time( )5. The word “it” in the sentence “it” wont seem so difficult” refers(指的是).A. the small childB. the second languageC. learning the second languageD. the best way to learn language(B)Dolphins are not fish. They are mammals(哺乳动物). They live in groups and speak to each other in their own language. But they are quite different from almost all land animals. Their brain(大脑)is as big as men’s and t hey live a long life-at least 20 or 30 years.Like some animals, dolphins use sounds to help them find their way around. They also use these sounds to talk to each other and to help them find food. They do not use their ears to receive sounds, but use the jaw-the lower part of the mouth.It si strange that dolphins are friendly to men, and for thousands of years,there are many stories about dolphins and men. In the 19 th century, in a dangerous part of the sea near New Zealand, there was a dolphin, the seaman liked him very much and gave him a very good name, Jack. From 1871 to 1903 a passenger on a boat with the name of The Penguin shot and hurt Jack. Luckily the dolphin didn’t die, and after a long time he was well again. He guided the ships through the area for nine more year, but he refused to help the boat The Penguin.Today, some people still kill dolphins, but many countries in the world now protect them. In these places, people are not allowed to kill them.( )6. The word jaw means in Chinese.A. 下颌B. 嘴巴C. 嘴唇D. 鼻子( )7. How do dolphins find their way?A. They use their noses to smell the way.B. They use their ears to hear the sounds.C. They use their eyes to see the way.D. They use sounds to find the way.( )8. Who was Jack?A. The writer.B. A dolphin.C. A seaman.D. The passenger.( )9. The dolphin guided the ships for .A. 32 yearsB. 9 yearsC. 41 yearsD. 23 years( )10. According to the passage, which of the following is NOT right?A. Dolphins are not fish.B. Dolphins don’t live in groups.C. Dolphins are kind and friendly to people.D. Dolphins can live a long life.Ⅳ. 情景交际根据对话内容,从方框中选出五个合适的句子补全对话,并将其字母填入题后横线上。
2019-2020年九年级上册期末考试试卷附参考答案

2019-2020年九年级上册期末考试试卷附参考答案温馨提示:亲爱的同学,本试卷满分150分,答题时间150分钟,试卷共分为第I卷和第Ⅱ卷,第I卷为77分,第Ⅱ卷为65分;卷面书写8分。
相信你通过九年时间的语文学习,一定会在本次考试中取得可喜的成绩!第Ⅰ卷(共77分)一、(6分)1.下列加点字的注音完全正确..的一项是(2分)()A.古刹.(chà)褴褛.(lǔ)言简意赅.(gāi)B.惬.意(qiè)惺.松(xīng)揠.苗助长(yà)C.贮.藏(zhù)尴尬.(gǎ)鸢.飞戾天(yuān)D.阴晦.(huì)婆娑.(sō)鄙夷不屑.(xiè)2.下列句子中有错别字....的一项是(2分)()A.北雁南飞,活跃在田间草际的昆虫也都销声匿迹。
B.有些人总认为矜持、含蓄才是美德,但在今天这样的时代里,直截了当的沟通更为重要。
C.我怀念着绿色,如同涸辙的鱼盼等着雨水!D.花丛中,两颗高大的古树,枝繁叶茂,绿荫如盖,根部护以石栏,显得与众不同。
3.依次填入下面各句横线处的词语,最恰当的一组是(2分)()①这一地区曾一度山洪,造成公路被毁、交通中断。
②北京市政府对城市建设布局做出了,在2008年前将每年增加800万平方米的绿地。
③商业广告不同于公益广告,其主要目的就是为了。
A.暴发计划盈利B.暴发规划营利C.爆发计划盈利D.爆发规划营利二、(5分)请你向你的同学推荐一篇课外精美的散文(或小说),并把你的推荐词写在美文推荐卡上(15字左右)三、(40分)阅读下面文字,分别回答问题[一](20分)黎明的眼睛三月清晨,把窗子推开,第一片阳光便飞到人们的全身。
对着阳光带进来的新鲜空气,任谁都要深吸一口,说:春天来了!就这样,春天从窗口走近我们。
但是,可不要忘记,不是从有房子那天起,我们就有了窗子!我们的兄弟,爱斯基摩人用冰块建筑的房子,像个白玉的钟罩一般,是没有什么窗子的。
2019--2020第一学期九年级数学期末考试及答案

2019-2020学年度第一学期期末调研考试九年级数学试卷注意:本试卷共8页,三道大题,26小题。
总分120分。
时间120分钟。
题号 一 二 20 21 22 23 24 25 26 总分 得分一、 选择题(本题共16小题,总分42分。
1~10小题,每题3分;11~16小题,每题2分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
请将正确选项的代号填写在下面的表格中)题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 答案1.“抛一枚均匀硬币,落地后正面朝上”这一事件是( ) A .必然事件 B .随机事件 C .确定事件D .不可能事件2. 如图,该图形围绕自己的旋转中心,按下列角度旋转后,不能与自身重合的是( ) A .72° B .108° C .144° D .216° 3.反比例函数ky x=的图象经过点P(-1,2),则这个函数的图象位于( ) A .第二、三象限 B .第一、三象限 C .第三、四象限 D .第二、四象限4.用配方法将方程0142=--x x 变形为m x =-2)2(,则m 的值是( )A. 4B. 5C. 6D. 75. 在下列四个图案中,既是轴对称图形,又是中心对称图形的是( )A.B.C.D.6. 一元二次方程220200x +=的根的情况是( )A .有两个相等的实根B .有两个不等的实根C .只有一个实根D .无实数根 7. 如图,在正方形网格上有两个相似三角形△ABC 和△EDF ,则∠BAC 的度数为( )得分 评卷人A .105°B .115°C .125°D .135°8. 已知三角形面积一定,则它的底边a 上的高h 与底边a 之间的函数关系图象是( )9. 下列对二次函数2y x x =-图象的描述,正确的是( )A .开口向下B .对称轴是y 轴C .经过原点D .在对称轴右侧部分是下降的 10. 参加一次聚会的每两人都握了一次手,所有人共握手10次。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
苏以数谏故 ,上使外将兵。今或闻无罪 ,二世杀之。百姓多闻其贤 ,未知其死也。项楚为楚将 ,
数有功 ,楚人怜之。或以为死 ,或以为亡。今诚以吾众 ,诈自称公子扶苏、项燕 ,为天下唱 ,宜多
应者。”吴广以为然。乃行卜。 卜者知其指意 ,曰 : “足下事皆成,有功。然足下卜之鬼乎 ? ”陈胜、
吴广喜 ,念鬼 , 曰 : “此教我先威众耳。”乃丹书帛曰: “陈胜王”,置人所罾鱼腹中。卒买鱼烹食 ,
用一句话概括出来。 (2 分)
答: 二、古诗文阅读(共 10 分)
读《陈涉世家》选段回答
8- 12 题
陈涉世家
二世元年七月,发闾左適戍渔阳,九百人屯大泽乡。陈胜、吴广皆次当行,为屯长。会
天大雨,倒不通,度已失期。失期,法皆斩。陈胜、吴广乃谋曰:
“今亡亦死,举大计亦死;
等死, 死国可乎?”陈胜曰 : “天下苦秦久矣。吾闻二世少子也 ,不当立 ,当立者乃公子扶苏。 扶
他学习非常认真专注。一次,他一边吃饭,一边学习,竟把练习纸放进了嘴里。他之所 以学习成绩优秀,是他刻苦学习的原因。②
他的妈妈年轻、漂亮、手巧、善良。在生活和学习上,同学一有困难总愿求他。这时候, 他总是微笑着说: “我们都是同学,应该互相帮助。 ”
虽然一点帮助不值得称道,但是,我们全班同学都从内心里由衷的感谢他。③ ( 1)修改加线的三个句子( 3 分) ① ② ③ 除了以上三处外,本文还有什么问题?请改正其中一处(多改以第一处记分)
! ”众皆
令军士更替吃饭。孔明一日上坛三次,下坛三次。 …… 将近三更时分,怨听风声响,旗幡转 动。瑜出帐看时,旗脚竟飘西北 —— 霎时同东南风大起。
( 1)以上选段出自中国古典名著《
》,作者是元末明初的小说家
。(1 分)
( 2)试用简洁的语言概括这个故事情节。 (1 分 )
答:
。
( 3)从上面语段看,孔明是一个怎样的人?请你从原著中再找出一个有关孔明的故事,
得鱼腹中书 ,固以怪之矣。又间令吴广之次所旁从祠中 ,夜篝火 ,狐鸣呼曰 : “大楚兴, 陈胜王”。
卒皆夜惊恐。旦日 ,卒中往往语 ,皆指目陈胜。
8.下面加点词语意义或用法相同的一项是 ( )(2 分 )
会天大雨
又间令吴广之次所旁丛神祠中
A
B
会宾客大宴 固以怪之矣
中间力拉崩倒之声 乃丹书帛曰 : 陈“胜王 ”
际,文天祥的 “人生自古谁无死,
。 ”的凛然正气,无不深深打动着我们的心,使
我们的精神得到陶冶。
3.用一组句式整齐。语言优美的句子(至少含有三个分句) 或者表达你对校园生活的某种情感。 ( 2 分)
,勾勒你眼中的校园生活,
示例 1:校园就是乐园,在这里,我们学习知识,探索奥秘;在这里,我们放飞心灵, 感受快乐;在这里我们建立友谊,共同成长。
C
D
扶苏以数谏故
卒买鱼烹食 ,得鱼腹中书
9.用现代汉语翻译下列句子( 2 分)
①今亡亦死,举大计亦死;等死,死国可乎?
②今诚以吾众诈自称公子扶苏、项燕,为天下唱,宜多应者。
2019-2020 年初三第一学期期末考试及答案
卷首寄语 ------ 同学们,经过近三年初中语文的学习,你一定有不少的收获吧!下面的
题目会让你对自己的学习有一个全面的评价,仔细审题,认真答题,你就会有出色的表现,
相信自己的实力,祝你成功!
A 卷( 100 分)
一、积累与运用(共 20 分)
1.给下列加点字注音,并改正句中的错别字。 (2 分) 一个衣服褴褛的年老水手拿小刀一下翘开牡蛎,递给两位先生,再由他们递给两位太
( 1 分)
6.如果你是丘吉尔,该怎样回答? (2 分 )
英国首相到美国访问,在众议院发表演说后走下讲台。一位反对他的女议员气冲冲地走
到他的面前说: “阁下,如果我是你的妻子的话,我会在你的咖啡里下毒药。
”邱吉尔平静地
看着她说: “
。”
7.名著阅读 (4 分 ) 阅读下面语段,回答问题。
孔明于十一月二十曰甲子吉辰,沭浴斋戒,身披道衣,跣足散发,来到坛前。吩咐守坛 将士: “不许擅离方位。不许交头接耳。不许失口乱言。不许失惊打怪。如违令者斩 领命。孔明缓步登坛,观瞻方位已定,焚香于炉,注水于盂,仰天暗祝。下坛入帐中少歇,
_____
4.我国古典四大名著中, 典型的人物和故事情节一定给你留下了深刻的印象,
其中 “协
理 荣 国 府 ”“煮 酒 论 英 雄 ”“风 雪 山 神 庙 ”“三 打 白 骨 精 ”等 故 事 和 主 人 公 分 别 是
_________________________
、
______________________
、
_________________________________ 、 _______________________________ ( 2 分)
5.下面是一名学生的习作《我的同学》的一部分,读后请按要求答题(
4 分)
我上初中以后,结识了一个叫王冬的同学。他个子大约一米六,头发清秀,双眼皮,戴
着一副眼睛。他尽管学习刻苦,但是乐于助人。①
示例 2:校园里, 长长的台阶记录着我们进步的脚印; 明亮的灯光注视着我们专注的神 情;热闹的操场承载着我们快乐的身影。
你的创意: _________________________________________________________________
__________________________________________________________________________
“
,愁云惨淡万里凝 (岑参 《白雪歌送武判官归京》 )”为我们呈现边塞风光; “海
内存知己,
。“是王勃对即将离别的友人的真诚劝慰, “但愿人长久,
。”
是苏轼对相隔两地亲人深情的祝愿;杜甫《望岳》抒写
“
,一览众山小 ”之豪情;
王安石《登飞来峰》悟出 “不畏浮云遮望眼,
。“的哲理;在国家受辱 .生灵涂炭之
太。 ①褴褛 ______________
② _____________ 改为 ____________
2.根据语境,在横线上填上诗文原句: (共 4 分)
漫步在文学艺术的长廊,品读古代优美诗词:
“乱花渐欲迷人眼,
(白居易
《钱塘湖春行》 )”引领我们欣赏早春美景; “
,长河落日圆 (王维 《使至塞上》 )”,
