2015年希望杯第二试试题(初三年级)
希望杯数学邀请赛九年级二试模拟试题
)
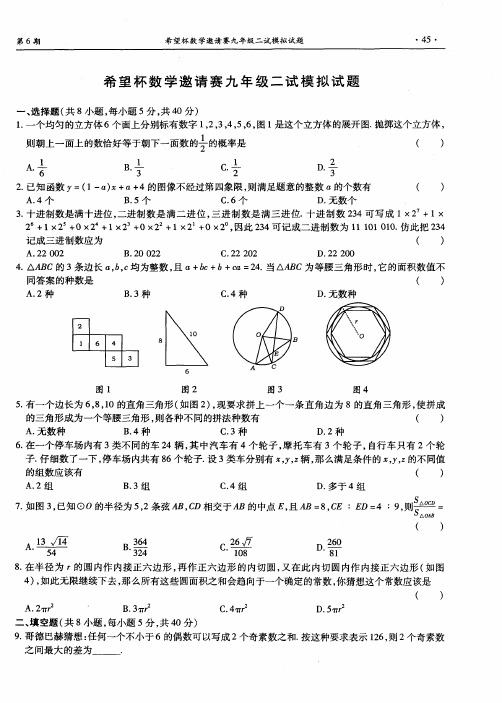
8 在半径 为 r . 的圆内作 内接正六边形 , 再作正六边形的 内切圆, 又在此 内切圆内作内接正六边形 ( 如图 4, ) 如此无限继续下去 , 那么所有这些圆面积之和会趋向于一个确定 的常数 , 你猜想这个常数应该是
(
A. r2 27r B
.
)
3 P =
C 4r2 ., r r
1. 123, ,95 0 将 , , … 4 ,O任意 分 成 1 O组 , 组 5个 数 , 组 中 有 1个 中位 数 , 这 1 中 位数 之 和 的最 大 每 每 则 O个 值是一 1. 个 长方 体 的长 、 、 1一 宽 高分 别 为 9c 6c 5c 先 从 这个 长方 体 上 尽 可 能 大地 切 下 一个 正 方 体 , 从 m, m, m. 再
一
、
1
则朝上一面上的数恰好等于朝下一面数的÷的概率是
' 1 1 , ,
(
)
A ÷ .
U
B÷ .
J
c÷ .
二
D ÷ .
J
2 已知 函数 Y 1 a x+ 4的图像不经过第 四象限 , . =( 一 ) 0+ 则满足题意的整数 口的个数有 ( ) A. 4个 B 5个 . C 6个 . D 无数 个 . 3 十进制 数 是 满 十进位 , 进制 数 是 满 二 进 位 , 进 制 数 是 满 三 进 位. 进 制 数 2 4可写 成 1× +1× . 二 三 十 3 2 2 + l ×2 +O ×2 + 1× 2 +O ×2 + l × 2 +O ×2 因此 2 4可 记 成 二进 制 数 为 1 11 . 。 3 1 0 0 仿此 把 2 4 0 3 记成三进制数应为 ( )
初中二年级历届“希望杯”二试解答题

初中二年1-17届“希望杯”二试解答题1.1、从自然数354 , , 3 , 2 , 1 中仸取178个数,试证:其中必有两个数,它们的差是177。
1.2、平面上有两个边长相等的正方形ABCD 和D C B A '''',且正方形D C B A ''''的顶点A '在正方形ABCD 的中心。
当正方形D C B A ''''绕A '转动时,两个正方形的重合部分的面积必然是一个定值。
这个结论对吗?证明你的判断。
1.3、用1,9,9,0四个数码组成的所有可能的四位数中,每一个这样的四位数与自然数n 之和被7除余数都不为1,将所有满足上述条件的自然数n 由小到大排成一列 <<<<4321n n n n ,试求:21n n ⋅之值。
2.1、已知两个正数的立方和是最小的质数,求证:这两个数之和不大于2。
2.2、一块四边形的地(如图2.2所示)(KG OH FK EO //,//)内有一段曲折的水渠,现在要把这段水渠EOHGKF 改成直的(即两边都是直线)。
但进水口EF 的宽度不能改变,新渠占地面积与原水渠面积相等,且要尽可能利用原水渠以节省工时,那么新渠的两条边应当怎么作?写出作法,幵加以证明。
A B 图2.23.1、若0 , , , >d c b a ,证明:在方程02212=+++cd x b a x , 02212=+++da x c b x ,02212=+++ab x d c x ,02212=+++bc x a d x 中,至少有两个方程有不相等的实数根。
3.2、(1)能否把1992 , , 3 , 2 , 1 这1992个数分成八组,使得第二组各数之和比第一组各数之和多10,第三组各数之和比第二组各数之和多10,…,最后第八组各数之和比第七组各数之和也多10?请加以说明。
2015年世界少年奥林匹克数学竞赛九年级海选赛试题含答案

九年级 第1页 九年级 第2页2015年世界少年奥林匹克数学竞赛九年级海选赛试题含答案绝密★启用前世界少年奥林匹克数学竞赛(中国区)选拔赛地方海选赛试题(2015年10月)选手须知:1、本卷共三部分,第一部分:填空题,共计50分;第二部分:计算题,共计12分;第三部分:解答题,共计58分。
2、答题前请将自己的姓名、学校、赛场、参赛证号码写在规定的位置。
3、比赛时不能使用计算工具。
4、比赛完毕时试卷和草稿纸将被收回。
九年级试题(A卷)(本试卷满分120分 ,考试时间90分钟 )一、填空题。
(每题5分,共计50分)1、两块三角形面板如图放置,等腰直角三角形板ABC 的斜边BC 与∠F=30°的直角三角板DEF 的直角边EF 重合,则∠a 的度数为 。
2、若a 、b 都为实数,且b = 20131-a + 2014a -1+ 2015 则a b= 。
3.设x 1,x 2是方程x 2 - x -2013 = 0 的两实数根,则x 13+2014x 22-2013= 。
4、已知三个实数x ,y ,z 中,x 与y 的平均数是127,y 与z 的和的31是78,x 与z 的和的41是52,则这三个数x ,y ,z 的平均数是 。
5、如图,矩形ABCD 中,已知AB=5,AD=12,P 是AD 上的动点,PE ⊥AC 与E ,PF ⊥BD 与F ,则PE+PF= 。
6、如图,在平面直角坐标系中,△ABC 是等腰直角三角形,∠ACB = Rt, CA ⊥x 轴,垂足为点A ,点B 在反比例函数y 1=x4(x>0)的图像上,反比例 函数y 2=x2(x>0)的图像经过点C ,交AB 于点D ,则点D 的坐标 。
7、若有理数x ,y ,z 满足2121=-+-+z y x (x+y+z )则(x-zy)2= 。
8、我国汉代数学家赵爽为了证明勾股定理,创制了一副"弦图",后人称其为"赵爽弦图"如图,也是由八个全等的直角三角形拼接而成,记图中正方形ABCD ,正方形EFGH,正方形MNKT 的面积,分别为S 1,S 2,S 3,若S 1+S 2+S 3 = 10 ,则S 2的值是 。
2015年全国初中数学联合竞赛(初三)试题及解答

第一试(A)
一、选择题(本题满分 42 分,每小题 7 分) 1. 设实数 a, b, c 满足: a b c 3, a2 b2 c2 4 ,则 A.0 【答】D. 【解析】 B.3 C.6
a 2 b2 b2 c 2 c 2 a 2 =( 2c 2a 2b
D.9
)
a 2 b2 b2 c 2 c 2 a 2 4 c 2 4 a 2 4 b2 (2 c) (2 a) (2 b) 9 . 2c 2a 2b 2c 2a 2b
2. 若抛物线 y x2 bx c 与 x 轴只有一个公共点, 且过 A(m, n) ,B(m 8, n) , 则 n ( A.8. 【答】 C 【解析】法一(LTX) : 依题意,设抛物线解析式为 y ( x h)2 , 因为它过 A(m, n) , B(m 8, n) , 所以 h m 4 ,故 n (m h)2 (4)2 16 ,选 C . 法二: 由题意, b 8 2m ,
2 2 2
)
A.3 【答】D.
B.6.
C .9
D.12
【解析】设 x y t ,则 x y t , 代入题设等式得 ( y t )2 ( y t ) y y 2 3 ,整理得 3 y 2 3ty t 2 3 0 . 由判别式 (3t )2 12(t 2 3) 3 得 2 3 t 2 3 ,故 ( x y)2 t 2 12 . 5.题目和解答与(A)卷第 4 题相同. 6.设 n 是小于 100 的正整数且使 2n2 3n 2 是 6 的倍数,则符合条件的所有正整数 n 的和 是( ) B.850 C.1536 D.1634
-年初一希望杯第二试试题及答案(word版)

2015 年初一希望杯第二试1、请你想好一个数。
将该数与2015之和乘以4,减去12,再将其差除以4,然后减去你想好的那个数,最后的结果等于()(A) 0 (B) 2008 (C) 2012 (D)20152、若a + 2015 = 0,则a − 2015的值是()(A) − 4030 (B) − 2015 (C) 0 (D)20153、如图1,MA//BN//CP,若BA =BC,∠MAC = 50°,∠NBC =150°,则∠ABC =()(A) 60°(B) 150°(C) 140°(D) 130°4、红光中学初一年级有3个班,已知一班、二班的平均人数与三班人数之和为45,二班、三班的平均人数与一班人数之和为48,一班、三班的平均人数与二班人数之和为47。
则三个班的总人数为()(A) 68 (B) 70 (C) 72 (D)745、As shown in the Fig.2,Points A,B and C on the number axis represent nonzero rational numbera ,b,and c respectively . If |a| + |a + b| + |b − c| = −c,then the point represent 0 is()(A) on the right side of A(B) on the left side of C(C) between B and C(D) between B and A(翻译)如图2,数轴上的点A,B,C代表非零数字a,b和c,如果|a| + |a +b| + |b − c| =−c,则代表0的点位于()(A) A点的右边(B) C点的左边(C) B , C之间(D) B , A之间6、如图3,正方形ABCD由四个相同的小长方形和一个小正方形EFGH组成。
历届(第1-23届)希望杯数学竞赛初一七年级真题及答案

“希望杯”全国数学竞赛(第1-23届)初一年级/七年级第一/二试题目录1.希望杯第一届(1990年)初中一年级第一试试题......................003-0052.希望杯第一届(1990年)初中一年级第二试试题......................010-0123.希望杯第二届(1991年)初中一年级第一试试题...... 0错误!未定义书签。
-0204.希望杯第二届(1991年)初中一年级第二试试题...... 0错误!未定义书签。
-0265.希望杯第三届(1992年)初中一年级第一试试题...... 0错误!未定义书签。
-0326.希望杯第三届(1992年)初中一年级第二试试题...... 0错误!未定义书签。
-0407.希望杯第四届(1993年)初中一年级第一试试题...... 0错误!未定义书签。
-0508.希望杯第四届(1993年)初中一年级第二试试题...... 0错误!未定义书签。
-0589.希望杯第五届(1994年)初中一年级第一试试题...... 0错误!未定义书签。
-06610.希望杯第五届(1994年)初中一年级第二试试题..... 0错误!未定义书签。
-07311.希望杯第六届(1995年)初中一年级第一试试题..... 0错误!未定义书签。
-080 12希望杯第六届(1995年)初中一年级第二试试题..... 0错误!未定义书签。
-08713.希望杯第七届(1996年)初中一年级第一试试题..... 0错误!未定义书签。
-09814.希望杯第七届(1996年)初中一年级第二试试题....... 错误!未定义书签。
-10515.希望杯第八届(1997年)初中一年级第一试试题....... 错误!未定义书签。
-11316.希望杯第八届(1997年)初中一年级第二试试题....... 错误!未定义书签。
-12017.希望杯第九届(1998年)初中一年级第一试试题....... 错误!未定义书签。
15年(二模)九年级数学试题

2014—2015学年度第二学期教学质量阶段性检测九年级数学试题(满分:120分时间:120分钟)友情提示:亲爱的同学,你好!今天是你展示才能的时候,只要你仔细审题、认真答题,你就会有出色的表现!第Ⅰ卷一、选择题:(本题满分24分,共有8道小题,每小题3分)请把唯一正确答案的字母标号涂在答题卡的相应位置1.12-的倒数是().A.2 B.12C.-2 D.12-2.下列图形中,中心对称图形有()个A .1 B. 2 C. 3 D.43.一种病毒的长度约为0.0000046mm,用科学记数法表示为().A.0.46×105-B.4.6 × 106-C. 46 ×106-D. 4.6×106 4.如图,AB是⊙O的直径,C、D是⊙O上的点,若∠ABC=64°,则∠BDC等于().A.26° B.64° C. 52° D. 128°D FECBA5.如图,在四边形ABCD中,∠A=90°,对角线BD平分∠ABC,若BC=5,AD=4,则△BCD 的面积为().A.6 B.10 C.12 D.20第4题OBDCAAB CD第5题图6.如图,在方格纸上△DEF 是由△ABC 绕定点P 顺时针旋转得到的。
如果用(2,1)表示方格纸上A 点的位置,(1,2)表示B 点的位置,那么点P 的位置为( )。
A .(5, 2) B .(2, 5) C .(2, 1) D .(1, 2)7.若反比例函数()0ky k x =≠的图象经过点A (-2, 1),则当x <-1时,函数值y 的取值范围是( ) .A .y >2 B. -2<y <0 C .y >-2 D .0<y <2 8.已知函数ax ax y +=2与函数y =xa,则它们在同一坐标系中的大致图象是( )第Ⅱ卷二、填空题:(本题满分18分,共有6道小题,每小题3分) 请把正确答案填写在答题卡的相应位置9.化简:01127(3.14)3π---+=() .10.某工厂生产某种产品,今年产量为200件,计划通过技术革新,使今后两年的产量都比前一年增长相同的百分数,这样三年的产量达到1400件,设这个百分数为x ,根据题意,可列方程为 __________________.11.在不透明的袋子中有黑棋子10枚和白棋子若干(它们除颜色外都相同),现随机从中摸出10枚记下颜色后放回,这样连续做了10次,记录了如下的数据:次数12 3 4 5 6 7 8 9 10 黑棋数 132342113根据以上数据,估算袋中的白棋子数量为 枚.12.如图,将边长为3cm 的正方形ABCD 沿 其对角线AC 剪开,再把△ABC 沿着AD 方向平移,得到△A 1B 1C 1,若两个三角形 重叠部分的面积是49cm 2,则△ABC 移动 的距离A A 1是 cm . 第12题图第8题1 3.如图所示的图案(阴影部分)是这样设计的:在△ABC 中,AB =AC =2cm ,∠ABC =30°,以A 为圆心,以AB 为半径作弧BEC ,以BC 为直径作半圆BFC ,则图案(阴影部分)的面积是 .(结果保留π)14.在直角坐标系中,正方形A 1B 1C 1O 1、A 2B 2C 2C 1、A 3B 3C 3C 2、…、A n B n C n C n -1按如图所示的方式放置,其中点A 1、A 2、A 3、…、A n 均在一次函数y kx b =+的图象上,点C 1、C 2、C 3、…、C n 均在x 轴上。
2015年中考二模名校考试数学试题及答案

2015年中考数学二模名校考试数学试题(卷)时间120分钟满分120分2015、2、28一、选择题(1-6小题,每小题2分7-16小题每小题3分,共42分)1.下列各数中,最小的数是()A.﹣2 B.﹣0.1 C.0D.|﹣1| 2.计算(﹣9)2﹣2×(﹣9)×1+12的值为()A.﹣98 B.﹣72 C.64 D.1003.下列式子正确的是()A.﹣(x﹣3)=﹣x﹣3 B. 5a﹣a=5C. 2﹣1=﹣2 D. 2<<34.如图,将一个正六边形分割成六个全等的等边三角形,其中有两个已涂灰,如果再随意涂灰一个空白三角形,则所有涂灰部分恰好成为一个轴对称图形的概率是()A.B.C.D.14题图 5题图 7题图5.如图,直线a、b及木条c在同一平面上,将木条c绕点O旋转到与直线a平行时,其最小旋转角为()A.100°B.90°C.80°D.70°6.下列一元二次方程中,无解的是()A. x2+4x+2=0 B.x2+4x+3=0 C.x2﹣4x+4=0 D.x2﹣4x+5=07.如图,Rt△ABC中,∠C=90°,∠B=45°,AD是∠CAB的平分线,DE⊥AB于E,AB=a,CD=m,则AC的长为()A. 2m B.a﹣m C.a D.a+m8.如图,在正方形网格中,△ABC的三个顶点及点D、E、F、G、H都在格点上,现以D、E、F、G、H中的三点为顶点画三角形,则下列与△ABC面积相等但不全等的三角形是()A.△EHD B.△EGF C.△EFH D.△HDF9.计算(﹣)÷的结果为()A.B.C.D.10.如图,平行四边形ABCD的顶点B,D都在反比例函数y=(x>0)的图象上,点D的坐标为(2,6),AB平行于x轴,点A的坐标为(0,3),将这个平行四边形向左平移2个单位、再向下平移3个单位后点C的坐标为()A.(1,3)B.(4,3)C.(1,4)D.(2,4)8题图 10题图11.张昆早晨去学校共用时15分钟.他跑了一段,走了一段,他跑步的平均速度是250m/分钟,步行的平均速度是80m/分钟;他家离学校的距离是2900m,如果他跑步的时间为x分钟,则列出的方程是()A. 250x+80(﹣x)=2900 B.80x+250(15﹣x)=2900C. 80x+250(﹣x)=2900 D.250x+80(15﹣x)=290012.已知⊙O及⊙O外一点P,过点P作出⊙O的一条切线(只有圆规和三角板这两种工具).以下是甲、乙两同学的作业:甲:①连接OP,作OP的垂直平分线l,交OP于点A;②以点A为圆心、OA为半径画弧、交⊙O于点M;③作直线PM,则直线PM即为所求(如图1).乙:①让直角三角板的一条直角边始终经过点P;②调整直角三角板的位置,让它的另一条直角边过圆心O,直角顶点落在⊙O上,记这时直角顶点的位置为点M;③作直线PM ,则直线PM 即为所求(如图2). 对于两人的作业,下列说法正确的是( ) A .甲对,乙不对 B . 甲不对,乙对 C . 两人都对 D . 两人都不对13.如图,直线l 经过点P (1,2),与坐标轴交于A (a ,0),B (0,b )两点(其中a <b ,如果a+b=6,那么tan∠ABO 的值为( )A .B . 1C .D . 213题图 14题图 16题图 14.如图,在⊙O 中,AB 为直径,点C 为圆上一点,将劣弧沿弦AC 翻折交AB 于点D ,连接CD .如果∠BAC=20°,则∠BDC=( )A . 80°B . 70°C . 60°D . 50° 15.对于实数m ,n ,定义一种运算“※”:m※n=m 2﹣mn ﹣3.下列说法错误的是( ) A . 0※1=﹣3 B . 方程x※2=0的根为x 1=﹣1,x 2=3 C .不等式组无解D . 函数y=x※(﹣2)的顶点坐标是(1,﹣4)16.如图1,S 是矩形ABCD 的AD 边上的一点,点E 以每秒kcm 的速度沿折线BS ﹣SD ﹣DC 匀速运动,同时点F 从点C 出发,以每秒1cm 的速度沿边CB 匀速运动,并且点F 运动到点B 时点E 也运动到点C .动点E ,F 同时停止运动.设点E ,F 出发t 秒时,△EBF的面积为ycm 2.已知y 与t 的函数图象如图2所示.其中曲线OM ,NP 为两段抛物线,MN 为线段.则下列说法:①点E 运动到点S 时,用了2.5秒,运动到点D 时共用了4秒; ②矩形ABCD 的两邻边长为BC=6cm ,CD=4cm ; ③sin∠ABS=;④点E 的运动速度为每秒2cm .其中正确的是( )A .①②③B .①③④C .①②④D . ②③④二、填空题(每小题3分,共12分.)17.在△ABC中,若|sinA﹣|+(1﹣tanB)2=0,则∠C的度数为_________ °.18.如图,已知点A、B、C在⊙O上,CD⊥OB于D,AB=2OD,若∠C=40°,则∠B=_________ °.18题图 19题图 20题图19.如图,一条4m宽的道路将矩形花坛分为一个直角三角形和一个直角梯形,根据图中数据,可知这条道路的占地面积为_________ m2.20.如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第60个点的横坐标为_________ .三、解答题(共66分)21.(9分)已知关于x,y的二元一次方程x﹣y=3a和x+3y=4﹣a.(1)如果是方程x﹣y=3a的一个解,求a的值;(2)当a=1时,求两方程的公共解;(3)若是已知方程的公共解,当x0≤1时,求y的取值范围.22.(10分)某中学对校园卫生进行清理,某班有13名同学参加这次卫生大扫除,按要求他们需要完成总面积为80m2的三项清扫工作,三项工作的面积比例如图1,每人每分钟完成各项的工作量如图2.(1)从统计图中可知:擦玻璃、擦课桌椅、扫地拖地的面积分别是_________ m2,_________ m2,_________ m2;(2)如果x人每分钟擦玻璃面积ym2,那么y关于x的函数关系式是_________ ;(3)完成扫地拖地的任务后,把13人分成两组,一组去擦玻璃,一组去擦课桌椅,怎样分配才能同时完成任务?23.(10分)河北省赵县A、B两村盛产雪花梨,A村有雪花梨200吨,B村有雪花梨300吨,现将这些雪花梨运到C、D两个冷藏仓库,已知C仓库可储存240吨,D仓库可储存260吨,从A村运往C、D两处的费用分别为40元/吨和45元/吨;从B村运往C、D两处的费用分别为25元/吨和32元/吨,设从A村运往C仓库的雪花梨为x吨,A、B两村往两仓库运雪花梨的运输费用分别为yA 元,yB元.C D 总计A x吨_________ 300吨B _________ _________ 400吨总计240吨260吨500吨(1)请填写下表,并求出yA ,yB与x之间的函数关系式:(2)当x为何值时,A村的运输费用比B村少?(3)请问怎样调运,才能使两村的运费之和最小?求出最小值.24.(11分)(1)如图1,已知△ABC,以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接BE,CD,请你完成图形,并证明:BE=CD;(尺规作图,不写作法,保留作图痕迹);(2)如图2,已知△ABC,以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE,CD,BE与CD有什么数量关系?简单说明理由;(3)运用(1)、(2)解答中所积累的经验和知识,完成下题:如图3,要测量池塘两岸相对的两点B,E的距离,已经测得∠ABC=45°,∠CAE=90°,AB=BC=100米,AC=AE,求BE的长.25.(12分)已知,抛物线y=ax2+x+c的顶点为M(﹣1,﹣2),它与x轴交于点B,C(点B在点C左侧).(1)求点B、点C的坐标;(2)将这个抛物线的图象沿x轴翻折,得到一个新抛物线,这个新抛物线与直线l:y=﹣4x+6交于点N.①求证:点N是这个新抛物线与直线l的唯一交点;②将新抛物线位于x轴上方的部分记为G,将图象G以每秒1个单位的速度向右平移,同时也将直线l以每秒1个单位的速度向上平移,记运动时间为t,请直接写出图象G 与直线l有公共点时运动时间t的范围.26.(3分)1)如图1、图2,点P是⊙O外一点,作直线OP,交⊙O于点M、N,则有结论:①点M是点P到⊙O的最近点;②点N是点P到⊙O的最远点.请你从①和②中选择一个进行证明.(注:图1和图2中的虚线为辅助线,可以直接利用)(2)如图,已知,点A、B分别是直角∠XOY的两边上的动点,并且线段AB=4,如果点T是线段AB的中点,则线段TO的长等于_________ ,所以,当点A和B在直角∠XOY 的两边上运动时,点O一定在以点_________ 为圆心,以线段_________ 为直径的圆上.(3)如图,△ABC的等边三角形,AB=4,直角∠XOY的两边OX,OY分别经过点A和点B (点O与点A、点B都不重合),连接OC,求OC的最大值与最小值.(4)如图,在直角坐标系xOy中,点A、B分别是x轴与y轴上的动点,并且线段AB 等于4为一定值.以AB为边作正方形ABCD,连接OC,则OC的最大值与最小值的乘积等于_________ .参考答案三、解答题(本大题共6个小题,共66分.解答应写出文字说明、证明过程或演算步骤)21.解:(1)将代入方程x﹣y=3a得:5+1=3a,∴a=2.(2)当a=1时,两方程为:由①得:x=3+y,代入②得:3+y+3y=3,∴y=0,∴x=3.所以方程组的公共解为:.(3)因为是已知方程的公共解,∴解得:,∵x≤1,∴2a+1≤1,∴a≤0,所以1﹣a≥1,≥1.∴y22.解:(1)擦玻璃的面积:80×20%=16(m2);擦课桌椅的面积:80×25%=20(m2);扫地拖地的面积:80×55%=44(m2);故答案为:16,22,44;(2)由题意可得,每人每分钟擦玻璃的面积为=,得y=x;故答案为:y=x;(3)设擦玻璃的人数为x人,则擦课桌的人数为(13﹣x)人,根据题意得:16÷x=20÷[0.5×(13﹣x)],即=,解得x=8,经检验x=8是原方程的解,则擦课桌椅的有:13﹣8=5(人),答:擦玻璃的8人,擦课桌椅的有5人.23.解:(1)填表如图所示,y=40x+45(200﹣x)=﹣5x+9000,Ay=25(240﹣x)+32(60+x)=7x+7920;B(2)∵A村的运输费用比B村少,∴﹣5x+9000<7x+7920,解得x>90,∵A村有雪花梨200吨,故200≥x>90吨时,A村的运输费用比B村少;(3)A、B两村的运输费用之和为:﹣5x+9000+7x+7920=2x+16920,∵2>0,∴运输费用随x的增大而增大,∵,∴x≤200,∴当x=0时,运输费用最小,为16920元.24.解:(1)完成图形,如图所示:证明:∵△ABD和△ACE都是等边三角形,∴AD=AB,AC=AE,∠BAD=∠CAE=60°,∴∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB,∵在△CAD和△EAB中,,∴△CAD≌△EAB(SAS),∴BE=CD;(2)BE=CD,理由同(1),∵四边形ABFD和ACGE均为正方形,∴AD=AB,AC=AE,∠BAD=∠CAE=90°,∴∠CAD=∠EAB,∵在△CAD和△EAB中,,∴△CAD≌△EAB(SAS),∴BE=CD;(3)由(1)、(2)的解题经验可知,过A作等腰直角三角形ABD,∠BAD=90°,则AD=AB=100米,∠ABD=45°,∴BD=100米,连接CD,则由(2)可得BE=CD,∵∠ABC=45°,∴∠DBC=90°,在Rt△DBC中,BC=100米,BD=100米,根据勾股定理得:CD==100米,则BE=CD=100米.25.解:(1)∵抛物线y=ax2+x+c的顶点为M(﹣1,﹣2),∴该抛物线的解析式为y=a(x+1)2﹣2.即:y=ax2+2ax+a﹣2.∴2a=1.解得 a=.故该抛物线的解析式是:y=x2+x﹣.当y=0时,x2+x﹣=0.解之得 x1=﹣3,x2=1.∴B(﹣3,0),C(1,0);(2)①证明:将抛物线y=x2+x﹣沿x轴翻折后的图象,即新图象,仍过点B、C,其顶点M′与点M关于x轴对称,则M′(﹣1,2).设新抛物线的解析式为:y=a′(x+1)2+2.∵y=a′(x+1)2+2过点C(1,0),∴a′(1+1)2+2=0,解得,a′=﹣.∴翻折后得到的新抛物线的解析式为:y=﹣x2﹣x+.当﹣4x+6=x2+x﹣时,有:x2﹣6x+9=0,解得,x1=x2=3,此时,y=﹣6.∴新抛物线y=﹣x2﹣x+与直线l有唯一的交点N(3,﹣6);②≤t≤6.附解答过程:∵点N是新抛物线y=﹣x2﹣x+与直线l有唯一的交点,∴直线l与新抛物线y=﹣x2﹣x+在x轴上方部分(即G)无交点,∴当直线l经过点C时产生第一个公共点,经过点B时是最后一个公共点,运动t秒时,点B的坐标为(﹣3+t,0),点C的坐标为(1+t,0),直线与x轴交点为(,0).∵当=﹣3+t时,t=6∴图象G与直线l有公共点时,≤t≤6.26.解:(1)①如图1,根据两点之间线段最短可得:PO≤PR+OR.∴PM+MO≤PR+OR.∵MO=RO,∴PM≤PR.∴点M是点P到⊙O的最近点.②如图2,根据两点之间线段最短可得:PS≤PO+OS.∵OS=ON,∴PS≤PO+ON,即PS≤PN.∴点N是点P到⊙O的最远点.(2)如图3,∵∠XOY=90°,点T是线段AB的中点,∴TO=AB=2.∴点O在以点T为圆心,以线段AB为直径的圆上.故答案为:2、T、AB.(3)取AB的中点T,连接TO、CT、OC,如图4.∵∠AOB=90°,点T是线段AB的中点,∴TO=AB=2.∵△ABC的等边三角形,点T是线段AB的中点,∴CT⊥AB,AT=BT=2.∴CT===2.根据两点之间线段最短可得:OC≤OT+CT,即OC≤2+2;CT≤OC+OT,即OC≥CT﹣OT,也即OC≥2﹣2.∴OC的最大值为2+2,OC的最小值为2﹣2.(4)取AB的中点T,连接TO、CO、CT,如图5.∵∠AOB=90°,点T是线段AB的中点,∴TO=AB=2.∵四边形ABCD是正方形,∴BC=AB=4,∠ABC=90°.∵点T是线段AB的中点,∴BT=AB=2.∴CT===2.根据两点之间线段最短可得:OC≤OT+CT,即OC≤2+2;CT≤OC+OT,即OC≥CT﹣OT,也即OC≥2﹣2.∴OC的最大值为2+2,OC的最小值为2﹣2.∵(2+2)(2﹣2)=20﹣4=16.∴OC的最大值与最小值的乘积等于16.故答案为:16.。
二十五届希望杯初三二试有答案

第二十五届 希望杯 全国数学邀请赛初三㊀第2试试题一㊁选择题(每小题4分,共40分.)1.I fb o t h a a n d c a r e r e a l n u m b e r s ,2a n d 3a r e t h e t w o s o l u t i o n s o f t h e e qu a t i o n a x 2-10x +c =0f o r x ,t h e n t h e v a l u e o f a +c i s ()(A )10.(B )12.(C )14.(D )16.图12.如图1,在әA B C 中,B C >C A >A B ,D ㊁E ㊁F 分别是A B ㊁B C ㊁C A 边上的点,D E ʊA C ,F D ʊC B ,若A D ʒD B =1ʒ2,则图中的相似三角形有()对.(A )3.(B )4.(C )5.(D )6.3.若a -b =4,a b +c 2+4=0,则a 的值是()(A )2.(B )3.(C )4.(D )5.4.将抛物线y =x 2先向左平移1个单位,再向下平移2个单位,则所得的抛物线的解析式是()(A )y =x 2-2x +1.(B )y =x 2+2x -1.(C )y =x 2+4x +3.(D )y =x 2-2x -1.5.若3x 2-x =1,则9x 4+12x 3-2x 2-7x +2014的值是()(A )2013.(B )2014.(C )2015.(D )2016.6.半径分别是1,2的☉O 1和☉O 2相外切,若半径是3的☉O 3和它们都相切,则满足条件的☉O 3的个数是()(A )6.(B )3.(C )4.(D )5.7.给如图2所示的无水游泳池注水,如果进水速度是均匀的,那么,泳池内水的高度h 随时间t 变化的图象可能是()图28.三角形内的一点和三角形三个顶点的连线将三角形分成三部分,若这三部分的面积比是1ʒ2ʒ3,则这样的点的个数是()(A )1.(B )3.(C )6.(D )9.9.G i v e n p o s i t i v e i n t e g e r m w h i c h i s n o l a r g e r t h a n 10,a n d m 2014+2014mc a nb ed i v i de db y5,t h e n t h en u m b e r o f s u c h m i s()图3(A )2.(B )3.(C )4.(D )5.10.如图3,在平面直角坐标系x O y 中,点A (2,0),M (0,33),N (5,23),N B ʅx 轴于点B ,P 为MN 上一动点,则P A +P B 的最小值为()(A )33.(B )23.(C )323.(D )343.二㊁填空题(每小题4分,共40分.)11.若y =a x 2+b x +c (a ʂ0)的图象如图4所示,则a b c 的值是(填: 正数 ㊁ 负数 或 0 ).12.若关于x 的方程x 2+p x +q =0有两个负根,则直线y =p x +q 不经过第象限.(填: 一 ㊁ 二 ㊁ 三 或 四 )13.已知{x +x y +y =6,x 2+y 2=12,则x 3+y 3的值是.14.在әA B C 中,A C =8,B C =6,øA C B =90ʎ,C D ʅA B 于点D ,若әA B C ㊁әA C D ㊁әB C D的内切圆的半径分别是r 1,r 2,r 3,则r 1+r 2+r 3的值是.15.若关于x 的方程x 2-(m +5)|x |+4=m 恰有3个实数解,则实数m =.16.在平面直角坐标系x O y 中,若直线x =-1,x =3,y =3,y =kx -2围成的四边形的面积是16,则k =.图4F i g .5图6图717.A ss h o w ni n F i g .5,t h e r ea r e3s q u a r e s i nt h er i g h tt r i a n gl e .T h es i d e so ft h et w o s m a l l e r s q u a r e s a r e a a n d4.T h e s i d eo f t h e s qu a r e i n t h em i d d l e i s x ,t h e n x =(i n t e r m s o f a ).18.如图6,在边长为2的正方形A B C D 内有等边三角形C D E ,A C 交D E 于点F ,则S әC F E =.19.如图7,将长为4,宽为2的长方形A B C D 绕顶点A 顺时针旋转90ʎ到达A B ᶄC ᶄD ᶄ,图中的两段弧线分别是顶点C ㊁D 经过的路径,则阴影部分的面积为.(π取3)20.长与宽的比是2ʒ1的长方形称为 特征长方形 .用宽分别为a 1,a 2,a 3,a 4,a 5(a 1<a 2<a 3<a 4<a 5)的5个 特征长方形 拼成的大长方形,记为(a 1,a 2,a 3,a 4,a 5),则大长方形(1,2,a 3,a 4,a 5)的面积最大是.三、解答题.21.(本题满分10分)如图8,在边长为1的正方形A B C D 中,以A 为圆心㊁A B 为半径的弧与以D C 为直径的半圆交于点E ,连结D E 并延长交B C 于F ,连结B E 并延长交D C 于G .(1)求D G ʒG C 的值;(2)求四边形E F C G 的面积.图8图9图1022.(本题满分15分)如图9,排球场总长18m ,设球网高为2m ,运动员站在离网3m 的线上(图中虚线所示)正对网前跳起将球水平击出.以击球点为原点,建立如图10的直角坐标系,球运动的轨迹方程是y =5x 2v2(x ,y 单位:m ),其中v 是球被击出时的速度(单位:m /s ).(1)设击球点在3m 线的正上方,高度为2.5m ,求使球既不触网也不出界的击球速度的范围;(2)若击球点在3m 线的正上方,当高度小于h (单位:m )时,无论水平击球的速度多大,球不是触网就是越界,求h .23.(本题满分15分)如图11,有一束光线,从中心为O 的圆环的A 点射入,在圆环内经过两次反射后从A 点射出;如图12,从A 点射入的光线经过三次反射后从A 点射出.图11图12图13图14(1)如图13,若从A 点射入的光线经过五次反射后从A 点射出,求从A 点射入的光线和圆环半径O A 的夹角α的度数;(2)如图14,若从A 点射入的光线和圆环半径O A 的夹角是50ʎ,则经过几次反射后光线从A 点射出?初三第2试答案21.(1)=2DG GC.(2)760CGEF S =.22.(1)击球速度的范围是v <<;(2)若击球点在3m 线的正上方3215m 处,则无论水平击球的速度多大,球不是触网就是越界.23.(1)60α=︒.(2)经过8次反射后,从A 点出来.。
2015年东城初三数学二模试题及答案

B
A
F E
C
D
19.若实数 a 满足 a 2a 1 0 ,计算 4(a 1)(a 1) 2a(a 2) 的值.
20. 已知关于 x 的方程 (k 1) x (k 1) x
2
1 0 有两个相等的实数根,求实数 k 的值. 4
21. A,B 两个火车站相距 360km.一列快车与一列普通列车分别从 A,B 两站同时出发相向而行,快车的 速度比普通列车的速度快 54km/h,当快车到达 B 站时,普通列车距离 A 站还有 135km.求快车和普通 列车的速度各是多少?
1 ,则 a 等于 3
A.1 B.2 C.3 D.4 7. 如图,将△ABC 沿 BC 方向向右平移 2cm 得到△DEF,若△ABC 的周长为 16cm,则四边形 ABFD 的周长 为
A. 16cm
B. 18cm
C. 20cm
D. 22cm
1
8. 如图, 在已知的△ABC 中, 按以下步骤作图: ①分别以 B, C 为圆心, 以大于
1 BC 2
C
M
的长为半径作弧,两弧相交于点 M,N;②作直线 MN 交 AB 于点 D,连接 CD.若 A CD=AC,∠B=25° ,则∠ACB 的度数为 D N A. 90° B. 95° C. 100° D. 105° 9.如果三角形的一个角是另一个角的 3 倍,那么我们称这个三角形为“智慧三角形”.下列各组数据中,能 作为一个智慧三角形三边长的一组是 A.1,2,3 B.1,1, C.1,1, D.1, , 2 10. 如图,矩形 ABCD 中,AB=3,BC=4,动点 P 从 A 点出发,按 A→B→C 的方向在 AB 和 BC 上移动,记 PA=x,点 D 到直线 PA 的距离为 y,则 y 关于 x 的函数图象大致是
2014-2015初三数学二模

2014-2015学年第二学期初三第二次统测数学试卷说明:本试卷满分120分,考试时间90分钟,请在答题卡上相应题目的答题区域内作答。
亲爱的同学,解题时请你认真审题,注意检查,祝你发挥最好的水平。
一.选择题(本大题10小题,每小题3分,共30分)在每小题列出的四个选项中,只有一个是正确的,请把答题卡上对应题目所选的选项涂黑.1.﹣的倒数是()AA.5.一个多边形的内角和是外角和的2倍,这个多边形的边数是()A.4 B.5 C.6 D.76. 一个不透明的布袋里装有7个只有颜色不同的球,其中4个红球,3个白球,从布袋中随机摸出一个球,摸出的球是红球的概率是()A.47B.37C.34D.137.下列哪组条件能判别四边形ABCD是平行四边形()A. AB∥CD,AD=BCB. AB=CD,AD=BCC. ∠A=∠B,∠C=∠DD. AB=AD,CB=CD8.关于x的一元二次方程x2+kx-1=0的解的情况是()A.有两个不相等实数解B.没有实数解C.有两个相等的实数解D.不能确定9. 已知一个等腰三角形的其中一个角的度数为50度,则该三角形顶角的度数为()A.50 B.80 C.50或80 D.6510. 二次函数cbxaxy++=2的图象如图所示,若cbaM++=24, baN+=2,abcP=,则()12. 某市约有4500000人,该数用科学记数法表示为__________;13. 如图,在平行四边形ABCD中,点E在AD上,且AE:ED=3:1,CE的延长线与BA的延长线交于点F,则S△AFE:S△E DC为__________;14. 不等式组⎩⎨⎧+<-≤1312205xxx的解集为__________;15. 已知O⊙的直径8cmAB C=,为O⊙上的一点,30BAC∠=°,则BC=__________;16.如图,等边ABC∆绕点A按顺时针旋转30度,得到''CAB∆,若ABC∆的边长为2,则图中阴影部分的面积等于__________.D CBA BA三、解答题(一)(本大题3小题,每小题6分,共18分) 17.计算:20)2(8)2015(16----+-+π18.解方程:xxx --=+-34231 19. 如图,在Rt △ABC 中,∠ACB =90°.(1)用尺规在边BC 上求作一点P ,使PA =PB (不写作法,保留作图痕迹) (2)连结AP ,若AP 刚好平分∠CAB,求∠B 的度数.四、解答题(二)(本大题3小题,每小题7分,共21分)20. 如图所示,从热气球C 上测定建筑物A 、B 底部的俯角分别为30°和60°,已知AB 间的距离为180米,CD 垂直于AB 于点D ,问:此时热气球的高度为多少?21. 有大小两种货车,2辆小货车和3辆大货车一次可以运货38吨,5辆小货车与6辆大货车一次可以运货80吨,问:(1)3辆小货车与5辆大货车一次可以运货多少吨?(2)通过计算说明,用4辆大货车和5辆小货车能否将32吨货物一次运走?22. 五一期间某公司组织部分员工到A 、B 、C 三地旅游,公司购买前往各地的车票种类、数量绘制成条形统计图,如图,根据统计图回答下列问题:(1)前往 A 地的车票有___ _张,前往C 地的车票占全部车票的_______%;(2)若公司决定采用随机抽取的方式把车票分配给 100 名员工,在看不到车票的条件下,每人抽取一张(所有车票的形状、大小、质地完全相同且充分洗匀),那么员工小王抽到去 B 地车票的概率为_____;(3)若最后剩下一张车票时,员工小张、小李都想要,决定采用抛掷一枚各面分别标有数字1,2,3,4的正四面体骰子的方法来确定,具体规则是:“每人各抛掷一次,若小张掷得着地一面的数字比小李掷得着地一面的数字大,车票给小张,否则给小李.”试用“列表法或画树状图”的方法分析,这张车票给谁的机会更大?五、解答题(三)(本大题3小题,每小题9分,共27分) 23.如图,一次函数b ax y +=与反比例函数xky =的图象交于M (-2,1),N (1,c )两点. (1)求k 、c 的值.(2)直接写出x 取何值时,一次函数的值大于反比例函数的值.(3)x 轴的正半轴上是否存在点A ,使得∆AMN 的面积为9,若存在,请求出点A 的坐标,若不存在,请说明理由。
2015年初三二模试卷 (1) 2

2015年初中毕业升学模拟考试英语试题本试题分两卷。
第I卷(客观题),第II卷(主观题)。
考试时间为100分钟。
试卷满分为90分。
注意事项:1.答卷前,考生务必用0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写在答题卡的相应位置上,并认真核对条形码上的姓名、准考证号是否与本人的相符合。
2.答客观题必须用2B铅笔将答题卡上对应题目的正确选项涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案。
答案不能答在试题卷上。
3.答主观题必须用0.5毫米黑色墨水签字笔作答,答案写在答题卡各题目指定区域内相应位置上。
如需改动,先划掉原来的答案,然后再写上新的答案。
不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.考生必须保持答题卡的整洁,考试结束后,将试卷和答题卡一并交回。
第I卷(客观题,共50分)一、单项填空在A、B、C、D四个选项中,选出可以填入空白处的最佳选项,并在答题卡上将该项涂黑。
(本大题共14分,每小题1分)1. ---Wow, ____useful and fashionable iphone5s you have bought!---Yes, it is ____ great help to me, ____ I must say it also cost me a lot.A what, a, butB what an, the, AndC What a, a , AndD How, a , But2. ---I hear the government is going to ___ the air quality with the new standard PM2.5,isn’t it?---Yes, ___ the air pollution will get more serious.A discover, thereforeB revise, anywayC review, howeverD test, otherwise3. _____ you can understand how the human body woks, you need to have some knowledge of chemistryA As soon asB ThoughC So thatD Since4. I think that “Duang” must be one of the words on the Internet this year.A. deepestB. widestC. hottestD. highest5. ---Why did you buy one more tie?you have got more than ten ties,---A man can never have _____ many ties.A. enoughB. tooC. soD. such6. —Mr. Ma has gone to Guangzhou on business.—Really? Do you know ?A. who did he go withB. when he came backC. how soon will he be backD. whether he went there by train7. Jack is dishonest. He always some excuses for doing something wrong.A. makes upB. sets upC. takes upD. picks up8. —Liu Xiang has announced the end of his sporting career.—. But I think he is still one of the greatest athletes in China.A. Don’t mention itB. That’s such a pityC. I can’t agree moreD. I’m afraid he couldn’t9. --- ________ David be the new chairperson of the Students’ Union?--- He _______ be, but I’m not sure.A. Can; can’tB. Can; mayC. May; mustD. May; mustn’t10. This problem worried her so much that she didn’t know ___________ with it..A. what she can doB. what she could dealC. how to doD. how to deal11. Roy made three kites, but ______ of them can fly high in the sky.A. neitherB. noneC. allD. either12. —Great! It’s one I have ever had.A. deliciousB. the least deliciousC. more deliciousD. the most delicious13. 11. How lucky Peter was! Some policemen arrived in time and ________ him out.A. tried to helpB. managed to helpC. tried helpingD. succeeded to help14. ---How would you like your tea?---_____________.A Very muchB As it comes, pleaseC I do not like teaD It tastes nice二、完形填空先通读下面的短文,掌握其大意,然后在A、B、C、D四个选项中选出可以填入相应空白处的最佳答案,并在答题卡上将该项涂黑。
2015北京初三数学二模试题及答案WORD

中考统一练习㈡数 学 2015.5考生须知1.本试卷共6页,共五道大题,25个小题,满分120分。
考试时间120分钟。
2.在试卷和答题卡上认真填写学校名称、姓名和考试编号。
3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效。
4.考试结束,请将本试卷和答题卡一并交回。
一、选择题(共8道小题,每小题4分,共32分) 下列各题均有四个选项,其中只有一个..是符合题意的. 1.21-的倒数是( ). A .2 B .2- C .21D . 21-2.根据中国汽车工业协会的统计,2011年上半年的中国汽车销量约为932.5万辆,同比增速3.35%.将932.5万辆用科学记数法表示为( )辆A .93.25×105B .0.9325×107C .9.325×106D .9.325×1023.若一个正多边形的每个内角都为135°,则这个正多边形的边数是( ). A .9 B .8 C .7 D .6 4.下列运算正确的是( ).A .22a a a =⋅B .22=÷a aC . 22423a a a +=D . ()33a a -=-5.如图所示,直线a ∥b ,直线c 与直线a ,b 分别相交于点A 、点B ,AM ⊥b ,垂足为点M ,若∠1=58°,则∠2的度数是( ).A .22B .30C .32D .426.某校抽取九年级的8名男生进行了1次体能测试,其成绩分别为90,75,90,85, 75,85,95,75,(单位:分)这次测试成绩的众数和中位数分别是 ( ).A .85,75B .75,85C .75,80D .75,757.已知圆锥的底面半径为3,母线长为4,则圆锥的侧面积等于( ).A .15πB .14π C.13π D .12π8.过正方体中有公共顶点的三条棱的中点切出一个平面,形成如图几何体,其正确展开图为( ) .A B C D 二、填空题(共4道小题,每小题4分,共16分)第5题图2a bcMB A 19.在函数3+=x y 中,自变量x 的取值范围是 .10.若()022=++-a b a ,则=+b a .11.把代数式142-+m m 化为()b a m ++2的形式,其中a 、b 为常数,则a +b = . 12.如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0)…根据这个规律探索可得,第20个点的坐标是__________;第90个点的坐标为____________.三、解答题(共6道小题,每小题5分,共30分) 13.()33602120---+︒-πcos解:14.解方程:2132+=+-a a a解:15. 已知4+=y x ,求代数式2524222-+-y xy x 的值.解:16.如图,在△ABC 中,AD 是中线,分别过点B 、C 作AD 及其延长线的垂线BE 、CF ,垂足分别为点E 、F .求证:BE =CF . 证明:17.如图,某场馆门前台阶的总高度CB 为0.9m ,为了方便残疾人行走,该场馆决定将其中一个门的门前台阶改造成供轮椅行走的斜坡,并且设计斜坡的倾斜角A ∠为8°,请计算从斜坡起点A 到台阶最高点D 的距离(即斜坡AD 的长).(结果精确到0.1m ,参考数据:sin 8°≈0.14,cos 8°≈0.99,tan 8°≈0.14)C ABD解:18.如图,平面直角坐标系中,直线AB 与x 轴交于点A (2,0),与y 轴交于点B ,点D 在直线AB 上.⑴求直线AB 的解析式;⑵将直线AB 绕点A 逆时针旋转30°,求旋转后的直线解析式.解:⑴⑵四、解答题(共4道小题,每小题均5分,共20分)19.如图1,已知平行四边形ABCD 中,对角线AC BD ,交于点O ,E 是BD 延长线上的点,且ACE △是等边三角形. ⑴求证:四边形ABCD 是菱形;⑵如图2,若2AED EAD ∠=∠,AC =6.求DE 的长.OBEACD OB EACD图1 图2 证明:⑴ ⑵ 20. 如图,⊙O 中有直径AB 、EF 和弦BC ,且BC 和EF 交于点D ,点D 是弦BC 的中点,CD =4,DF =8.⑴求⊙O 的半径及线段AD 的长; ⑵求sin ∠DAO 的值. 解:⑴ ⑵21.图①、图②反映是某综合商场今年1-4月份的商品销售额统计情况.观察图①和图②,解答下面问题:y x31D B O A FED BOA C⑴来自商场财务部的报告表明,商场1-4月份的销售总额一共是280万元,请你根据这一信息补全图①;⑵商场服装部4月份的销售额是多少万元;⑶小华观察图②后认为,4月份服装部的销售额比3月份减少了.你同意他的看法吗?为什么? 解:⑴ ⑵ ⑶22.⑴阅读下面材料并完成问题:已知:直线AD 与△ABC 的边BC 交于点D ,①如图1,当BD =DC 时,则S △ABD ________S △ADC .(填“=”或“<”或“>”)DBCADBCABCAD图1 图2 图3②如图2,当BD =21DC 时,则=∆ABD S ADC S ∆ . ③如图3,若AD ∥BC ,则有ABC S ∆ DBC S ∆ .(填“=”或“<”或“>”)⑵请你根据上述材料提供的信息,解决下列问题:过四边形ABCD 的一个顶点画一条直线,把四边形ABCD 的面积分成1︰2的两部分.(保留画图痕迹)BCAD五、解答题(共3道小题,23题7分,24题8分,25题7分,共22分)23.已知:关于x 的方程mx 2-3(m -1)x +2m -3=0.⑴当m 取何整数值时,关于x 的方程mx 2-3(m -1)x +2m -3=0的根都是整数; ⑵若抛物线32)1(32-+--=m x m mx y 向左平移一个单位后,过反比例函数)0(≠=k xky 上的一点(-1,3),①求抛物线32)1(32-+--=m x m mx y 的解析式; ②利用函数图象求不等式0>-kx x k 的解集.解:⑴⑵①② 24.探究问题:已知AD 、BE 分别为△ABC 的边BC 、AC 上的中线,且AD 、BE 交于点O .⑴△ABC 为等边三角形,如图1,则AO ︰OD = ;⑵当小明做完⑴问后继续探究发现,若△ABC 为一般三角形(如图2),⑴中的结论仍成立,请你给予证明.⑶运用上述探究的结果,解决下列问题:如图3,在△ABC 中,点E 是边AC 的中点,AD 平分∠BAC , AD ⊥BE 于点F ,若AD =BE =4. 求:△ABC 的周长.ODE ABCOE DBCA1 2 3 4 4 3 2 1xy O -1 -2 -3 -4 -4 -3-2-1D CF B EA图1 图2 图3解:⑴⑵⑶25.如图,在平面直角坐标系中,点P从原点O出发,沿x轴向右以每秒1个单位长的速度运动t(t>0)秒,抛物线y=x2+bx+c经过点O和点P.已知矩形ABCD的三个顶点为A(1,0)、B(1,-5)、D(4,0).⑴求c、b(可用含t的代数式表示);⑵当t>1时,抛物线与线段AB交于点M.在点P的运动过程中,你认为∠AMP的大小是否会变化?若变化,说明理由;若不变,求出∠AMP的值;⑶在矩形ABCD的内部(不含边界),把横、纵坐标都是整数的点称为“好点”.若抛物线将这些“好点”分成数量相等的两部分,请直接..写出t的取值范围.解:⑴⑵⑶参考答案一、选择题1 2 3 4 5 6 7 8 B C B D C B DB二、填空题9、x ≥-3 10、-4 11、-3 12、(6,4);(13,1) 三、解答题(共6道小题,每小题5分,共30分) 13.解:原式=3121232-+⨯----------------------------------------4分 =3---------------------------------------5分14.解:()()()()32322-=+-++a a a a a ---------------------------------------1分a a a a a364222-=--++ ---------------------------------------2分 24=a ---------------------------------------3分 21=a ---------------------------------------4分是原方程的根经检验:21=a∴是原方程的根21=a ---------------------------5分15.44=-∴+=y x y x 解:---------------------------------------1分原式=2524222-+-y xy x ---------------------------------------2分()2522--=y x ---------------------------------------4分7254242=-⨯==-时,原式当y x ---------------------------------------5分 16.证明: AD 是中线∴BD=CD ---------------------------------------1分 分别过点B 、C 作AD 及其延长线的垂线BE 、CFCFD E ∠=∠∴---------------------------------------2分中和在CFD BED ∆∆ ⎪⎩⎪⎨⎧∠=∠=∠=∠CDF BDE CDBD CFD E ()AAS CFD BED ∆≅∆∴-------------------------------4分 CF BE =∴---------------------------------------5分17.解:E AB DE D 于点作过⊥---------------------------------------1分 ,于B AB CB ⊥ DC ∥AB∴.90==CB DE ---------------------------------------2分A DE AD AED Rt sin =∆ 中,在---------------------------------------4分∴m AD 4.614.09.0≈= EC AD B∴从斜坡起点A 到台阶最高点D 的距离约为6.4m 。
希望杯历年真题集(九年级)-附答案

目录第二十二届“希望杯”全国数学邀请赛(第1试) (3)第二十三届“希望杯”全国数学邀请赛(第1试) (7)第二十三届“希望杯”全国数学邀请赛(第2试) (11)第二十四届“希望杯”全国数学邀请赛(第1试) (15)第二十四届“希望杯”全国数学邀请赛(第2试) (19)第二十五届“希望杯”全国数学邀请赛(第1试) (23)第二十五届“希望杯”全国数学邀请赛(第2试) (27)第二十六届“希望杯”全国数学邀请赛(第1试) (31)第二十六届“希望杯”全国数学邀请赛(第2试) (35)第二十七届“希望杯”全国数学邀请赛(第1试) (40)第二十八届“希望杯”全国数学邀请赛(第1试) (43)参考答案 (47)第二十二届“希望杯”全国数学邀请赛(第1试)一、选择题(每小题4分,共40分)1.假期里王老师有一个紧急通知,要用电话尽快通知给50个同学,假设每通知一个同学需要1分钟时间,同学接到电话后也可以相互通知,那么要使所有同学都接到通知最快需要的时间为( )A .8分钟B .7分钟C .6分钟D .5分钟 2.若关于x 的一元二次方程()2320a b x ax b +++=有唯一解,则这个解是( )A .23-B .32-C .23D .323.如图,已知////AD EF BC ,::1:2:4AD EF BC =,则梯形AEFD 与梯形EBCF 的面积之比为( )A .1:2B .1:3C .1:4D .2:34.一个兵乓球队有男队员6人,女队员5人,其中男、女左撇子分别有3人和2人,若从这个球队任意抽取2人,则抽到2个左撇子的概率是( )A .211 B .511 C .15D .251215.已知x ,y 都是负整数,且满足66xy x=-,则y 的最小值为( ) A .3- B .4- C .5- D .6-6.已知等腰ABC 中,,30AB AC BAC =∠=︒,AD 为BC 边上的高,P 点在AC 上,E 点在AD 上,若PE EC +的最小值为4,则ABC 的面积为( )A .8B .16C .32D .647.如图,AB 是圆O 的直径,点C 平分AB ,点D 平分AC ,DB 、CA 交于点E ,则DEEB的值( )A .13B .14 C .1 D8.已知直线()0y kx k =<与双曲线2y x=-交于点()11A x y ,和()22B x y ,两点,则122138x y x y -的值是( ) A .10- B .5- C .5 D .109.用一些棱长是1的小正方体堆成一个立体,下图分别是它的俯视图和主视图,则这个立体的表面积(含下底面面积)的值最小是( )A .42B .43C .44D .4610.如图,在ABC 中,BAC ∠、BCA ∠的平分线相交于点I ,若35B ∠=,BC AI AC =+,则BAC ∠的度数为( )A .60B .70C .80D .90二、A 组填空题(每小题4分,共40分)11.如图,正六边形的边向外延长一倍,连接端点后又构成一个大的正六边形,则小正六边形与大正六边形的面积之比为 ;12.若对于p 的任意值,抛物线2231y x px p =-++都过一个定点,则这个定点的坐标是 ; 13.如图,正方形ABCD 的边长为 4,E 点在BC 上,以E 为圆心,EC 为半径的半圆与以A 为圆心,AB 为半径的圆弧外切,则EC = ;14.在锐角ABC 中,54AB AC ==,,则BC 的取值范围是 ;15.袋中装有大小相同的黑球、白球、红球各2个,规定:取出一个黑球计0分,取出一个白球计1 分,取出一个红球计2分;在抽取这些球的时候,看不到球的颜色.甲先取出3个球,不再放回袋中,然后,乙取出剩余的3个球;取出球的总积分多者获胜.则甲乙成平局的概率为 ;16.不等式21x x a -+-≥对所有实数x 都成立,则 a 的最大值是 ; 17.如图,设M 是ABC 的重心,过M 的直线分别交边AB AC 、于P Q 、 两点,且APm PB=,AQ n QC =,则11m n+= ;18.已知抛物线()20y ax bx c c =++≠与x 轴的交点坐标为()()1,0,3,0-,当25x -≤≤时,y 的最大值为12,则该抛物线的解析式为 ;19.已知平面直角坐标系中有()1,3A ,()3,1B 两点,在x y 、轴上分别找一点C D 、,使四边形的周长最小,则最小周长为 ;20.明明用计算器求代数式()a b c +的值.他依次按出“,,,,,a b c ⨯+=”,显示11;当他依次按“,,,,b c a +⨯=”,显示14 (其中,,a b c 均为正整数).这时他才明白不按括号时,计算器先做乘法再做加法.那么如果他按键正确(该加括号时加括号)时,显示结果应为 ;三、B 组填空题(每小题 8 分,共 40 分)21.已知代数式22 342x xy y x by ---+-能分解为两个关于x y 、的一次式的乘积,则b = 或 ; 22.已知,,x y z 是三个非负实数,满足3252x y z x y z ++=+-=,,若2S x y z =+-,则S 的最大值为 最小值为 ;23.已知()2f x ax bx c =++,若()01f =,并且()()12f x f x x +-=,则()1f = ,()1f -= ,a = ,b = ;24.如图,在平面直角坐标系中,矩形OABC 的顶点A C 、分别在轴上,顶点B 在()14,8,点E F 、分别在OA 、 OB 、上.将AEF 沿EF 对折,使点A 落在线段BC 上的点D 处.经过抛物线()2220y ax abx ab c c =-++<顶点P 的每一条直线总平分矩形OABC 的面积.若点P 在线段DE 上,AF 的长为整数,且已知抛物线与线段EF 仅有一个交点,则点F 的坐标是 ,a 的取值范围是 ;25.某种在同一平面内进行传动的机械装置如左图,右图是它的示意图.其工作原理是:滑块Q 在平直滑道l 上可以左右滑动,在Q 滑动的过程 中,连杆PQ 也随之运动,并且PQ 带动连杆OP 绕定点O 摆动.在摆动过程中,两连杆的接点P 在以OP 为半径的O 上运动.数学兴趣小组为进一步研究其中所蕴含的数学知识,过点O 做 OH l ⊥于点H ,并测得4OH = 分米,3PQ = 分米,2OP = 分米.则点Q 在l 上 允许滑动的最大距离为 分米,点P在O 上的最大移动路线长为 分米;第二十三届“希望杯”全国数学邀请赛(第1试)一、选择题(每小题4分,共40分)1.如图1所示,一个正方体和一个圆柱体紧靠在一起,则它们的主视图是( )图1 A B C D2.完成一项工作,甲单独做需a 天,乙单独做需b 天,甲乙合作需c 天,则丙单做全部工作所需的天数是( )A .abc ab ac bc -- B .abc ab ac bc +- C .ab ac bcabc++ D .()ab c b a c --3.已知1,0,1x ≠-,则1111x x x x x x -+++-+的值可能是( ) A .比3大的数 B .比3-小的数 C .1,3±± D .比3-大,并且比3小的数4.如图,梯形ABCD 中,//AB CD ,两条对角线交于点E .已知ABE 的面积是a ,CDE 的面积是b ,则梯形ABCD 的面积是( )A .22a b +B )a b +C .2D .()2a b +5.已知a ,b 是实数,关于x 的不等式组的解集表示在数轴上如图所示,则这个不等式组是( )A .11ax bx >⎧⎨>⎩B .11ax bx >⎧⎨<⎩C .11ax bx <⎧⎨>⎩D .11ax bx <⎧⎨<⎩6.如图,AB BC ⊥,AB BC =,点D 在BC 上,以D 为直角顶点作等腰直角,则当D 从B 运动到C 的过程中,点E 的运动轨迹是( )A .圆弧B .抛物线C .线段D .双曲线7.已知实数1234,,,x x x x 满足条件1231234234134124x x x a x x x a x x x a x x x a ++=⎧⎪++=⎪⎨++=⎪⎪++=⎩其中1234a a a a <<<,则1234,,,x x x x 的大小关系是( )A .1234x x x x <<<B .2314x x x x <<<C .3214x x x x <<<D .4321x x x x <<< 8.已知23x ≤≤,则函数()21y x =-的取值范围是( )A .14y ≤≤和916y ≤≤B .116y ≤≤C .49y ≤≤D .19y ≤≤ 9.如图,已知梯形ABCD 中,//AB DC A C αβ∠=∠=,,,则:AD BC 等于( )A .sin :cos αβB .sin :sin αβC .sin :sin βαD .cos :sin αβ10.若关于x 的二次函数221y x mx =-+的图像与端点在()1,1-和()3,4的线段只有一个交点,则m 的取值可能是( )A .52B .13-C .12D .13二、A 组填空题(每小题4分,共40分)11.若两位数除以他的数字和等于7,则这样的两位数有 个. 12.已知21x y -=,则22425x y x y ---+= ;13.二次函数2y ax bx c =++的图象如图所示,已知2OB OA OA OC =<,,则,,a b c 满足的关系式是 ;14.如图,已知A B C 、、三点在同一个圆上,并且AB 是圆O 的直径,若点C 到AB 的距离5CD =,则圆O 的面积最小是;15.如图,在边长为1的正方形中,分别以四个顶点为圆心,作半径为1的圆弧,则图中阴影部分的面积是 ;16.如图,在梯形ABCD 中,2//76BA CD AD AB AB CD m BC m ⊥===,,,,,若以BC 为直径的圆与AD 没有公共点,则m 的取值范围是 ;17.设()f x 是关于x 的多项式,()f x 除以()21x +,余式是3;()2f x 除以()32x -,余式是4-,那么,()3f x 除以()242x x --,余式是 ;18.已知实数,a b 满足3a ab b ++=,若m a ab b =-+,则m 的取值范围是 ;19.Tom’s computer has password,which contains only numbers from 0 to 9.If the probability to guess the right password only one time is less than12012,then at least the password has digits. 20.Suppose point ()1,A m - is on the graph of the function 2y x=-,,,,B C D respectively,are point As symmetric points of x -axis,origin,y-axis.Then the area of the quadrilateral ABCD is ;三、B 组填空题(每小题8分,共40分) 21.反比例函数1k y x =和一次函数2y k x b =+的图象交于点2(3,)3M -和点()1,2N -,则1k = ,2k = ,一次函数的图象交x 轴于点 ;22.已知,a b 是实数,且2210a a -=,则a = ,b = ;23.已知,a b 是有理数,1x =是方程20x ax b -+=的一个解,则a 的值是 ,b 的值是 ; 24.如图,已知ABC 中,CD AB ⊥于点D ,26BD AD CD ==,,8cos 9ACD ∠=,BE 是AC 边上的高,则AD = ,BE = ;25.已知点A B Pa=︒,∠=,点M是上的动点,且使ABM为等腰三角形.若45、、是O上不同的三点,APB a则所有符合条件的点M有个,若满足题意的点M有2个,则a=;第二十三届 “希望杯”全国数学邀请赛(第2试)一、 选择题(每小题4分,共40分) 1.若反比例函数k y x =的图像经过点1,22⎛⎫- ⎪⎝⎭,则k 的值为( ) A .1- B .1 C .4- D .42.已知二次函数2y ax bx c =++的图像如图所示,则下列代数式的值恒为正值的是( )A .abcB .acC .bcD .ab3.若存在12x ≤≤,使得2120ax -->,则a 的取值范围是( )A .14a <-B .34a >C .1344a -<<D .14a <-或34a >4.直线k y x k=总是下列哪个函数图像的对称轴?( )A .y k x =B .ky x=C .2y kx =D .y kx = 5.若实数,,a b c 满足2222221,2,3,a b b c c a +=+=+=则ab bc ca ++的最小值为( )A .B .C .D 6.如图,双曲线(0)ky k x=>经过Rt AOB ∆的斜边AB 的中点C ,,AF AO ⊥,BF BO ⊥,AF BF 与双曲线分别交于点,D E ,若8,6,OA OB ==则四边形ODFE 的面积是( )A .12B .24C .36D .407.对于实数a ,规定[]a 表示不大于a 的最大整数,如[][]2.12, 1.52,=-=-则方程[][]224x y +=的解在xOy 坐标系中的图像是( )A B C D 8.某商店对于某个商品的销售量与获利做了统计,得到下表:若获利是销售量的二次函数,则该商店获利的最大值是( )A .9万元B .9.25万元C .9.5万元D .10万元9.如图,已知长方形ABCD 的边长32AB AD ==,,点E 在BC 边上,且AE EF ⊥,EF 交CD 于F ,设,BE x FC y ==,则当点E 从点B 运动到点C 时,y 关于x 的函数图像是( )A B C D10.若凸n 边形12n A A A 适合以下:(1)1100A ∠=,(2)18,1,2,,1,k k A A k n +∠=∠+=-则n 的值是( )A .5B .6C .7D .8 二、A 组填空题(每小题4分,共40分)11.若ABC ∆是半径为1的圆的内接三角形,BC =则A ∠= ; 12.方程11112012201420162018x x x x -=-----的解是x = ; 13.如图,P 是等边ABC ∆内一点,3,4,5,AP BP PC ===则APB ∠= ;14.边长为整数,且周长为2012的等腰三角形有 个.15.已知关于x 的一元二次方程222(1)(1)0x m x m --+-=有两个不相等的实根,αβ,若224,αβ+=则m = ; 16.已知ABC ∆的三个顶点的坐标分别为(1,5),(6,2),(1,2),A B C ----则ABC ∆外接圆半径的长度为 ;17.已知坐标平面xOy ,Rt ABC ∆中的直角顶点是A ,点B 与点O 重合,点C 在坐标轴上,则点C 的坐标是 ;18.已知350,x y z -+=并且230x y z ++=,则2222223323x y z xy yz zx x y z-+++-+-的值等于 ; 19.α和β是方程2210x x --=的两根,2α和2β是20x mx n ++=的两根,点(,)m n 在一次函数(3)y kx n =+-的图像上,则此函数的解析式是 .它的图像与xOy 坐标平面内的坐标轴围成的图形的面积是 ; 20.如图5,在直角梯形ABCD 中,,90,AB CD BAD ADC ∠=∠=∥两条对角线的交点为O ,O 与AD 相切,并与以AD 为直径的O '内切,已知AD 长为h ,则梯形ABCD 的面积是 ;三、解答题(每题都要写出推算过程) 21.解方程44(2)820x x +--=22.如图所示,已知二次函数28y x bx =-++的图像与x 轴交于,A B 两点,与y 轴交于点C ,且(4,0)B . (1)求二次函数的解析式及其图像的顶点D 的坐标;(2)若点(,0)M p 是x 轴上的一个动点,则当MC MD -取得最大值时,求p 的值;(3)如果点(,)E m n 是二次函数28y x bx =-++的图像上的一个动点,且ABE ∆是钝角三角形,求m 的取值范围.23.给你若干个边长都是1的正三角形,正方形,正五边形,正六边形,从其中任选两种(个数不限),将它们拼接,要求是:(1)使某边重合;(2)两种图形中的任何一种不得有公共部分.问:(1)用选出的两种图形围成正n 边形,如:用3个正方形和3个正六边形围成一个正三角形ABC (如下图). 请你再举两例,并作图说明.(2) 对于(1)中的正n 边形,求它的外接圆的半径.第二十四届“希望杯”全国数学邀请赛(第1试)一、选择题(每小题4分,共40分)1.若m n 、是方程210x -+=的两个根,则n mm n-的值是( )A .±B .±C .±D .±2.设O 的半径是5,点P 不在O 外,若点O 与P 的距离222OP m m =-+,则m 的取值范围是( ) A .1m <-或3m > B .13m -≤≤ C .1m ≤- D .3m ≥3.如图,O 内的点P 在弦AB 上,点C 在圆O 上,PC OP ⊥,若2BP =,6AP =,则CP 的长等于( )A .B .4C .D .4.如图是类似“羊头的”图案,它左右对称,由正方形,等腰直角三角形构成,如果标有数字“13”的正方形的边长是,那么标有数字“2”的等腰直角三角形的斜边的长是( )A .4B .C .2D .325.若m n 、()()m n n m +-的差的绝对值最小的整数是( ) A .55- B .56- C .16- D .15-6.如图,铁路MN 和公路PQ 在点O 处交汇,30QON ∠=︒,点A 在OQ 上,240AO = (米),当火车行驶时,周围200米以内未受到噪音的影响,现有一列火车沿MN 方向意72千米/时的速度行驶(火车的长度忽略不计),那么,A 处受噪音影像的时间为( )A .12秒B .16秒C .20秒D .24秒 7.InABC as shown in fig, ,,AB AC BD EC BE CF ===,if 50A ∠=︒,then the degree of DEF ∠ is ( )A .60︒B .65︒C .70︒D .75︒8.如图5,2O 的半径是1,正方形ABCD 的边长是6,点2O 是正方形ABCD 的中心,12O O 垂直AD 于P 点,128O O =,若将1O 绕点P 按顺时针方向旋转360°,在旋转过程中,与正方形ABCD 的边只有一个公共点的情况一共出现( )A .3次B .5次C .6次D .7次9.如图,在同一个平面直角坐标系内,二次函数()120y ax bx c a =++≠和一次函数()20y dx e d =+≠的图象相交于点(),A m n 和点(),B p q ,当12y y <时,用,m p 表示x 的取值范围,则是( )A .m x p <<B .x m <C .x p >D .x m >10.如图,在正方形ABCD 中,点M N 、分别在边AB BC 、上运动(不与正方形的顶点重合),2BN AM =,若图中的三个阴影三角形中至少有两个相似,则这样的点M 有( )A .1个B .2个C .3个D .4个二、A 组填空题(每小题4分,共40分)11.已知实数,a b 不相等,并且2215,15,a a b b +=+=则2211a b+= ; 12.If 111a m=-, 2111a a =-, 3211a a =-,...,then 2013a in terms of m is;13.如图,在3×2的方格纸上,以某三个格点为顶点的三角形中,等腰三角形共有 个.14.若实数,,x y z 使20x y z ++=和3250x y z ++=成立,并且0z ≠,则2222222457x y z xy x z xz -+--+的值是 ;15, ,则此三角形的面积是 ;16.已知抛物线2(0)y ax bx c c =++≠与x 轴的交点坐标为()1,0-,()3,0,当25x -≤≤时,y 的最大值为12,则该抛物线的解析式为 ;17.如图,直角梯形纸片ABCD 中,//AD BC ,AB BC ⊥,10AB =,25BC =,15AD =,以BD 为折痕,将ABD 折起,旋转180°后,点A 到点1A ,则凹五边形1BDCEA 的面积为 ;18.如图,将边长为a 的正方形ABCD 绕其顶点C 顺时针旋转45︒,得四边形A B C D '''',则图中阴影部分的面积是 ;19.If7,then the value range of real number a is ;20.如图,从边长为5的正方形纸片ABCD 中剪去直角EBF (点E 在边AB 上,点F 在边BC 上),EB BF +=则五边形AEFCD 的面积的最小值是 ;三、B 组填空题(每小题8分,共40分)21.下图是由若干个棱长为1厘米的正方形堆成的几何体,它的三视图中,面积最大的是 平方厘米,这个几何体的体积是 立方厘米22.如图,在ABC 中,502A AB AC ∠=︒==,,BD 是边AC 上的高,利用此图可求得tan15︒= ;BC = ;23.在直角坐标系内,如果一个点的横坐标和纵坐标都是整数,则称该点为整点,若凸n 边形的顶点都是整点,并且多边形内部及其边上没有其它整点,则n = ;24.如图,直角梯形中, 1.5213////90AB CD AF AD AB EF CD A ====∠=︒,,,,,,分别以AD FE ,所在的直线为x 轴、y 轴建立坐标系(,AD FE 为正方向)若抛物线过点B C 、,并且它的顶点M 在线段EF 上,则a = b = c = ;25.如图,ABC 中,90602B A AB AD ∠=︒∠=︒==,,,点M 在DC 上,以M 为圆心,以DM 为半径的半圆切边BC 于点N ,交MC 于点P ,则DM = 曲边的面积= ;附加题(每小题10分,共20分)1.若()326116f x x x ax =-+-可以被()23g x x =-整除,则a = 当()0f x >时,x 的取值范围是 ;2.有一堆黑,白围棋子,如果从中每次取出3枚黑子和2枚白子,当黑子被取完或剩下1枚或2枚时,则还剩35枚白子,如果每次取出5枚黑子和7枚白子,当白子被取完或剩下不足7枚时,则还剩下35枚黑子,那么这堆棋子中,原有黑子 枚,白子 枚;第二十四届“希望杯”全国数学邀请赛(第2试)一、选择题(每小题4分,共40分)1.如图,矩形ABCD 中,2AB =,1AD =,点M 在边DC 上,若AM 平分DMB ∠,则AMD ∠的大小是( )A .75B .60C .45D .302 )A .B .-C .D .-3.一个矩形被直线分成面积为,x y 的两部分,则y 与x 之间的函数关系只可能是( )A B C D 4.函数31x y x x-=-中,x 的取值范围是( ) A .0以外的一切实数 B .0,1-以外的一切实数 C .1±以外的一切实数 D .0,1±以外的一切实数5 )A .1B .2C .3D .4 6.代数式25x x -++( )A .有最小值,没有最大值B .有最大值,没有最小值C .既有最小值,也有最大值D .既没有最小值,也没有最大值7.如图,△ABC 中,AB=2,BC=4,CA=3,平行于BC 的直线l 过△ABC 的内心I ,分别交边AB AC 、于点D E 、,则ADE 的周长是( )A .5B .6C .7D .88.若动点)M x y (,到定点A 324⎛⎫⎪⎝⎭,的距离等于M 到直线54y =的距离,则动点)M x y (,的轨迹( )A .双曲线B .抛物线C .双曲线的一支D .一条直线9.不等式0a 的解是( ) A .0a ≠ B .1a >或1a <- C .1a >或10a -<< D .0a >或1a <-10.如图,ABC 中,1,2,90AB AC ABC ==∠=,若BD EF GH 、、都垂直于AC DE FG HI 、、、都垂直于BC ,则阴影HIC 的面积与ABC 的面积的比是( )A .634⎛⎫ ⎪⎝⎭ B .6324⎛⎫⨯ ⎪⎝⎭ C 634⎛⎫⎪⎝⎭D .62334⎛⎫⨯ ⎪⎝⎭二、填空题(每小题4分,共40分)112=的根是 ; 12.若正n 边形的一个外角为5︒,则n = ;13.已知关于x 的方程224220x x p p --++=的一个根为p ,则p = ;14.平面直角坐标系内,一只跳蚤停在点()5,0处,它要跳到点()6,0处,它每一跳都是飞越5个长度单位,并且总是跳到整点(坐标都是整数的点),也不从原路返回,那么,当它跳到点()6,0时,至少跳了 次 15.将一个圆分成三个相同的扇形,将其中一个卷成圆锥,锥顶对锥底圆周上任意两点的最大张角的余弦值是 ;16.将相同的平行四边形和相同的菱形镶嵌成如图所示的图案.设菱形中较小角为x 度,平行四边形中较大角为y 度,则y 与x 的关系式是 ;17.ABC 中,3,5,120AC BC ACB ==∠=,点M 平分AB ,则tan MCA ∠= ,MC = ;18.方程组3322181x y z x y z +=-⎧⎨+=-⎩的正整数解(),,x y z 是 ; 19.ABC 的三条高依次是643AD BE CF ===,,,则cos C = ,ABC 的面积是 ; 20.已知()f x 是一个多项式,若()f x 除以()1x -,余5;若()f x 除以()2x +,余2,则()f x 除以()()12x x -+,得到的余式是 ;三、解答题(每题都要写出推算过程) 21.(本题满分10分)已知二次函数24y mx x m =+++的图象在直线2y =-的上方. (1)求m 的取值范围;(2)当2m =时,求此二次函数的图象在x 轴上截得的线段长.22.(本题满分15分)一家商店销售某种计算器,开始按定价(小于200元的整数元)售出,后来按定价的六折售出,当售出200台时,共得款30498元.问:打折前,按定价售出了多少台?23.(本题满分15分)设()0)f x x =>(1)将()f x(a b ,是不同的整数)的形式;(2)求()f x 的最大值及相应的x 的值.第二十五届“希望杯”全国数学邀请赛(第1试)一、选择题(每小题4分,共40分)1.以下三角形中,与图1中的三角形相似的是( )图1 A B C D2.某商品原价200元,先降价%a ,又提价%a ,售价是182元,则下列关系式中正确的是( )A .()()2001%1%182a a -÷+=B .()()1821%1%200a a -÷+=C .()()2001%1%182a a +÷-=D .()()1821%1%200a a ÷-÷+= 3.一个几何体的三视图如图所示,则该几何体可能是下列四个选项中的( )主视图 左视图 俯视图A B C D4.若关于x 的一元二次方程()2223560m x x m m -++-+=的常数项为0,则m 的值是( )A .2B .3C .2或3D .0 5.方程20142014x x -=-的正整数解有( )A .2013个B .2014个C .2015个D .无穷多个6.在ABC 中,若AC =BC AB =ABC 的面积为( )A B . C .112D .67.Given equationx ,then the number of solutions for this equation is ( )A .0B .1C .2D .countless8.若()()6xx+=,则x =( )A .2B .2-C .2±D .12±9.如图,AB AC AD DE EC BC ====,,则ABC ∠的度数为( )A .30︒B .40︒C .45︒D .60︒ 10.如图,设AB 是O 的弦,CD 是O 的直径,且CD 与AB 相交,若CABOABm SS=-,OABn S=,则( )A .2m n >B .2m n =C .2m n <D .m 与2n 的大小关系无法确定. 二、A 组填空题(每小题4分,共40分)11.若2420y y ++=,则22224y y y =-+ ;12.如图,矩形ABCD 中,60AB =,23BD BC CD =+,则BC = ;13.InABC as shown in Fig., 40BAC ∠=︒.Both BD and CD are the interior angle bisectors of ABC which intersect atpoint D , BE and CE are exterior angle bisectors of ABC which intersect at point E ,then BDC BEC ∠-∠= °14.有1,2,5,10g g g g 的砝码各2个,从中任取2个放在已经平衡的天平的两端,则天平依然保持平衡的概率P = ;15.如图,将等边ABC 的外接圆对折,使点A 与弧BC 的中点F 重合,折痕与边AB AC 、分别交于点D E 、.若3BC =,则ADE 的面积是 ;16.如图,Rt ABC 中,9021C AC BC ∠=︒==,,,若以C 为圆心,CB 为半径的圆交AB 于点D ,则AD DB= ;17.在平面直角坐标系中,抛物线C 经过点()()3,87,8A B ,,且与x 轴恰有一个交点,则抛物线C 上纵坐标为32的两个点的距离为 ;18.如图,等边AFG 被线段BC DE ,分割成周长相等的三部分:等边三角形ACB 、梯形BCED 、梯形DEGF ,其面积分别为123S S S ,,,若263S =,则12S S -= ;19.如图,四边形ABCD 中,90571ABC CDA AD DC AB BC ∠=∠=︒====,,,,则BD = ; 20.正方体骰子的每个面内都写了一个正整数.随意地投掷这样的两个骰子,若朝上的两个面内的数的和为偶数的概率最小为P ,则P = ;三、B 组填空题(每小题8分,共40分.)21.若关于x 的方程()()()()2424x x p p --=--的两个实数根12x x ,是某直角三角形的两条直角边的长,则此直角三角形的面积最大是 ,此时P = ;22.If ,x y and z satisfy the equation x y z ++,then x y z ++= ,and xyz = ;23.若ABC 的三条边长,,a b c 满足2101261b c bc a a +==-+,,则ABC 的周长等于 ,面积等于 ;24.如图,在平面直角坐标系x O y --中,反比例函数()0ky x x=>的图象交矩形OBCD 的边BC 于点E ,交CD 于F 点,且14DF CD =,若四边形OECF 的面积为24,则k = ,OEFS= ;25.在直角坐标系xOy 中,抛物线2y ax bx c =++(,,a b c 是正整数)与x 轴有两个不同的交点()()12,0,,0A x B x .若1x 和2x 都大于1,则abc 的最小值是 ,此时a b c ++= ;第二十五届“希望杯”全国数学邀请赛(第2试)一、选择题(每小题4分,共40分)1.If both a and c are real numbers , 2and 3are the two solutions of the equation 2100ax x c -+= for x ,then the value of a c + is ( )A .10B .12C .14D .162.如图,在ABC 中,BC CA AB >>,D E F 、、分别是AB BC CA 、、边上的点,//,//DE AC FD CB ,若 :1:2AD DB =,则图中的相似三角形有( )对。
希望杯初三试题及答案

希望杯初三试题及答案一、选择题(每题3分,共30分)1. 下列哪项不是希望杯的特点?A. 面向初中生B. 强调数学思维C. 侧重于计算能力D. 每年举办一次答案:C2. 希望杯的举办时间通常是?A. 春季B. 夏季C. 秋季D. 冬季答案:A3. 希望杯的试题难度如何?A. 基础B. 中等C. 困难D. 非常困难答案:B4. 希望杯的奖项设置包括哪些?A. 一等奖、二等奖、三等奖B. 特等奖、一等奖、二等奖C. 金奖、银奖、铜奖D. 以上都是答案:A5. 希望杯的参赛资格是什么?A. 必须是初三学生B. 必须是数学竞赛获奖者C. 必须是学校推荐的学生D. 所有初三学生均可参加答案:D6. 希望杯的试题类型包括哪些?A. 选择题、填空题、解答题B. 选择题、计算题、解答题C. 选择题、填空题、证明题D. 选择题、填空题、计算题答案:A7. 希望杯的试题内容主要涉及哪些学科?A. 语文、数学、英语B. 数学、物理、化学C. 数学、历史、地理D. 数学、英语、物理答案:B8. 希望杯的试题评分标准是怎样的?A. 每题分值相同B. 根据难度不同分值不同C. 每题分值不同,但难度相同D. 根据答案的详细程度给分答案:B9. 希望杯的试题来源是什么?A. 官方指定教材B. 教师团队编写C. 学生自己出题D. 从历年试题中选择答案:B10. 希望杯的试题数量是多少?A. 10题B. 20题C. 30题D. 40题答案:C二、填空题(每题4分,共20分)1. 希望杯的试题通常由________个选择题和________个填空题组成。
答案:10,52. 希望杯的试题中,选择题的分值通常为________分,填空题的分值通常为________分。
答案:3,43. 希望杯的试题中,解答题的分值通常为________分,证明题的分值通常为________分。
答案:5,64. 希望杯的试题中,数学部分通常占总分的________%,物理部分通常占总分的________%。
“希望杯”全国数学邀请赛初三竞赛二试模拟卷

“希望杯”全国数学邀请赛初三竞赛二试模拟卷佚名【期刊名称】《中学教研:数学版》【年(卷),期】2009(000)006【总页数】3页(P45-47)【关键词】全国数学邀请赛;“希望杯”;模拟卷;竞赛;初三;数学课本;选择题;厚度【正文语种】中文【中图分类】G633.6一、选择题(每小题5分,满分40分)1、一张纸的厚度为0.07 mm,连续对折15次,这时它的厚度最接近于A.数学课本的厚度 B.书桌的高度 C.姚明的身高 D.三层楼的高度2、如图1,若直线x=1是二次函数y=ax2+bx+c的对称轴,则A.3bgt;2c B.a+b+clt;0 C.blt;a+c D.abcgt;03、已知直角坐标平面上的4个点P(-1,1),Q(1,5),R(2,7),S(4,14),其中有且只有3点在同一直线上,则不在这条直线上的点是A.R点 B.Q点 C.P点 D.S点4、一个长方体的长、宽、高分别为9 cm,6 cm,5 cm,先从这个长方体上尽可能大地切下一个正方体;再从剩余部分上又尽可能大地切下一个正方体;最后再从第2次剩余部分上又尽可能大地切下一个正方体,那么经过3次切割后剩余部分的体积为A.110 cm3 B.75 cm3 C.74 cm3 D.73 cm35、在半径为1的⊙O上任取一点A,连续以1为半径在⊙O上截取AB=BC=CD;分别以点A,D为圆心,点A到点C的距离为半径画弧,两弧相交于点E;又以点A为圆心,点O到点E的距离为半径画弧,交⊙O于点F.点F与点E在直线AD的2侧,则△ACF的面积是A. B. C. D.6、对于任意大于2的整数n,满足方程组的解的组数有A.n组 B.3组 C.2组 D.1组7、平面上有若干个点,其中任意3点都不在同一直线上.将这些点分成3组,并按下面的规则用线段连接:①在同一组的任意两点间都没有线段连接;②不在同一组的任意两点间一定有线段连接.平面上现有96条线段,则平面上至少有的点数是A.16点 B.17点 C.18点 D.19点8、将1,2,3,4,5这5个数排成一排,最后一个数是奇数,且使得其中任意连续3个数之和都能被这3个数中的第一个数整除,则满足要求的排法有A.2种 B.3种 C.4种 D.5种二、填空题(每小题5分,共40分)9、“北”、“京”、“奥”、“运”分别代表一个数字,4位数“”与它的各位数字的和为2 008,则这个4位数为________.10、若P是四边形ABCD内任意一点,且S△PAB+S△PCD=S四边形ABCD恒成立,则四边形ABCD的形状一定为________.图2 图311、己知方程组则x3=________.图2 图312、3位同学分别用m根长度相同的火柴棒,摆出了如图2,图3,图4的图案,各自恰好用完了这m根火柴棒.这些图案中的每个小正方形的边长均为一根火柴棒的长度,则m的最小值为________.13、如图5所示,直线l1⊥l2,垂足为点O,点A,B是直线l1上的2个点,且OB=2,AB=.直线l1绕点O按逆时针方向旋转,当旋转的角度α=60°时,在直线l2上可找到点P,使得△BPA是以∠B为顶角的等腰三角形,此时OP=________.14、在自然数的带余除法算式A÷B=C…1.己知A+B+C=2 015,则A=________.15、某班同学参加秋游约定条件,从a,b,c,d,e这5个风景点选择旅游点:(1)若去d,则也必须去b;(2)a,c两点至少去一个;(3)b,e两点只去一个;(4)a,e两点或都去,或都不去;(5)若去c,则a,d两点也必须去,则该班必去的风景点是________.16、某中学原有教室若干个,每个教室有相等数量的课桌,总课桌数为539张,今年学校新盖教学楼增加教室9个,全校课桌数增至1 080张,此时每个教室的课桌数仍然相等,且每个教室的课桌数都比以前增加,则现有教室有________个.三、解答题(每小题20分,共40分)17、己知a,b,c,d是非零实数,且满足a2+b2=1,c2+d2=1,ac+bd=0,则在下列几个等式中,哪几个是能够由上述条件推导出来的?请一一说明!(1)a2+c2=1;(2)ab+cd=0;(3)ad+cb=0.18、如图6,在直角坐标系中,已知点P0的坐标为(1,0),将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3,OP4,…,OPn(n为正整数).(1)求点P6的坐标及△P5OP6的面积;(2)我们规定:把点Pn(xn,yn)(n=0,1,2,3…)的横坐标xn、纵坐标yn都取绝对值后得到的新坐标(|xn|,|yn|),称之为点Pn的“绝对坐标”.根据图中点Pn的分布规律,请你猜想点Pn的“绝对坐标”,并写出来.1、C2、A3、D4、D5、D6、B7、B8、D9、2 003或1 985 10、平行四边形 11、1或-或- 12、52 13、OP=±1 14、1 849或1 609或1 921 15、e,a 16、2017、解 (1)由a2+b2=1,c2+d2=1,得又由ac+bd=0,得a2c2=b2d2,从而即得同理可得(2)由(a2+b2)(c2+d2)-(ac+bd)2=1,得又由(b2+d2)(a2+c2)-(ad-bc)2=0,可得因此(3)式(3)是不能推出的,只要举一个反例即可.取a=,b=-,c=,d=,此时,这4个非零实数对3个条件a2+b2=1,c2+d2=1,ac+bd=0,均得到了满足.但ad+cb≠0,这就表明式(3)不能成立,所以也是不能推出的.18、解 (1)根据旋转规律,点P6落在y轴的负半轴上,而点Pn到坐标原点的距离始终等于前一个点到原点距离的2倍,故其坐标为P6(0,26),即P6(0,64).又由已知,可得设P1(x1,y1),则从而又由=32,得从而(2)由题意知,OP0旋转8次之后回到x轴正半轴.在这8次中,点Pn分别落在坐标象限的平分线上或x轴或y轴上,但各点绝对坐标的横、纵坐标均为非负数,因此点Pn的坐标可分3类情况(令旋转次数为n):①当n=8k或n=8k+4时(其中k为自然数),点Pn落在x轴上,此时点Pn的绝对坐标为(2n,0);②当n=8k+1或n=8k+3或n=8k+5或n=8k+7时(其中k为自然数),点Pn落在各象限的平分线上,此时点Pn的绝对坐标为即(2n-1·,2n-1·).③当n=8k+2或n=8k+6(其中k为自然数)时,点Pn落在y轴上,此时点Pn的绝对坐标为(0,2n).。
初中二年级历届“希望杯”二试解答题

初中二年1-17届“希望杯”二试解答题1.1、从自然数354 , , 3 , 2 , 1 中任取178个数,试证:其中必有两个数,它们的差是177。
1.2、平面上有两个边长相等的正方形ABCD 和D C B A '''',且正方形D C B A ''''的顶点A '在正方形ABCD 的中心。
当正方形D C B A ''''绕A '转动时,两个正方形的重合部分的面积必然是一个定值。
这个结论对吗?证明你的判断。
1.3、用1,9,9,0四个数码组成的所有可能的四位数中,每一个这样的四位数与自然数n 之和被7除余数都不为1,将所有满足上述条件的自然数n 由小到大排成一列 <<<<4321n n n n ,试求:21n n ⋅之值。
2.1、已知两个正数的立方和是最小的质数,求证:这两个数之和不大于2。
2.2、一块四边形的地(如图2.2所示)(KG OH FK EO //,//)内有一段曲折的水渠,现在要把这段水渠EOHGKF 改成直的(即两边都是直线)。
但进水口EF 的宽度不能改变,新渠占地面积与原水渠面积相等,且要尽可能利用原水渠以节省工时,那么新渠的两条边应当怎么作?写出作法,并加以证明。
A B 图2.23.1、若0 , , , >d c b a ,证明:在方程02212=+++cd x b a x , 02212=+++da x c b x ,02212=+++ab x d c x ,02212=+++bc x a d x 中,至少有两个方程有不相等的实数根。
3.2、(1)能否把1992 , , 3 , 2 , 1 这1992个数分成八组,使得第二组各数之和比第一组各数之和多10,第三组各数之和比第二组各数之和多10,…,最后第八组各数之和比第七组各数之和也多10?请加以说明。
第15届 希望杯 初二 第二试

第二试 试题一、选择题 以下每题的四个结论中,仅有一个是正确的,请将正确答案的英文字母填在每题后的圆括号内.1.方程134x x ++-=的整数解有( ) A .2个B .3个C .5个D . 无穷多个2.若等式28339m n xx x x -=+--对任意的x (3x ±≠)恒成立,则mn =( ) A .8 B .8- C .16 D .16-3.若x z >,y z >,则下列各式中一定成立的是( ) A .4x y z +> B .3x y z +> C .2x y z +> D .x y z +>4.规定[]a 表示不超过a 的最大整数.当1x =-时,代数式3236mx nx -+的值为16,则23m n ⎡⎤-=⎢⎥⎣⎦( )A .4-B .3-C .3D .45.如图1,在平行四边形ABCD 中,AC 与BD 相交于O ,AE BD ⊥于E ,CF BD ⊥于F ,那么图中 的全等三角形共有( ) A .5对 B .6对 C .7对 D .8对OFE D CBA图 1CBA图 26.如图2,在直角扇形ABC 内,分别以AB 和AC 为直径作半圆,两条半圆弧相交于点D ,整个图形 被分成1S 、2S 、3S 、4S 四部分,则2S 和4S 的大小关系是( ) A .24S S <B .24S S =C .24S S >D .无法确定7.Given m is a real number ,and 11m m -=+,simplify an algebraic expression to( ) A .1m -B .1m -+C .1m -D .1m -+(英汉小词典simplify :化简;algebraic expression :代数式)8.初二⑴班共有35名学生,其中12的男生和13的女生骑自行车上学,那么该班骑自行车上学的学生 的人数最少是( ) A .9 B .10C .11D .129.李编辑昨天按时间顺序先后收到A 、B 、C 、D 、E 共5封电子邮件,如果他每次都是首先回复 最新收到的一封电子邮件,那么在下列顺序 ①BAECD ②CEDBA ③ACBED ④DCABE中,李编辑可能回复的邮件顺序是( ) A .①和② B .②和③ C .③和④D .①和④10.有A 、B 、C 三把刻度尺,它们的刻度都是从0到30个单位(单位长度各不相同),设三把尺子的0刻度和30刻度处到尺子边缘的长度可以忽略不计,现用其中的一把尺子量度另两把尺子的长度已知用C 尺量度,得到A 尺比B 尺长6个单位,得B 尺比C 尺长10个单位;则用B 尺量度,A 尺比C 尺( ) A .长15个单位 B .短15个单位 C .长5个单位 D .短5个单位(似题人:王永会 吉林省吉林市松花江中学132000)二、填空题11.若方程23100210021002x -=的根分别是1x 和2x ,则12x x += .12.分解因式:432234232a a b a b ab b ++++= .13.对于任意的自然数n ,有()f n =, 则()135999f f f f ++++= .14.1x ,2x ,3x ,4x ,5x ,6x 都是正数,且2345611x x x x x x =,1345622x x x x x x =,1245633x x x x xx =,1235644x x x x x x =,1234656x x x x x x =,1234569x x x x xx =,则123456x x x x x x = .15.(Figure 3)In a trapezoid ABCD ,13AE DE =,CE AD ⊥,CE is a bisector to BCD ∠,then the ratio of the area of a quadrilateral ABCE to that of a triangle CDE is .(英汉小词典 trapezoid :梯形;bisector :平分;ratio :比值;quadrilateral :四边形)16.已知a ,b ,c ,d 为正整数,且47b d a c -=,()711d b a c -+=,则ca的值是 ;17.一个直角三角形的三条边的长均为整数,已知它的一条直角边的长是18,那么另一条直角边的长 有种可能 18.“神舟”飞船由返回舱、轨道舱和推进舱三个舱组成,已知三个舱中每两个舱的长度之和分别为4859毫米、5000毫米和5741毫米,那么这三个舱中长度最大的是 毫米;长度最小的是 毫米.19.若()()()12213136x x y y z z ++--++-++=,则23x y z ++的最大值是 ,最小值是 .20.图4是某电台“市民热线”栏目一周内接到的热线电话的统计图,其中有关房产城建的热线电话有30个,那么有关环境保护的电话有 个;如果每年按52周计算,每周接到的热线电话数量相同,那么“市民热线”一年内接到的热线电话有 个.EDCB A图 3环境保护道路交通其它方面房产城建144°36°72°图 4三、解答题 要求写出简要步骤21.民航规定:旅客可以免费携带a 千克物品,若超过a 千克,则要收取一定的费用,当携带物品的重量为b 千克(b a >)时,所交费用为10200Q b =-(元).⑴ 小明携带了35千克的物品,重量大于a 千克,他应交多少费用? ⑵ 小王交了100元费用,他携带了多少千克物品?⑶ 若收费标准以超重部分的重量m (千克)计算,在保证所交费用Q 不变的情况下,试用m 表 示Q .22.如图5,一张矩形纸片ABCD 的边长分别为9厘米和3厘米,把顶点A 和C 叠合在一起,得到折痕EF .⑴ 证明四边形AECF 是菱形;⑵ 计算折痕EF 的长; ⑶ 求CEH △的面积.23.如图6,用水平线与竖直线将平面分成若干个边长为1的正方形格子,点O 、A 、B 均在正方形格子的顶点(格点)处,其中点O 与点A 位于同一水平线上,相距a 格,点O 与点B 位于同一竖直线上,相距b 格.⑴ 若5a =,4b =,则OAB △中(包括三条边)共有多少个格点?⑵ 若a ,b 互质,则在线段AB 上(不包括A 、B 两点)是否有格点?证明你的结论; ⑶ 若a ,b 互质,且8a b >>,OAB △中(包括三条边)共有67个格点,求a ,b 的值.OBA图 6H (D )FE D C (A)BA 图 5答 案一、选择题1.C【解析】 用数轴表示,方程中的未知数x 表示到1-与3的距离的和等于4的整数值,所以11x =-,20x =,31x =,42x =,53x =, 共有5个整数解,选C .2.D【解析】 因为3x ±≠,将原等式去分母得()()338m x m x x --+=,即()()38m n x m n x --+=, 所以80.m n m n -=⎧⎨+=⎩,解得44.m n =⎧⎨=-⎩,所以16mn =-,选D .3.C【解析】 因为x z >,y z >,将两式相加得2x y z +>,选C .此题易误选D ,因为z 可以是负数,所以x y z +>不一定成立.4.A【解析】 将1x =-代入323616mx nx -+=,得3210n m -=, 所以21033m n -=.因为10433-<-<-,所以243m n ⎡⎤-=-⎢⎥⎣⎦.选A .5.C【解析】 ABD CDB △△≌,ABE CDF △△≌,ABO CDO △△≌,AEO CFO △△≌,AED CFB △△≌,AOD COB △△≌,ACD CAB △△≌,共7对全等三角形,选C .6.B【解析】 如图7,连结AD 并延长交弧CB 于点E ,则点B 、D 、E 之间的阴影部分的面积是212S ,点A 、D 之间的阴影部分的面积是412S .设以AB 为半径的圆的面积为A S ,A 、B 、D 之间的空白部分面积为S .图 7因为21128A ABE S S S S S =-=-扇形;41128A ADB S S S S S =-=-扇形. 所以24S S =.选B .7.D【解析】 译文:若实数m 满足11m m -=+)A .1m -B .1m -+C .1m -D . 1m -+ 由条件11m m -=+,得 11m m --=.m 表示数轴上到1和0的距离的差等于1的数,可知0m ≤.11m m =-=-.选D .8.D【解析】 设初二⑴班有男生x 名,则女生有()35x -名,骑自行车上学的人数为35704112366x x x x-+++==+. 要使上式的值最小且为整数,则2x =,所以骑自行车上学的人数最少为4211126++=(人),选D . 9.B【解析】 解法1:在①中,E 前在面没有D ,接下来的回复的应是D 而不是C .在④中,C 前面没有B ,接下来回复的应是B 而不是A .所以,只有顺序②、③是可能的,选B .解法2:制5张卡片,分别注上A 、B 、C 、D 、E ,具体演示一下不难得出结果.10.A【解析】 设A 、B 、C 的实际长度分别为a ,b ,c ,则它们的单位长度分别为30a ,30b ,30c. 依题意有630510.303c c a b a a b c ⎧-=⋅=⎪⎪⎨⎪-=⋅=⎪⎩,设用B 量度时,A 比C 长x 个单位,则由12a c b -=,得1530a cx b -==(个单位),选A .二、填空题11.2004【解析】 原方程化为210021002x -=,整理得210021002x -=±,解得2110021002x =+,2210021002x =-, 所以122004x x +=.12.()222a b ab ++【解析】 原式()()42243322222a a b b a b ab a b =+++++()()()2222222a b ab a b ab =++++()222a b ab =++13.5 【解析】 因为()f n ===, 所以()()()()135999f f f f ++++3100022=++++5==.14.6【解析】 将六个等式相乘得()4412345612966x x x x x x ==,因为1x ,2x ,3x ,4x ,5x ,6x 都是正数, 所以1234566x x x x x x =.15.79∶【解析】 译文:如图3,梯形ABCD 中,13AE DE =,CE AD ⊥,CE 平分BCD ∠,则四边形ABCE 与三角形CDE 的面积之比是 .如图8,延长DA 、CB 相交于点G . 因为CE 平分BCD , 且CE AD ⊥,所以CDG △是等腰三角形,GA BCDE 图 8CD CG =.又AB DC ∥,13AE DE =,所以2133GA DE GD ==,所以19GAB GDC S S =△△,ABCE GEC GAB S S S =-△△ 1129GDC S ⎛⎫=- ⎪⎝⎭△, 718GDC S =△, 12DCE GDC S S =△△,所以79ABCE DCE S S =△∶∶.16.21;7 【解析】 由已知47b d a c -=,得47c d a b -=. 由()711d b a c -+=,得771c d a b -=+. 所以47771d d b b --=+, 整理得713d b d-=+.因为b 是正整数,所以703d d -≥,且73d d-是整数. 显然27d >-,故73d d -<,所以713d d-<,所以只有703d d -=,即7d =时,b 是整数,1b =.所以77211c d a b -==+,7d b=.17.2;80【解析】 设另一条直角边长为x ,斜边长为y ,由勾股定理,得22218x y +=,即()()324116221083814y x y x +-=⨯=⨯=⨯=⨯54636927121818=⨯=⨯=⨯=⨯.因为y x +和y x -相差2x ,所以它们的奇偶性相同,且y x y x +>-, 所以1622.y x y x +=⎧⎨-=⎩,和546.y x y x +=⎧⎨-=⎩,解得80x =或24.即x 的值有2种可能,它的最大值是80.18.2941;2059【解析】 设三个舱的长度分别为x 毫米,y 毫米和z 毫米,由题意知485950005741.x y y z z x +=⎧⎪+=⎨⎪+=⎩,,①②③ 由①+②+③,得()215600x y z ++=, 即7800x y z ++=, ④由④-②,得2800x =, 由④-③,得2059y =, 由④-①,得2941z =.所以三个舱中长度最大的是2941毫米,长度最小的是2059毫米.19.15;6-【解析】 因为123x x ++-≥,当12x -≤≤时等号成立;213y y -++≥,当12y -≤≤时等号成立; 314z z -++≥,当13z -≤≤时等号成立,由已知()()()12213136x x y y z z ++--++-++=,所以只有123x x ++-=,213y y -++=,314z z -++=.则当2x =,2y =,3z =时,23x y z ++最大,最大值为15; 当1x =-,1y =-,1z =-时,23x y z ++最小,最小值为6-.20.45;7800【解析】 由统计图可知,“环境保护”所占圆心角的大小为3601447236108︒-︒-︒-︒=︒,所以有关环境保护的热线电话有301084572⨯=(个); 每周接到的热线电话有3036015072⨯=(个); 全年的热线电话共有150527800⨯=(个).三、解答题21.【解析】 ⑴ 当携带的物品重量35b =千克时,应交的费用为3510200150Q =⨯-=(元).小明应交150元.⑵ 小王交了100Q =元的费用,设他携带了x 千克物品,则10200100x -=,解得30x =.因此,小王携带了30千克物品. ⑶ 已知最多可以免费携带a 千克物品,则102000a -=,解5是20a =,所以超重部分的重量为20m b a b =-=-, 即20b m =+,故所交费用为()10200102020010Q b m m =-=+-=(元)22.【解析】 ⑴ 如图9,因为AB CD ∥,所以AF CE ∥,CF HE ∥. 根据对称性,知CEH AED =∠∠, 因为D 、E 、C 三点共线, 所以A 、E 、H 三点共线.所以AE CF ∥,四边形AECF 是平行四边形, 又AF CF =,所以四边形AECF 是菱形.(也可通过AC 垂直平分EF 进行证明) ⑵ 设AF x =厘米,则CF x =厘米,()9BF x =-厘米. 在BCF △中,222CF BF BC =+, 所以()22293x x =-+,解得5x =,即5CF =厘米,4BF =厘米. 过E 作EM AB ⊥交AB 于M ,则1MF BM BF CE BF CF BF =-=-=-=厘米,3EM =厘米,所以EF = ⑶ 根据对称性,知CEH AED △△≌,所以12CEH AED S S DE AD ==⋅△△()12AF MF AD =-⋅ 14362=⨯⨯=(平方厘米) M ABC (A)D EFH (D )图 923.【解析】 ⑴ 如图10,5a =,4b =,OAB △中(包括三条边) 的格点的个数为1234616++++=(个)图 10⑵ 若a ,b 互质,假设线段AB 上存在某一点P (恰为格点),设点P 到OA 的距离为y ,到OB 的距离为x (x ,y 均为整数),则12AOB S ab =△,1122AOP BOP S S ay bx +=+△△.所以111222ab ay bx =+,即ab ay bx =+,()ay b a x =-. 因为a ,b 互质,所以a x -是a 的倍数,但与a x a -<矛盾,因此假设不正确, 即线段AB 上(除A 、B 两点外)不存在其他格点.⑶ 由⑵知,线段AB 上(除A 、B 两点外)不存在其他的格点.以OA 、OB 为边作一个矩形OACB ,则CAB △中格点的个数与OAB △中格点的个数相同,且只有A 、B 两点是公共的,在矩形OACB 中格点的个数为()()11a b ++. 因此()()112267134a b +++=⨯=,()()1113222311a b ++==⨯⨯⨯.由8a b >>,得112a +=,111b +=, 即11a =,10b =.。
