动量定理与动量守恒定律·典型例题解析
高考物理动量守恒定律试题经典及解析

5.(1)恒星向外辐射的能量来自于其内部发生的各种热核反应,当温度达到 108K 时,可
以发生“氦燃烧”。
①完成“氦燃烧”的核反应方程:
4 2
He
___
8 4
Be
γ
。
②
8 4
Be
是一种不稳定的粒子,其半衰期为
2.6×10-16s。一定质量的
8 4
Be
,经
7.8×10-16s
后所剩下的
8 4
Be
占开始时的
械能守恒定律有 m1gh=
1 2
m1 v02
(1
分)v0=
2gh ,解得:v0=4.0 m/s(1 分)
②设物块 B 受到的滑动摩擦力为 f,摩擦力做功为 W,则 f=μm2g(1 分)
W=-μm2gx 解得:W=-1.6 J(1 分)
③设物块 A 与物块 B 碰撞后的速度为 v1,物块 B 受到碰撞后的速度为 v,碰撞损失的机械
关数学知识辅助分析、求解。
4.装甲车和战舰采用多层钢板比采用同样质量的单层钢板更能抵御穿甲弹的射击.通过对 一下简化模型的计算可以粗略说明其原因.质量为 2m、厚度为 2d 的钢板静止在水平光滑 桌面上.质量为 m 的子弹以某一速度垂直射向该钢板,刚好能将钢板射穿.现把钢板分成 厚度均为 d、质量均为 m 的相同两块,间隔一段距离水平放置,如图所示.若子弹以相同 的速度垂直射向第一块钢板,穿出后再射向第二块钢板,求子弹射入第二块钢板的深 度.设子弹在钢板中受到的阻力为恒力,且两块钢板不会发生碰撞不计重力影
E
1 2
mv02
1 2
Mv2
M
m mv02
2M
E mc2
解得
m
高中物理-动量守恒定律经典例题详解

高中物理-动量守恒定律经典例题详解一 动量 冲量 动量定理1.篮球运动员通常伸出双手迎接传来的篮球.接球时,两手随球迅速收缩至胸前.这样做可以( )A .减小球对手的冲量B .减小球对手的冲击力C .减小球的动量变化量D .减小球的动能变化量答案B [解析] 由动量定理Ft =Δp 知,接球时两手随球迅速收缩至胸前,延长了手与球接触的时间,从而减小了球的动量变化率,减小了球对手的冲击力,选项B 正确.二 动量守恒定律2. 一弹丸在飞行到距离地面5 m 高时仅有水平速度v =2 m/s ,爆炸成为甲、乙两块水平飞出,甲、乙的质量比为3∶1,不计质量损失,重力加速度g 取10 m/s 2,则下列图中两块弹片飞行的轨迹可能正确的是A BC D答案B [解析] 弹丸在爆炸过程中,水平方向的动量守恒,有m 弹丸v 0=34m v 甲+14m v 乙,解得4v 0=3v 甲+v 乙,爆炸后两块弹片均做平抛运动,竖直方向有h =12gt 2,水平方向对甲、乙两弹片分别有x 甲=v 甲t ,x 乙=v 乙t ,代入各图中数据,可知B 正确.3.如图所示,竖直平面内的四分之一圆弧轨道下端与水平桌面相切,小滑块A 和B 分别静止在圆弧轨道的最高点和最低点.现将A 无初速释放,A 与B 碰撞后结合为一个整体,并沿桌面滑动.已知圆弧轨道光滑,半径R =0.2 m ;A 和B 的质量相等;A 和B 整体与桌面之间的动摩擦因数μ=0.2.重力加速度g 取10 m/s 2.求:(1) 碰撞前瞬间A 的速率v ;(2) 碰撞后瞬间A 和B 整体的速率v ′; (3) A 和B 整体在桌面上滑动的距离l .[答案] (1)2 m/s (2)1 m/s (3)0.25 m [解析] 设滑块的质量为m . (1)根据机械能守恒定律有mgR =12m v 2解得碰撞前瞬间A 的速率有v =2gR =2 m/s.(2)根据动量守恒定律有m v =2m v ′解得碰撞后瞬间A 和B 整体的速率v ′=12v =1 m/s.(3)根据动能定理有12(2m )v ′2=μ(2m )gl 解得A 和B 整体沿水平桌面滑动的距离l =v ′22μg=0.25 m . 4.质量为2 kg 的小车以2 m/s 的速度沿光滑的水平面向右运动,若将质量为0 .5 kg 的砂袋以3 m/s 的水平速度迎面扔上小车,则砂袋与小车一起运动的速度的大小和方向是( )A .1.0 m/s ,向右B .1.0 m/s ,向左C .2.2 m/s ,向右D .2.2 m/s ,向左答案D [解析] 忽略空气阻力和分离前后系统质量的变化,卫星和箭体整体分离前后动量守恒,则有(m 1+m 2)v 0=m 1v 1+m 2v 2,整理可得v 1=v 0+m 2m 1(v 0-v 2),故D 项正确. 5.冰壶运动深受观众喜爱,图X291甲为2014年2月第22届索契冬奥会上中国队员投掷冰壶的镜头.在某次投掷中,冰壶甲运动一段时间后与对方静止的冰壶乙发生正碰,如图乙.若两冰壶质量相等,则碰后两冰壶最终停止的位置,可能是图丙中的哪幅图( )图X291答案B [解析] 两个质量相等的冰壶发生正碰,碰撞前后都在同一直线上,选项A 错误;碰后冰壶A 在冰壶B 的左边,选项C 错误;碰撞过程中系统的动能可能减小,也可能不变,但不能增大,所以选项B 正确,选项D 错误.6.下图X292是“牛顿摆”装置,5个完全相同的小钢球用轻绳悬挂在水平支架上,5根轻绳互相平行,5个钢球彼此紧密排列,球心等高.用1、2、3、4、5分别标记5个小钢球.当把小球1向左拉起一定高度,如图甲所示,然后由静止释放,在极短时间内经过小球间的相互碰撞,可观察到球5向右摆起,且达到的最大高度与球1的释放高度相同,如图乙所示.关于此实验,下列说法中正确的是()图X292A.上述实验过程中,5个小球组成的系统机械能守恒,动量守恒B.上述实验过程中,5个小球组成的系统机械能不守恒,动量不守恒C.如果同时向左拉起小球1、2、3到相同高度(如图丙所示),同时由静止释放,经碰撞后,小球4、5一起向右摆起,且上升的最大高度高于小球1、2、3的释放高度D.如果同时向左拉起小球1、2、3到相同高度(如图丙所示),同时由静止释放,经碰撞后,小球3、4、5一起向右摆起,且上升的最大高度与小球1、2、3的释放高度相同答案D[解析] 5个小球组成的系统发生的是弹性正碰,系统的机械能守恒,系统在水平方向的动量守恒,总动量并不守恒,选项A、B错误;同时向左拉起小球1、2、3到相同的高度,同时由静止释放并与4、5碰撞后,由机械能守恒和水平方向的动量守恒知,小球3、4、5一起向右摆起,且上升的最大高度与小球1、2、3的释放高度相同,选项C错误,选项D正确.三动量综合问题7. 如图所示,水平地面上静止放置一辆小车A,质量m A=4 kg,上表面光滑,小车与地面间的摩擦力极小,可以忽略不计.可视为质点的物块B置于A的最右端,B的质量m B =2 kg.现对A施加一个水平向右的恒力F=10 N,A运动一段时间后,小车左端固定的挡板与B发生碰撞,碰撞时间极短,碰后A、B粘合在一起,共同在F的作用下继续运动,碰撞后经时间t=0.6 s,二者的速度达到v t=2 m/s.求:(1)A开始运动时加速度a的大小;(2)A、B碰撞后瞬间的共同速度v的大小;(3)A的上表面长度l.答案(1)2.5 m/s2(2)1 m/s(3)0.45 m[解析] (1)以A为研究对象,由牛顿第二定律有F=m A a①代入数据解得a=2.5 m/s2②(2)对A、B碰撞后共同运动t=0.6 s的过程,由动量定理得Ft=(m A+m B)v t-(m A+m B)v③代入数据解得v =1 m/s ④(3)设A 、B 发生碰撞前,A 的速度为v A ,对A 、B 发生碰撞的过程,由动量守恒定律有m A v A =(m A +m B )v ⑤A 从开始运动到与B 发生碰撞前,由动能定理有Fl =12m A v 2A ⑥ 由④⑤⑥式,代入数据解得l =0.45 m ⑦8.如图所示,质量分别为m A 、m B 的两个弹性小球A 、B 静止在地面上,B 球距地面的高度h =0.8 m ,A 球在B 球的正上方,先将B 球释放,经过一段时间后再将A 球释放,当A 球下落t =0.3 s 时,刚好与B 球在地面上方的P 点处相碰,碰撞时间极短,碰后瞬间A 球的速度恰为零,已知m B =3m A ,重力加速度大小g 取10 m/s 2,忽略空气阻力及碰撞中的动能损失.求:(1)B 球第一次到过地面时的速度; (2)P 点距离地面的高度.答案解:(ⅰ)设B 球第一次到达地面时的速度大小为v B ,由运动学公式有v B =2gh ①将h =0.8 m 代入上式,得v 1=4 m/s.②(ⅱ)设两球相碰前后,A 球的速度大小分别为v 1和v ′1(v ′1=0),B 球的速度分别为v 2和v ′2,由运动学规律可得v 1=gt ③由于碰撞时间极短,重力的作用可以忽略,两球相碰前后的动量守恒,总动能保持不变,规定向下的方向为正,有m A v 1+m B v 2=m B v ′2④12m A v 21+12m B v 22=12m v ′22⑤ 设B 球与地面相碰后速度大小为v ′B ,由运动学及碰撞的规律可得v ′B =v B ⑥设P 点距地面的高度为h ′,由运动学规律可得h ′=v ′2B -v 222g⑦联立②③④⑤⑥⑦式,并代入已知条件可得h ′=0.75 m .⑧9. 一中子与一质量数为A (A >1)的原子核发生弹性正碰.若碰前原子核静止,则碰撞前与碰撞后中子的速率之比为( )A.A +1A -1B.A -1A +1C.4A(A +1)2 D.(A +1)2(A -1)2答案A [解析] 本题考查完全弹性碰撞中的动量守恒、动能守恒.设碰撞前后中子的速率分别为v 1,v ′1,碰撞后原子核的速率为v 2,中子的质量为m 1,原子核的质量为m 2,则m 2=Am 1.根据完全弹性碰撞规律可得m 1v 1=m 2v 2+m 1v ′1,12m 1v 21=12m 2v 22+12m 1v ′21,解得碰后中子的速率v ′1=⎪⎪⎪⎪⎪⎪m 1-m 2m 1+m 2v 1=A -1A +1v 1,因此碰撞前后中子速率之比v 1v ′1=A +1A -1,A 正确.10.如图X296所示,竖直平面内的光滑水平轨道的左边与墙壁对接,右边与一个足够高的14光滑圆弧轨道平滑相连,木块A 、 B 静置于光滑水平轨道上,A 、B 的质量分别为1.5kg 和0.5 kg.现让A 以6 m/s 的速度水平向左运动,之后与墙壁碰撞,碰撞的时间为0.3 s ,碰后的速度大小变为4 m/s.当A 与B 碰撞后会立即粘在一起运动,g 取10 m/s 2,求:(1)在A 与墙壁碰撞的过程中,墙壁对A 的平均作用力的大小; (2)A 、B 滑上圆弧轨道的最大高度.图X296答案(1)50 N (2)0.45 m[解析] (1)设水平向右为正方向,当A 与墙壁碰撞时根据动量定理有 Ft =m A v ′1-m A ·(-v 1) 解得F =50 N.(2)设碰撞后A 、B 的共同速度为v ,根据动量守恒定律有 m A v ′1=(m A +m B )vA 、B 在光滑圆形轨道上滑动时,机械能守恒,由机械能守恒定律得 12(m A +m B )v 2=(m A +m B )gh 解得h =0.45 m.四 力学观点的综合应用11.如图的水平轨道中,AC 段的中点B 的正上方有一探测器,C 处有一竖直挡板,物体P 1沿轨道向右以速度v 1与静止在A 点的物体P 2碰撞,并接合成复合体P ,以此碰撞时刻为计时零点,探测器只在t 1=2 s 至t 2=4 s 内工作.已知P 1、P 2的质量都为m =1 kg ,P 与AC 间的动摩擦因数为μ=0.1,AB 段长L =4 m ,g 取10 m/s 2,P 1、P 2和P 均视为质点,P 与挡板的碰撞为弹性碰撞.(1)若v 1=6 m/s ,求P 1、P 2碰后瞬间的速度大小v 和碰撞损失的动能ΔE ;(2)若P 与挡板碰后,能在探测器的工作时间内通过B 点,求v 1的取值范围和P 向左经过A 点时的最大动能E .答案(1)3 m/s 9 J (2)10 m/s ≤v 1≤14 m/s 17 J [解析] (1)P 1、P 2碰撞过程动量守恒,有m v 1=2m v解得v =v 12=3 m/s碰撞过程中损失的动能为ΔE =12m v 21-12(2m )v 2解得ΔE =9 J.(2)由于P 与挡板的碰撞为弹性碰撞.故P 在AC 间等效为匀减速运动,设P 在AC 段加速度大小为a ,碰后经过B 点的速度为v 2 ,由牛顿第二定律和运动学规律,得μ(2m )g =2ma3L =v t -12at 2v 2=v -at解得v 1=2v =6L +μgt 2t v 2=6L -μgt 22t由于2 s ≤t ≤4 s 所以解得v 1的取值范围10 m/s ≤v 1≤14 m/sv 2的取值范围1 m/s ≤v 2≤5 m/s所以当v 2=5 m/s 时,P 向左经过A 点时有最大速度 v 3=v 22-2μgL则P 向左经过A 点时有最大动能E =12(2m )v 23=17 J. 12. 冰球运动员甲的质量为80.0 kg.当他以5.0 m/s 的速度向前运动时,与另一质量为100 kg 、速度为3.0 m/s 的迎面而来的运动员乙相撞.碰后甲恰好静止.假设碰撞时间极短,求:(1 )碰后乙的速度的大小; (2)碰撞中总机械能的损失. [答案] (1)1.0 m/s (2)1400 J[解析] (1)设运动员甲、乙的质量分别为m 、M ,碰前速度大小分别为v 、V ,碰后乙的速度大小为V ′.由动量守恒定律有m v -MV =MV ′①代入数据得V ′=1.0 m/s ②(2)设碰撞过程中总机械能的损失为ΔE ,应有12m v 2+12MV 2=12MV ′2+ΔE ③ 联立②③式,代入数据得ΔE =1400 J ④。
专题:动量定理 动量守恒定律

专题:动量定理动量守恒定律考点一:动量定理的理解及应用【典例1】质量的篮球从距地板高处由静止释放,与水平地板撞击后反弹上升的最大高度,从释放到弹跳至h高处经历的时间,忽略空气阻力,重力加速度,求:篮球与地板撞击过程中损失的机械能;篮球对地板的平均撞击力.强化训练一1.蹦床运动有“空中芭蕾“之称,某质量的运动员从空中落下,接着又能弹起高度,此次人与蹦床接触时间,取,求:运动员与蹦床接触时间内,所受重力的冲量大小I;运动员与蹦床接触时间内,受到蹦床平均弹力的大小F。
2.蹦床是运动员在一张绷紧的弹性网上蹦跳、翻滚并做各种空中动作的运动项目一个质量为60kg的运动员,从离水平网面高处自由下落,着网后沿竖直方向蹦回离水平网面高处已知运动员与网接触的时间为若把在这段时间内网对运动员的作用力当作恒力处理,求此力的大小取3.如图所示,物块A和B通过一根轻质不可伸长的细绳连接,跨放在质量不计的光滑定滑轮两侧,质量分别为、。
初始时A静止与水平地面上,B悬于空中。
先将B竖直向上再举高未触及滑轮然后由静止释放。
一段时间后细绳绷直绷直的时间极短,A、B以大小相等的速度一起运动,之后B恰好可以和地面接触。
取。
从释放到细绳绷直时的运动时间t;的最大速度v的大小;初始时B离地面的高度H。
4.某游乐园入口旁有一喷泉,喷出的水柱将一质量M的卡通玩具稳定地悬停在空中。
为计算方便起见,假设水柱从横截面积为S的喷口持续以速度竖直向上喷出;玩具底部为平板面积略大于;水柱冲击到玩具底板后,在竖直方向水的速度变为零,在水平方向朝四周均匀散开。
忽略空气阻力。
已知水的密度为,重力加速度大小为g。
求喷泉单位时间内喷出的水的质量;玩具在空中悬停时,其底面相对于喷口的高度。
考点二:动量守恒定律的理解及应用【典例2】在光滑水平面上静止有质量均为m的木板AB和滑块CD,木板AB上表面粗糙,滑块CD上表面是光滑的圆弧,他们紧靠在一起,如图所示一个可视为质点的物块P,质量也为m,它从木板AB的右端以初速度滑上木板,过B点时速度为,然后又滑上滑块CD,最终恰好能滑到滑块CD圆弧的最高点C处若物体P与木板AB间的动摩擦因数为,求:物块滑到B处时木板AB的速度的大小;木板AB的长度L;滑块CD最终速度的大小.【典例3】如图所示,在光滑的水平面上有一带半圆形光滑弧面的小车,质量为M,圆弧半径为R,从距车上表面高为H处静止释放一质量为m的小球,它刚好沿圆弧切线从A点落入小车,求小球到达车底B点时小车的速度和此过程中小车的位移;小球到达小车右边缘C点处,小球的速度.强化训练二1. 如图,在光滑的水平面上,有一质量为 的木板,木板上有质量为 的物块 它们都以 的初速度反向运动,它们之间有摩擦,且木板足够长,求:当木板向左的速度为 时,物块的速度是多大?木板的最终速度是多大?2. 如图所示,A 、B 两木块靠在一起放于光滑的水平面上,A 、B 的质量均为 。
动量冲量和动量定理典型例题精析

动量、冲量和动量定理·典型例题精析[例题1]质量为m的物体,在倾角为θ的光滑斜面上由静止开始下滑.如图7-1所示.求在时间t内物体所受的重力、斜面支持力以与合外力给物体的冲量.[思路点拨]依冲量的定义,一恒力的冲量大小等于这力大小与力作用时间的乘积,方向与这力的方向一致.所以物体所受各恒力的冲量可依定义求出.而依动量定理,物体在一段时间t内的动量变化量等于物体所受的合外力冲量,故合外力给物体的冲量又可依动量定理求出.[解题过程]依冲量的定义,重力对物体的冲量大小为I G=mg·t,方向竖直向下.斜面对物体的支持力的冲量大小为I N=N·t=mg·cosθ·t,方向垂直斜面向上.合外力对物体的冲量可分别用如下三种方法求出.(1)先根据平行四边形法如此求出合外力,再依定义求出其冲量.由图7-1(2)知,作用于物体上的合力大小为F=mg·sinθ,方向沿斜面向下.所以合外力的冲量大小I F=F·t=mg·sinθ·t.方向沿斜面向下.(2)合外力的冲量等于各外力冲量的矢量和,先求出各外力的冲量,然后依矢量合成的平行四边形法如此求出合外力的冲量.利用前面求出的重力与支持力冲量,由图7-1(3)知合外力冲量大小为方向沿斜面向下.或建立平面直角坐标系如图7-1(4),由正交分解法求出.先分别求出合外力冲量I F在x,y方向上分量I Fx,I Fy,再将其合成.(3)由动量定理,合外力的冲量I F等于物体的动量变化量Δp.I F=Δp=Δmv=mΔv=m(at)=mgsinθ·t.[小结] (1)计算冲量必须明确计算的是哪一力在哪一段时间内对物体的冲量.(2)冲量是矢量,求某一力的冲量除应给出其大小,还应给出其方向.(3)此题解提供了三种不同的计算合外力冲量的方法.[例题2]一质量为100g的小球从0.80m高处自由下落到一厚软垫上.假如从小球接触软垫到小球陷至最低点经历了0.20 s,如此这段时间内软垫对小球的冲量为多少(取g=10 m/s2,不计空气阻力)?[思路点拨]小球从落至软垫至陷到最低点,即速度变为零的过程中,受重力和软垫对它的作用力,软垫对球的作用力在此过程中是变力,但动量定理对于变力依然适用.因此可以用动量定理求软垫对球的冲量.[解题过程]小球落至软垫前,只受重力作用,故可由自由落体公式求出小球落至软垫时的速度大小为方向竖直向下.小球接触软垫后除受重力mg外,还受软垫对它的作用力F,在这两力合力冲量作用下,小球动量变为零(此时小球陷至最低点).取竖直向上为正方向,小球的初动量为p=-mv(负号表示小球刚与软垫接触时速度方向竖直向下,因而初动量方向竖直向下,与所取正方向相反,此处v仅表示小球速度的大小).小球的末动量 p′=0.由动量定理有解得小球自接触软垫起到陷至最低点这一过程中受到软垫平均作用大小为在这段时间内软垫对小球的冲量大小为方向竖直向上.[小结] (1)应用动量定理解题时,必须明确研究的哪一物体的哪一运动过程,因动量定理是针对一确定物体一确定过程而言.此题应用动量定理研究的是小球自落至软垫开始与其接触起至陷至最低点速度恰变为零这一过程.(2)在解决诸如此题和课本习题中用铁锤钉钉子这样的碰撞、打击一类问题时,物体所受的冲击力的变化极为迅速,难于用牛顿第二定律(结合运动学公式)求解,但用以力的冲量概念表述的动量定理解决起来如此极为方便.(3)在应用动量定理解决类似此题这样的碰撞、打击等问题时,不可随意忽略物体所受的重力,例如此题如忽略小球陷落过程中所受的重力,结果如此为I F·s,显然与正确结果有较大偏离,因而是错误的.[例题3]人从高台上跳下着地时,总是不自觉地先弯腿再站起来,为什么?[思路点拨]这是一道说明题,不要求给出计算结果,但对这类问题不应含混说上几句就算了事,而要做严格分析,即也要明确研究对象,确定研究过程,列出必要的方程,再做讨论,得出令人信服的结论.[解题过程]将人视为质量集中在重心的质点,分两种情况讨论:一为着地时不弯腿;一为着地时开始弯腿.台的高度一定,两种情况下,人着地时动量大小皆为p=mv,最后速度均变为零,因而动量为零.假如取竖直向上为正方向,两种情况下,人着地过程中的动量变化量均为Δp=0-(-mv)=mv.从开始着地到静止过程中,人受重力mg与地面作用力F,用F表示地面对人的作用力平均值,根据动量定理解得人着地过程中地面对人作用力的平均值由此式知,第一种情况,人落地后始终直立,人(视为质量集中于重的作用力,很容易造成伤害.第二种情况下,由于着地后弯腿,人的重心还要向下移动较长距离,速度经过较长时间变为零,Δt较大,故地面对[小结]解答说明、论证型的题目,首先要明确论点.如此题的论点是要求比拟人在两种不同情况下受到地面作用力大小.然后选择论据,论据的选择要正确有效,如此题选择的论据应是动量守恒,假如选择牛顿第二定律如此不能有效地论证.最后是论证,论证的过程即为推理的过程,推理要清晰严密.如此题就要先找出两种情况下,人的动量变化量Δp的关系与动量变化与所经历的时间Δt的关系,然后才能由动量定理推出两种情况下地面作用力F大小的关系.[例题4]质量m=5 kg的物体在恒定水平推力F=5 N的作用下,自静止开始在水平路面上运动,t1=2s后,撤去力F,物体又经t2=3 s停了下来,求物体运动中受水平面滑动摩擦力的大小.[思路点拨]此题中物体所经历的过程可分为两个阶段.第一阶段,物体在力F作用下自静止开始运动直至撤去力F;第二阶段,撤去力F后物体在滑动摩擦力f作用下减速运动,直至停下.如果用动量定理来求题,那么能否对包括两阶段在内的整个运动过程来应用定理呢?现给出两种方法求解这一问题:第一种方法,将整个运动过程分为两个阶段,分别用动量定理来处理.第二种方法,将整个运动作为一过程来应用动量定理.[解题过程]因物体在水平面上运动,故只需考虑物体在水平方向上受力即可,在撤去力F前,物体在水平方向上还受方向与物体运动方向相反的滑动摩擦力f,撤去力F后,物体只受摩擦力f.取物体运动方向为正方向.方法1设撤去力F时物体的运动速度为v.对于物体自静止开始运动至撤去力F这一过程,由动量定理有(F-f)t1=mv. (1)对于撤去力F直至物体停下这一过程,由动量定理有(-f)t2=0-mv. (2) 联立式(1)、(2)解得运动中物体所受滑动摩擦力大小为说明式(1)、(2)中f仅表示滑动摩擦力的大小,f前的负号表示f与所取正方向相反.方法2将物体整个运动过程视为在一变化的合外力作用下的运动过程.在时间t1内物体所受合外力为(F-f),在时间t2内物体所受合外力-f,整个运动时间t1+t2内,物体所受合外力冲量为(F-f)t1+(-f)t2.对物体整个运动过程应用动量定理有(F-f)t1+(-f)t2=0,说明冲量是矢量,由矢量运算法如此可知合外力对物体的冲量等于物体所受各外力冲量的矢量和.所以求物体运动过程中所受合外力冲量又可用下述方法得出:即先求物体在运动过程所受各外力冲量,再取其矢量和即为合外力冲量.例如,就此题中物体整个运动时间t1+t2内,力F的冲量为Ft1,力f的冲量为(-f)(t1+t2).整个运动过程中物体所受合外力冲量为Ft1+(-f)(t1+t2).这一结果与解法(2)给出的结果一样.[小结] (1)此题解法2再次明确动量定理适用于变力作用过程.(2)合外力在一段时间t内的冲量等于这段时间t内各分段时间t i(t=t1+t2+…+t i+…)内冲量的矢量和,又等于这段时间t内各外力对物体冲量的矢量和.(3)此题求解时,显然对整个过程应用动量定理来处理,解起来更为简捷.*[例题5]采煤中有一种方法是用高压水流将煤层击碎将煤采下.今有一采煤水枪,由枪口射出的高压水流速度为v,设水流垂直射向煤层的竖直外表,随即顺煤壁竖直流下,求水对煤层的压强(水的密度为ρ).[思路点拨]射向煤层的水流受到煤层的作用水平速度(因而动量)变为零后随即顺壁流下,如能求出此过程中煤层对水流的作用力,根据牛顿第三定律即可求出水对煤层的作用力,从而求水对煤层的压强.word[解题过程]设射向煤层水流截面为S,在时间Δt内有质量为ρSv·Δt的水撞击煤层,动量变为零,设煤层对水流作用力为F.取煤层对水作用力方向为正,对于上述这局部水由动量定理有F·Δt=0-(-ρSvΔt·v),得F=ρSv2.由牛顿第三定律知,水对煤层作用力大小F′=F=ρSv2,所以煤层外表受到水流压强为[小结]解决此类连续体产生的持续作用问题时,关键在于:①正确选取研究对象——Δt时间内动量发生变化的物质;②根据题意正确地表示出其质量与动量变化量.11 / 11。
动量定理题型及例题讲解

动量定理题型及例题讲解动量定理是物理学中的一个重要定理,它描述了力、质量和时间之间的关系。
动量定理指出,在一个惯性系中,外力的冲量等于物体动量的增量。
下面我将介绍动量定理的题型和例题讲解。
一、动量定理题型动量定理题型一般可分为以下三种:1. 动量守恒定律应用题动量守恒定律是指在一个系统内,若不存在外力作用,则系统的总动量保持不变。
在这类题型中,考生需要根据动量守恒定律,计算出系统的总动量,然后根据动量定理,求解外力对系统的作用。
2. 动量定理公式应用题在这类题型中,考生需要根据动量定理,计算出物体的动量增量,然后根据动量守恒定律,求解外力对物体的作用。
3. 碰撞问题应用题碰撞问题是物理学中的一个重要问题,它涉及到动量守恒定律和动量定理。
在这类题型中,考生需要根据动量守恒定律和动量定理,计算出碰撞前后物体的动量变化,然后根据碰撞原理,求解外力对物体的作用。
二、动量定理例题讲解下面我们来看几个动量定理的例题:1. 动量守恒定律应用题例题:一个质量为 2 千克的物体,以 5 米/秒的速度沿水平面滑行,如果在物体表面放置一个弹簧,求弹簧的弹力。
解析:根据动量守恒定律,由于物体的速度不变,系统的总动量守恒。
因此,外力的冲量等于物体的动量增量。
即:I = m * v其中,I 为外力的冲量,m 为物体的质量,v 为物体的速度。
根据题意,可知:I = m * v = 2 * 5 = 10 J因此,外力对物体的作用为:F = I / a = 10 / 1 = 10 N。
2. 动量定理公式应用题例题:一个质量为 2 千克的物体,以 5 米/秒的速度沿水平面滑行,如果在物体表面放置一个弹簧,求弹簧的弹力。
解析:根据动量定理,在外力作用期间,物体的动量增量为:p = m * v"其中,p 为物体的动量,m 为物体的质量,v"为物体的速度。
根据题意,可知:v" = v - at其中,a 为物体的水平加速度,t 为物体滑行的时间。
08 动量定理及动量守恒定律高考真题分项详解(原卷版)

十年高考分类汇编专题08动量定理及动量守恒定律(2011-2020)目录题型一、动量与动量定理的综合应用 (1)题型二、动量守恒定律与能量的综合应用模型一(碰撞类) (4)题型三、动量守恒定律与能量的综合应用模型二(弹簧类) (9)题型四、动量守恒定律与能量的综合应用模型三(反冲类) (10)题型五、动量守恒定律与能量的综合应用模型四(子弹木块、板块类) (12)题型六、动量守恒定律与能量的综合应用模型五(轨道类) (13)题型七、实验:验证动量守恒定律 (15)题型一、动量与动量定理的综合应用1.(2020江苏).一只质量为1.4kg的乌贼吸入0.1kg的水,静止在水中。
遇到危险时,它在极短时间内把吸入的水向后全部喷出,以2m/s的速度向前逃窜。
求该乌贼喷出的水的速度大小v。
2.(2020全国1).行驶中的汽车如果发生剧烈碰撞,车内的安全气囊会被弹出并瞬间充满气体。
若碰撞后汽车的速度在很短时间内减小为零,关于安全气囊在此过程中的作用,下列说法正确的是()A. 增加了司机单位面积的受力大小B. 减少了碰撞前后司机动量的变化量C. 将司机的动能全部转换成汽车的动能D. 延长了司机的受力时间并增大了司机的受力面积3.(2018全国2)高空坠物极易对行人造成伤害.若一个50 g的鸡蛋从一居民楼的25层坠下,与地面的撞击时间约为2 ms,则该鸡蛋对地面产生的冲击力约为()A. 10 NB. 102 NC. 103 ND. 104 N4.(2018北京)2022年将在我国举办第二十四届冬奥会,跳台滑雪是其中最具观赏性的项目之一.某滑道示意图如下,长直助滑道AB与弯曲滑道BC平滑衔接,滑道BC高h=10 m,C是半径R=20 m圆弧的最低点,质量m=60 kg的运动员从A处由静止开始匀加速下滑,加速度a=4.5 m/s2,到达B点时速度vB=30 m/s.取重力加速度g=10 m/s2.(1)求长直助滑道AB的长度L;(2)求运动员在AB段所受合外力的冲量的I大小;(3)若不计BC段的阻力,画出运动员经过C点时的受力图,并求其所受支持力FN的大小.5.(2018江苏)如图所示,悬挂于竖直弹簧下端的小球质量为m,运动速度的大小为v,方向向下.经过时间t,小球的速度大小为v,方向变为向上.忽略空气阻力,重力加速度为g,求该运动过程中,小球所受弹簧弹力冲量的大小.6.(2017全国3)一质量为2 kg的物块在合外力F的作用下从静止开始沿直线运动。
2020年高考物理二轮专题复习附解答:动量定理与动量守恒定律(解析版)

动量定理与动量守恒定律一、选择题1.高空坠物极易对行人造成伤害。
若一个50 g 的鸡蛋从一居民楼的25层坠下,与地面的碰撞时间约为2 ms ,则该鸡蛋对地面产生的冲击力约为A .10 NB .102 NC .103 ND .104 N解析 根据自由落体运动和动量定理有2gh =v 2(h 为25层楼的高度,约70 m),Ft =mv ,代入数据解得F ≈1×103 N ,所以C 正确。
答案 C2.(多选)在光滑的水平面上,原来静止的物体在水平力F 的作用下,经过时间t 、通过位移L 后,动量变为p 、动能变为E k ,以下说法正确的是A .在力F 的作用下,这个物体若是经过时间3t ,其动量将等于3pB .在力F 的作用下,这个物体若是经过位移3L ,其动量将等于3pC .在力F 的作用下,这个物体若是经过时间3t ,其动能将等于3E kD .在力F 的作用下,这个物体若是经过位移3L ,其动能将等于3E k解析 根据p =mv ,E k =12mv 2 联立解得p =2mE k根据动能定理FL =12mv 2,位移变为原来的3倍,动能变为原来的3倍,根据p =2mE k ,动量变为原来的3倍,故B 错误,D 正确。
根据动量定理Ft =mv ,时间变为原来的3倍,动量变为原来的3倍,根据E k =p 22m,知动能变为原来的9倍,故A 正确,C 错误。
答案 AD3.(多选)质量为m 的物块甲以3 m/s 的速度在光滑水平面上运动,有一轻弹簧固定在其左侧,另一质量也为m 的物块乙以4 m/s 的速度与甲相向运动,如图所示,两物块通过弹簧相互作用(未超出弹簧弹性限度)并最终弹开,则A.在压缩弹簧的过程中,两物块组成的系统动量守恒B.当两物块相距最近时,甲物块的速度为零C.甲物块的速率可能为5 m/sD.当甲物块的速率为1 m/s时,乙物块的速率可能为2 m/s解析在压缩弹簧的过程中,两物块组成的系统所受合外力为零,系统动量守恒,选项A正确;当两物块相距最近时,两物块速度相等,甲物块的速度不为零,选项B错误;若甲物块的速率为5 m/s,根据动量守恒定律可得此时乙物块的速率为6 m/s或4 m/s,两物块组成的系统机械能增大,违反了能量守恒定律,选项C错误;当甲物块的速率为1 m/s,方向向左时,选取向右为速度的正方向,根据动量守恒定律,m·4 m/s-m·3 m/s=mv-m·1 m/s,解得乙物块的速率v=2 m/s,选项D正确。
专题06 动量和动量定理(解析版)

专题06 动量和动量定理1.(2021届广东省汕头市金山中学高三期中)冰壶运动深受观众喜爱,图1为2014年2月第22届索契冬奥会上中国队员投掷冰壶的镜头.在某次投掷中,冰壶甲运动一段时间后与对方静止的冰壶乙发生正碰,如图2.若两冰壶质量相等,则碰后两冰壶最终停止的位置,可能是图中的哪幅图()A.B.C.D.【答案】B【解析】冰壶甲乙碰撞过程动量守恒,碰撞前系统动量水平向右,碰撞后合动量也必然水平向右,碰撞后冰壶在摩擦力作用下做匀减速直线运动,所以碰撞点即圆心到最后停靠点的连线代表碰撞后的速度方向,连线的长短代表碰撞后的速度大小.A图中,甲乙碰后的动量都斜向右上方,所以合动量不可能水平向右,不满足动量守恒定律选项A错.乙图中,碰撞后甲静止,乙水平向右运动,符合质量相等小球发生完全弹性碰撞的过程,选项B是可能的.选项C中,虽然甲乙动量都是水平向右,合动量也满足水平向右,但甲在后,乙在前,碰后甲不可能速度大于乙,即甲不可能在乙前面,选项C错,D选项,碰后甲的速度大于乙的速度,合动量水平向左,不符合动量守恒定律选项D错误。
2.(2021届湖南省衡阳市第八中学高三月考)如图所示,垫球是排球运动中通过手臂的迎击动作,使来球从垫击面上反弹出去的一项击球技术,若某次从垫击面上反弹出去竖直向上运动的排球,之后又落回到原位置,设整个运动过程中排球所受阻力大小不变,则( )A .球从击出到落回的时间内,重力的冲量为零B .球从击出到落回的时间内,空气阻力的冲量为零C .球上升阶段阻力的冲量小于下降阶段阻力的冲量D .若不计阻力,球上升阶段动量的变化等于下降阶段动量的变化 【答案】CD【解析】整个过程中,重力不为零,作用时间不为零,根据G I mgt =,可知,重力冲量不为零,故A 错误; 由于整个过程中,阻力都做负功,所以上升阶段的平均速度大于下降阶段的平均速度,即上升过程所用时间比下降过程所用时间少,根据f I ft =可知上升阶段阻力冲量小于下降阶段阻力冲量,整个过程中阻力冲量不为零,故B 错误,C 正确;若不计空气阻力,并规定向上为正方向,设初速度为0v ,上升阶段,初速度为0v ,末速度为零,动量变化量为1000p mv mv ∆=-=-,下降阶段,初速度为零,末速度为0v -,动量变化量为2000p mv mv -∆=-=-,两者相等,故D 正确。
08专题:动量定理与动量守恒定律专题(含答案)

08专题:动量定理与动量守恒定律专题1.(多选)(2017·全国卷Ⅲ)一质量为 2 kg 的物块在合外力F的作用下从静止开始沿直线运动。
F随时间t变化的图线如图所示,则( )A.t=1 s时物块的速率为1 m/sB.t=2 s时物块的动量大小为4 kg·m/sC.t=3 s时物块的动量大小为5 kg·m/sD.t=4 s时物块的速度为零2.质量为m的运动员从下蹲状态向上起跳,经时间t身体伸直并刚好离开水平地面,该过程中,地面对他的冲量大小为I,重力加速度大小为g.下列说法正确的是()A.运动员在加速上升过程中处于超重状态 B.运动员离开地面时的速度大小为I mC.该过程中,地面对运动员做的功为22ImD.该过程中,人的动量变化大小为I-mgt3.如图所示,abc是竖直面内的光滑固定轨道,ab段水平,长度为2R;bc段是半径为R的四分之一圆弧,与ab相切于b点.一质量为m的小球.始终受到与重力大小相等的水平外力F的作用,自a点处从静止开始向右运动,重力加速度大小为g.小球从a点开始运动到其轨迹最高点的过程中,以下说法正确的是()A.重力与水平外力合力的冲量等于小球的动量变化量B.小球对圆弧轨道b点和c点的压力大小都为5mgC.小球机械能的增量为3mgRD.小球在到达c点前的最大动能为21)mgR4.如图所示,在光滑水平面上停放着质量为m、装有光滑弧形槽的小车,一质量也为m的小球以水平初速度v0沿槽口向小车滑去,到达某一高度后,小球又返回右端,则( ) A.小球以后将向右做平抛运动B.小球将做自由落体运动C.此过程小球对小车做的功为20 2 mvD .小球在弧形槽内上升的最大高度为204gν 5.如图所示,甲、乙两名宇航员正在离空间站一定距离的地方执行太空维修任务。
某时刻甲、乙都以大小为v 0=2 m/s 的速度相向运动,甲、乙和空间站在同一直线上且可视为质点。
甲和他的装备总质量为M 1=90 kg ,乙和他的装备总质量为M 2=135 kg ,为了避免直接相撞,乙从自己的装备中取出一质量为m =45 kg 的物体A 推向甲,甲迅速接住A 后即不再松开,此后甲、乙两宇航员在空间站外做相对距离不变的同向运动,且安全“飘”向空间站(设甲、乙距离空间站足够远,速度均指相对空间站的速度)。
物理动量定理专项含解析

物理动量定理专项含解析一、高考物理精讲专题动量定理1.2022年将在我国举办第二十四届冬奥会,跳台滑雪是其中最具观赏性的项目之一.某滑道示意图如下,长直助滑道AB 与弯曲滑道BC 平滑衔接,滑道BC 高h =10 m ,C 是半径R =20 m 圆弧的最低点,质量m =60 kg 的运动员从A 处由静止开始匀加速下滑,加速度a =4.5 m/s 2,到达B 点时速度v B =30 m/s .取重力加速度g =10 m/s 2. (1)求长直助滑道AB 的长度L ;(2)求运动员在AB 段所受合外力的冲量的I 大小;(3)若不计BC 段的阻力,画出运动员经过C 点时的受力图,并求其所受支持力F N 的大小.【答案】(1)100m (2)1800N s ⋅(3)3 900 N 【解析】(1)已知AB 段的初末速度,则利用运动学公式可以求解斜面的长度,即2202v v aL -=可解得:221002v v L m a-==(2)根据动量定理可知合外力的冲量等于动量的该变量所以01800B I mv N s =-=⋅(3)小球在最低点的受力如图所示由牛顿第二定律可得:2Cv N mg m R-= 从B 运动到C 由动能定理可知:221122C B mgh mv mv =-解得;3900N N =故本题答案是:(1)100L m = (2)1800I N s =⋅ (3)3900N N =点睛:本题考查了动能定理和圆周运动,会利用动能定理求解最低点的速度,并利用牛顿第二定律求解最低点受到的支持力大小.2.如图1所示,水平面内的直角坐标系的第一象限有磁场分布,方向垂直于水平面向下,磁感应强度沿y 轴方向没有变化,与横坐标x 的关系如图2所示,图线是双曲线(坐标是渐近线);顶角θ=53°的光滑金属长导轨MON 固定在水平面内,ON 与x 轴重合,一根与ON 垂直的长导体棒在水平向右的外力作用下沿导轨MON 向右滑动,导体棒在滑动过程中始终保持与导轨良好接触,已知t =0时,导体棒位于顶角O 处;导体棒的质量为m =4kg ;OM 、ON 接触处O 点的接触电阻为R =0.5Ω,其余电阻不计,回路电动势E 与时间t 的关系如图3所示,图线是过原点的直线,求:(1)t =2s 时流过导体棒的电流强度的大小; (2)在1~2s 时间内导体棒所受安培力的冲量大小;(3)导体棒滑动过程中水平外力F (单位:N )与横坐标x (单位:m )的关系式. 【答案】(1)8A (2)8N s ⋅(3)32639F x =+【解析】 【分析】 【详解】(1)根据E-t 图象中的图线是过原点的直线特点,可得到t =2s 时金属棒产生的感应电动势为4V E =由欧姆定律得24A 8A 0.5E I R === (2)由图2可知,1(T m)x B =⋅ 由图3可知,E 与时间成正比,有E =2t (V )4EI t R== 因θ=53°,可知任意t 时刻回路中导体棒有效切割长度43x L =又由F BIL =安所以163F t 安=即安培力跟时间成正比所以在1~2s 时间内导体棒所受安培力的平均值163233N 8N2F +==故8N s I F t =∆=⋅安(3)因为43vE BLv Bx ==⋅所以1.5(m/s)v t =可知导体棒的运动时匀加速直线运动,加速度21.5m/s a =又212x at =,联立解得6F =+【名师点睛】本题的关键首先要正确理解两个图象的数学意义,运用数学知识写出电流与时间的关系,要掌握牛顿运动定律、闭合电路殴姆定律,安培力公式、感应电动势公式.3.如图甲所示,平面直角坐标系中,0≤x ≤l 、0≤y ≤2l 的矩形区域中存在交变匀强磁场,规定磁场垂直于纸面向里的方向为正方向,其变化规律如图乙所示,其中B 0和T 0均未知。
高中物理动量定理解题技巧及经典题型及练习题(含答案)含解析

高中物理动量定理解题技巧及经典题型及练习题(含答案)含解析一、高考物理精讲专题动量定理1.如图所示,光滑水平面上有一轻质弹簧,弹簧左端固定在墙壁上,滑块A以v0=12 m/s 的水平速度撞上静止的滑块B并粘在一起向左运动,与弹簧作用后原速率弹回,已知A、B 的质量分别为m1=0.5 kg、m2=1.5 kg。
求:①A与B撞击结束时的速度大小v;②在整个过程中,弹簧对A、B系统的冲量大小I。
【答案】①3m/s;②12N•s【解析】【详解】①A、B碰撞过程系统动量守恒,以向左为正方向由动量守恒定律得m1v0=(m1+m2)v代入数据解得v=3m/s②以向左为正方向,A、B与弹簧作用过程由动量定理得I=(m1+m2)(-v)-(m1+m2)v代入数据解得I=-12N•s负号表示冲量方向向右。
2.汽车碰撞试验是综合评价汽车安全性能的有效方法之一.设汽车在碰撞过程中受到的平均撞击力达到某个临界值F0时,安全气囊爆开.某次试验中,质量m1=1 600 kg的试验车以速度v1 = 36 km/h正面撞击固定试验台,经时间t1 = 0.10 s碰撞结束,车速减为零,此次碰撞安全气囊恰好爆开.忽略撞击过程中地面阻力的影响.(1)求此过程中试验车受到试验台的冲量I0的大小及F0的大小;(2)若试验车以速度v1撞击正前方另一质量m2 =1 600 kg、速度v2 =18 km/h同向行驶的汽车,经时间t2 =0.16 s两车以相同的速度一起滑行.试通过计算分析这种情况下试验车的安全气囊是否会爆开.【答案】(1)I0 = 1.6×104 N·s ,1.6×105 N;(2)见解析【解析】【详解】(1)v1 = 36 km/h = 10 m/s,取速度v1 的方向为正方向,由动量定理有-I0 =0-m1v1 ①将已知数据代入①式得I0 = 1.6×104 N·s ②由冲量定义有I0 = F0t1 ③将已知数据代入③式得 F 0 = 1.6×105 N ④(2)设试验车和汽车碰撞后获得共同速度v ,由动量守恒定律有m 1v 1+ m 2v 2 = (m 1+ m 2)v ⑤对试验车,由动量定理有 -Ft 2 = m 1v -m 1v 1 ⑥将已知数据代入⑤⑥式得F = 2.5×104 N ⑦可见F <F 0,故试验车的安全气囊不会爆开 ⑧3.如图所示,在倾角θ=37°的足够长的固定光滑斜面的底端,有一质量m =1.0kg 、可视为质点的物体,以v 0=6.0m/s 的初速度沿斜面上滑。
动量定理典型例题解析

动量定理(1)·典型例题解析【例1】 钉钉子时为什么要用铁锤而不用橡皮锤,而铺地砖时却用橡皮锤而不用铁锤?解析:钉钉子时用铁锤是因为铁锤形变很小,铁锤和钉子之间的相互作用时间很短,对于动量变化一定的铁锤,受到钉子的作用力很大,根据牛顿第三定律,铁锤对钉子的作用力也很大,所以能把钉子钉进去.橡皮锤形变较大,它和钉子之间的作用时间较长,同理可知橡皮锤对钉子的作用力较小,不容易把钉子钉进去.但在铺地砖时,需要较小的作用力,否则容易把地砖敲碎,因此铺地砖时用橡皮锤,不用铁锤.点拨:根据动量定理,利用对作用时间的调整来控制作用力的大小. 【例2】 如图50-1所示,质量为m 的小球以速度v 碰到墙壁上,被反弹回来的速度大小为2v/3,若球与墙的作用时间为t ,求小球与墙相碰过程中所受的墙壁给它的作用力.解析:取向左为正方向,根据动量定理,对小球有=--=,由于此过程中小球在竖直方向受力平衡,墙给它的作用力等于它所受的合外力,所以墙给它的作用力为=,方向向左.Ft m 23v (mv)mv F 5353mvt点拨:动量定理是矢量式,解题要选取正方向,动量定理中的F 是合外力. 【例3】 下列说法正确的是[ ]A .动量的方向与受力方向相同B .动量的方向与冲量的方向相同C .动量的增量的方向与受力方向相同D .动量变化率的方向与速度方向相同点拨:冲量的方向与力的方向相同,动量的方向与速度方向相同,动量增量的方向与冲量的方向相同,动量方向与冲量方向间无必然的联系.动量变化率(Δp/Δt)的方向与力的方向相同,力的方向与速度方向间无必然的联系.参考答案 C【例4】 在空间某处以相等的速率分别竖直上抛、竖直下抛、水平抛出质量相等三个小球,不计空气阻力,经相同的时间t(设小球均未落地),下列有关动量变化的判断正确的是[ ] A.作上抛运动的小球动量变化最大B.作下抛运动的小球动量变化最小C.三小球动量变化大小相等,方向相同D.三小球动量变化大小相等,方向不同点拨:三个小球都只有竖直方向的动量变化(作平抛运动的小球水平方向动量不变).可根据匀变速直线运动的速度公式,求出竖直方向的速度变化,从而直接求出动量变化加以比较.但如果转换思考角度,从动量定理出发从考虑重力的冲量来比较动量的变化可使问题简单明了.参考答案C跟踪反馈1.动量定理Ft=p′-p中的F是指[ ] A.物体所受的动力B.物体所受的除重力以外的其它力的合力C.重力和弹力的合力D.物体所受的合外力2.对任何运动的物体,用一不变的力制动使它停止运动,所需的时间决定于物体的[ ] A.速度B.加速度C.动量D.质量3.一个质量为m的小球以速率v垂直射向墙壁,被墙以等速率反向弹回.若球与墙的作用时间为t,则小球受到墙的作用力大小为[ ] A.mv/tB.2mv/tC.mv/2tD.04.人从高处跳到低处,为了安全,一般都是让脚尖先着地,接着让整个脚底着地,并让人下蹲,这样做是为了[ ] A.减小人受到的冲量B.减小人的动量变化C.延长与地面的作用时间,从而减小人受到的作用力D.延长与地面的作用时间,使人所受地面给他的弹力小于人所受的重力参考答案1.D 2.C 3.B 4.C。
压轴题07 动量定理及动量守恒(解析版)

压轴题07 动量定理及动量守恒一、考向分析二、压轴题要领热点题型一对动量定理的理解和基本应用1.对动量定理的理解(1)动量定理不仅适用于恒定的力,也适用于随时间变化的力.这种情况下,动量定理中的力F应理解为变力在作用时间内的平均值.(2)动量定理的表达式F·Δt=Δp是矢量式,运用它分析问题时要特别注意冲量、动量及动量变化量的方向,公式中的F是物体或系统所受的合力.2.用动量定理解题的基本思路3.动量定理的应用技巧(1)应用I=Δp求变力的冲量如果物体受到大小或方向改变的力的作用,则不能直接用I=Ft求冲量,可以求出该力作用下物体动量的变化Δp,等效代换得出变力的冲量I.(2)应用Δp=FΔt求动量的变化例如,在曲线运动中,速度方向时刻在变化,求动量变化(Δp=p2-p1)需要应用矢量运算方法,计算比较复杂.如果作用力是恒力,可以求恒力的冲量,等效代换得出动量的变化.热点题型二动量定理的综合应用1.应用动量定理解释的两类物理现象(1)当物体的动量变化量一定时,力的作用时间Δt越短,力F就越大,力的作用时间Δt越2022高考预计会以生活实例为命题背景,考查动量守恒定律在生活中的应用,复习时应侧重本知识和其他知识的综合应用,如与动力学、功和能、电磁学等知识综合考查。
题型既有选择题,也有计算题,难度中等或中等偏上。
在研究物体的受力与运动的关系时,不可避免地要引起能量和动量的变化,所以说动量和能量都是力学综合题中不可缺少的考点,这类考题综合性强,难度大,主要题型是计算题。
要知道碰撞的特点,能区分弹性碰撞,非完全弹性碰撞和完全非弹性碰撞。
长,力F就越小,如玻璃杯掉在水泥地上易碎,而掉在沙地上不易碎.(2)当作用力F一定时,力的作用时间Δt越长,动量变化量Δp越大,力的作用时间Δt越短,动量变化量Δp越小.2.应用动量定理解决两类问题(1)应用动量定理解决微粒类问题(2)应用动量定理解决流体类问题第一类是“吸收模型”,即流体与被碰物质接触后速度为零,第二类是“反弹模型”,即流体与被碰物质接触后以原速率反弹.设时间t内流体与被碰物质相碰的“粒子”数为n,每个“粒子”的动量为p,被碰物质对“粒子”的作用力为F,以作用力的方向为正,则“吸收模型”满足Ft=0-n(-p),“反弹模型”满足Ft=np-n(-p).“反弹模型”的动量变化量为“吸收模型”的动量变化量的2倍,解题时一定要明辨模型,避免错误.热点题型三动量守恒的理解和判断1.动量守恒定律适用条件(1)前提条件:存在相互作用的物体系.(2)理想条件:系统不受外力.(3)实际条件:系统所受合外力为0.(4)近似条件:系统内各物体间相互作用的内力远大于系统所受的外力.(5)方向条件:系统在某一方向上满足上面的条件,则此方向上动量守恒.2.动量守恒定律的表达式(1)m1v1+m2v2=m1v1′+m2v2′,相互作用的两个物体组成的系统,作用前的动量和等于作用后的动量和.(2)Δp 1=-Δp 2,相互作用的两个物体动量的增量等大反向.(3)Δp =0,系统总动量的增量为零.3.动量守恒定律的“五性”热点题型四 对碰撞现象中规律的分析1.碰撞遵守的规律 (1)动量守恒,即p 1+p 2=p ′1+p ′2.(2)动能不增加,即E k1+E k2≥E ′k1+E ′k2(3)速度要符合情景:如果碰前两物体同向运动,则后面的物体速度必大于前面物体的速度,即v 后>v 前,否则无法实现碰撞.碰撞后,原来在前面的物体的速度一定增大,且原来在前面的物体速度大于或等于原来在后面的物体的速度,即v ′前≥v ′后,否则碰撞没有结束.如果碰前两物体相向运动,则碰后两物体的运动方向不可能都不改变,除非两物体碰撞后速度均为零.2.碰撞模型类型(1)弹性碰撞两球发生弹性碰撞时应满足动量守恒和机械能守恒.以质量为m 1、速度为v 1的小球与质量为m 2的静止小球发生正面弹性碰撞为例,有 m 1v 1=m 1v ′1+m 2v ′212m 1v 21=12m 1v ′21+12m 2v ′22 解得v ′1=(m 1-m 2)v 1m 1+m 2,v ′2=2m 1v 1m 1+m 2. 结论:①当两球质量相等时,v ′1=0,v ′2=v 1,两球碰撞后交换了速度.②当质量大的球碰质量小的球时,v ′1>0,v ′2>0,碰撞后两球都沿速度v 1的方向运动. ③当质量小的球碰质量大的球时,v ′1<0,v ′2>0,碰撞后质量小的球被反弹回来. ④撞前相对速度与撞后相对速度大小相等.(2)完全非弹性碰撞①撞后共速.②有动能损失,且损失最多.三、压轴题速练1. 将一个质量为m 的小木块放在光滑的固定斜面上,使木块从斜面的顶端由静止开始向下滑动,滑到底端总共用时t ,如图所示,设在下滑的前一半时间内木块的动量变化为Δp 1,在后一半时间内其动量变化为Δp 2,则Δp 1∶Δp 2为( )A .1∶2B .1∶3C .1∶1D .2∶1【答案】C【解析】木块在下滑的过程中,一直受到的是重力与斜面支持力的作用,二力的合力大小恒定为F =mg sin θ,方向也始终沿斜面向下.由动量定理可得Δp 1∶Δp 2=(F ·t 1)∶(F ·t 2)=(mg sin θ·12t )∶(mg sin θ·12t )=1∶1,故选项C 正确. 2.一小球从水平地面上方无初速释放,与地面发生碰撞后反弹至速度为零,假设小球 与地面碰撞没有机械能损失,运动时的空气阻力大小不变,下列说法正确的是( ) A .上升过程中小球动量改变量等于该过程中空气阻力的冲量B .小球与地面碰撞过程中,地面对小球的冲量为零C .下落过程中小球动能的改变量等于该过程中重力做的功D .从释放到反弹至速度为零过程中小球克服空气阻力做的功等于重力做的功【答案】D【解析】根据动量定理可知,上升过程中小球动量改变量等于该过程中重力和空气阻力的合力的冲量,选项A 错误;小球与地面碰撞过程中,由动量定理得:Ft -mgt =mv 2-(-mv 1),可知地面对小球的冲量Ft 不为零,选项B 错误;下落过程中小球动能的改变量等于该过程中重力和空气阻力做功代数和,选项C 错误;由能量守恒关系可知,从释放到反弹至速度为零过程中小球克服空气阻力做的功等于重力做的功,选项D 正确;故选D.43.为估算池中睡莲叶面承受雨滴撞击产生的平均压强,小明在雨天将一圆柱形水杯置于露台,测得1小时内杯中水位上升了45 mm.查询得知,当时雨滴竖直下落速度约为12 m/s 据此估算该压强约为(设雨滴撞击睡莲后无反弹,不计雨滴重力,雨水的密度为1×103kg/m 3)( )A .0.15 PaB .0.54 PaC .1.5 PaD .5.4Pa【答案】A【解析】设雨滴受到支持面的平均作用力为F .设在Δt 时间内有质量为Δm 的雨水的速度由v =12 m/s 减为零.以向上为正方向,对这部分雨水应用动量定理:F Δt =0-(-Δmv )=Δmv ,得到F =Δm Δtv .设水杯横截面积为S ,对水杯里的雨水,在Δt 时间内水面上升Δh ,则有Δm =ρS Δh ,得F =ρSv Δh Δt .压强p =F S =ρv Δh Δt =1×103×12×45×10-33 600Pa =0.15 Pa. 4.一个质量为0.18 kg 的垒球,以25 m/s 的水平速度向左飞向球棒,被球棒打击后反向水平飞回,速度大小变为45 m/s.则这一过程中动量的变化量为( )A .大小为3.6 kg·m/s ,方向向左B .大小为3.6 kg·m/s ,方向向右C .大小为12.6 kg·m/s ,方向向左D .大小为12.6 kg·m/s ,方向向右【答案】D【解析】.选向左为正方向,则动量的变化量Δp =mv 1-mv 0=-12.6 kg·m/s ,大小为12.6 kg·m/s ,负号表示其方向向右,D 正确.5.高空坠物极易对行人造成伤害.若一个50 g 的鸡蛋从一居民楼的25层坠下,与地面的碰撞时间约为2 ms ,则该鸡蛋对地面产生的冲击力约为( )A .10 NB .102 NC .103 ND .104 N【答案】C【解析】.根据自由落体运动和动量定理有2gh =v 2(h 为25层楼的高度,约70 m),Ft =mv ,代入数据解得F ≈1×103 N ,所以C 正确.6.如图所示,足够长的固定光滑斜面倾角为θ,质量为m 的物体以速度v 从斜面底端冲上斜面,达到最高点后又滑回原处,所用时间为t .对于这一过程,下列判断正确的是( )A .斜面对物体的弹力的冲量为零B .物体受到的重力的冲量大小为mgtC .物体受到的合力的冲量大小为零D .物体动量的变化量大小为mg sin θ·t【答案】BD.【解析】由冲量的求解公式可知,斜面对物体的弹力的冲量为mg cos θ·t ,选项A 错误;物体受到的重力的冲量大小为mgt ,选项B 正确;物体回到斜面底端的速度仍为v ,方向与初速度方向相反,故根据动量定理可知,物体受到的合力的冲量大小为2mv ,选项C 错误;因整个过程中物体所受的合力为mg sin θ,则根据动量定理可知,物体动量的变化量大小为mg sin θ·t ,选项D 正确.7.如图所示,AB 为固定的光滑圆弧轨道,O 为圆心,AO 水平,BO 竖直,轨道半径为R ,将质量为m 的小球(可视为质点)从A 点由静止释放,在小球从A 点运动到B 点的过程中( )A .小球所受合力的冲量方向为弧中点指向圆心B .小球所受支持力的冲量为0C .小球所受重力的冲量大小为m 2gRD .小球所受合力的冲量大小为m 2gR【答案】D【解析】小球受到竖直向下的重力和垂直切面指向圆心的支持力,所以合力不指向圆心,故合力的冲量也不指向圆心,A 错误;小球的支持力不为零,作用时间不为零,故支持力的冲量不为零,B 错误;小球在运动过程中只有重力做功,所以根据机械能守恒可得mgR =12mv B 2,故v B =2gR ,根据动量定理可得I 合=Δp =mv B =m 2gR ,故C 错误,D 正确.8.小球质量为2m ,以速度v 沿水平方向垂直撞击墙壁,球被反方向弹回速度大小是45v ,球与墙撞击时间为t ,在撞击过程中,球对墙的平均冲力大小是( )A.2mv 5tB.8mv 5tC.18mv 5tD.2mv t【答案】C【解析】设初速度方向为正,则弹后的速度为-4v 5,则由动量定理可得Ft =-2m ×4v 5-2mv ,解得F =-18mv 5t,负号表示力的方向与初速度方向相反.由牛顿第三定律可知,球对墙的平均冲力为F ′=-F =18mv 5t,故选C. 9.质量为m 的物体, 以v 0的初速度沿斜面上滑,到达最高点后返回原处的速度大小为v t ,且v t =0.5v 0,则( )A .上滑过程中重力的冲量比下滑时小B .上滑时和下滑时支持力的冲量都等于零C .合力的冲量在整个过程中大小为32mv 0D .整个过程中物体的动量变化量为12mv 0 【答案】AC【解析】以v 0的初速度沿斜面上滑,返回原处时速度为v t =0.5v 0,说明斜面不光滑.设斜面长为l ,则上滑过程所需时间t 1=l v 02=2l v 0,下滑过程所需时间t 2=l v t 2=4l v 0,t 1<t 2,根据冲量的定义可知,上滑过程中重力的冲量比下滑时小,A 正确.上滑和下滑时支持力的冲量都不等于零,B 错误.对全过程应用动量定理,则I 合=Δp =-mv t -mv 0=-32mv 0,C 正确,D 错误.10.如图所示,一物体分别沿三个倾角不同的光滑斜面由静止开始从顶端下滑到底端C 、D 、E 处,三个过程中重力的冲量依次为I 1、I 2、I 3,动量变化量的大小依次为Δp 1、Δp 2、Δp 3,则有( )A .三个过程中,合力的冲量相等,动量的变化量相等B .三个过程中,合力做的功相等,动能的变化量相等C .I 1<I 2<I 3,Δp 1=Δp 2=Δp 3D .I 1<I 2<I 3,Δp 1<Δp 2<Δp 3【答案】ABC【解析】.由机械能守恒定律可知物体下滑到底端C 、D 、E 的速度大小v 相等,动量变化量的大小Δp =mv 相等,即Δp 1=Δp 2=Δp 3;根据动量定理,合力的冲量等于动量的变化量,故合力的冲量也相等,注意不是相同(方向不同);设斜面的高度为h ,从顶端A 下滑到底端C ,由h sin θ=12g sin θ·t 2得物体下滑的时间t =2h g sin 2θ,所以θ越小,sin 2θ越小,t 越大,重力的冲量I =mgt 就越大,故I 1<I 2<I 3,故A 、C 正确,D 错误;物体下滑过程中只有重力做功,故合力做的功相等,根据动能定理,动能的变化量相等,故B 正确.11.如图所示,甲木块的质量为m 1,以v 的速度沿光滑水平地面向前运动,正前方有一静止的、质量为m 2的乙木块,乙上连有一轻质弹簧.甲木块与弹簧接触后( )A .甲木块的动量守恒B .乙木块的动量守恒C .甲、乙两木块所组成系统的动量守恒D .甲、乙两木块所组成系统的动能守恒【答案】C【解析】:.两木块在光滑水平地面上相碰,且中间有弹簧,则碰撞过程系统的动量守恒,机械能也守恒,故选项A 、B 错误,选项C 正确;甲、乙两木块碰撞前、后动能总量不变,但碰撞过程中有弹性势能,故动能不守恒,只是机械能守恒,选项D 错误.12.有一个质量为3m 的爆竹斜向上抛出,到达最高点时速度大小为v 0、方向水平向右,在最高点爆炸成质量不等的两块,其中一块质量为2m ,速度大小为v ,方向水平向右,则另一块的速度是( )A .3v 0-vB .2v 0-3vC .3v 0-2vD .2v 0+v【答案】C【解析】:.在最高点水平方向动量守恒,由动量守恒定律可知,3mv 0=2mv +mv ′,可得另一块的速度为v ′=3v 0-2v ,对比各选项可知,答案选C.13.如图所示,两滑块A 、B 在光滑水平面上沿同一直线相向运动,滑块A 的质量为m ,速度大小为2v 0,方向向右,滑块B 的质量为2m ,速度大小为v 0,方向向左,两滑块发生弹性碰撞后的运动状态是( )A .A 和B 都向左运动B .A 和B 都向右运动C .A 静止,B 向右运动D .A 向左运动,B 向右运动【答案】D【解析】:.选向右为正方向,则A 的动量p A =m ·2v 0=2mv 0,B 的动量p B =-2mv 0.碰前A 、B 的动量之和为零,根据动量守恒,碰后A 、B 的动量之和也应为零,可知四个选项中只有选项D 符合题意.14.A 、B 两船的质量均为m ,都静止在平静的湖面上,现A 船中质量为12m 的人,以对地的水平速度v 从A 船跳到B 船,再从B 船跳到A 船……经n 次跳跃后,人停在B 船上,不计水的阻力,则( )A .A 、B 两船速度大小之比为2∶3B .A 、B (包括人)两船动量大小之比为1∶1C .A 、B (包括人)两船的动能之比为2∶3D .A 、B (包括人)两船的动能之比为1∶1【答案】:B【解析】:人和两船组成的系统动量守恒,两船原来静止,总动量为0,A 、B (包括人)两船的动量大小相等,选项B 正确;经过n 次跳跃后,A 船速度为v A 、B 船速度为v B ,则0=mv A -(m +m 2)v B ,解得v A v B =32,选项A 错误;A 船最后获得的动能为E k A =12mv A 2,B 船(包括人)最后获得的动能为E k B =12(m 2+m )v B 2=12(m 2+m )(23v A )2=23E k A ,所以E k A E k B =32,选项C 、D 错误.15.一弹丸在飞行到距离地面5 m 高时仅有水平速度v =2 m/s ,爆炸成为甲、乙两块水平飞出,甲、乙的质量比为3∶1.不计质量损失,重力加速度g 取10 m/s 2,则下列图中两块弹片飞行的轨迹可能正确的是( )【答案】:B【解析】:由h =12gt 2可知,爆炸后甲、乙两块做平抛运动的时间t =1 s ,爆炸过程中,爆炸力对沿原方向运动的一块的冲量沿运动方向,故这一块的速度必然增大,即v >2 m/s ,因此水平位移大于2 m ,C 、D 项错误;甲、乙两块在爆炸前后,水平方向不受外力,故水平方向动量守恒,即甲、乙两块的动量改变量大小相等,两块质量比为3∶1,所以速度变化量之比为1∶3,由平抛运动水平方向上,x =v 0t ,所以A 图中,v 乙=-0.5 m/s ,v 甲=2.5 m/s ,Δv 乙=2.5 m/s ,Δv 甲=0.5 m/s ,A 项错误;B 图中,v 乙=0.5 m/s ,v 甲=2.5 m/s ,Δv 乙=1.5 m/s ,Δv 甲=0.5 m/s ,B 项正确.16.2021年7月9日,斯诺克世界杯在江苏无锡落下帷幕,由丁俊晖和梁文博组成的中国A 队在决赛中1比3落后的不利形势下成功逆转,最终以4比3击败英格兰队,帮助中国斯诺克台球队获得了世界杯三连冠.如图所示为丁俊晖正在准备击球,设在丁俊晖这一杆中,白色球(主球)和花色球碰撞前、后都在同一直线上运动,碰前白色球的动量p A =5 kg·m/s ,花色球静止,白色球A 与花色球B 发生碰撞后,花色球B 的动量变为p ′B =4 kg·m/s ,则两球质量m A 与m B 间的关系可能是( )A .mB =m A B .m B =14m AC .m B =16m A D .m B =6m A 【答案】A【解析】:.由动量守恒定律得p A +p B =p ′A +p ′B ,解得p ′A =1 kg·m/s ,根据碰撞过程中总动能不增加,则有p 2A 2m A ≥p ′2A 2m A +p ′2B 2m B ,代入数据解得m B ≥23m A ,碰后两球同向运动,白色球A 的速度不大于花色球B 的速度,则p ′A m A ≤p ′B m B ,解得m B ≤4m A ,综上可得23m A ≤m B ≤4m A ,选项A 正确.17.如图所示,光滑水平面上有大小相同的A 、B 两球在同一直线上运动.两球质量关系为m B =2m A ,规定向右为正方向,A 、B 两球的动量均为6 kg·m/s ,运动中两球发生碰撞,碰撞后A 球的动量增量为-4 kg·m/s ,则( )A .该碰撞为弹性碰撞B .该碰撞为非弹性碰撞C .左方是A 球,碰撞后A 、B 两球速度大小之比为2∶5D .右方是A 球,碰撞后A 、B 两球速度大小之比为1∶10【答案】AC【解析】:.由m B =2m A ,p A =p B 知碰前v B <v A ,若右方为A 球,由于碰前动量都为6 kg·m/s ,即都向右运动,两球不可能相碰;若左方为A 球,设碰后二者速度分别为v ′A 、v ′B ,由题意知p ′A =m A v ′A =2 kg·m/s ,p ′B =m B v ′B =10 kg·m/s ,解得v ′A v ′B =25.碰撞后A 球动量变为2 kg·m/s ,B 球动量变为10 kg·m/s ,又m B =2m A ,由计算可知碰撞前后A 、B 两球动能之和不变,即该碰撞为弹性碰撞,选项A 、C 正确.18.如图所示,小车(包括固定在小车上的杆)的质量为M ,质量为m 的小球通过长度为L 的轻绳与杆的顶端连接,开始时小车静止在光滑的水平面上.现把小球从与O 点等高的地方释放(小球不会与杆相撞),小车向左运动的最大位移是( )A .2LM M +mB .2Lm M +mC .ML M +mD .mL M +m【答案】B【解析】:.分析可知小球在下摆过程中,小车向左加速,当小球从最低点向上摆动过程中,小车向左减速,当小球摆到右边且与O 点等高时,小车的速度减为零,此时小车向左的位移达到最大,小球相对于小车的位移为2L .小球和小车组成的系统在水平方向上动量守恒,设小球和小车在水平方向上的速度大小分别为v 1、v 2,有mv 1=Mv 2,故ms 1=Ms 2,s 1+s 2=2L ,其中s 1代表小球的水平位移大小,s 2代表小车的水平位移大小,因此s 2=2Lm M +m ,选项B 正确.19.如图所示,光滑水平直轨道上有三个质量均为m 的物块A 、B 、C .B 的左侧固定一轻弹簧(弹簧左侧的挡板质量不计).设A 以速度v 0朝B 运动,压缩弹簧;当A 、B 速度相等时,B 与C 恰好相碰并粘接在一起,然后继续运动.假设B 和C 碰撞过程时间极短.求从A 开始压缩弹簧直至与弹簧分离的过程中:(1)整个系统损失的机械能;(2)弹簧被压缩到最短时的弹性势能.【答案】:(1)116mv 02 (2)1348mv 02【解析】:(1)从A 压缩弹簧到A 与B 具有相同速度v 1时,对A 、B 与弹簧组成的系统,由动量守恒定律得mv 0=2mv 1①此时B 与C 发生完全非弹性碰撞,设碰撞后的瞬时速度为v 2,损失的机械能为ΔE .对B 、C 组成的系统,由动量守恒和能量守恒定律得mv 1=2mv 2②12mv 12=ΔE +12(2m )v 22③ 联立①②③式得ΔE =116mv 02④ (2)由②式可知v 2<v 1,A 将继续压缩弹簧,直至A 、B 、C 三者速度相同,设此速度为v 3,此时弹簧被压缩至最短,其弹性势能为E p .由动量守恒和能量守恒定律得mv 0=3mv 3⑤12mv 02-ΔE =12(3m )v 32+E p ⑥ 联立④⑤⑥式得E p =1348mv 02 20.如图所示,光滑冰面上静止放置一表面光滑的斜面体,斜面体右侧一蹲在滑板上的小孩和其面前的冰块均静止于冰面上。
动量守恒定律典型例题解析

动量守恒定律·典型例题解析【例1】 如图52-1所示,在光滑的水平面上,质量为m 1的小球以速度v 1追逐质量为m 2,速度为v 2的小球,追及并发生相碰后速度分别为v 1′和v 2′,将两个小球作为系统,试根据牛顿运动定律推导出动量守恒定律.解析:在两球相互作用过程中,根据牛顿第二定律,对小球1有:F==,对有′==.由牛顿第三定律得=m a m m F m a m F 1112222∆∆∆∆v t v t 12 -F ′,所以F ·Δt =-F ′·Δt ,m 1Δv 1=-m 2Δv 2,即m 1(v 1′-v 1)=-m 2(v 2′-v 2),整理后得:m 1v 1+m 2v 2=m 1v 1′+m 2v 2′,这表明以两小球为系统,系统所受的合外力为零时,系统的总动量守恒.点拨:动量守恒定律和牛顿运动定律是一致的,当系统内受力情况不明,或相互作用力为变力时,用牛顿运动定律求解很繁杂,而动量定理只管发生相互作用前、后的状态,不必过问相互作用的细节,因而避免了直接运用牛顿运动定律解题的困难,使问题简化.【例2】 把一支枪水平地固定在光滑水平面上的小车上,当枪发射出一颗子弹时,下列说法正确的是[ ]A .枪和子弹组成的系统动量守恒B .枪和车组成的系统动量守恒C .子弹、枪、小车这三者组成的系统动量守恒D .子弹的动量变化与枪和车的动量变化相同解析:正确答案为C点拨:在发射子弹时,子弹与枪之间,枪与车之间都存在相互作用力,所以将枪和子弹作为系统,或枪和车作为系统,系统所受的合外力均不为零,系统的动量不守恒,当将三者作为系统时,系统所受的合外力为零,系统的动量守恒,这时子弹的动量变化与枪和车的动量变化大小相等,方向相反.可见,系统的动量是否守恒,与系统的选取直接相关.【例3】 如图52-2所示,设车厢的长度为l ,质量为M ,静止于光滑的水平面上,车厢内有一质量为m 的物体以初速度v 0向右运动,与车厢壁来回碰撞n 次后,静止在车厢中,这时车厢的速度为_______,方向与v 0的方向_______.点拨:不论物体与车厢怎样发生作用,碰撞多少次,将物体与车厢作为系统,物体与车厢间作用力是内力,不改变系统的总动量,同时这一系统所受的合外力为零,系统的总动量守恒,以v 0为正方向,有mv 0=(M +m)v ′.【例4】 一辆列车的总质量为M ,在平直的水平轨道上以速度v 匀速行驶,突然最后一节质量为m 的车厢脱钩,假设列车所受的阻力与车的重量成正比,机车的牵引力不变,当脱钩的车厢刚好停止运动时,前面列车的速度为多大?点拨:以整列列车为系统,不管最后一节车厢是否脱钩,系统所受的外力在竖直方向上重力与轨道给系统的弹力相平衡,在运动方向上牵引力与系统所受的总的阻力相平衡,即系统所受的外力为零,总动量守恒.参考答案例,相同例-3 mv M +m 4 M M mv 0跟踪反馈1.在光滑水平面上有两个质量不等的物体,它们之间夹一被压缩的弹簧,开始时两物用细绳相连,烧断细绳后两物体[ ]A .在任何时刻加速度大小相等B .在任何时刻速度大小相等C .在任何时刻动量大小相等D .在任意一段时间内,弹簧对两物体的冲量相同2.沿一直线相向运动的甲、乙两质点,作用前动量分别是P 1=10kg ·m/s ,P 2=-18kg ·m/s ,作用后甲的动量为-1kg ·m/s ,不计任何外界阻力,则作用后乙的动量为[ ]A.-29kg·m/sB.29kg·m/sC.-7kg·m/sD.7kg·m/s3.质量为490g的木块静止在光滑水平面上,质量为10g的子弹以500m/s 的速度水平射入木块并嵌在其中,从子弹刚射入木块至与木块相对静止的过程中,木块增加的动量为_______kg·m/s,它们的共同运动速度为_______m/s.4.质量为120t的机车,向右匀速滑行与静止的质量均为60t的四节车厢挂接在一起运动,由于四节车厢的挂接,使机车的速度减小了3m/s,求机车在挂接前的速度.参考答案1.C 2.C 3.4.9;10 4.4.5m/s;方向向右。
动量和动量守恒定律解题技巧

动量和动量守恒定律解题技巧(一)动量及动量定理【例1】质量为m的小球从高处由静止开始落下,经t1秒落在泥塘上,在泥塘中下落t2秒后停住.求小球在泥塘中所受平均阻力.分析与解答取小球为研究对象,研究从下落到停在泥塘中的全过程.此过程中小球受重力冲量和阻力冲量.根据动量定理,有:可求出小球在泥塘中所受平均阻力为:【例2】滑块A和B用轻细线连接在一起后放在水平桌面上,水平恒力F作用在B上,使A、B一起由静止开始沿水平桌面滑动,如图5-4所示.已知滑块A、B与水平桌面之间滑动摩擦系数均为μ.力F作用t秒后A、B间连线断开,此后力F仍作用于B.试求:滑块A刚刚停住时,滑块B的速度多大?滑块A、B的质量分别为mA、mB.分析与解答(1)取滑块A、B为研究对象,研究A、B整体作加速运动的过程,根据动量定理,有:[F-μ(mA+mB)g]t = (mA+mB)v-0(2)研究滑块A,研究A作匀减速运动的过程,根据动量定理,有:-μmAgt′= 0-mAv将v代入上式,可求得滑块A作匀减速滑行时间为:(3)研究滑块A、B整体.研究从力F作用开始直至A停住的全过程.此过程中物体系统始终受到力F及摩擦力的冲量,根据动量定理,有[F-μ(mA+mB)g](t+t′) = mBvB将t′代入上式,可求出滑块A刚停住时滑块B的速度为上面例1、例2既可以用牛顿运动定律求解,也可以用功和能观点求解.此处用动量定理求解,使解题过程简化.通过对例题1、2分析,请读者体会前面所讲的几个方面应注意的问题.这里进一步说明的是,动量定理的研究对象可以是一个物体(质点),也可以是物体系统(质点组).例1的研究对象是一个物体,例2则是以研究物体系统为主.不论研究对象是物体还是物体系统,研究对象的动量变化都是由研究对象所受外力的冲量产生的.因此正确确定研究对象,正确分析研究对象所受力的冲量及其动量的变化,是应用动量定理分析、解决问题的基础.【例3】由高压水枪中竖直向上喷出的水柱,将一个质量为m的小铁盒开口向下倒顶在空中,如图5-5所示.已知水以恒定速率v0从横截面积为S的水枪中持续不变喷出,向上运动并冲击铁盒后,以不变的速率竖直返回,求稳定状态下铁盒距水枪口的高度h.分析与解答由水枪喷出的水作竖直上抛运动,当水柱上升到h高单位时间内,由水枪喷出的水的质量为Δm = ρv0S水柱喷射到铁盒上时,由于速度v减小,水柱与铁盒接触面积S′>S.由于水柱持续喷出,有Sv0 = S′v,所以单位时间内喷射到铁盒上水的质量保持Δm = ρv0S不变.取质量为Δm的水为研究对象,研究Δm与铁盒相互作用的过程.由于Δm 水中每一水滴与铁盒作用时间极短,可忽略作用过程中每一水滴所受重力影响.取向上为正方向,根据动量定理,有:f′Δt = -2ρv0Sv由于Δt = 1秒,可得Δm的水受铁盒作用力为:f′ = -2ρv0Sv铁盒所受Δm水的冲击力f=-f′=2ρv0Sv,处于稳定状态时,铁盒所受合外力为零,有2ρv0Sv= mg.将v代入上式,解得:</PGN0123.TXT/PGN>对于较复杂的问题,不仅仅要应用到动量定理的知识,还要涉及到所学的其它物理知识.综合运用所学知识解决问题是这部分知识的较高要求.(二)动量守恒定律物体间发生相互作用的过程中,如果没有外力作用,那么相互作用物体的总动量保持不变,这就是动量守恒定律.动量守恒定律是宏观世界和微观世界都遵守的共同规律,应用非常广泛.动量守恒定律的适用条件是相互作用的物体系统不受外力,当然,世界上真正满足不受外力的情况几乎是不存在的,应用动量守恒定律的主要是如下三种情况:①系统受到的合外力为零.②系统所受的外力比相互作用力(内力)小很多,以至可以忽略外力的影响,认为系统的总动量守恒.③系统总体上不满足动量守恒的条件,但在某一特定的方向上,系统不受外力,或所受的外力远小于内力,则系统沿这一方向的分动量守恒.碰撞是指两物体间的短暂作用,由于相互作用的时间极短,相互作用力很大,即使系统还受有摩擦、空气阻力等外力作用,也能满足相互作用的内力远大于外力的条件,因此各碰撞过程都可应用动量守恒定律求解.【例4】有N个质量均为m的人,站在质量为M的平板车上,开始时人与车均静止于光滑水平地面上.若这N个人都从平板车的后端以相对平板车为u 的水平速度从车上跳下,车向前方反冲前进.第一种情况是N个人同时跳车,第二种情况是N个人依次跳下,试求这两种情况中平板车最终行驶速度多大?分析与解答第一种情况中,设人跳车时车的速度为V,则人跳车时人相对地的速度v = u-V跳车过程中,人与车系统动量守恒,根据动量守恒定律,有MV-Nmv = 0第二种情况中,N个人依次跳车,第一个人跳车过程有[M+(N-1)m]V1-mv1 = 0v1 = u-V1.由上面两式解出第一个人跳车后,车的反冲速度为V1 = mu/(M+Nm)第二个人跳车过程有:[M+(N-2)m]V2-mv2 = [M+(N-1)m]V1v2 = u-V2依次分析每个人跳车过程,可得:将上面各结果相加,可得第二种情况中平板车最终的反冲速度为:由例4的分析可以看出,应用动量守恒定律解题时,各物体初、末速度都应是相对地面的.若题目中给出物体间相对速度,最好单独列出相对速度关系式,而在动量守恒定律中应列出对地的速度,避免由于速度关系引起混乱而出错误.对类似例4这种有多次相互作用的物理过程,要注意分析每一过程的特点及规律,还要找出前后过程之间的联系,才能对整个物理过程有全面掌握.根据对第二种情况的分析,读者可以进一步体会、类比质量连续变化的火箭发射问题.由例4的结果对比可知V<VN,读者可以由此结果体会在发射人造航天器时,为什么要采用多级火箭依次点火加速,而不采用这些多级火箭发动机同时点火加速的方式.【例5】人和冰车的总质量为M,另有一个质量为m的坚固木箱.开始时人坐在冰车上静止不动,某一时刻人将原来静止在冰面上的木箱以相对冰面的速度v0推向前方的固定弹性挡板,同时冰车反向滑动.木箱与挡板碰撞后又反向弹回.设碰撞挡板过程中木箱无机械能的损失,人接到木箱后再以同样相对于冰面的速度v0推向挡板……如此往复多次,试分析人推出木箱多少次后将不可能再接到木箱?已知M∶m = 31∶2,不计冰车及木箱与冰面之间的摩擦.分析与解答解法1:取人、冰车及木箱系统为研究对象.不论是第一次推出木箱,还是以后每次接到木箱再将其推出的过程,系统的动量都是守恒的.根据动量守恒定律,有:第一次推出木箱的过程0 = MV1-mv0第二次推出木箱的过程MV1+mv0 = MV2-mv0第三次推出木箱的过程MV2+mv0 = MV3-mv0……第n次推出木箱的过程</PGN0125.TXT/PGN>MVn-1+mv0 = MVn-mv0将以上各式相加,得到:(n-1)mv0 = MVn-nmv0即(2n-1)mv0 = MVn当Vn≥v0时,木箱追不上冰车,即人无法再接到木箱,此时2n-1 =MVn/mv0≥M/m取n = 9时,即人推出木箱9次后将不会再接到木箱.解法2:取人、冰车及木箱为研究对象,考虑研究对象与挡板之间的作用.木箱每碰挡板一次,其动量变化2mv0,即得到2mv0的冲量作用.对于研究对象,木箱每碰挡板一次,系统动量将增加2mv0.设人推出木箱n次后,冰车速度Vn≥v0,则此后人无法再接到木箱.研究人推出木箱n次的全过程,此过程中木箱共碰挡板(n-1)次,系统所受冲量为(n-1)2mv0,根据动量定理有:2(n-1)mv0 = (MVn-mv0)-0可以导出(2n-1)mv0 = MVn以下分析与解法1相同,故略去.同是一个问题,解法1用动量守恒定律求解,解法2用动量定理求解,请读者体会其中的差异:在解法1中,我们研究系统内物体之间相互作用过程,每次接到又推出木箱的过程中系统的动量是守恒的;在解法2中,我们并不考虑物体系统内的相互作用,而是考虑系统所受外界物体(挡板)的作用(这恰好是解法1中所没有考虑的),考虑了研究对象与外界物体作用的全过程.由以上例题分析应该重点体会、理解应用物理规律分析问题的方法和思路.【例6】一条质量为M,长为L的小船静止在平静的水面上,一个质量为m的人站立在船头.如果不计水对船运动的阻力,那么当人从船头走到船尾时,船的位移多大?分析与解答本题中人从船头走向船尾,不是匀速运动,但不管人的运动多么复杂,人与船组成的系统在水平方向上是满足动量守恒条件的(水对船的阻力不计).开始时人与船都静止,总动量为零,人运动过程中,船向相反方向运动,最后人停止在船尾,船也静止在水中.画出图5-6所示的示意图,人相对船的位移是L,但人对地的位移不是L.设船发</PGN0126.TXT/PGN>生的位移是x,由图中可以看出人对地的位移是L-x.设人运动过程中对地的速度(平均速度)是v,船对地的速度是V,根据动量守恒定律,有mv+MV = 0两边同乘以运动时间t,得mvt+MVt = 0由于Vt = x,vt = L-x即m(L-x)+Mx = 0其中负号是表示方向的.说明本题主要想说明应用动量守恒定律解题时参照物必须明确和统一,一般情况下,都以地面为参照物,各物体的始末速度都是对地的,如果忽略了这一点,不作如图5-6所示的分析,是解决不了这个问题的.【例7】一列火车在水平直铁轨上做匀速运动,总质量为M,速度为v,某时刻车后部有质量为m的一节车厢脱钩,司机并未发觉,又继续行驶了一般距离,这期间机车的牵引力保持不变,并且火车各部分所受的阻力跟运动速度无关.当司机发现时,后面脱钩的车厢的速度已减分析与解答火车原在铁轨上做匀速直线运动,说明它受力平衡,即牵引力与所受阻力大小相等.一节车厢脱钩后,由于牵引力保持不变,前面部分将做加速运动,后面部分将做减速运动,如果两部分分开考虑,将很繁琐,而做为一个系统,仍满足“合外力为零”的条件,因此可以应用动量守恒定律求解.设火车前面部分末速度为v′,根据动量守恒定律,有说明:选择本题是想说明动量守恒定律决不只限制在碰撞一类问题中应用,任何一个系统(包括像本题这样已经脱离接触、不再相互作用的系统),只要满足动量守恒的条件,总动量就守恒.(三)碰撞碰撞是两个物体在很短时间内发生相互作用的物理过程.不论是宏观物体间还是微观粒子间,碰撞现象是普遍存在的.由于碰撞的作用时间极短(例如两个钢</PGN0127.TXT/PGN>球碰撞相互作用的时间约为10-4秒),物体间相互作用力又非常大,通常物体所受外力(如重力、摩擦力)在这段时间内的影响可以忽略不计.此过程中参与相互碰撞作用的物体系统的总动量守恒,这就是我们对碰撞现象的基本认识之一.由于物体间作用力很大,而相互作用时间很短,碰撞时物体间相互作用力(通常称之为冲力)对物体作用效果的两个显著特点是使物体速度发生骤变而其位置变化极其微小以至我们认为其位置没有变化.这是我们对碰撞现象的另一基本认识.根据碰撞前后物体系统能量变化特点,碰撞可以分为完全弹性碰撞、完全非弹性碰撞和非弹性碰撞.在完全弹性碰撞中,系统动能在碰撞前后是不变的.而在完全非弹性碰撞和非弹性碰撞中,碰撞后系统总动能比碰撞前要减少,其中在完全非弹性碰撞中,系统损失的动能多于一般非弹性碰撞中系统损失的动能.【例8】一个质量是M = 0.5kg的斜面体A原静止在光滑的水平面上,一个质量m = 40g的小球B以水平速度v0 = 30m/s撞到A的斜面上,碰撞时间很短,碰后变为竖直向上运动,求物体A碰后的速度.分析与解答B与A的碰撞时间很短,说明碰撞过程中相互作用力很大,但A与B组成的系统总动量并不守恒,因为A与桌面间有弹力作用,这个弹力(支持力)属于反应力,在B与A相互作用的短暂过程中,支持力要发生很大变化,它不满足“外力内力”的条件,但这个外力是沿竖直方向的,在水平方向上,由于水平面是光滑的,因此A与B组成的系统,在水平方向上不受外力,水平方向上动量守恒.设A碰后的速度为v,而B碰后的水平分速为0,根据动量守恒定律,有0+mv0 = Mv+0,说明:本题是为了说明应用动量守恒定律解决问题的一般思路,首先要把相互作用的物体组成一个系统,看这个系统是否满足动量守恒的条件,然后分析相互作用前、后两个状态各自的动量,再列方程求解.【例9】质量为M的木块放在水平地面上,处于静止状态,木块与地面间摩擦系数为μ.一颗质量为m的子弹水平射入木块后,木块沿水平地面滑行了距离s后停住,如图5-8所示,试求:</PGN0128.TXT/PGN>(1)子弹射入木块前速度v0多大?(2)若子弹射入木块的深度为d,子弹与木块之间相互作用力多大?分析与解答(1)子弹射入木块的过程时间极短暂,子弹与木块相互作用力远远大于木板所受摩擦力,子弹与木块系统动量守恒,有mv0 = (m+M)v.子弹射入木块后以共同速度v在水平地面上滑行了距离为s,研究(2)子弹射入木块并停在其中,相互作用中系统动量守恒.由于相互作用过程中有摩擦力做功,系统动能减少.根据动量关系及动能关系,有由以上两式解得子弹与木块之间的相互作用力为f = μM(M+m)gs/md【例10】一个固定在平板车上不动的人用力将质量为m的铅球水平推出.第一次平板车被固定在水平地面上不动,球落地时水平射程为s0.第二次将平板车放在光滑水平地面上,人同样用力将球水平推出,这两次人推球消耗的能量相同.若人与平板车的总质量为M,试求:(1)第二次铅球落地时水平射程(相对于地面)多大?(2)铅球落地时,人与铅球水平方向相距多远?分析与解答(1)设人推铅球过程中做功消耗的能量为E,则第一第二次推出铅球过程中,车、人与铅球系统动量守恒,且推球过程中根据能量守恒,有:mv = MV由此可知,第二次球的水平射程为:此时人与球之间水平距离为:</PGN0129.TXT/PGN>上面例题中讨论的问题过程较复杂.而且不仅涉及到系统的动量,还同时涉及相互作用的物体系统的能量.对于类似的问题,首先要正确选择研究对象,正确将整个过程分几个阶段处理;其次要分析每一阶段物体相互作用的特点,找出各阶段的关系.通过上面例题分析还可以看到,不论是动量还是动能,都是对物体的机械运动状态的量度.在物体相互作用过程中,量度物体之间机械运动的“运动量”的转移和传递时,我们用动量及有关规律进行分析;若讨论在相互作用过程中,物体机械运动的“运动量”与其它运动形式(如热运动)的转化问题,则要应用动能及有关功和能的关系加以分析.。
高考物理动量守恒定律试题经典及解析

高考物理动量守恒定律试题经典及解析一、高考物理精讲专题动量守恒定律1.如图所示,一辆质量M=3 kg 的小车A 静止在光滑的水平面上,小车上有一质量m=l kg 的光滑小球B ,将一轻质弹簧压缩并锁定,此时弹簧的弹性势能为E p =6J ,小球与小车右壁距离为L=0.4m ,解除锁定,小球脱离弹簧后与小车右壁的油灰阻挡层碰撞并被粘住,求:①小球脱离弹簧时的速度大小;②在整个过程中,小车移动的距离。
【答案】(1)3m/s (2)0.1m 【解析】试题分析:(1)除锁定后弹簧的弹性势能转化为系统动能,根据动量守恒和能量守恒列出等式得 mv 1-Mv 2=022121122P E mv Mv =+ 代入数据解得:v 1=3m/s v 2=1m/s (2)根据动量守恒和各自位移关系得12x xm M t t=,x 1+x 2=L 代入数据联立解得:24Lx ==0.1m 考点:动量守恒定律;能量守恒定律.2.如图,光滑冰面上静止放置一表面光滑的斜面体,斜面体右侧一蹲在滑板上的小孩和其面前的冰块均静止于冰面上.某时刻小孩将冰块以相对冰面3 m/s 的速度向斜面体推出,冰块平滑地滑上斜面体,在斜面体上上升的最大高度为h="0.3" m (h 小于斜面体的高度).已知小孩与滑板的总质量为m 1="30" kg ,冰块的质量为m 2="10" kg ,小孩与滑板始终无相对运动.取重力加速度的大小g="10" m/s 2.(i )求斜面体的质量;(ii )通过计算判断,冰块与斜面体分离后能否追上小孩? 【答案】(i )20 kg (ii )不能 【解析】试题分析:①设斜面质量为M ,冰块和斜面的系统,水平方向动量守恒:222()m v m M v =+系统机械能守恒:22222211()22m gh m M v m v ++= 解得:20kg M =②人推冰块的过程:1122m v m v =,得11/v m s =(向右)冰块与斜面的系统:22223m v m v Mv '=+ 22222223111+222m v m v Mv ='解得:21/v m s =-'(向右) 因21=v v ',且冰块处于小孩的后方,则冰块不能追上小孩. 考点:动量守恒定律、机械能守恒定律.3.光滑水平轨道上有三个木块A 、B 、C ,质量分别为3A m m =、B C m m m ==,开始时B 、C 均静止,A 以初速度0v 向右运动,A 与B 相撞后分开,B 又与C 发生碰撞并粘在一起,此后A 与B 间的距离保持不变.求B 与C 碰撞前B 的速度大小.【答案】065B v v = 【解析】 【分析】 【详解】设A 与B 碰撞后,A 的速度为A v ,B 与C 碰撞前B 的速度为B V ,B 与C 碰撞后粘在一起的速度为v ,由动量守恒定律得: 对A 、B 木块:0A A A B B m v m v m v =+对B 、C 木块:()B B B C m v m m v =+由A 与B 间的距离保持不变可知A v v = 联立代入数据得:065B v v =.4.(1)恒星向外辐射的能量来自于其内部发生的各种热核反应,当温度达到108K 时,可以发生“氦燃烧”。
动量定理、动量守恒定理大题50题含问题详解
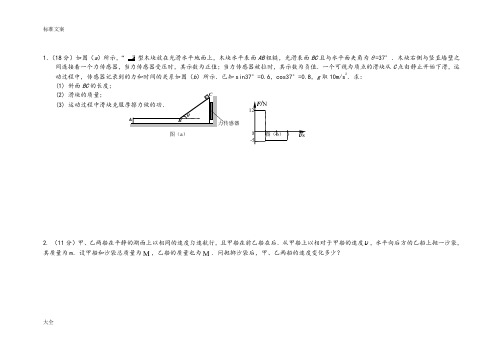
大全1.(18分)如图(a )所示,“ ”型木块放在光滑水平地面上,木块水平表面AB 粗糙,光滑表面BC 且与水平面夹角为θ=37°.木块右侧与竖直墙壁之间连接着一个力传感器,当力传感器受压时,其示数为正值;当力传感器被拉时,其示数为负值.一个可视为质点的滑块从C 点由静止开始下滑,运动过程中,传感器记录到的力和时间的关系如图(b )所示.已知sin37°=0.6,cos37°=0.8,g 取10m/s 2.求:(1) 斜面BC 的长度;(2) 滑块的质量;(3) 运动过程中滑块克服摩擦力做的功.2. (11分)甲、乙两船在平静的湖面上以相同的速度匀速航行,且甲船在前乙船在后.从甲船上以相对于甲船的速度 ,水平向后方的乙船上抛一沙袋,其质量为m .设甲船和沙袋总质量为M ,乙船的质量也为M .问抛掷沙袋后,甲、乙两船的速度变化多少?0 F/N t/s-5 12 1 2 3 图(b ) 图(a ) A θ B C 力传感器大全3.(2011·新课标全国卷)如图,A 、B 、C 三个木块的质量均为m 。
置于光滑的水平面上,B 、C 之间有一轻质弹簧,弹簧的两端与木块接触而不固连,将弹簧压紧到不能再压缩时用细线把B 和C 紧连,使弹簧不能伸展,以至于B 、C 可视为一个整体,现A 以初速v 0沿B 、C 的连线方向朝B 运动,与B 相碰并粘合在一起,以后细线突然断开,弹簧伸展,从而使C 与A ,B 分离,已知C 离开弹簧后的速度恰为v 0,求弹簧释放的势能。
【详解】设碰后A 、B 和C 的共同速度大小为v ,由动量守恒有,3mv=mv 0 ①设C 离开弹簧时,A 、B 的速度大小为v1,由动量守恒有,3mv=2mv 1+mv 0 ②设弹簧的弹性势能为Ep ,从细线断开到C 与弹簧分开的过程中机械能守恒,有,12 (3m )v 2+Ep=12 (2m )v 12+12mv 02 ③ 由①②③式得弹簧所释放的势能为Ep=13m v 024.一质量为2m 的物体P 静止于光滑水平地面上,其截面如图所示。
动量-动量守恒-知识点-例题详解

动量-动量守恒-知识点-例题详解(总25页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第七章动量动量守恒考纲要求1、动量、冲量、动量定理Ⅱ2、动量守恒定律Ⅱ说明:动量定理和动量守恒定律的应用只限于一维的情况知识网络:单元切块:按照考纲的要求,本章内容可以分成两部分,即:动量、冲量、动量定理;动量守恒定律。
其中重点是动量定理和动量守恒定律的应用。
难点是对基本概念的理解和对动量守恒定律的应用。
§1 动量、冲量和动量定理知识目标一、动量1、动量:运动物体的质量和速度的乘积叫做动量.是矢量,方向与速度方向相同;动量的合成与分解,按平行四边形法则、三角形法则.是状态量;通常说物体的动量是指运动物体某一时刻的动量,计算物体此时的动量应取这一时刻的瞬时速度。
是相对量;物体的动量亦与参照物的选取有关,常情况下,指相对地面的动量。
单位是kg·m/s;2、动量和动能的区别和联系①动量的大小与速度大小成正比,动能的大小与速度的大小平方成正比。
即动量相同而质量不同的物体,其动能不同;动能相同而质量不同的物体其动量不同。
②动量是矢量,而动能是标量。
因此,物体的动量变化时,其动能不一定变化;而物体的动能变化时,其动量一定变化。
③因动量是矢量,故引起动量变化的原因也是矢量,即物体受到外力的冲量;动能是标量,引起动能变化的原因亦是标量,即外力对物体做功。
④动量和动能都与物体的质量和速度有关,两者从不同的角度描述了运动物体的特性,且二者大小间存在关系式:P2=2mEk3、动量的变化及其计算方法动量的变化是指物体末态的动量减去初态的动量,是矢量,对应于某一过程(或某一段时间),是一个非常重要的物理量,其计算方法: (1)ΔP=P t 一P 0,主要计算P 0、P t 在一条直线上的情况。
(2)利用动量定理 ΔP=F ·t ,通常用来解决P 0、P t ;不在一条直线上或F 为恒力的情况。
动量定理、动量守恒判断

动量定理的理解与应用 【例题解析】排球运动是一项同学们喜欢的体育运动.为了了解排球的某些性能,某同学让排球从距地面高h 1=1.8m 处自由落下,测出该排球从开始下落到第一次反弹到最高点所用时间为t=1.3s ,第一次反弹的高度为h 2=1.25m .已知排球的质量为m=0.4kg ,g 取10m/s 2,不计空气阻力.求:①排球与地面的作用时间.②排球对地面的平均作用力的大小.【答案解析】 解:①设排球第一次落至地面经历的时间为t 1,第一次离开地面至反弹到最高点经历的时间为t 2,则有h 1=\frac{1}{2}gt 12,h 2=gt 22解得t 1=0.6s ,t 2=0.5s所以,排球与地面的作用时间为t 3=t ﹣t 1﹣t 2=0.2s②设排球第一次落地时的速度大小为v 1,第一次反弹离开地面时的速度大小为v 2,有v 1=gt 1=6m/s ,v 2=gt 2=5m/s设地面对排球的平均作用力为F ,选排球为研究对象,以向上的方向为正方向,则在它与地面碰撞的过程中,由动量定理有(F ﹣mg )t 3=mv 2﹣m (﹣v 1)代入数据解得F=26N 根据牛顿第三定律,排球对地面的平均作用力F′=26N1、(单选)物体在恒定的合力F 作用下做直线运动,在时间Δt 1 内速度由0增大到v ,在时间Δt 2内速度由v 增大到2v 。
设F 在Δt 1 内做的功是W 1,冲量是I 1;在Δt 2 内做的功是W 2,冲量是I 2;那么( )A.I 1<I 2,W 1=W 2B.I 1<I 2,W 1<W 2C.I 1=I 2,W 1=W 2D.I 1=I 2,W 1<W 2【解析】 I 1=F Δt 1=mv ,I 2=F Δt 2=2mv -mv =mv ,所以冲量相同,由动能定理W 1=12mv 2,W 2=12m ×4v 2-12mv 2=32mv 2,所以W 1<W 2,D 正确。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
动量定理与动量守恒定律·典型例题解析
【例1】 在光滑的水平面上有一质量为2m 的盒子,盒子中间有一质量为m 的物体,如图55-1所示.物体与盒底间的动摩擦因数为μ现给物体以水平速度v 0向右运动,当它刚好与盒子右壁相碰时,速度减为
v 02
,物体与盒子右壁相碰后即粘在右壁上,求:
(1)物体在盒内滑行的时间;
(2)物体与盒子右壁相碰过程中对盒子的冲量.
解析:(1)对物体在盒内滑行的时间内应用动量定理得:-μmgt =
m mv t 0·-,=v v g
0022 (2)物体与盒子右壁相碰前及相碰过程中系统的总动量都守恒,设碰
撞前瞬时盒子的速度为,则:=+=+.解得=,=.所以碰撞过程中物体给盒子的冲量由动量定理得=-=,方向向右.
v mv m
v 22mv (m 2m)v v v I 2mv 2mv mv /61001212210v v 0043
点拨:分清不同的物理过程所遵循的相应物理规律是解题的关键.
【例2】 如图55-2所示,质量均为M 的小车A 、B ,B 车上
挂有质量为的金属球,球相对车静止,若两车以相等的速率M 4
C C B 1.8m/s 在光滑的水平面上相向运动,相碰后连在一起,则碰撞刚结束时小车的速度多大?C 球摆到最高点时C 球的速度多大?
解析:两车相碰过程由于作用时间很短,C 球没有参与两车在水平方向的相互作用.对两车组成的系统,由动量守恒定律得(以向左为正):Mv -Mv =
2Mv 1两车相碰后速度v 1=0,这时C 球的速度仍为v ,向左,接着C 球向左上方摆动与两车发生相互作用,到达最高点时和两车
具有共同的速度,对和两车组成的系统,水平方向动量守恒,=++,解得==,方向向左.v C v (M M )v v v 0.2m /s 222M M 4419
点拨:两车相碰的过程,由于作用时间很短,可认为各物都没有发生位移,因而C 球的悬线不偏离竖直方向,不可能跟B 车发生水平方向的相互作用.在C 球上摆的过程中,作用时间较长,悬线偏离竖直方向,与两车发生相互作用使两车在水平方向的动量改变,这时只有将C 球和两车作为系统,水平方向的总动量才守恒.
【例3】 如图55-3所示,质量为m 的人站在质量为M 的小车的右端,处于静止状态.已知车的长度为L ,则当人走到小车的左端时,小车将沿光滑的水平面向右移动多少距离?
点拨:将人和车作为系统,动量守恒,设车向右移动的距离为s ,则人向左移动的距离为L -s ,取向右为正方向,根据动量守恒定律可得M ·s -m(L -s)=0,从而可解得s .注意在用位移表示动量守恒时,各位移都是相对地面的,并在选定正方向后位移有正、负之分.
参考答案
例例跟踪反馈...;;.×·3
m M +m L 4 M +m M
H [] 1 C 2h 300v 49.110N s 04M m M 【例4】 如图55-4所示,气球的质量为M 离地的高度为H ,在气球下方有一质量为m 的人拉住系在气球上不计质量的软绳,人和气球恰悬浮在空中处于静止状态,现人沿软绳下滑到达地面时软绳的下端恰离开地面,求软绳的长度.
点拨:人和气球组成的系统总动量守恒,人沿绳子到达地面的过程中向下发生的位移为H ,此过程中气球向上发生位移为s ,两位移大小之和等于所求的绳长.
参考答案
例例跟踪反馈...;;.×·3
m M +m L 4 M +m M
H [] 1 C 2h 300v 49.110N s 04M m M 跟踪反馈
1.如图55-5所示,质量为m 的小球悬挂在质量为M 的小车上,小车静止在光滑的水平面上,现将小球拉到悬线呈水平位置时自由释放,小球向下摆动后陷入固定在车上的一块橡皮泥中,则此后小车的状态是
[ ]
A .向右匀速运动
B .向左匀速运动
C .静止不动
D .左右来回运动
2.质量为m 的木块和质量为M 的金属块用细线系在一起,悬浮在深水中的某一位置处于静止状态,若细线断裂,木块向上浮起h 的高度时与金属块之间的距离为_______.
3.在光滑的水平面上有三个完全相同的小球排成一条直线,第2、3两个小球静止并靠在一起,如图55-6所示:第1个小球以速度v 0,射向它们并发生正碰,已知在不存在第3个球时第一个球与静止的第二个球碰后第一个球的
速度为零,第二个球速度为v 0,现存在第三个球,则正碰后三球的速度分别为_______、_______、_______.
4.质量为130t ,速度为2m/s 的机车,与一节静止在水平轨道上的质量为70t 的车厢挂接,求挂接过程中车厢所受的冲量多大.
参考答案 例例跟踪反馈..
.;;.×·3 m M +m L 4 M +m M H [] 1 C 2h 300v 49.110N s 04M m M。
