磁场的安培环路定理
§9.4 磁场的安培环路定理概述

思考:如图,平行的无限长直截流导线 A 和 B,电流强度均为 I, 垂直纸面向外,两根截流导线之间相距为 a,则 (1) AB 中点(p点)的磁感应强度 Bp 0 (2)磁感应强度B 沿图中环路L的线积分 l B dl 0I
2、求解具有某些对称性的磁场分布 求解条件:电流分布(磁场分布)具有某些对称性, 以便可以找到恰当的安培环路 L ,使积分
2018/10/30 重庆邮电大学理学院 7
L
B dl B 2r 0 I内
r R:
I
内
I
B内
P
B外
0 I 1 B外 2r r
r R:
2 I Ir 2 I r 2 内 R2 R
L
L
o
r
I
R
P
B
B内
0 Ir r 2 2R
(穿过L )
I I
i
1
2I2
(穿过L )
I 2I
i
1
2018/10/30
重庆邮电大学理学院
成立条件:稳恒电流的磁场
L : 场中任一闭合曲线 — 安培环路(规定绕向)
S2
S0
Ii
(穿 过L )
I
B:
i
: 穿过以 L 为边界的任意曲
面的电流的代数和. 与空间所有电流有关
S1
L
r
o
R
1 r
r
B 方向与 I 指向满足右旋关系
2018/10/30 重庆邮电大学理学院
8
练习:无限长均匀载流圆柱体(R , I )如图,求通过 截面 S( 2 R , h )的磁通量.
13.9 安培环路定理
r 1
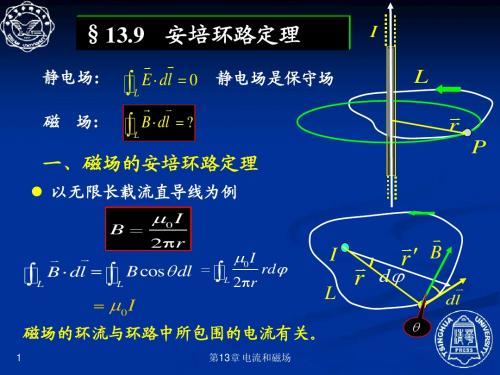
推广到一般情况
I3
电流分布
∫
说明: 说明:
L
B ⋅ dl = µ o ∑ I内
I1> 0
I2< 0
1)安培环路定理只适用于稳恒 ) 电流(闭合或伸展到∞ 电流(闭合或伸展到∞); 2) I 流向与 绕向成右手 ) 内 流向与L绕向成右手 关系时I 为正, 关系时 内为正, I内 流向与 绕向成左手 流向与L绕向成左手 关系时为负; 关系时为负; 3)环路上各点的磁场为所有 ) 电流的贡献; 电流的贡献; 4) 磁场是有旋场 )
I
n
I
B = µ0nI
管外场强仍为零。 管外场强仍为零。
7 第13章 电流和磁场
求无限大平面电流的磁场。 例3 求无限大平面电流的磁场。
?
解 平板上下两侧的磁场平行于 平板,且垂直于平板电流, 平板,且垂直于平板电流, 又是面对称的。 又是面对称的。 取回路,环量为 取回路,
I
B
b
P
a
d
B'
∫ B⋅dl = ∫
L
I
B = µ0N / 2πr I
0
若螺绕环的截面很小, 若螺绕环的截面很小,
N B = µ0 I = µ nI 内 0 2π r
若在外部再做一个环路, 若在外部再做一个环路,可得
r =r
N
o
R 1
h
R2
r
dr
∑Ii =0
螺绕环内的磁通量为
B =0 外
R 2
1
S
Φm = ∫ B⋅ dS = ∫R
R 1
§13.9 安培环路定理
静电场: 静电场 磁 场:
§7.3 磁场的安培环路定理

P. 1
二、安培环路定理
在稳恒磁场中,磁感强度B沿任意闭合路径的积分(即
环流)等于该路径所包围的电流强度代数和的μ0倍。
B dl 0 Ii
L
(L内)
L:称为安培回路。
安培 法国物理学家、数学家和化学家,
主要从事电动力学方面的研究。最先揭示 电过程和磁过程之间的起源关系,提出关 于磁性起源的纯电流概念。
过,求磁感应强度分布。已知 R。
解 B分布为柱对称,作同轴圆形安培回路。
r R : B dl B dl
L
L
I
r
L
B dl B 2 r L
B dl 0 I
L
B
0I 2 r
可等效成 ……
rR
L
Chapter 7. 稳恒电流与稳作恒者磁:场杨茂田 §7.6 磁场的安培环路定理
均匀地流过,求磁感应强度分布。
I
B
0I 2 r
o
R
R
r
(解毕 )
Chapter 7. 稳恒电流与稳作恒者磁:场杨茂田 §7.6 磁场的安培环路定理
P. 2
课堂练习 电流 I 从半径为R的无限长金属圆柱体的截面
均匀地流过,求磁感应强度分布。
提示:柱内外的 B 分布为柱对称,作同
轴圆形安培回路。
数为n,管内磁场为均匀磁场。求管内磁感应强度。
解 作矩形安培回路。
bcda
B dl
L
abcd
I
I B外 0
答案: B
0 I 2 R2
r
0I
2 r
(r Ra) (r Rd )
11-5真空中磁场的安培环路定理

0 I d d L 2 L 0 I 2
1 2
L1
L2
I
o I B 2 r
A
0
B
L2 L1
规定:与L绕向成右旋关系 Ii > 0 与L绕向成左旋关系 Ii < 0 例如:
I2
I1
I3
L
I4
I
L
I I I 1 2 3 i
0 I
2πr
r
B
B 外 方向与I指向满足右旋关系
B内 0
B外
O
R
r
练习:同轴的两筒状导线通有等值反向的电流I,
求 B 的分布。
(1) r R2 , B 0
0 I ( 2) R1 r R2 , B 2r
R2
R1
I
r I
( 3) r R1 , B 0
0 j B
2
0 j x arctg 2π z z 2
0 zj 1
o
x
0 j
2
解二、用安培环路定理
j
z
l
在对称性分析的基础上
x
选如图安培环路 得:B
由:
L
B dl 2lB 0 jl
0 j
2
思考:如果载Байду номын сангаас平面不是无限宽, 思考 能否用叠加原理求解? 能否用安培环路定理求解?
例4. 求无限长载流圆柱形导体的磁场分布. 对称性分析:
L
dI
r
dI dI o r dI
dB
dB
I
09.3磁场的安培环路定理

二、安培环路定理的应用
B dl 0 I i
当场源分布具有高度对称性时,利用安培环路定理
计算磁感应强度
1. 无限长载流圆柱导体
已知:I、R 电流沿轴向,在截面上均匀分布 分析对称性 电流分布——轴对称 磁场分布——轴对称
I
R
B 的方向判断如下:
B dl 0 I
任意积分回路
B dl B cos dl
B dl 0 I
回路不环绕电流
0 I cos dl 2r 0 I 0 I rd 2 2r 2
.
I
r
d
B dl
.
B dl 0
R2
R1
I
r I
(3) r R1 , B 0
电场、磁场中典型结论的比较
电荷均匀分布 长直线 长 直 圆 柱 面
长 直 圆 柱 体 内 外
电流均匀分布
E 2 0 r
E0
0 I B 2r
B0
内
外
E 2 0 r r E 2 2 0 R E 2 0 r
由环路内电流决定
B dl 0 I i 0 ( I 2 I 3 )
由环路内外电流产生 环路所包围的电流
I1 I4
l
I2
I3
不变
?
I4
B dl 0 I i 0 ( I 2 I 3 )
?
不变
?
I1
l
改变
I2
I1
I3
I2
I4
R2 NI 0 2. B dS hdr R1 2r 0 NIh R2 ln 2r R1
磁场高斯定理 安培环路定理
R
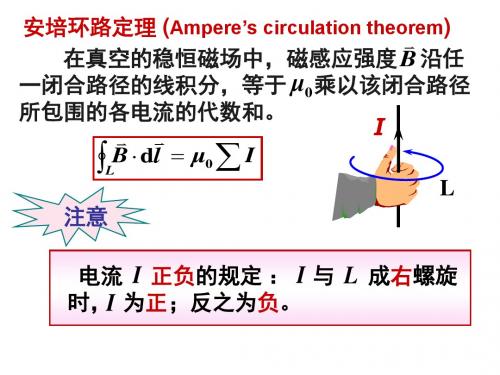
例题 无限大平板电流的磁场分布。设一无限大导体 薄平板垂直于纸面放置,其上有方向垂直于纸面朝外 的电流通过,面电流密度(即指通过与电流方向垂直 的单位长度的电流)到处均匀。大小为 j 。
解:视为无限多平行长 直电流的场。 分析求场点p的对称性 做 po 垂线,取对称的 长直电流元,其合磁场 方向平行于电流平面。
多电流情况
I1
I2
I3
B B1 B2 B3 B d l 0 ( I 2 I 3 )
l
l
以上结果对任意形状 的闭合电流(伸向无限远 的电流)均成立.
n B dl 0 Ii i 1
安培环路定理
2. 明确几点 (1) 电流正负规定:电流方向与环路方向满足 右手定则时电流 I取正;反之取负。 (2) B 是指环路上一点的磁感应强度,不是任 意点的,它是空间所有电流共同产生的。
I
a
b
B
B d l lb c d d a c B d l B d l B d l B d l Bab
a
得长直载流螺线管内的磁场: B μ0 nI 无限长载流螺线管内部磁场处处相等 , 外 部磁场为零。
B
b
l
在无限大均匀平面电流的两侧的磁场都为均 匀磁场,并且大小相等,但方向相反。
同轴电缆的内导体圆柱
半径为R1,外导体圆筒内外
半径分别为R2、 R3,电缆载 有电流I,求磁场的分布。
课堂练习
0 I B r r R1 2 2 R1 0 I B R1 r R2 2 r 2 2 0 I ( R3 r ) B r R2 2 2 2 r ( R3 R2 )
大学物理 5.4 磁场的安培环路定理
l
B
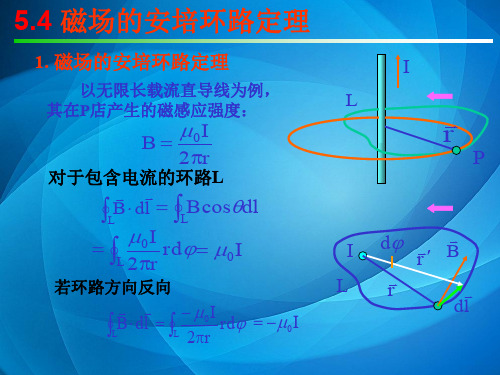
例2 载流长直螺线管磁场分布
如图,均匀密绕无限长直
螺线管通有电流为I,单位
长度匝数为n)
I
解:对称性分析—— 管内垂轴
b
Ba
平面上任意一点与 B轴平行
cd b c d a
(3)磁场是有旋场 —— 电流是磁场涡旋的轴心
B dl —— 不代表磁场力的功,仅是磁场与电流的关系
L
(4)安培环路定理只适用于闭合的载流导线,对于任 意设想的一段载流导线不成立
2. 安培环路定理的应用
在静电场中,当带电体具有一定对称性时 可以利用高斯定理很方便的计算其电场分布。 在恒定磁场中,如果电流分布具有某种对称性, 也可以利用安培环路定理计算电流磁场的分布。
由 于 这 时 I 内 =0 , 所 以 有 B=0 (在螺线环外)
l2
l1
可见,螺线环的磁场集中在
环内,环外无磁场。
对载流长直密绕螺线管,若线圈中通有电流强度为I的电
流,沿管长方向单位长度上的匝数为n,则由安培环路定理容
易求得:管内: B onI
说明
(1)积分回路绕行方向与电流方向呈右螺旋
关系
满足右螺旋关系时 Ii 0 反之 Ii 0
I
1
I
I
3
2l
I I
l
l B dl o ( I1 I2 ) l B dl o ( 2I I) oI
(2)公式中的 B 是环路上的磁感应强度,使
空间所有电流共同激发的。
L
B
LB
dr
64磁场的安培环路定理

例1.求无限长载流导体圆管(内外半径为R1, R2、电流I )的磁场。
解:电流分布——轴对称 产生的磁场——轴对称
r< R1
过场点作安培环路
B d l B cos 0d l =B2r =0
L
L
B=0
P•2
×
P•3
P•1
R1<r< R2 B d l =B2r L
•
•• ••
•• •
• •
B 圆柱外的
磁场分布 是以中心 轴线为轴 的对称分 布。
圆柱内:
I
•• ••
••••••••••••
•• • •• •• • ••
• • • •
• ••
• •• •
•• •• • r• •
••
•• • ••
•
•• •
••
•• •• •
圆柱内的磁场分布 也是以中心轴线为 轴的对称分布。
dal
L
AC
BlAC
B
CD
d Bb
dld
BB
DEb
d
l
0dBBalDE 0 0
I
Bdl
EA
n lACI
B
1 2
0nI
d
B
证毕!
D
P•
E
B dl
L
0
Ii
C
A
互动题:在以下四个环路的环流 B d l ? L
l1
I
I2
I1
l2
B dl
L
0
Ii
l3
I1 •
I2
l4
§6. 4 磁场的安培环路定理
第二十讲:§6.4磁场的安培环路定律

第二十讲: §6.4磁场的安培环路定理一、安培环路定理;是磁场与电流之间相互作用的基本定律之一 1、表述:在稳恒磁场中,B 沿任意闭合回路的积分等于该闭合回路所包围的电流的代数和乘以0μ 。
2、表达式:∑⎰=⋅iI d B 0μ两点说明:①∑i I 虽是闭合回路内所环绕的电流,且满足右手螺旋法则。
但是B 是与闭合回路内外电流有关,即B 是闭合回路内外电流共同作用的结果。
环路外的电流对 d B L ⋅⎰无贡献。
②当B 无对称性时,安培环路定理仍成立,只是B 不能提到积分号外面来,所以,利用安培环路定理不能求解B ,必须利用比-萨定律及叠加原理来进行求解。
二、安培环路定理的应用1、无限长圆柱载流导体的磁场分布∑⎰=⋅iI d B 0μR r :20122122RIr B r RIr B πμππμπ=⇒=⋅Rr :rI B I rB πμμπ220202=⇒=⋅☆如果是无限长圆面载流导体的磁场分布∑⎰=⋅iI d B 0μR r :00211=⇒=⋅B r B πRr :rI B I rB πμμπ220202=⇒=⋅2、长直载流螺线管内的磁场分布∑⎰=⋅iI d B 0μd B d B d B d B d addccbba⋅+⋅+⋅+⋅=⋅⎰⎰⎰⎰⎰BnIB I ab n ab B abd B 00B μμ=⇒=⇒=⋅⎰电流数密度:单位长度的电流数。
3、载流环形螺线管内的磁场分布∑⎰=⋅iI d B 0μr 2B d B Lπ==⋅⎰⎰d BnII rN B NI r 00022B μπμμπ==⇒=小结:磁场的安培环路定理 作业:P253预习:§6.5 磁场对运动电荷和载流导线的作用第二十讲: §6.4磁场的安培环路定理 作业:P2536-15 (1)a r <,由安培环路定理可得201220122aIrB raI r B πμππμπ==(2)b r a <<rIB Ir B πμμπ220202==(3)c r b <<)(2)()()(222220302222222203b c r r c I B I b c rc b c b r I I r B --=--=⎥⎦⎤⎢⎣⎡---=πμμππμπ(4)0,4=>B c r6-16 (1)如图示,过P 点作一半径为r 的圆形回路,圆心为O ,由安培环路定律可得 rNIB NI u r B πμπ2,200==故绕线环内磁感强度B 的大小与径向距离r 成反比。
磁场安培环路定理证明

磁场安培环路定理证明磁场安培环路定理是电磁学中的一个重要定理,它描述了磁场在电路中的分布和变化规律。
本文将对该定理进行全面详细的证明,包括定义、公式推导、实验验证以及应用等方面。
一、磁场安培环路定理的定义磁场安培环路定理是指:在任意闭合回路上,磁感应强度的积分等于该回路所包围电流的代数和。
即:∮B·dl=μ0I其中,∮B·dl表示沿闭合回路积分的磁感应强度;μ0为真空中的磁导率;I为该回路所包围电流的代数和。
二、公式推导为了证明上述定理,我们需要从麦克斯韦方程组入手,具体如下:1. 静电场高斯定理∮E·dS=Q/ε02. 静电场法拉第定律∮E·dl=-dΦ/dt3. 磁场高斯定理∮B·dS=04. 磁场法拉第定律∮B·dl=μ0I+μ0ε0(dΦE/dt)其中,E为电场强度;B为磁感应强度;S为任意闭合曲面;dl为曲线段微元;dS为曲面微元;Q为该曲面所包围的电荷量;ΦE为电通量;I为该回路所包围电流的代数和。
由于磁场高斯定理中∮B·dS=0,因此我们需要找到一种方法来消去第二个式子中的第二项,即使其等于零。
这时,我们可以利用安培环路定理来实现这一目标。
对于一个任意闭合回路,根据斯托克斯定理可得:∮B·dl=∫(∇×B)·dS其中,∇×B表示磁场强度的旋度运算符。
由于磁场是无旋场,因此有:∇×B=0将上式代入上式中,则有:∮B·dl=0但是,在真空中没有任何电流通过闭合回路时,根据安培定律可知:∮B·dl=μ0I因此,我们可以得到磁场安培环路定理:∮B·dl=μ0I三、实验验证为了验证磁场安培环路定理的正确性,我们可以进行如下实验:1. 实验器材:一个长直导线、一个螺线管、一个万用表和一些导线。
2. 实验步骤:(1) 将长直导线穿过螺线管的中心,将万用表连接到导线两端。
真空中磁场的安培环路定理表达式

真空中磁场的安培环路定理表达式
磁场的安培环路定理:
一、定义
1、安培环路定理:安培环路定理是物理和电学中一个重要的理论,它指出,在真空中 xyz 三个方向上,通过一定距离或一条环路的一个磁场线时,磁通环 mzmz 与安培数之间存在一种关系。
2、磁场线:磁场线是磁场的一种重要组成部分,每一条磁场线代表不同的磁场值。
二、表达式
安培环路定理表达式为:Mzmz= 2π i Φ,其中Φ是由偶然电磁现象形成的磁场的流过的安培数,i是圆的周长被用于测量的环路的距离。
三、推导
由于磁场力线总是有完整的封闭环路,根据磁感应定律,磁场中心点处将产生磁场,有M0=μ H 的关系,ΔH表示磁感应强度,μ是介质的磁导率,这时环路上的磁感应应该与安培数有关,于是就有了磁场安
培环路定理的表达式:Mzmz= 2π i Φ 。
四、应用
1、安培环路定理用于求解磁场的磁力矢量,可以准确测量磁场的强度、强度的方向以及磁场的变化情况。
2、可以用安培环路定理计算磁力矢量对电磁激励的结果,从而掌握不
同形状、尺寸和构造的电磁设备的性能和特性。
3、也可以用安培环路定理分析及设计空间电磁环境及其对周边子系统
的影响,更好地检测和预测管道、设备的运行状况。
磁场的安培环路定理公式

磁场的安培环路定理公式安培环路定理(Ampere's Circuital Law)是电磁学中的一个重要定理,描述了电流所产生的磁场的性质。
该定理是由法国科学家安德烈·玛丽·安培于1826年提出的。
安培环路定理公式可以用来计算闭合曲线上的磁场和电流之间的关系。
安培环路定理可以表述如下:在真空中,闭合曲线上的磁场的环流等于通过该闭合曲线所围成的面内的电流的代数和的N倍,即B·l=μ0·N·I。
其中,B表示磁场强度,单位为特斯拉(T);l表示闭合曲线的长度,单位为米(m);μ0表示真空中的磁导率(磁场的常量),约等于4π×10^-7N/A^2;N表示闭合曲线所围成的面内的匝数;I表示通过该闭合曲线所围成的面内的电流,单位为安培(A)。
这个公式表明了闭合曲线上的磁场强度与该闭合曲线所围成的面内电流的代数和成正比。
当电流的方向与闭合曲线所围成的面的法线方向相同时,为正;而当电流的方向与闭合曲线所围成的面的法线方向相反时,为负。
安培环路定理的应用非常广泛。
通过安培环路定理,我们可以计算出闭合曲线上的磁场强度,从而了解电流所产生的磁场的强度和分布情况。
此外,我们还可以通过安培环路定理来计算导线上的磁场,从而提前预测电流的影响范围和磁场的强度。
安培环路定理的一个重要应用是计算长直导线产生的磁场。
对于一根长度为l的直导线,安培环路定理公式可以简化为B=μ0·I/2πr,其中r为距离导线的垂直距离。
另一个应用是计算无限长薄直导线产生的磁场。
在这种情况下,合理的选择闭合曲线为无限大的圆形曲线,通过计算可以得到B=μ0·I/2r,其中r为距离导线的垂直距离。
安培环路定理还可以应用于计算线圈产生的磁场。
对于一个具有N匝的螺线管,安培环路定理的公式可以表示为B·2πr=μ0·N·I,其中B 为螺线管中心处的磁场强度,r为距离螺线管中心的距离。
磁场的安培环路定理

2B ab
利用安培环路定理求 B
B • dl 0n ab I
ba .........
cd
B 0 nI 2
板上下两侧为均匀磁场
讨论:如图,两块无限大载流导体薄板平行放置。 通有相反方向的电流。求磁场分布。
已知:导线中电流强度 I、单位长度导线匝数n
B 0 nI 2
0 两板外侧
B
B • dl 0nabI
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
B
B
0
nI
0
内 外
a
b
d
cI
3. 环形载流螺线管的磁场分布. . .
已知:I 、N、R1、R2
..
N——导线总匝数
. .
分析对称性
. .
R1
.
.
...
r
. ... ...
磁力线分布如图 作积分回路如图
. ...
.
.
R2 ..
.
.
.
.
...
0I 2r
rd
0I 2
2
B • dl 0I
3、回路不环绕电流
.
B • dl 0
B
d
r
dl
安培环路定理
意闭在合真曲空线中的的线稳 积分恒(电也流称磁场B中的,环磁流感)应,强等度于穿B过沿该任
闭合曲线的所有电流强度(即穿过以闭合曲线为边界
的任意曲面的电流强度)的代数和的
倍。即:
0
B • dl 0 Ii
I R
I
0
B
r
磁场中的安培环路定理

磁场中的安培环路定理磁场中的安培环路定理是电磁学中的一条重要定理,它描述了磁场中的电流与磁场的相互作用关系。
根据安培环路定理,一个封闭的电流环路所受的磁场力的总和等于该环路所包围的电流的总和乘以真空中的磁导率。
让我们来了解一下什么是磁场。
磁场是由电流或磁体产生的一种力场,它可以对其他电流或磁体施加力。
磁场的强度可以用磁感应强度B来表示,单位是特斯拉(T)。
磁感应强度的方向可以用磁力线来表示,磁力线是磁场中的力线,表示磁场的方向和强度。
在磁场中,当有电流通过一个导线时,该导线周围会形成一个磁场。
根据安培环路定理,沿着一个封闭的回路,该回路内的电流与回路所包围的磁场的相互作用力之和等于回路内电流的总和乘以磁导率的乘积。
这个定理可以用一个简单的公式来表示:∮B·dl=μ0I其中,∮B·dl表示环路所包围的磁场力的总和,μ0表示真空中的磁导率,I表示环路内电流的总和。
安培环路定理的应用非常广泛。
在电磁铁中,安培环路定理可以用来计算铁芯中的磁感应强度。
在计算电感的时候,我们也可以利用安培环路定理来计算电流所产生的磁场。
此外,在电磁感应中,安培环路定理也可以用来计算感应电动势。
为了更好地理解安培环路定理,我们可以通过一个简单的实例来说明。
假设有一个平面圆环,环上有电流I流过。
我们想要计算该圆环所包围的磁场力。
根据安培环路定理,我们可以选择一个闭合的路径,沿着该路径计算环所包围的磁场力的总和。
在这个例子中,我们可以选择圆环的周长作为路径。
然后,我们需要计算路径上的磁场力。
根据安培环路定理,路径上的磁场力等于路径内电流的总和乘以磁导率。
假设路径上的磁感应强度为B,根据安培环路定理,我们可以得到以下等式:B·2πr=μ0I其中,r表示圆环的半径。
通过这个等式,我们可以计算圆环所包围的磁场力。
总结一下,磁场中的安培环路定理是描述磁场中的电流与磁场的相互作用关系的定理。
根据该定理,一个封闭的电流环路所受的磁场力的总和等于该环路所包围的电流的总和乘以真空中的磁导率。
11-5真空中磁场的安培环路定理

2. 多根载流导线穿过环路 B B1 B2 Bn
I3
I2
I1
L
o I1 o I 2 o I n o I i
3.电流在环路之外 B d l B dl B dl
0 j B
2
0 j x arctg 2π z z 2
0 zj 1
o
x
0 j
2
解二、用安培环路定理
j
z
l
在对称性分析的基础上
x
选如图安培环路 得:B
由:
L
B dl 2lB 0 jl
0 j
2
思考:如果载流平面不是无限宽, 思考 能否用叠加原理求解? 能否用安培环路定理求解?
r R:
B外
I
内
I
1 2πr r
0 I
L
B
L
o rP
I 2πr
0
内
B
r
O
1 r
R
2 I Ir r R : I内 2 π r 2 2 πR R 0 Ir B内 r 2 2πR B方向与I指向满足右旋关系
思考: 无限长均匀载流直圆筒 思考 B–r曲线?
§11.5 真空中磁场的安培环路定理 一、 安培环路定理
1、安培环路定理:
在真空中恒定电流的磁场中,磁感应强度沿任意闭合 路径L 的线积分等于被此闭合路径所包围并穿过的电 流的代数和的 0 倍,而与路径的形状和大小无关。
L
B dl 0
(穿过L )
Ii
磁场的安培环路定理公式

磁场的安培环路定理公式磁场的安培环路定理是电磁学中的重要定理之一,它描述了磁场在闭合回路上的环路积分等于该回路所包围的电流的代数和的性质。
在分析磁场问题时,安培环路定理可以提供一个简便的方法来计算磁场的强度和方向。
安培环路定理的数学表达式为:∮B·dl = μ0·Ienc其中,∮B·dl表示磁场B沿闭合回路的环路积分,μ0是真空中的磁导率,其值约为4π×10^-7 T·m/A,Ienc表示回路所包围的电流的代数和。
通过安培环路定理,可以方便地计算磁场的分布情况。
下面将通过几个具体的例子来说明安培环路定理的应用。
例1:一根直导线的磁场考虑一根无限长的直导线,电流为I,要求计算离导线距离为d处的磁场强度B。
我们可以选择一个以导线为轴的圆形回路,根据安培环路定理,有∮B·dl = μ0·Ienc。
由于回路只包围了一段电流,所以Ienc = I。
回路的环路积分可以通过计算B在回路上的分量得到,由于B的方向在回路上是沿着回路的方向,所以B在回路上的分量为B·2πd,其中2πd是回路的周长。
因此,我们可以得到B·2πd =μ0·I,即B = μ0·I/(2πd)。
这就是直导线产生的磁场强度的公式。
例2:两根平行直导线的磁场考虑两根平行的无限长直导线,电流分别为I1和I2,距离为d,要求计算它们之间的磁场强度B。
同样地,我们可以选择一个以两根导线为边的矩形回路,根据安培环路定理,有∮B·dl = μ0·Ienc。
由于回路包围了两段电流,所以Ienc = I1 + I2。
回路的环路积分可以分为两部分,一部分是沿着左边导线的分量B1在回路上的环路积分,另一部分是沿着右边导线的分量B2在回路上的环路积分。
由于两根导线的方向相反,B1与B2的方向也相反,所以它们的环路积分相加为0。
因此,我们可以得到B1·2d + B2·2d = μ0·(I1 + I2),即B = μ0·(I1 + I2)/(2d)。
§7.3 磁场的安培环路定理

解 B分布为柱对称,作同轴圆形安培回路。
r
R
:
B
dr
B
dr
cos 00 B dl
L
L
L
I
r
B dl B 2 r
B
dr
L
0
I
L
B
0I 2 r
可等效成 ……
B
rR
L· 11 ·
Chapter 7. 恒定磁场
§7. 3 磁场的安培环路定理
三、安培环路定理的应用
对于某些对称性磁场,可选取适当的回路 L,使得 回路 L 上各点 B大小相等,方向与 dr相同,则:
B
dr
B
|
d
r
|
cos
0
o
B
|
dr
|
L
L
L
B
dr
0
Ii
B
L
( L内)
·9 ·
Chapter 7. 恒定磁场
§7. 3 磁场的安培环路定理
L
0I 2 r
dr
cos
0o
L
0I 2 r
dl 0I
B
L
L
r
B
dr
·2 ·
Chapter 7. 恒定磁场
§7. 3 磁场的安培环路定理
在磁感线平面内作一闭合回路L:
LB
dr
0I 2
磁场中的安培环路定理

磁场中的安培环路定理磁场中的安培环路定理是电磁学中的重要定律之一,它描述了通过一个封闭回路的磁场的总磁通量。
安培环路定理的数学表达式是∮B·dl = μ0·Ienc,在这个公式中,∮B·dl代表磁场矢量B沿着闭合回路的环路积分,μ0是真空中的磁导率,而Ienc则是通过回路的总电流。
安培环路定理的实质是一个电磁学中的基本定理,它与法拉第电磁感应定律一起共同组成了麦克斯韦方程组的一部分。
通过安培环路定理,我们可以更好地理解磁场的产生和变化规律,以及电磁感应现象的发生。
我们来讨论一下安培环路定理的基本原理。
根据这个定理,当一个导线中通过电流时,会在其周围产生一个磁场。
这个磁场的大小与电流的大小成正比,而方向则根据右手定则确定。
根据安培环路定理,如果我们沿着一个闭合回路进行环路积分,所得到的结果就是该回路内部的总磁通量。
在实际应用中,我们经常使用安培环路定理来求解磁场的大小和方向。
例如,在一个长直导线附近,我们可以通过安培环路定理来计算导线周围的磁场强度。
以导线为中心,选取一个圆形回路,通过环路积分可以得到磁场的大小。
根据安培环路定理,这个积分结果等于回路内部的总磁通量。
因此,我们可以通过这个方法来确定导线周围的磁场分布。
除了计算磁场的大小和方向,安培环路定理还可以用来推导其他相关的物理规律。
例如,当一个导体中有变化的电流时,根据安培环路定理,会产生一个变化的磁场。
这个磁场的变化又会导致周围的导体中产生感应电流。
这就是著名的法拉第电磁感应定律。
通过安培环路定理和法拉第电磁感应定律,我们可以更深入地研究电磁感应现象的本质和规律。
在实际应用中,安培环路定理也有很多重要的应用。
例如,在电磁铁中,我们可以利用安培环路定理来计算铁芯中的磁场强度。
通过调整电流的大小和方向,我们可以控制电磁铁的磁场强度,从而实现吸引或排斥其他磁性物体的目的。
此外,安培环路定理还可以应用在变压器、电动机等电磁设备的设计和分析中,帮助我们了解和优化这些设备的性能。
安培环路定理

结论
所以有: 从载流直导线中心O出发,可以作许多条射线,将环路分割成许多成对的线元,磁感强度对每对线元的标量 积之和,都有上式的结果,故即环路不包围电流时,B的环流值为零。 安培环路定理反映了磁场的基本规律。和静电场的环路定理相比较,稳恒磁场中B的环流,说明稳恒磁场的 性质和静电场不同,静电场是保守场,稳恒磁场是非保守场。
微分形式
根据开尔文-斯托克斯定理,这方程也可以写为微分形式。只有当电场不含时间的时候,也就是说,当电场 对于时间的偏微分等于零的时候,这方程才成立。采用国际单位制,这方程表示为
。 磁场的旋度等于(产生该磁场的)传导电流密度。
缺点
缺点
原版安培定律只适用于静磁学。在电动力学里,当物理量含时间,有些细节必须仔细检查。思考安培方程, ;
简介
积分形式
微分形式
ห้องสมุดไป่ตู้分形式
电流I在一个曲面上的通量,等于B场沿着的边缘闭合回路的路径积分。采用国际单位制,原版安培定律的积 分形式可以写为:
。
请注意到这方程有些模糊之处,需要特别澄清: 第一,边界曲线的正向与曲面的侧符合右手规则。 第二,(固定 )定理之成立与以为边界的的选择无关。
安培定律可由毕奥-萨伐尔定律和磁场的叠加性证明(请参阅毕奥-萨伐尔定律)。在静磁学中,安培定律的 角色与高斯定律在静电学的角色类似。当系统组态具有适当的对称性时,我们可以利用这对称性,使用安培定律 来便利地计算磁场。例如,当计算一条直线的载流导线或一个无限长螺线管的磁场时,可以采用圆柱坐标系来匹 配系统的圆柱对称性。
证明方法
对称环路 任意环路
不包围电流 结论
对称环路
在垂直于长直载流导线的平面内,以载流导线为圆心作一条半径为r的圆形环路l, 则在这圆周上任一点的磁感强度H的大小为 其方向与圆周相切.取环路的绕行方向为逆时针方向,取线元矢量dl,则H与dl间的夹角,H沿这一环路 l 的环流为 式中积分是环路的周长。 于是上式可写成为 从上式看到,H沿此圆形环路的环流只与闭合环路所包围的电流I有关,而与环路的大小、形状无关。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
③若I不穿过L,则 I =0
磁场的安培环路定理及应用
思考 求下列情况时的环流?
Bdl
L
0 (I1
I1
I1
I2)
(0 I1
I
)
2
I1
I2 I3
I1
L
I1
I3
I1 >0
L
I2<0
Bdl o(I1 I2 )
I1
I2
I3
L
Bdl o(I1 I3 )
n N
2 R1
B
0nI 0
内 外
磁场的安培环路定理及应用
练习:若螺绕环截面为方形,求通过螺绕环截面的磁通量 .
解: dS hdr
dm
B内
dS
0 NIh 2r
dr
m
dm
0 NIh 2
R2 dr r R1
N,I
h
R2
R1 dS
0 NIh ln R2
磁场的安培环路定理及应用
磁电场场的、安培磁环场路中定典理型及结应论用 的比较
长直线
长 直
内
圆
柱外
面
长 直
内
圆
柱 体
外
电荷均匀分布
E
2 0r
E0
E 2 0r
E
r 2 0 R2
E
2 0r
电流均匀分布
B 0I 2r
B0
B 0I 2r
B
0 Ir 2R 2
磁场的安培环 路定理及应用
磁场分布 B 的方向与 I 成右螺旋
轴对称 半径相同处大小相等 B dl Bdl 2rB
0 r R, r R,
I内
πr2 π R2
I
I内 I
B
0Ir
2π R2
B 0I
2π r
I
L1
r
0I B
2π R
R
L2 r
oR r
i 1
磁场的安培环路定理及应用
二、安培环路定理的说明
安培环路定理
n
B dl 0 Ii
i1
一闭合即路在径真的空积的分稳的恒值磁,场等中于,磁0感乘应以强该度闭合B 沿路任径
所包围的各电流的代数和.
注意1
电流 I 取正负的规定 : ① I与L成右螺旋时,I为正;
②I与L不是成右螺旋时,I为负;
l
MN
NO
OP
PM
利用安培环路定理求 B
B MN 0nMNI B 0nI
无限长载流螺线管内部磁场处处 相等 , 外部磁场为零.
B
0nI 0内 外磁场的安培环路定理及应用
② 求载流螺绕环内的磁场
已知:I 、N(导线总匝数
)、内径R1、外径R2
解 1) 对称性分析: 环内 B 线为同心圆,环外 B 为零.
电场有保守性,它是 保守场,或有势场
E dS
1
s
0
qi
电力线起于正电荷、
止于负电荷。
静电场是有源场
稳恒磁场
B dl 0 Ii i
磁场没有保守性,它是 非保守场,或无势场
B dS 0
磁力线闭合、 无自由磁荷
磁场是无源场
磁场的安培环路定理及应用
0I
rd
0I
d
2π r
2π
B dl
l
0I
磁场的安培环路定理及应用
3.电流在回路之外
B1
B2
d
I
r1
dl1
dl2
r2
l
B1
0I
2π r1
,
B2
0I
2π r2
B1
dl1
B2
dl2
0I
2π
d
B1 dl1 B2 dl2 0
1
S
0
q内 有源场
SB dS 0
无源场
环路定理
E dl 0 保守场 L
B dl ? ? L
恒电流磁场中,磁感应强度沿任意闭合
环路的积分等于此环路所包围的电流代
数和的 0倍。
B dl L
0
Ii
i
I
oR l
磁场的安培环路定理及应用
闭合路径包围的电流为电流
密度沿所包围的曲面的积分
Ii
j dS
S
i
安培环路定理微分形式
B μ0 j
注意4
安培环路定理揭示了磁场的基本性质之 一,磁场是有旋场,是非保守场,故磁 场中不能引入势能的概念。
磁场的安培环路定理及应用
静电场
E dl 0
磁场的安培环路定理及应用
思考
位置移动
I1 I2
I4
I3
l
不变
? ? B dl 0 Ii 0 (I2 I3 )
? 改变
不变
磁场的安培环路定理及应用
注意3
安培环路定理
n
B dl 0 Ii
i 1
当电流呈体分布时 B dl 0 S j dS
c
b
Bdl
cos 2
d
c
Bdl cos 0
da Bdl
cos
2
B ab B cd
2B ab
利用安培环路定理求
B
B dl 0n ab I
ba .........
cd
B 0 nI 2
板上下两侧为均匀磁场
磁场的安培环路定理及应用
2) 选回 路 .
d
Bdl
l
2 π rB
0NI
B 0 NI
r
2πr
令 L 2πr B 0 NI L
磁场的安培环路定理及应用
B
0 NI 2r
内
0 外
d
B
r
o R1 R2 r
讨论 若 R1、R2 R2 R1 或者 2r d 时,
螺绕环内可视为均匀场 .
磁场的安培环路定理及应用
一、安培环路定理的推导 (稳恒磁场、真空)
二、安培环路定理的说明 三、安培环路定理的应用
教材:10.4节 作业:练习15
I,N
o R1
R2
磁场的安培环路定理及应用
思考 一般方法:
用高斯定理和环路定理描述空间矢量场的性质。
比较 静电场 稳恒磁场
高斯定理
E dS
2
R1
h
I
R2
R1
磁场的安培环路定理及应用
小结:
1.熟悉典型问题结果
无限长直电流, 圆电流轴线上, 长直载流螺线管, 螺绕环 ...
2.总结出用安培环路定理求解磁场分布的思路
对称性分析 — 选环路 L并规定绕向.
— 由 L B dl 0 I内 求 B 分布.
L I
B dl 4oI
磁场的安培环路定理及应用
注意2
磁感应强度的环流只与环路内的电流有
关,但环路上一点的磁感应强度是由环
路内、外电流共同产生的。I1 I2
I4
I3
l
由环路内电流决定
B dl 0 Ii 0 (I2 I3 )
由环路内外电流产生 环路所包围的电流
练习:如图,两块无限大载流导体薄板平行放置。 通有相反方向的电流。求磁场分布。
已知:导线中电流强度 I、单位长度导线匝数n
B 0 nI 2
B 00nI
两板之间 两板之外
.........
磁场的安培环路定理及应用 (3)其它安培环路定理的应用举例
① 求长直密绕螺线管内磁场。已知:I、n(单位
长度导线的匝数)
解 1 ) 对称性分析螺旋管内为均匀场 , 方向沿
轴向;外部磁感强度趋于零 ,即 B 0 .
磁场的安培环路定理及应用
2 ) 选回路 L .
磁场 B 的方向与
M
NB
电流 I 成右螺旋.
计算环流
+++++ P
+
+ L+
++++ O
B dl B dl B dl B dl B dl
一、 安培环路定理(Ampere’s circulation theorem)的推导
1.最特殊情况
载流长直导线的磁感强
度为 B 0I
l
B
dl
2π R
0
2π
I dl R
I
B
dl
oR
l
B dl
0I
dl
l 2π R l
B dl
l
0I
l B d l 0
磁场的安培环路定理及应用
4.多电流情况
B B1 B2 B3
I1
I2
I3
Bdl
l
0(I2
I3)
【总结】以上结果可以推
