常见的分数与小数、百分数之间的互化
常见的分数、小数及百分数的互化,常用平方数、立方数及各种计算方法

1、C列分数化小数的记法:分子乘5,小数点向左移动两位.之巴公井开创作2、D、E两列分数化小数的记法:分子乘4,小数点向左移动两位罕见分数、小数互化表罕见的分数、小数及百分数的互化经常使用平方数罕见立方数罕见特殊数的乘积错位相加/减例:743×9=743×10-743=7430-743=6687A×9.9型速算技巧:A×9.9= A×10+A÷10;例:743×9.9=743×10-743÷10=7430-74.3=7355.7A×11型速算技巧:A×11= A×10+A;例:743×11=743×10+743=7430+743=8173A×101型速算技巧:A×101= A×100+A;例:743×101=743×100+743=75043乘/除以5、25、125的速算技巧:A×5型速算技巧:A×5=10A÷2;例:8739.45×5=8739.45×10÷2=87394.5÷2=43697.25 A÷5型速算技巧:A÷5=0.1A×2;例:36.843÷5=36.843×0.1×2=3.6843×2=7.3686A×25型速算技巧:A×25=100A÷4;例:7234×25=7234×100÷4=723400÷4=180850A÷25型速算技巧:A÷25=0.01A×4;例:3714÷25=3714×0.01×4=37.14×4=148.56A×125型速算技巧:A×5=1000A÷8;例:8736×125=8736×1000÷8=8736000÷8=1092000A÷125型速算技巧:A÷1255=0.001A×8;例:4115÷125=4115×0.001×8=4.115×8=32.92减半相加:例:3406×1.5=3406+3406÷2=3406+1703=5109“首数相同尾数互补”型两数乘积速算技巧:积的头=头×(头+1);积的尾=尾×尾例:23×27=首数均为2,尾数3与7的和是10,互补所以乘积的首数为2×(2+1)=6,尾数为3×7=21,即23×27=621本方法适合 11~99 所有平方的计算.11X11=121 21X21=4141 31X31=961 41X41=168112X12=148 22X22=484 32X32=1024 42X42=1764 52X52=2704从上面的计算我们可以得出公式:个位=个位×个位所得数的个位,如果满几十就向前进几,十位=个位×(十位上的数字×2)+进位所得数的末位,如果满几十就向前进几,百位=两个十位上的数字相乘+进位.例:26×26=个位=6×6=36,满 30 向前进 3;十位=6×(2×2)+3=27,满 20 向前=进 2;百位=2×2+2=6由此可见26×26=67623×23个位=3×3=9十位=3×(2×2)=12,写 2 进 1百位=2×2+进 1=5所以23×23=52946×46 个位=6×6= 36,写6进3十位=6×(4×2)+进 3= 5 1,写 1 进 5百位=4×4+进 5= 21,写 1 进 2所以46×46=2116如果没有满十就不用进位,计算更简便.例:13×13个位=3×3=9 十位=3×(1×2)=6 百位=1×1所以13×13=169规律:(1)完全平方数的个位数字只能是 0,1,4,5,6,9.(没有 2,3,7,8)两个整数的个位数字之和为 10,则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数,十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是 6;反之,如果完全平方数的个位数字是 6,则它的十位数字一定是奇数.(4)偶数的平方是 4 的倍数;奇数的平方是 4 的倍数加 1.(5)奇数的平方是 8n+1 型;偶数的平方为 8n 或 8n+4 型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被 5 整除的数的平方为5n±1 型,能被 5 整除的数的平方为 5n 型.(8)平方数的形式具有下列形式 16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有 2,5,8)(10)如果质数 p 能整除 a,但 p 的平方不能整除 a,则 a 不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.(12)一个正整数 n 是完全平方数的充沛需要条件是 n 有奇数个因数(包括 1 和 n).一个数如果是另一个整数的完全立方(即一个整数的三次方,或整数乘以它自己乘以它本身),那么我们就称这个数为完全立方数,也叫做立方数,如 0,1,8,27,64,125,216,343,512,729,1000 等.如果正整数 x,y,z 满足不定方程 x2+y2=z2 ,就称 x,y,z 为一组勾股数.x,y 肯定是一个为奇数另一个为偶数,不成能同时为奇数或同时为偶数.z 和z² 肯建都是奇数.五组罕见的勾股数:3²+4²=5²;5²+12²=13²;7²+24²=25²;8²+15²=17²;20²+21²=29²9+16=25;25+144=169;49+576=625; 64+225=289; 400+441=841记忆技巧:(a+b)²= a² + b² + 2ab (a-b)²=a² + b² -2ab|| | | | |a×a b×b 2×a×b a×a b×b 2×a×b例:13²=(10+3) ²=10²+3²+2×10×3=100+9+60=16988²=(90-2)²=90²+2²-2×90×2=8100+4-360=7744用处:①训练计算能力,使计算更快更准确;②估计某数的平方根所处的范围,在判定某个较年夜的数 n 是不是质数时可以缩小其可能因子的筛选范围,只需检查 3 到n 之间的所有质数是不是 n 的因子即可, 超越n的都不用检查了例如:判定2431是否为质数,因为49²=2401<2431<2500=50²,所以 49<2431.<50,2+4+3+1=10不能被3整除, 2341的个位既非0又非5,故只需检查7到 47之间的所有质数能否整除2431即可,而53,59,61,67……等更年夜的质数都不用检查了,实际上2431=11×13×17③增加对数字的熟悉水平,比如16²=256=28,32²=1024=210,64²=4096=212,另外一些特殊结构的数字应该牢记,如88²=7744, 11²=121,22²=484,(121 和 484 从左到右与从右到左看是一样的) 12²=144,21²=441,13²=169,31²=961,(a 左右倒置后a² 也左右倒置).小学单元换算一、长度(一) 什么是长度?长度是一维空间的怀抱.(二) 长度经常使用单元* 公里(km) * 米(m) * 分米(dm) * 厘米(cm) * 毫米(mm) * 微米(um)(三) 单元之间的换算1 微米=1000 纳米 1 毫米 =1000 微米 1 厘米=10 毫米1 分米 =10 厘米1 米 =1000 毫米1 千米 =1000 米1 米=10 分米=100 厘米二、面积(一)什么是面积面积,就是物体所占平面的年夜小.对峙体物体的概况的几多的丈量一般称概况积.(二)经常使用的面积单元* 平方毫米 * 平方厘米 * 平方分米 * 平方米 * 平方千米(三)面积单元的换算1 平方厘米 =100 平方毫米 1 平方分米=100 平方厘米1 平方米=100 平方分米1 公倾 =10000 平方米 1 平方公里 =1 平方千米=100 公顷1 公顷=0.01 平方千米≈15 亩 1 平方千米=1000000 平方米1 平方米=100 平方分米=10000 平方厘米三、体积和容积(一)什么是体积、容积体积,就是物体所占空间的年夜小.容积,箱子、油桶、仓库等所能容纳物体的体积,通常叫做它们的容积.(二)经常使用单元1 体积单元* 立方米 * 立方分米 * 立方厘米2 容积单元* 升 * 毫升(三)单元换算1 体积单元1 平方米 =100 平方分米 1 平方分米=100 平方厘米 1 平方厘米=100 平方毫米1 立方米=1000 立方分米 1 立方分米=1000 立方厘米2 容积单元1 升=1 立方米 1 升=1000 毫升1 毫升=1 立方厘米1 立方米=1000 升1 立方分米=1 升 1 立方厘米=1 毫升四、质量(一)什么是质量质量,就是暗示暗示物体有多重.(二)经常使用单元* 吨 t * 千克 kg * 克 g(三)经常使用换算1 吨(t)=1000 千克(kg)1 千克=1000 克(g)重量单元换算1 吨=1000 千克1 千克=1000 克1 千克=1 公斤五、时间(一)什么是时间是指有起点和终点的一段时间(二)经常使用单元世纪、年、月、日、时、分、秒(三)单元换算* 1 世纪=100 年 1 年=12 月 1 年=365 天平年一年=366 天闰年.一、三、五、七、八、十、十二是年夜月年夜月有 31 天四、六、九、十一是小月小月有 30 天平年 2 月有 28 天闰年 2 月有 29 天1 天= 24 小时 1 小时=60 分 1 分=60 秒 1秒=1000毫秒(ms) 1时=3600秒货币(一)什么是货币货币是充任一切商品的等价物的特殊商品.货币是价值的一般代表,可以购买任何另外商品.(二)经常使用单元* 元 * 角 * 分(三)单元换算1 元=10 角 1 角=10 分 1 元=100 分四则运算关系加法:一个加数=和-另一个加数减法:被减数=差+减数减数=被减数-差乘法:一个因数=积÷另一个因数除法:被除数=商×除数除数=被除数÷商两个规律1、除法的商不变规律:被除数和除数同时乘或除以相同的数(0 除外),商不变.2、乘法的积不变规律:如果一个因数乘几,另一个因数则除以几,那么它们的积不变.数学简便运算方法归类一、同级运算(没有括号),可以带着符号搬场a+b+c=a+c+ba-b-c=a-c-ba+b-c=a-c+b a-b+c=a+c-ba×b×c=a×c×b a÷b÷c=a÷c÷ba×b÷c=a÷c×ba÷b×c=a×c÷b二、有括号的同级运算,可以根据去括号的性质把括号去失落1、括号前面是“+”号或“×”号,去失落括号不变号.a+(b+c)=a+b+c a+(b-c)=a+b-c a×(b×c)=a×b×c a×(b÷c)=a×b÷c2、括号前面是“-”号或“÷”号,去失落括号要变号.a-(b+c)=a-b-c a-(b-c)=a-b+c a÷(b×c)=a÷b÷c a÷(b÷ c)=a÷b×c上面的式子从左到右可以去括号,那么从右到左就是添括号的方法了.自己认真观察发现没有括号的同级运算中添括号的性质哦. 三、乘法分配律:(a+b)×c=a×c+b×c 或(a-b)×c=a×c-b×c 乘法分配律的逆运用:a×c+a×b=(a+b)×c 或a×c-b×c=(a-b)×c两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加,这叫做乘法分配律.1.分配法(从左到右的用法) 括号里是加或减运算,与另一个数相乘,注意分配.2.提取公因式(从右到左的用法)注意相同因数的提取.3.注意构造,让算式满足乘法分配律的条件.四、借来还去法看到名字,就知道这个方法的含义.用此方法时,需要注意观察,发现规律.还要注意还哦 ,有借有还, 再借不难嘛.例:9999+999+99+9五、拆分法顾名思义,拆分法就是为了方便计算把一个数拆成几个数.这需要掌握一些“好朋友”,如:2 和 5,4 和 5,2 和 2.5,4 和 2.5,8 和 1.25 等.分拆还要注意不要改变数的年夜小哦. 例:3.2×12.5×25 1.25×88 3.6×0.25以上几种方法包括了小学数学罕见的简便运算的方法, 在选择简便方法的时候一定要注意简便方法的依据,千万不能没有依据的胡拉乱扯一通,有时候是出题者故意挖的陷阱,看似可以运用简便算法,实际上找不出可以简便运算的依据,这样的题只能依照运算顺序计算的.(例如 2.5×4÷ 2.5×4,看似加括号很简便,结果即是1,而实际上括号加在除号的后面是要变号的,所以本道题的简便方法是“没有括号的同级运算,可以带着符号搬场.2.5÷ 2.5×4×4)简便计算简便运算重在找依据1、运算定律:运算定律用字母暗示加法交换律 a+b=b+a加法结合律(a+b)+c=a+(b+c)乘法交换律a×b=b×a乘法结合律(a×b)×c=a×(b×c)乘法分配律(a+b)×c=a×c+b×c减法运算规律 a-b-c=a-(b+c)除法运算规律a÷b÷c=a÷(b×c)2、乘、除法的互化.(小技巧:符号是相反的;两个数相乘得“1”)(1)A÷0.1=A×10 (7)A÷0.01=A×100(2)A×0.1=A÷10 (8)A×0.01=A÷100(3)A÷0.2=A×5 (9)A÷0.25=A×4(4)A×0.2=A÷5 (10)A×0.25=A÷4(5)A÷0.5=A×2 (11)A÷0.125=A×8(6)A×0.5=A÷2 (12)A×0.125=A÷83、求近似数的方法.(1)四舍五入法. (2)进一法.(3)去尾法4、积与因数、商与被除数的年夜小比力:第 2 个因数>1,积>第 1 个因数;除数>1,商<被除数;第 2 个因数=1,积=第 1 个因数;除数=1,商=被除数;第 2 个因数<1,积<第 1 个因数. 除数<1,商>被除数;。
(完整版)常用的∏倍及分数、小数和百分数的互化及单位换算

1、熟练的掌握常见分数和小数的互化,对于提高运算速度,增强数感,有着很好的帮助。
2、记忆方法:(1)可以用一张卡片盖住左边的分数,看着小数说出与相等的分数,再交换。
(2)C 列分数化小数的记法:分子乘5,小数点向左移动两位。
(3)D 、E 两列分数化小数的记法:分子乘4,小数点向左移动两位。
常见分数、小数互化表0625.0161二、常用的分数、小数及百分数的互化常用平方数常用立方数:13=1 23=8 33=27 43=64 53=125 63=216 73=343 83=512 93=729 常用特殊数的乘积25×3=75 25×4=100 25×8=200 125×3=375125×4=500 125×8=1000 625×16=10000 37×3=111本方法适合11~99所有平方的计算。
11X11=121 21X21=4141 31X31=961 41X41=1681 51X51=260112X12=148 22X22=484 32X32=1024 42X42=1764 52X52=2704从上面的计算我们可以得出公式:个位=个位×个位所得数的个位,如果满几十就向前进几,十位=个位×(十位上的数字×2)+进位所得数的末位,如果满几十就向前进几,百位=两个十位上的数字相乘+进位。
例:26×26=因为6×6=36 所以26×26的个位就是6,满30向前进3;十位=6×(2×2)+3=27,所以26×26的十位就是7,满20向前=进2;百位=2×2+2=6由此可见26×26=676如果没有满十就不用进位,计算更简便。
例:13×13个位=3×3=9 十位=3×(1×2)=6 百位=1×1所以13×13=16923×23个位=3×3=9 十位=3×(2×2)=12写2进1 百位=2×2+进1=5所以23×23=52946×46个位=6×6=○36 写6进3 十位=6×(4×2)+进3=○51写1进5 百位=4×4+进5=○21 写1进2 所以26×26=2116规律:(1)完全平方数的个位数字只能是0,1,4,5,6,9.(没有2,3,7,8)两个整数的个位数字之和为10,则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数,十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6;反之,如果完全平方数的个位数字是6,则它的十位数字一定是奇数.(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)(10)如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.(12)一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n).一个数如果是另一个整数的完全立方(即一个整数的三次方,或整数乘以它本身乘以它本身),那么我们就称这个数为完全立方数,也叫做立方数,如0,1,8,27,64,125,216,343,512,729,1000等.如果正整数x,y,z满足不定方程x2+y2=z2 ,就称x,y,z为一组勾股数.x,y必然是一个为奇数另一个为偶数,不可能同时为奇数或同时为偶数.z和z2必定都是奇数.五组常见的勾股数:32+42=52;52+122=132;72+242=252;82+152=172;202+212=2929+16=25;25+144=169;49+576=625;64+225=289;400+441=841记忆技巧:(a+b)2= a2 + b2 + 2ab (a-b)2=a2 + b2 -2ab| | | | | |a×a b×b 2×a×b a×a b×b 2×a×b例:132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22-2×90×2=8100+4-360=7744用处:①训练计算能力,使计算更快更准确;②估计某数的平方根所处的范围,在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可,超过的都不必检查了.例如,判定2431是否为质数,因为492=2401<2431<2500=502,所以49<<50 ,2+4+3+1=10不能被3整除, 2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可,而53,59,61,67……等更大的质数都不用检查了,实际上2431=1117.③增加对数字的熟悉程度,比如162=256=28,322=1024=210,642=4096=212 ,另外一些特殊结构的数字应该牢记,如882=7744,112=121,222=484,(121和484从左到右与从右到左看是一样的)22222一、常用的π倍1π 3.14 17π53.38 92π254.342π 6.28 18π56.52 102π3143π9.42 19π59.66 112π379.944π12.56 20π62.8 122π452.165π15.7 21π65.94 132π530.666π18.84 22π69.08 142π615.447π21.98 23π72.22 152π706.58π25.12 24π75.36 162π803.849π28.26 25π78.5 172π907.4610π31.4 26π81.64 182π1017.3611π34.54 27π84.78 192π1133.5412π37.68 28π87.92 202π125613π40.82 29π91.06 212π1384.7414π43.96 30π94.2 222π1519.7615π47.1 62π113.04 232π1661.0616π50.24 72π153.86 242π1808.6482π200.96 252π1962.5小学单位换算一、长度(一)什么是长度?长度是一维空间的度量。
五年级必会的常用分数小数互化方法

100 4
100 4
2、百分数化成小数:去掉百分号,小数点向左移动两位;或者先化成分母
是 100、1000 的分数再化成小数。
例如:125%=1.25
26% 26 0.26 100
62.5% 62.5 625 0.625 100 1000
2
31 31 5 155 1.55 20 20 5 100
实际上,很多特殊分母的分数可以通过记忆一劳永逸。如下表:
分母 2 3 4 5 6 7
分数化成小数
1 0.5 2
1
0.3
3
2
0.6
3
1 0.25 2 1 0.5 3 0.75
4
42
4
1 0.2 5
2 0.4 5
3 0.6 4 0.8
分母是 2、4、5、8、10、20、25、50 等分数称作特殊分数,因为运用分数 的基本性质,这些分数的分子和分母同时乘 5、25、2、125、4 等后可以化成分
母是 10、100、1000 的分数,再化成一位、两位、三位小数就容易了。
例如: 4 4 4 16 0.16
25 25 4 100
5
5
1
0.16
2
1
0.3
3 1 0.5
4
2
0.6
5
0.8 3
6
63
62
63
6
1
0.14285
7
2
0. 2 8571
4
…你发现循环节数字排列规律了吗?
7
7
8
1 0.125 2 1 0.25 3 0.375 4 1 0.5 5 0.625
8
84
8
82
(完整版)分数、小数和百分数的互化表

一、常用的π倍二、常用的分数、小数及百分数的互化12 =0.5=50% 14 =0.25=25% 34=0.75=75% 15 =0.2=20% 25 =0.4=40% 35 =0.6=60% 45=0.8=80% 18 =0.125=12.5% 38 =0.375=37.5% 58 =0.625=62.5% 78=0.875=87.5% 110 =0.1=10% 116 =0.0625=6.25% 120 =0.05=5% 125=0.04=4% 140 =0.025=2.5% 150 =0.02=2% 1100=0.01=1%1、把6 kg 盐平均分成8包,每包重( )kg,每包重量是6kg 的( )。
2、一个数乘真分数,积一定小于这个数。
( )3、10米长的铁丝,如果用去1/4还剩( )米,如果用去1/4米,还剩( )米。
4、小明骑自行车一分钟可以行2/3千米,照这样计算,他行2千米要用多少分钟?5、一根钢管,用去它的40%后还剩12米,如果用去它的5/8,则剩下( )米。
6、一辆汽车每行8千米耗油3/5千克,平均每行1千米要耗油( ) 千克。
每千克汽油可以行驶( )千米。
7、一种钢材4/5米重1/25吨,这样的钢材每吨长( )米,每米重( )吨。
8、汽车从甲城开往乙城,已经行了全程的2/5,距离中点还有120千米。
那么甲乙两城相距多少千米?9、如果A:B=4:7,那么A=4,B=7。
( )。
10、1.5小时:1小时50分钟=( )。
11、用120厘米的铁丝做一个长方体的框架,长、宽、高的比是3:2:1。
这个长方体的长、宽、高分别是多少?12、用一根长36厘米长的铁丝围成一个长和宽的比是5:4的长方形,那么这个长方形的面积是多少?13、已知d=10cm,求半圆周长。
PS: 半圆的周长≠圆周长的一半;圆的周长要记清,3.14乘直径。
半圆周长要记清,5.14乘半径。
14、一只挂钟的分针长20cm,经过30分钟后,分针的尖端所走的路程是多少厘米?经过45 分钟呢?15、一只挂钟的时针长5cm,经过6小时,这个尖端移动了()厘米。
百分数,分数,小数之间的互化

百分数化小数的方法,百分数化分数的方法(一)百分数化小数的方法把百分数化成小数时,要把百分号去掉,同时把小数点向左移动两位.例:把160%和0.8%化成小数.[分析]把160%化成小数时,只要把百分号去掉,把160的小数点向左移动两位,变成1.6就可以了,0.8%也是如此.解答:160%=1.6 0.8%=0.008(二)百分数化分数的方法百分数化成分数时,先把百分数改写成分数,能约分的要约分成最简分数.例:把160%和0.8%化成分数.(三)求一个数的百分之几是多少的实际问题的方法求一个数的百分之几是多少,和我们以前学习的求一个数的几分之几的问题的解决办法一样,都是用乘法来计算.在计算时,要根据具体情境,把百分数转化成分数或小数,再计算.例:黄豆营养很丰富,其中的蛋白质含量约占36%,脂肪含量约占18.4%,碳水化合物含量约占25%,250克黄豆中,蛋白质、脂肪和碳水化合物的含量分别约有多少克?[分析]根据分数乘法意义,求250克黄豆中蛋白质、脂肪和碳水化合物的含量,就是求250克的36%、18.4%和25%各是多少,只要用250分别乘它们所占的百分之几就可以了,在计算时,把百分数化成分数或小数再计算.解答:250×36% 或250×36%=250×=250×0.36=90(克)=90(克)250×18.4% 或250×18.4%=250×=250×0.184=46(克)=46(克)250×25% 或250×25%=250×=250×0.25=62.5(克)=62.5(克)答:250克黄豆中,蛋白质、脂肪和碳水化合物的含量分别是90克,46克,62.5克.[总结]百分数化成分数、小数的方法:百分数化分数,先写成分母是100的分数形式,再化成最简分数;百分数化小数:百分号先去掉,小数点左移两位.这月我当家教学目标1、会用方程解决有关百分数的简单实际问题,体会百分数在现实生活中的应用价值.2、在经历数据调查的过程中,体会百分数与统计的联系.3、在计算过程中,培养节约意识.教学过程知识要点(一)用方程解决“已知一个数的百分之几是多少,求这个数”的问题的方法“已知一个数的百分之几是多少,求这个数,”同以前学习的“已知一个数的几分之几是多少,求这个数”的解题方法基本是一致的,都是先要找准单位“1”,然后根据数据关系列出方程,再解方程,百分数的题同以前学习的分数应用题基本一致,解题方法也相同,但在计算时一般要先把百分数化成小数或分数再计算.例:小红家月支出统计表如下:根据这个统计表,计算出小红家这个月一共花了多少钱,并把统计表填写完整.[分析]求小红家这个月一共花了多少钱,可以根据食品花了500元,占总支出的40%来求,因为总支出为单位“1”,而且未知,所以可以设总支出为x,列方程求出总支出.总支出求出来了,则水电气所花钱数占总支出的百分比也可求出,用125÷1250即可,因为书报费占总支出的2%,书报费也可求出,用1250×2%即可,合计中的总钱数既是总支出:1250元,而合计中的百分比则是100%.其他一项可用总支出减去其余几项既得.解:设小红家这个月一共花了x元.40%x=500x=500÷40%x=1250答:小红家这个月一共花了1250元.水电气占总支出的百分比为125÷1250=0.1=10%书报花了2%×1250=25(元)其它花了1250-25-100-125-500=500(元)其它占总支出的百分比为500÷1250=0.4=40%家庭月支出统计表如下:[提示]在计算后要把各种支出的百分比加起来,看是否等于100%,但是当计算百分比使用“四舍五入”法时,计算得出的百分比有一定的偏差,再将所有百分比相加时,所得结果往往不等于100%.(二)点燃你的思维1、某小学五年级有学生50人,有一天缺席1人,求这一天的出席率.[分析]求出席率,就是求出席的人数占总人数的百分之几,但是出席人数不知,所以要用总人数减去缺席的人数求出出席率.解答(50-1)÷50=49÷50=98%答:这一天的出席率是98%.又用酒精灌满,然后再倒出全部溶液的25%,再用酒精灌满,那么这时的酒精占全部溶液的百分之几?[分析]解决这道题关键在于求出最后酒精有多少,要求酒精有多少,我们可以求出倒出的水是多少.而题目中都用的是分数,所以找准每个分数的单位1就变得更加重要了.答:这时酒精占全部溶液的75%.生每人也植20×(1-25%)=15棵树,则现在每人植树的棵数都是15棵,共植树多少棵也就能求出来了.解答20×(1-25%)×400=6000(棵)答:共植树6000棵.【模拟试题】(答题时间:30分钟)一、把下面的百分数化成小数或整数.36.5% 0.4% 320%67.8% 126.85% 6.34%200% 7% 5000%(4)六年级一班有50名学生,今天的出勤率是98%,今天有()人缺勤.四、应用题.1、王师傅在第一季度生产了340个零件,合格率是85%,第二季度生产了480个零件,合格率是95%,求王师傅这两个季度生产的产品的合格率?2、火车原来的速度是每小时90千米,提速后,火车的速度是每小时100千米,提速了百分之几?3、五年级一班男同学占全班总数的60%,女同学比男同学要少百分之几?。
常见的分数、小数及百分数的互化,常用平方数、立方数及各种计算方法

1、C列分数化小数的记法:分子乘5,小数点向左移动两位。
之蔡仲巾千创作2、D、E两列分数化小数的记法:分子乘4,小数点向左移动两位A 列B列C列D列E列罕见分数、小数互化表罕见的分数、小数及百分数的互化除法除不尽(按四舍五入计算) 除法 比分数小数百分除法比分数小数百分1÷2 1:2 1/2 50% 1÷3 1:3 1/3 33% 1÷4 1:4 1/4 25% 2÷3 2:3 2/3 67% 1÷51:51/520%1÷61:61/617%2÷5 2:5 2/5 40% 5÷6 5:6 5/6 83% 3÷5 3:5 3/5 60% 1÷7 1:7 1/7 14% 4÷5 4:5 4/5 80% 2÷7 2:7 2/7 29% 1÷8 1:8 1/8 12.5% 3÷7 3:7 3/7 43% 3÷8 3:8 3/8 37.5% 4÷7 4:7 4/7 57% 5÷8 5:8 5/8 62.5% 5÷7 5:7 5/7 71% 7÷8 7:8 7/8 87.5% 6÷7 6:7 6/7 86% 1÷11:10 1/10 10% 1÷9 1:9 1/9 11%3÷13:10 3/10 30% 2÷9 2:9 2/9 22% 7÷17:10 7/10 70% 4÷9 4:9 4/9 44% 9÷19:10 9/10 90% 5÷9 5:9 5/9 56% 3÷2 3:2 3/2 150% 7÷9 7:9 7/9 78% 5÷4 5:4 5/4 125% 8÷9 8:9 8/9 89% 7÷5 7:5 7/5 140% 4÷3 4:3 4/3 133%备注除尽是指除数(前项、分子)除以除数(后项、分母)得商不出现循环(或无限循环)小数;除不尽与除尽相反,是无限循环小数。
常见的分数、小数及百分数的互化,常用平方数、立方数及各种计算方法

1、C列分数化小数的记法:分子乘5,小数点向左移动两位。
2、D、E两列分数化小数的记法:分子乘4,小数点向左移动两位常见分数、小数互化表常见的分数、小数及百分数的互化常用平方数常见立方数常见特殊数的乘积错位相加/减A×9型速算技巧:A×9= A×10-A;例:743×9=743×10-743=7430-743=6687A×型速算技巧:A×= A×10+A÷10;例:743×=743×10-743÷10==A×11型速算技巧:A×11= A×10+A;例:743×11=743×10+743=7430+743=8173A×101型速算技巧:A×101= A×100+A;例:743×101=743×100+743=75043乘/除以5、25、125的速算技巧:A×5型速算技巧:A×5=10A÷2;例:×5=×10÷2=÷2=A÷5型速算技巧:A÷5=×2;例:÷5=××2=×2=A×25型速算技巧:A×25=100A÷4;例:7234×25=7234×100÷4=723400÷4=180850A÷25型速算技巧:A÷25=×4;例:3714÷25=3714××4=×4=A×125型速算技巧:A×5=1000A÷8;例:8736×125=8736×1000÷8=8736000÷8=1092000A÷125型速算技巧:A÷1255=×8;例:4115÷125=4115××8=×8=减半相加:A×型速算技巧:A×=A+A÷2;例:3406×=3406+3406÷2=3406+1703=5109“首数相同尾数互补”型两数乘积速算技巧:积的头=头×(头+1);积的尾=尾×尾例:23×27=首数均为2,尾数3与7的和是10,互补所以乘积的首数为2×(2+1)=6,尾数为3×7=21,即23×27=621本方法适合11~99 所有平方的计算。
分数 小数 百分数之间互化的方法

分数小数百分数之间互化的方法之吉白夕凡创作
1.小数化成分数:原来有几位小数,就在1的后面写几个零作分母,把原来的小数去掉小数点作分子,能约分的要约分.
2.分数化成小数:用分母去除分子.能除尽的就化成有限小数,有的不克不及除尽,不克不及化成有限小数的,一般保存三位小数.
3.小数化成百分数:只要把小数点向右移动两位,同时在后面添上百分号.
4.百分数化成小数:把百分数化成小数,只要把百分号去掉,同时把小数点向左移动两位.
5.分数化成百分数:通常先把分数化成小数(除不尽时,通常保存三位小数),再把小数化成百分数.
6.百分数化成小数:先把百分数改写成分数,能约分的要约成最简分数.。
常见的分数、小数及百分数的互化,常用平方数、立方数及各种计算方法
常见的分数、⼩数及百分数的互化,常⽤平⽅数、⽴⽅数及各种计算⽅法1、C列分数化⼩数的记法:分⼦乘5,⼩数点向左移动两位。
2、D、E两列分数化⼩数的记法:分⼦乘4,⼩数点向左移动两位常见分数、⼩数互化表常见的分数、⼩数及百分数的互化常⽤平⽅数常见⽴⽅数常见特殊数的乘积错位相加/减A×9型速算技巧:A×9= A×10-A;例:743×9=743×10-743=7430-743=6687 A×型速算技巧:A×= A×10+A÷10;例:743×=743×10-743÷10==A×11型速算技巧:A×11= A×10+A;例:743×11=743×10+743=7430+743=8173 A×101型速算技巧:A×101= A×100+A;例:743×101=743×100+743=75043乘/除以5、25、125的速算技巧:A×5型速算技巧:A×5=10A÷2;例:×5=×10÷2=÷2=A÷5型速算技巧:A÷5=×2;例:÷5=××2=×2=A×25型速算技巧:A×25=100A÷4;例:7234×25=7234×100÷4=723400÷4=180850A÷25型速算技巧:A÷25=×4;例:3714÷25=3714××4=×4=A×125型速算技巧:A×5=1000A÷8;例:8736×125=8736×1000÷8=8736000÷8=1092000A÷125型速算技巧:A÷1255=×8;例:4115÷125=4115××8=×8=减半相加:A×型速算技巧:A×=A+A÷2;例:3406×=3406+3406÷2=3406+1703=5109“⾸数相同尾数互补”型两数乘积速算技巧:积的头=头×(头+1);积的尾=尾×尾例:23×27=⾸数均为2,尾数3与7的和是10,互补所以乘积的⾸数为2×(2+1)=6,尾数为3×7=21,即23×27=621本⽅法适合11~99 所有平⽅的计算。
(完整版)常见的分数、小数及百分数的互化,常用平方数、立方数及各种计算方法

1、C列分数化小数的记法:分子乘5,小数点向左移动两位。
2、D、E两列分数化小数的记法:分子乘4,小数点向左移动两位常见分数、小数互化表常见的分数、小数及百分数的互化错位相加/减A×9型速算技巧:A×9= A×10-A;例:743×9=743×10-743=7430-743=6687A×9.9型速算技巧:A×9.9= A×10+A÷10;例:743×9.9=743×10-743÷10=7430-74.3=7355.7A×11型速算技巧:A×11= A×10+A;例:743×11=743×10+743=7430+743=8173A×101型速算技巧:A×101= A×100+A;例:743×101=743×100+743=75043乘/除以5、25、125的速算技巧:A×5型速算技巧:A×5=10A÷2;例:8739.45×5=8739.45×10÷2=87394.5÷2=43697.25A÷5型速算技巧:A÷5=0.1A×2;例:36.843÷5=36.843×0.1×2=3.6843×2=7.3686A×25型速算技巧:A×25=100A÷4;例:7234×25=7234×100÷4=723400÷4=180850A÷25型速算技巧:A÷25=0.01A×4;例:3714÷25=3714×0.01×4=37.14×4=148.56A×125型速算技巧:A×5=1000A÷8;例:8736×125=8736×1000÷8=8736000÷8=1092000A÷125型速算技巧:A÷1255=0.001A×8;例:4115÷125=4115×0.001×8=4.115×8=32.92减半相加:A×1.5型速算技巧:A×1.5=A+A÷2;例:3406×1.5=3406+3406÷2=3406+1703=5109“首数相同尾数互补”型两数乘积速算技巧:积的头=头×(头+1);积的尾=尾×尾例:23×27=首数均为2,尾数3与7的和是10,互补所以乘积的首数为2×(2+1)=6,尾数为3×7=21,即23×27=621本方法适合11~99 所有平方的计算。
常见的分数、小数及百分数的互化,常用平方数、立方数及各种计算方法

1、C列分数化小数的记法:分子乘5,小数面背左移动二位.之阳早格格创做2、D、E二列分数化小数的记法:分子乘4,小数面背左移动二位罕睹分数、小数互化表罕睹的分数、小数及百分数的互化时常使用仄圆数罕睹坐圆数罕睹特殊数的乘积错位相加/减A×9型速算本领:A×9= A×10-A;例:743×9=743×10-743=7430-743=6687A×9.9型速算本领:A×9.9= A×10+A÷10;A×11型速算本领:A×11= A×10+A;例:743×11=743×10+743=7430+743=8173A×101型速算本领:A×101= A×100+A;例:743×101=743×100+743=75043乘/除以5、25、125的速算本领:A×5型速算本领:A×5=10A÷2;A÷5型速算本领:A÷5=0.1A×2;A×25型速算本领:A×25=100A÷4;例:7234×25=7234×100÷4=723400÷4=180850A÷25型速算本领:A÷25=0.01A×4;A×125型速算本领:A×5=1000A÷8;例:8736×125=8736×1000÷8=8736000÷8=1092000A÷125型速算本领:A÷1255=0.001A×8;减半相加:A×1.5型速算本领:A×1.5=A+A÷2;例:3406×1.5=3406+3406÷2=3406+1703=5109“尾数相共尾数互补”型二数乘积速算本领:积的头=头×(头+1);积的尾=尾×尾例:23×27=尾数均为2,尾数3与7的战是10,互补所以乘积的尾数为2×(2+1)=6,尾数为3×7=21,即23×27=621原要领符合11~99 所有仄圆的预计.11X11=121 21X21=4141 31X31=961 41X41=168112X12=148 22X22=484 32X32=1024 42X42=1764 52X52=2704从上头的预计咱们不妨得出公式:个位=个位×个位所得数的个位,如果谦几十便背前进几,十位=个位×(十位上的数字×2)+进位所得数的终位,如果谦几十便背前进几,百位=二个十位上的数字相乘+进位.例:26×26=个位=6×6=36,谦30 背前进3;十位=6×(2×2)+3=27,谦20 背前=进2;百位=2×2+2=6由此可睹26×26=67623×23个位=3×3=9十位=3×(2×2)=12,写2 进1百位=2×2+进1=5所以23×23=52946×46 个位=6×6= 36,写6进3十位=6×(4×2)+进3= 5 1,写1 进5百位=4×4+进5= 21,写1 进2所以46×46=2116如果不谦十便不必进位,预计更烦琐.例:13×13个位=3×3=9 十位=3×(1×2)=6 百位=1×1所以13×13=169程序:(1)真足仄圆数的个位数字只可是0,1,4,5,6,9.(不2,3,7,8)二个整数的个位数字之战为10,则它们的仄圆数的个位数字相共.(2)奇数的仄圆的个位数字是奇数,十位数字是奇数.(3)如果真足仄圆数的十位数字是奇数,则它的个位数字一定是6;反之,如果真足仄圆数的个位数字是6,则它的十位数字一定是奇数.(4)奇数的仄圆是4 的倍数;奇数的仄圆是4 的倍数加1.(5)奇数的仄圆是8n+1 型;奇数的仄圆为8n 或者8n+4 型.(6)真足仄圆数的形式必为下列二种之一:3n,3n+1.(7)不克不迭被5 整除的数的仄圆为5n±1 型,能被5 整除的数的仄圆为5n 型.(8)仄圆数的形式具备下列形式16n,16n+1,16n+4,16n+9.(9)真足仄圆数的诸位数字之战的个位数字只可是0,1,3,4,6,7,9.(不2,5,8)(10)如果量数p 能整除a,但是p 的仄圆不克不迭整除a,则a 不是真足仄圆数.(11)正在二个相邻的整数的仄圆数之间的所有整数皆不是真足仄圆数.(12)一个正整数n 是真足仄圆数的充分需要条件是n 有奇数个果数(包罗1 战n).一个数如果是另一个整数的真足坐圆(即一个整数的三次圆,或者整数乘以它自己乘以它原身),那么咱们便称那个数为真足坐圆数,也喊干坐圆数,如0,1,8,27,64,125,216,343,512,729,1000 等.如果正整数x,y,z 谦脚大概圆程x2+y2=z2 ,便称x,y,z 为一组勾股数.x,y 必定是一个为奇数另一个为奇数,不可能共时为奇数或者共时为奇数.z 战z²肯定皆是奇数.五组罕睹的勾股数:3²+4²=5²;5²+12²=13²;7²+24²=25²;8²+15²=17²;20²+21²=29²9+16=25;25+144=169;49+576=625;64+225=289;400+441=841影象本领:(a+b)²= a² + b² + 2ab (a-b)²=a² + b²-2ab|| | | | |a×a b×b 2×a×b a×a b×b 2×a×b例:13² =(10+3) ²=10²+3²+2×10×3=100+9+60=16988²=(90-2)²=90²+2²-2×90×2=8100+4-360=7744用处:①锻炼预计本领,使预计更快更准确;②预计某数的仄圆根所处的范畴,正在判决某个较大的数n 是不是量数时不妨缩小其大概果子的筛选范畴,只需查看3 到n之间的所有量数是不是n 的果子即可,超出n的皆不必查看了比圆:判决2431是可为量数,果为49²=2401<2431<2500=50²,所以49<2431.<50,2+4+3+1=10不克不迭被3整除, 2341的个位既非0又非5,故只需查看7到47之间的所有量数是可整除2431即可,而53,59,61,67……等更大的量数皆不必查看了,本量上2431=11×13×17③减少对于数字的认识程度,比圆16²=256=28,32²=1024=210,64²=4096=212,其余一些特殊结构的数字该当牢记,如88²=7744, 11²=121,22²=484,(121 战484 从左到左与从左到左瞅是一般的) 12²=144,21²=441,13²=169,31²=961,(a 安排颠倒后a²也安排颠倒).小教单位换算一、少度(一) 什么是少度?少度是一维空间的度量.(二) 少度时常使用单位* 公里(km) * 米(m) * 分米(dm) * 厘米(cm) * 毫米(mm) * 微米(um)(三) 单位之间的换算1 微米=1000 纳米1 毫米=1000 微米1 厘米=10 毫米1 分米=10 厘米1 米=1000 毫米1 千米=1000 米1 米=10 分米=100 厘米二、里积(一)什么是里积里积,便是物体所占仄里的大小.对于坐体物体的表面的几的丈量普遍称表面积.(二)时常使用的里积单位* 仄圆毫米* 仄圆厘米* 仄圆分米* 仄圆米* 仄圆千米(三)里积单位的换算1 仄圆厘米=100 仄圆毫米1 仄圆分米=100 仄圆厘米 1 仄圆米=100 仄圆分米1 公倾=10000 仄圆米1 仄圆公里=1 仄圆千米=100 公顷1 公顷=0.01 仄圆千米≈15 亩1 仄圆千米=1000000 仄圆米1 仄圆米=100 仄圆分米=10000 仄圆厘米三、体积战容积(一)什么是体积、容积体积,便是物体所占空间的大小.容积,箱子、油桶、堆栈等所能容纳物体的体积,常常喊干它们的容积.(二)时常使用单位1 体积单位* 坐圆米* 坐圆分米* 坐圆厘米2 容积单位* 降* 毫降(三)单位换算1 体积单位1 仄圆米=100 仄圆分米 1 仄圆分米=100 仄圆厘米1 仄圆厘米=100 仄圆毫米1 坐圆米=1000 坐圆分米 1 坐圆分米=1000 坐圆厘米2 容积单位1 降=1 坐圆米1 降=1000 毫降1 毫降=1 坐圆厘米1 坐圆米=1000 降1 坐圆分米=1 降 1 坐圆厘米=1 毫降四、品量(一)什么是品量品量,便是表示表示物体有多沉.(二)时常使用单位* 吨t * 千克kg * 克g(三)时常使用换算1 吨(t)=1000 千克(kg)1 千克=1000 克(g)沉量单位换算1 吨=1000 千克1 千克=1000 克1 千克=1 公斤五、时间(一)什么是时间是指有起面战终面的一段时间(二)时常使用单位世纪、年、月、日、时、分、秒(三)单位换算* 1 世纪=100 年1 年=12 月1 年=365 天仄年一年=366 天闰年.一、三、五、七、八、十、十二是大月大月有31 天四、六、九、十一是小月小月有30 天仄年2 月有28 天闰年2 月有29 天1 天= 24 小时 1 小时=60 分 1 分=60 秒1秒=1000毫秒(ms)1时=3600秒货币(一)什么是货币货币是充当十足商品的等价物的特殊商品.货币是价格的普遍代表,不妨买买所有别的商品.(二)时常使用单位* 元* 角* 分(三)单位换算1 元=10 角1 角=10 分1 元=100 分四则运算闭系加法:一个加数=战-另一个加数减法:被减数=好+减数减数=被减数-好乘法:一个果数=积÷另一个果数除法:被除数=商×除数除数=被除数÷商二个程序1、除法的商稳定程序:被除数战除数共时乘或者除以相共的数(0 除中),商稳定.2、乘法的积稳定程序:如果一个果数乘几,另一个果数则除以几,那么它们的积稳定.数教烦琐运算要领归类一、共级运算(不括号),不妨戴着标记搬场a+b+c=a+c+ba-b-c=a-c-ba+b-c=a-c+b a-b+c=a+c-ba×b×c=a×c×b a÷b÷c=a÷c÷ba×b÷c=a÷c×ba÷b×c=a×c÷b二、有括号的共级运算,不妨根据去括号的本量把括号去掉1、括号前里是“+”号或者“×”号,去掉括号稳定号.a+(b+c)=a+b+c a+(b-c)=a+b-c a×(b×c)=a×b×c a×(b÷c)=a×b÷c2、括号前里是“-”号或者“÷”号,去掉括号要变号.a-(b+c)=a-b-c a-(b-c)=a-b+c a÷(b×c)=a÷b÷c a÷(b÷ c)=a÷b×c 上头的式子从左到左不妨去括号,那么从左到左便是加括号的要领了.自己严肃瞅察创制不括号的共级运算中加括号的本量哦.三、乘法调配律:(a+b)×c=a×c+b×c 或者(a-b)×c=a×c-b×c乘法调配律的顺使用:a×c+a×b=(a+b)×c 或者a×c-b×c=(a-b)×c 二个数的战与一个数相乘,不妨先把它们与那个数分别相乘,再相加,那喊干乘法调配律.1.调配法(从左到左的用法) 括号里是加或者减运算,与另一个数相乘,注意调配.2.提与公果式(从左到左的用法)注意相共果数的提与.3.注意构制,让算式谦脚乘法调配律的条件.四、借去还去法瞅到名字,便知讲那个要领的含意.用此要领时,需要注意瞅察,创制程序.还要注意还哦,有借有还,再借不易嘛.例:9999+999+99+9五、拆分法瞅名思义,拆分法便是为了便当预计把一个数拆成几个数.那需要掌握一些“佳伙伴”,如:2 战5,4 战5,2 战2.5,4 战2.5,8 战1.25 等.分拆还要注意不要改变数的大小哦. 例:3.2×12.5×25 1.25×88 3.6×0.25以上几种要领包罗了小教数教罕睹的烦琐运算的要领,正在采用烦琐要领的时间一定要注意烦琐要领的依据,千万不克不迭不依据的胡推治扯一通,奇尔间是出题者蓄意掘的陷阱,瞅似不妨使用烦琐算法,本量上找不出不妨烦琐运算的依据,那样的题只可依照运算程序预计的.(比圆2.5×4÷2.5×4,瞅似加括号很烦琐,截止等于1,而本量上括号加正在除号的后里是要变号的,所以原讲题的烦琐要领是“不括号的共级运算,不妨戴着标记搬场.2.5÷ 2.5×4×4)烦琐预计烦琐运算沉正在找依据1、运算定律:运算定律用字母表示加法接换律a+b=b+a加法分离律(a+b)+c=a+(b+c)乘法接换律a×b=b×a乘法分离律(a×b)×c=a×(b×c)乘法调配律(a+b)×c=a×c+b×c减法运算程序a-b-c=a-(b+c)除法运算程序a÷b÷c=a÷(b×c)2、乘、除法的互化.(小本领:标记是好异的;二个数相乘得“1”)(1)A÷0.1=A×10 (7)A÷0.01=A×100(2)A×0.1=A÷10 (8)A×0.01=A÷100(3)A÷0.2=A×5 (9)A÷0.25=A×4(4)A×0.2=A÷5 (10)A×0.25=A÷4(5)A÷0.5=A×2 (11)A÷0.125=A×8(6)A×0.5=A÷2 (12)A×0.125=A÷83、供近似数的要领.(1)四舍五进法. (2)进一法.(3)去尾法4、积与果数、商与被除数的大小比较:第2 个果数>1,积>第1 个果数;除数>1,商<被除数;第2 个果数=1,积=第1 个果数;除数=1,商=被除数;第2 个果数<1,积<第1 个果数. 除数<1,商>被除数;。
常见的分数、小数及百分数的互化,常用平方数、立方数及各种计算方法

1、C列分数化小数的记法:分子乘5,小数点向左移动两位。
2、D、E两列分数化小数的记法:分子乘4,小数点向左移动两位常见分数、小数互化表常见的分数、小数及百分数的互化错位相加/减A×9型速算技巧:A×9= A×10-A;例:743×9=743×10-743=7430-743=6687A×9.9型速算技巧:A×9.9= A×10+A÷10;例:743×9.9=743×10-743÷10=7430-74.3=7355.7A×11型速算技巧:A×11= A×10+A;例:743×11=743×10+743=7430+743=8173A×101型速算技巧:A×101= A×100+A;例:743×101=743×100+743=75043乘/除以5、25、125的速算技巧:A×5型速算技巧:A×5=10A÷2;例:8739.45×5=8739.45×10÷2=87394.5÷2=43697.25A÷5型速算技巧:A÷5=0.1A×2;例:36.843÷5=36.843×0.1×2=3.6843×2=7.3686A×25型速算技巧:A×25=100A÷4;例:7234×25=7234×100÷4=723400÷4=180850A÷25型速算技巧:A÷25=0.01A×4;例:3714÷25=3714×0.01×4=37.14×4=148.56A×125型速算技巧:A×5=1000A÷8;例:8736×125=8736×1000÷8=8736000÷8=1092000A÷125型速算技巧:A÷1255=0.001A×8;例:4115÷125=4115×0.001×8=4.115×8=32.92减半相加:A×1.5型速算技巧:A×1.5=A+A÷2;例:3406×1.5=3406+3406÷2=3406+1703=5109“首数相同尾数互补”型两数乘积速算技巧:积的头=头×(头+1);积的尾=尾×尾例:23×27=首数均为2,尾数3与7的和是10,互补所以乘积的首数为2×(2+1)=6,尾数为3×7=21,即23×27=621本方法适合11~99 所有平方的计算。
小数,分数,百分数的互化

小数,分数,百分数的互化
小数、分数、百分数是数学中常用的表示方式,它们之间的转换可以帮助我们更好地理解数学概念和运算。
1. 小数转分数
将小数转换为分数,需要将小数部分的数字乘以适当的倍数,使其变为整数。
比如,0.5可以乘以2,变为1/2;0.75可以乘以4,变为3/4。
需要注意的是,分母要与乘数相同。
2. 分数转小数
将分数转换为小数,可以直接将分子除以分母。
比如,2/5可以计算得到0.4;3/8可以计算得到0.375。
3. 分数转百分数
将分数转换为百分数,需要将分数化为小数,然后将小数乘以100。
比如,2/5转换为百分数为40%;3/8转换为百分数为37.5%。
4. 百分数转分数
将百分数转换为分数,需要将百分数除以100,然后化为最简分数形式。
比如,60%可以除以100得到0.6,再将0.6化为最简分数形式得到3/5。
5. 小数转百分数
将小数转换为百分数,需要将小数乘以100。
比如,0.75转换为百分数为75%。
6. 百分数转小数
将百分数转换为小数,需要将百分数除以100。
比如,35%可以
除以100得到0.35。
分数、小数和百分数的互化表

一、常用的π倍二、常用的分数、小数及百分数的互化12 =0.5=50% 14 =0.25=25% 34=0.75=75% 15 =0.2=20% 25 =0.4=40% 35 =0.6=60% 45=0.8=80% 18 =0.125=12.5% 38 =0.375=37.5% 58 =0.625=62.5% 78=0.875=87.5% 110 =0.1=10% 116 =0.0625=6.25% 120 =0.05=5% 125=0.04=4% 140 =0.025=2.5% 150 =0.02=2% 1100=0.01=1%1、把6 kg 盐平均分成8包,每包重〔 〕kg,每包重量是6kg 的〔 〕。
2、一个数乘真分数,积一定小于这个数。
〔 〕3、10米长的铁丝,如果用去1/4还剩〔 〕米,如果用去1/4米,还剩〔 〕米。
4、小明骑自行车一分钟可以行2/3千米,照这样计算,他行2千米要用多少分钟?5、一根钢管,用去它的40%后还剩12米,如果用去它的5/8,那么剩下〔 〕米。
6、一辆汽车每行8千米耗油3/5千克,平均每行1千米要耗油〔 〕 千克。
每千克汽油可以行驶〔 〕千米。
7、一种钢材4/5米重1/25吨,这样的钢材每吨长〔 〕米,每米重〔 〕吨。
8、汽车从甲城开往乙城,已经行了全程的2/5,距离中点还有120千米。
那么甲乙两城相距多少千米?9、如果A:B=4:7,那么A=4,B=7。
〔 〕。
10、1.5小时:1小时50分钟=〔 〕。
11、用120厘米的铁丝做一个长方体的框架,长、宽、高的比是3:2:1。
这个长方体的长、宽、高分别是多少?12、用一根长36厘米长的铁丝围成一个长和宽的比是5:4的长方形,那么这个长方形的面积是多少?13、d=10cm,求半圆周长。
PS: 半圆的周长≠圆周长的一半;圆的周长要记清,3.14乘直径。
半圆周长要记清,5.14乘半径。
14、一只挂钟的分针长20cm,经过30分钟后,分针的尖端所走的路程是多少厘米?经过45 分钟呢?15、一只挂钟的时针长5cm,经过6小时,这个尖端移动了〔〕厘米。
(完整版)常见的分数、小数及百分数的互化,常用平方数、立方数及各种计算方法

1、C列分数化小数的记法:分子乘5,小数点向左移动两位。
2、D、E两列分数化小数的记法:分子乘4,小数点向左移动两位常见分数、小数互化表常见的分数、小数及百分数的互化错位相加/减A×9型速算技巧:A×9= A×10-A;例:743×9=743×10-743=7430-743=6687A×9.9型速算技巧:A×9.9= A×10+A÷10;例:743×9。
9=743×10-743÷10=7430—74.3=7355。
7A×11型速算技巧:A×11= A×10+A;例:743×11=743×10+743=7430+743=8173A×101型速算技巧:A×101= A×100+A;例:743×101=743×100+743=75043乘/除以5、25、125的速算技巧:A×5型速算技巧:A×5=10A÷2;例:8739。
45×5=8739.45×10÷2=87394。
5÷2=43697。
25A÷5型速算技巧:A÷5=0。
1A×2;例:36。
843÷5=36。
843×0.1×2=3.6843×2=7.3686A×25型速算技巧:A×25=100A÷4;例:7234×25=7234×100÷4=723400÷4=180850A÷25型速算技巧:A÷25=0.01A×4;例:3714÷25=3714×0.01×4=37.14×4=148.56A×125型速算技巧:A×5=1000A÷8;例:8736×125=8736×1000÷8=8736000÷8=1092000A÷125型速算技巧:A÷1255=0。
常见的分数小数及百分数的互化常用平方数立方数及各种计算方法

常见的分数小数及百分数的互化常用平方数立方数及各种计算方法一、常见的分数、小数及百分数的互化1.分数转小数:分数转化为小数的方法是将分子除以分母。
例如,将2/3转化为小数:2÷3=0.6667(保留四位小数)。
2.小数转分数:小数转化为分数的方法是将小数点后的数字作为分子,分母为10的幂次方。
例如,将0.75转化为分数:小数点后有两位数字,所以分母为10的2次方,即100,故0.75=75/100。
3.分数转百分数:分数转化为百分数的方法是将分子除以分母后乘以100。
例如,将3/5转化为百分数:3÷5×100=60%。
4.百分数转分数:百分数转化为分数的方法是将百分数除以100。
例如,将80%转化为分数:80÷100=4/55.百分数转小数:百分数转化为小数的方法是将百分数除以100。
例如,将75%转化为小数:75÷100=0.756.小数转百分数:小数转化为百分数的方法是将小数乘以100。
例如,将0.6转化为百分数:0.6×100=60%。
1.平方数:平方数是一个数的平方,即将一个数自乘得到的结果。
例如,4是一个平方数,因为4×4=16、常见的平方数有1、4、9、16、25、36、49、64、81、100等。
2.立方数:立方数是一个数的立方,即将一个数自乘两次得到的结果。
例如,3是一个立方数,因为3×3×3=27、常见的立方数有1、8、27、64、125、216、343、512、729、1000等。
3.计算方法:常见的计算方法包括加减乘除四则运算、乘方、开方等。
-加法:将两个数相加得到和的结果。
例如,3+4=7-减法:将一个数减去另一个数得到差的结果。
例如,8-5=3-乘法:将两个数相乘得到积的结果。
例如,2×6=12-除法:将一个数除以另一个数得到商的结果。
例如,9÷3=3-乘方:将一个数自乘多次得到的结果。
常见的分数、小数及百分数的互化,常用平方数、立方数及各种计算方法
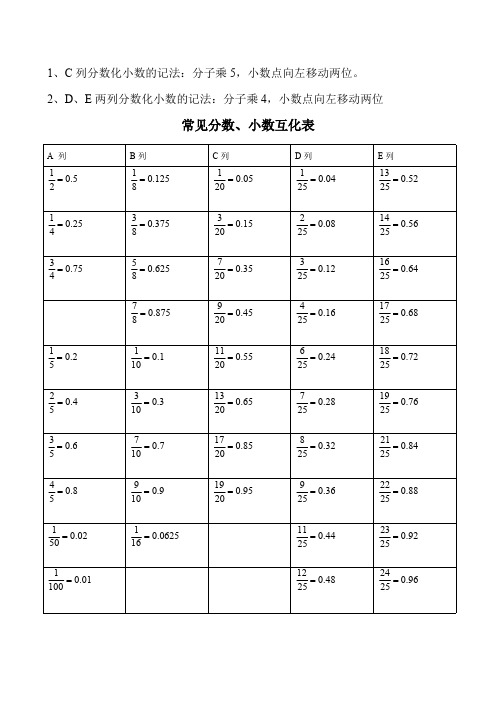
1、C 列分数化小数的记法:分子乘5,小数点向左移动两位。
2、D 、E 两列分数化小数的记法:分子乘4,小数点向左移动两位常见分数、小数互化表A 列B 列C 列D 列E 列5.021=125.081=05.0201=04.0251=52.02513=25.041=375.083=15.0203=08.0252=56.02514=75.043=625.085=35.0207=12.0253=64.02516=875.087=45.0209=16.0254=68.02517=2.051=1.0101=55.02011=24.0256=72.02518=4.052=3.0103=65.02013=28.0257=76.02519=6.053=7.0107=85.02017=32.0258=84.02521=8.054=9.0109=95.02019=36.0259=88.02522=02.0501=0625.0161=44.02511=92.02523=01.01001=48.02512=96.02524=常见的分数、小数及百分数的互化除法除不尽(按四舍五入计算)除法比分数小数百分除法比分数小数百分1÷21:21/20.550%1÷31:31/30.3333% 1÷41:41/40.2525%2÷32:32/30.6767% 1÷51:51/50.220%1÷61:61/60.1717% 2÷52:52/50.440%5÷65:65/60.8383% 3÷53:53/50.660%1÷71:71/70.1414% 4÷54:54/50.880%2÷72:72/70.2929% 1÷81:81/80.12512.5%3÷73:73/70.4343% 3÷83:83/80.37537.5%4÷74:74/70.5757% 5÷85:85/80.62562.5%5÷75:75/70.7171% 7÷87:87/80.87587.5%6÷76:76/70.8686% 1÷101:101/100.110%1÷91:91/90.1111% 3÷103:103/100.330%2÷92:92/90.2222% 7÷107:107/100.770%4÷94:94/90.4444% 9÷109:109/100.990%5÷95:95/90.5656% 3÷23:23/2 1.5150%7÷97:97/90.7878% 5÷45:45/4 1.25125%8÷98:98/90.8989% 7÷57:57/5 1.4140%4÷34:34/3 1.33133%备注除尽是指除数(前项、分子)除以除数(后项、分母)得商不出现循环(或无限循环)小数;除不尽与除尽相反,是无限循环小数。
常用分数、小数、百分数之间的互化
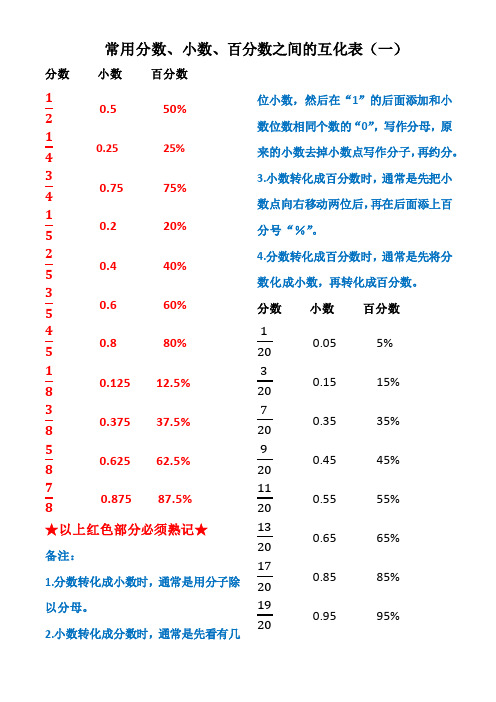
分数小数百分数120.5 50%140.25 25%340.75 75%150.2 20%250.4 40%350.6 60%450.8 80%180.125 12.5%380.375 37.5%580.625 62.5%780.875 87.5%★以上红色部分必须熟记★备注:1.分数转化成小数时,通常是用分子除以分母。
2.小数转化成分数时,通常是先看有几位小数,然后在“1”的后面添加和小数位数相同个数的“0”,写作分母,原来的小数去掉小数点写作分子,再约分。
3.小数转化成百分数时,通常是先把小数点向右移动两位后,再在后面添上百分号“%”。
4.分数转化成百分数时,通常是先将分数化成小数,再转化成百分数。
分数小数百分数1200.05 5%3200.15 15%7200.35 35%9200.45 45%11200.55 55%13200.65 65%17200.85 85%19200.95 95%分数小数百分数分数小数百分数1250.04 4%2250.08 8%3250.12 12%4250.16 16%6250.24 24%7250.28 28%8250.32 32%9250.36 36%11250.44 44%12 250.48 48%13250.52 52%14250.56 56%16250.64 64%17250.68 68%18250.72 72%19250.76 76%21250.84 84%22250.88 88%23250.92 92%24250.96 96%备注:1. 分母为20的分数转化成小数,先用分子乘以“5”,再把所得的积的小数点向左移动两位即可。
2. 分母为25的分数转化成小数,先用分子乘以“4”,再把所得的积的小数点向左移动两位即可。
常见的分数小数及百分数的互化经常使用平方数立方数及各类计算方式
一、C列分数化小数的记法:分子乘5,小数点向左移动两位。
二、D、E两列分数化小数的记法:分子乘4,小数点向左移动两位常见分数、小数互化表常见的分数、小数及百分数的互化错位相加/减A×9型速算技术:A×9= A×10-A;例:743×9=743×10-743=7430-743=6687A×9.9型速算技术:A×9.9= A×10+A÷10;例:743×9.9=743×10-743÷10=7430-74.3=7355.7A×11型速算技术:A×11= A×10+A;例:743×11=743×10+743=7430+743=8173A×101型速算技术:A×101= A×100+A;例:743×101=743×100+743=75043乘/除以五、2五、125的速算技术:A×5型速算技术:A×5=10A÷2;例:8739.45×5=8739.45×10÷2=87394.5÷2=43697.25A÷5型速算技术:A÷5=0.1A×2;例:36.843÷5=36.843×0.1×2=3.6843×2=7.3686A×25型速算技术:A×25=100A÷4;例:7234×25=7234×100÷4=723400÷4=180850A÷25型速算技术:A÷25=0.01A×4;例:3714÷25=3714×0.01×4=37.14×4=148.56A×125型速算技术:A×5=1000A÷8;例:8736×125=8736×1000÷8=8736000÷8=1092000A÷125型速算技术:A÷1255=0.001A×8;例:4115÷125=4115×0.001×8=4.115×8=32.92减半相加:A×1.5型速算技术:A×1.5=A+A÷2;例:3406×1.5=3406+3406÷2=3406+1703=5109“首数相同尾数互补”型两数乘积速算技术:积的头=头×(头+1);积的尾=尾×尾例:23×27=首数均为2,尾数3与7的和是10,互补因此乘积的首数为2×(2+1)=6,尾数为3×7=21,即23×27=621本方式适合11~99 所有平方的计算。
