冲激函数
冲激信号是偶函数,冲激偶信号是奇函数

冲激信号是偶函数,冲激偶信号是奇函数
冲激函数既不是偶函数也不是奇函数.是一个非正常函数,某种极限函数。
冲激偶函数是奇函数,关于原点对称,在全时域对其积分为零,即正、负两个冲激的面积相互抵消。
所以说冲激函数是偶函数,冲激偶就是奇函数
信号的分解,可以分解为冲激函数和阶跃函数的卷积,只不过对于阶跃函数而言会有一个初值的问题,这个初值产生原因就在于其对信号分解可以看成冲激函数与信号卷积的微分和积分(微分分配给f,积分分配给冲激函数),无论是先微分或者先积分,都会存在一个常数是无法确切表示的,需要有初值条件,从频域分析时,是因为存在微分性质使用时要保证是没有直流分量
在频域分析时,同样我们可以的得到一个有趣的结论,可以将任意信号分解为该信号的基函数的幅频特性曲线必没有0点,进一步拓展,一个有限长的信号,一定不能作为基函数表示任意信号(在时域来看这是显然的)。
冲激函数和冲激响应.
我们为什么要研究电路的冲激响应呢?这是由于电子、 通信与信息工程中使用的电信号十分复杂,我们需要知道 电路对任意输入信号的反映。而电路的冲激响应不仅能反 映出电路的特性,而且在知道线性时不变电路的冲激响应 后,可以通过一个积分运算求出电路在任意输入波形时的 零状态响应,从而求出电路的全响应。
* §6-6 冲激函数和冲激响应
一、 冲激函数
图6-38
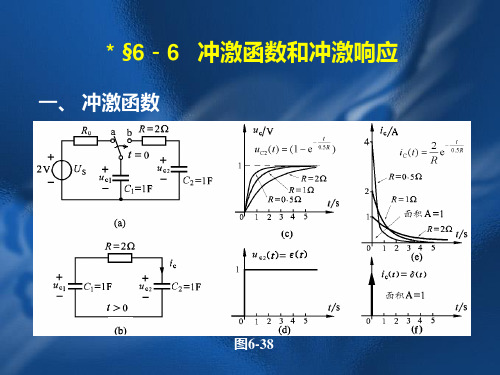
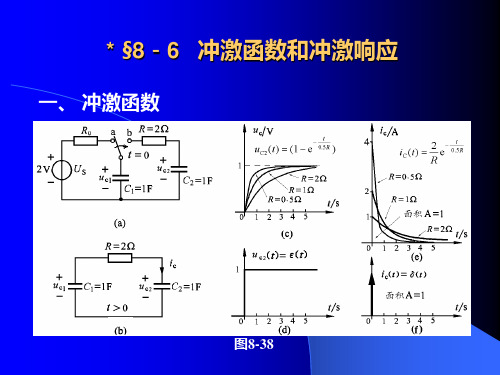
在介绍冲激函数之前,先看图6-38(a)所示电路,开关
原来倒向a点,由2V电压源对电容C1充电,使其电压达到 2V,电容上有2库仑电荷。开关在t=0时刻倒向b点后,将有
1库仑电荷从电容C1上移动到电容C2上,使电容上的电压逐 渐达到uC1()=uC2()=1V。
lim
0
P
(t
)
δ(t)
(6 34)
注意到响应波形的峰值h△(△)将随△减小而增加,我们
用罗比塔法则求h△(△)在△→0时的极限
lim
0
h
()
lim 0
f '() g ' ()
lim 0
(1/
τ)e 1
τ
1 τ
(6 35)
因此,图6-42(f)的波形趋于指数波形
h(t
)
1
e
t
0
t0 t0
当图(b)电路中电阻R趋于零时,电容电压uC2(t)波形趋 于一个单位阶跃,如图(d)所示。而电容电流iC(t)的波形将 变为初始值iC(0+)趋于无限大,时间常数无限小(波形的宽度 趋于零),而面积(电荷量)为一个单位的脉冲,这个极限的
波形称为单位冲激电流,用(t)表示。
当且仅当其满足以下两个性质时,一个无界的信号(t)
1.3_冲激函数
1
方法二: 0 0 1 f t(2t+2)反折 f (-2t+2)] .5 压缩 平移 f (t+2)
1
平移
2
t
另外应该还
方法三: f (t 方法一: 2) 压缩 f (2t) f (-2t)平移 f [-2(t-1)] 压缩 f (2t) 反折 1 f (2t 2) 平移 f [2(t+1)] 反折 f (-2t+2)
折叠信号的平移
f (t )
1
0
f (-t-1)= f [-(t+1)]将 已知 ff(t) 求 f (-t-1) (-t) 的波形向左移动 1。
f (t ) f (t 1)
平移
反折
1
平移
t
1
0
t
2
1
0
t
f (t 1)
1
0
反折
1
2
t
13
第一章第2讲
信号的平移与折叠
折叠信号的平移
任何偶函数的导数为奇函数。
第一章第2讲 5
举 例 1
下列各表达式中错误的是______ C 。
( A) ( B) (C ) ( D) (C )
f (t ) (t )dt f (0) f (t ) (t t0 )dt f (t0 ) f (t t0 ) (t )dt f (t0 ) f (t t0 ) (t t0 )dt f (0) f (t t0 ) (t )dt
1
0
平移 请同学们自己思考绘出图形。
1
0
t
0.5 0
第一章第2讲
冲激函数和冲激响应
h(t )
1
e
1
ε (t )
t
(8 - 32)
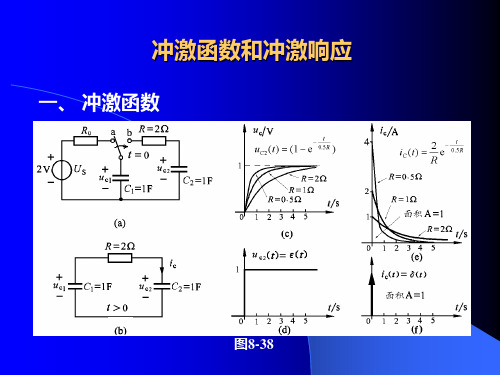
计算冲激响应的另一种方
法是先求出面积为1个单位
的矩形脉冲的响应,然后 求脉冲宽度趋于零的极限。
1 e h ( )
f ( ) g ( )
(8 33)
当△→0时,P(t)趋向于单
位冲激,如图(g)所示,即
lim P (t ) δ (t ) (8 34 )
1 s(t ) (1 e R
R - t L
) (t )
电感电流阶跃响应对时间求导得到iL(t)的冲激响应
t t t ds(t ) 1 1 1 h(t ) (1 e L ) (t ) e L (t ) e L (t ) dt R L L R R R
R t L R
2002年春节摄于成都人民公园
响应的一个方法是先求出电路的阶跃响应s(t),再将它对时
间求导即可得到冲激响应,即利用下式由电路的阶跃响应 计算出电路的冲激响应
ds ( t ) h (t ) dt
(8 31)
例如图8-35(a)所示RC串联电路的单位阶跃响应为
s(t ) (1 e
其冲激响应为
t RC
) ε (t )
t
当图(b)电路中电阻R趋于零时,电容电压uC2(t)波形趋 于一个单位阶跃,如图(d)所示。而电容电流iC(t)的波形将 变为初始值iC(0+)趋于无限大,时间常数无限小(波形的宽 度趋于零),而面积(电荷量)为一个单位的脉冲,这个极限
的波形称为单位冲激电流,用(t)表示。
当且仅当其满足以下两个性质时,一个无界的信号(t) 称为单位冲激函数
离散数学冲激函数

离散数学冲激函数冲击函数是离散数学中的一种重要函数,也称为脉冲响应函数或单位脉冲函数。
它常用符号δ(n)或δ[n]表示。
冲激函数具有以下特点:1.冲激函数在离散时间n=0时取值为1,其他时刻取值为0。
即δ(0)=1,δ(n)=0,n≠0。
2.冲激函数的取值是一个理想化的信号,它在瞬间时间内具有无限大的振幅和无限短的时间宽度。
冲激函数的定义可以通过极限的方式来理解。
当我们得到一个脉冲宽度为0、振幅趋近于无穷大的函数时,我们可以将其逼近为冲激函数。
冲激函数在离散时间系统中具有重要的作用,可以用于描述信号的性质、系统的响应以及信号的滤波特性。
它可以用来表示信号的单位样本,在系统的输入中起到触发输出的作用。
在信号处理中,冲激函数通常被用来表示单位冲激信号,即在一些特定时间发生的瞬时脉冲。
通过将冲激信号与待处理的信号进行卷积运算,我们可以得到系统对输入信号的响应。
此外,冲激函数还可以用于构造信号的频谱表示。
根据频谱分析理论,任意一个信号都可以表示为一系列冲激函数的叠加。
这种表示方式被广泛应用于数字信号处理、图像处理等领域。
在离散控制系统中,冲激函数用于描述系统的动态性能。
通过对冲激函数进行观测和分析,我们可以得到系统的传递函数、阶跃响应以及频率特性等关键参数。
总结起来,冲激函数在离散数学中具有重要的意义。
它是描述信号和系统性质的重要工具,可以用于构造信号的频谱表示,描述系统的动态性能,以及解决各种实际问题。
在实际应用中,冲激函数被广泛应用于数字信号处理、图像处理、控制系统和通信系统等领域。
冲激函数的特解范文

冲激函数的特解范文冲激函数是数学中的一种特殊函数,通常记为δ(t),也称为Dirac函数。
它在数学分析和工程应用中非常有用,尤其在处理信号问题时。
冲激函数的特解即是求解线性时不变系统微分方程的一个方法,下面将详细介绍冲激函数的特解的基本原理和应用。
首先,我们来了解一下冲激函数的基本性质。
冲激函数δ(t)在t=0的时刻取无穷大,并且在其他时刻都为零。
在数学上,可以将冲激函数定义为满足以下两个性质的极限函数:1.函数在t=0时的值为无穷大,即δ(0)=∞。
2.对任意的t≠0,函数的值为零,即δ(t)=0。
在实际应用中,由于冲激函数的定义非常特殊,它不是一个常用函数,而是作为一种数学工具来使用。
因此,我们通常可以将冲激函数理解为一个脉冲信号,它的幅值非常短暂且极大,然后迅速衰减为零。
这种特性使得冲激函数成为处理信号问题的重要工具。
接下来,我们来探讨冲激函数的特解的应用。
在信号处理和系统分析中,我们经常遇到线性时不变系统的微分方程,例如:d^n y(t) / dt^n + a_(n-1) d^(n-1) y(t) / dt^(n-1) + ... +a_0 y(t) = b_(n-1) d^(n-1) x(t) / dt^(n-1) + ... + b_0 x(t)其中,y(t)表示系统的响应,x(t)表示系统的输入信号,a_i和b_i表示系统的系数。
我们可以通过冲激函数的特解来求解这个微分方程。
假设系统的零状态响应为y_p(t),那么系统的总响应为y(t)=y_p(t)+y_c(t),其中y_c(t)是系统的零输入响应。
根据线性时不变系统的性质,我们可以将输入信号x(t)拆解为冲激函数的线性组合,即:x(t)=∫x(τ)δ(t-τ)dτ带入微分方程,我们可以得到:d^n y_p(t) / dt^n + a_(n-1) d^(n-1) y_p(t) / dt^(n-1) + ...+ a_0 y_p(t) = ∫ b_(n-1) d^(n-1) x(τ) / dt^(n-1) δ(t - τ)dτ + ... + b_0 x(t)根据冲激函数的性质,除了t=τ处的δ(t-τ)项之外,其他的冲激函数都为零。
冲激函数的卷积

冲激函数的卷积冲激函数(impulse function)是一种在数学和工程中经常出现的函数。
形式上,冲激函数是一个极小化了宽度但有无限高度的正态分布函数,通常表示为δ(t)。
冲激函数的主要特点是在t=0的地方等于无限值,且在其他地方都等于0。
当两个函数f(t)和g(t)做卷积运算时,结果可以写成下面的形式:f(t)*g(t) = ∫f(t-τ)g(τ)dτ在这个公式中,f(t)和g(t)可以是任何类型的函数,而τ是一个积分变量。
这个公式中包含的信息是f(t)的形状要和位于τ处的g(τ)的形状结合起来,可以想象它们的相对位置在不断地变化。
卷积运算的物理解释是将一个函数和一个滤波器(另一个函数)相乘,然后在一定时间内积分,得到的结果是输出信号。
在实际中,经常使用冲激函数来描述信号系统的行为。
因为冲激函数的一个重要特性是可以用来表示单位冲激响应函数(impulse response),即系统对单位冲激响应的输出。
另一个重要的特性是冲击函数具有筛选性质(selectivity property),即对于输入序列的每个分量,只有在t=0时能够对输出产生影响。
所以,当使用冲激函数对一个系统进行调试时,只需要生成一个单位冲激输入信号,通过观察系统的输出能够得到系统对每个分量响应的确认。
在卷积运算中,冲激函数具有独特的作用。
假设有一个函数f(t),我们将它和冲激函数做卷积运算,可以得到下面的形式:f(t)*δ(t) = ∫f(t-τ)δ(τ)dτ根据冲激函数的定义,只有在τ=0时δ(τ)才会取得其最大值。
再根据卷积运算的定义,当τ=t时f(t-τ)等于f(0),所以上式需要简化为:f(t)*δ(t) = f(0)这个结果非常有用。
它表示当一个信号与冲激函数做卷积运算时,得到的结果就是原始信号在t=0处的值。
这个性质在信号处理和控制系统设计中经常被用到。
举个例子,设有一个跃阶函数(step function)f(t),其表达式为:f(t) = 1,t>=0; f(t) = 0,t<0将f(t)和冲击函数δ(t)做卷积计算,可以得到下面的公式:f(t)*δ(t) = ∫f(t-τ)δ(τ)dτ = ∫1δ(τ)dτ = 1结果是1,这意味着在t=0处,f(t)的值为1。
冲激函数的定义

冲激函数的定义冲激函数是一种特殊的函数,它在数学和工程领域有着广泛的应用。
冲激函数在信号处理、控制理论、线性系统、微积分和物理学等领域都起着重要的作用。
本文将对冲激函数进行详细的定义和解释,以便读者更好理解其概念和应用。
1、什么是冲激函数冲激函数是数学中的一种特殊函数,也称为Dirac函数或Dirac delta函数。
冲激函数是在除零点外均为0,在零点附近无限大的函数。
冲激函数通常表示为δ(x),其中x为自变量。
冲激函数在x=0处的值无限大,但在除零点外的其他点的值都为0。
在物理学和工程领域,冲激函数可以通过一个实验来理解它的概念。
如果我们在时间轴上以极短的时间间隔内向电路中输入一个短暂的电压脉冲,那么电路将会产生一个极短的电流脉冲,这个电流脉冲就可以用一个冲激函数来描述。
2、冲激函数的重要性冲激函数在数学中的重要性很大。
它可以用在微积分、偏微分方程、傅里叶分析、抽象代数和泛函分析等领域。
在控制系统和信号处理领域,冲激函数也是非常重要的。
它可以用来描述系统的 impulse response(冲击响应)函数,冲激响应是控制系统和信号处理中非常常见的一种概念。
冲激函数还可以用来分析和设计滤波器和信号处理系统。
在物理学中,冲激函数可以用来描述质点、电荷或电流的瞬间变化情况。
冲激函数也可以用来描述物理学中的波函数,比如在量子力学中,波函数可以在测量时间点上采用Delta函数的形式。
冲激函数有一些非常重要的性质。
下面我们将对其中的一些最主要的进行介绍。
3.1 奇异性冲激函数在所有除零点外的点上取值为0,但在零点处取值为无穷大。
冲激函数在数学上是一个奇异函数,可能常常忽略它在除零点外的任何部分。
3.2 瞬时能量3.3 单位冲激函数3.4 积分性质冲激函数的积分性质十分重要。
因为冲激函数在所有除零点外的点上都为0,所以对于任意函数f(x),有:∫f(x)δ(x)dx=f(0)这意味着冲激函数的积分可以用来计算f(x)在零点处的值。
冲激函数

电路分析基础——第二部分:第九章内容回顾
内容回顾:
第七章:研究包含一个动态元件的一阶电路,它们用一阶
线性常系数常微分方程描述。一阶电路不同的响应形式根据 其初值和终值的相对大小而指数上升或衰减,变化的速度受 时间常数 ( = RC 或 = L/R) 的控制。
第八章:研究包含电感和电容两个动态元件的二阶电路,
电路分析基础——第二部分:第九章 目录
第九章 冲激函数在动态电路分 析中的应用
1 冲激函数
4 冲激响应
2 冲激函数的性质
5 由阶跃响应求冲激响应
3 电容电压和电感电流的跃变 6 线性非时变电路对任意输入 的响应——卷积积分
电路分析基础——第二部分:第九章内容回顾
内容回顾:
所有电路都是由动态电路和电阻电路两类电路组成的; 所有电路受到两类约束。即:
电路中的各支路电流、电压受到KVL、KCL的约束, 元件上的电流、电压受到元件VA全不同的电路,但 第一部分中的分析方法,几乎所有都能得到应用,当然, 动态电路还有其自己的方法; 电容和电感是基本的动态元件,它们都是储能元件。电容 通过存储电荷来存储电能,电感通过存储磁链来存储磁能。 电容的电压和电感的电流是它们最本质的变量,一般情况 下,它们都不能突变。……
t0 t
电路分析基础——第二部分:9-1
2/2
(t) 的其他工程逼近: (t) 除了矩形窄脉冲 p□(t)以外,还可以 有许多其他形式,如下面所示。关键是所包围的面积为 1。
pΔ(t)
1 Δ
pde(t)
1
2Δ
e–|t|/Δ
(t)
2Δ
–Δ 0
Δt
pcos(t)
4Δ
cos
2Δ
冲激函数

t
R L
e
R L
t
t
hu t
t
R L
Rt
e L
t
t=0时,有冲激
电压出现
19
§9-5 由阶跃响应求冲激响应
❖ 线性非时变电路有一个重要的性质:如果激励x产生
响应y,那末,
激励
dx dt
将产生响应为
dy dt
;
激励 xdt 将产生响应为 ydt K K为积分常数。
由图(b)求短路电流时,电流
可看成是电阻支路电流和电容支
路电流之和。
电阻支路的电流为(t)/Rl。阶 跃电压(t)作用于电容,意味着电
容电压发生跃变,因而电容支路
的电流为C1(t)。
is
t
t
R1
C1
t
R1 // R2 C1 C2
23
解答
运用叠加定理,阶跃电流作用于电路时,u2(t)的分量
❖ 计算冲激响应时,先计算由(t)产生的在t=0+时的初始
状态,然后求解由这一初始状态所产生的零输入响应。 此即为t>0时的冲激响应h(t)。
17
例9-8
试求电路中电流及电感电压的冲激响应。
解 把电感看作开路,作出t=0时的等效电路(b)。来自
冲激电源的冲激电压全部出现于电感两端。
关于冲激电压全部出现于电感可理解如下:如果冲激
f(t)=f(0),故得
f t t f 0 t
f
t
t
dt
f 0 tdt
冲激函数的傅里叶变换计算

冲激函数的傅里叶变换计算可以通过以下步骤进行: 1. 定义冲激函数:冲激函数通常用 δ(t) 表示,其中 t 表示时间。冲激函数在 t=0 时刻取 值为无穷大,其他时刻取值为零。
2. 冲激函数的傅里叶变换:冲激函数的傅里叶变换可以表示为 F(ω) = ∫[从负无穷到正无 穷] δ(t) * e^(-jωt) dt,其中 F(ω) 表示傅里叶变换后的结果,ω表示频率。
3. 计算傅里叶变换:由于冲激函数在 t=0 时刻取值为无穷大,而其他时刻取值为零,因 此可以将积分范围缩小为从 -ε 到 ε,其中 ε 为一个无穷小的正数。这样,傅里叶变换可以简 化为 F(ω) = ∫[从 -ε 到 ε] δ(t) * e^(-jωt) dt。
冲激函数的傅里叶变换计算
4. 计算结果:由于冲激函数在 t=0 时刻取值为无穷大,因此在积分范围内,只有当 t=0 时,δ(t) * e^(-jωt) 才有非零值。因此,傅里叶变换的结果可以表示为 F(ω) = ∫[从 -ε 到 ε] δ(t) * e^(-jωt) dt = e^(-jω*0) = 1,即冲激函数的傅里叶变换结果为常数1。
总结起来,冲激函数的傅里叶变换结果为常数1。这是因为冲激函数在时域上的特性导致 其频域上的傅里叶变换结果为常数。
ቤተ መጻሕፍቲ ባይዱ
8-6 冲激函数和冲激响应
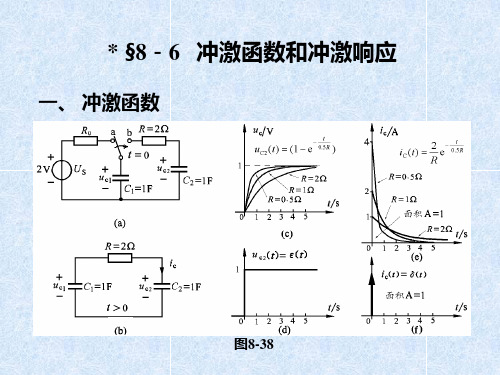
例如电压源电压US=20V,开关在t=5s时刻由a点倒向b 点,则冲激电流发生在 t=5s 时刻,根据式8-28,所产生的
冲激电流应该表示为
iS (t ) 10 δ (t 5)A
这个冲激电流使电容 C2 在 t = 5s 时刻,迅速获得10库 仑的电荷,使 1F 电容 C2 的电压压发生 10V 的跃变,由
h(t )
1
e
1
ε (t )
t
(8 32) -
计算冲激响应的另一种方
法是先求出面积为1个单位
的矩形脉冲的响应,然后 求脉冲宽度趋于零的极限。
1 e h ( )
f ( ) g ( )
(8 33)
当△→0时,P(t)趋向于单
位冲激,如图(g)所示,即
lim P (t ) δ (t ) (8 34 )
奇异值 δ = (t ) 0 ε 1 δ (t )dt 1 ε 2 t 0 t0 ε 1 0, ε
2
(8 28) 0
当图8-38(a)电路中电压源的电压增大时,从电容C1上 移动到电容C2的电荷量以及相应的电流脉冲的面积也将增 加,此时图(f)得到的冲激电流为A(t)。
uC2(5-)=0V 跃变到 uC2(5+)=10V。
q( t ) 1 t u C (t ) iS (t )dt 2 (t 5) V C 5
这是一个延迟的阶跃,如图(c)所示。由于冲激电流在 t=5s时刻,将10库仑电荷迅速投到5F电容的极板上,使电
容电压发生2V的跃变,由uC(5-)=0V跃变到uC(5+)=2V。
0
图8-42
注意到响应波形的峰值h△(△)将随△减小而增加,我 们用罗比塔法则求h△(△)在△→0时的极限
冲激函数及其性质

可以使用`title`和`xlabel`等函数为图形添加标题和坐标轴标签,以便更好地描述图 形。
计算卷积结果并展示图形
在MATLAB中,可以使用`conv` 函数计算两个序列的卷积结果。
将冲激信号与另一个信号进行卷 积运算,可以得到卷积后的结果
2023
PART 02
冲激函数性质分析
REPORTING
筛选性质
筛选性质定义
01
冲激函数具有筛选性质,即与任何函数相乘的结果都等于该函
数在冲激点的取值。
数学表达式
02
对于任意函数f(t),有f(t)*δ(t) = f(0)*δ(t)。
应用举例
03
在信号处理中,冲激函数可用于从复杂信号中提取特定时刻的
2023
冲激函数及其性质
https://
REPORTING
2023
目录
• 冲激函数基本概念 • 冲激函数性质分析 • 与其他函数关系探讨 • 在信号处理中应用举例 • MATLAB仿真实现冲激函数 • 总结回顾与拓展延伸
2023
PART 01
冲激函数基本概念
REPORTING
连续信号处理
在连续信号处理中,冲激函数可以表示为连续函 数的形式,通过求解冲激响应可以得到系统的输 出信号。
频域分析辅助工具
傅里叶变换
冲激函数在频域分析中具有重要的地位。通过傅里叶变换, 可以将时域信号转换为频域信号,进而分析信号的频谱特 性。
频域滤波器设计
利用冲激函数的频域特性,可以设计各种频域滤波器,实 现对信号频率成分的选择性过滤和处理。
线性叠加原理
冲激函数的特解

冲激函数的特解冲激函数是一种在数学和工程领域常用的特殊函数,它具有许多独特的性质和广泛的应用。
它的特解可谓是独具一格,发人深省。
冲激函数,顾名思义,形似一个瞬间突然增长到无穷大,然后迅速回到零的函数。
它可以用来描述一瞬间发生的现象,例如,当一个球体从高楼上自由下落时,撞到地面时的冲击力就可以用冲激函数来表示。
如果将这种冲击力视为一个“冲激”,那么在数学上,我们可以用冲激函数来模拟这个过程。
冲激函数在控制论、信号处理和物理学等领域有广泛的应用。
在控制论中,我们经常需要对系统的冲击响应进行分析和设计,例如自动驾驶汽车中的碰撞检测系统。
在信号处理中,冲激函数常常被用来描述信号的时域特性,例如在音频处理中,我们可以利用冲激函数来实现音频信号的均衡和滤波。
在物理学中,冲激函数可以用来描述电荷的分布、介质的传导和波的传播等现象。
冲激函数的特解与其它函数的特解有些不同之处。
在通常的微分方程中,我们需要给定一些初始条件来求解方程的特解,但对于冲激函数而言,其特解在冲激函数出现的瞬间即可得到。
这是因为冲激函数在出现瞬间的那一刻,它的值变为无穷大,而在其他时刻,它的值均为零。
因此,冲激函数的特解在出现时刻的性质决定了整个特解的形式。
冲激函数的特解具有高频调制和窄带性的特点。
高频调制意味着在时间轴上,冲激函数的特解的波峰和波谷之间的时间间隔非常短,从而可以观察到短时的冲击力。
窄带性意味着冲激函数的频率范围较窄,因此它对频率较低的信号有较强的敏感性,而对频率较高的信号则不敏感。
冲激函数的特解在工程实际中起到了重要的作用。
例如,在声学中,我们可以利用冲激函数的特解来精确测量音响系统的频率响应。
在通信中,我们可以使用冲激函数的特解来计算信道的冲击响应,从而实现可靠的信号传输。
在控制系统中,我们可以通过冲激函数的特解来设计控制器的增益和时间响应,从而实现系统的稳定性和性能优化。
总之,冲激函数的特解是一种生动而全面的数学工具,它在数学和工程领域发挥着重要的作用。
《电路分析》冲激函数和冲激响应
Rt
e L
(t)
R
e
Rt
L
(t)
L
(t)
R
e
Rt
L (t)
L
2002年春节摄于成都人民公园
当电阻R为不同数值时,电容上的电压uC2(t)以及电荷 移动所形成的电容电流iC(t),如图(c)和(e)所示。
由图8-38可见,当电路中的电阻分别为R=2、1、
0.5时,uC2(t)和iC(t)的波形如图所示。注意到电容C1上移
动到电容C2上的电荷量,即电容电流对时间的积分(电容电
流对时间轴之间的面积)均为1个单位,即
从以上叙述可以看出单位阶跃函数与单位冲激函数之存 在以下关系
δ (t) dε (t) dt
t
ε (t) δ ( )d -
(8 29) (8 30)
二、冲激响应
单位冲激信号作用下电路的零状态响应,称为电路的 冲激响应,用符号h(t)表示。计算任何线性时不变电路冲激 响应的一个方法是先求出电路的阶跃响应s(t),再将它对时 间求导即可得到冲激响应,即利用下式由电路的阶跃响应 计算出电路的冲激响应
如图(h)所示。利用单位阶跃函数(t),我们可以将式
(8-36)写为下式
h(t)
1
t
e
(t)
(8 37)
从以上讨论中可以看出,冲激电压或电流的作用就是 给动态元件提供一个初始储能(例如uC(0+)=1/C或iL(0+)=1/L),
即产生一个初始条件(例如f (0+)=1/)。此时刻以后电路响应
实际上是这些初始储能引起的零输入响应。
波形称为单位冲激电流,用(t)表示。
当且仅当其满足以下两个性质时,一个无界的信号(t)
04冲激信号

冲激函数主要内容由理想电路引入冲激函数12单位冲激函数的定义及波形任意冲激函数的定义及波形3如图所示用理想元件组成的电路,求电容电压、电容电流。
v C (t )=Eu (t )解电容电压0vC (t )tE注意:电容电压突变!−+E i C (t )。
v C (t )+−a。
bk 当t =0时,开关k 由a→b ,1、由理想电路引入冲激函数d v C (t)i C (t )=Cd t电容电流当t > 0或t < 0时,i C (t )=00v C (t )tE t = 0时,i C (t )=?电容电压1v C (t )=i C (τ) d τC⎰−∞t在t =0时,电容电压可导吗?在t =0时,电容电压v C (t )突变的原因是什么?问:在t =0时,电容电压可导吗?在t =0时,电容电压v C (t )突变的原因是什么?这样的物理现象可引入什么数学模型来描述?的时间积分有限的物理现象可以用冲激函数描述。
这种电流持续时间为零,电流幅度为无穷大,但电流问:答:2、单位冲激函数的定义及波形单位冲激函数的符号—— (t )单位冲激函数可由矩形脉冲面积保持为1,宽度τ→0的极限表示δ(t )=lim τ→0τ1u (t+) −u (t −)τ2τ20f (t )τ2τ21τ2−τ1τ11−τ11/τ−τ2τ2t单位冲激函数一般定义为δ(t )t(1)∞t = 00t ≠0δ(t ) =⎰∞−∞δ(t ) d t = 1幅度强度3、任意冲激信号(函数)的定义及波形任一时刻t = t 0、强度为A 的冲激函数记为A δ(t −t 0)∞t = t 00t ≠t 0A δ(t −t 0)(A )t 0tA δ(t −t 0) d t = A⎰∞−∞冲激函数由t −t 0=0→t=t 0A δ(t −t 0) =。
冲激函数

• t
ht
dst
dt
R
d dt
1
1t
e RC
•
t
R
t
t
e
1 RC
t
1 RC
1 t
e RC t
R
t t
1 RC
1 t
e RC t
1
1t
e RC
t
C
电容电压发生 了1/C的跃变
21
例9-12
试用诺顿定理求解补偿分压器 的输出压u2(t)。
解 诺顿定理能用于线性动态电路。ab 的左边部分可以用一个诺顿等效电路代 替,即可以用一个电流源与N0的并联组 合代替。 等效电流源的电流is(t)等于原电路中ab 端的短路电流,见图(b)。
17
例9-8
试求电路中电流及电感电压的冲激响应。
解 把电感看作开路,作出t=0时的等效电路(b)。来自冲激电源的冲激电 压全部出现于电感两端。
关于冲激电压全部出现于电感可理解如下:如果冲激电压出现于电阻, 则在电阻中将产生冲激电流,因而电感中也将有冲激电流,这样,电感 电压将为冲激偶电压,无法满足KVL。
4
其他形状脉冲的极限情况
❖ 冲激函数一般看成是矩形脉冲函数的极限情况,其他 形状脉冲的极限情况也可作为单位冲激的近似。
❖ 具有单位面积的三角形脉冲,当趋近于零时,可作 为单位冲激的近似。
5
负指数函数
f
t
0 Ae t
/
t0 t0
| Ae t / dt Ae t /
A
0
0
令 A 1,
t 0
在0-至0+期间,iC1(t)及iC2(t)中含有冲激电流,故得
冲激函数的一阶导数

冲激函数(也称为单位冲激函数或狄拉克冲激函数)用符号δ(t)表示。
它在t=0处为无穷大,其面积为1。
冲激函数的一阶导数是用导数的定义来理解,考虑极限:
δ′(t)=limΔt→0δ(t+Δt)−δ(t)
Δt
由于冲激函数在t=0处除了一个脉冲之外都是零,我们可以将这个极限化简为:
δ′(t)=limΔt→00−0
Δt
=0
因此,冲激函数的一阶导数是零,除了在t=0处的一个点外。
在这个点,导数未定义,因为冲激函数在t=0处不是光滑的。
需要注意的是,冲激函数和其导数在分布理论等数学领域有广泛的应用,但在普通函数的意义下,它们是一种广义函数,不容易在每个点上具有良好的定义。
