Mathematica 的动画制作
《Mathematica》使用手册

《Mathematica》使用手册Mathematica 使用手册1.简介1.1 Mathematica 简介1.2 Mathematica 的应用领域1.3 Mathematica 的基本特性2.安装与启动2.1 系统要求2.2 安装 Mathematica2.3 启动 Mathematica2.4 探索 Mathematica 界面2.5 设置用户首选项3.数值计算3.1 基本数值运算3.2 数值函数的使用3.3 数值积分与微分3.4 数值解方程3.5 特殊数值计算技巧4.符号计算4.1 符号数据类型4.2 符号运算与化简4.3 方程求解与解析解4.4 函数极限和级数展开4.5 矩阵与线性代数运算5.绘图与可视化5.1 绘制函数图像5.2 绘制二维与三维图形5.3 自定义图形选项5.4 绘制动态图形5.5 数据可视化6.编程与函数定义6.1 Mathematica 的编程语言 6.2 函数的定义与使用6.3 控制流程与条件判断6.4 模块化与函数封装6.5 文件读写与外部程序交互7.数据分析与统计7.1 数据导入与清洗7.2 数据处理与转换7.3 数据可视化与探索7.4 数值统计与假设检验7.5 机器学习与数据建模8.物理与工程应用8.1 经典力学模拟8.2 电磁场与电路分析8.3 量子力学与粒子物理8.4 工程建模与仿真8.5 数据分析在物理与工程中的应用9.MATLAB 兼容性与互操作9.1 导入与导出 MATLAB 数据9.2 运行 MATLAB 代码9.3 在 Mathematica 中调用 MATLAB 函数 9.4 在 MATLAB 中调用 Mathematica 函数9.5 MATLAB 兼容性的限制与注意事项10.Mathematica 社区与资源10.1 论坛和社区支持10.2 官方文档与教程10.3 第三方扩展包与资源10.4 在线学习资源10.5 Mathematica 社区的活动与会议本文档涉及附件:附件1:示例代码文件附件2:图形绘制示例文件附件3:数据分析样本数据集本文所涉及的法律名词及注释:1.版权:法律上对原创作品的保护权益。
Mathematica使用简介

a1 x2
6.
2 x+y → →
x2
a1 2x y
作用:例如对x求微分,得如下结果:
如果希望知道D的用法,怎么办? HELP 查看帮助命令
二、绘图命令
Plot[f,{x,xmin,xmax}] 从xmin到xmax绘制绘制f(x)的函数图 Plot[{f1,f2,f3,…},{x, xmin,xmax}] 同时绘制多个函数图
x cos t 例,单位圆的参数形式为 y sin t
则画圆操作如下: ParametricPlot[{Cos[t],Sin[t]},{t,-Pi,Pi}]
(ii)三维参数作图
ParametricPlot3D[参数形式函数,{自变量1,下限,上限}, {自变量2,下限,上 限},,选项]
数学表达式的二维格式输入
Expression input Edit菜单 a1 2 例:输入数学表 x 2x y 达式:
步骤 1. 2. 3. 4. 5. 按键顺序 x (ctrl+6) 2 → + a (ctrl+-) 1 (ctrl +/) (ctrl+2) 显示结果
x
x
x2
2
x2 a 1
2) 如果希望多个图形左右或上下排成一长图而 重叠,则可以用GraphicsArray 命令 Show[GraphicsArray[{g1, g2, …}]] 将图形横向并排 Show[GraphicsArray[{ {g1}, {g2}, …}]] 将图形纵向排列 Show[GraphicsArray[{ {g1, g2, …}, …}]] 将图形以二维矩阵的形式排列
5.
图形的合并与排列
《Mathematica》使用手册

《Mathematica》使用手册Mathematica使用手册=========================第一章:介绍Mathematica-------------------------------------1.1 Mathematica的概述Mathematica是一种强大的数学计算和数据处理软件,广泛应用于科学、工程、计算机科学等领域。
1.2 安装和启动本节介绍如何安装Mathematica软件并启动它。
1.3 界面和基本操作介绍Mathematica的界面和基本操作,包括工具栏、菜单、笔记本等。
第二章:基本语法和数据类型-------------------------------------2.1 表达式和运算符讲解Mathematica的表达式和运算符,包括数值运算、符号运算、逻辑运算等。
2.2 变量和函数介绍Mathematica中的变量和函数的定义和使用方法。
2.3 数据类型讲解Mathematica中的基本数据类型,包括数值类型、字符串类型、列表类型等。
第三章:图形绘制-------------------------------------3.1 绘制函数图像介绍使用Mathematica绘制函数图像的方法和技巧。
3.2 绘制二维图形讲解Mathematica中绘制二维图形的常用函数和参数设置。
3.3 绘制三维图形介绍Mathematica中绘制三维图形的方法,包括绘制曲面、绘制立体图形等。
第四章:方程求解和数值计算4.1 方程求解讲解Mathematica中方程求解的方法和技巧。
4.2 数值计算介绍Mathematica中数值计算的函数和用法。
4.3 微分方程求解讲解Mathematica中求解微分方程的方法和技巧。
第五章:数据分析和统计-------------------------------------5.1 数据导入和导出介绍Mathematica中的数据导入和导出方法。
Mathematica介绍

Mathematica介绍Mathematica 5.0使⽤简介Mathematica是美国Wolfram Research公司研制的⼀种数学软件, 集⽂本编辑、符号运算、数值计算、逻辑分析、图形、动画、声⾳于⼀体, 与Matlab、Maple⼀起被称为⽬前国际上最流⾏的三⼤数学软件. 它以符号运算见长, 同时具有强⼤的图形功能和⾼精度的数值计算功能. 在Mathematica中可以进⾏各种符号和数值运算, 包括微积分、线性代数、概率论和数理统计等数学各个分⽀中公式的推演、数值求解⾮线性⽅程、最优化问题等,可以绘制各种复杂的⼆维图形和三维图形,并能产⽣动画和声⾳.Mathematica系统与常见的⾼级程序设计语⾔相似, 都是通过⼤量的函数和命令来实现其功能的. 要灵活使⽤Mathematica, 就必须尽可能熟悉各种内部函数(包括内置函数和软件包函数). 由于篇幅限制, 本附录以2003年发布的Mathematica 5.0为基础, 简单分类介绍软件系统的基本功能, 及与微积分有关的函数(命令)的使⽤, 其他功能请读者⾃⾏查阅帮助或有关参考⽂献. 另外, 为节省篇幅, 本附录有时也将键盘输⼊和系统输出尽可能写在同⼀⾏, 并省略某些输出, 读者可上机演⽰观看结果1 启动与运⾏Mathematica是⼀个交互式的计算系统, 计算是在⽤户和Mathematica互相交互、传递信息数据的过程中完成的. Mathematica 系统所接受的命令都被称作表达式, 系统在接受了⼀个表达式之后就对它进⾏处理(即表达式求值), 然后再把计算结果返回. 1.1 启动假设在Windows环境下已安装好Mathematica 5.0, 那么进⼊系统的⽅法是: 在桌⾯上双击Mathematica图标(图1-1)或从“开始”菜单的“程序”下的“Mathematica 5”联级菜单下单击Mathematica图标(图1-2)均可.图1-1 图1-2启动了Mathematica后, 即进⼊Mathematica的⼯作环境----Notebook窗⼝(图1-3), 它像⼀张长长的草稿纸, ⽤户可以在上⾯输⼊⼀⾏或多⾏的表达式, 并可像处理其他计算机⽂件⼀样, 对它进⾏创建、打开、保存、修改和打印等操作.第⼀个打开的Notebook⼯作窗⼝, 系统暂时取名Untitled-1, 直到⽤户保存时重新命名为⽌, 必要时⽤户可同时打开多个⼯作窗⼝, 系统会依次暂时取名为Untitled-2、Untitled-3 .图1-3 Mathematica的⼯作窗⼝在⼯作窗⼝中, 你就可键⼊想计算的东西, ⽐如键⼊2+3, 然后同时按下Shift键和Enter键或者只按下数字键盘区(右⼩键盘区)的Enter键, 这时系统开始计算并输出计算结果5, 同时⾃动给输⼊和输出附上次序标识In[1]:=和Out[1]= ;若再输⼊第⼆个表达式a=1+Abs[-3]-2*Sin[Pi/2]后, 按Shift+Enter输出结果, 系统也会作类似处理, 窗⼝变化如图1-4.图1-4 完成运算后的Mathematica的窗⼝1.2 基本命令Mathematica的基本命令有如下两种形式:(1)表达式/ 执⾏表达式运算, 显⽰结果, 并将结果保存在Out[x]中;(2)变量=表达式/ 除(1)的功能外, 还对变量进⾏赋值.注意:命令⾏后⾯如果加上分号“;”, 那么就不显⽰运算结果.1.3 退出要退出Mathematica, 可单击关闭窗⼝按钮或从菜单“File”中选择“Exit”(或“Close”)或按Ctrl (或Alt)+F4, 这时如果窗⼝中还有未保留的内容, 系统会显⽰⼀对话框, 询问是否保存. 单击“否(N)”,则关闭窗⼝;单击“是(Y)”,则调出“SaveNotebook”对话框,等待你输⼊⽂件名, 保存“Notebook”的内容后再退出. 所保存的内容是以“.nb”为扩展名的Mathematica⽂件, 以后需要时, 可通过菜单“File”中的“Open”调⼊使⽤.1.4 使⽤联机帮助系统在使⽤Mathematica的过程中, 常常需要了解⼀个命令的详细⽤法, 或者想知道系统中是否有完成某⼀计算的命令, 联机帮助系统是最详细、最⽅便的资料库. 通常可使⽤如下两种求助⽅法:(1) 获取函数和命令的帮助在Notebook界⾯下, ⽤? 或?? 可向系统查询运算符、函数和命令的定义和⽤法. 例如查询函数Abs的⽤法可⽤Abs / 系统将给出调⽤Abs的格式及Abs命令的功能(如果⽤两个问号“??”, 则信息会更详细些);Abs* / 给出所有以Abs这三个字母开头的命令.(2) 使⽤Help菜单任何时候都可以通过按F1键或点击菜单项Help, 选择Help Browser调出帮助菜单, 供你选择浏览各种类的命令格式及功能.1.5 说明在输⼊时要注意如下⼏个规则:(1) 输⼊的字母严格区分⼤⼩写. 系统预定义变量和函数名第⼀字母⼀定要⽤⼤写(可参见表1-1和表1-2);(2) 变量名不能以数字开头, 当中也不能出现空格, 否则数字与字母之间或空格之间系统会默认是相乘关系, 例如x2可作变量名,但2x表⽰2*x;(3) 严格区分花括号、⽅括号与圆括号, 函数后⾯的表达式⼀定要放在⽅括号内, ⽽算术表达式中的括号只允许⽤圆括号(⽆论有多少层);(4) 数值计算时, 输出的结果将尽量保持精确值, 即结果中有时会含有分式、根式或函数的原形式. 例如In[1]:=1/2+1/3 Out[1]= 5 6In[2]:=Sqrt[4+8] Out[2]=In[3]:=Sin[1+2] Out[3]= Sin[3]这时, 若要得到⼩数表⽰的结果(近似数), 可在命令⾏后⾯加上“//N”或引⽤N函数, 函数格式为N[表达式, 有效数位]. 例如In[1]:=1/2+1/3 //N Out[1]= 0.833333In[2]:=N[Sqrt[4+8],10] Out[2]=3.464101615(5) 特殊字母、符号的输⼊,可使⽤热键(见表1-3), 当然也可利⽤符号输⼊平台: 先从菜单“File”中的“Palettes”打开基本输⼊⾯板“4 BasicInput”窗⼝(见图1-5), 点击相应的符号即可实现数学运算的输⼊.符号输⼊平台(菜单项“File→Palettes”)中含有9种输⼊⾯板, 利⽤它们可⼤⼤⽅便字符、命令、函数的输⼊, 尤其是“3 BasicCalculation”窗⼝(“基本计算⾯板”,可见图1-5), 其中含有常⽤的7⼤类函数的输⼊⾯板, 需要应⽤某类函数的栏⽬时, 只须点击相应栏⽬的左端折叠标志符号“ ”, 即变成展开标志符号“?”, 同时打开它所含下级的函数(类)输⼊⾯板, 最后找到所需的命令单击选定. 例如要输⼊⼀个2阶⽅阵, 可点击“File→Palettes→3 BasicCalculation →Lists andMatrices →Creating Lists and Matrices”,再点击选定“??”即可.图1-5 Mathematica的符号输⼊平台(6) 前⾯旧的命令⾏In[x], 可通过光标的上、下移动,对它进⾏编辑、修改再利⽤;对前⾯计算好的结果Out[x], 也可使⽤如下的⽅式调⽤:% / 代表上⾯最后⼀个输出结果;%% / 代表上⾯倒数第⼆个输出结果;%n / 代表上⾯第n个输出结果, 即Out[n].2 变量与函数变量和函数是Mathematica中⼴泛应⽤的重要概念, 对它们的操作命令⾮常丰富, 这⾥仅介绍⼏种基本的操作⽅法, 其它功能请读者随着学习的深⼊, ⾃⼰逐步去体会.2.1 变量赋值在Mathematica中, 运算符号“=”起赋值作⽤, 此处的“=”应理解为给它左边的变量赋⼀个值, 这个值可以是⼀个数值、⼀个数组、⼀个表达式,也可以是⼀个图形. 赋值有如下的基本形式:(1) 变量名=值/ 给⼀个变量赋值(2) 变量名1=变量名2=值/ 给⼆个变量赋相同值(3) {变量名1, 变量名2,…}={值1, 值2,…} / 给多个变量赋不同的值注意:变量⼀旦赋值后, 那么这个值将⼀直保留, 此后, ⽆论变量出现在何处, 都会⽤该值替代它, 直到你清除或再次定义它为⽌.对于已定义的变量, 当你不再使⽤它的时候, 为防⽌它影响以后的运算, 最好及时清除它的值.清除变量值命令有如下两种形式:(1)变量名=.(2)Clear[变量名列表] /列表中列出的是要清值的变量名,之间⽤逗号分开例如In[1]:= x=y=2 Out[1]= 2In[2]:= s=2x+3y Out[2]= 10In[3]:= x=.In[4]:= s=2x+3y Out[4]= 6+2x2.2 变量替换表达式中的变量名(未赋值)就像⼀个符号, 必要时我们可⽤新的内容替换它. 变量替换格式如下:(1) 表达式/.变量名->值(2) 表达式/.{变量名1->值1, 变量名2->值2,…}例如In[1]:= 1+2x+3y/.{x->2,y->s+1} Out[1]= 5+3(1+s)注意: 变量替换与变量赋值的差异在于, 变量替换是暂时性的, ⽽变量赋值是长久性的.2.3 定义函数Mathematica系统提供了⼤量的内部函数让⽤户选⽤(可参见表1-2), ⽤户若有需要也可以⾃⼰定义新函数, 这些⾃定义的函数会加⼊到当前的系统中, 如同内部函数⼀样可被随时调⽤. ⾃定义函数的⼀般形式是:函数名[⾃变量名_]=表达式或函数名[⾃变量名_]:=表达式注意:下划线“_”是在⾃变量名的右边, 它表⽰左边的⾃变量是形式参数. 类似地, 可定义不少于两个⾃变量(多元)函数. 如⼆元函数定义为函数名[⾃变量名1_, ⾃变量名2_]=表达式In[1]:= f[x_]=x+3;{f[x],f[y],f[2]} Out[1]= {3+x,3+y,5} In[2]:= g[x_,y_]=x^2-y^2;In[3]:= g[1,2] Out[3]= 43 表与矩阵表是指形式上由花括号括起来的若⼲个元素, 元素之间⽤逗号分隔. 在运算中可对表作整体操作, 也可对表中的单个元素操作. 表可以表⽰数学中的集合、向量和矩阵, 也可以表⽰数据库中的⼀组记录. 表中的元素可以是任何数据类型的数值、表达式,甚⾄是图形或表格.3.1 表的基本操作(1) 建表: 表中元素较少时, 可在给出表名时⼜定义表中元素, 格式如下表名(变量名)={元素1,元素2, …}这⾥, 元素可以是不同类型的数据.经常地, 使⽤建表函数快速建表:表名=Table[通项公式, {循环变量,循环初值,循环终值,步长}]其中, 当循环初值或步长是1时可以省略, 循环范围还可多重设置.例如In[1]:= A={1,2,3};2+3A Out[1]= {5,8,11}In[2]:= t=Table[i+j,{i,2},{j,3}] Out[2]={{2,3,4},{3,4,5}}(2) 元素处理: 处理表元素常⽤的格式(函数)有A[[i]] \ 取表A中的第i个元素Part[A{i,j,…}] 或A[[{i,j,…}]] \ 取表A中的第i,j,..元素组成新表Part[A,i]=值或A[[i]]=值\ 给表A的第i个元素重新赋值3.2 矩阵的基本操作矩阵是表的特殊形式(⼆维表), 所有标准的表操作都可⽤于矩阵操作, 除此⽽外, 它具有很多特殊的运算函数, 下⾯就简单介绍⼏类常⽤的函数.(1) 创建特殊矩阵函数(表3-1)(2) 截取矩阵块函数(表3-2)(3) 矩阵的基本运算函数(表3-3)注意:[1] 向量也是表的特殊形式(⼀维表), 对它的操作命令很多是与矩阵操作相类似的, 这⾥就不在另列. 且在Mathematica的实际应⽤中, 是不区分⾏向量还是列向量的.[2] 矩阵(向量)间的相乘要⽤点乘符号“.”表3-1 创建特殊矩阵4 符号运算Mathematica是在⼀个完全集成环境下的符号运算系统, 它具有强⼤的处理符号表达式的能⼒, 代数运算、微分、积分和微分⽅程求解等都是很典型的例⼦.4.1 代数运算(1) 展开格式: Expand[表达式]注: 对多项式按幂次展开; 对分式展开分⼦, 各项除以分母.(2) 分解因式格式: Factor[表达式]注: 对多项式进⾏因式分解; 对分式分⼦、分母各⾃因式分解.(3) 化简格式: Simplify[表达式]例如In[1]:= Expand[(1+2x)^2] Out[1]= 1+4x+4x2In[2]:= Factor[%] Out[2]= (1+2x)2In[3]:= Simplify[1/(1+1/(1+x))+1/(2(1-x))] Out[3]=11 222xx x++-+说明:代数运算还有很多操作函数, 读者必要时可从“File→Palettes→2 AlgebraicManipulation ”的窗⼝⾯板中选⽤.4.2 微分(1) ⼀阶导数格式: D[函数,⾃变量] / 函数关于指定⾃变量的导数(2) ⾼阶导数格式: D[函数,{⾃变量,n}] / 函数关于指定⾃变量的n阶导数(3) 混合偏导数格式: D[函数, x , y,…] / 函数关于⾃变量x , y,…的混合偏导数(4) 全微分格式: Dt[函数] / 函数关于各变量的全微分例如In[1]:= D[Sin[x],x] Out[1]= Cos[x]In[2]:= D[Sin[2x],{x,2}] Out[2]= -4Sin[2x]In[3]:= D[Sin[x*y],x,,y] Out[3]= Cos[xy]-xySin[xy]In[3]:= Dt[Sin[x*y],x,y] Out[3]= Cos[xy](yDt[x]+xDt[y])4.3 积分(1) 不定积分格式: Integrate[函数,⾃变量](2) 多重不定积分格式: Integrate [函数,⾃变量1,⾃变量2]或Integrate [函数,⾃变量1,⾃变量2,⾃变量3](3) 定积分格式: Integrate[函数,{⾃变量,下限,上限}]或NIntegrate[函数,{⾃变量,下限,上限}] / 数值积分(4) 多重定积分格式: Integrate[函数,{⾃变量1,下限1,上限1},…]或NIntegrate[函数,{⾃变量,下限,上限},…] / 数值积分例如In[1]:= Integrate[Sin[x]+1,x] Out[1]= x-Cos[x]In[2]:= Integrate[4x*y+1,x,y] Out[2]= xy+x2y2In[3]:= Integrate[Sin[x]+1,{x,0,1}] Out[3]= 2-Cos[1]In[4]:= NIntegrate[Sin[x]+1,{x,0,1}] Out[4]= 1.4597In[5]:= Integrate[4x*y+1,{x,0,1},{y,0,1}] Out[2]= 24.4 常微分⽅程的准确解在Mathematica中, 使⽤函数DSolve[]可以求解线性和⾮线性的常微分⽅程(组). 求特解时, 可将定解的条件作为⽅程的⼀部分.格式: DSolve[⽅程,未知函数,⾃变量]例如In[1]:= DSolve[y’[x]==2x,y[x],x] Out[1]={{y[x]->x2+C[1]}} In[2]:= DSolve[{y’[x]==2y[x],y[0]==3},y[x],x] Out[2]={{y[x]->3e2x }}In[3]:= DSolve[{y’[x]==z[x],z’[x]== -y[x]},{y[x],z[x]},x]Out[3]={{y[x]->C[1]Cos[x]+C[2]Sin[x], z[x]->C[2]Cos[x] -C[1]Sin[x]}}注: ⼤多数情况, 微分⽅程的精确解是不能⽤初等函数表⽰出来的, 这时, 只能求其数值解, 并结合作图功能画出解的⼤致图形, 这些内容后⾯再作介绍.4.5 幂级数展开格式: Series[函数表达式,{变量,展开点x0,阶数n}]例如In[1]:= Series [Sin[x],{x,0,5}] Out[1]=3560[] 6120x xx x -++注:去掉表达式中的误差项O[x]n 可调⽤Normal[] 函数.5 数值计算Mathematica的优势在于符号运算, 但对于数值问题, 它也提供了丰富的数值计算功能, 例如求和(有限或⽆限)、求极限值、解代数⽅程、求⾮线性⽅程数值解和求微分⽅程数值解等。
Mathematica使用说明

Mathematica 入门一、引 言Mathematica 是美国Wolfram 公司开发的一个功能强大的数学软件系统,它主要包括:数值计 算、符号计算、图形功能和程序设计. 本指导书力图在不大的篇幅中给读者提供该系统的一个简 要的介绍. 指导书是按Mathematica 4.0版本编写的, 但是也适用于Mathematica 的任何其它图形 界面的版本.Mathematica 在数值计算、符号运算和图形表示等方面都是强有力的工具,并且其命令句法惊 人地一致, 这个特性使得Mathematica 很容易使用.不必担心你还不太熟悉计算机.本入门将带你 迅速了解Mathematica 的基本使用过程, 但在下面的介绍中,我们假定读者已经知道如何安装及启动Mathematica. 此外,始终要牢记的几点是:● Mathematica 是一个敏感的软件. 所有的Mathematica 函数都以大写字母开头; ● 圆括号( ),花括号{ },方括号[ ]都有特殊用途, 应特别注意; ● 句号“.”,分号“;”,逗号“,”感叹号“!”等都有特殊用途, 应特别注意; ● 用主键盘区的组合键Shfit+Enter 或数字键盘中的Enter 键执行命令.二、一般介绍1. 输入与输出例1 计算 1+1:在打开的命令窗口中输入1+2+3并按组合键Shfit+Enter 执行上述命令,则屏幕上将显示:In[1] : =1+2+3 Out[1] =6这里In[1] : = 表示第一个输入,Out[1]= 表示第一个输出,即计算结果.2. 数学常数Pi 表示圆周率π; E 表示无理数e; I 表示虚数单位i ; Degree 表示π/180; Infinity 表示无穷大.注:Pi,Degree,Infinity 的第一个字母必须大写,其后面的字母必须小写.3. 算术运算Mathematica 中用“+”、“-”、“*”、“/” 和“^”分别表示算术运算中的加、减、乘、除和 乘方.例2 计算 π⋅⎪⎭⎫ ⎝⎛⋅+⎪⎭⎫⎝⎛⋅--213121494891100. 输入 100^(1/4)*(1/9)^(-1/2)+8^(-1/3)*(4/9)^(1/2)*Pi则输出 3103π+这是准确值. 如果要求近似值,再输入N[%] 则输出 10.543这里%表示上一次输出的结果,命令N[%]表示对上一次的结果取近似值. 还用 %% 表示上 上次输出的结果,用 %6表示Out[6]的输出结果.注:关于乘号*,Mathematica 常用空格来代替. 例如,x y z 则表示x*y*z,而xyz 表示字符 串,Mathematica 将它理解为一个变量名. 常数与字符之间的乘号或空格可以省略.4. 代数运算例3 分解因式 232++x x 输入 Factor[x^2+3x+2] 输出 )x 2)(x 1(++ 例4 展开因式 )2)(1(x x ++ 输入 Expand[(1+x)(2+x)] 输出 2x x 32++例5 通分 3122+++x x 输入 Together[1/(x+3)+2/(x+2)]输出 )x 3)(x 2(x38+++例6 将表达式)3)(2(38x x x+++ 展开成部分分式输入 Apart[(8+3x)/((2+x)(3+x))]输出 3x 12x 2+++ 例7 化简表达式 )3)(1()2)(1(x x x x +++++ 输入 Simplify[(1+x)(2+x)+(1+x)(3+x)]输出 2x 2x 75++三、函数1. 内部函数Mathematica 系统内部定义了许多函数,并且常用英文全名作为函数名,所有函数名的第一个 字母都必须大写,后面的字母必须小写. 当函数名是由两个单词组成时,每个单词的第一个字母都 必须大写,其余的字母必须小写. Mathematica 函数(命令)的基本格式为函数名[表达式,选项] 下面列举了一些常用函数:算术平方根x Sqrt[x] 指数函数x e Exp[x] 对数函数x a log Log[a,x]对数函数x ln Log[x]三角函数 Sin[x], Cos[x], Tan[x], Cot[x], Sec[x], Csc[x] 反三角函数ArcSin[x], ArcCos[x], ArcTan[x], ArcCot[x], AsrcSec[x], ArcCsc[x]双曲函数 Sinh[x], Cosh[x], Tanh[x], 反双曲函数 ArcSinh[x], ArcCosh[x], ArcTanh[x] 四舍五入函数 Round[x] (*取最接近x 的整数*) 取整函数 Floor[x] (*取不超过x 的最大整数*) 取模 Mod[m,n] (*求m/n 的模*)取绝对值函数 Abs[x] n 的阶乘 n! 符号函数 Sign[x] 取近似值 N[x,n] (*取x 的有n 位有效数字的近似值,当n 缺省时,n 的默认值 为6*)例8 求π的有6位和20位有效数字的近似值. 输入 N[Pi] 输出 3.14159输入 N[Pi, 20] 输出 3.1415926535897932285 注:第一个输入语句也常用另一种形式: 输入 Pi//N 输出 3.14159例9 计算函数值(1) 输入 Sin[Pi/3] 输出23 (2) 输入 ArcSin[.45] 输出 0.466765 (3) 输入 Round[-1.52] 输出 -2 例10 计算表达式)6.0arctan(226sin 2ln 1132+-+-e π 的值 输入 1/(1+Log[2])*Sin[Pi/6]-Exp[-2]/(2+2^(2/3))*ArcTan[.6] 输出 0.2749212. 自定义函数在Mathematica 系统内,由字母开头的字母数字串都可用作变量名,但要注意其中不能包含空 格或标点符号.变量的赋值有两种方式. 立即赋值运算符是“=”,延迟赋值运算符是“: =”. 定义函数使用 的符号是延迟赋值运算符“: =”.例11 定义函数 12)(23++=x x x f ,并计算)2(f ,)4(f ,)6(f . 输入Clear[f,x]; (*清除对变量f 原先的赋值*) f[x_]:=x^3+2*x^2+1; (*定义函数的表达式*) f[2] (*求)2(f 的值*)f[x]/.{x->4} (*求)4(f 的值,另一种方法*)x=6; (*给变量x 立即赋值6*)f[x] (*求)6(f 的值,又一种方法*)输出17 97 289注:本例1、2、5行的结尾有“;”,它表示这些语句的输出结果不在屏幕上显示.四、解方程在Mathematica 系统内,方程中的等号用符号“==”表示. 最基本的求解方程的命令为 Solve[eqns, vars]它表示对系数按常规约定求出方程(组)的全部解,其中eqns 表示方程(组),vars 表示所求未知变量. 例12 解方程0232=++x x 输入 Solve[x^2+3x+2==0, x] 输出 }}1x {},2x {{-→-→例13 解方程组 ⎩⎨⎧=+=+1dy cx by ax输入 Solve[{a x + b y == 0,c x + d y ==1}, {x,y}]输出 ⎭⎬⎫⎩⎨⎧⎭⎬⎫⎩⎨⎧+-→-→ad bc a y ,ad bc b x例14 解无理方程a x x =++-11输入 Solve[Sqrt[x-1]+ Sqrt[x+1] == a, x]输出 ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+→24a 4a 4x 很多方程是根本不能求出准确解的,此时应转而求其近似解. 求方程的近似解的方法有两种, 一种是在方程组的系数中使用小数,这样所求的解即为方程的近似解;另一种是利用下列专门用于 求方程(组)数值解的命令:NSolve[eqns, vars] (*求代数方程(组)的全部数值解*)FindRoot[eqns, {x, x0}, {y, y0} ,]后一个命令表示从点),,(00 y x 出发找方程(组)的一个近似解,这时常常需要利用图像法先大致确定所求根的范围,是大致在什么点的附近.例15 求方程013=-x 的近似解 输入 NSolve[x^3-1== 0, x]输出 {{→x -0.5-0.866025ii},{→x -0.5+0.866025ii},{→x 1.}} 输入 FindRoot[x^3-1==0,{x, .5}] 输出 {→x 1.}下面再介绍一个很有用的命令:Eliminate[eqns, elims] (*从一组等式中消去变量(组)elims*)例16从方程组 ⎪⎩⎪⎨⎧=+=-+-+=++11)1()1(1222222y x z y x z y x 消去未知数y 、z .输入Eliminate[{x^2+y^2+z^2 ==1,x^2+(y-1)^2 + (z-1)^2 ==1, x + y== 1},{y, z}] 输出 0x 3x 22==+-注:上面这个输入语句为多行语句,它可以像上面例子中那样在行尾处有逗号的地方将行与行 隔开, 来迫使Mathematica 从前一行继续到下一行在执行该语句. 有时候多行语句的意义不太明 确,通常发生在其中有一行本身就是可执行的语句的情形,此时可在该行尾放一个继续的记号“\”, 来迫使Mathematica 继续到下一行再执行该语句.五、保存与退出Mathematica 很容易保存Notebook中显示的内容,打开位于窗口第一行的File菜单,点击Save 后得到保存文件时的对话框,按要求操作后即可把所要的内容存为*.nb文件. 如果只想保存全部输入的命令,而不想保存全部输出结果,则可以打开下拉式菜单Kernel,选中Delete All Output,然后再执行保存命令. 而退出Mathematica与退出Word的操作是一样的.六、查询与帮助查询某个函数(命令)的基本功能,键入“?函数名”,想要了解更多一些,键入“??函数名”,例如, 输入?Plot则输出Plot[f,{x,xmin,xmax}] generates a plot of f as a functionof x from xmin to xmax. Plot[{f1,f2,…},{x,xmin,xmax}] plots several functions fi它告诉了我们关于绘图命令“Plot”的基本使用方法.例17 在区间]1,1y=的图形.[-上作出抛物线2x输入Plot[x^2,{x,-1,1}]则输出例18 .输入Plot[{Sin[x],Cos[x]},{x,0,2Pi}]则输出??Plot则Mathematica会输出关于这个命令的选项的详细说明,请读者试之.此外,Mathematica的Help菜单中提供了大量的帮助信息,其中Help菜单中的第一项Help Browser(帮助游览器)是常用的查询工具,读者若想了解更多的使用信息,则应自己通过Help菜单去学习.空间图形的画法(基础实验)实验目的 掌握用Mathematica 绘制空间曲面和曲线的方法. 熟悉常用空间曲线和空间曲面 的图形特征,通过作图和观察, 提高空间想像能力. 深入理解二次曲面方程及其图形.基本命令1.空间直角坐标系中作三维图形的命令Plot3D命令Plot3D 主要用于绘制二元函数),(y x f z =的图形. 该命令的基本格式为Plot3D[f[x,y],{x,x1,x2},{y,y1,y2},选项]其中f[x,y]是y x ,的二元函数, x1,x2表示x 的作图范围, y1,y2表示y 的作图范围.例如,输入Plot3D[x^2+y^2,{x,-2,2},{y,-2,2}]则输出函数22y x z +=在区域22,22≤≤-≤≤-y x 上的图形(图2.1)与Plot 命令类似, Plot3D 有许多选项. 其中常用的如PlotPoints 和ViewPoint. PlotPoints 的用 法与以前相同. 由于其默认值为PlotPoints->15, 常常需要增加一些点以使曲面更加精致, 可能要 用更多的时间才能完成作图. 选项ViewPoint 用于选择图形的视点(视角), 其默认值为 ViewPoint->{1.3,-2.4,2.0},需要时可以改变视点.2.利用参数方程作空间曲面或曲线的命令ParametricPlot3D 用于作曲面时, 该命令的基本格式为ParametricPlot3D[{x[u,v],y[u,v],z[u,v]},{u,u1,u2},{v,v1,v2},选项]其中x[u,v],y[u,v],z[u,v]是曲面的参数方程表示式. u1,u2是作图时参数u 的范围, v1,v2是参数v 的 范围.例如,对前面的旋转抛物面, 输入ParametricPlot3D[{u*Cos[v],u*Sin[v],u^2},{u,0,3},{v,0,2 Pi}]同样得到曲面22y x z +=的图形(图2.2).由于自变量的取值范围不同, 图形也不同. 不过, 后者比较好的反映了旋转曲面的特点, 因 而是常用的方法.又如, 以原点为中心, 2为半径的球面. 它是多值函数, 不能用命令Plot3D 作图. 但是, 它的 参数方程为,20,0,cos 2,sin sin 2,cos sin 2πθπϕϕθϕθϕ≤≤≤≤===z y x因此,只要输入ParametricPlot3D[{2 Sin[u]*Cos[v],2 Sin[u]*Sin[v],2 Cos[u]},{u,0,Pi},{v,0,2 Pi}]便作出了方程为22222=++y x z 的球面(图2.3)..用于作空间曲线时,ParametricPlot3D 的基本格式为ParametricPlot3D[{x[t],y[t],z[t]},{t,t1,t2},选项]其中x[t],y[t],z[t]是曲线的参数方程表示式. t1,t2是作图时参数t 的范围.例如, 空间螺旋线的参数方程为).80(10/,sin ,cos π≤≤===t t z t y t x输入ParametricPlot3D[{Cos[t],Sin[t],t/10,RGBColor[1,0,0]},{t,0,8 Pi}]则输出了一条红色的螺旋线(图2.4).在这个例子中,请读者注意选项RGBColor[1,0,0]的位置.用于作空间曲线时, ParametricPlot3D 的选项PlotPoints 的默认值是30, 选项ViewPoint 的默 认值没有改变.3.作三维动画的命令MoviPlot3D:无论在平面或空间, 先作出一系列的图形, 再连续不断地放映, 便得到动画. 例如, 输入调用作图软件包命令<<Graphics\Animation.m.执行后再输入MoviePlot3D[Cos[t*x]*Sin[t*y],{x,-Pi,Pi},{y,-Pi,Pi},{t,1,2},Frames->12]则作出了12幅曲面图, 选中任一幅图形, 双击它便可形成动画.实验举例一般二元函数作图例2.1 (教材 例2.1) 作出平面y x z 326--=的图形,其中20,30≤≤≤≤y x . 输入Plot3D[6-2x-3y,{x,0,3},{y,0,2}]则输出所作平面的图形(图2.5).如果只要位于第一卦限的部分, 则输入Plot3D[6-2x-3y,{x,0,3},{y,0,2},PlotRange->{0,6}]观察图形.2.6).图2.6例2.2 (教材 例2.2) 作出函数2214y x z ++=的图形.输入k[x_,y_]:=4/(1+x^2+y^2)Plot3D[k[x,y],{x,-2,2},{y,-2,2},PlotPoints->30,PlotRange->{0,4},BoxRatios->{1,1,1}]则输出函数的图形2.7. 观察图形, 理解选项PlotRange->{0,4}和BoxRatios->{1,1,1}的含义. 选项 BoxRatios 的默认值是{1,1,0.4}.例2.3 (教材 例2.3) 作出函数22y x xye z ---=的图形. 输入命令Plot3D[-x*y*Exp[-x^2-y^2],{x,-3,3},{y,-3,3},PlotPoints->30,AspectRatio->Automatic];则输出所求图形(图 图2.8例2.4 (教材 例2.4) 作出函数)94cos(22y x z +=的图形. 输入Plot3D[Cos[4x^2+9y^2],{x,-1,1},{y,-1,1},Boxed->False,Axes->Automatic,PlotPoints->30,Shading->False]则输出网格形式的曲面图2.9, 这是选项Shading->False 起的作用, 同时注意选项Boxed->False 的作用.二次曲面例2.5 (教材 例2.5) 作出椭球面1194222=++z y x 的图形. 这是多值函数, 用参数方程作图的命令ParametricPlot3D. 该曲面的参数方程为,cos ,sin sin 3,cos sin 2u z v u y v u x === (ππ20,0≤≤≤≤v u ).输入ParametricPlot3D[{2*Sin[u]*Cos[v],3*Sin[u]*Sin[v], Cos[u]},{u,0,Pi},{v,0,2 Pi},PlotPoints->30]则输出椭球面的图形, 可使图形更加光滑.图2.10例2.6 (教材 例2.6) 作出单叶双曲面1941222=-+z y x 的图形. 曲面的参数方程为,tan 3,cos sec 2,sin sec u z v u y v u x === (.20,2/2/πππ≤≤<<-v u )输入ParametricPlot3D[{Sec[u]*Sin[v],2*Sec[u]*Cos[v], 3*Tan[u]},{u,-Pi/4,Pi/4},{v,0,2 Pi},PlotPoints->30]图2.11例2.7 作双叶双曲面13.14.15.1222222-=-+z y x 的图形.曲面的参数方程是,csc 3.1,sin cot 4.1,cos cot 5.1u z v u y v u x ===其中参数πππ<<-≤<v u ,20时对应双叶双曲面的一叶, 参数πππ<<-<≤-v u ,02时对应双叶双曲面的另一叶. 输入sh1=ParametricPlot3D[{1.5*Cot[u]*Cos[v],1.4*Cot[u]*Sin[v],1.3/Sin[u]},{u,Pi/1000,Pi/2},{v,-Pi,Pi}, DisplayFunction->Identity];(*DisplayFunction->Identity 是使图形暂时不输出的选项*) sh2=ParametricPlot3D[{1.5*Cot[u]*Cos[v],1.4* Cot[u]*Sin[v],1.3/Sin[u]},{u,-Pi/2,-Pi/1000}, {v,-Pi,Pi},DisplayFunction->Identity];Show[sh1,sh2,DisplayFunction->$DisplayFunction](*命令Show[sh1,sh2]是把图形sh1,sh2放置在一起, DisplayFunction->$DisplayFunction 是恢复显示图形的选项*) 输出为图2.12.例2.8 可以证明: 函数xy z =的图形是双曲抛物面. 在区域22,22≤≤-≤≤-y x 上作出它的图形.输入Plot3D[x*y,{x,-2,2},{y,-2,2},BoxRatios->{1,1,2}, PlotPoints->30]输出图形略. 也可以用ParametricPlot3命令作出这个图形, 输入ParametricPlot3[{r*Cos[t],r*Sin[t],r^2*Cos[t] *Sin[t]},{r,0,2},{t,0,2 Pi},PlotPoints->30]输出为图2.13例2.9 (教材 例2.7) 作出圆环v z u v y u v x sin 7,sin )cos 38(,cos )cos 38(=+=+=,(πππ22/,2/30≤≤≤≤v u )的图形.输入ParametricPlot3D[{(8+3*Cos[v])*Cos[u],(8+3*Cos[v])*Sin[u],7*Sin[v]},{u,0,3*Pi/2},{v,Pi/2,2*Pi}];图2.14例2.10 画出参数曲面]2,001.0[],4,0[)5/2/ln(tan cos sin sin sin cos ∈∈⎪⎩⎪⎨⎧++===v u u v v z vu y v u x π的图形.输入命令ParametricPlot3D[{Cos[u]*Sin[v],Sin[u]Sin[v],Cos[v]+Log[Tan[v/2]+u/5]}, {u,0,4*Pi},{v,0.001,2}];则输出所求图形(图2.15).曲面相交例2.11 (教材 例2.8) 作出球面22222=++z y x 和柱面1)1(22=+-y x 相交的图形. 输入g1=ParametricPlot3D[{2 Sin[u]*Cos[v],2 Sin[u]*Sin[v],2 Cos[u]},{u,0,Pi},{v,0,2 Pi},DisplayFunction->Identity];g2=ParametricPlot3D[{2Cos[u]^2,Sin[2u],v},{u,-Pi/2,Pi/2},{v,-3,3},DisplayFunction->Identity];Show[g1,g2,DisplayFunction->$DisplayFunction]则输出所求图形(图2.16)例2.12 作出锥面222z y x =+和柱面1)1(22=+-y x 相交的图形. 输入g3=ParametricPlot3D[{r*Cos[t],r*Sin[t],r}, {r,-3,3},{t,0,2 Pi},DisplayFunction->Identity];Show[g2,g3,DisplayFunction->$DisplayFunction]输出为图2.17.图2.17例2.13 画出以平面曲线x y cos =为准线, 母线平等Z 轴的柱面的图形. 写出这一曲面的参数方程为⎪⎩⎪⎨⎧=∈-∈==s z R s t t y t x ],,[,cos ππ 取参数s 的范围为[0, 8]. 输入命令ParametricPlot3D[{t,Cos[t],s},{t,-Pi,Pi},{s,0,8}]则输出所求图形(图2.18).例2.14 (教材 例2.9) 作出曲面x y x y x z =+--=2222,1及xOy 面所围成的立体图形. 输入g1=ParametricPlot3D[{r*Cos[t], r*Sin[t],r^2},{t,0,2*Pi},{r,0,1},PlotPoints->30]; g2=ParametricPlot3D[{Cos[t]*Sin[r],Sin[t]Sin[r],Cos[r]+1},{t,0,2*Pi},{r,0,Pi/2},PlotPoints->30];Show[g1,g2]则输出所求图形(图图2.19例2.15 (教材 例2.10) 作出螺旋线t z t y t x 2,sin 10,cos 10===(R t ∈)在xOz 面上的正投影曲线的图形.所给螺旋线在xOz面上的投影曲线的参数方程为10==.,cosx2ztt输入ParametricPlot[{2t,10Cos[t]},{t,-2Pi,2Pi}];则输出所求图形(图图2.20注:将表示曲线的方程组, 消去其中一个变量, 即得到曲线在相应于这一变量方向上的正投影曲线的方程, 不考虑曲线所在平面, 它就是投影柱面方程; 对于参数方程, 只要注意将方程中并不存在的那个变元看成第二参数而添加第三个方程即可.例2.16 (教材例2.11) 作出默比乌斯带(单侧曲面)的图形.输入Clear[r,x,y,z];r[t_,v_]:=2+0.5*v*Cos[t/2];x[t_,v_]:=r[t,v]*Cos[t]y[t_,v_]:=r[t,v]*Sin[t]z[t_,v_]:=0.5*v*Sin[t/2];ParametricPlot3D[{x[t,v],y[t,v],z[t,v]},{t,0,2 Pi},{v,-1,1},PlotPoints->{40,4},Ticks->False]则输出所求图形(图空间曲线例2.17 (教材 例2.12) 作出空间曲线)60(2,sin ,cos π≤≤===t t z t t y t t x 的图形. 输入ParametricPlot3D[{t*Cos[t],t*Sin[t],2*t,RGBColor[1.0,0,0.5]},{t,0,6 Pi}]则输出所求图形(图图2.22例2.18 绘制参数曲线 ⎪⎩⎪⎨⎧===2/cos 2sin t z t y t x 的图形.输入命令ParametricPlot3D[{Sin[t],2Cos[t],t.2},{t,0,12}];则输出所求图形(图2.23).例2.19 绘制参数曲线 ⎪⎪⎩⎪⎪⎨⎧=+==t z t y t x arctan 211cos 2的图形.输入命令ParametricPlot3D[{Cos[t]^2,1/(1+2*t),ArcTan[t]},{t,0,8}]; 则输出所求图形(图2.24).动画制作例2.20 平面正弦曲线的运动. 输入Table[Plot[Sin[x+t*Pi],{x,0,6 Pi}],{t,0,2,1/8}]则作出了16幅具有不同相位的正弦曲线(输出图形略). 双击屏幕上某一幅画, 则可形成动画. 下面是动画的最后一幅图(图2.25).例2.21 (教材 例2.13) 作模拟水波纹运动的动画. 输入调用软件包命令<<Graphics\Animation.m执行后再输入MoviePlot3D[Sin[Sqrt[x^2+y^2]+t*2*Pi],{x,-8 Pi,8 Pi},{y,-8 Pi,8 Pi},{t,1,0},PlotPoints->50,AspectRatio->0.5,ViewPoint->{0.911,-1.682,2.791},Frames->12]则输出12幅具有不同相位的水面图形, 双击屏幕上任意一幅图, 均可观察动画效果. 下图是第一幅图(图2.26).图2.26例2.22 (教材 例2.14) 用动画演示由曲线],0[,sin π∈=z z y 绕z 轴旋转产生旋转曲面的过程.该曲线绕z 轴旋转所得旋转曲面的方程为,sin 222z y x =+ 其参数方程为])2,0[],,0[(,,sin sin ,cos sin ππ∈∈===u z z z u z y u z x输入For[i=1,i<=30,i++,ParametricPlot3D[{Sin[z]*Cos[u],Sin[z]*Sin[u],z},{z,0,Pi},{u,0,2*Pi*i/30},AspectRatio->1,AxesLabel->{"X","Y","Z"}]];则输出连续变化的30幅图形. 双击屏幕上任意一幅图, 均可观察动画效果. 下面是生成旋转曲面的过程中的第23幅图(图2.27).图2.27例2.23 将一张薄膜贴在1,0,1,0====y y x x 的方框上, 薄膜振动的函数取为)cos()sin()sin()cos 1)(cos 1(16),,(224141222t n m y m x n m n n m t y x u m n ππππππ+⋅-+=∑∑==其中t 为参数, 作出图形随t 的变动而引起薄膜振动的动画.初始位置是).0,,(y x u 通过t 的不同值得到多幅画面, 然后将这些图形连续地一张张显示出来, 即可达到运动的动画效果. 输入命令<<Graphics 'Animation '; Clear[x,y,t,m,n];u[x_,y_,t_]:=Sum[16*(1+Cos[n*Pi])*(1-Cos[m*Pi])*Sin[n*Pi*x]*Sin[m*Pi*y]*Cos[Sqrt[m^2+n^2]*Pi*t] /(m^2*n^2*Pi*2),{m,1,4},{n,1,4}]Animate[Plot3D[u[x,y,t],{x,0,1},{y,0,1}, PlotRange->{-8,8}],{t,0,1.75,0.25}];图2.28附录Ⅰ 大学数学实验指导书项目三 多元函数微积分实验1 多元函数微分学(基础实验)实验目的 掌握利用Mathematica 计算多元函数偏导数和全微分的方法, 掌握计算二元 函数极值和条件极值的方法. 理解和掌握曲面的切平面的作法. 通过作图和观察, 理解二元 函数的性质、方向导数、梯度和等高线的概念.基本命令1.求偏导数的命令D命令D 既可以用于求一元函数的导数, 也可以用于求多元函数的偏导数. 例如: 求),,(z y x f 对x 的偏导数, 则输入D[f[x,y,z],x] 求),,(z y x f 对y 的偏导数, 则输入D[f[x,y,z],y]求),,(z y x f 对x 的二阶偏导数, 则输入D[f[x,y,z],{x,2}] 求),,(z y x f 对y x ,的混合偏导数, 则输入D[f[x,y,z],x,y] …………2.求全微分的命令Dt该命令只用于求二元函数),(y x f 的全微分时, 其基本格式为Dt[f[x,y]]其输出的表达式中含有Dt[x],Dt[y], 它们分别表示自变量的微分d x ,d y . 若函数),(y x f 的表 达式中还含有其它用字符表示的常数, 例如a, 则Dt[f[x,y]]的输出中还会有Dt[a], 若采用选 项Constants->{a}, 就可以得到正确结果, 即只要输入Dt[f[x,y],Constants->{a}]3.在Oxy 平面上作二元函数),(y x f 的等高线的命令ContourPlot 命令的基本格式为ContourPlot[f[x,y],{x,x1,x2},{y,y1,y2}]例如,输入ContourPlot[x^2-y^2,{x,-2,2},{y,-2,2}]则输出函数22y x z -=的等高线图(图1.1). 该命令的选项比较多(详细的内容参见光盘中的实验案例库). 如选项Contours->15表示作15条等高线, 选项Contours->{0}表示只作函数值为0的等高线.实验举例求多元函数的偏导数与全微分例1.1 (教材 例1.1) 设),(cos )sin(2xy xy z +=求.,,,222yx zx z y z x z ∂∂∂∂∂∂∂∂∂输入Clear[z];z=Sin[x*y]+Cos[x*y]^2; D[z,x] D[z,y] D[z,{x,2}] D[z,x,y]则输出所求结果.y Cos x y2y Cos x y Sin x yx Cos x y 2x Cos x y Sin x y2y 2Cos x y 2y 2Sin x y 2y 2Sin x y2Cos x y 2x y Cos x y 2x y Sin x y 2Cos x y Sin x y2x y Sin x y2例1.2 设,)1(y xy z +=求yzx z ∂∂∂∂,和全微分dz.输入Clear[z];z=(1+x*y)^y;D[z,x] D[z,y]则有输出⎪⎪⎭⎫ ⎝⎛++++++-]1[1)1()1(12xy Log xy xy xy xy y y y再输入Dt[z]则得到输出⎪⎪⎭⎫⎝⎛+++++]1[][1])[][()1(xy Log y Dt xy y xDt x yDt y xy y 例1.3 (教材 例1.2) 设,)(y xy a z +=其中a 是常数, 求dz.输入Clear[z,a];z=(a+x*y)^y;wf=Dt[z,Constants->{a}]//Simplify则输出结果:(a+xy)-1+y (y 2Dt[x,Constants->{a}]+Dt[y,Constants->{a}](xy+(a+xy)Log[a+xy]))其中Dt[x,Constants->{a}]就是d x , Dt[y,Constants->{a}]就是d y . 可以用代换命令“/.”把它们 换掉. 输入wf/.{Dt[x,Constants->{a}]->dx,Dt[y,Constants->{a}]->dy}输出为(a+xy)-1+y (dxy 2+dy(xy+(a+xy)Log[a+xy]))例1.4 (教材 例1.3) 设v u e y v u e x u u cos ,sin -=+=,求.,,,yv x v y u x u ∂∂∂∂∂∂∂∂ 输入eq1=D[x==E^u+u*Sin[v],x,NonConstants->{u,v}](*第一个方程两边对x 求导数, 把u,v 看成x,y 的函数*) eq2=D[y==E^u-u*Cos[v],x,NonConstants->{u,v}](*第二个方程两边对x 求导数, 把u,v 看成x,y 的函数*) Solve[{eq1,eq2},{D[u,x,NonConstants->{u,v}],D[v,x,NonConstants->{u,v}]}]//Simplify(*解求导以后由eq1,eq2组成的方程组*)则输出}}][][1(][}],{tan ,,[,][][1][}],{tan ,,[{{v Sin E v Cos E u v Cos E v u ts NonCons x v D v Sin E v Cos E v Sin v u ts NonCons x u D u u u u u -+-->->-+->->-其中D[u,x,NonConstants->{u,v}]表示u 对x 的偏导数, 而D[v,x,NonCosnstants->{u,v}]表示v 对x 的偏导数. 类似地可求得u ,v 对y 的偏导数.微分学的几何应用例1.5 求出曲面222y x z +=在点(1,1)处的切平面、法线方程, 并画出图形.解(1) 画出曲面的图形. 曲面的参数方程为⎪⎩⎪⎨⎧=∈∈==2]2,0[],2,0[,cos 2/sin rz r u u r y u f x π 输入命令Clear[f];f[x_,y_]=2x^2+y^2;p1=Plot3D[f[x,y],{x,-2,2},{y,-2,2}];g1=ParametricPlot3D[{r*Sin[u]/Sqrt[2.],r*Cos[u],r^2}, {u,0,2*Pi},{r,0,2}] 则输出相应图形(图1.2).(2) 画出切平面的图形. 输入命令a=D[f[x,y],x]/.{x->1,y->1}; b=D[f[x,y],y]/.{x->1,y->1}; p[x_,y_]=f[1,1]+a(x-1)+b(y-1);g2=Plot3D[p[x,y],{x,-2,2},{y,-2,2}];则输出切平面方程为,012=-+y x 及相应图形(图1.3).(3) 画出法线的图形. 输入命令ly[x_]=1+b(x-1)/a;lz[x_]=f[1,1]-(x-1)/a;g3=ParametricPlot3D[{x,ly[x],lz[x]},{x,-2,2}]; Show[p1,g2,g3,AspectRatio->Automatic,ViewPoint->{-2.530,-1.025,2.000}];则输出相应图形(图1.4).例1.6 (教材 例1.4) 求曲面14),(22++=y x y x k 在点⎪⎭⎫⎝⎛2164,21,41处的切平面方程, 并把曲面和它的切平面作在同一图形里.输入Clear[k,z];k[x_,y_]=4/(x^2+y^2+1); (*定义函数k(x,y)*)kx=D[k[x,y],x]/.{x->1/4,y->1/2};(*求函数k(x,y)对x 的偏导数, 并代入在指定点的值*) ky=D[k[x,y],y]/.{x->1/4,y->1/2};(*求函数k(x,y)对y 的偏导数, 并代入在指定的值*) z=kx*(x-1/4)+ky*(y-1/2)+k[1/4,1/2]; (*定义在指定点的切平面函数*)再输入qm=Plot3D[k[x,y],{x,-2,2},{y,-2,2},PlotRange->{0,4}, BoxRatios->{1,1,1},PlotPoints->30, DisplayFunction->Identity]; qpm=Plot3D[z,{x,-2,2},{y,-2,2}, DisplayFunction->Identity];Show[qm,qpm,DisplayFunction->$DisplayFunction]则输出所求曲面与切平面的图形(图1.5).多元函数的极值例1.7 (教材 例1.5) 求x y x y x y x f 933),(2233-++-=的极值. 输入Clear[f];f[x_,y_]=x^3-y^3+3x^2+3y^2-9x; fx=D[f[x,y],x] fy=D[f[x,y],y]critpts=Solve[{fx==0,fy==0}]则分别输出所求偏导数和驻点:2236369y y x x -++-{{x->-3,y->0},{x->-3,y->2},{x->1,y->0},{x->1,y->2}}再输入求二阶偏导数和定义判别式的命令fxx=D[f[x,y],{x,2}]; fyy=D[f[x,y],{y,2}]; fxy=D[f[x,y],x,y]; disc=fxx*fyy-fxy^2输出为判别式函数2xy yy xx f f f -的形式:(6+6x)(6-6y)再输入data={x,y,fxx,disc,f[x,y]}/.critpts;TableForm[data,TableHeadings->{None,{ "x ", "y ", "fxx ", "disc ", "f "}}]最后我们得到了四个驻点处的判别式与xx f 的值并以表格形式列出.X y fxx disc f -3 0 -12 -72 27 -3 2 -12 72 31 1 0 12 72 -51 2 12 -72 -1易见,当2,3=-=y x 时,12-=xx f 判别式disc=72, 函数有极大值31; 当0,1==y x 时,12=xx f 判别式disc=72, 函数有极小值-5;当0,3=-=y x 和2,1==y x 时, 判别式disc=-72, 函数在这些点没有极值. 最后,把函数的等高线和四个极值点用图形表示出来,输入d2={x,y}/.critpts;g4=ListPlot[d2,PlotStyle->PointSize[0.02],DisplayFunction->Identity]; g5=ContourPlot[f[x,y],{x,-5,3},{y,-3,5},Contours->40,PlotPoints->60,ContourShading->False,Frame->False,Axes->Automatic,AxesOrigin->{0,0},DisplayFunction->Identity];Show[g4,g5,DisplayFunction->$DisplayFunction]则输出图1.6.从上图可见, 在两个极值点附近, 函数的等高线为封闭的. 在非极值点附近, 等高线不 封闭. 这也是从图形上判断极值点的方法.注:在项目一的实验4中,我们曾用命令FindMinimum 来求一元函数的极值, 实际上,也可 以用它求多元函数的极值, 不过输入的初值要在极值点的附近. 对本例,可以输入以下命令FindMinimum[f[x,y],{x,-1},{y,1}]则输出{-5.,{x->1.,y->-2.36603×10-8}}从中看到在0,1==y x 的附近函数),(y x f 有极小值-5, 但y 的精度不够好.例1.8 求函数22y x z +=在条件0122=-+++y x y x 下的极值. 输入Clear[f,g,la]; f[x_,y_]=x^2+y^2;g[x_,y_]=x^2+y^2+x+y-1; la[x_,y_,r_]=f[x,y]+r*g[x,y]; extpts=Solve[{D[la[x,y,r],x]==0,D[la[x,y,r],y]==0,D[la[x,y,r],r]==0}]得到输出⎭⎬⎫⎩⎨⎧⎭⎬⎫⎩⎨⎧+->-+->-+->-⎩⎨⎧⎭⎬⎫⎩⎨⎧-->--->--->-)31(21),31(21),33(31,)31(21),31(21),33(31y x r y x r再输入f[x,y]/.extpts//Simplify得到两个可能是条件极值的函数值}.32,32{-+但是否真的取到条件极值呢? 可利用等高线作图来判断.输入dian={x,y}/.Table[extpts[[s,j]],{s,1,2},{j,2,3}] g1=ListPlot[dian,PlotStyle->PointSize[0.03],DisplayFunction->Identity]cp1=ContourPlot[f[x,y],{x,-2,2},{y,-2,2},Contours->20,PlotPoints->60,ContourShading->False,Frame->False,Axes-> Automatic,AxesOrigin->{0,0},DisplayFunction->Identity]; cp2=ContourPlot[g[x,y],{x,-2,2},{y,-2,2},PlotPoints->60,Contours->{0},ContourShading-> False,Frame->False,Axes->Automatic,ContourStyle->Dashing[{0.01}],AxesOrigin->{0,0},DisplayFunction->Identity]; Show[g1,cp1,cp2,AspectRatio->1,DisplayFunction->$DisplayFunction]输出为⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+-+-⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧----)31(21,2321,)31(21,2321 及图1.7. 从图可见,在极值可疑点,2321,2321⎪⎪⎭⎫ ⎝⎛----⎪⎪⎭⎫ ⎝⎛+-+-2321,2321 处, 函数),(y x f z =的等高线与曲线0),(=y x g (虚线)相切. 函数),(y x f z =的等高线是一系列同心圆, 由里向外, 函数值在增大, 在)31(21),31(21--=--=y x 的附近观察, 可以得出),(y x f z =取条件极大的结论. 在),31(21+-=x )31(21+-=y 的附近观察, 可以得出),(y x f z =取条件极小的结论.梯度场例1.9 画出函数222),,(y x z z y x f --=的梯度向量. 解 输入命令<<Graphics`ContourPlot3D` <<Graphics`PlotField3D` <<Calculus`VectorAnalysis`SetCoordinates[Cartesian[x,y,z]];f=z^2-x^2-y^2;cp3d=ContourPlot3D[f,{x,-1.1,1.1},{y,-1.1,1.1},{z,-2,2},Contours->{1.0},Axes->Tr ue,AxesLabel->{"x","y","z"}];vecplot3d=PlotGradientField3D[f,{x,-1.1,1.1},{y,-1.1,1.1},{z,-2,2},PlotPoints->3,Ve ctorHeads->True];Show[vecplot3d, cp3d];则输出相应图形(图1.8)例1.10 在同一坐标面上作出⎪⎪⎭⎫⎝⎛++=2211),(y x x y x u 和 ,11),(22⎪⎪⎭⎫⎝⎛+-=y x y y x v 的等高线图(0>x ), 并给出它们之间的关系.解 输入命令<<Calculus`VectorAnalysis` <<Graphics`PlotField`SetCoordinates[Cartesian[x,y,z]];check[u_,v_]:={Grad[u][[1]]-Grad[v][[2]],Grad[v][[1]]+Grad[u][[2]]} u=x(1+1/(x^2+y^2));v=y(1-1/(x^2+y^2)); check[u,v]//Simplifyugradplot=PlotGradientField[u,{x,-2,2},{y,-2,2},DisplayFunction->Identity];uplot=ContourPlot[u,{x,-2,2},{y,-2,2},ContourStyle->GrayLevel[0],ContourShading->False,DisplayFunction->Identity,Contours->40,PlotPoints->40]; g1=Show[uplot,ugradplot,DisplayFunction->$DisplayFunction];vgradplot=PlotGradientField[v,{x,-2,2},{y,-2,2},DisplayFunction->Identity];vplot=ContourPlot[v,{x,-2,2},{y,-2,2},ContourStyle->GrayLevel[0.7],ContourShading->False,DisplayFunction->Identity,Contours->40,PlotPoints->40]; g2=Show[vplot,vgradplot,DisplayFunction->$DisplayFunction]; g3=Show[uplot,vplot,DisplayFunction->$DisplayFunction];g4=Show[ugradplot,vgradplot,DisplayFunction->$DisplayFunction];则输出相应图形(图1.9),其中(a) ),(y x u 的梯度与等高线图;(b) ),(y x v 的梯度与等高线图; (c) ),(y x u 与),(y x v 的等高线图; (d) ),(y x u 与),(y x v 的梯度图.图1.9从上述图中可以看出它们的等高线为一族正交曲线. 事实上, 有,,2222x v y x x y u y v y x x x u ∂∂-=+=∂∂∂∂=+=∂∂ 且,0=∇⋅∇v u 它们满足拉普拉斯方程022222222=∂∂+∂∂=∂∂+∂∂y vx v y u x u 例1.11 (教材 例1.6) 设,),()(22y x xe y x f +-=作出),(y x f 的图形和等高线, 再作出它的梯度向量gradf 的图形. 把上述等高线和梯度向量的图形叠加在一起, 观察它们之间的关系.输入调用作向量场图形的软件包命令<<Graphics\PlotField.m再输入Clear[f];f[x_,y_]=x*Exp[-x^2-y^2];dgx=ContourPlot[f[x,y],{x,-2,2},{y,-2,2},PlotPoints->60, Contours->25,ContourShading->False,Frame->False,Axes->Automatic,AxesOrigin->{0,0}] td=PlotGradientField[f[x,y],{x,-2,2},{y,-2,2},Frame->False] Show[dgx,td]输出为图1.10. 从图可以看到Oxy 平面上过每一点的等高线和梯度向量是垂直的, 且梯度的 方向是指向函数值增大的方向图1.10例1.12 求出函数244),(y xy x y x f +-=的极值, 并画出函数),(y x f 的等高线、驻点以及),(y x f -的梯度向量的图形.输入命令<<Graphics`PlotField`f=x^4-4*x*y+y^2;FindMinimum[f,{x,1},{y,1}]conplot=ContourPlot[f,{x,-2,2},{y,-3,3},ContourShading->False,PlotPoints->100,Contours->{-4,-2,0,2,4,10,20}];fieldplot=PlotGradientField[-f,{x,-2,2},{y,-3,3},ScaleFunction->(Tanh[#/5]&)];critptplot=ListPlot[{{-Sqrt[2],-2*Sqrt[2]},{0,0},{Sqrt[2],2*Sqrt[2]}},PlotStyle->{PointSize [0.03]}];Show[conplot,fieldplot,critptplot];则得到),(y x f 的最小值.4)82843.2,41421.1(-=f 以及函数的图形(图1.11).实验习题 1.设,xy e z =求.dz2.设),,(y xy f z =求.,,22222y x zy z x z ∂∂∂∂∂∂∂ 3.设),sin (cos ),(228/)(22y x e y x g y x+=+-求.,,2yx z y z x z ∂∂∂∂∂∂∂ 4.试用例1.5的方法求265433051830120),(xy x x x x y x f +++--=的极值. 5.求324y x z +=在01422=-+y x 条件下的极值.6.作出函数42210/)2(),(y x e y x f +-=的等高线和梯度线的图形, 并观察梯度线与等高线的 关系.实验2 多元函数积分学(基础实验)实验目的掌握用Mathematica 计算二重积分与三重积分的方法; 深入理解曲线积分、曲面积分的 概念和计算方法. 提高应用重积分和曲线、曲面积分解决各种问题的能力.基本命令1. 计算重积分的命令lntegrate 和NIntegrate 例如,计算dydx xy x ⎰⎰102, 输入Integrate[x*y^2,{x,0,1},{y,0,x}]则输出 151又如,计算dydx xy )sin(10102⎰⎰的近似值, 输入NIntegrate[Sin[x*y^2],{x,0,1},{y,0,1}] 则输出 0.160839注: Integrate 命令先对后边的变量积分.计算三重积分时,命令Integrate 的使用格式与计算二重积分时类似. 由此可见, 利用 Mathematica 计算重积分, 关键是确定各个积分变量的积分限. 2. 柱坐标系中作三维图形的命令CylindricalPlot3D使用命令Cylindricalplot3D, 首先要调出作图软件包. 输入 <<Graphics`ParametricPlot3D` 执行成功后便可继续下面的工作.使用命令Cylindricalplot3D 时,一定要把z 表示成r ,θ的函数. 例如,在直角坐标系中方 程22y x z +=是一旋转抛物面, 在柱坐标系中它的方程为2r z =. 因此,输入 CylindricalPlot3D[r^2,{r,0,2},{t,0,2Pi}] 则在柱坐标系中作出了该旋转抛物面的图形.3. 球面坐标系中作三维图形命令SphericalPlot3D使用命令SphericalPlot3D, 首先要调出作图软件包. 输入 <<Graphics`ParametricPlot3D` 执行成功后便可继续下面的工作.命令SphericalPlot3D 的基本格式为SphericalPlot3D[r[],θϕ, {}],,{},,,2121θθθϕϕϕ其中r[],θϕ是曲面的球面坐标方程, 使用时一定要把球面坐标中的r 表示成ϕ、θ的函数. 例如,在球面坐标系中作出球面,22222=++z y x 输入Sphericalplot3D[2,{u,0,pi},|v,0,2,pi|,plotpoints->40]则在球面坐标系中作出了该球面的图形. 4. 向量的内积用“.”表示两个向量的内积. 例如,输入 vecl={al,bl,cl} vec2={a2,b2,c2} 则定义了两个三维向量, 再输入 vec1. vec2 则得到它们的内积a1a2+b1b2+c1c2实验举例计算重积分例2.1 (教材 例2.1) 计算,2dxdy xyD⎰⎰ 其中D 为由,,2y x y x ==+ 2=y 所围成的有界区域.先作出区域D 的草图, 易直接确定积分限,且应先对x 积分, 因此, 输入 Integrate[x*y^2,{y,1,2},{x,2-y,Sqrt[y]}] 则输出所求二重积分的计算结果.120193例2.2 (教材 例2.2) 计算,)(22dxdy e Dy x⎰⎰+- 其中D 为.122≤+y x如果用直角坐标计算, 输入Clear[f,r];f[x,y]=Exp [-(x^2+y^2)];Integrate[f[x,y],{x,-1,1},{y,-Sqrt[1-x^2],Sqrt[1-x^2]}]则输出为dx x 1Erf e 211x 2⎥⎦⎤⎢⎣⎡-π⎰--其中Erf 是误差函数. 显然积分遇到了困难.如果改用极坐标来计算, 也可用手工确定积分限. 输入Integrate[(f[x,y]/.{x->r*Cos[t],y->r*Sin[t]})*r,{t,0,2 Pi},{r,0,1}] 则输出所求二重积分的计算结果eπ-π 如果输入NIntegrate[(f[x,y]/.{x->r*Cos[t],y->r*Sin[t]})*r,{t,0,2 Pi},{r,0,1}] 则输出积分的近似值1.98587例 2.3 (教材 例 2.3) 计算dxdydz z y x)(22++⎰⎰⎰Ω, 其中Ω由曲面222y x z --=与22y x z +=围成.先作出区域Ω的图形. 输入g1=ParametricPlot3D[{Sqrt[2]*Sin[fi]*Cos[th],Sqrt[2]*Sin[fi]*Sin[th], Sqrt[2]*Cos[fi]},{fi,0,Pi/4},{th,0,2Pi}] g2=ParametricPlot3D[{z*Cos[t],z*Sin[t],z},{z,0,1},{t,0,2Pi}] Show[g1,g2,ViewPoint->{1.3,-2.4,1.0}]则分别输出三个图形(图2.1(a), (b), (c)).考察上述图形, 可用手工确定积分限. 如果用直角坐标计算, 输入 g[x_,y_,z_]=x^2+y^2+z;Integrate[g[x,y,z],{x,-1,1},{y,-Sqrt[1-x^2], Sqrt[1-x^2]},{z,Sqrt[x^2+y^2],Sqrt[2-x^2-y^2]}] 执行后计算时间很长, 且未得到明确结果.现在改用柱面坐标和球面坐标来计算. 如果用柱坐标计算,输入Integrate[(g[x,y,z]/.{x->r*Cos[s],y->r*Sin[s]})*r, {r,0,1},{s,0,2Pi},{z,r,Sqrt[2-r^2]}]则输出π⎪⎪⎭⎫⎝⎛+-15281252 如果用球面坐标计算,输入Integrate[(g[x,y,z]/.{x->r*Sin[fi]*Cos[t],y->r*Sin[fi]*Sin[t],z->r*Cos[fi]})*r^2*Sin[fi],{s,0,2Pi},{fi,0,Pi/4},{r,0,Sqrt[2]}]则输出π⎪⎪⎭⎫ ⎝⎛+-321662551这与柱面坐标的结果相同.重积分的应用例2.4 求由曲面()y x y x f --=1,与()222,y x y x g --=所围成的空间区域Ω的体积.输入Clear[f,g];f[x_,y_]=1-x -y;g[x_,y_]=2-x^2-y^2;Plot3D[f[x,y],{x,-1,2},{y,-1,2}] Plot3D[g[x,y],{x,-1,2},{y,-1,2}] Show[%,%%]一共输出三个图形,首先观察到Ω的形状. 为了确定积分限, 要把两曲面的交线投影到Oxy 平面上输入 jx=Solve[f[x,y]==g[x,y],y] 得到输出 ⎭⎬⎫⎩⎨⎧⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛-++→⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛-+-→22445121,445121x x y x x y为了取出这两条曲线方程, 输入 y1=jx[[1,1,2]] y2=jx[[2,1,2]] 输出为⎪⎭⎫ ⎝⎛-+-2445121x x⎪⎭⎫ ⎝⎛-++2445121x x再输入tu1=Plot[y1,{x,-2,3},PlotStyle->{Dashing[{0.02}]},DisplayFunction->Identity];tu2=Plot[y2,{x,-2,3},DisplayFunction->Identity]; Show[tu1,tu2,AspectRatio->1, DisplayFunction-> $DisplayFunction]输出为图2.2, 由此可见,y 是下半圆(虚线),y 是上半圆,因此投影区域是一个圆.设21y y =的解为1x 与2x ,则21,x x 为x 的积分限. 输入 xvals=Solve[y1==y2,x]输出为 ()()⎭⎬⎫⎩⎨⎧⎭⎬⎫⎩⎨⎧+→⎭⎬⎫⎩⎨⎧-→6121,6121x x 为了取出21,x x , 输入x1=xvals[[1,1,2]]x2=xvals[[2,1,2]]输出为()6121- ()6121+。
Mathematica函数图形的绘制

Mathematica函数图形的绘制《微积分》课程第⼀章演⽰与实验函数图形的绘制by PengBo, Shanghai JiaoTong University⽤Mathematica绘制函数图形的基本⽅法使⽤Mathematica绘制函数图形是⾮常⽅便的,⼀般只需指定函数和绘图范围。
如果需要在⼀幅图上绘制多条曲线或改变曲线的线形,颜⾊,底⾊等属性或给图形增加标题等信息,只需要指定相应的选项即可。
(* 绘制[-Pi,Pi]内Sin(x)函数的图形 *)Plot[Sin[x],{x,-Pi,Pi}]-Graphics-(* 可以使⽤函数集合来同时绘制多条曲线,并可将结果赋给变量 *)p1 = Plot[{Sin[2 x],Cos[x]/2},{x,-Pi,Pi}]-Graphics-(* 绘制[-Pi,Pi]内Sin(2 x)+Cos(x)/2函数的图形,保存在变量p2中 *)p2 = Plot[Sin[2 x] + Cos[x]/2,{x,-Pi,Pi}]-Graphics-(* 可以使⽤Show函数叠加p1和p2 *)Show[p1,p2]-Graphics-(* 可以使⽤ PlotRange参数指定y轴的选取区域 *)Plot[Tan[x],{x,-Pi,Pi},PlotRange->{-5,5}]-Graphics-(* 可以使⽤PlotStyle选项改变线型 *)PlotStylePlot[{Sin[x],Sin[3 x]},{x,-Pi,Pi}, PlotStyle->{RGBColor[1,0,0],RGBColor[0,0,0]}]PlotStyle is an option for Plot, ParametricPlot and ListPlot. PlotStyle -> style specifies that all lines or points are to be generated with the specified graphics directive, or list of graphics directives. PlotStyle -> {{style1}, {style2}, ... } specifies that successive lines generated should use graphics directives style1, style2, ... .-Graphics-初等函数图形(* 指数函数 a<1 *)Plot[Evaluate[{(1/2)^x,(1/3)^x,(1/10)^x}],{x,-2,2},PlotStyle->{ RGBColor[1,0,0],RGBColor[0,1 ,0],RGBColor[0,0,1]}]-Graphics-(* 指数函数 a>1 *)Plot[Evaluate[{(2)^x,(3)^x,(10)^x}],{x,-2,2},PlotStyle->{ RGBColor[1,0,0],RGBColor[0,1,0],RG BColor[0,0,1]}]-Graphics-(* 对数函数, a>1 *)Plot[Evaluate[{Log[2,x],Log[3,x],Log[10,x]}],{x,0.0001,6},PlotStyle->{RGBColor[1,0,0],RGBColor[0,1,0],RGBColor[0,0,1]}]-Graphics-(* 对数函数, a<1 *)Plot[Evaluate[{Log[1/2 ,x],Log[1/3,x],Log[1/10,x]}],{x,0.0001,6},PlotStyle->{RGBColor[1,0,0],RGBColor[0,1,0],RGBColor[0,0,1]}]-Graphics-(* 幂函数, a>0 *)Plot[Evaluate[{x^2,x,x^(1/2)}],{x,0.0001,2},PlotStyle->{ RGBColor[1,0,0],RGBColor[0,1,0],RGB Color[0,0,1]}] -Graphics-(* 幂函数, a<0 *)Plot[Evaluate[{x^(-1/2),x^(-1),x^(-2)}],{x,0.0001,4},PlotRange->{0,4},PlotStyle->{ RGBColor[1,0,0],RGBColor[0,1,0],RGBColor[0,0,1]}]-Graphics-(* 基本三⾓函数 *)Plot[{Sin[x],Cos[x]},{x,-2Pi,2Pi}, PlotStyle->{RGBColor[1,0,0],RGBColor[0,1,0]}]-Graphics-(* 基本三⾓函数 *)Plot[{Tan[x],Cot[x]},{x,-2Pi,2Pi},PlotRange->{-5,5},PlotStyle->{RGBColor[1,0,0],RGBColor[0,1,0]}]-Graphics-(* 反三⾓函数 *)Plot[{ArcSin[x],ArcCos[x]},{x,-1,1}, PlotStyle->{RGBColor[1,0,0],RGBColor[0,1,0]}]-Graphics-(* 双曲三⾓函数 *)Plot[{Sinh[x],Cosh[x]},{x,-3,3}, PlotRange->{{-3,3},{-10,10}},PlotStyle->{RGBColor[1,0,0],RGBColor[0,1,0]}]-Graphics-(* 双曲三⾓函数 *)Plot[{Tanh[x],Coth[x]},{x,-4,4},PlotRange->{-4,4},PlotStyle->{RGBColor[1,0,0],RGBColor[0,1,0]}]-Graphics-⼀般函数绘图⽰例(* 直接在[-3,3]范围间作图,由于超出函数定义域,出现错误信息 *)Plot[Sqrt[4-x^2],{x,-3,3}]Plot::plnr: CompiledFunction[{x}, <<1>>, -CompiledCode-][x] is not a machine-size real number at x = -3..Plot::plnr: CompiledFunction[{x}, <<1>>, -CompiledCode-][x] is not a machine-size real number at x = -2.75.Plot::plnr: CompiledFunction[{x}, <<1>>, -CompiledCode-][x] is not a machine-size real number at x = -2.5.General::stop: Further output of Plot::plnr will be suppressed during this calculation.-Graphics-(* 经分析,定义域为 [-2,2],所以限定 x 轴范围为[-2,2] *)Plot[Sqrt[4-x^2],{x,-2,2}]-Graphics-(* 但我们看到的图形并不是圆,因为Mathematica⼀般将图象⽐例调整为黄⾦分割,以达到最佳的视觉效果。
Mathematica软件在数值分析中的动态可视化设计

Mathematica软件在数值分析中的动态可视化设计孔祥强【摘要】Using the Mathematica software programming ,the visualization of the compound Simpson formula for numerical integration is realized,and the dynamic calculation process of an example is presented. The interaction process to solve linear equations by the successive over-relaxation iteration method is designed , and the effect of the relaxation factor changes on the approximate solution is analyzed. A visual display of the special Newton iterative method for nonlinear equation roots is given , and the method of solving process through a numerical example is demonstrated. Using the Mathematica software in the course of numerical analysis , the intuitive and interactive of teaching content areenhanced ,and the students′interests and motivation in learning are stimulated.%利用Mathematica软件编程,实现了用复化Simpson公式求数值积分的可视化,动态演示了算例的计算过程;设计了用逐次超松弛迭代法求解线性方程组的交互过程,分析了松弛因子的改变对近似解的影响;给出了用一类特殊的牛顿迭代法求非线性方程根的可视化展示,通过算例演示了方法的求解过程。
Mathematica绘图部分

49
50
(2) Contours 用于给出等值线的数目.其值 为:
➢n 给出等值线的条数(默认值为10) ➢{z1,z2,…} 画出对应函数值为z1,z2,…
的等值线 注:利用指定函数值可以画出隐函数F(x,y)=0
的图形.
➢DensityPlot[f,{x,xmin,xmax},{y,ymin, ymax}] 其中f是二元函数的表达式
55
例 21
56
此函数有两个可选参数: (1) ColorFunction 意义同上
(2)Mesh 说明在曲面上是否画网格. 其值为:
➢True 画网格(默认值) ➢False 不画网格
57
6 外部绘制函数
Mathematica绘制二维图形的内部函数缺 少一些功能,如绘制极坐标图形,直方图和 向量场等.但是它有自带的绘图程序包.
58
例 22
极坐标系下做图
59
例 23
60
例 24
61
填充图的绘图命令
62
63
64
65
最后再给出一个绘制向量场的例子:
66
1 二元函数图形
数值 x i 带入求 xidxi ,当然出错.
解决的办法是使用函数Evaluate[f],告
知Mathematica首先求出表达式f的值.
7
例3:
8
2 可选参数
绘图函数的可选参数很多,一下介绍Plot 的常用可选参数.
可选参数分为两类:第一类参数能改变输 出图形的外观,但不影响图形自身的质量;第 二类参数则影响图形自身的质量.
➢Automatic 实际颜色与Windows的窗口背 景色一致,但利用Mathematica的直接打印功
MATH6循环命令动画

循环命令
❖ For语句 For[初始化,检测条件,增量,表达式]
执行初始化语句,然后重复计算表达式与增量,直到 检测条件的值为False
例:For[i=1,i<4,i=i+1,Print[i]]
For[i=1;t=0,i<=5,i++,Print[t=t+i]] (*i++等价于i=i+1*)
这里的计算顺序是检测条件,表达式,然后是增量。只要 检测条件的值为False,For循环就会结束。如果初始化、检 测条件,增量和表达式的由多个语句组成,那么用分号分开 相邻语句。
If[test,then,else,unknown]
同上,但如果test无法判断是T还是F时,则执行unknown
例: If[7,Print[a],Print[b],Print[c]]
g[x_]:=If[x>0,1,If[x==0,0,-1]
gx
(利用If命令可以更简洁的定义单位步阶函数)
1, x 0 0, x 0 1, x 0
双击任何一幅图像,就能看到动画的效果。
练习:试构造Sin[nx], n从1变到10的动画
❖ 练习
1. 试分别用Do循环,While循环,For循环计 算10!
2. 显示出从1到50的整数中不是2,3,5倍数 的那些整数。反之。
3. 对于从1到10之间的每个数k,如果k为偶数, 显示它的一半,如果k为奇数,显示它的两 倍。
例:f[x_]:=Which[x>=-1&&x<2,(x^2-1)/(x-
1),x>=2&&x<=5,5-x]
fx
x2 1 , 1x2
总结和分类Mathematica的画图功能

总结和分类Mathematica的画图功能一、引言简述Mathematica软件及其在数学和科学计算中的地位强调画图功能在Mathematica中的重要性二、Mathematica画图功能概述Mathematica画图功能的基本特点画图功能与其他数学软件的比较三、基本图形绘制点、线、面的绘制基本几何图形的绘制:圆形、矩形、多边形等四、函数图形绘制一元函数图形的绘制多元函数图形的绘制参数方程和极坐标方程图形的绘制五、数据可视化散点图、折线图、柱状图等常见图表的绘制高级数据可视化技术:热图、树状图、网络图等六、三维图形绘制三维空间中点、线、面的绘制三维函数图形的绘制复杂的三维几何体的绘制七、图形的变换与操作平移、旋转、缩放等图形变换图形的合并、拆分与组合图形的动画与交互八、颜色与样式的应用颜色的选择与应用图形样式的定制样式模板的使用九、图形的标注与解释文本标注、数值标注、符号标注图形的标题、图例、坐标轴标签交互式图形的注释与解释十、高级图形绘制技术隐函数图形的绘制轮廓图、等高线图的绘制动态图形与交互式图形的创建十一、图形的输出与导出图形的屏幕显示与打印图形的导出格式:PDF、EPS、PNG等图形的嵌入与分享十二、Mathematica画图功能的应用案例科学计算中的图形应用工程领域的图形应用教育与教学中的图形应用十三、Mathematica画图功能的局限性与改进当前画图功能的局限性用户反馈与改进建议未来画图功能的发展趋势十四、结语总结Mathematica画图功能的核心优势对Mathematica画图功能的综合评价十五、参考文献列出用于撰写文档的相关文献和资料。
Matlab如何制作和保存gif动图
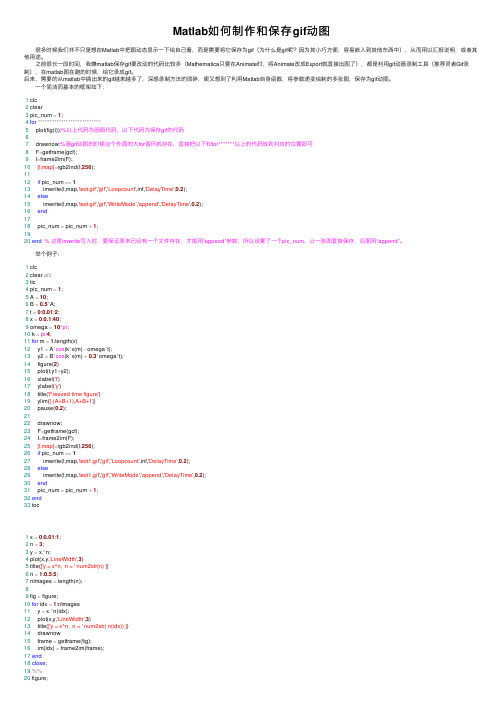
Matlab如何制作和保存gif动图 很多时候我们并不只是想在Matlab中把图动态显⽰⼀下给⾃⼰看,⽽是需要将它保存为gif(为什么是gif呢?因为其⼩巧⽅便,容易嵌⼊到其他东西中),从⽽⽤以汇报说明,或者其他⽤途。
之前很长⼀段时间,我嫌matlab保存gif要改动的代码⽐较多(Mathematica只要在Animate时,将Animate改成Export就直接出图了),都是利⽤gif动画录制⼯具(推荐灵者Gif录制),在matlab图在跑的时候,给它录成gif。
后来,需要的从matlab中搞出来的gif越来越多了,深感录制⽅法的琐碎,便⼜想到了利⽤Matlab⾃⾝函数,将参数递变绘制的多张图,保存为gif动图。
⼀个简洁⽽基本的框架如下:1 clc2 clear3 pic_num =1;4for***************************5 plot(fig(i));%以上代码为画图代码,以下代码为保存gif的代码67 drawnow;%画gif动图的时候这个外⾯的⼤for循环就存在,直接把以下和for*******以上的代码放到对应的位置即可8 F=getframe(gcf);9 I=frame2im(F);10[I,map]=rgb2ind(I,256);1112if pic_num ==113 imwrite(I,map,'test.gif','gif','Loopcount',inf,'DelayTime',0.2);14else15 imwrite(I,map,'test.gif','gif','WriteMode','append','DelayTime',0.2);16end1718 pic_num = pic_num +1;1920end % 这⾥imwrite写⼊时,要保证原来已经有⼀个⽂件存在,才能⽤“append”参数,所以设置了⼀个pic_num,让⼀张图直接保存,后⾯⽤“append”。
Mathematica5 制作动画教程

Mathematica5制作动画教程
friendfine@
Mathematica被美国Macword杂志誉为“不只是一个软件,更是一场划时代的革命”。
用Mathematica制作动画是相当精彩的一部分。
制作原理非常简单,它只是把mathematica绘制的图一张张快速地显示出来,从而形成动画。
制作动画会占用大量内存空间,如果您的计算机内存少于32M或执行过多次数学运算,建议您退出Mathematica,再重新运行。
下面我们用一个范例说明如何制作动画。
步骤如下:
(1)在Mathematica的工作区输入:
Table[Plot[Sin[x+z]Cos[z],{x,0,3Pi},PlotRange->{-1,1}],{z,0,2Pi,0.2}]
(2)执行上述命令,Mathematica便绘制出32张图。
(3)用鼠标左键双击其中的任一张(或者关闭其它图片,只保留最上面的一张,再用鼠标左键双击这张图片,便开始播放动画,如下图所示:
注意:在播放动画时,窗口的左下角会出现类似功能的录音机按钮,可以改变速度,方向和暂停。
如果要停止,只要用鼠标左键单击工作区内的任意一点即停止。
Mathematica用法IV

三维参数方程绘图也可以带有绘图参数,例如:
例:用参数方程绘制一个环形螺线管。
例:用参数方程绘出洛伦兹方程的数值解图像。
如果参数方程中有两个参数,将得到三维曲面。例如:
绘图时也可以把两幅图画在一起,做法如下:
例:用参数方程绘制一个蜗牛壳。
例2、把上图的散点连成线。
例3、画一个散点图,每个点都用“s”表示。
6、二维矢量场图形 如果某二维函数在平面区域内某点不仅有大小,
也有方向,则该函数构成矢量场。电场和磁场就是典 型的矢量场。矢量场在空间某点的大小和方向可以用 箭头表示,箭头的方向表示矢量场在该点的方向,箭 头的长度和矢量场在该点的大小成正比。
RevolutionPlot3D[r^2-3r,{r,0,2.2},{θ,0,2π}]
10、三维矢量场绘图
与绘制二维矢量场图形类似,在Mathematica中也可以 绘制三维矢量场图形。
输入<<Graphics`PlotField3D`,然后运行,即可调用矢 量图形软件包。常用的三维矢量场函数是PlotVectorField3D 和PlotGradientField3D。
4、Mathematica 作图
Mathematica具有强大的作图功能,它可以作二
维、三维和参数图形,也可以作出动态图形。
1. 一般二维图形 2. 二维参数作图 3. 等值线图和密度图 4. 极坐标图形 5. 散点图 6. 二维矢量场图形
7. 基本三维图形 8. 三维参数方程绘图 9. 三维球(柱)坐标绘图 10.三维矢量场图形 11.动态图形
1、一般二维图形
作二维图形的常用函数是Plot,它的用法如下:
探讨利用mathmatic动画演示功能解决实际问题

探讨利用mathmatic 动画演示功能解决实际问题简介:mathmatic 动画演示功能是mathmatic 软件很重要的一种应用与实际活动,运动问题的更能之一,可以利用编程解决一些,路径不定,速度不定的复杂相遇问题或轨道讨论,它的原理是:利用一串图形连续播放,客观地反映相互轨迹的交互关系,从而达到讨论、解决实际问题的目的。
关键词:mathmatic ,动画演示,追逐问题,正文:一. 问题的提出(1)、追逐问题问题提出:正方形的四个顶点各有一人.在某一时刻,四人同时出发以匀速v 按顺时针方向追赶下一个人. 如果他们始终保持对准目标,试求出每个人的行进路线.要求:结合实际问题,建立一个数学模型。
(2)、追击问题问题提出:一个慢跑者在平面上沿曲线 以恒定的速率v=2跑步,起点为(5,0),方向为逆时针。
这时有一只狗从原点出发,以恒定速率w =3跑向慢跑者,狗的运动方向始终指向慢跑者。
给出用计算机仿真这个追逐过程的主要步骤。
要求:结合实际问题,建立一个数学模型。
二. 问题的分析1、 对问题(1),分析如下:建立平面直角坐标系xoy ,取时间间隔为Δt, 在Δt 间隔中,每个人都沿2225x y +=直线行进, 计算每个人在一时刻t 的下一时刻t+Δt 的位置(坐标).设甲追逐乙,t 时刻甲的坐标为(xa ,ya),乙的坐标为(xb ,yb),则甲在t+Δt 的坐标为(xa+v Δt*cos α,ya+v Δt*sin α),其中由此得到这一问题的算法为:a) 赋初值:采样间隔Δt,行进速度v,及各点起始位置,终止时刻t;b) 确定循环次数n(Δt 的个数);c) i=1,2,3,4(人的编号)循环计算: j=1,2,3,…,n 循环计算:则有:d )分别连接四人各自对应时刻的对应点成一折线, 并将它们画在同一图中即四人的行进轨迹.2、 对问题(2),分析如下:建立平面直角坐标系xoy, 取时间间隔为dt, 在dt 间隔中狗沿直线行进,计算慢跑者和狗在一时刻t 的下一时刻t+dt 的位置坐标。
Mathcad操作指南

Mathcad操作指南基础部分 (3)LESSON 1. MATHCAD工具栏及面板 (11)LESSON 2:使用MATHCAD工作区域 (13)LESSON 3: 输入数学和文本 (14)LESSON 4: 使用MATHCAD模板及样式 (17)LESSON 5: 定义变量 (18)LESSON 6: 定义函数 (19)LESSON 7: 建立数学表达式 (21)LESSON 8: 编辑表达式 (23)LESSON 9: 定义变量范围 (25)LESSON 10: 定义矢量和矩阵 (28)LESSON 11: 图表 (32)LESSON 12:数字和文本格式 (39)LESSON 13: 结果格式化 (40)LESSON 14:单位运算 (43)LESSON 15:MATHCAD的编程 (44)在哪里可以得到更多帮助: (50)基础部分注意此稿包含的使用Mathcad 11版本的指南同从软件内置的指南相同。
最初的资料来源于Mathcad 7的专业版,更新了Mathcad 11版本新增加的内容。
因此, 有可能涉及到MathCad 7相关的信息,也可能在此稿中出现,标识符同MathCad 11版有些不同。
我们已经做了一些必要的编辑工作,用命令表格介绍材料,以满足FAMU - FSU 学院的机械工程系采用MathCad进行动力系统课程教育的需要。
如果未经著作拥有者许可仅限于本公司使用,不得提供给其他公司使用,MathSoft公司。
简介: Mathcad 优点Mathcad 是唯一的一个在同一张工作表集合了数学公式、数字、文本和图表的功能强大的工程应用工具。
和其它数学软件不同的是,Mathcad 是用和您一样的方式做数学。
那是因为它的操作界面就像是铅笔和纸张。
Mathcad的操作界面就是一个空白的工作区域,您可以在上面直接输入公式、图表或者是方程式,而且可以在任意的地方插入文字注解。
不像有些数学软件需要您会使用某种相关的语言,Mathcad 可以让您直接使用自然数学语言来进行工作。
用Mathcad制作烷烃构象模型旋转动画

用M a th c ad 制作烷烃构象模型旋转动画成志毅3刘素芳(中山大学中山医学院数学教研室广州510089)摘要: 用数学软件M a th cad 的函数处理和作图功能, 将描述烷烃构象的N e wm an 投影式制作成可以连续任意旋转角度的动画, 并将烷烃构象的能量曲线与其N e wm an 投影式的旋转同步变化, 动态描述直链烷烃的构象概念。
将动画制成通用视频文件, 可作为医用有机化学多媒体教学的课件元素。
关键词: 烷烃构象; 动画; 多媒体构象是烷烃C —C Ρ键旋转而产生的分子中原子或基团在空间的不同排列形式, 构象异构体是连续变化的。
通常用N ewm an 投影式来描述开链烷烃的构象, 由于书本上无法用N ewm an 投影式来表达构象的连续变化过程, 只给出几个典型异构体的投影式, 结合烷烃构象的能量曲线来说明分子的这种同分异构现象。
正是由于书本的局限性, 部分初学医用有机化学的学生会形成构象异构体只有书本上表示的那几种形式的错误概念。
我们在教学实践中尝试用多媒体手段来表达有机化学中一些有关分子动态过程的概念, 使学生能非常直观地接受这些概念, 简化了教师在课堂上的讲述。
目前制作多媒体动画文件的软件有很多, 但主流软件如f l a s h 等都是基于绘画来实现的, 这对一些实验装置的教学很有用, 但有机化学中一些有明确物理意义的概念, 如反应与活化能的关系, 分子的构象等用绘画来描述往往会不够准确, 这时就需要用到一些专业的软件。
考虑到要将分子构象的N ewm an 投影式与其构象的能量曲线同步变化, 我们采用数学专业软件来处理。
M a t h c ad 具有操作方便、直观灵活等特点, 有很强的函数处理和作图功能, 特别是该软件可以将作图的过程用动画表示出来, 非常适合用来制作多媒体课件1 。
有机化学教科书2 中一般都是以乙烷和正丁烷为例来讲述构象。
对乙烷来说, 两个碳原子的周围都是氢原子, 其构象能量曲线用简单的正弦函数就能描述。
用MATHCAD模拟振荡图及其动画制作

自评报告孙老师:您好!自此,有关《实验设计数据处理和计算机模拟》课程的学习要告一段落了。
在这短短的几周里,我充分利用了这次机会,好好的把一些计算机工具软件的基本操作学了一下。
以前,我只会用EXCELL做直线分析。
现在会用EXCELL做一些统计分析和数据处理了,这在实验后的数据处理中很重要。
,头几天,我做了关于阻力测定的实验,发现用EXCELL做数据处理的效果很不错。
至于ORIGIN和MATHCAD各有所长,用ORIGIN做曲线拟合的效果很好,但拟合后得出的方程往往很复杂,用MATHCAD解方程再好不过了。
把三者结合起来使用效果还是很不错的。
如用于求离心泵的扬程。
管路的特性方程可用伯努力方程求出,离心泵的特征方程可以根据实验数据,用EXCELL的多项式拟合功能获得(ORIGIN 拟合的效果虽好,但高斯方程很复杂),再用MATHCAD解这两个方程即可获得比较满意的解。
“师傅领进门,修行在个人”。
我以后会进一步加强使用这些软件的意识,多看些有关软件使用的书籍。
在实验数据处理,做化工原理作业等等的实战当中,发现他们的新用法,提高自己处理数据的水平!这几周的时间里,我感觉我的自学能力有待提高。
我从网上下了不少教程,但和当初学AUTOCAD一样,看的很少。
这几周也就是仅仅把从您的网站下的练习题,认认真真的练习了一下。
做论文时,才把MATHCAD的有关动画制作的内容学一下。
我今后自然要多在自学方面多加努力了。
对我的论文的质量:我不能说它有多少创新的成分,格式也不是那麽的正式,但通过做这个论文,我提高了很多,也解决了一些“技术问题”。
所以我还是希望我的论文能获得优的。
下面是我对本门课程的一些建议:一.这门课的开课时间是否可以再早一些。
如在大二上学期时就开。
我的理由是:(1)数据处理中使用的这几个软件的学习门槛不高,同时,学生的学习积极性很高,所以不存在太多的学习障碍。
(2)大二开的实验课很多,许多的实验都涉及到了数据处理,这本身就提供了很好的实战的机会。
动画

课件与作业_10_动画功能在Mathematica4.1及其以上版本的动画功能按以下步骤操作:第一步进入子程序软件包<<Graphics`Animation`第二步制作动画(命令与格式见下面例子),大致有三种情形:(1)围绕曲面的一个轴(类似于z轴)旋转一个曲面;(2)制作单一图像的动画,在作图的过程中,添加一个控制变量,由控制变量的变化,得到一系列图像,然后将这些图像像放电影一样连续显示,得到的效果就是动画;(3)制作多个图像的动画,将程序模块化。
首先,打开动画功能,执行下列命令:<<Graphics`Animation`例1旋转一个曲面。
(1)画出曲面:g = ParametricPlot3D[ { u*Sin[t], u*Cos[t], t/2 }, { t, 0, 10 }, { u, 0, 1}, Boxed->False, Axes->None]执行后,得到图像(2)旋转图像(可以从0o到360o旋转,也可以从360o到0o旋转)SpinShow[ g, Frames -> 10, SpinRange -> { 0 Degree, 360 Degree } ]其中的命令Frames -> 10表示执行以后得到10个图像,双击最后一个图像,图像就会转动起来。
例2作一个平面曲线的动画。
制作动画:Animate[ ParametricPlot[ { 8 ( 1 - Cos[ 2Pi*t + x ] )*Sin[x],8 ( 1- Cos[ 2Pi*t + x ] )*Cos[x] }, { x, 0, 2Pi } ], { t, 0, 1, 1/12 } ]执行后得到13个心脏线的图像,双击最后一个图像,图像就会转动起来。
其中{ x, 0, 2Pi }表示作图区间,{ t, 0, 1, 1/12 }表示作图控制变量,对t = 0, t = 0 + 1/12, t = 0 + 2/12, … , t = 0 + 12/12 依次作图,共13个图。
半无穷域绳波之自由端与固定端之Mathematica动画实用PPT文档

指導老師:陳正宗 終身特聘教授 簡報人員:賴佳宏
一維波動方程
•假設均勻且完全彈性之繩索,在兩點張力 及斜率分別為T1、tanα及T2、tanβ之作用 下、如圖
• ΣFy=0
數學模式
• ΣFx=0
數學模式
一維波動方程式
•ρ 為單位質量
•u 為繩索位移
•c為波速
數學模式
• 利用特徵線的概念 波動方程通解
• 代入初始條件
• D’Alembert’s solution
映像法-Huygens Principle
自由端
映像法-Huygens Principle
固定端
MathemΒιβλιοθήκη tica 語法半無窮域自由端
• 初始條件:
指導老師:陳正宗 終身特聘教授 映像法-Huygens Principle 自由端 Mathematica 語法 指導老師:陳正宗 終身特聘教授 半無窮域繩波之自由端與固定端之Mathematica動畫 映像法-Huygens Principle 固定端 半無窮域繩波之自由端與固定端之Mathematica動畫
Mathematica動畫
指導老師:陳正宗 終身特聘教授
假設均勻且完全彈性之繩索,在兩點張力及斜率分別為T1、tanα及T2、tanβ之作用下、如圖
半無窮域繩波之自由端與固定端之Mathematica動畫
映像法-Huygens Principle
自由端
D’Alembert’s solution
假設均勻且完全彈x性-5之,5繩 x索,6在兩點張力及斜率分別為T1、tanα及T2、tanβ之作用下、如圖
初假 M指始 a設導th位 均老em勻 師移a:且 :tic完 陳xa語全 正 法彈 宗07性,-o終xt之,身h6e繩特rwx索聘i,s教7e在授兩點張力及斜率分別為T1、tanα及T2、tanβ之作用下、如圖
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学动画制作
3、逻辑表达式 用逻辑运算符连接的表达式。逻辑运算符有三种 :! 逻辑非; && 逻辑与; || 逻辑或。逻辑量词:ForAll;Exists。 4、复合表达式 在 Mathematica 中,一个用分号隔开的表达式序列称为一个复合 表达式。运行一个复合表达式就是依次执行过程中的每个表达式,且 过程中最后一个表达式的值作为该复合表达式的值。例如: In[63]:=t=1;u=t + 4;Sin[u] (复合表达式) Out[63]=Sin[5] (显示 Sin[u]、函数求值:格式: f[1,2,-3]; 2、表达式求值:格式 expr/.{x1 ->ex1, x2 ->ex2,…} 或: Replace[expr, {x1 ->ex1, x2 ->ex2,…}]
数学动画制作
Mathematica 绘图
数学动画制作
一、绘图命令 Mathematica 可以根据给定的表达式或函数, 绘制曲线, 间曲面。 下面主要介绍平面曲线的绘制命令,根据表达式或函数的形式,有 不同的绘制命令。 1、直角坐标显式:y=f(x),绘图命令 fig=Plot[f(x),{x,x1,x2}, 绘图参数] fig=Plot[{f1(x),f2(x),…},{x,x1,x2},可选项] 2、直角坐标隐式:F(x,y)=0,绘图命令 fig=ImplicitPlot[F[x,y]==0,{x,x1,x2},绘图参数] 3、直角坐标参数式:x=x(t),y=y(t),绘图命令 fig=ParametricPlot[{x(t),y(t)},{t,t1,t2},绘图参数]
数学动画制作
数学软件的基本功能: 数值计算; 符号计算; 数学图像; 文字功能; 学习功能; 扩展功能;
数学动画制作
Mathematica 简介
数学动画制作
一、Mathematica 的变量 1、变量名规定: 英文字母开头的若干字母和数字表示的字符串。 变量名中的字符之间不能有空格。 2、变量类型: 在 Mathematica 中,使用变量不必规定类型。变量可以用来表 示任何对象,如存放一个方程式、一个图形或更复杂的关系式。对 一个变量 var,可以通过 Head[var]查看它的类型。 3、变量赋值: 可以通过 var= xxx 方式赋值,其中 xxx 是任意对象。
数学动画制作
二、几何体绘图 用 Graphics 可以绘制线、点、圆,圆弧等几何体。命令格式 Graphics[几何体类型,参数] 1、几何体类型有: 点:指定位置{x,y}的点:Point[{x,y}] 线:连接点 p1, p2, p3 的线:Line[{p1,p2,p3}] 箭头:连接点 p1, p2, p3 的线:Arrow[{p1,p2,p3}] 文字:在点 p 处写出文字:Text[text, p] 2、参数指定几何体的大小颜色等。
数学动画制作
二、Maple 它是由加拿大 Waterloo 大学开发的科学计算软件,拥有优秀的 符号计算和数值计算能力。并且其符号计算同时是 MATLAB 和 MathCAD 等软件的符号处理的核心。最新版本 Maple 2016.
数学动画制作
三、MathCAD 它是美国 PTC 公司旗下 MathSoft 子公司推出的一个交互式的数 学软件。MathCAD 是集科学编辑、数学计算、和仿真于一体的软 件,主要特点是输入界面比较友好,所见即所得。MathCAD 可视 作一个功能强大的计算器,没有复杂的使用规则。
数学动画制作
三、表达式 Mathematica 中有算术表达式、 关系表达式、 逻辑表达式及复合 表达式。 1、算术表达式: 由算术运算符(+、-、*、/、^连接常数、变量、函数构成的式 子。如:Sqrt[x]、2+3.2、3*x-Sin[y]、 都是算术表达式。 2、关系表达式 由关系符连接的表达式。关系运算符有六种:相等关系= =;不等 关系!=;>大于关系;>= 大于等于关系;<小于关系;<= 小于等 于关系。关系表达式的计算结果是三个逻辑值 True (真)、False(假) 和非真非假。
数学动画制作
二、表和数组 表是 Mathematica 中重要对象,表示数学中的集合、向量、矩 阵和各种记录。Mathematica 也提供丰富的处理表的函数。 1、表的形式:任何对象放入花括号中都可以组成表。 如:{var1,var2,……,var6},{{1,3,5}、{3,x,4}}都是表。 2、建表命令: 主要建表命令是 Table。 3、表的操作:Mathematica 提供很多表的运算函数。 在表 T 中取出第 n 个分量,格式 T[[n]]; 在表 T 的尾端插入元素 xx,Append[T, xx]; Apply[Plus, T]、Apply[Times, T],对表中所有元素求和、求积。
数学动画制作
四、动画制作 1、制作图像序列 因为抛物线形状是变动的,将抛物线参数化为:f = -a t^2 + 2.2 t; 参数 a 的取值范围为 1.2 到 1.6,取值间隔为 0.02;这样每次 a 取定 一个值, 就重复上面的步骤, 就能生成一个图像, 这样图像生成序列 T。 2、实现 将前面画图的步骤放入圆括号 ( ) , 将 f 换成 f = -a t^2 + 2.2 t, 然后定义个图像值的函数 Fig[a_]:=( )。 用 Table[Fig[a],{a,初值,终值,间隔}]生成序列 T。然后用 ListAnimate[T]播放。
数学动画制作
2、自定义函数: 自定义函数命令:f[x_,y_,var_]:=关于 x, y, var 的表达式。 方括号中的每个自变量名后一定要有一个下划线,定义要用“: =” 。 例如二元函数:z1[x_ ,y_ ]:=Tan[x/y]+y*Exp[5x]。 分段函数定义方式:用 Piecewise 定义,格式: Piecewise[{{val1,cond1},{val2,cond2},…}] 3、注意:函数和表达式的区别 z1[x_ ,y_ ]:=Tan[x/y]+y*Exp[5x]是函数,可以计算 z1[1,2] z2[x ,y ]=Tan[x/y]+y*Exp[5x]是表达式,计算 z2[1,2]无意义。
t 0
1 [ f (t )]2 dt 1.62 ,解出t0 ,代入曲线得到
数学动画制作
2、画图 画图范围取为:������������������������������������������������������ → {{−������. ������, ������. ������}, {−������. ������, ������. ������}}。 画抛物线:f1=Plot[f, {0, t0}, 其它参数]; 画 P 点:f2=Graphics[参数,Point[P 点坐标]]; 在 P 点左侧显示 P 字符:f3=Graphics[参数,Text[]]; 画 M 点:f4=Graphics[参数,Point[M 点坐标]]; 在 M 点左侧显示 M 字符:f5=Graphics[参数,Text[]];
数学动画制作 主要内容:
数学动画制作
符号计算数学软件介绍
数学动画制作
一、Mathematica 它是由世界著名物理学家 Stephen Wolfram 领导的 Wolfram Research 公司开发的科学计算软件。 它兼具强大的符号计算功能和 数值处理功能,被称为世界上最强大的通用计算系统。最新版本 10.02 中文版。
数学动画制作
fig=ParametricPlot[{{x1(t),y1(t)},{x2(t),y2(t)}},{t,t1,t2}, 绘 图 参数] 4、极坐标式:ρ=ρ(θ),绘图命令 PolarPlot[ρ(θ),{ θ, θ1, θ2}]
数学动画制作
二、平面图形的绘图参数 绘图命令包含许多参数,用于控制图像的显示样式,多数情况缺省 值就可以符合需要,但有时需要指定。全部参数可参考各绘图命令的 Options。下面给出几个重要参数。 1、PlotRange,用于制定绘图范围。格式: {{x1,x2},{y1,y2}}。 2、AspectRatio,指定图形的高宽比,默认为黄金比例。 3、Axes 显示坐标轴。 4、AxesLabel 指定坐标轴代表的变量。 6、Frame 指定图像是否显示外框。 7、 PlotStyle 用于指定线型, 包含很多参数, 如线的粗细, 线的虚实、 线的颜色等。
数学动画制作
1、数学准备
f 1.2t 2.2t 。 左端点 P 取原点: P {0,0};
抛物线:
2
右端点 M 按弧长选取:从 P 到 M 的抛物线弧长为 1.62; 弧长: s M 坐标。 在 P 点求导数,算出 P 点切线斜率 k1;点斜式算出切线方程; 在 M 点求导数,算出 M 点切线斜率 k2;点斜线式算出切线方程; 解方程算出两个切线的交点 Q;
数学动画制作
四、表达式的运算 1、表达式可以做各种运算,得到新的表达式,但是 Mathemetica 不 自动对表达式进行化简。常见的化简命令是: Simplify;FullSimplify
数学动画制作
五、函数 1、内部函数: Mathematica 有很丰富的内部函数,它们是 Mathematica 系 统自带的函数,函数名一般为数学中常使用的英文单词,只要输入 相应的函数名,就可以方便地使用这些函数。内部函数既有数学中 常用的函数,又有工程中用的特殊函数。 Mathematica 中函数自变量放入方括号 [ ],不能用圆括号( )。 了解内置函数的详细用法, 可以查看联机帮助系统。 选中函数名, 按 F1 即可获取函数帮助。
数学动画制作
二、基本流程 1、做什么样的动画,想象的效果是什么样的。 2、需要那些数学对象,对象的表示是什么样的。 3、画面坐标,范围。 4、实现; 5、调整; 6、等等。
