圆曲线、缓和曲线反推里程和偏距公式

缓和曲线圆曲线计算公式

缓和曲线、竖曲线、圆曲线、匝道（计算公式）一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x 求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”) 求：①线路匝道上点的坐标：xy②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x0时sgn(x)=1，当x=0时sgn(x)=0。

缓和曲线)计算公式

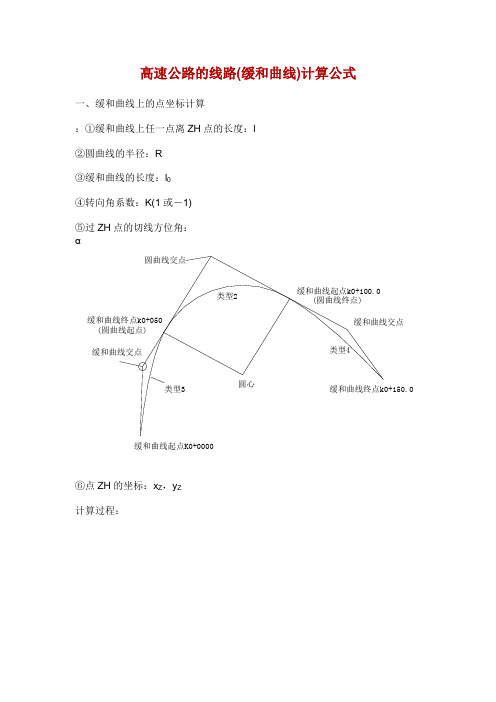
高速公路的线路(缓和曲线)计算公式一、缓和曲线上的点坐标计算：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，那么：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z，y Z为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，那么：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z，y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度〔或缓曲上任意点到缓曲起点的长度〕l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算：①第一坡度：i1(上坡为“＋〞，下坡为“－〞)②第二坡度：i2(上坡为“＋〞，下坡为“－〞)③变坡点桩号：S Z④变坡点高程：H Z⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程五、超高缓和过渡段的横坡计算：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点〔过渡段终点〕的间隔：x 求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－〞，右转为“＋〞)⑦曲线终点处曲率：P1(左转为“－〞，右转为“＋〞)求：①线路匝道上点的坐标：x,y ②待求点的切线方位角：αT计算过程：。

缓和曲线常用计算公式

一、缓和曲线常数1、内移距P ：3420268824Rl R l P n -= 2、切垂距m ：2302402R l l m -= 3、缓和曲线基本角：Rl R l πβ000902== 3、缓和曲线偏角： Rl R l πδ000306== 5、缓和曲线反偏角： Rl R l b π000603== 缓和曲线常数既有线元素，又有角元素，且均为圆曲线半径R 和缓和曲线长0l 的函数。

线元素要计算到mm ，角元素要计算到秒。

二、缓和曲线综合要素切线长：()m P R T +⎪⎭⎫ ⎝⎛+=2tan α 曲线长：()0022l R L +-=βα外视距：R P R E -⎪⎭⎫ ⎝⎛+=2cos 0α 切曲差：L T q -=2曲线综合要素均为线元素，且均为转向角 α、圆曲线半径R 和缓和曲线长0l 的函数。

曲线综合要素计算到cm 。

三、缓和曲线任意点偏角计算2020202902306Rl l Rl l Rl l Rl l t t t t t t πβπδ====0202603Rl l Rl l b t t t π==实际应用中，缓和曲线长0l 均选用10m 的倍数。

四、偏角法测设缓和曲线遇障碍 ()()T B B T l l l l Rl 2610+-=βδ ()()()()T F T F T F T F F l l l l Rl l l l l Rl 23026100+-=+-=πδ—B l 为靠近ZH(HZ)点的缓和曲线长； —T l 为置镜点的缓和曲线长；—F l 为远离ZH(HZ)点的缓和曲线长。

五、直角坐标法1、缓和曲线参数方程：5202401a a a l l R l x -= 30373033661l R l l Rl y a a a -= 2、圆曲线m R x b b +=αsin()P R y b b +-=αcos 1式中，b α为圆心O 到切线的垂线方向和到B 的半径方向所形成的圆心角，按下式计算:00βα+-=Rl l b b ()()T B B T l l l l Rl 2610+-=βδ ()()T B B T l l l l Rl 2300+-=π。

圆曲线偏角计算公式

圆曲线偏角计算公式90L/（∏R）L为置镜点到测点的距离缓和曲线偏角计算公式：573L2/（RLs60）L为置镜点（ZH，HZ）到测点的距离，Ls为缓和曲线总长HY，YH点的切线方向是：两倍的缓和曲线总偏角后视ZH，或HZ点曲线要素：切线长T=Rtg（a/2）a为转折角曲线长L=∏Ra/180 a为转折角，R为半径外矢距E=R/cos（a/2）-R a为转折角，R为半径切曲差q=2T-L竖曲线：曲线长L=R（i2-i1）i2i1分别为交点相邻两边的纵坡度切线长T= R（i2-i1）/2外矢距E=T2/（2R）前进方向坐标计算公式：（坐标增量）：X1=X+Dcosa D为距离ａ为方位角Y1=Y+Dsina后退方向坐标计算公式;Cx=X-DcosａCy=Y-Dsinａ直线段右侧坡脚点坐标计算公式：Ax1=AX+Dcos(ａ+90) Y 值同样直线段左侧坡脚点坐标计算公式：Ax1=AX+Dcos(ａ-90) Y值同样有已知两个坐标点计算方位角：例：A点坐标（X，Y），B点坐标（X1，Y1）A点方位角：tan-1a=（Y1-Y）/（X1-X）A，B两点间的距离AB=√（X-X1）2+（Y-Y1）2( 一).导线坐标计算的基本公式1.以纵坐标X的北端按顺时针方向到一直线的角度，称为该直线的方位角，通常以ａ表示。

有例说明，ａAB表示直线AB方向的坐标方位角，ａBA表示直线BA方向的坐标方位角，一般以直线的前进方向称为正方向，反之，称为反方向，直线AB的正、反方向的坐标方位角有如下关系：ａBA=ａAB加减180度2.坐标方位角的传递已知直线AB的方位角为ａAB，在B点测得到直线B1的折角￡左（或￡右），直线B1的方位角ａB1为：取左角￡左时，ａB1=ａAB+￡左—180度取右角￡右时，ａB1=ａAＢ—￡右＋１８０度若计算的ａB1<０度时应加３６０度若计算的ａB1>３６０度时应减３６０度３坐标的正运算设Ａ为已知点，其坐标ＸA、YA为已知，B是待定点。

缓和曲线常用计算公式

缓和曲线常用计算公式-CAL-FENGHAI.-(YICAI)-Company One1一、缓和曲线常数1、内移距P ：3420268824Rl R l P n -= 2、切垂距m ：2302402R l l m -= 3、缓和曲线基本角：Rl R l πβ000902== 3、缓和曲线偏角： Rl R l πδ000306== 5、缓和曲线反偏角： Rl R l b π000603== 缓和曲线常数既有线元素，又有角元素，且均为圆曲线半径R 和缓和曲线长0l 的函数。

线元素要计算到mm ，角元素要计算到秒。

二、缓和曲线综合要素切线长：()m P R T +⎪⎭⎫ ⎝⎛+=2tan α曲线长：()0022l R L +-=βα外视距：R P R E -⎪⎭⎫ ⎝⎛+=2cos 0α切曲差：L T q -=2曲线综合要素均为线元素，且均为转向角 α、圆曲线半径R 和缓和曲线长0l 的函数。

曲线综合要素计算到cm 。

三、缓和曲线任意点偏角计算2020202902306Rl l Rl l Rl l Rl l t t t t t t πβπδ====0202603Rl l Rl l b t t t π==实际应用中，缓和曲线长0l 均选用10m 的倍数。

1 四、偏角法测设缓和曲线遇障碍 ()()T B B T l l l l Rl 2610+-=βδ()()()()T F T F T F T F F l l l l Rl l l l l Rl 23026100+-=+-=πδ—B l 为靠近ZH(HZ)点的缓和曲线长； —T l 为置镜点的缓和曲线长； —F l 为远离ZH(HZ)点的缓和曲线长。

五、直角坐标法1、缓和曲线参数方程： 5202401a a a l l R l x -= 30373033661l R l l Rl y a a a -= 2、圆曲线m R x b b +=αsin()P R y b b +-=αcos 1 式中，b α为圆心O 到切线的垂线方向和到B 的半径方向所形成的圆心角，按下式计算:00βα+-=Rl l b b ()()T B B T l l l l Rl 2610+-=βδ ()()T B B T l l l l Rl 2300+-=π。

缓和曲线）计算公式

高速公路的线路(缓和曲线)计算公式一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z，y Z为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z，y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：S Z④变坡点高程：H Z⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x 求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y ②待求点的切线方位角：αT计算过程：。

曲线计算公式

Ls---缓和曲线长
2、缓和曲线偏角公式：
δn=30Ln2/RπLs
3、切线长T=m+(R+P)tan(β/2)
4、曲线长：
L=（Rπ(β-2β0）)/180+2Ls
5、外矢距E=(R+P)/cos(β/2Βιβλιοθήκη -R6、切曲差q=2T-L
7、切垂距m=Ls/2-Ls3/240R2
8、内移距P=Ls2/24R-Ls4/2688R3
一、圆曲线范围公式
已知：半径R.转向角β
1、切线长T=Rtan(β/2)
2、曲线长L=（Rπβ）/180
3、外矢距E=R(1/cos(β/2)-1)
4、切曲差q=2T-L
偏角公式δ=180C/2Rπ注C为所点弧长
二、缓和曲线范围公式
1、缓和曲线切线角βn=90Ln2/RπLs
Ln为所点n到直缓或缓直点曲线长
9、缓和曲线数学坐标公式：
X=Ls-Ln5/40R2Ls2
Y=Ln3/6RLs-Ln7/336R3Ls3
10、缓和曲线偏角公式：
δn=tan-1(y/x)
11、缓和曲线弦长公式:Ci=√(x2+y2)
Cc=Ln-Ln3/90R2+Ln5/3888R4(代数式
综合曲线中圆曲线范围坐标公式：
Xi=m+Li-Ls/2-(Li-Ls/2)3/6R2
Yi=p+(Li-Ls/2)2/2R-(Li-Ls/2)4/24R3
注：Li为圆曲线上任意点到ZH或HZ的曲线长（用于计算偏移值）
三、竖曲线计算公式
Y=X2/2R

高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式【精选】

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x 求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x<0时sgn(x)=-1，当x>0时sgn(x)=1，当x=0时sgn(x)=0。

2019高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式23708

高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式未知2009-12-27 21:40:34 本站高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z，y Z为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z，y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：S Z④变坡点高程：H Z⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”) 求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x<0时sgn(x)=-1，当x>0时sgn(x)=1，当x=0时sgn(x)=0。

公路缓和曲线计算公式讲解

公路缓和曲线计算公式讲解公路缓和曲线是指在设计公路线形时为了使车辆在曲线上能够顺利转弯而采用的一种曲线形式。

在公路设计中，缓和曲线的设计是非常重要的，因为它直接关系到车辆在曲线上的安全行驶和舒适性。

在本文中，我们将对公路缓和曲线的计算公式进行详细的讲解，希望能够帮助大家更好地理解和应用这一知识。

一、缓和曲线的类型。

在公路设计中，常见的缓和曲线类型有三种，分别是圆曲线、过渡曲线和螺旋曲线。

圆曲线是一种由圆弧组成的曲线形式，它的曲率是恒定的。

过渡曲线是一种由直线段和圆弧段组成的曲线形式，它的曲率是逐渐变化的。

螺旋曲线是一种由圆弧和直线段交替组成的曲线形式，它的曲率也是逐渐变化的。

在实际的公路设计中，我们需要根据具体的情况选择合适的缓和曲线类型，以确保车辆在曲线上的安全行驶和舒适性。

二、缓和曲线的计算公式。

1. 圆曲线的计算公式。

在公路设计中，圆曲线的计算是非常常见的。

圆曲线的计算公式如下：L = (V^2) / (127R)。

其中，L表示圆曲线的长度（单位，米），V表示车辆的设计速度（单位，公里/小时），R表示圆曲线的半径（单位，米）。

根据这个公式，我们可以计算出圆曲线的长度，从而确定圆曲线的位置和形状。

2. 过渡曲线的计算公式。

过渡曲线是一种由直线段和圆弧段组成的曲线形式，它的计算公式如下：L = (V^2) / (a)。

其中，L表示过渡曲线的长度（单位，米），V表示车辆的设计速度（单位，公里/小时），a表示过渡曲线的加速度（单位，米/秒^2）。

根据这个公式，我们可以计算出过渡曲线的长度，从而确定过渡曲线的位置和形状。

3. 螺旋曲线的计算公式。

螺旋曲线是一种由圆弧和直线段交替组成的曲线形式，它的计算公式比较复杂。

螺旋曲线的计算需要考虑曲线的曲率变化和车辆的行驶轨迹，因此通常需要借助计算机软件来进行精确计算。

三、缓和曲线的设计原则。

在公路设计中，缓和曲线的设计需要遵循一些基本原则，以确保车辆在曲线上的安全行驶和舒适性。

趋近法求算缓和曲线里程及偏距的计算原理

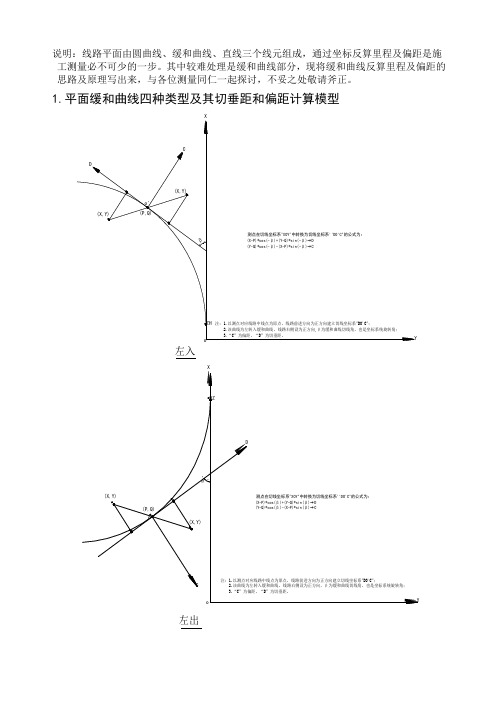
说明：线路平面由圆曲线、缓和曲线、直线三个线元组成，通过坐标反算里程及偏距是施工测量必不可少的一步。

其中较难处理是缓和曲线部分，现将缓和曲线反算里程及偏距的思路及原理写出来，与各位测量同仁一起探讨，不妥之处敬请斧正。

1.平面缓和曲线四种类型及其切垂距和偏距计算模型左入左出右入右出把以上左转曲线和右转曲线公式进行整理分析。

左转：入缓和曲线（X-P）*cos（-β）+（Y-Q）*sin（-β）→D（Y-Q）*cos（-β）-（X-P）*sin（-β）→C出缓和曲线（X-P）*cos（β）+（Y-Q）*sin（β）→D（Y-Q）*cos（β）-（X-P）*sin（β）→C右转：入缓和曲线（X-P）*cos（β）+（Y-Q）*sin（β）→D（Y-Q）*cos（β）-（X-P）*sin（β）→C出缓和曲线（X-P）*cos（-β）+（Y-Q）*sin（-β）→D（Y-Q）*cos（-β）-（X-P）*sin（-β）→C假设变量W为曲线方向判别符号，且规定W=1为右转，W=-1为左转，旋转角β=K,则以上公式简化为：入缓和曲线（X-P）×cos（W×K）+（Y-Q）×sin（W×K）→D（Y-Q）×cos（W×K）-（X-P）×sin（W×K）→C出缓和曲线（X-P）×cos（-W×K）+（Y-Q）×sin（-W×K）→D（Y-Q）×cos（-W×K）-（X-P）×sin（-W×K）→C2.趋近法求算缓和曲线里程及偏距(以上推导公式的应用)HHQX1 (计算入缓和曲线里程及偏距)程序清单:X:?Y:?W:（输入切线坐标和线路转向参数，1为左转，-1为右转X－S ZH→L：（测点对应缓和曲线长，估计值D O：S ZH+(L-L5÷(40×R2×l012)+ L9÷(3456×R4×l014))→P: W×(L3÷(6×R×l01)- L7÷(336×R3×l013))→Q:90×L2÷(π×R×l01)→K: (X-P)×cos(W×K)+(Y-Q)×sin(W×K)→D: (Y-Q)×cos(W×K)-(X-P)×sin(W×K)→C: L+D →L: LpWhile Abs(D)≥0.001: （循环语句。

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x 求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x<0时sgn(x)=-1，当x>0时sgn(x)=1，当x=0时sgn(x)=0。

缓和曲线、竖曲线、圆曲线、匝道计算公式

[转] 缓和曲线、竖曲线、圆曲线、匝道（计算公式）缓和曲线、竖曲线、圆曲线、匝道（计算公式）一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”) 求：①线路匝道上点的坐标：xy②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x0时sgn(x)=1，当x=0时sgn(x)=0。

趋近法求算缓和曲线里程及偏距的计算原理

说明：线路平面由圆曲线、缓和曲线、直线三个线元组成，通过坐标反算里程及偏距是施工测量必不可少的一步。

其中较难处理是缓和曲线部分，现将缓和曲线反算里程及偏距的思路及原理写出来，与各位测量同仁一起探讨，不妥之处敬请斧正。

1.平面缓和曲线四种类型及其切垂距和偏距计算模型左入左出右入右出把以上左转曲线和右转曲线公式进行整理分析。

左转：入缓和曲线（X-P）*cos（-β）+（Y-Q）*sin（-β）→D（Y-Q）*cos（-β）-（X-P）*sin（-β）→C出缓和曲线（X-P）*cos（β）+（Y-Q）*sin（β）→D（Y-Q）*cos（β）-（X-P）*sin（β）→C右转：入缓和曲线（X-P）*cos（β）+（Y-Q）*sin（β）→D（Y-Q）*cos（β）-（X-P）*sin（β）→C出缓和曲线（X-P）*cos（-β）+（Y-Q）*sin（-β）→D（Y-Q）*cos（-β）-（X-P）*sin（-β）→C假设变量W为曲线方向判别符号，且规定W=1为右转，W=-1为左转，旋转角β=K,则以上公式简化为：入缓和曲线（X-P）×cos（W×K）+（Y-Q）×sin（W×K）→D（Y-Q）×cos（W×K）-（X-P）×sin（W×K）→C出缓和曲线（X-P）×cos（-W×K）+（Y-Q）×sin（-W×K）→D（Y-Q）×cos（-W×K）-（X-P）×sin（-W×K）→C2.趋近法求算缓和曲线里程及偏距(以上推导公式的应用)HHQX1 (计算入缓和曲线里程及偏距)程序清单:X:?Y:?W:（输入切线坐标和线路转向参数，1为左转，-1为右转X－S ZH→L：（测点对应缓和曲线长，估计值D O：S ZH+(L-L5÷(40×R2×l012)+ L9÷(3456×R4×l014))→P: W×(L3÷(6×R×l01)- L7÷(336×R3×l013))→Q:90×L2÷(π×R×l01)→K: (X-P)×cos(W×K)+(Y-Q)×sin(W×K)→D: (Y-Q)×cos(W×K)-(X-P)×sin(W×K)→C: L+D →L: LpWhile Abs(D)≥0.001: （循环语句。

缓和曲线、圆曲线计算方法桥墩偏移量

缓和曲线计算方法(ZH～HY)桥墩偏移量首先计算直线段坐标方位角（即ZH～JD坐标方位角），及ZH 点坐标。

备用偏角公式：{30*L2/（π*RL S）缓和曲线}1、计算待求点偏角=（（L/10）2 *（57296/（RL S））/60。

其中L=待求点至ZH距离、R=圆曲线半径、L S =缓和曲线长。

2、待求点方位角=直线方位角±待求点偏角。

（曲线左转-偏角，曲线右转+偏角）3、待求点至ZH点弦长=L—L5/（90*R2*L S 2），其中L=待求点至ZH距离（里程）、R=圆曲线半径。

4、待求点坐标：X=ZH点X坐标+COS（待求点方位角）*弦长+ESIN(3偏角) Y= ZH点Y坐标+SIN（待求点方位角）*弦长±L7 /(336R3L S3)±ECOS(3偏角)说明：X增量无论曲线左右转都为正值，Y增量曲线左转为正右转为负。

红色部分为偏移位置至线路中线坐标增量。

圆曲线计算方法（HY～YH）偏移量注：（ZY-YZ）同理，方位角=用直线方位角-待求点偏角首先计算直线段坐标方位角（即Z H～JD坐标方位角），及HY 点坐标。

求出缓圆点（HY）偏角=（L S*90）/（π* R）。

1、2、求待求点偏角=（L*90）/（π* R）。

其中：L=待求点至HY距离（里程）、R=圆曲线半径、L S =缓和曲线长。

3、待求点至HY点弦长=2* R*SIN（待求点偏角）。

4、待求点方位角=直线方位角±HY点偏角±待求点偏角，（曲线左转-偏角，曲线右转+偏角）。

5、待求点坐标：X=HY点X坐标+COS（待求点方位角）*弦长Y=HY点Y坐标+SIN（待求点方位角）*弦长圆曲线计算左右边线坐标(偏移量计算)方位角=（待求点方位角±偏角±90º）。

X=该点中线X坐标+COS（左侧方位角）*（边线至中线距离+E）Y=该点中线Y坐标+SIN（左侧方位角）*（边线至中线距离+E）说明：{方位角=（待求点方位角±偏角±90º）}。

圆曲线和缓和曲线坐标推算公式附带例题

、直线上的坐标推算a c ――直线段起点M 到JD1的方位角二、圆曲线上任一点的坐标推算旳 180”①、圆曲线上任一点i 相对应的圆心角：「一二了兀R式中：Li ――圆曲线上任一点i 离开ZY 或YZ 点的弧长 ‘X 一Rsin^j Y i 一 R例题:已知一段圆曲线,R=3500m , Ls = 553.1m ，交点里程 K50+154.734 , ZY点到JD 方向方位角为 A=129 °3 ‘18.3 〃，右偏9 ° ‘15.8 〃，ZY 点里程 K49+877.607 , YZ 点里程 K50+430.707 ，起点坐标为 x = 389823.196 , y = 507787.251，求K50+200处中点坐标及左右各偏 12.5m 的坐标。

解：K50+200 处的曲线长度为 Li = 322.393m180 180圆曲线和缓和曲线坐标推算公式式中：Xm 、Ym ------- 直线段起点 M 坐标Li ---- 直线段上任意点i到线路起点M 的距离L i②、圆曲线上任一点i 的直角坐标: （1-COS 、）（可不计算）.③、圆曲线 ZY 或YZ 点到任一点的偏角:L i④、圆曲线 ZY 或YZ 点到任一点的弦长: 4C i = 2Rsin(~^) = 2Rsin( J ⑤、圆曲线 ZY 或YZ 点到任一点的弦长的方位角：ai 一 azy >jd 或yz 》jd - i⑥、所以圆曲线上任意点i 的坐标为:X j = X ZY 或 YZ C j COsqY j =YZY 或 YZC i sina iK50+200 相对应的方位角：a一二R L i- 一3500 322.393-5 16 39.52典 90°90°K50+200 相对应的偏角：十-=L尸 322.393=2 38j9.76，2 nR八 3500K50+200 到 zy 点的弦长：G =2Rsin =2 3500 sin2 38 19.76 = 322.279m zy 点到K50+200中桩的方位角：K50+200 左、右偏12.5m 的方位角：所以K50+200处的坐标为： K50+200左偏12.5m 的坐标为: K50+200右偏12.5m 的坐标为:三、缓和曲线上任一点的坐标推算切线角「尸去180X --------------兀缓和曲线上任意点i 的偏角: 二=丄3 6RL s180 缓和曲线ZH 或HZ 点到任意点i 的方位角为:ai=a ZH >jd 或HZrjd一 i缓和曲线上任意点i 的坐标为:( L 5 Xi = Li一 40R 2L ；i = _LL“ 6RL s缓和曲线ZH 或HZ 点到任意点所以缓和曲线上任意点i 的坐标为: i 的弦长：x 2y 2X i = X ZH 或HZ + C i cosqY j = Y ZH 或 HZ C i sina i例题:已知一段缓和曲线，ZH 点到JD 方向方位角为A=183 °7'08.9 〃，线路左偏 43 °「02 〃，ZH 点里程为 K52+001.615 , ZH 点坐标 x = 388071.927 ,y = 508789.089 , R = 960m , Ls = 120m ，求 K52+100 处的中点坐标及左右各偏12.5m 的坐标。

缓和曲线反算里程

缓和曲线反算里程、偏移Lbl A:｛XY｝↙L“LS”:R:S:T:B“ZH”:O“RHQXZHAO”:H“XO”:F“YO”:X:Y:Defm 20 ↙Lbl B:D=Abs(O-B):Z10=（O-B）/D：Z0=D-D5/(90L2R2):Z1=30D2/(лRLSZ10):Z7=Z1+T:Z2=Z7+2Z1:Z3=H+Z0Cos Z7:Z4=F+Z0Sin Z7:Pol(X-Z3,Y-Z4):Z5=(J-Z2)SZ10:Z6=I Cos Z5:Z8=Abs Z6:Z8≧0.001=>O=O+Z6Z10:Goto B:≠>Z“JSZHAO”=O+Z6Z10◣Z9“E”=I Sin Z5◣L“LS”——缓和曲线长度R——圆曲线半径S——偏角系数，左偏为-1，右偏为+1T——HZ或ZH点到JD方向的方位角B“ZH”——直缓或缓直点桩号O“RHQXZHAO”缓和曲线上任意一点桩号H“XO”F“YO”——HZ或ZH点桩号坐标X、Y——缓和曲线上任意一点实测坐标Z“JSZHAO”——计算出来的桩号Z9“E”计算出来的偏移距离，左负右正CASIO FX-4800计算器缓和曲线反算求里程程序编程公式：1、已知缓和曲线的起点（ZH\HZ）里程ZH和坐标(X0,Y0)，缓和曲线的长L0,缓和曲线上所求点坐标(X1,Y1),缓圆点或圆缓点处的半径R.2、求换和曲线上所求点里程DKI3、设：起点至所求点的弧长为L,起点至所求点的弦长为D则：D=√((X1-X0)^2+(Y1-Y0)^2)C=RL0R1=C/L------(1)D1=L-L^3/(90R1^2)+L^5 /(3888R1^4)-------(2)将(1)代入(2)式得：D1=L-L^5/(90C^2)+L^9/(3888C^4)――――（3）编程思路：用迭代法解一元高次方程(3)HFS------文件名Lb1 0：{ABEF}↙A”X0=” ：B”Y0=” ：E”R=” ：F”L0=”Lb1 1 ：{CDGK}↙C”X1=” ：D”Y1=” ：G”ZHorHZ=”：K”K=1or-1”I=0：J=0：Pol (C-A,D-B)T=EF：L=ILbl 2：L=L+0.001M=L-L^5÷(90T^2)+L^9÷(3888T^4)I-M<0.00001=>GOTO 3⊿GOTO 2Lbl 3 :N“DKI”=G+LK◢GOTO 1程序说明：1、本程序适用于：缓和曲线任意点坐标反算求其里程。

圆曲线和缓和曲线坐标推算公式(附带例题)

圆曲线和缓和曲线坐标推算公式一、直线上的坐标推算⎩⎨⎧++0i m i0i m i sina L Y Y cosa L X X ＝＝式中：Xm 、Ym ——直线段起点M 坐标Li ——直线段上任意点i 到线路起点M 的距离 a 0——直线段起点M 到JD1的方位角二、圆曲线上任一点的坐标推算①、圆曲线上任一点i 相对应的圆心角：i i L R180πϕ︒＝式中：Li ——圆曲线上任一点i 离开ZY 或YZ 点的弧长②、圆曲线上任一点i 的直角坐标：⎩⎨⎧-）（＝＝i iii cos 1R Y Rsin X ϕϕ（可不计算）.③、圆曲线ZY 或YZ 点到任一点i 的偏角：i ii L R902πϕ︒∆＝＝④、圆曲线ZY 或YZ 点到任一点i 的弦长：)sin(2)2sin(2C i i iR R ∆=ϕ＝⑤、圆曲线ZY 或YZ 点到任一点i 的弦长的方位角：i jd yz jd zy i a a ∆±→→或＝⑥、所以圆曲线上任意点i 的坐标为：⎩⎨⎧++i i YZ ZY iii YZ ZY i sina C Y Y cosa C X X 或或＝＝例题：已知一段圆曲线,R=3500m ，Ls ＝553.1m ，交点里程K50+154.734，ZY 点到JD 方向方位角为A=129°23′18.3″，右偏9°3′15.8″，ZY 点里程K49+877.607，YZ 点里程K50+430.707，起点坐标为x ＝389823.196，y ＝507787.251，求K50+200处中点坐标及左右各偏12.5m 的坐标。

解：K50+200处的曲线长度为Li ＝322.393mK50+200相对应的方位角："'︒⨯⨯︒︒52.39165393.3223500180L R 180i ＝＝＝ππa K50+200相对应的偏角："'︒⨯⨯︒︒∆76.19382393.322350090L R 902i ii ＝＝＝＝ππϕ K50+200到zy 点的弦长：m 279.32276.19382sin 35002Rsin 2C i i ＝＝＝"'︒⨯⨯∆ zy 点到K50+200中桩的方位角："'︒"'︒+"'︒∆+→06.38113276.193823.1823129a a i jd zy i ＝＝＝K50+200左、右偏12.5m 的方位角："'︒︒-"'︒︒-+82.5739449082.573913490a a ＝＝＝左i A "'︒︒+"'︒︒++82.57391349082.573913490a a ＝＝＝右i A 所以K50+200处的坐标为：⎩⎨⎧"'︒⨯++"'︒⨯++6484.50802606.381132sin 279.322251.507787sina C Y Y 4354.38960706.381132cos 279.322196.389823cosa C X X i i ZY ii i ZY i ＝＝＝＝＝＝K50+200左偏12.5m 的坐标为：⎩⎨⎧"'︒⨯++"'︒⨯++4656.50803582.573944sin 5.126484.508026sina 5.21Y Y 3256.38961682.573944cos 5.124354.389607cosa 5.21X X i i ＝＝＝＝＝＝左左左左 K50+200右偏12.5m 的坐标为：⎩⎨⎧"'︒⨯++"'︒⨯++5386.50803582.5739341sin 5.126484.508026sina 5.21Y Y 6482.38959882.5739341cos 5.124354.389607cosa 5.21X X i i ＝＝＝＝＝＝右右右右三、缓和曲线上任一点的坐标推算切线角：πβ︒⨯1802RL L s 2i i＝缓和曲线上任意点i 的偏角：πβδ︒⨯180RL 6L 3s 2i ii ＝＝缓和曲线ZH 或HZ 点到任意点i 的方位角为：i jd H Z jd ZH a a i δ±→→或＝缓和曲线上任意点i 的坐标为：⎪⎪⎩⎪⎪⎨⎧-s 3ii 2s 25i i i 6RL L y L 40R L L x ＝＝缓和曲线ZH 或HZ 点到任意点i 的弦长：22i yx C +＝所以缓和曲线上任意点i 的坐标为：⎩⎨⎧++i i HZ ZH iii HZ ZH i sina C Y Y cosa C X X 或或＝＝例题：已知一段缓和曲线，ZH 点到JD 方向方位角为A=183°17′08.9″，线路左偏43°31′02″，ZH 点里程为K52+001.615，ZH 点坐标x ＝388071.927，y ＝508789.089，R ＝960m ，Ls ＝120m ，求K52+100处的中点坐标及左右各偏12.5m 的坐标。

圆曲线、缓和曲线反推里程和偏距公式

缓和曲线圆曲线计算公式

缓和曲线)计算公式

缓和曲线常用计算公式

圆曲线偏角计算公式

缓和曲线常用计算公式

缓和曲线）计算公式

曲线计算公式

高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式【精选】

2019高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式23708

公路缓和曲线计算公式讲解

趋近法求算缓和曲线里程及偏距的计算原理

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)

缓和曲线、竖曲线、圆曲线、匝道计算公式

趋近法求算缓和曲线里程及偏距的计算原理

缓和曲线、 圆曲线计算方法桥墩偏移量

圆曲线和缓和曲线坐标推算公式附带例题

缓和曲线反算里程

圆曲线和缓和曲线坐标推算公式(附带例题)

缓和曲线、圆曲线计算方法桥墩偏移量