spss试验
spss分析实验报告

spss分析实验报告SPSS分析实验报告引言在社会科学研究领域,SPSS(Statistical Package for the Social Sciences)作为一种数据分析工具,被广泛应用于统计分析和数据挖掘。
本实验报告旨在通过SPSS软件对某项研究进行数据分析,探索其背后的数据模式和相关关系。
一、研究背景与目的本次研究旨在探究大学生的学习成绩与睡眠时间之间的关系。
学习成绩和睡眠时间是大学生日常生活中两个重要的方面,通过分析两者之间的关联,可以为学生提供科学的学习指导,提高学习效果。
二、研究设计与数据收集本研究采用问卷调查的方式,通过随机抽样的方法选取了500名大学生作为研究对象。
问卷内容包括学生的学习成绩和每日平均睡眠时间。
收集到的数据以Excel表格的形式整理并导入SPSS软件进行分析。
三、数据预处理在进行数据分析之前,需要对数据进行预处理。
首先,检查数据是否存在缺失值或异常值。
通过SPSS软件的数据清洗功能,将缺失值进行填补或删除,确保数据的完整性和准确性。
其次,对数据进行标准化处理,以消除不同变量之间的量纲差异。
四、描述性统计分析描述性统计分析是对数据的基本特征进行总结和描述。
通过SPSS软件的统计功能,可以计算出学生的学习成绩和睡眠时间的平均值、标准差、最大值、最小值等统计指标。
同时,可以绘制直方图、箱线图等图表来展示数据的分布情况。
五、相关性分析相关性分析是研究不同变量之间相关关系的一种方法。
本研究中,我们使用Pearson相关系数来衡量学习成绩和睡眠时间之间的线性相关性。
通过SPSS软件的相关性分析功能,可以得到相关系数的数值和显著性水平。
如果相关系数接近于1或-1,并且显著性水平小于0.05,则说明学习成绩和睡眠时间之间存在显著的相关关系。
六、回归分析回归分析是研究自变量对因变量影响程度的一种方法。
在本研究中,我们使用线性回归模型来探究睡眠时间对学习成绩的影响。
通过SPSS软件的回归分析功能,可以得到回归方程的系数、显著性水平和模型的拟合优度。
spss实验报告,心得体会

spss实验报告,心得体会篇一:SPSS实验报告SPSS应用——实验报告班级:统计0801班学号:1304080116 姓名: 宋磊指导老师:胡朝明2010.9.8一、实验目的:1、熟悉SPSS操作系统,掌握数据管理界面的简单的操作;2、熟悉SPSS结果窗口的常用操作方法,掌握输出结果在文字处理软件中的使用方法。
掌握常用统计图(线图、条图、饼图、散点、直方图等)的绘制方法;3、熟悉描述性统计图的绘制方法;4、熟悉描述性统计图的一般编辑方法。
掌握相关分析的操作,对显著性水平的基本简单判断。
二、实验要求:1、数据的录入,保存,读取,转化,增加,删除;数据集的合并,拆分,排序。
2、了解描述性统计的作用,并1掌握其SPSS的实现(频数,均值,标准差,中位数,众数,极差)。
3、应用SPSS生成表格和图形,并对表格和图形进行简单的编辑和分析。
4、应用SPSS做一些探索性分析(如方差分析,相关分析)。
三、实验内容:1、使用SPSS进行数据的录入,并保存: 职工基本情况数据:操作步骤如下:打开SPSS软件,然后在数据编辑窗口(Data View)中录入数据,此时变量名默认为var00001,var00002,…,var00007,然后在Variable View窗口中将变量名称更改即可。
具体结果如下图所示:输入后的数据为:将上述的数据进行保存:单击保存即可。
2、读取上述保存文件:选择菜单File--Open—Data;选择数据文件的类型,并输入文件名进行读取,出现如下窗口:选定职工基本情况.sav文件单击打开即可读取数据。
3、对上述数据新增一个变量工龄,其操作步骤为将当前数据单元确定在某变量上,选择菜单Data—Insert Variable,SPSS自动在当前数据单元所在列的前一列插入一2个空列,该列的变量名默认为var00016,数据类型为标准数值型,变量值均是系统缺失值,然后将数据填入修改。
结果如下图所示:篇二:SPSS相关分析实验报告本科教学实验报告(实验)课程名称:数据分析技术系列实验实验报告学生姓名:一、实验室名称:二、实验项目名称:相关分析三、实验原理相关关系是不完全确定的随机关系。
SPSS上机实验报告一
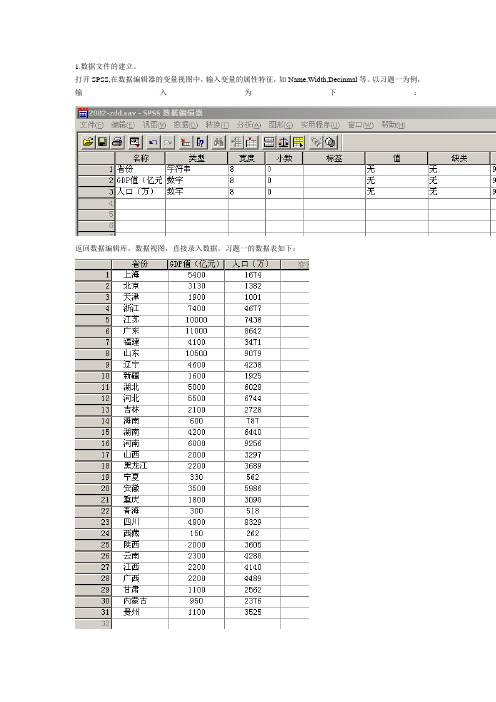
1.数据文件的建立。
打开SPSS,在数据编辑器的变量视图中,输入变量的属性特征,如Name,Width,Decinmal等。
以习题一为例,输入为下:返回数据编辑库,数据视图,直接录入数据。
习题一的数据表如下:点击Save,输入文件名将文件保存。
2.数据的整理数据编辑窗口的Date可提供数据整理功能。
其主要功能包括定义和编辑变量、观测量的命令,变量数据变换的命令,观测量数据整理的命令。
以习题一为例,将上图中的数据进行整理,以GDP值为参照,升序排列。
数据整理后的数据表为:整理后的数据,可以直观看出GDP值的排列。
3、频数分析。
以习题一为例(1).单击“分析→描述统计→频率”(2)打开“频率”对话框,选择GDP为变量(3)单击“统计量”按钮,打开“统计量”对话框.选择中值及中位数。
得到如下结果:(4)单击“分析→描述统计→探索”,打开“探索”对话框,选择GDP(亿元),输出为统计量。
结果如下:4、探索分析以习题2为例子:(1)单击“分析→统计描述→频率”,打开“频率”对话框,选择“身高”变量。
(2)选择统计量,分别选择百分数,均值,标准差,单击图标。
的如下结果:(3)单击“分析→统计描述→探索”,选择相应变量变量,单击“绘制”,选择如下图表,的如下结果:从上述图标可以看出,除了个别极端点以外,数据都围绕直线上下波动,可以看出,该组数据,在因子水平下符合正态分布。
4.交叉列联表分析:以习题3,原假设是吸烟与患病无关备择假设是吸烟与患病有关操作如下:单击“分析→统计描述→交叉表”,打开“交叉表”对话框,选择相应变量变量,单击精确,并选择“统计量”按钮,选择“卡方”作为统计量检验,然后单击“单元格”按钮,选择“观测值”和“期望值”进行计数。
得出分析结果如下:分析得出卡方值为7.469,,自由度是1,P值为0.004<0.05拒绝原假设,故有大于95%的把握认为吸烟和换慢性气管炎有关。
习题4:原假设是性别与安全性能的偏好无关备择假设是性别与安全性能的偏好有关操作如下:单击“分析→统计描述→交叉表”,打开“交叉表”对话框,选择相应行列变量然后选择“统计量”按钮,以“卡方”作为统计量检验.单击“单元格”按钮,选择“观测值”和“期望值”进行计数单击“确定”,得出分析结果如下:分析得出卡方值为19自由度是4,P值为0.001<0.05拒绝原假设,故有99.9%的把握认为性别与安全性能的偏好有关5实验作业补充。
SPSS分析报告(二)

SPSS实验分析报告二一、婆媳关系*住房条件检验(一)、提出原假设H0原假设: 婆媳关系的好坏程度与住房条件有关系(二)、两独立样本t检验结果及分析表(一)觀察值處理摘要觀察值有效遺漏總計N百分比N百分比N百分比婆媳关系* 住房条件600100.0%00.0%600100.0%由表(一)可知, 本次调查获得的有效样本为600份, 没有遗漏的个案。
表(二)婆媳关系*住房条件交叉列表住房条件總計差一般好婆媳关系紧张計數577860195預期計數48.868.378.0195.0婆媳关系內的%29.2%40.0%30.8%100.0%住房条件內的%38.0%37.1%25.0%32.5%佔總計的百分比9.5%13.0%10.0%32.5%殘差8.39.8-18.0一般計數458763195預期計數48.868.378.0195.0婆媳关系內的%23.1%44.6%32.3%100.0%住房条件內的%30.0%41.4%26.3%32.5%佔總計的百分比7.5%14.5%10.5%32.5%殘差-3.818.8-15.0好計數4845117210預期計數52.573.584.0210.0婆媳关系內的%22.9%21.4%55.7%100.0%住房条件內的%32.0%21.4%48.8%35.0%佔總計的百分比8.0%7.5%19.5%35.0%殘差-4.5-28.533.0總計計數150210240600預期計數150.0210.0240.0600.0婆媳关系內的%25.0%35.0%40.0%100.0%住房条件內的%100.0%100.0%100.0%100.0%佔總計的百分比25.0%35.0%40.0%100.0%由表(二)可知, 一共调查了600人, 其中婆媳关系紧张的组有195人, 占总人数的32.5%;婆媳关系一般的组有195人, 占总人数的32.5%;婆媳关系好的组有210人, 占总人数的35.0%;数据分布均匀。
spss分析实验报告

SPSS分析实验报告引言SPSS(统计包括社会科学)是一种常用的统计分析软件,广泛应用于社会科学领域的数据分析。
本文将以“step by step thinking”为思维导向,详细介绍如何使用SPSS进行实验数据的分析和结果解读。
步骤一:数据导入首先,我们需要将实验数据导入SPSS软件中。
打开SPSS软件,点击“文件”菜单,并选择“导入数据”。
选择数据文件所在位置,并按照指示完成数据导入过程。
确认数据导入完成后,我们可以开始进行下一步分析。
步骤二:数据清洗在进行实验数据分析之前,我们需要对数据进行清洗,以确保数据的准确性和可靠性。
数据清洗的步骤包括删除重复数据、处理缺失值和异常值等。
通过点击SPSS软件中的“数据”菜单,我们可以找到相应的数据清洗工具,并按照指示进行操作。
步骤三:描述性统计描述性统计是对数据进行总体特征描述的过程。
在SPSS软件中,我们可以使用“统计”菜单中的“描述统计”工具进行描述性统计分析。
该工具可以计算数据的均值、标准差、中位数等统计量,为后续的分析提供参考。
步骤四:检验假设在进行实验数据分析时,我们通常需要检验某些假设是否成立。
SPSS软件提供了多种假设检验工具,如t检验、方差分析等。
通过点击“分析”菜单,并选择相应的假设检验工具,我们可以输入所需的参数,并进行假设检验。
根据检验结果,我们可以判断实验数据是否支持或拒绝了我们的假设。
步骤五:相关性分析相关性分析用于研究两个或多个变量之间的关系。
SPSS软件中的“相关”工具可以计算出变量之间的相关系数,并绘制相应的相关图表。
通过相关性分析,我们可以了解变量之间的线性关系,并得出相关系数的显著性程度。
步骤六:回归分析回归分析是一种用于预测和解释变量之间关系的统计方法。
在SPSS软件中,我们可以使用“回归”工具进行回归分析。
通过输入自变量和因变量,并进行回归分析,我们可以得到回归方程和相关统计指标,进而进行预测和解释。
结果解读根据以上分析步骤,我们可以得到一系列实验数据的统计分析结果。
第一次SPSS实验

SPSS第一次作业一实验目的1、掌握均值比较,用于计算指定变量的综合描述统计量,2、掌握单样本T检验(One-Sample T Test),检验单个变量的均值与假设之间是否存在差异;3、掌握独立样本T检验(Independent-Samples Test),用于检验两组来自独立总体的样本,企图理综题的均值或中心位置是否一样4、掌握配对样本T检验(Paired-Samples Test),用于检验两个相关的样本是否来自具有相同均值的总体。
二、实验内容1、题目:某康体中心的减肥班学员入班时的体重数据和减肥训练一个月后的体重数据记录在数据文件data08-06中,试分析一个月的训练是否有效。
如果按性别分组分析结果又如何?如果按体重等级分组检查训练结果,结果会是怎样的?(此问题满足配对样本T检验(Paired-Samples T Test)的条件,因此用配对样本T检验来解决此问题。
)1.1问题:分析一个月的训练是否有效。
1)实验步骤:第1步数据组织;打开SPSS数据文件data08-06。
第2步打开主对话框;选择Analyse→Compare Means →Paired-Samples T Test ,打开同下图样的配对样本T检验主对话框。
2)运行结果:a)配对样本统计量Paired Samples Statistics表1.1.1b)配对样本相关关系Paired Samples Correlations表1.1.2c)配对样本T检验结果Paired Samples Test表1.1.33)结果分析:表1.1.1是对训练前后体重的单变量描述统计量,表中显示的事配对变量的变量标签,对数为1对。
Means给出训练前后的体重均值,分别为71.255与68.912。
N即观测量数目训练前后均为51。
Std.Deviation训练前后的标准差,分别为7.0989和7.2289Std.Deviation训练前后的均值标准误,分别为0.9940和1.0122 表1.1.2中给出训练前后体重之间的相关系数,Correlation为0.951,不相关的概率为0.000。
spss对数据进行相关性分析实验报告

spss对数据进行相关性分析实验报告一、实验目的与背景在统计学的研究中,相关性分析是一种常见的分析方法,用于研究两个或多个变量之间的关联程度。
本实验旨在使用SPSS软件对收集到的数据进行相关性分析,并探索变量之间的关系。
二、实验过程1. 数据收集:根据研究目的,我们收集了一份包含多个变量的数据集。
其中,变量包括A、B、C等。
2. 数据准备:在进行相关性分析之前,我们需要对数据进行准备。
首先,我们载入数据集到SPSS软件中。
然后,对于缺失数据,我们根据需要采取相应的填补或删除策略。
接着,我们进行数据的清洗和整理,以确保数据的准确性和一致性。
3. 相关性分析:使用SPSS软件,我们可以轻松地进行相关性分析。
在SPSS的分析菜单中,选择相关性分析功能,并设置相应的参数。
我们将选择Pearson相关系数,该系数用于衡量两个变量之间的线性相关关系。
此外,还可以选择其他类型的相关系数,如Spearman相关系数,用于非线性关系的探索。
设置参数后,我们点击“运行”按钮,即可得到相关性分析的结果。
4. 结果解读:SPSS将为我们提供一份详细的结果报告。
我们可以看到每对变量之间的相关系数及其显著性水平。
如果相关系数接近1或-1,并且P值低于显著性水平(通常为0.05),则可以得出两个变量之间存在显著的线性相关关系的结论。
此外,我们还可以通过散点图、线性回归等方法进一步分析相关性结果。
5. 结论与讨论:根据相关性分析的结果,我们可以得出结论并进行讨论。
如果发现两个变量之间存在显著的相关关系,我们可以进一步探究其原因和意义。
同时,我们还可以提出假设并设计更深入的实验,以验证和解释这些相关性。
三、结果与讨论根据我们的研究目的和数据集,通过SPSS软件进行的相关性分析显示了一些有意义的结果。
我们发现变量A与变量B之间存在显著的正相关关系(Pearson相关系数为0.7,P<0.05)。
这表明随着A的增加,B也会相应增加。
SPSS聚类分析实验报告

SPSS聚类分析实验报告一、实验目的本实验旨在通过SPSS软件对样本数据进行聚类分析,找出样本数据中的相似性,并将样本划分为不同的群体。
二、实验步骤1.数据准备:在SPSS软件中导入样本数据,并对数据进行处理,包括数据清洗、异常值处理等。
2.聚类分析设置:在SPSS软件中选择聚类分析方法,并设置分析参数,如距离度量方法、聚类方法、群体数量等。
3.聚类分析结果:根据分析结果,对样本数据进行聚类,并生成聚类结果。
4.结果解释:分析聚类结果,确定每个群体的特征,观察不同群体之间的差异性。
三、实验数据本实验使用了一个包含1000个样本的数据集,每个样本包含了5个变量,分别为年龄、性别、收入、教育水平和消费偏好。
下表展示了部分样本数据:样本编号,年龄,性别,收入,教育水平,消费偏好---------,------,------,------,---------,---------1,30,男,5000,大专,电子产品2,25,女,3000,本科,服装鞋包3,35,男,7000,硕士,食品饮料...,...,...,...,...,...四、实验结果1. 聚类分析设置:在SPSS软件中,我们选择了K-means聚类方法,并设置群体数量为3,距离度量方法为欧氏距离。
2.聚类结果:经过聚类分析后,我们将样本分为了3个群体,分别为群体1、群体2和群体3、每个群体的特征如下:-群体1:年龄偏年轻,女性居多,收入较低,教育水平集中在本科,消费偏好为服装鞋包。
-群体2:年龄跨度较大,男女比例均衡,收入中等,教育水平较高,消费偏好为电子产品。
-群体3:年龄偏高,男性居多,收入较高,教育水平较高,消费偏好为食品饮料。
3.结果解释:根据聚类结果,我们可以看到不同群体之间的差异性较大,每个群体都有明显的特征。
这些结果可以帮助企业更好地了解不同群体的消费习惯,为市场营销活动提供参考。
五、实验结论通过本次实验,我们成功地对样本数据进行了聚类分析,并得出了3个不同的群体。
spss实验一、实验步骤
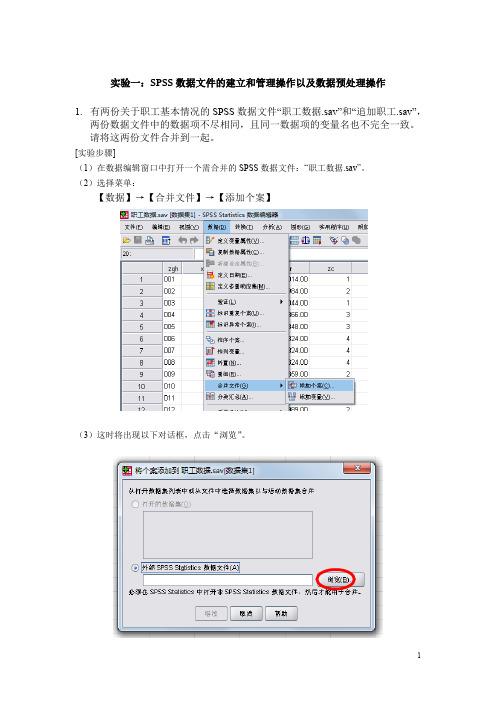
实验一:SPSS数据文件的建立和管理操作以及数据预处理操作1.有两份关于职工基本情况的SPSS数据文件“职工数据.sav”和“追加职工.sav”,两份数据文件中的数据项不尽相同,且同一数据项的变量名也不完全一致。
请将这两份文件合并到一起。
[实验步骤](1)在数据编辑窗口中打开一个需合并的SPSS数据文件:“职工数据.sav”。
(2)选择菜单:【数据】→【合并文件】→【添加个案】(3)这时将出现以下对话框,点击“浏览”。
(4)打开需进行纵向合并处理的SPSS数据文件“追加职工.sav”。
按“继续”后,显示纵向合并数据文件窗口。
(如下图)(5)对话框右边【新的活动数据集中的变量】框中显示的变量名是两个数据文件中的同名变量,对话框左边【非成对变量】框中显示的变量名是两个文件中的不同名变量。
其中,变量名后面的【*】表示该变量是当前数据编辑窗口中(“职工数据.sav”)的变量,【+】表示该变量是(2)“追加职工.sav”中指定的磁盘文件中的变量。
SPSS默认这些变量的含义不同,且不放入合并后的新文件中。
如果不接受这种默认,可选择其中的两个变量名并按【对】按钮指定配对,表示虽然它们的名称不同但数据含义是相同的,可进入合并后的数据文件中。
本题中,显然职称zc(*)和职称zc1(+)两个变量名需要按【对】按钮指定配对。
方法是:按住“Ctrl键”,同时鼠标点zc(*)和zc1(+),然后按【对】按钮,这时【新的活动数据集中的变量】框中出现“zc&zc1”变量名。
(6)把【非成对变量】框中显示的其他变量名全部标记,按右向箭头。
(7)按【确定】,完成操作。
2.根据“住房状况调查.sav”数据,通过数据排序功能分析本市户口和外地户口家庭的住房面积情况。
(按升序排列)[实验步骤](1)在数据编辑窗口中打开SPSS数据文件:“住房状况调查.sav”。
(2)选择菜单:【数据】→【排序个案】(3)指定主排序变量“户口状况”到【排序依据】框中,并选择【排序顺序】框中的选项指出该变量按升序还是降序排序。
SPSS操作实验手册

SPSS试验操作指导手册(2023版)2.SPSS数据整顿2.1 SPSS数据文献旳建立SPSS数据文献旳建立可以运用【File(文献)】菜单中旳命令来实现。
详细来说, SPSS提供了四种创立数据文献旳措施:●新建数据文献【File(文献)】→【New(新建)】→【Data(数据)】命令;●直接打开已经有数据文献【File(文献)】→【Open (打开)】→【Data(数据)】命令;●使用数据库查询;【File(文献)】→【Open Database(打开数据库)】→【New Query(新建查询)】命令, 弹出【Database Wizard(数据库向导)】对话框●从文本向导导入数据文献。
【File(文献)】→【Read Text Data(打开文本数据)】命令, 弹出【Open Data(打开数据)】对话框实例分析: 股票指数旳导入文献2-1.xls是上证指数从2023年1月4日至2023年10月16 日旳数据资料, 包括了开盘价、当日最高价、当日最低价和收盘价等选项, 请将该数据导入至SPSS中。
2.2 SPSS数据文献旳属性一种完整旳SPSS文献构造包括变量名称、变量类型、变量名标签、变量值标签等内容。
注意: SPSS数据文献中旳一列数据称为一种变量, 每个变量都应有一种变量名。
SPSS数据文献中旳一行数据称为一条个案或观测量(Case)2.2.1 实例分析: 员工满意度调查表旳数据属性设计1.实例内容为了提高员工旳工作积极性, 完善企业各方面管理制度, 并到达有旳放矢旳目旳, 某企业决定对我司员工进行不记名调查, 但愿理解员工对企业旳满意状况。
请根据该企业设计旳员工满意度调查题目(行政人事管理部分)旳特点, 设计该调查表数据在SPSS旳数据属性。
2.实例操作详细环节如下文献(2-2.sav.)Step01: 打开SPSS中旳Data View窗口, 录入或导入原始调查数据。
Step02:选择菜单栏中旳【File(文献)】→【Save (保留)】命令, 保留数据文献, 以免丢失。
spss对数据进行相关性分析实验报告

spss对数据进行相关性分析实验报告一、实验目的本次实验旨在运用 SPSS 软件对给定的数据进行相关性分析,以探究不同变量之间的关系,为进一步的研究和决策提供有价值的信息。
二、实验原理相关性分析是一种用于研究两个或多个变量之间线性关系强度和方向的统计方法。
常用的相关性系数包括皮尔逊(Pearson)相关系数、斯皮尔曼(Spearman)相关系数等。
皮尔逊相关系数适用于两个连续变量之间的线性关系分析,要求变量服从正态分布;斯皮尔曼相关系数则适用于有序变量或不满足正态分布的变量。
三、实验数据本次实验使用的数据来源于具体来源,包含了变量数量个变量,分别为变量名称 1、变量名称2……变量名称 n。
每个变量包含了样本数量个观测值。
四、实验步骤1、数据导入打开 SPSS 软件,选择“文件”菜单中的“打开”选项,找到并选中要分析的数据文件。
在弹出的对话框中,根据数据的格式选择相应的导入方式,如CSV、Excel 等。
2、变量定义在“变量视图”中,对导入的变量进行定义,包括变量名称、类型、宽度、小数位数等。
3、相关性分析选择“分析”菜单中的“相关”选项,在弹出的子菜单中选择“双变量”。
将需要分析相关性的变量选入“变量”框中。
根据变量的类型和分布特征,选择合适的相关性系数,如皮尔逊或斯皮尔曼相关系数。
点击“确定”按钮,运行相关性分析。
五、实验结果1、相关性系数矩阵输出的相关性系数矩阵显示了各个变量之间的相关性系数值。
系数值的范围在-1 到 1 之间,-1 表示完全负相关,1 表示完全正相关,0 表示无相关性。
2、显著性水平除了相关性系数值外,还输出了每个相关性系数的显著性水平(p 值)。
p 值小于 005 通常被认为相关性是显著的。
以下是对实验结果的具体分析:变量 1 与变量 2 的相关性分析:相关性系数为具体数值,表明变量 1 和变量 2 之间存在正/负相关关系。
p 值为具体数值,小于 005,说明这种相关性在统计上是显著的。
spss实验报告一,二
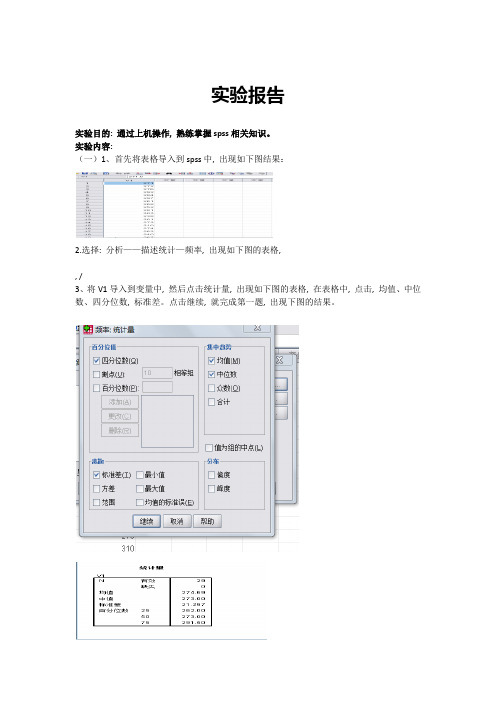
实验报告
实验目的: 通过上机操作, 熟练掌握spss相关知识。
实验内容:
(一)1、首先将表格导入到spss中, 出现如下图结果:
2.选择: 分析——描述统计—频率, 出现如下图的表格,
, /
3、将V1导入到变量中, 然后点击统计量, 出现如下图的表格, 在表格中, 点击, 均值、中位数、四分位数, 标准差。
点击继续, 就完成第一题, 出现下图的结果。
以上就是第一题的结果。
(二)
1.首先将表格导入到spss中, 如下图:
2.从上表中, 可知, 方法A要比B.C的只都要高, 可见平均值要高于B.C, 就应该对这三组进行平均值, 方差的计算进行比较。
选择: 分析——描述统计——描述, 出现如下图的表格:
将方法A.B.C分别导入到变量中, 然后点击选项这个按钮, 出现如下图的表格进行选择:
可以选择标准差, 最大值, 最小值, 均值, 然后点击继续, 则会出现结果, 通过对结果进行对比, 选择方案。
由图可知, 方法A的平均值高于B、C, 而且最小值也都大于B、C的最大值, 可知A的组装优越于B、C, 即使标准差大于B, 稳定性稍微差于B, 但总体上组装的结果要比B好, 所以要选择方案A。
第六章Spss实验报告
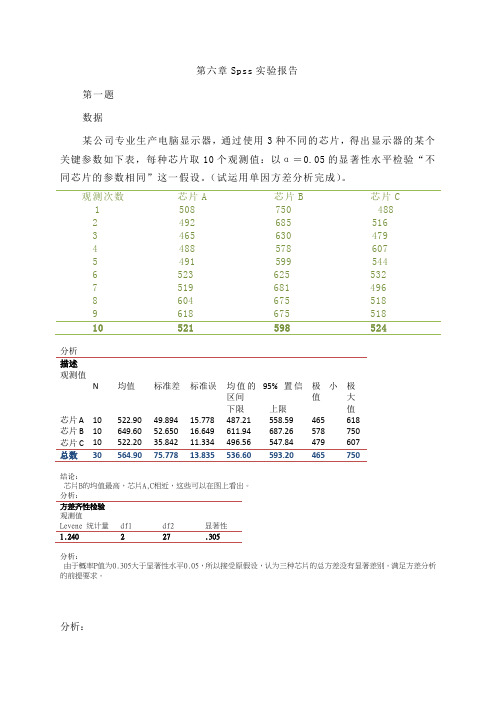
第六章Spss实验报告第一题数据某公司专业生产电脑显示器,通过使用3种不同的芯片,得出显示器的某个关键参数如下表,每种芯片取10个观测值:以α=0.05的显著性水平检验“不同芯片的参数相同”这一假设。
(试运用单因方差分析完成)。
观测次数芯片A 芯片B 芯片C1 508 750 4882 492 685 5163 465 630 4794 488 578 6075 491 599 5446 523 625 5327 519 681 4968 604 675 5189 618 675 51810 521 598 524分析描述观测值N均值标准差标准误均值的95% 置信区间极小值极大值下限上限芯片A10522.9049.89415.778487.21558.59465618芯片B10649.6052.65016.649611.94687.26578750芯片C10522.2035.84211.334496.56547.84479607总数30564.9075.77813.835536.60593.20465750结论:芯片B的均值最高,芯片A,C相近,这些可以在图上看出。
分析:方差齐性检验观测值Levene 统计量df1 df2 显著性1.240 2 27 .305分析:由于概率P值为0.305大于显著性水平0.05,所以接受原假设,认为三种芯片的总方差没有显著差别。
满足方差分析的前提要求。
分析:结论:对应的P值近似为0显著性水平为0.05,概率P小于0.05,拒绝原假设,认为三种不同的芯片有显著差异。
分析;多重比较观测值LSD(I) 芯片(J) 芯片均值差(I-J)标准误显著性95% 置信区间下限上限芯片A 芯片B -126.700*20.890 .000 -169.56 -83.84芯片C .700 20.890 .974 -42.16 43.56芯片B 芯片A 126.700*20.890 .000 83.84 169.56芯片C 127.400*20.890 .000 84.54 170.26芯片C 芯片A -.700 20.890 .974 -43.56 42.16芯片B -127.400*20.890 .000 -170.26 -84.54*. 均值差的显著性水平为 0.05。
SPSS实验报告——均值比较

实验报告一、实验目的1、掌握均值比较,用于计算指定变量的综合描述统计量2、掌握独立样本T检验(Independent Samples Test),用于检验两组来自独立总体的样本,企图理综题的均值或中心位置是否一样二、实验步骤第1步数据导入;打开“EG5-2城市和农村学生心理素质测试得分.sav”第2步确定要进行T检验的变量;选择Analyze→ Compare Means →Independent-Samples ,选择“p”变量作为检验变量,移入“Test Variable(s)”框中。
第4步确定分组变量;选择变量“group”作为分组变量,将其移入下图中的“Grouping variable”文本框中,并定义分组的变量值:Group1—1,Group2—2。
三、结果及分析两独立样本T检验的基本描述统计量分析:1、根据结果,方差齐性检验的p值为0.791,大于0.05,故应接受原假设。
2、因为方差相等,两独立样本T检验的结果应该看两独立样本T检验结果报中的Equal variances assumed”一行,第5列为相应的双尾检测概率(Sig.(2-tailed))为0.07,在显著性水平为0.05的情况下,T统计量的概率p值大于0.05,故接受原假设假设,即认为两样本的均值是相等的,在本题中,不能认为两组的成绩有显著性差异。
实验报告一、实验目的1、掌握均值比较,用于计算指定变量的综合描述统计量2、掌握配对样本T检验(Paired Samples Test),用于检验两个相关的样本是否来自具有相同均值的总体。
二、实验步骤第1步数据组织;打开“EG5-1学生培训前后心理测试得分.sav”第2步确定配对分析的变量选择Analyze→ Compare Means →Paired-Samples T Test,将变量“before”和“after”添加到“Paired Variables”框中,作为一对分析的配对变量三、结果及分析分析:表“paired samples test”显示,学生培训前后的平均成绩相差 -0.158,平均成绩差值的标准差为1.5048,差值标准差的标准误为0.4344.在置信水平为95%时平均值差值的置信区间为-1.114~0.798。
spss实验

目录1.实验一 SPSS的数据管理2.实验二描述性统计分析3.实验三均值检验4.实验四方差分析5.实验五聚类分析和判别分析6.实验六因子分析和主成分分析7.实验七相关分析和回归分析8.实验八非参数检验9.实验九绘制统计图实验三均值检验一、实验目的学习利用SPSS进行单样本、两独立样本以及成对样本的均值检验。
二、实验内容及步骤(一)描述统计(Means过程)实验内容:某医师测得血红蛋白值(g%)如表3.1,试利用Means过程作基本的描述性统计分析。
1.建立数据文件。
定义4个变量:ID、Gender、Age和HB,分别表示编号、性别、年龄和血红蛋白值。
2. 选择菜单“Analyze→Compare Means→Means”,弹出“Means”对话框。
在对话框左侧的变量列表中,选择变量“血红蛋白值”进入“Dependent List”列表框,选择变量“性别”进入“Independent List”,单击“Next”按钮,选择变量“年龄”进入“Independent List”。
3.单击“Options”按钮,在弹出的“选择描述统计量”对话框中设置输出的描述统计量。
4.单击“OK”按钮,得到输出结果。
(二)单样本T检验(One-Sample T Test过程)实验内容:某地区10年测得16-18岁人口的平均血红蛋白值为10.25。
现在抽查测量了该地区40个16-18岁人口的血红蛋白如表1,试分析该地区现在16-18岁人口的血红蛋白与10年前相比,是否有显著的差异?实验步骤:1.打开数据文件。
2. 选择菜单“Analyze→Compare Means→One-Sample T Test”。
弹出“One-Sample T Test”对话框。
3.在对话框左侧的变量列表中选择变量“血红蛋白”进入“Test Variable(s)”框;在“Test Value”编辑框中输入过去的平均血红蛋白值10.25.4.单击“OK”按钮,得到输出结果。
SPSS相关分析实验报告_实验报告_

SPSS相关分析实验报告篇一:spss对数据进行相关性分析实验报告实验一一.实验目的掌握用spss软件对数据进行相关性分析,熟悉其操作过程,并能分析其结果。
二.实验原理相关性分析是考察两个变量之间线性关系的一种统计分析方法。
更精确地说,当一个变量发生变化时,另一个变量如何变化,此时就需要通过计算相关系数来做深入的定量考察。
P值是针对原假设H0:假设两变量无线性相关而言的。
一般假设检验的显著性水平为0.05,你只需要拿p值和0.05进行比较:如果p值小于0.05,就拒绝原假设H0,说明两变量有线性相关的关系,他们无线性相关的可能性小于0.05;如果大于0.05,则一般认为无线性相关关系,至于相关的程度则要看相关系数R值,r越大,说明越相关。
越小,则相关程度越低。
而偏相关分析是指当两个变量同时与第三个变量相关时,将第三个变量的影响剔除,只分析另外两个变量之间相关程度的过程,其检验过程与相关分析相似。
三、实验内容掌握使用spss软件对数据进行相关性分析,从变量之间的相关关系,寻求与人均食品支出密切相关的因素。
(1)检验人均食品支出与粮价和人均收入之间的相关关系。
a.打开spss软件,输入“回归人均食品支出”数据。
b.在spssd的菜单栏中选择点击,弹出一个对话窗口。
C.在对话窗口中点击ok,系统输出结果,如下表。
从表中可以看出,人均食品支出与人均收入之间的相关系数为0.921,t检验的显著性概率为0.000<0.01,拒绝零假设,表明两个变量之间显著相关。
人均食品支出与粮食平均单价之间的相关系数为0.730,t检验的显著性概率为0.000<0.01,拒绝零假设,表明两个变量之间也显著相关。
(2)研究人均食品支出与人均收入之间的偏相关关系。
读入数据后:A.点击系统弹出一个对话窗口。
B.点击OK,系统输出结果,如下表。
从表中可以看出,人均食品支出与人均收入的偏相关系数为0.8665,显著性概率p=0.000<0.01,说明在剔除了粮食单价的影响后,人均食品支出与人均收入依然有显著性关系,并且0.8665<0.921,说明它们之间的显著性关系稍有减弱。
SPSS实验报告

通过计算诸如样本均值、中位数、样本方差等重要基本统计量,并辅助于SPSS 提供的图形功能,能够使分析者把握数据的基本特征和数据的整体分布形态,对进一步的统计判断和数据建模工作起到重要作用。
并且,通过例子学习描述性统计分析及其在 SPSS 中的实现,包括统计量的定义及计算、频率分析、描述性分析、探索性分析、交叉表分析和多重响应分析,能够使分析者更好的掌握基本的统计分析,即单变量频数分布的编制、基本统计量的计算以及数据的探索性分析等。
1.打开数据文件 data4-8.sav,完成以下统计分析。
(1)计算各科成绩的描述统计量:平均成绩、中位数、众数、标准差、方差、极差、最大值和最小值;①解决问题的原理:描述性分析②实验步骤:通过“分析-描述统计-描述”,打开“描述性”对话框,根据题目所需要的统计量进行设置。
③结果及分析:表中分析变量“成绩”的个案数、所有个案中的极大值、极小值、均值、标准差及方差。
(2)使用 Recode 命令生成一个新变量“成绩段”,其值为各科成绩的分段: 90~100 为 1,80~89 为 2,70~79 为 3,60~69 为4,60 分以下为 5,其值标签: 1—优, 2—良, 3—中, 4—及格, 5—不及格。
分段以后进行频数分析,统计各分数段的人数,最后生成条形图和饼图。
①解决问题的原理:频率分析。
②实验步骤:通过“分析-描述统计-频率”,打开“频率”对话框,根据题目所需要的统计量进行设置。
③结果及分析:有效1519242830323334363743495055频率11111211121111百分比2.22.22.22.22.24.42.22.22.24.42.22.22.22.2有效百分比2.22.22.22.22.24.42.22.22.24.42.22.22.2积累百分比2.24.46.78.911.115.617.820.022.226.728.931.133.3全距极小值83 15成绩有效的 N (列表状态) N4545标准差23.048极大值98方差531.210均值60.518.9 6.7 2.2 2.2 2.2 2.2 6.7 2.2 2.2 2.2 2.2 2.2 2.2 4.4 2.2 4.4 2.2 4.4 2.2 100.0表中显示了变量“成绩段”在各个取值上浮现的次数(频率)、其频率占所有个案中的百分比、有效百分比及积累百分比。
统计学原理SPSS实验报告
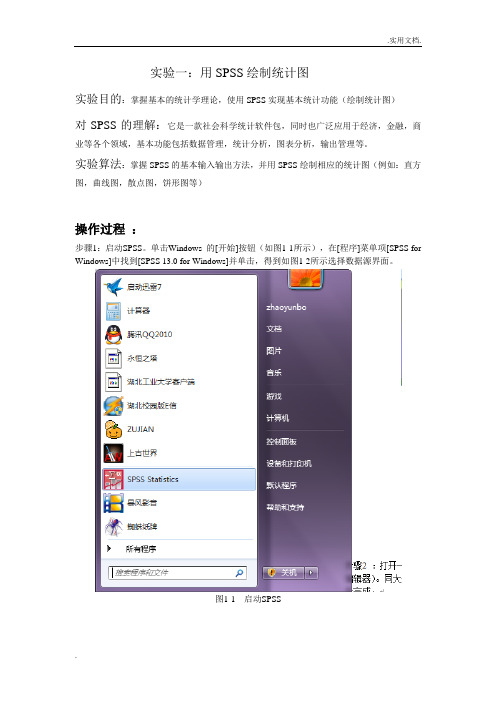
实验一:用SPSS绘制统计图实验目的:掌握基本的统计学理论,使用SPSS实现基本统计功能(绘制统计图)对SPSS的理解:它是一款社会科学统计软件包,同时也广泛应用于经济,金融,商业等各个领域,基本功能包括数据管理,统计分析,图表分析,输出管理等。
实验算法:掌握SPSS的基本输入输出方法,并用SPSS绘制相应的统计图(例如:直方图,曲线图,散点图,饼形图等)操作过程:步骤1:启动SPSS。
单击Windows 的[开始]按钮(如图1-1所示),在[程序]菜单项[SPSS for Windows]中找到[SPSS 13.0 for Windows]并单击,得到如图1-2所示选择数据源界面。
图1-1 启动SPSS图1-2 选择数据源界面步骤2 :打开一个空白的SPSS数据文件,如图1-3。
启动SPSS 后,出现SPSS 主界面(数据编辑器)。
同大多数Windows 程序一样,SPSS 是以菜单驱动的。
多数功能通过从菜单中选择完成。
图1-3 空白的SPSS数据文件步骤3:数据的输入。
打开SPSS以后,直接进入变量视图窗口。
SPSS的变量视图窗口分为data view和variable view两个。
先在variable view中定义变量,然后在data view里面直接输入自定义数据。
命名为mydata并保存在桌面。
如图1-4所示。
图1-4 数据的输入步骤4:调用Graphs菜单的Bar过程,绘制直条图。
直条图用直条的长短来表示非连续性资料(该资料可以是绝对数,也可以是相对数)的数量大小。
选择的数据源见表1。
步骤5:数据准备。
激活数据管理窗口,定义变量名:年龄标化发生率为RA TE,冠心病临床型为DISEASE,血压状态为BP。
RATE按原数据输入,DISEASE按冠状动脉机能不全=1、猝死=2、心绞痛=3、心肌梗塞=4输入,BP按正常=1、临界=2、异常=3输入。
步骤6:选Graphs菜单的Bar...过程,弹出Bar Chart定义选项框(图1-5)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Step 5:单击OK完成输出报表实验六:列形式摘要报表
对银行16位职员的身高数据进行列形式摘要报表分析。数据集casesummaries.sav
Step 1:
按Analyze-Report-Report Summaries in Columns的顺序单击, 打开 Summaries in Columns主对话框 将height变量入Data框,然后单击该文件中的Summary按钮,选中 Mean of Values项,按Continue返回。 挑选sex,grade变量入Break框
例:在xuelin.sav中建立新变量temp,令其值当血磷值大于1时为 2,否则为1
Step 1:选择菜单Transform—Compute,弹出Compute Variable
对话框,并进行输入,如下图输入“temp”和“1”后按“OK”
给目标变量赋值
需计算的变量名
软键盘
Step 2:再次选择菜单Transform—Compute,弹出Compute
未被纳入的变 量列表
被纳入合并后新数 据的变量列表 用于选入记录匹配使用 的关键变量。此处单击 左上面的ID,将其选入
用于定义关键 变量。此处选 中该复选框的 第一个。
运行结果如下图
Aggregate过程
按制定的分类变量对观测值进行分组,对每组记录的各变量求指定的描述 统计量。各零件的含义如下: 选择分组变量
出一个确认对话框,进行确认替换。
Transform中其他过程:
Recode过程
Recode过程用于从原变量值按照某种一一对应的关系生成新变量 值,可以将新值赋给原变量,也可以生成一个新变量。 作业:在xuelin.sav中生成新变量temp3,当血磷值小于1时取值为0, 1~2时取值为10,大于2时取值为20。 Categorize Variables过程 用于将连续性变量自动按要求分成等间距的几组。 作业:在xuelin.sav中将血磷值x按大小分成5个等级 Count过程 Count过程用于标识某个值或某些值在某个变量的取值中是否出现。 作业:在xuelin.sav中看有哪些记录的血磷值在2~3之间。 Rank Case过程 Rank Case过程是用来排序的一个专用过程。 作业:在xuelin.sav中分组计算血磷值的秩次
实验八:单样本T检验
随机抽查某区25名健康成年男子的脉搏(次/分)分别为65 65 67 67 69 69 70 70 71 71 72 72 74 76 76 78 78 79 79 80 80 81 81 82 82 ,已知健康成年男子的脉搏均 数为72次/分,比较该区健康成年男子的脉搏与已知健康成年男子的脉搏均数间 有无显著性差异。 Step1: 设变量为p,将25名健康成年男子的脉搏数输入spss. 数据集为maibo.sav Step2: 选择analyze→compare means→one-sample T test单击,出现onesample T test框,将p选入test variable框,test value框内填入72, Options不用,如下图示,
某市1995年110名7岁男童身高数据如下:数据集为nantong.sav
114.4 119.2 124.7 125.0 115.0 112.8 120.2 110.2 120.9 120.1 125.5 120.3 122.3 118.2 116.7 121.7 116.8 121.6 115.2 122.0 121.7 118.8 121.8 124.5 121.7 122.7 116.3 124.0 119.0 124.5 121.8 124.9 130.0 123.5 128.1 119.7 126.1 131.3 123.8 114.7 122.2 122.8 128.6 122.0 132.5 122.0 123.5 116.3 126.1 119.2 126.4 118.4 121.0 119.1 116.9 131.1 120.4 115.2 118.0 122.4 114.3 116.9 126.4 114.2 127.2 118.3 127.8 123.0 117.4 123.0 119.9 122.1 120.4 124.8 122.1 114.4 120.5 115.0 122.8 116.8 125.8 120.1 124.8 122.7 119.4 128.2 124.1 127.2 120.0 122.7 118.3 127.1 122.5 116.3 125.1 124.4 112.3 121.3 127.0 113.5 118.8 127.6 125.2 121.5 122.5 129.1 122.6 134.5 118.3 132.8
实验三:Data菜单操作
当我们需要对整个数据文件进行加工整理,比如根据统计分析的要求对数 据进行分组,合并,加权,筛选等操作。这些功能都集中在Data菜单中 一.Merge Files过程
用于合并数据文件,实际上包括了两个过程,分别对应了两种合并方式:
【纵向合并】
从外部数据文件中增加记录到当前数据文件中,称为纵向合并,用Add Case对话框 完成。 例:将数据集pkc2.sav中的记录添加到pkc1.sav中,注意在pkc2.sav中的变量xinbie对 应了pkc1.sav中的sex。 打开文件pkc1.sav,选择Data-Merge Files-Add Cases: 选中需要添加的数据文件pk2.sav并按OK,弹出如下对话框。
定义新产生的汇总变量 的名称和标签 定义一个新变量以存储同组 的记录数
选择被汇总的变量
定义汇总函数
定义一个新文件以存储汇 总的结果
用汇总的结果代替原 来的结果
其它Data菜单的各项命令
Define Dates : 自动生成时间变量,主要用于时间序列模型 Insert Variable: Insert Cases: Goto Cases: Sort Cases: 在当前列插入新变量 在当前行插入新记录。 到达指定记录号的记录 按选定的变量对观测值排序
Variable对话框,并在Numeric Expression框中输入2后按“if”按 钮,弹出对话框如下图,选择inlude if case satisfies condition项; 然后把x添加进该框,补充“>1”.最后按continue按钮。
Step 3:系统回到Compute Variable对话框,按“OK”,系统弹
不匹配变量 已经匹配变量
按住Crrl键选中需要匹配的两个变量再单击Pair钮对其进行强制匹配。 变量名以当前数据集的sex名为准,完成后按OK,操作就完成了
【横向合并】
从外部数据文件增加变量到当前数据文件,称为横向合并,用Add Variable对话框完成。 例:数据集brain1.sav包含了ID号1-90(有缺号)的病人的性别, 年龄和血小板值,brain2.sav则包含了11-100号病人的收缩压,舒 张压和迟发性脑损伤结果。将两个数据集按ID号合并,并尽可能多 的保留病人记录。 操作: Step 1:对两个数据集分别按ID号升序排列并存盘。 Step 2:从新打开brain1.sav。选择菜单Data-Merge Files- AddVariables,然后找到brain2.sav并打开,弹出对话框如下页左 图,并按下页右图选择选项。 Step 3:单击OK,系统就会进行相应的合并。
实验十六:非参数检验——成组设计两样本比较的秩和检验 实验十七:X²检验 实验十九: 判别分析 实验十八: 聚类分析 实验二十:因子分析
实验一:数据编辑操作 一.SPSS的界面
标题栏 当前数据域 输入数据域 数据显示区
定义变量栏
二.定义变量
单击左下脚的“variable view”,就会显示如左图的界面。我们 在其中进行定义,如右图
Step 1:这组数据只有一个变量,设为x,将其录入spss中,如示
Step2:选择analyze→descriptive statistics→explore出现如下界 面:
Step 3: 将变量x选入dependent list框,ok变黑,单击ok按 钮,即可得出如下结果
从结果中即可看出对该组数据的描述性统计结果: range:极差 22.3 最大132.5最小值110.2 算数平均数 mean121.8标准差std.deviation4.614.和描述其频数分布特征 的茎叶图.当然,用该菜单下的frenquencies 和descriptive也 能进行描述,但不能做出茎叶图。但frenquencies 可做出描 述其频数分布特征的柱状图。而descriptive不能描述频数分 布特征。 作业:用frenquencies 和descriptive过程对该数据集进行描 述统计
按Analyze-Report-Case Summaries的顺序单击,打开Summarie Case主对话框
将变量hight选入Variable框中作为摘要分析的变量,将sex,grade选入 Grouping框中作为分组变量。如下图
Step 4: Step 5 :
量。
清除Display cases复选框。 单击Statistics按钮,如下图所示选中需要输出的统计
Step 2:
选择Break框中的sex变量,单击Summary按钮,打开Summary Lines for sex对话框。并如下选择后按Continue回主对话框
Step 3:
Step 4:
选择Break框中的grade变量,单击Summary按钮,打开Summary Lines for grade对话框。并选择Mean of Values,Number of Cases复选框后按Continue回主对话框
实验一:数据编辑操作 实验三:Data菜单操作 实验五:行形式摘要报表 实验七:频数分布分析 实验九:两独立样本T检验 实验 十一:单因素方差分析 实验 十三:直线回归 实验十五:多元线性回归
