清华大学中学生标准学术能力诊断性测试2020届高三5月测试数学(理)试题(一卷) PDF版含答案
中学生标准学术能力诊断性测试2020年5月测试数学试卷答案

一、选择题:
1 2 3 4 5 6 78
C D B A B ADC
二、多项选择题:本大题共 4 小题,每小题 5 分,共 20 分.在每小题给出的四个选项中, 有多项符合题目要求.全部选对的得 5 分,选对但不全的得 3 分,有选错的得 0 分.
第3页 共 6 页
…………………5 分 …………………6 分
从而,平面 APD 和平面 PCD 的法向量分别为 r1 = ( 3, −1, 0), r2 = ( 3,1, 3)
…………………7 分
二面角 A − PD − C 的余弦值 =|r1 r2 | /(| r1 | | r2 |= 2 / (2
.
则当 n
2 时 Sn2
=
1 n2
1 n2 −1
=
1 2
n
1 −1
−
n
1 +
1
.
…………6 分
故当 n 2 时 S12 + S22 +
+
Sn2
1+
1 2
1 −
1 3
+
1 2
1 2
−
1 4
+
+
1 2
1 n −1
−
n
1 +1
第1页 共 6 页
=
1+
1 2
1 +
1 2
−
1 n
−
n
1 +1
P( X = 0) = 1 , P( X = 1) = (1)2 = 1 , P( X = 2) = (1)3 = 1 , P( X = 3) = (1)3 = 1
2020届清华大学中学生标准学术能力诊断性测试高三5月测试数学(理)试题(一卷)(解析版)

中学生标准学术能力诊断性测试2020年5月测试理科数学试卷(一卷)本试卷共150分,考试时间120分钟.一、选择题:本大题共12小题,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知集合{}2log (2)0A x x =->,{}245,B y y xx x A ==-+∈,则A B =U ( )A.[)3,+∞B.[)2,+∞ C.()2,+∞D.()3,+∞【答案】C 【分析】先解对数不等式求出集合A ,再根据二次函数的单调性求出集合B ,然后根据并集的定义求解即可.【详解】解:∵2log (2)0x ->, ∴21x ->,即3x >, ∴()3,A =+∞,∴()2245212y x x x =-+=-+>, ∴()2,B =+∞,∴A B =U ()2,+∞,故选:C .【点睛】本题主要考查集合的并集运算,考查对数不等式的解法,考查二次函数的值域,属于基础题. 2.在复平面内,复数231ii+-的虚部为( )C. D. 【答案】B 【分析】根据复数代数形式的除法运算和复数的模先化简该复数,再根据虚部的定义得出结论.【详解】解:∵)()()231111122ii i i i i i ++===+---+,∴复数231i i +-的虚部为,故选:B .【点睛】本题主要考查复数代数形式的除法运算,考查复数的模和虚部的定义,属于基础题.3.已知单位向量a r ,br满足22a b a b +=-r r r r ,则()()3a b a b -⋅+=r rr r ( )A. 1B. 2C. 3D. 4【答案】B 【分析】由22a b a b +=-r r r r 可得0a b ⋅=r r ,再根据平面向量的数量积的定义即可求出答案. 【详解】解:∵22a b a b +=-r r r r ,∴()()2222a ba b+=-r r r r ,化简得0a b ⋅=r r ,∵1a =r,1=r b ,∴()()223322a b a b a b a b -⋅+=-+⋅=r r r r rr r r ,故选:B .【点睛】本题主要考查平面向量数量积的定义及其应用,属于基础题.4.下列程序框图的算法思想源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入16a =,10b =,则程序中需要做减法的次数为( )A. 6B. 5C. 4D. 3【答案】C 【分析】由循环结构的特点,先判断,再执行,分别计算出当前的,a b 的值,即可得到结论. 【详解】解:由16a =,10b =,满足a b ¹,满足a b >,则16106a =-=; 满足a b ¹,不满足a b >,则1064b =-=; 满足a b ¹,满足a b >,则642a =-=; 满足a b ¹,不满足a b >,则422b =-=;不满足a b ¹,则输出2a =; 则程序中需要做减法的次数为4, 故选:C .【点睛】本题主要考查算法和程序框图,主要考查循环结构的理解和运用,以及赋值语句的运用,属于基础题. 5.在()()252211x x x ++-的展开式中,4x 的系数为( )A. 6-B. 6C. 10D. 4【答案】A 【分析】 因为()()()()2545221111x x x x x ++-+-=,且()41+x 的展开式的通项公式为14r r r T C x +=,()51x -的展开式的通项公式为()5151kk k k T C x -+=⋅-⋅,令4r k +=,由此可求出答案.【详解】解:∵()()()()2545221111x x x x x ++-+-=,∵()41+x 的展开式的通项公式为41441rrr r rr T C x C x -+=⋅⋅=,()51x -的展开式的通项公式为()5151kkk k T C x -+=⋅-⋅,则展开式中含4x 的项需满足4r k +=,∴展开式中4x 的系数为()()20413454511C C C C ⋅-+⋅-()()342231454511C C C C +⋅-+⋅-()540451C C +⋅-54060201=-+-+-6=-,故选:A .【点睛】本题主要考查二项展开式的通项公式的应用,考查计算能力与推理能力,属于中档题. 6.在三角形ABC 中,a ,b ,c 分别为角A ,B ,C 的对边,且满足22265b c a bc +=+,则sin 2B C +⎛⎫=⎪⎝⎭( )A.2C.5【答案】D 【分析】根据余弦定理结合题意得3cos 5A =,而sin cos 22B C A +⎛⎫= ⎪⎝⎭,再根据半角公式求解即可.【详解】解:∵22265bc a bc +=+,即22265a b c bc -=+,由余弦定理可得2222cos a b c bc A =+-, ∴62cos 5bc A bc =, ∴3cos 5A =,则02A π<<, ∵ABC π++=, ∴1cos 25sin cos 222B C A A ++⎛⎫===⎪⎝⎭, 故选:D .【点睛】本题主要考查余弦定理的应用,考查半角公式的应用,属于基础题.7.函数()32x e f x x -=-的部分图像大致是( )A. B. C. D.【答案】A 【分析】根据指数函数的值域和绝对值的几何意义可知()302x e f x x -=>-,再结合导数求出函数在()2,+∞上的单调性,由此可得出答案.【详解】解:根据指数函数的值域和绝对值的几何意义可知()302x e f x x -=>-,则C 、D 错; 当2x >时,()32x x e f x --=,()()()23'32x f x x e x ---=, 由()'0f x >得3x >,由()'0f x <得23x <<,∴函数()f x 在()2,3上单调递减,在()3,+∞上单调递增,则A 对,B 错;故选:A .【点睛】本题主要考查函数图象的识别,考查利用导数研究函数的单调性,属于中档题.8.已知函数()31663x x f x x x e e -=--+-,若211011f f a a ⎛⎫⎛⎫+≤ ⎪ ⎪+-⎝⎭⎝⎭,则a 的取值范围为( ) A. (][),12,-∞-⋃+∞ B. ()1,2-C.()()1,00,1-UD.()[)1,12,-+∞U【答案】D 【分析】先判断函数的奇偶性,再求导研究函数的单调性,再结合奇偶性与单调性解不等式即可.【详解】解:∵()31663x x f x x x e e -=--+-,定义域为R ,∴()()31663x x f x x x e f x e --=+-+=-, ∴函数()f x 为奇函数,∵()21660x x f'x x e e -=---<-,∴函数()f x 在R 上单调递减,∵211011f f a a ⎛⎫⎛⎫+≤ ⎪ ⎪+-⎝⎭⎝⎭ ∴21111f f a a ⎛⎫⎛⎫≤-⎪ ⎪+-⎝⎭⎝⎭,则21111f f a a ⎛⎫⎛⎫≤ ⎪ ⎪+⎝-⎝⎭⎭, ∴21111a a ≥+-, ∴()()2011a a a +-≥-, ∴()()20110a a a -≤⎧⎨+-<⎩或()()20110a a a -≥⎧⎨+->⎩,解得11a -<<,或2a ≥, 故选:D .【点睛】本题主要考查利用函数的奇偶性与单调性解不等式,考查利用导数研究函数的单调性,考查分式不等式的解法,属于中档题. 9.已知等差数列{}n a 满足:11a =,4164a a +=,则1912222a a a⨯⨯⋅⋅⋅⨯=( )A. 382B. 192C. 162D. 762【分析】根据等差数列的性质和求和公式可得()()1194161219191922a a a a a a a ++++⋅⋅⋅+==,由此可求出答案. 【详解】解:∵等差数列{}n a 满足:11a =,4164a a +=,∴()()119416121919193822a a a a a a a ++++⋅⋅⋅+===,∴191219123822222a a a a a a ++⋅⋅⋅+⨯⨯⋅⋅⋅⨯==,故选:A .【点睛】本题主要考查等差数列的性质的应用,考查等差数列的求和公式,属于基础题.10.已知椭圆()222210x y a b a b +=>>21y x =+相切,则a =( )A. 2D. 1【答案】D 【分析】由题意可得222b c e a a b c =⎪==⎨⎪⎪-=⎪⎩,解出即可.【详解】解:由题意有,以原点为圆心以椭圆短半轴长为半径的圆的方程为222x y b +=, 直线21y x =+的一般式为210x y -+=,又椭圆22221x y a b+=,∴222b c e a a b c =⎪==⎨⎪⎪-=⎪⎩,解得1a b c ⎧⎪=⎪⎪=⎨⎪⎪=⎪⎩,【点睛】本题主要考查椭圆的标准方程及其几何性质,考查直线与圆的位置关系,属于中档题.11.设()f x 为定义于[]1,1-上的偶函数,当[]0,1x ∈时,()12f x x =-,则方程()()22xf f x =的实数解的个数为( ) A. 8 B. 6C. 4D. 2【答案】A 【分析】由题意可知,()()f f x 为偶函数,()[]0,1f x ∈,则()()()12f f x f x =-141,02134,12x x x x ⎧-≤≤⎪⎪=⎨⎪-<≤⎪⎩,画出函数()()f f x 和22x y =在[]0,1上的图象,结合图象即可得出结论.【详解】解:当[]0,1x ∈时,()112,0212121,12x x f x x x x ⎧-≤≤⎪⎪=-=⎨⎪-<≤⎪⎩,∴()[]0,1f x ∈,∴当[]0,1x ∈时,()()()12f f x f x =-()()11212,0211221,12x x x x ⎧--≤≤⎪⎪=⎨⎪--<≤⎪⎩141,02134,12x x x x ⎧-≤≤⎪⎪=⎨⎪-<≤⎪⎩114,041141,421334,24343,14x x x x x x x x ⎧-≤≤⎪⎪⎪-<≤⎪=⎨⎪-<≤⎪⎪⎪-<≤⎩,又()()()()f f x f f x -=,∴()()ff x 为偶函数,且22x y =为偶函数,画出函数()()f f x 和22x y =在[]0,1上的图象如图,由图可知,函数()()f f x 和22x y =的图象在[]0,1上有4个交点,∴由偶函数的性质可知,函数()()f f x 和22x y =的图象在[]1,0-上有4个交点,∴函数()()f f x 和22x y =的图象在[]1,1-上有8个交点,即方程()()22x f f x =的实数解的个数为8,故选:A .【点睛】本题主要考查方程的根与函数的零点以及函数图象的交点之间的关系,考查转化与化归思想,考查分类讨论思想,考查数形结合思想,考查计算能力与推理能力,属于难题. 12.已知当[]0,1x ∈时,不等式()()22cos 11sin 0x x x x θθ--+->恒成立,则θ的取值范围为( )A. π5πππ1212k k θ+<<+(k 为任意整数) B. π5πππ66k k θ+<<+(k 为任意整数) C. π5π2π2π1212k k θ+<<+(k 为任意整数) D. π5π2π2π66k k θ+<<+(k 为任意整数) 【答案】C 【分析】可设不等式左边为()f x 并化简,求出()f x 的最小值,令其大于0,得到θ的取值范围即可.【详解】解:设()()22()cos 11sin f x x x x x θθ=--+-2(1sin cos )(2sin 1)sin x x θθθθ=++-++,①若1cos sin 0θθ++=,即3222k k θππππ=++或时,原不等式不恒成立; ②若1cos sin 0θθ++≠即3222k k θππππ≠++或时,()f x Q 在[0,1]的最小值为(0)f 或()1f 或2sin 1[]2(1cos sin )f θθθ+++,∴(0)0(1)02sin 1[]02(1cos sin )f f f θθθ⎧⎪>⎪⎪>⎨⎪+⎪>++⎪⎩, ∴sin 0cos 01sin 22θθθ⎧⎪>⎪>⎨⎪⎪>⎩,解得522()1212k k k Z πππθπ+<<+∈, 故选:C .【点睛】本题主要考查不等式恒成立的问题,考查三角函数的性质,考查分类讨论思想,考查计算能力与转化能力,属于难题.二、填空题:本大题共4小题. 13.设数列{}n a 满足14a=,210a =,215n a a -=,3n ∀≥,则201920181ln ln 2a a -=______. 【答案】ln 5 【分析】由题意可得,(()21lnln 5n n a a -=,化简整理得112112ln ln ln ln ln 522n n n n a a a a ---⎛⎫⎛⎫---= ⎪ ⎪⎝⎭⎝⎭,令11ln ln 2n n n b a a +=-,可得()122ln5ln5n n b b ---=-,由此可得ln 5n b =,从而可求出答案.【详解】解:∵215n a a -=,3n ∀≥,∴当3n ≥时,(()21lnln 5n n a a -=,即2112ln ln ln 52ln 2n n na a a --+=+, ∴1212ln 2ln ln ln 52n n n a a a ---+=,∴112112ln ln ln ln ln 522n n n n a a a a ---⎛⎫⎛⎫---= ⎪ ⎪⎝⎭⎝⎭, 令11ln ln 2n n n b a a +=-,则122ln 5n n b b ---=,且1211ln ln ln 52a b a =-=,∴()122ln5ln5n n b b ---=-,又1ln 50b -=, ∴ln 5n b =,即11lnln ln 52n n a a +-=, ∴201920181ln ln ln 52a a -=, 故答案为:ln 5.【点睛】本题主要考查数列递推公式的应用,考查推理能力与计算能力,考查转化与化归思想,属于中档题.14.设实数x ,y 满足02203x y x y x -≥⎧⎪++≥⎨⎪≤⎩,则22x y +的最大值为______.【答案】73 【分析】画出不等式组表示的可行域,利用目标函数的几何意义(到原点的距离的平方)转化求解即可. 【详解】解:不等式组的图象如图:22x y +的几何意义是可行域内的点和原点的距离的平方,显然A 到原点的距离最大,由2203x y x ++=⎧⎨=⎩,解得()3,8A -,则22xy +的最大值为:96473+=,故答案为:73.【点睛】本题主要考查线性规划的应用,利用目标函数的几何意义,通过数形结合是解决本题的关键,属于基础题.15.假设抛一枚质地均匀的色子,若抛出的点数为1、2或3,我们称为“小”,否则,若抛出的点数为4、5或6,则称为“大”.独立重复地抛这枚色子两次,已知两次都为“大”,则第1次抛出的点数为6的概率______. 【答案】13【分析】由题意可知,第1次抛出的点数为4、5或6,根据相互独立的事件的概率互不影响即可求出答案. 【详解】解:由题意可知,第1次抛出的点数为4、5或6, ∵独立重复地抛这枚色子两次,两次抛掷互不影响, ∴第1次抛出的点数为6的概率13p =, 故答案为:13. 【点睛】本题主要考查独立重复试验的应用,属于基础题. 16.已知定义于实数R 上的奇函数()f x 满足()'2f x >-,则不等式()()()2132ln 312f x x x x -<-+-的解集为______. 【答案】()0,1【分析】 设()()()()2132ln 312,0g x f x x x x x =----->,则()()()2132ln 312f x x x x -<-+-()0g x ⇔<,()()''14ln 46g x f x x x x =-+-+,令()4ln 46h x x x x =-+,则()'4ln h x x =,求导后可得()()12h x h ≥=,结合题意可得()'220g x >-+=,得函数()gx 在()0+∞,上单调递增,而()10g =,由此可求出解集. 【详解】解:设()()()()2132ln 312,0g x f x x x x x =----->,则()()()2132ln 312f x x x x -<-+-()0g x ⇔<,∵()()''14ln 46g x f x x x x =-+-+,令()4ln 46h x x x x =-+,则()'4ln h x x =,由()'0hx >得1x >,由()'0h x <得01x <<,∴当1x =时,函数()h x 取得极小值同时也是最小值()12h =,∵()'12fx ->-,()2h x ≥,∴()'220gx >-+=,∴函数()g x 在()0+∞,上单调递增, 又()()()()2111132ln13120gf =-----=, ∴由()0gx <得()()1g x g <,∴01x <<, 故答案为:()0,1.【点睛】本题主要考查利用导数研究函数的单调性,考查利用函数的单调性解不等式,考查计算能力与推理能力,属于难题.三、解答题:解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答. (一)必考题:17.设ABC V 中,()cos cos cos 0C A A B +=,内角A 、B 、C 对应的对边长分别为a 、b 、c .(1)求角B 的大小; (2)若2248a c +=,求ABC V 面积S 的最大值,并求出S 取得最大值时b 的值.【答案】(1)π3B =(2)面积S 的最大值为b =【分析】(1)在三角形中,()cos cos cos cos sin sin C A B A B A B =-+=-+,结合条件可得π2sin sin 03A B ⎛⎫-= ⎪⎝⎭,由此可求出答案;(2)由2248a c +=可得2ac ≤,则11sin 222S ac B =≤⋅=,此时2a =,1c =,再由余弦定理即可求出答案.【详解】解:(1)∵()cos coscos cos sin sin C A B A B A B =-+=-+,∴()cos cos cos sin cos cos C A A B A B A B +=-π2sin sin 03A B ⎛⎫=-= ⎪⎝⎭,∵sin 0A >,0πB <<,∴πsin 03B ⎛⎫-= ⎪⎝⎭,则π3B =; (2)因a ,0c >,2248a c +=,2244a c ac +≥,故2ac ≤,于是,11sin 22222S ac B =≤⋅⋅=,∴ABC V 面积S 的最大值为2, 且当S 取得最大值时,2ac =,2a c =,可得2a =,1c =,由余弦定理,2222cos 3b a c ac B =+-=,即得b =【点睛】本题主要考查余弦定理的应用,考查三角形的面积公式,考查重要不等式的应用,属于基础题. 18.如下为简化的计划生育模型:每个家庭允许生男孩最多一个,即某一胎若为男孩,则不能再生下一胎,而女孩可以多个.为方便起见,此处约定每个家庭最多可生育3个小孩,即若第一胎或前两胎为女孩,则继续生,但若第三胎还是女孩,则不能再生了.设每一胎生男生女等可能,且各次生育相互独立.依据每个家庭最多生育一个男孩的政策以及我们对生育女孩的约定,令X 为某一家庭所生的女孩数,Y 为此家庭所生的男孩数.(1)求X ,Y 的分布列,并比较它们数学期望的大小;(2)求概率()()PX D X >,其中()D X 为X 的方差.【答案】(1)分布列见解析:EX EY =(2)14【分析】 (1)易知X 的取值为0,1,2,3,Y 的取值为0,1,利用相互独立的事件的概率公式求出相应概率,由此可得分布列,再根据数学期望的计算公式求出期望,进而比较大小;(2)结合公式()()22)(D X E X EX =-求出方差,再根据互斥事件的概率加法公式即可求出结果. 【详解】解:(1)易知X 的取值为0,1,2,3,对应取值的概率为别为:()102P X ==,()211124P X ⎛⎫=== ⎪⎝⎭,()311228P X ⎛⎫=== ⎪⎝⎭,()311328P X ⎛⎫=== ⎪⎝⎭ 即得X 的分布列如下类似地,Y 的取值为0,1,对应取值的概率分别为:()()1038P Y P X ====,()()71108P Y P Y ==-==;得Y 的分布列如下:X0 1P18 78由X ,Y 的分布列可得它们的期望分别为:11117()012324888E X =⨯+⨯+⨯+⨯=,177()01888E Y =⨯+⨯=,因此()()E X E Y =;(2)()()22222221111771(012)32488864D XE X EX ⎛⎫=-=⨯+⨯+⨯+⨯-=⎪⎝⎭, 故()()()()71123644PX D X P X P X P X ⎛⎫>=>==+== ⎪⎝⎭. 【点睛】本题主要考查离散型随机变量的分布列及数学期望、方差,考查计算能力与推理能力,属于中档题. 19.如图,已知四棱锥P ABCD -的底面ABCD 为边长为2的菱形,PA ⊥平面ABCD ,2PA =,60ABC ∠=︒,F 为棱PC 上一点,且:1:3PF FC =.(1)求证:BD AF ⊥;(2)求二面角A PD C--余弦值;(3)求三棱锥F APD -的体积V . 【答案】(1)证明见解析;(2)77(3)36【分析】(1)由PA ⊥平面ABCD 得PA BD ⊥,又底面ABCD 为菱形可得AC BD ⊥,则BD ⊥平面PAC ,从而BD AF ⊥;(2)设菱形ABCD 的对角线交点为O ,以O 为原点,分别以OC u u u r 、OD uuu r的方向为x ,y 轴建立空间直角坐标系,借助空间向量求出平面法向量的夹角,从而求出答案;(3)由图可知P ACD F ACD V V V --=-,由题意可知三棱锥P ACD -的高为3342PA =,由此可求出答案. 【详解】解:(1)因PA ⊥平面ABCD ,故PA BD ⊥, 又因底面ABCD 为菱形,故AC BD ⊥,又PA AC A =I,,PA AC ⊂平面PAC ,∴BD ⊥平面PAC , 而AF⊂平面PAC ,∴BD AF ⊥;(2)设菱形ABCD 的对角线交点为O ,因AC BD ⊥,PA ⊥平面ABCD ,以O 为原点,分别以OC u u u r 、OD uuu r的方向为x ,y 轴建立如图所示的空间直角坐标系,则()1,0,0A-,()1,0,2P -,()3,0D ,()1,0,0C ,∴()0,0,2AP =u u u r,()3,0AD =u u u r ,()2,0,2PC =-u u u r,()3,0CD =-u u u r ,∴平面APD 和平面PCD 的一个法向量分别为()13,1,0r =-r,23,1,3r =u r,∴1212127cos ,27r r r r r r ⋅===⋅⨯r r r rr r ,由图可知二面角A PD C --的平面角为锐角, ∴二面角A PD C --7(3)由图可知,P ACD F ACD V V V --=-,因:1:3PF FC =,可知三棱锥P ACD -的高为3342PA =,∴1311232326ACD VS ⎛⎫=⨯⨯-==⎪⎝⎭△. 【点睛】本题主要考查线面垂直的判定与性质,考查二面角的求法,考查三棱锥的体积的求法,考查计算能力与推理能力,属于中档题.20.已知双曲线C :()222210,0x y a b a b-=>>的离心率3e =,其左焦点1F到此双曲线渐近线的距离为(1)求双曲线C 的方程; (2)若过点()2,0D的直线l 交双曲线C 于AB 两点,且以AB 为直径的圆E 过原点O ,求圆E 的圆心到抛物线24x y =的准线的距离.【答案】(1)2218y x -=(21+1【分析】(1)由题意可得2223c e a a b c ⎧==⎪=+=⎪⎩,解出即可; (2)由题意设直线AB的方程为2x my =+,联立直线与椭圆的方程并消元,设()11,Ax y ,()22,B x y ,可得韦达定理的结论,又以AB 为直径的圆过原点O 得12120x x y y+=,代入可求得2=±m ,根据中点坐标公式求得圆E 的圆心的纵坐标,从而可求出答案.【详解】解:(1)由题意可得2223c e a a b c ⎧==⎪=+=⎪⎩, 解得13a b c =⎧⎪=⎨⎪=⎩,∴双曲线C 的方程为2218y x -=;(2)易知直线AB 与x 轴不重合,设直线AB 的方程为2x my =+,联立方程22182y x x my ⎧-=⎪⎨⎪=+⎩,可得()228132240m y my -++=, 上述方程式的判别式()232830m ∆=+>,以及2810m -≠(否则直线l 不能与双曲线交两点), 设()11,Ax y ,()22,B x y ,则1223281m y y m +=--,1222481y y m =-, 同时可得()()()2212121212284222481m x x my my m y y m y y m +=++=+++=--,以AB 为直径的圆过原点O ,知12120x x y y +=,结合2810m -≠,可知28424m +=,=m , ∴圆E 的圆心即AB中点的纵坐标为12216281y y m m +=-=-, ∵抛物线24x y =的准线方程为1y =-,∴圆E 的圆心到抛物线24x y =的准线距离为1+1. 【点睛】本题主要考查椭圆的标准方程及其几何性质,考查直线与椭圆的位置关系,考查计算能力,考查转化与化归思想,属于中档题. 21.设函数()3ln aef x x b x=-+,0x >,其中e 为欧拉数,a ,b 为未知实数,且0a >.如果()0,e 和(),e ∞均为函数()f x 的单调区间.(1)求a ; (2)若函数()()3hx f x cx =+在()()0,,e e ⋃∞上有极值点,c 为实数,求c 的取值范围.【答案】(1)3a =(2)22,0,e e ⎛⎫⎛⎫-⋃∞ ⎪ ⎪⎝⎭⎝⎭【分析】(1)令()3ln 3ln ae aeg x xx x x=-=-,0x >,求导得函数()g x 在()0,∞上单调递增,设()0g x =的唯一根为0x ,则0x 满足003ln aex x =,由题设得0x e =, 由此可得答案; (2)由题意得存在()()00,,x e e ∈⋃∞,使得()0h x '=,再分类讨论结合一元二次方程根的分布即可求出答案.【详解】解:(1)令()3ln 3ln ae aeg x xx x x=-=-,0x >, ∴()23)0aeg x x x'=+>(因0a >,0x >), ∴函数()gx 在()0,∞上单调递增,设()0gx =的唯一根为0x ,即0x 满足003ln ae x x =,(利用3ln x ,ae x的函数图象很容易确定) 于是,当()00,x x ∈时,()0g x <,而当()0,x x ∈∞时,()0g x >, 从而,当()00,x x ∈时,()3ln aef x x b x =-+, 当()0,x x ∈∞时,()3ln aef x x b x=-+, 可知,()00,x 为()f x 的单调递减区间,()0,∞x 为()f x 的单调递增区间,进而,由题设得0x e =, 因此,003ln 3x x a e==; (2)若函数()()3hx f x cx =+在()()0,,e e ⋃∞上有极值点,则易知存在()()00,,x e e ∈⋃∞,使得()0h x '=,注意到()()()22333,0,333,,e c x e x xh x e c x e x x ⎧--+∈⎪⎪=⎨⎪++∈'∞⎪⎩,①若23330e c x x --+=在()0,e 上有根,等价于20ey y c +-=在1,e ⎛⎫∞ ⎪⎝⎭上有解,由一元二次方程根的分布可得,只需满足2110e c e e⎛⎫+-< ⎪⎝⎭,解得2c e >; ②若23330e c x x ++=在(),e ∞上有根,等价于20ey y c ++=在10,e ⎛⎫⎪⎝⎭上有解, 由一元二次方程根的分布可得,只需满足0c <且2110e c e e⎛⎫++> ⎪⎝⎭,解得20c e -<<;综上,c 的取值范围为22,0,e e ⎛⎫⎛⎫-⋃∞ ⎪ ⎪⎝⎭⎝⎭. 【点睛】本题主要考查利用导数研究函数的单调性,考查分类讨论思想,考查计算能力与推理能力,属于难题. (二)选考题:共10分.请考生在第22,23题中任选一题作答,如果多做,则按所做的第一题计分.作答时请写清题号.[选修4-5:不等式选讲] 22.设()f x 为定义于()0,1上的函数,满足:(1)对任意()0,1x ∈,都有()0f x >;(2)对任意x ,()0,1y ∈,都有()()()()121f x f x f y f y -+≤-. 求证:()f x 在()0,1上的导数恒为零.【答案】证明见解析; 【分析】由题意可得,对任意x ,()0,1y ∈,都有()f x ,()1f x -,()f y ,()10f y ->, 由()()()()121f x f x f y f y -+≤-得()()()()()()1121f x f y f y f x f y f y -+-≤-,令1x y=-,可得()()()()()()221210f x f x f x f x +---≤,即()()()210f x f x --≤,则()()1f x f x =-,于是()()()()121f x f x f y f y -+≤-化为()()22f x f y ≤,即()()f x f y ≤,同理,亦有()()f y f x ≤,则()()f x f y =,由此得证.【详解】证明:要证明()f x 在()0,1上的导数恒为零,等价于证明()f x 在()0,1上恒为常数;因对任意()0,1x ∈,都有()0f x >,故对任意x ,()0,1y ∈,都有()f x ,()1f x -,()f y ,()10f y ->,对任意x ,()0,1y ∈,都有()()()()121f x f x f y f y -+≤-, 故有()()()()()()1121f x f y f y f x f y f y -+-≤-,因上式对于任意()0,1x ∈都成立,故令1x y =-,可得()()()()()()221210f x f x f x f x +---≤,即()()()210f x f x --≤,∴()()1f x f x =-,()0,1x ∀∈,于是,()()()()121f x f x f y f y -+≤-可化为()()22f x f y ≤,即()()f x f y ≤,x ∀,()0,1y ∈, 同理,亦有()()f y f x ≤,x ∀,()0,1y ∈, 因此,x ∀,()0,1y ∈,()()f x f y =,即得证()f x 在()0,1上恒为一个常数,∴()f x 在()0,1上的导数恒为零.【点睛】本题主要考查抽象函数的导数的应用,考查转化与化归思想,考查计算能力,属于难题. [选修2-2,推理与证明] 23.设数列{}n a 为非负实数列,且满足1220k k k a a a ++-+≥,11ki i a =≤∑,1k =,2,….求证:1220k k a a k +≤-<,1k =,2,….【答案】证明见解析; 【分析】先证10k k a a --≥,1k=,2,…,反证法,若存在某个01k ≥,使得001k k a a +<,则有从0k a 起,非负数列{}n a 单调递增,从而得出矛盾,得到假设不成立; 再证122kk a a k+-<,1k =,2,…,令10k k k b a a +=-≥,则1k k k a a b ++=,有题意可知1k k b b +≥,再由条件可得到123123k b b b kb ≥+++⋅⋅⋅+()()1122k k k k k b b +≥++⋅⋅⋅+=,由此即可证明. 【详解】证明:先证10k k a a --≥,1k=,2,…,21若存在某个01k ≥,使得001k k a a +<,则有000001122k k k k k a a a a a ++++≤-+<,即从0k a 起,非负数列{}n a 单调递增, ∴1kii a =∑将随着k 的增加而趋于正无穷,不可能永远小于等于1, 即与11k ii a =≤∑,1k =,2,…矛盾, 故10k k a a +-≥,1k=,2,…; 再证122k k a a k+-<,1k =,2,…, 令10k k k b a a +=-≥,1k =,2,…,则1k k k a a b ++=,由1220k k k a a a ++-+≥可知1k k b b +≥,1k=,2,…, 又因123411ki k i a a a a a a =≥=++++⋅⋅⋅+∑12342k b a a a a =++++⋅⋅⋅+12323k b b a a =+++⋅⋅⋅+123123k k b b b kb ka +=+++⋅⋅⋅++12323k b b b kb ≥+++⋅⋅⋅+,故有()()1231123122k k k k k b b b kb k b b +≥+++⋅⋅⋅+≥++⋅⋅⋅+=, ∴()2221k b k k k ≤<+,即证得122k k a a k +-<,1k =,2,…; 综上:1220k k a a k +≤-<,1k =,2,…. 【点睛】本题主要考查反证法证明不等式,考查数列的递推公式的应用,考查推理能力与计算能力,属于难题.。
清华大学中学生标准学术能力诊断性测试2020届高三5月测试理综试题 Word版含答案
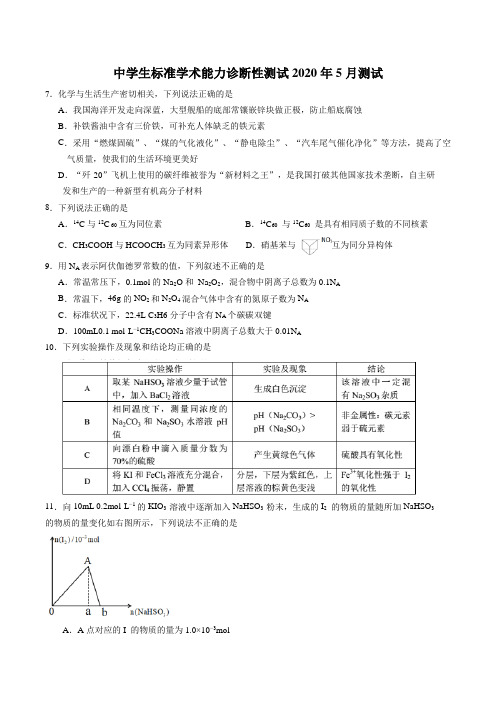
中学生标准学术能力诊断性测试2020年5月测试7.化学与生活生产密切相关,下列说法正确的是A.我国海洋开发走向深蓝,大型舰船的底部常镶嵌锌块做正极,防止船底腐蚀B.补铁酱油中含有三价铁,可补充人体缺乏的铁元素C.采用“燃煤固硫”、“煤的气化液化”、“静电除尘”、“汽车尾气催化净化”等方法,提高了空气质量,使我们的生活环境更美好D.“歼-20”飞机上使用的碳纤维被誉为“新材料之王”,是我国打破其他国家技术垄断,自主研发和生产的一种新型有机高分子材料8.下列说法正确的是A.14C与12C 60互为同位素B.14C60与12C60是具有相同质子数的不同核素C.CH3COOH与HCOOCH3互为同素异形体D.硝基苯与互为同分异构体9.用N A表示阿伏伽德罗常数的值,下列叙述不正确的是A.常温常压下,0.1mol的Na2O和Na2O2,混合物中阴离子总数为0.1N AB.常温下,46g的NO2和N2O4混合气体中含有的氮原子数为N AC.标准状况下,22.4L C3H6分子中含有N A个碳碳双键D.100mL0.1 mol·L−1CH3COONa溶液中阴离子总数大于0.01N A10.下列实验操作及现象和结论均正确的是11.向10mL 0.2mol·L−1的KIO3 溶液中逐渐加入NaHSO3 粉末,生成的I2的物质的量随所加NaHSO3的物质的量变化如右图所示,下列说法不正确的是A.A点对应的I 的物质的量为1.0×10−3molB.0a:ab=5:1C.当溶液中的n(I2)=5×10−4mol时,加入NaHSO3的物质的量可能为2.5×10−3mol或4.5×10−3mol D.由ab段反应可知,氧化性I2>HSO3−12.A、B、C、D为石墨电极,E、F分别为短周期相邻的两种活泼金属中的一种,且E能与NaOH 溶液反应。
按图接通线路,反应一段时间,当电路中通过1.0×10−3mol电子时,下列叙述正确的是A.U型管中的D端先变红,b烧杯中的溶液会变蓝B.a烧杯中最多有0.127gI2(KI足量)生成,甲池中的质量会减少0.04g(CuSO4溶液足量)C.A极产生气体的体积为5.6mL,甲池溶液的pH值为2D.E电极附近的溶液无明显现象产生13.常温下,将0.1mol·L−1的NaOH溶液逐渐加到5mL0.1mol·L−1的一元酸HA溶液中,测得混合溶液的BG(BG=-lg)与所加NaOH的体积的变化关系如图所示。
清华大学中学生标准学术能力诊断性测试2020届高三5月测试数学(理)试题(一卷)与答案

中学生标准学术能力诊断性测试2020年5月测试理科数学试卷(一卷)本试卷共150分,考试时间120分钟。
一、选择题:本大题共12小题,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知集合{}2log (2)0A x x =->,{}245,B y y x x x A ==-+∈,则A B ⋃=( ) A .[)3,∞B .[)2,∞C .()2,∞D .()3,∞2.在复平面内,复数231ii+-的虚部为( )A B C .D . 3.已知单位向量a ,b 满足22a b a b +=-,则()()3a b a b -⋅+=( ) A .1B .2C .3D .44.下列程序框图的算法思想源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入16a =,10b =,则程序中需要做减法的次数为( )A .6B .5C .4D .35.在()()252211x x x ++-的展开式中,4x 的系数为( )A .6-B .6C .10D .46.在三角形ABC 中,a ,b ,c 分别为角A ,B ,C 的对边,且满足22265b c a bc +=+,则sin 2B C +⎛⎫=⎪⎝⎭( )A .2B C .5D7.函数()32x e f x x -=-的部分图像大致是( )A .B .C .D .8.已知函数()31663x x f x x x e e -=--+-,若211011f f a a ⎛⎫⎛⎫+≤ ⎪ ⎪+-⎝⎭⎝⎭,则a 的取值范围为( ) A .(][),12,-∞-⋃+∞ B .()1,2- C .()()1,00,1-⋃ D .()[)1,1$2,-⋃+∞9.已知等差数列{}n a 满足:11a =,4164a a +=,则1912222a a a⨯⨯⋅⋅⋅⨯=( )A .382B .192C .162D .76210.已知椭圆()222210x y a b a b +=>>21y x =+相切,则a =( )A .2BCD .111.设()f x 为定义于[]1,1-上的偶函数,当[]0,1x ∈时,()12f x x =-,则方程()()22x f f x =的实数解的个数为( ) A .8B .6C .4D .212.已知当[]0,1x ∈时,不等式()()22cos 11sin 0x x x x θθ--+->恒成立,则θ的取值范围为( ) A .π5πππ1212k k θ+<<+(k 为任意整数) B .π5πππ66k k θ+<<+(k 为任意整数) C .π5π2π2π1212k k θ+<<+(k 为任意整数) D .π5π2π2π66k k θ+<<+(k 为任意整数) 二、填空题:本大题共4小题.13.设数列{}n a 满足14a =,210a =,215n n a a -=,3n ∀≥,则201920181ln ln 2a a -=______. 14.设实数x ,y 满足02203x y x y x -≥⎧⎪++≥⎨⎪≤⎩,则22x y +的最大值为______.15.假设抛一枚质地均匀的色子,若抛出的点数为1、2或3,我们称为“小”,否则,若抛出的点数为4、5或6,则称为“大”。
2020年5月清华大学中学生标准学术能力理科综合诊断性测试一卷

2020年5月清华大学中学生标准学术能力理科综合诊断性测试一卷本试卷共300分,考试时间150分钟。
可能用到的相对原子质量:H 1 O 16 C 12 N 14 Fe 56 Cr 52 S 32 I 127 Ba 137一、选择题:本题共13小题,每小题6分,共78分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.2019年诺贝尔生理医学奖授予了揭示“细胞如何感知和适应氧气”机理的三位科学家。
他们研究发现肾脏中有专门的细胞可以感受氧气水平的变化,当氧气供应不充足时,低氧诱导因子(HIF-1α)不被降解,细胞内积累的HIF-1α可促进促红细胞生成素(EPO)的合成;氧气供应充足时,HIF-1α合成后很快被降解,具体调节途径如下图所示。
请据图分析下列说法错误的是A.低氧时,HIF-1α进入细胞核联合ARNT与EPO基因调控序列结合,增强EPO基因的表达,使细胞合成更多的EPOB.若将细胞中的脯氨酸酰羟化酶基因敲除,EPO基因的表达水平会下降,细胞合成的EPO量减少C.正常条件下,人体细胞内HIF-1α的含量较低,在医学上可尝试通过提高HIF-1α的含量来治疗人类的贫血症D.高原反应时,EPO 会刺激骨髓中的造血干细胞,使其增殖分化生成大量红细胞,提高氧气的运输能力,该调节方式属于激素调节2.双脱氧核苷三磷酸(ddNTP)属于非天然核苷酸,是桑格-库森法测定DNA 序列的底物。
ddNTP 与脱氧核苷三磷酸(dNTP)的结构如下图所示,根据所学知识判断下列选项错误的是A.若X表示OH,该结构代表的物质dNTP可作为体内DNA分子复制的原料B.若将ddNTP加到正在复制的DNA反应体系中,ddNTP结合到子链后,子链的延伸会立即终止C.ddNTP、dNTP以及磷脂分子的元素组成都为C、H、O、N、PD.若X表示OH,碱基为A时,该物质可为细胞的各项生命活动直接提供能量3.细胞自噬有助于人类更好地了解细胞如何实现自身的循环利用,帮助细胞适应饥饿和应对感染等不良环境。
清华大学中学生标准学术能力诊断性测试2020届高三5月(THUSSAT)文科数学试题 (含答案)

32
3
2
所以 h = 3 . 2
………………12 分
20.解:设点 A( x1, y1 ) , B ( x2 , y2 ) ,中点 M (t,1) ,
直线 AB 的斜率为 k ,( k 斜率显然存在且不为 0 ).
由
x12 x22
= =
4 y1, 4 y2 ,
可得 ( x1 − x2 )( x1 + x2 ) = 4( y1 − y2 ) ,
第2页 共 5 页
y N
B M
OA
x
(第 20 题)
所以
x1
+
x2
=
4
y1 x1
− −
y2 x2
,故
2t
=
4k
,
………………3 分
(1)直线 MN : y −1 = − 1 ( x − t ) ,即 y −1 = − 1 ( x − 2k ) ,解得点 N (0,3) ;………6 分
k
k
(2)因为直线 AB 经过点 M (t,1) ,直线 AB 的斜率为 k ,
C.
1 e
,
+
D. (e, +)
( ) ( ) 7.数列 an 的前 n 项和 Sn = 2n2 − 3n n N* ,若 p + q = 5 p, q N* ,则 ap + aq =
A. 6
B. 8
C. 9
D.10
8.已知 x, y R ,“ x + y 1 且 x − y 1 ”是“ | x | + | y | 1”的
A.[2, 4)
B. (−1, +)
C.[2, +)
THUSSAT中学生标准学术能力测试诊断性测试2020年5月测试测试清华大学理科综合一卷试题参考答案

或: 若子代无低产植株,D 基因在 7 号正常染色体上 若子代出现低产植株,D 基因在 7 号异常染色体上
CH3
(3)
SO3H
CH3
SO3H (2 分,每个 1 分)
SO3H
避免苯环上对位的氢原子也被硝基取代使产物不纯(或减少副产物也得分)(1 分)
(4)
(2 分)
(5)13 (2 分) (6)
(2 分,写错 1 步扣 1 分)
第2页 共2页
案 答 考
术 学
参准
标
生
学
中
中学生标准学术能力诊断性测试 2020 年 5 月测试
洗涤(1 分) 灼烧(或煅烧)(1 分)
(2)V2O3+ Na2CO3+O2 = 煅烧 2NaVO3+CO2↑(不加↑不扣分,不加条件扣 1 分,2 分) (3)VO2++ H2O VO3-+2H+(反过来写也得分)(2 分) (4)6(2 分) 使 VO2++ H2O VO3-+2H+正向移动,VO2-更多地转化为 VO3+(1 分)
100%
(2 分)
80 233
(二) (1)HSO3Cl+H2O=HCl+H2SO4,HCl 气体在湿空气中形成盐酸小液滴(2 分) (2)控制浓盐酸的流量,使其缓慢流入浓硫酸中(1 分) 液体飞溅(或爆沸)(1 分) (3)①吸收剩余的气体 ②防止空气中水分进入 E(2 分,答对 1 点得 1 分) 27.(14 分) 答案: (1)AlO2-+CO2+2H2O=Al(OH)3↓+HCO3-(不加↓不扣分,2 分)
清华大学2020届5月高三中学生标准学术能力诊断性测试 理综答案

中学生标准学术能力测试中学生标准学术能力诊断性测试2020年5月测试理科综合-物理参考答案(一卷)二、选择题:本题共8小题,每小题6分,共48分。
在每小题给出的四个选项中,第14~18题只有一项符合题目要求,第19~21题有多项符合题目要求。
全部选对的得6分,选对但不全的得3分,有选错的得0分。
14 15 16 17 18 19 20 21B D D DC BD AD CD三、非选择题:共62分。
(一)必考题:共47分。
22 . (6分)答案:(1)1.050 (2分) (2)23 . (9分)答案:(2分) (3) (2分)(1)5409 ( 3 分)(2)实验电路如图所示,(3分)(3) (3分)24. (14分)解析:(1)设粒子不从MN 边界飞出的入射速度最小值为vmn, 对应的粒子在两个区域中做圆周运动的半径分别为r₁和r₂。
两圆心的连线与MN 的夹角为θ。
中学生标准学术能力测 试庄(x+2)sin θ=r ₂五+7cOS θ=h(1分)( 2 分 )( 1 分 )( 1 分 )( 1 分 )( 1 分 )(2)设粒子入射速度为v, 粒子在两区域中的运动半径分别为r ₁ 和 r ₂, 粒子第一次通过AB 时距离A 点为x ,由题意有(n=1,2,3 … …)x=√P²-(h-x)²可 得n<2.9则 n=1 时n=2 时25 . (18分)(1 分)( 1 分 )( 1 分 )( 1 分 )( 1 分 )( 1 分 )( 1 分 )解析:(1)由动能定理得:解得: d=8m( 1 分 )( 1 分 )②①THUSSAT中学生标准学术能力测试小物块通过D 点时,③( 1分)从C点至D 点,由机械能守恒定律得:④ ( 1 分)解得:R=2m ⑤( 1分)(2)由动能定理得:⑥( 1 分)由牛顿第二定律得:F-μmg=ma₁⑦(1分)μ₂mg- μ₃(M+m)g=Ma₂⑧( 1 分)设小物块从B点运动至C点所需时间为t,则vc=vg+at₁⑨(1分)木板到达凹槽右端时的速度v=a₂T₁⑩( 1 分)由题意可知v<vc 且a₂>0 ⑪( 1 分)解得②( 1 分)(3)当M=0.1kg时,由⑧得a₂=9m/s²设木板的长度为L, 则⑬( 1 分)解得L=3.5m ① ( 1 分)小物块离开D 点后做平抛运动,竖直方向 2 ⑮(1分)水平方向x=vo¹2 ⑩( 1 分)解得x = 4m ⑪( 1 分)由于x >L, 故小物块不能落在木板上⑩( 1 分)(二)选考题:共15分。
2020年5月诊断性测试理科数学答案(一卷)

中学生标准学术能力测试诊断性测试2020 年5 月测试理科数学(一卷)答案一.选择题:本大题共12 小题,每小题5 分,共60 分.在每小题给出的四个选项中,只有一项是符合题目要求的.1 2 3 4 5 6 7 8 9 10 11 12C D B C A D A D A D A C二.填空题:本大题共4 小题,每小题5 分,共20 分.13.(线下答案)ln 51 11 12( ) ( ) 12016 2016 (线上答案,均可得分)答案1:(2 )ln5 ln 2 5 22 22 22017 20171 11 1 1 2答案2:(2 )ln5 ln10 5 2 1022015 20162 2 22016 201714.7315.1 316.(0,1)三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:60分.17.解:(1)因cos C cos(A B) cos A cos B sin A sin B…………………2 分得cos C(cos A 3 sin A) cos B sin A cos B 3 sin A cos B2 s in A sin(B) 0 …………4 分3由于sin A0,0 B 可知B= …………………6 分3(2)因a,c0,a2 4c2 8,a2 4c2 4ac, 故ac 2 …………………8 分于是,1 1 3 3 S ac sin B2.2 2 2 2知△ABC面积S的最大值为 32…………………9 分且当S取得最大值时,ac2,a2c,可得a2,c 1. ………………10 分第1页共6 页由余弦定理,b2 a2 c2 2ac cos B3, 即得b 3. ………………12 分18.解:(1)易知X的取值为0,1,2,3,对应取值的概率为别为:1 1 1 1 1 1 1P(X0) , P(X1) ( ) , P(X2) ( ) , P(X3) ( )2 3 32 2 4 2 8 2 8即得X的分布列如下X0 1 2 3P 12141818…………4 分类似地,Y的取值为0,1,对应取值的概率分别为:1 7 P(Y0) P(Y3) , P(Y1) 1P(Y0) ,8 8 得Y的分布列如下:Y0 1P 1878…………6 分由X,Y的分布列可得它们的期望分别为:EX1 1 1 1 7 0123,2 4 8 8 8EY1 7 7 01;8 8 8因此EX EY. …………………8 分(2) 2 ( )2 02 1 12 1 22 1 32 1 (7)2 71 D(X)=EX EX2 4 8 8 8 64…………………10 分故71 1P(X D(X)) P(X) P(X2) P(X3) . …………………12 分64 419.解:(1)因PA平面ABCD,故PA BD. …………………1 分又因底面ABCD为菱形,故AC BD. …………………2 分又于是BD平面PAC. …………………3 分而AF平面PAC,因此BD AF. …………………4 分第2页共6 页(2)设菱形ABCD的对角线交点为O,因AC BD, PA平面ABCD,我们以O为原点,分别以OC、OD的方向为x, y轴的正方向可建立空间直角坐标系如图所示.由题设,易知下列各点的坐标:A (1, 0, 0), P (1, 0, 2), D(0, 3, 0),C(1, 0, 0) …………………5 分于是,可得向量AP (0, 0, 2) , AD (1, 3, 0) ,PC ,CD (1, 3, 0) …………………6 分(2, 0, 2)从而,平面APD和平面PCD的法向量分别为r 1 ( 3,1,0),r 2 ( 3,1, 3)…………………7 分7 二面角A PD C的余弦值r r r r=| | /(| | | | 2 / (2 7) ……8 分1 2 1 27(3)三菱锥F APD的体积V 三菱锥P ACD的体积V 三菱锥F ACD的体积V1 2三棱锥P ACD与三棱锥F ACD有相同的底面三角形ACD三棱锥F APD的高PA 2,因PF: FC 1:3,可知三棱锥P ACD的高为3 3 ,PA …………10 分4 2于是三菱锥F APD的体积 1 (2 3) 1 3 1 3V S△…12 分ACD3 2 3 2 620.解:(1)根据题意,我们有c | bc |e 3, 2 2,a a 2 b2且a 2 b 2 c2 可得b 2 2,a 1,c 3. …………………2 分于是可得双曲线C的方程为y2x 2 1. …………………3 分8(2)易知直线AB与x轴不重合,设直线AB的方程为x my 2.第3页共6 页联立方程联立方程2y2 1x8x my 2,可得(8m 2 1)y 2 32my 24 0. ………4 分上述方程式的判别式△=3(2 8m 2 3) 0, 以及8m 10(否则直线l不能与双2曲线交两点)设A(x, y),B(x, y) ,则1 12 232m24y y , y y ………………6 分1 2 2 1 2 28m 1 8m 1同时可得8m 42x x (my 2)(my 2) m y y 2m(y y ) 421 2 1 2 1 2 1 2 28m 1以AB为直径的圆过原点O,知x1x 2 y1 y 2 0 ,10结合8m 2 10,可知m 2 m …………………9 分8 4 24,2因抛物线x 2 4y的准线方程为y 1,且圆E的圆心即AB中点的纵坐标为y y 16m 8 101 22 8m 1 192. …………………10 分于是可得圆E的圆心到抛物线x 2 4y的准线距离为81019+1或810191. …12 分ae ae 3 ae21.解:(1)令g(x ) ln x 3 3ln x , x 0, g(x ) 0 (因a 0, x 0)x x x x2故函数g(x) 在(0,)单调递增. …………………2 分设g(x)=0的唯一根为x,即ae(利用3ln x, aex满足3ln x.0 0x x的函数图很容易确定)于是,当x(0, x)时,g(x ) 0,而当0 x(x,) 时,g(x ) 0. …………4 分0x x时,f(x) ae3ln x b,(0, )从而,当xx x时,f(x) 3ln x ae b.( , ) …………………6 分当x(0, x) 为f(x) 的单调递减区间,(0 , ) 为f(x) 的单调递增区间x可知,第4页共6 页进而,由题设得进而,由题设得x e…………………7 分03x ln x因此,a0 0 3.…………………8 分e(2 )若函数h(x ) f(x ) 3cx在(0,e) 上有极值点,则易知存在x(e,使得h(x ) 0. …………………9 分0 0, )3e 33c, x(0,e )x x2注意到h(x)3 3e3c, x(e, )x x2,故知有两种情形:①3e 3 在(0,e) 上有根,或等价于ey 2 y c 0在(1 ,)3c0 上有解,x x e2这只需e(1)2 1 c 0, 即得c 2…………………10 分e e e3 3 = 在(e,)上有根,或等价于ey 2 y+c 0在(0 1)e②,上有解,故需3c0x x e2满足c 0 且e(1)2 1 c 0, 从而 2 c 0.…………………11 分e e e2 2( ,0)综上,c的取值范围为…………………12 分e e(二)选考题:共10 分.请考生在第22,23 题中任选一题作答,如果多做,则按所做的第一题计分.作答时请写清题号.22.【选修4−4:坐标系与参数方程】(10 分)证明:要证明f(x) 在(0,1) 上的导数恒为零,等价于证明f(x) 在(0,1) 上恒为常数.因对任意x(0, 1),都有f(x ) 0,故对任意x, y(0,1) ,都有f(x), f (1x), f(y), f (1y ) 0.对任意x, y(0,1) ,都有f(x) f (1x )f(y) f (1y)2, 故有f(x) f (1y )f(y) f (1x ) 2 f(y) f (1y). (3)……………2 分因(3)对于任意x(0,1)都成立,故令x 1y,可得( f(x))2 ( f (1x))2 2 f(x) f (1x ) 0. ……………4 分第5页共6 页但注意到( f(x))2 ( f (1x))2 2 f(x) f (1x ) ( f(x)-f(1- x))2,我们有( f(x)-f(1- x))2 0,从而,f(x ) f(1- x ),x(0,1). ……………6 分f(x) f (1x) 于是,f(y) f (1y) 2 可化为f(x)2 2,即f(x ) f(y),x, y(0,1).…8 分f(y)同理,亦有f(y ) f(x ),x, y(0,1).因此,x, y(0, 1),f(x ) f(y). 即得证f(x) 在(0,1) 上恒为一个常数.……10 分23.【选修4−5:不等式选讲】(10 分)证明:先证a a 1 0,k 1, 2,…k k若存在某个k 0 1,使得a a ,则有k k0 0 1 a a a a a ,k k k k k0 1 0 0 1 0 2 0 2即从a 起,非负数列a单调递增,k n于是,ki a1i 将随着푘的增加而趋于正无穷,不可能永远小于等于1,即与,…ki1 a 1 k 1, 2,矛盾.故i a a 1 0,k 1, 2,………………3 分k k再证2a a ,k 1, 2, k k1 2kb a a 1 0,k 1, 2,…由令k k k a 2a a 0 可知k k 1 k 2b b 1,k 1, 2,………………5 分k kk又因1 i a b2a a a a b2b3a ai 1 2 3 4 k 1 2 3 k1b 2b 3b k b ka1 2 3 k k 1b 2b 3b kb1 2 3 k……………7 分k(k 1)故有1b 2b 3b kb (12 k)b b…………9 分1 2 3 k k k2从而,bk22k(k 1) k2.2即证得a a ,k 1, 2,……………10 分k k1 2k第6页共6 页。
2020届高三高中毕业生五月质量检测数学(理科)试卷(含答案)

2020届高中毕业生五月质量检测理科数学 2020.5.25 本试卷共5页,23题(含选考题).全卷满分150分.考试用时120分钟.★祝考试顺利★注意事项:1.答题前,先将自已的姓名、准考证号填写在试卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置.2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.写在试卷、草稿纸和答题卡上的非答题区域均无效.3.非选择题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内.写在试卷、草稿纸和答题卡上的非答题区域均无效.4.选考题的作答:先把所选题目的题号在答题卡指定的位置用2B 铅笔涂黑.答案写在答题卡上对应的答题区域内,写在试卷、草稿纸和答题卡上的非答题区域均无效.5.考试结束后,请将本试卷和答题卡一并上交.一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知复数z 满足,i i i z +=++12,则复数z= A .2+i B .1 +2i C .3 +i D .3-2i2.已知集合⎭⎬⎫⎩⎨⎧≤+-=031x x x A ,{}2<=x x B ,则A∩B= A .{}12<<-x x B .{}23<<-x x C .{}12≤<-x x D .{}12≤≤-x x3.设等比数列{}n a 的前n 项和为n S ,21=a ,02432=++a a a ,则5S =A .2B .0C . -2D . -44.若某几何体的三视图如下,则该几何体的体积为A .2B .4C .24D .D .34 5.在某项测量中,测量结果ξ服从正态分布)0)(,1(2>σσN ,若ξ在(0,2)内取值的概率为0.8,则ξ在),0(+∞内取值的概率为A .0.9B .0.1C .0.5D .0.46.已知函数)22)(3cos()(πϕπϕ<<-+=x x f 图象关于直线185π=x 对称,则函数f (x )在区间[0,π]上零点个数为A .1B .2C .3D .47.已知向量,是互相垂直的单位向量,向量满足1=⋅,1=⋅=A .2B .5C .3D .78.已知等差数列{}n a 满足:82521=+a a ,则21a a +的最大值为 A .2 C .4 B .3 D .59.已知直线21-=x y PQ :与y 轴交于P 点,与曲线)0(:2≥=y x y C 交于M Q ,成为线段PQ 上一点,过M 作直线t x =交C 于点N ,则△MNP 面积取到最大值时,t 的值为A .161B .41C .1D .45 10.已知函数)(1)(1R a eax e x f x ∈--=-的图象与x 轴有唯一的公共点,则实数a 的取值范围为 A .{}0≤a a B .⎭⎬⎫⎩⎨⎧=≤e a a a 10,或 C .{}e a a a =≤,或0 D .{}10=≤a a a ,或 11.已知A ,B 分别为双曲线1322=-Γy x :实轴的左右两个端点,过双曲线Γ的左焦点F 作直线PQ 交双曲线于P ,Q 两点(点P ,Q 异于A ,B ) ,则直线AP ,BQ 的斜率之比BQ AP k k :=A .31-B .3-C .32-D .23- 12.在四棱锥ABCD P -中,2=PA ,7===PD PC PB ,7==AD AB ,2==CD BC ,则四棱锥ABCD P -的体积为A .32B .3C .5D .3二、填空题:本题共4小题,每小题5分,共20分13.函数ln 1x y x =+在点P (1,0)处的切线方程为 . 14.一种药在病人血液中的量保持1500 mg 以上才有疗效;而低于500 mg 病人就有危险。
2020届高三5月质量检测数学理科试卷(解析版)

2020年高考数学模拟试卷(理科)(5月份)一、选择题(共12小题).1.已知全集U=R,集合A={x|﹣2<x<3},B={x|√2x−4≤2},则B∩(∁U A)=()A.[2,3]B.(﹣∞,﹣2]∪[2,+∞)C.(3,4]D.[3,4]2.已知复数z=a2−i+1(i为虚数单位,a∈R)为纯虚数,则实数a=()A.52B.−52C.0D.23.已知函数f(x)={e x,x<14−mx,x≥1,若f(m)=1,则实数m的值是()A.0B.√3C.0或√3D.0或√3或−√3 4.若l,m,n是三条不相同的直线,α,β是两个不同的平面,则下列命题中为真命题的是()A.若l∥m,m∥α,则l∥αB.若α⊥β,n⊥α,m∥n,则m∥βC.若α⊥β,l⊥α,m∥β,则l∥m D.若l⊥α,l∥n,n⊥β,则α∥β5.宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:“松长六尺,竹长两尺,松日自半,竹日自倍,何日竹逾松长?”如图是解决此问题的一个程序框图,其中a为松长、b为竹长,则菱形框与矩形框处应依次填()A .a <b ?;a =a +a2 B .a <b ?;a =a +2aC .a ≥b ?;a =a +a2D .a ≥b ?;a =a +2a6.在等比数列{a n }中,已知a 1a 3=4,a 9=256,则a 8=( ) A .128或﹣128B .128C .64或﹣64D .647.2020年新型肺炎疫情期间,山东省某市派遣包含甲,乙两人的12名医护人员支援湖北省黄冈市,现将这12人平均分成两组,分别分配到黄冈市区定点医院和黄冈市英山县医院,则甲、乙不在同一组的概率为( )A .511B .611C .12D .238.函数f (x )=5(x 2−cosx)e x +e−x 的大致图象是( )A .B .C .D .9.直线l :x ﹣y +√2=0将圆O :x 2+y 2=4分成的两部分的面积之比为( ) A .(4π−√3):(8π+√3) B .(4π﹣3√3):(8π+3√3) C .(2π﹣2√3):(10π+2√3)D .(2π﹣3√3):(10π+3√3)10.设无穷等差数列{a n }的各项都为正数,且其前n 项和为S n ,若S 2017=2017,则下列判断错误的是( ) A .a 1009=1B .a 1010≥1C .S 2016>2016D .S 2019≥201911.函数f (x )=sin (ωx +φ)(ω>0,|φ|<π2)的图象如图所示,先将函数f (x )图象上所有点的横坐标变为原来的6倍,纵坐标不变,再将所得函数的图象向左平移7π2个单位长度,得到函数g (x )的图象,则下列结论 正确的是( )A .函数g (x )是奇函数B .函数g (x )在区间[﹣2π,0]上单调递增C .函数g (x )图象关于(3π,0)对称D .函数g (x )图象关于直线x =﹣3π对称12.定义在[0,+∞)上的函数f (x )满足:f (x )+f '(x )=√x ex ,f(12)=√12e .其中f '(x )表示f (x )的导函数,若存在正数a ,使得f(x 2−x 4)≥1a +a 8e成立,则实数x 的取值范围是( ) A .[﹣1,2] B .(﹣∞,﹣1]∪[2,+∞) C .[﹣1,0]∪[1,2]D .[﹣2,﹣1]∪[1,2]二、填空题:本题共4小题,每小题5分,共20分.13.已知向量a →=(﹣2,1),b →=(4,3),c →=(﹣1,λ),若(a →+b →)∥c →,则λ= . 14.二项式(1x −3x 2)6的展开式中的常数项是 .(用数字作答) 15.在直三棱柱ABC ﹣A 1B 1C 1中,∠BAC =120°且AB =AC =3,BB 1=4,则此三棱柱外接球的表面积为 .16.已知椭圆C :x 2a +y 2b =1(a >b >0)的左、右焦点分别为F 1,F 2,且椭圆C 与双曲线C ':2x 2a −y 2=1共焦点,若椭圆C 与双曲线C '的一个交点M 满足|MF 1|•|MF 2|=2,则△MF 1F 2的面积是 .三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.17.在△ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,且cos(B+C)cosC=a 2b+c.(1)求角A 的大小;(2)若a =4√3,b =4√2,求△ABC 的面积.18.现有一种水上闯关游戏,共设有3个关口,如果在规定的时间内闯过了这3个关口,那么闯关成功,否则闯关失败,结束游戏.假定小张、小王、小李闯过任何一个关口的概率分别为23,12,12,且各关口能否顺利闯过相互独立.(1)求小张、小王、小李分别闯关成功的概率;(2)记小张、小王、小李三人中闯关成功的人数为X ,求X 的分布列及数学期望. 19.如图,四边形ABCD 为正方形,PA ∥CE ,AB =CE =12PA ,PA ⊥平面ABCD . (1)证明:PE ⊥平面DBE ;(2)求二面角B ﹣PD ﹣E 的正弦值的大小.20.已知抛物线C :y 2=4x 的焦点为F ,过点P (2,0)的直线l 交抛物线C 于A (x 1,y 1)和B (x 2,y 2)两点.(1)当x 1+x 2=8时,求直线l 的方程;(2)若过点P (2,0)且垂直于直线l 的直线l '与抛物线C 交于M ,N 两点,记△ABF 与△MNF 的面积分别为S 1与S 2,求S 1S 2的最小值.21.已知函数g (x )=e x ﹣ax 2﹣ax ,h (x )=e x ﹣2x ﹣lnx .其中e 为自然对数的底数. (1)若f (x )=h (x )﹣g (x ). ①讨论f (x )的单调性;②若函数f (x )有两个不同的零点,求实数a 的取值范围.(2)已知a >0,函数g (x )恰有两个不同的极值点x 1,x 2,证明:x 1+x 2<ln(4a 2).(二)选考题:共10分.请考生在第22、23两题中任选一题作答.如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程]22.以平面直角坐标系xOy 的原点为极点,x 轴的非负半轴为极轴并取相同的单位长度建立极坐标系,已知过点A (﹣1,﹣2)且斜率为1的直线l 1与曲线C :{x =3+4cosα,y =4+4sinα(α是参数)交于P ,Q 两点,与直线l 2:ρcos θ+2ρsin θ+4=0交于点N . (1)求曲线C 的普通方程与直线l 2的直角坐标方程;(2)若PQ 的中点为M ,比较|PQ |与|MN |的大小关系,并说明理由. [选修4-5:不等式选讲]23.已知函数f (x )=3|x ﹣2|﹣3.(1)求不等式13[f(x)+3]>|x +1|的解集;(2)若关于x 的不等式f (x )≥mx +m 恒成立,求实数m 的取值范围.参考答案一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集U =R ,集合A ={x |﹣2<x <3},B ={x |√2x −4≤2},则B ∩(∁U A )=( ) A .[2,3] B .(﹣∞,﹣2]∪[2,+∞) C .(3,4]D .[3,4]【分析】求出集合B ,∁U A ,由此能求出B ∩(∁U A ). 解:∵全集U =R ,集合A ={x |﹣2<x <3}, B ={x |√2x −4≤2}={x |2≤x ≤4}, ∴∁U A ={x |x ≤﹣2或x ≥3}, ∴B ∩(∁U A )={x |3≤x ≤4}, 故选:D .2.已知复数z =a2−i +1(i 为虚数单位,a ∈R )为纯虚数,则实数a =( ) A .52B .−52C .0D .2【分析】利用复数代数形式的乘除运算化简,再由实部为0,且虚部不为0列式求解. 解:∵z =a2−i +1=a(2+i)(2−i)(2+i)+1=2a+55+a5i 为纯虚数, ∴{2a+55=0a 5≠0,解得a =−52.故选:B .3.已知函数f(x)={e x,x<14−mx,x≥1,若f(m)=1,则实数m的值是()A.0B.√3C.0或√3D.0或√3或−√3【分析】讨论字母m的范围,求出f(m)的表达式,列出方程求出符合条件的m值.解:因为函数f(x)={e x,x<14−mx,x≥1,当m<1时,有f(m)=e m,e m=1解得m=0满足条件;当m≥1时,有f(m)=4﹣m2,∴4﹣m2=1解得m=√3(−√3舍)总之,m=√3或0;故选:C.4.若l,m,n是三条不相同的直线,α,β是两个不同的平面,则下列命题中为真命题的是()A.若l∥m,m∥α,则l∥αB.若α⊥β,n⊥α,m∥n,则m∥βC.若α⊥β,l⊥α,m∥β,则l∥m D.若l⊥α,l∥n,n⊥β,则α∥β【分析】对于A,l∥α或l⊂α;对于B,m∥β或m⊂β;对于C,l与m相交、平行或异面;对于D,由面面垂直的判定定理得α∥β.解:对于A,若l∥m,m∥α,则l∥α或l⊂α,故A错误;对于B,若α⊥β,n⊥α,m∥n,则m∥β或m⊂β,故B错误;对于C,若α⊥β,l⊥α,m∥β,则l与m相交、平行或异面,故C错误;对于D,若l⊥α,l∥n,n⊥β,则由面面垂直的判定定理得α∥β,故D正确.故选:D.5.宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:“松长六尺,竹长两尺,松日自半,竹日自倍,何日竹逾松长?”如图是解决此问题的一个程序框图,其中a为松长、b为竹长,则菱形框与矩形框处应依次填()A.a<b?;a=a+a2B.a<b?;a=a+2aC.a≥b?;a=a+a2D.a≥b?;a=a+2a【分析】由程序框图模拟程序的运行,结合题意即可得解.解:竹逾松长,意为竹子比松高,即a<b,但这是一个含当型循环结构的程序框图,当不满足条件时,退出循环,故菱形框中条件应为a≥b?,松日自半,则表示松每日增加一半,即矩形框应填a=a+a 2.故选:C.6.在等比数列{a n}中,已知a1a3=4,a9=256,则a8=()A .128或﹣128B .128C .64或﹣64D .64【分析】由已知结合等比数列的性质可求a 2,然后结合等比数列的通项公式即可求解. 解:由等比数列的性质可得,a 1a 3=a 22=4, ∴a 2=2或﹣2,∵a 9=256,当a 2=2时,q 7=128即q =2,则a 8=128, 当a 2=﹣2时,q 7=﹣128即q =﹣2,则a 8=﹣128, 故选:A .7.2020年新型肺炎疫情期间,山东省某市派遣包含甲,乙两人的12名医护人员支援湖北省黄冈市,现将这12人平均分成两组,分别分配到黄冈市区定点医院和黄冈市英山县医院,则甲、乙不在同一组的概率为( )A .511B .611C .12D .23【分析】设“甲、乙不在同一组”为事件M ,12名医护人员平均分配到两所医院的基本事件总数为n =C 126=924,甲、乙在同一组包含的基本事件个数m =2C 104=420,由此能求出甲、乙不在同一组的概率.解:设“甲、乙不在同一组”为事件M ,12名医护人员平均分配到两所医院的基本事件总数为n =C 126=924, 甲、乙在同一组包含的基本事件个数m =2C 104=420, ∴甲、乙不在同一组的概率P =1−mn =1−420924=611. 故选:B .8.函数f (x )=5(x 2−cosx)e x +e−x 的大致图象是( )A.B.C.D.【分析】直接利用函数的奇偶性及特殊点的函数值,运用排除法得解.解:函数的定义域为R,且f(−x)=5[(−x)2−cos(−x)]e−x+e x =5(x2−cosx)e x+e−x=f(x),∴函数f(x)为偶函数,故排除B选项;又f(0)=−52,故排除C选项;当|x|>1时,x2>cos x,故当|x|>1时,f(x)>0,故排除D选项.故选:A.9.直线l:x﹣y+√2=0将圆O:x2+y2=4分成的两部分的面积之比为()A.(4π−√3):(8π+√3)B.(4π﹣3√3):(8π+3√3)C.(2π﹣2√3):(10π+2√3)D.(2π﹣3√3):(10π+3√3)【分析】根据题意,设直线l与圆O:x2+y2=4交于点M、N,过点O作OP⊥MN,垂足为点P,求出|OP|的值,结合直线与圆的位置关系可得∠MON=2π3以及|MN|=2√3;进而计算可得S△MON和S扇形OMN的值,据此可得直线l将圆O分成的两部分的面积,计算即可得答案.解:根据题意,设直线l与圆O:x2+y2=4交于点M、N,过点O作OP⊥MN,垂足为点P,则点O到直线l的距离|OP|=|√2|1+1=1,又由圆O :x 2+y 2=4的半径|OM |=r =2,则∠MOP =π3,则∠MON =2π3; 同时|MP |=√|OM|2−|OP|2=√4−1=√3,则|MN |=2√3, 且S △MON =12×|OP |×|MN |=√3, 则S 扇形OMN =12×2π3×r 2=4π3, 则劣弧对应的弓形的面积S 1=4π3−√3,另一部分的面积S 2=πr 2﹣S 1=4π﹣(4π3−√3)=8π3+√3, 故两部分的面积之比S 1S 2=4π3−√38π3+√3=√38π+3√3=(4π﹣3√3):(8π+3√3);故选:B .10.设无穷等差数列{a n }的各项都为正数,且其前n 项和为S n ,若S 2017=2017,则下列判断错误的是( ) A .a 1009=1B .a 1010≥1C .S 2016>2016D .S 2019≥2019【分析】由S 2017=2017=2017(a 1+a 2017)2=2017a 1009,可得a 1009.由无穷等差数列{a n }的各项都为正数,可得公差d ≥0.进而判断出结论.解:S 2017=2017=2017(a 1+a 2017)2=2017a 1009,∴a 1009=1.∵无穷等差数列{a n }的各项都为正数,∴公差d ≥0.∴a 1010≥1. S 2016=2016(a 1+a 2016)21008(a 1009+a 1008)≤1008×2=2016,S 2019=S 2017+a 2018+a 2019≥2017+2=2019, 综上可得:只有C 错误. 故选:C .11.函数f (x )=sin (ωx +φ)(ω>0,|φ|<π2)的图象如图所示,先将函数f (x )图象上所有点的横坐标变为原来的6倍,纵坐标不变,再将所得函数的图象向左平移7π2个单位长度,得到函数g (x )的图象,则下列结论 正确的是( )A .函数g (x )是奇函数B .函数g (x )在区间[﹣2π,0]上单调递增C .函数g (x )图象关于(3π,0)对称D .函数g (x )图象关于直线x =﹣3π对称【分析】首先利用函数的图象求出函数的关系式,进一步利用函数的图象的伸缩变换和平移变换的应用求出函数g (x )的关系式,最后利用函数的性质的应用求出结果.解:根据T =4×(7π12−π3)=π,所以ω=2ππ=2,由于函数的图象过(7π12,−1),所以2×7π12+φ=2kπ+3π2,由于|φ|<π2,解得φ=π3, 故f (x )=sin (2x +π3),先将函数f (x )图象上所有点的横坐标变为原来的6倍,纵坐标不变,再将所得函数的图象向左平移7π2个单位长度,得到g (x )=sin[13×(x +7π2)+π3]=−cos 13x .①故函数g (x )为偶函数,故错误.②令13x ∈[2kπ,2kπ+π],所以x ∈[6k π,3π+6k π],故[﹣2π,0]⊄[6k π,3π+6k π],故错误. ③令13x =π2+kπ(k ∈Z ),解得x =3π2+3kπ(k ∈Z ),所以函数的对称中心为(3π2+3kπ,0)(k ∈Z ),故错误④令13x =kπ解得x =3k π,当k =﹣1时,x =﹣3π,故正确. 故选:D .12.定义在[0,+∞)上的函数f (x )满足:f (x )+f '(x )=√xex ,f(12)=√12e.其中f '(x )表示f (x )的导函数,若存在正数a ,使得f(x 2−x 4)≥1a +a 8e成立,则实数x 的取值范围是( ) A .[﹣1,2] B .(﹣∞,﹣1]∪[2,+∞) C .[﹣1,0]∪[1,2]D .[﹣2,﹣1]∪[1,2]【分析】由已知可得[e x f (x )]′=√x ,结合其结构特点考虑构造函数g (x )=e x f (x ),结合导数可判断相应函数的单调性,结合单调性即可求解不等式.解:由f (x )+f '(x )=√xex ,可得,e x [f(x)+f′(x)]=√x ,即[e x f (x )]′=√x ,令g (x )=e x f (x ),则f (x )=g(x)e x,且g′(x)=√x , 故f′(x)=√x−g(x)e x, 令h (x )=√x −g(x),x >0,则h′(x)=2x, 当x ∈(0,12)时,h ′(x )>0,h (x )单调递增,当x ∈(12,+∞)时,h ′(x )<0,h (x )单调递减,故h (x )max =h (12)=0,则f ′(x )≤0,故f (x )在(0,+∞)上单调递减,因为1a+a 8e≥√12e,当且仅当1a=a 8e即a =2√2e 时取等号,由题意f(x 2−x 4)≥√12e=f (12),因为f (x )在[0,+∞)上单调递减,则0≤x 2−x 4≤12,解可得,﹣1≤x ≤0或1≤x ≤2, 故选:C .二、填空题:本题共4小题,每小题5分,共20分.13.已知向量a →=(﹣2,1),b →=(4,3),c →=(﹣1,λ),若(a →+b →)∥c →,则λ= ﹣2 .【分析】根据题意,用坐标表示出a →+b →,根据两直线平行的坐标表示列式子计算即可得答案.解:由题,a→+b→=(2,4),c→=(−1,λ),∵(a→+b→)∥c→,∴2λ=﹣4,λ=﹣2.故答案为:﹣2.14.二项式(1x−3x2)6的展开式中的常数项是−1352.(用数字作答)【分析】先求出其通项公式,再令x的指数为0即可求解.解:因为二项式(1x−3x2)6的展开式得通项为:T r+1=∁6r•(1x)6﹣r•(−3x2)r=(−32)r•∁6r•x2r﹣6;令2r﹣6=0得r=3;故二项式(1x−3x2)6的展开式中的常数项是:(−32)3•∁63=−1352.故答案为:−135 2.15.在直三棱柱ABC﹣A1B1C1中,∠BAC=120°且AB=AC=3,BB1=4,则此三棱柱外接球的表面积为52π.【分析】由题意可知直三棱柱ABC﹣A1B1C1中,AB=AC=3,∠BAC=120°,AA1=4,底面ABC的小圆半径为2,连接两个底面中心的连线,中点与顶点的连线就是球的半径,即可求出三棱柱的外接球的表面积.解:由题意可知直三棱柱ABC ﹣A 1B 1C 1中,AB =AC =3,∠BAC =120°,AA 1=4, ∴底面小圆ABC 的半径r 满足:2r =3sin30°=6,即r =3, 连接两个底面中心的连线,中点与顶点的连线就是球的半径,外接球的半径为:R =√32+22=√13∴三棱柱的外接球的表面积为:4π•R 2=52π; 故答案为:52π.16.已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左、右焦点分别为F 1,F 2,且椭圆C 与双曲线C ':2x 2a 2−y 2=1共焦点,若椭圆C 与双曲线C '的一个交点M 满足|MF 1|•|MF 2|=2,则△MF 1F 2的面积是 1 .【分析】先将双曲线的方程化成标准形式,再由椭圆和双曲线的定义可得{|MF 1|+|MF 2|=2a |MF 1|−|MF 2|=2⋅√22a =√2a,解得{|MF 1|=2+√22a|MF 2|=2−√22a,再代入|MF 1|•|MF 2|=2,即可解得a 的值,从而得|MF 1|、|MF 2|和|F 1F 2|的长,由勾股定理可知,△MF 1F 2是直角三角形,因此S △MF 1F 2=12⋅|MF 1|⋅|MF 2|.解:将双曲线C ':2x 2a −y 2=1化成标准形式为x 2a 22−y 2=1,不妨设点M 在双曲线的右支上,则根据椭圆和双曲线的定义,有{|MF 1|+|MF 2|=2a |MF 1|−|MF 2|=2⋅√22a =√2a,解得{|MF 1|=2+√22a|MF 2|=2−√22a. ∵|MF 1|•|MF 2|=2, ∴2+√22a ⋅2−√22a =2,解得a =2或﹣2(舍负), ∴|MF 1|=2+√2,|MF 2|=2−√2,双曲线的焦距|F 1F 2|=2√a 22+1=2√3.显然有|MF1|2+|MF2|2=|F1F2|2,∴△MF1F2是直角三角形,∴S△MF1F2=12⋅|MF1|⋅|MF2|=12×(2+√2)×(2−√2)=1.故答案为:1.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.17.在△ABC中,a,b,c分别是角A,B,C的对边,且cos(B+C)cosC=a2b+c.(1)求角A的大小;(2)若a=4√3,b=4√2,求△ABC的面积.【分析】(1)由已知结合正弦定理及和差角公式进行化简可求cos A,进而可求A;(2)由已知结合余弦定理可求c,然后结合三角形的面积公式即可求解.解:(1)∵cos(B+C)cosC=a2b+c=−cosAcosC,由正弦定理可得,sinA2sinB+sinC =−cosAcosC,所以2sin B cos A+sin C cos A=﹣sin A cos C,所以2sin B cos A+sin C cos A+sin A cos C=0,即2sin B cos A+sin(C+A)=0,所以2sin B cos A+sin B=0,因为sin B≠0,故cos A=−1 2,因为A 为三角形的内角,故A =2π3, (2)∵a =4√3,b =4√2,由余弦定理可得,48=32+c 2−2×4√2c ×(−12), 解可得c =2√6−2√2,∴S △ABC =12bcsinA =12×4√2×(2√6−2√2)×√32=12﹣4√318.现有一种水上闯关游戏,共设有3个关口,如果在规定的时间内闯过了这3个关口,那么闯关成功,否则闯关失败,结束游戏.假定小张、小王、小李闯过任何一个关口的概率分别为23,12,12,且各关口能否顺利闯过相互独立.(1)求小张、小王、小李分别闯关成功的概率;(2)记小张、小王、小李三人中闯关成功的人数为X ,求X 的分布列及数学期望. 【分析】(1)记小张、小王、小李闯关成功的事件分别为:A ,B ,C ,求出概率. (2)易知X 的所有可能取值为:0,1,2,3;求出概率,得到随机变量的分布列,然后求解期望即可.解:(1)记小张、小王、小李闯关成功的事件分别为:A ,B ,C ,则P (A )=(23)3=827;P (B )=(12)3=18;P (C )=(12)3=18;(2)易知X 的所有可能取值为:0,1,2,3;P (X =0)=1927×78×78=9311728;P (X =1)=827×78×78+1927×18×78+1927×78×18=6581728; P (X =2)=827×18×78+827×78×18+1927×18×18=1311728, P (X =3)=827×18×18=81728.所有随机变量的分布列为:X0123P93117286581728131172881728故E(X)=0×9311728+1×6581728+2×1311728+3×81728=59108.19.如图,四边形ABCD为正方形,PA∥CE,AB=CE=12PA,PA⊥平面ABCD.(1)证明:PE⊥平面DBE;(2)求二面角B﹣PD﹣E的正弦值的大小.【分析】(1)连结AC,推导出BD⊥AC,PA⊥BD,PA⊥AD,从而BD⊥平面APEC,进而BD⊥PE,推导出PE⊥DE,由此能证明PE⊥平面DBE.(2)以A为原点,AD,AB,AP所在直线为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角B﹣PD﹣E的正弦值.【解答】(1)证明:连结AC,∵四边形ABCD是正方形,∴BD⊥AC,∵PA⊥平面ABCD,∴PA⊥BD,PA⊥AD,∵PA∩AC=A,∴BD⊥平面APEC,∵PE⊂平面APEC,∴BD⊥PE,设AB=1,则AD=1,PA=2,∴PD=√5,同理解得DE=√2,要梯形PACE中,解得PE=√3,∴PE2+DE2=PD2,∴PE⊥DE,∵BD ∩DE =D ,∴PE ⊥平面DBE .(2)解:以A 为原点,AD ,AB ,AP 所在直线为x ,y ,z 轴,建立空间直角坐标系, 令AB =1,则CE =,AP =2,∴P (0,0,2),E (1,1,1),D (1,0,0),B (0,1,0),EP →=(﹣1,﹣1,1),DP →=(﹣1,0,2),BP →=(0,﹣1,2),BD →=(1,﹣1,0),设平面DPE 的法向量n →=(x ,y ,z ),则{n →⋅EP →=−x −y +z =0n →⋅DP →=−x +2z =0,取z =1,得n →=(2,﹣1,1),设平面BPD 的法向量m →=(a ,b ,c ),则{m →⋅BD →=a −b =0m →⋅DP →=−a +2c =0,取c =1,得m →=(2,2,1),设二面角B ﹣PD ﹣E 的平面角为θ,则cos θ=|m →⋅n →||m →|⋅|n →|=√66,∴二面角B ﹣PD ﹣E 的正弦值sin θ=1−(66)2=√306.20.已知抛物线C:y2=4x的焦点为F,过点P(2,0)的直线l交抛物线C于A(x1,y1)和B(x2,y2)两点.(1)当x1+x2=8时,求直线l的方程;(2)若过点P(2,0)且垂直于直线l的直线l'与抛物线C交于M,N两点,记△ABF 与△MNF的面积分别为S1与S2,求S1S2的最小值.【分析】(1)判断直线l的斜率一定不为0,可设直线l的方程为x=my+2,联立抛物线的方程,运用韦达定理和直线方程,化简整理,解方程可得m,进而得到所求直线方程;(2)设直线l的方程为x=my+2,联立抛物线的方程,运用韦达定理和三角形的面积公式,可得S1,同理可得S2,化简整理,由基本不等式,可得S1S2的最小值.解:(1)直线l过定点P(2,0),在x轴上,且直线l与抛物线相交,则斜率一定不为0,可设直线l的方程为x=my+2,联立抛物线的方程y2=4x,可得y2﹣4my﹣8=0,可得y1+y2=4m,y1y2=﹣8,所以x1+x2=my1+2+my2+2=m(y1+y2)+4=4m2+4,因为x1+x2=8,所以4m2+4=8,解得m=±1,所以直线l的方程为x﹣y﹣2=0或x+y﹣2=0;(2)设直线l的方程为x=my+2,联立抛物线的方程可得y2﹣4my﹣8=0,可得y1+y2=4m,y1y2=﹣8,则S1=12|PF|•|y1﹣y2|=12√(y1+y2)2−4y1y2=12√16m2+32=2√m2+2,因为直线MN与直线l垂直,且当m=0时,直线l的方程为x=2,此时直线l'的方程为x=0,但此时直线l'与抛物线C没有两个交点,所以不符题意,所以m≠0,所以直线l的斜率为1m ,因此直线MN的斜率为﹣m(m≠0),由点斜式方程可得直线l'的方程为y﹣0=﹣m(x ﹣2),即mx+y﹣2m=0,联立抛物线的方程y2=4x,消去y,可得m2x2﹣(4m2+4)x+4m2=0,设M(x3,y3),N(x4,y4),可得x3+x4=4m 2+4m2,x3x4=4,则y3﹣y4=m(2﹣x3)﹣m(2﹣x4)=﹣m(x3﹣x4),因此|y3﹣y4|=|m|•|x3﹣x4|=|m|•√(x3+x4)2−4x3x4=|m|•√(4m2+4m2)2−4×4= |m|m2√(4+4m2)2−16m2=1|m|√16+32m2,所以S2=12|PF|•|y3﹣y4|=12×1×1|m|√16+32m2=2|m|√2m2+1,所以S1S2=2√m2+2•2 |m|√2m2+1=4√(m2+2)(2m2+1)m2=4√5+2m2+2m2≥4√5+2√2m2⋅2m2=4√5+2×2=12,当且仅当2m2=2m2即m=±1时等号恒成立,所以S1S2的最小值为12.21.已知函数g(x)=e x﹣ax2﹣ax,h(x)=e x﹣2x﹣lnx.其中e为自然对数的底数.(1)若f(x)=h(x)﹣g(x).①讨论f(x)的单调性;②若函数f(x)有两个不同的零点,求实数a的取值范围.(2)已知a>0,函数g(x)恰有两个不同的极值点x1,x2,证明:x1+x2<ln(4a2).【分析】(1)①求出f(x)并求导,解关于导函数的不等式即可得到单调区间;②显然a>0,分析可知只需f(x)的最小值小于0即可满足条件,进而得解;(2)依题意,将所证不等式转化为证明(x1−x2)ex1−x22>e x1−x2−1,再通过换元构造新函数即可得证.解:(1)f (x )=h (x )﹣g (x )=e x ﹣2x ﹣lnx ﹣e x +ax 2+ax =ax 2+(a ﹣2)x ﹣lnx (x >0),①f′(x)=2ax +(a −2)−1x =2ax 2+(a−2)x−1x =(2x+1)(ax−1)x(x >0), (i )当a ≤0时,f ′(x )<0,函数f (x )在(0,+∞)上递减;(ii )当a >0时,令f ′(x )>0,解得x >1a ;令f ′(x )<0,解得0<x <1a ,∴函数f (x )在(0,1a )递减,在(1a ,+∞)递增;综上,当a ≤0时,函数f (x )在(0,+∞)上单调递减;当a >0时,函数f (x )在(0,1a )上单调递减,在(1a ,+∞)上单调递增;②由①知,若a ≤0,函数f (x )在(0,+∞)上单调递减,不可能有两个不同的零点,故a >0;且当x →0时,f (x )→+∞;当x →+∞时,f (x )→+∞;故要使函数f (x )有两个不同的零点,只需f(x)min =f(1a )=a ⋅(1a )2+a−2a −ln 1a <0,即lna −1a+1<0, 又函数y =lnx −1x +1在(0,+∞)上为增函数,且ln1−11+1=0,故lna −1a+1<0的解集为(0,1).故实数a 的取值范围为(0,1);(2)证明:g ′(x )=e x ﹣2ax ﹣a ,依题意,{e x 1−2ax 1−a =0e x 2−2ax 2−a =0,两式相减得,2a =e x 1−e x 2x 1−x 2(x 1<x 2), 要证x 1+x 2<ln(4a 2),即证x 1+x 22<ln2a ,即证e x 1+x 22<e x 1−e x 2x 1−x 2,两边同除以e x 2,即证(x 1−x 2)ex 1−x 22>e x 1−x 2−1, 令t =x 1﹣x 2(t <0),即证te t 2−e t +1>0,令h(t)=te t 2−e t +1(t <0),则h′(t)=−e t 2[e t 2−(t 2+1)], 令p(t)=e t 2−(t 2+1),则p′(t)=12(e t 2−1), 当t <0时,p ′(t )<0,p (t )在(﹣∞,0)上递减,∴p (t )>p (0)=0,∴h ′(t )<0,∴h (t )在(﹣∞,0)上递减,∴h (t )>h (0)=0,即te t 2−e t +1>0,故x 1+x 2<ln(4a 2).(二)选考题:共10分.请考生在第22、23两题中任选一题作答.如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程]22.以平面直角坐标系xOy 的原点为极点,x 轴的非负半轴为极轴并取相同的单位长度建立极坐标系,已知过点A (﹣1,﹣2)且斜率为1的直线l 1与曲线C :{x =3+4cosα,y =4+4sinα(α是参数)交于P ,Q 两点,与直线l 2:ρcos θ+2ρsin θ+4=0交于点N .(1)求曲线C 的普通方程与直线l 2的直角坐标方程;(2)若PQ 的中点为M ,比较|PQ |与|MN |的大小关系,并说明理由.【分析】(1)直接利用转换关系,把参数方程极坐标方程和直角坐标方程之间进行转换. (2)利用一元二次方程根和系数关系式的应用和弦长公式的应用求出|MN |和|PQ |的长,进一步比较出结果.解:(1)曲线C :{x =3+4cosα,y =4+4sinα(α是参数)转换为直角坐标方程为(x ﹣3)2+(y ﹣4)2=16.直线l 2:ρcos θ+2ρsin θ+4=0根据{x =ρcosθy =ρsinθ转换为直角坐标方程为x +2y +4=0.(2)已知过点A (﹣1,﹣2)且斜率为1的直线l 1的直角坐标方程为x ﹣y ﹣1=0.所以{x −y −1=0(x −3)2+(y −4)2=16,整理得x 2﹣8x +9=0, 设点P (x 1,y 1),Q (x 2,y 2),所以中点M (x 1+x 22,y 1+y 22),根据一元二次方程根和系数关系式的应用,解得x 1+x 2=8,x 1x 2=9,整理得:M (4,3).联立{x +2y +4=0x −y −1=0,解得{x =−23y =−53,即N (−23,−53), 所以|MN |=√(−23−4)2+(−53−3)2=14√23. 根据弦长公式:|PQ |=√1+k 2|x 1−x 2|=√1+12⋅√(x 1+x 2)2−4x 1x 2=2√14.由于14√23−2√14=2√2(√499−√7)<0,所以|PQ |>|MN |.[选修4-5:不等式选讲]23.已知函数f (x )=3|x ﹣2|﹣3.(1)求不等式13[f(x)+3]>|x +1|的解集; (2)若关于x 的不等式f (x )≥mx +m 恒成立,求实数m 的取值范围.【分析】(1)不等式13[f(x)+3]>|x +1|化为|x ﹣2|>|x +1|,去掉绝对值求出x 的取值范围;(2)画出函数f (x )与函数y =mx +m 的图象,结合图象求出满足条件时m 的取值范围.解:(1)由函数f (x )=3|x ﹣2|﹣3,则不等式13[f(x)+3]>|x +1|可化为13[3|x ﹣2|﹣3+3]>|x +1|,得|x ﹣2|>|x +1|,等价于(x ﹣2)2>(x +1)2,整理得6x <3,解得x <12,所以所求不等式的解集为(﹣∞,12);(2)函数f (x )=3|x ﹣2|﹣3={3x −9,x ≥23−3x ,x <2; 画出函数f (x )={3x −9,x ≥23−3x ,x <2与函数y =mx +m 的图象,如图所示;由图象知函数y =f (x )图象的最低点N (2,﹣3),函数y =mx +m 可化为y =m (x +1),其图象恒过点M (﹣1,0),又直线MN的斜率为−3−02−(−1)=−1,.直线y=m(x+1)以M(﹣1,0)为中心,在直线l和MN之间转动时(含边界)满足条件;否则不满足条件;所以﹣3≤m≤﹣1,即不等式f(x)≥mx+m恒成立时,实数m的取值范围是[﹣3,﹣1].。
