常用工具箱
arcgis常用工具箱简明总结_范文模板及概述

arcgis常用工具箱简明总结范文模板及概述1. 引言1.1 概述本文主要介绍ArcGIS常用工具箱的简洁总结,以帮助读者更好地掌握和使用这些工具。
ArcGIS是由Esri公司开发的一款强大的地理信息系统软件,它提供了丰富的功能和工具,可以用于数据管理、空间分析、地图制作等多个领域。
1.2 文章结构本文按照以下结构进行组织:- 引言部分对文章进行概述,介绍文章内容和结构;- ArcGIS常用工具箱简介部分对工具箱进行整体概述,并说明其功能和注意事项;- 常用工具部分将工具箱划分为数据管理工具集合、空间分析工具集合以及地图制作和可视化工具集合等多个分类,并详细介绍其中常用的工具;- 结论部分对全文内容进行总结,并探讨ArcGIS在未来的发展趋势。
1.3 目的本文旨在向读者介绍ArcGIS常用工具箱,帮助读者快速了解各类工具的功能和使用方法。
通过学习本文内容,读者将能够更高效地利用ArcGIS进行数据处理、空间分析和地图制作,在实际应用中提升工作效率。
同时,本文也将展望ArcGIS 未来的发展趋势,帮助读者了解该软件在地理信息领域的前景。
2. ArcGIS常用工具箱简介2.1 工具箱概述ArcGIS工具箱是ArcGIS软件中的一个重要组成部分,它提供了一系列功能强大的工具,用于处理和分析地理数据。
工具箱中包含了各种各样的工具,涵盖了数据管理、空间分析、地图制作和可视化等多个方面。
通过使用这些工具,用户可以有效地完成与地理数据相关的任务。
2.2 工具箱功能ArcGIS工具箱的功能十分丰富多样。
以下是一些常见的功能:- 数据导入导出工具:提供了各种选项,使用户可以从不同格式(如shapefile、CSV文件等)导入或导出地理数据。
- 数据清理工具集合:包含了各种可以对数据进行清理和整理的工具,例如去除重复记录、删除空值等。
- 数据转换工具集合:提供了多种转换和转换操作,使用户可以将数据从一种格式或坐标系统转换为另一种格式或坐标系统。
【免费下载】MATLAB常用工具箱函数注释

1 线性代数
1.1 矩阵分析
Norm 矩阵或向量的范数 Null 零空间
Normest 估计矩阵的 2 范数 Orth 正交化
Rank 矩阵的秩
Rref 简化矩阵为梯形形式
Det 矩阵行列式的值 Subspace 两个子空间的夹角
1.2 线性方程
\和/ 线性方程求解
Inv
矩阵的逆
Poly 特征多项式
1.4 矩阵函数
Expm 矩阵指数 Sqrtm 矩阵平方根 Logm 矩阵对数 Funm 计算一般矩阵函数
2 曲线拟合工具箱函数
2.1 拟合数据预处理
Cftool
Lu
Ilu
LU 分解
不完全的 LU 分解
Luinc 不完全的 LU 分解
Qr
QR 分解
Lsqnonneg 非负线性最小二乘
Fittype 构造一个曲线拟合对象
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电,力根保通据护过生高管产中线工资敷艺料设高试技中卷术资配0料不置试仅技卷可术要以是求解指,决机对吊组电顶在气层进设配行备置继进不电行规保空范护载高高与中中带资资负料料荷试试下卷卷高问总中题体资,配料而置试且时卷可,调保需控障要试各在验类最;管大对路限设习度备题内进到来行位确调。保整在机使管组其路高在敷中正设资常过料工程试况中卷下,安与要全过加,度强并工看且作护尽下关可都于能可管地以路缩正高小常中故工资障作料高;试中对卷资于连料继接试电管卷保口破护处坏进理范行高围整中,核资或对料者定试对值卷某,弯些审扁异核度常与固高校定中对盒资图位料纸置试,.卷保编工护写况层复进防杂行腐设自跨备动接与处地装理线置,弯高尤曲中其半资要径料避标试免高卷错等调误,试高要方中求案资技,料术编试交写5、卷底重电保。要气护管设设装线备备置敷4高、调动设中电试作技资气高,术料课中并中3试、件资且包卷管中料拒含试路调试绝线验敷试卷动槽方设技作、案技术,管以术来架及避等系免多统不项启必方动要式方高,案中为;资解对料决整试高套卷中启突语动然文过停电程机气中。课高因件中此中资,管料电壁试力薄卷高、电中接气资口设料不备试严进卷等行保问调护题试装,工置合作调理并试利且技用进术管行,线过要敷关求设运电技行力术高保。中护线资装缆料置敷试做设卷到原技准则术确:指灵在导活分。。线对对盒于于处调差,试动当过保不程护同中装电高置压中高回资中路料资交试料叉卷试时技卷,术调应问试采题技用,术金作是属为指隔调发板试电进人机行员一隔,变开需压处要器理在组;事在同前发一掌生线握内槽图部内纸故,资障强料时电、,回设需路备要须制进同造行时厂外切家部断出电习具源题高高电中中源资资,料料线试试缆卷卷敷试切设验除完报从毕告而,与采要相用进关高行技中检术资查资料和料试检,卷测并主处且要理了保。解护现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
招聘面试常用工具箱

招聘面试常用工具箱目录电话访谈计划表 (4)电话面试:关键是4W+1H (4)电话面试三步曲 (5)电话面试实用小技巧 (7)提高你的电话面试技巧 (8)面试程序 (14)人员的招聘、筛选与录用 (15)销售经理当地人员招聘制度 (18)招聘方法与程序 (20)招聘分析报告 (22)招聘计划的程序和内容 (24)招聘流程制度 (26)招聘录用流程(二) (28)招聘录用流程(三) (29)招聘录用应届毕业生制度 (29)招聘录用制度(二) (32)招聘录用制度(六) (34)第二章招聘 (34)招聘录用制度(七) (35)招聘录用制度(三) (38)招聘录用制度(四) (40)招聘录用制度(五) (42)招聘录用制度(一) (44)招聘录用制度(八) (45)招聘面试管理制度 (48)招聘面试四步 (49)招聘启事的写作格式和内容 (50)招聘业务的基础建设——工作分析 (51)职位说明书编写的目的与作用 (52)众多名企用人标准 (53)专业技术人员职位任用办法 (56)HR经理怎样筛选应聘简历 (57)读透简历——如何通过简历获得有效信息 (57)关注简历细节,锤炼你的火眼金睛 (59)简历筛选模块导读 (60)乐百氏挑选简历的三道工序 (61)如何分析简历及确定部分面试问题 (62)如何筛选应届生简历 (64)筛选简历的八大妙招 (65)筛选简历的标准 (66)“筛选”应聘者的四种招数 (69)招聘企业挑选简历的6个标准 (69)咨询业简历筛选标准(简化版) (70)面试评价量表 (87)面谈构成表 (89)面谈记录表 (91)面谈考评表 (92)模拟应聘评估表 (92)企业招聘的事后评估 (93)人才素质模型和面试评估要点 (95)人才招聘评价的定量分析 (98)新员工甄选比较表 (99)员工招聘录用审批表 (100)招聘结果评估表:财会员 (101)招聘结果评估表:秘书 (102)招聘进程表 (103)招聘面试记录表 (103)招聘面试评估表(技术类) (104)招聘面试评估表(销售类) (105)招聘面试评估表(行政类) (107)招聘面试综合分析报告 (109)招聘人员测评表 (110)甄询记录表 (111)专业技能的级别描述及需求识别 (111)BEI面试注意事项 (112)H R实战:面试不能这样做 (113)HR主管必备5原则 (116)IBM经典面试题:考察逻辑分析能力 (118)标准化面试笔试编制过程图 (119)传统面试的七处硬伤 (120)创造力测试 (122)典型的面试方法——结构化面试 (127)非常规的面试方法 (128)结构化面试的组织实施程序 (133)结构化面试实例及评析 (135)典型的结构化面试题本及测评要点(样例二) (136)典型的结构化面试题本及评分标准(样例一) (138)跨国公司面试特点集锦 (140)面试操作实务步骤 (142)面试的13种提问方式 (143)面试的方式 (145)面试的过程 (146)面试的组织:观察与聆听 (150)面试发问的十四准则 (151)面试分类 (154)面试技巧101招 (157)面试交流——“行为事件访谈法” (162)面试时如何与应聘者谈薪资 (164)面试试题的编制设计程序 (166)面试中识别谎言的技巧 (182)面试主管常犯的八大错误 (186)名企面试鲜招迭起 (188)名企招聘怪题 (189)某著名IT外企招聘过程 (190)内部招聘应注意的六个问题 (195)招聘面试题 (196)人事部年度招聘计划报表 (198)企业招聘面试中的六个陷阱 (199)企业招聘中几种新的面试方法 (201)企业中层干部的选拔策略 (205)情景面试试题的设计技术 (205)情景面试样题点评分析 (206)情景模拟的操作程序 (208)情景模拟的七种形式 (210)人才招聘中的望闻问切 (214)标准制定模块导读 (216)MBTI倾向性与职位类别的匹配介绍 (219)标准化面试笔试编制过程图 (227)岗位评估方法简介 (227)面试实施的重点 (230)企业各层级岗位基本任职资格参考 (230)网络招聘与传统招聘方式的比较分析 (232)以能力为核心的人力资源盘点 (233)应聘面试谈话样本 (235)员工推荐表样本 (238)公司技术能力的知识检查表 (239)求职人员登记表 (241)人员需求估计表 (246)招聘计划下达及进度 (257)工作申请表范例 (258)大学求职者结构化面试表 (259)调动员工情况登记表 (260)关于应聘者情况的电话交流记录 (261)结构化面试模式 (262)面试时的100个关键问题 (267)聘任书 (271)校园招聘流程及面试题 (274)应聘人员复试表 (276)营销人员素质测评表 (277)员工报到通知书 (278)职业评估测验 (281)电话访谈计划表电话面试:关键是4W+1H按照字典中的解释,“phoneinterview”可以指对申请工作者或申请学校的人进行电话面谈、会谈,我们这里是指用人单位派人对应聘者通过电话进行交流沟通或者电话面试等。
MATLAB中常用的工具箱

6.1.1MA TLAB中常用的工具箱MA TLAB中常用的工具箱有:Matlab main toolbox——matlab主工具箱Control system toolbox——控制系统工具箱Communication toolbox——通信工具箱Financial toolbox——财政金融工具箱System identification toolbox——系统辨识工具箱Fuzzy logic toolbox ——模糊逻辑工具箱Higher-order spectral analysis toolbox——高阶谱分析工具箱Image processing toolbox——图像处理工具箱Lmi contral toolbox——线性矩阵不等式工具箱Model predictive contral toolbox——模型预测控制工具箱U-Analysis ang sysnthesis toolbox——u分析工具箱Neural network toolbox——神经网络工具箱Optimization toolbox——优化工具箱Partial differential toolbox——偏微分奉承工具箱Robust contral toolbox——鲁棒控制工具箱Spline toolbox——样条工具箱Signal processing toolbox——信号处理工具箱Statisticst toolbox——符号数学工具箱Symulink toolbox——动态仿真工具箱System identification toolbox——系统辨识工具箱Wavele toolbox——小波工具箱6.2优化工具箱中的函数1、最小化函数2、最小二乘问题3、方程求解函数4、演示函数中型问题方法演示函数大型文体方法演示函数。
常用维修工具的使用

常用维修工具的使用维修工具是进行各种机器或设备维护和修复的关键性物品。
好的维修工具可以帮助您更有效地完成维修工作,并缩短维修时间。
这里介绍一些维修行业常用的工具及其使用方法。
扳手扳手是维修工具箱中最常见的工具之一,用于拧紧或松开螺丝。
扳手的用途非常广泛,下面介绍两种常用扳手的类型和使用方法。
手动扳手手动扳手是最常用的扳手类型。
它们通常由一个可调节的开口和一个手柄组成,手柄的长度和形状可以根据工具的大小和使用者的需求进行调整。
在使用手动扳手时,打开开口并把它放在螺丝或螺母的六边形头上。
然后,通过向一个方向转动手柄来拧紧或松开螺丝或螺母。
请注意,使用手动扳手可能需要一些力来转动手柄,因此要确保使用正确的力度以避免受伤。
气动扳手气动扳手是自动化的扳手类型,通常由压缩空气驱动。
与手动扳手相比,它可以更快地松紧螺丝和螺母,并且需要更少的力量。
使用气动扳手时,需要将其与气体压力系统连接。
将开口放在螺丝或螺母的头上,打开扳手开关,会听到扳手发出高速旋转声。
然后,将扳手靠近螺丝或螺母,并将其旋转以拧紧或放松它们。
种类不同的钳子钳子是另一种常用的维修工具,用于夹住物体或松紧小型零部件。
本文介绍三种常见的钳子类型及其使用方法。
镊子镊子是最常用的钳子类型之一。
它们通常由两个钳爪和一个弹簧组成,可以使用它们来夹住和移动细小的物体或小型零件。
使用镊子时,将两个钳爪放在需要夹住的物体两端,然后轻轻收缩钳柄即可夹紧物体。
卡簧钳卡簧钳是一种专门用于安装和拆卸卡簧的钳子。
卡簧是一种类似于小弹簧的装置,它们扮演着在不同设备和机器中固定零部件的角色。
使用卡簧钳时,将卡簧夹在钳子两个爪子之间,然后将卡簧安装到相应的设备或机器上。
弯头钳弯头钳用于从难以触及位置夹住或移动物体。
它们的钳头非常细长,而且通常都是弯曲的。
使用弯头钳时,将钳子的爪子插入到需要夹住的物体中,然后使用钳柄控制钳爪的移动。
压紧工具压紧工具通常用于将断裂的电线或电缆连接起来。
关于PPT中控件工具箱

设置交互效果
通过设置控件的交互效果, 如点击、悬停等,提升用 户体验。
如何使用控件进行事件处理
了解事件类型
编写事件处理程序
了解PPT中常见的事件类型,如单击、 双击、鼠标悬停等。
根据需求编写事件处理程序,实现特 定的功能或效果。
绑定事件处理程序
将事件处理程序绑定到相应的控件上, 以便在事件发生时执行相应的操作。
关于PPT中的控件工具箱
• 控件工具箱简介 • 常用控件工具箱介绍 • 控件工具箱的使用技巧 • 控件工具箱的优化建议 • 控件工具箱的发展趋势与展望
01
控件工具箱简介
控件工具箱的定义
01
控件工具箱:在PowerPoint中, 控件工具箱是一组用于创建交互 式幻灯片的工具。
02
它允许用户在演示文稿中添加各 种类型的控件,如按钮、文本框 、下拉列表等,以实现更丰富的 演示效果和观众参与。
控件工具箱的功能与作用
功能
提供多种控件类型,如按钮、复 选框、文本框等,方便用户创建 交互式幻灯片。
作用
增强演示文稿的互动性和观众参 与度,使演示内容更加生动有趣 。
控件工具箱的分类与特点
分类
标准控件、ActiveX控件、表单控件 。
特点
易于使用工具箱介绍
控件工具箱将提供更多动态数据可视化工具,帮助用户快 速创建实时数据驱动的图表和图形。
控件工具箱与其他软件的集成与交互
1 2 3
与Office套件深度集成
控件工具箱将与Word、Excel等Office套件进行 更紧密的集成,实现数据和格式的共享与同步。
与Adobe系列软件的集成
通过与Adobe系列软件的集成,用户可以在控件 工具箱中直接导入和编辑Adobe设计软件创建的 内容。
初三物理电学工具箱

初三物理电学工具箱引言:在学习物理电学的过程中,使用适当的工具是非常重要的。
初三物理电学工具箱是初中学习物理电学课程时必备的工具箱,它包含了一些常用的工具,能够帮助学生更好地进行实验和观察。
下面将介绍一些常见的物理电学工具及其用途。
1. 电流计电流计是测量电流大小的仪器。
它通常由一个表盘和一个电流表针组成。
使用时,将电流计与电路连接,通过电流表针的偏转来判断电流的大小。
电流计在实验中起到了至关重要的作用,能够帮助学生观察和测量电流的强度,从而研究电流的特性。
2. 电压计电压计是测量电压大小的仪器。
它通常由一个表盘和一个电压表针组成。
使用时,将电压计与电路连接,通过电压表针的偏转来判断电压的大小。
电压计在实验中也具有重要的作用,能够帮助学生观察和测量电压的大小,从而研究电压的特性。
3. 电阻器电阻器是调节电阻大小的仪器。
它通常由一个旋钮和一个电阻器组成。
使用时,通过旋转电阻器上的旋钮,可以改变电阻器的电阻大小。
电阻器在实验中常用于调节电路中的电阻,从而研究电阻对电流和电压的影响。
4. 万用表万用表是一种多功能的电测仪器。
它可以测量电流、电压和电阻,还可以进行连续性测试和二极管测试等。
使用时,将万用表与电路连接,并选择相应的测量模式,即可进行各种电测操作。
万用表在实验和电路调试中非常实用,能够帮助学生进行各种电参数的测量和测试。
5. 电池电池是一种能够提供电能的装置。
它通常由一个正极、一个负极和一个电解质组成。
电池的正负极之间存在电势差,当电路与电池连接时,电势差会驱动电流的流动。
电池在物理电学实验中常用于提供电源,使电路能够正常工作。
6. 导线导线是用来传输电流的材料。
它通常由金属制成,具有良好的导电性能。
导线在实验中起到了连接电路的作用,能够将电流从一个电器元件传输到另一个电器元件。
导线的截面积和材料的电阻率会影响电流的大小和传输的效率。
7. 开关开关是控制电路通断的装置。
它通常由一个导电材料和一个可移动的触点组成。
第二章 常用操作和工具箱简介

第二章常用操作和工具箱简介本章主要介绍Photoshop的一些基本操作以及工具,包括对Photoshop的预置、常用操作和一些工具的用法,上一章中我们已经了解很多Photoshop的基础知识,那么在这一章中我们就来初步了解它的一些基础的操作及工具箱。
通过本章学习,你可以:◆了解和掌握Photoshop的常用操作◆认识和掌握Photosop的工具2.1 PhotoshopCS的基本操作开始学习Photoshop时一定要掌握其基本操作,之后才能容易掌握更高级的技巧。
2.1.1预置在第一次启动软件后,需要进行一些设置,以提高工作效率。
选择【编辑】/【预置】/【常规】命令或按快捷键Ctrl+K,预置中共有8个预设调板,可以进行如下一些设置。
1.增加历史记录的数目在处理图片过程中,系统会自动记录每步操作过程,可以让使用者还原或重做多个步骤。
默认的步骤是20步,如图1-4所示,提高这个数字就可以提高还原的步骤数目。
注意这个数字和内存是息息相关的,数字越大占用内存越大,如果系统内存低于128M,尽量不要做提高的改动。
2.改变笔刷的形状在绘画中如果想让绘制的位置更加准确,可以将绘画光标更改为“标准”或“精确”光标,不过通常情况下选择默认的“画笔大小”,如图2.1.1所示,可用鼠标单击选择。
图2.1.13.调整标尺和文字的单位标尺出现在现用窗口的顶部和左侧,可根据图片的制作目的,来进行标尺和文字的设定。
如果是用于印刷,可将标尺和文字的单位设置为通用尺寸单位(如英寸、厘米、毫米等);如果是用于屏幕显示(如网页图像、软件界面设计),可将单位设置为显示尺寸(像素),如图2.1.2所示。
图2.1.24.调整网格参考线参考线和网格出现在现用窗口的内部,它们是一种辅助线,可根据图片的整体来设置其颜色,通过右侧的色块更改默认的线条颜色。
其中网格线间隔可比照标尺和文字的设定来进行设置,如图2.1.3所示。
图2.1.35.更改暂存盘暂存盘是Photoshop软件系统在硬盘上开辟的一些空间,作用存放其临时文件。
MATLAB工具箱的使用

MATLAB工具箱的使用MATLAB®是一种强大的科学计算软件,广泛应用于各个领域的数学建模、数据分析、仿真和算法开发等工作中。
为了满足不同领域的需求,MATLAB提供了许多不同的工具箱。
这些工具箱包含了各种不同领域的函数和工具,可以帮助用户更加高效地进行数据处理、模拟和算法开发等工作。
下面将介绍几个常用的MATLAB工具箱,以及它们的使用方法:1.信号处理工具箱(Signal Processing Toolbox):这个工具箱提供了一系列处理数字信号的函数和工具。
用户可以使用这些函数和工具进行信号滤波、功率谱估计、频谱分析、时间频率分析等操作。
该工具箱还提供了许多基本信号处理算法,如滤波器设计、卷积和相关等。
例如,用户可以使用`filtfilt(`函数对信号进行零相移滤波,以去除噪声。
2.图像处理工具箱(Image Processing Toolbox):图像处理工具箱提供了一系列处理数字图像的函数和工具。
用户可以使用这些函数和工具进行图像的读取、显示、修改、增强和分析等操作。
该工具箱包含了许多常用的图像处理算法,如图像滤波、边缘检测、形态学处理和图像分割等。
例如,用户可以使用`imread(`函数读取图像,然后使用`imshow(`函数显示图像。
3.控制系统工具箱(Control System Toolbox):这个工具箱提供了一系列用于分析和设计控制系统的函数和工具。
用户可以使用这些函数和工具进行控制系统的建模、稳定性分析、根轨迹设计和频域分析等操作。
该工具箱还提供了许多常用的控制系统设计方法,如PID控制器设计和状态空间控制器设计等。
例如,用户可以使用`tf(`函数创建传递函数模型,然后使用`step(`函数绘制系统的阶跃响应。
4.优化工具箱(Optimization Toolbox):优化工具箱提供了一系列用于求解优化问题的函数和工具。
用户可以使用这些函数和工具进行线性规划、非线性规划和整数规划等操作。
基层管理者的工具箱29个常用管理工具

基层管理者的工具箱29个常用管理工具随着企业竞争日益激烈和工作环境的复杂性增加,基层管理者需要应对各种挑战和问题。
为了帮助他们更好地管理团队和提高工作效率,本文将介绍29个常用的管理工具,以帮助基层管理者更好地处理各种管理任务。
1. SWOT分析:通过分析组织的优势、劣势、机会和威胁,帮助管理者制定战略决策。
2. SMART目标设置:确保目标具体、可衡量、可实现、相关和时间限定,帮助管理者管理团队的期望。
3. 任务分解表:将大型任务拆分为小的可管理的任务,以便更好地组织和追踪进展。
4. 知识管理系统:建立一个集中存储和共享知识的系统,以便员工可以轻松地获取所需的信息。
5. 绩效评估工具:评估员工的绩效,识别他们的强项和待改进之处,并提供有针对性的反馈和支持。
6. 薪酬体系:建立一个公平的薪酬体系,激励员工的表现,并与市场相符。
7. 沟通计划:确定组织内和外的沟通渠道,并开展有效的沟通,以确保信息的流动和共享。
8. 团队建设活动:组织团队建设活动,增强团队凝聚力和协作精神。
9. 项目管理工具:使用项目管理工具,如甘特图和里程碑图,以便更好地计划、执行和监控项目。
10. 冲突管理策略:制定冲突解决和管理策略,以处理团队内部的冲突和分歧。
11. 培训和发展计划:为员工提供培训和发展机会,以促进他们的职业成长和技能提升。
12. 时间管理工具:使用时间管理工具,如日程表和任务列表,以更好地管理时间和提高工作效率。
13. 组织架构设计:设计合理的组织架构,明确职责和权责,以提高工作效率和组织效能。
14. 创新管理方法:采用创新管理方法,鼓励员工提出创新想法,并促进组织的创新和变革。
15. 目标管理系统:建立一个目标管理系统,确保员工的目标与组织的目标相一致,并进行监测和反馈。
16. 决策树:使用决策树分析和解决问题,帮助管理者做出准确和明智的决策。
17. 变革管理计划:制定变革管理计划,帮助组织顺利实施变革,并减少负面影响。
(完整版)常用战略工具箱

第三章常用战略工具箱第一节常用战略分析工具一.PEST分析工具用途:重要的战略分析工具,主要用于分析企业所处的宏观环境对于战略的影响。
其中PEST含义是分别代表四类影响企业战略制定的因素的字母缩写:政治的(Political)、经济的(Economic)、社会的(Social)、技术的(Technological)等.原理分析企业的宏观环境主要包括政治法律环境、经济环境、技术环境、社会环境和自然环境等五种环境。
对企业的宏观环境进行分析的方法称为PEST分析法,即政治、经济、社会和技术环境分析法。
宏观环境与企业的关系如图所示。
1.政治法律环境政治法律环境是指一个国家或地区的政治体制、政治形势、方针政策、法律法规等方面。
对于企业战略的影响。
国家政治体制与经济体制始终是相辅相成的互动形式,一个国家经济体制的选择是由政治力量决定的,尽管其背后仍是由经济力量所支配。
虽然市场竞争法则已迅速地被引入众多的行业,但对于关系到国计民生和意识形态的领域,政府的管制仍然发挥着重要的影响。
政府的政策还广泛地影响着企业的经营行动。
即使在市场经济比较成熟的发达国家,政府对市场与企业的干预几乎也有增无减,如最低工资限度、劳动保护、社会福利、进出口限制等等。
法律、法规作为国家意志的强制表现,对于规范市场与企业行为有着直接的作用。
立法在经济上的作用主要表现为维护公平竞争,维护消费者的利益,维护社会最大利益等三个方面。
市场经济越成熟的国家,往往在经济立法方面越完善。
对企业来说,影响企业战略的政治和法律因素主要有:*企业和政府之间的关系 *专利法*环境保护法 *政府财政支出*政府的法规 *政府换届*外交状况 *政府预算规模*产业政策 *其他等等对企业战略有重要意义的政治和法律变量有:*政府的管理与管制解除 *税法的改变*特种关税 *专利法的修改*专利数量 *劳动保护法*政府采购规模和政策 *公司法和合同法的修改*进出口限制 *财政与货币政策的变化以上各因素是从政治、法律角度出发将可能对于企业战略制定及战略实施产生的影响因素,例如国内产品型企业在进行国际化战略的同时须首先思考进入国家的政府经济政策、与我国的外交关系、打破壁垒的难易程度、政府对本国企业的保护力度、对于我国企业的支持力度、地区劳动法、税法、进出口政策等政治、法律的诸多因素。
MATLAB常用工具箱与函数库介绍

MATLAB常用工具箱与函数库介绍1. 统计与机器学习工具箱(Statistics and Machine Learning Toolbox):该工具箱提供了各种统计分析和机器学习算法的函数,包括描述统计、概率分布、假设检验、回归分析、分类与聚类等。
可以用于进行数据探索和建模分析。
2. 信号处理工具箱(Signal Processing Toolbox):该工具箱提供了一系列信号处理的函数和算法,包括滤波、谱分析、信号生成与重构、时频分析等。
可以用于音频处理、图像处理、通信系统设计等领域。
3. 控制系统工具箱(Control System Toolbox):该工具箱提供了控制系统设计与分析的函数和算法,包括系统建模、根轨迹设计、频域分析、状态空间分析等。
可以用于控制系统的设计和仿真。
4. 优化工具箱(Optimization Toolbox):该工具箱提供了各种数学优化算法,包括线性规划、非线性规划、整数规划、最优化等。
可以用于寻找最优解或最优化问题。
5. 图像处理工具箱(Image Processing Toolbox):该工具箱提供了图像处理和分析的函数和算法,包括图像滤波、边缘检测、图像分割、图像拼接等。
可以用于计算机视觉、医学影像处理等领域。
6. 神经网络工具箱(Neural Network Toolbox):该工具箱提供了神经网络的建模和训练工具,包括感知机、多层前馈神经网络、循环神经网络等。
可以用于模式识别、数据挖掘等领域。
7. 控制系统设计工具箱(Robust Control Toolbox):该工具箱提供了鲁棒控制系统设计与分析的函数和算法,可以处理不确定性和干扰的控制系统设计问题。
8. 信号系统工具箱(Signal Systems Toolbox):该工具箱提供了分析、设计和模拟线性时不变系统的函数和算法。
可以用于信号处理、通信系统设计等领域。
9. 符号计算工具箱(Symbolic Math Toolbox):该工具箱提供了符号计算的功能,可以进行符号表达式的运算、求解方程、求解微分方程等。
测试工程师的十大工具箱

测试工程师的十大工具箱在软件开发行业中,测试工程师起着至关重要的作用。
他们负责确保软件的质量和稳定性,以及发现并修复潜在的问题。
为了更好地完成测试任务,测试工程师通常会使用一系列工具来提高效率和准确性。
本文将介绍测试工程师使用的十大工具,以及它们各自的功能和优势。
1. 自动化测试工具自动化测试工具是测试工程师必备的利器之一。
它们能够模拟用户操作,自动执行测试用例,提高测试的覆盖率和效率。
常见的自动化测试工具包括Selenium、Appium和JUnit等。
它们可以用于Web应用、移动应用和后端服务等不同类型的软件测试。
2. 性能测试工具性能测试工具用于评估软件在各种负载情况下的性能表现。
通过模拟用户并发访问和大规模的数据处理,性能测试工具能够测量软件的响应时间、吞吐量和资源利用率等指标。
常用的性能测试工具有JMeter和LoadRunner等。
3. 缺陷管理工具缺陷管理工具帮助测试团队有效地追踪和管理软件中的缺陷。
它们提供了一个集中式的平台,方便测试人员报告缺陷、分配任务并跟踪缺陷的解决进度。
一些知名的缺陷管理工具包括JIRA和Bugzilla等。
4. 测试管理工具测试管理工具用于规划、组织和跟踪测试活动。
它们可以帮助测试团队制定测试计划、管理测试资源和生成测试报告。
一些常见的测试管理工具有TestRail和TestLink等。
5. API测试工具API测试工具用于测试软件的应用程序接口(API),以确保其功能正确性和性能稳定性。
这些工具能够模拟API请求,验证返回结果,并检查API的响应时间和错误处理能力等。
常用的API测试工具有Postman和SoapUI等。
6. 覆盖率分析工具覆盖率分析工具用于评估测试用例对源代码的覆盖程度。
它们能够分析测试用例执行过程中哪些代码被访问到,从而帮助测试工程师了解测试的完整性和有效性。
常见的覆盖率分析工具包括JaCoCo和Emma等。
7. 数据生成工具数据生成工具用于生成各种类型的测试数据,以满足不同的测试需求。
matlab常用工具箱
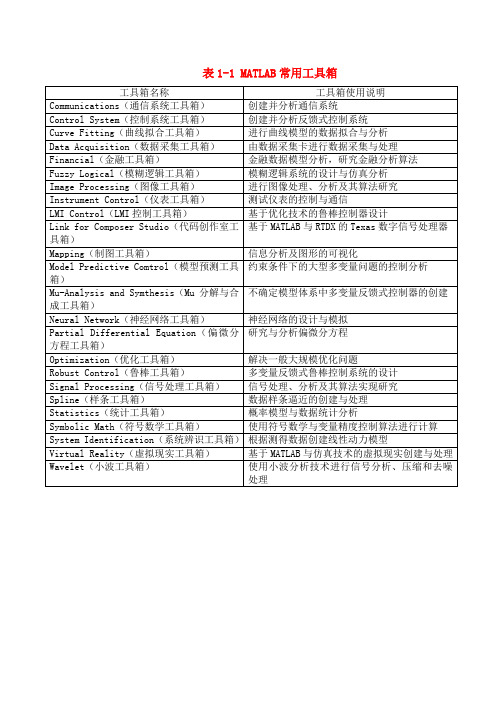
Financial(金融工具箱)
金融数据模型分析,研究金融分析算法
Fuzzy Logical(模糊逻辑工具箱)
模糊逻辑系统的设计与仿真分析
Image Processing(图像工具箱)
进行图像处理、分析及其算法研究
Instrument Control(仪表工具箱)
测试仪表的控制与通信
Optimization(优化工具箱)
解决一般大规模优化问题
Robust Control(鲁棒工具箱)
多变量反馈式鲁棒控制系统的设计
Signal Processing(信号处理工具箱)
信号处理、分析及其算法实现研究
Spline(样条工具箱)
数据样条逼近的创建与处理
Statistics(统计工具箱)
概率模型与数据统计分析
LMI Control(LMI控制工具箱)
基于优化技术的鲁棒控制器设计
Link for Composer Studio(代码创作室工具箱)
基于MATLAB与RTDX的Texas数字信号处理器
Mapping(制图工具箱)
信息分析及图形的可视化
Model Predictive Comtrol(模型预测工具箱)
表1-1 MATLAB常用工具箱
工具箱名称
工具箱使用说明
Communications(通信系统工具箱)
创建并分析通信系统
Control System(控制系统工具箱)
创建并分析反馈式控制系统
Curve Fitting(曲线拟合工具箱)
进行曲线模型的数据拟合与分析
Data Acquisition(数据采集工具箱)
约束条件下的大型多变量问题的控制分析
先闻CAD工具箱常用工具使用手册

先闻CAD工具箱常用工具使用手册目录先闻CAD工具箱常用工具简介 (5)功能介绍 (5)如何安装常用工具 (5)工具条命令介绍 (9)绘图 (9)1、设置 (9)1)基本设置 (9)2、型钢1)型钢截面 (9)2)型钢材料表 (10)3、常用 (11)1)标标注2D (11)2)标标注3D (11)3)梁简化-两点 (11)4)梁简化-线段 (11)5)梁简化-三点弧 (11)6)梁简化-圆弧 (11)4、快速绘图 (12)5、焊缝标注 (12)6、螺栓螺母 (13)7、锚栓 (14)1)Q235锚栓 (14)2)Q345锚栓 (14)钢构节点 (15)1、梁柱节点 (15)2、梁梁节点 (16)3、柱脚节点 (17)4、支撑及其他节点 (18)图形工具 (18)1、常用 (18)1)同类型快速选择 (18)2)Z坐标归零 (18)3)曲线比例分段 (18)4)曲线选点分段 (18)5)曲线交点分段 (18)6)双向偏移 (19)7)节点缩放 (19)8)长度/面积/体积 (19)9)合并为多义线 (19)10)多点标注 (19)11)线段角平分线 (19)12)曲线切线标记 (19)13)对象对齐 (19)14)对象排列 (19)15)解除标注关联 (19)16)标注不再关联 (19)17)相贯线3D (19)18)相贯线2D (19)2、旋转复制 (19)1)复制 (19)2)粘帖-多方向点 (19)3)粘帖-单方向点 (19)4)粘帖-曲线切向 (19)3、建模辅助 (20)1)平面曲线到空间(XY,XZ) (20)2)平面曲线到空间(XY,YZ) (20)3)空间曲线交点(Z) (20)4)空间曲线交点(X) (20)5)空间曲线交点(Y) (20)6)移动重复线段 (20)7)标记相近不重复端点 (20)8)标记端点接近曲线非端点 (20)9)合并线段相近端点 (20)10)线段端点取整 (20)11)用线段连接端点 (21)12)单曲面(Y) (21)13)单曲面(X) (21)文字工具 (21)1.单行文本合并 (21)2.数字累加 (21)3.文字选点分段 (21)4.文字对齐到曲线 (21)5.文字数字序列 (21)6.文字重复次数统计 (21)7.表达式求值 (21)显示工具 (22)1.显示/隐藏 (22)1)全部显示 (22)2)部分显示 (22)3)部分隐藏 (22)4)按层显示 (22)5)按层隐藏 (22)6)按颜色显示 (22)7)按颜色隐藏 (22)8)按线型显示 (22)9)按线型隐藏 (22)10)按类型显示 (22)11)按类型隐藏 (22)2.显示/隐藏 (22)1)锁定对象所在层 (22)2)解锁对象所在层 (22)3)所在层当前 (22)4)标注样式当前 (22)5)文本样式当前 (22)6)线型当前 (22)7)线型比例当前 (22)一、先闻CAD工具箱常用工具简介先闻CAD工具箱—常用工具是一款帮助技术人员解决CAD绘图中实际需求的辅助工具。
MATLAB常用工具箱与函数库介绍

MATLAB常用工具箱与函数库介绍1. 引言MATLAB是一款功能强大的数学软件,广泛应用于工程、科学、计算机科学等领域。
在MATLAB中,有许多常用的工具箱和函数库,可以帮助用户解决各种数学计算和数据处理问题。
本文将介绍几个常用的MATLAB工具箱和函数库,帮助读者更好地理解和使用这些工具。
2. 统计工具箱统计工具箱是MATLAB中一个重要的工具箱,用于统计数据的分析和处理。
这个工具箱提供了许多函数,如直方图、概率分布函数、假设检验等等。
读者可以使用统计工具箱来分析数据的分布特征、计算数据的均值和标准差、进行假设检验等。
3. 信号处理工具箱信号处理工具箱是MATLAB中用于处理信号的一个重要工具箱。
它提供了一些常用的函数,如滤波器、谱分析、窗函数等等。
利用信号处理工具箱,读者可以对信号进行滤波、频谱分析、窗函数设计等操作,帮助解决各种与信号处理相关的问题。
4. 优化工具箱优化工具箱是MATLAB中用于求解优化问题的一个重要工具箱。
它提供了一些常用的函数,如线性规划、非线性规划、整数规划等等。
利用优化工具箱,读者可以求解各种优化问题,如优化算法选择、变量约束等。
优化工具箱在生产、物流、金融等领域具有广泛的应用。
5. 控制系统工具箱控制系统工具箱是MATLAB中一个针对控制系统设计和分析的重要工具箱。
它提供了一些常用的函数,如系统模型构建、控制器设计、系统分析等。
利用控制系统工具箱,读者可以构建控制系统模型、设计控制器、进行系统稳定性分析等操作。
这个工具箱在自动化控制领域非常有用。
6. 图像处理工具箱图像处理工具箱是MATLAB中一个用于处理和分析图像的重要工具箱。
它提供了一些常用的函数,如图像滤波、边缘检测、图像分割等等。
利用图像处理工具箱,读者可以对图像进行滤波、边缘检测、目标分割等操作,帮助解决图像处理中的各种问题。
7. 符号计算工具箱符号计算工具箱是MATLAB中一个用于进行符号计算的重要工具箱。
搞调查做研究要带好“工具箱”共3篇

搞调查做研究要带好“工具箱”共3篇搞调查做研究要带好“工具箱”1搞调查做研究要带好“工具箱”在进行调查和研究的过程中,正确选择并使用各种方法和工具是非常重要的。
这需要研究人员具备丰富的专业知识和技能,同时也需要掌握各种工具和软件。
本文就从调查和研究的角度来提出一些工具箱中必备的“工具”。
一、问卷设计问卷设计是调查的关键步骤之一,因为它会直接影响到调查的可靠程度和有效性。
在此过程中,研究人员需要根据调查目的和研究问题,设计出合适的问卷。
在此,推荐使用以下工具:1. QuestionProQuestionPro是一款在线问卷设计和分析的工具,它具有易用、高效的特点。
这款工具提供了200多个问卷模版,可以快速完成问卷设计,同时也可自定义问卷。
此外,QuestionPro还提供了丰富的数据分析功能,支持多种数据导出、分享和协作。
2. SurveyMonkeySurveyMonkey是一款国际知名的在线问卷工具,被广泛用于商业和学术领域的调查研究中。
该工具可以轻松创建、发送和分析问卷,并可以随时跟踪回应率和反馈结果。
SurveyMonkey 也提供了一系列有用的功能,如逻辑跳转、调查随机化、多语言支持等。
二、数据收集数据收集是调查研究中最关键的环节之一。
恰当的数据收集方法和工具将直接影响研究结论和数据质量。
以下是一些推荐的数据收集工具:1. Google FormsGoogle Forms是一款易于使用的数据收集工具,可以帮助研究人员快速创建表格和问卷,并可以选择模版或自定义表格。
该工具还提供了多种问卷题型、逻辑跳转等高级功能,并且可以与谷歌表格等工具进行协作。
2. QualtricsQualtrics是一款专业的数据收集和分析工具,被广泛应用于学术和企业研究中。
该工具提供了多种数据采集方式,如邮寄、短信、在线等,也可以采用定向调查、CAPI、CATI等高级方法。
此外,Qualtrics还提供了丰富的数据分析和可视化功能,可以帮助研究人员更好地理解和展现数据结果。
工具箱的使用实训报告

通过本次工具箱使用实训,使学生了解和掌握常用工具箱的基本构造、功能和使用方法,提高学生实际操作能力,培养严谨的工作态度和良好的安全意识。
二、实训时间2022年X月X日至2022年X月X日三、实训地点XX职业技能培训中心四、实训工具1. 常用工具箱:包括螺丝刀、扳手、钳子、锤子、扳手、锉刀、电钻等。
2. 安全防护用品:安全帽、护目镜、手套等。
五、实训内容1. 工具箱的基本构造:了解工具箱的各个组成部分,如工具格、工具夹、工具套等,以及它们的功能和用途。
2. 常用工具的使用方法:(1)螺丝刀:学习不同类型螺丝刀的使用方法,包括一字螺丝刀、十字螺丝刀等,以及如何正确选择和使用螺丝刀。
(2)扳手:了解不同类型扳手的使用方法,如开口扳手、梅花扳手等,以及如何正确使用扳手。
(3)钳子:学习夹钳、钢丝钳等钳子的使用方法,以及如何正确握持和操作钳子。
(4)锤子:掌握不同类型锤子的使用方法,如木锤、钢锤等,以及如何正确使用锤子。
(5)锉刀:了解锉刀的种类和使用方法,以及如何正确使用锉刀进行表面处理。
(6)电钻:学习电钻的使用方法,包括钻头的选用、钻孔深度和速度的控制等。
3. 安全操作规范:学习工具箱使用过程中的安全操作规范,如正确佩戴安全防护用品、注意工具使用时的姿势和力度等。
1. 实训开始前,教师简要介绍实训目的、工具箱的基本构造和常用工具的使用方法。
2. 学生分组进行实训,每组由一名教师指导。
3. 学生按照实训内容,依次进行工具箱的使用操作,教师现场进行指导和纠正。
4. 学生完成实训操作后,进行互评和总结,教师对学生的操作进行点评和指导。
七、实训结果1. 学生能够熟练掌握常用工具箱的基本构造和常用工具的使用方法。
2. 学生在实训过程中,能够按照安全操作规范进行操作,提高安全意识。
3. 学生通过实训,培养了实际操作能力和严谨的工作态度。
八、实训总结本次工具箱使用实训,使学生了解了工具箱的基本构造和常用工具的使用方法,提高了学生的实际操作能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
content ch1ch2ch3ch4ch5ch6ch7ch8ch9ch10ch11ch12ch13ch14Mappingdownload Matlab的使用第十四章常用工具箱第一章一. 符號工具箱function Meaning Examplesym 宣告任一符號變數sym('x');sym('d1')syms 宣告諸多符號變數syms a b c d3pretty 一般數學化外形F=(1+x)^4/(1+x^2)+4/(1+x^2);pretty(F) simplify 簡化浮式simplify(F)expand 展開數學式p=expand((1+x)^4)horner 巢狀排列horner(p)factor 分解數學式factor(a^3+b^3-a*b-a*c-b*c+b^2+c^2)simple 嘗式不同方法以簡化數學式,並傳回最簡化式子syms xy;y=sqrt(cos(x)+i*sin(x));simple(y)subs 代換不同變數subs(p,x,2)collect 整理同次幕a=(x+3)(x-4);collect(a)double 將符號表示化簡為標準數值double(1/4*pi)vpa 取得任何十進位數目vpa(sqrt(16),100)taylor 泰勒式展開開始taylor(exp(x),8)gamma 求取gamma(Γ)函數之加合gamma(5)symsum 指數函數的級數展開之加合symsum(1/gamma(r),1,inf) zeta 求取Riemann Zeta函數之加合zeta(2)solve 求取多項式的解solve(x^3-7/2*x^2-17/2*x+5)diff 對任一函數進行符號式(偏)微分syms z,k; f=k*cos(z^4); diff(f,z) int 對函數進行符號式積分syms u; f=u^2*cos(u); int(f)dsolve 求取微分方程的解s=dsolve('(1+t^2)*Dy+2*t*y=cos(t),t(0)=0')laplace 求取函數之拉式轉換syms t; laplace(t^4) ztrans 求取函數Z轉換syms z n; ztrans(1/4^n) fourier 求取傅立葉轉換值y=fourier(cos(3*x)) ifourier 求取反傅立葉轉換值z=ifourier(y)符號式變數與表示法>> x=sym('x')x =x>> d1=sym('d1')d1 =d1>> syms a b c d3>> 1/(x+1)ans =1/(x+1)>> syms x y>> d=[x+1 x^2 x-y;1/x 3*y/x 1/(1+x); 2-x x/4 3/2] d =[ x+1, x^2, x-y][ 1/x, 3*y/x, 1/(x+1)][ 2-x, 1/4*x, 3/2]>> d(2,2)ans =3*y/x>> c=d(2,:)c =[ 1/x, 3*y/x, 1/(x+1)]>> e=(1+x)^4/(1+x^2)+4/(1+x^2)e =(x+1)^4/(1+x^2)+4/(1+x^2)>> pretty(e)4(x + 1) 4-------- + ------2 21 + x 1 + x>> simplify(e)ans =x^2+4*x+5 >> p=expand((1+x)^4) p =x^4+4*x^3+6*x^2+4*x+1>> horner(p)ans =1+(4+(6+(4+x)*x)*x)*x>> syms x;y=sqrt(cos(x)+i*sin(x)); >> simple(y)simplify:(cos(x)+i*sin(x))^(1/2) radsimp:(cos(x)+i*sin(x))^(1/2)combine(trig):(cos(x)+i*sin(x))^(1/2)factor:(cos(x)+i*sin(x))^(1/2)expand:(cos(x)+i*sin(x))^(1/2) combine:(cos(x)+i*sin(x))^(1/2)convert(exp):exp(i*x)^(1/2)convert(sincos):(cos(x)+i*sin(x))^(1/2)convert(tan):((1-tan(1/2*x)^2)/(1+tan(1/2*x)^2)+2*i*tan(1/2*x)/(1+tan(1/2*x)^2))^(1/ 2)collect(x):(cos(x)+i*sin(x))^(1/2)ans =exp(i*x)^(1/2)>> syms u v w>> fmv=pi*v*w/(u+v+w)fmv =pi*v*w/(u+v+w)>> subs(fmv,u,2*v)ans =pi*v*w/(3*v+w)>> subs(ans,v,1)ans =pi*w/(3+w)>> subs(ans,w,3)ans =1.5708>> syms x y>> f=3x+2*y^2>> f=3*x+2*y^2f =3*x+2*y^2>> subs(f,x,2*y)ans =6*y+2*y^2 >> subs(f,x,3)ans =9+2*y^2>> subs(ans,y,2)ans =17>> ff =3*x+2*y^2>> subs(f,y,x-3)ans =3*x+2*(x-3)^2>> collect(ans)ans =2*x^2-9*x+18>> factor(f)ans =3*x+2*y^2符號計算的變數精準度(vpa)級數展開與加合(raylor, gamma, zeta) 或Riemann Zeta函數(zeta):>> taylor(cos(exp(x)),4)cos(1)-sin(1)*x+(-1/2*cos(1)-1/2*sin(1))*x^2-1/2*cos(1)*x^3>> s=taylor(exp(x),8)s =1+x+1/2*x^2+1/6*x^3+1/24*x^4+1/120*x^5+1/720*x^6+1/5040*x^7 >> syms r>> symsum((0.1)^(r-1)/gamma(r),1,8)ans =55700614271/50400000000>> double(ans)ans =1.1052>> double(subs(s,x,0.1))ans =1.1052>> symsum(r*r,1,n)ans =1/3*(n+1)^3-1/2*(n+1)^2+1/6*n+1/6 >> factor(ans)ans =1/6*n*(n+1)*(2*n+1) >> symsum(r^3,1,n)ans =1/4*(n+1)^4-1/2*(n+1)^3+1/4*(n+1)^2>> factor(ans)ans =1/4*n^2*(n+1)^2>> symsum(1/r^2,1,inf)ans =1/6*pi^2>> zeta(2)1.6449>> zeta(3)ans =1.2021符號式矩陣運算符號式的解方程式(solve)>> syms x>> f1=x^2-4*x+3f1 =x^2-4*x+3>> solve(f1)ans =[ 1]>> f2=x^3-7/2*x^2-17/2*x+5f2 =x^3-7/2*x^2-17/2*x+5>> solve(f2)ans =[ 5][ 1/2][ -2] >> f3=x^3-7/(2*x^2)-17/(2*x)+5f3 =x^3-7/2/x^2-17/2/x+5>> [x,y]=solve('x^2+y^2=a','x^2-y^2=b') x =[ 1/2*(2*b+2*a)^(1/2)][ -1/2*(2*b+2*a)^(1/2)][ 1/2*(2*b+2*a)^(1/2)][ -1/2*(2*b+2*a)^(1/2)]y =[ 1/2*(-2*b+2*a)^(1/2)][ 1/2*(-2*b+2*a)^(1/2)][ -1/2*(-2*b+2*a)^(1/2)][ -1/2*(-2*b+2*a)^(1/2)] >> x.^2+y.^2,x.^2-y.^2 ans =[ a][ a][ a][ a]ans =[ b][ b][ b][ b]符號式微分(diff), ,, ,, ,>> syms x n>> f1=x^nf1 =x^n>> diff(f1)ans =x^n*n/x.>> f2=x^-1f2 =1/x>> diff(f2)ans =-1/x^2>> f3=log(x)f3 =log(x)>> diff(f3)ans =1/x >> syms e a >> f4=e^a*xf4 =e^a*x>> diff(f4)ans =e^a>> f5=e^(a*x) f5 =e^(a*x)>> diff(f5)ans =e^(a*x)*a*log(e) >> f6=a^xf6 =a^x>> diff(f6)ans =a^x*log(a)>> f7=sin(a*x)f7 =sin(a*x) >> diff(f7) ans =cos(a*x)*a>> f8=cos(a*x)f8 =cos(a*x)>> diff(f8)ans =-sin(a*x)*a>> f9=asin(x/a)f9 =asin(x/a)>> diff(f9)ans =1/a/(1-x^2/a^2)^(1/2) >> f10=sinh(a*x)f10 =sinh(a*x)>> diff(f10)ans =cosh(a*x)*a符號式積分(int)>> int(f1)ans =x^(n+1)/(n+1)>> int(f2)ans =log(x)>> int(f3)ans =x*log(x)-x >> int(f4) ans =1/2*e^a*x^2>> int(f5)ans =1/a/log(e)*e^(a*x) >> pretty(ans)(a x)e--------a log(e)>> int(f6)ans =1/log(a)*a^x >> int(f7) ans =-1/a*cos(a*x)>> int(f8)ans =sin(a*x)/a>> int(f9)ans =a*(x/a*asin(x/a)+(1-x^2/a^2)^(1/2))>> int(f10)ans =1/a*cosh(a*x)符號式偏微分(diff)>> syms u v w>> fmv=u*v*w/(u+v+w)fmv =u*v*w/(u+v+w)>> d=[diff(fmv,u) diff(fmv,v) diff(fmv,w)]d =[ v*w/(u+v+w)-u*v*w/(u+v+w)^2, u*w/(u+v+w)-u*v*w/(u+v+w)^2, u*v/(u+v+w)-u*v*w/(u+v+w)^2]>> diff(d(3),u)ans =v/(u+v+w)-u*v/(u+v+w)^2-v*w/(u+v+w)^2+2*u*v*w/(u+v+w)^3 >> pretty(ans)v u v v w u v w-------- - ------------ - ------------ + 2 ------------u + v + w 2 2 3(u + v + w) (u + v + w) (u + v + w)>> diff(d(2),w)ans =u/(u+v+w)-u*w/(u+v+w)^2-u*v/(u+v+w)^2+2*u*v*w/(u+v+w)^3>> diff(ans,u)ans =1/(u+v+w)-u/(u+v+w)^2-w/(u+v+w)^2+2*u*w/(u+v+w)^3-v/(u+v+w)^2+ 2*u*v/(u+v+w)^3+2*v*w/(u+v+w)^3-6*u*v*w/(u+v+w)^4符號式解常微分方程(dsolve)函數dsolve解微分方程式的一般呼叫如下:其中參數de1, de2, de3, ……den代表各別微分方程,需使用符號式變數;標準的matlab運算元與代表一階、二階、及高階的微分運算子為D1, D2, D3, ……Dn,以符號式表示;初值設定條件為in1, in2,in3, ……inn,代表微分方程的初值條件,若應變數為y,初始條件為,表示t=0時,y值為1,。
