层次分析法matlab程序
MatLab层次分析法代码

>>d=eig(A)%求全部特征值所组成的向量
e=max(eig(A));%最大特征值
v=null(A-e*eye(length(A)));%e对应特征向量
>>e
>>A=[13365957;1/31134746;1/31134746;1/61/31/311/241/22;1/51/41/421412;1/91/71/71/41/411/31/2;1/51/41/421312;1/71/61/61/21/221/21];
e=max(eig(A));%最大特征值
v=null(A-e*eye(length(A)));%e对应特征向量
>>e
e=
8.4243
>>v
v=
-0.7427
-0.3893
-0.2579
-0.0985
-0.2588
-0.0519
-0.3352
-0.1966
>>A=[13365957;1/31134746;1/31134746;1/61/31/311/241/22;1/51/41/421412;1/91/71/71/41/411/31/2;1/51/41/421312;1/71/61/61/21/221/21];
0.2579-0.0614+0.3195i-0.0614-0.3195i-0.0739-0.0916i-0.0739+0.0916i-0.1506-0.0176i-0.1506+0.0176i
(完整版)层次分析法计算权重在matlab中的实现

(完整版)层次分析法计算权重在matlab中的实现信息系统分析与设计作业层次分析法确定绩效评价权重在matlab中的实现小组成员:孙高茹、王靖、李春梅、郭荣1 程序简要概述编写程序一步实现评价指标特征值lam、特征向量w以及一致性比率CR的求解。
具体的操作步骤是:首先构造评价指标,用专家评定法对指标两两打分,构建比较矩阵,继而运用编写程序实现层次分析法在MATLAB中的应用。
通过编写MATLAB程序一步实现问题求解,可以简化权重计算方法与步骤,减少工作量,从而提高人力资源管理中绩效考核的科学化电算化。
2 程序在matlab中实现的具体步骤function [w,lam,CR] = ccfx(A)%A为成对比较矩阵,返回值w为近似特征向量% lam为近似最大特征值λmax,CR为一致性比率n=length(A(:,1));a=sum(A);B=A %用B代替A做计算for j=1:n %将A的列向量归一化B(:,j)=B(:,j)./a(j);ends=B(:,1);for j=2:ns=s+B(:,j);endc=sum(s);%计算近似最大特征值λmaxw=s./c;d=A*wlam=1/n*sum((d./w));CI=(lam-n)/(n-1);%一致性指标RI=[0,0,0.58,0.90,1.12,1.24,1.32,1.41,1.45,1.49,1.51];%RI为随机一致性指标CR=CI/RI(n);%求一致性比率if CR>0.1disp('没有通过一致性检验');else disp('通过一致性检验');endend3 案例应用我们拟构建公司员工绩效评价分析权重,完整操作步骤如下:3.1构建的评价指标体系我们将影响员工绩效评定的指标因素分为:打卡、业绩、创新、态度与品德。
3.2专家打分,构建两两比较矩阵A =1.0000 0.5000 3.0000 4.00002.0000 1.0000 5.00003.00000.3333 0.2000 1.0000 2.00000.2500 0.3333 0.5000 1.00003.3在MATLAB中运用编写好的程序实现直接在MATLAB命令窗口中输入[w,lam,CR]=ccfx(A)继而直接得出d =1.30352.00000.51450.3926w =0.31020.46910.12420.0966lam =4.1687CR =0.0625,通过一致性检验3.4解读程序结果根据程序求解中得出的特征向量,可以得出打卡、业绩、创新以及态度品德在员工绩效评价中所占的权重分别为:0.3102、0.4691、0.1242、0.0966。
matlab a计权算法

matlab a计权算法
MATLAB中的A计权算法指的是AHP(层次分析法)计算权重的
算法。
AHP是一种多准则决策分析方法,用于确定各准则对于特定
目标的相对重要性。
下面我会从多个角度来解释AHP算法在MATLAB
中的应用。
首先,AHP算法在MATLAB中的实现可以通过使用MathWorks提
供的AHP工具箱或者自行编写代码来完成。
AHP工具箱提供了一些
内置的函数和工具,可以帮助用户进行层次分析法的权重计算和一
致性检验。
用户可以通过调用这些函数来实现AHP算法的各个步骤,包括建立层次结构、构造判断矩阵、计算特征向量和一致性指标等。
其次,AHP算法的实现需要用户输入层次结构和判断矩阵。
在MATLAB中,用户可以通过定义层次结构和输入判断矩阵来进行AHP
算法的计算。
通过调用相应的函数,MATLAB可以帮助用户对判断矩
阵进行特征值分解,计算特征向量,进而得到每个准则的权重。
此外,AHP算法在MATLAB中的应用还可以包括对一致性检验的
实现。
AHP算法要求判断矩阵满足一致性,MATLAB提供了相应的函
数来对判断矩阵进行一致性检验,帮助用户评估判断矩阵的一致性
水平,从而确保AHP算法的可靠性和准确性。
总的来说,MATLAB提供了丰富的工具和函数来支持AHP算法的实现和应用。
用户可以通过调用这些函数来进行层次分析法的权重计算和一致性检验,从而应用AHP算法解决实际的决策问题。
希望这些信息能够帮助你更好地理解MATLAB中AHP算法的应用。
层次分析法判断矩阵求权值以及一致性检验程序

function [w,CR]=mycom(A,m,RI)[x,lumda]=eig(A);r=abs(sum(lumda));n=find(r==max(r));max_lumda_A=lumda(n,n);max_x_A=x(:,n);w=A/sum(A);CR=(max_lumda_A-m)/(m-1)/RI;end本matlab程序用于层次分析法中计算判断矩阵给出的权值已经进行一致性检验。
其中A为判断矩阵,不同的标度和评定A将不同。
m为A的维数RI为判断矩阵的平均随机一致性指标:根据m的不同值不同。
当CR<0.1时符合一致性检验,判断矩阵构造合理。
下面是层次分析法的简介,以及判断矩阵构造方法。
一.层次分析法的含义层次分析法(The analytic hierarchy process)简称AHP,在20世纪70年代中期由美国运筹学家托马斯·塞蒂(T.L.Saaty)正式提出。
它是一种定性和定量相结合的、系统化、层次化的分析方法。
由于它在处理复杂的决策问题上的实用性和有效性,很快在世界范围得到重视。
它的应用已遍及经济计划和管理、能源政策和分配、行为科学、军事指挥、运输、农业、教育、人才、医疗和环境等领域。
二.层次分析法的基本思路与人对一个复杂的决策问题的思维、判断过程大体上是一样的。
(1)层次分析法的原理层次分析法是将决策问题按总目标、各层子目标、评价准则直至具体的备投方案的顺序分解为不同的层次结构,然后得用求解判断矩阵特征向量的办法,求得每一层次的各元素对上一层次某元素的优先权重,最后再加权和的方法递阶归并各备择方案对总目标的最终权重,此最终权重最大者即为最优方案。
这里所谓“优先权重”是一种相对的量度,它表明各备择方案在某一特点的评价准则或子目标,标下优越程度的相对量度,以及各子目标对上一层目标而言重要程度的相对量度。
层次分析法比较适合于具有分层交错评价指标的目标系统,而且目标值又难于定量描述的决策问题。
matlab计算AHP层次分析法

matlab计算AHP层次分析法第一篇:matlab计算AHP层次分析法用matlab解决层次分析法AHP1、求矩阵最大特征值及特征向量用matlab求:输入:A=[1 1/2 2 1/4;2 1 1 1/3;1/2 1 1 1/3;4 3 3 1][x,y]=eig(A)得出:特征向量x=[0.2688 0.3334 0.2373 0.8720]最大特征值λmax=4.19642、一致性检验CI=(λmax-n)/(n-1)=(4.1964-4)/(4-1)=0.0655 CR=CI/RI=0.0655/0.9=0.0727(注:维数为4时,RI=0.9)CR=0.0727<0.1,矩阵一致性通过检验3、对最大特征值进行归一化处理,即可得到各指标权重(归一化:分项/分项之和)W=[0.157 0.195 0.139 0.510]第二篇:AHP层次分析法层次分析法层次分析法(The analytic hierarchy process,简称AHP),也称层级分析法什么是层次分析法层次分析法(The analytic hierarchy process)简称AHP,在20世纪70年代中期由美国运筹学家托马斯·塞蒂(T.L.Saaty)正式提出。
它是一种定性和定量相结合的、系统化、层次化的分析方法。
由于它在处理复杂的决策问题上的实用性和有效性,很快在世界范围得到重视。
它的应用已遍及经济计划和管理、能源政策和分配、行为科学、军事指挥、运输、农业、教育、人才、医疗和环境等领域。
层次分析法的基本思路与人对一个复杂的决策问题的思维、判断过程大体上是一样的。
不妨用假期旅游为例:假如有3个旅游胜地A、B、C供你选择,你会根据诸如景色、费用和居住、饮食、旅途条件等一些准则去反复比较这3个候选地点.首先,你会确定这些准则在你的心目中各占多大比重,如果你经济宽绰、醉心旅游,自然分别看重景色条件,而平素俭朴或手头拮据的人则会优先考虑费用,中老年旅游者还会对居住、饮食等条件寄以较大关注。
使用Matlab程序实现层次分析法(AHP)的简捷算法

使用Matlab程序实现层次分析法(AHP)的简捷算法作者:于晶来源:《科技风》2016年第16期摘要:层次分析法简便易懂,可操作性和实用性强,但是构造判断矩阵往往不容易,计算判断矩阵的特征值特别繁琐且易出错,得到的一致性检验不易调整,这些都给使用层次分析法带来困难,以往使用办公软件电子表格(Excel)的方法计算单层次排序和总层次排序,这种方法使得计算和一致性检验变得容易,文本使用Matlab程序使得计算变得更容易,也使得层次分析法在多个领域得到推广和应用。
关键词:层次分析法;Excel;matlab1 层次分析法(AHP法)的原理和解决思路层次分析法是对定性问题进行定量分析的一种简便、灵活而又实用的多准则决策方法。
它的原理是模拟人的决策过程,具有思路清晰、方法简便、适用面广、系统性强等特点。
是解决多目标、多准则、多层次复杂问题决策或者大型工程风险分析的有力工具。
层次分析法解决问题的思路就是用下一次因素的相对排序求得上一次因素的相对排序。
按照因素之间的相互影响和隶属关系将各层次因素聚类组合,形成一个递进有序的层次结构模型。
2 层次分析法的应用难点2.1合适的判断矩阵构造不易模型确定后,按照模型层次结构和模型的各因素的相对重要性,综合专家群体咨询意见,采用标度法[ 1 ],从数字1/9一9中选取恰当值,构造各层的判断矩阵,并使之尽量符合一致性检验,这一步成为问题的关键。
但实际上系统越复杂,判定矩阵的阶数就会越高,计算就会越困难。
2.2计算量大,步骤繁琐层次分析法首先要求的就是判断矩阵的最大特征值?姿max,及其正规化的特征向量w,向量w的分量wi是相应因素的单层次权值,这部分计算理论上基于线性代数知识,不用计算机也可以将其计算出来。
但实际上,当矩阵的阶数高于4阶时,人工计算就变得相当困难且易出错,如使用计算机计算,就容易得多,常用的方法有Basic语言,电子表格Excel等方法。
但计算量都有待改进。
层次分析法及matlab程序

层次分析法及Matlab程序一、层次分析法简介层次分析法(Analytic Hierarchy Process,简称AHP)是一种用于决策分析的工具,由美国数学家托马斯·L·萨蒂(Thomas L. Saaty)在1970年代创立。
AHP通过将决策问题划分为多个层次和多个因素,将主要因素和次要因素划分归纳,以定量化的方法分析各因素间优先级的关系,从而对决策方案进行综合评价。
AHP的基本原理是通过构造判断矩阵、计算判断矩阵的特征向量、确定权重,最终得到决策方案的优先级,从而找到最终的最优决策方案。
其主要优点是可定量化、简单易行,适用于大部分决策问题。
二、层次分析法的步骤AHP的具体步骤如下:1.确定决策目标;2.确定影响决策的因素,并将它们分成若干类别,即形成层次结构;3.为每个因素构建判断矩阵,评估每个因素的重要程度(用1~9的数字表示);4.将各判断矩阵进行一致性检验,并计算其权重;5.对计算得到的权重进行优先级排序,选出最优决策方案。
三、Matlab程序实现AHP计算在Matlab中,可以通过编写程序实现AHP的计算。
以下是一份简单的Matlab 程序,用于计算AHP的权重:% 输入判断矩阵A = [1 4 5;1/4 1 2;1/5 1/2 1];% 计算特征向量[V, D] = eig(A);[m, idx] = max(max(D));w = V(:,idx)';w = w/sum(w);% 一致性检验RI = [0 0 0.58 0.9 1.12 1.24 1.32 1.41 1.45 1.49];CR = (max(D) - 3)/2/RI(length(A));CI = sum(CR)/length(A);if CI < 0.1disp('一致性较好,权重为:');disp(w);elsedisp('一致性差,需重新评估判断矩阵!');end该程序用于计算一个3x3的判断矩阵的权重,并输出一致性检验的结果。
(完整版)层次分析法及matlab程序

层次分析法建模层次分析法(AHP-Analytic Hierachy process)---- 多目标决策方法70 年代由美国运筹学家T·L·Satty提出的,是一种定性与定量分析相结合的多目标决策分析方法论。
吸收利用行为科学的特点,是将决策者的经验判断给予量化,对目标(因素)结构复杂而且缺乏必要的数据情况下,採用此方法较为实用,是一种系统科学中,常用的一种系统分析方法,因而成为系统分析的数学工具之一。
传统的常用的研究自然科学和社会科学的方法有:机理分析方法:利用经典的数学工具分析观察的因果关系;统计分析方法:利用大量观测数据寻求统计规律,用随机数学方法描述(自然现象、社会现象)现象的规律。
基本内容:(1)多目标决策问题举例AHP建模方法(2)AHP建模方法基本步骤(3)AHP建模方法基本算法(3)AHP建模方法理论算法应用的若干问题。
参考书:1、姜启源,数学模型(第二版,第9章;第三版,第8章),高等教育出版社2、程理民等,运筹学模型与方法教程,(第10章),清华大学出版社3、《运筹学》编写组,运筹学(修订版),第11章,第7节,清华大学出版社一、问题举例:A.大学毕业生就业选择问题获得大学毕业学位的毕业生,“双向选择”时,用人单位与毕业生都有各自的选择标准和要求。
就毕业生来说选择单位的标准和要求是多方面的,例如:①能发挥自己的才干为国家作出较好贡献(即工作岗位适合发挥专长);②工作收入较好(待遇好);③生活环境好(大城市、气候等工作条件等);④单位名声好(声誉-Reputation);⑤工作环境好(人际关系和谐等)⑥发展晋升(promote, promotion)机会多(如新单位或单位发展有后劲)等。
问题:现在有多个用人单位可供他选择,因此,他面临多种选择和决策,问题是他将如何作出决策和选择?——或者说他将用什么方法将可供选择的工作单位排序?工作选择贡献收入发展声誉工作环境生活环境B.假期旅游地点选择暑假有3个旅游胜地可供选择。
层次分析法的程序

层次分析法的程序计算的Matlab 程序如下:clc,clearfid=fopen('txt3.txt','r');n1=6;n2=3;a=[];for i=1:n1tmp=str2num(fgetl(fid));a=[a;tmp]; %读准则层判断矩阵endfor i=1:n1str1=char(['b',int2str(i),'=[];']);str2=char(['b',int2str(i),'=[b',int2str(i),';tmp];']); eval(str1);for j=1:n2tmp=str2num(fgetl(fid));eval(str2); %读方案层的判断矩阵endri=[0,0,0.58,0.90,1.12,1.24,1.32,1.41,1.45]; %一致性指标[x,y]=eig(a);lamda=max(diag(y));num=find(diag(y)==lamda);w0=x(:,num)/sum(x(:,num));cr0=(lamda-n1)/(n1-1)/ri(n1)for i=1:n1[x,y]=eig(eval(char(['b',int2str(i)])));lamda=max(diag(y));num=find(diag(y)==lamda);w1(:,i)=x(:,num)/sum(x(:,num));cr1(i)=(lamda-n2)/(n2-1)/ri(n2);endcr1, ts=w1*w0, cr=cr1*w0主成分分析dataset=xlsread(‘d:\1\11.xls’)stdr=std(dataset);%求出各变量标准差[n,m]=size(dataset)%定义矩阵的行列数sddata=dataset./stdr(ones(n,1),:);%将原始数据集体标准化sddata %输出标准化数据[P,princ,eigenvalue,t2]=princomp(sddata); %调用主成分分析数据p3=P(:,1:3);%提取前三个主成分系数p3%输出前三个主成分系数sc=princ(:,1:3);%提出前三个主成分得分值sc%输出前三个主成分得分值eigenvalue%输出相关矩阵的各特征值e=eigenva lue(1:3)’%提取前三个特征根并转置M=e(ones(m,1),:).^0.5;%利用特征根构造变化矩阵compmat=p3.*M%求主成分载荷矩阵的前三列per=100*eigenvalue/sum(eigenvalue);%求出各个主成分的贡献率per%求出各个主成分的贡献率cumsum(per)%求出各个主成分的累计贡献率pareto(per)%将贡献率绘成直方图t2%输出各省市与平均位置的距离plot(eigenvalue,'r+')%绘制方差贡献散点图hold on%保持图形plot(eigenvalue,'g-');%绘制方差贡献山麓图hold off%关闭图形plot(princ(:,1),princ(:,2),'+'); %绘制2维分布散点图6、模型的优缺点。
Matlab求解层次分析法程序代码【求解步骤+代码】
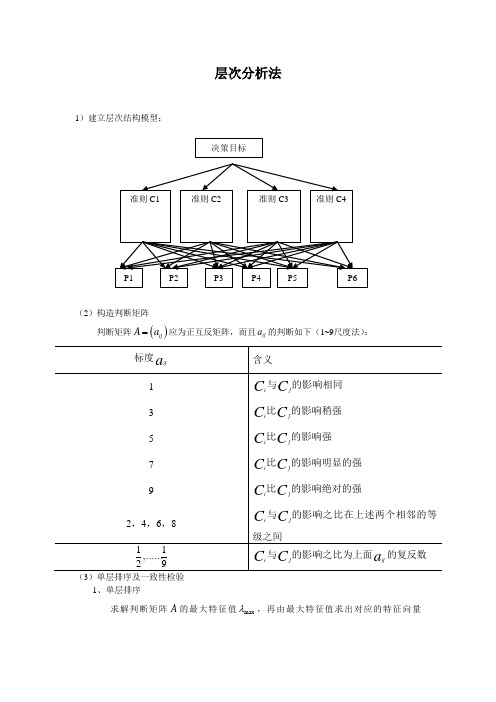
层次分析法1)建立层次结构模型:(2)构造判断矩阵判断矩阵()ij A a =应为正互反矩阵,而且ij a 的判断如下(1~9尺度法):(3)单层排序及一致性检验1、单层排序求解判断矩阵A 的最大特征值max λ,再由最大特征值求出对应的特征向量ω()max A ωλω=,并将ω标准化,即为同一层相对于上一层某一因素的权重,根据此权重的大小,便可确定该层因素的排序。
2、一致性检验取一致性指标max 1nCI n λ-=-,(n 为A 的阶数)令CR RI=,若0.1CR <,则认为A 具有一致性。
否则,需要对A 进行调整,直到具有满意的一致性为止。
(4)层次总排序及一致性检验假定准则层12,,,n C C C 排序完成,其权重分别为12,,,n a a a ,方案层P 包含m 个方案:12,,,m P P P 。
其相对于上一层的()1,2,,j C j n =对方案层P 中的m 个方案进行单层排序,其排序权重记为12,,,j j mj b b b ()1,2,,j n =,则方案层P 中第i 个方案Pi 的总排序权重为1nj ijj a b=∑,见下表:从而确定层的排序。
例:纯文本文件txt3.txt 中的数据格式如下:1 1 1 4 1 1/2 1 1 2 4 1 1/2 1 1/2 1 53 1/2 1/4 1/4 1/5 1 1/3 1/3 1 1 1/3 3 1 12 2 23 3 11 1/4 1/24 1 32 1/3 11 1/4 1/54 1 1/25 2 11 3 1/31/3 1 1/73 7 11 1/3 53 1 71/5 1/7 11 1 71 1 71/7 1/7 11 7 91/7 1 11/9 1 1matlab程序:>> fid=fopen('txt3.txt','r');n1=6;n2=3;a=[];for i=1:n1tmp=str2num(fgetl(fid));a=[a;tmp]; %读准则层判断矩阵endfor i=1:n1str1=char(['b',int2str(i),'=[];']);str2=char(['b',int2str(i),'=[b',int2str(i),';tmp];']); eval(str1);for j=1:n2tmp=str2num(fgetl(fid));eval(str2); %读方案层的判断矩阵endendri=[0,0,0.58,0.90,1.12,1.24,1.32,1.41,1.45]; %一致性指标[x,y]=eig(a);lamda=max(diag(y));num=find(diag(y)==lamda);w0=x(:,num)/sum(x(:,num));cr0=(lamda-n1)/(n1-1)/ri(n1)for i=1:n1[x,y]=eig(eval(char(['b',int2str(i)])));lamda=max(diag(y));num=find(diag(y)==lamda);w1(:,i)=x(:,num)/sum(x(:,num));cr1(i)=(lamda-n2)/(n2-1)/ri(n2);endcr1, ts=w1*w0, cr=cr1*w0层次分析法层次分析法层次分析法层次分析法层次分析法层次分析法层次分析法层次分析法层次分析法层次分析法层次分析法层次分析法层次分析法层次分析法层次分析法层次分析法层次分析法层次分析法层次分析法实例与步骤结合一个具体例子,说明层次分析法的基本步骤和要点。
MATLAB层次分析法
C11
C1
0
桥梁 D1
隧道 D2
渡船 D3
(1)过河效益层次结构
例3 横渡江 河、海峡方 案的抉择
经济代价 B1
过河的代价 A
社会代价 B2
环境代价 B3
投 操 冲冲 交 居 汽 对 对
入 作 击击 通 民 车 水 生
资 维 渡生 拥 搬 排 的 态
金 护 船活 挤 迁 放 污 的
C1 C2 业 方 C5 C6 物 染 破
关
献
入
展
誉
系
对外 贸易
位 置
供选择的岗位
例3 横渡江 河、海峡方 案的抉择
经济效益 B1
过河的效益 A
社会效益 B2
节 收岸 当 建安 交 自
省 入间 地 筑全 往 豪
时 C2 商 商 就 可 沟 感
间
业 业 业 靠 通 C8
C1
C3 C4 C5 C6 C7
环境效益 B3
舒进 美
适出 化
C9
方 便
Ci : C j aij
A
(aij )nn , aij
0,
a ji
1 aij
选 择
1 1/ 2 4 3 3
2
1
7
5
5
A~成对比较阵
旅 A 1/ 4 1/ 7
游 地
1/ 3
1/ 5
1/ 3 1/ 5
1 2
1/ 2 1
1/ 3
1
A是正互反阵
3 1 1
要由A确定C1,…, Cn对O的权向量
2
n
min
wi ( i1,,n ) i1
n j1 ln aij
ln wi wj
层次分析法判断矩阵

层次分析法判断矩阵层次分析法判断矩阵程序先确定判断矩阵;然后用以下程序就好了:%层次分析法的matlab程序%%%%diertimoxingyiclc,cleardisp(输入判断矩阵);% 在屏幕显示这句话A=input(A=);% 从屏幕接收判断矩阵[n,n]=size(A);% 计算A的维度,这里是方阵,这么写不太好x=ones(n,100);% x为n行100列全1的矩阵y=ones(n,100);% y同xm=zeros(1,100);% m为1行100列全0的向量m(1)=max(x(:,1));% x第一列中最大的值赋给m的第一个分量y(:,1)=x(:,1);% x的第一列赋予y 的第一列x(:,2)=A*y(:,1);% x的第二列为矩阵A*y(:,1)m(2)=max(x(:,2));% x 第二列中最大的值赋给m的第二个分量y(:,2)=x(:,2)/m(2);% x的第二列除以m(2)后赋给y的第二列p=0.0001;i=2;k=abs(m(2)-m(1));% 初始化p,i,k为m(2)-m(1)的绝对值while k>p% 当k>p是执行循环体i=i+1;% i 自加1x(:,i)=A*y(:,i-1);% x的第i列等于A*y的第i-1列m(i)=max(x(:,i));% m的第i个分量等于x第i列中最大的值y(:,i)=x(:,i)/m(i);% y的第i列等于x的第i列除以m的第i个分量k=abs(m(i)-m(i-1));% k等于m(i)-m(i-1)的绝对值enda=sum(y(:,i));% y的第i列的和赋予aw=y(:,i)/a;% y的第i 列除以at=m(i);% m的第i个分量赋给tdisp(权向量:);disp(w);% 显示权向量wdisp(最大特征值:);disp(t);% 显示最大特征值t %以下是一致性检验CI=(t-n)/(n-1);% t-维度再除以维度-1的值赋给CIRI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];% 计算的标准CR=CI/RI(n);% 计算一致性if CR摘要在定性问题的决策中,AHP是一种优秀的方法,其基础是对评价对象的两两比较,并用比较结果构造判断矩阵,而这些都依赖于决策者选用的偏好关系。
Matlab建模教程层次分析法

第八章 层次分析法层次分析法(Analytic Hierarchy Process ,简称AHP )是对一些较为复杂、较为模糊的问题作出决策的简易方法,它特别适用于那些难于完全定量分析的问题。
它是美国运筹学家T. L. Saaty 教授于70年代初期提出的一种简便、灵活而又实用的多准则决策方法。
§1 层次分析法的基本原理与步骤人们在进行社会的、经济的以及科学管理领域问题的系统分析中,面临的常常是一个由相互关联、相互制约的众多因素构成的复杂而往往缺少定量数据的系统。
层次分析法为这类问题的决策和排序提供了一种新的、简洁而实用的建模方法。
运用层次分析法建模,大体上可按下面四个步骤进行:(i )建立递阶层次结构模型;(ii )构造出各层次中的所有判断矩阵;(iii )层次单排序及一致性检验;(iv )层次总排序及一致性检验。
下面分别说明这四个步骤的实现过程。
1.1 递阶层次结构的建立与特点应用AHP 分析决策问题时,首先要把问题条理化、层次化,构造出一个有层次的结构模型。
在这个模型下,复杂问题被分解为元素的组成部分。
这些元素又按其属性及关系形成若干层次。
上一层次的元素作为准则对下一层次有关元素起支配作用。
这些层次可以分为三类:(i )最高层:这一层次中只有一个元素,一般它是分析问题的预定目标或理想结果,因此也称为目标层。
(ii )中间层:这一层次中包含了为实现目标所涉及的中间环节,它可以由若干个层次组成,包括所需考虑的准则、子准则,因此也称为准则层。
(iii )最底层:这一层次包括了为实现目标可供选择的各种措施、决策方案等,因此也称为措施层或方案层。
递阶层次结构中的层次数与问题的复杂程度及需要分析的详尽程度有关,一般地层次数不受限制。
每一层次中各元素所支配的元素一般不要超过9个。
这是因为支配的元素过多会给两两比较判断带来困难。
下面结合一个实例来说明递阶层次结构的建立。
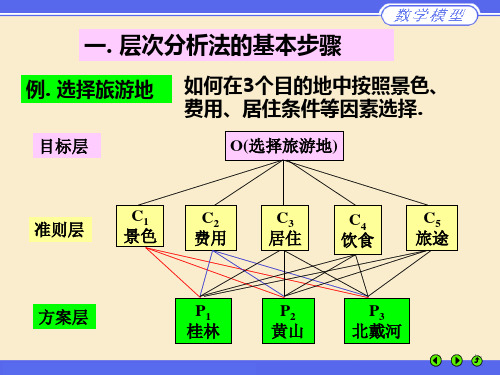
例1 假期旅游有1P 、2P 、3P 3个旅游胜地供你选择,试确定一个最佳地点。
(完整版)层次分析法计算权重在matlab中的实现

信息系统分析与设计作业层次分析法确定绩效评价权重在matlab中的实现小组成员:孙高茹、王靖、李春梅、郭荣1 程序简要概述编写程序一步实现评价指标特征值lam、特征向量w以及一致性比率CR的求解。
具体的操作步骤是:首先构造评价指标,用专家评定法对指标两两打分,构建比较矩阵,继而运用编写程序实现层次分析法在MATLAB中的应用。
通过编写MATLAB程序一步实现问题求解,可以简化权重计算方法与步骤,减少工作量,从而提高人力资源管理中绩效考核的科学化电算化。
2 程序在matlab中实现的具体步骤function [w,lam,CR] = ccfx(A)%A为成对比较矩阵,返回值w为近似特征向量% lam为近似最大特征值λmax,CR为一致性比率n=length(A(:,1));a=sum(A);B=A %用B代替A做计算for j=1:n %将A的列向量归一化B(:,j)=B(:,j)./a(j);ends=B(:,1);for j=2:ns=s+B(:,j);endc=sum(s);%计算近似最大特征值λmaxw=s./c;d=A*wlam=1/n*sum((d./w));CI=(lam-n)/(n-1);%一致性指标RI=[0,0,0.58,0.90,1.12,1.24,1.32,1.41,1.45,1.49,1.51];%RI为随机一致性指标CR=CI/RI(n);%求一致性比率if CR>0.1disp('没有通过一致性检验');else disp('通过一致性检验');endend3 案例应用我们拟构建公司员工绩效评价分析权重,完整操作步骤如下:3.1构建的评价指标体系我们将影响员工绩效评定的指标因素分为:打卡、业绩、创新、态度与品德。
3.2专家打分,构建两两比较矩阵A =1.0000 0.5000 3.0000 4.00002.0000 1.0000 5.00003.00000.3333 0.2000 1.0000 2.00000.2500 0.3333 0.5000 1.00003.3在MATLAB中运用编写好的程序实现直接在MATLAB命令窗口中输入[w,lam,CR]=ccfx(A)继而直接得出d =1.30352.00000.51450.3926w =0.31020.46910.12420.0966lam =4.1687CR =0.0625,通过一致性检验3.4解读程序结果根据程序求解中得出的特征向量,可以得出打卡、业绩、创新以及态度品德在员工绩效评价中所占的权重分别为:0.3102、0.4691、0.1242、0.0966。
基于Matlab的层次分析法及其运用浅析

度 )具体标度 方法如表 1所示。 ,
表 1 T..a t LS ay教授 的 1 9标度方法 -
底层 指 标 相 对 于 准 则 层 的 权 重 系数 , 而 有助 于 选 择 最 优 方案 , 序 从 程 流程如图 1 所示 , 其中的平行 四边形表示输入数据 , 菱形表示判断 , 根据 判 断结 果 的不 同 出现 2个 分 支 。 程 序 中 , 于 生成 判 断矩 阵 的部 分 程 序 如 下 : 用
表 2 平均 随机一致性指标 ,
在当前信息化 、 全球化 的大背景下 , 传统的手工计 算已不能满足 素, 因此在判断矩 阵不能通过一致性检 验时, 需要对 各指标问相互重 人们高效 率、 高准确度 的决策需求。 因此计算机辅助决策当仁不让地 要性程度重新进行赋值 , 直至其通过矩阵一致性检验。 其最大特征值 成为 了管理决策 的新工具、 方法。基于 此, 新 本文在充分发挥计算机 对应 的特征 向量 即为该指标相对于上一级指标的重要性排序。 强大运算功能的基础上 ,选用美国 Mah rs公司的集成数学建 tWok
基于 Malb的层次分析 法及 其运 用浅析 t a
郭 东硕 程 正敏 彭茜 ( 西南大学 经济管理学院)
满足同一层 次中各指标对 所有的下级指标均产生影响 的假定条件下 ,实现 了层次分析法的分析运算。 本程序允许 用户自由设定指标层次结构内的层次数以及各层次 内的指标数 , 通过程序的循环 , 用户只需输入 判断矩 阵的部 分数据 , 程序可依据层 次分析 法的计算流程 进行计算并作 出判断。 本程序可以方便地处理层 次分析法下较 大的运算量 , 解决层次分析法的效率问题 , 提高计算机辅助决策的时效性。 关键词 : t b层 次分析法 判断矩阵 决策 Mal a
层次分析法判断矩阵求权值和一致性查验程序

function [w,CR]=mycom(A,m,RI)[x,lumda]=eig(A);r=abs(sum(lumda));n=find(r==max(r));max_lumda_A=lumda(n,n);max_x_A=x(:,n);w=A/sum(A);CR=(max_lumda_A-m)/(m-1)/RI;end本matlab程序用于层次分析法中计算判断矩阵给出的权值已经进行一致性查验。
其中A为判断矩阵,不同的标度和评定A将不同。
m为A的维数RI为判断矩阵的平均随机一致性指标:按照m的不同值不同。
当CR<时符合一致性查验,判断矩阵构造合理。
下面是层次分析法的简介,和判断矩阵构造方式。
一.层次分析法的含义层次分析法(The analytic hierarchy process)简称AHP,在20世纪70年代中期由美国运筹学家()正式提出。
它是一种定性和定量相结合的、系统化、层次化的分析方式。
由于它在处置复杂的问题上的实用性和有效性,专门快活着界范围取得重视。
它的应用已遍及经济和、能源政策和分派、行为科学、军事指挥、运输、农业、教育、人材、医疗和环境等领域。
二.层次分析法的大体思路与人对一个复杂的决策问题的思维、判断进程大体上是一样的。
(1)层次分析法的原理层次分析法是将决策问题按总目标、各层子目标、评价准则直至具体的备投方案的顺序分解为不同的层次结构,然后得用求解判断矩阵特征向量的办法,求得每一层次的各元素对上一层次某元素的优先权重,最后再加权和的方式递阶归并各备择方案对总目标的最终权重,此最终权重最大者即为最优方案。
这里所谓“优先权重”是一种相对的量度,它表明各备择方案在某一特点的评价准则或子目标,标下优越程度的相对量度,和各子目标对上一层目标而言重要程度的相对量度。
层次分析法比较适合于具有分层交织评价指标的目标系统,而且目标值又难于定量描述的决策问题。
其用法是构造判断矩阵,求出其最大特征值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
disp('请输入判断矩阵A(n阶)');
A=input('A=');
[n,n]=size(A);
x=ones(n,100);
y=ones(n,100);
m=zeros(1,100);
m(1)=max(x(:,1));
y(:,1)=x(:,1);
x(:,2)=A*y(:,1);
m(2)=max(x(:,2));
y(:,2)=x(:,2)/m(2);
p=0.0001;i=2;k=abs(m(2)-m(1));
while k>p
i=i+1;
x(:,i)=A*y(:,i-1);
m(i)=max(x(:,i));
y(:,i)=x(:,i)/m(i);
k=abs(m(i)-m(i-1));
end
a=sum(y(:,i));
w=y(:,i)/a;
t=m(i);
disp(w);disp(t);
%以下是一致性检验
CI=(t-n)/(n-1);RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56
1.58 1.59];
CR=CI/RI(n);
if CR<0.10
disp('此矩阵的一致性可以接受!');
disp('CI=');disp(CI);
disp('CR=');disp(CR);
end
function AHPInit1(x,y)
%层次分析的初始化
%默认只有两层x为准则数,y为方案数
%CToT为准则对目标生成的比较阵
%EigOfCri为准则层的特征向量
%EigOfOpt为选项层的特征向量
EigOfCri=zeros(x,1);%准则层的特征向量
EigOfOpt=zeros(y,x);
dim=x;%维度
RI=[0 0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49 1.51];%RI标准%生成成对比较阵
for i=1:dim
CToT(i,:)=input('请输入数据:');
end
CToT %输出
pause,
tempmatrix=zeros(x+1);
tempmatrix=AHP1(dim,CToT);
EigOfCri=tempmatrix(1:x);
ci1=tempmatrix(1+x);
EigOfCri
ci1
pause,
matrix=cell(x);%元胞数组
ci=zeros(1,x);
dim=y;
for k=1:x
matrix{k}=zeros(dim,dim);
%生成成对比较阵
for i=1:dim
matrix{k}(i,:)=input('请输入数据:'); end
%判断该比较阵是不是一致阵
tempmatrix=zeros(y+1);
tempmatrix=AHP1(dim,matrix{k}); EigOfOpt(:,k)=tempmatrix(1:y);
ci(k)=tempmatrix(y+1);
EigOfOpt(:,k)
ci(k)
pause,
end
%下面进行组合一致性检查
RI=[0 0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49 1.51]; CR=ci1/RI(x)+ci*EigOfCri/RI(y);
CR
if CR>0.1
disp('组合一致性不通过,请重新评分')
return
end
%下面根据比较阵的结果进行组合
result=EigOfOpt*EigOfCri;
result
function f=AHP1(dim,CmpMatrix)
RI=[0 0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49 1.51]; %判断该比较阵是不是一致阵
%判断该比较阵是不是一致阵
[V,D]=eig(CmpMatrix);%求得特征向量和特征值
%求出最大特征值和它所对应的特征向量
tempNum=D(1,1);
pos=1;
for h=1:dim
if D(h,h)>tempNum
tempNum=D(h,h);
pos=h;
end
end
eigVector=V(:,pos);
maxeig=D(pos,pos);
maxeig
dim
CI=(maxeig-dim)/(dim-1);
CR=CI/RI(dim);
if CR>0.1
disp('准则对目标影响度评分生成的矩阵不是一致阵,请重新评分') return
end
CI
%归一化
sum=0;
for h=1:dim
sum=sum+eigVector(h);
end
sum
pause,
for h=1:dim
eigVector(h)=eigVector(h)/sum;
end
f=[eigVector;CI];。
