数据结构习题课-数据结构习题课4
严蔚敏版数据结构习题及参考答案

习题1一、单项选择题A1.数据结构是指()。
A.数据元素的组织形式B.数据类型C.数据存储结构D.数据定义C2.数据在计算机存储器内表示时,物理地址与逻辑地址不相同的,称之为()。
A.存储结构B.逻辑结构C.链式存储结构D.顺序存储结构D3.树形结构是数据元素之间存在一种()。
A.一对一关系B.多对多关系C.多对一关系D.一对多关系B4.设语句x++的时间是单位时间,则以下语句的时间复杂度为()。
for(i=1; i<=n; i++)for(j=i; j<=n; j++)x++;A.O(1)B.O(2n)C.O(n)D.O(3n)CA5.算法分析的目的是(1),算法分析的两个主要方面是(2)。
(1) A.找出数据结构的合理性 B.研究算法中的输入和输出关系C.分析算法的效率以求改进D.分析算法的易懂性和文档性(2) A.空间复杂度和时间复杂度 B.正确性和简明性C.可读性和文档性D.数据复杂性和程序复杂性6.计算机算法指的是(1),它具备输入,输出和(2)等五个特性。
(1) A.计算方法 B.排序方法C.解决问题的有限运算序列D.调度方法(2) A.可行性,可移植性和可扩充性 B.可行性,确定性和有穷性C.确定性,有穷性和稳定性D.易读性,稳定性和安全性7.数据在计算机内有链式和顺序两种存储方式,在存储空间使用的灵活性上,链式存储比顺序存储要()。
A.低B.高C.相同D.不好说8.数据结构作为一门独立的课程出现是在()年。
A.1946B.1953C.1964D.19689.数据结构只是研究数据的逻辑结构和物理结构,这种观点()。
A.正确B.错误C.前半句对,后半句错D.前半句错,后半句对10.计算机内部数据处理的基本单位是()。
A.数据B.数据元素C.数据项D.数据库二、填空题1.数据结构按逻辑结构可分为两大类,分别是______________和_________________。
数据结构课后习题答案第四章

第四章一、简述下列每对术语的区别:空串和空白串;串常量和串变量;主串和子串;静态分配的顺序串和动态分配的顺序串;目标串和模式串;有效位移和无效位移。
答:●空串是指不包含任何字符的串,它的长度为零。
空白串是指包含一个或多个空格的串,空格也是字符。
●串常量是指在程序中只可引用但不可改变其值的串。
串变量是可以在运行中改变其值的。
●主串和子串是相对的,一个串中任意个连续字符组成的串就是这个串的子串,而包含子串的串就称为主串。
●静态分配的顺序串是指串的存储空间是确定的,即串值空间的大小是静态的,在编译时刻就被确定。
动态分配的顺序串是在编译时不分配串值空间,在运行过程中用malloc和free等函数根据需要动态地分配和释放字符数组的空间(这个空间长度由分配时确定,也是顺序存储空间)。
●目标串和模式串:在串匹配运算过程中,将主串称为目标串,而将需要匹配的子串称为模式串,两者是相对的。
●有效位移和无效位移:在串定位运算中,模式串从目标的首位开始向右位移,每一次合法位移后如果模式串与目标中相应的字符相同,则这次位移就是有效位移(也就是从此位置开始的匹配成功),反之,若有不相同的字符存在,则此次位移就是无效位移(也就是从此位置开始的匹配失败)。
二、假设有如下的串说明:char s1[30]="Stocktom,CA", s2[30]="March 5 1999", s3[30], *p;(1)在执行如下的每个语句后p的值是什么?p=stchr(s1,'t'); p=strchr(s2,'9'); p=strchr(s2,'6');(2)在执行下列语句后,s3的值是什么?strcpy(s3,s1); strcat(s3,","); strcat(s3,s2);(3)调用函数strcmp(s1,s2)的返回值是什么?(4)调用函数strcmp(&s1[5],"ton")的返回值是什么?(5)调用函数stlen(strcat(s1,s2))的返回值是什么?解:(1) stchr(*s,c)函数的功能是查找字符c在串s中的位置,若找到,则返回该位置,否则返回NULL。
数据结构教程李春葆课后答案第4章串

8. 采用顺序结构存储串,设计一个实现串通配符匹配的算法 pattern_index(),其中的 通配符只有‘?’ ,它可以和任一个字符匹配成功。例如,pattern_index("?re","there are") 返回的结果是 2。 解:采用 BF 算法的穷举法的思路,只需要增加对‘?’字符的处理功能。对应的算法 如下:
void maxsubstr(SqString s,SqString &t) { int maxi=0,maxlen=0,len,i,j,k; i=0; while (i<s.length) //从下标为 i 的字符开始 { j=i+1; //从 i 的下一个位置开始找重复子串 while (j<s.length) { if (s.data[i]==s.data[j]) //找一个子串,其起始下标为 i,长度为 len { len=1; for(k=1;s.data[i+k]==s.data[j+k];k++) len++; if (len>maxlen) //将较大长度者赋给 maxi 与 maxlen { maxi=i; maxlen=len; } j+=len; } else j++; } i++; //继续扫描第 i 字符之后的字符 } t.length=maxlen; //将最长重复子串赋给 t for (i=0;i<maxlen;i++) t.data[i]=s.data[maxi+i]; }
SqString CommChar(SqString s1,SqString s2) { SqString s3; int i,j,k=0; for (i=0;i<s1.length;i++) { for (j=0;j<s2.length;j++) if (s2.data[j]==s1.data[i]) break; if (j<s2.length) //s1.data[i]是公共字符 { s3.data[k]=s1.data[i]; k++; } } s3.length=k; return s3; }
数据结构答案第4章

⑴二维数组A的每个元素是由6个字符组成的串,行下标的范围从0~8,列下标的范围是从0~9,则存放A至少需要()个字节,A的第8列和第5行共占()个字节,若A按行优先方式存储,元素A[8][5]的起始地址与当A按列优先方式存储时的()元素的起始地址一致。
A 90 B 180 C 240 D 540 E 108 F 114 G 54
⑵二维数组A中行下标从10到20,列下标从5到10,按行优先存储,每个元素占4个存储单元,A[10][5]的存储地址是1000,则元素A[15][10]的存储地址是()。
【解答】1140
【分析】数组A中每行共有6个元素,元素A[15][10]的前面共存储了(15-10)×6+5个元素,每个元素占4个存储单元,所以,其存储地址是1000+140=1140。
Head(Tail(Tail(Head(ST))))=奖金
⑵工资表ST的头尾表示法如图4-7所示。7.若在矩阵A中存在一个元素ai,j(0≤i≤n-1,0≤j≤m-1),该元素是第i行元素中最小值且又是第j列元素中最大值,则称此元素为该矩阵的一个马鞍点。假设以二维数组存储矩阵A,试设计一个求该矩阵所有马鞍点的算法,并分析最坏情况下的时间复杂度。
⑵因为k和i, j之间是一一对应的关系,k+1是当前非零元素的个数,整除即为其所在行号,取余表示当前行中第几个非零元素,加上前面零元素所在列数就是当前列号,即:
(完整word)北邮C++数据结构课后习题 习题4参考答案

习题41.填空题(1)已知二叉树中叶子数为50,仅有一个孩子的结点数为30,则总结点数为(___________)。
答案:129(2)4个结点可构成(___________)棵不同形态的二叉树。
答案:12(3)设树的度为5,其中度为1~5的结点数分别为6、5、4、3、2个,则该树共有(___________)个叶子。
答案:31(4)在结点个数为n(n〉1)的各棵普通树中,高度最小的树的高度是(___________),它有(___________)个叶子结点,(___________)个分支结点。
高度最大的树的高度是(___________),它有(___________)个叶子结点,(___________)个分支结点。
答案:2 n—1 1 n 1 n-1(5)深度为k的二叉树,至多有(___________)个结点。
答案:2k-1(6)有n个结点并且其高度为n的二叉树的数目是(___________)。
答案:2n—1(7)设只包含根结点的二叉树的高度为1,则高度为k的二叉树的最大结点数为(___________),最小结点数为(___________)。
答案:2k-1 k(8)将一棵有100个结点的完全二叉树按层编号,则编号为49的结点为X,其双亲PARENT(X)的编号为().答案:24(9)已知一棵完全二叉树中共有768个结点,则该树中共有(___________)个叶子结点。
答案:384(10)已知一棵完全二叉树的第8层有8个结点,则其叶子结点数是(___________).答案:68(11)深度为8(根的层次号为1)的满二叉树有(___________)个叶子结点。
答案:128(12)一棵二叉树的前序遍历是FCABED,中序遍历是ACBFED,则后序遍历是(___________).答案:ABCDEF(13)某二叉树结点的中序遍历序列为ABCDEFG,后序遍历序列为BDCAFGE,则该二叉树结点的前序遍历序列为(___________),该二叉树对应的树林包括(___________)棵树。
数据结构习题集答案(C语言版严蔚敏)第四章串

第四章串4.10void String_Reverse(Stringtype s,Stringtype &r)//求s的逆串r{StrAssign(r,''); //初始化r为空串for(i=Strlen(s);i;i--){StrAssign(c,SubString(s,i,1));StrAssign(r,Concat(r,c)); //把s的字符从后往前添加到r中}}//String_Reverse4.11void String_Subtract(Stringtype s,Stringtype t,Stringtype &r)//求所有包含在串s中而t中没有的字符构成的新串r{StrAssign(r,'');for(i=1;i<=Strlen(s);i++){StrAssign(c,SubString(s,i,1));for(j=1;j<i&&StrCompare(c,SubString(s,j,1));j++); //判断s的当前字符c是否第一次出现if(i==j){for(k=1;k<=Strlen(t)&&StrCompare(c,SubString(t,k,1));k++); //判断当前字符是否包含在t中if(k>Strlen(t)) StrAssign(r,Concat(r,c));}}//for}//String_Subtract4.12int Replace(Stringtype &S,Stringtype T,Stringtype V);//将串S中所有子串T替换为V,并返回置换次数{for(n=0,i=1;i<=Strlen(S)-Strlen(T)+1;i++) //注意i的取值范围if(!StrCompare(SubString(S,i,Strlen(T)),T)) //找到了与T匹配的子串{ //分别把T的前面和后面部分保存为head和tailStrAssign(head,SubString(S,1,i-1));StrAssign(tail,SubString(S,i+Strlen(T),Strlen(S)-i-Strlen(T)+1));StrAssign(S,Concat(head,V));StrAssign(S,Concat(S,tail)); //把head,V,tail连接为新串i+=Strlen(V); //当前指针跳到插入串以后n++;}//ifreturn n;}//Replace分析:i+=Strlen(V);这一句是必需的,也是容易忽略的.如省掉这一句,则在某些情况下,会引起不希望的后果,虽然在大多数情况下没有影响.请思考:设S='place', T='ace', V='face',则省掉i+=Strlen(V);运行时会出现什么结果?4.13int Delete_SubString(Stringtype &s,Stringtype t)//从串s中删除所有与t相同的子串,并返回删除次数{for(n=0,i=1;i<=Strlen(s)-Strlen(t)+1;i++)if(!StrCompare(SubString(s,i,Strlen(t)),t)){StrAssign(head,SubString(S,1,i-1));StrAssign(tail,SubString(S,i+Strlen(t),Strlen(s)-i-Strlen(t)+1));StrAssign(S,Concat(head,tail)); //把head,tail连接为新串n++;}//ifreturn n,}//Delete_SubString4.14Status NiBoLan_to_BoLan(Stringtype str,Stringtype &new)//把前缀表达式str转换为后缀式new{Initstack(s); //s的元素为Stringtype类型for(i=1;i<=Strlen(str);i++){r=SubString(str,i,1);if(r为字母) push(s,r);else{if(StackEmpty(s)) return ERROR;pop(s,a);if(StackEmpty(s)) return ERROR;pop(s,b);StrAssign(t,Concat(r,b));StrAssign(c,Concat(t,a)); //把算符r,子前缀表达式a,b连接为新子前缀表达式cpush(s,c);}}//forpop(s,new);if(!StackEmpty(s)) return ERROR;return OK;}//NiBoLan_to_BoLan分析:基本思想见书后注释3.23.请读者用此程序取代作者早些时候对3.23题给出的程序.4.15void StrAssign(Stringtype &T,char chars&#;)//用字符数组chars给串T赋值,Stringtype的定义见课本{for(i=0,T[0]=0;chars[i];T[0]++,i++) T[i+1]=chars[i];}//StrAssign4.16char StrCompare(Stringtype s,Stringtype t)//串的比较,s>t时返回正数,s=t时返回0,s<t时返回负数{for(i=1;i<=s[0]&&i<=t[0]&&s[i]==t[i];i++);if(i>s[0]&&i>t[0]) return 0;else if(i>s[0]) return -t[i];else if(i>t[0]) return s[i];else return s[i]-t[i];}//StrCompare4.17int String_Replace(Stringtype &S,Stringtype T,Stringtype V);//将串S中所有子串T替换为V,并返回置换次数{for(n=0,i=1;i<=S[0]-T[0]+1;i++){for(j=i,k=1;T[k]&&S[j]==T[k];j++,k++);if(k>T[0]) //找到了与T匹配的子串:分三种情况处理{if(T[0]==V[0])for(l=1;l<=T[0];l++) //新子串长度与原子串相同时:直接替换S[i+l-1]=V[l];else if(T[0]<V[0]) //新子串长度大于原子串时:先将后部右移{for(l=S[0];l>=i+T[0];l--)S[l+V[0]-T[0]]=S[l];for(l=1;l<=V[0];l++)S[i+l-1]=V[l];}else //新子串长度小于原子串时:先将后部左移{for(l=i+V[0];l<=S[0]+V[0]-T[0];l++)S[l]=S[l-V[0]+T[0]];for(l=1;l<=V[0];l++)S[i+l-1]=V[l];}S[0]=S[0]-T[0]+V[0];i+=V[0];n++;}//if}//forreturn n;}//String_Replace4.18typedef struct {char ch;int num;} mytype;void StrAnalyze(Stringtype S)//统计串S中字符的种类和个数{mytype T[MAXSIZE]; //用结构数组T存储统计结果for(i=1;i<=S[0];i++){c=S[i];j=0;while(T[j].ch&&T[j].ch!=c) j++; //查找当前字符c是否已记录过if(T[j].ch) T[j].num++;else T[j]={c,1};}//forfor(j=0;T[j].ch;j++)printf("%c: %d\n",T[j].ch,T[j].num);}//StrAnalyze4.19void Subtract_String(Stringtype s,Stringtype t,Stringtype &r)//求所有包含在串s中而t中没有的字符构成的新串r{r[0]=0;for(i=1;i<=s[0];i++){c=s[i];for(j=1;j<i&&s[j]!=c;j++); //判断s的当前字符c是否第一次出现if(i==j){for(k=1;k<=t[0]&&t[k]!=c;k++); //判断当前字符是否包含在t中if(k>t[0]) r[++r[0]]=c;}}//for}//Subtract_String4.20int SubString_Delete(Stringtype &s,Stringtype t)//从串s中删除所有与t相同的子串,并返回删除次数{for(n=0,i=1;i<=s[0]-t[0]+1;i++){for(j=1;j<=t[0]&&s[i+j-1]==t[i];j++);if(j>m) //找到了与t匹配的子串{for(k=i;k<=s[0]-t[0];k++) s[k]=s[k+t[0]]; //左移删除s[0]-=t[0];n++;}}//forreturn n;}//Delete_SubString4.21typedef struct{char ch;LStrNode *next;} LStrNode,*LString; //链串结构void StringAssign(LString &s,LString t)//把串t赋值给串s{s=malloc(sizeof(LStrNode));for(q=s,p=t->next;p;p=p->next){r=(LStrNode*)malloc(sizeof(LStrNode));r->ch=p->ch;q->next=r;q=r;}q->next=NULL;}//StringAssignvoid StringCopy(LString &s,LString t)//把串t复制为串s.与前一个程序的区别在于,串s业已存在.{for(p=s->next,q=t->next;p&&q;p=p->next,q=q->next){p->ch=q->ch;pre=p;}while(q){p=(LStrNode*)malloc(sizeof(LStrNode));p->ch=q->ch;pre->next=p;pre=p;}p->next=NULL;}//StringCopychar StringCompare(LString s,LString t)//串的比较,s>t时返回正数,s=t时返回0,s<t时返回负数{for(p=s->next,q=t->next;p&&q&&p->ch==q->ch;p=p->next,q=q->next);if(!p&&!q) return 0;else if(!p) return -(q->ch);else if(!q) return p->ch;else return p->ch-q->ch;}//StringCompareint StringLen(LString s)//求串s的长度(元素个数){for(i=0,p=s->next;p;p=p->next,i++);return i;}//StringLenLString * Concat(LString s,LString t)//连接串s和串t形成新串,并返回指针{p=malloc(sizeof(LStrNode));for(q=p,r=s->next;r;r=r->next){q->next=(LStrNode*)malloc(sizeof(LStrNode));q=q->next;q->ch=r->ch;}//for //复制串sfor(r=t->next;r;r=r->next){q->next=(LStrNode*)malloc(sizeof(LStrNode));q=q->next;q->ch=r->ch;}//for //复制串tq->next=NULL;return p;}//ConcatLString * Sub_String(LString s,int start,int len)//返回一个串,其值等于串s从start位置起长为len的子串{p=malloc(sizeof(LStrNode));q=p;for(r=s;start;start--,r=r->next); //找到start所对应的结点指针rfor(i=1;i<=len;i++,r=r->next){q->next=(LStrNode*)malloc(sizeof(LStrNode));q=q->next;q->ch=r->ch;} //复制串tq->next=NULL;return p;}//Sub_String4.22void LString_Concat(LString &t,LString &s,char c)//用块链存储结构,把串s插入到串t的字符c 之后{p=t.head;while(p&&!(i=Find_Char(p,c))) p=p->next; //查找字符cif(!p) //没找到{t.tail->next=s.head;t.tail=s.tail; //把s连接在t的后面}else{q=p->next;r=(Chunk*)malloc(sizeof(Chunk)); //将包含字符c的节点p分裂为两个for(j=0;j<i;j++) r->ch[j]='#'; //原结点p包含c及其以前的部分for(j=i;j<CHUNKSIZE;j++) //新结点r包含c以后的部分{r->ch[j]=p->ch[j];p->ch[j]='#'; //p的后半部分和r的前半部分的字符改为无效字符'#'}p->next=s.head;s.tail->next=r;r->next=q; //把串s插入到结点p和r之间}//elset.curlen+=s.curlen; //修改串长s.curlen=0;}//LString_Concatint Find_Char(Chunk *p,char c)//在某个块中查找字符c,如找到则返回位置是第几个字符,如没找到则返回0{for(i=0;i<CHUNKSIZE&&p->ch[i]!=c;i++);if(i==CHUNKSIZE) return 0;else return i+1;}//Find_Char4.23int LString_Palindrome(LString L)//判断以块链结构存储的串L是否为回文序列,是则返回1,否则返回0{InitStack(S);p=S.head;i=0;k=1; //i指示元素在块中的下标,k指示元素在整个序列中的序号(从1开始) for(k=1;k<=S.curlen;k++){if(k<=S.curlen/2) Push(S,p->ch[i]); //将前半段的字符入串else if(k>(S.curlen+1)/2){Pop(S,c); //将后半段的字符与栈中的元素相匹配if(p->ch[i]!=c) return 0; //失配}if(++i==CHUNKSIZE) //转到下一个元素,当为块中最后一个元素时,转到下一块{p=p->next;i=0;}}//forreturn 1; //成功匹配}//LString_Palindrome4.24void HString_Concat(HString s1,HString s2,HString &t)//将堆结构表示的串s1和s2连接为新串t{if(t.ch) free(t.ch);t.ch=malloc((s1.length+s2.length)*sizeof(char));for(i=1;i<=s1.length;i++) t.ch[i-1]=s1.ch[i-1];for(j=1;j<=s2.length;j++,i++) t.ch[i-1]=s2.ch[j-1];t.length=s1.length+s2.length;}//HString_Concat4.25int HString_Replace(HString &S,HString T,HString V)//堆结构串上的置换操作,返回置换次数{for(n=0,i=0;i<=S.length-T.length;i++){for(j=i,k=0;k<T.length&&S.ch[j]==T.ch[k];j++,k++);if(k==T.length) //找到了与T匹配的子串:分三种情况处理{if(T.length==V.length)for(l=1;l<=T.length;l++) //新子串长度与原子串相同时:直接替换S.ch[i+l-1]=V.ch[l-1];else if(T.length<V.length) //新子串长度大于原子串时:先将后部右移{for(l=S.length-1;l>=i+T.length;l--)S.ch[l+V.length-T.length]=S.ch[l];for(l=0;l<V.length;l++)S[i+l]=V[l];}else //新子串长度小于原子串时:先将后部左移{for(l=i+V.length;l<S.length+V.length-T.length;l++)S.ch[l]=S.ch[l-V.length+T.length];for(l=0;l<V.length;l++)S[i+l]=V[l];}S.length+=V.length-T.length;i+=V.length;n++;}//if}//forreturn n;}//HString_Replace4.26Status HString_Insert(HString &S,int pos,HString T)//把T插入堆结构表示的串S的第pos个字符之前{if(pos<1) return ERROR;if(pos>S.length) pos=S.length+1;//当插入位置大于串长时,看作添加在串尾S.ch=realloc(S.ch,(S.length+T.length)*sizeof(char));for(i=S.length-1;i>=pos-1;i--)S.ch[i+T.length]=S.ch[i]; //后移为插入字符串让出位置for(i=0;i<T.length;i++)S.ch[pos+i-1]=T.ch[pos]; //插入串TS.length+=T.length;return OK;}//HString_Insert4.27int Index_New(Stringtype s,Stringtype t)//改进的定位算法{i=1;j=1;while(i<=s[0]&&j<=t[0]){if((j!=1&&s[i]==t[j])||(j==1&&s[i]==t[j]&&s[i+t[0]-1]==t[t[0]])){ //当j==1即匹配模式串的第一个字符时,需同时匹配其最后一个i=i+j-2;j=1;}else{i++;j++;}}//whileif(j>t[0]) return i-t[0];}//Index_New4.28void LGet_next(LString &T)//链串上的get_next算法{p=T->succ;p->next=T;q=T;while(p->succ){if(q==T||p->data==q->data){p=p->succ;q=q->succ;p->next=q;}else q=q->next;}//while}//LGet_nextLStrNode * LIndex_KMP(LString S,LString T,LStrNode *pos)//链串上的KMP匹配算法,返回值为匹配的子串首指针{p=pos;q=T->succ;while(p&&q){if(q==T||p->chdata==q->chdata){p=p->succ;q=q->succ;}else q=q->next;}//whileif(!q){for(i=1;i<=Strlen(T);i++)p=p->next;return p;} //发现匹配后,要往回找子串的头return NULL;}//LIndex_KMP4.30void Get_LRepSub(Stringtype S)//求S的最长重复子串的位置和长度{for(maxlen=0,i=1;i<S[0];i++)//串S2向右移i格{for(k=0,j=1;j<=S[0]-i;j++)//j为串S2的当前指针,此时串S1的当前指针为i+j,两指针同步移动{if(S[j]==S[j+i]) k++; //用k记录连续相同的字符数else k=0; //失配时k归零if(k>maxlen) //发现了比以前发现的更长的重复子串{lrs1=j-k+1;lrs2=mrs1+i;maxlen=k; //作记录}}//forif(maxlen){printf("Longest Repeating Substring length:%d\n",maxlen);printf("Position1:%d Position 2:%d\n",lrs1,lrs2);}else printf("No Repeating Substring found!\n");}//Get_LRepSub分析:i代表"错位值".本算法的思想是,依次把串S的一个副本S2向右错位平移1格,2格,3格,...与自身S1相匹配,如果存在最长重复子串,则必然能在此过程中被发现.用变量lrs1,lrs2,maxlen 来记录已发现的最长重复子串第一次出现位置,第二次出现位置和长度.题目中未说明"重复子串"是否允许有重叠部分,本算法假定允许.如不允许,只需在第二个for语句的循环条件中加上k<=i即可.本算法时间复杂度为O(Strlen(S)^2).4.31void Get_LPubSub(Stringtype S,Stringtype T)//求串S和串T的最长公共子串位置和长度{if(S[0]>=T[0]){StrAssign(A,S);StrAssign(B,T);}else{StrAssign(A,T);StrAssign(B,S);} //为简化设计,令S和T中较长的那个为A,较短的那个为Bfor(maxlen=0,i=1-B[0];i<A[0];i++){if(i<0) //i为B相对于A的错位值,向左为负,左端对齐为0,向右为正{jmin=1;jmax=i+B[0];}//B有一部分在A左端的左边else if(i>A[0]-B[0]){jmin=i;jmax=A[0];}//B有一部分在A右端的右边else{jmin=i;jmax=i+B[0];}//B在A左右两端之间.//以上是根据A和B不同的相对位置确定A上需要匹配的区间(与B重合的区间)的端点:jmin,jmax.for(k=0,j=jmin;j<=jmax;j++){if(A[j]==B[j-i]) k++;else k=0;if(k>maxlen){lps1=j-k+1;lps2=j-i-k+1;maxlen=k;}}//for}//forif(maxlen){if(S[0]>=T[0]){lpsS=lps1;lpsT=lps2;}else{lpsS=lps2;lpsT=lps1;} //将A,B上的位置映射回S,T上的位置printf("Longest Public Substring length:%d\n",maxlen);printf("Position in S:%d Position in T:%d\n",lpsS,lpsT);}//ifelse printf("No Repeating Substring found!\n");}//Get_LPubSub分析:本题基本思路与上题同.唯一的区别是,由于A,B互不相同,因此B不仅要向右错位,而且还要向左错位,以保证不漏掉一些情况.当B相对于A的位置不同时,需要匹配的区间的计算公式也各不相同,请读者自己画图以帮助理解.本算法的时间复杂度是o(strlrn(s)*strlen(t))。
数据结构 习题课

算 法
练习5 若已知非空线性链表第一个结点的指针为list, 请 写一个算法, 将该链表中数据域值最小的那个 移到链表的最前端。
list
35 67 18
…
52
10
14
71
…
82
65
q
p
^
list=q;
list
35 67 18
s->link=q->link;
…
52 10 14 71
…
82
65
s
q
^
(删除表中第i元素)
寻找满足条件的元素,即从表中第一个 元素开始到最后那个元素,反复比较相邻的 两个元素是否相同,若相同,删除其中一个, 否则,比较下一对相邻元素。
for(j=i+1; j<n; j++) A[j−1]=A[j]; n--;
(删除表中第i元素)
void DEL( ElemType A[ ], int &n ) { int j, i=0; 比较相邻元素 while(i<n-1) if(A[i]!=A[i+1]) i++; else { for(j=i+1; j<n; j++) A[j−1]=A[j]; n– – ; } } 删除一个元素
list
35 68 59 28
q->link=list;
… q p r r sp qp
r=p; p=p->link;
void REMOVE(LinkList &list ) { 算法 LinkList q=list,s,r; p=list → link; r=list; while (p!=NULL) { if (p→data<q→data) then 寻找值最小结点 { s=r; q=p; } r=p; O (链表长度) p=p→link; // 找到值最小的那个结点 ,地址由q记录 // } if (q!=list) then // 若值最小的结点不是链表最前面那个结点 // { s→link=q→link; q→link=list; list=q ; list s q } } … … 28 39 35 82
数据结构习题和答案

数据结构习题和答案习题课填空1、对于⼀棵⼆叉树,若⼀个结点的编号为i,则它的左孩⼦结点的编号为,双亲结点的编号为。
2、向⼀个长度为n的向量中删除第i个元素(1≤i≤n)时,需向前移动个元素。
3、在⼀棵⼆叉树中,若双分⽀结点数为5个,单分⽀结点数为6个,则叶⼦结点数为个。
4、为了实现折半查找,线性表必须采⽤⽅法存储。
顺序5、⼀种抽象数据类型包括数据对象和。
6、在以L为表头指针的带表头附加结点的单链表和循环单链表中,判断链表为空的条件分别为__________和_______。
7、数据结构被形式地定义为(D, R),其中D是的有限集合,R是D上的有限集合。
8、队列的插⼊操作在进⾏,删除操作在进⾏。
9、⼆叉搜索树的中序遍历得到的结点序列为____ ____。
10、在顺序表中插⼊或删除⼀个元素,需要平均移动元素,具体移动的元素个数与有关。
11、栈的特点是。
12、在单链表中,除了⾸元结点外,任⼀结点的存储位置由。
13、在⼀个具有n个顶点的⽆向图中,要连通所有顶点则⾄少需要条边。
14、深度为k(设根的层数为1)的完全⼆叉树⾄少有个结点,⾄多有个结点。
15、⼀棵深度为6的满⼆叉树有个分⽀结点和个叶⼦结点。
16、⼀个算法的效率可分为效率和效率。
17、队列的特点是。
18、⼀棵深度为5的满⼆叉树中的结点数为个。
19、在⼀个具有n个顶点的⽆向完全图中,包含有________条边,在⼀个具有n个顶点的有向完全图中,包含有________条边。
简答题1、已知⼀组元素为(38,26,62,94,35,50,28,55),画出按元素排列顺序输⼊⽣成的⼀棵⼆叉搜索树。
答:2、假设有⼆维数组A[0..5,0..7],每个元素⽤相邻的6个字节存储,存储器按字节编址。
已知A的起始存储位置(基地址)为1000,计算:(1)末尾元素A57的第⼀个字节地址为;(2)若按列存储时,元素A47的第⼀个字节地址为。
(3) 数组A的体积(存储量);(4) 若按⾏存储时,元素A14的第⼀个字节地址为。
数据结构课后习题及答案

填空题(10 * 1’ = 10’)一、概念题2.2.当对一个线性表经常进行的是插入和删除操作时,采用链式存储结构为宜。
2.3.当对一个线性表经常进行的是存取操作,而很少进行插入和删除操作时,最好采用顺序存储结构。
2.6.带头结点的单链表L中只有一个元素结点的条件是L->Next->Next==Null。
3.6.循环队列的引入,目的是为了克服假溢出。
4.2.长度为0的字符串称为空串。
4.5.组成串的数据元素只能是字符。
4.8.设T和P是两个给定的串,在T中寻找等于P的子串的过程称为模式匹配,又称P为模式。
7.2.为了实现图的广度优先搜索,除一个标志数组标志已访问的图的结点外,还需要队列存放被访问的结点实现遍历。
5.7.广义表的深度是广义表中括号的重数7.8.有向图G可拓扑排序的判别条件是有无回路。
7.9.若要求一个稠密图的最小生成树,最好用Prim算法求解。
8.8.直接定址法法构造的哈希函数肯定不会发生冲突。
9.2.排序算法所花费的时间,通常用在数据的比较和交换两大操作。
1.1.通常从正确性﹑可读性﹑健壮性﹑时空效率等几个方面评价算法的(包括程序)的质量。
1.2.对于给定的n元素,可以构造出的逻辑结构有集合关系﹑线性关系树形关系﹑图状关系四种。
1.3.存储结构主要有顺序存储﹑链式存储﹑索引存储﹑散列存储四种。
1.4.抽象数据类型的定义仅取决于它的一组逻辑特性,而与存储结构无关,即不论其内部结构如何变化,只要它的数学特性不变,都不影响其外部使用。
1.5.一个算法具有五大特性:有穷性﹑确定性﹑可行性,有零个或多个输入﹑有一个或多个输入。
2.8.在双向链表结构中,若要求在p指针所指的结点之前插入指针为s所指的结点,则需执行下列语句:s->prior= p->prior; s->next= p; p->prior- next= s; p->prior= s;。
2.9.在单链表中设置头结点的作用是不管单链表是否为空表,头结点的指针均不空,并使得对单链表的操作(如插入和删除)在各种情况下统一。
数据结构课程习题集第1页共25页

《数据结构》课程习题集第 1 页(共 25 页)一、. 选择题. 1. 算法的计算量的大小称为计算的()。
A.效率 B. 复杂性 C. 现实性 D. 难度.2. 算法的时间复杂度取决于().A.问题的规模 B. 待处理数据的初态 C. A和B D. 难确定.3. 下面关于算法说法错误的是()A.算法最终必须由计算机程序实现B.为解决某问题的算法同为该问题编写的程序含义是相同的C. 算法的可行性是指指令不能有二义性D. 以上几个都是错误的.4.从逻辑上可以把数据结构分为()两大类。
A.动态结构、静态结构 B.顺序结构、链式结构C.线性结构、非线性结构 D.初等结构、构造型结构.5.以下数据结构中,哪一个是线性结构()?A.广义表 B. 二叉树 C. 稀疏矩阵 D. 串.6.下述哪一条是顺序存储结构的优点?()A.存储密度大 B.插入运算方便C.删除运算方便 D.可方便地用于各种逻辑结构的存储表示.7.下面关于线性表的叙述中,错误的是哪一个?()A.线性表采用顺序存储,必须占用一片连续的存储单元。
B.线性表采用顺序存储,便于进行插入和删除操作。
C.线性表采用链接存储,不必占用一片连续的存储单元。
D.线性表采用链接存储,便于插入和删除操作。
.8.若某线性表最常用的操作是存取任一指定序号的元素和在最后进行插入和删除运算,则利用()存储方式最节省时间。
A.顺序表 B.双链表 C.带头结点的双循环链表 D.单循环链表.9.设一个链表最常用的操作是在末尾插入结点和删除尾结点,则选用( )最节省时间。
A. 单链表B.单循环链表C. 带尾指针的单循环链表D.带头结点的双循环链表.10. 链表不具有的特点是().A.插入、删除不需要移动元素 B.可随机访问任一元素C.不必事先估计存储空间 D.所需空间与线性长度成正比.11. 设一个栈的输入序列是 1,2,3,4,5,则下列序列中,是栈的合法输出序列的是()。
A. 5 1 2 3 4B. 4 5 1 3 2C. 4 3 1 2 5D. 3 2 1 5 4.12. 某堆栈的输入序列为a, b,c ,d,下面的四个序列中,不可能是它的输出序列的是()。
数据结构课后习题(第4-5章)

【课后习题】第4章 串 第5章 数组和广义表网络工程2010级( )班 学号: 姓名:题 号 一 二 三 四 总分 得 分一、填空题(每空1分,共30分)1. 串有三种机内表示方法: 、 和 ,其中前两种属于顺序存储结构,第三种属于 。
2. 若n 为主串长度,m 为子串长度,则串的BF (朴素)匹配算法最坏的情况下需要比较字符的总次数为 ,T(n)= 。
3. 是任意串的子串;任意串S 都是S 本身的子串,除S 本身外,S 的其他子串称为S 的 。
4. 设数组a[1…50, 1…60]的基地址为1000,每个元素占2个存储单元,若以行序为主序顺序存储,则元素a[32,58]的存储地址为 。
5. 对于数组,比较适于采用 结构够进行存储。
6. 广义表的深度是指_______。
7. 将一个100100 A 的三对角矩阵,按行优先存入一维数组B[297]中,A 中元素66,66A 在B 数组中的位置k 为 。
8. 注意:a i,j 的k 为 2(i-1)+j-1,(i=1时j=1,2;1<i<=n 时,j=i-1,i,i+1) 。
9. 称为空串; 称为空白串。
10. 求串T 在主串S 中首次出现的位置的操作是 ,其中 称为目标串, 称为模式。
11. 对称矩阵的下三角元素a[i,j],存放在一维数组V 的元素V[k]中(下标都是从0开始), 12. k 与i ,j 的关系是:k= 。
13. 在n 维数组中每个元素都受到 个条件的约束。
14. 同一数组中的各元素的长度 。
15. 三元素组表中的每个结点对应于稀疏矩阵的一个非零元素,它包含有三个数据项,分别表示该元素的 、 和 。
16.稀疏矩阵中有n个非零元素,则其三元组有行。
17.求下列广义表操作的结果:18.(1)GetHead【((a,b),(c,d))】=== ;19.(2)GetHead【GetTail【((a,b),(c,d))】】=== ;20.(3)GetHead【GetTail【GetHead【((a,b),(c,d))】】】=== ;21.(4)GetTail【GetHead【GetTail【((a,b),(c,d))】】】=== ;22.广义表E=(a,(b,E)),则E的长度= ,深度= ;二、判断题(如果正确,在下表对应位置打“√”,否则打“⨯”。
数据结构课后题答案(1-4章)

数据结构部分课后习题答案第一章1.1数据的逻辑结构是从具体问题中抽象出来的数学模型,体现了事物的组成和事物之间的逻辑关系。
数据的存储结构主要用来解决各种逻辑结构在计算机中物理存储表示的问题。
1.2事前分析和事后统计事前分析:优点,程序不必运行,所得结果只依赖于算法本身缺点,不够精确事后统计:优点,精确缺点,必须运行程序,所得结果依赖于硬件、环境等因素考虑赋值、运算操作执行的次数第3行赋值2次第6行赋值执行n次,加法执行n次所以,总共2n+2次操作,算法复杂度为O(n)1.4y= y + i * j 执行次数:1.5第二章2.9内存中一片连续空间(不妨假设地址从1到m)提供给两个栈S1和S2使用,怎样分配这部分存储空间,使得对任一个栈,仅当这部分空间全满时才发生上溢。
答:S1和S2共享内存中一片连续空间(地址1到m),可以将S1和S2的栈底设在两端,两栈顶向共享空间的中心延伸,仅当两栈顶指针相邻(两栈顶指针值之差的绝对值等于1)时,判断为栈满,当一个栈顶指针为0,另一个栈顶指针m+1时为两栈均空。
2.10线性表是数据项组成的一种有限且有序的序列,各元素之间呈线性关系。
从逻辑结构来说,栈和队列与线性表相同,都是典型的线性结构。
与线性表不同的是,栈和队列的操作特殊,受到一定的限制,仅允许在线性表的一端或两端进行。
栈是限定仅在一端进行插入删除的线性表,无论插入、删除还是读取都在一端进行,按后进先出的原则。
队列的元素只能从一端插入,从另一端删除,按先进先出的原则进行数据的存取。
2.11共有132种合法序列。
235641序列可以。
154623序列不可以。
对于每一个数来说,必须进栈一次、出栈一次。
我们把进栈设为状态‘1’,出栈设为状态‘0’。
n个数的所有状态对应n个1和n个0组成的2n位二进制数。
由于等待入栈的操作数按照1‥n的顺序排列、入栈的操作数b大于等于出栈的操作数a(a≤b),因此输出序列的总数目=由左而右扫描由n个1和n个0组成的2n位二进制数,1的累计数不小于0的累计数的方案种数。
数据结构练习题(1-4章)

数据结构练习题习题1 绪论1.1 单项选择题1. 数据结构是一门研究非数值计算的程序设计问题中,数据元素的①、数据信息在计算机中的②以及一组相关的运算等的课程。
①A.操作对象B.计算方法C.逻辑结构D.数据映象②A.存储结构B.关系C.运算D.算法2. 数据结构DS(Data Struct)可以被形式地定义为DS=(D,R),其中D是①的有限集合,R是D上的②有限集合。
①A.算法B.数据元素C.数据操作D.数据对象②A.操作B.映象C.存储D.关系3. 在数据结构中,从逻辑上可以把数据结构分成。
A.动态结构和静态结构B.紧凑结构和非紧凑结构C.线性结构和非线性结构D.内部结构和外部结构4. 算法分析的目的是①,算法分析的两个主要方面是②。
①A. 找出数据结构的合理性 B. 研究算法中的输入和输出的关系C. 分析算法的效率以求改进D. 分析算法的易懂性和文档性②A. 空间复杂性和时间复杂性 B. 正确性和简明性C. 可读性和文档性D. 数据复杂性和程序复杂性5. 计算机算法指的是①,它必具备输入、输出和②等五个特性。
① A. 计算方法 B. 排序方法C. 解决问题的有限运算序列D. 调度方法②A. 可行性、可移植性和可扩充性 B. 可行性、确定性和有穷性C. 确定性、有穷性和稳定性D. 易读性、稳定性和安全性1.2 填空题(将正确的答案填在相应的空中)1. 数据逻辑结构包括、、和四种类型,树形结构和图形结构合称为。
2. 在线性结构中,第一个结点前驱结点,其余每个结点有且只有个前驱结点;最后一个结点后续结点,其余每个结点有且只有个后续结点。
3. 在树形结构中,树根结点没有结点,其余每个结点有且只有个直接前驱结点,叶子结点没有结点,其余每个结点的直接后续结点可以。
4. 在图形结构中,每个结点的前驱结点数和后续结点数可以。
5. 线性结构中元素之间存在关系,树形结构中元素之间存在关系,图形结构中元素之间存在关系。
数据结构(c语言版)课后习题答案完整版

第1章 绪论5.选择题:CCBDCA6.试分析下面各程序段的时间复杂度。
.试分析下面各程序段的时间复杂度。
(1)O (1) (2)O (m*n ) (3)O (n 2) (4)O (log 3n )(5)因为x++共执行了n-1+n-2+……+1= n(n-1)/2,所以执行时间为O (n 2) (6)O(n )第2章 线性表1.选择题.选择题babadbcabdcddac 2.算法设计题.算法设计题(6)设计一个算法,通过一趟遍历在单链表中确定值最大的结点。
)设计一个算法,通过一趟遍历在单链表中确定值最大的结点。
ElemType Max (LinkList L ){if(L->next==NULL) return NULL; pmax=L->next; //假定第一个结点中数据具有最大值假定第一个结点中数据具有最大值 p=L->next->next;while(p != NULL ){//如果下一个结点存在if(p->data > pmax->data) pmax=p; p=p->next; }return pmax->data;(7)设计一个算法,通过遍历一趟,将链表中所有结点的链接方向逆转,仍利用原表的存储空间。
的存储空间。
void inverse(LinkList &L) { // 逆置带头结点的单链表 Lp=L->next; L->next=NULL; while ( p) {q=p->next; // q 指向*p 的后继 p->next=L->next;L->next=p; // *p 插入在头结点之后 p = q; }}、空间(n)、空间(10)已知长度为n的线性表A采用顺序存储结构,请写一时间复杂度为O(n)的数据元素。
复杂度为O(1)的算法,该算法删除线性表中所有值为item的数据元素。
数据结构课后习题答案-完整版

数据结构课后习题答案-完整版下面是《数据结构课后习题答案-完整版》的内容:---第一章:数组1. 题目:给定一个整数数组,判断是否存在两个元素之和等于目标值。
答案:使用双指针法,首先将数组排序,然后设置左指针指向数组头部,右指针指向数组尾部。
如果左指针和右指针指向的元素之和小于目标值,则左指针右移;如果大于目标值,则右指针左移;如果等于目标值,则找到了两个元素之和等于目标值的情况。
2. 题目:给定一个整数数组和一个目标值,找出数组中和为目标值的两个数的下标。
答案:使用哈希表,在遍历数组的过程中,将每个元素的值和下标存储在哈希表中。
遍历到当前元素时,检查目标值与当前元素的差值是否在哈希表中,如果存在,则找到了两个数的下标。
---第二章:链表1. 题目:给定一个链表,判断链表中是否存在环。
答案:使用快慢指针法,定义两个指针,一个指针每次向前移动一个节点,另一个指针每次向前移动两个节点。
如果存在环,则两个指针必定会相遇。
2. 题目:给定一个链表,删除链表的倒数第N个节点。
答案:使用双指针法,定义两个指针,一个指针先移动N个节点,然后两个指针同时向前移动,直到第一个指针到达链表尾部。
此时第二个指针指向的节点即为要删除的节点。
---第三章:栈和队列1. 题目:设计一个栈,使得可以在常数时间内获取栈中的最小元素。
答案:使用辅助栈来保存当前栈中的最小元素。
每次压栈操作时,将当前元素与辅助栈的栈顶元素比较,只有当前元素较小才将其压入辅助栈。
2. 题目:设计一个队列,使得可以在常数时间内获取队列中的最大元素。
答案:使用双端队列来保存当前队列中的最大值。
每次入队操作时,将当前元素与双端队列的末尾元素比较,只有当前元素较大才将其压入双端队列。
---第四章:树和二叉树1. 题目:给定一个二叉树,判断它是否是平衡二叉树。
答案:通过递归遍历二叉树的每个节点,计算每个节点的左子树高度和右子树高度的差值。
如果任意节点的差值大于1,则该二叉树不是平衡二叉树。
数据结构课后习题答案第四章

第四章串一、单项选择题1.B2. B3.B4.C5. C二、填空题1.空、字符2.由空格字符(ASCII值32)所组成的字符串空格个数3.长度、相等、子、主4.55.011223126.(1)char s[ ] (2) j++ (3) i >= j7.[题目分析]本题算法采用顺序存储结构求串s和串t的最大公共子串。
串s用i指针(1<=i<=s.len)。
t串用j指针(1<=j<=t.len)。
算法思想是对每个i(1<=i<=s.len,即程序中第一个WHILE循环),来求从i开始的连续字符串与从j(1<=j<=t.len,即程序中第二个WHILE循环)开始的连续字符串的最大匹配。
程序中第三个(即最内层)的WHILE循环,是当s中某字符(s[i])与t中某字符(t[j])相等时,求出局部公共子串。
若该子串长度大于已求出的最长公共子串(初始为0),则最长公共子串的长度要修改。
(1) i+k<=s.len && j+k<=t.len && s[i+k]==t[j+k] //所有注释同上(a)(2) con=0 (3) j+=k (4) j++ (5) i++三、应用题1.空格是一个字符,其ASCII码值是32。
空格串是由空格组成的串,其长度等于空格的个数。
空串是不含任何字符的串,即空串的长度是零。
2.(a)A+B “ mule”(b)B+A “mule ”(c)D+C+B “myoldmule”(d)SUBSTR(B,3,2) “le”(e)SUBSTR(C,1,0) “”(f)LENGTH(A) 2(g)LENGTH(D) 2(h)INDEX(B,D) 0(i)INDEX(C,”d”) 3(j)INSERT(D,2,C) “myold”(k)INSERT(B,1,A) “m ule”(l)DELETE(B,2,2) “me”(m)DELETE(B,2,0) “mule”3.朴素的模式匹配(Brute-Force)时间复杂度是O(m*n),KMP算法有一定改进,时间复杂度达到O(m+n)。
数据结构课后习题部分参考答案

数据结构课后习题部分参考答案第一章一、选择题1.C 2.C 3.A 4.D 5.B二、判断题1.╳2.╳ 3.╳ 4.╳5.∨三、简答题1.常见逻辑结构:集合结构,数据元素之间的关系仅仅是属于同一个集合。
线性结构,除第一个元素只有一个直接后继、最后一个元素只有一个直接前驱,其余元素有且只有唯一一个直接前驱、有且只有唯一一个直接后继,数据元素之间存在一对一的关系。
树形结构,树中只有唯一一个根元素,除根元素之外,其余元素只有一个直接前驱,但可以有多个直接后继元素,数据元素之间存在一对多的关系。
图形结构,元素之间关系任意,数据元素之间存在多对多的关系。
常用的存储结构:顺序存储,把逻辑上相邻的元素存储在物理位置相邻的存储单元中,由此得到的存储表示称为顺序存储结构。
通常用数组实现。
链式存储,对逻辑上相邻的元素不要求其物理位置相邻,元素间的逻辑关系通过附加的指针字段来表示,由此得到的存储表示称为链式存储结构。
通常用指针来实现。
除上述两种方法外,有时为了查找方便还采用索引存储方法和散列存储方法。
索引存储:在存储结点信息的同时,还建立附加的索引表来标识结点的地址。
散列存储:根据元素的关键码确定元素存储位置的存储方式。
2.算法与程序的区别:程序不一定满足有穷性(如操作系统);程序中的指令必须是机器可执行的,算法中的指令则无此限制;算法代表了对问题的解,程序则是算法在计算机上的特定的实现(一个算法若用程序设计语言来描述,它才是一个程序);数据结构+算法=程序。
3.例如有一张学生成绩表,记录了一个班的学生各门课的成绩。
按学生的姓名为一行记成的表。
这个表就是一个数据结构。
每个记录就是一个结点,对于整个表来说,只有一个开始结点和一个终端结点,其他的结点则各有一个也只有一个直接前趋和直接后继。
这几个关系就确定了这个表的逻辑结构——线形结构。
那么我们怎样把这个表中的数据存储到里呢? 用高级语言如何表示各结点之间的关系呢? 是用一片连续的内存单元来存放这些记录(顺序存储)还是随机存放各结点数据再用指针进行链接(链式存储)呢? 这就是存储结构的问题,我们都是从高级语言的层次来讨论这个问题的。
数据结构课后题答案(第4章).
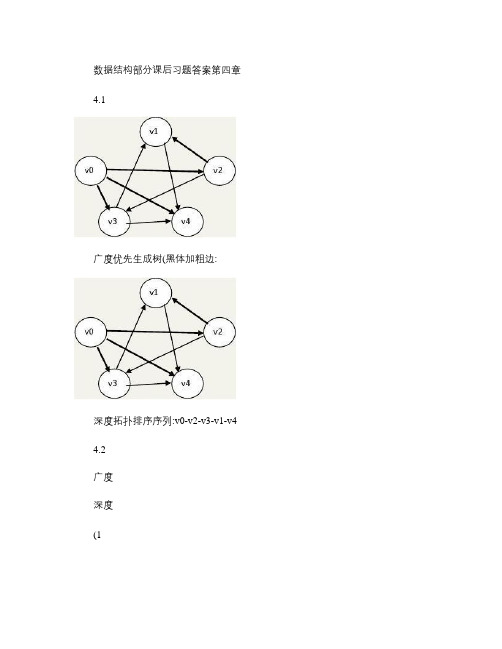
数据结构部分课后习题答案第四章4.1广度优先生成树(黑体加粗边:深度拓扑排序序列:v0-v2-v3-v1-v4 4.2广度深度(1(2加边顺序a-b b-e e-d d-f f-c4.3、如图所示为一个有6个顶点{u1,u2,u3,u4,u5,u6}的带权有向图的邻接矩阵。
根据此邻接矩阵画出相应的带权有向图,利用dijkstra 算法求第一个顶点u1到其余各顶点的最短路径,并给出计算过程。
带权有向图:4.4证明在图中边权为负时Dijkstra算法不能正确运行若允许边上带有负权值,有可能出现当与S(已求得最短路径的顶点集,归入S内的结点的最短路径不再变更内某点(记为a以负边相连的点(记为b确定其最短路径时,它的最短路径长度加上这条负边的权值结果小于a原先确定的最短路径长度,而此时a在Dijkstra算法下是无法更新的。
4.5P.198 图中的权值有负值不会影响prim和kruskal的正确性如图:KRUSKAL求解过程:4.6 Dijkstra算法如何应用到无向图?答:Dijkstra算法通常是运用在带非负权值的有向图中,但是无向图其实就是两点之间两条有向边权值相同的特殊的有向图,这样就能将Dijkstra算法运用到无向图中。
4.7用FLOYD算法求出任意两顶点的最短路径(如图A(6所示。
A(0= A(1= A(2=A(3= A(4=A(5= A(6= V1 到 V2、V3、V4、V5、V6 往返路径长度分别为 5,9,5,9,9,最长为 9,总的往返路程为 37 同理 V2 到 V1、V3、V4、V5、V6 分别为 5,8,4,4,13,最长为 13,总和 34 V3 对应分别为 9,8,12,8,9,最长为 12,总和为 46 V4 对应分别为 5,4,12,4,9,最长为 12,总和为 34 V5 对应分别为9,4,8,4,9,最长为 9,总和为 34 V6 对应分别为 9,13,9,9,9,最长为13,总和为 49 题目要求娱乐中心“距其它各结点的最长往返路程最短” ,结点V1, V5 最长往返路径最短都是 9。
(完整版)数据结构课后习题答案

第1章绪论1 •简述下列概念:数据、数据元素、数据项、数据对象、数据结构、逻辑结构、存储结构、抽象数据类型。
答案:数据:是客观事物的符号表示,指所有能输入到计算机中并被计算机程序处理的符号的总称。
如数学计算中用到的整数和实数,文本编辑所用到的字符串,多媒体程序处理的图形、图像、声音、动画等通过特殊编码定义后的数据。
数据元素:是数据的基本单位,在计算机中通常作为一个整体进行考虑和处理。
在有些情况下,数据元素也称为元素、结点、记录等。
数据元素用于完整地描述一个对象,如一个学生记录,树中棋盘的一个格局(状态)、图中的一个顶点等。
数据项:是组成数据元素的、有独立含义的、不可分割的最小单位。
例如,学生基本信息表中的学号、姓名、性别等都是数据项。
数据对象:是性质相同的数据元素的集合,是数据的一个子集。
例如:整数数据对象是集合N={0,士1,士2,…},字母字符数据对象是集合C={ ‘ A', ‘ B…,‘ Z,‘ a'b ',…,‘ z ' },学生基本信息表也可是一个数据对象。
数据结构:是相互之间存在一种或多种特定关系的数据元素的集合。
换句话说,数据结构是带“结构”的数据元素的集合,“结构”就是指数据元素之间存在的关系。
逻辑结构:从逻辑关系上描述数据,它与数据的存储无关,是独立于计算机的。
因此,数据的逻辑结构可以看作是从具体问题抽象出来的数学模型。
存储结构:数据对象在计算机中的存储表示,也称为物理结构。
抽象数据类型:由用户定义的,表示应用问题的数学模型,以及定义在这个模型上的一组操作的总称。
具体包括三部分:数据对象、数据对象上关系的集合和对数据对象的基本操作的集合。
2 •试举一个数据结构的例子,叙述其逻辑结构和存储结构两方面的含义和相互关系。
答案:例如有一张学生基本信息表,包括学生的学号、姓名、性别、籍贯、专业等。
每个学生基本信息记录对应一个数据元素,学生记录按顺序号排列,形成了学生基本信息记录的线性序列。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分析:其他解题思路
对树做层次遍历,每遍历一层树的深度+1.
最后访问节点的层数即为树的深度。
关键:将队列中的结点结构变为
(结点,该结点的层数i) 。
A A
B
BCD E FG
EC FD G
算法Depth3(t. d) //思想:对树做层次遍历,每遍历 一层树的深度+1.
IF t = THEN (d ← -1. RETURN) //判断t是否为 CREATEQ(Q). Q (t,0) . //创建辅助队列, 根结点入队 WHILE NOT(IsEmpty(Q)) DO ( //利用队列Q遍历第d层
{ TreeNode * p = new TreeNode(nodes[0]); Queue q( size ); q.QInsert( p ); for ( int i = 0, j = 1; i < size; j += degrees[i++] ) { p = q.QDelete( p ); Children( p, nodes + j, degrees[i], q ); }
(p, flag) NS IF flag = 0 THEN ( // p尚未访问
NS (p, 1) q ← FirstChild(p) WHILE q ≠ DO (
NS (q, 0). q←NextBrother(q). ) ) ELSE ( // p已访问 IF p = THEN RS -1 // 递归出口
depth(t) =
ìïïï íïïïïî
-1 1+ max{depth( 为t的子节点}
p)
|
p
t= L 否则
分析:解题思路
A BCD E FG
A
B EC
FD G
后根遍历:节点访问为计算以该 节点为根的树形高度
算法 Depth(t. d) // 递归算法 D1[递归出口]
IF t = THEN (d← -1. RETURN) D2[递归调用]
结点
(p, d) Q.
WHILE p ≠ DO ( IF FirstChild(p)≠NULL THEN
Q (FirstChild(p), d+1). p ← NextBrother(p) .
) )▌
第12题
• 构造权值为{5, 13, 21, 7, 18, 30, 41}的哈夫曼树。
第12题分析
算法Similar(t1, t2) /*判断两棵二叉树是否相似,t1、 t2表示两棵树的根节点。若相似,返回值为true,否 则为false*/
S1[递归出口] IF t1=NULL AND t2=NULL THEN RETURN true. IF t1=NULL OR t2=NULL THEN RETURN false.
}
void Children(TreeNode * parent, char * nodes, int d, Queue & q )
{ if ( d == 0 ) { parent->child = NULL; return; } parent->child = new TreeNode( nodes[0] ); TreeNode * ch = parent->child; q.QInsert(ch); for ( int i = 1; i < d; i++) { ch->sibling = new TreeNode( nodes[i] ); ch = ch->sibling; q.QInsert(ch); } ch->sibling = NULL;
p ← FirstChild(t). max ← -1. // max为各子树最大深度 WHILE p ≠ DO (
Depth(p. dp). IF dp > max THEN max ← dp. p ← NextBrother(p). ) d← 1 + max. RETURN. ▌
算法 Depth2(t. d) // 迭代算法 CREATES(NS). CREATES(RS). NS (t, 0) WHILE NS is nonempty DO (
节点都在右子树中节点之前出现,因此,在三种遍历中l1均在l2 之前。
第5题
• 编写一算法,判别给定二叉树是否为完全二叉树。
分析
• 一棵二叉树是完全二叉树当且仅当其满足如下 的条件: (1)任意节点不能有右孩子无左孩子; (2)若节点不含两个子节点,按照层次序列其 后的节点都没有子节点。
参考答案 (层次遍历)
57
{5, 13, 21, 7, 18, 30, 41}
第14题
• 已知一棵树的层次遍历序列及相应的每个节点的次数序 列,请写出构造此树的左02201000
A BCD E FGH
I
参考答案
TreeNode * Level2Tree( char * nodes, int * degrees, int size )
• 判断以下命题是否为真?若真,请证明之;否则,举出 反例。 一棵二叉树形的所有的叶结点,在先根次序、中根次序 和后根次序下的排列都按相同的相对位置出现。
分析
A B
C
D
E FG H
IJ
KL
先根: A B C E I F J D G H K L 中根: E I C F J B G D K H L A 后根: I E J F C G K L H D B A
S2[递归调用] RETURN Similar(left(t1),left(t2)) AND Similar(right(t1),right(t2)). ▌
时间复杂度为O(min(n1, n2))
第8题
• 对于下图所示的树
- (a)对其进行先根和后根遍历。 - (b)给出其在自然对应下的二叉树。
A
• 首先,在森林中取权值最小的两个根结点s和n,合成一 棵二叉树,新生成的结点T1,作为这两个结点的父结点, T1的权值是两个子结点的权值之和;
• 对新的森林重复上一步操作,直至森林中只有唯一的根 结点时,终止操作。
第12题答案
0 135 1
55 01
80 01
25 30 39 41
01
01
12 13 18 21 01
参考答案
int height(BinTreeNode<T>* t) {
if ( t==NULL ) return -1; return 1+max(height(t->left),height(t->right)); } void path(BinTreeNode<T>* t) { while ( t != NULL ){
cout << t->data << “ ” <<endl; if (height(t->left)>height(t->right)) t=t->left; else t=t->right; } }
第7题
• 编写算法判断两棵二叉树T和T’是否相似。两棵二叉树 相似是指它们具有相同结构。
参考答案
if (p->right != NULL) return false; else if (p->left != NULL) Q.Insert(p->left); while (!Q.Empty()) { //看剩余节点是否有孩子
p=Q.Delete(); if ( p->left ! = NULL || p->right != NULL)
bool IsComplete(BinTreeNode * t) {
Queue Q; if ( t == NULL ) return true; else Q.Insert(t); while ( true ) {
p=Q.Delete(); if (p->left == NULL || p->right == NULL) break; // Q.Insert(p->left); Q.Insert(p->right); } // 待续
B
C
D
EF G H I
KG J
第8题参考答案
• (a)对其进行先根和后根遍历。 先根遍历:ABEKGJFCGDHI 后根遍历:KGJEFBGCHIDA
• (b)
A
B
E
C D
F
K
G
G J
H I
第10题
• 对以左儿子—右兄弟链接表示的树,编写计算树的深度的 算法。
分析:解题思路
A
BCD
E FG
后根遍历
}
THE END
return false; } return true; }
第6题
• 编写算法求任意二叉树中一条最长的路径,并输出此路 径上各结点的值。
分析
• 给定一棵树,如果左子树的高度大于右子树的高度,则 最长路径的第一条边肯定是根节点的左分支,否则,第 一条边是根节点的右分支。以此类推,可以找到第二条 边到最后一条边。
算法 Depth2(t. d)[续] ELSE ( // 结果综合 p ← FirstChild(t). max ← -1 WHILE p ≠ DO ( dp RS IF dp > Max THEN max←dp. p←NextBrother(p). ) RS max+1 )
) ) d RS. ▌
参考答案
使用数学归纳法进行证明。令h为二叉树高度; • h=0时,命题成立 • 假设 h <= k 时命题成立,往证h=k+1时命题也成立。当 h =
k+1 时,对任意两个叶结点l1,l2,有三种情况:
