Pages from EViews 6 Users Guide II
Eviews2章EViews工作界面介绍(基础教程)

EViews统计分析基础教程
二、基本对象
1.对象的建立
工作文件(Workfile)是对象的集合,EViews中的所 有信息都存储在对象中,共有17种不同类型的对象, 存储不同类型的信息。
EViews统计分析基础教程
二、基本对象
1.对象的建立 建立新对象可选择主菜单中的“Object” |“New Object”选项或选择工作文件工具栏中的“Object” |“New Object”选项,均可以打开如下图所示的对话 框。
EViews统计分析基础教程
第2章 EViews工作界面介绍
重点内容: • EViews工作文件的操作 • EViews对象的操作
EViews统计分析基础教程
一、工作文件
1.工作文件的建立 首先单击主菜单栏中的File选项,在下拉菜单中选择 “New”|“Workfile”选项,将弹出下图所示的对话框。
工具栏
EViews统计分析基础教程
一、工作文件
2.工作文件窗口
新建立的工作文件窗口只包含两个对象,一个是 “ resid”(残差),一个是“ c”(系数向量), 新建立的这两个对象的取值分别为“0”和“NA”(空 值 )。残差(resid)和系数向量(c)前面的符号为该对 象的图标,不同类型的对象均有各自不同的类型图 标。
EViews统计分析基础教程
一、工作文件
4. 工作文件的功能键
3 Object(对象) 其功能与第1章中所介绍的主菜单中的“Object”功能相 同。 4 Save(保存) 用来保存当前的工作文件,与主菜单中的 “File”|“Save”功能相同。 5 Fetch(提取) 可将以文件形式存储的对象调入当前工作文件中。 “Browse”按钮选择对象所在的路径,然后在“Objects to fetch ”中输入所要提取的对象名称,再单击“OK” 按钮即可。”作用相同。
Eviews操作指导

Eviews上机指导第一节Eviews简介1、Eviews是什么2、运行Eviews3、Eviews的窗口4、Eviews的主要功能5、关闭Eviews第二节单方程计量经济模型Eviews操作案例一、创建工作文件二、输入和编辑数据三、图形分析四、OLS估计参数五、预测六、非线性回归模型的估计七、异方差检验与解决办法八、自相关检验与解决办法第三节联立方程计量经济模型Eviews操作第一节 Eviews简介Eviews是Econometrics Views的缩写,直译为计量经济学观察,通常称为计量经济学软件包。
它的本意是对社会经济关系与经济活动的数量规律,采用计量经济学方法与技术进行“观察”。
计量经济学研究的核心是设计模型、收集资料、估计模型、检验模型、应用模型(结构分析、经济预测、政策评价)。
Eviews是完成上述任务比较得力的必不可少的工具。
正是由于Eviews等计量经济学软件包的出现,使计量经济学取得了长足的进步,发展成为一门较为实用与严谨的经济学科。
1、Eviews是什么Eviews是美国QMS公司研制的在Windows下专门从事数据分析、回归分析和预测的工具。
使用Eviews可以迅速地从数据中寻找出统计关系,并用得到的关系去预测数据的未来值。
Eviews的应用范围包括:科学实验数据分析与评估、金融分析、宏观经济预测、仿真、销售预测和成本分析等。
Eviews是专门为大型机开发的、用以处理时间序列数据的时间序列软件包的新版本。
Eviews的前身是1981年第1版的Micro TSP。
目前最新的版本是Eviews4.0。
我们以Eviews3.1版本为例,介绍经济计量学软件包使用的基本方法和技巧。
虽然Eviews是经济学家开发的,而且主要用于经济学领域,但是从软件包的设计来看,Eviews的运用领域并不局限于处理经济时间序列。
即使是跨部门的大型项目,也可以采用Eviews进行处理。
Eviews处理的基本数据对象是时间序列,每个序列有一个名称,只要提及序列的名称就可以对序列中所有的观察值进行操作,Eviews允许用户以简便的可视化的方式从键盘或磁盘文件中输入数据,根据已有的序列生成新的序列,在屏幕上显示序列或打印机上打印输出序列,对序列之间存在的关系进行统计分析。
Eviews操作教程_完整版

Eviews操作教程_完整版1.EVIEWS基础 (3)1.1. E VIEWS简介 (3)1.2. E VIEWS的启动、主界⾯和退出 (3)1.3. E VIEWS的操作⽅式 (6)1.4. E VIEWS应⽤⼊门 (6)1.5. E VIEWS常⽤的数据操作 (15)2.⼀元线性回归模型 (24)2.1. ⽤普通最⼩⼆乘估计法建⽴⼀元线性回归模型 (24) 2.2. 模型的预测 (30)2.3. 结构稳定性的C HOW检验 (34)3. 多元线性回归 (39)3.1. ⽤OLS建⽴多元线性回归模型 (39)3.2. 函数形式误设的RESET检验 (45)4. ⾮线性回归 (48)4.1. ⽤直接代换法对含有幂函数的⾮线性模型的估计 (48) 4.2. ⽤间接代换法对含有对数函数的⾮线性模型的估计 (50) 4.3. ⽤间接代换法对CD函数的⾮线性模型的估计 (53)4.4. NLS对可线性化的⾮线性模型的估计 (55)4.5. NLS对不可线性化的⾮线性模型的估计 (58)4.6. ⼆元选择模型 (62)5. 异⽅差 (68)5.1. 异⽅差的⼽得菲尔德——匡特检验 (68)5.2. 异⽅差的WHITE检验 (72)5.3. 异⽅差的处理 (75)6. ⾃相关 (79)6.1. ⾃相关的判别 (79)6.2. ⾃相关的修正 (83)7. 多重共线性 (87)7.1. 多重共线性的检验 (87)7.2. 多重共线性的处理 (92)8. 虚拟变量 (94)8.1. 虚拟⾃变量的应⽤ (94)8.2. 虚拟变量的交互作⽤ (99)8.3. ⼆值因变量:线性概率模型 (101)9. 滞后变量模型 (106)9.1. ⾃回归分布滞后模型的估计 (106)9.2. 多项式分布滞后模型的参数估计 (111)10. 联⽴⽅程模型 (116)10.1. 联⽴⽅程模型的单⽅程估计⽅法 (116)10.2. 联⽴⽅程模型的系统估计⽅法 (120)2..1.Eviews基础1.1.Eviews简介Eviews:Econometric Views(经济计量视图),是美国QMS公司(Quantitative Micro Software Co.,⽹址为/doc/8e38170bbed126fff705cc1755270722192e59b1.html )开发的运⾏于Windows环境下的经济计量分析软件。
企业模拟竞技协会手册 Eviews 6
序目录方便面的故事技篇市场分析一、内部分析法所谓内部分析,就是通过分析自身的销售数据,来预测未来销售的方法。
(一)Eviews 6 的应用Eviews 6 是一款十分强大的实用数据分析工具。
它的使用方法很多,受我们自身知识水平所限,这里我们只介绍一种常用的初级应用方法,至于这么做的原因,以及如何修正序列相关性等等等等都不予介绍。
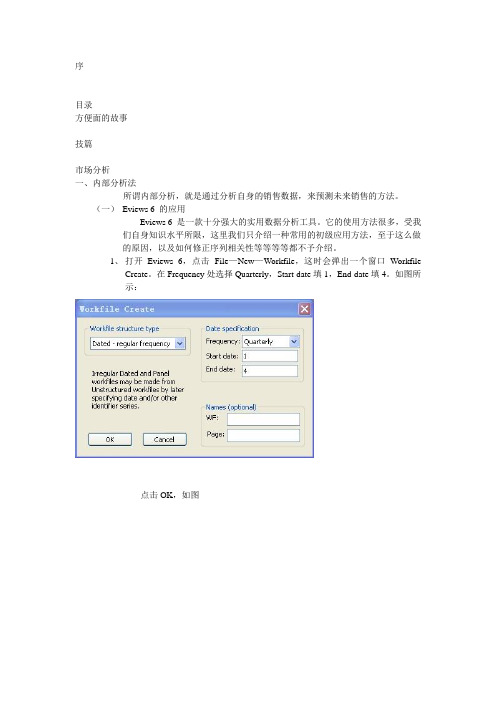
1、打开Eviews 6,点击File—New—Workfile,这时会弹出一个窗口WorkfileCreate。
在Frequency处选择Quarterly,Start date填1,End date填4。
如图所示:点击OK,如图这里意味着你已经创建了一个4年的Eviews文件,共有16个季节。
2、输入命令“data y x1 x2 x3”,回车这里的意思是创建原始数据。
如图所示接下来,就要把原始数据输入进去了。
我们把Y定义为需求,价格定义为x1,促销定义为x2,广告定义为x3。
这些数据可以在比赛平台里的时间序列数据里面找到。
我用1836赛区前15期的数据演示,录入后如图所示。
3、输入命令“ls log(y) c log(x1) log(x2) log(x3) log(x3(-1)) ar(1)”,回车这里的意思是使用最小二乘法,并且对原始数据取对数,且广告滞后一期,建立数学模型。
结果如图所示。
注意,在这里懂得理解分析结果至关重要。
第一,要检查模型的经济意义是否过关。
C为常数,可以不必理会。
LOG(X1)为价格,此时它的系数为-6.880721,为负数,通过经济检验。
因为价格与需求一定是负相关的关系。
同理可得,促销LOG(X2)的系数-.0054312为负数,没有通过检验。
广告LOG(X3)的系数0.971834为正数,通过了检验。
经济检验通不过有几种原因。
(1)样本太少。
(2)样本质量不好。
如果价格变化幅度总是很大,广告促销变化也很不稳定,就会出现模型计算不符合实际。
EVIEW操作指南.
EVIEW操作指南Eviews入门首先是打开Eviews软件,可以双击桌面上的图标,或者从windows开始菜单中寻找Eviews,如图F1-1。
图F1-1打开Eviews打开Eviews后,可以看到下面的窗口,图F1-2图F1-2 Eviews窗口关于Eviews的操作可以点击F1-2的Help打开Eviews后,第一项任务就是建立一个新Workfile或者打开一个已有的Workfile,单击File,然后光标放在New上,最后单击Workfile。
如图F1-3图F1-3建立新Workfile得到一个workfile对话框,图F1-4图F1-4 workfile对话框对话框中选择数据的频率:年、半年、季度、月度、周、天(5天一周或7天1周)、没有周期填写开始日期和结束日期:日期格式年:1997,季度:1997:1,月度:1997:01周和天:8:10:1997表示1997年8月10号—美式8:10:1997表示1997年10月8号—欧式如何选择欧式和美式呢?从Eviews窗口点击Options再点击Frequency conversion-dates…图F1-4建立了一个频率是月度数据的workfile。
填写完后点OK,一个新Workfile就建好了。
见图F1-5。
保存该workfile,单击workfile窗口的save命令,选择保存位置即可。
F1-5 Workfile窗口打开一个已经存在的Workfile,见图F1-6图F1-6 打开已经存在的Workfile2 输入输出数据,如果是新建立的workfile,第二件事就是输入数据。
1)直接输入数据,见F1-7在Eviews窗口下,单击Quick,再单击Empty group(edit seriest),直接输数值即可。
最后单击“ser01”,输入希望的名字,按回车键;F1-7直接输入数据注意在该窗口中命令行有一个Edit+/-,如图F1-7,1997:07后面的单元格是蓝色的则不能输入数据,这时可以点一下Edit+/-就可以变成如图所示的空白格,输完数据后,为了避免不小心改变数据,可以再点一下Edit+/-,这时数据就不能被修改了。
EVIEWS6

《EVIEWS6.0计量经济与时间序列分析班》详细目录第一讲:eviews入门知识点1:Eviews工作界面介绍知识点2:Eviews工作文件及常用对象介绍知识点3:变量的建立,变量中数据的录入(手动录入和复制粘贴)知识点4:删除变量或观察值知识点5:样本区间的调整知识点6:变量的排序知识点7:通过数学运算生成新的变量(取自然对数,一阶差分等常见运算)知识点8:工作文件的保存与EViews软件的退出知识点9:如何调用已保存过的工作文件数据说明案例1:本案例中所采用的数据均来自中国经济信息网,数据区间为1978-2008 北京市城镇家庭年平均每人可支配收入(x1)北京市城镇家庭平均每人全年消费性支出(y1)北京市居民消费价格指数(1978=100)(index)案例2:上证综指日收盘价(2003-1-6,2009-6-29)第二讲 Eviews图形对象介绍一、关于单个变量的作图知识点1:单变量的折线图,钉形图、柱形图。
知识点2:对于图形的修饰(给图形设置背景,给图形添加网格线,改变折线图的颜色,在图形中添加文本、直线和阴影)案例数据说明:2003年1月6日-2009年6月26日上证综指日收盘价。
二、关于多个变量的作图知识点1:多变量折线图(左右两个纵坐标显示不同的变量,做变量标准化后的折线图,折线交叉或不交叉的设置,如何编辑图例)案例数据说明:1978年-2008年北京市城镇居民收入和消费性支出数据(已经经过物价调整的)。
知识点2:多变量的扇形图案例说明:1985年和1998年城镇居民家庭8项支出占总支出的比重。
知识点3:做多变量的散点图(如何修改横轴和纵轴的标签)案例数据说明:1978年-2008年北京市城镇居民收入和消费性支出数据(已经经过物价调整的)。
知识点4:做多变量的面积图(直观的看人口增长率)案例数据说明:1980年-2008年中国人口出生率和死亡率。
第三讲描述性统计分析一、序列窗口下的描述性统计分析知识点1:如何以建立组对象的方式将数据导入到Eviews中去(第二种导入数据的方式)。
Eviews6.0操作关键方法记录本

1.用Eviews 6.0生产一个0均值的序列或对数数列1.1.用途及原理原序列非常的不稳定,不稳定序列可以取均值或者对数数列,让其趋于稳定,才能做预测或者拟合. 对于平稳随机过程,我们已经建立了一整套的处理方法。
由于平稳序列的均值、方差、协方差等数字特征并不伴随着时间的推移而变化,且其数字特征具有遍历性,因此可以基于时间序列在过去时点上的信息,建立拟合模型,用于预测时间序列在未来时点上的特征或者可能出现的情景。
但在经济实践中,诸如国内生产总值之类的实际经济统计时间序列经常呈现出系统性地上涨或下降的趋势。
有些时间序列还具有周期性波动的特征,例如社会零售总额的月度时间序列数据等。
诸如此类的时间序列样本数据不可能生成于平稳随机过程,从而可看成来自于非平稳随机过程的样本数据。
然而,非平稳时间序列的数字特征会伴随着时间的推移而变化,亦即其在不同时点上的统计规律性互不相同,且不具有遍历性,因此不能基于序列既往的信息来推测其在未来的可能情景。
于是我们必须建立一套处理非平稳随机过程的专门方法。
其中,设法将其平稳化是处理非平稳随机过程的基本思路。
1.2操作方法实验操作数据基于甘蔗产量ExcelGZCL取对数数列变量窗口下操作如下:相对于原数列取0均值序列操作如下:第一步,找出原数列的Mean(均值),操作如上。
结果如下。
Mean:均值 Median:中值(中位数) Max Min:最大值,最小值Std.Dev:样本标准差 Skewness:偏度(直观看来就是密度函数曲线尾部的相对长度,即曲线峰波往哪边偏,偏的是多少,BS)Kurtosis:峰度(峰度是用来反映频数分布曲线顶端尖峭或扁平程度的指)第二步,利用Mean数值做出O均值序列。
操作如下:出现以下窗口:输入命令:X=GZCL-Mean(输入Mean代表的具体数值)确定后,既可得到相对于原序列的,0均值序列在对时间序列进行拟合的时候,如果用二次或者n次函数或其他函数方式进行拟合。
Eview6
3、输入数据
在EViews软件主窗口或工作文件窗口点击Objects-New创建一个新序列。再从工作文件目录中选取并双击所创建的新序列就可以展示该对象,选择Edit+/-,进入编辑状态,输入数据。用同样的方式可以输入序列y
EViews软件的基本操作
二、实验过程记录:
1、在主菜单上依次点击File-New-Workfile,即选择新建对象的类型为工作文件,
将弹出一个对话框,由用户选择数据Undated or irregular——非时间序列数据
2、工作文件窗口是EViews的子窗口,工作文件一开始其中就包含了两个对象,一个
4、将显示一个数组(group)窗口,此时可以按全屏幕编辑方式输入每个变量的统计资料。也可以将Excel文件中的数据用copy和paste命令复制过来。
5、绘图
可以在命令行中输入scat x y来绘制x对y的散点图。
实验操作成绩(百分制)__________实验指导教师签字:__________
实验报告成绩(百分制)__________实验指导教师签字:__________
Eviews 操作步骤

Eviews 操作步骤:一、数据下载(百度国泰安)1、关于指数下载步骤:数据中心→单表查询→股票市场→指数信息2、字段选择指数代码如下:000001 上证指数000002 上证A股指数000003 上证B股指数399001 深成指数399106 深圳综合指数3991007 深圳综合A指数3、时间选择:2010.1.1~2017.9.204、条件筛选:指数代码→选条件→条件值→添加5、预览数据6、下载数据下载格式:.xsl下载详情→下载二、货币量下载1、数据中心→单表查询→经济研究系列→宏观经济→金融业2、字段:M0、M1、M23、时间:2010.1.1-2017.9.204、下载详情→下载5、居民消费指数和国内贷款总量的下载步骤:经济研究系列→宏观经济→固定资产投资三、EVIEWS数据导入File→Open→Foreign data as workfile→rename→File→Save as四、单位根检验Quick→Series Statistics→Unit root test→Seires name(输入如m等)→ok→选择level(1st different、2st different)分别检验,看显著性水平和p值五、VAR 模型Quick→Estimate VAR→Endogenous→输入shz、M0、M1、M2、LOAN→lag Internval →填两个数12或14等(确认找AIC最小的数)→确立六、脉冲影应函数在上面输出结果工具栏:Impulse(或view→impulse response)→display format(选如:mutiple sraphs)→选择冲击变量如:M0→在response中选入shz→ok七、方差分解:在六的结果中→View→variance→decomposition of:shz、m0、m1、m2、loan→ok八、协整检验:1、五、六、七中任选一结果→VIEW→cointegratiom→display format(选table)→decomposition of:shz、m0、m1、m2、loan→ok2、两个变量(两步法):Quick→Estimation Equation→Equationg specification shz、m0等→ok3、Pro→make residual series(保存残差)→name for residual series(命名)→ok→view→unit root test→ok九、格兰杰因果检验:Quick→group statistics→granger causality test→series list(输变量,可以多个变量)十、保存输出结果→freez(然后编辑)→保存。
Eviews6.0面板数据操作指南
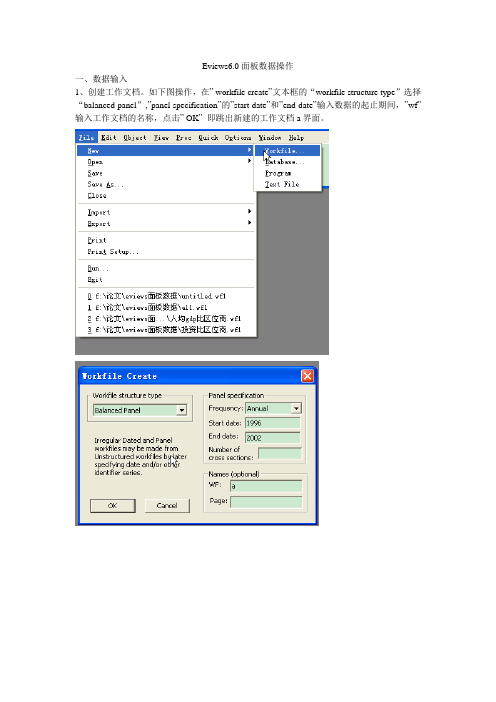
Eviews6.0面板数据操作一、数据输入1、创建工作文档。
如下图操作,在” workfile create”文本框的“workfile structure type”选择“balanced panel”,”panel specification”的”start date”和”end date”输入数据的起止期间,”wf”输入工作文档的名称,点击” OK”即跳出新建的工作文档a界面。
2、创建新对象。
操作如下图。
在”new object”文本框的”type of object”选择”pool”,”name for object ”输入新对象的名称。
创建成功后的界面如下面第3张图所示。
3、输入数据。
双击”workfile”界面的,跳出”pool”界面,输入个体。
一般输入方式为如下:若上海输入_sh,北京输入_bj,…。
个体输入完成后,点击该界面的键,在跳出的”series list”输入变量名称,注意变量后要加问号。
格式如下:y? x?。
点击”OK”后,跳出数据输入界面,如下面第4张图所示。
在这个界面上点击键,即可以输入或者从EXCEL处复制数据。
在输入数据后,记得保存数据。
保存操作如下:在跳出的“workfile save”文本框选择“ok”即可,则自动保存到我的文档。
然后在“workfile”界面如下会显示保存路径:d:\my documents\a.wf1。
若要保存到自己选择的路径下面,则在保存时选择“save as”,在跳出的文本框里选择自己要保存的路径以及命名文件名称。
4、单位根检验。
一般回归前要检验面板数据是否存在单位根,以检验数据的平稳性,避免伪回归,或虚假回归,确保估计的有效性。
单位根检验时要分变量检验。
(补充:网上对面板数据的单位根检验和协整检验存在不同意见,一般认为时间区间较小的面板数据无需进行这两个检验。
)(1)生成数据组。
如下图操作。
点击”make group”后在跳出的”series list”里输入要单位根检验的变量,完成后就会跳出如下图3所示的组数据。
EVIEWS6软件安装说明
EVIEWS 6 软件安装说明1、解压缩Eviews6.RAR文件到指定目录,得到Eviews6文件夹。
2、进入EViews6文件夹,双击Autorun.exe文件。
3、单击第一个选项,安装Eviews6.0。
如图1所示。
图1 安装Eviews64、单击Next→Yes→选择安装路径(推荐使用默认路径),如图2所示。
图2 选择安装路径5、点击Next,在图3所示对话框中输入demo,之后点击next。
图3 输入序列号6、选择安装插件(如图4),点击Next。
开始安装软件。
图4 选择安装插件7、等待软件安装完成,有三个提示:均选择Yes即可。
如图5所示。
单击Finish。
图5 软件安装结束对话框8、运行Upgrade文件夹中的EViews6Patch_061807.exe文件,将已安装的软件升级到2007年6月18日。
一路Next,直到安装完成。
如图6所示。
图6 安装EViews6Patch_0618079、将Crack文件夹中的eviews.6.b1807-fix.exe文件复制到程序目录下,执行该文件,按patch后进行安装,单Exit退出。
如图7所示。
图7 安装eviews.6.b1807-fix.exe10、运行Eviews.exe文件,选Eviews Registration….,如图8所示。
记下Machine ID,(可以通过复制此ID号保存到剪贴板上),见图9。
图8 选择Eviews Registration….图9 获取Machine ID11、单击图9对话框中的Exit without registering 按钮,关闭EviewsResgistration对话框。
关闭Eviews6程序。
12、鼠标右键单击Crack文件夹中的Eviews 6.reg文件,在弹出的菜单中选择打开方式…,使用记事本打开此文件。
如图10。
图10 用记事本打开Eviews 6.reg 文件 13、 将第10步中所得的Machine ID 覆盖现有ID (User~!至 !60C45678 –之间的部分),现有ID 如图11所示的选定部分。
eviews软件使用说明

EViews软件使用说明一、EViews软件的特点EViews(Econometric Views)软件是美国QMS公司研制的MicroTSP软件的Windows版本。
除了TSP软件所具有的特点之外,EViews软件还有以下特点:1.具有Windows软件的操作风格允许用户通过鼠标在标准的Windows窗口、菜单、对话框上操作,处理结果直接显示在窗口之中,并且可以利用标准的Windows技术(如复制、粘贴等)去进一步处理这些结果。
因此,只要熟悉Windows环境下的软件操作,将会很快掌握EViews软件的基本操作方法。
2.采用了面向对象的软件设计思想EViews软件将计量经济分析的基本元素(如序列、数据、矩阵等)和分析结果(如方程、图形、系统等)都视为“对象”,每一个对象都用相应的窗口来表示。
通过对每一个对象不同侧面的观察,来分析对象的属性和特征,揭示不同对象之间的关系。
3.具有灵活的操作方式为了便于用户操作,EViews软件提供了三种操作方式,一是菜单驱动方式;利用系统提供的命令菜单可以很方便地完成有关操作。
二是命令输入方式;系统专门设置了命令输入窗口,以便用户在此窗口中直接键入有关命令,而且在命令字后边可以添加命令参数。
三是程序运行方式,将有关命令序列编制成程序之后,运行该程序则以批处理方式完成一组命令的操作,这种方式适用于经常使用的重复操作。
另外,EViews软件还在各个对象窗口中设置了常用命令的命令按钮。
这些方式使得EViews软件的操作非常方便灵活。
4.反映了计量经济学的最新研究成果由于EViews软件是由计量经济学家研制、并且专门用于计量经济分析的专用软件,所以软件中反映了计量经济学理论、方法研究的发展情况。
在EViews 2.0版中,检验方法包括异方差性的white检验、自相关性的BG检验、因果关系的Granger检验、协整的单位根检验等等;估计方法包括ARCH模型、GMM模型、向量自回归模型的估计和三段最小二乘估计法等系统估计方法。
Eviews的基本操作
建立eviews文件
1、双击eviews
2、file\new\workfile
3、在对话框中选择unstructured
4、在上述对话框中输入样本容量和文件名(文件名可不填)
5、save as
原始数据的录入
1、双击eviews文件
2、object\new object
3、选择series
4、命名
5、点击edit+/-
6、录入数据(可以直接复制excel中的数据)
1、双击文件consp序列(即被解释变量的序列)
2、quick\estimate equation
3、在对话框依次输入:
被解释变量 c 解释变量(注意两个变量的字母表示必须一致,后面也是如此)
显示回归分析
4、view\representations
显示回归分析结果,即公式
散点图
输入数据:单击“Quick”,选择“Empty Group”,出现“Group”窗口,将第一列取
名为gdpp,第二列取名为consp,然后输入数据
(obs在1上面,在第二个obs中输入两个变量名,数据会自动录入)
(二)绘制散点图:
单击“Quick”,选择“Graph”, 在“Graph”里选择“Scatter ”,点击“OK”,出现“Series List”对话框,输入gdpp consp(有空格),点击“OK”。
出现散点图。
如下图:
如果要模型做出来,则在下图状态下
选择view——>graph——>scatter——>scattered with regression,点击ok,即出现。
eviews各模块英文翻译(1)

1、主界面:File——文件Edit——编辑Object——对象View——查看Proc——过程(处理)Quick——快速Options——选项Window——窗口Help——帮助2、File——文件New——新建Open——打开Save——保存Save As——另存为、Close——关闭Import——输入Export——出口Print——打印Print Setup——打印设置Run——运行Exit——退出Undo——撤销Cut——剪切Copy——复制Paste——粘贴Paste Special——选择性粘贴Delete——删除Find——查找Replace——替换Next——下一个Insert Text File——插入文本文件4、Object——对象New Object——新对象Fetch From DB——从数据库中获取···Store to DB——储存在数据库中···Copy Object——复制对象Name——命名Delete——删除Freeze Output——冻结结果Print——打印View Options——查看选项Sample——样本Generate Series——生成序列Show——展示Graph——图表Empty Group(Edit Series)——空集Series Statistics——序列统计Group Statistics——集合统计Estimate Equation——估计方程Estimate VAR——估计VAR6、Options——选项General Options——常规选项Graphics defaults——默认图像Database Registry——数据库注册表后续的会陆续上传··。
Eviews软件基本操作
Eviews 软件基本操作一、工作文件及建立(一)主窗口简介启动Eviews 软件,进入主窗口。
如下图所示:1、标题栏:窗口的顶部是标题栏。
2、菜单栏:标题栏下是菜单栏。
菜单栏上共有9个选项: File ,Edit ,Objects ,View ,Procs ,Quick ,Options ,Window ,Help 。
用鼠标点击可打开下拉式菜单,显示该部分的具体功能。
File 包含一些文件的常用操作命令。
如:建立(New )、打开(open )、保存(Save /Save As )、关闭(Close )、读入(Import )、读出(Export )、打印(Print )、运行程序(Run )、退出 Eviews (Exit )。
常用的有新建工作文件,打开工作文件,保存工作文件,输入输出数据文件。
Edit 一般情况下只有复制功能,即拷贝(Copy )和粘贴(Paste )功能。
在某些特殊的窗口,该菜单项还包括剪切(Cut )、删除(Delete )、查找(Find )、替换(Replace )等操作。
objects 提供有关对象的基本操作。
包括建立新对象(New Objects )、从数据库获取使新对象(Fetch /Update From DB )、将工作文件中的对象存储到数据库(Store to DB )、复制对象(Copy Selected )、重命名(Rename )、删除(Delete )。
View 其功能随窗口的不同而变化,主要涉及变量的各种查看方式。
Procs 它的功能也是随窗口的不同而变化,其主要功能为变量的预算过程。
Quick 提供快速统计分析过程。
Options 系统参数设定选项。
Window 在使用Eviews 的过程中将会有多个子窗口。
该菜单提供子窗口的切换和关闭功能。
命令窗信息栏路径主显示窗口图1主窗口Help帮助功能。
提供索引方式和目录方式的帮助功能。
3、命令窗口:菜单栏下是命令窗口。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Appendix D. Estimation and Solution OptionsEViews estimates the parameters of a wide variety of nonlinear models, from nonlinear least squares equations, to maximum likelihood models, to GMM specifications. These types of nonlinear estimation problems do not have closed form solutions and must be estimatedusing iterative methods. EViews also solves systems of non-linear equations. Again, there are no closed form solutions to these problems, and EViews must use an iterative method to obtain a solution.Below, we provide details on the algorithms used by EViews in dealing with nonlinear esti-mation and solution, and the optional settings that we provide to allow you to control esti-mation.Our discussion here is necessarily brief. For additional details, we direct you to the quitereadable discussions in Press, et al. (1992), Quandt (1983), Thisted (1988), and Amemiya (1983).Setting Estimation OptionsWhen you estimate an equation in EViews, you enter specification information into theSpecification tab of the Equation Estimation dialog. Clicking on the Options tab displays a dialog that allows you to set various options to control the estimation procedure. The con-tents of the dialog will differ depending upon the options available for a particular estima-tion procedure.The default settings for the options will be taken from the global options (“EstimationDefaults” on page767), or from the options used previously to estimate the object.The Options tab for binarymodels is depicted here. Forother estimator and estimationtechniques (e.g. systems) thedialog will differ to reflect thedifferent estimation optionsthat are available.Starting Coefficient Val-uesIterative estimation proceduresrequire starting values for thecoefficients of the model. Thereare no general rules for select-626—Appendix D. Estimation and Solution Optionsing starting values for parameters. Obviously, the closer to the true values, the better, so if you have reasonable guesses for parameter values, these can be useful. In some cases, you can obtain starting values by estimating a restricted version of the model. In general, how-ever, you may have to experiment to find good starting values.EViews follows three basic rules for selecting starting values:•For nonlinear least squares type problems, EViews uses the values in the coefficient vector at the time you begin the estimation procedure as starting values.•For system estimators and ARCH, EViews uses starting values based upon preliminary single equation OLS or TSLS estimation. In the dialogs for these estimators, the drop-down menu for setting starting values will not appear.•For selected estimation techniques (binary, ordered, count, censored and truncated), EViews has built-in algorithms for determining the starting values using specific infor-mation about the objective function. These will be labeled in the Starting coefficientvalues combo box as EViews supplied.In the latter two cases, you may change this default behavior by selecting an item from the Starting coefficient values drop down menu. Y ou may choose fractions of the default start-ing values, zero, or arbitrary User Supplied.If you select User Supplied, EViews will use the values stored in the C coefficient vector at the time of estimation as starting values. T o see the starting values, double click on the coef-ficient vector in the workfile directory. If the values appear to be reasonable, you can close the window and proceed with estimating your model.If you wish to change the starting values, first make certain that the spreadsheet view of the coefficient vector is in edit mode, then enter the coefficient values. When you are finished setting the initial values, close the coefficient vector window and estimate your model.Y ou may also set starting coefficient values from the command window using the PARAM command. Simply enter the P ARAM keyword, followed by pairs of coefficients and theirdesired values:param c(1) 153 c(2) .68 c(3) .15sets C(1)=153, C(2)=.68, and C(3)=.15. All of the other elements of the coefficient vector are left unchanged.Lastly, if you want to use estimated coefficients from another equation, select Proc/Update Coefs from Equation from the equation window toolbar.For nonlinear least squares problems or situations where you specify the starting values,bear in mind that:Setting Estimation Options—627•The objective function must be defined at the starting values. For example, if your objective function contains the expression 1/C(1), then you cannot set C(1) to zero. Similarly, if the objective function contains LOG(C(2)), then C(2) must be greater than zero.• A poor choice of starting values may cause the nonlinear least squares algorithm to fail. EViews begins nonlinear estimation by taking derivatives of the objective func-tion with respect to the parameters, evaluated at these values. If these derivatives are not well behaved, the algorithm may be unable to proceed.If, for example, the starting values are such that the derivatives are all zero, you will immediately see an error message indicating that EViews has encountered a “Near Singular Matrix”, and the estimation procedure will stop.•Unless the objective function is globally concave, iterative algorithms may stop at a local optimum. There will generally be no evidence of this fact in any of the output from estimation.If you are concerned with the possibility of local optima, you may wish to select vari-ous starting values and see whether the estimates converge to the same values. One common suggestion is to estimate the model and then randomly alter each of the esti-mated coefficients by some percentage, then use these new coefficients as starting val-ues in estimation.Iteration and Convergence OptionsThere are two common iteration stopping rules: based on the change in the objective func-tion, or based on the change in parameters. The convergence rule used in EViews is based upon changes in the parameter values. This rule is generally conservative, since the change in the objective function may be quite small as we approach the optimum (this is how we choose the direction), while the parameters may still be changing.The exact rule in EViews is based on comparing the norm of the change in the parameters with the norm of the current parameter values. More specifically, the convergence test is:(40.13)where is the vector of parameters, is the 2-norm of , and tol is the specified toler-ance. However, before taking the norms, each parameter is scaled based on the largestobserved norm across iterations of the derivative of the least squares residuals with respect to that parameter. This automatic scaling system makes the convergence criteria more robust to changes in the scale of the data, but does mean that restarting the optimization from the final converged values may cause additional iterations to take place, due to slight changes in the automatic scaling value when started from the new parameter values.v i 1+()v i ()–2v i ()2----------------------------------tol £v x 2x628—Appendix D. Estimation and Solution OptionsThe estimation process achieves convergence if the stopping rule is reached using the toler-ance specified in the Convergence edit box of the Estimation Dialog or the EstimationOptions Dialog. By default, the box will be filled with the tolerance value specified in the global estimation options, or if the estimation object has previously been estimated, it will be filled with the convergence value specified for the last set of estimates.EViews may stop iterating even when convergence is not achieved. This can happen for two reasons. First, the number of iterations may have reached the prespecified upper bound. In this case, you should reset the maximum number of iterations to a larger number and try iterating until convergence is achieved.Second, EViews may issue an error message indicating a “Failure to improve”after a number of iterations. This means that even though the parameters continue to change, EViews could not find a direction or step size that improves the objective function. This can happen when the objective function is ill-behaved; you should make certain that your model is identified.Y ou might also try other starting values to see if you can approach the optimum from other directions.Lastly, EViews may converge, but warn you that there is a singularity and that the coeffi-cients are not unique. In this case, EViews will not report standard errors or t-statistics for the coefficient estimates.Derivative Computation OptionsIn many EViews estimation procedures, you can specify the form of the function for themean equation. For example, when estimating a regression model, you may specify an arbi-trary nonlinear expression in the coefficients. In these cases, when estimating the model, EViews will compute derivatives of the user-specified function.EViews uses two techniques for evaluating derivatives: numeric (finite difference) and ana-lytic. The approach that is used depends upon the nature of the optimization problem and any user-defined settings:•In most cases, EViews offers the user the choice of computing either analytic or numeric derivatives. By default, EViews will fill the options dialog with the globalestimation settings. If the Use numeric only setting is chosen, EViews will only com-pute the derivatives using finite difference methods. If this setting is not checked,EViews will attempt to compute analytic derivatives, and will use numeric derivativesonly where necessary.•EViews will ignore the numeric derivative setting and use an analytic derivative whenever a coefficient derivative is a constant value.•For some procedures where the range of specifications allowed is limited (e.g., V ARs, pools), EViews always uses analytic first and/or second derivatives, whatever the val-ues of these settings.Optimization Algorithms—629•The derivatives with respect to the AR coefficients in an ARMA specification are always computed analytically while those with respect to the MA coefficients arecomputed numerically.•In a limited number of cases, EViews will always use numeric derivatives. For exam-ple, selected GARCH (see “Derivative Methods” on page192) and state space modelsalways use numeric derivatives. As noted above, MA coefficient derivatives arealways computed numerically.•Logl objects always use numeric derivatives unless you provide the analytic deriva-tives in the specification.Where relevant, the estimationoptions dialog allows you tocontrol the method of takingderivatives. For example, theoptions dialog for standardregression allows you to over-ride the use of EViews analyticderivatives, and to choosebetween favoring speed oraccuracy in the computation ofany numeric derivatives (notethat the additional LS and TSLSoptions are discussed in detailin Chapter25. “AdditionalRegression Methods,” begin-ning on page23).Computing the more accurate numeric derivatives requires additional objective functionevaluations. While the algorithms may change in future versions, at present, EViews com-putes numeric derivatives using either a one-sided finite difference (favor speed), or using a four-point routine using Richardson extrapolation (favor precision). Additional details are provided in Kincaid and Cheney (1996).Analytic derivatives will often be faster and more accurate than numeric derivatives, espe-cially if the analytic derivatives have been simplified and carefully optimized to removecommon subexpressions. Numeric derivatives will sometimes involve fewer floating point operations than analytic, and in these circumstances, may be faster.Optimization AlgorithmsGiven the importance of the proper setting of EViews estimation options, it may prove useful to review briefly various basic optimization algorithms used in nonlinear estimation. Recall630—Appendix D. Estimation and Solution Optionsthat the problem faced in non-linear estimation is to find the values of parameters that optimize (maximize or minimize) an objective function .Iterative optimization algorithms work by taking an initial set of values for the parameters, say , then performing calculations based on these values to obtain a better set of param-eter values, . This process is repeated for , and so on until the objective func-tion no longer improves between iterations.There are three main parts to the optimization process: (1) obtaining the initial parameter values, (2) updating the candidate parameter vector at each iteration, and (3) determining when we have reached the optimum.If the objective function is globally concave so that there is a single maximum, any algo-rithm which improves the parameter vector at each iteration will eventually find this maxi-mum (assuming that the size of the steps taken does not become negligible). If the objective function is not globally concave, different algorithms may find different local maxima, but all iterative algorithms will suffer from the same problem of being unable to tell apart a local and a global maximum.The main thing that distinguishes different algorithms is how quickly they find the maxi-mum. Unfortunately, there are no hard and fast rules. For some problems, one method may be faster, for other problems it may not. EViews provides different algorithms, and will often let you choose which method you would like to use.The following sections outline these methods. The algorithms used in EViews may bebroadly classified into three types: second derivative methods, first derivative methods, and derivative free methods. EViews’ second derivative methods evaluate current parameter val-ues and the first and second derivatives of the objective function for every observation. First derivative methods use only the first derivatives of the objective function during the itera-tion process. As the name suggests, derivative free methods do not compute derivatives.Second Derivative MethodsFor binary, ordered, censored, and count models, EViews can estimate the model using Newton-Raphson or quadratic hill-climbing.Newton-RaphsonCandidate values for the parameters may be obtained using the method of Newton-Raphson by linearizing the first order conditions at the current parameter values, :(40.14)where is the gradient vector , and is the Hessian matrix .v F v ()v 0()v 1()v 2()v 3()F v v 1()∂F ∂v §v i ()g i ()H i ()v i 1+()v i ()–()+0=v i 1+()v i ()H i ()1–g i ()–=g ∂F ∂v §H ∂2F ∂v 2§Optimization Algorithms—631If the function is quadratic, Newton-Raphson will find the maximum in a single iteration. If the function is not quadratic, the success of the algorithm will depend on how well a local quadratic approximation captures the shape of the function.Quadratic hill-climbing (Goldfeld-Quandt)This method, which is a straightforward variation on Newton-Raphson, is sometimes attrib-uted to Goldfeld and Quandt. Quadratic hill-climbing modifies the Newton-Raphson algo-rithm by adding a correction matrix (or ridge factor) to the Hessian. The quadratic hill-climbing updating algorithm is given by:(40.15)where is the identity matrix and is a positive number that is chosen by the algorithm.The effect of this modification is to push the parameter estimates in the direction of the gra-dient vector. The idea is that when we are far from the maximum, the local quadraticapproximation to the function may be a poor guide to its overall shape, so we may be better off simply following the gradient. The correction may provide better performance at loca-tions far from the optimum, and allows for computation of the direction vector in cases where the Hessian is near singular.For models which may be estimated using second derivative methods, EViews uses qua-dratic hill-climbing as its default method. Y ou may elect to use traditional Newton-Raphson, or the first derivative methods described below, by selecting the desired algorithm in the Options menu.Note that asymptotic standard errors are always computed from the unmodified Hessian once convergence is achieved.First Derivative MethodsSecond derivative methods may be computationally costly since we need to evaluate the elements of the second derivative matrix at every iteration. Moreover, second derivatives calculated may be difficult to compute accurately. An alternative is to employ methods which require only the first derivatives of the objective function at the parameter values.For general nonlinear models (nonlinear least squares, ARCH and GARCH, nonlinear system estimators, GMM, State Space), EViews provides two first derivative methods: Gauss-New-ton/BHHH or Marquardt.Gauss-Newton/BHHHThis algorithm follows Newton-Raphson, but replaces the negative of the Hessian by an approximation formed from the sum of the outer product of the gradient vectors for each observation’s contribution to the objective function. For least squares and log likelihood v i 1+()v i ()H ˜i ()1–g i ()–=where H ˜i ()–H i ()–a I +=I a k k 1+()2§632—Appendix D. Estimation and Solution Optionsfunctions, this approximation is asymptotically equivalent to the actual Hessian when evalu-ated at the parameter values which maximize the function. When evaluated away from the maximum, this approximation may be quite poor.The algorithm is referred to as Gauss-Newton for general nonlinear least squares problems, and often attributed to Berndt, Hall, Hall and Hausman (BHHH ) for maximum likelihood problems.The advantages of approximating the negative Hessian by the outer product of the gradient are that (1) we need to evaluate only the first derivatives, and (2) the outer product is neces-sarily positive semi-definite. The disadvantage is that, away from the maximum, thisapproximation may provide a poor guide to the overall shape of the function, so that more iterations may be needed for convergence.MarquardtThe Marquardt algorithm modifies the Gauss-Newton algorithm in exactly the same manner as quadratic hill climbing modifies the Newton-Raphson method (by adding a correction matrix (or ridge factor) to the Hessian approximation).The ridge correction handles numerical problems when the outer product is near singular and may improve the convergence rate. As above, the algorithm pushes the updated param-eter values in the direction of the gradient.For models which may be estimated using first derivative methods, EViews uses Marquardt as its default method. Y ou may elect to use traditional Gauss-Newton via the Options menu.Note that asymptotic standard errors are always computed from the unmodified (Gauss-Newton) Hessian approximation once convergence is achieved.Choosing the step sizeAt each iteration, we can search along the given direction for the optimal step size. EViews performs a simple trial-and-error search at each iteration to determine a step size that improves the objective function. This procedure is sometimes referred to as squeezing or stretching .Note that while EViews will make a crude attempt to find a good step, is not actually optimized at each iteration since the computation of the direction vector is often moreimportant than the choice of the step size. It is possible, however, that EViews will be unable to find a step size that improves the objective function. In this case, EViews will issue an error message.EViews also performs a crude trial-and-error search to determine the scale factor for Mar-quardt and quadratic hill-climbing methods.l l aNonlinear Equation Solution Methods—633Derivative free methodsOther optimization routines do not require the computation of derivatives. The grid search is a leading example. Grid search simply computes the objective function on a grid of parame-ter values and chooses the parameters with the highest values. Grid search is computation-ally costly, especially for multi-parameter models.EViews uses (a version of) grid search for the exponential smoothing routine.Nonlinear Equation Solution MethodsWhen solving a nonlinear equation system, EViews first analyzes the system to determine if the system can be separated into two or more blocks of equations which can be solved sequentially rather than simultaneously. Technically, this is done by using a graph represen-tation of the equation system where each variable is a vertex and each equation provides a set of edges. A well known algorithm from graph theory is then used to find the strongly connected components of the directed graph.Once the blocks have been determined, each block is solved for in turn. If the block contains no simultaneity, each equation in the block is simply evaluated once to obtain values for each of the variables.If a block contains simultaneity, the equations in that block are solved by either a Gauss-Seidel or Newton method, depending on how the solver options have been set.Gauss-SeidelBy default, EViews uses the Gauss-Seidel method when solving systems of nonlinear equa-tions. Suppose the system of equations is given by:(40.16)where are the endogenous variables and are the exogenous variables.The problem is to find a fixed point such that . Gauss-Seidel employs an itera-tive updating rule of the form:.(40.17)to find the solution. At each iteration, EViews solves the equations in the order that they appear in the model. If an endogenous variable that has already been solved for in that iter-ation appears later in some other equation, EViews uses the value as solved in that iteration. For example, the k -th variable in the i -th iteration is solved by:x 1f 1x 1x 2ºx N z ,,,,()=x 2f 2x 1x 2ºx N z ,,,,()=x N f N x 1x 2ºx N z ,,,,()=x z x f x z ,()=x i 1+()f x i ()z ,()=634—Appendix D. Estimation and Solution Options.(40.18)The performance of the Gauss-Seidel method can be affected be reordering of the equations. If the Gauss-Seidel method converges slowly or fails to converge, you should try moving the equations with relatively few and unimportant right-hand side endogenous variables so that they appear early in the model.Newton's MethodNewton’s method for solving a system of nonlinear equations consists of repeatedly solving a local linear approximation to the system.Consider the system of equations written in implicit form:(40.19)where is the set of equations, is the vector of endogenous variables and is the vector of exogenous variables.In Newton’s method, we take a linear approximation to the system around some values and :(40.20)and then use this approximation to construct an iterative procedure for updating our current guess for :(40.21)where raising to the power of -1 denotes matrix inversion.The procedure is repeated until the changes in between periods are smaller than a speci-fied tolerance.Note that in contrast to Gauss-Seidel, the ordering of equations under Newton does not affect the rate of convergence of the algorithm.Broyden's MethodBroyden's Method is a modification of Newton's method which tries to decrease the calcula-tional cost of each iteration by using an approximation to the derivatives of the equation sys-tem rather than the true derivatives of the equation system when calculating the Newton step. That is, at each iteration, Broyden's method takes a step:(40.22)x k i ()f k x 1i ()x 2i ()ºx k 1–i ()x k i 1–()x k 1+i 1–()ºx ,,,N i 1–()z ,,,,,()=F x z ,()0=F x z x ∗z ∗F x z ,()F x ∗z ∗,()x ∂∂F x ∗z ∗,()x D +0==x x t 1+x t x ∂∂F x t z ∗,()1–F x t z ∗,()–=x x t 1+x t J t 1–F x t z ∗,()–=References—635where is the current approximation to the matrix of derivatives of the equation system.As well as updating the value of at each iteration, Broyden's method also updates the existing Jacobian approximation, , at each iteration based on the difference between the observed change in the residuals of the equation system and the change in the residuals pre-dicted by a linear approximation to the equation system based on the current Jacobianapproximation.In particular, Broyden's method uses the following equation to update :(40.23)where . This update has a number of desirable properties (see Chapter 8 of Dennis and Schnabel (1983) for details).In EViews, the Jacobian approximation is initialized by taking the true derivatives of the equation system at the starting values of . The updating procedure given above is repeated until changes in between periods become smaller than a specified tolerance. In some cases the method may stall before reaching a solution, in which case a fresh set of deriva-tives of the equation system is taken at the current values of , and the updating is contin-ued using these derivatives as the new Jacobian approximation.Broyden's method shares many of the properties of Newton's method including the fact that it is not dependent on the ordering of equations in the system and that it will generally con-verge quickly in the vicinity of a solution. In comparison to Newton's method, Broyden's method will typically take less time to perform each iteration, but may take more iterations to converge to a solution. In most cases Broyden's method will take less overall time to solve a system than Newton's method, but the relative performance will depend on the structure of the derivatives of the equation system.ReferencesAmemiya, Takeshi (1983). “Nonlinear Regression Models,” Chapter 6 in Z. Griliches and M. D. Intriliga-tor (eds.), Handbook of Econometrics, Volume 1, Amsterdam: Elsevier Science Publishers B.V . Dennis, J. E. and R. B. Schnabel (1983). “Secant Methods for Systems of Nonlinear Equations,” Numeri-cal Methods for Unconstrained Optimization and Nonlinear Equations . Prentice-Hall, London.Kincaid, David, and Ward Cheney (1996). Numerical Analysis , 2nd edition , Pacific Grove, CA: Brooks/Cole Publishing Company.Press, W . H., S. A. T eukolsky, W . T. Vetterling, and B. P. Flannery (1992). Numerical Recipes in C , 2ndedition , Cambridge University Press.Quandt, Richard E. (1983). “Computational Problems and Methods,” Chapter 12 in Z. Griliches and M.D. Intriligator (eds.), Handbook of Econometrics, Volume 1, Amsterdam: Elsevier Science Publish-ers B.V .Thisted, Ronald A. (1988). Elements of Statistical Computing , New Y ork: Chapman and Hall.J t x J t J J t 1+J t F x t 1+z ∗,()F x t z ∗,()–J t D x –()D x ¢D x ¢D x ----------------------------------------------------------------------------------------+=D x x t 1+x t –=x x x。
