材料力学课后作业5-11章
材料力学课后习题答案5章

∑ Fy = 0,FS左 + F + qdx − FS右 = 0
保留有限量,略去微量 qdx 后,得
FS右 − FS左 = F 为了更一般地反映 F 作用处剪力的突变情况(把向下的 F 也包括在内),可将上式改写为
FS右 − FS左 = F
(a)
1
仍据题图 a,由
∑MC
= 0,M 右
−
F
(
dx 2
5-7 .........................................................................................................................................................3
5-11 .....................................................................................................................................................10
5-13 .....................................................................................................................................................11
− Me
−
qdx(
dx 2
)
−
FS左
0
保留有限量,略去一阶和二阶微量后,得
M右 −M左 = Me
为了更一般地反映 M e 作用处弯矩的突变情况(把逆钟向的 M e 也包括在内),可将上式改写
材料力学课后答案

由平衡方程,解得:
FBy 5KN; M B 13KN m
微分法画弯矩图
( M B 13KN m; M C M C 3KN m; M D 0)
2.根据强度要求确定 b
max WZ 2 bh 2 3 WZ b 6 3 M
弯矩图
M
(+)
x
3.绘制挠曲轴略图并计算wmax, A , B 令 dw 0 得 x l (0 x l ) 2 dx 所以 wmax w x l
2
挠曲轴略图
w
5ql 4 384 EI
x0
(-)
B
ql 3 24 EI
x
由式(3)知 A
max
M max ymax 176MPa IZ
max
M WZ
K
M max yK 132MPa IZ
3
5-5.图示简支梁,由 NO18 工字钢制成,在集度为q的均匀载荷作用下测得横截 4 面C底边的纵向正应变 =3.0 10 ,试计算梁内的最大弯曲正应力,已知刚的弹 FAy FBy 性模量E=200GPa,a=1m。
M yA Wy 6 M yA M zA 6M zA Wz 2b b 2 b (2b) 2
由 max 解得 b 35.6mm 故
h 2b 71.2mm
14
2.截面为圆形,确定d 由分析图及叠加原理可知: 在1,3区边缘某点分别有最大拉应力,最大压应力 其值均为:
I Z I Z 1 2 I Z 2 1.02 104 m4
2.画弯矩图 由平衡方程得 微分法画弯矩图
FCy 10KN; M C 10KN m
材料力学习题

材料力学作业册学院:专业:年级:班级:学号:姓名:前言本作业题册是为适应当前我校教学特色而统一筛选出来的题集,入选题目共计72个,教师可根据学时情况有选择性的布置作业。
本题册中列出的题目仅是学习课程的最基本的作业要求,老师根据情况可适当增加部分作业,部分学生如果有考研或者其他方面更高的学习要求,请继续训练其他题目。
本题册仅用于学生课程训练之练习,任何人不得将其用于商业目的,违者将追究其法律责任。
由于时间仓促,并限于编者水平有限,缺点和错误在所难免,恳请大家提出修改建议。
王钦亭wangqt@ 2013年2月27日目录第一章绪论 (1)第二章拉伸与压缩 (2)第三章扭转 (7)第四章弯曲应力 (11)第五章弯曲变形 (18)第六章简单超静定问题 (20)第七章应力状态与强度理论 (25)第八章组合变形与连接件计算 (32)第九章压杆稳定 (36)第十章能量法 (41)第十一章动荷载.交变应力 (49)附录I 截面的几何性质 (53)第一章绪论1-1 材料力学的中所讲的构件失效是指哪三方面的失效?1-2 可变形固体的基本假设有哪些?1-3 材料力学中研究的“杆”,有什么样的几何特征?1-4 材料力学中,杆件的基本变形有哪些?第二章 拉伸与压缩2-1(SXFV5-2-1)试求图示各杆1-1和2-2横截面上的轴力,并作轴力图。
2-2(SXFV5-2-2)一打入地基内的木桩如图所示,沿杆轴单位长度的摩擦力为2f kx (k 为常数),试作木桩的轴力图。
A2-3(SXFV5-2-3)石砌桥墩的墩身高=10 m l ,其横截面尺寸如图所示。
荷载 1 000 kN F =,材料的密度33=2.3510 kg/m ρ⨯。
试求墩身底部横截面上的压应力。
2-4(SXFV5-2-6)一木桩受力如图所示。
柱的横截面为边长200 mm 的正方形,材料可认为符合胡克定律,其纵向弹性模量10 GPa E =。
如不计柱的自重,试求: (1)作轴力图;(2)各段柱横截面上的应力; (3)各段柱的纵向线应变; (4)柱端A 的位移。
材料力学课后作业5-11章
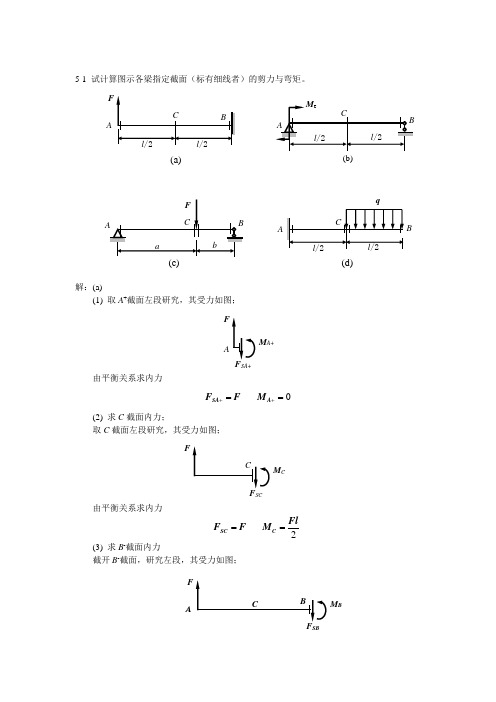
5-1 试计算图示各梁指定截面(标有细线者)的剪力与弯矩。
解:(a)(1) 取A +截面左段研究,其受力如图;由平衡关系求内力0SA A F F M ++==(2) 求C 截面内力;取C 截面左段研究,其受力如图;由平衡关系求内力2SC C Fl F F M ==(3) 求B -截面内力截开B -截面,研究左段,其受力如图;qAC Bl /2l /2(d)A M e (b)BCl /2l /2a B C Ab (c)F C B l /2 l /2 (a)FFA F SA+M A+C FF SCM CACB F F SBM B由平衡关系求内力SB B F F M Fl ==(b)(1) 求A 、B 处约束反力eA B M R R l==(2) 求A +截面内力;取A +截面左段研究,其受力如图;eSA A A e M F R M M l++=-=-= (3) 求C 截面内力;取C 截面左段研究,其受力如图;22e e SC A A e A M Ml F R M M R l +=-=-=-⨯= (4) 求B 截面内力;取B 截面右段研究,其受力如图;0eSB B B M F R M l=-=-= (c)(1) 求A 、B 处约束反力R AA M eB CR BA M e R AF SA M A+A M eC R AF SCM CB R BF SBM BR AB CAF R BA B Fb FaR R a b a b==++ (2) 求A +截面内力;取A +截面左段研究,其受力如图;0SA A A FbF R M a b++===+ (3) 求C -截面内力;取C -截面左段研究,其受力如图;SC A C A Fb FabF R M R a a b a b--===⨯=++ (4) 求C +截面内力;取C +截面右段研究,其受力如图;SC B C B Fa FabF R M R b a b a b++=-=-=⨯=++ (5) 求B -截面内力;取B -截面右段研究,其受力如图;0SB B B FaF R M a b--=-=-=+ (d)(1) 求A +截面内力取A +截面右段研究,其受力如图;A R A F SA+M A+ R A A CF SC-M C- B CR BF SC+M C+ B R B F SB-M B- qACBF SA+M A+-233 22248SA A l ql l l ql F q M q ++=⨯==-⨯⨯=-(3) 求C -截面内力;取C -截面右段研究,其受力如图;222248SC C l ql l l ql F q M q --=⨯==-⨯⨯=-(4) 求C +截面内力;取C +截面右段研究,其受力如图;222248SC C l ql l l ql F q M q ++=⨯==-⨯⨯=-(5) 求B -截面内力;取B -截面右段研究,其受力如图;0 0SB B F M --==5-6qCBF SC- M C-qCBF SC+ M C+BF SB-M B--5-85-116-4 图示悬臂梁,横截面为矩形,承受载荷F 1与F 2作用,且F 1=2F 2=5 kN ,试计算梁内的最大弯曲正应力,及该应力所在截面上K 点处的弯曲正应力。
第五章 习题解答(材料力学课件)-PPT文档资料

换后最大扭矩将由1.5kN m减小为1kN m
4. 解 :
AC
AB
3
BC
T1 l 1 T 2 l 2 G Ip G Ip
3
1.5 1 0 1.2 0 .5 1 0 0 .8 9 4 80 10 0 .0 5 32 0 .0 4 4 8 4 ra d A、 B两 轮 互 换 位 置 后 , 轴 两 端 的 相 对 扭 转 角 为 1.0 1 0 1.2 0 .5 1 0 0 .8 9 80 10 0 .0 5 4 32 0 .0 1 6 3 ra d
m
x
l
XT5TU1
1 0 .解 : 轴 的 扭 矩 图 如 下 图 , 最 大 扭 矩 T . k N m m a x 05 T m a x 由 强 度 条 件 m [] 得 轴 的 直 径 a x 3 d 1 6 1 6 T m a x 3 d 5 03 . m m []
m
A
B
m
C
D
mD
即
1 2m 解 得 m 05 . 5 7 m D 4 4 A 端 的 反 力 偶 m m .4 3m A m D 04
4
(m ) 4m D m D 2
m D 2 0
内、外层横截面上剪应力的计算公式分别为 T1 m T2 2m 1 , 2 I p1 I p1 2 I p 2 I p2 I p1 2 I p 2
1 9 .解 : 此 为 一 次 静 不 定 问 题 。 解 除端 D 约 束 , 代 之 以 反 力 偶 m D 由 变 形 协 调 条 件 A A 0 , 得 D B B C C D ( m ml )A m m D B Dl B C Dl C D 0 G IpA G IpB IpC B C G D
材料力学第五版孙训方版课后习题答案高等教育出版社

材料力学 高等教育出版社 孙训方[习题2-2]一打入基地内的木桩如图所示,杆轴单位长度的摩擦力f=kx**2,试做木桩的后力图。
解:由题意可得:33233110,,3/()3/(/)ll N fdx F kl F k F l F x Fx l dx F x l =====⎰⎰1有3[习题2-3] 石砌桥墩的墩身高m l 10=,其横截面面尺寸如图所示。
荷载kN F 1000=,材料的密度3/35.2m kg =ρ,试求墩身底部横截面上的压应力。
解:墩身底面的轴力为:g Al F G F N ρ--=+-=)(2-3图)(942.31048.935.210)114.323(10002kN -=⨯⨯⨯⨯+⨯--=墩身底面积:)(14.9)114.323(22m A =⨯+⨯=因为墩为轴向压缩构件,所以其底面上的正应力均匀分布。
MPa kPa m kNA N 34.071.33914.9942.31042-≈-=-==σ[习题2-7] 图示圆锥形杆受轴向拉力作用,试求杆的伸长。
2-7图解:取长度为dx 截离体(微元体)。
则微元体的伸长量为:)()(x EA Fdxl d =∆ ,⎰⎰==∆l lx A dxE F dx x EA F l 00)()( lxr r r r =--121,22112112d x l d d r x l r r r +-=+⋅-=,2211222)(u d x ld d x A ⋅=⎪⎭⎫ ⎝⎛+-=ππ,dx ld d du d x l d d d 2)22(12112-==+- du d d ldx 122-=,)()(22)(221212udu d d l du u d d l x A dx -⋅-=⋅-=ππ 因此,)()(2)()(202100u du d d E Fl x A dx E F dx x EA F l l l l⎰⎰⎰--===∆π lld x l d d d d E Fl u d d E Fl 011221021221)(21)(2⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+--=⎥⎦⎤⎢⎣⎡-=ππ ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+--=21221)(2111221d d l l d d d d E Fl π ⎥⎦⎤⎢⎣⎡--=122122)(2d d d d E Fl π214d Ed Fl π=[习题2-10] 受轴向拉力F 作用的箱形薄壁杆如图所示。
材料力学作业(8-11)

第八章 应力应变状态分析一、选择或填空题1、过受力构件内任一点,取截面的不同方位,各个面上的( )。
A 、正应力相同,切应力不同;B 、正应力不同,切应力相同;C 、正应力相同,切应力相同;D 、正应力不同,切应力不同。
2、在单元体的主平面上( )。
A 、正应力一定最大;B 、正应力一定为零;C 、切应力一定最小;D 、切应力一定为零。
3、图示矩形截面悬臂梁,A-A 为任意横截面,1点位于截面上边缘,3点位于中性层,则1、2、3点的应力状态单元体分别为( )。
A-AA B C4、图示单元体,其最大主应力为( )A 、σ;B 、2σ;C 、3σ;D 、4σ。
5、下面 单元体表示构件A 点的应力状态。
6、图示单元体,如果MPa 30=ασ,则βσ=( ) A 、100Mpa ; B 、50Mpa ; C 、20MPa ; D 、0MPa 。
(C)7、图示单元体应力状态,沿x 方向的线应变εx 可表示为( )A 、Eyσ; B 、)(1y x E μσσ−;C 、)(1x y E μσσ− ;D 、Gτ。
8、图示应力圆对应于单元体( )。
9、已知单元体及应力圆如图所示,σ1所在主平面的法线方向为( )。
A 、n 1;B 、 n 2;C 、n 3;D 、n4。
二、计算题1、已知应力状态如图所示,试用解析法计算图中指定截面上的正应力和切应力。
2、试画图示应力状态的三向应力圆,并求主应力、最大正应力和最大切应力。
3、边长为20mm的钢立方块置于刚性模中,在顶面受力F=14kN作用。
已知材料的泊松比为0.3,求立方体各个面上的正应力。
4、图示矩形截面梁某截面上的弯矩和剪力分别为M=10 kN.m,Q=120 kN。
试绘出截面上1、2、3、4各点的应力状态单元体,并求其主应力。
第九章 强度理论一、选择题或填空题 1、在冬天严寒天气下,水管中的水会受冻而结冰。
根据低温下水管和冰所受力情况可知( )。
A 、冰先破裂而水管完好;B 、水管先破裂而冰完好;C 、冰与水管同时破裂;D 、不一定何者先破裂。
(完整版)材料力学课后习题答案
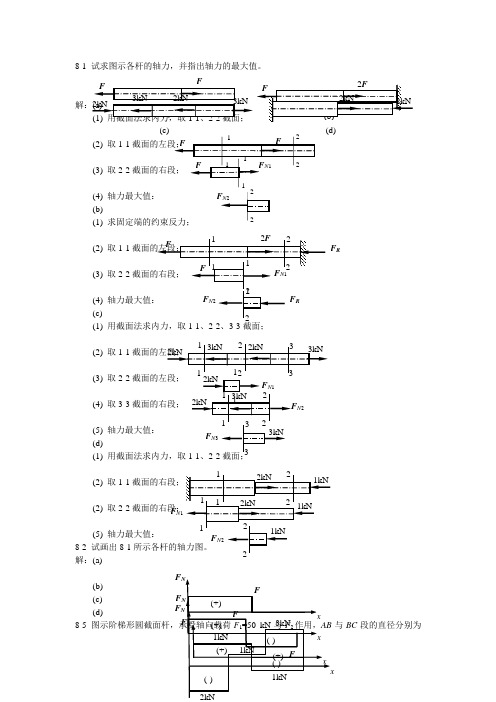
8-1 试求图示各杆的轴力,并指出轴力的最大值。
(2) 取1-1(3) 取2-2(4) 轴力最大值: (b)(1) 求固定端的约束反力; (2) 取1-1(3) 取2-2(4) (c)(1) 用截面法求内力,取1-1、2-2、3-3截面;(2) 取1-1(3) 取2-2 (4) 取3-3截面的右段;(5) 轴力最大值: (d)(1) 用截面法求内力,取1-1、(2) 取1-1(2) 取2-2(5) 轴力最大值: 8-2 试画出8-1解:(a) (b) (c) (d) 8-5与BC 段的直径分别为(c) (d)F RN 2F N 3 F N 1F F Fd 1=20 mm 和d 2=30 mm ,如欲使AB 与BC 段横截面上的正应力相同,试求载荷F 2之值。
解:(1) 用截面法求出(2) 求1-1、2-28-6 题8-5段的直径d 1=40 mm ,如欲使AB 与BC 段横截面上的正应力相同,试求BC 段的直径。
解:(1)用截面法求出1-1、2-2截面的轴力;(2) 求1-1、2-2截面的正应力,利用正应力相同;8-7 图示木杆,承受轴向载荷F =10 kN 作用,杆的横截面面积A =1000 mm 2,粘接面的方位角θ= 450,试计算该截面上的正应力与切应力,并画出应力的方向。
解:(1) (2) 8-14 2=20 mm ,两杆F =80 kN 作用,试校核桁架的强度。
解:(1) 对节点A(2) 列平衡方程 解得: (2) 8-15 图示桁架,杆1A 处承受铅直方向的载荷F 作用,F =50 kN ,钢的许用应力[σS ] =160 MPa ,木的许用应力[σW ] =10 MPa 。
解:(1) 对节点A (2) 84 mm 。
8-16 题8-14解:(1) 由8-14得到的关系;(2) 取[F ]=97.1 kN 。
8-18 图示阶梯形杆A 2=100 mm 2,E =200GPa ,试计算杆AC 的轴向变形 解:(1) (2) AC 8-22 图示桁架,杆1与杆2的横截面面积与材料均相同,在节点A 处承受载荷F 作用。
材料力学作业题解_第5-9章

1
ρ
于是,有
=
M EI EI
M=
代入弯曲正应力公式,得
ρ
σ max =
Mymax Eymax = I ρ
空心圆截面比实心圆截面最大正应力减少了
5.4 矩形截面悬臂梁如图所示,已知 l = 4 m , 确定此梁横截面的尺寸。 解:梁的最大弯矩发生在固定端处,其值为
b 3 = , q = 10 kN/m , [σ ] = 10 MPa 。试 h 5
q A
l
M max =
梁的强度条件
1 2 1 ql = ×10 × 42 =80 (kN ⋅ m) 2 2 M 80 ×106 = = ≤ [σ ] 1 2 W bh 6
m
n
8
m
22
n
13
发生,应加以比较,方可决定割刀内的最大正应力。 n-n 截面
2.5
4
1 WI = × 2.5 × 132 =70.4 (mm3 ) 6
M I = 1× 103 × 8=8 ×103 (N ⋅ mm)
σI =
n-n 截面
M I 8 ×103 = = 114 (MPa ) WI 70.4
− = σ max
C 截面
+ σ max =
10 × 106 ×158 = 26.3 (MPa)<[σ t ]=40 MPa 60.1× 106 10 × 106 × (230 − 158) = 12 (MPa)<[σ c ]=160 MPa 60.1×106
河海大学-材料力学第5章弯曲应力作业参考解答

IZ
=
2 × ( 1 × 60 ×1403 12
+ 60 ×140 × (70 - (76.82 - 50))2 )
+ 1 × 280 ×503 + 280 ×50 × (76.82 - 50 / 2)2 = 9.9´107 mm4 12
(3)b-b 处切应力
t b-b
=
FS
S
* z
Izb
=
27.5kN ´ (60 ´100 ´ 63.18mm3 ) 9.9 ´107 ´108 mm4 ´ 60mm
解:
A
A
z
z
A
z
y
y
y
5-23 求图所示梁的最大容许荷载 q。梁的容许正应力为 3.5MPa,容许切应力为 0.7MPa,胶 结处的容许切应力为 0.35MPa。
yc
解:(1)求内力
最大剪力为 Fs max
=
0.5ql
= 0.3q ,最大弯矩为 M z max
=
1 8
ql
2
= 0.045q 。
(2)确定形心位置及计算惯性矩
£ 0.7 ´106
解得: q £ 3.97kN / m 。
(5) 粘结处应力强度条件
t max
=
Fs
max
S
* z
Izb
=
0.3q ´ 25´ 25´ 25´10-9 3.32 ´10-6 ´ 25´10-3
£ 0.35´106
解得: q £ 6.2kN / m 。
最后容许荷载为 q £ 3.97kN / m 。
第 5 章作业参考解答
本章主要公式
梁平面纯弯曲时曲率与弯矩和弯曲刚度的关系: 1 = M r EI z
《材料力学》第五章课后习题参考答案

错误原因及避免方法
错误原因
1. 对材料力学的基本原理理解不深入,导致选择错误的公式或方法进行 计算。
2. 计算过程中出现数值错误或单位不统一等问题,导致结果偏差较大。
错误原因及避免方法
• 对计算结果缺乏分析和讨论,无法判断其 合理性和准确性。
错误原因及避免方法
01
避免方法
02
03
04
1. 加强对材料力学基本原理 的学习和理解,掌握各种公式 和方法的适用范围和条件。
题目一
分析并比较不同材料在拉伸过程中的力学行为差异。
题目二
讨论材料疲劳破坏的机理及影响因素。
要求
掌握材料在拉伸过程中的应力-应变曲线,理解弹性模量 、屈服强度、抗拉强度等概念,能够运用所学知识分析不 同材料的力学行为。
要求
了解材料疲劳破坏的基本概念,掌握疲劳破坏的机理和影 响因素,能够运用所学知识分析实际工程中的疲劳破坏问 题。
知识点综合运用
弹性力学基础
运用弹性力学的基本原理,分析 材料在弹性阶段的力学行为,计
算弹性模量等参数。
塑性力学基础
运用塑性力学的基本原理,分析材 料在塑性阶段的力学行为,理解屈 服强度、抗拉强度等概念。
疲劳破坏理论
运用疲劳破坏的基本理论,分析材 料在交变应力作用下的力学行为, 讨论疲劳破坏的机理和影响因素。
加强实践应用
除了理论学习外,我还计划通过 实践应用来加深对材料力学的理 解。例如,可以尝试利用所学知 识解决实际工程问题,或者参加 相关的实验和课程设计等。
拓展相关学科领域
材料力学是一门基础学科,与其他学 科领域有着密切的联系。因此,我计 划拓展相关学科领域的学习,如结构 力学、弹性力学等,以便更全面地了 解材料的力学性能和工程应用。
材料力学课后作业
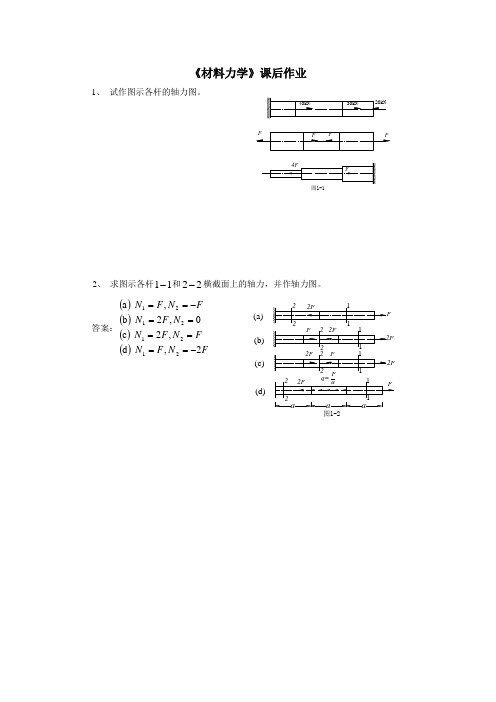
《材料力学》课后作业1、 试作图示各杆的轴力图。
2、 求图示各杆11-和22-横截面上的轴力,并作轴力图。
答案:()()()()FN F N F N F N N F N F N F N 2, d ,2 c 0,2 b , a 21212121-======-==3、 求图示阶梯状直杆横截面11-、22-和33-上的轴力,并作轴力图。
如横截面面积21mm 200=A ,2300=A 答案:25kN,10kN,10kN,20332211==-=-=-=-=σσσN N N4、 图示一混合屋架结构的计算简图。
屋架的上弦用钢筋混凝土制成。
下面的拉杆和中间竖向撑杆用角钢构成,其截面均为两个875⨯的等边角钢。
已知屋面承受集度为kN/m 20=q 的竖直均布荷载。
求拉杆AE 和EG 横截面上的应力。
答案:1-4MPa 8.154MPa,1.159==AE σσ5图,并求端点D 的位移。
答案:EAFlD 3=∆6、 一木柱受力如图所示。
柱的横截面为边长mm 200的正方形,材料可认为符合胡克定律,其弹性模量GPa 100=E 。
如不计柱的自重,试求下列各项:(1)作轴力图;(2)各段柱横截面上的应力; (3)各段柱的纵向线应变; (4)柱的总变形。
答案:()()mm35.1 )4(65.0,1025.0 (3)5.6MPa,5.2 2kN260 1CB 3AC CB -=∆-=⨯-=-=-==-l N AC CB εεσσ最大压力7、 简易起重设备的计算简图如图所示。
已知斜杆AB 用两根不等边角钢44063⨯⨯组成。
如钢的许用应力[]170=σ斜杆AB 是否满足强度条件?答案:MPa 74=AB σ8、力[]MPa 170=σ,试选择AB答案:101002 ⨯∠杆AB9、(1)刚性梁AB 用两根钢杆AC 、BD 悬挂着,受力如图所示。
已知钢杆AC 和BD 的直径分别为m m 251=d 和m m 182=d ,钢的许用应力[]MPa 170=σ,弹性模量GPa 210=E ,试校核钢杆的强度,并计算钢杆的变形AC l ∆、DB l ∆及A 、B 两点的竖直位移A ∆、B ∆。
材料力学作业

材料力学作业Company number:【0089WT-8898YT-W8CCB-BUUT-202108】第一章 绪论1. 试求图示结构m-m 和n-n 两截面上的内力,并指出AB 和BC 两杆的变形属于何类基本变形。
2. 拉伸试样上A ,B 两点的距离l 称为标距。
受拉力作用后,用变形仪量出两点距离的增量为mm l 2105-⨯=∆。
若l 的原长为l =100mm ,试求A 与B 两点间的平均应变m ε。
第二章 轴向拉伸和压缩与剪切 一、选择题1.等直杆受力如图,其横截面面积A=1002mm ,则横截面mk上的正应力为( )。
(A)50MPa(压应力); (B)40MPa(压应力); (C)90MPa(压应力); (D)90MPa(拉应力)。
2.低碳钢拉伸经过冷作硬化后,以下四种指标中哪种得到提高( ): (A)强度极限; (B)比例极限;(C)断面收缩率; (D)伸长率(延伸率)。
3.图示等直杆,杆长为3a ,材料的抗拉刚度为EA ,受力如图。
杆中点横截面的铅垂位移为( )。
(A)0;(B)Pa/(EA);(C)2 Pa/(EA);(D)3 Pa/(EA)。
4.图示铆钉联接,铆钉的挤压应力bs σ是( )。
(A )2P/(2d π); (B )P/2dt;(C)P/2bt; (D)4p/(2d π)。
5.铆钉受力如图,其压力的计算有( )(A )bs σ=p/(td);(B)bs σ=p/(dt/2);(C)bs σ=p/(πdt/2);(D)bs σ=p/(πdt/4)。
6.图示A 和B 的直径都为d,则两面三刀者中最大剪应力为( )(A)4bp/(2d απ); (B)4(αb +)P/(2d απ); (C)4(a b +)P/(2b d π); (D)4αP/(2b d π). 7.图示两木杆(I 和II )连接接头,承受轴向拉力作用,错误的是( ).(A )1-1截面偏心受拉; (B )2-2为受剪面;(C )3-3为挤压面; (D )4-4为挤压面。
材料力学作业习题
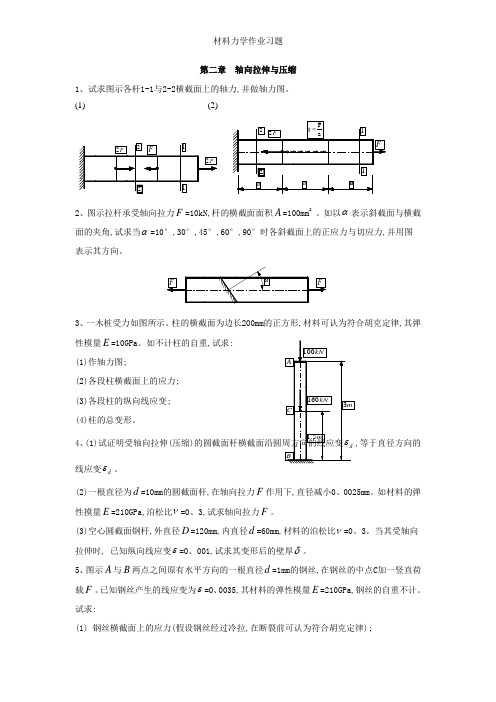
第二章 轴向拉伸与压缩1、试求图示各杆1-1与2-2横截面上的轴力,并做轴力图。
(1) (2)2、图示拉杆承受轴向拉力F =10kN,杆的横截面面积A =100mm 2。
如以α表示斜截面与横截面的夹角,试求当α=10°,30°,45°,60°,90°时各斜截面上的正应力与切应力,并用图表示其方向。
3、一木桩受力如图所示。
柱的横截面为边长200mm 的正方形,材料可认为符合胡克定律,其弹性模量E =10GPa 。
如不计柱的自重,试求:(1)作轴力图;(2)各段柱横截面上的应力; (3)各段柱的纵向线应变;(4)柱的总变形。
4、(1)试证明受轴向拉伸(压缩)等于直径方向的线应变d ε。
(2)一根直径为d =10mm 的圆截面杆,在轴向拉力F 作用下,直径减小0、0025mm 。
如材料的弹性摸量E =210GPa,泊松比ν=0、3,试求轴向拉力F 。
(3)空心圆截面钢杆,外直径D =120mm,内直径d =60mm,材料的泊松比ν=0、3。
当其受轴向拉伸时, 已知纵向线应变ε=0、001,试求其变形后的壁厚δ。
5、图示A 与B 两点之间原有水平方向的一根直径d =1mm 的钢丝,在钢丝的中点C 加一竖直荷载F 。
已知钢丝产生的线应变为ε=0、0035,其材料的弹性模量E =210GPa,钢丝的自重不计。
试求:(1) 钢丝横截面上的应力(假设钢丝经过冷拉,在断裂前可认为符合胡克定律);(2) 钢丝在C点下降的距离∆;(3) 荷载F的值。
6、简易起重设备的计算简图如图所示、一直斜杆AB应用两根63mm×40mm×4mm不等边角钢组[σ=170MPa。
试问在提起重量为P=15kN的重物时,斜杆AB就是否满足强成,钢的许用应力]度条件?7、一结构受力如图所示,杆件AB,AD均由两根等边角钢组成。
已知材料的许用应力[σ=170MPa,试选择杆AB,AD的角钢型号。
材料力学课后习题答案11章

S z (η2 ) = 2.5 × 10 − 5 + (0.010η2 )(0.050 −
S z ,max (η 2 ) = 3.75 × 10 −5 m 3
η2
2
)
τ1 =
FSy S z , max (η1 ) 5 × 103 × 2.5 × 10 −5 N = = 3.75 × 106 Pa = 3.75MPa I zδ 3.333 × 10 − 6 × 0.010m 2 FSy S z , max (η2 ) I zδ 5 × 103 × 3.75 × 10 −5 N = = 5.63 × 106 Pa = 5.63MPa −6 2 3.333 × 10 × 0.010m
2 = 2.5 × 10 −5 + 2.5 × 10 −4 η 2 − 5 × 10 −3 η 2
τ 1, max =
FSy S z , max (η1 ) I zδ 1
=
5 × 103 × 1.25 × 10 −5 N = 3.00 ×106 Pa = 3.00MPa 2.08 × 10 − 6 × 0.010m 2
S z , A (ω ) =
δ
2 yA =
0.010 × 0.050 2 m 3 = 1.25 × 10 − 5 m 3 2
= 1.875 × 10 −4 m 3
据公式
τ (η ) =
得
FS S z (ω ) I zδ
40 × 10 3 × 1.25 × 10 −5 N τA = = 1.499 × 10 6 Pa = 1.499MPa −5 2 3.335 × 10 × 0.010m
[
]
11-6
试指出图示截面的剪心位置。
题 11-6 图 解: (a)双对称截面,剪心与形心重合; (b)角钢形截面,剪心在二边条中心线相交处; (c)T 形截面,剪心在翼缘中心线与腹板中心线相交处。
材料力学作业参考解答

2-3答:以B点为研究对象,由平面汇交力系的平衡条件
2-2求下列结构中指定杆内的应力。已知(a)图中杆的横截面面积A1=A2=1150mm2;
解:(1)分析整体,作示力图
:
(2)取部分分析,示力图见(b)
:
(3)分析铰E,示力图见(c)
:
2-3求下列各杆内的最大正应力。
(3)图(c)为变截面拉杆,上段AB的横截面积为40mm2,下段BC的横截面积为30mm2,杆材料的ρg=78kN/m3。
解:(1)求①、②杆轴力
由平衡方程可以求出:
(2)求杆的变形
(压缩)
(拉伸)
(压缩)
(3)由几何关系: (下降)
2-9答:任一截面上轴力为F,由
得面积为
伸长量为
2-11图示一挡水墙示意图,其中AB杆支承着挡水墙,各部分尺寸均已示于图中。若AB杆为圆截面,材料为松木,其容许应力[σ]=11MPa,试求AB杆所需的直径。
:
(2)由强度条件求
2-14图示AB为刚性杆,长为3a。A端铰接于墙壁上,在C、B两处分别用同材料、同面积的①、②两杆拉住,使AB杆保持水平。在D点作用荷载F后,求两杆内产生的应力。设弹性模量为E,横截面面积为A。
解:
1.本题为超静定问题,
见图(a),设AB杆产生角位移 ,则
,
2.由Hooke定律:
由平衡条件可知:
所以B,C截面相对位移为
3-1试作下列各杆的扭矩图。
3-2一直径d=60mm的圆杆,其两端受外力偶矩T=2kN·m的作用而发生扭转。试求横截面上1,2,3点处的切应力和最大切应变,并在此三点处画出切应力的方向。(G=80GPa)。
解:横截面上切应力大小沿半径线性分布,方向垂直半径
材料力学第五版(刘鸿文主编)课后习题答案课件

材料力学的基本单位
总结词
材料力学的基本单位包括长度单位、质量单 位、时间单位和力的单位。这些单位是国际 单位制中的基本单位,用于描述和度量材料 力学中的各种物理量。
详细描述
在材料力学中,需要用到各种物理量来描述 和度量材料的机械行为。因此,选择合适的 单位非常重要。长度单位通常采用米(m) ,质量单位采用千克(kg),时间单位采 用秒(s),力的单位采用牛顿(N)。这 些单位是国际单位制中的基本单位,具有通 用性和互换性,可以方便地用于描述和度量 材料力学中的各种物理量,如应变、应力、 弹性模量等。同时,这些单位的选择也符合 国际惯例,有利于学术交流和技术合作。
材料力学第五版(刘鸿文 主编)课后习题答案课件
• 材料力学基础概念 • 材料力学基本公式 • 课后习题答案解析 • 材料力学实际应用 • 材料力学的未来发展
01
材料力学基础概念
材料力学定义与性质
总结词
材料力学是研究材料在各种外力作用下 产生的应变、应力、强度、刚度和稳定 性等机械行为的科学。其性质包括材料 的弹性、塑性、脆性等,以及材料的强 度、刚度、稳定性等机械性能。
02
材料力学基本公式
拉伸与压缩
•·
应变公式: $epsilon = frac{Delta L}{L}$,其中 $epsilon$是应变,$Delta L$是长度变化量,$L$是
原始长度。
描述了材料在拉伸和压缩过程中的应力、应变 关系。
应力公式: $sigma = frac{F}{A}$,其中 $sigma$是应力,$F$是作用在物体上的力, $A$是受力面积。
习题二答案解析
问题2
说明应力分析和应变分析在材料力学中的重要性。
答案
材料力学第五版课后习题答案修订版

材料力学第五版课后习题答案Company number:【WTUT-WT88Y-W8BBGB-BWYTT-19998】二、轴向拉伸和压缩2-1试求图示各杆1-1和2-2横截面上的轴力,并作轴力图。
(a)解:;;(b)解:;;(c)解:;。
(d)解:。
2-2 试求图示等直杆横截面1-1,2-2和3-3上的轴力,并作轴力图。
若横截面面积,试求各横截面上的应力。
解:2-3试求图示阶梯状直杆横截面1-1,2-2和3-3上的轴力,并作轴力图。
若横截面面积,,,并求各横截面上的应力。
解:2-4 图示一混合屋架结构的计算简图。
屋架的上弦用钢筋混凝土制成。
下面的拉杆和中间竖向撑杆用角钢构成,其截面均为两个75mm×8mm的等边角钢。
已知屋面承受集度为的竖直均布荷载。
试求拉杆AE和EG横截面上的应力。
解:=1)求内力取I-I分离体得(拉)取节点E为分离体,故(拉)2)求应力75×8等边角钢的面积A=11.5 cm2(拉)(拉)2-5(2-6)图示拉杆承受轴向拉力,杆的横截面面积。
如以表示斜截面与横截面的夹角,试求当,30,45,60,90时各斜截面上的正应力和切应力,并用图表示其方向。
解:2-6(2-8) 一木桩柱受力如图所示。
柱的横截面为边长200mm的正方形,材料可认为符合胡克定律,其弹性模量E=10 GPa。
如不计柱的自重,试求:(1)作轴力图;(2)各段柱横截面上的应力;(3)各段柱的纵向线应变;(4)柱的总变形。
解:(压)(压)2-7(2-9)一根直径、长的圆截面杆,承受轴向拉力,其伸长为。
试求杆横截面上的应力与材料的弹性模量E。
解:2-8(2-11)受轴向拉力F作用的箱形薄壁杆如图所示。
已知该杆材料的弹性常数为E,,试求C与D两点间的距离改变量。
解:横截面上的线应变相同因此2-9(2-12) 图示结构中,AB为水平放置的刚性杆,杆1,2,3材料相同,其弹性模量E=210GPa,已知,,,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5-1 试计算图示各梁指定截面(标有细线者)的剪力与弯矩。
解:(a)(1) 取A +截面左段研究,其受力如图;由平衡关系求内力0SA A F F M ++==(2) 求C 截面内力;取C 截面左段研究,其受力如图;由平衡关系求内力2SC C Fl F F M ==(3) 求B -截面内力截开B -截面,研究左段,其受力如图;qAC Bl /2l /2(d)A M e (b)BCl /2l /2a B C Ab (c)F C B l /2 l /2 (a)FFA F SA+M A+C FF SCM CACB F F SBM B由平衡关系求内力SB B F F M Fl ==(b)(1) 求A 、B 处约束反力eA B M R R l==(2) 求A +截面内力;取A +截面左段研究,其受力如图;eSA A A e M F R M M l++=-=-= (3) 求C 截面内力;取C 截面左段研究,其受力如图;22e e SC A A e A M Ml F R M M R l +=-=-=-⨯= (4) 求B 截面内力;取B 截面右段研究,其受力如图;0eSB B B M F R M l=-=-= (c)(1) 求A 、B 处约束反力R AA M eB CR BA M e R AF SA M A+A M eC R AF SCM CB R BF SBM BR AB CAF R BA B Fb FaR R a b a b==++ (2) 求A +截面内力;取A +截面左段研究,其受力如图;0SA A A FbF R M a b++===+ (3) 求C -截面内力;取C -截面左段研究,其受力如图;SC A C A Fb FabF R M R a a b a b--===⨯=++ (4) 求C +截面内力;取C +截面右段研究,其受力如图;SC B C B Fa FabF R M R b a b a b++=-=-=⨯=++ (5) 求B -截面内力;取B -截面右段研究,其受力如图;0SB B B FaF R M a b--=-=-=+ (d)(1) 求A +截面内力取A +截面右段研究,其受力如图;A R A F SA+M A+ R A A CF SC-M C- B CR BF SC+M C+ B R B F SB-M B- qACBF SA+M A+-233 22248SA A l ql l l ql F q M q ++=⨯==-⨯⨯=-(3) 求C -截面内力;取C -截面右段研究,其受力如图;222248SC C l ql l l ql F q M q --=⨯==-⨯⨯=-(4) 求C +截面内力;取C +截面右段研究,其受力如图;222248SC C l ql l l ql F q M q ++=⨯==-⨯⨯=-(5) 求B -截面内力;取B -截面右段研究,其受力如图;0 0SB B F M --==5-6qCBF SC- M C-qCBF SC+ M C+BF SB-M B--5-85-116-4 图示悬臂梁,横截面为矩形,承受载荷F 1与F 2作用,且F 1=2F 2=5 kN ,试计算梁内的最大弯曲正应力,及该应力所在截面上K 点处的弯曲正应力。
解:(1) 画梁的弯矩图(2) 最大弯矩(位于固定端):max 7.5 M kN(3) 计算应力: 最大应力:(+)7.5kN x M5kN 401m F 1C yF 2 80 Kz30K 点的应力:6-5 图示梁,由No22槽钢制成,弯矩M =80 N.m ,并位于纵向对称面(即x-y 平面)内。
试求梁内的最大弯曲拉应力与最大弯曲压应力。
解:(1) 查表得截面的几何性质:4020.3 79 176 z y mm b mm I cm ===(2) 最大弯曲拉应力(发生在下边缘点处)()30max880(7920.3)10 2.67 17610x M b y MPa I σ-+-⋅-⨯-⨯===⨯ (3) 最大弯曲压应力(发生在上边缘点处)30max88020.3100.92 17610x M y MPa I σ---⋅⨯⨯===⨯6-8 图示简支梁,由No28工字钢制成,在集度为q 的均布载荷作用下,测得横截面C 底边的纵向正应变ε=3.0×10-4,试计算梁内的最大弯曲正应力,已知钢的弹性模量E =200 Gpa ,a =1 m 。
解:(1) 求支反力31 44A B R qa R qa == (2) 画内力图6max max max227.510176 408066ZM M MPabh W σ⨯====⨯6max max 337.51030132 ********K ZM y M y MPa bh I σ⋅⋅⨯⨯====⨯M M yzy 0 b C A B aa qCε R A R B(3) 由胡克定律求得截面C 下边缘点的拉应力为:49max 3.010******* C E MPa σε+-=⋅=⨯⨯⨯=也可以表达为:2max4C C z zqa MW W σ+== (4) 梁内的最大弯曲正应力:2maxmax max 993267.5 8C zz qa M MPa W W σσ+==== 6-16 图示槽形截面悬臂梁,F =10 kN ,M e =70 kNm ,许用拉应力[σ+]=35 MPa ,许用压应力[σ-]=120 MPa ,试校核梁的强度。
解:(1) 截面形心位置及惯性矩:112212(150250)125(100200)15096 (150250)(100200)C A y A y y mm A A ⋅+⋅⨯⋅+-⨯⋅===+⨯+-⨯x(+)x(-)3qa/4F Sqa/4qa 2/49qa 2/32My100 3m F m M e25 25 50 200z CCA3322841505025200(15050)(25)2(25200)(150)12121.0210 zCC C I y y mm ⎡⎤⨯⨯=+⨯⋅-++⨯⋅-⎢⎥⎣⎦=⨯ (2) 画出梁的弯矩图(3) 计算应力A +截面下边缘点处的拉应力及上边缘点处的压应力分别为:68(250)4010(25096)60.4 1.0210C A A zCM y MPa I σ+++⋅-⨯-===⨯ 6840109637.61.0210CA A zCM y MPa I σ-++⋅⨯⨯===⨯ A -截面下边缘点处的压应力为68(250)3010(25096)45.3 1.0210C A A zCM y MPa I σ---⋅-⨯-===⨯ 可见梁内最大拉应力超过许用拉应力,梁不安全。
6-20 图示外伸梁,承受载荷F 作用。
已知载荷F =20KN ,许用应力[σ]=160 Mpa ,试选择工字钢型号。
解:(1) 求约束力:5 25 A B R kNm R kNm ==(2) 画弯矩图:(3) 依据强度条件选择工字钢型号Mx40kNm30kNm(+)(-)10kNmBA F 4m 1m R A RB xM20kNm(-)[]6max max2010160 M MPa W Wσσ⨯==≤=解得:3125 W cm ≥查表,选取No16工字钢8-910-3 图示矩形截面钢杆,用应变片测得其上、下表面的轴向正应变分别为εa=1.0×10-3与εb=0.4×10-3,材料的弹性模量E=210Gpa。
试绘横截面上的正应力分布图。
并求拉力F 及偏心距e的数值。
解:(1) 杆件发生拉弯组合变形,依据胡克定律知:33331.010******** 0.4102101084 a a b b E MPa E MPaσεσε--=⋅=⨯⨯⨯==⋅=⨯⨯⨯=横截面上正应力分布如图:(2) 上下表面的正应力还可表达为:22210 6846a b M N F e F MPa b h W A b hM N F e F MPa b h W A b h σσ⋅=+=+=⋅⋅⋅=-+=-+=⋅⋅将b 、h 数值代入上面二式,求得:18.38 1.785 F mm e mm ==10-9 图示钢质拐轴,承受集中载荷F 作用。
试根据第三强度理论确定轴AB 的直径。
已知载荷F=1kN ,许用应力[σ]=160Mpa 。
解:扭矩弯矩由得:Fεa 525εbFe σb σa所以,10-13 图示齿轮传动轴,用钢制成。
在齿轮Ⅰ上,作用有径向力、切向力;在齿轮Ⅱ上,作用有切向力、径向力。
若许用应力[σ]=100Mpa,试根据第四强度理论确定轴径。
求解思路:作、、图。
从图中可以看出,危险截面为B截面。
其内力分量为:由第四强度理论得:411-12 图示活塞杆,用硅钢制成,其直径d=40mm,外伸部分的最大长度l=1m,弹性模量E=210Gpa,=100。
试确定活塞杆的临界载荷。
解:看成是一端固定、一端自由。
此时,而,所以,。
用大柔度杆临界应力公式计算。
11-15 图示矩形截面压杆,有三种支持方式。
杆长l=300mm,截面宽度b=20mm,高度h=12mm,弹性模量E=200Gpa,=50,=0,中柔度杆的临界应力公式为:试计算它们的临界载荷,并进行比较。
解:,,,(a)(b)(c)从计算结果看出,第三种支持方式的临界载荷最大。
