《隧道结构计算》PPT课件
隧道结构计算

一.基本资料惠家庙公路隧道,结构断面尺寸如下图,内轮廓半径为 6.12m ,二衬 厚度为 0.45m 。
围岩为 V 级,重度为19.2kN/m3,围岩弹性抗力系数为 1.6×105kN/m3,二衬材料为 C25 混凝土,弹性模量为 28.5GPa ,重度 为 23kN/m 3。
考虑到初支和二衬分别承担部分荷载,二衬作为安全储备,对其围岩压力进行折减,对本隧道按照 60%进行折减。
求二衬内力,作出内力图,偏心距分布图。
1)V1级围岩,二衬为素混凝土,做出安全系数分布图,对二衬安全性进行验算。
2)V2级围岩,二衬为钢筋混凝土,混凝土保护层厚度 0.035m ,按结构设计原理对其进行配筋设计。
二.荷载确定1.围岩竖向均布压力:q=0.6×0.45⨯12-S γω式中: S —围岩级别,此处S=5;γ--围岩重度,此处γ=19.2KN/3m ;ω--跨度影响系数,ω=1+i(m l -5),毛洞跨度m l =13.14+2⨯0.06=13.26m ,其中0.06m 为一侧平均超挖量,m l =5—15m 时,i=0.1,此处ω=1+0.1⨯(13.26-5)=1.826。
所以,有:q=0.6×0.451-52⨯⨯19.2⨯1.826=151.456(kPa )此处超挖回填层重忽略不计。
2.围岩水平均布压力:e=0.4q=0.4⨯151.456=60.582(kPa ) 三.衬砌几何要素 5.3.1 衬砌几何尺寸内轮廓线半径126.12m , 8.62m r r ==内径12,r r 所画圆曲线的终点截面与竖直轴的夹角1290,98.996942φφ=︒=︒; 拱顶截面厚度00.45m,d = 墙底截面厚度n 0.45m d =此处墙底截面为自内轮廓半径2r 的圆心向内轮廓墙底做连线并延长至与外轮廓相交,其交点到内轮廓墙底间的连线。
外轮廓线半径:110 6.57m R r d =+= 2209.07m R r d =+=拱轴线半径:'1200.5 6.345m r r d =+= '2200.58.845m r r d =+=拱轴线各段圆弧中心角:1290,8.996942θθ=︒=︒5.3.2 半拱轴线长度S 及分段轴长S ∆分段轴线长度:'11190π 3.14 6.3459.9667027m 180180S r θ︒==⨯⨯=︒︒'2228.996942π 3.148.845 1.3888973m 180180S r θ︒==⨯⨯=︒︒半拱线长度:1211.3556000m S S S =+=将半拱轴线等分为8段,每段轴长为:11.3556 1.4194500m 88S S ∆===5.3.3 各分块接缝(截面)中心几何要素(1)与竖直轴夹角i α11'1180 1.4194518012.8177296π 6.345πS r αθ∆︒︒=∆=⨯=⨯=︒ 21112.817729612.817729625.6354592ααθ=+∆=︒+︒=︒ 32125.635459212.817729638.4531888ααθ=+∆=︒+︒=︒43138.453188812.817729651.2709184ααθ=+∆=︒+︒=︒54151.270918412.817729664.0886480ααθ=+∆=︒+︒=︒ 65164.088648012.817729676.9063776ααθ=+∆=︒+︒=︒ 76176.906377612.817729689.7241072ααθ=+∆=︒+︒=︒2'2180 1.419451809.2748552π8.845πS r θ∆︒︒∆=⨯=⨯=︒ 87289.72410729.194855298.996942ααθ=+∆=︒+︒=︒另一方面,8129012.817729698.996942αθθ=+=︒+︒=︒ 角度闭合差Δ≈0。
隧道工程第5章-隧道支护结构计算课件.ppt

e
ue
a
e
(4
3
)
a
e
e
(14
15
)
e
2 2
4
14
3
1
4
2
10
当基础无扩展时,墙顶位移为:
0 cp
uc0p
M
0 cp
1
M c0pu1
H
0
cp
2
H c0pu2
eeuee00
墙顶截面的弯矩Mc、水平力Hc、转角c、水平位移uc为:
Mc Hc
c
M
0 cp
X1
X2
另一种是开挖后,洞室围岩产生塑性区,此时洞室都要 采用承载的支护结构,支护结构对洞室围岩应力状态和位移 状态产生影响。
根据弹性力学和岩体力学可得,隧道壁的径向位移与支护阻 力之间的关系式:
u
பைடு நூலகம்
|r r0
r0 2G
(Hc
sin
C
cos)[(1
sin )
Hc C cot pa C cot
1sin
心某一距离的各点,其应力值是相同的,因此围岩中的塑性 区必然是个圆形区域。令这个圆形塑性区的半径为R0,那么
在塑性区与弹性区的交界面上(即在r=R0处),塑性区的应力 p与弹性区的应力 e一定保持平衡,同时,交界面上的应力
既要满足弹性条件,又要满足塑性条件,可得到在r=R0处:
围岩弹塑性区
p r
p
替,便可得到变位积分的近似计算公式:
ik
S E
ip
S E
MiMk
M
I iM
p
I
11
S E
隧道工程第6章 隧道结构计算

8
9
6.3 半衬砌的计算
拱圈直接支承在坑道围岩侧壁上时,称为半衬砌, 如图6.3所示。常适合于坚硬和较完整的围岩(Ⅱ、Ⅲ 级)中,或用先拱后墙法施工时,在拱圈已作好,但马 口尚未开挖前,拱圈也处于半衬砌工作状态。 6.3.1 计算图式、基本结构及正则方程 道路隧道中的拱圈,一般矢跨比不大,在垂直荷载 作用下拱圈向坑道内变形,为自由变形,不产生弹性抗 力。由于支承拱圈的围岩是弹性的,即拱圈支座是弹性 的,在拱脚反力的作用下围岩表面将发生弹性变形,使 拱脚产生角位移和线位移。
24
6.4 曲墙式衬砌计算
在衬砌承受较大的垂直方向和水平方向的围岩压力 时,常常采用曲墙式衬砌形式。它由拱圈、曲边墙和底 板组成,有向上的底部压力时设仰拱。曲墙式衬砌常用 于Ⅳ耀Ⅵ级围岩中,拱圈和曲边墙作为一个整体按无铰 拱计算,施工时仰拱是在无铰拱业已受力之后修建的, 因此,一般不考虑仰拱对衬砌内力的影响。 6.4.1 计算图式在主动荷载作用下,顶部衬砌向隧 道内变形而形成脱离区,两侧衬砌向围岩方向变形,引 起围岩对衬砌的被动弹性抗力,形成抗力区,如图6.11 所示。抗力图形分布规律按结构变形特征作以下假定:
3
③作用与反作用模型,即荷载—结构模型。例如, 弹性地基圆环计算和弹性地基框架计算等计算法; ④连续介质模型,包括解析法和数值法。数值计算 法目前主要是有限单元法。从各国的地下结构设计实践 看,目前在设计隧道的结构体系时,主要采用两类计算 模型:一类是以支护结构作为承载主体,围岩作为荷载 同时考虑其对支护结构的变形约束作用的模型;另一类 则相反,视围岩为承载主体,支护结构则为约束围岩变 形的模型。
18
19
视为自由变形得到的计算结果。 由于没有考虑弹性抗力,所以弯矩是比较大的,因此截 面也较厚。如果围岩较坚硬,或者拱的形状较尖,则可 能有弹性抗力。衬砌背后的密实回填是提供弹性抗力的 必要条件,但是拱部的回填相当困难,不容易做到密实。 仅在起拱线以上1耀1.5m 范围内的超挖部分,由于是用 与拱圈同级的混凝土回填的,可以做到密实以外,其余 部分的回填则比较松散,不能有效地提供弹性抗力。拱 脚处无径向位移,故弹性抗力为零,最大值在上述的1 耀1.5m 处,中间的分布规律较复杂,为简化计算可以 假定为按直线分布。考虑弹性抗力的拱圈计算,可参考 曲墙式衬砌进行。
隧道结构设计
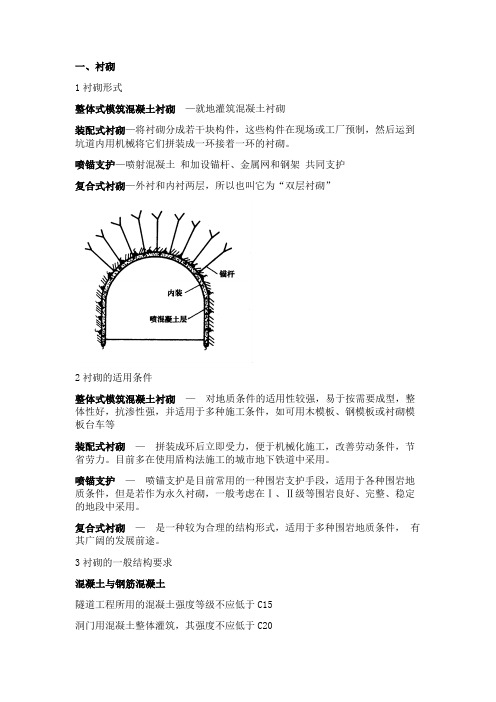
一、衬砌1衬砌形式整体式模筑混凝土衬砌—就地灌筑混凝土衬砌装配式衬砌—将衬砌分成若干块构件,这些构件在现场或工厂预制,然后运到坑道内用机械将它们拼装成一环接着一环的衬砌。
喷锚支护—喷射混凝土和加设锚杆、金属网和钢架共同支护复合式衬砌—外衬和内衬两层,所以也叫它为“双层衬砌”2衬砌的适用条件整体式模筑混凝土衬砌—对地质条件的适用性较强,易于按需要成型,整体性好,抗渗性强,并适用于多种施工条件,如可用木模板、钢模板或衬砌模板台车等装配式衬砌—拼装成环后立即受力,便于机械化施工,改善劳动条件,节省劳力。
目前多在使用盾构法施工的城市地下铁道中采用。
喷锚支护—喷锚支护是目前常用的一种围岩支护手段,适用于各种围岩地质条件,但是若作为永久衬砌,一般考虑在Ⅰ、Ⅱ级等围岩良好、完整、稳定的地段中采用。
复合式衬砌—是一种较为合理的结构形式,适用于多种围岩地质条件,有其广阔的发展前途。
3衬砌的一般结构要求混凝土与钢筋混凝土隧道工程所用的混凝土强度等级不应低于C15洞门用混凝土整体灌筑,其强度不应低于C20强度等级对于衬砌段不应低于C20,对于洞门不应低于C15片石混凝土在岩层较好地段的边墙衬砌,可采用片石混凝土(片石的掺量不应超过总体积的20%)。
当起拱线以上1m以外部位有超挖时,其超挖部分也可用片石混凝土进行回填。
选用的石料要坚硬,其强度等级不应低于MU40,有裂隙和易风化的石料不应采用。
石料和混凝土预制块石料或混凝土预制块用强度等级不低于M10的水泥砂浆砌筑衬砌。
石料的强度等级不应低于MU60,并且有裂隙和易风化的石料不应采用。
混凝土预制块强度等级不应低于MU20。
喷射混凝土喷射混凝土的强度等级采用C20,所用的水泥应优先采用硅酸盐水泥或普通硅酸盐水泥喷射钢纤维混凝土中的钢纤维宜采用普通碳素钢制成,等效直径为0.3~0.5㎜的方形或圆形断面,长度宜为20~25㎜锚杆锚杆的杆体宜用20 MnSi钢筋,也可采用Q235钢筋;缝管式锚杆宜采用16 MnSi钢管,亦可采用Q235钢管;锚杆直径宜为18~22㎜,垫板可采用Q235钢板。
隧道衬砌结构计算

03
弹性模量表示材料抵抗弹性变形的能力,泊松比则表示横向变
形的程度。
衬砌结构材料的耐久性和可靠性
环境因素
衬砌结构材料应能耐受地下水、土壤中的化学物质、侵蚀性气体 等环境因素的侵蚀,保持长期性能稳定。
耐久性设计
衬砌结构材料的耐久性应通过合理的耐久性设计和施工质量控制来 保证,包括选择合适的材料、采取有效的防排水措施等。
计算内容
防水层的厚度、材料性能、抗渗压力等。
计算方法
采用理论分析和实验验证相结合的方法,综合考虑水压、地质条件 和施工工艺等因素进行计算。
感谢您的观看
THANKS
抗震加固措施
根据抗震设计结果,采取相应的加固措施提 高衬砌结构的抗震性能。
03 隧道衬砌结构材料与性能
衬砌结构材料的种类和特性
混凝土
混凝土是隧道衬砌结构中最常用 的材料之一,具有抗压强度高、 耐久性好、成本低等优点。根据 需要可加入添加剂,如防水剂、
膨胀剂等。
钢材
钢材用于隧道衬砌结构中的受力 构件,如型钢、钢板等。具有强 度高、塑性好、耐腐蚀等特点。
可靠性评估
衬砌结构材料的可靠性应通过科学的方法进行评估,以便及时发现 和处理潜在的安全隐患,确保隧道运营安全。
04
计算目的
确保隧道衬砌结构的安全性和稳定性,满足公路行车 要求。
计算内容
衬砌厚度、混凝土抗压强度、抗剪强度、抗弯强度等。
计算方法
采用有限元分析法,结合实际地质资料和荷载条件进 行计算。
衬砌结构设计的基本原则
安全可靠
衬砌结构设计应满足安全可靠 的要求,能够承受围岩压力、 水压力等作用,保证隧道结构
的稳定性。
经济合理
衬砌结构设计应考虑工程成本 ,选择合适的材料和结构形式 ,以达到经济合理的目标。
隧道结构体系的计算模型与方法

隧道结构体系的计算模型与方法王丽琴主讲第五章隧道结构体系设计原理与方法第一节概述第二节围岩的二次应力场和位移场第三节隧道围岩与支护结构的共同作用第四节支护结构的设计原则第五节围岩压力第六节隧道结构体系的计算模型第七节隧道结构体系设计计算方法王丽琴主讲第六节隧道结构体系的计算模型一、计算模型的建立原则二、常用的计算模型王丽琴主讲一、计算模型的建立原则地下结构的力学模型必须符合下列条件:与实际工作状态一致能反映围岩的实际状态以及与支护结构的接触状态荷载假定应与在修建隧道过中(各作业阶段)中荷载发生的情况一致算出的应力状态要与经过长时间使用的结构所发生的应力变化和破坏现象一致材料性质和数学表达要等价。
王丽琴主讲目前,地下结构设计方法可以归纳为以下四种设计模型:①工程类比模型:参照过去隧道工程实践经验进行设计②监控量测模型:以现场量测和实验室试验为主的实用设计方法例如通过洞周位移和衬砌应力的量测不断优化支护参数③荷载结构模型:即作用与反作用模型例如假定弹性抗力法、弹性地基梁法和弹性链杆法④地层结构模型:即连续介质模型包括解析法、数值法、特征曲线法和剪切滑移破坏法。
数值计算法目前主要是有限单元法。
王丽琴主讲第一类模型:以支护结构作为承载主体围岩作为荷载主要来源同时考虑其对支护结构的变形起约束作用传统结构力学模型第二类模型:与上述模型相反是以围岩为承载主体支护结构则约束和限制围岩向隧道内变形。
现代岩体力学模型二、常用的计算模型从各国的地下结构设计实践看目前在设计隧道的结构体系时主要采用两类计算模型:王丽琴主讲第七节隧道结构体系设计计算方法一、结构力学方法二、岩体力学方法三、以围岩分级为基础的经验设计方法四、监控设计方法(信息化设计和施工)王丽琴主讲这一类计算模型主要适用于围岩因过分变形而发生松弛和崩塌支护结构主动承担围岩“松动”压力的情况。
属于这一类模型的计算方法有:弹性连续框架(含拱形)法假定抗力法和弹性地基梁(含曲梁和圆环)法等。
隧道工程(第六讲-隧道支护结构设计)

半拱形结构计算 典型方程的建立 正对称的结构,作用有正对称的荷载,利用对称性,从拱顶切开,取基本结构如右图
结构力学设计方法
计算关键: 拱顶单位位移和荷载位移的计算; 拱脚位移的计算。
半拱形结构计算
结构力学设计方法
拱顶单位位移和荷载位移的计算: 根据结构力学中位移计算方法,可求的某一点在单位力作用下,沿k方向的位移(忽略剪力作用)为:
结构力学设计方法
曲墙拱形结构计算
1. 求主动荷载作用下的衬砌内力
结构力学设计方法
曲墙拱形结构计算 1. 求主动荷载作用下的衬砌内力
结构力学设计方法
曲墙拱形结构计算 求单位弹性反力作用下的衬砌内力
结构力学设计方法
曲墙拱形结构计算
3. 位移及最大弹性反力值的计算
①主动荷载作用下最大抗力点h点位移的计算
结构力学设计方法
直墙拱形结构计算
计算原理
③附加一个方程:墙顶变位 ④拱圈内力的计算:在原理上与弹性固定的高拱结构完全相同 ,只是计及墙顶变位 ⑤边墙:作为弹性地基上的直梁来计算
结构力学设计方法
直墙拱形结构计算
计算原理
弹性地基梁,按其换算长度l的不同,可分为3种情况: ① 长梁 l≥2.75 ② 短梁 1<l<2.75 ③ 刚性梁 1≥l l为梁的长度(即边墙高度),为弹性地基梁的弹性特征值
结构力学设计方法
4.衬砌内力计算及校核计算结果的正确性
曲墙拱形结构计算
③ 按变形协调条件,校核整个计算过程:
直墙拱形结构计算 结构 拱圈支承在弹性地基梁上的弹性固定无铰拱; 边墙双向弹性地基梁 计算原理
结构力学设计方法
结构力学设计方法
直墙拱形结构计算 计算原理 ②弹性反力 拱圈:任意截面弹性反力荷载图形假设为二次抛物线,作用方向为径向;计算公式如下; 边墙:用弹性地基梁的方法计算
隧道-结构计算分析课件

一、计算原则和依据1、采用ANSYS有限元通用程序(注:该程序是目前唯一通过ISO9001国际认证的有限元计算分析程序)对竹篱晒网隧道进行结构受力及变形分析。
2、采用地层-结构模型对暗挖隧道的受力和变形进行分析。
3、分析对象为纵向宽1m的隧道结构和地层。
4、依据《竹篱晒网隧道施工图设计文件》、《公路路隧道设计规范》等建立计算模型。
二、计算内容对竹篱晒网隧道的计算,分别取洞口段、洞身段中V、IV、III级围岩进行计算,取断面计算如下:1、出洞段KY2+760(V级围岩,采用双侧壁法施工);2、洞身段KY2+480(IV级围岩,采用环形台阶法施工);3、洞身段KY2+500(III级围岩,采用台阶法施工)。
三、结构计算模型、荷载1、计算模型采用隧道与地层共同作用的地层-结构模式,模拟分析施工过程地层和结构的受力及变形特点。
计算模型所取范围是:水平方向取隧道两侧3倍洞跨,而竖直方向,仰拱以下地层,以洞跨的3倍为限,即从仰拱至地层下3倍洞跨深度范围,隧道拱顶以上地层:V级围岩取至地面,IV 、III 级围岩根据计算高度取值。
计算中地层及初期支护(初衬喷砼及钢架除外)采用了DP 材料的弹塑性实体单元模拟,而初衬(钢架喷砼)、二次衬砌采用弹性梁模拟,为使点和点之间位移协调,初衬和地层之间用约束方程联系、初衬和二衬之间用只传递轴向压力的链杆连接。
ANSYS 程序中,采用单元的“生”(KILL )、“死”(ALIVE )来模拟衬砌和临时支撑的施作和拆除过程,当单元“死”时,受力体系不受其影响,“死”单元的应力、应变不计(即内力为0),而后被激“活”的单元不计以前自身应变,也就是说,“活”的单元只对以后应力发生变化时产生作用。
2、计算荷载模拟开挖过程中,先计算初始应力,每开挖一步形成“毛洞”时,释放一部分初始应力,施作支护时释放余下的初始应力。
有限元计算中,采用莫尔—库仑屈服准则对结构的开挖过程进行弹塑性分析。
也即采用 Drucker-Prager (DP )模型计算结构非线形的变形特性。
隧道结构设计隧道工程结构构造设计课件(ppt 43页)

柱式拱形明洞门路堑式
翼墙式拱形明洞门路堑式
台阶式拱形明洞门(半路堑式)
台阶式拱形明洞门(偏压式)
2、棚式明洞
当山坡坍方,落石数量较少,山体侧压力不大,或因受地 质、地形条件的限制,难以修建拱形明洞时,可采用棚式明洞
棚式明洞的类型主要取决于外侧边墙的结构形式。通常有 墙式、刚架式,柱式和悬臂式(不修建外墙时)等 ※ 墙式棚洞(墙式棚式明洞)
大拱脚薄边墙衬砌
曲墙式衬砌
3、曲墙式衬砌 ※ 适用范围 ※ 作用 ① 地质条件较差,为抵御底鼓压力,配以仰拱使
衬砌形成环状封闭结构;
② 基础地基较好,可采用无仰拱的曲墙式衬砌。
4、喷混凝土衬砌、喷锚衬砌及复合式衬砌
① 要求用光面爆破开挖,使洞室周边平顺光滑, 成型准确,减少超欠挖。适当的时间喷混凝土,即 为喷混凝土衬砌;
环框式洞门
3、隧道洞门构造
⑴ 洞门仰坡坡脚至洞门墙背后的水平距离不小于1.5m,水 沟沟底与衬砌拱顶外缘的高度不应小于1.0 m,洞门墙顶应高 出仰坡脚0.5m以上。
⑵ 洞门墙基基底埋入土质地基的深度不应小于1.0m,嵌入 岩石地基的深度不应小于0.5m ,墙基底埋设的深度应大于墙 边各种沟、槽基础底埋设的深度;
路堑对称型明洞
路堑偏压型明洞
※ 路堑偏压型
适用于两侧山坡高差较大的路堑,高侧边坡有坍塌,落石 或泥石流;低侧边坡明洞墙顶以下部分为挖方,且能满足外侧 边墙嵌入基岩要求的地段
※ 半路堑偏压型
适用于半路堑靠山侧边坡较高,有坍塌、落石或泥石流等 不良地质现象,而外侧地面较为宽敞和稳定,上部填土坡面线 能与地面相交以平衡山侧压力的地段
③ 增加底部和墙部的支护抵抗力,防止内挤而产生剪切破坏。
隧道支护结构计算-计算模型及方法

5.1.1 隧道结构计算的发展历史
2. 1900—1960年代
其后,不同学者和工程师们在设计隧道衬砌时采 用不同的假定来计及围岩对衬砌变形所产生的抗力, 其中温克尔(winker)局部变形理论得到了广泛应用。
与此同时,将村砌和围岩视作连续介质模型进行 分析的方法也得到了发展,其中的代表学者是H.卡 斯特勒(1960)。
5.1.2 隧道工程的力学特点
1.荷载的模糊性 隧道工程是在自然状态下的岩土地质中开挖的,隧
道周边围岩的地质环境对隧道支护结构的计算起着决定 性的作用。地面结构的荷载比较明确,而且荷载的量级 不大;而隧道结构的荷载取决于当地的地应力,但是地 应力难以进行准确测试,这就使得隧道工程的计算精度 受到影响。
8
5.1.1 隧道结构计算的发展历史
2. 1900—1960年代
1950年代以来,喷射混凝土和锚杆被广泛用作初期支护。 人们逐渐认识到,这种支护能在保证围岩稳定的同时允许 其有一定程度的变形,使围岩内部应力得到调整从而发挥 其自持作用,因此可以将内层衬砌的厚度减小很多。
3. 20世纪60年代以来
1960年代中期,随着数字电子计算机的更新和岩土本构 定律研究的进展,隧道工程分析方法进入了以有限元法为 代表的数值分析时期。这方面的代表性学者是:0.C.辛克 维奇等(1968)
12
5.1.2 隧道工程的力学特点
3.围岩—支护结构承载体系 ◆围岩不仅是荷载,同时又是承载体 ◆地层压力由围岩和支护结构共同承受 ◆充分发挥围岩自身承载力的重要性 4.设计参数受施工方法和施作时机的影响很大
隧道工程支护结构安全与否,既要考虑到支护结 构能否承载,又要考虑围岩是否失稳。
5.隧道与地面结构受力的不同点 存在围岩抗力的作用
隧道结构设计—内轮廓

★ 内轮廓线 ★ 结构轴线 ★ 截面厚度
00
设计步骤
净空限界
内轮廓
结构轴线
截面厚度
断面优化
内轮廓符合 净空限界, 减小洞室体
积
结构轴线 尽可能地 符合压力
线
满足强度要求
采用的施工 方法能确保 断面形状及 尺寸有利于 隧道的稳定
圆形轮廓绘制步骤
1
隧道内轮廓线绘制方法
2
00
3
连接ab、ac、ad,作三条 线的垂直平分线,分别交隧 道几何中心线O1、O2、O3
取O1、O2、O3 中距离路 面最高的点O1,连接O1a 并延长至A使Aa=10cm
以O1为圆心,O1A为 半径作圆,所得的圆形 就是所求的圆形轮廓线
直墙式轮廓线绘制步骤
1
2
3
在几何中线G点上方找到点H, HG=1~1.2m,e点位于GH之 间且He=10cm,作de的垂直 平分线交隧道几何中线于点Q1
c. 车辆两端向曲线外侧的偏移
L — 标准车辆长度,我国为26m,则
则总加宽值:
d总
d内1+d内2+d
外=
4050 R
2.7E
4400 R
8450 R
2.7E
d. 隧道中线与线路中线偏离距离
• 双线铁路隧道加宽计算
a. d内及d外计算与单线加宽值相同 b. 当外侧线路外轨超高大于内侧线路外轨超高时:
隧道建筑结构
单元思维导图知识点梳理 隧道限界与净空 隧道衬砌构造 隧道洞门与明洞
隧道附属建筑 小结
隧道限界与净空
Subtitle Here
Subtitle Here
铁路隧道限界与净空 公路隧道限界与净空
006第六章隧道衬砌结构计算PPT课件

福建工程爆破协会 福建省福州市
柳河路36号(省委党校北侧)
21
二、非对称问题解
对非对称问题、需取全拱为基本结构,拱的内力及拱脚 变位的正负号规定与对称问题相同,计算简图与基本结 构如图9-8所示。
图9-8福建计工算程简爆破图协及会 基福建本省结福构州市
荷载等。
福建工程爆破协会 福建省福州市
柳河路36号(省委党校北侧)
5
2. 荷载的组合
对于一个特定的地下建筑结构,上述几种荷载不一定都存在, 也不可能同时作用在某衬砌上。设计中应根据实际可能出现的 情况进行荷载组合。
所谓荷载组合,即是将有可能同时作用在衬砌上的荷载进行编 组。并取其最不利者作为设计荷载、求得最危险截面中所产生 的最大内力值,作为选择截面时的依据。
6.1 概述
隧道结构是地下建筑结构的重要组成部分,它的 结构形式可根据地层的类别、使用功能和施工水 平等选择。
按结构形式的不同,隧道结构可分为: 1、半衬砌结构; 2、厚拱薄墙衬砌结构; 3、直墙拱形衬砌结构; 4、曲墙结构; 5、复合衬砌结构;
6、连拱隧道结构。
福建工程爆破协会 福建省福州市
力法方程和衬砌内力 6.4.3 最大抗力的计算 6.4.5 衬砌最终内力计算及校核
福建工程爆破协会 福建省福州市
柳河路36号(省委党校北侧)
25
6.4.1 计算图式
地下结构所承受的荷载,按其作用特点及其使用中可能出现的情况分为 以下三类,即:主要荷载,附加荷载和特殊荷载。
(1)主要荷载:长期及经常作用的荷载:结构自重;回填土层重量;围岩 压力;弹性抗力;地下水静水压力和使用荷载。围岩压力是衬砌承受的主 要静荷载。弹性抗力是地下结构所特有的一种被动荷载。使用荷载是在使 用过程中,作用在衬砌上的荷载,如吊车荷载、设备重量、地下贮油库的 油压力、车辆、人员等荷重。
第6章隧道结构计算ppt课件

6.4 隧道洞门计算
6.4.3 洞门计算内容
1. 计算内容 ①墙身偏心及强度; ②绕墙趾的抗倾覆性(墙趾:墙身外表面与基底面的交点); ③沿基底滑动的稳定性; ④基底应力检算。
6.4 隧道洞门计算
6.4.3 洞门计算内容
2. 洞门端墙及挡(翼)墙检算规定
墙身截面压应力
墙身截面偏心距 e 基底应力
1 主动荷载模式 适于软弱岩层,如:
明挖地铁 明洞工程
6.2 结构力学方法
2 主动荷载+弹性抗力模式
适于各类围岩在实际应用中,该模式基本能反映出 支护结构的实际受力状况。
6.2 结构力学方法
3 实际荷载模式
它采用量测仪器实地量测作用在衬砌上的荷载值,某种 实测荷载只能适用于类似情况。
6.2 结构力学方法
作为结构设计荷载
的设计状态
支护 围岩变形过大,松动坍 支护与围岩共同作用,共同变形所 阻力 塌所产生的松动压力 产生的接触形变压力
支护 开挖
临时支撑+整体式厚衬砌
初期支护+二次衬砌
分部开挖, 钻爆法+中小型机械
大断面开挖, 钻爆法+大中型机械掘进
6.2 结构力学方法
6.2.1 基本原理
支护和围岩分开考虑,支护是承载的主体,视围岩为荷载 来源和支护的弹性支承,荷载处理有三种模式:主动荷载,主 动荷载+被动抗力,实际荷载。
图3.2 弹性地基梁的受力和变形
隧道衬砌结构计算的矩阵位移法
基本原理
矩阵位移法又叫直接刚度法,它是以结构节点位移 为基本未知量,联接在同一节点各单元的节点位移应该 相等,并等于该点的结构节点位移(变形协调条件); 同时作用于某一结构节点的荷载必须与该节点上作用的 各个单元的节点力相平衡(静力平衡条件)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6.1 概述
1、隧道结构环境及其简化 2、隧道结构体系的计算模型
1、隧道结构环境及其简化
⑴ 隧道结构与地面结构的区别 隧道结构工程特性、设计原则和
方法与地面结构完全不同
⑴ 隧道结构与地面结构的区别
● 隧道结构是由周边围岩和支护 结构两者组成共同的并相互作用的 结构体系
● 周边围岩在很大程度上是隧道 结构承载的主体
⑵ 隧道结构计算的简化问题
● 进入本世纪后,通过长期观测, 发现围岩不仅对衬砌施加压力,同 时还约束着衬砌的变形。围岩对衬 砌变形的约束,对改善衬砌结构的 受力状态有利,不容忽视
⑶ 局部变形理论和共同变形理论
● 局部变形理论:是以温克尔 (E.Winkler)假定为基础的。它认 为应力和变形之间呈线性关系,即为 围岩弹性抗力系数
2、隧道结构体系的计算模型
● 以工程类比为主的经验设计法; ● 以现场量测和试验为主的实用设计法 ● 荷载—结构模型方法 ● 岩体力学模型方法,包括解析法和数 值法。
从各国的地下结构设计实践看,目前主要采 用两类计算模型:
● 一类是以支护结构作为承载主体,结构力学 模型,又称为荷载-结构模型 ;
cos2 i cos2 h
h
i
1
yi'
y
' h
2
h
⑹ 忽略衬砌与围岩之间的摩擦力
⑺ 墙脚支承在弹性岩体上,可发生转动 和垂直位移(无水平位移)
2 、主动荷载作用下的力法方程和衬砌内力
X 1p11 X 2 p12 1p ap 0 X 1p 21 X 2 p 22 2 p f ap uap 0
6.3 半衬砌的计算
● 适合于坚硬 和较完整的围 岩(Ⅱ、Ⅲ级);
1、基本假定
⑴ 在垂直荷载作用下拱圈向隧道内变形为自由 变形,不产生弹性抗力 ;
⑵ 拱脚产生角位移和线位移,并使拱圈内力发 生改变,计算中除按固端无铰拱考虑外,还必 须考虑拱脚位移的影响
1、基本假定
⑶ 拱脚没有径向位移,只有切向位移; ⑷ 对称的垂直分位移对拱圈内力不产生影响; ⑸ 拱脚的转角 a 和切向位移的水平分位移 ua 是必须考虑的
城市地下空间工程系
2010年2月
本章学习要求: (1)熟悉公路隧道的荷载类型及其隧道 结构的计算模型简化方法; (2)掌握半衬砌和曲墙式衬砌结构内力 计算方法; (3)了解公路隧道的数值分析方法。
第6章 隧道结构计算
6.1 概述 6.2 隧道衬砌上的荷载类型及其组合 6.3 半衬砌的计算 6.4 曲墙式衬砌计算 6.5 直墙式衬砌计算 6.6 衬砌截面强度验算 6.7 单元刚度矩阵 6.8 结构刚度方程
11
落石冲击力
12
偶然
地震力
荷载
荷载组合:
● 结构自重+围岩压力+附加恒载(基本) ● 结构自重+土压力+公路荷载+附加恒载 ● 结构自重+土压力+附加恒载+施工荷载
+温度作用力 ● 结构自重+土压力+附加恒载+地震作用
附加恒载:伴随隧道运营的各种设备设施的荷载等。
6.3 半衬砌的计算
拱圈直接 支承在隧道围 岩侧壁上时, 称为半衬砌
Ni
X2
cos i
N
0 ip
x
6.4 曲墙式衬砌计算
6.4 曲墙式衬砌计算
● 常用于Ⅳ~Ⅵ级围岩;
● 拱圈和曲边墙作为一个整体按无铰 拱计算 ;
● 施工时仰拱是在无铰拱业已受力之 后修建的,不考虑仰拱对衬砌内力的 影响 ;
1 计算假设
⑴ 在主动荷载作用下,顶部衬砌向隧道 内变形而形成脱离区,两侧衬砌向围岩方 向变形,引起围岩对衬砌的被动弹性抗力
式中: ik , ip 是基本结构的单位位移和主动荷载位移;1
是墙底单位转角; 衬砌的矢高。
0 ap
为基本结构墙底的荷载转角;f
为
求得 X 1p , X 2 p 后,在主动荷载作用下, 衬砌内力即可计算:
M ip
X1p
X 2 p yi
M
0 ip
N ip
X2p
cos i
N
0 ip
在具体进行计算时,还需进一步确定被动抗
● 在十九世纪末,隧道衬砌结构 是作为超静定弹性拱计算的,但仅 考虑作用在衬砌上的围岩压力,忽 视了围岩对衬砌的约束作用
⑵ 隧道结构计算的简化问题
● 弹性抗力:衬砌在受力过程中的 变形,一部分结构有离开围岩形成 “脱离区”的趋势,另一部分压紧围 岩形成所谓“抗力区”,在抗力区内, 约束着衬砌变形的围岩相应地产生被 动抵抗力
ik
S E
MiMk J
ip
S E
M
i
M
0 p
EJ
3、拱脚位移计算
⑴ 单位力矩作用时
a
1
Ma Wa
6 bha2
1
1
ka
Байду номын сангаас
6 k a bha2
ha
a
a a
ha
1
1
ha
12 k a bha
1 ka J a
ua 0
2
ha 为拱脚截面厚度;Wa 为拱脚截面的截面模量; k a 是拱脚围岩基底弹性抗力系数; J a 为拱脚
X1 (11 1 ) X 2 (12 f1 ) 1 a 0 X1 ( 21 f1 ) X 2 ( 22 f 2 1 ) 2 f a 0
4、在单位抗力作用下的内力
解出 X1 及 X 2 后,即可求出衬砌在单位抗力图为荷 载单独作用下任一截面内力:
M i
X 1
X 2 yi
● 被动荷载是因结构变形压缩围岩而引起 的围岩被动抵抗力,即弹性抗力,它对结 构变形起限制作用。
2、隧道结构上的荷载及其类型
《公路隧道设计规范》JTG D70-2004将 隧道结构上荷载仿照桥规分为:
● 永久荷载 ● 可变荷载 ● 偶然荷载
隧规P28:表6.1.1 作用在隧道结构上的荷载
编号
荷载类型
● 另一类则相反,视围岩为承载主体,支护结 构则为约束围岩变形的模型 ,即岩体力学模型 或称为围岩—结构模型。
6.2 隧道衬砌上的荷载类型
1、隧道结构上的基本荷载 2、隧道结构上的荷载及其类型
1、基本荷载
(1)围岩压力 (2)结构自重力
2、隧道结构上的荷载及其类型
按其性质可以区分为两大类:
● 主动荷载是主动作用于结构、并引起结 构变形的荷载;
可以求得 hp 和 h
hp
M p ( yh y) ds s
EJ
E
Mp J
( yh
y)
h
M (( yh y)) ds s
EJ
E
M J
( yh
y)
4、在单位抗力作用下的内力
将抗力图 h 1 视为外荷载单独作用时,未知力X1 及 X 2 可以参照X 1p 及 X 2 p 的求法得出
⑶ 局部变形理论和共同变形理论
● 共同变形理论把围岩视为弹性半 无限体,考虑相邻质点之间变形的 相互影响。
人 工 喷 射 混 凝 土 的 场 景
2、隧道结构体系的计算模型
计算模型的如何建立? 隧道结构计算如何简化? 不同简化计算结果差异大!
2、隧道结构体系的计算模型
国际隧道协会(ITA) 认为,目前 采用的地下结构设计方法可以归纳为 以下4种设计模型:
2、基本结构
a ,ua
u
uβ
L/2
f
3、正则方程
X 1 11 X 2 12 1p a 0
f
X 1 21 X 2 22 a 2 p f a ua 0
β
u
u
uβ
L/2
式中: ik 是单位变位,即在基本结构上,因X k 1
作用时,在 X i方向上所产生的变位;ip为荷载变 位,即基本结构因外荷载作用,在Xi 方向的变位;
hp
M pMh EJ
ds
yah ap
s E
M pMh J
yah ap
h
M M EJ
h
ds
yah a
s E
M Mh J
yah a
● h点所对应的 h 90 ,则该点的径向位移
约等于水平位移
● 拱顶截面的垂直位移对h点径向位移的影响 可以忽略不计
按照结构力学方法,在h点加一单位力 p 1,
荷载名称
1
围岩压力
2
永久荷载
结构自重力
(恒载)
3
填土压力 水压力
4
混凝土收缩和徐变影响力
5
可
6
变
荷
7
载
8
9
10
基本 可变 荷载
其它 可变 荷载
公路车辆荷载,人群荷载 立交公路车辆荷载及其所产生的冲击力和土压力
立交铁路列车活载及其所产生的冲击力和土压力 立交渡槽流水压力 温度变化的影响力 冻胀力 施工荷载
1)
X 2 (12
2
f1 ) (1p
0 ap
)
0
X 1 ( 21
u1
f1 )
X 2 ( 22
u2
fu1
f 2
f
2 1) (2 p
f
0 ap
u
0 ap
)
0
a11 X1 a12 X 2 a10 0 a21 X1 a22 X 2 a20 0
X1
a22a10 a12a20 a122 a11a22
力 h的大小,这需要利用最大抗力点h处的变
形协调条件。
h hp h h h k h
h
k hp 1 k h
h hp h h h k h
h
k hp 1 k h
3、最大抗力值的计算
●先求出 hp 和 h h
