第一章 作业答案
中级经济法·基础班·课后作业·第一章

第一章课后作业一、单项选择题1.下列各项中,表述不正确的是()。
A.经济法是一个新兴的法律部门B.经济法是市场经济进入垄断阶段以后产生的C.经济法为中国法律体系中的一个独立的法律部门D.与经济有关的法都是经济法2.下列各项中,属于宏观调控法的是()。
A.反垄断法B.反不正当竞争法C.金融法D.消费者保护法3.下列法的形式中,属于国家根本大法的是()。
A.《中华人民共和国全国人民代表大会组织法》B.《中华人民共和国立法法》C.《中华人民共和国宪法》D.《中华人民共和国刑法》4.下列各项中,属于行政法规制定主体的是()。
A.全国人大及其常委会B.国务院C.省、自治区、直辖市以及较大的市的人大及其常委会D.国务院的各部、委、行、署以及具有行政管理职能的直属机构5.下列各项,关于经济法主体的表述正确的是()。
A.经济法主体只能是组织,不能是个人B.经济法主体只能是立法机关或执法机关,不能是各类企业或非营利性组织C.同一主体可以因其参加不同的法律关系,成为多个法律领域的主体D.外国人不可能成为我国经济法的主体6.关于经济法主体资格的取得,下列说法中,不正确的是()。
A.经济法主体资格取得的法律依据具有差异性B.经济法主体资格的取得具有多源性C.受控主体和受制主体主要由民商法确定其资格D.经济法规范不可以限定受控主体和受制主体的主体资格或资质条件等7.下列经济法主体的行为中,不属于宏观调控行为的是()。
A.金融调控行为B.财税调控行为C.金融市场规制行为D.计划调控行为8.从经济法主体行为效果角度出发,可以将经济法主体的行为分为()。
A.单方行为和双方行为B.抽象行为和具体行为C.积极行为和消极行为D.自为行为和代理行为9.下列各项中,关于经济法主体权利和义务的表述,不正确的是()。
A.经济法主体的职权可以放弃B.经济法主体的权利可以放弃C.职权和权力都要依法行使D.职责和义务都要依法履行10.下列各项中,不属于经济法主体权利义务的特殊性的是()。
欧美电影文化12张答案

欧美电影文化答案第一章作业答案1【单选题】(1分)艺术的一个功能是(A)A.使看不见的东西看见B.源于生活,高于生活2【单选题】(1分)“我怕丧失对他人的兴趣”。
是波兰导演(B)的名言。
A.瓦伊达B.基耶斯洛夫斯基3【单选题】(1分)电影保存了时间是指(B)A.让时间停止B.人的生命经验4【单选题】(1分)电影是继文学、戏剧、绘画、雕塑、音乐、舞蹈之后的(A)A.第七种艺术B.第六种艺术5【单选题】(1分)《云上的日子》的导演是(B)A.帕索里尼B.米开朗琪罗-安东尼奥尼6【单选题】(1分)《云上的日子》中有一段对白,“十二刀,一切真实都在其中,可是如果我要拍有三刀就够了,这样显得更真实。
”这说明(A)A.再现真实不同于客观的真实B.没有真实7【单选题】(1分)维姆-文德斯说,“我完全拒斥故事。
因为在我看来他们除了带来谎言外别无所有。
而最大的谎言就是故事总是表现出事实上并不存在的有头有尾的一致性和连贯性,而现实根本不是这样的。
然而,因为我们对这些谎言的需求又是如此的贪婪,以致于使得我们即或用没有故事的片断来对抗也是毫无疑义的。
也就是说,故事是不可能(表现真实)的,而我们又不可能没有故事。
”这段话说明(A)A.电影是对我们生命经验的再现和理解B.电影纯属虚构故事而已8【单选题】(1分)《阳光灿烂的日子》的导演是(B)A.张艺谋B.姜文9【单选题】(1分)《美国往事》的导演是(B)A.科波拉B.莱昂内10【单选题】(1分)《红、白、蓝》三部曲的导演是(B)A.波兰斯基B.基耶斯洛夫斯基11【单选题】(1分)看电影的活动是(A)A.它既是集体性的同时又是极端个人化的,是凝聚社会去剧院的习俗和阅读小说似的个人主义者白日梦的混合物。
B.仅仅就是娱乐12【单选题】(1分)电影艺术是(B)A.影像的艺术B.视觉与听觉的合一,时间和空间的保留与再现,是时、空、光、电的合一。
电影本身还包含着看电影,所以电影院和观众都是电影的要素13【单选题】(1分)《阿甘正传》是一部关于(A)的电影。
国开《管理学基础》章节自测题作业答案

国开《管理学基础》章节自测题作业答案第一章一、单项选择题目1在管理的各项职能中,最具有规范性、技术性的职能是()。
A.控制题目2人们常说“管理是一门艺术”,强调的是()。
A.管理的实践性题目3“管理就是决策”是下列哪位经济学家的观点?()C.西蒙题目4当管理者接待来访者、参加剪彩仪式等社会活动时,他行使的是()的角色。
A.精神领袖题目5组织是管理的基本职能之一,它是由()三个基本要素构成。
A.目标、部门和关系二、多项选择题目6管理作为一种特殊的实践活动,具有其独特的性质,比如()。
管理具有二重性,管理具有科学性,管理具有艺术性题目7明茨伯格通过实证研究发现:管理者在组织中扮演十种角色,这些角色被分为()。
人际关系角色,信息传递角色,决策制定角色题目8根据管理二重性的原理,与自然属性相联系的是()。
生产力,社会化大生产题目9管理者在行使各种管理职能、扮演三类管理角色时,必须具备以下技能:如()。
技术技能,人际技能,概念技能题目10下列选项中,()属于管理者所扮演的决策角色。
企业家角色,干扰应对者角色,资源分配者角色,谈判者角色三、判断正误题目11一般来说,组织规模越大,管理者必须应对的环境因素的数量越多。
()对题目12控制的实质就是使实践符合于计划,计划就是控制的标准。
()对题目13事先对未来行为所作的安排就是预测,它是人们有意识的活动。
()错题目14处于不同管理层次上管理者,其履行的管理职能也是不同的。
()错题目15从教材给“管理”所下定义中,可以得出这样的结论,管理的对象就是组织的各种资源。
()错第二章一、单项选择题目1西方早期的管理思想中,()是最早研究专业化和劳动分工的经学家。
正确答案是:亚当•斯密题目2管理科学学派中所运用的科学技术方法,来源于()。
正确答案是:军队题目3泰罗科学管理理论的中心问题是()。
正确答案是:提高劳动生产率题目4企业流程再造强调()的理念。
正确答案是:顾客为导向和服务至上题目5古典管理理论对人性的基本假设,认为人是()。
稳态第1-3章作业答案

1. 某变压器额定容量为 31.5MVA,变比为 110/38.5kV, Pk=200kW,Uk(%)=10.5,P0=86kW,I0(%)=2.7, 试求变压器参数并画出等值电路。若以100MVA及变压 器额定电压为基值,求各参数的标么值。
1、解:一般归算至高压侧即可
RT
Pk
U
2 N
1000 SN2
200 1000
1102 31.52
2.44()
XT
Uk
%U
2 N
100 SN
10.51102 100 31.5
40.33()
GT
P0
1000
U
2 N
86 1000 1102
7.11106 (S)
BT
I0% S 100 U
N 2 N
2.7 100
31.5 1102
7.03105 (S)
4
第二次堂测答案:
SA2 S2 +SA2 29.586+j16.771 MVA
UA2
PA2
6 QA2 UA
12
29.58610 16.77112 110
3.443
U2 UA UA2 106.557
(3)求变比 线路1-2无功潮流为0,
Q12 QA1 QC Q1 0
QC Q1 QA1 7.6
8.60 104
BT*
BT
U
2 N
SN
7.03105 1102
100
8.51103
注意:标幺值没有单位
11
❖ 2.三相三绕组降压变压器的型号为SFPSL120000/220,额定容量为 120000/120000/60000/kVA,额定电压为 220/121/11kV,Pk(1-2)=601kW,Pk(13)=182.5kW,Pk(2-3)=132.5kW,Uk(12)(%)=14.85, Uk(1-3)(%)=28.25, Uk(23)(%)=7.96,P0=135kW,I0(%)=0.663,求该变 压器的参数,并做出等值电路。
第1章部分作业答案

第一章 部分作业答案1.5.9 在图1.10中,五个元件代表电源或负载。
电流和电压的参考方向如图中所示,今通过实验测量得知:A I 41-=,A I 62=,A I 103=,V U 1401=,V U 902-=,V U 603=,V U 804-=,V U 305=(1)试标出各电流的实际方向和各电压的实际极性(可另画一图);(2)是判断哪些元件是电源?哪些是负载?(3)计算各元件的功率,电源发出的功率和负载取用的功率是否平衡?解:(1)各电流的实际方向和各电压的实际极性如右画所示:(2)元件1、元件2是电源,元件3、元件4和元件5是负载。
(3)W I U P 560)4(140111-=-⨯==,W I U P 5406)90(222-=⨯-==W I U P 6001060333=⨯==,W I U P 320)4()80(144=-⨯-==W I U P 180630255=⨯==∵0180320600)540()560(=+++-+-=∑P∴电源发出的功率和负载取用的功率平衡。
1.5.10 在图1.11中,已知mA I 31=,mA I 12=。
试确定电路元件3中的电流3I 和其两端电压3U ,并说明它是电源还是负载。
检验整个电路的功率是否平衡。
解:mA I I I 231123-=-=-=, V R I U U 60201802223=⨯-=-=元件3是电源mW I U P U 90330111=⨯==,mW I U P U 80180222-=⨯-=-= mW I U P 120)2(60333-=-⨯==,mW R I P R 9010321211=⨯== mW R I P R 2020122222=⨯==∵02090)120()80(90=++-+-+=∑P∴整个电路的功率平衡。
1.5.11 有一直流电源,其额定功率W P N 200=,额定电压V U N 50=,内阻Ω=5.0o R ,负载电阻R 可以调节,其电路如图1.5.1所示。
测量学作业答案

测量学作业第一次作业:第一章~第三章第一章作业1.测量学的基本任务是什么?答:确定地面点的点位。
2.测量工作中常采用哪几种基准面?各自定义和作用是什么?答:(1)大地水准面:由静止的海水面扩展延伸而形成的闭合曲面。
作用:测量外业工作的基准面。
(2)旋转椭球面:椭圆绕其短轴旋转而成的闭合曲面,其形状和大小可由长半径a,短半径b,以及扁率a ba-=α确定。
作用:精确确定地面点的点位的基准面。
(3)圆球面:计算精度要求不高时,近似代替椭球面进行计算的基准面。
作用:近似确定地面点的点位的基准面。
(4)水平面:小范围内(一般在R=10km),近似代替大地水准面进行计算的基准面。
作用:近似确定地面点的点位的基准面。
3.测量学里可以选用哪几种坐标系各自如何表示地面点的位置4.答: a) 地理坐标系:研究和测量整个地球的形状和大小,或进行大面积的测量工作时,可采用地理坐标系。
i.大地地理坐标系:用大地经度 L 和大地纬度B来表示。
ii.天文地理坐标系:用天文经度和天文纬度来表示。
b)平面直角坐标系:在R=10km的范围内,以水平面作为该区的基准面,直接将地面点沿铅垂线投影到水平面上。
c)高斯平面直角坐标系:以中央子午线的投影线为X轴,赤道的投影线为Y轴,两轴的交点为坐标原点O而建立起来的平面直角坐标系。
5.水准面是不是水平面在什么范围内可将水准面当作水平面处理为什么答:(1)水准面不是水平面。
水准面:由静止的海水面扩展延伸而形成的闭合曲面。
水平面:近似代替大地水准面进行计算的基准面。
(2)当测量的半径在10公里以内时,进行角度测量和距离测量时可用水平面代替水准面。
(3)原因:球面三角形化为平面三角形时每个角的球面角超影响为23/RP=''ε,P为平面三角形的面积,当三角形的边长为10km时,算得。
因此,在半径为10km的面积内进行普通测量时,水平面代替水准面所产生的水平角度误差可以忽略不计。
6.测定地面点位置的基本观测元素是什么?答:水平角、水平距离和高差(高程)是确定地面点空间位置的三个基本观测要素。
物理初二第一章练习题答案

物理初二第一章练习题答案1. 速度和加速度的关系根据物理学的基本概念,速度是物体运动的一个重要参量,而加速度则表示物体速度变化的快慢。
在初二的物理学习中,我们常常需要研究速度和加速度之间的关系。
以下是第一章练习题的答案:题目1:一个从静止开始的物体以恒定的加速度3 m/s²沿着一条直线运动,求它在5秒后的速度是多少?答案:根据物理学中的加速度公式v = u + at,其中v是末速度,u是初速度,a是加速度,t是时间。
给定初速度u=0,加速度a=3 m/s²,时间t=5秒。
代入公式计算可得v = 0 + 3 × 5 = 15 m/s。
题目2:一辆汽车在道路上以25 m/s的速度匀速行驶,经过10秒后它的位置是多少?答案:根据物理学中的位移公式s = ut,其中s是位移,u是速度,t 是时间。
给定速度u=25 m/s,时间t=10秒。
代入公式计算可得s = 25 ×10 = 250 m。
题目3:一个物体的速度从10 m/s增加到20 m/s,经过2秒的时间,求它的加速度是多少?答案:根据物理学中的加速度公式a = (v - u) / t,其中a是加速度,v是末速度,u是初速度,t是时间。
给定初速度u=10 m/s,末速度v=20 m/s,时间t=2秒。
代入公式计算可得a = (20 - 10) / 2 = 5 m/s²。
2. 动量守恒定律在物理学中,动量守恒定律是一个重要的原理,它指出在一个系统内,所有物体的总动量在没有外力作用的情况下保持不变。
以下是第一章练习题中涉及到动量守恒定律的答案:题目1:一辆质量为1000 kg的小轿车以20 m/s的速度向东行驶,和一辆质量为1500 kg的卡车以15 m/s的速度向东行驶发生碰撞,碰撞后两车结合在一起,求结合后的速度是多少?答案:根据动量守恒定律,碰撞前的总动量等于碰撞后的总动量。
小轿车的动量为mv1,卡车的动量为mv2,碰撞后的总动量为(m1 +m2)v。
第一章 金属的晶体结构作业 答案

第一章金属的晶体结构1、试用金属键的结合方式,解释金属具有良好的导电性、正的电阻温度系数、导热性、塑性和金属光泽等基本特性.答:(1)导电性:在外电场的作用下,自由电子沿电场方向作定向运动。
(2)正的电阻温度系数:随着温度升高,正离子振动的振幅要加大,对自由电子通过的阻碍作用也加大,即金属的电阻是随温度的升高而增加的。
(3)导热性:自由电子的运动和正离子的振动可以传递热能。
(4) 延展性:金属键没有饱和性和方向性,经变形不断裂。
(5)金属光泽:自由电子易吸收可见光能量,被激发到较高能量级,当跳回到原位时辐射所吸收能量,从而使金属不透明具有金属光泽。
2、填空:1)金属常见的晶格类型是面心立方、体心立方、密排六方。
2)金属具有良好的导电性、导热性、塑性和金属光泽主要是因为金属原子具有金属键的结合方式。
3)物质的原子间结合键主要包括金属键、离子键和共价键三种。
4)大部分陶瓷材料的结合键为共价键。
5)高分子材料的结合键是范德瓦尔键。
6)在立方晶系中,某晶面在x轴上的截距为2,在y轴上的截距为1/2;与z轴平行,则该晶面指数为(( 140 )).7)在立方晶格中,各点坐标为:A (1,0,1),B (0,1,1),C (1,1,1/2),D(1/2,1,1/2),那么AB晶向指数为(ī10),OC晶向指数为(221),OD晶向指数为(121)。
8)铜是(面心)结构的金属,它的最密排面是(111 )。
9) α-Fe、γ-Fe、Al、Cu、Ni、Cr、V、Mg、Zn中属于体心立方晶格的有(α-Fe 、 Cr、V ),属于面心立方晶格的有(γ-Fe、Al、Cu、Ni ),属于密排六方晶格的有( Mg、Zn )。
3、判断1)正的电阻温度系数就是指电阻随温度的升高而增大。
(√)2)金属具有美丽的金属光泽,而非金属则无此光泽,这是金属与非金属的根本区别。
(×)3) 晶体中原子偏离平衡位置,就会使晶体的能量升高,因此能增加晶体的强度。
国际经济学作业答案

第一章练习与答案1.为什么说在决定生产和消费时,相对价格比绝对价格更重要?答案提示:当生产处于生产边界线上,资源则得到了充分利用,这时,要想增加某一产品的生产,必须降低另一产品的生产,也就是说,增加某一产品的生产是有机会机本(或社会成本)的。
生产可能性边界上任何一点都表示生产效率和充分就业得以实现,但究竟选择哪一点,则还要看两个商品的相对价格,即它们在市场上的交换比率。
相对价格等于机会成本时,生产点在生产可能性边界上的位置也就确定了。
所以,在决定生产和消费时,相对价格比绝对价格更重要。
2.仿效图1—6和图1—7,试推导出Y商品的国民供给曲线和国民需求曲线。
答案提示:3.在只有两种商品的情况下,当一个商品达到均衡时,另外一个商品是否也同时达到均衡?试解释原因。
答案提示:4.如果生产可能性边界是一条直线,试确定过剩供给(或需求)曲线。
答案提示:5.如果改用Y商品的过剩供给曲线(B国)和过剩需求曲线(A国)来确定国际均衡价格,那么所得出的结果与图1—13中的结果是否一致?答案提示:国际均衡价格将依旧处于贸易前两国相对价格的中间某点。
6.说明贸易条件变化如何影响国际贸易利益在两国间的分配。
答案提示:一国出口产品价格的相对上升意味着此国可以用较少的出口换得较多的进口产品,有利于此国贸易利益的获得,不过,出口价格上升将不利于出口数量的增加,有损于出口国的贸易利益;与此类似,出口商品价格的下降有利于出口商品数量的增加,但是这意味着此国用较多的出口换得较少的进口产品。
对于进口国来讲,贸易条件变化对国际贸易利益的影响是相反的。
7.如果国际贸易发生在一个大国和一个小国之间,那么贸易后,国际相对价格更接近于哪一个国家在封闭下的相对价格水平?答案提示:贸易后,国际相对价格将更接近于大国在封闭下的相对价格水平。
8.根据上一题的答案,你认为哪个国家在国际贸易中福利改善程度更为明显些?答案提示:小国。
9*.为什么说两个部门要素使用比例的不同会导致生产可能性边界曲线向外凸?答案提示:第二章答案1.根据下面两个表中的数据,确定(1)贸易前的相对价格;(2)比较优势型态。
第一章作业答案

1.写出下列单体形成聚合物的反应式。
说明属于何类聚合反应。
(1) CH2CHCl(2)CH2CHCOOH(3)OH(CH2)5COOH(4) CH2CH2CH2O(5) H2N(CH2)6NH2+HOOC(CH2)8COOH(6) OCN(CH2)6NCO+HO(CH2)4OH解:(1)nCH22CHCl CH2CHCln单体自由基聚合聚氯乙烯重复单元结构单元单体单元(2)nCH2CH2CHCOOH CH2CHCOOHn单体自由基聚合聚丙烯酸重复单元结构单元单体单元(3)nHO(CH2)5O(CH2)5CO+ nH2On单体缩聚反应聚己(内)酯O(CH2)5CO为重复单元和结构单元,无单体单元。
(4)nCH2CH2CH2O CH2CH2CH2O n单体开环聚合聚氧杂环丁烷CH2CH2CH2O为重复单元、结构单元、单体单元。
(5)nH2N(CH2)10NH2 + nHOOC(CH2)8COOH H NH(CH2)10NHCO(CH2)8CO OH+(2n-1)H2On缩聚反应聚癸二酰癸二胺H2N(CH2)10NH2和HOOC(CH2)8COOH为单体。
NH(CH2)10NHCO(CH2)8CO为重复单元,NH(CH2)10NH和CO(CH2)8CO分别为结构单元,无单体单元。
(6)nOCN(CH 2)6NCO+nHO(CH 2)4 O(CH 2)4OCONH(CH 2)6NHCOn聚氨酯②为聚加成反应,无单体单元。
O(CH 2)4OCONH(CH 2)6NHCO 为重复单元,H O(CH 2)4OH 和OCN(CH 2)6NCO 为单体。
2.简述高分子科学所包括的分支领域。
解:高分子化学、高分子物理、高分子工艺与工程学、功能高分子。
3.解释名词:结构单元、聚合度、高分子化合物。
结构单元:聚合物链中与单体相对应的最小结构单位。
聚合度:聚合物分子所含有的结构单元的数目。
高分子化合物:是一种或多种原子或原子团经无数次重复连接而成的分子所组成的化合物。
高中生物 第1章答案

第一章答案:
第1节细胞是生命活动的基本单位
一、细胞学说
1、施莱登和施旺
2、①细胞是一个有机体,一切动植物都由细胞发育而来,并由细胞和细胞产物所构成
②细胞是一个相对独立的单位,既有它自己的生命,又对与其他细胞共同组成的整体生命起作用。
③新细胞是由老细胞分裂产生的。
3、①:动物和植物的统一性生物界的统一性②:细胞水平
二、细胞是基本的生命系统
1、病毒,活细胞,寄生,核酸(DNA 或RNA),蛋白质
2、基本单位
3、细胞、组织、器官、系统、个体、种群、群落、生态系统、生物圈
4、系统、个体、细胞
5、细胞
6、同种生物所有个体
7、所有生物(动物、植物、微生物)
8、生物群落、无机环境
第 2 节细胞的多样性和统一性
一、高倍镜的使用步骤1 低倍镜、视野中央2 转换器 3 光圈、反光镜、4 细准焦
螺旋
二、显微镜使用常识1 大,暗,少。
小,亮,多。
2 有,长。
无,短。
3 物镜、目镜。
长度或宽度
三、细胞种类
细胞内有无以核膜为界限的细胞核
1、染色体核糖体细胞壁
2、细胞核
3、细菌
4、真菌
5、有无细胞结构RNA 病毒、RNA 病毒、DNA 病毒。
西南交通大学理论力学作业答案①
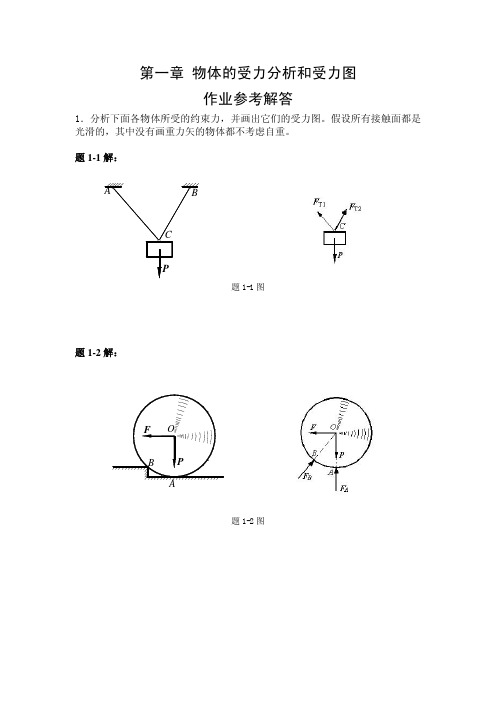
第一章物体的受力分析和受力图
作业参考解答
1.分析下面各物体所受的约束力,并画出它们的受力图。
假设所有接触面都是光滑的,其中没有画重力矢的物体都不考虑自重。
题1-1解:
题1-1图
题1-2解:
题1-2图
题1-3解:
题1-3图题1-4解:
题1-4图
2.分析下列各刚体系统中每个物体及整体的受力情况,并画出它们的受力图。
图中没有画上重力矢的物体都不考虑自重,并假设所有接触面都是光滑的。
题2-1解:
题2-2解:
题2-3解:
题2-4解:
3.分析下列结构中每根杆件(不含销钉)及整体的受力情况,并画出它们的受
力图。
图中没有画上重力矢的杆件都不考虑自重。
解:
题3图
F Cx
F Cy
F A
By
F Bx
′
ABy
A。
第一次作业答案

第一章《软件工程概述》作业答案一、名词解释1.软件软件是计算机程序以及开发、使用和维护程序所需要的所有文档。
软件是包括程序、数据及其相关文档的完整集合。
2.软件危机软件生产的进度、数量、质量、成本满足不了社会对软件的需求量和希望的现象,称为“软件危机”。
软件工程IEEE[IEE93]:软件工程是将系统的、规范的、可度量的工程化方法应用于软件开发、运行和维护的全过程及上述方法的研究。
4.软件生存周期软件生存周期是指一个软件从提出开发要求开始直到不再使用(报废)为止的整个时期。
5.软件过程模型软件过程指为获得高质量软件所需要完成的一系列任务以及完成这些任务的工作步骤。
过程还规定了运用的方法的顺序、应该交付的文档资料、为保证软件质量和协调变化所需要采取的管理措施、任务完成的标志等。
软件过程模型也叫软件生存期模型、软件工程范型,是软件过程的一种抽象表示。
二、填空题1、在信息处理和计算机领域内,一般认为软件是程序、数据和文档的集合。
2、软件生产的发展经历了程序设计时代、程序系统时代和软件工程时代,各时代的生产方式分别是个体、作方式和工程化。
3、软件生存周期的8个阶段分别是问题定义、可行性研究、需求分析、概要设计、详细设计、编码与模块测试、综合测试、维护。
4、软件工程是利用工程化的原理和方法来进行开发、维护和管理软件的一门学科。
5、描述软件开发过程中各种活动如何执行的模型称为软件过程模型。
6、瀑布模型不适应需求可变的软件开发,只有到最后才能见到整个软件系统。
7、软件产品的生产主要是研制,软件产品的成本主要体现在人力成本上。
8、软件工程面临的问题有软件费用、可靠性、可维护性、生产率。
三、单项选择题1、软件文档是( C )。
A.程序B.工具C.文书和资料D.数据2、软件是一种( B )性工业产品A.理论B.知识(或逻辑)C.消耗D.体力3、与计算机科学的理论研究不同,软件工程是一门( B )的学科。
A.理论性 B.工程性 C.原理性 D.心理性4、软件工程与计算机科学的性质不同,软件工程着重于( B )A.理论研究 B.建造软件系统 C.原理探讨 D.原理的理论5、软件工程学科出现的直接原因是( C )。
自动控制原理课后习题答案

du3 (t) dt
(R1C2
1)u3 (t)
R1R2C1C2
d 2V (t) dt 2
(R1C1
R2C2
R1C2 )
dV (t) dt
( R1C2
1)V (t)
G(S ) u3 (s) R1R2C1C2 S 2 (R1C1 R2C2 R1C2 )S (R1C2 1)
V (s)
R1R2C1C2 S 2 (R1C1 R2C2 )S (R1C2 1)
第三章:作业3.5
试用Routh稳定判据判断下列(a)(b)(c)(d)(e)特征方程描述的系统的稳 定性,若不稳定说明右半复数平面或虚轴上的根的个数。
解:(a) s5+6s4+3s3+2s2+s+1=0
1
3
6
2
16
5
2
16
-1
-(1/-1)×1×16=16
1 1
一行同乘分母6 一行同乘分母16 一行同乘2/246
没有互不接触回路: ∑LbLc = ∑LdLeLf = ···=0 特征式:△(s)=1-[L1 + L2+ L3]=1+G2(s) G3(s)G6(s)+G3(s) G4(s)G5(s)+ G1(s) G2(s) G3(s) G4(s) G7(s) 余子式:△1 (s)=1
H(s)=y(s)/u(s)= Q1(s)/ △(s)
的控制方法。
• 反馈控制原理-通过反馈信息形成反馈控制作用的原理,称为反馈控制原理。
3、反馈控制系统的基本构成及特点?
简答:反馈控制系统由被控对象和控制器两大部分组成。
控制器又主要由以下基本元件构成:
运筹学课程作业答案

工厂5
工厂9 工厂6
工厂3
8
线性规划 Linear Programming(LP)
3. 河流污染治理规划问题
曾几何时长江水, 哺育华夏代代人, 谁知后代疏珍惜, 清清江水黑如泥。
工厂2 工厂8
工厂7
工厂1 工厂3
工厂4
工厂5
工厂9
工厂6
今日认识未为晚, 吾辈齐心治环境, 线性规划大有用, 定让江水绿如蓝。 9
10
线性规划 Linear Programming(LP)
背景资料:
表-1 污水排放量
单位:万m3
化工厂1
1.2
化工厂4
2
化工厂7
2
化工厂2
1
化工厂5
1
化工厂8
0.8
化工厂3
3
化工厂6
1
化工厂9
1.5
表-2 流经各化工厂的河流流量
单位:万m3
化工厂1
500
化工厂4 1200 化工厂7 1200
化工厂2
6
第一章作业
3. 河流污染治理规划问题 曾几何时长江水, 哺育华夏代代人, 谁知后代疏珍惜, 清清江水黑如泥。
7
线性规划 Linear Programming(LP)
案 例 河流污染治理规划问题
曾几何时长江水, 哺育华夏代代人, 谁知后代疏珍惜, 清清江水黑如泥。
工厂1
工厂2 工厂8
工厂7
工厂4
5
▪ ▪
对化工厂7应有—— 3 (2-X7)+ 0.8(1.5-X9) / 1200 ≦ 0.2%
13
线性规划 Linear Programming(LP)
▪ 对化工厂4应有——
国科大应用光学作业答案_1-7_汇总

1、根据费马原理证明反射定律。
答案:略2、某国产玻璃的n C=1.51389, n d=1.5163, n F=1.52195,计算其阿贝数,并查出该玻璃的牌号。
答案:V=64.06、K93、求图1-5的入射角i1。
答案:25.81︒4、已知入射光线A的三个方向余弦为cosα、cosβ、cosγ,反射光线A'的三个方向余弦为cosα'、cosβ'、cosγ',求法线方向。
答案:cosα'-cosα、cosβ'-cosβ、cosγ'-cosγ5、有一光线o o=+A i j入射于n=1和n'=1.5的平面分界面上,平面cos60cos30的法线为o oN i j,求反射光线A'和折射光线A''。
cos30cos60=+答案:略6、有一光线以60︒的入射角入射于n=点反射和折射的光线间的夹角。
答案:90︒7、在水中深度为y处有一发光点Q,作QO面垂直于水面,求射出水面折射线的延长线与QO交点Q '的深度y'与入射角i的关系。
答案:'y=1、一个玻璃球直径为400mm,玻璃折射率为1.5。
球中有两个小气泡,一个在球心,一个在1/2半径处。
沿两气泡连线方向,在球的两侧观察这两个气泡,它们应在什么位置?如在水中观察(水的折射率为1.33)时,它们又应在什么位置?答案:空气中:80mm、200mm;400mm、200mm水中:93.99mm、200mm;320.48mm、200mm2、一个折射面r=150mm, n=1, n'=1.5,当物距l=∞, -1000mm, -100mm, 0, 100mm, 150mm, 1000mm时,横向放大率各为多少?答案:0、-3/7、3/2、1、3/4、2/3、3/133、一个玻璃球直径为60mm,玻璃折射率为1.5,一束平行光射到玻璃球上,其汇聚点在何处?答案:l'=15mm4、一玻璃棒(n=1.5),长500mm,两端面为凸的半球面,半径分别为r1=50mm, r2= -100mm,两球心位于玻璃棒的中心轴线上。
第一章作业参考答案

第一章作业答案1-1 地面空气的主要成分是什么?矿井空气与地面空气有何区别?N2(78%) O2(20.96%) CO2(0.03%) Ar(1%) 其他稀有气体(0.01%)地面空气进入井下后,因发生物理和化学两种变化,使其成分种类增多,各种成分浓度改变1-2 氧气有哪些性质?造成矿井空气中氧浓度减少的主要原因有哪些?物理性质:氧是无色、无臭、无味、无毒和无害的气体,比重为1.105,是人和其他动物呼吸所必需的物质化学性质:氧是很活跃的元素,易使其他物质氧化,并能助燃主要原因:煤、岩、坑木等缓慢氧化耗氧,煤层自燃,人员呼吸,爆破。
1-3矿井空气中常见的有害气体有哪些?《规程》对矿井空气中有害气体的最高容许浓度有哪些具体规定?1-4CO的主要来源。
CO是无色、无臭、无味的有毒有害气体,比重为0.967,比空气轻,不易溶于水,当浓度在13~75%时可发生爆炸;CO比O2与血色素亲和力大250~300倍,它能够驱逐人体血液中的氧气使血液缺氧致命;井下爆炸工作、火区氧化、机械润滑油高温分解等都能产生CO。
1-5 什么是矿井气候?简述井下空气温度的变化规律。
矿井气候指井内的温度、湿度、风速等条件在金进风路线上:冬季,冷空气进入井下,冷气温与地温进行热交换,风流吸热,地温散热,因地温随深度增加且风流下行受压缩,故沿线气温逐渐升高;夏季,与冬季情况相反,沿线气温逐渐降低在采掘工作面内:由于物质氧化程度大,机电设备多,人员多以及爆破工作等,致使产生较大热量,对风流起着加热的作用,气温逐渐上升,而且常年变化不大。
1-8《规程》对矿井空气的质量有哪些具体规定?采掘工作面进风流中的氧气浓度不得低于20%;二氧化碳浓度不得超过0.5%;总回风流二氧化碳浓度不得超过0.75%。
当采掘工作面风流中二氧化碳浓度达到1.5%或采区,采掘工作面回风道中二氧化碳浓度超过1.5%时,必须停工处理。
1-9某矿一采煤工作面CO2的绝对涌出量为7.56m3/min,当供风量为850m3/min 时,该工作面回风流中CO2的浓度是多少?能否正常工作?取一分钟,工作面总风量为7.56 +850=862.56m3CO2总量为: 7.56+850×0.04%=7.90m3所以CO2的浓度为: 7.90÷862.56=0.92%>0.75%所以,不能进行正常工作。
会计学第一章作业 答案

会计学第一章总论班级姓名学号一、单项选择题1.会计是以( B )为主要计量单位,核算与监督一个单位经济活动的经济管理工作。
A. 实物B. 货币C. 工时D. 劳动耗费2.按期计提固定资产折旧是以(C )为基本前提的。
A. 会计主体B. 权责发生制C. 会计分期D. 货币计量3.企业会计核算的基础是(B )。
A. 收付实现制B. 权责发生制C. 实地盘存制D. 现金收付制4.企业本月收到上期产品赊销款80000元;本期销售产品60000元,收到货款10000元,余款尚未收到。
按权责发生制原则,本月实现的产品销售收入为(B )元。
A. 80000B. 60000C. 90000D. 100005.企业将融资租赁方式租入的设备确认为固定资产,是基于(B )要求的考虑。
A. 重要性B. 实质重于形式C. 明晰性D. 谨慎性6.业务收支以外币为主的企业,会计核算可以选用一种外币作为记账本位币,但其编制的财务会计报告应折算为(C )反映。
A. 记账本位币B. 功能货币C. 人民币D. 某种外币7.正确地划分投资者和被投资者经济活动范围的界限,是会计核算(B )基本假设的要求。
A. 会计分期B. 会计主体C. 持续经营D. 货币计量8.会计分期是建立在(B )基础之上的。
A. 会计主体B. 持续经营C. 会计核算D. 货币计量9.( D )界定了从事会计工作和提供会计信息的空间范围。
A.会计职能 B。
会计对象 C。
会计内容 D。
会计主体10.( A )作为会计核算的基本前提,就是将一个会计主体持续经营的生产经营活动划分为若干个相等的会计期间。
A.会计分期B.会计主体C.会计年度D.持续经营11.为避免损失发生时对企业正常经营的影响,企业应对可能发生的损失做出合理预计。
这体现的会计信息质量特征是(C )A.实质重于形式B.权责发生制C.谨慎性D.重要性12.下列(B )不属于会计核算的方法。
A.成本计算B.会计分析C.复式记账D.登记账簿13.下列项目中,属于企业资产的是(C )。
汽车制造工艺学习题答案

第一章作业答案1、解释名词术语工艺过程、工序、工步、试切法、静调整法、加工经济精度答:工艺过程:在生产过程中,改变生产对象的形状、尺寸、相对位置和性质,使其成为成品或半成品的过程,称为工艺过程。
工序:一个或一组工人,在一个工作地(机械设备)上对同一个或同时对几个工件所连续完成的那一部分工艺过程,称为工序。
划分工序的依据是加工是否连续完成和工作地是否改变。
工步:在一次安装或工位中,加工表面、加工工具和切削用量中的转速及进给量不变的情况下,所连续完成的那一部分工序,称为工步。
静调整法:先调整好刀具和工件在机床上的相对位置,并在一批零件的加工过程中保持这个位置不变,以保证工件被加工尺寸的方法。
比试切法生产率高,而且加工尺寸的稳定性也好,适合于成批大量生产。
加工经济精度:在正常生产条件下,每种加工方法所能保证的公差等级,称为加工经济精度。
2、汽车零件切削加工时,零件尺寸精度的获得方法有几种?答:有四种:(1)试切法:通过试切—测量—调整—再试切,反复进行到被加工尺寸达到要求为止的加工方法。
常用于单件小批生产。
(2)静调整法:先调整好刀具和工件在机床上的相对位置,并在一批零件的加工过程中保持这个位置不变,以保证工件被加工尺寸的方法。
比试切法生产率高,而且加工尺寸的稳定性也好,适合于成批大量生产。
(3)定尺寸刀具法:是利用刀具的相应尺寸来保证加工尺寸的。
如用钻头、铰刀直接保证被加工孔的尺寸。
(4)主动和自动测量法:是在一些精密机床上加工工件尺寸的同时,利用检测装置测量和控制被加工表面尺寸的一种方法。
3、汽车零件加工时,零件形状的获得方法有几种?答:有三种:(1)轨迹法:是靠刀具运动轨迹来获得所需要的工件形状的一种方法。
(2)成形法:是使用成形刀具加工,获得工件表面的方法。
(3)展成法:在加工时刀具和工件做展成运动,刀刃包络出被加工表面的形状,称为展成法、范成法或滚切法。
8、在大批大量和单件小批生产时,汽车零件尺寸分别采用什么方法获得?答:大批大量生产中,汽车零件尺寸多采用静调整法、定尺寸刀具法和主动及自动测量法来保证;单件小批生产中多采用试切法和定尺寸刀具法来保证尺寸精度。
(完整版)概率统计章节作业答案

第一章 随机事件与概率一、单项选择题1.掷一枚骰子,设A ={出现奇数点},B ={出现1或3点},则下列选项正确的是( B ).A. AB ={出现奇数点}B. AB ={出现5点}C. B ={出现5点}D. A B =ΩU2.设A 、B 为任意两个随机事件,则下列选项中错误的是 ( A ).A. ()A B B A +-=B. ()A B B A B A AB +-=-=-C. ()A B B A B -+=+D.AB AB A +=3.将一枚匀称的硬币投掷两次,令A i ={第i 次正面向上}(i =1,2),则“至少有一次正面向上”可表示为( D ).A.1212A A A A UB.12A AC.12A AD.12A A U4.某人向一目标射击3次,设A i 表示“第i 次射击命中目标”(i =1,2,3),则3次都没有命中目标表示为( A ).A.123A A AB.123A A A ++C.123A A AD.123A A A5.设A 与B 为互为对立事件,且()0,()0P A P B >>,则下列各式中错误的是( A).A.(|)0P A B =B. (|)0P B A =C. ()0P AB =D. ()1P A B =U6.设事件A 与B 相互独立,P (A )=0.2, P (B )=0.4, 则(|)P A B =( D ).A. 0.2B. 0.4C. 0.6D. 0.87.已知事件A 与B 互不相容, P (A )>0, P (B )>0, 则( C ).A.()1P A B =UB.()()()P AB P A P B =C. ()0P AB =D.()0P AB >8.设P (A )=0, B 为任一事件, 则 ( C ).A.A =ΦB.A B ⊂C.A 与B 相互独立D. A 与B 互不相容9.已知P (A )=0.4, P (B )=0.5, 且A B ⊂,则P (A |B )= ( C ).A. 0B. 0.4C. 0.8D. 110.设A 与B 为两事件, 则AB = ( B ).A.A BB. A B UC. A B ID. A B I11.设事件A B ⊂, P (A )=0.2, P (B )=0.3,则()P A B =U ( A ).A. 0.3B. 0.2C. 0.5D. 0.4412.设事件A 与B 互不相容, P (A )=0.4, P (B )=0.2, 则P (A|B )=( D ).A. 0.08B. 0.4C. 0.2D. 013.设A , B 为随机事件, P (B )>0, P (A |B )=1, 则必有 ( A ).A.()()P A B P A =UB.A B ⊂C. P (A )=P (B )D. P (AB )=P (A )14.从1,2,3,4,5中任意取3个数字,则这3个数字中不含5的概率为 ( A ).A. 0.4B. 0.2C. 0.25D. 0.7515.某学习小组有10名同学,其中6名男生、4名女生,从中任选4人参加社会活动,则4人中恰好2男2女的概率为( A ).A.37B.0.4C. 0.25D.16 16.某种动物活20年的概率为0.8,活25年的概率为0.6,现有一只该种动物已经活了20年,它能活到25年的概率是 ( B ).A. 0.48B. 0.75C. 0.6D. 0.817.将两封信随机地投到4个邮筒内,则前两个邮筒内各有一封信的概率为( A ).A. 0.125B. 0.25C. 0.5D. 0.418.一批产品的合格品率为96%,而合格品中有75%是优质品,从该批产品中任取一件恰好是优质品的概率为( A ).A. 0.72B. 0.75C. 0.96D. 0.7819.设有10个产品,其中7个正品,3个次品,现从中任取4个产品,则这4个都是正品的概率为( C ).A. 710B. 44710C. 47410C C D. 4710⨯ 20.设有10个产品,其中8个正品,2个次品,现从中抽取3次,每次任取1个,取后放回,则取到的3个产品都是正品的概率为( C ).A. 810B. 38310C C C. 33810 D. 38310C 21.某人打靶的命中率为0.4,现独立地射击5次,则5次中恰有2次命中的概率为( C ).A. 20.4B. 30.6C. 22350.40.6CD. 23250.40.6C22.随机地抛掷质地匀称的6枚骰子,则至少有一枚骰子出现6点的概率为( D ).A.15615()66CB.156151()66C - C.15651()66C D.651()6- 23.把3个不同的球分别放在3个不同的盒子中,则出现2个空盒的概率为(A ).A. 19B. 12C. 23D. 13 24.从1,2,3,4,5,6六个数字中,等可能地、有放回地连续抽取4个数字,则取到的4个数字完全不同的概率为( A ).A.518B.4!6!C.4446AAD.44!625.某人每次射击命中目标的概率为p(0<p<1),他向目标连续射击,则第一次未中第二次命中的概率为( D ).A. p2B. (1-p)2C. 1-2pD. p(1-p)二、填空题1.一个盒子中有6颗黑棋子、9颗白棋子,从中任取两颗,则这两颗棋子是不同色的概率为18/35 .2.甲乙两人,每人扔两枚均匀硬币,则两人所扔硬币均未出现正面的概率为1/16 .3.设袋中有5个红球、3个白球和2个黑球,从袋中任取3个球,则恰好取到1个红球、1个白球和1个黑球的概率为0.25 .4.从数字1,2,…,10中有放回地任取4个数字,则数字10恰好出现两次的概率为0.0486 .5.甲乙丙三人各自独立地向一目标射击一次,三人的命中率分别是0.5,0.6,0.7,则目标被击中的概率为0.94 .6.甲袋中装有两白一黑共3个球,乙袋中装有一白两黑共3个球,从甲袋中任取一球放入乙袋中,再从乙袋中任取一球,则取到白球的概率为5/12 .7.设事件A与B互不相容,P(A)=0.2, P(B)=0.3, 则()P A BU= 0.5 .8.设事件A与B相互独立,且P(A+B)=0.6, P(A)=0.2, 则P(B)= 0.5 .9.设()0.3,(|)0.6P A P B A==,则P(AB)= 0.42 .10.设11()()(),()(),()046P A P B P C P AB P AC P BC======,则P(A+B+C)=5/12 .11.已知P (A )=0.7, P (A -B )=0.3, 则()P AB = 0.6 .12.某射手对一目标独立射击4次,每次射击的命中率为0.5,则4次射击中恰好命中3次的概率为 0.25 .13.已知P (A )=0.4, P (B )=0.8, P (B|A )=0.25, 则P (A|B )= 0.125 .14.设111(),(|),(|)432P A P B A P A B ===,则()P A B U = 1/3 . 15.一批产品的废品率为4%,而正品中的一等品率为60%,从这批产品中任取一件是一等品的概率为 0.576 .16.甲、乙两门高射炮彼此独立地向一架飞机各发一炮,甲、乙击中飞机的概率分别为0.4,0.5,则飞机至少被击中一炮的概率为 0.7 .三、计算题1.设P (A )=0.4, P (B )=0.2, (|)0.3P B A =, 求P (AB )以及P (A |B ).解:由(|)0.3P B A =得:()0.3,()P AB P A =即()()0.31()P B P AB P A -=-, 解得:P (AB )=0.02. 从而, ()0.02(|)0.1()0.2P AB P A B P B ===.2.已知,()0.2,()0.3,A B P A P B ⊂==求:(1)(),()P A P B ;(2)P (AB );(3)()P AB ;(4) ()P A B U ;(5)P (B -A ).(1)由概率的性质,知()1()0.8,P A P A =-=()1()0.7P B P B =-=;(2)因为A B ⊂,所以AB A =,P (AB )=P (A )=0.2; (3)()P AB =P (A -AB )=P (A )-P (AB )=P (A )-P (A )=0;(4) 因为A B ⊂,所以A B B =U , ()P A B U =P (B )=0.3;或者,()P A B U =P (A )+P (B )-P (AB )=0.2+0.3-0.2=0.3;3.若事件A 与B 互不相容,P (A )=0.6, P (A+B )=0.9, 求:(1)()P AB ;(2)(|)P A B ;(3)()P AB .解:(1) 因A 与B 互不相容,故AB =Φ,P (AB )=0,所以()P AB =1-P (AB )=1;(2) 因A 与B 互不相容,由加法公式:P (A+B )=P (A )+P (B ),得P (B )=0.3,从而 (|)P A B =()()()0.661()0.77()P AB P A P AB P B P B -===-; (3) ()P AB =1()1()10.90.1P AB P A B -=-+=-=.4.已知事件A 与B 相互独立,且P (A )=0.4, P (A+B )=0.6, 求(1)P (B );(2) ()P AB ;(3)P (A|B ).解:(1)因为事件A 与B 相互独立,所以P (AB )=P (A )P (B ),()()()()()()()()P A B P A P B P AB P A P B P A P B +=+-=+-0.6=0.4+P (B )-0.4P (B ),解得:P (B )=13; (2) 因为事件A 与B 相互独立,所以A 与B 也相互独立,故()P AB =4()()15P A P B =; (3) 因为事件A 与B 相互独立,所以P (A|B )=P (A )=0.4.四、应用题 1.一批产品共有50个,其中40个一等品、6个二等品、4个三等品,现从中任取3个产品,求3个产品中至少有2个产品等级相同的概率.解:设A “3个产品中至少有2个产品等级相同”,A “3个产品等级都不同”,由古典概率定义,得111406435012()0.049245C C C P A C ==≈,从而 ()10.0490.951P A =-=.2.10把钥匙中有3把能打开门,现从中任取2把,求能打开门的概率.解:A “取出2把钥匙能打开门”,由古典概率知:1123732108()15C C C P A C +==.3.将5双不同的鞋子混放在一起,从中任取4只,求这4只鞋子至少能配成一双的概率.解:A “4只鞋子中至少能配成一双”,则A “4只鞋子都不同”.由古典概率得:41111522224108()21C C C C C P A C ==,故13()1()21P A P A =-=. 4.从0,1,2,3这4个数中任取3个进行排列,求取得的三个数字排成的数是三位数且是偶数的概率.解:A “排成的数是三位数且是偶数”,A 0“排成的三位数末位是0”,A 2“排成的三位数末位是2”,则A =A 0+A 2,且A 0与A 2互不相容,因为230342!1(),3!4C P A C ==11222341(),3!6C C P A C == 所以,015()()()12P A P A P A =+=. 5.一批零件共100个,次品率为10%,每次从中任取一个零件,取出的零件不再放回去,求下列事件的概率:(1)第三次才取得合格品;(2)如果取得一个合格品后就不再取零件,在三次内取得合格品.解:设A i “第i 次取到合格品”(i =1,2,3),则(1)第三次才取到合格品的概率为:12312131210990()()(|)(|)0.00831009998P A A A P A P A A P A A A ==⨯⨯≈. (2)A “三次内取得合格品”,则112123A A A A A A A =++,所求概率为: 112123()()()()P A P A P A A P A A A =++1121121312()()(|)()(|)(|)P A P A P A A P A P A A P A A A =++90109010990100100991009998=+⨯+⨯⨯0.9993.≈ 6.盒子中有8个红球和4个白球,每次从盒子中任取一球,不放回地抽取两次,试求:(1) 两次取出的都是红球的概率;(2)在第一次取出白球的条件下,第二次取出红球的概率;(3)第二次取到红球的概率.解:A 1“第一次取出的是红球”,A 2“第二次取出的是红球”,则(1)由乘法公式得,两次取出的都是红球的概率为:121218714()()(|)121133P A A P A P A A ==⨯=; (2)在第一次取出白球的条件下,第二次取出红球的概率为:218(|)11P A A =; (3)由全概率公式得,第二次取到红球的概率为:2121121()()(|)()(|)P A P A P A A P A P A A =+7.某工厂有三台设备生产同一型号零件,每台设备的产量分别占总产量的25%,35%,40%,而各台设备的废品率分别是0.05,0.04,0.02,今从全厂生产的这种零件中任取一件,求此件产品是废品的概率.解:设A i “第i 台设备生产的零件”(i =1,2),B “产品是废品”,由题意知:P (A 1)=25%,P (A 2)=35%,P (A 3)=40%,P (B |A 1)=0.05, P (B |A 2)=0.04, P (B |A 3)=0.02,由全概率公式得,产品是废品的概率为:112233()()(|)()(|)()(|)P B P A P B A P A P B A P A P B A =++25%0.0535%0.0440%0.020.0345=⨯+⨯+⨯=.8.两台车床加工同一种零件,加工出来的零件放在一起,已知第一台出现废品的概率是0.03,第二台出现废品的概率是0.02,且第一台加工的零件比第二台加工的零件多一倍.(1)求任取一个零件是合格品的概率;(2)如果取出的是废品,求它是由第二台车床加工的概率.解:设B “零件是合格品”,A “第一台车床加工的零件”,则A “第二台车床加工的零件”,由题意知:21(),()33P A P A ==. (1)由全概率公式得:()()(|)()(|)P B P A P B A P A P B A =+21(10.03)(10.02)0.97333=⨯-+⨯-≈; (2)由贝叶斯公式得,如果取出的是废品,求它是由第二台车床加工的概率为:10.02()()(|)3(|)0.252.921()()13P A B P A P B A P A B P B P B ⨯====--9.已知5%的男人和0.25%的女人是色盲,假设男人女人各占一半.现随机地挑选一人,求:(1)此人恰是色盲的概率是多少?(2)若随机挑选一人,此人是色盲,问他是男人的概率多大?(3)若随机挑选一人,此人不是色盲,问他是男人的概率多大?解:设B “色盲患者”,A “随机挑选一人是男人”,由题设知:11(),(),(|)5%,(|)0.25%22P A P A P B A P B A ====,则 (1)由全概率公式得,随机挑选一人是色盲的概率为:()()(|)()(|)P B P A P B A P A P B A =+115%0.25%0.0262522=⨯+⨯=; (2)由贝叶斯公式得,随机选一人是色盲,他是男人的概率为:15%()()(|)2(|)0.952()()0.02625P AB P A P B A P A B P B P B ⨯===≈; (3)由贝叶斯公式得,随机选一人不是色盲,他是男人的概率为:195%()()(|)2(|)0.48781()0.97375()P AB P A P B A P A B P B P B ⨯===≈-. 10.现有10张考签,其中4张是难签,甲、乙、丙三人抽签考试(取后不放回),甲先乙次丙最后,求下列事件的概率:(1)甲乙都抽到难签;(2)甲没有抽到难签,而乙抽到难签;(3)甲乙丙都抽到难签;(4)证明:甲乙丙抽到难签的机会均等.解:设A ,B ,C 分别表示“甲、乙、丙抽到难签”,则(1)甲乙都抽到难签的概率为:432()()(|)10915P AB P A P B A ==⨯=; (2)甲没有抽到难签,而乙抽到难签的概率为:644()()(|)10915P AB P A P B A ==⨯=; (3)甲乙丙都抽到难签的概率为:4321()()(|)(|)109830P ABC P A P B A P C AB ==⨯⨯=; (4)由古典概率知,甲抽到难签的概率为:4()0.410P A ==. 由全概率公式得,乙抽到难签的概率为:()()(|)()(|)P B P A P B A P A P B A =+43640.4109109=⨯+⨯=. 丙抽到难签的概率为:()()(|)()(|)()(|)()(|)P C P AB P C AB P AB P C AB P AB P C AB P AB P C AB =+++ 4326434636541098109810981098=⨯⨯+⨯⨯+⨯⨯+⨯⨯=0.4. 得,P (A )=P (B )=P (C )=0.4,所以,甲乙丙抽到难签的机会均等,各占40%.11.三个人向同一敌机射击,设三人命中飞机的概率分别为0.4,0.5和0.7.若三人中只有一人击中,飞机被击落的概率为0.2;若有两人击中,飞机被击落的概率为0.6;若三人都击中,则飞机必被击落.求飞机被击落的概率.解:设A i 表示“三人中恰有i 人击中飞机”,i =0,1,2,3.B “飞机被击落”. A 0, A 1, A 2, A 3构成完备事件组,且0()(10.4)(10.5)(10.7)0.09P A =-⨯--=,1()0.4(10.5)(10.7)(10.4)0.5(10.7)(10.4)(10.5)0.70.36P A =⨯-⨯-+-⨯⨯-+-⨯-⨯=, 2()0.40.5(10.7)0.4(10.5)0.7(10.4)0.50.70.41P A =⨯⨯-+⨯-⨯+-⨯⨯=, 3()0.40.50.70.14P A =⨯⨯=.由题设知:0123(|)0,(|)0.2,(|)0.6,(|)1P B A P B A P B A P B A ====.故,由全概率公式得,飞机被击落的概率为:00112233()()(|)()(|)()(|)()(|)P B P A P B A P A P B A P A P B A P A P B A =+++ 0.0900.360.20.410.60.1410.458=⨯+⨯+⨯+⨯=.12.在上题中,假设三人的射击水平相当,命中率都是0.6,其他条件不变,再求飞机被击落的概率.解:设A i 表示“三人中恰有i 人击中飞机”,i =0,1,2,3.B “飞机被击落”. A 0, A 1, A 2, A 3构成完备事件组,且由贝努里公式得:00303()0.60.40.064P A C =⨯⨯=,1213()0.60.40.288P A C =⨯⨯=, 2223()0.60.40.432P A C =⨯⨯=,3333()0.60.216P A C =⨯=.由题设知:0123(|)0,(|)0.2,(|)0.6,(|)1P B A P B A P B A P B A ====. 故由全概率公式得,飞机被击落的概率为:30()()(|)i i i P B P A P B A ==∑0.06400.2880.20.4320.60.21610.5328=⨯+⨯+⨯+⨯=13.已知一批产品中有95%是合格品,检查产品质量时,一个合格品被误判为次品的概率为0.02,一个次品被误判为合格品的概率为0.03,求:(1)任意抽查一个产品,它被判为合格品的概率;(2)一个经检查被判为合格的产品,它确实是合格品的概率.解:设A “产品是合格品”,B “经检查产品被判为合格品”,且由题意知:P (A )=95%, ()195%5%,(|)10.020.98,(|)0.03P A P B A P B A =-==-==.则(1)由全概率公式得,任意抽查一个产品,它被判为合格品的概率为: ()()(|)()(|)P B P A P B A P A P B A =+ 95%0.985%0.030.9325=⨯+⨯=;(2)由贝叶斯公式得,一个经检查被判为合格的产品,它确实是合格品的概率为:()0.950.98(|)0.9984()0.9325P AB P A B P B ⨯==≈. 14.一个工人看管三台机床,在一小时内机床不需要工人看管的概率第一台为0.9,第二台为0.8,第三台为0.7,且三台机床是否需要看管彼此独立.求在一小时内三台机床中最多有一台需要工人看管的概率.解:设A i “第i 台机床需要看管”,i =1,2,3. “三台机床中最多有一台需要工人看管”表示为123123123123A A A A A A A A A A A A +++,且这4个事件两两互不相容,由加法与独立性知,所求的概率为: 123123123123()P A A A A A A A A A A A A +++ 123123123123()()()()P A A A P A A A P A A A P A A A =+++123123123123()()()()()()()()()()()()P A P A P A P A P A P A P A P A P A P A P A P A =+++0.10.80.70.90.20.70.90.80.30.90.80.70.902=⨯⨯+⨯⨯+⨯⨯+⨯⨯=15.加工某一零件共需经过三道工序,设第一、第二、第三道工序的次品率分别是2%,3%,5%.假定各道工序是互不影响的,问加工出来的零件的次品率是多少?解:设A i “第i 道工序加工出次品”,i =1,2,3.则加工出来的零件是次品表示为A 1+A 2+A 3,且A 1,A 2,A 3相互独立,从而123,,A A A 也相互独立. 所求概率为:123123123(++)1()1()()()P A A A P A A A P A P A P A =-=- 1(12%)(13%)(15%)0.09693=----=.16.甲、乙、丙三人独立地破译一密码,他们各自能破译出的概率分别是0.4,0.6,0.7,求此密码被破译的概率.解:设A ,B ,C 分别表示“甲、乙、丙破译出密码”,则A+B+C 表示“密码被破译”,且A ,B ,C 相互独立,从而,,A B C 也相互独立,故所求概率为:(++)1()1()()()P A B C P A B C P A P B P C =-=- 1(10.4)(10.6)(10.7)0.928=----=.17.有甲、乙两批种子,发芽率分别为0.8和0.7,各在两批中随机取一粒,求: (1)两粒种子都能发芽的概率; (2)至多有一粒种子能发芽的概率; (3)至少有一粒种子能发芽的概率.解:设A ,B 分别表示“甲、乙种子发芽”,由题设知:()0.8,()0.7,()10.80.2,()10.70.3P A P B P A P B ===-==-=. (1)两粒种子都能发芽的概率为:()()()0.80.70.56P AB P A P B ==⨯=; (2)至多有一粒种子能发芽的概率为:()()()()P AB AB A B P AB P AB P A B ++=++ ()()()()()()P A P B P A P B P A P B =++ 0.80.30.20.70.20.30.44=⨯+⨯+⨯=; (3)至少有一粒种子能发芽的概率为:()()()()()()()()P A B P A P B P AB P A P B P A P B =+-=+-U0.80.70.80.70.94=+-⨯=.18.一批产品有70%的一级品,进行重复抽样检查,共抽取5件样品,求: (1)取出5件样品中恰有2件一级品的概率p 1; (2)取出5件样品中至少有2件一级品的概率p 2; (3)取出5件样品中至少有一件一级品的概率p 3.解:该问题是参数p =0.7的5重贝努里试验,由贝努里公式得: (1)取出5件样品中恰有2件一级品的概率p 1=22350.70.30.1323C ⨯⨯=; (2)取出5件样品中至少有2件一级品的概率为:p 2=55520.70.3k k k k C -=⨯⨯∑=005145510.70.30.70.30.96922C C -⨯⨯-⨯⨯=; (3)取出5件样品中至少有一件一级品的概率为: p 3=55510.70.3k k k k C -=⨯⨯∑=005510.70.30.99757C -⨯⨯=.19.一射手对一目标独立地射击4次,若至少命中一次的概率为8081, 求射手射击一次命中目标的概率..解:设射手射击一次命中目标的概率为p ,由贝努里定理知,4次射击中至少有一次命中目标的概率为:41(1)p --,由题设知:4801(1)81p --=,解得:23p =.20.一射手对一目标独立地射击, 每次射击命中率为p , 求射击到第4次时恰好两次命中的概率.解:射手射击到第4次恰好有两次命中目标,即第四次命中,而前三次中恰有一次命中,由贝努里定理知,所求概率为:12223(1)3(1)P pC p p p p =-=-. 五、证明题1.设0<P (B )<1,证明事件A 与B 相互独立的充分必要条件是(|)(|)P A B P A B =. 证:必要性 设事件A 与B 相互独立,则P (AB )=P (A )P (B ),P (A|B )=P (A ), 又()()()()()(|)()1()1()()P AB P A AB P A P A P B P A B P A P B P B P B --====--, 所以,(|)(|)P A B P A B =.充分性 若(|)(|)P A B P A B =,则()()()()()()1()1()()P AB P AB P A AB P A P AB P B P B P B P B --===--, 对上式两端化简,得:()()()P AB P A P B =,所以A 与B 相互独立2.证明条件概率的下列性质:(1)若P (B )>0,则0(|)1,(|)1,(|)0P A B P B P B ≤≤Ω=Φ=;(2)若A 与B 互不相容,()0P C >,则(|)(|)(|)P A B C P A C P B C =+U ; (3)(|)1(|)P A B P A B =-. 证:(1)因为()(|)()P AB P A B P B =,而0()()P AB P B ≤≤,所以,0(|)1P A B ≤≤,且()()(|)1()()P B P B P B P B P B ΩΩ===,()()(|)0()()P B P P B P B P B ΦΦΦ===; (2)若A 与B 互不相容,则AC 与BC 也互不相容,从而 ()()()(|)(|)(|)()()P AC BC P AC P BC P A B C P A C P B C P C P C +===+U U ;(3)由性质(2)得:(|)(|)(|)P A A B P A B P A B =+U ,又A A =ΩU ,由性质(1)知,(|)1P B Ω=,所以,(|)(|)1P A B P A B +=,即(|)1(|)P A B P A B =-第二章 随机变量及其概率分布 一、单项选择题1.设随机变量X 的分布律为则P {X <1}=( C ).A. 0B. 0.2C. 0.3D. 0.5 2.设随机变量X 的概率分布为 则a =( D ).A. 0.2B. 0.3C. 0.1D. 0.43.设随机变量X 的概率密度为2,1(),0,1cx f x x x ⎧>⎪=⎨⎪≤⎩则常数c =( D ).A. 1-B.12 C. -12D. 1 4.设随机变量X 的概率密度为3,01(),0,ax x f x ⎧≤≤⎪=⎨⎪⎩其它则常数a =( D ).A.14 B. 12C. 3D. 4 5.下列函数中可作为某随机变量的概率密度函数的是 (A ).A.2100,1000,100x x x ⎧>⎪⎨⎪≤⎩ B.10,00,0x xx ⎧>⎪⎨⎪≤⎩ C. 1,020,x -≤≤⎧⎨⎩其它D.113,2220,x ⎧≤≤⎪⎨⎪⎩其它6.设函数()f x 在区间[,]a b 上等于sin x ,而在此区间外等于0;若()f x 可以作为某连续型随机变量的概率密度函数,则区间[,]a b 为 ( A ).A. [0,]2πB. [0,]πC. [,0]2π-D. 3[0,]2π7.下列函数中,可以作为某随机变量X 的分布函数的是 ( C ).A. 0,00.3,01()0.2,121,2x x F x x x <⎧⎪≤<⎪=⎨≤<⎪⎪≥⎩B. 0.5,0()0.8,011,1x x F x x x <⎧⎪=≤<⎨⎪≥⎩C. 0,00.1,05()0.6,561,6x x F x x x <⎧⎪≤<⎪=⎨≤<⎪⎪≥⎩ D. 0,2()sin ,021,0x F x x x x ππ⎧<-⎪⎪⎪=-≤<⎨⎪≥⎪⎪⎩8.设()F x 是随机变量X 的分布函数,则 ( B ). A. ()F x 一定连续 B. ()F x 一定右连续 C. ()F x 是不增的 D. ()F x 一定左连续9.设()()F x P X x =≤是随机变量X 的分布函数,则下列结论错误的是(D ).A.()F x 是定义在(,)-∞+∞上的函数B.lim ()lim ()1x x F x F x →+∞→-∞-=C.()()()P a X b F b F a <≤=-D.对一切实数x ,都有0<()F x <110.设随机变量的概率分布为2()(),(1,2,3...)3k P X k a k ===,则常数a =( B ).A. 1B. 12C. 2D. 12-11.已知随机变量X 的分布律为()F x 是X 的分布函数,则F (2.5)=( B ). A. 0.7 B. 0.8 C. 0.1 D. 112.随机变量X 的概率密度2,01()0,x x f x <<⎧=⎨⎩其它,则11{}22P X -≤≤=( A ).A.14B.13C.12D.3413.已知随机变量X 的分布律为 若随机变量Y =X 2,则P {Y =1}=( C ).A. 0.1B. 0.3C. 0.4D. 0.2 14.设随机变量X ~B (4, 0.2),则P {X >3}=( A ).A. 0.0016B. 0.0272C. 0.4096D. 0.819215.设随机变量X ~N (1,4),Y =2X +1,Y ~ ( C). A. N (1, 4) B. N (0, 1) C. N (3, 16) D. N (3, 9) 16.设2~(,)X N μσ,()x Φ是N (0, 1)的分布函数,则()P a X b ≤≤= ( D ). A.()()b a Φ-Φ B.()()b a Φ+ΦC.22()()b a μμσσ--Φ-Φ D.()()b a μμσσ--Φ-Φ17.设X ~N (-1,4),()x Φ是N (0, 1)的分布函数,则P (-2<X <0)= ( A ).A.12()12Φ- B.(0)(2)Φ-Φ- C.1(2)2Φ- D.(2)(0)Φ-Φ18.设X ~N (0,1),()x ϕ是X 的概率密度函数,则(0)ϕ= (C ). A. 0 B. 0.5C.D. 1 19.设X 服从均匀分布U[0,5],Y =3X +2,则Y 服从 ( B ). A. U[0, 5] B. U[2, 17] C. U[2, 15] D. U[0, 17] 20.某种商品进行有奖销售,每购买一件有0.1的中奖率.现某人购买了20件该商品,用随机变量X 表示中奖的件数,则X 的分布为 ( D ).A.正态分布B.指数分布C.泊松分布D.二项分布 21.设X 服从参数2λ=的泊松分布,()F x 是X 的分布函数,则下列正确的选项是 ( B ).A.2(1)F e -=B.2(0)F e -=C.P (X =0)=P (X =1)D.2(1)2P X e -≤= 22.设X 服从参数λ的泊松分布,且2(1)(3)3P X P X ===,则λ= ( C ). A. 1 B. 2 C. 3 D. 4二、填空题1.若2()1P X x β≤=-,1()1P X x α≥=-,其中x 1<x 2, 则12()P x X x ≤≤= 1 .2.设随机变量X 的概率分布为记Y =X 2, 则P (Y =4)= 0.5 .3.若X 是连续型随机变量, 则P (X =1)= 0 .4.设随机变量X 的分布函数为F (x ), 已知F (2)=0.5, F (-3)=0.1, 则(32)P X -<≤= 0.4 .5.设随机变量X的分布函数为212()xt F x edt --∞=⎰,则其密度函数为 .6.设连续型随机变量X 的分布函数为0,0()sin ,021,2x F x x x x ππ⎧⎪<⎪⎪=≤<⎨⎪⎪≥⎪⎩, 其密度函数为()f x ,则()6f π= 1/2 .7.设随机变量X 的分布函数为1,0()0,x e x F x x -⎧-≥=⎨<⎩, 则当x >0时, X 的概率密度()f x = 1 . .8.设随机变量X 的分布律为则(01)P X ≤≤= 0.6 .9.设随机变量X ~N (3, 4), 则(45)P X <<= 0.148 . (其中(1)0.8413,(0.5)0.6915Φ=Φ=)10.设随机变量X 服从参数为6的泊松分布, 写出其概率分布律 P(X=K)=6K/K! K=0,1,2,3 .11.若随机变量X ~B (4, 0.5), 则(1)P X ≥= 15/16 .12.若随机变量X ~U (0, 5),且Y =2X ,则当010y ≤≤时, Y 的概率密度()Y f y = 1/10 .13.设随机变量X ~N (0, 4),则(0)P X ≥= 0.5 .14.设随机变量X ~U (-1, 1),则1(||)2P X ≤= 0.5 .15.设随机变量X 在[2, 4]上服从均匀分布,则(23)P X <<= 0.5 .16.设随机变量X ~N (-1, 4),则1~2X Y +=N(0,1) . 17.设随机变量X 的分布律为(),0,1,2, (3)k aP X k k ===,则a = 2/3 .18.设连续型随机变量X 的概率密度为1,02()0,kx x f x +<<⎧=⎨⎩其它,则k =-1/2 .19.若随机变量X ~N (1, 16),Y =2X -1,则Y ~ N(1,64) . 20.若随机变量X ~U (1, 6),Y =3X +2,则Y ~ U(5,20) . 三、计算题1.设连续型随机变量X 的分布函数为20,0(),011,1x F x x x x <⎧⎪=≤<⎨⎪≥⎩,求X 的概率密度函数.解:由分布函数与概率密度函数之间的关系()()F x f x '=知,当0<x <1时, 2()()2f x x x '==,当1x ≥或0x ≤时,()f x =0,所以,X 的概率密度为2,01()0,x x f x <<⎧=⎨⎩其它.2.设X 服从参数p =0.2的0-1分布,求X 的分布函数及P (X <0.5). 解:X 的分布律为当0x <时,()()F x P X x =≤=0;当01x ≤<时,()()F x P X x =≤=(0)0.8P X ==;当1x ≥时,()()F x P X x =≤=(0)(1)0.80.21P X P X =+==+=.所以,X 的分布函数为0,0()0.8,011,1x F x x x <⎧⎪=≤<⎨⎪≥⎩;而P (X <0.5)= P (X =0)=0.8.3.设随机变量X ~U (a , b ),求X 的密度函数与分布函数.解:X 的密度函数为1,()0,a xb f x b a ⎧<<⎪=-⎨⎪⎩其它;分布函数()()x F x f t dt -∞=⎰,当x a <时,()()xF x f t dt -∞=⎰00xdt -∞==⎰;当a x b ≤<时,()()x F x f t dt -∞=⎰10a xax adt dt b a b a-∞-=+=--⎰⎰; 当x b ≥时,()()x F x f t dt -∞=⎰1001abx ab dt dt dt b a-∞=++=-⎰⎰⎰.所以,X 的分布函数为0,(),1,x a x a F x a x b b ax b <⎧⎪-⎪=≤<⎨-⎪≥⎪⎩.4.设随机变量X ~N (3, 4),求:(1)P (2<X <3);(2) P (-4<X <10);(3) P (|X|>2);(4)P (X >3).解:(1)P (2<X <3)=3323(3)(2)()()22F F ---=Φ-Φ(0)(0.5)=Φ-Φ- (0)[1(0.5)]=Φ--Φ=0.1915;(2) P (-4<X <10)=10343(10)(4)()()22F F -----=Φ-Φ=(3.5)( 3.5)2(3.5)1Φ-Φ-=Φ-=0.9996; (3) P (|X|>2)=1(||2)P X -≤=1(22)1[(2)(2)]P X F F --≤≤=---=23231[()()]22----Φ-Φ=(0.5)(2.5)1Φ-Φ+=0.6977; (4)P (X >3)=1(3)P X -≤=331(3)1()1(0)2F --=-Φ=-Φ=0.5.5.已知随机变量X 的密度函数为2,01()0,kx x f x ⎧<<=⎨⎩其它,求:(1)常数k ;(2)分布函数;(3)(10.5)P X -<<..解:(1)因为()1f x dx +∞-∞=⎰,所以123100|133k kkx dx x ===⎰,故k =3. 即随机变量X 的概率密度为23,01()0,x x f x ⎧<<=⎨⎩其它;(2)当0x <时,()()xF x f t dt -∞=⎰=0,当01x ≤<时,()()xF x f t dt -∞=⎰=023003xdt t dt x -∞+=⎰⎰,当1x ≥时,()()x F x f t dt -∞=⎰=012010301xdt t dt dt -∞++=⎰⎰⎰所以,随机变量X 的分布函数为30,0(),011,1x F x x x x <⎧⎪=≤<⎨⎪≥⎩;(3)(10.5)P X -<<3(0.5)(1)0.500.125F F =--=-=;6.设随机变量X 的概率密度为,011(),1220,x x f x x <<⎧⎪⎪=≤<⎨⎪⎪⎩其它,求X 的分布函数.解:当0x <时,()()xF x f t dt -∞=⎰=0;当01x ≤<时,()()xF x f t dt -∞=⎰=020102xdt tdt x -∞+=⎰⎰;当12x ≤<时,()()x F x f t dt -∞=⎰=010111022x dt tdt dt x -∞++=⎰⎰⎰;当2x ≥时,()()x F x f t dt -∞=⎰=01201210012xdt tdt dt dt -∞+++=⎰⎰⎰⎰.所以,随机变量X 的分布函数为20,01,012()1,1221,2x x x F x x x x <⎧⎪⎪≤<⎪=⎨⎪≤<⎪⎪≥⎩.7.设随机变量X~,01()2,120,x x f x x x ≤<⎧⎪=-≤<⎨⎪⎩其它,求:(1)1()2P X ≥;(2)13()22P X <<.解:(1)1()2P X ≥=+1211122()(2)f x dx xdx x dx ∞=+-⎰⎰⎰=2122112117|(2)|228x x x +-=; (2)13()22P X <<=3312211122()(2)f x dx xdx x dx =+-⎰⎰⎰=32122112113|(2)|224x x x +-=.8.设随机变量X 在[0,5]上服从均匀分布,求方程24420x Xx X +++=有实根的概率.解:X ~1,05()50,x f x ⎧≤≤⎪=⎨⎪⎩其它,而方程24420x Xx X +++=有实根的充分必要条件是21616(2)0X X ∆=-+≥,即220X X --≥,故所求概率为:2{20}(1)(2)P X X P X P X --≥=≤-+≥=0+5215dx ⎰=0.6.9.设随机变量X 的分布律为求:(1)Y =2X 的分布律;(2)Z =|X |的概率分布;(3)X 2的分布律.解:(1)由X 的分布律知,Y 的取值为-2,0,2,4.且(2)(1)0.1P Y P X =-==-=,(0)(0)0.2P Y P X ====, (2)(1)0.3P Y P X ====,(4)(2)0.4P Y P X ====. 所以,Y 的分布律为(2)Z =|X |的取值为0,1,2.2(0)(0)0.2P X P X ====,2(1)(1)(1)0.4P X P X P X ===-+==,2(4)(2)0.4P X P X ====.所以,X 2的分布律为:10.设X ~U [0,4], Y =3X +1,求Y 的概率密度.解:X ~1,04()40,x f x ⎧≤≤⎪=⎨⎪⎩其它,Y =3X +1的取值范围是[1,13].Y 的分布函数131()()(31)()()3y Y y F y P Y y P X y P X f x dx --∞-=≤=+≤=≤=⎰ 当1y <时,有103y -<,13()00y Y F y dx --∞==⎰;当113y ≤<时,有1043y -≤<,103011()0412y Y y F y dx dx --∞-=+=⎰⎰; 当13y ≥时,有143y -≥,1043041()0014y Y F y dx dx dx --∞=++=⎰⎰⎰.11.已知随机变量X ~N (1,4),Y =2X +3,求Y 的概率密度..解:X~2(1)8(),()x f x x --=-∞<<+∞,建立Y 的分布函数与X 的分布函数之间的关系.因为:33()()(23)()()22Y X y y F y P Y y P X y P X F --=≤=+≤=≤=, 两边对y 求导:3313()()()()2222Y X X y y y f y F f ---''=⋅=223(1)(5)2832y y -----==,即Y ~N (5,16).12.已知X 服从参数1λ=的指数分布,Y =2X -1,求Y 的概率密度.解:由题设知,X ~,0()0,0x e x f x x -⎧>=⎨≤⎩,方法1 11()()(21)()()22Y X y y F y P Y y P X y P X F ++=≤=-≤=≤=, 两边对y 求导:1111()()()()2222Y X X y y y f y F f +++''=⋅=, 又因为12121,012,1()210,10,02y y X y e y e y f y y +-+-⎧+>⎧⎪+⎪⎪>-==⎨⎨+⎪⎪≤-⎩≤⎪⎩,所以,Y 的概率密度为:121,1()20,1y Y e y f y y +-⎧>-⎪=⎨⎪≤-⎩.四、应用题1.一批零件中有10个合格品和2个废品,安装机器时,从这批零件中任取一个,如果每次取出废品后不再放回,用X 表示在取得合格品以前已取出的废品的个数,求:(1)随机变量X 的分布律;(2)随机变量X 的分布函数.解:(1)随机变量X 的可能取值为0,1,2,且105(0)126P X ===,2105(1)121133P X ==⨯=,21101(2)12111066P X ==⨯⨯=, 得到X 的分布律为:(2)X 的可能取值0,1,2将分布函数F (x )的定义域(,)-∞+∞分为四部分: 当0x <时,()()0F x P X x =≤=,当01x ≤<时,()()F x P X x =≤5(0)6P X ===,当12x ≤<时,()()F x P X x =≤65(0)(1)66P X P X ==+==, 当2x ≤时,()()F x P X x =≤(0)(1)(2)1P X P X P X ==+=+==. 从而得到X 的分布函数为:0,05,016()65,12661,2x x F x x x <⎧⎪⎪≤<⎪=⎨⎪≤<⎪⎪≥⎩.2.袋中有标号为1,2,2,3,3,3的六个球,从中任取一个球,求所取出的球的号码X 的概率分布及分布函数..解:X 的可能取值为1,2,3.且1(1)6P X ==,21(2)63P X ===,31(3)62P X ===, 所以,X 的概率分布为:当1x <时,()()0F x P X x =≤=,当12x ≤<时,()()F x P X x =≤1(1)6P X ===,当23x ≤<时,()()F x P X x =≤1(1)(2)2P X P X ==+==, 当3x ≥时,()()F x P X x =≤(1)(2)(3)1P X P X P X ==+=+==. 从而得到X 的分布函数为:0,11,126()1,2321,3x x F x x x <⎧⎪⎪≤<⎪=⎨⎪≤<⎪⎪≥⎩3. 袋中有标号为1,2,2,3,3,3的六个球,从中任取两个球,X 表示取出的两个球的最大号码,求X 的概率分布..解:X 的所有可能的取值为2,3.且112122261(2)5C C C P X C +===,112333264(3)5C C C P X C +===, 从而得到X 的概率分布为:4.设一批产品共1000个,其中40个是次品,随机抽取100个样品,按下列两种方式抽样,分别求样品中次品数X 的概率分布.(1)不放回抽样; (2)有放回抽样.解:(1)不放回抽样,X 的可能取值为0,1,2,…,40.{X =k }表示100个样品中恰好有k 个次品,则100401000401001000()k kC C P X k C --==,得到X 的概率分布为: 100409601001000(),0,1,2,...,40.k kC C P X k k C -=== (2)有放回抽样,X 的可能取值为0,1,2,…,100.由于有放回抽样,抽取100个样品可看作进行了100重贝努里试验,且每次抽到次品的概率都是0.04,抽到正品的概率为0.96,X ~B (100,0.04).则X 的概率分布为:100100()0.040.96,0,1,2,...,100.kk k P X k C k -===5.抛掷一枚质地不均匀的硬币,每次正面出现的概率为13,连续抛掷10次,以X 表示正面出现的次数,求X 的分布律.由题设知,X ~B (10,13). 则X 的分布律为:101012()()(),0,1,2,...,10.33k k kP X k C k -===6.有一繁忙的交通路口,每天有大量的汽车经过,设每辆汽车在一天的某段时间内出事故的概率为0.0001.在某天的该段时间内有1000辆汽车经过,问出事故的次数不小于2的概率.解:设X 表示1000辆汽车通过路口时出事故的次数,由题意知,X ~B (1000,0.0001).由于n =1000很大,p =0.0001很小,故利用泊松分布近似代替二项分布计算.其中,10000.00010.1np λ==⨯=,0.10.1(),0,1,2,...!k P X k e k k -=≈=, 查泊松分布表可得,所求概率为:7.以电话交换台每分钟收到的呼唤次数服从参数为4的泊松分布,求: (1)每分钟恰有4次呼唤的概率; (2)每分钟的呼唤次数至少有4次的概率.解:设X 表示电话交换台每分钟收到的呼唤次数,由题意知,X ~P (4),其分布律为:44(),0,1,2...!k P X k e k k -===,则(1)每分钟恰有4次呼唤的概率444(4)0.1953674!P X e -===;(2)每分钟的呼唤次数至少有4次的概率444(4)0.56653!k k P X e k ∞-=≥==∑8.袋中装有8个球,其中3个红球、5个白球,现从袋中任取3个球,求取出红球数的概率分布.解:X 表示取出3个球中含有红球的个数,则X 的可能取值为0,1,2,3. 且35385(0)28C P X C ===,12353815(1)28C C P X C ===,21353815(2)56C C P X C ===,33381(3)56C P X C ===,于是,X 的概率分布为:9.已知某类电子元件的寿命X (单位:小时)服从指数分布,其概率密度为110001,0()10000,0x e x f x x -⎧>⎪=⎨⎪≤⎩, 一台仪器装有3个此种类型的电子元件,其中任意一个损坏时仪器便不能正常工作,假设3个电子元件损坏与否相互独立.试求:(1)一个此类电子元件能工作1000小时以上的概率p 1; (2)一台仪器能正常工作到1000小时以上的概率p 2. 解:(1)一个此类电子元件能工作1000小时以上的概率为:p 1=11110001000100010001(1000)|1000x x P X e dx e e --+∞+∞-≥==-=⎰; (2)一台仪器能正常工作到1000小时以上,需要这3个电子元件的寿命都在1000小时以上,由独立性知,所求概率为:p 2=33[(1000)]P X e -≥=.10.公共汽车车门的高度是按男子与车门顶碰头的机会在0.01以下来设计的.设男子身高X 服从170μ=(厘米),6σ=(厘米)的正态分布,即2~(170,6)X N .问车门高度应如何确定?解:设车门高度为h 厘米,由题意知,()0.01P X h >≤,即()0.99P X h ≤≥. 因为X ~N (170,36),所以170()()()0.996h P X h F h -≤==Φ≥, 查表得:(2.33)0.99010.99Φ=>,所以1702.336h -=,解得h =183.98. 设计车门的高度为183.98厘米时,可使男子与车门碰头的机会不超过0.01.五、综合题1.设10件产品中有2件次品,现进行连续无放回抽样,直至取到正品为止,求:(1)抽样次数X 的概率分布; (2)X 的分布函数F (x ); (3)(2),(13)P X P X >-<<. .解:(1)X 的可能取值为1,2,3.且84(1)105P X ===,288(2)10945P X ==⨯=,2181(3)109845P X ==⨯⨯=. 所以,X 的概率分布为:(2)当1x <时,()()0F x P X x =≤=, 当12x ≤<时,4()()(1)5F x P X x P X =≤===, 当23x ≤<时,44()()(1)(2)45F x P X x P X P X =≤==+==, 当3x ≥时,()()(1)(2)(3)1F x P X x P X P X P X =≤==+=+==. 所以,X 的分布函数为:0,14,125()44,23451,3x x F x x x <⎧⎪⎪≤<⎪=⎨⎪≤<⎪⎪≥⎩;(3)(2)(1)(2)(3)1P X P X P X P X >-==+=+==; 或(2)1(2)1(2)101P X P X F >-=-≤=-=-=.8(13)(2)45P X P X <<===.2.司机通过某高速路收费站等候的时间X (单位:分钟)服从参数15λ=的指数分布.(1)求某司机在此收费站等候时间超过10分钟的概率p ;(2)若该司机一个月要经过此收费站两次,用Y 表示等候时间超过10分钟的次数,写出Y 的分布律,并求(1)P Y ≥.解:(1)由题设知,151,0~()50,0x e x X f x x -⎧>⎪=⎨⎪≤⎩,则司机在此收费站等候时间超过10分钟的概率为:125101(10)5x p P X e dx e -+∞-=>==⎰; (2)由题意知,2~(2,)Y B e -,Y 的分布律为:22222222()()(1)(1),0,1,2.k k k k k k P Y k C e e C e e k ------==-=-= 2224(1)1(0)1(1)2P Y P Y e e e ---≥=-==--=-.3.甲乙丙三人独立地等1,2,3路公共汽车,他们等车的时间(单位:分钟)都服从[0,5]上的均匀分布,求三人中至少有两人等车不超过2分钟的概率.解:设一个人等车的时间为X ,由题设知,X ~U [0,5],其密度函数:1,05()50,x f x ⎧≤≤⎪=⎨⎪⎩其它. 则一个人等车不超过2分钟的概率为:221(2)()0.45p P X f x dx dx -∞=≤===⎰⎰. 设Y 表示三人中等车时间不超过2分钟的人数,则Y ~B (3,0.4),则三人中至少有两人等车不超过2分钟的概率为:223333(2)(2)(3)0.40.60.4P Y P Y P Y C C ≥==+==+=0.352.4.设测量距离时产生的随机误差X ~N (0,102)(单位:米),现作三次独立测量,记Y 为三次测量中误差绝对值大于19.6的次数,已知(1.96)0.975.Φ=(1)求每次测量中误差绝对值大于19.6的概率p ; (2)问Y 服从何种分布,并写出其分布律;(3)求三次测量中至少有一次误差绝对值大于19.6的概率. 解:(1) p =(||19.6)1(||19.6)P X P X >=-≤019.601(||)1[2(1.96)1]1010X P --=-≤=-Φ-=0.05. (2)由题意知,Y ~B (3, 0.05),Y 的分布律为:33()0.050.95,0,1,2,3.k k k P X k C k -===(3)三次测量中至少有一次误差绝对值大于19.6的概率为: 3(1)1(0)10.95P Y P Y ≥=-==-=0.142625.5.设顾客在某银行的窗口等待服务的时间X (单位:分钟)服从参数110λ=的指数分布.某顾客在窗口等待服务,若超过10分钟,他就离开.他一个月要到银行5次,以Y 表示他未等到服务而离开窗口的次数.(1)写出Y 的分布律;(2)求该顾客一个月至少有一次未等到服务而离开窗口的概率.解:(1)由题设知,等待服务的时间X ~1101,0()100,0x e x f x x -⎧>⎪=⎨⎪≤⎩,顾客离开银行的概率为:1110101(10)10x p P X e dx e -+∞-=>==⎰.由题意知,Y ~B (5,e -1),其分布律为:1155()()(1),0,1,...,5.k k k P Y k C e e k ---==-=(2)所求概率为(1)P Y ≥=151(0)1(1)P Y e --==--0.899≈.6.设连续型随机变量X 的分布函数为:20,0(),011,1x F x Ax x x <⎧⎪=≤<⎨⎪≥⎩,求:(1)系数A ; (2)X 的概率密度; (3)(0.30.7)P X <≤; (4)Y =X 2的概率密度.解:(1)由F (x )的连续性知,11lim ()lim ()(1)x x F x F x F -+→→==,有21lim 1x Ax -→=,得1A =; (2)X 的概率密度2,01()()0,x x f x F x <<⎧'==⎨⎩其它;(3)(0.30.7)P X <≤22(0.7)(0.3)0.70.30.4F F =-=-=,或(0.30.7)P X <≤=0.720.70.30.32|0.4xdx x ==⎰; (4)因为20Y X =≥,所以,当0y <时,()()0Y F y P Y y =≤=, 当01y ≤<时,2()()()(Y F y P Y y P X y P X =≤=≤=≤≤()f x dx xdx y ===,当1y ≥时,101()(()21Y F y P X f x dx xdx dx =≤≤==+=⎰所以,X 的分布函数为:0,0(),011,1Y y F y y y y <⎧⎪=≤<⎨⎪≥⎩,X 的概率密度为:1,01()0,Y y f y <<⎧=⎨⎩其它.7.连续型随机变量X 的分布函数为()arctan ,()F x A B x x =+-∞<<+∞,求:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
4
• ※<习题一> 为使氦氖激光器的相干长度达到1km,它 的单色性Δλ/λ应是多少?
解:
Lc
Cc
C v v
C Lc
C vv C
v 0.6328106 6.3281010
v Lc
1000
A
5
※<习题二>
(1)一质地均匀的材料对光的吸收为0.01mm-1,光通 过10cm长的该材料后,出射光强为入射光强的百分之几? (2)一光束通过长度为1m的均匀激活的工作物质,如果 出射光强是入射光强的两倍,试求该物质的增益系
※<习题七> 如 等 (于果2)1工0为作5S使物-受质1激,的跃试某迁问一几:跃率(迁比1波)自长该发为跃跃1迁迁00的几n受m率的激大远辐三紫射倍外爱,光因腔,斯内自坦的发系单跃数色迁B能1几0量是率密多A度少10ρ? 应为多少?
※<习题八>
如 6u果m受(激红辐外射光爱)因;斯(坦2)系λ数=B60100=n1m0(19m可3见s-光3w)-;1,(试3计)00K时, n2/n1=?
当λ=1um、T=300K时,n2/n1=?
当λ=1um、n2/n1=0.1时,T=?
解: 根据玻尔兹曼分布知
n i g ie K E T in n ij g g ije E K i T E jg g ije K h v Tg g ije K h T c
A
2
※<习题五> 设一对激光能级为E2和E1(g1=g2),两能级间的跃迁频率为ν(相应 的波长为λ),能级上的粒子数密度分别为n2和n1,试求 当ν=3000MHz、T=300K时, n2/n1=? 当λ=1um、T=300K时,n2/n1=? 当λ=1um、n2/n1=0.1时,T=?
※<习题六> 假 是什定么工光作范物围质?的折射率η=1.73,试问ν为多大时,A21/B21=1J*S/m3 ,这
0.60nm(x射线),自发辐射跃迁几率A10和自发辐射寿命。又如果光强I=
10W/mm2,试求受激跃迁几率W10。
解:
Aul Bul8ch3v3 Bul8 3 hA1 ul
• 1)λ=6um
AB c h v A u l u l8 3 3 1 0 1 9 8 ( 6 6 . 6 1 2 0 9 6 ) 3 1 0 3 4 2 s 1 1 u l 1 . 2 9 6 1 0 3 s
• 解: 1) II0el
I el e0.0110010.3679=376.79%
I0
e
• 2)由题意知
不 考 虑
2I0 I0eGZ I 2 eGZ eG
损
I0
考 虑
2I0 I0eGZ Z
损 I 2 eGZ Z eG10
耗
I0
耗 G ln 2 0 .6 9 3 1 m -1 A
Aul
Bul
8hv3 c3
Aul Bul
8hv3 c3
1
v C / n 3 108 / 1.73 6.792 1018 3 8h 3 8 6.629 1034
cv/n2.5541011m
为Υ射线
A
10
※<习题七> 如果工作物质的某一跃迁波长为100nm的远紫外光,自发跃迁几率A10 等于105S-1,试问:(1)该跃迁的受激辐射爱因斯坦系数B10是多少? (2)为使受激跃迁几率比自发跃迁几率大三倍,腔内的单色能量密度 ρ应为多少?
第一章 作业
A
1
※<习题一> 为使氦氖激光器的相干长度达到1km,它的单色性Δλ/λ 应是多少?
※<习题二> (1)一质地均匀的材料对光的吸收为0.01mm-1,光通过 10cm长的该材料后,出射光强为入射光强的百分之几?(2) 一光束通过长度为1m的均匀激活的工作物质,如果出射光强是 入射光强的两倍,试求该物质的增益系数。
(2)λ=600nm
AB c h v A u l u l8 3 3 1 0 1 9 8 ( 6 6 . 6 1 2 0 9 7 ) 3 1 0 3 4 5 s 1 1 u l 1 . 2 9 6 1 0 6 s
(3)λ=60nm
AB c h v A u l u l8 3 3 1 0 1 9 8 ( 6 6 . 6 1 2 0 9 8 ) 3 1 0 3 4 8 s 1 1 u l 1 . 2 9 6 1 0 9 s
•
解:1)
Aul
Bul
8hv3 c3
Bul
Aul
c3 8hv3
105
3 8h
6.00221015s1
• 2)
Aul
Bul
8hv3 c3
13Bul
24hv3 c3
24h 3
4.998110-11Jms
A
11
※<习题八>
如果受激辐射爱因斯坦系数B10=1019m3s-1w-1,试计算在(1)λ=6um(红外 光);(2)λ=600nm(可见光);(3)λ=60nm(远紫外光);(4)λ=
当λ=0.5um
n h P v P h c 6 .6 2 8 1 1 5 0 3 1 4 0 3 7 1 0 8 2 .5 1 4 6 1 0 1 8
当v=3000mHZ n h P v A 6 .6 2 8 1 0 1 3 4 3 1 0 9 5 .0 2 9 2 1 70 2 3
G ln 2 10 10.6931m6-1
※<习题三>
如果激光器和微波激射器分别在λ =10um,
λ=5×10-1um和ν=3000MHz输出1W连
续功率,试问每秒钟从激光上能级向下能
级跃迁的粒子数是多少?
解:
由
E
o
p
hv
h
c
知
P n h v
当λ=10um
n h P v P h c 6 .6 2 8 1 1 0 1 0 3 4 53 1 0 8 5 .0 2 9 2 1 0 1 9
解: 1)
I eGZ e5 148.41 I0
2)
I(z0dz)I(z0)eG(z)dz
L
G(z)dz I(L)I0ez0
L
I0e0 G(z)dz
LA1cos(2kz)dz
0
2
I e0
ALAsin2kL
I0e2 4K
A
14
• ※<习题十一> 试证明,由于自发辐射,原子在E2能级的 平均寿命τs=1/A21
外 射光寿)命;。(又如4)果λ光=强0.6I=0n1m0W(/xm射m线2,)试,求自受发激辐跃射迁跃几迁率几W率10A。10和自发辐
A
3
※<习题九> 由两个全反射镜组成的稳定光学谐振腔,腔长为0.5m, 腔内振荡光的中心波长为6328A,试求该光的频带宽度 Δλ的近似值。
※<习题十> (1)一光束入射到长为10cm,增益系数为0.5cm-1的工 作物质中,求出射光强对入射光强的比值;(2)一初始 光它强的为增I益0波系长数为为λG的=光A束co入s射2kz到(长0≤为zL≤的L工)作,物式质中中A和,k如为果 常数。试求从工作物质出射的光强I的表达式。
12
※<习题九> 由两个全反射镜组成的稳定光学谐振腔,腔长为0.5m, 腔内振荡光的中心波长为6328A,试求该光的频带宽度 Δλ的近似值。
解:由驻波条件知
q 2nL 1
q 1 1580278.129
而q只能取正整数,所以q在1580278附近对应的λ
(λ 1580277 -λ 1580279)/2=4.0X10-13m
※<习题四>
设一光子的波长=5×10-1um,单色性 =10-7,试求光
子位置的不确定量 Δx。若光子的波长变为5×10-4um
(x射线)和5×10-18um(射线),则相应的 Δx又是多
少?
h mc2
解: 光子能量: 光子动量:
p mc
hv c
h
光子质量: 所以
m
c2
h
c2
p h h h h h h 1 0 7 h 1 0 7 h 1 0 7 m M / 2 / 2 2 2 / 4 2 1 0 1 4 2 / 4 ( 1 1 0 1 4 / 4 )
n1
当λ=1um、n2/n1=0.1时
hc
1.38 10 23 10 6
T
6257.617K
Klnn2 6.629A 10 343 108lnn2
9
n 1
n 1
※<习题六> 假定工作物质的折射率η=1.73,试问ν为多大时,A21/B21=1J*S/m3 ,这是什么 光范围?
解: 由爱因斯坦三个系数之间的关系知道
• 见课本
A
15
由海森堡理论知
x p 2 h x 2 h p 2 1 0 7
5×10-1um
x21070.7958m
5×10-4um x2 1077.958104m
5×10-18um
x2 10 A77.9581018m
8
※<习题五> 设一对激光能级为E2和E1(g1=g2),两能级间的跃迁频率为ν(相应的波长为λ), 能级上的粒子数密度分别为n2和n1,试求
(4)λ=0.60nm
AB c h v A u l u l8 3 3 1 0 1 9 8 ( 6 6 . 6 1 2 0 9 1 0 ) 3 1 0 3 4 1 4 s 1 1 u l 1 . 2 9 6 1 0 1 5 s
I s W10:
W 1 0 B 1 0 B 1 0C A1 0 1 9 1 3 0 1 1 0 0 8 6 3 . 3 3 3 3 1 0 1 7 1
