相对定向和绝对定向的解析过程(全面)

三、相对定向元素的计算过程
量测 5 个以上的同名点（定向点） 明显点 1、2点：左、右片的像主点 人工量测：六个标准点位 3、5点：X=0，Y值最大 4、6点：X=b，Y值最大
3
4
X
1
2
5
6
相对定向标准点位
计算框图：以连续像对的相对定向为例
输入像点坐标 （x1,y1）,（x2,y2） 确定初始值bu=(x1-x2)1 φ 2=ω 2=κ 2=μ =ν =0 计算右片旋转矩阵R2 计算像点的像空间辅助坐 标(u1 v1 w1)和(u2 v2 w2) 逐点计算误差方程式系数 和常数项 否
相对定向的过程
初始状态
最终状态 两个投
影器
中间状态
地面模型 地形图
投影光线 不相交
－交叉 改变立体像片 对的相对位置， 使光线相交 所有光线
对对相交
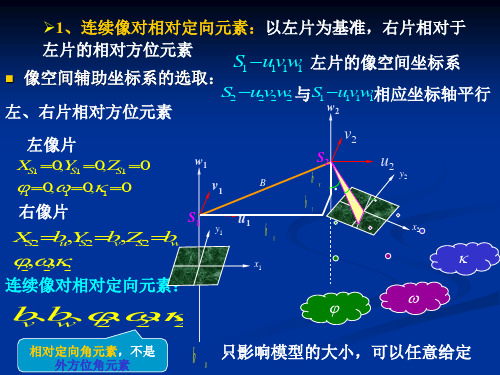
1、连续像对相对定向元素：以左片为基准，右片相对于 左片的相对方位元素 S1 u1v1w1 左片的像空间坐标系 像空间辅助坐标系的选取： S2 u2v2 w2 与 S1 u1v1w1相应坐标轴平行 w2 左、右片相对方位元素 v2 左像片 S2 w1 u2 X S1 0, YS1 0, Z S1 0 y b B w v1 1 0, 1 0, 1 0 bv 右像片 S u
w1 w2
v1
S1 u1
y1
v2 b
S2
X S1 0, YS1 0, Z S1 0
u2
1 , 1 0, 1
右像片
X S 2 bu b, YS 2 bv 0, Z S 2 bw 0
y2
x2
1
1 2
1、1、2、2、2
2 2
2 , 2 , 2
单独像对相对定向元素：

二、解析法相对定向原理 解求相对定向元素，建立立体模型 特征：恢复两张像片的相对位置，同名射线对对相交
S2 S1 b a2 a1
数学模型描述：同名射线对对相交
数学描述：三射线共面
S1S2、 S1a1、 S2a2
三矢量共面，混合积为零
S1S2 (S1a1 S2a2 ) 0
bu w2 bwu2 投影系数： N1 u1w2 u2 w1 bu w1 bwu1 N2 u1w2 u2 w11
A
相对定向：
5 个元素
它只确定两个影像的相对位置，但 是不能确定它们的绝对位置
例如
或
或
模型点在像空间辅助坐标系坐标
绝对定向－－ 确定模型在空间的绝对位置
由相对定向 建立的 地面模型
非线性函数，线性化，按泰勒级数展开，取小值一次项
F F F F F F F0 d d d2 d2 d 2 0 2 2 2
F0 : 相对定向元素的近似值及给定的bu带入得到的函数F的近似值
d 、d 、d2、d2、d2：相对定向元素近似值的改正数
结束 是 改正数 小于限差否？
否 是
求未知数新值 解法方程，求改正数
所有定向 点计算完否？
四、模型点坐标的计算（模型点在像空间辅助坐标系坐标）
解出相对定向元素后，只能求出像点在像空间辅助坐标系 w2 中的坐标 v2 w1
v1
u1 x1 v y 1 1 w1 f
2
X S 2 bu , YS 2 bv , Z S 2 bw
1
y1
1
bu
x2
2 , 2 , 2 连续像对相对定向元素：
x1

bv、bw、2、2、 2
相对定向角元素，不是 外方位角元素
bu
只影响模型的大小，可以任意给定
2、单独像对相对定向元素： 像空间辅助坐标系 S1 u1v1w1 的选取： u轴：摄影基线 v轴：垂直于左片的主核面 w轴：在左片的主核面内， UW平面：左主核面 左、右片相对方位元素 左像片
F F ：偏导数，系数 2
为简便计算，做一些近似（线性化过程仅考虑一次小值项）：
u2 1 － 2 －2 x2 v 1 y － 2 2 2 2 1 w2 2 2 f
Q用严密式计算
w2
v1 s1
w1 v1 u1
u2
u1
N1v1
N2v2
同名光线相交
相对定向完成
建立像对的立体几何模型 相对定向 元素
同名光线对对相交
模型点上下视差为0
单独法解析相对定向原理
w1
1 、 1 1、1
的函数
w2v1S1 y1源自Bv2u1 a1(u1 ,v1 ,w1)
x1 S2
u2
单独像对的相对定向 1、1、2、2、2
误差方程：VQ Qf v1 v f 2 w1 w2 u1v2 uv vv u u d1 2 1 d2 f (1 1 2 )d2 1 d1 2 d 2 Q w2 w1 w1w2 w1 w2
相对定向: 特点：不考虑模型的比例尺，不需要野外控制点 连续像对法相对定向的特征：前一像对右像片的相对定 向角元素，对后一像对而言，是左像片的角元素，已成为 已知值。适用于航带 单独像对法相对定向适用于单模型
共面条件方程式
A
连续法解析相对定向原理
连续像对法相对定向元素
bv、bw、2、2、 2
S1S2 (S1a1 S2a2 ) 0
共面条件方程坐标式
bu 只影响模型比例尺
bv bw ？ 待求
bu u1 u2
bv v1 v2
bw w1 0 w2
2 , 2 , 2
的函数
u1 x1 v y 1 1 w1 f
u2 x2 v R y 2 2 2 w2 f
b
S1
S2
u2
u1
a1
a2
模型点在像空间辅助坐标系坐标
U1 N1u1 bu N 2u2 V1 N1v1 bv N 2v2 W1 N1w1 bw N 2 w2
( AT PA) X AT PL
法方程
0 d 1 d 2 d 3 2 2 d 2 d 2 d 2
0 1 2 3
X ( A A) A L
T T
1
2 2 d 2 d 2 d 2
0 1 2 3
2 2 d 2 d 2 d 2
0 1 2 3
常数项的几何意义
Q N1v1 N2v2 bv
Q为定向点在 模型上的上下 视差 当一个立体像 对完成相对定 向，同名光线 相交， Q＝0 当一个立体像 对未完成相对 定向，即同名 光线不相交， Q＝0 w1
v2
u2 0 0 1 x2 f y 0 v 0 0 0 2 2 2 w2 1 0 0 f x2
F bu u1 2 u2 2
a1 cos cos sin sin sin c3 cos cos
u2 x2 v R y 2 2 2 w2 f
都化为角度形式：
b
s1
bu


bw bv
s2
bv bu tan bu bu bw tan bu cos bu bv bw 1 u1 v1 w1 0 F bu u1 v1 w1 0 u2 v2 w2 u2 v2 w2
y2
u1 x1 v R y 1 1 1 w1 f
x2
a2(u2 ,v2 ,w2)
b u1 u2
0 v1 v2
0 w1 0 w2
A
2 , 2 , 2
的函数
u2 x2 v R y 2 2 2 w2 f

做近似
v1 v2 , w1 w2 w1u 2 u1 w2 u1v2 令 bu w1 N2
bu u 2 v1 v1 N2 F0 N 2 Q bu w1
整理得
u2v2 v2 2 v2 Q N 2 d2 ( w2 ) N 2 d2 u2 N 2 d 2 bu d bu d w2 w2 w2 F0 N 2 bu w2 bwu2 bu w1 bwu1 Q v1 v2 bv N1v1 N 2v2 bv bu w1 u1w2 u2 w1 u1w2 u2 w1
视Q为观测值，列误差方程：
F F0
F F F F F d d d2 d2 d 2 0 2 2 2
u2 v2 v2 2 v vQ N 2 d2 ( w2 ) N 2 d 2 u2 N 2 d 2 bu d 2 bu d Q w2 w2 w2 d 2 d 2 T V AX l V a b c d e d 2 l V VQ1 VQ2 VQn d d a1 b1 c1 d1 e1 T T A X d2 d 2 d 2 d d L l1 l2 ln 0 d 1 d 2 d 3 an bn cn d n en
坐标原点的 平移量
模型比例尺 缩放系数
模型点在像空间辅助 坐标系中的坐标
七个绝对定向元素
、、、、X S、YS、ZS
解析法绝对定向：利用已知的地面控制点，解求绝对定向元素
F F F F F F F d d d d dX s dYs dZ s X s Ys Z s dX S 视U、V、W为观测值 dY S W 0 V dZ S VU lU 1 0 0 U 0 1 0 V d l V 0 W U V V V 0 0 0 1 W U d VW lW d 控制点坐标 绝对定向元素初值带入 d 计算的近似值 F F0